A New Approach to the Dynamic Maintenance of Maximal Points in a Plane*
|
|
|
- Joshua Lawrence
- 6 years ago
- Views:
Transcription
1 Discrete Comput Geom 5: (1990) 1990 Springer-Verlag New York~Inc.~ A New Approach to the Dynamic Maintenance of Maximal Points in a Plane* Greg N. Frederickson and Susan Rodger Department of Computer Sciences, Purdue University, West Lafayette, IN 47907, USA Abstract. A point p~ = (x~, y~) in the x-y plane is maximal if there is no point pj=(xj, yj) such that xj>x, and yj>y~. We present a simple data structure, a dynamic contour search tree, which contains all the points in the plane and maintains an embedded linked list of maximal points so that m maximal points are accessible in O(m) time. Our data structure dynamically maintains the set of points so that insertions take O(log n) time, a speedup of O(log n) over previous results, and deletions take O((log n) 2) time. 1. Introduction Given a set S of points in the x-y plane, pi = (xt, Yi) E S is a maximal point if there is no pj = (xi, Yi) e S such that Pi <Pj (Pi <P~ iff x~ <x i and y~ <yj). The set of maximal points of S form what we call an m-contour. In this paper we present a dynamic contour search tree, a data structure to represent contour information for a search tree. This data structure is quite natural, and is simpler than previous data structures for solving the dynamic version of the m-contour problem. The dynamic contour search tree stores the points of the set S in the leaves of the tree and stores various search information in the internal nodes. The m-contour is maintained as a linked list embedded in this structure, so that it can be accessed in O(m) time where m is the number of maximal points. Our data structure dynamically maintains the set of points so that insertions take O(log n) time, a speedup of O(log n) over previous results, and deletions take O((log n) 2) time. * The research of thefirst author was partially supported by the National Science Foundation under Grant No. DCR and by the Office of Naval Research on Contract No. N K The research of the second author was partially supported by the Office of Naval Research on Contract No. N K-0689.
2 366 G.N. Fredenckson and S. Rodger In addition, the query of whether a new point lies inside or outside of the m-contour can be determined in O(log n) time. For a static set of n points, Kung et al. [1] have shown that the m-contour can be computed in O(n log n) time. One method for constructing the m- contour proceeds by examining all the points, one at a time, and building the m-contour from the points examined thus far. If a point is not on the m-contour then the point is discarded. In the dynamic version of this problem, those points in the set S which are not maximal points must be saved, because deleting a point on the m-contour can result in a point which was not maximal becoming maximal. Overmars and van Leeuwen [2] use a balanced binary search tree in which the points from S are stored in the leaves of the tree and each internal node has a concatenable queue associated with it. The concatenable queue at the root contains all the maximal points and the other concatenable queues contain the remaining points. In the data structure of Overmars and van Leeuwen, the m-contour can be listed in O(m) time, and the query of whether a new point lies inside or outside of the m-contour can be determined in O(log n) time. However, Overmars and van Leeuwen's insertions and deletions consist of tearing apart concatenable queues and rebuilding them at each internal node along a path, causing insertions and deletions to take O((log n) 2) time. With our data structure, insertions and deletions consist of updating O(1) search information at each internal node along a path, causing insertions to take O(log n) time. Willard and Lueker [4] have shown how to perform range queries in k dimensions on trees of bounded balance with worst-case times of O((log n) k-l) for update and query operations. Applying their data structure to the maximal point problem in two dimensions results in efficient worst-case update and query times of O(log n). However, since their data structure is designed specifically for range queries, it has no scheme for representing the m-contour. There appears to be no efficient way to list out the m-contour. The dynamic contour search tree must be balanced in order to get the O(log n) search time. We use the balancing scheme of the red-black binary search trees of Tarjan [3] since they use the minimum number of rotations to keep the tree balanced. Each rotation in the dynamic contour search tree requires O(log n) time to update the search information at the three nodes possibly affected by the rotation. Thus it is crucial to use the red-black binary search trees which have O(1) rotations per update in order to achieve the O(log n) time for insertions. 2. Definitions and Searching Operations The m-contour of a set of points S in the plane is composed of the maximal points of S. These maximal points form a "staircase" in which all the remaining points of S lie to the left and below the staircase. An example set of points, and the staircase for them, are given in Fig. l(a). The inside region of the m-contour is the region dominated by the m-contour. That is, a point p, is inside the m-contour
3 A New Approach to the Dynamic Maintenance of Maximal Points in a Plane I 1 5 o2 +3,T 8 (a).6 I (b) Fig. 1. (a) The m-contour. (b) The corresponding dynamic contour search tree without the next_down pointers shown. The embedded m-contour is emphasized. if and only if there is a maximal point pj such that p~ <pj. The outside region of the m-contour is the region that is not dominated by the m-contour. The data structure we propose to maintain the m-contour dynamically is a balanced binary tree with all the points of the set S sorted by the x-coordinate and stored in the leaves of the tree. Each leaf node contains three fields: x, y, and transfer. The internal nodes of the tree are used to search for points and to represent the m-contour. Each internal node v contains six fields: right, left, max_x, max_y, next_down, and next_in_contour. Right(v) is the right child of internal node v and similarly left(v) is the left child of v. Max_x(v) points to the leaf containing the point with the largest x-coordinate of all the points in v's subtree. We use max_x(v) in the search for a point via its x-coordinate. Max_y(v) points to the leaf containing the point with the largest y-coordinate of all the points in v's subtree. We use max_y(v) when updating certain information after an insertion or deletion. Next_down(v) of node v points to the closest descendant node w that has a max_y(right(w)) = max_y(right(v)). If no such w exists, then next_down(v) points to the leaf node w that max_y(right(v)) points to. We use next_down(v) in Sections 3 and 4 to reset transfer pointers in O(1) time. Next_in_contour(v) for internal node v contains a pointer to the descendant leaf in the tree which represents the nearest point that is to the left and above of max_y(right(v)) in the plane. If max_y(right(v)) points to the leaf for Pi = (x, yi) then next_in_contour(v) will point to some point pj = (xj, yj) which has the largest x-coordinate xj such that xj < x~ and yj > y~. It is possible for several internal nodes to have the same max_y(right(v)) values. Of these nodes, only the node v closest to the root will have its next_in_contour(v) pointer set to the next contour point; the others will set their next_in_contour pointers to NULL. Transfer(w), where w is a leaf containing the point Pi = (xi, Yi), is a pointer to the highest ancestor v that has a y(max_y(right(v))) value equal to y~. Transfer(w) together with the next_down pointers of all the nodes v whose max_y(right(v)) = p~ form a circularly linked list in the tree. A dynamic contour search tree for the set of points in Fig. l(a) is given in Fig. l(b). Downward arrows are next_in_contour pointers, upward arrows are transfer pointers, and a label beside an interior node v is the max_y(right(v))
4 368 G.N. Frederickson and S. Rodger Fig. 2. A circular linked list for p~ formed by a transfer pointer and three next_down pointers. value. Next_down pointers are not shown. Figure 2 shows the circularly linked list of the transfer pointer for the point p~ and the next_down pointers of the nodes v whose max_y(right(v))=p~. The m-contour can easily be produced from this data structure by traversing a linked list consisting of alternating next_in_contour and transfer pointers. Note that the rightmost point on the m-contour will always be a point p~ = (xi, y~) with the largest x-coordinate. Starting from p, we can trace through the m-contour that is represented in the tree by alternately following transfer and next_in_contour pointers. This list is emboldened in Fig. l(b). Theorem 2.1. The points of the m-contour can be listed using the dynamic contour search tree in O( m ) time where m is the number of maximal points. Proof. The rightmost leaf w in the search tree contains the fightmost point p~ = (x, y~) on the m-contour since the leaves are sorted by x-coordinates and x~ is the largest x-value of any point. Transfer(w) points to its highest ancestor v that has a y(max_y(right(v))) value of y~. No point in v's fight subtree has a larger y-value. To find the next maximal point, examine next_in_contour(v). It points to the leaf u containing the point Pk = (Xk, Yk) such that xk = (maxxj such that xj<x~ and yj>y~). Thus by starting with the rightmost leaf and tracing the transfer and next_in_contour pointers, the m-contour can be listed in O(m) time. [] An arbitrary point p~ = (xj, y~) ~ S can be tested easily to see whether p~ lies inside or outside of the m-contour. Any point that lies inside the m-contour is dominated by some maximal point. A simple search of the dynamic contour search tree would find a maximal point p~ that dominates Pi if pj lies inside the m-contour. Otherwise, pj will be found to lie outside the m-contour. Initialize v to the root. Let p~ = (xi, yt) be the point at the leaf pointed to by max_y(right(v)). Figure 3 shows four quadrants with respect to p~. The point pj must lie in one
5 A New Approach to the Dynamic Maintenance of Maximal Points in a Plane 369 IV Pi III II Fig. 3. Quadrants with respect to the point p~. of these quadrants. If xj > x~ and yj > y~ then the point pj lies outside of the m-contour (quadrant I), as we shall show. If xj < x~ and yj < Yi then the point pj is dominated by p~ and lies inside the m-contour (quadrant III). If xj <xi and y~ > y~ then recursively apply the search to v's left subtree (quadrant IV). If xj > xi and yj <y~ then recursively apply the search to v's right subtree (quadrant II). If a leaf is reached, then pj was not dominated by any point and thus lies outside the m-contour. Theorem 2.2. Using the above procedure, an arbitrary point pj will be found to lie inside or outside the m-contour in O(log n) time. Proof. Suppose pj lies outside the m-contour. No point dominates pj so either pj is found to lie clearly outside of the m-contour (quadrant I) or a leaf is reached during the search indicating that no points dominate pj. Suppose pj lies inside the m-contour. Then there is at least one point on the m-contour which dominates pj. Let Pk be the maximal point to the fight of pj that has the largest y-value. There is an internal node w in the dynamic contour search tree with its max_y(right(w)) equal to Pk such that the leaf position in the tree that would he reached in searching for pj is in w's left subtree. Thus, there is an internal node along the search path from the root to p2 whose max_y(right(w)) value would determine that pj is inside the m-contour. Figure 4(a) shows the point pj dominated by three maximal points and Fig. 4(b) shows the node w in the dynamic contour search tree. Starting at the root of the tree, the search proceeds toward the node w. Let v be the current internal node in our search and let p~ = (x~, y~) be the point at the leaf pointed to by max_y(right(v)). If p~ dominates pj then our search stops. Otherwise, if p~ is a contour point, then w is either in v's left subtree if Xk < X~ or in v's fight subtree if x~ > x~ and the search continues accordingly toward w.
6 370 G.N. Frederickson and S. Rodger... ] Pk Q ~ root "PJ ~.4. (a) T Position of pj (a) The m-contour. (b) The corresponding dynamic contour search tree. (b) If Pi is not a contour point, then there are no contour points in v's right subtree. The node w is not in v's right subtree since if it was then pi would be a contour point. Thus w is in v's left subtree and p/s position in the tree is to the left of p~. The search continues via the left child of v. It cannot happen that pi <pj, so the point pj cannot lie in quadrant I with respect to p,~. Thus either the search halts before reaching w, or it halts at w. The search clearly takes O(log n) time. [] 3. Insertions Given the dynamic contour search tree for a set of n points, suppose we want to add an additional point pj to the set. The point pj will be inserted into the dynamic contour search tree. If p~ is outside the current m-contour, then pj will become a new point on the m-contour, otherwise pj will become an interior point. To maintain balance in the dynamic contour search tree after each insertion, we use the balancing scheme of the red-black binary search trees of Tarjan [3]. Each rotation performed during balancing will take O(log n) time to update the fields of the node involved. Thus is it crucial to use the red-black trees since they have O(1) rotations per insertion. To insert the point p~ = (xj, yj) into the dynamic contour search tree, we use the insertion procedure for red-black trees, and update other fields as the insertion is performed. First search for the leaf position of p~, a leaf node containing the point p~ = (xi, y~). On the way down to find the insertion position, update max_x(v) and max_y(v) for each node o on the path by comparing it with pj. Also on the way down, identify each node v such that max_y(right(v)) will change to point to pj. Each of these will have its next_in_contour pointer set to NULL except for the one closest to the root. For this node v, we compute its next_in_contour pointer as follows. The next_in_contour value of v will point to a leaf in v's left subtre. It cannot point to a leaf in v's right subtree because then it would be pointing to a y.value which is larger than y(max_y(right(v))). To calculate v's next_in_contour pointer,
7 A New Approach to the Dynamic Maintenance of Maximal Points in a Plane 371 traverse down a path in v's left subtree. At each internal node w, if y(max_y(right(w))) is greater than y(max_y(right(v))), then traverse down w's right subtree, else traverse down w's left subtree. If a leaf containing the point Pk is reached such that yk >y(max_y(right(v))), then set v's next_in_contour pointer to point to this leaf. Otherwise set v's next_in_contour pointer to NULL because there is no point in the subtree that is above and to the left in the plane. As mentioned above, there may be several nodes v such that the value max_y(right(v)) will change to point to pj. If max_y(right(v)) was previously pointing to Pk, then transfer(w) for the leaf node w containing the point Pk is pointing to V as v must be the node closest to the root with a max_y(right(v)) = Pk. Next_down(v) points to the next node u closest to the root with a max_y(right(u))=pk, so when max_y(right(v)) changes to point to pj, next_down(v) is used to update transfer(w) quickly. Next_down(v) will be updated as soon as the node it will point to is reached. For nodes on the path between the root and the new leaf for pj, their next_in_contour pointer could possibly change to pj if p~ is in quadrant IV with respect to them and pj is closer than the point they are currently pointing to. A simple comparison at each node on the way down the path should tell whether the next_in_contour pointer should be changed to point to pj. Upon reaching p~, replace p~ by an internal node and two leaves, one for pj and one for Pi. The transfer pointer of the leaf p~ should be set to point to the internal node v which is the closest internal node to the root with a max_y(right(v)) value of p~. Once pj is inserted in a leaf, the insertion path is retraced updating the balance information. This will halt at some node with O(1) rotations performed. These rotations may aliect three internal nodes that would need to recalculate their fields at a cost of O(log n). In Fig. 5(a) the change to the m-contour is shown when point P9 is inserted into the set of points from Fig. 1. The corresponding dynamic contour search tree is shown in Fig. 5(b). ~ 1 J9 9,, (a) (b) Fig. 5. (a) The m-contour after inserting point 9. (b) The corresponding dynamic contour search tree with the embedded m-contour emphasized.
8 372 G.N. Frederickson and S. Rodger Theorem 3.1. Inserting a point p into a search tree with n leaves takes O(log n) time. Proof. To add the new point pj involves a search from the root to a leaf which takes O(log n) time. At each internal node on the way down the path, updating max_x and max_y takes O(1) time. There is one next_in_contour pointer which must be calculated at a cost of O(log n) time. The remaining next_in_contour pointers that change are set to NULL or are set to point to the leaf pj and thus can be calculated in O(1) time. Transfer and next_down pointers are updated in O(1) time by adding or deleting a node from a linked list. Balance information at each internal node can be calculated in O(1) time. Each rotation affects at most three internal nodes. Their fields can be recalculated in O(log n) time. Since there are O(1) rotations per insertion, the total time for balancing is O(log n) time. Thus the time to insert the point pj into the search tree takes O(log n) time. [] Corollary 3.1. The search tree for a set of n points can be built in O( n log n) time. Proof. Apply the insertion procedure above for each point. [] 4. Deletions Given the dynamic contour search tree for a set of n points, suppose we want to delete a point pj from the set. If pj was a point on the m-contour then the new m-contour will be updated when pj is deleted by updating the dynamic contour search tree. Even if pj was not on the m-contour, some work may be needed to update the dynamic contour search tree. To delete the point pj = (xj, yj) from the dynamic contour search tree, we use the deletion procedure for the red-black trees. First find the leaf w containing the point pj. Leaf w will be the child of some internal node v. Let u be the other child of v and let p(v) be the parent of v. Remove w and v and let u become a child of p(v). Now proceed back up the path, updating values at the internal nodes. Updating max_x(v) and max_y (v) at each internal node v along the path takes O(1) time per node. Updating transfer and next_down pointers also takes O(1) time per node along the path. Some next_in_contour pointers may need to be recalculated. If any internal node v had y(max_y(right(v)))=yj then this node would receive a new max_y(right(v)) value. Nodes with y(max_y(right(v)))=yj must lie along the search path from the root to pj. If the y(max_y(right(v))) value of a node v changes, then the next_in_contour pointer of the node could possibly change, so its next_in_contour pointer must be recalculated. In addition, if any next_in_contour pointer was pointing at pg, then these next_in_contour pointers need to be recalculated because p~ will be deleted. Only nodes along the path from the root to pj can have next_in_contour pointers pointing to pj since next_in_contour pointers must point to a descendant leaf. Next_in_contour pointers should be recalculated on the way back up to the root.
9 A New Approach to the Dynamic Maintenance of Maximal Points in a Plane o3, ) > (a) (b) Fig. 6. (a) The m-contour before the deletion of point 9. (b) The corresponding contour search tree before deleting point 9. Also on the way back up the path, update the balance information using the balancing scheme of the red-black binary search trees. There may be O(1) rotations needed to balance the tree. At most three internal nodes will be affected by a rotation and need their fields recalculated. After performing a rotation, continue on up the path updating the remaining nodes on the path. Figure 6(a) and (b) gives a set of points and an associated dynamic contour search tree. Figure 7(a) and (b) gives the set of points and the associated dynamic contour search tree after point P9 is deleted. Theorem 4,1. Deleting a point from a search tree with n leaves takes O((log n) 2) time. Proof. To delete the leaf pj from the dynamic contour search tree involves a search from the root to the leaf p~ which takes O(log n) time. After removing the point pj, the same path must be traversed back up to the root, updating the fields at each internal node along the way. At most O(log n) nodes will need to...,9 2.I I (a) Fig. 7. (a) The m-contour after the deletion of point 9. (b) The corresponding contour search tree after deleting point 9. (b)
10 374 G.N. Frederickson and S. Rodger recalculate next_in_contour pointers. It takes O(log n) time to recalculate one next_in_contour pointer so the total time in recalculating the next_in_contour pointers is O((log n) 2) time. Updating max_x, max_y, transfer, next_down, and the balance information takes O ( 1 ) time at each node. There will be O (1) rotations and it will take O(log n) time to recalculate the fields of the nodes affected by the rotation. Thus the total time to delete point pj from the search structure is O((log n) 2) time. [] References 1. H. T. Kung, F. Luccio, and F. P. Preparata, On finding the maxima of a set of vectors, J. Assoc. Comput. Mach. 22, 4 (1975), M. H. Overmars and J. L. van Leeuwen, Maintenance of configurations in the plane, J. Comp. System Sci. 23 (1981), R. E. Tarjan, Updating a balanced search tree in O(1) rotations, Inform. Process. Lett. 16 (1983), D. E. Willard and G. S. Lueker, Adding range restriction capability to dynamic data structures, J. Assoc. Comput. Mach. 32, 3 (1985), Received July 16, 1987.
Binary Trees, Binary Search Trees
 Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
Computational Geometry
 Range trees Range queries Database queries salary G. Ometer born: Aug 16, 1954 salary: $3,500 A database query may ask for all employees with age between a 1 and a 2, and salary between s 1 and s 2 19,500,000
Range trees Range queries Database queries salary G. Ometer born: Aug 16, 1954 salary: $3,500 A database query may ask for all employees with age between a 1 and a 2, and salary between s 1 and s 2 19,500,000
Binary Trees. BSTs. For example: Jargon: Data Structures & Algorithms. root node. level: internal node. edge.
 Binary Trees 1 A binary tree is either empty, or it consists of a node called the root together with two binary trees called the left subtree and the right subtree of the root, which are disjoint from
Binary Trees 1 A binary tree is either empty, or it consists of a node called the root together with two binary trees called the left subtree and the right subtree of the root, which are disjoint from
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Binary Search Trees > = 2014 Goodrich, Tamassia, Goldwasser. Binary Search Trees 1
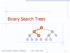 Binary Search Trees < > = Binary Search Trees 1 Ordered Dictionary (Map) ADT get (k): record with key k put (k,data): add record (k,data) remove (k): delete record with key k smallest(): record with smallest
Binary Search Trees < > = Binary Search Trees 1 Ordered Dictionary (Map) ADT get (k): record with key k put (k,data): add record (k,data) remove (k): delete record with key k smallest(): record with smallest
Is Research For Me? CRAW UndergraduateWorkshop Grace Hopper Celebration of Women in Computing 2010 September 29, 2010 Atlanta, GA
 Is Research For Me? CRAW UndergraduateWorkshop Grace Hopper Celebration of Women in Computing 2010 September 29, 2010 Atlanta, GA Abrita Susanna Susan Ellen Chakravarty Ricco Rodger Walker 1 Can we solve
Is Research For Me? CRAW UndergraduateWorkshop Grace Hopper Celebration of Women in Computing 2010 September 29, 2010 Atlanta, GA Abrita Susanna Susan Ellen Chakravarty Ricco Rodger Walker 1 Can we solve
Point Enclosure and the Interval Tree
 C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 8 Date: March 3, 1993 Scribe: Dzung T. Hoang Point Enclosure and the Interval Tree Point Enclosure We consider the 1-D
C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 8 Date: March 3, 1993 Scribe: Dzung T. Hoang Point Enclosure and the Interval Tree Point Enclosure We consider the 1-D
Planar Point Location
 C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 04 Date: February 15, 1993 Scribe: John Bazik Planar Point Location 1 Introduction In range searching, a set of values,
C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 04 Date: February 15, 1993 Scribe: John Bazik Planar Point Location 1 Introduction In range searching, a set of values,
Can we solve a research problem in. Is Research For Me? Where do you find a research problem? Is research challenging and frustrating?
 Is Research For Me? CRAW UndergraduateWorkshop Grace Hopper Celebration of Women in Computing 2010 September 29, 2010 Atlanta, GA Abrita Susanna Susan Ellen Chakravarty Ricco Rodger Walker 1 Can we solve
Is Research For Me? CRAW UndergraduateWorkshop Grace Hopper Celebration of Women in Computing 2010 September 29, 2010 Atlanta, GA Abrita Susanna Susan Ellen Chakravarty Ricco Rodger Walker 1 Can we solve
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
T consists of finding an efficient implementation of access,
 968 IEEE TRANSACTIONS ON COMPUTERS, VOL. 38, NO. 7, JULY 1989 Multidimensional Balanced Binary Trees VIJAY K. VAISHNAVI A bstract-a new balanced multidimensional tree structure called a k-dimensional balanced
968 IEEE TRANSACTIONS ON COMPUTERS, VOL. 38, NO. 7, JULY 1989 Multidimensional Balanced Binary Trees VIJAY K. VAISHNAVI A bstract-a new balanced multidimensional tree structure called a k-dimensional balanced
Heap: A binary heap is a complete binary tree in which each, node other than root is smaller than its parent. Heap example: Fig 1. NPTEL IIT Guwahati
 Heap sort is an efficient sorting algorithm with average and worst case time complexities are in O(n log n). Heap sort does not use any extra array, like merge sort. This method is based on a data structure
Heap sort is an efficient sorting algorithm with average and worst case time complexities are in O(n log n). Heap sort does not use any extra array, like merge sort. This method is based on a data structure
CSE 502 Class 16. Jeremy Buhler Steve Cole. March A while back, we introduced the idea of collections to put hash tables in context.
 CSE 502 Class 16 Jeremy Buhler Steve Cole March 17 2015 Onwards to trees! 1 Collection Types Revisited A while back, we introduced the idea of collections to put hash tables in context. abstract data types
CSE 502 Class 16 Jeremy Buhler Steve Cole March 17 2015 Onwards to trees! 1 Collection Types Revisited A while back, we introduced the idea of collections to put hash tables in context. abstract data types
Lecture 6: Analysis of Algorithms (CS )
 Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
CIS265/ Trees Red-Black Trees. Some of the following material is from:
 CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
CMSC 754 Computational Geometry 1
 CMSC 754 Computational Geometry 1 David M. Mount Department of Computer Science University of Maryland Fall 2005 1 Copyright, David M. Mount, 2005, Dept. of Computer Science, University of Maryland, College
CMSC 754 Computational Geometry 1 David M. Mount Department of Computer Science University of Maryland Fall 2005 1 Copyright, David M. Mount, 2005, Dept. of Computer Science, University of Maryland, College
Computational Geometry
 Windowing queries Windowing Windowing queries Zoom in; re-center and zoom in; select by outlining Windowing Windowing queries Windowing Windowing queries Given a set of n axis-parallel line segments, preprocess
Windowing queries Windowing Windowing queries Zoom in; re-center and zoom in; select by outlining Windowing Windowing queries Windowing Windowing queries Given a set of n axis-parallel line segments, preprocess
Range Searching and Windowing
 CS 6463 -- Fall 2010 Range Searching and Windowing Carola Wenk 1 Orthogonal range searching Input: n points in d dimensions E.g., representing a database of n records each with d numeric fields Query:
CS 6463 -- Fall 2010 Range Searching and Windowing Carola Wenk 1 Orthogonal range searching Input: n points in d dimensions E.g., representing a database of n records each with d numeric fields Query:
1. Meshes. D7013E Lecture 14
 D7013E Lecture 14 Quadtrees Mesh Generation 1. Meshes Input: Components in the form of disjoint polygonal objects Integer coordinates, 0, 45, 90, or 135 angles Output: A triangular mesh Conforming: A triangle
D7013E Lecture 14 Quadtrees Mesh Generation 1. Meshes Input: Components in the form of disjoint polygonal objects Integer coordinates, 0, 45, 90, or 135 angles Output: A triangular mesh Conforming: A triangle
Computational Optimization ISE 407. Lecture 16. Dr. Ted Ralphs
 Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Balanced search trees. DS 2017/2018
 Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
1 Divide and Conquer Approach
 Comp 163: Computational Geometry Tufts University, Spring 005 Professor Diane Souvaine Scribe: Katelyn Mann Dynamic Convex Hull and Order Decomposable Problems 1 Divide and Conquer Approach In order to
Comp 163: Computational Geometry Tufts University, Spring 005 Professor Diane Souvaine Scribe: Katelyn Mann Dynamic Convex Hull and Order Decomposable Problems 1 Divide and Conquer Approach In order to
Binary Heaps in Dynamic Arrays
 Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Trees. (Trees) Data Structures and Programming Spring / 28
 Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
HEAPS ON HEAPS* Downloaded 02/04/13 to Redistribution subject to SIAM license or copyright; see
 SIAM J. COMPUT. Vol. 15, No. 4, November 1986 (C) 1986 Society for Industrial and Applied Mathematics OO6 HEAPS ON HEAPS* GASTON H. GONNET" AND J. IAN MUNRO," Abstract. As part of a study of the general
SIAM J. COMPUT. Vol. 15, No. 4, November 1986 (C) 1986 Society for Industrial and Applied Mathematics OO6 HEAPS ON HEAPS* GASTON H. GONNET" AND J. IAN MUNRO," Abstract. As part of a study of the general
13.4 Deletion in red-black trees
 Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Computational Geometry
 Range searching and kd-trees 1 Database queries 1D range trees Databases Databases store records or objects Personnel database: Each employee has a name, id code, date of birth, function, salary, start
Range searching and kd-trees 1 Database queries 1D range trees Databases Databases store records or objects Personnel database: Each employee has a name, id code, date of birth, function, salary, start
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
1 The range query problem
 CS268: Geometric Algorithms Handout #12 Design and Analysis Original Handout #12 Stanford University Thursday, 19 May 1994 Original Lecture #12: Thursday, May 19, 1994 Topics: Range Searching with Partition
CS268: Geometric Algorithms Handout #12 Design and Analysis Original Handout #12 Stanford University Thursday, 19 May 1994 Original Lecture #12: Thursday, May 19, 1994 Topics: Range Searching with Partition
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Dynamic Euclidean Minimum Spanning Trees and Extrema of Binary Functions
 Dynamic Euclidean Minimum Spanning Trees and Extrema of Binary Functions David Eppstein Department of Information and Computer Science University of California, Irvine, CA 92717 Abstract We maintain the
Dynamic Euclidean Minimum Spanning Trees and Extrema of Binary Functions David Eppstein Department of Information and Computer Science University of California, Irvine, CA 92717 Abstract We maintain the
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
CS711008Z Algorithm Design and Analysis
 CS711008Z Algorithm Design and Analysis Lecture 7. Binary heap, binomial heap, and Fibonacci heap Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / 108 Outline
CS711008Z Algorithm Design and Analysis Lecture 7. Binary heap, binomial heap, and Fibonacci heap Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / 108 Outline
CS711008Z Algorithm Design and Analysis
 CS700Z Algorithm Design and Analysis Lecture 7 Binary heap, binomial heap, and Fibonacci heap Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / Outline Introduction
CS700Z Algorithm Design and Analysis Lecture 7 Binary heap, binomial heap, and Fibonacci heap Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / Outline Introduction
Organizing Spatial Data
 Organizing Spatial Data Spatial data records include a sense of location as an attribute. Typically location is represented by coordinate data (in 2D or 3D). 1 If we are to search spatial data using the
Organizing Spatial Data Spatial data records include a sense of location as an attribute. Typically location is represented by coordinate data (in 2D or 3D). 1 If we are to search spatial data using the
CSCI2100B Data Structures Heaps
 CSCI2100B Data Structures Heaps Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction In some applications,
CSCI2100B Data Structures Heaps Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction In some applications,
l Heaps very popular abstract data structure, where each object has a key value (the priority), and the operations are:
 DDS-Heaps 1 Heaps - basics l Heaps very popular abstract data structure, where each object has a key value (the priority), and the operations are: l insert an object, find the object of minimum key (find
DDS-Heaps 1 Heaps - basics l Heaps very popular abstract data structure, where each object has a key value (the priority), and the operations are: l insert an object, find the object of minimum key (find
An Algorithm for Enumerating all Directed Spanning Trees in a Directed Graph
 (C) Springer Verlag, Lecture Notes on Computer Sience An Algorithm for Enumerating all Directed Spanning Trees in a Directed Graph Takeaki UNO Department of Systems Science, Tokyo Institute of Technology,
(C) Springer Verlag, Lecture Notes on Computer Sience An Algorithm for Enumerating all Directed Spanning Trees in a Directed Graph Takeaki UNO Department of Systems Science, Tokyo Institute of Technology,
CSCI2100B Data Structures Trees
 CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
Lecture 26. Introduction to Trees. Trees
 Lecture 26 Introduction to Trees Trees Trees are the name given to a versatile group of data structures. They can be used to implement a number of abstract interfaces including the List, but those applications
Lecture 26 Introduction to Trees Trees Trees are the name given to a versatile group of data structures. They can be used to implement a number of abstract interfaces including the List, but those applications
CSCI Trees. Mark Redekopp David Kempe
 CSCI 104 2-3 Trees Mark Redekopp David Kempe Trees & Maps/Sets C++ STL "maps" and "sets" use binary search trees internally to store their keys (and values) that can grow or contract as needed This allows
CSCI 104 2-3 Trees Mark Redekopp David Kempe Trees & Maps/Sets C++ STL "maps" and "sets" use binary search trees internally to store their keys (and values) that can grow or contract as needed This allows
Algorithms. Deleting from Red-Black Trees B-Trees
 Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Lecture 3 February 9, 2010
 6.851: Advanced Data Structures Spring 2010 Dr. André Schulz Lecture 3 February 9, 2010 Scribe: Jacob Steinhardt and Greg Brockman 1 Overview In the last lecture we continued to study binary search trees
6.851: Advanced Data Structures Spring 2010 Dr. André Schulz Lecture 3 February 9, 2010 Scribe: Jacob Steinhardt and Greg Brockman 1 Overview In the last lecture we continued to study binary search trees
SFU CMPT Lecture: Week 9
 SFU CMPT-307 2008-2 1 Lecture: Week 9 SFU CMPT-307 2008-2 Lecture: Week 9 Ján Maňuch E-mail: jmanuch@sfu.ca Lecture on July 8, 2008, 5.30pm-8.20pm SFU CMPT-307 2008-2 2 Lecture: Week 9 Binary search trees
SFU CMPT-307 2008-2 1 Lecture: Week 9 SFU CMPT-307 2008-2 Lecture: Week 9 Ján Maňuch E-mail: jmanuch@sfu.ca Lecture on July 8, 2008, 5.30pm-8.20pm SFU CMPT-307 2008-2 2 Lecture: Week 9 Binary search trees
CMPSCI 250: Introduction to Computation. Lecture #14: Induction and Recursion (Still More Induction) David Mix Barrington 14 March 2013
 CMPSCI 250: Introduction to Computation Lecture #14: Induction and Recursion (Still More Induction) David Mix Barrington 14 March 2013 Induction and Recursion Three Rules for Recursive Algorithms Proving
CMPSCI 250: Introduction to Computation Lecture #14: Induction and Recursion (Still More Induction) David Mix Barrington 14 March 2013 Induction and Recursion Three Rules for Recursive Algorithms Proving
Heaps. 2/13/2006 Heaps 1
 Heaps /13/00 Heaps 1 Outline and Reading What is a heap ( 8.3.1) Height of a heap ( 8.3.) Insertion ( 8.3.3) Removal ( 8.3.3) Heap-sort ( 8.3.) Arraylist-based implementation ( 8.3.) Bottom-up construction
Heaps /13/00 Heaps 1 Outline and Reading What is a heap ( 8.3.1) Height of a heap ( 8.3.) Insertion ( 8.3.3) Removal ( 8.3.3) Heap-sort ( 8.3.) Arraylist-based implementation ( 8.3.) Bottom-up construction
Data Structures. Outline. Introduction Linked Lists Stacks Queues Trees Deitel & Associates, Inc. All rights reserved.
 Data Structures Outline Introduction Linked Lists Stacks Queues Trees Introduction dynamic data structures - grow and shrink during execution Linked lists - insertions and removals made anywhere Stacks
Data Structures Outline Introduction Linked Lists Stacks Queues Trees Introduction dynamic data structures - grow and shrink during execution Linked lists - insertions and removals made anywhere Stacks
1 Tree Sort LECTURE 4. OHSU/OGI (Winter 2009) ANALYSIS AND DESIGN OF ALGORITHMS
 OHSU/OGI (Winter 2009) CS532 ANALYSIS AND DESIGN OF ALGORITHMS LECTURE 4 1 Tree Sort Suppose a sequence of n items is given. We can sort it using TreeInsert and DeleteMin: TreeSort Initialize an empty
OHSU/OGI (Winter 2009) CS532 ANALYSIS AND DESIGN OF ALGORITHMS LECTURE 4 1 Tree Sort Suppose a sequence of n items is given. We can sort it using TreeInsert and DeleteMin: TreeSort Initialize an empty
B-Trees. Based on materials by D. Frey and T. Anastasio
 B-Trees Based on materials by D. Frey and T. Anastasio 1 Large Trees n Tailored toward applications where tree doesn t fit in memory q operations much faster than disk accesses q want to limit levels of
B-Trees Based on materials by D. Frey and T. Anastasio 1 Large Trees n Tailored toward applications where tree doesn t fit in memory q operations much faster than disk accesses q want to limit levels of
8. Binary Search Tree
 8 Binary Search Tree Searching Basic Search Sequential Search : Unordered Lists Binary Search : Ordered Lists Tree Search Binary Search Tree Balanced Search Trees (Skipped) Sequential Search int Seq-Search
8 Binary Search Tree Searching Basic Search Sequential Search : Unordered Lists Binary Search : Ordered Lists Tree Search Binary Search Tree Balanced Search Trees (Skipped) Sequential Search int Seq-Search
Computational Geometry
 Windowing queries Windowing Windowing queries Zoom in; re-center and zoom in; select by outlining Windowing Windowing queries Windowing Windowing queries Given a set of n axis-parallel line segments, preprocess
Windowing queries Windowing Windowing queries Zoom in; re-center and zoom in; select by outlining Windowing Windowing queries Windowing Windowing queries Given a set of n axis-parallel line segments, preprocess
Binary Tree. Preview. Binary Tree. Binary Tree. Binary Search Tree 10/2/2017. Binary Tree
 0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
Rank-Pairing Heaps. Bernard Haeupler Siddhartha Sen Robert E. Tarjan. SIAM JOURNAL ON COMPUTING Vol. 40, No. 6 (2011), pp.
 Rank-Pairing Heaps Bernard Haeupler Siddhartha Sen Robert E. Tarjan Presentation by Alexander Pokluda Cheriton School of Computer Science, University of Waterloo, Canada SIAM JOURNAL ON COMPUTING Vol.
Rank-Pairing Heaps Bernard Haeupler Siddhartha Sen Robert E. Tarjan Presentation by Alexander Pokluda Cheriton School of Computer Science, University of Waterloo, Canada SIAM JOURNAL ON COMPUTING Vol.
Three-Dimensional Layers of Maxima 1. Adam L. Buchsbaum 2 and Michael T. Goodrich 3. Fractional cascading, Layers of maxima, Planar point location.
 Algorithmica (004) 39: 75 86 DOI: 0.007/s00453-004-08-5 Algorithmica 004 Springer-Verlag New York, LLC Three-Dimensional Layers of Maxima Adam L. Buchsbaum and Michael T. Goodrich 3 Abstract. We present
Algorithmica (004) 39: 75 86 DOI: 0.007/s00453-004-08-5 Algorithmica 004 Springer-Verlag New York, LLC Three-Dimensional Layers of Maxima Adam L. Buchsbaum and Michael T. Goodrich 3 Abstract. We present
Range-Aggregate Queries Involving Geometric Aggregation Operations
 Range-Aggregate Queries Involving Geometric Aggregation Operations Saladi Rahul, Ananda Swarup Das, K. S. Rajan, and Kannan Srinathan {srahul,anandaswarup}@research.iiit.ac.in {rajan, srinathan}@iiit.ac.in
Range-Aggregate Queries Involving Geometric Aggregation Operations Saladi Rahul, Ananda Swarup Das, K. S. Rajan, and Kannan Srinathan {srahul,anandaswarup}@research.iiit.ac.in {rajan, srinathan}@iiit.ac.in
Priority Queues. 1 Introduction. 2 Naïve Implementations. CSci 335 Software Design and Analysis III Chapter 6 Priority Queues. Prof.
 Priority Queues 1 Introduction Many applications require a special type of queuing in which items are pushed onto the queue by order of arrival, but removed from the queue based on some other priority
Priority Queues 1 Introduction Many applications require a special type of queuing in which items are pushed onto the queue by order of arrival, but removed from the queue based on some other priority
ICS 691: Advanced Data Structures Spring Lecture 3
 ICS 691: Advanced Data Structures Spring 2016 Prof. Nodari Sitchinava Lecture 3 Scribe: Ben Karsin 1 Overview In the last lecture we started looking at self-adjusting data structures, specifically, move-to-front
ICS 691: Advanced Data Structures Spring 2016 Prof. Nodari Sitchinava Lecture 3 Scribe: Ben Karsin 1 Overview In the last lecture we started looking at self-adjusting data structures, specifically, move-to-front
Lecture 3: Art Gallery Problems and Polygon Triangulation
 EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
l So unlike the search trees, there are neither arbitrary find operations nor arbitrary delete operations possible.
 DDS-Heaps 1 Heaps - basics l Heaps an abstract structure where each object has a key value (the priority), and the operations are: insert an object, find the object of minimum key (find min), and delete
DDS-Heaps 1 Heaps - basics l Heaps an abstract structure where each object has a key value (the priority), and the operations are: insert an object, find the object of minimum key (find min), and delete
Trees, Binary Trees, and Binary Search Trees
 COMP171 Trees, Binary Trees, and Binary Search Trees 2 Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search,
COMP171 Trees, Binary Trees, and Binary Search Trees 2 Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search,
1 Static-to-Dynamic Transformations
 You re older than you ve ever been and now you re even older And now you re even older And now you re even older You re older than you ve ever been and now you re even older And now you re older still
You re older than you ve ever been and now you re even older And now you re even older And now you re even older You re older than you ve ever been and now you re even older And now you re older still
Data Structures Lesson 9
 Data Structures Lesson 9 BSc in Computer Science University of New York, Tirana Assoc. Prof. Marenglen Biba 1-1 Chapter 21 A Priority Queue: The Binary Heap Priority Queue The priority queue is a fundamental
Data Structures Lesson 9 BSc in Computer Science University of New York, Tirana Assoc. Prof. Marenglen Biba 1-1 Chapter 21 A Priority Queue: The Binary Heap Priority Queue The priority queue is a fundamental
Lecture 7. Transform-and-Conquer
 Lecture 7 Transform-and-Conquer 6-1 Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more convenient instance of the same problem (instance simplification)
Lecture 7 Transform-and-Conquer 6-1 Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more convenient instance of the same problem (instance simplification)
Lecture: Analysis of Algorithms (CS )
 Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
where is a constant, 0 < <. In other words, the ratio between the shortest and longest paths from a node to a leaf is at least. An BB-tree allows ecie
 Maintaining -balanced Trees by Partial Rebuilding Arne Andersson Department of Computer Science Lund University Box 8 S-22 00 Lund Sweden Abstract The balance criterion dening the class of -balanced trees
Maintaining -balanced Trees by Partial Rebuilding Arne Andersson Department of Computer Science Lund University Box 8 S-22 00 Lund Sweden Abstract The balance criterion dening the class of -balanced trees
Orthogonal range searching. Range Trees. Orthogonal range searching. 1D range searching. CS Spring 2009
 CS 5633 -- Spring 2009 Orthogonal range searching Range Trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 5633 Analysis of Algorithms 1 Input: n points in d dimensions
CS 5633 -- Spring 2009 Orthogonal range searching Range Trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 5633 Analysis of Algorithms 1 Input: n points in d dimensions
Lecture 23: Binary Search Trees
 Lecture 23: Binary Search Trees CS 62 Fall 2017 Kim Bruce & Alexandra Papoutsaki 1 BST A binary tree is a binary search tree iff it is empty or if the value of every node is both greater than or equal
Lecture 23: Binary Search Trees CS 62 Fall 2017 Kim Bruce & Alexandra Papoutsaki 1 BST A binary tree is a binary search tree iff it is empty or if the value of every node is both greater than or equal
Optimum Alphabetic Binary Trees T. C. Hu and J. D. Morgenthaler Department of Computer Science and Engineering, School of Engineering, University of C
 Optimum Alphabetic Binary Trees T. C. Hu and J. D. Morgenthaler Department of Computer Science and Engineering, School of Engineering, University of California, San Diego CA 92093{0114, USA Abstract. We
Optimum Alphabetic Binary Trees T. C. Hu and J. D. Morgenthaler Department of Computer Science and Engineering, School of Engineering, University of California, San Diego CA 92093{0114, USA Abstract. We
Discussion 2C Notes (Week 8, February 25) TA: Brian Choi Section Webpage:
 Discussion 2C Notes (Week 8, February 25) TA: Brian Choi (schoi@cs.ucla.edu) Section Webpage: http://www.cs.ucla.edu/~schoi/cs32 Trees Definitions Yet another data structure -- trees. Just like a linked
Discussion 2C Notes (Week 8, February 25) TA: Brian Choi (schoi@cs.ucla.edu) Section Webpage: http://www.cs.ucla.edu/~schoi/cs32 Trees Definitions Yet another data structure -- trees. Just like a linked
lecture notes September 2, How to sort?
 .30 lecture notes September 2, 203 How to sort? Lecturer: Michel Goemans The task of sorting. Setup Suppose we have n objects that we need to sort according to some ordering. These could be integers or
.30 lecture notes September 2, 203 How to sort? Lecturer: Michel Goemans The task of sorting. Setup Suppose we have n objects that we need to sort according to some ordering. These could be integers or
A Fast Algorithm for Optimal Alignment between Similar Ordered Trees
 Fundamenta Informaticae 56 (2003) 105 120 105 IOS Press A Fast Algorithm for Optimal Alignment between Similar Ordered Trees Jesper Jansson Department of Computer Science Lund University, Box 118 SE-221
Fundamenta Informaticae 56 (2003) 105 120 105 IOS Press A Fast Algorithm for Optimal Alignment between Similar Ordered Trees Jesper Jansson Department of Computer Science Lund University, Box 118 SE-221
CMPS 2200 Fall 2017 B-trees Carola Wenk
 CMPS 2200 Fall 2017 B-trees Carola Wenk 9/18/17 CMPS 2200 Intro. to Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
CMPS 2200 Fall 2017 B-trees Carola Wenk 9/18/17 CMPS 2200 Intro. to Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
Commando: Solution. Solution 3 O(n): Consider two decisions i<j, we choose i instead of j if and only if : A S j S i
 Commando: Solution Commando: Solution Solution 1 O(n 3 ): Using dynamic programming, let f(n) indicate the maximum battle effectiveness after adjustment. We have transfer equations below: n f(n) = max
Commando: Solution Commando: Solution Solution 1 O(n 3 ): Using dynamic programming, let f(n) indicate the maximum battle effectiveness after adjustment. We have transfer equations below: n f(n) = max
B-Trees and External Memory
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 and External Memory 1 1 (2, 4) Trees: Generalization of BSTs Each internal node
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 and External Memory 1 1 (2, 4) Trees: Generalization of BSTs Each internal node
Describe how to implement deque ADT using two stacks as the only instance variables. What are the running times of the methods
 Describe how to implement deque ADT using two stacks as the only instance variables. What are the running times of the methods 1 2 Given : Stack A, Stack B 3 // based on requirement b will be reverse of
Describe how to implement deque ADT using two stacks as the only instance variables. What are the running times of the methods 1 2 Given : Stack A, Stack B 3 // based on requirement b will be reverse of
Lecture 13 Thursday, March 18, 2010
 6.851: Advanced Data Structures Spring 2010 Lecture 13 Thursday, March 18, 2010 Prof. Erik Demaine Scribe: David Charlton 1 Overview This lecture covers two methods of decomposing trees into smaller subtrees:
6.851: Advanced Data Structures Spring 2010 Lecture 13 Thursday, March 18, 2010 Prof. Erik Demaine Scribe: David Charlton 1 Overview This lecture covers two methods of decomposing trees into smaller subtrees:
Transform & Conquer. Presorting
 Transform & Conquer Definition Transform & Conquer is a general algorithm design technique which works in two stages. STAGE : (Transformation stage): The problem s instance is modified, more amenable to
Transform & Conquer Definition Transform & Conquer is a general algorithm design technique which works in two stages. STAGE : (Transformation stage): The problem s instance is modified, more amenable to
Search Trees - 2. Venkatanatha Sarma Y. Lecture delivered by: Assistant Professor MSRSAS-Bangalore. M.S Ramaiah School of Advanced Studies - Bangalore
 Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
8.1. Optimal Binary Search Trees:
 DATA STRUCTERS WITH C 10CS35 UNIT 8 : EFFICIENT BINARY SEARCH TREES 8.1. Optimal Binary Search Trees: An optimal binary search tree is a binary search tree for which the nodes are arranged on levels such
DATA STRUCTERS WITH C 10CS35 UNIT 8 : EFFICIENT BINARY SEARCH TREES 8.1. Optimal Binary Search Trees: An optimal binary search tree is a binary search tree for which the nodes are arranged on levels such
B-Trees and External Memory
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 B-Trees and External Memory 1 (2, 4) Trees: Generalization of BSTs Each internal
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 B-Trees and External Memory 1 (2, 4) Trees: Generalization of BSTs Each internal
Binary Trees
 Binary Trees 4-7-2005 Opening Discussion What did we talk about last class? Do you have any code to show? Do you have any questions about the assignment? What is a Tree? You are all familiar with what
Binary Trees 4-7-2005 Opening Discussion What did we talk about last class? Do you have any code to show? Do you have any questions about the assignment? What is a Tree? You are all familiar with what
Balanced Trees Part One
 Balanced Trees Part One Balanced Trees Balanced search trees are among the most useful and versatile data structures. Many programming languages ship with a balanced tree library. C++: std::map / std::set
Balanced Trees Part One Balanced Trees Balanced search trees are among the most useful and versatile data structures. Many programming languages ship with a balanced tree library. C++: std::map / std::set
Data Structures Question Bank Multiple Choice
 Section 1. Fundamentals: Complexity, Algorthm Analysis 1. An algorithm solves A single problem or function Multiple problems or functions Has a single programming language implementation 2. A solution
Section 1. Fundamentals: Complexity, Algorthm Analysis 1. An algorithm solves A single problem or function Multiple problems or functions Has a single programming language implementation 2. A solution
Dictionaries. Priority Queues
 Red-Black-Trees.1 Dictionaries Sets and Multisets; Opers: (Ins., Del., Mem.) Sequential sorted or unsorted lists. Linked sorted or unsorted lists. Tries and Hash Tables. Binary Search Trees. Priority Queues
Red-Black-Trees.1 Dictionaries Sets and Multisets; Opers: (Ins., Del., Mem.) Sequential sorted or unsorted lists. Linked sorted or unsorted lists. Tries and Hash Tables. Binary Search Trees. Priority Queues
A Comparison of Data Structures for Dijkstra's Single Source Shortest Path Algorithm. Shane Saunders
 A Comparison of Data Structures for Dijkstra's Single Source Shortest Path Algorithm Shane Saunders November 5, 1999 Abstract Dijkstra's algorithm computes the shortest paths between a starting vertex
A Comparison of Data Structures for Dijkstra's Single Source Shortest Path Algorithm Shane Saunders November 5, 1999 Abstract Dijkstra's algorithm computes the shortest paths between a starting vertex
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Binary Search Tree (3A) Young Won Lim 6/2/18
 Binary Search Tree (A) /2/1 Copyright (c) 2015-201 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2
Binary Search Tree (A) /2/1 Copyright (c) 2015-201 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2
On k-dimensional Balanced Binary Trees*
 journal of computer and system sciences 52, 328348 (1996) article no. 0025 On k-dimensional Balanced Binary Trees* Vijay K. Vaishnavi Department of Computer Information Systems, Georgia State University,
journal of computer and system sciences 52, 328348 (1996) article no. 0025 On k-dimensional Balanced Binary Trees* Vijay K. Vaishnavi Department of Computer Information Systems, Georgia State University,
Operations on Heap Tree The major operations required to be performed on a heap tree are Insertion, Deletion, and Merging.
 Priority Queue, Heap and Heap Sort In this time, we will study Priority queue, heap and heap sort. Heap is a data structure, which permits one to insert elements into a set and also to find the largest
Priority Queue, Heap and Heap Sort In this time, we will study Priority queue, heap and heap sort. Heap is a data structure, which permits one to insert elements into a set and also to find the largest
Splay Trees. (Splay Trees) Data Structures and Programming Spring / 27
 Splay Trees (Splay Trees) Data Structures and Programming Spring 2017 1 / 27 Basic Idea Invented by Sleator and Tarjan (1985) Blind rebalancing no height info kept! Worst-case time per operation is O(n)
Splay Trees (Splay Trees) Data Structures and Programming Spring 2017 1 / 27 Basic Idea Invented by Sleator and Tarjan (1985) Blind rebalancing no height info kept! Worst-case time per operation is O(n)
Efficient pebbling for list traversal synopses
 Efficient pebbling for list traversal synopses Yossi Matias Ely Porat Tel Aviv University Bar-Ilan University & Tel Aviv University Abstract 1 Introduction 1.1 Applications Consider a program P running
Efficient pebbling for list traversal synopses Yossi Matias Ely Porat Tel Aviv University Bar-Ilan University & Tel Aviv University Abstract 1 Introduction 1.1 Applications Consider a program P running
CSE Data Structures and Introduction to Algorithms... In Java! Instructor: Fei Wang. Binary Search Trees. CSE2100 DS & Algorithms 1
 CSE 2100 Data Structures and Introduction to Algorithms...! In Java!! Instructor: Fei Wang! Binary Search Trees 1 R-10.6, 10.7!!! Draw the 11-entry hash table that results from using the hash function
CSE 2100 Data Structures and Introduction to Algorithms...! In Java!! Instructor: Fei Wang! Binary Search Trees 1 R-10.6, 10.7!!! Draw the 11-entry hash table that results from using the hash function
A red-black tree is a balanced binary search tree with the following properties:
 Binary search trees work best when they are balanced or the path length from root to any leaf is within some bounds. The red-black tree algorithm is a method for balancing trees. The name derives from
Binary search trees work best when they are balanced or the path length from root to any leaf is within some bounds. The red-black tree algorithm is a method for balancing trees. The name derives from
13.4 Deletion in red-black trees
 The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
Lecture 9 March 4, 2010
 6.851: Advanced Data Structures Spring 010 Dr. André Schulz Lecture 9 March 4, 010 1 Overview Last lecture we defined the Least Common Ancestor (LCA) and Range Min Query (RMQ) problems. Recall that an
6.851: Advanced Data Structures Spring 010 Dr. André Schulz Lecture 9 March 4, 010 1 Overview Last lecture we defined the Least Common Ancestor (LCA) and Range Min Query (RMQ) problems. Recall that an
CSE373: Data Structures & Algorithms Lecture 5: Dictionary ADTs; Binary Trees. Linda Shapiro Spring 2016
 CSE373: Data Structures & lgorithms Lecture 5: Dictionary DTs; Binary Trees Linda Shapiro Spring 2016 Today s Outline nnouncements - Homework 1 due TODY at 11:59 pm - Homework 2 out (paper and pencil assignment)
CSE373: Data Structures & lgorithms Lecture 5: Dictionary DTs; Binary Trees Linda Shapiro Spring 2016 Today s Outline nnouncements - Homework 1 due TODY at 11:59 pm - Homework 2 out (paper and pencil assignment)
Garbage Collection: recycling unused memory
 Outline backtracking garbage collection trees binary search trees tree traversal binary search tree algorithms: add, remove, traverse binary node class 1 Backtracking finding a path through a maze is an
Outline backtracking garbage collection trees binary search trees tree traversal binary search tree algorithms: add, remove, traverse binary node class 1 Backtracking finding a path through a maze is an
CS350: Data Structures AVL Trees
 S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
Balanced Trees Part Two
 Balanced Trees Part Two Outline for Today Recap from Last Time Review of B-trees, 2-3-4 trees, and red/black trees. Order Statistic Trees BSTs with indexing. Augmented Binary Search Trees Building new
Balanced Trees Part Two Outline for Today Recap from Last Time Review of B-trees, 2-3-4 trees, and red/black trees. Order Statistic Trees BSTs with indexing. Augmented Binary Search Trees Building new
