Algebra 1 STAAR EOC Review #9 Reporting Category 5: Quadratic and Other Nonlinear Functions
|
|
|
- Antonia Nicholson
- 6 years ago
- Views:
Transcription
1 Name Class Date RC9 A.09B Algebra 1 STAAR EOC Review #9 Reporting Category 5: Quadratic and Other Nonlinear Functions 1. Which shows the functions correctly listed in order from widest to narrowest graph? 1 3 y 7x, y x, y x, y 5x y x, y x, y 5x, y 7x y x, y x, y 5x, y 7x y 7x, y 5x, y x, y x 7 4 A. B. C. D. A.9bcd 5. Which lists the functions of the form y = ax in order from the widest to the narrowest graph? F. G. H. J.. How is the graph of y = x different from the graph of y = 3x? 6. The graph of y = 0.x is shown below. F. The graph of y = x opens downward and is wider than the graph of y = 3x. G. The graph of y = x opens downward and is narrower than the graph of y = 3x. H. The graph of y = x opens upward and is wider than the graph of y = 3x. 3. Which equation will produce the widest parabola when graphed? A. y = x B. y = -6x C. y = -0.6x D. y = 0.x 4. Barbara graphs a family of equations of the form y = ax + 1. How does each new graph compare to the previous graph as Barbara increases the value 1 1 of a from to 1 to 1 and finally to? Which of the following equations represents a graph that is wider than the graph of y = 0.x? F. y = 0.3x G. y = 0.x + 1 H. y = 0.1x J. y = 0.x - 1 A. Each new graph is above the previous graph. B. Each new graph is wider than the previous graph. C. Each new graph is narrower than the previous graph.
2 RC 5 A.09C 7. In the graph of the function y = x + 5, which describes the shift in the vertex of the parabola if, in the function, 5 is changed to -? 1. Which graph shows a function y = x + c when c < -1? F. A. 3 units up B. 7 units up C. 3 units down D. 7 units down 8. What is the effect on the graph of the equation y = x + 1 when it is changed to y = x + 5? F. The slope of the graph changes. G. The curve translates in the positive x direction. H. The graph is congruent, and the vertex of the graph moves up the y-axis. J. The graph narrows. G. 9. How does the graph of y = x differ from the graph of y = x - 4? A. The graph of y = x - 4 is wider than the graph of y = x. B. The graph of y = x - 4 is shifted to the left of the graph of y = x. C. The graph of y = x - 4 is shifted down from the graph of y = x. D. The graph of y = x - 4 is narrower than the graph of y = x. H. 10. The graph of y = 11x + c is a parabola with a vertex at the origin. Which of the following is true about the value of c? F. c > 0 G. c < 0 H. c = 0 J. c = 11 J. 11. If the graph of y = 19x + 31 is translated up 15 units, which of the following equations will best describe the resulting graph? A. y = 34x + 31 B. y = 34x + 46 C. y = 19x + 46 D. y = 19x + 16
3 13. The graph of the function y = x 3 is shown below. 16. The graph of the form y = ax + c is shown below. If the graph of the original function is shifted 5 units up, which of the following equations best represents the translation of each point on the curve? A. y = x + 5 B. y = x + C. y = x - D. y = x What is the effect on the graph of the equation y = x -.5 when the equation is changed to y = x +.5? F. The graph of y = x +.5 is a reflection of y = x -.5 across the x- axis. G. The graph of y = x +.5 is a translation of the graph of y = x -.5. H. The graph of y = x +.5 is a reflection of y = x -.5 across the y- axis. J. The graph of y = x +.5 is a dilation of the graph of y = x How does the graph of y = 3x 5 compare with the graph of y = 3x + 8? A. The graph of y = 3x - 5 is 3 units above the graph of y = 3x + 8. B. The graph of y = 3x - 5 is 13 units below the graph of y = 3x + 8. C. The graph of y = 3x - 5 is 3 units to the right of the graph of y = 3x + 8. D. The graph of y = 3x - 5 is 13 units to the left of the graph of y = 3x + 8. If the graph is translated only up or down to include the ordered pair (6, 7), which of the following equations best represents the resulting graph? F. G. H. J. 17. The function y = 5x represents a function of the form y = ax + c. If the value of c is multiplied by 4, how does the graph of the new function compare to the graph of the original function? A. The graph of the new function is a reflection of the graph of the original function across the x-axis. B. The graph of the new function is a translation down of the graph of the original function. C. The graph of the new function is the same as the graph of the original function.
4 RC 5 A.09D 18. The graph below shows h, the height in meters of a model rocket, versus t, the time in seconds after the rocket is launched. From the graph, what conclusion can be made about the flight of the rocket? 0. Which of the following is the vertex of the graph of the equation y = x + x + 3? F. The rocket reached its maximum height after.5 seconds. G. At 0 seconds the rocket was meters off the ground. H. The height of the rocket was 0 meters when it was launched. J. The rocket was in flight for 5 seconds. F. (0, 3) G. ( 1, 0) H. (1, 4) J. (3, 0) 1. The graph below represents the relationship between the density of water and the temperature of water. 19. Look at the equation shown below. Which of the following statements is true for the graphs of all the equations given? A. The graphs are congruent and open downward. B. The graphs open upward and are symmetrical about the y-axis. C. The graphs are congruent and are listed from narrowest to widest. D. The graphs open downward and are symmetrical about the y-axis. According to the graph, which of the following intervals best represents the temperature at which the density of water is greater than kilograms per cubic meter? A. Less than 1 C B. Between 0 C and 4 C C. Between 4 C and 8 C D. Between 1 C and 7 C
5 . The graph of a quadratic function is shown below. 4. If the graph of a function of the form has a vertex located above the origin and opens downward, which of the following must be true about the values of a and c? F. a < 0 and c > 0 G. a > 0 and c > 0 H. a < 0 and c < 0 J. a > 0 and c < 0 5. An object was dropped from a height of 50 meters and fell to the ground. The graph below shows the change in h, the object s height in meters, with respect to t, the time in seconds. A. The graph has a y-intercept at (0, 8). B. The graph has a maximum point at (-1, 9). C. The graph has an x-intercept at (, 0). D. The graph has the y-axis as a line of symmetry. 3. Which statement best describes the sales of this CD? According to the graph, which time interval best represents when the object was at 140 meters above the ground? A. Between 3 seconds and 3.5 seconds B. Between 3.75 seconds and 4 seconds C. Between 3.5 seconds and 3.75 seconds D. Between 3.5 seconds and 3.5 seconds F. Sales rapidly increased, reached a peak, and then gradually decreased. G. Sales gradually increased, reached a peak, and then leveled off. H. Sales rapidly increased, reached a peak, and then rapidly decreased. J. Sales remained constant throughout the time period.
6
3.1 INTRODUCTION TO THE FAMILY OF QUADRATIC FUNCTIONS
 3.1 INTRODUCTION TO THE FAMILY OF QUADRATIC FUNCTIONS Finding the Zeros of a Quadratic Function Examples 1 and and more Find the zeros of f(x) = x x 6. Solution by Factoring f(x) = x x 6 = (x 3)(x + )
3.1 INTRODUCTION TO THE FAMILY OF QUADRATIC FUNCTIONS Finding the Zeros of a Quadratic Function Examples 1 and and more Find the zeros of f(x) = x x 6. Solution by Factoring f(x) = x x 6 = (x 3)(x + )
8-4 Transforming Quadratic Functions
 8-4 Transforming Quadratic Functions Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up For each quadratic function, find the axis of symmetry and vertex, and state whether the function opens upward
8-4 Transforming Quadratic Functions Warm Up Lesson Presentation Lesson Quiz Algebra 1 Warm Up For each quadratic function, find the axis of symmetry and vertex, and state whether the function opens upward
Warm-Up Exercises. Find the x-intercept and y-intercept 1. 3x 5y = 15 ANSWER 5; y = 2x + 7 ANSWER ; 7
 Warm-Up Exercises Find the x-intercept and y-intercept 1. 3x 5y = 15 ANSWER 5; 3 2. y = 2x + 7 7 2 ANSWER ; 7 Chapter 1.1 Graph Quadratic Functions in Standard Form A quadratic function is a function that
Warm-Up Exercises Find the x-intercept and y-intercept 1. 3x 5y = 15 ANSWER 5; 3 2. y = 2x + 7 7 2 ANSWER ; 7 Chapter 1.1 Graph Quadratic Functions in Standard Form A quadratic function is a function that
UNIT 3 EXPRESSIONS AND EQUATIONS Lesson 3: Creating Quadratic Equations in Two or More Variables
 Guided Practice Example 1 Find the y-intercept and vertex of the function f(x) = 2x 2 + x + 3. Determine whether the vertex is a minimum or maximum point on the graph. 1. Determine the y-intercept. The
Guided Practice Example 1 Find the y-intercept and vertex of the function f(x) = 2x 2 + x + 3. Determine whether the vertex is a minimum or maximum point on the graph. 1. Determine the y-intercept. The
CHAPTER 6 Quadratic Functions
 CHAPTER 6 Quadratic Functions Math 1201: Linear Functions is the linear term 3 is the leading coefficient 4 is the constant term Math 2201: Quadratic Functions Math 3201: Cubic, Quartic, Quintic Functions
CHAPTER 6 Quadratic Functions Math 1201: Linear Functions is the linear term 3 is the leading coefficient 4 is the constant term Math 2201: Quadratic Functions Math 3201: Cubic, Quartic, Quintic Functions
Objective. 9-4 Transforming Quadratic Functions. Graph and transform quadratic functions.
 Warm Up Lesson Presentation Lesson Quiz Warm Up For each quadratic function, find the axis of symmetry and vertex, and state whether the function opens upward or downward. 1. y = x 2 + 3 2. y = 2x 2 x
Warm Up Lesson Presentation Lesson Quiz Warm Up For each quadratic function, find the axis of symmetry and vertex, and state whether the function opens upward or downward. 1. y = x 2 + 3 2. y = 2x 2 x
3x 2 + 7x + 2. A 8-6 Factor. Step 1. Step 3 Step 4. Step 2. Step 1 Step 2 Step 3 Step 4
 A 8-6 Factor. Step 1 3x 2 + 7x + 2 Step 2 Step 3 Step 4 3x 2 + 7x + 2 3x 2 + 7x + 2 Step 1 Step 2 Step 3 Step 4 Factor. 1. 3x 2 + 4x +1 = 2. 3x 2 +10x + 3 = 3. 3x 2 +13x + 4 = A 8-6 Name BDFM? Why? Factor.
A 8-6 Factor. Step 1 3x 2 + 7x + 2 Step 2 Step 3 Step 4 3x 2 + 7x + 2 3x 2 + 7x + 2 Step 1 Step 2 Step 3 Step 4 Factor. 1. 3x 2 + 4x +1 = 2. 3x 2 +10x + 3 = 3. 3x 2 +13x + 4 = A 8-6 Name BDFM? Why? Factor.
6.4 Vertex Form of a Quadratic Function
 6.4 Vertex Form of a Quadratic Function Recall from 6.1 and 6.2: Standard Form The standard form of a quadratic is: f(x) = ax 2 + bx + c or y = ax 2 + bx + c where a, b, and c are real numbers and a 0.
6.4 Vertex Form of a Quadratic Function Recall from 6.1 and 6.2: Standard Form The standard form of a quadratic is: f(x) = ax 2 + bx + c or y = ax 2 + bx + c where a, b, and c are real numbers and a 0.
F.BF.B.3: Graphing Polynomial Functions
 F.BF.B.3: Graphing Polynomial Functions 1 Given the graph of the line represented by the equation f(x) = 2x + b, if b is increased by 4 units, the graph of the new line would be shifted 4 units 1) right
F.BF.B.3: Graphing Polynomial Functions 1 Given the graph of the line represented by the equation f(x) = 2x + b, if b is increased by 4 units, the graph of the new line would be shifted 4 units 1) right
This is called the vertex form of the quadratic equation. To graph the equation
 Name Period Date: Topic: 7-5 Graphing ( ) Essential Question: What is the vertex of a parabola, and what is its axis of symmetry? Standard: F-IF.7a Objective: Graph linear and quadratic functions and show
Name Period Date: Topic: 7-5 Graphing ( ) Essential Question: What is the vertex of a parabola, and what is its axis of symmetry? Standard: F-IF.7a Objective: Graph linear and quadratic functions and show
3.1 Investigating Quadratic Functions in Vertex Form
 Math 2200 Date: 3.1 Investigating Quadratic Functions in Vertex Form Degree of a Function - refers to the highest exponent on the variable in an expression or equation. In Math 1201, you learned about
Math 2200 Date: 3.1 Investigating Quadratic Functions in Vertex Form Degree of a Function - refers to the highest exponent on the variable in an expression or equation. In Math 1201, you learned about
Writing Equivalent Forms of Quadratic Functions Adapted from Walch Education
 Writing Equivalent Forms of Quadratic Functions Adapted from Walch Education Recall The standard form, or general form, of a quadratic function is written as f(x) = ax 2 + bx + c, where a is the coefficient
Writing Equivalent Forms of Quadratic Functions Adapted from Walch Education Recall The standard form, or general form, of a quadratic function is written as f(x) = ax 2 + bx + c, where a is the coefficient
Section 9.3 Graphing Quadratic Functions
 Section 9.3 Graphing Quadratic Functions A Quadratic Function is an equation that can be written in the following Standard Form., where a 0. Every quadratic function has a U-shaped graph called a. If the
Section 9.3 Graphing Quadratic Functions A Quadratic Function is an equation that can be written in the following Standard Form., where a 0. Every quadratic function has a U-shaped graph called a. If the
Unit 2: Functions and Graphs
 AMHS Precalculus - Unit 16 Unit : Functions and Graphs Functions A function is a rule that assigns each element in the domain to exactly one element in the range. The domain is the set of all possible
AMHS Precalculus - Unit 16 Unit : Functions and Graphs Functions A function is a rule that assigns each element in the domain to exactly one element in the range. The domain is the set of all possible
Polynomial and Rational Functions. Copyright Cengage Learning. All rights reserved.
 2 Polynomial and Rational Functions Copyright Cengage Learning. All rights reserved. 2.1 Quadratic Functions Copyright Cengage Learning. All rights reserved. What You Should Learn Analyze graphs of quadratic
2 Polynomial and Rational Functions Copyright Cengage Learning. All rights reserved. 2.1 Quadratic Functions Copyright Cengage Learning. All rights reserved. What You Should Learn Analyze graphs of quadratic
Algebra II Quadratic Functions
 1 Algebra II Quadratic Functions 2014-10-14 www.njctl.org 2 Ta b le o f C o n te n t Key Terms click on the topic to go to that section Explain Characteristics of Quadratic Functions Combining Transformations
1 Algebra II Quadratic Functions 2014-10-14 www.njctl.org 2 Ta b le o f C o n te n t Key Terms click on the topic to go to that section Explain Characteristics of Quadratic Functions Combining Transformations
Algebra II Notes Transformations Unit 1.1. Math Background
 Lesson. - Parent Functions and Transformations Math Background Previously, you Studied linear, absolute value, exponential and quadratic equations Graphed linear, absolute value, exponential and quadratic
Lesson. - Parent Functions and Transformations Math Background Previously, you Studied linear, absolute value, exponential and quadratic equations Graphed linear, absolute value, exponential and quadratic
2. The diagram shows part of the graph of y = a (x h) 2 + k. The graph has its vertex at P, and passes through the point A with coordinates (1, 0).
 Quadratics Vertex Form 1. Part of the graph of the function y = d (x m) + p is given in the diagram below. The x-intercepts are (1, 0) and (5, 0). The vertex is V(m, ). (a) Write down the value of (i)
Quadratics Vertex Form 1. Part of the graph of the function y = d (x m) + p is given in the diagram below. The x-intercepts are (1, 0) and (5, 0). The vertex is V(m, ). (a) Write down the value of (i)
Amplifying an Instructional Task Algebra II Example
 Original Task The student is expected to write the equation of a parabola using given attributes, including vertex, focus, directrix, axis of symmetry, and direction of opening. A(4)(B) Write the equations
Original Task The student is expected to write the equation of a parabola using given attributes, including vertex, focus, directrix, axis of symmetry, and direction of opening. A(4)(B) Write the equations
3.1 Quadratic Functions in Vertex Form
 3.1 Quadratic Functions in Vertex Form 1) Identify quadratic functions in vertex form. 2) Determine the effect of a, p, and q on the graph of a quadratic function in vertex form where y = a(x p)² + q 3)
3.1 Quadratic Functions in Vertex Form 1) Identify quadratic functions in vertex form. 2) Determine the effect of a, p, and q on the graph of a quadratic function in vertex form where y = a(x p)² + q 3)
Quadratic Functions, Part 1
 Quadratic Functions, Part 1 A2.F.BF.A.1 Write a function that describes a relationship between two quantities. A2.F.BF.A.1a Determine an explicit expression, a recursive process, or steps for calculation
Quadratic Functions, Part 1 A2.F.BF.A.1 Write a function that describes a relationship between two quantities. A2.F.BF.A.1a Determine an explicit expression, a recursive process, or steps for calculation
MAC Rev.S Learning Objectives. Learning Objectives (Cont.) Module 4 Quadratic Functions and Equations
 MAC 1140 Module 4 Quadratic Functions and Equations Learning Objectives Upon completing this module, you should be able to 1. understand basic concepts about quadratic functions and their graphs.. complete
MAC 1140 Module 4 Quadratic Functions and Equations Learning Objectives Upon completing this module, you should be able to 1. understand basic concepts about quadratic functions and their graphs.. complete
Properties of Quadratic functions
 Name Today s Learning Goals: #1 How do we determine the axis of symmetry and vertex of a quadratic function? Properties of Quadratic functions Date 5-1 Properties of a Quadratic Function A quadratic equation
Name Today s Learning Goals: #1 How do we determine the axis of symmetry and vertex of a quadratic function? Properties of Quadratic functions Date 5-1 Properties of a Quadratic Function A quadratic equation
It is than the graph of y= x if a > 1.
 Chapter 8 Quadratic Functions and Equations Name: Instructor: 8.1 Quadratic Functions and Their Graphs Graphs of Quadratic Functions Basic Transformations of Graphs More About Graphing Quadratic Functions
Chapter 8 Quadratic Functions and Equations Name: Instructor: 8.1 Quadratic Functions and Their Graphs Graphs of Quadratic Functions Basic Transformations of Graphs More About Graphing Quadratic Functions
Replacing f(x) with k f(x) and. Adapted from Walch Education
 Replacing f(x) with k f(x) and f(k x) Adapted from Walch Education Graphing and Points of Interest In the graph of a function, there are key points of interest that define the graph and represent the characteristics
Replacing f(x) with k f(x) and f(k x) Adapted from Walch Education Graphing and Points of Interest In the graph of a function, there are key points of interest that define the graph and represent the characteristics
Quadratic Functions (Section 2-1)
 Quadratic Functions (Section 2-1) Section 2.1, Definition of Polynomial Function f(x) = a is the constant function f(x) = mx + b where m 0 is a linear function f(x) = ax 2 + bx + c with a 0 is a quadratic
Quadratic Functions (Section 2-1) Section 2.1, Definition of Polynomial Function f(x) = a is the constant function f(x) = mx + b where m 0 is a linear function f(x) = ax 2 + bx + c with a 0 is a quadratic
Section 6.2: Properties of Graphs of Quadratic Functions. Vertex:
 Section 6.2: Properties of Graphs of Quadratic Functions determine the vertex of a quadratic in standard form sketch the graph determine the y intercept, x intercept(s), the equation of the axis of symmetry,
Section 6.2: Properties of Graphs of Quadratic Functions determine the vertex of a quadratic in standard form sketch the graph determine the y intercept, x intercept(s), the equation of the axis of symmetry,
Algebra I. Slide 1 / 137. Slide 2 / 137. Slide 3 / 137. Quadratic & Non-Linear Functions. Table of Contents
 Slide 1 / 137 Slide 2 / 137 Algebra I Quadratic & Non-Linear Functions 2015-11-04 www.njctl.org Table of Contents Slide 3 / 137 Click on the topic to go to that section Key Terms Explain Characteristics
Slide 1 / 137 Slide 2 / 137 Algebra I Quadratic & Non-Linear Functions 2015-11-04 www.njctl.org Table of Contents Slide 3 / 137 Click on the topic to go to that section Key Terms Explain Characteristics
Unit 3, Lesson 3.1 Creating and Graphing Equations Using Standard Form
 Unit 3, Lesson 3.1 Creating and Graphing Equations Using Standard Form Imagine the path of a basketball as it leaves a player s hand and swooshes through the net. Or, imagine the path of an Olympic diver
Unit 3, Lesson 3.1 Creating and Graphing Equations Using Standard Form Imagine the path of a basketball as it leaves a player s hand and swooshes through the net. Or, imagine the path of an Olympic diver
Unit #3: Quadratic Functions Lesson #13: The Almighty Parabola. Day #1
 Algebra I Unit #3: Quadratic Functions Lesson #13: The Almighty Parabola Name Period Date Day #1 There are some important features about the graphs of quadratic functions we are going to explore over the
Algebra I Unit #3: Quadratic Functions Lesson #13: The Almighty Parabola Name Period Date Day #1 There are some important features about the graphs of quadratic functions we are going to explore over the
2.5: GRAPHS OF EXPENSE AND REVENUE FUNCTIONS OBJECTIVES
 Section 2.5: GRAPHS OF EXPENSE AND REVENUE FUNCTIONS OBJECTIVES Write, graph and interpret the expense function. Write, graph and interpret the revenue function. Identify the points of intersection of
Section 2.5: GRAPHS OF EXPENSE AND REVENUE FUNCTIONS OBJECTIVES Write, graph and interpret the expense function. Write, graph and interpret the revenue function. Identify the points of intersection of
Quadratic Functions CHAPTER. 1.1 Lots and Projectiles Introduction to Quadratic Functions p. 31
 CHAPTER Quadratic Functions Arches are used to support the weight of walls and ceilings in buildings. Arches were first used in architecture by the Mesopotamians over 4000 years ago. Later, the Romans
CHAPTER Quadratic Functions Arches are used to support the weight of walls and ceilings in buildings. Arches were first used in architecture by the Mesopotamians over 4000 years ago. Later, the Romans
A function: A mathematical relationship between two variables (x and y), where every input value (usually x) has one output value (usually y)
 SESSION 9: FUNCTIONS KEY CONCEPTS: Definitions & Terminology Graphs of Functions - Straight line - Parabola - Hyperbola - Exponential Sketching graphs Finding Equations Combinations of graphs TERMINOLOGY
SESSION 9: FUNCTIONS KEY CONCEPTS: Definitions & Terminology Graphs of Functions - Straight line - Parabola - Hyperbola - Exponential Sketching graphs Finding Equations Combinations of graphs TERMINOLOGY
QUADRATIC FUNCTIONS. PROTOTYPE: f(x) = ax 2 + bx + c. (1) The leading coefficient a 0 is called the shape parameter.
 QUADRATIC FUNCTIONS PROTOTYPE: f(x) = ax 2 + bx + c. (1) The leading coefficient a 0 is called the shape parameter. SHAPE-VERTEX FORMULA One can write any quadratic function (1) as f(x) = a(x h) 2 + k,
QUADRATIC FUNCTIONS PROTOTYPE: f(x) = ax 2 + bx + c. (1) The leading coefficient a 0 is called the shape parameter. SHAPE-VERTEX FORMULA One can write any quadratic function (1) as f(x) = a(x h) 2 + k,
Quadratic Functions. *These are all examples of polynomial functions.
 Look at: f(x) = 4x-7 f(x) = 3 f(x) = x 2 + 4 Quadratic Functions *These are all examples of polynomial functions. Definition: Let n be a nonnegative integer and let a n, a n 1,..., a 2, a 1, a 0 be real
Look at: f(x) = 4x-7 f(x) = 3 f(x) = x 2 + 4 Quadratic Functions *These are all examples of polynomial functions. Definition: Let n be a nonnegative integer and let a n, a n 1,..., a 2, a 1, a 0 be real
Module 3: Graphing Quadratic Functions
 Haberman MTH 95 Section V Quadratic Equations and Functions Module 3 Graphing Quadratic Functions In this module, we'll review the graphing quadratic functions (you should have studied the graphs of quadratic
Haberman MTH 95 Section V Quadratic Equations and Functions Module 3 Graphing Quadratic Functions In this module, we'll review the graphing quadratic functions (you should have studied the graphs of quadratic
KEY Algebra: Unit 10 Graphing Quadratic Equations & other Relations
 Name: KEY Algebra: Unit 10 Graphing Quadratic Equations & other Relations Date: Test Bank Part I: Answer all 15 questions in this part. Each correct answer will receive credits. No partial credit will
Name: KEY Algebra: Unit 10 Graphing Quadratic Equations & other Relations Date: Test Bank Part I: Answer all 15 questions in this part. Each correct answer will receive credits. No partial credit will
9.1: GRAPHING QUADRATICS ALGEBRA 1
 9.1: GRAPHING QUADRATICS ALGEBRA 1 OBJECTIVES I will be able to graph quadratics: Given in Standard Form Given in Vertex Form Given in Intercept Form What does the graph of a quadratic look like? https://www.desmos.com/calculator
9.1: GRAPHING QUADRATICS ALGEBRA 1 OBJECTIVES I will be able to graph quadratics: Given in Standard Form Given in Vertex Form Given in Intercept Form What does the graph of a quadratic look like? https://www.desmos.com/calculator
Algebra 1: Quadratic Functions Review (Ch. 9 part 1)
 Name: Class: Date: ID: A Algebra 1: Quadratic Functions Review (Ch. 9 part 1) 1. Find the rule of a parabola that has the Ê 1 x-intercepts at ( 6,0) and,0 ˆ 3 ËÁ. 6. 2. Find the rule of a parabola that
Name: Class: Date: ID: A Algebra 1: Quadratic Functions Review (Ch. 9 part 1) 1. Find the rule of a parabola that has the Ê 1 x-intercepts at ( 6,0) and,0 ˆ 3 ËÁ. 6. 2. Find the rule of a parabola that
Section 18-1: Graphical Representation of Linear Equations and Functions
 Section 18-1: Graphical Representation of Linear Equations and Functions Prepare a table of solutions and locate the solutions on a coordinate system: f(x) = 2x 5 Learning Outcome 2 Write x + 3 = 5 as
Section 18-1: Graphical Representation of Linear Equations and Functions Prepare a table of solutions and locate the solutions on a coordinate system: f(x) = 2x 5 Learning Outcome 2 Write x + 3 = 5 as
Graphing Absolute Value Functions
 Graphing Absolute Value Functions To graph an absolute value equation, make an x/y table and plot the points. Graph y = x (Parent graph) x y -2 2-1 1 0 0 1 1 2 2 Do we see a pattern? Desmos activity: 1.
Graphing Absolute Value Functions To graph an absolute value equation, make an x/y table and plot the points. Graph y = x (Parent graph) x y -2 2-1 1 0 0 1 1 2 2 Do we see a pattern? Desmos activity: 1.
Quadratic Equations. Learning Objectives. Quadratic Function 2. where a, b, and c are real numbers and a 0
 Quadratic Equations Learning Objectives 1. Graph a quadratic function using transformations. Identify the vertex and axis of symmetry of a quadratic function 3. Graph a quadratic function using its vertex,
Quadratic Equations Learning Objectives 1. Graph a quadratic function using transformations. Identify the vertex and axis of symmetry of a quadratic function 3. Graph a quadratic function using its vertex,
Section 9.1 Identifying Quadratic Functions Section 9.2 Characteristics of Quadratics
 1 Algebra 1, Quadratic Notes Name Learning Targets: Section 9.1 Identifying Quadratic Functions Section 9.2 Characteristics of Quadratics Identify quadratic functions and determine whether they have a
1 Algebra 1, Quadratic Notes Name Learning Targets: Section 9.1 Identifying Quadratic Functions Section 9.2 Characteristics of Quadratics Identify quadratic functions and determine whether they have a
MAC Learning Objectives. Module 4. Quadratic Functions and Equations. - Quadratic Functions - Solving Quadratic Equations
 MAC 1105 Module 4 Quadratic Functions and Equations Learning Objectives Upon completing this module, you should be able to: 1. Understand basic concepts about quadratic functions and their graphs. 2. Complete
MAC 1105 Module 4 Quadratic Functions and Equations Learning Objectives Upon completing this module, you should be able to: 1. Understand basic concepts about quadratic functions and their graphs. 2. Complete
Unit 6 Quadratic Functions
 Unit 6 Quadratic Functions 12.1 & 12.2 Introduction to Quadratic Functions What is A Quadratic Function? How do I tell if a Function is Quadratic? From a Graph The shape of a quadratic function is called
Unit 6 Quadratic Functions 12.1 & 12.2 Introduction to Quadratic Functions What is A Quadratic Function? How do I tell if a Function is Quadratic? From a Graph The shape of a quadratic function is called
Student Exploration: Quadratics in Polynomial Form
 Name: Date: Student Exploration: Quadratics in Polynomial Form Vocabulary: axis of symmetry, parabola, quadratic function, vertex of a parabola Prior Knowledge Questions (Do these BEFORE using the Gizmo.)
Name: Date: Student Exploration: Quadratics in Polynomial Form Vocabulary: axis of symmetry, parabola, quadratic function, vertex of a parabola Prior Knowledge Questions (Do these BEFORE using the Gizmo.)
5.1 Introduction to the Graphs of Polynomials
 Math 3201 5.1 Introduction to the Graphs of Polynomials In Math 1201/2201, we examined three types of polynomial functions: Constant Function - horizontal line such as y = 2 Linear Function - sloped line,
Math 3201 5.1 Introduction to the Graphs of Polynomials In Math 1201/2201, we examined three types of polynomial functions: Constant Function - horizontal line such as y = 2 Linear Function - sloped line,
Section 4.4: Parabolas
 Objective: Graph parabolas using the vertex, x-intercepts, and y-intercept. Just as the graph of a linear equation y mx b can be drawn, the graph of a quadratic equation y ax bx c can be drawn. The graph
Objective: Graph parabolas using the vertex, x-intercepts, and y-intercept. Just as the graph of a linear equation y mx b can be drawn, the graph of a quadratic equation y ax bx c can be drawn. The graph
2.2 Transformers: More Than Meets the y s
 10 SECONDARY MATH II // MODULE 2 STRUCTURES OF EXPRESSIONS 2.2 Transformers: More Than Meets the y s A Solidify Understanding Task Writetheequationforeachproblembelow.Useasecond representationtocheckyourequation.
10 SECONDARY MATH II // MODULE 2 STRUCTURES OF EXPRESSIONS 2.2 Transformers: More Than Meets the y s A Solidify Understanding Task Writetheequationforeachproblembelow.Useasecond representationtocheckyourequation.
Algebra II Lesson 4.1 and 4.2 Review
 Name: Class: Date: Algebra II Lesson 4.1 and 4.2 Review 1. Graph y = 1 4 x 2. a. c. b. d. Graph. 2. y = x 2 3 a. c. b. d. 1 Name: 3. y = 3x 2 + x + 1 a. c. b. d. 4. y = 2x 2 + x + 3 5. How would you translate
Name: Class: Date: Algebra II Lesson 4.1 and 4.2 Review 1. Graph y = 1 4 x 2. a. c. b. d. Graph. 2. y = x 2 3 a. c. b. d. 1 Name: 3. y = 3x 2 + x + 1 a. c. b. d. 4. y = 2x 2 + x + 3 5. How would you translate
Lesson 1: Analyzing Quadratic Functions
 UNIT QUADRATIC FUNCTIONS AND MODELING Lesson 1: Analyzing Quadratic Functions Common Core State Standards F IF.7 F IF.8 Essential Questions Graph functions expressed symbolically and show key features
UNIT QUADRATIC FUNCTIONS AND MODELING Lesson 1: Analyzing Quadratic Functions Common Core State Standards F IF.7 F IF.8 Essential Questions Graph functions expressed symbolically and show key features
Parabolas have a, a middle point. For
 Key Ideas: 3.1A Investigating Quadratic Functions in Vertex Form: y = a(x ± p) ± q Date: Graph y x using the count method. Quick way to graph: Use a basic count: Start at vertex: in this case (0,0) Graph
Key Ideas: 3.1A Investigating Quadratic Functions in Vertex Form: y = a(x ± p) ± q Date: Graph y x using the count method. Quick way to graph: Use a basic count: Start at vertex: in this case (0,0) Graph
A I only B II only C II and IV D I and III B. 5 C. -8
 1. (7A) Points (3, 2) and (7, 2) are on the graphs of both quadratic functions f and g. The graph of f opens downward, and the graph of g opens upward. Which of these statements are true? I. The graphs
1. (7A) Points (3, 2) and (7, 2) are on the graphs of both quadratic functions f and g. The graph of f opens downward, and the graph of g opens upward. Which of these statements are true? I. The graphs
QUADRATICS Graphing Quadratic Functions Common Core Standard
 H Quadratics, Lesson 6, Graphing Quadratic Functions (r. 2018) QUADRATICS Graphing Quadratic Functions Common Core Standard Next Generation Standard F-IF.B.4 For a function that models a relationship between
H Quadratics, Lesson 6, Graphing Quadratic Functions (r. 2018) QUADRATICS Graphing Quadratic Functions Common Core Standard Next Generation Standard F-IF.B.4 For a function that models a relationship between
Properties of Graphs of Quadratic Functions
 H e i g h t (f t ) Lesson 2 Goal: Properties of Graphs of Quadratic Functions Identify the characteristics of graphs of quadratic functions: Vertex Intercepts Domain and Range Axis of Symmetry and use
H e i g h t (f t ) Lesson 2 Goal: Properties of Graphs of Quadratic Functions Identify the characteristics of graphs of quadratic functions: Vertex Intercepts Domain and Range Axis of Symmetry and use
Section 7.2 Characteristics of Quadratic Functions
 Section 7. Characteristics of Quadratic Functions A QUADRATIC FUNCTION is a function of the form " # $ N# 1 & ;# & 0 Characteristics Include:! Three distinct terms each with its own coefficient:! An x
Section 7. Characteristics of Quadratic Functions A QUADRATIC FUNCTION is a function of the form " # $ N# 1 & ;# & 0 Characteristics Include:! Three distinct terms each with its own coefficient:! An x
Exploring Quadratic Graphs
 Exploring Quadratic Graphs The general quadratic function is y=ax 2 +bx+c It has one of two basic graphs shapes, as shown below: It is a symmetrical "U"-shape or "hump"-shape, depending on the sign of
Exploring Quadratic Graphs The general quadratic function is y=ax 2 +bx+c It has one of two basic graphs shapes, as shown below: It is a symmetrical "U"-shape or "hump"-shape, depending on the sign of
Name: Algebra. Unit 8. Quadratic. Functions
 Name: Algebra Unit 8 Quadratic Functions Quadratic Function Characteristics of the Graph: Maximum Minimum Parent Function Equation: Vertex How many solutions can there be? They mean what? What does a do?
Name: Algebra Unit 8 Quadratic Functions Quadratic Function Characteristics of the Graph: Maximum Minimum Parent Function Equation: Vertex How many solutions can there be? They mean what? What does a do?
Algebra II Quadratic Functions and Equations - Extrema Unit 05b
 Big Idea: Quadratic Functions can be used to find the maximum or minimum that relates to real world application such as determining the maximum height of a ball thrown into the air or solving problems
Big Idea: Quadratic Functions can be used to find the maximum or minimum that relates to real world application such as determining the maximum height of a ball thrown into the air or solving problems
+ bx + c = 0, you can solve for x by using The Quadratic Formula. x
 Math 33B Intermediate Algebra Fall 01 Name Study Guide for Exam 4 The exam will be on Friday, November 9 th. You are allowed to use one 3" by 5" index card on the exam as well as a scientific calculator.
Math 33B Intermediate Algebra Fall 01 Name Study Guide for Exam 4 The exam will be on Friday, November 9 th. You are allowed to use one 3" by 5" index card on the exam as well as a scientific calculator.
1. Answer: x or x. Explanation Set up the two equations, then solve each equation. x. Check
 Thinkwell s Placement Test 5 Answer Key If you answered 7 or more Test 5 questions correctly, we recommend Thinkwell's Algebra. If you answered fewer than 7 Test 5 questions correctly, we recommend Thinkwell's
Thinkwell s Placement Test 5 Answer Key If you answered 7 or more Test 5 questions correctly, we recommend Thinkwell's Algebra. If you answered fewer than 7 Test 5 questions correctly, we recommend Thinkwell's
EXERCISE SET 10.2 MATD 0390 DUE DATE: INSTRUCTOR
 EXERCISE SET 10. STUDENT MATD 090 DUE DATE: INSTRUCTOR You have studied the method known as "completing the square" to solve quadratic equations. Another use for this method is in transforming the equation
EXERCISE SET 10. STUDENT MATD 090 DUE DATE: INSTRUCTOR You have studied the method known as "completing the square" to solve quadratic equations. Another use for this method is in transforming the equation
Name: Chapter 7 Review: Graphing Quadratic Functions
 Name: Chapter Review: Graphing Quadratic Functions A. Intro to Graphs of Quadratic Equations: = ax + bx+ c A is a function that can be written in the form = ax + bx+ c where a, b, and c are real numbers
Name: Chapter Review: Graphing Quadratic Functions A. Intro to Graphs of Quadratic Equations: = ax + bx+ c A is a function that can be written in the form = ax + bx+ c where a, b, and c are real numbers
UNIT 5 QUADRATIC FUNCTIONS Lesson 7: Building Functions Instruction
 Prerequisite Skills This lesson requires the use of the following skills: multiplying linear expressions factoring quadratic equations finding the value of a in the vertex form of a quadratic equation
Prerequisite Skills This lesson requires the use of the following skills: multiplying linear expressions factoring quadratic equations finding the value of a in the vertex form of a quadratic equation
0.4 Family of Functions/Equations
 0.4 Family of Functions/Equations By a family of functions, we are referring to a function definition such as f(x) = mx + 2 for m = 2, 1, 1, 0, 1, 1, 2. 2 2 This says, work with all the functions obtained
0.4 Family of Functions/Equations By a family of functions, we are referring to a function definition such as f(x) = mx + 2 for m = 2, 1, 1, 0, 1, 1, 2. 2 2 This says, work with all the functions obtained
9.1 Linear Inequalities in Two Variables Date: 2. Decide whether to use a solid line or dotted line:
 9.1 Linear Inequalities in Two Variables Date: Key Ideas: Example Solve the inequality by graphing 3y 2x 6. steps 1. Rearrange the inequality so it s in mx ± b form. Don t forget to flip the inequality
9.1 Linear Inequalities in Two Variables Date: Key Ideas: Example Solve the inequality by graphing 3y 2x 6. steps 1. Rearrange the inequality so it s in mx ± b form. Don t forget to flip the inequality
Transformations with Quadratic Functions KEY
 Algebra Unit: 05 Lesson: 0 TRY THIS! Use a calculator to generate a table of values for the function y = ( x 3) + 4 y = ( x 3) x + y 4 Next, simplify the function by squaring, distributing, and collecting
Algebra Unit: 05 Lesson: 0 TRY THIS! Use a calculator to generate a table of values for the function y = ( x 3) + 4 y = ( x 3) x + y 4 Next, simplify the function by squaring, distributing, and collecting
But a vertex has two coordinates, an x and a y coordinate. So how would you find the corresponding y-value?
 We will work with the vertex, orientation, and x- and y-intercepts of these functions. Intermediate algebra Class notes More Graphs of Quadratic Functions (section 11.6) In the previous section, we investigated
We will work with the vertex, orientation, and x- and y-intercepts of these functions. Intermediate algebra Class notes More Graphs of Quadratic Functions (section 11.6) In the previous section, we investigated
Lesson 3.1 Vertices and Intercepts. Important Features of Parabolas
 Lesson 3.1 Vertices and Intercepts Name: _ Learning Objective: Students will be able to identify the vertex and intercepts of a parabola from its equation. CCSS.MATH.CONTENT.HSF.IF.C.7.A Graph linear and
Lesson 3.1 Vertices and Intercepts Name: _ Learning Objective: Students will be able to identify the vertex and intercepts of a parabola from its equation. CCSS.MATH.CONTENT.HSF.IF.C.7.A Graph linear and
Quadratic Functions. Chapter Properties of Quadratic Functions... p Investigating Quadratic Functions... p. 6 in Vertex Form: Part 1
 Chapter 3 Quadratic Functions 3. Properties of Quadratic Functions........... p. 1 3.1 Investigating Quadratic Functions........... p. 6 in Vertex Form: Part 1 3.1 Investigating Quadratic Functions...........
Chapter 3 Quadratic Functions 3. Properties of Quadratic Functions........... p. 1 3.1 Investigating Quadratic Functions........... p. 6 in Vertex Form: Part 1 3.1 Investigating Quadratic Functions...........
Quadratic Forms Formula Vertex Axis of Symmetry. 2. Write the equation in intercept form. 3. Identify the Vertex. 4. Identify the Axis of Symmetry.
 CC Algebra II Test # Quadratic Functions - Review **Formulas Name Quadratic Forms Formula Vertex Axis of Symmetry Vertex Form f (x) = a(x h) + k Standard Form f (x) = ax + b x + c x = b a Intercept Form
CC Algebra II Test # Quadratic Functions - Review **Formulas Name Quadratic Forms Formula Vertex Axis of Symmetry Vertex Form f (x) = a(x h) + k Standard Form f (x) = ax + b x + c x = b a Intercept Form
Solving Simple Quadratics 1.0 Topic: Solving Quadratics
 Ns Solving Simple Quadratics 1.0 Topic: Solving Quadratics Date: Objectives: SWBAT (Solving Simple Quadratics and Application dealing with Quadratics) Main Ideas: Assignment: Square Root Property If x
Ns Solving Simple Quadratics 1.0 Topic: Solving Quadratics Date: Objectives: SWBAT (Solving Simple Quadratics and Application dealing with Quadratics) Main Ideas: Assignment: Square Root Property If x
QUESTIONS 1 10 MAY BE DONE WITH A CALCULATOR QUESTIONS ARE TO BE DONE WITHOUT A CALCULATOR. Name
 QUESTIONS 1 10 MAY BE DONE WITH A CALCULATOR QUESTIONS 11 5 ARE TO BE DONE WITHOUT A CALCULATOR Name 2 CALCULATOR MAY BE USED FOR 1-10 ONLY Use the table to find the following. x -2 2 5-0 7 2 y 12 15 18
QUESTIONS 1 10 MAY BE DONE WITH A CALCULATOR QUESTIONS 11 5 ARE TO BE DONE WITHOUT A CALCULATOR Name 2 CALCULATOR MAY BE USED FOR 1-10 ONLY Use the table to find the following. x -2 2 5-0 7 2 y 12 15 18
MATHS METHODS QUADRATICS REVIEW. A reminder of some of the laws of expansion, which in reverse are a quick reference for rules of factorisation
 MATHS METHODS QUADRATICS REVIEW LAWS OF EXPANSION A reminder of some of the laws of expansion, which in reverse are a quick reference for rules of factorisation a) b) c) d) e) FACTORISING Exercise 4A Q6ace,7acegi
MATHS METHODS QUADRATICS REVIEW LAWS OF EXPANSION A reminder of some of the laws of expansion, which in reverse are a quick reference for rules of factorisation a) b) c) d) e) FACTORISING Exercise 4A Q6ace,7acegi
Unit 6 Part I. Quadratic Functions 2/9/2017 2/23/2017
 Unit 6 Part I Quadratic Functions 2/9/2017 2/23/2017 By DeviantArt user MagicFiretrucks Name: By the end of this unit, you will be able to Analyze the characteristics of graphs of quadratic functions Graph
Unit 6 Part I Quadratic Functions 2/9/2017 2/23/2017 By DeviantArt user MagicFiretrucks Name: By the end of this unit, you will be able to Analyze the characteristics of graphs of quadratic functions Graph
Section 3.3. Analyzing Graphs of Quadratic Functions
 Section 3.3 Analyzing Graphs of Quadratic Functions Introduction Definitions A quadratic function is a function with the form f (x) = ax 2 + bx + c, where a 0. Definitions A quadratic function is a function
Section 3.3 Analyzing Graphs of Quadratic Functions Introduction Definitions A quadratic function is a function with the form f (x) = ax 2 + bx + c, where a 0. Definitions A quadratic function is a function
POLYNOMIALS Graphing Polynomial Functions Common Core Standard
 K Polynomials, Lesson 6, Graphing Polynomial Functions (r. 2018) POLYNOMIALS Graphing Polynomial Functions Common Core Standard Next Generation Standard F-BF.3 Identify the effect on the graph of replacing
K Polynomials, Lesson 6, Graphing Polynomial Functions (r. 2018) POLYNOMIALS Graphing Polynomial Functions Common Core Standard Next Generation Standard F-BF.3 Identify the effect on the graph of replacing
Parabolas have a, a middle point. For. In this example, the equation of the axis of symmetry is
 5.1/5.A Investigating Quadratic Functions in Standard Form: y = a(x ± h) ± k y x Graph y x using a table of values x -3 - -1 0 1 3 Graph Shape: the graph shape is called a and occurs when the equation
5.1/5.A Investigating Quadratic Functions in Standard Form: y = a(x ± h) ± k y x Graph y x using a table of values x -3 - -1 0 1 3 Graph Shape: the graph shape is called a and occurs when the equation
Algebra 2B CH 5. WYNTK & TEST Algebra 2B What You Need to Know , Test
 Algebra 2B CH 5 NAME: WYNTK 5.1 5.3 & 5.7 5.8 TEST DATE: HOUR: Algebra 2B What You Need to Know 5.1 5.3, 5.7-5.8 Test A2.5.1.2 Be able to use transformations to graph quadratic functions and answer questions.
Algebra 2B CH 5 NAME: WYNTK 5.1 5.3 & 5.7 5.8 TEST DATE: HOUR: Algebra 2B What You Need to Know 5.1 5.3, 5.7-5.8 Test A2.5.1.2 Be able to use transformations to graph quadratic functions and answer questions.
7.1A Investigating Quadratic Functions in Vertex (Standard) Form: y = a(x±p) 2 ±q. Parabolas have a, a middle point. For
 7.1A Investigating Quadratic Functions in Vertex (Standard) Form: y = a(x±p) ±q y x Graph y x using a table of values x -3 - -1 0 1 3 Graph Shape: the graph shape is called a and occurs when the equation
7.1A Investigating Quadratic Functions in Vertex (Standard) Form: y = a(x±p) ±q y x Graph y x using a table of values x -3 - -1 0 1 3 Graph Shape: the graph shape is called a and occurs when the equation
Warm Up. Factor the following numbers and expressions. Multiply the following factors using either FOIL or Box Method
 Warm Up Factor the following numbers and expressions 1. 36 2. 36x 3 + 48x 2 + 24x Multiply the following factors using either FOIL or Box Method 3. (3x 2)(x 1) 4. (x 2)(x + 3) Objectives Recognize standard
Warm Up Factor the following numbers and expressions 1. 36 2. 36x 3 + 48x 2 + 24x Multiply the following factors using either FOIL or Box Method 3. (3x 2)(x 1) 4. (x 2)(x + 3) Objectives Recognize standard
Lecture 5. If, as shown in figure, we form a right triangle With P1 and P2 as vertices, then length of the horizontal
 Distance; Circles; Equations of the form Lecture 5 y = ax + bx + c In this lecture we shall derive a formula for the distance between two points in a coordinate plane, and we shall use that formula to
Distance; Circles; Equations of the form Lecture 5 y = ax + bx + c In this lecture we shall derive a formula for the distance between two points in a coordinate plane, and we shall use that formula to
Math 2201 Unit 4: Quadratic Functions. 16 Hours
 Math 2201 Unit 4: Quadratic Functions 16 Hours 6.1: Exploring Quadratic Relations Quadratic Relation: A relation that can be written in the standard form y = ax 2 + bx + c Ex: y = 4x 2 + 2x + 1 ax 2 is
Math 2201 Unit 4: Quadratic Functions 16 Hours 6.1: Exploring Quadratic Relations Quadratic Relation: A relation that can be written in the standard form y = ax 2 + bx + c Ex: y = 4x 2 + 2x + 1 ax 2 is
Unit 2: Function Transformation Chapter 1. Basic Transformations Reflections Inverses
 Unit 2: Function Transformation Chapter 1 Basic Transformations Reflections Inverses Section 1.1: Horizontal and Vertical Transformations A transformation of a function alters the equation and any combination
Unit 2: Function Transformation Chapter 1 Basic Transformations Reflections Inverses Section 1.1: Horizontal and Vertical Transformations A transformation of a function alters the equation and any combination
For every input number the output involves squaring a number.
 Quadratic Functions The function For every input number the output involves squaring a number. eg. y = x, y = x + 3x + 1, y = 3(x 5), y = (x ) 1 The shape parabola (can open up or down) axis of symmetry
Quadratic Functions The function For every input number the output involves squaring a number. eg. y = x, y = x + 3x + 1, y = 3(x 5), y = (x ) 1 The shape parabola (can open up or down) axis of symmetry
Review for Quarter 3 Cumulative Test
 Review for Quarter 3 Cumulative Test I. Solving quadratic equations (LT 4.2, 4.3, 4.4) Key Facts To factor a polynomial, first factor out any common factors, then use the box method to factor the quadratic.
Review for Quarter 3 Cumulative Test I. Solving quadratic equations (LT 4.2, 4.3, 4.4) Key Facts To factor a polynomial, first factor out any common factors, then use the box method to factor the quadratic.
II. Functions. 61. Find a way to graph the line from the problem 59 on your calculator. Sketch the calculator graph here, including the window values:
 II Functions Week 4 Functions: graphs, tables and formulas Problem of the Week: The Farmer s Fence A field bounded on one side by a river is to be fenced on three sides so as to form a rectangular enclosure
II Functions Week 4 Functions: graphs, tables and formulas Problem of the Week: The Farmer s Fence A field bounded on one side by a river is to be fenced on three sides so as to form a rectangular enclosure
Let s review some things we learned earlier about the information we can gather from the graph of a quadratic.
 Section 6: Quadratic Equations and Functions Part 2 Section 6 Topic 1 Observations from a Graph of a Quadratic Function Let s review some things we learned earlier about the information we can gather from
Section 6: Quadratic Equations and Functions Part 2 Section 6 Topic 1 Observations from a Graph of a Quadratic Function Let s review some things we learned earlier about the information we can gather from
Section 6.2 Properties of Graphs of Quadratic Functions soln.notebook January 12, 2017
 Section 6.2: Properties of Graphs of Quadratic Functions 1 Properties of Graphs of Quadratic Functions A quadratic equation can be written in three different ways. Each version of the equation gives information
Section 6.2: Properties of Graphs of Quadratic Functions 1 Properties of Graphs of Quadratic Functions A quadratic equation can be written in three different ways. Each version of the equation gives information
OpenStax-CNX module: m Quadratic Functions. OpenStax OpenStax Precalculus. Abstract
 OpenStax-CNX module: m49337 1 Quadratic Functions OpenStax OpenStax Precalculus This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 4.0 In this section, you
OpenStax-CNX module: m49337 1 Quadratic Functions OpenStax OpenStax Precalculus This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 4.0 In this section, you
REMARKS. 8.2 Graphs of Quadratic Functions. A Graph of y = ax 2 + bx + c, where a > 0
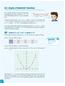 8. Graphs of Quadratic Functions In an earlier section, we have learned that the graph of the linear function = m + b, where the highest power of is 1, is a straight line. What would the shape of the graph
8. Graphs of Quadratic Functions In an earlier section, we have learned that the graph of the linear function = m + b, where the highest power of is 1, is a straight line. What would the shape of the graph
Quadratic Functions. Full Set of Notes. No Solutions
 Quadratic Functions Full Set of Notes No Solutions Graphing Quadratic Functions The graph of a quadratic function is called a parabola. Applications of Parabolas: http://www.doe.virginia.gov/div/winchester/jhhs/math/lessons/calc2004/appparab.html
Quadratic Functions Full Set of Notes No Solutions Graphing Quadratic Functions The graph of a quadratic function is called a parabola. Applications of Parabolas: http://www.doe.virginia.gov/div/winchester/jhhs/math/lessons/calc2004/appparab.html
Sketching graphs of polynomials
 Sketching graphs of polynomials We want to draw the graphs of polynomial functions y = f(x). The degree of a polynomial in one variable x is the highest power of x that remains after terms have been collected.
Sketching graphs of polynomials We want to draw the graphs of polynomial functions y = f(x). The degree of a polynomial in one variable x is the highest power of x that remains after terms have been collected.
Algebra Ch Graphing ax 2 + c. Mr. Deyo
 Algebra Ch. 10.1 Graphing ax 2 + c Mr. Deyo Learning Target By the end of the period, students will graph quadratic equations in the form of ax 2 + c. They will demonstrate this by completing Four Square
Algebra Ch. 10.1 Graphing ax 2 + c Mr. Deyo Learning Target By the end of the period, students will graph quadratic equations in the form of ax 2 + c. They will demonstrate this by completing Four Square
Worksheet: Transformations of Quadratic Functions
 Worksheet: Transformations of Quadratic Functions Multiple Choice Identif the choice that best completes the statement or answers the question.. Which correctl identifies the values of the parameters a,
Worksheet: Transformations of Quadratic Functions Multiple Choice Identif the choice that best completes the statement or answers the question.. Which correctl identifies the values of the parameters a,
Notes Rules for Transformations of Functions If f x is the original functions, a > 0 and c > 0.
 9.1.2 Parabola Investigation Do Now 1. Vertical means and horizontal is. 2. Another word for compress is. 3. Given the statement 0 < a < 1, a represents numbers like 4. Given the statement a > 1, a represents
9.1.2 Parabola Investigation Do Now 1. Vertical means and horizontal is. 2. Another word for compress is. 3. Given the statement 0 < a < 1, a represents numbers like 4. Given the statement a > 1, a represents
GSE Algebra 1 Name Date Block. Unit 3b Remediation Ticket
 Unit 3b Remediation Ticket Question: Which function increases faster, f(x) or g(x)? f(x) = 5x + 8; two points from g(x): (-2, 4) and (3, 10) Answer: In order to compare the rate of change (roc), you must
Unit 3b Remediation Ticket Question: Which function increases faster, f(x) or g(x)? f(x) = 5x + 8; two points from g(x): (-2, 4) and (3, 10) Answer: In order to compare the rate of change (roc), you must
Final Exam Review Algebra Semester 1
 Final Exam Review Algebra 015-016 Semester 1 Name: Module 1 Find the inverse of each function. 1. f x 10 4x. g x 15x 10 Use compositions to check if the two functions are inverses. 3. s x 7 x and t(x)
Final Exam Review Algebra 015-016 Semester 1 Name: Module 1 Find the inverse of each function. 1. f x 10 4x. g x 15x 10 Use compositions to check if the two functions are inverses. 3. s x 7 x and t(x)
CHAPTER 2 - QUADRATICS
 CHAPTER 2 - QUADRATICS VERTEX FORM (OF A QUADRATIC FUNCTION) f(x) = a(x - p) 2 + q Parameter a determines orientation and shape of the parabola Parameter p translates the parabola horizontally Parameter
CHAPTER 2 - QUADRATICS VERTEX FORM (OF A QUADRATIC FUNCTION) f(x) = a(x - p) 2 + q Parameter a determines orientation and shape of the parabola Parameter p translates the parabola horizontally Parameter
Integrated Math 1 Honors Module 10 Structures of Expressions Ready, Set, Go! Homework Solutions
 1 Integrated Math 1 Honors Module 10 Structures of Expressions Ready, Set, Go! Homework Solutions Adapted from The Mathematics Vision Project: Scott Hendrickson, Joleigh Honey, Barbara Kuehl, Travis Lemon,
1 Integrated Math 1 Honors Module 10 Structures of Expressions Ready, Set, Go! Homework Solutions Adapted from The Mathematics Vision Project: Scott Hendrickson, Joleigh Honey, Barbara Kuehl, Travis Lemon,
