New Mexico Tech Hyd 510
|
|
|
- William Stone
- 5 years ago
- Views:
Transcription
1 Numerics Motivation Modeling process (JLW) To construct a model we assemble and synthesize data and other information to formulate a conceptual model of the situation. The model is conditioned on the science or policy issue to be addressed, or the engineering problem to be solved, not just the hydrological setting. That is, the model can change with the issue or problem. The conceptual model is then translated into mathematical form, usually as a differential equation, but perhaps as an algebraic or integral equation, or in a statistical or probability framework. Analytical or numerical methods can be applied to solve the model, the choice of method depending on the complexity of the model and how it is to be used. Numerical methods provide greater flexibility and range of application, and these days they offer convenience as well. (Hybrid numerical-analytical approaches are also possible.) Assuming a numerical method is selected, the mathematics are transformed to numerical form, for example descretizing time and space. The numerical form must then be programmed, usually using a scientific/engineering language like Fortran, but more and more these days using a higher level language like Matlab. The numerical model, as programmed, must then be tested to ensure that it is performing as designed (model verification and validation). The program is then applied to the issue or problem at hand to produce a numerical solution. The numerical solution is post-processed to provide and present the desired information, and tested with the data. (At this stage the conceptual model is often revised, in order to do a better job representing reality. Here we assume that the conceptual model is accepted.) That information is then interpreted within the context of the issue or problem. For example, many engineering applications involve the design of something. The model is used to test and revise the design, in order to improve its performance. (JLW) In outline form the process (ignoring feedbacks, such as changing the conceptual model) is something like: 1. Data 2. Conceptualization 3. Mathematical Model 4. Numerical Solution Method(s) 5. Programing, including testing the program 6. Solution 7. Post-processing and interpretation Need for discretization When we adopt a numerical approach to a solution we replace the continuous function f(x) and its independent variable x, with the function f examined at only a few points, x i, where i =1, 2, 3, n is an index representing those points, and n is the number of points. In the continuous space of x, there are an infinity of points x and in the space of funciton f there could be an infinity of values f (if f and x are one-to-one). But computers can t handle an infinite number of values. Instead, they can deal only with finite numbers. So, along x we pick certain points x i that interest us, hopefully close enough to preserve a decide representation of f, and we perform numerical (not symbolic) calculations using those points. 112
2 Numerics Backgound (Most of this is material in Kreyszig, Section 19.1) Floating-Point Form of Numbers (text, section 19.1) Fixed point numbers = fixed number of decimals after the decimal point. 3D: 3= number of the digits after the decimal point e.g., , 0.014, 1.000, are all 3D Floating point numbers = number of significant digits are fixed, the decimal point is floating 4S: 4= number of significant digits e.g., x10 3, x10-13, x10-1 or 6.247x10 2, Any floating point number can be written as (1) a = ±m 10 n, 0.1 m 1, n integer Machine numbers On a computer, since m is limited to k digits (e.g., k=8) and n is limited, this gives the (machine number) representation as (2) a = ±m 10 n, m = 0.d 1 d 2 d 3 d k, d 1 >0. with a limited range of exponent n, depending on machine word length and whether the program is using machine single precision (e.g., -38 < n < 38) or software double precision. Values of n outside this range lead to underflow (number is too small) or overflow (number is too big and the computation crashes). Roundoff (text, section 19.1) Roundoff error is due to rounding a number to k decimals. Rules for rounding up and down leading to rounding error calculation: Let a = fl(a) in (2), where fl is the floating point approximation of a in (1). Then the roundoff rules give m- m ±½ 10 -k. Since m 0.1, this implies (when a 0) 113
3 Accuracy in tables Largely, look-up-tables (LUT) of function values, like sin x, have been replaced in computers with series, polynomial or other approximations. Yet LUTs are still used. In hydrology we find that we have a choice of using LUTs of certain functions or the data itself. Examples are equations of state (EOS) relating fluid density to pressure and temperature, and relative permeability relating porous media permeability to fluid saturation. If the typical functions don t fit the data well, the data itself, as a LUT, is often used. If the table shows k significant digits, it is assumed that any value a ~ in the table deviates from the exact value a by, at most ±½ unit in the kth digit. Algorithm (Numerical) Stability (text, section 19.1) Stable: Small changes in initial conditions should only cause small changes in results. Unstable: Small changes lead to significant deviation of results. Consider first theoretical stability, i.e., of the equations themselves. A system may be naturally unstable. Such conditions occur commonly in hydrology and related sciences, e.g., thermal convection cells; turbulence; and viscous, gravity, or dissolution fingering. The mathematics for these problems is ill conditioned. Instead, let s consider only problems which are well conditioned, with stable mathematical solutions. These are more common in hydrology. Even if the mathematics is well conditioned the numerical scheme used to solve it (approximately) may itself be unstable. Numerical instability can be avoided by changing algorithms (wholesale or just increase the order of the algorithm) or, with the same algorithm, increasing discretization resolution (e.g., more points x i ; i.e., make n bigger). Some algorithms are stable only within certain ranges, which must be respected. Errors of Numeric Results (text, section 19.1) Numerical results are approximations, that is, they are not exact but involve errors. - Experimental (data) errors - Roundoff errors - Truncation errors Truncation errors result from truncating approximations (e.g., reducing their order), not truncating digits (that is, instead, related to roundoff). Examples of truncation error are found in series solutions, Taylor series approximation of a derivative, and numerical integration. Error Let a ~ be the approximate value of a quantity whose exact value is a. (4) Error of a ~ : ε = a a~ or 114
4 (4 ) a = a~ + ε True value of a = Approximation + Error Examples: a ~ =10.5 and a= 10.2, then ε = Caution: there are other errors referred to the literature. Examples are and a ~ a. a a~ (absolute error), Relative error (5)(5 ) ε a a~ Error ε ε r = = = a a Relative Error a~ Error bounds. In practice one gets an error bound, that is a number β such that ε β hence Or for the relative error, a bound β r such that ε β r r hence a a~ a a~ a β r β Basic error principle Always accompany a numerical method with an error estimate, both in testing the method in general, and in every single application. Use a theoretical error estimate and/or error estimation by comparison. Loss of significant digits A calculation often has fewer (and never more) significant digits than the numbers from which it was obtained. Choose your steps carefully to minimize this issue. 115
5 Solution of equations by iteration (text, section 19.2) Consider the equation (1) f ( x) = 0 which could be an algebraic or transcendental equation, or a differential or integral equation. If (1) is non-linear then we often solve it by iteration. That is, we guess a solution (a value of x) and test it to see if it satisfies (1). If not we guess a new solution and repeat until we are satisfied, that is the solution converges, or we give up, perhaps because the solution diverges. Formal iterative methods use different methods to construct the next guess. Some are better than others, but the better ones are more expensive to use. Suppose a method converges but does so slowly. Another, higher order method may (often will) converge faster. The higher the order the method, the more information it uses, so that higher order methods are more expensive per step. There is a tradeoff between the number of steps and the expense of each step in determining optimal iterative method for a given problem. In general, with a more non-linear the problem you should use a higher order method. We visited one of these methods, Newton s method, during our review of calculus. We ll visit it and two other often used iteration methods below. We ll start with fixed point iteration, a lower order method, before revisiting Newton s method, and its cousin the secant method, which are of higher order. In general, these are likely the only sophisticated methods you will encounter in practice. In these three methods you make an initial guess of x, call it x 0, and use that to linearize (1). You then solve the remaining linear equation for x 2, your new estimate of x. That estimate x 2 is used to relinearize (1) and solve for a third estimate x 3, so on recursively, until you converge or give up. All three methods are used in hydrologic codes, primarily to solve non-linear differential equations. The unsaturated (and non-linear) code HYDRUS ( a popular code used in our vadose zone classes, research and application, uses fixed point iteration. The popular groundwater flow code MODFLOW is nonlinear when it deals with phreatic aquifers. It too uses fixed point iteration ( The proprietary code MODFLOW- SURFAC ( was originally developed to tackle non-linear problems that MODFLOW can t handle, like mine dewatering and water table recovery. It uses Newton s method. The multiphysics code COMSOL Multiphysics code (see Hyd510 web links page) uses Newton iteration, even for linear problems. They figure that it takes just one iteration to converge for a linear problem, so why bother with all the extra baggage of special routines for those special (special to them, since they mainly attack non-linear problems) linear cases. 116
6 Fixed Point Iteration (text, section 19.2) Using algebra expend f as f ( x) = x g( x). Then rewrite (1) as (2) x = g(x) The exact solution, s, is where these two curves, for x and g(x), intersect. Then choose an x 0, and compute x 1 =g(x 0 ), x 2 =g(x 1 ), etc., or in general (3) x n+ 1 = g( xn ) n = 0, 1, 2. A solution x of (2) is called a fixed point of g. (1) can be converted to several different versions of (2). 117
7 Newton s Method (text, section 19.2) 118
8 Secant Method (text, section 19.2) 119
Introduction to Computational Mathematics
 Introduction to Computational Mathematics Introduction Computational Mathematics: Concerned with the design, analysis, and implementation of algorithms for the numerical solution of problems that have
Introduction to Computational Mathematics Introduction Computational Mathematics: Concerned with the design, analysis, and implementation of algorithms for the numerical solution of problems that have
Computational Methods. Sources of Errors
 Computational Methods Sources of Errors Manfred Huber 2011 1 Numerical Analysis / Scientific Computing Many problems in Science and Engineering can not be solved analytically on a computer Numeric solutions
Computational Methods Sources of Errors Manfred Huber 2011 1 Numerical Analysis / Scientific Computing Many problems in Science and Engineering can not be solved analytically on a computer Numeric solutions
CS321 Introduction To Numerical Methods
 CS3 Introduction To Numerical Methods Fuhua (Frank) Cheng Department of Computer Science University of Kentucky Lexington KY 456-46 - - Table of Contents Errors and Number Representations 3 Error Types
CS3 Introduction To Numerical Methods Fuhua (Frank) Cheng Department of Computer Science University of Kentucky Lexington KY 456-46 - - Table of Contents Errors and Number Representations 3 Error Types
Truncation Errors. Applied Numerical Methods with MATLAB for Engineers and Scientists, 2nd ed., Steven C. Chapra, McGraw Hill, 2008, Ch. 4.
 Chapter 4: Roundoff and Truncation Errors Applied Numerical Methods with MATLAB for Engineers and Scientists, 2nd ed., Steven C. Chapra, McGraw Hill, 2008, Ch. 4. 1 Outline Errors Accuracy and Precision
Chapter 4: Roundoff and Truncation Errors Applied Numerical Methods with MATLAB for Engineers and Scientists, 2nd ed., Steven C. Chapra, McGraw Hill, 2008, Ch. 4. 1 Outline Errors Accuracy and Precision
Mathematical preliminaries and error analysis
 Mathematical preliminaries and error analysis Tsung-Ming Huang Department of Mathematics National Taiwan Normal University, Taiwan August 28, 2011 Outline 1 Round-off errors and computer arithmetic IEEE
Mathematical preliminaries and error analysis Tsung-Ming Huang Department of Mathematics National Taiwan Normal University, Taiwan August 28, 2011 Outline 1 Round-off errors and computer arithmetic IEEE
Computational Economics and Finance
 Computational Economics and Finance Part I: Elementary Concepts of Numerical Analysis Spring 2015 Outline Computer arithmetic Error analysis: Sources of error Error propagation Controlling the error Rates
Computational Economics and Finance Part I: Elementary Concepts of Numerical Analysis Spring 2015 Outline Computer arithmetic Error analysis: Sources of error Error propagation Controlling the error Rates
Computational Economics and Finance
 Computational Economics and Finance Part I: Elementary Concepts of Numerical Analysis Spring 2016 Outline Computer arithmetic Error analysis: Sources of error Error propagation Controlling the error Rates
Computational Economics and Finance Part I: Elementary Concepts of Numerical Analysis Spring 2016 Outline Computer arithmetic Error analysis: Sources of error Error propagation Controlling the error Rates
Review of Calculus, cont d
 Jim Lambers MAT 460/560 Fall Semester 2009-10 Lecture 4 Notes These notes correspond to Sections 1.1 1.2 in the text. Review of Calculus, cont d Taylor s Theorem, cont d We conclude our discussion of Taylor
Jim Lambers MAT 460/560 Fall Semester 2009-10 Lecture 4 Notes These notes correspond to Sections 1.1 1.2 in the text. Review of Calculus, cont d Taylor s Theorem, cont d We conclude our discussion of Taylor
LECTURE 0: Introduction and Background
 1 LECTURE 0: Introduction and Background September 10, 2012 1 Computational science The role of computational science has become increasingly significant during the last few decades. It has become the
1 LECTURE 0: Introduction and Background September 10, 2012 1 Computational science The role of computational science has become increasingly significant during the last few decades. It has become the
Error in Numerical Methods
 Error in Numerical Methods By Brian D. Storey This section will describe two types of error that are common in numerical calculations: roundoff and truncation error. Roundoff error is due to the fact that
Error in Numerical Methods By Brian D. Storey This section will describe two types of error that are common in numerical calculations: roundoff and truncation error. Roundoff error is due to the fact that
Scientific Computing: An Introductory Survey
 Scientific Computing: An Introductory Survey Chapter 1 Scientific Computing Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
Scientific Computing: An Introductory Survey Chapter 1 Scientific Computing Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
2.1.1 Fixed-Point (or Integer) Arithmetic
 x = approximation to true value x error = x x, relative error = x x. x 2.1.1 Fixed-Point (or Integer) Arithmetic A base 2 (base 10) fixed-point number has a fixed number of binary (decimal) places. 1.
x = approximation to true value x error = x x, relative error = x x. x 2.1.1 Fixed-Point (or Integer) Arithmetic A base 2 (base 10) fixed-point number has a fixed number of binary (decimal) places. 1.
Computing Basics. 1 Sources of Error LECTURE NOTES ECO 613/614 FALL 2007 KAREN A. KOPECKY
 LECTURE NOTES ECO 613/614 FALL 2007 KAREN A. KOPECKY Computing Basics 1 Sources of Error Numerical solutions to problems differ from their analytical counterparts. Why? The reason for the difference is
LECTURE NOTES ECO 613/614 FALL 2007 KAREN A. KOPECKY Computing Basics 1 Sources of Error Numerical solutions to problems differ from their analytical counterparts. Why? The reason for the difference is
AM205: lecture 2. 1 These have been shifted to MD 323 for the rest of the semester.
 AM205: lecture 2 Luna and Gary will hold a Python tutorial on Wednesday in 60 Oxford Street, Room 330 Assignment 1 will be posted this week Chris will hold office hours on Thursday (1:30pm 3:30pm, Pierce
AM205: lecture 2 Luna and Gary will hold a Python tutorial on Wednesday in 60 Oxford Street, Room 330 Assignment 1 will be posted this week Chris will hold office hours on Thursday (1:30pm 3:30pm, Pierce
Computational Methods CMSC/AMSC/MAPL 460. Representing numbers in floating point and associated issues. Ramani Duraiswami, Dept. of Computer Science
 Computational Methods CMSC/AMSC/MAPL 460 Representing numbers in floating point and associated issues Ramani Duraiswami, Dept. of Computer Science Class Outline Computations should be as accurate and as
Computational Methods CMSC/AMSC/MAPL 460 Representing numbers in floating point and associated issues Ramani Duraiswami, Dept. of Computer Science Class Outline Computations should be as accurate and as
COS 323: Computing for the Physical and Social Sciences
 COS 323: Computing for the Physical and Social Sciences COS 323 People: Szymon Rusinkiewicz Sandra Batista Victoria Yao Course webpage: http://www.cs.princeton.edu/cos323 What s This Course About? Numerical
COS 323: Computing for the Physical and Social Sciences COS 323 People: Szymon Rusinkiewicz Sandra Batista Victoria Yao Course webpage: http://www.cs.princeton.edu/cos323 What s This Course About? Numerical
What we need to know about error: Class Outline. Computational Methods CMSC/AMSC/MAPL 460. Errors in data and computation
 Class Outline Computational Methods CMSC/AMSC/MAPL 460 Errors in data and computation Representing numbers in floating point Ramani Duraiswami, Dept. of Computer Science Computations should be as accurate
Class Outline Computational Methods CMSC/AMSC/MAPL 460 Errors in data and computation Representing numbers in floating point Ramani Duraiswami, Dept. of Computer Science Computations should be as accurate
Today s class. Roots of equation Finish up incremental search Open methods. Numerical Methods, Fall 2011 Lecture 5. Prof. Jinbo Bi CSE, UConn
 Today s class Roots of equation Finish up incremental search Open methods 1 False Position Method Although the interval [a,b] where the root becomes iteratively closer with the false position method, unlike
Today s class Roots of equation Finish up incremental search Open methods 1 False Position Method Although the interval [a,b] where the root becomes iteratively closer with the false position method, unlike
Scientific Computing. Error Analysis
 ECE257 Numerical Methods and Scientific Computing Error Analysis Today s s class: Introduction to error analysis Approximations Round-Off Errors Introduction Error is the difference between the exact solution
ECE257 Numerical Methods and Scientific Computing Error Analysis Today s s class: Introduction to error analysis Approximations Round-Off Errors Introduction Error is the difference between the exact solution
Computational Methods CMSC/AMSC/MAPL 460. Representing numbers in floating point and associated issues. Ramani Duraiswami, Dept. of Computer Science
 Computational Methods CMSC/AMSC/MAPL 460 Representing numbers in floating point and associated issues Ramani Duraiswami, Dept. of Computer Science Class Outline Computations should be as accurate and as
Computational Methods CMSC/AMSC/MAPL 460 Representing numbers in floating point and associated issues Ramani Duraiswami, Dept. of Computer Science Class Outline Computations should be as accurate and as
Roundoff Errors and Computer Arithmetic
 Jim Lambers Math 105A Summer Session I 2003-04 Lecture 2 Notes These notes correspond to Section 1.2 in the text. Roundoff Errors and Computer Arithmetic In computing the solution to any mathematical problem,
Jim Lambers Math 105A Summer Session I 2003-04 Lecture 2 Notes These notes correspond to Section 1.2 in the text. Roundoff Errors and Computer Arithmetic In computing the solution to any mathematical problem,
Math 340 Fall 2014, Victor Matveev. Binary system, round-off errors, loss of significance, and double precision accuracy.
 Math 340 Fall 2014, Victor Matveev Binary system, round-off errors, loss of significance, and double precision accuracy. 1. Bits and the binary number system A bit is one digit in a binary representation
Math 340 Fall 2014, Victor Matveev Binary system, round-off errors, loss of significance, and double precision accuracy. 1. Bits and the binary number system A bit is one digit in a binary representation
Calculus I Review Handout 1.3 Introduction to Calculus - Limits. by Kevin M. Chevalier
 Calculus I Review Handout 1.3 Introduction to Calculus - Limits by Kevin M. Chevalier We are now going to dive into Calculus I as we take a look at the it process. While precalculus covered more static
Calculus I Review Handout 1.3 Introduction to Calculus - Limits by Kevin M. Chevalier We are now going to dive into Calculus I as we take a look at the it process. While precalculus covered more static
CHAPTER 2 SENSITIVITY OF LINEAR SYSTEMS; EFFECTS OF ROUNDOFF ERRORS
 CHAPTER SENSITIVITY OF LINEAR SYSTEMS; EFFECTS OF ROUNDOFF ERRORS The two main concepts involved here are the condition (of a problem) and the stability (of an algorithm). Both of these concepts deal with
CHAPTER SENSITIVITY OF LINEAR SYSTEMS; EFFECTS OF ROUNDOFF ERRORS The two main concepts involved here are the condition (of a problem) and the stability (of an algorithm). Both of these concepts deal with
Basics of Computation. PHY 604:Computational Methods in Physics and Astrophysics II
 Basics of Computation Basics of Computation Computers store information and allow us to operate on it. That's basically it. Computers have finite memory, so it is not possible to store the infinite range
Basics of Computation Basics of Computation Computers store information and allow us to operate on it. That's basically it. Computers have finite memory, so it is not possible to store the infinite range
Scientific Computing: An Introductory Survey
 Scientific Computing: An Introductory Survey Chapter 1 Scientific Computing Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
Scientific Computing: An Introductory Survey Chapter 1 Scientific Computing Prof. Michael T. Heath Department of Computer Science University of Illinois at Urbana-Champaign Copyright c 2002. Reproduction
ME 261: Numerical Analysis. ME 261: Numerical Analysis
 ME 261: Numerical Analysis 3. credit hours Prereq.: ME 163/ME 171 Course content Approximations and error types Roots of polynomials and transcendental equations Determinants and matrices Solution of linear
ME 261: Numerical Analysis 3. credit hours Prereq.: ME 163/ME 171 Course content Approximations and error types Roots of polynomials and transcendental equations Determinants and matrices Solution of linear
COS 323: Computing for the Physical and Social Sciences
 COS 323: Computing for the Physical and Social Sciences COS 323 Professor: Szymon Rusinkiewicz TAs: Mark Browning Fisher Yu Victoria Yao Course webpage http://www.cs.princeton.edu/~cos323/ What s This
COS 323: Computing for the Physical and Social Sciences COS 323 Professor: Szymon Rusinkiewicz TAs: Mark Browning Fisher Yu Victoria Yao Course webpage http://www.cs.princeton.edu/~cos323/ What s This
NUMERICAL ANALYSIS USING SCILAB: NUMERICAL STABILITY AND CONDITIONING
 powered by NUMERICAL ANALYSIS USING SCILAB: NUMERICAL STABILITY AND CONDITIONING In this Scilab tutorial we provide a collection of implemented examples on numerical stability and conditioning. Level This
powered by NUMERICAL ANALYSIS USING SCILAB: NUMERICAL STABILITY AND CONDITIONING In this Scilab tutorial we provide a collection of implemented examples on numerical stability and conditioning. Level This
Introduction to numerical algorithms
 Introduction to numerical algorithms Given an algebraic equation or formula, we may want to approximate the value, and while in calculus, we deal with equations or formulas that are well defined at each
Introduction to numerical algorithms Given an algebraic equation or formula, we may want to approximate the value, and while in calculus, we deal with equations or formulas that are well defined at each
Lecture Notes to Accompany. Scientific Computing An Introductory Survey. What is scientific computing?
 Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Scientific Computing What is scientific computing? Design and analysis of algorithms for solving
Lecture Notes to Accompany Scientific Computing An Introductory Survey Second Edition by Michael T. Heath Scientific Computing What is scientific computing? Design and analysis of algorithms for solving
Review Questions 26 CHAPTER 1. SCIENTIFIC COMPUTING
 26 CHAPTER 1. SCIENTIFIC COMPUTING amples. The IEEE floating-point standard can be found in [131]. A useful tutorial on floating-point arithmetic and the IEEE standard is [97]. Although it is no substitute
26 CHAPTER 1. SCIENTIFIC COMPUTING amples. The IEEE floating-point standard can be found in [131]. A useful tutorial on floating-point arithmetic and the IEEE standard is [97]. Although it is no substitute
SYSTEMS OF NONLINEAR EQUATIONS
 SYSTEMS OF NONLINEAR EQUATIONS Widely used in the mathematical modeling of real world phenomena. We introduce some numerical methods for their solution. For better intuition, we examine systems of two
SYSTEMS OF NONLINEAR EQUATIONS Widely used in the mathematical modeling of real world phenomena. We introduce some numerical methods for their solution. For better intuition, we examine systems of two
fractional quantities are typically represented in computers using floating point format this approach is very much similar to scientific notation
 Floating Point Arithmetic fractional quantities are typically represented in computers using floating point format this approach is very much similar to scientific notation for example, fixed point number
Floating Point Arithmetic fractional quantities are typically represented in computers using floating point format this approach is very much similar to scientific notation for example, fixed point number
Isotropic Porous Media Tutorial
 STAR-CCM+ User Guide 3927 Isotropic Porous Media Tutorial This tutorial models flow through the catalyst geometry described in the introductory section. In the porous region, the theoretical pressure drop
STAR-CCM+ User Guide 3927 Isotropic Porous Media Tutorial This tutorial models flow through the catalyst geometry described in the introductory section. In the porous region, the theoretical pressure drop
Floating-Point Arithmetic
 Floating-Point Arithmetic Raymond J. Spiteri Lecture Notes for CMPT 898: Numerical Software University of Saskatchewan January 9, 2013 Objectives Floating-point numbers Floating-point arithmetic Analysis
Floating-Point Arithmetic Raymond J. Spiteri Lecture Notes for CMPT 898: Numerical Software University of Saskatchewan January 9, 2013 Objectives Floating-point numbers Floating-point arithmetic Analysis
Outline. Numerical Analysis Basics. Some Higher-Level Languages. Programming Languages. BASIC and VBA MATLAB
 umerical Analysis Basics Larry Caretto Mechanical Engineering 39 umerical Analysis of Engineering Systems February 5, 214 Outline Programming Languages Binary umbers and Data Types Limits on the size and
umerical Analysis Basics Larry Caretto Mechanical Engineering 39 umerical Analysis of Engineering Systems February 5, 214 Outline Programming Languages Binary umbers and Data Types Limits on the size and
And Now to Something Completely Different: Finding Roots of Real Valued Functions
 And Now to Something Completely Different: Finding Roots of Real Valued Functions Four other Oysters followed them, And yet another four; And thick and fast they came at last, And more, and more, and more{
And Now to Something Completely Different: Finding Roots of Real Valued Functions Four other Oysters followed them, And yet another four; And thick and fast they came at last, And more, and more, and more{
Using Arithmetic of Real Numbers to Explore Limits and Continuity
 Using Arithmetic of Real Numbers to Explore Limits and Continuity by Maria Terrell Cornell University Problem Let a =.898989... and b =.000000... (a) Find a + b. (b) Use your ideas about how to add a and
Using Arithmetic of Real Numbers to Explore Limits and Continuity by Maria Terrell Cornell University Problem Let a =.898989... and b =.000000... (a) Find a + b. (b) Use your ideas about how to add a and
Imaging of flow in porous media - from optimal transport to prediction
 Imaging of flow in porous media - from optimal transport to prediction Eldad Haber Dept of EOS and Mathematics, UBC October 15, 2013 With Rowan Lars Jenn Cocket Ruthotto Fohring Outline Prediction is very
Imaging of flow in porous media - from optimal transport to prediction Eldad Haber Dept of EOS and Mathematics, UBC October 15, 2013 With Rowan Lars Jenn Cocket Ruthotto Fohring Outline Prediction is very
Introduction to Computer Programming with MATLAB Calculation and Programming Errors. Selis Önel, PhD
 Introduction to Computer Programming with MATLAB Calculation and Programming Errors Selis Önel, PhD Today you will learn Numbers, Significant figures Error analysis Absolute error Relative error Chopping
Introduction to Computer Programming with MATLAB Calculation and Programming Errors Selis Önel, PhD Today you will learn Numbers, Significant figures Error analysis Absolute error Relative error Chopping
Numerical Methods 5633
 Numerical Methods 5633 Lecture 2 Marina Krstic Marinkovic mmarina@maths.tcd.ie School of Mathematics Trinity College Dublin Marina Krstic Marinkovic 1 / 15 5633-Numerical Methods Organisational Assignment
Numerical Methods 5633 Lecture 2 Marina Krstic Marinkovic mmarina@maths.tcd.ie School of Mathematics Trinity College Dublin Marina Krstic Marinkovic 1 / 15 5633-Numerical Methods Organisational Assignment
2 Computation with Floating-Point Numbers
 2 Computation with Floating-Point Numbers 2.1 Floating-Point Representation The notion of real numbers in mathematics is convenient for hand computations and formula manipulations. However, real numbers
2 Computation with Floating-Point Numbers 2.1 Floating-Point Representation The notion of real numbers in mathematics is convenient for hand computations and formula manipulations. However, real numbers
Numerical Computing: An Introduction
 Numerical Computing: An Introduction Gyula Horváth Horvath@inf.u-szeged.hu Tom Verhoeff T.Verhoeff@TUE.NL University of Szeged Hungary Eindhoven University of Technology The Netherlands Numerical Computing
Numerical Computing: An Introduction Gyula Horváth Horvath@inf.u-szeged.hu Tom Verhoeff T.Verhoeff@TUE.NL University of Szeged Hungary Eindhoven University of Technology The Netherlands Numerical Computing
lecture 8 Groundwater Modelling -1
 The Islamic University of Gaza Faculty of Engineering Civil Engineering Department Water Resources Msc. Groundwater Hydrology- ENGC 6301 lecture 8 Groundwater Modelling -1 Instructor: Dr. Yunes Mogheir
The Islamic University of Gaza Faculty of Engineering Civil Engineering Department Water Resources Msc. Groundwater Hydrology- ENGC 6301 lecture 8 Groundwater Modelling -1 Instructor: Dr. Yunes Mogheir
Solve Non-Linear Parabolic Partial Differential Equation by Spline Collocation Method
 Solve Non-Linear Parabolic Partial Differential Equation by Spline Collocation Method P.B. Choksi 1 and A.K. Pathak 2 1 Research Scholar, Rai University,Ahemdabad. Email:pinalchoksey@gmail.com 2 H.O.D.
Solve Non-Linear Parabolic Partial Differential Equation by Spline Collocation Method P.B. Choksi 1 and A.K. Pathak 2 1 Research Scholar, Rai University,Ahemdabad. Email:pinalchoksey@gmail.com 2 H.O.D.
MAT128A: Numerical Analysis Lecture Two: Finite Precision Arithmetic
 MAT128A: Numerical Analysis Lecture Two: Finite Precision Arithmetic September 28, 2018 Lecture 1 September 28, 2018 1 / 25 Floating point arithmetic Computers use finite strings of binary digits to represent
MAT128A: Numerical Analysis Lecture Two: Finite Precision Arithmetic September 28, 2018 Lecture 1 September 28, 2018 1 / 25 Floating point arithmetic Computers use finite strings of binary digits to represent
Accuracy versus precision
 Accuracy versus precision Accuracy is a consistent error from the true value, but not necessarily a good or precise error Precision is a consistent result within a small error, but not necessarily anywhere
Accuracy versus precision Accuracy is a consistent error from the true value, but not necessarily a good or precise error Precision is a consistent result within a small error, but not necessarily anywhere
Homogenization and numerical Upscaling. Unsaturated flow and two-phase flow
 Homogenization and numerical Upscaling Unsaturated flow and two-phase flow Insa Neuweiler Institute of Hydromechanics, University of Stuttgart Outline Block 1: Introduction and Repetition Homogenization
Homogenization and numerical Upscaling Unsaturated flow and two-phase flow Insa Neuweiler Institute of Hydromechanics, University of Stuttgart Outline Block 1: Introduction and Repetition Homogenization
Errors in Computation
 Theory of Errors Content Errors in computation Absolute Error Relative Error Roundoff Errors Truncation Errors Floating Point Numbers Normalized Floating Point Numbers Roundoff Error in Floating Point
Theory of Errors Content Errors in computation Absolute Error Relative Error Roundoff Errors Truncation Errors Floating Point Numbers Normalized Floating Point Numbers Roundoff Error in Floating Point
Computational Mathematics: Models, Methods and Analysis. Zhilin Li
 Computational Mathematics: Models, Methods and Analysis Zhilin Li Chapter 1 Introduction Why is this course important (motivations)? What is the role of this class in the problem solving process using
Computational Mathematics: Models, Methods and Analysis Zhilin Li Chapter 1 Introduction Why is this course important (motivations)? What is the role of this class in the problem solving process using
Reals 1. Floating-point numbers and their properties. Pitfalls of numeric computation. Horner's method. Bisection. Newton's method.
 Reals 1 13 Reals Floating-point numbers and their properties. Pitfalls of numeric computation. Horner's method. Bisection. Newton's method. 13.1 Floating-point numbers Real numbers, those declared to be
Reals 1 13 Reals Floating-point numbers and their properties. Pitfalls of numeric computation. Horner's method. Bisection. Newton's method. 13.1 Floating-point numbers Real numbers, those declared to be
1.2 Numerical Solutions of Flow Problems
 1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
(Refer Slide Time: 02:59)
 Numerical Methods and Programming P. B. Sunil Kumar Department of Physics Indian Institute of Technology, Madras Lecture - 7 Error propagation and stability Last class we discussed about the representation
Numerical Methods and Programming P. B. Sunil Kumar Department of Physics Indian Institute of Technology, Madras Lecture - 7 Error propagation and stability Last class we discussed about the representation
Chapter 3. Errors and numerical stability
 Chapter 3 Errors and numerical stability 1 Representation of numbers Binary system : micro-transistor in state off 0 on 1 Smallest amount of stored data bit Object in memory chain of 1 and 0 10011000110101001111010010100010
Chapter 3 Errors and numerical stability 1 Representation of numbers Binary system : micro-transistor in state off 0 on 1 Smallest amount of stored data bit Object in memory chain of 1 and 0 10011000110101001111010010100010
Introduction to Numerical Computing
 Statistics 580 Introduction to Numerical Computing Number Systems In the decimal system we use the 10 numeric symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 to represent numbers. The relative position of each symbol
Statistics 580 Introduction to Numerical Computing Number Systems In the decimal system we use the 10 numeric symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 to represent numbers. The relative position of each symbol
Introduction to C omputational F luid Dynamics. D. Murrin
 Introduction to C omputational F luid Dynamics D. Murrin Computational fluid dynamics (CFD) is the science of predicting fluid flow, heat transfer, mass transfer, chemical reactions, and related phenomena
Introduction to C omputational F luid Dynamics D. Murrin Computational fluid dynamics (CFD) is the science of predicting fluid flow, heat transfer, mass transfer, chemical reactions, and related phenomena
CS321. Introduction to Numerical Methods
 CS31 Introduction to Numerical Methods Lecture 1 Number Representations and Errors Professor Jun Zhang Department of Computer Science University of Kentucky Lexington, KY 40506 0633 August 5, 017 Number
CS31 Introduction to Numerical Methods Lecture 1 Number Representations and Errors Professor Jun Zhang Department of Computer Science University of Kentucky Lexington, KY 40506 0633 August 5, 017 Number
Most nonzero floating-point numbers are normalized. This means they can be expressed as. x = ±(1 + f) 2 e. 0 f < 1
 Floating-Point Arithmetic Numerical Analysis uses floating-point arithmetic, but it is just one tool in numerical computation. There is an impression that floating point arithmetic is unpredictable and
Floating-Point Arithmetic Numerical Analysis uses floating-point arithmetic, but it is just one tool in numerical computation. There is an impression that floating point arithmetic is unpredictable and
6.1 Evaluate Roots and Rational Exponents
 VOCABULARY:. Evaluate Roots and Rational Exponents Radical: We know radicals as square roots. But really, radicals can be used to express any root: 0 8, 8, Index: The index tells us exactly what type of
VOCABULARY:. Evaluate Roots and Rational Exponents Radical: We know radicals as square roots. But really, radicals can be used to express any root: 0 8, 8, Index: The index tells us exactly what type of
Floating-Point Numbers in Digital Computers
 POLYTECHNIC UNIVERSITY Department of Computer and Information Science Floating-Point Numbers in Digital Computers K. Ming Leung Abstract: We explain how floating-point numbers are represented and stored
POLYTECHNIC UNIVERSITY Department of Computer and Information Science Floating-Point Numbers in Digital Computers K. Ming Leung Abstract: We explain how floating-point numbers are represented and stored
Floating-Point Numbers in Digital Computers
 POLYTECHNIC UNIVERSITY Department of Computer and Information Science Floating-Point Numbers in Digital Computers K. Ming Leung Abstract: We explain how floating-point numbers are represented and stored
POLYTECHNIC UNIVERSITY Department of Computer and Information Science Floating-Point Numbers in Digital Computers K. Ming Leung Abstract: We explain how floating-point numbers are represented and stored
1. Fill in the right hand side of the following equation by taking the derivative: (x sin x) =
 7.1 What is x cos x? 1. Fill in the right hand side of the following equation by taking the derivative: (x sin x = 2. Integrate both sides of the equation. Instructor: When instructing students to integrate
7.1 What is x cos x? 1. Fill in the right hand side of the following equation by taking the derivative: (x sin x = 2. Integrate both sides of the equation. Instructor: When instructing students to integrate
Chapter One. Numerical Algorithms
 Chapter One Numerical Algorithms The word algorithm derives from the name of the Persian mathematician (Abu Ja far Muhammad ibn Musa) Al- Khwarizmi who lived from about 790 CE to about 840 CE. He wrote
Chapter One Numerical Algorithms The word algorithm derives from the name of the Persian mathematician (Abu Ja far Muhammad ibn Musa) Al- Khwarizmi who lived from about 790 CE to about 840 CE. He wrote
Lesson 4: Numerical Computations; Newton's method
 Lesson 4: Numerical Computations; Newton's method restart; Catastrophic cancellation in the quadratic formula One case where roundoff error can be severe is if you subtract two numbers that are very close
Lesson 4: Numerical Computations; Newton's method restart; Catastrophic cancellation in the quadratic formula One case where roundoff error can be severe is if you subtract two numbers that are very close
Binary floating point encodings
 Week 1: Wednesday, Jan 25 Binary floating point encodings Binary floating point arithmetic is essentially scientific notation. Where in decimal scientific notation we write in floating point, we write
Week 1: Wednesday, Jan 25 Binary floating point encodings Binary floating point arithmetic is essentially scientific notation. Where in decimal scientific notation we write in floating point, we write
An interesting related problem is Buffon s Needle which was first proposed in the mid-1700 s.
 Using Monte Carlo to Estimate π using Buffon s Needle Problem An interesting related problem is Buffon s Needle which was first proposed in the mid-1700 s. Here s the problem (in a simplified form). Suppose
Using Monte Carlo to Estimate π using Buffon s Needle Problem An interesting related problem is Buffon s Needle which was first proposed in the mid-1700 s. Here s the problem (in a simplified form). Suppose
2 Computation with Floating-Point Numbers
 2 Computation with Floating-Point Numbers 2.1 Floating-Point Representation The notion of real numbers in mathematics is convenient for hand computations and formula manipulations. However, real numbers
2 Computation with Floating-Point Numbers 2.1 Floating-Point Representation The notion of real numbers in mathematics is convenient for hand computations and formula manipulations. However, real numbers
New Rules of ME Ph.D. Qualifying Exams 1/8
 New Rules of ME Ph.D. Qualifying Exams 1/8 Qualifying Examination The student must pass a Qualifying Examination before the Dissertation Director, the Interdisciplinary Committee, and the courses for the
New Rules of ME Ph.D. Qualifying Exams 1/8 Qualifying Examination The student must pass a Qualifying Examination before the Dissertation Director, the Interdisciplinary Committee, and the courses for the
1.3 Floating Point Form
 Section 1.3 Floating Point Form 29 1.3 Floating Point Form Floating point numbers are used by computers to approximate real numbers. On the surface, the question is a simple one. There are an infinite
Section 1.3 Floating Point Form 29 1.3 Floating Point Form Floating point numbers are used by computers to approximate real numbers. On the surface, the question is a simple one. There are an infinite
Lecture 1 Contracts. 1 A Mysterious Program : Principles of Imperative Computation (Spring 2018) Frank Pfenning
 Lecture 1 Contracts 15-122: Principles of Imperative Computation (Spring 2018) Frank Pfenning In these notes we review contracts, which we use to collectively denote function contracts, loop invariants,
Lecture 1 Contracts 15-122: Principles of Imperative Computation (Spring 2018) Frank Pfenning In these notes we review contracts, which we use to collectively denote function contracts, loop invariants,
Groundwater in Hydrologic Cycle
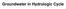 Groundwater in Hydrologic Cycle Types of Terrestrial Water Surface Water Soil Moisture Ground water Pores Full of Combination of Air and Water Unsaturated Zone / Zone of Aeration / Vadose (Soil Water)
Groundwater in Hydrologic Cycle Types of Terrestrial Water Surface Water Soil Moisture Ground water Pores Full of Combination of Air and Water Unsaturated Zone / Zone of Aeration / Vadose (Soil Water)
Section 1.4 Mathematics on the Computer: Floating Point Arithmetic
 Section 1.4 Mathematics on the Computer: Floating Point Arithmetic Key terms Floating point arithmetic IEE Standard Mantissa Exponent Roundoff error Pitfalls of floating point arithmetic Structuring computations
Section 1.4 Mathematics on the Computer: Floating Point Arithmetic Key terms Floating point arithmetic IEE Standard Mantissa Exponent Roundoff error Pitfalls of floating point arithmetic Structuring computations
Bindel, Fall 2016 Matrix Computations (CS 6210) Notes for
 1 Logistics Notes for 2016-09-07 1. We are still at 50. If you are still waiting and are not interested in knowing if a slot frees up, let me know. 2. There is a correction to HW 1, problem 4; the condition
1 Logistics Notes for 2016-09-07 1. We are still at 50. If you are still waiting and are not interested in knowing if a slot frees up, let me know. 2. There is a correction to HW 1, problem 4; the condition
Introduction to Design Optimization
 Introduction to Design Optimization James T. Allison University of Michigan, Optimal Design Laboratory June 23, 2005 1 Introduction Technology classes generally do a good job of helping students learn
Introduction to Design Optimization James T. Allison University of Michigan, Optimal Design Laboratory June 23, 2005 1 Introduction Technology classes generally do a good job of helping students learn
The Bisection Method versus Newton s Method in Maple (Classic Version for Windows)
 The Bisection Method versus (Classic Version for Windows) Author: Barbara Forrest Contact: baforres@uwaterloo.ca Copyrighted/NOT FOR RESALE version 1.1 Contents 1 Objectives for this Lab i 2 Approximate
The Bisection Method versus (Classic Version for Windows) Author: Barbara Forrest Contact: baforres@uwaterloo.ca Copyrighted/NOT FOR RESALE version 1.1 Contents 1 Objectives for this Lab i 2 Approximate
: What is Finite Element Analysis (FEA)?
 Q: What is Finite Element Analysis (FEA)? A1: It is a numerical technique for finding approximate solutions of partial differential equations (PDE) as well as of integral equations. The solution approach
Q: What is Finite Element Analysis (FEA)? A1: It is a numerical technique for finding approximate solutions of partial differential equations (PDE) as well as of integral equations. The solution approach
Improved Attack on Full-round Grain-128
 Improved Attack on Full-round Grain-128 Ximing Fu 1, and Xiaoyun Wang 1,2,3,4, and Jiazhe Chen 5, and Marc Stevens 6, and Xiaoyang Dong 2 1 Department of Computer Science and Technology, Tsinghua University,
Improved Attack on Full-round Grain-128 Ximing Fu 1, and Xiaoyun Wang 1,2,3,4, and Jiazhe Chen 5, and Marc Stevens 6, and Xiaoyang Dong 2 1 Department of Computer Science and Technology, Tsinghua University,
Outline. 1 Scientific Computing. 2 Approximations. 3 Computer Arithmetic. Scientific Computing Approximations Computer Arithmetic
 Outline 1 2 3 Michael T. Heath 2 / 46 Introduction Computational Problems General Strategy What is scientific computing? Design and analysis of algorithms for numerically solving mathematical problems
Outline 1 2 3 Michael T. Heath 2 / 46 Introduction Computational Problems General Strategy What is scientific computing? Design and analysis of algorithms for numerically solving mathematical problems
A-SSE.1.1, A-SSE.1.2-
 Putnam County Schools Curriculum Map Algebra 1 2016-2017 Module: 4 Quadratic and Exponential Functions Instructional Window: January 9-February 17 Assessment Window: February 20 March 3 MAFS Standards
Putnam County Schools Curriculum Map Algebra 1 2016-2017 Module: 4 Quadratic and Exponential Functions Instructional Window: January 9-February 17 Assessment Window: February 20 March 3 MAFS Standards
Objectives. look at floating point representation in its basic form expose errors of a different form: rounding error highlight IEEE-754 standard
 Floating Point Objectives look at floating point representation in its basic form expose errors of a different form: rounding error highlight IEEE-754 standard 1 Why this is important: Errors come in two
Floating Point Objectives look at floating point representation in its basic form expose errors of a different form: rounding error highlight IEEE-754 standard 1 Why this is important: Errors come in two
computational Fluid Dynamics - Prof. V. Esfahanian
 Three boards categories: Experimental Theoretical Computational Crucial to know all three: Each has their advantages and disadvantages. Require validation and verification. School of Mechanical Engineering
Three boards categories: Experimental Theoretical Computational Crucial to know all three: Each has their advantages and disadvantages. Require validation and verification. School of Mechanical Engineering
CITS2401 Computer Analysis & Visualisation
 FACULTY OF ENGINEERING, COMPUTING AND MATHEMATICS CITS2401 Computer Analysis & Visualisation SCHOOL OF COMPUTER SCIENCE AND SOFTWARE ENGINEERING Topic 13 Revision Notes CAV review Topics Covered Sample
FACULTY OF ENGINEERING, COMPUTING AND MATHEMATICS CITS2401 Computer Analysis & Visualisation SCHOOL OF COMPUTER SCIENCE AND SOFTWARE ENGINEERING Topic 13 Revision Notes CAV review Topics Covered Sample
Definition. A Taylor series of a function f is said to represent function f, iff the error term converges to 0 for n going to infinity.
 Definition A Taylor series of a function f is said to represent function f, iff the error term converges to 0 for n going to infinity. 120202: ESM4A - Numerical Methods 32 f(x) = e x at point c = 0. Taylor
Definition A Taylor series of a function f is said to represent function f, iff the error term converges to 0 for n going to infinity. 120202: ESM4A - Numerical Methods 32 f(x) = e x at point c = 0. Taylor
1. Practice the use of the C ++ repetition constructs of for, while, and do-while. 2. Use computer-generated random numbers.
 1 Purpose This lab illustrates the use of looping structures by introducing a class of programming problems called numerical algorithms. 1. Practice the use of the C ++ repetition constructs of for, while,
1 Purpose This lab illustrates the use of looping structures by introducing a class of programming problems called numerical algorithms. 1. Practice the use of the C ++ repetition constructs of for, while,
Classes of Real Numbers 1/2. The Real Line
 Classes of Real Numbers All real numbers can be represented by a line: 1/2 π 1 0 1 2 3 4 real numbers The Real Line { integers rational numbers non-integral fractions irrational numbers Rational numbers
Classes of Real Numbers All real numbers can be represented by a line: 1/2 π 1 0 1 2 3 4 real numbers The Real Line { integers rational numbers non-integral fractions irrational numbers Rational numbers
CHAPTER 1. Introduction
 ME 475: Computer-Aided Design of Structures 1-1 CHAPTER 1 Introduction 1.1 Analysis versus Design 1.2 Basic Steps in Analysis 1.3 What is the Finite Element Method? 1.4 Geometrical Representation, Discretization
ME 475: Computer-Aided Design of Structures 1-1 CHAPTER 1 Introduction 1.1 Analysis versus Design 1.2 Basic Steps in Analysis 1.3 What is the Finite Element Method? 1.4 Geometrical Representation, Discretization
DOWNLOAD PDF BIG IDEAS MATH VERTICAL SHRINK OF A PARABOLA
 Chapter 1 : BioMath: Transformation of Graphs Use the results in part (a) to identify the vertex of the parabola. c. Find a vertical line on your graph paper so that when you fold the paper, the left portion
Chapter 1 : BioMath: Transformation of Graphs Use the results in part (a) to identify the vertex of the parabola. c. Find a vertical line on your graph paper so that when you fold the paper, the left portion
Lecture 1 Contracts : Principles of Imperative Computation (Fall 2018) Frank Pfenning
 Lecture 1 Contracts 15-122: Principles of Imperative Computation (Fall 2018) Frank Pfenning In these notes we review contracts, which we use to collectively denote function contracts, loop invariants,
Lecture 1 Contracts 15-122: Principles of Imperative Computation (Fall 2018) Frank Pfenning In these notes we review contracts, which we use to collectively denote function contracts, loop invariants,
MS213: Numerical Methods Computing Assignments with Matlab
 MS213: Numerical Methods Computing Assignments with Matlab SUBMISSION GUIDELINES & ASSIGNMENT ADVICE 1 Assignment Questions & Supplied Codes 1.1 The MS213 Numerical Methods assignments require students
MS213: Numerical Methods Computing Assignments with Matlab SUBMISSION GUIDELINES & ASSIGNMENT ADVICE 1 Assignment Questions & Supplied Codes 1.1 The MS213 Numerical Methods assignments require students
The following information is for reviewing the material since Exam 3:
 Outcomes List for Math 121 Calculus I Fall 2010-2011 General Information: The purpose of this Outcomes List is to give you a concrete summary of the material you should know, and the skills you should
Outcomes List for Math 121 Calculus I Fall 2010-2011 General Information: The purpose of this Outcomes List is to give you a concrete summary of the material you should know, and the skills you should
Simulation in Computer Graphics. Particles. Matthias Teschner. Computer Science Department University of Freiburg
 Simulation in Computer Graphics Particles Matthias Teschner Computer Science Department University of Freiburg Outline introduction particle motion finite differences system of first order ODEs second
Simulation in Computer Graphics Particles Matthias Teschner Computer Science Department University of Freiburg Outline introduction particle motion finite differences system of first order ODEs second
Computer Simulations
 Computer Simulations A practical approach to simulation Semra Gündüç gunduc@ankara.edu.tr Ankara University Faculty of Engineering, Department of Computer Engineering 2014-2015 Spring Term Ankara University
Computer Simulations A practical approach to simulation Semra Gündüç gunduc@ankara.edu.tr Ankara University Faculty of Engineering, Department of Computer Engineering 2014-2015 Spring Term Ankara University
COURSE: NUMERICAL ANALYSIS. LESSON: Methods for Solving Non-Linear Equations
 COURSE: NUMERICAL ANALYSIS LESSON: Methods for Solving Non-Linear Equations Lesson Developer: RAJNI ARORA COLLEGE/DEPARTMENT: Department of Mathematics, University of Delhi Page No. 1 Contents 1. LEARNING
COURSE: NUMERICAL ANALYSIS LESSON: Methods for Solving Non-Linear Equations Lesson Developer: RAJNI ARORA COLLEGE/DEPARTMENT: Department of Mathematics, University of Delhi Page No. 1 Contents 1. LEARNING
Computer Arithmetic Floating Point
 Computer Arithmetic Floating Point Chapter 3.6 EEC7 FQ 25 About Floating Point Arithmetic Arithmetic basic operations on floating point numbers are: Add, Subtract, Multiply, Divide Transcendental operations
Computer Arithmetic Floating Point Chapter 3.6 EEC7 FQ 25 About Floating Point Arithmetic Arithmetic basic operations on floating point numbers are: Add, Subtract, Multiply, Divide Transcendental operations
1.00 Lecture 19. Numerical Methods: Root Finding
 1.00 Lecture 19 Numerical Methods: Root Finding short int Remember Java Data Types Type byte long float double char boolean Size (bits) 8 16 32 64 32 64 16 1-128 to 127-32,768 to 32,767-2,147,483,648 to
1.00 Lecture 19 Numerical Methods: Root Finding short int Remember Java Data Types Type byte long float double char boolean Size (bits) 8 16 32 64 32 64 16 1-128 to 127-32,768 to 32,767-2,147,483,648 to
Floating-point numbers. Phys 420/580 Lecture 6
 Floating-point numbers Phys 420/580 Lecture 6 Random walk CA Activate a single cell at site i = 0 For all subsequent times steps, let the active site wander to i := i ± 1 with equal probability Random
Floating-point numbers Phys 420/580 Lecture 6 Random walk CA Activate a single cell at site i = 0 For all subsequent times steps, let the active site wander to i := i ± 1 with equal probability Random
Numerical computing. How computers store real numbers and the problems that result
 Numerical computing How computers store real numbers and the problems that result The scientific method Theory: Mathematical equations provide a description or model Experiment Inference from data Test
Numerical computing How computers store real numbers and the problems that result The scientific method Theory: Mathematical equations provide a description or model Experiment Inference from data Test
Lecture 03 Approximations, Errors and Their Analysis
 AM702 Applied Computational Methods c ecture 03 Approximations, rrors and heir Analysis Approximations and rrors c Approximation is unavoidable in mathematical modeling the real world phenomena Approximation
AM702 Applied Computational Methods c ecture 03 Approximations, rrors and heir Analysis Approximations and rrors c Approximation is unavoidable in mathematical modeling the real world phenomena Approximation
CPSC 340: Machine Learning and Data Mining. Robust Regression Fall 2015
 CPSC 340: Machine Learning and Data Mining Robust Regression Fall 2015 Admin Can you see Assignment 1 grades on UBC connect? Auditors, don t worry about it. You should already be working on Assignment
CPSC 340: Machine Learning and Data Mining Robust Regression Fall 2015 Admin Can you see Assignment 1 grades on UBC connect? Auditors, don t worry about it. You should already be working on Assignment
