QUADRIC SURFACES IN HYPERBOLIC SPACE*
|
|
|
- Ophelia Simpson
- 5 years ago
- Views:
Transcription
1 QUADRIC SURFACES IN HYPERBOLIC SPACE* BY JULIAN LOWELL COOLIDGE Introduction. The object of this paper is to classify quadric surfaces in a three-dimensional space of constant negative curvature, and to exhibit some of their more striking metrical properties. The system of coordinates used is the usual projective one, and, as we shall always take a tetrahedron of reference self-con jugate with regard to the Absolute, the equation of the latter will appear in the form x\ -f x\ + x\ x\ = 0. The first broad line of demarcation is naturally between those surfaces which have a vanishing discriminant, and those which have a non-vanishing one. We shall occupy ourselves only with surfaces of the latter type. The next great division is into ruled surfaces, non-ruled ones, and surfaces whose equations are definite forms. This classification depends upon the signs of the discriminant and its leading minors, according to certain familiar principles. We then come to the metrical properties of quadrics. These arise from the various possible relations to the Absolute, so that the next problem is that of the classification of the mutual relations of two quadrics. This has been successfully solved by a number of writers, in particular, by Hesse f and Clebsch. J Yet from the strict point of view of a dweller in a hyperbolic space this last classification is not wholly satisfactory, for it is at once too inclusive and too ill-defined. It is too inclusive, for we are interested only in real surfaces, and must distinguish between real and imaginary curves of intersection. The Absolute has no real generators, so that we must exclude those cases where the two surfaces cut in one or more generators. It is not sharp enough, for if we search for the shape of our surface, we wish to know whether the curve which it cuts from the Absolute the absolute curve, let us say and the corresponding focal developable are real 01- imaginary ; whether there be real vertices to the common self-conjugate tetrahedron ; etc. Furthermore, we care not at all for those surfaces, analyt- * Presented to the Society April 26, Received for publication September 1, t Hesse, Vorlesungen über Geometrie des Raumes, third ed., supplement 4, section 4. X Clebsch, Vorlesungm übtr Geometrie, vol. 2, 2te Abtheilung, sections 10 and Trans. Am. Math. Woc. 11
2 162 J. L. COOLIDGE: QUADRIC SURFACES [April ically real, which lie entirely in the ultra-infinite or ideal portion of space. Nevertheless, it will be convenient to take Clebsch's classification as the basis of our work, and to use his numbering of the various cases for convenience of reference. 1. Central quadrics. Let us begin with case 1 (Clebsch) where the absolute curve is a twisted quartic. There are four cones, called the central cones, passing through this curve, whose vertices may all be real, or two may be conjugate imaginary. The important point is that they can not all be imaginary. Consider the'question as follows. The vertices of the cones are also the vertices of the common selfconjugate tetrahedron of the surface and Absolute. If two vertices be conjugate imaginary points, the line joining them will be real, and the opposite edge, the polar of the first, will be real also. Now if we have two mutually polar lines with regard to a non-ruled quadric such as the Absolute, the one will fail to meet it in real points and, hence, bear an elliptic involution of conjugate points. This involution must have a real pair common with the involution of points conjugate with regard to the other surface * and these will be the two real vertices on that line. We shall at first restrict ourselves to the case where the four vertices are real. If O be such a vertex and a line through it meet the absolute in Q Ql and the given surface in PPX, we see, using yon Staudt's symbol of projectivity, QOQxP a Qx O QPX A QPX Qx O. Remembering Cayley's projective definition of distance, we see from this that OP = PxO or O is a centre to the surface. The surface has one actual, and three ideal centres. The opposite planes are planes of symmetry. Let us now be more specific, and call those quadrics which cut the Absolute in a real curve, hyperboloids, and those which fail to meet it ellipsoids. We shall need to consider, not only the curve, but the focal developable. An ellipsoid is actual only when the developable is imaginary ; in the case of the hyperboloid, the nature of the developable determines the shape of the surface, A non-ruled hyperboloid is concave towards its centre when the developable is real, otherwise convex ; a ruled hyperboloid is two-sheeted in the former, and one-sheeted in the latter case. These indications will enable us to write the equations of the five central surfaces. Ellipsoid, Ojx\ -f a2x\ + a3x\ a4cc2 = 0, al > «2 > a3 > at > 0. Concave, non-ruled, hyperboloid, ayx] + a2cc2 + a3x\ a4;c4 = 0, ax > a2 > ai > a3 > 0. * VON SHUDI, Beiträge zur Geometrie der Lage, p. 52.
3 1903] IN HYPERBOLIC SPACE 163 Convex, non-ruled, hyperboloid, axx\ a2x\ a3x\ a x\ = 0, ax > a4 > a2 > a3 > 0. Two sheeted ruled hyperboloid, axx\ -f a2x\ a3x\ atx\ = 0, ax > a4 > a2 > 0. One sheeted ruled hyperboloid, ^a;2 + a2x\ a3x\ a4x] = 0, at > a2 > a4 > 0. What are the Cayleyan characteristics of the twisted quartic? * The osculating developable is of class 12 and order 8 ; there are 16 stationary planes, 38 lines in every plane which lie in two osculating planes, 2 lines meeting the curve twice pass through every point, 16 points in every plane lie on two tangents to the curve, and 8 planes through every point touch the curve twice. In interpreting these, let us remember that a conic having double contact with the Absolute comes under the general head of circle. If the chord of contact be ideal, the centre is actual, and we have a proper circle ; if the chord be actual, the centre is ideal, and the curve is the locus of points at a fixed distance from the chord, an equi-dista*nt curve, let us say. When the chord is tangent to the Absolute, the curve has four-point contact, and is called a horocycle: it is an orthogonal trajectory of a set of parallel lines. With these facts in view we see that: Through every point will pass 12 planes cutting the surface in osculating parabolas ;f Through every line will pass 8 planes of parabolic section ; 16 planes cut the surface in horocycles ; Every point is the centre of one section ; 16 points in every plane are the centres of circular sections ; Through every point pass 8 planes of circular section. Of these statistics, the most interesting are the ones that deal with cyclic and horocyclic sections. The circular sections are in planes tangent to the four central cones, the ray of tangency forming the chord of contact of circle and Absolute. Let us look more closely at the question of real and imaginary circles, for only the former possess any geometrical interest. To be precise we will start with the following hyperboloid: axx\ -f a2x\ a3x\ a x\ = 0, ax > a2 > a4 > 0. * Salmon, Geometry of Three Dimensions, p fstoby, American Journal of Mathematics, vol. 5 (1882), p. 358, calls this curve a " semi circular parabola."
4 164. J. L. COOLIDGE: quadric surfaces [April The equations of the four central cones are : 1) («i - ajxl + K - a*)xl - («s + at)xl =. vertex at ( 0, 0, 0, 1 ), surrounds ( 0, 0, 1, 0 ) ; 2) («! + a3)x\ + (a2+ a3)x\ (a3 + aja;2 = 0, vertex at ( 0, 0, 1, 0 ), surrounds ( 0, 0, 0, 1 ) ; 3) (a, - a2)x\ - (a2 + a3)x23 - (o4 - a2)x\ = 0, vertex at ( 0, 1, 0, 0 ), surrounds ( 0, 0, 1, 0 ) ; 4) (a2 ax)x22 (a3 + ax)x23 (ai ax)x\ = 0, vertex at ( 1, 0, 0, 0 ), surrounds ( 0, 0, 0, 1 ) ; for each cone surrounds a vertex opposite to a face it cuts in imaginary lines. If two cones surround one another's vertices, every ray of each meets two rays of the other. This is the case with cones 1 and 2, hence every ray of 2 meets the Absolute in real points. A plane tangent to either of these cones will cut the surface in an equidistant curve. Cone 3 has real rays in x4 = 0, hence some of its rays fail to meet the Absolute in real points. In the plane x3 = 0 cone 4 has the lines (x2 V ax a2 + xav ax at)(x2v ax a2 xa\/ ax a4) =.0, which are both ideal. Some rays of this cone also do not meet the Absolute. Let us next consider the point (0,1,0,1). It lies without cones 1, 2, 3, but within cone 4 and is on the Absolute. Then every point on the Absolute will be situated in that same way, or else be within the first three cones, and without the last one ; for the question of externality is not altered as we move about the Absolute until we cross the curve, when the relation to each cone is reversed. There are also, clearly, points within the Absolute, actual points, which are without three cones, and within the fourth ; but none which are without all four. For if there were such a point, we could pass thence to any other point outside all the cones, say a point in the close vicinity of ( 1, 0, 0, 0 ) without ever being inside any cone, but this is impossible as at some time during our journey, we should have to pierce the Absolute. There are, however, actual points within all four cones. It is noticeable, by similar reasoning, that no actual point is without both cones 3 and 4. Summing up, we reach this theorem : The maximum number of real planes of circular section through an actual point is six; in only two of these can we have proper circles.
5 1903] IN HYPERBOLIC SPACE 165 It will be found that a like result holds in the case of the other hyperboloids. For the ellipsoid but two of the cones are real, one surrounding all actual points, the other surrounding none. There are thus two planes of circular section through each actual point, and these cut the surface in proper circles. Let us now look at the sixteen horocyclic sections. The points of osculation with the absolute curve lie by fours in the faces of the tetrahedron.* Two faces will cut the curve in imaginary points and two in real ones, so that the hyperboloid has eight real horocyclic sections. The ellipsoid, naturally, has none. A system of quadrics touching the same focal developable may properly be called a confocal system. The theorems connected therewith bear the closest analogy to the corresponding ones in Euclidean geometry. The quadrics touching the four planes of symmetry degenerate into conies, called the focal conies ; each passes through two foci of the other. When the focal developable is imaginary, we may employ the usual proceeding and show that through each actual point will pass an ellipsoid, a ruled, and a non-ruled hyperboloid. When the developable is real we are driven to employ some other procedure, for instance the following. Through an actual point will pass two pairs of conjugate imaginary planes touching all of the confocal surfaces, hence there are three real mutually perpendicular planes which are conjugate with regard to the whole system. The generators at this point of the three quadrics meeting there are the pairs of intersections of the four planes first mentioned, only one pair being real. This shows that when the developable is real, through an actual point will pass one ruled and two non-ruled hyperboloids. Our general class of central surfaces includes also those with two imaginary centres. These centres will lie on a line cutting the surface, the Absolute, and the two real central cones in pairs of an elliptic involution. The absolute curve and focal developable will both be real. The central cones will bear tó one another the relation of cones 3 and 4 in the preceding discussion, so that through no actual point may we pass more than two real planes of circular section. Three confocals will pass through a point, and two focal conies will be real, though in the ideal region. To form the equation, we may assume that ( 1, 0,0,0) and ( 0, 1, 0, 0 ) are the poles of xx = 0 and x2 = 0, respectively ; furthermore, the surface must cut x3 = 0, cc4 = 0 in a pair of points separated by (0,0,1,1), (0,0,1, 1 ). We thus get axx\ + a2x\ + a3x\ 2bx3x^ + a x\ =0, (2&)2 > (a3 -f a4)2. The surface is ruled if ax a2 > 0. * SchröTEB, Baumkurven 4' " Ordnung, p. 85.
6 166 J. L. COOLIDGE: QUADRIC SURFACES [April 2. Paraboloids. Under this general heading, we shall include all those surfaces which touch the Absolute. The first are those that come under case 2 and have a nodal quartic as their absolute curve. There will be hyperbolic and elliptic sub-cases, according as the rest of the curve is real or imaginary. The properties of the latter may be quickly deduced from those of the ellipsoid. Two real planes of circular section will pass through an actual point, there are no horocyclic sections, and the developable is imaginary. The hyperbolic paraboloids may be ruled or otherwise. Two centres coalesce at the node, two others lie in the tangent plane there and are, hence, real. The node may be an intersection of two branches of the curve, or an isolated point, but this difference is immaterial for our purposes. There will be, as before, a distinction between those surfaces which have a real, and those which have an imaginary focal developable ; the nodal tangent plane counting double in either case. When the developable is real, we shall have three real focal conies, otherwise but two. Three confocal surfaces will pass through a point. To find the simplest form of equation, we may assume once more that the product terms in xx and x2 vanish, and that the surface touches x3 «4 = 0 at(0, 0, 1, 1). We easily get axx\ + a2x\ + a3x\ + (a4 a3)x3cc4 a4x\ = 0. The criteria for the various sub-cases are obtained by regarding the sign of the discriminant and the question of reality for the cone from the node to the absolute curve and the focal conic in the special tangent plane. We thus get : Elliptic paraboloid, 2«, 1 2a2\a3+a^ «3>«4> - Tubular, hyperbolic paraboloid, non-ruled, a1a2>0, ai>a3>0, 2ax>a3 + ar Cup-shaped, hyperbolic paraboloid, non-ruled, o}<0» a3>a4>0. Open, ruled, hyperbolic paraboloid, a3>a4>0, a2<0<2a1<a3 +a4. Gathered, ruled, hyperbolic paraboloid, 2a1>a3 + a4>0, a3>a4>0>a2.
7 1903] IN HYPERBOLIC SPACE 167 Somewhat different results will be obtained under case 3 where the absolute curve has a cusp. Both curve and developable are necessarily real, there are two horocycles, and two real focal conies. The equation may be written as that of the most general quadric cutting the Absolute in the same curve as a cone whose vertex is at ( 0, 0, 1, 1 ), and which touches x3 x4 = 0 along the intersection with xx 0, the polar of (1,0,0,0). We obtain : axx\ + x\ + 2a2x2(x3 x4) + (a3 + l)cc2 2a3x3x4 + (a3 l)x4 = 0. Writing the discriminant, we see that the surface is ruled if ax < 0. In case 7 the absolute curve is two conies touching one another. Sub-cases arise through the option of real or imaginary conies. When the conies are real, there is one real central cone, so that two circular sections may pass through an actual point, the curve being, however, strictly speaking, an equidistant one. When the conies are imaginary, the cone is still real, but surrounds all actual points, as we see by a continuous change to the case where the two conies coalesce ; there are no real circular sections. The number of horocycles is, in either case, singly infinite. The focal developable becomes imaginary with the conies ; also, when the conies are real, if the surface be ruled. The developable is, in fact, two quadric cones. To write the equations of the horocyclic paraboloids, we may take the vertex of the one central cone at ( 1, 0, 0, 0 ), and have the planes of the conies harmonically separated by xx = 0 and a;s íc4 = 0. So we get axx\ +x\ + (x3 - xf) [(1 + a)x3 + (1 - a)xf] = 0. The hyperbolic case will arise if ( 1 ax )/a > 0. The surface is ruled if ax < 0. Closely allied to this is case 10 where the absolute curve is a conic and two imaginary straight lines meeting on it. The conic must be real, since its plane is real and actual ; the surface cannot be ruled. There is a singly infinite set of horocyclic sections, but no circular ones. The focal developable will be a cone and two imaginary generators. The equation takes the simple form : x\ -f x\ -f x\ -f rxx(x3 xf) x\ = Surfaces of revolution. The next case, 6, is where the absolute curve is two intersecting conies. We shall restrict ourselves at first to the case where the line of intersection of the planes of the conies is ideal. The sections in planes through this line will be circles. Their centres will lie on the polar of the line, and their planes will be perpendicular thereunto, so that the surface is one of revolution. There will
8 168 J. L. COOLIDGE: quadric surfaces [April be no horocyclic sections, and the developable will be a pair of cones. There will be four sub-cases : 1) The planes of the conies are both ideal. 2) The planes of the conies are both imaginary. 3) The planes of the conies are both actual. 4) One plane is actual and one ideal. The first two suppositions give us ellipsoids. There is, however, an important distinction which arises from the following consideration. In an ellipse, the real cofnmon chords with the Absolute are perpendicular to the minor axis. The first sub-case will then be the oblate spheroid, while the second is the prolate. In neither case are there additional circular sections. Under the third supposition we may get both ruled and non-ruled hyperboloids and among the latter there will be some which are convex to the centre, while others are concave. The first are obtained by rotating a convex hyperbola about the conjugate axis, the second by rotating it about the transverse axis, and the third by rotating a concave hyperbola. In writing the equations we may take x3 = 0, cc4 = 0 as our ideal line. The typical equation is X, + X\ + G3Xl a4xl = 0 The criteria are : Prolate spheroid, a3 > 1 > a4 > 0. Oblate spheroid, 1 > a3 > a4 > 0. Concave hyperboloid of revolution, a3 > a4 > 1. Convex hyperboloid of revolution, a3 < a4 < 0. Ruled hyperboloid of revolution, a3 < 0 < a4 < 1. Sub-case 4 is a very different configuration. The surface can not be ruled, and we easily see that it is obtained by rotating a semi-hyperbola about its line of symmetry. The focal developable consists of two cones, one being real. In finding the equation, we may take x3 = 0 as the plane of the real conic : the other plane is to meet it in the same line as b4 = 0. This gives : X\ + x2 + asxl bx3xi xl = 0, b2 > ( a3 1 )2. There are some more special surfaces of revolution which naturally come before us at this point. In case 8 we have a conic and two intersecting lines as our absolute curve. The plane of the conic may be actual or ideal. The focal developable consists of a cone, together with the two lines. The surface is a paraboloid of revolution, obtained by rotating a parabola about its line of symmetry.
9 1903] IN HYPERBOLIC SPACE 169 There will be elliptic and hyperbolic paraboloids ; the latter divided between tubular ones and cup-shaped ones, for which last the Absolute touches an ideal sheet of the surface. These, like the elliptic ones, yield an imaginary developable. In finding the equation, we may assume that the absolute curve lies in the planes x3 ce4 = 0, «4 = 0 for the elliptic case, and x3 x4 = 0, x3 = 0 for the other. Hence x\+x\ + x\ + ( at 1 )x3x4 a x\ = 0, x\ + x\ + a3x + (l-a3)x3x4-xl=:0. For the elliptic paraboloid we must have d\ < 1 to insure an actual surface. The hyperbolic paraboloid will be tubular if 1 > a3 > 0. The last surface of revolution is the remarkable one coming under case 9. The absolute curve is two pairs of edges of a tetrahedron ; a plane through one of the remaining real edges will cut the surface in a circle or equidistant curve. The surface may be obtained by rotating an equidistant curve about its line of symmetry, or moving a circle of constant radius along a line through its centre, perpendicular to its plane. It is the simplest type of canal surface, and is the exact analogue of Clifford's surface of parallel lines in elliptic space.* The equation is : x2 + xl + a(xl-xl) = Q. 4. Surfaces of translation. The surface last considered serves as a natural bridge to our next class, where the planes of the two conies forming the absolute curve intersect in an actual line. Such a surface will be cut by every plane through this line in an equidistant curve, and is described by moving a conic of constant magnitude in such a way that its axes trace fixed planes whose intersection is ever perpendicular to the plane of the conic ; the analogue, from one point of view, of a right cylinder in Euclidean space. There will be elliptic and hyperbolic sub-cases. For the former we shall have two real central cones, whereof but one surrounds all actual points, so that through every actual point will pass two planes cutting the surface in proper circles. When the surface is hyperbolic there are two real cones situated like 2 and 4 in the discussion of 1 ; no actual point lies without both, and they will yield, at best, two equidistant curves in planes through a chosen point. In finding the equation, we may assume that the planes of the conies are harmonically separated by xx = 0, x2 = 0, giving axx\ -f a2x\ + x\ x\ = 0. *Cf. Klein, Zur nicht-euklidische Geometrie, Mathematische Annalen, vol. 37 (1890)
10 170 J. L. COOLIDGE: QUADRIC SURFACES IN HYPERBOLIC SPACE We shall have an ellipsoid if ax > a2 > 1. We shall have a hyperboloid if a1>l>«2, ruled if os2<0. The ruled surface will be obtained by transporting a convex hyperbola, otherwise we get the non-ruled surface. 5. Spheres. There remain to us only those surfaces which come under the general head of spheres. In case 12 the absolute curve is a conic counting twice. If the conic lie in an ideal plane, every section of the surface will be a circle, and we have a sphere whose centre is the pole of the plane. When the plane of the conic is actual, the perpendicular distance thence to the surface is constant, and we have an equidistant surface. The respective equations will be: x\+xl + x\ a4x2 = 0, l>a4>0; x\ + x22 + a3x\ x\ = 0, «3 > 1 In case 13 the absolute curve is a pair of straight lines counted twice. Every plane through their intersection will cut the surface in a horocycle, other planes will cut it in circles. This is the horocyclic surface of zero curvature. Its equation will be: Harvard x\ + x\ + (a+ l)x\ 2ax3xi + (a \)x\= 0, a>0. University, September, 1902.
Quadric Surfaces. Philippe B. Laval. Today KSU. Philippe B. Laval (KSU) Quadric Surfaces Today 1 / 24
 Quadric Surfaces Philippe B. Laval KSU Today Philippe B. Laval (KSU) Quadric Surfaces Today 1 / 24 Introduction A quadric surface is the graph of a second degree equation in three variables. The general
Quadric Surfaces Philippe B. Laval KSU Today Philippe B. Laval (KSU) Quadric Surfaces Today 1 / 24 Introduction A quadric surface is the graph of a second degree equation in three variables. The general
Quadric Surfaces. Philippe B. Laval. Spring 2012 KSU. Philippe B. Laval (KSU) Quadric Surfaces Spring /
 .... Quadric Surfaces Philippe B. Laval KSU Spring 2012 Philippe B. Laval (KSU) Quadric Surfaces Spring 2012 1 / 15 Introduction A quadric surface is the graph of a second degree equation in three variables.
.... Quadric Surfaces Philippe B. Laval KSU Spring 2012 Philippe B. Laval (KSU) Quadric Surfaces Spring 2012 1 / 15 Introduction A quadric surface is the graph of a second degree equation in three variables.
Chapter 15: Functions of Several Variables
 Chapter 15: Functions of Several Variables Section 15.1 Elementary Examples a. Notation: Two Variables b. Example c. Notation: Three Variables d. Functions of Several Variables e. Examples from the Sciences
Chapter 15: Functions of Several Variables Section 15.1 Elementary Examples a. Notation: Two Variables b. Example c. Notation: Three Variables d. Functions of Several Variables e. Examples from the Sciences
Quadric Surfaces. Six basic types of quadric surfaces: ellipsoid. cone. elliptic paraboloid. hyperboloid of one sheet. hyperboloid of two sheets
 Quadric Surfaces Six basic types of quadric surfaces: ellipsoid cone elliptic paraboloid hyperboloid of one sheet hyperboloid of two sheets hyperbolic paraboloid (A) (B) (C) (D) (E) (F) 1. For each surface,
Quadric Surfaces Six basic types of quadric surfaces: ellipsoid cone elliptic paraboloid hyperboloid of one sheet hyperboloid of two sheets hyperbolic paraboloid (A) (B) (C) (D) (E) (F) 1. For each surface,
12.6 Cylinders and Quadric Surfaces
 12 Vectors and the Geometry of Space 12.6 and Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. and We have already looked at two special types of surfaces:
12 Vectors and the Geometry of Space 12.6 and Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. and We have already looked at two special types of surfaces:
Math 155, Lecture Notes- Bonds
 Math 155, Lecture Notes- Bonds Name Section 10.1 Conics and Calculus In this section, we will study conic sections from a few different perspectives. We will consider the geometry-based idea that conics
Math 155, Lecture Notes- Bonds Name Section 10.1 Conics and Calculus In this section, we will study conic sections from a few different perspectives. We will consider the geometry-based idea that conics
What you will learn today
 What you will learn today Conic Sections (in 2D coordinates) Cylinders (3D) Quadric Surfaces (3D) Vectors and the Geometry of Space 1/24 Parabolas ellipses Hyperbolas Shifted Conics Conic sections result
What you will learn today Conic Sections (in 2D coordinates) Cylinders (3D) Quadric Surfaces (3D) Vectors and the Geometry of Space 1/24 Parabolas ellipses Hyperbolas Shifted Conics Conic sections result
1.6 Quadric Surfaces Brief review of Conic Sections 74 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE. Figure 1.18: Parabola y = 2x 2
 7 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE Figure 1.18: Parabola y = x 1.6 Quadric Surfaces Figure 1.19: Parabola x = y 1.6.1 Brief review of Conic Sections You may need to review conic sections for
7 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE Figure 1.18: Parabola y = x 1.6 Quadric Surfaces Figure 1.19: Parabola x = y 1.6.1 Brief review of Conic Sections You may need to review conic sections for
THE GEOMETRY OF MOVEMENT.
 4 76 THE GEOMETRY OF MOVEMENT. [J u ty? THE GEOMETRY OF MOVEMENT. Geometrie der Bewegung in synlhetischer Darstellung. Von Dr. ARTHUR SCHOENFLIES. Leipzig, B. G. Teubner, 1886. 8vo, pp. vi + 194. La Géométrie
4 76 THE GEOMETRY OF MOVEMENT. [J u ty? THE GEOMETRY OF MOVEMENT. Geometrie der Bewegung in synlhetischer Darstellung. Von Dr. ARTHUR SCHOENFLIES. Leipzig, B. G. Teubner, 1886. 8vo, pp. vi + 194. La Géométrie
4 = 1 which is an ellipse of major axis 2 and minor axis 2. Try the plane z = y2
 12.6 Quadrics and Cylinder Surfaces: Example: What is y = x? More correctly what is {(x,y,z) R 3 : y = x}? It s a plane. What about y =? Its a cylinder surface. What about y z = Again a cylinder surface
12.6 Quadrics and Cylinder Surfaces: Example: What is y = x? More correctly what is {(x,y,z) R 3 : y = x}? It s a plane. What about y =? Its a cylinder surface. What about y z = Again a cylinder surface
Planes Intersecting Cones: Static Hypertext Version
 Page 1 of 12 Planes Intersecting Cones: Static Hypertext Version On this page, we develop some of the details of the plane-slicing-cone picture discussed in the introduction. The relationship between the
Page 1 of 12 Planes Intersecting Cones: Static Hypertext Version On this page, we develop some of the details of the plane-slicing-cone picture discussed in the introduction. The relationship between the
Section 12.2: Quadric Surfaces
 Section 12.2: Quadric Surfaces Goals: 1. To recognize and write equations of quadric surfaces 2. To graph quadric surfaces by hand Definitions: 1. A quadric surface is the three-dimensional graph of an
Section 12.2: Quadric Surfaces Goals: 1. To recognize and write equations of quadric surfaces 2. To graph quadric surfaces by hand Definitions: 1. A quadric surface is the three-dimensional graph of an
Quadric surface. Ellipsoid
 Quadric surface Quadric surfaces are the graphs of any equation that can be put into the general form 11 = a x + a y + a 33z + a1xy + a13xz + a 3yz + a10x + a 0y + a 30z + a 00 where a ij R,i, j = 0,1,,
Quadric surface Quadric surfaces are the graphs of any equation that can be put into the general form 11 = a x + a y + a 33z + a1xy + a13xz + a 3yz + a10x + a 0y + a 30z + a 00 where a ij R,i, j = 0,1,,
Cylinders and Quadric Surfaces A cylinder is a three dimensional shape that is determined by
 Cylinders and Quadric Surfaces A cylinder is a three dimensional shape that is determined by a two dimensional (plane) curve C in three dimensional space a line L in a plane not parallel to the one in
Cylinders and Quadric Surfaces A cylinder is a three dimensional shape that is determined by a two dimensional (plane) curve C in three dimensional space a line L in a plane not parallel to the one in
Multivariable Calculus
 Multivariable Calculus Chapter 10 Topics in Analytic Geometry (Optional) 1. Inclination of a line p. 5. Circles p. 4 9. Determining Conic Type p. 13. Angle between lines p. 6. Parabolas p. 5 10. Rotation
Multivariable Calculus Chapter 10 Topics in Analytic Geometry (Optional) 1. Inclination of a line p. 5. Circles p. 4 9. Determining Conic Type p. 13. Angle between lines p. 6. Parabolas p. 5 10. Rotation
Systems of Spheres connected with the Tetrahedron.
 108 Systems of Spheres connected with the Tetrahedron. By J. A THIRD, M.A. [References in square brackets are to my paper on Systems of Circles analogous to Tucker Circles.] 1. If A a and B 3 (Fig. 17),
108 Systems of Spheres connected with the Tetrahedron. By J. A THIRD, M.A. [References in square brackets are to my paper on Systems of Circles analogous to Tucker Circles.] 1. If A a and B 3 (Fig. 17),
Unit 12 Topics in Analytic Geometry - Classwork
 Unit 1 Topics in Analytic Geometry - Classwork Back in Unit 7, we delved into the algebra and geometry of lines. We showed that lines can be written in several forms: a) the general form: Ax + By + C =
Unit 1 Topics in Analytic Geometry - Classwork Back in Unit 7, we delved into the algebra and geometry of lines. We showed that lines can be written in several forms: a) the general form: Ax + By + C =
Standard Equation of a Circle
 Math 335 Trigonometry Conics We will study all 4 types of conic sections, which are curves that result from the intersection of a right circular cone and a plane that does not contain the vertex. (If the
Math 335 Trigonometry Conics We will study all 4 types of conic sections, which are curves that result from the intersection of a right circular cone and a plane that does not contain the vertex. (If the
ASSIGNMENT BOOKLET. Bachelor s Degree Programme. Analytical Geometry
 ASSIGNMENT BOOKLET MTE-05 Bachelor s Degree Programme Analytical Geometry (Valid from st January, 0 to st December, 0) School of Sciences Indira Gandhi National Open University Maidan Garhi New Delhi-0068
ASSIGNMENT BOOKLET MTE-05 Bachelor s Degree Programme Analytical Geometry (Valid from st January, 0 to st December, 0) School of Sciences Indira Gandhi National Open University Maidan Garhi New Delhi-0068
Vectors and the Geometry of Space
 Vectors and the Geometry of Space In Figure 11.43, consider the line L through the point P(x 1, y 1, z 1 ) and parallel to the vector. The vector v is a direction vector for the line L, and a, b, and c
Vectors and the Geometry of Space In Figure 11.43, consider the line L through the point P(x 1, y 1, z 1 ) and parallel to the vector. The vector v is a direction vector for the line L, and a, b, and c
Pre-Calculus Guided Notes: Chapter 10 Conics. A circle is
 Name: Pre-Calculus Guided Notes: Chapter 10 Conics Section Circles A circle is _ Example 1 Write an equation for the circle with center (3, ) and radius 5. To do this, we ll need the x1 y y1 distance formula:
Name: Pre-Calculus Guided Notes: Chapter 10 Conics Section Circles A circle is _ Example 1 Write an equation for the circle with center (3, ) and radius 5. To do this, we ll need the x1 y y1 distance formula:
CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS
 CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS Big IDEAS: 1) Writing equations of conic sections ) Graphing equations of conic sections 3) Solving quadratic systems Section: Essential Question 8-1 Apply
CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS Big IDEAS: 1) Writing equations of conic sections ) Graphing equations of conic sections 3) Solving quadratic systems Section: Essential Question 8-1 Apply
CONSTRUCTIVE THEORY OF THE UNICURSAL CUBIC
 CONSTRUCTIVE THEORY OF THE UNICURSAL CUBIC BY SYNTHETIC METHODS* BY D. N. LEHMER 1. Schroeter's f classic work on the general cubic leaves little to be desired in point of symmetry and generality. It is
CONSTRUCTIVE THEORY OF THE UNICURSAL CUBIC BY SYNTHETIC METHODS* BY D. N. LEHMER 1. Schroeter's f classic work on the general cubic leaves little to be desired in point of symmetry and generality. It is
274 Curves on Surfaces, Lecture 5
 274 Curves on Surfaces, Lecture 5 Dylan Thurston Notes by Qiaochu Yuan Fall 2012 5 Ideal polygons Previously we discussed three models of the hyperbolic plane: the Poincaré disk, the upper half-plane,
274 Curves on Surfaces, Lecture 5 Dylan Thurston Notes by Qiaochu Yuan Fall 2012 5 Ideal polygons Previously we discussed three models of the hyperbolic plane: the Poincaré disk, the upper half-plane,
Chapter 11. Parametric Equations And Polar Coordinates
 Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
The point (x, y) lies on the circle of radius r and center (h, k) iff. x h y k r
 NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
Ex. 1-3: Put each circle below in the correct equation form as listed!! above, then determine the center and radius of each circle.
 Day 1 Conics - Circles Equation of a Circle The circle with center (h, k) and radius r is the set of all points (x, y) that satisfies!! (x h) 2 + (y k) 2 = r 2 Ex. 1-3: Put each circle below in the correct
Day 1 Conics - Circles Equation of a Circle The circle with center (h, k) and radius r is the set of all points (x, y) that satisfies!! (x h) 2 + (y k) 2 = r 2 Ex. 1-3: Put each circle below in the correct
KEMATH1 Calculus for Chemistry and Biochemistry Students. Francis Joseph H. Campeña, De La Salle University Manila
 KEMATH1 Calculus for Chemistry and Biochemistry Students Francis Joseph H Campeña, De La Salle University Manila January 26, 2015 Contents 1 Conic Sections 2 11 A review of the coordinate system 2 12 Conic
KEMATH1 Calculus for Chemistry and Biochemistry Students Francis Joseph H Campeña, De La Salle University Manila January 26, 2015 Contents 1 Conic Sections 2 11 A review of the coordinate system 2 12 Conic
Substituting a 2 b 2 for c 2 and using a little algebra, we can then derive the standard equation for an ellipse centred at the origin,
 Conics onic sections are the curves which result from the intersection of a plane with a cone. These curves were studied and revered by the ancient Greeks, and were written about extensively by both Euclid
Conics onic sections are the curves which result from the intersection of a plane with a cone. These curves were studied and revered by the ancient Greeks, and were written about extensively by both Euclid
Conic Sections. College Algebra
 Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
Functions of Several Variables
 . Functions of Two Variables Functions of Several Variables Rectangular Coordinate System in -Space The rectangular coordinate system in R is formed by mutually perpendicular axes. It is a right handed
. Functions of Two Variables Functions of Several Variables Rectangular Coordinate System in -Space The rectangular coordinate system in R is formed by mutually perpendicular axes. It is a right handed
Geometry Vocabulary Math Fundamentals Reference Sheet Page 1
 Math Fundamentals Reference Sheet Page 1 Acute Angle An angle whose measure is between 0 and 90 Acute Triangle A that has all acute Adjacent Alternate Interior Angle Two coplanar with a common vertex and
Math Fundamentals Reference Sheet Page 1 Acute Angle An angle whose measure is between 0 and 90 Acute Triangle A that has all acute Adjacent Alternate Interior Angle Two coplanar with a common vertex and
Ellipse, Hyperbola and Their Conjunction
 Ellipse, Hyperbola and Their Conjunction arxiv:1805.02111v1 [math.ho] 5 May 2018 Arkadiusz Kobiera Warsaw University of Technology Abstract The article presents simple analysis of cones which are used
Ellipse, Hyperbola and Their Conjunction arxiv:1805.02111v1 [math.ho] 5 May 2018 Arkadiusz Kobiera Warsaw University of Technology Abstract The article presents simple analysis of cones which are used
Descriptive Geometry 2
 By Pál Ledneczki Ph.D. 2007 Spring Semester 1 Conic Sections Ellipse Parabola Hyperbola 2007 Spring Semester 2 Intersection of Cone and Plane: Ellipse The intersection of a cone of revolution and a plane
By Pál Ledneczki Ph.D. 2007 Spring Semester 1 Conic Sections Ellipse Parabola Hyperbola 2007 Spring Semester 2 Intersection of Cone and Plane: Ellipse The intersection of a cone of revolution and a plane
Chapter 9. Linear algebra applications in geometry
 Chapter 9. Linear algebra applications in geometry C.O.S. Sorzano Biomedical Engineering August 25, 2013 9. Linear algebra applications in geometry August 25, 2013 1 / 73 Outline 9 Linear algebra applications
Chapter 9. Linear algebra applications in geometry C.O.S. Sorzano Biomedical Engineering August 25, 2013 9. Linear algebra applications in geometry August 25, 2013 1 / 73 Outline 9 Linear algebra applications
Unit 3 Functions of Several Variables
 Unit 3 Functions of Several Variables In this unit, we consider several simple examples of multi-variable functions, quadratic surfaces and projections, level curves and surfaces, partial derivatives of
Unit 3 Functions of Several Variables In this unit, we consider several simple examples of multi-variable functions, quadratic surfaces and projections, level curves and surfaces, partial derivatives of
Section 2.5. Functions and Surfaces
 Section 2.5. Functions and Surfaces ² Brief review for one variable functions and curves: A (one variable) function is rule that assigns to each member x in a subset D in R 1 a unique real number denoted
Section 2.5. Functions and Surfaces ² Brief review for one variable functions and curves: A (one variable) function is rule that assigns to each member x in a subset D in R 1 a unique real number denoted
Chapter 10. Exploring Conic Sections
 Chapter 10 Exploring Conic Sections Conics A conic section is a curve formed by the intersection of a plane and a hollow cone. Each of these shapes are made by slicing the cone and observing the shape
Chapter 10 Exploring Conic Sections Conics A conic section is a curve formed by the intersection of a plane and a hollow cone. Each of these shapes are made by slicing the cone and observing the shape
LIBRARY UNIVERSITY OF ILLINOIS7'^esAnGsyauu- m 2 m
 m 2 m LIBRARY UNIVERSITY OF ILLINOIS7'^esAnGsyauu- URBANA ^ ^ UNIVERSITY OF ILLINOIS BULLETIN Vol. XVIII Issued Weekly NOVEMBER 22, 1920 No, 12 Entered as second-class matter December 11, 1912, at the
m 2 m LIBRARY UNIVERSITY OF ILLINOIS7'^esAnGsyauu- URBANA ^ ^ UNIVERSITY OF ILLINOIS BULLETIN Vol. XVIII Issued Weekly NOVEMBER 22, 1920 No, 12 Entered as second-class matter December 11, 1912, at the
10.2: Parabolas. Chapter 10: Conic Sections. Conic sections are plane figures formed by the intersection of a double-napped cone and a plane.
 Conic sections are plane figures formed b the intersection of a double-napped cone and a plane. Chapter 10: Conic Sections Ellipse Hperbola The conic sections ma be defined as the sets of points in the
Conic sections are plane figures formed b the intersection of a double-napped cone and a plane. Chapter 10: Conic Sections Ellipse Hperbola The conic sections ma be defined as the sets of points in the
Chapter 10. Homework
 Chapter 0 Homework Lesson 0- pages 538 5 Exercises. 2. Hyperbola: center (0, 0), y-intercepts at ±, no x-intercepts, the lines of symmetry are the x- and y-axes; domain: all real numbers, range: y 5 3
Chapter 0 Homework Lesson 0- pages 538 5 Exercises. 2. Hyperbola: center (0, 0), y-intercepts at ±, no x-intercepts, the lines of symmetry are the x- and y-axes; domain: all real numbers, range: y 5 3
ENTIRELY CIRCULAR QUARTICS IN THE PSEUDO-EUCLIDEAN PLANE
 Acta Math. Hungar., 134 (4) (2012), 571 582 DOI: 10.1007/s10474-011-0174-3 First published online November 29, 2011 ENTIRELY CIRCULAR QUARTICS IN THE PSEUDO-EUCLIDEAN PLANE E. JURKIN and N. KOVAČEVIĆ Faculty
Acta Math. Hungar., 134 (4) (2012), 571 582 DOI: 10.1007/s10474-011-0174-3 First published online November 29, 2011 ENTIRELY CIRCULAR QUARTICS IN THE PSEUDO-EUCLIDEAN PLANE E. JURKIN and N. KOVAČEVIĆ Faculty
CIRCULAR QUARTICS IN THE ISOTROPIC PLANE GENERATED BY PROJECTIVELY LINKED PENCILS OF CONICS
 Acta Math. Hungar., 130 (1 2) (2011), 35 49 DOI: 10.1007/s10474-010-0038-2 First published online November 3, 2010 CIRCULAR QUARTICS IN THE ISOTROPIC PLANE GENERATED BY PROJECTIVELY LINKED PENCILS OF CONICS
Acta Math. Hungar., 130 (1 2) (2011), 35 49 DOI: 10.1007/s10474-010-0038-2 First published online November 3, 2010 CIRCULAR QUARTICS IN THE ISOTROPIC PLANE GENERATED BY PROJECTIVELY LINKED PENCILS OF CONICS
9.3 Hyperbolas and Rotation of Conics
 9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
We start by looking at a double cone. Think of this as two pointy ice cream cones that are connected at the small tips:
 Math 1330 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text. We start
Math 1330 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text. We start
Conic Sections and Analytic Geometry
 Chapter 9 Conic Sections and Analytic Geometry Chapter 9 Conic Sections and Analytic Geometry 9.1 The Ellipse 9.2 The Hyperbola 9.3 The Parabola 9.4 Rotation of Axes 9.5 Parametric Equations 9.6 Conic
Chapter 9 Conic Sections and Analytic Geometry Chapter 9 Conic Sections and Analytic Geometry 9.1 The Ellipse 9.2 The Hyperbola 9.3 The Parabola 9.4 Rotation of Axes 9.5 Parametric Equations 9.6 Conic
PARAMETRIC EQUATIONS AND POLAR COORDINATES
 10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES A coordinate system represents a point in the plane by an ordered pair of numbers called coordinates. PARAMETRIC EQUATIONS
10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES A coordinate system represents a point in the plane by an ordered pair of numbers called coordinates. PARAMETRIC EQUATIONS
8.3 Technology: Loci and Conics
 8.3 Technology: Loci and Conics The diagram shows a double cone. The two cones have one point in common. The intersection of a double cone and a plane is called a conic section or a conic. The circle,
8.3 Technology: Loci and Conics The diagram shows a double cone. The two cones have one point in common. The intersection of a double cone and a plane is called a conic section or a conic. The circle,
1 Solution of Homework
 Math 3181 Dr. Franz Rothe February 2, 2012 All3181\4080_spr12h1.tex Name: Use the back pages for extra space due date: February 10 1 Solution of Homework Figure 1: A neutral construction of the tangents
Math 3181 Dr. Franz Rothe February 2, 2012 All3181\4080_spr12h1.tex Name: Use the back pages for extra space due date: February 10 1 Solution of Homework Figure 1: A neutral construction of the tangents
OPTICAL RAY TRACING PROGRAM. A simple program has been written which will enable the non-expert to
 OPTICAL RAY TRACING PROGRAM SLAC-TN-71-19 E. A. Taylor July 1971 Introduction: A simple program has been written which will enable the non-expert to trace rays through a variety of geometric optical elements.
OPTICAL RAY TRACING PROGRAM SLAC-TN-71-19 E. A. Taylor July 1971 Introduction: A simple program has been written which will enable the non-expert to trace rays through a variety of geometric optical elements.
Glossary of dictionary terms in the AP geometry units
 Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
Chapter 3. Quadric hypersurfaces. 3.1 Quadric hypersurfaces Denition.
 Chapter 3 Quadric hypersurfaces 3.1 Quadric hypersurfaces. 3.1.1 Denition. Denition 1. In an n-dimensional ane space A; given an ane frame fo;! e i g: A quadric hypersurface in A is a set S consisting
Chapter 3 Quadric hypersurfaces 3.1 Quadric hypersurfaces. 3.1.1 Denition. Denition 1. In an n-dimensional ane space A; given an ane frame fo;! e i g: A quadric hypersurface in A is a set S consisting
ü 12.1 Vectors Students should read Sections of Rogawski's Calculus [1] for a detailed discussion of the material presented in this section.
![ü 12.1 Vectors Students should read Sections of Rogawski's Calculus [1] for a detailed discussion of the material presented in this section. ü 12.1 Vectors Students should read Sections of Rogawski's Calculus [1] for a detailed discussion of the material presented in this section.](/thumbs/75/71742148.jpg) Chapter 12 Vector Geometry Useful Tip: If you are reading the electronic version of this publication formatted as a Mathematica Notebook, then it is possible to view 3-D plots generated by Mathematica
Chapter 12 Vector Geometry Useful Tip: If you are reading the electronic version of this publication formatted as a Mathematica Notebook, then it is possible to view 3-D plots generated by Mathematica
Module 3: Stand Up Conics
 MATH55 Module 3: Stand Up Conics Main Math concepts: Conic Sections (i.e. Parabolas, Ellipses, Hyperbolas), nd degree equations Auxilliary ideas: Analytic vs. Co-ordinate-free Geometry, Parameters, Calculus.
MATH55 Module 3: Stand Up Conics Main Math concepts: Conic Sections (i.e. Parabolas, Ellipses, Hyperbolas), nd degree equations Auxilliary ideas: Analytic vs. Co-ordinate-free Geometry, Parameters, Calculus.
Demo of some simple cylinders and quadratic surfaces
 Demo of some simple cylinders and quadratic surfaces Yunkai Zhou Department of Mathematics Southern Methodist University (Prepared for Calculus-III, Math 2339) Acknowledgement: The very nice free software
Demo of some simple cylinders and quadratic surfaces Yunkai Zhou Department of Mathematics Southern Methodist University (Prepared for Calculus-III, Math 2339) Acknowledgement: The very nice free software
12 - THREE DIMENSIONAL GEOMETRY Page 1 ( Answers at the end of all questions ) = 2. ( d ) - 3. ^i - 2. ^j c 3. ( d )
 - THREE DIMENSIONAL GEOMETRY Page ( ) If the angle θ between the line x - y + x + y - z - and the plane λ x + 4 0 is such that sin θ, then the value of λ is - 4-4 [ AIEEE 00 ] ( ) If the plane ax - ay
- THREE DIMENSIONAL GEOMETRY Page ( ) If the angle θ between the line x - y + x + y - z - and the plane λ x + 4 0 is such that sin θ, then the value of λ is - 4-4 [ AIEEE 00 ] ( ) If the plane ax - ay
Copyright. Anna Marie Bouboulis
 Copyright by Anna Marie Bouboulis 2013 The Report committee for Anna Marie Bouboulis Certifies that this is the approved version of the following report: Poincaré Disc Models in Hyperbolic Geometry APPROVED
Copyright by Anna Marie Bouboulis 2013 The Report committee for Anna Marie Bouboulis Certifies that this is the approved version of the following report: Poincaré Disc Models in Hyperbolic Geometry APPROVED
Course Number: Course Title: Geometry
 Course Number: 1206310 Course Title: Geometry RELATED GLOSSARY TERM DEFINITIONS (89) Altitude The perpendicular distance from the top of a geometric figure to its opposite side. Angle Two rays or two line
Course Number: 1206310 Course Title: Geometry RELATED GLOSSARY TERM DEFINITIONS (89) Altitude The perpendicular distance from the top of a geometric figure to its opposite side. Angle Two rays or two line
ALGEBRA II UNIT X: Conic Sections Unit Notes Packet
 Name: Period: ALGEBRA II UNIT X: Conic Sections Unit Notes Packet Algebra II Unit 10 Plan: This plan is subject to change at the teacher s discretion. Section Topic Formative Work Due Date 10.3 Circles
Name: Period: ALGEBRA II UNIT X: Conic Sections Unit Notes Packet Algebra II Unit 10 Plan: This plan is subject to change at the teacher s discretion. Section Topic Formative Work Due Date 10.3 Circles
We start by looking at a double cone. Think of this as two pointy ice cream cones that are connected at the small tips:
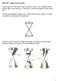 Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Math 126C: Week 3 Review
 Math 126C: Week 3 Review Note: These are in no way meant to be comprehensive reviews; they re meant to highlight the main topics and formulas for the week. Doing homework and extra problems is always the
Math 126C: Week 3 Review Note: These are in no way meant to be comprehensive reviews; they re meant to highlight the main topics and formulas for the week. Doing homework and extra problems is always the
Design and Communication Graphics
 An approach to teaching and learning Design and Communication Graphics Solids in Contact Syllabus Learning Outcomes: Construct views of up to three solids having curved surfaces and/or plane surfaces in
An approach to teaching and learning Design and Communication Graphics Solids in Contact Syllabus Learning Outcomes: Construct views of up to three solids having curved surfaces and/or plane surfaces in
Accelerated Pre-Calculus Unit 1 Task 1: Our Only Focus: Circles & Parabolas Review
 Accelerated Pre-Calculus Unit 1 Task 1: Our Only Focus: Circles & Parabolas Review Name: Date: Period: For most students, you last learned about conic sections in Analytic Geometry, which was a while ago.
Accelerated Pre-Calculus Unit 1 Task 1: Our Only Focus: Circles & Parabolas Review Name: Date: Period: For most students, you last learned about conic sections in Analytic Geometry, which was a while ago.
SPECIAL TECHNIQUES-II
 SPECIAL TECHNIQUES-II Lecture 19: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Method of Images for a spherical conductor Example :A dipole near aconducting sphere The
SPECIAL TECHNIQUES-II Lecture 19: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Method of Images for a spherical conductor Example :A dipole near aconducting sphere The
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Moore Catholic High School Math Department
 Moore Catholic High School Math Department Geometry Vocabulary The following is a list of terms and properties which are necessary for success in a Geometry class. You will be tested on these terms during
Moore Catholic High School Math Department Geometry Vocabulary The following is a list of terms and properties which are necessary for success in a Geometry class. You will be tested on these terms during
Answer Key: Three-Dimensional Cross Sections
 Geometry A Unit Answer Key: Three-Dimensional Cross Sections Name Date Objectives In this lesson, you will: visualize three-dimensional objects from different perspectives be able to create a projection
Geometry A Unit Answer Key: Three-Dimensional Cross Sections Name Date Objectives In this lesson, you will: visualize three-dimensional objects from different perspectives be able to create a projection
16.6 Parametric Surfaces and Their Areas
 SECTION 6.6 PARAMETRIC SURFACES AND THEIR AREAS i j k (b) From (a), v = w r = =( ) i +( ) j +( ) k = i + j i j k (c) curl v = v = = () () i + ( ) () j + () ( ) k =[ ( )] k = k =w 9. For any continuous
SECTION 6.6 PARAMETRIC SURFACES AND THEIR AREAS i j k (b) From (a), v = w r = =( ) i +( ) j +( ) k = i + j i j k (c) curl v = v = = () () i + ( ) () j + () ( ) k =[ ( )] k = k =w 9. For any continuous
Geometry. Cluster: Experiment with transformations in the plane. G.CO.1 G.CO.2. Common Core Institute
 Geometry Cluster: Experiment with transformations in the plane. G.CO.1: Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of
Geometry Cluster: Experiment with transformations in the plane. G.CO.1: Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of
Conic Sections. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Conic Sections MATH 211, Calculus II J. Robert Buchanan Department o Mathematics Spring 2018 Introduction The conic sections include the parabola, the ellipse, and the hyperbola. y y y x x x Parabola A
Conic Sections MATH 211, Calculus II J. Robert Buchanan Department o Mathematics Spring 2018 Introduction The conic sections include the parabola, the ellipse, and the hyperbola. y y y x x x Parabola A
Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 2 4 x 0
 Pre-Calculus Section 1.1 Completing the Square Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 4 x 0. 3x 3y
Pre-Calculus Section 1.1 Completing the Square Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 4 x 0. 3x 3y
Sphere-geometric aspects of bisector surfaces
 Sphere-geometric aspects of bisector surfaces Martin eternell Vienna University of Technology, AGGM 2006, arcelona, September 2006 1 Definition Smooth oriented objects and
Sphere-geometric aspects of bisector surfaces Martin eternell Vienna University of Technology, AGGM 2006, arcelona, September 2006 1 Definition Smooth oriented objects and
Special Quartics with Triple Points
 Journal for Geometry and Graphics Volume 6 (2002), No. 2, 111 119. Special Quartics with Triple Points Sonja Gorjanc Faculty of Civil Engineering, University of Zagreb V. Holjevca 15, 10010 Zagreb, Croatia
Journal for Geometry and Graphics Volume 6 (2002), No. 2, 111 119. Special Quartics with Triple Points Sonja Gorjanc Faculty of Civil Engineering, University of Zagreb V. Holjevca 15, 10010 Zagreb, Croatia
How to Project Spherical Conics into the Plane
 How to Project pherical Conics into the Plane Yoichi Maeda maeda@keyakiccu-tokaiacjp Department of Mathematics Tokai University Japan Abstract: In this paper, we will introduce a method how to draw the
How to Project pherical Conics into the Plane Yoichi Maeda maeda@keyakiccu-tokaiacjp Department of Mathematics Tokai University Japan Abstract: In this paper, we will introduce a method how to draw the
Calculation of the Focal Length of an Offset Satellite Dish Antenna
 Calculation of the Focal Length of an Offset Satellite Dish Antenna by John A R Legon, B.Sc. Given an offset satellite dish or antenna without LNB bracket or documentation, it is useful to be able to determine
Calculation of the Focal Length of an Offset Satellite Dish Antenna by John A R Legon, B.Sc. Given an offset satellite dish or antenna without LNB bracket or documentation, it is useful to be able to determine
Montclair Public Schools Math Curriculum Unit Planning Template Unit # SLO # MC 2 MC 3
 Subject Geometry High Honors Grade Montclair Public Schools Math Curriculum Unit Planning Template Unit # Pacing 8-10 9 10 weeks Unit Circles, Conic Sections, Area & 3-D Measurements Name Overview Unit
Subject Geometry High Honors Grade Montclair Public Schools Math Curriculum Unit Planning Template Unit # Pacing 8-10 9 10 weeks Unit Circles, Conic Sections, Area & 3-D Measurements Name Overview Unit
Conic Sections: Parabolas
 Conic Sections: Parabolas Why are the graphs of parabolas, ellipses, and hyperbolas called 'conic sections'? Because if you pass a plane through a double cone, the intersection of the plane and the cone
Conic Sections: Parabolas Why are the graphs of parabolas, ellipses, and hyperbolas called 'conic sections'? Because if you pass a plane through a double cone, the intersection of the plane and the cone
Mathematics High School Geometry
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Name. Center axis. Introduction to Conic Sections
 Name Introduction to Conic Sections Center axis This introduction to conic sections is going to focus on what they some of the skills needed to work with their equations and graphs. year, we will only
Name Introduction to Conic Sections Center axis This introduction to conic sections is going to focus on what they some of the skills needed to work with their equations and graphs. year, we will only
Special sextics with a quadruple line
 MATHEMATICAL COMMUNICATIONS 85 Math. Commun., Vol. 14, No. 1, pp. 85-102 2009) Special sextics with a quadruple line Sonja Gorjanc 1, and Vladimir Benić 1 1 Faculty of Civil Engineering, University of
MATHEMATICAL COMMUNICATIONS 85 Math. Commun., Vol. 14, No. 1, pp. 85-102 2009) Special sextics with a quadruple line Sonja Gorjanc 1, and Vladimir Benić 1 1 Faculty of Civil Engineering, University of
Algebra II. Slide 1 / 181. Slide 2 / 181. Slide 3 / 181. Conic Sections Table of Contents
 Slide 1 / 181 Algebra II Slide 2 / 181 Conic Sections 2015-04-21 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 181 Review of Midpoint and Distance Formulas Introduction
Slide 1 / 181 Algebra II Slide 2 / 181 Conic Sections 2015-04-21 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 181 Review of Midpoint and Distance Formulas Introduction
Common Core Cluster. Experiment with transformations in the plane. Unpacking What does this standard mean that a student will know and be able to do?
 Congruence G.CO Experiment with transformations in the plane. G.CO.1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point,
Congruence G.CO Experiment with transformations in the plane. G.CO.1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point,
The Manifold of Planes that Intersect Four Straight Lines in Points of a Circle
 Journal for Geometry and Graphics Volume 8 (2004), No. 1, 59 68. The Manifold of Planes that Intersect Four Straight Lines in Points of a Circle Hans-Peter Schröcker Institute of Discrete Mathematics and
Journal for Geometry and Graphics Volume 8 (2004), No. 1, 59 68. The Manifold of Planes that Intersect Four Straight Lines in Points of a Circle Hans-Peter Schröcker Institute of Discrete Mathematics and
arxiv: v2 [math.mg] 24 Jul 2013
![arxiv: v2 [math.mg] 24 Jul 2013 arxiv: v2 [math.mg] 24 Jul 2013](/thumbs/74/70304288.jpg) Solution of Sondow s problem: a synthetic proof of the tangency property of the parbelos Emmanuel Tsukerman arxiv:1210.5580v2 [math.mg] 24 Jul 2013 Abstract In a recent paper titled The parbelos, a parabolic
Solution of Sondow s problem: a synthetic proof of the tangency property of the parbelos Emmanuel Tsukerman arxiv:1210.5580v2 [math.mg] 24 Jul 2013 Abstract In a recent paper titled The parbelos, a parabolic
volume & surface area of a right circular cone cut by a plane parallel to symmetrical axis (Hyperbolic section)
 From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter December 25, 2016 volume & surface area of a right circular cone cut by a plane parallel to symmetrical axis (Hyperbolic section) Harish
From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter December 25, 2016 volume & surface area of a right circular cone cut by a plane parallel to symmetrical axis (Hyperbolic section) Harish
Geometry and Gravitation
 Chapter 15 Geometry and Gravitation 15.1 Introduction to Geometry Geometry is one of the oldest branches of mathematics, competing with number theory for historical primacy. Like all good science, its
Chapter 15 Geometry and Gravitation 15.1 Introduction to Geometry Geometry is one of the oldest branches of mathematics, competing with number theory for historical primacy. Like all good science, its
Geometry: Conic Sections
 Conic Sections Introduction When a right circular cone is intersected by a plane, as in figure 1 below, a family of four types of curves results. Because of their relationship to the cone, they are called
Conic Sections Introduction When a right circular cone is intersected by a plane, as in figure 1 below, a family of four types of curves results. Because of their relationship to the cone, they are called
EXTREME POINTS AND AFFINE EQUIVALENCE
 EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
Key Idea. It is not helpful to plot points to sketch a surface. Mainly we use traces and intercepts to sketch
 Section 12.7 Quadric surfaces 12.7 1 Learning outcomes After completing this section, you will inshaallah be able to 1. know what are quadric surfaces 2. how to sketch quadric surfaces 3. how to identify
Section 12.7 Quadric surfaces 12.7 1 Learning outcomes After completing this section, you will inshaallah be able to 1. know what are quadric surfaces 2. how to sketch quadric surfaces 3. how to identify
Chapter 9 Topics in Analytic Geometry
 Chapter 9 Topics in Analytic Geometry What You ll Learn: 9.1 Introduction to Conics: Parabolas 9.2 Ellipses 9.3 Hyperbolas 9.5 Parametric Equations 9.6 Polar Coordinates 9.7 Graphs of Polar Equations 9.1
Chapter 9 Topics in Analytic Geometry What You ll Learn: 9.1 Introduction to Conics: Parabolas 9.2 Ellipses 9.3 Hyperbolas 9.5 Parametric Equations 9.6 Polar Coordinates 9.7 Graphs of Polar Equations 9.1
15. GEOMETRY AND COORDINATES
 15. GEOMETRY AND COORDINATES We define. Given we say that the x-coordinate is while the y- coordinate is. We can view the coordinates as mappings from to : Coordinates take in a point in the plane and
15. GEOMETRY AND COORDINATES We define. Given we say that the x-coordinate is while the y- coordinate is. We can view the coordinates as mappings from to : Coordinates take in a point in the plane and
A Transformation Based on the Cubic Parabola y = x 3
 Journal for Geometry and Graphics Volume 10 (2006), No. 1, 15 21. A Transformation Based on the Cubic Parabola y = x 3 Eugeniusz Korczak ul. św. Rocha 6B m. 5, PL 61-142 Poznań, Poland email: ekorczak@math.put.poznan.pl
Journal for Geometry and Graphics Volume 10 (2006), No. 1, 15 21. A Transformation Based on the Cubic Parabola y = x 3 Eugeniusz Korczak ul. św. Rocha 6B m. 5, PL 61-142 Poznań, Poland email: ekorczak@math.put.poznan.pl
Workshop 2 in Minkowski Geometry: Conic sections Shadowing Euclidean and Minkowski Geometry
 Workshop at IME-10 July 2004 econd part Workshop 2 in Minkowski Geometry: onic sections hadowing Euclidean and Minkowski Geometry In the second part of the workshop we will investigate conic sections in
Workshop at IME-10 July 2004 econd part Workshop 2 in Minkowski Geometry: onic sections hadowing Euclidean and Minkowski Geometry In the second part of the workshop we will investigate conic sections in
We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance.
 Solid geometry We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance. First, note that everything we have proven for the
Solid geometry We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance. First, note that everything we have proven for the
Make geometric constructions. (Formalize and explain processes)
 Standard 5: Geometry Pre-Algebra Plus Algebra Geometry Algebra II Fourth Course Benchmark 1 - Benchmark 1 - Benchmark 1 - Part 3 Draw construct, and describe geometrical figures and describe the relationships
Standard 5: Geometry Pre-Algebra Plus Algebra Geometry Algebra II Fourth Course Benchmark 1 - Benchmark 1 - Benchmark 1 - Part 3 Draw construct, and describe geometrical figures and describe the relationships
Designing Cylinders with Constant Negative Curvature
 Designing Cylinders with Constant Negative Curvature Ulrich Pinkall Abstract. We describe algorithms that can be used to interactively construct ( design ) surfaces with constant negative curvature, in
Designing Cylinders with Constant Negative Curvature Ulrich Pinkall Abstract. We describe algorithms that can be used to interactively construct ( design ) surfaces with constant negative curvature, in
Chapter. Implicit Function Graphs
 Chapter 14 Implicit Function Graphs You can graph any one of the following types of implicit functions using the calculator s built-in functions. Parabolic graph Circle graph Elliptical graph Hyperbolic
Chapter 14 Implicit Function Graphs You can graph any one of the following types of implicit functions using the calculator s built-in functions. Parabolic graph Circle graph Elliptical graph Hyperbolic
The Law of Reflection
 If the surface off which the light is reflected is smooth, then the light undergoes specular reflection (parallel rays will all be reflected in the same directions). If, on the other hand, the surface
If the surface off which the light is reflected is smooth, then the light undergoes specular reflection (parallel rays will all be reflected in the same directions). If, on the other hand, the surface
PUBLISHED BY THE UNIVERSITY OF ILLINOIS, URBANA
 UNIVERSITY OF ILLINOIS URBANA LIBRARY UNIVERSITY OF ILLINOIS BULLETIN Issued Weekly Vol XX June 18, 1923 No. 42 [Entered as second-class matter December 11, 1912, at the post office at Urbana, Illinois,
UNIVERSITY OF ILLINOIS URBANA LIBRARY UNIVERSITY OF ILLINOIS BULLETIN Issued Weekly Vol XX June 18, 1923 No. 42 [Entered as second-class matter December 11, 1912, at the post office at Urbana, Illinois,
Summary of Formulas: see
 To review the Conic Sections, Identify them and sketch them from the given equations, watch the following set of YouTube videos. They are followed by several practice problems for you to try, covering
To review the Conic Sections, Identify them and sketch them from the given equations, watch the following set of YouTube videos. They are followed by several practice problems for you to try, covering
