CIRCULAR QUARTICS IN THE ISOTROPIC PLANE GENERATED BY PROJECTIVELY LINKED PENCILS OF CONICS
|
|
|
- Clarence Anderson
- 5 years ago
- Views:
Transcription
1 Acta Math. Hungar., 130 (1 2) (2011), DOI: /s First published online November 3, 2010 CIRCULAR QUARTICS IN THE ISOTROPIC PLANE GENERATED BY PROJECTIVELY LINKED PENCILS OF CONICS E. JURKIN Faculty of Mining, Geology and Petroleum Engineering, University of Zagreb, Pierottijeva 6, Zagreb, Croatia (Received October 19, 2009; revised March 24, 2010; accepted June 2, 2010) Abstract. A curve in the isotropic plane is circular if it passes through the absolute point F. Its degree of circularity is defined as the number of its intersection points with the absolute line f falling into the absolute point F. A curve of order four can be obtained as a locus of the intersections of corresponding conics of projectively linked pencils of conics. In this paper the conditions that the pencils and the projectivity have to fulfill in order to obtain a circular quartic of a certain degree of circularity have been determined analytically. The quartics of all degrees of circularity and all types (depending on their position with respect to the absolute figure) can be constructed using these results. The results have first been stated for any projective plane and then their isotropic interpretation has been given. 1. Introduction An isotropic plane I 2 is a real projective plane where the metric is induced by a real line f and a real point F, incidental with it [6], [7]. The ordered pair (f,f) iscalledtheabsolute figure of the isotropic plane. All straight lines through the absolute point F are called isotropic lines, and all points incidental with f are called isotropic points. There are seven types of regular conics classified depending on their position with respect to the absolute figure, [1], [6]: ellipse (imaginary or real), hyperbola (of 1 st or 2 nd type), special hyperbola, parabola and circle. A curve in the isotropic plane is circular if it passes through the absolute point [8]. Its degree of circularity is defined as the number of its intersection points with the absolute line f falling into the absolute point. If it does not share any common point with the absolute line except the absolute point, it is entirely circular [5]. Key words and phrases: isotropic plane, circular quartic, projectivity, pencils of conics Mathematics Subject Classification: 51M15, 51N /$20.00 c 2010 Akadémiai Kiadó, Budapest, Hungary
2 36 E. JURKIN A circular curve of order four can be 1, 2, 3 or 4-circular. The absolute line can intersect it, touch it, osculate or hyperosculate it at the absolute point. The absolute point can be simple, double or triple point of the curve. Due to that for each degree of circularity we distinguish several types of quartics. In [2] the conditions for obtaining circular quartics by automorphic inversion have been derived. But, it has been shown that it is not possible to construct quartics of all types by using this transformation. The aim of this paper is to construct circular quartics by using two projectively linked pencils of conics and to classify them depending on their position with respect to the absolute figure. It will be shown that it is possible to obtain quartics of all degrees of circularity and for each degree it is possible to construct quartics of all types. 1-circular quartics pass through the absolute point F and meet the absolute line f in three further points. Those three points can be different, two of them can fall together (the line touches the curve at a simple (ordinary) point or the line intersects the curve in a double point) or all three fall together (the line osculates the curve at a simple point, the line touches the curve at a double point or the line intersects the curve in a triple point). 2- circular quartics touch f at F or they have a double point at F. The other two intersection points can be different or fall together. 3-circular quartics osculate f at F, touch it at a double point or intersect it in a triple point falling into F. 4-circular quartics do not share any common point with f except F. They are called entirely circular quartics of the isotropic plane. The absolute point can be a simple point at which the line hyperosculates the curve, a double point at which the line osculates the curve, a double point at which both tangents coincide with the absolute line or a triple point at which the line touches the curve. 2. Projectively linked pencils of conics A curve of order four can be defined as a locus of the intersections of pairs of corresponding conics in projectively linked pencils of conics [4]. Let A, B, C and D be basic conics (symmetric 3 3-matrices) of projectively linked pencils A + λb and C + λd. This projectivity maps the conic A to C, B to D and A + λb to C + λd. Some calculation delivers the equation F( x) x B x x C x x A x x D x =0 of the quartic k. The quartic k passes through the following sixteen points: four basic points of the pencil [A, B], four basic points of the pencil [C, D], four intersection points of A and C and four intersection points of B and D. Remark. We have to be aware of the fact that proportional symmetric matrices A, B, C, D and αa, βb, γc, δd represent the same four conics,
3 CIRCULAR QUARTICS IN THE ISOTROPIC PLANE 37 but the corresponding quartics are different. For defining the projectivity beside A, C and B, D we need one more pair of conics. We will now search for the conditions that the pencils and the projectivity have to fulfill in order to obtain a circular quartic of a certain type. The results will be first stated for a projective plane and then their isotropic interpretation will be given. Let us start with a point y on the quartic k. We can assume that it is an intersection point of the basic conics A and C and we have y A y =0, y C y = 0. The tangential behavior in this point on k is usually being studied by observing the intersections of k with arbitrary straight lines through y. Such a line q will be spanned by y and a further point z. It can be parametrized by q... y + t z, t R. We compute the intersections of k and q: They belong to the zeros of the following polynomial of degree 4 in t (1) p(t) =F( y + t z) =2t[ y B y y C z y A z y D y] + t 2 [ y B y z C z +4 y B z y C z 4 y A z y D z z A z y D y] +2t 3 [ y B z z C z + z B z y C z y A z z D z z A z y D z] + t 4 [ z B z z C z z A z z D z]. The equation of the tangent of k at the regular (simple) point y is (2) y B y y C z y A z y D y =0 as t = 0 has to be zero of multiplicity 2 of the polynomial p, and y is the intersection of k and q with multiplicity 2. We now will discuss the following three cases: y B,D, y B, y D, y B,D. If y lies on B and D, then the coefficient of t of the polynomial (1) vanishes. Therefore, t = 0 is zero of multiplicity 2 for every point z of the plane. In other words, if two projectively linked pencils have a common basic point, it is a singular point of the quartic k. If y lies on B, but not on D, in general case (when A is a regular conic) the tangent of k at y contains the points z with y A z y D y =0.
4 38 E. JURKIN Obviously the tangent of k at y is the tangent of A at y. If A is a singular conic with a singular point y (A = a a, y a, a), the above-mentioned equation is satisfied for every z. This means that y is a singular point on k. If A is a singular conic, but y is not its singular point (A = a a, y a, y a), the tangent of k at y is given by the equation y A z =0. If we interpret y as the absolute point F and the basic conic A as a special hyperbola, the quartic k is 1-circular (Fig. 1). By choosing a circle for the conic A, we will obtain 2-circular quartic k touching the absolute line at the absolute point (Fig. 2). It is easy to conclude that by proper choice of basic conics it is also possible to get 1-circular quartics that intersect the absolute line in three points beside the absolute point, or they intersect it in one point and touch it at another, and 2-circular quartics that touch the absolute line at the absolute point and intersect it in two points or touch it at one more. Fig. 1 It follows that if y is a basic point of one of the projectively linked pencils, the tangent of the quartic at y is identical with the tangent of the conic of the pencil linked to the conic of the second pencil which passes through y. Fig. 1 displays a 1-circular quartic k. It is generated by the projectivity linking a pencil of special hyperbolas [A, B] with two basic points on absolute line f and a pencil [C, D] with two basic points at F, while C is a
5 CIRCULAR QUARTICS IN THE ISOTROPIC PLANE 39 special hyperbola. The projectivity is defined by three corresponding pairs: A C, B D and V V,whereV is a singular conic formed by two lines, while the absolute line is one of them. The constructive determination of interlinking pairs of conics of pencils [A, B], [C, D] uses the induced projectivities on the lines p, p. Fig. 2 The quartic k shown in Fig. 2 is 2-circular. It is a result of projectively linked pencils [A, B], [C, D] with the following properties: A is a circle, [C, D] is a pencil of parabolas with a common isotropic point, C is a singular conic. Four intersection points of k and f form their two points of contact. We can state: Theorem 1. Let A, B, C be circular and D a non-circular conic of the isotropic plane with the absolute figure (f,f) and let π :[A, B] [C, D] be a projectivity mapping a conic A + λb to a conic C + λd. The result of π is a quartic k which is 1-circular iff A is a special hyperbola or a singular conic with a regular point F not containing f, and a 2-circular quartic touching f at F iff A is a circle or a singular conic with aregularpointf containing f. The tangent y A z = 0 can also osculate the quartic k. To gain y as the intersection of q and k with multiplicity 3, the coefficient of the polynomial (1) of t 2 has to equal zero. Therefore, osculation is characterized by the condition (3) y B y z C z +4 y B z y C z 4 y A z y D z z A z y D y =0,
6 40 E. JURKIN for all z, y A z = 0, while hyperosculation is characterized by (3) and the condition (4) y B z z C z + z B z y C z y A z z D z z A z y D z =0, for all z, y A z =0. If A is a singular conic with non-singular point y, A = a a, y a, y a, then y A z = 0 is the equation of the line a. The condition (3) is fulfilled iff y B z y C z =0forevery z a ( y A z = 0) i.e. iff one of the conics B, C touches a. Depending on whether [A, B] is a pencil of circles or parabolas (and C is passing through F ) the constructed quartic k is either 3-circular or 1-circular having the absolute line as an inflexion tangent. The tangent y A z = 0 will hyperosculate the quartic k iff for every z on the tangent the equality y B z z C z + z B z y C z = 0 holds. This is fulfilled iff both conics B and C touch a. By choosing for [A, B] a pencil of isotropic circles and for [C, D] apencil of conics with a circle C as basic conic, while D is non-circular, an entirely circular quartic k will be obtained, Fig. 3. Fig. 3 Nowwestudythelastcasewhen y is not a basic point of either of the pencils of conics. The tangent of k at y given by the equation (2) is a linear combination of the tangents of the conics A, C at that point. If A is a singular conic with the singular point y, the tangent of k at y is the tangent of C. The conic C should not be a singular conic with the singular point y at the same time, as the quartic would have a singularity in y in this case.
7 CIRCULAR QUARTICS IN THE ISOTROPIC PLANE 41 If A is a singular conic with a regular point y, (A = a a, y a, y a), the line a is the tangent of k at y iff C touches a. The tangent y A z = 0 of a regular conic A is the tangent of the quartic k as well, iff C touches A or C is a singular conic with the singular point y. The following theorem is an immediate consequence of our previous results: Theorem 2. Let A, C be circular and B, D non-circular conics of the isotropic plane and let A and C have a point of contact at the absolute point. Let π :[A, B] [C, D] be a projectivity that maps the conics A + λb to the conics C + λd. The result of π is a quartic k which is 1-circular iff A and C are special hyperbolas. k is a 2-circular quartic touching f at F iff A and C are circles. A necessary condition to gain y as a double point is (5) y B y y C z y A z y D y =0, z as then t = 0 is a zero of multiplicity 2 of the polynomial (1) for all z (and for all lines q passing through y). The equations of the tangents at y are determined by (6) y B y z C z +4 y B z y C z 4 y A z y D z z A z y D y =0. The same three cases will be discussed again: y B,D, y B, y D, y B,D. If both B and D pass through y, the condition (5) is fulfilled. equation (6) is reduced to The y B z y C z y A z y D z =0. If A is a singular conic having y as a singular point, the tangents to k are given by y B z y C z =0. This implies the following: If the conics of one pencil touch each other at the common basic point y, one of the tangents to the quartic at that point coincides with the common tangent of conics. The other tangent to the quartic coincides with the tangent of the conic from the second pencil that is linked to a singular conic with the singular point y from the first pencil. Defining y as the absolute point F and the conics B, C as special hyperbolas results in a 2-circular quartic k with double point in F.Ifoneofthe conics B, C is a special hyperbola and the other is a circle, k is a 3-circular
8 42 E. JURKIN quartic touching f at the double point F.IfB and C are circles, the result is a 4-circular quartic having F as the double point at which both tangents coincide with the absolute line. If A is not a singular conic with the singular point y and either B or C is a singular conic with the singular point y, the tangents of k at y are given by the equation y A z y D z =0. We will obtain a 2-circular, 3-circular or 4-circular quartic depending on whether we choose A and D to be special hyperbolas, one of them to be a special hyperbola and the other a circle, or both to be circles. If A is not a singular conic with the singular point y and neither B nor C is a singular conic with the singular point y, one of the tangents to k is the tangent to A at y iff y B z = α y A z or y C z = α y A z, i.e. iff B touches A or C touches A. Let us suppose this first case. Then B αa is a singular conic with a singular point y. Now the tangents of k at y are y A z[α y C z y D z] =0. In the case of C, D touching each other at y, the second tangent at that point coincides with the common tangent to the conics of the pencil [C, D] (Fig. 4). Both tangents coincide with the tangent to A iff B touches A and the conic corresponding to the singular conic B αa touches A. Particularly, that holds if C, D touch A, B (Fig. 5). Therefore, if we consider y to be the absolute point F, the pencils of conics have to be pencils of special hyperbolas. The result of this projectivity will be a 2-circular quartic intersecting the absolute line in two further points. Those points can be different or can coincide forming either a double point or a point of contact of k with f. If we consider one of the pencils [A, B], [C, D] to be a pencil of special hyperbolas and the other as a pencil of circles, the absolute line f will touch the 3-circular quartic at the double point F. Further, if we consider both pencils to be pencils of circles, a 4-circular quartic k with tangents coincident with f at the double point F, will be generated. With suitable choice of projectively linked pencils of conics 1-circular and 2-circular quartics having double points in an isotropic point (different from F ) can also be obtained. The quartic k shown in Fig. 4 is 3-circular. It is generated by a projectively linked pencil of circles [A, B] and a pencil of special hyperbolas [C, D] touching at the absolute point F. If a pencil of hyperbolas had been chosen instead of a pencil of circles, and a pencil of hyperbolas having a common basic point in an isotropic point
9 CIRCULAR QUARTICS IN THE ISOTROPIC PLANE 43 Fig. 4 Fig. 5 instead of a pencil of special hyperbolas, and if we had defined the projectivity in the way that the singular conic V (containing f as its part) from the first pencil is mapped to a special hyperbola V from the second, the constructed quartic would be 1-circlar. The quartic k shown in Fig. 5 is obtained by two projectively linked pencils of circles and therefore is 4-circular.
10 44 E. JURKIN If pencils of special hyperbolas touching at the absolute point had been chosen instead of the pencils of circles, the constructed quartic would be 2-circlar. Previous studies lead us to: Theorem 3. Let A, B, C, D be circular conics of the isotropic plane with the absolute figure (f,f). Let π :[A, B] [C, D] be the projectivity which maps the conics A + λb to the conics C + λd. The result of π is a quartic k having F as a double point. If A, B are circles, k touches f at F (k is 3-circular quartic). The quartic k is entirely circular iff the conic corresponding to the singular conic with the singular point F from [A, B] is acircle. Let us observe the possibility of gaining inflexion in the double point. One of the tangents at the common basic point y of the pencils will osculate one branch of the quartic if the following equality holds for all z on the tangent y B z z C z + z B z y C z y A z z D z z A z y D z =0. This condition is fulfilled in the case when A is a singular conic, A = a a, y a, y a, B touches A, andc either touches A or is a singular conic with the singular point y. These assumptions provide the line a with the equation y A z = 0 as an inflexion tangent at y. Let us now discuss the case of y lying on A, B, C but not on D. The condition (5) is reduced to y A z =0, z which characterizes A as a singular conic (pair of lines {a, a} intersecting in y). It follows that the conics of the pencil [A, B] touch each other in the basic point y. The tangents of k at y are determined by 4 y B z y C z z A z y D y =0. Since A is a singular conic, z A z is a product of linear factors in the coordinates of z, i.e. z A z =(α 0 z 0 + α 1 z 1 + α 2 z 2 )(α 0 z 0 + α 1 z 1 + α 2 z 2 ). If one of the conics B, C is a singular conic with the singular point y, the tangents to k coincide with a, a. We conclude: If one of the pencils of conics is a pencil of pairs of lines with the vertex in a point different from the basic points of the second pencil, that vertex will be a double point of the quartic. There is only one conic from the second pencil passing through the vertex of the first. The pair of lines corresponding to that conic is the pair of tangents to the quartic at the double point.
11 CIRCULAR QUARTICS IN THE ISOTROPIC PLANE 45 We can also state: If the conics from first pencil touch each other at a point y not being a basic point of the second pencil and the singular conic with the singular point y from the first pencil is mapped to the singular conic with the singular point y from the second pencil, then k has y as a double point at which tangents coincide with the singular conic with the singular point y from the first pencil. Particularly, if a = a, a cusp will occur in the double point. If none of B, C is a singular conic with the singular point y, oneofthe tangents to k will be one of the lines a, a iff one of the conics B, C touches that line. If B touches a, y B z = βa, the pencil [A, B] contains conics osculating each other at y. The tangents are: a[4β y C z y D y a] =0. The tangent a osculates the quartic iff for all z a the equality y B z z C z + z B z y C z y A z z D z z A z y D z =0 holds as in that case t = 0 is the zero of the polynomial (1) with multiplicity 2. This condition is obviously fulfilled iff C touches a, too. Fig. 6 By identifying a with the absolute line f and y with the absolute point F an entirely circular quartic will be obtained (Fig. 6).
12 46 E. JURKIN If the conic A is a double line touched by the conics B, C, both tangents to k coincide with that line. We conclude: Theorem 4. Let A, B, C be circular and D non-circular conic of the isotropic plane with the absolute figure (f,f) and let π :[A, B] [C, D] be the projectivity mapping the conics A + λb to the conics C + λd. The result of π is a quartic k having a double point in F iff A is a pair of isotropic lines. If [A, B] is a pencil of circles osculating at F, k touches f at F (i.e. k is 3-circular). Let us now consider the case of y on A, C but not on B,D. If A is a singular conic with the singular point y, the condition (5) is fulfilled iff C is a singular conic with the singular point y. The tangents at the double point are determined by y B y z C z z A z y D y =0. Obviously, the lines of which A consists cannot be the tangents to k. If A is not a singular conic with the singular point y, the condition (5) is fulfilled iff y is a singular point of the conic y B y C y D y A. It follows that C necessarily touches A, however that condition is not sufficient. It is left to us to observe the case of a triple point on k. The necessary condition to gain a triple point at y is that the coefficients of the polynomial (1)nexttot and t 2 vanish: (7) y B y y C z y A z y D y =0, y B y z C z +4 y B z y C z 4 y A z y D z z A z y D y =0, z. The tangents are given by (8) y B z z C z + z B z y C z y A z z D z z A z y D z =0. If y is a basic point of the pencils [A, B], [C, D], the condition (7) is reduced to (9) y B z y C z y A z y D z =0, z. Now we will discuss the following two cases: Either A is or is not a singular conic with a singular point y. In the first case the condition above is fulfilled iff at least one of the conics B, C is a singular conic with a singular point y. We arrive at three subcases:
13 CIRCULAR QUARTICS IN THE ISOTROPIC PLANE 47 (1) B, C are singular conics with a singular point y. Tangents to the quartic are described by z A z y D z =0,orwrittenintheotherway a a y D z =0, where a, a are lines forming A or more precisely linear factors representing them. A cusp will occur iff either D touches a (or a) ora = a. Therefore, [A, B] is a pencil of degenerated conics (pairs of lines) and [C, D] is a pencil of conics touching at the vertex y. One of the tangents at thetriplepoint y is the common tangent of the conics from [C, D]. The other two tangents coincide with the lines from the first pencil that are linked to the singular conic with the singular point y from the second pencil. (2) The conic B = b b, y b, b. Tangents are now b b y C z a a y D z =0. One of the tangents coincide with a iff C touches a. (3) The conic C = c c, y c, c. Tangents are determined by y B z c c a a y D z =0. One of the tangents coincides with a iff B touches a. This leads to the statement: If the conics of one pencil have a common tangent at the point y and if the conics of the second pencil have a common tangent at the point y (not necessarily the same line) and if a singular conic with a singular point y from the first pencil is linked to a singular conic with a singular point y from the second pencil, then the common basic point is a triple point of a quartic. Furthermore, if y is the intersection of the conics from one pencil with multiplicity 3, their common tangent will be tangent to the quartic. Fig. 7 presents an entirely circular quartic generated by the projectively linked pencil of pairs of isotropic line and a pencil of circles. By exchanging [C, D] with a pencil of special hyperbolas, we will obtain a 3-circular quartic. It is also possible to get a 1-circular quartic if we interpret [C, D] asapencil of special hyperbolas with one further basic point on the absolute line and at the same time [A, B] is a pencil of pairs of lines with the vertex in the isotropic point. In the case when A is not a singular conic with a singular point y, it necessarily follows from (9) that either y B z = ω y A z or y C z = ω y A z holds. Let us suppose y B z = ω y A z which implies that the conics from [A, B] intersect in y with multiplicity 2 and y is a singular point on the singular conic B ωa from that pencil. The condition (7) becomes y A z [ω y C z y D z] =0, z
14 48 E. JURKIN Fig. 7 and is equivalent to the fact that y is the singular point on the singular conic D ωc from the pencil [C, D]. We are now in a position to conclude: y is a triple point of the quartic k iff the singular conic with the singular point y from [A, B] is mapped to the singular conic with the singular point y from [C, D]. The tangents to k at y are given by y A z [ z (D ωc) z] y C z [ z (B ωa) z] =0. Since the equations of the singular conics can be written as the products of linear factors in the coordinates of z, z (B ωa) z = h h, z (D ωc) z = g g, the equation above is transformed into y A z g g y C z h h =0. One of the tangents to the quartic is identical to the common tangent to the conics from the first pencil iff one of the lines y C z =0,h =0,h =0is identical to the line y A z = 0. Similarly, a tangent to the quartic is identical with the common tangent to the conics from the second pencil iff one of the lines y A z =0,g =0,g = 0 is the line y C z =0. Therefore: In the case when the conics from one pencil osculate each other (and the conics from the second pencil touch each other), one tangent to the quartic at the triple point coincides with the common tangent to the conics from that pencil.
15 CIRCULAR QUARTICS IN THE ISOTROPIC PLANE 49 If both pencils have the same common tangent, the tangent will be the tangent to the quartic at the triple point. Giving isotropic interpretation to these results we can state: Theorem 5. Let A, B and C, D be conics of the isotropic plane with F as an intersection point with multiplicity 2. Let π :[A, B] [C, D] be the projectivity which maps the conic A + λb to the conic C + λd. The result of π is a quartic k having a triple point in F iff the singular conic with the singular point F from [A, B] is mapped to the singular conic with a singular point F from [C, D]. The quartic k is entirely circular iff one of the pencils contains isotropic circles osculating at F or both pencils are pencils of circles. 3. Conclusion We did not observe all the possible cases of projectively linked pencils of conics, but those that we did observe allow us to construct the quartics of all degrees of circularity and all types. Remarks. 1. In this paper we have observed the projectivity π :[A, B] [C, D]. Fixing B = C and studying the projectivity π :[A, B] [B,D] in the same manner would allow us to construct almost all types of circular quartics. The problem in this less general case appears when we try to find the conditions for obtaining a quartic osculating the absolute line. It is caused by the fact that if y is an intersection of A and B with multiplicity n, then it is an intersection of A and k with multiplicity 2n. 2. Similar observations have been made in [3] for the entirely circular quartics in the hyperbolic plane. References [1] J. Beban-Brkić, Isometric invariants of conics in the isotropic plane Classification of conics, J. Geom. Graph., 6 (2002), [2] E. Jurkin, Automorphic inversion and circular quartics in isotropic plane, KoG, 12 (2008), [3] E. Jurkin and O. Röschel, Envelopes of absolute quadratic systems of conics of the hyperbolic plane I, Math. Pannonica, 19 (2008), [4] E.F.Kummer,Über einige besondere Arten von Flächen vierten Grades, Berl. Monatsber. (1872), [5] D. Palman, Vollständig zirkuläre Kurven 4. Ordnung der isotropen Ebene, Rad Hrvat. Akad. Znan. Umjet., 10 (1991), [6] H. Sachs, Ebene Isotrope Geometrie, Wieweg (Braunschweig Wiesbaden, 1987). [7] H. Sachs, Vollständig zirkuläre Kurven n-ter Ordnung der isotropen Ebene, Stud. Sci. Math. Hung., 24 (1989), [8] V. Szirovicza, Circular Cubics ina Isotropic and Hyperbolic Plane, PhD thesis (Zagreb, 2001) (in Croatian).
ENTIRELY CIRCULAR QUARTICS IN THE PSEUDO-EUCLIDEAN PLANE
 Acta Math. Hungar., 134 (4) (2012), 571 582 DOI: 10.1007/s10474-011-0174-3 First published online November 29, 2011 ENTIRELY CIRCULAR QUARTICS IN THE PSEUDO-EUCLIDEAN PLANE E. JURKIN and N. KOVAČEVIĆ Faculty
Acta Math. Hungar., 134 (4) (2012), 571 582 DOI: 10.1007/s10474-011-0174-3 First published online November 29, 2011 ENTIRELY CIRCULAR QUARTICS IN THE PSEUDO-EUCLIDEAN PLANE E. JURKIN and N. KOVAČEVIĆ Faculty
Special Quartics with Triple Points
 Journal for Geometry and Graphics Volume 6 (2002), No. 2, 111 119. Special Quartics with Triple Points Sonja Gorjanc Faculty of Civil Engineering, University of Zagreb V. Holjevca 15, 10010 Zagreb, Croatia
Journal for Geometry and Graphics Volume 6 (2002), No. 2, 111 119. Special Quartics with Triple Points Sonja Gorjanc Faculty of Civil Engineering, University of Zagreb V. Holjevca 15, 10010 Zagreb, Croatia
Diagonal triangle of a non-tangential quadrilateral in the isotropic plane
 MATHEMATICAL COMMUNICATIONS 157 Math. Commun. 16(011) 157 168. Diagonal triangle of a non-tangential quadrilateral in the isotropic plane Jelena Beban-Brkić 1 Marija Šimić and Vladimir Volenec 3 1 Faculty
MATHEMATICAL COMMUNICATIONS 157 Math. Commun. 16(011) 157 168. Diagonal triangle of a non-tangential quadrilateral in the isotropic plane Jelena Beban-Brkić 1 Marija Šimić and Vladimir Volenec 3 1 Faculty
The focus and the median of a non-tangential quadrilateral in the isotropic plane
 MATHEMATICAL COMMUNICATIONS 117 Math. Commun., Vol. 15, No. 1, pp. 117-17 (010) The focus and the median of a non-tangential quadrilateral in the isotropic plane Vladimir Volenec 1,, Jelena Beban-Brkić
MATHEMATICAL COMMUNICATIONS 117 Math. Commun., Vol. 15, No. 1, pp. 117-17 (010) The focus and the median of a non-tangential quadrilateral in the isotropic plane Vladimir Volenec 1,, Jelena Beban-Brkić
Shape Control of Cubic H-Bézier Curve by Moving Control Point
 Journal of Information & Computational Science 4: 2 (2007) 871 878 Available at http://www.joics.com Shape Control of Cubic H-Bézier Curve by Moving Control Point Hongyan Zhao a,b, Guojin Wang a,b, a Department
Journal of Information & Computational Science 4: 2 (2007) 871 878 Available at http://www.joics.com Shape Control of Cubic H-Bézier Curve by Moving Control Point Hongyan Zhao a,b, Guojin Wang a,b, a Department
Special sextics with a quadruple line
 MATHEMATICAL COMMUNICATIONS 85 Math. Commun., Vol. 14, No. 1, pp. 85-102 2009) Special sextics with a quadruple line Sonja Gorjanc 1, and Vladimir Benić 1 1 Faculty of Civil Engineering, University of
MATHEMATICAL COMMUNICATIONS 85 Math. Commun., Vol. 14, No. 1, pp. 85-102 2009) Special sextics with a quadruple line Sonja Gorjanc 1, and Vladimir Benić 1 1 Faculty of Civil Engineering, University of
Planes Intersecting Cones: Static Hypertext Version
 Page 1 of 12 Planes Intersecting Cones: Static Hypertext Version On this page, we develop some of the details of the plane-slicing-cone picture discussed in the introduction. The relationship between the
Page 1 of 12 Planes Intersecting Cones: Static Hypertext Version On this page, we develop some of the details of the plane-slicing-cone picture discussed in the introduction. The relationship between the
GEOMETRY OF CURVES CHAPMAN & HALL/CRC. Boca Raton London New York Washington, D.C.
 GEOMETRY OF CURVES JOHN W. RUTTER CHAPMAN & HALL/CRC Boca Raton London New York Washington, D.C. Contents Introduction 0.1 Cartesian coordinates 0.2 Polar coordinates 0.3 The Argand diagram 0.4 Polar equations
GEOMETRY OF CURVES JOHN W. RUTTER CHAPMAN & HALL/CRC Boca Raton London New York Washington, D.C. Contents Introduction 0.1 Cartesian coordinates 0.2 Polar coordinates 0.3 The Argand diagram 0.4 Polar equations
Transversal Surfaces of Ruled Surfaces in the Pseudo-Galilean Space
 Sitzungsber. Abt. II (2004) 213: 23 32 Transversal Surfaces of Ruled Surfaces in the Pseudo-Galilean Space By Željka Milin Šipuš and Blaženka Divjak (Vorgelegt in der Sitzung der math.-nat. Klasse am 22.
Sitzungsber. Abt. II (2004) 213: 23 32 Transversal Surfaces of Ruled Surfaces in the Pseudo-Galilean Space By Željka Milin Šipuš and Blaženka Divjak (Vorgelegt in der Sitzung der math.-nat. Klasse am 22.
CK 12 Algebra II with Trigonometry Concepts 1
 10.1 Parabolas with Vertex at the Origin Answers 1. up 2. left 3. down 4.focus: (0, 0.5), directrix: y = 0.5 5.focus: (0.0625, 0), directrix: x = 0.0625 6.focus: ( 1.25, 0), directrix: x = 1.25 7.focus:
10.1 Parabolas with Vertex at the Origin Answers 1. up 2. left 3. down 4.focus: (0, 0.5), directrix: y = 0.5 5.focus: (0.0625, 0), directrix: x = 0.0625 6.focus: ( 1.25, 0), directrix: x = 1.25 7.focus:
90 C. R. WYLIE, JR. [February,
 90 C. R. WYLIE, JR. [February, CURVES BELONGING TO PENCILS OF LINEAR LINE COMPLEXES IN 5 4 BY C. R. WYLIE, JR. 1. Introduction. It has been demonstrated in at least two ways* that every curve in 53, whose
90 C. R. WYLIE, JR. [February, CURVES BELONGING TO PENCILS OF LINEAR LINE COMPLEXES IN 5 4 BY C. R. WYLIE, JR. 1. Introduction. It has been demonstrated in at least two ways* that every curve in 53, whose
CONSTRUCTIVE THEORY OF THE UNICURSAL CUBIC
 CONSTRUCTIVE THEORY OF THE UNICURSAL CUBIC BY SYNTHETIC METHODS* BY D. N. LEHMER 1. Schroeter's f classic work on the general cubic leaves little to be desired in point of symmetry and generality. It is
CONSTRUCTIVE THEORY OF THE UNICURSAL CUBIC BY SYNTHETIC METHODS* BY D. N. LEHMER 1. Schroeter's f classic work on the general cubic leaves little to be desired in point of symmetry and generality. It is
THE GEOMETRY OF MOVEMENT.
 4 76 THE GEOMETRY OF MOVEMENT. [J u ty? THE GEOMETRY OF MOVEMENT. Geometrie der Bewegung in synlhetischer Darstellung. Von Dr. ARTHUR SCHOENFLIES. Leipzig, B. G. Teubner, 1886. 8vo, pp. vi + 194. La Géométrie
4 76 THE GEOMETRY OF MOVEMENT. [J u ty? THE GEOMETRY OF MOVEMENT. Geometrie der Bewegung in synlhetischer Darstellung. Von Dr. ARTHUR SCHOENFLIES. Leipzig, B. G. Teubner, 1886. 8vo, pp. vi + 194. La Géométrie
CS-9645 Introduction to Computer Vision Techniques Winter 2019
 Table of Contents Projective Geometry... 1 Definitions...1 Axioms of Projective Geometry... Ideal Points...3 Geometric Interpretation... 3 Fundamental Transformations of Projective Geometry... 4 The D
Table of Contents Projective Geometry... 1 Definitions...1 Axioms of Projective Geometry... Ideal Points...3 Geometric Interpretation... 3 Fundamental Transformations of Projective Geometry... 4 The D
The Manifold of Planes that Intersect Four Straight Lines in Points of a Circle
 Journal for Geometry and Graphics Volume 8 (2004), No. 1, 59 68. The Manifold of Planes that Intersect Four Straight Lines in Points of a Circle Hans-Peter Schröcker Institute of Discrete Mathematics and
Journal for Geometry and Graphics Volume 8 (2004), No. 1, 59 68. The Manifold of Planes that Intersect Four Straight Lines in Points of a Circle Hans-Peter Schröcker Institute of Discrete Mathematics and
Chapter 3. Quadric hypersurfaces. 3.1 Quadric hypersurfaces Denition.
 Chapter 3 Quadric hypersurfaces 3.1 Quadric hypersurfaces. 3.1.1 Denition. Denition 1. In an n-dimensional ane space A; given an ane frame fo;! e i g: A quadric hypersurface in A is a set S consisting
Chapter 3 Quadric hypersurfaces 3.1 Quadric hypersurfaces. 3.1.1 Denition. Denition 1. In an n-dimensional ane space A; given an ane frame fo;! e i g: A quadric hypersurface in A is a set S consisting
Chapter 9. Linear algebra applications in geometry
 Chapter 9. Linear algebra applications in geometry C.O.S. Sorzano Biomedical Engineering August 25, 2013 9. Linear algebra applications in geometry August 25, 2013 1 / 73 Outline 9 Linear algebra applications
Chapter 9. Linear algebra applications in geometry C.O.S. Sorzano Biomedical Engineering August 25, 2013 9. Linear algebra applications in geometry August 25, 2013 1 / 73 Outline 9 Linear algebra applications
ADDITION LAW ON ELLIPTIC CURVES
 ADDITION LAW ON ELLIPTIC CURVES JORDAN HISEL Abstract. This paper will explore projective spaces and elliptic curves. Addition on elliptic curves is rather unintuitive, but with a rigorous definition,
ADDITION LAW ON ELLIPTIC CURVES JORDAN HISEL Abstract. This paper will explore projective spaces and elliptic curves. Addition on elliptic curves is rather unintuitive, but with a rigorous definition,
Almost Curvature Continuous Fitting of B-Spline Surfaces
 Journal for Geometry and Graphics Volume 2 (1998), No. 1, 33 43 Almost Curvature Continuous Fitting of B-Spline Surfaces Márta Szilvási-Nagy Department of Geometry, Mathematical Institute, Technical University
Journal for Geometry and Graphics Volume 2 (1998), No. 1, 33 43 Almost Curvature Continuous Fitting of B-Spline Surfaces Márta Szilvási-Nagy Department of Geometry, Mathematical Institute, Technical University
Isoparametric Curve of Quadratic F-Bézier Curve
 J. of the Chosun Natural Science Vol. 6, No. 1 (2013) pp. 46 52 Isoparametric Curve of Quadratic F-Bézier Curve Hae Yeon Park 1 and Young Joon Ahn 2, Abstract In this thesis, we consider isoparametric
J. of the Chosun Natural Science Vol. 6, No. 1 (2013) pp. 46 52 Isoparametric Curve of Quadratic F-Bézier Curve Hae Yeon Park 1 and Young Joon Ahn 2, Abstract In this thesis, we consider isoparametric
Projective 2D Geometry
 Projective D Geometry Multi View Geometry (Spring '08) Projective D Geometry Prof. Kyoung Mu Lee SoEECS, Seoul National University Homogeneous representation of lines and points Projective D Geometry Line
Projective D Geometry Multi View Geometry (Spring '08) Projective D Geometry Prof. Kyoung Mu Lee SoEECS, Seoul National University Homogeneous representation of lines and points Projective D Geometry Line
On the Quartic Curve having two double points. By K. OGURA.( READ JANUARY 18, 1908.)
 230 K. OGURA: [VOL. W. On the Quartic Curve having two double points. By K. OGURA.( READ JANUARY 18, 1908.) 1. Any point (x1 x2 x3) on a quartic curve having two double points P, P' can be expressed by
230 K. OGURA: [VOL. W. On the Quartic Curve having two double points. By K. OGURA.( READ JANUARY 18, 1908.) 1. Any point (x1 x2 x3) on a quartic curve having two double points P, P' can be expressed by
Generation of lattices of points for bivariate interpolation
 Generation of lattices of points for bivariate interpolation J. M. Carnicer and M. Gasca Departamento de Matemática Aplicada. University of Zaragoza, Spain Abstract. Principal lattices in the plane are
Generation of lattices of points for bivariate interpolation J. M. Carnicer and M. Gasca Departamento de Matemática Aplicada. University of Zaragoza, Spain Abstract. Principal lattices in the plane are
The Manifold of Planes that Intersect Four Straight Lines in Points of a Circle
 The Manifold of Planes that Intersect Four Straight Lines in Points of a Circle Hans-Peter Schröcker Institute of Discrete Mathematics and Geometry Vienna University of Technology March 7, 2004 Our topic
The Manifold of Planes that Intersect Four Straight Lines in Points of a Circle Hans-Peter Schröcker Institute of Discrete Mathematics and Geometry Vienna University of Technology March 7, 2004 Our topic
volume & surface area of a right circular cone cut by a plane parallel to symmetrical axis (Hyperbolic section)
 From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter December 25, 2016 volume & surface area of a right circular cone cut by a plane parallel to symmetrical axis (Hyperbolic section) Harish
From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter December 25, 2016 volume & surface area of a right circular cone cut by a plane parallel to symmetrical axis (Hyperbolic section) Harish
Rational Bezier Curves
 Rational Bezier Curves Use of homogeneous coordinates Rational spline curve: define a curve in one higher dimension space, project it down on the homogenizing variable Mathematical formulation: n P(u)
Rational Bezier Curves Use of homogeneous coordinates Rational spline curve: define a curve in one higher dimension space, project it down on the homogenizing variable Mathematical formulation: n P(u)
ON SWELL COLORED COMPLETE GRAPHS
 Acta Math. Univ. Comenianae Vol. LXIII, (1994), pp. 303 308 303 ON SWELL COLORED COMPLETE GRAPHS C. WARD and S. SZABÓ Abstract. An edge-colored graph is said to be swell-colored if each triangle contains
Acta Math. Univ. Comenianae Vol. LXIII, (1994), pp. 303 308 303 ON SWELL COLORED COMPLETE GRAPHS C. WARD and S. SZABÓ Abstract. An edge-colored graph is said to be swell-colored if each triangle contains
A Transformation Based on the Cubic Parabola y = x 3
 Journal for Geometry and Graphics Volume 10 (2006), No. 1, 15 21. A Transformation Based on the Cubic Parabola y = x 3 Eugeniusz Korczak ul. św. Rocha 6B m. 5, PL 61-142 Poznań, Poland email: ekorczak@math.put.poznan.pl
Journal for Geometry and Graphics Volume 10 (2006), No. 1, 15 21. A Transformation Based on the Cubic Parabola y = x 3 Eugeniusz Korczak ul. św. Rocha 6B m. 5, PL 61-142 Poznań, Poland email: ekorczak@math.put.poznan.pl
Cremona transformations
 Synopsis for Tuesday, November 1 Cremona transformations Let N be a net with base-points. It gives a generically one-to-one map of P 2 into N blowing up the base-points and blowing-down the lines joining
Synopsis for Tuesday, November 1 Cremona transformations Let N be a net with base-points. It gives a generically one-to-one map of P 2 into N blowing up the base-points and blowing-down the lines joining
A COINCIDENCE BETWEEN GENUS 1 CURVES AND CANONICAL CURVES OF LOW DEGREE
 A COINCIDENCE BETWEEN GENUS 1 CURVES AND CANONICAL CURVES OF LOW DEGREE AARON LANDESMAN 1. A COINCIDENCE IN DEGREES 3, 4, AND 5 Describing equations for the low degree canonical embeddings are a very classical
A COINCIDENCE BETWEEN GENUS 1 CURVES AND CANONICAL CURVES OF LOW DEGREE AARON LANDESMAN 1. A COINCIDENCE IN DEGREES 3, 4, AND 5 Describing equations for the low degree canonical embeddings are a very classical
Chapter 9 Topics in Analytic Geometry
 Chapter 9 Topics in Analytic Geometry What You ll Learn: 9.1 Introduction to Conics: Parabolas 9.2 Ellipses 9.3 Hyperbolas 9.5 Parametric Equations 9.6 Polar Coordinates 9.7 Graphs of Polar Equations 9.1
Chapter 9 Topics in Analytic Geometry What You ll Learn: 9.1 Introduction to Conics: Parabolas 9.2 Ellipses 9.3 Hyperbolas 9.5 Parametric Equations 9.6 Polar Coordinates 9.7 Graphs of Polar Equations 9.1
9.3 Hyperbolas and Rotation of Conics
 9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
2 Solution of Homework
 Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Chapter 6. Curves and Surfaces. 6.1 Graphs as Surfaces
 Chapter 6 Curves and Surfaces In Chapter 2 a plane is defined as the zero set of a linear function in R 3. It is expected a surface is the zero set of a differentiable function in R n. To motivate, graphs
Chapter 6 Curves and Surfaces In Chapter 2 a plane is defined as the zero set of a linear function in R 3. It is expected a surface is the zero set of a differentiable function in R n. To motivate, graphs
Math 155, Lecture Notes- Bonds
 Math 155, Lecture Notes- Bonds Name Section 10.1 Conics and Calculus In this section, we will study conic sections from a few different perspectives. We will consider the geometry-based idea that conics
Math 155, Lecture Notes- Bonds Name Section 10.1 Conics and Calculus In this section, we will study conic sections from a few different perspectives. We will consider the geometry-based idea that conics
On the classification of real algebraic curves and surfaces
 On the classification of real algebraic curves and surfaces Ragni Piene Centre of Mathematics for Applications and Department of Mathematics, University of Oslo COMPASS, Kefermarkt, October 2, 2003 1 Background
On the classification of real algebraic curves and surfaces Ragni Piene Centre of Mathematics for Applications and Department of Mathematics, University of Oslo COMPASS, Kefermarkt, October 2, 2003 1 Background
Shape Modeling and Geometry Processing
 252-0538-00L, Spring 2018 Shape Modeling and Geometry Processing Discrete Differential Geometry Differential Geometry Motivation Formalize geometric properties of shapes Roi Poranne # 2 Differential Geometry
252-0538-00L, Spring 2018 Shape Modeling and Geometry Processing Discrete Differential Geometry Differential Geometry Motivation Formalize geometric properties of shapes Roi Poranne # 2 Differential Geometry
QUADRIC SURFACES IN HYPERBOLIC SPACE*
 QUADRIC SURFACES IN HYPERBOLIC SPACE* BY JULIAN LOWELL COOLIDGE Introduction. The object of this paper is to classify quadric surfaces in a three-dimensional space of constant negative curvature, and to
QUADRIC SURFACES IN HYPERBOLIC SPACE* BY JULIAN LOWELL COOLIDGE Introduction. The object of this paper is to classify quadric surfaces in a three-dimensional space of constant negative curvature, and to
Envelopes Computational Theory and Applications
 Envelopes Computational Theory and Applications Category: survey Abstract for points, whose tangent plane maps to a line under the projection. These points form the so-called Based on classical geometric
Envelopes Computational Theory and Applications Category: survey Abstract for points, whose tangent plane maps to a line under the projection. These points form the so-called Based on classical geometric
CGT 581 G Geometric Modeling Curves
 CGT 581 G Geometric Modeling Curves Bedrich Benes, Ph.D. Purdue University Department of Computer Graphics Technology Curves What is a curve? Mathematical definition 1) The continuous image of an interval
CGT 581 G Geometric Modeling Curves Bedrich Benes, Ph.D. Purdue University Department of Computer Graphics Technology Curves What is a curve? Mathematical definition 1) The continuous image of an interval
Linear Systems of Conics
 Synopsis for Tuesday, November 6 and Thursday, November 8 Linear Systems of Conics As we have already noted, the linear space of global sections Γ(2H) of the divisor 2H on P 2 consists of all the conics.
Synopsis for Tuesday, November 6 and Thursday, November 8 Linear Systems of Conics As we have already noted, the linear space of global sections Γ(2H) of the divisor 2H on P 2 consists of all the conics.
Alternative interpretation of the Plücker quadric s ambient space and its application
 Alternative interpretation of the Plücker quadric s ambient space and its application Georg Nawratil Institute of Discrete Mathematics and Geometry Funded by FWF Project Grant No. P24927-N25 18th ICGG,
Alternative interpretation of the Plücker quadric s ambient space and its application Georg Nawratil Institute of Discrete Mathematics and Geometry Funded by FWF Project Grant No. P24927-N25 18th ICGG,
A1:Orthogonal Coordinate Systems
 A1:Orthogonal Coordinate Systems A1.1 General Change of Variables Suppose that we express x and y as a function of two other variables u and by the equations We say that these equations are defining a
A1:Orthogonal Coordinate Systems A1.1 General Change of Variables Suppose that we express x and y as a function of two other variables u and by the equations We say that these equations are defining a
The equal tangents property
 The equal tangents property J. Jerónimo-Castro, G. Ruiz-Hernández and S. Tabachnikov April 29, 2012 Abstract Let M be a C 2 -smooth strictly convex closed surface in R 3 and denote by H the set of points
The equal tangents property J. Jerónimo-Castro, G. Ruiz-Hernández and S. Tabachnikov April 29, 2012 Abstract Let M be a C 2 -smooth strictly convex closed surface in R 3 and denote by H the set of points
Definition 2 (Projective plane). A projective plane is a class of points, and a class of lines satisfying the axioms:
 Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana
 University of Groningen Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish
University of Groningen Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish
The point (x, y) lies on the circle of radius r and center (h, k) iff. x h y k r
 NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
Workshop 2 in Minkowski Geometry: Conic sections Shadowing Euclidean and Minkowski Geometry
 Workshop at IME-10 July 2004 econd part Workshop 2 in Minkowski Geometry: onic sections hadowing Euclidean and Minkowski Geometry In the second part of the workshop we will investigate conic sections in
Workshop at IME-10 July 2004 econd part Workshop 2 in Minkowski Geometry: onic sections hadowing Euclidean and Minkowski Geometry In the second part of the workshop we will investigate conic sections in
Module 3: Stand Up Conics
 MATH55 Module 3: Stand Up Conics Main Math concepts: Conic Sections (i.e. Parabolas, Ellipses, Hyperbolas), nd degree equations Auxilliary ideas: Analytic vs. Co-ordinate-free Geometry, Parameters, Calculus.
MATH55 Module 3: Stand Up Conics Main Math concepts: Conic Sections (i.e. Parabolas, Ellipses, Hyperbolas), nd degree equations Auxilliary ideas: Analytic vs. Co-ordinate-free Geometry, Parameters, Calculus.
Bezier Curves. An Introduction. Detlef Reimers
 Bezier Curves An Introduction Detlef Reimers detlefreimers@gmx.de http://detlefreimers.de September 1, 2011 Chapter 1 Bezier Curve Basics 1.1 Linear Interpolation This section will give you a basic introduction
Bezier Curves An Introduction Detlef Reimers detlefreimers@gmx.de http://detlefreimers.de September 1, 2011 Chapter 1 Bezier Curve Basics 1.1 Linear Interpolation This section will give you a basic introduction
Conics, Parametric Equations, and Polar Coordinates. Copyright Cengage Learning. All rights reserved.
 10 Conics, Parametric Equations, and Polar Coordinates Copyright Cengage Learning. All rights reserved. 10.5 Area and Arc Length in Polar Coordinates Copyright Cengage Learning. All rights reserved. Objectives
10 Conics, Parametric Equations, and Polar Coordinates Copyright Cengage Learning. All rights reserved. 10.5 Area and Arc Length in Polar Coordinates Copyright Cengage Learning. All rights reserved. Objectives
An Introduction to Belyi Surfaces
 An Introduction to Belyi Surfaces Matthew Stevenson December 16, 2013 We outline the basic theory of Belyi surfaces, up to Belyi s theorem (1979, [1]), which characterizes these spaces as precisely those
An Introduction to Belyi Surfaces Matthew Stevenson December 16, 2013 We outline the basic theory of Belyi surfaces, up to Belyi s theorem (1979, [1]), which characterizes these spaces as precisely those
Ellipse, Hyperbola and Their Conjunction
 Ellipse, Hyperbola and Their Conjunction arxiv:1805.02111v1 [math.ho] 5 May 2018 Arkadiusz Kobiera Warsaw University of Technology Abstract The article presents simple analysis of cones which are used
Ellipse, Hyperbola and Their Conjunction arxiv:1805.02111v1 [math.ho] 5 May 2018 Arkadiusz Kobiera Warsaw University of Technology Abstract The article presents simple analysis of cones which are used
Sphere-geometric aspects of bisector surfaces
 Sphere-geometric aspects of bisector surfaces Martin eternell Vienna University of Technology, AGGM 2006, arcelona, September 2006 1 Definition Smooth oriented objects and
Sphere-geometric aspects of bisector surfaces Martin eternell Vienna University of Technology, AGGM 2006, arcelona, September 2006 1 Definition Smooth oriented objects and
Name: Date: 1. Match the equation with its graph. Page 1
 Name: Date: 1. Match the equation with its graph. y 6x A) C) Page 1 D) E) Page . Match the equation with its graph. ( x3) ( y3) A) C) Page 3 D) E) Page 4 3. Match the equation with its graph. ( x ) y 1
Name: Date: 1. Match the equation with its graph. y 6x A) C) Page 1 D) E) Page . Match the equation with its graph. ( x3) ( y3) A) C) Page 3 D) E) Page 4 3. Match the equation with its graph. ( x ) y 1
PUBLISHED BY THE UNIVERSITY OF ILLINOIS, URBANA
 UNIVERSITY OF ILLINOIS URBANA LIBRARY UNIVERSITY OF ILLINOIS BULLETIN Issued Weekly Vol XX June 18, 1923 No. 42 [Entered as second-class matter December 11, 1912, at the post office at Urbana, Illinois,
UNIVERSITY OF ILLINOIS URBANA LIBRARY UNIVERSITY OF ILLINOIS BULLETIN Issued Weekly Vol XX June 18, 1923 No. 42 [Entered as second-class matter December 11, 1912, at the post office at Urbana, Illinois,
MAT 3271: Selected Solutions to the Assignment 6
 Chapter 2: Major Exercises MAT 3271: Selected Solutions to the Assignment 6 1. Since a projective plan is a model of incidence geometry, Incidence Axioms 1-3 and Propositions 2.1-2.5 (which follow logically
Chapter 2: Major Exercises MAT 3271: Selected Solutions to the Assignment 6 1. Since a projective plan is a model of incidence geometry, Incidence Axioms 1-3 and Propositions 2.1-2.5 (which follow logically
LIBRARY UNIVERSITY OF ILLINOIS7'^esAnGsyauu- m 2 m
 m 2 m LIBRARY UNIVERSITY OF ILLINOIS7'^esAnGsyauu- URBANA ^ ^ UNIVERSITY OF ILLINOIS BULLETIN Vol. XVIII Issued Weekly NOVEMBER 22, 1920 No, 12 Entered as second-class matter December 11, 1912, at the
m 2 m LIBRARY UNIVERSITY OF ILLINOIS7'^esAnGsyauu- URBANA ^ ^ UNIVERSITY OF ILLINOIS BULLETIN Vol. XVIII Issued Weekly NOVEMBER 22, 1920 No, 12 Entered as second-class matter December 11, 1912, at the
INTERSECTION OF CURVES FACTS, COMPUTATIONS, APPLICATIONS IN BLOWUP*
 South Bohemia Mathematical Letters Volume 24, (2016), No. 1, 10-16. INTERSECTION OF CURVES FACTS, COMPUTATIONS, APPLICATIONS IN BLOWUP* PAVEL CHALMOVIANSKÝ abstrakt. We deal with application of intersection
South Bohemia Mathematical Letters Volume 24, (2016), No. 1, 10-16. INTERSECTION OF CURVES FACTS, COMPUTATIONS, APPLICATIONS IN BLOWUP* PAVEL CHALMOVIANSKÝ abstrakt. We deal with application of intersection
Conics, Parametric Equations, and Polar Coordinates. Copyright Cengage Learning. All rights reserved.
 10 Conics, Parametric Equations, and Polar Coordinates Copyright Cengage Learning. All rights reserved. 10.5 Area and Arc Length in Polar Coordinates Copyright Cengage Learning. All rights reserved. Objectives
10 Conics, Parametric Equations, and Polar Coordinates Copyright Cengage Learning. All rights reserved. 10.5 Area and Arc Length in Polar Coordinates Copyright Cengage Learning. All rights reserved. Objectives
Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 2 4 x 0
 Pre-Calculus Section 1.1 Completing the Square Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 4 x 0. 3x 3y
Pre-Calculus Section 1.1 Completing the Square Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 4 x 0. 3x 3y
Multiple View Geometry in Computer Vision
 Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 More on Single View Geometry Lecture 11 2 In Chapter 5 we introduced projection matrix (which
Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 More on Single View Geometry Lecture 11 2 In Chapter 5 we introduced projection matrix (which
MATHEMATICS 105 Plane Trigonometry
 Chapter I THE TRIGONOMETRIC FUNCTIONS MATHEMATICS 105 Plane Trigonometry INTRODUCTION The word trigonometry literally means triangle measurement. It is concerned with the measurement of the parts, sides,
Chapter I THE TRIGONOMETRIC FUNCTIONS MATHEMATICS 105 Plane Trigonometry INTRODUCTION The word trigonometry literally means triangle measurement. It is concerned with the measurement of the parts, sides,
COMPUTER AIDED ENGINEERING DESIGN (BFF2612)
 COMPUTER AIDED ENGINEERING DESIGN (BFF2612) BASIC MATHEMATICAL CONCEPTS IN CAED by Dr. Mohd Nizar Mhd Razali Faculty of Manufacturing Engineering mnizar@ump.edu.my COORDINATE SYSTEM y+ y+ z+ z+ x+ RIGHT
COMPUTER AIDED ENGINEERING DESIGN (BFF2612) BASIC MATHEMATICAL CONCEPTS IN CAED by Dr. Mohd Nizar Mhd Razali Faculty of Manufacturing Engineering mnizar@ump.edu.my COORDINATE SYSTEM y+ y+ z+ z+ x+ RIGHT
Tangency of Conics and Quadrics
 Proc. of the 6th WSEAS Int. Conf. on Signal Processing, Computational Geometry & Artificial Vision, Elounda, Greece, August 21-23, 26 (pp21-29) Tangency of Conics and Quadrics SUDANTHI N. R. WIJEWICKREMA,
Proc. of the 6th WSEAS Int. Conf. on Signal Processing, Computational Geometry & Artificial Vision, Elounda, Greece, August 21-23, 26 (pp21-29) Tangency of Conics and Quadrics SUDANTHI N. R. WIJEWICKREMA,
Chapter 11. Parametric Equations And Polar Coordinates
 Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
Singularity Loci of Planar Parallel Manipulators with Revolute Joints
 Singularity Loci of Planar Parallel Manipulators with Revolute Joints ILIAN A. BONEV AND CLÉMENT M. GOSSELIN Département de Génie Mécanique Université Laval Québec, Québec, Canada, G1K 7P4 Tel: (418) 656-3474,
Singularity Loci of Planar Parallel Manipulators with Revolute Joints ILIAN A. BONEV AND CLÉMENT M. GOSSELIN Département de Génie Mécanique Université Laval Québec, Québec, Canada, G1K 7P4 Tel: (418) 656-3474,
Topics in geometry Exam 1 Solutions 7/8/4
 Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
PG TRB MATHS /POLYTECNIC TRB MATHS NATIONAL ACADEMY DHARMAPURI
 PG TRB MATHS /POLYTECNIC TRB MATHS CLASSES WILL BE STARTED ON JULY 7 th Unitwise study materials and question papers available contact: 8248617507, 7010865319 PG TRB MATHS DIFFERENTIAL GEOMETRY TOTAL MARKS:100
PG TRB MATHS /POLYTECNIC TRB MATHS CLASSES WILL BE STARTED ON JULY 7 th Unitwise study materials and question papers available contact: 8248617507, 7010865319 PG TRB MATHS DIFFERENTIAL GEOMETRY TOTAL MARKS:100
CURRICULUM MAP. Course / Subject: Precalculus Grade: 11/12 Teacher: Kelly, Kirk, McCollick, Palkovics, Roderick Month: September (19 days)
 Month: September (19 days) - Change from radian to degree measure, & vice versa - Find angles that are coterminal with a given angle - Find reference angle for a given angle Angles & Their Measure (Section
Month: September (19 days) - Change from radian to degree measure, & vice versa - Find angles that are coterminal with a given angle - Find reference angle for a given angle Angles & Their Measure (Section
MOTION OF A LINE SEGMENT WHOSE ENDPOINT PATHS HAVE EQUAL ARC LENGTH. Anton GFRERRER 1 1 University of Technology, Graz, Austria
 MOTION OF A LINE SEGMENT WHOSE ENDPOINT PATHS HAVE EQUAL ARC LENGTH Anton GFRERRER 1 1 University of Technology, Graz, Austria Abstract. The following geometric problem originating from an engineering
MOTION OF A LINE SEGMENT WHOSE ENDPOINT PATHS HAVE EQUAL ARC LENGTH Anton GFRERRER 1 1 University of Technology, Graz, Austria Abstract. The following geometric problem originating from an engineering
A new CAS-touch with touching problems
 A new CAS-touch with touching problems T 3 - Conference, Oostende, August 00 Dr. René Hugelshofer, Switzerland rene@hugelshofer.net Parameters provide Maths with a new dynamic and lead sometimes to astonishing
A new CAS-touch with touching problems T 3 - Conference, Oostende, August 00 Dr. René Hugelshofer, Switzerland rene@hugelshofer.net Parameters provide Maths with a new dynamic and lead sometimes to astonishing
MATH 1020 WORKSHEET 10.1 Parametric Equations
 MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
Free-form curve design by knot alteration
 6 th International Conference on Applied Informatics Eger, Hungary, January 27 31, 2004. Free-form curve design by knot alteration Imre Juhásza, Miklós Hoffmannb a b Department of Descriptive Geometry,
6 th International Conference on Applied Informatics Eger, Hungary, January 27 31, 2004. Free-form curve design by knot alteration Imre Juhásza, Miklós Hoffmannb a b Department of Descriptive Geometry,
Control point based representation of inellipses of triangles
 Annales Mathematicae et Informaticae 40 (2012) pp. 37 46 http://ami.ektf.hu Control point based representation of inellipses of triangles Imre Juhász Department of Descriptive Geometry, University of Miskolc,
Annales Mathematicae et Informaticae 40 (2012) pp. 37 46 http://ami.ektf.hu Control point based representation of inellipses of triangles Imre Juhász Department of Descriptive Geometry, University of Miskolc,
Objectives and Homework List
 MAC 1140 Objectives and Homework List Each objective covered in MAC1140 is listed below. Along with each objective is the homework list used with MyMathLab (MML) and a list to use with the text (if you
MAC 1140 Objectives and Homework List Each objective covered in MAC1140 is listed below. Along with each objective is the homework list used with MyMathLab (MML) and a list to use with the text (if you
We start by looking at a double cone. Think of this as two pointy ice cream cones that are connected at the small tips:
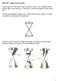 Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Chapter 15: Functions of Several Variables
 Chapter 15: Functions of Several Variables Section 15.1 Elementary Examples a. Notation: Two Variables b. Example c. Notation: Three Variables d. Functions of Several Variables e. Examples from the Sciences
Chapter 15: Functions of Several Variables Section 15.1 Elementary Examples a. Notation: Two Variables b. Example c. Notation: Three Variables d. Functions of Several Variables e. Examples from the Sciences
The Convex Hull of a Space Curve
 The Convex Hull of a Space Curve Bernd Sturmfels, UC Berkeley (joint work with Kristian Ranestad) The Mathematics of Klee & Grünbaum: 100 Years in Seattle Friday, July 30, 2010 Convex Hull of a Trigonometric
The Convex Hull of a Space Curve Bernd Sturmfels, UC Berkeley (joint work with Kristian Ranestad) The Mathematics of Klee & Grünbaum: 100 Years in Seattle Friday, July 30, 2010 Convex Hull of a Trigonometric
On the Dimension of the Bivariate Spline Space S 1 3( )
 On the Dimension of the Bivariate Spline Space S 1 3( ) Gašper Jaklič Institute of Mathematics, Physics and Mechanics University of Ljubljana Jadranska 19, 1000 Ljubljana, Slovenia Gasper.Jaklic@fmf.uni-lj.si
On the Dimension of the Bivariate Spline Space S 1 3( ) Gašper Jaklič Institute of Mathematics, Physics and Mechanics University of Ljubljana Jadranska 19, 1000 Ljubljana, Slovenia Gasper.Jaklic@fmf.uni-lj.si
Vectors and the Geometry of Space
 Vectors and the Geometry of Space In Figure 11.43, consider the line L through the point P(x 1, y 1, z 1 ) and parallel to the vector. The vector v is a direction vector for the line L, and a, b, and c
Vectors and the Geometry of Space In Figure 11.43, consider the line L through the point P(x 1, y 1, z 1 ) and parallel to the vector. The vector v is a direction vector for the line L, and a, b, and c
ON THE NUMBER OF CONNECTED COMPONENTS IN THE SPACE OF CLOSED NONDEGENERATE CURVES ON S"
 BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY Volume 25, Number 1, July 1991 ON THE NUMBER OF CONNECTED COMPONENTS IN THE SPACE OF CLOSED NONDEGENERATE CURVES ON S" B. Z. SHAPIRO AND M. Z.
BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY Volume 25, Number 1, July 1991 ON THE NUMBER OF CONNECTED COMPONENTS IN THE SPACE OF CLOSED NONDEGENERATE CURVES ON S" B. Z. SHAPIRO AND M. Z.
Blending curves. Albert Wiltsche
 Journal for Geometry and Graphics Volume 9 (2005), No. 1, 67 75. Blenng curves Albert Wiltsche Institute of Geometry, Graz University of Technology Kopernikusgasse 24, A-8010 Graz, Austria email: wiltsche@tugraz.at
Journal for Geometry and Graphics Volume 9 (2005), No. 1, 67 75. Blenng curves Albert Wiltsche Institute of Geometry, Graz University of Technology Kopernikusgasse 24, A-8010 Graz, Austria email: wiltsche@tugraz.at
CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS
 CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS Big IDEAS: 1) Writing equations of conic sections ) Graphing equations of conic sections 3) Solving quadratic systems Section: Essential Question 8-1 Apply
CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS Big IDEAS: 1) Writing equations of conic sections ) Graphing equations of conic sections 3) Solving quadratic systems Section: Essential Question 8-1 Apply
Technische Universität München Zentrum Mathematik
 Technische Universität München Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Bernhard Werner Projective Geometry SS 28 https://www-m.ma.tum.de/bin/view/lehre/ss8/pgss8/webhome Solutions for Worksheet
Technische Universität München Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Bernhard Werner Projective Geometry SS 28 https://www-m.ma.tum.de/bin/view/lehre/ss8/pgss8/webhome Solutions for Worksheet
COMPUTER AIDED GEOMETRIC DESIGN. Thomas W. Sederberg
 COMPUTER AIDED GEOMETRIC DESIGN Thomas W. Sederberg January 31, 2011 ii T. W. Sederberg iii Preface This semester is the 24 th time I have taught a course at Brigham Young University titled, Computer Aided
COMPUTER AIDED GEOMETRIC DESIGN Thomas W. Sederberg January 31, 2011 ii T. W. Sederberg iii Preface This semester is the 24 th time I have taught a course at Brigham Young University titled, Computer Aided
Lecture 11 COVERING SPACES
 Lecture 11 COVERING SPACES A covering space (or covering) is not a space, but a mapping of spaces (usually manifolds) which, locally, is a homeomorphism, but globally may be quite complicated. The simplest
Lecture 11 COVERING SPACES A covering space (or covering) is not a space, but a mapping of spaces (usually manifolds) which, locally, is a homeomorphism, but globally may be quite complicated. The simplest
x 6 + λ 2 x 6 = for the curve y = 1 2 x3 gives f(1, 1 2 ) = λ actually has another solution besides λ = 1 2 = However, the equation λ
 Math 0 Prelim I Solutions Spring 010 1. Let f(x, y) = x3 y for (x, y) (0, 0). x 6 + y (4 pts) (a) Show that the cubic curves y = x 3 are level curves of the function f. Solution. Substituting y = x 3 in
Math 0 Prelim I Solutions Spring 010 1. Let f(x, y) = x3 y for (x, y) (0, 0). x 6 + y (4 pts) (a) Show that the cubic curves y = x 3 are level curves of the function f. Solution. Substituting y = x 3 in
A Conic Associated with Euler Lines
 Forum Geometricorum Volume 6 (2006) 17 23. FRU GE ISSN 1534-1178 onic ssociated with Euler Lines Juan Rodríguez, Paula anuel, and Paulo Semião bstract. We study the locus of a point for which the Euler
Forum Geometricorum Volume 6 (2006) 17 23. FRU GE ISSN 1534-1178 onic ssociated with Euler Lines Juan Rodríguez, Paula anuel, and Paulo Semião bstract. We study the locus of a point for which the Euler
HOSTOS COMMUNITY COLLEGE DEPARTMENT OF MATHEMATICS. College Algebra with Trigonometric Functions
 HOSTOS COMMUNITY COLLEGE DEPARTMENT OF MATHEMATICS Math 150 College Algebra with Trigonometric Functions CREDIT HOURS: 4.0 EQUATED HOURS: 4.0 CLASS HOURS: 4.0 PREREQUISITE: Passing Mat 15 or mat 20 or
HOSTOS COMMUNITY COLLEGE DEPARTMENT OF MATHEMATICS Math 150 College Algebra with Trigonometric Functions CREDIT HOURS: 4.0 EQUATED HOURS: 4.0 CLASS HOURS: 4.0 PREREQUISITE: Passing Mat 15 or mat 20 or
STEINER TREE CONSTRUCTIONS IN HYPERBOLIC SPACE
 STEINER TREE CONSTRUCTIONS IN HYPERBOLIC SPACE DENISE HALVERSON AND DON MARCH Abstract. Methods for the construction of Steiner minimal trees for n fixed points in the hyperbolic plane are developed. A
STEINER TREE CONSTRUCTIONS IN HYPERBOLIC SPACE DENISE HALVERSON AND DON MARCH Abstract. Methods for the construction of Steiner minimal trees for n fixed points in the hyperbolic plane are developed. A
On a Geometric Locus in Taxicab Geometry
 Forum Geometricorum Volume 14 014) 117 11 FORUM GEOM ISSN 1534-1178 On a Geometric Locus in Taxicab Geometry Bryan Brzycki Abstract In axiomatic geometry, the taxicab model of geometry is important as
Forum Geometricorum Volume 14 014) 117 11 FORUM GEOM ISSN 1534-1178 On a Geometric Locus in Taxicab Geometry Bryan Brzycki Abstract In axiomatic geometry, the taxicab model of geometry is important as
Gergonne and Nagel Points for Simplices in the n-dimensional Space
 Journal for Geometry and Graphics Volume 4 (2000), No. 2, 119 127. Gergonne and Nagel Points for Simplices in the n-dimensional Space Edwin Koźniewsi 1, Renata A. Górsa 2 1 Institute of Civil Engineering,
Journal for Geometry and Graphics Volume 4 (2000), No. 2, 119 127. Gergonne and Nagel Points for Simplices in the n-dimensional Space Edwin Koźniewsi 1, Renata A. Górsa 2 1 Institute of Civil Engineering,
4 = 1 which is an ellipse of major axis 2 and minor axis 2. Try the plane z = y2
 12.6 Quadrics and Cylinder Surfaces: Example: What is y = x? More correctly what is {(x,y,z) R 3 : y = x}? It s a plane. What about y =? Its a cylinder surface. What about y z = Again a cylinder surface
12.6 Quadrics and Cylinder Surfaces: Example: What is y = x? More correctly what is {(x,y,z) R 3 : y = x}? It s a plane. What about y =? Its a cylinder surface. What about y z = Again a cylinder surface
Honors Precalculus: Solving equations and inequalities graphically and algebraically. Page 1
 Solving equations and inequalities graphically and algebraically 1. Plot points on the Cartesian coordinate plane. P.1 2. Represent data graphically using scatter plots, bar graphs, & line graphs. P.1
Solving equations and inequalities graphically and algebraically 1. Plot points on the Cartesian coordinate plane. P.1 2. Represent data graphically using scatter plots, bar graphs, & line graphs. P.1
Conic Sections. College Algebra
 Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
A New Class of Quasi-Cubic Trigonometric Bezier Curve and Surfaces
 A New Class of Quasi-Cubic Trigonometric Bezier Curve and Surfaces Mridula Dube 1, Urvashi Mishra 2 1 Department of Mathematics and Computer Science, R.D. University, Jabalpur, Madhya Pradesh, India 2
A New Class of Quasi-Cubic Trigonometric Bezier Curve and Surfaces Mridula Dube 1, Urvashi Mishra 2 1 Department of Mathematics and Computer Science, R.D. University, Jabalpur, Madhya Pradesh, India 2
Graphing Techniques. Domain (, ) Range (, ) Squaring Function f(x) = x 2 Domain (, ) Range [, ) f( x) = x 2
 Graphing Techniques In this chapter, we will take our knowledge of graphs of basic functions and expand our ability to graph polynomial and rational functions using common sense, zeros, y-intercepts, stretching
Graphing Techniques In this chapter, we will take our knowledge of graphs of basic functions and expand our ability to graph polynomial and rational functions using common sense, zeros, y-intercepts, stretching
Preferred directions for resolving the non-uniqueness of Delaunay triangulations
 Preferred directions for resolving the non-uniqueness of Delaunay triangulations Christopher Dyken and Michael S. Floater Abstract: This note proposes a simple rule to determine a unique triangulation
Preferred directions for resolving the non-uniqueness of Delaunay triangulations Christopher Dyken and Michael S. Floater Abstract: This note proposes a simple rule to determine a unique triangulation
Chapter 5. Projections and Rendering
 Chapter 5 Projections and Rendering Topics: Perspective Projections The rendering pipeline In order to view manipulate and view a graphics object we must find ways of storing it a computer-compatible way.
Chapter 5 Projections and Rendering Topics: Perspective Projections The rendering pipeline In order to view manipulate and view a graphics object we must find ways of storing it a computer-compatible way.
