Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.1/30
|
|
|
- Myrtle Eaton
- 5 years ago
- Views:
Transcription
1 Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs Sergiy Butenko Department of Industrial Engineering Texas A&M University College Station, TX Joint work with P. Pardalos, I. Sergienko, V. Shylo, and P. Stetsyuk Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.1/30
2 Outline Introduction Maximum clique/independent set problems Error-correcting codes Lower bound for codes correcting one error on the Z-channel Conclusion Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.2/30
3 Introduction Definitions: G = (V, E) is a simple undirected graph, V = {1, 2,..., n}. G = (V, E), is the complement graph of G = (V, E), where E = {(i, j) i, j V, i j and (i, j) / E}. For S V, G(S) = (S, E S S) the subgraph induced by S. Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.3/30
4 Introduction Example: V = {1, 2, 3, 4, 5} E = {(1,2), (1,3), (1,4), (2,3), (2,4), (3,4), (3,5), (4,5)} Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.4/30
5 Introduction S = {1, 3, 5} Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.4/30
6 Introduction S = {1, 3, 5} G(S) : Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.4/30
7 Introduction S = {1, 3, 5} G(S) : Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.4/30
8 Introduction A subset I V is called an independent set (stable set, vertex packing) if G(I) has no edges. A subset C V is called a clique if G(C) is complete, i.e. it has all possible edges. An independent set (clique) is said to be maximal, if it is not a subset of any larger independent set (clique); maximum, if there is no larger independent set (clique) in the graph. Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.5/30
9 Introduction Example: Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.6/30
10 Introduction A maximal clique: {3, 4, 5} Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.6/30
11 Introduction The maximum clique: {1, 2, 3, 4} Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.6/30
12 Introduction α(g) the independence (stability) number of G. ω(g) the clique number of G. V C V is a vertex cover if every edge has at least one endpoint in V C. I is a maximum independent set of G I is a maximum clique of Ḡ V \ I is a minimum vertex cover of G. MC, MIS and MVC problems are NP-hard Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.7/30
13 Error-correcting Codes Given: Find: Set B n of all binary vectors of length n; For u B n denote by F e (u) = { } v : u error e v A subset C B n is said to be an e-correcting code if F e (u) F e (v) = for all u, v C, u v. The largest correcting code. Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.8/30
14 Error-correcting Codes Example: Single Deletion Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.9/30
15 Error-correcting Codes X Example: Single Deletion Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.9/30
16 Error-correcting Codes X X Example: Single Deletion Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.9/30
17 Error-correcting Codes We construct the following graph G n = (V n, E (e) n ): V n = B n ; (u, v) E (e) n if and only if u v and F e (u) F e (v). Then a correcting code corresponds to an independent set in G n. Hence, the largest e-correcting code can be found by solving the maximum independent set problem in the considered graph. Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.10/30
18 Error-correcting Codes Single-Deletion-Correcting Codes (1dc); Two-Deletion-Correcting Codes (2dc); Codes For Correcting a Single Transposition, Excluding the End-Around Transposition (1tc); Codes For Correcting a Single Transposition, Including the End-Around Transposition (1et); Codes For Correcting One Error on the Z-Channel (1zc). njas/doc/graphs.html (Neil Sloane s webpage) Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.11/30
19 Error-correcting Codes Preprocessing: Simplicial vertices are removed and connected components are considered separately. Clique Partitioning: We partition the set of vertices V of G as follows: k V = C i, i=1 where C i - cliques such that C i C j =, i j. Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.12/30
20 Error-correcting Codes An upper bound: s. t. O C (G) = max n i=1 x i i C j x i 1, j = 1,..., m x 0. where C j C is a maximal clique, C- a set of maximal cliques, C = m. Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.13/30
21 Error-correcting Codes Branch-and-Bound algorithm Branching: Based on the fact that the number of vertices from a clique that can be included in an independent set is always equal to 0 or 1. Bounding: We use a heuristic solution as a lower bound and O C (G) as an upper bound. Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.14/30
22 Error-correcting Codes Exact Solutions Found. Graph V E α(g) 1dc dc ltc ltc ltc let let let Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.15/30
23 One Error on the Z-Channel p p A scheme of the Z-channel Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.16/30
24 One Error on the Z-Channel n Lower bound Upper bound Varshamov (1973), Constantin and Rao (1979), Delsarte and Piret (1981), Etzion and Östergard (1998) Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.17/30
25 One Error on the Z-Channel The asymmetric distance d A (x, y) between vectors x, y B n is defined as follows: d A (x, y) = max{n(x, y), N(y, x)}, where N(x, y) = {i : (x i = 0) (y i = 1)}. It is related to the Hamming distance d H (x, y) = n x i y i = N(x, y) + N(y, x) by the expression i=1 2d A (x, y) = d H (x, y) + w(x) w(y) Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.18/30
26 One Error on the Z-Channel The minimum asymmetric distance for a code C B n is defined as = min {d A (x, y) x, y C, x y}. Rao and Chawla (1975): A code C with the minimum asymmetric distance can correct at most ( 1) asymmetric errors. We consider = 2. Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.19/30
27 One Error on the Z-Channel The partitioning method (Van Pul and Etzion, 1989) V (n) = m i=1 I i, I i is an independent set, I i Ij =, i j. Π(n) = (I 1, I 2,..., I m ). The index vector of partition Π(n): π(n) = ( I 1, I 2,..., I m ), We assume that I 1 I 2... I m. Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.20/30
28 One Error on the Z-Channel Constant weight codes of weight w Construct a graph G(n, w) ( n ) w vertices x and y are adjacent iff d H (x, y) < 4 an independent set partition Π(n, w) = (I w 1, I w 2,..., I w m) (each ind. set is a subcode with minimum Hamming distance 4) Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.21/30
29 One Error on the Z-Channel The direct product Π(n 1 ) Π(n 2, w) of a partition of asymmetric codes Π(n 1 ) = (I 1, I 2,..., I m1 ) and a partition of constant weight codes Π(n 2, w) = (I w 1, I w 2,..., I w m 2 ) is the set of vectors C = {(u, v) : u I i, v I w i, 1 i m}, where m = min{m 1, m 2 }. Etzion and Östergard (1998): C is a code of length n = n 1 + n 2 with minimum asymmetric distance 2, i.e. a code correcting one error on the Z-channel of length n = n 1 + n 2. Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.22/30
30 One Error on the Z-Channel A procedure for finding a code C of length n and minimum asymmetric distance 2: 1. Choose n 1 and n 2 such that n 1 + n 2 = n. 2. Choose ɛ = 0 or Compute Π(n 1 ) and Π(n 2, 2i + ɛ), i = 0,..., n 2 /2. 4. Set C = n 2 /2 i=0 (Π(n 1 ) Π(n 2, 2i + ɛ)). Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.23/30
31 One Error on the Z-Channel INPUT: G = (V, E); OUTPUT: I 1, I 2,..., I m. 0. i=0; 1. while G for j = 1 to k end Find a maximal independent set IS j ; if IS j < IS j 1 break end Construct graph G; Find a maximal independent set MIS = {IS i1,..., IS ip } of G; I i+q = IS iq, q = 1,..., p; p G = G G(I i+q ); i = i + p; q=1 Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.24/30
32 One Error on the Z-Channel Π(n, 0) consists of one (zero) codeword, Π(n, 1) consists of n codes of size 1, Π(n, 2) consists of n 1 codes of size n/2 for even n, Index vectors of Π(n, w) and Π(n, n w) are equal; Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.25/30
33 One Error on the Z-Channel Partitions of asymmetric codes found. n # Partition index vector Norm m ,34, 34, 33, 30, 29, 26, 25, , 62, 62, 61, 58, 56, 53, 46, 29, 18, , 62, 62, 62, 58, 56, 53, 43, 32, 16, , 62, 62, 61, 58, 56, 52, 46, 31, 17, , 62, 62, 62, 58, 56, 52, 43, 33, 17, , 62, 62, 62, 58, 56, 54, 42, 31, 15, , 110, 110, 109, 105, 100, 99, 88, 75, 59, 37, 16, , 110, 110, 109, 105, 101, 96, 87, 77, 60, 38, 15, , 110, 110, 108, 106, 99, 95, 89, 76, 60, 43, 15, , 110, 110, 108, 105, 100, 96, 88, 74, 65, 38, 17, Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.26/30
34 One Error on the Z-Channel Partitions of constant weight codes obtained k w Partition index-vector Norm m , 30, 30, 30, 26, 25, 22, 15, , 51, 51, 51, 49, 48, 48, 42, 42, 37, 23, , 51, 51, 51, 49, 48, 48, 45, 39, 36, 22, , 51, 51, 51, 49, 48, 48, 45, 41, 32, 22, , 132, 120, 120, 110, 94, 90, 76, 36, , 91, 88, 87, 84, 82, 81, 79, 76, 73, 66, 54, 38, , 90, 88, 85, 84, 83, 81, 79, 76, 72, 67, 59, 34, 11, , 273, 265, 257, 250, 231, 229, 219, 211, , 184, 156, 127, 81, 35, 4 Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.27/30
35 One Error on the Z-Channel Example: n = 18, n 1 = 8, n 2 = 10. Π(8) = {36, 34, 34, 33, 30, 29, 26, 25, 9}; Π(10, 4) = {30, 30, 30, 30, 26, 25, 22, 15, 2}. Π(8) Π(10, 0) = Π(8) Π(10, 10) = 36 1 = 36; Π(8) Π(10, 2) = Π(8) Π(10, 8) = = 1280; Π(8) Π(10, 4) = Π(8) Π(10, 6) = = 6580; The total is 2( ) = codewords. Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.28/30
36 One Error on the Z-Channel Improved lower bounds. Previous results by: (a)-etzion (1991); (b)- Etzion and Östergard (1998) Lower bound n new previous (a) (b) (b) (b) (b) (b) Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.29/30
37 Conclusion Improved lower bounds and exact solutions for the size of largest error-correcting codes were obtained. Structural properties (automorphisms,...) of the considered graphs can be utilized more efficiently to reduce problem size. We used computational approach. Can the problem be solved analytically? Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.30/30
Network Based Models For Analysis of SNPs Yalta Opt
 Outline Network Based Models For Analysis of Yalta Optimization Conference 2010 Network Science Zeynep Ertem*, Sergiy Butenko*, Clare Gill** *Department of Industrial and Systems Engineering, **Department
Outline Network Based Models For Analysis of Yalta Optimization Conference 2010 Network Science Zeynep Ertem*, Sergiy Butenko*, Clare Gill** *Department of Industrial and Systems Engineering, **Department
On the Complexity of Broadcast Scheduling. Problem
 On the Complexity of Broadcast Scheduling Problem Sergiy Butenko, Clayton Commander and Panos Pardalos Abstract In this paper, a broadcast scheduling problem (BSP) in a time division multiple access (TDMA)
On the Complexity of Broadcast Scheduling Problem Sergiy Butenko, Clayton Commander and Panos Pardalos Abstract In this paper, a broadcast scheduling problem (BSP) in a time division multiple access (TDMA)
The Maximum Clique Problem
 November, 2012 Motivation How to put as much left-over stuff as possible in a tasty meal before everything will go off? Motivation Find the largest collection of food where everything goes together! Here,
November, 2012 Motivation How to put as much left-over stuff as possible in a tasty meal before everything will go off? Motivation Find the largest collection of food where everything goes together! Here,
ON THE COMPLEXITY OF THE BROADCAST SCHEDULING PROBLEM
 ON THE COMPLEXITY OF THE BROADCAST SCHEDULING PROBLEM SERGIY I. BUTENKO, CLAYTON W. COMMANDER, AND PANOS M. PARDALOS Abstract. In this paper, a Broadcast Scheduling Problem (bsp) in a time division multiple
ON THE COMPLEXITY OF THE BROADCAST SCHEDULING PROBLEM SERGIY I. BUTENKO, CLAYTON W. COMMANDER, AND PANOS M. PARDALOS Abstract. In this paper, a Broadcast Scheduling Problem (bsp) in a time division multiple
Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes
 Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes J.-F. Couturier 1 P. Heggernes 2 D. Kratsch 1 P. van t Hof 2 1 LITA Université de Lorraine F-57045 Metz France 2 University
Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes J.-F. Couturier 1 P. Heggernes 2 D. Kratsch 1 P. van t Hof 2 1 LITA Université de Lorraine F-57045 Metz France 2 University
Introduction to Graph Theory
 Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
Small Survey on Perfect Graphs
 Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
CS388C: Combinatorics and Graph Theory
 CS388C: Combinatorics and Graph Theory David Zuckerman Review Sheet 2003 TA: Ned Dimitrov updated: September 19, 2007 These are some of the concepts we assume in the class. If you have never learned them
CS388C: Combinatorics and Graph Theory David Zuckerman Review Sheet 2003 TA: Ned Dimitrov updated: September 19, 2007 These are some of the concepts we assume in the class. If you have never learned them
Colouring graphs with no odd holes
 Colouring graphs with no odd holes Paul Seymour (Princeton) joint with Alex Scott (Oxford) 1 / 17 Chromatic number χ(g): minimum number of colours needed to colour G. 2 / 17 Chromatic number χ(g): minimum
Colouring graphs with no odd holes Paul Seymour (Princeton) joint with Alex Scott (Oxford) 1 / 17 Chromatic number χ(g): minimum number of colours needed to colour G. 2 / 17 Chromatic number χ(g): minimum
On the Approximability of Modularity Clustering
 On the Approximability of Modularity Clustering Newman s Community Finding Approach for Social Nets Bhaskar DasGupta Department of Computer Science University of Illinois at Chicago Chicago, IL 60607,
On the Approximability of Modularity Clustering Newman s Community Finding Approach for Social Nets Bhaskar DasGupta Department of Computer Science University of Illinois at Chicago Chicago, IL 60607,
Math 776 Graph Theory Lecture Note 1 Basic concepts
 Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Stanford University CS359G: Graph Partitioning and Expanders Handout 18 Luca Trevisan March 3, 2011
 Stanford University CS359G: Graph Partitioning and Expanders Handout 8 Luca Trevisan March 3, 20 Lecture 8 In which we prove properties of expander graphs. Quasirandomness of Expander Graphs Recall that
Stanford University CS359G: Graph Partitioning and Expanders Handout 8 Luca Trevisan March 3, 20 Lecture 8 In which we prove properties of expander graphs. Quasirandomness of Expander Graphs Recall that
Computability Theory
 CS:4330 Theory of Computation Spring 2018 Computability Theory Other NP-Complete Problems Haniel Barbosa Readings for this lecture Chapter 7 of [Sipser 1996], 3rd edition. Sections 7.4 and 7.5. The 3SAT
CS:4330 Theory of Computation Spring 2018 Computability Theory Other NP-Complete Problems Haniel Barbosa Readings for this lecture Chapter 7 of [Sipser 1996], 3rd edition. Sections 7.4 and 7.5. The 3SAT
Matchings and Covers in bipartite graphs
 Matchings and Covers in bipartite graphs A bipartite graph, also called a bigraph, is a set of graph vertices decomposed into two disjoint sets such that no two graph vertices within the same set are adjacent.
Matchings and Covers in bipartite graphs A bipartite graph, also called a bigraph, is a set of graph vertices decomposed into two disjoint sets such that no two graph vertices within the same set are adjacent.
Graph Theory S 1 I 2 I 1 S 2 I 1 I 2
 Graph Theory S I I S S I I S Graphs Definition A graph G is a pair consisting of a vertex set V (G), and an edge set E(G) ( ) V (G). x and y are the endpoints of edge e = {x, y}. They are called adjacent
Graph Theory S I I S S I I S Graphs Definition A graph G is a pair consisting of a vertex set V (G), and an edge set E(G) ( ) V (G). x and y are the endpoints of edge e = {x, y}. They are called adjacent
Let G = (V, E) be a graph. If u, v V, then u is adjacent to v if {u, v} E. We also use the notation u v to denote that u is adjacent to v.
 Graph Adjacent Endpoint of an edge Incident Neighbors of a vertex Degree of a vertex Theorem Graph relation Order of a graph Size of a graph Maximum and minimum degree Let G = (V, E) be a graph. If u,
Graph Adjacent Endpoint of an edge Incident Neighbors of a vertex Degree of a vertex Theorem Graph relation Order of a graph Size of a graph Maximum and minimum degree Let G = (V, E) be a graph. If u,
Graph Theory: Introduction
 Graph Theory: Introduction Pallab Dasgupta, Professor, Dept. of Computer Sc. and Engineering, IIT Kharagpur pallab@cse.iitkgp.ernet.in Resources Copies of slides available at: http://www.facweb.iitkgp.ernet.in/~pallab
Graph Theory: Introduction Pallab Dasgupta, Professor, Dept. of Computer Sc. and Engineering, IIT Kharagpur pallab@cse.iitkgp.ernet.in Resources Copies of slides available at: http://www.facweb.iitkgp.ernet.in/~pallab
Extremal Graph Theory: Turán s Theorem
 Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
Lecture 6: Graph Properties
 Lecture 6: Graph Properties Rajat Mittal IIT Kanpur In this section, we will look at some of the combinatorial properties of graphs. Initially we will discuss independent sets. The bulk of the content
Lecture 6: Graph Properties Rajat Mittal IIT Kanpur In this section, we will look at some of the combinatorial properties of graphs. Initially we will discuss independent sets. The bulk of the content
Bipartite Roots of Graphs
 Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Decomposition of log-linear models
 Graphical Models, Lecture 5, Michaelmas Term 2009 October 27, 2009 Generating class Dependence graph of log-linear model Conformal graphical models Factor graphs A density f factorizes w.r.t. A if there
Graphical Models, Lecture 5, Michaelmas Term 2009 October 27, 2009 Generating class Dependence graph of log-linear model Conformal graphical models Factor graphs A density f factorizes w.r.t. A if there
Vertex coloring, chromatic number
 Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
How many colors are needed to color a map?
 How many colors are needed to color a map? Is 4 always enough? Two relevant concepts How many colors do we need to color a map so neighboring countries get different colors? Simplifying assumption (not
How many colors are needed to color a map? Is 4 always enough? Two relevant concepts How many colors do we need to color a map so neighboring countries get different colors? Simplifying assumption (not
Introduction to Combinatorial Algorithms
 Fall 2009 Intro Introduction to the course What are : Combinatorial Structures? Combinatorial Algorithms? Combinatorial Problems? Combinatorial Structures Combinatorial Structures Combinatorial structures
Fall 2009 Intro Introduction to the course What are : Combinatorial Structures? Combinatorial Algorithms? Combinatorial Problems? Combinatorial Structures Combinatorial Structures Combinatorial structures
Graphs: Introduction. Ali Shokoufandeh, Department of Computer Science, Drexel University
 Graphs: Introduction Ali Shokoufandeh, Department of Computer Science, Drexel University Overview of this talk Introduction: Notations and Definitions Graphs and Modeling Algorithmic Graph Theory and Combinatorial
Graphs: Introduction Ali Shokoufandeh, Department of Computer Science, Drexel University Overview of this talk Introduction: Notations and Definitions Graphs and Modeling Algorithmic Graph Theory and Combinatorial
Network Clustering. Balabhaskar Balasundaram, Sergiy Butenko
 Network Clustering Balabhaskar Balasundaram, Sergiy Butenko Department of Industrial & Systems Engineering Texas A&M University College Station, Texas 77843, USA. Introduction Clustering can be loosely
Network Clustering Balabhaskar Balasundaram, Sergiy Butenko Department of Industrial & Systems Engineering Texas A&M University College Station, Texas 77843, USA. Introduction Clustering can be loosely
MapReduce Algorithms. Barna Saha. March 28, 2016
 MapReduce Algorithms Barna Saha March 28, 2016 Complexity Model for MapReduce Minimum Spanning Tree in MapReduce Computing Dense Subgraph in MapReduce Complexity Model for MapReduce:MRC i Input: finite
MapReduce Algorithms Barna Saha March 28, 2016 Complexity Model for MapReduce Minimum Spanning Tree in MapReduce Computing Dense Subgraph in MapReduce Complexity Model for MapReduce:MRC i Input: finite
Chordal graphs MPRI
 Chordal graphs MPRI 2017 2018 Michel Habib habib@irif.fr http://www.irif.fr/~habib Sophie Germain, septembre 2017 Schedule Chordal graphs Representation of chordal graphs LBFS and chordal graphs More structural
Chordal graphs MPRI 2017 2018 Michel Habib habib@irif.fr http://www.irif.fr/~habib Sophie Germain, septembre 2017 Schedule Chordal graphs Representation of chordal graphs LBFS and chordal graphs More structural
Junction Trees and Chordal Graphs
 Graphical Models, Lecture 6, Michaelmas Term 2011 October 24, 2011 Decomposability Factorization of Markov distributions Explicit formula for MLE Consider an undirected graph G = (V, E). A partitioning
Graphical Models, Lecture 6, Michaelmas Term 2011 October 24, 2011 Decomposability Factorization of Markov distributions Explicit formula for MLE Consider an undirected graph G = (V, E). A partitioning
Vertex coloring, chromatic number
 Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
The Structure of Bull-Free Perfect Graphs
 The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
Decision Problems. Observation: Many polynomial algorithms. Questions: Can we solve all problems in polynomial time? Answer: No, absolutely not.
 Decision Problems Observation: Many polynomial algorithms. Questions: Can we solve all problems in polynomial time? Answer: No, absolutely not. Definition: The class of problems that can be solved by polynomial-time
Decision Problems Observation: Many polynomial algorithms. Questions: Can we solve all problems in polynomial time? Answer: No, absolutely not. Definition: The class of problems that can be solved by polynomial-time
Maximum Differential Graph Coloring
 Maximum Differential Graph Coloring Sankar Veeramoni University of Arizona Joint work with Yifan Hu at AT&T Research and Stephen Kobourov at University of Arizona Motivation Map Coloring Problem Related
Maximum Differential Graph Coloring Sankar Veeramoni University of Arizona Joint work with Yifan Hu at AT&T Research and Stephen Kobourov at University of Arizona Motivation Map Coloring Problem Related
INDEPENDENT SET PROBLEMS AND ODD-HOLE-PRESERVING GRAPH REDUCTIONS. A Dissertation JEFFREY S. WARREN
 INDEPENDENT SET PROBLEMS AND ODD-HOLE-PRESERVING GRAPH REDUCTIONS A Dissertation by JEFFREY S. WARREN Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment of the requirements
INDEPENDENT SET PROBLEMS AND ODD-HOLE-PRESERVING GRAPH REDUCTIONS A Dissertation by JEFFREY S. WARREN Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment of the requirements
W4231: Analysis of Algorithms
 W4231: Analysis of Algorithms 11/23/99 NP-completeness of 3SAT, Minimum Vertex Cover, Maximum Independent Set, Boolean Formulae A Boolean formula is an expression that we can build starting from Boolean
W4231: Analysis of Algorithms 11/23/99 NP-completeness of 3SAT, Minimum Vertex Cover, Maximum Independent Set, Boolean Formulae A Boolean formula is an expression that we can build starting from Boolean
Computational problems. Lecture 2: Combinatorial search and optimisation problems. Computational problems. Examples. Example
 Lecture 2: Combinatorial search and optimisation problems Different types of computational problems Examples of computational problems Relationships between problems Computational properties of different
Lecture 2: Combinatorial search and optimisation problems Different types of computational problems Examples of computational problems Relationships between problems Computational properties of different
CS270 Combinatorial Algorithms & Data Structures Spring Lecture 19:
 CS270 Combinatorial Algorithms & Data Structures Spring 2003 Lecture 19: 4.1.03 Lecturer: Satish Rao Scribes: Kevin Lacker and Bill Kramer Disclaimer: These notes have not been subjected to the usual scrutiny
CS270 Combinatorial Algorithms & Data Structures Spring 2003 Lecture 19: 4.1.03 Lecturer: Satish Rao Scribes: Kevin Lacker and Bill Kramer Disclaimer: These notes have not been subjected to the usual scrutiny
CSC 373: Algorithm Design and Analysis Lecture 4
 CSC 373: Algorithm Design and Analysis Lecture 4 Allan Borodin January 14, 2013 1 / 16 Lecture 4: Outline (for this lecture and next lecture) Some concluding comments on optimality of EST Greedy Interval
CSC 373: Algorithm Design and Analysis Lecture 4 Allan Borodin January 14, 2013 1 / 16 Lecture 4: Outline (for this lecture and next lecture) Some concluding comments on optimality of EST Greedy Interval
Triple Connected Domination Number of a Graph
 International J.Math. Combin. Vol.3(2012), 93-104 Triple Connected Domination Number of a Graph G.Mahadevan, Selvam Avadayappan, J.Paulraj Joseph and T.Subramanian Department of Mathematics Anna University:
International J.Math. Combin. Vol.3(2012), 93-104 Triple Connected Domination Number of a Graph G.Mahadevan, Selvam Avadayappan, J.Paulraj Joseph and T.Subramanian Department of Mathematics Anna University:
Comparing the Best Maximum Clique Finding Algorithms, Which are Using Heuristic Vertex Colouring
 Comparing the Best Maximum Clique Finding Algorithms, Which are Using Heuristic Vertex Colouring DENISS KUMLANDER Department of Informatics Tallinn University of Technology Raja St.15, 12617 Tallinn ESTONIA
Comparing the Best Maximum Clique Finding Algorithms, Which are Using Heuristic Vertex Colouring DENISS KUMLANDER Department of Informatics Tallinn University of Technology Raja St.15, 12617 Tallinn ESTONIA
Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees
 Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees Wei Wang joint with Zishen Yang, Xianliang Liu School of Mathematics and Statistics, Xi an Jiaotong University Dec 20, 2016
Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees Wei Wang joint with Zishen Yang, Xianliang Liu School of Mathematics and Statistics, Xi an Jiaotong University Dec 20, 2016
Graph Theory. Probabilistic Graphical Models. L. Enrique Sucar, INAOE. Definitions. Types of Graphs. Trajectories and Circuits.
 Theory Probabilistic ical Models L. Enrique Sucar, INAOE and (INAOE) 1 / 32 Outline and 1 2 3 4 5 6 7 8 and 9 (INAOE) 2 / 32 A graph provides a compact way to represent binary relations between a set of
Theory Probabilistic ical Models L. Enrique Sucar, INAOE and (INAOE) 1 / 32 Outline and 1 2 3 4 5 6 7 8 and 9 (INAOE) 2 / 32 A graph provides a compact way to represent binary relations between a set of
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Using Constraint Programming to Solve the Maximum Clique Problem
 Using Constraint Programming to Solve the Maximum Clique Problem Jean-Charles Régin ILOG Sophia Antipolis Les Taissounières HB, 1681 route des Dolines, 06560 Valbonne, France regin@ilog.fr Abstract. This
Using Constraint Programming to Solve the Maximum Clique Problem Jean-Charles Régin ILOG Sophia Antipolis Les Taissounières HB, 1681 route des Dolines, 06560 Valbonne, France regin@ilog.fr Abstract. This
NP-Completeness. Algorithms
 NP-Completeness Algorithms The NP-Completeness Theory Objective: Identify a class of problems that are hard to solve. Exponential time is hard. Polynomial time is easy. Why: Do not try to find efficient
NP-Completeness Algorithms The NP-Completeness Theory Objective: Identify a class of problems that are hard to solve. Exponential time is hard. Polynomial time is easy. Why: Do not try to find efficient
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
CS 441 Discrete Mathematics for CS Lecture 26. Graphs. CS 441 Discrete mathematics for CS. Final exam
 CS 441 Discrete Mathematics for CS Lecture 26 Graphs Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Final exam Saturday, April 26, 2014 at 10:00-11:50am The same classroom as lectures The exam
CS 441 Discrete Mathematics for CS Lecture 26 Graphs Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Final exam Saturday, April 26, 2014 at 10:00-11:50am The same classroom as lectures The exam
Vertical decomposition of a lattice using clique separators
 Vertical decomposition of a lattice using clique separators Anne Berry, Romain Pogorelcnik, Alain Sigayret LIMOS UMR CNRS 6158 Ensemble Scientifique des Cézeaux Université Blaise Pascal, F-63 173 Aubière,
Vertical decomposition of a lattice using clique separators Anne Berry, Romain Pogorelcnik, Alain Sigayret LIMOS UMR CNRS 6158 Ensemble Scientifique des Cézeaux Université Blaise Pascal, F-63 173 Aubière,
How many colors are needed to color a map?
 How many colors are needed to color a map? Is 4 always enough? Two relevant concepts How many colors do we need to color a map so neighboring countries get different colors? Simplifying assumption (not
How many colors are needed to color a map? Is 4 always enough? Two relevant concepts How many colors do we need to color a map so neighboring countries get different colors? Simplifying assumption (not
Abstract. A graph G is perfect if for every induced subgraph H of G, the chromatic number of H is equal to the size of the largest clique of H.
 Abstract We discuss a class of graphs called perfect graphs. After defining them and getting intuition with a few simple examples (and one less simple example), we present a proof of the Weak Perfect Graph
Abstract We discuss a class of graphs called perfect graphs. After defining them and getting intuition with a few simple examples (and one less simple example), we present a proof of the Weak Perfect Graph
GRAPH THEORY LECTURE 3 STRUCTURE AND REPRESENTATION PART B
 GRAPH THEORY LECTURE 3 STRUCTURE AND REPRESENTATION PART B Abstract. We continue 2.3 on subgraphs. 2.4 introduces some basic graph operations. 2.5 describes some tests for graph isomorphism. Outline 2.3
GRAPH THEORY LECTURE 3 STRUCTURE AND REPRESENTATION PART B Abstract. We continue 2.3 on subgraphs. 2.4 introduces some basic graph operations. 2.5 describes some tests for graph isomorphism. Outline 2.3
Minimal dominating sets in graph classes: combinatorial bounds and enumeration
 Minimal dominating sets in graph classes: combinatorial bounds and enumeration Jean-François Couturier 1, Pinar Heggernes 2, Pim van t Hof 2, and Dieter Kratsch 1 1 LITA, Université Paul Verlaine - Metz,
Minimal dominating sets in graph classes: combinatorial bounds and enumeration Jean-François Couturier 1, Pinar Heggernes 2, Pim van t Hof 2, and Dieter Kratsch 1 1 LITA, Université Paul Verlaine - Metz,
Multiagent Graph Coloring: Pareto Efficiency, Fairness and Individual Rationality By Yaad Blum, Jeffrey S. Rosenchein
 Multiagent Graph Coloring: Pareto Efficiency, Fairness and Individual Rationality By Yaad Blum, Jeffrey S. Rosenchein Presented by: Simina Brânzei Outline Introduction Background Coloring from an Economics
Multiagent Graph Coloring: Pareto Efficiency, Fairness and Individual Rationality By Yaad Blum, Jeffrey S. Rosenchein Presented by: Simina Brânzei Outline Introduction Background Coloring from an Economics
On connected domination in unit ball graphs
 Noname manuscript No. (will be inserted by the editor) On connected domination in unit ball graphs Sergiy Butenko Sera Kahruman-Anderoglu Oleksii Ursulenko Received: date / Accepted: date Abstract Given
Noname manuscript No. (will be inserted by the editor) On connected domination in unit ball graphs Sergiy Butenko Sera Kahruman-Anderoglu Oleksii Ursulenko Received: date / Accepted: date Abstract Given
Algorithms for the Bin Packing Problem with Conflicts
 Algorithms for the Bin Packing Problem with Conflicts Albert E. Fernandes Muritiba *, Manuel Iori, Enrico Malaguti*, Paolo Toth* *Dipartimento di Elettronica, Informatica e Sistemistica, Università degli
Algorithms for the Bin Packing Problem with Conflicts Albert E. Fernandes Muritiba *, Manuel Iori, Enrico Malaguti*, Paolo Toth* *Dipartimento di Elettronica, Informatica e Sistemistica, Università degli
On Clique Relaxation Models in Network Analysis
 On Clique Relaxation Models in Network Analysis Jeffrey Pattillo Department of Mathematics, Texas A&M University, College Station, TX 77843-3131, jeff.pattillo@gmail.com Nataly Youssef Operations Research
On Clique Relaxation Models in Network Analysis Jeffrey Pattillo Department of Mathematics, Texas A&M University, College Station, TX 77843-3131, jeff.pattillo@gmail.com Nataly Youssef Operations Research
Junction tree propagation - BNDG 4-4.6
 Junction tree propagation - BNDG 4-4. Finn V. Jensen and Thomas D. Nielsen Junction tree propagation p. 1/2 Exact Inference Message Passing in Join Trees More sophisticated inference technique; used in
Junction tree propagation - BNDG 4-4. Finn V. Jensen and Thomas D. Nielsen Junction tree propagation p. 1/2 Exact Inference Message Passing in Join Trees More sophisticated inference technique; used in
Ultraconnected and Critical Graphs
 Brigham Young University BYU ScholarsArchive All Theses and Dissertations 2004-05-05 Ultraconnected and Critical Graphs Jason Nicholas Grout Brigham Young University - Provo Follow this and additional
Brigham Young University BYU ScholarsArchive All Theses and Dissertations 2004-05-05 Ultraconnected and Critical Graphs Jason Nicholas Grout Brigham Young University - Provo Follow this and additional
arxiv: v1 [cs.it] 9 Feb 2009
![arxiv: v1 [cs.it] 9 Feb 2009 arxiv: v1 [cs.it] 9 Feb 2009](/thumbs/72/67165571.jpg) On the minimum distance graph of an extended Preparata code C. Fernández-Córdoba K. T. Phelps arxiv:0902.1351v1 [cs.it] 9 Feb 2009 Abstract The minimum distance graph of an extended Preparata code P(m)
On the minimum distance graph of an extended Preparata code C. Fernández-Córdoba K. T. Phelps arxiv:0902.1351v1 [cs.it] 9 Feb 2009 Abstract The minimum distance graph of an extended Preparata code P(m)
Research Question Presentation on the Edge Clique Covers of a Complete Multipartite Graph. Nechama Florans. Mentor: Dr. Boram Park
 Research Question Presentation on the Edge Clique Covers of a Complete Multipartite Graph Nechama Florans Mentor: Dr. Boram Park G: V 5 Vertex Clique Covers and Edge Clique Covers: Suppose we have a graph
Research Question Presentation on the Edge Clique Covers of a Complete Multipartite Graph Nechama Florans Mentor: Dr. Boram Park G: V 5 Vertex Clique Covers and Edge Clique Covers: Suppose we have a graph
Fast-Mixed Searching and Related Problems on Graphs
 Fast-Mixed Searching and Related Problems on Graphs Boting Yang Department of Computer Science University of Regina May 27, 2012 GRASCan 2012, Ryerson University 1 Outline Fast searching and mixed searching
Fast-Mixed Searching and Related Problems on Graphs Boting Yang Department of Computer Science University of Regina May 27, 2012 GRASCan 2012, Ryerson University 1 Outline Fast searching and mixed searching
Introduction to Algorithms. Lecture 24. Prof. Patrick Jaillet
 6.006- Introduction to Algorithms Lecture 24 Prof. Patrick Jaillet Outline Decision vs optimization problems P, NP, co-np Reductions between problems NP-complete problems Beyond NP-completeness Readings
6.006- Introduction to Algorithms Lecture 24 Prof. Patrick Jaillet Outline Decision vs optimization problems P, NP, co-np Reductions between problems NP-complete problems Beyond NP-completeness Readings
P = NP; P NP. Intuition of the reduction idea:
 1 Polynomial Time Reducibility The question of whether P = NP is one of the greatest unsolved problems in the theoretical computer science. Two possibilities of relationship between P and N P P = NP; P
1 Polynomial Time Reducibility The question of whether P = NP is one of the greatest unsolved problems in the theoretical computer science. Two possibilities of relationship between P and N P P = NP; P
Ton Kloks and Yue-Li Wang. Advances in Graph Algorithms. October 10, y X z
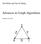 Ton Kloks and Yue-Li Wang Advances in Graph Algorithms October 10, 2013 x Z Y < y X z
Ton Kloks and Yue-Li Wang Advances in Graph Algorithms October 10, 2013 x Z Y < y X z
COMP 355 Advanced Algorithms Approximation Algorithms: VC and TSP Chapter 11 (KT) Section (CLRS)
 COMP 355 Advanced Algorithms Approximation Algorithms: VC and TSP Chapter 11 (KT) Section 35.1-35.2(CLRS) 1 Coping with NP-Completeness Brute-force search: This is usually only a viable option for small
COMP 355 Advanced Algorithms Approximation Algorithms: VC and TSP Chapter 11 (KT) Section 35.1-35.2(CLRS) 1 Coping with NP-Completeness Brute-force search: This is usually only a viable option for small
1 The Traveling Salesperson Problem (TSP)
 CS 598CSC: Approximation Algorithms Lecture date: January 23, 2009 Instructor: Chandra Chekuri Scribe: Sungjin Im In the previous lecture, we had a quick overview of several basic aspects of approximation
CS 598CSC: Approximation Algorithms Lecture date: January 23, 2009 Instructor: Chandra Chekuri Scribe: Sungjin Im In the previous lecture, we had a quick overview of several basic aspects of approximation
Paths. Path is a sequence of edges that begins at a vertex of a graph and travels from vertex to vertex along edges of the graph.
 Paths Path is a sequence of edges that begins at a vertex of a graph and travels from vertex to vertex along edges of the graph. Formal Definition of a Path (Undirected) Let n be a nonnegative integer
Paths Path is a sequence of edges that begins at a vertex of a graph and travels from vertex to vertex along edges of the graph. Formal Definition of a Path (Undirected) Let n be a nonnegative integer
A Survey of the Algorithmic Properties of Simplicial, Upper Bound and Middle Graphs
 Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 10, no. 2, pp. 159 190 (2006) A Survey of the Algorithmic Properties of Simplicial, Upper Bound and Middle Graphs Grant A. Cheston Tjoen
Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 10, no. 2, pp. 159 190 (2006) A Survey of the Algorithmic Properties of Simplicial, Upper Bound and Middle Graphs Grant A. Cheston Tjoen
HW Graph Theory SOLUTIONS (hbovik) - Q
 1, Diestel 9.3: An arithmetic progression is an increasing sequence of numbers of the form a, a+d, a+ d, a + 3d.... Van der Waerden s theorem says that no matter how we partition the natural numbers into
1, Diestel 9.3: An arithmetic progression is an increasing sequence of numbers of the form a, a+d, a+ d, a + 3d.... Van der Waerden s theorem says that no matter how we partition the natural numbers into
A Computational Study of Conflict Graphs and Aggressive Cut Separation in Integer Programming
 A Computational Study of Conflict Graphs and Aggressive Cut Separation in Integer Programming Samuel Souza Brito and Haroldo Gambini Santos 1 Dep. de Computação, Universidade Federal de Ouro Preto - UFOP
A Computational Study of Conflict Graphs and Aggressive Cut Separation in Integer Programming Samuel Souza Brito and Haroldo Gambini Santos 1 Dep. de Computação, Universidade Federal de Ouro Preto - UFOP
Solutions to Exercises 9
 Discrete Mathematics Lent 2009 MA210 Solutions to Exercises 9 (1) There are 5 cities. The cost of building a road directly between i and j is the entry a i,j in the matrix below. An indefinite entry indicates
Discrete Mathematics Lent 2009 MA210 Solutions to Exercises 9 (1) There are 5 cities. The cost of building a road directly between i and j is the entry a i,j in the matrix below. An indefinite entry indicates
Lecture 5: Exact inference
 Lecture 5: Exact inference Queries Inference in chains Variable elimination Without evidence With evidence Complexity of variable elimination which has the highest probability: instantiation of all other
Lecture 5: Exact inference Queries Inference in chains Variable elimination Without evidence With evidence Complexity of variable elimination which has the highest probability: instantiation of all other
Graph and Digraph Glossary
 1 of 15 31.1.2004 14:45 Graph and Digraph Glossary A B C D E F G H I-J K L M N O P-Q R S T U V W-Z Acyclic Graph A graph is acyclic if it contains no cycles. Adjacency Matrix A 0-1 square matrix whose
1 of 15 31.1.2004 14:45 Graph and Digraph Glossary A B C D E F G H I-J K L M N O P-Q R S T U V W-Z Acyclic Graph A graph is acyclic if it contains no cycles. Adjacency Matrix A 0-1 square matrix whose
Approximation Algorithms for Geometric Intersection Graphs
 Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
CS242: Probabilistic Graphical Models Lecture 2B: Loopy Belief Propagation & Junction Trees
 CS242: Probabilistic Graphical Models Lecture 2B: Loopy Belief Propagation & Junction Trees Professor Erik Sudderth Brown University Computer Science September 22, 2016 Some figures and materials courtesy
CS242: Probabilistic Graphical Models Lecture 2B: Loopy Belief Propagation & Junction Trees Professor Erik Sudderth Brown University Computer Science September 22, 2016 Some figures and materials courtesy
The Maximum Common Subgraph Problem: Faster Solutions via Vertex Cover
 The Maximum Common Subgraph Problem: Faster Solutions via Vertex Cover Faisal N. Abu-Khzam Division of Computer Science and Mathematics Lebanese American University Beirut, Lebanon faisal.abukhzam@lau.edu.lb
The Maximum Common Subgraph Problem: Faster Solutions via Vertex Cover Faisal N. Abu-Khzam Division of Computer Science and Mathematics Lebanese American University Beirut, Lebanon faisal.abukhzam@lau.edu.lb
THE CONNECTED COMPLEMENT DOMINATION IN GRAPHS V.MOHANASELVI 1. Assistant Professor of Mathematics, Nehru Memorial College, Puthanampatti,
 THE CONNECTED COMPLEMENT DOMINATION IN GRAPHS V.MOHANASELVI 1 Assistant Professor of Mathematics, Nehru Memorial College, Puthanampatti, Tiruchirappalli-621 00 S.DHIVYAKANNU 2 Assistant Professor of Mathematics,
THE CONNECTED COMPLEMENT DOMINATION IN GRAPHS V.MOHANASELVI 1 Assistant Professor of Mathematics, Nehru Memorial College, Puthanampatti, Tiruchirappalli-621 00 S.DHIVYAKANNU 2 Assistant Professor of Mathematics,
CSC2420 Fall 2012: Algorithm Design, Analysis and Theory
 CSC2420 Fall 2012: Algorithm Design, Analysis and Theory Allan Borodin September 27, 2012 1 / 23 Lecture 3 1 We will first do the analysis of the Greedy α revocable priority algorithm for the WISP problem
CSC2420 Fall 2012: Algorithm Design, Analysis and Theory Allan Borodin September 27, 2012 1 / 23 Lecture 3 1 We will first do the analysis of the Greedy α revocable priority algorithm for the WISP problem
Graphs and Discrete Structures
 Graphs and Discrete Structures Nicolas Bousquet Louis Esperet Fall 2018 Abstract Brief summary of the first and second course. É 1 Chromatic number, independence number and clique number The chromatic
Graphs and Discrete Structures Nicolas Bousquet Louis Esperet Fall 2018 Abstract Brief summary of the first and second course. É 1 Chromatic number, independence number and clique number The chromatic
Eternal Domination: Criticality and Reachability
 Eternal Domination: Criticality and Reachability William F. Klostermeyer School of Computing University of North Florida Jacksonville, FL 32224-2669 wkloster@unf.edu Gary MacGillivray Department of Mathematics
Eternal Domination: Criticality and Reachability William F. Klostermeyer School of Computing University of North Florida Jacksonville, FL 32224-2669 wkloster@unf.edu Gary MacGillivray Department of Mathematics
arxiv: v1 [cs.ds] 8 Jan 2019
![arxiv: v1 [cs.ds] 8 Jan 2019 arxiv: v1 [cs.ds] 8 Jan 2019](/thumbs/93/113547113.jpg) Subset Feedback Vertex Set in Chordal and Split Graphs Geevarghese Philip 1, Varun Rajan 2, Saket Saurabh 3,4, and Prafullkumar Tale 5 arxiv:1901.02209v1 [cs.ds] 8 Jan 2019 1 Chennai Mathematical Institute,
Subset Feedback Vertex Set in Chordal and Split Graphs Geevarghese Philip 1, Varun Rajan 2, Saket Saurabh 3,4, and Prafullkumar Tale 5 arxiv:1901.02209v1 [cs.ds] 8 Jan 2019 1 Chennai Mathematical Institute,
CS 4407 Algorithms. Lecture 8: Circumventing Intractability, using Approximation and other Techniques
 CS 4407 Algorithms Lecture 8: Circumventing Intractability, using Approximation and other Techniques Prof. Gregory Provan Department of Computer Science University College Cork CS 4010 1 Lecture Outline
CS 4407 Algorithms Lecture 8: Circumventing Intractability, using Approximation and other Techniques Prof. Gregory Provan Department of Computer Science University College Cork CS 4010 1 Lecture Outline
Graph Theory. Connectivity, Coloring, Matching. Arjun Suresh 1. 1 GATE Overflow
 Graph Theory Connectivity, Coloring, Matching Arjun Suresh 1 1 GATE Overflow GO Classroom, August 2018 Thanks to Subarna/Sukanya Das for wonderful figures Arjun, Suresh (GO) Graph Theory GATE 2019 1 /
Graph Theory Connectivity, Coloring, Matching Arjun Suresh 1 1 GATE Overflow GO Classroom, August 2018 Thanks to Subarna/Sukanya Das for wonderful figures Arjun, Suresh (GO) Graph Theory GATE 2019 1 /
COMP260 Spring 2014 Notes: February 4th
 COMP260 Spring 2014 Notes: February 4th Andrew Winslow In these notes, all graphs are undirected. We consider matching, covering, and packing in bipartite graphs, general graphs, and hypergraphs. We also
COMP260 Spring 2014 Notes: February 4th Andrew Winslow In these notes, all graphs are undirected. We consider matching, covering, and packing in bipartite graphs, general graphs, and hypergraphs. We also
Grundy chromatic number of the complement of bipartite graphs
 Grundy chromatic number of the complement of bipartite graphs Manouchehr Zaker Institute for Advanced Studies in Basic Sciences P. O. BOX 45195-159 Zanjan, Iran E-mail: mzaker@iasbs.ac.ir Abstract A Grundy
Grundy chromatic number of the complement of bipartite graphs Manouchehr Zaker Institute for Advanced Studies in Basic Sciences P. O. BOX 45195-159 Zanjan, Iran E-mail: mzaker@iasbs.ac.ir Abstract A Grundy
CMSC Honors Discrete Mathematics
 CMSC 27130 Honors Discrete Mathematics Lectures by Alexander Razborov Notes by Justin Lubin The University of Chicago, Autumn 2017 1 Contents I Number Theory 4 1 The Euclidean Algorithm 4 2 Mathematical
CMSC 27130 Honors Discrete Mathematics Lectures by Alexander Razborov Notes by Justin Lubin The University of Chicago, Autumn 2017 1 Contents I Number Theory 4 1 The Euclidean Algorithm 4 2 Mathematical
Exact Algorithms for NP-hard problems
 24 mai 2012 1 Why do we need exponential algorithms? 2 3 Why the P-border? 1 Practical reasons (Jack Edmonds, 1965) For practical purposes the difference between algebraic and exponential order is more
24 mai 2012 1 Why do we need exponential algorithms? 2 3 Why the P-border? 1 Practical reasons (Jack Edmonds, 1965) For practical purposes the difference between algebraic and exponential order is more
Lecture 5: Exact inference. Queries. Complexity of inference. Queries (continued) Bayesian networks can answer questions about the underlying
 given that Maximum a posteriori (MAP query: given evidence 2 which has the highest probability: instantiation of all other variables in the network,, Most probable evidence (MPE: given evidence, find an
given that Maximum a posteriori (MAP query: given evidence 2 which has the highest probability: instantiation of all other variables in the network,, Most probable evidence (MPE: given evidence, find an
These notes present some properties of chordal graphs, a set of undirected graphs that are important for undirected graphical models.
 Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
The complement of PATH is in NL
 340 The complement of PATH is in NL Let c be the number of nodes in graph G that are reachable from s We assume that c is provided as an input to M Given G, s, t, and c the machine M operates as follows:
340 The complement of PATH is in NL Let c be the number of nodes in graph G that are reachable from s We assume that c is provided as an input to M Given G, s, t, and c the machine M operates as follows:
Acyclic Network. Tree Based Clustering. Tree Decomposition Methods
 Summary s Join Tree Importance of s Solving Topological structure defines key features for a wide class of problems CSP: Inference in acyclic network is extremely efficient (polynomial) Idea: remove cycles
Summary s Join Tree Importance of s Solving Topological structure defines key features for a wide class of problems CSP: Inference in acyclic network is extremely efficient (polynomial) Idea: remove cycles
Math 778S Spectral Graph Theory Handout #2: Basic graph theory
 Math 778S Spectral Graph Theory Handout #: Basic graph theory Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved the Königsberg Bridge problem: Is it possible
Math 778S Spectral Graph Theory Handout #: Basic graph theory Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved the Königsberg Bridge problem: Is it possible
STAT 598L Probabilistic Graphical Models. Instructor: Sergey Kirshner. Exact Inference
 STAT 598L Probabilistic Graphical Models Instructor: Sergey Kirshner Exact Inference What To Do With Bayesian/Markov Network? Compact representation of a complex model, but Goal: efficient extraction of
STAT 598L Probabilistic Graphical Models Instructor: Sergey Kirshner Exact Inference What To Do With Bayesian/Markov Network? Compact representation of a complex model, but Goal: efficient extraction of
THE INSULATION SEQUENCE OF A GRAPH
 THE INSULATION SEQUENCE OF A GRAPH ELENA GRIGORESCU Abstract. In a graph G, a k-insulated set S is a subset of the vertices of G such that every vertex in S is adjacent to at most k vertices in S, and
THE INSULATION SEQUENCE OF A GRAPH ELENA GRIGORESCU Abstract. In a graph G, a k-insulated set S is a subset of the vertices of G such that every vertex in S is adjacent to at most k vertices in S, and
Traveling Salesman Problem (TSP) Input: undirected graph G=(V,E), c: E R + Goal: find a tour (Hamiltonian cycle) of minimum cost
 Traveling Salesman Problem (TSP) Input: undirected graph G=(V,E), c: E R + Goal: find a tour (Hamiltonian cycle) of minimum cost Traveling Salesman Problem (TSP) Input: undirected graph G=(V,E), c: E R
Traveling Salesman Problem (TSP) Input: undirected graph G=(V,E), c: E R + Goal: find a tour (Hamiltonian cycle) of minimum cost Traveling Salesman Problem (TSP) Input: undirected graph G=(V,E), c: E R
Conflict Graphs for Combinatorial Optimization Problems
 Conflict Graphs for Combinatorial Optimization Problems Ulrich Pferschy joint work with Andreas Darmann and Joachim Schauer University of Graz, Austria Introduction Combinatorial Optimization Problem CO
Conflict Graphs for Combinatorial Optimization Problems Ulrich Pferschy joint work with Andreas Darmann and Joachim Schauer University of Graz, Austria Introduction Combinatorial Optimization Problem CO
DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI
 DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI Department of Computer Science and Engineering CS6702 - GRAPH THEORY AND APPLICATIONS Anna University 2 & 16 Mark Questions & Answers Year / Semester: IV /
DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI Department of Computer Science and Engineering CS6702 - GRAPH THEORY AND APPLICATIONS Anna University 2 & 16 Mark Questions & Answers Year / Semester: IV /
Lecture 4: Walks, Trails, Paths and Connectivity
 Lecture 4: Walks, Trails, Paths and Connectivity Rosa Orellana Math 38 April 6, 2015 Graph Decompositions Def: A decomposition of a graph is a list of subgraphs such that each edge appears in exactly one
Lecture 4: Walks, Trails, Paths and Connectivity Rosa Orellana Math 38 April 6, 2015 Graph Decompositions Def: A decomposition of a graph is a list of subgraphs such that each edge appears in exactly one
Lecture 19 Thursday, March 29. Examples of isomorphic, and non-isomorphic graphs will be given in class.
 CIS 160 - Spring 2018 (instructor Val Tannen) Lecture 19 Thursday, March 29 GRAPH THEORY Graph isomorphism Definition 19.1 Two graphs G 1 = (V 1, E 1 ) and G 2 = (V 2, E 2 ) are isomorphic, write G 1 G
CIS 160 - Spring 2018 (instructor Val Tannen) Lecture 19 Thursday, March 29 GRAPH THEORY Graph isomorphism Definition 19.1 Two graphs G 1 = (V 1, E 1 ) and G 2 = (V 2, E 2 ) are isomorphic, write G 1 G
Junction Trees and Chordal Graphs
 Graphical Models, Lecture 6, Michaelmas Term 2009 October 30, 2009 Decomposability Factorization of Markov distributions Explicit formula for MLE Consider an undirected graph G = (V, E). A partitioning
Graphical Models, Lecture 6, Michaelmas Term 2009 October 30, 2009 Decomposability Factorization of Markov distributions Explicit formula for MLE Consider an undirected graph G = (V, E). A partitioning
