The Maximum Clique Problem
|
|
|
- Rolf Wright
- 5 years ago
- Views:
Transcription
1 November, 2012
2 Motivation How to put as much left-over stuff as possible in a tasty meal before everything will go off?
3 Motivation Find the largest collection of food where everything goes together! Here, we have the choice:
4 Motivation Find the largest collection of food where everything goes together! Here, we have the choice:
5 Motivation Find the largest collection of food where everything goes together! Here, we have the choice:
6 Motivation Find the largest collection of food where everything goes together! Here, we have the choice:
7 Outline s 4
8 Graph (G): a network of vertices (V(G)) and edges (E(G)). Graph Complement (G): the graph with the same vertex set of G but whose edge set consists of the edges not present in G. Complete Graph: every pair of vertices is connected by an edge. A Clique in an undirected graph G=(V,E) is a subset of the vertex set C V,such that for every two vertices in C, there exists an edge connecting the two.
9
10 Maximum Clique: A Clique of the largest possible size in a given graph. The clique number, ω (G), is the cardinality of the maximum clique. Maximal Clique: A Clique that cannot be extended by including one more adjacent vertex. Independent Set: a subset of the vertices such that no two vertices in the subset are connected by an edge of G. Vertex cover: a subset of the vertices of G which contains at least one of the two endpoints of each edge.
11
12 Maximum Clique Problem Does there exist an integer k such that G contains an clique of cardinality k? What is the clique in G with maximum cardinality? What is the clique number of G?
13 Equivalent Problems Maximum Independent Set Problem in G
14 Equivalent Problems Minimum Vertex Cover Problem in G
15 Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound NP-hard A problem is NP-hard if solving it in polynomial time would make it possible to solve all problems in the class of NP problems in polynomial time. All 3 versions of the Maximum Clique problem are known to be NP-hard for general graphs.
16 Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound NP : the class of decision problem which can be solved by a non-deterministic polynomial algorithm. P: the class of problems which can be solved by a deterministic polynomial algorithm. NP-hard: the class of problems to which every NP problem reduces. NP-complete (NPC): the class of problems which are NP-hard and belong to NP.
17 Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound Method to Solve Maximum Clique Problem Non polynomial-time algorithms. Polynomial-time algorithms providing approximate solutions. Polynomial-time algorithms providing exact solutions to graphs of special classes. Two effective algorithms for dealing with NP-complete Problems: backtracking, branch and bound
18 Bron Kerbosch Algorithm Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound The Algorithm was Designed and Published in 1973 by the Dutch scientists Joep Kerbosch and Coenradd Bron. Bron Kerbosch Algorithm is for Finding the Maximal Cliques in undirected graph. It is known to be one of the most efficient algorithm which uses recursive backtracking to find Cliques is practically proven. The Bron Kerbosch Algorithm uses the vertex in graph and its neighbour with few functions to generate some effective results.
19 Without Pivoting Strategy Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound BronKerbosch(R, P, X ) if {P = X = } Report R as the Maximal Clique for each vertex v in P BronKerbosch(R {v}, P N {v}, X N {v}) P := P\ {v} X := X {v}
20 With Pivoting Strategy Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound BronKerbosch(R, P, X ) if {P = X = } Report R as the Maximal Clique Choose Pivot Vertex u in P X for each vertex v in P BronKerbosch(R {v}, P N {v}, X N {v}) P := P\ {v} X := X {v}
21 Example Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound
22 Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound R = X =, P = (1, 2, 3, 4, 5, 6) Choosing the pivot element u as 4. 4 in P\N(v) = (1, 2, 3, 4, 5, 6) \ (1, 2, 3, 5, 6) = 4 in 4 Finds the values of R new, P new, X new P new = P N (v); R new = R v; X new = X N (v) R new = 4; P new = (1, 2, 3, 5, 6) ; X new = BronKerbosch(4,(1,2,3,5,6), ) BronKerbosch((4,1),(2,3), ) BronKerbosch((4,1,2),, ) Report (4,1,2) as one of the Maximal Clique
23 Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound BronKerbosch(4,(1,2,3,5,6), ) BronKerbosch((4,3),(1), ) BronKerbosch((4,3,1),, ) Report (4,3,1) as one of the other Maximal Clique. BronKerbosch(4,(1,2,3,5,6), ) BronKerbosch((4,2),(1,5), ) BronKerbosch((4,2,5),, ) Report (4,2,5) as an other Maximal Clique. BronKerbosch(4,(1,2,3,5,6), ) BronKerbosch((4,6),, ) Report (4,6) as the Maximal Clique.
24 Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound This backtracking algorithm is a method for finding all the sub sets in an undirected graph G. Given a graph G with V vertices and E edges, G=(V,E) Let us take an integer variable k. This algorithm is used in scientific and engineering applications. This algorithm is a Depth First Search algorithm. The algorithm for finding k-clique in an undirected graph is a NP-complete problem.
25 Example Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound
26 Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound
27 Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound
28 Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound List out all the possibilities in the subgraph and check for each and every edge. Check for a subgraph in which every node is connected to every other node. Check for all possible Cliques in the graphs. Check the size of clique whether it is equal to k or not.
29 Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound Any n-vertex graph has at most 3 n/3 Maximal Cliques The worst-case running time of the BronKerbosch algorithm (with a pivot strategy that minimizes the number of recursive calls made at each step) is O(3 n/3 ) This Backtracking algorithm runs in polynomial time if size of k is fixed. If k is varying then it is in exponencial time Running time of the algorithm is O (nk), where k = O(log n)
30 Bron Kerbosch Algorithm Backtracking Algorithm Time Complexity Brand-and-Bound f (x) = n x i min i=1 x i + x j 1, (i, j) E x {0, 1} n f (x) = x T Ax min x {0, 1} n, wherea = A G I
31 Scheduling Coding Theory: Hamming and Johnson Graphs Map Labeling Computer Vision and Pattern Recognition
32 Problem: finding maximum cliques of a graph efficiently Hard task (in terms of memory and runtime) Bron-Kerbosch algorithm is one efficient solution Several applications
33 References 1. D.-Z. Du and P.M.Pardalos Handbook of Combinatorial Optimization. Kluwer Academic Publishers, http : //en.wikipedia.org/wiki/clique - problem.
34 Thank you for your attention!
NP Completeness. Andreas Klappenecker [partially based on slides by Jennifer Welch]
![NP Completeness. Andreas Klappenecker [partially based on slides by Jennifer Welch] NP Completeness. Andreas Klappenecker [partially based on slides by Jennifer Welch]](/thumbs/76/73396698.jpg) NP Completeness Andreas Klappenecker [partially based on slides by Jennifer Welch] Overview We already know the following examples of NPC problems: SAT 3SAT We are going to show that the following are
NP Completeness Andreas Klappenecker [partially based on slides by Jennifer Welch] Overview We already know the following examples of NPC problems: SAT 3SAT We are going to show that the following are
P = NP; P NP. Intuition of the reduction idea:
 1 Polynomial Time Reducibility The question of whether P = NP is one of the greatest unsolved problems in the theoretical computer science. Two possibilities of relationship between P and N P P = NP; P
1 Polynomial Time Reducibility The question of whether P = NP is one of the greatest unsolved problems in the theoretical computer science. Two possibilities of relationship between P and N P P = NP; P
Introduction to Combinatorial Algorithms
 Fall 2009 Intro Introduction to the course What are : Combinatorial Structures? Combinatorial Algorithms? Combinatorial Problems? Combinatorial Structures Combinatorial Structures Combinatorial structures
Fall 2009 Intro Introduction to the course What are : Combinatorial Structures? Combinatorial Algorithms? Combinatorial Problems? Combinatorial Structures Combinatorial Structures Combinatorial structures
Graphs: Introduction. Ali Shokoufandeh, Department of Computer Science, Drexel University
 Graphs: Introduction Ali Shokoufandeh, Department of Computer Science, Drexel University Overview of this talk Introduction: Notations and Definitions Graphs and Modeling Algorithmic Graph Theory and Combinatorial
Graphs: Introduction Ali Shokoufandeh, Department of Computer Science, Drexel University Overview of this talk Introduction: Notations and Definitions Graphs and Modeling Algorithmic Graph Theory and Combinatorial
Decision Problems. Observation: Many polynomial algorithms. Questions: Can we solve all problems in polynomial time? Answer: No, absolutely not.
 Decision Problems Observation: Many polynomial algorithms. Questions: Can we solve all problems in polynomial time? Answer: No, absolutely not. Definition: The class of problems that can be solved by polynomial-time
Decision Problems Observation: Many polynomial algorithms. Questions: Can we solve all problems in polynomial time? Answer: No, absolutely not. Definition: The class of problems that can be solved by polynomial-time
The complement of PATH is in NL
 340 The complement of PATH is in NL Let c be the number of nodes in graph G that are reachable from s We assume that c is provided as an input to M Given G, s, t, and c the machine M operates as follows:
340 The complement of PATH is in NL Let c be the number of nodes in graph G that are reachable from s We assume that c is provided as an input to M Given G, s, t, and c the machine M operates as follows:
Comparing the Best Maximum Clique Finding Algorithms, Which are Using Heuristic Vertex Colouring
 Comparing the Best Maximum Clique Finding Algorithms, Which are Using Heuristic Vertex Colouring DENISS KUMLANDER Department of Informatics Tallinn University of Technology Raja St.15, 12617 Tallinn ESTONIA
Comparing the Best Maximum Clique Finding Algorithms, Which are Using Heuristic Vertex Colouring DENISS KUMLANDER Department of Informatics Tallinn University of Technology Raja St.15, 12617 Tallinn ESTONIA
Introduction to Algorithms. Lecture 24. Prof. Patrick Jaillet
 6.006- Introduction to Algorithms Lecture 24 Prof. Patrick Jaillet Outline Decision vs optimization problems P, NP, co-np Reductions between problems NP-complete problems Beyond NP-completeness Readings
6.006- Introduction to Algorithms Lecture 24 Prof. Patrick Jaillet Outline Decision vs optimization problems P, NP, co-np Reductions between problems NP-complete problems Beyond NP-completeness Readings
Best known solution time is Ω(V!) Check every permutation of vertices to see if there is a graph edge between adjacent vertices
 Hard Problems Euler-Tour Problem Undirected graph G=(V,E) An Euler Tour is a path where every edge appears exactly once. The Euler-Tour Problem: does graph G have an Euler Path? Answerable in O(E) time.
Hard Problems Euler-Tour Problem Undirected graph G=(V,E) An Euler Tour is a path where every edge appears exactly once. The Euler-Tour Problem: does graph G have an Euler Path? Answerable in O(E) time.
Improving network robustness
 Improving network robustness using distance-based graph measures Sander Jurgens November 10, 2014 dr. K.A. Buchin Eindhoven University of Technology Department of Math and Computer Science dr. D.T.H. Worm
Improving network robustness using distance-based graph measures Sander Jurgens November 10, 2014 dr. K.A. Buchin Eindhoven University of Technology Department of Math and Computer Science dr. D.T.H. Worm
Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs p.1/30
 Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs Sergiy Butenko Department of Industrial Engineering Texas A&M University College Station, TX 77843
Computing Largest Correcting Codes and Their Estimates Using Optimization on Specially Constructed Graphs Sergiy Butenko Department of Industrial Engineering Texas A&M University College Station, TX 77843
NP-Completeness. Algorithms
 NP-Completeness Algorithms The NP-Completeness Theory Objective: Identify a class of problems that are hard to solve. Exponential time is hard. Polynomial time is easy. Why: Do not try to find efficient
NP-Completeness Algorithms The NP-Completeness Theory Objective: Identify a class of problems that are hard to solve. Exponential time is hard. Polynomial time is easy. Why: Do not try to find efficient
REDUCING GRAPH COLORING TO CLIQUE SEARCH
 Asia Pacific Journal of Mathematics, Vol. 3, No. 1 (2016), 64-85 ISSN 2357-2205 REDUCING GRAPH COLORING TO CLIQUE SEARCH SÁNDOR SZABÓ AND BOGDÁN ZAVÁLNIJ Institute of Mathematics and Informatics, University
Asia Pacific Journal of Mathematics, Vol. 3, No. 1 (2016), 64-85 ISSN 2357-2205 REDUCING GRAPH COLORING TO CLIQUE SEARCH SÁNDOR SZABÓ AND BOGDÁN ZAVÁLNIJ Institute of Mathematics and Informatics, University
Vertex Cover is Fixed-Parameter Tractable
 Vertex Cover is Fixed-Parameter Tractable CS 511 Iowa State University November 28, 2010 CS 511 (Iowa State University) Vertex Cover is Fixed-Parameter Tractable November 28, 2010 1 / 18 The Vertex Cover
Vertex Cover is Fixed-Parameter Tractable CS 511 Iowa State University November 28, 2010 CS 511 (Iowa State University) Vertex Cover is Fixed-Parameter Tractable November 28, 2010 1 / 18 The Vertex Cover
Some graph theory applications. communications networks
 Some graph theory applications to communications networks Keith Briggs Keith.Briggs@bt.com http://keithbriggs.info Computational Systems Biology Group, Sheffield - 2006 Nov 02 1100 graph problems Sheffield
Some graph theory applications to communications networks Keith Briggs Keith.Briggs@bt.com http://keithbriggs.info Computational Systems Biology Group, Sheffield - 2006 Nov 02 1100 graph problems Sheffield
Honour Thy Neighbour Clique Maintenance in Dynamic Graphs
 Honour Thy Neighbour Clique Maintenance in Dynamic Graphs Thorsten J. Ottosen Department of Computer Science, Aalborg University, Denmark nesotto@cs.aau.dk Jiří Vomlel Institute of Information Theory and
Honour Thy Neighbour Clique Maintenance in Dynamic Graphs Thorsten J. Ottosen Department of Computer Science, Aalborg University, Denmark nesotto@cs.aau.dk Jiří Vomlel Institute of Information Theory and
Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees
 Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees Wei Wang joint with Zishen Yang, Xianliang Liu School of Mathematics and Statistics, Xi an Jiaotong University Dec 20, 2016
Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees Wei Wang joint with Zishen Yang, Xianliang Liu School of Mathematics and Statistics, Xi an Jiaotong University Dec 20, 2016
Graph Theory and Optimization Approximation Algorithms
 Graph Theory and Optimization Approximation Algorithms Nicolas Nisse Université Côte d Azur, Inria, CNRS, I3S, France October 2018 Thank you to F. Giroire for some of the slides N. Nisse Graph Theory and
Graph Theory and Optimization Approximation Algorithms Nicolas Nisse Université Côte d Azur, Inria, CNRS, I3S, France October 2018 Thank you to F. Giroire for some of the slides N. Nisse Graph Theory and
Combinatorial Optimization
 Combinatorial Optimization Frank de Zeeuw EPFL 2012 Today Introduction Graph problems - What combinatorial things will we be optimizing? Algorithms - What kind of solution are we looking for? Linear Programming
Combinatorial Optimization Frank de Zeeuw EPFL 2012 Today Introduction Graph problems - What combinatorial things will we be optimizing? Algorithms - What kind of solution are we looking for? Linear Programming
On Covering a Graph Optimally with Induced Subgraphs
 On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
Approximation Basics
 Milestones, Concepts, and Examples Xiaofeng Gao Department of Computer Science and Engineering Shanghai Jiao Tong University, P.R.China Spring 2015 Spring, 2015 Xiaofeng Gao 1/53 Outline History NP Optimization
Milestones, Concepts, and Examples Xiaofeng Gao Department of Computer Science and Engineering Shanghai Jiao Tong University, P.R.China Spring 2015 Spring, 2015 Xiaofeng Gao 1/53 Outline History NP Optimization
Parallelizing Maximal Clique Enumeration in Haskell
 Parallelizing Maximal Clique Enumeration in Haskell Andres Löh (joint work with Toni Cebrián) Well-Typed LLP 7 February 2012 Background: The Parallel GHC Project The Parallel GHC Project Currently the
Parallelizing Maximal Clique Enumeration in Haskell Andres Löh (joint work with Toni Cebrián) Well-Typed LLP 7 February 2012 Background: The Parallel GHC Project The Parallel GHC Project Currently the
Deleting edges to save cows - an application of treewidth
 Deleting edges to save cows - an application of treewidth UCLA, 14th February 2017 Kitty Meeks Joint work with Jessica Enright (University of Stirling) 2/13 The animal contact network 3/13 The animal contact
Deleting edges to save cows - an application of treewidth UCLA, 14th February 2017 Kitty Meeks Joint work with Jessica Enright (University of Stirling) 2/13 The animal contact network 3/13 The animal contact
Using Constraint Programming to Solve the Maximum Clique Problem
 Using Constraint Programming to Solve the Maximum Clique Problem Jean-Charles Régin ILOG Sophia Antipolis Les Taissounières HB, 1681 route des Dolines, 06560 Valbonne, France regin@ilog.fr Abstract. This
Using Constraint Programming to Solve the Maximum Clique Problem Jean-Charles Régin ILOG Sophia Antipolis Les Taissounières HB, 1681 route des Dolines, 06560 Valbonne, France regin@ilog.fr Abstract. This
Lecture 3, Review of Algorithms. What is Algorithm?
 BINF 336, Introduction to Computational Biology Lecture 3, Review of Algorithms Young-Rae Cho Associate Professor Department of Computer Science Baylor University What is Algorithm? Definition A process
BINF 336, Introduction to Computational Biology Lecture 3, Review of Algorithms Young-Rae Cho Associate Professor Department of Computer Science Baylor University What is Algorithm? Definition A process
COMP 355 Advanced Algorithms Approximation Algorithms: VC and TSP Chapter 11 (KT) Section (CLRS)
 COMP 355 Advanced Algorithms Approximation Algorithms: VC and TSP Chapter 11 (KT) Section 35.1-35.2(CLRS) 1 Coping with NP-Completeness Brute-force search: This is usually only a viable option for small
COMP 355 Advanced Algorithms Approximation Algorithms: VC and TSP Chapter 11 (KT) Section 35.1-35.2(CLRS) 1 Coping with NP-Completeness Brute-force search: This is usually only a viable option for small
NP-Complete Problems
 1 / 34 NP-Complete Problems CS 584: Algorithm Design and Analysis Daniel Leblanc 1 1 Senior Adjunct Instructor Portland State University Maseeh College of Engineering and Computer Science Winter 2018 2
1 / 34 NP-Complete Problems CS 584: Algorithm Design and Analysis Daniel Leblanc 1 1 Senior Adjunct Instructor Portland State University Maseeh College of Engineering and Computer Science Winter 2018 2
Improved Algorithms for Min Cuts and Max Flows in Undirected Planar Graphs
 Improved Algorithms for Min Cuts and Max Flows in Undirected Planar Graphs Giuseppe F. Italiano Università di Roma Tor Vergata Joint work with Yahav Nussbaum, Piotr Sankowski and Christian Wulff-Nilsen
Improved Algorithms for Min Cuts and Max Flows in Undirected Planar Graphs Giuseppe F. Italiano Università di Roma Tor Vergata Joint work with Yahav Nussbaum, Piotr Sankowski and Christian Wulff-Nilsen
Dr. Amotz Bar-Noy s Compendium of Algorithms Problems. Problems, Hints, and Solutions
 Dr. Amotz Bar-Noy s Compendium of Algorithms Problems Problems, Hints, and Solutions Chapter 1 Searching and Sorting Problems 1 1.1 Array with One Missing 1.1.1 Problem Let A = A[1],..., A[n] be an array
Dr. Amotz Bar-Noy s Compendium of Algorithms Problems Problems, Hints, and Solutions Chapter 1 Searching and Sorting Problems 1 1.1 Array with One Missing 1.1.1 Problem Let A = A[1],..., A[n] be an array
Approximation Algorithms
 Approximation Algorithms Frédéric Giroire FG Simplex 1/11 Motivation Goal: Find good solutions for difficult problems (NP-hard). Be able to quantify the goodness of the given solution. Presentation of
Approximation Algorithms Frédéric Giroire FG Simplex 1/11 Motivation Goal: Find good solutions for difficult problems (NP-hard). Be able to quantify the goodness of the given solution. Presentation of
CS270 Combinatorial Algorithms & Data Structures Spring Lecture 19:
 CS270 Combinatorial Algorithms & Data Structures Spring 2003 Lecture 19: 4.1.03 Lecturer: Satish Rao Scribes: Kevin Lacker and Bill Kramer Disclaimer: These notes have not been subjected to the usual scrutiny
CS270 Combinatorial Algorithms & Data Structures Spring 2003 Lecture 19: 4.1.03 Lecturer: Satish Rao Scribes: Kevin Lacker and Bill Kramer Disclaimer: These notes have not been subjected to the usual scrutiny
Combinatorial Algorithms. Unate Covering Binate Covering Graph Coloring Maximum Clique
 Combinatorial Algorithms Unate Covering Binate Covering Graph Coloring Maximum Clique Example As an Example, let s consider the formula: F(x,y,z) = x y z + x yz + x yz + xyz + xy z The complete sum of
Combinatorial Algorithms Unate Covering Binate Covering Graph Coloring Maximum Clique Example As an Example, let s consider the formula: F(x,y,z) = x y z + x yz + x yz + xyz + xy z The complete sum of
Algorithms for the Bin Packing Problem with Conflicts
 Algorithms for the Bin Packing Problem with Conflicts Albert E. Fernandes Muritiba *, Manuel Iori, Enrico Malaguti*, Paolo Toth* *Dipartimento di Elettronica, Informatica e Sistemistica, Università degli
Algorithms for the Bin Packing Problem with Conflicts Albert E. Fernandes Muritiba *, Manuel Iori, Enrico Malaguti*, Paolo Toth* *Dipartimento di Elettronica, Informatica e Sistemistica, Università degli
Network Based Models For Analysis of SNPs Yalta Opt
 Outline Network Based Models For Analysis of Yalta Optimization Conference 2010 Network Science Zeynep Ertem*, Sergiy Butenko*, Clare Gill** *Department of Industrial and Systems Engineering, **Department
Outline Network Based Models For Analysis of Yalta Optimization Conference 2010 Network Science Zeynep Ertem*, Sergiy Butenko*, Clare Gill** *Department of Industrial and Systems Engineering, **Department
Complexity Results on Graphs with Few Cliques
 Discrete Mathematics and Theoretical Computer Science DMTCS vol. 9, 2007, 127 136 Complexity Results on Graphs with Few Cliques Bill Rosgen 1 and Lorna Stewart 2 1 Institute for Quantum Computing and School
Discrete Mathematics and Theoretical Computer Science DMTCS vol. 9, 2007, 127 136 Complexity Results on Graphs with Few Cliques Bill Rosgen 1 and Lorna Stewart 2 1 Institute for Quantum Computing and School
31.6 Powers of an element
 31.6 Powers of an element Just as we often consider the multiples of a given element, modulo, we consider the sequence of powers of, modulo, where :,,,,. modulo Indexing from 0, the 0th value in this sequence
31.6 Powers of an element Just as we often consider the multiples of a given element, modulo, we consider the sequence of powers of, modulo, where :,,,,. modulo Indexing from 0, the 0th value in this sequence
Practice Final Exam 1
 Algorithm esign Techniques Practice Final xam Instructions. The exam is hours long and contains 6 questions. Write your answers clearly. You may quote any result/theorem seen in the lectures or in the
Algorithm esign Techniques Practice Final xam Instructions. The exam is hours long and contains 6 questions. Write your answers clearly. You may quote any result/theorem seen in the lectures or in the
Antibandwidth of Hamming graphs
 Antibandwidth of Hamming graphs Štefan Dobrev Rastislav Královič Dana Pardubská Ľubomír Török Imrich Vrťo Workshop on Discrete Mathematics Vienna, November 19-22, 2008 Antibandwidth problem Consists of
Antibandwidth of Hamming graphs Štefan Dobrev Rastislav Královič Dana Pardubská Ľubomír Török Imrich Vrťo Workshop on Discrete Mathematics Vienna, November 19-22, 2008 Antibandwidth problem Consists of
P and NP (Millenium problem)
 CMPS 2200 Fall 2017 P and NP (Millenium problem) Carola Wenk Slides courtesy of Piotr Indyk with additions by Carola Wenk CMPS 2200 Introduction to Algorithms 1 We have seen so far Algorithms for various
CMPS 2200 Fall 2017 P and NP (Millenium problem) Carola Wenk Slides courtesy of Piotr Indyk with additions by Carola Wenk CMPS 2200 Introduction to Algorithms 1 We have seen so far Algorithms for various
Notes for Lecture 24
 U.C. Berkeley CS170: Intro to CS Theory Handout N24 Professor Luca Trevisan December 4, 2001 Notes for Lecture 24 1 Some NP-complete Numerical Problems 1.1 Subset Sum The Subset Sum problem is defined
U.C. Berkeley CS170: Intro to CS Theory Handout N24 Professor Luca Trevisan December 4, 2001 Notes for Lecture 24 1 Some NP-complete Numerical Problems 1.1 Subset Sum The Subset Sum problem is defined
Approximation Algorithms for Geometric Intersection Graphs
 Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
Ton Kloks and Yue-Li Wang. Advances in Graph Algorithms. October 10, y X z
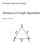 Ton Kloks and Yue-Li Wang Advances in Graph Algorithms October 10, 2013 x Z Y < y X z
Ton Kloks and Yue-Li Wang Advances in Graph Algorithms October 10, 2013 x Z Y < y X z
CS 231: Algorithmic Problem Solving
 CS 231: Algorithmic Problem Solving Naomi Nishimura Module 7 Date of this version: January 28, 2019 WARNING: Drafts of slides are made available prior to lecture for your convenience. After lecture, slides
CS 231: Algorithmic Problem Solving Naomi Nishimura Module 7 Date of this version: January 28, 2019 WARNING: Drafts of slides are made available prior to lecture for your convenience. After lecture, slides
Chapter 9 Graph Algorithms
 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures Chapter 9 Graph s 2 Definitions Definitions an undirected graph is a finite set
Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures Chapter 9 Graph s 2 Definitions Definitions an undirected graph is a finite set
Unit 8: Coping with NP-Completeness. Complexity classes Reducibility and NP-completeness proofs Coping with NP-complete problems. Y.-W.
 : Coping with NP-Completeness Course contents: Complexity classes Reducibility and NP-completeness proofs Coping with NP-complete problems Reading: Chapter 34 Chapter 35.1, 35.2 Y.-W. Chang 1 Complexity
: Coping with NP-Completeness Course contents: Complexity classes Reducibility and NP-completeness proofs Coping with NP-complete problems Reading: Chapter 34 Chapter 35.1, 35.2 Y.-W. Chang 1 Complexity
Maximizing edge-ratio is NP-complete
 Maximizing edge-ratio is NP-complete Steven D Noble, Pierre Hansen and Nenad Mladenović February 7, 01 Abstract Given a graph G and a bipartition of its vertices, the edge-ratio is the minimum for both
Maximizing edge-ratio is NP-complete Steven D Noble, Pierre Hansen and Nenad Mladenović February 7, 01 Abstract Given a graph G and a bipartition of its vertices, the edge-ratio is the minimum for both
Introduction to Graph Theory
 Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
XLVI Pesquisa Operacional na Gestão da Segurança Pública
 Setembro de 014 Approximation algorithms for simple maxcut of split graphs Rubens Sucupira 1 Luerbio Faria 1 Sulamita Klein 1- IME/UERJ UERJ, Rio de JaneiroRJ, Brasil rasucupira@oi.com.br, luerbio@cos.ufrj.br
Setembro de 014 Approximation algorithms for simple maxcut of split graphs Rubens Sucupira 1 Luerbio Faria 1 Sulamita Klein 1- IME/UERJ UERJ, Rio de JaneiroRJ, Brasil rasucupira@oi.com.br, luerbio@cos.ufrj.br
CS 534: Computer Vision Segmentation II Graph Cuts and Image Segmentation
 CS 534: Computer Vision Segmentation II Graph Cuts and Image Segmentation Spring 2005 Ahmed Elgammal Dept of Computer Science CS 534 Segmentation II - 1 Outlines What is Graph cuts Graph-based clustering
CS 534: Computer Vision Segmentation II Graph Cuts and Image Segmentation Spring 2005 Ahmed Elgammal Dept of Computer Science CS 534 Segmentation II - 1 Outlines What is Graph cuts Graph-based clustering
Stanford University CS261: Optimization Handout 1 Luca Trevisan January 4, 2011
 Stanford University CS261: Optimization Handout 1 Luca Trevisan January 4, 2011 Lecture 1 In which we describe what this course is about and give two simple examples of approximation algorithms 1 Overview
Stanford University CS261: Optimization Handout 1 Luca Trevisan January 4, 2011 Lecture 1 In which we describe what this course is about and give two simple examples of approximation algorithms 1 Overview
On the Max Coloring Problem
 On the Max Coloring Problem Leah Epstein Asaf Levin May 22, 2010 Abstract We consider max coloring on hereditary graph classes. The problem is defined as follows. Given a graph G = (V, E) and positive
On the Max Coloring Problem Leah Epstein Asaf Levin May 22, 2010 Abstract We consider max coloring on hereditary graph classes. The problem is defined as follows. Given a graph G = (V, E) and positive
Chapter 9 Graph Algorithms
 Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures 3 Definitions an undirected graph G = (V, E) is a
Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures 3 Definitions an undirected graph G = (V, E) is a
Extremal Graph Theory: Turán s Theorem
 Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
GRAPH THEORY and APPLICATIONS. Factorization Domination Indepence Clique
 GRAPH THEORY and APPLICATIONS Factorization Domination Indepence Clique Factorization Factor A factor of a graph G is a spanning subgraph of G, not necessarily connected. G is the sum of factors G i, if:
GRAPH THEORY and APPLICATIONS Factorization Domination Indepence Clique Factorization Factor A factor of a graph G is a spanning subgraph of G, not necessarily connected. G is the sum of factors G i, if:
Exact Algorithms for NP-hard problems
 24 mai 2012 1 Why do we need exponential algorithms? 2 3 Why the P-border? 1 Practical reasons (Jack Edmonds, 1965) For practical purposes the difference between algebraic and exponential order is more
24 mai 2012 1 Why do we need exponential algorithms? 2 3 Why the P-border? 1 Practical reasons (Jack Edmonds, 1965) For practical purposes the difference between algebraic and exponential order is more
Xiao, M. (Mingyu); Lin, W. (Weibo); Dai, Y. (Yuanshun); Zeng, Y. (Yifeng)
 TeesRep - Teesside's Research Repository A Fast Algorithm to Compute Maximum k-plexes in Social Network Analysis Item type Authors Citation Eprint Version Publisher Additional Link Rights Meetings and
TeesRep - Teesside's Research Repository A Fast Algorithm to Compute Maximum k-plexes in Social Network Analysis Item type Authors Citation Eprint Version Publisher Additional Link Rights Meetings and
The strong chromatic number of a graph
 The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
Maximum Clique Conformance Measure for Graph Coloring Algorithms
 Maximum Clique Conformance Measure for Graph Algorithms Abdulmutaleb Alzubi Jadarah University Dept. of Computer Science Irbid, Jordan alzoubi3@yahoo.com Mohammad Al-Haj Hassan Zarqa University Dept. of
Maximum Clique Conformance Measure for Graph Algorithms Abdulmutaleb Alzubi Jadarah University Dept. of Computer Science Irbid, Jordan alzoubi3@yahoo.com Mohammad Al-Haj Hassan Zarqa University Dept. of
Graph Theory: Introduction
 Graph Theory: Introduction Pallab Dasgupta, Professor, Dept. of Computer Sc. and Engineering, IIT Kharagpur pallab@cse.iitkgp.ernet.in Resources Copies of slides available at: http://www.facweb.iitkgp.ernet.in/~pallab
Graph Theory: Introduction Pallab Dasgupta, Professor, Dept. of Computer Sc. and Engineering, IIT Kharagpur pallab@cse.iitkgp.ernet.in Resources Copies of slides available at: http://www.facweb.iitkgp.ernet.in/~pallab
Graphs (MTAT , 6 EAP) Lectures: Mon 14-16, hall 404 Exercises: Wed 14-16, hall 402
 Graphs (MTAT.05.080, 6 EAP) Lectures: Mon 14-16, hall 404 Exercises: Wed 14-16, hall 402 homepage: http://courses.cs.ut.ee/2012/graafid (contains slides) For grade: Homework + three tests (during or after
Graphs (MTAT.05.080, 6 EAP) Lectures: Mon 14-16, hall 404 Exercises: Wed 14-16, hall 402 homepage: http://courses.cs.ut.ee/2012/graafid (contains slides) For grade: Homework + three tests (during or after
Approximation Algorithms
 Chapter 8 Approximation Algorithms Algorithm Theory WS 2016/17 Fabian Kuhn Approximation Algorithms Optimization appears everywhere in computer science We have seen many examples, e.g.: scheduling jobs
Chapter 8 Approximation Algorithms Algorithm Theory WS 2016/17 Fabian Kuhn Approximation Algorithms Optimization appears everywhere in computer science We have seen many examples, e.g.: scheduling jobs
Mathematical and Algorithmic Foundations Linear Programming and Matchings
 Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
On the Complexity of Broadcast Scheduling. Problem
 On the Complexity of Broadcast Scheduling Problem Sergiy Butenko, Clayton Commander and Panos Pardalos Abstract In this paper, a broadcast scheduling problem (BSP) in a time division multiple access (TDMA)
On the Complexity of Broadcast Scheduling Problem Sergiy Butenko, Clayton Commander and Panos Pardalos Abstract In this paper, a broadcast scheduling problem (BSP) in a time division multiple access (TDMA)
Research Question Presentation on the Edge Clique Covers of a Complete Multipartite Graph. Nechama Florans. Mentor: Dr. Boram Park
 Research Question Presentation on the Edge Clique Covers of a Complete Multipartite Graph Nechama Florans Mentor: Dr. Boram Park G: V 5 Vertex Clique Covers and Edge Clique Covers: Suppose we have a graph
Research Question Presentation on the Edge Clique Covers of a Complete Multipartite Graph Nechama Florans Mentor: Dr. Boram Park G: V 5 Vertex Clique Covers and Edge Clique Covers: Suppose we have a graph
Partha Sarathi Mandal
 MA 515: Introduction to Algorithms & MA353 : Design and Analysis of Algorithms [3-0-0-6] Lecture 39 http://www.iitg.ernet.in/psm/indexing_ma353/y09/index.html Partha Sarathi Mandal psm@iitg.ernet.in Dept.
MA 515: Introduction to Algorithms & MA353 : Design and Analysis of Algorithms [3-0-0-6] Lecture 39 http://www.iitg.ernet.in/psm/indexing_ma353/y09/index.html Partha Sarathi Mandal psm@iitg.ernet.in Dept.
Approximation slides 1. An optimal polynomial algorithm for the Vertex Cover and matching in Bipartite graphs
 Approximation slides 1 An optimal polynomial algorithm for the Vertex Cover and matching in Bipartite graphs Approximation slides 2 Linear independence A collection of row vectors {v T i } are independent
Approximation slides 1 An optimal polynomial algorithm for the Vertex Cover and matching in Bipartite graphs Approximation slides 2 Linear independence A collection of row vectors {v T i } are independent
Module 6 NP-Complete Problems and Heuristics
 Module 6 NP-Complete Problems and Heuristics Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 97 E-mail: natarajan.meghanathan@jsums.edu Optimization vs. Decision
Module 6 NP-Complete Problems and Heuristics Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 97 E-mail: natarajan.meghanathan@jsums.edu Optimization vs. Decision
Chapter 10 Part 1: Reduction
 //06 Polynomial-Time Reduction Suppose we could solve Y in polynomial-time. What else could we solve in polynomial time? don't confuse with reduces from Chapter 0 Part : Reduction Reduction. Problem X
//06 Polynomial-Time Reduction Suppose we could solve Y in polynomial-time. What else could we solve in polynomial time? don't confuse with reduces from Chapter 0 Part : Reduction Reduction. Problem X
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
SEARCH ALGORITHMS NOTES FOR THE ADVANCED ALGORITHM CLASS
 SEARCH ALGORITHMS NOTES FOR THE ADVANCED ALGORITHM CLASS GIUSEPPE PERSIANO Contents 1. Model 1 2. Exhaustive Search 2 3. Backtrack 3 3.1. Backtrack for Sudoku 4 3.2. Backtrack for Vertex Cover 4 4. Branch
SEARCH ALGORITHMS NOTES FOR THE ADVANCED ALGORITHM CLASS GIUSEPPE PERSIANO Contents 1. Model 1 2. Exhaustive Search 2 3. Backtrack 3 3.1. Backtrack for Sudoku 4 3.2. Backtrack for Vertex Cover 4 4. Branch
Conflict Graphs for Combinatorial Optimization Problems
 Conflict Graphs for Combinatorial Optimization Problems Ulrich Pferschy joint work with Andreas Darmann and Joachim Schauer University of Graz, Austria Introduction Combinatorial Optimization Problem CO
Conflict Graphs for Combinatorial Optimization Problems Ulrich Pferschy joint work with Andreas Darmann and Joachim Schauer University of Graz, Austria Introduction Combinatorial Optimization Problem CO
Matchings and Covers in bipartite graphs
 Matchings and Covers in bipartite graphs A bipartite graph, also called a bigraph, is a set of graph vertices decomposed into two disjoint sets such that no two graph vertices within the same set are adjacent.
Matchings and Covers in bipartite graphs A bipartite graph, also called a bigraph, is a set of graph vertices decomposed into two disjoint sets such that no two graph vertices within the same set are adjacent.
Randomized Graph Algorithms
 Randomized Graph Algorithms Vasileios-Orestis Papadigenopoulos School of Electrical and Computer Engineering - NTUA papadigenopoulos orestis@yahoocom July 22, 2014 Vasileios-Orestis Papadigenopoulos (NTUA)
Randomized Graph Algorithms Vasileios-Orestis Papadigenopoulos School of Electrical and Computer Engineering - NTUA papadigenopoulos orestis@yahoocom July 22, 2014 Vasileios-Orestis Papadigenopoulos (NTUA)
Maximum Clique Problem. Team Bushido bit.ly/parallel-computing-fall-2014
 Maximum Clique Problem Team Bushido bit.ly/parallel-computing-fall-2014 Agenda Problem summary Research Paper 1 Research Paper 2 Research Paper 3 Software Design Demo of Sequential Program Summary Of the
Maximum Clique Problem Team Bushido bit.ly/parallel-computing-fall-2014 Agenda Problem summary Research Paper 1 Research Paper 2 Research Paper 3 Software Design Demo of Sequential Program Summary Of the
Introduction to Algorithms
 Introduction to Algorithms 6.046J/18.401 Lecture 21 Prof. Piotr Indyk P vs NP (interconnectedness of all things) A whole course by itself We ll do just two lectures More in 6.045, 6.840J, etc. Introduction
Introduction to Algorithms 6.046J/18.401 Lecture 21 Prof. Piotr Indyk P vs NP (interconnectedness of all things) A whole course by itself We ll do just two lectures More in 6.045, 6.840J, etc. Introduction
Dynamic programming. Trivial problems are solved first More complex solutions are composed from the simpler solutions already computed
 Dynamic programming Solves a complex problem by breaking it down into subproblems Each subproblem is broken down recursively until a trivial problem is reached Computation itself is not recursive: problems
Dynamic programming Solves a complex problem by breaking it down into subproblems Each subproblem is broken down recursively until a trivial problem is reached Computation itself is not recursive: problems
CSE 417 Branch & Bound (pt 4) Branch & Bound
 CSE 417 Branch & Bound (pt 4) Branch & Bound Reminders > HW8 due today > HW9 will be posted tomorrow start early program will be slow, so debugging will be slow... Review of previous lectures > Complexity
CSE 417 Branch & Bound (pt 4) Branch & Bound Reminders > HW8 due today > HW9 will be posted tomorrow start early program will be slow, so debugging will be slow... Review of previous lectures > Complexity
11/22/2016. Chapter 9 Graph Algorithms. Introduction. Definitions. Definitions. Definitions. Definitions
 Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Chapter 9 Graph Algorithms
 Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
Welcome to the course Algorithm Design
 Welcome to the course Algorithm Design Summer Term 2011 Friedhelm Meyer auf der Heide Lecture 13, 15.7.2011 Friedhelm Meyer auf der Heide 1 Topics - Divide & conquer - Dynamic programming - Greedy Algorithms
Welcome to the course Algorithm Design Summer Term 2011 Friedhelm Meyer auf der Heide Lecture 13, 15.7.2011 Friedhelm Meyer auf der Heide 1 Topics - Divide & conquer - Dynamic programming - Greedy Algorithms
UML CS Algorithms Qualifying Exam Fall, 2003 ALGORITHMS QUALIFYING EXAM
 NAME: This exam is open: - books - notes and closed: - neighbors - calculators ALGORITHMS QUALIFYING EXAM The upper bound on exam time is 3 hours. Please put all your work on the exam paper. (Partial credit
NAME: This exam is open: - books - notes and closed: - neighbors - calculators ALGORITHMS QUALIFYING EXAM The upper bound on exam time is 3 hours. Please put all your work on the exam paper. (Partial credit
The Maximum Common Subgraph Problem: Faster Solutions via Vertex Cover
 The Maximum Common Subgraph Problem: Faster Solutions via Vertex Cover Faisal N. Abu-Khzam Division of Computer Science and Mathematics Lebanese American University Beirut, Lebanon faisal.abukhzam@lau.edu.lb
The Maximum Common Subgraph Problem: Faster Solutions via Vertex Cover Faisal N. Abu-Khzam Division of Computer Science and Mathematics Lebanese American University Beirut, Lebanon faisal.abukhzam@lau.edu.lb
Interval Graphs. Joyce C. Yang. Nicholas Pippenger, Advisor. Arthur T. Benjamin, Reader. Department of Mathematics
 Interval Graphs Joyce C. Yang Nicholas Pippenger, Advisor Arthur T. Benjamin, Reader Department of Mathematics May, 2016 Copyright c 2016 Joyce C. Yang. The author grants Harvey Mudd College and the Claremont
Interval Graphs Joyce C. Yang Nicholas Pippenger, Advisor Arthur T. Benjamin, Reader Department of Mathematics May, 2016 Copyright c 2016 Joyce C. Yang. The author grants Harvey Mudd College and the Claremont
Assignment No 2 (Group B)
 Assignment No 2 (Group B) 1 Problem Statement : Concurrent Implementation of Travelling Salesman Problem. 2 Objective : To develop problem solving abilities using Mathematical Modeling. To apply algorithmic
Assignment No 2 (Group B) 1 Problem Statement : Concurrent Implementation of Travelling Salesman Problem. 2 Objective : To develop problem solving abilities using Mathematical Modeling. To apply algorithmic
3 INTEGER LINEAR PROGRAMMING
 3 INTEGER LINEAR PROGRAMMING PROBLEM DEFINITION Integer linear programming problem (ILP) of the decision variables x 1,..,x n : (ILP) subject to minimize c x j j n j= 1 a ij x j x j 0 x j integer n j=
3 INTEGER LINEAR PROGRAMMING PROBLEM DEFINITION Integer linear programming problem (ILP) of the decision variables x 1,..,x n : (ILP) subject to minimize c x j j n j= 1 a ij x j x j 0 x j integer n j=
Approximability Results for the p-center Problem
 Approximability Results for the p-center Problem Stefan Buettcher Course Project Algorithm Design and Analysis Prof. Timothy Chan University of Waterloo, Spring 2004 The p-center
Approximability Results for the p-center Problem Stefan Buettcher Course Project Algorithm Design and Analysis Prof. Timothy Chan University of Waterloo, Spring 2004 The p-center
v 2 v 3 v 1 v 0 K 3 K 1
 It is Hard to Know when Greedy is Good for Finding Independent Sets Hans L. Bodlaender, Dimitrios M. Thilikos, Koichi Yamazaki Department of Computer Science, Utrecht University, P.O. Box 80.089, 3508
It is Hard to Know when Greedy is Good for Finding Independent Sets Hans L. Bodlaender, Dimitrios M. Thilikos, Koichi Yamazaki Department of Computer Science, Utrecht University, P.O. Box 80.089, 3508
Solution of Maximum Clique Problem. by Using Branch and Bound Method
 Applied Mathematical Sciences, Vol. 8, 2014, no. 2, 81-90 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.310601 Solution of Maximum Clique Problem by Using Branch and Bound Method Mochamad
Applied Mathematical Sciences, Vol. 8, 2014, no. 2, 81-90 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/ams.2014.310601 Solution of Maximum Clique Problem by Using Branch and Bound Method Mochamad
Outline Purpose How to analyze algorithms Examples. Algorithm Analysis. Seth Long. January 15, 2010
 January 15, 2010 Intuitive Definitions Common Runtimes Final Notes Compare space and time requirements for algorithms Understand how an algorithm scales with larger datasets Intuitive Definitions Outline
January 15, 2010 Intuitive Definitions Common Runtimes Final Notes Compare space and time requirements for algorithms Understand how an algorithm scales with larger datasets Intuitive Definitions Outline
Let G = (V, E) be a graph. If u, v V, then u is adjacent to v if {u, v} E. We also use the notation u v to denote that u is adjacent to v.
 Graph Adjacent Endpoint of an edge Incident Neighbors of a vertex Degree of a vertex Theorem Graph relation Order of a graph Size of a graph Maximum and minimum degree Let G = (V, E) be a graph. If u,
Graph Adjacent Endpoint of an edge Incident Neighbors of a vertex Degree of a vertex Theorem Graph relation Order of a graph Size of a graph Maximum and minimum degree Let G = (V, E) be a graph. If u,
Practical Fixed-Parameter Algorithms for Graph-Modeled Data Clustering
 Practical Fixed-Parameter Algorithms for Graph-Modeled Data Clustering Sebastian Wernicke* Institut für Informatik, Friedrich-Schiller-Universität Jena, Ernst-Abbe-Platz 2, D-07743 Jena, Fed. Rep. of Germany
Practical Fixed-Parameter Algorithms for Graph-Modeled Data Clustering Sebastian Wernicke* Institut für Informatik, Friedrich-Schiller-Universität Jena, Ernst-Abbe-Platz 2, D-07743 Jena, Fed. Rep. of Germany
!!" '!" Fall 2003 ICS 275A - Constraint Networks 2
 chapter 10 1 !"!!" # $ %&!" '!" Fall 2003 ICS 275A - Constraint Networks 2 ( Complexity : O(exp(n)) Fall 2003 ICS 275A - Constraint Networks 3 * bucket i = O(exp( w )) DR time and space : O( n exp( w *
chapter 10 1 !"!!" # $ %&!" '!" Fall 2003 ICS 275A - Constraint Networks 2 ( Complexity : O(exp(n)) Fall 2003 ICS 275A - Constraint Networks 3 * bucket i = O(exp( w )) DR time and space : O( n exp( w *
Stanford University CS359G: Graph Partitioning and Expanders Handout 18 Luca Trevisan March 3, 2011
 Stanford University CS359G: Graph Partitioning and Expanders Handout 8 Luca Trevisan March 3, 20 Lecture 8 In which we prove properties of expander graphs. Quasirandomness of Expander Graphs Recall that
Stanford University CS359G: Graph Partitioning and Expanders Handout 8 Luca Trevisan March 3, 20 Lecture 8 In which we prove properties of expander graphs. Quasirandomness of Expander Graphs Recall that
Grundy chromatic number of the complement of bipartite graphs
 Grundy chromatic number of the complement of bipartite graphs Manouchehr Zaker Institute for Advanced Studies in Basic Sciences P. O. BOX 45195-159 Zanjan, Iran E-mail: mzaker@iasbs.ac.ir Abstract A Grundy
Grundy chromatic number of the complement of bipartite graphs Manouchehr Zaker Institute for Advanced Studies in Basic Sciences P. O. BOX 45195-159 Zanjan, Iran E-mail: mzaker@iasbs.ac.ir Abstract A Grundy
NP-Complete Problems
 NP-omplete Problems P and NP Polynomial time reductions Satisfiability Problem, lique Problem, Vertex over, and ominating Set 10/19/2009 SE 5311 FLL 2009 KUMR 1 Polynomial lgorithms Problems encountered
NP-omplete Problems P and NP Polynomial time reductions Satisfiability Problem, lique Problem, Vertex over, and ominating Set 10/19/2009 SE 5311 FLL 2009 KUMR 1 Polynomial lgorithms Problems encountered
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs { }
 motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
Module 6 NP-Complete Problems and Heuristics
 Module 6 NP-Complete Problems and Heuristics Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu P, NP-Problems Class
Module 6 NP-Complete Problems and Heuristics Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu P, NP-Problems Class
Learning decomposable models with a bounded clique size
 Learning decomposable models with a bounded clique size Achievements 2014-2016 Aritz Pérez Basque Center for Applied Mathematics Bilbao, March, 2016 Outline 1 Motivation and background 2 The problem 3
Learning decomposable models with a bounded clique size Achievements 2014-2016 Aritz Pérez Basque Center for Applied Mathematics Bilbao, March, 2016 Outline 1 Motivation and background 2 The problem 3
8 NP-complete problem Hard problems: demo
 Ch8 NPC Millennium Prize Problems http://en.wikipedia.org/wiki/millennium_prize_problems 8 NP-complete problem Hard problems: demo NP-hard (Non-deterministic Polynomial-time hard), in computational complexity
Ch8 NPC Millennium Prize Problems http://en.wikipedia.org/wiki/millennium_prize_problems 8 NP-complete problem Hard problems: demo NP-hard (Non-deterministic Polynomial-time hard), in computational complexity
Polynomial-Time Approximation Algorithms
 6.854 Advanced Algorithms Lecture 20: 10/27/2006 Lecturer: David Karger Scribes: Matt Doherty, John Nham, Sergiy Sidenko, David Schultz Polynomial-Time Approximation Algorithms NP-hard problems are a vast
6.854 Advanced Algorithms Lecture 20: 10/27/2006 Lecturer: David Karger Scribes: Matt Doherty, John Nham, Sergiy Sidenko, David Schultz Polynomial-Time Approximation Algorithms NP-hard problems are a vast
