Network Optimization Problems. Chapter 6: Hillier and Hillier
|
|
|
- Luke Davis
- 5 years ago
- Views:
Transcription
1 Network Optimization Problems Chapter 6: Hillier and Hillier
2 Agenda Minimum-Cost Flow Problems Case Study: Distribution Unlimited Co. Maximum Flow Problems Case Study: BMZ Company Shortest Path Problems Case Study: Littletown Fire Department Minimum Spanning Tree Problems Case Study: The Modern Corp. Problem
3 Minimum-Cost Flow Problems These problems are also known as distribution network problems which were seen in chapter 3. Your objective is to distribute goods from a supply source to an ultimate demand destination with potential distribution centers in-between.
4 Needed Terminology A network in this case is a representation of the model for a minimum-cost flow model that has flow passing through it. Circles in the network are known as nodes. These nodes can be broken-up into supply nodes, demand nodes, and transshipment nodes. A supply node is a node where the net amount of flow generated (outflow minus inflow) is a fixed positive number.
5 Needed Terminology Cont. A demand node is a node where the net amount of flow generated (outflow minus inflow) is a fixed negative number. A transshipment node is a node where the net amount of flow generated (outflow minus inflow) is a fixed at zero. Having the outflow equal to the inflow is known as conservation of flow.
6 Needed Terminology Cont. Arcs are lines from node to node which represent the direction in which flow can occur. Capacity of an arc represents the maximum amount of flow that can be sent through an arc. Flow is defined as an amount that is sent through an arc.
7 Assumptions of the Minimum- Cost Flow Problem There is at least one supply node. There is at least one demand node. Any node that is not a supply node or a demand node is a transshipment node. Flow through an arc is only allowed in the direction the arc is pointing, where the maximum amount of flow is dictated by its capacity.
8 Assumptions of the Minimum- Cost Flow Problem The network has enough arcs with sufficient capacity to move all the flows from the supply nodes to the demand nodes. The cost of the flows through the arc are proportional to the amounts sent through the arc. The cost of each flow is known. The objective is to minimize the cost of the flows from the supply nodes to the demand nodes.
9 Feasible Solution and Integer Properties Feasible Solution Property A minimum-cost flow problem is said to have a feasible solution if and only if the sum of the supplies is equal to the sum of the demands. Integer Solution Property A minimum-cost flow problem will have an integer solution as long as all its supplies, demands, and arc capacities have integer values.
10 Case Study: Distribution Unlimited Co. Distribution Unlimited Co. (DUC) has two factories producing a product that needs to be shipped to two warehouses. Factory 1 produces 80 units Factory 2 produces 70 units Warehouse 1 needs 60 units Warehouse 2 needs 90 units DUC has one distribution center that both factories can ship to.
11 Case Study: Distribution Unlimited Co. Cont. DUC has the ability for factory 1 to ship to warehouse 1 or the distribution center. DUC has the ability for factory 2 to ship to warehouse 2 or the distribution center. The distribution center can ship to either warehouses. Shipments to and from distribution centers are limited to a 50 unit maximum amount for each route.
12 Case Study: Distribution Unlimited Co. Cont. Unit Cost For Shipments Distribution Warehouse 1 Warehouse 2 Center Factory 1 $300 $700 N/A Factory 2 $400 N/A $900 Distribution Center N/A $200 $400
13 Case Study: Distribution Unlimited Co. Cont. Maximum Amount of Shipments to Each Source Distribution Warehouse 1 Warehouse 2 Center Factory N/A Factory 2 50 N/A 50 Distribution Center N/A 50 50
14 Case Study: Distribution Unlimited Co. Cont. DUC wants to find the cheapest shipping plan to transport is supply from the factories to the demand of the warehouses.
15 Representation of Distribution Unlimited Co. Problem 80 units produced F1 W1 60 units needed DC 70 units produced F2 W2 90 units needed
16 Representation of Distribution Unlimited Co. Problem Cont. [80] [- 60] F1 $700 W1 $300 $200 [50] [0] [50] DC F2 $400 [50] $900 $400 [50] W2 [70] [- 90]
17 Mathematical Model of Distribution Unlimited Co * 1 200* * 2 400* 1 300* * 2 1, 2 2, 2 1 1, 1 DCW DCW W F DC F DC F W F Min DCW DCW W F DC F DC F W F
18 Mathematical Model of Distribution Unlimited Co. Cont. Constraints : F1DC + F2DC - DCW1- DCW2 = 0 F1W1+ DCW1 = 60 F2W2 + DCW2 = 90 F1W1+ F1DC = 80 F2W2 + F2DC = 70 F1DC, F2DC, DCW1, DCW2 50 F1DC, F2DC, DCW1, DCW2, F1W1, F2W2 0
19 SUMIF Function in Excel The SUMIF function takes a range and compares it to a some condition. If the condition is true, then the function will add to the running sum the corresponding value in another range. If the condition is false, then the function will not add to the running sum the corresponding value in another range. SUMIF(Range A, condition, Range B) If you put in a value or a number, the function checks for equality.
20 A Note on Solutions While the Simplex Method can solve minimum-cost flow problems, it is not the most efficient algorithm to use. The most efficient algorithm is the the Network Simplex Method. Unfortunately with Excel s Solver, the network Simplex cannot be utilized because Solver does not currently have the algorithm.
21 Maximum Flow Problems The objective of a maximum flow problem is to find a plan that maximizes the flow through the network. The characteristics of the maximum flow problem are similar to those of the minimum-cost flow problem.
22 Assumptions of the Maximum Flow Problem All flow originates from a single node known as the source. All flow terminates at a single node known as the sink. All remaining nodes are transshipment nodes. Flow through the arc is only allowed by the direction of the flow arrow.
23 Assumptions of the Maximum Flow Problem Maximum flow through an arc is dictated by the capacity of the arc. All arcs extending from the source node point away from the source node. All arcs coming to the sink node point towards the sink node. The objective is to maximize the total flow from the source to the sink. The total flow can be either measured by the amount entering the sink or the amount leaving the source.
24 Differences Between Minimum- Cost and Maximum Flow In the minimum-cost model, the supply nodes and demand nodes have fixed amounts, whereas the maximum flow problem has a variable amount. In the minimum-cost model, there can be multiple demand and supply nodes, whereas the maximum flow model has only one supply node and one demand node.
25 Case Study: BMZ Company BMZ is a car company that is trying to get as many cars from its factory in Stuttgart to the Los Angeles market. BMZ can send cars across rail to three shipping points to the US: Rotterdam Bordeaux Lisbon
26 Case Study: BMZ Company Cont. From the Rotterdam terminal, cars can be shipped to a port in New York. From Bordeaux, cars can be shipped to either New York or New Orleans. From Lisbon, cars can be shipped to New Orleans. Once the cars are in New York and New Orleans, the cars will be shipped to the LA market. Each route for shipment has a limited amount of cars that it can handle.
27 Case Study: BMZ Company Cont. Maximum Shipments Allowed Rotterdam Bordeaux Lisbon New York New Orleans Los Angeles Stuttgart N/A N/A N/A Rotterdam N/A N/A N/A 60 N/A N/A Bordeaux N/A N/A N/A N/A Lisbon N/A N/A N/A N/A 30 N/A New York N/A N/A N/A N/A N/A 80 New Orleans N/A N/A N/A N/A N/A 70
28 BMZ Company Visual Diagram [60 units max.] RO Rotterdam New York [80 units max.] NY [50 units max.] {40 units max.] BO ST [70 units max.] Stuttgart Bordeaux [40 units max.] [50 units max.] LA New Orleans Los Angeles [70 units max] NO [30 units max.] LI Lisbon
29 Mathematical Formulation 70 80, 30, 50, 40, 60, 40, 70, 50, STRO Constraints :,,,,,,,, + NOLA NYLA LINO BONO BONY RONY STLI STBO NOLA NYLA Max NOLA NYLA LINO BONO BONY RONY STLI STBO STRO
30 Mathematical Formulation Cont. 0 0,,, 0,,, STRO, STRO Constraints Cont.: = + = + = + = = = NOLA LINO BONO NOLA NYLA LINO STLI BONO BONY STBO RONY NOLA LINO BONO NYLA RONY BONY LINO STLI BONO BONY STBO RONY
31 Shortest Path Problems In the shortest path problem the objective is to find the shortest path from an origin node to a destination node.
32 Assumptions of the Shortest Path Problem You need to choose a path that starts at an origin node and ends at a destination node and follows a particular path. The key to these types of problems is that ordering of the solution matters. The lines connecting nodes in the shortest path problem are known as links and usually are bidirectional. Arcs are also allowed.
33 Assumptions of the Shortest Path Problem Cont. Associated with each link is a nonnegative number known as the length. Lengths can be considered time, costs, distance, etc. The objective is to find the shortest path from the origin node to the destination node.
34 Case Study: Littletown Fire Department Littletown Fire Department is trying to find the fastest route through the county to reach a specific farming community. The fire department would like to know what is the shortest path to get from the fire department to the farming community.
35 Diagram of Littletown s Problem 8 6 A F 4 Fire Station C 1 B D 3 E H G Farming Community
36 Minimum Spanning Tree Problems (Not in textbook) Minimum spanning tree problems are problems where you are trying to find the most efficient network. You start out with nodes that have potential links and you must decide whether a link from two nodes should exist. The objective in spanning tree problems are to link all the nodes directly or indirectly to each other with the smallest amount of resources used.
37 Needed Terminology Tree A tree is a network that does not have any paths that begin and end at the same node. Spanning Tree It is a tree that provides a path between every pair of nodes, i.e., it spans the tree.
38 Assumptions of the Minimum Spanning Tree Problem You are given the nodes of the network, but not the links. You are given all the costs related to linking nodes together. You must put enough links into the network to link every pair of nodes so that the nodes are either directly or indirectly linked. The objective is to choose the links that satisfy the above at the cheapest cost.
39 Algorithm for a Minimum Spanning Tree Problem The Greedy Algorithm Step 1: Select the cheapest potential link. Step 2: Select the cheapest potential link between a node that already has a link with one that does not have a link. Step 3: Continue step two until all nodes have been directly or indirectly linked. Note: Ties may be broken arbitrarily.
40 Notes on Minimum Spanning Trees The number of links in a spanning tree are one less than the number of nodes. Each node is directly connected by a single link to at least one other node. It is possible to have multiple minimum spanning trees.
41 Case Study: The Modern Corp. Problem Modern Corp is trying to provide fiber-optic network to all its major centers. The company only needs to make sure that the centers are directly or indirectly linked to each other. They want to link the centers with the cheapest amount of links. The potential links are given on the next slide.
42 The Modern Corp. Problem A B C 7 4 E 5 G D 4 F
NETWORK OPTIMIZATION MODELS
 NETWORK OPTIMIZATION MODELS Network models Transportation, electrical and communication networks pervade our daily lives. Network representation are widely used in: Production, distribution, project planning,
NETWORK OPTIMIZATION MODELS Network models Transportation, electrical and communication networks pervade our daily lives. Network representation are widely used in: Production, distribution, project planning,
Overview. H. R. Alvarez A., Ph. D.
 Network Modeling Overview Networks arise in numerous settings: transportation, electrical, and communication networks, for example. Network representations also are widely used for problems in such diverse
Network Modeling Overview Networks arise in numerous settings: transportation, electrical, and communication networks, for example. Network representations also are widely used for problems in such diverse
Network Optimization Models. Chapter 10: Hillier and Lieberman Chapter 8: Decision Tools for Agribusiness Dr. Hurley s AGB 328 Course
 Network Optimization Models Chapter 10: Hillier and Lieberman Chapter 8: Decision Tools for Agribusiness Dr. Hurley s AGB 328 Course Terms to Know Nodes, Arcs, Directed Arc, Undirected Arc, Links, Directed
Network Optimization Models Chapter 10: Hillier and Lieberman Chapter 8: Decision Tools for Agribusiness Dr. Hurley s AGB 328 Course Terms to Know Nodes, Arcs, Directed Arc, Undirected Arc, Links, Directed
1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes:
 1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes: x 1 = -8.75-3.1 x 2 + 4.2 x 3 + 7 x 5-8 x 6 2. What constraint is added? 3. What do you need
1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes: x 1 = -8.75-3.1 x 2 + 4.2 x 3 + 7 x 5-8 x 6 2. What constraint is added? 3. What do you need
Introduction to Management Science (8th Edition, Bernard W. Taylor III) Chapter 12 Network Flow Models. Chapter 12 - Network Flow Models 1
 Introduction to Management Science (8th Edition, Bernard W. Taylor III) Chapter 12 Network Flow Models Chapter 12 - Network Flow Models 1 Chapter Topics The Shortest Route Problem The Minimal Spanning
Introduction to Management Science (8th Edition, Bernard W. Taylor III) Chapter 12 Network Flow Models Chapter 12 - Network Flow Models 1 Chapter Topics The Shortest Route Problem The Minimal Spanning
Linear Programming: Basic Concepts. Chapter 2: Hillier and Hillier
 Linear Programming: Basic Concepts Chapter 2: Hillier and Hillier Agenda Define Linear Programming The Case of the Wyndor Glass Co. A Maximization Problem Developing a Mathematical Representation of Wyndor
Linear Programming: Basic Concepts Chapter 2: Hillier and Hillier Agenda Define Linear Programming The Case of the Wyndor Glass Co. A Maximization Problem Developing a Mathematical Representation of Wyndor
Lecture 8 Network Flow Models
 Lecture 8 Andrew Nunekpeku / Charles Jackson Fall 2011 Outline 1 1 Assignment 4 When we ask for the solution of an LP, we typically mean tell me the values of the decision variables or what is the plan?
Lecture 8 Andrew Nunekpeku / Charles Jackson Fall 2011 Outline 1 1 Assignment 4 When we ask for the solution of an LP, we typically mean tell me the values of the decision variables or what is the plan?
Chapter 10: Network Flow Programming
 Chapter 10: Network Flow Programming Linear programming, that amazingly useful technique, is about to resurface: many network problems are actually just special forms of linear programs! This includes,
Chapter 10: Network Flow Programming Linear programming, that amazingly useful technique, is about to resurface: many network problems are actually just special forms of linear programs! This includes,
IV. Special Linear Programming Models
 IV. Special Linear Programming Models Some types of LP problems have a special structure and occur so frequently that we consider them separately. A. The Transportation Problem - Transportation Model -
IV. Special Linear Programming Models Some types of LP problems have a special structure and occur so frequently that we consider them separately. A. The Transportation Problem - Transportation Model -
Introduction to Mathematical Programming IE406. Lecture 16. Dr. Ted Ralphs
 Introduction to Mathematical Programming IE406 Lecture 16 Dr. Ted Ralphs IE406 Lecture 16 1 Reading for This Lecture Bertsimas 7.1-7.3 IE406 Lecture 16 2 Network Flow Problems Networks are used to model
Introduction to Mathematical Programming IE406 Lecture 16 Dr. Ted Ralphs IE406 Lecture 16 1 Reading for This Lecture Bertsimas 7.1-7.3 IE406 Lecture 16 2 Network Flow Problems Networks are used to model
APPM 4120/5120 Exam #2 Practice Solutions Spring 2015
 APPM 4120/5120 Exam #2 Practice Solutions Spring 2015 You are not allowed to use textbooks, class notes. Problem #1 (20 points): Consider the following activity-on-arc project network, where the 12 arcs
APPM 4120/5120 Exam #2 Practice Solutions Spring 2015 You are not allowed to use textbooks, class notes. Problem #1 (20 points): Consider the following activity-on-arc project network, where the 12 arcs
4. Linear Programming
 /9/08 Systems Analysis in Construction CB Construction & Building Engineering Department- AASTMT by A h m e d E l h a k e e m & M o h a m e d S a i e d. Linear Programming Optimization Network Models -
/9/08 Systems Analysis in Construction CB Construction & Building Engineering Department- AASTMT by A h m e d E l h a k e e m & M o h a m e d S a i e d. Linear Programming Optimization Network Models -
Lecture notes on Transportation and Assignment Problem (BBE (H) QTM paper of Delhi University)
 Transportation and Assignment Problems The transportation model is a special class of linear programs. It received this name because many of its applications involve determining how to optimally transport
Transportation and Assignment Problems The transportation model is a special class of linear programs. It received this name because many of its applications involve determining how to optimally transport
Network Flow Models. Chapter Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall
 Network Flow Models Chapter 7 7-1 Chapter Topics The Shortest Route Problem The Minimal Spanning Tree Problem The Maximal Flow Problem 7-2 Network Components A network is an arrangement of paths (branches)
Network Flow Models Chapter 7 7-1 Chapter Topics The Shortest Route Problem The Minimal Spanning Tree Problem The Maximal Flow Problem 7-2 Network Components A network is an arrangement of paths (branches)
Notes on Network Optimization CE 4920 Stephen Boyles Fall 2009
 Notes on Network Optimization CE 9 Stephen Boyles Fall 9 Introduction and Preliminaries From this point on, the remaining course material takes on a more tangible form than nonlinear or linear programming
Notes on Network Optimization CE 9 Stephen Boyles Fall 9 Introduction and Preliminaries From this point on, the remaining course material takes on a more tangible form than nonlinear or linear programming
Optimization Methods in Management Science
 Optimization Methods in Management Science MIT 15.053 Recitation 9 TAs: Giacomo Nannicini, Ebrahim Nasrabadi Problem 1 We apply Dijkstra s algorithm to the network given below to find the shortest path
Optimization Methods in Management Science MIT 15.053 Recitation 9 TAs: Giacomo Nannicini, Ebrahim Nasrabadi Problem 1 We apply Dijkstra s algorithm to the network given below to find the shortest path
Ch.07 Shortest Route, Minimal Spanning Tree, and Maximal Flow Models. Management Science / Prof. Bonghyun Ahn
 Ch.07 Shortest Route, Minimal Spanning Tree, and Maximal Flow Models Management Science / Prof. Bonghyun Ahn Chapter Topics Network Components The Shortest Route Problem The Minimal Spanning Tree Problem
Ch.07 Shortest Route, Minimal Spanning Tree, and Maximal Flow Models Management Science / Prof. Bonghyun Ahn Chapter Topics Network Components The Shortest Route Problem The Minimal Spanning Tree Problem
Unit.9 Integer Programming
 Unit.9 Integer Programming Xiaoxi Li EMS & IAS, Wuhan University Dec. 22-29, 2016 (revised) Operations Research (Li, X.) Unit.9 Integer Programming Dec. 22-29, 2016 (revised) 1 / 58 Organization of this
Unit.9 Integer Programming Xiaoxi Li EMS & IAS, Wuhan University Dec. 22-29, 2016 (revised) Operations Research (Li, X.) Unit.9 Integer Programming Dec. 22-29, 2016 (revised) 1 / 58 Organization of this
Transportation Planning: The maximum flow problem
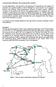 Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
Prepared By. Handaru Jati, Ph.D. Universitas Negeri Yogyakarta.
 Prepared By Handaru Jati, Ph.D Universitas Negeri Yogyakarta handaru@uny.ac.id Chapter 8 Using The Excel Solver To Solve Mathematical Programs Chapter Overview 8.1 Introduction 8.2 Formulating Mathematical
Prepared By Handaru Jati, Ph.D Universitas Negeri Yogyakarta handaru@uny.ac.id Chapter 8 Using The Excel Solver To Solve Mathematical Programs Chapter Overview 8.1 Introduction 8.2 Formulating Mathematical
Linear Programming Motivation
 Linear Programming Motivation CS 9 Staff September, 00 The slides define a combinatorial optimization problem as: Given a set of variables, each associated with a value domain, and given constraints over
Linear Programming Motivation CS 9 Staff September, 00 The slides define a combinatorial optimization problem as: Given a set of variables, each associated with a value domain, and given constraints over
Application of Bounded Variable Simplex Algorithm in Solving Maximal Flow Model
 Dhaka Univ. J. Sci. (): 9-, 3 (January) Application of Bounded Variable Simplex Algorithm in Solving Maximal Flow Model Sohana Jahan, Marzia Yesmin and Fatima Tuj Jahra Department of Mathematics,University
Dhaka Univ. J. Sci. (): 9-, 3 (January) Application of Bounded Variable Simplex Algorithm in Solving Maximal Flow Model Sohana Jahan, Marzia Yesmin and Fatima Tuj Jahra Department of Mathematics,University
Linear programming II João Carlos Lourenço
 Decision Support Models Linear programming II João Carlos Lourenço joao.lourenco@ist.utl.pt Academic year 2012/2013 Readings: Hillier, F.S., Lieberman, G.J., 2010. Introduction to Operations Research,
Decision Support Models Linear programming II João Carlos Lourenço joao.lourenco@ist.utl.pt Academic year 2012/2013 Readings: Hillier, F.S., Lieberman, G.J., 2010. Introduction to Operations Research,
CSC 8301 Design & Analysis of Algorithms: Linear Programming
 CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
CSCI 5654 (Fall 2013): Network Simplex Algorithm for Transshipment Problems.
 CSCI 5654 (Fall 21): Network Simplex Algorithm for Transshipment Problems. Sriram Sankaranarayanan November 14, 21 1 Introduction e will present the basic ideas behind the network Simplex algorithm for
CSCI 5654 (Fall 21): Network Simplex Algorithm for Transshipment Problems. Sriram Sankaranarayanan November 14, 21 1 Introduction e will present the basic ideas behind the network Simplex algorithm for
Copyright 2007 Pearson Addison-Wesley. All rights reserved. A. Levitin Introduction to the Design & Analysis of Algorithms, 2 nd ed., Ch.
 Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
2/25/2016. Minimal Spanning Tree Problem. Minimal Spanning Tree Problem. Example: Minimal Spanning Tree. Example: Minimal Spanning Tree
 // OPERATIONAL RESEARCH II Agustina Eunike, ST., MT., MBA. Industrial Engineering University of Brawijaya MINIMAL SPANNING TREE PROBLEM Minimal Spanning Tree Problem A tree is a set of connected arcs that
// OPERATIONAL RESEARCH II Agustina Eunike, ST., MT., MBA. Industrial Engineering University of Brawijaya MINIMAL SPANNING TREE PROBLEM Minimal Spanning Tree Problem A tree is a set of connected arcs that
Introduction to Linear Programming. Chapter 3: Hillier and Lieberman Chapter 3: Decision Tools for Agribusiness Dr. Hurley s AGB 328 Course
 Introduction to Linear Programming Chapter 3: Hillier and Lieberman Chapter 3: Decision Tools for Agribusiness Dr Hurley s AGB 328 Course Terms to Know Simplex Method, Feasible Region, Slope- Intercept
Introduction to Linear Programming Chapter 3: Hillier and Lieberman Chapter 3: Decision Tools for Agribusiness Dr Hurley s AGB 328 Course Terms to Know Simplex Method, Feasible Region, Slope- Intercept
ME 391Q Network Flow Programming
 ME 9Q Network Flow Programming Final Exam, Summer 00. ( Points) The figure below shows an undirected network. The parameters on the edges are the edge lengths. Find the shortest path tree using Dijkstra
ME 9Q Network Flow Programming Final Exam, Summer 00. ( Points) The figure below shows an undirected network. The parameters on the edges are the edge lengths. Find the shortest path tree using Dijkstra
Fundamentals of Operations Research. Prof. G. Srinivasan. Department of Management Studies. Indian Institute of Technology, Madras. Lecture No.
 Fundamentals of Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture No. # 13 Transportation Problem, Methods for Initial Basic Feasible
Fundamentals of Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture No. # 13 Transportation Problem, Methods for Initial Basic Feasible
Chalmers University of Technology. Network Models. April 11, Birgit Grohe
 Chalmers University of Technology Applied Optimisation lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Network Models - Examples Many different problems can be formulated as graph/network models:
Chalmers University of Technology Applied Optimisation lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Network Models - Examples Many different problems can be formulated as graph/network models:
Network Models - Examples. Network Models. Definition and Terminology. The Minimum Spanning Tree (MST) Problem
 Chalmers University of Technology Applied Optimisa- Network Models - Examples tion lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Many different problems can be formulated as graph/network models:
Chalmers University of Technology Applied Optimisa- Network Models - Examples tion lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Many different problems can be formulated as graph/network models:
ORF 307: Lecture 14. Linear Programming: Chapter 14: Network Flows: Algorithms
 ORF 307: Lecture 14 Linear Programming: Chapter 14: Network Flows: Algorithms Robert J. Vanderbei April 10, 2018 Slides last edited on April 10, 2018 http://www.princeton.edu/ rvdb Agenda Primal Network
ORF 307: Lecture 14 Linear Programming: Chapter 14: Network Flows: Algorithms Robert J. Vanderbei April 10, 2018 Slides last edited on April 10, 2018 http://www.princeton.edu/ rvdb Agenda Primal Network
Network optimization: An overview
 Network optimization: An overview Mathias Johanson Alkit Communications 1 Introduction Various kinds of network optimization problems appear in many fields of work, including telecommunication systems,
Network optimization: An overview Mathias Johanson Alkit Communications 1 Introduction Various kinds of network optimization problems appear in many fields of work, including telecommunication systems,
Dynamic modelling and network optimization
 Dynamic modelling and network optimization Risto Lahdelma Aalto University Energy Technology Otakaari 4, 25 Espoo, Finland risto.lahdelma@aalto.fi Risto Lahdelma Feb 4, 26 Outline Dynamic systems Dynamic
Dynamic modelling and network optimization Risto Lahdelma Aalto University Energy Technology Otakaari 4, 25 Espoo, Finland risto.lahdelma@aalto.fi Risto Lahdelma Feb 4, 26 Outline Dynamic systems Dynamic
of optimization problems. In this chapter, it is explained that what network design
 CHAPTER 2 Network Design Network design is one of the most important and most frequently encountered classes of optimization problems. In this chapter, it is explained that what network design is? The
CHAPTER 2 Network Design Network design is one of the most important and most frequently encountered classes of optimization problems. In this chapter, it is explained that what network design is? The
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn
 Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
The Islamic University of Gaza Faculty of Commerce Quantitative Analysis - Dr. Samir Safi Midterm #2-28/4/2014
 The Islamic University of Gaza Faculty of Commerce Quantitative Analysis - Dr. Samir Safi Midterm #2-28/4/2014 Name TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1)
The Islamic University of Gaza Faculty of Commerce Quantitative Analysis - Dr. Samir Safi Midterm #2-28/4/2014 Name TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false. 1)
Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem
 Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem Uncapacitated Networks: Basic primal and dual solutions Flow conservation constraints
Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem Uncapacitated Networks: Basic primal and dual solutions Flow conservation constraints
15.082J and 6.855J. Lagrangian Relaxation 2 Algorithms Application to LPs
 15.082J and 6.855J Lagrangian Relaxation 2 Algorithms Application to LPs 1 The Constrained Shortest Path Problem (1,10) 2 (1,1) 4 (2,3) (1,7) 1 (10,3) (1,2) (10,1) (5,7) 3 (12,3) 5 (2,2) 6 Find the shortest
15.082J and 6.855J Lagrangian Relaxation 2 Algorithms Application to LPs 1 The Constrained Shortest Path Problem (1,10) 2 (1,1) 4 (2,3) (1,7) 1 (10,3) (1,2) (10,1) (5,7) 3 (12,3) 5 (2,2) 6 Find the shortest
TIM 206 Lecture Notes Integer Programming
 TIM 206 Lecture Notes Integer Programming Instructor: Kevin Ross Scribe: Fengji Xu October 25, 2011 1 Defining Integer Programming Problems We will deal with linear constraints. The abbreviation MIP stands
TIM 206 Lecture Notes Integer Programming Instructor: Kevin Ross Scribe: Fengji Xu October 25, 2011 1 Defining Integer Programming Problems We will deal with linear constraints. The abbreviation MIP stands
ADMS 3330 FALL 2008 EXAM All Multiple choice Exam (See Answer Key on last page)
 MULTIPLE CHOICE. Choose the letter corresponding to the one alternative that best completes the statement or answers the question. 1. Which of the following are assumptions or requirements of the transportation
MULTIPLE CHOICE. Choose the letter corresponding to the one alternative that best completes the statement or answers the question. 1. Which of the following are assumptions or requirements of the transportation
Material handling and Transportation in Logistics. Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena
 Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
Mathematical Tools for Engineering and Management
 Mathematical Tools for Engineering and Management Lecture 8 8 Dec 0 Overview Models, Data and Algorithms Linear Optimization Mathematical Background: Polyhedra, Simplex-Algorithm Sensitivity Analysis;
Mathematical Tools for Engineering and Management Lecture 8 8 Dec 0 Overview Models, Data and Algorithms Linear Optimization Mathematical Background: Polyhedra, Simplex-Algorithm Sensitivity Analysis;
Lesson 08 Linear Programming
 Lesson 08 Linear Programming A mathematical approach to determine optimal (maximum or minimum) solutions to problems which involve restrictions on the variables involved. 08 - Linear Programming Applications
Lesson 08 Linear Programming A mathematical approach to determine optimal (maximum or minimum) solutions to problems which involve restrictions on the variables involved. 08 - Linear Programming Applications
COT 6936: Topics in Algorithms! Giri Narasimhan. ECS 254A / EC 2443; Phone: x3748
 COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
TRANSPORTATION AND ASSIGNMENT PROBLEMS
 TRANSPORTATION AND ASSIGNMENT PROBLEMS Transportation problem Example P&T Company produces canned peas. Peas are prepared at three canneries (Bellingham, Eugene and Albert Lea). Shipped by truck to four
TRANSPORTATION AND ASSIGNMENT PROBLEMS Transportation problem Example P&T Company produces canned peas. Peas are prepared at three canneries (Bellingham, Eugene and Albert Lea). Shipped by truck to four
Transportation Problems
 Transportation Problems Transportation is considered as a special case of LP Reasons? it can be formulated using LP technique so is its solution 1 (to p2) Here, we attempt to firstly define what are them
Transportation Problems Transportation is considered as a special case of LP Reasons? it can be formulated using LP technique so is its solution 1 (to p2) Here, we attempt to firstly define what are them
CSE 417 Network Flows (pt 4) Min Cost Flows
 CSE 417 Network Flows (pt 4) Min Cost Flows Reminders > HW6 is due Monday Review of last three lectures > Defined the maximum flow problem find the feasible flow of maximum value flow is feasible if it
CSE 417 Network Flows (pt 4) Min Cost Flows Reminders > HW6 is due Monday Review of last three lectures > Defined the maximum flow problem find the feasible flow of maximum value flow is feasible if it
BCN Decision and Risk Analysis. Syed M. Ahmed, Ph.D.
 Linear Programming Module Outline Introduction The Linear Programming Model Examples of Linear Programming Problems Developing Linear Programming Models Graphical Solution to LP Problems The Simplex Method
Linear Programming Module Outline Introduction The Linear Programming Model Examples of Linear Programming Problems Developing Linear Programming Models Graphical Solution to LP Problems The Simplex Method
Simulation. Lecture O1 Optimization: Linear Programming. Saeed Bastani April 2016
 Simulation Lecture O Optimization: Linear Programming Saeed Bastani April 06 Outline of the course Linear Programming ( lecture) Integer Programming ( lecture) Heuristics and Metaheursitics (3 lectures)
Simulation Lecture O Optimization: Linear Programming Saeed Bastani April 06 Outline of the course Linear Programming ( lecture) Integer Programming ( lecture) Heuristics and Metaheursitics (3 lectures)
Lecture 2 Generalized Representation of a Transportation Network
 Lecture 2 Generalized Representation of a Transportation Network Professor Anna Nagurney John F. Smith Memorial Professor and Director Virtual Center for Supernetworks Isenberg School of Management University
Lecture 2 Generalized Representation of a Transportation Network Professor Anna Nagurney John F. Smith Memorial Professor and Director Virtual Center for Supernetworks Isenberg School of Management University
What is Network Analyst?
 What is Network Analyst? Extension for analyzing transportation networks Four network solvers Route Closest Facility Service Area Uses Network Datasets Origin-Destination (OD) Cost Matrix Specialized layers
What is Network Analyst? Extension for analyzing transportation networks Four network solvers Route Closest Facility Service Area Uses Network Datasets Origin-Destination (OD) Cost Matrix Specialized layers
We have already seen the transportation problem and the assignment problem. Let us take the transportation problem, first.
 Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 19 Network Models In this lecture, we will discuss network models. (Refer
Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 19 Network Models In this lecture, we will discuss network models. (Refer
Solutions for Operations Research Final Exam
 Solutions for Operations Research Final Exam. (a) The buffer stock is B = i a i = a + a + a + a + a + a 6 + a 7 = + + + + + + =. And the transportation tableau corresponding to the transshipment problem
Solutions for Operations Research Final Exam. (a) The buffer stock is B = i a i = a + a + a + a + a + a 6 + a 7 = + + + + + + =. And the transportation tableau corresponding to the transshipment problem
SOLVING THE TRANSPORTATION PROBLEM WITH PIECEWISE-LINEAR CONCAVE COST FUNCTIONS
 Review of the Air Force Academy No.2 (34)/2017 SOLVING THE TRANSPORTATION PROBLEM WITH PIECEWISE-LINEAR CONCAVE COST FUNCTIONS Tatiana PAȘA, Valeriu UNGUREANU Universitatea de Stat, Chișinău, Moldova (pasa.tatiana@yahoo.com,
Review of the Air Force Academy No.2 (34)/2017 SOLVING THE TRANSPORTATION PROBLEM WITH PIECEWISE-LINEAR CONCAVE COST FUNCTIONS Tatiana PAȘA, Valeriu UNGUREANU Universitatea de Stat, Chișinău, Moldova (pasa.tatiana@yahoo.com,
= 5. x 3,1. x 1,4. x 3,7 =15. =10 x 6,3 = 8
 Network Programming Exam CSE 8 (NTU# QN M) November, Updated December, Exam Instructions ffl This take-home" exam is open book and notes. ffl The submitted exam must be your original work, achieved with
Network Programming Exam CSE 8 (NTU# QN M) November, Updated December, Exam Instructions ffl This take-home" exam is open book and notes. ffl The submitted exam must be your original work, achieved with
MULTIMEDIA UNIVERSITY FACULTY OF ENGINEERING PEM2046 ENGINEERING MATHEMATICS IV TUTORIAL
 A. Linear Programming (LP) MULTIMEDIA UNIVERSITY FACULTY OF ENGINEERING PEM046 ENGINEERING MATHEMATICS IV TUTORIAL. Identify the optimal solution and value: (a) Maximize f = 0x + 0 x (b) Minimize f = 45x
A. Linear Programming (LP) MULTIMEDIA UNIVERSITY FACULTY OF ENGINEERING PEM046 ENGINEERING MATHEMATICS IV TUTORIAL. Identify the optimal solution and value: (a) Maximize f = 0x + 0 x (b) Minimize f = 45x
Konigsberg Bridge Problem
 Graphs Konigsberg Bridge Problem c C d g A Kneiphof e D a B b f c A C d e g D a b f B Euler s Graph Degree of a vertex: the number of edges incident to it Euler showed that there is a walk starting at
Graphs Konigsberg Bridge Problem c C d g A Kneiphof e D a B b f c A C d e g D a b f B Euler s Graph Degree of a vertex: the number of edges incident to it Euler showed that there is a walk starting at
A compromise method for solving fuzzy multi objective fixed charge transportation problem
 Lecture Notes in Management Science (2016) Vol. 8, 8 15 ISSN 2008-0050 (Print), ISSN 1927-0097 (Online) A compromise method for solving fuzzy multi objective fixed charge transportation problem Ratnesh
Lecture Notes in Management Science (2016) Vol. 8, 8 15 ISSN 2008-0050 (Print), ISSN 1927-0097 (Online) A compromise method for solving fuzzy multi objective fixed charge transportation problem Ratnesh
AMPL Network Optimization
 AMPL Network Optimization ORLAB Operations Research Laboratory Borzou Rostami Politecnico di Milano, Italy December 14, 2011 Network Optimization Shortest path models Consider the problem of finding the
AMPL Network Optimization ORLAB Operations Research Laboratory Borzou Rostami Politecnico di Milano, Italy December 14, 2011 Network Optimization Shortest path models Consider the problem of finding the
Foundations of Operations Research Introduction to AMPL and Modellisation
 Foundations of Operations Research Introduction to AMPL and Modellisation Pierre Hosteins hosteins@di.unito.it Politecnico di Milano November 14th 2013 Transportation Problem and Integrality Property Graph
Foundations of Operations Research Introduction to AMPL and Modellisation Pierre Hosteins hosteins@di.unito.it Politecnico di Milano November 14th 2013 Transportation Problem and Integrality Property Graph
Graph Algorithms Maximum Flow Applications
 Chapter 5 Graph Algorithms Maximum Flow Applications Algorithm Theory WS 202/3 Fabian Kuhn Maximum Flow Applications Maximum flow has many applications Reducing a problem to a max flow problem can even
Chapter 5 Graph Algorithms Maximum Flow Applications Algorithm Theory WS 202/3 Fabian Kuhn Maximum Flow Applications Maximum flow has many applications Reducing a problem to a max flow problem can even
Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras
 Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 28 Chinese Postman Problem In this lecture we study the Chinese postman
Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 28 Chinese Postman Problem In this lecture we study the Chinese postman
OIM 413 Logistics and Transportation Lecture 2: Representation of a Transportation Network
 OIM 413 Logistics and Transportation Lecture 2: Representation of a Transportation Network Professor Anna Nagurney John F. Smith Memorial Professor and Director Virtual Center for Supernetworks Department
OIM 413 Logistics and Transportation Lecture 2: Representation of a Transportation Network Professor Anna Nagurney John F. Smith Memorial Professor and Director Virtual Center for Supernetworks Department
Introduction. Chapter 15. Optimization Modeling: Applications. Integer Programming. Manufacturing Example. Three Types of ILP Models
 Chapter 5 Optimization Modeling: Applications Integer Programming Introduction When one or more variables in an LP problem must assume an integer value we have an Integer Linear Programming (ILP) problem.
Chapter 5 Optimization Modeling: Applications Integer Programming Introduction When one or more variables in an LP problem must assume an integer value we have an Integer Linear Programming (ILP) problem.
Chapter 16. Greedy Algorithms
 Chapter 16. Greedy Algorithms Algorithms for optimization problems (minimization or maximization problems) typically go through a sequence of steps, with a set of choices at each step. A greedy algorithm
Chapter 16. Greedy Algorithms Algorithms for optimization problems (minimization or maximization problems) typically go through a sequence of steps, with a set of choices at each step. A greedy algorithm
CMPSCI 311: Introduction to Algorithms Practice Final Exam
 CMPSCI 311: Introduction to Algorithms Practice Final Exam Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question. Providing more detail including
CMPSCI 311: Introduction to Algorithms Practice Final Exam Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question. Providing more detail including
INEN 420 Final Review
 INEN 420 Final Review Office Hours: Mon, May 2 -- 2:00-3:00 p.m. Tues, May 3 -- 12:45-2:00 p.m. (Project Report/Critiques due on Thurs, May 5 by 5:00 p.m.) Tuesday, April 28, 2005 1 Final Exam: Wednesday,
INEN 420 Final Review Office Hours: Mon, May 2 -- 2:00-3:00 p.m. Tues, May 3 -- 12:45-2:00 p.m. (Project Report/Critiques due on Thurs, May 5 by 5:00 p.m.) Tuesday, April 28, 2005 1 Final Exam: Wednesday,
Final Exam Spring 2003
 .8 Final Exam Spring Name Instructions.. Please answer all questions in the exam books that are provided.. Please budget your time carefully. It is often a good idea to read the entire exam first, so that
.8 Final Exam Spring Name Instructions.. Please answer all questions in the exam books that are provided.. Please budget your time carefully. It is often a good idea to read the entire exam first, so that
PBW 654 Applied Statistics - I Urban Operations Research. Unit 3. Network Modelling
 PBW 54 Applied Statistics - I Urban Operations Research Unit 3 Network Modelling Background So far, we treated urban space as a continuum, where an entity could travel from any point to any other point
PBW 54 Applied Statistics - I Urban Operations Research Unit 3 Network Modelling Background So far, we treated urban space as a continuum, where an entity could travel from any point to any other point
Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras
 Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 18 All-Integer Dual Algorithm We continue the discussion on the all integer
Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 18 All-Integer Dual Algorithm We continue the discussion on the all integer
Network Analysis. Links, nodes, trees, graphs, paths and cycles what does it all mean? Minimal spanning tree shortest route maximum flow
 Network Analysis Minimal spanning tree shortest route maximum flow Links, nodes, trees, graphs, paths and cycles what does it all mean? Real OR in action! 1 Network Terminology Graph - set of points (nodes)
Network Analysis Minimal spanning tree shortest route maximum flow Links, nodes, trees, graphs, paths and cycles what does it all mean? Real OR in action! 1 Network Terminology Graph - set of points (nodes)
Fundamentals of Integer Programming
 Fundamentals of Integer Programming Di Yuan Department of Information Technology, Uppsala University January 2018 Outline Definition of integer programming Formulating some classical problems with integer
Fundamentals of Integer Programming Di Yuan Department of Information Technology, Uppsala University January 2018 Outline Definition of integer programming Formulating some classical problems with integer
Approximation Algorithms
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Approximation Algorithms Tamassia Approximation Algorithms 1 Applications One of
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Approximation Algorithms Tamassia Approximation Algorithms 1 Applications One of
CSE 40/60236 Sam Bailey
 CSE 40/60236 Sam Bailey Solution: any point in the variable space (both feasible and infeasible) Cornerpoint solution: anywhere two or more constraints intersect; could be feasible or infeasible Feasible
CSE 40/60236 Sam Bailey Solution: any point in the variable space (both feasible and infeasible) Cornerpoint solution: anywhere two or more constraints intersect; could be feasible or infeasible Feasible
Computational Methods in IS Research Fall Graph Algorithms Network Flow Problems
 Computational Methods in IS Research Fall 2017 Graph Algorithms Network Flow Problems Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Network Flow Problems
Computational Methods in IS Research Fall 2017 Graph Algorithms Network Flow Problems Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Network Flow Problems
CSE 417 Network Flows (pt 3) Modeling with Min Cuts
 CSE 417 Network Flows (pt 3) Modeling with Min Cuts Reminders > HW6 is due on Friday start early bug fixed on line 33 of OptimalLineup.java: > change true to false Review of last two lectures > Defined
CSE 417 Network Flows (pt 3) Modeling with Min Cuts Reminders > HW6 is due on Friday start early bug fixed on line 33 of OptimalLineup.java: > change true to false Review of last two lectures > Defined
Fundamentals of Operations Research. Prof. G. Srinivasan. Department of Management Studies. Indian Institute of Technology Madras.
 Fundamentals of Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology Madras Lecture No # 06 Simplex Algorithm Initialization and Iteration (Refer Slide
Fundamentals of Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology Madras Lecture No # 06 Simplex Algorithm Initialization and Iteration (Refer Slide
Greedy Homework Problems
 CS 1510 Greedy Homework Problems 1. (2 points) Consider the following problem: INPUT: A set S = {(x i, y i ) 1 i n} of intervals over the real line. OUTPUT: A maximum cardinality subset S of S such that
CS 1510 Greedy Homework Problems 1. (2 points) Consider the following problem: INPUT: A set S = {(x i, y i ) 1 i n} of intervals over the real line. OUTPUT: A maximum cardinality subset S of S such that
Primal Simplex Algorithm for the Pure Minimal Cost Flow Problem
 Primal Simplex Algorithm for the Pure Minimal Cost Flow Problem Algorithm This section describes the adaptation of the primal simplex algorithm for solving a pure network flow program; that is, the problem
Primal Simplex Algorithm for the Pure Minimal Cost Flow Problem Algorithm This section describes the adaptation of the primal simplex algorithm for solving a pure network flow program; that is, the problem
Integer Programming. Xi Chen. Department of Management Science and Engineering International Business School Beijing Foreign Studies University
 Integer Programming Xi Chen Department of Management Science and Engineering International Business School Beijing Foreign Studies University Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 1 / 42
Integer Programming Xi Chen Department of Management Science and Engineering International Business School Beijing Foreign Studies University Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 1 / 42
A Computer Oriented Method for Solving Transportation Problem
 Dhaka Univ. J. Sci. 63(1): 1-7, 015 (January) A Computer Oriented Method for Solving Transportation Problem Sharmin Afroz and M. Babul Hasan* Department of Mathematics, Dhaka University, Dhaka-1000, Bangladesh
Dhaka Univ. J. Sci. 63(1): 1-7, 015 (January) A Computer Oriented Method for Solving Transportation Problem Sharmin Afroz and M. Babul Hasan* Department of Mathematics, Dhaka University, Dhaka-1000, Bangladesh
OPERATIONS RESEARCH. Linear Programming Problem
 OPERATIONS RESEARCH Chapter 1 Linear Programming Problem Prof. Bibhas C. Giri Department of Mathematics Jadavpur University Kolkata, India Email: bcgiri.jumath@gmail.com 1.0 Introduction Linear programming
OPERATIONS RESEARCH Chapter 1 Linear Programming Problem Prof. Bibhas C. Giri Department of Mathematics Jadavpur University Kolkata, India Email: bcgiri.jumath@gmail.com 1.0 Introduction Linear programming
Linear Programming. L.W. Dasanayake Department of Economics University of Kelaniya
 Linear Programming L.W. Dasanayake Department of Economics University of Kelaniya Linear programming (LP) LP is one of Management Science techniques that can be used to solve resource allocation problem
Linear Programming L.W. Dasanayake Department of Economics University of Kelaniya Linear programming (LP) LP is one of Management Science techniques that can be used to solve resource allocation problem
Department of Mathematics Oleg Burdakov of 30 October Consider the following linear programming problem (LP):
 Linköping University Optimization TAOP3(0) Department of Mathematics Examination Oleg Burdakov of 30 October 03 Assignment Consider the following linear programming problem (LP): max z = x + x s.t. x x
Linköping University Optimization TAOP3(0) Department of Mathematics Examination Oleg Burdakov of 30 October 03 Assignment Consider the following linear programming problem (LP): max z = x + x s.t. x x
18 Spanning Tree Algorithms
 November 14, 2017 18 Spanning Tree Algorithms William T. Trotter trotter@math.gatech.edu A Networking Problem Problem The vertices represent 8 regional data centers which need to be connected with high-speed
November 14, 2017 18 Spanning Tree Algorithms William T. Trotter trotter@math.gatech.edu A Networking Problem Problem The vertices represent 8 regional data centers which need to be connected with high-speed
Using the Graphical Method to Solve Linear Programs J. Reeb and S. Leavengood
 PERFORMANCE EXCELLENCE IN THE WOOD PRODUCTS INDUSTRY EM 8719-E October 1998 $2.50 Using the Graphical Method to Solve Linear Programs J. Reeb and S. Leavengood A key problem faced by managers is how to
PERFORMANCE EXCELLENCE IN THE WOOD PRODUCTS INDUSTRY EM 8719-E October 1998 $2.50 Using the Graphical Method to Solve Linear Programs J. Reeb and S. Leavengood A key problem faced by managers is how to
Problem set 2. Problem 1. Problem 2. Problem 3. CS261, Winter Instructor: Ashish Goel.
 CS261, Winter 2017. Instructor: Ashish Goel. Problem set 2 Electronic submission to Gradescope due 11:59pm Thursday 2/16. Form a group of 2-3 students that is, submit one homework with all of your names.
CS261, Winter 2017. Instructor: Ashish Goel. Problem set 2 Electronic submission to Gradescope due 11:59pm Thursday 2/16. Form a group of 2-3 students that is, submit one homework with all of your names.
Using the Simplex Method to Solve Linear Programming Maximization Problems J. Reeb and S. Leavengood
 PERFORMANCE EXCELLENCE IN THE WOOD PRODUCTS INDUSTRY EM 8720-E October 1998 $3.00 Using the Simplex Method to Solve Linear Programming Maximization Problems J. Reeb and S. Leavengood A key problem faced
PERFORMANCE EXCELLENCE IN THE WOOD PRODUCTS INDUSTRY EM 8720-E October 1998 $3.00 Using the Simplex Method to Solve Linear Programming Maximization Problems J. Reeb and S. Leavengood A key problem faced
The University of Sydney MATH 2009
 The University of Sydney MTH 009 GRPH THORY Tutorial 10 Solutions 004 1. In a tournament, the score of a vertex is its out-degree, and the score sequence is a list of all the scores in non-decreasing order.
The University of Sydney MTH 009 GRPH THORY Tutorial 10 Solutions 004 1. In a tournament, the score of a vertex is its out-degree, and the score sequence is a list of all the scores in non-decreasing order.
Chapter 1 Introduction to Optimization
 Chapter 1 Introduction to Optimization Chapter Contents OVERVIEW................................... 15 DATA FLOW................................... 16 PROC LP................................... 17 PROC
Chapter 1 Introduction to Optimization Chapter Contents OVERVIEW................................... 15 DATA FLOW................................... 16 PROC LP................................... 17 PROC
The k-center problem Approximation Algorithms 2009 Petros Potikas
 Approximation Algorithms 2009 Petros Potikas 1 Definition: Let G=(V,E) be a complete undirected graph with edge costs satisfying the triangle inequality and k be an integer, 0 < k V. For any S V and vertex
Approximation Algorithms 2009 Petros Potikas 1 Definition: Let G=(V,E) be a complete undirected graph with edge costs satisfying the triangle inequality and k be an integer, 0 < k V. For any S V and vertex
Linear Programming. Readings: Read text section 11.6, and sections 1 and 2 of Tom Ferguson s notes (see course homepage).
 Linear Programming Learning Goals. Introduce Linear Programming Problems. Widget Example, Graphical Solution. Basic Theory: Feasible Set, Vertices, Existence of Solutions. Equivalent formulations. Outline
Linear Programming Learning Goals. Introduce Linear Programming Problems. Widget Example, Graphical Solution. Basic Theory: Feasible Set, Vertices, Existence of Solutions. Equivalent formulations. Outline
OPTIMIZAÇÃO E DECISÃO 09/10
 OPTIMIZAÇÃO E DECISÃO 09/10 PL #7 Integer Programming Alexandra Moutinho (from Hillier & Lieberman Introduction to Operations Research, 8 th edition) Problem 1 Pawtucket University is planning to buy new
OPTIMIZAÇÃO E DECISÃO 09/10 PL #7 Integer Programming Alexandra Moutinho (from Hillier & Lieberman Introduction to Operations Research, 8 th edition) Problem 1 Pawtucket University is planning to buy new
Linear Programming. Widget Factory Example. Linear Programming: Standard Form. Widget Factory Example: Continued.
 Linear Programming Widget Factory Example Learning Goals. Introduce Linear Programming Problems. Widget Example, Graphical Solution. Basic Theory:, Vertices, Existence of Solutions. Equivalent formulations.
Linear Programming Widget Factory Example Learning Goals. Introduce Linear Programming Problems. Widget Example, Graphical Solution. Basic Theory:, Vertices, Existence of Solutions. Equivalent formulations.
Linear Programming CISC4080, Computer Algorithms CIS, Fordham Univ. Linear Programming
 Linear Programming CISC4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang! Linear Programming In a linear programming problem, there is a set of variables, and we want to assign real values
Linear Programming CISC4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang! Linear Programming In a linear programming problem, there is a set of variables, and we want to assign real values
4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Mathematical programming (optimization) problem: min f (x) s.t. x X R n set of feasible solutions with linear objective function
4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Mathematical programming (optimization) problem: min f (x) s.t. x X R n set of feasible solutions with linear objective function
Artificial Intelligence
 Artificial Intelligence Shortest Path Problem G. Guérard Department of Nouvelles Energies Ecole Supérieur d Ingénieurs Léonard de Vinci Lecture 3 GG A.I. 1/42 Outline 1 The Shortest Path Problem Introduction
Artificial Intelligence Shortest Path Problem G. Guérard Department of Nouvelles Energies Ecole Supérieur d Ingénieurs Léonard de Vinci Lecture 3 GG A.I. 1/42 Outline 1 The Shortest Path Problem Introduction
CMPSCI611: The Simplex Algorithm Lecture 24
 CMPSCI611: The Simplex Algorithm Lecture 24 Let s first review the general situation for linear programming problems. Our problem in standard form is to choose a vector x R n, such that x 0 and Ax = b,
CMPSCI611: The Simplex Algorithm Lecture 24 Let s first review the general situation for linear programming problems. Our problem in standard form is to choose a vector x R n, such that x 0 and Ax = b,
