NETWORK OPTIMIZATION MODELS
|
|
|
- Lesley Conley
- 5 years ago
- Views:
Transcription
1 NETWORK OPTIMIZATION MODELS Network models Transportation, electrical and communication networks pervade our daily lives. Network representation are widely used in: Production, distribution, project planning, facilities location, resource management, financial planning, etc. Algorithms and software are being used to solve huge network problems on a routine basis. Many network problems are special cases of linear programming problems. 4
2 Prototype example Seervada Park has a limited amount of sightseeing and backpack hiking. O: entrance of the park. T: station with scenic wonder. 42 Park problems Determine route from park entrance to station T with smallest total distance for the operation of trams. Telephone lines must be installed under the roads to establish communication among all the stations. This should be accomplished with a minimum total distance of lines. Route the various trips of trams to maximize the number of trips per day without violating the limits of any road. 43 2
3 Typical networks Nodes Arcs Flow Intersections Roads Vehicles Airports Air lanes Aircraft Switching points Wires, channels Messages Pumping stations Pipes Fluids Work centers Material-handling sources Jobs 44 Terminology of networks Network is a set of points (nodes or vertices) and a set of lines (arcs or links or edges or branches) connecting certain pairs of the nodes. Example: road system of Seervada Park has 7 nodes and 2 arcs. Flow in only one direction is a directed arc. Flow allowed in either directions: undirected arc or link. Network with only directed arcs is a directed network. 45 3
4 Terminology of networks Network with only undirected arcs is an undirected network. A path between two nodes is a sequence of distinct arcs connecting these nodes. A directed path from node i to node j is a sequence of connecting arcs whose direction is toward node j. Anundirected path from node i to node j is a sequence of connecting arcs whose direction (if any) can be either toward or away from node j. 46 Example Distribution Unlimited Co. produces the same new product at two different factories. Products must be shipped to two warehouses (a distribution center is available). 47 4
5 Example of a directed network 48 Terminology of networks A path that begins and ends at the same node is a cycle. Two nodes are connected if the network contains at least one undirected path between them. A connected network is a network where every pair of nodes is connected. A tree is a connected network (for some subset of the n nodes of the original network) that contains no undirected cycles. 49 5
6 Terminology of networks A spanning tree is a connected network for all n nodes of the original network that contains no undirected cycles. Spanning tree has exactly n arcs. The maximum amount of flow that can be carried on a directed arc is the arc capacity. Supply node: the flow out of the node exceeds the flow into the node. The reverse in a demand node. Transshipment node: node where the amount of flow out equals the amount of flow in. 5 Growing tree one arc a time a) Nodes without arcs b) Tree with one arc c) Tree with two arcs d) Tree with three arcs e) A spanning tree 5 6
7 Shortest-path problem Consider an undirected and connected network with the special nodes called origin and destination. Eachlink (undirected arc) has an associated distance. Objective: find the shortest path from the origin to the destination. Algorithm: starting from the origin, successively identifies the shortest path to each of the nodes in the ascending order of their distances from the origin. The problem is solved when the destination is reached. 52 Algorithm for shortest-path problem Objective of nth iteration: find the nth nearest node to the origin (n =, 2, ) until the nth nearest node is reached. Input for the nth iteration: n nearest nodes to the origin, including their shortest path and distance to the origin (these are the solved nodes). Candidates for the nth nearest node: each solved that is directly connected to unsolved nodes provides one candidate the unsolved node with the shortest connecting link. 53 7
8 Algorithm for shortest-path problem Calculation of the nth nearest node: for each solved and its candidate, add the distance between them to the distance of the shortest path from the origin to this solved node. The candidate with the smallest total distance is the nth nearest node, and its shortest path is the one generating this distance. 54 Example: Seervada park n Solved nodes directly connected to unsolved nodes Closest connected unsolved node Total distance involved nth nearest node Minimum distance Last connection 55 8
9 Example: Seervada park n Solved nodes directly connected to unsolved nodes Closest connected unsolved node Total distance involved nth nearest node Minimum distance Last connection O A 2 A 2 OA 2,3 O C 4 C 4 OC A B = 4 B 4 AB A D = 9 4 B E = 7 E 7 BE C E = 8 A D = 9 5 B D = 8 D 8 BD E D 7 + = 8 D 8 ED 6 D T = 3 T 3 DT E T = 4 56 Solution 57 9
10 Using simplex to solve the problem Seervada Park Shortest-Path Problem From To On Route Distance Nodes Net Flow Supply/Demand Range Name Cells O A 2 O = Distance F4:F7 O B 5 A = From B4:B7 O C 4 B = NetFlow I4:I A B 2 C = Nodes H4:H A D 7 D = OnRoute D4:D7 B C E = SupplyDemand K4:K B D 4 T - = - To C4:C7 B E 3 TotalDistance D9 C B C E 4 D E D T 5 E D E T 7 Total Distance 3 58 Using simplex to solve the problem 59
11 Applications of shortest path Main applications:. Minimize the total distance traveled. 2. Minimize the total cost of a sequence of activities. 3. Minimize the total time of a sequence of activities. 4. Combination of the previous three. What happens if the network is directed? How to optimize from the source to all other nodes? How to find the shortest path from every node to every other node? 6 Minimum spanning tree problem Also for undirected and connected networks. A positive length (distance, cost, time, etc.) is associated with each link. Both the shortest path problem and the minimum spanning tree choose a set of links that satisfy a certain property. Objective: find the shortest total length that provide a path between each pair of nodes. 6
12 Minimum spanning tree problem Definitions: Nodes of the network are given, as well as potential links and positive length for each if it is inserted in the network. The network should insert links in order to have a path between each pair of nodes. These links must minimize the total length of the links inserted into the network. 62 Properties A network with n nodes requires n links to provide a path between each pair of nodes. The n links form a spanning tree. Which is a spanning tree: (a), (b) or (c)? 63 2
13 Applications Design of telecommunication networks: fiber-optic, computer, leased-line telephone cable television, etc. Design of a lightly used transportation network to minimize the total cost of providing the links. Design of a network of high-voltage electrical power transmission lines. Design of a network of wiring on electrical equipment to minimize the total length of wire. Design of a network of pipelines to connect locations. 64 Algorithm for minimum spanning tree Can be solved in a straightforward way using a greedy algorithm.. Select any node, and connect it to the nearest distinct node. 2. Identify the unconnected node that is closest to a connected node, and connect the two nodes. Repeat this step until all nodes have been connected. Tie breaking: can be done arbitrarily. It can indicate that more than one optimal solution exist. 65 3
14 Application to Seervada park Total length of the links: 4. Verify that the choice of the initial node does not affect the final solution. 66 Maximum flow problems Third problem in Seervada Park: route the tram trips from the park entrance to the scenic wonder to maximize the number of trips per day. Outgoing trips allowed per day: 67 4
15 Feasible solution One solution (not optimal): 5 trams using the route O B E T tram using O B C E T tram using O B C E D T 68 Definition of maximum flow problem All flows through a directed and connected network from the source to the sink. All remaining nodes are transshipment nodes. Flow through an arc in only allowed in the direction indicated by the arrowhead. Maximum amount of flow is given by the capacity of that node. Objective: maximize the total amount of flow from the source to the sink. 69 5
16 Applications Maximize the flow through a company s distribution network from its factories to its costumers. Maximize the flow through a company s supply network from its vendors (suppliers) to its factories. Maximize the flow of oil through a system of pipelines. Maximize the flow of water through a system aqueducts. Maximize the flow of vehicles through a transportation network. 7 Some applications For some applications, the flow may be originated at more than one node, and the may also terminate at more than one node. More than one source: include a dummy source with capacity equal to the maximum flow. More than one sink: include a dummy sink with capacity equal to the maximum flow. Maximum flow problem is a linear programming problem; can be solved by the simplex method. However, the augmented path algorithm is more efficient. 7 6
17 Augmented path algorithm Every arc is changed from a directed to an undirected arc: O 7 B O 7 B Residual network shows the residual capacities for assigning additional flows: O 2 5 B 72 Seervada Park residual network Augmenting path is a directed path from the source to the sink, such that every path has strictly positive residual capacity. 73 7
18 Iteration of augmented path algorithm. Identify an augmenting path (directed path from source to sink with positive residual capacity). 2. Residual capacity c * is the minimum of residual capacities of the arcs. Increase the flow by c *. 3. Decrease c * the residual capacity of each arc on this augmented path. Increase c * the residual capacity of each arc in the opposite direction. Return to Step. Several augmented paths can be chosen. Its choice is important for the efficiency of large-scale networks. 74 Application to Seervada Park Initial residual network: 75 8
19 Iteration Iteration : one of several augmenting paths is O B E T residual capacity is min{7, 6, 5} = Iteration 2 Iteration 2: assign a flow of 3 to the augmenting path O A D T
20 Iterations 3 and 4 Iteration 3: assign flow of to augmenting path O A B D T Iteration 4: assign flow of 2 to augmenting path O B D T Iterations 5 and 6 Iteration 5: assign flow of to augmenting path O C E D T Iteration 6: assign flow of to augmenting path O C E T
21 Iteration 7 Iteration 7: assign flow of to augmenting path O C E B D T Optimal solution After iteration 7 there are no more augmenting paths. Optimal flow pattern is: 8 2
22 Finding an augmenting path This can be difficult, especially for large networks. Procedure: Find all nodes that can be reached from the source along a single arc with strictly positive residual capacity. For each reached node, find all new nodes from this node that can be reached along an arc with strictly positive residual capacity. Repeat this successively with the new nodes as they are reached. 82 Example in Seervada Park Residual network after Iteration 6 is given, as well as the possible augmenting path
23 How to recognize the optimal? Using the maximum-flow min-cut theorem. Cut: any set of directed arcs containing at least one arc from every directed path from the source to the sink. Cut value: sum of the arc capacities of the arcs (in the specified direction) of the cut. Maximum-flow min-cut theorem: for any network with a single source and sink, the maximum feasible flow from the source to the sink equals the minimum cut value for all cuts of the network. 84 Maximum-flow min-cut theorem F is the amount of flow from the source to the sink for any feasible flow pattern. Example: value of cut is = 4. This is the maximum value of F, so this is the minimum cut
24 Using simplex to solve the problem Seervada Park Maximum Flow Problem From To Flow Capacity Nodes Net Flow Supply/Demand Range Name Cells O A 3 <= 5 O 4 Capacity F4:F5 O B 7 <= 7 A = Flow D4:D5 O C 4 <= 4 B = From B4:B5 A B <= C = MaximumFlow D7 A D 3 <= 3 D = NetFlow I4:I B C <= 2 E = Nodes H4:H B D 4 <= 4 T -4 SupplyDemand K5:K9 B E 3 <= 5 To C4:C5 C E 4 <= 4 D T 8 <= 9 E D <= E T 6 <= 6 Maximum Flow 4 86 Using simplex to solve the problem 87 24
25 Minimum cost flow problem It contains a large number of applications and it can be solved extremely efficiently. Like the maximum flow problem, it considers flow through a network with limited arc capacities. Like the shortest-path problem, it considers a cost (or distance) for flow through an arc. Like the transportation problem or assignment problem, it can consider multiple sources (supply nodes) and multiple destinations (demand nodes) for the flow, again with associated costs. 88 Minimum cost flow problem The four previous problems are all special cases of the minimum cost flow problem. This problem can be formulated as a linear programming problem, solved using a streamlined version of the simplex method: network simplex method 89 25
26 Definition of minimum cost flow problem. The network is a directed and connected network. 2. At least one of the nodes is a supply node. 3. At least one of the other nodes is a demand node. 4. All the remaining nodes are transshipment nodes. 5. Flow through an arc is in the direction of the arrow. Maximum amount of flow is the capacity of the arc. 6. Network has enough arcs with sufficient capacity such that all flow generated at supply nodes reach the demand nodes. 7. Cost of flow through each arc is proportional to the amount of that flow. 8. Objective: minimize the total cost (profit) of sending the available supply through the network to satisfy the demand. 9 Applications Kind of application Supply nodes Transshipment nodes Demand nodes Operation of a distributed network Sources of goods Intermediate storage facilities Customers Solid waste management Sources of solid waste Processing facilities Landfill locations Operation of a supply network Vendors Intermediate warehouses Processing facilities Coordinating product mixes at plants Plants Production of a specific product Market for a specific product Cash flow management Sources of cash at a specific time Short-term investment options Needs for cash at a specific time 9 26
27 Formulation of the model Decision variables: x ij = flow through arc i j Given information: c ij = cost per unit flow through arc i j u ij = arc capacity for arc i j b i = net flow generated at node i Value of b i depends on nature of node i: b i > if node i is a supply node b i < if node i is a demand node b i = if node i is a transshipment node 92 Formulation of the model n n i j minimize Z cx, subject to n n ij ij ij ji i j j node constraints x x b, for each node i, and x u, for each arc i j ij ij 93 27
28 Minimum cost flow problem Feasible solutions property: necessary condition for a minimum flow problem to have feasible solutions: n i b i If this condition does not hold, a dummy source or a dummy destination is needed. Integer solutions property: when every b i and u ij have integer values, al the basic variables in every basic feasible (BF) solution also have integer values. 94 Example Distribution network for the Distribution Unlimited Co
29 Example Linear programming problem: minimize Z 2xAB 4xAC 9xAD 3xBC xce 3xDE 2 xed, subject to xab xac xad xab xbc 5 4 x x x AC BC CE x x x 3 AD DE ED x x x 6 CE DE ED and x, x 8, all x. AB CE ij 96 Using simplex to solve the problem Distribution Unlimited Co. Minimum Cost Flow Problem From To Ship Capacity Unit Cost Nodes Net Flow Supply/Demand Range Name Cells A B <= 2 A 5 = 5 From B4:B A C 4 4 B 4 = 4 NetFlow J4:J8 A D 9 C = Nodes I4:I8 B C 4 3 D -3 = -3 Ship D4:D C E 8 <= 8 E -6 = -6 SupplyDemand L4:L8 D E 3 To C4:C E D 2 2 TotalCost D2 UnitCost G4:G Total Cost
30 Using simplex to solve the problem 98 Special cases Transportation problem. A supply node is provided for each source and a demand node for each destination. No transshipment nodes are included. Assignment problem. As in the transportation problem and Number of supply nodes equal to number of demand nodes b i = for supply nodes and b i = for demand nodes. Transshipment problem. A minimum cost flow problem with unlimited arc capacities: u ij =. 99 3
31 Special cases Shortest-path problem A supply node with the supply of is provided for the origin A demand node with the demand of is provided for the destination. Rest of nodes are transshipment nodes. Each undirected link is replaced by a pair of directed arcs in opposite directions (c ij = c ji ). No arc capacities are imposed: u ij = +. 2 Example of shortest-path problem 2 3
32 Special cases Maximum flow problem Already provided with one supply node (source) and one demand node (sink). Set c ij = for all existing arcs (absence of costs). Select F, which is a safe upper bound of the maximum feasible flow through the network, and assign it as a supply and a demand. Add an arc from the supply node to the demand node and assign a cost, c ij = M, as well as unlimited capacity, u ij =. 22 Example of maximum flow problem 23 32
33 Network simplex method Highly streamlined version of the simplex method for solving minimum cost flow problems. Goes from one BF solution to another one using the network itself (without using the simplex tableau). There is a correspondence between BF solutions and feasible spanning trees. See example in Hillier s book, OR and IOR examples, and computational implementations
Overview. H. R. Alvarez A., Ph. D.
 Network Modeling Overview Networks arise in numerous settings: transportation, electrical, and communication networks, for example. Network representations also are widely used for problems in such diverse
Network Modeling Overview Networks arise in numerous settings: transportation, electrical, and communication networks, for example. Network representations also are widely used for problems in such diverse
Network Optimization Models. Chapter 10: Hillier and Lieberman Chapter 8: Decision Tools for Agribusiness Dr. Hurley s AGB 328 Course
 Network Optimization Models Chapter 10: Hillier and Lieberman Chapter 8: Decision Tools for Agribusiness Dr. Hurley s AGB 328 Course Terms to Know Nodes, Arcs, Directed Arc, Undirected Arc, Links, Directed
Network Optimization Models Chapter 10: Hillier and Lieberman Chapter 8: Decision Tools for Agribusiness Dr. Hurley s AGB 328 Course Terms to Know Nodes, Arcs, Directed Arc, Undirected Arc, Links, Directed
Network Analysis. Links, nodes, trees, graphs, paths and cycles what does it all mean? Minimal spanning tree shortest route maximum flow
 Network Analysis Minimal spanning tree shortest route maximum flow Links, nodes, trees, graphs, paths and cycles what does it all mean? Real OR in action! 1 Network Terminology Graph - set of points (nodes)
Network Analysis Minimal spanning tree shortest route maximum flow Links, nodes, trees, graphs, paths and cycles what does it all mean? Real OR in action! 1 Network Terminology Graph - set of points (nodes)
Network Optimization Problems. Chapter 6: Hillier and Hillier
 Network Optimization Problems Chapter 6: Hillier and Hillier Agenda Minimum-Cost Flow Problems Case Study: Distribution Unlimited Co. Maximum Flow Problems Case Study: BMZ Company Shortest Path Problems
Network Optimization Problems Chapter 6: Hillier and Hillier Agenda Minimum-Cost Flow Problems Case Study: Distribution Unlimited Co. Maximum Flow Problems Case Study: BMZ Company Shortest Path Problems
Lecture 8 Network Flow Models
 Lecture 8 Andrew Nunekpeku / Charles Jackson Fall 2011 Outline 1 1 Assignment 4 When we ask for the solution of an LP, we typically mean tell me the values of the decision variables or what is the plan?
Lecture 8 Andrew Nunekpeku / Charles Jackson Fall 2011 Outline 1 1 Assignment 4 When we ask for the solution of an LP, we typically mean tell me the values of the decision variables or what is the plan?
Lecture notes on Transportation and Assignment Problem (BBE (H) QTM paper of Delhi University)
 Transportation and Assignment Problems The transportation model is a special class of linear programs. It received this name because many of its applications involve determining how to optimally transport
Transportation and Assignment Problems The transportation model is a special class of linear programs. It received this name because many of its applications involve determining how to optimally transport
TRANSPORTATION AND ASSIGNMENT PROBLEMS
 TRANSPORTATION AND ASSIGNMENT PROBLEMS Transportation problem Example P&T Company produces canned peas. Peas are prepared at three canneries (Bellingham, Eugene and Albert Lea). Shipped by truck to four
TRANSPORTATION AND ASSIGNMENT PROBLEMS Transportation problem Example P&T Company produces canned peas. Peas are prepared at three canneries (Bellingham, Eugene and Albert Lea). Shipped by truck to four
Chalmers University of Technology. Network Models. April 11, Birgit Grohe
 Chalmers University of Technology Applied Optimisation lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Network Models - Examples Many different problems can be formulated as graph/network models:
Chalmers University of Technology Applied Optimisation lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Network Models - Examples Many different problems can be formulated as graph/network models:
Network Models - Examples. Network Models. Definition and Terminology. The Minimum Spanning Tree (MST) Problem
 Chalmers University of Technology Applied Optimisa- Network Models - Examples tion lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Many different problems can be formulated as graph/network models:
Chalmers University of Technology Applied Optimisa- Network Models - Examples tion lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Many different problems can be formulated as graph/network models:
COT 6936: Topics in Algorithms! Giri Narasimhan. ECS 254A / EC 2443; Phone: x3748
 COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
Introduction to Mathematical Programming IE406. Lecture 16. Dr. Ted Ralphs
 Introduction to Mathematical Programming IE406 Lecture 16 Dr. Ted Ralphs IE406 Lecture 16 1 Reading for This Lecture Bertsimas 7.1-7.3 IE406 Lecture 16 2 Network Flow Problems Networks are used to model
Introduction to Mathematical Programming IE406 Lecture 16 Dr. Ted Ralphs IE406 Lecture 16 1 Reading for This Lecture Bertsimas 7.1-7.3 IE406 Lecture 16 2 Network Flow Problems Networks are used to model
Material handling and Transportation in Logistics. Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena
 Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
Network Flow Models. Chapter Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall
 Network Flow Models Chapter 7 7-1 Chapter Topics The Shortest Route Problem The Minimal Spanning Tree Problem The Maximal Flow Problem 7-2 Network Components A network is an arrangement of paths (branches)
Network Flow Models Chapter 7 7-1 Chapter Topics The Shortest Route Problem The Minimal Spanning Tree Problem The Maximal Flow Problem 7-2 Network Components A network is an arrangement of paths (branches)
APPM 4120/5120 Exam #2 Practice Solutions Spring 2015
 APPM 4120/5120 Exam #2 Practice Solutions Spring 2015 You are not allowed to use textbooks, class notes. Problem #1 (20 points): Consider the following activity-on-arc project network, where the 12 arcs
APPM 4120/5120 Exam #2 Practice Solutions Spring 2015 You are not allowed to use textbooks, class notes. Problem #1 (20 points): Consider the following activity-on-arc project network, where the 12 arcs
Source. Sink. Chapter 10: Iterative Programming Maximum Flow Problem. CmSc250 Intro to Algorithms
 Chapter 10: Iterative Programming Maximum Flow Problem CmSc20 Intro to Algorithms A flow network is a model of a system where some material is produced at its source, travels through the system, and is
Chapter 10: Iterative Programming Maximum Flow Problem CmSc20 Intro to Algorithms A flow network is a model of a system where some material is produced at its source, travels through the system, and is
Notes on Network Optimization CE 4920 Stephen Boyles Fall 2009
 Notes on Network Optimization CE 9 Stephen Boyles Fall 9 Introduction and Preliminaries From this point on, the remaining course material takes on a more tangible form than nonlinear or linear programming
Notes on Network Optimization CE 9 Stephen Boyles Fall 9 Introduction and Preliminaries From this point on, the remaining course material takes on a more tangible form than nonlinear or linear programming
1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes:
 1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes: x 1 = -8.75-3.1 x 2 + 4.2 x 3 + 7 x 5-8 x 6 2. What constraint is added? 3. What do you need
1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes: x 1 = -8.75-3.1 x 2 + 4.2 x 3 + 7 x 5-8 x 6 2. What constraint is added? 3. What do you need
Introduction to Management Science (8th Edition, Bernard W. Taylor III) Chapter 12 Network Flow Models. Chapter 12 - Network Flow Models 1
 Introduction to Management Science (8th Edition, Bernard W. Taylor III) Chapter 12 Network Flow Models Chapter 12 - Network Flow Models 1 Chapter Topics The Shortest Route Problem The Minimal Spanning
Introduction to Management Science (8th Edition, Bernard W. Taylor III) Chapter 12 Network Flow Models Chapter 12 - Network Flow Models 1 Chapter Topics The Shortest Route Problem The Minimal Spanning
CSC 8301 Design & Analysis of Algorithms: Linear Programming
 CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
Solutions for Operations Research Final Exam
 Solutions for Operations Research Final Exam. (a) The buffer stock is B = i a i = a + a + a + a + a + a 6 + a 7 = + + + + + + =. And the transportation tableau corresponding to the transshipment problem
Solutions for Operations Research Final Exam. (a) The buffer stock is B = i a i = a + a + a + a + a + a 6 + a 7 = + + + + + + =. And the transportation tableau corresponding to the transshipment problem
Integer Programming. Xi Chen. Department of Management Science and Engineering International Business School Beijing Foreign Studies University
 Integer Programming Xi Chen Department of Management Science and Engineering International Business School Beijing Foreign Studies University Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 1 / 42
Integer Programming Xi Chen Department of Management Science and Engineering International Business School Beijing Foreign Studies University Xi Chen (chenxi0109@bfsu.edu.cn) Integer Programming 1 / 42
Graphs and Network Flows IE411. Lecture 13. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
Chapter 10: Network Flow Programming
 Chapter 10: Network Flow Programming Linear programming, that amazingly useful technique, is about to resurface: many network problems are actually just special forms of linear programs! This includes,
Chapter 10: Network Flow Programming Linear programming, that amazingly useful technique, is about to resurface: many network problems are actually just special forms of linear programs! This includes,
Dynamic modelling and network optimization
 Dynamic modelling and network optimization Risto Lahdelma Aalto University Energy Technology Otakaari 4, 25 Espoo, Finland risto.lahdelma@aalto.fi Risto Lahdelma Feb 4, 26 Outline Dynamic systems Dynamic
Dynamic modelling and network optimization Risto Lahdelma Aalto University Energy Technology Otakaari 4, 25 Espoo, Finland risto.lahdelma@aalto.fi Risto Lahdelma Feb 4, 26 Outline Dynamic systems Dynamic
Transportation Planning: The maximum flow problem
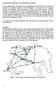 Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
0.0.1 Network Analysis
 Graph Theory 0.0.1 Network Analysis Prototype Example: In Algonquian Park the rangers have set up snowmobile trails with various stops along the way. The system of trails is our Network. The main entrance
Graph Theory 0.0.1 Network Analysis Prototype Example: In Algonquian Park the rangers have set up snowmobile trails with various stops along the way. The system of trails is our Network. The main entrance
56:272 Integer Programming & Network Flows Final Exam -- December 16, 1997
 56:272 Integer Programming & Network Flows Final Exam -- December 16, 1997 Answer #1 and any five of the remaining six problems! possible score 1. Multiple Choice 25 2. Traveling Salesman Problem 15 3.
56:272 Integer Programming & Network Flows Final Exam -- December 16, 1997 Answer #1 and any five of the remaining six problems! possible score 1. Multiple Choice 25 2. Traveling Salesman Problem 15 3.
of optimization problems. In this chapter, it is explained that what network design
 CHAPTER 2 Network Design Network design is one of the most important and most frequently encountered classes of optimization problems. In this chapter, it is explained that what network design is? The
CHAPTER 2 Network Design Network design is one of the most important and most frequently encountered classes of optimization problems. In this chapter, it is explained that what network design is? The
Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret
 Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret Greedy Algorithms (continued) The best known application where the greedy algorithm is optimal is surely
Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret Greedy Algorithms (continued) The best known application where the greedy algorithm is optimal is surely
Optimization Methods in Management Science
 Optimization Methods in Management Science MIT 15.053 Recitation 9 TAs: Giacomo Nannicini, Ebrahim Nasrabadi Problem 1 We apply Dijkstra s algorithm to the network given below to find the shortest path
Optimization Methods in Management Science MIT 15.053 Recitation 9 TAs: Giacomo Nannicini, Ebrahim Nasrabadi Problem 1 We apply Dijkstra s algorithm to the network given below to find the shortest path
CSCI 5654 (Fall 2013): Network Simplex Algorithm for Transshipment Problems.
 CSCI 5654 (Fall 21): Network Simplex Algorithm for Transshipment Problems. Sriram Sankaranarayanan November 14, 21 1 Introduction e will present the basic ideas behind the network Simplex algorithm for
CSCI 5654 (Fall 21): Network Simplex Algorithm for Transshipment Problems. Sriram Sankaranarayanan November 14, 21 1 Introduction e will present the basic ideas behind the network Simplex algorithm for
IV. Special Linear Programming Models
 IV. Special Linear Programming Models Some types of LP problems have a special structure and occur so frequently that we consider them separately. A. The Transportation Problem - Transportation Model -
IV. Special Linear Programming Models Some types of LP problems have a special structure and occur so frequently that we consider them separately. A. The Transportation Problem - Transportation Model -
4. Linear Programming
 /9/08 Systems Analysis in Construction CB Construction & Building Engineering Department- AASTMT by A h m e d E l h a k e e m & M o h a m e d S a i e d. Linear Programming Optimization Network Models -
/9/08 Systems Analysis in Construction CB Construction & Building Engineering Department- AASTMT by A h m e d E l h a k e e m & M o h a m e d S a i e d. Linear Programming Optimization Network Models -
PBW 654 Applied Statistics - I Urban Operations Research. Unit 3. Network Modelling
 PBW 54 Applied Statistics - I Urban Operations Research Unit 3 Network Modelling Background So far, we treated urban space as a continuum, where an entity could travel from any point to any other point
PBW 54 Applied Statistics - I Urban Operations Research Unit 3 Network Modelling Background So far, we treated urban space as a continuum, where an entity could travel from any point to any other point
Final Exam Spring 2003
 .8 Final Exam Spring Name Instructions.. Please answer all questions in the exam books that are provided.. Please budget your time carefully. It is often a good idea to read the entire exam first, so that
.8 Final Exam Spring Name Instructions.. Please answer all questions in the exam books that are provided.. Please budget your time carefully. It is often a good idea to read the entire exam first, so that
Easter Term OPTIMIZATION
 DPK OPTIMIZATION Easter Term Example Sheet It is recommended that you attempt about the first half of this sheet for your first supervision and the remainder for your second supervision An additional example
DPK OPTIMIZATION Easter Term Example Sheet It is recommended that you attempt about the first half of this sheet for your first supervision and the remainder for your second supervision An additional example
Module 10. Network Simplex Method:
 Module 10 1 Network Simplex Method: In this lecture we shall study a specialized simplex method specifically designed to solve network structured linear programming problems. This specialized algorithm
Module 10 1 Network Simplex Method: In this lecture we shall study a specialized simplex method specifically designed to solve network structured linear programming problems. This specialized algorithm
Copyright 2007 Pearson Addison-Wesley. All rights reserved. A. Levitin Introduction to the Design & Analysis of Algorithms, 2 nd ed., Ch.
 Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Network optimization: An overview
 Network optimization: An overview Mathias Johanson Alkit Communications 1 Introduction Various kinds of network optimization problems appear in many fields of work, including telecommunication systems,
Network optimization: An overview Mathias Johanson Alkit Communications 1 Introduction Various kinds of network optimization problems appear in many fields of work, including telecommunication systems,
Department of Mathematics Oleg Burdakov of 30 October Consider the following linear programming problem (LP):
 Linköping University Optimization TAOP3(0) Department of Mathematics Examination Oleg Burdakov of 30 October 03 Assignment Consider the following linear programming problem (LP): max z = x + x s.t. x x
Linköping University Optimization TAOP3(0) Department of Mathematics Examination Oleg Burdakov of 30 October 03 Assignment Consider the following linear programming problem (LP): max z = x + x s.t. x x
TIM 206 Lecture Notes Integer Programming
 TIM 206 Lecture Notes Integer Programming Instructor: Kevin Ross Scribe: Fengji Xu October 25, 2011 1 Defining Integer Programming Problems We will deal with linear constraints. The abbreviation MIP stands
TIM 206 Lecture Notes Integer Programming Instructor: Kevin Ross Scribe: Fengji Xu October 25, 2011 1 Defining Integer Programming Problems We will deal with linear constraints. The abbreviation MIP stands
Lesson 08 Linear Programming
 Lesson 08 Linear Programming A mathematical approach to determine optimal (maximum or minimum) solutions to problems which involve restrictions on the variables involved. 08 - Linear Programming Applications
Lesson 08 Linear Programming A mathematical approach to determine optimal (maximum or minimum) solutions to problems which involve restrictions on the variables involved. 08 - Linear Programming Applications
NCSS Statistical Software
 Chapter 491 Introduction Given a directed network defined by nodes, arcs, and flow capacities, this procedure finds the maximum flow that can occur between a source node and a sink node. An example of
Chapter 491 Introduction Given a directed network defined by nodes, arcs, and flow capacities, this procedure finds the maximum flow that can occur between a source node and a sink node. An example of
Network Flow. November 23, CMPE 250 Graphs- Network Flow November 23, / 31
 Network Flow November 23, 2016 CMPE 250 Graphs- Network Flow November 23, 2016 1 / 31 Types of Networks Internet Telephone Cell Highways Rail Electrical Power Water Sewer Gas... CMPE 250 Graphs- Network
Network Flow November 23, 2016 CMPE 250 Graphs- Network Flow November 23, 2016 1 / 31 Types of Networks Internet Telephone Cell Highways Rail Electrical Power Water Sewer Gas... CMPE 250 Graphs- Network
Methods and Models for Combinatorial Optimization Modeling by Linear Programming
 Methods and Models for Combinatorial Optimization Modeling by Linear Programming Luigi De Giovanni, Marco Di Summa 1 Linear programming models Linear programming models are a special class of mathematical
Methods and Models for Combinatorial Optimization Modeling by Linear Programming Luigi De Giovanni, Marco Di Summa 1 Linear programming models Linear programming models are a special class of mathematical
Solving NP-hard Problems on Special Instances
 Solving NP-hard Problems on Special Instances Solve it in poly- time I can t You can assume the input is xxxxx No Problem, here is a poly-time algorithm 1 Solving NP-hard Problems on Special Instances
Solving NP-hard Problems on Special Instances Solve it in poly- time I can t You can assume the input is xxxxx No Problem, here is a poly-time algorithm 1 Solving NP-hard Problems on Special Instances
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn
 Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
56:272 Integer Programming & Network Flows Final Examination -- December 14, 1998
 56:272 Integer Programming & Network Flows Final Examination -- December 14, 1998 Part A: Answer any four of the five problems. (15 points each) 1. Transportation problem 2. Integer LP Model Formulation
56:272 Integer Programming & Network Flows Final Examination -- December 14, 1998 Part A: Answer any four of the five problems. (15 points each) 1. Transportation problem 2. Integer LP Model Formulation
Introduction to Mathematical Programming IE406. Lecture 20. Dr. Ted Ralphs
 Introduction to Mathematical Programming IE406 Lecture 20 Dr. Ted Ralphs IE406 Lecture 20 1 Reading for This Lecture Bertsimas Sections 10.1, 11.4 IE406 Lecture 20 2 Integer Linear Programming An integer
Introduction to Mathematical Programming IE406 Lecture 20 Dr. Ted Ralphs IE406 Lecture 20 1 Reading for This Lecture Bertsimas Sections 10.1, 11.4 IE406 Lecture 20 2 Integer Linear Programming An integer
8. The Postman Problems
 8. The Postman Problems The Chinese postman problem (CPP) A postal carrier must pick up the mail at the post office, deliver the mail along blocks on the route, and finally return to the post office. To
8. The Postman Problems The Chinese postman problem (CPP) A postal carrier must pick up the mail at the post office, deliver the mail along blocks on the route, and finally return to the post office. To
BCN Decision and Risk Analysis. Syed M. Ahmed, Ph.D.
 Linear Programming Module Outline Introduction The Linear Programming Model Examples of Linear Programming Problems Developing Linear Programming Models Graphical Solution to LP Problems The Simplex Method
Linear Programming Module Outline Introduction The Linear Programming Model Examples of Linear Programming Problems Developing Linear Programming Models Graphical Solution to LP Problems The Simplex Method
OIM 413 Logistics and Transportation Lecture 2: Representation of a Transportation Network
 OIM 413 Logistics and Transportation Lecture 2: Representation of a Transportation Network Professor Anna Nagurney John F. Smith Memorial Professor and Director Virtual Center for Supernetworks Department
OIM 413 Logistics and Transportation Lecture 2: Representation of a Transportation Network Professor Anna Nagurney John F. Smith Memorial Professor and Director Virtual Center for Supernetworks Department
Network Flow. The network flow problem is as follows:
 Network Flow The network flow problem is as follows: Given a connected directed graph G with non-negative integer weights, (where each edge stands for the capacity of that edge), and two distinguished
Network Flow The network flow problem is as follows: Given a connected directed graph G with non-negative integer weights, (where each edge stands for the capacity of that edge), and two distinguished
Introduction. Linear because it requires linear functions. Programming as synonymous of planning.
 LINEAR PROGRAMMING Introduction Development of linear programming was among the most important scientific advances of mid-20th cent. Most common type of applications: allocate limited resources to competing
LINEAR PROGRAMMING Introduction Development of linear programming was among the most important scientific advances of mid-20th cent. Most common type of applications: allocate limited resources to competing
Lecture 2 Generalized Representation of a Transportation Network
 Lecture 2 Generalized Representation of a Transportation Network Professor Anna Nagurney John F. Smith Memorial Professor and Director Virtual Center for Supernetworks Isenberg School of Management University
Lecture 2 Generalized Representation of a Transportation Network Professor Anna Nagurney John F. Smith Memorial Professor and Director Virtual Center for Supernetworks Isenberg School of Management University
Lecture and notes by: Sarah Fletcher and Michael Xu November 3rd, Multicommodity Flow
 Multicommodity Flow 1 Introduction Suppose we have a company with a factory s and a warehouse t. The quantity of goods that they can ship from the factory to the warehouse in a given time period is limited
Multicommodity Flow 1 Introduction Suppose we have a company with a factory s and a warehouse t. The quantity of goods that they can ship from the factory to the warehouse in a given time period is limited
Unit.9 Integer Programming
 Unit.9 Integer Programming Xiaoxi Li EMS & IAS, Wuhan University Dec. 22-29, 2016 (revised) Operations Research (Li, X.) Unit.9 Integer Programming Dec. 22-29, 2016 (revised) 1 / 58 Organization of this
Unit.9 Integer Programming Xiaoxi Li EMS & IAS, Wuhan University Dec. 22-29, 2016 (revised) Operations Research (Li, X.) Unit.9 Integer Programming Dec. 22-29, 2016 (revised) 1 / 58 Organization of this
CMPSCI 311: Introduction to Algorithms Practice Final Exam
 CMPSCI 311: Introduction to Algorithms Practice Final Exam Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question. Providing more detail including
CMPSCI 311: Introduction to Algorithms Practice Final Exam Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question. Providing more detail including
ME 391Q Network Flow Programming
 ME 9Q Network Flow Programming Final Exam, Summer 00. ( Points) The figure below shows an undirected network. The parameters on the edges are the edge lengths. Find the shortest path tree using Dijkstra
ME 9Q Network Flow Programming Final Exam, Summer 00. ( Points) The figure below shows an undirected network. The parameters on the edges are the edge lengths. Find the shortest path tree using Dijkstra
Simulation. Lecture O1 Optimization: Linear Programming. Saeed Bastani April 2016
 Simulation Lecture O Optimization: Linear Programming Saeed Bastani April 06 Outline of the course Linear Programming ( lecture) Integer Programming ( lecture) Heuristics and Metaheursitics (3 lectures)
Simulation Lecture O Optimization: Linear Programming Saeed Bastani April 06 Outline of the course Linear Programming ( lecture) Integer Programming ( lecture) Heuristics and Metaheursitics (3 lectures)
Computational Methods in IS Research Fall Graph Algorithms Network Flow Problems
 Computational Methods in IS Research Fall 2017 Graph Algorithms Network Flow Problems Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Network Flow Problems
Computational Methods in IS Research Fall 2017 Graph Algorithms Network Flow Problems Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Network Flow Problems
Ch.07 Shortest Route, Minimal Spanning Tree, and Maximal Flow Models. Management Science / Prof. Bonghyun Ahn
 Ch.07 Shortest Route, Minimal Spanning Tree, and Maximal Flow Models Management Science / Prof. Bonghyun Ahn Chapter Topics Network Components The Shortest Route Problem The Minimal Spanning Tree Problem
Ch.07 Shortest Route, Minimal Spanning Tree, and Maximal Flow Models Management Science / Prof. Bonghyun Ahn Chapter Topics Network Components The Shortest Route Problem The Minimal Spanning Tree Problem
Graphs Definitions. Gunnar Gotshalks. GraphDefinitions 1
 Graphs Definitions GraphDefinitions 1 Examples of Graphs Street maps» Vertices are the intersections» Edges are the streets Power line network» Vertices are the houses & power stations» Edges are the power
Graphs Definitions GraphDefinitions 1 Examples of Graphs Street maps» Vertices are the intersections» Edges are the streets Power line network» Vertices are the houses & power stations» Edges are the power
Minimum Spanning Tree
 Chapter 478 Minimum Spanning Tree Introduction A minimum spanning tree links all nodes (points or vertices) of a network with the minimum length of all arcs. This procedure finds the minimum spanning tree
Chapter 478 Minimum Spanning Tree Introduction A minimum spanning tree links all nodes (points or vertices) of a network with the minimum length of all arcs. This procedure finds the minimum spanning tree
Discrete Covering. Location. Problems. Louis. Luangkesorn. Housekeeping. Dijkstra s Shortest Path. Discrete. Covering. Models.
 Network Design Network Design Network Design Network Design Office Hours Wednesday IE 079/079 Logistics and Supply Chain Office is closed Wednesday for building renovation work. I will be on campus (or
Network Design Network Design Network Design Network Design Office Hours Wednesday IE 079/079 Logistics and Supply Chain Office is closed Wednesday for building renovation work. I will be on campus (or
Methods and Models for Combinatorial Optimization Exact methods for the Traveling Salesman Problem
 Methods and Models for Combinatorial Optimization Exact methods for the Traveling Salesman Problem L. De Giovanni M. Di Summa The Traveling Salesman Problem (TSP) is an optimization problem on a directed
Methods and Models for Combinatorial Optimization Exact methods for the Traveling Salesman Problem L. De Giovanni M. Di Summa The Traveling Salesman Problem (TSP) is an optimization problem on a directed
Chapter 20. Minimal Spanning Tree CONTENT 20.1 A MINIMAL SPANNING TREE ALGORITHM
 Chapter 0 Minimal Spanning Tree CONTENT 0. A MINIMAL SPANNING TREE ALGORITHM 0_ch0_ptg0_Web.indd 0/0/ :9 PM 0- Chapter 0 Minimal Spanning Tree In network terminology, the minimal spanning tree problem
Chapter 0 Minimal Spanning Tree CONTENT 0. A MINIMAL SPANNING TREE ALGORITHM 0_ch0_ptg0_Web.indd 0/0/ :9 PM 0- Chapter 0 Minimal Spanning Tree In network terminology, the minimal spanning tree problem
Fundamentals of Integer Programming
 Fundamentals of Integer Programming Di Yuan Department of Information Technology, Uppsala University January 2018 Outline Definition of integer programming Formulating some classical problems with integer
Fundamentals of Integer Programming Di Yuan Department of Information Technology, Uppsala University January 2018 Outline Definition of integer programming Formulating some classical problems with integer
Maximum flows & Maximum Matchings
 Chapter 9 Maximum flows & Maximum Matchings This chapter analyzes flows and matchings. We will define flows and maximum flows and present an algorithm that solves the maximum flow problem. Then matchings
Chapter 9 Maximum flows & Maximum Matchings This chapter analyzes flows and matchings. We will define flows and maximum flows and present an algorithm that solves the maximum flow problem. Then matchings
2/25/2016. Minimal Spanning Tree Problem. Minimal Spanning Tree Problem. Example: Minimal Spanning Tree. Example: Minimal Spanning Tree
 // OPERATIONAL RESEARCH II Agustina Eunike, ST., MT., MBA. Industrial Engineering University of Brawijaya MINIMAL SPANNING TREE PROBLEM Minimal Spanning Tree Problem A tree is a set of connected arcs that
// OPERATIONAL RESEARCH II Agustina Eunike, ST., MT., MBA. Industrial Engineering University of Brawijaya MINIMAL SPANNING TREE PROBLEM Minimal Spanning Tree Problem A tree is a set of connected arcs that
DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI
 DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI Department of Computer Science and Engineering CS6702 - GRAPH THEORY AND APPLICATIONS Anna University 2 & 16 Mark Questions & Answers Year / Semester: IV /
DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI Department of Computer Science and Engineering CS6702 - GRAPH THEORY AND APPLICATIONS Anna University 2 & 16 Mark Questions & Answers Year / Semester: IV /
Tuesday, April 10. The Network Simplex Method for Solving the Minimum Cost Flow Problem
 . Tuesday, April The Network Simplex Method for Solving the Minimum Cost Flow Problem Quotes of the day I think that I shall never see A poem lovely as a tree. -- Joyce Kilmer Knowing trees, I understand
. Tuesday, April The Network Simplex Method for Solving the Minimum Cost Flow Problem Quotes of the day I think that I shall never see A poem lovely as a tree. -- Joyce Kilmer Knowing trees, I understand
CS 4407 Algorithms Lecture 5: Graphs an Introduction
 CS 4407 Algorithms Lecture 5: Graphs an Introduction Prof. Gregory Provan Department of Computer Science University College Cork 1 Outline Motivation Importance of graphs for algorithm design applications
CS 4407 Algorithms Lecture 5: Graphs an Introduction Prof. Gregory Provan Department of Computer Science University College Cork 1 Outline Motivation Importance of graphs for algorithm design applications
Linear programming II João Carlos Lourenço
 Decision Support Models Linear programming II João Carlos Lourenço joao.lourenco@ist.utl.pt Academic year 2012/2013 Readings: Hillier, F.S., Lieberman, G.J., 2010. Introduction to Operations Research,
Decision Support Models Linear programming II João Carlos Lourenço joao.lourenco@ist.utl.pt Academic year 2012/2013 Readings: Hillier, F.S., Lieberman, G.J., 2010. Introduction to Operations Research,
CS 537: Introduction to Operating Systems Fall 2015: Midterm Exam #1
 CS 537: Introduction to Operating Systems Fall 2015: Midterm Exam #1 This exam is closed book, closed notes. All cell phones must be turned off. No calculators may be used. You have two hours to complete
CS 537: Introduction to Operating Systems Fall 2015: Midterm Exam #1 This exam is closed book, closed notes. All cell phones must be turned off. No calculators may be used. You have two hours to complete
Linear Programming. Course review MS-E2140. v. 1.1
 Linear Programming MS-E2140 Course review v. 1.1 Course structure Modeling techniques Linear programming theory and the Simplex method Duality theory Dual Simplex algorithm and sensitivity analysis Integer
Linear Programming MS-E2140 Course review v. 1.1 Course structure Modeling techniques Linear programming theory and the Simplex method Duality theory Dual Simplex algorithm and sensitivity analysis Integer
Introduction. Chapter 15. Optimization Modeling: Applications. Integer Programming. Manufacturing Example. Three Types of ILP Models
 Chapter 5 Optimization Modeling: Applications Integer Programming Introduction When one or more variables in an LP problem must assume an integer value we have an Integer Linear Programming (ILP) problem.
Chapter 5 Optimization Modeling: Applications Integer Programming Introduction When one or more variables in an LP problem must assume an integer value we have an Integer Linear Programming (ILP) problem.
Math 96--Radicals #1-- Simplify; Combine--page 1
 Simplify; Combine--page 1 Part A Number Systems a. Whole Numbers = {0, 1, 2, 3,...} b. Integers = whole numbers and their opposites = {..., 3, 2, 1, 0, 1, 2, 3,...} c. Rational Numbers = quotient of integers
Simplify; Combine--page 1 Part A Number Systems a. Whole Numbers = {0, 1, 2, 3,...} b. Integers = whole numbers and their opposites = {..., 3, 2, 1, 0, 1, 2, 3,...} c. Rational Numbers = quotient of integers
OPERATIONS RESEARCH. Transportation and Assignment Problems
 OPERATIONS RESEARCH Chapter 2 Transportation and Assignment Problems Prof Bibhas C Giri Professor of Mathematics Jadavpur University West Bengal, India E-mail : bcgirijumath@gmailcom MODULE-3: Assignment
OPERATIONS RESEARCH Chapter 2 Transportation and Assignment Problems Prof Bibhas C Giri Professor of Mathematics Jadavpur University West Bengal, India E-mail : bcgirijumath@gmailcom MODULE-3: Assignment
OPERATIONS RESEARCH. Linear Programming Problem
 OPERATIONS RESEARCH Chapter 1 Linear Programming Problem Prof. Bibhas C. Giri Department of Mathematics Jadavpur University Kolkata, India Email: bcgiri.jumath@gmail.com 1.0 Introduction Linear programming
OPERATIONS RESEARCH Chapter 1 Linear Programming Problem Prof. Bibhas C. Giri Department of Mathematics Jadavpur University Kolkata, India Email: bcgiri.jumath@gmail.com 1.0 Introduction Linear programming
Algorithm Design Methods. Some Methods Not Covered
 Algorithm Design Methods Greedy method. Divide and conquer. Dynamic Programming. Backtracking. Branch and bound. Some Methods Not Covered Linear Programming. Integer Programming. Simulated Annealing. Neural
Algorithm Design Methods Greedy method. Divide and conquer. Dynamic Programming. Backtracking. Branch and bound. Some Methods Not Covered Linear Programming. Integer Programming. Simulated Annealing. Neural
Graphs and Network Flows IE411 Lecture 20
 Graphs and Network Flows IE411 Lecture 20 Dr. Ted Ralphs IE411 Lecture 20 1 Network Simplex Algorithm Input: A network G = (N, A), a vector of capacities u Z A, a vector of costs c Z A, and a vector of
Graphs and Network Flows IE411 Lecture 20 Dr. Ted Ralphs IE411 Lecture 20 1 Network Simplex Algorithm Input: A network G = (N, A), a vector of capacities u Z A, a vector of costs c Z A, and a vector of
Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem
 Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem Uncapacitated Networks: Basic primal and dual solutions Flow conservation constraints
Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem Uncapacitated Networks: Basic primal and dual solutions Flow conservation constraints
3 INTEGER LINEAR PROGRAMMING
 3 INTEGER LINEAR PROGRAMMING PROBLEM DEFINITION Integer linear programming problem (ILP) of the decision variables x 1,..,x n : (ILP) subject to minimize c x j j n j= 1 a ij x j x j 0 x j integer n j=
3 INTEGER LINEAR PROGRAMMING PROBLEM DEFINITION Integer linear programming problem (ILP) of the decision variables x 1,..,x n : (ILP) subject to minimize c x j j n j= 1 a ij x j x j 0 x j integer n j=
Graphs and Network Flows IE411. Lecture 21. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
15.082J and 6.855J. Lagrangian Relaxation 2 Algorithms Application to LPs
 15.082J and 6.855J Lagrangian Relaxation 2 Algorithms Application to LPs 1 The Constrained Shortest Path Problem (1,10) 2 (1,1) 4 (2,3) (1,7) 1 (10,3) (1,2) (10,1) (5,7) 3 (12,3) 5 (2,2) 6 Find the shortest
15.082J and 6.855J Lagrangian Relaxation 2 Algorithms Application to LPs 1 The Constrained Shortest Path Problem (1,10) 2 (1,1) 4 (2,3) (1,7) 1 (10,3) (1,2) (10,1) (5,7) 3 (12,3) 5 (2,2) 6 Find the shortest
Application of Bounded Variable Simplex Algorithm in Solving Maximal Flow Model
 Dhaka Univ. J. Sci. (): 9-, 3 (January) Application of Bounded Variable Simplex Algorithm in Solving Maximal Flow Model Sohana Jahan, Marzia Yesmin and Fatima Tuj Jahra Department of Mathematics,University
Dhaka Univ. J. Sci. (): 9-, 3 (January) Application of Bounded Variable Simplex Algorithm in Solving Maximal Flow Model Sohana Jahan, Marzia Yesmin and Fatima Tuj Jahra Department of Mathematics,University
Achieving Efficiency in Gas Pipeline Connection: Evidence from Ghana
 International Journal of Business and Social Research Volume 06, Issue 05, 2016 Achieving Efficiency in Gas Pipeline Connection: Evidence from Ghana Anthony Kudjo Gborgenu *, Frank B. K. Twenefour 1, Mathias
International Journal of Business and Social Research Volume 06, Issue 05, 2016 Achieving Efficiency in Gas Pipeline Connection: Evidence from Ghana Anthony Kudjo Gborgenu *, Frank B. K. Twenefour 1, Mathias
Combinatorial Optimization
 Combinatorial Optimization Frank de Zeeuw EPFL 2012 Today Introduction Graph problems - What combinatorial things will we be optimizing? Algorithms - What kind of solution are we looking for? Linear Programming
Combinatorial Optimization Frank de Zeeuw EPFL 2012 Today Introduction Graph problems - What combinatorial things will we be optimizing? Algorithms - What kind of solution are we looking for? Linear Programming
LECTURES 3 and 4: Flows and Matchings
 LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
6 ROUTING PROBLEMS VEHICLE ROUTING PROBLEMS. Vehicle Routing Problem, VRP:
 6 ROUTING PROBLEMS VEHICLE ROUTING PROBLEMS Vehicle Routing Problem, VRP: Customers i=1,...,n with demands of a product must be served using a fleet of vehicles for the deliveries. The vehicles, with given
6 ROUTING PROBLEMS VEHICLE ROUTING PROBLEMS Vehicle Routing Problem, VRP: Customers i=1,...,n with demands of a product must be served using a fleet of vehicles for the deliveries. The vehicles, with given
CLASS: II YEAR / IV SEMESTER CSE CS 6402-DESIGN AND ANALYSIS OF ALGORITHM UNIT I INTRODUCTION
 CLASS: II YEAR / IV SEMESTER CSE CS 6402-DESIGN AND ANALYSIS OF ALGORITHM UNIT I INTRODUCTION 1. What is performance measurement? 2. What is an algorithm? 3. How the algorithm is good? 4. What are the
CLASS: II YEAR / IV SEMESTER CSE CS 6402-DESIGN AND ANALYSIS OF ALGORITHM UNIT I INTRODUCTION 1. What is performance measurement? 2. What is an algorithm? 3. How the algorithm is good? 4. What are the
Lecture 3: Totally Unimodularity and Network Flows
 Lecture 3: Totally Unimodularity and Network Flows (3 units) Outline Properties of Easy Problems Totally Unimodular Matrix Minimum Cost Network Flows Dijkstra Algorithm for Shortest Path Problem Ford-Fulkerson
Lecture 3: Totally Unimodularity and Network Flows (3 units) Outline Properties of Easy Problems Totally Unimodular Matrix Minimum Cost Network Flows Dijkstra Algorithm for Shortest Path Problem Ford-Fulkerson
Jessica Su (some parts copied from CLRS / last quarter s notes)
 1 Max flow Consider a directed graph G with positive edge weights c that define the capacity of each edge. We can identify two special nodes in G: the source node s and the sink node t. We want to find
1 Max flow Consider a directed graph G with positive edge weights c that define the capacity of each edge. We can identify two special nodes in G: the source node s and the sink node t. We want to find
Homework Assignment #3 Graph
 CISC 4080 Computer Algorithms Spring, 2019 Homework Assignment #3 Graph Some of the problems are adapted from problems in the book Introduction to Algorithms by Cormen, Leiserson and Rivest, and some are
CISC 4080 Computer Algorithms Spring, 2019 Homework Assignment #3 Graph Some of the problems are adapted from problems in the book Introduction to Algorithms by Cormen, Leiserson and Rivest, and some are
OPTIMIZATION. joint course with. Ottimizzazione Discreta and Complementi di R.O. Edoardo Amaldi. DEIB Politecnico di Milano
 OPTIMIZATION joint course with Ottimizzazione Discreta and Complementi di R.O. Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-16-17.shtml
OPTIMIZATION joint course with Ottimizzazione Discreta and Complementi di R.O. Edoardo Amaldi DEIB Politecnico di Milano edoardo.amaldi@polimi.it Website: http://home.deib.polimi.it/amaldi/opt-16-17.shtml
Notes for Lecture 24
 U.C. Berkeley CS170: Intro to CS Theory Handout N24 Professor Luca Trevisan December 4, 2001 Notes for Lecture 24 1 Some NP-complete Numerical Problems 1.1 Subset Sum The Subset Sum problem is defined
U.C. Berkeley CS170: Intro to CS Theory Handout N24 Professor Luca Trevisan December 4, 2001 Notes for Lecture 24 1 Some NP-complete Numerical Problems 1.1 Subset Sum The Subset Sum problem is defined
looking ahead to see the optimum
 ! Make choice based on immediate rewards rather than looking ahead to see the optimum! In many cases this is effective as the look ahead variation can require exponential time as the number of possible
! Make choice based on immediate rewards rather than looking ahead to see the optimum! In many cases this is effective as the look ahead variation can require exponential time as the number of possible
Maximum flow problem CE 377K. March 3, 2015
 Maximum flow problem CE 377K March 3, 2015 Informal evaluation results 2 slow, 16 OK, 2 fast Most unclear topics: max-flow/min-cut, WHAT WILL BE ON THE MIDTERM? Most helpful things: review at start of
Maximum flow problem CE 377K March 3, 2015 Informal evaluation results 2 slow, 16 OK, 2 fast Most unclear topics: max-flow/min-cut, WHAT WILL BE ON THE MIDTERM? Most helpful things: review at start of
LEAST COST ROUTING ALGORITHM WITH THE STATE SPACE RELAXATION IN A CENTRALIZED NETWORK
 VOL., NO., JUNE 08 ISSN 896608 00608 Asian Research Publishing Network (ARPN). All rights reserved. LEAST COST ROUTING ALGORITHM WITH THE STATE SPACE RELAXATION IN A CENTRALIZED NETWORK Y. J. Lee Department
VOL., NO., JUNE 08 ISSN 896608 00608 Asian Research Publishing Network (ARPN). All rights reserved. LEAST COST ROUTING ALGORITHM WITH THE STATE SPACE RELAXATION IN A CENTRALIZED NETWORK Y. J. Lee Department
