A Polynomial Algorithm for Submap Isomorphism: Application to Searching Patterns in Images
|
|
|
- Malcolm Flowers
- 5 years ago
- Views:
Transcription
1 A Polynomial Algorithm for Submap Isomorphism: Application to Searching Patterns in Images Guillaume Damiand, Colin de la Higuera, Jean-Christophe Janodet, Emilie Samuel, Christine Solnon GbR 009
2 Motivations Search patterns in images Model images graphs (RAGs, Delaunay triangulation,...) Search patterns subgraph isomorphism NP-complete in the general case... but do we consider the right problem when graphs model images? Is there a subgraph isomorphism???
3 Motivations Search patterns in images Model images graphs (RAGs, Delaunay triangulation,...) Search patterns subgraph isomorphism NP-complete in the general case... but do we consider the right problem when graphs model images? Yes but... the two graphs look rather different! Graphs modeling images are planar and are embedded in planes. Let us compare planar embeddings of graphs!
4 Motivations Search patterns in images Model images graphs (RAGs, Delaunay triangulation,...) Search patterns subgraph isomorphism NP-complete in the general case... but do we consider the right problem when graphs model images? Yes but... the two graphs look rather different! Graphs modeling images are planar and are embedded in planes. Let us compare planar embeddings of graphs!
5 Overview of the talk 1 Motivations Combinatorial maps 3 Map isomorphism: definition and algorithm 4 Submap isomorphism: definition and algorithm 5 Back to plane graphs plane subgraph isomorphism 6 Experimental results 7 Further work
6 D Combinatorial maps (1/3) From plane graphs to D combinatorial maps Each edge is decomposed into linked darts Faces are defined by dart successions Plane graph Combinatorial map
7 D Combinatorial maps (/3) Definition [Lienhardt91] A D combinatorial map is defined by M = (D, β 1, β ) such that D = finite set of darts β 1 = permutation on D β = involution on D Notation: β 0 β β β
8 D Combinatorial maps (3/3) Open maps Some darts may be i-sewn with ɛ (ex.: 5, 6, 7, 14, 15, 10 et 1) By definition, 0 i, β i (ɛ) = ɛ Connected maps for every pair of darts (d, d ), there exists a path (d 1,..., d k ) st d 1 = d and d k = d 1 i < k, j i {0, 1, }, d i+1 = β ji (d i )
9 Overview of the talk 1 Motivations Combinatorial maps 3 Isomorphism of combinatorial maps 4 Submap isomorphism 5 Back to plane graphs 6 Experimental results 7 Further work
10 Map isomorphism Definition [Cori75, Lienhardt94] M = (D, β 1, β ) and M = (D, β 1, β ) are isomorphic if there exists a bijection f : D D such that d D, i {1, }, f (β i (d)) = β i (f (d)). function testisomorphism(m, M ) [Cori75] Input: connected open maps M and M Output: returns true iff M and M are isomorphic Choose d 0 D For each dart d 0 D do : f traverseandmatch(m, M, d 0, d 0 ) If f is an isomorphism function between M and M then return true return false
11 Map traversal and construction of f function traverseandmatch(m, M, d 0, d 0 ) Input: maps M and M and darts d D and d D Output: returns a matching f : D {epsilon} D {epsilon} For each dart d D do: f [d] nil f [d 0 ] d 0 Let S be an empty stack Push d 0 in S While S is not empty do f [ɛ] ɛ return f Pop a dart d from S For i {0, 1, } do If β i (d) ɛ and f [β i (d)] = nil then f [β i (d)] β i (f [d]) Push β i (d) in S
12 Complexity and correction Complexity in O( D ) At most D map traversals Each traversal is in O( D ) Correction If testisomorphism(m, M ) returns true, then M and M are isomorphic check that f is an isomorphism function before returning true If M and M are isomorphic then testisomorphism(m, M ) returns true the traversal is determined by the order β i are used to discover new darts
13 Overview of the talk 1 Motivations Combinatorial maps 3 Isomorphism of combinatorial maps 4 Submap isomorphism 5 Back to plane graphs 6 Experimental results 7 Further work
14 Submap isomorphism Definition M = (D, β 1, β ) is isomorphic to a submap of M = (D, β 1, β ) if there exists an injection f : D {ɛ} D {ɛ} such that f (ɛ) = ɛ and d D, i {1, } : if β i (d) ɛ then β i (f (d)) = f (β i(d)) if β i (d) = ɛ then, either β i (f (d)) = ɛ, or f 1 (β i (f (d))) is empty. a b r 1 M M M M is a submap of M M is not a submap of M because β (1) = β () = ɛ but β (f (1)) = f ()
15 Algorithm for submap isomorphism function testsubisomorphism(m, M ) Input: open connected maps M and M Output: returns true iff M is isomorphic to a submap of M Choose d 0 D For every dart d 0 D do : f traverseandmatch(m, M, d 0, d 0 ) If f is a subisomorphism function between M and M then return true return false Complexity in O( D D ) There are at most D map traversals Each traversal is in O( D )
16 Example with wrong initial darts 1 1 1
17 Example with wrong initial darts
18 Example with wrong initial darts
19 Example with wrong initial darts
20 Example with wrong initial darts All darts of the pattern are discovered end of TraverseAndMatch The matching isn t a subisomorphism testsubiso tries another dart
21 Example with good initial darts 1 1 1
22 Example with good initial darts
23 Example with good initial darts
24 Example with good initial darts
25 Example with good initial darts All darts of the pattern are discovered end of TraverseAndMatch The matching is a subisomorphism testsubiso returns true
26 Overview of the talk 1 Motivations Combinatorial maps 3 Isomorphism of combinatorial maps 4 Submap isomorphism 5 Back to plane graphs 6 Experimental results 7 Further work
27 From plane graphs to combinatorial maps (1/3)...or how to use submap isomorphism to solve some subgraph isomorphism problems... Compact plane subgraph isomorphism Plane graph embedding of a planar graph in a plane G 1 and G are plane-isomorphic if there exists a bijection f : N 1 N which preserves edges and topology G 1 is a compact plane subgraph of G if G 1 is plane isomorphic to a compact subgraph remove nodes and edges adjacent to the unbounded face Yes 5 No
28 From plane graphs to combinatorial maps (/3) Modeling a plane graph with a D map Associate a face in the map with every face of the graph Non plane isomorphic Non isomorphic maps?
29 From plane graphs to combinatorial maps (/3) Modeling a plane graph with a D map Associate a face in the map with every face of the graph Non plane isomorphic Non isomorphic maps
30 From plane graphs to combinatorial maps (/3) Modeling a plane graph with a D map Associate a face in the map with every face of the graph except the unbounded face open map w.r.t. β only (and only for one face) topological disk Non plane isomorphic Non isomorphic maps Non isomorphic maps
31 From plane graphs to combinatorial maps (3/3) Precondition for using test(sub)isomorphism(m, M ) M and M must be connected plane graphs must be connected......and their unbounded face must be bounded by an elementary cycle Yes 5 No a polynomial algorithm to solve compact plane subgraph isomorphism when unbounded faces are bounded by elementary cycles...
32 Overview of the talk 1 Motivations Combinatorial maps 3 Isomorphism of combinatorial maps 4 Submap isomorphism 5 Back to plane graphs 6 Experimental results 7 Further work
33 Experimental results (1/) Original image Combinatorial map of the segmented image (435 nodes, 4057 edges) => find the car in 60ms Corner points connected by Delaunay triangulation (140 nodes, 404 edges) => find the car in 10ms
34 Experimental results (/) Comparison with Vflib (induced subgraph isomorphism) g x x nodes randomly embedded in the plane + Delaunay triangulation sg i,j% subgraph of g i with j% of the nodes sg i,5% sg i,10% sg i,0% sg i,33% sg i,50% g i vf map vf map vf map vf map vf map g g g Vflib and map do not solve the same problem...but they (nearly always) find the same solutions
35 Overview of the talk 1 Motivations Combinatorial maps 3 Isomorphism of combinatorial maps 4 Submap isomorphism 5 Back to plane graphs 6 Experimental results 7 Further work
36 Further work Dealing with holes in subgraphs Solving subgraph isomorphism in polynomial time for graphs with a polynomial number of topologically different embeddings in n dimensional spaces identify such classes of graphs Mining frequent submaps Definition of Error tolerant similarity measures Maximum common submap Map edit distance integrate geometric and color information
Signatures of Combinatorial Maps
 Signatures of Combinatorial Maps No Author Given No Institute Given Abstract. In this paper, we address the problem of computing a canonical representation of an n-dimensional combinatorial map. For that,
Signatures of Combinatorial Maps No Author Given No Institute Given Abstract. In this paper, we address the problem of computing a canonical representation of an n-dimensional combinatorial map. For that,
Polynomial Algorithms for Subisomorphism of nd Open Combinatorial Maps
 Polynomial Algorithms for Subisomorphism of nd Open Combinatorial Maps Guillaume Damiand a, Christine Solnon a Colin de la Higuera b Jean-Christophe Janodet c Émilie Samuel c a Université de Lyon, CNRS
Polynomial Algorithms for Subisomorphism of nd Open Combinatorial Maps Guillaume Damiand a, Christine Solnon a Colin de la Higuera b Jean-Christophe Janodet c Émilie Samuel c a Université de Lyon, CNRS
Polynomial Algorithm for Submap Isomorphism: Application to searching patterns in images
 Polynomial Algorithm for Submap Isomorphism: Application to searching patterns in images Guillaume Damiand, Colin De La Higuera, Jean-Christophe Janodet, Émilie Samuel, Christine Solnon To cite this version:
Polynomial Algorithm for Submap Isomorphism: Application to searching patterns in images Guillaume Damiand, Colin De La Higuera, Jean-Christophe Janodet, Émilie Samuel, Christine Solnon To cite this version:
Map Edit Distance vs Graph Edit Distance for Matching Images
 Map Edit Distance vs Graph Edit Distance for Matching Images Camille Combier 1,2, Guillaume Damiand 3,2, and Christine Solnon 3,2 1 Université Lyon 1, LIRIS, UMR 5205 CNRS, 69622 Villeurbanne, France 2
Map Edit Distance vs Graph Edit Distance for Matching Images Camille Combier 1,2, Guillaume Damiand 3,2, and Christine Solnon 3,2 1 Université Lyon 1, LIRIS, UMR 5205 CNRS, 69622 Villeurbanne, France 2
Extracting Plane Graphs from Images
 Extracting Plane Graphs from Images Émilie Samuel, Colin De La Higuera, Jean-Christophe Janodet To cite this version: Émilie Samuel, Colin De La Higuera, Jean-Christophe Janodet. Extracting Plane Graphs
Extracting Plane Graphs from Images Émilie Samuel, Colin De La Higuera, Jean-Christophe Janodet To cite this version: Émilie Samuel, Colin De La Higuera, Jean-Christophe Janodet. Extracting Plane Graphs
An intuitionistic proof of a discrete form of the Jordan Curve Theorem formalized in Coq with combinatorial hypermaps
 An intuitionistic proof of a discrete form of the Jordan Curve Theorem formalized in Coq with combinatorial hypermaps Jean-François Dufourd 1 1 LSIIT, UMR CNRS 7005, Université de Strasbourg, France Galapagos
An intuitionistic proof of a discrete form of the Jordan Curve Theorem formalized in Coq with combinatorial hypermaps Jean-François Dufourd 1 1 LSIIT, UMR CNRS 7005, Université de Strasbourg, France Galapagos
Embedded Subgraph Isomorphism and Related Problems
 Embedded Subgraph Isomorphism and Related Problems Graph isomorphism, subgraph isomorphism, and maximum common subgraph can be solved in polynomial time when constrained by geometrical information, in
Embedded Subgraph Isomorphism and Related Problems Graph isomorphism, subgraph isomorphism, and maximum common subgraph can be solved in polynomial time when constrained by geometrical information, in
Computing Linkless and Flat Embeddings of Graphs in R 3
 Computing Linkless and Flat Embeddings of Graphs in R 3 Stephan Kreutzer Technical University Berlin based on joint work with Ken-ichi Kawarabayashi, Bojan Mohar and Bruce Reed Graph Theory @ Georgie Tech
Computing Linkless and Flat Embeddings of Graphs in R 3 Stephan Kreutzer Technical University Berlin based on joint work with Ken-ichi Kawarabayashi, Bojan Mohar and Bruce Reed Graph Theory @ Georgie Tech
Topological Model for 3D Image Representation: Definition and Incremental Extraction Algorithm
 Topological Model for 3D Image Representation: Definition and Incremental Extraction Algorithm Guillaume Damiand To cite this version: Guillaume Damiand. Topological Model for 3D Image Representation:
Topological Model for 3D Image Representation: Definition and Incremental Extraction Algorithm Guillaume Damiand To cite this version: Guillaume Damiand. Topological Model for 3D Image Representation:
Surfaces Beyond Classification
 Chapter XII Surfaces Beyond Classification In most of the textbooks which present topological classification of compact surfaces the classification is the top result. However the topology of 2- manifolds
Chapter XII Surfaces Beyond Classification In most of the textbooks which present topological classification of compact surfaces the classification is the top result. However the topology of 2- manifolds
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Computer Vision and Image Understanding
 Computer Vision and Image Understanding 116 (2012) 1168 1177 Contents lists available at SciVerse ScienceDirect Computer Vision and Image Understanding journal homepage: www.elsevier.com/locate/cviu A
Computer Vision and Image Understanding 116 (2012) 1168 1177 Contents lists available at SciVerse ScienceDirect Computer Vision and Image Understanding journal homepage: www.elsevier.com/locate/cviu A
Planar Graphs. 1 Graphs and maps. 1.1 Planarity and duality
 Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Finite Math Linear Programming 1 May / 7
 Linear Programming Finite Math 1 May 2017 Finite Math Linear Programming 1 May 2017 1 / 7 General Description of Linear Programming Finite Math Linear Programming 1 May 2017 2 / 7 General Description of
Linear Programming Finite Math 1 May 2017 Finite Math Linear Programming 1 May 2017 1 / 7 General Description of Linear Programming Finite Math Linear Programming 1 May 2017 2 / 7 General Description of
54 Years of Graph Isomorphism Testing
 54 Years of Graph Isomorphism Testing Brendan McKay Australian National University isomorphism 1 isomorphism 2 The concept of isomorphism We have some objects consisting of some finite sets and some relations
54 Years of Graph Isomorphism Testing Brendan McKay Australian National University isomorphism 1 isomorphism 2 The concept of isomorphism We have some objects consisting of some finite sets and some relations
Algorithmic Semi-algebraic Geometry and its applications. Saugata Basu School of Mathematics & College of Computing Georgia Institute of Technology.
 1 Algorithmic Semi-algebraic Geometry and its applications Saugata Basu School of Mathematics & College of Computing Georgia Institute of Technology. 2 Introduction: Three problems 1. Plan the motion of
1 Algorithmic Semi-algebraic Geometry and its applications Saugata Basu School of Mathematics & College of Computing Georgia Institute of Technology. 2 Introduction: Three problems 1. Plan the motion of
Capturing Topology in Graph Pattern Matching
 Capturing Topology in Graph Pattern Matching Shuai Ma, Yang Cao, Wenfei Fan, Jinpeng Huai, Tianyu Wo University of Edinburgh Graphs are everywhere, and quite a few are huge graphs! File systems Databases
Capturing Topology in Graph Pattern Matching Shuai Ma, Yang Cao, Wenfei Fan, Jinpeng Huai, Tianyu Wo University of Edinburgh Graphs are everywhere, and quite a few are huge graphs! File systems Databases
Tiled top-down pyramids and segmentation of large histological images
 Tiled top-down pyramids and segmentation of large histological images Romain Goffe, Luc Brun, Guillaume Damiand To cite this version: Romain Goffe, Luc Brun, Guillaume Damiand. Tiled top-down pyramids
Tiled top-down pyramids and segmentation of large histological images Romain Goffe, Luc Brun, Guillaume Damiand To cite this version: Romain Goffe, Luc Brun, Guillaume Damiand. Tiled top-down pyramids
Polar Duality and Farkas Lemma
 Lecture 3 Polar Duality and Farkas Lemma October 8th, 2004 Lecturer: Kamal Jain Notes: Daniel Lowd 3.1 Polytope = bounded polyhedron Last lecture, we were attempting to prove the Minkowsky-Weyl Theorem:
Lecture 3 Polar Duality and Farkas Lemma October 8th, 2004 Lecturer: Kamal Jain Notes: Daniel Lowd 3.1 Polytope = bounded polyhedron Last lecture, we were attempting to prove the Minkowsky-Weyl Theorem:
Introduction III. Graphs. Motivations I. Introduction IV
 Introduction I Graphs Computer Science & Engineering 235: Discrete Mathematics Christopher M. Bourke cbourke@cse.unl.edu Graph theory was introduced in the 18th century by Leonhard Euler via the Königsberg
Introduction I Graphs Computer Science & Engineering 235: Discrete Mathematics Christopher M. Bourke cbourke@cse.unl.edu Graph theory was introduced in the 18th century by Leonhard Euler via the Königsberg
CONTRACTIONS OF PLANAR GRAPHS
 Marcin Kamiński Brussels Daniël Paulusma Durham Dimitrios Thilikos Athens ESA 2010 CONTAINMENT RELATIONS \v \e /e 2 CONTAINMENT RELATIONS \v \e /e induced subgraph subgraph minor contraction induced minor
Marcin Kamiński Brussels Daniël Paulusma Durham Dimitrios Thilikos Athens ESA 2010 CONTAINMENT RELATIONS \v \e /e 2 CONTAINMENT RELATIONS \v \e /e induced subgraph subgraph minor contraction induced minor
Extraction of tiled top-down irregular pyramids from large images
 Extraction of tiled top-down irregular pyramids from large images Romain Goffe 1 Guillaume Damiand 2 Luc Brun 3 1 SIC-XLIM, Université de Poitiers, CNRS, UMR6172, Bâtiment SP2MI, F-86962, Futuroscope Chasseneuil,
Extraction of tiled top-down irregular pyramids from large images Romain Goffe 1 Guillaume Damiand 2 Luc Brun 3 1 SIC-XLIM, Université de Poitiers, CNRS, UMR6172, Bâtiment SP2MI, F-86962, Futuroscope Chasseneuil,
Introduction to Combinatorial Algorithms
 Fall 2009 Intro Introduction to the course What are : Combinatorial Structures? Combinatorial Algorithms? Combinatorial Problems? Combinatorial Structures Combinatorial Structures Combinatorial structures
Fall 2009 Intro Introduction to the course What are : Combinatorial Structures? Combinatorial Algorithms? Combinatorial Problems? Combinatorial Structures Combinatorial Structures Combinatorial structures
Quadratic and cubic b-splines by generalizing higher-order voronoi diagrams
 Quadratic and cubic b-splines by generalizing higher-order voronoi diagrams Yuanxin Liu and Jack Snoeyink Joshua Levine April 18, 2007 Computer Science and Engineering, The Ohio State University 1 / 24
Quadratic and cubic b-splines by generalizing higher-order voronoi diagrams Yuanxin Liu and Jack Snoeyink Joshua Levine April 18, 2007 Computer Science and Engineering, The Ohio State University 1 / 24
Formal study of plane Delaunay triangulation
 Formal study of plane Delaunay triangulation Jean-François Dufourd 1 Yves Bertot 2 1 LSIIT, UMR CNRS 7005, Université de Strasbourg, France 2 INRIA, Centre de Sophia-Antipolis Méditerranée, France (Thanks:
Formal study of plane Delaunay triangulation Jean-François Dufourd 1 Yves Bertot 2 1 LSIIT, UMR CNRS 7005, Université de Strasbourg, France 2 INRIA, Centre de Sophia-Antipolis Méditerranée, France (Thanks:
Graph Isomorphism. Algorithms and networks
 Graph Isomorphism Algorithms and networks Today Graph isomorphism: definition Complexity: isomorphism completeness The refinement heuristic Isomorphism for trees Rooted trees Unrooted trees Graph Isomorphism
Graph Isomorphism Algorithms and networks Today Graph isomorphism: definition Complexity: isomorphism completeness The refinement heuristic Isomorphism for trees Rooted trees Unrooted trees Graph Isomorphism
Discrete mathematics II. - Graphs
 Emil Vatai April 25, 2018 Basic definitions Definition of an undirected graph Definition (Undirected graph) An undirected graph or (just) a graph is a triplet G = (ϕ, E, V ), where V is the set of vertices,
Emil Vatai April 25, 2018 Basic definitions Definition of an undirected graph Definition (Undirected graph) An undirected graph or (just) a graph is a triplet G = (ϕ, E, V ), where V is the set of vertices,
Persistent Homology Computation Using Combinatorial Map Simplification
 Persistent Homology Computation Using Combinatorial Map Simplification Guillaume Damiand 1, Rocio Gonzalez-Diaz 2 1 CNRS, Université de Lyon, LIRIS, UMR5205, F-69622 France 2 Universidad de Sevilla, Dpto.
Persistent Homology Computation Using Combinatorial Map Simplification Guillaume Damiand 1, Rocio Gonzalez-Diaz 2 1 CNRS, Université de Lyon, LIRIS, UMR5205, F-69622 France 2 Universidad de Sevilla, Dpto.
Learning Characteristic Structured Patterns in Rooted Planar Maps
 Learning Characteristic Structured Patterns in Rooted Planar Maps Satoshi Kawamoto Yusuke Suzuki Takayoshi Shoudai Abstract Exting the concept of ordered graphs, we propose a new data structure to express
Learning Characteristic Structured Patterns in Rooted Planar Maps Satoshi Kawamoto Yusuke Suzuki Takayoshi Shoudai Abstract Exting the concept of ordered graphs, we propose a new data structure to express
Subsea: An efficient heuristic algorithm for subgraph isomorphism
 Subsea: An efficient heuristic algorithm for subgraph isomorphism V. Lipets, N. Vanetik, E. Gudes Dept. of Computer Science, Ben-Gurion University { lipets, orlovn, ehud } @cs.bgu.ac.il Abstract We present
Subsea: An efficient heuristic algorithm for subgraph isomorphism V. Lipets, N. Vanetik, E. Gudes Dept. of Computer Science, Ben-Gurion University { lipets, orlovn, ehud } @cs.bgu.ac.il Abstract We present
Performance of general graph isomorphism algorithms Sara Voss Coe College, Cedar Rapids, IA
 Performance of general graph isomorphism algorithms Sara Voss Coe College, Cedar Rapids, IA I. Problem and Motivation Graphs are commonly used to provide structural and/or relational descriptions. A node
Performance of general graph isomorphism algorithms Sara Voss Coe College, Cedar Rapids, IA I. Problem and Motivation Graphs are commonly used to provide structural and/or relational descriptions. A node
Invariant Measures. The Smooth Approach
 Invariant Measures Mathieu Desbrun & Peter Schröder 1 The Smooth Approach On this show lots of derivatives tedious expressions in coordinates For what? only to discover that there are invariant measures
Invariant Measures Mathieu Desbrun & Peter Schröder 1 The Smooth Approach On this show lots of derivatives tedious expressions in coordinates For what? only to discover that there are invariant measures
Notation Index. Probability notation. (there exists) (such that) Fn-4 B n (Bell numbers) CL-27 s t (equivalence relation) GT-5.
 Notation Index (there exists) (for all) Fn-4 Fn-4 (such that) Fn-4 B n (Bell numbers) CL-27 s t (equivalence relation) GT-5 ( n ) k (binomial coefficient) CL-15 ( n m 1,m 2,...) (multinomial coefficient)
Notation Index (there exists) (for all) Fn-4 Fn-4 (such that) Fn-4 B n (Bell numbers) CL-27 s t (equivalence relation) GT-5 ( n ) k (binomial coefficient) CL-15 ( n m 1,m 2,...) (multinomial coefficient)
Graphs: Introduction. Ali Shokoufandeh, Department of Computer Science, Drexel University
 Graphs: Introduction Ali Shokoufandeh, Department of Computer Science, Drexel University Overview of this talk Introduction: Notations and Definitions Graphs and Modeling Algorithmic Graph Theory and Combinatorial
Graphs: Introduction Ali Shokoufandeh, Department of Computer Science, Drexel University Overview of this talk Introduction: Notations and Definitions Graphs and Modeling Algorithmic Graph Theory and Combinatorial
15-451/651: Design & Analysis of Algorithms October 11, 2018 Lecture #13: Linear Programming I last changed: October 9, 2018
 15-451/651: Design & Analysis of Algorithms October 11, 2018 Lecture #13: Linear Programming I last changed: October 9, 2018 In this lecture, we describe a very general problem called linear programming
15-451/651: Design & Analysis of Algorithms October 11, 2018 Lecture #13: Linear Programming I last changed: October 9, 2018 In this lecture, we describe a very general problem called linear programming
A Generic and Parallel Algorithm for 2D Image Discrete Contour Reconstruction
 A Generic and Parallel Algorithm for 2D Image Discrete Contour Reconstruction Guillaume Damiand, David Coeurjolly To cite this version: Guillaume Damiand, David Coeurjolly. A Generic and Parallel Algorithm
A Generic and Parallel Algorithm for 2D Image Discrete Contour Reconstruction Guillaume Damiand, David Coeurjolly To cite this version: Guillaume Damiand, David Coeurjolly. A Generic and Parallel Algorithm
Computational Geometry for Imprecise Data
 Computational Geometry for Imprecise Data November 30, 2008 PDF Version 1 Introduction Computational geometry deals with algorithms on geometric inputs. Historically, geometric algorithms have focused
Computational Geometry for Imprecise Data November 30, 2008 PDF Version 1 Introduction Computational geometry deals with algorithms on geometric inputs. Historically, geometric algorithms have focused
Bijective Links on Planar Maps via Orientations
 Bijective Links on Planar Maps via Orientations Éric Fusy Dept. Math, University of British Columbia. p.1/1 Planar maps Planar map = graph drawn in the plane without edge-crossing, taken up to isotopy
Bijective Links on Planar Maps via Orientations Éric Fusy Dept. Math, University of British Columbia. p.1/1 Planar maps Planar map = graph drawn in the plane without edge-crossing, taken up to isotopy
Recent PTAS Algorithms on the Euclidean TSP
 Recent PTAS Algorithms on the Euclidean TSP by Leonardo Zambito Submitted as a project for CSE 4080, Fall 2006 1 Introduction The Traveling Salesman Problem, or TSP, is an on going study in computer science.
Recent PTAS Algorithms on the Euclidean TSP by Leonardo Zambito Submitted as a project for CSE 4080, Fall 2006 1 Introduction The Traveling Salesman Problem, or TSP, is an on going study in computer science.
CS 860 Fall Lecture 6. Anna Lubiw, U. Waterloo. one more paper on dynamic graphs (connectivity rather than shortest paths)
 one more paper on dynamic graphs (connectivity rather than shortest paths) Efficient edge splitting-off algorithms maintaining all-pairs edge-connectivities LC Lau, CK Yung - Integer Programming and Combinatorial
one more paper on dynamic graphs (connectivity rather than shortest paths) Efficient edge splitting-off algorithms maintaining all-pairs edge-connectivities LC Lau, CK Yung - Integer Programming and Combinatorial
However, this is not always true! For example, this fails if both A and B are closed and unbounded (find an example).
 98 CHAPTER 3. PROPERTIES OF CONVEX SETS: A GLIMPSE 3.2 Separation Theorems It seems intuitively rather obvious that if A and B are two nonempty disjoint convex sets in A 2, then there is a line, H, separating
98 CHAPTER 3. PROPERTIES OF CONVEX SETS: A GLIMPSE 3.2 Separation Theorems It seems intuitively rather obvious that if A and B are two nonempty disjoint convex sets in A 2, then there is a line, H, separating
CS 372: Computational Geometry Lecture 10 Linear Programming in Fixed Dimension
 CS 372: Computational Geometry Lecture 10 Linear Programming in Fixed Dimension Antoine Vigneron King Abdullah University of Science and Technology November 7, 2012 Antoine Vigneron (KAUST) CS 372 Lecture
CS 372: Computational Geometry Lecture 10 Linear Programming in Fixed Dimension Antoine Vigneron King Abdullah University of Science and Technology November 7, 2012 Antoine Vigneron (KAUST) CS 372 Lecture
The Active Bijection in Graphs, Hyperplane Arrangements, and Oriented Matroids
 The Active Bijection in Graphs, Hyperplane Arrangements, and Oriented Matroids. The Fully Optimal Basis of a Bounded Region Emeric Gioan Michel Las Vergnas published in European Journal of Combinatorics
The Active Bijection in Graphs, Hyperplane Arrangements, and Oriented Matroids. The Fully Optimal Basis of a Bounded Region Emeric Gioan Michel Las Vergnas published in European Journal of Combinatorics
Edge-disjoint Spanning Trees in Triangulated Graphs on Surfaces and application to node labeling 1
 Edge-disjoint Spanning Trees in Triangulated Graphs on Surfaces and application to node labeling 1 Arnaud Labourel a a LaBRI - Universite Bordeaux 1, France Abstract In 1974, Kundu [4] has shown that triangulated
Edge-disjoint Spanning Trees in Triangulated Graphs on Surfaces and application to node labeling 1 Arnaud Labourel a a LaBRI - Universite Bordeaux 1, France Abstract In 1974, Kundu [4] has shown that triangulated
As a consequence of the operation, there are new incidences between edges and triangles that did not exist in K; see Figure II.9.
 II.4 Surface Simplification 37 II.4 Surface Simplification In applications it is often necessary to simplify the data or its representation. One reason is measurement noise, which we would like to eliminate,
II.4 Surface Simplification 37 II.4 Surface Simplification In applications it is often necessary to simplify the data or its representation. One reason is measurement noise, which we would like to eliminate,
gspan: Graph-Based Substructure Pattern Mining
 University of Illinois at Urbana-Champaign February 3, 2017 Agenda What motivated the development of gspan? Technical Preliminaries Exploring the gspan algorithm Experimental Performance Evaluation Introduction
University of Illinois at Urbana-Champaign February 3, 2017 Agenda What motivated the development of gspan? Technical Preliminaries Exploring the gspan algorithm Experimental Performance Evaluation Introduction
Shape Similarity based on a Treelet Kernel with Edition
 Shape Similarity based on a Treelet Kernel with Edition joint work S. Bougleux, L. Brun, M. Mokhtari F.-X. Dupé Introduction Context 2D shapes given by continuous functions of their boundaries binary functions
Shape Similarity based on a Treelet Kernel with Edition joint work S. Bougleux, L. Brun, M. Mokhtari F.-X. Dupé Introduction Context 2D shapes given by continuous functions of their boundaries binary functions
Heuristics and Really Hard Instances for Subgraph Isomorphism Problems
 Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence (IJCAI-6) Heuristics and Really Hard Instances for Subgraph Isomorphism Problems Ciaran McCreesh and Patrick Prosser
Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence (IJCAI-6) Heuristics and Really Hard Instances for Subgraph Isomorphism Problems Ciaran McCreesh and Patrick Prosser
Bijective counting of tree-rooted maps and connection with shuffles of parenthesis systems
 Bijective counting of tree-rooted maps and connection with shuffles of parenthesis systems Olivier Bernardi Abstract The number of tree-rooted maps, that is, tree-covered rooted planar maps, with n edges
Bijective counting of tree-rooted maps and connection with shuffles of parenthesis systems Olivier Bernardi Abstract The number of tree-rooted maps, that is, tree-covered rooted planar maps, with n edges
Bijective counting of tree-rooted maps and shuffles of parenthesis systems
 Bijective counting of tree-rooted maps and shuffles of parenthesis systems Olivier Bernardi Submitted: Jan 24, 2006; Accepted: Nov 8, 2006; Published: Jan 3, 2006 Mathematics Subject Classifications: 05A15,
Bijective counting of tree-rooted maps and shuffles of parenthesis systems Olivier Bernardi Submitted: Jan 24, 2006; Accepted: Nov 8, 2006; Published: Jan 3, 2006 Mathematics Subject Classifications: 05A15,
The Topology of Bendless Orthogonal Three-Dimensional Graph Drawing. David Eppstein Computer Science Dept. Univ. of California, Irvine
 The Topology of Bendless Orthogonal Three-Dimensional Graph Drawing David Eppstein Computer Science Dept. Univ. of California, Irvine Graph drawing: visual display of symbolic information Vertices and
The Topology of Bendless Orthogonal Three-Dimensional Graph Drawing David Eppstein Computer Science Dept. Univ. of California, Irvine Graph drawing: visual display of symbolic information Vertices and
Reference Sheet for CO142.2 Discrete Mathematics II
 Reference Sheet for CO14. Discrete Mathematics II Spring 017 1 Graphs Defintions 1. Graph: set of N nodes and A arcs such that each a A is associated with an unordered pair of nodes.. Simple graph: no
Reference Sheet for CO14. Discrete Mathematics II Spring 017 1 Graphs Defintions 1. Graph: set of N nodes and A arcs such that each a A is associated with an unordered pair of nodes.. Simple graph: no
Efficient Subgraph Matching by Postponing Cartesian Products
 Efficient Subgraph Matching by Postponing Cartesian Products Computer Science and Engineering Lijun Chang Lijun.Chang@unsw.edu.au The University of New South Wales, Australia Joint work with Fei Bi, Xuemin
Efficient Subgraph Matching by Postponing Cartesian Products Computer Science and Engineering Lijun Chang Lijun.Chang@unsw.edu.au The University of New South Wales, Australia Joint work with Fei Bi, Xuemin
Notation Index 9 (there exists) Fn-4 8 (for all) Fn-4 3 (such that) Fn-4 B n (Bell numbers) CL-25 s ο t (equivalence relation) GT-4 n k (binomial coef
 Notation 9 (there exists) Fn-4 8 (for all) Fn-4 3 (such that) Fn-4 B n (Bell numbers) CL-25 s ο t (equivalence relation) GT-4 n k (binomial coefficient) CL-14 (multinomial coefficient) CL-18 n m 1 ;m 2
Notation 9 (there exists) Fn-4 8 (for all) Fn-4 3 (such that) Fn-4 B n (Bell numbers) CL-25 s ο t (equivalence relation) GT-4 n k (binomial coefficient) CL-14 (multinomial coefficient) CL-18 n m 1 ;m 2
Part II. Graph Theory. Year
 Part II Year 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2017 53 Paper 3, Section II 15H Define the Ramsey numbers R(s, t) for integers s, t 2. Show that R(s, t) exists for all s,
Part II Year 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2017 53 Paper 3, Section II 15H Define the Ramsey numbers R(s, t) for integers s, t 2. Show that R(s, t) exists for all s,
Graph Theory. Part of Texas Counties.
 Graph Theory Part of Texas Counties. We would like to visit each of the above counties, crossing each county only once, starting from Harris county. Is this possible? This problem can be modeled as a graph.
Graph Theory Part of Texas Counties. We would like to visit each of the above counties, crossing each county only once, starting from Harris county. Is this possible? This problem can be modeled as a graph.
Cluster algebras and infinite associahedra
 Cluster algebras and infinite associahedra Nathan Reading NC State University CombinaTexas 2008 Coxeter groups Associahedra and cluster algebras Sortable elements/cambrian fans Infinite type Much of the
Cluster algebras and infinite associahedra Nathan Reading NC State University CombinaTexas 2008 Coxeter groups Associahedra and cluster algebras Sortable elements/cambrian fans Infinite type Much of the
Graph Algorithms Using Depth First Search
 Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
751 Problem Set I JWR. Due Sep 28, 2004
 751 Problem Set I JWR Due Sep 28, 2004 Exercise 1. For any space X define an equivalence relation by x y iff here is a path γ : I X with γ(0) = x and γ(1) = y. The equivalence classes are called the path
751 Problem Set I JWR Due Sep 28, 2004 Exercise 1. For any space X define an equivalence relation by x y iff here is a path γ : I X with γ(0) = x and γ(1) = y. The equivalence classes are called the path
Mathematical and Algorithmic Foundations Linear Programming and Matchings
 Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Graph Grammars. Marc Provost McGill University February 18, 2004
 Graph Grammars Marc Provost McGill University marc.provost@mail.mcgill.ca February 18, 2004 Abstract This presentation introduces graph transformations. Typeset by FoilTEX Structure of the talk Graph Theory
Graph Grammars Marc Provost McGill University marc.provost@mail.mcgill.ca February 18, 2004 Abstract This presentation introduces graph transformations. Typeset by FoilTEX Structure of the talk Graph Theory
Flavor of Computational Geometry. Convex Hull in 2D. Shireen Y. Elhabian Aly A. Farag University of Louisville
 Flavor of Computational Geometry Convex Hull in 2D Shireen Y. Elhabian Aly A. Farag University of Louisville February 2010 Agenda Introduction Definitions of Convexity and Convex Hulls Naïve Algorithms
Flavor of Computational Geometry Convex Hull in 2D Shireen Y. Elhabian Aly A. Farag University of Louisville February 2010 Agenda Introduction Definitions of Convexity and Convex Hulls Naïve Algorithms
Planarity. 1 Introduction. 2 Topological Results
 Planarity 1 Introduction A notion of drawing a graph in the plane has led to some of the most deep results in graph theory. Vaguely speaking by a drawing or embedding of a graph G in the plane we mean
Planarity 1 Introduction A notion of drawing a graph in the plane has led to some of the most deep results in graph theory. Vaguely speaking by a drawing or embedding of a graph G in the plane we mean
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs { }
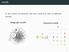 motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
Reliable Location with Respect to the Projection of a Smooth Space Curve
 Reliable Location with Respect to the Projection of a Smooth Space Curve Rémi Imbach Marc Pouget INRIA Nancy Grand Est, LORIA laboratory, Nancy, France. firstname.name@inria.fr Guillaume Moroz Abstract
Reliable Location with Respect to the Projection of a Smooth Space Curve Rémi Imbach Marc Pouget INRIA Nancy Grand Est, LORIA laboratory, Nancy, France. firstname.name@inria.fr Guillaume Moroz Abstract
Trees. 3. (Minimally Connected) G is connected and deleting any of its edges gives rise to a disconnected graph.
 Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Computational Geometry Lecture Duality of Points and Lines
 Computational Geometry Lecture Duality of Points and Lines INSTITUTE FOR THEORETICAL INFORMATICS FACULTY OF INFORMATICS 11.1.2016 Duality Transforms We have seen duality for planar graphs and duality of
Computational Geometry Lecture Duality of Points and Lines INSTITUTE FOR THEORETICAL INFORMATICS FACULTY OF INFORMATICS 11.1.2016 Duality Transforms We have seen duality for planar graphs and duality of
In class 75min: 2:55-4:10 Thu 9/30.
 MATH 4530 Topology. In class 75min: 2:55-4:10 Thu 9/30. Prelim I Solutions Problem 1: Consider the following topological spaces: (1) Z as a subspace of R with the finite complement topology (2) [0, π]
MATH 4530 Topology. In class 75min: 2:55-4:10 Thu 9/30. Prelim I Solutions Problem 1: Consider the following topological spaces: (1) Z as a subspace of R with the finite complement topology (2) [0, π]
Voronoi Diagrams, Delaunay Triangulations and Polytopes
 Voronoi Diagrams, Delaunay Triangulations and Polytopes Jean-Daniel Boissonnat MPRI, Lecture 2 Computational Geometry Learning Voronoi, Delaunay & Polytopes MPRI, Lecture 2 1 / 43 Voronoi diagrams in nature
Voronoi Diagrams, Delaunay Triangulations and Polytopes Jean-Daniel Boissonnat MPRI, Lecture 2 Computational Geometry Learning Voronoi, Delaunay & Polytopes MPRI, Lecture 2 1 / 43 Voronoi diagrams in nature
CSC2420 Fall 2012: Algorithm Design, Analysis and Theory
 CSC2420 Fall 2012: Algorithm Design, Analysis and Theory Allan Borodin September 27, 2012 1 / 23 Lecture 3 1 We will first do the analysis of the Greedy α revocable priority algorithm for the WISP problem
CSC2420 Fall 2012: Algorithm Design, Analysis and Theory Allan Borodin September 27, 2012 1 / 23 Lecture 3 1 We will first do the analysis of the Greedy α revocable priority algorithm for the WISP problem
Subgraph Isomorphism. Artem Maksov, Yong Li, Reese Butler 03/04/2015
 Subgraph Isomorphism Artem Maksov, Yong Li, Reese Butler 03/04/2015 Similar Graphs The two graphs below look different but are structurally the same. Definition What is Graph Isomorphism? An isomorphism
Subgraph Isomorphism Artem Maksov, Yong Li, Reese Butler 03/04/2015 Similar Graphs The two graphs below look different but are structurally the same. Definition What is Graph Isomorphism? An isomorphism
Kurt Mehlhorn, MPI für Informatik. Curve and Surface Reconstruction p.1/25
 Curve and Surface Reconstruction Kurt Mehlhorn MPI für Informatik Curve and Surface Reconstruction p.1/25 Curve Reconstruction: An Example probably, you see more than a set of points Curve and Surface
Curve and Surface Reconstruction Kurt Mehlhorn MPI für Informatik Curve and Surface Reconstruction p.1/25 Curve Reconstruction: An Example probably, you see more than a set of points Curve and Surface
Introduction to Immersion, Embedding, and the Whitney Embedding Theorems
 Introduction to Immersion, Embedding, and the Whitney Embedding Theorems Paul Rapoport November 23, 2015 Abstract We give an overview of immersion in order to present the idea of embedding, then discuss
Introduction to Immersion, Embedding, and the Whitney Embedding Theorems Paul Rapoport November 23, 2015 Abstract We give an overview of immersion in order to present the idea of embedding, then discuss
4. Simplicial Complexes and Simplicial Homology
 MATH41071/MATH61071 Algebraic topology Autumn Semester 2017 2018 4. Simplicial Complexes and Simplicial Homology Geometric simplicial complexes 4.1 Definition. A finite subset { v 0, v 1,..., v r } R n
MATH41071/MATH61071 Algebraic topology Autumn Semester 2017 2018 4. Simplicial Complexes and Simplicial Homology Geometric simplicial complexes 4.1 Definition. A finite subset { v 0, v 1,..., v r } R n
Surfaces, meshes, and topology
 Surfaces from Point Samples Surfaces, meshes, and topology A surface is a 2-manifold embedded in 3- dimensional Euclidean space Such surfaces are often approximated by triangle meshes 2 1 Triangle mesh
Surfaces from Point Samples Surfaces, meshes, and topology A surface is a 2-manifold embedded in 3- dimensional Euclidean space Such surfaces are often approximated by triangle meshes 2 1 Triangle mesh
Computing NodeTrix Representations of Clustered Graphs
 Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 22, no. 2, pp. 139 176 (2018) DOI: 10.7155/jgaa.00461 Computing NodeTrix Representations of Clustered Graphs Giordano Da Lozzo Giuseppe
Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 22, no. 2, pp. 139 176 (2018) DOI: 10.7155/jgaa.00461 Computing NodeTrix Representations of Clustered Graphs Giordano Da Lozzo Giuseppe
Graph Crossing Number and Isomorphism SPUR Final Paper, Summer 2012
 Graph Crossing Number and Isomorphism SPUR Final Paper, Summer 2012 Mark Velednitsky Mentor Adam Bouland Problem suggested by Adam Bouland, Jacob Fox MIT Abstract The polynomial-time tractability of graph
Graph Crossing Number and Isomorphism SPUR Final Paper, Summer 2012 Mark Velednitsky Mentor Adam Bouland Problem suggested by Adam Bouland, Jacob Fox MIT Abstract The polynomial-time tractability of graph
Incremental Updating of 3D Topological Maps to Describe Videos
 Incremental Updating of 3D Topological Maps to Describe Videos Guillaume Damiand, Sylvain Brandel, Donatello Conte To cite this version: Guillaume Damiand, Sylvain Brandel, Donatello Conte. Incremental
Incremental Updating of 3D Topological Maps to Describe Videos Guillaume Damiand, Sylvain Brandel, Donatello Conte To cite this version: Guillaume Damiand, Sylvain Brandel, Donatello Conte. Incremental
On ɛ-unit distance graphs
 On ɛ-unit distance graphs Geoffrey Exoo Department of Mathematics and Computer Science Indiana State University Terre Haute, IN 47809 g-exoo@indstate.edu April 9, 003 Abstract We consider a variation on
On ɛ-unit distance graphs Geoffrey Exoo Department of Mathematics and Computer Science Indiana State University Terre Haute, IN 47809 g-exoo@indstate.edu April 9, 003 Abstract We consider a variation on
Monotone Paths in Geometric Triangulations
 Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
INTRODUCTION TO GRAPH THEORY. 1. Definitions
 INTRODUCTION TO GRAPH THEORY D. JAKOBSON 1. Definitions A graph G consists of vertices {v 1, v 2,..., v n } and edges {e 1, e 2,..., e m } connecting pairs of vertices. An edge e = (uv) is incident with
INTRODUCTION TO GRAPH THEORY D. JAKOBSON 1. Definitions A graph G consists of vertices {v 1, v 2,..., v n } and edges {e 1, e 2,..., e m } connecting pairs of vertices. An edge e = (uv) is incident with
Testing Maximal 1-planarity of Graphs with a Rotation System in Linear Time
 Testing Maximal 1-planarity of Graphs with a Rotation System in Linear Time Peter Eades 1, Seok-Hee Hong 1, Naoki Katoh 2, Giuseppe Liotta 3, Pascal Schweitzer 4, and Yusuke Suzuki 5 1 University of Sydney,
Testing Maximal 1-planarity of Graphs with a Rotation System in Linear Time Peter Eades 1, Seok-Hee Hong 1, Naoki Katoh 2, Giuseppe Liotta 3, Pascal Schweitzer 4, and Yusuke Suzuki 5 1 University of Sydney,
Discovering Frequent Geometric Subgraphs
 Discovering Frequent Geometric Subgraphs Michihiro Kuramochi and George Karypis Department of Computer Science/Army HPC Research Center University of Minnesota 4-192 EE/CS Building, 200 Union St SE Minneapolis,
Discovering Frequent Geometric Subgraphs Michihiro Kuramochi and George Karypis Department of Computer Science/Army HPC Research Center University of Minnesota 4-192 EE/CS Building, 200 Union St SE Minneapolis,
Invariant Measures of Convex Sets. Eitan Grinspun, Columbia University Peter Schröder, Caltech
 Invariant Measures of Convex Sets Eitan Grinspun, Columbia University Peter Schröder, Caltech What will we measure? Subject to be measured, S an object living in n-dim space convex, compact subset of R
Invariant Measures of Convex Sets Eitan Grinspun, Columbia University Peter Schröder, Caltech What will we measure? Subject to be measured, S an object living in n-dim space convex, compact subset of R
P = NP; P NP. Intuition of the reduction idea:
 1 Polynomial Time Reducibility The question of whether P = NP is one of the greatest unsolved problems in the theoretical computer science. Two possibilities of relationship between P and N P P = NP; P
1 Polynomial Time Reducibility The question of whether P = NP is one of the greatest unsolved problems in the theoretical computer science. Two possibilities of relationship between P and N P P = NP; P
Neighborhood-Preserving Translations on Graphs
 Neighborhood-Preserving Translations on Graphs Nicolas Grelier, Bastien Pasdeloup, Jean-Charles Vialatte and Vincent Gripon Télécom Bretagne, France name.surname@telecom-bretagne.eu arxiv:1606.02479v1
Neighborhood-Preserving Translations on Graphs Nicolas Grelier, Bastien Pasdeloup, Jean-Charles Vialatte and Vincent Gripon Télécom Bretagne, France name.surname@telecom-bretagne.eu arxiv:1606.02479v1
Simulations of the quadrilateral-based localization
 Simulations of the quadrilateral-based localization Cluster success rate v.s. node degree. Each plot represents a simulation run. 9/15/05 Jie Gao CSE590-fall05 1 Random deployment Poisson distribution
Simulations of the quadrilateral-based localization Cluster success rate v.s. node degree. Each plot represents a simulation run. 9/15/05 Jie Gao CSE590-fall05 1 Random deployment Poisson distribution
Three applications of Euler s formula. Chapter 10
 Three applications of Euler s formula Chapter 10 A graph is planar if it can be drawn in the plane R without crossing edges (or, equivalently, on the -dimensional sphere S ). We talk of a plane graph if
Three applications of Euler s formula Chapter 10 A graph is planar if it can be drawn in the plane R without crossing edges (or, equivalently, on the -dimensional sphere S ). We talk of a plane graph if
Lecture 1 Discrete Geometric Structures
 Lecture 1 Discrete Geometric Structures Jean-Daniel Boissonnat Winter School on Computational Geometry and Topology University of Nice Sophia Antipolis January 23-27, 2017 Computational Geometry and Topology
Lecture 1 Discrete Geometric Structures Jean-Daniel Boissonnat Winter School on Computational Geometry and Topology University of Nice Sophia Antipolis January 23-27, 2017 Computational Geometry and Topology
Lecture notes for Topology MMA100
 Lecture notes for Topology MMA100 J A S, S-11 1 Simplicial Complexes 1.1 Affine independence A collection of points v 0, v 1,..., v n in some Euclidean space R N are affinely independent if the (affine
Lecture notes for Topology MMA100 J A S, S-11 1 Simplicial Complexes 1.1 Affine independence A collection of points v 0, v 1,..., v n in some Euclidean space R N are affinely independent if the (affine
Approximation Algorithms for Geometric Intersection Graphs
 Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
INTRODUCTION TO THE HOMOLOGY GROUPS OF COMPLEXES
 INTRODUCTION TO THE HOMOLOGY GROUPS OF COMPLEXES RACHEL CARANDANG Abstract. This paper provides an overview of the homology groups of a 2- dimensional complex. It then demonstrates a proof of the Invariance
INTRODUCTION TO THE HOMOLOGY GROUPS OF COMPLEXES RACHEL CARANDANG Abstract. This paper provides an overview of the homology groups of a 2- dimensional complex. It then demonstrates a proof of the Invariance
Basics of Graph Theory
 Basics of Graph Theory 1 Basic notions A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. Simple graphs have their
Basics of Graph Theory 1 Basic notions A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. Simple graphs have their
PTAS for geometric hitting set problems via Local Search
 PTAS for geometric hitting set problems via Local Search Nabil H. Mustafa nabil@lums.edu.pk Saurabh Ray saurabh@cs.uni-sb.de Abstract We consider the problem of computing minimum geometric hitting sets
PTAS for geometric hitting set problems via Local Search Nabil H. Mustafa nabil@lums.edu.pk Saurabh Ray saurabh@cs.uni-sb.de Abstract We consider the problem of computing minimum geometric hitting sets
A NEW ALGORITHM FOR INDUCED SUBGRAPH ISOMORPHISM
 U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 1, 2016 ISSN 1223-7027 A NEW ALGORITHM FOR INDUCED SUBGRAPH ISOMORPHISM Nadia M. G. AL-SAIDI 1, Nuha A. RAJAB 2, and Hayder N. ABDUL- RAHMAN 3 Many algorithms
U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 1, 2016 ISSN 1223-7027 A NEW ALGORITHM FOR INDUCED SUBGRAPH ISOMORPHISM Nadia M. G. AL-SAIDI 1, Nuha A. RAJAB 2, and Hayder N. ABDUL- RAHMAN 3 Many algorithms
Chapter 12 and 11.1 Planar graphs, regular polyhedra, and graph colorings
 Chapter 12 and 11.1 Planar graphs, regular polyhedra, and graph colorings Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 12: Planar Graphs Math 184A / Fall 2017 1 / 45 12.1 12.2. Planar graphs Definition
Chapter 12 and 11.1 Planar graphs, regular polyhedra, and graph colorings Prof. Tesler Math 184A Fall 2017 Prof. Tesler Ch. 12: Planar Graphs Math 184A / Fall 2017 1 / 45 12.1 12.2. Planar graphs Definition
The following is a summary, hand-waving certain things which actually should be proven.
 1 Basics of Planar Graphs The following is a summary, hand-waving certain things which actually should be proven. 1.1 Plane Graphs A plane graph is a graph embedded in the plane such that no pair of lines
1 Basics of Planar Graphs The following is a summary, hand-waving certain things which actually should be proven. 1.1 Plane Graphs A plane graph is a graph embedded in the plane such that no pair of lines
Vertex Cover is Fixed-Parameter Tractable
 Vertex Cover is Fixed-Parameter Tractable CS 511 Iowa State University November 28, 2010 CS 511 (Iowa State University) Vertex Cover is Fixed-Parameter Tractable November 28, 2010 1 / 18 The Vertex Cover
Vertex Cover is Fixed-Parameter Tractable CS 511 Iowa State University November 28, 2010 CS 511 (Iowa State University) Vertex Cover is Fixed-Parameter Tractable November 28, 2010 1 / 18 The Vertex Cover
Lecture 5 CLASSIFICATION OF SURFACES
 Lecture 5 CLASSIFICATION OF SURFACES In this lecture, we present the topological classification of surfaces. This will be done by a combinatorial argument imitating Morse theory and will make use of the
Lecture 5 CLASSIFICATION OF SURFACES In this lecture, we present the topological classification of surfaces. This will be done by a combinatorial argument imitating Morse theory and will make use of the
Search Algorithms. IE 496 Lecture 17
 Search Algorithms IE 496 Lecture 17 Reading for This Lecture Primary Horowitz and Sahni, Chapter 8 Basic Search Algorithms Search Algorithms Search algorithms are fundamental techniques applied to solve
Search Algorithms IE 496 Lecture 17 Reading for This Lecture Primary Horowitz and Sahni, Chapter 8 Basic Search Algorithms Search Algorithms Search algorithms are fundamental techniques applied to solve
