DEVELOPING A THREE-DIMENSIONAL TOPOLOGICAL DATA MODEL
|
|
|
- Ashlie Brooks
- 5 years ago
- Views:
Transcription
1 DEVELOPING A THREE-DIMENSIONAL TOPOLOGICAL DATA MODEL Saadi MESGARI International Institute for Aerospace Survey and Earth Sciences (ITC) The Netherlands Mesgari@itc.nl Working Group IC/16 KEY WORDS: Data models, Topology, Topological, 3D, Spatial Objects, Cell Complex, Overlay ABSTRACT In this study, a topological data model is defined based on cell-complexes to represent the geometry of spatial objects and their topological relations. It is discussed how a spatial object can be fragmented into simple cells and represented by a regular cell-complex. Such a cell-complex can describe both the geometry and internal topological structure of a spatial object. In other words, the regular cell-complex is both an approximation of the geometry of the spatial object and a topological equivalent of it. Topological relations between n-dimensional (0 n 3) spatial objects will be defined based on the integration (overlay) of regular cell-complexes representing spatial objects in a 3-dimensional space R 3. The result is a more general cell-complex called Generalized Singular (GS) cell-complex, which consists of cells of different dimensions. The direct consequence of integrating spatial objects is the intersection of their cells. Some types of singularity, which are caused by the intersection of cells, along with the way they should be handled are discussed. The only type of singularity we allow in the GS cell-complex happens when a higher-dimensional cell contains lower-dimensional cells that are not part of its boundary cycles. The reason why we should not allow other types of singularity is discussed. Finally, the rules governing the GS cell-complex are described. 1 INTRODUCTION Compared to the traditional maps, spatial analysis of thematic data is improved efficiently by digital co-registration and overlaying analysis capabilities of 2D GISs. Many analyses, predictions and simulations that never could be done using maps is now possible using 2D GISs. However, many applications require the modeling and analysis of 3D phenomena, which are not properly supported by 2D GISs. Many systems have already been developed for modeling spatial objects and simulating their movements and behavior in 3D space. However, because of their shortcoming in representing the topological relations between objects, such systems are not capable of many spatial analyses that are expected from a GIS. Therefore, there is a need for a 3D topological data model to represent both the 3D geometry and topological relations of spatial objects. Developing such a data model is not a trivial and simple extension of the available 2D topological data models. The geometry of spatial objects can be much more complicated in a 3D than in a 2D space. In addition, the relations between spatial objects in 3D space are of more types. Development of a 3D spatial data model should be based on the study of geometry and relations of spatial objects in 3D space. 2 CELLS, BUILDING BLOCKS OF SPATIAL OBJECTS The first applications of cells and cell-complexes were in topology, which is the most general form of geometry. Topologists use cells and cell-complexes for the fragmentation of spaces they study. This fragmentation is to simplify the calculation of very general characteristics (topological properties) of those spaces. With the development of computer science and technology, several systems such as CAD/CAM, Computer Graphics and GIS emerged to represent spatial objects for different applications. Such spatial objects are usually complex. To overcome this complexity, in those systems also, spatial objects are fragmented and represented as cell-complexes composed of simple International Archives of Photogrammetry and Remote Sensing. Vol. XXXIII, Part B4. Amsterdam
2 primitives (cells) of different dimensions. In this research we follow the same approach and fragment spatial objects into primitive cells of proper dimensions. In the followings, we use some terms from topology such as manifold, manifold with boundary, n-disk and topologically equivalent without defining them. For the definitions of these terms, reader can refer to Croom (1978), Singer and Thorpe (1967) and Stillwell (1980). We define a Generalized Regular n-dimensional cell (GR n-cell) as a connected part of a Euclidean n-manifold (n-dimensional manifold) with one or more subdivided (n-1)-manifold boundary cycles (2 n 3). We exclude the 0-cell from this definition simply because we can not assume a 0-manifold with subdivided (-1)-dimensional manifold boundary cycles. A GR 0-cell is simply defined as a single point. A 1-cell is also excluded from that definition for the same reason; i.e. we do not have any 0-manifold to be the boundary of the 1- cell. A 1-cell can be defined as a connected part of a Euclidean 1-manifold with exactly two 0-cells as its boundary. It means that 1-cells and 2-cells do not have any curvature or folding. A 1-cell is a straight segment and a 2-cell is a part of a flat surface possibly with some inner boundaries. In the rest of the thesis, whenever it is more convenient, we use the more familiar terms of node, arc, facet and body instead of GR 0-cell, GR 1-cell, GR 2-cell and GR 3-cell respectively. The definition of GR cell includes any connected part of an Euclidean n-manifold with the only condition that any of its boundary cycles should be a subdivided (n-1)-manifold. We use the term subdivided to note that such a manifold boundary is also represented by a generalized regular (n-1)-dimensional cell-complex (we define these terms latter), which actually subdivides the boundary (n-1)-manifold into a bunch of cells. We name our cell generalized because it extends and incorporates the simplicial and regular CW complexes used in topology. In addition, we call it regular because the subdivided manifold boundary cycles form the (n-1)-skeleton of the cell and so are regular. Figure 1 shows some examples of cells that are in accordance with the definition of GR cell. Figure 1: Some examples of the Generalized Regular cells 3 SPATIAL OBJECTS REPRESENTED AS REGULAR CELL-COMPLEXES 3.1 Spatial Objects Usually, we use the term spatial objects for any object or phenomenon that spatially extends through the 3-dimensional space (the physical world we live in). Basically, such an object, no matter how thin and small, occupies some parts of the 3-dimensional space ant so inherent the dimension from that space. It means that, all spatial objects we are dealing with are actually 3-dimensional. However, sometimes a spatial object is much more extended in one or more dimensions than in the others. For example, although a water supply pipe is a cylinder (a 3-dimensional object) and has volume, but still its diameter is negligible in comparison with its length. Therefore, in spatial data modeling the image of such object can be considered as a 1-dimensional spatial object. Similarly, a spatial object can be considered and represented as a 2-dimensional object. An object that is small enough, regarding the scale or in comparison with other objects around it, can be considered as a 0-dimensional spatial object. Therefore, in the followings, whenever we say that a spatial object is n-dimensional, 0 n 2, we mean that the extension of different parts of it along one or more dimensions are insignificant. 648 International Archives of Photogrammetry and Remote Sensing. Vol. XXXIII, Part B4. Amsterdam 2000.
3 To be more clear and specific about the concepts that will be discussed in the following, we assume a spatial object to be uni-dimensional, i.e. composed of parts of the same dimension. In reality, an object can be multi-dimensional, i.e. composed of parts of different dimensions. If an object is multi-dimensional, it can be divided into some unidimensional spatial objects. For example, a house with all its assets is a multi-dimensional object that can be divided into some 3D, 2D and 1D spatial objects. Later, all these uni-dimensional spatial objects can be aggregated to build up the multi-dimensional object of the house. Figure 2 represents some examples of uni-dimensional spatial objects. (a) (b) (c) (d) Figure 2: Examples of uni-dimensional spatial objects: a 0-dimensional spatial object is represented by a single node. Spatial objects of dimensions 1, 2 and 3 are represented as GR cell-complexes, in which the points with non-manifold neighborhood are highlighted. Because of such non-manifold points, none of these objects can be represented by a single cell. 3.2 Generalized Regular Cell-Complex Any such spatial object, although uni-dimensional, still can be geometrically complex and might have complex topological relations with other objects. To overcome those complexities, any such uni-dimensional spatial object is fragmented into GR cells and represented by a cell-complex consisting of those GR cells. Usually a cell-complex is defined in the same way as a simplicial complex. We define a Generalized Regular (GR) cell-complex U as a set of GR cells if the following conditions are satisfied: The set U is finite. If U contains a GR cell then it also contains all the faces of this cell. The intersection of two GR cells of U is either empty or a common face of them. 3.3 Geometry of Spatial Objects and handling Curvature and Folding Although topology is also a part of geometry, we exclusively define the geometry of cells and objects as their shape, size, orientation and positional information. The geometry of a spatial object can be determined based on the geometry of cells in the cell-complex representing it. The geometry of each cell is also determined from the geometry of its lowerdimensional boundary cells, down to the lowest-dimensional cells (nodes). Therefore, all the shape, size, orientation and positional information about objects are stored in the coordinates of their nodes. In the definition of GR cell given by Pigot (1995), he allowed a cell to be a topologically equivalent of a part of the Euclidean manifold. With such a definition, an arc or facet can be curved and/or folded and still be topologically equivalent to a part of the Euclidean 1-manifolds or 2-manifolds. It is obvious that curvature and folding are meaningless for nodes and bodies in a three-dimensional space. Allowing the curvature and folding in an arc or facet, its geometry can not be always defined simply based on the geometry of its boundary cells. Only in the case of a folded arc, it seams possible to use the same method as used in 2-dimensional GISs. That is, to have a list of coordinates associated with the arc to represent the intermediate points between the two end nodes of the arc. Our intention in using cells and cell-complexes is to represent not only the topological relations between spatial objects, but also their geometrical structure. Therefore, we modified our definition of GR cell by allowing it to be only a part of the Euclidean manifold and not a topological equivalent of it. Such a definition explicitly limits the arcs and facets to be straight and flat respectively. International Archives of Photogrammetry and Remote Sensing. Vol. XXXIII, Part B4. Amsterdam
4 3.4 Subdividing a Spatial Objects into GR Cells With the above results, we can determine how and where a spatial object should be fragmented in order to be represented by a set of simple cells. As is shown in Figure 2(a), a 0-dimensional spatial object can be simply represented by a single node. A 1-dimensional spatial object should be fragmented at any point with a neighborhood that is not topologically equivalent to a 1-disk. Such points are where three or more line-segments are intersecting. In the Figure 2(b), such non-1-manifold points are highlighted. Also, for the sake of consistency and homogeneity, we selected not to use the list of intermediate point coordinates, explained above. Therefore, at any folding point the object will be fragmented. The curvature can be approximated by a set of arcs. A 2-dimensional spatial object is also shown in Figure 2(c). Similar to 1-dimensional case, such an object is fragmented at the non-2-manifold points, which are depicted in the Figure as a highlighted arc. In addition, it is fragmented at any folding line. A Curved facet can be replaced by a collection of flat facets. Finally, a 3-dimensional object can be subdivided at any non-3-manifold point such as those highlighted in the Figure2(d). 4 TOPOLOGICAL RELATIONS BETWEEN CELLS AND BETWEEN CELL-COMPLEXES Topological relations can be divided into two types, the relations between the cells in a cell complex and the relations between different cell complexes representing spatial objects. What we need for spatial analyses and queries in a GIS are the topological relations between spatial objects (cell complexes) themselves. Studies done by Egenhofer and Herring (1991), Egenhofer and Mark (1995) and others show how numerous and complex the topological relations between spatial objects are. Usually, to calculate the relations between spatial objects, in 2D-GIS the union of cell complexes representing spatial objects is calculated. It means that, the cell complexes representing spatial objects are embedded together in a Euclidean 2-manifold and the topological relations between their cells are calculated again. Then the relations between spatial objects can be derived from the relations among their cells. For example, when we want to query if a river is going through a forest, we only need to check if any of the arcs representing the river has the facets of the forest as both its coboundaries. We select the same approach as the above. GR cell-complexes representing spatial objects of different dimensions are embedded together (overlaid) in a 3-dimensional Euclidean manifold. The Euclidean 3-dimensional manifold represents the 3-dimensional space of spatial objects. The result is a more general cell complex, which does not obey the rules described in the definition of the GR cell-complexes. We call it a Generalized Singular (GS) cellcomplex in contrast to GR cell-complexes. The definition of such a cell-complex and its difference with GR cellcomplex will be discussed later. The immediate consequence of such integration is that cells of different spatial objects might intersect each other. So, whenever the interior of a cell is crossed (cut) by another cell, at the intersection points new cells will be created (if such a cell does not exist already) and one or both of intersecting cells will be subdivided. Then simple topological relations between all cells in this GS cell-complex should be calculated. The result is that, latter, complicated topological relations between spatial objects can be derived from simpler topological relations among their cells in the GS cell-complex. 5 OVERLAY OF SPATIAL OBJECTS As was explained, when overlaying GR cell-complexes representing spatial objects some cells intersect each other and sometimes in the intersection points new cells should be created. For example when two arcs are intersecting in their interiors, in the intersection point a new node is created; also, when an arc is intersecting the interior of a facet, in the intersection point a new node is created. Usually the creation of such new cells have two consequences. Any of the two intersecting cells either will contain the new cell or will be subdivided by the new cell. The criterion for any intersecting cell to be subdivided or not is its continuity after the intersection. Here, we call a k - cell continuous if we can draw a path between any two points of it, completely inside it and without crossing any j -cell inside it (j < k). If by the creation of a new cell at the intersection points, the intersecting cell remains continuous then it will not be subdivided and the new cell will be embedded in it. For example, when an arc is crossing through the interior of a facet, i.e. when they intersect in one point in their interiors, at the intersection point a new node will be 650 International Archives of Photogrammetry and Remote Sensing. Vol. XXXIII, Part B4. Amsterdam 2000.
5 created. Having such a new node created, the arc will not be continuous anymore and will be subdivided into two smaller arcs adjacent in the new node. In contrast, the facet will remain continuous. Therefore, it will not be subdivided by the node and the node will be contained in it. The relation between the two new arcs (subdivision of the first arc) and the facet is based on the new intersection node, which is both a common boundary of the arcs and a dangling node inside the facet. When two cells intersect, it is not always necessary to create new cells in the intersection points. Sometimes the intersection is in an existing cell, which might be part of the boundary of one or both of the intersecting cells. For example, a facet can touch the interior of another facet, i.e. a boundary arc/node of one facet can be in the interior of the other one. Calculating the union (overlay) of spatial objects represented as GR cell-complexes should be based on the following general rules: The intersection of two cells should always be a cell (or some cells) of the cell-complex. If the intersection of two cells is not of the same dimension as both of them and already a cell exists at the intersection of the two cells, then we only need to define the relation of the intersection cell with the two intersecting cells. An example is when two cells intersect in a part of the boundary of one or both of them) If the intersection of two cells is not of the same dimension as both of them and there is not any cell at the intersection of the two cells (i.e. if the two cells intersect each other in their interiors), then at the intersection points new cell (cells) should be created. By the creation of the new cell, if any of the two intersecting cells become discontinuous, then that cell should be subdivided into two smaller cells, which are adjacent to each other at the new cell. Otherwise, the new cell will be contained inside that intersecting cell. Two cells that are equal, i.e. cover each other completely, will be represented as only one cell in the GS cellcomplex. One cell can not be completely covered by (contained in) another cell of the same dimension. In such a case, the containing cell will be subdivided into two parts that are shared and not shared with the smaller cell. The two shared (matching) parts will be equalized (represented by one cell). Such a subdivision might cause the creation of cyclic singularity, which will be explained latter. However, a cell can be completely contained in another cell of a higher dimension without demolishing the continuity of the higher-dimensional cell, e.g. an arc can be inside a facet but a facet can not be inside another facet. If the intersection of two cells is not equal to any of them but is of the same dimension as both of them, e.g. when two bodies overlap each other in a part of their volumes, then the two cells should be subdivided such that the intersection part becomes a new and separated cell. 6 SINGULARITIES RESULTED FROM THE OVERLAY OF SPATIAL OBJECTS When we have the union of spatial objects of the same dimension, the result of intersections is another cell-complex composed of cells of the same dimension, with the only difference that they are more subdivided. For example, when cell-complexes composed of 2-cells and representing 2-dimensional spatial objects are combined, the result of intersection is another cell-complex in which the 2-cells are subdivided into smaller 2-cells. Sometimes, we have the integration of spatial objects of different dimensions, which are represented as cell-complexes with cells of different dimensions. The result of integration will be a cell-complex consisting of multi-dimensional cells. So, for example, there might be 2-cells that have dangling and/or internal 1-dimensional and 0-dimensional cell-complexes. Such situations are referred to as singularity. Obviously, those dangling and isolated internal cell-complexes are not part of the boundary of the 2-cell. They simply are parts of cell-complexes representing other spatial objects. Despite this fact, in early works of Corbett (1975) and Corbett (1979), such dangling and internal cells were considered as part of the boundary of the cell in order to describe the neighborhoods of cells in such singularities. Corbett (1979) defined a regular cell as the image of a one-to-one, onto and continuous transformation (homeomorphism) applied to both the interior and boundary of the n-disk (n-ball). In contrast to this, he defined a singular cell as an image of the n-disk, in which the one-to-one condition of the transformation is relaxed. The consequence of this relaxation is that some points in the boundary of the n-cell can be identified. In other words, the boundary of a singular cell is the image of a continuous mapping applied to the boundary cycle of a regular cell that results in the identification of sets of points. The effect of such identifications is singularity, i.e. singularity is the set of points whose neighborhoods are no longer homeomorphic to the 1-disk. He distinguishes among three types of singularities for 2-cells: cyclic, acyclic and interior. International Archives of Photogrammetry and Remote Sensing. Vol. XXXIII, Part B4. Amsterdam
6 Figure 3 shows some examples of such singularities. In Figure 3(a), we have a regular 2-cell, which has a boundary cycle homeomorphic to the boundary of a 2-disk. Notice that the boundary of a 2-disk is a 1-dimensional sphere, which is a 1-manifold. Figure 3(b) shows a mapping applied to the regular cell that identifies two points in the boundary of the regular cell. The result is a 2-cell with a cyclic singularity, i.e. it has a new 1-cycle as part of its boundary and attached to its outer boundary. The problem with such a boundary is that in the identified points the boundary is not a 1-manifold anymore. Similarly, by applying another continuous mapping and identifying some other points in the boundary of the 2-cell Figure 3(c) will be resulted. This Figure shows a 2-cell with acyclic singularity, which is a 2-cell with an internal tree structure composed of 1-cells. Finally, by the identification of more points Figure 3(d) is resulted, which shows a 2- cell with interior singularity. (a) (b) (c) (d) Figiure 3: Examples of singularity: (a) a regular 2-cell, (b) a 2-cell with cyclic singularity, (c) a 2-cell with acyclic singularity and (d) a 2-cell with interior singularity. Corbett (1979) assumed singularities as part of the boundary of the singular cell by allowing the boundary of a singular cell to be a pseudomanifold. A pseudomanifold is a figure in which almost all points obey the manifold conditions and is formed by gluing (identifying) some points of a manifold. Pigot (1995) followed the same approach and defined a generalized singular k-cell as a Euclidean k -manifold with i subdivided (k-1) -pseudomanifold boundary cycles (i 1). The j-cells (j k-1) in the subdivided (k-1)-pseudomanifold boundary cycles are a subset of the (k-1)-skeleton. Having defined such a singular cell, he defined the generalized singular cell-complex as a complex composed of such singular cells. Such a cell-complex is the union of cell-complexes representing spatial objects. In this research, we take a different approach. In our model, we have only GR cells and not any singular cell. Instead, when integrating cell-complexes that represent spatial objects of different dimensions, the regular cells are allowed to have dangling or isolated cells of lower-dimensions in their interiors. So, in our approach dangling and internal structures are considered as being contained inside the higher-dimensional cell and not part of its boundary. Such an approach has two advantages compared with the other one: First, it is more intuitive and more representative of the real relation between the higher-dimensional cell and the dangling/internal cells inside it. We should remember that, essentially, the boundary is supposed to be the border between the interior and the exterior of an object or cell. However, when a k-cell has some dangling or internal j-cells (j k-1) inside it, the whole k-dimensional neighborhoods of those j-cells are at the interior of the k-cell. Second, in our approach the boundary of a regular k-cell is enforced to be a (k-1)-manifold. As it will be explained latter, this manifold condition can be checked using the co-boundary orderings. In fact, this condition is the basis of topological consistency checks to differentiate between correct and incorrect cells (Mesgari et all, 1998). In the other approach, checking the condition of the boundary being a pseudomanifold is not as easy as in our approach. Because, basically, the class of pseudomanifolds is much more general than the class of manifolds and the neighborhood of points in singularities are more complex than regular points. We explained that in our approach, the dangling and internal structures inside a cell are not assumed as part of its boundary and still the boundary of such a cell should be a manifold. However, in order to be consistent with other approaches to the problem of integrating spatial objects, still we refer to such situations as acyclic and interior singularities. Nevertheless, these situations are in contradiction to a general rule of regular cell-complexes (the rule that cells intersect only along their boundaries). Therefore, we refer to the multi-dimensional cell-complex resulted from the integration of spatial objects of different dimensions, which has such singularities, as the Generalized Singular cellcomplex. The two types of acyclic and interior singularities are allowed in our model by accepting a cell to be inside another cell of a higher dimension. In this regard, cyclic singularity is different from the other two types. The problem with this singularity is that in the identified points the boundary is not a manifold anymore, and so, the cell can not be a GR cell 652 International Archives of Photogrammetry and Remote Sensing. Vol. XXXIII, Part B4. Amsterdam 2000.
7 anymore. This type of singularity is usually created by the subdivision of a regular cell that is shared (covered) partly by a smaller cell of the same dimension, as explained in section 5. We eliminate cyclic singularities by subdividing such a singular cell into two new GR cells. 7 GENERALIZED SINGULAR CELL-COMPLEX REPRESENTING THE OVERLAY OF SPATIAL OBJECTS From the above discussions, it can be concluded that the union of spatial objects can not be realized without accepting some types of singularities. We discussed how the overlapping and containment relations between cells (and consequently spatial objects) of the same dimension can be represented by subdividing them into shared and non-shared parts. The same can not be done for cells (and so objects) of different dimensions and as a result we encounter some types of singularities. From the rules described in section 5 and above discussions, the definition of the GS cellcomplex, which is the result of integrating spatial objects of different dimensions, can be concluded. We define a Generalized Singular (GS) Cell-Complex as a set of generalized regular cells X if the following conditions are satisfied: 1. The set X is finite. 2. If X contains a cell, then it also contains all the faces of the cell. 3. Not only the boundary, but also the interior of a cell can be intersected by another cell, with the only condition that the intersection should be in some cells of X. 4. Any k-cell of X, although having singularities, is continuous, i.e. it should always be possible to draw a path between any two points of the k-cell, completely inside it, without crossing any j-cell inside it (j < k). 5. Two cells of X of the same dimensions can not intersect each other in a part of their interiors that is of the same dimension as the two cells. We adopt the first two conditions from the regular cell-complexes. Condition 1 is simply to prevent the assumption of infinite number of cells; usually the cell-complexes we want to create in GIS are satisfying this condition. Condition 2 prevents the creation and existence of a cell without all its faces (boundaries and boundaries of boundaries etc.) existing. Before we create a cell, all its faces should be created and they should be part of the cell-complex. This condition also guarantees that we do not delete a cell when it is still part of the boundary of another cell. First, the higher-dimensional cell should be deleted and only then, a part of its boundary can be deleted. Condition 3 is to allow the acyclic and interior singularities, when the interior of the higher-dimensional cell is intersected by the other cell. Previously it was explained that the definition of the generalized regular cell does not allow the presence of cyclic singularities because the cells in GS cell-complex should be GR cells. Based on this condition, whenever arcs and facets cross each other, in the intersection points new cells should be created (if not existent already) and added to the cellcomplex. Condition 4 is to enforce the continuity of cells. Previous condition enforces the existence or creation of a cell in the intersection of two cells. Condition 4 suggests that whenever any of the two intersecting cells becomes discontinuous by creating the new cell, we should subdivide that intersecting cell. Finally, condition 5 is to prevent the overlapping and containment relations between cells of the same dimension. These five conditions along with the definition of GR cell are enough to check and ensure the correctness of the GS cell-complex such that it represents the topological relations between cells of spatial objects. In some other parts of this research, different types of topological relations between cells of the singular cell-complex are studied. Those topological relations are represented by a modified version of the cell-tuple data structure of Brisson (1990). The modifications are necessary to cover the singular situations. Also some topological operators are designed and are going to be formally specified for the construction of cells in the GS cell-complex. More explanation about these parts of the research is out of the scope of this article. 8 CONCLUSIONS The geometry and topological structure of spatial objects of different dimensions were represented by regular cellcomplexes of proper dimensions. To determine the topological relations between them, spatial objects are integrated in a more general cell-complex, which includes some types of singularities. Singularities are the result of intersection International Archives of Photogrammetry and Remote Sensing. Vol. XXXIII, Part B4. Amsterdam
8 between cells of different dimensions in their interiors. Different types of singularities were studied. The rules governing the general cell-complex that represent the integration of spatial objects were determined. REFERENCES Brisson, E., (1990). Representation of d Dimensional Geometric Objects. PhD Thesis, University of Washington, Seattle, USA. Corbett, J. P., Topological Principles in Cartography. In: The Proceedings of AUTOCARTO-2, Reston, Virginia, pp Corbett, J. P., Topological Principles in Cartography. Technical Paper 48, U.S. Bureau of the Census, USA. Croom, F. H., Basic concepts of Algebraic Topology. Springer-Verlag, New York Inc. Egenhofer, M. J. and Herring, J. R., Categorizing binary topological relations between regions, lines and points in geographic databases, Technical Report, Department of Surveying Engineering, University of Maine, Orono, ME. Egenhofer, M. J. and Mark, D. M., Modelling conceptual neighbourhoods of topological line-region relations. International Journal of Geographical Information Systems, 9(5), pp Mesgari, S., Kainz, W. and de By, R. A., D Topological Data Modeling for Public Utilities. In: Proceedings of the First Conference of the Association of Geographical Information Laboratories in Europe (AGILE), ITC, The Netherlands. Pigot, S., A Topological Model for a 3-Dimensional Spatial Information System. PhD thesis, University of Tasmania, Australia. Singer, I. M. and Thorpe, J. A., Lecture Notes on Elementary Topology and Geometry. Springer-Verlag, New York. Stillwell, J., Classical Topology and Computational Group Theory. Springer-Verlag, New York Inc. 654 International Archives of Photogrammetry and Remote Sensing. Vol. XXXIII, Part B4. Amsterdam 2000.
OPERATORS FOR CELL TUPLE-BASED SPATIOTEMPORAL DATA MODEL
 OPERTORS FOR CELL TUPLE-BSED SPTIOTEMPORL DT MODEL le Raza ESRI 80 New York Street, Redlands, California 97-800, US Tel.: +-909-79-85 (ext. 009) Fax: +-909-07-067 araza@esri.com Commission IV, WG IV/ KEY
OPERTORS FOR CELL TUPLE-BSED SPTIOTEMPORL DT MODEL le Raza ESRI 80 New York Street, Redlands, California 97-800, US Tel.: +-909-79-85 (ext. 009) Fax: +-909-07-067 araza@esri.com Commission IV, WG IV/ KEY
DERIVING SPATIOTEMPORAL RELATIONS FROM SIMPLE DATA STRUCTURE
 DERIVING SPATIOTEMPORAL RELATIONS FROM SIMPLE DATA STRUCTURE Ale Raza ESRI 380 New York Street, Redlands, California 9373-800, USA Tel.: +-909-793-853 (extension 009) Fax: +-909-307-3067 araza@esri.com
DERIVING SPATIOTEMPORAL RELATIONS FROM SIMPLE DATA STRUCTURE Ale Raza ESRI 380 New York Street, Redlands, California 9373-800, USA Tel.: +-909-793-853 (extension 009) Fax: +-909-307-3067 araza@esri.com
CLASSIFICATION OF SURFACES
 CLASSIFICATION OF SURFACES JUSTIN HUANG Abstract. We will classify compact, connected surfaces into three classes: the sphere, the connected sum of tori, and the connected sum of projective planes. Contents
CLASSIFICATION OF SURFACES JUSTIN HUANG Abstract. We will classify compact, connected surfaces into three classes: the sphere, the connected sum of tori, and the connected sum of projective planes. Contents
1. Introduction to Constructive Solid Geometry (CSG)
 opyright@010, YZU Optimal Design Laboratory. All rights reserved. Last updated: Yeh-Liang Hsu (010-1-10). Note: This is the course material for ME550 Geometric modeling and computer graphics, Yuan Ze University.
opyright@010, YZU Optimal Design Laboratory. All rights reserved. Last updated: Yeh-Liang Hsu (010-1-10). Note: This is the course material for ME550 Geometric modeling and computer graphics, Yuan Ze University.
The Construction of a Hyperbolic 4-Manifold with a Single Cusp, Following Kolpakov and Martelli. Christopher Abram
 The Construction of a Hyperbolic 4-Manifold with a Single Cusp, Following Kolpakov and Martelli by Christopher Abram A Thesis Presented in Partial Fulfillment of the Requirement for the Degree Master of
The Construction of a Hyperbolic 4-Manifold with a Single Cusp, Following Kolpakov and Martelli by Christopher Abram A Thesis Presented in Partial Fulfillment of the Requirement for the Degree Master of
Geometric and Thematic Integration of Spatial Data into Maps
 Geometric and Thematic Integration of Spatial Data into Maps Mark McKenney Department of Computer Science, Texas State University mckenney@txstate.edu Abstract The map construction problem (MCP) is defined
Geometric and Thematic Integration of Spatial Data into Maps Mark McKenney Department of Computer Science, Texas State University mckenney@txstate.edu Abstract The map construction problem (MCP) is defined
Solids as point set. Solid models. Solid representation schemes (cont d) Solid representation schemes. Solid representation schemes (cont d)
 Solid models Solid models developed to address limitations of wireframe modeling. Attempt was to create systems which create only complete representations. Modelers would support direct creation of 3D
Solid models Solid models developed to address limitations of wireframe modeling. Attempt was to create systems which create only complete representations. Modelers would support direct creation of 3D
Lecture 0: Reivew of some basic material
 Lecture 0: Reivew of some basic material September 12, 2018 1 Background material on the homotopy category We begin with the topological category TOP, whose objects are topological spaces and whose morphisms
Lecture 0: Reivew of some basic material September 12, 2018 1 Background material on the homotopy category We begin with the topological category TOP, whose objects are topological spaces and whose morphisms
Planar Graphs. 1 Graphs and maps. 1.1 Planarity and duality
 Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Lecturer 2: Spatial Concepts and Data Models
 Lecturer 2: Spatial Concepts and Data Models 2.1 Introduction 2.2 Models of Spatial Information 2.3 Three-Step Database Design 2.4 Extending ER with Spatial Concepts 2.5 Summary Learning Objectives Learning
Lecturer 2: Spatial Concepts and Data Models 2.1 Introduction 2.2 Models of Spatial Information 2.3 Three-Step Database Design 2.4 Extending ER with Spatial Concepts 2.5 Summary Learning Objectives Learning
Class #2. Data Models: maps as models of reality, geographical and attribute measurement & vector and raster (and other) data structures
 Class #2 Data Models: maps as models of reality, geographical and attribute measurement & vector and raster (and other) data structures Role of a Data Model Levels of Data Model Abstraction GIS as Digital
Class #2 Data Models: maps as models of reality, geographical and attribute measurement & vector and raster (and other) data structures Role of a Data Model Levels of Data Model Abstraction GIS as Digital
Embedding a graph-like continuum in some surface
 Embedding a graph-like continuum in some surface R. Christian R. B. Richter G. Salazar April 19, 2013 Abstract We show that a graph-like continuum embeds in some surface if and only if it does not contain
Embedding a graph-like continuum in some surface R. Christian R. B. Richter G. Salazar April 19, 2013 Abstract We show that a graph-like continuum embeds in some surface if and only if it does not contain
Lecture 6: GIS Spatial Analysis. GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University
 Lecture 6: GIS Spatial Analysis GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University 1 Spatial Data It can be most simply defined as information that describes the distribution
Lecture 6: GIS Spatial Analysis GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University 1 Spatial Data It can be most simply defined as information that describes the distribution
Lecture notes for Topology MMA100
 Lecture notes for Topology MMA100 J A S, S-11 1 Simplicial Complexes 1.1 Affine independence A collection of points v 0, v 1,..., v n in some Euclidean space R N are affinely independent if the (affine
Lecture notes for Topology MMA100 J A S, S-11 1 Simplicial Complexes 1.1 Affine independence A collection of points v 0, v 1,..., v n in some Euclidean space R N are affinely independent if the (affine
Topic: Orientation, Surfaces, and Euler characteristic
 Topic: Orientation, Surfaces, and Euler characteristic The material in these notes is motivated by Chapter 2 of Cromwell. A source I used for smooth manifolds is do Carmo s Riemannian Geometry. Ideas of
Topic: Orientation, Surfaces, and Euler characteristic The material in these notes is motivated by Chapter 2 of Cromwell. A source I used for smooth manifolds is do Carmo s Riemannian Geometry. Ideas of
Chapter 12 Solid Modeling. Disadvantages of wireframe representations
 Chapter 12 Solid Modeling Wireframe, surface, solid modeling Solid modeling gives a complete and unambiguous definition of an object, describing not only the shape of the boundaries but also the object
Chapter 12 Solid Modeling Wireframe, surface, solid modeling Solid modeling gives a complete and unambiguous definition of an object, describing not only the shape of the boundaries but also the object
Simplicial Hyperbolic Surfaces
 Simplicial Hyperbolic Surfaces Talk by Ken Bromberg August 21, 2007 1-Lipschitz Surfaces- In this lecture we will discuss geometrically meaningful ways of mapping a surface S into a hyperbolic manifold
Simplicial Hyperbolic Surfaces Talk by Ken Bromberg August 21, 2007 1-Lipschitz Surfaces- In this lecture we will discuss geometrically meaningful ways of mapping a surface S into a hyperbolic manifold
A Flavor of Topology. Shireen Elhabian and Aly A. Farag University of Louisville January 2010
 A Flavor of Topology Shireen Elhabian and Aly A. Farag University of Louisville January 2010 In 1670 s I believe that we need another analysis properly geometric or linear, which treats place directly
A Flavor of Topology Shireen Elhabian and Aly A. Farag University of Louisville January 2010 In 1670 s I believe that we need another analysis properly geometric or linear, which treats place directly
The Charney-Davis conjecture for certain subdivisions of spheres
 The Charney-Davis conjecture for certain subdivisions of spheres Andrew Frohmader September, 008 Abstract Notions of sesquiconstructible complexes and odd iterated stellar subdivisions are introduced,
The Charney-Davis conjecture for certain subdivisions of spheres Andrew Frohmader September, 008 Abstract Notions of sesquiconstructible complexes and odd iterated stellar subdivisions are introduced,
TOWARDS A 3D SPATIAL QUERY LANGUAGE FOR BUILDING INFORMATION MODELS
 TOWARDS A D SPATIAL QUERY LANGUAGE FOR BUILDING INFORMATION MODELS André Borrmann 1, Christoph van Treeck 1, and Ernst Rank 1 ABSTRACT The paper introduces the concept of a spatial query language for building
TOWARDS A D SPATIAL QUERY LANGUAGE FOR BUILDING INFORMATION MODELS André Borrmann 1, Christoph van Treeck 1, and Ernst Rank 1 ABSTRACT The paper introduces the concept of a spatial query language for building
[8] that this cannot happen on the projective plane (cf. also [2]) and the results of Robertson, Seymour, and Thomas [5] on linkless embeddings of gra
![[8] that this cannot happen on the projective plane (cf. also [2]) and the results of Robertson, Seymour, and Thomas [5] on linkless embeddings of gra [8] that this cannot happen on the projective plane (cf. also [2]) and the results of Robertson, Seymour, and Thomas [5] on linkless embeddings of gra](/thumbs/85/93035794.jpg) Apex graphs with embeddings of face-width three Bojan Mohar Department of Mathematics University of Ljubljana Jadranska 19, 61111 Ljubljana Slovenia bojan.mohar@uni-lj.si Abstract Aa apex graph is a graph
Apex graphs with embeddings of face-width three Bojan Mohar Department of Mathematics University of Ljubljana Jadranska 19, 61111 Ljubljana Slovenia bojan.mohar@uni-lj.si Abstract Aa apex graph is a graph
Lecture 17: Solid Modeling.... a cubit on the one side, and a cubit on the other side Exodus 26:13
 Lecture 17: Solid Modeling... a cubit on the one side, and a cubit on the other side Exodus 26:13 Who is on the LORD's side? Exodus 32:26 1. Solid Representations A solid is a 3-dimensional shape with
Lecture 17: Solid Modeling... a cubit on the one side, and a cubit on the other side Exodus 26:13 Who is on the LORD's side? Exodus 32:26 1. Solid Representations A solid is a 3-dimensional shape with
Euler s Theorem. Brett Chenoweth. February 26, 2013
 Euler s Theorem Brett Chenoweth February 26, 2013 1 Introduction This summer I have spent six weeks of my holidays working on a research project funded by the AMSI. The title of my project was Euler s
Euler s Theorem Brett Chenoweth February 26, 2013 1 Introduction This summer I have spent six weeks of my holidays working on a research project funded by the AMSI. The title of my project was Euler s
DERIVING TOPOLOGICAL RELATIONSHIPS BETWEEN SIMPLE REGIONS WITH HOLES
 DERIVING TOPOLOGICAL RELATIONSHIPS BETWEEN SIMPLE REGIONS WITH HOLES Mark McKenney, Reasey Praing, and Markus Schneider Department of Computer and Information Science & Engineering, University of Florida
DERIVING TOPOLOGICAL RELATIONSHIPS BETWEEN SIMPLE REGIONS WITH HOLES Mark McKenney, Reasey Praing, and Markus Schneider Department of Computer and Information Science & Engineering, University of Florida
LECTURE 2 SPATIAL DATA MODELS
 LECTURE 2 SPATIAL DATA MODELS Computers and GIS cannot directly be applied to the real world: a data gathering step comes first. Digital computers operate in numbers and characters held internally as binary
LECTURE 2 SPATIAL DATA MODELS Computers and GIS cannot directly be applied to the real world: a data gathering step comes first. Digital computers operate in numbers and characters held internally as binary
γ 2 γ 3 γ 1 R 2 (b) a bounded Yin set (a) an unbounded Yin set
 γ 1 γ 3 γ γ 3 γ γ 1 R (a) an unbounded Yin set (b) a bounded Yin set Fig..1: Jordan curve representation of a connected Yin set M R. A shaded region represents M and the dashed curves its boundary M that
γ 1 γ 3 γ γ 3 γ γ 1 R (a) an unbounded Yin set (b) a bounded Yin set Fig..1: Jordan curve representation of a connected Yin set M R. A shaded region represents M and the dashed curves its boundary M that
Geometric Modeling Mortenson Chapter 11. Complex Model Construction
 Geometric Modeling 91.580.201 Mortenson Chapter 11 Complex Model Construction Topics Topology of Models Connectivity and other intrinsic properties Graph-Based Models Emphasize topological structure Boolean
Geometric Modeling 91.580.201 Mortenson Chapter 11 Complex Model Construction Topics Topology of Models Connectivity and other intrinsic properties Graph-Based Models Emphasize topological structure Boolean
4.0 DIGITIZATION, EDITING AND STRUCTURING OF MAP DATA
 .0 DIGITIZATION, EDITING AND STRUCTURING OF MAP DATA The process of digitizing existing maps is a transformation from one analog) form of information to another digital) form. Data input is the operation
.0 DIGITIZATION, EDITING AND STRUCTURING OF MAP DATA The process of digitizing existing maps is a transformation from one analog) form of information to another digital) form. Data input is the operation
Topological Decompositions for 3D Non-manifold Simplicial Shapes
 Topological Decompositions for 3D Non-manifold Simplicial Shapes Annie Hui a,, Leila De Floriani b a Dept of Computer Science, Univerity of Maryland, College Park, USA b Dept of Computer Science, University
Topological Decompositions for 3D Non-manifold Simplicial Shapes Annie Hui a,, Leila De Floriani b a Dept of Computer Science, Univerity of Maryland, College Park, USA b Dept of Computer Science, University
Engineering designs today are frequently
 Basic CAD Engineering designs today are frequently constructed as mathematical solid models instead of solely as 2D drawings. A solid model is one that represents a shape as a 3D object having mass properties.
Basic CAD Engineering designs today are frequently constructed as mathematical solid models instead of solely as 2D drawings. A solid model is one that represents a shape as a 3D object having mass properties.
Pacific Journal of Mathematics
 Pacific Journal of Mathematics SIMPLIFYING TRIANGULATIONS OF S 3 Aleksandar Mijatović Volume 208 No. 2 February 2003 PACIFIC JOURNAL OF MATHEMATICS Vol. 208, No. 2, 2003 SIMPLIFYING TRIANGULATIONS OF S
Pacific Journal of Mathematics SIMPLIFYING TRIANGULATIONS OF S 3 Aleksandar Mijatović Volume 208 No. 2 February 2003 PACIFIC JOURNAL OF MATHEMATICS Vol. 208, No. 2, 2003 SIMPLIFYING TRIANGULATIONS OF S
Lecture 5: Simplicial Complex
 Lecture 5: Simplicial Complex 2-Manifolds, Simplex and Simplicial Complex Scribed by: Lei Wang First part of this lecture finishes 2-Manifolds. Rest part of this lecture talks about simplicial complex.
Lecture 5: Simplicial Complex 2-Manifolds, Simplex and Simplicial Complex Scribed by: Lei Wang First part of this lecture finishes 2-Manifolds. Rest part of this lecture talks about simplicial complex.
Topological Model for 3D Image Representation: Definition and Incremental Extraction Algorithm
 Topological Model for 3D Image Representation: Definition and Incremental Extraction Algorithm Guillaume Damiand To cite this version: Guillaume Damiand. Topological Model for 3D Image Representation:
Topological Model for 3D Image Representation: Definition and Incremental Extraction Algorithm Guillaume Damiand To cite this version: Guillaume Damiand. Topological Model for 3D Image Representation:
751 Problem Set I JWR. Due Sep 28, 2004
 751 Problem Set I JWR Due Sep 28, 2004 Exercise 1. For any space X define an equivalence relation by x y iff here is a path γ : I X with γ(0) = x and γ(1) = y. The equivalence classes are called the path
751 Problem Set I JWR Due Sep 28, 2004 Exercise 1. For any space X define an equivalence relation by x y iff here is a path γ : I X with γ(0) = x and γ(1) = y. The equivalence classes are called the path
Lecture 7: Jan 31, Some definitions related to Simplical Complex. 7.2 Topological Equivalence and Homeomorphism
 CS 6170 Computational Topology: Topological Data Analysis University of Utah Spring 2017 School of Computing Lecture 7: Jan 31, 2017 Lecturer: Prof. Bei Wang Scribe: Avani Sharma,
CS 6170 Computational Topology: Topological Data Analysis University of Utah Spring 2017 School of Computing Lecture 7: Jan 31, 2017 Lecturer: Prof. Bei Wang Scribe: Avani Sharma,
Generalized life and motion configurations reasoning model
 Generalized life and motion configurations reasoning model Pierre Hallot & Roland Billen Geomatics Unit, University of Liege, 17 Allée du 6-Août, B-4000 Liege, Belgium {P.Hallot, rbillen}@ulg.ac.be Abstract.
Generalized life and motion configurations reasoning model Pierre Hallot & Roland Billen Geomatics Unit, University of Liege, 17 Allée du 6-Août, B-4000 Liege, Belgium {P.Hallot, rbillen}@ulg.ac.be Abstract.
A convenient way to construct large simplicial complexes is through specifying sets and recording their intersection patterns.
 III.2 Convex Set Systems 53 III.2 Convex Set Systems A convenient way to construct large simplicial complexes is through specifying sets and recording their intersection patterns. Nerves. Let F be a finite
III.2 Convex Set Systems 53 III.2 Convex Set Systems A convenient way to construct large simplicial complexes is through specifying sets and recording their intersection patterns. Nerves. Let F be a finite
EULER S FORMULA AND THE FIVE COLOR THEOREM
 EULER S FORMULA AND THE FIVE COLOR THEOREM MIN JAE SONG Abstract. In this paper, we will define the necessary concepts to formulate map coloring problems. Then, we will prove Euler s formula and apply
EULER S FORMULA AND THE FIVE COLOR THEOREM MIN JAE SONG Abstract. In this paper, we will define the necessary concepts to formulate map coloring problems. Then, we will prove Euler s formula and apply
Fractals: Self-Similarity and Fractal Dimension Math 198, Spring 2013
 Fractals: Self-Similarity and Fractal Dimension Math 198, Spring 2013 Background Fractal geometry is one of the most important developments in mathematics in the second half of the 20th century. Fractals
Fractals: Self-Similarity and Fractal Dimension Math 198, Spring 2013 Background Fractal geometry is one of the most important developments in mathematics in the second half of the 20th century. Fractals
GIS Data Models. 4/9/ GIS Data Models
 GIS Data Models 1 Conceptual models of the real world The real world can be described using two conceptually different models: 1. As discrete objects, possible to represent as points, lines or polygons.
GIS Data Models 1 Conceptual models of the real world The real world can be described using two conceptually different models: 1. As discrete objects, possible to represent as points, lines or polygons.
G 6i try. On the Number of Minimal 1-Steiner Trees* Discrete Comput Geom 12:29-34 (1994)
 Discrete Comput Geom 12:29-34 (1994) G 6i try 9 1994 Springer-Verlag New York Inc. On the Number of Minimal 1-Steiner Trees* B. Aronov, 1 M. Bern, 2 and D. Eppstein 3 Computer Science Department, Polytechnic
Discrete Comput Geom 12:29-34 (1994) G 6i try 9 1994 Springer-Verlag New York Inc. On the Number of Minimal 1-Steiner Trees* B. Aronov, 1 M. Bern, 2 and D. Eppstein 3 Computer Science Department, Polytechnic
ON DECOMPOSITION OF FUZZY BԐ OPEN SETS
 ON DECOMPOSITION OF FUZZY BԐ OPEN SETS 1 B. Amudhambigai, 2 K. Saranya 1,2 Department of Mathematics, Sri Sarada College for Women, Salem-636016, Tamilnadu,India email: 1 rbamudha@yahoo.co.in, 2 saranyamath88@gmail.com
ON DECOMPOSITION OF FUZZY BԐ OPEN SETS 1 B. Amudhambigai, 2 K. Saranya 1,2 Department of Mathematics, Sri Sarada College for Women, Salem-636016, Tamilnadu,India email: 1 rbamudha@yahoo.co.in, 2 saranyamath88@gmail.com
Simplicial Complexes: Second Lecture
 Simplicial Complexes: Second Lecture 4 Nov, 2010 1 Overview Today we have two main goals: Prove that every continuous map between triangulable spaces can be approximated by a simplicial map. To do this,
Simplicial Complexes: Second Lecture 4 Nov, 2010 1 Overview Today we have two main goals: Prove that every continuous map between triangulable spaces can be approximated by a simplicial map. To do this,
layers in a raster model
 layers in a raster model Layer 1 Layer 2 layers in an vector-based model (1) Layer 2 Layer 1 layers in an vector-based model (2) raster versus vector data model Raster model Vector model Simple data structure
layers in a raster model Layer 1 Layer 2 layers in an vector-based model (1) Layer 2 Layer 1 layers in an vector-based model (2) raster versus vector data model Raster model Vector model Simple data structure
Geometric and Solid Modeling. Problems
 Geometric and Solid Modeling Problems Define a Solid Define Representation Schemes Devise Data Structures Construct Solids Page 1 Mathematical Models Points Curves Surfaces Solids A shape is a set of Points
Geometric and Solid Modeling Problems Define a Solid Define Representation Schemes Devise Data Structures Construct Solids Page 1 Mathematical Models Points Curves Surfaces Solids A shape is a set of Points
M. Andrea Rodríguez-Tastets. I Semester 2008
 M. -Tastets Universidad de Concepción,Chile andrea@udec.cl I Semester 2008 Outline refers to data with a location on the Earth s surface. Examples Census data Administrative boundaries of a country, state
M. -Tastets Universidad de Concepción,Chile andrea@udec.cl I Semester 2008 Outline refers to data with a location on the Earth s surface. Examples Census data Administrative boundaries of a country, state
Computational Geometry
 Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
Michał Kukieła. Rescalings and the coreduction homology algorithm for cubical complexes. Uniwersytet M. Kopernika w Toruniu
 Michał Kukieła Uniwersytet M. Kopernika w Toruniu Rescalings and the coreduction homology algorithm for cubical complexes Praca semestralna nr 3 (semestr letni 2011/12) Opiekun pracy: prof. dr hab. Marian
Michał Kukieła Uniwersytet M. Kopernika w Toruniu Rescalings and the coreduction homology algorithm for cubical complexes Praca semestralna nr 3 (semestr letni 2011/12) Opiekun pracy: prof. dr hab. Marian
Data Models and Data processing in GIS
 PDHonline Course L155G (5 PDH) Data Models and Data processing in GIS Instructor: Steve Ramroop, Ph.D. 2012 PDH Online PDH Center 5272 Meadow Estates Drive Fairfax, VA 22030-6658 Phone & Fax: 703-988-0088
PDHonline Course L155G (5 PDH) Data Models and Data processing in GIS Instructor: Steve Ramroop, Ph.D. 2012 PDH Online PDH Center 5272 Meadow Estates Drive Fairfax, VA 22030-6658 Phone & Fax: 703-988-0088
Computer Aided Engineering Design Prof. Anupam Saxena Department of Mechanical Engineering Indian Institute of Technology, Kanpur.
 (Refer Slide Time: 00:28) Computer Aided Engineering Design Prof. Anupam Saxena Department of Mechanical Engineering Indian Institute of Technology, Kanpur Lecture - 6 Hello, this is lecture number 6 of
(Refer Slide Time: 00:28) Computer Aided Engineering Design Prof. Anupam Saxena Department of Mechanical Engineering Indian Institute of Technology, Kanpur Lecture - 6 Hello, this is lecture number 6 of
A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3
 A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3 ANDREW J. HANSON AND JI-PING SHA In this paper we present a systematic and explicit algorithm for tessellating the algebraic surfaces (real 4-manifolds) F
A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3 ANDREW J. HANSON AND JI-PING SHA In this paper we present a systematic and explicit algorithm for tessellating the algebraic surfaces (real 4-manifolds) F
Maps as Numbers: Data Models
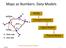 Maps as Numbers: Data Models vertices E Reality S E S arcs S E Conceptual Models nodes E Logical Models S Start node E End node S Physical Models 1 The Task An accurate, registered, digital map that can
Maps as Numbers: Data Models vertices E Reality S E S arcs S E Conceptual Models nodes E Logical Models S Start node E End node S Physical Models 1 The Task An accurate, registered, digital map that can
A Distributed Approach to Fast Map Overlay
 A Distributed Approach to Fast Map Overlay Peter Y. Wu Robert Morris University Abstract Map overlay is the core operation in many GIS applications. We briefly survey the different approaches, and describe
A Distributed Approach to Fast Map Overlay Peter Y. Wu Robert Morris University Abstract Map overlay is the core operation in many GIS applications. We briefly survey the different approaches, and describe
Hyperbolic Geometry on the Figure-Eight Knot Complement
 Hyperbolic Geometry on the Figure-Eight Knot Complement Alex Gutierrez Arizona State University December 10, 2012 Hyperbolic Space Hyperbolic Space Hyperbolic space H n is the unique complete simply-connected
Hyperbolic Geometry on the Figure-Eight Knot Complement Alex Gutierrez Arizona State University December 10, 2012 Hyperbolic Space Hyperbolic Space Hyperbolic space H n is the unique complete simply-connected
Introduction to Immersion, Embedding, and the Whitney Embedding Theorems
 Introduction to Immersion, Embedding, and the Whitney Embedding Theorems Paul Rapoport November 23, 2015 Abstract We give an overview of immersion in order to present the idea of embedding, then discuss
Introduction to Immersion, Embedding, and the Whitney Embedding Theorems Paul Rapoport November 23, 2015 Abstract We give an overview of immersion in order to present the idea of embedding, then discuss
Solid Modelling. Graphics Systems / Computer Graphics and Interfaces COLLEGE OF ENGINEERING UNIVERSITY OF PORTO
 Solid Modelling Graphics Systems / Computer Graphics and Interfaces 1 Solid Modelling In 2D, one set 2D line segments or curves does not necessarily form a closed area. In 3D, a collection of surfaces
Solid Modelling Graphics Systems / Computer Graphics and Interfaces 1 Solid Modelling In 2D, one set 2D line segments or curves does not necessarily form a closed area. In 3D, a collection of surfaces
Using level-2 fuzzy sets to combine uncertainty and imprecision in fuzzy regions
 Using level-2 fuzzy sets to combine uncertainty and imprecision in fuzzy regions Verstraete Jörg Abstract In many applications, spatial data need to be considered but are prone to uncertainty or imprecision.
Using level-2 fuzzy sets to combine uncertainty and imprecision in fuzzy regions Verstraete Jörg Abstract In many applications, spatial data need to be considered but are prone to uncertainty or imprecision.
CSG obj. oper3. obj1 obj2 obj3. obj5. obj4
 Solid Modeling Solid: Boundary + Interior Volume occupied by geometry Solid representation schemes Constructive Solid Geometry (CSG) Boundary representations (B-reps) Space-partition representations Operations
Solid Modeling Solid: Boundary + Interior Volume occupied by geometry Solid representation schemes Constructive Solid Geometry (CSG) Boundary representations (B-reps) Space-partition representations Operations
Discrete Morse Theory on Simplicial Complexes
 Discrete Morse Theory on Simplicial Complexes August 27, 2009 ALEX ZORN ABSTRACT: Following [2] and [3], we introduce a combinatorial analog of topological Morse theory, and show how the introduction of
Discrete Morse Theory on Simplicial Complexes August 27, 2009 ALEX ZORN ABSTRACT: Following [2] and [3], we introduce a combinatorial analog of topological Morse theory, and show how the introduction of
Life and motion configuration
 Life and motion configuration Pierre Hallot, Roland Billen 1 1 Geomatics Unit, University of Liège, 17 allée du 6 Août, B-4000 Liège, Belgium {P.Hallot, rbillen}@ulg.ac.be 1 INTRODUCTION Spatio-temporality
Life and motion configuration Pierre Hallot, Roland Billen 1 1 Geomatics Unit, University of Liège, 17 allée du 6 Août, B-4000 Liège, Belgium {P.Hallot, rbillen}@ulg.ac.be 1 INTRODUCTION Spatio-temporality
Computing intersections in a set of line segments: the Bentley-Ottmann algorithm
 Computing intersections in a set of line segments: the Bentley-Ottmann algorithm Michiel Smid October 14, 2003 1 Introduction In these notes, we introduce a powerful technique for solving geometric problems.
Computing intersections in a set of line segments: the Bentley-Ottmann algorithm Michiel Smid October 14, 2003 1 Introduction In these notes, we introduce a powerful technique for solving geometric problems.
The orientability of small covers and coloring simple polytopes. Nishimura, Yasuzo; Nakayama, Hisashi. Osaka Journal of Mathematics. 42(1) P.243-P.
 Title Author(s) The orientability of small covers and coloring simple polytopes Nishimura, Yasuzo; Nakayama, Hisashi Citation Osaka Journal of Mathematics. 42(1) P.243-P.256 Issue Date 2005-03 Text Version
Title Author(s) The orientability of small covers and coloring simple polytopes Nishimura, Yasuzo; Nakayama, Hisashi Citation Osaka Journal of Mathematics. 42(1) P.243-P.256 Issue Date 2005-03 Text Version
Topological Relationships between a Circular Spatially Extended Point and a Line: Spatial Relations and their Conceptual Neighborhoods
 IAENG International Journal of Computer Science, 36:4, IJCS_36_4_7 Topological Relationships between a Circular Spatially Extended oint and a Line: Spatial Relations and their Conceptual hoods aribel Yasmina
IAENG International Journal of Computer Science, 36:4, IJCS_36_4_7 Topological Relationships between a Circular Spatially Extended oint and a Line: Spatial Relations and their Conceptual hoods aribel Yasmina
Geodesic and curvature of piecewise flat Finsler surfaces
 Geodesic and curvature of piecewise flat Finsler surfaces Ming Xu Capital Normal University (based on a joint work with S. Deng) in Southwest Jiaotong University, Emei, July 2018 Outline 1 Background Definition
Geodesic and curvature of piecewise flat Finsler surfaces Ming Xu Capital Normal University (based on a joint work with S. Deng) in Southwest Jiaotong University, Emei, July 2018 Outline 1 Background Definition
Finite-Resolution Simplicial Complexes
 1 Finite-Resolution Simplicial Complexes Werner Hölbling, Werner Kuhn, Andrew U. Frank Department of Geoinformation Technical University Vienna Gusshausstrasse 27-29, A-1040 Vienna (Austria) frank@geoinfo.tuwien.ac.at
1 Finite-Resolution Simplicial Complexes Werner Hölbling, Werner Kuhn, Andrew U. Frank Department of Geoinformation Technical University Vienna Gusshausstrasse 27-29, A-1040 Vienna (Austria) frank@geoinfo.tuwien.ac.at
Decomposition of the figure-8 knot
 CHAPTER 1 Decomposition of the figure-8 knot This book is an introduction to knots, links, and their geometry. Before we begin, we need to define carefully exactly what we mean by knots and links, and
CHAPTER 1 Decomposition of the figure-8 knot This book is an introduction to knots, links, and their geometry. Before we begin, we need to define carefully exactly what we mean by knots and links, and
Categorizing Binary Topological Relations Between Regions, Lines, and Points in Geographic Databases
 Categorizing Binary Topological elations Between egions, 3 Lines, and Points in Geographic Databases Max J. Egenhofer University of Maine, National Center for Geographic Information and Analysis and Department
Categorizing Binary Topological elations Between egions, 3 Lines, and Points in Geographic Databases Max J. Egenhofer University of Maine, National Center for Geographic Information and Analysis and Department
Don t just read it; fight it! Ask your own questions, look for your own examples, discover your own proofs. Is the hypothesis necessary?
 Don t just read it; fight it! Ask your own questions, look for your own examples, discover your own proofs. Is the hypothesis necessary? Is the converse true? What happens in the classical special case?
Don t just read it; fight it! Ask your own questions, look for your own examples, discover your own proofs. Is the hypothesis necessary? Is the converse true? What happens in the classical special case?
6.001 Notes: Section 8.1
 6.001 Notes: Section 8.1 Slide 8.1.1 In this lecture we are going to introduce a new data type, specifically to deal with symbols. This may sound a bit odd, but if you step back, you may realize that everything
6.001 Notes: Section 8.1 Slide 8.1.1 In this lecture we are going to introduce a new data type, specifically to deal with symbols. This may sound a bit odd, but if you step back, you may realize that everything
Tilings of the Euclidean plane
 Tilings of the Euclidean plane Yan Der, Robin, Cécile January 9, 2017 Abstract This document gives a quick overview of a eld of mathematics which lies in the intersection of geometry and algebra : tilings.
Tilings of the Euclidean plane Yan Der, Robin, Cécile January 9, 2017 Abstract This document gives a quick overview of a eld of mathematics which lies in the intersection of geometry and algebra : tilings.
A CONSISTENCY MAINTENANCE OF SHARED BOUNDARY AFTER POLYGON GENERALIZATION
 CO-182 A CONSISTENCY MAINTENANCE OF SHARED BOUNDARY AFTER POLYGON GENERALIZATION AI T.(1), ZHANG W.(2) (1) Wuhan University, WUHAN CITY, CHINA ; (2) Zhongnan University of Economics and Law, WUHAN CITY,
CO-182 A CONSISTENCY MAINTENANCE OF SHARED BOUNDARY AFTER POLYGON GENERALIZATION AI T.(1), ZHANG W.(2) (1) Wuhan University, WUHAN CITY, CHINA ; (2) Zhongnan University of Economics and Law, WUHAN CITY,
Topological Data Analysis - I. Afra Zomorodian Department of Computer Science Dartmouth College
 Topological Data Analysis - I Afra Zomorodian Department of Computer Science Dartmouth College September 3, 2007 1 Acquisition Vision: Images (2D) GIS: Terrains (3D) Graphics: Surfaces (3D) Medicine: MRI
Topological Data Analysis - I Afra Zomorodian Department of Computer Science Dartmouth College September 3, 2007 1 Acquisition Vision: Images (2D) GIS: Terrains (3D) Graphics: Surfaces (3D) Medicine: MRI
Restricted-Orientation Convexity in Higher-Dimensional Spaces
 Restricted-Orientation Convexity in Higher-Dimensional Spaces ABSTRACT Eugene Fink Derick Wood University of Waterloo, Waterloo, Ont, Canada N2L3G1 {efink, dwood}@violetwaterlooedu A restricted-oriented
Restricted-Orientation Convexity in Higher-Dimensional Spaces ABSTRACT Eugene Fink Derick Wood University of Waterloo, Waterloo, Ont, Canada N2L3G1 {efink, dwood}@violetwaterlooedu A restricted-oriented
Topological Relationships Between Map Geometries
 Topological Relationships Between Map Geometries Mark McKenney and Markus Schneider University of Florida, Department of Computer and Information Sciences {mm7,mschneid}@cise.ufl.edu Abstract. The importance
Topological Relationships Between Map Geometries Mark McKenney and Markus Schneider University of Florida, Department of Computer and Information Sciences {mm7,mschneid}@cise.ufl.edu Abstract. The importance
Mathematical Research Letters 1, (1994) MÖBIUS CONE STRUCTURES ON 3-DIMENSIONAL MANIFOLDS. Feng Luo
 Mathematical Research Letters 1, 257 261 (1994) MÖBIUS CONE STRUCTURES ON 3-DIMENSIONAL MANIFOLDS Feng Luo Abstract. We show that for any given angle α (0, 2π), any closed 3- manifold has a Möbius cone
Mathematical Research Letters 1, 257 261 (1994) MÖBIUS CONE STRUCTURES ON 3-DIMENSIONAL MANIFOLDS Feng Luo Abstract. We show that for any given angle α (0, 2π), any closed 3- manifold has a Möbius cone
INTRODUCTION TO 3-MANIFOLDS
 INTRODUCTION TO 3-MANIFOLDS NIK AKSAMIT As we know, a topological n-manifold X is a Hausdorff space such that every point contained in it has a neighborhood (is contained in an open set) homeomorphic to
INTRODUCTION TO 3-MANIFOLDS NIK AKSAMIT As we know, a topological n-manifold X is a Hausdorff space such that every point contained in it has a neighborhood (is contained in an open set) homeomorphic to
1 Point Set Topology. 1.1 Topological Spaces. CS 468: Computational Topology Point Set Topology Fall 2002
 Point set topology is something that every analyst should know something about, but it s easy to get carried away and do too much it s like candy! Ron Getoor (UCSD), 1997 (quoted by Jason Lee) 1 Point
Point set topology is something that every analyst should know something about, but it s easy to get carried away and do too much it s like candy! Ron Getoor (UCSD), 1997 (quoted by Jason Lee) 1 Point
FACES OF CONVEX SETS
 FACES OF CONVEX SETS VERA ROSHCHINA Abstract. We remind the basic definitions of faces of convex sets and their basic properties. For more details see the classic references [1, 2] and [4] for polytopes.
FACES OF CONVEX SETS VERA ROSHCHINA Abstract. We remind the basic definitions of faces of convex sets and their basic properties. For more details see the classic references [1, 2] and [4] for polytopes.
Smallworld Core Spatial Technology 4 Spatial data is more than maps tracking the topology of complex network models
 Smallworld Core Spatial Technology 4 Spatial data is more than maps tracking the topology of complex network models 2004 General Electric Company. All Rights Reserved GER-4230 (10/04) Abstract Spatial
Smallworld Core Spatial Technology 4 Spatial data is more than maps tracking the topology of complex network models 2004 General Electric Company. All Rights Reserved GER-4230 (10/04) Abstract Spatial
4. Simplicial Complexes and Simplicial Homology
 MATH41071/MATH61071 Algebraic topology Autumn Semester 2017 2018 4. Simplicial Complexes and Simplicial Homology Geometric simplicial complexes 4.1 Definition. A finite subset { v 0, v 1,..., v r } R n
MATH41071/MATH61071 Algebraic topology Autumn Semester 2017 2018 4. Simplicial Complexes and Simplicial Homology Geometric simplicial complexes 4.1 Definition. A finite subset { v 0, v 1,..., v r } R n
A Genus Bound for Digital Image Boundaries
 A Genus Bound for Digital Image Boundaries Lowell Abrams and Donniell E. Fishkind March 9, 2005 Abstract Shattuck and Leahy [4] conjectured and Abrams, Fishkind, and Priebe [1],[2] proved that the boundary
A Genus Bound for Digital Image Boundaries Lowell Abrams and Donniell E. Fishkind March 9, 2005 Abstract Shattuck and Leahy [4] conjectured and Abrams, Fishkind, and Priebe [1],[2] proved that the boundary
MA651 Topology. Lecture 4. Topological spaces 2
 MA651 Topology. Lecture 4. Topological spaces 2 This text is based on the following books: Linear Algebra and Analysis by Marc Zamansky Topology by James Dugundgji Fundamental concepts of topology by Peter
MA651 Topology. Lecture 4. Topological spaces 2 This text is based on the following books: Linear Algebra and Analysis by Marc Zamansky Topology by James Dugundgji Fundamental concepts of topology by Peter
and this equivalence extends to the structures of the spaces.
 Homeomorphisms. A homeomorphism between two topological spaces (X, T X ) and (Y, T Y ) is a one - one correspondence such that f and f 1 are both continuous. Consequently, for every U T X there is V T
Homeomorphisms. A homeomorphism between two topological spaces (X, T X ) and (Y, T Y ) is a one - one correspondence such that f and f 1 are both continuous. Consequently, for every U T X there is V T
2D image segmentation based on spatial coherence
 2D image segmentation based on spatial coherence Václav Hlaváč Czech Technical University in Prague Center for Machine Perception (bridging groups of the) Czech Institute of Informatics, Robotics and Cybernetics
2D image segmentation based on spatial coherence Václav Hlaváč Czech Technical University in Prague Center for Machine Perception (bridging groups of the) Czech Institute of Informatics, Robotics and Cybernetics
Morphological Image Processing
 Morphological Image Processing Morphology Identification, analysis, and description of the structure of the smallest unit of words Theory and technique for the analysis and processing of geometric structures
Morphological Image Processing Morphology Identification, analysis, and description of the structure of the smallest unit of words Theory and technique for the analysis and processing of geometric structures
Introduction :- Storage of GIS Database :- What is tiling?
 Introduction :- GIS storage and editing subsystems provides a variety of tools for storing and maintaining the digital representation of a study area. It also provide tools for examining each theme for
Introduction :- GIS storage and editing subsystems provides a variety of tools for storing and maintaining the digital representation of a study area. It also provide tools for examining each theme for
Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS
 Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS Definition 1.1. Let X be a set and T a subset of the power set P(X) of X. Then T is a topology on X if and only if all of the following
Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS Definition 1.1. Let X be a set and T a subset of the power set P(X) of X. Then T is a topology on X if and only if all of the following
Teichmüller Space and Fenchel-Nielsen Coordinates
 Teichmüller Space and Fenchel-Nielsen Coordinates Nathan Lopez November 30, 2015 Abstract Here we give an overview of Teichmüller space and its realization as a smooth manifold through Fenchel- Nielsen
Teichmüller Space and Fenchel-Nielsen Coordinates Nathan Lopez November 30, 2015 Abstract Here we give an overview of Teichmüller space and its realization as a smooth manifold through Fenchel- Nielsen
Manifolds. Chapter X. 44. Locally Euclidean Spaces
 Chapter X Manifolds 44. Locally Euclidean Spaces 44 1. Definition of Locally Euclidean Space Let n be a non-negative integer. A topological space X is called a locally Euclidean space of dimension n if
Chapter X Manifolds 44. Locally Euclidean Spaces 44 1. Definition of Locally Euclidean Space Let n be a non-negative integer. A topological space X is called a locally Euclidean space of dimension n if
Surfaces: notes on Geometry & Topology
 Surfaces: notes on Geometry & Topology 1 Surfaces A 2-dimensional region of 3D space A portion of space having length and breadth but no thickness 2 Defining Surfaces Analytically... Parametric surfaces
Surfaces: notes on Geometry & Topology 1 Surfaces A 2-dimensional region of 3D space A portion of space having length and breadth but no thickness 2 Defining Surfaces Analytically... Parametric surfaces
COMPUTER DESIGN OF REPEATING HYPERBOLIC PATTERNS
 COMPUTER DESIGN OF REPEATING HYPERBOLIC PATTERNS Douglas Dunham University of Minnesota Duluth Department of Computer Science 1114 Kirby Drive Duluth, Minnesota 55812-2496 USA ddunham@d.umn.edu Abstract:
COMPUTER DESIGN OF REPEATING HYPERBOLIC PATTERNS Douglas Dunham University of Minnesota Duluth Department of Computer Science 1114 Kirby Drive Duluth, Minnesota 55812-2496 USA ddunham@d.umn.edu Abstract:
Extension as the background of substance a formal approach
 Extension as the background of substance a formal approach Bart lomiej Skowron Wroc law University The Pontifical University of John Paul II, Kraków bartlomiej.skowron@gmail.com February 11, 2013 Presentation
Extension as the background of substance a formal approach Bart lomiej Skowron Wroc law University The Pontifical University of John Paul II, Kraków bartlomiej.skowron@gmail.com February 11, 2013 Presentation
Representing Geography
 Data models and axioms Chapters 3 and 7 Representing Geography Road map Representing the real world Conceptual models: objects vs fields Implementation models: vector vs raster Vector topological model
Data models and axioms Chapters 3 and 7 Representing Geography Road map Representing the real world Conceptual models: objects vs fields Implementation models: vector vs raster Vector topological model
External Memory Algorithms and Data Structures Fall Project 3 A GIS system
 External Memory Algorithms and Data Structures Fall 2003 1 Project 3 A GIS system GSB/RF November 17, 2003 1 Introduction The goal of this project is to implement a rudimentary Geographical Information
External Memory Algorithms and Data Structures Fall 2003 1 Project 3 A GIS system GSB/RF November 17, 2003 1 Introduction The goal of this project is to implement a rudimentary Geographical Information
Determining Differences between Two Sets of Polygons
 Determining Differences between Two Sets of Polygons MATEJ GOMBOŠI, BORUT ŽALIK Institute for Computer Science Faculty of Electrical Engineering and Computer Science, University of Maribor Smetanova 7,
Determining Differences between Two Sets of Polygons MATEJ GOMBOŠI, BORUT ŽALIK Institute for Computer Science Faculty of Electrical Engineering and Computer Science, University of Maribor Smetanova 7,
SOME 024: Computer Aided Design. E. Rozos
 SOME 024: Computer Aided Design E. Rozos Introduction to CAD theory part 2 Lesson structure Why Solid modelling Solid modelling methods Representation based Manufacturing based Solid modelling storage
SOME 024: Computer Aided Design E. Rozos Introduction to CAD theory part 2 Lesson structure Why Solid modelling Solid modelling methods Representation based Manufacturing based Solid modelling storage
Elementary Combinatorial Topology
 Elementary Combinatorial Topology Frédéric Meunier Université Paris Est, CERMICS, Ecole des Ponts Paristech, 6-8 avenue Blaise Pascal, 77455 Marne-la-Vallée Cedex E-mail address: frederic.meunier@cermics.enpc.fr
Elementary Combinatorial Topology Frédéric Meunier Université Paris Est, CERMICS, Ecole des Ponts Paristech, 6-8 avenue Blaise Pascal, 77455 Marne-la-Vallée Cedex E-mail address: frederic.meunier@cermics.enpc.fr
Assignment 8; Due Friday, March 10
 Assignment 8; Due Friday, March 10 The previous two exercise sets covered lots of material. We ll end the course with two short assignments. This one asks you to visualize an important family of three
Assignment 8; Due Friday, March 10 The previous two exercise sets covered lots of material. We ll end the course with two short assignments. This one asks you to visualize an important family of three
Topological Issues in Hexahedral Meshing
 Topological Issues in Hexahedral Meshing David Eppstein Univ. of California, Irvine Dept. of Information and Computer Science Outline I. What is meshing? Problem statement Types of mesh Quality issues
Topological Issues in Hexahedral Meshing David Eppstein Univ. of California, Irvine Dept. of Information and Computer Science Outline I. What is meshing? Problem statement Types of mesh Quality issues
What is a... Manifold?
 What is a... Manifold? Steve Hurder Manifolds happens all the time! We just have to know them when we see them. Manifolds have dimension, just like Euclidean space: 1-dimension is the line, 2-dimension
What is a... Manifold? Steve Hurder Manifolds happens all the time! We just have to know them when we see them. Manifolds have dimension, just like Euclidean space: 1-dimension is the line, 2-dimension
