Fast, Accurate Spectral Clustering Using Locally Linear Landmarks
|
|
|
- Nathan Byrd
- 5 years ago
- Views:
Transcription
1 Fast, Accurate Spectral Clustering Using Locally Linear Landmarks Max Vladymyrov Google, Inc. Miguel Á. Carreira-Perpiñán EECS, UC Merced Abstract For problems of image or video segmentation, where clusters have a complex structure, a leading method is spectral clustering. It works by encoding the similarity between pairs of points into an affinity matrix and applying k-means in its loworder eigenspace, where the clustering structure is enhanced. When the number of points is large, an approximation is necessary to limit the runtime even if the affinity matrix is sparse. This is commonly done with the Nyström formula, where one solves an eigenproblem using affinities between a subset of the data points (landmarks) and then estimates the eigenvectors over the entire data by interpolation. In practice, this can still require many landmarks to achieve reasonably accurate solutions, and applies only for explicitly defined affinity kernels. In this paper we propose two ideas: the Locally Linear Landmarks technique, where one solves a reduced spectral problem over landmarks that involves the entire, original affinity matrix; and a fast, good initialization for k-means. We show both approximation error and runtime are considerably reduced, even though fewer landmarks are used. We apply it to spectral clustering and to several variants of it that involve complex affinities: constrained clustering, affinity aggregation, neighborhood graphs based on tree ensembles, and video segmentation. Spectral clustering (SC; [28], [36]) is a popular method that has been used for many problems in machine learning and computer vision, such as image or motion segmentation [28], [12], [25]. It uses graph structure that can discover complex clusters in data better than model-based algorithms such as Gaussian mixture. The use of pairwise affinities allows for construction of different similarity measures, ranging from simple Gaussian affinities based on the pixel location and color and/or texture, to using edge and contour information or approaches involving information at multiple scales and semisupervised learning [28], [18], [22], [16]. The clustering structure in the original space is amplified in the projections of the data on the eigenspace of the graph, so that a simple clustering algorithm (e.g. k-means) can help locating the clusters efficiently. One disadvantage of SC is its computational cost. With large number of points N, computing and storing a full N N affinity matrix is impractical. Using a sparse matrix reduces the complexity, but the runtime can still be high for large N, because of the need to solve a sparse large eigenproblem. In addition, for high-dimensional input data, achieving good clustering solutions requires the use of a neighborhood graph because of the concentration of measure. In this case, one seeks an approximate solution. The most common way to Part of this work was done while M.V. was a PhD student at UC Merced. do this is based on subsampling. Here, one selects a small subset of points (landmarks) from the input, solves the eigenproblem for them, and approximates the full eigenproblem with an out-of-sample mapping, most commonly the Nyström formula [37], [3]. By using sufficiently many landmarks, the approximation error can be reduced to an acceptable level while keeping the runtime lower than that of the full problem. One problem with the subsampling approach is that the solution for the landmarks is obtained using only the affinities between the landmarks themselves, while the rest of the points are used only in the out-of-sample formula. Hence, for few landmarks the eigenproblem solution will have a large error, and so will the extension to all the points. One can use more landmarks, but at the cost of larger runtime. This is also problematic if a user wants to use a small bandwidth in the affinity kernel, because in order for two landmarks to interact they have to be within reach of each other. Additionally, the Nyström method requires a continuous kernel function that generates the affinity matrix, which is not always available. Many of the popular variants of SC, such as proximity graphs [7], constrained spectral clustering (CSC; [20]) and affinity aggregation for spectral clustering (AASC; [15]) are using custom affinity matrices that are not generated from a continuous kernel. A different way to avoid this problem while still using a small number of landmarks is to use the connection between pairs of points, not just between the landmarks. This was proposed by Vladymyrov and Carreira-Perpiñán [35] in the context of manifold learning. Their locally linear landmarks (LLL) method solves a reduced spectral problem for landmarks, where the reduced affinities involve the entire original affinity matrix, rather than just the affinities between the landmarks. This is useful for problems with big and sparse affinity matrices, for which subsampling methods would need a lot of landmarks to get the structure right. In this paper we analyze the application of LLL algorithm for different variations of spectral clustering. We show that the algorithm is particularly beneficial for problems of image and motion segmentation, with speed and accuracy benefits that sometime larger than LLL has for manifold learning, which is the original application of the algorithm. We also show that LLL can be used for effective approximation of custom non-gaussian affinity matrices. Such affinities arise in order to improve the quality of the Gaussian affinities [7], add
2 additional must- and cannot-link constraints [20] or aggregate different features into one unified affinity [15]. For each of those affinities we derive a custom fast and accurate algorithm that benefits from the structure of the approximation used by LLL. For these custom-based affinities, it is difficult to apply Nyström and other approximations. Based on our knowledge, we are the first one to propose to scale up affinity aggregation and constrained SC algorithms. We analyze the assumptions of LLL for the context of SC. Different from Vladymyrov and Carreira-Perpiñán [35] who concentrated on the manifold learning, the structure of the data in clustering is very different. While in manifold learning it is ok for the clustering information to be smoothed out in order to reveal the manifold structure, in clustering it is important to emphasize the discontinues between points from different clusters. In section IV and the experiments we validate the assumptions imposed in LLL for SC. Finally, we also provide a simple but very effective way to accelerate the k-means step by using a good initialization based on the landmarks solution. Our approach is robust, parameter-free and fast, essentially reducing the cost of the algorithm to a single k-means iteration over the full dataset. In the experiments we show that our approach gives faster yet accurate solution with respect to the both exact SC and its variations and compares favorably to the Nyström extension. It is able to efficiently solve a motion segmentation problem using spatio-temporal affinities with N = variables. It took the algorithm under 10 minutes to get meaningful solution, while for Nyström we were not able to get good results at all. I. THE SPECTRAL CLUSTERING PROBLEM There exist several formulations of SC, depending on what kind of affinities are used, type of normalization applied to the graph Laplacian, etc [36]. Here we use the most common one, which approximates the normalized cut criterion [28]. Given a (sparse) affinity matrix W R N N defined on data points Y = (y 1,...,y n ) of D N: 1) Find K dimensional spectral embedding: min X tr ( XLX T), s.t. XDX T = I, XD1 = 0, (1) where L = D W is a graph Laplacian defined for a degree matrix D = diag( N m=1 w nm) and X R K N is a data projection. 2) Obtain the final clustering by running k-means on the normalized projections ˆX ij = X ij /( j X2 ij )1/2. The solution to the spectral embedding problem (1) is given by X = U T K D 1 2, where U K = (u 1,...,u K ) are 2,...,K + 1 trailing eigenvectors of the N N matrix C = D 1 2LD 1 2. This eigendecomposition is a bottleneck and scales as O(N 3 ). In case of sparse affinities and small number of clusters K, one can possibly use iterative methods, such as power method or Krylov subspace methods [13], however the complexity still can be expensive. Our goal is to approximate the solution of this spectral problem, and thus to achieve a fast approximation to final clustering result. As we will show, we can also speed up step 2 with no error. II. RELATED WORK The most widespread approach to approximate the solution of a spectral problem, in particular spectral clustering, is to solve the problem for a subset of points (landmarks) and then to estimate the solution for the remaining points. For example, the Nyström formula [37], [3] has been widely applied to approximate the solution of SC [4], [12]. The formula nonlinearly interpolates the landmarks using the kernel that was used to construct the affinities. The projection x of a new point y can be found using the interpolation x k = 1 L λ k n=1 X nkk(y,y i ), where an out-of-sample kernel K is defined as K(a,b) = K(a,b)/ D a D b, with K(a, b) as a data-dependent kernel (e.g. Gaussian) and D a = L K(a,y n=1 n ), D b = L K(y n=1 n,b). Nyström formula gives fast results, with cost being proportional to O(KL 2 ) to compute the embedding of landmarks and O(N LK) to compute the projection of N out-of-sample points. However, the quality of the method is not the best, since landmarks projection only uses a small subsample of the affinity matrix, basically ignoring the rest of the available information. In addition, the algorithm relies on the existence of the data-dependent kernel K(a,b) which is not always available. K-means-based approximate spectral clustering (KASP; [38]) replaces the original data with a subsample, while maintaining the mapping between the original data and the subsample points. Then, the SC is run on the subsample and the final clustering assignment to the original points comes from the cluster assignment of the corresponding subsample point. For the subsampling algorithm Yan et al [38] chose k- means and Random Projection trees. Similar to Nyström, the subsample matrix does not use the structure of the original data. Laplacian eigenmaps latent variable model (LELVM; [6]) approximates SC based on the idea of adding new point to the subset embedding and solving the spectral problem for that new point. The final formula takes the form of a Nadaraya- Watson estimator jointly constructed on the feature vectors and embedding projections. Landmark Spectral Clustering (LSC; [8]) uses the Anchor- Graphs [19], where a smaller affinity matrix is built between landmarks and points that approximate a full N N affinity. This approach, however, does not solve the problem (1), in the sense that it does not approximate a given spectral problem and thus the clustering defined by it. Multi-grid spectral clustering methods [9], [17] approximate the eigendecomposition specifically for the problem of image segmentation. The eigenspectrum of the Laplacian is defined using a random chain matrix expressed as Markov chain propagation model with a certain probability distribution, which can be fine scaled using a kernel matrix. Multi-scale approximation [10] was also proposed in the context of image
3 segmentation and is restricted to data defined on an image grid. It approximates a dense affinity matrix as a weighted sum of affinities connected at different scales, which allows faster computation. Maire and Yu [21] combine both multiscale and multi-grid techniques together. These algorithms are specialized for data having a form of an image grid and may not apply to unstructured, high-dimensional data. In comparison to the proposed LLL-based algorithm, they do not benefit from savings when having to solve multiple SC problems on the same dataset but with different affinities (as in affinity aggregation or model selection over the affinity parameters). In addition, these methods are far more complex to implement than Nyström or LLL, and require several user parameters that are nontrivial to set (e.g. scale splits and their weights in multi-split SC or initial kernel size, coarse schedule for multi-grid methods). III. ACCELERATING THE SPECTRAL CLUSTERING USING LOCALLY LINEAR LANDMARKS LLL approximates (1) by constructing matrices à and B defined for a set of landmarks, but using the structure of the whole data. For L N landmarks Ỹ = (ỹ 1,...ỹ L ) from Y, LLL approximates each point as a linear combination of K Z nearest landmarks Y ỸZ, where a reconstruction matrix Z R L N is a column matrix of the nearest K Z landmarks of each point (K Z nonzero entries per column). Thus, this approximation preserves the locality of the data and the matrix Z corresponds to the proximity of the data points to the nearby landmarks. We can solve for Z using min Z Y ỸZ 2, s.t. 1 T Z = 1 T, where the constraint comes from the translational invariance of Z. The solution to this optimization problem is found for each point separately by first solving the linear system L k=1 (y n ỹ i )(y n ỹ j )z nk = 1 and then rescaling the weights so they sum to one. Further, LLL assumes that this local reconstruction matrix Z also approximates the points in the projection space: X XZ. (2) Now, the spectral embedding problem (1) takes a form min Xtr( Xà X T ) s.t. X B XT = I, (3) with L L reduced affinity matrices à = ZLZ T, B = ZDZ T. (4) This problem has the same form as the original problem (1), but defined on a smaller-size reduced affinities à and B. LLL basically solves a smaller embedding problem for the landmarks using smaller reduced affinities that incorporate the structure of the original affinity. After the landmarks are projected, the rest of the points can be found using reconstruction (2). Notice, that à and B do not have the same form as the original matrices L and D. For example, A may or may not have a form of graph Laplacian, B may not be diagonal those matrices just approximate L and D. The cost of LLL is based on four parts: computing Z is O(NDK 2 Z ); à and B are O(cK Z N), where c depends on the sparsity of W; K eigenvectors takes O(KL 2 ); and Error 10 6 Random LLL kmeans Runtime Error 1.4 x 105 LLL Rand. subset kmeans Number of Iterations Fig. 1. Left: 20 runs of k-means initialized at random (red), with LLL (green) and with k-means++ (blue). Right: k-means initialized with LLL landmarks and 50 other subsets of L points. the final projection (2) is O(LdN). The total cost is O ( (K Z c+ld+dk 2 Z )N +KL2 ) ) which is linear in N. As one can see from the form of the approximation (3) LLL requires feature vectors, but the majority of (spectral) clustering applications do use features. a) Accelerating the k-means clustering step: LLL approximation gives us the K-dimensional projections X of the original data Y (using (2)). Next step is to run k-means on X to obtain the final K clusters. This problem is nonconvex and, to avoid local optima, a common strategy is to use multiple restarts with different initializations and pick the result with the lowest error. We can speed up the k-means step by capitalizing on the fact that the landmarks themselves provide a reasonable clustering, and there are fewer landmarks than points. Instead of running k-means for the whole dataset m times, we run it just on the landmarks, pick the best solution and feed its centroids as an initialization to k-means on the entire data. Thus, k-means is run just once on the full problem, but with an initialization that is much better than random. The cost is O(mLK 2 + NK 2 ) and when L N the speed-up over the O(mNK 2 ) of the naive k-means step is proportional to m. Also, we can afford to run many restarts to increase the chance of finding a good local optimum. The idea of seeding for initialization of k-means is not new [11], [30]. However, our approximation makes sense in the context of LLL, since instead of the random sample of points, our sample comes from the landmark location. Those landmarks are acting as the reference points to the rest of the data for the local linear reconstruction (2). Therefore, the landmarks have more chance to be inside the cluster than on its boundary. Fig. 1 on the left shows the decrease of k-means objective function for the clustering N = points to 6 classes using LLL (see motion segmentation example below). Red curves correspond to randomly initialized restarts of full k- means and a green curve is a single full k-mean initialized from the best of m = 20 different restarts of k-means on LLL landmarks. We also compare to the kmeans++ [2], which picks centroids greedily one at a time so they are widely separated. Overall it took 0.5 seconds to run k-means using LLL landmarks and 5.3 seconds for a single run of a full k- means. In comparison, 20 restarts of full k-means took 91.3 seconds. On the inset we can see that only one out of 20 runs
4 Bad assign. Good assign. Input Y Approx. eigenvectors Fig. 2. Left column: dataset Y with 5 landmarks selected far from the cluster boundary (top row) and closer (bottom row). Right column: final eigenvectors form LLL. The color of the points are the same if they share two nearest landmark assignment. of k-means converged to that solution. This means that using smaller number of restarts m we could end up only with more expensive, but also worse solution that using LLL landmarks. In the right plot of fig. 1 we show k-means error using LLL landmarks versus k-means using 50 different subsets of L random points from Y. While LLL landmarks do not give the best result among random subsets (see the inset), the error is lower then most of the random subsets. IV. IS LOCAL LINEARITY A GOOD ASSUMPTION FOR CLUSTERING? Comparing to the original motivation of Vladymyrov and Carreira-Perpiñán [35] that propose LLL to be used for manifold learning, the desired properties of SC in the projection space are different. For clustering, we do not need to preserve the manifold structure, but rather separate the points into clusters. Let us consider the following ideal clustering situation with SC. The eigenvectors are piecewise constant with same values for points in each cluster. A clustering solution is also a piecewise constant function. The approximate solution (from LLL) for the landmarks eigenvectors is piecewise constant as well, corresponding to the same clusters. The LLL outof-sample formula (2) is a linear combination of the nearest landmarks eigenvector value. Then we have two cases: (1) if the nearest landmarks to the test point are in the same cluster, their eigenvectors values ( cluster labels ) are equal and (2) will predict that same eigenvector value, which is correct. This will happen with the test points in the interior of each cluster, i.e. nearly everywhere if the cluster boundaries are narrow. (2) if the nearest landmarks to the test point are not all in the same cluster, their eigenvector values ( cluster labels ) are not all equal and the formula will predict an average of those values, giving more weight to the landmarks that are closer to the test point. The resulting predicted eigenvector value will be smoothed out, since it averages different labels. This will happen with test points in the boundary between different clusters. How narrow are the cluster boundaries depends on the number of landmarks. The more landmarks, the narrower the boundaries, since this is the region where points have nearest neighboring landmarks from different clusters. In fig. 2 we show the example of two cases above. The dataset on the left consists of points along a line separated into two clusters. Exact SC solves this problem given sufficiently narrow bandwidth of the kernel, such that the points on the side of one cluster won t be affected by the points on the side of the other. For LLL, there is one more constraint. If the test point is reconstructed by landmarks from different clusters (such as dark red points in the top plots) the target eigenvector will be smoothed out. Good assignment (as the one on the bottom), gives much better approximation. We expect the a piecewise linear model of LLL to match perfectly the piecewise constant clustering model except at discontinuities (cluster boundaries). These points are difficult for SC in the first place, i.e. their exact eigenvector value will be less pure than at points in the interior of a cluster. LLL might have troubles with small clusters, because they will get fewer landmarks. However, SC tends not to produce small clusters, since it approximates the Normalized Cut objective function [28], which discourages this. V. USING MORE COMPLEX AFFINITIES One of the important benefits of LLL is that it can use any affinity matrix and with any explicit or implicit kernel that generates it. Comparing to that, Nyström method requires well defined data-independent kernel function that generates the affinities [4], and, to our knowledge, was applied only to the Gaussian kernel [32], [12]. Landmark Spectral Clustering [8] is also not applicable because their approximation constructs their own affinity matrix. Finally, the vector quantization techniques (such as the algorithm of Yan et al [38]) also cannot be easily applied for this problem, since the affinities are built between the subset of points, while in this section we consider specifically the affinities that involve the whole dataset. Apart from expensive eigendecomposition that can be alleviated with LLL, the custom affinities involve large overhead in their computation, which can become a bottleneck by itself. For each of those cases we investigate how the structure of LLL can help the computation of the affinities and propose custom algorithm that can reduce the cost of both the computation of the affinities and the eigendecomposition. Our analysis comes naturally given the structure of LLL and does not involve additional approximations. Based on our knowledge, the algorithms below have been never applied on large matrices before. Slightly abusing the notation, in this section we are going to call W the modified affinities of currently described algorithm. A. Constrained Spectral Clustering In constrained spectral clustering (CSC) user additionally provides must and cannot link constraints between some of the data points. Lu and Carreira-Perpiñán [20] propose the algorithm for including this information inside the affinity matrix. Original affinity information is assumed to be interpreted as a covariance matrix of a zero-mean Gaussian process, which acts as a prior on the labels. The pairwise constraints serve as noisy observations. The modified affinities are then computed using the Bayes rule as the posterior probability of the labels given the pairwise constraints. The final expression for the modified affinities: W = (W 1 +M) 1 = W W(I+MW) 1 MW, (5)
5 Sparsity Level, % Sliding window size 20 W W Number of constraints Fig. 3. Sparsity of the original W and constrained W affinity matrices for cameraman image. Left: as a sliding window increases with 10 random constraints (must and cannot), right: as a number of constraint increase with the sliding window radius equals to 5. Experiments were repeated 5 times with different random sets of constraints. where M contains the constraint information: m i ǫ + ci 2 m ǫ if i = j 2 c 1 ǫ (i,j) M M ij = 2 m. 1 ǫ (i,j) C 2 c 0 otherwise Here m i and c i are the number of must- and cannot-links respectively for point i, ǫ m and ǫ c are the importance of the constraints with respect to the affinity (with ǫ 0 implying harder constraints). The modified affinity W is able to capture constrains well with two drawbacks: (1) computing the inverse in (5) scales as O(N 3 ) and (2) W is much denser than W. The first problem can be solved efficiently by reorganizing the points, such that the constrained ones appear first: M = ( M 1:2R 0 0 0), where R is the number of constraints and M 1:2R ( has a size of at most 2R 2R. Then, I + M1:2RW MW = 1:2R+I 1:2R M 1:2RW 2R+1:N 0 I 2R+1:N ), where we split ( W = (W 1:2R ) W 2R+1:N ) T. Now, for the inverse: ( A 0 B I ) 1 = A 1 A 1 B 0 I. Thus, the only matrix to be inverted is a small 2R 2R matrix A = M 1:2R W 1:2R +I 1:2R, which is always invertible due to the added identity. The second problem makes things complicated. Adding many constraints to the original affinity can make it much denser than the original one, as a result of which not only the subsequent eigendecomposition is much more complicated to do, but even storing the matrix can be problematic. In fig. 3 we show how the sparsity level of W changes with respect to two different variables: the sparsity of W and the number of constrains R. For both cases the constrained affinity matrix becomes dense very fast. With LLL we can a huge benefit of computing the constrained affinitywwithout ever evaluating the original affinity W, thus removing both of the problems above. Using (5) we can expand the reduces affinities (4) as ZLZ T = ZDZ T ZWZ T = Zdiag(W1)Z T Zdiag(WQW1))Z T ZWZ T +ZWQWZ T, where Q = (I+MW) 1 M is N N matrix, but only with N L nonzero rows (due to the sparsity of M). Therefore, instead of computing L and then computing the reduced affinity, we can precompute ZW in O(cNL), where c is the constant that depends on the sparsity of W, and solve for diagonal matrix in the second term by multiplying the elements from right to left. Overall, the complexity of computing the affinity is O(cN L) and it avoids direct computation and storage of dense matrix W. B. Affinity Aggregation for Spectral Clustering In many situations using just a single affinity matrix built on top of Euclidean distance features does not give satisfactory performance. A practitioner has to try many different features with many different parameters in order to get good performance. Huang et al [15] propose an affinity aggregation spectral clustering (AASC) that combines multiple affinities in a single SC framework. For K affinity matrices W (1),...,W (K) and the weighting coefficients v = (v 1,...,v k ) the AASC minimizes the following: min X,v XLX T, s.t. XDX T = I,v T 1 = 1, (6) where L = D W and W is an aggregated affinity matrix W = K k=1 v2 k W(k). To solve (6) the algorithm alternates between minimizing over v and X. With respect to v, the problem is a 1D root-finding problem that can be solved with a few Newton iterations. With v fixed, the objective function is a standard SC objective with affinity W. The algorithm works well in combining affinity matrices resulting from different features, however it is too expensive for large problems, requiring an eigendecomposition of N N matrix for every iteration. In addition, the aggregate affinity matrix is denser than the input affinities. Similarly to the case above, we can use the structure of LLL to solve the problems with dense affinity. The reduced affinity (4) takes the form: L = ZLZ T = ZDZ T ZWZ T = Z( K k=1 v2 k W(k) 1)Z T Z( K k=1 v2 k W(k) )Z T = K k=1 v2 k ZD(k) Z T K k=1 v2 k ZW(k) Z T. We can benefit from precomputing Z and reduced affinity matrices ZW (k) Z T just once in the beginning. Then, each iteration would just involve recomputing a weighted sum and eigendecomposition of small L L matrix. VI. EXPERIMENTS Here we are going to provide an extensive experimental analysis on benefits of LLL for spectral clustering problem. We are going to evaluate the algorithm for a classical settings of image segmentation with Gaussian affinity matrix. Then we will show how LLL can be useful for the problem of model selection of hyper-parameters. After that we are going to describe three different experiments with custom non- Gaussian affinity matrices. In the end, we are going to show the scalability of our approximation by applying it to the motion segmentation problem with N = data points. All the algorithms in this paper use an affinity matrix as an input. Since we cannot explicitly compute the full affinity matrix, we can approximate it with a sparse N N matrix
6 Proj. error exact LLL Nystrom LSC LELVM KASP Clust. error # of landmarks Runtime, s # of landmarks Runtime, s # of landmarks Fig. 4. Image segmentation of cameraman. Projection and clustering errors with respect to the number of landmarks and the runtime. Dashed vertical black line represents the results of exact spectral clustering. Clustering 1st eigenvector 2nd eigenvector 3rd eigenvector 4th eigenvector 5th eigenvector 10 2 Runtime, s e 1% t = 56.8 L = Nyström e 10% t = 0.67 L = 1550 e 1% t = 1.82 L = 2475 LLL e 10% t = 0.9 L = 14 Exact e = 0% t = 66.6 N = Fig. 5. Clustering results and leading eigenvectors for exact spectral clustering, LLL and Nyström. For each row, left columns give the clustering error e, the runtime t and the number of landmarks L needed to produce the results. computed e.g. with a neighborhood graph. Constructing such a graph requires finding nearest neighbors for every point, which is costly. However, for some cases this matrix can be approximated using a domain knowledge. For example, for image segmentation the features can represent color, intensity or texture information, but also a spatial ordering (such as the coordinates of the pixels). Thus, we can compute the approximate nearest neighbors for each point using a sliding window approach, where for each pixel we define its neighbors as points that fall in a square window with a side r centered at a given datapoint. We can get additional savings by using similar approach to find nearest landmarks for LLL. Because the number of closest landmarks K Z is quite low in practice (we used K Z = K + 1, as in Vladymyrov and Carreira-
7 Class. error (exact), % Class. error (LLL), % Runtime (exact), s. Runtime (LLL), s σ k W k W k W k W Fig. 6. Model selection of the Gaussian affinities using exact spectral clustering and LLL approximation with different values of bandwidth σ and number of nearest neighbors k W. First two plots show the classification error and last two show the runtime. Notice that the error pattern in very similar for exact and LLL, but the runtime is an order of magnitude smaller. Perpiñán [35]), chances are that the closest landmarks can be found within the sliding window neighborhood of a given point. For few points for which this is not the case, we retrieve to computing the distance to all landmarks and truncate it to achieve the K Z closest ones. The solution of the spectral embedding (both exact and approximate) results in K-dimensional projections matrix X (on which k-means is run after the normalization). We characterize the error incurred by our algorithm in three different ways. (1) Projection error between the unnormalized exact and LLL eigenvectors, defined as proc( X) X F / X F, where we apply Procrustes alignment to remove the influence of translations, rotations and scaling of the eigenvectors. (2) Clustering error between final clusters of exact and LLL SC. To align the clusters we used the Hungarian algorithm [5] and report the fraction of misclassified points. (3) Classification error (when ground truth is available). We report all errors as % (0% exact match, 100% total mismatch). To compute the eigendecomposition we used the MATLAB routine eigs(). All the experiments were performed on a single core machine. A. Classical Spectral Clustering We show the runtime, the proj. and clust. errors as number of landmarks grow. We compared LLL with Nyström method, Landmark Spectral Clustering (LSC; [8]), LELVM [6] and KASP [38]. We applied the approximations to cameraman grayscale image (N = , D = 3) 5 times with different number of randomly chosen landmarks logarithmically spaced from L = 8 to L = N 10. We used sparse Gaussian affinities constructed using a sliding window over the pixels with a side r = (1681 nearest neighbors for each point) withσ = 20. In fig. 4 we show the results. Nyström method gives poor performance for a L < 200 because the affinity matrix has isolated points that are not connected to any of the landmarks. As L grows, the error improves, but slowly. LLL gives good performance for any L, with both proj. and clust. error decreasing steadily and consistently with the increase of L. There are other ways to compute the error (angle between the subspaces defined by the eigenvectors, NMI [31] etc.) We observed that the error that they give is very similar to the one we use. 80 In fig. 5 we show the final clustering and the largest normalized eigenvectors of the exact clustering and LLL and Nyström approximations that achieve 10% and 1% clustering error. With respect to the exact algorithm, clustering performance of LLL is visually identical for both clustering results and eigenvectors, but with LLL being 30 faster. B. Model Selection As a preprocessing step, the spectral clustering algorithm needs to compute the affinity matrix. It should be a good representation of the underlying data, which requires careful parameter selection. For example, for the Gaussian affinities, it is crucial to find a good value of the bandwidth σ as well as the number of neighbors k W that one wishes to preserve. There is no universal rule that allows a user to pick the best values for those parameters. Ng et al [24] simply suggest choosing them by trying several values until satisfiable result is achieved. Apart from that, couple of heuristic has been proposed that can improve the results. Zelnik-Manor and Perona [39] claim that the results can be improved by setting bandwidth individually per each point of the dataset and computing the Gaussian affinity between points y n and y m as w nm = exp( yn ym 2 σ nσ m ). The paper suggests to use distance to k nearest neighbor to set individual σ n, for n = 1,...,N. Entropic affinities [14], [34] compute individual bandwidth for each point, such that the perplexity, or the effective number of neighbors, is equal to K. While each of the methods above can result in a good affinity matrix, they all depend on some parameter(s) that need to be tuned (nearest neighbor, perplexity etc.). This can lead to multiple restarts of the whole algorithms, which is expensive. To reduce this cost, we can use LLL for spectral clustering to perform the model selection. Because LLL uses complete affinity matrix, its parameters are also shared between exact method and LLL. Notice that it is not the case for the subset methods (e.g. Nyström), that use smaller affinity matrix which may require different parameter settings for the best performance. The algorithm that we propose is as follows: instead of running full exact spectral clustering several times for different parameter values, we can first try them out with LLL approximation. Then, the best parameters for LLL 8 6
8 will roughly correspond to the best parameters for the exact spectral clustering. In fig. 6 we show the search for the parameters of the simple Gaussian affinities for digits from MNIST. We run exact spectral clustering and LLL approximation with 1000 landmarks using 20 different values for σ and k W chosen on a logarithmic scale from 1 to Left two plots correspond to the classification error for the exact and LLL spectral clustering respectively. Notice that the error has similar pattern for both exact and approximate clustering. Also, for k W = 1 exact clustering fails, because the affinity matrix decouples into many disconnected components. LLL reduced affinity matrix brings those components together again and gives meaningful error. Right two plots show the runtime of exact spectral clustering and LLL respectively with LLL being more than 10 faster than the exact one (notice different ranges of the color bar). C. Constrained Spectral Clustering We applied CSC to a problem of figure/ground segmentation of an image from BSDS500 dataset [1]. To show the scalability, we tested the algorithm using the same image with 3 different sizes: small, 1 2 medium and large. We used the following bandwidths: σ = 8 for small, σ = 20 for medium and σ = for large image. In all the cases, the sliding window size is equal to σ. We used L = 730 landmarks for small image, L = 2100 for medium and L = 3890 for large. We first run the original SC that was able to separate the flower from the background (see fig. 7 for the LLL approximation of the large size image. Then, for the CSC we introduced constraints that separate the petals from the center of the flower (see green and red lines in fig. 7). Below we show the runtimes for both exact and LLL approximations: SC CSC Image Size Exact LLL Exact LLL Small Medium Large LLL gives 10 speed up with almost no compromise on the quality (both proj. and reconst. errors are less then 1% for SC and CSC). For large image exact method run out of memory during the computation of W. In comparison, LLL was able to handle large-scale input with no problem. D. Affinity Aggregation for Spectral Clustering We tested the algorithm on a subset of CMU-PIE [29], where each point is a cropped image of the face in the near frontal position (poses C05, C07, C09, C27, C29). We had points each with 96 dimensions that correspond to 67 people. Following Huang et al [15], we used three types of features: Local binary pattern (LBP; [26]) with uniform LBP using 8 neighbors and radius of 1; Gabor texture [23] with filters generated for 5 scales and 8 orientations; and eigenface [33] using top 90% eigenvectors. All the affinities were computed with Gaussian kernel with 1000 nearest neighbors. To chose the best bandwidth σ we used LLL for the model selection (similar to the way we describe above). We run LLL with L = 1000 landmarks for 20 different values spaced logarithmically between10 and10 7. The best values were: for LBP, 10 for Gabor filter and 42 for the eigenfaces. Notice the scatter of final values. Without LLL, it would be hard to predict those values by random guessing. In the table I we show the classification error and the runtime of the exact eigendecomposition and LLL approximation using 5 different tries of randomly chosen landmarks. Using the affinity matrices individually, LLL performs almost as well as exact method, but 10 faster. For AASC the resulting error of LLL is also about the same as the exact method, but faster. In fig. 9 we show the classification error decrease per iterations. LLL follows the exact method closely with a very similar error. E. Proximity Graph Carreira-Perpiñán and Zemel [7] define affinity as an ensemble of multiple affinities constructed using minimum spanning tree on a neighborhood graph perturbed with noise. Constructed this way, the affinities tend to be more robust to shortcuts between distant parts of the manifold. In fig. 10 we show the results of the image segmentation for the grayscale image of the house using LLL for spectral clustering with 3000 landmarks and K Z = 5. We used a graph ensemble of 10 affinities constructed with MST with every point perturbed using uniform random jitter with standard deviation 0.4 d, where d is a mean distance to the available neighbors of that point. For comparison, we also show the results of traditional Gaussian affinities (with bandwidth σ = 5). Both affinities use a neighborhood graph defined with sliding window with r = 10. Graph ensemble gives better results than Gaussian affinities. In particular, sky, windows and shadow of the house is better clustered using the former affinities. F. Motion Segmentation We also applied SC for motion segmentation in video. We used a dataset of 41 video frames of a person walking around a room. Each frame is represented as RGB image. Following [27], we used both spatial and temporal features, with each datapoint given by six coordinates: two for the location on the image plane, one for the number of the frame and three for the color intensity. Overall this gives N = points in D = 6 dimensions. The neighborhood graph can be easily defined by connecting points along both spatial and temporal domain. For spatial, we used a sliding window with a side r = 30. For temporal, we connected each pixel with the same pixel and its adjacent pixels of the previous and the next frames. It gives a neighborhood graph with 963 neighbors for each point. Then we build a Gaussian affinities with bandwidth σ = 15 for each pair of neighbors. Overall, it took 6.8 minutes to build this affinity matrix.
9 Original image SC with LLL CSC with LLL Fig. 7. Figure/ground segmentation of a flower image using SC and CSC (see eq. (5)) Classification error, % Exact LLL Number of iterations Fig. 9. Classification error for AASC obj. function. TABLE I CLUSTERING OF THE FACES FROM CMU-PIE DATASET USING SEPARATE FEATURES AND COMBINED FEATURES WITH EXACT SC AND LLL APPROXIMATION. LLL IS AVERAGED OVER 10 RUNS WITH RANDOM SET OF 1000 LANDMARKS. Single affinities Combined Features LBP Gabor filter Eigenface AASC Class. error, % Exact LLL 44±1 49±2 56±1 39±3 Runtime, s Exact LLL 8.15± ± ± ±2.1 Proj. error, % 4±0.8 3±1 1±0.5 3±2 Input LLL Nys. full Nys. sparse 1st frame 20th frame 41st frame Fig. 8. Spatio-temporal segmentation of41 frame video with resolution We shows 3 frames from the original video. Rows shows the result of clustering with LLL and Nyström methods applied on full or sparse affinities. It took 3 minutes for LLL to find a solution with L = 5000 randomly chosen landmarks with 1 minute spent on computing the entries of Z and 1 minute to compute the reduce affinities (4). Also, as we showed above (fig. 1), k-means with 20 restarts took 1.5 minutes which is comparable to the runtime of LLL. We tried using larger number of landmarks, but the results did not change much. For Nyström we first tried using the same sparse affinities as we did for LLL. However, with so few non-zeros, it is impossible to cover the entire dataset even with thousands of landmarks. We end up trying landmarks before running out of memory. Even for such graph we still got 35 singleton points. We also applied Nyström that approximates full affinities by computing the Gaussian kernel between all the point in the subset. This requires computing eigendecomposition of full L L matrix and evaluating an out-of-sample kernel for N L non-landmark points, which are quite costly. For L = 3000 these two steps already took more time than the runtime of the LLL and the results were still not as good as LLL. In fig. 8 we show two frames from the input and their segmentation for LLL and Nyström. The clusters for LLL correspond to the meaningful objects (e.g. floor, person, wall) and are consistent from frame to frame. Interestingly, the pants and the shirt of the person ended up in the same cluster, albeit having very different colors. Nyström results are much worse. Using the full affinities, it is possible to find some useful clusters (e.g. person s torso), but the rest do not represent any good features. Nyström with sparse affinities does not show almost any meaningful segmentation. VII. DISCUSSION A further speedup not explored here is the use of multiprocessors. The basic operations required are: (1) the computation of the sparse affinity matrix (itself possibly involving constructing a nearest-neighbor graph and computing the affinity values); (2) the computation of the weights Z; (3) the construction of the reduced spectral problem (involving matrix products); (4) the computation of the landmark eigenvectors; (5) the out-of-sample extension of the eigenvectors to the full data; (6) the random k-means restarts on the landmarks; and (7) the final k-means on the entire data. Most of these steps are easily parallelizable, in particular the more expensive ones that involve the entire, O(N), dataset. VIII. CONCLUSION Our contribution is to speed up the eigenproblem and k- means steps of spectral clustering with small approximation
10 Original image Graph ensemble affinities Gaussian affinities Fig. 10. Image segmentation of house image (shown on the left) into four clusters using graph ensemble affinities from [7] (center plot) and Gaussian affinities (right plot). Notice that the former segments the sky, the shadow in a separate cluster. errors, both with kernel-based affinities and with more complex affinities used by variants of spectral clustering. In the spectral problem, LLL provides two crucial advantages. 1) It uses all the available affinity information in constructing the landmark eigenproblem, but preserving the fast computation properties of subsampling methods. Because fewer landmarks are necessary, this makes it possible to achieve both smaller error and runtime than with the Nyström method. 2) LLL does not rely on an explicitly defined affinity kernel, unlike the the Nyström method, so it applies to variants such as constrained spectral clustering. In the k-means clustering, we run many restarts on the landmarks at little overhead. This gives a good initialization for k-means on the entire data, which then converges in very few iterations, considerably reducing the overall runtime, and is more likely to find a good optimum. Good results can be obtained for over 700K points in 10 minutes in a single processor. Since most of the required operations are easily parallelizable, in particular the more expensive ones involving the entire data, this could enable the application of spectral clustering to quite larger datasets. REFERENCES [1] P. Arbelaez, M. Maire, C. Fowlkes, and J. Malik. Contour detection and hierarchical image segmentation. PAMI, 33(5): , May [2] D. Arthur and S. Vassilvitskii. k-means++: The advantages of careful seeding. In SODA, p , Jan [3] C. T. H. Baker. The Numerical Treatment of Integral Equations. Clarendon Press, [4] Y. Bengio, O. Delalleau, N. Le Roux, J.-F. Paiement, P. Vincent, and M. Ouimet. Learning eigenfunctions links spectral embedding and kernel PCA. Neural Computation, 16(10): , Oct [5] R. Burkard, M. Dell Amico, and S. Martello. Assignment Problems. Other Titles in Applied Mathematics. SIAM Publ., [6] M. Á. Carreira-Perpiñán and Z. Lu. The Laplacian Eigenmaps Latent Variable Model. In AISTATS, p , [7] M. Á. Carreira-Perpiñán and R. S. Zemel. Proximity graphs for clustering and manifold learning. In NIPS, p , [8] X. Chen and D. Cai. Large scale spectral clustering with landmark-based representation. In AAAI, p , [9] C. Chennubhotla and A. Jepson. Hierarchical eigensolver for transition matrices in spectral methods. In NIPS, p , [10] T. Cour, F. Bénézit, and J. Shi. Spectral segmentation with multiscale graph decomposition. In CVPR, p , [11] V. Faber. Clustering and the continuous k-means algorithm. Los Alamos Science, 22: , [12] C. Fowlkes, S. Belongie, F. Chung, and J. Malik. Spectral grouping using the Nyström method. PAMI, 26(2): , [13] G. H. Golub and C. F. van Loan. Matrix Computations. Johns Hopkins University Press, Baltimore, third edition, [14] G. Hinton and S. T. Roweis. Stochastic neighbor embedding. In NIPS, p , [15] H.-C. Huang, Y.-Y. Chuang, and C.-S. Chen. Affinity aggregation for spectral clustering. In Proc. CVPR, p , [16] T. H. Kim, K. M. Lee, and S. U. Lee. Learning full pairwise affinities for spectral segmentation. PAMI, 35(7): , [17] D. Kushnir, M. Galun, and A. Brandt. Efficient multilevel eigensolvers with applications to data analysis tasks. PAMI, 32(8): , [18] T. Leung and J. Malik. Contour continuity in region-based image segmentation. In ECCV, p , [19] W. Liu, J. He, and S.-F. Chang. Large graph construction for scalable semi-supervised learning. In ICML, [20] Z. Lu and M. Á. Carreira-Perpiñán. Constrained spectral clustering through affinity propagation. In CVPR, [21] M. Maire and S. X. Yu. Progressive multigrid eigensolvers for multiscale spectral segmentation. In ICCV, p , [22] J. Malik, S. Belongie, T. Leung, and J. Shi. Contour and texture analysis for image segmentation. IJCV, 43(1):7 27, [23] B. S. Manjunath and W.-Y. Ma. Texture features for browsing and retrieval of image data. PAMI, 18(8): , [24] A. Y. Ng, M. I. Jordan, and Y. Weiss. On spectral clustering: Analysis and an algorithm. In NIPS, volume 14, p Cambridge, MA, [25] P. Ochs and T. Brox. Higher order motion models and spectral clustering. In CVPR, p , [26] T. Ojala, M. Pietikäinen, and T. Mäenpää. Gray scale and rotation invariant texture classification with local binary patterns. In ECCV, p , [27] J. Shi and J. Malik. Motion segmentation and tracking using normalized cuts. In ICCV, p , [28] J. Shi and J. Malik. Normalized cuts and image segmentation. PAMI, 22(8): , [29] T. Sim, S. Baker, and M. Bsat. The CMU pose, illumination, and expression database. PAMI, 25(12): , [30] D. Steinley and M. J. Brusco. Initializing k-means batch clustering: A critical evaluation of several techniques. Journal of Classification, 24(1):99 121, [31] A. Strehl and J. Ghosh. Cluster ensembles a knowledge reuse framework for combining multiple partitions. JMLR, 3: , [32] A. Talwalkar, S. Kumar, and H. Rowley. Large-scale manifold learning. In CVPR, [33] M. A. Turk and A. Pentland. Eigenfaces for recognition. J. Cognitive Neurosci., 3(1):71 86, [34] M. Vladymyrov and M. Á. Carreira-Perpiñán. Entropic affinities: Properties and efficient numerical computation. In ICML, p , Atlanta, GA, [35] M. Vladymyrov and M. Á. Carreira-Perpiñán. Locally Linear Landmarks for large-scale manifold learning. In ECML, p , [36] U. von Luxburg. A tutorial on spectral clustering. Statistics and Computing, 17(4): , Dec [37] C. K. I. Williams and M. Seeger. Using the Nyström method to speed up kernel machines. In NIPS, volume 13, p , [38] D. Yan, L. Huang, and M. I. Jordan. Fast approximate spectral clustering. In SIGKDD, p , [39] L. Zelnik-Manor and P. Perona. Self-tuning spectral clustering. In NIPS, p , 2005.
Fast, Accurate Spectral Clustering Using Locally Linear Landmarks
 Fast, Accurate Spectral Clustering Using Locally Linear Landmarks Max Vladymyrov Google Inc. Miguel Á. Carreira-Perpiñán EECS, UC Merced May 17, 2017 Spectral clustering Focus on the problem of Spectral
Fast, Accurate Spectral Clustering Using Locally Linear Landmarks Max Vladymyrov Google Inc. Miguel Á. Carreira-Perpiñán EECS, UC Merced May 17, 2017 Spectral clustering Focus on the problem of Spectral
Locally Linear Landmarks for large-scale manifold learning
 Locally Linear Landmarks for large-scale manifold learning Max Vladymyrov and Miguel Á. Carreira-Perpiñán Electrical Engineering and Computer Science University of California, Merced http://eecs.ucmerced.edu
Locally Linear Landmarks for large-scale manifold learning Max Vladymyrov and Miguel Á. Carreira-Perpiñán Electrical Engineering and Computer Science University of California, Merced http://eecs.ucmerced.edu
Large-Scale Face Manifold Learning
 Large-Scale Face Manifold Learning Sanjiv Kumar Google Research New York, NY * Joint work with A. Talwalkar, H. Rowley and M. Mohri 1 Face Manifold Learning 50 x 50 pixel faces R 2500 50 x 50 pixel random
Large-Scale Face Manifold Learning Sanjiv Kumar Google Research New York, NY * Joint work with A. Talwalkar, H. Rowley and M. Mohri 1 Face Manifold Learning 50 x 50 pixel faces R 2500 50 x 50 pixel random
Spectral Clustering X I AO ZE N G + E L HA M TA BA S SI CS E CL A S S P R ESENTATION MA RCH 1 6,
 Spectral Clustering XIAO ZENG + ELHAM TABASSI CSE 902 CLASS PRESENTATION MARCH 16, 2017 1 Presentation based on 1. Von Luxburg, Ulrike. "A tutorial on spectral clustering." Statistics and computing 17.4
Spectral Clustering XIAO ZENG + ELHAM TABASSI CSE 902 CLASS PRESENTATION MARCH 16, 2017 1 Presentation based on 1. Von Luxburg, Ulrike. "A tutorial on spectral clustering." Statistics and computing 17.4
Locally Linear Landmarks for Large-Scale Manifold Learning
 Locally Linear Landmarks for Large-Scale Manifold Learning Max Vladymyrov and Miguel Á. Carreira-Perpiñán Electrical Engineering and Computer Science, University of California, Merced, USA {mvladymyrov,mcarreira-perpinan}@ucmerced.edu
Locally Linear Landmarks for Large-Scale Manifold Learning Max Vladymyrov and Miguel Á. Carreira-Perpiñán Electrical Engineering and Computer Science, University of California, Merced, USA {mvladymyrov,mcarreira-perpinan}@ucmerced.edu
The K-modes and Laplacian K-modes algorithms for clustering
 The K-modes and Laplacian K-modes algorithms for clustering Miguel Á. Carreira-Perpiñán Electrical Engineering and Computer Science University of California, Merced http://faculty.ucmerced.edu/mcarreira-perpinan
The K-modes and Laplacian K-modes algorithms for clustering Miguel Á. Carreira-Perpiñán Electrical Engineering and Computer Science University of California, Merced http://faculty.ucmerced.edu/mcarreira-perpinan
Visual Representations for Machine Learning
 Visual Representations for Machine Learning Spectral Clustering and Channel Representations Lecture 1 Spectral Clustering: introduction and confusion Michael Felsberg Klas Nordberg The Spectral Clustering
Visual Representations for Machine Learning Spectral Clustering and Channel Representations Lecture 1 Spectral Clustering: introduction and confusion Michael Felsberg Klas Nordberg The Spectral Clustering
Learning to Recognize Faces in Realistic Conditions
 000 001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050
000 001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050
Technical Report. Title: Manifold learning and Random Projections for multi-view object recognition
 Technical Report Title: Manifold learning and Random Projections for multi-view object recognition Authors: Grigorios Tsagkatakis 1 and Andreas Savakis 2 1 Center for Imaging Science, Rochester Institute
Technical Report Title: Manifold learning and Random Projections for multi-view object recognition Authors: Grigorios Tsagkatakis 1 and Andreas Savakis 2 1 Center for Imaging Science, Rochester Institute
Locally Linear Landmarks for Large-Scale Manifold Learning
 Max Vladymyrov MVLADYMYROV@UCMERCED.EDU Miguel Á. Carreira-Perpiñán MCARREIRA-PERPINAN@UCMERCED.EDU Electrical Engineering and Computer Science, School of Engineering, University of California, Merced
Max Vladymyrov MVLADYMYROV@UCMERCED.EDU Miguel Á. Carreira-Perpiñán MCARREIRA-PERPINAN@UCMERCED.EDU Electrical Engineering and Computer Science, School of Engineering, University of California, Merced
Supervised texture detection in images
 Supervised texture detection in images Branislav Mičušík and Allan Hanbury Pattern Recognition and Image Processing Group, Institute of Computer Aided Automation, Vienna University of Technology Favoritenstraße
Supervised texture detection in images Branislav Mičušík and Allan Hanbury Pattern Recognition and Image Processing Group, Institute of Computer Aided Automation, Vienna University of Technology Favoritenstraße
Clustering CS 550: Machine Learning
 Clustering CS 550: Machine Learning This slide set mainly uses the slides given in the following links: http://www-users.cs.umn.edu/~kumar/dmbook/ch8.pdf http://www-users.cs.umn.edu/~kumar/dmbook/dmslides/chap8_basic_cluster_analysis.pdf
Clustering CS 550: Machine Learning This slide set mainly uses the slides given in the following links: http://www-users.cs.umn.edu/~kumar/dmbook/ch8.pdf http://www-users.cs.umn.edu/~kumar/dmbook/dmslides/chap8_basic_cluster_analysis.pdf
Fast and Adaptive Pairwise Similarities for Graph Cuts-based Image Segmentation
 Fast and Adaptive Pairwise Similarities for Graph Cuts-based Image Segmentation Baris Sumengen UC, Santa Barbara Santa Barbara, CA 931 sumengen@ece.ucsb.edu Luca Bertelli UC, Santa Barbara Santa Barbara,
Fast and Adaptive Pairwise Similarities for Graph Cuts-based Image Segmentation Baris Sumengen UC, Santa Barbara Santa Barbara, CA 931 sumengen@ece.ucsb.edu Luca Bertelli UC, Santa Barbara Santa Barbara,
Spectral Clustering. Presented by Eldad Rubinstein Based on a Tutorial by Ulrike von Luxburg TAU Big Data Processing Seminar December 14, 2014
 Spectral Clustering Presented by Eldad Rubinstein Based on a Tutorial by Ulrike von Luxburg TAU Big Data Processing Seminar December 14, 2014 What are we going to talk about? Introduction Clustering and
Spectral Clustering Presented by Eldad Rubinstein Based on a Tutorial by Ulrike von Luxburg TAU Big Data Processing Seminar December 14, 2014 What are we going to talk about? Introduction Clustering and
Image Coding with Active Appearance Models
 Image Coding with Active Appearance Models Simon Baker, Iain Matthews, and Jeff Schneider CMU-RI-TR-03-13 The Robotics Institute Carnegie Mellon University Abstract Image coding is the task of representing
Image Coding with Active Appearance Models Simon Baker, Iain Matthews, and Jeff Schneider CMU-RI-TR-03-13 The Robotics Institute Carnegie Mellon University Abstract Image coding is the task of representing
CS 664 Segmentation. Daniel Huttenlocher
 CS 664 Segmentation Daniel Huttenlocher Grouping Perceptual Organization Structural relationships between tokens Parallelism, symmetry, alignment Similarity of token properties Often strong psychophysical
CS 664 Segmentation Daniel Huttenlocher Grouping Perceptual Organization Structural relationships between tokens Parallelism, symmetry, alignment Similarity of token properties Often strong psychophysical
Color Image Segmentation
 Color Image Segmentation Yining Deng, B. S. Manjunath and Hyundoo Shin* Department of Electrical and Computer Engineering University of California, Santa Barbara, CA 93106-9560 *Samsung Electronics Inc.
Color Image Segmentation Yining Deng, B. S. Manjunath and Hyundoo Shin* Department of Electrical and Computer Engineering University of California, Santa Barbara, CA 93106-9560 *Samsung Electronics Inc.
Region-based Segmentation
 Region-based Segmentation Image Segmentation Group similar components (such as, pixels in an image, image frames in a video) to obtain a compact representation. Applications: Finding tumors, veins, etc.
Region-based Segmentation Image Segmentation Group similar components (such as, pixels in an image, image frames in a video) to obtain a compact representation. Applications: Finding tumors, veins, etc.
Diffusion Wavelets for Natural Image Analysis
 Diffusion Wavelets for Natural Image Analysis Tyrus Berry December 16, 2011 Contents 1 Project Description 2 2 Introduction to Diffusion Wavelets 2 2.1 Diffusion Multiresolution............................
Diffusion Wavelets for Natural Image Analysis Tyrus Berry December 16, 2011 Contents 1 Project Description 2 2 Introduction to Diffusion Wavelets 2 2.1 Diffusion Multiresolution............................
Object Classification Problem
 HIERARCHICAL OBJECT CATEGORIZATION" Gregory Griffin and Pietro Perona. Learning and Using Taxonomies For Fast Visual Categorization. CVPR 2008 Marcin Marszalek and Cordelia Schmid. Constructing Category
HIERARCHICAL OBJECT CATEGORIZATION" Gregory Griffin and Pietro Perona. Learning and Using Taxonomies For Fast Visual Categorization. CVPR 2008 Marcin Marszalek and Cordelia Schmid. Constructing Category
Clustering K-means. Machine Learning CSEP546 Carlos Guestrin University of Washington February 18, Carlos Guestrin
 Clustering K-means Machine Learning CSEP546 Carlos Guestrin University of Washington February 18, 2014 Carlos Guestrin 2005-2014 1 Clustering images Set of Images [Goldberger et al.] Carlos Guestrin 2005-2014
Clustering K-means Machine Learning CSEP546 Carlos Guestrin University of Washington February 18, 2014 Carlos Guestrin 2005-2014 1 Clustering images Set of Images [Goldberger et al.] Carlos Guestrin 2005-2014
Learning independent, diverse binary hash functions: pruning and locality
 Learning independent, diverse binary hash functions: pruning and locality Ramin Raziperchikolaei and Miguel Á. Carreira-Perpiñán Electrical Engineering and Computer Science University of California, Merced
Learning independent, diverse binary hash functions: pruning and locality Ramin Raziperchikolaei and Miguel Á. Carreira-Perpiñán Electrical Engineering and Computer Science University of California, Merced
Targil 12 : Image Segmentation. Image segmentation. Why do we need it? Image segmentation
 Targil : Image Segmentation Image segmentation Many slides from Steve Seitz Segment region of the image which: elongs to a single object. Looks uniform (gray levels, color ) Have the same attributes (texture
Targil : Image Segmentation Image segmentation Many slides from Steve Seitz Segment region of the image which: elongs to a single object. Looks uniform (gray levels, color ) Have the same attributes (texture
MSA220 - Statistical Learning for Big Data
 MSA220 - Statistical Learning for Big Data Lecture 13 Rebecka Jörnsten Mathematical Sciences University of Gothenburg and Chalmers University of Technology Clustering Explorative analysis - finding groups
MSA220 - Statistical Learning for Big Data Lecture 13 Rebecka Jörnsten Mathematical Sciences University of Gothenburg and Chalmers University of Technology Clustering Explorative analysis - finding groups
EE795: Computer Vision and Intelligent Systems
 EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 FDH 204 Lecture 14 130307 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Stereo Dense Motion Estimation Translational
EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 FDH 204 Lecture 14 130307 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Stereo Dense Motion Estimation Translational
Selecting Models from Videos for Appearance-Based Face Recognition
 Selecting Models from Videos for Appearance-Based Face Recognition Abdenour Hadid and Matti Pietikäinen Machine Vision Group Infotech Oulu and Department of Electrical and Information Engineering P.O.
Selecting Models from Videos for Appearance-Based Face Recognition Abdenour Hadid and Matti Pietikäinen Machine Vision Group Infotech Oulu and Department of Electrical and Information Engineering P.O.
Learning and Inferring Depth from Monocular Images. Jiyan Pan April 1, 2009
 Learning and Inferring Depth from Monocular Images Jiyan Pan April 1, 2009 Traditional ways of inferring depth Binocular disparity Structure from motion Defocus Given a single monocular image, how to infer
Learning and Inferring Depth from Monocular Images Jiyan Pan April 1, 2009 Traditional ways of inferring depth Binocular disparity Structure from motion Defocus Given a single monocular image, how to infer
Sparse Manifold Clustering and Embedding
 Sparse Manifold Clustering and Embedding Ehsan Elhamifar Center for Imaging Science Johns Hopkins University ehsan@cis.jhu.edu René Vidal Center for Imaging Science Johns Hopkins University rvidal@cis.jhu.edu
Sparse Manifold Clustering and Embedding Ehsan Elhamifar Center for Imaging Science Johns Hopkins University ehsan@cis.jhu.edu René Vidal Center for Imaging Science Johns Hopkins University rvidal@cis.jhu.edu
Segmentation & Clustering
 EECS 442 Computer vision Segmentation & Clustering Segmentation in human vision K-mean clustering Mean-shift Graph-cut Reading: Chapters 14 [FP] Some slides of this lectures are courtesy of prof F. Li,
EECS 442 Computer vision Segmentation & Clustering Segmentation in human vision K-mean clustering Mean-shift Graph-cut Reading: Chapters 14 [FP] Some slides of this lectures are courtesy of prof F. Li,
Machine Learning A W 1sst KU. b) [1 P] Give an example for a probability distributions P (A, B, C) that disproves
![Machine Learning A W 1sst KU. b) [1 P] Give an example for a probability distributions P (A, B, C) that disproves Machine Learning A W 1sst KU. b) [1 P] Give an example for a probability distributions P (A, B, C) that disproves](/thumbs/93/111796408.jpg) Machine Learning A 708.064 11W 1sst KU Exercises Problems marked with * are optional. 1 Conditional Independence I [2 P] a) [1 P] Give an example for a probability distribution P (A, B, C) that disproves
Machine Learning A 708.064 11W 1sst KU Exercises Problems marked with * are optional. 1 Conditional Independence I [2 P] a) [1 P] Give an example for a probability distribution P (A, B, C) that disproves
Segmentation Computer Vision Spring 2018, Lecture 27
 Segmentation http://www.cs.cmu.edu/~16385/ 16-385 Computer Vision Spring 218, Lecture 27 Course announcements Homework 7 is due on Sunday 6 th. - Any questions about homework 7? - How many of you have
Segmentation http://www.cs.cmu.edu/~16385/ 16-385 Computer Vision Spring 218, Lecture 27 Course announcements Homework 7 is due on Sunday 6 th. - Any questions about homework 7? - How many of you have
On Order-Constrained Transitive Distance
 On Order-Constrained Transitive Distance Author: Zhiding Yu and B. V. K. Vijaya Kumar, et al. Dept of Electrical and Computer Engineering Carnegie Mellon University 1 Clustering Problem Important Issues:
On Order-Constrained Transitive Distance Author: Zhiding Yu and B. V. K. Vijaya Kumar, et al. Dept of Electrical and Computer Engineering Carnegie Mellon University 1 Clustering Problem Important Issues:
Feature Selection for fmri Classification
 Feature Selection for fmri Classification Chuang Wu Program of Computational Biology Carnegie Mellon University Pittsburgh, PA 15213 chuangw@andrew.cmu.edu Abstract The functional Magnetic Resonance Imaging
Feature Selection for fmri Classification Chuang Wu Program of Computational Biology Carnegie Mellon University Pittsburgh, PA 15213 chuangw@andrew.cmu.edu Abstract The functional Magnetic Resonance Imaging
Unsupervised learning in Vision
 Chapter 7 Unsupervised learning in Vision The fields of Computer Vision and Machine Learning complement each other in a very natural way: the aim of the former is to extract useful information from visual
Chapter 7 Unsupervised learning in Vision The fields of Computer Vision and Machine Learning complement each other in a very natural way: the aim of the former is to extract useful information from visual
Digital Image Processing. Prof. P. K. Biswas. Department of Electronic & Electrical Communication Engineering
 Digital Image Processing Prof. P. K. Biswas Department of Electronic & Electrical Communication Engineering Indian Institute of Technology, Kharagpur Lecture - 21 Image Enhancement Frequency Domain Processing
Digital Image Processing Prof. P. K. Biswas Department of Electronic & Electrical Communication Engineering Indian Institute of Technology, Kharagpur Lecture - 21 Image Enhancement Frequency Domain Processing
Appearance Manifold of Facial Expression
 Appearance Manifold of Facial Expression Caifeng Shan, Shaogang Gong and Peter W. McOwan Department of Computer Science Queen Mary, University of London, London E1 4NS, UK {cfshan, sgg, pmco}@dcs.qmul.ac.uk
Appearance Manifold of Facial Expression Caifeng Shan, Shaogang Gong and Peter W. McOwan Department of Computer Science Queen Mary, University of London, London E1 4NS, UK {cfshan, sgg, pmco}@dcs.qmul.ac.uk
Clustering. SC4/SM4 Data Mining and Machine Learning, Hilary Term 2017 Dino Sejdinovic
 Clustering SC4/SM4 Data Mining and Machine Learning, Hilary Term 2017 Dino Sejdinovic Clustering is one of the fundamental and ubiquitous tasks in exploratory data analysis a first intuition about the
Clustering SC4/SM4 Data Mining and Machine Learning, Hilary Term 2017 Dino Sejdinovic Clustering is one of the fundamental and ubiquitous tasks in exploratory data analysis a first intuition about the
The Analysis of Parameters t and k of LPP on Several Famous Face Databases
 The Analysis of Parameters t and k of LPP on Several Famous Face Databases Sujing Wang, Na Zhang, Mingfang Sun, and Chunguang Zhou College of Computer Science and Technology, Jilin University, Changchun
The Analysis of Parameters t and k of LPP on Several Famous Face Databases Sujing Wang, Na Zhang, Mingfang Sun, and Chunguang Zhou College of Computer Science and Technology, Jilin University, Changchun
Segmentation and Tracking of Partial Planar Templates
 Segmentation and Tracking of Partial Planar Templates Abdelsalam Masoud William Hoff Colorado School of Mines Colorado School of Mines Golden, CO 800 Golden, CO 800 amasoud@mines.edu whoff@mines.edu Abstract
Segmentation and Tracking of Partial Planar Templates Abdelsalam Masoud William Hoff Colorado School of Mines Colorado School of Mines Golden, CO 800 Golden, CO 800 amasoud@mines.edu whoff@mines.edu Abstract
3D Human Motion Analysis and Manifolds
 D E P A R T M E N T O F C O M P U T E R S C I E N C E U N I V E R S I T Y O F C O P E N H A G E N 3D Human Motion Analysis and Manifolds Kim Steenstrup Pedersen DIKU Image group and E-Science center Motivation
D E P A R T M E N T O F C O M P U T E R S C I E N C E U N I V E R S I T Y O F C O P E N H A G E N 3D Human Motion Analysis and Manifolds Kim Steenstrup Pedersen DIKU Image group and E-Science center Motivation
CSE 6242 A / CS 4803 DVA. Feb 12, Dimension Reduction. Guest Lecturer: Jaegul Choo
 CSE 6242 A / CS 4803 DVA Feb 12, 2013 Dimension Reduction Guest Lecturer: Jaegul Choo CSE 6242 A / CS 4803 DVA Feb 12, 2013 Dimension Reduction Guest Lecturer: Jaegul Choo Data is Too Big To Do Something..
CSE 6242 A / CS 4803 DVA Feb 12, 2013 Dimension Reduction Guest Lecturer: Jaegul Choo CSE 6242 A / CS 4803 DVA Feb 12, 2013 Dimension Reduction Guest Lecturer: Jaegul Choo Data is Too Big To Do Something..
Application of Spectral Clustering Algorithm
 1/27 Application of Spectral Clustering Algorithm Danielle Middlebrooks dmiddle1@math.umd.edu Advisor: Kasso Okoudjou kasso@umd.edu Department of Mathematics University of Maryland- College Park Advance
1/27 Application of Spectral Clustering Algorithm Danielle Middlebrooks dmiddle1@math.umd.edu Advisor: Kasso Okoudjou kasso@umd.edu Department of Mathematics University of Maryland- College Park Advance
EE 701 ROBOT VISION. Segmentation
 EE 701 ROBOT VISION Regions and Image Segmentation Histogram-based Segmentation Automatic Thresholding K-means Clustering Spatial Coherence Merging and Splitting Graph Theoretic Segmentation Region Growing
EE 701 ROBOT VISION Regions and Image Segmentation Histogram-based Segmentation Automatic Thresholding K-means Clustering Spatial Coherence Merging and Splitting Graph Theoretic Segmentation Region Growing
Geometric Registration for Deformable Shapes 3.3 Advanced Global Matching
 Geometric Registration for Deformable Shapes 3.3 Advanced Global Matching Correlated Correspondences [ASP*04] A Complete Registration System [HAW*08] In this session Advanced Global Matching Some practical
Geometric Registration for Deformable Shapes 3.3 Advanced Global Matching Correlated Correspondences [ASP*04] A Complete Registration System [HAW*08] In this session Advanced Global Matching Some practical
Improving Image Segmentation Quality Via Graph Theory
 International Symposium on Computers & Informatics (ISCI 05) Improving Image Segmentation Quality Via Graph Theory Xiangxiang Li, Songhao Zhu School of Automatic, Nanjing University of Post and Telecommunications,
International Symposium on Computers & Informatics (ISCI 05) Improving Image Segmentation Quality Via Graph Theory Xiangxiang Li, Songhao Zhu School of Automatic, Nanjing University of Post and Telecommunications,
Image Segmentation continued Graph Based Methods
 Image Segmentation continued Graph Based Methods Previously Images as graphs Fully-connected graph node (vertex) for every pixel link between every pair of pixels, p,q affinity weight w pq for each link
Image Segmentation continued Graph Based Methods Previously Images as graphs Fully-connected graph node (vertex) for every pixel link between every pair of pixels, p,q affinity weight w pq for each link
Segmentation. Bottom Up Segmentation
 Segmentation Bottom up Segmentation Semantic Segmentation Bottom Up Segmentation 1 Segmentation as clustering Depending on what we choose as the feature space, we can group pixels in different ways. Grouping
Segmentation Bottom up Segmentation Semantic Segmentation Bottom Up Segmentation 1 Segmentation as clustering Depending on what we choose as the feature space, we can group pixels in different ways. Grouping
CS 664 Slides #11 Image Segmentation. Prof. Dan Huttenlocher Fall 2003
 CS 664 Slides #11 Image Segmentation Prof. Dan Huttenlocher Fall 2003 Image Segmentation Find regions of image that are coherent Dual of edge detection Regions vs. boundaries Related to clustering problems
CS 664 Slides #11 Image Segmentation Prof. Dan Huttenlocher Fall 2003 Image Segmentation Find regions of image that are coherent Dual of edge detection Regions vs. boundaries Related to clustering problems
10-701/15-781, Fall 2006, Final
 -7/-78, Fall 6, Final Dec, :pm-8:pm There are 9 questions in this exam ( pages including this cover sheet). If you need more room to work out your answer to a question, use the back of the page and clearly
-7/-78, Fall 6, Final Dec, :pm-8:pm There are 9 questions in this exam ( pages including this cover sheet). If you need more room to work out your answer to a question, use the back of the page and clearly
Hashing with Graphs. Sanjiv Kumar (Google), and Shih Fu Chang (Columbia) June, 2011
 Hashing with Graphs Wei Liu (Columbia Columbia), Jun Wang (IBM IBM), Sanjiv Kumar (Google), and Shih Fu Chang (Columbia) June, 2011 Overview Graph Hashing Outline Anchor Graph Hashing Experiments Conclusions
Hashing with Graphs Wei Liu (Columbia Columbia), Jun Wang (IBM IBM), Sanjiv Kumar (Google), and Shih Fu Chang (Columbia) June, 2011 Overview Graph Hashing Outline Anchor Graph Hashing Experiments Conclusions
Behavioral Data Mining. Lecture 18 Clustering
 Behavioral Data Mining Lecture 18 Clustering Outline Why? Cluster quality K-means Spectral clustering Generative Models Rationale Given a set {X i } for i = 1,,n, a clustering is a partition of the X i
Behavioral Data Mining Lecture 18 Clustering Outline Why? Cluster quality K-means Spectral clustering Generative Models Rationale Given a set {X i } for i = 1,,n, a clustering is a partition of the X i
The goals of segmentation
 Image segmentation The goals of segmentation Group together similar-looking pixels for efficiency of further processing Bottom-up process Unsupervised superpixels X. Ren and J. Malik. Learning a classification
Image segmentation The goals of segmentation Group together similar-looking pixels for efficiency of further processing Bottom-up process Unsupervised superpixels X. Ren and J. Malik. Learning a classification
INF 4300 Classification III Anne Solberg The agenda today:
 INF 4300 Classification III Anne Solberg 28.10.15 The agenda today: More on estimating classifier accuracy Curse of dimensionality and simple feature selection knn-classification K-means clustering 28.10.15
INF 4300 Classification III Anne Solberg 28.10.15 The agenda today: More on estimating classifier accuracy Curse of dimensionality and simple feature selection knn-classification K-means clustering 28.10.15
Time and Space Efficient Spectral Clustering via Column Sampling
 Time and Space Efficient Spectral Clustering via Column Sampling Mu Li Xiao-Chen Lian James T. Kwok Bao-Liang Lu, 3 Department of Computer Science and Engineering, Shanghai Jiao Tong University, Shanghai
Time and Space Efficient Spectral Clustering via Column Sampling Mu Li Xiao-Chen Lian James T. Kwok Bao-Liang Lu, 3 Department of Computer Science and Engineering, Shanghai Jiao Tong University, Shanghai
Computer Vision I. Announcements. Fourier Tansform. Efficient Implementation. Edge and Corner Detection. CSE252A Lecture 13.
 Announcements Edge and Corner Detection HW3 assigned CSE252A Lecture 13 Efficient Implementation Both, the Box filter and the Gaussian filter are separable: First convolve each row of input image I with
Announcements Edge and Corner Detection HW3 assigned CSE252A Lecture 13 Efficient Implementation Both, the Box filter and the Gaussian filter are separable: First convolve each row of input image I with
Stacked Denoising Autoencoders for Face Pose Normalization
 Stacked Denoising Autoencoders for Face Pose Normalization Yoonseop Kang 1, Kang-Tae Lee 2,JihyunEun 2, Sung Eun Park 2 and Seungjin Choi 1 1 Department of Computer Science and Engineering Pohang University
Stacked Denoising Autoencoders for Face Pose Normalization Yoonseop Kang 1, Kang-Tae Lee 2,JihyunEun 2, Sung Eun Park 2 and Seungjin Choi 1 1 Department of Computer Science and Engineering Pohang University
Spectral clustering Lecture 3
 Spectral clustering Lecture 3 Vasileios Zografos zografos@isy.liu.se Klas Nordberg klas@isy.liu.se Contents Computer Vision Laboratory Applications of spectral clustering Mainly computer vision (image,
Spectral clustering Lecture 3 Vasileios Zografos zografos@isy.liu.se Klas Nordberg klas@isy.liu.se Contents Computer Vision Laboratory Applications of spectral clustering Mainly computer vision (image,
Segmentation and Grouping April 19 th, 2018
 Segmentation and Grouping April 19 th, 2018 Yong Jae Lee UC Davis Features and filters Transforming and describing images; textures, edges 2 Grouping and fitting [fig from Shi et al] Clustering, segmentation,
Segmentation and Grouping April 19 th, 2018 Yong Jae Lee UC Davis Features and filters Transforming and describing images; textures, edges 2 Grouping and fitting [fig from Shi et al] Clustering, segmentation,
COMP 551 Applied Machine Learning Lecture 16: Deep Learning
 COMP 551 Applied Machine Learning Lecture 16: Deep Learning Instructor: Ryan Lowe (ryan.lowe@cs.mcgill.ca) Slides mostly by: Class web page: www.cs.mcgill.ca/~hvanho2/comp551 Unless otherwise noted, all
COMP 551 Applied Machine Learning Lecture 16: Deep Learning Instructor: Ryan Lowe (ryan.lowe@cs.mcgill.ca) Slides mostly by: Class web page: www.cs.mcgill.ca/~hvanho2/comp551 Unless otherwise noted, all
Data fusion and multi-cue data matching using diffusion maps
 Data fusion and multi-cue data matching using diffusion maps Stéphane Lafon Collaborators: Raphy Coifman, Andreas Glaser, Yosi Keller, Steven Zucker (Yale University) Part of this work was supported by
Data fusion and multi-cue data matching using diffusion maps Stéphane Lafon Collaborators: Raphy Coifman, Andreas Glaser, Yosi Keller, Steven Zucker (Yale University) Part of this work was supported by
Face Recognition using Eigenfaces SMAI Course Project
 Face Recognition using Eigenfaces SMAI Course Project Satarupa Guha IIIT Hyderabad 201307566 satarupa.guha@research.iiit.ac.in Ayushi Dalmia IIIT Hyderabad 201307565 ayushi.dalmia@research.iiit.ac.in Abstract
Face Recognition using Eigenfaces SMAI Course Project Satarupa Guha IIIT Hyderabad 201307566 satarupa.guha@research.iiit.ac.in Ayushi Dalmia IIIT Hyderabad 201307565 ayushi.dalmia@research.iiit.ac.in Abstract
Motion Estimation. There are three main types (or applications) of motion estimation:
 Members: D91922016 朱威達 R93922010 林聖凱 R93922044 謝俊瑋 Motion Estimation There are three main types (or applications) of motion estimation: Parametric motion (image alignment) The main idea of parametric motion
Members: D91922016 朱威達 R93922010 林聖凱 R93922044 謝俊瑋 Motion Estimation There are three main types (or applications) of motion estimation: Parametric motion (image alignment) The main idea of parametric motion
APPROXIMATE SPECTRAL LEARNING USING NYSTROM METHOD. Aleksandar Trokicić
 FACTA UNIVERSITATIS (NIŠ) Ser. Math. Inform. Vol. 31, No 2 (2016), 569 578 APPROXIMATE SPECTRAL LEARNING USING NYSTROM METHOD Aleksandar Trokicić Abstract. Constrained clustering algorithms as an input
FACTA UNIVERSITATIS (NIŠ) Ser. Math. Inform. Vol. 31, No 2 (2016), 569 578 APPROXIMATE SPECTRAL LEARNING USING NYSTROM METHOD Aleksandar Trokicić Abstract. Constrained clustering algorithms as an input
Cluster Analysis. Mu-Chun Su. Department of Computer Science and Information Engineering National Central University 2003/3/11 1
 Cluster Analysis Mu-Chun Su Department of Computer Science and Information Engineering National Central University 2003/3/11 1 Introduction Cluster analysis is the formal study of algorithms and methods
Cluster Analysis Mu-Chun Su Department of Computer Science and Information Engineering National Central University 2003/3/11 1 Introduction Cluster analysis is the formal study of algorithms and methods
Occluded Facial Expression Tracking
 Occluded Facial Expression Tracking Hugo Mercier 1, Julien Peyras 2, and Patrice Dalle 1 1 Institut de Recherche en Informatique de Toulouse 118, route de Narbonne, F-31062 Toulouse Cedex 9 2 Dipartimento
Occluded Facial Expression Tracking Hugo Mercier 1, Julien Peyras 2, and Patrice Dalle 1 1 Institut de Recherche en Informatique de Toulouse 118, route de Narbonne, F-31062 Toulouse Cedex 9 2 Dipartimento
Robust Pose Estimation using the SwissRanger SR-3000 Camera
 Robust Pose Estimation using the SwissRanger SR- Camera Sigurjón Árni Guðmundsson, Rasmus Larsen and Bjarne K. Ersbøll Technical University of Denmark, Informatics and Mathematical Modelling. Building,
Robust Pose Estimation using the SwissRanger SR- Camera Sigurjón Árni Guðmundsson, Rasmus Larsen and Bjarne K. Ersbøll Technical University of Denmark, Informatics and Mathematical Modelling. Building,
Non-linear dimension reduction
 Sta306b May 23, 2011 Dimension Reduction: 1 Non-linear dimension reduction ISOMAP: Tenenbaum, de Silva & Langford (2000) Local linear embedding: Roweis & Saul (2000) Local MDS: Chen (2006) all three methods
Sta306b May 23, 2011 Dimension Reduction: 1 Non-linear dimension reduction ISOMAP: Tenenbaum, de Silva & Langford (2000) Local linear embedding: Roweis & Saul (2000) Local MDS: Chen (2006) all three methods
Head Frontal-View Identification Using Extended LLE
 Head Frontal-View Identification Using Extended LLE Chao Wang Center for Spoken Language Understanding, Oregon Health and Science University Abstract Automatic head frontal-view identification is challenging
Head Frontal-View Identification Using Extended LLE Chao Wang Center for Spoken Language Understanding, Oregon Health and Science University Abstract Automatic head frontal-view identification is challenging
Markov Random Fields and Gibbs Sampling for Image Denoising
 Markov Random Fields and Gibbs Sampling for Image Denoising Chang Yue Electrical Engineering Stanford University changyue@stanfoed.edu Abstract This project applies Gibbs Sampling based on different Markov
Markov Random Fields and Gibbs Sampling for Image Denoising Chang Yue Electrical Engineering Stanford University changyue@stanfoed.edu Abstract This project applies Gibbs Sampling based on different Markov
COSC160: Detection and Classification. Jeremy Bolton, PhD Assistant Teaching Professor
 COSC160: Detection and Classification Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Problem I. Strategies II. Features for training III. Using spatial information? IV. Reducing dimensionality
COSC160: Detection and Classification Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Problem I. Strategies II. Features for training III. Using spatial information? IV. Reducing dimensionality
Clustering. CS294 Practical Machine Learning Junming Yin 10/09/06
 Clustering CS294 Practical Machine Learning Junming Yin 10/09/06 Outline Introduction Unsupervised learning What is clustering? Application Dissimilarity (similarity) of objects Clustering algorithm K-means,
Clustering CS294 Practical Machine Learning Junming Yin 10/09/06 Outline Introduction Unsupervised learning What is clustering? Application Dissimilarity (similarity) of objects Clustering algorithm K-means,
Applied Bayesian Nonparametrics 5. Spatial Models via Gaussian Processes, not MRFs Tutorial at CVPR 2012 Erik Sudderth Brown University
 Applied Bayesian Nonparametrics 5. Spatial Models via Gaussian Processes, not MRFs Tutorial at CVPR 2012 Erik Sudderth Brown University NIPS 2008: E. Sudderth & M. Jordan, Shared Segmentation of Natural
Applied Bayesian Nonparametrics 5. Spatial Models via Gaussian Processes, not MRFs Tutorial at CVPR 2012 Erik Sudderth Brown University NIPS 2008: E. Sudderth & M. Jordan, Shared Segmentation of Natural
Computer Vision I. Announcement. Corners. Edges. Numerical Derivatives f(x) Edge and Corner Detection. CSE252A Lecture 11
 Announcement Edge and Corner Detection Slides are posted HW due Friday CSE5A Lecture 11 Edges Corners Edge is Where Change Occurs: 1-D Change is measured by derivative in 1D Numerical Derivatives f(x)
Announcement Edge and Corner Detection Slides are posted HW due Friday CSE5A Lecture 11 Edges Corners Edge is Where Change Occurs: 1-D Change is measured by derivative in 1D Numerical Derivatives f(x)
Introduction to spectral clustering
 Introduction to spectral clustering Denis Hamad LASL ULCO Denis.Hamad@lasl.univ-littoral.fr Philippe Biela HEI LAGIS Philippe.Biela@hei.fr Data Clustering Data clustering Data clustering is an important
Introduction to spectral clustering Denis Hamad LASL ULCO Denis.Hamad@lasl.univ-littoral.fr Philippe Biela HEI LAGIS Philippe.Biela@hei.fr Data Clustering Data clustering Data clustering is an important
Classification and Detection in Images. D.A. Forsyth
 Classification and Detection in Images D.A. Forsyth Classifying Images Motivating problems detecting explicit images classifying materials classifying scenes Strategy build appropriate image features train
Classification and Detection in Images D.A. Forsyth Classifying Images Motivating problems detecting explicit images classifying materials classifying scenes Strategy build appropriate image features train
Outline. Segmentation & Grouping. Examples of grouping in vision. Grouping in vision. Grouping in vision 2/9/2011. CS 376 Lecture 7 Segmentation 1
 Outline What are grouping problems in vision? Segmentation & Grouping Wed, Feb 9 Prof. UT-Austin Inspiration from human perception Gestalt properties Bottom-up segmentation via clustering Algorithms: Mode
Outline What are grouping problems in vision? Segmentation & Grouping Wed, Feb 9 Prof. UT-Austin Inspiration from human perception Gestalt properties Bottom-up segmentation via clustering Algorithms: Mode
CS 4495 Computer Vision. Segmentation. Aaron Bobick (slides by Tucker Hermans) School of Interactive Computing. Segmentation
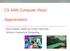 CS 4495 Computer Vision Aaron Bobick (slides by Tucker Hermans) School of Interactive Computing Administrivia PS 4: Out but I was a bit late so due date pushed back to Oct 29. OpenCV now has real SIFT
CS 4495 Computer Vision Aaron Bobick (slides by Tucker Hermans) School of Interactive Computing Administrivia PS 4: Out but I was a bit late so due date pushed back to Oct 29. OpenCV now has real SIFT
Biometrics Technology: Image Processing & Pattern Recognition (by Dr. Dickson Tong)
 Biometrics Technology: Image Processing & Pattern Recognition (by Dr. Dickson Tong) References: [1] http://homepages.inf.ed.ac.uk/rbf/hipr2/index.htm [2] http://www.cs.wisc.edu/~dyer/cs540/notes/vision.html
Biometrics Technology: Image Processing & Pattern Recognition (by Dr. Dickson Tong) References: [1] http://homepages.inf.ed.ac.uk/rbf/hipr2/index.htm [2] http://www.cs.wisc.edu/~dyer/cs540/notes/vision.html
Lecture 16 Segmentation and Scene understanding
 Lecture 16 Segmentation and Scene understanding Introduction! Mean-shift! Graph-based segmentation! Top-down segmentation! Silvio Savarese Lecture 15 -! 3-Mar-14 Segmentation Silvio Savarese Lecture 15
Lecture 16 Segmentation and Scene understanding Introduction! Mean-shift! Graph-based segmentation! Top-down segmentation! Silvio Savarese Lecture 15 -! 3-Mar-14 Segmentation Silvio Savarese Lecture 15
Image Segmentation. Selim Aksoy. Bilkent University
 Image Segmentation Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr Examples of grouping in vision [http://poseidon.csd.auth.gr/lab_research/latest/imgs/s peakdepvidindex_img2.jpg]
Image Segmentation Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr Examples of grouping in vision [http://poseidon.csd.auth.gr/lab_research/latest/imgs/s peakdepvidindex_img2.jpg]
CS 543: Final Project Report Texture Classification using 2-D Noncausal HMMs
 CS 543: Final Project Report Texture Classification using 2-D Noncausal HMMs Felix Wang fywang2 John Wieting wieting2 Introduction We implement a texture classification algorithm using 2-D Noncausal Hidden
CS 543: Final Project Report Texture Classification using 2-D Noncausal HMMs Felix Wang fywang2 John Wieting wieting2 Introduction We implement a texture classification algorithm using 2-D Noncausal Hidden
Machine Learning for Signal Processing Clustering. Bhiksha Raj Class Oct 2016
 Machine Learning for Signal Processing Clustering Bhiksha Raj Class 11. 13 Oct 2016 1 Statistical Modelling and Latent Structure Much of statistical modelling attempts to identify latent structure in the
Machine Learning for Signal Processing Clustering Bhiksha Raj Class 11. 13 Oct 2016 1 Statistical Modelling and Latent Structure Much of statistical modelling attempts to identify latent structure in the
Image Segmentation. Selim Aksoy. Bilkent University
 Image Segmentation Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr Examples of grouping in vision [http://poseidon.csd.auth.gr/lab_research/latest/imgs/s peakdepvidindex_img2.jpg]
Image Segmentation Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr Examples of grouping in vision [http://poseidon.csd.auth.gr/lab_research/latest/imgs/s peakdepvidindex_img2.jpg]
Big-data Clustering: K-means vs K-indicators
 Big-data Clustering: K-means vs K-indicators Yin Zhang Dept. of Computational & Applied Math. Rice University, Houston, Texas, U.S.A. Joint work with Feiyu Chen & Taiping Zhang (CQU), Liwei Xu (UESTC)
Big-data Clustering: K-means vs K-indicators Yin Zhang Dept. of Computational & Applied Math. Rice University, Houston, Texas, U.S.A. Joint work with Feiyu Chen & Taiping Zhang (CQU), Liwei Xu (UESTC)
Digital Geometry Processing
 Digital Geometry Processing Spring 2011 physical model acquired point cloud reconstructed model 2 Digital Michelangelo Project Range Scanning Systems Passive: Stereo Matching Find and match features in
Digital Geometry Processing Spring 2011 physical model acquired point cloud reconstructed model 2 Digital Michelangelo Project Range Scanning Systems Passive: Stereo Matching Find and match features in
Supplementary Material: The Emergence of. Organizing Structure in Conceptual Representation
 Supplementary Material: The Emergence of Organizing Structure in Conceptual Representation Brenden M. Lake, 1,2 Neil D. Lawrence, 3 Joshua B. Tenenbaum, 4,5 1 Center for Data Science, New York University
Supplementary Material: The Emergence of Organizing Structure in Conceptual Representation Brenden M. Lake, 1,2 Neil D. Lawrence, 3 Joshua B. Tenenbaum, 4,5 1 Center for Data Science, New York University
Motion and Tracking. Andrea Torsello DAIS Università Ca Foscari via Torino 155, Mestre (VE)
 Motion and Tracking Andrea Torsello DAIS Università Ca Foscari via Torino 155, 30172 Mestre (VE) Motion Segmentation Segment the video into multiple coherently moving objects Motion and Perceptual Organization
Motion and Tracking Andrea Torsello DAIS Università Ca Foscari via Torino 155, 30172 Mestre (VE) Motion Segmentation Segment the video into multiple coherently moving objects Motion and Perceptual Organization
Clustering: Classic Methods and Modern Views
 Clustering: Classic Methods and Modern Views Marina Meilă University of Washington mmp@stat.washington.edu June 22, 2015 Lorentz Center Workshop on Clusters, Games and Axioms Outline Paradigms for clustering
Clustering: Classic Methods and Modern Views Marina Meilă University of Washington mmp@stat.washington.edu June 22, 2015 Lorentz Center Workshop on Clusters, Games and Axioms Outline Paradigms for clustering
Network Traffic Measurements and Analysis
 DEIB - Politecnico di Milano Fall, 2017 Introduction Often, we have only a set of features x = x 1, x 2,, x n, but no associated response y. Therefore we are not interested in prediction nor classification,
DEIB - Politecnico di Milano Fall, 2017 Introduction Often, we have only a set of features x = x 1, x 2,, x n, but no associated response y. Therefore we are not interested in prediction nor classification,
A FRAMEWORK FOR ANALYZING TEXTURE DESCRIPTORS
 A FRAMEWORK FOR ANALYZING TEXTURE DESCRIPTORS Timo Ahonen and Matti Pietikäinen Machine Vision Group, University of Oulu, PL 4500, FI-90014 Oulun yliopisto, Finland tahonen@ee.oulu.fi, mkp@ee.oulu.fi Keywords:
A FRAMEWORK FOR ANALYZING TEXTURE DESCRIPTORS Timo Ahonen and Matti Pietikäinen Machine Vision Group, University of Oulu, PL 4500, FI-90014 Oulun yliopisto, Finland tahonen@ee.oulu.fi, mkp@ee.oulu.fi Keywords:
Clustering Part 4 DBSCAN
 Clustering Part 4 Dr. Sanjay Ranka Professor Computer and Information Science and Engineering University of Florida, Gainesville DBSCAN DBSCAN is a density based clustering algorithm Density = number of
Clustering Part 4 Dr. Sanjay Ranka Professor Computer and Information Science and Engineering University of Florida, Gainesville DBSCAN DBSCAN is a density based clustering algorithm Density = number of
Image Segmentation continued Graph Based Methods. Some slides: courtesy of O. Capms, Penn State, J.Ponce and D. Fortsyth, Computer Vision Book
 Image Segmentation continued Graph Based Methods Some slides: courtesy of O. Capms, Penn State, J.Ponce and D. Fortsyth, Computer Vision Book Previously Binary segmentation Segmentation by thresholding
Image Segmentation continued Graph Based Methods Some slides: courtesy of O. Capms, Penn State, J.Ponce and D. Fortsyth, Computer Vision Book Previously Binary segmentation Segmentation by thresholding
Analysis: TextonBoost and Semantic Texton Forests. Daniel Munoz Februrary 9, 2009
 Analysis: TextonBoost and Semantic Texton Forests Daniel Munoz 16-721 Februrary 9, 2009 Papers [shotton-eccv-06] J. Shotton, J. Winn, C. Rother, A. Criminisi, TextonBoost: Joint Appearance, Shape and Context
Analysis: TextonBoost and Semantic Texton Forests Daniel Munoz 16-721 Februrary 9, 2009 Papers [shotton-eccv-06] J. Shotton, J. Winn, C. Rother, A. Criminisi, TextonBoost: Joint Appearance, Shape and Context
Segmentation and Grouping
 Segmentation and Grouping How and what do we see? Fundamental Problems ' Focus of attention, or grouping ' What subsets of pixels do we consider as possible objects? ' All connected subsets? ' Representation
Segmentation and Grouping How and what do we see? Fundamental Problems ' Focus of attention, or grouping ' What subsets of pixels do we consider as possible objects? ' All connected subsets? ' Representation
Mesh Segmentation Using Laplacian Eigenvectors and Gaussian Mixtures
 Manifold Learning and its Applications: Papers from the AAAI Fall Symposium (FS-09-04) Mesh Segmentation Using Laplacian Eigenvectors and Gaussian Mixtures Avinash Sharma, Radu Horaud, David Knossow and
Manifold Learning and its Applications: Papers from the AAAI Fall Symposium (FS-09-04) Mesh Segmentation Using Laplacian Eigenvectors and Gaussian Mixtures Avinash Sharma, Radu Horaud, David Knossow and
EE795: Computer Vision and Intelligent Systems
 EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 WRI C225 Lecture 04 130131 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Histogram Equalization Image Filtering Linear
EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 WRI C225 Lecture 04 130131 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Histogram Equalization Image Filtering Linear
CPSC 340: Machine Learning and Data Mining. Principal Component Analysis Fall 2017
 CPSC 340: Machine Learning and Data Mining Principal Component Analysis Fall 2017 Assignment 3: 2 late days to hand in tonight. Admin Assignment 4: Due Friday of next week. Last Time: MAP Estimation MAP
CPSC 340: Machine Learning and Data Mining Principal Component Analysis Fall 2017 Assignment 3: 2 late days to hand in tonight. Admin Assignment 4: Due Friday of next week. Last Time: MAP Estimation MAP
Generalized Principal Component Analysis CVPR 2007
 Generalized Principal Component Analysis Tutorial @ CVPR 2007 Yi Ma ECE Department University of Illinois Urbana Champaign René Vidal Center for Imaging Science Institute for Computational Medicine Johns
Generalized Principal Component Analysis Tutorial @ CVPR 2007 Yi Ma ECE Department University of Illinois Urbana Champaign René Vidal Center for Imaging Science Institute for Computational Medicine Johns
Based on Raymond J. Mooney s slides
 Instance Based Learning Based on Raymond J. Mooney s slides University of Texas at Austin 1 Example 2 Instance-Based Learning Unlike other learning algorithms, does not involve construction of an explicit
Instance Based Learning Based on Raymond J. Mooney s slides University of Texas at Austin 1 Example 2 Instance-Based Learning Unlike other learning algorithms, does not involve construction of an explicit
Bumptrees for Efficient Function, Constraint, and Classification Learning
 umptrees for Efficient Function, Constraint, and Classification Learning Stephen M. Omohundro International Computer Science Institute 1947 Center Street, Suite 600 erkeley, California 94704 Abstract A
umptrees for Efficient Function, Constraint, and Classification Learning Stephen M. Omohundro International Computer Science Institute 1947 Center Street, Suite 600 erkeley, California 94704 Abstract A
