Intro to Linear Programming. The problem that we desire to address in this course is loosely stated below.
|
|
|
- Chastity Manning
- 5 years ago
- Views:
Transcription
1 . Introduction Intro to Linear Programming The problem that we desire to address in this course is loosely stated below. Given a number of generators make price-quantity offers to sell (each provides their individual supply function) a number of loads make price-quantity bids to buy (each provides their individual demand function) there is an electric network that imposes physical restrictions, including: o sum of generation=sum of demand o flows on circuits<maimum flow for circuit we want to maimize the social surplus U(P)-C(P) where U(P) is the composite utility function for consumers, C(P) is the composite cost function for suppliers, and P is the real power injection vector of the network nodes (positive for generation, negative for load). It is sometimes convenient to recognize a couple of things about the form of optimization problems.
2 . Maimization of a function is equivalent to minimization of the negated function, that is ma f() is the same as min (-f()). An inequality constraint may be equivalently written as g()>b or -g()<b And so we can say that in general, we want to solve a problem like this: min f ( ) s.t. h( ) c g( ) b () We have already seen how to do this when f(), h(), and g() are nonlinear but conve (form Lagrangian, take KKT conditions, solve for variables). We now want to consider what happens when f, h, and g are all linear functions in. When this is the case, the optimization problem of (), generally called a mathematical program, becomes a special type of mathematical program called a linear program. We will motivate our interest with an eample.
3 . Eample 4 6 ) ( ma s.t. f Let s apply our standard procedure to this problem. Form Lagrangian (ignoring inequality constraint): 6) ( ), ( F Apply first-order conditions: 6 F F F The first two equations result in a contradiction, and the three equations taken together do not provide a solution for and. Our procedure failed. What happened? Let s see if we can graphically inspect the situation. Fig. illustrates the contours of increasing objective function together with the equality constraint.
4 Fig. : Sample problem In considering Fig., we see that we can push f as far negative as we please (causing the contours to move down and to the left), minimizing it more and more, and there will always be an intersection point with the equality constraint. This shows that there is no solution to our problem. We might say that the solution is unbounded. This can happen with linear programs. However, recall that we are considering only the equality constraint, i.e., the problem we considered for which there is no solution is: 4
5 5 6 ) ( ma s.t. f But let s consider our original, full problem, with the inequality constraint as well, repeated here for convenience. 4 6 ) ( ma s.t. f Form Lagrangian (this time with inequality constraint): 4) ( 6) ( ), ( F Observe, in contrast to our previous work where we had an inequality constraint epressed as g()> b and we subtracted the term corresponding to the inequality, now we have an inequality constraint epressed as g()<b and we add the term corresponding to it. The KKT conditions then become: 4 6 F F F F 4) (
6 6 The left-hand set of equations is a set of linear equations we can solve as: 4 6 having solution 6 We plot it in Figure. Fig. : With inequality constraint
7 The feasible region associated with the inequality constraint is below the dotted line. The feasible region for the problem is below the dotted line and on the thick one (the equality constraint). So we see that the feasible region for the problem includes everything on the thick line to the right of the intersection point. Now, recall that we are maimizing the objective. Therefore we want to choose a solution that has the largest possible value of f but is in the feasible region. This means, in terms of Fig., we want to choose the contour that is highest (most upwards to the right) but feasible. The location of the solution to the problem is immediate: =6, =. The contour which passes through this point is not obvious from Fig., but it is between f= and f=, probably about f=8. We can get it eactly by evaluating f at the solution: f ( ) (6) 8 which agrees eactly with our estimate. We will call any constraint comprising the feasible region boundary an active constraint. 7
8 One important observation for this problem: the solution occurred at a point where two active constraints intersect. Let s do another eample. This time, we will work on a maimization problem.. Eample [] Resource allocation is a kind of problem where one desires to optimize some objective subject to constraints on a set of resources. It is a very common kind of problem in many different industries, including the electric power industry. Consider a manufacturer of materials X and Y. Each materials produced requires a certain amount of time from three different people, and each person can allocate their time to producing item X or item Y or some combination of the two. A unit of material requires contributions from all three people, i.e., no individual can make either material on their own. The following table time contributions for each person to make each type of material. Person Material X 4 min 4 min min Y min min 4 min 8
9 Each person works a standard 8 hour day, and so has a maimum amount of time per day of 8 6=48 minutes. The profit per unit of item X and Y is $5 and $8, respectively. We desire to maimize daily profits. Let and y denote the number of each item produced in a day. The problem will be, then, as follows: ma f (, y) 5 8y Subject to y 48 (person ) y 48 (person ) 4y 48 (person ) 4 4 y The first three constraints are due to the limit on the resource (time) for each person. The 4 th and 5 th constraints are due to the fact that we cannot produce a negative number of items. There are many possible solutions to this problem. Consider, for eample, if we limit ourselves to producing only item X or item Y, but not both. 9
10 Produce only item X. In this case, y= and the constraints become: 4 48 (person ) 4 48 (person ) 48 4 (person ) To maimize the objective function, we want to produce the maimum amount of items we can. And so the solution is clearly = (and y=). The objective then, becomes 5()=$6. Produce only item Y. In this case, = and the constraints become: y 48 y 6 (person ) y 48 y 5 (person ) 4y 48 y (person ) Again, to maimize the objective function, we want to produce the maimum amount of items we can. And so the solution is clearly y=5 (and =). The objective then, becomes 8(5)=$. Conclusion: Producing only Y is better than producing only X, and if we have only these two options, we will produce only Y.
11 However, is it possible that we might make an even higher profit by producing some of each? Fig. plots the inequality constraints. We can identify the feasible region. Fig. : Constraints for Eample It is now interesting to plot the contours of increasing objective function, that is, we will plot the function for increasing values of f. f (, y) 5 8y
12 f 5 8y y f 5 8 We have plotted the contours for values of f=,,, 7. Fig. 4: Constraints with contours for Eample From Fig. 4, we observe that the f= contour appears to be the contour of maimum f which contains a point in the feasible region. One should observe from Fig. 4 that the optimal point must occur at either the point (,5) or the point of
13 intersection between the two active constraints, which is (.74,.74). Because the slope of our contours are less than the slope of the constraint boundary 4+y=48, if a contour crosses the 4+y=48 constraint boundary within the feasible region, then there will necessarily be another point to the left of the crossing which will be interior (feasible, but not on a boundary) to the feasible region. This means it will be possible to move to a contour of higher f which still has at least one point in the feasible region. By this argument, then, if a contour passes through the intersection point (.74,.74), then it is possible to move to a contour of higher f which still has one point in the feasible region. Because the optimal point must occur at either (, 5) or (.74,.74), we know now that it must occur at (, 5). Again, we notice: the solution occurred at a point where two active constraints intersect. 4. Eample
14 Let s try a slightly different problem, as follows: ma f (, y) 9 8y Subject to y 48 (person ) y 48 (person ) 4y 48 (person ) 4 4 y Figure 6 shows the feasible region together with contours of increasing f. 4
15 Fig. 6: Constraints with contours for Eample From Fig. 6, we see that the point (.74,.74) must be the optimal point, and the maimum value of f will be about f=5 (evaluation of the above point yields f=5.4). Again, we notice: the solution occurred at a point where two active constraints intersect. 5. Eample 4 Let s again change our problem slightly, as follows: 5
16 ma f (, y) 5 8y Subject to y 48 (person ) y 48 (person ) 4y 48 (person ) 4 4 y Figure 7 shows the feasible region together with contours of increasing f. Fig. 7: Constraints with contours for Eample 6
17 From Fig. 7, we see that the point (, ) must be the optimal point, and the maimum value of f will be f=8. Again, as in all previous cases, we notice: the solution occurred at a point where two active constraints intersect. This last observation is no coincidence. It always happens in a LP. That is: The solution to an LP is always at a point where active constraints intersect. We will call such intersection points corner points. Therefore we see that our solution will always be at a corner point. This provides us with a basis for solution to LPs: Search the corner points! [] W. Claycombe and W. Sullivan, Foundations of Mathematical Programming, Reston Publishing Company, Reston Virginia. 7
4 Linear Programming (LP) E. Amaldi -- Foundations of Operations Research -- Politecnico di Milano 1
 4 Linear Programming (LP) E. Amaldi -- Foundations of Operations Research -- Politecnico di Milano 1 Definition: A Linear Programming (LP) problem is an optimization problem: where min f () s.t. X n the
4 Linear Programming (LP) E. Amaldi -- Foundations of Operations Research -- Politecnico di Milano 1 Definition: A Linear Programming (LP) problem is an optimization problem: where min f () s.t. X n the
Linear Mathematical Programming (LP)
 Linear Mathematical Programming (LP) A MP is LP if : The objective function is linear where The set is defined by linear equality or inequality constraints c f T ) = ( ],..., [ n T c c c = = n b A where
Linear Mathematical Programming (LP) A MP is LP if : The objective function is linear where The set is defined by linear equality or inequality constraints c f T ) = ( ],..., [ n T c c c = = n b A where
Chapter 4 Section 1 Graphing Linear Inequalities in Two Variables
 Chapter 4 Section 1 Graphing Linear Inequalities in Two Variables Epressions of the tpe + 2 8 and 3 > 6 are called linear inequalities in two variables. A solution of a linear inequalit in two variables
Chapter 4 Section 1 Graphing Linear Inequalities in Two Variables Epressions of the tpe + 2 8 and 3 > 6 are called linear inequalities in two variables. A solution of a linear inequalit in two variables
Graphical Analysis. Figure 1. Copyright c 1997 by Awi Federgruen. All rights reserved.
 Graphical Analysis For problems with 2 variables, we can represent each solution as a point in the plane. The Shelby Shelving model (see the readings book or pp.68-69 of the text) is repeated below for
Graphical Analysis For problems with 2 variables, we can represent each solution as a point in the plane. The Shelby Shelving model (see the readings book or pp.68-69 of the text) is repeated below for
LINEAR PROGRAMMING. Chapter Overview
 Chapter 12 LINEAR PROGRAMMING 12.1 Overview 12.1.1 An Optimisation Problem A problem which seeks to maximise or minimise a function is called an optimisation problem. An optimisation problem may involve
Chapter 12 LINEAR PROGRAMMING 12.1 Overview 12.1.1 An Optimisation Problem A problem which seeks to maximise or minimise a function is called an optimisation problem. An optimisation problem may involve
February 10, 2005
 15.053 February 10, 2005 The Geometry of Linear Programs the geometry of LPs illustrated on DTC Announcement: please turn in homework solutions now with a cover sheet 1 Goal of this Lecture 3 mathematical
15.053 February 10, 2005 The Geometry of Linear Programs the geometry of LPs illustrated on DTC Announcement: please turn in homework solutions now with a cover sheet 1 Goal of this Lecture 3 mathematical
1.1 What is Microeconomics?
 1.1 What is Microeconomics? Economics is the study of allocating limited resources to satisfy unlimited wants. Such a tension implies tradeoffs among competing goals. The analysis can be carried out at
1.1 What is Microeconomics? Economics is the study of allocating limited resources to satisfy unlimited wants. Such a tension implies tradeoffs among competing goals. The analysis can be carried out at
Using Linear Programming for Management Decisions
 Using Linear Programming for Management Decisions By Tim Wright Linear programming creates mathematical models from real-world business problems to maximize profits, reduce costs and allocate resources.
Using Linear Programming for Management Decisions By Tim Wright Linear programming creates mathematical models from real-world business problems to maximize profits, reduce costs and allocate resources.
Simplex Method. Introduction:
 Introduction: Simple Method In the previous chapter, we discussed about the graphical method for solving linear programming problems. Although the graphical method is an invaluable aid to understand the
Introduction: Simple Method In the previous chapter, we discussed about the graphical method for solving linear programming problems. Although the graphical method is an invaluable aid to understand the
In other words, we want to find the domain points that yield the maximum or minimum values (extrema) of the function.
 1 The Lagrange multipliers is a mathematical method for performing constrained optimization of differentiable functions. Recall unconstrained optimization of differentiable functions, in which we want
1 The Lagrange multipliers is a mathematical method for performing constrained optimization of differentiable functions. Recall unconstrained optimization of differentiable functions, in which we want
Linear Programming has been used to:
 Linear Programming Linear programming became important during World War II: used to solve logistics problems for the military. Linear Programming (LP) was the first widely used form of optimization in
Linear Programming Linear programming became important during World War II: used to solve logistics problems for the military. Linear Programming (LP) was the first widely used form of optimization in
OPERATIONS RESEARCH. Linear Programming Problem
 OPERATIONS RESEARCH Chapter 1 Linear Programming Problem Prof. Bibhas C. Giri Department of Mathematics Jadavpur University Kolkata, India Email: bcgiri.jumath@gmail.com 1.0 Introduction Linear programming
OPERATIONS RESEARCH Chapter 1 Linear Programming Problem Prof. Bibhas C. Giri Department of Mathematics Jadavpur University Kolkata, India Email: bcgiri.jumath@gmail.com 1.0 Introduction Linear programming
Linear Programming. L.W. Dasanayake Department of Economics University of Kelaniya
 Linear Programming L.W. Dasanayake Department of Economics University of Kelaniya Linear programming (LP) LP is one of Management Science techniques that can be used to solve resource allocation problem
Linear Programming L.W. Dasanayake Department of Economics University of Kelaniya Linear programming (LP) LP is one of Management Science techniques that can be used to solve resource allocation problem
Module 4 Lecture Notes 1. Use of software for solving linear programming problems
 Optimization Methods: Linear Programming Applications Software Module 4 Lecture Notes Use of software for solving linear programming problems Introduction In this class, use of software to solve linear
Optimization Methods: Linear Programming Applications Software Module 4 Lecture Notes Use of software for solving linear programming problems Introduction In this class, use of software to solve linear
Solutions to assignment 3
 Math 9 Solutions to assignment Due: : Noon on Thursday, October, 5.. Find the minimum of the function f, y, z) + y + z subject to the condition + y + z 4. Solution. Let s define g, y, z) + y + z, so the
Math 9 Solutions to assignment Due: : Noon on Thursday, October, 5.. Find the minimum of the function f, y, z) + y + z subject to the condition + y + z 4. Solution. Let s define g, y, z) + y + z, so the
Linear Programming Applications. Software for Linear Programming
 Linear Programming Applications Software for Linear Programming Objectives Use of software to solve LP problems MMO Software with eample Graphical Method Simple Method Simple method using optimization
Linear Programming Applications Software for Linear Programming Objectives Use of software to solve LP problems MMO Software with eample Graphical Method Simple Method Simple method using optimization
Chapter 3: Section 3-2 Graphing Linear Inequalities
 Chapter : Section - Graphing Linear Inequalities D. S. Malik Creighton Universit, Omaha, NE D. S. Malik Creighton Universit, Omaha, NE Chapter () : Section - Graphing Linear Inequalities / 9 Geometric
Chapter : Section - Graphing Linear Inequalities D. S. Malik Creighton Universit, Omaha, NE D. S. Malik Creighton Universit, Omaha, NE Chapter () : Section - Graphing Linear Inequalities / 9 Geometric
Chapter 15 Introduction to Linear Programming
 Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Lesson 08 Linear Programming
 Lesson 08 Linear Programming A mathematical approach to determine optimal (maximum or minimum) solutions to problems which involve restrictions on the variables involved. 08 - Linear Programming Applications
Lesson 08 Linear Programming A mathematical approach to determine optimal (maximum or minimum) solutions to problems which involve restrictions on the variables involved. 08 - Linear Programming Applications
Introduction to Linear Programming. Algorithmic and Geometric Foundations of Optimization
 Introduction to Linear Programming Algorithmic and Geometric Foundations of Optimization Optimization and Linear Programming Mathematical programming is a class of methods for solving problems which ask
Introduction to Linear Programming Algorithmic and Geometric Foundations of Optimization Optimization and Linear Programming Mathematical programming is a class of methods for solving problems which ask
Section 4.1 Max and Min Values
 Page 1 of 5 Section 4.1 Ma and Min Values Horizontal Tangents: We have looked at graphs and identified horizontal tangents, or places where the slope of the tangent line is zero. Q: For which values does
Page 1 of 5 Section 4.1 Ma and Min Values Horizontal Tangents: We have looked at graphs and identified horizontal tangents, or places where the slope of the tangent line is zero. Q: For which values does
MA30SA Applied Math Unit D - Linear Programming Revd:
 1 Introduction to Linear Programming MA30SA Applied Math Unit D - Linear Programming Revd: 120051212 1. Linear programming is a very important skill. It is a brilliant method for establishing optimum solutions
1 Introduction to Linear Programming MA30SA Applied Math Unit D - Linear Programming Revd: 120051212 1. Linear programming is a very important skill. It is a brilliant method for establishing optimum solutions
Linear Programming: Introduction
 CSC 373 - Algorithm Design, Analysis, and Complexity Summer 2016 Lalla Mouatadid Linear Programming: Introduction A bit of a historical background about linear programming, that I stole from Jeff Erickson
CSC 373 - Algorithm Design, Analysis, and Complexity Summer 2016 Lalla Mouatadid Linear Programming: Introduction A bit of a historical background about linear programming, that I stole from Jeff Erickson
Chapter 7. Linear Programming Models: Graphical and Computer Methods
 Chapter 7 Linear Programming Models: Graphical and Computer Methods To accompany Quantitative Analysis for Management, Eleventh Edition, by Render, Stair, and Hanna Power Point slides created by Brian
Chapter 7 Linear Programming Models: Graphical and Computer Methods To accompany Quantitative Analysis for Management, Eleventh Edition, by Render, Stair, and Hanna Power Point slides created by Brian
BCN Decision and Risk Analysis. Syed M. Ahmed, Ph.D.
 Linear Programming Module Outline Introduction The Linear Programming Model Examples of Linear Programming Problems Developing Linear Programming Models Graphical Solution to LP Problems The Simplex Method
Linear Programming Module Outline Introduction The Linear Programming Model Examples of Linear Programming Problems Developing Linear Programming Models Graphical Solution to LP Problems The Simplex Method
Econ 172A - Slides from Lecture 2
 Econ 205 Sobel Econ 172A - Slides from Lecture 2 Joel Sobel September 28, 2010 Announcements 1. Sections this evening (Peterson 110, 8-9 or 9-10). 2. Podcasts available when I remember to use microphone.
Econ 205 Sobel Econ 172A - Slides from Lecture 2 Joel Sobel September 28, 2010 Announcements 1. Sections this evening (Peterson 110, 8-9 or 9-10). 2. Podcasts available when I remember to use microphone.
Controlling Air Pollution. A quick review. Reclaiming Solid Wastes. Chapter 4 The Simplex Method. Solving the Bake Sale problem. How to move?
 ESE Operations Research 9// Controlling Air Pollution Technology can be use fully () or fractional thereof A quick review ESE Operations Research Reclaiming Solid Wastes Chapter The Simple Method ESE Operations
ESE Operations Research 9// Controlling Air Pollution Technology can be use fully () or fractional thereof A quick review ESE Operations Research Reclaiming Solid Wastes Chapter The Simple Method ESE Operations
What is the reasonable domain of this volume function? (c) Can there exist a volume of 0? (d) Estimate a maximum volume for the open box.
 MA 15800 Lesson 11 Summer 016 E 1: From a rectangular piece of cardboard having dimensions 0 inches by 0 inches, an open bo is to be made by cutting out identical squares of area from each corner and,
MA 15800 Lesson 11 Summer 016 E 1: From a rectangular piece of cardboard having dimensions 0 inches by 0 inches, an open bo is to be made by cutting out identical squares of area from each corner and,
2.1. Definition: If a < b, then f(a) < f(b) for every a and b in that interval. If a < b, then f(a) > f(b) for every a and b in that interval.
 1.1 Concepts: 1. f() is INCREASING on an interval: Definition: If a < b, then f(a) < f(b) for every a and b in that interval. A positive slope for the secant line. A positive slope for the tangent line.
1.1 Concepts: 1. f() is INCREASING on an interval: Definition: If a < b, then f(a) < f(b) for every a and b in that interval. A positive slope for the secant line. A positive slope for the tangent line.
MATLAB Simulink Modeling and Simulation of Recurrent Neural Network for Solving Linear Programming Problems
 International Conference on Mathematical Computer Engineering - ICMCE - 8 MALAB Simulink Modeling and Simulation of Recurrent Neural Network for Solving Linear Programming Problems Raja Das a a School
International Conference on Mathematical Computer Engineering - ICMCE - 8 MALAB Simulink Modeling and Simulation of Recurrent Neural Network for Solving Linear Programming Problems Raja Das a a School
Linear Programming Problems
 Linear Programming Problems Two common formulations of linear programming (LP) problems are: min Subject to: 1,,, 1,2,,;, max Subject to: 1,,, 1,2,,;, Linear Programming Problems The standard LP problem
Linear Programming Problems Two common formulations of linear programming (LP) problems are: min Subject to: 1,,, 1,2,,;, max Subject to: 1,,, 1,2,,;, Linear Programming Problems The standard LP problem
Precalculus Notes Unit 1 Day 1
 Precalculus Notes Unit Day Rules For Domain: When the domain is not specified, it consists of (all real numbers) for which the corresponding values in the range are also real numbers.. If is in the numerator
Precalculus Notes Unit Day Rules For Domain: When the domain is not specified, it consists of (all real numbers) for which the corresponding values in the range are also real numbers.. If is in the numerator
5-8. Systems of Linear Inequalities. Vocabulary. Lesson. Mental Math
 Lesson 5-8 Systems of Linear Inequalities Vocabulary feasible set, feasible region BIG IDEA The solution to a system of linear inequalities in two variables is either the empty set, the interior of a polygon,
Lesson 5-8 Systems of Linear Inequalities Vocabulary feasible set, feasible region BIG IDEA The solution to a system of linear inequalities in two variables is either the empty set, the interior of a polygon,
Section 18-1: Graphical Representation of Linear Equations and Functions
 Section 18-1: Graphical Representation of Linear Equations and Functions Prepare a table of solutions and locate the solutions on a coordinate system: f(x) = 2x 5 Learning Outcome 2 Write x + 3 = 5 as
Section 18-1: Graphical Representation of Linear Equations and Functions Prepare a table of solutions and locate the solutions on a coordinate system: f(x) = 2x 5 Learning Outcome 2 Write x + 3 = 5 as
Introduction. Linear because it requires linear functions. Programming as synonymous of planning.
 LINEAR PROGRAMMING Introduction Development of linear programming was among the most important scientific advances of mid-20th cent. Most common type of applications: allocate limited resources to competing
LINEAR PROGRAMMING Introduction Development of linear programming was among the most important scientific advances of mid-20th cent. Most common type of applications: allocate limited resources to competing
+ Solving Linear Inequalities. Mr. Smith IM3
 + Solving Linear Inequalities Mr. Smith IM3 + Inequality Symbols < > Less than Greater than Less than or equal to Greater than or equal to Not equal to + Linear Inequality n Inequality with one variable
+ Solving Linear Inequalities Mr. Smith IM3 + Inequality Symbols < > Less than Greater than Less than or equal to Greater than or equal to Not equal to + Linear Inequality n Inequality with one variable
CME307/MS&E311 Theory Summary
 CME307/MS&E311 Theory Summary Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/~yyye http://www.stanford.edu/class/msande311/
CME307/MS&E311 Theory Summary Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/~yyye http://www.stanford.edu/class/msande311/
3.6-Rational Functions & Their Graphs
 .6-Rational Functions & Their Graphs What is a Rational Function? A rational function is a function that is the ratio of two polynomial functions. This definition is similar to a rational number which
.6-Rational Functions & Their Graphs What is a Rational Function? A rational function is a function that is the ratio of two polynomial functions. This definition is similar to a rational number which
Appendix F: Systems of Inequalities
 A0 Appendi F Sstems of Inequalities Appendi F: Sstems of Inequalities F. Solving Sstems of Inequalities The Graph of an Inequalit The statements < and are inequalities in two variables. An ordered pair
A0 Appendi F Sstems of Inequalities Appendi F: Sstems of Inequalities F. Solving Sstems of Inequalities The Graph of an Inequalit The statements < and are inequalities in two variables. An ordered pair
Fundamentals of Operations Research. Prof. G. Srinivasan. Department of Management Studies. Indian Institute of Technology, Madras. Lecture No.
 Fundamentals of Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture No. # 13 Transportation Problem, Methods for Initial Basic Feasible
Fundamentals of Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture No. # 13 Transportation Problem, Methods for Initial Basic Feasible
Unconstrained and Constrained Optimization
 Unconstrained and Constrained Optimization Agenda General Ideas of Optimization Interpreting the First Derivative Interpreting the Second Derivative Unconstrained Optimization Constrained Optimization
Unconstrained and Constrained Optimization Agenda General Ideas of Optimization Interpreting the First Derivative Interpreting the Second Derivative Unconstrained Optimization Constrained Optimization
These notes are in two parts: this part has topics 1-3 above.
 IEEM 0: Linear Programming and Its Applications Outline of this series of lectures:. How can we model a problem so that it can be solved to give the required solution 2. Motivation: eamples of typical
IEEM 0: Linear Programming and Its Applications Outline of this series of lectures:. How can we model a problem so that it can be solved to give the required solution 2. Motivation: eamples of typical
Chapter II. Linear Programming
 1 Chapter II Linear Programming 1. Introduction 2. Simplex Method 3. Duality Theory 4. Optimality Conditions 5. Applications (QP & SLP) 6. Sensitivity Analysis 7. Interior Point Methods 1 INTRODUCTION
1 Chapter II Linear Programming 1. Introduction 2. Simplex Method 3. Duality Theory 4. Optimality Conditions 5. Applications (QP & SLP) 6. Sensitivity Analysis 7. Interior Point Methods 1 INTRODUCTION
II. Linear Programming
 II. Linear Programming A Quick Example Suppose we own and manage a small manufacturing facility that produced television sets. - What would be our organization s immediate goal? - On what would our relative
II. Linear Programming A Quick Example Suppose we own and manage a small manufacturing facility that produced television sets. - What would be our organization s immediate goal? - On what would our relative
Chapter 2 An Introduction to Linear Programming
 Chapter 2 An Introduction to Linear Programming MULTIPLE CHOICE 1. The maximization or minimization of a quantity is the a. goal of management science. b. decision for decision analysis. c. constraint
Chapter 2 An Introduction to Linear Programming MULTIPLE CHOICE 1. The maximization or minimization of a quantity is the a. goal of management science. b. decision for decision analysis. c. constraint
Chapter 4 Linear Programming
 Chapter Objectives Check off these skills when you feel that you have mastered them. From its associated chart, write the constraints of a linear programming problem as linear inequalities. List two implied
Chapter Objectives Check off these skills when you feel that you have mastered them. From its associated chart, write the constraints of a linear programming problem as linear inequalities. List two implied
6.5. SYSTEMS OF INEQUALITIES
 6.5. SYSTEMS OF INEQUALITIES What You Should Learn Sketch the graphs of inequalities in two variables. Solve systems of inequalities. Use systems of inequalities in two variables to model and solve real-life
6.5. SYSTEMS OF INEQUALITIES What You Should Learn Sketch the graphs of inequalities in two variables. Solve systems of inequalities. Use systems of inequalities in two variables to model and solve real-life
Linear programming II João Carlos Lourenço
 Decision Support Models Linear programming II João Carlos Lourenço joao.lourenco@ist.utl.pt Academic year 2012/2013 Readings: Hillier, F.S., Lieberman, G.J., 2010. Introduction to Operations Research,
Decision Support Models Linear programming II João Carlos Lourenço joao.lourenco@ist.utl.pt Academic year 2012/2013 Readings: Hillier, F.S., Lieberman, G.J., 2010. Introduction to Operations Research,
Simulation. Lecture O1 Optimization: Linear Programming. Saeed Bastani April 2016
 Simulation Lecture O Optimization: Linear Programming Saeed Bastani April 06 Outline of the course Linear Programming ( lecture) Integer Programming ( lecture) Heuristics and Metaheursitics (3 lectures)
Simulation Lecture O Optimization: Linear Programming Saeed Bastani April 06 Outline of the course Linear Programming ( lecture) Integer Programming ( lecture) Heuristics and Metaheursitics (3 lectures)
Chapter 4. Linear Programming
 Chapter 4 Linear Programming For All Practical Purposes: Effective Teaching Occasionally during the semester remind students about your office hours. Some students can perceive that they are bothering
Chapter 4 Linear Programming For All Practical Purposes: Effective Teaching Occasionally during the semester remind students about your office hours. Some students can perceive that they are bothering
2.5: GRAPHS OF EXPENSE AND REVENUE FUNCTIONS OBJECTIVES
 Section 2.5: GRAPHS OF EXPENSE AND REVENUE FUNCTIONS OBJECTIVES Write, graph and interpret the expense function. Write, graph and interpret the revenue function. Identify the points of intersection of
Section 2.5: GRAPHS OF EXPENSE AND REVENUE FUNCTIONS OBJECTIVES Write, graph and interpret the expense function. Write, graph and interpret the revenue function. Identify the points of intersection of
11 Linear Programming
 11 Linear Programming 11.1 Definition and Importance The final topic in this course is Linear Programming. We say that a problem is an instance of linear programming when it can be effectively expressed
11 Linear Programming 11.1 Definition and Importance The final topic in this course is Linear Programming. We say that a problem is an instance of linear programming when it can be effectively expressed
a) Alternative Optima, b) Infeasible(or non existing) solution, c) unbounded solution.
 Unit 1 Lesson 5. : Special cases of LPP Learning Outcomes Special cases of linear programming problems Alternative Optima Infeasible Solution Unboundedness In the previous lecture we have discussed some
Unit 1 Lesson 5. : Special cases of LPP Learning Outcomes Special cases of linear programming problems Alternative Optima Infeasible Solution Unboundedness In the previous lecture we have discussed some
Linear Programming. Formulation and Graphical Solution
 Linear Programming Formulation and Graphical Solution A Two Variable Model Simple LP with two decision variables Two dimensional model is hardly useful in the real world systems which normally encompass
Linear Programming Formulation and Graphical Solution A Two Variable Model Simple LP with two decision variables Two dimensional model is hardly useful in the real world systems which normally encompass
4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Mathematical programming (optimization) problem: min f (x) s.t. x X R n set of feasible solutions with linear objective function
4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Mathematical programming (optimization) problem: min f (x) s.t. x X R n set of feasible solutions with linear objective function
UNIT 6 MODELLING DECISION PROBLEMS (LP)
 UNIT 6 MODELLING DECISION This unit: PROBLEMS (LP) Introduces the linear programming (LP) technique to solve decision problems 1 INTRODUCTION TO LINEAR PROGRAMMING A Linear Programming model seeks to maximize
UNIT 6 MODELLING DECISION This unit: PROBLEMS (LP) Introduces the linear programming (LP) technique to solve decision problems 1 INTRODUCTION TO LINEAR PROGRAMMING A Linear Programming model seeks to maximize
Introduction to Optimization
 Introduction to Optimization Constrained Optimization Marc Toussaint U Stuttgart Constrained Optimization General constrained optimization problem: Let R n, f : R n R, g : R n R m, h : R n R l find min
Introduction to Optimization Constrained Optimization Marc Toussaint U Stuttgart Constrained Optimization General constrained optimization problem: Let R n, f : R n R, g : R n R m, h : R n R l find min
Mathematics for Business and Economics - I. Chapter7 Linear Inequality Systems and Linear Programming (Lecture11)
 Mathematics for Business and Economics - I Chapter7 Linear Inequality Systems and Linear Programming (Lecture11) A linear inequality in two variables is an inequality that can be written in the form Ax
Mathematics for Business and Economics - I Chapter7 Linear Inequality Systems and Linear Programming (Lecture11) A linear inequality in two variables is an inequality that can be written in the form Ax
Ahigh school curriculum in Algebra 2 contains both solving systems of linear equations,
 The Simplex Method for Systems of Linear Inequalities Todd O. Moyer, Towson University Abstract: This article details the application of the Simplex Method for an Algebra 2 class. Students typically learn
The Simplex Method for Systems of Linear Inequalities Todd O. Moyer, Towson University Abstract: This article details the application of the Simplex Method for an Algebra 2 class. Students typically learn
8.NS.1 8.NS.2. 8.EE.7.a 8.EE.4 8.EE.5 8.EE.6
 Standard 8.NS.1 8.NS.2 8.EE.1 8.EE.2 8.EE.3 8.EE.4 8.EE.5 8.EE.6 8.EE.7 8.EE.7.a Jackson County Core Curriculum Collaborative (JC4) 8th Grade Math Learning Targets in Student Friendly Language I can identify
Standard 8.NS.1 8.NS.2 8.EE.1 8.EE.2 8.EE.3 8.EE.4 8.EE.5 8.EE.6 8.EE.7 8.EE.7.a Jackson County Core Curriculum Collaborative (JC4) 8th Grade Math Learning Targets in Student Friendly Language I can identify
Tuesday, April 10. The Network Simplex Method for Solving the Minimum Cost Flow Problem
 . Tuesday, April The Network Simplex Method for Solving the Minimum Cost Flow Problem Quotes of the day I think that I shall never see A poem lovely as a tree. -- Joyce Kilmer Knowing trees, I understand
. Tuesday, April The Network Simplex Method for Solving the Minimum Cost Flow Problem Quotes of the day I think that I shall never see A poem lovely as a tree. -- Joyce Kilmer Knowing trees, I understand
Example 1: Given below is the graph of the quadratic function f. Use the function and its graph to find the following: Outputs
 Quadratic Functions: - functions defined by quadratic epressions (a 2 + b + c) o the degree of a quadratic function is ALWAYS 2 - the most common way to write a quadratic function (and the way we have
Quadratic Functions: - functions defined by quadratic epressions (a 2 + b + c) o the degree of a quadratic function is ALWAYS 2 - the most common way to write a quadratic function (and the way we have
CME307/MS&E311 Optimization Theory Summary
 CME307/MS&E311 Optimization Theory Summary Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/~yyye http://www.stanford.edu/class/msande311/
CME307/MS&E311 Optimization Theory Summary Yinyu Ye Department of Management Science and Engineering Stanford University Stanford, CA 94305, U.S.A. http://www.stanford.edu/~yyye http://www.stanford.edu/class/msande311/
QUADRATIC FUNCTIONS Investigating Quadratic Functions in Vertex Form
 QUADRATIC FUNCTIONS Investigating Quadratic Functions in Verte Form The two forms of a quadratic function that have been eplored previousl are: Factored form: f ( ) a( r)( s) Standard form: f ( ) a b c
QUADRATIC FUNCTIONS Investigating Quadratic Functions in Verte Form The two forms of a quadratic function that have been eplored previousl are: Factored form: f ( ) a( r)( s) Standard form: f ( ) a b c
Some Advanced Topics in Linear Programming
 Some Advanced Topics in Linear Programming Matthew J. Saltzman July 2, 995 Connections with Algebra and Geometry In this section, we will explore how some of the ideas in linear programming, duality theory,
Some Advanced Topics in Linear Programming Matthew J. Saltzman July 2, 995 Connections with Algebra and Geometry In this section, we will explore how some of the ideas in linear programming, duality theory,
Section 4.1: Maximum and Minimum Values
 Section 4.: Maimum and Minimum Values In this chapter, we shall consider further applications of the derivative. The main application we shall consider is using derivatives to sketch accurate graphs of
Section 4.: Maimum and Minimum Values In this chapter, we shall consider further applications of the derivative. The main application we shall consider is using derivatives to sketch accurate graphs of
A Short SVM (Support Vector Machine) Tutorial
 A Short SVM (Support Vector Machine) Tutorial j.p.lewis CGIT Lab / IMSC U. Southern California version 0.zz dec 004 This tutorial assumes you are familiar with linear algebra and equality-constrained optimization/lagrange
A Short SVM (Support Vector Machine) Tutorial j.p.lewis CGIT Lab / IMSC U. Southern California version 0.zz dec 004 This tutorial assumes you are familiar with linear algebra and equality-constrained optimization/lagrange
Chapter 2--An Introduction to Linear Programming
 Chapter 2--An Introduction to Linear Programming 1. The maximization or minimization of a quantity is the A. goal of management science. B. decision for decision analysis. C. constraint of operations research.
Chapter 2--An Introduction to Linear Programming 1. The maximization or minimization of a quantity is the A. goal of management science. B. decision for decision analysis. C. constraint of operations research.
Chapter 2 - An Introduction to Linear Programming
 True / False 1. Increasing the right-hand side of a nonbinding constraint will not cause a change in the optimal solution. TOPICS: Introduction 2. In a linear programming problem, the objective function
True / False 1. Increasing the right-hand side of a nonbinding constraint will not cause a change in the optimal solution. TOPICS: Introduction 2. In a linear programming problem, the objective function
Chapter 1 Linear Programming. Paragraph 4 The Simplex Algorithm
 Chapter Linear Programming Paragraph 4 The Simplex Algorithm What we did so far By combining ideas of a specialized algorithm with a geometrical view on the problem, we developed an algorithm idea: Find
Chapter Linear Programming Paragraph 4 The Simplex Algorithm What we did so far By combining ideas of a specialized algorithm with a geometrical view on the problem, we developed an algorithm idea: Find
Algebra Reviews & LP Graphic Solutions
 Algebra Reviews & LP Graphic Solutions Given Constraints to Draw Straight Lines and Identify Feasible Region Draw Straight Lines for Each Constraint: From Equ(1), Set X = 0, Y = 3, a(0, 3); Set Y = 0,
Algebra Reviews & LP Graphic Solutions Given Constraints to Draw Straight Lines and Identify Feasible Region Draw Straight Lines for Each Constraint: From Equ(1), Set X = 0, Y = 3, a(0, 3); Set Y = 0,
UNIT 2 LINEAR PROGRAMMING PROBLEMS
 UNIT 2 LINEAR PROGRAMMING PROBLEMS Structure 2.1 Introduction Objectives 2.2 Linear Programming Problem (LPP) 2.3 Mathematical Formulation of LPP 2.4 Graphical Solution of Linear Programming Problems 2.5
UNIT 2 LINEAR PROGRAMMING PROBLEMS Structure 2.1 Introduction Objectives 2.2 Linear Programming Problem (LPP) 2.3 Mathematical Formulation of LPP 2.4 Graphical Solution of Linear Programming Problems 2.5
Design and Analysis of Algorithms (V)
 Design and Analysis of Algorithms (V) An Introduction to Linear Programming Guoqiang Li School of Software, Shanghai Jiao Tong University Homework Assignment 2 is announced! (deadline Apr. 10) Linear Programming
Design and Analysis of Algorithms (V) An Introduction to Linear Programming Guoqiang Li School of Software, Shanghai Jiao Tong University Homework Assignment 2 is announced! (deadline Apr. 10) Linear Programming
The problem. Needed for contract. 10% Reduction. Resources available
 As part of May 2010 s P2 paper, a question was asked (Q6) which required candidates to prepare a graph showing the optimum production plan for the organisation in question. In his post examination guide
As part of May 2010 s P2 paper, a question was asked (Q6) which required candidates to prepare a graph showing the optimum production plan for the organisation in question. In his post examination guide
CLEMSON ALGEBRA PROJECT UNIT 4: INEQUALITIES IN TWO VARIABLES
 CLEMSON ALGEBRA PROJECT UNIT 4: INEQUALITIES IN TWO VARIABLES PROBLEM 1: GIFT GIVING Gift-giving season is approaching and you wish to purchase gifts for four relatives and si friends. The amount you spend
CLEMSON ALGEBRA PROJECT UNIT 4: INEQUALITIES IN TWO VARIABLES PROBLEM 1: GIFT GIVING Gift-giving season is approaching and you wish to purchase gifts for four relatives and si friends. The amount you spend
Graphing Linear Inequalities in Two Variables.
 Many applications of mathematics involve systems of inequalities rather than systems of equations. We will discuss solving (graphing) a single linear inequality in two variables and a system of linear
Many applications of mathematics involve systems of inequalities rather than systems of equations. We will discuss solving (graphing) a single linear inequality in two variables and a system of linear
Applied Lagrange Duality for Constrained Optimization
 Applied Lagrange Duality for Constrained Optimization Robert M. Freund February 10, 2004 c 2004 Massachusetts Institute of Technology. 1 1 Overview The Practical Importance of Duality Review of Convexity
Applied Lagrange Duality for Constrained Optimization Robert M. Freund February 10, 2004 c 2004 Massachusetts Institute of Technology. 1 1 Overview The Practical Importance of Duality Review of Convexity
LINEAR PROGRAMMING (LP), GRAPHICAL PRESENTATION GASPAR ASAMPANA
 LINEAR PROGRAMMING (LP), GRAPHICAL PRESENTATION GASPAR ASAMPANA INTRODUCTION Linear Programming a is combination of a linear objective function and set of linear constraints. The linear constraints express
LINEAR PROGRAMMING (LP), GRAPHICAL PRESENTATION GASPAR ASAMPANA INTRODUCTION Linear Programming a is combination of a linear objective function and set of linear constraints. The linear constraints express
x Boundary Intercepts Test (0,0) Conclusion 2x+3y=12 (0,4), (6,0) 0>12 False 2x-y=2 (0,-2), (1,0) 0<2 True
 MATH 34 (Finite Mathematics or Business Math I) Lecture Notes MATH 34 Module 3 Notes: SYSTEMS OF INEQUALITIES & LINEAR PROGRAMMING 3. GRAPHING SYSTEMS OF INEQUALITIES Simple Systems of Linear Inequalities
MATH 34 (Finite Mathematics or Business Math I) Lecture Notes MATH 34 Module 3 Notes: SYSTEMS OF INEQUALITIES & LINEAR PROGRAMMING 3. GRAPHING SYSTEMS OF INEQUALITIES Simple Systems of Linear Inequalities
Here are some guidelines for solving a linear programming problem in two variables in which an objective function is to be maximized or minimized.
 Appendi F. Linear Programming F F. Linear Programming Linear Programming: A Graphical Approach Man applications in business and economics involve a process called optimization, in which ou are asked to
Appendi F. Linear Programming F F. Linear Programming Linear Programming: A Graphical Approach Man applications in business and economics involve a process called optimization, in which ou are asked to
A9.1 Linear programming
 pplications 9. Linear programming 9. Linear programming efore ou start You should be able to: show b shading a region defined b one or more linear inequalities. Wh do this? Linear programming is an eample
pplications 9. Linear programming 9. Linear programming efore ou start You should be able to: show b shading a region defined b one or more linear inequalities. Wh do this? Linear programming is an eample
Lecture 3: Linear Classification
 Lecture 3: Linear Classification Roger Grosse 1 Introduction Last week, we saw an example of a learning task called regression. There, the goal was to predict a scalar-valued target from a set of features.
Lecture 3: Linear Classification Roger Grosse 1 Introduction Last week, we saw an example of a learning task called regression. There, the goal was to predict a scalar-valued target from a set of features.
SUGGESTED SOLUTION CA FINAL MAY 2017 EXAM
 SUGGESTED SOLUTION CA FINAL MAY 2017 EXAM ADVANCED MANAGEMENT ACCOUNTING Test Code - F M J 4 0 1 6 BRANCH - (MULTIPLE) (Date : 11.02.2017) Head Office : Shraddha, 3 rd Floor, Near Chinai College, Andheri
SUGGESTED SOLUTION CA FINAL MAY 2017 EXAM ADVANCED MANAGEMENT ACCOUNTING Test Code - F M J 4 0 1 6 BRANCH - (MULTIPLE) (Date : 11.02.2017) Head Office : Shraddha, 3 rd Floor, Near Chinai College, Andheri
Sections 4.3, 4.5 & 4.6: Graphing
 Sections 4.3, 4.5 & 4.6: Graphing In this section, we shall see how facts about f () and f () can be used to supply useful information about the graph of f(). Since there are three sections devoted to
Sections 4.3, 4.5 & 4.6: Graphing In this section, we shall see how facts about f () and f () can be used to supply useful information about the graph of f(). Since there are three sections devoted to
Linear Programming: Model Formulation and Graphical Solution
 Linear Programming: Model Formulation and Graphical Solution Chapter 2 Chapter Topics Model Formulation A Maximization Model Example Graphical Solutions of Linear Programming Models A Minimization Model
Linear Programming: Model Formulation and Graphical Solution Chapter 2 Chapter Topics Model Formulation A Maximization Model Example Graphical Solutions of Linear Programming Models A Minimization Model
Matrix Representations
 CONDENSED LESSON 6. Matri Representations In this lesson, ou Represent closed sstems with transition diagrams and transition matrices Use matrices to organize information Sandra works at a da-care center.
CONDENSED LESSON 6. Matri Representations In this lesson, ou Represent closed sstems with transition diagrams and transition matrices Use matrices to organize information Sandra works at a da-care center.
The total cost function is linear. The fixed cost is $3482 and the total cost to produce 20 Trinkets is $4004. Find the total cost function.
 1. Finding the equation of a line. 1. Find two points (x 1, y 1 ), (x 2, y 2 ) and compute the slope m = y 2 y 1 x 2 x 1. 2. The line equation is y = m(x x 1 ) + y 2 (expand to get in the form y = mx +
1. Finding the equation of a line. 1. Find two points (x 1, y 1 ), (x 2, y 2 ) and compute the slope m = y 2 y 1 x 2 x 1. 2. The line equation is y = m(x x 1 ) + y 2 (expand to get in the form y = mx +
REMARKS. 8.2 Graphs of Quadratic Functions. A Graph of y = ax 2 + bx + c, where a > 0
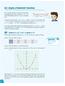 8. Graphs of Quadratic Functions In an earlier section, we have learned that the graph of the linear function = m + b, where the highest power of is 1, is a straight line. What would the shape of the graph
8. Graphs of Quadratic Functions In an earlier section, we have learned that the graph of the linear function = m + b, where the highest power of is 1, is a straight line. What would the shape of the graph
Graphing Linear Equations and Inequalities: Graphing Linear Equations and Inequalities in One Variable *
 OpenStax-CNX module: m18877 1 Graphing Linear Equations and Inequalities: Graphing Linear Equations and Inequalities in One Variable * Wade Ellis Denny Burzynski This work is produced by OpenStax-CNX and
OpenStax-CNX module: m18877 1 Graphing Linear Equations and Inequalities: Graphing Linear Equations and Inequalities in One Variable * Wade Ellis Denny Burzynski This work is produced by OpenStax-CNX and
Vertical and Horizontal Translations
 SECTION 4.3 Vertical and Horizontal Translations Copyright Cengage Learning. All rights reserved. Learning Objectives 1 2 3 4 Find the vertical translation of a sine or cosine function. Find the horizontal
SECTION 4.3 Vertical and Horizontal Translations Copyright Cengage Learning. All rights reserved. Learning Objectives 1 2 3 4 Find the vertical translation of a sine or cosine function. Find the horizontal
Open and Closed Sets
 Open and Closed Sets Definition: A subset S of a metric space (X, d) is open if it contains an open ball about each of its points i.e., if x S : ɛ > 0 : B(x, ɛ) S. (1) Theorem: (O1) and X are open sets.
Open and Closed Sets Definition: A subset S of a metric space (X, d) is open if it contains an open ball about each of its points i.e., if x S : ɛ > 0 : B(x, ɛ) S. (1) Theorem: (O1) and X are open sets.
Fractions. 7th Grade Math. Review of 6th Grade. Slide 1 / 306 Slide 2 / 306. Slide 4 / 306. Slide 3 / 306. Slide 5 / 306.
 Slide 1 / 06 Slide 2 / 06 7th Grade Math Review of 6th Grade 2015-01-14 www.njctl.org Slide / 06 Table of Contents Click on the topic to go to that section Slide 4 / 06 Fractions Decimal Computation Statistics
Slide 1 / 06 Slide 2 / 06 7th Grade Math Review of 6th Grade 2015-01-14 www.njctl.org Slide / 06 Table of Contents Click on the topic to go to that section Slide 4 / 06 Fractions Decimal Computation Statistics
CHAPTER 12: LINEAR PROGRAMMING
 CHAPTER 12: LINEAR PROGRAMMING Previous Years Board Exam (Important Questions & Answers) MARKS WEIGHTAGE 06 marks 1. A cottage industry manufactures pedestal lamps and wooden shades, each requiring the
CHAPTER 12: LINEAR PROGRAMMING Previous Years Board Exam (Important Questions & Answers) MARKS WEIGHTAGE 06 marks 1. A cottage industry manufactures pedestal lamps and wooden shades, each requiring the
Introduction to Linear Programing Problems
 Paper: Linear Programming and Theory of Games Lesson: Introduction to Linear Programing Problems Lesson Developers: DR. MANOJ KUMAR VARSHNEY, College/Department: Department of Statistics, Hindu College,
Paper: Linear Programming and Theory of Games Lesson: Introduction to Linear Programing Problems Lesson Developers: DR. MANOJ KUMAR VARSHNEY, College/Department: Department of Statistics, Hindu College,
LINEAR PROGRAMMING INTRODUCTION 12.1 LINEAR PROGRAMMING. Three Classical Linear Programming Problems (L.P.P.)
 LINEAR PROGRAMMING 12 INTRODUCTION ou are familiar with linear equations and linear inequations in one and two variables. They can be solved algebraically or graphically (by drawing a line diagram in case
LINEAR PROGRAMMING 12 INTRODUCTION ou are familiar with linear equations and linear inequations in one and two variables. They can be solved algebraically or graphically (by drawing a line diagram in case
Math : Differentiation
 EP-Program - Strisuksa School - Roi-et Math : Differentiation Dr.Wattana Toutip - Department of Mathematics Khon Kaen University 00 :Wattana Toutip wattou@kku.ac.th http://home.kku.ac.th/wattou. Differentiation
EP-Program - Strisuksa School - Roi-et Math : Differentiation Dr.Wattana Toutip - Department of Mathematics Khon Kaen University 00 :Wattana Toutip wattou@kku.ac.th http://home.kku.ac.th/wattou. Differentiation
6th Grade Report Card Mathematics Skills: Students Will Know/ Students Will Be Able To...
 6th Grade Report Card Mathematics Skills: Students Will Know/ Students Will Be Able To... Report Card Skill: Use ratio reasoning to solve problems a ratio compares two related quantities ratios can be
6th Grade Report Card Mathematics Skills: Students Will Know/ Students Will Be Able To... Report Card Skill: Use ratio reasoning to solve problems a ratio compares two related quantities ratios can be
Modelling of LP-problems (2WO09)
 Modelling of LP-problems (2WO09) assignor: Judith Keijsper room: HG 9.31 email: J.C.M.Keijsper@tue.nl course info : http://www.win.tue.nl/ jkeijspe Technische Universiteit Eindhoven meeting 1 J.Keijsper
Modelling of LP-problems (2WO09) assignor: Judith Keijsper room: HG 9.31 email: J.C.M.Keijsper@tue.nl course info : http://www.win.tue.nl/ jkeijspe Technische Universiteit Eindhoven meeting 1 J.Keijsper
Section 2.2: Absolute Value Functions, from College Algebra: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a
 Section.: Absolute Value Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Section.: Absolute Value Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
2.2 Absolute Value Functions
 . Absolute Value Functions 7. Absolute Value Functions There are a few was to describe what is meant b the absolute value of a real number. You ma have been taught that is the distance from the real number
. Absolute Value Functions 7. Absolute Value Functions There are a few was to describe what is meant b the absolute value of a real number. You ma have been taught that is the distance from the real number
