Unconstrained and Constrained Optimization
|
|
|
- Winfred Joshua Porter
- 5 years ago
- Views:
Transcription
1 Unconstrained and Constrained Optimization
2 Agenda General Ideas of Optimization Interpreting the First Derivative Interpreting the Second Derivative Unconstrained Optimization Constrained Optimization
3 Optimization There are two ways of eamining optimization. Minimization In this case you are looking for the lowest point on the function. Maimization In this case you are looking for the highest point on the function. 3
4 Needed Terminology Critical Point A point * on a function is said to be a critical point if when you evaluate the derivative of the function at the point *, then the derivative at that point is zero, i.e., f (*) 0. 4
5 What observations can you make about the attributes of a minimum? 5
6 Questions Regarding the Minimum What is the sign of the slope when you are to the left of the minimum point? Another way of saying this is what is f () when < *? Note: * denotes the point where the function is at a minimum. 6
7 Questions Regarding the Minimum Cont. What is the sign of the slope when you are to the right of the minimum point? Another way of saying this is what is f () when > *? What is the sign of the slope when you at the minimum point? Another way of saying this is what is f () when *? 7
8 Graphical Representation of a Minimum y 0 y f()
9 What observations can you make about the attributes of a maimum? 9
10 Questions Regarding the Maimum What is the sign of the slope when you are to the left of the maimum point? Another way of saying this is what is f () when < *? Note: * denotes the point where the function is at a maimum. 0
11 Questions Regarding the Maimum Cont. What is the sign of the slope when you are to the right of the maimum point? Another way of saying this is what is f () when > *? What is the sign of the slope when you at the maimum point? Another way of saying this is what is f () when *?
12 Graphical Representation of a Maimum y 6 y f()
13 Interpreting the First Derivative The first derivative of a function as was shown previously is the slope of the curve evaluated at a particular point. In essence it tells you the instantaneous rate of change of the function at the given particular point. Knowing the slope of the function can tell you where a maimum or a minimum eists on a curve. Why? 3
14 Question Can the derivative tell you whether you are at a maimum or a minimum? The answer is yes if you eamine the slope of the function around the critical point, i.e., the point where the derivative is zero. An easier way of eamining whether you have a maimum or a minimum is to eamine the second derivative of the function. 4
15 The Second Derivative The second derivative of a function f() is the derivative of the function f (), where f () is the derivative of f(). The second derivative can tell you whether the function is concave or conve at the critical point. The second derivative can be denoted by f (). 5
16 Concavity and the Second Derivative The maimum of a function f() occurs when a critical point * is at a concave portion of the function. This is equivalent to saying that f (*) < 0. If f () < 0 for all, then the function is said to be concave. 6
17 Conveity and the Second Derivative The minimum of a function f() occurs when a critical point * is at a conve portion of the function. This is equivalent to saying that f (*) > 0. If f () > 0 for all, then the function is said to be conve. 7
18 Special Case of the Second Derivative Suppose you have a function f() that has a maimum at *. What does it mean when the second derivative is equal to zero, i.e., f (*) 0? This is a point where the second derivative may not be able to tell you whether you have a maimum or a minimum. Usually in this case you will get a saddle point/point of inflection where the point is neither a maimum nor a minimum. 8
19 Eample of Special Case of the Second Derivative Suppose y f() 3, then f () 3 and f () 6, This implies that * 0 and f (*0) 0. y yf() 3 9
20 Unconstrained Optimization An unconstrained optimization problem is one where you only have to be concerned with the objective function you are trying to optimize. An objective function is a function that you are trying to optimize. None of the variables in the objective function are constrained. 0
21 First and Second Order Condition For a Maimum The first order condition for a maimum at a point * on the function f() is when f (*) 0. The second order condition for a maimum at a point * on the function f() is when f (*) < 0.
22 First and Second Order Condition For a Minimum The first order condition for a minimum at a point * on the function f() is when f (*) 0. The second order condition for a minimum at a point * on the function f() is when f (*) > 0.
23 Eample of Using First and Second Order Conditions Suppose you have the following function: f() Then the first order condition to find the critical points is: f () This implies that the critical points are at and 3. 3
24 Eample of Using First and Second Order Conditions Cont. The net step is to determine whether the critical points are maimums or minimums. These can be found by using the second order condition. f () 6 6(-) 4
25 Eample of Using First and Second Order Conditions Cont. Testing implies: f () 6(-) -6 < 0. Hence at, we have a maimum. Testing 3 implies: f (3) 6(3-) 6 > 0. Hence at 3, we have a minimum. Are these the ultimate maimum and minimum of the function f()? 5
26 Relative Vs. Absolute Etremum A relative etremum is a point that is locally greater or lesser than all points around it. A relative etrema can be found by using the first order condition. An absolute etremum is a point that is either absolutely greater than or less than all other points, i.e., f(*) > f() for all not equal to * for a maimum and f(*) < f() for all not equal to * for a minimum. 6
27 Finding the Absolute Etremum To find the absolute etremum, you need to compare all the critical points on the function, as well as, any potential end points of the function like and -. When evaluating a polynomial function at, the value of the function at takes the value of the at the highest ordered variable. 7
28 Finding the Absolute Etremum Cont. Some properties of : + - is undefined c*, where c is any value greater than zero * * (- ) - From the previous eample, the relative etremum points occur at -,, 3, and. The absolute maimum occurs at and the absolute minimum occurs at -. 8
29 9 Unconstrained Optimization: Two Variables Suppose you have a function y f(, ), then to find the critical points, you can use the following first order condition: 0 ), ( 0 ), ( * * * * f f f f
30 Unconstrained Optimization: Two Variables Cont. The second order condition are more comple where you have to eamine the second derivative of each of the variables, as well as, the cross derivative. 30
31 Cross Partial Derivative Suppose you have a function y f(, ), then the cross partial derivative can be represented as: 3 ), ( ), ( ), ( y f f y f f y f f j i j i j i
32 Cross Partial Derivative Eample Suppose you have a function y f(, ) + +3, then: 3 y y
33 Constrained Optimization Constrained Optimization is said to occur when one or more of the variables in the objective function is constrained by some function. Hence a constrained optimization problem will have an objective functions and a set of constraints. 33
34 Constrained Optimization Cont. The Constrained Optimization problem where you are trying to maimize can be set-up as the following: Maimize an objective function f() with respect to given a set of constraints g()c. ma w. r. t. f ( ) subject to g( ) c 34
35 Eample of Constrained Optimization Suppose that you want to maimize f() 5 -, subject to the constraint that. Since is the constraint, the answer to this is trivial where *. 35
36 Constrained Optimization: Two Variables The Constrained Optimization problem where you are trying to maimize can be set-up as the following: Maimize an objective function f(, ) with respect to, given a set of constraints g(, ) c. ma w r. t.,. f (, ) subject to g(, ) c 36
37 Eample of Constrained Optimization: Two Variables Suppose you want to maimize y f(, ) with respect to and given that To solve this problem, we can turn this constrained problem into an unconstrained problem. 37
38 Eample of Constrained Optimization: Two Variables Cont. If we solve the constraint for as a function of we get 600. Plugging into the objective function gives the following new unconstrained maimization problem. Maimize (600 ) w.r.t.. The first order condition is Which implies *50. Which implies *
39 Motivating the Lagrange Method In the previous problem, we made a substitution to turn the constrained optimization problem into an unconstrained problem. While this made solving the problem easier, there may be times when you have multiple constraints or potentially inequality constraints that make changing the constrained into the unconstrained difficult or impossible. 39
40 Motivating the Lagrange Method Cont. Another way of solving the above problem is using Lagrange s method. The Lagrange method uses what is called a Lagrange multiplier λ to transform the problem. The Lagrange multiplier tells us how much will be added to the optimization problem if the constraint was relaed by one unit. 40
41 4 Setting-Up the Lagrange The Constrained Optimization problem where you are trying to maimize can be set-up as the following: Maimize an objective function f(, ) with respect to and given a set of constraints g(, ) c. )), ( ( ), ( ),, ( minimum problem a If ) ), ( ( ), ( ),, ( maimum problem a If g c f L c g f L + + λ λ λ λ
42 Solving the Lagrange Problem To solve the Lagrange problem, you need to optimize L(,, λ) with respect to,, and λ. This is equivalent to using the first and second order conditions. 4
43 43 Eample of Lagrange Suppose you want to maimize y f(, ) with respect to and given that This implies: L 0 L 0 L First Order Conditions 600) ( ),, ( L λ λ λ λ λ
Math RE - Calculus I Application of the derivative (1) Curve Sketching Page 1 of 9
 Math 201-103-RE - Calculus I Application of the derivative (1) Curve Sketching Page 1 of 9 Critical numbers - Increasing and decreasing intervals - Relative Etrema Given f(), the derivatives f () and f
Math 201-103-RE - Calculus I Application of the derivative (1) Curve Sketching Page 1 of 9 Critical numbers - Increasing and decreasing intervals - Relative Etrema Given f(), the derivatives f () and f
3.5 - Concavity. a concave up. a concave down
 . - Concavity 1. Concave up and concave down For a function f that is differentiable on an interval I, the graph of f is If f is concave up on a, b, then the secant line passing through points 1, f 1 and,
. - Concavity 1. Concave up and concave down For a function f that is differentiable on an interval I, the graph of f is If f is concave up on a, b, then the secant line passing through points 1, f 1 and,
Section 4.4 Concavity and Points of Inflection
 Section 4.4 Concavit and Points of Inflection In Chapter 3, ou saw that the second derivative of a function has applications in problems involving velocit and acceleration or in general rates-of-change
Section 4.4 Concavit and Points of Inflection In Chapter 3, ou saw that the second derivative of a function has applications in problems involving velocit and acceleration or in general rates-of-change
2.1. Definition: If a < b, then f(a) < f(b) for every a and b in that interval. If a < b, then f(a) > f(b) for every a and b in that interval.
 1.1 Concepts: 1. f() is INCREASING on an interval: Definition: If a < b, then f(a) < f(b) for every a and b in that interval. A positive slope for the secant line. A positive slope for the tangent line.
1.1 Concepts: 1. f() is INCREASING on an interval: Definition: If a < b, then f(a) < f(b) for every a and b in that interval. A positive slope for the secant line. A positive slope for the tangent line.
MA 220 Lesson 28 Notes Section 3.3 (p. 191, 2 nd half of text)
 MA 220 Lesson 28 Notes Section 3.3 (p. 191, 2 nd half of tet) The property of the graph of a function curving upward or downward is defined as the concavity of the graph of a function. Concavity if how
MA 220 Lesson 28 Notes Section 3.3 (p. 191, 2 nd half of tet) The property of the graph of a function curving upward or downward is defined as the concavity of the graph of a function. Concavity if how
4 Using The Derivative
 4 Using The Derivative 4.1 Local Maima and Minima * Local Maima and Minima Suppose p is a point in the domain of f : f has a local minimum at p if f (p) is less than or equal to the values of f for points
4 Using The Derivative 4.1 Local Maima and Minima * Local Maima and Minima Suppose p is a point in the domain of f : f has a local minimum at p if f (p) is less than or equal to the values of f for points
4.4. Concavity and Curve Sketching. Concavity
 4.4 Concavit and Curve Sketching 267 4.4 Concavit and Curve Sketching f' decreases CONCAVE DOWN 3 f' increases 0 CONCAVE UP FIGURE 4.25 The graph of ƒsd = 3 is concave down on s - q, 0d and concave up
4.4 Concavit and Curve Sketching 267 4.4 Concavit and Curve Sketching f' decreases CONCAVE DOWN 3 f' increases 0 CONCAVE UP FIGURE 4.25 The graph of ƒsd = 3 is concave down on s - q, 0d and concave up
MA 131 Lecture Notes Chapter 4 Calculus by Stewart
 MA 131 Lecture Notes Chapter 4 Calculus by Stewart 4.1) Maimum and Minimum Values 4.3) How Derivatives Affect the Shape of a Graph A function is increasing if its graph moves up as moves to the right and
MA 131 Lecture Notes Chapter 4 Calculus by Stewart 4.1) Maimum and Minimum Values 4.3) How Derivatives Affect the Shape of a Graph A function is increasing if its graph moves up as moves to the right and
3.5 - Concavity 1. Concave up and concave down
 . - Concavit. Concave up and concave down Eample: The graph of f is given below. Determine graphicall the interval on which f is For a function f that is differentiable on an interval I, the graph of f
. - Concavit. Concave up and concave down Eample: The graph of f is given below. Determine graphicall the interval on which f is For a function f that is differentiable on an interval I, the graph of f
This handout will discuss three kinds of asymptotes: vertical, horizontal, and slant.
 CURVE SKETCHING This is a handout that will help you systematically sketch functions on a coordinate plane. This handout also contains definitions of relevant terms needed for curve sketching. ASYMPTOTES:
CURVE SKETCHING This is a handout that will help you systematically sketch functions on a coordinate plane. This handout also contains definitions of relevant terms needed for curve sketching. ASYMPTOTES:
Math 295: Exam 3 Name: Caleb M c Whorter Solutions Fall /16/ Minutes
 Math 295: Eam 3 Name: Caleb M c Whorter Solutions Fall 2018 11/16/2018 50 Minutes Write your name on the appropriate line on the eam cover sheet. This eam contains 10 pages (including this cover page)
Math 295: Eam 3 Name: Caleb M c Whorter Solutions Fall 2018 11/16/2018 50 Minutes Write your name on the appropriate line on the eam cover sheet. This eam contains 10 pages (including this cover page)
Module 3 Graphing and Optimization
 Module 3 Graphing and Optimization One of the most important applications of calculus to real-world problems is in the area of optimization. We will utilize the knowledge gained in the previous chapter,
Module 3 Graphing and Optimization One of the most important applications of calculus to real-world problems is in the area of optimization. We will utilize the knowledge gained in the previous chapter,
Graph Sketching. Review: 1) Interval Notation. Set Notation Interval Notation Set Notation Interval Notation. 2) Solving Inequalities
 Lesson. Graph Sketching Review: ) Interval Notation Set Notation Interval Notation Set Notation Interval Notation a) { R / < < 5} b) I (, 3) ( 3, ) c){ R} d) I (, ] (0, ) e){ R / > 5} f) I [ 3,5) ) Solving
Lesson. Graph Sketching Review: ) Interval Notation Set Notation Interval Notation Set Notation Interval Notation a) { R / < < 5} b) I (, 3) ( 3, ) c){ R} d) I (, ] (0, ) e){ R / > 5} f) I [ 3,5) ) Solving
Optimization Methods: Optimization using Calculus-Stationary Points 1. Module - 2 Lecture Notes 1
 Optimization Methods: Optimization using Calculus-Stationary Points 1 Module - Lecture Notes 1 Stationary points: Functions of Single and Two Variables Introduction In this session, stationary points of
Optimization Methods: Optimization using Calculus-Stationary Points 1 Module - Lecture Notes 1 Stationary points: Functions of Single and Two Variables Introduction In this session, stationary points of
MA123, Chapter 6: Extreme values, Mean Value Theorem, Curve sketching, and Concavity
 MA123, Chapter 6: Etreme values, Mean Value Theorem, Curve sketching, and Concavit Chapter Goals: Appl the Etreme Value Theorem to find the global etrema for continuous function on closed and bounded interval.
MA123, Chapter 6: Etreme values, Mean Value Theorem, Curve sketching, and Concavit Chapter Goals: Appl the Etreme Value Theorem to find the global etrema for continuous function on closed and bounded interval.
dt Acceleration is the derivative of velocity with respect to time. If a body's position at time t is S = f(t), the body's acceleration at time t is
 APPLICATIN F DERIVATIVE INTRDUCTIN In this section we eamine some applications in which derivatives are used to represent and interpret the rates at which things change in the world around us. Let S be
APPLICATIN F DERIVATIVE INTRDUCTIN In this section we eamine some applications in which derivatives are used to represent and interpret the rates at which things change in the world around us. Let S be
1.1 What is Microeconomics?
 1.1 What is Microeconomics? Economics is the study of allocating limited resources to satisfy unlimited wants. Such a tension implies tradeoffs among competing goals. The analysis can be carried out at
1.1 What is Microeconomics? Economics is the study of allocating limited resources to satisfy unlimited wants. Such a tension implies tradeoffs among competing goals. The analysis can be carried out at
Mth Test 3 Review Stewart 8e Chapter 4. For Test #3 study these problems, the examples in your notes, and the homework.
 For Test #3 study these problems, the eamples in your notes, and the homework. I. Absolute Etrema A function, continuous on a closed interval, always has an absolute maimum and absolute minimum. They occur
For Test #3 study these problems, the eamples in your notes, and the homework. I. Absolute Etrema A function, continuous on a closed interval, always has an absolute maimum and absolute minimum. They occur
Graphing Functions. 0, < x < 0 1, 0 x < is defined everywhere on R but has a jump discontinuity at x = 0. h(x) =
 Graphing Functions Section. of your tetbook is devoted to reviewing a series of steps that you can use to develop a reasonable graph of a function. Here is my version of a list of things to check. You
Graphing Functions Section. of your tetbook is devoted to reviewing a series of steps that you can use to develop a reasonable graph of a function. Here is my version of a list of things to check. You
Sections 4.3, 4.5 & 4.6: Graphing
 Sections 4.3, 4.5 & 4.6: Graphing In this section, we shall see how facts about f () and f () can be used to supply useful information about the graph of f(). Since there are three sections devoted to
Sections 4.3, 4.5 & 4.6: Graphing In this section, we shall see how facts about f () and f () can be used to supply useful information about the graph of f(). Since there are three sections devoted to
Derivatives and Graphs of Functions
 Derivatives and Graphs of Functions September 8, 2014 2.2 Second Derivatives, Concavity, and Graphs In the previous section, we discussed how our derivatives can be used to obtain useful information about
Derivatives and Graphs of Functions September 8, 2014 2.2 Second Derivatives, Concavity, and Graphs In the previous section, we discussed how our derivatives can be used to obtain useful information about
Supplemental Problems MAT (Prepared by Prof. Urmi Ghosh-Dastidar)
 Supplemental Problems MAT 3770 (Prepared by Prof. Urmi Ghosh-Dastidar) 1. Use Lagrange Multiplier methods to find the stationary values of z: (a) z = y, subject to + y = (b) z = (y+4), subject to + y =
Supplemental Problems MAT 3770 (Prepared by Prof. Urmi Ghosh-Dastidar) 1. Use Lagrange Multiplier methods to find the stationary values of z: (a) z = y, subject to + y = (b) z = (y+4), subject to + y =
Further Differentiation
 Worksheet 39 Further Differentiation Section Discriminant Recall that the epression a + b + c is called a quadratic, or a polnomial of degree The graph of a quadratic is called a parabola, and looks like
Worksheet 39 Further Differentiation Section Discriminant Recall that the epression a + b + c is called a quadratic, or a polnomial of degree The graph of a quadratic is called a parabola, and looks like
Use Derivatives to Sketch the Graph of a Polynomial Function.
 Applications of Derivatives Curve Sketching (using derivatives): A) Polynomial Functions B) Rational Functions Lesson 5.2 Use Derivatives to Sketch the Graph of a Polynomial Function. Idea: 1) Identify
Applications of Derivatives Curve Sketching (using derivatives): A) Polynomial Functions B) Rational Functions Lesson 5.2 Use Derivatives to Sketch the Graph of a Polynomial Function. Idea: 1) Identify
Section 4.3: Derivatives and the Shapes of Curves
 1 Section 4.: Derivatives and the Shapes of Curves Practice HW from Stewart Textbook (not to hand in) p. 86 # 1,, 7, 9, 11, 19, 1,, 5 odd The Mean Value Theorem If f is a continuous function on the closed
1 Section 4.: Derivatives and the Shapes of Curves Practice HW from Stewart Textbook (not to hand in) p. 86 # 1,, 7, 9, 11, 19, 1,, 5 odd The Mean Value Theorem If f is a continuous function on the closed
Critical and Inflection Points
 Critical and Inflection Points 1 Finding and Classifying Critical Points A critical point is a point on the graph where the tangent slope is horizontal, (0) or vertical, ( ). or not defined like the minimum
Critical and Inflection Points 1 Finding and Classifying Critical Points A critical point is a point on the graph where the tangent slope is horizontal, (0) or vertical, ( ). or not defined like the minimum
MAC 2311 Chapter 3 Review Materials (Part 1) Topics Include Max and Min values, Concavity, Curve Sketching (first and second derivative analysis)
 MAC Chapter Review Materials (Part ) Topics Include Ma and Min values, Concavit, Curve Sketching (first and second derivative analsis) MULTIPLE CHOICE. Choose the one alternative that best completes the
MAC Chapter Review Materials (Part ) Topics Include Ma and Min values, Concavit, Curve Sketching (first and second derivative analsis) MULTIPLE CHOICE. Choose the one alternative that best completes the
2.2 Absolute Value Functions
 . Absolute Value Functions 7. Absolute Value Functions There are a few was to describe what is meant b the absolute value of a real number. You ma have been taught that is the distance from the real number
. Absolute Value Functions 7. Absolute Value Functions There are a few was to describe what is meant b the absolute value of a real number. You ma have been taught that is the distance from the real number
4 Linear Programming (LP) E. Amaldi -- Foundations of Operations Research -- Politecnico di Milano 1
 4 Linear Programming (LP) E. Amaldi -- Foundations of Operations Research -- Politecnico di Milano 1 Definition: A Linear Programming (LP) problem is an optimization problem: where min f () s.t. X n the
4 Linear Programming (LP) E. Amaldi -- Foundations of Operations Research -- Politecnico di Milano 1 Definition: A Linear Programming (LP) problem is an optimization problem: where min f () s.t. X n the
10. f(x) = 3 2 x f(x) = 3 x 12. f(x) = 1 x 2 + 1
 Relations and Functions.6. Eercises To see all of the help resources associated with this section, click OSttS Chapter b. In Eercises -, sketch the graph of the given function. State the domain of the
Relations and Functions.6. Eercises To see all of the help resources associated with this section, click OSttS Chapter b. In Eercises -, sketch the graph of the given function. State the domain of the
Math 1314 Lesson 12 Curve Analysis (Polynomials) This lesson will cover analyzing polynomial functions using GeoGebra.
 Math 1314 Lesson 12 Curve Analysis (Polynomials) This lesson will cover analyzing polynomial functions using GeoGebra. Suppose your company embarked on a new marketing campaign and was able to track sales
Math 1314 Lesson 12 Curve Analysis (Polynomials) This lesson will cover analyzing polynomial functions using GeoGebra. Suppose your company embarked on a new marketing campaign and was able to track sales
Calculus & Its Applications Larry J. Goldstein David Lay Nakhle I. Asmar David I. Schneider Thirteenth Edition
 Calculus & Its Applications Larr J. Goldstein David La Nakhle I. Asmar David I. Schneider Thirteenth Edition Pearson Education Limited Edinburgh Gate Harlow Esse CM20 2JE England and Associated Companies
Calculus & Its Applications Larr J. Goldstein David La Nakhle I. Asmar David I. Schneider Thirteenth Edition Pearson Education Limited Edinburgh Gate Harlow Esse CM20 2JE England and Associated Companies
ABSOLUTE EXTREMA AND THE MEAN VALUE THEOREM
 61 LESSON 4-1 ABSOLUTE EXTREMA AND THE MEAN VALUE THEOREM Definitions (informal) The absolute maimum (global maimum) of a function is the -value that is greater than or equal to all other -values in the
61 LESSON 4-1 ABSOLUTE EXTREMA AND THE MEAN VALUE THEOREM Definitions (informal) The absolute maimum (global maimum) of a function is the -value that is greater than or equal to all other -values in the
Section 2.2: Absolute Value Functions, from College Algebra: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a
 Section.: Absolute Value Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Section.: Absolute Value Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Section 4.1 Max and Min Values
 Page 1 of 5 Section 4.1 Ma and Min Values Horizontal Tangents: We have looked at graphs and identified horizontal tangents, or places where the slope of the tangent line is zero. Q: For which values does
Page 1 of 5 Section 4.1 Ma and Min Values Horizontal Tangents: We have looked at graphs and identified horizontal tangents, or places where the slope of the tangent line is zero. Q: For which values does
DM6 Support Vector Machines
 DM6 Support Vector Machines Outline Large margin linear classifier Linear separable Nonlinear separable Creating nonlinear classifiers: kernel trick Discussion on SVM Conclusion SVM: LARGE MARGIN LINEAR
DM6 Support Vector Machines Outline Large margin linear classifier Linear separable Nonlinear separable Creating nonlinear classifiers: kernel trick Discussion on SVM Conclusion SVM: LARGE MARGIN LINEAR
Section 4.1: Maximum and Minimum Values
 Section 4.: Maimum and Minimum Values In this chapter, we shall consider further applications of the derivative. The main application we shall consider is using derivatives to sketch accurate graphs of
Section 4.: Maimum and Minimum Values In this chapter, we shall consider further applications of the derivative. The main application we shall consider is using derivatives to sketch accurate graphs of
Section 4.3: How Derivatives Affect the Shape of the Graph
 Section 4.3: How Derivatives Affect the Shape of the Graph What does the first derivative of a function tell you about the function? Where on the graph below is f x > 0? Where on the graph below is f x
Section 4.3: How Derivatives Affect the Shape of the Graph What does the first derivative of a function tell you about the function? Where on the graph below is f x > 0? Where on the graph below is f x
Augmented Lagrangian Methods
 Augmented Lagrangian Methods Mário A. T. Figueiredo 1 and Stephen J. Wright 2 1 Instituto de Telecomunicações, Instituto Superior Técnico, Lisboa, Portugal 2 Computer Sciences Department, University of
Augmented Lagrangian Methods Mário A. T. Figueiredo 1 and Stephen J. Wright 2 1 Instituto de Telecomunicações, Instituto Superior Técnico, Lisboa, Portugal 2 Computer Sciences Department, University of
Constrained Optimization and Lagrange Multipliers
 Constrained Optimization and Lagrange Multipliers MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Constrained Optimization In the previous section we found the local or absolute
Constrained Optimization and Lagrange Multipliers MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Constrained Optimization In the previous section we found the local or absolute
What is the reasonable domain of this volume function? (c) Can there exist a volume of 0? (d) Estimate a maximum volume for the open box.
 MA 15800 Lesson 11 Summer 016 E 1: From a rectangular piece of cardboard having dimensions 0 inches by 0 inches, an open bo is to be made by cutting out identical squares of area from each corner and,
MA 15800 Lesson 11 Summer 016 E 1: From a rectangular piece of cardboard having dimensions 0 inches by 0 inches, an open bo is to be made by cutting out identical squares of area from each corner and,
To find the intervals on which a given polynomial function is increasing/decreasing using GGB:
 To find the intervals on which a given polynomial function is increasing/decreasing using GGB: 1. Use GGB to graph the derivative of the function. = ; 2. Find any critical numbers. (Recall that the critical
To find the intervals on which a given polynomial function is increasing/decreasing using GGB: 1. Use GGB to graph the derivative of the function. = ; 2. Find any critical numbers. (Recall that the critical
Intro to Linear Programming. The problem that we desire to address in this course is loosely stated below.
 . Introduction Intro to Linear Programming The problem that we desire to address in this course is loosely stated below. Given a number of generators make price-quantity offers to sell (each provides their
. Introduction Intro to Linear Programming The problem that we desire to address in this course is loosely stated below. Given a number of generators make price-quantity offers to sell (each provides their
Review Guide for MAT220 Final Exam Part I. Thursday December 6 th during regular class time.
 Review Guide for MAT0 Final Exam Part I. Thursday December 6 th during regular class time. Part is worth 50% of your Final Exam grade. YOUR Syllabus approved calculator can be used on this part of the
Review Guide for MAT0 Final Exam Part I. Thursday December 6 th during regular class time. Part is worth 50% of your Final Exam grade. YOUR Syllabus approved calculator can be used on this part of the
22. LECTURE 22. I can define critical points. I know the difference between local and absolute minimums/maximums.
 . LECTURE Objectives I can define critical points. I know the difference between local and absolute minimums/maximums. In many physical problems, we re interested in finding the values (x, y) that maximize
. LECTURE Objectives I can define critical points. I know the difference between local and absolute minimums/maximums. In many physical problems, we re interested in finding the values (x, y) that maximize
Section 3.6 Rational Functions
 Section 3.6 Rational Functions DEFINITION: A rational function is a function of the form r() = P() Q() where P() and Q() are polynomials with Q() 0. EXAMPLE: f() = 1, g() = 7 4+3, h() = 2 +5+11 2 4 + 3
Section 3.6 Rational Functions DEFINITION: A rational function is a function of the form r() = P() Q() where P() and Q() are polynomials with Q() 0. EXAMPLE: f() = 1, g() = 7 4+3, h() = 2 +5+11 2 4 + 3
Now each of you should be familiar with inverses from your previous mathematical
 5. Inverse Functions TOOTLIFTST: Knowledge of derivatives of basic functions, including power, eponential, logarithmic, trigonometric, and inverse trigonometric functions. Now each of you should be familiar
5. Inverse Functions TOOTLIFTST: Knowledge of derivatives of basic functions, including power, eponential, logarithmic, trigonometric, and inverse trigonometric functions. Now each of you should be familiar
Augmented Lagrangian Methods
 Augmented Lagrangian Methods Stephen J. Wright 1 2 Computer Sciences Department, University of Wisconsin-Madison. IMA, August 2016 Stephen Wright (UW-Madison) Augmented Lagrangian IMA, August 2016 1 /
Augmented Lagrangian Methods Stephen J. Wright 1 2 Computer Sciences Department, University of Wisconsin-Madison. IMA, August 2016 Stephen Wright (UW-Madison) Augmented Lagrangian IMA, August 2016 1 /
4.3 Maximum and Minimum Values of a Function
 MA: Prepared b Asst.Prof.Dr. Archara Pacheenburawana 83 4.3 Maimum and Minimum Values of a Function Some of the most important applications of differential calculus are optimization problems, in which
MA: Prepared b Asst.Prof.Dr. Archara Pacheenburawana 83 4.3 Maimum and Minimum Values of a Function Some of the most important applications of differential calculus are optimization problems, in which
NOTES: ALGEBRA FUNCTION NOTATION
 STARTER: 1. Graph f by completing the table. f, y -1 0 1 4 5 NOTES: ALGEBRA 4.1 FUNCTION NOTATION y. Graph f 4 4 f 4 4, y --5-4 - - -1 0 1 y A Brief Review of Function Notation We will be using function
STARTER: 1. Graph f by completing the table. f, y -1 0 1 4 5 NOTES: ALGEBRA 4.1 FUNCTION NOTATION y. Graph f 4 4 f 4 4, y --5-4 - - -1 0 1 y A Brief Review of Function Notation We will be using function
Chapter 3: Section 3-2 Graphing Linear Inequalities
 Chapter : Section - Graphing Linear Inequalities D. S. Malik Creighton Universit, Omaha, NE D. S. Malik Creighton Universit, Omaha, NE Chapter () : Section - Graphing Linear Inequalities / 9 Geometric
Chapter : Section - Graphing Linear Inequalities D. S. Malik Creighton Universit, Omaha, NE D. S. Malik Creighton Universit, Omaha, NE Chapter () : Section - Graphing Linear Inequalities / 9 Geometric
3 Limits Involving Infinity: Asymptotes LIMITS INVOLVING INFINITY. 226 Chapter 3 Additional Applications of the Derivative
 226 Chapter 3 Additional Applications of the Derivative 52. Given the function f() 2 3 3 2 2 7, complete the following steps: (a) Graph using [, ] b [, ] and [, ] b [ 2, 2]2. (b) Fill in the following
226 Chapter 3 Additional Applications of the Derivative 52. Given the function f() 2 3 3 2 2 7, complete the following steps: (a) Graph using [, ] b [, ] and [, ] b [ 2, 2]2. (b) Fill in the following
Rational functions and graphs. Section 2: Graphs of rational functions
 Rational functions and graphs Section : Graphs of rational functions Notes and Eamples These notes contain subsections on Graph sketching Turning points and restrictions on values Graph sketching You can
Rational functions and graphs Section : Graphs of rational functions Notes and Eamples These notes contain subsections on Graph sketching Turning points and restrictions on values Graph sketching You can
30. Constrained Optimization
 30. Constrained Optimization The graph of z = f(x, y) is represented by a surface in R 3. Normally, x and y are chosen independently of one another so that one may roam over the entire surface of f (within
30. Constrained Optimization The graph of z = f(x, y) is represented by a surface in R 3. Normally, x and y are chosen independently of one another so that one may roam over the entire surface of f (within
SUMMARY OF PROPERTY 1 PROPERTY 5
 SUMMARY OF PROPERTY 1 PROPERTY 5 There comes a time when putting a puzzle together that we start to see the final image. The same is true when we represent the first five (5) FUNction Summary Properties
SUMMARY OF PROPERTY 1 PROPERTY 5 There comes a time when putting a puzzle together that we start to see the final image. The same is true when we represent the first five (5) FUNction Summary Properties
Downloaded from
 1 Class XI: Math Chapter 13: Limits and Derivatives Chapter Notes Key-Concepts 1. The epected value of the function as dictated by the points to the left of a point defines the left hand it of the function
1 Class XI: Math Chapter 13: Limits and Derivatives Chapter Notes Key-Concepts 1. The epected value of the function as dictated by the points to the left of a point defines the left hand it of the function
Math Stuart Jones. 4.3 Curve Sketching
 4.3 Curve Sketching In this section, we combine much of what we have talked about with derivatives thus far to draw the graphs of functions. This is useful in many situations to visualize properties of
4.3 Curve Sketching In this section, we combine much of what we have talked about with derivatives thus far to draw the graphs of functions. This is useful in many situations to visualize properties of
Lecture 25 Nonlinear Programming. November 9, 2009
 Nonlinear Programming November 9, 2009 Outline Nonlinear Programming Another example of NLP problem What makes these problems complex Scalar Function Unconstrained Problem Local and global optima: definition,
Nonlinear Programming November 9, 2009 Outline Nonlinear Programming Another example of NLP problem What makes these problems complex Scalar Function Unconstrained Problem Local and global optima: definition,
Finding Asymptotes KEY
 Unit: 0 Lesson: 0 Discontinuities Rational functions of the form f ( are undefined at values of that make 0. Wherever a rational function is undefined, a break occurs in its graph. Each such break is called
Unit: 0 Lesson: 0 Discontinuities Rational functions of the form f ( are undefined at values of that make 0. Wherever a rational function is undefined, a break occurs in its graph. Each such break is called
Section 4: Extreme Values & Lagrange Multipliers.
 Section 4: Extreme Values & Lagrange Multipliers. Compiled by Chris Tisdell S1: Motivation S2: What are local maxima & minima? S3: What is a critical point? S4: Second derivative test S5: Maxima and Minima
Section 4: Extreme Values & Lagrange Multipliers. Compiled by Chris Tisdell S1: Motivation S2: What are local maxima & minima? S3: What is a critical point? S4: Second derivative test S5: Maxima and Minima
CONCAVITY AND INFLECTION POINTS
 CONCAVITY AND INFLECTION POINTS Find the Second Derivative of the function, f. Set the Second Derivative equal to zero and solve. Determine whether the Second Derivative is undefined for any x-values.
CONCAVITY AND INFLECTION POINTS Find the Second Derivative of the function, f. Set the Second Derivative equal to zero and solve. Determine whether the Second Derivative is undefined for any x-values.
TABLE OF CONTENTS CHAPTER 1 LIMIT AND CONTINUITY... 26
 TABLE OF CONTENTS CHAPTER LIMIT AND CONTINUITY... LECTURE 0- BASIC ALGEBRAIC EXPRESSIONS AND SOLVING EQUATIONS... LECTURE 0- INTRODUCTION TO FUNCTIONS... 9 LECTURE 0- EXPONENTIAL AND LOGARITHMIC FUNCTIONS...
TABLE OF CONTENTS CHAPTER LIMIT AND CONTINUITY... LECTURE 0- BASIC ALGEBRAIC EXPRESSIONS AND SOLVING EQUATIONS... LECTURE 0- INTRODUCTION TO FUNCTIONS... 9 LECTURE 0- EXPONENTIAL AND LOGARITHMIC FUNCTIONS...
WebAssign hw2.3 (Homework)
 WebAssign hw2.3 (Homework) Current Score : / 98 Due : Wednesday, May 31 2017 07:25 AM PDT Michael Lee Math261(Calculus I), section 1049, Spring 2017 Instructor: Michael Lee 1. /6 pointsscalc8 1.6.001.
WebAssign hw2.3 (Homework) Current Score : / 98 Due : Wednesday, May 31 2017 07:25 AM PDT Michael Lee Math261(Calculus I), section 1049, Spring 2017 Instructor: Michael Lee 1. /6 pointsscalc8 1.6.001.
Chapter 3 Path Optimization
 Chapter 3 Path Optimization Background information on optimization is discussed in this chapter, along with the inequality constraints that are used for the problem. Additionally, the MATLAB program for
Chapter 3 Path Optimization Background information on optimization is discussed in this chapter, along with the inequality constraints that are used for the problem. Additionally, the MATLAB program for
Section 1.5 Transformation of Functions
 Section.5 Transformation of Functions 6 Section.5 Transformation of Functions Often when given a problem, we try to model the scenario using mathematics in the form of words, tables, graphs and equations
Section.5 Transformation of Functions 6 Section.5 Transformation of Functions Often when given a problem, we try to model the scenario using mathematics in the form of words, tables, graphs and equations
MATH CALCULUS & STATISTICS/BUSN - PRACTICE EXAM #3 - FALL DR. DAVID BRIDGE
 MATH 2053 - CALCULUS & STATISTICS/BUSN - PRACTICE EXAM #3 - FALL 2007 - DR. DAVID BRIDGE MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Use a calculator
MATH 2053 - CALCULUS & STATISTICS/BUSN - PRACTICE EXAM #3 - FALL 2007 - DR. DAVID BRIDGE MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Use a calculator
a) y = x 3 + 3x 2 2 b) = UNIT 4 CURVE SKETCHING 4.1 INCREASING AND DECREASING FUNCTIONS
 UNIT 4 CURVE SKETCHING 4.1 INCREASING AND DECREASING FUNCTIONS We read graphs as we read sentences: left to right. Plainly speaking, as we scan the function from left to right, the function is said to
UNIT 4 CURVE SKETCHING 4.1 INCREASING AND DECREASING FUNCTIONS We read graphs as we read sentences: left to right. Plainly speaking, as we scan the function from left to right, the function is said to
MATH 19520/51 Class 10
 MATH 19520/51 Class 10 Minh-Tam Trinh University of Chicago 2017-10-16 1 Method of Lagrange multipliers. 2 Examples of Lagrange multipliers. The Problem The ingredients: 1 A set of parameters, say x 1,...,
MATH 19520/51 Class 10 Minh-Tam Trinh University of Chicago 2017-10-16 1 Method of Lagrange multipliers. 2 Examples of Lagrange multipliers. The Problem The ingredients: 1 A set of parameters, say x 1,...,
Section 1.6: Graphs of Functions, from College Algebra: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative
 Section.6: Graphs of Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Section.6: Graphs of Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
You Try: Find the x-intercepts of f ( x) Find the roots (zeros, x-intercepts) of 2. x x. x 2. x 8 x x 2 8x 4 4x 32
 1 Find the roots (zeros, -intercepts) of 1 3. 1a Find the -intercepts of 5 1 We are looking for the solutions to Method 1: Factoring Using Guess & heck Using an rea Model, fill in a Generic Rectangle with
1 Find the roots (zeros, -intercepts) of 1 3. 1a Find the -intercepts of 5 1 We are looking for the solutions to Method 1: Factoring Using Guess & heck Using an rea Model, fill in a Generic Rectangle with
Solutions to assignment 3
 Math 9 Solutions to assignment Due: : Noon on Thursday, October, 5.. Find the minimum of the function f, y, z) + y + z subject to the condition + y + z 4. Solution. Let s define g, y, z) + y + z, so the
Math 9 Solutions to assignment Due: : Noon on Thursday, October, 5.. Find the minimum of the function f, y, z) + y + z subject to the condition + y + z 4. Solution. Let s define g, y, z) + y + z, so the
Limits. f(x) and lim. g(x) g(x)
 Limits Limit Laws Suppose c is constant, n is a positive integer, and f() and g() both eist. Then,. [f() + g()] = f() + g() 2. [f() g()] = f() g() [ ] 3. [c f()] = c f() [ ] [ ] 4. [f() g()] = f() g()
Limits Limit Laws Suppose c is constant, n is a positive integer, and f() and g() both eist. Then,. [f() + g()] = f() + g() 2. [f() g()] = f() g() [ ] 3. [c f()] = c f() [ ] [ ] 4. [f() g()] = f() g()
Chapter 3 Numerical Methods
 Chapter 3 Numerical Methods Part 1 3.1 Linearization and Optimization of Functions of Vectors 1 Problem Notation 2 Outline 3.1.1 Linearization 3.1.2 Optimization of Objective Functions 3.1.3 Constrained
Chapter 3 Numerical Methods Part 1 3.1 Linearization and Optimization of Functions of Vectors 1 Problem Notation 2 Outline 3.1.1 Linearization 3.1.2 Optimization of Objective Functions 3.1.3 Constrained
Calculus Limits Images in this handout were obtained from the My Math Lab Briggs online e-book.
 Calculus Limits Images in this handout were obtained from the My Math Lab Briggs online e-book. A it is the value a function approaches as the input value gets closer to a specified quantity. Limits are
Calculus Limits Images in this handout were obtained from the My Math Lab Briggs online e-book. A it is the value a function approaches as the input value gets closer to a specified quantity. Limits are
The Limit Concept. Introduction to Limits. Definition of Limit. Example 1. Example 2. Example 3 4/7/2015
 4/7/015 The Limit Concept Introduction to Limits Precalculus 1.1 The notion of a it is a fundamental concept of calculus. We will learn how to evaluate its and how they are used in the two basic problems
4/7/015 The Limit Concept Introduction to Limits Precalculus 1.1 The notion of a it is a fundamental concept of calculus. We will learn how to evaluate its and how they are used in the two basic problems
FINAL EXAM (PRACTICE A) MATH 265
 UNIVERSITY OF CALGARY FACULTY OF SCIENCE DEPARTMENT OF MATHEMATICS & STATISTICS FINAL EXAM (PRACTICE A) MATH 265 NAME STUDENT ID EXAMINATION RULES 1. This is a closed book eamination. 2. Calculators are
UNIVERSITY OF CALGARY FACULTY OF SCIENCE DEPARTMENT OF MATHEMATICS & STATISTICS FINAL EXAM (PRACTICE A) MATH 265 NAME STUDENT ID EXAMINATION RULES 1. This is a closed book eamination. 2. Calculators are
Linear Mathematical Programming (LP)
 Linear Mathematical Programming (LP) A MP is LP if : The objective function is linear where The set is defined by linear equality or inequality constraints c f T ) = ( ],..., [ n T c c c = = n b A where
Linear Mathematical Programming (LP) A MP is LP if : The objective function is linear where The set is defined by linear equality or inequality constraints c f T ) = ( ],..., [ n T c c c = = n b A where
Unit 2 Functions Analyzing Graphs of Functions (Unit 2.2)
 Unit 2 Functions Analzing Graphs of Functions (Unit 2.2) William (Bill) Finch Mathematics Department Denton High School Introduction Domain/Range Vert Line Zeros Incr/Decr Min/Ma Avg Rate Change Odd/Even
Unit 2 Functions Analzing Graphs of Functions (Unit 2.2) William (Bill) Finch Mathematics Department Denton High School Introduction Domain/Range Vert Line Zeros Incr/Decr Min/Ma Avg Rate Change Odd/Even
Solve the following system of equations. " 2x + 4y = 8 # $ x 3y = 1. 1 cont d. You try:
 1 Solve the following system of equations. " 2x + 4y = 8 # $ x 3y = 1 Method 1: Substitution 1. Solve for x in the second equation. 1 cont d Method 3: Eliminate y 1. Multiply first equation by 3 and second
1 Solve the following system of equations. " 2x + 4y = 8 # $ x 3y = 1 Method 1: Substitution 1. Solve for x in the second equation. 1 cont d Method 3: Eliminate y 1. Multiply first equation by 3 and second
9. p(x) = x 3 8x 2 5x p(x) = x 3 + 3x 2 33x p(x) = x x p(x) = x 3 + 5x x p(x) = x 4 50x
 Section 6.3 Etrema and Models 593 6.3 Eercises In Eercises 1-8, perform each of the following tasks for the given polnomial. i. Without the aid of a calculator, use an algebraic technique to identif the
Section 6.3 Etrema and Models 593 6.3 Eercises In Eercises 1-8, perform each of the following tasks for the given polnomial. i. Without the aid of a calculator, use an algebraic technique to identif the
Math 111 Lecture Notes
 A function f is even if for ever in the domain of f it holds that f( ) = f(). Visuall, an even function is smmetric about the -ais. A function f is odd if for ever in the domain of f it holds that f( )
A function f is even if for ever in the domain of f it holds that f( ) = f(). Visuall, an even function is smmetric about the -ais. A function f is odd if for ever in the domain of f it holds that f( )
Optimization Methods: Optimization using Calculus Kuhn-Tucker Conditions 1. Module - 2 Lecture Notes 5. Kuhn-Tucker Conditions
 Optimization Methods: Optimization using Calculus Kuhn-Tucker Conditions Module - Lecture Notes 5 Kuhn-Tucker Conditions Introduction In the previous lecture the optimization of functions of multiple variables
Optimization Methods: Optimization using Calculus Kuhn-Tucker Conditions Module - Lecture Notes 5 Kuhn-Tucker Conditions Introduction In the previous lecture the optimization of functions of multiple variables
minimize ½(x 1 + 2x 2 + x 32 ) subject to x 1 + x 2 + x 3 = 5
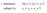 minimize ½(x 1 2 + 2x 2 2 + x 32 ) subject to x 1 + x 2 + x 3 = 5 In this Chapter We will study a new theory for constrained optimization Local optimality condition Easier to implement Deeper insights
minimize ½(x 1 2 + 2x 2 2 + x 32 ) subject to x 1 + x 2 + x 3 = 5 In this Chapter We will study a new theory for constrained optimization Local optimality condition Easier to implement Deeper insights
Simplex Method. Introduction:
 Introduction: Simple Method In the previous chapter, we discussed about the graphical method for solving linear programming problems. Although the graphical method is an invaluable aid to understand the
Introduction: Simple Method In the previous chapter, we discussed about the graphical method for solving linear programming problems. Although the graphical method is an invaluable aid to understand the
Convex Functions & Optimization
 672 Conve Functions & Optimization Aashray Yadav Abstract - My research paper is based on the recent work in interior-point methods, specifically those methods that keep track of both the primal and dual
672 Conve Functions & Optimization Aashray Yadav Abstract - My research paper is based on the recent work in interior-point methods, specifically those methods that keep track of both the primal and dual
ICM ~Unit 4 ~ Day 2. Section 1.2 Domain, Continuity, Discontinuities
 ICM ~Unit 4 ~ Day Section 1. Domain, Continuity, Discontinuities Warm Up Day Find the domain, -intercepts and y-intercepts. 1. 3 5. 1 9 3. Factor completely. 6 4 16 3 4. Factor completely. 8 7 Practice
ICM ~Unit 4 ~ Day Section 1. Domain, Continuity, Discontinuities Warm Up Day Find the domain, -intercepts and y-intercepts. 1. 3 5. 1 9 3. Factor completely. 6 4 16 3 4. Factor completely. 8 7 Practice
1-1. Functions. Lesson 1-1. What You ll Learn. Active Vocabulary. Scan Lesson 1-1. Write two things that you already know about functions.
 1-1 Functions What You ll Learn Scan Lesson 1- Write two things that ou alread know about functions. Lesson 1-1 Active Vocabular New Vocabular Write the definition net to each term. domain dependent variable
1-1 Functions What You ll Learn Scan Lesson 1- Write two things that ou alread know about functions. Lesson 1-1 Active Vocabular New Vocabular Write the definition net to each term. domain dependent variable
In other words, we want to find the domain points that yield the maximum or minimum values (extrema) of the function.
 1 The Lagrange multipliers is a mathematical method for performing constrained optimization of differentiable functions. Recall unconstrained optimization of differentiable functions, in which we want
1 The Lagrange multipliers is a mathematical method for performing constrained optimization of differentiable functions. Recall unconstrained optimization of differentiable functions, in which we want
Module 12 Rational Functions and Rational Equations
 MAC 1105 Module 12 Rational Functions and Rational Equations Learning Objective Upon completing this module, you should be able to: 1. Identify a rational function and state its domain. 2. Find and interpret
MAC 1105 Module 12 Rational Functions and Rational Equations Learning Objective Upon completing this module, you should be able to: 1. Identify a rational function and state its domain. 2. Find and interpret
MAC What is a Rational Function? Module 12. Rational Functions and Rational Equations. Learning Objective
 MAC 1105 Module 12 Rational Functions and Rational Equations Learning Objective Upon completing this module, you should be able to: 1. Identify a rational function and state its domain. 2. Find and interpret
MAC 1105 Module 12 Rational Functions and Rational Equations Learning Objective Upon completing this module, you should be able to: 1. Identify a rational function and state its domain. 2. Find and interpret
Situation 3. Parentheses vs. Brackets. Colleen Foy
 Situation 3 Parentheses vs. Brackets Colleen Foy Prompt: Students were finding the domain and range of various functions. Most of the students were comfortable with the set builder notation, but when asked
Situation 3 Parentheses vs. Brackets Colleen Foy Prompt: Students were finding the domain and range of various functions. Most of the students were comfortable with the set builder notation, but when asked
Relating Graphs of f and f
 Relating Graphs of f and f Do Now: Answer each of the following questions. 1. When the function, f, is increasing, what does that mean about the derivative, f? 2. When the function, f, is decreasing, what
Relating Graphs of f and f Do Now: Answer each of the following questions. 1. When the function, f, is increasing, what does that mean about the derivative, f? 2. When the function, f, is decreasing, what
f x How can we determine algebraically where f is concave up and where f is concave down?
 Concavity - 3.5 1. Concave up and concave down Definition For a function f that is differentiable on an interval I, the graph of f is a. If f is concave up on a, b, then the secant line passing through
Concavity - 3.5 1. Concave up and concave down Definition For a function f that is differentiable on an interval I, the graph of f is a. If f is concave up on a, b, then the secant line passing through
3.6-Rational Functions & Their Graphs
 .6-Rational Functions & Their Graphs What is a Rational Function? A rational function is a function that is the ratio of two polynomial functions. This definition is similar to a rational number which
.6-Rational Functions & Their Graphs What is a Rational Function? A rational function is a function that is the ratio of two polynomial functions. This definition is similar to a rational number which
Answers to Worksheet 5, Math 272
 Answers to Worksheet 5, Math 7 1. Calculate the directional derivative of the function f(, y, z) = cos y sin z at the point a = (1, π/, 5π/6) in the direction u = (3, 0, 1). The gradient of f at a is (
Answers to Worksheet 5, Math 7 1. Calculate the directional derivative of the function f(, y, z) = cos y sin z at the point a = (1, π/, 5π/6) in the direction u = (3, 0, 1). The gradient of f at a is (
MATH 115: Review for Chapter 1
 MATH 115: Review for Chapter 1 Can you use the Distance Formula to find the distance between two points? (1) Find the distance d P, P between the points P and 1 1, 6 P 10,9. () Find the length of the line
MATH 115: Review for Chapter 1 Can you use the Distance Formula to find the distance between two points? (1) Find the distance d P, P between the points P and 1 1, 6 P 10,9. () Find the length of the line
Local and Global Minimum
 Local and Global Minimum Stationary Point. From elementary calculus, a single variable function has a stationary point at if the derivative vanishes at, i.e., 0. Graphically, the slope of the function
Local and Global Minimum Stationary Point. From elementary calculus, a single variable function has a stationary point at if the derivative vanishes at, i.e., 0. Graphically, the slope of the function
Limits, Continuity, and Asymptotes
 LimitsContinuity.nb 1 Limits, Continuity, and Asymptotes Limits Limit evaluation is a basic calculus tool that can be used in many different situations. We will develop a combined numerical, graphical,
LimitsContinuity.nb 1 Limits, Continuity, and Asymptotes Limits Limit evaluation is a basic calculus tool that can be used in many different situations. We will develop a combined numerical, graphical,
Lines and Their Slopes
 8.2 Lines and Their Slopes Linear Equations in Two Variables In the previous chapter we studied linear equations in a single variable. The solution of such an equation is a real number. A linear equation
8.2 Lines and Their Slopes Linear Equations in Two Variables In the previous chapter we studied linear equations in a single variable. The solution of such an equation is a real number. A linear equation
9. p(x) = x 3 8x 2 5x p(x) = x 3 + 3x 2 33x p(x) = x x p(x) = x 3 + 5x x p(x) = x 4 50x
 Section 6.3 Etrema and Models 593 6.3 Eercises In Eercises 1-8, perform each of the following tasks for the given polnomial. i. Without the aid of a calculator, use an algebraic technique to identif the
Section 6.3 Etrema and Models 593 6.3 Eercises In Eercises 1-8, perform each of the following tasks for the given polnomial. i. Without the aid of a calculator, use an algebraic technique to identif the
