Module 3: Stand Up Conics
|
|
|
- Flora Melton
- 5 years ago
- Views:
Transcription
1 MATH55 Module 3: Stand Up Conics Main Math concepts: Conic Sections (i.e. Parabolas, Ellipses, Hyperbolas), nd degree equations Auxilliary ideas: Analytic vs. Co-ordinate-free Geometry, Parameters, Calculus. Parabolas Problem a. A parabola is defined as the set of points equidistant from a given line (the directrix of the parabola) and a given point (the focus) which is not on the directrix. Let d > 0. Derive the equation of the parabola with directrix y = - d and focus (0, d). Modify for directrix y = d and focus ( 0, - d). Solution. (x,y) d d - d - d (x,y) For the first case, by the distance formula, (x 0) + (y d) = y + d. Squaring gives x + y dy + d = y + dy + d. Simplifying gives x = dy, or y = d x. For the second case, (x 0) + (y + d) = d y. The same steps give us y = d x. Summarizing, these parabolas are y = ±ax, where the positive parameter a = d. The midpoint between the focus and the directrix is the vertex ( the origin in these examples) and the line of symmetry through the vertex and perpendicular to the directrix is the axis of the parabola. Vertical (North-South) parabolas such as these can be translated to move the vertex to (h, k) as usual: y k = a(x h), or as a function y = a(x h) + k = ax ahx + (ah + k). Horizontal (East-West) parabolas with vertex at ( h, k )can be obtained by interchanging x and y : x h = a(y k), or as a function x = a(y k) + h = ay aky + (ak + h). In all cases, the common length from focus to vertex, and vertex to directrix, is d = a.
2 Problem b. Find vertex, focus, axis, intercepts, and sketch the graph for y + 6y x 5 = 0. Notice that it is horizontal, since the y term is squared. Solution. [Completing the square]. We complete the square in y: (y + 3y +?) (?) x 5 = 0. We want? = ( 3) in order to make a perfect square. Then: 0 = (y + 3y + 9 ) (9 ) x 5 = (y + 3 ) x 9 which we can now solve for x: x = (y + 3 ) 9, or x + 9 = (y + 3 ). Thus, the vertex is ( 9, 3 ), and the axis is the horizontal line y = 3. Now, a =, so it opens to the right, and the focal distance is d = a =, so the focus is ( 8, 3 ). Setting y = 0 gives x-intercept 5, and setting x = 0 gives y + 6y 5 = 0, and then the quadratic formula gives y- intercepts y = 6 ± 36 ()( 5) 6 ± 76 = = 3 ± , Solution. [Use Calculus to find the vertex]. We can solve for x, x = y + 3y 5. We immediately have a = and so d = ¼ and parabola opens right. The vertex is the point where dx/dy = 0, we can simply compute y + 3 = 0, y = 3 and then plug in to get the x co-ordinate x = ( 3 ) + 3( 3 ) 5 = 9, then the focus is ( 9 +, 3 ) = ( 8, 3 ). The intercepts can be found as is the first solution. y + 6y x 5 = axis y = - 3/ - 3
3 Problem c. A car is driving on toward the vertex on a parabolic road. There is a wall running along the axis of the parabola, and a laser pointer is mounted on the wall side the car, perpendicular to the car s direction. At what point on the wall is the laser pointing as the car reaches the vertex? Solution. Let the parabola open upwards with vertex (0,0). Then its equation is y = ax for some positive a. Since the laser is perpendicular to the car s path, the point on the wall where the laser shines is the y-intercept of the normal line to the parabola. So,if we let y N denote the y-intercept of the normal line at point P on the parabola, then we are seeking lim y. N P (0,0) At the point (x 0, y 0 ), on the parabola y = ax, the slope of the tangent line is y (x 0 ) = ax 0 and so the slope of the normal line is. Thus the equation of the normal line is ax 0 y y 0 = (x x 0 ). Since y 0 = ax 0, the normal line is y = x + ax 0 ax 0 a + ax 0. Then the y-intercept of the normal line is y N = 0 + ax 0 a + ax 0 = a + ax 0. Finally, as the car approaches the origin, we have lim y N = lim x 0 0 x 0 0 a + ax 0 = a So, if the car is driving on the parabola y = ax, the limiting point of the laser image on the wall is at a distance a from the vertex. Since the focus is at from the vertex, we could also state the result a (in a co-ordinate-free way) by saying the limiting point is twice as far from the vertex as is the focus. Picture shows case a = with the limiting intercept y = x P = (x 0, y 0 )
4 II. Ellipses and Hyperbolas Problem a. Consider the equation x 5 + y =, whose graph is an ellipse. 9 i) Find intercepts, x and y extents, symmetries, critical points and sketch the graph. ii) Let (x, y ) be a point on the graph.. Find the sum: the distance from (x, y) to (-,0) plus distance from (x, y) to (,0). Solution (i). The graph is symmetric about x-axis, y-axis, and origin since replacing x and/or y by its negation gives an equivalent equation. The intercepts are (±5,0) and (0,±3), and since both terms on the left side are non-negative and sum to, then neither term can be more than. So x 5 x 5 5 x 5 and similarly 3 y 3. Differentiating gives x 5 + y 9 y = 0, so y = x(9) 5(y) = 9x. This gives vertical and horizontal tangents at 5y (±5,0) and (0,±3) respectively, and also shows that the curve is decreasing in the first quadrant where x and y are both positive. By the symmetries, then, the graph must look like: x 5 + y 9 = Another way to view this ellipse is to consider the stretching transformation T(x,y)= (5x, 3y) which moves a point 5 times further from the y-axis and 3 times further from the x-axis. We apply T to the unit circle x + y = by substituting (x, y) T (x, y) = (x / 5, y / 3) to obtain the equation x 5 + y =. So this ellipse amounts to the unit circle 9 stretched by factors of 5 horizontally and 3 vertically. ii) The two distances whose sum we want to find are shown. By the distance formula, and using the fact that (x, y) is on the ellipse, we have the sum of the distances is: (x + ) + y + (x ) + y = (x + 8x + 6) + (9 (9 / 5)x ) + (x 8x + 6) + (9 (9 / 5)x ) (6 / 5)x + 8x (6 / 5)x 8x + 5 = (( / 5)x + 5) + (( / 5)x 5). Now we must be careful! Since 5 x 5, then - ( / 5)x, so ( / 5)x 5 is negative and (/5)x+5 is positive. So the desired sum is ( / 5)x + 5 (( / 5)x 5) = 0. So the sum is equal to 0 for all points on this ellipse. Thus an alternative definition of this ellipse is: The set of points (x, y ) whose sum of distances to (-,0) and (, 0) is 0. Geometrically, it s the set of points whose sum of distances, to two fixed points eight units apart, is 0.
5 The points ( -, 0) and (,0) are the foci of this ellipse. The center is (0,0) and the distances a=5 and b=3 are the semi-major axis and the semi-minor axis respectively. The common sum of distances is twice the semi-major axis (in our case, 0 = x 5). Notice that the distance from the center to a focus in our example is c =, and that a = b + c in our example. This is always the case, although we won t take the time for a complete derivation. We can interchange x and y to get a congruent ellipse centered at (0,0) whose major axis runs vertically, with foci are at (0,±) and intercepts (0,±5) and (±3,0). And of course, we can translate the ellipse to have ( h, k ) as its center. Summarizing: An ellipse is the set of points in a plane whose sum of distances to two given points, called the foci, is (x h) (y k) a given constant. The equation of an upright ellipse can be written as + = where: a b (h, k ) is the center (i.e. the midpoint between the foci), and we take a and b positive. The x-extent is (h a,h + a) and the y-extent is ( k b, k + b). The larger of a and b is the semi-major axis M, the smaller is the semi-minor axis m. The common sum of distances is M [either a or b]. (if a = b, then the ellipse is a circle of radius a = b ). (h ± c, k) where c = a b if a b The foci are at. The distance between foci is c. (h, k ± c) where c = b a if b a The eccentricity of the ellipse is e = c / M = c / (semi-major axis); then 0 e <. (eccentricity=0 is a circle, eccentricity near means very elongated) Problem b. Find the equation, and sketch, the set of points whose sum of distances to the origin and (0,6) is. Solution: We have a vertical (i.e. N-S) ellipse with foci (0,0) and (0,6), so the center is (0,3) and c = 3. For the major axis, b= so b = 6. Then a = b c = 36 9 = 7, so a = 3 3. So the equation is: x (y 3) + = ; the x extent is [ 3 3, 3 3], and the y extent is [-3,9] The intercepts are (±9 /,0), (0,-3), and (0,6). Eccentricity is 3 / 6 = x (y 3) + =
6 Problem c. Sketch the graph x 6 + y 9 asymptotes. = indicating interesting features such as symmetries and Solution. We have symmetry about the x-axis, y-axis and the origin by replacing variables with their negations.. Since x 6 = y 9, then y 9 0, i.e. y 9, so either y 3 or y 3. On the other hand, x can be any real number since we have y = ±3 + x /6 = ±3 x + 6 and any x will work. Also, we see that for large x, y will be like ± 3 x, so we suspect those lines may be asymptotes. Looking at the derivative, we have x / 6 + y y / 9 = 0, so y' = 9x. So there are horizontal tangents at x=0 and 6y the curve is increasing in the first quadrant. The graph, shows the curve as well as the lines y = ± 3 x.: 6 x 6 + y 9 = Lastly, we note that if we define the points (0,5) and (0,-5) as the foci of this hyperbola, then all points on the hyperbola have the difference of their distances from the foci equal to 6 (HW problem).
7 So a hyperbola can be defined geometrically as the set of points for which the difference of distances to two fixed points, called the foci of the hyperbola, is constant. As usual, we can interchange x and y to obtain a congruent East-West hyperbola, and we can translate the center to ( h, k ) as well. Combining everything, we have (x h) (y k) The equation of an upright hyperbola can be written as ± = (**) : a b (h, k ) is the center (i.e. the midpoint between the foci), and we take a and b positive. The distance between the foci is c, where c = a + b. The asymptotes go through the center and have slopes ± b a. The following statements refer to East West hyperbolas (i.e. x term is positive in (**)) The x-extent is (,h a] [h + a, ), the y extent is R. The length a from the center to the extreme points is the semi-major axis. The common difference of distances is a ( i.e. twice the semi-major axis). The eccentricity is c / a, which is always bigger than for a hyperbola. For North-South hyperbolas, interchange a and b, x and y, h and k in these four statements. III. Second Order polynomials Problem a. Consider the graph of the equation Ax + y x = 0 where A is a parameter. Determine those values of A for which it is an ellipse, parabola, hyperbola, and for those A, find its orientation. Solution. First notice that for any value of A, the curve goes through the origin (0, 0 ) and has a vertical tangent at (0,0) [vertical tangent verification is left to the reader] We try to put the equation in our standard form by completing the square. A(x A x + A ) + y = A A(x A ) + y =. Now multiply by A to get a on the right: A A (x A ) + Ay =. Finally write the coefficients in the denominators: (x / A) ( + y A ) ( A ) =. We let r = A, then we have (x r) r + y r =. First, if A > 0, then r > 0 and we have an ellipse centered at (r, 0) with a = r, b = r. For A > (i.e. r < ), a = r < r = b so the ellipses are N-S oriented. As A decreases (r increases) towards, both vertical and horizontal semi-axes grow, but the horizontal one grows faster ( r vs. r ) so the shape is more circular. At A = (i.e. r=), we have the circle of radius centered at (,0), and for 0 < A <, then r > and so a > b and hence the ellipses are oriented E-W.
8 As A decreases toward 0, r grows large and the ellipses become larger and more eccentric. The graph shows the ellipses for A =,, 0.5, 0.5, 0.5 ( i.e. r = /,,,, 0/3 ) y What happens when A reaches 0? The equation becomes y = x, a parabola with vertex at the origin, focus at (/,0), which opens to the right. Lastly, we look at the case where A < 0. Let S = - / A, so S > 0 and the equation is 0 = x S + y x = S (x + Sx + S ) + S + y Continuing, we get S (x + (x + S) + y S) = S, and hence y = which is standard form. S S These hyperbolas are East-West (since x-term is positive), centered at (-S, 0), semi-major axis S = /A, so the critical points are (0,0) and (-S, 0). The asymptotes have slope ±S / S = A. So, as A grows large negative, the hyperbolas become wider, and (as S approaches 0), the left piece moves closer to the origin. Ax + y x = 0 for A =,, 0.5, 0, -0.5, - hyperbolas (A < 0) 3 x parabola (A = 0) ellipses (A > 0) A picture of the parameter line and the behaviors for various values of A: A EW hyperbolas parabola EW ellipses circle NS ellipses
The point (x, y) lies on the circle of radius r and center (h, k) iff. x h y k r
 NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 2 4 x 0
 Pre-Calculus Section 1.1 Completing the Square Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 4 x 0. 3x 3y
Pre-Calculus Section 1.1 Completing the Square Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 4 x 0. 3x 3y
Conic Sections. College Algebra
 Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS
 CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS Big IDEAS: 1) Writing equations of conic sections ) Graphing equations of conic sections 3) Solving quadratic systems Section: Essential Question 8-1 Apply
CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS Big IDEAS: 1) Writing equations of conic sections ) Graphing equations of conic sections 3) Solving quadratic systems Section: Essential Question 8-1 Apply
Algebra II. Slide 1 / 181. Slide 2 / 181. Slide 3 / 181. Conic Sections Table of Contents
 Slide 1 / 181 Algebra II Slide 2 / 181 Conic Sections 2015-04-21 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 181 Review of Midpoint and Distance Formulas Introduction
Slide 1 / 181 Algebra II Slide 2 / 181 Conic Sections 2015-04-21 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 181 Review of Midpoint and Distance Formulas Introduction
Pre-Calculus Guided Notes: Chapter 10 Conics. A circle is
 Name: Pre-Calculus Guided Notes: Chapter 10 Conics Section Circles A circle is _ Example 1 Write an equation for the circle with center (3, ) and radius 5. To do this, we ll need the x1 y y1 distance formula:
Name: Pre-Calculus Guided Notes: Chapter 10 Conics Section Circles A circle is _ Example 1 Write an equation for the circle with center (3, ) and radius 5. To do this, we ll need the x1 y y1 distance formula:
Chapter 10. Exploring Conic Sections
 Chapter 10 Exploring Conic Sections Conics A conic section is a curve formed by the intersection of a plane and a hollow cone. Each of these shapes are made by slicing the cone and observing the shape
Chapter 10 Exploring Conic Sections Conics A conic section is a curve formed by the intersection of a plane and a hollow cone. Each of these shapes are made by slicing the cone and observing the shape
Multivariable Calculus
 Multivariable Calculus Chapter 10 Topics in Analytic Geometry (Optional) 1. Inclination of a line p. 5. Circles p. 4 9. Determining Conic Type p. 13. Angle between lines p. 6. Parabolas p. 5 10. Rotation
Multivariable Calculus Chapter 10 Topics in Analytic Geometry (Optional) 1. Inclination of a line p. 5. Circles p. 4 9. Determining Conic Type p. 13. Angle between lines p. 6. Parabolas p. 5 10. Rotation
We start by looking at a double cone. Think of this as two pointy ice cream cones that are connected at the small tips:
 Math 1330 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text. We start
Math 1330 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text. We start
Unit 12 Topics in Analytic Geometry - Classwork
 Unit 1 Topics in Analytic Geometry - Classwork Back in Unit 7, we delved into the algebra and geometry of lines. We showed that lines can be written in several forms: a) the general form: Ax + By + C =
Unit 1 Topics in Analytic Geometry - Classwork Back in Unit 7, we delved into the algebra and geometry of lines. We showed that lines can be written in several forms: a) the general form: Ax + By + C =
, minor axis of length 12. , asymptotes y 2x. 16y
 Math 4 Midterm 1 Review CONICS [1] Find the equations of the following conics. If the equation corresponds to a circle find its center & radius. If the equation corresponds to a parabola find its focus
Math 4 Midterm 1 Review CONICS [1] Find the equations of the following conics. If the equation corresponds to a circle find its center & radius. If the equation corresponds to a parabola find its focus
Ex. 1-3: Put each circle below in the correct equation form as listed!! above, then determine the center and radius of each circle.
 Day 1 Conics - Circles Equation of a Circle The circle with center (h, k) and radius r is the set of all points (x, y) that satisfies!! (x h) 2 + (y k) 2 = r 2 Ex. 1-3: Put each circle below in the correct
Day 1 Conics - Circles Equation of a Circle The circle with center (h, k) and radius r is the set of all points (x, y) that satisfies!! (x h) 2 + (y k) 2 = r 2 Ex. 1-3: Put each circle below in the correct
ALGEBRA II UNIT X: Conic Sections Unit Notes Packet
 Name: Period: ALGEBRA II UNIT X: Conic Sections Unit Notes Packet Algebra II Unit 10 Plan: This plan is subject to change at the teacher s discretion. Section Topic Formative Work Due Date 10.3 Circles
Name: Period: ALGEBRA II UNIT X: Conic Sections Unit Notes Packet Algebra II Unit 10 Plan: This plan is subject to change at the teacher s discretion. Section Topic Formative Work Due Date 10.3 Circles
Summary of Formulas: see
 To review the Conic Sections, Identify them and sketch them from the given equations, watch the following set of YouTube videos. They are followed by several practice problems for you to try, covering
To review the Conic Sections, Identify them and sketch them from the given equations, watch the following set of YouTube videos. They are followed by several practice problems for you to try, covering
Standard Equation of a Circle
 Math 335 Trigonometry Conics We will study all 4 types of conic sections, which are curves that result from the intersection of a right circular cone and a plane that does not contain the vertex. (If the
Math 335 Trigonometry Conics We will study all 4 types of conic sections, which are curves that result from the intersection of a right circular cone and a plane that does not contain the vertex. (If the
Geometry: Conic Sections
 Conic Sections Introduction When a right circular cone is intersected by a plane, as in figure 1 below, a family of four types of curves results. Because of their relationship to the cone, they are called
Conic Sections Introduction When a right circular cone is intersected by a plane, as in figure 1 below, a family of four types of curves results. Because of their relationship to the cone, they are called
Algebra II. Midpoint and Distance Formula. Slide 1 / 181 Slide 2 / 181. Slide 3 / 181. Slide 4 / 181. Slide 6 / 181. Slide 5 / 181.
 Slide 1 / 181 Slide 2 / 181 lgebra II onic Sections 2015-04-21 www.njctl.org Slide 3 / 181 Slide 4 / 181 Table of ontents click on the topic to go to that section Review of Midpoint and istance Formulas
Slide 1 / 181 Slide 2 / 181 lgebra II onic Sections 2015-04-21 www.njctl.org Slide 3 / 181 Slide 4 / 181 Table of ontents click on the topic to go to that section Review of Midpoint and istance Formulas
Chapter 11. Parametric Equations And Polar Coordinates
 Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
Mid-Chapter Quiz: Lessons 7-1 through 7-3
 Write an equation for and graph a parabola with the given focus F and vertex V 1. F(1, 5), V(1, 3) Because the focus and vertex share the same x coordinate, the graph is vertical. The focus is (h, k +
Write an equation for and graph a parabola with the given focus F and vertex V 1. F(1, 5), V(1, 3) Because the focus and vertex share the same x coordinate, the graph is vertical. The focus is (h, k +
Substituting a 2 b 2 for c 2 and using a little algebra, we can then derive the standard equation for an ellipse centred at the origin,
 Conics onic sections are the curves which result from the intersection of a plane with a cone. These curves were studied and revered by the ancient Greeks, and were written about extensively by both Euclid
Conics onic sections are the curves which result from the intersection of a plane with a cone. These curves were studied and revered by the ancient Greeks, and were written about extensively by both Euclid
Unit 8, Ongoing Activity, Little Black Book of Algebra II Properties
 Unit 8, Ongoing Activity, Little Black Book of Algebra II Properties Little Black Book of Algebra II Properties Unit 8 Conic Sections 8.1 Circle write the definition, provide examples of both the standard
Unit 8, Ongoing Activity, Little Black Book of Algebra II Properties Little Black Book of Algebra II Properties Unit 8 Conic Sections 8.1 Circle write the definition, provide examples of both the standard
Math 155, Lecture Notes- Bonds
 Math 155, Lecture Notes- Bonds Name Section 10.1 Conics and Calculus In this section, we will study conic sections from a few different perspectives. We will consider the geometry-based idea that conics
Math 155, Lecture Notes- Bonds Name Section 10.1 Conics and Calculus In this section, we will study conic sections from a few different perspectives. We will consider the geometry-based idea that conics
Algebra II Lesson 10-5: Hyperbolas Mrs. Snow, Instructor
 Algebra II Lesson 10-5: Hyperbolas Mrs. Snow, Instructor In this section, we will look at the hyperbola. A hyperbola is a set of points P in a plane such that the absolute value of the difference between
Algebra II Lesson 10-5: Hyperbolas Mrs. Snow, Instructor In this section, we will look at the hyperbola. A hyperbola is a set of points P in a plane such that the absolute value of the difference between
Accelerated Pre-Calculus Unit 1 Task 1: Our Only Focus: Circles & Parabolas Review
 Accelerated Pre-Calculus Unit 1 Task 1: Our Only Focus: Circles & Parabolas Review Name: Date: Period: For most students, you last learned about conic sections in Analytic Geometry, which was a while ago.
Accelerated Pre-Calculus Unit 1 Task 1: Our Only Focus: Circles & Parabolas Review Name: Date: Period: For most students, you last learned about conic sections in Analytic Geometry, which was a while ago.
1.) Write the equation of a circle in standard form with radius 3 and center (-3,4). Then graph the circle.
 Welcome to the world of conic sections! http://www.youtube.com/watch?v=bfonicn4bbg Some examples of conics in the real world: Parabolas Ellipse Hyperbola Your Assignment: Circle -Find at least four pictures
Welcome to the world of conic sections! http://www.youtube.com/watch?v=bfonicn4bbg Some examples of conics in the real world: Parabolas Ellipse Hyperbola Your Assignment: Circle -Find at least four pictures
Name. Center axis. Introduction to Conic Sections
 Name Introduction to Conic Sections Center axis This introduction to conic sections is going to focus on what they some of the skills needed to work with their equations and graphs. year, we will only
Name Introduction to Conic Sections Center axis This introduction to conic sections is going to focus on what they some of the skills needed to work with their equations and graphs. year, we will only
Pre-Calculus. 2) Find the equation of the circle having (2, 5) and (-2, -1) as endpoints of the diameter.
 Pre-Calculus Conic Review Name Block Date Circles: 1) Determine the center and radius of each circle. a) ( x 5) + ( y + 6) = 11 b) x y x y + 6 + 16 + 56 = 0 ) Find the equation of the circle having (,
Pre-Calculus Conic Review Name Block Date Circles: 1) Determine the center and radius of each circle. a) ( x 5) + ( y + 6) = 11 b) x y x y + 6 + 16 + 56 = 0 ) Find the equation of the circle having (,
Assignment Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Assignment.1-.3 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. 1) The arch beneath a bridge is semi-elliptical, a one-way
Assignment.1-.3 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. 1) The arch beneath a bridge is semi-elliptical, a one-way
KEMATH1 Calculus for Chemistry and Biochemistry Students. Francis Joseph H. Campeña, De La Salle University Manila
 KEMATH1 Calculus for Chemistry and Biochemistry Students Francis Joseph H Campeña, De La Salle University Manila January 26, 2015 Contents 1 Conic Sections 2 11 A review of the coordinate system 2 12 Conic
KEMATH1 Calculus for Chemistry and Biochemistry Students Francis Joseph H Campeña, De La Salle University Manila January 26, 2015 Contents 1 Conic Sections 2 11 A review of the coordinate system 2 12 Conic
13.1 2/20/2018. Conic Sections. Conic Sections: Parabolas and Circles
 13 Conic Sections 13.1 Conic Sections: Parabolas and Circles 13.2 Conic Sections: Ellipses 13.3 Conic Sections: Hyperbolas 13.4 Nonlinear Systems of Equations 13.1 Conic Sections: Parabolas and Circles
13 Conic Sections 13.1 Conic Sections: Parabolas and Circles 13.2 Conic Sections: Ellipses 13.3 Conic Sections: Hyperbolas 13.4 Nonlinear Systems of Equations 13.1 Conic Sections: Parabolas and Circles
Figures adapted from Mathworld.wolfram.com and vectosite.net.
 MTH 11 CONIC SECTIONS 1 The four basic types of conic sections we will discuss are: circles, parabolas, ellipses, and hyperbolas. They were named conic by the Greeks who used them to describe the intersection
MTH 11 CONIC SECTIONS 1 The four basic types of conic sections we will discuss are: circles, parabolas, ellipses, and hyperbolas. They were named conic by the Greeks who used them to describe the intersection
9.3 Hyperbolas and Rotation of Conics
 9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
Conic Sections: Parabolas
 Conic Sections: Parabolas Why are the graphs of parabolas, ellipses, and hyperbolas called 'conic sections'? Because if you pass a plane through a double cone, the intersection of the plane and the cone
Conic Sections: Parabolas Why are the graphs of parabolas, ellipses, and hyperbolas called 'conic sections'? Because if you pass a plane through a double cone, the intersection of the plane and the cone
PreCalculus Chapter 9 Practice Test Name:
 This ellipse has foci 0,, and therefore has a vertical major axis. The standard form for an ellipse with a vertical major axis is: 1 Note: graphs of conic sections for problems 1 to 1 were made with the
This ellipse has foci 0,, and therefore has a vertical major axis. The standard form for an ellipse with a vertical major axis is: 1 Note: graphs of conic sections for problems 1 to 1 were made with the
Assignment 3/17/15. Section 10.2(p 568) 2 12 (E) (E)
 Section 10.2 Warm Up Assignment 3/17/15 Section 10.2(p 568) 2 12 (E) 24 40 (E) Objective We are going to find equations for parabolas identify the vertex, focus, and directrix of a parabola The parabola
Section 10.2 Warm Up Assignment 3/17/15 Section 10.2(p 568) 2 12 (E) 24 40 (E) Objective We are going to find equations for parabolas identify the vertex, focus, and directrix of a parabola The parabola
Chapter 10 Test Review
 Name: Class: Date: Chapter 10 Test Review Short Answer 1. Write an equation of a parabola with a vertex at the origin and a focus at ( 2, 0). 2. Write an equation of a parabola with a vertex at the origin
Name: Class: Date: Chapter 10 Test Review Short Answer 1. Write an equation of a parabola with a vertex at the origin and a focus at ( 2, 0). 2. Write an equation of a parabola with a vertex at the origin
Chapter 9 Topics in Analytic Geometry
 Chapter 9 Topics in Analytic Geometry What You ll Learn: 9.1 Introduction to Conics: Parabolas 9.2 Ellipses 9.3 Hyperbolas 9.5 Parametric Equations 9.6 Polar Coordinates 9.7 Graphs of Polar Equations 9.1
Chapter 9 Topics in Analytic Geometry What You ll Learn: 9.1 Introduction to Conics: Parabolas 9.2 Ellipses 9.3 Hyperbolas 9.5 Parametric Equations 9.6 Polar Coordinates 9.7 Graphs of Polar Equations 9.1
MATH 110 analytic geometry Conics. The Parabola
 1 MATH 11 analytic geometry Conics The graph of a second-degree equation in the coordinates x and y is called a conic section or, more simply, a conic. This designation derives from the fact that the curve
1 MATH 11 analytic geometry Conics The graph of a second-degree equation in the coordinates x and y is called a conic section or, more simply, a conic. This designation derives from the fact that the curve
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 Pre-Calculus Mid Term Review. January 2014 Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Use the graph of the function f, plotted with a solid
Pre-Calculus Mid Term Review. January 2014 Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Use the graph of the function f, plotted with a solid
7. r = r = r = r = r = 2 5
 Exercise a: I. Write the equation in standard form of each circle with its center at the origin and the given radius.. r = 4. r = 6 3. r = 7 r = 5 5. r = 6. r = 6 7. r = 0.3 8. r =.5 9. r = 4 0. r = 3.
Exercise a: I. Write the equation in standard form of each circle with its center at the origin and the given radius.. r = 4. r = 6 3. r = 7 r = 5 5. r = 6. r = 6 7. r = 0.3 8. r =.5 9. r = 4 0. r = 3.
Warm-Up. Write the standard equation of the circle with the given radius and center. 1) 9; (0,0) 2) 1; (0,5) 3) 4; (-8,-1) 4) 5; (4,2)
 Warm-Up Write the standard equation of the circle with the given radius and center. 1) 9; (0,0) ) 1; (0,5) 3) 4; (-8,-1) 4) 5; (4,) 8.4 Graph and Write Equations of Ellipses What are the major parts of
Warm-Up Write the standard equation of the circle with the given radius and center. 1) 9; (0,0) ) 1; (0,5) 3) 4; (-8,-1) 4) 5; (4,) 8.4 Graph and Write Equations of Ellipses What are the major parts of
Quadratic Functions. *These are all examples of polynomial functions.
 Look at: f(x) = 4x-7 f(x) = 3 f(x) = x 2 + 4 Quadratic Functions *These are all examples of polynomial functions. Definition: Let n be a nonnegative integer and let a n, a n 1,..., a 2, a 1, a 0 be real
Look at: f(x) = 4x-7 f(x) = 3 f(x) = x 2 + 4 Quadratic Functions *These are all examples of polynomial functions. Definition: Let n be a nonnegative integer and let a n, a n 1,..., a 2, a 1, a 0 be real
Algebra II Chapter 10 Conics Notes Packet. Student Name Teacher Name
 Algebra II Chapter 10 Conics Notes Packet Student Name Teacher Name 1 Conic Sections 2 Identifying Conics Ave both variables squared?' No PARABOLA y = a(x- h)z + k x = a(y- k)z + h YEs Put l'h squared!'erms
Algebra II Chapter 10 Conics Notes Packet Student Name Teacher Name 1 Conic Sections 2 Identifying Conics Ave both variables squared?' No PARABOLA y = a(x- h)z + k x = a(y- k)z + h YEs Put l'h squared!'erms
What you will learn today
 What you will learn today Conic Sections (in 2D coordinates) Cylinders (3D) Quadric Surfaces (3D) Vectors and the Geometry of Space 1/24 Parabolas ellipses Hyperbolas Shifted Conics Conic sections result
What you will learn today Conic Sections (in 2D coordinates) Cylinders (3D) Quadric Surfaces (3D) Vectors and the Geometry of Space 1/24 Parabolas ellipses Hyperbolas Shifted Conics Conic sections result
1. Answer: x or x. Explanation Set up the two equations, then solve each equation. x. Check
 Thinkwell s Placement Test 5 Answer Key If you answered 7 or more Test 5 questions correctly, we recommend Thinkwell's Algebra. If you answered fewer than 7 Test 5 questions correctly, we recommend Thinkwell's
Thinkwell s Placement Test 5 Answer Key If you answered 7 or more Test 5 questions correctly, we recommend Thinkwell's Algebra. If you answered fewer than 7 Test 5 questions correctly, we recommend Thinkwell's
2.) Write the standard form of the equation of a circle whose endpoints of diameter are (4, 7) and (2,3).
 Ch 10: Conic Sections Name: Objectives: Students will be able to: -graph parabolas, hyperbolas and ellipses and answer characteristic questions about these graphs. -write equations of conic sections Dec
Ch 10: Conic Sections Name: Objectives: Students will be able to: -graph parabolas, hyperbolas and ellipses and answer characteristic questions about these graphs. -write equations of conic sections Dec
Exploring Quadratic Graphs
 Exploring Quadratic Graphs The general quadratic function is y=ax 2 +bx+c It has one of two basic graphs shapes, as shown below: It is a symmetrical "U"-shape or "hump"-shape, depending on the sign of
Exploring Quadratic Graphs The general quadratic function is y=ax 2 +bx+c It has one of two basic graphs shapes, as shown below: It is a symmetrical "U"-shape or "hump"-shape, depending on the sign of
Name: Date: 1. Match the equation with its graph. Page 1
 Name: Date: 1. Match the equation with its graph. y 6x A) C) Page 1 D) E) Page . Match the equation with its graph. ( x3) ( y3) A) C) Page 3 D) E) Page 4 3. Match the equation with its graph. ( x ) y 1
Name: Date: 1. Match the equation with its graph. y 6x A) C) Page 1 D) E) Page . Match the equation with its graph. ( x3) ( y3) A) C) Page 3 D) E) Page 4 3. Match the equation with its graph. ( x ) y 1
UNIT 3 EXPRESSIONS AND EQUATIONS Lesson 3: Creating Quadratic Equations in Two or More Variables
 Guided Practice Example 1 Find the y-intercept and vertex of the function f(x) = 2x 2 + x + 3. Determine whether the vertex is a minimum or maximum point on the graph. 1. Determine the y-intercept. The
Guided Practice Example 1 Find the y-intercept and vertex of the function f(x) = 2x 2 + x + 3. Determine whether the vertex is a minimum or maximum point on the graph. 1. Determine the y-intercept. The
Name: Class: Date: Conics Multiple Choice Pre-Test. Multiple Choice Identify the choice that best completes the statement or answers the question.
 Name: Class: Date: Conics Multiple Choice Pre-Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1 Graph the equation x 2 + y 2 = 36. Then describe the
Name: Class: Date: Conics Multiple Choice Pre-Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1 Graph the equation x 2 + y 2 = 36. Then describe the
Conics. By: Maya, Dietrich, and Jesse
 Conics By: Maya, Dietrich, and Jesse Exploring Conics (This is basically the summary too) A conic section curve formed by intersection of a plane and double cone: by changing plane, one can create parabola,
Conics By: Maya, Dietrich, and Jesse Exploring Conics (This is basically the summary too) A conic section curve formed by intersection of a plane and double cone: by changing plane, one can create parabola,
Chapter 8.1 Conic Sections/Parabolas. Honors Pre-Calculus Rogers High School
 Chapter 8.1 Conic Sections/Parabolas Honors Pre-Calculus Rogers High School Introduction to Conic Sections Conic sections are defined geometrically as the result of the intersection of a plane with a right
Chapter 8.1 Conic Sections/Parabolas Honors Pre-Calculus Rogers High School Introduction to Conic Sections Conic sections are defined geometrically as the result of the intersection of a plane with a right
P.5 Rational Expressions
 P.5 Rational Expressions I Domain Domain: Rational expressions : Finding domain a. polynomials: b. Radicals: keep it real! i. sqrt(x-2) x>=2 [2, inf) ii. cubert(x-2) all reals since cube rootscan be positive
P.5 Rational Expressions I Domain Domain: Rational expressions : Finding domain a. polynomials: b. Radicals: keep it real! i. sqrt(x-2) x>=2 [2, inf) ii. cubert(x-2) all reals since cube rootscan be positive
8.2 Graph and Write Equations of Parabolas
 8.2 Graph and Write Equations of Parabolas Where is the focus and directrix compared to the vertex? How do you know what direction a parabola opens? How do you write the equation of a parabola given the
8.2 Graph and Write Equations of Parabolas Where is the focus and directrix compared to the vertex? How do you know what direction a parabola opens? How do you write the equation of a parabola given the
) 2 + (y 2. x 1. y c x2 = y
 Graphing Parabola Parabolas A parabola is a set of points P whose distance from a fixed point, called the focus, is equal to the perpendicular distance from P to a line, called the directrix. Since this
Graphing Parabola Parabolas A parabola is a set of points P whose distance from a fixed point, called the focus, is equal to the perpendicular distance from P to a line, called the directrix. Since this
Chapter 10. Homework
 Chapter 0 Homework Lesson 0- pages 538 5 Exercises. 2. Hyperbola: center (0, 0), y-intercepts at ±, no x-intercepts, the lines of symmetry are the x- and y-axes; domain: all real numbers, range: y 5 3
Chapter 0 Homework Lesson 0- pages 538 5 Exercises. 2. Hyperbola: center (0, 0), y-intercepts at ±, no x-intercepts, the lines of symmetry are the x- and y-axes; domain: all real numbers, range: y 5 3
Section 7.2 Characteristics of Quadratic Functions
 Section 7. Characteristics of Quadratic Functions A QUADRATIC FUNCTION is a function of the form " # $ N# 1 & ;# & 0 Characteristics Include:! Three distinct terms each with its own coefficient:! An x
Section 7. Characteristics of Quadratic Functions A QUADRATIC FUNCTION is a function of the form " # $ N# 1 & ;# & 0 Characteristics Include:! Three distinct terms each with its own coefficient:! An x
Look up partial Decomposition to use for problems #65-67 Do Not solve problems #78,79
 Franklin Township Summer Assignment 2017 AP calculus AB Summer assignment Students should use the Mathematics summer assignment to identify subject areas that need attention in preparation for the study
Franklin Township Summer Assignment 2017 AP calculus AB Summer assignment Students should use the Mathematics summer assignment to identify subject areas that need attention in preparation for the study
Graphing Techniques. Domain (, ) Range (, ) Squaring Function f(x) = x 2 Domain (, ) Range [, ) f( x) = x 2
 Graphing Techniques In this chapter, we will take our knowledge of graphs of basic functions and expand our ability to graph polynomial and rational functions using common sense, zeros, y-intercepts, stretching
Graphing Techniques In this chapter, we will take our knowledge of graphs of basic functions and expand our ability to graph polynomial and rational functions using common sense, zeros, y-intercepts, stretching
MATH 1020 WORKSHEET 10.1 Parametric Equations
 MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
We start by looking at a double cone. Think of this as two pointy ice cream cones that are connected at the small tips:
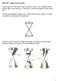 Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Study Guide and Review
 Graph the hyperbola given by each equation. 30. = 1 The equation is in standard form, and h = 6 and k = 3. Because a 2 = 30 and b 2 = 8, a = 5.5 and b =. The values of a and b can be used to find c. c
Graph the hyperbola given by each equation. 30. = 1 The equation is in standard form, and h = 6 and k = 3. Because a 2 = 30 and b 2 = 8, a = 5.5 and b =. The values of a and b can be used to find c. c
A function: A mathematical relationship between two variables (x and y), where every input value (usually x) has one output value (usually y)
 SESSION 9: FUNCTIONS KEY CONCEPTS: Definitions & Terminology Graphs of Functions - Straight line - Parabola - Hyperbola - Exponential Sketching graphs Finding Equations Combinations of graphs TERMINOLOGY
SESSION 9: FUNCTIONS KEY CONCEPTS: Definitions & Terminology Graphs of Functions - Straight line - Parabola - Hyperbola - Exponential Sketching graphs Finding Equations Combinations of graphs TERMINOLOGY
MATHS METHODS QUADRATICS REVIEW. A reminder of some of the laws of expansion, which in reverse are a quick reference for rules of factorisation
 MATHS METHODS QUADRATICS REVIEW LAWS OF EXPANSION A reminder of some of the laws of expansion, which in reverse are a quick reference for rules of factorisation a) b) c) d) e) FACTORISING Exercise 4A Q6ace,7acegi
MATHS METHODS QUADRATICS REVIEW LAWS OF EXPANSION A reminder of some of the laws of expansion, which in reverse are a quick reference for rules of factorisation a) b) c) d) e) FACTORISING Exercise 4A Q6ace,7acegi
Unit 5: Quadratic Functions
 Unit 5: Quadratic Functions LESSON #5: THE PARABOLA GEOMETRIC DEFINITION DIRECTRIX FOCUS LATUS RECTUM Geometric Definition of a Parabola Quadratic Functions Geometrically, a parabola is the set of all
Unit 5: Quadratic Functions LESSON #5: THE PARABOLA GEOMETRIC DEFINITION DIRECTRIX FOCUS LATUS RECTUM Geometric Definition of a Parabola Quadratic Functions Geometrically, a parabola is the set of all
Chapter. Implicit Function Graphs
 Chapter 14 Implicit Function Graphs You can graph any one of the following types of implicit functions using the calculator s built-in functions. Parabolic graph Circle graph Elliptical graph Hyperbolic
Chapter 14 Implicit Function Graphs You can graph any one of the following types of implicit functions using the calculator s built-in functions. Parabolic graph Circle graph Elliptical graph Hyperbolic
Conic Sections and Analytic Geometry
 Chapter 9 Conic Sections and Analytic Geometry Chapter 9 Conic Sections and Analytic Geometry 9.1 The Ellipse 9.2 The Hyperbola 9.3 The Parabola 9.4 Rotation of Axes 9.5 Parametric Equations 9.6 Conic
Chapter 9 Conic Sections and Analytic Geometry Chapter 9 Conic Sections and Analytic Geometry 9.1 The Ellipse 9.2 The Hyperbola 9.3 The Parabola 9.4 Rotation of Axes 9.5 Parametric Equations 9.6 Conic
CK 12 Algebra II with Trigonometry Concepts 1
 10.1 Parabolas with Vertex at the Origin Answers 1. up 2. left 3. down 4.focus: (0, 0.5), directrix: y = 0.5 5.focus: (0.0625, 0), directrix: x = 0.0625 6.focus: ( 1.25, 0), directrix: x = 1.25 7.focus:
10.1 Parabolas with Vertex at the Origin Answers 1. up 2. left 3. down 4.focus: (0, 0.5), directrix: y = 0.5 5.focus: (0.0625, 0), directrix: x = 0.0625 6.focus: ( 1.25, 0), directrix: x = 1.25 7.focus:
= ( )= To find the domain, we look at the vertical asymptote(s) (where denominator equals zero) , =0
 Precalculus College Algebra Review for Final Name It is also a good idea to go back through your old tests and quizzes to review. 1. Find (+1) given ()=3 +1 2. Determine () given ()=+2 and ()= (+1)=3(+1)
Precalculus College Algebra Review for Final Name It is also a good idea to go back through your old tests and quizzes to review. 1. Find (+1) given ()=3 +1 2. Determine () given ()=+2 and ()= (+1)=3(+1)
Practice Test - Chapter 7
 Write an equation for an ellipse with each set of characteristics. 1. vertices (7, 4), ( 3, 4); foci (6, 4), ( 2, 4) The distance between the vertices is 2a. 2a = 7 ( 3) a = 5; a 2 = 25 The distance between
Write an equation for an ellipse with each set of characteristics. 1. vertices (7, 4), ( 3, 4); foci (6, 4), ( 2, 4) The distance between the vertices is 2a. 2a = 7 ( 3) a = 5; a 2 = 25 The distance between
Pure Math 30: Explained!
 www.puremath30.com 5 Conics Lesson Part I - Circles Circles: The standard form of a circle is given by the equation (x - h) +(y - k) = r, where (h, k) is the centre of the circle and r is the radius. Example
www.puremath30.com 5 Conics Lesson Part I - Circles Circles: The standard form of a circle is given by the equation (x - h) +(y - k) = r, where (h, k) is the centre of the circle and r is the radius. Example
3.1 INTRODUCTION TO THE FAMILY OF QUADRATIC FUNCTIONS
 3.1 INTRODUCTION TO THE FAMILY OF QUADRATIC FUNCTIONS Finding the Zeros of a Quadratic Function Examples 1 and and more Find the zeros of f(x) = x x 6. Solution by Factoring f(x) = x x 6 = (x 3)(x + )
3.1 INTRODUCTION TO THE FAMILY OF QUADRATIC FUNCTIONS Finding the Zeros of a Quadratic Function Examples 1 and and more Find the zeros of f(x) = x x 6. Solution by Factoring f(x) = x x 6 = (x 3)(x + )
x y 2 2 CONIC SECTIONS Problem 1
 CONIC SECTIONS Problem For the equations below, identify each conic section If it s a parabola, specify its vertex, focus and directrix If it s an ellipse, specify its center, vertices and foci If it s
CONIC SECTIONS Problem For the equations below, identify each conic section If it s a parabola, specify its vertex, focus and directrix If it s an ellipse, specify its center, vertices and foci If it s
3. Solve the following. Round to the nearest thousandth.
 This review does NOT cover everything! Be sure to go over all notes, homework, and tests that were given throughout the semester. 1. Given g ( x) i, h( x) x 4x x, f ( x) x, evaluate the following: a) f
This review does NOT cover everything! Be sure to go over all notes, homework, and tests that were given throughout the semester. 1. Given g ( x) i, h( x) x 4x x, f ( x) x, evaluate the following: a) f
Conic Sections. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Conic Sections MATH 211, Calculus II J. Robert Buchanan Department o Mathematics Spring 2018 Introduction The conic sections include the parabola, the ellipse, and the hyperbola. y y y x x x Parabola A
Conic Sections MATH 211, Calculus II J. Robert Buchanan Department o Mathematics Spring 2018 Introduction The conic sections include the parabola, the ellipse, and the hyperbola. y y y x x x Parabola A
Section 4.4: Parabolas
 Objective: Graph parabolas using the vertex, x-intercepts, and y-intercept. Just as the graph of a linear equation y mx b can be drawn, the graph of a quadratic equation y ax bx c can be drawn. The graph
Objective: Graph parabolas using the vertex, x-intercepts, and y-intercept. Just as the graph of a linear equation y mx b can be drawn, the graph of a quadratic equation y ax bx c can be drawn. The graph
Math 125 Little Book Homework Chapters 7, 10, 11, and 12
 Math 125 Little Book Homework Chapters 7, 10, 11, and 12 Do NOT copy the book follow the guidelines given for each section. NO CREDIT will be given if you copy the book! You earn 2 points if you turn in
Math 125 Little Book Homework Chapters 7, 10, 11, and 12 Do NOT copy the book follow the guidelines given for each section. NO CREDIT will be given if you copy the book! You earn 2 points if you turn in
Math 2 Coordinate Geometry Part 3 Inequalities & Quadratics
 Math 2 Coordinate Geometry Part 3 Inequalities & Quadratics 1 DISTANCE BETWEEN TWO POINTS - REVIEW To find the distance between two points, use the Pythagorean theorem. The difference between x 1 and x
Math 2 Coordinate Geometry Part 3 Inequalities & Quadratics 1 DISTANCE BETWEEN TWO POINTS - REVIEW To find the distance between two points, use the Pythagorean theorem. The difference between x 1 and x
Preview Notes. Systems of Equations. Linear Functions. Let y = y. Solve for x then solve for y
 Preview Notes Linear Functions A linear function is a straight line that has a slope (m) and a y-intercept (b). Systems of Equations 1. Comparison Method Let y = y x1 y1 x2 y2 Solve for x then solve for
Preview Notes Linear Functions A linear function is a straight line that has a slope (m) and a y-intercept (b). Systems of Equations 1. Comparison Method Let y = y x1 y1 x2 y2 Solve for x then solve for
Z+z 1 X2 Y2. or y, Graph / 4 25 jj y=±x. x2+y 2=
 Conic Sections Understanding the graphs of conic sections is made easier if you first begin with the simplest form of a conic section. These would be the graphs that are centered at the origin. If we can
Conic Sections Understanding the graphs of conic sections is made easier if you first begin with the simplest form of a conic section. These would be the graphs that are centered at the origin. If we can
1.6 Quadric Surfaces Brief review of Conic Sections 74 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE. Figure 1.18: Parabola y = 2x 2
 7 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE Figure 1.18: Parabola y = x 1.6 Quadric Surfaces Figure 1.19: Parabola x = y 1.6.1 Brief review of Conic Sections You may need to review conic sections for
7 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE Figure 1.18: Parabola y = x 1.6 Quadric Surfaces Figure 1.19: Parabola x = y 1.6.1 Brief review of Conic Sections You may need to review conic sections for
3, 10,( 2, 4) Name. CP Algebra II Midterm Review Packet Unit 1: Linear Equations and Inequalities. Solve each equation. 3.
 Name CP Algebra II Midterm Review Packet 018-019 Unit 1: Linear Equations and Inequalities Solve each equation. 1. x. x 4( x 5) 6x. 8x 5(x 1) 5 4. ( k ) k 4 5. x 4 x 6 6. V lhw for h 7. x y b for x z Find
Name CP Algebra II Midterm Review Packet 018-019 Unit 1: Linear Equations and Inequalities Solve each equation. 1. x. x 4( x 5) 6x. 8x 5(x 1) 5 4. ( k ) k 4 5. x 4 x 6 6. V lhw for h 7. x y b for x z Find
Buds Public School, Dubai
 Buds Public School, Dubai Subject: Maths Grade: 11 AB Topic: Statistics, Probability, Trigonometry, 3D, Conic Section, Straight lines and Limits and Derivatives Statistics and Probability: 1. Find the
Buds Public School, Dubai Subject: Maths Grade: 11 AB Topic: Statistics, Probability, Trigonometry, 3D, Conic Section, Straight lines and Limits and Derivatives Statistics and Probability: 1. Find the
2.1 Quadraticsnts.notebook. September 10, 2018
 1 A quadratic function is a polynomial function of second degree. The graph of a quadratic function is called a parabola. 2 Standard Form: Intercept Form: Vertex Form: f(x) = a(x h) 2 + k vertex: (h, k)
1 A quadratic function is a polynomial function of second degree. The graph of a quadratic function is called a parabola. 2 Standard Form: Intercept Form: Vertex Form: f(x) = a(x h) 2 + k vertex: (h, k)
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Precalculus Fall 204 Midterm Review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find an equation in standard form for the hyperbola that
Precalculus Fall 204 Midterm Review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find an equation in standard form for the hyperbola that
Chapter 3: The Parabola
 Chapter 3: The Parabola SSMth1: Precalculus Science and Technology, Engineering and Mathematics (STEM) Mr. Migo M. Mendoza Chapter 3: The Parabola Lecture 7: Introduction to Parabola Lecture 8: Converting
Chapter 3: The Parabola SSMth1: Precalculus Science and Technology, Engineering and Mathematics (STEM) Mr. Migo M. Mendoza Chapter 3: The Parabola Lecture 7: Introduction to Parabola Lecture 8: Converting
Section 1.1 The Distance and Midpoint Formulas
 Section 1.1 The Distance and Midpoint Formulas 1 y axis origin x axis 2 Plot the points: ( 3, 5), (0,7), ( 6,0), (6,4) 3 Distance Formula y x 4 Finding the Distance Between Two Points Find the distance
Section 1.1 The Distance and Midpoint Formulas 1 y axis origin x axis 2 Plot the points: ( 3, 5), (0,7), ( 6,0), (6,4) 3 Distance Formula y x 4 Finding the Distance Between Two Points Find the distance
Put your initials on the top of every page, in case the pages become separated.
 Math 1201, Fall 2016 Name (print): Dr. Jo Nelson s Calculus III Practice for 1/2 of Final, Midterm 1 Material Time Limit: 90 minutes DO NOT OPEN THIS BOOKLET UNTIL INSTRUCTED TO DO SO. This exam contains
Math 1201, Fall 2016 Name (print): Dr. Jo Nelson s Calculus III Practice for 1/2 of Final, Midterm 1 Material Time Limit: 90 minutes DO NOT OPEN THIS BOOKLET UNTIL INSTRUCTED TO DO SO. This exam contains
Each point P in the xy-plane corresponds to an ordered pair (x, y) of real numbers called the coordinates of P.
 Lecture 7, Part I: Section 1.1 Rectangular Coordinates Rectangular or Cartesian coordinate system Pythagorean theorem Distance formula Midpoint formula Lecture 7, Part II: Section 1.2 Graph of Equations
Lecture 7, Part I: Section 1.1 Rectangular Coordinates Rectangular or Cartesian coordinate system Pythagorean theorem Distance formula Midpoint formula Lecture 7, Part II: Section 1.2 Graph of Equations
Slide 2 / 222. Algebra II. Quadratic Functions
 Slide 1 / 222 Slide 2 / 222 Algebra II Quadratic Functions 2014-10-14 www.njctl.org Slide 3 / 222 Table of Contents Key Terms Explain Characteristics of Quadratic Functions Combining Transformations (review)
Slide 1 / 222 Slide 2 / 222 Algebra II Quadratic Functions 2014-10-14 www.njctl.org Slide 3 / 222 Table of Contents Key Terms Explain Characteristics of Quadratic Functions Combining Transformations (review)
Today is the last day to register for CU Succeed account AND claim your account. Tuesday is the last day to register for my class
 Today is the last day to register for CU Succeed account AND claim your account. Tuesday is the last day to register for my class Back board says your name if you are on my roster. I need parent financial
Today is the last day to register for CU Succeed account AND claim your account. Tuesday is the last day to register for my class Back board says your name if you are on my roster. I need parent financial
CHAPTER 6 Quadratic Functions
 CHAPTER 6 Quadratic Functions Math 1201: Linear Functions is the linear term 3 is the leading coefficient 4 is the constant term Math 2201: Quadratic Functions Math 3201: Cubic, Quartic, Quintic Functions
CHAPTER 6 Quadratic Functions Math 1201: Linear Functions is the linear term 3 is the leading coefficient 4 is the constant term Math 2201: Quadratic Functions Math 3201: Cubic, Quartic, Quintic Functions
y 1 ) 2 Mathematically, we write {(x, y)/! y = 1 } is the graph of a parabola with 4c x2 focus F(0, C) and directrix with equation y = c.
 Ch. 10 Graphing Parabola Parabolas A parabola is a set of points P whose distance from a fixed point, called the focus, is equal to the perpendicular distance from P to a line, called the directrix. Since
Ch. 10 Graphing Parabola Parabolas A parabola is a set of points P whose distance from a fixed point, called the focus, is equal to the perpendicular distance from P to a line, called the directrix. Since
WHAT YOU SHOULD LEARN
 GRAPHS OF EQUATIONS WHAT YOU SHOULD LEARN Sketch graphs of equations. Find x- and y-intercepts of graphs of equations. Use symmetry to sketch graphs of equations. Find equations of and sketch graphs of
GRAPHS OF EQUATIONS WHAT YOU SHOULD LEARN Sketch graphs of equations. Find x- and y-intercepts of graphs of equations. Use symmetry to sketch graphs of equations. Find equations of and sketch graphs of
Walt Whitman High School SUMMER REVIEW PACKET. For students entering AP CALCULUS BC
 Walt Whitman High School SUMMER REVIEW PACKET For students entering AP CALCULUS BC Name: 1. This packet is to be handed in to your Calculus teacher on the first day of the school year.. All work must be
Walt Whitman High School SUMMER REVIEW PACKET For students entering AP CALCULUS BC Name: 1. This packet is to be handed in to your Calculus teacher on the first day of the school year.. All work must be
Planes Intersecting Cones: Static Hypertext Version
 Page 1 of 12 Planes Intersecting Cones: Static Hypertext Version On this page, we develop some of the details of the plane-slicing-cone picture discussed in the introduction. The relationship between the
Page 1 of 12 Planes Intersecting Cones: Static Hypertext Version On this page, we develop some of the details of the plane-slicing-cone picture discussed in the introduction. The relationship between the
Quadratic Functions CHAPTER. 1.1 Lots and Projectiles Introduction to Quadratic Functions p. 31
 CHAPTER Quadratic Functions Arches are used to support the weight of walls and ceilings in buildings. Arches were first used in architecture by the Mesopotamians over 4000 years ago. Later, the Romans
CHAPTER Quadratic Functions Arches are used to support the weight of walls and ceilings in buildings. Arches were first used in architecture by the Mesopotamians over 4000 years ago. Later, the Romans
Math 136 Exam 1 Practice Problems
 Math Exam Practice Problems. Find the surface area of the surface of revolution generated by revolving the curve given by around the x-axis? To solve this we use the equation: In this case this translates
Math Exam Practice Problems. Find the surface area of the surface of revolution generated by revolving the curve given by around the x-axis? To solve this we use the equation: In this case this translates
Chapter 10: Parametric And Polar Curves; Conic Sections
 206 Chapter 10: Parametric And Polar Curves; Conic Sections Summary: This chapter begins by introducing the idea of representing curves using parameters. These parametric equations of the curves can then
206 Chapter 10: Parametric And Polar Curves; Conic Sections Summary: This chapter begins by introducing the idea of representing curves using parameters. These parametric equations of the curves can then
Properties of Quadratic functions
 Name Today s Learning Goals: #1 How do we determine the axis of symmetry and vertex of a quadratic function? Properties of Quadratic functions Date 5-1 Properties of a Quadratic Function A quadratic equation
Name Today s Learning Goals: #1 How do we determine the axis of symmetry and vertex of a quadratic function? Properties of Quadratic functions Date 5-1 Properties of a Quadratic Function A quadratic equation
