A Comprehensive, Step-by-Step Tutorial on Computing Dubin s Curves. Andy Giese
|
|
|
- Alban Richard
- 5 years ago
- Views:
Transcription
1 A Comprehensive, Step-by-Step Tutorial on Computing Dubin s Curves Andy Giese October 1, 2012
2 Introduction Imagine you have a point, a single little dot on a piece of paper. What s the quickest way to go from that point to another point on the piece of paper? You sigh and answer A straight line because it s completely obvious; even first graders know that. Now let s imagine your have an open parking lot, with a human standing in it. What s the quickest way for the human to get from one side of the parking lot to the other? The answer is again obvious to you, so you get a little annoyed and half-shout A straight-line again, duh!. Okay, okay, enough toss-up questions. Now what if I gave you a car in the parking lot and asked you what was the quickest way for that car to get into a parking spot? Hmm, a little harder now. You can t say a straight line because what if the car isn t facing directly towards the parking space? Cars don t just slide horizontally and then turn in place, so planning for them seems to be a lot more difficult than for a human. But! We can make planning for a car just about as easy as for a human if we consider the car to be a special type of car we ll call a Dubin s Car. Interested in knowing how? Then read on! In robotics, we would consider our human from the example above to be a type of holonomic agent. Don t let this terminology scare you; I ll explain it all. A holonomic agent can simply be considered an agent who we have full control over. That is, if we treat the human as a point in the x-y plane, we are able to go from any coordinate to any other coordinate always. Humans 1
3 can turn on a dime, walk straight forward, side-step, walk backwards, etc. They really have full control over their coordinates. A car however, is not holonomic because we don t have full control over it at all times. Therefore we call a car a type of nonholonomic agent. Cars can only turn about some minimal radius circle, therefore they can t move straight towards a point just barely to their left or right. As you can imagine, planning paths for nonholonomic agents is much more difficult than for holonomic ones. Let s simplify our model of our car. How about this: it can only move forwards never backwards, and it s always moving at a unit velocity so we don t have to worry about braking or accelerating. What I just described is known as a Dubin s Car, and planning shortest paths for it is a well studied problem in robotics and control theory. What makes the Dubin s car attractive is that its shortest paths can be solved exactly using relatively simple geometry, whereas planning for many other dynamical systems requires some pretty high level and complicated matrix operations. The Dubin s Car was introduced into the literature by Lester Dubins, a famous mathematician and statistician, in a paper published in The cars essentially have only 3 controls: turn left at maximum, turn right at maximum, and go straight. All the paths traced out by the Dubin s car are combinations of these three controls. Let s name the controls: turn left at maximum will be L, turn right at maximum will be R, and go straight will be S. We can make things even more general: left and right turns both describe curves, so lets group them under a single category that we ll call C ( curve ). Lester Dubins proved in his paper that there are only 6 combinations of these controls that describe ALL the shortest paths, and they are: RSR, LSL, RSL, LSR, RLR, and LRL. Using our more general terminology, there s only two classes: CSC and CCC. Despite being relatively well studied, with all sorts of geometric proofs out there and qualitative statements about what the shortest paths look like, I could not find one single source on the internet that described in depth how to actually compute these shortest paths! So what that we know the car can try to turn left for some amount of time, then move straight, and then move right I want to know exactly how much I need to turn, and how long I need to turn for. And if you re like me in the least, you tend to forget some geometry that you learned in high school, so doing these computations isn t as trivial for you like all the other online sources make it out to be. If you re looking for the actual computations needed to compute these shortest paths, then you ve come to the right place. The following will be my longest article to-date, and is basically a how-to guide on computing the geometry required for the Dubin s shortest paths. 2
4 Overview Let sfirsttalkaboutthedynamicsofoursystem, andthendescribeingeneral terms what the shortest paths look like. Afterwards, I ll delve into the actual calculations. Car-like robots all have one thing in common they have a minimum turning radius. Think of this minimum turning radius as a circle next to the car that, try as it might, the robot can only go around the circle s circumference if it turns as hard as it can. The radius of this circle, r min is the car s minimum turning radius. This radius is determined by the physics of the car the maximum angle the tires can deviate from forward, and the car s wheelbase, or the length from the front axle to rear axle. Marco Monster has a really good descriptive article that talks about these car dynamics. Car Dynamics I already mentioned that the Dubin s car could only move forward at a unit velocity, and by forward I mean it can t change gears into reverse. Let s describe the vehicle dynamics more formally. A Car s configuration can be describe by the triplet x, y, θ. Define the car s velocity (actually speed, because it will be a scalar quantity) as v. When a car is moving at velocity v about a circle of radius r turn, it will have angular velocity ω = v r turn. Now let s define how our system evolves over time. If you know even just the basics of differential equations, this will be cake for you. If not, I ll explain. When we want to describe how our system evolves over time, we use notation like ẋ to talk about how our x coordinate changes over time. In basic vector math, if our car is at position A = (x 1,y 1 ) with θ = θ 1, and we move straight forward for a single timestep, then our new configuration is B = (x 1 +vcos(θ 1 ),y 1 +vsin(θ 1 ),θ 1 ) Note how our x coordinate changes as a function of cos(θ). Therefore, we d say that ẋ = cos(θ). A full system description would read like this: ẋ = cos(θ) ẏ = sin(θ) θ = ω = v r turn 3
5 I d like to point out that this equation is linear in that the car s new position is changing to be some straight line away from the previous one. In reality, this is not the case; cars are nonlinear systems. Therefore, the dynamics I described above are merely an approximation of the true system dynamics. Linear systems are much easier to handle, and if we do things right, they can approximate the true dynamics so well that you d never be able to tell the difference. The dynamics equations translate nicely into update equations. These update equations describe what actually happens each time you want to update the car s configuration. That is, if you re stepping through your simulator, at each timestep you d want to update the car. As the Dubin s car only has unit velocity, we ll replace all instances of v with 1. x new = x prev +δ cos(θ) y new = y prev +δ sin(θ) θ new = θ prev + δ r turn Note that I actually replaced instances of v with the symbol δ. What s with that? Well, remember when I said that our dynamics are a linear approximation of a nonlinear system? Every time we update, we are moving thecaralongaline. Ifweonlymove averyshort amountonthisline, thenwe approximate turnsmorefinely. Thinkofit thisway: Youaretrying todrawa circle using a series of evenly-spaced points. If you only use 3 points, you get a triangle. If you use 4 you get a square, and 8 you get an octagon. As you add more and more points you get something that more closely resembles the circle. This is the same concept. δ essentially tells us the amount of spacing between our points. If it is really small, then the points are close together and we get overall motion that looks closer to reality. High-level Description of Dubin s curves In this section I ll briefly go over what each of the 6 trajectories (RSR, LSR, RSL, LSR, RLR,LRL) lookslike. (Disclaimer: I do not claim to be an artist, and as such the figures you see that I drew in the following sections are NOT to scale; they serve to illustrate all the geometry being discussed.) CSC Trajectories The CSC trajectories include RSR, LSR, RSL, and LSR a turn followed by a straight line followed by another turn (Shown in Figure 1. 4
6 Pick a position and orientation for your start and goal configurations. Draw your start and goal configurations as points in the plane with arrows extending out in the direction the car is facing. Next, draw circles to the left and right of the car with radius r min. The circles should be tangent at the location of the car. Draw tangent lines from the circles at the starting configuration to the circles at the goal configuration. In the next section I ll discuss how to compute this, but for now just draw them. For each pair of circles (RR), (LL), (RL), (LR), there should be four possible tangent lines, but note that there is only one valid line for each pair (Shown in Figure 2. That is, for the RR circles, only one line extending from the agent s circle meets the goal s circle such that everything is going in the correct direction. Therefore, for any of the CSC Trajectories, there is a unique tangent line to follow. This tangent line makes up the S portion of the trajectory. The points at which the line is tangent to the circles are the points the agent must pass through to complete its trajectory. Therefore, solving these trajectories basically boils down to correctly computing these tangents. Figure 1: A RSR Trajectory CCC Trajectories CCC Trajectories are slightly different. They consist of a turn in one direction followed by a turn in the opposite direction, and then another turn in the original direction, like the RLR Trajectory shown in Figure 3. They are only valid when the agent and its goal are relatively close to each other, else one circle would need to have a radius larger than r min, and if we must do that, then the CCC Trajectory is sub-optimal. For the Dubin s Car there are only 2 CCC Trajectories: RLR and LRL. Computing the tangent lines between RR or LL circles won t help us this 5
7 Figure 2: Valid Tangent Lines time around. The third circle that we turn about is still tangent to the agent and goal turning circles, but these tangent points are not the same as those from tangent line calculations. Therefore, solving these trajectories boils down to correctly computing the location of this third tangent circle. Figure 3: A RLR Trajectory Tangent Line Construction In this section, I will discuss the geometry in constructing tangent lines between two circles. First I ll discuss how to do so geometrically, and then I ll show how to do so in a more efficient, vector-based manner. Given: two circles C 1 and C 2, with radii of r 1 and r 2 respectively. Consider the center of C 1 as p 1 = (x 1,y 1 ), the center of C 2 as p 2 = (x 2,y 2 ) and so on (Figure 4). 6
8 Figure 4: Setup for computing tangents Method 1: Geometrically computing tangents Inner tangents 1. First draw a vector V 1 from p 1 to p 2. V1 = (x 2 x 1,y 2 y 1 ). This vector has a magnitude of D = (x 2 x 1 ) 2 +(y 2 y 1 ) 2 2. Construct acirclec 3 centeredatthemidpoint ofv 1 withradiusr 3 = D. 2 That is, ( x1 +x 2 p 3 =, y ) 1 +y (Figure 5). Figure 5: Steps 1 and 2 7
9 3. Construct a circle C 4 centered at C 1 s center, with radius r 4 = r 1 +r 2 (Figure 6). Figure 6: Step 3 4. Construct a vector V 2 from p 1 to the top point, p t = (x t,y t ) of intersection between C 3 and C 4. If we can compute this vector, then we can get the first tangent point because V 2 is pointing at it in addition to p t. For visual reference, see Figure 7. Figure 7: Step 4 5. This is accomplished by first drawing a triangle from p 1 to p 3 to p t like the one shown in Figure 8. The segments p 1 p 3 and p 3 p t have magnitude r 4 = D 2. Thesegmentp 1p t hasmagnituder 3 = r 1 +r 2. Weareinterested in the angle γ = p t p 1 p 3 8
10 γ willgiveustheanglethatvector V 1 thatwouldneedtorotatethrough to point in the same direction as vector V 2 = (p t p 1 ) We obtain the full amount of rotation about the x axis, θ for V 2, by the equation θ = γ +atan2 ( V1 ) (Note: the atan2() function first takes the y-component, and then the x-component) p t is therefore obtained by traversing V 2 for a distance of r 4. That is, x t = x 1 +(r 1 +r 2 ) cos(θ) y t = y 1 +(r 1 +r 2 ) sin(θ) Figure 8: Step 5 6. To find the first inner tangent point p it1 on C 1, we follow a similar procedure to how we obtained p t we travel along V 2 from p 1, but we only go a distance of r 1. Because we know p t, we are now able to actually compute V 2 = (p t p 1 ). Now, we need to normalize V 2 and thenmultiply itbyr 1 toachieve avector V 3 top it1 fromp 1. (Remember that, to normalize a vector, you divide each element by the vector s magnitude V 3 = V 2 V 2 r 1. p it1 follows simply: p it1 = p 1 + V 3. It may be a bit of an abuse of notation to add a vector to a point, but when we add the components of the point to the components of the vector, we get our new point and everything works out. 9
11 7. Now that we have p t, we can draw a vector V 4 from p t to p 2 like in Figure 9. Note that this vector is parallel to an inner tangent between C 1 and C 2 V4 = (p 2 p t ). We can take advantage of its magnitude and direction to find aninner tangent point on C 2. Given that we ve already calculated p it1, getting its associated tangent point on C 2, p it2 is as easy as:. p it2 = p it1 + V 4 Figure 9: Step 7 I hope this is clear enough for you to be able to compute the other inner tangent point. The trick is to use the bottom intersection point between C 3 and C 4, and then work everything out exactly the same to get p it3 and p it4, which define the other inner tangent line. Outer tangents Constructing outer tangents is very similar to constructing the inner tangents. Given the same two circles C 1 and C 2 as before, and assuming r 1 r 2 Remember how we started off by making C 4 centered at p 1 with radius r 4 = r 1 + r 2? Well this time around we ll construct it a bit differently. C 4 is centered at p 1 as before, but this time it has radius r 4 = r 1 r 2 Follow the steps we performed for the interior tangent points, constructing C 3 on the midpoint of V 1 exactly the same as before. Find the intersection between C 3 and C 4 to get p t just as before as well. After we ve gone through 10
12 all thesteps asbeforeuptothepointwhere we ve obtained V 2, we canget the first outer tangent point p ot1 by following V 2 a distance of r 1 just as before. I just wanted to note that the magnitude of V 2 before normalization is r 4 < r 1 instead of r 4 > r 1. To get p ot2, the accompanying tangent point on C 2, we perform addition: p ot2 = p ot1 + V 4 This is exactly the same as before. In essence, the only step that changes between calculating outer tangents as opposed to inner tangents is how C 4 is constructed; all other steps remains exactly the same. Method 2: A Vector-based Approach Now that we understand geometrically how to get tangent lines between two circles, I ll show you a more efficient way to do so using vectors that has no need for constructing circles C 3 or C 4. We didn t work through the example in the previous section we had to work up to Step 7 so that you could have some intuition on why the following vector method works. 1. Draw your circles C 1 and C 2 as before (Figure 4). 2. Draw vector V 1 from p 1 to p 2. This has magnitude D as before. 3. Draw a vector V 2 between your tangent points. In this case, it s easier to start with outer tangent points, which we ll call p ot1 and p ot2. So, V 2 = p ot2 p ot1. 4. Draw a unit vector perpendicular to V 2. We ll call it ˆn (normal vector). Figure 10 depicts our setup. In the general case, the radii of C 1 and C 2 will not be equivalent, but for us it will. This method works for both cases. 5. Let s consider some relationships between these vectors. The dot product between V 2 and ˆn is 0 because the vectors are perpendicular. ˆn ˆn = 1 because ˆn is a unit vector. We can modify vector V 1 to be parallel to V 2 quite easily by subtracting V 1 = (r 1 r 2 ) ˆn 11
13 Figure 10: Setup for computing tangents via the vector method Why does this work? For some intuition, consider Step 7 in the previous section: We drew a vector from p t to C 2 s center, and then I stated that the vector was parallel to the vector between the tangent points. Well, both points were equidistant from their respective tangents; we need to move p t a distance of r 2 to get to the first tangent point. Likewise, we need to translate p 2 (the center of the other circle) down the same amount of distance. Using the head-to-tail method of vector addition, you can see that we modified V 1 to be this same vector! Now that I ve convinced you that this modification causes V 1 to be parallel to V 2, the following statement holds: ˆn ( V1 ((r 2 r 1 ) ˆn) ) = 0 Simplifying the above equation by distributing ˆn: ˆn V 1 +r 1 r 2 = 0 Further simplifying the equation: ˆn V 1 = r 2 r 1 Let s normalize V 1 by dividing by its magnitude, D. This doesn t change the dot product between V 1 and ˆn because the vectors are still perpendicular, but we also have to divide the right-hand side by D: V 1 D ˆn = r 2 r 1 D I ll refer to the normalized V 1 Simply as ˆV 1 from here on. 12
14 Now we can solve for ˆn because it is the only unknown in the equations: ˆV 1 ˆn = r 2 r 1 D and ˆn ˆn = 1 The dot product between two vectors A and B is defined as: A B = A B cos(θ) Where θ is the angle between them. Therefore, in the equation ˆV 1 ˆn = r 2 r 1 D r 2 r 1 is the angle between ˆV D 1 and ˆn. Because it s constant, and I don t want to keep re-typing it, let s define c = r 2 r 1 (constant). D Nowallthatremainsistorotate ˆV 1 throughtheanglec, anditwill be equivalent to ˆn. Rotating a vector is a well known operation in mathematics. ˆn = (n x,n y ) is, therefore: n x = v 1x c v 1y 1 c 2 n y = v 1x 1 c 2 +v 1y c Remember that c is the cosine of the angle between ˆV 1 and ˆn, so therefore, the sine of the angle is 1 c 2 because cos 2 (θ)+sin 2 (θ) = 1 6. Knowing ˆn as well as V 2 (remember when we modified V 1 to be to V 2?), allows us to very easily calculate the tangent points by first going from the center of C 1 along ˆn for a distance of r 1, and then from there, following V 2 to get the second tangent point. The other tangent points are easily calculated from this vector-based formalism, and it s much faster to do than all the geometry transformations we did with Method 1. Refer to freely available code online for how to actually implement the vector method. 13
15 Computing CSC curves The only reason we needed to compute tangent points between circles is so that we could find the S portion of our CSC curves. Knowing the tangent pointsonourcirclesweneedtoplanto, computing CSCpathssimplybecome a matter of turning on a minimum turning radius until the first tangent point is reached, travelling straight until the second tangent point is reached, and then turning again at a minimum turning radius until the goal configuration is reached. There s really just one gotcha one needs to worry about this step, and that has to do with the directionality of the circles. When an agent wants to traverse the arc of a circle between two points on the circle s circumference, it must follow the circle s direction. That is, an agent cannot turn left (positive) on a right-turn-only (negative) circle. This can become an issue when computing the arc lengths between points on a circle. The thing about all your trigonometry functions is that they will only return you the short angle between things. With directed circles, though, very often you want to actually be traversing the long angle between two points on the circle. Fortunately there is a simple fix. Computing Arc Lengths Given: A circle C 1 centered at p 1 with points p 2 and p 3 along its circumference, radius r 1, and circle directionality d, which can be left or right. Arc lengths of circles are computed by multiplying the radius of the circle by the angle θ between the points along the circumference. Therefore arc length, L = r 1 θ, and θ can be naïvely computed using the law of cosines after you compute the Euclidean distance between the points. I say naïvely because this method will only give you the shorter arc length, which will not always be correct for your directed circles (Figure 11). A better strategy would be to generate vectors from the center of the circle to the points along the circumference. That is, V1 = p 2 p 1 and V 2 = p 3 p 1. Let s assume that the arc you want to traverse is from p 2 to p 3 with direction d. We can use the atan2() function to compute the small angle between the points as before, but the difference is that atan2() gives us directional information. Thatis, θ = atan2 ( V3 ) atan2 ( V2 ) will bepositiveornegative depending onwhat direction V 1 rotatedtoendupat V 2. Apositive rotation is a left turn and a negative rotation is a right turn. We can check the sign of this angle against d. If our angle s sign disagrees with the direction 14
16 Figure 11: A scenario where the arc length on a directed circle is actually the larger of the two between the points we d like to turn, we ll correct it by either adding or subtracting 2π. That is: Algorithm 1 ArcLength θ = atan2 ( V2 ) atan2 ( V1 ) if θ < 0 and d = left then θ = θ+2π else if θ > 0 and d = right then θ = θ 2π end if return θ r 1 With a function like this to compute your arc lengths, you will now very easily be able to compute the duration of time to apply your turn left or turn right controls within a circle. The geometry of CSC trajectories RSR, LSL, RSL, and LSR trajectories are all calculated similarly to each other, so I ll only describe the RSR trajectory (Figure 12). Given starting configuration s = x 1,y 1,θ 1 and goal configuration g = x 2,y 2,θ 2, we wish to compute a trajectory that consists of first turning right (negative) at a minimum turning radius, driving straight, and then turning right (negative) again at minimum turning radius until the goal configuration is reached. Assume that the minimum turning radius is r min 15
17 First, we must calculate the circles about which the agent will turn a circle of minimum radius C 1 to the right of s as well as a circle of minimum radius C 2 to the right of g. The center of C 1, becomes ( ( p c1 = x 1 +r min cos θ 1 π ) (,y 1 +r min sin θ 1 π )) 2 2. Similarly, the center of C 2 becomes ( ( p c2 = x 2 +r min cos θ 2 π ) (,y 1 +r min sin θ 2 π )) 2 2. Figure 12: Using what we ve learned to compute a RSR trajectory Now that we ve obtained the circles about which the agent will turn, we need to find the outer tangent points we can traverse. I demonstrated earlier how one would go about calculating all the tangent points given two circles. For an RR circle, though, only one set of outer tangents is valid. If you implement your tangent-pt computing function appropriately, it will always return tangent points in a reliable manner. At this point, I ll assume you are able to obtain the proper tangent points for a right-circle to right-circle connection. Your tangent point function should return points p ot1 and p ot2 which respectively define the appropriate tangent points on C 1, the agent s right-turn circle and C 2, the query configurations right-turn circle. Now that we ve calculated geometrically the points we need to travel through, we need to transform them into a control the agent can understand. Such a control should be in the form of do this action at this timestep. For thedubin s car, thisispretty easy. Ifwe defineacontrol asapairof(steering angle, timesteps), then we can define a RSR trajectory as an array of 3 controls, ( steeringmax, timesteps1), (0, timesteps2), and ( steeringmax, timesteps3). We still need to compute the number of timesteps, but this isn t so bad. 16
18 We know x 1,y 1, the position of our starting configuration, as well as p ot1 our outer tangent point. Both of these points lie on the circumference of the minimum turning-radius right-turn only circle to the right of the s, the starting configuration. Now we can take advantage of our ArcLength function to compute the distance between the two points given a right-turn. Typically, simulations don t update entire seconds at once, but rather some some δ. This is a type of integration called Euler integration that allows us to closely approximate the actual trajectory the car should follow, though not perfectly so. Because we ve defined the Dubin s car s update function as a linear function of the form ẋ = cos(θ) ẏ = sin(θ) θ = 1 r turn then we actually travel in a straight line from timestep to timestep. A big δ therefore results in a poor approximation of reality. As δ approaches 0, though, we more closely approximate reality. Typically a delta in the range of [0.01,0.05] is appropriate, but you may need finer or coarser control. Accounting for δ, our update equations become: x new = x prev +δ cos(θ) y new = y prev +δ sin(θ) θ new = θ prev + δ r turn Now that we have decided on a value for δ, we can compute the number of timesteps to apply each steering angle. Given the length of an arc L (computed using the ArcLength function, or just simply the magnitude of the tangent line) timesteps x = L δ. Computing the other trajectories now becomes a matter or getting the right tangent points to plan towards. The RSR and LSL trajectories will use outer tangents while the RSL and LSR trajectories use the inner tangents. 17
19 Computing CCC trajectories Two of the Dubin s shortest paths don t use the tangent lines at all. These are the RLR and LRL trajectories, which consist of three tangential, minimum radius turning circles. Very often, these trajectories aren t even valid because of the small proximity that s and g must be to each other for such an arrangement of the three circles to be possible. If the distance between the agent and query configurations turning circles is less than 4r min, then a CCC curve is valid. I say less than 4r min, because if the distance were equal, then a CSC trajectory is more optimal. For CCC trajectories, we must calculate the location of the third circle, as well as its tangent points to the circles near s and g. To be more concrete, I ll address the LRL case, shown in Figure 13. Consider theminimum-radius turningcircletothe left ofstobec 1 and the minimum-radius turning circle to the left of g to be to C 2. Our task is now to compute C 3, a minimum-radius turning circle tangent to both C 1 and C 2 plus the points p t1 and p t2 which are respective points of intersection between C 1 and C 3, and between C 2 and C 3. Let p 1,p 2,p 3 be the centers of C 1,C 2, and C 3, respectively. We can form the triangle p 1,p 2,p 3 using these points. Because C 3 is tangent to both C 1 and C 2, we already know the lengths of all three sides. Figure 13: Computing a RLR trajectory Segments p 1 p 3 and p 2 p 3 have length 2r min and segment p 1 p 2 has length D = (x 2 x 1 ) 2 +(y 2 y 1 ) 2. We are interested in the angle θ = p 2 p 1 p 3 because that is the angle that the line between C 1 and C 2 ( V 1 = p 2 p 1 ) must 18
20 rotate to face the center of C 3, which will allow us to calculate p 3. Using the law of cosines, we can determine that ( ) D θ = cos 1 4r m in In a LRL trajectory, we re interested in a C 3 that is left of C 1. At the moment, we have an angle, θ that represents the amount of rotation that vector V 1 = (p 2 p 1 ) must rotate to point at the center of C 3. However, θ s valueisonlyvalidif V 1 isparalleltothex-axis. Otherwise, weneedtoaccount for the amount V 1 is rotated with the atan2() function atan2 ( V1 ). For a LRL trajectory, we want to add θ to this value, but for an RLR trajectory we want to subtract θ from it to obtain a circle to the right of C 1. Remember that we consider left, or counter-clockwise turns to be positive. Now that theta represents the absolute amount of rotation, we can compute p 3 = (x 1 +2r min cos(θ),y 1 +2r min sin(θ)) Computing thetangentpointsp t1 andp t2 becomeseasy; wecandefinevectors from the p 3 to p 1 and p 2, and walk down them a distance of r min. As an example, I ll calculate p t1. First, obtain the vector V 2 from p 3 to p 1 ; V2 = p 1 p 3. Next, change the vector s magnitude to r min by normalizing it and multiplying by r min (or just dividing its components by 2, as its magnitude should already be 2r min ). Next, compute p t1 using the new V 2 ; V 2 = V 2 V 2 r min p t1 = p 3 + V 2 Computing p t2 follows a similar procedure. At this point we have everything we need for our CCC trajectory! We have three arcs as before, from (x 1,y 1 ) to p t1. From p t1 to p t2, and from p t2 to (x 2,y 2 ). One can compute arc lengths and duration as before to finish things off. Conclusions So now that we ve computed all of the shortest paths for the Dubin s Car, what can we do next? Well, you could use them to write a car simulator. 19
21 The paths are very quick to compute, but are what s known as open-loop trajectories. An open-loop trajectory is only valid if you apply the desired controls exactly as stated. Even if you used a computer to control your car, this would still only work perfectly in simulation. In the real-world, we have all kinds of sources for error that we represent as uncertainty in our controls. If a human driver tried to apply our Dubin s shortest path controls, they wouldn t end up exactly on target, would they? Perhaps in a later article I will discuss motion planning under uncertainty, but for now I defer you to the internet. Another application we could use these shortest path calculations for would be something known as a rapidly exploring random tree, or RRT. An RRT uses the know-how of planning between two points to build a map of sorts in the environment. The resulting map is a tree structure with a root at our start, and the paths one gets from the tree can look pretty good; imagine a car deftly maneuvering around things in its way. RRTs are a big topic of research right now, and Steven LaValle has a wealth of information about them. Following from the Dubin s RRT, you might one day use a much more complicated car-like robot. For this complicated car-like robot you may want to also use an RRT. Remember when I said that the resulting structure of an RRT looks like a tree with its root at our start? Well, to grow this tree, one has to continue adding points to it, and part of that process is determining which point in the tree to connect to. Typically this is done by just choosing the closest point in the tree. Closest usually means, the shortest line between myself and any point in the tree. For a lot of robots (holonomic especially), this straight-line distance is just fine, but for car-like (nonholonomic) robots it may not be good enough, because you can t always move on a straight line between start and goal. Therefore, you could use the length of the Dubin s shortest path instead of the straight-line shortest path as your measure of distance! (We re using the Dubin s shortest paths as a distance metric ). In reality, the Dubin s shortest paths are not a true distance metric because they are not symmetric, which means that the distance from A to B isn t always the same as the distance from B to A. Because the Dubin s car can only move forward, it isn t symmetric. However, if you expanded the Dubin s car to be able to move backwards, you d have created a Reeds-Shepp car, and the Reeds-Shepp shortest paths are symmetric. 1 1 I d like to thank my classmate and colleague Jory Denny for his help with LaTeX and in editing this article 20
Basics of Computational Geometry
 Basics of Computational Geometry Nadeem Mohsin October 12, 2013 1 Contents This handout covers the basic concepts of computational geometry. Rather than exhaustively covering all the algorithms, it deals
Basics of Computational Geometry Nadeem Mohsin October 12, 2013 1 Contents This handout covers the basic concepts of computational geometry. Rather than exhaustively covering all the algorithms, it deals
Linear algebra deals with matrixes: two-dimensional arrays of values. Here s a matrix: [ x + 5y + 7z 9x + 3y + 11z
 Basic Linear Algebra Linear algebra deals with matrixes: two-dimensional arrays of values. Here s a matrix: [ 1 5 ] 7 9 3 11 Often matrices are used to describe in a simpler way a series of linear equations.
Basic Linear Algebra Linear algebra deals with matrixes: two-dimensional arrays of values. Here s a matrix: [ 1 5 ] 7 9 3 11 Often matrices are used to describe in a simpler way a series of linear equations.
Polar Coordinates. 2, π and ( )
 Polar Coordinates Up to this point we ve dealt exclusively with the Cartesian (or Rectangular, or x-y) coordinate system. However, as we will see, this is not always the easiest coordinate system to work
Polar Coordinates Up to this point we ve dealt exclusively with the Cartesian (or Rectangular, or x-y) coordinate system. However, as we will see, this is not always the easiest coordinate system to work
Here are some of the more basic curves that we ll need to know how to do as well as limits on the parameter if they are required.
 1 of 10 23/07/2016 05:15 Paul's Online Math Notes Calculus III (Notes) / Line Integrals / Line Integrals - Part I Problems] [Notes] [Practice Problems] [Assignment Calculus III - Notes Line Integrals Part
1 of 10 23/07/2016 05:15 Paul's Online Math Notes Calculus III (Notes) / Line Integrals / Line Integrals - Part I Problems] [Notes] [Practice Problems] [Assignment Calculus III - Notes Line Integrals Part
CALCULUS II. Parametric Equations and Polar Coordinates. Paul Dawkins
 CALCULUS II Parametric Equations and Polar Coordinates Paul Dawkins Table of Contents Preface... ii Parametric Equations and Polar Coordinates... 3 Introduction... 3 Parametric Equations and Curves...
CALCULUS II Parametric Equations and Polar Coordinates Paul Dawkins Table of Contents Preface... ii Parametric Equations and Polar Coordinates... 3 Introduction... 3 Parametric Equations and Curves...
Final Report: Dynamic Dubins-curve based RRT Motion Planning for Differential Constrain Robot
 Final Report: Dynamic Dubins-curve based RRT Motion Planning for Differential Constrain Robot Abstract This project develops a sample-based motion-planning algorithm for robot with differential constraints.
Final Report: Dynamic Dubins-curve based RRT Motion Planning for Differential Constrain Robot Abstract This project develops a sample-based motion-planning algorithm for robot with differential constraints.
Vector Calculus: Understanding the Cross Product
 University of Babylon College of Engineering Mechanical Engineering Dept. Subject : Mathematics III Class : 2 nd year - first semester Date: / 10 / 2016 2016 \ 2017 Vector Calculus: Understanding the Cross
University of Babylon College of Engineering Mechanical Engineering Dept. Subject : Mathematics III Class : 2 nd year - first semester Date: / 10 / 2016 2016 \ 2017 Vector Calculus: Understanding the Cross
LIGHT: Two-slit Interference
 LIGHT: Two-slit Interference Objective: To study interference of light waves and verify the wave nature of light. Apparatus: Two red lasers (wavelength, λ = 633 nm); two orange lasers (λ = 612 nm); two
LIGHT: Two-slit Interference Objective: To study interference of light waves and verify the wave nature of light. Apparatus: Two red lasers (wavelength, λ = 633 nm); two orange lasers (λ = 612 nm); two
Geometry and Gravitation
 Chapter 15 Geometry and Gravitation 15.1 Introduction to Geometry Geometry is one of the oldest branches of mathematics, competing with number theory for historical primacy. Like all good science, its
Chapter 15 Geometry and Gravitation 15.1 Introduction to Geometry Geometry is one of the oldest branches of mathematics, competing with number theory for historical primacy. Like all good science, its
Unit 1, Lesson 1: Moving in the Plane
 Unit 1, Lesson 1: Moving in the Plane Let s describe ways figures can move in the plane. 1.1: Which One Doesn t Belong: Diagrams Which one doesn t belong? 1.2: Triangle Square Dance m.openup.org/1/8-1-1-2
Unit 1, Lesson 1: Moving in the Plane Let s describe ways figures can move in the plane. 1.1: Which One Doesn t Belong: Diagrams Which one doesn t belong? 1.2: Triangle Square Dance m.openup.org/1/8-1-1-2
Grade 6 Math Circles October 16 & Non-Euclidean Geometry and the Globe
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Kinematics, Kinematics Chains CS 685
 Kinematics, Kinematics Chains CS 685 Previously Representation of rigid body motion Two different interpretations - as transformations between different coord. frames - as operators acting on a rigid body
Kinematics, Kinematics Chains CS 685 Previously Representation of rigid body motion Two different interpretations - as transformations between different coord. frames - as operators acting on a rigid body
Geometric Computations for Simulation
 1 Geometric Computations for Simulation David E. Johnson I. INTRODUCTION A static virtual world would be boring and unlikely to draw in a user enough to create a sense of immersion. Simulation allows things
1 Geometric Computations for Simulation David E. Johnson I. INTRODUCTION A static virtual world would be boring and unlikely to draw in a user enough to create a sense of immersion. Simulation allows things
Section 4.1: Introduction to Trigonometry
 Section 4.1: Introduction to Trigonometry Review of Triangles Recall that the sum of all angles in any triangle is 180. Let s look at what this means for a right triangle: A right angle is an angle which
Section 4.1: Introduction to Trigonometry Review of Triangles Recall that the sum of all angles in any triangle is 180. Let s look at what this means for a right triangle: A right angle is an angle which
Table of Laplace Transforms
 Table of Laplace Transforms 1 1 2 3 4, p > -1 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Heaviside Function 27 28. Dirac Delta Function 29 30. 31 32. 1 33 34. 35 36. 37 Laplace Transforms
Table of Laplace Transforms 1 1 2 3 4, p > -1 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Heaviside Function 27 28. Dirac Delta Function 29 30. 31 32. 1 33 34. 35 36. 37 Laplace Transforms
Non-holonomic Planning
 Non-holonomic Planning Jane Li Assistant Professor Mechanical Engineering & Robotics Engineering http://users.wpi.edu/~zli11 Recap We have learned about RRTs. q new q init q near q rand But the standard
Non-holonomic Planning Jane Li Assistant Professor Mechanical Engineering & Robotics Engineering http://users.wpi.edu/~zli11 Recap We have learned about RRTs. q new q init q near q rand But the standard
Study Guide - Geometry
 Study Guide - Geometry (NOTE: This does not include every topic on the outline. Take other steps to review those.) Page 1: Rigid Motions Page 3: Constructions Page 12: Angle relationships Page 14: Angle
Study Guide - Geometry (NOTE: This does not include every topic on the outline. Take other steps to review those.) Page 1: Rigid Motions Page 3: Constructions Page 12: Angle relationships Page 14: Angle
Kinematics of Machines Prof. A. K. Mallik Department of Mechanical Engineering Indian Institute of Technology, Kanpur. Module - 3 Lecture - 1
 Kinematics of Machines Prof. A. K. Mallik Department of Mechanical Engineering Indian Institute of Technology, Kanpur Module - 3 Lecture - 1 In an earlier lecture, we have already mentioned that there
Kinematics of Machines Prof. A. K. Mallik Department of Mechanical Engineering Indian Institute of Technology, Kanpur Module - 3 Lecture - 1 In an earlier lecture, we have already mentioned that there
Math 5320, 3/28/18 Worksheet 26: Ruler and compass constructions. 1. Use your ruler and compass to construct a line perpendicular to the line below:
 Math 5320, 3/28/18 Worksheet 26: Ruler and compass constructions Name: 1. Use your ruler and compass to construct a line perpendicular to the line below: 2. Suppose the following two points are spaced
Math 5320, 3/28/18 Worksheet 26: Ruler and compass constructions Name: 1. Use your ruler and compass to construct a line perpendicular to the line below: 2. Suppose the following two points are spaced
Background for Surface Integration
 Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
by Kevin M. Chevalier
 Precalculus Review Handout.4 Trigonometric Functions: Identities, Graphs, and Equations, Part I by Kevin M. Chevalier Angles, Degree and Radian Measures An angle is composed of: an initial ray (side) -
Precalculus Review Handout.4 Trigonometric Functions: Identities, Graphs, and Equations, Part I by Kevin M. Chevalier Angles, Degree and Radian Measures An angle is composed of: an initial ray (side) -
Graphics and Interaction Transformation geometry and homogeneous coordinates
 433-324 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
433-324 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates
 COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
2-D Geometry for Programming Contests 1
 2-D Geometry for Programming Contests 1 1 Vectors A vector is defined by a direction and a magnitude. In the case of 2-D geometry, a vector can be represented as a point A = (x, y), representing the vector
2-D Geometry for Programming Contests 1 1 Vectors A vector is defined by a direction and a magnitude. In the case of 2-D geometry, a vector can be represented as a point A = (x, y), representing the vector
Reflections and Refractions in Ray Tracing
 Reflections and Refractions in Ray Tracing Bram de Greve (bram.degreve@gmail.com) 10th October 2004 When you re writing a ray tracer, soon or late you ll stumble on the problem of reflection and refraction.
Reflections and Refractions in Ray Tracing Bram de Greve (bram.degreve@gmail.com) 10th October 2004 When you re writing a ray tracer, soon or late you ll stumble on the problem of reflection and refraction.
To graph the point (r, θ), simply go out r units along the initial ray, then rotate through the angle θ. The point (1, 5π 6. ) is graphed below:
 Polar Coordinates Any point in the plane can be described by the Cartesian coordinates (x, y), where x and y are measured along the corresponding axes. However, this is not the only way to represent points
Polar Coordinates Any point in the plane can be described by the Cartesian coordinates (x, y), where x and y are measured along the corresponding axes. However, this is not the only way to represent points
Motion Control (wheeled robots)
 Motion Control (wheeled robots) Requirements for Motion Control Kinematic / dynamic model of the robot Model of the interaction between the wheel and the ground Definition of required motion -> speed control,
Motion Control (wheeled robots) Requirements for Motion Control Kinematic / dynamic model of the robot Model of the interaction between the wheel and the ground Definition of required motion -> speed control,
Grade 6 Math Circles October 16 & Non-Euclidean Geometry and the Globe
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
ACT Math test Trigonometry Review
 Many students are a little scared of trig, but the ACT seems to overcompensate for that fact by testing trig in an extremely straightforward way. ACT trig is basically all about right triangles. When it
Many students are a little scared of trig, but the ACT seems to overcompensate for that fact by testing trig in an extremely straightforward way. ACT trig is basically all about right triangles. When it
1.7 Limit of a Function
 1.7 Limit of a Function We will discuss the following in this section: 1. Limit Notation 2. Finding a it numerically 3. Right and Left Hand Limits 4. Infinite Limits Consider the following graph Notation:
1.7 Limit of a Function We will discuss the following in this section: 1. Limit Notation 2. Finding a it numerically 3. Right and Left Hand Limits 4. Infinite Limits Consider the following graph Notation:
Time Optimal Trajectories for Bounded Velocity Differential Drive Robots
 Time Optimal Trajectories for Bounded Velocity Differential Drive Robots Devin J. Balkcom Matthew T. Mason Robotics Institute and Computer Science Department Carnegie Mellon University Pittsburgh PA 53
Time Optimal Trajectories for Bounded Velocity Differential Drive Robots Devin J. Balkcom Matthew T. Mason Robotics Institute and Computer Science Department Carnegie Mellon University Pittsburgh PA 53
Grade 6 Math Circles November 6 & Relations, Functions, and Morphisms
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Relations Let s talk about relations! Grade 6 Math Circles November 6 & 7 2018 Relations, Functions, and
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Relations Let s talk about relations! Grade 6 Math Circles November 6 & 7 2018 Relations, Functions, and
Robotics Project. Final Report. Computer Science University of Minnesota. December 17, 2007
 Robotics Project Final Report Computer Science 5551 University of Minnesota December 17, 2007 Peter Bailey, Matt Beckler, Thomas Bishop, and John Saxton Abstract: A solution of the parallel-parking problem
Robotics Project Final Report Computer Science 5551 University of Minnesota December 17, 2007 Peter Bailey, Matt Beckler, Thomas Bishop, and John Saxton Abstract: A solution of the parallel-parking problem
Detailed instructions for video analysis using Logger Pro.
 Detailed instructions for video analysis using Logger Pro. 1. Begin by locating or creating a video of a projectile (or any moving object). Save it to your computer. Most video file types are accepted,
Detailed instructions for video analysis using Logger Pro. 1. Begin by locating or creating a video of a projectile (or any moving object). Save it to your computer. Most video file types are accepted,
ACT Math test Plane Geometry Review
 Plane geometry problems account for 14 questions on the ACT Math Test that s almost a quarter of the questions on the Subject Test. If you ve taken high school geometry, you ve probably covered all of
Plane geometry problems account for 14 questions on the ACT Math Test that s almost a quarter of the questions on the Subject Test. If you ve taken high school geometry, you ve probably covered all of
Chapter 10 Motion Planning
 Chapter 10 Motion Planning 10.1 Introduction Part 1 1 10.1 Introduction Outline 10.1.1 Introducing Motion Planning 10.1.2 Formulation of Motion Planning 10.1.3 Obstacle Free Motion Planning Summary 2 Hierarchy
Chapter 10 Motion Planning 10.1 Introduction Part 1 1 10.1 Introduction Outline 10.1.1 Introducing Motion Planning 10.1.2 Formulation of Motion Planning 10.1.3 Obstacle Free Motion Planning Summary 2 Hierarchy
A lg e b ra II. Trig o n o m e tric F u n c tio
 1 A lg e b ra II Trig o n o m e tric F u n c tio 2015-12-17 www.njctl.org 2 Trig Functions click on the topic to go to that section Radians & Degrees & Co-terminal angles Arc Length & Area of a Sector
1 A lg e b ra II Trig o n o m e tric F u n c tio 2015-12-17 www.njctl.org 2 Trig Functions click on the topic to go to that section Radians & Degrees & Co-terminal angles Arc Length & Area of a Sector
3D Transformations and Complex Representations. Computer Graphics CMU /15-662, Fall 2016
 3D Transformations and Complex Representations Computer Graphics CMU 15-462/15-662, Fall 2016 Quiz 4: Trees and Transformations Student solutions (beautiful!): Rotations in 3D What is a rotation, intuitively?
3D Transformations and Complex Representations Computer Graphics CMU 15-462/15-662, Fall 2016 Quiz 4: Trees and Transformations Student solutions (beautiful!): Rotations in 3D What is a rotation, intuitively?
Trigonometry. 9.1 Radian and Degree Measure
 Trigonometry 9.1 Radian and Degree Measure Angle Measures I am aware of three ways to measure angles: degrees, radians, and gradians. In all cases, an angle in standard position has its vertex at the origin,
Trigonometry 9.1 Radian and Degree Measure Angle Measures I am aware of three ways to measure angles: degrees, radians, and gradians. In all cases, an angle in standard position has its vertex at the origin,
Algebra II. Slide 1 / 162. Slide 2 / 162. Slide 3 / 162. Trigonometric Functions. Trig Functions
 Slide 1 / 162 Algebra II Slide 2 / 162 Trigonometric Functions 2015-12-17 www.njctl.org Trig Functions click on the topic to go to that section Slide 3 / 162 Radians & Degrees & Co-terminal angles Arc
Slide 1 / 162 Algebra II Slide 2 / 162 Trigonometric Functions 2015-12-17 www.njctl.org Trig Functions click on the topic to go to that section Slide 3 / 162 Radians & Degrees & Co-terminal angles Arc
ACT SparkNotes Test Prep: Plane Geometry
 ACT SparkNotes Test Prep: Plane Geometry Plane Geometry Plane geometry problems account for 14 questions on the ACT Math Test that s almost a quarter of the questions on the Subject Test If you ve taken
ACT SparkNotes Test Prep: Plane Geometry Plane Geometry Plane geometry problems account for 14 questions on the ACT Math Test that s almost a quarter of the questions on the Subject Test If you ve taken
(Refer Slide Time 3:31)
 Digital Circuits and Systems Prof. S. Srinivasan Department of Electrical Engineering Indian Institute of Technology Madras Lecture - 5 Logic Simplification In the last lecture we talked about logic functions
Digital Circuits and Systems Prof. S. Srinivasan Department of Electrical Engineering Indian Institute of Technology Madras Lecture - 5 Logic Simplification In the last lecture we talked about logic functions
This blog addresses the question: how do we determine the intersection of two circles in the Cartesian plane?
 Intersecting Circles This blog addresses the question: how do we determine the intersection of two circles in the Cartesian plane? This is a problem that a programmer might have to solve, for example,
Intersecting Circles This blog addresses the question: how do we determine the intersection of two circles in the Cartesian plane? This is a problem that a programmer might have to solve, for example,
Algebra II Trigonometric Functions
 Slide 1 / 162 Slide 2 / 162 Algebra II Trigonometric Functions 2015-12-17 www.njctl.org Slide 3 / 162 Trig Functions click on the topic to go to that section Radians & Degrees & Co-terminal angles Arc
Slide 1 / 162 Slide 2 / 162 Algebra II Trigonometric Functions 2015-12-17 www.njctl.org Slide 3 / 162 Trig Functions click on the topic to go to that section Radians & Degrees & Co-terminal angles Arc
Math Fundamentals for Statistics (Math 52) Unit 3: Addition and Subtraction. Scott Fallstrom and Brent Pickett The How and Whys Guys.
 Math Fundamentals for Statistics (Math 52) Unit 3: Addition and Subtraction Scott Fallstrom and Brent Pickett The How and Whys Guys Unit 3 Page 1 3.1: Place Value (Addition Preview) Our system is a base-ten,
Math Fundamentals for Statistics (Math 52) Unit 3: Addition and Subtraction Scott Fallstrom and Brent Pickett The How and Whys Guys Unit 3 Page 1 3.1: Place Value (Addition Preview) Our system is a base-ten,
In this chapter, we will investigate what have become the standard applications of the integral:
 Chapter 8 Overview: Applications of Integrals Calculus, like most mathematical fields, began with trying to solve everyday problems. The theory and operations were formalized later. As early as 70 BC,
Chapter 8 Overview: Applications of Integrals Calculus, like most mathematical fields, began with trying to solve everyday problems. The theory and operations were formalized later. As early as 70 BC,
To graph the point (r, θ), simply go out r units along the initial ray, then rotate through the angle θ. The point (1, 5π 6
 Polar Coordinates Any point in the plane can be described by the Cartesian coordinates (x, y), where x and y are measured along the corresponding axes. However, this is not the only way to represent points
Polar Coordinates Any point in the plane can be described by the Cartesian coordinates (x, y), where x and y are measured along the corresponding axes. However, this is not the only way to represent points
Trigonometry I -- Answers -- Trigonometry I Diploma Practice Exam - ANSWERS 1
 Trigonometry I -- Answers -- Trigonometry I Diploma Practice Exam - ANSWERS www.puremath.com Formulas These are the formulas for Trig I you will be given on your diploma. a rθ sinθ cosθ tan θ cotθ cosθ
Trigonometry I -- Answers -- Trigonometry I Diploma Practice Exam - ANSWERS www.puremath.com Formulas These are the formulas for Trig I you will be given on your diploma. a rθ sinθ cosθ tan θ cotθ cosθ
Chapter 3: Kinematics Locomotion. Ross Hatton and Howie Choset
 Chapter 3: Kinematics Locomotion Ross Hatton and Howie Choset 1 (Fully/Under)Actuated Fully Actuated Control all of the DOFs of the system Controlling the joint angles completely specifies the configuration
Chapter 3: Kinematics Locomotion Ross Hatton and Howie Choset 1 (Fully/Under)Actuated Fully Actuated Control all of the DOFs of the system Controlling the joint angles completely specifies the configuration
Jane Li. Assistant Professor Mechanical Engineering Department, Robotic Engineering Program Worcester Polytechnic Institute
 Jane Li Assistant Professor Mechanical Engineering Department, Robotic Engineering Program Worcester Polytechnic Institute (3 pts) How to generate Delaunay Triangulation? (3 pts) Explain the difference
Jane Li Assistant Professor Mechanical Engineering Department, Robotic Engineering Program Worcester Polytechnic Institute (3 pts) How to generate Delaunay Triangulation? (3 pts) Explain the difference
Vector Addition. Qty Item Part Number 1 Force Table ME-9447B 1 Mass and Hanger Set ME Carpenter s level 1 String
 rev 05/2018 Vector Addition Equipment List Qty Item Part Number 1 Force Table ME-9447B 1 Mass and Hanger Set ME-8979 1 Carpenter s level 1 String Purpose The purpose of this lab is for the student to gain
rev 05/2018 Vector Addition Equipment List Qty Item Part Number 1 Force Table ME-9447B 1 Mass and Hanger Set ME-8979 1 Carpenter s level 1 String Purpose The purpose of this lab is for the student to gain
Here are a couple of warnings to my students who may be here to get a copy of what happened on a day that you missed.
 Preface Here are my online notes for my Algebra course that I teach here at Lamar University, although I have to admit that it s been years since I last taught this course. At this point in my career I
Preface Here are my online notes for my Algebra course that I teach here at Lamar University, although I have to admit that it s been years since I last taught this course. At this point in my career I
3D Rotations and Complex Representations. Computer Graphics CMU /15-662, Fall 2017
 3D Rotations and Complex Representations Computer Graphics CMU 15-462/15-662, Fall 2017 Rotations in 3D What is a rotation, intuitively? How do you know a rotation when you see it? - length/distance is
3D Rotations and Complex Representations Computer Graphics CMU 15-462/15-662, Fall 2017 Rotations in 3D What is a rotation, intuitively? How do you know a rotation when you see it? - length/distance is
(Refer Slide Time: 00:04:20)
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture 8 Three Dimensional Graphics Welcome back all of you to the lectures in Computer
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture 8 Three Dimensional Graphics Welcome back all of you to the lectures in Computer
Section 10.1 Polar Coordinates
 Section 10.1 Polar Coordinates Up until now, we have always graphed using the rectangular coordinate system (also called the Cartesian coordinate system). In this section we will learn about another system,
Section 10.1 Polar Coordinates Up until now, we have always graphed using the rectangular coordinate system (also called the Cartesian coordinate system). In this section we will learn about another system,
Lagrange Multipliers and Problem Formulation
 Lagrange Multipliers and Problem Formulation Steven J. Miller Department of Mathematics and Statistics Williams College Williamstown, MA 01267 Abstract The method of Lagrange Multipliers (and its generalizations)
Lagrange Multipliers and Problem Formulation Steven J. Miller Department of Mathematics and Statistics Williams College Williamstown, MA 01267 Abstract The method of Lagrange Multipliers (and its generalizations)
Math 3C Section 9.1 & 9.2
 Math 3C Section 9.1 & 9.2 Yucheng Tu 11/14/2018 1 Unit Circle The unit circle comes to the stage when we enter the field of trigonometry, i.e. the study of relations among the sides and angles of an arbitrary
Math 3C Section 9.1 & 9.2 Yucheng Tu 11/14/2018 1 Unit Circle The unit circle comes to the stage when we enter the field of trigonometry, i.e. the study of relations among the sides and angles of an arbitrary
What You ll See in This Chapter. Word Cloud. René Descartes. Introduction. Ian Parberry University of North Texas. Fletcher Dunn
 What You ll See in This Chapter Chapter 1: Cartesian Coordinate Systems Fletcher Dunn Valve Software Ian Parberry University of North Texas This chapter describes the basic concepts of 3D math. It is divided
What You ll See in This Chapter Chapter 1: Cartesian Coordinate Systems Fletcher Dunn Valve Software Ian Parberry University of North Texas This chapter describes the basic concepts of 3D math. It is divided
Let s start with occluding contours (or interior and exterior silhouettes), and look at image-space algorithms. A very simple technique is to render
 1 There are two major classes of algorithms for extracting most kinds of lines from 3D meshes. First, there are image-space algorithms that render something (such as a depth map or cosine-shaded model),
1 There are two major classes of algorithms for extracting most kinds of lines from 3D meshes. First, there are image-space algorithms that render something (such as a depth map or cosine-shaded model),
GCSE Maths: Formulae you ll need to know not
 GCSE Maths: Formulae you ll need to know As provided by AQA, these are the formulae required for the new GCSE These will not be given in the exam, so you will need to recall as well as use these formulae.
GCSE Maths: Formulae you ll need to know As provided by AQA, these are the formulae required for the new GCSE These will not be given in the exam, so you will need to recall as well as use these formulae.
INTRODUCTION TO LINE INTEGRALS
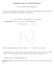 INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
Math Section 4.2 Radians, Arc Length, and Area of a Sector
 Math 1330 - Section 4.2 Radians, Arc Length, and Area of a Sector The word trigonometry comes from two Greek roots, trigonon, meaning having three sides, and meter, meaning measure. We have already defined
Math 1330 - Section 4.2 Radians, Arc Length, and Area of a Sector The word trigonometry comes from two Greek roots, trigonon, meaning having three sides, and meter, meaning measure. We have already defined
(Refer Slide Time: 00:02:00)
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 18 Polyfill - Scan Conversion of a Polygon Today we will discuss the concepts
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 18 Polyfill - Scan Conversion of a Polygon Today we will discuss the concepts
SMMG October 14 th, 2006 featuring Dr. Michael Starbird Circles, Rings, and Tractors: Clever Cleaving for Finding Formulas
 SMMG October 14 th, 2006 featuring Dr. Michael Starbird Circles, Rings, and Tractors: Clever Cleaving for Finding Formulas 1. The Polygon Sweep a) On one of the colored pieces of construction paper you
SMMG October 14 th, 2006 featuring Dr. Michael Starbird Circles, Rings, and Tractors: Clever Cleaving for Finding Formulas 1. The Polygon Sweep a) On one of the colored pieces of construction paper you
CCNY Math Review Chapters 5 and 6: Trigonometric functions and graphs
 Ch 5. Trigonometry 6. Angles 6. Right triangles 6. Trig funs for general angles 5.: Trigonometric functions and graphs 5.5 Inverse functions CCNY Math Review Chapters 5 and 6: Trigonometric functions and
Ch 5. Trigonometry 6. Angles 6. Right triangles 6. Trig funs for general angles 5.: Trigonometric functions and graphs 5.5 Inverse functions CCNY Math Review Chapters 5 and 6: Trigonometric functions and
Math for Geometric Optics
 Algebra skills Math for Geometric Optics general rules some common types of equations units problems with several variables (substitution) Geometry basics Trigonometry Pythagorean theorem definitions,
Algebra skills Math for Geometric Optics general rules some common types of equations units problems with several variables (substitution) Geometry basics Trigonometry Pythagorean theorem definitions,
Common Core Standards Addressed in this Resource
 Common Core Standards Addressed in this Resource N-CN.4 - Represent complex numbers on the complex plane in rectangular and polar form (including real and imaginary numbers), and explain why the rectangular
Common Core Standards Addressed in this Resource N-CN.4 - Represent complex numbers on the complex plane in rectangular and polar form (including real and imaginary numbers), and explain why the rectangular
2D and 3D Transformations AUI Course Denbigh Starkey
 2D and 3D Transformations AUI Course Denbigh Starkey. Introduction 2 2. 2D transformations using Cartesian coordinates 3 2. Translation 3 2.2 Rotation 4 2.3 Scaling 6 3. Introduction to homogeneous coordinates
2D and 3D Transformations AUI Course Denbigh Starkey. Introduction 2 2. 2D transformations using Cartesian coordinates 3 2. Translation 3 2.2 Rotation 4 2.3 Scaling 6 3. Introduction to homogeneous coordinates
2.3 Circular Functions of Real Numbers
 www.ck12.org Chapter 2. Graphing Trigonometric Functions 2.3 Circular Functions of Real Numbers Learning Objectives Graph the six trigonometric ratios as functions on the Cartesian plane. Identify the
www.ck12.org Chapter 2. Graphing Trigonometric Functions 2.3 Circular Functions of Real Numbers Learning Objectives Graph the six trigonometric ratios as functions on the Cartesian plane. Identify the
Lecture 13: Geometry Steven Skiena. skiena
 Lecture 13: Geometry Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.sunysb.edu/ skiena Geometry This chapter will deal with programming
Lecture 13: Geometry Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.sunysb.edu/ skiena Geometry This chapter will deal with programming
Trig for right triangles is pretty straightforward. The three, basic trig functions are just relationships between angles and sides of the triangle.
 Lesson 10-1: 1: Right ngle Trig By this point, you ve probably had some basic trigonometry in either algebra 1 or geometry, but we re going to hash through the basics again. If it s all review, just think
Lesson 10-1: 1: Right ngle Trig By this point, you ve probably had some basic trigonometry in either algebra 1 or geometry, but we re going to hash through the basics again. If it s all review, just think
Polar Coordinates
 Polar Coordinates 7-7-2 Polar coordinates are an alternative to rectangular coordinates for referring to points in the plane. A point in the plane has polar coordinates r,θ). r is roughly) the distance
Polar Coordinates 7-7-2 Polar coordinates are an alternative to rectangular coordinates for referring to points in the plane. A point in the plane has polar coordinates r,θ). r is roughly) the distance
Unit 13: Periodic Functions and Trig
 Date Period Unit 13: Periodic Functions and Trig Day Topic 0 Special Right Triangles and Periodic Function 1 Special Right Triangles Standard Position Coterminal Angles 2 Unit Circle Cosine & Sine (x,
Date Period Unit 13: Periodic Functions and Trig Day Topic 0 Special Right Triangles and Periodic Function 1 Special Right Triangles Standard Position Coterminal Angles 2 Unit Circle Cosine & Sine (x,
CMPUT 412 Motion Control Wheeled robots. Csaba Szepesvári University of Alberta
 CMPUT 412 Motion Control Wheeled robots Csaba Szepesvári University of Alberta 1 Motion Control (wheeled robots) Requirements Kinematic/dynamic model of the robot Model of the interaction between the wheel
CMPUT 412 Motion Control Wheeled robots Csaba Szepesvári University of Alberta 1 Motion Control (wheeled robots) Requirements Kinematic/dynamic model of the robot Model of the interaction between the wheel
Class #10 Wednesday, November 8, 2017
 Graphics In Excel Before we create a simulation, we need to be able to make a drawing in Excel. The techniques we use here are also used in Mathematica and LabVIEW. Drawings in Excel take place inside
Graphics In Excel Before we create a simulation, we need to be able to make a drawing in Excel. The techniques we use here are also used in Mathematica and LabVIEW. Drawings in Excel take place inside
Math Dr. Miller - Constructing in Sketchpad (tm) - Due via by Friday, Mar. 18, 2016
 Math 304 - Dr. Miller - Constructing in Sketchpad (tm) - Due via email by Friday, Mar. 18, 2016 As with our second GSP activity for this course, you will email the assignment at the end of this tutorial
Math 304 - Dr. Miller - Constructing in Sketchpad (tm) - Due via email by Friday, Mar. 18, 2016 As with our second GSP activity for this course, you will email the assignment at the end of this tutorial
In section 8.1, we began by introducing the sine function using a circle in the coordinate plane:
 Chapter 8.: Degrees and Radians, Reference Angles In section 8.1, we began by introducing the sine function using a circle in the coordinate plane: y (3,3) θ x We now return to the coordinate plane, but
Chapter 8.: Degrees and Radians, Reference Angles In section 8.1, we began by introducing the sine function using a circle in the coordinate plane: y (3,3) θ x We now return to the coordinate plane, but
Research in Computational Differential Geomet
 Research in Computational Differential Geometry November 5, 2014 Approximations Often we have a series of approximations which we think are getting close to looking like some shape. Approximations Often
Research in Computational Differential Geometry November 5, 2014 Approximations Often we have a series of approximations which we think are getting close to looking like some shape. Approximations Often
Solution Guide for Chapter 21
 Solution Guide for Chapter 21 Here are the solutions for the Doing the Math exercises in Girls Get Curves! DTM from p. 74-75 2. Find the surface area of a pyramid with slant height 5 in, whose Base is
Solution Guide for Chapter 21 Here are the solutions for the Doing the Math exercises in Girls Get Curves! DTM from p. 74-75 2. Find the surface area of a pyramid with slant height 5 in, whose Base is
1
 Zeros&asymptotes Example 1 In an early version of this activity I began with a sequence of simple examples (parabolas and cubics) working gradually up to the main idea. But now I think the best strategy
Zeros&asymptotes Example 1 In an early version of this activity I began with a sequence of simple examples (parabolas and cubics) working gradually up to the main idea. But now I think the best strategy
Trigonometry and the Unit Circle. Chapter 4
 Trigonometry and the Unit Circle Chapter 4 Topics Demonstrate an understanding of angles in standard position, expressed in degrees and radians. Develop and apply the equation of the unit circle. Solve
Trigonometry and the Unit Circle Chapter 4 Topics Demonstrate an understanding of angles in standard position, expressed in degrees and radians. Develop and apply the equation of the unit circle. Solve
TEAMS National Competition High School Version Photometry Solution Manual 25 Questions
 TEAMS National Competition High School Version Photometry Solution Manual 25 Questions Page 1 of 15 Photometry Questions 1. When an upright object is placed between the focal point of a lens and a converging
TEAMS National Competition High School Version Photometry Solution Manual 25 Questions Page 1 of 15 Photometry Questions 1. When an upright object is placed between the focal point of a lens and a converging
Chapter 15 Right Triangle Trigonometry
 Chapter 15 Right Triangle Trigonometry Sec. 1 Right Triangle Trigonometry The most difficult part of Trigonometry is spelling it. Once we get by that, the rest is a piece of cake. efore we start naming
Chapter 15 Right Triangle Trigonometry Sec. 1 Right Triangle Trigonometry The most difficult part of Trigonometry is spelling it. Once we get by that, the rest is a piece of cake. efore we start naming
Unit Circle. Project Response Sheet
 NAME: PROJECT ACTIVITY: Trigonometry TOPIC Unit Circle GOALS MATERIALS Explore Degree and Radian Measure Explore x- and y- coordinates on the Unit Circle Investigate Odd and Even functions Investigate
NAME: PROJECT ACTIVITY: Trigonometry TOPIC Unit Circle GOALS MATERIALS Explore Degree and Radian Measure Explore x- and y- coordinates on the Unit Circle Investigate Odd and Even functions Investigate
Solution Guide for Chapter 20
 Solution Guide for Chapter 0 Here are the solutions for the Doing the Math exercises in Girls Get Curves! DTM from p. 351-35. In the diagram SLICE, LC and IE are altitudes of the triangle!sci. L I If SI
Solution Guide for Chapter 0 Here are the solutions for the Doing the Math exercises in Girls Get Curves! DTM from p. 351-35. In the diagram SLICE, LC and IE are altitudes of the triangle!sci. L I If SI
SNAP Centre Workshop. Introduction to Trigonometry
 SNAP Centre Workshop Introduction to Trigonometry 62 Right Triangle Review A right triangle is any triangle that contains a 90 degree angle. There are six pieces of information we can know about a given
SNAP Centre Workshop Introduction to Trigonometry 62 Right Triangle Review A right triangle is any triangle that contains a 90 degree angle. There are six pieces of information we can know about a given
Integral Geometry and the Polynomial Hirsch Conjecture
 Integral Geometry and the Polynomial Hirsch Conjecture Jonathan Kelner, MIT Partially based on joint work with Daniel Spielman Introduction n A lot of recent work on Polynomial Hirsch Conjecture has focused
Integral Geometry and the Polynomial Hirsch Conjecture Jonathan Kelner, MIT Partially based on joint work with Daniel Spielman Introduction n A lot of recent work on Polynomial Hirsch Conjecture has focused
CURVES OF CONSTANT WIDTH AND THEIR SHADOWS. Have you ever wondered why a manhole cover is in the shape of a circle? This
 CURVES OF CONSTANT WIDTH AND THEIR SHADOWS LUCIE PACIOTTI Abstract. In this paper we will investigate curves of constant width and the shadows that they cast. We will compute shadow functions for the circle,
CURVES OF CONSTANT WIDTH AND THEIR SHADOWS LUCIE PACIOTTI Abstract. In this paper we will investigate curves of constant width and the shadows that they cast. We will compute shadow functions for the circle,
Presented, and Compiled, By. Bryan Grant. Jessie Ross
 P a g e 1 Presented, and Compiled, By Bryan Grant Jessie Ross August 3 rd, 2016 P a g e 2 Day 1 Discovering Polar Graphs Days 1 & 2 Adapted from Nancy Stephenson - Clements High School, Sugar Land, Texas
P a g e 1 Presented, and Compiled, By Bryan Grant Jessie Ross August 3 rd, 2016 P a g e 2 Day 1 Discovering Polar Graphs Days 1 & 2 Adapted from Nancy Stephenson - Clements High School, Sugar Land, Texas
Trigonometric ratios provide relationships between the sides and angles of a right angle triangle. The three most commonly used ratios are:
 TRIGONOMETRY TRIGONOMETRIC RATIOS If one of the angles of a triangle is 90º (a right angle), the triangle is called a right angled triangle. We indicate the 90º (right) angle by placing a box in its corner.)
TRIGONOMETRY TRIGONOMETRIC RATIOS If one of the angles of a triangle is 90º (a right angle), the triangle is called a right angled triangle. We indicate the 90º (right) angle by placing a box in its corner.)
SPECIAL TECHNIQUES-II
 SPECIAL TECHNIQUES-II Lecture 19: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Method of Images for a spherical conductor Example :A dipole near aconducting sphere The
SPECIAL TECHNIQUES-II Lecture 19: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Method of Images for a spherical conductor Example :A dipole near aconducting sphere The
Lecture 3: Linear Classification
 Lecture 3: Linear Classification Roger Grosse 1 Introduction Last week, we saw an example of a learning task called regression. There, the goal was to predict a scalar-valued target from a set of features.
Lecture 3: Linear Classification Roger Grosse 1 Introduction Last week, we saw an example of a learning task called regression. There, the goal was to predict a scalar-valued target from a set of features.
Modeling a Gear Standard Tools, Surface Tools Solid Tool View, Trackball, Show-Hide Snaps Window 1-1
 Modeling a Gear This tutorial describes how to create a toothed gear. It combines using wireframe, solid, and surface modeling together to create a part. The model was created in standard units. To begin,
Modeling a Gear This tutorial describes how to create a toothed gear. It combines using wireframe, solid, and surface modeling together to create a part. The model was created in standard units. To begin,
Planar Graphs and Surfaces. Graphs 2 1/58
 Planar Graphs and Surfaces Graphs 2 1/58 Last time we discussed the Four Color Theorem, which says that any map can be colored with at most 4 colors and not have two regions that share a border having
Planar Graphs and Surfaces Graphs 2 1/58 Last time we discussed the Four Color Theorem, which says that any map can be colored with at most 4 colors and not have two regions that share a border having
MATHEMATICS FOR ENGINEERING TRIGONOMETRY
 MATHEMATICS FOR ENGINEERING TRIGONOMETRY TUTORIAL SOME MORE RULES OF TRIGONOMETRY This is the one of a series of basic tutorials in mathematics aimed at beginners or anyone wanting to refresh themselves
MATHEMATICS FOR ENGINEERING TRIGONOMETRY TUTORIAL SOME MORE RULES OF TRIGONOMETRY This is the one of a series of basic tutorials in mathematics aimed at beginners or anyone wanting to refresh themselves
Chapter 4: Trigonometry
 Chapter 4: Trigonometry Section 4-1: Radian and Degree Measure INTRODUCTION An angle is determined by rotating a ray about its endpoint. The starting position of the ray is the of the angle, and the position
Chapter 4: Trigonometry Section 4-1: Radian and Degree Measure INTRODUCTION An angle is determined by rotating a ray about its endpoint. The starting position of the ray is the of the angle, and the position
Use Parametric notation. Interpret the effect that T has on the graph as motion.
 Learning Objectives Parametric Functions Lesson 3: Go Speed Racer! Level: Algebra 2 Time required: 90 minutes One of the main ideas of the previous lesson is that the control variable t does not appear
Learning Objectives Parametric Functions Lesson 3: Go Speed Racer! Level: Algebra 2 Time required: 90 minutes One of the main ideas of the previous lesson is that the control variable t does not appear
Kinematics of Machines Prof. A. K. Mallik Department of Mechanical Engineering Indian Institute of Technology, Kanpur. Module 10 Lecture 1
 Kinematics of Machines Prof. A. K. Mallik Department of Mechanical Engineering Indian Institute of Technology, Kanpur Module 10 Lecture 1 So far, in this course we have discussed planar linkages, which
Kinematics of Machines Prof. A. K. Mallik Department of Mechanical Engineering Indian Institute of Technology, Kanpur Module 10 Lecture 1 So far, in this course we have discussed planar linkages, which
Developmental Math An Open Program Unit 7 Geometry First Edition
 Developmental Math An Open Program Unit 7 Geometry First Edition Lesson 1 Basic Geometric Concepts and Figures TOPICS 7.1.1 Figures in 1 and 2 Dimensions 1 Identify and define points, lines, line segments,
Developmental Math An Open Program Unit 7 Geometry First Edition Lesson 1 Basic Geometric Concepts and Figures TOPICS 7.1.1 Figures in 1 and 2 Dimensions 1 Identify and define points, lines, line segments,
Unit 2: Locomotion Kinematics of Wheeled Robots: Part 3
 Unit 2: Locomotion Kinematics of Wheeled Robots: Part 3 Computer Science 4766/6778 Department of Computer Science Memorial University of Newfoundland January 28, 2014 COMP 4766/6778 (MUN) Kinematics of
Unit 2: Locomotion Kinematics of Wheeled Robots: Part 3 Computer Science 4766/6778 Department of Computer Science Memorial University of Newfoundland January 28, 2014 COMP 4766/6778 (MUN) Kinematics of
