Light Scattering by Individual and Groups of Spheroidal Particles
|
|
|
- Arabella May
- 5 years ago
- Views:
Transcription
1 Light Sattering by Individual and Groups of Spheroidal Partiles Diploma paper by Peter Alsholm Lund Reports on Atomi Physis, LRAP-200 Lund, August 1996
2 Abstrat In order to simulate the light propagation in illuminated samples ontaining suspensions of spheroidal partiles, taking into onsideration size, shape, onentration and different orientations, a Monte Carlo omputer program was developed. The program, based on an old Monte Carlo program, was able to treat samples of finite extension laterally, as well as in depth. The omputations of the angular sattering of eah partile, were made by separate programs based on the T-matrix theory. Modifiations of existing programs for this purpose were performed, enabling sattering alulations for partiles with larger size parameters. Simulations were made by using a sample with properties similar to human blood, i.e. a suspension of erythroytes, approximated by oblate spheroids, as sattering partiles. These results were then finally ompared with measurements and results obtained by the original Monte Carlo program. 3
3 Contents Abstrat... 3 I. Introdution Theory Sattering from one partile Eletri time-harmoni fields The T-matrix method Multiple sattering The original Monte Carlo method Material and methods The T-matrix omputer programs The original omputer program Tl Modifiations of program Tl The original omputer program T Modifiations of program Tl The Monte Carlo omputer programs The original Monte Carlo program Modifiations due to boundary onditions Implementation of speifi sattering objets Testing program MCMLBOUN, due to boundary onditions Testing limitations and auray Evaluations and tests of the programs EXTENDT3 and TMMCML Comparison with the original Monte Carlo model Results Testing program MCMLBOUN, due to boundary onditions Testing limitations and auray Evaluations and tests of the programs EXTENDT3 and TMMCML Comparison with the original Monte Carlo model Disussion and onlusions Comments to the tests and evaluations Testing program MCMLBOUN, due to boundary onditions Testing limitations and auray Evaluations and tests of the programs EXTENDT3 and TMMCML Comparison with the original Monte Carlo model Summary and onluding remarks Future Aknowledgements Referenes Appendix A: The T -matrix omputer programs A. I. Computer ode listing inluding omments A.l.l. EXTENDTI A.1.2. EXTENDT A.1.3. MCDATA A.2. Flow harts A.2.1. EXTENDTI A.2.2. EXTENDT A.2.3. MCDA TA
4 Appendix B: The Monte Carlo omputer programs B.l. Computer ode listing B.l.1. MCMLBOUN B mml.h B mmlmain B mmlio B mmlgo B.1.2. TMMCML B mml.h B mmlmain B mmlio B mmlgo B.2. List of speifi modifiations... l38 B.2.1. Modifiations from MCML to MCMLBOUN B.2.2. Modifiations from MCMLBOUN to TMMCML B.3. Flow harts Appendix C: How to run the programs C.1. EXTENDT C.2. EXTENDT C.3. MCDATA C.4. MCMLBOUN C.5. TMMCML Appendix D: Speial funtions D.l. Bessel and Hankel funtions D.2. Assoiated Legendre funtions
5 1. Introdution The knowledge of light interating with biologial tissue is important when developing new diagnosti methods and medial treatments utilizing lasers. The more these methods are refined, the more detailed studies of the propagation of light in tissue are required. In diagnosing diseases suh as aner and arterioslerosis, using lasers, the fluoresene, inelasti or elasti sattered light, transmitted through or refleted by the tissue is analyzed. Distintions in the obtained spetra originate from deviations in optial properties, whih makes it possible to differentiate between healthy and malignant tissue. When laser light is used to treat medial disorders, e.g. in obliteration of port wine stains or aner ell destrution using photodynami therapy (PDT) 1, the energy of the laser light is transformed into heat energy or indues hemial reations. In order to optimize the results of these treatments, the understanding of light propagation properties in tissue is essential. When light propagates, two proesses - absorption and sattering - our to various extents due to the medium. A ommon way of desribing the optial properties of the medium is by the absorption oeffiient, fl., the sattering oeffiient, f.!,, and the anisotropy oeffiient, g. The absorption and sattering oeffiients desribe the probability per unit path length of a photon being absorbed or sattered, respetively. The g-fator is defined by the mean value of the osine of the sattering angle. These optial parameters an be used as input parameters for Monte Carlo simulations 2, to obtain the distribution of light transmitted through or refleted by the medium. In the Monte Carlo method, the paths of a large number of photons are simulated in a randomized manner using the known geometry and optial oeffiients. In a previous work 3, the optial properties of human blood were measured in onjuntion with slow heating. Sudden hanges in g-fator and sattering oeffiient were observed simultaneously as the red blood ells were transformed from spheroidal into spherial shape. Other authors 4 ' 5 have studied the light sattering by one erythroyte and indiated that the ell shape influenes the propagation of light. The sattering proess in the Monte Carlo model has also been ritiized 6, when simulating the light distribution in human blood. The purpose of this work is to study the angular sattering by one spheroidal partile, the influene of size, shape, onentration and orientation of spheroidal partiles distributed in a homogenous non-absorbing medium and to develop a omputer program taking these harateristis into onsideration, when evaluating the propagation of light. The study inludes in partiular partiles with the size of erythroytes. For alulations of the angular sattering by one spheroidal partile, the T-matrix method is an effetive tool, desribed and used in this work. Nevertheless, the idea is that the developed program will be used not only for investigations of light propagating in human blood, but also in any tissue or media in general, using other shapes and sizes of the sattering partiles. Interesting results of investigations of the optial and printing properties of paper, orrelated to the strutures of fibres and pores 7, have also given inspiration to this work and might be another appliation of this model. 7
6 2. Theory 2.1. Sattering from one partile Eletri time-harmoni fields The time-dependent eletri field of a uniform plane wave in spae an be expressed as E(t,z) = Re(E(kz) e-iw') (2.1) Re( ) extrats the real part of a omplex variable. The omplex field E(kz) is written as E(kz) = E ei(kz-ple k = 2n:n/A 0 e ' 0 (2.2) where z is the position in the diretion of propagation ez, <p is the phase at z = 0, n represents the omplex index of refration and A 0 the free spae wavelength. The notation ee symbolizes the unity vetor in the diretion of thee-field (eel_ ej The intensity (time-averaged power per unit area) is determined by I Re(ExH) I=- JEJ Re(-.) 2 2 ~ ( stands for the omplex onjugate) (2.3) H represents the magneti field and is proportional to E. The two fields are perpendiular to eah other and to the propagating diretion. Thus, the intensity is proportional to IEI 2 The omplex variable ~ symbolizes the impedane of the medium. When a plane wave is sattered by a partile, a sattered wave is generated. Far from the partile, the time-independent sattered eletri field an be expressed as eikr E(kr) = E - o r (2.4) and is hene termed the far-field. The amplitude of the near-field has a stronger r dependene and deays faster The T -matrix method Assuming a partile is illuminated by the inident eletri field Ei. This field then indues an internal field Eint and a sattered field denoted by E, The inident field is a plane-wave in the k-diretion: This expression an be expanded as k = ke k (2.5) 8
7 Ei(kr) = E 0 L Dv[avMv(kr) + bvnv(kr)] (2.6) v where v = ( r,m,n) is the triple index for spherial harmoni funtions ( r indiates whether the harmoni funtion is odd (o) or even (e), m represents the azimuthal mode and n the expansion-oeffiient). Mv and Nv are Bessel-radial dependent vetor spherial funtions in the two polarization diretions and Dv is a normalization onstant. The inident field expansion oeffiients av and bv are obtained by evaluating different ombinations of trigonometri funtions and assoiated Legendre-funtions P: (os 8). For example, aemn is determined by n Pm(osS) d m aeiilll=4ie [-eesin(m~)m n. S -e$os(m~)-(pn(os8))] (2.7) e sm ds where e and ~ indiate the diretion of k and e8 and e~ are unity vetors in these diretions. The oeffiients a, b and b are expressed in a similar way. Jakson 8 has ornn eiiul ornn made a more detailed desription about spherial wave-expansion of plane waves. In the same way as the inident field, the internal and sattered field an be expanded: Eint(rnkr) = E 0 L DJ.l[J.lMJ.l(rnkr) + dj.lnj.l(rnkr)] j.l (2.8) v (2.9) The vetor spherial funtions M and N have a Bessel-radial dependene in equation (2.8) and a Hankel-radial dependene in equation (2.9). The oeffiients J.l, dj.l, fv and gv are unknown and the refrative index of the partile relative the surrounding medium is denoted by m. Beause of the linearity of Maxwell's equations, the relation between the different expansion oeffiients is linear. Thus, when the oeffiients av and bv are known as well as the shape and size of the partile, it is possible to determine J.L and dj.l : (2.10) fv and gv are alulated in the same way: (2.11) Thus, this relation an be expressed as
8 [] ~ -[ B-nnmx I A -nnmx n -[ :~] ~ I:~] (2.12) T-nnmx where T-matrix is a shorter name for the so alled transition-matrix. Obviously, the T matrix an be used to alulate fv and gv and thus the sattered field. The elements of the A- and B- matries onsist of surfae-integrals ontaining produts of spherial funtions. The integrals have to be numerially determined over the surfae of the partile for every v = (r,m,n) ombination. If the partile is axi-symmetri simplifiations an be made so that the surfae integrals an be redued to onedimensional integrals ontaining ombinations of Bessel-, Hankel-, assoiated Legendreand trigonometri funtions. As the elements are independent of the inident and sattered fields, it's enough to ompute the T -matrix one for a speifi sattering partile at a fixed wavelength. In the ase of a sphere, the T-matrix will be diagonal and expliit expressions an be obtained for the diagonal elements. These expressions will be idential with the ones obtained in Mie-sattering. When E, is evaluated, the far-field F is defined by eikr E (kr) = F(8,~)- r (2.13) in the limit kr -7 oo. Fe and F~ are the two omponents of F. By replaing the Hankel-funtions with asymptoti expressions (in the kr -7 oo limit), an expliit form off an be obtained 9 For example, for ee inident polarization, Fe is evaluated by i-(n+l) Pm(os8) Fe = -- os(m~) m ( n. 8 ) D f + k Sill mn ornn i-n pm (os 8) pm 1 (os 8) + -k os(m~) [n os 8 ( n. 8 ) - (n+m) ( n-. 8 )] Dmngemn (2.14) Sill Sill The differential sattering ross setion, expressing the sattered intensity in a speifi diretion relative the intensity of the inident field, an then be determined: r/8,~)= IF(8,~)!E/ (2.15) The total sattering ross setion inludes all sattering diretions and is given by a, = 1tk 2 L Dv ( lfvl 2 + lgi) (2.16) v By using the optial theorem 10, the total extintion ross setion 0" 0, whih desribes how muh the inident field is influened by the partile, an be expressed as 10
9 (2.17) F is evaluated in the diretion straight forward and e 0 is the polarization unity vetor of the inident field. Im( ) extrats the imaginary part. Finally, the absorption ross setion is defined by a =a- a a e s (2.18) By dividing the ross setions by 1ta 2, where a is a harateristi dimension of the partile, normalized ross setions an be alulated. Other authors 9 ' have desribed the T-matrix method more extensively and speifi properties of the T-matrix are analyzed by Waterman Multiple sattering The original Monte Carlo method Light propagation in turbid media an be simulated using Monte Carlo methods 2 In those, photons or photon pakages are sent on a random walk through the tissue. The phase and polarization of the photons are not taken into onsideration in this method, due to their random behaviour after multiple sattering in the tissue. The wave phenomena of the photon are thus ignored and the photon is treated as a partile. The path of every photon pakage is simulated until it is emerged or absorbed. When a large amount of photon pakages are used, good statisti results of the light distribution in the tissue an be obtained. The omputer ode MCML, written by Wang and Jaques 2, is a program based on the Monte Carlo method, where the distribution of absorbed light in a medium, ontaining layers with different optial parameters and refrative indies, an be omputed as well as the distributions of refleted and transmitted light. When the photon pakage enters the media, it is assigned an initial weight W. This weight will be redued eah time the photon pakage interats with the media. The fration ~ W whih is subtrated from the initial weight is given by ~ w = _!.! ;:.'--- w I.! a + lls (2.19) The path length, S, between the points of interation is S = _-_ln_(_i_-_r_) I.! a + lls (2.20) where R represents a random number between 0 and I. I I
10 In every interation point a new diretion of the photon pakage 1s obtained. The azimuthal angle~ is alulated by ~ = 2rR (2.21) where R is assigned a new random value between 0 and 1. In order to determine the defletion angle 8, the Henyey-Greenstein phase funtion 14 is utilized. This funtion, often used in tissue optis, is in fat a probability distribution expressed as 1-g2 p os e) = ::----=-----=-=- 4rO + g2-2g os 8)312 (2.22) where the anisotropy oeffiient g is in the range between -1 and 1. Complete bak and forward sattering are desribed by g = -1 and g = 1, respetively and g = 0 represents isotropi sattering. The defletion angle 8, assumed to be distributed aording to the Henyey-Greenstein distribution an then be determined by using a new random value R, between 0 and 1: 1 2 l+g2 -( -g )2 1-g+2gR os e = :: ;; 2g (2.23) A speial routine is used in the program to determine when the photon pakage is totally absorbed. To ensure the onservation of energy, a roulette routine is used if the photon weight falls below a partiular threshold value. The photon pakage survives at a ertain probability, m, and is then assigned the value of m times the old weight. It is otherwise terminated. The MCML-program finally also takes are of the proesses ourring when a photon pakage hits a boundary between two layers with different optial properties, using Snell's law and Fresnel's formulas 15 The Monte Carlo method is disussed more rigorously by Keijzer 16 12
11 3. Material and methods 3.1. The T -matrix omputer programs A series of omputer programs, written in FORTRAN, whih an be utilized for determination of the sattering and absorption harateristis of the fmite- thikness slab, infmite irular ylinder, general axi-symmetri partile and sphere, is developed by Barber and Hill 9 In this work two of their programs, T1 and T3, were modified to be able to ompute the angular sattering of oblate spheroids with larger size parameters as for example the erythroyte. A short desription of the originally programs as well as the neessary modifiations are desribed below The original omputer program Tl Input parameters to T1 are: 2a: 2b: x = ka = 2rna!A.o: aovrb =alb: mr,mi: nrank : ntheta: ase 0: ase 1 : ase 2: The diameter of the spheroidal partile along the symmetry axis. The diameter of the spheroidal partile perpendiular to the symmetry axis. The size parameter. Axial ratio. The real and imaginary part of the relative index of refration. Number of expansion oeffiients (number of terms in eq. 2.6). Number of integration points in the one-dimensional integrals in the alulation of the elements of the A- and B-matries. The program Tl heks the onvergene over ntheta. The program Tl heks the onvergene over nrank. The program Tl heks the onvergene over m. (m is the number of azimuthal modes). In order to evaluate a orret T-matrix, a suffiient amount of expansion oeffiients, integration points and azimuthal modes are needed depending on the size and shape of the sattering partile 17 Large partiles and oblate- and prolate-shaped partiles with a onsiderable axial ratio require larger values of nrank and ntheta, ompared to small and spherial-shaped partiles. The possibility of obtaining a onverged solution depends on the omputer apaity and the number of preision variables. The program T1 first heks the number of expansion oeffiients, integration points and azimuthal modes needed to obtain a onverged solution for a speifi sattering partile in a speifi surrounding medium and then it determines the T-matrix. Figure 3.1 shows a ross setional piture of one possible sattering partile. The partile must be axi-symmetri and fulfil the equation a r(8) = r======= (3.1) 13
12 Figure 3.1. A ross setional piture of a sattering oblate-shaped spheroid. The partile is rotational symmetri around its semiminor axis. The diameter of the partile along this axis equals 2a. When determining onvergene over nrank and ntheta for a speifi partile, the inident field is assumed along the synunetry axis and the azimuthal modem an be set to one, as all the other azimuthal modes then are zero. Convergene is verified when the angular sattering outputs for nrank and nrank -1 or nth eta and ntheta+4, respetively, orrespond with a ertain auray. The obtained values of nrank: and ntheta are then used when evaluating onvergene over m. In this ase (2), the inident field is assumed along a diretion 45 degrees from the synunetry axis (the most ompliated ase). The program alulates and ompares the angular sattering for inreasing m-values until onvergene is obtained or m > nrank: (whih means that no onverged solution exists). By the use of ase 2, the T-matrix is determined, but onvergene over nrank and nth eta must first have been obtained to be sure that the determination is orret. The number of rows (or olumns) in this matrix equals twie nrank:. When the T-rnatrix finally is stored it an be used to ompute various ross setions and resulting sattered fields in different diretions Modifiations of program Tl Using a larger T-matrix, more integration-points and extended pretston variables, onverged solutions are possible for partiles with larger size parameters and axial ratios. Extended preision uses a signifiane of 32 digits instead of normally 8 digits. The extended preision variables are neessary, as the round-off-errors in the ill-onditioned proess of alulating the integrals in the A- and B-rnatries (2.12) beome inreasingly signifiant for these kind of partiles. The DEC OSF/1 ompiler, used in this work, applies extended preision for real variables, but only double preision (16 digits) for eah part of a omplex variable. With these fats in mind, some modifiations of the Tl-program have been done: The maximum size of the matries used to evaluate the T-matrix has been inreased. The real variables have been delared reall6 (extended preision). The omplex variables have been split up into two real variables, through ritial parts of the program. The auray in the integration routine has been inreased, as there are values with more digits to pay attention to. The auray when a solution is aepted as being onverged has been inreased. The original program requires an auray of 1.0% in 8 of 10 angles, whereas the modified version requires 0.1% in all angles. 14
13 However, one onsequene of these modifiations is that the index of refration must be real, whih results in that no absorption ross setion an be evaluated. This an be adjusted by splitting all omplex variables in the program into two real ones. To prove the orretness of the modifiations, omparing tests were performed for partiles whih have a onverged solution in both the original and the modified program. Additional tests were made to hek that the obtained T-matries still fulfil the ondition of energy onservation 11 : TT + Re(T) = 0 ( symbolizes the omplex onjugate). The modified omputer program is alled EXTENDTl and is able to alulate aurate T matries, even for partiles with the dimension of a human blood ell The original omputer program T3 Program T3 uses the T-matrix, obtained from program Tl, to alulate the differential sattering ross setions in all sattering diretions. The input parameters to this program are: angint: anginp: anglab: npnts: The angle between the symmetry axis of the partile and the inident wave. The orientation of the partile relative a referene frame in the plane perpendiular to the symmetry axis. The orientation of the polarization diretion. The number of points in whih the angular sattering is evaluated is npnts2. The normalized differential sattering ross setions as a funtion of the sattering angles e and~ are put in a vetor and stored in the file T3.DA T. The graphial representation is a planar grid as shown in figure 3.2. The defletion angle e is mapped along the radius r in the graph (8 = oo when r = 0 and e = 180 when r = 1) and~ is mapped in the normal way using ylindrial oordinates. The logarithm of the normalized differential sattering ross setion at eah grid-point is alulated and stored in the vetor starting in the orner (X,Y) = (-1,-1), ontinuing by inreasing X until X= 1 (onstant Y), followed by the same proedure for the next Y -value et. The value of the grid points outside the unit irle is set to the logarithm of the bak sattering value. X=[-1,1] Figure 3.2. The representation of the sattering angles (8,p) on a planar grid. 15
14 Modifiations of program T3 The modified version of T3, alled EXTENDT3, is able to use the modified T-matrix. No further modifiations have been made in this program. In program MCDA T A, an additional modified version of T3, probability distributions of the sattering angles are omputed instead of the normalized differential sattering ross setions. One probability distribution is obtained for eah of a ertain number of inident angles. The number of inident angles, uniformly distributed between 0 and 90, is an input parameter (nbrangin) and the variable anginp from program T3 is initially always set to zero. The input parameter npnts is replaed by the two parameters nbrths and nbrphs, whih desribe the number of spherial oordinate angles 8 and ~' respetively, uniformly distributed in spae, in whih the sattering probability shall be evaluated for every inident angle. Thus, these variables indiate the resolution of the probability distribution. When evaluating the distribution for one inident angle, the normalized differential sattering ross setions are first determined for all ombinations of 8 and ~' and the probability of sattering in a ertain diretion is obtained by normalization with the sum of the sattering in all other diretions, and with the relative area this sattering diretion represents. The obtained probability values are then stored in the file MC.DAT, making it easy to implement a program utilizing these values. A further desription of the tehnial details of the implementation is found in Appendix C The Monte Carlo omputer programs The original Monte Carlo program As mentioned before, the standard C omputer ode MCML 2 an be used to simulate the distributions of refleted, absorbed and transmitted light of a speified illuminated medium. The medium onsists of a number of infinitely wide parallel layers, eah with partiular optial properties. The optial parameters (!-!.,!l, and g), index of refration and thikness of eah layer are input parameters to the program, as well as the number of photon pakages and variables defining the resolution of the light distribution. The variables dr and da represent the radial and angular resolution, respetively, and dz is the resolution along the axis parallel to the inident beam. The output file, obtained from the program, ontains the angularly and spatially resolved frations as well as the total frations of refleted, absorbed and transmitted light. Other terms, used in the output file are the refletane per unit area and transmittane per unit area. These terms atually represent the probabilities of detetion of a photon per unit area 2 The refletane per unit area at a speifi distane r from the entre of the sample is thus alulated by dividing the total photon weight deteted at this distane by the total number of photon pakage and the area of an annular ring Lla = 2n:r dr. The transmittane per unit area is alulated in a orresponding way. Speular refletane is the amount of light, refleted from the outer boundary of the sample, without interating the with medium. The remaining refletane is alled diffuse refletane. Io
15 Modifiations due to boundary onditions To be able to model the light distribution of samples, whih have a finite extension, a modified version of the omputer program is needed. The modified version MCMLBOUN assumes that the sample is laterally surrounded by glass layers, as shown in figure 3.3. The proesses ourring when the photon pakage hits the surrounding glass are the same as when it hits a boundary between two layers. As glass is non-sattering, photons propagating in this glass, away from the sample, will never turn bak. The lateral dimension of the sample and the refrative index of the surrounding glass are new input parameters. inident beam glass layer laterally laterally surrounding sample surrounding glass layer glass layer glass layer Figure 3.3. The ross setional geometry for a sample and surrounding glass layers, used in program MCMLBOUN Implementation of speifi sattering objets An additional modified version, TMMCML, has been developed within this work. This version is based on the assumption of speifi sattering objets, spheroidal partiles, are distributed in the medium. The optial parameters in the original version are replaed, in the input file as well as in the program, by the orientation of the sattering objets and the mean distane between them. Standard deviations of these new parameters, assuming Gaussian distributions, are also defined in the input file. The two main differenes between this version and the original one, are the proess of the photon pakage making a new step and the alulation of the new photon diretion from an interation point. The interation points are in this ase equal to the sattering partiles. The step of the photon pakage before a new interation ours is obtained from a Gaussian distribution 18, where the mean distane and standard deviation are defined in the input file as mentioned before. A new sattering objet is hit and the angle between the symmetry axis of the sattering spheroid and the inident diretion of the photon pakage is evaluated. A new diretion of the photon pakage is then obtained using a random number and the data base in MC.DA T. This data base ontains the probability of sattering in different diretions for several inident angles, as mentioned in hapter The name of the data base, as well as the resolution of inident and sattering diretions are defined by the user as input parameters. If the sattering objets are spheres, only one inident angle is needed. These modifiations also require a modifiation of the absorbing proess. A new variable, the normalized absorption ross setion, is defined in the input 17
16 file and speifies the relative weight of the inident photon pakage being absorbed by the sattering objet. The input parameters of one layer in program TMMCML is summarized below. meanstep: meanstepdev : absross: bux, buy, buz : st. dev : d: The mean distane between the partiles. The standard deviation of this distane. The normalized absorption ross setion. (The part of the light absorbed by one partile.) The diretion of the diretion of the partile symmetry axis (the buz-diretion is parallel with the inident field). The standard deviation of these diretions. The thikness 3.3. l;'esting program MCMLBOUN, due to boundary onditions Monte Carlo simulations, using the program MCMLBOUN aounting for lateral boundary effets, were performed for four samples with idential optial properties but different lateral extensions. The results were ompared with eah other and with results from an original Monte Carlo simulation in order to investigate the influene of boundary onditions, as the original Monte Carlo method assumes an infinite medium, but the extension of experimental samples are finite. The optial properties were hosen to be similar to those of human tissue 19 and the thikness of the sample was hosen lose to experimentally used values 20 The sizes of the samples were em x em, 5 em x 3 em, 1 em x 1 em and 0.1 em x 0.1 em. Table 3.1 shows further input parameters. # No. of photons # dz, dr #No. of dz, dr, da # Number of layers 3 # layer n mua mus g thikness # n for medium above 1 #layer #layer #layer # n for medium below 1 # n for surrounding glass 1.5 Table 3.1. Input parameters of the tests in setion 3.3, investigating the influene of boundary onditions. The variables mua and mus represent the absorption and sattering oeffiients f.la and f.ls, n is the refrative index and g is the anisotropy fator. The radial and angular resolutions are desribed by dz, dr and da. The length unit is always em Testing limitations and auray Several different omparisons have been made, using the modified programs EXTENDT 1, EXTENDT3 and MCDA T A. The alulations were mainly performed for partiles with sizes and properties similar to erythroytes and a surrounding medium 18
17 similar to blood plasma. The parameters (hapter and 3.1.3), ommon in all the tests using these programs, were thus n = (refrative index of blood plasma 21 ), rnr = (refrative index of a blood ell relative the blood plasma 22 ), mi = 0 (the imaginary refrative index of a blood ell, whih is negligible when evaluating the sattered field 23 ) and A 0 = nm (wavelength of a He-Ne laser 24 ). The variable ntheta (number of integration points) was always assigned the value of twie nrank:. In this setion, tests were made to study the limits in size and shape of the partile in order to obtain a onverged solution, as well as the influene of different polarization diretions of the inident light and the number of inident and sattering angles needed to obtain a suffiient auray. In the last-mentioned study, the program TMMCML was exeuted for four different values of the variable nbrths, whih represents the number of sattering defletion angles 8, in whih the differential sattering ross setion shall be determined. The values assigned to this variable were 46, 91, 181 and 721, respetively, and the remaining input parameters of these simulations are speified in table 3.2. The sattering partiles were spheres with a volume equal to a blood ell This volume equals m3 22, whih leads to ka = 37.67, alb = 1 and requires nrank: = 50, where nrank represents the number of expansion oeffiients in eq. 2.6, 2.8 and 2.9. The orientation of polarization (anglab) was set to zero as well as the inident angles (angint and anginp), whih are arbitrary in the ase of a sphere. # nbran_gin and nbrphs 1 37 # No. of photons # dz, dr #No. of dz, dr, da # x size and y_ size 5E+06 5E+06 # Number of layers 3 #layer n m-step m-dev. abs. thikness # n for medium above 1 #laver #layer #layer # n for medium below 1 # n for surrounding glass 1.5 Table 3.2. Input parameters of the TMMCML-tests in setion 3.4, performed to study the neessary auray of the variable nbrths (number of sattering defletion angles 8). The length unit is em Evaluations and tests of the programs EXTENDT3 and TMMCML Test 1. In order to investigate the influene of partile size on the light sattering by one partile as well as on the marosopial light distribution, exeutions of the programs EXTENDT3 and TMMCML were made for spheres of three different sizes as sattering partiles. One sphere with a volume equal to a blood ell (V = m3, ka = 37.67, a/b = 1 and nrank"" 50), one larger sphere (V = m3, ka = 60 and nrank "" 100) and one 19
18 smaller sphere (V = 14 ~m3, ka = 20 and nrank = 30). The three variables angint, anginp (inident angles) and anglab (polarization diretion) were set to zero. The variable npnts was assigned the value of 181 (the number of evaluated sattering angles is npnts2). The normalized differential sattering ross setions in various diretions for the spheres were alulated using program EXTENDT3. The logarithms of the obtained ross setions were then plotted in three-dimensional graphs utilizing a small MA TLAB program. The input parameters of program TMMCML, used for the alulation of the marosopial light distribution, are found in table 3.3. The g-fator (average value of the osine of the sattering defletion angle 8) was alulated for the three spheres using a small FORTRAN program. # nbrangin, nbrths and nbrphs # No. of photons # dz, dr #No. of dz, dr, da # x size and y_ size 5E+06 5E+06 #Number of layers 3 #layer n m-ste_p m-dev. abs. thikness # n for medium above 1 #layer #layer #layer # n for medium below 1 # n for surrounding glass 1.5 Table 3.3. Input parameters of the TMMCML-simulations in test I, made to study the influene of partile size on the marosopi light distribution. The length unit is em. Test 2. The influene of shape and orientation of sattering partiles were investigated in this test. The normalized differential sattering ross setions in various diretions for an oblate spheroid with the dimension of an erythroyte were alulated using program EXTENDT3. The values of V = 94 ~m3 and b = 3.91 ~m 22 result in alb= and ka = These dimensions require nrank = 66 (number of expansion oeffiients). Computations were made for three different inident angles, angint = 0, 45 and 90. The variables anginp and anglab were set to zero and npnts = 181. Three-dimensional graphs were plotted to show the angular sattering and the small FORTRAN program, mentioned before, was used to find the anisotropy fator g, in the different ases. The influene of partile shape and orientation on the marosopial light distribution was analyzed by omparing the output data from program TMMCML, using spheres and the reently desribed oblate spheroids in various orientations as sattering partiles. The volume of the spheres were equal to human blood ells (94 ~m3) and further properties were desribed in test 1. One simulation was made with the spheres and six with different orientations of the spheroids, desribed in table 3.4. Remaining input parameters were unhanged from test 1, exept the variable nbrangin, whih had a value of 91 in the ase of spheroids. The absorption ross setion was assumed to be independent of the shape of t h e partie. I e zs. 20
19 spheroid spheroid spheroid spheroid spheroid spheroid sphere # bux rand sphere # buy rand sphere # buz rand sphere #st. dev sphere Table 3.4. The orientation of the sattering spheroids in the seven samples in test 2. The parameters (bux, buy, buz) represent the diretion of the symmetry axis of the spheroids and this axis is parallel with the inident light beam in the ase of (bux, buy, buz) = (0, 0, I). The standard deviation of this diretion is denoted by st. dev. in the table and rand. indiates randomized orientation. If st. dev. equals zero, all spheroids have exatly the same diretion. In ase of spheres, no orientation is needed. The outlines of a normal blood ell 22 and an oblate spheroid with an equal volume are drawn in figure 3.4 and blood ell mirometer Figure 3.4. The dimension of a blood ell. 21
20 blood ell approximated by an oblate spheroid ~------~------~~------~------~ mirometer 2 4 Figure 3.5. The dimension of a blood ell approximated by a volume equivalent oblate spheroid. Test 3 was performed to investigate the influene of the distane between the sattering partiles on the transmitted and refleted light obtained from TMMCML-simulations. Two different distanes were used. In the first ase, the average distane was assigned a value of 0.2 em and in the seond a value of 0.05 em. The standard deviation was 20% of the average distane in both ases. The same partiles and orientations as in the previous test were utilized. Table 3.5. displays the remaining input parameters. # dz, dr #No. of dz, dr, da # x size and y_ size # Number of layers 3 # layer n abs. thikness # n for medium above 1 #layer #layer #layer # n for medium below 1 # n for surroundinq glass 1.5 Table 3.5. Input parameters oftmmcml-simulations in test 3, investigating the influene of the distane betvveen the sattering partiles on the light distribution. The length unit is em. 22
21 3.6. Comparison with the original Monte Carlo model A omparison between an original Monte Carlo simulation and a simulation with sattering spheres using TMMCML was made, where the extension and thikness of the sample were very large, in order to obtain multiple sattering for all photons. The properties of the spheres were still unhanged (volume equal to an erythroytes). The mean distane between two interation points and the absorption during an interation were idential in the two simulations and the g-fator in the original Monte Carlo program was assigned the mean value of the osine of the sattering defletion angle 8 (0.9940), obtained by a small FORTRAN program from the sattering probability distribution of one sphere. In order to save time, the original Monte Carlo program was used instead of MCMLBOUN, as the lateral extension of the samples were assumed to be large. Table 3.6a and 3.6b present the input parameters. #No. of photons # dz, dr # No. of dz, dr, da #Number of layers 3 # One line for eah layer n mua mus g thikness # n for medium above 1 # layer #layer #layer # n for medium below 1 Table 3.6a. Input parameters of the original Monte Carlo simulations in setion 3.6. # nbrangin, nbrths and nbrphs # No. of photons # dz, dr # No. of dz, dr, da # x size andy_ size 5E+06 5E+06 #Number of layers 3 # layer n m-step m-dev. abs. thikness # n for medium above 1 #layer #layer E #layer # n for medium below 1 # n for surrounding glass 1.5 Table 3.6b. Input parameters of the TMMCML-simulations in setion
22 4. Results The results and omparisons of the alulations and simulations, using the modified omputer programs will be presented in this hapter. In all diagrams and tables, the length unit is em. Refletane per unit area has onsequently the unit m Testing program MCMLBOUN, due to boundary onditions The distributions of refleted and transmitted light obtained when exeuting the program MCMLBOUN for four samples with different lateral extensions are shown in figures 4.1 and 4.2, as well as the orresponding result from an original Monte Carlo simulation. Table 4.1 presents the total refleted, absorbed and transmitted parts and table 4.2 indiates the time of eah simulation. The differene in refleted and transmitted light between the original Monte Carlo simulation and the two largest samples (10000 em x em and 5 em x 3 em) in the MCMLBOUN-simulations never exeeds 3%, exept lose to origo. Regarding the total amounts, this deviation is muh less than 1%. From the results of the simulations using samples with sizes less than 1 em x 1 em a larger deviation an be observed, up to 25% at some radial distanes. 2,50E =--=------~ , Refletane per unit area 2,00E original MC -m em em ' 5 em 3 em 1,50E ::,::; em 1 em 1,00E em 0.1 em 5,00E-01 O,OOE+OO t _:~~~~di:~~f::=:!ej~=j~~~~ 0 0,05 0,1 0,15 r (em) 0,2 0,25 0,3 Figure 4.1. The refletane per unit area versus the radial distane from the entre of the sample. The filled rhombs orrespond to the result of the original Monte Carlo program. The other symbols orrespond to results of program MCMLBOUN, where the sizes of the samples are desribed in the figure. The used parameter were fla= 2.6 m-1, Jl:;:. = 267 m-1 and g = The thikness was 0.05 em. 24
23 3,00E+01 2,50E+01 2,00E original MC em em.. =.... sem3em,.v.';:-:f.v.v 1 em 1 em ~0.1 em0.1 em 1,50E+01 1,00E+01 5,00E+00 O,OOE+OO.J t-=...::E~~~~~!'e- ++~----ltj 0 0,02 0,04 0,06 0,08 0,1 r(m) 0,12 0,14 0,16 0,18 0,2 Figure 4.2. The transmittane per unit area versus the radial distane from the entre of the sample. The filled rhombs orrespond to the result of the original Monte Carlo program. The other symbols orrespond to results of program MCMLBOUN, where the sizes of the samples are desribed in the figure. The used parameter were J.la= 2.6 m-1, J.ls = 267 m-1 and g = The thikness was 0.05 em. orig. MC em 5.0 em 1.0 em 0.1 em IO nfi nite) em 3.0 em 1.0 em 0.1 em #Speular refletane # Diffuse refletane #Absorbed fration #Transmittane Table 4.1. The parts of refleted, absorbed and transmitted light for the five different sizes of the samples used in the tests desribed in setion 3.3, investigating the influene of boundary onditions. orig. MC em 5.0 em 1.0 em 0.1 em (infinite) em 3.0 em 1.0 em 0.1 em t=2152s t=3683s t=3092s t=2167s t=11 08s Table 4.2. The simulation time for the five different sizes of the samples used in the tests desribed in setion 3.3, investigating the influene of boundary onditions Testing limitations and auray When testing whih sizes and shapes of partiles, possible for obtaining a onverged solution in program EXTENDTl, the minimal axial ratio obtained for ka = 19.6 was alb= 0.34, the largest size parameter for alb = was ka = 22 and the highest possible value of the relative refrative index for this kind of partiles was mr = Converged 25
24 solutions were obtained for prolate partiles with about 2% larger volumes than the orresponding oblate partiles. Tests were also performed indiating that the angular sattering for two inident angles separated by 1 deviate less than 1%. Results obtained with different polarization diretions of the inident light showed the same small deviation. The obtained radial resolutions of the refletane per unit area and transmittane per unit area from the TMMCML-simulations when testing the output resolution needed by hanging the variable nbrths (the number of sattering defletion angles 8) are shown in figures 4.3 and 4.4. The total amounts are shown in table 4.3. The differenes in total amounts of refleted and transmitted light are less than 2%, omparing nbrths = 46 and nbrths = 721. Investigating radial resolution of the light, the deviation is below 6%, exept lose to origo. 1,40E-04 -r ~~~~------:~ ""j 1,20E-04 1,OOE-04 8,00E-05 6,00E-05 4,00E-05 2,00E-05 O,OOE+OO t (~; ~L-:==< ~A it\.. ~''\.. ~:::<.. -:~ ''==\ --y:~'vv \,:~ Refletane per unit area -+-nbrts = 46 ~nbrths = 91...,.. nbrths = ;::,:;;... nbrths = ~''"- f~w--y.~j. D f} -f'~ O P- F>. f:}- f'i- H \\:.EL.i"U,:~<:=&.:{1"f.'=::1=<.H:-----! r (em) Figure 4.3. The refletane per unit area versus the radial distane from the entre of the sample in the tests desribed in setion 3.4, investigating the auray needed. The symbols in the graph orrespond to nbrths = 46, 91, 181 and 721, respetively, where nbrths represents the number of sattering defletion angles e. The mean distane between the partiles was 0.1 em and the sample thikness was 100 em. 26
25 1,00E-05_ T...( ::::~-~----~ """'l :::::l" Transmittane per unit area --+- nbrths = 46 ~nbrths=91...:.. nbrths = 181 :::::"' S,OOE-06 ~~';' 4,00E-06 ~~-.., N' -- nbrths = 721 i,~;~\ f r (em) 250 Figure 4.4. The transmittane per unit area versus the radial distane from the entre of the sample in the tests desribed in setion 3.4, investigating the auray needed. The symbols in the graph orrespond to nbrths = 46, 91, 181 and 721, respetively, where nbrths represents the number of sattering defletion angles e. The mean distane between the partiles was 0.1 em and the sample thikness was 100 em. nbrthsc=46 nbrthsc=91 nbrths=181 nbrthsc=721 # Speular refletane # Diffuse refletane #Absorbed fration #Transmittane Table 4.3. The parts of refleted, absorbed and transmitted light for the four values of nbrths in the tests desribed in setion 3.4, investigating the auray needed of the variable nbrths (the number of sattering defletion angles 8) Evaluations and tests of the programs EXTENDT3 and TMMCML Test 1. This test was made in order to investigate the influene of partile size on light sattering and distribution. The three following pages ontain three-dimensional graphs, with the logarithm of the normalized differential sattering ross setion plotted versus the sattering angles aording to the rules desribed in setion (8 along the radius), for the spheres with size parameters ka = 20.0 (V = m3), ka = 37.7 (V = 94 ~-tm3) and ka = 60.0 (V = 390 ~-tm3), respetively. Figure 4.5 shows the sattering probability versus the sattering defletion angle e for these three spheres and the radially resolved refletane and transmittane per unit area obtained from the TMMCML-simulations are presented in figures 4.6 and 4.7. Corresponding total amounts are found in table 4.4. The g-values obtained from the FORTRAN program were g = (ka = 20), g = (ka = 37.7) and g = (ka = 60). 27
26 TEST 1 Logarithm of the normalized differential sattering ross setion of a sphere. The volume is 14 J..lm y -1-1 X
27 TEST 1 Logarithm of the normalized differential sattering ross setion of a sphere. The volume is 94 ~m y -1-1 X
28 TEST 1 Logarithm of the normalized differential sattering ross setion of a sphere. The volume is 390 ~m y -1-1 X
29 3,00E-01 _,..,~~~~~~~~~~ ;ati~ii1(;1r\;~~jitt~~~-~---,::=====:-l sattering probability --+-ka = 37 _ 7 2,50E m-ka = :... ka = ,00E-01 1,50E-01 1,OOE theta (degrees) Figure 4.5. The sattering probability versus the defletion angle 8,for three spheres with size parameters ka = 37.7, 60.0 and 20.0, respetively (test I). e = 0 represents the sattering probability between 0 o and 0.5, whereas e = I o represents the interval between 0.5 and I.5 et. 4,00E-04 -r--~----~--~-:::-~~-~-~ ~-~-~ Refletane per unit area 3,50E ka = ,00E-04 2,50E-04 ~ka=37.7. ka=60.0 2,00E-04 1,50E-04 1,OOE-04 5,00E-05 0,00E n f'}. +~~~-""~~~ "8'\;;;;,f~l~;~- {'4-f.:: r (em) 100 Figure 4.6. The refletane per unit area versus the radial distane from the entre of the sample obtained from the TMMCML-simulations in test I. The rhombs, squares and triangles orrespond to sattering spheres ofvolumes I4f.1m3 (ka = 20.0), 94 f.1m3 (ka = 37.7) and 390 j..lm3 (ka = 60.0), respetively. The mean distane between the partiles was O.I em and the sample thikness was 100 em. 31
30 9,00E-06 -,-~--~~-~:::::-~~~~~~~~----~~~~~~..., Transmittane per unit area S,OOE-06 7,00E-06 6,00E-06 5,00E-06 ~ka= ka= 37.7.,:... ka = ,00E-06 3,00E-06 2,00E-06 1,00E-06 O,OOE+OO L ~:~~~;11fl;jj~-~~~! ! Figure 4.7. The transmittane per unit area versus the radial distane from the entre of the sample obtained from the TMMCML-simulations in test I. The rhombs, squares and triangles orrespond to sattering spheres ofvolumes I4J.lm3 (ka = 20.0), 94 J.lm3 (ka = 37.7) and 390 J.lm3 (ka = 60.0), respetively. The mean distane between the partiles was 0.1 em and the sample thikness was IOO em. r {em) ka = 20.0 ka = 37.7 ka = 60.0 #Speular refletane #Diffuse refletane #Absorbed fration #Transmittane Table 4.4. The parts of refleted, absorbed and transmitted light obtained by TMMCMLsimulations in test I, investigating the influene of partile size on the light distribution. Test 2. In this test the influene of partile shape and orientation on light sattering and distribution was studied. Three-dimensional graphs, with the logarithm of the normalized differential sattering ross setion plotted versus the sattering angles aording to the rules desribed in setion 3.1.3, are presented on the three following pages for an oblate spheroid with the dimension of a human blood ell. The inident angles are 0, 45 and 90, respetively. These pitures show muh smaller variations for the sattering azimuthal angle ~, than for the defletion angle e. Figure 4.8 shows the sattering probability versus the sattering defletion angle 8, for these three ases and the obtained orresponding g-values were , and , respetively. 32
31 symmetry axis inident light 8 -,- 0 sattered light TEST 2 Logarithm of the normalized differential sattering ross setion of an oblate spheroid. The inident angle is ~ y X 0 0.5
32 symmetry axis sattered light TEST 2 Logarithm of the normalized differential sattering ross setion of an oblate spheroid. The inident angle is y -1-1 X
33 symmetry axis inident light sattered ligfi TEST 2 Logarithm of the normalized differential sattering ross setion of an oblate spheroid. The inident angle is y X 0 0.5
34 4,00E-01,...,-~----~-""""':'~~'T:"" r""'1~r:""'"'"-----~ , sattering probability 3,50E-01 3,00E-01 2,50E-01 2,00E-01 1,50E oblate spheroid, inident angle= 0... oblate spheroid, inident angle = 45 degrees oblate spheroid, inident angle= 90 degrees < { sphere (equal volume) 1,OOE-01 5,00E-02 -~::~ O,OOE+OO T theta (degrees) Figure 4. 8a. The sattering probability versus the defletion angle e for three different orientations of an oblate spheroid with the dimension of a blood ell. The inident angles are 0~ 45 and 90~ respetively. The ross symbols represent the sattering probability by a sphere with an equal volume ( 94 Jlm3 ). e = 0 represents the sattering probability between 0 and 0.5~ whereas e = I 0 represents the interval between 0.5 and 1.5 et. 1,20E-02 -r ~~--~~~ ""'""""'1 ~attering probability ,OOE-02. oblate spheroid, inident angle = 0... oblate spheroid, inident angle= 45 degrees S,OOE oblate spheroid, inident angle= 90 degrees 6,00E-03 ~ =:: sphere (equal volume) 4,00E-03 2,00E-03 O,OOE+OO ~~-~~~~~~~~ theta (degrees) 45 Figure 4.8b. Continuation of figure 4.8afor larger radial distanes. The radially resolved transmittane per unit area obtained from the TMMCMLsimulations for the different orientations of the spheroids are presented in figure 4.9. Corresponding total amounts are found in table 4.5. The different symbols in the graph in figure 4.9 and the different olumns in table 4.5 represent the different orientations of the sattering spheroids. 36
35 Orientation ran do- (1,0,0) (0, 1,0) (0,0,1) (1,1,1) (1,1,1) spheres mized st.dev.=0.5 #Speular refletane #Diffuse refletane #Absorbed fration #Transmit tane Table 4.5. The parts of refleted, absorbed and transmitted light obtained by the TMMCMLsimulation in test 2, using different orientations of the sattering spheroidal partiles. Eah olumn represents one sample ontaining spheroidal partiles and the partiles have different orientations in the different samples. The orientation of the partile symmetry axis is desribed by the three values on the first row, where the diretion ( 0, 0, 1) is parallel with the inident light. If there is a deviation in the orientation, this is denoted by st.dev. The last olumn orresponds to sattering spheres with an equal volume. 6.00E-04,_...~~~~--~o:""""'-~~---~--~~~~~--~-~ Transmittane per unit area 5.00E E oblate spheroids (randomized)...-oblate spheroids (1,0,0) '='::: oblate spheroids (0, 1,0) 1.00E-04 X oblate spheroids (0,0, 1) ---oblate spheroids ( 1, 1, 1)._oblate spheroids (1, 1,1; st. dev. = 0.5) -+-spheres O.OOE+OO ~-l=:oo=l~..;...:=:~o..,...+o-ooolooo...,f,~::::~~-==~ -- &ll&ai-4...,._j r (em) Figure 4.9a. The transmittane per unit area versus the radial distane from the entre of the sample in the TMMCML-simulations in test 2, using samples ontaining spheroids in different orientations in the different ases. The different symbols represent the orientations of the sattering spheroidal partiles. The small strokes in the lower part of the figure represent the transmittane per unit area obtained by a simulation using spheres of equal volume as sattering partiles. 37
36 7,00E-06 6,00E-06 5,00E-06 4,00E-06 3,00E-06 2,00E-06 1,OOE-06 Transmittane per unit area -+-oblate spheroids (randomized) ~oblate spheroids ( 1,0,0) oblate spheroids (0, 1,0)...,';:::;... oblate spheroids (0,0, 1) -lir- oblate spheroids ( 1,1, 1) -e-oblate spheroids (1, 1,1; st.dev. = 0.5)...J--spheres O,OOE+OO r (em) Figure 4.9b. Continuation of figure 4.9afor larger radial distanes ,00E-07 6,00E-07 5,00E oblate spheroids (randomized) ~oblate spheroids ( 1,0,0) oblate spheroids (0, 1,0). ';:::;',... oblate spheroids (0,0, 1) 4,00E-07 3,00E-07 2,00E-07 1,OOE-07 O,OOE+OO.J t--~,f~~~lll!hMI!Jlllii8i~~~~fdr.iMJM i!l~iti~liiiil..l r(m) Figure 4.9. Continuation of figure 4.9b for larger radial distanes. Test 3. The amounts of refleted, absorbed and transmitted light obtained by two TMMCML simulations, using different average distanes, 0.2 em and 0.05 em, between the sattering partiles, are shown in tables 4.6 and
37 Orientation ran do- (1,0,0) (0, 1,0) {0,0, 1) (1,1,1) (1,1,1) spheres mized st.dev.=0.5 #Speular refletane #Diffuse refletane #Absorbed fration #Trans mittane Table 4.6. The parts of refleted, absorbed and transmitted light obtained by the TMMCML-simulations in test 3, investigating the influene of the distane between the sattering partiles on the light distribution. The results orrespond to a simulation where meanstep = 0.2 em. Different orientations of the sattering spheroidal partiles were used. The last olumn orresponds to sattering spheres with an equal volume. The sample thikness was 5 em. Orientation ran do- (1,0,0) (0, 1,0) (0,0,1) (1,1,1) (1,1,1) spheres mized st.dev.=0.5 #Speular refletane #Diffuse refletane #Absorbed fration #Trans mittane Table 4.7. The parts of refleted, absorbed and transmitted light obtained by the TMMCML-simulations in test 3, investigating the influene of the distane between the sattering partiles on the light distribution. The results orrespond to a simulation where meanstep = 0.05 em. Different orientations of the sattering spheroidal partiles were used. The last olumn orresponds to sattering spheres with an equal volume. The sample thikness was 5 em. Obviously, the refleted and transmitted parts of the light inrease when the distane between the sattering partiles inreases. The absorbed part dereases Comparison with original Monte Carlo model A three-dimensional piture representing the Henyey-Greenstein phase funtion is shown on next page. The representation of the sattering angles on a planar grid was desribed in setion (the sattering defletion angle 8 along the radius). The probability values in eah grid point are normalized in order to obtain a normalized total sattering ross setion equal to the sphere with a volume of an erythroyte (rsf'ra2 = 3.1). 39
38 Henyey-Greenstein distribution for g = y X 0
39 The radial resolutions of the refleted and transmitted light for the simulation of the original Monte Carlo program are shown in figures 4.10 and 4.11, as well as the results from the orresponding TMMCML-simulation, using spheres as sattering partiles. The refleted, absorbed and transmitted parts of the light are displayed in table ,50E =-"'7."""""":"" ,., ~ Refletane per unit area 3,00E-04 2,50E-04 2,00E original MC... TMMCML 1,50E-04 1,00E-04 5,00E-05 O,OOE+OO l ~----! r (em) Figure 4.1 Oa. The refletane per unit area versus the radial distane from the entre of the sample, omparing the original Monte Carlo model with the TMMCML program, using spheres as sattering partiles. The rhombs orrespond to the original MCML program and the squares to TMMCML. The sample thikness was 200 em and the optial properties in the original program were Jla = m-1, J.ls = m-1 and g = Corresponding parameters in the modified version were meanstep = 0.1 em (meanstepdev = 0.02 em) and absross = ,60E =--::::-~----..,., """! Refletane per unit area 1,40E-05 1,20E-05 1,00E original MC... TMMCML S,OOE-06 6,00E-06 4,00E-06 2,00E f--~~~~~-llill!llllilllllll!iii!~!llliil-illllll!llliil-illllllllll illllllllll!lllllllllilllliiillllllliiillliiiiiiiiiii J O,OOE+OO r (em) Figure 4.10b. Continuation of figure 4.10afor larger radial distanes. 41
40 2,00E-06, ,."'""-;"~ ~: ""> Transmittane per unit area 1,SOE-06 1,60E-06 1,40E-06 1,20E-06 1,00E-06 S,OOE-07 6,00E-07 4,00E-07 2,00E original MC... TMMCML O,OOE+OO ! r (em) Figure The transmittane per unit area versus the radial distane from the entre of the sample, omparing the original Monte Carlo model with the TMMCML program, using spheres as sattering partiles. The rhombs orrespond to the original MCML program and the squares to TMMCML. original MC TMMCML #Speular refletane # Diffuse refletane # Absorbed fration # Transmittane Table 4.8. The parts of refleted, absorbed and transmitted light obtained by simulations of the original Monte Carlo program and the TMMCML program, using spheres as sattering partiles. The differene in transmitted and refleted light is less than 5% at all radial distanes exept lose to origo. The simulation time in the modified version is almost four times that used by the original program (34.0 hours for the modified program and 9.6 hours for the original program). 42
41 5. Disussion and onlusions 5.1. Comments to the tests and evaluations Testing program MCMLBOUN, due to boundary onditions The onlusion of this test, when investigating the influene of the lateral extension of the sample on the light distribution, is that for normal experimentally used tissue samples of ommon thikness, in the order of millimetres, the extension of the sample ought to be at least a few entimetres in eah diretion, if the original Monte Carlo program, assuming infinitely wide layers, should be a orret model. Higher values of ~s and lower values of g require larger samples. The refrative indies of the sample and the surrounding medium influene the neessary size of the sample as well, as a big differene between these two indies results in more light refleted bak towards the surrounding medium into the sample instead of esape in the borders. The tests onfirm reasonable results by the program MCMLBOUN and the fat that this modified version requires more simulation time for samples, possible to approximate as infinite than the original program. The inrease in simulation time depends on more neessary omputations in MCMLBOUN, as the distane from the position of the photon pakage to three different boundaries, instead of one in the original program, must be alulated for every new step. The small deviations in refletane per unit area lose to origo in figure 4.1, depend on the low number of photons emerged in this area Testing limitations and auray These tests, investigating needed auray, assure that it is suffiient to assign the number of sattering defletion angles, nbrths, a value of 46, when the sattering partiles are spheres. The results show also that the number of inident angles, nbrangin does not need to exeed 91 and that the polarization diretion of the inident light is arbitrary. With these fats in mind together with the smaller dependene of the azimuthal sattering angle (test 2 in setion 4.2) and information of the omputer apaity, reasonable input parameters to program TMMCML are nbrangin = 91, nbrths = 181 and nbrphs = 37. The last parameter represents the number of azimuthal sattering angles. The small deviations lose to origo in the distributions of transmitted and refleted light (figures 4.3 and 4.4) depend on the low number of emerged photons in these areas. Finally, the limits of size and shape of the sattering partiles in order to obtain onverged solutions by program EXTENDT1 agree very well with those obtained by Mishhenko et. al. 26, and are muh better than the values ahieved by Hill et. al. 27, probably using non-extended variables Evaluations and tests of the programs EXTENDT3 and TMMCML Test 1 shows the well-known phenomenon 28, that large spheres tend to satter more light in the forward diretion than small ones, omparing three spheres with size parameters ka = 20.0, 37.7 and 60.0 (V = 14 j.lm3, 94 ~m3 and 390 ~m3). The three-dimensional figures on pages 28-30, as well as the sattering probability distribution in figure 4.5 indiate this property. The obtained g-values (0.9891, and ) for the three spheres, respetively, show that this value is lower for the largest sphere than for the sphere with a size parameter of The g-fator, whih only desribes the mean value of the osine of 43
42 the sattering defletion angle 8, is thus no suffiient quantity of desribing the distribution of light sattered by a partile. Neither is the forward sattering. The osillating patterns of the sattering probability distributions depend on interferene phenomena. The TMMCML-simulations made for the three mentioned spheres, as sattering partiles, were mainly performed to hek the program TMMCML rather than to obtain any exat results. The mean distane between two sattering partiles and the absorption in eah of these partiles were assumed to be equal in these three simulations. The first assumption results in different volume proportions of partiles in relation to surrounding medium and the seond is wrong, while the absorption ross setion is volume dependene 9 Nevertheless, the TMMCML-simulations manifest the fat, that more light is forward sattered when larger partiles are used (figures 4.6 and 4.7). The high value of refletane per unit area in origo (figure 4.6) for the largest sphere is probably due to the higher omplete bak satter value for this partile. The program TMMCML yields thus reasonable results in well aordane with general sattering theory 28 When omparing the results of sattering by an oblate spheroidal partile, for three different inident angles (0, 45 and 90 ) in test 2, it is evident that a smaller inident angle results in more light sattered straight forward than a larger inident angle. This is shown in the three-dimensional figures on pages 33-35, the sattering probability distribution in figure 4.8, as well as indiated by the obtained g-values (0.9967, and in the three ases, respetively) and is due to the larger area of the partile perpendiular to the diretion of the inident wave for a smaller inident angle 30 The bak sattering for an inident angle of 0 is about 100 times higher than that for the ase of 45. When the inident angle is 90, the bak sattering is also quite high. These results may depend on the higher refletane in straight opposite diretion, whih ours when the light falls perpendiular towards a surfae, than for the ase of slant inident light, e.g. 45. However, influene on the probability of bak sattering of partile size and shape is very irregular 30 and is hard to predit. Another disovery, from the three-dimensional figures is that the sattering dependene of the azimuthal angle ~' seems to be muh less than that of the defletion angle 8. Not totally negligible, though. Several interesting fats are shown in the results of the TMMCML-simulations in test 2, using oblate spheroids in different orientations as sattering partiles. The most remarkable property is the muh lower amounts of refleted light and higher amounts of transmitted light, obtained when the oblate spheroids were used as sattering objets ompared to when spheres were used, irrespetive of the orientations of the spheroids (see table 4.5). This observation has earlier been desribed and disussed in ase of randomly oriented spheroids 25 The total amount of absorbed light, whih indiates the interation sites and events of the photons in the medium is also muh less in the ase of spheroids. The results presented in table 4.5, show that the absorbed fration of light using spheroids was about half the fration obtained, when using spheres as sattering partiles. When omparing two simulations with the same orientation of the partiles with an unertainty (normal distribution with a given standard deviation) in the diretion in one of them (blak stars and filled irles in figure 4.9), the total transmittane and the light transmitted lose to origo are higher in the standard deviation ase. Far from origo, the non-standard deviation ase yields more transmitted light. This is probably a onsequene of one the light has been sattered in a quite large angle, it tends to ontinue in this diretion as it is more probable. In the standard deviation ase, the photon pakage will 44
43 have a higher probability to hit a spheroid at an angle with lower g-fator (i.e. at an inident angle lose to 90 ), than in the non-standard deviation ase. The probability of sattering in wide angles will therefore be higher and more sattering events result in wide sattering angles. This an lead to that it is more rare that photons are transmitted far from the entre of the sample. The results of two simulations using spheroids oriented with their symmetry axis in the two diretions perpendiular to the inident beam, respetively (squares and triangles in figure 4.9) are almost idential, whih is expeted due to the axial symmetry of the partile. If the symmetry axis of the spheroids is parallel to the inident light (grey stars in figure 4.9), both the total refletane and the total transmittane will be higher. This is in agreement with the results from three-dimensional pitures (pages 33-35) of the angular sattering by an oblate spheroid for different inident angles. They show higher values of forward sattering as well as bak sattering for an inident angle of 0 than for other angles ( 45 and 90 ). The fat that a sample with randomly oriented spheroids (filled rhombs in figure 4.9) results in more light transmitted straight forward than for spheroids with their symmetry axis parallel to the inident light (grey stars in figure 4.9) seems rather onfusing at first sight, as the highest g-fator is obtained for an inident angle of 0. Nevertheless, taking into onsideration that the total amount of transmitted light is lower in the latter ase, due to the high probability of bak sattering and the fats mentioned before, that one the light has been sattered in quite a large angle, it tends to ontinue in this diretion more probable in the latter ase than in the first, this phenomenon an seem reasonable. Even more surprising seems a omparison between the results of the TMMCML-simulations using spheres (small grey strokes in figure 4.9) and spheroids oriented with their symmetry axis in the diretion perpendiular to the inident beam, as sattering partiles. Results from test 1 and test 2, obtained using a small FORTRAN program, shows g = for the spheres and g = for the spheroids, when the inident angle equals 90. Thus, less light would atually be sattered in the forward diretion using spheroids oriented with the symmetry axis perpendiular to the inident beam than in the ase with spheres. However, the anisotropy fator, g, desribes only the mean value of the osine of the defletion sattering angle 8, but not the sattering probability distribution. In fat, the sattering probability of a sattering angle between 5 and 35 is muh higher for this kind of spheroids than for spheres, whih an be seen in figure 4.8. The inident angle is around 90 only in the first interation points and ausing other diretions of the inident angle at later interations. The explanation onerning samples with no deviations in the orientations of the spheroids is also most likely in this ase, due to the high transmission far from origo, using the spheroids as sattering partiles (grey stars in figure 4.9). Comparing the results of test 3, where two different distanes (0.2 em and 0.05 em) between the partiles in TMMCML-simulations, reasonable results are obtained i.e. more absorption and less transmission for the shorter partile distane due to more interation oasions. The higher amounts of refleted light for samples ontaining spheroids, with larger distane in-between are probably due to higher amounts of light refleted in the lowest boundary, whih is transmitted through the sample one more. 45
44 Comparison with original Monte Carlo model When simulating multiple light sattering by exeuting TMMCML with sattering spheres and the original Monte Carlo program with idential values of the g-fator, the mean distane between two interation points and the absorption during an interation, the results show that light distribution is independent the sattering phase funtion Henyey Greenstein versus T-matrix omputation for spheres if the photons are sattered many times. The deviation in the distribution of refleted light lose to origo (figure 4.10), is mainly aused by photons, not multiple sattered. The small deviations in the transmittane diagram (figure 4.11) might be due to the low number of photons in this areas. The differene in simulation time indiates the more ompliated omputations of the sattering events, required by the TMMCML program Summary and onluding remarks The modified programs have been used to simulate the distributions of transmitted and refleted light of samples with a finite extension ontaining spheroidal sattering partiles and the results presented here orrespond well with those by others within this field 25 ' 26 ' 28 ' 30 One purpose of this work was to get a more aurate model for prediting light propagation in human blood. The main disadvantage of the developed model is the large distane between the sattering partiles needed due to the assumption of far-field (eq. 2.13). The original Monte Carlo model used, is a onventional way of desribing light propagation in tissue 20 ' 3 L 32, in spite of its insuffiient desription on the mirosopi level. Monte Carlo simulations, using the Henyey-Greenstein funtion, has been proved to be in a good agreement to measured values of refleted and transmitted light in human tissue 33 The most important assumption by the Monte Carlo model is that the light satters aording to the Henyey-Greenstein funtion. In the tests made during this work, no agreement have been obtained between the results of the program TMMCML with oblate spheroids as sattering partiles and the original Monte Carlo program with orresponding input parameters. One explanation for the ase of short distanes between the blood ells (normal human blood) might be that this distane is muh too small to assume that the inident field of one ell is equal to the sattered far-field from the previous ell. Nevertheless, this annot be the whole truth, as there is no agreement when the distane between the ells is inreased (Test 2). One possible reason to this fat is that the original Monte Carlo method and the Henyey Greenstein phase funtion maybe are no longer valid in extremely diluted blood, in spite of a sample thikness resulting in multiple sattering. Thus, the modified model would in this ase be a better desription of the light propagation. The Monte Carlo model might even not be valid for blood at all, in spite of its good agreement for tissue in general. Another reason to the mentioned disagreements ould be that the shape deviation between a blood ell and an oblate spheroid might influene the sattering proess too muh to make suh an approximation. This an be due to different distribution of light sattering, different diffration and ourrene of interferene 20 or some resonane phenomenon taking plae. Finally, the assumptions made in the work suh as angular resolution of inident and sattered field, disregarding of the light polarization and negleted dependene of partile light absorption on the angular sattering, might have influened the results. 46
45 Measurements made on slightly diluted blood 5, also indiate higher values of refletane in proportion to transmittane than ever obtained by TMMCML simulations, with orresponding sample sizes and distanes between the sattering spheroids. However, no measurements are made at the low onentrations required for aurate T-matrix omputations. Nevertheless, some optial measurements on human blood qualitatively agree with the simulations in this work. The transmitted light for instane derease when the blood ells were transformed from spheroidal into spherial shape 3 This is in line with the results obtained from the simulations (figure 4.5) showing less transmitted light from the sample with spherial partiles than from the one ontaining volume equivalent spheroids. Agreements is also obtained between measurements showing more refleted and less transmitted light with inreasing blood flow 3 \ when the ells are less randomly oriented and the results from simulations with totally randomized versus well aligned spheroids showing more transmitted light for the former (Table 4.5) Future As mentioned before, the omputer programs, developed during this work, an be used to evaluate the sattering in various diretions from large spheroidal partiles, as well as the distributions of transmitted and refleted light of a sample ontaining a lot of suh partiles in different orientations. These programs an hopefully be of use when suh results are needed to interpret measurements and to understand whih partile parameters influene the distributions of sattered light. The number of possible shapes and sizes of the sattering partiles has inreased onsiderably due to this work, and the appliation field has thus expanded. In order to ontinue the investigations of sattering by blood ells and light distribution in human blood, some possible further works are suggested: To establish an expliit expression, r(8) (see figure 3.1 ), of the shape of the blood ell (figure 3.4) and to obtain a onverged solution for suh a partile by the program Tl. The first part would be possible, modifying an available impliit expression 22, while the onvergene probably requires more advaned omputers and further programming efforts. Another modifiation of the programs Tl and T2 9, in order to obtain the absorption ross setions for different inident angles and the angular sattering without negleting the absorption. Measured values of the imaginary refrative index of a blood ell are available 23 and using a ompiler with extended preision for omplex variables, the neessary modifiations should be few. Measurements of transmitted and refleted light, from a sample ontaining blood, or another suspensions with spheroidal partiles diluted to suh an extension that the assumption of far-field, desribed earlier, is fulfilled. The idea would be to ompare the results obtained by the program TMMCML with measured values. 47
46 6. Aknowledgements First of all, I would like to thank my supervisor Annika Nilsson for her good advies, positive attitude to the emerged problems and for always having time for all my questions. Speial thanks to Anders Karlsson at the Department of Eletromagneti Theory, Lund Institute of Tehnology, who shared his knowledge about the T-matrix method and the belonging omputer programs. Many thanks to Stefan Andersson-Engels for taking part in stimulating disussions, as well as the outlining of this projet and to Jorgen Carlsson who helped me, with the largesaled alulations on his omputer. I am grateful to my family, who has supported me during my work. Finally, I would like to thank Professor Sune Svanberg, who woke my interest for appliations of atomi physis and all the other staff members at the division, for helping me solving different kind of problems and many pleasant onversations. 48
47 7. Referenes 1. B. W. Henderson and T. J. Dougherty, Photodynami Therapy - Basi priniple and linial appliations (Marel Dekker, INC. New York, USA, 1992). 2. L. Wang and S. L. Jaques, "Monte Carlo modeling of light transport in multi-layered tissues in standard C", (1992). 3. A. M. K. Nilsson, G. W. Luassen, W. Verkruysse, S. Andersson-Engels and M. J. C. van Gernert, "Changes in optial properties of human whole blood in vitro due to slow heating", submitted to Photohem. Photobiol. (1996). 4. J. M. Steinke and A. P. Shepherd, "Comparison of Mie theory and the light sattering of red blood ells", Appl. Opt. 27, (1988). 5. S. Kashima, A. Sohda, Y. Yagyu and T. Ohsawa, "Determination of deformability of erythroytes by hange in sattering ross setion", Japanese Journal of Applied Physis part 1 34, (1994). 6. H. Hahn, A. Roggan, D. Shadel, U. Stok, H. Baumler and F. Wondrazek, "Die Optishen Eigenshaften von diken Shihten zirkulierenden Humanblutes", Minimal Invasive Medizin 7, (1996). 7. J. Carlsson, P. Hellentin, L. Malmqvist and W. Persson, "The propagation of light in paper: modelling and Monte Carlo simulations", submitted to JPPS (1995). 8. J.D. Jakson, Classial eletrodynamis (John Wiley & Sons, In. USA, 1975). 9. P. W. Barber and S. C. Hill, Light sattering by partiles: Computational Methods. (World Sientifi Publishing Co. Pte. Ltd. Signapore, 1990). 10. G. Kristensson, Spridnings- oh antennteori (Lund, 1995) (in Swedish). 11. P. C. Waterman, "New formulation of aousti sattering", The Journal of the Aoustial soiety of Ameria 45, (1968). 12. W. E. Vargas, "Visible and near infrared optial properties of pigmented films", Dissertation thesis UPTEC R (Institute of Tehnology, Uppsala university, Uppsala, 1995). 13. P. C. Waterman, "Symmetry, unitarity and geometry in eletromagneti sattering", Physial review D 3, (1970). 14. L. G. Henyey and J. L. Greenstein, "Diffuse radiation in the galaxy", Astrophysis Journal93, (1941). 15. E. Heht, Optis (Addison-Wesley Publishing Company, Reading, Massahusetts, USA, 1987). 49
48 16. M. Keijzer, "Light transport for medial laser treatments", Ph.D. Thesis (Tehnishe Universiteit Delft, the Netherlands, 1993). 17. M. I. Mishhenk:o, "Light sattering by size-shape distributions of randomly oriented axially symmetri partiles of a size omparable to a wavelength", Appl. Opt. 32, (1993). 18. W. H. Press, S. A. Teukolsky, W. T. Vetterling and B.P. Flannery, Numerial reipes inc (Cambridge University Press, Cambridge, 1992). 19. W. F. Cheong, S. A. Prahl and A. J. Welh, "A review of the optial properties of biologial tissues", IEEE J. Quant. Eletr. 26, (1990). 20. R. Graaf, A. C. M. Dassel, M. H. Koelink, F. F. M. de Mul, J. G. Aarnoudse and W. G. Zijlstra, "Optial properties of human dermis in vitro and in vivo", Appl. Opt. 32, (1993). 21. G. J. Streekstra, A. G. Hoekstra, E.-J. Nijhof and R. M. Heethaar, "Light sattering by red blood ells in ektaytometry: Fraunhofer versus anomalous diffration", Appl. Opt. 32, (1993). 22. E. Evans and Y. Fung, "Improved measurements of the erythroyte geometry", Mirovasular researh 4, (1972). 23. L. Reynolds, C. Johnson and A. Ishimaru, "Diffuse refletane from a finite blood medium: appliations to the modeling of fiber opti atheters", Appl. Opt. 15, (1976). 24. S. Svanberg, Atomi and moleular spetrosopy (Springer Verlag, Heidelberg, Germany, 1992). 25. S. Asano and M. Sato, "Light sattering by randomly oriented spheroidal partiles", Appl. Opt. 19, (1980). 26. M. I. Mishhenk:o and L. D. Travis, "T-matrix omputations of light sattering by large spheroidal partiles", Optis Comm. 109, (1994). 27. S. C. Hill, A. C. Hill and P. W. Barber, "Light sattering by size/shape distributions of soil partiles and spheroids", Appl. Opt. 23, (1984). 28. P. Latimer and B. E. Pyle, "Light sattering at various angles. Theoretial preditions of the effets of partile volume hanges", Biophysial Journal12, (1971). 29. H. C. van de Hulst, Light sattering by small partiles (Wiley, New York, 1957). 30. S. Asano, "Light sattering properties of spheroidal partiles", Appl. Opt. 18, (1979). 50
49 31. A. M. K. Nilsson, R. Berg and S. Andersson-Engels, "Measurements of the optial properties of tissue in onjuntion with photodynami therapy", Appl. Opt. 34, (1995). 32. A. Roggan, H. Albreht, K. Dorshel, 0. Minet and G. J. MUller, "Experimental set-up and Monte-Carlo model for the determination of optial tissue properties in the wavelength range nm", SPIE 2323, (1995). 33. S. L. Jaques, C. A. Alter and S. A. Prahl, "Angular dependene of HeNe laser light sattering by human dermis", Lasers Life Si. 1, (1987). 34. L. G. Lindberg and P. A. Oberg, "Optial Properties of blood in motion", Opt. Eng. 32, (1993). 35. G. Artken, Mathematial methods for physiists (Aademi Press, INC. San Diego, California, 1985). 51
50 APPENDIX A: The T -matrix omputer programs A.l. Computer ode listing inluding omments The omputer ode listing of the three modified T-matrix omputer programs, inludes some omments of the speifi modifiations. Remarks are inserted in the programs EXTENDTl and MCDATA where modifiations of the Tl- and EXTENDT3-programs have been made. When hanging program T3 to EXTENDT3, only general modifiations have been made and they are all desribed in the beginning of program EXTENDT3. Original omments in program Tl and T3, whih are not valid in the modified versions, are removed. A.l.l. EXTENDTl : program EXTENDT1 Light Sattering by Partiles: Computational Methods by P.W. Barber and S.C. Hill opyright () 1990 by World Sientifi Publishing Co Pte Ltd Modi fi tjoi1s 1996 by P. Al shol.m and A. Nilsson alulate the sattering by axisymmetri dieletri objets onvergene test over three parameters: nrank : number of terms (matrix order) ntheta: number of integration steps nm : number of azimuthal modes m inputs: nrank matrix order ntheta = integration steps i = onvergene ase ntheta ( = 0 ), nrank x = size parameter (ka) aovrb = alb ratio 1 ), or nm ( 2 ) em omplex index of refration, (real, imag) (imag is positive for absorption) EXTENDT1 An auray of 32 digits is needed to obtain onverged solutions for large satterers. The DEC OSF/1 ompiler uses 32 digits for real variables(real16) and (16+16) digits for eah part of a omplex variable(double omplex). We have to split the omplex variables into two real variables. These modifiations have been made: no imaginary part of refrative index (erased everywhere) all real variables are delared real16 all variables whih have no imaginary part, if the refration index is real, are also delared real16 all omplex variables whih are used before returning from prssm are split up in a real and an imaginary part. Both parts are delared real16 at the end of prssm, the ritial region is passed and the omplex variables an be delared double omplex EXTENDT1 arrays are expanded to nrank = 200 and ntheta = 1000 maximum -1-1 alulate [TJ [BJ [A] { [A] ' [B] '}' use transposed matries to permit the effiient -1-1 [ ] [ ] operation rather than [ ] [ ] (1) obtain the transposed matries [A] ' and [B]' -1 (2) alulate [T]' = [A]' [B]' (3) transpose [T]' to obtain [T] EXTENDT1 52
51 The size of a,b,a2,b2,aa2,bb2,are,aim bre,bim,breold,areold,tmat is 12nrankmax)~2 The size of mxnrm,ls,ab1,ab2, fg1, fg2 is (nrankmax) The size of bslmp,hankelre,hankelim is (nrankmax+1j The size of as,wt is (nthetamax) The ommon-bloks have been hanged and split up, in order to prevent ompiler warnings EXTENDT1 0.0 is hanged to O.qO mplx(o.o,o.oj is hanged to mplx(o.do,o.doj 1.0e-05 is hanged to 1.0q-05 et. impliit real16 (a-h,o-z) double omplex a,b ommon dtr,rtd,pi ommon /mtxom/ nrank,nranki,a(400,400j,b(400,400) ommon /mtxom2/ mxnrm(200) ommon /mvom/ nm,kmv ommon/mvom2/ mv,twm,prodm ommon /thtom/ theta,sinth,osth,x ommon /uvom/ angint,anginp,utheta,uphi,aovrb,mr,mi,i ommon /mtxom3/ a2(400,400),b2(400,400) real16 wt(1000),as(1000),pnmllg(201),bslmp(201) real16 hankelre(201),hankelim(201),aa2(400,400),bb2(400,400) set program onstants EXTENDT1 : no imaginary refration index nrankmax,nthetamax: new variables better auray of pi,dtr et. nrankmax = 200 nthetamax = 1000 pi = dtr =pi/180.q0 rtd=180.q0/pi pi2 = pi/2.q0 write(6,200) write ( 6, ) 'enter nrank, ntheta, ase' read(5,) nrank,ntheta,i nranki = nrank+1 nr2 = 2nrank write(6,210) WtiL.~((1,) '..:onl.t_~l X, LlUVlLJ,!Ill' read(5,) x,aovrb,mr set the index of refration for an exp(-iwt) time variation EXTENDT1 : The refration index is always real mi is erased em, den et. are delared real16 em = mr den = m2 utheta and uphi are the amplitudes of the inident field in the theta (parallel) and phi (perpendiular) diretions utheta = 1.q0/sqrt(2.q0) uphi = 1.q0/sqrt(2.q0) onvergene over m (i = 2) requires nrank azimuthal modes, a nonsymmetri orientation, and a file for the matries EXTENDT1 : status='unknown' is added in the open arguments, to prevent ompil.er warnings mtxsav = 0 if(i.eq.2) then nm = nrank angint = pi/4.q0 anginp = pi/4.q0 write(6,220) write(6,) 'enter1 (save [TJ) or2 (save [A])' read(5,j mtxsav if(mtxsav.eq.1) then open(unit=11,file='t',form='unformatted',status='unknown') else open(unit=11,file='a',form='unformatted',status='unknown') end if rewind 11 onvergene over ntheta (i = 0) or nrank (i = 1) requires one azimuthal mode (m = 1) and a symmetri orientation else nm = 1 angint anginp end if O.qO 0.qO write(6,230) nm,nrank,ntheta,i writ.e(6,240) x,aovrb,mr dthjlpr = anyinl rld angppr = anginprtd write(6,250) utheta,uphi,angtpr,angppr 53
52 = 10 onvergene over ntheta (i = 0) requires solutions for two values of ntheta it " 1 ifli.eq.o) it = 2 do 160 ion= 1,it set the integration points and weighting values all gauss(wt,as,ntheta,o.q0,pi21 enter a loop for eah azimuthal mode m do 150 im = 1,nm set m-dependent variables kmv = im-1 i f! nm. eq. 1 1 kmv = 1 :::m\r = real (kmv) m2 = mv2 prodm = 1.q0 if(kmv.eq.o) then em = l.qo else em= 2.q0 quanm = mv do 10 i quanm prodm ontinue end if qem = 2.q0/em twm = 2.q0mv 1,kmv quanm+l.qo quanmprodm/2.q0 set indies for matrix ompression when n < m note: useful only when m > 1 j = kmv-1 flij.lt.oj ij = 0 jt = 2ij ns = nrank-ij ns2 = 2ns initialize all matrix elements to zero EXTENDT1 : Different initialization do iii 1,2nrankmax do jj 1,2nrankmax a2 I i, j j j I = 0. qo b21 i,jjj) = O.qO enddo enddo enter a loop to integrate over the surfae (theta is the integration variable) do 50 ithta = 1,ntheta theta = as(ithta) sinth = sin(theta) osth = os(theta) alulate the assoiated Legendre funtions at eah integration point all genlgp(pnmllg,nrankij alulate kr and it's derivative at eah integration point urrent shape desriptor is for a spheroid: a < b : oblate, a = 0 : sphere, a > b : prolate dimension = 2a (along the symmetry axis) x 2b EXTENDT1 : (omment) All axisymmetri partiles an be treated, (not only prelates and oblates) but it will be harder to obtain onverged solutions. The expression of r(theta) is needed. qb = r(theta)/a dkr = x(d(qb)/dtheta) x = ka (input parameter) 2a is the dimension along the symmetry axis. 2a is NOT the dimension along semimajor axis!! qb = 1.q0/sqrt(osth2+(aovrbsinth)2) kr = xqb dkr = -xosthsinth(aovrb2-1.q0)qb3 alulate the Hankel funtions (real argument) and Bessel funtions (omplex argument) at eah integration point EXTENDT1 : two variables, hankelre and hankelim, are used instead of hankel and hbkre,hbkim instead of hbk 54
53 EXTEl-.JDTl EXTENDTl bslmp is always real, while refration index is real. In Tl bslmp was delared omplex dn,h,bk,bbk,sa,sb,kpr are real all besh(kr,hankelre,hankelim,nranki) kpr = mkr all besj (kpr,bslmp,nranki) d = dkrsinth wtsin = 2.qOwt(ithta)sinth enter a loop for eah row of the matrix EXTENDTl: h is the imaginary hankel-element-quota, while it's only used in the a2-alulation (the imaginary part of AJ dn 40 irow ~ l,nrnnk if(irow.le.ij) go to 40 irowl = irowtnrank row= real(irow) rowm = mvtrow rawl = row+l.qo br = hankelre(irow)/hankelre(irow+l) h = hankelim(irow) /hankelim(irow+l) enter a loop for eah olumn of the matrix do 30 iol = l,nrank if(iol.le.ij) go to 30 ioll = ioltnrank ol = real(iol) olm = mv+ol oll = oltl.qo alulate variable ombinations rij = rowtol rssij rowol mro = m2tqemrssijosth2 pnroo = pnmllg(irow)pnmllg(iol) pnrol = pnmllg(irow)pnmllg(iol+l) pnrlo = pnmllg(irowtl)pnmllg(iol) pnrll = pnmllg(irow+ljpnmllg(ioltl) bla = rowosthpnrll-rowmpnrol blb = olosthpnrll-olmpnrlo bk = mbslmp(iol)/bslmp(ioltl) bbk = hankelre(irowtl)bslmp(iol+l)wtsin hbkre = hankelre(irow+l)bslmp(ioltl)wtsin hbkim = hankelim(irowtl)bslmp(iol+l)wtsin 1 alulate the [A)' and [B)' submatries, e.g., I I I I ' I I (K + em J) 1-(I +em Ll I [A) I I = I ' I I (L + em I J I (J + em KJ I I I I I EXTENDTl : a2 and b2 are used instead and A = mplx(b2,a21 ll <:mp 1 xi 1.>2, 0. II) Thus, modifiations have been made in the a2 expressions (hbkim instead of hbk) simplifiation for mi ttor- symmetri partiles: if (irow+iol) is even then the I and L elements are zero if (irow+iol) is odd then the J and K elements are zero if(mod( (irowtiol),2).ne.o) then inrement the -(I + em LJ' submatrix element if(kmv.ne.o) then bl = bla+blb sa = pnrll (rowrowlbktolollh-rssij(rij+2.q0)/kr)d sa= (kr(l.qothbk)-olh-rowbktrssij/kriblkr+sa a2(iol-ij,irowl-ijt)=a2(iol-ij,irowl-ijt)+mvsahbkim sb = sa+(br-h)(olollpnrlldt ibkkr-oljblkrj b2(iol-ij,irowl-ijt) = b2(iol-ij,irowl-ijt)+mvsbbbk inrement the I L + em I J ' submatrix element = (dn-l.q0jblkr2 a2(ioll-ijt,irow-ijl=a2(ioll-ijt,irow-ij)-mv(sat) 1 hbkim/m b2(ioll-ijt,irow-ij) = b2(ioll-ijt,irow-ij)- 1 mv(sb+lbbk/m end if else inrement the (J + em Kl' submatrix element 55
54 a12 = mropnrll-qem(rowolmosthpnrlo+ 1 olrowmosthpnrol-rowmolmpnroo) a22 = a12kr2 bla = olollbla blb = rowrowlblb sa tkr(bk-dnh)+dnrow-ol)a12kr+(bla-dnblb)qemd a2( oll-ijt,irowl-ijt)=a2(ioll-ijt,irowl-ijt)+sahbkim/m b2i oll-ijt,irowl-ijt) = b2(ioll-ijt,irowl-ijt) 1 +(sa-(br-h)dna22ibbk/m 1 inrement the ( K + em J I ' submatrix element sa tkr(bk-h)+row-ol)a12kr+(bla-blb)qemd a2t ol-ij,irow-ijj = a2(iol-ij,irow-ij)+sahbkim b2 l ol- ij, irow-ij I =b2 l iol-ij, irow-ij) + (sa- (br-hj a22 I bbk end i ontinue ontinue ontinue ':dj,:ulate the normal.lzation fator do 70 irow = l,nrank iflirow.le.ijl go to 70 row= real(irow) iflkmv_eq.oj then mxnrm(irow-ijl=(2.q0row+l-q0j'14-q0row(row+1.q0)) else if l i row. l t. kmv J then m; :nnnl irow ij I l.qo else ib = irow-kmv+l ie = irow+kmv ftki = l.qo fprod = real(ib) do 60 l = ib,ie ftki = ftkifprod fprod = fprod+l.qo end if end if ontinue ontinue mxnrm I i row-- i j I em(2.q0row+l.q0)/ (4.qOrow(row+l.q0)ftkiJ onvergene over nrank (i = 11 requires that the [A] 'and [B]' matries be stored for a seond iteration with nrank = nrank - 1 EXTENDT1 : a2(,) and b2(,j are stored instead of [A] ' and [B] ' if(i.eq.1) then do 80 ii l,nr2 do 75 j 1, nr2 aa2 ( i j ) = a2 ( i i, j j J bb2 I i, j I = b2 Iii, j j J ontinue ontinue end if for onvergene over nm (i = 21 save the [A] matrix and normalization onstants for later use in internal field programs EXTENDT1 : [A]' is stored in the a2(,1- and b2(,)-arrays. transpose and store in the a(,l array if(i.eq.2.and.mtxsav.eq.2) then do 90 ir = 1,ns2 do 85 jr = 1,ns2 a(ir,jr) = mplx(b2(jr,ir),a2(jr,ir)) ontinue ontinue write(111 aa end if -1 alulate [T]' = [A]' [B]' all prssm(ns2) [T]' is stored in the b(,j array transpose [T] ' to obtain [T] do 100 ir = l,ns2 do 95 jr = 1,ns2 a(ir,jr) = b(jr,ir) ontinue ontinue for onvergene over nm (i = 2) save the [T] matrix and normalization onstants for later use in sattering programs 56
55 ; the [T] matrix is stored in the a(,) array if(i.eq.2.and.mtxsav.eq.1) write(11) a,mxnrm alulate the angular sattering and effiienies all addpr onvergene over nrank (i = 1) requires a seond solution with nrank = nrank-1 if(i.eq.1) then restore the original [A] ' and [B] ' matries EXTENDT1 : a2(,) and b2(,) are restored do 110 ii do 105 1,nr2 j = 1,nr2 a2(ii, j) = aa2tii,jj) b2 ( i i' j ) = bb2 ( i i ' j j ) Jntinue ontinue dni.,'t 2 the last rovl and olumn of eah submatrix to redue nrank to nrank - 1 EXTENDT1 : the a2- and b2- submatries are used instead of A and B nr2m = nr2-1 nr2 = 2(nrank-1J do 120 ir = 1,nr2m do 115 jr = nrank,nr2 a2(ir,jr) = a2(ir,jr+1) b2 (ir, jr) = b2 (ir, jr+1) ontinue ontinue do 130 jr = 1, nr2 do 125 ir nrank,nr2 a2(ir,jr) = a2(ir+1,jr) b2(ir,jr) = b2(ir+1,jr) ontinue ontinue nranki = nrank nrank = nrank-1 write(6,230) nm,nrank,ntheta,i -1 alulate [T]' = [A]' [B]' all prssm(nr2) [T]' is stored in the b(,) array transpose [T] ' to obtain [T] do 140 ir = 1,nr2 do 135 jr = 1,nr2 a(ir,jr) = b(jr,ir) ontinue ontinue alulate the angular sattering and effiienies all addpr end if ontinue onvergene over ntheta (i = 0) requires a solution for a seond value of ntheta if(i.eq.o.and.ion.eq.1) then ntheta = ntheta+4 write(6,230) nm,nrank,ntheta,i end if ontinue stop format ( '... ', I, 1 onvergene test- save the matries,/, 2 [T] is written to file ''t''.',/, 3 [A] is written to file ''a''. ',/, 4 parameters are in file ''ase''. ',/, 5 I... I I I/ I 6 'nrank: number of terms',/, 7 'ntheta: number of integration steps',/, 8 'onvergene ase: ntheta (0), nrank (1), nm (2) ',/) format(/, 'x: size parameter',/, 1 'aovrb: a/b ratio',/, 2 'index of refration:',/) format(/, 'save [T] or [A] matrix',/) format(/, 'nm',i8,3x, 'nrank',i6,3x, 'ntheta',i8,3x, 'i',i12) format( 'ka', fb. 3, 3x, 'aovrb', f6. 3, 3x, 'mr', f12. 3, 3x) format ( 'utht', f6. 3, 3x, 'uphi', f7. 3, 3x, 'angint', fb. 3, 3x, 1 'anginp', fb. 3) end subroutine gauss(wt,as,n,aa,bb) alulate absissas and weights for n-point Gaussian 57
56 ,.. 10 quadrature over integration limits of aa to bb aa = lower integration limit bb = upper integration limit n = number of integration points as = absissas wt = weights a well-doumented program whih performs the same funtion is given in Chapter 4.5 of W.H. Press, B.P. Flannery, S.A. Teukolsky and W.T. Vetterling, Numerial Reipes The Art of Sientifi Computing (Cambridge University Press, Cambridge, 1986) the results (either program) ompare with Table 25.4 in M. Abramowitz and I.A. Stegun, Handbook of Mathematial Funtions (National Bureau of Standards, Washington, 1964) impliit real16 (a-h,o-z) real16 wt(n),as(n) data pi/ / data onst,tol/ ,1.0q-31/ the tolerane (tol) may be dereased to 1.0d-10 or less when double preision variables are used EXTENDT1: the tolerane (tol) is dereased to 1.0q-31 data 1, 2, 3, 4/. 125, , , I if(n.eq.1) then as(1i = l.q0/sqrt(3.q0) wt 11 I = 1. qo return end if en= real(n) ndiv2 = n/2 np1 = n+1 nnl = nln+1.q0) appft = 1.q0/sqrt((n+.5)2+onst) on1 =.5ibb-aa) on2 =.5(bb+aa) do 30 k = 1,ndiv2 b = (real(k)-.25)pi bisq = l.q0/b2 bfroot = b(1.q0+bisq(1+bisq(2+bisq(3+4bisq)))) xi = os(appftbfroot) x = xi pm2 = 1.q0 pm1 = x do 20 in = 2, n rn = real(in) p = ((2.qOrn-1.q0)xpm1-lrn-1.qOJpm2)/rn pm2 = pm1 pm1 = p ontinue pm1 = pm2 aux = 1.q0/(1.q0-x2) der1p = n(pm1-xp)aux der2p = (2.q0xder1p-nn1p)aux ratio = p/der1p xi= x-ratio(1.q0+ratioder2p/(2.q0der1p)) if(abs(xi-xl.gt.tol) go to 10 as(k) = -xi wt(k) = 2.q0(1.q0-xi2)/(npm1)2 as(np1-k) = -as(k) wt(np1-k) = wt(k) ontinue if(mod(n,2).ne.o) then as(ndiv2+1) = O.qO nm1 = n-1 nm2 = n-2 prod = en do 40 k = 1,nm2,2 prod= prodreal(nm1-k)/real(n-k) ontinue wt(ndiv2+1) = 2.q0/prod2 end if do 50 k = 1,n as(k) = on1as(k)+on2 wt(k) = on1wt(k) ontinue return end subroutine genlgp(pnmllg,n) alulate assoiated Legendre funtions (argument os(theta)) divided by sin(theta) for eah azimuthal mode m generate first two orders by formula and remaining orders by reursion pnmllg = assoiated Legendre funtion/sin(theta) sinth = sin(theta), osth = os(theta) n = number of orders (0 to n-1) the order of the assoiated Legendre funtions is inremented by one in the pnmllg(l array impliit real16 (a-h,o-z) 58
57 10 20 ommon /mvom/ nm,kmv ommon /mvom2/ mv,twm,prodm ommon /thtom/ theta,sinth,osth,x real16 pnmllg(n) dtwm = twmtl.qo alulate for the speial ase theta = 0 degrees or 180 degrees - note that for theta = 180 degrees, osth = -1, but theta is set to 0 degrees prior to subroutine entry if theta 0 degrees and m.ne.1 all funtions are zero ifltheta.eq.o.and.kmv.ne.1) then do 10 ilg = 1,n pnmllg(ilg) = O.qO ontinue return end if it theta= 0 degrees and m.eq.1 alulate orders 0,1,2 if (theta. eq. 0. and. kmv. eq. 1 1 then pnmllg111 = O.qO pnmllgl21 = l.qo pla = 1.q0 plb = 3.q0osth pnmllg = plb ibeg = 4 if theta.ne.o degrees and m.eq.o alulate orders 0 and 1 else if(kmv.eq.o) then pla = 1.q0/sinth plb = osthpla pnmllg I 1 I = pla pnmllg 12 I = plb ibeg = 3 if theta.ne.o degrees and m.ne.o alulate first two nonzero orders - the assoiated Legendre funtion is zero tor orders less than the azimuthal mode m else do 20 ilg = 1,kmv pnmllglilg) = O.qO ontinue pla = prodmsinthlkmv-1) 30 pnmllg(kmv+11 = pla plb = dtwmosthpla pnmllg(kmv+21 = plb ibeg = kmv+3 end if reur upward to obtain all remaining orders if(ibeg.gt.n) return nmul = real12ibeg-3) nm = 2.q0 nmm = dtwm do 30 ilgr = ibeg,n pl = (nmulosthplb-nmmpla)/nm pnmllg(ilgr) = pl pla = plb plb = pl nmul = nmult2.q0 nm = nm+1.q0 nmm = nmm+1.q0 ontinue return end subroutine beshlx,hankelre,hankelim,n) alulate Hankel funtions bj = Bessel funtion of the first kind by = Bessel funtion of the seond kind x = real argument n =number of orders (0 to n-1) the order of the funtions is inremented by one in the bj (I,by() and hankelre/im(l arrays arrays are set for n = 201 (nrank+11 maximum EXTENDT1 : hankelre and hankelim are used instead of hankel in T1 impliit real16 (a-h,o-z) real16 hankelre(n),hankelim(n) real16 bj(201),by(201),t(3) by() alulation- obtain the zeroeth and first order funtions a= sin(x)/x by(1) = -COSIX)/X byl21 = byl11/x-a 59
58 obtain the higher order funtions by upward reursion do 10 n = 3,n rn=real(n~2) bytnl = (2.q0rn+l.q0)by(n~l)/x-by(n~2J ontinue nst t 131 tt21 bj (I alulation~ n+int((l0l.q0+x).5) set the starting order for downward reursion the t(j array is used to reur down to the two highest order funtions that are needed set starting values for the two highest orders nst and nst~l = O.qO l.oq~35 reur dovmward to obtain orders n~l do 20 i ri = realtil till t(31 = t(21 t i 2 I t I 1 I ontinue = nst-l,n~l,-1 (2.q0ri+l.q0)tl21/x~t(3) ontinue downward reursion to order zero bj :nl = t(31 bj(n-11 = tl21 do 30 i = n-2,1,~1 ri = realtil bjtil = (2.qOri+l.qOIbjti+lJ/x-bjii+21 onti.nue and n~2 alulate the sale fator and the funtions alpha = a/bj ill do 40 k = l,n hankelrelki hankelim(kl ontinue return end bj iklalpha by lkl subroutine besj (z,bslmp,n) alulate Bessel funtions of the first kind bslmp = Bessel funtion of the first kind n = number of orders 10 to n-1) the order of the Bessel funtions is inremented by one in the bslmp() array EXTENDTl : bslmp is delared real (no absorption) z is also real (no absorption), x = z impliit real16 (a-h,o-z) real16 bslmp(n),t(3) set the starting order for downward reursion EXTENDTl n has been added to nst to prevent that the loop(l0) will not be entered x = abs(z) nst = n+int(x+4.05x q0+(10l.q0+xj.5) the t() array is used to reur down to the two highest order funtions that are needed set starting values for the two highest orders nst and nst-1 t i 3 I = 0. qo t(21 = l.oq~35 reur downward to obtain orders n~l do 10 i = nst~l,n-1,-1 ri = realiil till (2.q0ri+l.q01 t(21 /z--t(3) t(3) = t(2) t(2) = t(1) ontinue and n-2 ontinue downward reursion to order zero bslmp(n) = t(3) bslmp(n-1) = t(2) do 20 i = n~2,1,-l ri = real(i) bslmp(i) = (2.qOri+l.qO)bslmp(i+lJ/z-bslmpli+21 ontinue alulate the sale fator and the funtions 60
59 30 alpha= sin(z)/(zbslmp(1) I rlo 30 k l,n bslmp(k) = bslmp(k)alpha ontinue return end subroutine prssm(n) ~1 alulate [T]' = [A]' [B]' using Gauss~Jordan impliit real16 (a~h,o~z) double omplex a,b ommon /mtxom/ nr,nri,a(400,400),b(400,400) ommon / mtxom2 I mxnrm ( I ommon/mtxom3/ a2i400,400),b2(400,4001 real16 ls(400),are(400,400),aim(400,400),bre(400,400) real16 bim(400, 400), areoldi400, 400), breold (400, 4001 redution EXTENDT1: are,aim,bre,bim are used (are= real(a) et.) d:j ii = l,n do jj = l,n are I U, j j I aim(ii, jj I bre(ii,jj) bim(ii,jj) enddo enddo b2 I i, j j I a2(i,jjl b2 I i, j j I O.qO start redution of [a] do 6 0 i 1, n searh for the maximum element in the ith row of [a] EXTENDT1 : areijmax, aimijmax (real16) are used instead of aijmax (omplex) in T1 areijmax are(i,11 aimijmax aimli,11 jmax = 1 do 10 j = 2,n if i 1 are ( i, j 1 2 +aim 1 i, j I 2 I. gt. 1 a rei j max 2 +aimi j max 2 I I then areijmax aimi jrnax jmax = j end if are(i,jj aimli,ji ontinue on = areijmax2+aimijmax2 normalize the ith row of [a] and [b] by aijmax EXTENDTl: on,areold,breold are used in order to simplify I Tl: a(i,j) = a(i,jl/aijmax; b(i,jl = b(i,j)/aijmax) 1 do 20 j = l,n areold(i,j)=are(i,j) breold(i,j)=bre(i,j) are(i,jl=lare(i,j)areijmax+aim(i,j)aimijmax)/on aim(i,jl=laim(i,j)areijmax~areold(i,j)aimijmax)/on bre(i,j)=lbre(i,j)areijmax+bim(i,j)aimijmax)/on bim(i,j)=(bim(i,j)areijmax~breold(i,j)aimijmaxl/on ontinue use row transformations to obtain zeros above and below the jmax element of the ith row of [a] apply the same row transformations to [b] do 50 k = l,n if(k.ne.i) then aratre = ~are(k,jmaxj aratim = ~aim(k,jmaxi = l,n areold I i, j I = are! i, j I if (abs (are I i, j I 2+aim(i, j) 21.gt. 0.qO) then are(k,j) = aratreare(i,jj~aratimaim(i,j)+are(k,jj aim(k,jl = aratimareold(i,jj+aratreaim(i,jj+aim(k,j) end if do 30 j ontinue are (k, jmax) aim(k, jmax) O.qO O.qO do 40 j = l,n breold(i,j)=breli,j! if (abs (bre (i, j I >-2+bim(i, j I 2 I.gt. 0.qO) then bre(k,j) aratrebre(i,j)~aratimbim(i,j)+bre(k,j) bim(k,j) = aratimbreold(i,j)+aratrebim(i,j)+bim(k,j) end if ontinue end if ontinue store row ounter IiI in array l s ( 1, suh tha l ls() ontains the loation of the pivot (unity) 61
60 element of eah olumn (after redution) ls ( jmax) = i ontinue the redution of (a] is omplete - perform row interhanges as indiated in array ls() do 90 i = l,n k: = i put the integer value in ls(k) into k: if k is less than i, then that row has already been involved in an interhange so iterate k: = ls(k:) until a value of k: greater than i (orresponding to a row stored above the ith row) is obtained k: = ls (k:i if(k:.lt.i) go to 70 if ( k. gt. 0 I then do 80 j=l,n aratre = bre(i,j) aratim = bim(i,jl bre I i, j I = bre ( k:, j I bim(i,j) = bim(k:,j) bre(k:,j) = aratre bim(k:,j) = aratim ontinue end if ontinue EXTENDTl : the ritial region is passed and the double omplex T-matrix an be stored in b(,j do i = l,n do j = l,n bli,j) = mplx(bre(i,jl,bim(i,j) J end do enddo ['T]' is stored in the b(,) array return end subroutine genang(n,tang,pang,osb,sinb) alulate sattering angles in the partile frame orresponding to sattering angles in the laboratory frame alulate the elements of the transform matrix for the polarization vetors impliit real16 (a-h,o-z) ommon dtr,rtd,pi ommon /uvom/ angint,anginp,utheta,uphi,aovrb,mr,mi,i real16 tang(n),pang(n),osb(n),sinb(n) dltang sint ost sinp osp dltang alulation assumes sattering over degrees = pi/real(n-1) sin(angint) os(angint) sin(anginp) os(anginp) alulate sattering angles in the partile frame orresponding to sattering angles in the laboratory frame do 10 i = l,n ts = dltangreal(i-11 ps = O.qO sints = sinlts) osts= os(ts) osps = os (psi x = -ospostsintsosps+sintosts y = sinpsintsosps z = ospsintsintsosps+ostosts alulate the theta sattering angles in the partile frame r = sqrt(x2+y21 tang(i) = O.qO if(z.ne.o.qo.or.r.ne.o.qo) tang(i) = atan2(r,z) alulate the phi sattering angles in the partile frame pang(il = O.qO if(x.ne.o.qo.or.y.ne.o.qoj pang(i) = atan2(y,xj if(pang(i).lt.o.qoi pang(i) = 2.q0pi+pang(i) alulate the elements of the transform matrix for the polarization vetors sint = sine (partile theta orientation angle) 62
61 10 ost sinp osp sints osts osps osine (partile theta orientation angle) sine (partile phi orientation angle) osine (partile phi orientation angle) sine (theta sattering angle in laboratory frame) osine (theta sattering angle in laboratory frame) osine (phi sattering angle in laboratory frame) pang(i) = phi sattering angle in partile frame osb(i) = ospssinpostsin(pang(i)) 1 -ospsospos(pang(i)) sinb(i) = ostsospsospostsin(pang(i)) 1 +sintssintsin(pang(i))+ostsospssinpos(pang(i)) ontinue return end subroutine addpr onvergene test the differential sattering ross setion and alulate the sattering, absorption and extintion effiienies alulations are performed in the partile frame and written in the laboratory frame impliit real16 (a-h,o-z) double omplex tmat,b,i,l,2,im,abl(400),ab2(400) double omplex aans(l0,2),fg1(400),fg2(400) ommon dtr,rtd,pi ommon /mtxom/ nrank:,nrank:i,tmat(400,400),b(400,400) ommon /mtxom2/ mxnrmt200) ommon /mvom/ nm,k:mv ommon /mvom2/ mv,twm,prodm ommon /thtom/ theta,sinth,osth,x ommon /uvom/ angint,anginp,utheta,uphi,aovrb,mr,mi,i real16 tang(10),pang(loj,osb(10),sinb(10),pnmllg(201) real16 oldh(10),oldv(10),lrtot(40) equivalene (aans,lrtot) logial first data first/.true./ set onstants and alulate the oordinate transformation variables the first time the subroutine is entered if I first) then i = (O.dO,l.dO) snorm = l.q0/(pix2) all genang(10,tang,pang,osb,sinb) 10 transform the inident field polarization vetor from the laboratory frame to the partile frame uul = theta omponent and uu2 = phi omponent uul = osb(l)utheta-sinb(l)uphi uu2 = sinb(1jutheta+osb(1)uphi end if lear the result aumulators when i = 0 or i = 1 and the first time the subroutine is entered for i = 2 if(i.le.1.or.k:mv.eq.o) then s = O.qO do 10 i = 1,40 lrtot(i) = O.qO ontinue nr2 = 2nrank: end if set indies for matrix ompression when n < m note: useful only when m > 1 ij = k:mv-1 if(ij.lt.oj ij-= 0 ijt = 2ij ns = nrank:-ij ns2 = 2ns alulate the assoiated Legendre funtions for the inident angle = tang(1) in the partile frame theta = tang(1) osth = os(theta) sinth = sin(theta) if(tang(1).eq.pi) then theta = O.qO osth = -l.qo end if all genlgp(pnmllg,nrank:i) alulate the inident field oeffiients: ab1() =theta polarization ab2() =phi polarization note: ab1() and ab2() used in sattered field programs are i times ab1() and ab2() used in internal field programs 63
62 do 20 n = l,nrank ifln.le.ij) go to 20 nr- JJ t!jtank en= real(n) nl = n+l l = 4.q0in 2 = 4.q0inl pl = nosthpnmllg(nl)-(n+mv)pnmllg(n) p2 = mvpnmllglnll ablin-ij) = lp2uul abl(np-ijt) = -2pluul ab21n-ij) = -lpluu2 ab2(np-ijt) = 2p2uu2 ontinue the sattered field oeffiients= -[T] times the inident field oeffiients fg21ns+ll to fg2(ns21 is -g(omn) do 4 0 i = l, ns2 fgl li I ~ O.qO [g2 IiI 0. qo do 30 j = l,ns2 fgj I i 1 = fgl IiI - tma t I i, j I abl ( j I fg2(i) = fg2(ij-tmat(i,jjab2(j) ontinue ontinue evaluate the sattered field at eah sattering angle theta = tang() and phi = pang() in the partile frame results are aumulated in aans(,j for eah azimuthal mode m aans = kf, where F is a omponent of the vetor far-field amplitude do 60 iu = 1,10 alulate the assoiated Legendre funtions at eah sattering angle theta = tang(iu) sinth = sin(theta) osth = os(theta) if(tang(iul.eq.pil then theta = O.qO osth = -l.qo end if all genlgp(pnmllg,nrankil phi = mvpang(iu) osphi = os(phil sinphi = sin(phil do 50 n = 1,nrank if(n.le.ij) go to 50 en= real(n) np = n+nrank nl = n+1 pl = nosthpnmllg(nl)-(n+mv)pnmllg(nl p2 = mvpnmllg(nll aa = sinphip1 bb = osphip1 = sinphip2 dd = osphip2 im = i(-n1) nij = n-ij npijt = np-ijt solve for the theta polarized sattered field in the partile frame aans I j u, 11 = aans (iu, 11 +im I fgl lnij I ddti tgl (npijt) bb 1 -fg2(nij)-ifg2(npijt)aalmxnrm(nij) solve for the phi polarized sattered field in the partile frame fg2(npijt) is -g(omn) per (3.12bi aans(iu,2) 1 ontinue ontinue aans(iu,2)-im(fgl(nij)aa+ifg1(npijt) +fg2(nijlbb+ifg21npijtlddlmxnrm(nijl write the sattering results in the laboratory frame h = horizontal (parallel) or theta polarization v = vertial (perpendiular) or phi polarization write(6,100i kmv nonv = 0 monv = 0 do 70 jup = 1,10 ang = 20.real(jup-1J h = snormabs (osb ( jup) a ans 1 jup, 11 tsinb ( jup; a ans ( jup, 2) I 2 v = snormabs(osb(jup)aans(jup,2)-sinb(juplaans(jup,l1j2 write(6,1101 ang,h,v test for onvergene at eah sattering angle 64
63 70 80 ift.not.first) then if labs i 1. qo-oldh (jup) /hi.le.1. Oq-03 I nonv if(abs(l.qo-oldv(jup)/v).le.1.0q-03) monv end if oldh(jup) = h oldv(jup) = v ontinue nonv+1 monv+1 alulate the normalized (pia2j extintion (ex), sattering (s) and absorption lab) ross setions the ex alulation an be performed in either r-eferene frame - use the partile frame EXTENDTl : imag instead of aimag while double omplex is used ex= (imag(aans(1,1))uu1+imag(aans(l,21 )uu2) 1 4.q0/x2 the s alulation is independent ot the referene frame results are aumulated for eah azimuthal mode m dn 80 n = ] 1 Tl.S I I f.! I l I I I ~ : s = s+ labs ( fgl (n) I 2+abs ( fgl (npj 1 ~ +abs I fg2 (n) i 2+ab.s I fg2 (npl I 2 I mxnrm(n) ontinue s = s/x2 absorption s = extintion s - ab = ex~s iftab.lt.l.oq-08) ab = O.qO write(6,120j s,ab,ex sattering s test for omplete onvergene of solution at 8 out of 10 angles for eah polarization if onverged - stop if not onverged - return EXTENDT1 : status='unknown' is added in the open argument to prevent ompiler warnings EXTENDT1 requires solution in all 10 angles with an auray of if(nonv.ge.10.and.monv.ge.10) then write(6,1 'solution has onverged' ifli.eq.2j t.hen open I uni t=12, file=' ase', status=' unknown' 1 rewind 12 nt = kmv+1 write(12,130) nt,nrank,x,aovrb,mr lose(unit=12j lose(unit=11j end if else first =. fa1 ~e. telurn end if stop 100 format(/,12x,' m =,i3,' ',/, 1 1 2x, 'differential sattering ross setion',/, 1 1x, 'angle', 9x, 'parallel', 8x, 'perpendiular',/) 110 format(f6.2,2(5x,1pe13.4j format I I,' sat xset = ', 1pe13. 4, I, ' abs xset = le13.4,/,' ext xset = ',el3.4) 130 format(2i4,4f8.4j end A.l.2. EXTENDT3 program EXTENDT3 Light Sattering by Partiles: Computational Methods by P.W. Barber and S.C. Hill opyright () 1990 by World Sientifi Publishing Co Pte Ltd Modifiations 1996 by P. Alsholm and A. Nilsson alulate the differential sattering ross setion in all diretions by projeting the surfae of a spherial surfae onto a retangular oordinate system. ths: the theta sattering angle, is projeted onto the radius r in the retangular plane r = ths/180 degrees (r varies from 0 to 11 when r > 1, set sattering to baksatter value phs: the phi sattering angle, is the azimuthal angle in the spherial and retangular oordinate systems 65
64 ,-. X X X X X X X X X X X X X X X X X start at (X,y) = (-1,-1) and ontinue in the+ x diretion then inrement y by dlt and ontinue at (-1,-1+dlt) inputs: angint anginp anglab npnts EXTENDT3: omplex ----> double omplex real -----> real16 alog - --> qlog.0 -- >.qo (mplx(o.do,o.doii nrankmax = 200 ommon-bloks are hanged open-arguments are hanged theta orientation in the laboratory frame phi orientation in the laboratory frame angle of the E-field polarization vetor in the x-y plane number of grid points = npnts x npnts impliit real16 (a-h,o-z) double omplex tmat,aans ommon dtr,rtd,pi ommon /mtxom/ nrank,nranki,tmat(400,400) ommon ;mt.xom2/ mxnrmi200,201) ommon /mvom/ nm,kmv ommon /mvom2/ mv,twm,prodm ommon /thtom/ theta,sinth,osth,x ommon,. uvom/ angint,anginp,utheta,uphi,i ommon /uvom2/ ths -:.mmon ioutom/ total dimension mx(200),a(loooi set program onstants dtr = y rtd = pi = read from file: the T-matrix and normalization onstants nrank = number of terms (matrix order) nm = number of azimuthal modes m X = size parameter (ka) open(unit=11,file='t',form='unformatted',st.atus='unknown') rewind 11 open(unit=12,file='ase',status='unknown'j rewind 12 read(12,100j nm,nrank,x lose(unit=121 nranki = nrank+1 write(6,110) write(6,) 'enter angint,anginp,anglab,npnts' read(5,) angint,anginp,anglab,npnts alulation for angint = 0 or 180 degrees uses m = 1 only set the do 30 and do 50 loop indies for m = 1 only read the stored arrays one to skip over the T-matrix and normalization onstants for m = 0 if(angint.eq.o.q0.or.angint..eq.180.q0) then nl = 2 nh = 2 i = 1 read(11) tmat,mx alulation for angint not 0 or 180 degrees ( all m 1 set the do 30 and do 50 loop indies for all m else nl = 1 nh = nm i = 2 end if angint = angintdtr anginp = anginpdtr anglab = anglabdtr tp = anginp utheta and uphi are the amplitudes of the inident field in the theta (parallel) and phi (perpendiular) diretions utheta = os(anglab) 66
65 10 = = uphi = sinlanglab) alulate the sattered field expansion oeffiients and the baksatter enter a loop for eah azimuthal mode m do 30 im = nl,nh set m-dependent variables kmv = im-1 mv = reallkmvj prodm = l.qo if(kmv.gt.o) then quanm = do 10 i quanm prodm ont :Lnue end if twm = 2.q0mv ij = kmv-1 if(ij.lt.oi ij 0 ns = nrank--ij mv 1, kmv quanm+1.q0 quanmprodm/2.q0 read the T-matrix and normalization onstants for eah m read(lll tmat,mx do 20 k = 1,ns mxnrm(k,iml = mx(kj ontinue alulate the sattered field expansion oeffiients and sum the baksatter over all azimuthal modes all addpr ontinue lose(unit=l1j alulate the logarithm of the total baksatter differential sattering ross setion bksat qloglo(total) open(un t=9, file='t3.dat',status='unknown'i rewind alulate the differential sattering ross setion over a retangular grid orresponding 40 to the surfae of a sphere dlt = 2.q0/real(npnts-1J set starting y grid value (yg) enter loop to vary y values yg = -l.qo do 70 ig = l,npnts set starting x grid value (xgl enter loop to vary x values xg = -l.qo do 60 jg = l,npnts r = sqrt(xg2+yg21 if I r. lt. 1. qo I then alulate the theta and phi sattering angles for radii within the unit irle on the retangular grid ths = rpi phs = O.qO iflabslxg).gt.o.qo.or.abs(yg).gt.o.qoj phs = atan2(yg,xg) rotate the phi orientation angle anginp with phs so that the sattering at the angle phs an be obtained in the phi = zero degree plane in the laboratory frame anginp = tp-phs if(anginp.lt.o.qoj anginp = anginp+2.q0pi enter a loop for eah azimuthal mode m do 50 im = nl,nh set m-dependent onstants kmv = im-1 mv = real lkmv) prodm = 1.q0 iflkmv.gt.o) then quanm = do 40 i quanm prodm ontinue end if mv l,kmv quanm+l.qo quanmprodm/2.q0 67
66 .50 = sr, llo twm = 2.q0mv alulate the differential sattering ross setion at eah grid point - press is an alternate entry to subroutine addpr for sattered field alulations using the previously alulated expansion oeffiients all press ontinue alulate the logarithm of the total differential sattering ross setion at (xg,yg) and store in array a() a(jg) = qlog10(total) else set the differential sattering ross setion to the baksatter value for all grid points on or outside the unit irle a(jg) = bksat end if inrement x value xg = xg+dlt ontinue write out data for all xg values (for given yg value! write(9,120) (a(j),j=1,npnts) inrement y value yg = yg+dlt ontinue lose(unit=9) stop forrnat(2i4, f8.4) format ( '... ', I, 1 alulate sattered intensity in all diretions.,:, 2 output is written to t3.dat. ',I, 3 '... ',I I, 4 'angint: theta orientation in the lab frame, degrees',/, 5 'anginp: phi orientation in the lab frame, degrees'/, 6 'anglab: angle of thee-field polarization',/, vetor in the x-y plane, degrees',/, 8 'npnts: number of grid points (npnts x npnts) ',/) format(e14.6) end subroutine genlgp(pnmllg,n) alulate assoiated Legendre funtions (argument os(theta)) divided by sin(theta) for eah azimuthal mode m generate first two orders by formula and remaining orders by reursion pnmllg = assoiated Legendre funtionlsin(theta) sinth = sin(theta), osth = os(theta) n = number of orders (0 to n-1) the order of the assoiated Legendre funtions is inremented by one in the pnmllg() array impliit real16 (a-h,o-zl ommon lmvom/ nrn,kmv ommon lmvom2/ mv,twm,prodm ommon lthtom/ t.heta,sint.h,osth,x dimension pnmllg(n) dtwm = twm+1.q0 alulate for the speial ase theta = 0 degrees or 180 degrees- note that for theta= 180 degrees, osth = -1, but theta is set to 0 degrees prior to subroutine ent..1 y if theta = 0 degrees and m.ne.1 all funtions are zero if(theta.eq.o.and.kmv.ne.l) then do 10 ilg = 1,n pnmllg(ilg) = O.qO ontinue return end if if theta= 0 degrees and m.eq.1 alulate orders 0,1,2 if(theta.eq.o.and.kmv.eq.1) then pnmllg(1) = O.qO pnmllg(2) = 1.q0 pla = l.qo plb = 3.q0osth pnmllg(3) = plb ibeg = 4 68
67 20 30 tl 1_/t :~Ld.!le.O degrees and rn.eq.o <al ~Uldte orders I) and 1 else if(kmv.eq.o; then pla = 1.q0/sinth plb = osthpla pnrnllg I 1 I = pla pnrnllgi21 = plb ibeg = 3 if theta.ne.o degrees and rn.ne.o alulate first two nonzero orders - the assoiated Legendre funtion is zero for orders less than the azimuthal mode m else do 20 ilg = l,krnv ptunl]g(ilg) = O.qO ontinue pia = prodmsinthlkrnv-11 pllrnll,j(ktnvd) pla plb = dtwmosthpla pnrnllg(kmv+2j = plb ibeg = kmv+3 end if reur upward to obtain all remaining orders iflibeg.gt.n) return nmul = real(2ibeg-3) nm = 2.q0 nmm = dtwm do 30 ilgr = ibeg,n pl = (nmulosthplb-nmmpla)/nrn pnmllgiilgr) = pl pla = plb plb = pl nmul = nmul+2.q0 nm = nm+l.qo nmm = nmm+l.qo ontinue return end subroutine genang(n,tang,pang,osb,sinbi alulate sattering angles in the partile frame orres ponding to sattering angles in the laboratory frame alulate the elements of the transform matrix for the polarization vetors impliit reall6 (a-h,o-z; ommon dtr,rtd,pi ommon /uvom/ angint,anginp,utheta,uphi,i ommon /uvom2/ ths sint = sin(angint) ost = os(angint) sinp = sin(anginp) osp = os(anginp) alulate sattering angles in the partile frame orresponding to sattering angles in the laboratory frame ps = O.qO sints = sin(ths) osts = os(thsl osps = os (psi x = -ospostsintsosps+sintosts y = sinpsintsosps z = ospsintsintsosps+ostosts alulate the theta sattering angles in the partile frame r = sqrt(x2+y2) tang = O.qO if(z.ne.o.qo.or.r.ne.o.qo) tang= atan2(r,z) alulate the phi sattering angles in the partile frame pang = O.qO if(x.ne.o.qo.or.y.ne.o.qo) pang= atan2(y,xj if(pang.lt.o.qoj pang= 2.qOpi+pang alulate the elements of the transform matrix matrix for the polarization vetors the transform matrix is needed only for the inident polarization vetor ( ase n = 1 if ( n. eq.1 I then osb = -osp sinb = sinp end if return end subroutine addpr alulate the sattered field expansion oeffiients and the differential sattering ross setion at angles 69
68 :::.: tang, pang in the partile frame orresponding to angles ths, phs in the laboratory frame entry at addpr alulates the inident field expansion oeffiients and sattered field expansion oeffiients whih only need to be alulated one for eah m entry at press uses the previously alulated sattered field expansion oeffiients to alulate the differential sattering ross setion alulations are performed in the partile frame impliit real16 (a-h,o-z) double omplex tmat,abl(400),ab2(400),i,l,2,im,aans double omplex fg1(400,2011, fg2(400,2011 ommon dtr,rtd,pi ommon imtxom/ nrank,nranki,tmat(400,400j ommon, mtxom2 / mxnrm , ommon /Cm'..rom/ nm,kmv ommon /mvom2/ mv,twm,prodm ommon ;thtom/ theta,sinth,osth,x ommon ;uvom/ angint,anginp,utheta,uphi,i ommon,;uvom2/ ths ommon /:Jut:Jm; total dimension pnmllg(201),aans{2) logial first. data first /.true.; on first entry set the onstants and: Ill alulate the inident field diretion thtin in the partile frame 121 transform the inident field polarization vetor from the laboratory frame to the partile frame uu1 = theta omponent and uu2 = phi omponent 131 set the baksatter angle ths to 180 degrees if I first) then i = IO.dO,l.dO) nr2 = 2nrank snorm = 1.q0/lpix21 ths = O.qO all genangl1,tang,pang,osb,sinb) thtin = tang uu1 = osbutheta-sinbuphi uu2 = sinbutheta+osbuphi ths = pi first =. false. end if 10 set indies for matrix ompression when n < m note: useful only when m > 1 j = kmv.. l f(ij.lt.o) ij = 0 jt = 2ij ns = nrank-ij ns2 = 2ns alulate the assoiated Legendre funtions for the inident angle = thtin in the partile frame theta thtin sinth = sinltheta) osth = osltheta) all genlgp lpnmllg, nranki I alulate the inident field oeffiients: ab1() =theta polarization ab211 =phi polarization note: ab111 and ab2t) used in sattered field programs are j times ab1ij and ab211 used in internal field programs do 10 n = l,nrank if In. 1 e. i j I go to l 0 np = n+nrank en realln) nl = n+1 l = 4.d0in 2 4.d0inl pl = nosthpnmllg(n1)-ln+mv)pnmllglni p2 = mvpnmllglnll abl(n-ij) = 1p2uul ab1(np-ijt) = -2pluul ab2(n-ij) = -lpluu2 ab2(np-ijt) = 2p2uu2 ontinue the sattered field oeffiients = -[T] times the inident field oeffiients store the oeffiients for all azimuthal modes fg2(nst1) to fg21ns2) is -g(omn) do 30 i = l,ns2 fglli,kmv+ll = O.dO fg2(i,kmv+l) = O.dO do 20 j = l,ns2 70
69 20 30 fgl li,kmv+l) fg21i,kmv+1) ontinue ont~inue fg11i,kmv+1)-tmatli,j)ab11j) fg21i,kmv+1)-tmatli,j)ab21j) alternate entry to alulate the differential sattering ross setion using the previously alulated sattered field expansion oeffiients entry press lear the result aumulators and alulate the oordinate transformation variables for eah new grid point if I i. eq. 1. or. kmv. eq. 0) then aans(l) = O.qO aans(2) = O.qO all genangl2,tang,pang,osb,sinb) end if set indies for matrix ompression when n < m note: useful only when m > 1 j = kmv-1 f(ij.lt.o) ij = 0 jt = 2ij evaluate the sattered field at eah sattering angle thea = tang and phi = pang in the partile frame results are aumulated in aans(j for eah azimuthal mode m aans = kf, where F is a omponent of the vetor far-field amplitude alulate the assoiated Legendre funtions at eah sattering angle theta ang sinth sin(theta) osth os(theta) ifltang.eq.pi) then theta = O.qO osth = -1.q0 40 end if all genlgplpnmllg,nranki) phi = mvpang sinphi = sin(phi) osphi = os(phi) do 40 n = 1,nrank if(n.le.ij) go to 40 np = n+nrank n1 = n+1 en = real In) p1 = nosthpnmllgln1)-(n+mv)pnmllg(n) p2 = mvpnmllg 1 n1) aa = sinphip1 bb = osphip1 = sinphip2 dd = osphip2 im = i I ~ n1) nij = n-ij npijt = np-ijt solve for the theta polarized sattered field in the partile frame a ans I 1) ~ a ans I 1) +im 1 fg1 (nij, kmv+1! ddt i fgl lnpij t, kmv+lj bb 1 - fg2 (nij, kmvd) -i fg2 I npij t, kmv+1 I aa I mxnrm I ni j, kmv+l I solve for the phi polarized sattered field in the partile frame fg2(npijt) is -g(omn) per (3.12bi aans(2) = aans(2)-im(fg1(nij,kmv+11aa+ifg1(npijt,kmv+1) 1 +fg2 (nij, k~mv+1) bb+ifg2 (npijt,kmv+1) ddl mxnrm(nij,kmv+1) ontinue normalize the onverged results and alulate the total differential sattering ross setion (both polarizations) in the partile frame (same as in the laboratory frame) if(i.eq.lor.kmv.eq. (nm-1)) then total= snorm(abs(aansl11 J2+abs(aansl2) 12! end if return end 71
70 A.l.3. MCDATA = = = = program HCD.Z\TA Light Sattering by Partiles: Computational Methods by P.W. Barber and S.C. Hill opyright () 1990 by World Sientifi Publishing Co Pte Ltd Modifiations 1996 by P. Alsholm and A. Nilsson The original program T3 alulates the differential sattering ross setion in all diretions by projeting the surfae of a spherial surfae onto a retangular oordinate system. (See omments in the T3-ode) Til liv rn< difiol inn W'Tll\1'7\ th-~ f'i l :ll ility nf ;-,C]tlPJ-irr l i11.tll.jj!_(_;i_:li.ull j_~_; JUd [ -! r!ll llli _;Llllt_ 1_!]_ ill :...~i.j ~;IJL thet.a angles. The inident phi angle tangi.npj.i.s always zero Output is written to m.dat ::omment.s are inluded, where HCD.Z\T.Z\ differs from EXTENDT3 I npu I 1. HCDA'f'.i\: nbrangint = number of different theta orientations in the laboratory frame (number of inident angles) I[O,dth,90]; dth = 90/(nbrangint-11 anglab = angle of the E-field polarization vetor in the x-y plane nbrths number of ths (theta sattering angle) ([O,dths,180) dths = 180/(nbrths-1) I nbrphs number of phs (phi sattering angle) i[o,dphs,180) dphs = 180/inbrphs-111 MCDATA : one loop for all angint = [O,dth,90]; dth = 90/(nbrangint-1) nbrangint is a new variable algoritm: for angint = O,dth,90 bksat (ths=180) for ths = O,dths,180-dths if ths = 0 then dths=lbo/inbrths-1) forwsat else for phs = O,dphs,l80 dphs=lbo/inbrphs-1) a(th,phl =probability of sattering in this diretion end end end The preision of the output is inreased. The size and dimension of the array a 1 1 is inreased. A new ommonblok is reated ontaining the variable first in order to reset this variable for every new angint first is delared in the main program as well impliit_ re;-:tllt; (rl h,.-!-7.) double ont_p1ex trnal, adns logial first ommon dtr,rtd,pi ommon /mtxom/ nrank, nranki, tmat 14 00, ommon /mtxom2/ mxnrml200,20li ommon I mv::(_)jti/ nm, kmv ommon /mvom2/ mv,twm,prodm ommon /thtom/ theta,sinth,osth,x ommon /uvom/ angint,anginp,utheta,uph.i.,i ommon /uvom2/ ths ommon /outom/ total ommon /newblok/ first dimension mx(200),a(361,361) set program onstants dtr = rtd = pi = read from file: the T-matrix and normalization onstants nrank number of terms (matrix order) nm number of azimuthal modes m X size parameter (ka) MCDATA: new input parameters new variables (dtheta, dphiold, forwelem) 72
71 open(unit=12,file='ase',status='unknown'j rewind 12 read(12,100) nm,nrank,x lose(unit=12j nranki = nrank+1 write(6,110) write(6,j 'enter nbrangint,anglab,nbrths,nbrphs' read(5,) nbrangint,anglab,nbrths,nbrphs dtheta = pi/(nbrths - 11 dphiold = pi/(nbrphs- 11 forwelem = 2pi(1.d0- os(dtheta/211 alulation for angint = 0 or 180 degrees uses m = 1 only set the do 30 and do 50 loop indies for m = 1 only read the stored arrays one to skip over the T-matrix and normalization onstants for m = 0 MCDATA: one loop 180) for eah inident angle nbrangint = 1 is used for spheres (angint doesn't matter) nbrangint <> 1, angint is uniformly distributed [0,90] the t-file is opened and losed inside eah loop anginp is set to zero angint is written to stdout first is set to 'true' in the beginning of eah loop open(unit=9,file='m.dat',status='unknown') rewind 9 do 80 iangint = 1,nbrangint if (nbrangint.eq.11 then angint = O.qO else angint 90.q01iangint-1J/(nbrangint-11 end if anginp = O.qO write(,) (angint) open(unit=11,file='t', form='unformatted',status='unknown') rewind 11 first =.true. if(angint.eq.o.qo) then nl = 2 nh = 2 i = 1 read(111 tmat,mx alulation for angint not 0 or 180 degrees I all m I set the do 30 and do 50 loop indies for all m 10 MCDATA: angint is shifted to prevent underflow else nl = 1 nh = nm i = 2 angint = angint - end if angint = angintdtr anginp = anginpdtr anglab = anglabdtr tp = anginp 1.0q-3 utheta and uphi are the amplitudes of the inident field in the theta (parallel) and phi (perpendiular) diretions utheta = os(anglab) uphi = sin(anglab) alulate the sattered field expansion oeffiients and the baksatter enter a loop for eah azimuthal mode m do 30 im = nl,nh set m-dependent variables kmv = im-1 mv = realikmv) prodm = 1.q0 if(kmv.gt.oj then quanm = do 10 i quanm prodm ontinue end if twm = 2.q0mv ij = kmv-1 if(ij.lt.oj ij = 0 ns = nrank-ij mv 1,kmv quanm+l.qo quanmprodm/2.q0 read the T-matri.x and normalization onstants for eah m read(111 tmat,mx do 20 k = 1,ns mxnrm(k,im) = mx(k) 73
72 20 jq ::: ont.inue alulate the sattered field expansion oeffiients and sum the baksatter over all azimuthal modes all addpr onr-. 1 r1up luse(utlit.=ll) alulate the logarithm of the total baksatter differential sattering ross setion HCO.Z\TA: bksat. = total no logarithm. alulate the differential sattering ross setions.. MCDATA: enter a loop to vary ths values do 70 ig = l,nbrths-1. t 1CDATA: enter a loop to vary phs values do 60 jg = l,nbrphs alulate the theta and phi sattering angles ~1CDATA: the ombination ths = 0. 0 and phs <> 0. 0 is not neessary. if (ig.ne.1.or.jg.eq.1) then ths = pi(ig-1)/(nbrths-1) phs = pi(jg-1)/(nbrphs-1) rotate the phi orientation angle anginp with phs so that the sattering at the angle phs an be obtained in the phi = zero degree plane in the laboratory frame anginp = tp-phs if(anginp.lt.o.qo) anginp = anginp+2.q0pi enter a loop for eah azimuthal mode m do 50 im = nl,nh set m-dependent onstants kmv = im-1 mv = real(kmv) prodm = l.qo if(kmv.gt.o) then quanm = mv do 40 i quanm prodm ontinue end if twm = 2.q0mv l,krnv quanmtl.qo quanmprodm/2.q0 alulate the differential sattering ross setion at eah grid point - press is an alternate entry to subroutine addpr for sattered field alulations using the previously alulated expansion oeffiients all press ontinue MCDATA: alulate the total differential sattering ross setion at (ths,phs) and store in array a(,) if ths = 0 : forward sattering else : justify the intensity aording to the area with the fator dphiold/dphinew dphiold: the phi angle between two phs dphinew: the phi angle for a surfae element with an area equal to the area of the forward (and bak) sattering surfae element (forwelem) dphinew is theta-dependent the fator 2 is multiplied to a(,) while this value symbolizes the sattering of both phi and 360-phi This fator is not used for phi=o, phi=180 or theta=o if (ig.eq.l) then forwsat = total else i = ig - 1 dphinew = forwelem/(os( (i-0.5)dtheta) - os((i+0.5)dtheta)) a(ig,jg) = 2totaldphiold/dphinew if (jg.eq.l.or.jg.eq.nbrphs) then a(ig,jg) = a(ig,jg)/2 74
73 60 70 end if end if end if MCDATA: inrement phs value ontinue MCDATA: ontinue inrement ths value THIS PART IS ONLY FOR MCDATA : a(,) ontains differential sattering ross-setions (dss) in different sattering angels bksat and forwsat symbolizes bak- and forward sattering sum : summation of all dss divide a by sum to get a probability of sattering in different sattering angels hek is used to be sure that the probability of sattering in all diretions together is exatly 1.q0 sum = bksat do i = 2,nbrths-1 do j = l,nbrphs sum= sum+ a(i,j) enddo enddo sum = sum + forwsat bksat = bksat/sum val = bksat do i = 2,nbrths-1 do j = l,nbrphs a(i,j) = a(i,j)/sum +val val = a(i,j) enddo enddo forwsat = forwsat/sum + val hek = forwsat do i = 2,nbrths-1 do j = l,nbrphs a(i,j) = a(i,j)/hek enddo enddo bksat = bksat/hek MCDATA: write out the baksatter value and the a() values. forwsat = 1.q0-a(nbrths-1,nbrphs) write(9,120) bksat do i = 2,nbrths-1 write(9,120) (a(i,j),j=1,nbrphs) enddo ontinue lose(unit=91 stop format(2i4,f8.4) format ('... ',I, 1 alulate sattered intensity in all diretions.',/, 2 ' output is written to m.dat.',/, 3 I... ~ I I II 1 4 'nbrangint: number of different inident theta angles',/, 5 'anglab: angle of thee-field polarization',/, 6 vetor in the x-y plane, degrees',/, 7 'nbrths: number of sattering angles (theta)',/, 8 'nbrphs: number of sattering angles (phil',/). MCDATA: the preision of the ouput is inreased format(e14.91 end subroutine genlgp(pnmllg,nl alulate assoiated Legendre funtions (argument os(theta) I divided by sin( theta) for eah azimuthal mode m generate first two orders by formula and remaining orders by reursion pnmllg = assoiated Legendre funtion/sin(thetal sinth = sin(theta), osth = os(thetal n = number of orders (0 to n-11 the order of the assoiated Legendre funtions is inremented by one in the pnmllg() array impliit real16 (a-h,o-zl ommon /mvom/ nm,kmv ommon /mvom2/ mv,twm,prodm ommon /thtom/ theta,sinth,osth,x dimension pnmllg(n) dtwm = twm+l.qo 75
74 10 20 alulate for the speial ase theta = 0 degrees or 180 degrees - note that for theta = 180 degrees, osth = -1, but theta is set to 0 degrees prior to subroutine entry if theta = 0 degrees and m.ne.1 all funtions are zero if(theta.eq.o.and.kmv.ne.1) then do 10 ilg = 1,n pnmllg(ilgl = O.qO ontinue return end if if theta = 0 degrees and m.eq.1 alulate orders 0,1,2 if(theta.eq.o.and.kmv.eq.11 then pnmllgi1j = O.qO pnmllg(21 = 1.q0 pla = 1. qo plb = 3.q0osth pnmllg I 3 I = plb ibeg = 4 if theta.ne.o degrees and m.eq.o alulate orders 0 and 1 else if(kmv.eq.o) then pla = l.qo/sinth plb = osthpla pnmllg(11 = pla pnmllg ( 2 I = plb ibeg = 3 if theta.ne.o degrees and m.ne.o alulate first two nonzero orders - the assoiated Legendre funtion is zero for orders less than the azimuthal mode m else do 20 ilg = 1,kmv pnmllg(ilgl = O.qO ontinue pla = prodmsinth(kmv-11 pnmllg(kmv+1) = pla plb = dtwmosthpla pnmllg(kmv+21 = plb ibeg = knlv+3 end if 30 reur upward to obtain all remaining orders if(ibeg.gt.n) return nmul = real(2ibeg-3) nm = 2.q0 nmm = dtwm do 30 ilgr = ibeg,n pl = (nmulosthplb-nmmplal/nm pnmllg(ilgr) = pl pla = plb plb = pl nmul = nmul+2.q0 nm = nm+1.q0 nmm = nmm+1.q0 ontinue return end subroutine genang(n,tang,pang,osb,sinb) alulate sattering angles in the partile frame orresponding to sattering angles in the laboratory frame alulate the elements of t.he transform matrix for the polarization vetors impliit real16 (a-h,o-z) ommon dtr,rtd,pi ommon /uvom/ angint,anginp,utheta,uphi,i ommon /uvom2/ ths sint = sin(angintl ost = os(angint) sinp = sin(anginpl osp = os(anginp) alulate sattering angles in the partile frame orresponding to sattering angles in the laboratory frame ps = 0.qO sints = sin(thsl osts = os(thsl osps = os (ps) x = -ospostsintsosps+sintosts y = sinpsintsosps z = ospsintsintsosps+ostosts alulate the theta sattering angles in the partile frame r = sqrt(x2+y21 tang = O.qO 76
75 if(z.ne.o.qo.or.r.ne.o.qoi tang= atan2(r,z) alulate the phi sattering angles in the partile frame pang = O.qO if(x.ne.o.qo.or.y.ne.o.qo) pang= atan2(y,x) if(pang.lt.o.qo) pang= 2.qOpi+pang alulate the elements of the transform matrix matrix for the polarization vetors the transform matrix is needed only for the inident polarization vetor I ase n = 1 if (n. eq.1 I then osb = -osp sinb = sinp end if return end subroutine addpr alulate the sattered field expansion oeffiients and the differential sattering ross setion at angles tang, pang in the partile frame orresponding to angles ths, phs in the laboratory frame entry at addpr alulates the inident field expansion oeffiients and sattered field expansion oeffiients whih only need to be alulated one for eah m entry at press uses the previously alulated sattered field expansion oeffiients to alulate the differential sattering ross setion alulations are performed in the partile frame t lcdata: the variable first an be set in the main program a new ommonblok for the variable first is reated first is delared in another way impliit real16 (a-h,o-zl double omplex tmat,ab1(400),ab2(4001,i,1,2,im,aans(2) double omplex fg1(400,201),fg2(400,201) logial first ommon dtr,rtd,pi ommon /mtxom/ nrank,nranki,tmat(400,400) ommon /mtxom2/ mxnrm(200,201i ommon /mvom/ nm,kmv ommon lmvom2/ mv,twm,prodm ommon /thtom/ theta,sinth,osth,x ommon iuvom/ angint,anginp,utheta,uphi,i ommon /uvom2/ ths ommon /outom/ total ommon /newblok/ first dimension pnmllg(201) on first entry set the onstants and: (11 alulate the inident field diretion thtin in the partile frame (2) transform the inident field polarization vetor from the laboratory frame to the partile frame uu1 = theta omponent and uu2 = phi omponent (3) set the baksatter angle ths to 180 degrees if(first) then i = (O.dO,l.dOi nr2 = 2nrank snorm = 1.q0/(pix21 ths = O.qO all genang(l,tang,pang,osb,sinb) thtin ~ t.ang uu1 = osbutheta-sinbuphi uu2 = sinbutheta+osbuphi ths = pi first =. false. end if set indies for matrix ompression when n < m note: useful only when m > 1 j = kmv-1 f(ij.lt.oi ij = 0 jt = 2ij ns = nrank-ij ns2 = 2ns alulate the assoiated Legendre funtions for the inident angle = thtin in the partile frame theta = thtin sinth = sin(theta) osth = os(theta) all genlgp(pnmllg,nranki) alulate the inident field oeffiients: abl(l =theta polarization ab2() =phi polarization note: ab1() and ab2il used in sattered 77
76 field programs are j times ab11j and ab21j used in internal field programs do 10 n = 1,nrank ifln.le.ij) go to 10 np = n+nrank en= reallnl n1 n dOin 2 4.dOinl pl = nosthpnmllgln1)-ln+mvjpnmllglnl p2 = mvpnmllgln1) ab11n-ij) = lp2uu1 abl(np-ijt) = -2p1uu1 ab2(n-ij) = -lp1uu2 ab2(np-ijt) = 2p2uu2 ontinue the sattered field oeffiients= -[T] times the inident field oeffiients store the oeffiients for all azimuthal modes fg2 lns+ll to fg2 lns2) is -g(omnl do 30 i = l,ns2 fg1(i,kmv+11 = (O.dO,O.dO) fg2(i,kmv+ll = IO.dO,O.dO) do 20 j = 1,ns2 fg1(i,kmv+l) fg21i,kmv+1j ontinue ontinue fg11i,kmv+1)-tmat(i,j)ab11jj fg2(i,kmv+1)-tmat(i,j)ab2(j) alternate entry to alulate the differential sattering ross setion using the previously alulated sattered field expansion oeffiients entry press lear the result aumulators and alulate the oordinate transformation variables for eah new grid point if(i.eq.1.or.kmv.eq.o) then aans(l) = (O.dO,O.dOJ aans(2j = (O.dO,O.dO) all genang(2,tang,pang,osb,sinb) end if set indies for matrix ompression when n < m note: useful only when m > 1 j = kmv-1 flij.lt.oj ij = 0 jt = 2ij evaluate the sattered field at eah sattering angle theta = tang and phi = pang in the partile frame results are aumulated in aans(j for eah azimuthal mode m aans = kf, where F is a omponent of the vetor far-field amplitude alulate the assoiated Legendre funtions at eah sattering angle theta = tang sinth = sin(theta) osth = os(theta) if(tang.eq.pi) then theta = O.qO osth = -l.qo end if all genlgplpnmllg,nranki) phi = mvpang sinphi = sinlphil osphi = os(phi) do 40 n = l,nrank ifln.le.ij) go to 40 np = n+nrank n1 = n+1 en = real In! p1 = nosthpnmllgln1j-in+mvjpnmllg(n) p2 = mvpnmllg(nl) aa = sinphipl bb = osphip1 = sinphip2 dd = osphip2 im = i I -nl) nij = n-ij npijt = np-ijt solve for the theta polarized sattered field in the partile frame aansl11 = aans11j+imlfg1(nij,kmv+1idd+ifgl lnpijt,kmv+1jbb 1 -fg21nij,kmv+1j-ifg21npijt,kmv+1)aa)mxnrmlnij,kmv+11 78
77 40 solve for the phi polarized sattered field in the partile frame fg2(npijt) is -g(omn) per (3.12b) aans(2) = aans(2)-imlfg1(nij,kmv+1)aa+ifg1(npijt,kmv+1) 1 +fg2(nij,kmv+1)bb+ifg2(npijt,kmv+l)dd)mxnrm(nij,kmv+l) ontinue normalize the onverged results and alulate the total differential sattering ross setion (both polarizations) in the partile frame (same as in the laboratory frame) if(i.eq.1.or.kmv.eq. (nm-1)) then total= snorm(abs(aans(1) )2+abs(aans(2) )2) end if return end 79
78 A.2. A.2.1. Flow harts EXTENDTl set program onstants (nrank,ntheta,ase,ka,alb,n) ase=2 ase 1,0 angint=n/4 anginp=n/4 m azimuthal modes ~ ~ angint=o anginp=o one azimuthal mode L GAUSS (alulates the integration-points and their weights) r set m-dependent variables For eah integration-point: A(,)= 0, B(,) = 0 GENLGP alulates the assoiated Legendre-funtion I BESHIBESJ alulates the Hankel/Bessel-funtion ~ for itheta = 1, ntheta GENLGP f and g are funtions of Hankel, Bessel, (eah integration-point) BESH Legendre and trigonometri funtions BESJ for row = 1, 2nrank f+~(row,ol) = A(row,ol) + f(itheta) for ol = 1, 2nrank ~ B(row,ol) = B(row,ol) + g(itheta) alulate normalization fator ase: 2 ase=1l ase=o I save A,B I! PRCSSM (alulates T=K 1 B) ~ jsavyj ADDPRC (alulates r and angular sattering) (heks onvergene (not the first time)) restore A and B nrank = nrank-1 1 ntheta = ntheta+4l l + onverged no or m>=nrank first -+ yes first-+ + ~seond ~seond Write result and show if a onverged solution is obtained I 80
79 A.2.2. EXTENDT3 set program onstants I theta = 0 or 1t else m= 1 m=nm forim= 1, m read T -matrix values and normalization onstants I T.. ~ T alulate the logarithm of ADDPRC GENLGP the normalized sattering (alulates the sattering expansion : (alulates the assoiated ross setion oeffiients, one for eah m) Legendre funtion) in bak satter diretion... 1' PRCSSM (alulates the differential sattering ross setions, one for eah sattering angle) : GENANG (alulates the sattering angles, orresponding to the referene frame) r.-t theta and phi ~ for eah grid point if- are omputed The expansion oeffiients are already omputed. ADDPRC doesn't need to be entered. write the logarithm of the normalized differential sattering ross setions in file t3.dat as desribed in hapter 3. 81
80 A.2.3. MCDATA set program onstants! for iangint = 1, nbrangint anginp = 0 angint = n:/2iangint/(nbrangint-1) = 0 if nbrangint = 1 (sphere) I angint = 0 or 1t else m= 1 m=nm for im = 1, m l read T -matrix values and normalization onstants I! T ompute the differential ADDPRC GENLGP sattering ross setion (alulates the sattering expansion ~ (alulates the assoiated in bak satter diretion oeffiients, one for eah m) Legendre funtion) f:-t theta and phi t--1. T PRCSSM (alulates the differential sattering ross setions, one for eah sattering angle) ~ GENANG (alulates the sattering angles, orresponding to the referene frame) for eah The expansion oeffiients are already evaluated. grid point are alulated ADDPRC does not need to be entered. ompute the sattering probability in all grid points I + write the probability values in file m.dat as desribed in hapter 3. 82
81 APPENDIX B: The Monte Carlo omputer programs B.l. Computer ode listing B.l.l. BOUNMCML B.l.l.l. mml.h! Monte Carlo simulation of photon distribution in multi~layered turbid media in ANSI Standard C. Starting Date: 10/1991. Current Date: 6/1992. Lihong Wang, Ph. D. Steven L. Jaques, Ph. D. Laser Biology Researh Laboratory~ 17 M.n. Anderson Caner Conter University of Texas 1515 Holombe Blvd. Houston, TX USA This program was based on: Ill The Pasal ode written by Marleen Keijzer and Steven L. Jaques in this laboratory in 1989, whih deals with multi~layered turbid media. (21 Algorithm for semi~infinite turbid medium by S.A. Prahl, M. Keijzer, S.L. Jaques, A.J. Welh, SPIE Institute Series Vol. IS 5 (1989), and by A.N. Witt, The Astrophysial journal Supplement Series 35, 1~ ). Major modifiations inlude: Conform to ANSI Standard C. Removal of limit on number of array elements, beause arrays in this program are dynamially alloated. This means that the program an aept any number of layers or gridlines as long as the memory permits. Avoiding global variables whenever possible. This program has not used global variables so far. Grouping variables logially using strutures. Top~down design, keep eah subroutine lear & short. Refletane and transmittane are angularly resolved. Modifiations 1996 by P. Alsholm and A. Nilsson inluding lateral boundaries. 'lr: General Naming Conventions: Preproessor names: all apital letters, e.g. #define PREPROCESSORS Globals: first letter of eah word is apital, no undersores, e.g. short GlobalVar; Dummy variables: first letter of ealj word is apital, and words are onneted by undersores, e.g. void NieFuntion(har Dummy_Var);! Loal variables: by undersores, e.g. short loal_var; Funtion names or data types: Dimension of length: em. #inlude <math.h> #inlude <stdlib.h> #inlude <stdio.h> #inlude <stddef.h> #inlude <time.h> #inlude <string.h> #inlude <type.h> all lower ases, words are onneted same as Globals. #define PI #define WEIGHT 1E~4 / Critial weight for roulette. / 83
82 #define CHANCE 0.1 #define STRLEN 256 llrj,f.i nr' llu,j,,,.,,, dtar #define SIGN(X) ((X)>=O 7 1:-1)! Chane of roulette survival. /! String length. /! Stutures / / Struture used to desribe a photon paket.! typedef strut { double x, y,z; double ux, uy, uz; double H; Boolean dead; short layer; double s; double sleft; PhotonStrut;! Cartesian oordinates. [em} I! diretional osines of a photon. /! weight. I! 1 if photon is terminated. / / index to layer where the photon /! paket resides. /! urrent step size. [em}. I!step size left. dimensionless [-}. I.. Struture used to desribe the geometry and optial properties of a layer. zo and z1 are the z oordinates for the upper boundary and lower boundary respetively. os_rito and os_rit1 are the osines of the ritial angle of total internal refletion for the upper boundary and lower boundary respetively. os_ritxy is the osine of the ritial angle of total internal refletion for the boundary to the surrounding glass. They are set to zero if no total internal refletion exists. They are used for omputation speed.! typedef strut { double z 0, z 1 ; double n; double mua; double mus; double g; double os_rito, Layerstrut; I z oordinates of a layer. [em] I I refrative index of a layer. I I absorption oeffiient. [11m] I I sattering oeffiient. [1/m] I I anisotropy. I os_rit1, os_ritxy;! Input parameters for eah independent run. z and r are for the ylindrial rnjrdinale system. [em] a is for the angle alpha between the photon exiting diretion and the surfae normal. [radian] The grid line separations in z, r, and alpha diretions are dz, dr, and da respetively. The numbers of grid lines in z, r, and alpha diretions are nz, nr, and na respetively. The member layerspes will point to an array of strutures whih store parameters of eah layer. This array has (number_layers + 3) elements. One element is for a layer. The layers 0 and (num_layers + 1) are for top ambient medium and the bottom ambient medium respetively. The layer (num_layers + 2) i.s for the surrounding glass.! typedef strut { har out_fname[strlen]; har out_f format; long num_photons; double Wth; double dz; double dr; double da; short nz; short nr; short na; short num_layers; double x_size, y_size; Layerstrut layerspes; Inputstrut; I output file name. I I output file format. ' I / 'A' for.z\.scii, I I 'B' for binary. I I to be traed. I! play roulette if photon /!weight< Wth./ I z grid separation. [em] I! r grid separation. [em] I I alpha grid separation. / / [radian} I I array range O.. nz-1. I /array range O.. nr-1. I I array range O.. na-1. I! number of layers. I I dimension of the sample. / I layer parameters. I! Strutures for soring physial quantities. z and r represent z and r oordinates of the ylindrial oordinate system. [em] a is the angle alpha between the photon exiting diretion and the normal to the surfaes. [radian] 84
83 See omments of the Inputstrut. see manual for the physial quantities. / typedef strut { double Rsp;! speular refletane. [-) / double Rd ra;! 2D distribution of diffuse / double Rd_r;! refletane. [1/ (m2 sr))! ld radial distribution of diffuse /! refletane. [1/m2] / double Rd_a; / ld angular distribution of diffuse /! refletane. [1/sr] I double Rd; / total diffuse refletane. [ -] I double A_rz; f 2D probability density in turbid /! media over r & z. [1/m3] double A_z; / 1D probability density over z. I! [1/m] I double A_l; / eah layer's absorption/ double A; / probability. [-] I! total absorption probability. [-] / I I double Tt_ra; / 2D distribution of total I double Tt_r; / transmittane. [1/ (m2 sr)] I! ld radial. distribution of /! transmittane. [1/m2) ; double Tt_a; / ld angular distribution of /! transmittane. [1/sr] I double Tt;! total transmittane. [ -] I outstrut;! Routine prototypes for dynami memory alloation and release of arrays and matries. Modified from Numerial Reipes in C.! double AlloVetor(short, short); double AlloMatrix(short, short, short, short); void FreeVetor(double, short, short); void FreeMatrix(double, short, short, short, short) ; void nrerror(har ); B mmlmain. / main program for Monte Carlo simulation of photon distribution in multi-layered turbid media.! / THINKCPROFILER is defined to generate profiler alls in Think. If 1, remember to turn on "Generate profiler alls" in the options menu.! #define THINKCPROFILER 0 /GNU does not support difftime() and CLOCKS PER_SEC./ #define GNUCC 0 #if THINKCPROFILER #inlude <profile.h> #inlude <onsole.h> #endif #inlude "mml.h" / Delare before they are used in main(). I FILE GetFile(har ); short ReadNumRuns(FILE ) ; void ReadParm(FILE, Inputstrut ) ; void ChekParm(FILE, Inputstrut ); void InitOutputData(InputStrut, Outstrut I; void FreeData(InputStrut, OutStrut ); double Rspeular(Layerstrut ) ; void LaunhPhoton(double, Layerstrut, PhotonStrut ); void HopDropSpin(Inputstrut,PhotonStrut,Outstrut ); void sumsaleresult(inputstrut, OutStrut ); void WriteResult(Inputstrut, OutStrut, har );! If F = 0, reset the lok and return 0. If F = 1, pass the user time to Msg and print Msg on sreen, return the real time sine F=O. If F = 2, same as F=1 exept no printing. Note that lok() and time() return user time and real time respetively. User time is whatever the system alloates to the running of the program; real time is wall-lok Lime. In a time-shared system, 85
84 Ll!~y llo.,dj not be the same. lok() only hold 16 bit integer, whih is about lok tiks.! time t PunhTime(har F, har Msg) { #if GNUCC return( OJ; #else stati lok_t uto; stati time t double sees; har s [ STRLEN] ; rto; ifif==0) uto = lok( I; rto = time(nulli; return(oi;! user time referene. / / real time referene. / else ifif==lj sees= (lok() - uto)/(double)clocks_per_sec; if (ses<oi ses=o; / lok() an overflow. / sprintf(s, "User time: %8.0lf se= %8.2lf hr. %s\n", sees, ses/3600.0, Msg); puts Is); strpy(msg, s); return(difftime(time(null), rt0)); else if(f==21 return(difftime(time(null), rto)i; else return(oi; #endif ) / Print the urrent time and the estimated finishing time. Pl is the number of omputed photon pakets. Pt is the total number of photon pakets. / void PreditDoneTime(long P1, long Pt) { time_t now, done_time; strut tm date; har s[80]; now= time(null); date= loaltime(&now); strftime(s, 80, "%H:%M %x, date); printf("now %s, ", s); done time = now + I time_t J I Punh Time ( 2, "" J I Pt-Pl J I (double I P1 J; date = loaltime(&done_timej; strftime(s, 80, "%H:%M%x", date); printf("end %s\n", s); / Report estimated time, number of photons and runs left after alulating 10 photons or every 1/10 of total number of photons. Num_Runs is the number of runs left. Pi is the index to the urrent photon, ounting down. Pt is the total number of photons.! void Reportstatus 1 short Num Runs, long Pi, long Pt I { if(pt-pi == 10 II Pi10%Pt == 0 && Pi!= Pt) print f ( "%ld photons & %hd runs left, ", Pi, Num_Runs 1 ; PreditDoneTime(Pt-Pi, Ptl;! Report time and write results.! void ReportResult (Inputstrut In_Parm, Outstrut out Parml { har time_report[strlen]; strpy(time_report, " Simulation time of this run.'); PunhTime(1, time_reportl; SumSaleResult(In_Parm, &Out_Parm); WriteResult(In_Parm, Out Parm, time_report);! Get the file name of the input data file from the argument to the ommand line.! void GetFnameFromArgv(int arg, har argv[ l, har input_filename) if(arg>=2) { / filename in ommand line / strpylinput_filename, argv[1]1; 86
85 else input_filename[oj I \0 I;! Exeute Monte Carlo simulation for one independent run.! void DoOneRun(short NumRuns, Inputstrut In_Ptr) { register long i photon;! index to photon. Outstrut out parm; Photonstrut photon; register for speed./!distribution of photons./ #if THINKCPROFILER InitProfile(200,200); eho2file("prof.rpt",0, stdout); #endif InitOutputData(In_Ptr, &out parm); out parm.rsp = Rspeular(In_Ptr->layerspes); i photon = I n Ptr->num photons; Punh Time ( 0, " " ) ; do { ReportStatus(NumRuns, i photon, In_Ptr->num photons); LaunhPhoton(out parm.rsp, In_Ptr->layerspes, &photon) do HopDropSpin(In_Ptr, &photon, &out parm); while (!photon.dead); while(--i photon); #if THINKCPROFILER exit (OJ; #endif ReportResul t ( In_Ptr, out parm) ; FreeData(In_Ptr, &out parm); / The argument to the ommand line is filename, if any. Maintosh does not support ommand line.! har main ( int arg, har argv []) { har input_filename[strlen]; FILE input_file ptr; short num_runs;! number of independent runs.,' InputStrut in parm; ShowVersion ( "Version 1. 0, 19 92" ) ; GetFnameFromArgv(arg, argv, input_filename); input_file_ptr = GetFile(input_filenameJ; ChekParm(input_file_ptr, &in parm); num_runs = ReadNumRuns (input file ptr); while(num_runs--j ReadParm(input_file ptr, &in parm); DoOneRun (num_runs, &in parm); flose(input_file ptr); return ( 0 J; B.l.l.3. mmlio. / Input/output of data.! #inlude "mml.h"! Struture used to hek against dupliated file names. / strut NameList { } ; har name[strlen]; strut NameList next; typedef strut NameList NameNode; typedef NameNode NameLink;! Center a string aording to the olumn width. 87
86 I har CenterStrtshort Wid, har InStr, har OutStr) s i ;~ ~~ t! number of spaes to be filled /! befote Ir1Str. nspaes = (Wid- strlen(instrl )/2; iftnspaes<oi nspaes = 0; strpy(outstr, ""); while(nspaes--1 strat(outstr, stratioutstr, Instr); returntoutstr);! Print. some messages before starting simulation. e.g. author, address, program version, year.! #define COLWIDTH 80 void ShowVersianthar version) har str[strlen]; CenterStr(COLWIDTH, "Monte Carlo Simulation of Multi-layered Turbid Media", str); puts(str); puts!""); CenterStr ( COLWIDTH, "Lihong Wang, Ph. D. ", str) ; puts(str); CenterStriCOLWIDTH, "Steven L. Jaques, Ph. D.", str); puts 1 strl; CenterStr(COLWIDTH, "Laser Biology Researh Laboratory- 17",str); puts(strl; CenterStr(COLWIDTH, "M.D. Anderson Caner Center", str) puts(stri; CenterStr(COLWIDTH, "University of Texas", str); putststr); "I; CenterStr(COLWIDTH, "Houston, TX 77030", str); puts(str); CenterStr (COLWIDTH, puts(strl; puts(""); "Fax: I 713 I ", str); CenterStr(COLWIDTH, version, str); puts I str); CenterStr(COLWIDTH, "modified 1996, PA- mmlboun", str); puts(strl; puts I"" I; puts("\n\n\n\n"); #undef COLWIDTH / Get a filename and open it far reading, retry until the file an be opened. ' terminates the program. If Fname!=NULL, try Fname first.! FILE GetFile(har Fname; { FILE file=null; Boolean firsttime=l; do { iflfirsttime && Fname[OJ!='\0' 1! use the filename from ommand line / firsttime = 0; else { printf("input filename(or. to exit):"); sanf( %s", Fname); 11 firsttime = 0; if(strlen(fname) exit I 1) ; file = fopen(fname, "r"); while(file ==NULL); return( file); 1 && Fname[O] '. ')! exit if no filename entered. /!~ 88
87 Kill the ith har (ounting from 0), push the following hars forward by one. / void KillChar(size_t i, har Str) { size_t sl = str.len(str); for(;i<sl;i++l Str(i] = Str[i+l];! Eliminate the hars in a string whih are not printing hars or spaes. Spaes inlude ' '\f', '\t' et. Return 1 if no nonprinting hars found, otherwise return 0.! Boolean ChekChar(har Str) { Boolean found = 0;! found bad har. I size_t sl = strlenistrl; ;;j :-:.--, I 11; while (i<sli if (Slr[i]<O I I Str[i]>255J nrerror("non-ascii file\n"); else iflisprint(str[i]l I I isspae(str[i]) 1 i++; else { found = 1; KillChar1i., Str); sl--; return (found!;! Return 1 if this line is a omment line in whih the first non-spae harater is "#". Also return 1 if this line is spae line.! Boolean CommentLine(har Buf) { size_t spn, spn; spn = strspn(buf, " \t"); I length spanned by spae or tab hars. I spn = strspn(buf, '#\n"l; I length before the 1st # or return. / if(spn == spn) return(l); else return(o); / omment line or spae line. / I the line has data. I! Skip spae or omment lines and return a data line only. / har FindDataLine(FILE File_Ptr) { har buf [STRLEN]; bu f [ 0 J = ' \ 0 ' ; do { I skip spae or omment lines./ if(fgets(buf, 255, File_Ptr) == NULL) printf("inomplete data\n"); bu f [ 0 J = ' \ 0 ' ; hn~ak; else ChekChar(bufl; while(commentline(buf)); return (buf);! Skip file version, then read number of runs.! short ReadNumRuns(FILE File_Ptr) { har buf[strlen]; short n=o; FindDataLine(File_Ptr); I skip file version. I strpy(buf, FindDataLine(File_Ptr)); if(buf[0]=='\0') nrerror('reading number of runs\n"); ssanf(buf, '%hd",&n); return (n) ;! 89
88 Read the file name and the file format. The file format an be either A for ASCII or B for binary.! void ReadFnameFormat(FILE File_Ptr, InputStrut In_Ptr) { har buf [STRLEN];! read in file name and format. / strpy(buf, FindDataLine(File_Ptr)); if I bu f [ 0 J ==' \0' ) nrerror("reading file name and format.\n"); ssanf (but, "%s %", In_Ptr->out_fname, & ( In_Ptr->out_f format 1 1 ; if(toupper(in_ptr->out_fformatl!= 'B' I In Ptr->out fformat = 'A'; 'k Read the number of photons. / void ReadNumPhotons(FILE File_Ptr, Inputstrut In_Ptr) { har buf [STRLEN]; / read in number of photons. / strpy(buf, FindDataLine(File_Ptr) I; iflbuf[oj=='\0') nrerror I "Reading number of photons. \n" I ; ssanf (buf, "%ld", &In_Ptr->num_photonsl; if1in_ptr->num_photons<=0) nrerror I "Nonpositi ve number of photons. \n' I;! Read the members dz and dr.! void ReadDzDriFILE File_Ptr, Inputstrut In_Ptrl har buf [STRLEN];! read in dz, dr. / strpy(buf, FindDataLine(File_Ptr)); if(buf[0]=='\0') nrerror("reading dz, dr.\n"); ssanf(buf, "%lf%lf", &In_Ptr->dz, &In_Ptr->dr); ifiin_ptr->dz<=oi nrerror("nonpositive dz.\n"j; if I In_Ptr->dr<=O 1 nrerror ( "Nonposi ti ve dr. \n") ;! Read the members nz, nr, na.! void ReadNzNrNaiFILE File_Ptr, Inputstrut In_Ptrl { har buf[strlen];! read in number of dz, dr, da. / strpy(buf, FindDataLine(File_Ptr)l; if(buf[0]=='\0') nrerror I "Reading number of dz, dr, da' s. \n ) ; ssanf(buf, '%hd%hd%hd', &In_Ptr->nz, &In_Ptr->nr, &In_Ptr->nal; if(in_ptr->nz<=o) nrerror("nonpositive number of dz's.\n"l; iflln_ptr->nr<=o) nrerror("nonpositive number of dr's.\n"); if(in_ptr->na<=o) nrerror("nonpositive number of da's.\n"l; In_Ptr->da = 0.5PI/In_Ptr->na; / Read the members x_size and y_size.! void ReadXSizeYSize(FILE File_Ptr, Inputstrut In_Ptr) { har buf [STRLEN];! read in x_size, y_size. / strpy(buf, FindDataLine(File_Ptr)J; iflbuf[0]=='\0') nrerror("reading x_size, y_size.\n'j; ssanf(buf, "%lf%lf", &In_Ptr->x_size, &In_Ptr->y_size); if ( In_Ptr->x_size<=O) nrerror ( "Nonpositive x_size. \n" 1; if ( In_Ptr->y_size<=O) nrerror I "Nonposi tive y_size. \n") ;! Read the number of layers.! void ReadNumLayers(FILE File_Ptr, Inputstrut In_Ptr) { har buf [STRLEN];! read in number of layers. / strpy(buf, FindDataLine(File Ptrl); if(buf[ol=='\0') nrerror I" Readi.ng number of layers. \n" 1 ; ssanf (buf, "%hd", &In_Ptr- >num._layers); 90
89 if(in_ptr->num_layers<=oi nre{ror ( "Nonposi ti ve number of layers. \n" I ;! Read the refrative index n of the ambient. / void ReadAmbient(FILE File_Ptr, Layerstrut Layer_Ptr, har side) har buf[strlen], msg[strlen]; double n; strpy(buf, FindDataLine(File_Ptr) I; if ( bu f [ 0 J ==' \0' I { sprintf (msg, "Rading n of %s ambient. \n", side); nrerror (msg); ssanf(buf, "%lf", &n I; if(n<=oi nrerror("wrong n.\n"); Layer_Ptr->n = n;! Read the parameters of one layer. Return 1 if error deteted. Return 0 otherwise. Z_Ptr is the z oordinate of the urrent layer, whih is used to onvert thikness of layer to z oordinates of the two boundaries of the layer.! Boolean ReadOneLayer(FILE File_Ptr, har buf[strlen]; double d, n, mua, mus, g; Layerstrut Layer_Ptr, double Z_Ptr) / d is thikness. / strpy(buf, FindDataLine(File_Ptrl I; if(buf[ol=='\0'1 returnl11; /error. / ssanf(buf, "%lf%lf%lf%lf%lf", &n, &.mua, &mus, &g, &d); if (d<o I I n<=o I I mua<o I I mus<o I I g<o I I g>1 I return(11;! error. / Layer_Ptr->n = n; Layer_Ptr->mua mua; Layer_Ptr->mus mus; Layer_Ptr->g g; Layer_Ptr->zO Z_Ptr += d; Layer_Ptr->z1 return(o); Z_Ptr; Z_Ptr;! Read and set the parameters of the surrounding glass. Return 1 if error deteted. Return 0 otherwise. Z_Ptr is the z oordinate of the urrent layer, whih is used to onvert thikness of layer to z oordinates of the two boundaries of the layer.! Boolean ReadsurrGlass(FILE File_Ptr, har buf [STRLEN]; double n; strpy(buf, FindDataLine(File_Ptr)J; if(buf[0]=='\0') return(1); /error./ ssanf (buf, "%lf', &n); if (n<=oi return ( 1 I; Layer_Ptr->n Layer_Ptr->mua Layer_Ptr->mus Layer_Ptr->zO Layer_Ptr >zl return(oi; n; = 0.0; = 0. 0; 0. 0; = Z Ptr;!error./ Layerstrut Layer_Ptr, double Z_Ptr) / Read the parameters of one layer at a time.! void ReadLayerSpes(FILE File_Ptr, short Num_Layers, Layerstrut Layerspes_PPI 91
90 har msg[strlen]; short i=o; double z = 0.0; I z oordinate of the urrent layer. I Alloate an array for the layer parameters. I layer 0 and layer Num_Layers + 1 are for ambient. I Layerspes_PP = (LayerStrut ) mallo ((unsigned) (Num_Layers+3) sizeof (LayerStrut)) if 1! 1 Layerspes_PP) ) nrerror 1 "alloation failure in ReadLayerSpes () "); ReadAmbient i File_Ptr, & 1 i Layerspes_PPJ [ i]), "top" J; for(i=l; i<=num_layers; i++) if(readonelayer(file_ptr, &(ILayerspes_PPJ [i]), &z)) sprintflmsg, "Error reading %hd of %hd layers\n", i, Num_Layers 1 ; nrerr,r (msg) EeadAmbi ent ( Fi le_ptr, & ( ( Layerspes_PP I [ i] I, "bot tom") ; if 1 P.eadSurrGlass I File_Ptr, & I I Layerspes_PP 1 [ i+ll I, &z J) sprintf(msg, "Error reading surrounding glass"); nrerror (msg);!~' Compute the ritial angles for total int.ernal refletion aording to the relative refrative index of the layer. All layers are proessed. / void CritialAnglel short Num_Layers, LayerStrut Layerspes_PPI short i=o; double nl, n2; for(i=l; i<=num_layers; i++) n1 = (Layerspes_PPI[i].n; n2 = (Layerspes_PPI [i-1].n; (Layerspes_PP) [i].os_rito = n1>n2? sqrt(l.o- n2n21(n1nl) I : 0.0; n2 = ILayerspes_PP) [i+1].n; (Layerspes_PPI [i].os_rit1 = n1>n2? sqrt(1.0- n2n21(n1nl) I 0.0; n2 = 1 Layerspes_PPI [Num_Layers+2 J.n; (Layerspes_PP) [i].os_ritxy = n1>n2? sqrt(1.0 - n2n211nln11 I 0.0; n1 = I Layerspes_PP I [Num_Layers+2 J. n; I surrounding glass. I n2 = (Layerspes_PP) [OJ.n; ( Layerspes_PP) [Num_Layers+2]. os_rito = n1>n2? sqrt(1.0- n2n211n1n1)) : 0.0; n2 = ( Layerspes_PP) [Num_Layers+1]. n; I Layerspes_PP) [Num_Layers+2]. os_ri t1 = n1 >n2? sqrt(l.o- n2n21(n1nl) I : 0.0;! Read in the input parameters for one run.! void ReadParmiFILE File_Ptr, Inputstrut In_Ptr) { In Ptr->Wth WEIGHT; ReadFnameFormat(File_Ptr, In_Ptr); ReadNumPhotons I Fi le Ptr, In_Ptr 1 ; ReadDzDr(File_Ptr, In_Ptr); ReadNzNrNa(File_Ptr, In_Ptr); ReadXSizeYSi ze ( Fi le_ptr, In_Ptr) ; ReadNumLayers (File Ptr, In Ptr); ReadLayerSpes(File_Ptr, In_Ptr->num_layers, &In_Ptr->layerspes) CritialAngle(ln_Ptr->num_layers, &In_Ptr->layerspes); / Return 1, if the name in the name list. Return 0, otherwise.! Boolean NameinList(har Name, NameLink List) { while (List!=NULL) if(strmp(name, List->name) 01 return I 1 I ; List = List->next; ) ; return(o);! Add the name to the name list.! void AddNameToList(har Name, NameLink Llst Ptrl { NameLink list = List_Ptr; 92
91 if I list "'- NULL) { / first node. I List Ptr = list = (NameLink)mallo(sizeof(NameNode)); strpy(list->name, Name); list->next = NULL; else! Move to the last node. / while(list->next!=null) list = list->next;! subsequent nodes. / / Append a node to the list. / list->next = (NameLink)mallo(sizeof(NameNode)); list = list->next; strpy(list->name, Name); list->next = NULL; / Chek against dupliated file names. A linked list is set up to store the file names used in this input data file. / Boolean FnameTaken(har fname, NameLink List Ptr) { if(nameinlisttfname, List_Plr)) return ill; else { AddllameToLi st ( fname, List_Ptr) ; return(o);! Free eah node in the file name list. / void FreeFnameList(NameLink List) { NameLink next; while(list!=null) next = List->next; free (List); List = next; '~ Chek the input parameters for eah run.! void ChekParm(FILE File_Ptr, Inputstrut In_Ptrl { short i_run; short num_runs; / number of independent runs. / NameLink head = NULL; Boolean name_taken;/ output files share the same /! file name./ har msg[strlen]; num_runs = ReadNumRuns(File_Ptr); for(i_run=l; i_run<=num_runs; i_run++) printf('cheking input data for run %hd\n", i_run); ReadParm(File_Ptr, In_Ptr); name_ taken = FnameTaken 1 In Ptr-- >ou t_fname, &head) ; if (name_taken) sprintf (msg, "file name %s dupliated. \n", In_Ptr->out_fnamel; free(in_ptr->layerspes); if(name_taken) nrerror(msg); FreeFnameList(head); rewind(file_ptr); / Alloate the arrays in OutStrut for one run, and array elements are automatially initialized to zeros.! void InitOutputData(Inputstrut In_Parm, outstrut Out_Ptr) short nz In_Parm. nz; short nr In_Parm.nr; short na = In_Parm.na; short nl = In_Parm.num_layers; / remember to use nl+2 beause of 2 for ambient. / if (nz<=o I I nr<=o I I na<=o I I nl<=o J nrerror("wrong grid parameters.\n"j;! Init pure numbers. / Out_Ptr->Rsp = 0.0; Out Ptr->Rd = 0.0; Out Ptr->A = 0.0; Out Ptr->Tt 0. 0; 93
92 ! Alloate the arrays and the matries.! Out_Ptr->Rd_ra = AlloMatrix(O,nr-1,0,na-11 Out Ptr->Rd r AlloVetor(O,nr-11 out Ptr->Rd a = AlloVetor(O,na-11; out_ptr->a_rz Out Ptr->A_z out Ptr->A_l Out Ptr->Tt ra out Ptr->Tt r Out Ptr->Tt a AlloMatrix(O,nr-1,0,nz-11 AlloVetor(O,nz-11; AlloVetor(O,nl+11; AlloMatrix(O,nr-1,0,na-11 AlloVetor(O,nr-11 AlloVetor(O,na-11;! Undo what InitOutputOata did. i.e. free the data alloations.,! void freeoata(lnputstrut In_Parm, OutStrut Out Ptrl short nz In_Parm.nz; short nr In_Parm.nr; short na = In_Parm.na; short nl = In_Parm.num_layers; / remember t.o use nl+2 beause of 2 for ambient. / free(in_parm.layerspesj; freer-latrix 1 Out_Ptr- >Rd_ra, 0, nr-1, 0, na -1 I FreeVetor(Out_Ptr->Rd_r, O,nr-11 FreeVetor(Out_Ptr->Rd_a, O,na-11; FreeMatrix(Out_Ptr->.Z\._rz, 0, nr-1, O,nz-11 FreeVetor(Out_Ptr->A_z, 0, nz-11; FreeVetor(Out_Ptr->A_l, O,nl+11; FreeMatrix(Out_Ptr->Tt_ra, O,nr-1,0,na-1J FreeVetor(Out_Ptr->Tt_r, O,nr-11 FreeVetor(Out_Ptr->Tt_a, O,na-11; / Get 10 array elements by summing the 20 array elements. / void Sum20Rd(InputStrut In_Parm, Outstrut out PtrJ { short nr = In_Parm.nr; short na = In_Parm.na; short ir, ia; double sum; for(ir=o; ir<nr; ir++l sum= 0.0; for(ia=o; ia<na; ia++l sum += Out_Ptr->Rd_ra[ir] [ia]; Out_Ptr->Rd_r[ir] = sum; for(ia=o; ia<na; ia++l sum= 0.0; for(ir=o; ir<nr; ir++l sum+= Out_Pt.r->Rd_ra[ir] [ia]; Out_Ptr->Rd_a[ia] = sum; sum= 0.0; for(ir=o; ir<nr; ir++l sum+= out Ptr->Pd_r[ir]; Out Ptr->Pd = sum;! Peturn the index to the layer aording to the index to the grid line system in z diretion (IzJ. Use the enter of box. j /(I short IzToLayer(short Iz, InputStrut In_ParmJ ( short i=1; / index to layer. / short num_layers = In_Parm.num_layers; double dz = In_Parm.dz; while( (Iz+0.5Jdz >= In_Parm.layerspes[i].zl && i<num_layersl i++; return(i)! Get 10 array elements by summing the 20 array elements.! void sum20a ( InputStrut In_Parm, OutStrut Out Ptr 1 ( short nz = In_Parm.nz; short nr = In_Parm.nr; short iz,ir; double sum; for(iz=o; iz<nz; iz++l sum= 0.0; for(ir=o; ir<nr; ir++l sum += Out Ptr->A_rz [ir] [iz] 94
93 Out_Ptr->A_z[iz] sum; sum= 0.0; for(iz=o; iz<nz; iz++) sum+= Out_Ptr->A_z[iz]; out_ptr->a_l[iztolayer(iz, In_Parm) J += out_ptr->a_z[iz]; out Ptr->A = sum;!~ Get ld array elements by summing the 2D array elements. ~/ void Sum2DTt(InputStrut In_Parm, OutStrut Out_Ptr) { short nr = In_Parm.nr; short na = In_Parm.na; short ir,ia; double sum; for(ir=o; ir<nr; ir++) sum = 0.0; for(ii1 O; iil<na; ia++) sum ~ out PLr->'l'L rlirj =sum; Out_Ptr >'l'l ra[ir[ [ia]; for(ia=o; ia<na; ia++l sum= 0.0; for(ir=o; ir<nr; ir++l sum+= Out_Ptr->Tt_ra[ir] [ia]; Out_Ptr->Tt_a[ia] = sum; sum= 0.0; for(ir=o; ir<nr; ir++l sum+= Out_Ptr->Tt_r[ir]; Out Ptr->Tt = sum;! Sale Rd and Tt properly. "a" stands for angle alpha. Sale Rd(r,a) and Tt(r,a) by (area perpendiular to photon diretion) x(solid angle)x(no. of photons). or [2PIrdros(a)]x[2PIsin(a)da]x[No. of photons] or [2PIPIdrdarsin(2aJ]x[No. of photons] Sale Rd(r) and Tt(r) by (area on the surfae)x(no. of photons). Sale Rd(a) and Tt(a) by (solid angle)x(no. of photons).! void salerdtt(inputstrut In_Parm, OutStrut Out_Ptr) { short nr = In_Parm.nr; short na = In_Parm.na; double dr = In_Parm.dr; double da = In_Parm.da; short ir,ia; double sale1, sale2; sale1 = 4.0.PIPIdrsin(da/21 In_Parm.num_photons;!The fator (ir+0.5)sin(2al to be added. / for(ir=o; ir<nr; ir++l for(ia=o; ia<na; ia++l sale2 = 1.0/((ir+0.5)sinl2.0(ia+0.5)da)sale1); Out_Ptr->Rd_ra[ir] [ia] = sale2; Out._Ptr->Tt_rafirl fia) ~ s :ale2; sale1 = 2.0PIdrdrIn_Parm.num_photons;!area is 2PI[(ir+0.5Jdr]dr./! ir+o.s to be added. / for(ir=o; ir<nr; ir++l { sale2 = 1.0/((ir+0.5)sale11; Out_Ptr->Rd_r[irl = sale2; Out_Ptr->Tt_r[ir] = sale2; sale1 = 2.0PIdaIn_Parm.num_photons; /solid angle is 2PIsin(a)da. sin(a) to be added. I for(ia=o; ia<na; ia++l { sale2 = 1.0/(sin((ia+0.5ida)sale1); Out_Ptr->Rd_a[ia] = sale2; Out_Ptr->Tt_a[ia] = sale2; sale2 = 1.0/(double)In_Parm.num_photons; Out_Ptr->Rd = sale2; Out Ptr->Tt = sale2; 95
94 ! Sale absorption arrays properly. / void SaleA(Inputstrut In_Parm, OutStrut Out Ptrl { short nz = In_Parm.nz; short nr = In_Parm.nr; double dz = In_Parm.dz; double dr = In_Parm.dr; short nl = In_Parm.num_layers; short iz, ir; short il; double salel; I Sale A_rz. / salel = 2 _ OPIdrdrdzIn_Parm.num pholons;!volume is 2pi(irt0.5idrdrdz.' / ir+o.s to be added. / for{iz=o; iz<nz; iz++} forlir=o; i.r<nr; ir++l 0111 f'll -,\ n:[ir[[i;[ I i r t 0. S I ;.l I I ; Sale.b.. z_ 1 seal eel L. o,- l,dzln_parrn.num_ph )tjn:); for(iz=o; iz<nz; izt+) Out_Ptr->.l;_z[iz] = salel; : Sale.2.,_1.. Z\.void int/int. / salel = 1.0/tdouble)In_Parm.num photons; forlil=o; il<=nl+l; il++) Out_Ptr->.Z\._1 [i.l] = salel; Out Ptr->A =salel; k~~'~ kkkk Sum and sale results of urrent ru11. / void sumsaleresultiinputstrut In_Parm, OutStrut out Ptr)!Get 10 & 00 results. / sum2drd1in_parm, Out_Ptr); Sum2DA(In_Parm, Out_Ptr); Sum2DTt(In_Parm, Out_Ptr); SaleRdTt(In Farm, Out_Ptr); SaleA(In_Parm, Out_Ptr);! Write the version number as the first string in the file. Use hars only so that they an be read as either ASCII or binary. / void WriteVersion(FILE file, har Version) { fprintf(file, "%s \t# Version number of the file format. \n\n", Version); fprintf (file, fprintf I file, fprinlf I file, fprintflfile, "####\n# Data ategories inlude: \n"); "# InParm, RAT, \n" J ; "# A_l, A_z, Rd_r, Rd_a, rt_r, Tt_a, \n" 1; "# A_rz, Rd_ra, Tt ra \n####\n\n");!~ Write the input parameters to the file.! void Writf'Tnl'.lrrniPTI.F fi 1:, Trq ttl ~llll t 111 J\11111) { short i; fprintf(file, "InParm \t\t\t# Input parameters. em is used.\n"l; fprintflfile, "%s \ta\t\t# output file name, ASCII.\n", In_Parm. out fname I; fprintf I file, "%ld \t\t\t\t# No. of photons\n", In_Parm.num photons); fprintflfile, "%G\t%G\t\t\t# dz, dr [em] \n", InParm.dz, In Parm.drl fprint fll i I, "'i.ltd\1 'i,ll<l\1 'i,]t l\1 \Ill II.,J L, II,,j,'- 11", In_Parm.nz, ln_parm.nr, In_Parm.na); fprintflfile, "%G\t%G\t\t\t# x_size and y_size.\n\n", In_Parm.x size, In Parm.y_size); fprintf I file, "%hd\t\t\t\t\t# Number of layers\n", In_Parm. num_layers) ; fprintf I file, "#n\trnua\tmus\tg\td\t# One line for eah layer\n"j fprintf I file, "%G\t\t\t\t\t# n for medium above\n", In_Parm.layerspes[O].n); for I i=l; i<=ln_parm. num layers; i++ I 96
95 LayerStrut s; s = In_Parm.layerspes[i]; fprintf (file, '%G\t%G\t%G\t%G\t%G\t# layer %hd\n', s.n, s.mua, s.mus, s.g, s.zl-s.zo, ij; fprintf(file, "%G\t\t\t\t\t# n for medium below\n", In_Parm.layerspes[i].n); fprintf(file, "%G\t\t\t\t\t# n for surrounding glass\n\n", In_Parm.layerspes[i+l].n);! Write refletane, absorption, transmission.! void WriteRATIFILE file, outstrut Out ParmJ { fprintf (file, "RAT #Refletane, absorption, transmission. \n" I; / flag. / fprintf(file, "%-14.6G \t#speular refletane [-]\n", Out_Parm.Rsp); fprintf(file, "%-14.6G \t#diffuse refletane [-]\n", Out_Parm.Rd); fprintf(file, "%-14.6G \t#absorbed fration [-]\n", Out_Parm.AI; fprintf(file, "%-14.6G \t#transmittane (-]\n", Out_Parm.Tt); fprintf(file, "\n");! Write absorption as a funtion of layer.! void WriteA_layer(FILE file, short Num_Layers, Outstrut Out Parmi short i; fprintf (file, "A_l #Absorption as a funtion of layer. [-]\n");! r1:1q. / for(i=1; i<=num_layers; i++) fprintf(file, "%12.4G\n", Out_Parm.A_l[i]); fprintf(file, "\n"l;! 5 numbers eah line. / void WriteRd_ra(FILE file, short ir, ia; short Nr, short Na, OutStrut Out Parmi fprintf (file, '%s\n%s\n%s\n%s\n%s\n%s\n", / flag. / "# Rd[r][ang1e]. [1/(m2sr)].", '# Rd [ 0] [ 0], [ 0 l [ 1],.. [ 0] [na-1] ", '# Rd[1][0], [1][1],.. [1][na-1]', II I H # ~ "# Rd[nr-1] [OJ, [nr-1] (1],.. [nr-1] [na-1] ", 'Rd_ra" I; for(ir=o;ir<nr;ir++l for(ia=o;ia<na;ia++l { fprintf(file, '%12.4E ", Out_Parm.Rd_ra[ir][ia]); if( (irna + ia + 1)%5 == 01 fprintf(file, "\n"l; fprintf(file, "\n"l;! 1 number eah line.! void WriteRd_r(FILE file, short Nr, outstrut out_parm) short ir; fprintf (file, 'Rd_r #Rd[OL [lj,.. Rd[nr-1]. [1/m2]\n"l; I flag. / for(ir=o;ir<nr;ir++l fprintf(file, "%12.4E\n', Out_Parm.Rd_r[ir]); fprintf(file, "\n'l;! 1 number eah line.! void WriteRd_a(FILE file, 97
96 short ia; short Na, outstrut out Parmi fprintf 1 file, "Rd_a #RdiO], 11],.. Rdlna-1]. lsr-1]\n"l;! flag. / for(ia=o;ia<na;ia++l fprintf(file, "%12.4E\n", Out_Parm.Rd_alia]); fprintf 1 file, "\n" I;! S numbers eah line. void WriteTt_ra(FILE file, shorl Nr, short Na, OutStrut Out Parmi short ir, ia; fprintf (file, "%s\n%s\n%s\n%s\n%s\n%s\ti 11 1 / flag. / "# Tt[r][angle]. [1/(m2sr)].", "# Tt I 0 J I 0 J, I 0 J [ 1 J,.. [ 0 J [ na -1 J ", " # Tt I 1 I I 0 I, I 1 J I 1 J,.. I 1 J Ina -1 J ", "#... "' "# Tt[nr-1] [OJ, [nr-1] [1],.. [nr-1] lna-1] ", "Tt_ra" I; fortir=o;ir<nr;ir++l for(ia=o;ia<na;ia++l fprintf(file, "%12.4E" Out_Parm.Tt_ra[ir][ia]); if( (irj.ja + ia + 1)%5 == 0) fprintflfile, "\n"); short iz, ir; fprintf I file, 11 %s\n%s\n%s\n%s\n%s\n%s\n 11, / flag~ / " # A I r J [ z J. [ 1 I m3 J ", "# AIOJIO], [0][1],.. [0][nz-1]", "# A[1][0], [1][1],.. [1J[nz-1]", II# II I "# A[nr-1] [0], [nr-1] [1],.. [nr-1] [nz-1] ", "A_rz" I; for(ir=o;ir<nr;ir++l for(iz=o;iz<nz;iz++) fprintf(file, "%12.4E " Out_Parm.A _rz[ir] liz] 1; if( li.rnz + iz + 1)%5 == 01 fprint.f(file, "\n"l; fprintf(file, "\n"); / 1 number eah line.! void WriteA Z(FILE file, short Nz, Outstrut Out~Parm) short iz; fprintf I file, "A_z #A[O], [1],.. A[nz-1]. 11/m]\n"); / flag. / for(iz=o;iz<nz;iz++) fprintf(file, "%12.4E\n", Out_Parm.A_z[iz]l; fprintf(file, "\n"); fprintf 1 file, "\n" J;! 5 numbers eah line.! void WriteA rzifile file, short Nr, short Nz, OutStrut Out_ParmJ! 1 number eah line.! void WriteTt r(file file, short Nr, OutStrut out Parmi short ir; fprintf(file, 98
97 "Tt_r #Tt[O], [1],.. Tt[nr-1]. [1/m2]\n"); /flag./ for(ir=o;ir<nr;ir++) fprintf(file, "%12.4E\n", Out_Parm.Tt_r[ir]); fprintf(file, "\n");! 1 number eah line.! void WriteTt a(file file, short Na, outstrut Out Parmi short ia; fprintf(file, "Tt a #Tt[O], [1],.. Tt[na-1]. [sr-1]\n"); /flag./ for(ia=o;ia<na;ia++l fprintf(file, "%12.4E\n", Out_Parm.Tt_a[ia]); fprintf(file, "\n"); / void WriteP.esult(InputStrut In_Parm, OutStrut Out_Parm, har TimeReport) FILE file; file= fopen(in_parm.out_fname, "w"); if( file== NULL) nrerror("cannot open file to write.\n"); if(toupper(in_parm.out_fformat) WriteVersion(file, "A1"); else Wri teversion (file, B1") ; fprint f (file, "# %s", TimeReport) ; fprintf(file, "\n"); 'A'J WriteinParm(file, In_Parm); WriteRAT(file, Out_Parm);! refletane, absorption, transmittane. /! 10 arrays. / WriteA_layer(file, In_Parm.num_layers, Out_Parm); WriteA_z(file, In_Parm.nz, Out_Parm); WriteRd_r(file, In_Parm.nr, Out Parmi; WriteRd_a(fi1e, In_Parm.na, Out_Parml; WriteTt_r (file, In_Parm.nr, Out_Parrn); WriteTt_a(file, In_Parm.na, Out_Parm);! 20 arrays. / WriteA_rz (file, In_Parm.nr, In_Parm.nz, out_parml; WriteRd_ra(file, In_Parm.nr, In_Parm.na, Out_Parm); WriteTt_ra(file, In_Parm.nr, In_Parm.na, Out_Parm); flose(file); B.l.1.4. mmlgo.! Launh, move, and reord photon weight.! #inlude "mml.h" #define STANDARDTEST 0! testing program using fixed rnd seed. / #define PARTIALREFLECTION 0! 1=split photon, O=statistial refletion. / #define COSZERO ( E-12)! osine of about 1e-6 rad. / #define COS90D 1.0E-6! osine of about e-6 rad. / / A random number generator from Numerial Reipes in C.! 99
98 #define MRIG #define MS~ED #define MZ 0 #define FAC 1.0E-9 float ran3(int idumj { stati int inext,inextp; stati long ma[56]; stati int iff=o; long mj,mk; int i 1 ii,k; if I idum < 0 I I iff == 0 J { iff=1; mj=mseed-(idum < 0? -idum mj %= MBIG; ma[55]=mj; mk=l; for (i=1;i<=54;i++j i. t-:- ( ~ 1 1. J 9i s~l; mali i I ~/llf:; mk=mj-mk; if (mk < MZJ mk += MBIG; mj=ma[ii); idum); Generate a random number between 0 and 1. Take a number as seed the first time entering the funtion. The seed is limited to 1<<15. We found that when idum is too large, ran3 may return numbers beyond 0 and 1. / double RandomNum(voidJ { stati Boolean first_time=1; stati int idum; / seed for ran3. / if I first_timej #if STANDARDTEST / Use fixed seed to test the program. / idum = - 1; #else idum = -(int)time(null)%(1<<151; / use 16-bit integer as the seed. / #endif ran3 (&idum); first time = 0; idum = l; return( (double) ran3 (&iduml J; for I k=l; k<.4; k++ I for li=l;i<.=55;i++l rna[i] -= rna[1+ (i+30i % 55]; if (ma[i] < MZJ ma(i] += MBIG; inext=o; inextp=31; idum=1; if (++ next == 56) inext=l; if I++ nextp == 56) inextp=l; mj=ma[ next] -ma[inextp]; if (mj < MZJ mj += MBIG; rna [ inext] =mj; return mjfac; #undef MBIG #unde f!4seed #undef MZ #undef Fl\.C!! Compute the speular refletion. If the first layer is a turbid medium, use the Fresnel refletion from the boundary of the first layer as the speular refletane. If the first layer is glass, multiple refletions in the first layer is onsidered to get the speular refletane. The subroutine assumes the Layerspes array is orretly initialized.! double Rspeular(LayerStrut Layerspes_PtrJ { double rl, r2; / diret refletions from the 1st and 2nd layers. / double temp; temp =(Layerspes_Ptr[O].n- Layerspes_Ptr[l].n) /(Layerspes_Ptr[O].n + Layerspes_Ptr[1].n); r1 = temptemp; 100
99 if( (Layerspes_Ptr[l].mua == 0.0) && (Layerspes_Ptr[l].mus == 0.0)) { /glass layer. I temp= (Layerspes_Ptr[l].n- Layerspes_Ptr[2].n) IILayerspes_Ptr[l].n + Layerspes_Ptr[2].n); r2 = temptemp; rl = r1 + (l-rl)(l-rl)r2/(1-rlr2); return (r1);! Initialize a photon paket. / void LaunhPhoton(double Rspeular, LayerStrut Layerspes_Ptr, PhotonStrut Photon_Ptr) Photon_Ptr->w = Rspeular; Photon_Ptr->dead = 0; Photon_Ptr->layer = 1; Photon_Ptr->s = 0; Photon Ptr->sleft= 0; Phot.on Ptr- >X Photon_Ptr->y Photon_Ptr->z Photon_Ptr->ux Photon_Ptr->uy Photon Ptr->uz 0. 0; 0. 0; 0. 0; 0. 0; 0. 0; 1. 0; if( (Layerspes_Ptr[l).mua 0.0) && (Layerspes_Ptr[l].mus Photon Ptr->layer = 2; 0. 0 I I { / glass layer. / Photon_Ptr->z = Layerspes_Ptr[2].zO;! Choose (sample) a new theta angle for photon propagation aording to the anisotropy. If anisotropy g is 0, then os(theta) = 2rand-l. otherwise sample aording to the Henyey-Greenstein funtion. Returns the osine of the polar defletion angle theta. / double SpinTheta(double g) double ost; if(g == 0.0) ost = 2RandomNum() -1; else { double temp= (l-gg)/(1-g+2grandomnum(ll; ost= ll+gg- temptempl/12g); return(ost); / Choose a new diretion for photon propagation by sampling the polar defletion angle theta and the azimuthal angle psi. Note: theta: 0 - pi so sin(thetal is always positive feel free to use sqrt() for os(thetal. psi: 0-2pi for 0-pi sin(psi) is j for pi-2pi sin(psi) is - / void Spin(double g, PhotonStrut Photon_Ptr) double ost, sint;! osine and sine of the / I polar defletion angle theta. I double osp, sinp;! osine and sine of the I / azimuthal angle psi. / double ux Photon_Ptr->ux; double uy Photon_Ptr->uy; double uz Photon_Ptr->uz; double psi; ost = SpinTheta(g); sint = sqrt(l.o - ostost);! sqrt() is faster than sin(). I psi = 2.0PIRandomNum();! spin psi 0-2pi. I osp = os (psi) ; if (psi<pi) sinp = sqrt(l.o- osposp); / sqrt() is faster than sin(). I else sinp = - sqrt ( osposp); 101
100 if(fabs(uz) > COSZERO)! normal inident. / Photon_Ptr->ux sintosp; Photon_Ptr->uy = sintsinp; Photon_Ptr->uz = ostsign(uz); / SIGN() is faster than division. / else { / regular inident. I double temp = sqrt(1.0 - uzuz); Photon_Ptr->ux = sint(uxuzosp- uysinp) /temp + uxost; Photon_Ptr->uy sint(uyuzosp + uxsinp) ;'temp + uyost; Photon_Ptr->uz -sintosptemp + uzost;! hitase 1,2 or 3 for boundary perp. to x-, y- or z-diretion. / if(uz>0.0) dl zbound = (In_Ptr->layerspes[layer].z1 - Photon_Ptr->z I /uz;! dl_zbound>o. I else if(uz<o.oi dl_zbound = (In_Ptr->layerspes[layer].zO - Photon_Ptr->z I /uz; / dl zbound>o. / dl_b = dl_zbound; hitase = 3; i f I ux! = 0. 0 I dl_xbound = ((In_Ptr->x_size)SIGN(ux)/2- Photon_Ptr->x)/ux; if (dl_xbound<dl_b) dl_b = dl_xbound; hitase = 1;! Move the photon s away in the urrent layer of medium. / void Hop(PhotonStr~t Photon_.Pt r I { double s = Photon_Ptr->s; Photon_Ptr->x += sphoton_ptr->ux; Photon_Ptr->y += sphoton_ptr->uy; Photon Ptr->z += sphoton_ptr->uz; if I uy! = 0. 0 I dl_ybound = I (In_Ptr->y_size) SIGN(uy) /2 - if ( dl_ybound<dl_b) dl_b ~ dl_ybound; hitase = 2; Photon Ptr->s = dl_b; return(hilase); Photon_Ptr->y) /uy;! Return the photon step size in glass. The step size is the distane between the urrent position and the nearest boundary in the photon diretion. uz! = 0 / short StepSizeinGlass(PhotonStrut double dl_.b; double dl_xbound; double dl_ybound; double dl_zbound; / distane to / distane to / distane to / distane to short layer = Photon_Ptr->layer; double ux = Photon_Ptr->ux; double uy = Photon_Ptr->uy; double uz = Photon_Ptr->uz; short hitase; / the boundary Photon_Ptr, InputStrut In_Ptr) nearest boundary. / boundary perp. to x-diretion. / boundary perp. toy-diretion. / boundary perp. to z-diretion. / whih is hit. /! Return the photon step size in surrouning glass, The step size is the distane between the urrent position and the boundary, perp. to z-diretion, in the photon diretion. uz! = 0 / void StepSizeinSurrGlass(PhotonStrut Photon_Ptr, Inputstrut In_Ptrl double dl_b; / distane to boundary. / short layer = Photon_Ptr->layer; double uz = Photon_Ptr ->UZ; if(uz>0.0) dl_b = (In_Ptr->layerspes[layer].z1 - Photon Ptr->z) /uz; else if(uz<o.o) dl_b = ( In_Ptr->layerspes [layer]. zo! dl_b>o. / 102
101 Photon_Ptr->s dl_b; - Photon_Ptr->Z)/UZ;! dl_b>o. I! Pik a step size for a photon paket when it is in tissue. If the member sleft is zero, make a new step size with: -log(rnd)/(mua+mus). Otherwise, pik up the leftover in sleft. Layer is the index to layer. In_Ptr is the input parameters.! void StepSizeinTissue(PhotonStrut Photon_Ptr, InputStrut short layer = Photon_Ptr->layer; double mua In_Ptr->layerspes[layer].mua; double mus = In_Ptr->layerspes[layer].mus; if(photon_ptr->sleft double rnd; 0.0)! make a new step. / do rnd = RandomNum(); while( rnd <= 0.0 );!avoid zero.! Photon_Ptr->s = -log(rndlllmua+musl; else { / take the leftover. I Photon_Ptr->s = Photon_Ptr->sleftl(mua+musl; Photon_Ptr->sleft = 0.0; In_Ptr)! Chek if the step will hit a boundary. Return 1, 2 or 3 if a boundary is hit. Return 0 otherwise. If the projeted step hits the boundary, the members s and sleft of Photon_Ptr are updated.! short HitBoundary(PhotonStrut double dl_b; double dl_xbound; double dl_ybound; double dl_zbound; Photon_Ptr, InputStrut! distane to nearest boundary. I distane to boundary perp. to I distane to boundary perp. to I distane to boundary perp. to In_Ptrl I x-diretion. I y-diretion. I z-diretion. I short layer = Photon_Ptr->layer; double ux = Photon_Ptr->ux; double uy = Photon_Ptr->uy; double uz = Photon_Ptr->uz; short hitase; I the boundary whih is hit. I I hitase = 1,2 or 3 for boundary perp. to x-, y- or z-diretion. I I hitase = 0 if no boundary is hit I double maxdl_xybound = sqrt(pow(in_ptr->x_size, pow(in_ptr->y_size, pow(in_ptr->layerspes[layer].z1 -In Pt.r >layen;pe~;[layerj.z0,2.0ij; I The longest possible palh in this layer. I if(uz>o.oi dl_zbound = (In_Ptr->layerspes[layer].z1 - Photon_Ptr->z I /uz; I dl zbound>o. I else if(uz<o.oi dl zbound = (In_Ptr->layerspes [layer]. zo - Photon_Ptr->zl luz; I dl zbound>o. / if (UZ =-= 0.0) dl_b = maxdl_xybound; else { dl_b = dl zbound; hitase = 3; i f I ux! = o. o I { dl_xbound = ((In_Ptr->x_sizel SIGN (uxl!2 - if ( dl xbound<dl_b I { dl_b = dl_xbound; hitase = 1; Photon_Ptr->xl ;ux; if ( uy! = 0. 0 J { dl_ybound = ((In_Ptr->y_sizeiSIGN(uyJ/2- Photon_Ptr->yl/uy; if (dl_ybound<dl_bl { dl_b = dl_ybound; hitase = 2; if(photon_ptr->s > dl_bl I rossing. I double mut = In_Ptr->layerspes[layer].mua + In_Ptr->layerspes[layer].mus; Photon_Ptr->sleft = (Photon_Ptr->s- dl_blmut; Photon_Ptr->s = dl_b; else hi tease 0; 103
102 return I hi tease 1 ;! Drop photon weight inside the tissue (not glass). The photon is assumed not dead. The weight drop is dw wmua/(mua+mus) The dropped weight is assigned to the absorption array elements. / void Drop I InputStrut In_Ptr, Photonstrut OutStrut Photon_Ptr, Out PtrJ double dwa; / absorbed weight./ double x = Photon_Ptr->x; double y = Photon_Ptr->y; short i::1 ir; / index to z & r. short layer ::: Photon_Ptr->layer; double mual mus; ' ompute array indies., 1 i z = I short I I Photon_Ptr->z /In_Ptr->dz I ; if(iz>in_ptr->nz-1) iz=in_ptr->nz-1; ir = (short) (sqrt(xx+yy) /In_Ptr->dr); if!, ir>in_ptr- >nr-1; i r=in_ptr- >nr-1;! update photon weight. / mua = In_Ptr->layerspes[layer].mua; mus = In_Ptr->layerspes[layer].mus; dwa = Photon_Ptr->w mua/(mua+musj; Photon_Ptr->w -= dwa; / assign dwa to the absorption array element. / Out Ptr->A rz[lr] [iz] += dwa; / The photon weight is small, and the photon paket tries to survive a roulette.! void Roulette(PhotonStrut Photon_Ptr) ( lf(photon_ptr->w == 0.0) Photon_Ptr->dead = 1; else if(randomnum() <CHANCE)/ survived the roulette./ Photon Ptr->w I= CHANCE; else Photon Ptr->dead = 1;! Compute the Fresnel refletane. double r; Make sure that the osine of the inident angle al is positive, and the ase when the angle is greater than the ritial angle is ruled out. Avoid trigonometri funtion operations as muh as possible, beause they are omputation-intensive.! double RFresnel(double nl,! inident refrative index./ double n2, / transmit refrative index./ double al, / osine of the inident /! angle. 0<al<90 degrees. I double a2 PlrJ / pointer to the /! osine of the transmission / / angle. a2>0. if(nl==n2j a2_ptr r = 0.0; al; else if(al>coszero) a2_ptr = al; r = (n2-nlj I (n2+nli; r = r; else if(al<cos90d) a2_ptr = 0.0; r = 1.0;! mathed boundary. /! normal inident. /!very slant./ else ( / general. / double sal, sa2;! sine of the inident and transmission angles. / double a2; sal= sqrt(l-alall; sa2 = nlsal/n2; if (sa2>=1. 0) (! double hek for total internal refletion. / a2_ptr = 0.0; r = 1. 0; 104
103 else double ap, am; I osines of the sum ap or I I differene am of the two I I angles. ap = a1ta2 I I am= a1 - a2. I double sap, sam; I sines. I a2 Ptr = a2 = sqrt(1-sa2sa2); ap = a1a2 - sa1sa2; I C+ = am = ala2 + sa1sa2; I - = sap = sa1a2 + a1sa2; I S+ = sam = sa1a2 - a1sa2; I s- = - + s + s - ss. I ss. I s. I s. I r = O.Ssamsam(amam+apapJI(sapsapamam) I rearranged for speed. / returntrl; / Reord the photon weight exiting the first layer(uz<o), no matter whether the layer is glass or not, to the refletion array. Update the photon weight as well. / void ReordR(double Refl, I refletane. I InputStrut Photonstrut In_Ptr, Photon_Ptr, Outstrut Out_PtrJ double x = Photon_Ptr->x; double y = Photon_Ptr->y; short ir, ia; I index to r & angle. I ir = (short) (sqrt (xx+yy) IIn_Ptr->dr); if(ir>in_ptr->nr-1) ir=in_ptr->nr-1; ia = (short) (aos(-photon_ptr->uz)/in_ptr->da); i. f ( ia>in_ptr->na-1) ia=in_ptr->na-1; I assign photon to the refletion array element. / out_ptr->rd_ra [ir] [ia] += Photon_Ptr->w (1. 0- Refl); Photon_Ptr- >W = Refl;! Reord the photon weight exiting the last layer(uz>oj, no matter whether the layer is glass or not, to the transmittane array. Update the photon weight as well.! void ReordT(double Refl, Inputstrut Photonstrut outstrut Out Ptrl double x = Photon_Ptr->x; double y = Photon_Ptr->y; short ir, ia; / index to r & angle. / ir = (short) (sqrt(xx+yy)/in Ptr->dr); if ( ir>in_ptr->nr-1) i r=in Ptr >nr-1; ia = (short) (aos(photon_ptr->uz) /In_Ptr->da); if ( ia>in_ptr->na-1 l ia=in_ptr->na- 1; In_Ptr, Photon_Ptr,! assign photon to the t.ransm.i t tane array element. 1 Out_Ptr->Tt_ra [ ir l [ ia l + =' Photon_Ptr->w ( 1. 0-Refl) ; Photon_Ptr->w = Refl; / Deide whether the photon will be transmitted or refleted on the upper boundary (uz<o) of the urrent layer. If "layer" is the first or surrounding layer, the photon paket will be partially transmitted and partially refleted if PARTIALREFLECTION is set to 1, or the photon paket will be either transmitted or refleted determined statistially if PARTIALREFLECTION is set to 0. Reord the transmitted photon weight as refletion. If 'layer is not the first or surrounding layer and the photon paket is transmitted, move the photon to 'layer-1'. Update the photon parmameters.! void CrossUpOrNot(InputStrut In_Ptr, Photonstrut Photon_Pt.r, 105
104 outstrut out_ptr) double uz = Photon_Ptr->uz; I z diretional osine. I double uzl; I osines of transmission alpha, always positive. I double r=o.o; I refletane. I short layer = Photon_Ptr->layer; double ni = In Ptr->layerspes[layer].n; double nt = In_Ptr->layerspes[layer-1].n; I Get r. I if( - uz <= In_Ptr->layerspes[layer].os_ritO) r=l. 0; I total internal refletion. I else if (layer == In_Ptr->num_layers + 2) I surr. glass. I r = RFresnel(In_Ptr->layerspes[layer].n, In_Ptr->layerspes(O].n, -uz, &uzl); else r = RFresnel(In_Ptr->layerspes[layer].n, In_Ptr->layerspes[layer-l].n, -uz, &uzl); if (r == 1.0 && layer == In_Ptr->num_layers + 2) Photon_Ptr->dead = 1; I total internal refletion. I I in surrounding glass. I #if PARTIALREFLECTION if( (layer == 1 I I layer== In_Ptr->num_layers + 21 && r<l. 0) { I partially transmitted. I Photon_Ptr->uz = -uzl; I transmitted photon. I ReordR(r, In_Ptr, Photon_Ptr, Out_Ptr); Photon_Ptr->uz = -uz; I refleted photon. / else if(randomnum() > r) {I transmitted. I Photon_Ptr->layer--; Photon_Ptr->UX = nilnt; Photon_Ptr->uy = nilnt; Photon_Ptr->UZ = -uzl; else I refleted. I Photon_Ptr->uz = -uz; #else if (RandomNum( 1 > r) { I transmitted. I if (layer == 1 I I layer In_Ptr->num_layers + 2) { Photon_Ptr->uz = -uzl; ReordR(O.O, In_Ptr, Photon_Ptr, Out_Ptr); Photon_Ptr->dead = 1; else { Photon_Ptr->layer--; Photon_Ptr->ux = nilnt; Photon_Ptr->uy = nilnt; Photon_Ptr->uz = -uzl; else Photon_Ptr->uz #endif -uz; I refleted. I if (r == 1.0 && layer == In_Ptr->num_layers + 2) Photon_Ptr->dead = 1; I total internal refletion in surrounding glass. / / Deide whether the photon will be transmitted or be refleted on the bottom boundary (uz>o) of the urrent layer. If the photon is transmitted, move the photon to "layer+l". If "layer" is the last or surrounding layer, reord the transmitted weight as transmittane. See omments for CrossUpOrNot. Update the photon parmameters.! void CrossDnOrNot(InputStrut In_Ptr, Photonstrut outstrut double uz = Photon_Ptr->uz; I z diretional osine. ; double uzl; / osines of transmission alpha. I double r=o.o; I refletane. / short layer = Photon_Ptr->layer; double ni = In_Ptr->layerspes[layer].n; double nt = In_Ptr->layerspes[layer+ll.n; Photon_Ptr, Out_Ptr) I Get r. I if( uz <= In_Ptr->layerspes[layer].os_ritl) r=l.o; internal refletion. I else if (layer == In_Ptr->num_layers + 2) / surr. glass. / r = RFresnel(In_Ptr->layerspes[layer].n, In_Ptr->layerspes[layer-l].n, uz, &uzl); else r = RFresnel(In_Ptr->layerspes[layer].n, In_Ptr ->layerspes [ layer+ll. n, uz, &uzl) ; #if PARTIALREFLECTION if((layer == In_Ptr->num_layers I I layer== In_Ptr->num_layers + 2) && r<l. 0) { Photon_Ptr->uz = uzl; ReordT(r, In_Ptr, Photon_Ptr, out_ptr); Photon_Ptr->uz = -uz;! total 106
105 else if(randomnum() > r) {/ transmitted. / Photon_Ptr->layer++; Photon_Ptr->ux = ni/nt; Photon_Ptr->uy = ni/nt; Photon_Ptr->uz = uzl; else! refleted. / Photon Ptr->uz = -uz; #else if(randomnum() > r) { / transmitted. / if (layer == In_Ptr->num_layers I I layer == In_Ptr->num_layers + 2) Photon_Ptr->uz = uzl; ReordT(O.O, In_Ptr, Photon_Ptr, out_ptr); Photon_Ptr->dead = 1; else { Photon_Ptr->layer++; Photon_Ptr->ux = ni/nt; Photon_Ptr->uy = ni/nt; Photon_Ptr->uz = uzl; else! refleted. / Ptwt on Pt:.r-->117. = -U7.; #endif }! Deide whether the photon will be transmitted or be refleted on the boundary perpendiular to the x-diretion If the photon is transmitted, move the photon to the surrounded glass layer. Update the photon parmameters. / void CrossXOrNot(Inputstrut In_Ptr, Photonstrut outstrut Photon_Ptr, Out Ptr) double ux = Photon Ptr->ux; / x diretional osine. / double uxl; / osines of transmission alpha. / double r=o.o;! refletane. / short layer = Photon_Ptr->layer; double ni = In_Ptr->layerspes[layer).n; double nt = In_Ptr->layerspes[In_Ptr->num_layers + 2).n; / Get r. / if( fabs(ux) <= In_Ptr->layerspes[layer].os_ritxy) r=l.o; / total internal refletion. / else r = RFresnel(In_Ptr->layerspes[layer].n, In_Ptr->layerspes[In_Ptr->num_layers+2].n, fabs(ux), &uxl); if(randomnum(} > r) { / transmitted to surrounding glass. / Photon_Ptr->layer = In_Ptr->num_layers+2; Photon_Ptr->UX = uxlsign(ux); Photon_Ptr->uy = ni/nt; Photon_Ptr->uz = ni/nt; } else / refleted. ' Photon Ptr->ux -ux; / Deide whether the photon will be transmitted or be refleted on the boundary perpendiular to the y-diretion If the photon is transmitted, move the photon to the surrounded glass layer. Update the photon parmameters. / void CrossYOrNot(InputStrut In Ptr, l'ilolutl~:l lttt 1'1 Jo. >LtJI I_ I 'I I ' OutStrut Out_Ptr) double uy = Photon_Ptr->uy; / x diretional osine. / double uyl; / osines of transmission alpha. / double r=o.o; / refletane. / short layer = Photon_Ptr->layer; double ni = In_Ptr->layerspes[layer].n; double nt = In_Ptr->layerspes[In_Ptr->num_layers + 2].n;! Get r.! if( fabs(uy) <= In_Ptr->layerspes[layer].os_ritxy) r=l.o; / total internal refletion. / else r = RFresnel(In_Ptr->layerspes[layer].n, In_Ptr->layerspes[In_Ptr->num_layers+2].n, fabs(uy), &uyl); if(randomnum(} > r) { / transmitted to surrounding glass. / Photon_Ptr->layer = In_Ptr->num_layers+2; Photon_Ptr->uy = uylsign(uy); Photon_Ptr->ux = ni/nt; Photon_Ptr->uz = ni/nt; } 107
106 else / refleted. / Photon_Ptr->uy -uy; / void CrossOrNot(InputStrut In_Ptr, Photonstrut Photon_Ptr, outstrut Out_Ptr, short hitase) if (hitase == 1) CrossXOrNot(In_Ptr, Photon_Ptr, Out_Ptr) else if lhitase == 21 CrossYOrNot(In_Ptr, Photon_Ptr, Out Ptrl else if 1 hi tease == 3 I { if(photon_ptr->uz < 0.01 CrossUpOrNot(In_Ptr, Photon_Ptr, Out_PtrJ; else CrossDnOrNot(In_Ptr, Photon_Ptr, Out_Ptrl; /~ Set a step size, move the photon, drop some weight, hoose a new photon diretion for propagation. When a step size is long enough for the photon to hit an interfae, this step is divided into two steps. First, move the photon to the boundary free of absorption or sattering, then deide whether the photon is refleted or transmitted. Then move the photon in the urrent or transmission medium with the unfinished stepsize to interation site. If the unfinished stepsize is still too long, repeat the above proess.! void HopDropSpininTissueiinputStrut InPtr, PhotonStrut OuLStrut Photon_Ptr, Out_Ptrl short. hi.tase; /the boundary whih i; hit ;ia Move the photon paket in glass layer. Horizontal photons are killed beause they will never interat with tissue again. / 'F~id HopinGlassi_InputStrut In_Ptr, short Photonstrut Photon_Ptr, OutStrut Out Ptrl hitase; 1 the boundary whih is hit. if(photon_ptr->uz == 0.01! horizontal photon in glass is killed. ; Photon_Ptr->dead = 1; else { ifiphoton_ptr->layer == In_Ptr->num_layers + 21! surrounding glass / StepsizeinSurrGlass(Photon_Ptr, In_Ptrl; hitase = 3; / always in surrounding glass / Hop(Photon_Ptrl; CrossOrNotiin_Ptr, Photon_Ptr, Out_Ptr, hitasel; else { ; glass layer whih is not the surrounding glass layer / hitase = StepSizeinGlassiPhoton_Ptr, In_Ptrl; HopiPhoton_Ptrl; CrossOrNotiin_Ptr, Photon_Ptr, Out_Ptr, hitasel; / hitase = 0 if no b~rujary is hit : StepSizein'I'issueiPhoton_Ptr, In Pte;; hi tease = Hi tboundary 1 Photon_Pr.r, In Pt r i ; iflhitase>oi HopiPhoton_Ptrl;! move to boundary plane. I CrossOrNot(In_Ptr, Photon_Ptr, Out_Ptr, hitasel; else { Hop ( Photon_Pt r I ; Drop(In_Ptr, Photon_Ptr, Out_Ptr); Spin ( In_Pt. r- >layerspes [ Photon_Ptr->layer]. g, Phot.on_Pt.r I ; /! void HopDropSpiniinputStrut short layer = Photon_Ptr->layer; if( IIn_Ptr->layerspes[layer].mua && 1 In_Pt.r >layerspes [layer]. mus In_Ptr, PhotonStrut Out.Strut 0. 0 I 0. 0 I I Photon_Ptr, Out Ptrl 108
107 / glass layer. I HopinGlass(In_Ptr, Photon_Ptr, Out_Ptr); else HopDropSpininTissue(In_Ptr, Photon_Ptr, Out_Ptr); if( Photon_Ptr->w < In_Ptr->Wth && Roulette(Photon_Ptr);!Photon_Ptr->dead) B.1.2. B TMMCML mml.h Monte Carlo simulation of photon distribution in multi-layered media ontaining sattering partiles in ANSI Standard. Starting Date: Current Date: 8/1996. Lihong Wang, Ph. D. Steven L. Jaques, Ph. D. Laser Biology Researh Laboratory - 17 M.D. Anderson Caner Center University of Texas 1515 Holombe Blvd. Houston, TX US.Z\ This program was based on: ill The Pasal ode written by Marleen Keijzer and Steven L. Jaques in this laboratory in 1989, whih deals with multi-layered turbid media. 121 Algorithm for semi-infinite turbid medium by S.A. Prahl, M. Keijzer, S.L. Jaques, A.J. Welh, SPIE Institute Series VoL IS 5 (1989), and by A.N. Witt, The Astrophysial journal Supplement Series 35, 1-6 (1977). Major modifiations inlude: Conform to ANSI Standard. Removal of limit on number of array elements, beause arrays in this program are dynamially alloated. This means that the program an aept any number of layers or gridlines as long as the memory permits. Avoiding global variables whenever possible. This program has not used global variables so far. Grouping variables logially using strutures.,. / Top-down design, keep eah subroutine lear & short. Refletane and transmittane are angularly resolved. Modifiations when inluding sattering partiles made 1996 by P. Alsholm and A. Nilsson. General Naming Conventions: Preproessor names: all apital letters, e.g. #define PREPROCESSORS Globals: first letter of eah word is apital, no undersores, e.g. short GlobalVar; Dummy variables: first letter CJt eah word is apit.a.l, and words are onneted by undersores, e.g. void NieFuntion(har Dummy_Var); Loal variables: all lower ases, words are onneted by undersores, e.g. short loal_var; Funtion names or data types: same as Globals. Dimension of length: em. #inlude <math.h> #inlude <stdlib.h> #inlude <stdio.h> #inlude <stddef.h> #inlude <time.h> #inlude <string.h> #inlude <type.h> #define PI #define WEIGHT le-4 #define CHANCE 0.1 I Critial weight for roulette. I / Chane of roulette survival. / 109
108 #define STELE!l 256 I String length. / #define Boolean har #define SIGN(XI ((XI>=O? 1:-11! Stutures / / Struture used to desribe a photon paket. / typedef strut ( double x, y,z; double ux, uy, uz; double w; Boolean dead; short layer; double s; double sleft; Ph :=,tonsttut; I Cartesian oordinates. [em] / / diretional osines of a photon. /! weight. I! 1 if photon is terminated.! I index to layer where the photon/ I paket resides. /! urrent step size. [em]. / / step size left. dimensionless i Struture used to desribe the geometry and optial properties of a layer. zo and z1 are the z oordinates for the upper boundary and lower boundary respetively. os rito and os rit1 are the osines of the ritial angle of total internal refletion for the upper boundary and lower boundary respetively. os_ritxy is analogous for the boundary to the surrounding glass. They are set to zero if no total internal refletion exists. They are used for omputation speed. / typedef strut ( double zo, z1;! z oordinates of a layer. [em] I double n; / refrative index of a layer. I double absross; double meanstep; double meanstepdev; double bux;! double buy;! double buz;! double dev; I I absorption ross setion. [-] I / the step length. [em]/! deviation of step length. [em] I orientation of blood ell. I orientation of blood ell. I orientation of blood ell. I deviation of that orientation. [ ] I double os_rito, os_rit1, os_ritxy; Layerstrut; [ -J. I! Input parameters for eah independent run. z and r are for the ylindrial oordinate system. [em] a is for the angle alpha between the photon exiting diretion and the surfae normal. [radian] The grid line separations in z, r, and alpha diretions are dz, dr, and da respetively. The numbers of grid lines in z, r, and alpha diretions are nz, nr, and na respetively. The member layerspes will point to an array of strutures whih store parameters of eah layer. This array has (number_layers + 3 I elements. One element is for a layer. The layers 0 and (num_layers + 1 I are for top ambient medium and the bottom ambient medium respetively. The layer (num_layers + 21 is for the surrounding glass.! typedef strut ( har har out_fname [STRLEN]; out fformat; I output file name. ; / output file format. ; I 'A'! 'B' for ASCII, I for binary. I har dat_fname[strleni; /data base file name./ short nbrangint; I data base parameter, number of inident. angels. I short nbrths; I data base parameter, number of sattering theta. I short nbrpss; I data base parameter, number of sattering psi. I double valmatrix; I data base values. I long num photons; I to be traed. I double Wth; I play roulette if photon I /weight< Wth./ double dz; double dr; double da; short nz; short nr; short na; short num_layers; double x_size, y.size; Layerstrut layerspes; Inputstrut; I z grid separation. [em] I I r grid separation. [em] I I alpha grid separation. I I [radian] I I array range 0.. nz-1. I I array range 0.. nr-1. I / array range 0.. na-1. I / number of layers. I! dimension of the sample. [em] /! layer parameters. / 110
109 / Strutures for soring physial quantities. z and r represent z and r oordinates of the ylindrial oordinate system. [em] a is the angle alpha between the photon exiting diretion and the normal to the surfaes. [radian] See omments of the InputStrut. See manual for the physial quantities. / typedef strut { double Rsp; double Rd_ra; double Rd_r; I speular refletane. [-] I! 2D distribution of diffuse / /refletane. [1/(m2 sr)]! 1D radial distribution of diffuse / double Rd_a; / refletane. [1/m2] /! 1D angular distribution of diffuse /! refletane. [1/sr] I double Rd; / total diffuse refletane. [- J I I double A_rz;! 2D probability density in turbid /! media over r & z. [1/m3] double A 7. -~'! 1D probability density over z. I! [1 /em] I I I double A_l; / eah layer's absorption / double A; / probability. [- J I! total absorption probability. [- J ; I double Tt_ra;! 2D distribution of total I double Tt r;! transmittane. [ 1 I I m2 sr) J I! 1D radial distribution of I double Tt_a;! transmittane. [ 1/m2]! 1D angular distribution of I I! transmittane. [1/sr] I double Tt; / total transmittane. [-I I outstrut;! Routine prototypes for dynami memory alloation and release of arrays and matries. / double double void void void Modified from Numerial Reipes in C. AlloVetor(short, short); AlloMatrix(short, short, short, short); FreeVetor(double, short, short); FreeMatrix(double short, short, short, nrerror(har short); ); B.l.2.2. mmlmain. / main program for Monte Carlo simulation of photon distribution in multi-layered turbid media. / / THINKCPROFILER is defined to generate profiler alls in Think. If 1, remember to turn on "Generate profiler alls" in the options menu. / #define THINKCPROFILER 0 /GNU does not support difftime() and CLOCKS PER SEC./ #define GNUCC 0 Nif THINKCPROFILER»inlude <pro[ile.h> #inlude <onsole.h> #endif #inlude "mml.h"! Delare before they are used in main().! void ShowVersion(har ); FILE GetFile(har ); short ReadNumRuns(FILE ) ; void ReadParmiFILE, lnputstrul ) ; void ChekParm(FILE, InputStrut ) ; void ReadDataBase(FILE, InputStrut ) ; void InitOutputData(Inputstrut, Outstrut ); void FreeData(InputStrut, Outstrut ); double Rspeular(LayerStrut ) ; void LaunhPhoton(double, LayerStrut, PhotonStrut ); void HopDropSpin(InputStrut,PhotonStrut,Outstrut J void SumSaleResult(Inputstrut, outstrut ); void WriteResult(InputSt.rut, Outstrut, har);!kk~'k++ Ill
110 If F 0. eset the lak and return 0. If F = 1, pass the user time to Msg and print Msg on sreen, return the real time sine F=O. If F = 2, same as F=1 exept no printing. Note that lok() and time() return user time and real time respetively. User time is whatever the system alloates to the running of the program; real time is wall-lok time. In a time-shared system, they need not be the same. lok,) only hold 16 bit integer, whih is about lok tiks. / t1me t PunhTlme(har F, har Msg) ( #if GNUCC return(oj; #else stati lok t uto; stati time t double sees; har s[stelen); rto; ifif==oi uto = lok(); rto = timetnulli returnioi;! user time referene. /! real time referene. / else ifif==1j sees= (lok() - uto)/(double)clocks_pee_sec; if (ses<o) ses=o; /lok() an overflow. / sprintf(s, "User time: %8.0lf se= %8.2lf hr. %s\n", sees, ses/3600.0, Msg); puts(sj; strpy (Msg, s); return(difftime(time(null), rto) J; else if(f==21 return(difftime(time(nulli, rto)); else return IOJ; #endif ) / Print the urrent time and the estimated finishing time. P1 is the number of omputed photon pakets. Pt is the total number of photon pakets. / void PreditDoneTime(long P1, long Pti ( time_t now, done_time; strut tm date; har s[80); now= time(null); date = loaltime(&now); strftime (s, 80, "%H:%M %x", date); printf("now %s, ", s); done time = now + (time_tl (PunhTime (2, "" 1 ( Pt-P1) I (double) P11 date = loaltime(&done_time); strftime(s, 80, "%H:%M%x", date); printf("end %s\n", s);!,. Report estimated time, number of photons and runs left after alulating 10 photons or every 1/10 of total number of photons. Num_Euns is the number of runs left. Pi is the index to the urrent photon, ounting down. Pt i.s the total number of photons.! void F.eportStatus(short Num_Euns,long Pi,long Ptl ( if(pt-pi == 10 I I Pi10%Pt == 0 && Pi!= Pt) printf("%ld photons & %hd runs left, ",Pi, Num_Runs); PreditDoneTime(Pt-Pi, Pt);! Report time and write results.! void ReportResult(InputStrut In_Parm, outstrut Out_Parml { har time report [ STRLEN); strpy(time_report, " Simulation time of this run. "I; PunhTime(1, time_report); SumSaleF.esult(In_Parm, &Out_ParmJ; WriteResult(In_Parm, Out_Parm, time_report); 112
111 jk Get the file name of the input data file from the argument to the ommand line.! void GetFnameFromArgv(int arg, har argv [ J, har input_filename) if(arg>=21 { / filename in ommand line / strpy(input_filename, argv[l]j; else input_filename[oj 1 \0 I;! Exeute Monte Carlo simulation for one independent run. / void DoOneRun(short NumRuns, InputStrut In_Ptr) { register long i_photon;! index to photon. register for speed./ outstrut out _parm; / distribution of photons. I PhotonStrut photon; #if THINKCPROFILER InitProfile\200,200); eho2file("prof.rpt",o, stdout); #endif InitOutputData{In_Ptr, &out_parm); out_parm.rsp = Rspeular(In_Ptr- >layerspes); i_photon = In_Ptr->num_photons; PunhTime{O, ""I; do { ReportStatus(NumRuns, i_photon, In_Ptr->num_photonsJ; LaunhPhoton{out_parm.Rsp, In_Ptr->layerspes, &photon); do HopDropSpin ( In_Ptr, &photon, &.out_parm) ; while (!photon. dead); while(--i_photon); #if THINKCPROFILER exit(o); #end if ReportResult(In_Ptr, out_parm); FreeData(In_Ptr, &out_parml; / The argument to the ommand line is filename, if any. Maintosh does not support ommand line.! har main(int arg, har ar gv[ J) { har input_filename[strlen]; FILE input_file_ptr; short num_runs; / number of independent runs. / InputStrut in_parm; ShowVersi.on ("Version 1. 0, 1992' I ; GetFnameFromArgv ( arg, argv, input_t i.lename) ; input_file_ptr = GetFile(input_filename); ChekParm(input_file_ptr, &in_parm); num_runs = ReadNumRuns ( input_file_ptr); while(num_runs--) ReadDataBase(input_file_ptr, &in_parmj; ReadParm(input_file_ptr, &in_parm); DoOneRun(num_runs, &in_parm); flose(input_file_ptr); return( OJ; B mmlio.! Input/output of data.! #inlude "mml.h"! Struture used to hek against dupliated file names.! strut NameList { har name[strlen]; strut NameList next; 113
112 }; typedef strut NameList NameNode; typedef NameNode NameLink;! Center a string aording to the olumn width. / har CenterStr(short Wid, har rnstr, har outstr) size t nspaes; nspaes = (Wid- strlen(instr) )/2; if(nspaes<o) nspaes = 0;! number of spaes to be filled /! before InStr. / strpy 1 Outstr, "") ; while(nspaes--) strat(outstr, " "); strat(outstr, InStr); return (Outstr);! Print some messages before starting simulation. e.g. author, address, program version, year.! #define COLWIDTH 80 void ShowVrrsion(rhRr vprsion) har str[strlen]; CenterStr(COLWIDTH, "Monte Carlo Simulation of Multi-layered Turbid Media", str); puts(str); puts I""); CenterStr(COLWIDTH, "Lihong Wang, Ph. D.", str); puts(str); Centerstr(COLWIDTH, "Steven L. Jaques, Ph. D.", str); puts(str); puts(str); Centerstr(COLWIDTH, "M.D. Anderson Caner Center", str); puts(str); Centerstr(COLWIDTH, "University of Texas, str); puts(str); CenterStr(COLWIDTH, "Houston, TX 77030", str); puts(str); CenterStr(COLWIDTH, "Fax: (713) ", str); puts(str); puts I" ); Centerstr(COLWIDTH, version, str); puts I str); CenterStr(COLWIDTH, 'Modified 1996, PA- tmmml", str); puts(str); puts (" "); puts("\n\n\n\n"); } #undef COLWIDTH lk Get a filename and open it for reading, retry until the file an be opened. ' terminates the program. If Fname!=NULL, try Fname first. / FTLF. GetFi10(har Fnam<") { FILE file=null; Boolean firsttime=1; do { if(firsttime && Fname[0]!='\0')! use the filename from ommand line / firsttime = 0; else { printf("input filename(or. to exit):"); sanf("%s", Fname); firsttime = 0; CenterStr(COLWIDTH, "Laser Biology Researh Laboratory- 17",str); if(strlen(fname) exit (1); 1 && Fname [ 0 J == '. ' )! exit if no filename entered. / 114
113 file= fopen(fname, "r") while(file ==NULL) return I file); ' Kill the ith har (ounting from 0), push the following hars forward by one.! void Klll=har(slze t i, har Str) { s1zetsl strlen(strl; for(;i<sl;i++l Str[i) = Str[i+l); ' Eliminate the hars in a string whih are not printing hars or spaes. Spaes inlude '\f', '\t' et. EeLurn 1.i. [ no nonprinling hars four1d, olherwise ret. urn 0.! Boolean Chekhar(har Str) Boolean found= 0;!found bad har./ size_t sl = strlen(str) size t i=o; while I i<sli if IStr[i)<O II Str[i]>255) nrerror("non-ascii file\n"l; else if(isprint(str[i)j I I isspae(str[i) I I i++; else ( found = 1; KillCharli, str) sl--; return (found)! Return 1 if this line is a omment line in whih the first non-spae harater is "#". Also return 1 if this line is spae line. / Boolean CommentLine(har Bufl { size t spn, spn; spn = strspn(buf, "\t");! length spanned by spae or tab hars. I spn = strspn(buf, "#\n"); I length before the 1st # or return. I if(spn == spnl! omment line or spae line. / return(l); else I the line has data. / return(oj;! Skip spae or omment lines and return a data line only. k! har FindDataLine(FILE File_PtrJ ( har buf[strlen); bu f [ 0 ] = ' \0 ' ; do { / skip spae or omment lines. / if(fgets(buf, 255, File_Ptr) ==NULL) printf ("Inomplete data\n" 1; bu f [ 0 J = ' \ 0 ' ; break; else ChekChar ( bu f I ; while(commentline(bufj) return(bufl;! Skip file version, then read number of runs.! short ReadNumRuns (FILE File Ptr) { har buf[strlen); short n=o; FindDataLine(File_Ptr)! skip the fil version. I ' 115
114 strpy (buf, if I bu f [ 0 J = = ' ssanfibuf, return(n); inddataline(file_ptr) I; 0'1 nrerror("reading number of runs\n"l; %hd",&n);! Plae the data base values in a matrix. Valmatrix 1 i, j I j = [ 1, nbrangint] The different inident angles [O,PI/2]. i [l,num_rows]: num_rows = (nbrths-2)nbrpss-1) Valmatrixll,l bak sattering probability. Valmatrix(2,J Valmatrix(1,1 probability of sattering in diretion theta= 1/(nbrths-11, psi = 0. Valmatrix(n,l - Valmatrix(n-1,1 probability of sattering in diretion theta I (n-21%nbrpss+1)/(nbrths-1) psi = I (n-2)/nbrpss)/(nbrths-1). Valmatrix((num_rows,) 1- forward sattering probability. For forward and bak sattering, psi is arbitrary.! void PlaeOataint1atrix(InputStrut In_Ptr) ( short short short short short short double har FILE nbrths = In_Ptr->nbrths; nbrpss = In_Ptr->nbrpss; thetaol = 1; num_thetaol = In_Ptr->nbrangint; row = 0; num_rows; value; bu f [ STP.LEN] ; Datfile_Ptr; num_rows = (nbrths-2)nbrpss + 1;! number of data values for eah inident angle aording / ' to the remarks in HCDATA.FOR. / In Ptr->valmatrix Allot1atrixl1,num_rows,1,num_thetaol); Datfile_Ptr = fopen(in_ptr->dat_fname, "r"); if (num_thetaol==ll ( / sphere. / for (row=1; row <= num_rows; row++) ( strpy(buf, FindDataLine(Oatfile_Ptr) ); if(buf[0]=='\0'1 nrerror('reading data base value.\n"l; ssanf(buf, "%lf", &value); In_Ptr->valmatrix[row] [thetaol] = value; else ( / spheroid. / for (thetaol=1; thetaol<=num_thetaol; thetaol++l for (row=l; row<= num_rows; row++l { strpy(buf, FindDataLine(Datfile_Ptr) I; if I bu f [ 0 l ==' \0' I nrerror("reading data base value.\n"); ssanf (buf, "%lf", &value); In Ptr-->valmatrix[row] [thetaol] =value; flose (Oat file_ptr);! Read the data base.! void ReadDataBase (FILE Fi.le_Ptr, Inputstrut In_ Ptr) { har buf[strlen]; / read in file name, nbrangint. / strpy(buf, FindDataLine(File_Ptr) 1; if(buf[ol=='\0' 1 nrerror("reading data base parameters.\n"); ssanf (buf, "%s %hd", In Ptr->dat_fname, &In_Ptr->nbrangi.ntl; if(in_ptr->nbrangint<=oi nrerror("nonpositive number of angles.\n");! read in nbrths, nbrpss. / strpy(buf, FindDataLine(File_Ptr) I; iflbuf[0]=='\0' I nrerror("reading data base parameters.\n"); ssanf(buf, "%hd %hd", &In_Ptr->nbrths, &In_Ptr->nbrpss); if I In_Ptr->nbrths<=1 I I In_Ptr->nbrpss<=1 1 nrerror I "Wrong number of angles. \n" I ; PlaeDatalnt1atrix(In_Ptr); / Read the file name and the file format. 116
115 The file format an be either A for ASCII or B for binary.! void ReadFnameFormat(FILE File_Ptr, Inputstrut In_Ptr) { hnr hiif[s'rrf.fn];! read in file name and format. / strpy(buf, FindDataLine(File_Ptr)); if(buf[0]=='\0') nrerror("reading file name and format.\n"); ssanf(bu[, "%s %", In_Ptr->out_fname, &(In_Ptr->out_fformat) ) ; if ( toupper ( In_Ptr- >ou t_f format)! = 'B' ) In_Ptr->out fformat = 'A'; / Read the number of photons.! void ReadNumPhotons(FILE File_Ptr, InputStruL In_Ptr) { har buf[strf.en];! read in number of photons. / strpylbuf, FindDataLineiFile_Ptr)); i I I I''' I I 0 I ' \0 ' I nrerrori"reading number of photons.\n"); ssanflbuf, "%lei", &In Ptr->nnmphotonsl; l L 1 lri_plt->num_jjlwtons,~o) nrerror I "Nonposi ti ve number of photons. \n" I ;! Read the members dz and dr.! void ReadDzDriFILE File_Ptr, Inputstrut In_Ptr) { har buf [STRLEN]; / read in dz, dr. / strpy(buf, FindDataLine(File_Ptr)); iflbuf[ol=='\0') nrerrori"reading dz, dr.\n"); ssanf (buf, "%lf%lf", &In_Ptr->dz, &In_Ptr->dr); if(in_ptr->dz<=ol nrerror("nonpositive dz.\n"); if ( In_Ptr->dr<=O) nrerror ( "Nonposi ti ve dr. \n"); / Read the members nz, nr, na.! void ReadNzNrNa(FILE File_Ptr, InputStrut In_Ptr) { har buf[strlen]; / read in number of dz, dr, da. / strpy(buf, FindDataLine(File_Ptr)); iflbuf[0]=='\0') nrerror ("Reading number of dz, dr, da' s. \n"); ssanf(buf, "%hd%hd%hd', &In_Ptr->nz, &In_Ptr->nr, &In_Ptr->nal; if(in_ptr->nz<=o) nrerror ( "Nonposi ti ve number of dz' s. \n') ; if(in_ptr->nr<=o) nrerror ( "Nonposi ti ve number of dr' s. \n"); if(in_ptr->na<=o) nrerror ( "Nonposi ti ve number of da' s. \n ) ; In_Ptr->da = O.SPI/In_Ptr->na;! Read the members x size and y_size.! void ReadXSizeYSizel~lLE File_PLr, lrrputstrul ln_ptrl { har buf[s'l'rlen];! read in x_size, y_size. / strpylbnf, F'indDatili.in,o(F'i l0 Ptr) 1; iflbuf[oj=='\0') nrerrori"reading x_size, y_size.\n"); ssanf(buf, "%lf%lf", &In_Ptr->x_size, &In_Ptr->y_sizel; if (In_Ptr->x_size<=O) nrerror ( "Nonpositive x_size. \n'); if (In_Ptr->y_size<=O) nrerror ( "Nonpositive y_size. \n");! Read the number of layers. / void ReadNumLayers(FILE File_Ptr, Inputstrut In_Ptr) { har buf [STRLEN]; / read in number of layers. / strpy(buf, FindDataLine(File_Ptr) ); if(buf[ol=='\0') nrerror ('Reading number of layers. \n"); ssanf(buf, '%hd', &In_Ptr->num layers); if(in_ptr->num_layers<=o) nrerror I "Nonposi ti ve number of layers. \n" 1 ; 117
116 ! Read the refrative index n of the ambient. / void ReadAmbientiFILE File_Ptr, LayerStrut Layer_Ptr, har side) har buf[strlen], msg[strlen]; double n; strpy(buf, FindDataLine(File_Ptr) I; iflbuf[0]=='\0'1 sprintf (msg, "Rading n of %s ambient. \n", side); nrerror (msg); ssanf (buf, "%lf%lf%lf%lf%lf%lf%lf%lf%lf", &n, &meanstep, &absross, &bux, &buy, &buz, &dev, &d); if (d<o I I n<=o I I meanstep<o I I meanstepdev<o I I absross<o I I dev<o I I dev>1 I returnl11; / error. I Layer_Ptr->n = n; Layer_Ptr->meanstep = meanstep; Layer_Ptr- >meanstepdev = meanstepdev; Layer_Ptr->absross = absross; temp= sqrt(buxbux+buybuy+buzbuzj; if (temp== 0.0) { / no orientation. / Layer_Ptr->dev = 1.0; Layer_Ptr->bux = 0.0; Layer_Ptr->buy 0.0; Layer_Ptr->buz = 0.0; &meanstepdev, ssanf(buf, "%lf", &n I; ifln<=oi nrerror("wrong n.\n"l; Layer_Ptr->n = n;! Read the parameters of one layer. Return if error deteted. Return 0 otherwise. else { Layer_Ptr->bux Layer_Ptr->buy Layer_Ptr->buz Layer_Ptr->dev Layer_Ptr >ZO Z_Ptr += d; Layer_Ptr >zl bux/temp; buy/temp; buz/temp; dev; Z_Ptr; Z Ptr;! normalization.! Z_Ptr is the z oordinate of the urrent layer, whih is used to onvert thikness of layer to z oordinates of the two boundaries of the layer. / Boolean ReadOneLayeriFILE File_Ptr, Layerstrut Layer_Ptr, double Z Ptr) har bu E [ STI-\LEI1] ; double d; I thikness. / double n;! index of refration. / double meanstep; / mean distane between partiles. / double meanstepdev;/ standard deviation. / double absross; / absorbed part in eah partile. / double bux, buy, buz; / orientation of the partile. ; double dev; / deviation ( ]; 1.0 : no orientation at all./ double temp; strpy(buf, FindDataLine(File_Ptr) I; if(buf[0]=='\0'1 returnlll; /error./ return(o);! Read and set the parameters of the surrounding glass. Return 1 if error deteted. Return 0 otherwise. Z_Ptr is the z oordinate of the urrent layer, whih is used to onvert thikness of layer to z oordinates of the two boundaries of the layer.! Boolean ReadSurrGlass(FILE File_Ptr, har buf [STRLEN]; double n; strpy(buf, FindDataLine(File_Ptr) 1; Layerstrut Layer_Ptr, double Z Ptr) 118
117 iflbuf[0]=='\0') returnllj; /error.! ssanflbuf, "%lf", &nl; ifln<=oj return (1 J ; Layer_Ptr->n = n; Layer_Ptr->meanstep Layer_Ptr->zO Layer Ptr->zl return IOJ; = 0.0; 0. 0; = Z_Ptr;! error. /! Read the parameters of one layer at a time. / void ReadLayerSpesiFILE File_Ptr, short Num_Layers, LayerStrut Layerspes_PPI har msg [ STRLEN] ; short i=o; doubje z 0. 0;! z oordinate of the urrent layer. 1 Alloate an array for the layer parameters. / layer 0 and layer Num_Layers + 1 are for ambient. / Num_Layers + 2 is for the surrounding glass. / Layerspes_PP = ILayerStrut I mallo 1 1 unsigned) INum_Layers+ 3 I si zeof I LayerStrut I I i E I! I Layerspes_PPJ J nrerrorl"alloation failure in ReadLayerSpesl) "I; ReadAmbientiFile_Ptr, &IILayerspes_PPJ[i]i, "top"); forli=l; i<=num_layers; i++j if I ReadOneLayer I File_Ptr, & I I Layerspes_PP I [ i l I, &z I I sprintf lmsg, "Error reading %hd of %hd layers\n", i, Num_Layers); nrerror lmsg); ReadAmbientiFile_Ptr, &IILayerspes_PPI [i]), "bottom"); if (ReadSurrGlass I File_Ptr, & I I Layerspes_PPI [ i+l] J, &z J J sprint f I msg, "Error reading surrounding glass" J ; nrerror lmsg);! Compute the ritial angles for total internal refletion aording to the relative refrative index of the layer. All layers are proessed.! void CritialAngle( short Num_Layers, short i=o; double nl, n2; for(i=l; i<=num_layers; i++l nl = (Layerspes_PPJ [i].n; n2 = (Layerspes_PPJ [i-ll.n; (Layerspes_PPJ [i].os_rito = nl>n2? sqrt(l.o- n2n2/ln1nl)) : 0.0; n2 = (Layerspes_PP) [i+l].n; ( Layerspes_PP I [ i J os_ri tl = nl >n2? sqrt(l.o - n2n2/lnln1j) : 0.0; n2 = ( Layerspes_PPI [Num_Layers+2]. n; (Layerspes_PPI [i].os_ritxy = nl>n2? sqrt(l.o- n2n2/(n1n11l : 0.0; LayerStrut Layerspes_PPJ nl = ILayerspes_PPJ [Num_Layers+2).n; / surrounding glass / n2 = ILayerspes_.PPI [O].n; I Layerspes_PP J [Num_Layers+2]. os_.ri to " nl >n2? sqrtll.o- n2n2/(n1n11 1 : 0.0; n2 = I Layerspes_PPI [Num_Layers+l]. n; (Layerspes_PPI [Num_Layers+2].os rit1 = nl>n2? sqrt(l.o- n2n2/(nln1ji: 0.0; / Read in the input parameters for one run.! void ReadParm(FILE File_Ptr, InputStrut In_Ptr) { In_Pt.r->Wth = WEIGHT; ReadFnameFormat(File_Ptr, In_Ptrl; ReadNumPhotonsiFile_Ptr, In_Ptrl; ReadDzDr(File_Ptr, In_Ptrl; ReadNzNrNa(File_Ptr, In_PtrJ; ReadXSizeYSize(File_Ptr, In_Ptrl; ReadNumLayers(File_Ptr, In_Ptr); ReadLayerSpes(File_Ptr, In_Ptr->num_layers, &In_Ptr->layerspesl ; Cri tialangle ( In_Ptr->num_layers, &In._Ptr->layerspes J ; 119
118 ! Return 1, if the name in the name list. Return 0, otherwise.! Boolean NameinList(har Name, NameLink List) { while (List!=NULL) if(strmp(name, List->name) OJ return Ill; List = List->next; }; return( OJ;! Add the name to the name list.! void AddNameToLtst(har Name, NameLink List Ptrl { NameLink list = List_Ptr; HillsL NULL) { / (irst node./ List Ptr =list= (NameLinklmallo(si.zeof(NameNode)); strrpyllisl->name, Name); lisl->n~xt = NULL; else { / subsequent nodes. / ' Move to the last node. / while(list->next!=null) list = list->next;! Append a node to the list. / list->next = (NameLink)mallo(sizeof(NameNode) J; list = list->next; strpy(list->name, Name); list->next = NULL;! Chek against dupliated file names. A linked list is set up to store the file names used in this input data file. / Boolean FnameTaken(har fname, NameLink List Ptrl { if(nameinlist(fname, List_Ptrll return ill; else AddNameToList(fname, List_Ptr); return(o);! Free eah node in the file name list. / void FreeFnameList(NameLink List) { NameLink next; while(list!=null) next = List->next; free(list); List next;!~k Chek Lh ~ input parameters for eah run.! void ChekPanniFILE File_Pt.r, Inputstrut In Ptrl ( short i_run; short num_runs;!'number of independent runs./ NameLink head = NULL; Boolean name_taken;/ output files share the same /! file name./ har msg[strlen]; num_runs = ReadNumRuns{File_Ptr); for{i_run=l; i_run<=num_runs; i run++) printf("cheking input data for run %hd\n", i_run); FindDataLine(File_PtrJ;! skip the data base parameters./ FindDataLine(File_Ptr); / " / ReadParm(File_Ptr, In_Ptr); name_ taken = FnameTaken I In_Ptr->out fname, &head) ; if (name_ taken) sprint.f(msg, "file name %s dupliated.\n", In_Ptr->out_fname); Eree(In_Ptr->layerspes); if(name_taken) nrerror(msg); FreeFnameList(head); rewind(file_ptr); 120
119 / remember to use nl+2 beause of 2 for ambient. /! Alloate the arrays in OutStrut for one run, and array elements are automatially initialized to zeros.! void InitOutputData(InputStrut In_Parm, OutStrut out_ptr) short nz In_Parm.nz; short nr = In_Parm.nr; short na = In_Parm.na; short nl = In_Parm.num_layers; / remember to use nl+2 beause of 2 for ambient. / if(nz<=o II nr<=o II na<=o II nl<=ol nrerror("wrong grid parameters.\n");! Init. pure numbers. / out._ptr->rsp = 0.0; Out_Ptr->Rd = 0.0; Out_Ptr->A = 0.0; Out Ptr->Tt = 0.0; / Alloate the arrays and the matries. / Out Ptr->Rd ra = AlloMatrix(O,nr-1,0,na-l); Out Ptr->Rd r = AlloVetor(O,nr-1); Out Ptr->Rd_a = AlloVetor(O,na-1); Out_Ptr->A_rz out Ptr->A z Out_Ptr->A_l AlloMatrix(O,nr-1,0,nz-1); AlloVetor(O,nz-1); AlloVetor(O,nl+1); num_rows = (In_Parm.nbrths-2)In_Parm.nbrpss + 1; / number of data values for eah inident angle aording /! to the remarks in MCDATA.FOR. / free(in_parm.layerspes); FreeMatrix(Out_Ptr->Rd_ra, O,nr-1,0,na-1); FreeVetor(Out_Ptr->Rd_r, O,nr-1); FreeVetor (Out_Pt.r->Rd a, 0, na-11; FreeMatrix(Out_Ptr->A rz, 0, nr-1, O,nz-11; FreeVetor(Out_Ptr->A_z, 0, nz-1); FreeVetor(Out_Ptr->A_l, O,nl+1); FreeMatrix(Out_Ptr->Tt_ra, O,nr-1,0,na-1); FreeVetor(Out_Ptr->Tt._r, O,nr-1); FreeVetor(Out_Pt.r->Tt_a, O,na-11; FreeMatrix(In_Parm.valmatrix,1,num_rows,1,num_thetaol); / Get 1D array elements by summing the 20 array elements.! void sum2drd ( Inputstrut In Parm, outstrut Out_Ptr 1 { short nr = In_Parm.nr; short na = In_Parm.na; short ir,ia; double sum; Out Ptr->Tt_ra out_ptr->tt r Out Ptr->Tt a AlloMatrix(O,nr-1,0,na-1); AlloVetor(O,nr-1); AlloVet.or(O,na-1); for(ir=o; ir<nr; ir++l sum = 0. 0; for(ia=o; ia<na; iah-) sum += Out_Ptr->Rd_ra[ir] [ia]; out_ptr->rd_r[ir] = sum;! Undo what InitoutputData did. i.e. free the data alloations.! void FreeData(InputStrut In_Parm, Outstrut out Ptr) { short num_thetaol=in_parm.nbrangint; short num_rows; short nz = In_Parm.nz; short nr = In_Parm.nr; short na = In_Parm.na; short nl = In_Parm.num_layers; for(ia=o; ia<na; ia++) sum = 0.0; for(ir=o; ir<nr; irt+l sum+= Out_Ptr->Rd_ra[ir] [ia]; out_ptr->rd_a[ia] = sum; sum = 0.0; for(ir=o; ir<nr; ir++l sum+= Out_Ptr->Rd_r[ir]; Out_Ptr->Rd = sum; 121
120 ' Return the index to the layer aording to the index to the grid line system in z diretion (Iz). Use the enter of box.! short IzToLayer(short Iz, InputStrut In_ParmJ { short i=l; / index to layer. / short num layers = In_Parm. num_layers; double dz = In_Parm.dz; while( (lzto.sidz >= In_Parm.layerspes[i].zl && i<num_layers) i++; return(i);! Get ld array elements by summing the 2D array elements. / void sum2da(inputstrut In_Parm, OutStrut Out_Ptr) { short nz = In_Parm.nz; short nr ~ In_Parm.nr; short iz,ir; double sum; for(iz=o; iz<nz; iz++) sum= 0.0; for(ir=o; ir<nr; ir++) sum+= Out_Ptr ->A_rz[ir] [iz]; Out_Ptr->A_z[iz] = sum; sum= 0.0; for(iz=o; iz<nz; iz++) sum+= out_ptr->a_z[iz]; Out_Ptr->A_l[IzToLayer(iz, In_ParmJ l += Out_Ptr->A_z[iz]; out Ptr->A = sum; / Get ld array elements by summing the 2D array elements.! void Sum2DTt(InputStrut In_Parm, Outstrut out_ptr) { short nr short na In_Parm.nr; In_Parm.na; short ir,ia; double sum; for(ir=o; ir<nr; i r++j sum= 0.0; for(ia=o; ia<na; ia++) sum+= Out_Ptr->Tt_ra[ir] [ia]; Out_Ptr->Tt_r[ir] = sum; for(ia=o; ia<na; ia++) sum= 0.0; for(ir=o; ir<nr; ir++) sum+= Out_Ptr->Tt_ra[ir][i.a); Out_Ptr->Tt_a[ia\ = sum; sum= 0.0; for(ir=o; ir<nr; ir++j sum+= out_ptr->tt_r[ir]; Out Ptr->Tt = sum;!~ Sale Rd and Tt properly. "a" stands for angle alpha. Sale Rdlr,al and Tt(r,a) by (area perpendiular to photon diretion) X("olid di!<,jll')xij- J..,..:>[ J>iJ >il'i!l:). or [2PIrdros(a) )x[2pisin(a)da]x[no. of photons] or [2PIPIdrdarsin(2aJ ]x[no. of photons] Sale Rdlrl and Ttlrl by (area on the surfae)x(no. of photons). Sale Rd(a) and Tt(a) by (solid angle)x(no. of photons).! void SaleRdTt(InputStrut In_Parm, outstrut { short nr = In_Parm.nr; short na = In_Parm.na; double dr = In_Parm.dr; double da = In_Parm.da; short ir,ia; double salel, sale2; salel = 4.0PIPIdrsin(da/2)In_Parm.num_photons;!The fator (ir+0.5)sin(2a) to be added. / Out_Ptr J 122
121 for(ir=o; ir<nr; ir++) for(ia=o; ia<na; ia++) sale2 = 1.0/((ir+O.S)sin(2.0(ia+0.5)da)salel); out_ptr->rd_ra[ir] [ia] = sale2; out PLr >'ft_ra[ir] [ia] = sale2; sale1 = 2.0PIdrdrIn_Parm.num_photons;!area is 2PI[(ir+0.5)dr]dr./! ir+o.s to be added. / for(ir=o; ir<nr; ir++) sale2 = 1.0/( (ir+0.5)sale1); Out_Ptr->Rd_r[irl = sale2; out_ptr->tt_r[ir] = sale2; sale1 = 2.0PIdaIn_Parm.num_photons;! solid angle is 2PIsin(a)da. sin(a) to be added. / for(ia=o; ia<na; ia++) sale2 = 1.0/(sin((ia+O.S)da)salel); Out_Ptr->Rd_a[ia] = sale2; Out_Ptr->Tt_a[ia] = sale2; sale2 = 1.0/(double)In_Parm.num_photons; Out Ptr->Rd = sale2; Out Ptr->Tt = sale2; for(iz=o; iz<nz; iz++) for(ir=o; ir<nr; ir++) Out_Ptr->A_rz[ir] [iz] I= (ir+o.s)sale1;! Sale A z.! salel = 1.0/(dzIn_Parm.num_photons); for(iz=o; iz<nz; iz++) out_ptr->a_z[iz] = sale1; / Sale A_l. Avoid int/int. / salel = 1.0/(double)In_Parm.num_photons; for(il=o; il<=nl+1; ilh) out_ptr->a_l[il] = sale1; out_ptr->a =salel; / sum and sale results of urrent run. / void SumSaleResult(InputStrut In_Parm, outstrut out_ptr)! Get ld & OD results. / sum2drd(in_parm, Out_Ptr); Sum2DA(In_Parm, Out_Ptr); Sum2DTt (In Parm, Out Ptr); SaleRdTt(In_Parm, Out_Ptr); SaleA(In_Parm, Out_Ptr);! Sale absorption arrays properly. / void SaleA(InputStrut In_Parm, Outstrut Out PtrJ { short nz = In_Parm.nz; short nr = In_Parm.nr; double dz = In_Parm.dz; double dr = In_Parm.dr; short nl = In_Parm.num_layers; short iz,ir; short il; double sale1;! Sale A_rz. / sale1 = 2.0PIdrdrdzIn_Parm.num_photons; /volume is 2pi(ir+0.5)drdrdz./ ' ir+o.s to be added. / / Write the version number as the first string in the file. Use hars only so that they an be read as either ASCII or binary. / void WriteVersion(FILE file, har Version) { fprintf (file, "%s \t# Version number of the file format. \n\n", Version); fprintf(file, '####\n# Data ategories inlude: \n"); fprintf(file, '# InParm, RAT, \n'); fprintf(file, "# A_l, A_z, Rd_r, Rd a, Tt_r, Tt_a, \n"); fprintf(file, "# A_rz, Rd_ra, Tt_ra \n####\n\n');!~ 123
122 Write the input parameters to the file.! void WriteinParmiFILE file, InputStrut In Parmi { short i; fprintflfile, "InParm \t\t\tl Input parameters. em is used.\n"); fprintf I file, "%s \taitn output file name, ASCII.\n", In_Parm.out_fname); fprintflfile, "%s 't\t\t# data base file name\n', In_Parm.dat_fname); fprintf I file, '%hd\t%hd\t%hd\t\t# data base param.\n", In_Parm.nbrangint, In_Parm.nbrths, In_Parm.nbrpss); fprintf I file, "%ld.t t'.t.\t#!jo. of photons\n", In_Parm.num_photons); fprintflfile, "%G,t%G\t\t\t# dz, dr [m]\n", In_Parm.dz,In Parm.drl; fprinl({tije, "%hd\t%hd\t%hd\t',tll Ilo. of dz, dr, da.\n', In_Par-m.nz, In_Parm.nr, In_Parm.naJ; fprintf 1 file, '%G\t%G\t,t\t# x s1ze and y size. \n\n", In_Parm.x~_size, In_Parm.y_size;; fprintf I file, '%hd\t\t'.t'.t\t\t\t\t\t# Number of layers\n", In_Parm.num_layers); fprintf I file, "#n\tmstep\tdev\tabs\tbux\tbuy\tbuz\tdev\td\t# layer\n"l fprintf I file, 11 %G',t',t\,t\t',t\t\t\t\t# n for medium above\d 11, In_Parm.layerspes [ 0]. n); forli=l; i<=in_parm.num_layers; i++l LayerStrut s; s = In_Parm.layerspes[i]; fprintflfile, '%G\t%G\t%G\t%G\t%.3G\t%.3G\t%.3G\t%G\t%G\t# layer %hd\n", s.n, s.meanstep, s.meanstepdev, s.absross, s.bux, s.buy, s.buz, s.dev, s.zl-s.zo, i); fprintflfile, '%G\t\t\t\t\t\t\t\t\t# n for medium below\n', In_Parm.layerspes[i].n); fprintflfile, '%G\t\t\t\t\t\t\t\t\t# n for surrounding glass\n\n", In_Parm.layerspes[i+ll.n);! Write refletane, absorption, transmission.! void WriteRATIFILE file, Outstrut out Parmi { fprintflfile, "RAT\t\t\t #Refletane, absorption, transmission..n" 1;! flag. / fprintflfile, '%-14.6G \t#speular refletane [-]\n', out_parm.rsp); fprintflfile, '%-14.6G \t#diffuse refletane [-]\n', out_parm.rd); fprintf{file, '%-14.6G \t#absorbed fration [-]\n", Out_Parm.AI; fprintflfile, "%-14.6G \t#transmittane [-]\n', Out_Parm.Tt); fprintflfile, "\n");! Write absorption as a funtion of layer. ~! void WriteA_layer(FILE file, short i; short Num_Layers, OutStrut Out~Parm) fprintf I file, "A_l #Absorption as a funtion of layer. (-J\n"l;!flag./ forli=l; i<=num_layers; i++l fprintflfile, "%12.4G\n", Out_Parm.A_l[i]l; fprintf{file, "\n"l; / 5 numbers eah line. / void WriteRd_ra(FILE file, short Nr, short Na, Outstrut Out_Parm) short ir, ia; fprinte I file, "%s\n%s\n%s\n%s\n%s\n%s\n",! flag. I 124
123 "II Rd[r][angle]. [11(m2sr)].", "# Rd [ 0] [ 0], [ 0] [ 1],.. [ 0] [ na -1] ", " # Rd [ 1 J [ 0 J, [ 1 J [ 1 J,.. [ 1 J [ na -1 J ", "# "# Rd[nr-1] [0], [nr-1] [1],.. [nr-1] [na-1] ", "Rd_ra"); for(ir=o;ir<nr;ir++) for(ia=o;ia<na;ia++) fprintf(file, "%12.4E " Out_Parm.Rd_ra[ir] [ia]); if( (irna + ia + 1)%5 == 0) fprintf(file, "\n"); fprintf(file, "\n"); I ~ j.. ' ), ~ j..; -A- A: A -A 1 number eah line. I Wril~Hd r(file file, short Nr, OutStrut Out_Parm) short ir; iprinli (file, "Rd r #Rd[O), [1],.. Rd[nr-1]. [11m2]\n"); I flag. I for(ir=o;ir<nr;ir++) fprintf(file, "%12.4E\n", Out_Parm.Rd_r[ir]); fprintf(file, "\n");! 5 numbers eah line.! void WriteTt_ra(FILE file, short Nr, short Na, OutStrut Out Parm) short ir, ia; fprintf(file, "%s\n%s\n%s\n%s\n%s\n%s\n", I flag. I " # Tt [ r] [angle]. [ 1 I ( rn2.s r) J. ", "# Tt [ 0] [ 0 J, [ 0] [ 1],.. [ 0] [ na -1] ", "# Tt [ 1] [ 0 J, [ 1 J [ 1],.. [ 1] [ na -1 J ", "# --- "' "# Tt[nr-1] [OJ, [nr-1] [1],.. [nr-1] [na-1] ", "Tt_ra"); for(ir=o;ir<nr;ir++) for(ia=o;ia<na;ia++) { fprintf(file, "%12.4E out_parm.tt_ra[ir][ia]); if( (irna + ia + 1)%5 == 0) fprintf(file, "\n"); fprintf(file, "\n"); fprintf(file, "\n");! 1 number eah line. I void WriteRd_a(FILE file, short Na, OutStrut Out_Parm) short ia; fprintf(file, "Rd a #Rd[O], [1],.. Rd[na-1]. [sr-1]\n"); I flag. I for(ia=o;ia<na;ia++) fprintf(file, "%12.4E\n", Out_Parm.Rd_a[ia]);! 5 numbers eah line.! void WriteA_rz(FILE file, short Nr, short Nz, OutStrut Out_Parrn) short iz, ir; fprintf (file, "%s\n%s\n%s\n%s\n%s\n%s\n", I flag. I " # A [ r J [ z J [ 1 1 m3 J ", "# A[O][O], [0][1],.. [0][nz-1]", "# A[1J[O], [1][1],.. [1][nz-1]", "# --- "' "# A[nr-1][0], [nr-l][l],.. [nr-l][nz-1]", "A_rz"); 125
124 for(ir=o;ir<nr;ir++) for(iz=o;iz<nz;iz++) { fprintf(file, "%12.4E" Out_Parm.A_rz[ir] [iz]); if( (irnz + iz + 1)%5 == 0) fprintf(file, "\n"); fprintf(file, "\n"); / 1 number eah line. / void WriteA_z(FILE file, short Nz, OutStrut Out Farm) short iz; fprintf(file, "A_z #A[O], [l],.. A[nz-1]. [1/m]\n"); / flag. / for(iz=o;iz<nz;iz++) fprintf(file, "%12.4E\n", Out_Farm.A_z[iz]); fprintf(file, "\n");! void WriteTt_a(FILE file, short Na, OutStrut Out_Farm) short ia; fprintf (file, "Tt a #Tt[O], [l],.. Tt[na-1]. [sr-1]\n"); /flag./ for(ia=o;ia<na;ia++) fprintf(file, "%12.4E\n", Out_Farm.Tt_a[ia]); fprintf(file, "\n");! / void WriteResult(InputStrut In_Farm, OutStrut out_farm, har TimeReport) FILE file; file= fopen(in_farm.out_fname, "w"); if(file ==NULL) nrerror("cannot open file to write.\n");! 1 number eah line.! void WriteTt_r(FILE file, short Nr, OutStrut Out Farm) if(toupper(in_farm.out_fformat) == WriteVersion(file, "Al"); else WriteVersion(file, "Bl"); fprintf (file, fprintf (file, "# %s", TimeReport); "\n"); 'A') short ir; fprintf(file, "Tt r #Tt[O], [l],.. Tt[nr-1]. [1/m2]\n"); /flag./ for(ir=o;ir<nr;ir++) fprintf(file, "%12.4E\n", Out_Farm.Tt_r[ir]); fprintf(file, "\n");! 1 number eah line. WriteinParm(file, In_Parm); WriteRAT(file, out_parm);! refletane, absorption, transmittane. / / ld arrays. / WriteA_layer(file, In_Farm.num_layers, Out_Farm); WriteA_z(file, In_Parm.nz, out_farm); WriteRd_r(file, In_Farm.nr, Out_Farm); WriteRd_a(file, In_Farm.na, Out_Farm); WriteTt_r(file, In_Parm.nr, Out_Farm); WriteTt_a(file, In_Parm.na, Out Farm);! 2D arrays. / WriteA_rz(file, In_Parm.nr, In_Farm.nz, Out_Farm); 126
125 WriteRd_ra(file, In_Parm.nr, In_Parm.na, Out_Parm); WriteTt_ra(file, In_Parm.nr, In_Parm.na, Out_Parm); flose I file); B.l.2.4. mmlgo.! Launh, move, and reord photon weight.! #inlude "mml.h" #define STANDARDTEST 0! testing program using fixed rnd seed. / #define PARTIALREFLECTION 0! l=split photon, O=statistial refletion. / #define COSZERO ( E-12)! osine of about 1e-6 rad. / #define COS90D 1.0E-6 / or;j I1.: uf aboul 1. ~7 l;_-c r ad.!! A random number generator from Numerial Reipes in. / #define MBIG #define MSEED #define MZ 0 #define FAC l.oe-9 float ran3(int idum) { stati int inext,inextp; stati long ma[56]; stati int iff=o; long mj,mk; int i,ii,k; if lidum < 0 II iff == 0) iff=l; mj=mseed-iidum < 0? -idum mj %= MBIG; ma[55]=mj; mk=1; for (i=l;i<=54;i++) idum); ii=l21i) %55; ma[ii] =mk; mk=mj-mk; if (mk < MZ) mk += MBIG; mj=ma[ii]; } for lk=1;k<=4;k++) for (i=1;i<=55;i++) { ma[i] -= ma[1+(i+30)% 55]; if (ma[i] < MZ) ma[i] += t1big; inext=o; inextp=31; idum=1; if (++inext =-= 56) inext=1; if (+tinexlp == 56) inextp=l; mj=ma[inext]-ma[inextp]; if (mj < MZ) mj += t1big; ma[inext]=mj; return mjfac; #undef MBIG #undef MSEED #undef MZ #undef FAC / Generate a random number between 0 and 1. Take a number as seed the first time entering the funtion. The seed is limited to 1<<15. We found that when idum is too large, ran3 may return numbers beyond 0 and 1.! double RandomNum(voidJ { stati Boolean first_time=1; stati int idum; / seed for ran3. / if(first timel { 127
126 #if STANDAFDTEST /Use fixed seed to test the program. / idum - 1; #else idum -(inlltime(nulli%11<<151; ; use 16-bit integer as the seed. I #endif ran3 (&iduml; first_time = 0; idum = 1; return ( (double) ran3 (&iduml I; ' Compute the speular refletion. If the first layer is a turbid medium, use the Fresnel refletion from the boundary of the first layer as the speular refletane. If the first layer is glass, multiple refletions in the first layer is onsidered to get the speular refletane. The subroutine assumes the Layerspes array is orretly initialized. / double Rspeular(Layerstrut Layerspes_Ptrl double rl, r2; / diret refletions from the 1st and 2nd layers. / double temp; temp =(Layerspes_Ptr[O].n- Layerspes_Ptr[l].nl /(Layerspes_Ptr[OJ.n + Layerspes_Ptr[l].nl; rl = temptemp; if(layerspes_ptr[l].meanstep == 0.01 { /glass layer. / temp = (Layerspes_Ptr[l].n - Layerspes_Ptr[2].nl /(Layerspes_Ptr[l].n + Layerspes_Ptr[2].n); r2 = temptemp; rl = rl + 11-r1)(1-r1Jr2/ll-r1r2); return i rl I ;! Initialize a photon paket.! void LaunhPhoton(double Rspeular, LayerStrut Layerspes_Ptr, PhotonStrut Photon Ptrl Photon_Ptr->w Photon_Ptr->dead = 0; Photon_Ptr->layer = 1; Photon_Ptr->s = 0; Photon Ptr->sleft= 0; Photon Ptr->x Photon_Ptr->y Photon_Ptr->z Photon_Ptr->ux Photon_Ptr->uy Photon Ptr->uz 0. 0; 0. 0; 0. 0; Rspeular; if(layerspes_ptr[l].meanstep == 0.01 { / glass layer. I Photon_Ptr- >layer = 2; Photon_Ptr->z = Layerspes_Ptr[2].zO; / Calulate a value from a normal (Gaussian) distribution, aording to Numerial Reipes in C. Meanvalue = 0, standard deviation = dev.! double GaussDevStep(double dev) { double fa, r, vl, v2, gaussdev; stati double StepGset; stati short Stepiset = 0; if(stepiset == 01 do { v1 = 2RandomNum(l - 1.0; v2 = 2RandomNumll - 1.0; r = vlvl+v2v2; } while (r>=lo II r==0.0); fa = sqrt(-2.0devdevlog(rl/rl; StepGset vlfa; gaussdev = v2fa; Stepiset = 1; } else { Stepiset gaussdev 0. StepGset; 128
127 return(gaussdev);! Calulate a value from a normal (Gaussian) distribution, aording to Numerial Reipes in. Meanvalue = 0, standard deviation = dev. / double GaussDevSpin(double dev) { double fa, r, v1, v2, gaussdev; stati double SpinGset; stati short Spiniset = 0; if(spiniset == 0) do { vl = 2RandomNum() - 1.0; v2 = 2RandomNum() - 1.0; r = v1v1+v2v2; } while (r>=1.0 I I r==0.0); fa = sqrt(-2.0devdevlog(r)lr); SpinGset = v1fa; gaussdev = v2fa; Spiniset = 1; ) else { Spiniset = 0; gaussdev = SpinGset; return(gaussdev); ;w Choose a new diretion for photon propagation by sampling the polar defletion angle theta and the azimuthal angle psi. Note: theta: 0 - pi so sin(theta) is always positive feel free to use sqrt I) for os (theta). psi: 0-2pi for 0-pi sin (psi) is + for pi-2pi sin(psi) is -! void SpiniinputStrut In_Ptr, PhotonStrut Photon Ptr) short layer = Photon_Ptr->layer; double ost, sint; I osine and sine of the polar defletion angle theta. ' double osp, sinp; / osine and sine of the azimuthal angle psi. / double ux = Photon_Ptr->ux; /photon diretion. / double uy = Photon_Ptr->uy; I photon diretion. I double uz = Photon_Ptr->uz; I photon diretion. I double bux ; I spheroid diretion. / double buy ; I spheroid diretion. / double buz ; I spheroid diretion. / double angin; I the inident angle. / double theta; I sattering angle. / double psi; I sattering angle. / double dev = In_Ptr->layerspes[layer].dev; short thetaol; short thetaolshort; double thetaoldouble; double rnd = Rando~'um(); short num_rows; short num_thetaol = In_Ptr->nbrangint; short nbrths = In Ptr ->nbrths; short nbrpss = In_Ptr->nbrpss; short ipsi, itheta; short i; double temp; num_rows = (nbrths-2)nbrpss + 1; I number of data values for eah inident angle aording / I to the remarks in MCDATA.FOR. / if (num_thetaol - - 1) thetaol = 1; else { if (dev==l. 0) do { bux buy buz temp I sphere. I I independent of inident angle. / I spheroid. I! randomly oriented spheroids. / os(pirandomnum()); os(pirandomnum()); os(pirandomnum() ); sqrt(buxbux+buybuy+buzbuz); while (temp== 0.0); else { I orientation and deviation. I bux = In_Ptr->layerspes[layer].bux; buy = In_Ptr->layerspes[layer].buy; buz = In_Ptr->layerspes[layer].buz; temp = 1.0; if I dev! = 0. 0 ) 129
128 do { r.... u;-: buy buz temp - Lux + GaussDevSpin(dev); buy + GaussDevSpin(dev); buz + GaussDevSpin(dev); sqrt(buxbux+buybuy+buzbuz); } while (temp 0.0); angin = aosl (uxbux+uybuy+uzbuz)ltempl; I the inident angle angin is the angle between the photon diretion I! and the symmetry axis of the partile. I if (angin>pi/2 I angin = PI-angin; thetaolshort=(angin/(pii21 )(num_thetaol-1)+1; thetaoldouble=(angini(pii21 )(num_thetaol-11+1; if (thetaoldouble - thetaolshort < 0.51 thetaol = thetaolshort; else thetaol thetaolshort + 1; / The disrete sattering diretions are evaluated and /! spread out ontinuously. /! integer value. I I real value. I if (ttt L Irt f't 1 >valnratri: :[num row:l[t.li 'llc lll(.". [nw. ~.;att.rirtj- / theta= PI0.5RandomNum()/(nbrths-1); psi = PI RandomNum ( 1 ; I psi is arbitrary- I else if (rnd<in_ptr->valmatrix[1] [thetaol]j { I bak sattering. / theta= PI- PIO.SRando~~um(JI(nbrths-1); psi = PIRandomNum(J; I psi is arbitrary. I else { i 2; wh le (In_Ptr->valmatrix[i] [thetaol]<rndl ++; itheta = (i-2jinbrpss+1;! itheta = [0,1,nbrths-ll ==>theta= [0,1/(nbrths-1),PI] / ipsi = I i. -2 J %nbrpss;! ipsi = [O,l,nbrpss-1] ==>psi = [0,1/(nbrpss-11,PI] / theta= PI(itheta+(RandomNum()-0.5))/(nbrths-1); psi= PI(ipsi+(RandomNum(J-0.511/(nbrpss-1); if ( Rando~~um ( 1 > 0 _ 5) psi = 2PI - psi; / symmetry property / ost = os(thetaj; sint = sqrt(1.0- ostost); I sqrt() is faster than sin()- I osp = os(psi); if (psi<pi I sinp = sqrt(1.0- osposp);! sqrt() is faster than sin( I. I else sinp sqrt(1.0 - osposp); if(fabs(uz) > COSZERO) { I normal inident. / Photon_Ptr->ux = sintosp; Photon_Ptr->uy = sintsinp; Photon_Ptr->uz = ostsign(uz); I SIGN() is faster than division. / else { I regular inident_ I double temp = sqrt(1.0 - uzuzj; Photon_Ptr->ux = sint(uxuzosp- uysinp) /temp + uxost; Photon_Ptr->uy sint(uyuzosp + uxsinpj /temp + uyost; Photon Ptr->uz - sintosptemp + uzost;! Move the photon s away in the urrent layer of medium. I void Hop(Photonstrut Photon_PtrJ { double s = Photon_Ptr->s; Photon_Ptr- >x += sphoton_ptr->ux; Photon_Ptr->y t= sphoton_ptr->uy; Photon_Ptr->Z += sphoton_ptr->uz;! Return the photon step size in glass and the boundary whih is hit. The step size is the distane between the urrent position and the nearest boundary in the photon diretion. uz!= 0 130
129 ! short StepSizeinGlass(PhotonStrut Photon_Ptr, Inputstrut In Ptr) double dl_b; / distane to nearest boundary. / double dl_xbound; / distane to boundary perp. to x-diretion. / double dl_ybound; / distane to boundary perp. toy-diretion. / double dl_zbound; / distane to boundary perp. to z-diretion. / short layer = Photon_Ptr->layer; double ux = Photon_Ptr->UX; double uy Photon_Ptr->uy; double uz = Photon_Ptr->uz; short hitase; / the boundary whih is hit. / hitase = 1,2 or 3 for boundary perp. to the /,. x-, y- or z-diretions. /! distane to the nearest boundary. / if(uz>0.0) dl zbound = iln_ptr->layerspes[layer].z1 - Photon_Ptr->z)luz; / dl zbound>o. I else if(uz<o.oj dl zbound = (In_Ptr->layerspes[layer].zO - Photon_Ptr->z I /uz; / dl zbound>o. I dl_b = dl_zbound; hitase = 3; i f I ux! = 0. 0 I dl_xbound = ((In_Ptr->x_sizeiSIGN(ux)/2- Photon_Ptr->xl/ux; if ( dl_xbound<dl_b I ( dl_b = dl_xbound; hitase = 1; if I uy! = 0. 0 I dl_ybound = ((In_Ptr->y_sizeiSIGN(uyJ/2- Photon_Ptr->yl/uy; if (dl_ybound<dl_b) dl_b = dl_ybound; hitase = 2; Photon Ptr->s return(hitasel; dl_b;! Return the photon step size in surrouning glass, The step size is the distane between the urrent position and the boundary, perp. to z-diretion, in the photon diretion. uz! = 0 / void StepSizeinSurrGlass(Photonstrut Photon_Ptr, InputStrut double dl_b; / distane to boundary. I short layer = Photon_Ptr->layer; double uz = Photon_Ptr->uz; In_Ptr) if(uz>o.oi dl_b = 1In Ptr->layerspes[layer].z1 - Photon_Ptr->zlluz; I dl b>o. I else i.f(uz<o.oi dl_b = (In_Ptr->layerspes[layer].zO - Photon_Ptr->zlluz; I dl b>o. I Photon_Ptr->s dl_b;! Pik a step size for a photon paket when it is in tissue. If the member sleft is zero, make a new step. Otherwise, pik up the leftover in sleft. Layer is the index to layer. In_Ptr is the input parameters. sale is used instead of mut in the original MCML.! void StepSizeinTissue(PhotonStrut Photon_Ptr, InputStrut In_Ptrl short layer = Photon_Ptr->layer; double meanstep = In_Ptr->layerspes[layer].meanstep; double sale = In_Ptr->layerspes[layer].meanstep; double meanstepdev = In_Ptr-->layerspes[layer].meanstepdev; double stepdev; I standard deviation of meanstep. I do stepdev = GaussDevStep(meanstepdev); while (stepdev<-meanstepl21; I meanstep+stepdev must not be to small. I meanstep = meanstep + stepdev; if(photon_ptr->sleft == 0.01 ( I make a new step. / Photon_Ptr->s = meanstep; else ( / take the leftover. / Photon Ptr->s = Photon_Ptr->sleft/sale; 131
130 Photon_Ptr->sleft 0. 0; / Chek if the step will hit a boundary. Return 1, 2 or 3 if a boundary is hit. Return 0 otherwise. If the projeted step hits the boundary, the members s and sleft of Photon_Ptr are updated. sale is used instead of mua+mut in the original program.! short HitBoundary(PhotonStrut Photon_Pt r, InputStrut In_Ptr) double dl_b; ; distane to nearest boundary.! double dl_xbound; / distane to boundary perp. to x-diretion. / double dl_ybound; / distane to boundary perp. toy-diretion. / double dl ~bound; / distane to boundary perp. to z-diretion. / short layer = Photon_Ptr->layer; double ux = Photon Ptr->UX; double uy = Photon Ptr->uy; double uz = Photon Ptr->uz; short hitase; / the boundary whih is hit. /! hitase = 1,2 or 3 for boundary perp. to the x-, y- or z-diretions. /! hitase = 0 if no boundary is hit. / double maxdl_xybound = sqrt(pow(in_ptr->x_size,2.0) + pow(in_ptr->y_size,2.0) + pow(ln_ptr->layrsps[ luyer].zl - In_Ptr->layerspes[layer].z0,2.0) );! The longest possible path in this layer. / if(uz>0.0) ( I l ~ '. I!', 11 r 1' I I 111 I'll -l.!y'>i"i"'''"[i;ty l [.~:1 - PhoLon_Ptr >Z) /uz; / dl zbound>o. I else if(uz<o.o) dl zbound = (In_Ptr->layerspes[layer].zO - Photon_Ptr->z)/uz; / dl zbound>o. / if (UZ == 0.0) dl b = maxdl_xybound; else { dl_b = dl_zbound; hitase = 3; if(ux!= 0.0) dl_xbound = IIIn_Ptr->x_size)SIGN(ux)/2- Photon_Ptr->x)lux; if (dl_xbound<dl_b) dl_b = dl_xbound; hitase 1; } if ( uy! = 0. 0) { dl_ybound = ( (In_Ptr->y_size) SIGN(uy) /2 - if (dl_ybound<dl_b) { dl_b = dl_ybound; hitase = 2; if(photon_ptr->s > dl_b) I rossing. I double sale = In_Ptr->layerspes[layer].meanstep; Photon_Ptr->sleft = (Photon_Ptr->s - dl b) sale; Photon_Ptr->s = dl_b; else hitase = 0; return(hitase); Photon_Ptr->y) /uy; / Drop photon weight inside the tissue (not glass). The photon is assumed not dead. The weight drop is dwa = absross w. The dropped weight is assigned to Lite absorption array elements.! void Drop(Inputstrut In_Ptr, PhotonStrut Phnt on_ Pt. r, ()Ill ::I I II I IIIII double dwa; / absorbed weight. I double x = Photon_Ptr->x; double y = Photon_Ptr->y; short iz, ir; I index to z & r. / short layer = Photon_Ptr->layer; double absross; I ompute array indies. I iz = (short) (Photon_Ptr->z/In_Ptr->dzl; if(iz>in_ptr->nz-11 iz=in_ptr->nz-1; ir =(short) (sqrt(xx+yy)iin_ptr->drl; if ( ir>in_ptr->nr-11 ir=in_ptr->nr-1; 1'1 I I 132
131 / update photon weight. / absross = In_Ptr->layerspes[layer].absross; dwa = Photon_Ptr->w absross; Photon_Ptr->w -= dwa; / assign dwa to the absorption array element. / Out_Ptr->A_rz[ir] [iz] += dwa; / The photon weight is small, and the photon paket tries to survive a roulette.! void Roulette(PhotonStrut Photon_Ptr) { if(photon_ptr->w == 0.0) Photon_Ptr->dead = 1; else if(randomnum() <CHANCE) / survived the roulette./ Photon_Ptr->w I= CHANCE; else Photon_Ptr->dead = 1;! Compute the Fresnel refletane. degrees. / double r; Make sure that the osine of the inident angle al is positive, and the ase when the angle is greater than the ritial angle is ruled out. Avoid trigonometri funtion operations as muh as possible, beause they are omputation-intensive.! double RFresnel(duble nl, / inident refrative index./ double n2, / transmit refrative index./ double al, / osine of the inident / / angle. 0<al<90 double a2_ptr) / pointer to the /! osine of the transmission /! angle. a2>0. / a2_ptr = al; r = (n2-nl)/(n2+nl); r = r; else if(al<cos90d) a2_ptr = 0.0; r = 1.0;! very slant. / else { / general. / double sal, sa2;! sine of the inident and transmission angles. / double a2; sal = sqrt(l-alal); sa2 = nlsal/n2; if I sa2>=1. 0 I {! double hek for total internal refletion. / a2_ptr = 0.0; r = 1.0; else double ap, am; / osines of the sum ap or /! differene am of the two /! angles. ap = al+a2 /! am= al - a2. / double sap, sam;/ sines. / a2 Ptr = a2 = sqrt(l-sa2sa21; ap am sap sam r = returnlrl; ala2 - salsa2; / + ss. / ala2 + salsa2; / - + ss. I sala2 + alsa2; / S+ = s t s. / sala2 - alsa2; / s- = s - s. / O.Ssamsam(amam+apap)/(sapsapamam);! rearranged for speed. /! Reord the photon weight exiting the first layer(uz<o), no matter whether the layer is glass or not, to the refletion array. if(nl==n2) a2 Ptr r = 0.0; al; else if(al>coszero)! mathed boundary. /! normal inident. / Update the photon weight as well.! void ReordR(double Refl, / refletane. / Inputstrut PhotonStrut In_Ptr, Photon_Ptr, 133
132 Outstrut out_ptr) double x = Photon_Ptr->x; double y = Photon_Ptr->y; short ir, ia; / index to r & angle. / ir = (short) (sqrt(xx+yy)/in_ptr->dr); if(ir>in_ptr->nr-1) ir=in_ptr->nr-1; ia = (short) (aos(-photon_ptr->uz)/in_ptr->da); if(ia>in_ptr->na-1) ia=in_ptr->na-1;! assign photon to the refletion array element. / Out_Ptr->Rd_ra[ir] [ia] += Photon_Ptr->w(1.0-Refl); Photon_Ptr->w = Refl;! Reord the photon weight exiting the last layer(uz>o), no matter whether the layer is glass or not, to the transmittane array. Update the photon weight as well. / void ReordT(double Refl, InputStrut PhotonStrut OutStrut Out_Ptr) double x = Photon_Ptr->x; double y = Photon_Ptr->y; short ir, ia; / index to r & angle. / ir = (short 1 ( sqrt (xx+yy)!in_ptr->dr) ; if(ir>in_ptr->nr-1) ir=in_ptr->nr-1; ia = (short) (aos(photon_ptr->uz)/in_ptr->da); if(ia>in_ptr->na-1) ia=in_ptr->na-1; In_Ptr, Photon_Ptr,! assign photon to the transmittane array element. / out_ptr->tt ra[ir] [ia] += Photon_Ptr->w(1.0-Refll; Photon Ptr->w = Refl;! Deide whether the photon will be transmitted or refleted on the upper boundary (uz<oj of the urrent layer. If "layer' is the first or surrounding layer, the photon paket will be partially transmitted and partially refleted if PARTIALREFLECTION is set to 1, or the photon paket will be either transmitted or refleted determined statistially if PARTIALREFLECTION is set to 0. Reord the transmitted photon weight as refletion. If "layer" is not the first or surrounding layer and the photon paket is transmitted, move the photon to "layer-1". Update the photon parmameters.! void CrossUpOrNot(lnputStrut In_Ptr, PhotonStrut outstrut PhotoQ_Ptr, Out Ptr) double uz = Photon Ptr->uz; / z diretional osine. / double uz1; / osines of transmission alpha, always positive. / double r=o.o;! refletane. / short layer = Photon_Ptr->layer; double ni = In_Ptr->layerspes[layer].n; double nt = In_Ptr->layerspes[layer-1].n; / Get r. / if( - uz <= In_Ptr->layerspes[layer].os_ritO) r=1.0; / total internal refletion. / else if (layer == In_Ptr->num_layers + 2) / surr. glass. / r = RFresnel(In_Ptr->layerspes[layer].n, In_Ptr->layerspes[O].n, -uz, &uz1); else r = RFresnel(In_Ptr->layerspes[layer].n, In_Ptr->layerspes[layer-1].n, -uz, &uzl); if (r == 1.0 && layer == In_Ptr->num_layers + 21 Photon_Ptr->dead = 1; / total internal refletion in surrounding medium.! #if PARTIALREFLECTION if( (layer == 1 I I layer == In_Ptr->num_layers + 2) && r<1.0) {! partially transmitted. / Photon_Ptr->uz = -uz1; / transmitted photon. / ReordR(r, In_Ptr, Photon_Ptr, Out_Ptr); Photon_Ptr->uz = -uz; / refleted photon. / else if (RandomNum() > r) {/ transmitted. I Photon_Ptr->layer--; 134
133 Photon_Ptr->UX = nilnt; Photon_Ptr->uy = nilnt; Photon_Ptr->uz = -uz1; else I refleted. I Photon Ptr->uz = -uz;»else if(randomnum() > r) { I transmitted. I if ( layer==1 I I layer == In_Ptr->num_layers + 2) { Photon_Ptr->uz = -uz1; ReordR(O.O, In_Ptr, Photon_Ptr, Out_Ptrl; Photon Ptr->dead = 1; else { Photon_Ptr->layer--; Photon_Ptr->ux = nilnt; Photon_Ptr->uy = nilnt; Photon_Ptr->uz = -uz1; else I refleted. I Photon Ptr->uz -uz;»endif )!~~k~ Deide whether the photon will be transmitted or be reflet~~ on the bottom boundary (uz>o) of the urrent layer. If the photon is transmitted, move the photon to 'layer+l'. If 'layer' is the last or surrounding layer, reord the transmitted weight as transmittane. See omments for CrossUpOrNot. r=1.0; I total internal refletion. / else if (layer== In_Ptr->num_layers + 2) I surr. glass. / r = RFresnel(In_Ptr->Jayerspes[layer].n, In_Ptr->layerspes [ layer-1]. n, uz, &.uz1 1 ; else r = RFresnel(In_Ptr->layerspes[layer].n, In_Ptr->1ayerspes[layer+1].n, uz, &uzll; #if PARTIALREFLECTION if(layer == In_Ptr->num_layers I I layer -- In_Ptr->num_layers + 2) && r<l. 0) { Photon_Ptr->uz = uz1; ReordT(r, In_Ptr, Photon_Ptr, Out_Ptr); Photon_Ptr->uz = -uz; else if(randomnum() > r) (! transmitted. / Photon_Ptr->layertt; Photon_Ptr->ux = ni/nt; Photon_Ptr->uy = ni/nt; Photon Ptr->uz = uzl; else I refleted. / Photon_Ptr->uz = -uz; #else if(randomnum() >r) / transmitted. I if(lily''t Tn.. l'l.r ~ tllltn.. lily''l" II 1;1'/C>t [n_i.'lr dwtn li-''/'"t' ' 1 21 Photon_Ptr->UZ = uzl; ReordT(O.O, In_Ptr, Photon_Ptr, out_ptr); Photon Pt r- >dead ' 1 ; else { Photon_Ptr->layer++; Photon_Ptr->ux = ni/nt; Photon_Ptr->uy = ni/nt; Photon_Ptr->uz = uzl; Update the photon parmameters. / void CrossDnOrNot(Inputstrut In_Ptr, PhotonStrut OutStrut Photon_Ptr, Out_Ptr) else Photon_Ptr->uz #endif } -UZi I refleted. / double uz = Photon_Ptr->uz; / z diretional osine. I double uz1; I osines of transmission alpha. I double r=o.o; I refletane. I short layer = Photon_Ptr->layer; double ni = In_Ptr->layerspes[layer].n; double nt = In_Ptr->layerspes[layer+1].n; I Get r. / if( uz <= In_Ptr->layerspes[layer].os_rit1)! Deide whether the photon will be transmitted or be refleted on the boundary perpendiular to the x-diretion. If the photon is transmitted, move the photon to the surrounded glass layer. Update the photon parmameters. 135
134 ! void CrossXOrNot(InputStrut In_Ptr, PhotonStruL Outstrut Photon_Pt r, Out Ptrl double ux = Photon_Ptr->ux; / x diretional osine. / double uxl; / osines of transmission alpha. / double r=o.o;! refletane. / short layer = Photon_Ptr->layer; double ni In_Ptr->layerspes[layer].n; double nt = In_Ptr->layerspes[In_Ptr->num_layers+2].n;! Get r.! if( fabs(ux) <= In_Ptr->layerspes[layer].os_ritxy) r=l.o; / total internal refletion. / else r = RFresnel(In_Ptr->layerspes[layer].n, In_Ptr->layerspes[In_Ptr->num_layers+2].n, fabs(ux), &uxll; ll(eanjumnumll > rl ( ; LransttLiLL-2d Lo surroundi.ny glass./ Photon Pt r- >layer = In_Ptr->num_layers+2; l'il<>l '11 1'1 I 11:<0 11:-:1 ::J(~N(II: :); tjlh...jl<...jil yt_~_.. _...uy :~ rti/nl; Photon Ptr->uz = ni/nt; else Photon Ptr->ux -ux; / refleted. I! Deide whether the photon will be transmitted or be refleted on the boundary perpendiular to the y-diretion. If the photon is transmitted, move the photon to the surrounded glass layer. Update the photon parmameters.! void CrossYOrNot(InputStrut In_Ptr, PhotonStrut OutStrut double double double short double double uy = Photon_Ptr->uy; / x diretional osine. / uyl; / osines of transmission alpha. / r=o.o; / refletane. / layer = Photon_Ptr->layer; ni = In_Ptr->layerspes[layer].n; nt = In_Ptr->layerspes[In_Ptr->num_layers+2].n; Photon_Ptr, Out_Ptr)! Get r. / if( fabs(uy) <= In_Ptr->layerspes[layer].os_ritxy) r=1.0; / total internal refletion. / else r = RFresnel(In_Ptr->layerspes[layer].n, In_Ptr->layerspes[In Ptr->num_layers+2].n, fabs(uy), &uyl); if(randomnum() > r) { / transmitted to surrounding glass. / Photon_Ptr->layer = In_Ptr->num_layers+2; Photon_Ptr->uy = uylsign(uy); Photon_Ptr->ux = ni/nt; Photon_Ptr->uz = ni/nt; } else! refleted. / Photon_Ptr->uy = - uy;!! V >i d C! o::::ot N 'I I IIIJ>Ill ~:1 Ill 1 Ill 1'1 1, PhoLonStrul. l'hul:on_ptr, OutStrut Out_Ptr, :: ],,. 1 1 It i I.";. I if (hitase -== li CrossXOrNot I ln_ptr, Photon_Ptr, Out_Pt. r 1 ; else if lhitase == 2) CrossYOrNot(In_Ptr, Photon_Ptr, Out_Ptr); else if lhitase == 3) ( if(photon_ptr->uz < 0.0) CrossUpOrNot(In_Ptr, Photon_Ptr, out_ptr); else CrossDnOrNot(In_Ptr, Photon_Ptr, Out_Ptr);! Move the photon paket in glass layer. Horizontal photons are killed beause they will never interat with tissue again.! void HopinGlass(InputStrut In_Ptr, PhotonStrut Photon_Ptr, Outstrut Out Ptr) short hitase; / the boundary whih is hi.t 11,2 or 3). I ifiphoton_ptr->uz == 0.0)! horizontal photon in glass is killed. / Photon_Ptr->dead = 1; 136
135 if(photon_ptr->layer == In_Ptr->num_layers + 2) I surrounding glass. I StepSizeinsurrGlass(Photon_Ptr, In_Ptr); hitase = 3; I always in surrounding glass. I Hop(Photon_Ptr); CrossOrNot(In_Ptr, Photon_Ptr, Out_Ptr, hitase); else { I glass layer whih is not the surrounding glass layer. I hitase = StepSizeinGlass(Photon_Ptr, In_Ptr); Hop(Photon_Ptr); CrossOrNot(In_Ptr, Photon_Ptr, Out_Ptr, hitase); / Set a step size, move the photon, drop some weight, hoose a new photon diretion for propagation.,. When a step size is long enough for the photon to hit an interfae, this step is divided into two steps. First, move the photon to the boundary free of absorption or sattering, then deide whether the photon is refleted or transmitted. Then move the photon in the urrent or transmission medium with the unfinished stepsize to interation site. If the unfinished stepsize is still too long, repeat the above proess.! void HopDropSpininTissue(InputStrut In_Ptr, PhotonStrut OutStrut short hitase; I the boundary whih is hit (1,2,3). I Photon_Ptr, out_ptr) I hitase = 0 if no boundary is hit. I StepSizeinTissue(Photon_Ptr, In_Ptr); hitase = HitBoundary(Photon_Ptr, In_Ptr); if(hitase>o) Hop(Photon_Ptr); I move to boundary plane. I CrossOrNot(In_Ptr, Photon_Ptr, Out_Ptr, hitase); else { Hop(Photon_Ptr); Drop(In_Ptr, Photon_Ptr, Out_Ptr); Spin(In_Ptr, Photon_Ptr); / I void HopDropSpin(Inputstrut In_Ptr, Photonstrut Photon_Ptr, outstrut out_ptr) short layer = Photon_Ptr->layer; if(in_ptr->layerspes[layer].meanstep == 0.0) I glass layer. I HopinGlass(In_Ptr, Photon_Ptr, Out_Ptr); else HopDropSpininTissue(In_Ptr, Photon_Ptr, out_ptr); if( Photon_Ptr->w < In_Ptr->Wth && Roulette(Photon_Ptr);!Photon_Ptr->dead) 137
136 B.2. B.2.1. List of speifi modifiations Modifiations from MCML to MCMLBOUN The input file: The lateral extension of the plane layers of the sample, x_size and y _size, are defined on a row below the row defining the variables nz, nr and na. The refrative index of the surrounding glass~is defined on a row next to the rows ontaining the parameters of the different layers and ambients. mml.h: A variable os_ritxy is delared (data type: double) in the struture of Layerstrut. The two variables x_size and y_size are delared (data type: double) in the struture of Inputstrut. mmlio.: The funtion ShowVersion shows a modified version. A new funtion ReadXSize YSize, reading the variables x_size and y _size, is written after the funtion ReadNzNrNa. An additional funtion ReadSurrGlass, reading and setting the parameters of the surrounding glass, is inluded after the funtion ReadOneLayer. The number of elements in the array named Layerspes is inreased by one due to the surrounding glass. The argument of the mallo ommando in the funtion ReadLayerSpes is thus hanged. The funtion ReadLayerSpes alls the funtion ReadSurrGlass. The surrounding glass is thus defined as the layer with index (num_layers + 2). The alulation of the ritial angles for total internal refletion for the different layers relative the surrounding glass (os_ritxy) are added in the funtion CritialAngle as well as the ritial angles for the surrounding glass relative the ambient. The funtion ReadXSize YSize is alled after the funtion ReadNzNrNa from the funtion ReadParm. A modifiation of the funtion WritelnParm, arranges the new input parameters in the output file. mmlgo.: The data type of the funtion StepSizelnGlass is hanged to short. The funtion returns the values (1, 2, 3) due to the hit boundary (perpendiular to x-, y- or z-axis). The implementation of the path length to the boundary is not modified. The funtion HitBoundary is modified in the same way, but when no boundary was hit, the value returned is zero. In order to handle photon pakages propagating in the surrounding glass, a funtion alled StepSizelnSurrGlass has been written. The two funtions CrossUpOrNot and CrossDnOrNot are modified to work in the surrounding glass too. Photon pakages whih are totally refleted in the surrounding glass are killed in CrossUpOrNot. Two new funtions, similar to the two previous mentioned, hek if the photon pakages are refleted or transmitted when hitting the boundary to the surrounding 138
137 glass. This funtions are alled CrossXOrNot and CrossYOrNot and are introdued diretly after CrossDnOrNot. A new argument, hitase (data type: short), is delared in the funtion CrossOrNot. If hitase equals 1 or 2, CrossXOrNot or CrossYOrNot is alled respetively. If hitase equals 3, the funtion ontinues as in the original version. The funtion HoplnGlass alls StepSizelnGlass or StepSizelnSurrGlass depending on the position of the photon pakage. When the funtion CrossOrNot is alled, the value of the variable hitase obtained from the funtion StepSizelnGlass, is inluded in the argument. The new variable hitase is used in a similar way in the funtion HopDropSpinlnTissue, but its value is obtained from the funtion HitBoundary. The funtion CrossOrNot is alled when hitase differs from zero. mmlmain.: The funtion ShowVersion is delared in the main program in order to avoid ompiler warnings. B.2.2. Modifiations from MCMLBOUN to TMMCML The input file: The name of the file with the data base, and the values of the variables (datatype: short) nbrangint, nbrths and nbrpss are written before the normal input parameters of eah run. The three variables represent the number of inident angles (ei), sattered defletion angles es) and sattered azimuthal angles (ps), respetively, uniformly distributed. These values must agree with those onneted to the data base, to obtain the right result. The mean distane between the sattering objets (meanstep), the standard deviation of this value (meanstepdev), the normalized absorption ross setion (absross), the diretion of the symmetry axis of the sattering objets (bux, buy, buz) and the standard deviation of this diretion (dev) are written on a new row for eah layer. The length unit is em. mml.h: The parameters belonging to the data base (dat_fname, nbrangint, nbrths, nbrpss and valmatrix) are delared in the struture of lnputstrut. The array dat_fname (data type: har) ontains the name of the data base file. The two-dimensional array valmatrix (data type: double) is used to store the values from the data base. The parameters of eah layer (datatype: double) are delared in the struture of LayerStrut, replaing of the old ones (mua, mus and g). mmlio.: The funtion Show Version shows a modified version. The new parameters are read instead of the old ones in the funtion ReadOneLayer and are written to the output file by the modified funtion WritelnParm. The funtion ReadSurrGlass assigns meanstep = 0 instead of!-la = 1-ls = 0. Two new funtions, ReadDataBase and PlaeDatalnMatrix, alloate memory spae for a two-dimensional array (matrix), read the data base values and put them in the array. 139
138 In the funtion ChekParm a ommando FindDataLine is added to prevent the data base to be read twie. This saves time but the data base parameters will not be heked before the program starts. To free the alloated memory used to the data base values, another FreeMatrix ommando is added in the funtion FreeData. mmlgo.: The funtions Rspeular, LaunhPhoton and HopDropSpin hek if meanstep = 0 instead of!-la= 1-ls = 0. By using the variables meanstep and meanstepdev and the new funtion StepGaussDev, the funtion StepSizeinTissue evaluates a step length of the photon pakage instead of the old expression using 1-la and 1-ls In this funtion and in the funtion HitBoundary a variable sale is defined, orresponding to the variable 1-lt in the original program when alulating the value of the variable sleft. The funtion Drop dereases the weight of the photon pakage by a fator absross instead of the quotient 1-la"llt The funtion Spin is ompletely hanged. The funtion SpinTheta is removed and the new funtion SpinGaussDev handles the Gaussian distributed diretions of the sattering objets. The variable gin the argument of Spin is replaed by the struture variable In_Ptr. This modifiation is also made in the all from the funtion HopDropSpinlnTissue. mmlmain.: The funtion ReadDataBase is delared and alled. B.3. Flow harts Flow harts of the Monte Carlo programs are presented on the following three pages. The hart of the original Monte Carlo program is first shown, followed by the two modified versions MCMLBOUN and TMMCML. Squares symbolizing new routines in the modified versions are filled and squares for modified routines are shaded. 140
139 I i ~1 I MCML-MAIN I Runn ~ 7. i / / / / I 7 :!.-S_h_o_w_V_L._e-rs-i<-m-,1 GetFname I GetFile ChekParm ~ReadNumRunsl ~ L D ne~ll photons ReadParm oo~ _ \ I I I I I / I I I I \ Read Read Read Read Read Read Critial Init Rspe- Punh Report Launh Hop Report Free Fname Num DzDr NzNr Num Layer Angle Output ular Time Status photon Dr?p!\ Result Data i \) format Photons Na Layers Spes Data Spm I I ~ I Read ~ ~ Skapa oh Initiera Read Read I O:a matriser Starttid Predit fotone, '--tintil Photon Ambient one Ambient! Done ko ensera Ptr-dead=l layer Time fi ev. glas - ~ ~ ' J..LS=J..La=O else, ,. HopDropSpin HopmGlass. T" Roulett Ill ISSUe j I ReordR (Rd_ra)} / StepSize StepSize Yes inglass intissue 1 2 Hop (x,y,z, Hop (x,y,z, ttotal) ttotal) J..LZ<O CrossUporNot. Yes No. J.lX,J.lY,J.lZ, , L j "---~---'-- j ReordT (Tt_ra) I
140 Fname II Nurn format Photons Read DzDr NzNr Na Init Output Data Rspeu1ar Punh Time Report II Launh Status photon Numberoflayers= Numberoflayers+ 1 Skapa oh O:a matriser Starttid I Predit Done Time Rou1ett l::!:;;:;!!i!,i(:,::::::l::~:::::;:.::::;:::::;::i::::::::::;::~:l~:,::i::i: ReordR (Rd _ ra)('lf layer= layer 1
141 ReadParm Do~1 photons Read Read Read Read Read Fname Num DzDr NzNr XSize format Photons Na YSize ;;Jlr r n tl :~:(...::... :.., all II ~..:... :.:t:~~~:~ Num Layer An 1 Output lr-11 ~:~:~:~:m_~~iif~:~:::~:~'::~: funh T' me g e ~.,,,,,,,,,, ''''''''''''''''''' 1 Layers Spes 21 ~ 1 Skapaoh O:a matriser Starttid Numberoflayers= Numberoflayers+ 1 Roulett if SurrG1ass Step Size insurrg1ass ReordR (Rd _ra) {1flayer=1ayerl
Introduction to Seismology Spring 2008
 MIT OpenCourseWare http://ow.mit.edu 1.510 Introdution to Seismology Spring 008 For information about iting these materials or our Terms of Use, visit: http://ow.mit.edu/terms. 1.510 Leture Notes 3.3.007
MIT OpenCourseWare http://ow.mit.edu 1.510 Introdution to Seismology Spring 008 For information about iting these materials or our Terms of Use, visit: http://ow.mit.edu/terms. 1.510 Leture Notes 3.3.007
with respect to the normal in each medium, respectively. The question is: How are θ
 Prof. Raghuveer Parthasarathy University of Oregon Physis 35 Winter 8 3 R EFRACTION When light travels from one medium to another, it may hange diretion. This phenomenon familiar whenever we see the bent
Prof. Raghuveer Parthasarathy University of Oregon Physis 35 Winter 8 3 R EFRACTION When light travels from one medium to another, it may hange diretion. This phenomenon familiar whenever we see the bent
Particle Swarm Optimization for the Design of High Diffraction Efficient Holographic Grating
 Original Artile Partile Swarm Optimization for the Design of High Diffration Effiient Holographi Grating A.K. Tripathy 1, S.K. Das, M. Sundaray 3 and S.K. Tripathy* 4 1, Department of Computer Siene, Berhampur
Original Artile Partile Swarm Optimization for the Design of High Diffration Effiient Holographi Grating A.K. Tripathy 1, S.K. Das, M. Sundaray 3 and S.K. Tripathy* 4 1, Department of Computer Siene, Berhampur
Drawing lines. Naïve line drawing algorithm. drawpixel(x, round(y)); double dy = y1 - y0; double dx = x1 - x0; double m = dy / dx; double y = y0;
 Naïve line drawing algorithm // Connet to grid points(x0,y0) and // (x1,y1) by a line. void drawline(int x0, int y0, int x1, int y1) { int x; double dy = y1 - y0; double dx = x1 - x0; double m = dy / dx;
Naïve line drawing algorithm // Connet to grid points(x0,y0) and // (x1,y1) by a line. void drawline(int x0, int y0, int x1, int y1) { int x; double dy = y1 - y0; double dx = x1 - x0; double m = dy / dx;
The Alpha Torque and Quantum Physics
 The Alpha Torque and Quantum Physis Zhiliang Cao, Henry Cao williamao15000@yahoo.om, henry.gu.ao@gmail.om July 18, 010 Abstrat In the enter of the unierse, there isn t a super massie blak hole or any speifi
The Alpha Torque and Quantum Physis Zhiliang Cao, Henry Cao williamao15000@yahoo.om, henry.gu.ao@gmail.om July 18, 010 Abstrat In the enter of the unierse, there isn t a super massie blak hole or any speifi
Electromagnetic Waves
 Eletromagneti Waves Physis 6C Eletromagneti (EM) waves are produed by an alternating urrent in a wire. As the harges in the wire osillate bak and forth, the eletri field around them osillates as well,
Eletromagneti Waves Physis 6C Eletromagneti (EM) waves are produed by an alternating urrent in a wire. As the harges in the wire osillate bak and forth, the eletri field around them osillates as well,
We P9 16 Eigenray Tracing in 3D Heterogeneous Media
 We P9 Eigenray Traing in 3D Heterogeneous Media Z. Koren* (Emerson), I. Ravve (Emerson) Summary Conventional two-point ray traing in a general 3D heterogeneous medium is normally performed by a shooting
We P9 Eigenray Traing in 3D Heterogeneous Media Z. Koren* (Emerson), I. Ravve (Emerson) Summary Conventional two-point ray traing in a general 3D heterogeneous medium is normally performed by a shooting
Year 11 GCSE Revision - Re-visit work
 Week beginning 6 th 13 th 20 th HALF TERM 27th Topis for revision Fators, multiples and primes Indies Frations, Perentages, Deimals Rounding 6 th Marh Ratio Year 11 GCSE Revision - Re-visit work Understand
Week beginning 6 th 13 th 20 th HALF TERM 27th Topis for revision Fators, multiples and primes Indies Frations, Perentages, Deimals Rounding 6 th Marh Ratio Year 11 GCSE Revision - Re-visit work Understand
Analysis of input and output configurations for use in four-valued CCD programmable logic arrays
 nalysis of input and output onfigurations for use in four-valued D programmable logi arrays J.T. utler H.G. Kerkhoff ndexing terms: Logi, iruit theory and design, harge-oupled devies bstrat: s in binary,
nalysis of input and output onfigurations for use in four-valued D programmable logi arrays J.T. utler H.G. Kerkhoff ndexing terms: Logi, iruit theory and design, harge-oupled devies bstrat: s in binary,
An Event Display for ATLAS H8 Pixel Test Beam Data
 An Event Display for ATLAS H8 Pixel Test Beam Data George Gollin Centre de Physique des Partiules de Marseille and University of Illinois April 17, 1999 g-gollin@uiu.edu An event display program is now
An Event Display for ATLAS H8 Pixel Test Beam Data George Gollin Centre de Physique des Partiules de Marseille and University of Illinois April 17, 1999 g-gollin@uiu.edu An event display program is now
Pre-Critical incidence
 Seismi methods: Refration I Refration reading: Sharma p58-86 Pre-Critial inidene Refletion and refration Snell s Law: sin i sin R sin r P P P P P P where p is the ray parameter and is onstant along eah
Seismi methods: Refration I Refration reading: Sharma p58-86 Pre-Critial inidene Refletion and refration Snell s Law: sin i sin R sin r P P P P P P where p is the ray parameter and is onstant along eah
ICCGLU. A Fortran IV subroutine to solve large sparse general systems of linear equations. J.J. Dongarra, G.K. Leaf and M. Minkoff.
 http://www.netlib.org/linalg/ig-do 1 of 8 12/7/2009 11:14 AM ICCGLU A Fortran IV subroutine to solve large sparse general systems of linear equations. J.J. Dongarra, G.K. Leaf and M. Minkoff July, 1982
http://www.netlib.org/linalg/ig-do 1 of 8 12/7/2009 11:14 AM ICCGLU A Fortran IV subroutine to solve large sparse general systems of linear equations. J.J. Dongarra, G.K. Leaf and M. Minkoff July, 1982
Rotation Invariant Spherical Harmonic Representation of 3D Shape Descriptors
 Eurographis Symposium on Geometry Proessing (003) L. Kobbelt, P. Shröder, H. Hoppe (Editors) Rotation Invariant Spherial Harmoni Representation of 3D Shape Desriptors Mihael Kazhdan, Thomas Funkhouser,
Eurographis Symposium on Geometry Proessing (003) L. Kobbelt, P. Shröder, H. Hoppe (Editors) Rotation Invariant Spherial Harmoni Representation of 3D Shape Desriptors Mihael Kazhdan, Thomas Funkhouser,
Learning Convention Propagation in BeerAdvocate Reviews from a etwork Perspective. Abstract
 CS 9 Projet Final Report: Learning Convention Propagation in BeerAdvoate Reviews from a etwork Perspetive Abstrat We look at the way onventions propagate between reviews on the BeerAdvoate dataset, and
CS 9 Projet Final Report: Learning Convention Propagation in BeerAdvoate Reviews from a etwork Perspetive Abstrat We look at the way onventions propagate between reviews on the BeerAdvoate dataset, and
The Minimum Redundancy Maximum Relevance Approach to Building Sparse Support Vector Machines
 The Minimum Redundany Maximum Relevane Approah to Building Sparse Support Vetor Mahines Xiaoxing Yang, Ke Tang, and Xin Yao, Nature Inspired Computation and Appliations Laboratory (NICAL), Shool of Computer
The Minimum Redundany Maximum Relevane Approah to Building Sparse Support Vetor Mahines Xiaoxing Yang, Ke Tang, and Xin Yao, Nature Inspired Computation and Appliations Laboratory (NICAL), Shool of Computer
Triangles. Learning Objectives. Pre-Activity
 Setion 3.2 Pre-tivity Preparation Triangles Geena needs to make sure that the dek she is building is perfetly square to the brae holding the dek in plae. How an she use geometry to ensure that the boards
Setion 3.2 Pre-tivity Preparation Triangles Geena needs to make sure that the dek she is building is perfetly square to the brae holding the dek in plae. How an she use geometry to ensure that the boards
A Novel Validity Index for Determination of the Optimal Number of Clusters
 IEICE TRANS. INF. & SYST., VOL.E84 D, NO.2 FEBRUARY 2001 281 LETTER A Novel Validity Index for Determination of the Optimal Number of Clusters Do-Jong KIM, Yong-Woon PARK, and Dong-Jo PARK, Nonmembers
IEICE TRANS. INF. & SYST., VOL.E84 D, NO.2 FEBRUARY 2001 281 LETTER A Novel Validity Index for Determination of the Optimal Number of Clusters Do-Jong KIM, Yong-Woon PARK, and Dong-Jo PARK, Nonmembers
Plot-to-track correlation in A-SMGCS using the target images from a Surface Movement Radar
 Plot-to-trak orrelation in A-SMGCS using the target images from a Surfae Movement Radar G. Golino Radar & ehnology Division AMS, Italy ggolino@amsjv.it Abstrat he main topi of this paper is the formulation
Plot-to-trak orrelation in A-SMGCS using the target images from a Surfae Movement Radar G. Golino Radar & ehnology Division AMS, Italy ggolino@amsjv.it Abstrat he main topi of this paper is the formulation
A radiometric analysis of projected sinusoidal illumination for opaque surfaces
 University of Virginia tehnial report CS-21-7 aompanying A Coaxial Optial Sanner for Synhronous Aquisition of 3D Geometry and Surfae Refletane A radiometri analysis of projeted sinusoidal illumination
University of Virginia tehnial report CS-21-7 aompanying A Coaxial Optial Sanner for Synhronous Aquisition of 3D Geometry and Surfae Refletane A radiometri analysis of projeted sinusoidal illumination
MATH STUDENT BOOK. 12th Grade Unit 6
 MATH STUDENT BOOK 12th Grade Unit 6 Unit 6 TRIGONOMETRIC APPLICATIONS MATH 1206 TRIGONOMETRIC APPLICATIONS INTRODUCTION 3 1. TRIGONOMETRY OF OBLIQUE TRIANGLES 5 LAW OF SINES 5 AMBIGUITY AND AREA OF A TRIANGLE
MATH STUDENT BOOK 12th Grade Unit 6 Unit 6 TRIGONOMETRIC APPLICATIONS MATH 1206 TRIGONOMETRIC APPLICATIONS INTRODUCTION 3 1. TRIGONOMETRY OF OBLIQUE TRIANGLES 5 LAW OF SINES 5 AMBIGUITY AND AREA OF A TRIANGLE
Gray Codes for Reflectable Languages
 Gray Codes for Refletable Languages Yue Li Joe Sawada Marh 8, 2008 Abstrat We lassify a type of language alled a refletable language. We then develop a generi algorithm that an be used to list all strings
Gray Codes for Refletable Languages Yue Li Joe Sawada Marh 8, 2008 Abstrat We lassify a type of language alled a refletable language. We then develop a generi algorithm that an be used to list all strings
NONLINEAR BACK PROJECTION FOR TOMOGRAPHIC IMAGE RECONSTRUCTION. Ken Sauer and Charles A. Bouman
 NONLINEAR BACK PROJECTION FOR TOMOGRAPHIC IMAGE RECONSTRUCTION Ken Sauer and Charles A. Bouman Department of Eletrial Engineering, University of Notre Dame Notre Dame, IN 46556, (219) 631-6999 Shool of
NONLINEAR BACK PROJECTION FOR TOMOGRAPHIC IMAGE RECONSTRUCTION Ken Sauer and Charles A. Bouman Department of Eletrial Engineering, University of Notre Dame Notre Dame, IN 46556, (219) 631-6999 Shool of
Extracting Partition Statistics from Semistructured Data
 Extrating Partition Statistis from Semistrutured Data John N. Wilson Rihard Gourlay Robert Japp Mathias Neumüller Department of Computer and Information Sienes University of Strathlyde, Glasgow, UK {jnw,rsg,rpj,mathias}@is.strath.a.uk
Extrating Partition Statistis from Semistrutured Data John N. Wilson Rihard Gourlay Robert Japp Mathias Neumüller Department of Computer and Information Sienes University of Strathlyde, Glasgow, UK {jnw,rsg,rpj,mathias}@is.strath.a.uk
Rapid, accurate particle tracking by calculation of radial symmetry centers
 Rapid, aurate partile traing by alulation of radial symmetry enters Raghuveer Parthasarathy Supplementary Text and Figures Supplementary Figures Supplementary Figure 1 Supplementary Figure Supplementary
Rapid, aurate partile traing by alulation of radial symmetry enters Raghuveer Parthasarathy Supplementary Text and Figures Supplementary Figures Supplementary Figure 1 Supplementary Figure Supplementary
FUZZY WATERSHED FOR IMAGE SEGMENTATION
 FUZZY WATERSHED FOR IMAGE SEGMENTATION Ramón Moreno, Manuel Graña Computational Intelligene Group, Universidad del País Vaso, Spain http://www.ehu.es/winto; {ramon.moreno,manuel.grana}@ehu.es Abstrat The
FUZZY WATERSHED FOR IMAGE SEGMENTATION Ramón Moreno, Manuel Graña Computational Intelligene Group, Universidad del País Vaso, Spain http://www.ehu.es/winto; {ramon.moreno,manuel.grana}@ehu.es Abstrat The
INTERPOLATED AND WARPED 2-D DIGITAL WAVEGUIDE MESH ALGORITHMS
 Proeedings of the COST G-6 Conferene on Digital Audio Effets (DAFX-), Verona, Italy, Deember 7-9, INTERPOLATED AND WARPED -D DIGITAL WAVEGUIDE MESH ALGORITHMS Vesa Välimäki Lab. of Aoustis and Audio Signal
Proeedings of the COST G-6 Conferene on Digital Audio Effets (DAFX-), Verona, Italy, Deember 7-9, INTERPOLATED AND WARPED -D DIGITAL WAVEGUIDE MESH ALGORITHMS Vesa Välimäki Lab. of Aoustis and Audio Signal
Pipelined Multipliers for Reconfigurable Hardware
 Pipelined Multipliers for Reonfigurable Hardware Mithell J. Myjak and José G. Delgado-Frias Shool of Eletrial Engineering and Computer Siene, Washington State University Pullman, WA 99164-2752 USA {mmyjak,
Pipelined Multipliers for Reonfigurable Hardware Mithell J. Myjak and José G. Delgado-Frias Shool of Eletrial Engineering and Computer Siene, Washington State University Pullman, WA 99164-2752 USA {mmyjak,
CleanUp: Improving Quadrilateral Finite Element Meshes
 CleanUp: Improving Quadrilateral Finite Element Meshes Paul Kinney MD-10 ECC P.O. Box 203 Ford Motor Company Dearborn, MI. 8121 (313) 28-1228 pkinney@ford.om Abstrat: Unless an all quadrilateral (quad)
CleanUp: Improving Quadrilateral Finite Element Meshes Paul Kinney MD-10 ECC P.O. Box 203 Ford Motor Company Dearborn, MI. 8121 (313) 28-1228 pkinney@ford.om Abstrat: Unless an all quadrilateral (quad)
represent = as a finite deimal" either in base 0 or in base. We an imagine that the omputer first omputes the mathematial = then rounds the result to
 Sientifi Computing Chapter I Computer Arithmeti Jonathan Goodman Courant Institute of Mathemaial Sienes Last revised January, 00 Introdution One of the many soures of error in sientifi omputing is inexat
Sientifi Computing Chapter I Computer Arithmeti Jonathan Goodman Courant Institute of Mathemaial Sienes Last revised January, 00 Introdution One of the many soures of error in sientifi omputing is inexat
Orientation of the coordinate system
 Orientation of the oordinate system Right-handed oordinate system: -axis by a positive, around the -axis. The -axis is mapped to the i.e., antilokwise, rotation of The -axis is mapped to the -axis by a
Orientation of the oordinate system Right-handed oordinate system: -axis by a positive, around the -axis. The -axis is mapped to the i.e., antilokwise, rotation of The -axis is mapped to the -axis by a
Using Augmented Measurements to Improve the Convergence of ICP
 Using Augmented Measurements to Improve the onvergene of IP Jaopo Serafin, Giorgio Grisetti Dept. of omputer, ontrol and Management Engineering, Sapienza University of Rome, Via Ariosto 25, I-0085, Rome,
Using Augmented Measurements to Improve the onvergene of IP Jaopo Serafin, Giorgio Grisetti Dept. of omputer, ontrol and Management Engineering, Sapienza University of Rome, Via Ariosto 25, I-0085, Rome,
PhysicsAndMathsTutor.com 12
 PhysisAndMathsTutor.om M. (a) sin θ = or.33 sin θ =.47 sin44 or sin 0.768 () θ = 50.5, 50., 50.35 ( ) () answer seen to > sf (b) refrats towards normal () 44 shown () () (TIR) only when ray travels from
PhysisAndMathsTutor.om M. (a) sin θ = or.33 sin θ =.47 sin44 or sin 0.768 () θ = 50.5, 50., 50.35 ( ) () answer seen to > sf (b) refrats towards normal () 44 shown () () (TIR) only when ray travels from
timestamp, if silhouette(x, y) 0 0 if silhouette(x, y) = 0, mhi(x, y) = and mhi(x, y) < timestamp - duration mhi(x, y), else
 3rd International Conferene on Multimedia Tehnolog(ICMT 013) An Effiient Moving Target Traking Strateg Based on OpenCV and CAMShift Theor Dongu Li 1 Abstrat Image movement involved bakground movement and
3rd International Conferene on Multimedia Tehnolog(ICMT 013) An Effiient Moving Target Traking Strateg Based on OpenCV and CAMShift Theor Dongu Li 1 Abstrat Image movement involved bakground movement and
Coupling of MASH-MORSE Adjoint Leakages with Spaceand Time-Dependent Plume Radiation Sources
 ORNL/TM-2000/335 oupling of MASH-MORSE Adjoint Leakages with Spaeand Time-Dependent Plume Radiation Soures. O. Slater J. M. Barnes J. O. Johnson J. P. Renier R. T. Santoro DOUMENT AVAILABILITY Reports
ORNL/TM-2000/335 oupling of MASH-MORSE Adjoint Leakages with Spaeand Time-Dependent Plume Radiation Soures. O. Slater J. M. Barnes J. O. Johnson J. P. Renier R. T. Santoro DOUMENT AVAILABILITY Reports
1. The collection of the vowels in the word probability. 2. The collection of real numbers that satisfy the equation x 9 = 0.
 C HPTER 1 SETS I. DEFINITION OF SET We begin our study of probability with the disussion of the basi onept of set. We assume that there is a ommon understanding of what is meant by the notion of a olletion
C HPTER 1 SETS I. DEFINITION OF SET We begin our study of probability with the disussion of the basi onept of set. We assume that there is a ommon understanding of what is meant by the notion of a olletion
Measurement of the stereoscopic rangefinder beam angular velocity using the digital image processing method
 Measurement of the stereosopi rangefinder beam angular veloity using the digital image proessing method ROMAN VÍTEK Department of weapons and ammunition University of defense Kouniova 65, 62 Brno CZECH
Measurement of the stereosopi rangefinder beam angular veloity using the digital image proessing method ROMAN VÍTEK Department of weapons and ammunition University of defense Kouniova 65, 62 Brno CZECH
Smooth Trajectory Planning Along Bezier Curve for Mobile Robots with Velocity Constraints
 Smooth Trajetory Planning Along Bezier Curve for Mobile Robots with Veloity Constraints Gil Jin Yang and Byoung Wook Choi Department of Eletrial and Information Engineering Seoul National University of
Smooth Trajetory Planning Along Bezier Curve for Mobile Robots with Veloity Constraints Gil Jin Yang and Byoung Wook Choi Department of Eletrial and Information Engineering Seoul National University of
arxiv: v1 [cs.db] 13 Sep 2017
![arxiv: v1 [cs.db] 13 Sep 2017 arxiv: v1 [cs.db] 13 Sep 2017](/thumbs/96/126543346.jpg) An effiient lustering algorithm from the measure of loal Gaussian distribution Yuan-Yen Tai (Dated: May 27, 2018) In this paper, I will introdue a fast and novel lustering algorithm based on Gaussian distribution
An effiient lustering algorithm from the measure of loal Gaussian distribution Yuan-Yen Tai (Dated: May 27, 2018) In this paper, I will introdue a fast and novel lustering algorithm based on Gaussian distribution
Simulation of Crystallographic Texture and Anisotropie of Polycrystals during Metal Forming with Respect to Scaling Aspects
 Raabe, Roters, Wang Simulation of Crystallographi Texture and Anisotropie of Polyrystals during Metal Forming with Respet to Saling Aspets D. Raabe, F. Roters, Y. Wang Max-Plank-Institut für Eisenforshung,
Raabe, Roters, Wang Simulation of Crystallographi Texture and Anisotropie of Polyrystals during Metal Forming with Respet to Saling Aspets D. Raabe, F. Roters, Y. Wang Max-Plank-Institut für Eisenforshung,
The Mathematics of Simple Ultrasonic 2-Dimensional Sensing
 The Mathematis of Simple Ultrasoni -Dimensional Sensing President, Bitstream Tehnology The Mathematis of Simple Ultrasoni -Dimensional Sensing Introdution Our ompany, Bitstream Tehnology, has been developing
The Mathematis of Simple Ultrasoni -Dimensional Sensing President, Bitstream Tehnology The Mathematis of Simple Ultrasoni -Dimensional Sensing Introdution Our ompany, Bitstream Tehnology, has been developing
MPhys Final Year Project Dissertation by Andrew Jackson
 Development of software for the omputation of the properties of eletrostati eletro-optial devies via both the diret ray traing and paraxial approximation tehniques. MPhys Final Year Projet Dissertation
Development of software for the omputation of the properties of eletrostati eletro-optial devies via both the diret ray traing and paraxial approximation tehniques. MPhys Final Year Projet Dissertation
the data. Structured Principal Component Analysis (SPCA)
 Strutured Prinipal Component Analysis Kristin M. Branson and Sameer Agarwal Department of Computer Siene and Engineering University of California, San Diego La Jolla, CA 9193-114 Abstrat Many tasks involving
Strutured Prinipal Component Analysis Kristin M. Branson and Sameer Agarwal Department of Computer Siene and Engineering University of California, San Diego La Jolla, CA 9193-114 Abstrat Many tasks involving
A DYNAMIC ACCESS CONTROL WITH BINARY KEY-PAIR
 Malaysian Journal of Computer Siene, Vol 10 No 1, June 1997, pp 36-41 A DYNAMIC ACCESS CONTROL WITH BINARY KEY-PAIR Md Rafiqul Islam, Harihodin Selamat and Mohd Noor Md Sap Faulty of Computer Siene and
Malaysian Journal of Computer Siene, Vol 10 No 1, June 1997, pp 36-41 A DYNAMIC ACCESS CONTROL WITH BINARY KEY-PAIR Md Rafiqul Islam, Harihodin Selamat and Mohd Noor Md Sap Faulty of Computer Siene and
Chemical, Biological and Radiological Hazard Assessment: A New Model of a Plume in a Complex Urban Environment
 hemial, Biologial and Radiologial Haard Assessment: A New Model of a Plume in a omplex Urban Environment Skvortsov, A.T., P.D. Dawson, M.D. Roberts and R.M. Gailis HPP Division, Defene Siene and Tehnology
hemial, Biologial and Radiologial Haard Assessment: A New Model of a Plume in a omplex Urban Environment Skvortsov, A.T., P.D. Dawson, M.D. Roberts and R.M. Gailis HPP Division, Defene Siene and Tehnology
Cluster-Based Cumulative Ensembles
 Cluster-Based Cumulative Ensembles Hanan G. Ayad and Mohamed S. Kamel Pattern Analysis and Mahine Intelligene Lab, Eletrial and Computer Engineering, University of Waterloo, Waterloo, Ontario N2L 3G1,
Cluster-Based Cumulative Ensembles Hanan G. Ayad and Mohamed S. Kamel Pattern Analysis and Mahine Intelligene Lab, Eletrial and Computer Engineering, University of Waterloo, Waterloo, Ontario N2L 3G1,
Chapter 2: Introduction to Maple V
 Chapter 2: Introdution to Maple V 2-1 Working with Maple Worksheets Try It! (p. 15) Start a Maple session with an empty worksheet. The name of the worksheet should be Untitled (1). Use one of the standard
Chapter 2: Introdution to Maple V 2-1 Working with Maple Worksheets Try It! (p. 15) Start a Maple session with an empty worksheet. The name of the worksheet should be Untitled (1). Use one of the standard
A Unified Subdivision Scheme for Polygonal Modeling
 EUROGRAPHICS 2 / A. Chalmers and T.-M. Rhyne (Guest Editors) Volume 2 (2), Number 3 A Unified Subdivision Sheme for Polygonal Modeling Jérôme Maillot Jos Stam Alias Wavefront Alias Wavefront 2 King St.
EUROGRAPHICS 2 / A. Chalmers and T.-M. Rhyne (Guest Editors) Volume 2 (2), Number 3 A Unified Subdivision Sheme for Polygonal Modeling Jérôme Maillot Jos Stam Alias Wavefront Alias Wavefront 2 King St.
Supplementary Material: Geometric Calibration of Micro-Lens-Based Light-Field Cameras using Line Features
 Supplementary Material: Geometri Calibration of Miro-Lens-Based Light-Field Cameras using Line Features Yunsu Bok, Hae-Gon Jeon and In So Kweon KAIST, Korea As the supplementary material, we provide detailed
Supplementary Material: Geometri Calibration of Miro-Lens-Based Light-Field Cameras using Line Features Yunsu Bok, Hae-Gon Jeon and In So Kweon KAIST, Korea As the supplementary material, we provide detailed
1. Inversions. A geometric construction relating points O, A and B looks as follows.
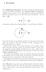 1. Inversions. 1.1. Definitions of inversion. Inversion is a kind of symmetry about a irle. It is defined as follows. he inversion of degree R 2 entered at a point maps a point to the point on the ray
1. Inversions. 1.1. Definitions of inversion. Inversion is a kind of symmetry about a irle. It is defined as follows. he inversion of degree R 2 entered at a point maps a point to the point on the ray
HIGHER ORDER full-wave three-dimensional (3-D) large-domain techniques in
 FACTA UNIVERSITATIS (NIŠ) SER.: ELEC. ENERG. vol. 21, no. 2, August 2008, 209-220 Comparison of Higher Order FEM and MoM/SIE Approahes in Analyses of Closed- and Open-Region Eletromagneti Problems Milan
FACTA UNIVERSITATIS (NIŠ) SER.: ELEC. ENERG. vol. 21, no. 2, August 2008, 209-220 Comparison of Higher Order FEM and MoM/SIE Approahes in Analyses of Closed- and Open-Region Eletromagneti Problems Milan
Adapting K-Medians to Generate Normalized Cluster Centers
 Adapting -Medians to Generate Normalized Cluster Centers Benamin J. Anderson, Deborah S. Gross, David R. Musiant Anna M. Ritz, Thomas G. Smith, Leah E. Steinberg Carleton College andersbe@gmail.om, {dgross,
Adapting -Medians to Generate Normalized Cluster Centers Benamin J. Anderson, Deborah S. Gross, David R. Musiant Anna M. Ritz, Thomas G. Smith, Leah E. Steinberg Carleton College andersbe@gmail.om, {dgross,
Video Data and Sonar Data: Real World Data Fusion Example
 14th International Conferene on Information Fusion Chiago, Illinois, USA, July 5-8, 2011 Video Data and Sonar Data: Real World Data Fusion Example David W. Krout Applied Physis Lab dkrout@apl.washington.edu
14th International Conferene on Information Fusion Chiago, Illinois, USA, July 5-8, 2011 Video Data and Sonar Data: Real World Data Fusion Example David W. Krout Applied Physis Lab dkrout@apl.washington.edu
On - Line Path Delay Fault Testing of Omega MINs M. Bellos 1, E. Kalligeros 1, D. Nikolos 1,2 & H. T. Vergos 1,2
 On - Line Path Delay Fault Testing of Omega MINs M. Bellos, E. Kalligeros, D. Nikolos,2 & H. T. Vergos,2 Dept. of Computer Engineering and Informatis 2 Computer Tehnology Institute University of Patras,
On - Line Path Delay Fault Testing of Omega MINs M. Bellos, E. Kalligeros, D. Nikolos,2 & H. T. Vergos,2 Dept. of Computer Engineering and Informatis 2 Computer Tehnology Institute University of Patras,
13.1 Numerical Evaluation of Integrals Over One Dimension
 13.1 Numerial Evaluation of Integrals Over One Dimension A. Purpose This olletion of subprograms estimates the value of the integral b a f(x) dx where the integrand f(x) and the limits a and b are supplied
13.1 Numerial Evaluation of Integrals Over One Dimension A. Purpose This olletion of subprograms estimates the value of the integral b a f(x) dx where the integrand f(x) and the limits a and b are supplied
Acoustic Links. Maximizing Channel Utilization for Underwater
 Maximizing Channel Utilization for Underwater Aousti Links Albert F Hairris III Davide G. B. Meneghetti Adihele Zorzi Department of Information Engineering University of Padova, Italy Email: {harris,davide.meneghetti,zorzi}@dei.unipd.it
Maximizing Channel Utilization for Underwater Aousti Links Albert F Hairris III Davide G. B. Meneghetti Adihele Zorzi Department of Information Engineering University of Padova, Italy Email: {harris,davide.meneghetti,zorzi}@dei.unipd.it
特集 Road Border Recognition Using FIR Images and LIDAR Signal Processing
 デンソーテクニカルレビュー Vol. 15 2010 特集 Road Border Reognition Using FIR Images and LIDAR Signal Proessing 高木聖和 バーゼル ファルディ Kiyokazu TAKAGI Basel Fardi ヘンドリック ヴァイゲル Hendrik Weigel ゲルド ヴァニーリック Gerd Wanielik This paper
デンソーテクニカルレビュー Vol. 15 2010 特集 Road Border Reognition Using FIR Images and LIDAR Signal Proessing 高木聖和 バーゼル ファルディ Kiyokazu TAKAGI Basel Fardi ヘンドリック ヴァイゲル Hendrik Weigel ゲルド ヴァニーリック Gerd Wanielik This paper
And, the (low-pass) Butterworth filter of order m is given in the frequency domain by
 Problem Set no.3.a) The ideal low-pass filter is given in the frequeny domain by B ideal ( f ), f f; =, f > f. () And, the (low-pass) Butterworth filter of order m is given in the frequeny domain by B
Problem Set no.3.a) The ideal low-pass filter is given in the frequeny domain by B ideal ( f ), f f; =, f > f. () And, the (low-pass) Butterworth filter of order m is given in the frequeny domain by B
Algorithms, Mechanisms and Procedures for the Computer-aided Project Generation System
 Algorithms, Mehanisms and Proedures for the Computer-aided Projet Generation System Anton O. Butko 1*, Aleksandr P. Briukhovetskii 2, Dmitry E. Grigoriev 2# and Konstantin S. Kalashnikov 3 1 Department
Algorithms, Mehanisms and Proedures for the Computer-aided Projet Generation System Anton O. Butko 1*, Aleksandr P. Briukhovetskii 2, Dmitry E. Grigoriev 2# and Konstantin S. Kalashnikov 3 1 Department
An Optimized Approach on Applying Genetic Algorithm to Adaptive Cluster Validity Index
 IJCSES International Journal of Computer Sienes and Engineering Systems, ol., No.4, Otober 2007 CSES International 2007 ISSN 0973-4406 253 An Optimized Approah on Applying Geneti Algorithm to Adaptive
IJCSES International Journal of Computer Sienes and Engineering Systems, ol., No.4, Otober 2007 CSES International 2007 ISSN 0973-4406 253 An Optimized Approah on Applying Geneti Algorithm to Adaptive
Department of Electrical and Computer Engineering University of Wisconsin Madison. Fall
 Department of Eletrial and Computer Engineering University of Wisonsin Madison ECE 553: Testing and Testable Design of Digital Systems Fall 2014-2015 Assignment #2 Date Tuesday, September 25, 2014 Due
Department of Eletrial and Computer Engineering University of Wisonsin Madison ECE 553: Testing and Testable Design of Digital Systems Fall 2014-2015 Assignment #2 Date Tuesday, September 25, 2014 Due
Cracked Hole Finite Element Modeling
 Craked Hole Finite Element Modeling (E-20-F72) Researh Report Submitted to: Lokheed Martin, Program Manager: Dr. Stephen P. Engelstad Prinipal Investigator: Dr. Rami M. Haj-Ali Shool of Civil and Environmental
Craked Hole Finite Element Modeling (E-20-F72) Researh Report Submitted to: Lokheed Martin, Program Manager: Dr. Stephen P. Engelstad Prinipal Investigator: Dr. Rami M. Haj-Ali Shool of Civil and Environmental
Outline: Software Design
 Outline: Software Design. Goals History of software design ideas Design priniples Design methods Life belt or leg iron? (Budgen) Copyright Nany Leveson, Sept. 1999 A Little History... At first, struggling
Outline: Software Design. Goals History of software design ideas Design priniples Design methods Life belt or leg iron? (Budgen) Copyright Nany Leveson, Sept. 1999 A Little History... At first, struggling
Algorithms for External Memory Lecture 6 Graph Algorithms - Weighted List Ranking
 Algorithms for External Memory Leture 6 Graph Algorithms - Weighted List Ranking Leturer: Nodari Sithinava Sribe: Andi Hellmund, Simon Ohsenreither 1 Introdution & Motivation After talking about I/O-effiient
Algorithms for External Memory Leture 6 Graph Algorithms - Weighted List Ranking Leturer: Nodari Sithinava Sribe: Andi Hellmund, Simon Ohsenreither 1 Introdution & Motivation After talking about I/O-effiient
Detecting Moving Targets in Clutter in Airborne SAR via Keystoning and Multiple Phase Center Interferometry
 Deteting Moving Targets in Clutter in Airborne SAR via Keystoning and Multiple Phase Center Interferometry D. M. Zasada, P. K. Sanyal The MITRE Corp., 6 Eletroni Parkway, Rome, NY 134 (dmzasada, psanyal)@mitre.org
Deteting Moving Targets in Clutter in Airborne SAR via Keystoning and Multiple Phase Center Interferometry D. M. Zasada, P. K. Sanyal The MITRE Corp., 6 Eletroni Parkway, Rome, NY 134 (dmzasada, psanyal)@mitre.org
BSPLND, A B-Spline N-Dimensional Package for Scattered Data Interpolation
 BSPLND, A B-Spline N-Dimensional Pakage for Sattered Data Interpolation Mihael P. Weis Traker Business Systems 85 Terminal Drive, Suite Rihland, WA 995-59-946-544 mike@vidian.net Robert R. Lewis Washington
BSPLND, A B-Spline N-Dimensional Pakage for Sattered Data Interpolation Mihael P. Weis Traker Business Systems 85 Terminal Drive, Suite Rihland, WA 995-59-946-544 mike@vidian.net Robert R. Lewis Washington
Define - starting approximation for the parameters (p) - observational data (o) - solution criterion (e.g. number of iterations)
 Global Iterative Solution Distributed proessing of the attitude updating L. Lindegren (21 May 2001) SAG LL 37 Abstrat. The attitude updating algorithm given in GAIA LL 24 (v. 2) is modified to allow distributed
Global Iterative Solution Distributed proessing of the attitude updating L. Lindegren (21 May 2001) SAG LL 37 Abstrat. The attitude updating algorithm given in GAIA LL 24 (v. 2) is modified to allow distributed
Review (Law of sines and cosine) cosines)
 Date:03/7,8/01 Review 6.1-6. Objetive: Apply the onept to use the law of the sines and osines to solve oblique triangles Apply the onept to find areas using the law of sines and osines Agenda: Bell ringer
Date:03/7,8/01 Review 6.1-6. Objetive: Apply the onept to use the law of the sines and osines to solve oblique triangles Apply the onept to find areas using the law of sines and osines Agenda: Bell ringer
BENDING STIFFNESS AND DYNAMIC CHARACTERISTICS OF A ROTOR WITH SPLINE JOINTS
 Proeedings of ASME 0 International Mehanial Engineering Congress & Exposition IMECE0 November 5-, 0, San Diego, CA IMECE0-6657 BENDING STIFFNESS AND DYNAMIC CHARACTERISTICS OF A ROTOR WITH SPLINE JOINTS
Proeedings of ASME 0 International Mehanial Engineering Congress & Exposition IMECE0 November 5-, 0, San Diego, CA IMECE0-6657 BENDING STIFFNESS AND DYNAMIC CHARACTERISTICS OF A ROTOR WITH SPLINE JOINTS
Calculation of typical running time of a branch-and-bound algorithm for the vertex-cover problem
 Calulation of typial running time of a branh-and-bound algorithm for the vertex-over problem Joni Pajarinen, Joni.Pajarinen@iki.fi Otober 21, 2007 1 Introdution The vertex-over problem is one of a olletion
Calulation of typial running time of a branh-and-bound algorithm for the vertex-over problem Joni Pajarinen, Joni.Pajarinen@iki.fi Otober 21, 2007 1 Introdution The vertex-over problem is one of a olletion
Exploring the Commonality in Feature Modeling Notations
 Exploring the Commonality in Feature Modeling Notations Miloslav ŠÍPKA Slovak University of Tehnology Faulty of Informatis and Information Tehnologies Ilkovičova 3, 842 16 Bratislava, Slovakia miloslav.sipka@gmail.om
Exploring the Commonality in Feature Modeling Notations Miloslav ŠÍPKA Slovak University of Tehnology Faulty of Informatis and Information Tehnologies Ilkovičova 3, 842 16 Bratislava, Slovakia miloslav.sipka@gmail.om
Numerical simulation of hemolysis: a comparison of Lagrangian and Eulerian modelling
 Modelling in Mediine and Biology VI 361 Numerial simulation of hemolysis: a omparison of Lagrangian and Eulerian modelling S. Pirker 1, H. Shima 2 & M. Stoiber 2 1 Johannes Kepler University, 4040 Linz,
Modelling in Mediine and Biology VI 361 Numerial simulation of hemolysis: a omparison of Lagrangian and Eulerian modelling S. Pirker 1, H. Shima 2 & M. Stoiber 2 1 Johannes Kepler University, 4040 Linz,
End mills are widely used in industry for high-speed machining. End milling cutters are C H A P T E R 2
 C H A P T E R End Mill End mills are widely used in industry for high-speed mahining. End milling utters are multi-point milling utters with utting edges both on the fae end as well as on the periphery,
C H A P T E R End Mill End mills are widely used in industry for high-speed mahining. End milling utters are multi-point milling utters with utting edges both on the fae end as well as on the periphery,
PARAMETRIC SAR IMAGE FORMATION - A PROMISING APPROACH TO RESOLUTION-UNLIMITED IMAGING. Yesheng Gao, Kaizhi Wang, Xingzhao Liu
 20th European Signal Proessing Conferene EUSIPCO 2012) Buharest, Romania, August 27-31, 2012 PARAMETRIC SAR IMAGE FORMATION - A PROMISING APPROACH TO RESOLUTION-UNLIMITED IMAGING Yesheng Gao, Kaizhi Wang,
20th European Signal Proessing Conferene EUSIPCO 2012) Buharest, Romania, August 27-31, 2012 PARAMETRIC SAR IMAGE FORMATION - A PROMISING APPROACH TO RESOLUTION-UNLIMITED IMAGING Yesheng Gao, Kaizhi Wang,
Defect Detection and Classification in Ceramic Plates Using Machine Vision and Naïve Bayes Classifier for Computer Aided Manufacturing
 Defet Detetion and Classifiation in Cerami Plates Using Mahine Vision and Naïve Bayes Classifier for Computer Aided Manufaturing 1 Harpreet Singh, 2 Kulwinderpal Singh, 1 Researh Student, 2 Assistant Professor,
Defet Detetion and Classifiation in Cerami Plates Using Mahine Vision and Naïve Bayes Classifier for Computer Aided Manufaturing 1 Harpreet Singh, 2 Kulwinderpal Singh, 1 Researh Student, 2 Assistant Professor,
Abstract. Key Words: Image Filters, Fuzzy Filters, Order Statistics Filters, Rank Ordered Mean Filters, Channel Noise. 1.
 Fuzzy Weighted Rank Ordered Mean (FWROM) Filters for Mixed Noise Suppression from Images S. Meher, G. Panda, B. Majhi 3, M.R. Meher 4,,4 Department of Eletronis and I.E., National Institute of Tehnology,
Fuzzy Weighted Rank Ordered Mean (FWROM) Filters for Mixed Noise Suppression from Images S. Meher, G. Panda, B. Majhi 3, M.R. Meher 4,,4 Department of Eletronis and I.E., National Institute of Tehnology,
Gradient based progressive probabilistic Hough transform
 Gradient based progressive probabilisti Hough transform C.Galambos, J.Kittler and J.Matas Abstrat: The authors look at the benefits of exploiting gradient information to enhane the progressive probabilisti
Gradient based progressive probabilisti Hough transform C.Galambos, J.Kittler and J.Matas Abstrat: The authors look at the benefits of exploiting gradient information to enhane the progressive probabilisti
Time delay estimation of reverberant meeting speech: on the use of multichannel linear prediction
 University of Wollongong Researh Online Faulty of Informatis - apers (Arhive) Faulty of Engineering and Information Sienes 7 Time delay estimation of reverberant meeting speeh: on the use of multihannel
University of Wollongong Researh Online Faulty of Informatis - apers (Arhive) Faulty of Engineering and Information Sienes 7 Time delay estimation of reverberant meeting speeh: on the use of multihannel
An Alternative Approach to the Fuzzifier in Fuzzy Clustering to Obtain Better Clustering Results
 An Alternative Approah to the Fuzziier in Fuzzy Clustering to Obtain Better Clustering Results Frank Klawonn Department o Computer Siene University o Applied Sienes BS/WF Salzdahlumer Str. 46/48 D-38302
An Alternative Approah to the Fuzziier in Fuzzy Clustering to Obtain Better Clustering Results Frank Klawonn Department o Computer Siene University o Applied Sienes BS/WF Salzdahlumer Str. 46/48 D-38302
Query Evaluation Overview. Query Optimization: Chap. 15. Evaluation Example. Cost Estimation. Query Blocks. Query Blocks
 Query Evaluation Overview Query Optimization: Chap. 15 CS634 Leture 12 SQL query first translated to relational algebra (RA) Atually, some additional operators needed for SQL Tree of RA operators, with
Query Evaluation Overview Query Optimization: Chap. 15 CS634 Leture 12 SQL query first translated to relational algebra (RA) Atually, some additional operators needed for SQL Tree of RA operators, with
UCSB Math TI-85 Tutorials: Basics
 3 UCSB Math TI-85 Tutorials: Basis If your alulator sreen doesn t show anything, try adjusting the ontrast aording to the instrutions on page 3, or page I-3, of the alulator manual You should read the
3 UCSB Math TI-85 Tutorials: Basis If your alulator sreen doesn t show anything, try adjusting the ontrast aording to the instrutions on page 3, or page I-3, of the alulator manual You should read the
A {k, n}-secret Sharing Scheme for Color Images
 A {k, n}-seret Sharing Sheme for Color Images Rastislav Luka, Konstantinos N. Plataniotis, and Anastasios N. Venetsanopoulos The Edward S. Rogers Sr. Dept. of Eletrial and Computer Engineering, University
A {k, n}-seret Sharing Sheme for Color Images Rastislav Luka, Konstantinos N. Plataniotis, and Anastasios N. Venetsanopoulos The Edward S. Rogers Sr. Dept. of Eletrial and Computer Engineering, University
Performance of Histogram-Based Skin Colour Segmentation for Arms Detection in Human Motion Analysis Application
 World Aademy of Siene, Engineering and Tehnology 8 009 Performane of Histogram-Based Skin Colour Segmentation for Arms Detetion in Human Motion Analysis Appliation Rosalyn R. Porle, Ali Chekima, Farrah
World Aademy of Siene, Engineering and Tehnology 8 009 Performane of Histogram-Based Skin Colour Segmentation for Arms Detetion in Human Motion Analysis Appliation Rosalyn R. Porle, Ali Chekima, Farrah
Unsupervised Stereoscopic Video Object Segmentation Based on Active Contours and Retrainable Neural Networks
 Unsupervised Stereosopi Video Objet Segmentation Based on Ative Contours and Retrainable Neural Networks KLIMIS NTALIANIS, ANASTASIOS DOULAMIS, and NIKOLAOS DOULAMIS National Tehnial University of Athens
Unsupervised Stereosopi Video Objet Segmentation Based on Ative Contours and Retrainable Neural Networks KLIMIS NTALIANIS, ANASTASIOS DOULAMIS, and NIKOLAOS DOULAMIS National Tehnial University of Athens
Detecting Outliers in High-Dimensional Datasets with Mixed Attributes
 Deteting Outliers in High-Dimensional Datasets with Mixed Attributes A. Koufakou, M. Georgiopoulos, and G.C. Anagnostopoulos 2 Shool of EECS, University of Central Florida, Orlando, FL, USA 2 Dept. of
Deteting Outliers in High-Dimensional Datasets with Mixed Attributes A. Koufakou, M. Georgiopoulos, and G.C. Anagnostopoulos 2 Shool of EECS, University of Central Florida, Orlando, FL, USA 2 Dept. of
Semi-Supervised Affinity Propagation with Instance-Level Constraints
 Semi-Supervised Affinity Propagation with Instane-Level Constraints Inmar E. Givoni, Brendan J. Frey Probabilisti and Statistial Inferene Group University of Toronto 10 King s College Road, Toronto, Ontario,
Semi-Supervised Affinity Propagation with Instane-Level Constraints Inmar E. Givoni, Brendan J. Frey Probabilisti and Statistial Inferene Group University of Toronto 10 King s College Road, Toronto, Ontario,
Fitting conics to paracatadioptric projections of lines
 Computer Vision and Image Understanding 11 (6) 11 16 www.elsevier.om/loate/viu Fitting onis to paraatadioptri projetions of lines João P. Barreto *, Helder Araujo Institute for Systems and Robotis, Department
Computer Vision and Image Understanding 11 (6) 11 16 www.elsevier.om/loate/viu Fitting onis to paraatadioptri projetions of lines João P. Barreto *, Helder Araujo Institute for Systems and Robotis, Department
Parallelization and Performance of 3D Ultrasound Imaging Beamforming Algorithms on Modern Clusters
 Parallelization and Performane of 3D Ultrasound Imaging Beamforming Algorithms on Modern Clusters F. Zhang, A. Bilas, A. Dhanantwari, K.N. Plataniotis, R. Abiprojo, and S. Stergiopoulos Dept. of Eletrial
Parallelization and Performane of 3D Ultrasound Imaging Beamforming Algorithms on Modern Clusters F. Zhang, A. Bilas, A. Dhanantwari, K.N. Plataniotis, R. Abiprojo, and S. Stergiopoulos Dept. of Eletrial
Chromaticity-matched Superimposition of Foreground Objects in Different Environments
 FCV216, the 22nd Korea-Japan Joint Workshop on Frontiers of Computer Vision Chromatiity-mathed Superimposition of Foreground Objets in Different Environments Yohei Ogura Graduate Shool of Siene and Tehnology
FCV216, the 22nd Korea-Japan Joint Workshop on Frontiers of Computer Vision Chromatiity-mathed Superimposition of Foreground Objets in Different Environments Yohei Ogura Graduate Shool of Siene and Tehnology
CUTTING FORCES AND CONSECUTIVE DEFORMATIONS AT MILLING PARTS WITH THIN WALLS
 Proeedings of the International Conferene on Manufaturing Systems ICMaS Vol. 4, 2009, ISSN 1842-3183 University POLITEHNICA of Buharest, Mahine and Manufaturing Systems Department Buharest, Romania CUTTING
Proeedings of the International Conferene on Manufaturing Systems ICMaS Vol. 4, 2009, ISSN 1842-3183 University POLITEHNICA of Buharest, Mahine and Manufaturing Systems Department Buharest, Romania CUTTING
Graph-Based vs Depth-Based Data Representation for Multiview Images
 Graph-Based vs Depth-Based Data Representation for Multiview Images Thomas Maugey, Antonio Ortega, Pasal Frossard Signal Proessing Laboratory (LTS), Eole Polytehnique Fédérale de Lausanne (EPFL) Email:
Graph-Based vs Depth-Based Data Representation for Multiview Images Thomas Maugey, Antonio Ortega, Pasal Frossard Signal Proessing Laboratory (LTS), Eole Polytehnique Fédérale de Lausanne (EPFL) Email:
Lecture Notes of Möbuis Transformation in Hyperbolic Plane
 Applied Mathematis, 04, 5, 6-5 Published Online August 04 in SiRes http://wwwsirporg/journal/am http://dxdoiorg/0436/am04555 Leture Notes of Möbuis Transformation in Hyperboli Plane Rania B M Amer Department
Applied Mathematis, 04, 5, 6-5 Published Online August 04 in SiRes http://wwwsirporg/journal/am http://dxdoiorg/0436/am04555 Leture Notes of Möbuis Transformation in Hyperboli Plane Rania B M Amer Department
1. Introduction. 2. The Probable Stope Algorithm
 1. Introdution Optimization in underground mine design has reeived less attention than that in open pit mines. This is mostly due to the diversity o underground mining methods and omplexity o underground
1. Introdution Optimization in underground mine design has reeived less attention than that in open pit mines. This is mostly due to the diversity o underground mining methods and omplexity o underground
Optimization of Two-Stage Cylindrical Gear Reducer with Adaptive Boundary Constraints
 5 JOURNAL OF SOFTWARE VOL. 8 NO. 8 AUGUST Optimization of Two-Stage Cylindrial Gear Reduer with Adaptive Boundary Constraints Xueyi Li College of Mehanial and Eletroni Engineering Shandong University of
5 JOURNAL OF SOFTWARE VOL. 8 NO. 8 AUGUST Optimization of Two-Stage Cylindrial Gear Reduer with Adaptive Boundary Constraints Xueyi Li College of Mehanial and Eletroni Engineering Shandong University of
Mean Deviation Similarity Index: Efficient and Reliable Full-Reference Image Quality Evaluator
 1 Mean Deviation Similarity Index: Effiient and Reliable Full-Referene Image Quality Evaluator Hossein Ziaei Nafhi, Atena Shahkolaei, Rahid Hedjam, and Mohamed Cheriet, Senior Member, IEEE two images of
1 Mean Deviation Similarity Index: Effiient and Reliable Full-Referene Image Quality Evaluator Hossein Ziaei Nafhi, Atena Shahkolaei, Rahid Hedjam, and Mohamed Cheriet, Senior Member, IEEE two images of
Projections. Let us start with projections in 2D, because there are easier to visualize.
 Projetions Let us start ith projetions in D, beause there are easier to visualie. Projetion parallel to the -ais: Ever point in the -plane ith oordinates (, ) ill be transformed into the point ith oordinates
Projetions Let us start ith projetions in D, beause there are easier to visualie. Projetion parallel to the -ais: Ever point in the -plane ith oordinates (, ) ill be transformed into the point ith oordinates
Colouring contact graphs of squares and rectilinear polygons de Berg, M.T.; Markovic, A.; Woeginger, G.
 Colouring ontat graphs of squares and retilinear polygons de Berg, M.T.; Markovi, A.; Woeginger, G. Published in: nd European Workshop on Computational Geometry (EuroCG 06), 0 Marh - April, Lugano, Switzerland
Colouring ontat graphs of squares and retilinear polygons de Berg, M.T.; Markovi, A.; Woeginger, G. Published in: nd European Workshop on Computational Geometry (EuroCG 06), 0 Marh - April, Lugano, Switzerland
Reading Object Code. A Visible/Z Lesson
 Reading Objet Code A Visible/Z Lesson The Idea: When programming in a high-level language, we rarely have to think about the speifi ode that is generated for eah instrution by a ompiler. But as an assembly
Reading Objet Code A Visible/Z Lesson The Idea: When programming in a high-level language, we rarely have to think about the speifi ode that is generated for eah instrution by a ompiler. But as an assembly
Automatic Physical Design Tuning: Workload as a Sequence Sanjay Agrawal Microsoft Research One Microsoft Way Redmond, WA, USA +1-(425)
 Automati Physial Design Tuning: Workload as a Sequene Sanjay Agrawal Mirosoft Researh One Mirosoft Way Redmond, WA, USA +1-(425) 75-357 sagrawal@mirosoft.om Eri Chu * Computer Sienes Department University
Automati Physial Design Tuning: Workload as a Sequene Sanjay Agrawal Mirosoft Researh One Mirosoft Way Redmond, WA, USA +1-(425) 75-357 sagrawal@mirosoft.om Eri Chu * Computer Sienes Department University
3-D IMAGE MODELS AND COMPRESSION - SYNTHETIC HYBRID OR NATURAL FIT?
 3-D IMAGE MODELS AND COMPRESSION - SYNTHETIC HYBRID OR NATURAL FIT? Bernd Girod, Peter Eisert, Marus Magnor, Ekehard Steinbah, Thomas Wiegand Te {girod eommuniations Laboratory, University of Erlangen-Nuremberg
3-D IMAGE MODELS AND COMPRESSION - SYNTHETIC HYBRID OR NATURAL FIT? Bernd Girod, Peter Eisert, Marus Magnor, Ekehard Steinbah, Thomas Wiegand Te {girod eommuniations Laboratory, University of Erlangen-Nuremberg
Reading Object Code. A Visible/Z Lesson
 Reading Objet Code A Visible/Z Lesson The Idea: When programming in a high-level language, we rarely have to think about the speifi ode that is generated for eah instrution by a ompiler. But as an assembly
Reading Objet Code A Visible/Z Lesson The Idea: When programming in a high-level language, we rarely have to think about the speifi ode that is generated for eah instrution by a ompiler. But as an assembly
