Figure 1: An Area Voronoi Diagram of a typical GIS Scene generated from the ISPRS Working group III/3 Avenches data set. 2 ARRANGEMENTS 2.1 Voronoi Di
|
|
|
- Darcy Scott
- 6 years ago
- Views:
Transcription
1 Qualitative Spatial Relations using Arrangements for Complex Images M. Burge and W. Burger Johannes Kepler University, Department of Systems Science Computer Vision Laboratory, A-4040 Linz, Austria July 2, 1997 Abstract A new spatial relation called arrangements has been previously proposed (H.M. Tagare et al., \Arrangement: A Spatial Relation Between Parts for Evaluating Similarity of Tomographic Section," IEEE PAMI, 17 (9), pp. 880{893, 1995) to describe how embedded parts in an image are surrounded by their neighbors. Arrangements can be derived directly from the sequence of Voronoi cells bordering an embedded part in an image. It has been show that it is possible to compare any two arrangements, caused by the embedding of the same parts, by use of the Diagonal Exchange Operator and the Voronoi Flower diagram. However, the algorithms previously proposed is practical only for very small sets of embedded parts because of both the expensive operation of computing the prerequisite area Voronoi tessellation and the exponential search complexity (in terms of the number of edges in the Voronoi tessellation) required to compute the distance metric. We present a new algorithm for computing arrangements eciently for complex images containing a large number of embedded parts. Motivated by the new algorithm, we propose the use of arrangements for the indexing and retrieval of complex technical diagrams which may contain many similar parts. 1 INTRODUCTION In the rst part of the paper the theoretical foundation for arrangements is presented. The Voronoi diagram is introduced and the necessary generalization for machine vision to area based attractors is shown. The basic theory allowing for the comparing two Voronoi diagrams with the same parts is shown. It is based upon using a series of applications of the diagonal exchange operator to convert each diagram into it's canonical Voronoi ower diagram. After establishing the theoretical foundation for the comparison of the diagrams, a method for computing the distance metric based on the exchange tree is shown. This method is shown to be exponential in complexity and therefore unsuited for our usage. A new algorithm for the computation of arrangements for real world images with many parts is presented in the second part of the paper. Motivated by the new algorithm the nal section discusses the retrieval of complex technical diagrams based upon their arrangements.
2 Figure 1: An Area Voronoi Diagram of a typical GIS Scene generated from the ISPRS Working group III/3 Avenches data set. 2 ARRANGEMENTS 2.1 Voronoi Diagram Voronoi neighborhoods provide an intuitively appealing denition of the neighborhood of an embedded part, namely, the neighborhood which corresponds to that portion of the Euclidean plane which is closer to any given part than to any other. The advantages of dening neighborhoods in this way has been shown by Ahuja[1] in 1982 and more recently by Okabe, Boots, and Sugihara[2]. To achieve similar results in the general case, one solution is to use a generalized Voronoi diagram which is suited to arbitrarily shaped image elements and still exhibits the desired properties of the normal Voronoi tessellation. Generalized Voronoi diagrams are dened by generalizing ordinary Voronoi diagrams with respect to either the distance measure (e.g. Euclidean, Manhattan), the space (e.g. two dimensional Cartesian, three dimensional spherical), or the generator set (e.g. point, area). The point based Voronoi tessellation[2] is unsuited to image understanding as the useful primitives are not the individual pixels corresponding to geometric points, but groups of pixels corresponding to segments, arcs, ellipses, or polygonal objects. Rather a generalized Voronoi tessellation (which we will call the area Voronoi tessellation) using an Euclidean distance measure, a two dimensional Cartesian space, and an area generator set is a good choice. O(n log n) algorithms for certain generalized tessellation have been presented by several authors including Yap[3] for curves, and Mayya and Rajan[4] for polygons, and the approximated area based Voronoi tessellation for generic shapes of Burge and Monagan[5]. 2.2 Area Based Voronoi Diagram We use the denition of the area Voronoi tessellation presented by Okabe Boots, and Sugihara[2], which is as follows. Given that A x ; : : : ; A n are parts and that p and q are locations in the image, we can dene the distance, d a (p; A i ), from p to A i as: 2
3 d a (p; A i ) = min q2a i d (p; q) (1) where this represents the minimum Euclidean distance from p to any location in A i. Using this d a, they dene the area Voronoi region, V a (A i ), as the set of locations from which the distance to A i is less than or equal to the distance to any other areas: V a (A i ) = fpjd a (p; A i ) d a (p; A j ) ; j 6= i; j = 1; : : : ; ng: (2) For brevity we will let N i = V a (A i ), and the area Voronoi tessellation is then the set V = fn x ; : : : ; N i g. An example of an area Voronoi diagram can be seen in Figure 1 generated from the ISPRS Working group III/3 Avenches data set. 2.3 Mathematical Foundation for Comparing Arrangements Tagare et al. [6] have previously laid the mathematical foundation for the comparison of two Voronoi diagrams, V x and V y with the same parts. They have shown that one can convert V x into V y using a series of applications of the diagonal exchange operator, call this sequence x, to convert rst V x into it's ower, F x, and then V y to it's ower, F y. They have show that when V x and V y have the same parts, then their ower diagrams are equivalent, F x = F y, and the sequence to convert V x into V y is the combination of the sequence, x, to convert V x into it's ower and the inverse of the sequence,?1 y, to convert V y into it's ower, that is: x (V x ) = F x = F y = y (V y ) x (V x ) = y (V y )?1 y ( x (V x )) = V y Listing the adjacent cells of a given cell in counterclockwise order produces the sequence termed the arrangement of N 0. Given a section of a Voronoi diagram with the following arrangements: N0 N1 N2 Before N3 N 0 : N 2 ; N 1 N 1 : N 0 ; N 2 ; N 3 N 2 : N 3 ; N 1 ; N 0 N 3 : N 1 ; N 2 N0 N1 N2 After N3 N 0 : N 2 ; N 3 ; N 1 N 1 : N 0 ; N 3 N 2 : N 3 ; N 0 N 3 : N 1 ; N 0 ; N 2 Figure 2: Application of the Diagonal Exchange Operator to a Voronoi conguration. 3
4 In Figure 2 on the left side the initial conguration of a section of a Voronoi diagram is shown, and it's arrangement. The right side shows the resulting gure and it's arrangement after the application of the diagonal exchange operator. The operator works locally, that is after application of the operator only the relation between the four parts are aected while the rest of the diagram remains the same. Another characteristic of the operator is that it is reversible, applying it twice to the same edge results in the original diagram, or more generally applying it an even number of times results in no change and an odd number of times is equivalent to applying it once. If a sequence of exchanges,, applied to V 1 results in V 2 then application of the inverse of this sequence,?1, to V 2 results in V 1. It is not obvious the order in which to apply the diagonal exchange operator to convert V 1 into V 2. Tagare shows that such a sequence does exist, and gives a constructive algorithm for nding it. This involves the used of the ower diagram, which is a canonical representation of a Voronoi diagram with n parts, he shows that any Voronoi diagram of n parts can be reduced using the diagonal exchange operator to the canonical diagram of size n. 2.4 Exchange Tree Tagare proved constructively that their exists a sequence of diagonal exchange operators,, to convert any two Voronoi diagrams, V 1 and V 2, with the same parts into one another, but this sequence does not meet the criterion of a distance, notably it is not necessarily minimum length. To use the diagonal exchange operator as a distance measure, d(v x ; V y ), one must be able to compute the size of the minimum length sequence between V x and V y. The diagonal exchange tree was proposed by Tagare[6] to compute this distance. It is a tree rooted at V x with each exchangeable edge of V x represented by a branch from V x to the node consisting of the new Voronoi diagram formed by the application of the diagonal exchange operator to that edge of V x, the tree continues recursively for each of these new Voronoi diagrams. Since every possible sequence of operators exists as a path in the tree, then it is guaranteed that V y exists in the tree. The distance measure can be computed using a breadth rst search of the tree to nd the number of levels from V x to V y in the tree. Even with some simple pruning rules arising from the nature of the diagonal exchange operator, this tree will be exponential on the order of the number of edges of V x. As the only way to nd V y in the tree is by breadth rst search, and since the tree grows exponentially, the search time will also be exponential. The exchange tree can not be used for computing the distance, d(v x ; V y ), when the number of parts, and consequentially the number of edges, is at all large. As an example the number of parts in Tagare's examples[6] is never larger than 5 and no more than one part is allowed to be dierent between the sets. As a result a new method of calculating the distance metric for a large number of parts must be found. 4
5 Figure 3: Computing Arrangements from the point set representation of the parts. The left shows the complete Delaunay triangulation while the right shows the nal Area Voronoi tessellation after application of rule (3) to remove certain Delaunay triangles, arrangements are calculated directly at this stage. 3 COMPUTING ARRANGEMENTS OF MANY PARTS To compute arrangements for complex images containing many parts it suces to compute an approximation of the area Voronoi tessellation which is topologically correct. One of two methods are commonly used to create an approximation to the area Voronoi tessellation. The rst method is to represent each part of the image as a point, typically it's centroid, and to then calculate the point tessellation based on this point list. This results in a poor approximation of the area tessellation but is useful in some domains, particularly those in which the parts are circular. The second method is to sample the edges of the parts and to compute the point tessellation based upon this point set. Then each Voronoi edge is examined to determine if it intersects a part, and if so, it is removed. This is an expensive process; the representation of the Voronoi edges, e.g. as a list of points, segments, or curves, determines the complexity of the process. If for example we represent the Voronoi edges with a sequence of points, then we must examine each point of each edge for an intersection with each part. The algorithm we present in this paper improves on this by rst constructing the Delaunay triangulation, the dual of the Voronoi tessellation, and concurrently removing those Delaunay edges which would give rise to Voronoi edges which would intersect with the parts. The test for removal of these edges is performed in constant time. We begin with an image in which each pixel is labeled as either belonging to an embedded part or to the background. We allow embedded parts to exhibit any shape but require that they be contiguous. Each part is sampled along its boundary at key points to obtain a list of representative boundary points. Using these points, the Delaunay triangulation is computed. The Delaunay triangulation of the points is then be processed to remove those Delaunay quads (two adjacent Delaunay triangles) which originate from the same part. Intuitively, 5
6 these are the Delaunay triangles which are within an part, and therefore would not be present in the area Voronoi tessellation. More specically, the Delaunay triangles are removed if the following rule evaluates to true: ((C(V a ) = C(V b )) ^ (C(V b ) = C(V c ))) _ ((C(V b ) = C(V d )) ^ (C(V d ) = C(V c ))) (3) where, V a 6= V b 6= V c 6= V d and given a vertex V x of a Delaunay triangle, C(V x ) is a function which returns the label of the part upon which the vertex is located. We have observed that as the visual complexity of the image elements increases, the overall percentage of Delaunay triangles that we can remove increases, for images such as those shown, an average of 36% of the Delaunay triangles can be removed using rule (3), resulting in more ecent computation of the Area Voronoi tessellation. The algorithm creates an approximation to the true tessellation which is dependent upon the sampling rate selected, with higher rates corresponding to better approximations. Even at relatively low sampling rates, the topology of the created tessellation is correct and sucient for computing arrangements. For details of the algorithm and analysis of the complexity please see Burge and Monagan's 1995 paper on the construction of Area Voronoi Diagrams.[5]. At this point arrangements can be calculated directly from the area Voronoi diagram of the parts. For each part, the Voronoi cells adjacent to it listed in a counter clockwise order are the arrangements of that part. 4 ARRANGEMENTS FOR IMAGE RETRIEVAL Given a set of technical diagrams in which the parts have been previously labeled we wish to retrieve diagrams containing a certain combination, or assembly, of parts. Due to industrial standardization technical diagrams of mechanical devices contain many of the same parts, eg. bolts, gaskets, nuts, tubes, and so forth. Important assemblies are made up of combinations of standardized parts in dierent arrangements. The retrieval of all diagrams containing a specic assembly is a common problem in industry, and one can not simply query the system for all diagrams containing instances of 10 bolts, 2 gaskets, 3 tubes and a distributor. Arrangements can be used as a method of retrieval when not only the parts, but the spatial arrangement of them is important. The problem of nding the arrangement corresponding to an assembly in a large technical diagram is similar to that of \word spotting" in speech recognition. In Figure 4 the \word" we wish to spot is shown in the middle. The \word" in the same arrangement can be found in both the left and right images. In the right image it is in a dierent orientation, but still in the same arrangement. Partial matches can also be found, such as in the lower left hand corner of the right image. It should be pointed out that we are not searching based on the shape of the Voronoi cells, which we have found in previous research[7] to be too variable 1, but on the arrangement of the cells. We are currently experimenting with a dynamic programming algorithm we have developed based upon evidence collection[8] and partial string matching[9]. 1 Note for instance the shape of the Voronoi cell of the large pipe in both images, it of course varies based upon the spatial arrangement and shape of it's neighbors. 6
7 Section (A) Assembly Section (B) N0 N1 N2 N3 N3 N0 N2 N1 Arrangement of Labeled Parts N 0 : N 1 ; N 2 N 1 : N 2 ; N 0 N 2 : N 0 ; N 1 ; N 3 N 3 : N 2 Arrangement of Labeled Parts N 0 : N 1 ; N 2 N 1 : N 2 ; N 0 N 2 : N 3 ; N 0 ; N 1 N 3 : N 2 Figure 4: Retrieving technical diagrams based on similar assemblies. Both Right and Left sections contain the assembly shown in the Middle. The arrangements for the assembly in each section are shown underneath, note that string rotations within an arrangement, as in N 2, are considered equivalent. 5 CONCLUSION The mathematical basis for the comparison of images with the same parts using arrangements was summarized. It was shown that the previously developed algorithm for computing the distance metric has exponential complexity in the number of edges of the Voronoi diagram and is therefore unsuited for use in images with many parts. The problem of computing arrangements for images with many parts was introduced and a new algorithm to solve it was presented. Searching for assemblies of parts in collections of complex technical diagrams was shown as a motivation for the usage of arrangements of many parts. 6 BIOGRAPHY Mark Burge received the BS degree from Ohio Wesleyan University in 1990 and the MS degree from The Ohio State University in 1993, both in computer science. In 1993 he joined the computer science department of The Swiss Federal Institute of Technology in Zurich and is currently a research assistant at the Johannes Kepler University in Austria. Wilhelm Burger received the MS degree from the University of Utah in 1985 and the PhD from Johannes Kepler University in Linz, Austria, in He is the head of the computer vision group within the Dept. of Systems Science at Johannes Kepler University. This work was supported in part by the Austrian Science Foundation (FWF) under grant S
8 References [1] N. Ahuja. Dot pattern processing using voronoi neighborhoods. IEEE PAMI, 4(3):336{343, [2] A. Okabe, B. Boots, and K. Sugihara. Nearest neighbourhood operations with generalized Voronoi diagrams: a review. International Journal of Geographical Information Systems, 8(1):43{71, January-February [3] C. Yap. An O(n log n) algorithm for the voronoi diagram of a set of simple curve segments. Discrete Computational Geometry, 2:365{393, [4] N. Mayya and V.T. Rajan. Voronoi diagrams of polygons: A framework for shape representation. In CVPR94, pages 638{643, [5] M. Burge and G. Monagan. Using the voronoi tessellation for grouping words and multipart symbols in documents. In VISION GEOMETRY IV, volume 2573, pages 116{123, San Diego, California, July SPIE. Online at [6] H. Tagare, F. Vos, C. Jae, and J. Duncan. Arrangement: A spatial relation between parts for evaluating similarity of tomographic section. IEEE Trans. Pattern Analysis and Machine Intelligence, 9(17):880{893, [7] M. Burge and G. Monagan. Extracting words and multi-part symbols in graphics rich documents. In 8th ICIAP, Lecture Notes in Computer Science, pages 533{538, San Remo, Italy, September 13{ IAPR, Springer Verlag. Online at [8] A.K. Jain and R. Homan. Evidence-based recognition of 3D objects. PAMI, 10(6):783{802, November [9] D. Sanko and J. Kruskal. Time Warps, String Edits, and Macromolecules: The Theory and practice of sequence comparison. Addison-Wesley, Inc., Reading, Massachusetts,
Conjectures concerning the geometry of 2-point Centroidal Voronoi Tessellations
 Conjectures concerning the geometry of 2-point Centroidal Voronoi Tessellations Emma Twersky May 2017 Abstract This paper is an exploration into centroidal Voronoi tessellations, or CVTs. A centroidal
Conjectures concerning the geometry of 2-point Centroidal Voronoi Tessellations Emma Twersky May 2017 Abstract This paper is an exploration into centroidal Voronoi tessellations, or CVTs. A centroidal
Voronoi Diagrams in the Plane. Chapter 5 of O Rourke text Chapter 7 and 9 of course text
 Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
2) For any triangle edge not on the boundary, there is exactly one neighboring
 Triangulating Trimmed NURBS Surfaces Chang Shu and Pierre Boulanger Abstract. This paper describes techniques for the piecewise linear approximation of trimmed NURBS surfaces. The problem, called surface
Triangulating Trimmed NURBS Surfaces Chang Shu and Pierre Boulanger Abstract. This paper describes techniques for the piecewise linear approximation of trimmed NURBS surfaces. The problem, called surface
Algorithm That Mimics Human Perceptual Grouping of Dot Patterns
 Algorithm That Mimics Human Perceptual Grouping of Dot Patterns G. Papari and N. Petkov Institute of Mathematics and Computing Science, University of Groningen, P.O.Box 800, 9700 AV Groningen, The Netherlands
Algorithm That Mimics Human Perceptual Grouping of Dot Patterns G. Papari and N. Petkov Institute of Mathematics and Computing Science, University of Groningen, P.O.Box 800, 9700 AV Groningen, The Netherlands
Dominating Sets in Planar Graphs 1
 Dominating Sets in Planar Graphs 1 Lesley R. Matheson 2 Robert E. Tarjan 2; May, 1994 Abstract Motivated by an application to unstructured multigrid calculations, we consider the problem of asymptotically
Dominating Sets in Planar Graphs 1 Lesley R. Matheson 2 Robert E. Tarjan 2; May, 1994 Abstract Motivated by an application to unstructured multigrid calculations, we consider the problem of asymptotically
Fast Computation of Generalized Voronoi Diagrams Using Graphics Hardware
 Fast Computation of Generalized Voronoi Diagrams Using Graphics Hardware paper by Kennet E. Hoff et al. (University of North Carolina at Chapel Hill) presented by Daniel Emmenegger GDV-Seminar ETH Zürich,
Fast Computation of Generalized Voronoi Diagrams Using Graphics Hardware paper by Kennet E. Hoff et al. (University of North Carolina at Chapel Hill) presented by Daniel Emmenegger GDV-Seminar ETH Zürich,
Progress in Image Analysis and Processing III, pp , World Scientic, Singapore, AUTOMATIC INTERPRETATION OF FLOOR PLANS USING
 Progress in Image Analysis and Processing III, pp. 233-240, World Scientic, Singapore, 1994. 1 AUTOMATIC INTERPRETATION OF FLOOR PLANS USING SPATIAL INDEXING HANAN SAMET AYA SOFFER Computer Science Department
Progress in Image Analysis and Processing III, pp. 233-240, World Scientic, Singapore, 1994. 1 AUTOMATIC INTERPRETATION OF FLOOR PLANS USING SPATIAL INDEXING HANAN SAMET AYA SOFFER Computer Science Department
Enumeration of Full Graphs: Onset of the Asymptotic Region. Department of Mathematics. Massachusetts Institute of Technology. Cambridge, MA 02139
 Enumeration of Full Graphs: Onset of the Asymptotic Region L. J. Cowen D. J. Kleitman y F. Lasaga D. E. Sussman Department of Mathematics Massachusetts Institute of Technology Cambridge, MA 02139 Abstract
Enumeration of Full Graphs: Onset of the Asymptotic Region L. J. Cowen D. J. Kleitman y F. Lasaga D. E. Sussman Department of Mathematics Massachusetts Institute of Technology Cambridge, MA 02139 Abstract
6. Concluding Remarks
 [8] K. J. Supowit, The relative neighborhood graph with an application to minimum spanning trees, Tech. Rept., Department of Computer Science, University of Illinois, Urbana-Champaign, August 1980, also
[8] K. J. Supowit, The relative neighborhood graph with an application to minimum spanning trees, Tech. Rept., Department of Computer Science, University of Illinois, Urbana-Champaign, August 1980, also
BMVC 1996 doi: /c.10.41
 On the use of the 1D Boolean model for the description of binary textures M Petrou, M Arrigo and J A Vons Dept. of Electronic and Electrical Engineering, University of Surrey, Guildford GU2 5XH, United
On the use of the 1D Boolean model for the description of binary textures M Petrou, M Arrigo and J A Vons Dept. of Electronic and Electrical Engineering, University of Surrey, Guildford GU2 5XH, United
Chapter 7 Spatial Operation
 7.1 Introduction Chapter 7 Spatial Operation Q: What is spatial operation? A: Spatial operation is computational manipulation of spatial objects that deepen our understanding of spatial phenomena. In spatial
7.1 Introduction Chapter 7 Spatial Operation Q: What is spatial operation? A: Spatial operation is computational manipulation of spatial objects that deepen our understanding of spatial phenomena. In spatial
A Cell-centered, Agent-based Method that utilizes a Delaunay and Voronoi Environment in 2- and 3-Dimensions
 A Cell-centered, Agent-based Method that utilizes a Delaunay and Voronoi Environment in 2- and 3-Dimensions Ryan C. Kennedy 1, Glen E.P. Ropella 2, C. Anthony Hunt 1 1 Department of Bioengineering and
A Cell-centered, Agent-based Method that utilizes a Delaunay and Voronoi Environment in 2- and 3-Dimensions Ryan C. Kennedy 1, Glen E.P. Ropella 2, C. Anthony Hunt 1 1 Department of Bioengineering and
N. Hitschfeld. Blanco Encalada 2120, Santiago, CHILE.
 Generalization of modied octrees for geometric modeling N. Hitschfeld Dpto. Ciencias de la Computacion, Univ. de Chile Blanco Encalada 2120, Santiago, CHILE E-mail: nancy@dcc.uchile.cl Abstract. This paper
Generalization of modied octrees for geometric modeling N. Hitschfeld Dpto. Ciencias de la Computacion, Univ. de Chile Blanco Encalada 2120, Santiago, CHILE E-mail: nancy@dcc.uchile.cl Abstract. This paper
Fuzzy Voronoi Diagram
 Fuzzy Voronoi Diagram Mohammadreza Jooyandeh and Ali Mohades Khorasani Mathematics and Computer Science, Amirkabir University of Technology, Hafez Ave., Tehran, Iran mohammadreza@jooyandeh.info,mohades@aut.ac.ir
Fuzzy Voronoi Diagram Mohammadreza Jooyandeh and Ali Mohades Khorasani Mathematics and Computer Science, Amirkabir University of Technology, Hafez Ave., Tehran, Iran mohammadreza@jooyandeh.info,mohades@aut.ac.ir
UPEM Master 2 Informatique SIS. Digital Geometry. Topic 2: Digital topology: object boundaries and curves/surfaces. Yukiko Kenmochi.
 UPEM Master 2 Informatique SIS Digital Geometry Topic 2: Digital topology: object boundaries and curves/surfaces Yukiko Kenmochi October 5, 2016 Digital Geometry : Topic 2 1/34 Opening Representations
UPEM Master 2 Informatique SIS Digital Geometry Topic 2: Digital topology: object boundaries and curves/surfaces Yukiko Kenmochi October 5, 2016 Digital Geometry : Topic 2 1/34 Opening Representations
Planar Graphs. 1 Graphs and maps. 1.1 Planarity and duality
 Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Chapter 8. Voronoi Diagrams. 8.1 Post Oce Problem
 Chapter 8 Voronoi Diagrams 8.1 Post Oce Problem Suppose there are n post oces p 1,... p n in a city. Someone who is located at a position q within the city would like to know which post oce is closest
Chapter 8 Voronoi Diagrams 8.1 Post Oce Problem Suppose there are n post oces p 1,... p n in a city. Someone who is located at a position q within the city would like to know which post oce is closest
u 0+u 2 new boundary vertex
 Combined Subdivision Schemes for the design of surfaces satisfying boundary conditions Adi Levin School of Mathematical Sciences, Tel-Aviv University, Tel-Aviv 69978, Israel. Email:fadilev@math.tau.ac.ilg
Combined Subdivision Schemes for the design of surfaces satisfying boundary conditions Adi Levin School of Mathematical Sciences, Tel-Aviv University, Tel-Aviv 69978, Israel. Email:fadilev@math.tau.ac.ilg
Isosurface Rendering. CSC 7443: Scientific Information Visualization
 Isosurface Rendering What is Isosurfacing? An isosurface is the 3D surface representing the locations of a constant scalar value within a volume A surface with the same scalar field value Isosurfaces form
Isosurface Rendering What is Isosurfacing? An isosurface is the 3D surface representing the locations of a constant scalar value within a volume A surface with the same scalar field value Isosurfaces form
Fast Distance Transform Computation using Dual Scan Line Propagation
 Fast Distance Transform Computation using Dual Scan Line Propagation Fatih Porikli Tekin Kocak Mitsubishi Electric Research Laboratories, Cambridge, USA ABSTRACT We present two fast algorithms that approximate
Fast Distance Transform Computation using Dual Scan Line Propagation Fatih Porikli Tekin Kocak Mitsubishi Electric Research Laboratories, Cambridge, USA ABSTRACT We present two fast algorithms that approximate
13.472J/1.128J/2.158J/16.940J COMPUTATIONAL GEOMETRY
 13.472J/1.128J/2.158J/16.940J COMPUTATIONAL GEOMETRY Lecture 23 Dr. W. Cho Prof. N. M. Patrikalakis Copyright c 2003 Massachusetts Institute of Technology Contents 23 F.E. and B.E. Meshing Algorithms 2
13.472J/1.128J/2.158J/16.940J COMPUTATIONAL GEOMETRY Lecture 23 Dr. W. Cho Prof. N. M. Patrikalakis Copyright c 2003 Massachusetts Institute of Technology Contents 23 F.E. and B.E. Meshing Algorithms 2
Robot Motion Planning Using Generalised Voronoi Diagrams
 Robot Motion Planning Using Generalised Voronoi Diagrams MILOŠ ŠEDA, VÁCLAV PICH Institute of Automation and Computer Science Brno University of Technology Technická 2, 616 69 Brno CZECH REPUBLIC Abstract:
Robot Motion Planning Using Generalised Voronoi Diagrams MILOŠ ŠEDA, VÁCLAV PICH Institute of Automation and Computer Science Brno University of Technology Technická 2, 616 69 Brno CZECH REPUBLIC Abstract:
Chapter 11 Arc Extraction and Segmentation
 Chapter 11 Arc Extraction and Segmentation 11.1 Introduction edge detection: labels each pixel as edge or no edge additional properties of edge: direction, gradient magnitude, contrast edge grouping: edge
Chapter 11 Arc Extraction and Segmentation 11.1 Introduction edge detection: labels each pixel as edge or no edge additional properties of edge: direction, gradient magnitude, contrast edge grouping: edge
Surfaces: notes on Geometry & Topology
 Surfaces: notes on Geometry & Topology 1 Surfaces A 2-dimensional region of 3D space A portion of space having length and breadth but no thickness 2 Defining Surfaces Analytically... Parametric surfaces
Surfaces: notes on Geometry & Topology 1 Surfaces A 2-dimensional region of 3D space A portion of space having length and breadth but no thickness 2 Defining Surfaces Analytically... Parametric surfaces
coding of various parts showing different features, the possibility of rotation or of hiding covering parts of the object's surface to gain an insight
 Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
Topic 6 Representation and Description
 Topic 6 Representation and Description Background Segmentation divides the image into regions Each region should be represented and described in a form suitable for further processing/decision-making Representation
Topic 6 Representation and Description Background Segmentation divides the image into regions Each region should be represented and described in a form suitable for further processing/decision-making Representation
CAD & Computational Geometry Course plan
 Course plan Introduction Segment-Segment intersections Polygon Triangulation Intro to Voronoï Diagrams & Geometric Search Sweeping algorithm for Voronoï Diagrams 1 Voronoi Diagrams Voronoi Diagrams or
Course plan Introduction Segment-Segment intersections Polygon Triangulation Intro to Voronoï Diagrams & Geometric Search Sweeping algorithm for Voronoï Diagrams 1 Voronoi Diagrams Voronoi Diagrams or
International Journal of Computer Science Trends and Technology (IJCST) Volume 3 Issue 1, Jan-Feb 2015
 RESEARCH ARTICLE Comparison between Square Pixel Structure and Hexagonal Pixel Structure in Digital Image Processing Illa Singh 1, Ashish Oberoi 2 M.Tech 1, Final Year Student, Associate Professor2 Department
RESEARCH ARTICLE Comparison between Square Pixel Structure and Hexagonal Pixel Structure in Digital Image Processing Illa Singh 1, Ashish Oberoi 2 M.Tech 1, Final Year Student, Associate Professor2 Department
Chapter 3. Sukhwinder Singh
 Chapter 3 Sukhwinder Singh PIXEL ADDRESSING AND OBJECT GEOMETRY Object descriptions are given in a world reference frame, chosen to suit a particular application, and input world coordinates are ultimately
Chapter 3 Sukhwinder Singh PIXEL ADDRESSING AND OBJECT GEOMETRY Object descriptions are given in a world reference frame, chosen to suit a particular application, and input world coordinates are ultimately
Data Mining Classification: Alternative Techniques. Lecture Notes for Chapter 4. Instance-Based Learning. Introduction to Data Mining, 2 nd Edition
 Data Mining Classification: Alternative Techniques Lecture Notes for Chapter 4 Instance-Based Learning Introduction to Data Mining, 2 nd Edition by Tan, Steinbach, Karpatne, Kumar Instance Based Classifiers
Data Mining Classification: Alternative Techniques Lecture Notes for Chapter 4 Instance-Based Learning Introduction to Data Mining, 2 nd Edition by Tan, Steinbach, Karpatne, Kumar Instance Based Classifiers
LATEST TRENDS on APPLIED MATHEMATICS, SIMULATION, MODELLING
 3D surface reconstruction of objects by using stereoscopic viewing Baki Koyuncu, Kurtuluş Küllü bkoyuncu@ankara.edu.tr kkullu@eng.ankara.edu.tr Computer Engineering Department, Ankara University, Ankara,
3D surface reconstruction of objects by using stereoscopic viewing Baki Koyuncu, Kurtuluş Küllü bkoyuncu@ankara.edu.tr kkullu@eng.ankara.edu.tr Computer Engineering Department, Ankara University, Ankara,
Study on Delaunay Triangulation with the Islets Constraints
 Intelligent Information Management, 2010, 2, 375-379 doi:10.4236/iim.2010.26045 Published Online June 2010 (http://www.scirp.org/journal/iim) Study on Delaunay Triangulation with the Islets Constraints
Intelligent Information Management, 2010, 2, 375-379 doi:10.4236/iim.2010.26045 Published Online June 2010 (http://www.scirp.org/journal/iim) Study on Delaunay Triangulation with the Islets Constraints
A Flavor of Topology. Shireen Elhabian and Aly A. Farag University of Louisville January 2010
 A Flavor of Topology Shireen Elhabian and Aly A. Farag University of Louisville January 2010 In 1670 s I believe that we need another analysis properly geometric or linear, which treats place directly
A Flavor of Topology Shireen Elhabian and Aly A. Farag University of Louisville January 2010 In 1670 s I believe that we need another analysis properly geometric or linear, which treats place directly
Lecture 6: GIS Spatial Analysis. GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University
 Lecture 6: GIS Spatial Analysis GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University 1 Spatial Data It can be most simply defined as information that describes the distribution
Lecture 6: GIS Spatial Analysis GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University 1 Spatial Data It can be most simply defined as information that describes the distribution
ROBOT MOTION USING DELAUNAY TRIANGULATION
 ROBOT MOTION USING DELAUNAY TRIANGULATION by Ioana-Maria Ileană Abstract. Robot motion is nowadays studied from a lot of different perspectives. This paper is based on the assumption of a fully known environment,
ROBOT MOTION USING DELAUNAY TRIANGULATION by Ioana-Maria Ileană Abstract. Robot motion is nowadays studied from a lot of different perspectives. This paper is based on the assumption of a fully known environment,
CPSC 695. Geometric Algorithms in Biometrics. Dr. Marina L. Gavrilova
 CPSC 695 Geometric Algorithms in Biometrics Dr. Marina L. Gavrilova Biometric goals Verify users Identify users Synthesis - recently Biometric identifiers Courtesy of Bromba GmbH Classification of identifiers
CPSC 695 Geometric Algorithms in Biometrics Dr. Marina L. Gavrilova Biometric goals Verify users Identify users Synthesis - recently Biometric identifiers Courtesy of Bromba GmbH Classification of identifiers
Development of Reverse Engineering System for Machine Engineering Using 3D Bit-map Data. Tatsuro Yashiki* and Tarou Takagi*
 Development of Reverse Engineering System for Machine Engineering Using 3D Bit-map Data Tatsuro Yashiki* and Tarou Takagi* *Power & Industrial Systems R&D Laboratory, Hitachi, Ltd. Abstract In this paper,
Development of Reverse Engineering System for Machine Engineering Using 3D Bit-map Data Tatsuro Yashiki* and Tarou Takagi* *Power & Industrial Systems R&D Laboratory, Hitachi, Ltd. Abstract In this paper,
Roadmap Methods vs. Cell Decomposition in Robot Motion Planning
 Proceedings of the 6th WSEAS International Conference on Signal Processing, Robotics and Automation, Corfu Island, Greece, February 16-19, 007 17 Roadmap Methods vs. Cell Decomposition in Robot Motion
Proceedings of the 6th WSEAS International Conference on Signal Processing, Robotics and Automation, Corfu Island, Greece, February 16-19, 007 17 Roadmap Methods vs. Cell Decomposition in Robot Motion
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass
 Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
Data Representation in Visualisation
 Data Representation in Visualisation Visualisation Lecture 4 Taku Komura Institute for Perception, Action & Behaviour School of Informatics Taku Komura Data Representation 1 Data Representation We have
Data Representation in Visualisation Visualisation Lecture 4 Taku Komura Institute for Perception, Action & Behaviour School of Informatics Taku Komura Data Representation 1 Data Representation We have
COMPUTING CONSTRAINED DELAUNAY
 COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS IN THE PLANE By Samuel Peterson, University of Minnesota Undergraduate The Goal The Problem The Algorithms The Implementation Applications Acknowledgments
COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS IN THE PLANE By Samuel Peterson, University of Minnesota Undergraduate The Goal The Problem The Algorithms The Implementation Applications Acknowledgments
Visualizing and Animating Search Operations on Quadtrees on the Worldwide Web
 Visualizing and Animating Search Operations on Quadtrees on the Worldwide Web František Brabec Computer Science Department University of Maryland College Park, Maryland 20742 brabec@umiacs.umd.edu Hanan
Visualizing and Animating Search Operations on Quadtrees on the Worldwide Web František Brabec Computer Science Department University of Maryland College Park, Maryland 20742 brabec@umiacs.umd.edu Hanan
the number of states must be set in advance, i.e. the structure of the model is not t to the data, but given a priori the algorithm converges to a loc
 Clustering Time Series with Hidden Markov Models and Dynamic Time Warping Tim Oates, Laura Firoiu and Paul R. Cohen Computer Science Department, LGRC University of Massachusetts, Box 34610 Amherst, MA
Clustering Time Series with Hidden Markov Models and Dynamic Time Warping Tim Oates, Laura Firoiu and Paul R. Cohen Computer Science Department, LGRC University of Massachusetts, Box 34610 Amherst, MA
Path-planning by Tessellation of Obstacles
 Path-planning by Tessellation of Obstacles Tane Pendragon and Lyndon While School of Computer Science & Software Engineering, The University of Western Australia, Western Australia 6009 email: {pendrt01,
Path-planning by Tessellation of Obstacles Tane Pendragon and Lyndon While School of Computer Science & Software Engineering, The University of Western Australia, Western Australia 6009 email: {pendrt01,
Delaunay Triangulation
 Delaunay Triangulation Steve Oudot slides courtesy of O. Devillers MST MST MST use Kruskal s algorithm with Del as input O(n log n) Last: lower bound for Delaunay Let x 1, x 2,..., x n R, to be sorted
Delaunay Triangulation Steve Oudot slides courtesy of O. Devillers MST MST MST use Kruskal s algorithm with Del as input O(n log n) Last: lower bound for Delaunay Let x 1, x 2,..., x n R, to be sorted
Triangulation and Convex Hull. 8th November 2018
 Triangulation and Convex Hull 8th November 2018 Agenda 1. Triangulation. No book, the slides are the curriculum 2. Finding the convex hull. Textbook, 8.6.2 2 Triangulation and terrain models Here we have
Triangulation and Convex Hull 8th November 2018 Agenda 1. Triangulation. No book, the slides are the curriculum 2. Finding the convex hull. Textbook, 8.6.2 2 Triangulation and terrain models Here we have
The Relative Neighbourhood Graph. of a Finite Planar Set. Godfried T. Toussaint
 The Relative Neighbourhood Graph of a Finite Planar Set Godfried T. Toussaint Published in Pattern Recognition, Vol. 12, 1980, pp. 261-268. Winner of an Outstanding Paper Award given by the Pattern Recognition
The Relative Neighbourhood Graph of a Finite Planar Set Godfried T. Toussaint Published in Pattern Recognition, Vol. 12, 1980, pp. 261-268. Winner of an Outstanding Paper Award given by the Pattern Recognition
Techniques. IDSIA, Istituto Dalle Molle di Studi sull'intelligenza Articiale. Phone: Fax:
 Incorporating Learning in Motion Planning Techniques Luca Maria Gambardella and Marc Haex IDSIA, Istituto Dalle Molle di Studi sull'intelligenza Articiale Corso Elvezia 36 - CH - 6900 Lugano Phone: +41
Incorporating Learning in Motion Planning Techniques Luca Maria Gambardella and Marc Haex IDSIA, Istituto Dalle Molle di Studi sull'intelligenza Articiale Corso Elvezia 36 - CH - 6900 Lugano Phone: +41
G 6i try. On the Number of Minimal 1-Steiner Trees* Discrete Comput Geom 12:29-34 (1994)
 Discrete Comput Geom 12:29-34 (1994) G 6i try 9 1994 Springer-Verlag New York Inc. On the Number of Minimal 1-Steiner Trees* B. Aronov, 1 M. Bern, 2 and D. Eppstein 3 Computer Science Department, Polytechnic
Discrete Comput Geom 12:29-34 (1994) G 6i try 9 1994 Springer-Verlag New York Inc. On the Number of Minimal 1-Steiner Trees* B. Aronov, 1 M. Bern, 2 and D. Eppstein 3 Computer Science Department, Polytechnic
Module 4: Index Structures Lecture 16: Voronoi Diagrams and Tries. The Lecture Contains: Voronoi diagrams. Tries. Index structures
 The Lecture Contains: Voronoi diagrams Tries Delaunay triangulation Algorithms Extensions Index structures 1-dimensional index structures Memory-based index structures Disk-based index structures Classification
The Lecture Contains: Voronoi diagrams Tries Delaunay triangulation Algorithms Extensions Index structures 1-dimensional index structures Memory-based index structures Disk-based index structures Classification
Tiling Three-Dimensional Space with Simplices. Shankar Krishnan AT&T Labs - Research
 Tiling Three-Dimensional Space with Simplices Shankar Krishnan AT&T Labs - Research What is a Tiling? Partition of an infinite space into pieces having a finite number of distinct shapes usually Euclidean
Tiling Three-Dimensional Space with Simplices Shankar Krishnan AT&T Labs - Research What is a Tiling? Partition of an infinite space into pieces having a finite number of distinct shapes usually Euclidean
The convex hull of a set Q of points is the smallest convex polygon P for which each point in Q is either on the boundary of P or in its interior.
 CS 312, Winter 2007 Project #1: Convex Hull Due Dates: See class schedule Overview: In this project, you will implement a divide and conquer algorithm for finding the convex hull of a set of points and
CS 312, Winter 2007 Project #1: Convex Hull Due Dates: See class schedule Overview: In this project, you will implement a divide and conquer algorithm for finding the convex hull of a set of points and
Average case analysis of dynamic geometric optimization
 Average case analysis of dynamic geometric optimization David Eppstein Department of Information and Computer Science University of California, Irvine, CA 92717 May 19, 1995 Abstract We maintain the maximum
Average case analysis of dynamic geometric optimization David Eppstein Department of Information and Computer Science University of California, Irvine, CA 92717 May 19, 1995 Abstract We maintain the maximum
[8] that this cannot happen on the projective plane (cf. also [2]) and the results of Robertson, Seymour, and Thomas [5] on linkless embeddings of gra
![[8] that this cannot happen on the projective plane (cf. also [2]) and the results of Robertson, Seymour, and Thomas [5] on linkless embeddings of gra [8] that this cannot happen on the projective plane (cf. also [2]) and the results of Robertson, Seymour, and Thomas [5] on linkless embeddings of gra](/thumbs/85/93035794.jpg) Apex graphs with embeddings of face-width three Bojan Mohar Department of Mathematics University of Ljubljana Jadranska 19, 61111 Ljubljana Slovenia bojan.mohar@uni-lj.si Abstract Aa apex graph is a graph
Apex graphs with embeddings of face-width three Bojan Mohar Department of Mathematics University of Ljubljana Jadranska 19, 61111 Ljubljana Slovenia bojan.mohar@uni-lj.si Abstract Aa apex graph is a graph
Graph-theoretic Issues in Remote Sensing and Landscape Ecology
 EnviroInfo 2002 (Wien) Environmental Communication in the Information Society - Proceedings of the 16th Conference Graph-theoretic Issues in Remote Sensing and Landscape Ecology Joachim Steinwendner 1
EnviroInfo 2002 (Wien) Environmental Communication in the Information Society - Proceedings of the 16th Conference Graph-theoretic Issues in Remote Sensing and Landscape Ecology Joachim Steinwendner 1
Using Semi-Regular 4 8 Meshes for Subdivision Surfaces
 Using Semi-Regular 8 Meshes for Subdivision Surfaces Luiz Velho IMPA Instituto de Matemática Pura e Aplicada Abstract. Semi-regular 8 meshes are refinable triangulated quadrangulations. They provide a
Using Semi-Regular 8 Meshes for Subdivision Surfaces Luiz Velho IMPA Instituto de Matemática Pura e Aplicada Abstract. Semi-regular 8 meshes are refinable triangulated quadrangulations. They provide a
6.854J / J Advanced Algorithms Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
DATA MODELS IN GIS. Prachi Misra Sahoo I.A.S.R.I., New Delhi
 DATA MODELS IN GIS Prachi Misra Sahoo I.A.S.R.I., New Delhi -110012 1. Introduction GIS depicts the real world through models involving geometry, attributes, relations, and data quality. Here the realization
DATA MODELS IN GIS Prachi Misra Sahoo I.A.S.R.I., New Delhi -110012 1. Introduction GIS depicts the real world through models involving geometry, attributes, relations, and data quality. Here the realization
The Farthest Point Delaunay Triangulation Minimizes Angles
 The Farthest Point Delaunay Triangulation Minimizes Angles David Eppstein Department of Information and Computer Science UC Irvine, CA 92717 November 20, 1990 Abstract We show that the planar dual to the
The Farthest Point Delaunay Triangulation Minimizes Angles David Eppstein Department of Information and Computer Science UC Irvine, CA 92717 November 20, 1990 Abstract We show that the planar dual to the
Localization in Graphs. Richardson, TX Azriel Rosenfeld. Center for Automation Research. College Park, MD
 CAR-TR-728 CS-TR-3326 UMIACS-TR-94-92 Samir Khuller Department of Computer Science Institute for Advanced Computer Studies University of Maryland College Park, MD 20742-3255 Localization in Graphs Azriel
CAR-TR-728 CS-TR-3326 UMIACS-TR-94-92 Samir Khuller Department of Computer Science Institute for Advanced Computer Studies University of Maryland College Park, MD 20742-3255 Localization in Graphs Azriel
all the vertices). between u and v in the subgraph is at most t necessary to endow them with additional properties,
 The Visibility Graph Contains a Bounded-Degree Spanner Gautam Das Abstract Given a collection of polygonal obstacles with n vertices on the place, and any t > 1, we present an O(n log n) time algorithm
The Visibility Graph Contains a Bounded-Degree Spanner Gautam Das Abstract Given a collection of polygonal obstacles with n vertices on the place, and any t > 1, we present an O(n log n) time algorithm
CSC Computer Graphics
 // CSC. Computer Graphics Lecture Kasun@dscs.sjp.ac.lk Department of Computer Science University of Sri Jayewardanepura Polygon Filling Scan-Line Polygon Fill Algorithm Span Flood-Fill Algorithm Inside-outside
// CSC. Computer Graphics Lecture Kasun@dscs.sjp.ac.lk Department of Computer Science University of Sri Jayewardanepura Polygon Filling Scan-Line Polygon Fill Algorithm Span Flood-Fill Algorithm Inside-outside
Outline of the presentation
 Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
M. Andrea Rodríguez-Tastets. I Semester 2008
 M. -Tastets Universidad de Concepción,Chile andrea@udec.cl I Semester 2008 Outline refers to data with a location on the Earth s surface. Examples Census data Administrative boundaries of a country, state
M. -Tastets Universidad de Concepción,Chile andrea@udec.cl I Semester 2008 Outline refers to data with a location on the Earth s surface. Examples Census data Administrative boundaries of a country, state
EULER S FORMULA AND THE FIVE COLOR THEOREM
 EULER S FORMULA AND THE FIVE COLOR THEOREM MIN JAE SONG Abstract. In this paper, we will define the necessary concepts to formulate map coloring problems. Then, we will prove Euler s formula and apply
EULER S FORMULA AND THE FIVE COLOR THEOREM MIN JAE SONG Abstract. In this paper, we will define the necessary concepts to formulate map coloring problems. Then, we will prove Euler s formula and apply
(Master Course) Mohammad Farshi Department of Computer Science, Yazd University. Yazd Univ. Computational Geometry.
 1 / 17 (Master Course) Mohammad Farshi Department of Computer Science, Yazd University 1392-1 2 / 17 : Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars, Algorithms and Applications, 3rd Edition,
1 / 17 (Master Course) Mohammad Farshi Department of Computer Science, Yazd University 1392-1 2 / 17 : Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars, Algorithms and Applications, 3rd Edition,
Determining Differences between Two Sets of Polygons
 Determining Differences between Two Sets of Polygons MATEJ GOMBOŠI, BORUT ŽALIK Institute for Computer Science Faculty of Electrical Engineering and Computer Science, University of Maribor Smetanova 7,
Determining Differences between Two Sets of Polygons MATEJ GOMBOŠI, BORUT ŽALIK Institute for Computer Science Faculty of Electrical Engineering and Computer Science, University of Maribor Smetanova 7,
x1_nearest x2_nearest Implicit Surface:[ f(x)=0,b(x)= false ]
![x1_nearest x2_nearest Implicit Surface:[ f(x)=0,b(x)= false ] x1_nearest x2_nearest Implicit Surface:[ f(x)=0,b(x)= false ]](/thumbs/88/115374031.jpg) Marching Triangles: Delaunay Implicit Surface Triangulation A.Hilton 1 and J.Illingworth Vision, Speech and Signal Processing Group, Department of Electronic and Electrical Engineering University of Surrey,
Marching Triangles: Delaunay Implicit Surface Triangulation A.Hilton 1 and J.Illingworth Vision, Speech and Signal Processing Group, Department of Electronic and Electrical Engineering University of Surrey,
Representation of 2D objects with a topology preserving network
 Representation of 2D objects with a topology preserving network Francisco Flórez, Juan Manuel García, José García, Antonio Hernández, Departamento de Tecnología Informática y Computación. Universidad de
Representation of 2D objects with a topology preserving network Francisco Flórez, Juan Manuel García, José García, Antonio Hernández, Departamento de Tecnología Informática y Computación. Universidad de
Geometric and Thematic Integration of Spatial Data into Maps
 Geometric and Thematic Integration of Spatial Data into Maps Mark McKenney Department of Computer Science, Texas State University mckenney@txstate.edu Abstract The map construction problem (MCP) is defined
Geometric and Thematic Integration of Spatial Data into Maps Mark McKenney Department of Computer Science, Texas State University mckenney@txstate.edu Abstract The map construction problem (MCP) is defined
Proceedings of the 5th WSEAS International Conference on Telecommunications and Informatics, Istanbul, Turkey, May 27-29, 2006 (pp )
 A Rapid Algorithm for Topology Construction from a Set of Line Segments SEBASTIAN KRIVOGRAD, MLADEN TRLEP, BORUT ŽALIK Faculty of Electrical Engineering and Computer Science University of Maribor Smetanova
A Rapid Algorithm for Topology Construction from a Set of Line Segments SEBASTIAN KRIVOGRAD, MLADEN TRLEP, BORUT ŽALIK Faculty of Electrical Engineering and Computer Science University of Maribor Smetanova
Maps as Numbers: Data Models
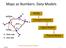 Maps as Numbers: Data Models vertices E Reality S E S arcs S E Conceptual Models nodes E Logical Models S Start node E End node S Physical Models 1 The Task An accurate, registered, digital map that can
Maps as Numbers: Data Models vertices E Reality S E S arcs S E Conceptual Models nodes E Logical Models S Start node E End node S Physical Models 1 The Task An accurate, registered, digital map that can
Computational Geometry. Algorithm Design (10) Computational Geometry. Convex Hull. Areas in Computational Geometry
 Computational Geometry Algorithm Design (10) Computational Geometry Graduate School of Engineering Takashi Chikayama Algorithms formulated as geometry problems Broad application areas Computer Graphics,
Computational Geometry Algorithm Design (10) Computational Geometry Graduate School of Engineering Takashi Chikayama Algorithms formulated as geometry problems Broad application areas Computer Graphics,
COMPUTER DESIGN OF REPEATING HYPERBOLIC PATTERNS
 COMPUTER DESIGN OF REPEATING HYPERBOLIC PATTERNS Douglas Dunham University of Minnesota Duluth Department of Computer Science 1114 Kirby Drive Duluth, Minnesota 55812-2496 USA ddunham@d.umn.edu Abstract:
COMPUTER DESIGN OF REPEATING HYPERBOLIC PATTERNS Douglas Dunham University of Minnesota Duluth Department of Computer Science 1114 Kirby Drive Duluth, Minnesota 55812-2496 USA ddunham@d.umn.edu Abstract:
AMS Sectional Meeting, Richmond VA Special Session on Mathematics and the Arts
 AMS Sectional Meeting, Richmond VA Special Session on Mathematics and the Arts Hyperbolic Truchet Tilings: First Steps Douglas Dunham University of Minnesota Duluth Duluth, Minnesota USA Outline A brief
AMS Sectional Meeting, Richmond VA Special Session on Mathematics and the Arts Hyperbolic Truchet Tilings: First Steps Douglas Dunham University of Minnesota Duluth Duluth, Minnesota USA Outline A brief
Simultaneously flippable edges in triangulations
 Simultaneously flippable edges in triangulations Diane L. Souvaine 1, Csaba D. Tóth 2, and Andrew Winslow 1 1 Tufts University, Medford MA 02155, USA, {dls,awinslow}@cs.tufts.edu 2 University of Calgary,
Simultaneously flippable edges in triangulations Diane L. Souvaine 1, Csaba D. Tóth 2, and Andrew Winslow 1 1 Tufts University, Medford MA 02155, USA, {dls,awinslow}@cs.tufts.edu 2 University of Calgary,
Non-Bayesian Classifiers Part I: k-nearest Neighbor Classifier and Distance Functions
 Non-Bayesian Classifiers Part I: k-nearest Neighbor Classifier and Distance Functions Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr CS 551, Fall 2017 CS 551,
Non-Bayesian Classifiers Part I: k-nearest Neighbor Classifier and Distance Functions Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr CS 551, Fall 2017 CS 551,
from Range Data Edvaldo M. Bispo, Andrew W. Fitzgibbon and Robert B. Fisher Dept. of Articial Intelligence, University of Edinburgh,
 Visually Salient 3D Model Acquisition from Range Data Edvaldo M. Bispo, Andrew W. Fitzgibbon and Robert B. Fisher Dept. of Articial Intelligence, University of Edinburgh, 5 Forrest Hill, Edinburgh EH1
Visually Salient 3D Model Acquisition from Range Data Edvaldo M. Bispo, Andrew W. Fitzgibbon and Robert B. Fisher Dept. of Articial Intelligence, University of Edinburgh, 5 Forrest Hill, Edinburgh EH1
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into
 2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
Aspect-Ratio Voronoi Diagram with Applications
 Aspect-Ratio Voronoi Diagram with Applications Tetsuo Asano School of Information Science, JAIST (Japan Advanced Institute of Science and Technology), Japan 1-1 Asahidai, Nomi, Ishikawa, 923-1292, Japan
Aspect-Ratio Voronoi Diagram with Applications Tetsuo Asano School of Information Science, JAIST (Japan Advanced Institute of Science and Technology), Japan 1-1 Asahidai, Nomi, Ishikawa, 923-1292, Japan
CSG obj. oper3. obj1 obj2 obj3. obj5. obj4
 Solid Modeling Solid: Boundary + Interior Volume occupied by geometry Solid representation schemes Constructive Solid Geometry (CSG) Boundary representations (B-reps) Space-partition representations Operations
Solid Modeling Solid: Boundary + Interior Volume occupied by geometry Solid representation schemes Constructive Solid Geometry (CSG) Boundary representations (B-reps) Space-partition representations Operations
CS133 Computational Geometry
 CS133 Computational Geometry Voronoi Diagram Delaunay Triangulation 5/17/2018 1 Nearest Neighbor Problem Given a set of points P and a query point q, find the closest point p P to q p, r P, dist p, q dist(r,
CS133 Computational Geometry Voronoi Diagram Delaunay Triangulation 5/17/2018 1 Nearest Neighbor Problem Given a set of points P and a query point q, find the closest point p P to q p, r P, dist p, q dist(r,
Autonomous and Mobile Robotics Prof. Giuseppe Oriolo. Motion Planning 1 Retraction and Cell Decomposition
 Autonomous and Mobile Robotics Prof. Giuseppe Oriolo Motion Planning 1 Retraction and Cell Decomposition motivation robots are expected to perform tasks in workspaces populated by obstacles autonomy requires
Autonomous and Mobile Robotics Prof. Giuseppe Oriolo Motion Planning 1 Retraction and Cell Decomposition motivation robots are expected to perform tasks in workspaces populated by obstacles autonomy requires
The Crust and Skeleton Applications in GIS
 The Crust and Skeleton Applications in GIS Christopher Gold and Maciek Dakowicz School of Computing, University of Glamorgan Pontypridd CF37 1DL Wales UK christophergold@voronoi.com Abstract This paper
The Crust and Skeleton Applications in GIS Christopher Gold and Maciek Dakowicz School of Computing, University of Glamorgan Pontypridd CF37 1DL Wales UK christophergold@voronoi.com Abstract This paper
Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1
 CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
Optimum Alphabetic Binary Trees T. C. Hu and J. D. Morgenthaler Department of Computer Science and Engineering, School of Engineering, University of C
 Optimum Alphabetic Binary Trees T. C. Hu and J. D. Morgenthaler Department of Computer Science and Engineering, School of Engineering, University of California, San Diego CA 92093{0114, USA Abstract. We
Optimum Alphabetic Binary Trees T. C. Hu and J. D. Morgenthaler Department of Computer Science and Engineering, School of Engineering, University of California, San Diego CA 92093{0114, USA Abstract. We
and implemented in parallel on a board with 3 Motorolla DSP's. This board, part of the DMA machine, has been designed and built jointly by INRIA
 In Vision-based Vehicle Guidance, Springer, New York, 1992 edited by I. Masaki, Chapter 13, pages 268--283 Obstacle Avoidance and Trajectory Planning for an Indoors Mobile Robot Using Stereo Vision and
In Vision-based Vehicle Guidance, Springer, New York, 1992 edited by I. Masaki, Chapter 13, pages 268--283 Obstacle Avoidance and Trajectory Planning for an Indoors Mobile Robot Using Stereo Vision and
Ray shooting from convex ranges
 Discrete Applied Mathematics 108 (2001) 259 267 Ray shooting from convex ranges Evangelos Kranakis a, Danny Krizanc b, Anil Maheshwari a;, Jorg-Rudiger Sack a, Jorge Urrutia c a School of Computer Science,
Discrete Applied Mathematics 108 (2001) 259 267 Ray shooting from convex ranges Evangelos Kranakis a, Danny Krizanc b, Anil Maheshwari a;, Jorg-Rudiger Sack a, Jorge Urrutia c a School of Computer Science,
EE 584 MACHINE VISION
 EE 584 MACHINE VISION Binary Images Analysis Geometrical & Topological Properties Connectedness Binary Algorithms Morphology Binary Images Binary (two-valued; black/white) images gives better efficiency
EE 584 MACHINE VISION Binary Images Analysis Geometrical & Topological Properties Connectedness Binary Algorithms Morphology Binary Images Binary (two-valued; black/white) images gives better efficiency
Graph projection techniques for Self-Organizing Maps
 Graph projection techniques for Self-Organizing Maps Georg Pölzlbauer 1, Andreas Rauber 1, Michael Dittenbach 2 1- Vienna University of Technology - Department of Software Technology Favoritenstr. 9 11
Graph projection techniques for Self-Organizing Maps Georg Pölzlbauer 1, Andreas Rauber 1, Michael Dittenbach 2 1- Vienna University of Technology - Department of Software Technology Favoritenstr. 9 11
How Do Computers Solve Geometric Problems? Sorelle Friedler, University of Maryland - College Park
 How Do Computers Solve Geometric Problems? Sorelle Friedler, University of Maryland - College Park http://www.cs.umd.edu/~sorelle Outline Introduction Algorithms Computational Geometry Art Museum Problem
How Do Computers Solve Geometric Problems? Sorelle Friedler, University of Maryland - College Park http://www.cs.umd.edu/~sorelle Outline Introduction Algorithms Computational Geometry Art Museum Problem
Surface segmentation for improved isotropic remeshing
 J. Edwards (Univ. of Texas) IMR 2012 1 / 20 Surface segmentation for improved isotropic remeshing John Edwards, Wenping Wang, Chandrajit Bajaj Department of Computer Science The University of Texas at
J. Edwards (Univ. of Texas) IMR 2012 1 / 20 Surface segmentation for improved isotropic remeshing John Edwards, Wenping Wang, Chandrajit Bajaj Department of Computer Science The University of Texas at
reasonable to store in a software implementation, it is likely to be a signicant burden in a low-cost hardware implementation. We describe in this pap
 Storage-Ecient Finite Field Basis Conversion Burton S. Kaliski Jr. 1 and Yiqun Lisa Yin 2 RSA Laboratories 1 20 Crosby Drive, Bedford, MA 01730. burt@rsa.com 2 2955 Campus Drive, San Mateo, CA 94402. yiqun@rsa.com
Storage-Ecient Finite Field Basis Conversion Burton S. Kaliski Jr. 1 and Yiqun Lisa Yin 2 RSA Laboratories 1 20 Crosby Drive, Bedford, MA 01730. burt@rsa.com 2 2955 Campus Drive, San Mateo, CA 94402. yiqun@rsa.com
Geometry Vocabulary. acute angle-an angle measuring less than 90 degrees
 Geometry Vocabulary acute angle-an angle measuring less than 90 degrees angle-the turn or bend between two intersecting lines, line segments, rays, or planes angle bisector-an angle bisector is a ray that
Geometry Vocabulary acute angle-an angle measuring less than 90 degrees angle-the turn or bend between two intersecting lines, line segments, rays, or planes angle bisector-an angle bisector is a ray that
Lecture Tessellations, fractals, projection. Amit Zoran. Advanced Topics in Digital Design
 Lecture Tessellations, fractals, projection Amit Zoran Advanced Topics in Digital Design 67682 The Rachel and Selim Benin School of Computer Science and Engineering The Hebrew University of Jerusalem,
Lecture Tessellations, fractals, projection Amit Zoran Advanced Topics in Digital Design 67682 The Rachel and Selim Benin School of Computer Science and Engineering The Hebrew University of Jerusalem,
Triangle Graphs and Simple Trapezoid Graphs
 JOURNAL OF INFORMATION SCIENCE AND ENGINEERING 18, 467-473 (2002) Short Paper Triangle Graphs and Simple Trapezoid Graphs Department of Computer Science and Information Management Providence University
JOURNAL OF INFORMATION SCIENCE AND ENGINEERING 18, 467-473 (2002) Short Paper Triangle Graphs and Simple Trapezoid Graphs Department of Computer Science and Information Management Providence University
ON DIFFERENCE CORDIAL GRAPHS
 Mathematica Aeterna, Vol. 5, 05, no., 05-4 ON DIFFERENCE CORDIAL GRAPHS M. A. Seoud Department of Mathematics, Faculty of Science Ain Shams University, Cairo, Egypt m.a.seoud@hotmail.com Shakir M. Salman
Mathematica Aeterna, Vol. 5, 05, no., 05-4 ON DIFFERENCE CORDIAL GRAPHS M. A. Seoud Department of Mathematics, Faculty of Science Ain Shams University, Cairo, Egypt m.a.seoud@hotmail.com Shakir M. Salman
6. Object Identification L AK S H M O U. E D U
 6. Object Identification L AK S H M AN @ O U. E D U Objects Information extracted from spatial grids often need to be associated with objects not just an individual pixel Group of pixels that form a real-world
6. Object Identification L AK S H M AN @ O U. E D U Objects Information extracted from spatial grids often need to be associated with objects not just an individual pixel Group of pixels that form a real-world
Transactions on Information and Communications Technologies vol 18, 1998 WIT Press, ISSN
 Environmental mapping made simple Christopher Gold Geomatics Research Centre, Laval University, Quebec City, Quebec, Canada G1K 7P4. Christopher. Gold@scg. ulaval.ca Abstract In environmental applications
Environmental mapping made simple Christopher Gold Geomatics Research Centre, Laval University, Quebec City, Quebec, Canada G1K 7P4. Christopher. Gold@scg. ulaval.ca Abstract In environmental applications
A technique for adding range restrictions to. August 30, Abstract. In a generalized searching problem, a set S of n colored geometric objects
 A technique for adding range restrictions to generalized searching problems Prosenjit Gupta Ravi Janardan y Michiel Smid z August 30, 1996 Abstract In a generalized searching problem, a set S of n colored
A technique for adding range restrictions to generalized searching problems Prosenjit Gupta Ravi Janardan y Michiel Smid z August 30, 1996 Abstract In a generalized searching problem, a set S of n colored
