x1_nearest x2_nearest Implicit Surface:[ f(x)=0,b(x)= false ]
|
|
|
- Lilian Blankenship
- 5 years ago
- Views:
Transcription
1 Marching Triangles: Delaunay Implicit Surface Triangulation A.Hilton 1 and J.Illingworth Vision, Speech and Signal Processing Group, Department of Electronic and Electrical Engineering University of Surrey, Guildford. GU2 5XH. U.K. a.hilton@surrey.ac.uk Abstract A new surface-based approach to triangulation of an implicit surface called `Marching Triangles' (MT) is introduced in this paper. MT enables reconstruction of an ecient triangular mesh representation of an open manifold implicit surface of arbitrary topology. The surface-based approach polygonises the implicit surface by growing a triangulated mesh according to the local geometry and topology. A local 3D Delaunay Surface Constraint is introduced to ensure that the triangulated mesh is locally Delaunay and is a correct surface approximation of the manifold surface. The resulting triangulation is globally Delaunay with uniform triangle shape providing an ecient representation of the implicit surface. MT overcomes several limitations of previous volume-based implicit surface polygonisation techniques. Volume-based approaches, such as Marching Cubes (MC), intersect the surface with a volumetric decomposition of the space. This results in highly inecient representation due to non-uniform triangle shape. MT also enables polygonisation of open manifolds, dynamic integration of new data into an existing triangulation, reduced computational cost and correct approximation of complex geometry. Results are presented for the polygonisation of implicit surfaces dened parametrically and from surface measurements of real objects. Implicit surface representation of real objects is based on the geometric fusion of multiple range images. The Marching Triangles algorithm leads to both representational and computational costs a factor of 3 5 lower than previous volume based approaches such as MC. 1 Introduction 1.1 Volume-Based Implicit Surface Polygonisation Polygonisation of implicitly dened surfaces has attracted considerable interest for visualisation in many elds including computer graphics and medical imaging. Implicit surface polygonisation based on a uniform subdivision of space are widely used [6]. These approaches are volume-based as they use a volumetric decomposition of the space to polygonise the implicit surface. A polygonal representation is constructed by intersecting the implicit surface with cubic or tetrahedral cells. Vertices in the polygonal representation are positioned at the intersection of the edges of the volume decomposition with the implicit surface. Each polygon is then subdivided into a set of triangles. The surface to volume intersection produces a highly non-uniform distribution of triangle shape and size, resulting in a highly inecient representation of the implicit surface geometry. Representation accuracy is dependent on the size of the spatial subdivision. The use of a uniform spatial subdivision limits the maximum polygon size to the size of the volume cell. This results in polygonal representations which are highly inecient for the geometric accuracy obtained. Typical medical images result in meshes of order 10 6 triangles. Adaptive spatial subdivision and mesh optimisation techniques have been proposed to obtain more ecient representations from volume-based techniques. A comparative evaluation of volume-based algorithms is given in [7]. 1 Supported by EPSRC GR/K04569 `Finite Element Snakes for Depth Data Fusion'
2 1.2 Surface-Based Implicit Surface Polygonisation In this paper we present an alternative to previous volume-based implicit surface polygonisation approaches. A surface-based approach called `Marching Triangles' (MT) is introduced which enables implicit surface polygonisation based on the local surface geometry and topology. Surface-based approaches, as dened by Boissonnat [2], allow mesh vertices to be placed according to the local surface geometry. A 3D Delaunay constraint is introduced which ensures the connectivity between mesh vertices is locally Delaunay and correctly approximates the implicit surface. The resulting triangulation is an accurate and ecient representation of the implicit surface. The triangulation is an approximation of the Delaunay triangulation for the set of mesh vertices on a manifold surface. The Delaunay triangulation is an optimal geometric structure which gives uniform triangle shape, resulting in an ecient representation. The resulting triangulation is therefore directly suitable for applications such as visualisation or nite element analysis. In this paper we introduce the Marching Triangles (MT) algorithm for implicit surface triangulation with approximately uniform triangle size and shape. Results are compared with the volume-based Marching Cubes (MC) approach to implicit surface polygonisation with uniform spatial decomposition [1]. MT with an adaptive distribution of triangle size according to the local surface curvature will be investigated in future work. The motivation for this work is the reconstruction of 3D models of real objects from multi-view sets of range image surface measurements. Recent research [5, 3] has resulted in the geometric fusion of multi-view range images into a single implicit surface representation. Reliable geometric fusion in regions of complex geometry is achieved by constraints on the local surface geometry and topology based on measurement uncertainty [5]. In previous work the MC approach was used to reconstruct a triangulated model from the implicit surface representation. This approach has several limitations: the surface is a closed manifold; all data are required a priori; the resulting triangulation is highly non-uniform; the method is computationally expensive and reconstruction of object geometry is limited by the cube size. MT was developed to overcome these limitations. 2 Implicit Representation of an Open Manifold Surface An implicit surface is dened as the zero-set, f(~x) = 0, of a eld function, f(~x), where ~x is a point in 3D space R 3. A closed manifold surface is a 2-manifold in R 3 of arbitrary topology which is geometrically continuous in position. An open manifold surface has geometric discontinuities in position i.e. holes. Implicit representation of a manifold surface, S, can be achieved by dening a scalar eld function, f(~x), to be the distance to the nearest point on the surface, ~x nearest, where f(~x nearest ) = 0: f(~x) = j~x nearest?~xj. Signed eld function representations are commonly required for implicit surface polygonisation algorithms, such as Marching Cubes, because they dene points as either `inside', f(~x) < 0, or `outside', f(~x) > 0, a closed manifold surface S. A change in the sign of the eld function between two points indicates that the manifold surface must intersect a straight line between those points at least once. A signed eld function can be evaluated for a closed manifold surface, S, from the surface normal orientation, ~n nearest, at the nearest point, ~x nearest as: f(~x) = (~x? ~x nearest ):~n nearest. Representation of an open manifold surface requires explicit representation of the discontinuity boundary. A boundary function b(~x) is dened which is `false' if the nearest point is internal to the surface and `true' if the nearest point is on the boundary. Thus an open manifold surface, S, is represented in an implicit form as the set of points for which [f(~x) = 0; b(~x) =`false']. Representation of an open manifold surface, S, is illustrated for a cross-section in gure 1. Field function evaluation is shown for two points x 1 and x 2 with nearest points internal to the surface, b(x 1 ) =`false', and on the surface boundary, b(x 2 ) =`true'. In the implicit surface-based geometric fusion approach [5] information on surface boundary, b(~x), and orientation, ~n nearest, is available when evaluating the eld function f(~x) at no additional computational cost. For parametric implicit surface functions this information is dened implicitly in the continuous eld function, f(~x), and may be found by a numerical scheme such as gradient decent. This is analogous to edge intersection techniques used in volume-based implicit surface polygonisation schemes.
3 x1:[f(x1),b(x1)= false ] x2:[f(x2),b(x2)= true ] n1_nearest n2_nearest x1_nearest x2_nearest Implicit Surface:[ f(x)=0,b(x)= false ] Figure 1: Field function evaluation 3 Delaunay Triangulation on a Manifold Surface This section denes the theoretical basis of a local 3D procedure for constructing a triangulated polyhedral model, M = ft 0 :::T N g, of an unknown object surface, S. We introduce a 3D surface-based constraint for the Delaunay triangulation of a set of points, X = f~x 1 :::~x i :::~x N g, on an arbitrary topology manifold surface, S, where each point ~x i is a vector, (x; y; z), displacement from the origin in R 3. The 3D Delaunay triangulation of an arbitrary point set X is composed of tetrahedral volumes, T ijkl = T (~x i ; ~x j ; ~x k ; ~x l ), such that there exists a sphere which passes through each vertex, (~x i ; ~x j ; ~x k ; ~x l ), of T ijkl which does not contain any other interior points of X. Each tetrahedra is composed of four triangular faces, (T ijk ; T ilj ; T lik ; T jkl ). In the case where the points, X, lie on a manifold surface, S, Boissonnat [2] derives the following important property which must be satised for the Delaunay triangulation D(X) to contain a polyhedron, M(X), which is a correct approximation of the surface S. Polyhedron, M(X), is a simple manifold composed of a connected subset of the faces of the Delaunay triangulation, D(X). Correct approximation requires that the polyhedron, M(X), respect the relative locations of the points, X,on the surface S. This requires that M(X) is dieomorphic to a curved polyhedron M C (X) tightly stretched on the surface S through the points X. Thus each triangle T in M(X) must be dieomorphic to a curved triangle T C on M C (X). Dieomorphism between two surface patches A and B can be dened as the existence of a projection that relates each point on A and B and respects their relative locations. A triangle T ijk which is locally dieomorphic to the manifold surface S is a face in the 3D Delaunay triangulation D(X) provided the following property is satised: Delaunay Face Property: Triangle T (~x i ; ~x j ; ~x k ) is a face in the 3D Delaunay triangulation D(X) provided there exists a circumsphere passing through each triangle vertex, (~x i ; ~x j ; ~x k ), that does not contain any other interior point of X. The above property follows from the denition of the Delaunay triangulation. A proof for the Delaunay triangulation in R 2 is given by O'Rouke [8] and extends to R 3. The Delaunay Face Property requires that the set X of points on a manifold surface must be suciently dense to satisfy the above constraint. This requires that in regions of high curvature or for thin parts the maximum spacing between measurements is determined by the amount of free space around the surface. The Delaunay face constraint is illustrated in Figure 2 for a polyhedral approximation M(X) of the manifold surface S. The sphere passing through the vertices of triangle, T ijk does not contain any other point in X. If the above face property is satised for all T in a polyhedron M(X) which is dieomorphic to surface, S, then the Delaunay triangulation D(X) must contain the polyhedron M(X). Consequently if M(X) is in D(X) then it inherits the optimal geometric properties of the Delaunay triangulation. Thus M(X)
4 Manifold Surface, S Polyhedral approximation M(X) C Empty Cirum-sphere x_i Tijk x_k x_j Figure 2: Delaunay face property is a Delaunay triangulation of the manifold surface, S, for the point set X. The Delaunay triangulation denes an optimal geometric structure which is symmetric, isotropic and closely related to the metric of the surface. Distances on the triangulation M(X) approximate the distance on the manifold surface S. In particular the triangulation maximises the minimum angle of any triangle. This is analogous to the 2D Delaunay triangulation of a point set where the points, X, lie on a 2-manifold surface in R 3 rather than the plane R 2. 4 Delaunay Surface Constraint Reconstruction of a triangulated polyhedron that correctly approximates the surface and is geometrically optimal requires two conditions to be satised. Each triangle T in M(X) must: 1. Respect the relative locations of points X on the surface S. 2. Satisfy the Delaunay Face Property. In this section we use the above conditions to derive a surface-based approach to triangulation of a manifold implicit surface. We start with a partial model, M 0 (X 0 ), which is a correct approximation of part of the surface S and is also a polyhedron in the Delaunay triangulation D(X 0 ), as dened in the previous section. We dene a local procedure for adding triangular elements, T new, to the boundary of, M 0, such that the resulting triangulation M = fm 0 ; T new g is also a correct approximation of S and is locally Delaunay. Given an edge e(~x i ; ~x j ) on the boundary of the existing model we nd a new point ~x new on the surface region adjacent to e outside the boundary of the existing model. Thus the triangle T new = T (~x i ; ~x j ; ~x new ) is a correct local approximation of the surface. For the triangle T new to be added to the model M 0 the following constraint must be satised: 3D Delaunay Surface Constraint: A triangle, T (~x i ; ~x j ; ~x new ), may only be added to the mesh boundary, at edge e(~x i ; ~x j ), if no part of the existing model, M 0, with the same surface orientation is inside the sphere passing through the triangle vertices, x, about the centre, c T, where c T is the circum-centre of the triangle vertices, (~x i ; ~x j ; ~x new ), in the plane of the triangle, T. Surface points of the same orientation are dened by a positive normal dot product, n T :n M 0 > 0. The Delaunay surface constraint is illustrated in Figure 3. This constraint guarantees that triangle T new uniquely approximates the local surface in the mesh M(X). Thus the mesh M(X) does not over-fold or self-intersect. The resulting triangulation will correctly represent the surface topology and approximate the surface geometry. The above constraint is an approximation of the Delaunay Face Property. An approximation is required as the Delaunay Face Property does not constrain the centre of the empty circum-sphere. Implementation
5 r i C k j Figure 3: 3D Delaunay Surface Constraint of the exact Delaunay Face Property would require a search for an empty sphere with centre on the line equi-distant from the triangle vertices. Constraining the centre of the circum-sphere to be the centre of the circum-circle in the triangle plane, c T, enables the Delaunay Face Property to be satised. However, this imposes a hard constraint that free-space around the surface must be greater than the radius of the circum-sphere. Relaxation of this constraint is achieved by allowing parts of the existing model, M 0 (X 0 ), with opposite orientation to intersect the sphere. This allows triangulation of complex geometries such as thin surface sections and region of high curvature. The resulting triangulation is locally approximately a Delaunay triangulation of the manifold surface S. This constraint ensures that the triangle T new is locally a Delaunay triangulation of the manifold surface, S. This ensures that the resulting triangulated model M, is approximately globally Delaunay, Fortune [4]. Thus the resulting model M(X) will approximate the optimal geometric properties of the Delaunay triangulation D(X) for the point set X. In particular the resulting triangulation will have the desirable properties of neighbourhood symmetry and isotropy. This constraint does not impose any restrictions on the mesh vertex position. In particular mesh vertices are not restricted to lie at measurement points unlike previous algorithms [2, 9]. This facilitates the design of a new algorithm which positions mesh vertices according to local surface geometry. 5 Marching Triangles Algorithm An implicit surface triangulation algorithm can now be developed based on the local 3D Delaunay surface constraint. Given an implicit surface representation, [f(~x); b(~x)], of an arbitrary topology open manifold surface the triangulation algorithm proceeds as follows. Firstly an initial seed model, M(X) = M 0 (X 0 ), is dened. This may be either a single triangular seed element or a previously constructed model to which we wish to incorporate new measurements. The current model M(X) is represented as a list of edges and vertices. The algorithm is implemented as a single pass through the edge list. New edges introduced by the addition of new elements to the model are appended to the end of the edge list. The algorithm does not terminate until all model edges have been tested once. The algorithm proceeds by testing each edge, e bound = e(~x i ; ~x j ), on the current model boundary, M: 1. Estimate a new vertex position, ~x proj, by projecting a constant distance, l proj, perpendicular to the mid-point of the boundary edge, e bound, in the plane of the model boundary element, T bound = T (~x j ; ~x i ; ~x k ). 2. Evaluate the new vertex position, ~x new, on the implicit surface as the nearest point to ~x proj : ~x new = ~x nearest where f(~x nearest ) = Terminate the mesh growing (8) for the edge e bound if either: (a) Nearest point is on the boundary b(~x new ) =`true'. (b) Implicit surface normal orientation, n new, of T new = T (~x i ; ~x j ; ~x new ) is opposite to the model orientation n bound of the boundary triangle T bound : n bound :n new < Apply 3D Delaunay Surface Constraint to T new. 5. If T new passes the 3D Delaunay Surface Constraint
6 i proj j i C j prev k (a) Step 1: Estimate new vertex position (b) Step 4:Delaunay constaint for new next overlap i C i C j k (c) Step 6:Delaunay constraint for next (d) Step 7:Delaunay constraint for overlap Figure 4: Illustration in 2D of key steps in the Marching Triangles algorithm (a) add vertex ~x new to the vertex list. (b) add triangle T new to the mesh M. (c) add edges e(~x j ; ~x new ) and e(~x new ; ~x i ) to the end of the edge list. 6. If T new fails the Local Delaunay Surface Constraint then apply steps 4&5 to adjacent boundary vertices, T new = T prev = T (~x i ; ~x j ; ~x prev ) or T new = T next = T (~x i ; ~x j ; ~x next ). 7. If T new, T next and T prev all fail the Local Delaunay Surface Constraint then if the Delaunay circumsphere for T new (~x i ; ~x j ; ~x new ) overlaps a boundary triangle, T overlap, on an existing part of the model, M(X) with the same orientation as the boundary triangle, T bound, such that n bound :n overlap > 0, then apply steps 4&5 with T new = T (~x i ; ~x j ; ~x overlap ) where ~x overlap is the nearest boundary vertex on T overlap. 8. Testing of edge e bound terminates when one or no new triangles have been added to the model, M. The mesh growing algorithm dened above enables triangulation of a manifold implicit surface of arbitrary topology and geometry. The principal steps of the MT algorithm are illustrated in Figure 4. Steps (1) and (2) estimate a possible new vertex position, x new, on the implicit surface, f(~x new ). Projection by a constant distance ensures approximately uniform triangle size. Step (3) ensures that the new triangle, T new, is a correct approximation of the local surface. New mesh vertices must correspond to non-boundary points on the implicit surface, step (3a). This constraint ensures that the the boundaries of geometric discontinuities in an open manifold implicit surface are correctly reconstructed. Step (3b) ensures that the local model geometry corresponds to the implicit surface geometry. This is required where the estimated vertex position, ~x proj, may erroneously correspond to a dierent part of the object surface. This may occur for thin object parts with the simple estimation scheme of step (1). An adaptive scheme for estimation of new vertex positions based on local surface properties such as curvature would reduce incorrect correspondences. Step (4) ensures that the new triangle, T new, locally satises the Delaunay circumsphere constraint. Hence, the resulting triangulation is locally Delaunay. Step (5) adds a triangle satisfying the Delaunay constraint to the mesh. New boundary edges are appended to the end of the edge list to ensure that the mesh growing algorithm will test them prior to termination. Step (6) allows the local connection of existing model vertices to form a continuous surface representation. Step (7) is required to eliminate cracks in the implicit surface where the estimated triangles on adjacent boundary regions overlap. This occurs for mesh growing where dierent parts of the triangulation meet due to the open manifold surface topology. Step (8) terminates testing for edge e bound after one or no triangles have been added. The mesh growing algorithm then applies steps (1 to 8) to the next boundary edge in the edge list. The `Marching Triangles' mesh growing algorithm reconstructs a triangulation which is a correct approximation of the implicit surface and is locally Delaunay. The resulting triangulated mesh, M(X), approximates the optimal geometric properties of the Delaunay triangulation for the set of vertices X on the surface S.
7 (a) 5 triangles (b) 10 triangles (c) 50 triangles (d) 100 triangles (e) 1498 triangles Figure 5: Marching Triangles for a sphere: (a d) intermediate meshes, (e) nal model Application of the MT algorithm to a parametrically dened implicit surface representation of a sphere is illustrated in Figure 5. The algorithm is initialised as a single triangular seed on the implicit surface. The mesh growing then proceeds to add elements to the mesh boundary. Figures 5(a d) show snapshots of the mesh growing procedure for 5,10,50 and 100 triangles. The algorithm terminates when no more triangles can be added to the mesh boundary 5(e) 1498 triangles. In this case the implicit surface is closed and terminates when no boundary edges exist. MT does not impose any constraint on the position of new vertices. In particular mesh vertices are not constrained to lie at measurement points unlike previous mesh growing procedures [2, 9]. This facilitates adaptive mesh growing by evaluating the projected distance, l proj, according to the local surface geometry. Results presented in this paper are for a constant projection distance which enables a uniform distribution of triangle size and shape. In principle an adaptive Marching Triangles algorithm could be implemented where the projection distance is derived from local surface properties such as curvature. If the implicit surface is composed of several disconnected surface regions then a `seed' mesh is required for each region. An analogous scheme is required with previous volume-based implicit surface polygonisation algorithms such as MC [1] and mesh growing algorithms [9]. The MT algorithm allows either `static' or `dynamic' integration. This is advantageous in situations where the implicit surface is constructed for the geometric fusion of multiple sets of measurements [3, 5]. Dynamic integration allows the addition of new measurements into an existing model. MT enables the extension of an existing model boundary if new measurements modify the implicit surface in an adjacent region. Dynamic integration is possible as the mesh growing algorithm acts directly on the existing triangulated model. Previous volumetric approaches polygonise the implicit surface by the intersection with a volume cell. Dynamic integration is therefore not possible unless the intermediate volumetric data structure is maintained. 6 Algorithm Performance 6.1 Computational Complexity The computational complexity of implicit surface polygonisation algorithms can be dened in terms of the number of eld function evaluations. The time complexity of the MT algorithm depends on the number of edges, N E in the polyhedral model, M. The addition of new elements to each edge in the model is considered when it is on the boundary of an intermediate partial model. Testing of a candidate triangle to be added to the model boundary requires two implicit surface function evaluations. One to dene the nearest point on the surface and the second to determine model overlap. The Euler formula [8] for a trianglated mesh denes the relationship between the number of edges, N E, nodes, N N, faces, N F, and handles, N H : N N? N E + NF = 2? 2N H. It follows that if the number of handles is small the number of nodes and faces is the same order as the number of edges O(N N ) = O(N E ) = O(N F ). For MT with a constant projection distance, l proj, the element edge length and area are approximately constant. Therefore, the computational complexity is proportional to the area of the manifold surface S. In addition the number of elements in the nal representation is proportional to the surface area. The computational complexity of the volume-based MC approach depends on the number of cubes visited. This depends on the number of cells intersected by the implicit surface. The lower bound on the number of cells occurs for a at implicit surface aligned with the volumetric subdivision. In this
8 Object Model Size Time(s) (SUN Sparc 10) MT MC MT MC Sphere Torus Jack Telephone Rabbit Teapot Soldier Table 1: Comparison of Marching Triangles and Cubes case the lower bound on the number of cells visited is proportional to the area of the surface. For a curved surface the number of cells visited is proportional to a factor times the area of the surface. On average approximately two implicit surface function evaluations are required per cube visited. Thus the computational complexity of the MT algorithm is equal to the lower bound of the complexity for the MC algorithm. 6.2 Representation Cost The same representation accuracy for surface S is achieved if the constant cube size for MC is equal to the constant projection distance for the MT algorithm. The MC algorithm generates at least two triangles per cube. This denes the lower limit for the number of triangles which is proportional to the implicit surface area. In general for a curved surface the number of triangles for the MC algorithm will be considerably larger than the lower limit [7]. For MT the number of triangles will always be proportional to the area of the surface as the positioning of vertices is based on the local surface geometry. The number of triangles is approximately geometrically optimal for a given manifold surface as it approximates the metric of the surface,s, due to the local Delaunay constraint. Hence the number of triangles for MT is equal to the lower bound of the MC algorithm for the same representation accuracy. In practice the number of triangles is signicantly lower for MT due to the uniform distribution of triangle shape. 6.3 Geometric Limitations The MT algorithm reconstructs the correct topology of implicit surface features larger than the constant projection distance, l proj. Assuming the implicit surface correctly represents the local topology then the lower limit for correct topology reconstruction is the projection distance. The 3D Delaunay Surface Constraint does not impose any limitations on the distance between adjacent surfaces. The use of this constraint enables correct reconstruction of arbitrarily thin object parts and crease edges. The MT algorithm eliminates limitations on surface geometry inherent in previous mesh growing algorithms [2, 9]. The cell size for volume-based algorithms imposes similar limitations on reconstruction of correct topology [7]. Features or thin objects smaller than the cell size may result in incorrect reconstruction and spurious artifacts. 7 Results Direct comparison of the representational and computational eciency of the MT and MC has been performed for polygonisation of implicit surfaces derived from synthetic models and real object measurements. Throughout this comparison the MT projection distance, l proj, is equal to the MC voxel size to obtain the same geometric representation accuracy. 7.1 Parametric Implicit Surfaces Results for three parametric implicit surfaces derived from algebraic expressions for a sphere, torus and jack are given in Table 1. Figure 6 gives a comparison of the reconstructed triangulated mesh using the
9 MT and MC approaches. Representation costs for MT are a factor of 3 7 lower for all shapes. The sphere and torus gives the greatest dierence in representation cost between MT and MC due to the smoothly curved surfaces. The computational cost for MT is reduced by a factor of 3 compared to MC. This is due to the use of a surface-based approach where the cost is directly proportional to the surface area. Comparison of the reconstructed meshes illustrates the improvement in representation eciency due to uniform triangle shape achieved with the MT approach. Results demonstrate that both the representation and computational cost are signicantly lower for the MT approach for the same representation accuracy and visulisation quality. 7.2 Implicit Surfaces from Geometric Fusion Results for the MT implicit surfaces polygonisation of surface measurements of real objects are illustrated in Figure 7. Implicit surface representations were obtained by geometric fusion of multiple range images [5]. The telephone and bunny data sets were measured using a Cyberware range sensor [3] and the teapot and soldier data sets are from an NRCC range sensor [10]. Each data sets contains approximately 10 range images. The teapot and soldier data sets are taken from multiple viewpoints in the horizontal plane, resulting in regions of no data for horizontal surfaces and occluded regions.the MT projection distance and MC cube size are equal to the sampling resolution of the range images. Results demonstrate accurate reconstruction of both surface geometry and topology. Small holes, thin surface regions, crease edges and regions of high curvature are correctly reconstructed. The relative representation and computation costs for MC and MT at the same resolution are given in Table 1. The representational costs are a factor of 2 7 lower for MT compared to MC. Objects with smooth surfaces result in a greater reduction in representation cost for the same geometric accuracy. The computational cost for MT is a factor of 3 10 lower than MC as it is directly proportional to the surface area. A comparison of the MT and MC reconstructed mesh for a region of the bunny head is presented in Figure 8. This illustrates that the MT representation eciency is signicantly better due to the uniform triangle shape. 8 Conclusions A new `surface-based' approach to implicit surface polgonisation has been presented called `Marching Triangles' MT. A local `3D Delaunay Surface Constraint' is used to control mesh growing across a manifold surface in R 3. The manifold surface is open or closed and of arbitrary topology. The MT algorithm ensures that the reconstructed triangulated mesh: 1. Is a correct approximation of the surface geometry and topology. 2. Is locally a Delaunay triangulation of the manifold surface. The use of a constraint based on the Delaunay triangulation results in a representation with optimal geometric properties. In particular ecient representation is achieved due to uniform triangle shape. Comparison with `volume-based' implicit surface polygonisation algorithms such as Marching Cubes demonstrates signicant improvement in both representation and computation costs for the same accuracy. Theoretical analysis shows that both costs are equal to the lower bound of the Marching Cubes algorithms. Geometric limitations on reconstruction of the correct surface topology are similar to those with previous volume-based approaches. Results for polygonisation of implicit surfaces dened parametrically and from surface measurements of real objects give a factor of 3 5 improvement in both representation and computation costs. The MT approach also has several potential advantages over previous volume-based approaches. Firstly it allows accurate polygonisation of open manifold surfaces through the use of an implicit boundary function. Secondly dynamic integration of new implicit surface regions into an existing model is achieved. This is important for applications such as fusion of multiple range images of real objects as it allows continuous updating of the model based on new measurements. The MT approach does not impose any restrictions on the mesh vertex position unlike previous mesh growing algorithms [2, 9]. This allows ecient representation with approximately uniform element shape. Future work will investigate adaptive implicit surface polygonisation based on local geometric properties such as surface curvature.
10 (a) Marching Triangles (b) Marching Cubes Figure 6: Parametric Implicit Surface Polygonisation
11 Figure 7: Marching Triangle Reconstruction of 3D Models for Real Objects (a) Marching Triangles (b) Marching Cubes Figure 8: Real Object Implicit Surface Polygonisation
12 References [1] J. Bloomenthal. An implicit surface polygonizer. Graphics Gems ed. Heckbert,P.S., 4: , [2] J.D. Boissonnat. Geometric structures for three-dimensional shape representation. ACM Transactions on Graphics, 3(4): , [3] B. Curless and M. Levoy. A volumetric method for building complex models from range images. In Computer Graphics Proceedings, SIGGRAPH, [4] S. Fortune. Voronoi diagrams and deluanay triangulations. In Computing in Euclidean Geometry, eds. Du, D.-Z. and Hwang, F., pages , [5] A. Hilton, A.J. Stoddart, J. Illingworth, and T. Windeatt. Reliable surface reconstruction from multiple range images. In 4th European Conference on Computer Vision, pages Springer, [6] W.E. Lorensen and H.E. Cline. Marching cubes: A high resolution 3d surface construction algorithm. Computer Graphics, 21(4): , [7] P. Ning and J. Bloomenthal. An evaluation of implicit surface tilers. IEEE Computer Graphics and Applications, 13(November):33 41, [8] J. O'Rouke. Computational Geometry in C. Cambridge University Press, [9] M. Rutishauser, M. Stricker, and M. Trobina. Merging range images of arbitrarily shaped objects. In Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, pages , [10] M. Soucy and D. Laurendeau. A dynamic integration algorithm to model surfaces from multiple range images. Machine Vision and Applications, 8:53{62, 1995.
LATEST TRENDS on APPLIED MATHEMATICS, SIMULATION, MODELLING
 3D surface reconstruction of objects by using stereoscopic viewing Baki Koyuncu, Kurtuluş Küllü bkoyuncu@ankara.edu.tr kkullu@eng.ankara.edu.tr Computer Engineering Department, Ankara University, Ankara,
3D surface reconstruction of objects by using stereoscopic viewing Baki Koyuncu, Kurtuluş Küllü bkoyuncu@ankara.edu.tr kkullu@eng.ankara.edu.tr Computer Engineering Department, Ankara University, Ankara,
Isosurface Rendering. CSC 7443: Scientific Information Visualization
 Isosurface Rendering What is Isosurfacing? An isosurface is the 3D surface representing the locations of a constant scalar value within a volume A surface with the same scalar field value Isosurfaces form
Isosurface Rendering What is Isosurfacing? An isosurface is the 3D surface representing the locations of a constant scalar value within a volume A surface with the same scalar field value Isosurfaces form
2) For any triangle edge not on the boundary, there is exactly one neighboring
 Triangulating Trimmed NURBS Surfaces Chang Shu and Pierre Boulanger Abstract. This paper describes techniques for the piecewise linear approximation of trimmed NURBS surfaces. The problem, called surface
Triangulating Trimmed NURBS Surfaces Chang Shu and Pierre Boulanger Abstract. This paper describes techniques for the piecewise linear approximation of trimmed NURBS surfaces. The problem, called surface
Generating 3D Meshes from Range Data
 Princeton University COS598B Lectures on 3D Modeling Generating 3D Meshes from Range Data Robert Kalnins Robert Osada Overview Range Images Optical Scanners Error sources and solutions Range Surfaces Mesh
Princeton University COS598B Lectures on 3D Modeling Generating 3D Meshes from Range Data Robert Kalnins Robert Osada Overview Range Images Optical Scanners Error sources and solutions Range Surfaces Mesh
Multi-Scale Free-Form Surface Description
 Multi-Scale Free-Form Surface Description Farzin Mokhtarian, Nasser Khalili and Peter Yuen Centre for Vision Speech and Signal Processing Dept. of Electronic and Electrical Engineering University of Surrey,
Multi-Scale Free-Form Surface Description Farzin Mokhtarian, Nasser Khalili and Peter Yuen Centre for Vision Speech and Signal Processing Dept. of Electronic and Electrical Engineering University of Surrey,
Geometric Representations. Stelian Coros
 Geometric Representations Stelian Coros Geometric Representations Languages for describing shape Boundary representations Polygonal meshes Subdivision surfaces Implicit surfaces Volumetric models Parametric
Geometric Representations Stelian Coros Geometric Representations Languages for describing shape Boundary representations Polygonal meshes Subdivision surfaces Implicit surfaces Volumetric models Parametric
Topology Preserving Tetrahedral Decomposition of Trilinear Cell
 Topology Preserving Tetrahedral Decomposition of Trilinear Cell Bong-Soo Sohn Department of Computer Engineering, Kyungpook National University Daegu 702-701, South Korea bongbong@knu.ac.kr http://bh.knu.ac.kr/
Topology Preserving Tetrahedral Decomposition of Trilinear Cell Bong-Soo Sohn Department of Computer Engineering, Kyungpook National University Daegu 702-701, South Korea bongbong@knu.ac.kr http://bh.knu.ac.kr/
Outline of the presentation
 Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
Processing 3D Surface Data
 Processing 3D Surface Data Computer Animation and Visualisation Lecture 12 Institute for Perception, Action & Behaviour School of Informatics 3D Surfaces 1 3D surface data... where from? Iso-surfacing
Processing 3D Surface Data Computer Animation and Visualisation Lecture 12 Institute for Perception, Action & Behaviour School of Informatics 3D Surfaces 1 3D surface data... where from? Iso-surfacing
CSG obj. oper3. obj1 obj2 obj3. obj5. obj4
 Solid Modeling Solid: Boundary + Interior Volume occupied by geometry Solid representation schemes Constructive Solid Geometry (CSG) Boundary representations (B-reps) Space-partition representations Operations
Solid Modeling Solid: Boundary + Interior Volume occupied by geometry Solid representation schemes Constructive Solid Geometry (CSG) Boundary representations (B-reps) Space-partition representations Operations
Scalar Algorithms: Contouring
 Scalar Algorithms: Contouring Computer Animation and Visualisation Lecture tkomura@inf.ed.ac.uk Institute for Perception, Action & Behaviour School of Informatics Contouring Scaler Data Last Lecture...
Scalar Algorithms: Contouring Computer Animation and Visualisation Lecture tkomura@inf.ed.ac.uk Institute for Perception, Action & Behaviour School of Informatics Contouring Scaler Data Last Lecture...
Shape and Appearance from Images and Range Data
 SIGGRAPH 2000 Course on 3D Photography Shape and Appearance from Images and Range Data Brian Curless University of Washington Overview Range images vs. point clouds Registration Reconstruction from point
SIGGRAPH 2000 Course on 3D Photography Shape and Appearance from Images and Range Data Brian Curless University of Washington Overview Range images vs. point clouds Registration Reconstruction from point
Surface Modeling. Polygon Tables. Types: Generating models: Polygon Surfaces. Polygon surfaces Curved surfaces Volumes. Interactive Procedural
 Surface Modeling Types: Polygon surfaces Curved surfaces Volumes Generating models: Interactive Procedural Polygon Tables We specify a polygon surface with a set of vertex coordinates and associated attribute
Surface Modeling Types: Polygon surfaces Curved surfaces Volumes Generating models: Interactive Procedural Polygon Tables We specify a polygon surface with a set of vertex coordinates and associated attribute
Processing 3D Surface Data
 Processing 3D Surface Data Computer Animation and Visualisation Lecture 17 Institute for Perception, Action & Behaviour School of Informatics 3D Surfaces 1 3D surface data... where from? Iso-surfacing
Processing 3D Surface Data Computer Animation and Visualisation Lecture 17 Institute for Perception, Action & Behaviour School of Informatics 3D Surfaces 1 3D surface data... where from? Iso-surfacing
Space Subdivision for the Adaptive Edge Spinning Polygonization
 Space Subdivision for the Adaptive Edge Spinning Polygonization MARTIN CERMAK 1, VACLAV SKALA Department of Computer Science and Engineering University of West Bohemia in Pilsen Univerzitni 8, 306 14 Plzen
Space Subdivision for the Adaptive Edge Spinning Polygonization MARTIN CERMAK 1, VACLAV SKALA Department of Computer Science and Engineering University of West Bohemia in Pilsen Univerzitni 8, 306 14 Plzen
A Method of Automated Landmark Generation for Automated 3D PDM Construction
 A Method of Automated Landmark Generation for Automated 3D PDM Construction A. D. Brett and C. J. Taylor Department of Medical Biophysics University of Manchester Manchester M13 9PT, Uk adb@sv1.smb.man.ac.uk
A Method of Automated Landmark Generation for Automated 3D PDM Construction A. D. Brett and C. J. Taylor Department of Medical Biophysics University of Manchester Manchester M13 9PT, Uk adb@sv1.smb.man.ac.uk
03 - Reconstruction. Acknowledgements: Olga Sorkine-Hornung. CSCI-GA Geometric Modeling - Spring 17 - Daniele Panozzo
 3 - Reconstruction Acknowledgements: Olga Sorkine-Hornung Geometry Acquisition Pipeline Scanning: results in range images Registration: bring all range images to one coordinate system Stitching/ reconstruction:
3 - Reconstruction Acknowledgements: Olga Sorkine-Hornung Geometry Acquisition Pipeline Scanning: results in range images Registration: bring all range images to one coordinate system Stitching/ reconstruction:
Project Updates Short lecture Volumetric Modeling +2 papers
 Volumetric Modeling Schedule (tentative) Feb 20 Feb 27 Mar 5 Introduction Lecture: Geometry, Camera Model, Calibration Lecture: Features, Tracking/Matching Mar 12 Mar 19 Mar 26 Apr 2 Apr 9 Apr 16 Apr 23
Volumetric Modeling Schedule (tentative) Feb 20 Feb 27 Mar 5 Introduction Lecture: Geometry, Camera Model, Calibration Lecture: Features, Tracking/Matching Mar 12 Mar 19 Mar 26 Apr 2 Apr 9 Apr 16 Apr 23
Surface Reconstruction. Gianpaolo Palma
 Surface Reconstruction Gianpaolo Palma Surface reconstruction Input Point cloud With or without normals Examples: multi-view stereo, union of range scan vertices Range scans Each scan is a triangular mesh
Surface Reconstruction Gianpaolo Palma Surface reconstruction Input Point cloud With or without normals Examples: multi-view stereo, union of range scan vertices Range scans Each scan is a triangular mesh
Computing 3D Geometry Directly From Range Images
 Computing 3D Geometry Directly From Range Images Sarah F. Frisken and Ronald N. Perry Mitsubishi Electric Research Laboratories Geometry from Range Data A Classic Approach Subject Range images Range surfaces
Computing 3D Geometry Directly From Range Images Sarah F. Frisken and Ronald N. Perry Mitsubishi Electric Research Laboratories Geometry from Range Data A Classic Approach Subject Range images Range surfaces
Efficient Representation and Extraction of 2-Manifold Isosurfaces Using kd-trees
 Efficient Representation and Extraction of 2-Manifold Isosurfaces Using kd-trees Alexander Greß and Reinhard Klein University of Bonn Institute of Computer Science II Römerstraße 164, 53117 Bonn, Germany
Efficient Representation and Extraction of 2-Manifold Isosurfaces Using kd-trees Alexander Greß and Reinhard Klein University of Bonn Institute of Computer Science II Römerstraße 164, 53117 Bonn, Germany
Data Representation in Visualisation
 Data Representation in Visualisation Visualisation Lecture 4 Taku Komura Institute for Perception, Action & Behaviour School of Informatics Taku Komura Data Representation 1 Data Representation We have
Data Representation in Visualisation Visualisation Lecture 4 Taku Komura Institute for Perception, Action & Behaviour School of Informatics Taku Komura Data Representation 1 Data Representation We have
Contours & Implicit Modelling 1
 Contouring & Implicit Modelling Visualisation Lecture 8 Institute for Perception, Action & Behaviour School of Informatics Contours & Implicit Modelling 1 Brief Recap Contouring Implicit Functions lecture
Contouring & Implicit Modelling Visualisation Lecture 8 Institute for Perception, Action & Behaviour School of Informatics Contours & Implicit Modelling 1 Brief Recap Contouring Implicit Functions lecture
Inside hole. Inside wire. Input: and. d y. Inside vertex. Outside loop
 Energy-Minimizing Approach to Meshing Curved Wire-Frame Models Atsushi Yamada Kenji Shimada Takayuki Itoh Tokyo Research Laboratory, IBM Japan, Ltd., 1623-14, Shimotsuruma, Yamato-shi, Kanagawa-ken 242,
Energy-Minimizing Approach to Meshing Curved Wire-Frame Models Atsushi Yamada Kenji Shimada Takayuki Itoh Tokyo Research Laboratory, IBM Japan, Ltd., 1623-14, Shimotsuruma, Yamato-shi, Kanagawa-ken 242,
Processing 3D Surface Data
 Processing 3D Surface Data Computer Animation and Visualisation Lecture 15 Institute for Perception, Action & Behaviour School of Informatics 3D Surfaces 1 3D surface data... where from? Iso-surfacing
Processing 3D Surface Data Computer Animation and Visualisation Lecture 15 Institute for Perception, Action & Behaviour School of Informatics 3D Surfaces 1 3D surface data... where from? Iso-surfacing
Outline. Reconstruction of 3D Meshes from Point Clouds. Motivation. Problem Statement. Applications. Challenges
 Reconstruction of 3D Meshes from Point Clouds Ming Zhang Patrick Min cs598b, Geometric Modeling for Computer Graphics Feb. 17, 2000 Outline - problem statement - motivation - applications - challenges
Reconstruction of 3D Meshes from Point Clouds Ming Zhang Patrick Min cs598b, Geometric Modeling for Computer Graphics Feb. 17, 2000 Outline - problem statement - motivation - applications - challenges
Computational Geometry
 Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
Geometric Modeling in Graphics
 Geometric Modeling in Graphics Part 10: Surface reconstruction Martin Samuelčík www.sccg.sk/~samuelcik samuelcik@sccg.sk Curve, surface reconstruction Finding compact connected orientable 2-manifold surface
Geometric Modeling in Graphics Part 10: Surface reconstruction Martin Samuelčík www.sccg.sk/~samuelcik samuelcik@sccg.sk Curve, surface reconstruction Finding compact connected orientable 2-manifold surface
Design Intent of Geometric Models
 School of Computer Science Cardiff University Design Intent of Geometric Models Frank C. Langbein GR/M78267 GR/S69085/01 NUF-NAL 00638/G Auckland University 15th September 2004; Version 1.1 Design Intent
School of Computer Science Cardiff University Design Intent of Geometric Models Frank C. Langbein GR/M78267 GR/S69085/01 NUF-NAL 00638/G Auckland University 15th September 2004; Version 1.1 Design Intent
Triangular Meshes from 3-D Image and Point Data. Gerhard Roth and Eko Wibowoo. Institute for Information Technology, Building M 50, Montreal Road
 An Ecient Volumetric Method for Building Closed Triangular Meshes from 3-D Image and Point Data Gerhard Roth and Eko Wibowoo Institute for Information Technology, Building M 50, Montreal Road National
An Ecient Volumetric Method for Building Closed Triangular Meshes from 3-D Image and Point Data Gerhard Roth and Eko Wibowoo Institute for Information Technology, Building M 50, Montreal Road National
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass
 Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
coding of various parts showing different features, the possibility of rotation or of hiding covering parts of the object's surface to gain an insight
 Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
Volume Illumination, Contouring
 Volume Illumination, Contouring Computer Animation and Visualisation Lecture 0 tkomura@inf.ed.ac.uk Institute for Perception, Action & Behaviour School of Informatics Contouring Scaler Data Overview -
Volume Illumination, Contouring Computer Animation and Visualisation Lecture 0 tkomura@inf.ed.ac.uk Institute for Perception, Action & Behaviour School of Informatics Contouring Scaler Data Overview -
Homework 1: Implicit Surfaces, Collision Detection, & Volumetric Data Structures. Loop Subdivision. Loop Subdivision. Questions/Comments?
 Homework 1: Questions/Comments? Implicit Surfaces,, & Volumetric Data Structures Loop Subdivision Shirley, Fundamentals of Computer Graphics Loop Subdivision SIGGRAPH 2000 course notes Subdivision for
Homework 1: Questions/Comments? Implicit Surfaces,, & Volumetric Data Structures Loop Subdivision Shirley, Fundamentals of Computer Graphics Loop Subdivision SIGGRAPH 2000 course notes Subdivision for
Figure 1: An Area Voronoi Diagram of a typical GIS Scene generated from the ISPRS Working group III/3 Avenches data set. 2 ARRANGEMENTS 2.1 Voronoi Di
 Qualitative Spatial Relations using Arrangements for Complex Images M. Burge and W. Burger Johannes Kepler University, Department of Systems Science Computer Vision Laboratory, A-4040 Linz, Austria burge@cast.uni-linz.ac.at
Qualitative Spatial Relations using Arrangements for Complex Images M. Burge and W. Burger Johannes Kepler University, Department of Systems Science Computer Vision Laboratory, A-4040 Linz, Austria burge@cast.uni-linz.ac.at
Introduction to Computer Graphics. Modeling (3) April 27, 2017 Kenshi Takayama
 Introduction to Computer Graphics Modeling (3) April 27, 2017 Kenshi Takayama Solid modeling 2 Solid models Thin shapes represented by single polygons Unorientable Clear definition of inside & outside
Introduction to Computer Graphics Modeling (3) April 27, 2017 Kenshi Takayama Solid modeling 2 Solid models Thin shapes represented by single polygons Unorientable Clear definition of inside & outside
Survey of Surface Reconstruction Algorithms
 Journal of Signal and Information Processing, 2014, 5, 63-79 Published Online August 2014 in SciRes. http://www.scirp.org/journal/jsip http://dx.doi.org/10.4236/jsip.2014.53009 Survey of Surface Reconstruction
Journal of Signal and Information Processing, 2014, 5, 63-79 Published Online August 2014 in SciRes. http://www.scirp.org/journal/jsip http://dx.doi.org/10.4236/jsip.2014.53009 Survey of Surface Reconstruction
Curvature Estimation on Smoothed 3-D Meshes
 Curvature Estimation on Smoothed 3-D Meshes Peter Yuen, Nasser Khalili and Farzin Mokhtarian Centre for Vision, Speech and Signal Processing School of Electronic Engineering, Information Technology and
Curvature Estimation on Smoothed 3-D Meshes Peter Yuen, Nasser Khalili and Farzin Mokhtarian Centre for Vision, Speech and Signal Processing School of Electronic Engineering, Information Technology and
Outline. Visualization Discretization Sampling Quantization Representation Continuous Discrete. Noise
 Fundamentals Data Outline Visualization Discretization Sampling Quantization Representation Continuous Discrete Noise 2 Data Data : Function dependent on one or more variables. Example Audio (1D) - depends
Fundamentals Data Outline Visualization Discretization Sampling Quantization Representation Continuous Discrete Noise 2 Data Data : Function dependent on one or more variables. Example Audio (1D) - depends
Tiling Three-Dimensional Space with Simplices. Shankar Krishnan AT&T Labs - Research
 Tiling Three-Dimensional Space with Simplices Shankar Krishnan AT&T Labs - Research What is a Tiling? Partition of an infinite space into pieces having a finite number of distinct shapes usually Euclidean
Tiling Three-Dimensional Space with Simplices Shankar Krishnan AT&T Labs - Research What is a Tiling? Partition of an infinite space into pieces having a finite number of distinct shapes usually Euclidean
Volume Illumination and Segmentation
 Volume Illumination and Segmentation Computer Animation and Visualisation Lecture 13 Institute for Perception, Action & Behaviour School of Informatics Overview Volume illumination Segmentation Volume
Volume Illumination and Segmentation Computer Animation and Visualisation Lecture 13 Institute for Perception, Action & Behaviour School of Informatics Overview Volume illumination Segmentation Volume
Contours & Implicit Modelling 4
 Brief Recap Contouring & Implicit Modelling Contouring Implicit Functions Visualisation Lecture 8 lecture 6 Marching Cubes lecture 3 visualisation of a Quadric toby.breckon@ed.ac.uk Computer Vision Lab.
Brief Recap Contouring & Implicit Modelling Contouring Implicit Functions Visualisation Lecture 8 lecture 6 Marching Cubes lecture 3 visualisation of a Quadric toby.breckon@ed.ac.uk Computer Vision Lab.
Mesh Repairing and Simplification. Gianpaolo Palma
 Mesh Repairing and Simplification Gianpaolo Palma Mesh Repairing Removal of artifacts from geometric model such that it becomes suitable for further processing Input: a generic 3D model Output: (hopefully)a
Mesh Repairing and Simplification Gianpaolo Palma Mesh Repairing Removal of artifacts from geometric model such that it becomes suitable for further processing Input: a generic 3D model Output: (hopefully)a
Voronoi diagram and Delaunay triangulation
 Voronoi diagram and Delaunay triangulation Ioannis Emiris & Vissarion Fisikopoulos Dept. of Informatics & Telecommunications, University of Athens Computational Geometry, spring 2015 Outline 1 Voronoi
Voronoi diagram and Delaunay triangulation Ioannis Emiris & Vissarion Fisikopoulos Dept. of Informatics & Telecommunications, University of Athens Computational Geometry, spring 2015 Outline 1 Voronoi
Special Topics in Visualization
 Special Topics in Visualization Final Project Report Dual contouring of Hermite Data Submitted By S M Shahed Nejhum 8589-1199 May 19, 2008 Introduction Iso-surface extraction from 3D volumetric data is
Special Topics in Visualization Final Project Report Dual contouring of Hermite Data Submitted By S M Shahed Nejhum 8589-1199 May 19, 2008 Introduction Iso-surface extraction from 3D volumetric data is
Shape Modeling and Geometry Processing
 252-0538-00L, Spring 2018 Shape Modeling and Geometry Processing Discrete Differential Geometry Differential Geometry Motivation Formalize geometric properties of shapes Roi Poranne # 2 Differential Geometry
252-0538-00L, Spring 2018 Shape Modeling and Geometry Processing Discrete Differential Geometry Differential Geometry Motivation Formalize geometric properties of shapes Roi Poranne # 2 Differential Geometry
A Volumetric Method for Building Complex Models from Range Images
 A Volumetric Method for Building Complex Models from Range Images Brian Curless Marc Levoy Computer Graphics Laboratory Stanford University Introduction Goal Given a set of aligned, dense range images,
A Volumetric Method for Building Complex Models from Range Images Brian Curless Marc Levoy Computer Graphics Laboratory Stanford University Introduction Goal Given a set of aligned, dense range images,
Complex Models from Range Images. A Volumetric Method for Building. Brian Curless. Marc Levoy. Computer Graphics Laboratory. Stanford University
 A Volumetric Method for Building Complex Models from Range Images Computer Graphics Laboratory Stanford University Brian Curless Marc Levoy Introduction Goal Given a set of aligned, dense range images,
A Volumetric Method for Building Complex Models from Range Images Computer Graphics Laboratory Stanford University Brian Curless Marc Levoy Introduction Goal Given a set of aligned, dense range images,
SURFACE CONSTRUCTION USING TRICOLOR MARCHING CUBES
 SURFACE CONSTRUCTION USING TRICOLOR MARCHING CUBES Shaojun Liu, Jia Li Oakland University Rochester, MI 4839, USA Email: sliu2@oakland.edu, li4@oakland.edu Xiaojun Jing Beijing University of Posts and
SURFACE CONSTRUCTION USING TRICOLOR MARCHING CUBES Shaojun Liu, Jia Li Oakland University Rochester, MI 4839, USA Email: sliu2@oakland.edu, li4@oakland.edu Xiaojun Jing Beijing University of Posts and
In this lecture we introduce the Gauss-Bonnet theorem. The required section is The optional sections are
 Math 348 Fall 2017 Lectures 20: The Gauss-Bonnet Theorem II Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams.
Math 348 Fall 2017 Lectures 20: The Gauss-Bonnet Theorem II Disclaimer. As we have a textbook, this lecture note is for guidance and supplement only. It should not be relied on when preparing for exams.
Topological Equivalence between a 3D Object and the Reconstruction of its Digital Image
 to appear in IEEE PAMI Topological Equivalence between a 3D Object and the Reconstruction of its Digital Image Peer Stelldinger, Longin Jan Latecki and Marcelo Siqueira Abstract Digitization is not as
to appear in IEEE PAMI Topological Equivalence between a 3D Object and the Reconstruction of its Digital Image Peer Stelldinger, Longin Jan Latecki and Marcelo Siqueira Abstract Digitization is not as
ACCURACY EVALUATION OF 3D RECONSTRUCTION FROM CT-SCAN IMAGES FOR INSPECTION OF INDUSTRIAL PARTS. Institut Francais du Petrole
 ACCURACY EVALUATION OF 3D RECONSTRUCTION FROM CT-SCAN IMAGES FOR INSPECTION OF INDUSTRIAL PARTS H. Delingette y,o.seguin z,r.perrocheau z,p.menegazzi z yinria Sophia-Antipolis 2004, Route des Lucioles
ACCURACY EVALUATION OF 3D RECONSTRUCTION FROM CT-SCAN IMAGES FOR INSPECTION OF INDUSTRIAL PARTS H. Delingette y,o.seguin z,r.perrocheau z,p.menegazzi z yinria Sophia-Antipolis 2004, Route des Lucioles
Surface Curvature Estimation for Edge Spinning Algorithm *
 Surface Curvature Estimation for Edge Spinning Algorithm * Martin Cermak and Vaclav Skala University of West Bohemia in Pilsen Department of Computer Science and Engineering Czech Republic {cermakm skala}@kiv.zcu.cz
Surface Curvature Estimation for Edge Spinning Algorithm * Martin Cermak and Vaclav Skala University of West Bohemia in Pilsen Department of Computer Science and Engineering Czech Republic {cermakm skala}@kiv.zcu.cz
Geometric Modeling Mortenson Chapter 11. Complex Model Construction
 Geometric Modeling 91.580.201 Mortenson Chapter 11 Complex Model Construction Topics Topology of Models Connectivity and other intrinsic properties Graph-Based Models Emphasize topological structure Boolean
Geometric Modeling 91.580.201 Mortenson Chapter 11 Complex Model Construction Topics Topology of Models Connectivity and other intrinsic properties Graph-Based Models Emphasize topological structure Boolean
Efficient Representation and Extraction of 2-Manifold Isosurfaces Using kd-trees
 Efficient Representation and Extraction of 2-Manifold Isosurfaces Using kd-trees Alexander Greß gress@cs.uni-bonn.de Reinhard Klein rk@cs.uni-bonn.de University of Bonn Institute of Computer Science II
Efficient Representation and Extraction of 2-Manifold Isosurfaces Using kd-trees Alexander Greß gress@cs.uni-bonn.de Reinhard Klein rk@cs.uni-bonn.de University of Bonn Institute of Computer Science II
Spectral Surface Reconstruction from Noisy Point Clouds
 Spectral Surface Reconstruction from Noisy Point Clouds 1. Briefly summarize the paper s contributions. Does it address a new problem? Does it present a new approach? Does it show new types of results?
Spectral Surface Reconstruction from Noisy Point Clouds 1. Briefly summarize the paper s contributions. Does it address a new problem? Does it present a new approach? Does it show new types of results?
Topological estimation using witness complexes. Vin de Silva, Stanford University
 Topological estimation using witness complexes, Acknowledgements Gunnar Carlsson (Mathematics, Stanford) principal collaborator Afra Zomorodian (CS/Robotics, Stanford) persistent homology software Josh
Topological estimation using witness complexes, Acknowledgements Gunnar Carlsson (Mathematics, Stanford) principal collaborator Afra Zomorodian (CS/Robotics, Stanford) persistent homology software Josh
implicit surfaces, approximate implicitization, B-splines, A- patches, surface fitting
 24. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE ZBYNĚK ŠÍR FITTING OF PIECEWISE POLYNOMIAL IMPLICIT SURFACES Abstrakt In our contribution we discuss the possibility of an efficient fitting of piecewise
24. KONFERENCE O GEOMETRII A POČÍTAČOVÉ GRAFICE ZBYNĚK ŠÍR FITTING OF PIECEWISE POLYNOMIAL IMPLICIT SURFACES Abstrakt In our contribution we discuss the possibility of an efficient fitting of piecewise
Correctness. The Powercrust Algorithm for Surface Reconstruction. Correctness. Correctness. Delaunay Triangulation. Tools - Voronoi Diagram
 Correctness The Powercrust Algorithm for Surface Reconstruction Nina Amenta Sunghee Choi Ravi Kolluri University of Texas at Austin Boundary of a solid Close to original surface Homeomorphic to original
Correctness The Powercrust Algorithm for Surface Reconstruction Nina Amenta Sunghee Choi Ravi Kolluri University of Texas at Austin Boundary of a solid Close to original surface Homeomorphic to original
(Discrete) Differential Geometry
 (Discrete) Differential Geometry Motivation Understand the structure of the surface Properties: smoothness, curviness, important directions How to modify the surface to change these properties What properties
(Discrete) Differential Geometry Motivation Understand the structure of the surface Properties: smoothness, curviness, important directions How to modify the surface to change these properties What properties
IMAGE-BASED RENDERING
 IMAGE-BASED RENDERING 1. What is Image-Based Rendering? - The synthesis of new views of a scene from pre-recorded pictures.!"$#% "'&( )*+,-/.). #0 1 ' 2"&43+5+, 2. Why? (1) We really enjoy visual magic!
IMAGE-BASED RENDERING 1. What is Image-Based Rendering? - The synthesis of new views of a scene from pre-recorded pictures.!"$#% "'&( )*+,-/.). #0 1 ' 2"&43+5+, 2. Why? (1) We really enjoy visual magic!
Lecture 17: Solid Modeling.... a cubit on the one side, and a cubit on the other side Exodus 26:13
 Lecture 17: Solid Modeling... a cubit on the one side, and a cubit on the other side Exodus 26:13 Who is on the LORD's side? Exodus 32:26 1. Solid Representations A solid is a 3-dimensional shape with
Lecture 17: Solid Modeling... a cubit on the one side, and a cubit on the other side Exodus 26:13 Who is on the LORD's side? Exodus 32:26 1. Solid Representations A solid is a 3-dimensional shape with
u 0+u 2 new boundary vertex
 Combined Subdivision Schemes for the design of surfaces satisfying boundary conditions Adi Levin School of Mathematical Sciences, Tel-Aviv University, Tel-Aviv 69978, Israel. Email:fadilev@math.tau.ac.ilg
Combined Subdivision Schemes for the design of surfaces satisfying boundary conditions Adi Levin School of Mathematical Sciences, Tel-Aviv University, Tel-Aviv 69978, Israel. Email:fadilev@math.tau.ac.ilg
GEOMETRIC TOOLS FOR COMPUTER GRAPHICS
 GEOMETRIC TOOLS FOR COMPUTER GRAPHICS PHILIP J. SCHNEIDER DAVID H. EBERLY MORGAN KAUFMANN PUBLISHERS A N I M P R I N T O F E L S E V I E R S C I E N C E A M S T E R D A M B O S T O N L O N D O N N E W
GEOMETRIC TOOLS FOR COMPUTER GRAPHICS PHILIP J. SCHNEIDER DAVID H. EBERLY MORGAN KAUFMANN PUBLISHERS A N I M P R I N T O F E L S E V I E R S C I E N C E A M S T E R D A M B O S T O N L O N D O N N E W
Free-form 3D object reconstruction from range images. C. Schütz, T. Jost, H. Hügli
 Free-form 3D object reconstruction from range images C. Schütz, T. Jost, H. Hügli Institute for Microtechnology University of Neuchatel, rue Breguet 2 CH-2000 Neuchatel, Switzerland email: christian.schutz@imt.unine.ch
Free-form 3D object reconstruction from range images C. Schütz, T. Jost, H. Hügli Institute for Microtechnology University of Neuchatel, rue Breguet 2 CH-2000 Neuchatel, Switzerland email: christian.schutz@imt.unine.ch
Supplementary Materials for
 advances.sciencemag.org/cgi/content/full/4/1/eaao7005/dc1 Supplementary Materials for Computational discovery of extremal microstructure families The PDF file includes: Desai Chen, Mélina Skouras, Bo Zhu,
advances.sciencemag.org/cgi/content/full/4/1/eaao7005/dc1 Supplementary Materials for Computational discovery of extremal microstructure families The PDF file includes: Desai Chen, Mélina Skouras, Bo Zhu,
3D Object Representation. Michael Kazhdan ( /657)
 3D Object Representation Michael Kazhdan (601.457/657) 3D Objects How can this object be represented in a computer? 3D Objects This one? H&B Figure 10.46 3D Objects This one? H&B Figure 9.9 3D Objects
3D Object Representation Michael Kazhdan (601.457/657) 3D Objects How can this object be represented in a computer? 3D Objects This one? H&B Figure 10.46 3D Objects This one? H&B Figure 9.9 3D Objects
Solid Modelling. Graphics Systems / Computer Graphics and Interfaces COLLEGE OF ENGINEERING UNIVERSITY OF PORTO
 Solid Modelling Graphics Systems / Computer Graphics and Interfaces 1 Solid Modelling In 2D, one set 2D line segments or curves does not necessarily form a closed area. In 3D, a collection of surfaces
Solid Modelling Graphics Systems / Computer Graphics and Interfaces 1 Solid Modelling In 2D, one set 2D line segments or curves does not necessarily form a closed area. In 3D, a collection of surfaces
The Ball-Pivoting Algorithm for Surface Reconstruction
 The Ball-Pivoting Algorithm for Surface Reconstruction 1. Briefly summarize the paper s contributions. Does it address a new problem? Does it present a new approach? Does it show new types of results?
The Ball-Pivoting Algorithm for Surface Reconstruction 1. Briefly summarize the paper s contributions. Does it address a new problem? Does it present a new approach? Does it show new types of results?
Development of Reverse Engineering System for Machine Engineering Using 3D Bit-map Data. Tatsuro Yashiki* and Tarou Takagi*
 Development of Reverse Engineering System for Machine Engineering Using 3D Bit-map Data Tatsuro Yashiki* and Tarou Takagi* *Power & Industrial Systems R&D Laboratory, Hitachi, Ltd. Abstract In this paper,
Development of Reverse Engineering System for Machine Engineering Using 3D Bit-map Data Tatsuro Yashiki* and Tarou Takagi* *Power & Industrial Systems R&D Laboratory, Hitachi, Ltd. Abstract In this paper,
Shape from Silhouettes I
 Shape from Silhouettes I Guido Gerig CS 6320, Spring 2015 Credits: Marc Pollefeys, UNC Chapel Hill, some of the figures and slides are also adapted from J.S. Franco, J. Matusik s presentations, and referenced
Shape from Silhouettes I Guido Gerig CS 6320, Spring 2015 Credits: Marc Pollefeys, UNC Chapel Hill, some of the figures and slides are also adapted from J.S. Franco, J. Matusik s presentations, and referenced
1 Appendix to notes 2, on Hyperbolic geometry:
 1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
Other Voronoi/Delaunay Structures
 Other Voronoi/Delaunay Structures Overview Alpha hulls (a subset of Delaunay graph) Extension of Voronoi Diagrams Convex Hull What is it good for? The bounding region of a point set Not so good for describing
Other Voronoi/Delaunay Structures Overview Alpha hulls (a subset of Delaunay graph) Extension of Voronoi Diagrams Convex Hull What is it good for? The bounding region of a point set Not so good for describing
Voronoi Diagram. Xiao-Ming Fu
 Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
Zipper Unfoldings of Polyhedral Complexes
 Zipper Unfoldings of Polyhedral Complexes Erik D. Demaine Martin L. Demaine Anna Lubiw Arlo Shallit Jonah L. Shallit Abstract We explore which polyhedra and polyhedral complexes can be formed by folding
Zipper Unfoldings of Polyhedral Complexes Erik D. Demaine Martin L. Demaine Anna Lubiw Arlo Shallit Jonah L. Shallit Abstract We explore which polyhedra and polyhedral complexes can be formed by folding
Appendix E Calculating Normal Vectors
 OpenGL Programming Guide (Addison-Wesley Publishing Company) Appendix E Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use
OpenGL Programming Guide (Addison-Wesley Publishing Company) Appendix E Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use
SOME 024: Computer Aided Design. E. Rozos
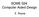 SOME 024: Computer Aided Design E. Rozos Introduction to CAD theory part 2 Lesson structure Why Solid modelling Solid modelling methods Representation based Manufacturing based Solid modelling storage
SOME 024: Computer Aided Design E. Rozos Introduction to CAD theory part 2 Lesson structure Why Solid modelling Solid modelling methods Representation based Manufacturing based Solid modelling storage
Calculating the Distance Map for Binary Sampled Data
 MITSUBISHI ELECTRIC RESEARCH LABORATORIES http://www.merl.com Calculating the Distance Map for Binary Sampled Data Sarah F. Frisken Gibson TR99-6 December 999 Abstract High quality rendering and physics-based
MITSUBISHI ELECTRIC RESEARCH LABORATORIES http://www.merl.com Calculating the Distance Map for Binary Sampled Data Sarah F. Frisken Gibson TR99-6 December 999 Abstract High quality rendering and physics-based
N. Hitschfeld. Blanco Encalada 2120, Santiago, CHILE.
 Generalization of modied octrees for geometric modeling N. Hitschfeld Dpto. Ciencias de la Computacion, Univ. de Chile Blanco Encalada 2120, Santiago, CHILE E-mail: nancy@dcc.uchile.cl Abstract. This paper
Generalization of modied octrees for geometric modeling N. Hitschfeld Dpto. Ciencias de la Computacion, Univ. de Chile Blanco Encalada 2120, Santiago, CHILE E-mail: nancy@dcc.uchile.cl Abstract. This paper
Egemen Tanin, Tahsin M. Kurc, Cevdet Aykanat, Bulent Ozguc. Abstract. Direct Volume Rendering (DVR) is a powerful technique for
 Comparison of Two Image-Space Subdivision Algorithms for Direct Volume Rendering on Distributed-Memory Multicomputers Egemen Tanin, Tahsin M. Kurc, Cevdet Aykanat, Bulent Ozguc Dept. of Computer Eng. and
Comparison of Two Image-Space Subdivision Algorithms for Direct Volume Rendering on Distributed-Memory Multicomputers Egemen Tanin, Tahsin M. Kurc, Cevdet Aykanat, Bulent Ozguc Dept. of Computer Eng. and
CS354 Computer Graphics Surface Representation IV. Qixing Huang March 7th 2018
 CS354 Computer Graphics Surface Representation IV Qixing Huang March 7th 2018 Today s Topic Subdivision surfaces Implicit surface representation Subdivision Surfaces Building complex models We can extend
CS354 Computer Graphics Surface Representation IV Qixing Huang March 7th 2018 Today s Topic Subdivision surfaces Implicit surface representation Subdivision Surfaces Building complex models We can extend
Extracting consistent and manifold interfaces from multi-valued volume data sets
 Extracting consistent and manifold interfaces from multi-valued volume data sets Stephan Bischoff, Leif Kobbelt Lehrstuhl für Informatik 8, RWTH Aachen, 52056 Aachen Email: {bischoff,kobbelt}@informatik.rwth-aachen.de
Extracting consistent and manifold interfaces from multi-valued volume data sets Stephan Bischoff, Leif Kobbelt Lehrstuhl für Informatik 8, RWTH Aachen, 52056 Aachen Email: {bischoff,kobbelt}@informatik.rwth-aachen.de
A Hybrid Hole-filling Algorithm
 A Hybrid Hole-filling Algorithm by Junhui Long A thesis submitted to the School of Computing in conformity with the requirements for the degree of Master of Science Queen s University Kingston, Ontario,
A Hybrid Hole-filling Algorithm by Junhui Long A thesis submitted to the School of Computing in conformity with the requirements for the degree of Master of Science Queen s University Kingston, Ontario,
What is visualization? Why is it important?
 What is visualization? Why is it important? What does visualization do? What is the difference between scientific data and information data Cycle of Visualization Storage De noising/filtering Down sampling
What is visualization? Why is it important? What does visualization do? What is the difference between scientific data and information data Cycle of Visualization Storage De noising/filtering Down sampling
Topological Data Analysis - I. Afra Zomorodian Department of Computer Science Dartmouth College
 Topological Data Analysis - I Afra Zomorodian Department of Computer Science Dartmouth College September 3, 2007 1 Acquisition Vision: Images (2D) GIS: Terrains (3D) Graphics: Surfaces (3D) Medicine: MRI
Topological Data Analysis - I Afra Zomorodian Department of Computer Science Dartmouth College September 3, 2007 1 Acquisition Vision: Images (2D) GIS: Terrains (3D) Graphics: Surfaces (3D) Medicine: MRI
Data sharing of shape model with VRML environment
 Data sharing of shape model with VRML environment K. G. Kobayasht, K. Ujihara, M. Hayamizu, and M. Fujii" Japan Society for Precision Engineering Toyama Prefectural University, Dept. of Mech. Systems Eng.
Data sharing of shape model with VRML environment K. G. Kobayasht, K. Ujihara, M. Hayamizu, and M. Fujii" Japan Society for Precision Engineering Toyama Prefectural University, Dept. of Mech. Systems Eng.
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 24 Solid Modelling
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 24 Solid Modelling Welcome to the lectures on computer graphics. We have
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 24 Solid Modelling Welcome to the lectures on computer graphics. We have
Pose estimation of two-pose 3D models using the base tangent plane and stability constraints
 Pose estimation of two-pose 3D models using the base tangent plane and stability constraints Soon-Yong Park and Murali Subbarao Department of Electrical and Computer Engineering State University of New
Pose estimation of two-pose 3D models using the base tangent plane and stability constraints Soon-Yong Park and Murali Subbarao Department of Electrical and Computer Engineering State University of New
Computer Graphics Ray Casting. Matthias Teschner
 Computer Graphics Ray Casting Matthias Teschner Outline Context Implicit surfaces Parametric surfaces Combined objects Triangles Axis-aligned boxes Iso-surfaces in grids Summary University of Freiburg
Computer Graphics Ray Casting Matthias Teschner Outline Context Implicit surfaces Parametric surfaces Combined objects Triangles Axis-aligned boxes Iso-surfaces in grids Summary University of Freiburg
A Flavor of Topology. Shireen Elhabian and Aly A. Farag University of Louisville January 2010
 A Flavor of Topology Shireen Elhabian and Aly A. Farag University of Louisville January 2010 In 1670 s I believe that we need another analysis properly geometric or linear, which treats place directly
A Flavor of Topology Shireen Elhabian and Aly A. Farag University of Louisville January 2010 In 1670 s I believe that we need another analysis properly geometric or linear, which treats place directly
Definitions. Topology/Geometry of Geodesics. Joseph D. Clinton. SNEC June Magnus J. Wenninger
 Topology/Geometry of Geodesics Joseph D. Clinton SNEC-04 28-29 June 2003 Magnus J. Wenninger Introduction Definitions Topology Goldberg s polyhedra Classes of Geodesic polyhedra Triangular tessellations
Topology/Geometry of Geodesics Joseph D. Clinton SNEC-04 28-29 June 2003 Magnus J. Wenninger Introduction Definitions Topology Goldberg s polyhedra Classes of Geodesic polyhedra Triangular tessellations
CSC Computer Graphics
 // CSC. Computer Graphics Lecture Kasun@dscs.sjp.ac.lk Department of Computer Science University of Sri Jayewardanepura Polygon Filling Scan-Line Polygon Fill Algorithm Span Flood-Fill Algorithm Inside-outside
// CSC. Computer Graphics Lecture Kasun@dscs.sjp.ac.lk Department of Computer Science University of Sri Jayewardanepura Polygon Filling Scan-Line Polygon Fill Algorithm Span Flood-Fill Algorithm Inside-outside
Texture Mapping using Surface Flattening via Multi-Dimensional Scaling
 Texture Mapping using Surface Flattening via Multi-Dimensional Scaling Gil Zigelman Ron Kimmel Department of Computer Science, Technion, Haifa 32000, Israel and Nahum Kiryati Department of Electrical Engineering
Texture Mapping using Surface Flattening via Multi-Dimensional Scaling Gil Zigelman Ron Kimmel Department of Computer Science, Technion, Haifa 32000, Israel and Nahum Kiryati Department of Electrical Engineering
Curvature-Adaptive Remeshing with Feature Preservation of Manifold Triangle Meshes with Boundary
 Curvature-Adaptive Remeshing with Feature Preservation of Manifold Triangle Meshes with Boundary Master s Project Tanja Munz Master of Science Computer Animation and Visual Effects 24th August, 2015 Abstract
Curvature-Adaptive Remeshing with Feature Preservation of Manifold Triangle Meshes with Boundary Master s Project Tanja Munz Master of Science Computer Animation and Visual Effects 24th August, 2015 Abstract
Brain Surface Conformal Spherical Mapping
 Brain Surface Conformal Spherical Mapping Min Zhang Department of Industrial Engineering, Arizona State University mzhang33@asu.edu Abstract It is well known and proved that any genus zero surface can
Brain Surface Conformal Spherical Mapping Min Zhang Department of Industrial Engineering, Arizona State University mzhang33@asu.edu Abstract It is well known and proved that any genus zero surface can
Fuzzy Voronoi Diagram
 Fuzzy Voronoi Diagram Mohammadreza Jooyandeh and Ali Mohades Khorasani Mathematics and Computer Science, Amirkabir University of Technology, Hafez Ave., Tehran, Iran mohammadreza@jooyandeh.info,mohades@aut.ac.ir
Fuzzy Voronoi Diagram Mohammadreza Jooyandeh and Ali Mohades Khorasani Mathematics and Computer Science, Amirkabir University of Technology, Hafez Ave., Tehran, Iran mohammadreza@jooyandeh.info,mohades@aut.ac.ir
274 Curves on Surfaces, Lecture 5
 274 Curves on Surfaces, Lecture 5 Dylan Thurston Notes by Qiaochu Yuan Fall 2012 5 Ideal polygons Previously we discussed three models of the hyperbolic plane: the Poincaré disk, the upper half-plane,
274 Curves on Surfaces, Lecture 5 Dylan Thurston Notes by Qiaochu Yuan Fall 2012 5 Ideal polygons Previously we discussed three models of the hyperbolic plane: the Poincaré disk, the upper half-plane,
Implicit Surfaces & Solid Representations COS 426
 Implicit Surfaces & Solid Representations COS 426 3D Object Representations Desirable properties of an object representation Easy to acquire Accurate Concise Intuitive editing Efficient editing Efficient
Implicit Surfaces & Solid Representations COS 426 3D Object Representations Desirable properties of an object representation Easy to acquire Accurate Concise Intuitive editing Efficient editing Efficient
L1 - Introduction. Contents. Introduction of CAD/CAM system Components of CAD/CAM systems Basic concepts of graphics programming
 L1 - Introduction Contents Introduction of CAD/CAM system Components of CAD/CAM systems Basic concepts of graphics programming 1 Definitions Computer-Aided Design (CAD) The technology concerned with the
L1 - Introduction Contents Introduction of CAD/CAM system Components of CAD/CAM systems Basic concepts of graphics programming 1 Definitions Computer-Aided Design (CAD) The technology concerned with the
Modeling, Combining, and Rendering Dynamic Real-World Events From Image Sequences
 Modeling, Combining, and Rendering Dynamic Real-World Events From Image s Sundar Vedula, Peter Rander, Hideo Saito, and Takeo Kanade The Robotics Institute Carnegie Mellon University Abstract Virtualized
Modeling, Combining, and Rendering Dynamic Real-World Events From Image s Sundar Vedula, Peter Rander, Hideo Saito, and Takeo Kanade The Robotics Institute Carnegie Mellon University Abstract Virtualized
