EM225 Projective Geometry Part 2
|
|
|
- Solomon Rogers
- 6 years ago
- Views:
Transcription
1 EM225 Projective Geometry Part 2 eview In projective geometry, we regard figures as being the same if they can be made to appear the same as in the diagram below. In projective geometry: a projective point or Point is a line through the origin a projective line or Line is a plane through the origin. In order to obtain diagrams that we can draw and interpret in the usual way, we need to intersect these rays through the origin with a plane, called an embedding plane. projective point with no representative on the embedding plane projective point with a representative on the embedding plane embedding plane Properties of projective Points and Lines Property 1 Any two distinct Points lie on (or determine) a unique Line. Point Line Point EM225 Projective Geometry 2 Page 1
2 Property 2 Any two distinct Lines intersect in a unique Point. Line Point Line Projective Geometry Theorems In projective geometry, distances, angles and parallelism are not preserved, so any theorems which involve these notions are not theorems of projective geometry. Example The following (add the words yourself!) is not a theorem of projective geometry. However, lines and intersections are preserved (provided we remember that any pair of lines intersect even parallel lines) so theorems that only involve these notions may be regarded as projective geometry theorems. We will look at two such theorems. Desargues Theorem Let P and P be two triangles such that the three lines PP, and meet at a point. Let P and P meet at a point and meet at a point P and P meet at a point. Then,, are collinear. P P EM225 Projective Geometry 2 Page 2
3 Pappus Theorem Let P,, lie on a line and let P,, lie on a line. Let P and P meet at a point and meet at a point P and P meet at a point. Then,, are collinear. P P Homogeneous Coordinates In projective geometry, projective Points are lines through the origin. Consider the line through the point (1, 2, 3). Any (Euclidean) point on the line is of the form (a, 2a, 3a) for some real number a. For example, (1, 2, 3), (3, 6, 9), ( 2, 4, 6), (π, 2π, 3π) all lie on the line. z 3a (a, 2a, 3a) a 2a y x This projective Point is represented by (a, 2a, 3a) for any real number a. We say the Point has homogeneous coordinates [a, 2a, 3a] for any real number a. The homogeneous coordinates of a point are not uniquely determined any non-zero multiple will do. Thus the Point above has homogeneous coordinates [1, 2, 3] = [3, 6, 9] = [ 2, 4, 6] = [π, 2π, 3π] =. uestion: where does this Point meet the embedding plane z = 1? EM225 Projective Geometry 2 Page 3
4 uestion: if the embedding plane is the plane z = 1, what are the homogeneous coordinates of ideal points? z y 1 x uestion: which of the following homogeneous coordinates represent the same projective Point? [1.5, 2, 2.5], [3, 5, 7], [3, 4, 5], [ 6, 10, 14], [1, 5/3, 7/3], [2, 3, 4]. In summary: a projective Point has homogeneous coordinates [a, b, c] this represents the line through the origin and the point (a, b, c) any non-zero multiple of the homogeneous coordinates are also homogeneous coordinates [a, b, c] = [ka, kb, kc] for any k 0. Projective lines A plane through the origin has equation of the form px + qy + rz = 0. z x px + qy + rz = 0 y EM225 Projective Geometry 2 Page 4
5 If (x, y, z) satisfies px + qy + rz = 0 then so will (ka, kb, kc) for any k 0. Therefore the equation of a projective Line is px + qy + rz = 0 provided x, y, z represent homogeneous coordinates of a Point. Examples 1. The xy-plane has equation z = 0. The xz-plane has equation y = 0. The yz-plane has equation x = The plane that passes through the origin and points (1, 1, 0) and (1, 0, 1) has equation x y z = 0. This is easy! Any equation of the form px + qy + rz = 0 which is satisfied by the coordinates (1, 1, 0) and (1, 0, 1) will do, so we just need to spot a suitable equation. 3. Find the equation of the plane that passes through the origin and points (1, 1, 2) and (0, 1, 1). Intersection Point of two projective Lines To find the Point of intersection of two Lines, solve the equations of the Lines simultaneously. Examples 1. Find the projective Point that is the intersection of the projective Lines x + y + z = 0 and 2x y + 3z = 0. Solution x+ y+ z = 0 2x y+ 3z = 0 Add 3x + 4z = 0 Let z = 3; then x = 4. Then, substituting into x + y + z = 0 gives y = 1. Therefore the Point of intersection is [ 4, 1, 3]. 2. Find the projective Point that is the intersection of the projective Lines Solution ou should obtain [1, 3, 4]. x y + z = 0 and x + 3y 2z = 0. EM225 Projective Geometry 2 Page 5
6 Projective transformations A perspectivity from is a mapping of the projective plane to itself such that P maps to P when, P, P are collinear. Projective plane Projective plane A projective transformation is a composition of perspectivities. Compare with: a Euclidean transformation of the plane is a composition of translations, rotations and reflections. Fundamental theorem of Projective Geometry Let ABCD and A B C D be any two quadrilaterals. Then there exists a unique projective transformation that maps ABCD to A B C D. In other words, any four points (no three of which are collinear) map to any other four points (no three of which are collinear). Colloquially: all quadrilaterals are projectively equivalent. A D A C B C D B Compare with Euclidean geometry: transformations of Euclidean geometry can map any point to any other point (use a translation). But, for pairs of points, there exists a Euclidean transformation from one pair to another pair if and only if they are the same distance apart. d A d B P EM225 Projective Geometry 2 Page 6
7 Conic sections All conics are projectively the same this is because each conic is the intersection of a (double) cone with some embedding plane. In other words, projective geometry cannot see the difference between a line pair, a circle, an ellipse, a parabola and a hyperbola. For Pappus theorem this is great news! Since Pappus theorem is a projective geometry theorem, once we have proved the theorem in the case of a line pair, we get for free the corresponding result for any conic. The following diagram illustrates the ellipse version of the theorem. P P Proof of Pappus Theorem. Suppose we have the configuration show on page 3. Since PP is a quadrilateral, we can choose a projective transformation that maps it to any other quadrilateral. For simplicity, we shall map it to the quadrilateral with homogeneous coordinates [1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 1, 1]. Thus we may assume that the figure is that given below. We shall calculate the homogeneous coordinates of Points and equations of Lines. Line P P : [1, 0, 0], : [0, 1, 0]. Therefore P has equation z = 0. Point is a point on the line z = 0; hence z has coordinates [α, β, 0] or, if we scale suitably, [1, a, 0] Line P P : [0, 0, 1], : [1, 1, 1] so P has equation x y = 0 or x = y. Point is a point on x = y. It has coordinates [α, α, β] = [1, 1, b]. EM225 Projective Geometry 2 Page 7
8 P [1,0,0] [0,1,0] [1,a,0] z = 0 [0,0,1] P [1,1,1] [1,1,b] x = y Line P P : [1, 0, 0], : [1, 1, 1] so P has equation Line P P : [0, 0, 1], : [0, 1, 0] so P has equation Point P has equation P has equation is the Point Line P P : [1, 0, 0], : [1, 1, b] so P has equation Line P P : [0, 0, 1], : [1, a, 0] so P has equation Point P has equation P has equation is the Point Line : [0, 1, 0], : [1, 1, b] so has equation Line : [1, 1, 1], : [1, a, 0] so has equation Point has equation has equation is the Point Line : : so has equation (ab a)x + y z = 0. The crunch Does lie on the line? Exercises Construct Desargues theorem in Cabri. Construct Pappus theorem (lines version) in Cabri. Construct Pappus theorem (general conic version) in Cabri. EM225 Projective Geometry 2 Page 8
9 P [1,0,0] [0,1,0] [1,a,0] z = 0 [0,0,1] P [1,1,1] [1,1,b] x = y Line P P : [1, 0, 0], : [1, 1, 1] so P has equation y = z. Line P P : [0, 0, 1], : [0, 1, 0] so P has equation x = 0 Point P has equation y = z P has equation x = 0 is the Point [0, 1, 1] Line P P : [1, 0, 0], : [1, 1, b] so P has equation by = z Line P P : [0, 0, 1], : [1, a, 0] so P has equation ax = y Point P has equation by = z P has equation ax = y is the Point [1, a, ab] Line : [0, 1, 0], : [1, 1, b] so has equation bx = z Line : [1, 1, 1], : [1, a, 0] so has equation y = ax + (1 a)z Point has equation bx = z has equation y = ax + (1 a)z x = 1 z = b y = a + b ab is the Point [1, a + b ab, b] Line : [0, 1, 1], : [1, a, ab] so has equation (ab a)x + y z = 0. The crunch Does lie on the line? (ab a)x + y z = ab a + a + b ab b = 0 so lies on the line. Therefore,, are collinear. EM225 Projective Geometry 2 Page 9
TECHNISCHE UNIVERSITÄT BERLIN WS2005 Fachbereich 3 - Mathematik Prof. Dr. U. Pinkall / Charles Gunn Abgabe:
 TECHNISCHE UNIVERSITÄT BERLIN WS2005 Fachbereich 3 - Mathematik Prof. Dr. U. Pinkall / Charles Gunn Abgabe: 27.10.2005 1. Übung Geometrie I (Lines in P 2 (R), Separation, Desargues) 1. Aufgabe Line equations
TECHNISCHE UNIVERSITÄT BERLIN WS2005 Fachbereich 3 - Mathematik Prof. Dr. U. Pinkall / Charles Gunn Abgabe: 27.10.2005 1. Übung Geometrie I (Lines in P 2 (R), Separation, Desargues) 1. Aufgabe Line equations
CS-9645 Introduction to Computer Vision Techniques Winter 2019
 Table of Contents Projective Geometry... 1 Definitions...1 Axioms of Projective Geometry... Ideal Points...3 Geometric Interpretation... 3 Fundamental Transformations of Projective Geometry... 4 The D
Table of Contents Projective Geometry... 1 Definitions...1 Axioms of Projective Geometry... Ideal Points...3 Geometric Interpretation... 3 Fundamental Transformations of Projective Geometry... 4 The D
3D Computer Vision II. Reminder Projective Geometry, Transformations
 3D Computer Vision II Reminder Projective Geometry, Transformations Nassir Navab" based on a course given at UNC by Marc Pollefeys & the book Multiple View Geometry by Hartley & Zisserman" October 21,
3D Computer Vision II Reminder Projective Geometry, Transformations Nassir Navab" based on a course given at UNC by Marc Pollefeys & the book Multiple View Geometry by Hartley & Zisserman" October 21,
Transformations Part If then, the identity transformation.
 Transformations Part 2 Definition: Given rays with common endpoint O, we define the rotation with center O and angle as follows: 1. If then, the identity transformation. 2. If A, O, and B are noncollinear,
Transformations Part 2 Definition: Given rays with common endpoint O, we define the rotation with center O and angle as follows: 1. If then, the identity transformation. 2. If A, O, and B are noncollinear,
Projective spaces and Bézout s theorem
 Projective spaces and Bézout s theorem êaû{0 Mijia Lai 5 \ laimijia@sjtu.edu.cn Outline 1. History 2. Projective spaces 3. Conics and cubics 4. Bézout s theorem and the resultant 5. Cayley-Bacharach theorem
Projective spaces and Bézout s theorem êaû{0 Mijia Lai 5 \ laimijia@sjtu.edu.cn Outline 1. History 2. Projective spaces 3. Conics and cubics 4. Bézout s theorem and the resultant 5. Cayley-Bacharach theorem
Basic Euclidean Geometry
 hapter 1 asic Euclidean Geometry This chapter is not intended to be a complete survey of basic Euclidean Geometry, but rather a review for those who have previously taken a geometry course For a definitive
hapter 1 asic Euclidean Geometry This chapter is not intended to be a complete survey of basic Euclidean Geometry, but rather a review for those who have previously taken a geometry course For a definitive
Notes on Spherical Geometry
 Notes on Spherical Geometry Abhijit Champanerkar College of Staten Island & The Graduate Center, CUNY Spring 2018 1. Vectors and planes in R 3 To review vector, dot and cross products, lines and planes
Notes on Spherical Geometry Abhijit Champanerkar College of Staten Island & The Graduate Center, CUNY Spring 2018 1. Vectors and planes in R 3 To review vector, dot and cross products, lines and planes
Problem 3.1 (Building up geometry). For an axiomatically built-up geometry, six groups of axioms needed:
 Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
CHAPTER 2 REVIEW COORDINATE GEOMETRY MATH Warm-Up: See Solved Homework questions. 2.2 Cartesian coordinate system
 CHAPTER 2 REVIEW COORDINATE GEOMETRY MATH6 2.1 Warm-Up: See Solved Homework questions 2.2 Cartesian coordinate system Coordinate axes: Two perpendicular lines that intersect at the origin O on each line.
CHAPTER 2 REVIEW COORDINATE GEOMETRY MATH6 2.1 Warm-Up: See Solved Homework questions 2.2 Cartesian coordinate system Coordinate axes: Two perpendicular lines that intersect at the origin O on each line.
Geometry Definitions, Postulates, and Theorems. Chapter 3: Parallel and Perpendicular Lines. Section 3.1: Identify Pairs of Lines and Angles.
 Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
Chapter 10. Homework
 Chapter 0 Homework Lesson 0- pages 538 5 Exercises. 2. Hyperbola: center (0, 0), y-intercepts at ±, no x-intercepts, the lines of symmetry are the x- and y-axes; domain: all real numbers, range: y 5 3
Chapter 0 Homework Lesson 0- pages 538 5 Exercises. 2. Hyperbola: center (0, 0), y-intercepts at ±, no x-intercepts, the lines of symmetry are the x- and y-axes; domain: all real numbers, range: y 5 3
Definition 2 (Projective plane). A projective plane is a class of points, and a class of lines satisfying the axioms:
 Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Co-ordinate Geometry
 Co-ordinate Geometry 1. Find the value of P for which the points (1, -), (2, -6) and (p, -1) are collinear 2. If the point P (x, y) is equidistant from the points A (1,) and B(4, 1). Prove that 2x+y =
Co-ordinate Geometry 1. Find the value of P for which the points (1, -), (2, -6) and (p, -1) are collinear 2. If the point P (x, y) is equidistant from the points A (1,) and B(4, 1). Prove that 2x+y =
Robot Vision: Projective Geometry
 Robot Vision: Projective Geometry Ass.Prof. Friedrich Fraundorfer SS 2018 1 Learning goals Understand homogeneous coordinates Understand points, line, plane parameters and interpret them geometrically
Robot Vision: Projective Geometry Ass.Prof. Friedrich Fraundorfer SS 2018 1 Learning goals Understand homogeneous coordinates Understand points, line, plane parameters and interpret them geometrically
Projective 2D Geometry
 Projective D Geometry Multi View Geometry (Spring '08) Projective D Geometry Prof. Kyoung Mu Lee SoEECS, Seoul National University Homogeneous representation of lines and points Projective D Geometry Line
Projective D Geometry Multi View Geometry (Spring '08) Projective D Geometry Prof. Kyoung Mu Lee SoEECS, Seoul National University Homogeneous representation of lines and points Projective D Geometry Line
7. The Gauss-Bonnet theorem
 7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
UNIT 5: GEOMETRIC AND ALGEBRAIC CONNECTIONS. Apply Geometric Concepts in Modeling Situations
 UNIT 5: GEOMETRIC AND ALGEBRAIC CONNECTIONS This unit investigates coordinate geometry. Students look at equations for circles and use given information to derive equations for representations of these
UNIT 5: GEOMETRIC AND ALGEBRAIC CONNECTIONS This unit investigates coordinate geometry. Students look at equations for circles and use given information to derive equations for representations of these
Multivariable Calculus
 Multivariable Calculus Chapter 10 Topics in Analytic Geometry (Optional) 1. Inclination of a line p. 5. Circles p. 4 9. Determining Conic Type p. 13. Angle between lines p. 6. Parabolas p. 5 10. Rotation
Multivariable Calculus Chapter 10 Topics in Analytic Geometry (Optional) 1. Inclination of a line p. 5. Circles p. 4 9. Determining Conic Type p. 13. Angle between lines p. 6. Parabolas p. 5 10. Rotation
Isometries. 1 Identifying Isometries
 Isometries 1 Identifying Isometries 1. Modeling isometries as dynamic maps. 2. GeoGebra files: isoguess1.ggb, isoguess2.ggb, isoguess3.ggb, isoguess4.ggb. 3. Guessing isometries. 4. What can you construct
Isometries 1 Identifying Isometries 1. Modeling isometries as dynamic maps. 2. GeoGebra files: isoguess1.ggb, isoguess2.ggb, isoguess3.ggb, isoguess4.ggb. 3. Guessing isometries. 4. What can you construct
2 Solution of Homework
 Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Perspective Mappings. Contents
 Perspective Mappings David Eberly, Geometric Tools, Redmond WA 98052 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License. To view a copy
Perspective Mappings David Eberly, Geometric Tools, Redmond WA 98052 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License. To view a copy
.(3, 2) Co-ordinate Geometry Co-ordinates. Every point has two co-ordinates. Plot the following points on the plane. A (4, 1) D (2, 5) G (6, 3)
 Co-ordinate Geometry Co-ordinates Every point has two co-ordinates. (3, 2) x co-ordinate y co-ordinate Plot the following points on the plane..(3, 2) A (4, 1) D (2, 5) G (6, 3) B (3, 3) E ( 4, 4) H (6,
Co-ordinate Geometry Co-ordinates Every point has two co-ordinates. (3, 2) x co-ordinate y co-ordinate Plot the following points on the plane..(3, 2) A (4, 1) D (2, 5) G (6, 3) B (3, 3) E ( 4, 4) H (6,
How to Project Spherical Conics into the Plane
 How to Project pherical Conics into the Plane Yoichi Maeda maeda@keyakiccu-tokaiacjp Department of Mathematics Tokai University Japan Abstract: In this paper, we will introduce a method how to draw the
How to Project pherical Conics into the Plane Yoichi Maeda maeda@keyakiccu-tokaiacjp Department of Mathematics Tokai University Japan Abstract: In this paper, we will introduce a method how to draw the
Unit 12 Topics in Analytic Geometry - Classwork
 Unit 1 Topics in Analytic Geometry - Classwork Back in Unit 7, we delved into the algebra and geometry of lines. We showed that lines can be written in several forms: a) the general form: Ax + By + C =
Unit 1 Topics in Analytic Geometry - Classwork Back in Unit 7, we delved into the algebra and geometry of lines. We showed that lines can be written in several forms: a) the general form: Ax + By + C =
9.3 Hyperbolas and Rotation of Conics
 9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
The angle measure at for example the vertex A is denoted by m A, or m BAC.
 MT 200 ourse notes on Geometry 5 2. Triangles and congruence of triangles 2.1. asic measurements. Three distinct lines, a, b and c, no two of which are parallel, form a triangle. That is, they divide the
MT 200 ourse notes on Geometry 5 2. Triangles and congruence of triangles 2.1. asic measurements. Three distinct lines, a, b and c, no two of which are parallel, form a triangle. That is, they divide the
Projective geometry for Computer Vision
 Department of Computer Science and Engineering IIT Delhi NIT, Rourkela March 27, 2010 Overview Pin-hole camera Why projective geometry? Reconstruction Computer vision geometry: main problems Correspondence
Department of Computer Science and Engineering IIT Delhi NIT, Rourkela March 27, 2010 Overview Pin-hole camera Why projective geometry? Reconstruction Computer vision geometry: main problems Correspondence
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES. V : Introduction to non Euclidean geometry
 FIGURES FOR SOLUTIONS TO SELECTED EXERCISES V : Introduction to non Euclidean geometry V.1 : Facts from spherical geometry V.1.1. The objective is to show that the minor arc m does not contain a pair of
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES V : Introduction to non Euclidean geometry V.1 : Facts from spherical geometry V.1.1. The objective is to show that the minor arc m does not contain a pair of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Multiple View Geometry in Computer Vision
 Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Projective 3D Geometry (Back to Chapter 2) Lecture 6 2 Singular Value Decomposition Given a
Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 Projective 3D Geometry (Back to Chapter 2) Lecture 6 2 Singular Value Decomposition Given a
Double Integrals, Iterated Integrals, Cross-sections
 Chapter 14 Multiple Integrals 1 ouble Integrals, Iterated Integrals, Cross-sections 2 ouble Integrals over more general regions, efinition, Evaluation of ouble Integrals, Properties of ouble Integrals
Chapter 14 Multiple Integrals 1 ouble Integrals, Iterated Integrals, Cross-sections 2 ouble Integrals over more general regions, efinition, Evaluation of ouble Integrals, Properties of ouble Integrals
EQUATIONS OF ALTITUDES, MEDIANS, and PERPENDICULAR BISECTORS
 EQUATIONS OF ALTITUDES, MEDIANS, and PERPENDICULAR BISECTORS Steps to Find the Median of a Triangle: -Find the midpoint of a segment using the midpoint formula. -Use the vertex and midpoint to find the
EQUATIONS OF ALTITUDES, MEDIANS, and PERPENDICULAR BISECTORS Steps to Find the Median of a Triangle: -Find the midpoint of a segment using the midpoint formula. -Use the vertex and midpoint to find the
Lesson 19: The Graph of a Linear Equation in Two Variables is a Line
 Lesson 19: The Graph of a Linear Equation in Two Variables is a Line Classwork Exercises Theorem: The graph of a linear equation y = mx + b is a non-vertical line with slope m and passing through (0, b),
Lesson 19: The Graph of a Linear Equation in Two Variables is a Line Classwork Exercises Theorem: The graph of a linear equation y = mx + b is a non-vertical line with slope m and passing through (0, b),
Review Exercise. 1. Determine vector and parametric equations of the plane that contains the
 Review Exercise 1. Determine vector and parametric equations of the plane that contains the points A11, 2, 12, B12, 1, 12, and C13, 1, 42. 2. In question 1, there are a variety of different answers possible,
Review Exercise 1. Determine vector and parametric equations of the plane that contains the points A11, 2, 12, B12, 1, 12, and C13, 1, 42. 2. In question 1, there are a variety of different answers possible,
The statement implies that any three intersection points of two distinct planes lie on a line.
 Math 3181 Dr. Franz Rothe February 23, 2015 All3181\3181_spr15ts1.tex 1 Solution of Test Name: Problem 1.1. The second part of Hilbert s Proposition 1 states: Any two different planes have either no point
Math 3181 Dr. Franz Rothe February 23, 2015 All3181\3181_spr15ts1.tex 1 Solution of Test Name: Problem 1.1. The second part of Hilbert s Proposition 1 states: Any two different planes have either no point
Three Dimensional Geometry. Linear Programming
 Three Dimensional Geometry Linear Programming A plane is determined uniquely if any one of the following is known: The normal to the plane and its distance from the origin is given, i.e. equation of a
Three Dimensional Geometry Linear Programming A plane is determined uniquely if any one of the following is known: The normal to the plane and its distance from the origin is given, i.e. equation of a
Chapter 15: Functions of Several Variables
 Chapter 15: Functions of Several Variables Section 15.1 Elementary Examples a. Notation: Two Variables b. Example c. Notation: Three Variables d. Functions of Several Variables e. Examples from the Sciences
Chapter 15: Functions of Several Variables Section 15.1 Elementary Examples a. Notation: Two Variables b. Example c. Notation: Three Variables d. Functions of Several Variables e. Examples from the Sciences
Drill Exercise - 1. Drill Exercise - 2. Drill Exercise - 3
 Drill Exercise -. Find the distance between the pair of points, (a sin, b cos ) and ( a cos, b sin ).. Prove that the points (a, 4a) (a, 6a) and (a + 3 a, 5a) are the vertices of an equilateral triangle.
Drill Exercise -. Find the distance between the pair of points, (a sin, b cos ) and ( a cos, b sin ).. Prove that the points (a, 4a) (a, 6a) and (a + 3 a, 5a) are the vertices of an equilateral triangle.
A Communications Network???
 A Communications Network??? A Communications Network What are the desirable properties of the switching box? 1. Every two users must be connected at a switch. 2. Every switch must "look alike". 3. The
A Communications Network??? A Communications Network What are the desirable properties of the switching box? 1. Every two users must be connected at a switch. 2. Every switch must "look alike". 3. The
Applications of Triple Integrals
 Chapter 14 Multiple Integrals 1 Double Integrals, Iterated Integrals, Cross-sections 2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals
Chapter 14 Multiple Integrals 1 Double Integrals, Iterated Integrals, Cross-sections 2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals
Mathematics High School Geometry
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
I can identify, name, and draw points, lines, segments, rays, and planes. I can apply basic facts about points, lines, and planes.
 Page 1 of 9 Are You Ready Chapter 1 Pretest & skills Attendance Problems Graph each inequality. 1. x > 3 2. 2 < x < 6 3. x > 1 or x < 0 Vocabulary undefined term point line plane collinear coplanar segment
Page 1 of 9 Are You Ready Chapter 1 Pretest & skills Attendance Problems Graph each inequality. 1. x > 3 2. 2 < x < 6 3. x > 1 or x < 0 Vocabulary undefined term point line plane collinear coplanar segment
3D Computer Vision II. Reminder Projective Geometry, Transformations. Nassir Navab. October 27, 2009
 3D Computer Vision II Reminder Projective Geometr, Transformations Nassir Navab based on a course given at UNC b Marc Pollefes & the book Multiple View Geometr b Hartle & Zisserman October 27, 29 2D Transformations
3D Computer Vision II Reminder Projective Geometr, Transformations Nassir Navab based on a course given at UNC b Marc Pollefes & the book Multiple View Geometr b Hartle & Zisserman October 27, 29 2D Transformations
Math 451: Euclidean and Non-Euclidean Geometry MWF 3pm, Gasson 204 Homework 8 Solutions
 Math 451: Euclidean and Non-Euclidean Geometry MWF 3pm, Gasson 204 Homework 8 Solutions Exercises from Chapter 2: 5.5, 5.10, 5.13, 5.14 Exercises from Chapter 3: 1.2, 1.3, 1.5 Exercise 5.5. Give an example
Math 451: Euclidean and Non-Euclidean Geometry MWF 3pm, Gasson 204 Homework 8 Solutions Exercises from Chapter 2: 5.5, 5.10, 5.13, 5.14 Exercises from Chapter 3: 1.2, 1.3, 1.5 Exercise 5.5. Give an example
Downloaded from Class XI Chapter 12 Introduction to Three Dimensional Geometry Maths
 A point is on the axis. What are its coordinates and coordinates? If a point is on the axis, then its coordinates and coordinates are zero. A point is in the XZplane. What can you say about its coordinate?
A point is on the axis. What are its coordinates and coordinates? If a point is on the axis, then its coordinates and coordinates are zero. A point is in the XZplane. What can you say about its coordinate?
Exercises for Chapter Three You know you've got to exercise your brain just like your muscles. Will Rogers ( )
 Exercises for Chapter Three You know you've got to exercise your brain just like your muscles. Will Rogers (1879 1935) Investigation Exercise 3.1. (a) Construct a tessellation. (Directions for construction.)
Exercises for Chapter Three You know you've got to exercise your brain just like your muscles. Will Rogers (1879 1935) Investigation Exercise 3.1. (a) Construct a tessellation. (Directions for construction.)
Common Core Specifications for Geometry
 1 Common Core Specifications for Geometry Examples of how to read the red references: Congruence (G-Co) 2-03 indicates this spec is implemented in Unit 3, Lesson 2. IDT_C indicates that this spec is implemented
1 Common Core Specifications for Geometry Examples of how to read the red references: Congruence (G-Co) 2-03 indicates this spec is implemented in Unit 3, Lesson 2. IDT_C indicates that this spec is implemented
Module 1 Session 1 HS. Critical Areas for Traditional Geometry Page 1 of 6
 Critical Areas for Traditional Geometry Page 1 of 6 There are six critical areas (units) for Traditional Geometry: Critical Area 1: Congruence, Proof, and Constructions In previous grades, students were
Critical Areas for Traditional Geometry Page 1 of 6 There are six critical areas (units) for Traditional Geometry: Critical Area 1: Congruence, Proof, and Constructions In previous grades, students were
Objectives. Cabri Jr. Tools
 ^Åíáîáíó=T oéñäéåíáçåë áå=íüé=mä~åé Objectives To use the Reflection tool on the Cabri Jr. application To investigate the properties of a reflection To extend the concepts of reflection to the coordinate
^Åíáîáíó=T oéñäéåíáçåë áå=íüé=mä~åé Objectives To use the Reflection tool on the Cabri Jr. application To investigate the properties of a reflection To extend the concepts of reflection to the coordinate
274 Curves on Surfaces, Lecture 5
 274 Curves on Surfaces, Lecture 5 Dylan Thurston Notes by Qiaochu Yuan Fall 2012 5 Ideal polygons Previously we discussed three models of the hyperbolic plane: the Poincaré disk, the upper half-plane,
274 Curves on Surfaces, Lecture 5 Dylan Thurston Notes by Qiaochu Yuan Fall 2012 5 Ideal polygons Previously we discussed three models of the hyperbolic plane: the Poincaré disk, the upper half-plane,
Interpretations and Models. Chapter Axiomatic Systems and Incidence Geometry
 Interpretations and Models Chapter 2.1-2.4 - Axiomatic Systems and Incidence Geometry Axiomatic Systems in Mathematics The gold standard for rigor in an area of mathematics Not fully achieved in most areas
Interpretations and Models Chapter 2.1-2.4 - Axiomatic Systems and Incidence Geometry Axiomatic Systems in Mathematics The gold standard for rigor in an area of mathematics Not fully achieved in most areas
Geometry: Conic Sections
 Conic Sections Introduction When a right circular cone is intersected by a plane, as in figure 1 below, a family of four types of curves results. Because of their relationship to the cone, they are called
Conic Sections Introduction When a right circular cone is intersected by a plane, as in figure 1 below, a family of four types of curves results. Because of their relationship to the cone, they are called
DO NOW Geometry Regents Lomac Date. due. Similar by Transformation Construction
 DO NOW Geometry Regents Lomac 2014-2015 Date. due. Similar by Transformation Construction (DN) What defines a similarity transformation? Name Per LO: I can construct a similarity transformation. (1) compass,
DO NOW Geometry Regents Lomac 2014-2015 Date. due. Similar by Transformation Construction (DN) What defines a similarity transformation? Name Per LO: I can construct a similarity transformation. (1) compass,
5200/7200 Fall 2007 Concurrence theorems for triangles
 5200/7200 Fall 2007 Concurrence theorems for triangles There are two basic concurrence theorems for triangles that hold in neutral geometry, that of medians and of angle bisectors, but it seems hard to
5200/7200 Fall 2007 Concurrence theorems for triangles There are two basic concurrence theorems for triangles that hold in neutral geometry, that of medians and of angle bisectors, but it seems hard to
On a Method in Algebra and Geometry
 On a Method in Algebra and Geometry Felix Lazebnik Department of Mathematical Sciences University of Delaware Newark, DE 976 Often applications of a well-known fact or method are more exciting than the
On a Method in Algebra and Geometry Felix Lazebnik Department of Mathematical Sciences University of Delaware Newark, DE 976 Often applications of a well-known fact or method are more exciting than the
Conic Sections. College Algebra
 Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
Vectors and the Geometry of Space
 Vectors and the Geometry of Space In Figure 11.43, consider the line L through the point P(x 1, y 1, z 1 ) and parallel to the vector. The vector v is a direction vector for the line L, and a, b, and c
Vectors and the Geometry of Space In Figure 11.43, consider the line L through the point P(x 1, y 1, z 1 ) and parallel to the vector. The vector v is a direction vector for the line L, and a, b, and c
Computer Vision I - Appearance-based Matching and Projective Geometry
 Computer Vision I - Appearance-based Matching and Projective Geometry Carsten Rother 05/11/2015 Computer Vision I: Image Formation Process Roadmap for next four lectures Computer Vision I: Image Formation
Computer Vision I - Appearance-based Matching and Projective Geometry Carsten Rother 05/11/2015 Computer Vision I: Image Formation Process Roadmap for next four lectures Computer Vision I: Image Formation
Conic Sections: Parabolas
 Conic Sections: Parabolas Why are the graphs of parabolas, ellipses, and hyperbolas called 'conic sections'? Because if you pass a plane through a double cone, the intersection of the plane and the cone
Conic Sections: Parabolas Why are the graphs of parabolas, ellipses, and hyperbolas called 'conic sections'? Because if you pass a plane through a double cone, the intersection of the plane and the cone
Topics in geometry Exam 1 Solutions 7/8/4
 Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
Buds Public School, Dubai
 Buds Public School, Dubai Subject: Maths Grade: 11 AB Topic: Statistics, Probability, Trigonometry, 3D, Conic Section, Straight lines and Limits and Derivatives Statistics and Probability: 1. Find the
Buds Public School, Dubai Subject: Maths Grade: 11 AB Topic: Statistics, Probability, Trigonometry, 3D, Conic Section, Straight lines and Limits and Derivatives Statistics and Probability: 1. Find the
Lesson 20: Exploiting the Connection to Cartesian Coordinates
 : Exploiting the Connection to Cartesian Coordinates Student Outcomes Students interpret complex multiplication as the corresponding function of two real variables. Students calculate the amount of rotation
: Exploiting the Connection to Cartesian Coordinates Student Outcomes Students interpret complex multiplication as the corresponding function of two real variables. Students calculate the amount of rotation
Technische Universität München Zentrum Mathematik
 Technische Universität München Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Bernhard Werner Projective Geometry SS 208 https://www-m0.ma.tum.de/bin/view/lehre/ss8/pgss8/webhome Solutions for
Technische Universität München Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Bernhard Werner Projective Geometry SS 208 https://www-m0.ma.tum.de/bin/view/lehre/ss8/pgss8/webhome Solutions for
Conic Sections. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Conic Sections MATH 211, Calculus II J. Robert Buchanan Department o Mathematics Spring 2018 Introduction The conic sections include the parabola, the ellipse, and the hyperbola. y y y x x x Parabola A
Conic Sections MATH 211, Calculus II J. Robert Buchanan Department o Mathematics Spring 2018 Introduction The conic sections include the parabola, the ellipse, and the hyperbola. y y y x x x Parabola A
Unit 6: Connecting Algebra and Geometry Through Coordinates
 Unit 6: Connecting Algebra and Geometry Through Coordinates The focus of this unit is to have students analyze and prove geometric properties by applying algebraic concepts and skills on a coordinate plane.
Unit 6: Connecting Algebra and Geometry Through Coordinates The focus of this unit is to have students analyze and prove geometric properties by applying algebraic concepts and skills on a coordinate plane.
8.G Cutting a rectangle into two congruent triangles
 8.G Cutting a rectangle into two congruent triangles Task ABCD AC Below is a picture of rectangle with diagonal. ACD 180 D A A C C a. Draw the image of triangle when it is rotated about vertex. Call the
8.G Cutting a rectangle into two congruent triangles Task ABCD AC Below is a picture of rectangle with diagonal. ACD 180 D A A C C a. Draw the image of triangle when it is rotated about vertex. Call the
Visual Recognition: Image Formation
 Visual Recognition: Image Formation Raquel Urtasun TTI Chicago Jan 5, 2012 Raquel Urtasun (TTI-C) Visual Recognition Jan 5, 2012 1 / 61 Today s lecture... Fundamentals of image formation You should know
Visual Recognition: Image Formation Raquel Urtasun TTI Chicago Jan 5, 2012 Raquel Urtasun (TTI-C) Visual Recognition Jan 5, 2012 1 / 61 Today s lecture... Fundamentals of image formation You should know
PARABOLA SYNOPSIS 1.S is the focus and the line l is the directrix. If a variable point P is such that SP
 PARABOLA SYNOPSIS.S is the focus and the line l is the directrix. If a variable point P is such that SP PM = where PM is perpendicular to the directrix, then the locus of P is a parabola... S ax + hxy
PARABOLA SYNOPSIS.S is the focus and the line l is the directrix. If a variable point P is such that SP PM = where PM is perpendicular to the directrix, then the locus of P is a parabola... S ax + hxy
UNIVERSITI TEKNOLOGI MALAYSIA SSE 1893 ENGINEERING MATHEMATICS TUTORIAL 5
 UNIVERSITI TEKNOLOGI MALAYSIA SSE 189 ENGINEERING MATHEMATIS TUTORIAL 5 1. Evaluate the following surface integrals (i) (x + y) ds, : part of the surface 2x+y+z = 6 in the first octant. (ii) (iii) (iv)
UNIVERSITI TEKNOLOGI MALAYSIA SSE 189 ENGINEERING MATHEMATIS TUTORIAL 5 1. Evaluate the following surface integrals (i) (x + y) ds, : part of the surface 2x+y+z = 6 in the first octant. (ii) (iii) (iv)
12.6 Cylinders and Quadric Surfaces
 12 Vectors and the Geometry of Space 12.6 and Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. and We have already looked at two special types of surfaces:
12 Vectors and the Geometry of Space 12.6 and Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. and We have already looked at two special types of surfaces:
Assignment 3/17/15. Section 10.2(p 568) 2 12 (E) (E)
 Section 10.2 Warm Up Assignment 3/17/15 Section 10.2(p 568) 2 12 (E) 24 40 (E) Objective We are going to find equations for parabolas identify the vertex, focus, and directrix of a parabola The parabola
Section 10.2 Warm Up Assignment 3/17/15 Section 10.2(p 568) 2 12 (E) 24 40 (E) Objective We are going to find equations for parabolas identify the vertex, focus, and directrix of a parabola The parabola
Problem 2.1. Complete the following proof of Euclid III.20, referring to the figure on page 1.
 Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
1.6 Quadric Surfaces Brief review of Conic Sections 74 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE. Figure 1.18: Parabola y = 2x 2
 7 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE Figure 1.18: Parabola y = x 1.6 Quadric Surfaces Figure 1.19: Parabola x = y 1.6.1 Brief review of Conic Sections You may need to review conic sections for
7 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE Figure 1.18: Parabola y = x 1.6 Quadric Surfaces Figure 1.19: Parabola x = y 1.6.1 Brief review of Conic Sections You may need to review conic sections for
Chapter 10. Exploring Conic Sections
 Chapter 10 Exploring Conic Sections Conics A conic section is a curve formed by the intersection of a plane and a hollow cone. Each of these shapes are made by slicing the cone and observing the shape
Chapter 10 Exploring Conic Sections Conics A conic section is a curve formed by the intersection of a plane and a hollow cone. Each of these shapes are made by slicing the cone and observing the shape
Inversive Plane Geometry
 Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
The point (x, y) lies on the circle of radius r and center (h, k) iff. x h y k r
 NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
1.8 Coordinate Geometry. Copyright Cengage Learning. All rights reserved.
 1.8 Coordinate Geometry Copyright Cengage Learning. All rights reserved. Objectives The Coordinate Plane The Distance and Midpoint Formulas Graphs of Equations in Two Variables Intercepts Circles Symmetry
1.8 Coordinate Geometry Copyright Cengage Learning. All rights reserved. Objectives The Coordinate Plane The Distance and Midpoint Formulas Graphs of Equations in Two Variables Intercepts Circles Symmetry
Geometry: Semester 1 Midterm
 Class: Date: Geometry: Semester 1 Midterm Multiple Choice Identify the choice that best completes the statement or answers the question. 1. The first two steps for constructing MNO that is congruent to
Class: Date: Geometry: Semester 1 Midterm Multiple Choice Identify the choice that best completes the statement or answers the question. 1. The first two steps for constructing MNO that is congruent to
Geometric transformations assign a point to a point, so it is a point valued function of points. Geometric transformation may destroy the equation
 Geometric transformations assign a point to a point, so it is a point valued function of points. Geometric transformation may destroy the equation and the type of an object. Even simple scaling turns a
Geometric transformations assign a point to a point, so it is a point valued function of points. Geometric transformation may destroy the equation and the type of an object. Even simple scaling turns a
DISCOVERING CONICS WITH. Dr Toh Pee Choon NIE 2 June 2016
 DISCOVERING CONICS WITH Dr Toh Pee Choon MTC @ NIE 2 June 2016 Introduction GeoGebra is a dynamic mathematics software that integrates both geometry and algebra Open source and free to download www.geogebra.org
DISCOVERING CONICS WITH Dr Toh Pee Choon MTC @ NIE 2 June 2016 Introduction GeoGebra is a dynamic mathematics software that integrates both geometry and algebra Open source and free to download www.geogebra.org
Algebra II. Slide 1 / 181. Slide 2 / 181. Slide 3 / 181. Conic Sections Table of Contents
 Slide 1 / 181 Algebra II Slide 2 / 181 Conic Sections 2015-04-21 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 181 Review of Midpoint and Distance Formulas Introduction
Slide 1 / 181 Algebra II Slide 2 / 181 Conic Sections 2015-04-21 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 181 Review of Midpoint and Distance Formulas Introduction
Unit 2A: Angle Pairs and Transversal Notes
 Unit 2A: Angle Pairs and Transversal Notes Day 1: Special angle pairs Day 2: Angle pairs formed by transversal through two nonparallel lines Day 3: Angle pairs formed by transversal through parallel lines
Unit 2A: Angle Pairs and Transversal Notes Day 1: Special angle pairs Day 2: Angle pairs formed by transversal through two nonparallel lines Day 3: Angle pairs formed by transversal through parallel lines
Shadows in Computer Graphics
 Shadows in Computer Graphics Steven Janke November 2014 Steven Janke (Seminar) Shadows in Computer Graphics November 2014 1 / 49 Shadows (from Doom) Steven Janke (Seminar) Shadows in Computer Graphics
Shadows in Computer Graphics Steven Janke November 2014 Steven Janke (Seminar) Shadows in Computer Graphics November 2014 1 / 49 Shadows (from Doom) Steven Janke (Seminar) Shadows in Computer Graphics
We start by looking at a double cone. Think of this as two pointy ice cream cones that are connected at the small tips:
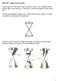 Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Multiple View Geometry in Computer Vision
 Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 More on Single View Geometry Lecture 11 2 In Chapter 5 we introduced projection matrix (which
Multiple View Geometry in Computer Vision Prasanna Sahoo Department of Mathematics University of Louisville 1 More on Single View Geometry Lecture 11 2 In Chapter 5 we introduced projection matrix (which
Mathematics (www.tiwariacademy.com)
 () Miscellaneous Exercise on Chapter 10 Question 1: Find the values of k for which the line is (a) Parallel to the x-axis, (b) Parallel to the y-axis, (c) Passing through the origin. Answer 1: The given
() Miscellaneous Exercise on Chapter 10 Question 1: Find the values of k for which the line is (a) Parallel to the x-axis, (b) Parallel to the y-axis, (c) Passing through the origin. Answer 1: The given
A Correlation of Pearson Mathematics Geometry Common Core, 2015 To the Missouri Learning Standards for Mathematics Geometry
 A Correlation of Pearson Mathematics Common Core, 2015 To the Missouri Learning Standards for Mathematics A Correlation of Common Core 2015 To the Introduction This document demonstrates how Pearson, Common
A Correlation of Pearson Mathematics Common Core, 2015 To the Missouri Learning Standards for Mathematics A Correlation of Common Core 2015 To the Introduction This document demonstrates how Pearson, Common
On the Cyclic Quadrilaterals with the Same Varignon Parallelogram
 Forum Geometricorum Volume 18 (2018) 103 113. FORUM GEOM ISSN 1534-1178 On the Cyclic Quadrilaterals with the Same Varignon Parallelogram Sándor Nagydobai Kiss Abstract. The circumcenters and anticenters
Forum Geometricorum Volume 18 (2018) 103 113. FORUM GEOM ISSN 1534-1178 On the Cyclic Quadrilaterals with the Same Varignon Parallelogram Sándor Nagydobai Kiss Abstract. The circumcenters and anticenters
GEOMETRY R Unit 2: Angles and Parallel Lines
 GEOMETRY R Unit 2: Angles and Parallel Lines Day Classwork Homework Friday 9/15 Unit 1 Test Monday 9/18 Tuesday 9/19 Angle Relationships HW 2.1 Angle Relationships with Transversals HW 2.2 Wednesday 9/20
GEOMETRY R Unit 2: Angles and Parallel Lines Day Classwork Homework Friday 9/15 Unit 1 Test Monday 9/18 Tuesday 9/19 Angle Relationships HW 2.1 Angle Relationships with Transversals HW 2.2 Wednesday 9/20
Section 12.1 Translations and Rotations
 Section 12.1 Translations and Rotations Any rigid motion that preserves length or distance is an isometry. We look at two types of isometries in this section: translations and rotations. Translations A
Section 12.1 Translations and Rotations Any rigid motion that preserves length or distance is an isometry. We look at two types of isometries in this section: translations and rotations. Translations A
Section 13.5: Equations of Lines and Planes. 1 Objectives. 2 Assignments. 3 Lecture Notes
 Section 13.5: Equations of Lines and Planes 1 Objectives 1. Find vector, symmetric, or parametric equations for a line in space given two points on the line, given a point on the line and a vector parallel
Section 13.5: Equations of Lines and Planes 1 Objectives 1. Find vector, symmetric, or parametric equations for a line in space given two points on the line, given a point on the line and a vector parallel
PARCC Review 1. Select the drop-down menus to correctly complete each sentence.
 Name PARCC Review 1. Select the drop-down menus to correctly complete each sentence. The set of all points in a plane that are equidistant from a given point is called a The given point is called the Radius
Name PARCC Review 1. Select the drop-down menus to correctly complete each sentence. The set of all points in a plane that are equidistant from a given point is called a The given point is called the Radius
Section 12.2: Quadric Surfaces
 Section 12.2: Quadric Surfaces Goals: 1. To recognize and write equations of quadric surfaces 2. To graph quadric surfaces by hand Definitions: 1. A quadric surface is the three-dimensional graph of an
Section 12.2: Quadric Surfaces Goals: 1. To recognize and write equations of quadric surfaces 2. To graph quadric surfaces by hand Definitions: 1. A quadric surface is the three-dimensional graph of an
Suggested problems - solutions
 Suggested problems - solutions Quadrilaterals Material for this section references College Geometry: A Discovery Approach, 2/e, David C. Kay, Addison Wesley, 2001. In particular, see section 3.7, pp 190-193.
Suggested problems - solutions Quadrilaterals Material for this section references College Geometry: A Discovery Approach, 2/e, David C. Kay, Addison Wesley, 2001. In particular, see section 3.7, pp 190-193.
Transactions in Euclidean Geometry
 Transactions in Euclidean Geometry Volume 207F Issue # 4 Table of Contents Title Author Square Construction Katherine Bertacini, Rachelle Feldmann, & Kaelyn Koontz Squares and Rectangles Rachelle Feldmann
Transactions in Euclidean Geometry Volume 207F Issue # 4 Table of Contents Title Author Square Construction Katherine Bertacini, Rachelle Feldmann, & Kaelyn Koontz Squares and Rectangles Rachelle Feldmann
f (Pijk ) V. may form the Riemann sum: . Definition. The triple integral of f over the rectangular box B is defined to f (x, y, z) dv = lim
 Chapter 14 Multiple Integrals..1 Double Integrals, Iterated Integrals, Cross-sections.2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals.3
Chapter 14 Multiple Integrals..1 Double Integrals, Iterated Integrals, Cross-sections.2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals.3
Make geometric constructions. (Formalize and explain processes)
 Standard 5: Geometry Pre-Algebra Plus Algebra Geometry Algebra II Fourth Course Benchmark 1 - Benchmark 1 - Benchmark 1 - Part 3 Draw construct, and describe geometrical figures and describe the relationships
Standard 5: Geometry Pre-Algebra Plus Algebra Geometry Algebra II Fourth Course Benchmark 1 - Benchmark 1 - Benchmark 1 - Part 3 Draw construct, and describe geometrical figures and describe the relationships
1 Affine and Projective Coordinate Notation
 CS348a: Computer Graphics Handout #9 Geometric Modeling Original Handout #9 Stanford University Tuesday, 3 November 992 Original Lecture #2: 6 October 992 Topics: Coordinates and Transformations Scribe:
CS348a: Computer Graphics Handout #9 Geometric Modeling Original Handout #9 Stanford University Tuesday, 3 November 992 Original Lecture #2: 6 October 992 Topics: Coordinates and Transformations Scribe:
Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1
 Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1 by Zvezdelina Stankova Berkeley Math Circle Director September 29 and October 13, 2010 Note: We shall work on the problems below
Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1 by Zvezdelina Stankova Berkeley Math Circle Director September 29 and October 13, 2010 Note: We shall work on the problems below
Drill Exercise - 1. Drill Exercise - 2. Drill Exercise - 3
 Drill Exercise - 1 1. Find the distance between the pair of points, (a sin, b cos ) and ( a cos, b sin ). 2. Prove that the points (2a, 4a) (2a, 6a) and (2a + 3 a, 5a) are the vertices of an equilateral
Drill Exercise - 1 1. Find the distance between the pair of points, (a sin, b cos ) and ( a cos, b sin ). 2. Prove that the points (2a, 4a) (2a, 6a) and (2a + 3 a, 5a) are the vertices of an equilateral
