L20 MPI Example, Numerical Integration. Let s now consider a real problem to write a parallel code for. Let s take the case of numerical integration.
|
|
|
- Ethan Jefferson
- 6 years ago
- Views:
Transcription
1 Geophysical Computing L20-1 L20 MPI Example, Numerical Integration 1. Numerical Integration Let s now consider a real problem to write a parallel code for. Let s take the case of numerical integration. In 1-dimension the definite integral is defined as: b E = f(x)dx a And we can use the mean value theorem to approximate this integral by: N (b a) E N = N f(x i) Where the points x i should cover the entire interval of integration. In the limit of large N, E N should approach the exact value of E. But, this is crude. Instead let s consider how to do this as a Monte Carlo simulation. Monte Carlo methods typically use random sampling to investigate the problem. Hence, the term Monte Carlo comes from the Monte Carlo casino located in Monaco. For illustration let s calculate the integral of: i=1 f(x) = cos 2 x Let s just consider the interval from 0 to π. analytically as E = π/2 ~ We can determine the value of this integral If we let f max be the maximum value of the function, and x max be the maximum range to calculate the integral over, we can define a rectangle with area x max f max.
2 Geophysical Computing L20-2 The integral of our function would just be the area of this rectangle that occurs under the curve. That is the red area in the figure above. To use a Monte-Carlo estimate we basically just hang a picture of this function up on the wall and randomly throw darts at it. Then we tabulate the number of darts that fall above the curve and the number of darts that fall below the curve. For example, let s assume we threw the following 5 darts, marked by circles. Here the two red darts fell below the curve, and the three black darts fell above the curve. We would estimate the integral as: E N = # below curve Total # darts (f max x max ) E N = 2 (1 π) = Not a great first guess. But, let s keep throwing darts. Let s do this a bit more automatically, and write a Fortran90 code to do it for us.
3 Geophysical Computing L20-3 PROGRAM monte IMPLICIT NONE REAL(KIND=8), DIMENSION(:), ALLOCATABLE :: xrand, yrand REAL(KIND=8) :: xmax, fmax, fr, En INTEGER(KIND=4) :: N, Kseed, J, Nbelow N = 1000 xmax = fmax = 1.0 ALLOCATE(xrand(N)) ALLOCATE(yrand(N)) Kseed = 1 CALL RANDOM_SEED(SIZE=Kseed) CALL RANDOM_NUMBER(xrand(:)) CALL RANDOM_NUMBER(yrand(:)) xrand(:) = xrand(:)*xmax yrand(:) = yrand(:)*fmax Nbelow = 0 DO J=1,N fr = (cos(xrand(j)))**2 IF (yrand(j) <= fr) THEN Nbelow = Nbelow + 1!estimate integral En = (float(nbelow)/float(n))*(fmax*xmax) write(*,*) En write(*,*) Nbelow OPEN(UNIT=1,FILE='darts.xy') DO J=1,N write(1,*) xrand(j), yrand(j) CLOSE(1) END PROGRAM monte Here are the actual positions using 1,000 darts from the above code:
4 Geophysical Computing L20-4 In this case, I got 483 darts below the curve (red darts), and an estimate of the integral as: E N = 483 (1 π) = Which is a much better estimate, but not quite good enough yet. Now, try running the code more times and fill in the following table. Be sure to add to the code an estimate of the error. N E N Error (%) 1,000 10, ,000 1,000,000 Where the error is defined as: Error = E actual E estimated E actual 100% Obviously, to improve on our estimate we need to throw more darts. So how can we do this efficiently? Well let s let multiple processors work on the problem simultaneously. 2. Parallel Monte Carlo Approach So, to write this as a parallel application one needs to think about how to go about the problem. In this case, it seems quite simple. We just let each processor throw the same number of darts at the dartboard, making sure that each processor is throwing a different set of darts, and tabulate all of the darts thrown that lie under the curve. First, let s consider for a brief moment a thing or two about random numbers. How are they generated? Are they really random? Well, the answer is in general no, because you need to have a program generate the numbers, i.e., an algorithm, and thus the numbers are pseudorandom. For, example check out the cellular automaton RULE 30 from Wolfram (just Wikipedia Rule 30), which is a pretty simple way of generating random numbers. If we call the random number generator in Fortran as we did above,
5 Geophysical Computing L20-5 CALL RANDOM_NUMBER(xrand(:)) This will return the same numbers every time. But, calling it again and again, will produce new sets of numbers. Hence, for our parallel application we will try multiple random number calls. OK, so let s set up the problem. If we were doing this on four processors we might think about this as follows: I did this as above for 4 cases, each with 1,000 dart throws with a different random seed in each case and got the # of darts below the curve as indicated. Then, the integral estimate would be: E N = ( ) (1 π) = ( ) Which is a minor improvement. So, let s pursue this in a more generalized sense, and write a code that allows us to use a variable number of processors. We will just modify the code above to achieve this. PROGRAM monte USE mpi IMPLICIT NONE REAL(KIND=8), DIMENSION(:), ALLOCATABLE :: xrand, yrand REAL(KIND=8) :: xmax, fmax, fr, En INTEGER(KIND=4) :: N, Kseed, J, Nbelow, Ntotal, Nbtemp INTEGER(KIND=4) :: mpi_ierr, nprocs, myrank INTEGER(KIND=4) :: mstatus(mpi_status_size)! Initialize the MPI environment CALL MPI_Init(mpi_ierr) CALL MPI_Comm_size(MPI_COMM_WORLD,nprocs,mpi_ierr)
6 Geophysical Computing L20-6 CALL MPI_Comm_rank(MPI_COMM_WORLD,myrank,mpi_ierr)! Initialize parameters N = 1000 xmax = fmax = 1.0!Allocate memory ALLOCATE(xrand(N)) ALLOCATE(yrand(N))! Populate random numbers differently for each rank Kseed = 1 DO J= 1,(myrank+1) CALL RANDOM_SEED(SIZE=Kseed) CALL RANDOM_NUMBER(xrand(:)) CALL RANDOM_NUMBER(yrand(:)) xrand(:) = xrand(:) * xmax yrand(:) = yrand(:) * fmax!now calculate Nbelow on each processor Nbelow = 0 DO J=1,N fr = (cos(xrand(j)))**2 IF (yrand(j) <= fr) THEN Nbelow = Nbelow + 1!write out value of Nbelow for each rank write(*,*) "myrank= ", myrank, "Nbelow= ", Nbelow! Now tabulate all of the Nbelows and total throws onto rank 0! First send the messages IF (myrank > 0) THEN CALL MPI_Send(Nbelow,1,MPI_INTEGER,0,myrank,MPI_COMM_WORLD,mpi_ierr)! Now receive them on rank 0 IF (myrank == 0) THEN Ntotal = N DO J=1,(nprocs-1) CALL MPI_Recv(Nbtemp,1,MPI_INTEGER,J,J,MPI_COMM_WORLD,mstatus,mpi_ierr) Ntotal = Ntotal + N Nbelow = Nbelow + Nbtemp
7 Geophysical Computing L20-7 write(*,*) "Ntotal= ", Ntotal, "Nbelow= ", Nbelow!estimate integral IF (myrank == 0) THEN En = (float(nbelow)/float(ntotal))*(fmax*xmax) write(*,*) "En= ", En CALL MPI_Finalize(mpi_ierr) END PROGRAM monte 3. Homework Calculate the following integrals: π a) sin 2 (π cos 3θ) cos 2 θdθ 0 b) 10 x 3 dx 0 x π c) sin 4 (3x) dx 0
Monte Carlo Techniques. Professor Stephen Sekula Guest Lecture PHY 4321/7305 Sep. 3, 2014
 Monte Carlo Techniques Professor Stephen Sekula Guest Lecture PHY 431/7305 Sep. 3, 014 What are Monte Carlo Techniques? Computational algorithms that rely on repeated random sampling in order to obtain
Monte Carlo Techniques Professor Stephen Sekula Guest Lecture PHY 431/7305 Sep. 3, 014 What are Monte Carlo Techniques? Computational algorithms that rely on repeated random sampling in order to obtain
Computational modeling
 Computational modeling Lecture 8 : Monte Carlo Instructor : Cedric Weber Course : 4CCP1000 Integrals, how to calculate areas? 2 Integrals, calculate areas There are different ways to calculate areas Integration
Computational modeling Lecture 8 : Monte Carlo Instructor : Cedric Weber Course : 4CCP1000 Integrals, how to calculate areas? 2 Integrals, calculate areas There are different ways to calculate areas Integration
2.9 Linear Approximations and Differentials
 2.9 Linear Approximations and Differentials 2.9.1 Linear Approximation Consider the following graph, Recall that this is the tangent line at x = a. We had the following definition, f (a) = lim x a f(x)
2.9 Linear Approximations and Differentials 2.9.1 Linear Approximation Consider the following graph, Recall that this is the tangent line at x = a. We had the following definition, f (a) = lim x a f(x)
Polar Coordinates. Chapter 10: Parametric Equations and Polar coordinates, Section 10.3: Polar coordinates 27 / 45
 : Given any point P = (x, y) on the plane r stands for the distance from the origin (0, 0). θ stands for the angle from positive x-axis to OP. Polar coordinate: (r, θ) Chapter 10: Parametric Equations
: Given any point P = (x, y) on the plane r stands for the distance from the origin (0, 0). θ stands for the angle from positive x-axis to OP. Polar coordinate: (r, θ) Chapter 10: Parametric Equations
Computational modeling
 Computational modeling Lecture 5 : Monte Carlo Integration Physics: Integration The Monte Carlo method Programming: Subroutine Differences Subroutine/Function The Fortran random number subroutine Monte
Computational modeling Lecture 5 : Monte Carlo Integration Physics: Integration The Monte Carlo method Programming: Subroutine Differences Subroutine/Function The Fortran random number subroutine Monte
Professor Stephen Sekula
 Monte Carlo Techniques Professor Stephen Sekula Guest Lecture PHYS 4321/7305 What are Monte Carlo Techniques? Computational algorithms that rely on repeated random sampling in order to obtain numerical
Monte Carlo Techniques Professor Stephen Sekula Guest Lecture PHYS 4321/7305 What are Monte Carlo Techniques? Computational algorithms that rely on repeated random sampling in order to obtain numerical
Polar Coordinates. Chapter 10: Parametric Equations and Polar coordinates, Section 10.3: Polar coordinates 28 / 46
 Polar Coordinates Polar Coordinates: Given any point P = (x, y) on the plane r stands for the distance from the origin (0, 0). θ stands for the angle from positive x-axis to OP. Polar coordinate: (r, θ)
Polar Coordinates Polar Coordinates: Given any point P = (x, y) on the plane r stands for the distance from the origin (0, 0). θ stands for the angle from positive x-axis to OP. Polar coordinate: (r, θ)
1. Practice the use of the C ++ repetition constructs of for, while, and do-while. 2. Use computer-generated random numbers.
 1 Purpose This lab illustrates the use of looping structures by introducing a class of programming problems called numerical algorithms. 1. Practice the use of the C ++ repetition constructs of for, while,
1 Purpose This lab illustrates the use of looping structures by introducing a class of programming problems called numerical algorithms. 1. Practice the use of the C ++ repetition constructs of for, while,
Math 11 Fall 2016 Section 1 Monday, October 17, 2016
 Math 11 Fall 16 Section 1 Monday, October 17, 16 First, some important points from the last class: f(x, y, z) dv, the integral (with respect to volume) of f over the three-dimensional region, is a triple
Math 11 Fall 16 Section 1 Monday, October 17, 16 First, some important points from the last class: f(x, y, z) dv, the integral (with respect to volume) of f over the three-dimensional region, is a triple
Parallel Techniques. Embarrassingly Parallel Computations. Partitioning and Divide-and-Conquer Strategies
 slides3-1 Parallel Techniques Embarrassingly Parallel Computations Partitioning and Divide-and-Conquer Strategies Pipelined Computations Synchronous Computations Asynchronous Computations Load Balancing
slides3-1 Parallel Techniques Embarrassingly Parallel Computations Partitioning and Divide-and-Conquer Strategies Pipelined Computations Synchronous Computations Asynchronous Computations Load Balancing
Problem #3 Daily Lessons and Assessments for AP* Calculus AB, A Complete Course Page Mark Sparks 2012
 Problem # Daily Lessons and Assessments for AP* Calculus AB, A Complete Course Page 490 Mark Sparks 01 Finding Anti-derivatives of Polynomial-Type Functions If you had to explain to someone how to find
Problem # Daily Lessons and Assessments for AP* Calculus AB, A Complete Course Page 490 Mark Sparks 01 Finding Anti-derivatives of Polynomial-Type Functions If you had to explain to someone how to find
4.7 Approximate Integration
 4.7 Approximate Integration Some anti-derivatives are difficult to impossible to find. For example, 1 0 e x2 dx or 1 1 1 + x3 dx We came across this situation back in calculus I when we introduced the
4.7 Approximate Integration Some anti-derivatives are difficult to impossible to find. For example, 1 0 e x2 dx or 1 1 1 + x3 dx We came across this situation back in calculus I when we introduced the
An interesting related problem is Buffon s Needle which was first proposed in the mid-1700 s.
 Using Monte Carlo to Estimate π using Buffon s Needle Problem An interesting related problem is Buffon s Needle which was first proposed in the mid-1700 s. Here s the problem (in a simplified form). Suppose
Using Monte Carlo to Estimate π using Buffon s Needle Problem An interesting related problem is Buffon s Needle which was first proposed in the mid-1700 s. Here s the problem (in a simplified form). Suppose
AP * Calculus Review. Area and Volume
 AP * Calculus Review Area and Volume Student Packet Advanced Placement and AP are registered trademark of the College Entrance Examination Board. The College Board was not involved in the production of,
AP * Calculus Review Area and Volume Student Packet Advanced Placement and AP are registered trademark of the College Entrance Examination Board. The College Board was not involved in the production of,
Name: Signature: Section and TA:
 Name: Signature: Section and TA: Math 7. Lecture 00 (V. Reiner) Midterm Exam I Thursday, February 8, 00 This is a 50 minute exam. No books, notes, calculators, cell phones or other electronic devices are
Name: Signature: Section and TA: Math 7. Lecture 00 (V. Reiner) Midterm Exam I Thursday, February 8, 00 This is a 50 minute exam. No books, notes, calculators, cell phones or other electronic devices are
The Plan: Basic statistics: Random and pseudorandom numbers and their generation: Chapter 16.
 Scientific Computing with Case Studies SIAM Press, 29 http://www.cs.umd.edu/users/oleary/sccswebpage Lecture Notes for Unit IV Monte Carlo Computations Dianne P. O Leary c 28 What is a Monte-Carlo method?
Scientific Computing with Case Studies SIAM Press, 29 http://www.cs.umd.edu/users/oleary/sccswebpage Lecture Notes for Unit IV Monte Carlo Computations Dianne P. O Leary c 28 What is a Monte-Carlo method?
Monte Carlo Simulations
 Monte Carlo Simulations DESCRIPTION AND APPLICATION Outline Introduction Description of Method Cost Estimating Example Other Considerations Introduction Most interesting things are probabilistic (opinion)
Monte Carlo Simulations DESCRIPTION AND APPLICATION Outline Introduction Description of Method Cost Estimating Example Other Considerations Introduction Most interesting things are probabilistic (opinion)
Math (Spring 2009): Lecture 5 Planes. Parametric equations of curves and lines
 Math 18.02 (Spring 2009): Lecture 5 Planes. Parametric equations of curves and lines February 12 Reading Material: From Simmons: 17.1 and 17.2. Last time: Square Systems. Word problem. How many solutions?
Math 18.02 (Spring 2009): Lecture 5 Planes. Parametric equations of curves and lines February 12 Reading Material: From Simmons: 17.1 and 17.2. Last time: Square Systems. Word problem. How many solutions?
Scientific Computing with Case Studies SIAM Press, Lecture Notes for Unit IV Monte Carlo
 Scientific Computing with Case Studies SIAM Press, 2009 http://www.cs.umd.edu/users/oleary/sccswebpage Lecture Notes for Unit IV Monte Carlo Computations Dianne P. O Leary c 2008 1 What is a Monte-Carlo
Scientific Computing with Case Studies SIAM Press, 2009 http://www.cs.umd.edu/users/oleary/sccswebpage Lecture Notes for Unit IV Monte Carlo Computations Dianne P. O Leary c 2008 1 What is a Monte-Carlo
Ph3 Mathematica Homework: Week 8
 Ph3 Mathematica Homework: Week 8 Eric D. Black California Institute of Technology v1.1 Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin. For, as has
Ph3 Mathematica Homework: Week 8 Eric D. Black California Institute of Technology v1.1 Anyone who considers arithmetical methods of producing random digits is, of course, in a state of sin. For, as has
A small review, Second Midterm, Calculus 3, Prof. Montero 3450: , Fall 2008
 A small review, Second Midterm, Calculus, Prof. Montero 45:-4, Fall 8 Maxima and minima Let us recall first, that for a function f(x, y), the gradient is the vector ( f)(x, y) = ( ) f f (x, y); (x, y).
A small review, Second Midterm, Calculus, Prof. Montero 45:-4, Fall 8 Maxima and minima Let us recall first, that for a function f(x, y), the gradient is the vector ( f)(x, y) = ( ) f f (x, y); (x, y).
Random Number Generator of STMC and simple Monte Carlo Integration
 Random Number Generator of STMC and simple Monte Carlo Integration Bernd Berg FSU MCMC Course, August 26, September 2, 2008 Random Numbers and Fortran Code According to Marsaglia and collaborators a list
Random Number Generator of STMC and simple Monte Carlo Integration Bernd Berg FSU MCMC Course, August 26, September 2, 2008 Random Numbers and Fortran Code According to Marsaglia and collaborators a list
Function f. Function f -1
 Page 1 REVIEW (1.7) What is an inverse function? Do all functions have inverses? An inverse function, f -1, is a kind of undoing function. If the initial function, f, takes the element a to the element
Page 1 REVIEW (1.7) What is an inverse function? Do all functions have inverses? An inverse function, f -1, is a kind of undoing function. If the initial function, f, takes the element a to the element
Chapter Four: Loops II
 Chapter Four: Loops II Slides by Evan Gallagher & Nikolay Kirov Chapter Goals To understand nested loops To implement programs that read and process data sets To use a computer for simulations Processing
Chapter Four: Loops II Slides by Evan Gallagher & Nikolay Kirov Chapter Goals To understand nested loops To implement programs that read and process data sets To use a computer for simulations Processing
CALCULUS LABORATORY ACTIVITY: Numerical Integration, Part 1
 CALCULUS LABORATORY ACTIVITY: Numerical Integration, Part 1 Required tasks: Tabulate values, create sums Suggested Technology: Goals Spreadsheet: Microsoft Excel or Google Docs Spreadsheet Maple or Wolfram
CALCULUS LABORATORY ACTIVITY: Numerical Integration, Part 1 Required tasks: Tabulate values, create sums Suggested Technology: Goals Spreadsheet: Microsoft Excel or Google Docs Spreadsheet Maple or Wolfram
Inverse and Implicit functions
 CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
Monte Carlo Methods. Named by Stanislaw Ulam and Nicholas Metropolis in 1940s for the famous gambling casino in Monaco.
 Monte Carlo Methods Named by Stanislaw Ulam and Nicholas Metropolis in 1940s for the famous gambling casino in Monaco. Used in numerous applications. Any method that uses random numbers to solve a problem
Monte Carlo Methods Named by Stanislaw Ulam and Nicholas Metropolis in 1940s for the famous gambling casino in Monaco. Used in numerous applications. Any method that uses random numbers to solve a problem
MAT137 Calculus! Lecture 31
 MAT137 Calculus! Lecture 31 Today: Next: Integration Methods: Integration Methods: Trig. Functions (v. 9.10-9.12) Rational Functions Trig. Substitution (v. 9.13-9.15) (v. 9.16-9.17) Integration by Parts
MAT137 Calculus! Lecture 31 Today: Next: Integration Methods: Integration Methods: Trig. Functions (v. 9.10-9.12) Rational Functions Trig. Substitution (v. 9.13-9.15) (v. 9.16-9.17) Integration by Parts
Integration. Volume Estimation
 Monte Carlo Integration Lab Objective: Many important integrals cannot be evaluated symbolically because the integrand has no antiderivative. Traditional numerical integration techniques like Newton-Cotes
Monte Carlo Integration Lab Objective: Many important integrals cannot be evaluated symbolically because the integrand has no antiderivative. Traditional numerical integration techniques like Newton-Cotes
L14 Supercomputing - Part 2
 Geophysical Computing L14-1 L14 Supercomputing - Part 2 1. MPI Code Structure Writing parallel code can be done in either C or Fortran. The Message Passing Interface (MPI) is just a set of subroutines
Geophysical Computing L14-1 L14 Supercomputing - Part 2 1. MPI Code Structure Writing parallel code can be done in either C or Fortran. The Message Passing Interface (MPI) is just a set of subroutines
Euler s Method for Approximating Solution Curves
 Euler s Method for Approximating Solution Curves As you may have begun to suspect at this point, time constraints will allow us to learn only a few of the many known methods for solving differential equations.
Euler s Method for Approximating Solution Curves As you may have begun to suspect at this point, time constraints will allow us to learn only a few of the many known methods for solving differential equations.
f (Pijk ) V. may form the Riemann sum: . Definition. The triple integral of f over the rectangular box B is defined to f (x, y, z) dv = lim
 Chapter 14 Multiple Integrals..1 Double Integrals, Iterated Integrals, Cross-sections.2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals.3
Chapter 14 Multiple Integrals..1 Double Integrals, Iterated Integrals, Cross-sections.2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals.3
Introduction to Parallel Programming Message Passing Interface Practical Session Part I
 Introduction to Parallel Programming Message Passing Interface Practical Session Part I T. Streit, H.-J. Pflug streit@rz.rwth-aachen.de October 28, 2008 1 1. Examples We provide codes of the theoretical
Introduction to Parallel Programming Message Passing Interface Practical Session Part I T. Streit, H.-J. Pflug streit@rz.rwth-aachen.de October 28, 2008 1 1. Examples We provide codes of the theoretical
13 Distribution Ray Tracing
 13 In (hereafter abbreviated as DRT ), our goal is to render a scene as accurately as possible. Whereas Basic Ray Tracing computed a very crude approximation to radiance at a point, in DRT we will attempt
13 In (hereafter abbreviated as DRT ), our goal is to render a scene as accurately as possible. Whereas Basic Ray Tracing computed a very crude approximation to radiance at a point, in DRT we will attempt
MAT203 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS
 MAT203 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT203 covers essentially the same material as MAT201, but is more in depth and theoretical. Exam problems are often more sophisticated in scope and difficulty
MAT203 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT203 covers essentially the same material as MAT201, but is more in depth and theoretical. Exam problems are often more sophisticated in scope and difficulty
y= sin( x) y= cos( x)
 . The graphs of sin(x) and cos(x). Now I am going to define the two basic trig functions: sin(x) and cos(x). Study the diagram at the right. The circle has radius. The arm OP starts at the positive horizontal
. The graphs of sin(x) and cos(x). Now I am going to define the two basic trig functions: sin(x) and cos(x). Study the diagram at the right. The circle has radius. The arm OP starts at the positive horizontal
PHYSICS 115/242 Homework 5, Solutions X = and the mean and variance of X are N times the mean and variance of 12/N y, so
 PHYSICS 5/242 Homework 5, Solutions. Central limit theorem. (a) Let y i = x i /2. The distribution of y i is equal to for /2 y /2 and zero otherwise. Hence We consider µ y y i = /2 /2 σ 2 y y 2 i y i 2
PHYSICS 5/242 Homework 5, Solutions. Central limit theorem. (a) Let y i = x i /2. The distribution of y i is equal to for /2 y /2 and zero otherwise. Hence We consider µ y y i = /2 /2 σ 2 y y 2 i y i 2
Sample some Pi Monte. Introduction. Creating the Simulation. Answers & Teacher Notes
 Sample some Pi Monte Answers & Teacher Notes 7 8 9 10 11 12 TI-Nspire Investigation Student 45 min Introduction The Monte-Carlo technique uses probability to model or forecast scenarios. In this activity
Sample some Pi Monte Answers & Teacher Notes 7 8 9 10 11 12 TI-Nspire Investigation Student 45 min Introduction The Monte-Carlo technique uses probability to model or forecast scenarios. In this activity
Programming with MPI
 Programming with MPI p. 1/?? Programming with MPI Introduction Nick Maclaren nmm1@cam.ac.uk April 2010 Programming with MPI p. 2/?? Why Use MPI? CPUs got faster at 40% per annum until 2003 Since then,
Programming with MPI p. 1/?? Programming with MPI Introduction Nick Maclaren nmm1@cam.ac.uk April 2010 Programming with MPI p. 2/?? Why Use MPI? CPUs got faster at 40% per annum until 2003 Since then,
Chapter Four: Loops. Slides by Evan Gallagher. C++ for Everyone by Cay Horstmann Copyright 2012 by John Wiley & Sons. All rights reserved
 Chapter Four: Loops Slides by Evan Gallagher The Three Loops in C++ C++ has these three looping statements: while for do The while Loop while (condition) { statements } The condition is some kind of test
Chapter Four: Loops Slides by Evan Gallagher The Three Loops in C++ C++ has these three looping statements: while for do The while Loop while (condition) { statements } The condition is some kind of test
Simulation. Chapter Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall
 Simulation Chapter 14 14-1 Chapter Topics The Monte Carlo Process Computer Simulation with Excel Spreadsheets Simulation of a Queuing System Continuous Probability Distributions Statistical Analysis of
Simulation Chapter 14 14-1 Chapter Topics The Monte Carlo Process Computer Simulation with Excel Spreadsheets Simulation of a Queuing System Continuous Probability Distributions Statistical Analysis of
3.1 The Inverse Sine, Cosine, and Tangent Functions
 3.1 The Inverse Sine, Cosine, and Tangent Functions Let s look at f(x) = sin x The domain is all real numbers (which will represent angles). The range is the set of real numbers where -1 sin x 1. However,
3.1 The Inverse Sine, Cosine, and Tangent Functions Let s look at f(x) = sin x The domain is all real numbers (which will represent angles). The range is the set of real numbers where -1 sin x 1. However,
1 Programs for double integrals
 > restart; Double Integrals IMPORTANT: This worksheet depends on some programs we have written in Maple. You have to execute these first. Click on the + in the box below, then follow the directions you
> restart; Double Integrals IMPORTANT: This worksheet depends on some programs we have written in Maple. You have to execute these first. Click on the + in the box below, then follow the directions you
1. Suppose that the equation F (x, y, z) = 0 implicitly defines each of the three variables x, y, and z as functions of the other two:
 Final Solutions. Suppose that the equation F (x, y, z) implicitly defines each of the three variables x, y, and z as functions of the other two: z f(x, y), y g(x, z), x h(y, z). If F is differentiable
Final Solutions. Suppose that the equation F (x, y, z) implicitly defines each of the three variables x, y, and z as functions of the other two: z f(x, y), y g(x, z), x h(y, z). If F is differentiable
x y
 10. LECTURE 10 Objectives I understand the difficulty in finding an appropriate function for a data set in general. In some cases, I can define a function type that may fit a data set well. Last time,
10. LECTURE 10 Objectives I understand the difficulty in finding an appropriate function for a data set in general. In some cases, I can define a function type that may fit a data set well. Last time,
What is the Monte Carlo Method?
 Program What is the Monte Carlo Method? A bit of history Applications The core of Monte Carlo: Random realizations 1st example: Initial conditions for N-body simulations 2nd example: Simulating a proper
Program What is the Monte Carlo Method? A bit of history Applications The core of Monte Carlo: Random realizations 1st example: Initial conditions for N-body simulations 2nd example: Simulating a proper
VARIANCE REDUCTION TECHNIQUES IN MONTE CARLO SIMULATIONS K. Ming Leung
 POLYTECHNIC UNIVERSITY Department of Computer and Information Science VARIANCE REDUCTION TECHNIQUES IN MONTE CARLO SIMULATIONS K. Ming Leung Abstract: Techniques for reducing the variance in Monte Carlo
POLYTECHNIC UNIVERSITY Department of Computer and Information Science VARIANCE REDUCTION TECHNIQUES IN MONTE CARLO SIMULATIONS K. Ming Leung Abstract: Techniques for reducing the variance in Monte Carlo
Tutorial using BEAST v2.4.1 Troubleshooting David A. Rasmussen
 Tutorial using BEAST v2.4.1 Troubleshooting David A. Rasmussen 1 Background The primary goal of most phylogenetic analyses in BEAST is to infer the posterior distribution of trees and associated model
Tutorial using BEAST v2.4.1 Troubleshooting David A. Rasmussen 1 Background The primary goal of most phylogenetic analyses in BEAST is to infer the posterior distribution of trees and associated model
3.7. Vertex and tangent
 3.7. Vertex and tangent Example 1. At the right we have drawn the graph of the cubic polynomial f(x) = x 2 (3 x). Notice how the structure of the graph matches the form of the algebraic expression. The
3.7. Vertex and tangent Example 1. At the right we have drawn the graph of the cubic polynomial f(x) = x 2 (3 x). Notice how the structure of the graph matches the form of the algebraic expression. The
Section Polar Coordinates. or 4 π (restricting θ to the domain of the lemniscate). So, there are horizontal tangents at ( 4 3
 Section 10.3 Polar Coordinates 66. r = e θ x = r cos θ = e θ cos θ, y = r sin θ = e θ sin θ. = eθ sin θ+e θ cos θ = e θ (sin θ+cos θ), dx = eθ cos θ e θ sin θ = e θ (cos θ sin θ). Let 1 = 0 sin θ = cos
Section 10.3 Polar Coordinates 66. r = e θ x = r cos θ = e θ cos θ, y = r sin θ = e θ sin θ. = eθ sin θ+e θ cos θ = e θ (sin θ+cos θ), dx = eθ cos θ e θ sin θ = e θ (cos θ sin θ). Let 1 = 0 sin θ = cos
LECTURE 18 - OPTIMIZATION
 LECTURE 18 - OPTIMIZATION CHRIS JOHNSON Abstract. In this lecture we ll describe extend the optimization techniques you learned in your first semester calculus class to optimize functions of multiple variables.
LECTURE 18 - OPTIMIZATION CHRIS JOHNSON Abstract. In this lecture we ll describe extend the optimization techniques you learned in your first semester calculus class to optimize functions of multiple variables.
In this chapter, we will investigate what have become the standard applications of the integral:
 Chapter 8 Overview: Applications of Integrals Calculus, like most mathematical fields, began with trying to solve everyday problems. The theory and operations were formalized later. As early as 70 BC,
Chapter 8 Overview: Applications of Integrals Calculus, like most mathematical fields, began with trying to solve everyday problems. The theory and operations were formalized later. As early as 70 BC,
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14 Scan Converting Lines, Circles and Ellipses Hello everybody, welcome again
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14 Scan Converting Lines, Circles and Ellipses Hello everybody, welcome again
MONTE CARLO EVALUATION OF DEFINITE INTEGRALS
 MISN-0-355 MONTE CARLO EVALUATION OF DEFINITE INTEGRALS by Robert Ehrlich MONTE CARLO EVALUATION OF DEFINITE INTEGRALS y 1. Integrals, 1-2 Dimensions a. Introduction.............................................1
MISN-0-355 MONTE CARLO EVALUATION OF DEFINITE INTEGRALS by Robert Ehrlich MONTE CARLO EVALUATION OF DEFINITE INTEGRALS y 1. Integrals, 1-2 Dimensions a. Introduction.............................................1
Jim Lambers MAT 169 Fall Semester Lecture 33 Notes
 Jim Lambers MAT 169 Fall Semester 2009-10 Lecture 33 Notes These notes correspond to Section 9.3 in the text. Polar Coordinates Throughout this course, we have denoted a point in the plane by an ordered
Jim Lambers MAT 169 Fall Semester 2009-10 Lecture 33 Notes These notes correspond to Section 9.3 in the text. Polar Coordinates Throughout this course, we have denoted a point in the plane by an ordered
4-6 Inverse Trigonometric Functions
 Find the exact value of each expression, if it exists. 29. The inverse property applies, because lies on the interval [ 1, 1]. Therefore, =. 31. The inverse property applies, because lies on the interval
Find the exact value of each expression, if it exists. 29. The inverse property applies, because lies on the interval [ 1, 1]. Therefore, =. 31. The inverse property applies, because lies on the interval
INTRODUCTION TO LINE INTEGRALS
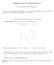 INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
Two-dimensional Totalistic Code 52
 Two-dimensional Totalistic Code 52 Todd Rowland Senior Research Associate, Wolfram Research, Inc. 100 Trade Center Drive, Champaign, IL The totalistic two-dimensional cellular automaton code 52 is capable
Two-dimensional Totalistic Code 52 Todd Rowland Senior Research Associate, Wolfram Research, Inc. 100 Trade Center Drive, Champaign, IL The totalistic two-dimensional cellular automaton code 52 is capable
Ordinary differential equations solving methods
 Radim Hošek, A07237 radhost@students.zcu.cz Ordinary differential equations solving methods Problem: y = y2 (1) y = x y (2) y = sin ( + y 2 ) (3) Where it is possible we try to solve the equations analytically,
Radim Hošek, A07237 radhost@students.zcu.cz Ordinary differential equations solving methods Problem: y = y2 (1) y = x y (2) y = sin ( + y 2 ) (3) Where it is possible we try to solve the equations analytically,
4 Visualization and. Approximation
 4 Visualization and Approximation b A slope field for the differential equation y tan(x + y) tan(x) tan(y). It is not always possible to write down an explicit formula for the solution to a differential
4 Visualization and Approximation b A slope field for the differential equation y tan(x + y) tan(x) tan(y). It is not always possible to write down an explicit formula for the solution to a differential
Monte Carlo Integration and Random Numbers
 Monte Carlo Integration and Random Numbers Higher dimensional integration u Simpson rule with M evaluations in u one dimension the error is order M -4! u d dimensions the error is order M -4/d u In general
Monte Carlo Integration and Random Numbers Higher dimensional integration u Simpson rule with M evaluations in u one dimension the error is order M -4! u d dimensions the error is order M -4/d u In general
Physics 736. Experimental Methods in Nuclear-, Particle-, and Astrophysics. - Statistical Methods -
 Physics 736 Experimental Methods in Nuclear-, Particle-, and Astrophysics - Statistical Methods - Karsten Heeger heeger@wisc.edu Course Schedule and Reading course website http://neutrino.physics.wisc.edu/teaching/phys736/
Physics 736 Experimental Methods in Nuclear-, Particle-, and Astrophysics - Statistical Methods - Karsten Heeger heeger@wisc.edu Course Schedule and Reading course website http://neutrino.physics.wisc.edu/teaching/phys736/
Lecture 7: the quotient topology
 Lecture 7: the quotient topology Saul Glasman September 21, 2016 Why couldn t we say that a homeomorphism was just a continuous bijection? Why did we have to explicitly require the inverse to be continuous
Lecture 7: the quotient topology Saul Glasman September 21, 2016 Why couldn t we say that a homeomorphism was just a continuous bijection? Why did we have to explicitly require the inverse to be continuous
Solution Notes. COMP 151: Terms Test
 Family Name:.............................. Other Names:............................. ID Number:............................... Signature.................................. Solution Notes COMP 151: Terms
Family Name:.............................. Other Names:............................. ID Number:............................... Signature.................................. Solution Notes COMP 151: Terms
VARIOUS ESTIMATIONS OF π AS DEMONSTRATIONS OF THE MONTE CARLO METHOD
 DEPARTMENT OF MATHEMATICS TECHNICAL REPORT VARIOUS ESTIMATIONS OF π AS DEMONSTRATIONS OF THE MONTE CARLO METHOD JAMIE McCREARY Under the supervision of DR. MICHAEL ALLEN July 2001 No. 2001-4 TENNESSEE
DEPARTMENT OF MATHEMATICS TECHNICAL REPORT VARIOUS ESTIMATIONS OF π AS DEMONSTRATIONS OF THE MONTE CARLO METHOD JAMIE McCREARY Under the supervision of DR. MICHAEL ALLEN July 2001 No. 2001-4 TENNESSEE
FUNCTIONS AND MODELS
 1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS In this section, we assume that you have access to a graphing calculator or a computer with graphing software. FUNCTIONS AND MODELS 1.4 Graphing Calculators
1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS In this section, we assume that you have access to a graphing calculator or a computer with graphing software. FUNCTIONS AND MODELS 1.4 Graphing Calculators
NUMERICAL INTEGRATION - TRAPEZIUM RULE
 Mathematics Revision Guides Numerical Integration using the Trapezium Rule Page of M.K. HOME TUITION Mathematics Revision Guides Level: A-Level Year NUMERICAL INTEGRATION - TRAPEZIUM RULE Version :.4 Date:
Mathematics Revision Guides Numerical Integration using the Trapezium Rule Page of M.K. HOME TUITION Mathematics Revision Guides Level: A-Level Year NUMERICAL INTEGRATION - TRAPEZIUM RULE Version :.4 Date:
Applications of MPI I
 Applications of MPI I N-Dimensional Integration Using Monte Carlo Techniques Gürsan ÇOBAN 4.06.202 Outline Numerical Integration Techniques Monte Carlo Techniques for Numerical Integration Some MPI Examples
Applications of MPI I N-Dimensional Integration Using Monte Carlo Techniques Gürsan ÇOBAN 4.06.202 Outline Numerical Integration Techniques Monte Carlo Techniques for Numerical Integration Some MPI Examples
Homework: Study 6.1 # 1, 5, 7, 13, 25, 19; 3, 17, 27, 53
 January, 7 Goals:. Remember that the area under a curve is the sum of the areas of an infinite number of rectangles. Understand the approach to finding the area between curves.. Be able to identify the
January, 7 Goals:. Remember that the area under a curve is the sum of the areas of an infinite number of rectangles. Understand the approach to finding the area between curves.. Be able to identify the
Math 2250 Lab #3: Landing on Target
 Math 2250 Lab #3: Landing on Target 1. INTRODUCTION TO THE LAB PROGRAM. Here are some general notes and ideas which will help you with the lab. The purpose of the lab program is to expose you to problems
Math 2250 Lab #3: Landing on Target 1. INTRODUCTION TO THE LAB PROGRAM. Here are some general notes and ideas which will help you with the lab. The purpose of the lab program is to expose you to problems
Perfect square numbers are formed when we multiply a number (factor) by itself, or square a number. 9 is a perfect square, and 3 is it s factor.
 Math Unit 1: Square Roots and Surface Area. Review from Grade 8: Perfect Squares What is a perfect square? Perfect square numbers are formed when we multiply a number (factor) by itself, or square a number.
Math Unit 1: Square Roots and Surface Area. Review from Grade 8: Perfect Squares What is a perfect square? Perfect square numbers are formed when we multiply a number (factor) by itself, or square a number.
WebAssign Lesson 1-2a Area Between Curves (Homework)
 WebAssign Lesson 1-2a Area Between Curves (Homework) Current Score : / 30 Due : Thursday, June 26 2014 11:00 AM MDT Jaimos Skriletz Math 175, section 31, Summer 2 2014 Instructor: Jaimos Skriletz 1. /3
WebAssign Lesson 1-2a Area Between Curves (Homework) Current Score : / 30 Due : Thursday, June 26 2014 11:00 AM MDT Jaimos Skriletz Math 175, section 31, Summer 2 2014 Instructor: Jaimos Skriletz 1. /3
Monte Carlo Simulation. Ben Kite KU CRMDA 2015 Summer Methodology Institute
 Monte Carlo Simulation Ben Kite KU CRMDA 2015 Summer Methodology Institute Created by Terrence D. Jorgensen, 2014 What Is a Monte Carlo Simulation? Anything that involves generating random data in a parameter
Monte Carlo Simulation Ben Kite KU CRMDA 2015 Summer Methodology Institute Created by Terrence D. Jorgensen, 2014 What Is a Monte Carlo Simulation? Anything that involves generating random data in a parameter
Math 21a Tangent Lines and Planes Fall, What do we know about the gradient f? Tangent Lines to Curves in the Plane.
 Math 21a Tangent Lines and Planes Fall, 2016 What do we know about the gradient f? Tangent Lines to Curves in the Plane. 1. For each of the following curves, find the tangent line to the curve at the point
Math 21a Tangent Lines and Planes Fall, 2016 What do we know about the gradient f? Tangent Lines to Curves in the Plane. 1. For each of the following curves, find the tangent line to the curve at the point
MAC2313 Final A. a. The vector r u r v lies in the tangent plane of S at a given point. b. S f(x, y, z) ds = R f(r(u, v)) r u r v du dv.
 MAC2313 Final A (5 pts) 1. Let f(x, y, z) be a function continuous in R 3 and let S be a surface parameterized by r(u, v) with the domain of the parameterization given by R; how many of the following are
MAC2313 Final A (5 pts) 1. Let f(x, y, z) be a function continuous in R 3 and let S be a surface parameterized by r(u, v) with the domain of the parameterization given by R; how many of the following are
MTH 122 Calculus II Essex County College Division of Mathematics and Physics 1 Lecture Notes #11 Sakai Web Project Material
 MTH Calculus II Essex County College Division of Mathematics and Physics Lecture Notes # Sakai Web Project Material Introduction - - 0 - Figure : Graph of y sin ( x y ) = x cos (x + y) with red tangent
MTH Calculus II Essex County College Division of Mathematics and Physics Lecture Notes # Sakai Web Project Material Introduction - - 0 - Figure : Graph of y sin ( x y ) = x cos (x + y) with red tangent
B. Examples Set up the integral(s) needed to find the area of the region bounded by
 Math 176 Calculus Sec. 6.1: Area Between Curves I. Area between the Curve and the x Axis A. Let f(x) 0 be continuous on [a,b]. The area of the region between the graph of f and the x-axis is A = f ( x)
Math 176 Calculus Sec. 6.1: Area Between Curves I. Area between the Curve and the x Axis A. Let f(x) 0 be continuous on [a,b]. The area of the region between the graph of f and the x-axis is A = f ( x)
P1 REVISION EXERCISE: 1
 P1 REVISION EXERCISE: 1 1. Solve the simultaneous equations: x + y = x +y = 11. For what values of p does the equation px +4x +(p 3) = 0 have equal roots? 3. Solve the equation 3 x 1 =7. Give your answer
P1 REVISION EXERCISE: 1 1. Solve the simultaneous equations: x + y = x +y = 11. For what values of p does the equation px +4x +(p 3) = 0 have equal roots? 3. Solve the equation 3 x 1 =7. Give your answer
Page 129 Exercise 5: Suppose that the joint p.d.f. of two random variables X and Y is as follows: { c(x. 0 otherwise. ( 1 = c. = c
 Stat Solutions for Homework Set Page 9 Exercise : Suppose that the joint p.d.f. of two random variables X and Y is as follows: { cx fx, y + y for y x, < x < otherwise. Determine a the value of the constant
Stat Solutions for Homework Set Page 9 Exercise : Suppose that the joint p.d.f. of two random variables X and Y is as follows: { cx fx, y + y for y x, < x < otherwise. Determine a the value of the constant
ACTIVITY 8. The Bouncing Ball. You ll Need. Name. Date. 1 CBR unit 1 TI-83 or TI-82 Graphing Calculator Ball (a racquet ball works well)
 . Name Date ACTIVITY 8 The Bouncing Ball If a ball is dropped from a given height, what does a Height- Time graph look like? How does the velocity change as the ball rises and falls? What affects the shape
. Name Date ACTIVITY 8 The Bouncing Ball If a ball is dropped from a given height, what does a Height- Time graph look like? How does the velocity change as the ball rises and falls? What affects the shape
3.1 Maxima/Minima Values
 3.1 Maxima/Minima Values Ex 1: Find all critical points for the curve given by f (x)=x 5 25 3 x3 +20x 1 on the interval [-3, 2]. Identify the min and max values. We're guaranteed max and min points if
3.1 Maxima/Minima Values Ex 1: Find all critical points for the curve given by f (x)=x 5 25 3 x3 +20x 1 on the interval [-3, 2]. Identify the min and max values. We're guaranteed max and min points if
F dr = f dx + g dy + h dz. Using that dz = q x dx + q y dy we get. (g + hq y ) x (f + hq x ) y da.
 Math 55 - Vector alculus II Notes 14.7 tokes Theorem tokes Theorem is the three-dimensional version of the circulation form of Green s Theorem. Let s quickly recall that theorem: Green s Theorem: Let be
Math 55 - Vector alculus II Notes 14.7 tokes Theorem tokes Theorem is the three-dimensional version of the circulation form of Green s Theorem. Let s quickly recall that theorem: Green s Theorem: Let be
Secondary Math 3- Honors. 7-4 Inverse Trigonometric Functions
 Secondary Math 3- Honors 7-4 Inverse Trigonometric Functions Warm Up Fill in the Unit What You Will Learn How to restrict the domain of trigonometric functions so that the inverse can be constructed. How
Secondary Math 3- Honors 7-4 Inverse Trigonometric Functions Warm Up Fill in the Unit What You Will Learn How to restrict the domain of trigonometric functions so that the inverse can be constructed. How
Topic 6: Calculus Integration Volume of Revolution Paper 2
 Topic 6: Calculus Integration Standard Level 6.1 Volume of Revolution Paper 1. Let f(x) = x ln(4 x ), for < x
Topic 6: Calculus Integration Standard Level 6.1 Volume of Revolution Paper 1. Let f(x) = x ln(4 x ), for < x
R f da (where da denotes the differential of area dxdy (or dydx)
 Math 28H Topics for the second exam (Technically, everything covered on the first exam, plus) Constrained Optimization: Lagrange Multipliers Most optimization problems that arise naturally are not unconstrained;
Math 28H Topics for the second exam (Technically, everything covered on the first exam, plus) Constrained Optimization: Lagrange Multipliers Most optimization problems that arise naturally are not unconstrained;
Volumes of Solids of Revolution Lecture #6 a
 Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
MATH 261 EXAM III PRACTICE PROBLEMS
 MATH 6 EXAM III PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam 3 typically has 5 (not 6!) problems on it, with no more than one problem of any given
MATH 6 EXAM III PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam 3 typically has 5 (not 6!) problems on it, with no more than one problem of any given
Math Girls rock! Math Club for Young Women Project 2. Geometric Probability and Buffon s Needle Problem
 Math Club for Young Women http://www.uvu.edu/csh/mathematics/mgr/ Project 2 Geometric Probability and Buffon s Needle Problem Project 2 Coordinators: Prof. Carolyn Hamilton (e-mail: HamiltCa@uvu.edu) Prof.
Math Club for Young Women http://www.uvu.edu/csh/mathematics/mgr/ Project 2 Geometric Probability and Buffon s Needle Problem Project 2 Coordinators: Prof. Carolyn Hamilton (e-mail: HamiltCa@uvu.edu) Prof.
The diagram above shows a sketch of the curve C with parametric equations
 1. The diagram above shows a sketch of the curve C with parametric equations x = 5t 4, y = t(9 t ) The curve C cuts the x-axis at the points A and B. (a) Find the x-coordinate at the point A and the x-coordinate
1. The diagram above shows a sketch of the curve C with parametric equations x = 5t 4, y = t(9 t ) The curve C cuts the x-axis at the points A and B. (a) Find the x-coordinate at the point A and the x-coordinate
Not for reproduction
 x=a GRAPHING CALCULATORS AND COMPUTERS (a, d ) y=d (b, d ) (a, c ) y=c (b, c) (a) _, by _, 4 x=b FIGURE 1 The viewing rectangle a, b by c, d _4 4 In this section we assume that you have access to a graphing
x=a GRAPHING CALCULATORS AND COMPUTERS (a, d ) y=d (b, d ) (a, c ) y=c (b, c) (a) _, by _, 4 x=b FIGURE 1 The viewing rectangle a, b by c, d _4 4 In this section we assume that you have access to a graphing
MITOCW ocw f99-lec07_300k
 MITOCW ocw-18.06-f99-lec07_300k OK, here's linear algebra lecture seven. I've been talking about vector spaces and specially the null space of a matrix and the column space of a matrix. What's in those
MITOCW ocw-18.06-f99-lec07_300k OK, here's linear algebra lecture seven. I've been talking about vector spaces and specially the null space of a matrix and the column space of a matrix. What's in those
Monte Carlo Simula/on and Copula Func/on. by Gerardo Ferrara
 Monte Carlo Simula/on and Copula Func/on by Gerardo Ferrara Introduc)on A Monte Carlo method is a computational algorithm that relies on repeated random sampling to compute its results. In a nutshell,
Monte Carlo Simula/on and Copula Func/on by Gerardo Ferrara Introduc)on A Monte Carlo method is a computational algorithm that relies on repeated random sampling to compute its results. In a nutshell,
Random Numbers Random Walk
 Random Numbers Random Walk Computational Physics Random Numbers Random Walk Outline Random Systems Random Numbers Monte Carlo Integration Example Random Walk Exercise 7 Introduction Random Systems Deterministic
Random Numbers Random Walk Computational Physics Random Numbers Random Walk Outline Random Systems Random Numbers Monte Carlo Integration Example Random Walk Exercise 7 Introduction Random Systems Deterministic
Parametric Surfaces. Substitution
 Calculus Lia Vas Parametric Surfaces. Substitution Recall that a curve in space is given by parametric equations as a function of single parameter t x = x(t) y = y(t) z = z(t). A curve is a one-dimensional
Calculus Lia Vas Parametric Surfaces. Substitution Recall that a curve in space is given by parametric equations as a function of single parameter t x = x(t) y = y(t) z = z(t). A curve is a one-dimensional
Math 250A (Fall 2009) - Lab I: Estimate Integrals Numerically with Matlab. Due Date: Monday, September 21, INSTRUCTIONS
 Math 250A (Fall 2009) - Lab I: Estimate Integrals Numerically with Matlab Due Date: Monday, September 21, 2009 4:30 PM 1. INSTRUCTIONS The primary purpose of this lab is to understand how go about numerically
Math 250A (Fall 2009) - Lab I: Estimate Integrals Numerically with Matlab Due Date: Monday, September 21, 2009 4:30 PM 1. INSTRUCTIONS The primary purpose of this lab is to understand how go about numerically
Name: Teacher: Pd: Algebra 2/Trig: Trigonometric Graphs (SHORT VERSION)
 Algebra 2/Trig: Trigonometric Graphs (SHORT VERSION) In this unit, we will Learn the properties of sine and cosine curves: amplitude, frequency, period, and midline. Determine what the parameters a, b,
Algebra 2/Trig: Trigonometric Graphs (SHORT VERSION) In this unit, we will Learn the properties of sine and cosine curves: amplitude, frequency, period, and midline. Determine what the parameters a, b,
Proceedings of the Third International DERIVE/TI-92 Conference
 Using the TI-92 and TI-92 Plus to Explore Derivatives, Riemann Sums, and Differential Equations with Symbolic Manipulation, Interactive Geometry, Scripts, Regression, and Slope Fields Sally Thomas, Orange
Using the TI-92 and TI-92 Plus to Explore Derivatives, Riemann Sums, and Differential Equations with Symbolic Manipulation, Interactive Geometry, Scripts, Regression, and Slope Fields Sally Thomas, Orange
David Appleyard Department of Mathematics and Computer Science Carleton College North eld, Minnesota 55057
 David Appleyard Department of Mathematics and Computer Science Carleton College North eld, Minnesota 55057 After turning your calculator on, press F1 then 8 to clear the home screen. #1. Find lim ³1+ x
David Appleyard Department of Mathematics and Computer Science Carleton College North eld, Minnesota 55057 After turning your calculator on, press F1 then 8 to clear the home screen. #1. Find lim ³1+ x
The Fundamental Theorem of Calculus Using the Rule of Three
 The Fundamental Theorem of Calculus Using the Rule of Three A. Approimations with Riemann sums. The area under a curve can be approimated through the use of Riemann (or rectangular) sums: n Area f ( k
The Fundamental Theorem of Calculus Using the Rule of Three A. Approimations with Riemann sums. The area under a curve can be approimated through the use of Riemann (or rectangular) sums: n Area f ( k
Math Circle Intermediate Group October 30, 2016 Geometric Probability
 Math Circle Intermediate Group October 30, 2016 Geometric Probability Warm up problems 1. Show that A \ (B [ C) =(A \ B) [ (A \ C) using Venn diagrams. 2. Show that A [ (B \ C) =(A [ B) \ (A [ C) using
Math Circle Intermediate Group October 30, 2016 Geometric Probability Warm up problems 1. Show that A \ (B [ C) =(A \ B) [ (A \ C) using Venn diagrams. 2. Show that A [ (B \ C) =(A [ B) \ (A [ C) using
