6.4 Maximum Flow. overview Ford-Fulkerson implementations applications
|
|
|
- Norah Kelley
- 6 years ago
- Views:
Transcription
1 6.4 Maximum Flow overview Ford-Fulkerson implementations applications Algorithms, 4 th Edition Robert Sedgewick and Kevin Wayne Copyright April 18, :02:27 AM
2 Mincut problem Given. A weighted digraph with identified source s and target t. Def. A cut is a partition of the vertices into two disjoint sets. Def. An st-cut is a cut that places s in one of its sets (C s ) and t in the other (C t ). Def. An st-cut s weight is the sum of the weights of its st-crossing edges. Minimum st-cut (mincut) problem. Find an st-cut of minimal weight. edges from Cs to Ct Note: don t count edges from Ct to Cs 2
3 Typical mincut application Find cheapest way to cut connection between s and t. s t 3
4 Mincut application (1950s) Rail network connecting Soviet Union with Eastern European countries Free world goal: Know how to cut supplies if cold war turns into real war (map declassified by Pentagon in 1999). 4
5 Potential mincut application (2010s) Facebook graph Government-in-power s goal: Cut off communication to specified set of people. 5
6 Maxflow problem Flow network. Weighted digraph with a source s (indegree 0) and sink t (outdegree 0) An edge s weight is its capacity (positive) Add additional flow variable to each edge(no greater than its capacity) Maximum st-flow (maxflow) problem: Assign flows to edges that Maintain local equilibrium: inflow = outflow at every vertex (except s and t). Maximize total flow into t. 6
7 2 out A physical model Oil flowing in pipes all flow goes down (just to simplify diagrams) local equilibrium at each vertex 4 in s 2 out t room for improvement? 7
8 Typical maxflow application Find best way to distribute goods from s to t. s t 8
9 Maxflow application (1950s) Rail network connecting Soviet Union with Eastern European countries flow capacity Soviet Union goal: Know how to maximize flow of supplies to Eastern Europe. 9
10 Potential mincut application (2010s) Facebook graph Free world goal: Maximize flow of information to specified set of people. 10
11 Overview (summary) Given. A weighted digraph, source s and target t. Minimum st-cut (mincut) problem. Find an st-cut of minimal weight. Maximum st-flow (maxflow) problem: Assign flows to edges that Maintain local equilibrium: inflow = outflow at every vertex (except s and t). Maximize total flow into t. Remarkable fact. These two problems are equivalent! Two very rich algorithmic problems Cornerstone problems in combintorial optimixation Beautiful mathematical duality 11
12 Maxflow / mincut applications Maxflow/mincut is a widely applicable problem-solving model Data mining. Open-pit mining. Project selection. Image processing. Airline scheduling. Bipartite matching. Baseball elimination. Distributed computing. Egalitarian stable matching. Security of statistical data. Network connectivity/reliability. Many many more... 12
13 overview APIs Ford Fulkerson implementations applications 13
14 APIs (cf. EdgeWeightedDigraph, DirectedEdge) manipulate flow values (stay tuned) 14
15 Flow edge: implementation in Java (cf. DirectedEdge) public class FlowEdge { private final int v; private final int w; private final double capacity; private double flow; // from // to // capacity // flow flow variable } public FlowEdge(int v, int w, double capacity, double flow) { this.v = v; this.w = w; this.capacity = capacity; this.flow = flow; } public int from() { return v; } public int to() { return w; } public double capacity() { return capacity; } public double flow() { return flow; } public int other(int vertex) { if (vertex == v) return w; else if (vertex == w) return v; else throw new RuntimeException("Illegal endpoint"); } public double residualcapacityto(int vertex) {...} public void addresidualflowto(int vertex, double delta) {...} stay tuned 15
16 Flow network representation A flow network is an array of bags of flow edges. tinyfn.txt V 6 E adj[] Flow network representation references to the same Edge object Bag objects 16
17 Flow network: implementation in Java (cf. EdgeWeightedDigraph) public class FlowNetwork { private final int V; private int E; private Bag<FlowEdge>[] adj; public FlowNetwork(int V) { this.v = V; this.e = 0; adj = (Bag<FlowEdge>[]) new Bag[V]; for (int v = 0; v < V; v++) adj[v] = new Bag<FlowEdge>(); } array of bags of flow edges constructor public int V() { return V; } public int E() { return E; } public void addedge(flowedge e) { E++; int v = e.from(); int w = e.to(); adj[v].add(e); adj[w].add(e); } public Iterable<FlowEdge> adj(int v) { return adj[v]; } add edge (to both adj lists) iterator for adjacent edges } 17
18 Typical client code: check that a flow is feasible private boolean localeq(flownetwork G, int v) { // Check local equilibrium at v. double EPSILON = 1E-11; double netflow = 0.0; for (FlowEdge e : G.adj(v)) if (v == e.from()) netflow -= e.flow(); else netflow += e.flow(); return Math.abs(netflow) < EPSILON; } private boolean isfeasible(flownetwork G) { for (int v = 0; v < G.V(); v++) for (FlowEdge e : G.adj(v)) if (e.flow() < 0 e.flow() > e.capacity()) return false; for (int v = 0; v < G.V(); v++) if (v!=s && v!= t &&!localeq(g, v)) return false; check that each flow is nonnegative and no greater than capacity check local equilibrium at each vertex } return true; 18
19 APIs Ford Fulkerson implementations applications 19
20 Idea: increase flow along augmenting paths s t
21 Idea: increase flow along augmenting paths s t 21
22 Idea: increase flow along augmenting paths s t = 10 22
23 Idea: increase flow along augmenting paths s t = 20 23
24 Idea: increase flow along augmenting paths Problem: Can get stuck with no way to add more flow to t. s +5 t 24
25 Idea: increase flow along augmenting paths Problem: Can get stuck with no way to add more flow to t. Solution: Go backwards along an edge with flow (removing some flow). +5 s t 25
26 Idea: increase flow along augmenting paths Augmenting paths in general increase flow on forward edge (if not full) decrease flow on backward edge (if not empty) s t = 25 26
27 Idea: increase flow along augmenting paths s t = 28 27
28 Idea: increase flow along augmenting paths Eventually all paths from s to t are blocked by either a full forward edge empty backward edge s t maxflow value = 28 28
29 Ford-Fulkerson algorithm Generic method for solving maxflow problem. Start with 0 flow everywhere. Find an augmenting path. Increase the flow on that path, by as much as possible. Repeat until no augmenting paths are left. Questions. Q. Does this process give a maximum flow? A. Yes! It also finds a mincut (!!). [Classic result] Q. How do we find an augmenting path? A. Easy. Adapt standard graph-searching methods. Q. How many augmenting paths (does the process even terminate)? A. Difficult to know: depends on graph model, search method. 29
30 Mincut problem (revisited) Given. A weighted digraph with identified source s and target t. Def. A cut is a partition of the vertices into two disjoint sets. Def. An st-cut is a cut that places s in one of its sets (C s ) and t in the other (C t ). Def. An st-cut s weight is the sum of the weights of its st-crossing edges. Mincut problem. Find an st-cut of minimal weight. edges from Cs to Ct 22 s s s 23 t 29 t t Note: don t count edges from Ct to Cs 30
31 Mincut problem (revisited with slight change in terminology) Given. A weighted flow network digraph with identified source s and target t. Def. A cut is a partition of the vertices into two disjoint sets. Def. An st-cut is a cut that places s in one of its sets (C s ) and t in the other (C t ). Def. An st-cut s capacity weight is the sum of the capacities weights of its st-crossing edges. Mincut problem. Find an st-cut of minimal weight. capacity. edges from Cs to Ct s s s t 29 Amazing fact. Mincut and maxflow problems are equivalent. t t 31
32 Relationship between flows and cuts Def. The flow across an st-cut is the sum of the flows on its st-crossing edges minus the sum of the flows of its ts-crossing edges. Thm. For any st-flow, the flow across every st-cut equals the value of the flow. s C s Pf. By induction on the size of C t. true when C t = {t}. true by local equilibrium when moving a vertex from C s to C t C t t difference between inflow and outflow is flow across cut inflow to t is value of the flow Corollary 1. Outflow from s = inflow to t = value. Corollary 2. No st-flow s value can exceed the capacity of any st-cut. 32
33 Relationship between flows and cuts (example) For any st-flow, the flow across every st-cut equals the value of the flow Shortest augmenting paths in a larger flow network 4 Shortest augmenting paths in a larger flow n 33
34 Maxflow-mincut theorem Thm. The following three conditions are equivalent for any st-flow f: i. There exists an st-cut whose capacity equals the value of the flow f. ii. f is a maxflow. iii. There is no augmenting path with respect to f. Pf. i. implies ii. [no flow s value can exceed any cut s capacity] ii. implies iii. by contradiction [aug path would give higher-value flow, so f could not be maximal]. iii. implies i. C s : set of all vertices connected to s by an undirected path with no full forward or empty backward edges. C t : all other vertices. capacity = flow across [st-crossing edges full, ts-crossing edges empty]. = value of f [capacity of any cut = value of f]. 34
35 FF termination Eventually all paths from s to t are blocked by either a full forward edge empty backward edge s t maxflow value = 28 mincut capacity = 28 Mincut: Consider only paths with no full forward or empty backward edges. C s is the set of vertices reachable from s; C t is the set of remaining vertices. 35
36 Maxflow/mincut application (1950s) bottleneck is mincut (all forward edges full) value of flow = = 163,000 tons 36
37 Integrality property Corollary to maxflow-mincut theorem. When capacities are integers, there exists an integer-valued maxflow, and the Ford Fulkerson algorithm finds it. Pf. Flow increases by augmenting path value, which is either unused capacity in a forward edge or flow in a backwards edge [and always an integer]. s t = 25 Bottom line: Ford-Fulkerson always works when weights are integers. Note: When weights are not integers, it could converge to the wrong value! 37
38 Possible strategies for augmenting paths FF algorithm: any strategy for choosing augmenting paths will give a maxflow. [Caveat: Can have convergence problems when weights are not integers.] Shortest path? aug path with fewest number of edges DFS path? This lecture (guaranteed to converge) Random path? Fattest path? max capacity aug path All easy to implement Define residual graph Find paths in residual graph. Performance depends on network properties (stay tuned) 38
39 Shortest augmenting path 39
40 Fattest augmenting path 40
41 Random augmenting path 41
42 Bad case for Ford-Fulkerson Bad news: Even when weights are integers, number of augmenting paths could be equal to the value of the maxflow. s U U 1 U U t Good news: This case is easily avoided [use shortest augmenting path]. 42
43 s t
44 first iteration s t = 1
45 second iteration s backwards edge t = 2
46 third iteration s t = 3
47 fourth iteration s backwards edge t = 4
48 ...
49 (2i-1)st iteration s t 2i = 2i 1
50 (2i)th iteration s backwards edge t 2i = 2i
51 Bad case for Ford-Fulkerson Bad news: Even when weights are integers, number of augmenting paths could be equal to the value of the maxflow. s U U 1 U U t Good news: This case is easily avoided [use shortest augmenting path]. 51
52 Flow network representation (revisited) Residual digraph. Another view of a flow network drawing with flow flow representation residual network backward edge (flow) capacity flow Anatomy of a network-flow problem (revisited) forward edge (remaining capacity) Finding an augmenting path is equivalent to finding a path in residual digraph. 52
53 Residual network implementation public class FlowEdge { private final int v; private final int w; private final double capacity; private double flow; // from // to // capacity // flow public double residualcapacityto(int vertex) { if (vertex == v) return flow; else if (vertex == w) return capacity - flow; else throw new RuntimeException("Illegal endpoint"); } public void addresidualflowto(int vertex, double delta) { if (vertex == v) flow -= delta; else if (vertex == w) flow += delta; else throw new RuntimeException("Illegal endpoint"); } } v w v capacity - flow w flow 53
54 Ford-Fulkerson: Java implementation public class FordFulkerson { private boolean[] marked; // true if s->v path in residual digraph private FlowEdge[] edgeto; // last edge on s->v path private double value; public FordFulkerson(FlowNetwork G, int s, int t) { value = 0; while (hasaugmentingpath(g, s, t)) { double bottle = Double.POSITIVE_INFINITY; for (int v = t; v!= s; v = edgeto[v].other(v)) bottle = Math.min(bottle, edgeto[v].residualcapacityto(v)); for (int v = t; v!= s; v = edgeto[v].other(v)) edgeto[v].addresidualflowto(v, bottle); compute bottleneck capacity augment flow } } value += bottle; public double hasaugmentingpath(flownetwork G, int s, int t) { /* See next slide. */ } public double value() { return value; } public boolean incut(int v) { return marked[v]; } 54
55 Finding a shortest augmenting path (cf. breadth-first search) private boolean hasaugmentingpath(flownetwork G, int s, int t) { edgeto = new FlowEdge[G.V()]; marked = new boolean[g.v()]; Queue<Integer> q = new Queue<Integer>(); q.enqueue(s); marked[s] = true; while (!q.isempty()) { int v = q.dequeue(); } for (FlowEdge e : G.adj(v)) { int w = e.other(v); if (e.residualcapacityto(w) > 0 &&!marked[w]) { edgeto[w] = e; marked[w] = true; q.enqueue(w); } } is there a path from s to w in the residual graph? save last edge on path, mark w, and add w to the queue return marked[t]; } 55
56 Analysis of Ford-Fulkerson (shortest augmenting path) Thm. Ford-Fulkerson (shortest augmenting path) uses at most EV/2 augmenting paths. Pf. [see text] Cor. Ford-Fulkerson (shortest augmenting path) examines at most E 2 V/2 edges. Pf. Each BFS examines at most E edges. 56
57 Summary: possible strategies for augmenting paths All easy to implement Define residual graph Find paths in residual graph. Shortest path: Use BFS. DFS path: Use DFS. Fattest path: Use a PQ, ala shortest paths. Random path: Use a randomized queue. Performance depends on network properties how many augmenting paths? how many edges examined to find each augmenting path? 57
58 Analysis of maxflow algorithms (Yet another) holy grail for mathematicians/theoretical computer scientists. For sparse graphs with E edges, integer capacities (max U). year method worst case order of growth discovered by 1951 simplex O ( E 3 U ) Dantzig 1955 augmenting paths O ( E 2 U ) Ford-Fulkerson 1970 shortest aug path O ( E 3 ) Edmunds-Karp 1970 fattest aug path O ( E 2 log E log U ) Edmunds-Karp 1973 capacity scaling O ( E 2 log U ) Dinitz-Gabow 1983 preflow-push O ( E 2 log E ) Sleator-Tarjan 1997 length function O ( E 3/2 ) Goldberg-Rao ~ 2011 electrical flow O ( E 4/3 ) *? O ( E ) ~ Christiano-Kelner-Madry- Spielman-Teng ~ ignore log factors * approximation Warning: Worst-case order-of-growth analysis is generally not useful for predicting or comparing algorithm performance in practice. 58
59 O-notation considered harmful (Lecture 2 revisited) Facebook and Google: Huge sparse graphs are of interest ( edges). Time to solve maxflow: ~ Algorithm A: O(E3/2). ~ Algorithm B: O(E4/3).* ~ ignore log factors * approximation algorithm Q. Which algorithm should Facebook and Google be interested in? A. Who knows? These mathematical results are not relevant! Upper bound on worst case [may never take stated time]. Unknown constants [most published maxflow algs never are implemented]. E1/6 savings likely offset by ignored log factors [40-50 vs ]. Performance for practical graph models likely unknown [and not studied]. Approximation algorithm [cost of accuracy may be too high]. 59
60 O-notation considered harmful Source? Schrijver s authoritative survey attributes T. E. Harris (author of the Soviet rail network report) as the first to formulate the problem in
61 O-notation considered harmful up to 100 if the constant-factor costs were the same for both algorithms and if the internet were the worst case for both algorithms, which there is no reason to believe. The algorithm has not been implemented or tested on graphs the size of the internet (or at all, for that matter). The algorithm would have to be implemented and tested before any claim to immediate practicality could be assessed. Moreover, these mathematical results are approximate, ignoring factors that could run into the hundreds for the internet graph. The algorithm also computes an approximation to the maxflow, not the actual maxflow, and slows down as the approximation improves. It is likely that simpler approaches involving parallelism will be used in practice. 61
62 Summary Minimum st-cut (mincut) problem. Find an st-cut of minimal weight. Maximum st-flow (maxflow) problem: Assign flows to edges that Maintain local equilibrium: inflow = outflow at every vertex (except s and t). Maximize total flow into t. Proven successful approaches. Ford-Fulkerson (various augmenting-path strategies). Preflow-push (various versions). Open research challenges. Practice: Solve maxflow/mincut problems for real networks in linear time. Theory: Prove it for worst-case networks. 62
63 APIs Ford Fulkerson implementations applications 63
64 Maxflow / mincut applications Maxflow/mincut is a widely applicable problem-solving model Data mining. Open-pit mining. Project selection. Image processing. Airline scheduling. Bipartite matching. Baseball elimination. Distributed computing. Egalitarian stable matching. Security of statistical data. Network connectivity/reliability. Many many more... 64
65 Bipartite matching problem N students apply for N jobs Each get several offers Is there a way to match all student to jobs? Alice Adobe Amazon Facebook Bob Adobe Amazon Yahoo Carol Facebook Google IBM Dave Adobe Amazon Eliza Google IBM Yahoo Frank IBM Yahoo Adobe Alice Bob Dave Amazon Alice Bob Dave Facebook Alice Carol Google Carol Eliza IBM Carol Eliza Frank Yahoo Bob Eliza Frank 65
66 Network flow formulation of bipartite matching To formulate a bipartite matching problem as a network flow problem create s, t, one vertex for each student, and one vertex for each job add edge from s to each student add edge from each job to t add edge from student to each job offered s give all edges capacity s 66
67 Bipartite matching problem formulated as a network flow problem Alice Adobe Amazon Facebook Bob Adobe Amazon Yahoo Carol Facebook Google IBM Dave Adobe Amazon Eliza Google IBM Yahoo Frank IBM Yahoo Adobe Alice Bob Dave Amazon Alice Bob Dave Facebook Alice Carol Google Carol Eliza IBM Carol Eliza Frank Yahoo Bob Eliza Frank 1 s s 1-1 correspondence between maxflow solution and bipartite matching solution 67
68 Maxflow solution (FF shortest augmenting path) 68
69 Maxflow solution (FF shortest augmenting path) 69
70 Maxflow solution (FF shortest augmenting path) 70
71 Maxflow solution (FF shortest augmenting path) 71
72 Maxflow solution (FF shortest augmenting path) path w back e 72
73 Maxflow solution (FF shortest augmenting path) path with back edges 73
74 Maxflow solution s ts 74
75 Maxflow solution corresponds directly to matching solution Alice Adobe Amazon Facebook Bob Adobe Amazon Yahoo Carol Facebook Google IBM Dave Adobe Amazon Eliza Google IBM Yahoo Frank IBM Yahoo Adobe Alice Bob Dave Amazon Alice Bob Dave Facebook Alice Carol Google Carol Eliza IBM Carol Eliza Frank Yahoo Bob Eliza Frank 1 s ts Alice Bob Carol Dave Eliza Frank Amazon Yahoo Facebook Adobe Google IBM 75
76 Overview (summary) Given. A weighted digraph, source s and target t. Minimum st-cut (mincut) problem. Find an st-cut of minimal weight. Maximum st-flow (maxflow) problem: Assign flows to edges that Maintain local equilibrium: inflow = outflow at every vertex (except s and t). Maximize total flow into t. Remarkable fact. These two problems are equivalent! Two very rich algorithmic problems Cornerstone problems in combinatorial optimisation Beautiful mathematical duality Still much to be learned! 76
Algorithms. Algorithms 4.4 SHORTEST PATHS. APIs properties Bellman Ford algorithm Dijkstra s algorithm ROBERT SEDGEWICK KEVIN WAYNE
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.4 SHORTEST PATHS Algorithms F O U R T H E D I T I O N APIs properties Bellman Ford algorithm Dijkstra s algorithm ROBERT SEDGEWICK KEVIN WAYNE https://algs4.cs.princeton.edu
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.4 SHORTEST PATHS Algorithms F O U R T H E D I T I O N APIs properties Bellman Ford algorithm Dijkstra s algorithm ROBERT SEDGEWICK KEVIN WAYNE https://algs4.cs.princeton.edu
4.4 Shortest Paths. Dijkstra's algorithm implementation acyclic networks negative weights. Reference: Algorithms in Java, 4 th edition, Section 4.
 4.4 Shortest Paths Dijkstra's algorithm implementation acyclic networks negative weights Reference: Algorithms in Java, 4 th edition, Section 4.4 Algorithms in Java, 4 th Edition Robert Sedgewick and Kevin
4.4 Shortest Paths Dijkstra's algorithm implementation acyclic networks negative weights Reference: Algorithms in Java, 4 th edition, Section 4.4 Algorithms in Java, 4 th Edition Robert Sedgewick and Kevin
CS/COE 1501 cs.pitt.edu/~bill/1501/ Network Flow
 CS/COE 1501 cs.pitt.edu/~bill/1501/ Network Flow Defining network flow Consider a directed, weighted graph G(V, E) Weights are applied to edges to state their capacity c(u, w) is the capacity of edge (u,
CS/COE 1501 cs.pitt.edu/~bill/1501/ Network Flow Defining network flow Consider a directed, weighted graph G(V, E) Weights are applied to edges to state their capacity c(u, w) is the capacity of edge (u,
CMSC 132: Object-Oriented Programming II. Shortest Paths
 CMSC 13: Object-Oriented Programming II Shortest Paths 1 Quiz 1 One advantage of adjacency list representation over adjacency matrix representation of a graph is that in adjacency list representation,
CMSC 13: Object-Oriented Programming II Shortest Paths 1 Quiz 1 One advantage of adjacency list representation over adjacency matrix representation of a graph is that in adjacency list representation,
Algorithms. Algorithms. Algorithms 4.3 MINIMUM SPANNING TREES
 Announcements Algorithms ROBERT SEDGEWICK KEVIN WAYNE Exam Regrades Due by Wednesday s lecture. Teaching Experiment: Dynamic Deadlines (WordNet) Right now, WordNet is due at PM on April 8th. Starting Tuesday
Announcements Algorithms ROBERT SEDGEWICK KEVIN WAYNE Exam Regrades Due by Wednesday s lecture. Teaching Experiment: Dynamic Deadlines (WordNet) Right now, WordNet is due at PM on April 8th. Starting Tuesday
Algorithms. Algorithms 4.3 MINIMUM SPANNING TREES. introduction cut property edge-weighted graph API Kruskal s algorithm Prim s algorithm
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction cut property edge-weighted graph API Kruskal s algorithm
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction cut property edge-weighted graph API Kruskal s algorithm
Network Flow. The network flow problem is as follows:
 Network Flow The network flow problem is as follows: Given a connected directed graph G with non-negative integer weights, (where each edge stands for the capacity of that edge), and two distinguished
Network Flow The network flow problem is as follows: Given a connected directed graph G with non-negative integer weights, (where each edge stands for the capacity of that edge), and two distinguished
Copyright 2007 Pearson Addison-Wesley. All rights reserved. A. Levitin Introduction to the Design & Analysis of Algorithms, 2 nd ed., Ch.
 Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Algorithms. Algorithms 4.3 MINIMUM SPANNING TREES. introduction cut property edge-weighted graph API Kruskal s algorithm Prim s algorithm context
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs4.cs.princeton.edu introduction cut property edge-weighted
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs4.cs.princeton.edu introduction cut property edge-weighted
Algorithms 4.3 MINIMUM SPANNING TREES. edge-weighted graph API greedy algorithm Kruskal's algorithm Prim's algorithm advanced topics
 4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N edge-weighted graph API greedy algorithm Kruskal's algorithm Prim's algorithm advanced topics R O B E R T S E D G E W I C K K E V I N W A
4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N edge-weighted graph API greedy algorithm Kruskal's algorithm Prim's algorithm advanced topics R O B E R T S E D G E W I C K K E V I N W A
Index. stack-based, 400 A* algorithm, 325
 Index Abstract transitive closure, 174-175, 217-221 Active vertex, 411 Acyclic graph. See Digraph; Directed acyclic graph (DAG) Acyclic network, 313-321, 334-335 maxflow, 427-429 Adjacency-lists representation,
Index Abstract transitive closure, 174-175, 217-221 Active vertex, 411 Acyclic graph. See Digraph; Directed acyclic graph (DAG) Acyclic network, 313-321, 334-335 maxflow, 427-429 Adjacency-lists representation,
! Interesting and broadly useful abstraction. ! Challenging branch of computer science and discrete math. ! Hundreds of graph algorithms known.
 Undirected Graphs Undirected Graphs Graph. Set of objects with pairwise connections. Why study graph algorithms?! Interesting and broadly useful abstraction.! Challenging branch of computer science and
Undirected Graphs Undirected Graphs Graph. Set of objects with pairwise connections. Why study graph algorithms?! Interesting and broadly useful abstraction.! Challenging branch of computer science and
Algorithms. Algorithms 4.3 MINIMUM SPANNING TREES. introduction greedy algorithm edge-weighted graph API Kruskal's algorithm Prim's algorithm context
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs4.cs.princeton.edu introduction greedy algorithm edge-weighted
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs4.cs.princeton.edu introduction greedy algorithm edge-weighted
CMSC 132: Object-Oriented Programming II
 CMSC 132: Object-Oriented Programming II DIRECTED GRAPHS Graphs slides are modified from COS 126 slides of Dr. Robert Sedgewick. 1 Directed graphs Digraph Set of vertices connected pairwise by directed
CMSC 132: Object-Oriented Programming II DIRECTED GRAPHS Graphs slides are modified from COS 126 slides of Dr. Robert Sedgewick. 1 Directed graphs Digraph Set of vertices connected pairwise by directed
Lecture 3: Graphs and flows
 Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
Algorithms. Algorithms. Algorithms 4.3 MINIMUM SPANNING TREES
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE. MINIMUM SPANNING TREES. MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs.cs.princeton.edu introduction greedy
Algorithms ROBERT SEDGEWICK KEVIN WAYNE. MINIMUM SPANNING TREES. MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs.cs.princeton.edu introduction greedy
Source. Sink. Chapter 10: Iterative Programming Maximum Flow Problem. CmSc250 Intro to Algorithms
 Chapter 10: Iterative Programming Maximum Flow Problem CmSc20 Intro to Algorithms A flow network is a model of a system where some material is produced at its source, travels through the system, and is
Chapter 10: Iterative Programming Maximum Flow Problem CmSc20 Intro to Algorithms A flow network is a model of a system where some material is produced at its source, travels through the system, and is
Directed Graphs. digraph API digraph search transitive closure topological sort strong components. Directed graphs
 Directed graphs Digraph. Set of vertices connected pairwise by oriented edges. Directed Graphs digraph API digraph search transitive closure topological sort strong components References: Algorithms in
Directed graphs Digraph. Set of vertices connected pairwise by oriented edges. Directed Graphs digraph API digraph search transitive closure topological sort strong components References: Algorithms in
Tutorial for Algorithm s Theory Problem Set 5. January 17, 2013
 Tutorial for Algorithm s Theory Problem Set 5 January 17, 2013 Exercise 1: Maximum Flow Algorithms Consider the following flow network: a) Solve the maximum flow problem on the above network by using the
Tutorial for Algorithm s Theory Problem Set 5 January 17, 2013 Exercise 1: Maximum Flow Algorithms Consider the following flow network: a) Solve the maximum flow problem on the above network by using the
Algorithms. Algorithms 4.3 MINIMUM SPANNING TREES. introduction greedy algorithm edge-weighted graph API Kruskal's algorithm Prim's algorithm context
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs4.cs.princeton.edu introduction greedy algorithm edge-weighted
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs4.cs.princeton.edu introduction greedy algorithm edge-weighted
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn
 Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
graph G not connected
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE. MINIMUM SPANNING TREES. MINIMUM SPANNING TREES introduction introduction Algorithms F O U R T H E D I T I O N greedy algorithm edge-weighted graph API Kruskal's
Algorithms ROBERT SEDGEWICK KEVIN WAYNE. MINIMUM SPANNING TREES. MINIMUM SPANNING TREES introduction introduction Algorithms F O U R T H E D I T I O N greedy algorithm edge-weighted graph API Kruskal's
Algorithms. Algorithms 4.3 MINIMUM SPANNING TREES. introduction greedy algorithm edge-weighted graph API Kruskal's algorithm Prim's algorithm context
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs4.cs.princeton.edu introduction greedy algorithm edge-weighted
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.3 MINIMUM SPANNING TREES Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs4.cs.princeton.edu introduction greedy algorithm edge-weighted
Undirected Graphs. graph API maze exploration depth-first search breadth-first search connected components challenges.
 Undirected graphs Graph. Set of vertices connected pairwise by edges. Undirected Graphs References: Algorithms in Java, Chapters and Why study graph algorithms? Interesting and broadly useful abstraction.
Undirected graphs Graph. Set of vertices connected pairwise by edges. Undirected Graphs References: Algorithms in Java, Chapters and Why study graph algorithms? Interesting and broadly useful abstraction.
Network Design and Optimization course
 Effective maximum flow algorithms Modeling with flows Network Design and Optimization course Lecture 5 Alberto Ceselli alberto.ceselli@unimi.it Dipartimento di Tecnologie dell Informazione Università degli
Effective maximum flow algorithms Modeling with flows Network Design and Optimization course Lecture 5 Alberto Ceselli alberto.ceselli@unimi.it Dipartimento di Tecnologie dell Informazione Università degli
7. NETWORK FLOW II. Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley Copyright 2013 Kevin Wayne
 7. NETWORK FLOW II Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley Copyright 203 Kevin Wayne http://www.cs.princeton.edu/~wayne/kleinberg-tardos bipartite matching disjoint paths extensions
7. NETWORK FLOW II Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley Copyright 203 Kevin Wayne http://www.cs.princeton.edu/~wayne/kleinberg-tardos bipartite matching disjoint paths extensions
Graph Traversals. Ric Glassey
 Graph Traversals Ric Glassey glassey@kth.se Overview Graph Traversals Aim: Develop alternative strategies to moving through a graph by visiting vertices and travelling along edges Maze example Depth-first
Graph Traversals Ric Glassey glassey@kth.se Overview Graph Traversals Aim: Develop alternative strategies to moving through a graph by visiting vertices and travelling along edges Maze example Depth-first
CS261: Problem Set #1
 CS261: Problem Set #1 Due by 11:59 PM on Tuesday, April 21, 2015 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Turn in your solutions by
CS261: Problem Set #1 Due by 11:59 PM on Tuesday, April 21, 2015 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Turn in your solutions by
UNDIRECTED GRAPHS BBM ALGORITHMS DEPT. OF COMPUTER ENGINEERING
 BBM - ALGORIHMS DEP. O COMPUER ENGINEERING UNDIRECED GRAPHS Acknowledgement: he course slides are adapted from the slides prepared by R. Sedgewick and K. Wayne of Princeton Uniersity. Undirected Graphs
BBM - ALGORIHMS DEP. O COMPUER ENGINEERING UNDIRECED GRAPHS Acknowledgement: he course slides are adapted from the slides prepared by R. Sedgewick and K. Wayne of Princeton Uniersity. Undirected Graphs
Undirected Graphs. introduction Graph API maze exploration depth-first search breadth-first search connected components challenges.
 Undirected Graphs Graph. Set of vertices connected pairwise by edges. Undirected Graphs Why study graph algorithms? Interesting and broadly useful abstraction. Challenging branch of computer science and
Undirected Graphs Graph. Set of vertices connected pairwise by edges. Undirected Graphs Why study graph algorithms? Interesting and broadly useful abstraction. Challenging branch of computer science and
Lecture 11: Maximum flow and minimum cut
 Optimisation Part IB - Easter 2018 Lecture 11: Maximum flow and minimum cut Lecturer: Quentin Berthet 4.4. The maximum flow problem. We consider in this lecture a particular kind of flow problem, with
Optimisation Part IB - Easter 2018 Lecture 11: Maximum flow and minimum cut Lecturer: Quentin Berthet 4.4. The maximum flow problem. We consider in this lecture a particular kind of flow problem, with
Maximum Flow. Flow Networks. Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms. Example Flow Network
 Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms Maximum Flow Flow Networks A flow network is a directed graph where: Each edge (u,v) has a capacity c(u,v) 0. If (u,v)
Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms Maximum Flow Flow Networks A flow network is a directed graph where: Each edge (u,v) has a capacity c(u,v) 0. If (u,v)
! Vertex = species. ! Edge = from prey to predator.
 irected Graphs irected Graphs igraph. Set of objects with oriented pairwise connections. x. One-way street, hyperlink. Reference: Chapter 19, Algorithms in Java, 3 rd dition, Robert Sedgewick. Robert Sedgewick
irected Graphs irected Graphs igraph. Set of objects with oriented pairwise connections. x. One-way street, hyperlink. Reference: Chapter 19, Algorithms in Java, 3 rd dition, Robert Sedgewick. Robert Sedgewick
GRAPHS Lecture 17 CS2110 Spring 2014
 GRAPHS Lecture 17 CS2110 Spring 2014 These are not Graphs 2...not the kind we mean, anyway These are Graphs 3 K 5 K 3,3 = Applications of Graphs 4 Communication networks The internet is a huge graph Routing
GRAPHS Lecture 17 CS2110 Spring 2014 These are not Graphs 2...not the kind we mean, anyway These are Graphs 3 K 5 K 3,3 = Applications of Graphs 4 Communication networks The internet is a huge graph Routing
Homework 3 Solutions
 CS3510 Design & Analysis of Algorithms Section A Homework 3 Solutions Released: 7pm, Wednesday Nov 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope
CS3510 Design & Analysis of Algorithms Section A Homework 3 Solutions Released: 7pm, Wednesday Nov 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope
CSE 417 Network Flows (pt 4) Min Cost Flows
 CSE 417 Network Flows (pt 4) Min Cost Flows Reminders > HW6 is due Monday Review of last three lectures > Defined the maximum flow problem find the feasible flow of maximum value flow is feasible if it
CSE 417 Network Flows (pt 4) Min Cost Flows Reminders > HW6 is due Monday Review of last three lectures > Defined the maximum flow problem find the feasible flow of maximum value flow is feasible if it
4.2 Directed Graphs. digraph API digraph search topological sort strong components
 4.2 Directed Graphs digraph API digraph search topological sort strong components Algorithms, 4 th Edition Robert Sedgewick and Kevin Wayne Copyright 2002 2010 November 8, 2010 8:43:22 PM Directed graphs
4.2 Directed Graphs digraph API digraph search topological sort strong components Algorithms, 4 th Edition Robert Sedgewick and Kevin Wayne Copyright 2002 2010 November 8, 2010 8:43:22 PM Directed graphs
Network flows and Menger s theorem
 Network flows and Menger s theorem Recall... Theorem (max flow, min cut strong duality). Let G be a network. The maximum value of a flow equals the minimum capacity of a cut. We prove this strong duality
Network flows and Menger s theorem Recall... Theorem (max flow, min cut strong duality). Let G be a network. The maximum value of a flow equals the minimum capacity of a cut. We prove this strong duality
CS2 Algorithms and Data Structures Note 9
 CS2 Algorithms and Data Structures Note 9 Graphs The remaining three lectures of the Algorithms and Data Structures thread will be devoted to graph algorithms. 9.1 Directed and Undirected Graphs A graph
CS2 Algorithms and Data Structures Note 9 Graphs The remaining three lectures of the Algorithms and Data Structures thread will be devoted to graph algorithms. 9.1 Directed and Undirected Graphs A graph
Algorithms. Algorithms 4.2 DIRECTED GRAPHS. introduction digraph API depth-first search breadth-first search topological sort strong components
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs4.cs.princeton.edu introduction digraph API depth-first search breadth-first
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE http://algs4.cs.princeton.edu introduction digraph API depth-first search breadth-first
GRAPH DECOMPOSITION BASED ON DEGREE CONSTRAINTS. March 3, 2016
 GRAPH DECOMPOSITION BASED ON DEGREE CONSTRAINTS ZOÉ HAMEL March 3, 2016 1. Introduction Let G = (V (G), E(G)) be a graph G (loops and multiple edges not allowed) on the set of vertices V (G) and the set
GRAPH DECOMPOSITION BASED ON DEGREE CONSTRAINTS ZOÉ HAMEL March 3, 2016 1. Introduction Let G = (V (G), E(G)) be a graph G (loops and multiple edges not allowed) on the set of vertices V (G) and the set
Notes for Lecture 20
 U.C. Berkeley CS170: Intro to CS Theory Handout N20 Professor Luca Trevisan November 13, 2001 Notes for Lecture 20 1 Duality As it turns out, the max-flow min-cut theorem is a special case of a more general
U.C. Berkeley CS170: Intro to CS Theory Handout N20 Professor Luca Trevisan November 13, 2001 Notes for Lecture 20 1 Duality As it turns out, the max-flow min-cut theorem is a special case of a more general
Transportation Planning: The maximum flow problem
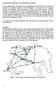 Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
GRAPHS (Undirected) Graph: Set of objects with pairwise connections. Why study graph algorithms?
 GRAPHS (Undirected) Graph: Set of objects with pairwise connections. Why study graph algorithms? Interesting and broadly useful abstraction. Challenging branch of computer science and discrete math. Hundreds
GRAPHS (Undirected) Graph: Set of objects with pairwise connections. Why study graph algorithms? Interesting and broadly useful abstraction. Challenging branch of computer science and discrete math. Hundreds
Network Flow. November 23, CMPE 250 Graphs- Network Flow November 23, / 31
 Network Flow November 23, 2016 CMPE 250 Graphs- Network Flow November 23, 2016 1 / 31 Types of Networks Internet Telephone Cell Highways Rail Electrical Power Water Sewer Gas... CMPE 250 Graphs- Network
Network Flow November 23, 2016 CMPE 250 Graphs- Network Flow November 23, 2016 1 / 31 Types of Networks Internet Telephone Cell Highways Rail Electrical Power Water Sewer Gas... CMPE 250 Graphs- Network
Graphs. Edges may be directed (from u to v) or undirected. Undirected edge eqvt to pair of directed edges
 (p 186) Graphs G = (V,E) Graphs set V of vertices, each with a unique name Note: book calls vertices as nodes set E of edges between vertices, each encoded as tuple of 2 vertices as in (u,v) Edges may
(p 186) Graphs G = (V,E) Graphs set V of vertices, each with a unique name Note: book calls vertices as nodes set E of edges between vertices, each encoded as tuple of 2 vertices as in (u,v) Edges may
Minimum cut application (RAND 1950s)
 Minimum cut application (RAND 950s) Free world goal. Cut supplies (if Cold War turns into real war). rail network connecting Soviet Union with Eastern European countries (map declassified by Pentagon in
Minimum cut application (RAND 950s) Free world goal. Cut supplies (if Cold War turns into real war). rail network connecting Soviet Union with Eastern European countries (map declassified by Pentagon in
Algorithms. Algorithms 4.2 DIRECTED GRAPHS. introduction digraph API depth-first search breadth-first search topological sort strong components
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE https://algs4.cs.princeton.edu introduction digraph API depth-first search
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE https://algs4.cs.princeton.edu introduction digraph API depth-first search
Algorithms. Algorithms 4.2 DIRECTED GRAPHS. introduction digraph API digraph search topological sort strong components ROBERT SEDGEWICK KEVIN WAYNE
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
Institute of Operating Systems and Computer Networks Algorithms Group. Network Algorithms. Tutorial 1: Flashback and Fast Forward
 Institute of Operating Systems and Computer Networks Algorithms Group Network Algorithms Tutorial 1: Flashback and Fast Forward Christian Rieck Staff Lecture: Dr. Christian Scheffer scheffer@ibr.cs.tu-bs.de
Institute of Operating Systems and Computer Networks Algorithms Group Network Algorithms Tutorial 1: Flashback and Fast Forward Christian Rieck Staff Lecture: Dr. Christian Scheffer scheffer@ibr.cs.tu-bs.de
Reductions. Linear Time Reductions. Desiderata. Reduction. Desiderata. Classify problems according to their computational requirements.
 Desiderata Reductions Desiderata. Classify problems according to their computational requirements. Frustrating news. Huge number of fundamental problems have defied classification for decades. Desiderata'.
Desiderata Reductions Desiderata. Classify problems according to their computational requirements. Frustrating news. Huge number of fundamental problems have defied classification for decades. Desiderata'.
Undirected Graphs. DSA - lecture 6 - T.U.Cluj-Napoca - M. Joldos 1
 Undirected Graphs Terminology. Free Trees. Representations. Minimum Spanning Trees (algorithms: Prim, Kruskal). Graph Traversals (dfs, bfs). Articulation points & Biconnected Components. Graph Matching
Undirected Graphs Terminology. Free Trees. Representations. Minimum Spanning Trees (algorithms: Prim, Kruskal). Graph Traversals (dfs, bfs). Articulation points & Biconnected Components. Graph Matching
Algorithms. Algorithms 4.2 DIRECTED GRAPHS. introduction digraph API digraph search topological sort strong components ROBERT SEDGEWICK KEVIN WAYNE
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
Graphs. Tessema M. Mengistu Department of Computer Science Southern Illinois University Carbondale Room - Faner 3131
 Graphs Tessema M. Mengistu Department of Computer Science Southern Illinois University Carbondale tessema.mengistu@siu.edu Room - Faner 3131 1 Outline Introduction to Graphs Graph Traversals Finding a
Graphs Tessema M. Mengistu Department of Computer Science Southern Illinois University Carbondale tessema.mengistu@siu.edu Room - Faner 3131 1 Outline Introduction to Graphs Graph Traversals Finding a
Your data structure should implement all operations in logarithmic time (or better) as a function of the size of the queue.
 1. Write a method isbst(node t) that checks that the binary subtree at t is a binary search tree. The method should return true if t is the root of a binary search tree and false otherwise. Assume Node
1. Write a method isbst(node t) that checks that the binary subtree at t is a binary search tree. The method should return true if t is the root of a binary search tree and false otherwise. Assume Node
Mathematical and Algorithmic Foundations Linear Programming and Matchings
 Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Lecture 23: Maximum Flows and Minimum Cuts [Fa 13] the other hand, any flow that leaves one vertex must enter another vertex, so we must have
![Lecture 23: Maximum Flows and Minimum Cuts [Fa 13] the other hand, any flow that leaves one vertex must enter another vertex, so we must have Lecture 23: Maximum Flows and Minimum Cuts [Fa 13] the other hand, any flow that leaves one vertex must enter another vertex, so we must have](/thumbs/83/87248485.jpg) Optimization Lecture 23: Maximum Flows and Minimum Cuts [Fa 13] A process cannot be understood by stopping it. Understanding must move with the flow of the process, must join it and flow with it. The First
Optimization Lecture 23: Maximum Flows and Minimum Cuts [Fa 13] A process cannot be understood by stopping it. Understanding must move with the flow of the process, must join it and flow with it. The First
LECTURES 3 and 4: Flows and Matchings
 LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
Algorithms. Algorithms 4.2 DIRECTED GRAPHS. introduction digraph API digraph search topological sort strong components ROBERT SEDGEWICK KEVIN WAYNE
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
Network Flow and Matching
 Chapter 4 Network Flow and Matching In this chapter, we examine the network flow problem, a graph problem to which many problems can be reduced. In fact, some problems that don t even appear to be graph
Chapter 4 Network Flow and Matching In this chapter, we examine the network flow problem, a graph problem to which many problems can be reduced. In fact, some problems that don t even appear to be graph
Lecture 10,11: General Matching Polytope, Maximum Flow. 1 Perfect Matching and Matching Polytope on General Graphs
 CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 2009) Lecture 10,11: General Matching Polytope, Maximum Flow Lecturer: Mohammad R Salavatipour Date: Oct 6 and 8, 2009 Scriber: Mohammad
CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 2009) Lecture 10,11: General Matching Polytope, Maximum Flow Lecturer: Mohammad R Salavatipour Date: Oct 6 and 8, 2009 Scriber: Mohammad
Jessica Su (some parts copied from CLRS / last quarter s notes)
 1 Max flow Consider a directed graph G with positive edge weights c that define the capacity of each edge. We can identify two special nodes in G: the source node s and the sink node t. We want to find
1 Max flow Consider a directed graph G with positive edge weights c that define the capacity of each edge. We can identify two special nodes in G: the source node s and the sink node t. We want to find
CSE 417 Network Flows (pt 3) Modeling with Min Cuts
 CSE 417 Network Flows (pt 3) Modeling with Min Cuts Reminders > HW6 is due on Friday start early bug fixed on line 33 of OptimalLineup.java: > change true to false Review of last two lectures > Defined
CSE 417 Network Flows (pt 3) Modeling with Min Cuts Reminders > HW6 is due on Friday start early bug fixed on line 33 of OptimalLineup.java: > change true to false Review of last two lectures > Defined
COT 6936: Topics in Algorithms! Giri Narasimhan. ECS 254A / EC 2443; Phone: x3748
 COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 4 Graphs Definitions Traversals Adam Smith 9/8/10 Exercise How can you simulate an array with two unbounded stacks and a small amount of memory? (Hint: think of a
Algorithm Design and Analysis LECTURE 4 Graphs Definitions Traversals Adam Smith 9/8/10 Exercise How can you simulate an array with two unbounded stacks and a small amount of memory? (Hint: think of a
Network Flow. By: Daniel Pham, Anthony Huber, Shaazan Wirani
 Network Flow By: Daniel Pham, Anthony Huber, Shaazan Wirani Questions 1. What is a network flow? 2. What is the Big O notation of the Ford-Fulkerson method? 3. How to test if the Hungarian algorithm is
Network Flow By: Daniel Pham, Anthony Huber, Shaazan Wirani Questions 1. What is a network flow? 2. What is the Big O notation of the Ford-Fulkerson method? 3. How to test if the Hungarian algorithm is
UNDIRECTED GRAPHS TODAY BBM ALGORITHMS DEPT. OF COMPUTER ENGINEERING. Undirected graphs. Graph applications
 BBM - ALGORIHMS ODAY DEP. O COMPUER ENGINEERING UNDIRECED GRAPHS Undirected Graphs Graph API Depth-first search Challenges Acknowledgement: he course slides are adapted from the slides prepared by R. Sedgewick
BBM - ALGORIHMS ODAY DEP. O COMPUER ENGINEERING UNDIRECED GRAPHS Undirected Graphs Graph API Depth-first search Challenges Acknowledgement: he course slides are adapted from the slides prepared by R. Sedgewick
Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem
 Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem Uncapacitated Networks: Basic primal and dual solutions Flow conservation constraints
Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem Uncapacitated Networks: Basic primal and dual solutions Flow conservation constraints
CSE 421 Applications of DFS(?) Topological sort
 CSE 421 Applications of DFS(?) Topological sort Yin Tat Lee 1 Precedence Constraints In a directed graph, an edge (i, j) means task i must occur before task j. Applications Course prerequisite: course
CSE 421 Applications of DFS(?) Topological sort Yin Tat Lee 1 Precedence Constraints In a directed graph, an edge (i, j) means task i must occur before task j. Applications Course prerequisite: course
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 5 Exploring graphs Adam Smith 9/5/2008 A. Smith; based on slides by E. Demaine, C. Leiserson, S. Raskhodnikova, K. Wayne Puzzles Suppose an undirected graph G is connected.
Algorithm Design and Analysis LECTURE 5 Exploring graphs Adam Smith 9/5/2008 A. Smith; based on slides by E. Demaine, C. Leiserson, S. Raskhodnikova, K. Wayne Puzzles Suppose an undirected graph G is connected.
Cuts, Connectivity, and Flow
 Cuts, Connectivity, and Flow Vertex Cut and Connectivity A separating set or vertex cut of a graph G is a set S V(G) such that G S G S has more than one component A graph G is k-connected if every vertex
Cuts, Connectivity, and Flow Vertex Cut and Connectivity A separating set or vertex cut of a graph G is a set S V(G) such that G S G S has more than one component A graph G is k-connected if every vertex
COMP4128 Programming Challenges
 Network Networks Network COMP4128 Programming Challenges School of Computer Science and Engineering UNSW Australia Table of Contents 2 Network 1 Networks Networks 2 3 4 5 6 networks 3 Network Networks
Network Networks Network COMP4128 Programming Challenges School of Computer Science and Engineering UNSW Australia Table of Contents 2 Network 1 Networks Networks 2 3 4 5 6 networks 3 Network Networks
Minimum Cost Edge Disjoint Paths
 Minimum Cost Edge Disjoint Paths Theodor Mader 15.4.2008 1 Introduction Finding paths in networks and graphs constitutes an area of theoretical computer science which has been highly researched during
Minimum Cost Edge Disjoint Paths Theodor Mader 15.4.2008 1 Introduction Finding paths in networks and graphs constitutes an area of theoretical computer science which has been highly researched during
CSC 8301 Design & Analysis of Algorithms: Linear Programming
 CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
Today. Maximum flow. Maximum flow. Problem
 5 Maximum Flow (slides 1 4) Today Maximum flow Algorithms and Networks 2008 Maximum flow problem Applications Briefly: Ford-Fulkerson; min cut max flow theorem Preflow push algorithm Lift to front algorithm
5 Maximum Flow (slides 1 4) Today Maximum flow Algorithms and Networks 2008 Maximum flow problem Applications Briefly: Ford-Fulkerson; min cut max flow theorem Preflow push algorithm Lift to front algorithm
Algorithms: Lecture 10. Chalmers University of Technology
 Algorithms: Lecture 10 Chalmers University of Technology Today s Topics Basic Definitions Path, Cycle, Tree, Connectivity, etc. Graph Traversal Depth First Search Breadth First Search Testing Bipartatiness
Algorithms: Lecture 10 Chalmers University of Technology Today s Topics Basic Definitions Path, Cycle, Tree, Connectivity, etc. Graph Traversal Depth First Search Breadth First Search Testing Bipartatiness
Solving problems on graph algorithms
 Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
and 6.855J March 6, Maximum Flows 2
 5.08 and.855j March, 00 Maximum Flows Network Reliability Communication Network What is the maximum number of arc disjoint paths from s to t? How can we determine this number? Theorem. Let G = (N,A) be
5.08 and.855j March, 00 Maximum Flows Network Reliability Communication Network What is the maximum number of arc disjoint paths from s to t? How can we determine this number? Theorem. Let G = (N,A) be
g(s, w) g(w, s) (in gross model).
 1 Maximum Flow 1.1 Definitions Tarjan: Data Structures and Network Algorithms Ford and Fulkerson, Flows in Networks, 1962 (paper 1956) Ahuja, Magnanti, Orlin Network Flows. Problem: do min-cost. Problem:
1 Maximum Flow 1.1 Definitions Tarjan: Data Structures and Network Algorithms Ford and Fulkerson, Flows in Networks, 1962 (paper 1956) Ahuja, Magnanti, Orlin Network Flows. Problem: do min-cost. Problem:
Directed Graph and Binary Trees
 and Dr. Nahid Sultana December 19, 2012 and Degrees Paths and Directed graphs are graphs in which the edges are one-way. This type of graphs are frequently more useful in various dynamic systems such as
and Dr. Nahid Sultana December 19, 2012 and Degrees Paths and Directed graphs are graphs in which the edges are one-way. This type of graphs are frequently more useful in various dynamic systems such as
Matching Theory. Figure 1: Is this graph bipartite?
 Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
Basic Graph Search. Algorithms and Data Structures, Fall Rasmus Pagh. Based on slides by Kevin Wayne, Princeton
 Algorithms and Data Structures, Fall Basic Graph Search Rasmus Pagh Based on slides by Kevin Wayne, Princeton Algorithms, th Edition Robert Sedgewick and Kevin Wayne Copyright Mid-term evaluation Thanks
Algorithms and Data Structures, Fall Basic Graph Search Rasmus Pagh Based on slides by Kevin Wayne, Princeton Algorithms, th Edition Robert Sedgewick and Kevin Wayne Copyright Mid-term evaluation Thanks
Combinatorial Search. permutations backtracking counting subsets paths in a graph. Overview
 Overview Exhaustive search. Iterate through all elements of a search space. Combinatorial Search Backtracking. Systematic method for examining feasible solutions to a problem, by systematically eliminating
Overview Exhaustive search. Iterate through all elements of a search space. Combinatorial Search Backtracking. Systematic method for examining feasible solutions to a problem, by systematically eliminating
PERFECT MATCHING THE CENTRALIZED DEPLOYMENT MOBILE SENSORS THE PROBLEM SECOND PART: WIRELESS NETWORKS 2.B. SENSOR NETWORKS OF MOBILE SENSORS
 SECOND PART: WIRELESS NETWORKS 2.B. SENSOR NETWORKS THE CENTRALIZED DEPLOYMENT OF MOBILE SENSORS I.E. THE MINIMUM WEIGHT PERFECT MATCHING 1 2 ON BIPARTITE GRAPHS Prof. Tiziana Calamoneri Network Algorithms
SECOND PART: WIRELESS NETWORKS 2.B. SENSOR NETWORKS THE CENTRALIZED DEPLOYMENT OF MOBILE SENSORS I.E. THE MINIMUM WEIGHT PERFECT MATCHING 1 2 ON BIPARTITE GRAPHS Prof. Tiziana Calamoneri Network Algorithms
PERFECT MATCHING THE CENTRALIZED DEPLOYMENT MOBILE SENSORS THE PROBLEM SECOND PART: WIRELESS NETWORKS 2.B. SENSOR NETWORKS OF MOBILE SENSORS
 SECOND PART: WIRELESS NETWORKS.B. SENSOR NETWORKS THE CENTRALIZED DEPLOYMENT OF MOBILE SENSORS I.E. THE MINIMUM WEIGHT PERFECT MATCHING ON BIPARTITE GRAPHS Prof. Tiziana Calamoneri Network Algorithms A.y.
SECOND PART: WIRELESS NETWORKS.B. SENSOR NETWORKS THE CENTRALIZED DEPLOYMENT OF MOBILE SENSORS I.E. THE MINIMUM WEIGHT PERFECT MATCHING ON BIPARTITE GRAPHS Prof. Tiziana Calamoneri Network Algorithms A.y.
4.2 Directed Graphs. vertex of outdegree 3 and indegree 1 digraph API digraph search topological sort strong components. directed path from 0 to 2
 Directed graphs. Directed Graphs Digraph. Set of vertices connected pairwise by directed edges. vertex of outdegree and indegree 1 digraph API digraph search topological sort strong components directed
Directed graphs. Directed Graphs Digraph. Set of vertices connected pairwise by directed edges. vertex of outdegree and indegree 1 digraph API digraph search topological sort strong components directed
Maximum flows & Maximum Matchings
 Chapter 9 Maximum flows & Maximum Matchings This chapter analyzes flows and matchings. We will define flows and maximum flows and present an algorithm that solves the maximum flow problem. Then matchings
Chapter 9 Maximum flows & Maximum Matchings This chapter analyzes flows and matchings. We will define flows and maximum flows and present an algorithm that solves the maximum flow problem. Then matchings
Algorithms. Algorithms 4.2 DIRECTED GRAPHS. introduction digraph API digraph search topological sort strong components ROBERT SEDGEWICK KEVIN WAYNE
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
Algorithms. Algorithms 4.2 DIRECTED GRAPHS. introduction digraph API digraph search topological sort strong components ROBERT SEDGEWICK KEVIN WAYNE
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
Algorithms. Algorithms 4.2 DIRECTED GRAPHS. introduction digraph API digraph search topological sort strong components ROBERT SEDGEWICK KEVIN WAYNE
 Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
Algorithms ROBERT SEDGEWICK KEVIN WAYNE 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N ROBERT SEDGEWICK KEVIN WAYNE introduction digraph API digraph search topological sort strong components
GRAPHS Lecture 19 CS2110 Spring 2013
 GRAPHS Lecture 19 CS2110 Spring 2013 Announcements 2 Prelim 2: Two and a half weeks from now Tuesday, April16, 7:30-9pm, Statler Exam conflicts? We need to hear about them and can arrange a makeup It would
GRAPHS Lecture 19 CS2110 Spring 2013 Announcements 2 Prelim 2: Two and a half weeks from now Tuesday, April16, 7:30-9pm, Statler Exam conflicts? We need to hear about them and can arrange a makeup It would
Graph Algorithms. Chapter 22. CPTR 430 Algorithms Graph Algorithms 1
 Graph Algorithms Chapter 22 CPTR 430 Algorithms Graph Algorithms Why Study Graph Algorithms? Mathematical graphs seem to be relatively specialized and abstract Why spend so much time and effort on algorithms
Graph Algorithms Chapter 22 CPTR 430 Algorithms Graph Algorithms Why Study Graph Algorithms? Mathematical graphs seem to be relatively specialized and abstract Why spend so much time and effort on algorithms
Algorithms 4.2 DIRECTED GRAPHS. digraph API digraph search topological sort strong components
 4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N digraph API digraph search topological sort strong components R O B E R T S E D G E W I C K K E V I N W A Y N E Algorithms, 4 Robert Sedgewick and
4.2 DIRECTED GRAPHS Algorithms F O U R T H E D I T I O N digraph API digraph search topological sort strong components R O B E R T S E D G E W I C K K E V I N W A Y N E Algorithms, 4 Robert Sedgewick and
CS 361 Data Structures & Algs Lecture 13. Prof. Tom Hayes University of New Mexico
 CS 361 Data Structures & Algs Lecture 13 Prof. Tom Hayes University of New Mexico 10-5-2010 1 Last Time Spanning Trees BFS DFS Testing Bipartiteness 2 Today Inside BFS Running Time Implementation Degrees
CS 361 Data Structures & Algs Lecture 13 Prof. Tom Hayes University of New Mexico 10-5-2010 1 Last Time Spanning Trees BFS DFS Testing Bipartiteness 2 Today Inside BFS Running Time Implementation Degrees
arxiv: v2 [cs.ds] 14 Sep 2010
![arxiv: v2 [cs.ds] 14 Sep 2010 arxiv: v2 [cs.ds] 14 Sep 2010](/thumbs/94/120844286.jpg) Multiple-source single-sink maximum flow in directed planar graphs in O(n 1.5 log n) time arxiv:1008.5332v2 [cs.ds] 14 Sep 2010 Philip N. Klein and Shay Mozes Brown University October 28, 2018 Abstract
Multiple-source single-sink maximum flow in directed planar graphs in O(n 1.5 log n) time arxiv:1008.5332v2 [cs.ds] 14 Sep 2010 Philip N. Klein and Shay Mozes Brown University October 28, 2018 Abstract
Minimum Spanning Tree (undirected graph)
 1 Minimum Spanning Tree (undirected graph) 2 Path tree vs. spanning tree We have constructed trees in graphs for shortest path to anywhere else (from vertex is the root) Minimum spanning trees instead
1 Minimum Spanning Tree (undirected graph) 2 Path tree vs. spanning tree We have constructed trees in graphs for shortest path to anywhere else (from vertex is the root) Minimum spanning trees instead
Graphs and Network Flows IE411. Lecture 13. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
Network Flows. 1. Flows deal with network models where edges have capacity constraints. 2. Shortest paths deal with edge costs.
 Network Flows. Flows deal with network models where edges have capacity constraints. 2. Shortest paths deal with edge costs. 4 u v 2 5 s 6 5 t 4 x 2 y 3 3. Network flow formulation: A network G = (V, E).
Network Flows. Flows deal with network models where edges have capacity constraints. 2. Shortest paths deal with edge costs. 4 u v 2 5 s 6 5 t 4 x 2 y 3 3. Network flow formulation: A network G = (V, E).
COS 226 Algorithms and Data Structures Spring Second Written Exam
 COS 226 Algorithms and Data Structures Spring 2018 Second Written Exam This exam has 7 questions (including question 0) worth a total of 80 points. You have 80 minutes. This exam is preprocessed by a computer,
COS 226 Algorithms and Data Structures Spring 2018 Second Written Exam This exam has 7 questions (including question 0) worth a total of 80 points. You have 80 minutes. This exam is preprocessed by a computer,
Problem Set 7 Solutions
 Design and Analysis of Algorithms March 0, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 7 Solutions Problem Set 7 Solutions
Design and Analysis of Algorithms March 0, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 7 Solutions Problem Set 7 Solutions
