Efficient Fourier transformation of unstructured meshes and application to MRI simulation. Alejandro Martinez
|
|
|
- Lilian Cummings
- 5 years ago
- Views:
Transcription
1 Efficient Fourier transformation of unstructured meshes and application to MRI simulation by Alejandro Martinez A thesis submitted in conformity with the requirements for the degree of Master of Mechanical Engineering Graduate Department of Mechanical and Industrial Engineering University of Toronto Copyright c 2014 by Alejandro Martinez
2 Abstract Efficient Fourier transformation of unstructured meshes and application to MRI simulation Alejandro Martinez Master of Mechanical Engineering Graduate Department of Mechanical and Industrial Engineering University of Toronto 2014 This thesis demonstrates different ways to compute the MRI signal in finite element magnetic resonance imaging or FE-MRI. For linear elements the MRI signal can be found analytically. The error metric for linear elements to calculate the signal with a fixed error in k-space using an adaptive Gaussian quadrature is derived using finite element function derivatives and is then extended for use in quadratic elements. The feasibility of using the numerical steepest descent (NSD) method, which is designed to compute oscillatory integrals like the MRI signal equation, was also studied. The method was found to compute the MRI signal faster than adaptive Gauss quadrature for quadratic surface elements using typical MRI imaging parameters. The feasibility of NSD is discussed for volumetric quadratic elements and for different mesh geometries. ii
3 Dedication For my love, Helena Violet Kelly, with gratitude for your love and support iii
4 Acknowledgements I would like to thank prof. Steinman. and prof. Huybrechs and the other members of the examination committee prof. Nachman and prof. Mandelis for their support and discussions. I would also like to thank my family for all their love and support. iv
5 Contents 1 Introduction Motivation Introduction to MRI theory and simulation Signal generation Slice selection Spatial encoding Signal acquisition and reconstruction Image resolution Image artefacts Literature review Analytic solutions Simulators using magnetization maps Simulators using T 1, T 2 and proton density maps Finite element based simulators Bloch equation simulators MRI acquisition within the FE-MRI library Research objectives Adaptive Gauss quadrature for FE-MRI elements Introduction v
6 2.2 Gauss quadrature to compute oscillatory integrals Computing oscillatory integrals in higher dimensions Error estimation for tri3 elements Error estimation for tri6 elements Error estimation for tet4 elements Error estimation for tet10 elements Algorithm details and implementation Introduction FE-MRI software architecture K-space acquisition algorithm Cycles per element quadrature table Calculation of quadrature rules Slice profile simulation for volumetric meshes Additions and improvements to current FE-MRI functions Results and discussion Introduction Validation of optimal algorithm for tri3 elements Validation of optimal algorithm for tri6 elements Validation of optimal algorithm for tet4 elements Validation of optimal algorithm for tet10 elements Computation time comparison between linear and quadratic surface discretizations Simulation of MRI acquisition of a carotid artery Feasibility of NSD for faster signal calculation Introduction Approximate evaluation of oscillatory integrals vi
7 5.1.2 Adaptive quadrature Filon method Levin method Numerical steepest descent Experiment using NSD for quadratic surface elements NSD decomposition for quadratic surface elements Algorithm details Results and discussion Conclusions Summary of work Future directions A Generation of Gauss quadratures 77 A.1 Introduction A.2 The Golub-Welsch algorithm A.3 Sample C++ quadrature code B Mesh generation with same discretization error 88 B.1 Introduction B.2 Discretization error when using quadratic elements B.3 Discretization error when using linear elements B.4 MATLAB implementation C Implementation of NSD algorithm 97 C.1 Introduction C.2 G 1 decomposition C.3 Steepest descent paths for G C.4 Steepest descent paths for F vii
8 Bibliography 108 viii
9 List of Tables 1.1 Values used for fig Finite element types used in this thesis K-space error error maps and histograms for all the element types implemented. Notice that the x-axis for the histograms in in terms of n, where error = 10 n Test meshes for each element type and their simulated MRI images. For the meshes with quadratic elements one of the elements is selected to show the blue edges shown are between element nodes and do not delineate a quadratic element Total computation times in seconds and time ratios for different k-space extents for an error threshold of Total computation times in seconds and time ratios for different k-space extents for an error threshold of A.1 Fejer quadrature points and weighs ix
10 List of Figures 1.1 Measured (top) and simulated (bottom) magnetization and T 2 maps of an artery wall Transformation of a plane wave in local coordinates in the standard triangle to the unit square tri3 domain s and vertices in global and local coordinate systems with a given K space vector The plane formed by the gradient of g with respect to ξ 1 and the location of its possible maximum absolute values in domain s. In this case the maximum absolute value of the gradient is at ξ 1 = ξ 2 = Flowchart of the main FE-MRI algorithm K-space error as a function of k-space location for a tet4 unit cube with a quadrature order of Number of k-space points as a function of n where error = 10 n for a tet4 unit cube with a quadrature order of Mesh of segmented artery (a) and its MRI reconstruction (b) K-space computation time maps in milliseconds for different adaptive algorithms and error thresholds. The time ratios between the algorithms is also shown x
11 B.1 Discretization of a circle using quadratic curve segments. The quantity to be minimized is proportional to the area between the lines B.2 Discretization of a circle using line segments. The quantity to be minimized is proportional to the area between the lines xi
12 Chapter 1 Introduction 1.1 Motivation MRI simulators are primarily used to determine the origin of acquisition errors and to design and optimize new pulse sequences. For example in [1], an MRI simulator is used to design and optimize a MRI pulse sequence for the characterization of artherosclerotic plaque. They are also used for education and training [2]. The motivation of this thesis is to design an adaptive Gauss quadrature to evaluate the MRI signal equation for unstructured meshes and to design and test an algorithm using numerical steepest descent (NSD) [3], [4], [5], [6]. Using NSD one can compute the Fourier transform of a mesh faster than other approaches like numeric quadrature [7]. The algorithm was tested using parameters needed for simulating an MRI acquisition. These results are then used to implement and improve upon new functions in the FE-MRI library [7] which can be used to simulate MRI acquisition. 1.2 Introduction to MRI theory and simulation In this section, an introduction to magnetic resonance imaging (MRI) will be given with emphasis on signal acquisition, its Fourier transform approximation (k-space) and image 1
13 Chapter 1. Introduction 2 artefacts. The introduction will have an emphasis on imaging and reconstruction methods that are based on the Fourier transform and for 2D imaging. This introduction will also aidthe reader in understanding how in some cases anmri acquisition of anobject can be simulated by the Fourier transform and inversion of a set of points or elements weighted by the actual material properties of said element such as in the FE-MRI library. The MRI acquisition process can be separated into the following steps: 1. Signal generation: generating a net magnetization in an object 2. Slice selection: selectively exciting a plane with a given thickness if a 2D acquisition is desired 3. Spacial encoding: spatially encoding the signal in that plane 4. Signal acquisition and reconstruction: acquiring a radio frequency signal and reconstructing the image These steps will be described in detail in the subsequent subsections. This introduction is based on the following sources: [8], [9], [10]. An overview is given next. MRI works by aligning nuclei in an object along their spin axes more in one direction than another. This spin is a magnetic and quantum effect but it can be described in the same way as a spinning top. This is done by a very strong fixed magnetic field B 0. Then another moving magnetic field that is perpendicular to the fixed field called B 1 tips the spins and they precess around the original fixed field. The amount of tipping depends on how long the B 1 field is applied. The speed of precession is dependant on the strength of B 0. The B 1 field can be chosen in a way that allows for selective excitation of a slice perpendicular to the z axis. Another smaller fixed gradient field G x (i.e B = B 0 +G x x) is superimposed on B 0 to cause a gradient in the total fixed field. The precessing spins emit radio waves that can be picked up by a coil. The signal s frequency and magnitude are related to the spatial location of the spins along the x axis and the amount of spins
14 Chapter 1. Introduction 3 in that given location. Hence an image of the spin distributions can be reconstructed by taking the inverse Fourier transform of the signal. To obtain a 2D distribution of spins, the locations along the y-axis can be encoded by using a gradient field G y applied before the measurement is taking place, so that the phase of each spin depends on the location along the y-axis. The readout coils which do the measurement can measure the phase, magnitude and frequency of the signal which means the 2D distribution of spins in a slice can be determined Signal generation The coordinate axes that will be used in this and subsequent sections are only used for convenience and consistency with MRI literature. Some nuclei in living things, like in hydrogen atoms ( 1 H), can have nuclear spin angular momentum. These types of nuclei will be referred to as spins. The most common spin used for MRI is 1 H since it is a component of water and the human body is mostly water. Spins can be described as small bar magnets oriented randomly in a given material. When the spins are exposed to a static magnetic field, some spins will align with the magnetic field and others align in the opposite direction to it and in both orientations they will rotate around the z axis with an angular frequency given by the Larmor equation: ω = γb 0 (1.1) Where γ is the gyromagnetic ratio which for a particle is the ratio between its magnetic dipole moment and its angular momentum. For 1 H, γ/2π = MHz/T [10]. A group of spins in an object with the same γ value are commonly referred to as isochromats. B 0 is the applied magnetic field referred to as the static field and it points in the positive z-axis. Slightly more spins will align in the same direction as B 0 because a spin is more
15 Chapter 1. Introduction 4 likely to take the lower energy state than a higher energy state. The net magnetization is simply the spins oriented towards the positive z-axis minus the ones oriented towards the negative z-axis and it is given by the following equation: M 0 z = M = γ2 2 B 0 N s 4KT s (1.2) Where is Plank s constant divided by 2π, N s is the number of spins, K is Boltzmann constant and T s is absolute temperature of the spins. The derivation of equation 1.2 is similar to the one used in [11] to determine the properties of a simple paramagnetic solid. More information is given in [10] and [11]. Equation 1.2 only applies to so called spin-1/2 systems like 1 H isochromats. The spins also can be made to rotate with other magnetic fields with respect to any line in the x-y plane but only by discrete angles; it is a quantum mechanical effect. However since the net magnetization is a sum of billions of spins in the whole object, the angle of rotation for the magnetization can be assumed to be continuous and a classical description analogous to a precessing spinning top can be used. After applying the static field, the net magnetization will point in the same direction. The equation that describes the time-dependent behaviour of M in the presence of an applied magnetic field is called the Bloch equation and it is given by: d M dt = γ M B M xî M yĵ T 2 M zî M 0ˆk T 1 (1.3) Where B is the total applied magnetic field, M x z are the components of M and T1 and T 2 are the longitudinal and transverse relaxation times respectively. The range of values for the relaxation times for 1 H are T 1 [100,1500] ms and T 1 [100,1500] ms [10]. Let us introduce a transverse magnetic field that oscillates at the Larmor frequency:
16 Chapter 1. Introduction 5 B 1 (t) = 2B1 e (t)cos(ωt+ϕ)î (1.4) Where B1(t) e is called an envelope function that for example can have a value of B 1 from time 0 to some time τ p and 0 otherwise. τ p is simply the amount of time the B 1 field is applied. It is also referred to as the pulse width. It will be shown later in this Section that the useful factor is only the integral of B1 e(t) from 0 to τ p and not its shape. The value ϕ is an initial phase angle. This longitudinal magnetic field can be decomposed into fields rotating in opposite directions about the z-axis. One of the terms rotates in the opposite direction as the processing spins and has a negligible effect. Therefore the effective field that needs to be considered is: B 1 (t) = B1 e (t)[cos(ωt+ϕ)î sin(ωt+ϕ)ĵ] (1.5) The magnetization vector 1.5 can be transformed into a vector in the Larmor-rotating frame with the following coordinate transformations: î cos(ωt)î sin(ωt)ĵ ĵ sin(ωt)î+cos(ωt)ĵ ˆk ˆk (1.6) Using the transformation 1.6, the magnetic field 1.5 becomes: B 1,rot (t) = B e 1 (t)î (1.7)
17 Chapter 1. Introduction 6 Whichisexpectedsincethevector i + j isspinningaroundthez-axisinthesamedirection and angular speed as the original B 1 (t) vector. If the pulse width is small compared to both relaxation times, the effect of B 1 (t) on the magnetization M is described by the first term of the Bloch equation. As will be shown below, it is also advantageous to transform that term into the Larmor-rotating frame. The transformed Bloch equation for a short exitation using the transformation 1.6 is: M rot t = γ M rot B eff (1.8) Where B eff = B rot + ω/γ is referred to as the effective magnetic field. Since the total rotating field is B 0 k + B e 1 (t)î, the motion of the bulk magnetization vector will be described by: M t = γ M rot B e 1(t) i (1.9) Notice that equation 1.9 will be equal to zero(i.e the bulk magnetization does not precess) if the only field present is the original B 0 k magnetization. The solution to equation 1.9 up to the pulse width time τ p with the initial condition M(0) = M 0 z is the following: M x (t) = 0 (1.10) M y (t) = Mz 0 sin(α) (1.11) M z (t) = Mz 0 cos(α) (1.12)
18 Chapter 1. Introduction 7 Where α is referred to as the flip angle and its given by: α = t 0 γb1 e (u)du (1.13) If the envelope function is rectangular then α = γb 1 t. So in this case the bulk magnetization tips away from the z axis about x or precesses (since its tipping but also rotating about z in the laboratory frame) at an angular velocity of γb 1. Also notice that as long as the area under B 1 (t) is the same, the bulk magnetization will tip to the same final angle Slice selection Since the envelope function B1(t) e can have any shape and still produce the desired tip angleaslong asitsareaisconstant, it canbeused toselectively excite aslice oftheobject being imaged. For simplicity we will assume the slice is perpendicular to the z axis. If we apply a gradient to the B 0 field as a function of the z component of location while the spins are being tipped, their positions will be spatially encoded by their resonant frequencies with the following frequency selection function; 1, f f c < f p(f) = 0, otherwise (1.14) Where: f c = f 0 + γ 2π G zz 0 (1.15)
19 Chapter 1. Introduction 8 f = γ 2π G z z (1.16) To obtain the time signal needed to produce the corresponding frequency spectrum, the Fourier transform can be applied on equation 1.14: B 1 (t) p(f)e 2πift dt = fsinc(π ft)e 2πifct (1.17) From equation 1.18, we get the envelope function: B1 e (t) = Asinc(π ft) (1.18) Where the constant A depends on the desired spin tip angle. This pulse is not possible to apply in practice so it is truncated from time 0 to some time τ p, with the center of the sinc function at τ p / Spatial encoding One can use the static field B 0 to encode spatial information in the final MRI signal. A simple way of achieving this is with a constant gradient field such as: ω(x) = ω 0 +γg x x (1.19) So now the field B 0 pointing along the z-axis changes magnitude along x. After tipping the spins uniformly along a slice in the z-axis to 90 for example, this gradient can be used to spatially encode a signal using both phase and frequency. This is needed because
20 Chapter 1. Introduction 9 the image signal in 2D acquisition is: s(t) = m(x,y)e iγ(gxx+gyy)t dxdy (1.20) Which is the Fourier transform of the object s magnetization, m(x, y), on the particular slice being imaged: M(k x,k y ) = m(x,y)e 2πi(kxx+kyy) dxdy (1.21) Where the Fourier coordinates for general G gradients are given by: k x = γ 2π t 0 G x (u) du (1.22) k y = γ 2π t 0 G y (u) du (1.23) In the MRI literature Fourier space is referred to as k-space. Phase encoding can be achieved as follows: first tip all spins 90 in the same direction using the B 1 (t) field discussed in Section 1.2.1, then apply a gradient field which happens along a line in the x-y plane (the magnetic field is still pointing in the z-axis) for a small time T pe which stands for phase encoding time. After T pe seconds, the spins will have a phase proportional to their location. For example if the G gradient that happens along the y-axis and is constant then the phase of the signal as a function of y is: φ(y) = γg y yt pe (1.24)
21 Chapter 1. Introduction 10 If the signal is acquired right after T pe for a very short time interval, we would obtain the sum of the magnetizations for each line that contains the same phase. However, if we apply yet another gradient field such as G x while recording the signal every t seconds, we will also obtain the magnetization along those lines as a function of the frequency, i.e the spatial information along the line has been frequency encoded. This procedure is referred to as a pulse sequence. The sequence described above is referred to as spin-wrap imaging and it is one of the most commonly used sequences because it results in equally spaced points in k-space on a grid which can be easily transformed into an image using the fast Fourier transform Signal acquisition and reconstruction Equation 1.20 for the MRI signal is obtained from radio waves given off by the object being imaged which are measured by coils in the MRI machine. The signal from the coils is then converted to a digital signal and its phase and frequency components are determined. If the signal is sampled in k-space at uniform intervals such as in spin-warp imaging, the signal can be obtained applying the inverse discrete Fourier transform of the discrete version of the signal equation. This method can take O(N 2 ) operations. The same transform can be performed in O(Nlog 2 N) operations using the fast Fourier transform or FFT. FFT is the reconstruction method most likely used in MRI equipment. Other transforms are available for k-space acquisition that is sampled radially such as the Radon transform. For more information refer to [9] Image resolution When the MRI signal is being acquired, k-space is recorded at discrete time intervals. Using equations 1.23 and 1.22 the k-space spacing is:
22 Chapter 1. Introduction 11 k y = γ 2π G yt y (1.25) k x = γ 2π G x,max t (1.26) Because of the Fourier sampling theorem [9], the field of view of the image should be the following: FOV x = 1 K x (1.27) Which also applies for the y and z axes. The spatial resolution of the image in the x axis is the field of view divided by the number of readout samples: x = FOV x N read = 1 k x N read (1.28) While the spatial resolution in the y axis is the field of view divided by the number of phase encoding steps: y = FOV y N pe = 1 k y N pe (1.29) Notice the above relations apply only to spin-warp imaging. They do not apply to other pulse sequences that sample k-space non-uniformly.
23 Chapter 1. Introduction Image artefacts Image artefacts arise in MRI acquisition either due to insufficient or inaccurate data or both. The motivation of this thesis is to provide a tool to simulate MRI such that the cause of image errors can be understood and also to design and test protocols such as the resolution and how it affects the measurement accuracy of some anatomic feature similar to [12] for example. With this in mind, the following image errors are described together with their causes and how they can be simulated in general or in the FE-MRI library. Gibbs or truncation artefact The Gibbs or truncation artefact is seen as spurious ringing around sharp discontinuities in the reconstructed image. If the image is a smooth function, the inverse transform of the signal equation uniformly converges to the true image when the number of samples N for a given FOV. However if the function is discontinuous, the inverse transform will have ringing with an overshoot and an undershoot of about 9% of the difference at the discontinuity. Surprisingly the overshoot and undershoot percent value is constant regardless of N. However the period of the ringing will decrease with higher N values. If the signal was not truncated to a finite number of N samples then the ringing period would be zero and the exact image would be reconstructed hence the name truncation artefact. This artefact can be made to appear on any simulated MRI acquisition simply by using a low enough number of N samples. Aliasing Aliasing happens when k-space is under-sampled. The artefact is a wraparound of the image in the direction that is being under-sampled. This can be clearly understood by the relationship between the true image function and its Fourier series reconstruction [9]:
24 Chapter 1. Introduction 13 Î = n= I ( x n ) x k x (1.30) Where the term 1/ k x = FOV x. This error can be readily be simulated by simply using an FOV value that is smaller than the object size along the same direction. This error can be eliminated simply by choosing an FOV value larger than the object being imaged. Chemical shift artefacts Chemical shift artefacts happen when an object with different isochromats is being imaged. Different isochromats will have a different γ value. Since spatial position is frequency encoded in the readout direction when an MRI signal is being obtained, signals coming from two different isochromats in the same location such as water and fat will end up in different locations along the frequency encode signal. The artefact will look like a region of the object such as fat which is not being explicitly imaged will be shifted compared to the rest of the image features. The frequency shift due to the different isochromat is given by [9]: ω c = γδb 0 (1.31) The frequency bandwidth of a pixel in k-space is: ω x = γg x (1.32) Since the pixel bandwidth is proportional to the pixel length, the spatial displacement in units of a pixel is:
25 Chapter 1. Introduction 14 δ x = ω c ω x = δb 0 G x (1.33) And the spatial shift will be: x c = δ x x = δb 0 G (1.34) Therefore an effective way to reduce the chemical shift is to use a strong readout gradient. In practise this will also reduce the signal to noise ratio of the acquired signal. Therefore an optimal value for G has to be determined. This error can be simulated simply by obtaining the k-space or each isochromat separately and then adding the signal. Motion artefacts A type of very obvious motion artefact that happens when the whole object being scanned is in motion is called ghosting. It can be clearly identified by copies of the object being imaged along the direction of motion and with a lower contrast than the actual image. This error happens when the object moves along the phase-encoding direction. For example, assuming the object moves at a constant speed v x along the x-direction and there is a constant phase encoding gradient G x applied for some time interval τ starting from time t n, the phase shift is the following: φ = γ tn+τ t n G n (x+v x t) dt = γg n xτ +γg n v x τ(t n +τ/2) = 2πk n x+2πk n v x (t n +τ/2) (1.35)
26 Chapter 1. Introduction 15 So the motion induced phase shift is: φ m = 2πk n v x t n +2πk n v x τ/2 (1.36) Since the time τ is much smaller than the total acquisition time up to that point, the second term of equation 1.36 can in most cases be omitted. Equation 1.36 without the second term can be obtained directly by applying the Fourier shift theorem to the MRI signal equation. For constant v x, G x and a negligible τ, the signal equation is: s m (k,t) = e 2πiknvxt s(k,t) (1.37) Equation 1.37 has the same phase shift as the one given in equation To simulate this error, either equation 1.37 can be applied directly to the simulated k-space map for a constant speed v x or the object can be translated a certain distance based on v x in the x direction and then its corresponding k-space points calculated to simulate the error. A further discussion on other types of motion artefacts is given in [9]. Flow artefacts Flow artefacts are caused by the motion of fluids such as blood in the living tissue being imaged. The main feature of these errors is a loss or gain of signal intensity where the flow is taking place like inside an artery [13]. The only simulation method that has been used successfully for these types of error is to either measure the flow directly using other imaging methods or to simulate the flow using computational fluid dynamics (CFD). Then a certain number of streamlines are extracted from the flow field. Afterwards the individual effect of spins moving along the streamlines is computed to obtain an MRI
27 Chapter 1. Introduction 16 signal. References [13] and [14] use this method of simulation. Since a set of discrete spins are used to simulate a continuum fluid are used, the number of spins needed and the related computation time is high. 1.3 Literature review The different MRI simulation methods can be grouped into the following types: 1. Analytic solutions 2. Simulators using magnetization maps 3. Simulators using T 1, T 2 and proton density maps 4. Finite element simulators 5. Bloch equation simulators The order on the list is based on increasing physical accuracy of the models in most cases at the expense of computation time. Except for some Bloch equation simulators, the other types use the Fourier transform of a pre-described signal therefore they technically are not simulators in the sense that they are not simulating a full MRI machine. A full simulation would require modelling both the object using the Bloch equation and the MRI components such as the coils and the B 0 magnet. However the methods described below will be referred to as simulations since they do still crudely simulate the object and parts of the MRI machine. Each type is described in the following sections.
28 Chapter 1. Introduction Analytic solutions In some situations, an analytic solution for k-space can be found. The author co-authored a paper, [12], where MRI acquisition of an artery was performed to determine how the total arterial wall thickness obtained from the segmentation of the MRI image depends on the T 2 values of the arterial layers (intima, media and adventitia) and T E. To test if this is due to a partial volume effect (a low resolution) or because of the different T 2 values of each layer, an analytic k-space was constructed for each of the 4 acquired images by adding the k-spaces of 4 concentric circles. Then the obtained images were segmented. The values used are given in the following table: Layer r o (mm) p TE=17ms p TE=34ms p TE=51ms p TE=68ms arterial blood intima media adventitia background N/A Table 1.1: Values used for fig. 1.1 Wherer o andpintable1.1standstheouterradiusfortheimageintensity. Theimage intensity is in arbitrary units; the actual value depends on the specific MRI scanner. The thickness changes as a function of T E closely match the experimental results. T E is called the echo time and is simply the time where the spins are allowed to relax after a RF filed is applied. Then a mono-exponential fit was performed (p = e T E/T 2, where p is the image intensity at a pixel) on the 4 simulated images to get a T 2 map; it also closely matches the T 2 map obtained from the actual MRI images. For the mono-exponential fit, if a pixel had p values lower than on all the 4 images, it was not taken into consideration and was given an arbitrary value of 0. The measured and simulated magnetization and T 2 maps are shown in Figure 1.1. The magnetization image shown has a magnetization normalized to 1. This image weighted with different magnetization values based on the echo time and the T 2 decay are
29 Chapter 1. Introduction Image y axis (mm) Image y axis (mm) T2 (ms) Image x axis (mm) Image x axis (mm) Figure 1.1: Measured (top) and simulated (bottom) magnetization and T 2 maps of an artery wall used in the paper. To obtain the k-space, corresponding to a simplified artery, 4 circle k- spaces were added, this can be done since the Fourier transform is a linear transform [9]. If the artery is long compared to its radius, a 2D Fourier transform can be used instead of the Fourier transform for a cylinder. If image and k-space coordinates are changed to cylindrical coordinates: r = ( x) 2 +( y) 2, θ = tan 1 ( x/ y), k r = kx 2 +k2 y and φ = tan 1 (k x /k y ). Therefore: K x x+k y y = k r r(cosφcosθ+sinφsinθ) = k r rcos(θ φ) (1.38)
30 Chapter 1. Introduction 19 Then the Fourier transform of a circle with unit radius and height is given in cylindrical coordinates as follows: F circlesimple (k r ) = 1 0 [ 2π ] r e 2πikrrcos(θ φ) dθ dr (1.39) 0 The integral can be simplified in cylindrical coordinates since the function for a cycle is circularly symmetric. The solution of equation 1.39 is given in terms of the first order Bessel function of the first kind J 1 [9] and its the following: F circlesimple (k r ) = J 1(2πk r ) k r (1.40) In the case of k r = 0, a Taylor series can be taken of equation 1.40 about k r = 0, and simplified to yield: F circlesimple (0) = π (1.41) Applying the scaling and linearity properties of the Fourier transform [9] to equations 1.40 and 1.41 yield the following equations for an arbitrary image intensity (h) and radius (r): F circle (k r ) = hr J 1(2πrk r ) k r (1.42) F circle (0) = hr 2 π (1.43)
31 Chapter 1. Introduction 20 This k-space is implemented in the FE-MRI library as a python script. An example of its use in Unix is given below: femri2dcylinderkspace -fov fovcenter matrix mvalue 1.0 -slicethickness 0.0 -radius 3.0 -center pipe femrikspacetoimage -dimensionality 2 -ofile circleimage.vti Both in the magnetization maps derived from measurements and the analytic model it was found that the mean wall thickness obtained by segmentation decreases with echo time because ofthesmall T 2 time ofthe adventitia. Therefore a short echo time should be included to properly image it. This layer plays an important role in plaque development [12] Simulators using magnetization maps In [15], artefacts due to relaxation, linear flow and motion after an RF-pulse are added to the k-space of the magnetization also called proton density map. Some limitations of this method are not able to simulate errors due to non-linear gradients and motion during and RF-pulse, since they are considered to be momentary Simulators using T 1, T 2 and proton density maps In[2], the T 1, T 2 and protondensity mapsare Fouriertransformed andchanged according to limited properties of MRI pulse sequences. Although the method is computationally fast and can simulate wraparound and simple motion artefacts accurately, by design it cannot simulate errors related to signal generation. This type of simulation is used in [1] to optimize a MRI pulse sequence for the characterization of atherosclerotic plaque.
32 Chapter 1. Introduction Finite element based simulators Finite element based simulators also use a magnetization map and can include T 1, T 2 maps, however they use the finite element discretization which allows the magnetization to vary continuously within the object. The elements used for this thesis are shown in Table 1.2. The names given in the figure will be used in the rest of the thesis. Both types of simulators have to transform the magnetization map into the Fourier domain. The Fourier transformation is then done in two different ways: discretizing the object into a set of points and then performing an FFT, or discretizing the object into elements with continuous values inside them as stated above and then computing exactly or approximating to a given error the Fourier transform for each element. The total acquired signal using the finite element discretization is the following: S tot ( k) = m [ f m (T 1,T 2,ρ) e ] s e ( k) (1.44) Where m stands for materials with different T 1, T 2, or ρ values, and e stands for all the elements representing the object. The advantage of this method is that if the error incurred by the finite element discretization is low enough, the error between the actual k-space values of the object and the simulated values can be either zero or can be made as low as is required (depending on the allowable computation time) depending on the element type. Also this approach can be faster than Fourier transform simulators if one starts with a mesh of a complex object, ideally an unstructured mesh to minimize antialiasing or stair-step effects, and takes into account the interpolation step to obtain a structured grid. This last operation scales as O(E) where E is the number of finite elements which also scales with the mesh volume [16]. Publications using this approach are [17] and [18]. In [17], the linear elements tri3 and tet4 are integrated analytically. If the magnetization inside a certain region of an object can be assumed to be constant
33 Chapter 1. Introduction 22 Gauss theorem can be used to transform the signal equation into a surface integral [19]: s e ( k) = me 2πi k x d x element = m element = im 2π k k i k x 2π k k e 2πi d x k ˆn(x)e 2πi k x ds (1.45) surface Where ds is an infinitesimal surface area and ˆn(x) is the unit normal pointing outwards from the closed surface. The normal is constant for a given linear element but varies with the global coordinates for quadratic elements. As explained in [19], this method is more efficient than volumetric integration of the signal equation in the following three ways. No volumetric meshing step is needed where volume elements are constructed from the surface mesh. The number of elements over which integration is performed is reduced and scales with the surface area of the shape and not its volume. Also fewer integration points are needed for surface vs. volume elements for the same integration order. The analytic solution for tri3 in [17] can also be adapted to solve equation 1.45 exactly. This method also reduces the storage requirements for the phantom compared to Fourier transform simulation methods that require a structured grid with a resolution greater than the nominal element size of the mesh [19]. The drawback of this method is that one has to decide in how many parts and object should be segmented so that the difference between material properties within each part is kept to a minimum. The advantage of FE-MRI over voxel based methods is that if the imaging resolution approaches the voxel size then stair-step errors will be produced. These error are also referred to as partial volume effects. This does not happen if an unstructured mesh with continuous changes in material properties within each element are used. These property makes this simulation method ideally suited to study how changing MRI imaging
34 Chapter 1. Introduction 23 parameters affect the image quality. With voxel based methods the image quality might show errors that are due to the simulation itself Bloch equation simulators Bloch equation simulators such as [20] and [21] allow for close to all possible computation of errors seen in MRI such as the errors due to static field inhomogeneity. However, the excessive time needed to compute one voxel means that not enough voxels can be used such that there will be voxel discretization artefacts [20]. 1.4 MRI acquisition within the FE-MRI library The volumetric and surface integration steps described in Subsection have been implemented in the FE-MRI library for all the elements in Table 1.2. The main advantage compared to simulators using a structured grid of T 1, T 2 and proton density values is that the interpolation step is not needed if one has an unstructured mesh. If one only has a surface mesh and can assume these values are constant, the Fourier transform of the surface mesh can be computed directly from it as explained in Subsection This is a fair assumption since organs with the same tissue types will have the same isochromats. Also the Fourier transform can be calculated exactly for linear elements such as tri3 and tet4, or with a desired image error for quadratic elements tri6 and tet Research objectives In previous work, [18], an error metric for linear elements was derived and used for an adaptive Gauss quadrature to compute 1.44 and The error metric is an estimate of the error between the calculated and exact signal for a given element and k-space value. The error metric is used to estimate the number of points for an adaptive Gauss
35 Chapter 1. Introduction 24 quadrature that integrates the MRI signal for each element in an unstructured grid. This was implemented by prof. Steinman and Luca Antiga in the FE-MRI library. The contributions of this thesis are as follows: 1. A derivation of the error metric found in [18] using the element s shape functions and k-space values and derivations of error metrics for three more element types including quadratic elements 2. An addition to FE-MRI that can estimate errors of Gauss quadratures in many dimensions from the error obtained in one dimension using a result in [22] and additions to FE-MRI that allow it to compute the MRI signal using the new elements 3. A test to see if the most promising of the methods to compute highly oscillatory integrals (NSD) could be used instead of adaptive Gauss quadrature which is currently used in FE-MRI The next Chapters explain in detail each of the above contributions.
36 Chapter 1. Introduction 25 Element diagram Name Nodes Shorthand Linear triangle 3 tri3 Quadratic triangle 6 tri6 Linear tetrahedron 4 tet4 Quadratic tetrahedron 10 tet10 Table 1.2: Finite element types used in this thesis
37 Chapter 2 Adaptive Gauss quadrature for FE-MRI elements 2.1 Introduction To obtain a signal with a uniform error in k-space, an adaptive Gauss quadrature scheme can be used. Gauss quadrature is a method of numerical integration where the function to be integrated is evaluated at some point called a quadrature point and multiplied by a weight for each point called a quadrature weight. The sum of all these products is an estimate of the integral: 1 1 f(x)w(x) dx = N w i f(x i )+E (2.1) i=1 Where f(x) is the function to be evaluated and w i and x i are the quadrature points and weights. W(x) is another function that has a constant form. A gauss quadrature is a special quadrature for numerical integration that allows the exact integration of f(x) for a given W(x) such as 1 or e x if f(x) is a polynomial of degree 2N 1 or less. If the function is smooth in the sense that it can be approximated by a polynomial (such as a 26
38 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 27 sinusoid), the integration error will be low. Gaussian quadrature can be readily extended for higher dimensions. These quadratures are referred to as product rules. Although these are easily derived from 1D rules, they require more function evaluations than is necessary to integrate over higher dimensional domains. Optimal Gauss weights and point locations exist for linear tetrahedral domains, but are only available for low integration orders and are not easily derived for higher orders. Non-optimal rules use more Gauss points and weights than optimal rules but they are easier to extend to arbitrary integration orders. The parametric representation of finite elements allows them to be integrated in a standard local tetrahedral domain. One can do a coordinate transformation referred to as a Duffy transformation [23] that maps the quadrature points and weights of the quadrature product rule to the same local standard tetrahedral domain. One of the integrals we would like to compute is the MRI signal equation for volumetric finite elements which is the following: s e ( k) = m( x) e 2πi k x d x = element 1 1 ξ1 1 ξ1 ξ J m( ξ ) e 2πi k x d ξ (2.2) The term J is the element s Jacobian which is given by: J = det x ξ 1 x ξ 2 x ξ 3 y ξ 1 y ξ 2 y ξ 3 z ξ 1 z ξ 2 z ξ 3 (2.3) As can be seen from 2.2, the higher the magnitude of the k-space vector, the more
39 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 28 oscillatory the integral is which can only be approximated by a higher order polynomial for a given approximation error. Therefore on average more quadrature points will be needed to compute with a fixed error when the magnitude of the k-space vector is higher. The global coordinates in terms of local coordinates are: x j = n N i ( ξ ) x ij (2.4) i=1 And the magnetization in local coordinates is given by: m( ξ) = n N i ( ξ ) m i (2.5) i=1 The terms N i ( ξ ) are called the element s shape functions and they are polynomials and n is the number of element nodes which are shown in Table 1.2. The term x ij is the j component of node i. So the integral is a 3D polynomial multiplied by a sinusoid. The MRI signal equation for surface elements as derived in Subsection is the following: s e ( k) = im 2π k k = im 2π k k = im 2π k k surface 1 1 ξ ξ1 0 k ˆn(x)e 2πi k x ds 0 J k ˆn(x)e 2πi k x d ξ (2.6) k n(x)e 2πi k x d ξ (2.7) The vector ˆn(x) is the unit normal pointing outwards from the element which is part of a closed surface. The unit normal is given by:
40 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 29 ˆn(x) = n(x) n(x) = x x ξ 1 ξ 2 x x ξ 1 ξ 2 (2.8) The simplification from equation 2.6 to equation 2.7 can be made since the denominator in equation 2.8 is also the element s Jacobian for surface elements. Again the integral is a polynomial multiplied by a sinusoid. By changing variables to change the integration domain to the standard tetrahedron, the same product quadrature rules can be used each time. Each element signal is then weighted with the appropriate material properties and added to get the full MRI signal as shown in equation To find out the number of quadrature points needed for both integrals, an estimate of the error for a given number of quadrature points is needed. Since the integration is carried out in the same standard domain with a fixed size, the error is only related to the maximum local frequency. 2.2 Gauss quadrature to compute oscillatory integrals The maximum local oscillation of a function will determine the minimum distance between quadrature points such that the Nyquist criteria is followed and the equation can be approximated properly in that area. We can then use a Gauss quadrature with enough points to guarantee a given accuracy at that point and the rest of the function since the oscillation everywhere else will be lower. Gauss quadrature also has the advantage of integrating the magnetization term exactly since it is described by a polynomial in finite elements. A way of estimating the maximum local oscillation is as follows: Consider the following 1D function:
41 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 30 y = e ig(x) (2.9) The equation can be approximated at x 0 by taking the Taylor series of g(x) at x 0 and substituting the result back into equation 2.9: y = e ig(x 0) e ig (x 0 )(x x 0 ) e i1 2 g (x 0 )(x x 0 ) 2... (2.10) The term that is non-constant and will usually have the the highest oscillation frequency is e ig (x 0 )(x x 0 ). This term produces a frequency of g (x 0 ). To determine the maximum local frequency of y to perform a numerical integration from a standard domain such as 0 to 1 one should therefore determine the following: max freq = max g (x),x [0,1] (2.11) 2.3 Computing oscillatory integrals in higher dimensions In 2D, if a product rule using Gauss quadrature is used with the same number of points in both coordinates axes to integrate a function in the unit square, the error will be dependant on the maximum local frequency in the unit square in the directions of the coordinate axes. Therefore this value will be given by: ( ) g max freq = max η 1, g η 2,x s (2.12)
42 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 31 Where η 1 and η 2 are the unit square coordinates and s is the boundary of the unit square. 2.4 Error estimation for tri3 elements The integration in local coordinates for triangular elements in the finite element method and FE-MRI is done using a Gauss quadrature product rule for the unit square where the point coordinates are transformed using the Duffy coordinate transform [23] to a unit triangle. This is the same as transforming g in the triangle to the unit square and integrating it with a Gauss quadrature product rule in the unit square. So to find the maximum oscillation in the standard triangle one should find how the maximum absolutevaluesofthegradientsofthefunctiong intheunitsquarerelatetothemaximum absolute values of the gradients of g in the unit triangle. Although there are symmetric quadrature rules for triangles that are optimal in the Gauss-quadrature sense such as [24], their computation requires finding a non-linear least square solution for a system of polynomial equations which in [24] could only be done numerically up to 20 points per dimension due to round-off error. Also the estimation of the quadrature error is very non-trivial [25]. For a survey of different cubature (quadrature rules for 2 and higher dimensions) formulas over triangles refer to [25]. To find these relationship lets look more closely at what happens to a plane wave (produced by the MRI signal equation with a given k-space vector for example) in local coordinates in the standard triangle when it is transformed to the standard square. Such a transformation is shown in Figure 2.1. In this case the gradient of g from the plane wave is constant in local coordinates along both coordinate axes. This gradient is also proportional to the number of cycles in the direction of each coordinate axes. The number of cycles is also proportional to the
43 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements ξ2 0.5 η ξ η 1 Figure 2.1: Transformation of a plane wave in local coordinates in the standard triangle to the unit square number of red crests or blue troughs for a given length along a given direction. We can see that the magnitude of the gradient along η 1 remains the same as the gradient along ξ 1 in the unit square at ξ 2 = 0 and decreases to 0 when ξ 2 increases to 1. We can also see that the magnitude of the gradient along η 2 appears to remain the same as the gradient along ξ 2 in the unit square at ξ 1 = 0. However in this case when ξ 1 increases from 0 to 1, the gradient decreases to 0 and increases again to what appears to be the gradient along the edge from (0,1) to (0,1) of the standard triangle. These observations can be made precise as follows. Based on the derivation in [23] for the standard square with ( 1, 1) bounds, the Duffy coordinate transform between the standard triangle and square used in FE-MRI is the following: ξ 1 = η 1 (1 η 2 ) (2.13) ξ 2 = η 2 (2.14)
44 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 33 Using the chain rule for a multi-varied function we can relate the gradients of g in the unit square to the ones in the unit triangle as follows: g η 1 = g ξ 1 ξ 1 η 1 + g ξ 2 ξ 2 η 1 = g ξ 1 (1 η 2 ) (2.15) g η 2 = g ξ 1 ξ 1 η 2 + g ξ 2 ξ 2 η 2 = g ξ 2 g ξ 1 η 1 (2.16) The maximum absolute value of equation 2.15 will happen when η 2 is 0 and the maximum absolute value of equation 2.16 will happen when η 1 is 0 is either 0 or 1. When η 1 = 0 the gradient is along the same direction as the side from (0,1) to (1,0) in the standard triangle. In the MRI signal equation g is k x x + k y y or K x. In finite element analysis, for triangular linear elements in 2D, the global coordinates are related to local coordinates in the following way: x = n N i x i, y = i=1 n N i y i (2.17) i=1 Where n is number of points in the element x i,y i are the global coordinates of point i and N i are the element s shape functions. For the tri3 element they are given by: N 1 = ξ 1, N 2 = ξ 2, N 3 = 1 ξ 1 ξ 2 (2.18)
45 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 34 Using the element s shape functions the maximum oscillation in the ξ 1 and ξ 2 directions can be determined by: g x y = k x +k y = K e 31 (2.19) ξ 1 ξ 1 ξ 1 g ξ 2 = k x x ξ 2 +k y y ξ 2 = K e 32 (2.20) Where e ij is a vector from element vertices i to j in global coordinates. Using the above two results yields: g g = K e 32 K e 31 = K e 12 (2.21) ξ 2 ξ 1 Note that these values are constant in local coordinates since the partial derivatives of the shape functions for linear finite elements are constant, therefore checking their maximum value in domain s is not necessary. These are the same error metrics used in [18]. In [18] the error metric is arrived at by observing that it should be invariant with respect to element size and shape and the k-space vector. These results can be interpreted as the dot product of the k space vector in local coordinates with each of the standard triangle side vectors expressed in terms of ξ 1 and ξ 2 which give the oscillation frequency per unit length in the local coordinate axes. The domain s in global and local coordinates is given in Figure 2.2. Since the k space vector in global coordinates is the following:
46 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 35 y (0,1) x (0,0) (1,0) Figure 2.2: tri3 domain s and vertices in global and local coordinate systems with a given K space vector K = k x = k y g x g y (2.22) The k space vector in local coordinates is given by: K l = g ξ 1 g ξ 2 = x ξ 1 x ξ 2 y ξ 1 y ξ 2 g x g y = JK (2.23) Where J is the element s Jacobian. Using the above result, the maximum oscillation estimates can be written as follows: g ξ 1 = K l (1,0) = K l ˆξ 1 (2.24) g ξ 2 = K l (0,1) = K l ˆξ 2 (2.25) g ξ 2 g ξ 1 = K l ( 1,1) = K l (ˆξ 2 ˆξ 1 ) (2.26)
47 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 36 Where ˆξ 1, ˆξ 2 and ˆξ 2 ˆξ 1 are the standard triangle side vectors. For the tri3 surface element the same results hold, except that the element sides e ij and the k-space vector are in three dimensions. In this case the local k-space vector in the still 2D local domain is a projection of the original k-space vector. 2.5 Error estimation for tri6 elements For quadratic elements equation 2.12 still applies, however the values of the gradients of g with respect to ξ 1 and ξ 2 in local coordinates will vary linearly with ξ 1 and ξ 2. The boundary s in local coordinates for tri6 is the same as the one for the tri3 element. Since the gradient of g for a given local coordinate g (ξ 1,ξ 2 ) is a plane in the space formed by ξ 2 and ξ 2 and the possible values of g (ξ 1,ξ 2 ), therefore the maximum absolute value of g (ξ 2,ξ 2 ) will be at one of the vertices of the standard triangular boundary. Therefore equation 2.12 will have to be computed 3 times for each gradient for a total of 3 x 3 = 9 gradients. A plane formed by the gradient of g in one of the 3 coordinates and the possible maximum absolute values are shown in Figure 2.3. The number of gradients that need to be computed is the number of gradients times the number of element vertices which is 9. The computation time will be lower if the gradients with respect to ξ 1 and ξ 2 are computed first and then the results are used to compute the gradient given by equation 2.16 with ξ 1 = 1. These gradients can be computed even faster by storing and reusing some of the intermediate results. The needed computations for the tri6 element are as follows. The
48 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 37 Figure 2.3: The plane formed by the gradient of g with respect to ξ 1 and the location of its possible maximum absolute values in domain s. In this case the maximum absolute value of the gradient is at ξ 1 = ξ 2 = 0 element s shape functions are as follows: N 1 = ζ(2ζ 1) N 2 = ξ(2ξ 1) N 3 = η(2η 1) N 4 = 4ξζ N 5 = 4ξη N 6 = 4ηζ (2.27) For the gradient in the ξ 1 direction:
49 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 38 g x y = k x +k y (2.28) ξ 1 ξ 1 ξ 1 = k x 6 = K i=1 [ x y N i ξ 1 x i +k y 6 i=1 N i ξ 1 y i (2.29) ] N ξ 1 (2.30) Where K is a 1 by 2 matrix, [x y] T is a 2 by 6 matrix with the element s node coordinates and N/ ξ 1 is a 6 by 1 matrix. The same result applies for the gradient in the ξ 2 direction. The matrices N/ ξ 1 and N/ ξ 2 can be precomputed for all elements by evaluating them at the local domain vertices (0,0),(1,0),(0,1). Half of the entries in these matrices are 0 therefore it is more useful to calculate the product [x y] T N/ ξ 1 directly. 2.6 Error estimation for tet4 elements For linear tetrahedral elements, to estimate the quadrature error, one has to estimate the maximum oscillation frequency in the standard cube given by equation ( ) g max freq = max η 1, g η 2, g η 3,x s (2.31) Where η 1 3 are the unit cube coordinates and s is the boundary of the unit cube. The Duffy transformation for the unit cube, again based on the derivation in [23] for the standard cube with ( 1, 1) bounds is the following:
50 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 39 ξ 1 = η 1 (1 η 3 )[1 η 2 (1 η 3 )] (2.32) ξ 2 = η 2 (1 η 3 ) (2.33) ξ 3 = η 3 (2.34) The derivation can be understood as using the 2D transformation recursively in two of the coordinate axes to collapse the standard cube into the standard tetrahedron. Using equations 2.32, 2.33 and 2.34, the gradients of g with respect to the standard cube coordinates are the following: g η 1 = g ξ 1 (1 η 3 )[1 η 2 (1 η 3 )] (2.35) g η 2 = g ξ 1 η 1 (1 η 3 ) 2 + g ξ 2 (1 η 3 ) (2.36) g η 3 = g ξ 1 η 1 [2η 2 (1 η 3 ) 1] g ξ 2 η 2 + g ξ 3 (2.37) Since the values of ξ 1 3 can only vary from 0 to 1, the maximum absolute value of the following gradients will determine the maximum oscillation frequency of g: g ξ 1, g ξ 2, g ξ 3 (2.38) g ξ 2 g ξ 1, g g, ξ 3 ξ 2 g ξ 3 g ξ 1 (2.39)
51 Chapter 2. Adaptive Gauss quadrature for FE-MRI elements 40 g g g, ξ 3 ξ 2 ξ 1 g g + g (2.40) ξ 3 ξ 2 ξ 1 The gradients shown in 2.38 and 2.39 are gradients along all the side edges of the standard tetrahedron as shown in the 2D case for the triangle. However the gradients shown in 2.40 which are derived from equation 2.37 are not related to any side of the standard tetrahedron, and would not have been taken into account in the maximum frequency calculation if extended the results for 2D elements (that the gradients along all the element side edges determine the maximum oscillation frequency) directly to 3D elements. 2.7 Error estimation for tet10 elements For quadratic tetrahedral elements equation 2.31 still applies, however their values will vary linearly on ξ 1 3 like in the tri6 element. The boundary s for tet10 is the same as the one for the tet4 element. To estimate the maximum frequency gradients 2.38, 2.39 and 2.40 should be calculated at the standard tetrahedron vertices. The gradient calculations can be performed faster if all the components of the gradients are computed before hand and then used for gradients 2.39 and Also the values of some of the intermediate steps can be stored and reused like in the case of the tri6 element.
52 Chapter 3 Algorithm details and implementation 3.1 Introduction The FE-MRI algorithm simulates either a 2D or 3D MRI signal acquisition. If a 2D signal is required the program computes a given number of k-space planes depending on the slice thickness and the needed resolution. If not the program computes a given k-space volume. If using an acquisition with a fixed number of quadrature points, the program computes the needed Gauss quadrature and uses that quadrature for all elements and k-space values. If the adaptive quadrature is used, the program computes all the Gauss quadratures requested, then it computes the ones needed for all the element/kspace point combinations and uses the appropriate ones in order to keep the k-space image error constant. If more quadrature points are needed in some elements the user is warned. Then the user can either use the result knowing some points at the edge of k-space might have a slightly higher image error or he/she can run the function again with more quadrature points. This is a useful feature if the computation time even using the adaptive algorithm with all the needed quadratures is prohibitive. 41
53 Chapter 3. Algorithm details and implementation FE-MRI software architecture TheFE-MRIlibraryisimplemented asasetofpythonfunctionsthatcanbeusedthrough a command line interface by typing a script in Linux or Unix. An example of a script that can be typed in the Unix command line after installing the FE-MRI library is given below: femritrisurfmeshkspace -ifile modifiedquadsphere.vtu -dimensionality 2 -fov fovcenter matrix useoptimal 1 -error qorder 59 -sliceprofile quadratic -slicethickness 6 --pipe femrikspacezeropadding -padding pipe femrikspacetoimage --pipe vmtkimageviewer The above script reads an unstructured mesh of a sphere-like closed surface composed of tri6 elements. Then a 2D acquisition is performed with a field-of-view of 30, a 32 by 32 k-space matrix and a quadratic slice profile in k-space. This is done using the optimal algorithmwhichcanuseagaussquadratureuptoorder59orpointsperdimension. Then the k-space is zero-padded and transformed back into an image which is displayed on the screen. Since the size of the shape is 40 by 40 by 40 units, the resulting image displays an aliasing error. In FE-MRI information from one function can be used into the next needed function without writing files by using the pipe command. Some of the python functions call C++ functions to perform the needed computations. Both languages are used together so the user is able to both use fast and efficient C++ functions while being able to easily customize either the script or the python functions. The C++ functions can also be modified if needed however it is usually harder to modify that a python script. Both the python and C++ functions use data structures and visualization functions from the visualization toolkit or VTK 1 and the vascular modelling toolkit or VMTK 2 1 Visualization toolkit website: 2 Vascular modelling toolkit website:
54 Chapter 3. Algorithm details and implementation 43 libraries. The mesh used in the example script above is in VTK s.vtu format. The FE-MRI acquisition algorithm and its related C++ functions are shown in Figure 3.1. The algorithm shown in Figure 3.1 is implemented in the vtkfemritetvolnumerickspacegenerator C++ class for meshes composed of tet4 and tet10 elements. The algorithm can use a mesh with both elements present. The same is the case for a surface mesh when it is used by its C++ class vtkfemritrisurfnumerickspacegenerator, it can contain both tri3 and tri6 elements. The class contains a set of data structures such as the k-space and functions that operate on them. This class is used to declare an object (an instance of a class) that then can call other objects declared using the classes vtkfemrivoltetquadratureordercalculator and vtkfemrigaussarbquadrature which compute a list of the cycles per element as described in Chapter 2 and their corresponding number of quadrature points to obtain a desired image error and the needed quadratures respectively. 3.3 K-space acquisition algorithm The k-space signal acquisition in the flowchart in Figure 3.1 is done using Algorithm 1. The k-space acquisition algorithm shown in Algorithm 1 starts by calculating the maximum cycles/element from all the k-space point and element combinations. This is done using a design table generated for a user specified error. The design table used for the optimal algorithm is a table that contains all the number of quadrature rules required and its corresponding cycles per element for a given error. Then it computes and stores all quadratures from orders 1 to the order needed for the maximum cycles/element to get the required error if the optimal algorithm will be used. The quadratures are calculated by the vtkfemrigaussarbquadrature C++ class. Then the algorithm loops through all the k-space values needed and all the elements in the mesh and uses the given Gauss quadrature to compute the MRI signal. One thing to take into account in the algorithm
55 Chapter 3. Algorithm details and implementation 44 Start Read mesh and MRI acquisition parameters Dimensionality? 3D 2D Find location and boundary of slices Set slice magnetization profile k-space aquisition Yes More slices? No, or 3D acquisition Output k-space file and/or send data to next python function Stop Figure 3.1: Flowchart of the main FE-MRI algorithm
56 Chapter 3. Algorithm details and implementation 45 is to make sure the magnetization and the Jacobian are being evaluated exactly. If the optimal algorithm is used, for k-space vectors with a low magnitude the number of quadrature points needed will be lower than the ones needed to compute the polynomial composed of the Jacobian multiplied by the magnetization. This is because even if the sinusoidal term is close to a straight line at low magnitudes of the k-space vector, needing only an order of 1 for example, one still wants enough quadrature order to compute the quadrature of the polynomial composed of the Jacobian multiplied by the magnetization. Algorithm 1 K-space acquisition algorithm if optimal algorithm then make design table relating cycles/element to quadrature order at desired image error compute Gauss quadratures from order 1 to specified order end if for each needed k-space location k do set S(k) = 0 for each element e do if optimal algorithm then calculate cycles/element from k and e set Gauss quadrature to get desired error for calculated cycles/element using design table else set to user-defined Gauss quadrature end if if order of Gauss quadrature < order of magnetization and Jacobian then set Gauss quadrature to same order as magnetization and Jacobian end if obtain Gauss points p obtain corresponding Gauss weights w set s(k) = 0 for each p do evaluate s(k) = s(k)+w m(p) exp(k,p) end for evaluate S(k) = S(k)+f(T 1,T 2,ρ) s(k) end for end for
57 Chapter 3. Algorithm details and implementation Cycles per element quadrature table The algorithm to find the design table is shown in Algorithm 2. Algorithm 2 Design table algorithm compute max cycles/element (max cpe) for all k-space points and elements for 1 to max number of quadrature points specified, n do set point list, pointlist(n) = n set start cpe to 0, cpe = 0 set error to 0 while error < error threshold do add cpe interval to cpe, cpe = cpe+dcpe get exact integral, I e (cpe) obtain Gauss points p obtain corresponding Gauss weights w set I c = 0 for each p do evaluate I c = I c +w exp(cpe,p) end for evaluate error = mag(i e ) mag(i c ) dim(e) end while set cpe list, cpelist(n) = cpe end for if max cpe > cpelist(max n) then display warning end if The algorithm is carried out in the vtkfemriquadratureordercalculator C++ class. The algorithm first calculates the maximum cycles/element from the mesh and the MRI acquisition parameters. Then it loops over all the quadratures from 1 to a number specified by the user, storing each number in pointlist. Within that loop it cycles thought increasing cycle/element values, until the error is above the user defined value. Then the cycles/element are stored in the corresponding entry in cpelist. The integral being computed is akin to a 1D MRI signal equation: I = 1 0 e 2πik (3.1)
58 Chapter 3. Algorithm details and implementation 47 Where k is the cycles/element. The exact solution of its magnitude is: mag(i e ) = 1 2 2cos(2πk) (3.2) 2πk The error is defined as follows: E = mag(i e ) mag(i c ) dim(e) (3.3) Where I c is an approximation of equation 3.1 calculated using Gauss quadrature and dim(e) is the dimensionality of the elements that the mesh is composed of. Note that the algorithm could have looped over the cycles/element first. However this could have caused some integrals computed with the quadrature rule to have a lower error simply because they are not being sampled properly by the points; the Nyquist criteria is not followed with that loop ordering. With the current loop ordering the oscillatory integral gets more oscillatory while the number of quadrature points is kept the same, making sure that once the error is larger than the threshold there were also enough points to sample the function. The only difference between the algorithm when computing it for 2D or 3D elements is that the 1D error is multiplied by 2 and 3 respectively. This is because the error of a product rule if using the same number of quadrature points in all dimensions can be estimated to first order as the error in one dimension times the number of dimensions of the product rule [22]. So the algorithm finds the error in one dimension and multiplies it by the number of dimensions to get an error estimate for the product rule which is then used to evaluate the element signal s(k) in Algorithm 1.
59 Chapter 3. Algorithm details and implementation Calculation of quadrature rules The quadrature rules are computed for the design table and the k-space acquisition calculations done in the C++ classes vtkfemrivoltetquadratureordercalculator and vtkfemritrisurfnumerickspacegenerator. Both classes make an object which is an instance of the class vtkfemriquadratureordercalculator. The class can produce Gauss-Laguerre and Gauss-Jacobi quadratures. The class also computes all the product rules needed by all the classes. These quadratures have different weighting functions W(x) as shown in equation 2.1. This allows one to make a product rule that integrates the Jacobian from the Duffy transformation exactly. Therefore the only error comes from the transformed coordinates in the oscillatory term. That is why the derived error metrics in Chapter 2 only take into account that term. The details of how the quadratures are computed are given in Appendix A. The author has added a simpler design table calculation, all the error metrics in Chapter 2 and a new class that can compute an arbitrary number of quadrature points and weights for the relevant Gauss quadratures. 3.6 Slice profile simulation for volumetric meshes A method to simulate an arbitrary slice profile could be to adaptively subdivide the elements inside the slice to linearly approximate the slice. This is referred to in the finite element literature as h-refinement. Another approach is to use a higher polynomial order for the elements inside the slice to adaptively get a more accurate simulation. This method is referred to as p-refinement. While those methods will give an accurate solution, they are computationally expensive. A more practical method that does not require modifying the mesh or the elements is to weigh the s(k) signal in Algorithm 1 after it is evaluated with a quadrature point, by using the location of the quadrature point and the required slice profile. For example, if one requires a quadratic slice profile along the z-direction, the weighting based on the location of the quadrature point within
60 Chapter 3. Algorithm details and implementation 49 the slice is the following: m = 1 4 t 2(p z z 0 ) 2 (3.4) Where m is the weighting, t is the slice thickness, z 0 is the slice origin location and p z is the z-component of the quadrature point. Everywhere else the weighting is 0. An ideal slice profile is simulated simply by making the weighting 1 within the slice and 0 otherwise. Notice this method does not compromise the accuracy of the result given by the quadrature since the weighting convoluted with the magnetization distribution forms a new function that the quadrature is integrating. The ideal, quadratic and a trapezoidal slice simulation was already implemented in the C++ class vtkfemritetvol- NumericKSpaceGenerator of the FE-MRI library. 3.7 Additions and improvements to current FE-MRI functions The new error metrics in Chapter 2 have been implemented as C++ functions in the FE- MRI library. The code has been improved by removing the normalization and Jacobian calculation step for surface elements which are the same value for a given quadrature point and cancel each other. The algorithm to find the design table shown in Algorithm 2 was rewritten using dynamically allocated C++ arrays instead of vtk arrays to make its execution faster and to aid in readability. Also instead of having a lookup table for the quadrature weights up to a certain number of points, the user can specify how many points can be used. The points are calculated from first principles once and stored at the beginning of the calculation. The details of the quadrature point and weights calculation can be found in Appendix A. If the program needs more points to calculate a certain
61 Chapter 3. Algorithm details and implementation 50 k-space point there is a warning shown that recommends using more points and running the function again. If not the program uses the maximum number of points available. The memory to store the points is dynamically allocated and the points are stored in a contiguous memory block for faster access. This is done in C++ as follows: inline double** newquadraturematrix(int numps) { double *matrix = new double[numps*(numps+1)*(2*numps+1)/6]; double **m = new double *[numps]; for(int i = 0; i < numps; i++) { m[i] = &matrix[i*(i+1)*(2*i+1)/6]; } return m; } The above function returns an array of pointers in m to the memory block named matrix, which contains all the points from 1 to numps. The actual number of points is the sum of the square of the the 1 to numps series since we are storing Gauss quadrature product rules which in this case are for 2D surface elements. The series needed and its result is shown below: n x=1 x 2 = n(n+1)(2n+1) 6 (3.5) This type of sum can be found using finite calculus [26]. Also the computation time has been cut in close to half by computing only half of k-space using the property [9]: s e ( k) = s e (k) (3.6)
62 Chapter 3. Algorithm details and implementation 51 Where s e (k) isthe complex conjugate ofthe original MRIsignal. Equation 3.6 applies for the Fourier transform of a real signal. However in actual MRI acquisition this constraint cannot be exploited because of object motion and magnetic field inhomogeneities [9]. In the case of a simulated signal object motion can be added later to the simulated signal by adding a motion dependent phase to the computed k-space for example.
63 Chapter 4 Results and discussion 4.1 Introduction This chapter shows the k-space error maps and error histograms for meshes with each of the element types discussed in this thesis. This is done to confirm the efficacy of the algorithms in Chapter 3. Also the MRI acquisition of an anatomically realistic carotid artery was simulated to show the potential uses of the surface FE-MRI algorithm. The desired error threshold for all elements tested was Validation of optimal algorithm for tri3 elements To validate the optimal algorithm for tri3 elements first the k-space error map and a histogram of the errors found in Table 4.1 for the adaptive algorithm were computed for a deformed unit cube. The deformed cube mesh and its simulated MRI image is shown in Table 4.2. The histogram shows a sharp peak at an error of A sharp peak is expected since the oscillation due to the k-space value is constant within each element. The lower value for the error might be due to the error estimate for product rules given in [22] being a conservative estimate. The shape was chosen because it was easy to generate in the Paraview program starting with a meshed cube. Paraview is 52
64 Chapter 4. Results and discussion 53 based on VTK and can produce files that can be read by the FE-MRI library. Then the shape was made asymmetric by moving the nodes. This was done to highlight any possible errors in the algorithm which might not be evident by imaging a symmetric object. The imaging parameters are as follows: FOV = 2.5 x 2.5, image size = 32 x 32 pixels. The magnetization value is 1 throughout. The exact image was computed using the exact algorithm available for surface linear elements in FE-MRI. As an example, the exact k-space using the analytic solution for the tri3 element was obtained by typing the following line in Unix: vmtkmeshtosurface -ifile cubesurf.vtu --pipe vmtksurfacenormals -cellnormals 1 --pipe femrinumericsurfacekspace -useexact 1 -dimensionality 2 -fov fovcenter matrix okspacefile exactkspace.vti Notice that the python function also requires the outward normals. The adaptive algorithm for tri3 elements was obtained using the following line: femritrisurfmeshkspace -ifile cubesurf.vtu -dimensionality 2 -fov fovcenter matrix useoptimal 1 -qorder 59 -error okspacefile voltetkspace.vti
65 Chapter 4. Results and discussion 54 Element type K-space error map Histogram 0 1 tri3 y kspace location log10(abs(kspaceerror)) Fraction of k space points x kspace location Absolute error 0 1 tri6 y kspace location log10(abs(kspaceerror)) Fraction of k space points x kspace location Absolute error 0 1 tet4 y kspace location log10(abs(kspaceerror)) Fraction of k space points x kspace location Absolute error 0 1 tet10 y kspace location log10(abs(kspaceerror)) Fraction of k space points x kspace location Absolute error Table 4.1: K-space error error maps and histograms for all the element types implemented. Notice that the x-axis for the histograms in in terms of n, where error = 10 n
66 Chapter 4. Results and discussion 55 Element type Test mesh MRI image of test mesh tri3 tri6 tet4 tet10 Table 4.2: Test meshes for each element type and their simulated MRI images. For the meshes with quadratic elements one of the elements is selected to show the blue edges shown are between element nodes and do not delineate a quadratic element
67 Chapter 4. Results and discussion Validation of optimal algorithm for tri6 elements To validate the optimal algorithm for tri6 elements as with the tri3 element, first the k-space error map and a histogram of the errors found in Table 4.1 for the adaptive algorithm were computed for a deformed sphere mesh. The histogram shows a peak at an error of 10 4 and also at an error of This can be explained by the oscillation due to the k-space value calculated using the error metric. This value is the maximum one within an element, therefore other parts of the element might have a lower oscillation and the signal in that region will be computed with more quadrature points than is needed to get the desired error threshold. The deformed sphere mesh and its simulated MRI image is shown in Table 4.2. The shape was chosen because it was easy to generate in the Paraview program starting with a meshed sphere. Then the shape was made asymmetric by moving the nodes of two of the elements. This was done to highlight any possible errors in the algorithm which might not be evident by imaging a symmetric object. The imaging parameters are as follows: FOV = 30 x 30, image size = 32 x 32 pixels. The magnetization value is 1 throughout. The exact image was computed by computing the k-space with a quadrature order of Validation of optimal algorithm for tet4 elements To illustrate the increasing error as the k-space vector magnitude increases, which is very noticeable for volumetric elements, first the k-space error map and a histogram of the errors for a tet4 unit cube are computed for the algorithm using the same number of quadrature points in all k-space locations. The unit cube mesh and its simulated MRI image is shown in Table 4.2. The shape chosen is a cube since it has a simple analytic Fourier transform and it can be exactly discretized by linear tetrahedral elements. The imaging parameters are as follows: FOV = 2.5 x 2.5, image size = 32 x 32 pixels. The magnetization value is 1 throughout and the quadrature order used is 14. As expected
68 Chapter 4. Results and discussion 57 the error increases when the k-space vector magnitude is high if the same quadrature order is used for all k-space points as shown in Figure 4.1. As can be seen from the error histogram in Figure 4.2, the number of k-space points with a given error goes up linearly with the logarithm of the error. This can be explained by the fact that the design curves calculated by Algorithm 2 seem to approximate a line at large cycles/element values. Also the number of points in k-space with a given k-space vector magnitude scales linearly with that magnitude. Logarithm of the kspace abs error for mesh of unit cube y kspace location log10(abs(kspaceerror)) x kspace location 14 Figure 4.1: K-space error as a function of k-space location for a tet4 unit cube with a quadrature order of 14 To validate the optimal algorithm for tet4 elements the same mesh was run with the same imaging parameters with the adaptive algorithm. As can be seen from k-space error map in Table 4.1, the error is 10 4 for most of k-space or is lower. Also its histogram in Table 4.1 displays a clear peak at 10 4 error.
69 Chapter 4. Results and discussion Fraction of k space points Absolute error Figure 4.2: Number of k-space points as a function of n where error = 10 n for a tet4 unit cube with a quadrature order of Validation of optimal algorithm for tet10 elements To validate the optimal algorithm for tet10 elements the shape chosen is a cube for the same reasons as with the tet4 element. The cube can also be discretized exactly with tet10 elements. However in this case to test the adaptive algorithm with curved elements the middle nodes of the elements were shifted in the z-direction from 0.5 to 0.7. So although all the elements have a curved side, they still form a cube. The curved sides are all within the cube and the sides which are also edges of the cube are straight. The tet10 cube mesh and its simulated MRI image is shown in Table 4.2. Note that the edges seen in the mesh are between the element nodes and do not delineate an element. This is how Paraview displays quadratic elements. The same mesh was run with the same imaging
70 Chapter 4. Results and discussion 59 parameters as for the tet4 element test with the adaptive algorithm. As can be seen from k-space error map in Table 4.1, the error is 10 2 for most of k-space or is lower. Also its histogram in Table 4.1 displays a peak at an error of 10 3 and also at an erro of This higher spread in the histogram towards lower errors can be explained in the same way as it was explained for tri6 elements Computation time comparison between linear and quadratic surface discretizations So far the errors being calculated are the errors due to integrating the MRI signal equation. However error is also introduced when the original object such as a voxelized shape is discretized using finite elements. To compare both algorithms for linear and quadratic elements a discretization using linear and quadratic elements can be found with the same discretization error and then compute the k-space using the same k-space image error with the given adaptive algorithm and find out how their computation times differ. The discretization error between an object with an arbitrary shape and magnetization and its discretization can be computed as: [ F = mdiscrete ( x) m actual ( x)] 2 (4.1) V If the object has a constant thickness and magnetization, eq. 4.1 can be written to account just for the difference in cross sectional shape: [ F = mdiscrete m actual ] 2 (4.2) A
71 Chapter 4. Results and discussion 60 For a simple shape such as a cylinder, equation 4.2 and its discretization into linear and quadratic finite elements can be computed exactly using cylindrical coordinates: F = 2π 0 [ rdiscrete (θ) r actual (θ) ] 2 (4.3) Where the integral is one dimensional since the shape can be described by a curve in cylindrical coordinates. We would like a discretization that minimizes the area difference between the actual and discretized shapes. The cross sectional area of the cylinder (a circle) can be cut into pie finite elements and a discretization for linear and quadratic elements with the same discretization error can be found. The details of this calculation are given in Appendix B. As an example, for a cylinder with a radius of 1 and discretized into 4 quadratic pie slices such that the discretization error of its cross section is minimum, the number of linear pie slices that produces the same discretization error is 22. This result compares favourably with [27], which graphs the maximum MRI image intensity error for both linear and quadratic pie slices using a large fixed number of quadrature points. This is essentially the same as comparing both discretizations to the original shape being imaged. The number of linear slices needed to get the same error as 4 quadratic slices is 26, which is close to 22 and slightly higher since the slice edges are made to intercept the circle s edges and not chosen to minimize the discretization error, therefore more elements are needed to get the same error. The shape imaged in the paper is also a cylinder with a uniform magnetization. The radius of both cylinders is 0.5 but the number of slices should be the same regardless of the size of the cylinder since the error scales with the cylinder s size.
72 Chapter 4. Results and discussion Simulation of MRI acquisition of a carotid artery A simulation of MRI acquisition and reconstruction of a carotid artery was carried out using the FE-MRI algorithm for tri6 elements. The imaging parameters used were the following: field of view: [ ] and number of sampling points: [ ]. The number of quadratic triangular surface elements is The number of quadrature points per dimension used for all elements is 4. The mesh of the segmented image using vmtk and the simulated MRI reconstruction are shown in Figure 4.3. (a) (b) Figure 4.3: Mesh of segmented artery (a) and its MRI reconstruction (b) The final image was zero padded with [ ] zeros. The reconstructed image shows some pixelation and some ringing artefact.
73 Chapter 5 Feasibility of NSD for faster signal calculation 5.1 Introduction After developing an algorithm in Chapter 2 that uses an adaptive quadrature to evaluate FE-MRI elements, other methods were investigated to calculate the element s k-space value (an oscillatory integral) with less number of quadrature evaluations. There are a family of methods that allow one to calculate an oscillatory integral with a given error with less number of quadrature points if one increases the minimum local oscillation. The method most suitable for FE-MRI elements is numerical steepest descent or NSD. An adaptive algorithm using this method was designed and simulated. Then the results were compared to the algorithm described in Chapter 2 for tri6 elements. The algorithm was tested using parameters needed for simulating an MRI acquisition Approximate evaluation of oscillatory integrals An oscillatory integral has the following form: 62
74 Chapter 5. Feasibility of NSD for faster signal calculation 63 I = b a f(x)e iωg(x) (5.1) In the first section the limitations of Gaussian quadrature are explained. In the subsequent sections the family of methods that, in principle, require less quadrature points for a fixed error as ω is increased are described Adaptive quadrature When either uniform, Simpson s or Gauss quadrature is used, the number of points used depends on the minimum local frequency of oscillatory term within the integration domain due to Nyquist criteria. Gauss quadrature is the most desirable method since it approximates the term f in equation 5.1 exactly and approximates the oscillatory term g with a low error. However the error depends both on Nyquist criteria and how closely a sinusoid function can be approximated by a polynomial. For all the quadrature methods above the number of quadrature points needed will increase with increasing ω for a fixed error Filon method A simple method described in [28] is simply to approximate f(x) in equation 5.1 by a polynomial and simply find the integral by pre-computing the moments: m = b a x m e iωg(x) dx (5.2) This method is very effective when f(x) is a smooth function and the moments can be easily found. Although the method could provide the exact solution for the integrals for the tri6 element, the oscillator g(x) will be different for every element and k-space
75 Chapter 5. Feasibility of NSD for faster signal calculation 64 value. So computing the moments is as hard as the original problem. Also there are no known analytic solutions for all the needed moments if g(x) is a quadratic such as the MRI signal equation for quadratic elements in local coordinates Levin method Another method by Levin described in [29] and [30] is as follows. Suppose f(x) can be expressed as follows: f(x) = iωg (x)p(x)+p (x), a x b (5.3) Then equation 5.1 can be found directly as: I = = b a b a (iωg (x)p(x)+p (x))e iωg(x) d dx (p(x)eiωg(x) )dx = p(b)e iωg(b) p(b)e iωg(a) (5.4) Although the general solution of p(x) has the following general form: p(x) = e iωg(x) [ x a ] f(x)e iωg(t) dt+c (5.5) which is also a highly oscillatory integral, in [29] it is shown that there is a slowly oscillatory solution that can be found by the collocation method without any initial conditions for equation 5.3 [29]. This method was not considered for further investigation since it requires solving a linear system to find the collocation weights in 2D and can
76 Chapter 5. Feasibility of NSD for faster signal calculation 65 only be used for rectangular domains Numerical steepest descent Numerical steepest descent or NSD [5], [4] is a method to evaluate integrals of the same form as 5.1. NSD can be used to evaluate an oscillatory integral by changing the integration boundaries in the complex plane by using a change of variables. This will yield the same integration value because of Cauchy s integral theorem. A good introduction to Cauchy s theorem and its applications can be found in [31]. However now the integral becomes the sum of complex constant terms multiplied by a rapidly decaying non-oscillatory integral that can be evaluated using Gauss quadrature. The quadrature error of the new integrals evaluated with the same number of quadrature points actually decreases with increasing ω. For example, if g(x) = x the integral can be decomposed as follows: b a f(x)e iωx = ie iωa f(a+ip)e ωp dp ie iωb f(b+ip)e ωp dp (5.6) 0 0 Instead of integrating from a to b along the real line, the integration is carried out from a to positive infinity in the direction of the complex axis then to (b, ) and then back to (b,0). The general decomposition is shown below: g(h a (p)) = g(a)+ip p [0, ) h a (0) = a (5.7) 0 f(h a (p))h a (p)eiω(g(a)+ip) dp = e iωg(a) f(h a (p))h a(p)e ωp (5.8) 0
77 Chapter 5. Feasibility of NSD for faster signal calculation 66 Where h a(p) is the partial derivative of h a (p) with respect to p. As shown in the conditions shown in 5.7, the paths in the complex plane have to be chosen such that the equation of the path parametrized by p has to be equal to g(a)+ip when its substituted in the oscillator term g(x). Also the paths have to be equal to the original integration limits when p = 0. The path also has to go through stationary points which are points where g (x) = 0. the method can be used recursively for integration in n dimensions [6]. 5.2 Experiment using NSD for quadratic surface elements Using NSD, a general algorithm to integrate oscillatory integrals in the standard simplex was developed. Then the algorithm was simulated and compared to the one developed in Chapter 2. The simulation was carried out as follows: first calculate the exact integral for every element and k-space point. Then calculate the same integrals using adaptive Gauss quadrature and also record the time needed for each. Do this for a range of numbers of quadrature points. Then calculate the same integrals again with NSD and record the integration time. As with the adaptive Gauss quadrature algorithm, use the same number of quadrature points in all dimensions. Then calculate the exact integration time of the Gauss quadrature algorithm simply by adding all the times for each integral where the error between the calculated and exact value is the desired one. The NSD computation times were used to simulate and calculate the time needed for Algorithm 3 to compute the full k-space signal. Where r time is the time ratio between what it takes to evaluate one quadrature point after carrying out the decomposition for NSD compared to evaluating one point with Gauss quadrature. This value will be greater than 1 since we are evaluating the function
78 Chapter 5. Feasibility of NSD for faster signal calculation 67 Algorithm 3 NSD algorithm if optimal algorithm then make design table for desired image error for Gauss and NSD compute Gauss quadratures from order 1 to specified order end if for each needed k-space location k do set S(k) = 0 for each element e do if optimal algorithm then if num points for Gauss quad > r time num points for NSD then use NSD quadrature else use Gauss quadrature end if end if if order of Gauss quadrature < order of magnetization and Jacobian then set Gauss quadrature to same order as magnetization and Jacobian end if obtain Gauss points p obtain corresponding Gauss weights w set s(k) = 0 for each p do evaluate s(k) = s(k)+w m(p) exp(k,p) end for evaluate S(k) = S(k)+f(T 1,T 2,ρ) s(k) end for end for
79 Chapter 5. Feasibility of NSD for faster signal calculation 68 f(x) (another 2D polynomial) in the complex plane and the decomposition will produce a sum of integrals that will need to be evaluated. Notice that the actual adaptive Gauss quadrature algorithm was not used since it is assumed that it could take a negligible amount of time to estimate the errors for each element and k-space location. By simulating the NSD algorithm the speed of the algorithm compared to the adaptive Gauss algorithm could be determined (and decide if programming the actual NSD algorithm is worth pursuing) without having to derive and program the error estimates for NSD NSD decomposition for quadratic surface elements Using equations 2.17 and 2.27 in the MRI signal equation, the oscillator g(x) in 5.1 will be a 2D quadratic function: g(x,y) = a 1 x 2 +a 2 y 2 +a 3 xy +a 4 x+a 5 y +a 6 (5.9) Where a 1 6 areconstants thatdepend ontheelement geometryandthek-spacevalue. Therefore a suitable NSD decomposition should be found for all possible values of a 1 6 including when some of them are close to 0. The full algorithm will be described in the next section. In this section the different cases on their own and the extension to the 2D standard simplex will be discussed. The first thing to consider is the sign of the oscillator. This will change the direction of the steepest descent paths. For example, if g(x) = x then the decomposition is the following: b a f(x)e iωx = ie iωa f(a ip)e ωp dp+ie iωb f(b ip)e ωp dp (5.10) 0 0 Which is the same as the one shown in equation 5.6 but with the paths going and
80 Chapter 5. Feasibility of NSD for faster signal calculation 69 coming back from negative infinity in the direction of the complex axis. If g(x) is a quadratic, there might be a stationary point within the integration domain. In that case the steepest descent path has to go through it. For example, if g(x) = x 2 then the stationary point is at the origin and the decomposition is: 1 1 f(x)e iωx2 =e iω f(h 1,1 (p))e ωp h 1,1(p)dp f(h 0,1 (p))e ωp h 0,1(p)dp f(h 0,2 (p))e ωp h 0,2(p)dp e iω f(h 1,2 (p))e ωp h 1,2(p)dp (5.11) With the following steepest descent paths: h 1,1 (p) = 1+ip h 0,1 (p) = ip h 0,2 (p) = ip h 1,2 (p) = 1+ip (5.12) Where h a,b (p) is the path starting at a in the direction given by one of the 2 solutions to the quadratic equation obtained by solving g(h a (p)) = g(a)+ip for h a (p). The value b specifies which solution is used. The equation has two solutions that can give a path towards either the positive or negative imaginary axis and it is evaluated at -1,0 or 1 to yield the 4 paths needed to have a closed loop as required by Cauchy s theorem. This example is easily extended to the a general quadratic function. The outer terms of 5.11 can be evaluated using Gauss-Laguerre quadrature with the simple substitution u = ωp. For the inner terms another quadrature has to be used since
81 Chapter 5. Feasibility of NSD for faster signal calculation 70 it has a weak singularity. This can be seen when the third term in 5.11 is written in full: 0 f(h 0,2 (p))e ωp h 0,2 (p)dp = i 2 0 f( ip)e ωp 1 ip dp (5.13) By doing the substitution ωp = u 2, the term becomes: i ω 0 f ( ) i ω u e u2 du (5.14) Which can be integrated using a half-range Gauss-Hermite quadrature. Both of the quadratures discussed can be calculated for any number of points as shown in Appendix A. The method can be used recursively by decomposing the integral with respect to one dimension and then with respect to the next dimension so one is integrating along a manifold of steepest descent [6]. For the standard simplex the integral is the following: S = 1 1 x 0 0 f(x,y)e iωg(x,y) dydx (5.15) If there are no stationary points along y then the integral is equal to: S = 1 0 G(x,0) G(x,1 x)dx (5.16) With: G(x,y) = e iωg(x,y) 0 f(x,v y (x,q)) v y q (x,q)e ωq dq (5.17) And v y (x,q) being the solution to: g(x,v y (x,q)) = g(x,y)+qi. Applying the decom-
82 Chapter 5. Feasibility of NSD for faster signal calculation 71 position again if there are no stationary points along x will yield: S = [F 1 (0,0) F 1 (1,0)] [F 2 (0,0) F 2 (1,1)] (5.18) With: F(x,y) = e iωg(x,y) 0 0 f(u x (p),v y (u x (p),q)) u x(p) p v y (u x (p),q) e ω(q+p) dqdp q (5.19) All the above functions can be evaluated with Gauss product rules composed of Gauss-Laguerre and half-range Gauss-Hermite quadratures. If the oscillation is really low, product rules that are also composed of the standard Gauss-Legendre quadrature were used in the NSD algorithm Algorithm details A naive implementation of an algorithm checking for all the cases outlined in the previous section could be to use symbolic computation in C++ using the CINaC library for example. However the computation time could be prohibitive. Instead the algorithm uses the constants a 1 6 to determine what decompositions need to be made in each dimension and then passes the relevant a constants and calculated values to the next sub function. All the possible combinations are included in the program. The program checks for the full decomposition in each dimension if: the oscillator has a low oscillation on the 0 to 1 interval of the standard simplex (then it uses Gauss-Legendre quadrature), if the oscillator is linear and not quadratic (then the paths in equation 5.6 are used), if the oscillator is quadratic (then use quadratic paths) and if the oscillator has a stationary point within the integration interval if it is quadratic (then the paths in equation 5.11 are used). The
83 Chapter 5. Feasibility of NSD for faster signal calculation 72 program also checks if the path directions should be switched depending on the sign of the a constants. The decompositions are evaluated using functions for each type of path. Each one of the path functions also has an input variable to evaluate it at either of the decided directions in the complex plane. The relevant parts of the code with comments are in Appendix C. 5.3 Results and discussion The results of the simulation applied to the deformed sphere mesh used in Section 4.3 are shown in Figure 5.1. The extent of the mesh is -1 to 1 in all dimensions. The total times taken for both the adaptive Gauss quadrature and NSD for different errors are shown in Tables 5.1 and 5.2. K-space extent (x and y) Algorithm -2 to 2-4 to 4-6 to 6-8 to 8 Gauss quadrature Gauss quadrature with NSD Time ratio Table 5.1: Total computation times in seconds and time ratios for different k-space extents for an error threshold of 10 2 K-space extent (x and y) Algorithm -2 to 2-4 to 4-6 to 6-8 to 8 Gauss quadrature Gauss quadrature with NSD Time ratio Table 5.2: Total computation times in seconds and time ratios for different k-space extents for an error threshold of 10 3 As can be seen from Tables 5.1 and 5.2, the NSD algorithm is faster for higher resolutions and for lower error thresholds. However the difference in speed between both algorithms for physically relevant MRI acquisition simulations is not high. Since typical simulationsliketheoneshownin4.3takelessthanhalfanhoura28%(1 1/1.384 = 0.28)
84 Chapter 5. Feasibility of NSD for faster signal calculation 73 decrease in computation time for a uniform k-space error of 1% is not significant. This can be understood more clearly with the following equation: λ l e = α 2δ l e (5.20) Where λ is the maximum k-space wavelength, l e is a characteristic element size, δ is the resolution and α is a constant close to 1 dependant of the element geometry. The inverse of the value of equation 5.20 is the cycles per element value described in [7]. For MRI simulation the resolution or imaging pixel size will be on the order or greater than the element size therefore the cycles per element value will be low. Therefore although the element signal equation is an oscillatory integral and the examples shown in [6] show NSD to be much more efficient than Gauss quadrature at even low oscillation values, the adaptive Gauss quadrature algorithm described in Chapter 2 is the most appropriate algorithm to compute the element signal equation in FE-MRI. This conclusion also applies for NSD for volumetric elements since the number of terms in the decomposition can be 4 times higher and finding the stationary points in a standard tetrahedron is more difficult than finding them in the standard triangle.
85 Figure 5.1: K-space computation time maps in milliseconds for different adaptive algorithms and error thresholds. The time ratios between the algorithms is also shown Chapter 5. Feasibility of NSD for faster signal calculation 74
86 Chapter 6 Conclusions 6.1 Summary of work In this thesis a derivation of Simedrea s error metric [18] was derived from an estimate of the maximum oscillation frequency produced by the oscillatory term of the MRI signal equation. The metric was then extended to triangular and tetrahedral quadratic elements. The metric was used to design an algorithm to obtain a k-space with a uniform image error for linear and quadratic triangular and tetrahedral elements. The algorithm for both volumetric and surface meshes was implemented in the FE-MRI library. Also changes were made to the algorithms in the library to make them faster and to be able to generate an arbitrary number of quadrature rules. Another algorithm using NSD to calculate a k-space with a uniform error for tri6 elements was simulated and was shown to have a performance increase for normally used MRI acquisition parameters. 6.2 Future directions The maximum frequency estimate found in this thesis could be extended to rectangular and prismatic finite elements. Since the local domain of integration is a square and a cube, the extra gradients that need to be calculated taking into account the Duffy 75
87 Chapter 6. Conclusions 76 transformation are not necessary. The reason error metrics for triangular finite elements were only considered in this thesis is because triangular elements are the preferred element type whensegmenting anmedical imageor performingacfdsimulation oftheflow ofan artery for example. Also segmentation and meshing programs for those types of elements are not as common compared to triangular or tetrahedral element based programs. The surface MRI signal algorithm could also be adopted for a surface composed of Non- Uniform Rational B-Splines or NURBS which is the representation used in CAD models. By using the same surface discretization as the original CAD model, the meshing step to approximate the surface is not needed. NURBS surfaces have already been used in finite element simulations such as in [32], where a scattering problem is simulated using a volumetric mesh with finite elements in the interior of the problem domain and NURBS surface elements on its surface. The use of NURBS surfaces in finite element analysis is also referred to as isogeometric analysis [33]. The finite element approach for MRI simulation could be extended to simulate the signal acquisition process itself, by implementing a Bloch equation solver using finite elements. Also motion artefacts might be simulated more accurately if the motion of the object is represented by finite elements with moving vertices. The NSD algorithm could be a viable alternative to one using an adaptive Gauss quadrature if extended for higher order and volumetric elements or NURBS surfaces, however the number of stationary points that need to be located also increase with element order. The FE-MRI library will be released as open-source software on GitHub 1 so that anyone working on MRI research will be able to use it, add other algorithms to simulate MRI signal acquisition and add algorithms to modify the computed k-space to simulate an acquisition error of interest. 1 GitHub website:
88 Appendix A Generation of Gauss quadratures A.1 Introduction To generate an arbitrary amount of quadrature points and weights in FE-MRI and for NSD, different Gaussian quadratures need to be calculated. Some of them standard and others non-standard. The outline of this appendix is as follows: first all the types of integrals that need quadrature rules are presented, then a general outline for finding the quadrature rules is presented and the C++ code is given that solves integral of type A.7 which is used in some functions of the FE-MRI library. The integrals that need to be integrated are of the following types: 0 f(x)e x2s dx (A.1) f(x)e x2s dx (A.2) 0 f(x)e x2s+1 dx (A.3) f(x)e x2s+1 dx (A.4) 0 f(x)e x dx (A.5) 0 f(x)x α e x dx (A.6) 77
89 Appendix A. Generation of Gauss quadratures f(x)(1 x) α (1+x) β dx (A.7) Integral types A.1 and A.3 are needed for the methods in [5] to be useful while types A.2 and A.4 are used to reduce the amount of computations required for the integrals related to the stationary points. Type A.5 is just a special case of A.3. Its quadrature is called Gauss-Laguerre. It is written as a separate type since its recurrence coefficients are explicitly know and there might be faster methods to find its related quadrature. The calculation can be performed more efficiently if the related quadrature is found for the specific case of A.5 instead of A.3. Type A.6 s quadrature rule is called General Gauss-Laguerre. It is only used to deal with some types of singularities that occur when the methods in [5] are used. Type A.7 is the Gauss-Jacobi rule which is used to obtain arbitrary 3D product rules for the adaptive Gauss quadrature scheme used for tet10 elements in the FE-MRI library. The appropriate quadrature points and weights are found in the following steps: 1. Find the recurrence coefficients of the two coefficient recurrence equation corresponding of the orthogonal polynomials that also correspond to the integral types 1 to 5 2. Find the eigenvalues of the related Jacobian matrix which are equal to the quadrature points 3. Solve the related linear system to find the eigenvectors and use them to find the corresponding weights The recurrence coefficients of the recurrence equation corresponding of the orthogonal polynomials can be found using one of the following methods: find the recurrence equation analytically using the three coefficient recurrence equation and/or other recurrence
90 Appendix A. Generation of Gauss quadratures 79 equations for orthogonal polynomials (such as Rodrigue s formula) or using Stieltjes procedure or using Lanczos algorithm. Lanczos algorithm is unstable except in a few cases [34]. The detail one has to be aware of is what kind of recurrence equation you need to go to the next step (finding the eigenvalues of the related Jacobian matrix). One of the main results of Gaussian quadrature theory is that the zeros of the corresponding orthogonal polynomials are the quadrature weights. Using that result in [35] it is shown that the coefficients of the two term recurrence relation for the corresponding monic polynomials can be used to get the quadrature weights. Unfortunately most recurrence equations in the literature have three coefficients. For example, the recurrence relation that produces the Laguerre polynomials corresponding to equation A.5 usually given is: L 0 (x) = 1 L 1 (x) = 1 x L n+1 (x) = 1 n+1 ((2n+1 x)l n(x) nl n 1 (x)) (A.8) Which can also be written in the form: xl n (x) = a n+1 L n+1 (x)+b n L n (x)+a n p n 1 (x) for n > 1 (A.9) What is needed for the related eigenvalue problem is a two coefficient relation for the related monic orthogonal polynomials (polynomials with a leading coefficient of 1). These are also the polynomials produced by Stieltjes algorithm. For example, the first three monic orthogonal polynomials related to the Laguerre polynomials above are:
91 Appendix A. Generation of Gauss quadratures 80 l 0 (x) = 1 l 1 (x) = x 1 (A.10) l 2 (x) = x 2 4x+2 Their recurrence relation is the following: l k+1 (x) = (x α n )l n (x) β n l n 1 (x) for n > 1 (A.11) Since Laguerre polynomials are also orthonormal ([36]): α 0 = 1 β 0 = any number (not used) α n = b n = 2n+1 (A.12) β n = a 2 n = n2 for n > 0 As it was mentioned before the coefficients can be either derived analytically using the three coefficient recurrence equation and/or other recurrence equations for orthogonal polynomials (such as Rodrigue s formula) or using Stieltjes algorithm. The coefficient values froma.12 canbeused to check animplementation tofindaquadraturefor integral A.5. Stieltjes algorithm (described in [34]) was used to check the coefficients from A.12. For evaluating the integrals needed in Stieltjes algorithm a Fejer type quadrature was used since it is recommended and described in [37]. The authors of [5] also used the same quadrature. They used the following MATLAB codes from the companion website to [37]: fejer.m, stieltjes.m and quadgp.m. This algorithm works for integral types A.1
92 Appendix A. Generation of Gauss quadratures 81 to A.5, but it is computationally intensive and finding its error is not trivial. It could be a better option to find the recurrence coefficients using known functions (such as the gamma function) that can be evaluated to a certain number of decimal places. This issue is discussed later. The Fejer points and weights for a 6 point quadrature are given in Table A.1. Fejer point Fejer weight Table A.1: Fejer quadrature points and weighs Stieltjes algorithm needs to carry out integrations using the same range as integral types A.1toA.6. Forexample, forintegral typea.5, in[37] thereisafractionaltransform that allows you to evaluate the following integral: 0 f(x) dx (A.13) As this integral: 1 1 f(φ(τ))φ (τ)dτ (A.14) Using the following transform: φ(τ) = 1+τ 1 τ (A.15)
93 Appendix A. Generation of Gauss quadratures 82 A.2 The Golub-Welsch algorithm Step 2 is done using a result found by Golub and Welsch, and described in [35]. The use of this result to calculate a quadrature is called the Golub-Welsch algorithm. The result states that the zeros of the orthogonal polynomials, corresponding to the quadrature points, are the eigenvalues of a symmetric tridiagonal matrix with the first coefficient in A.12 in the main diagonal, evaluated from k = 0 to n, and the square root of the second coefficient in A.12 in the side diagonals, evaluated from k = 1 to n where n is the number of quadrature points/weights needed. This matrix is also called a Jacobian matrix. The eigenvalues can then be found fairly efficiently with the QR algorithm. It is an iterative procedure that produces new tridiagonal matrices that converge on a diagonal matrix, and the eigenvalues of a diagonal matrix are its diagonal entries. There are various methods to increase this convergence but the most common are explicit and implicit shifting, deflation and subdivision. Unfortunately, the QR method does not work for integral type A.2 for example since α n = 0 for all n. The quadrature points and weights for these integrals were calculated beforehand in MATLAB using the function eig() and only needed to be included in the FE-MRI function that estimated the NSD computation time to simulate an MRI signal. After finding the eigenvalues of the Jacobian matrix, the eigenvectors can be found and then used to find the weights for each quadrature point as done in [35]. If the eigenvector A.16 corresponds to eigenvalue/quadrature point i. x i = [x 1, x 2,...,x n ] T (A.16) Then the quadrature weight is given by equation A.17.
94 Appendix A. Generation of Gauss quadratures 83 w i = x2 1 x i 2 0 e xr dx (A.17) Completing step 3. It is mentioned in [35] that as the Jacobian is iterated, the matrix Q converges to the values of its normalized eigenvectors in its rows. Extracting the eigenvectors from Q directly may not be successful possibly due to round-off error. Another solution is to make the first entry of A.16 equal to 1. It can be any value since A.16 will be normalized to find the weights. Then the system (since its only based on a tridiagonal matrix) can be solved by direct row by row substitution. Also A.17 reduces to: w i = 1 1+x x 2 n 0 e xr dx (A.18) The related quadrature for integral type A.7 is calculated for an arbitrary amount of points and weights (also using the MATLAB functions in the companion website to [37]) in C++ using VTK functions and it is included in the FE-MRI library. A.3 Sample C++ quadrature code The code to find any number of quadrature points and weights for the integral type A.7 with β = 0 is given below. //This function finds the quadrature points and weights for //Gauss-Jacobi quadrature with beta = 0 //Interval [0,1]. Transformation done using a change of variables //For more information consult Gautschi s book:
95 Appendix A. Generation of Gauss quadratures 84 //Numerical Analysis: An Introduction, section 2.4 void vtkfemrigaussarbquadrature::initialize1djacobi(int alpha) { if (this->quadraturepoints) { this->quadraturepoints->delete(); this->quadraturepoints = NULL; } this->quadraturepoints = vtkdoublearray::new(); if (this->quadratureweights) { this->quadratureweights->delete(); this->quadratureweights = NULL; } this->quadratureweights = vtkdoublearray::new(); //Added Golub s method to get an arbitary number of gauss points int numps; //Number of points int i; //Variable used for for loops //Zeroth moment of weight function //(just the integral of the weight function on quad interval) double m_0 = 1.0/(alpha+1.0); double lengthsquared; //Variable used to calculate weight //Calculate max number of points needed based on max quad order if(this->order % 2 == 0)
96 Appendix A. Generation of Gauss quadratures 85 else numps = (this->order + 2)/2; numps = (this->order + 1)/2; this->quadraturepoints ->SetNumberOfTuples(numPs); this->quadratureweights->setnumberoftuples(numps); //Fill points and weights using the GolubWelsch algorithm double* points = this->quadraturepoints->getpointer(0); double* weights = this->quadratureweights->getpointer(0); //Make 0 matrix to apply Golub-Welsch algorithm //using the JacobiN function in vtkmath.h double **A = vtknewmatrix(numps,numps); vtkzeromatrix(a,numps,numps); //Include in A the square root of 2 term recurrence //coefficients in the lower and upper diagonals for(i = 0; i < numps; i++) { A[i][i] = -alpha*alpha/(2.0*(i+1.0)+alpha)/(2.0*(i+1.0)-2.0+alpha); if(i < numps-1) A[i+1][i] = A[i][i+1] = sqrt( 4.0*(i+1.0)*(i+1.0)*(i+1.0+alpha)*(i+1.0+alpha) / ((2.0*(i+1.0)+alpha)*(2.0*(i+1.0)+alpha)*(2.0*(i+1.0) + alpha+1.0)*(2.0*(i+1.0)+alpha-1.0)));
97 Appendix A. Generation of Gauss quadratures 86 } //Find points using JacobiN function double *qpoints = new double[numps]; double **eigenvectors = vtknewmatrix(numps,numps); vtkmath::jacobin(a, numps, qpoints, eigenvectors); //Put found points (from 0 to 1) in point array taking into account //they are ordered from positive to negative for(i = 0; i < numps; i++) points[i] = (qpoints[numps-1 - i] + 1.0)/2.0; //Calculate weights //(first component of normalized evect^2 times first moment of W) for(i = 0; i < numps; i++) weights[i] = m_0*eigenvectors[0][numps-1-i]*eigenvectors[0][numps-1-i]; //Delete matrices when done using them vtkdeletematrix(a); delete [] qpoints; vtkdeletematrix(eigenvectors); } The first part of the code calculates the two term recurrence coefficients given by simple functions and uses them to make the tridiagonal matrix A. Then the eigenvalues and eigenvectors of A are calculated using the VTK function vtkmath::jacobin() and the eigenvalues are ordered and stored as the quadrature points. This function uses the Jacobi eigenvalue algorithm which is an alternative method to the QR method and is available in the VTK library. Then equation A.18 corresponding to the integral type A.7
98 Appendix A. Generation of Gauss quadratures 87 with β = 0 is used to calculate the quadrature weights from the calculated eigenvectors. The function uses three small inline functions above the function in the same file taken from the file vtkthinplatesplinetransform.cxx within the VTK C++ library. They are vtknewmatrix(), vtkdeletematrix() and vtkzeromatrix() and allow one to easily use of matrices within C++.
99 Appendix B Mesh generation with same discretization error B.1 Introduction In order to compare the computation expense of calculating the MRI signal of two different discretizations like the linear and quadratic tetrahedral in this thesis, the discretization error should be equal. Although this is not possible for a typical mesh, it can be achieved for a simple geometry with curved features such as a cylinder. The points and connectivity matrices for these two meshes with the same discretization error were calculated as follows: first the number of slices with quadratic tetrahedral elements were chosen, then the points on the curved side are chosen such that the difference in volume in a radial least square sense is minimized and finally the number of linear slices and their points that will produce that same difference are calculated. 88
100 Appendix B. Mesh generation with same discretization error 89 B.2 Discretization error when using quadratic elements To simplify the analysis, one should start with half of the slice which has one side on the x axis, the other side in the positive xy quadrant and its corner at the origin. The angle between the two is simply θ N = 2π/(2N) where N is the number of slices. For the quadratic elements there will be points along the lines made by the two sides. The quadratic element will have a curve in the xy plane that is given by x = a+by 2 were a positive and b is negative. The arc and its approximation is shown in Figure B.1. y x Figure B.1: Discretization of a circle using quadratic curve segments. The quantity to be minimized is proportional to the area between the lines This curve in radial coordinates is given by: r q (θ,a,b) = cosθ+ cos 2 θ 4absin 2 θ 2bsin 2 θ (B.1)
101 Appendix B. Mesh generation with same discretization error 90 One wants the best discretization possible which means that the least squares area difference between an arc with the same radius as the cylinder and the quadratic curve in radial coordinates between 0 and θ N should be minimized: minf = θn 0 [ rq (θ,a,b) R ] 2 (B.2) This is done by choosing the right a and b values. The usual procedure of differentiating the integrand of B.2 by a and b, integrating and solving for the variables is cumbersome if not impossible to do analytically. The equations found involve elliptic integrals with no closed form solution and solving two non-linear equations to find a and b. It is much simpler to use a simple derivative free minimization algorithm to minimize F and integrate it numerically to find the approximate values for a and b. The calculations were done in MATLAB. Since the integrand has a weak singularity at θ = 0 due to sin 2 θ, a simple adaptive two point Gaussian quadrature algorithm by Brian Bradie was used for the integration. 1 The application of Classic Quadrature rules does not require evaluating the integral limits. The adaptive integration method in function quad.m available in MATLAB will not work since it uses a recursive adaptive Simpson quadrature which needs to evaluate the integral limits. The initial guesses for a and b are a value close to R for a like a = 1.01R and for b equation B.5 can be solved for b with r = R and θ = θ N. Because of the accurate initial guess and the low dimensionality of the problem, a simple pattern search method called compass search [38] was used to minimize the integral. 2 After the a and b values are found, they are used to find the radii at θ = 0 and θ = θ N which are a (by definition) and equation B.5 at θ = θ N respectively. Also the value of F is stored. 1 The MATLAB function can be fund at: 2 The MATLAB function can be found at: compass_search/compass_search.html
102 Appendix B. Mesh generation with same discretization error 91 B.3 Discretization error when using linear elements The same derivation can be carried out for linear elements. Starting again with half a slice in the same location in the x-y plane, one side of the linear element should approximate an arc with the same radius as the cylinder. The arc and its approximation is shown in Figure B.2. y x Figure B.2: Discretization of a circle using line segments. The quantity to be minimized is proportional to the area between the lines Because of symmetry, the line is a vertical line in the x-y plane and its given by: r l (θ,a,b) = a cosθ (B.3) To get the best possible fit again the function to the minimized is: minf = θn 0 [ rl (θ,a,b) R ] 2 (B.4)
MRI Physics II: Gradients, Imaging
 MRI Physics II: Gradients, Imaging Douglas C., Ph.D. Dept. of Biomedical Engineering University of Michigan, Ann Arbor Magnetic Fields in MRI B 0 The main magnetic field. Always on (0.5-7 T) Magnetizes
MRI Physics II: Gradients, Imaging Douglas C., Ph.D. Dept. of Biomedical Engineering University of Michigan, Ann Arbor Magnetic Fields in MRI B 0 The main magnetic field. Always on (0.5-7 T) Magnetizes
Steen Moeller Center for Magnetic Resonance research University of Minnesota
 Steen Moeller Center for Magnetic Resonance research University of Minnesota moeller@cmrr.umn.edu Lot of material is from a talk by Douglas C. Noll Department of Biomedical Engineering Functional MRI Laboratory
Steen Moeller Center for Magnetic Resonance research University of Minnesota moeller@cmrr.umn.edu Lot of material is from a talk by Douglas C. Noll Department of Biomedical Engineering Functional MRI Laboratory
XI Signal-to-Noise (SNR)
 XI Signal-to-Noise (SNR) Lecture notes by Assaf Tal n(t) t. Noise. Characterizing Noise Noise is a random signal that gets added to all of our measurements. In D it looks like this: while in D
XI Signal-to-Noise (SNR) Lecture notes by Assaf Tal n(t) t. Noise. Characterizing Noise Noise is a random signal that gets added to all of our measurements. In D it looks like this: while in D
The SIMRI project A versatile and interactive MRI simulator *
 COST B21 Meeting, Lodz, 6-9 Oct. 2005 The SIMRI project A versatile and interactive MRI simulator * H. Benoit-Cattin 1, G. Collewet 2, B. Belaroussi 1, H. Saint-Jalmes 3, C. Odet 1 1 CREATIS, UMR CNRS
COST B21 Meeting, Lodz, 6-9 Oct. 2005 The SIMRI project A versatile and interactive MRI simulator * H. Benoit-Cattin 1, G. Collewet 2, B. Belaroussi 1, H. Saint-Jalmes 3, C. Odet 1 1 CREATIS, UMR CNRS
Imaging Notes, Part IV
 BME 483 MRI Notes 34 page 1 Imaging Notes, Part IV Slice Selective Excitation The most common approach for dealing with the 3 rd (z) dimension is to use slice selective excitation. This is done by applying
BME 483 MRI Notes 34 page 1 Imaging Notes, Part IV Slice Selective Excitation The most common approach for dealing with the 3 rd (z) dimension is to use slice selective excitation. This is done by applying
Exam 8N080 - Introduction MRI
 Exam 8N080 - Introduction MRI Friday January 23 rd 2015, 13.30-16.30h For this exam you may use an ordinary calculator (not a graphical one). In total there are 6 assignments and a total of 65 points can
Exam 8N080 - Introduction MRI Friday January 23 rd 2015, 13.30-16.30h For this exam you may use an ordinary calculator (not a graphical one). In total there are 6 assignments and a total of 65 points can
Edge and local feature detection - 2. Importance of edge detection in computer vision
 Edge and local feature detection Gradient based edge detection Edge detection by function fitting Second derivative edge detectors Edge linking and the construction of the chain graph Edge and local feature
Edge and local feature detection Gradient based edge detection Edge detection by function fitting Second derivative edge detectors Edge linking and the construction of the chain graph Edge and local feature
MRI image formation 8/3/2016. Disclosure. Outlines. Chen Lin, PhD DABR 3. Indiana University School of Medicine and Indiana University Health
 MRI image formation Indiana University School of Medicine and Indiana University Health Disclosure No conflict of interest for this presentation 2 Outlines Data acquisition Spatial (Slice/Slab) selection
MRI image formation Indiana University School of Medicine and Indiana University Health Disclosure No conflict of interest for this presentation 2 Outlines Data acquisition Spatial (Slice/Slab) selection
Computational Aspects of MRI
 David Atkinson Philip Batchelor David Larkman Programme 09:30 11:00 Fourier, sampling, gridding, interpolation. Matrices and Linear Algebra 11:30 13:00 MRI Lunch (not provided) 14:00 15:30 SVD, eigenvalues.
David Atkinson Philip Batchelor David Larkman Programme 09:30 11:00 Fourier, sampling, gridding, interpolation. Matrices and Linear Algebra 11:30 13:00 MRI Lunch (not provided) 14:00 15:30 SVD, eigenvalues.
Module 4. K-Space Symmetry. Review. K-Space Review. K-Space Symmetry. Partial or Fractional Echo. Half or Partial Fourier HASTE
 MRES 7005 - Fast Imaging Techniques Module 4 K-Space Symmetry Review K-Space Review K-Space Symmetry Partial or Fractional Echo Half or Partial Fourier HASTE Conditions for successful reconstruction Interpolation
MRES 7005 - Fast Imaging Techniques Module 4 K-Space Symmetry Review K-Space Review K-Space Symmetry Partial or Fractional Echo Half or Partial Fourier HASTE Conditions for successful reconstruction Interpolation
1.2 Numerical Solutions of Flow Problems
 1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
Slide 1. Technical Aspects of Quality Control in Magnetic Resonance Imaging. Slide 2. Annual Compliance Testing. of MRI Systems.
 Slide 1 Technical Aspects of Quality Control in Magnetic Resonance Imaging Slide 2 Compliance Testing of MRI Systems, Ph.D. Department of Radiology Henry Ford Hospital, Detroit, MI Slide 3 Compliance Testing
Slide 1 Technical Aspects of Quality Control in Magnetic Resonance Imaging Slide 2 Compliance Testing of MRI Systems, Ph.D. Department of Radiology Henry Ford Hospital, Detroit, MI Slide 3 Compliance Testing
Midterm Review
 Midterm Review - 2017 EE369B Concepts Noise Simulations with Bloch Matrices, EPG Gradient Echo Imaging 1 About the Midterm Monday Oct 30, 2017. CCSR 4107 Up to end of C2 1. Write your name legibly on this
Midterm Review - 2017 EE369B Concepts Noise Simulations with Bloch Matrices, EPG Gradient Echo Imaging 1 About the Midterm Monday Oct 30, 2017. CCSR 4107 Up to end of C2 1. Write your name legibly on this
MATH 31A HOMEWORK 9 (DUE 12/6) PARTS (A) AND (B) SECTION 5.4. f(x) = x + 1 x 2 + 9, F (7) = 0
 FROM ROGAWSKI S CALCULUS (2ND ED.) SECTION 5.4 18.) Express the antiderivative F (x) of f(x) satisfying the given initial condition as an integral. f(x) = x + 1 x 2 + 9, F (7) = 28.) Find G (1), where
FROM ROGAWSKI S CALCULUS (2ND ED.) SECTION 5.4 18.) Express the antiderivative F (x) of f(x) satisfying the given initial condition as an integral. f(x) = x + 1 x 2 + 9, F (7) = 28.) Find G (1), where
Math 113 Exam 1 Practice
 Math Exam Practice January 6, 00 Exam will cover sections 6.-6.5 and 7.-7.5 This sheet has three sections. The first section will remind you about techniques and formulas that you should know. The second
Math Exam Practice January 6, 00 Exam will cover sections 6.-6.5 and 7.-7.5 This sheet has three sections. The first section will remind you about techniques and formulas that you should know. The second
Advanced Image Reconstruction Methods for Photoacoustic Tomography
 Advanced Image Reconstruction Methods for Photoacoustic Tomography Mark A. Anastasio, Kun Wang, and Robert Schoonover Department of Biomedical Engineering Washington University in St. Louis 1 Outline Photoacoustic/thermoacoustic
Advanced Image Reconstruction Methods for Photoacoustic Tomography Mark A. Anastasio, Kun Wang, and Robert Schoonover Department of Biomedical Engineering Washington University in St. Louis 1 Outline Photoacoustic/thermoacoustic
White Pixel Artifact. Caused by a noise spike during acquisition Spike in K-space <--> sinusoid in image space
 White Pixel Artifact Caused by a noise spike during acquisition Spike in K-space sinusoid in image space Susceptibility Artifacts Off-resonance artifacts caused by adjacent regions with different
White Pixel Artifact Caused by a noise spike during acquisition Spike in K-space sinusoid in image space Susceptibility Artifacts Off-resonance artifacts caused by adjacent regions with different
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Calculus III-Final review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the corresponding position vector. 1) Define the points P = (-,
Calculus III-Final review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the corresponding position vector. 1) Define the points P = (-,
(a Scrhon5 R2iwd b. P)jc%z 5. ivcr3. 1. I. ZOms Xn,s. 1E IDrAS boms. EE225E/BIOE265 Spring 2013 Principles of MRI. Assignment 8 Solutions
 EE225E/BIOE265 Spring 2013 Principles of MRI Miki Lustig Assignment 8 Solutions 1. Nishimura 7.1 P)jc%z 5 ivcr3. 1. I Due Wednesday April 10th, 2013 (a Scrhon5 R2iwd b 0 ZOms Xn,s r cx > qs 4-4 8ni6 4
EE225E/BIOE265 Spring 2013 Principles of MRI Miki Lustig Assignment 8 Solutions 1. Nishimura 7.1 P)jc%z 5 ivcr3. 1. I Due Wednesday April 10th, 2013 (a Scrhon5 R2iwd b 0 ZOms Xn,s r cx > qs 4-4 8ni6 4
Compressed Sensing And Joint Acquisition Techniques In Mri
 Wayne State University Wayne State University Theses 1-1-2013 Compressed Sensing And Joint Acquisition Techniques In Mri Rouhollah Hamtaei Wayne State University, Follow this and additional works at: http://digitalcommons.wayne.edu/oa_theses
Wayne State University Wayne State University Theses 1-1-2013 Compressed Sensing And Joint Acquisition Techniques In Mri Rouhollah Hamtaei Wayne State University, Follow this and additional works at: http://digitalcommons.wayne.edu/oa_theses
A Novel Iterative Thresholding Algorithm for Compressed Sensing Reconstruction of Quantitative MRI Parameters from Insufficient Data
 A Novel Iterative Thresholding Algorithm for Compressed Sensing Reconstruction of Quantitative MRI Parameters from Insufficient Data Alexey Samsonov, Julia Velikina Departments of Radiology and Medical
A Novel Iterative Thresholding Algorithm for Compressed Sensing Reconstruction of Quantitative MRI Parameters from Insufficient Data Alexey Samsonov, Julia Velikina Departments of Radiology and Medical
Diffusion MRI Acquisition. Karla Miller FMRIB Centre, University of Oxford
 Diffusion MRI Acquisition Karla Miller FMRIB Centre, University of Oxford karla@fmrib.ox.ac.uk Diffusion Imaging How is diffusion weighting achieved? How is the image acquired? What are the limitations,
Diffusion MRI Acquisition Karla Miller FMRIB Centre, University of Oxford karla@fmrib.ox.ac.uk Diffusion Imaging How is diffusion weighting achieved? How is the image acquired? What are the limitations,
ELEC Dr Reji Mathew Electrical Engineering UNSW
 ELEC 4622 Dr Reji Mathew Electrical Engineering UNSW Review of Motion Modelling and Estimation Introduction to Motion Modelling & Estimation Forward Motion Backward Motion Block Motion Estimation Motion
ELEC 4622 Dr Reji Mathew Electrical Engineering UNSW Review of Motion Modelling and Estimation Introduction to Motion Modelling & Estimation Forward Motion Backward Motion Block Motion Estimation Motion
Image Sampling and Quantisation
 Image Sampling and Quantisation Introduction to Signal and Image Processing Prof. Dr. Philippe Cattin MIAC, University of Basel 1 of 46 22.02.2016 09:17 Contents Contents 1 Motivation 2 Sampling Introduction
Image Sampling and Quantisation Introduction to Signal and Image Processing Prof. Dr. Philippe Cattin MIAC, University of Basel 1 of 46 22.02.2016 09:17 Contents Contents 1 Motivation 2 Sampling Introduction
Geometric Representations. Stelian Coros
 Geometric Representations Stelian Coros Geometric Representations Languages for describing shape Boundary representations Polygonal meshes Subdivision surfaces Implicit surfaces Volumetric models Parametric
Geometric Representations Stelian Coros Geometric Representations Languages for describing shape Boundary representations Polygonal meshes Subdivision surfaces Implicit surfaces Volumetric models Parametric
Field Maps. 1 Field Map Acquisition. John Pauly. October 5, 2005
 Field Maps John Pauly October 5, 25 The acquisition and reconstruction of frequency, or field, maps is important for both the acquisition of MRI data, and for its reconstruction. Many of the imaging methods
Field Maps John Pauly October 5, 25 The acquisition and reconstruction of frequency, or field, maps is important for both the acquisition of MRI data, and for its reconstruction. Many of the imaging methods
surface Image reconstruction: 2D Fourier Transform
 2/1/217 Chapter 2-3 K-space Intro to k-space sampling (chap 3) Frequenc encoding and Discrete sampling (chap 2) Point Spread Function K-space properties K-space sampling principles (chap 3) Basic Contrast
2/1/217 Chapter 2-3 K-space Intro to k-space sampling (chap 3) Frequenc encoding and Discrete sampling (chap 2) Point Spread Function K-space properties K-space sampling principles (chap 3) Basic Contrast
Image Sampling & Quantisation
 Image Sampling & Quantisation Biomedical Image Analysis Prof. Dr. Philippe Cattin MIAC, University of Basel Contents 1 Motivation 2 Sampling Introduction and Motivation Sampling Example Quantisation Example
Image Sampling & Quantisation Biomedical Image Analysis Prof. Dr. Philippe Cattin MIAC, University of Basel Contents 1 Motivation 2 Sampling Introduction and Motivation Sampling Example Quantisation Example
= f (a, b) + (hf x + kf y ) (a,b) +
 Chapter 14 Multiple Integrals 1 Double Integrals, Iterated Integrals, Cross-sections 2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals
Chapter 14 Multiple Integrals 1 Double Integrals, Iterated Integrals, Cross-sections 2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals
f xx (x, y) = 6 + 6x f xy (x, y) = 0 f yy (x, y) = y In general, the quantity that we re interested in is
 1. Let f(x, y) = 5 + 3x 2 + 3y 2 + 2y 3 + x 3. (a) Final all critical points of f. (b) Use the second derivatives test to classify the critical points you found in (a) as a local maximum, local minimum,
1. Let f(x, y) = 5 + 3x 2 + 3y 2 + 2y 3 + x 3. (a) Final all critical points of f. (b) Use the second derivatives test to classify the critical points you found in (a) as a local maximum, local minimum,
Guidelines for proper use of Plate elements
 Guidelines for proper use of Plate elements In structural analysis using finite element method, the analysis model is created by dividing the entire structure into finite elements. This procedure is known
Guidelines for proper use of Plate elements In structural analysis using finite element method, the analysis model is created by dividing the entire structure into finite elements. This procedure is known
2.1 Signal Production. RF_Coil. Scanner. Phantom. Image. Image Production
 An Extensible MRI Simulator for Post-Processing Evaluation Remi K.-S. Kwan?, Alan C. Evans, and G. Bruce Pike McConnell Brain Imaging Centre, Montreal Neurological Institute, McGill University, Montreal,
An Extensible MRI Simulator for Post-Processing Evaluation Remi K.-S. Kwan?, Alan C. Evans, and G. Bruce Pike McConnell Brain Imaging Centre, Montreal Neurological Institute, McGill University, Montreal,
SUPPLEMENTARY FILE S1: 3D AIRWAY TUBE RECONSTRUCTION AND CELL-BASED MECHANICAL MODEL. RELATED TO FIGURE 1, FIGURE 7, AND STAR METHODS.
 SUPPLEMENTARY FILE S1: 3D AIRWAY TUBE RECONSTRUCTION AND CELL-BASED MECHANICAL MODEL. RELATED TO FIGURE 1, FIGURE 7, AND STAR METHODS. 1. 3D AIRWAY TUBE RECONSTRUCTION. RELATED TO FIGURE 1 AND STAR METHODS
SUPPLEMENTARY FILE S1: 3D AIRWAY TUBE RECONSTRUCTION AND CELL-BASED MECHANICAL MODEL. RELATED TO FIGURE 1, FIGURE 7, AND STAR METHODS. 1. 3D AIRWAY TUBE RECONSTRUCTION. RELATED TO FIGURE 1 AND STAR METHODS
Computer Vision 2. SS 18 Dr. Benjamin Guthier Professur für Bildverarbeitung. Computer Vision 2 Dr. Benjamin Guthier
 Computer Vision 2 SS 18 Dr. Benjamin Guthier Professur für Bildverarbeitung Computer Vision 2 Dr. Benjamin Guthier 1. IMAGE PROCESSING Computer Vision 2 Dr. Benjamin Guthier Content of this Chapter Non-linear
Computer Vision 2 SS 18 Dr. Benjamin Guthier Professur für Bildverarbeitung Computer Vision 2 Dr. Benjamin Guthier 1. IMAGE PROCESSING Computer Vision 2 Dr. Benjamin Guthier Content of this Chapter Non-linear
MRI Imaging Options. Frank R. Korosec, Ph.D. Departments of Radiology and Medical Physics University of Wisconsin Madison
 MRI Imaging Options Frank R. Korosec, Ph.D. Departments of Radiolog and Medical Phsics Universit of Wisconsin Madison f.korosec@hosp.wisc.edu As MR imaging becomes more developed, more imaging options
MRI Imaging Options Frank R. Korosec, Ph.D. Departments of Radiolog and Medical Phsics Universit of Wisconsin Madison f.korosec@hosp.wisc.edu As MR imaging becomes more developed, more imaging options
Diffusion Wavelets for Natural Image Analysis
 Diffusion Wavelets for Natural Image Analysis Tyrus Berry December 16, 2011 Contents 1 Project Description 2 2 Introduction to Diffusion Wavelets 2 2.1 Diffusion Multiresolution............................
Diffusion Wavelets for Natural Image Analysis Tyrus Berry December 16, 2011 Contents 1 Project Description 2 2 Introduction to Diffusion Wavelets 2 2.1 Diffusion Multiresolution............................
Regularized Estimation of Main and RF Field Inhomogeneity and Longitudinal Relaxation Rate in Magnetic Resonance Imaging
 Regularized Estimation of Main and RF Field Inhomogeneity and Longitudinal Relaxation Rate in Magnetic Resonance Imaging by Amanda K. Funai A dissertation submitted in partial fulfillment of the requirements
Regularized Estimation of Main and RF Field Inhomogeneity and Longitudinal Relaxation Rate in Magnetic Resonance Imaging by Amanda K. Funai A dissertation submitted in partial fulfillment of the requirements
Commutative filters for LES on unstructured meshes
 Center for Turbulence Research Annual Research Briefs 1999 389 Commutative filters for LES on unstructured meshes By Alison L. Marsden AND Oleg V. Vasilyev 1 Motivation and objectives Application of large
Center for Turbulence Research Annual Research Briefs 1999 389 Commutative filters for LES on unstructured meshes By Alison L. Marsden AND Oleg V. Vasilyev 1 Motivation and objectives Application of large
(Refer Slide Time: 0:32)
 Digital Image Processing. Professor P. K. Biswas. Department of Electronics and Electrical Communication Engineering. Indian Institute of Technology, Kharagpur. Lecture-57. Image Segmentation: Global Processing
Digital Image Processing. Professor P. K. Biswas. Department of Electronics and Electrical Communication Engineering. Indian Institute of Technology, Kharagpur. Lecture-57. Image Segmentation: Global Processing
Role of Parallel Imaging in High Field Functional MRI
 Role of Parallel Imaging in High Field Functional MRI Douglas C. Noll & Bradley P. Sutton Department of Biomedical Engineering, University of Michigan Supported by NIH Grant DA15410 & The Whitaker Foundation
Role of Parallel Imaging in High Field Functional MRI Douglas C. Noll & Bradley P. Sutton Department of Biomedical Engineering, University of Michigan Supported by NIH Grant DA15410 & The Whitaker Foundation
Clinical Importance. Aortic Stenosis. Aortic Regurgitation. Ultrasound vs. MRI. Carotid Artery Stenosis
 Clinical Importance Rapid cardiovascular flow quantitation using sliceselective Fourier velocity encoding with spiral readouts Valve disease affects 10% of patients with heart disease in the U.S. Most
Clinical Importance Rapid cardiovascular flow quantitation using sliceselective Fourier velocity encoding with spiral readouts Valve disease affects 10% of patients with heart disease in the U.S. Most
Section Parametrized Surfaces and Surface Integrals. (I) Parametrizing Surfaces (II) Surface Area (III) Scalar Surface Integrals
 Section 16.4 Parametrized Surfaces and Surface Integrals (I) Parametrizing Surfaces (II) Surface Area (III) Scalar Surface Integrals MATH 127 (Section 16.4) Parametrized Surfaces and Surface Integrals
Section 16.4 Parametrized Surfaces and Surface Integrals (I) Parametrizing Surfaces (II) Surface Area (III) Scalar Surface Integrals MATH 127 (Section 16.4) Parametrized Surfaces and Surface Integrals
Central Slice Theorem
 Central Slice Theorem Incident X-rays y f(x,y) R x r x Detected p(, x ) The thick line is described by xcos +ysin =R Properties of Fourier Transform F [ f ( x a)] F [ f ( x)] e j 2 a Spatial Domain Spatial
Central Slice Theorem Incident X-rays y f(x,y) R x r x Detected p(, x ) The thick line is described by xcos +ysin =R Properties of Fourier Transform F [ f ( x a)] F [ f ( x)] e j 2 a Spatial Domain Spatial
Edge detection. Convert a 2D image into a set of curves. Extracts salient features of the scene More compact than pixels
 Edge Detection Edge detection Convert a 2D image into a set of curves Extracts salient features of the scene More compact than pixels Origin of Edges surface normal discontinuity depth discontinuity surface
Edge Detection Edge detection Convert a 2D image into a set of curves Extracts salient features of the scene More compact than pixels Origin of Edges surface normal discontinuity depth discontinuity surface
Phase Difference Reconstruction. Outline
 Advanced MRI Phase Difference Reconstruction Faik Can MERAL Outline Introduction Quantitative Description Arctangent operation ATAN2 Phased-Array Multiple Coil Data Correction of Predictable Phase Errors
Advanced MRI Phase Difference Reconstruction Faik Can MERAL Outline Introduction Quantitative Description Arctangent operation ATAN2 Phased-Array Multiple Coil Data Correction of Predictable Phase Errors
MATH 2400, Analytic Geometry and Calculus 3
 MATH 2400, Analytic Geometry and Calculus 3 List of important Definitions and Theorems 1 Foundations Definition 1. By a function f one understands a mathematical object consisting of (i) a set X, called
MATH 2400, Analytic Geometry and Calculus 3 List of important Definitions and Theorems 1 Foundations Definition 1. By a function f one understands a mathematical object consisting of (i) a set X, called
A THESIS SUBMITTED TO THE GRADUATE SCHOOL IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE MASTER OF SCIENCE
 Exploring the Feasibility of the Detection of Neuronal Activity Evoked By Dendrite Currents Using MRI A THESIS SUBMITTED TO THE GRADUATE SCHOOL IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE
Exploring the Feasibility of the Detection of Neuronal Activity Evoked By Dendrite Currents Using MRI A THESIS SUBMITTED TO THE GRADUATE SCHOOL IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE
PHASE-SENSITIVE AND DUAL-ANGLE RADIOFREQUENCY MAPPING IN. Steven P. Allen. A senior thesis submitted to the faculty of. Brigham Young University
 PHASE-SENSITIVE AND DUAL-ANGLE RADIOFREQUENCY MAPPING IN 23 NA MAGNETIC RESONANCE IMAGING by Steven P. Allen A senior thesis submitted to the faculty of Brigham Young University in partial fulfillment
PHASE-SENSITIVE AND DUAL-ANGLE RADIOFREQUENCY MAPPING IN 23 NA MAGNETIC RESONANCE IMAGING by Steven P. Allen A senior thesis submitted to the faculty of Brigham Young University in partial fulfillment
Generalized barycentric coordinates
 Generalized barycentric coordinates Michael S. Floater August 20, 2012 In this lecture, we review the definitions and properties of barycentric coordinates on triangles, and study generalizations to convex,
Generalized barycentric coordinates Michael S. Floater August 20, 2012 In this lecture, we review the definitions and properties of barycentric coordinates on triangles, and study generalizations to convex,
Evaluations of k-space Trajectories for Fast MR Imaging for project of the course EE591, Fall 2004
 Evaluations of k-space Trajectories for Fast MR Imaging for project of the course EE591, Fall 24 1 Alec Chi-Wah Wong Department of Electrical Engineering University of Southern California 374 McClintock
Evaluations of k-space Trajectories for Fast MR Imaging for project of the course EE591, Fall 24 1 Alec Chi-Wah Wong Department of Electrical Engineering University of Southern California 374 McClintock
Chapter 3 Set Redundancy in Magnetic Resonance Brain Images
 16 Chapter 3 Set Redundancy in Magnetic Resonance Brain Images 3.1 MRI (magnetic resonance imaging) MRI is a technique of measuring physical structure within the human anatomy. Our proposed research focuses
16 Chapter 3 Set Redundancy in Magnetic Resonance Brain Images 3.1 MRI (magnetic resonance imaging) MRI is a technique of measuring physical structure within the human anatomy. Our proposed research focuses
used to describe all aspects of imaging process: input scene f, imaging system O, and output image g.
 SIMG-716 Linear Imaging Mathematics I 03 1 Representations of Functions 1.1 Functions Function: rule that assigns one numerical value (dependent variable) to each of a set of other numerical values (independent
SIMG-716 Linear Imaging Mathematics I 03 1 Representations of Functions 1.1 Functions Function: rule that assigns one numerical value (dependent variable) to each of a set of other numerical values (independent
Contents. MATH 32B-2 (18W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables. 1 Homework 1 - Solutions 3. 2 Homework 2 - Solutions 13
 MATH 32B-2 (8) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Homework - Solutions 3 2 Homework 2 - Solutions 3 3 Homework 3 - Solutions 9 MATH 32B-2 (8) (L) G. Liu / (TA) A. Zhou Calculus
MATH 32B-2 (8) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Homework - Solutions 3 2 Homework 2 - Solutions 3 3 Homework 3 - Solutions 9 MATH 32B-2 (8) (L) G. Liu / (TA) A. Zhou Calculus
Partial k-space Reconstruction
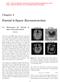 Chapter 2 Partial k-space Reconstruction 2.1 Motivation for Partial k- Space Reconstruction a) Magnitude b) Phase In theory, most MRI images depict the spin density as a function of position, and hence
Chapter 2 Partial k-space Reconstruction 2.1 Motivation for Partial k- Space Reconstruction a) Magnitude b) Phase In theory, most MRI images depict the spin density as a function of position, and hence
Vector Visualization. CSC 7443: Scientific Information Visualization
 Vector Visualization Vector data A vector is an object with direction and length v = (v x,v y,v z ) A vector field is a field which associates a vector with each point in space The vector data is 3D representation
Vector Visualization Vector data A vector is an object with direction and length v = (v x,v y,v z ) A vector field is a field which associates a vector with each point in space The vector data is 3D representation
Background for Surface Integration
 Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Non-Cartesian Parallel Magnetic Resonance Imaging
 Non-Cartesian Parallel Magnetic Resonance Imaging Dissertation zur Erlangung des naturwissenschaftlichen Doktorgrades der Bayerischen Julius-Maximilians-Universität Würzburg vorgelegt von Robin Heidemann
Non-Cartesian Parallel Magnetic Resonance Imaging Dissertation zur Erlangung des naturwissenschaftlichen Doktorgrades der Bayerischen Julius-Maximilians-Universität Würzburg vorgelegt von Robin Heidemann
Computer Graphics. Texture Filtering & Sampling Theory. Hendrik Lensch. Computer Graphics WS07/08 Texturing
 Computer Graphics Texture Filtering & Sampling Theory Hendrik Lensch Overview Last time Texture Parameterization Procedural Shading Today Texturing Filtering 2D Texture Mapping Forward mapping Object surface
Computer Graphics Texture Filtering & Sampling Theory Hendrik Lensch Overview Last time Texture Parameterization Procedural Shading Today Texturing Filtering 2D Texture Mapping Forward mapping Object surface
used to describe all aspects of imaging process: input scene f, imaging system O, and output image g.
 SIMG-716 Linear Imaging Mathematics I 03 1 Representations of Functions 1.1 Functions Function: rule that assigns one numerical value (dependent variable) to each of a set of other numerical values (independent
SIMG-716 Linear Imaging Mathematics I 03 1 Representations of Functions 1.1 Functions Function: rule that assigns one numerical value (dependent variable) to each of a set of other numerical values (independent
Intensity Transformations and Spatial Filtering
 77 Chapter 3 Intensity Transformations and Spatial Filtering Spatial domain refers to the image plane itself, and image processing methods in this category are based on direct manipulation of pixels in
77 Chapter 3 Intensity Transformations and Spatial Filtering Spatial domain refers to the image plane itself, and image processing methods in this category are based on direct manipulation of pixels in
SYNTHETIC SCHLIEREN. Stuart B Dalziel, Graham O Hughes & Bruce R Sutherland. Keywords: schlieren, internal waves, image processing
 8TH INTERNATIONAL SYMPOSIUM ON FLOW VISUALIZATION (998) SYNTHETIC SCHLIEREN Keywords: schlieren, internal waves, image processing Abstract This paper outlines novel techniques for producing qualitative
8TH INTERNATIONAL SYMPOSIUM ON FLOW VISUALIZATION (998) SYNTHETIC SCHLIEREN Keywords: schlieren, internal waves, image processing Abstract This paper outlines novel techniques for producing qualitative
ENGINEERING TRIPOS PART IIA FINITE ELEMENT METHOD
 ENGINEERING TRIPOS PART IIA LOCATION: DPO EXPERIMENT 3D7 FINITE ELEMENT METHOD Those who have performed the 3C7 experiment should bring the write-up along to this laboratory Objectives Show that the accuracy
ENGINEERING TRIPOS PART IIA LOCATION: DPO EXPERIMENT 3D7 FINITE ELEMENT METHOD Those who have performed the 3C7 experiment should bring the write-up along to this laboratory Objectives Show that the accuracy
Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder]
![Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder] Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder]](/thumbs/93/111713975.jpg) Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder] Preliminaries Recall: Given a smooth function f:r R, the function
Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder] Preliminaries Recall: Given a smooth function f:r R, the function
Strömningslära Fluid Dynamics. Computer laboratories using COMSOL v4.4
 UMEÅ UNIVERSITY Department of Physics Claude Dion Olexii Iukhymenko May 15, 2015 Strömningslära Fluid Dynamics (5FY144) Computer laboratories using COMSOL v4.4!! Report requirements Computer labs must
UMEÅ UNIVERSITY Department of Physics Claude Dion Olexii Iukhymenko May 15, 2015 Strömningslära Fluid Dynamics (5FY144) Computer laboratories using COMSOL v4.4!! Report requirements Computer labs must
Tomographic Image Reconstruction in Noisy and Limited Data Settings.
 Tomographic Image Reconstruction in Noisy and Limited Data Settings. Syed Tabish Abbas International Institute of Information Technology, Hyderabad syed.abbas@research.iiit.ac.in July 1, 2016 Tabish (IIIT-H)
Tomographic Image Reconstruction in Noisy and Limited Data Settings. Syed Tabish Abbas International Institute of Information Technology, Hyderabad syed.abbas@research.iiit.ac.in July 1, 2016 Tabish (IIIT-H)
Advanced Imaging Trajectories
 Advanced Imaging Trajectories Cartesian EPI Spiral Radial Projection 1 Radial and Projection Imaging Sample spokes Radial out : from k=0 to kmax Projection: from -kmax to kmax Trajectory design considerations
Advanced Imaging Trajectories Cartesian EPI Spiral Radial Projection 1 Radial and Projection Imaging Sample spokes Radial out : from k=0 to kmax Projection: from -kmax to kmax Trajectory design considerations
Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras. Lecture - 36
 Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras Lecture - 36 In last class, we have derived element equations for two d elasticity problems
Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras Lecture - 36 In last class, we have derived element equations for two d elasticity problems
Partial k-space Recconstruction
 Partial k-space Recconstruction John Pauly September 29, 2005 1 Motivation for Partial k-space Reconstruction a) Magnitude b) Phase In theory, most MRI images depict the spin density as a function of position,
Partial k-space Recconstruction John Pauly September 29, 2005 1 Motivation for Partial k-space Reconstruction a) Magnitude b) Phase In theory, most MRI images depict the spin density as a function of position,
Following on from the two previous chapters, which considered the model of the
 Chapter 5 Simulator validation Following on from the two previous chapters, which considered the model of the simulation process and how this model was implemented in software, this chapter is concerned
Chapter 5 Simulator validation Following on from the two previous chapters, which considered the model of the simulation process and how this model was implemented in software, this chapter is concerned
Parametric Surfaces. Substitution
 Calculus Lia Vas Parametric Surfaces. Substitution Recall that a curve in space is given by parametric equations as a function of single parameter t x = x(t) y = y(t) z = z(t). A curve is a one-dimensional
Calculus Lia Vas Parametric Surfaces. Substitution Recall that a curve in space is given by parametric equations as a function of single parameter t x = x(t) y = y(t) z = z(t). A curve is a one-dimensional
Alaska Mathematics Standards Vocabulary Word List Grade 7
 1 estimate proportion proportional relationship rate ratio rational coefficient rational number scale Ratios and Proportional Relationships To find a number close to an exact amount; an estimate tells
1 estimate proportion proportional relationship rate ratio rational coefficient rational number scale Ratios and Proportional Relationships To find a number close to an exact amount; an estimate tells
Computer Vision I. Announcements. Fourier Tansform. Efficient Implementation. Edge and Corner Detection. CSE252A Lecture 13.
 Announcements Edge and Corner Detection HW3 assigned CSE252A Lecture 13 Efficient Implementation Both, the Box filter and the Gaussian filter are separable: First convolve each row of input image I with
Announcements Edge and Corner Detection HW3 assigned CSE252A Lecture 13 Efficient Implementation Both, the Box filter and the Gaussian filter are separable: First convolve each row of input image I with
Measuring Lengths The First Fundamental Form
 Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
18.02 Final Exam. y = 0
 No books, notes or calculators. 5 problems, 50 points. 8.0 Final Exam Useful formula: cos (θ) = ( + cos(θ)) Problem. (0 points) a) (5 pts.) Find the equation in the form Ax + By + z = D of the plane P
No books, notes or calculators. 5 problems, 50 points. 8.0 Final Exam Useful formula: cos (θ) = ( + cos(θ)) Problem. (0 points) a) (5 pts.) Find the equation in the form Ax + By + z = D of the plane P
Dynamic Image and Fieldmap Joint Estimation Methods for MRI Using Single-Shot Trajectories
 Dynamic Image and Fieldmap Joint Estimation Methods for MRI Using Single-Shot Trajectories by Antonis Matakos A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor
Dynamic Image and Fieldmap Joint Estimation Methods for MRI Using Single-Shot Trajectories by Antonis Matakos A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor
Supplementary methods
 Supplementary methods This section provides additional technical details on the sample, the applied imaging and analysis steps and methods. Structural imaging Trained radiographers placed all participants
Supplementary methods This section provides additional technical details on the sample, the applied imaging and analysis steps and methods. Structural imaging Trained radiographers placed all participants
Magnetic Resonance Angiography
 Magnetic Resonance Angiography Course: Advance MRI (BIOE 594) Instructors: Dr Xiaohong Joe Zhou Dr. Shadi Othman By, Nayan Pasad Phase Contrast Angiography By Moran 1982, Bryan et. Al. 1984 and Moran et.
Magnetic Resonance Angiography Course: Advance MRI (BIOE 594) Instructors: Dr Xiaohong Joe Zhou Dr. Shadi Othman By, Nayan Pasad Phase Contrast Angiography By Moran 1982, Bryan et. Al. 1984 and Moran et.
Computer Graphics. Sampling Theory & Anti-Aliasing. Philipp Slusallek
 Computer Graphics Sampling Theory & Anti-Aliasing Philipp Slusallek Dirac Comb (1) Constant & δ-function flash Comb/Shah function 2 Dirac Comb (2) Constant & δ-function Duality f(x) = K F(ω) = K (ω) And
Computer Graphics Sampling Theory & Anti-Aliasing Philipp Slusallek Dirac Comb (1) Constant & δ-function flash Comb/Shah function 2 Dirac Comb (2) Constant & δ-function Duality f(x) = K F(ω) = K (ω) And
Chapter 11 Image Processing
 Chapter Image Processing Low-level Image Processing Operates directly on a stored image to improve or enhance it. Stored image consists of a two-dimensional array of pixels (picture elements): Origin (0,
Chapter Image Processing Low-level Image Processing Operates directly on a stored image to improve or enhance it. Stored image consists of a two-dimensional array of pixels (picture elements): Origin (0,
CHAPTER 1. Introduction
 ME 475: Computer-Aided Design of Structures 1-1 CHAPTER 1 Introduction 1.1 Analysis versus Design 1.2 Basic Steps in Analysis 1.3 What is the Finite Element Method? 1.4 Geometrical Representation, Discretization
ME 475: Computer-Aided Design of Structures 1-1 CHAPTER 1 Introduction 1.1 Analysis versus Design 1.2 Basic Steps in Analysis 1.3 What is the Finite Element Method? 1.4 Geometrical Representation, Discretization
Motion. 1 Introduction. 2 Optical Flow. Sohaib A Khan. 2.1 Brightness Constancy Equation
 Motion Sohaib A Khan 1 Introduction So far, we have dealing with single images of a static scene taken by a fixed camera. Here we will deal with sequence of images taken at different time intervals. Motion
Motion Sohaib A Khan 1 Introduction So far, we have dealing with single images of a static scene taken by a fixed camera. Here we will deal with sequence of images taken at different time intervals. Motion
EE225E/BIOE265 Spring 2011 Principles of MRI. Assignment 5. Solutions
 EE225E/BIOE265 Spring 211 Principles of MRI Miki Lustig Handout Assignment 5 Solutions 1. Matlab Exercise: 2DFT Pulse sequence design. In this assignment we will write functions to design a 2DFT pulse
EE225E/BIOE265 Spring 211 Principles of MRI Miki Lustig Handout Assignment 5 Solutions 1. Matlab Exercise: 2DFT Pulse sequence design. In this assignment we will write functions to design a 2DFT pulse
AQA GCSE Maths - Higher Self-Assessment Checklist
 AQA GCSE Maths - Higher Self-Assessment Checklist Number 1 Use place value when calculating with decimals. 1 Order positive and negative integers and decimals using the symbols =,, , and. 1 Round to
AQA GCSE Maths - Higher Self-Assessment Checklist Number 1 Use place value when calculating with decimals. 1 Order positive and negative integers and decimals using the symbols =,, , and. 1 Round to
Image Acquisition Systems
 Image Acquisition Systems Goals and Terminology Conventional Radiography Axial Tomography Computer Axial Tomography (CAT) Magnetic Resonance Imaging (MRI) PET, SPECT Ultrasound Microscopy Imaging ITCS
Image Acquisition Systems Goals and Terminology Conventional Radiography Axial Tomography Computer Axial Tomography (CAT) Magnetic Resonance Imaging (MRI) PET, SPECT Ultrasound Microscopy Imaging ITCS
6. Find the equation of the plane that passes through the point (-1,2,1) and contains the line x = y = z.
 Week 1 Worksheet Sections from Thomas 13 th edition: 12.4, 12.5, 12.6, 13.1 1. A plane is a set of points that satisfies an equation of the form c 1 x + c 2 y + c 3 z = c 4. (a) Find any three distinct
Week 1 Worksheet Sections from Thomas 13 th edition: 12.4, 12.5, 12.6, 13.1 1. A plane is a set of points that satisfies an equation of the form c 1 x + c 2 y + c 3 z = c 4. (a) Find any three distinct
Math D Printing Group Final Report
 Math 4020 3D Printing Group Final Report Gayan Abeynanda Brandon Oubre Jeremy Tillay Dustin Wright Wednesday 29 th April, 2015 Introduction 3D printers are a growing technology, but there is currently
Math 4020 3D Printing Group Final Report Gayan Abeynanda Brandon Oubre Jeremy Tillay Dustin Wright Wednesday 29 th April, 2015 Introduction 3D printers are a growing technology, but there is currently
Image Processing
 Image Processing 159.731 Canny Edge Detection Report Syed Irfanullah, Azeezullah 00297844 Danh Anh Huynh 02136047 1 Canny Edge Detection INTRODUCTION Edges Edges characterize boundaries and are therefore
Image Processing 159.731 Canny Edge Detection Report Syed Irfanullah, Azeezullah 00297844 Danh Anh Huynh 02136047 1 Canny Edge Detection INTRODUCTION Edges Edges characterize boundaries and are therefore
1. Fill in the right hand side of the following equation by taking the derivative: (x sin x) =
 7.1 What is x cos x? 1. Fill in the right hand side of the following equation by taking the derivative: (x sin x = 2. Integrate both sides of the equation. Instructor: When instructing students to integrate
7.1 What is x cos x? 1. Fill in the right hand side of the following equation by taking the derivative: (x sin x = 2. Integrate both sides of the equation. Instructor: When instructing students to integrate
Image Processing. Application area chosen because it has very good parallelism and interesting output.
 Chapter 11 Slide 517 Image Processing Application area chosen because it has very good parallelism and interesting output. Low-level Image Processing Operates directly on stored image to improve/enhance
Chapter 11 Slide 517 Image Processing Application area chosen because it has very good parallelism and interesting output. Low-level Image Processing Operates directly on stored image to improve/enhance
9-1 GCSE Maths. GCSE Mathematics has a Foundation tier (Grades 1 5) and a Higher tier (Grades 4 9).
 9-1 GCSE Maths GCSE Mathematics has a Foundation tier (Grades 1 5) and a Higher tier (Grades 4 9). In each tier, there are three exams taken at the end of Year 11. Any topic may be assessed on each of
9-1 GCSE Maths GCSE Mathematics has a Foundation tier (Grades 1 5) and a Higher tier (Grades 4 9). In each tier, there are three exams taken at the end of Year 11. Any topic may be assessed on each of
Tomographic reconstruction of shock layer flows
 Tomographic reconstruction of shock layer flows A thesis submitted for the degree of Doctor of Philosophy at The Australian National University May 2005 Rado Faletič Department of Physics Faculty of Science
Tomographic reconstruction of shock layer flows A thesis submitted for the degree of Doctor of Philosophy at The Australian National University May 2005 Rado Faletič Department of Physics Faculty of Science
Birkdale High School - Higher Scheme of Work
 Birkdale High School - Higher Scheme of Work Module 1 - Integers and Decimals Understand and order integers (assumed) Use brackets and hierarchy of operations (BODMAS) Add, subtract, multiply and divide
Birkdale High School - Higher Scheme of Work Module 1 - Integers and Decimals Understand and order integers (assumed) Use brackets and hierarchy of operations (BODMAS) Add, subtract, multiply and divide
MA 243 Calculus III Fall Assignment 1. Reading assignments are found in James Stewart s Calculus (Early Transcendentals)
 MA 43 Calculus III Fall 8 Dr. E. Jacobs Assignments Reading assignments are found in James Stewart s Calculus (Early Transcendentals) Assignment. Spheres and Other Surfaces Read. -. and.6 Section./Problems
MA 43 Calculus III Fall 8 Dr. E. Jacobs Assignments Reading assignments are found in James Stewart s Calculus (Early Transcendentals) Assignment. Spheres and Other Surfaces Read. -. and.6 Section./Problems
EECS 556 Image Processing W 09. Interpolation. Interpolation techniques B splines
 EECS 556 Image Processing W 09 Interpolation Interpolation techniques B splines What is image processing? Image processing is the application of 2D signal processing methods to images Image representation
EECS 556 Image Processing W 09 Interpolation Interpolation techniques B splines What is image processing? Image processing is the application of 2D signal processing methods to images Image representation
MATH 234. Excercises on Integration in Several Variables. I. Double Integrals
 MATH 234 Excercises on Integration in everal Variables I. Double Integrals Problem 1. D = {(x, y) : y x 1, 0 y 1}. Compute D ex3 da. Problem 2. Find the volume of the solid bounded above by the plane 3x
MATH 234 Excercises on Integration in everal Variables I. Double Integrals Problem 1. D = {(x, y) : y x 1, 0 y 1}. Compute D ex3 da. Problem 2. Find the volume of the solid bounded above by the plane 3x
Recent Developments in Model-based Derivative-free Optimization
 Recent Developments in Model-based Derivative-free Optimization Seppo Pulkkinen April 23, 2010 Introduction Problem definition The problem we are considering is a nonlinear optimization problem with constraints:
Recent Developments in Model-based Derivative-free Optimization Seppo Pulkkinen April 23, 2010 Introduction Problem definition The problem we are considering is a nonlinear optimization problem with constraints:
PHASE-ENCODED, RAPID, MULTIPLE-ECHO (PERME) NUCLEAR MAGNETIC RESONANCE IMAGING
 PHASE-ENCODED, RAPID, MULTIPLE-ECHO (PERME) NUCLEAR MAGNETIC RESONANCE IMAGING Mark Steven Lawton Master of Engineering Thesis Lawrence Berkeley Laboratory University of California Berkeley, California
PHASE-ENCODED, RAPID, MULTIPLE-ECHO (PERME) NUCLEAR MAGNETIC RESONANCE IMAGING Mark Steven Lawton Master of Engineering Thesis Lawrence Berkeley Laboratory University of California Berkeley, California
NUFFT for Medical and Subsurface Image Reconstruction
 NUFFT for Medical and Subsurface Image Reconstruction Qing H. Liu Department of Electrical and Computer Engineering Duke University Duke Frontiers 2006 May 16, 2006 Acknowledgment Jiayu Song main contributor
NUFFT for Medical and Subsurface Image Reconstruction Qing H. Liu Department of Electrical and Computer Engineering Duke University Duke Frontiers 2006 May 16, 2006 Acknowledgment Jiayu Song main contributor
5 Applications of Definite Integrals
 5 Applications of Definite Integrals The previous chapter introduced the concepts of a definite integral as an area and as a limit of Riemann sums, demonstrated some of the properties of integrals, introduced
5 Applications of Definite Integrals The previous chapter introduced the concepts of a definite integral as an area and as a limit of Riemann sums, demonstrated some of the properties of integrals, introduced
Noise Model. Important Noise Probability Density Functions (Cont.) Important Noise Probability Density Functions
 Others -- Noise Removal Techniques -- Edge Detection Techniques -- Geometric Operations -- Color Image Processing -- Color Spaces Xiaojun Qi Noise Model The principal sources of noise in digital images
Others -- Noise Removal Techniques -- Edge Detection Techniques -- Geometric Operations -- Color Image Processing -- Color Spaces Xiaojun Qi Noise Model The principal sources of noise in digital images
