PARAMETRIC EQUATIONS AND POLAR COORDINATES
|
|
|
- Marcia Daniels
- 5 years ago
- Views:
Transcription
1 9 ARAMETRIC EQUATIONS AND OLAR COORDINATES So far we have described plane curves b giving as a function of f or as a function of t or b giving a relation between and that defines implicitl as a function of f,. In this chapter we discuss two new methods for describing curves. Some curves, such as the ccloid, are best handled when both and are given in terms of a third variable t called a parameter f t, tt. Other curves, such as the cardioid, have their most convenient description when we use a new coordinate sstem, called the polar coordinate sstem. 9. ARAMETRIC CURVES FIGURE C (, )={ f(t), g(t)} Module 9.A gives an animation of the relationship between motion along a parametric curve f t, tt and motion along the graphs of f and t as functions of t. Imagine that a particle moves along the curve C shown in Figure. It is impossible to describe C b an equation of the form f because C fails the Vertical Line Test. But the - and -coordinates of the particle are functions of time and so we can write f t and tt. Such a pair of equations is often a convenient wa of describing a curve and gives rise to the following definition. Suppose that and are both given as functions of a third variable t (called a parameter) b the equations f t tt (called parametric equations). Each value of t determines a point,, which we can plot in a coordinate plane. As t varies, the point, f t, tt varies and traces out a curve C, which we call a parametric curve. The parameter t does not necessaril represent time and, in fact, we could use a letter other than t for the parameter. But in man applications of parametric curves, t does denote time and therefore we can interpret, f t, tt as the position of a particle at time t. EXAMLE Sketch and identif the curve defined b the parametric equations t t t SOLUTION Each value of t gives a point on the curve, as shown in the table. For instance, if t, then, and so the corresponding point is,. In Figure we plot the points, determined b several values of the parameter t and we join them to produce a curve. t t= t= t= (, ) t=3 t=_ t=4 8 t=_ 48 FIGURE
2 SECTION 9. ARAMETRIC CURVES 483 This equation in and describes where the particle has been, but it doesn t tell us when the particle was at a particular point. The parametric equations have an advantage the tell us when the particle was at a point. The also indicate the direction of the motion. A particle whose position is given b the parametric equations moves along the curve in the direction of the arrows as t increases. Notice that the consecutive points marked on the curve appear at equal time intervals but not at equal distances. That is because the particle slows down and then speeds up as t increases. It appears from Figure that the curve traced out b the particle ma be a parabola. This can be confirmed b eliminating the parameter t as follows. We obtain t from the second equation and substitute into the first equation. This gives t t 4 3 and so the curve represented b the given parametric equations is the parabola 4 3. (8, 5) No restriction was placed on the parameter t in Eample, so we assumed that t could be an real number. But sometimes we restrict t to lie in a finite interval. For instance, the parametric curve t t t t 4 (, ) shown in Figure 3 is the part of the parabola in Eample that starts at the point, and ends at the point 8, 5. The arrowhead indicates the direction in which the curve is traced as t increases from to 4. In general, the curve with parametric equations FIGURE 3 f t tt a t b π t= (cos t, sin t) has initial point f a, ta and terminal point f b, tb. V EXAMLE What curve is represented b the following parametric equations? t=π t t= (, ) t=π cos t sin t t SOLUTION If we plot points, it appears that the curve is a circle. We can confirm this impression b eliminating t. Observe that 3π t= cos t sin t FIGURE 4 t=, π, π (, ) Thus the point, moves on the unit circle. Notice that in this eample the parameter t can be interpreted as the angle (in radians) shown in Figure 4. As t increases from to, the point, cos t, sin t moves once around the circle in the counterclockwise direction starting from the point,. EXAMLE 3 What curve is represented b the given parametric equations? sin t cos t t SOLUTION Again we have sin t cos t FIGURE 5 so the parametric equations again represent the unit circle. But as t increases from to, the point, sin t, cos t starts at, and moves twice around the circle in the clockwise direction as indicated in Figure 5.
3 484 CHATER 9 ARAMETRIC EQUATIONS AND OLAR COORDINATES r (h, k) FIGURE 6 =h+r cos t, =k+r sin t Eamples and 3 show that different sets of parametric equations can represent the same curve. Thus we distinguish between a curve, which is a set of points, and a parametric curve, in which the points are traced in a particular wa. EXAMLE 4 Find parametric equations for the circle with center h, k and radius r. SOLUTION If we take the equations of the unit circle in Eample and multipl the epressions for and b r, we get r cos t, r sin t. You can verif that these equations represent a circle with radius r and center the origin traced counterclockwise. We now shift h units in the -direction and k units in the -direction and obtain parametric equations of the circle (Figure 6) with center h, k and radius r: h r cos t k r sin t t (_, ) (, ) V EXAMLE 5 Sketch the curve with parametric equations sin t, sin t. FIGURE 7 SOLUTION Observe that sin t and so the point, moves on the parabola. But note also that, since sin t, we have, so the parametric equations represent onl the part of the parabola for which. Since sin t is periodic, the point, sin t, sin t moves back and forth infinitel often along the parabola from, to,. (See Figure 7.) GRAHING DEVICES Most graphing calculators and computer graphing programs can be used to graph curves defined b parametric equations. In fact, it s instructive to watch a parametric curve being drawn b a graphing calculator because the points are plotted in order as the corresponding parameter values increase. 3 EXAMLE 6 Use a graphing device to graph the curve 4 3. SOLUTION If we let the parameter be t, then we have the equations _3 3 t 4 3t t FIGURE 8 _3 Using these parametric equations to graph the curve, we obtain Figure 8. It would be possible to solve the given equation 4 3 for as four functions of and graph them individuall, but the parametric equations provide a much easier method. In general, if we need to graph an equation of the form t, we can use the parametric equations tt t Notice also that curves with equations f (the ones we are most familiar with graphs of functions) can also be regarded as curves with parametric equations t f t
4 SECTION 9. ARAMETRIC CURVES Graphing devices are particularl useful for sketching complicated curves. For instance, the curves shown in Figures 9,, and would be virtuall impossible to produce b hand..5 _ _ _.5 _ FIGURE 9 =t+ sin t =t+ cos 5t FIGURE =.5 cos t-cos 3t =.5 sin t-sin 3t FIGURE =sin(t+cos t) =cos(t+sin t) THE CYCLOID An animation in Module 9.B shows how the ccloid is formed as the circle moves. EXAMLE 7 The curve traced out b a point on the circumference of a circle as the circle rolls along a straight line is called a ccloid (see Figure ). If the circle has radius r and rolls along the -ais and if one position of is the origin, find parametric equations for the ccloid. FIGURE SOLUTION We choose as parameter the angle of rotation of the circle when is at the origin). Suppose the circle has rotated through radians. Because the circle has been in contact with the line, we see from Figure 3 that the distance it has rolled from the origin is O r r C(r, r) Q T OT arc T r Therefore, the center of the circle is Cr, r. Let the coordinates of be,. Then from Figure 3 we see that OT Q r r sin r sin FIGURE 3 TC QC r r cos r cos Therefore, parametric equations of the ccloid are r sin r cos One arch of the ccloid comes from one rotation of the circle and so is described b. Although Equations were derived from Figure 3, which illustrates the case, it can be seen that these equations are still valid for other values of (see Eercise 33).
5 486 CHATER 9 ARAMETRIC EQUATIONS AND OLAR COORDINATES A Although it is possible to eliminate the parameter from Equations, the resulting Cartesian equation in and is ver complicated and not as convenient to work with as the parametric equations. ccloid FIGURE 4 FIGURE 5 B One of the first people to stud the ccloid was Galileo, who proposed that bridges be built in the shape of ccloids and who tried to find the area under one arch of a ccloid. Later this curve arose in connection with the brachistochrone problem: Find the curve along which a particle will slide in the shortest time (under the influence of gravit) from a point A to a lower point B not directl beneath A. The Swiss mathematician John Bernoulli, who posed this problem in 696, showed that among all possible curves that join A to B, as in Figure 4, the particle will take the least time sliding from A to B if the curve is part of an inverted arch of a ccloid. The Dutch phsicist Hugens had alread shown that the ccloid is also the solution to the tautochrone problem; that is, no matter where a particle is placed on an inverted ccloid, it takes the same time to slide to the bottom (see Figure 5). Hugens proposed that pendulum clocks (which he invented) should swing in ccloidal arcs because then the pendulum takes the same time to make a complete oscillation whether it swings through a wide or a small arc. 9. EXERCISES 4 Sketch the curve b using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as t increases.. st, t 4t,. cos t, t cos t, 3. 5 sin t, t, 4. e t t, e t t, t 5 t t t 5 8 (a) Sketch the curve b using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as t increases. (b) Eliminate the parameter to find a Cartesian equation of the curve. 5. 3t 5, t 6. 3t, 7. st, t 8. t, t 3 t. sec, tan, 3. e t, t 4. cos, cos 5 8 Describe the motion of a particle with position, as t varies in the given interval cos t, sin t, t 3 6. sin t, 4 cos t, t sin t, cos t, 8. sin t, cos t, t 5 t 9 Use the graphs of f t and tt to sketch the parametric curve f t, tt. Indicate with arrows the direction in which the curve is traced as t increases (a) Eliminate the parameter to find a Cartesian equation of the curve. (b) Sketch the curve and indicate with an arrow the direction in which the curve is traced as the parameter increases. 9. sin, cos,. 4 cos, 5 sin,. sin t, csc t, t. _ t t t t
6 SECTION 9. ARAMETRIC CURVES Match the parametric equations with the graphs labeled I VI. Give reasons for our choices. (Do not use a graphing device.) (a) t 3 t, t t (b) t 3, t (c) sin 3t, sin 4t (d) t sin t, t sin 3t (e) sint sin t, cost cos t (f) cos t, sint sin 5t I IV t II V ; 3. Graph the curve ; 4. Graph the curves 5 and and find their points of intersection correct to one decimal place. 5. (a) Show that the parametric equations t where t, describe the line segment that joins the points, and,. (b) Find parametric equations to represent the line segment from, 7 to 3,. ; 6. Use a graphing device and the result of Eercise 5(a) to draw the triangle with vertices A,, B4,, and C, Find parametric equations for the path of a particle that moves along the circle 4 in the manner described. (a) Once around clockwise, starting at, (b) Three times around counterclockwise, starting at, (c) Halfwa around counterclockwise, starting at, 3 ; 8. (a) Find parametric equations for the ellipse a b. [Hint: Modif the equations of the circle in Eample.] III VI t t (b) Use these parametric equations to graph the ellipse when a 3 and b,, 4, and 8. (c) How does the shape of the ellipse change as b varies? ; 9 3 Use a graphing calculator or computer to reproduce the picture Compare the curves represented b the parametric equations. How do the differ? 3. (a) t 3, t (b) t 6, t 4 (c) e 3t, e t 3. (a) t, t (b) cos t, sec t (c) e t, e t 33. Derive Equations for the case. 34. Let be a point at a distance d from the center of a circle of radius r. The curve traced out b as the circle rolls along a straight line is called a trochoid. (Think of the motion of a point on a spoke of a biccle wheel.) The ccloid is the special case of a trochoid with d r. Using the same parameter as for the ccloid and assuming the line is the -ais and when is at one of its lowest points, show that parametric equations of the trochoid are r d sin Sketch the trochoid for the cases d r and d r. 35. If a and b are fied numbers, find parametric equations for the curve that consists of all possible positions of the point in the figure, using the angle as the parameter. Then eliminate the parameter and identif the curve. a b O r d cos 4 3 8
7 488 CHATER 9 ARAMETRIC EQUATIONS AND OLAR COORDINATES 36. A curve, called a witch of Maria Agnesi, consists of all possible positions of the point in the figure. Show that parametric equations for this curve can be written as Sketch the curve. a cot =a ; 37. Suppose that the position of one particle at time t is given b 3 sin t cos t t and the position of a second particle is given b 3 cos t (a) Graph the paths of both particles. How man points of intersection are there? (b) Are an of these points of intersection collision points? In other words, are the particles ever at the same place at the same time? If so, find the collision points. (c) Describe what happens if the path of the second particle is given b 3 cos t sin t t 38. If a projectile is fired with an initial velocit of v meters per second at an angle above the horizontal and air resis- a O a sin A sin t C t tance is assumed to be negligible, then its position after t seconds is given b the parametric equations v cos t where t is the acceleration due to gravit ( 9.8 ms ). (a) If a gun is fired with and v 5 ms, when will the bullet hit the ground? How far from the gun will it hit the ground? What is the maimum height reached b the bullet? ; (b) Use a graphing device to check our answers to part (a). Then graph the path of the projectile for several other values of the angle to see where it hits the ground. Summarize our findings. (c) Show that the path is parabolic b eliminating the parameter. ; 39. Investigate the famil of curves defined b the parametric equations t, t 3 ct. How does the shape change as c increases? Illustrate b graphing several members of the famil. ; 4. The swallowtail catastrophe curves are defined b the parametric equations ct 4t 3, ct 3t 4. Graph several of these curves. What features do the curves have in common? How do the change when c increases? ; 4. The curves with equations a sin nt, b cos t are called Lissajous figures. Investigate how these curves var when a, b, and n var. (Take n to be a positive integer.) ; 4. Investigate the famil of curves defined b the parametric equations sin t c sin t 3 v sin t tt cos t c sin t How does the shape change as c changes? In particular, ou should identif the transitional values of c for which the basic shape of the curve changes. 9. CALCULUS WITH ARAMETRIC CURVES Having seen how to represent curves b parametric equations, we now appl the methods of calculus to these parametric curves. In particular, we solve problems involving tangents, areas, and arc length. TANGENTS Suppose f and t are differentiable functions and we want to find the tangent line at a point on the parametric curve f t, tt where is also a differentiable function of. Then the Chain Rule gives d dt d d d dt
PARAMETRIC EQUATIONS AND POLAR COORDINATES
 ARAETRIC EQUATINS AND LAR CRDINATES arametric equations and polar coordinates enable us to describe a great variet of new curves some practical, some beautiful, some fanciful, some strange. So far we have
ARAETRIC EQUATINS AND LAR CRDINATES arametric equations and polar coordinates enable us to describe a great variet of new curves some practical, some beautiful, some fanciful, some strange. So far we have
5/27/12. Objectives. Plane Curves and Parametric Equations. Sketch the graph of a curve given by a set of parametric equations.
 Objectives Sketch the graph of a curve given by a set of parametric equations. Eliminate the parameter in a set of parametric equations. Find a set of parametric equations to represent a curve. Understand
Objectives Sketch the graph of a curve given by a set of parametric equations. Eliminate the parameter in a set of parametric equations. Find a set of parametric equations to represent a curve. Understand
Lecture 34: Curves defined by Parametric equations
 Curves defined by Parametric equations When the path of a particle moving in the plane is not the graph of a function, we cannot describe it using a formula that express y directly in terms of x, or x
Curves defined by Parametric equations When the path of a particle moving in the plane is not the graph of a function, we cannot describe it using a formula that express y directly in terms of x, or x
is a plane curve and the equations are parametric equations for the curve, with parameter t.
 MATH 2412 Sections 6.3, 6.4, and 6.5 Parametric Equations and Polar Coordinates. Plane Curves and Parametric Equations Suppose t is contained in some interval I of the real numbers, and = f( t), = gt (
MATH 2412 Sections 6.3, 6.4, and 6.5 Parametric Equations and Polar Coordinates. Plane Curves and Parametric Equations Suppose t is contained in some interval I of the real numbers, and = f( t), = gt (
Polar Functions Polar coordinates
 548 Chapter 1 Parametric, Vector, and Polar Functions 1. What ou ll learn about Polar Coordinates Polar Curves Slopes of Polar Curves Areas Enclosed b Polar Curves A Small Polar Galler... and wh Polar
548 Chapter 1 Parametric, Vector, and Polar Functions 1. What ou ll learn about Polar Coordinates Polar Curves Slopes of Polar Curves Areas Enclosed b Polar Curves A Small Polar Galler... and wh Polar
Module 2, Section 2 Graphs of Trigonometric Functions
 Principles of Mathematics Section, Introduction 5 Module, Section Graphs of Trigonometric Functions Introduction You have studied trigonometric ratios since Grade 9 Mathematics. In this module ou will
Principles of Mathematics Section, Introduction 5 Module, Section Graphs of Trigonometric Functions Introduction You have studied trigonometric ratios since Grade 9 Mathematics. In this module ou will
Parametric Equations: Motion in a Plane Notes for Section 6.3. are parametric equations for the curve.
 Parametric Equations: Motion in a Plane Notes for Section 6.3 In Laman s terms: Parametric equations allow us to put and into terms of a single variable known as the parameter. Time, t, is a common parameter
Parametric Equations: Motion in a Plane Notes for Section 6.3 In Laman s terms: Parametric equations allow us to put and into terms of a single variable known as the parameter. Time, t, is a common parameter
10.1 Curves Defined by Parametric Equations
 10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? There are 2 ways to describe it: x 2 + y 2 = 1 and x = cos θ y = sin θ When
10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? There are 2 ways to describe it: x 2 + y 2 = 1 and x = cos θ y = sin θ When
To sketch the graph we need to evaluate the parameter t within the given interval to create our x and y values.
 Module 10 lesson 6 Parametric Equations. When modeling the path of an object, it is useful to use equations called Parametric equations. Instead of using one equation with two variables, we will use two
Module 10 lesson 6 Parametric Equations. When modeling the path of an object, it is useful to use equations called Parametric equations. Instead of using one equation with two variables, we will use two
PARAMETRIC EQUATIONS AND POLAR COORDINATES
 10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES A coordinate system represents a point in the plane by an ordered pair of numbers called coordinates. PARAMETRIC EQUATIONS
10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES A coordinate system represents a point in the plane by an ordered pair of numbers called coordinates. PARAMETRIC EQUATIONS
Unit 4 Trigonometry. Study Notes 1 Right Triangle Trigonometry (Section 8.1)
 Unit 4 Trigonometr Stud Notes 1 Right Triangle Trigonometr (Section 8.1) Objective: Evaluate trigonometric functions of acute angles. Use a calculator to evaluate trigonometric functions. Use trigonometric
Unit 4 Trigonometr Stud Notes 1 Right Triangle Trigonometr (Section 8.1) Objective: Evaluate trigonometric functions of acute angles. Use a calculator to evaluate trigonometric functions. Use trigonometric
9.1 Parametric Curves
 Math 172 Chapter 9A notes Page 1 of 20 9.1 Parametric Curves So far we have discussed equations in the form. Sometimes and are given as functions of a parameter. Example. Projectile Motion Sketch and axes,
Math 172 Chapter 9A notes Page 1 of 20 9.1 Parametric Curves So far we have discussed equations in the form. Sometimes and are given as functions of a parameter. Example. Projectile Motion Sketch and axes,
3.9 Differentials. Tangent Line Approximations. Exploration. Using a Tangent Line Approximation
 3.9 Differentials 3 3.9 Differentials Understand the concept of a tangent line approimation. Compare the value of the differential, d, with the actual change in,. Estimate a propagated error using a differential.
3.9 Differentials 3 3.9 Differentials Understand the concept of a tangent line approimation. Compare the value of the differential, d, with the actual change in,. Estimate a propagated error using a differential.
: = Curves Defined by Parametric Equations. Ex: Consider the unit circle from Trigonometry. What is the equation of that circle?
 10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? of 8* * # 2+-12=1 There are 2 ways to describe it: x 2 + y 2 = 1 x = cos!
10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? of 8* * # 2+-12=1 There are 2 ways to describe it: x 2 + y 2 = 1 x = cos!
Introduction to Trigonometric Functions. Peggy Adamson and Jackie Nicholas
 Mathematics Learning Centre Introduction to Trigonometric Functions Pegg Adamson and Jackie Nicholas c 998 Universit of Sdne Acknowledgements A significant part of this manuscript has previousl appeared
Mathematics Learning Centre Introduction to Trigonometric Functions Pegg Adamson and Jackie Nicholas c 998 Universit of Sdne Acknowledgements A significant part of this manuscript has previousl appeared
Precalculus 2 Section 10.6 Parametric Equations
 Precalculus 2 Section 10.6 Parametric Equations Parametric Equations Write parametric equations. Graph parametric equations. Determine an equivalent rectangular equation for parametric equations. Determine
Precalculus 2 Section 10.6 Parametric Equations Parametric Equations Write parametric equations. Graph parametric equations. Determine an equivalent rectangular equation for parametric equations. Determine
10 Polar Coordinates, Parametric Equations
 Polar Coordinates, Parametric Equations ½¼º½ ÈÓÐ Ö ÓÓÖ Ò Ø Coordinate systems are tools that let us use algebraic methods to understand geometry While the rectangular (also called Cartesian) coordinates
Polar Coordinates, Parametric Equations ½¼º½ ÈÓÐ Ö ÓÓÖ Ò Ø Coordinate systems are tools that let us use algebraic methods to understand geometry While the rectangular (also called Cartesian) coordinates
12 Polar Coordinates, Parametric Equations
 54 Chapter Polar Coordinates, Parametric Equations Polar Coordinates, Parametric Equations Just as we describe curves in the plane using equations involving x and y, so can we describe curves using equations
54 Chapter Polar Coordinates, Parametric Equations Polar Coordinates, Parametric Equations Just as we describe curves in the plane using equations involving x and y, so can we describe curves using equations
REMARKS. 8.2 Graphs of Quadratic Functions. A Graph of y = ax 2 + bx + c, where a > 0
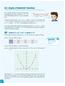 8. Graphs of Quadratic Functions In an earlier section, we have learned that the graph of the linear function = m + b, where the highest power of is 1, is a straight line. What would the shape of the graph
8. Graphs of Quadratic Functions In an earlier section, we have learned that the graph of the linear function = m + b, where the highest power of is 1, is a straight line. What would the shape of the graph
Chapter 11. Parametric Equations And Polar Coordinates
 Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
SECTION 6-8 Graphing More General Tangent, Cotangent, Secant, and Cosecant Functions
 6-8 Graphing More General Tangent, Cotangent, Secant, and Cosecant Functions 9 duce a scatter plot in the viewing window. Choose 8 for the viewing window. (B) It appears that a sine curve of the form k
6-8 Graphing More General Tangent, Cotangent, Secant, and Cosecant Functions 9 duce a scatter plot in the viewing window. Choose 8 for the viewing window. (B) It appears that a sine curve of the form k
x=2 26. y 3x Use calculus to find the area of the triangle with the given vertices. y sin x cos 2x dx 31. y sx 2 x dx
 4 CHAPTER 6 APPLICATIONS OF INTEGRATION 6. EXERCISES 4 Find the area of the shaded region.. =5-. (4, 4) =. 4. = - = (_, ) = -4 =œ + = + =.,. sin,. cos, sin,, 4. cos, cos, 5., 6., 7.,, 4, 8., 8, 4 4, =_
4 CHAPTER 6 APPLICATIONS OF INTEGRATION 6. EXERCISES 4 Find the area of the shaded region.. =5-. (4, 4) =. 4. = - = (_, ) = -4 =œ + = + =.,. sin,. cos, sin,, 4. cos, cos, 5., 6., 7.,, 4, 8., 8, 4 4, =_
Unit 13: Periodic Functions and Trig
 Date Period Unit 13: Periodic Functions and Trig Day Topic 0 Special Right Triangles and Periodic Function 1 Special Right Triangles Standard Position Coterminal Angles 2 Unit Circle Cosine & Sine (x,
Date Period Unit 13: Periodic Functions and Trig Day Topic 0 Special Right Triangles and Periodic Function 1 Special Right Triangles Standard Position Coterminal Angles 2 Unit Circle Cosine & Sine (x,
MAC Learning Objectives. Module 12 Polar and Parametric Equations. Polar and Parametric Equations. There are two major topics in this module:
 MAC 4 Module 2 Polar and Parametric Equations Learning Objectives Upon completing this module, you should be able to:. Use the polar coordinate system. 2. Graph polar equations. 3. Solve polar equations.
MAC 4 Module 2 Polar and Parametric Equations Learning Objectives Upon completing this module, you should be able to:. Use the polar coordinate system. 2. Graph polar equations. 3. Solve polar equations.
MAT1B01: Curves defined by parametric equations
 MAT1B01: Curves defined by parametric equations Dr Craig 24 October 2016 My details: acraig@uj.ac.za Consulting hours: Thursday 11h20 12h55 Friday 11h30 13h00 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
MAT1B01: Curves defined by parametric equations Dr Craig 24 October 2016 My details: acraig@uj.ac.za Consulting hours: Thursday 11h20 12h55 Friday 11h30 13h00 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
PARAMETERIZATIONS OF PLANE CURVES
 PARAMETERIZATIONS OF PLANE CURVES Suppose we want to plot the path of a particle moving in a plane. This path looks like a curve, but we cannot plot it like we would plot any other type of curve in the
PARAMETERIZATIONS OF PLANE CURVES Suppose we want to plot the path of a particle moving in a plane. This path looks like a curve, but we cannot plot it like we would plot any other type of curve in the
Chapter 10 Homework: Parametric Equations and Polar Coordinates
 Chapter 1 Homework: Parametric Equations and Polar Coordinates Name Homework 1.2 1. Consider the parametric equations x = t and y = 3 t. a. Construct a table of values for t =, 1, 2, 3, and 4 b. Plot the
Chapter 1 Homework: Parametric Equations and Polar Coordinates Name Homework 1.2 1. Consider the parametric equations x = t and y = 3 t. a. Construct a table of values for t =, 1, 2, 3, and 4 b. Plot the
20 Calculus and Structures
 0 Calculus and Structures CHAPTER FUNCTIONS Calculus and Structures Copright LESSON FUNCTIONS. FUNCTIONS A function f is a relationship between an input and an output and a set of instructions as to how
0 Calculus and Structures CHAPTER FUNCTIONS Calculus and Structures Copright LESSON FUNCTIONS. FUNCTIONS A function f is a relationship between an input and an output and a set of instructions as to how
Edexcel Mechanics 2 Kinematics of a particle. Section 1: Projectiles
 Edecel Mechanics Kinematics of a particle Section 1: Projectiles Notes and Eamples These notes contain subsections on Investigating projectiles Modelling assumptions General strateg for projectile questions
Edecel Mechanics Kinematics of a particle Section 1: Projectiles Notes and Eamples These notes contain subsections on Investigating projectiles Modelling assumptions General strateg for projectile questions
2. Find RS and the component form of RS. x. b) θ = 236, v = 35 y. b) 4i 3j c) 7( cos 200 i+ sin 200. a) 2u + v b) w 3v c) u 4v + 2w
 Pre Calculus Worksheet 6.1 For questions 1-3, let R = ( 5, 2) and S = (2, 8). 1. Sketch the vector RS and the standard position arrow for this vector. 2. Find RS and the component form of RS. 3. Show algebraicall
Pre Calculus Worksheet 6.1 For questions 1-3, let R = ( 5, 2) and S = (2, 8). 1. Sketch the vector RS and the standard position arrow for this vector. 2. Find RS and the component form of RS. 3. Show algebraicall
10.2 Calculus with Parametric Curves
 CHAPTER 1. PARAMETRIC AND POLAR 1 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t +sin() y t + cos() (a) Find the cartesian
CHAPTER 1. PARAMETRIC AND POLAR 1 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t +sin() y t + cos() (a) Find the cartesian
The Quadratic function f(x) = x 2 2x 3. y y = x 2 2x 3. We will now begin to study the graphs of the trig functions, y = sinx, y = cosx and y = tanx.
 Chapter 7 Trigonometric Graphs Introduction We have alread looked at the graphs of various functions : The Linear function f() = The Quadratic function f() = The Hperbolic function f() = = = = We will
Chapter 7 Trigonometric Graphs Introduction We have alread looked at the graphs of various functions : The Linear function f() = The Quadratic function f() = The Hperbolic function f() = = = = We will
Use Parametric notation. Interpret the effect that T has on the graph as motion.
 Learning Objectives Parametric Functions Lesson 3: Go Speed Racer! Level: Algebra 2 Time required: 90 minutes One of the main ideas of the previous lesson is that the control variable t does not appear
Learning Objectives Parametric Functions Lesson 3: Go Speed Racer! Level: Algebra 2 Time required: 90 minutes One of the main ideas of the previous lesson is that the control variable t does not appear
Polar Coordinates. Chapter 10: Parametric Equations and Polar coordinates, Section 10.3: Polar coordinates 28 / 46
 Polar Coordinates Polar Coordinates: Given any point P = (x, y) on the plane r stands for the distance from the origin (0, 0). θ stands for the angle from positive x-axis to OP. Polar coordinate: (r, θ)
Polar Coordinates Polar Coordinates: Given any point P = (x, y) on the plane r stands for the distance from the origin (0, 0). θ stands for the angle from positive x-axis to OP. Polar coordinate: (r, θ)
To graph the point (r, θ), simply go out r units along the initial ray, then rotate through the angle θ. The point (1, 5π 6. ) is graphed below:
 Polar Coordinates Any point in the plane can be described by the Cartesian coordinates (x, y), where x and y are measured along the corresponding axes. However, this is not the only way to represent points
Polar Coordinates Any point in the plane can be described by the Cartesian coordinates (x, y), where x and y are measured along the corresponding axes. However, this is not the only way to represent points
Jim Lambers MAT 169 Fall Semester Lecture 33 Notes
 Jim Lambers MAT 169 Fall Semester 2009-10 Lecture 33 Notes These notes correspond to Section 9.3 in the text. Polar Coordinates Throughout this course, we have denoted a point in the plane by an ordered
Jim Lambers MAT 169 Fall Semester 2009-10 Lecture 33 Notes These notes correspond to Section 9.3 in the text. Polar Coordinates Throughout this course, we have denoted a point in the plane by an ordered
MATH 1020 WORKSHEET 10.1 Parametric Equations
 MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
Unit 6 Introduction to Trigonometry The Unit Circle (Unit 6.3)
 Unit Introduction to Trigonometr The Unit Circle Unit.) William Bill) Finch Mathematics Department Denton High School Introduction Trig Functions Circle Quadrental Angles Other Angles Unit Circle Periodic
Unit Introduction to Trigonometr The Unit Circle Unit.) William Bill) Finch Mathematics Department Denton High School Introduction Trig Functions Circle Quadrental Angles Other Angles Unit Circle Periodic
Try It. Implicit and Explicit Functions. Video. Exploration A. Differentiating with Respect to x
 SECTION 5 Implicit Differentiation Section 5 Implicit Differentiation Distinguish between functions written in implicit form an eplicit form Use implicit ifferentiation to fin the erivative of a function
SECTION 5 Implicit Differentiation Section 5 Implicit Differentiation Distinguish between functions written in implicit form an eplicit form Use implicit ifferentiation to fin the erivative of a function
: = Curves Defined by Parametric Equations. Ex: Consider the unit circle from Trigonometry. What is the equation of that circle?
 10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? of 8* * # 2+-121 There are 2 ways to describe it: x 2 + y 2 1 x cos! : 9
10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? of 8* * # 2+-121 There are 2 ways to describe it: x 2 + y 2 1 x cos! : 9
48. Logistic Growth (BC) Classwork
 48. Logistic Growth (BC) Classwork Using the exponential growth model, the growth of a population is proportion to its current size. The differential equation for exponential growth is dp = kp leading
48. Logistic Growth (BC) Classwork Using the exponential growth model, the growth of a population is proportion to its current size. The differential equation for exponential growth is dp = kp leading
13.2. General Angles and Radian Measure. What you should learn
 Page 1 of 1. General Angles and Radian Measure What ou should learn GOAL 1 Measure angles in standard position using degree measure and radian measure. GOAL Calculate arc lengths and areas of sectors,
Page 1 of 1. General Angles and Radian Measure What ou should learn GOAL 1 Measure angles in standard position using degree measure and radian measure. GOAL Calculate arc lengths and areas of sectors,
Transformations of Functions. 1. Shifting, reflecting, and stretching graphs Symmetry of functions and equations
 Chapter Transformations of Functions TOPICS.5.. Shifting, reflecting, and stretching graphs Smmetr of functions and equations TOPIC Horizontal Shifting/ Translation Horizontal Shifting/ Translation Shifting,
Chapter Transformations of Functions TOPICS.5.. Shifting, reflecting, and stretching graphs Smmetr of functions and equations TOPIC Horizontal Shifting/ Translation Horizontal Shifting/ Translation Shifting,
Implicit and Explicit Functions
 60_005.q //0 :5 PM Page SECTION.5 Implicit Differentiation Section.5 EXPLORATION Graphing an Implicit Equation How coul ou use a graphing utilit to sketch the graph of the equation? Here are two possible
60_005.q //0 :5 PM Page SECTION.5 Implicit Differentiation Section.5 EXPLORATION Graphing an Implicit Equation How coul ou use a graphing utilit to sketch the graph of the equation? Here are two possible
Let be a function. We say, is a plane curve given by the. Let a curve be given by function where is differentiable with continuous.
 Module 8 : Applications of Integration - II Lecture 22 : Arc Length of a Plane Curve [Section 221] Objectives In this section you will learn the following : How to find the length of a plane curve 221
Module 8 : Applications of Integration - II Lecture 22 : Arc Length of a Plane Curve [Section 221] Objectives In this section you will learn the following : How to find the length of a plane curve 221
x y 2 2 CONIC SECTIONS Problem 1
 CONIC SECTIONS Problem For the equations below, identify each conic section If it s a parabola, specify its vertex, focus and directrix If it s an ellipse, specify its center, vertices and foci If it s
CONIC SECTIONS Problem For the equations below, identify each conic section If it s a parabola, specify its vertex, focus and directrix If it s an ellipse, specify its center, vertices and foci If it s
LESSON 3.1 INTRODUCTION TO GRAPHING
 LESSON 3.1 INTRODUCTION TO GRAPHING LESSON 3.1 INTRODUCTION TO GRAPHING 137 OVERVIEW Here s what ou ll learn in this lesson: Plotting Points a. The -plane b. The -ais and -ais c. The origin d. Ordered
LESSON 3.1 INTRODUCTION TO GRAPHING LESSON 3.1 INTRODUCTION TO GRAPHING 137 OVERVIEW Here s what ou ll learn in this lesson: Plotting Points a. The -plane b. The -ais and -ais c. The origin d. Ordered
Name: Date: 1. Match the equation with its graph. Page 1
 Name: Date: 1. Match the equation with its graph. y 6x A) C) Page 1 D) E) Page . Match the equation with its graph. ( x3) ( y3) A) C) Page 3 D) E) Page 4 3. Match the equation with its graph. ( x ) y 1
Name: Date: 1. Match the equation with its graph. y 6x A) C) Page 1 D) E) Page . Match the equation with its graph. ( x3) ( y3) A) C) Page 3 D) E) Page 4 3. Match the equation with its graph. ( x ) y 1
Date Lesson Text TOPIC Homework. Getting Started Pg. 314 # 1-7. Radian Measure and Special Angles Sine and Cosine CAST
 UNIT 5 TRIGONOMETRIC FUNCTIONS Date Lesson Text TOPIC Homework Oct. 0 5.0 (50).0 Getting Started Pg. # - 7 Nov. 5. (5). Radian Measure Angular Velocit Pg. 0 # ( 9)doso,,, a Nov. 5 Nov. 5. (5) 5. (5)..
UNIT 5 TRIGONOMETRIC FUNCTIONS Date Lesson Text TOPIC Homework Oct. 0 5.0 (50).0 Getting Started Pg. # - 7 Nov. 5. (5). Radian Measure Angular Velocit Pg. 0 # ( 9)doso,,, a Nov. 5 Nov. 5. (5) 5. (5)..
Contents. How You May Use This Resource Guide
 Contents How You Ma Use This Resource Guide ii 0 Trigonometric Formulas, Identities, and Equations Worksheet 0.: Graphical Analsis of Trig Identities.............. Worksheet 0.: Verifing Trigonometric
Contents How You Ma Use This Resource Guide ii 0 Trigonometric Formulas, Identities, and Equations Worksheet 0.: Graphical Analsis of Trig Identities.............. Worksheet 0.: Verifing Trigonometric
A Quick Review of Trigonometry
 A Quick Review of Trigonometry As a starting point, we consider a ray with vertex located at the origin whose head is pointing in the direction of the positive real numbers. By rotating the given ray (initial
A Quick Review of Trigonometry As a starting point, we consider a ray with vertex located at the origin whose head is pointing in the direction of the positive real numbers. By rotating the given ray (initial
Appendix C: Review of Graphs, Equations, and Inequalities
 Appendi C: Review of Graphs, Equations, and Inequalities C. What ou should learn Just as ou can represent real numbers b points on a real number line, ou can represent ordered pairs of real numbers b points
Appendi C: Review of Graphs, Equations, and Inequalities C. What ou should learn Just as ou can represent real numbers b points on a real number line, ou can represent ordered pairs of real numbers b points
Trigonometry Review Day 1
 Name Trigonometry Review Day 1 Algebra II Rotations and Angle Terminology II Terminal y I Positive angles rotate in a counterclockwise direction. Reference Ray Negative angles rotate in a clockwise direction.
Name Trigonometry Review Day 1 Algebra II Rotations and Angle Terminology II Terminal y I Positive angles rotate in a counterclockwise direction. Reference Ray Negative angles rotate in a clockwise direction.
Graphs and Functions
 CHAPTER Graphs and Functions. Graphing Equations. Introduction to Functions. Graphing Linear Functions. The Slope of a Line. Equations of Lines Integrated Review Linear Equations in Two Variables.6 Graphing
CHAPTER Graphs and Functions. Graphing Equations. Introduction to Functions. Graphing Linear Functions. The Slope of a Line. Equations of Lines Integrated Review Linear Equations in Two Variables.6 Graphing
8.6 Three-Dimensional Cartesian Coordinate System
 SECTION 8.6 Three-Dimensional Cartesian Coordinate Sstem 69 What ou ll learn about Three-Dimensional Cartesian Coordinates Distance and Midpoint Formulas Equation of a Sphere Planes and Other Surfaces
SECTION 8.6 Three-Dimensional Cartesian Coordinate Sstem 69 What ou ll learn about Three-Dimensional Cartesian Coordinates Distance and Midpoint Formulas Equation of a Sphere Planes and Other Surfaces
10.2 Calculus with Parametric Curves
 CHAPTER 1. PARAMETRIC AND POLAR 91 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t + sin() y t + cos() (a) Find the Cartesian
CHAPTER 1. PARAMETRIC AND POLAR 91 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t + sin() y t + cos() (a) Find the Cartesian
Glossary alternate interior angles absolute value function Example alternate exterior angles Example angle of rotation Example
 Glossar A absolute value function An absolute value function is a function that can be written in the form, where is an number or epression. alternate eterior angles alternate interior angles Alternate
Glossar A absolute value function An absolute value function is a function that can be written in the form, where is an number or epression. alternate eterior angles alternate interior angles Alternate
Essential Question What are the characteristics of the graph of the tangent function?
 8.5 Graphing Other Trigonometric Functions Essential Question What are the characteristics of the graph of the tangent function? Graphing the Tangent Function Work with a partner. a. Complete the table
8.5 Graphing Other Trigonometric Functions Essential Question What are the characteristics of the graph of the tangent function? Graphing the Tangent Function Work with a partner. a. Complete the table
7-5 Parametric Equations
 3. Sketch the curve given by each pair of parametric equations over the given interval. Make a table of values for 6 t 6. t x y 6 19 28 5 16.5 17 4 14 8 3 11.5 1 2 9 4 1 6.5 7 0 4 8 1 1.5 7 2 1 4 3 3.5
3. Sketch the curve given by each pair of parametric equations over the given interval. Make a table of values for 6 t 6. t x y 6 19 28 5 16.5 17 4 14 8 3 11.5 1 2 9 4 1 6.5 7 0 4 8 1 1.5 7 2 1 4 3 3.5
Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves
 Block #1: Vector-Valued Functions Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves 1 The Calculus of Moving Objects Problem.
Block #1: Vector-Valued Functions Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves 1 The Calculus of Moving Objects Problem.
In this chapter, we will investigate what have become the standard applications of the integral:
 Chapter 8 Overview: Applications of Integrals Calculus, like most mathematical fields, began with trying to solve everyday problems. The theory and operations were formalized later. As early as 70 BC,
Chapter 8 Overview: Applications of Integrals Calculus, like most mathematical fields, began with trying to solve everyday problems. The theory and operations were formalized later. As early as 70 BC,
5.6 Translations and Combinations of Transformations
 5.6 Translations and Combinations of Transformations The highest tides in the world are found in the Ba of Fund. Tides in one area of the ba cause the water level to rise to 6 m above average sea level
5.6 Translations and Combinations of Transformations The highest tides in the world are found in the Ba of Fund. Tides in one area of the ba cause the water level to rise to 6 m above average sea level
Math 370 Exam 5 Review Name
 Math 370 Exam 5 Review Name Graph the ellipse and locate the foci. 1) x2 6 + y2 = 1 1) Objective: (9.1) Graph Ellipses Not Centered at the Origin Graph the ellipse. 2) (x + 2)2 + (y + 1)2 9 = 1 2) Objective:
Math 370 Exam 5 Review Name Graph the ellipse and locate the foci. 1) x2 6 + y2 = 1 1) Objective: (9.1) Graph Ellipses Not Centered at the Origin Graph the ellipse. 2) (x + 2)2 + (y + 1)2 9 = 1 2) Objective:
The diagram above shows a sketch of the curve C with parametric equations
 1. The diagram above shows a sketch of the curve C with parametric equations x = 5t 4, y = t(9 t ) The curve C cuts the x-axis at the points A and B. (a) Find the x-coordinate at the point A and the x-coordinate
1. The diagram above shows a sketch of the curve C with parametric equations x = 5t 4, y = t(9 t ) The curve C cuts the x-axis at the points A and B. (a) Find the x-coordinate at the point A and the x-coordinate
2.3 Circular Functions of Real Numbers
 www.ck12.org Chapter 2. Graphing Trigonometric Functions 2.3 Circular Functions of Real Numbers Learning Objectives Graph the six trigonometric ratios as functions on the Cartesian plane. Identify the
www.ck12.org Chapter 2. Graphing Trigonometric Functions 2.3 Circular Functions of Real Numbers Learning Objectives Graph the six trigonometric ratios as functions on the Cartesian plane. Identify the
Section 9.3: Functions and their Graphs
 Section 9.: Functions and their Graphs Graphs provide a wa of displaing, interpreting, and analzing data in a visual format. In man problems, we will consider two variables. Therefore, we will need to
Section 9.: Functions and their Graphs Graphs provide a wa of displaing, interpreting, and analzing data in a visual format. In man problems, we will consider two variables. Therefore, we will need to
CALCULUS II. Parametric Equations and Polar Coordinates. Paul Dawkins
 CALCULUS II Parametric Equations and Polar Coordinates Paul Dawkins Table of Contents Preface... ii Parametric Equations and Polar Coordinates... 3 Introduction... 3 Parametric Equations and Curves...
CALCULUS II Parametric Equations and Polar Coordinates Paul Dawkins Table of Contents Preface... ii Parametric Equations and Polar Coordinates... 3 Introduction... 3 Parametric Equations and Curves...
(i) Find the exact value of p. [4] Show that the area of the shaded region bounded by the curve, the x-axis and the line
![(i) Find the exact value of p. [4] Show that the area of the shaded region bounded by the curve, the x-axis and the line (i) Find the exact value of p. [4] Show that the area of the shaded region bounded by the curve, the x-axis and the line](/thumbs/90/103919535.jpg) H Math : Integration Apps 0. M p The diagram shows the curve e e and its maimum point M. The -coordinate of M is denoted b p. (i) Find the eact value of p. [] (ii) Show that the area of the shaded region
H Math : Integration Apps 0. M p The diagram shows the curve e e and its maimum point M. The -coordinate of M is denoted b p. (i) Find the eact value of p. [] (ii) Show that the area of the shaded region
Parametric and Polar Curves
 Chapter 2 Parametric and Polar Curves 2.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves Parametric Equations So far we ve described a curve by giving an equation that the coordinates
Chapter 2 Parametric and Polar Curves 2.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves Parametric Equations So far we ve described a curve by giving an equation that the coordinates
Updated: August 24, 2016 Calculus III Section Math 232. Calculus III. Brian Veitch Fall 2015 Northern Illinois University
 Updated: August 24, 216 Calculus III Section 1.2 Math 232 Calculus III Brian Veitch Fall 215 Northern Illinois University 1.2 Calculus with Parametric Curves Definition 1: First Derivative of a Parametric
Updated: August 24, 216 Calculus III Section 1.2 Math 232 Calculus III Brian Veitch Fall 215 Northern Illinois University 1.2 Calculus with Parametric Curves Definition 1: First Derivative of a Parametric
MAT01B1: Curves defined by parametric equations
 MAT01B1: Curves defined by parametric equations Dr Craig 10 October 2018 My details: acraig@uj.ac.za Consulting hours: Monday 14h40 15h25 Thursday 11h20 12h55 Friday 11h20 12h55 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
MAT01B1: Curves defined by parametric equations Dr Craig 10 October 2018 My details: acraig@uj.ac.za Consulting hours: Monday 14h40 15h25 Thursday 11h20 12h55 Friday 11h20 12h55 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
Think About. Unit 5 Lesson 3. Investigation. This Situation. Name: a Where do you think the origin of a coordinate system was placed in creating this
 Think About This Situation Unit 5 Lesson 3 Investigation 1 Name: Eamine how the sequence of images changes from frame to frame. a Where do ou think the origin of a coordinate sstem was placed in creating
Think About This Situation Unit 5 Lesson 3 Investigation 1 Name: Eamine how the sequence of images changes from frame to frame. a Where do ou think the origin of a coordinate sstem was placed in creating
Parametric and Polar Curves
 Chapter 2 Parametric and Polar Curves 2.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves Parametric Equations So far we ve described a curve by giving an equation that the coordinates
Chapter 2 Parametric and Polar Curves 2.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves Parametric Equations So far we ve described a curve by giving an equation that the coordinates
Parametric and Polar Curves
 Chapter 2 Parametric and Polar Curves 2.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves Parametric Equations So far we ve described a curve by giving an equation that the coordinates
Chapter 2 Parametric and Polar Curves 2.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves Parametric Equations So far we ve described a curve by giving an equation that the coordinates
turn counterclockwise from the positive x-axis. However, we could equally well get to this point by a 3 4 turn clockwise, giving (r, θ) = (1, 3π 2
 Math 133 Polar Coordinates Stewart 10.3/I,II Points in polar coordinates. The first and greatest achievement of modern mathematics was Descartes description of geometric objects b numbers, using a sstem
Math 133 Polar Coordinates Stewart 10.3/I,II Points in polar coordinates. The first and greatest achievement of modern mathematics was Descartes description of geometric objects b numbers, using a sstem
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
4.1 Angles and Angle Measure. 1, multiply by
 4.1 Angles and Angle Measure Angles can be measured in degrees or radians. Angle measures without units are considered to be in radians. Radian: One radian is the measure of the central angle subtended
4.1 Angles and Angle Measure Angles can be measured in degrees or radians. Angle measures without units are considered to be in radians. Radian: One radian is the measure of the central angle subtended
8.5. Quadratic Function A function f is a quadratic function if f(x) ax 2 bx c, where a, b, and c are real numbers, with a 0.
 8.5 Quadratic Functions, Applications, and Models In the previous section we discussed linear functions, those that are defined b firstdegree polnomials. In this section we will look at quadratic functions,
8.5 Quadratic Functions, Applications, and Models In the previous section we discussed linear functions, those that are defined b firstdegree polnomials. In this section we will look at quadratic functions,
AREA OF A SURFACE OF REVOLUTION
 AREA OF A SURFACE OF REVOLUTION h cut r πr h A surface of revolution is formed when a curve is rotated about a line. Such a surface is the lateral boundar of a solid of revolution of the tpe discussed
AREA OF A SURFACE OF REVOLUTION h cut r πr h A surface of revolution is formed when a curve is rotated about a line. Such a surface is the lateral boundar of a solid of revolution of the tpe discussed
dt Acceleration is the derivative of velocity with respect to time. If a body's position at time t is S = f(t), the body's acceleration at time t is
 APPLICATIN F DERIVATIVE INTRDUCTIN In this section we eamine some applications in which derivatives are used to represent and interpret the rates at which things change in the world around us. Let S be
APPLICATIN F DERIVATIVE INTRDUCTIN In this section we eamine some applications in which derivatives are used to represent and interpret the rates at which things change in the world around us. Let S be
5-2 Verifying Trigonometric Identities
 5- Verifying Trigonometric Identities Verify each identity. 1. (sec 1) cos = sin 3. sin sin 3 = sin cos 4 5. = cot 7. = cot 9. + tan = sec Page 1 5- Verifying Trigonometric Identities 7. = cot 9. + tan
5- Verifying Trigonometric Identities Verify each identity. 1. (sec 1) cos = sin 3. sin sin 3 = sin cos 4 5. = cot 7. = cot 9. + tan = sec Page 1 5- Verifying Trigonometric Identities 7. = cot 9. + tan
Differential Geometry MAT WEEKLY PROGRAM 1-2
 15.09.014 WEEKLY PROGRAM 1- The first week, we will talk about the contents of this course and mentioned the theory of curves and surfaces by giving the relation and differences between them with aid of
15.09.014 WEEKLY PROGRAM 1- The first week, we will talk about the contents of this course and mentioned the theory of curves and surfaces by giving the relation and differences between them with aid of
Answers. Investigation 4. ACE Assignment Choices. Applications
 Answers Investigation ACE Assignment Choices Problem. Core Other Connections, ; Etensions ; unassigned choices from previous problems Problem. Core, 7 Other Applications, ; Connections ; Etensions ; unassigned
Answers Investigation ACE Assignment Choices Problem. Core Other Connections, ; Etensions ; unassigned choices from previous problems Problem. Core, 7 Other Applications, ; Connections ; Etensions ; unassigned
Math 259 Winter Unit Test 1 Review Problems Set B
 Math 259 Winter 2009 Unit Test 1 Review Problems Set B We have chosen these problems because we think that they are representative of many of the mathematical concepts that we have studied. There is no
Math 259 Winter 2009 Unit Test 1 Review Problems Set B We have chosen these problems because we think that they are representative of many of the mathematical concepts that we have studied. There is no
Chapter 5. An Introduction to Trigonometric Functions 1-1
 Chapter 5 An Introduction to Trigonometric Functions Copyright (c) The McGraw-Hill Companies, Inc. Permission required for reproduction or display. 1-1 5.1 A half line or all points extended from a single
Chapter 5 An Introduction to Trigonometric Functions Copyright (c) The McGraw-Hill Companies, Inc. Permission required for reproduction or display. 1-1 5.1 A half line or all points extended from a single
APPLICATIONS OF INTEGRATION
 6 APPLICATIONS OF INTEGRATION The volume of a sphere is the limit of sums of volumes of approimating clinders. In this chapter we eplore some of the applications of the definite integral b using it to
6 APPLICATIONS OF INTEGRATION The volume of a sphere is the limit of sums of volumes of approimating clinders. In this chapter we eplore some of the applications of the definite integral b using it to
GRAPHS AND GRAPHICAL SOLUTION OF EQUATIONS
 GRAPHS AND GRAPHICAL SOLUTION OF EQUATIONS 1.1 DIFFERENT TYPES AND SHAPES OF GRAPHS: A graph can be drawn to represent are equation connecting two variables. There are different tpes of equations which
GRAPHS AND GRAPHICAL SOLUTION OF EQUATIONS 1.1 DIFFERENT TYPES AND SHAPES OF GRAPHS: A graph can be drawn to represent are equation connecting two variables. There are different tpes of equations which
Volumes of Solids of Revolution Lecture #6 a
 Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
INTRODUCTION TO LINE INTEGRALS
 INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
STRAND G: Relations, Functions and Graphs
 UNIT G Using Graphs to Solve Equations: Tet STRAND G: Relations, Functions and Graphs G Using Graphs to Solve Equations Tet Contents * * Section G. Solution of Simultaneous Equations b Graphs G. Graphs
UNIT G Using Graphs to Solve Equations: Tet STRAND G: Relations, Functions and Graphs G Using Graphs to Solve Equations Tet Contents * * Section G. Solution of Simultaneous Equations b Graphs G. Graphs
Pre-calculus Chapter 4 Part 1 NAME: P.
 Pre-calculus NAME: P. Date Day Lesson Assigned Due 2/12 Tuesday 4.3 Pg. 284: Vocab: 1-3. Ex: 1, 2, 7-13, 27-32, 43, 44, 47 a-c, 57, 58, 63-66 (degrees only), 69, 72, 74, 75, 78, 79, 81, 82, 86, 90, 94,
Pre-calculus NAME: P. Date Day Lesson Assigned Due 2/12 Tuesday 4.3 Pg. 284: Vocab: 1-3. Ex: 1, 2, 7-13, 27-32, 43, 44, 47 a-c, 57, 58, 63-66 (degrees only), 69, 72, 74, 75, 78, 79, 81, 82, 86, 90, 94,
4.6 Graphs of Other Trigonometric Functions
 .6 Graphs of Other Trigonometric Functions Section.6 Graphs of Other Trigonometric Functions 09 Graph of the Tangent Function Recall that the tangent function is odd. That is, tan tan. Consequentl, the
.6 Graphs of Other Trigonometric Functions Section.6 Graphs of Other Trigonometric Functions 09 Graph of the Tangent Function Recall that the tangent function is odd. That is, tan tan. Consequentl, the
Polar Coordinates. OpenStax. 1 Dening Polar Coordinates
 OpenStax-CNX module: m53852 1 Polar Coordinates OpenStax This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License 4.0 Abstract Locate points
OpenStax-CNX module: m53852 1 Polar Coordinates OpenStax This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License 4.0 Abstract Locate points
3.2 Exercises. rise y (ft) run x (ft) Section 3.2 Slope Suppose you are riding a bicycle up a hill as shown below.
 Section 3.2 Slope 261 3.2 Eercises 1. Suppose ou are riding a biccle up a hill as shown below. Figure 1. Riding a biccle up a hill. a) If the hill is straight as shown, consider the slant, or steepness,
Section 3.2 Slope 261 3.2 Eercises 1. Suppose ou are riding a biccle up a hill as shown below. Figure 1. Riding a biccle up a hill. a) If the hill is straight as shown, consider the slant, or steepness,
MA 154 PRACTICE QUESTIONS FOR THE FINAL 11/ The angles with measures listed are all coterminal except: 5π B. A. 4
 . If θ is in the second quadrant and sinθ =.6, find cosθ..7.... The angles with measures listed are all coterminal except: E. 6. The radian measure of an angle of is: 7. Use a calculator to find the sec
. If θ is in the second quadrant and sinθ =.6, find cosθ..7.... The angles with measures listed are all coterminal except: E. 6. The radian measure of an angle of is: 7. Use a calculator to find the sec
Investigation Free Fall
 Investigation Free Fall Name Period Date You will need: a motion sensor, a small pillow or other soft object What function models the height of an object falling due to the force of gravit? Use a motion
Investigation Free Fall Name Period Date You will need: a motion sensor, a small pillow or other soft object What function models the height of an object falling due to the force of gravit? Use a motion
Graphing f ( x) = ax 2 + c
 . Graphing f ( ) = a + c Essential Question How does the value of c affect the graph of f () = a + c? Graphing = a + c Work with a partner. Sketch the graphs of the functions in the same coordinate plane.
. Graphing f ( ) = a + c Essential Question How does the value of c affect the graph of f () = a + c? Graphing = a + c Work with a partner. Sketch the graphs of the functions in the same coordinate plane.
ENGI Parametric & Polar Curves Page 2-01
 ENGI 3425 2. Parametric & Polar Curves Page 2-01 2. Parametric and Polar Curves Contents: 2.1 Parametric Vector Functions 2.2 Parametric Curve Sketching 2.3 Polar Coordinates r f 2.4 Polar Curve Sketching
ENGI 3425 2. Parametric & Polar Curves Page 2-01 2. Parametric and Polar Curves Contents: 2.1 Parametric Vector Functions 2.2 Parametric Curve Sketching 2.3 Polar Coordinates r f 2.4 Polar Curve Sketching
4.4. Concavity and Curve Sketching. Concavity
 4.4 Concavit and Curve Sketching 267 4.4 Concavit and Curve Sketching f' decreases CONCAVE DOWN 3 f' increases 0 CONCAVE UP FIGURE 4.25 The graph of ƒsd = 3 is concave down on s - q, 0d and concave up
4.4 Concavit and Curve Sketching 267 4.4 Concavit and Curve Sketching f' decreases CONCAVE DOWN 3 f' increases 0 CONCAVE UP FIGURE 4.25 The graph of ƒsd = 3 is concave down on s - q, 0d and concave up
PROJECTILE. 5) Define the terms Velocity as related to projectile motion: 6) Define the terms angle of projection as related to projectile motion:
 1) Define Trajectory a) The path traced by particle in air b) The particle c) Vertical Distance d) Horizontal Distance PROJECTILE 2) Define Projectile a) The path traced by particle in air b) The particle
1) Define Trajectory a) The path traced by particle in air b) The particle c) Vertical Distance d) Horizontal Distance PROJECTILE 2) Define Projectile a) The path traced by particle in air b) The particle
