Red-black tree. Background and terminology. Uses and advantages
|
|
|
- Melvin Phillips
- 5 years ago
- Views:
Transcription
1 Red-black tree A red-black tree is a type of self-balancing binary search tree, a data structure used in computer science, typically used to implement associative arrays. The original structure was invented in 1972 by Rudolf Bayer who called them "symmetric binary B-trees", but acquired its modern name in a paper in 1978 by Leo J. Guibas and Robert Sedgewick. It is complex, but has good worst-case running time for its operations and is efficient in practice: it can search, insert, and delete in O(log n) time, where n is the number of elements in the tree. Background and terminology A red-black tree is a special type of binary tree, which is a structure used in computer science to organize pieces of comparable data, such as numbers. Each piece of data is stored in a node. One of the nodes always functions as our starting place, and is not the child of any node; we call this the root node or root. It has up to two "children", other nodes to which it connects. Each of these children can have up to two children of its own, and so on. The root node thus has a path connecting it to any other node in the tree. If a node has no children, we call it a leaf node, since intuitively it is at the periphery of the tree. A subtree is the portion of the tree that can be reached from a certain node, considered as a tree itself. In red-black trees, the leaves are assumed to be null, that is, they do not contain any data. As red-black trees are also binary search trees, they satisfy the constraint that every node contains a value less than or equal to all nodes in its left subtree, and greater than or equal to all nodes in its right subtree. This makes it quick to search the tree for a given value, and allows efficient in-order traversal of elements. Uses and advantages Red-black trees, along with AVL trees, offer the best possible worst-case guarantees for insertion time, deletion time, and search time. Not only does this make them valuable in time-sensitive applications such as real-time applications, but it makes them valuable building blocks in other data structures which provide worst-case guarantees; for example, many data structures used in computational geometry can be based on red-black trees. Red-black trees are also particularly valuable in functional programming, where they are one of the most common persistent data structures, used to construct associative arrays and sets which can retain previous versions after mutations. The persistent version of redblack trees requires O(log n) space for each insertion or deletion, in addition to time.
2 Red-black trees are an isometry of trees. In other words, for every tree, there exists at least one red-black tree with data elements in the same order. The insertion and deletion operations on trees are also equivalent to color-flipping and rotations in red-black trees. This makes trees an important tool for understanding the logic behind red-black trees, and this is why many introductory algorithm texts introduce trees just before red-black trees, even though trees are not often used in practice. Properties A red-black tree is a binary search tree where each node has a color attribute, the value of which is either red or black. In addition to the ordinary requirements imposed on binary search trees, we make the following additional requirements of any valid red-black tree: 1. A node is either red or black. 2. The root is black. 3. All leaves are black. (This includes the NIL children) 4. Both children of every red node are black. (i.e. Every red node must have a black parent.) 5. All paths from any given node to its leaf nodes contain the same number of black nodes. These constraints enforce a critical property of red-black trees: that the longest possible path from the root to a leaf is no more than twice as long as the shortest possible path. The result is that the tree is roughly balanced. Since operations such as inserting, deleting, and finding values requires worst-case time proportional to the height of the tree, this theoretical upper bound on the height allows red-black trees to be efficient in the worst-case, unlike ordinary binary search trees. To see why these properties guarantee this, it suffices to note that no path can have two red nodes in a row, due to property 4. The shortest possible path has all black nodes, and the longest possible path alternates between red and black nodes. Since all maximal paths have the same number of black nodes, by property 5, this shows that no path is more than twice as long as any other path.
3 In many presentations of tree data structures, it is possible for a node to have only one child, and leaf nodes contain data. It is possible to present red-black trees in this paradigm, but it changes several of the properties and complicates the algorithms. For this reason, in this article we use "nil leaves" or "null leaves", which contain no data and merely serve to indicate where the tree ends, as shown above. These nodes are often omitted in drawings, resulting in a tree which seems to contradict the above principles, but which in fact does not. A consequence of this is that all internal (non-leaf) nodes have two children, although one or more of those children may be a null leaf. Some explain a red-black tree as a binary search tree whose edges, instead of nodes, are colored in red or black, but this does not make any difference. The color of a node in our terminology corresponds to the color of the edge connecting the node to its parent, except that the root node is always black in our terminology (property 2) whereas the corresponding edge does not exist. Operations Read-only operations on a red-black tree require no modification from those used for binary search trees, because every red-black tree is a specialization of a simple binary search tree. However, the immediate result of an insertion or removal may violate the properties of a red-black tree. Restoring the red-black properties requires a small number (O(log n) or amortized O(1)) of color changes (which are very quick in practice) and no more than three tree rotations (two for insertion). Although insert and delete operations are complicated, their times remain O(log n). Insertion We begin by adding the node as we would in a simple binary search tree and coloring it red. What happens next depends on the color of other nearby nodes. We will use the term uncle node to refer to the sibling of a node's parent, as in human family trees. Note that: Property 3 (All leaves, including nils, are black) always holds. Property 4 (Both children of every red node are black) is threatened only by adding a red node, repainting a black node red, or a rotation. Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) is threatened only by adding a black node, repainting a red node black, or a rotation. Note: We'll use the label N for the node being inserted, P for N's parent node, G for N's grandparent, and U for N's uncle. Note, that in between some cases, we exchange the roles and labels of the nodes, but in each case, every label continues to represent the same node it represented at the beginning of the case. Any color shown in the diagram is either assumed in its case or implied by these assumptions.
4 We'll demonstrate each case with example C code. The uncle and grandparent nodes can be found by these functions: node grandparent(node n) { return n->parent->parent; node uncle(node n) { if (n->parent == grandparent(n)->left) return grandparent(n)->right; return grandparent(n)->left; Case 1: The new node N is at the root of the tree. In this case, we repaint it black to satisfy Property 2 (The root is black). Since this adds one black node to every path at once, Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) is not violated. void insert_case1(node n) { if (n->parent == NULL) n->color = BLACK; insert_case2(n); Case 2: The new node's parent P is black, so Property 4 (Both children of every red node are black) is not invalidated. In this case, the tree is still valid. Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) is threatened, because the new node N has two black leaf children, but because N is red, the paths through each of its children have the same number of black nodes as the path through the leaf it replaced, which was black, and so this property remains satisfied. void insert_case2(node n) { if (n->parent->color == BLACK) return; /* Tree is still valid */ insert_case3(n); Note: In the following cases we can assume that N has a grandparent node G, because its parent P is red, and if it were the root, it would be black. Thus, N also has an uncle node U, although it may be a leaf in cases 4 and 5.
5 Case 3: If both the parent P and the uncle U are red, then we can repaint them both black and repaint the grandparent G red (to maintain Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes)). Now our new red node N has a black parent. Since any path through the parent or uncle must pass through the grandparent, the number of black nodes on these paths has not changed. However, the grandparent G may now violate properties 2 (The root is black) or 4 (Both children of every red node are black). To fix this, we perform this entire procedure recursively on G from case 1. Note that this is the only recursive call, and it occurs prior to any rotations, which proves that a constant number of rotations occur. void insert_case3(node n) { if (uncle(n)!= NULL && uncle(n)->color == RED) { n->parent->color = BLACK; uncle(n)->color = BLACK; grandparent(n)->color = RED; insert_case1(grandparent(n)); insert_case4(n); Note: In the remaining cases, we assume the parent node P is the left child of its parent. If it is the right child, left and right should be reversed throughout cases 4 and 5. The code samples take care of this. Case 4: The parent P is red but the uncle U is black; also, the new node N is the right child of P, and P in turn is the left child of its parent G. In this case, we can perform a left rotation that switches the roles of the new node N and its parent P; then, we deal with the former parent node P using Case 5 (relabeling N and P). This causes some paths (those in the tree labelled "1") to pass through the new node where they did not before, but both these nodes are red, so Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) is not violated. void insert_case4(node n) { if (n == n->parent->right && n->parent == grandparent(n)->left) { rotate_left(n->parent); n = n->left; if (n == n->parent->left && n->parent == grandparent(n)- >right) { rotate_right(n->parent); n = n->right; insert_case5(n);
6 Case 5: The parent P is red but the uncle U is black, the new node N is the left child of P, and P is the left child of its parent G. In this case, we perform a right rotation on the grandparent G; the result is a tree where the former parent P is now the parent of both the new node N and the former grandparent G. We know that G is black, since its former child P could not have been red otherwise. We then switch the colors of P and G, and the resulting tree satisfies Property 4 (Both children of every red node are black). Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) also remains satisfied, since all paths that went through any of these three nodes went through G before, and now they all go through P. In each case, this is the only black node of the three. void insert_case5(node n) { n->parent->color = BLACK; grandparent(n)->color = RED; if (n == n->parent->left && n->parent == grandparent(n)->left) { rotate_right(grandparent(n)); { /* Here, n == n->parent->right && n->parent == grandparent(n)- >right */ rotate_left(grandparent(n)); Note that inserting is actually in-place, since all the calls above use tail recursion. Removal In a normal binary search tree, when deleting a node with two non-leaf children, we find either the maximum element in its left subtree or the minimum element in its right subtree, and move its value into the node being deleted (as shown here). We then delete the node we copied the value from, which must have less than two non-leaf children. Because merely copying a value does not violate any red-black properties, this reduces the problem of deleting to the problem of deleting a node with at most one child. It doesn't matter whether this node is the node we originally wanted to delete or the node we copied the value from. For the remainder of this discussion we can assume we're deleting a node with at most one non-leaf child, which we'll call its child (if it has only leaf children, let one of them be its child). If we are deleting a red node, we can simply replace it with its child, which must be black. All paths through the deleted node will simply pass through one less red
7 node, and both the deleted node's parent and child must be black, so properties 3 (All leaves, including nils, are black) and 4 (Both children of every red node are black) still hold. Another simple case is when the deleted node is black and its child is red. Simply removing a black node could break Properties 4 (Both children of every red node are black) and 5 (All paths from any given node to its leaf nodes contain the same number of black nodes), but if we repaint its child black, both of these properties are preserved. The complex case is when both the node to be deleted and its child are black. We begin by replacing the node to be deleted with its child. We will call (or label) this child (in its new position) N, and its sibling (its new parent's other child) S. In the diagrams below, we will also use P for N's new parent, S L for S's left child, and S R for S's right child (it can be shown that S cannot be a leaf). Note: In between some cases, we exchange the roles and labels of the nodes, but in each case, every label continues to represent the same node it represented at the beginning of the case. Any color shown in the diagram is either assumed in its case or implied by these assumptions. White represents an unknown color (either red or black). We will find the sibling using this function: node sibling(node n) { if (n == n->parent->left) return n->parent->right; return n->parent->left; Note: In order that the tree remains well-defined, we need that every null leaf remains a leaf after all transformations (that it won't have any children). If the node we are deleting has a non-leaf (non-null) child N, it is easy to see that the property is satisfied. If, on the other hand, N would be a null leaf, it can be verified from the diagrams (or code) for all the cases that the property is satisfied as well. We can perform the steps outlined above with the following code, where the function replace_node substitutes child into n's place in the tree. For convenience, code in this section will assume that null leaves are represented by actual node objects rather than NULL (the code in the Insertion section works with either representation). void delete_one_child(node n) { /* Precondition: n has at most one non-null child */ node child = (is_leaf(n->right))? n->left : n->right; replace_node(n, child); if (n->color == BLACK) { if (child->color == RED) child->color = BLACK; delete_case1(child);
8 free(n); Note: If N is a null leaf and we don't want to represent null leaves as actual node objects, we can modify the algorithm by first calling delete_case1() on its parent (the node that we delete, n in the code above) and deleting it afterwards. We can do this because the parent is black, so it behaves in the same way as a null leaf (and is sometimes called a 'phantom' leaf). And we can safely delete it at the end as n will remain a leaf after all operations, as shown above. If both N and its original parent are black, then deleting this original parent causes paths which proceed through N to have one fewer black node than paths that do not. As this violates Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes), the tree must be rebalanced. There are several cases to consider: Case 1: N is the new root. In this case, we're done. We removed one black node from every path, and the new root is black, so the properties are preserved. void delete_case1(node n) { if (n->parent == NULL) return; delete_case2(n); Note: In cases 2, 5, and 6, we assume N is the left child of its parent P. If it is the right child, left and right should be reversed throughout these three cases. Again, the code examples take both cases into account. Case 2: S is red. In this case we reverse the colors of P and S, and then rotate left at P, turning S into N's grandparent. Note that P has to be black as it had a red child. Although all paths still have the same number of black nodes, now N has a black sibling and a red parent, so we can proceed to step 4, 5, or 6. (Its new sibling is black because it was once the child of the red S.) In later cases, we will relabel S to be N's new sibling. void delete_case2(node n) { if (sibling(n)->color == RED) { n->parent->color = RED; sibling(n)->color = BLACK; if (n == n->parent->left) rotate_left(n->parent); rotate_right(n->parent); delete_case3(n);
9 Case 3: P, S, and S's children are black. In this case, we simply repaint S red. The result is that all paths passing through S, which are precisely those paths not passing through N, have one less black node. Because deleting N's original parent made all paths passing through N have one less black node, this evens things up. However, all paths through P now have one fewer black node than paths that do not pass through P, so Property 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) is still violated. To correct this, we perform the rebalancing procedure on P, starting at case 1. void delete_case3(node n) { if (n->parent->color == BLACK && sibling(n)->color == BLACK && sibling(n)->left->color == BLACK && sibling(n)->right->color == BLACK) { sibling(n)->color = RED; delete_case1(n->parent); delete_case4(n); Case 4: S and S's children are black, but P is red. In this case, we simply exchange the colors of S and P. This doesn't affect the number of black nodes on paths not going through N, but it does add one to the number of black nodes on paths going through N, making up for the deleted black node on those paths. void delete_case4(node n) { if (n->parent->color == RED && sibling(n)->color == BLACK && sibling(n)->left->color == BLACK &&
10 sibling(n)->right->color == BLACK) { sibling(n)->color = RED; n->parent->color = BLACK; delete_case5(n); Case 5: S is black, S's left child is red, S's right child is black, and N is the left child of its parent. In this case we rotate right at S, so that S's left child becomes S's parent and N's new sibling. We then exchange the colors of S and its new parent. All paths still have the same number of black nodes, but now N has a black sibling whose right child is red, so we fall into case 6. Neither N nor its parent are affected by this transformation. (Again, for case 6, we relabel S to be N's new sibling.) void delete_case5(node n) { if (n == n->parent->left && sibling(n)->color == BLACK && sibling(n)->left->color == RED && sibling(n)->right->color == BLACK) { sibling(n)->color = RED; sibling(n)->left->color = BLACK; rotate_right(sibling(n)); if (n == n->parent->right && sibling(n)->color == BLACK && sibling(n)->right->color == RED && sibling(n)->left->color == BLACK) { sibling(n)->color = RED; sibling(n)->right->color = BLACK; rotate_left(sibling(n)); delete_case6(n);
11 Case 6: S is black, S's right child is red, and N is the left child of its parent P. In this case we rotate left at P, so that S becomes the parent of P and S's right child. We then exchange the colors of P and S, and make S's right child black. The subtree still has the same color at its root, so Properties 4 (Both children of every red node are black) and 5 (All paths from any given node to its leaf nodes contain the same number of black nodes) are not violated. However, N now has one additional black ancestor: either P has become black, or it was black and S was added as a black grandparent. Thus, the paths passing through N pass through one additional black node. Meanwhile, if a path does not go through N, then there are two possibilities: It goes through N's new sibling. Then, it must go through S and P, both formerly and currently, and they've only exchanged colors. Thus the path contains the same number of black nodes. It goes through N's new uncle, S's right child. Then, it formerly went through S, S's parent, and S's right child, but now only goes through S, which has assumed the color of its former parent, and S's right child, which has changed from red to black. The net effect is that this path goes through the same number of black nodes. Either way, the number of black nodes on these paths does not change. Thus, we have restored Properties 4 (Both children of every red node are black) and 5 (All paths from any given node to its leaf nodes contain the same number of black nodes). The white node in the diagram can be either red or black, but must refer to the same color both before and after the transformation. void delete_case6(node n) { sibling(n)->color = n->parent->color; n->parent->color = BLACK; if (n == n->parent->left) { /* Here, sibling(n)->right->color == RED */ sibling(n)->right->color = BLACK; rotate_left(n->parent); { /* Here, sibling(n)->left->color == RED */ sibling(n)->left->color = BLACK; rotate_right(n->parent);
12 Again, the function calls all use tail recursion, so the algorithm is in-place. Additionally, no recursive calls will be made after a rotation, so a constant number of rotations (up to 3) are made. Proof of asymptotic bounds A red black tree which contains n internal nodes has a height of O(log(n)). Definitions: h(v) = height of subtree rooted at node v bh(v) = the number of black nodes (not counting v if it is black) from v to any leaf in the subtree (called the black-height). bh(v) Lemma: A subtree rooted at node v has at least 2 1 Proof of Lemma (by induction height): Basis: h(v) = 0 internal nodes. If v has a height of zero then it must be nil, therefore bh(v) = 0. So: bh(v) = 2 1 = 1 1 = 0 bh(v) Inductive Hypothesis: v such that h(v) = k, has 2 1 bh(v') such that h(v') = k+1 has 2 1 internal nodes. internal nodes implies that v' Since v' has h(v') > 0 it is an internal node. As such it has two children which have a black-height of either bh(v') or bh(v')-1 (depending on whether v' is red or black). By the bh(v') 1 inductive hypothesis each child has at least 2 1 internal nodes, so v' has: bh(v') 1 bh(v') 1 bh(v') = 2 1 internal nodes. Using this lemma we can now show that the height of the tree is logarithmic. Since at least half of the nodes on any path from the root to a leaf are black (property 4 of a red black tree), the black-height of the root is at least h(root)/2. By the lemma we get: Therefore the height of the root is O(log(n)).
Properties of red-black trees
 Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Algorithms. Red-Black Trees
 Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Balanced search trees. DS 2017/2018
 Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
Self-Balancing Search Trees. Chapter 11
 Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Red-black trees (19.5), B-trees (19.8), trees
 Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
Algorithms. Deleting from Red-Black Trees B-Trees
 Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Red-Black Trees. Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood
 Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
Balanced search trees
 Balanced search trees Ordinary binary search trees have expected height Θ(log n) if items are inserted and deleted in random order, but for other orders the height can be Θ(n). This is undesirable, since
Balanced search trees Ordinary binary search trees have expected height Θ(log n) if items are inserted and deleted in random order, but for other orders the height can be Θ(n). This is undesirable, since
Define the red- black tree properties Describe and implement rotations Implement red- black tree insertion
 Red black trees Define the red- black tree properties Describe and implement rotations Implement red- black tree insertion We will skip red- black tree deletion October 2004 John Edgar 2 Items can be inserted
Red black trees Define the red- black tree properties Describe and implement rotations Implement red- black tree insertion We will skip red- black tree deletion October 2004 John Edgar 2 Items can be inserted
A red-black tree is a balanced binary search tree with the following properties:
 Binary search trees work best when they are balanced or the path length from root to any leaf is within some bounds. The red-black tree algorithm is a method for balancing trees. The name derives from
Binary search trees work best when they are balanced or the path length from root to any leaf is within some bounds. The red-black tree algorithm is a method for balancing trees. The name derives from
Outline. Definition. 2 Height-Balance. 3 Searches. 4 Rotations. 5 Insertion. 6 Deletions. 7 Reference. 1 Every node is either red or black.
 Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
13.4 Deletion in red-black trees
 Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
13.4 Deletion in red-black trees
 The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
Trees. (Trees) Data Structures and Programming Spring / 28
 Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Part 2: Balanced Trees
 Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
Balanced Search Trees. CS 3110 Fall 2010
 Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Search Trees - 2. Venkatanatha Sarma Y. Lecture delivered by: Assistant Professor MSRSAS-Bangalore. M.S Ramaiah School of Advanced Studies - Bangalore
 Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
10.2 AVL Trees. Definition of an AVL Tree. 438 Chapter 10. Search Trees
 438 Chapter 10. Search Trees 10. AVL Trees In theprevioussection,wediscussedwhatshouldbeanefficientmapdatastructure, but the worst-case performance it achieves for the various operations is linear time,
438 Chapter 10. Search Trees 10. AVL Trees In theprevioussection,wediscussedwhatshouldbeanefficientmapdatastructure, but the worst-case performance it achieves for the various operations is linear time,
B Tree. Also, every non leaf node must have at least two successors and all leaf nodes must be at the same level.
 B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
CSCI2100B Data Structures Trees
 CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
Some Search Structures. Balanced Search Trees. Binary Search Trees. A Binary Search Tree. Review Binary Search Trees
 Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Search Structures. Kyungran Kang
 Search Structures Kyungran Kang (korykang@ajou.ac.kr) Ellis Horowitz, Sartaj Sahni and Susan Anderson-Freed, Fundamentals of Data Structures in C, 2nd Edition, Silicon Press, 2007. Contents Binary Search
Search Structures Kyungran Kang (korykang@ajou.ac.kr) Ellis Horowitz, Sartaj Sahni and Susan Anderson-Freed, Fundamentals of Data Structures in C, 2nd Edition, Silicon Press, 2007. Contents Binary Search
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Data Structures and Algorithms
 Data Structures and Algorithms Searching Red-Black and Other Dynamically BalancedTrees PLSD210 Searching - Re-visited Binary tree O(log n) if it stays balanced Simple binary tree good for static collections
Data Structures and Algorithms Searching Red-Black and Other Dynamically BalancedTrees PLSD210 Searching - Re-visited Binary tree O(log n) if it stays balanced Simple binary tree good for static collections
CMPT 225. Red black trees
 MPT 225 Red black trees Red-black Tree Structure red-black tree is a BST! Each node in a red-black tree has an etra color field which is red or black In addition false nodes are added so that every (real)
MPT 225 Red black trees Red-black Tree Structure red-black tree is a BST! Each node in a red-black tree has an etra color field which is red or black In addition false nodes are added so that every (real)
Lecture 5. Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
 Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Balanced Binary Search Trees
 Balanced Binary Search Trees Why is our balance assumption so important? Lets look at what happens if we insert the following numbers in order without rebalancing the tree: 3 5 9 12 18 20 1-45 2010 Pearson
Balanced Binary Search Trees Why is our balance assumption so important? Lets look at what happens if we insert the following numbers in order without rebalancing the tree: 3 5 9 12 18 20 1-45 2010 Pearson
9/29/2016. Chapter 4 Trees. Introduction. Terminology. Terminology. Terminology. Terminology
 Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Search Trees. Undirected graph Directed graph Tree Binary search tree
 Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Data Structures Lesson 7
 Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
Binary Search Trees. Analysis of Algorithms
 Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
CHAPTER 10 AVL TREES. 3 8 z 4
 CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CS350: Data Structures Red-Black Trees
 Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
COSC160: Data Structures Balanced Trees. Jeremy Bolton, PhD Assistant Teaching Professor
 COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
AVL Trees. (AVL Trees) Data Structures and Programming Spring / 17
 AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
Graduate Algorithms CS F-07 Red/Black Trees
 Graduate Algorithms CS673-2016F-07 Red/lack Trees David Galles Department of Computer Science University of San Francisco 07-0: inary Search Trees inary Trees For each node n, (value stored at node n)
Graduate Algorithms CS673-2016F-07 Red/lack Trees David Galles Department of Computer Science University of San Francisco 07-0: inary Search Trees inary Trees For each node n, (value stored at node n)
CSE100. Advanced Data Structures. Lecture 8. (Based on Paul Kube course materials)
 CSE100 Advanced Data Structures Lecture 8 (Based on Paul Kube course materials) CSE 100 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
CSE100 Advanced Data Structures Lecture 8 (Based on Paul Kube course materials) CSE 100 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
Lecture 6: Analysis of Algorithms (CS )
 Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
AVL Trees Goodrich, Tamassia, Goldwasser AVL Trees 1
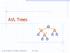 AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
Red-Black, Splay and Huffman Trees
 Red-Black, Splay and Huffman Trees Kuan-Yu Chen ( 陳冠宇 ) 2018/10/22 @ TR-212, NTUST AVL Trees Review Self-balancing binary search tree Balance Factor Every node has a balance factor of 1, 0, or 1 2 Red-Black
Red-Black, Splay and Huffman Trees Kuan-Yu Chen ( 陳冠宇 ) 2018/10/22 @ TR-212, NTUST AVL Trees Review Self-balancing binary search tree Balance Factor Every node has a balance factor of 1, 0, or 1 2 Red-Black
Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms
 Department of Informatics, University of Zürich Vertiefungsarbeit Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms Mirko Richter Matrikelnummer: 12-917-175 Email: mirko.richter@uzh.ch
Department of Informatics, University of Zürich Vertiefungsarbeit Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms Mirko Richter Matrikelnummer: 12-917-175 Email: mirko.richter@uzh.ch
Balanced Binary Search Trees. Victor Gao
 Balanced Binary Search Trees Victor Gao OUTLINE Binary Heap Revisited BST Revisited Balanced Binary Search Trees Rotation Treap Splay Tree BINARY HEAP: REVIEW A binary heap is a complete binary tree such
Balanced Binary Search Trees Victor Gao OUTLINE Binary Heap Revisited BST Revisited Balanced Binary Search Trees Rotation Treap Splay Tree BINARY HEAP: REVIEW A binary heap is a complete binary tree such
Fundamental Algorithms
 WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
Introduction. for large input, even access time may be prohibitive we need data structures that exhibit times closer to O(log N) binary search tree
 Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
COMP251: Red-black trees
 COMP251: Red-black trees Jérôme Waldispühl School of Computer Science McGill University Based on (Cormen et al., 2002) Based on slides from D. Plaisted (UNC) The running Rme of inserrons in BST trees with
COMP251: Red-black trees Jérôme Waldispühl School of Computer Science McGill University Based on (Cormen et al., 2002) Based on slides from D. Plaisted (UNC) The running Rme of inserrons in BST trees with
Analysis of Algorithms
 Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Note that this is a rep invariant! The type system doesn t enforce this but you need it to be true. Should use repok to check in debug version.
 Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
BRONX COMMUNITY COLLEGE of the City University of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE
 BRONX COMMUNITY COLLEGE of the City University of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI Section E01 AVL Trees AVL Property While BST structures have average performance of Θ(log(n))
BRONX COMMUNITY COLLEGE of the City University of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI Section E01 AVL Trees AVL Property While BST structures have average performance of Θ(log(n))
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Lecture 21: Red-Black Trees
 15-150 Lecture 21: Red-Black Trees Lecture by Dan Licata April 3, 2012 Last time, we talked about the signature for dictionaries: signature ORDERED = sig type t val compare : t * t -> order signature DICT
15-150 Lecture 21: Red-Black Trees Lecture by Dan Licata April 3, 2012 Last time, we talked about the signature for dictionaries: signature ORDERED = sig type t val compare : t * t -> order signature DICT
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
ECE 242 Data Structures and Algorithms. Trees IV. Lecture 21. Prof.
 ECE 22 Data Structures and Algorithms http://www.ecs.umass.edu/~polizzi/teaching/ece22/ Trees IV Lecture 2 Prof. Eric Polizzi Summary previous lectures Implementations BST 5 5 7 null 8 null null 7 null
ECE 22 Data Structures and Algorithms http://www.ecs.umass.edu/~polizzi/teaching/ece22/ Trees IV Lecture 2 Prof. Eric Polizzi Summary previous lectures Implementations BST 5 5 7 null 8 null null 7 null
Uses for Trees About Trees Binary Trees. Trees. Seth Long. January 31, 2010
 Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
Balanced Trees Part Two
 Balanced Trees Part Two Outline for Today Recap from Last Time Review of B-trees, 2-3-4 trees, and red/black trees. Order Statistic Trees BSTs with indexing. Augmented Binary Search Trees Building new
Balanced Trees Part Two Outline for Today Recap from Last Time Review of B-trees, 2-3-4 trees, and red/black trees. Order Statistic Trees BSTs with indexing. Augmented Binary Search Trees Building new
Assume you are given a Simple Linked List (i.e. not a doubly linked list) containing an even number of elements. For example L = [A B C D E F].
![Assume you are given a Simple Linked List (i.e. not a doubly linked list) containing an even number of elements. For example L = [A B C D E F]. Assume you are given a Simple Linked List (i.e. not a doubly linked list) containing an even number of elements. For example L = [A B C D E F].](/thumbs/79/79282263.jpg) Question Assume you are given a Simple Linked List (i.e. not a doubly linked list) containing an even number of elements. For example L = [A B C D E F]. a) Draw the linked node structure of L, including
Question Assume you are given a Simple Linked List (i.e. not a doubly linked list) containing an even number of elements. For example L = [A B C D E F]. a) Draw the linked node structure of L, including
Advanced Algorithms. Class Notes for Thursday, September 18, 2014 Bernard Moret
 Advanced Algorithms Class Notes for Thursday, September 18, 2014 Bernard Moret 1 Amortized Analysis (cont d) 1.1 Side note: regarding meldable heaps When we saw how to meld two leftist trees, we did not
Advanced Algorithms Class Notes for Thursday, September 18, 2014 Bernard Moret 1 Amortized Analysis (cont d) 1.1 Side note: regarding meldable heaps When we saw how to meld two leftist trees, we did not
CIS265/ Trees Red-Black Trees. Some of the following material is from:
 CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
Lecture: Analysis of Algorithms (CS )
 Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
2-3 Tree. Outline B-TREE. catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } ADD SLIDES ON DISJOINT SETS
 Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
COMP171. AVL-Trees (Part 1)
 COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
AVL Trees / Slide 2. AVL Trees / Slide 4. Let N h be the minimum number of nodes in an AVL tree of height h. AVL Trees / Slide 6
 COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
On k-dimensional Balanced Binary Trees*
 journal of computer and system sciences 52, 328348 (1996) article no. 0025 On k-dimensional Balanced Binary Trees* Vijay K. Vaishnavi Department of Computer Information Systems, Georgia State University,
journal of computer and system sciences 52, 328348 (1996) article no. 0025 On k-dimensional Balanced Binary Trees* Vijay K. Vaishnavi Department of Computer Information Systems, Georgia State University,
10/23/2013. AVL Trees. Height of an AVL Tree. Height of an AVL Tree. AVL Trees
 // AVL Trees AVL Trees An AVL tree is a binary search tree with a balance condition. AVL is named for its inventors: Adel son-vel skii and Landis AVL tree approximates the ideal tree (completely balanced
// AVL Trees AVL Trees An AVL tree is a binary search tree with a balance condition. AVL is named for its inventors: Adel son-vel skii and Landis AVL tree approximates the ideal tree (completely balanced
AVL Tree Definition. An example of an AVL tree where the heights are shown next to the nodes. Adelson-Velsky and Landis
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
We will show that the height of a RB tree on n vertices is approximately 2*log n. In class I presented a simple structural proof of this claim:
 We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
Solutions. Suppose we insert all elements of U into the table, and let n(b) be the number of elements of U that hash to bucket b. Then.
 Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
Binary Trees, Binary Search Trees
 Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Search Trees. COMPSCI 355 Fall 2016
 Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Analysis of Algorithms
 Analysis of Algorithms Concept Exam Code: 16 All questions are weighted equally. Assume worst case behavior and sufficiently large input sizes unless otherwise specified. Strong induction Consider this
Analysis of Algorithms Concept Exam Code: 16 All questions are weighted equally. Assume worst case behavior and sufficiently large input sizes unless otherwise specified. Strong induction Consider this
AVL Trees (10.2) AVL Trees
 AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
Multi-way Search Trees. (Multi-way Search Trees) Data Structures and Programming Spring / 25
 Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
(2,4) Trees. 2/22/2006 (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
(2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
Chapter 22 Splay Trees
 Chapter 22 Splay Trees Introduction Splay trees support all the operations of binary trees. But they do not guarantee Ο(log N) worst-case performance. Instead, its bounds are amortized, meaning that although
Chapter 22 Splay Trees Introduction Splay trees support all the operations of binary trees. But they do not guarantee Ο(log N) worst-case performance. Instead, its bounds are amortized, meaning that although
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
CS102 Binary Search Trees
 CS102 Binary Search Trees Prof Tejada 1 To speed up insertion, removal and search, modify the idea of a Binary Tree to create a Binary Search Tree (BST) Binary Search Trees Binary Search Trees have one
CS102 Binary Search Trees Prof Tejada 1 To speed up insertion, removal and search, modify the idea of a Binary Tree to create a Binary Search Tree (BST) Binary Search Trees Binary Search Trees have one
Section 4 SOLUTION: AVL Trees & B-Trees
 Section 4 SOLUTION: AVL Trees & B-Trees 1. What 3 properties must an AVL tree have? a. Be a binary tree b. Have Binary Search Tree ordering property (left children < parent, right children > parent) c.
Section 4 SOLUTION: AVL Trees & B-Trees 1. What 3 properties must an AVL tree have? a. Be a binary tree b. Have Binary Search Tree ordering property (left children < parent, right children > parent) c.
Multiway Search Trees. Multiway-Search Trees (cont d)
 Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
Trees. Introduction & Terminology. February 05, 2018 Cinda Heeren / Geoffrey Tien 1
 Trees Introduction & Terminology Cinda Heeren / Geoffrey Tien 1 Review: linked lists Linked lists are constructed out of nodes, consisting of a data element a pointer to another node Lists are constructed
Trees Introduction & Terminology Cinda Heeren / Geoffrey Tien 1 Review: linked lists Linked lists are constructed out of nodes, consisting of a data element a pointer to another node Lists are constructed
V Advanced Data Structures
 V Advanced Data Structures B-Trees Fibonacci Heaps 18 B-Trees B-trees are similar to RBTs, but they are better at minimizing disk I/O operations Many database systems use B-trees, or variants of them,
V Advanced Data Structures B-Trees Fibonacci Heaps 18 B-Trees B-trees are similar to RBTs, but they are better at minimizing disk I/O operations Many database systems use B-trees, or variants of them,
Search Trees (Ch. 9) > = Binary Search Trees 1
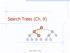 Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Red-Black trees are usually described as obeying the following rules :
 Red-Black Trees As we have seen, the ideal Binary Search Tree has height approximately equal to log n, where n is the number of values stored in the tree. Such a BST guarantees that the maximum time for
Red-Black Trees As we have seen, the ideal Binary Search Tree has height approximately equal to log n, where n is the number of values stored in the tree. Such a BST guarantees that the maximum time for
Chapter 4: Trees. 4.2 For node B :
 Chapter : Trees. (a) A. (b) G, H, I, L, M, and K.. For node B : (a) A. (b) D and E. (c) C. (d). (e).... There are N nodes. Each node has two pointers, so there are N pointers. Each node but the root has
Chapter : Trees. (a) A. (b) G, H, I, L, M, and K.. For node B : (a) A. (b) D and E. (c) C. (d). (e).... There are N nodes. Each node has two pointers, so there are N pointers. Each node but the root has
Best-Case upper limit on the time for insert/delete/find of an element for a BST withnelements?
 S673-2016F-07 Red/lack Trees 1 07-0: inary Search Trees inary Trees For each node n, (value stored at node n)>(value stored in left subtree) For each node n, (value stored at node n)
S673-2016F-07 Red/lack Trees 1 07-0: inary Search Trees inary Trees For each node n, (value stored at node n)>(value stored in left subtree) For each node n, (value stored at node n)
12 July, Red-Black Trees. Red-Black Trees
 1 BST work well if the data is inserted into the tree in random order. They work much slower if the data is inserted in already sorted order. When the values to be inserted are already ordered, a binary
1 BST work well if the data is inserted into the tree in random order. They work much slower if the data is inserted in already sorted order. When the values to be inserted are already ordered, a binary
Multiway Search Trees
 Multiway Search Trees Intuitive Definition A multiway search tree is one with nodes that have two or more children. Within each node is stored a given key, which is associated to an item we wish to access
Multiway Search Trees Intuitive Definition A multiway search tree is one with nodes that have two or more children. Within each node is stored a given key, which is associated to an item we wish to access
(2,4) Trees Goodrich, Tamassia (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
(2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
Treaps. 1 Binary Search Trees (BSTs) CSE341T/CSE549T 11/05/2014. Lecture 19
 CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
CS521 \ Notes for the Final Exam
 CS521 \ Notes for final exam 1 Ariel Stolerman Asymptotic Notations: CS521 \ Notes for the Final Exam Notation Definition Limit Big-O ( ) Small-o ( ) Big- ( ) Small- ( ) Big- ( ) Notes: ( ) ( ) ( ) ( )
CS521 \ Notes for final exam 1 Ariel Stolerman Asymptotic Notations: CS521 \ Notes for the Final Exam Notation Definition Limit Big-O ( ) Small-o ( ) Big- ( ) Small- ( ) Big- ( ) Notes: ( ) ( ) ( ) ( )
Abstract Relaxed balancing of search trees was introduced with the aim of speeding up the updates and allowing a high degree of concurrency. In a rela
 Chromatic Search Trees Revisited Institut fur Informatik Report 9 Sabine Hanke Institut fur Informatik, Universitat Freiburg Am Flughafen 7, 79 Freiburg, Germany Email: hanke@informatik.uni-freiburg.de.
Chromatic Search Trees Revisited Institut fur Informatik Report 9 Sabine Hanke Institut fur Informatik, Universitat Freiburg Am Flughafen 7, 79 Freiburg, Germany Email: hanke@informatik.uni-freiburg.de.
A dictionary interface.
 A dictionary interface. interface Dictionary { public Data search(key k); public void insert(key k, Data d); public void delete(key k); A dictionary behaves like a many-to-one function. The search method
A dictionary interface. interface Dictionary { public Data search(key k); public void insert(key k, Data d); public void delete(key k); A dictionary behaves like a many-to-one function. The search method
Figure 4.1: The evolution of a rooted tree.
 106 CHAPTER 4. INDUCTION, RECURSION AND RECURRENCES 4.6 Rooted Trees 4.6.1 The idea of a rooted tree We talked about how a tree diagram helps us visualize merge sort or other divide and conquer algorithms.
106 CHAPTER 4. INDUCTION, RECURSION AND RECURRENCES 4.6 Rooted Trees 4.6.1 The idea of a rooted tree We talked about how a tree diagram helps us visualize merge sort or other divide and conquer algorithms.
Section 1: True / False (1 point each, 15 pts total)
 Section : True / False ( point each, pts total) Circle the word TRUE or the word FALSE. If neither is circled, both are circled, or it impossible to tell which is circled, your answer will be considered
Section : True / False ( point each, pts total) Circle the word TRUE or the word FALSE. If neither is circled, both are circled, or it impossible to tell which is circled, your answer will be considered
CS 380 ALGORITHM DESIGN AND ANALYSIS
 CS 380 ALGORITHM DESIGN AND ANALYSIS Lecture 12: Red-Black Trees Text Reference: Chapters 12, 13 Binary Search Trees (BST): Review Each node in tree T is a object x Contains attributes: Data Pointers to
CS 380 ALGORITHM DESIGN AND ANALYSIS Lecture 12: Red-Black Trees Text Reference: Chapters 12, 13 Binary Search Trees (BST): Review Each node in tree T is a object x Contains attributes: Data Pointers to
We assume uniform hashing (UH):
 We assume uniform hashing (UH): the probe sequence of each key is equally likely to be any of the! permutations of 0,1,, 1 UH generalizes the notion of SUH that produces not just a single number, but a
We assume uniform hashing (UH): the probe sequence of each key is equally likely to be any of the! permutations of 0,1,, 1 UH generalizes the notion of SUH that produces not just a single number, but a
V Advanced Data Structures
 V Advanced Data Structures B-Trees Fibonacci Heaps 18 B-Trees B-trees are similar to RBTs, but they are better at minimizing disk I/O operations Many database systems use B-trees, or variants of them,
V Advanced Data Structures B-Trees Fibonacci Heaps 18 B-Trees B-trees are similar to RBTs, but they are better at minimizing disk I/O operations Many database systems use B-trees, or variants of them,
