Florida State University Libraries
|
|
|
- Toby Webster
- 5 years ago
- Views:
Transcription
1 Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2011 Parallel Grid Generation and Multi- Resolution Methods for Climate Modeling Applications Douglas W. (Douglas William) Jacobsen Follow this and additional works at the FSU Digital Library. For more information, please contact
2 THE FLORIDA STATE UNIVERSITY COLLEGE OF ARTS AND SCIENCES PARALLEL GRID GENERATION AND MULTI-RESOLUTION METHODS FOR CLIMATE MODELING APPLICATIONS By DOUGLAS W. JACOBSEN A Dissertation submitted to the Department of Scientific Computing in partial fulfillment of the requirements for the degree of Doctor of Philosophy Degree Awarded: Summer Semester, 2011
3 The members of the committee approve the dissertation of Douglas W. Jacobsen defended on June 14th, Max Gunzburger Professor Directing Thesis Doron Nof University Representative Janet Peterson Committee Member Gordon Erlebacher Committee Member Michael Navon Committee Member John Burkardt Committee Member Approved: Todd Ringler Committee Member Max Gunzburger, Chair, Department of Scientific Computing Joseph Travis, Dean, College of Arts and Sciences The Graduate School has verified and approved the above-named committee members. ii
4 I would like to dedicate this dissertation to my loving and supportive wife who helped me significantly through all of my school work. Also, I would like to thank my parents and brothers for their continued support. iii
5 ACKNOWLEDGMENTS I would like to thank Dan Voss, Geoff Womeldorff, Mark Peterson, Michael Duda, and Phil Jones for many useful discussions. The work contained in this dissertation was supported by the US Department of Energy under grant numbers DE-SC and DE-FG02-07ER iv
6 TABLE OF CONTENTS List of Tables List of Figures Abstract vii viii xiii 1 Introduction Personal Contributions Parallel SCVT Generator Background Delaunay Triangulations Voronoi Tessellations Stereographic Projections Parallel Algorithm Details Convergence Criteria Initial Conditions Parallel SCVT Generator Results Quasi-Uniform Results Variable Resolution Results Grid Generator Performance Numerical Model Background Shallow-Water Equations and Numerical Method Shallow-Water Test Cases Non-linear Geostrophic Flow (TC2) Zonal Flow Over an Isolated Mountain (TC5) Barotropic Instability (BTI) Numerical Model Results Shallow-Water Model Setup Shallow Water Test Case Results Shallow Water Test Case Shallow Water Test Case Barotropic Instability Test Case v
7 6 Adaptive Mesh Refinement Background AMR Background SCVT-AMR Framework Adaptive Mesh Refinement Results Point Suite Point Suite Discussion Future Work Bibliography Biographical Sketch vi
8 LIST OF TABLES 3.1 Timing results for MPI-SCVT with bisection and Monte Carlo initial conditions and the speedup of bisection relative to Monte Carlo initial conditions Comparison of STRIPACK with Serial and Parallel versions of MPI- SCVT using final triangulations Comparison of STRIPACK with serial and parallel versions of MPI- SCVT using per iteration triangulations Timings based on the domain decomposition used. Uniform uses a coarse quasi-uniform SCVT to define region centers and their associated radii, and sorts using a simple dot product. x16 uses a coarse x16 SCVT to define region centers and their associated radii, and sorts using a simple dot product. Voronoi uses a coarse x16 SCVT to define region centers and their associated radii, and sorts using a Voronoi cell based sort Table of grid sizes and spacings for quasi-uniform grids used in shallowwater exploration Minimum values and grid spacing factors Approximate mesh resolutions (km) of the fine-mesh (dx f ) and coarsemesh (dx c ) regions of the global domain for the x1 through x16 meshes as a function of the number of grid points Error norms associated with the suite of AMR meshes based on the 642 grid point reference mesh. Presented are L 2 and L norms of the error in the thickness field, compared to a T511 reference simulation Error norms for AMR grids based on 2562 grid point reference mesh. L 2 and L norms are computed with the thickness field relative to a T511 simulation vii
9 LIST OF FIGURES 2.1 Cross-sectional illustration of a stereographic projection from a sphere into a tangent plane Domain Decomposition Example. Figure 2.2(a) is an SCVT used for a 12 processor domain decomposition, where Figure 2.2(b) is a generator Delaunay triangulation computed using the 12 generator SCVT for parallelization. Each colored ring represents a regions radius R k, where region centers T k are the Voronoi cell center, at the center of each pentagonal structure in Figure 2.2(a) Triangulations in a plane after Stereographic projection. 2.3(a) is the triangulation before (2.8) is applied, and 2.3(b) is after it is applied Triangle division used for integrating Voronoi cells using only the Delaunay triangulation without any adjacency information. Kite sections contribute to the Voronoi cell centered at the vertex that is part of the kite. A, B, C vertices are generators in the point set, where the point at the center of the triangle is the circumcenter of this triangle. Triangular regions that are colored similarly contribute to the same vertex Timings for a STRIPACK based SCVT Generator at 162, 642, 10242, and generators. The red solid line represents the time spent in STRIPACK computing a triangulation, where the green dashed line represents the time spent integrating the Voronoi cells outside of STRIPACK in one iteration of Lloyd s algorithm. Timings in this figure were computed using an Intel Core 2 Duo T8100 CPU with 3GB of RAM. 24 viii
10 3.2 Timings for various portions of MPI-SCVT using 2 processors and 2 regions. As the problem size increases the slope of both the triangulation (Red-Solid) and the integration (Green-Dashed) remain constant. The triangulation doesn t become more expensive than the integration until after roughly generators, as compared to Figure 3.1 where triangulation was more expensive after only 2562 generators. Also, a triangulation using generators costs roughly the same using MPI-SCVT and 2 processors as a triangulation using generators in STRIPACK Timing results from MPI-SCVT vs. number of processors. Constant problem size, shown as parallelization is increased. Red solid lines represent the cost of computing a triangulation, where green dashed lines represent the cost of integrating all Voronoi cells, and blue dotted lines represent the cost of communicating each region s updated point set to its neighbors Density function that creates a grid with resolutions that differ by a factor of 16 between the coarse and the fine region. The maximum value of the density function is 1, where the minimum value is ( 1 16 ) Figures show a variable resolution grid created using a density function with the format defined in (3.1). All three figures are of the same grid, only the viewing perspective is changed. Figure 3.5(a) shows the coarse region of the grid, 3.5(b) shows the transition region of the grid, and 3.5(c) shows the fine region of the grid Number of points each processor has to triangulate. 3.6(a) uses a quasiuniform SCVT for its decomposition, with a simple dot product. 3.6(b) uses a x16 SCVT for its decomposition, with a simple dot product. 3.6(c) uses a x16 SCVT for its decomposition, with a more complicated sort based on the region s Voronoi diagram Scalability results based on number of generators. Green is a linear reference where Red is the Speedup computed using parallel version of MPI-SCVT against a serial version Four members of a family of meshes constructed from (3.1). Each mesh uses 2562 grid points and only differ in the setting of the parameter γ. x1, x2, x4 and x16 shown in the top-left, top-right, bottom-left and bottom-right, respectively ix
11 4.2 C-grid staggering of variables for the finite-volume scheme used in MPAS. Fluid thickness, topography, and kinetic energy are stored at Voronoi cell centers. The normal component of the velocity field is defined at the mid-point of line segments connecting cell centers. Vorticity related fields such as relative, absolute, and potential vorticity are stored at Voronoi cell vertices. Derived fields, ĥe, ˆq e, and F e must be reconstructed at each velocity point The fluid height, h i + b i, at day 15 for TC5. Starting at the upper left and moving clockwise shows results from the X1, X2, X16 and X4 meshes using cells. The black oval denotes the location of the mountain. The figures are generated by filling each Voronoi cell with a single color, i.e. there is no interpolation due to rendering. This allows the coarse-mesh grid cells to be seen in the X4 and X16 simulations. All results are plotted with an identical color scheme with a maximum of 5975 m and a minimum of 5025 m Log 10 of the relative change in available total energy for TC5 as a function of time for the x1, x2, x4, x8 and x16 meshes with grid points Globally averaged potential enstrophy as a function of time for x1, x2, x4, x8, and x16 meshes with grid points. Simulations are run for 15 days. Figures show decreasing potential enstrophy for x1 and x2 meshes, and increasing potential enstrophy for x4, x8, and x16 meshes Log 10 of the relative change in available potential enstrophy for TC5 as a function of time for the x1, x2, x4, x8 and x16 meshes with grid points The L 2 error of the thickness field at day 15 for TC5 shown for the x1, x2, x4, x8 and x16 meshes. Figure 5.5(a) shows errors as a function of number of generators, and figure 5.5(b) shows errors as a function of coarse-mesh grid spacing. Error norms are computed against a T511 reference solution The L 2 error of the thickness field at day 12 for TC2 for the x1, x2, x4, x8andx16meshes. Figure5.6(a)showserrorsasafunctionofnumberof generators, and Figure 5.6(b) shows errors as a function of coarse-mesh grid spacing. Error norms are computed against the analytic initial conditions x
12 5.7 Each panel depicts the relative vorticity field at day 6 for a barotropicallyunstable jet using cells. The panels differ only in the mesh used in the simulation. The vertical extent of each panel covers the northern hemisphere. The horizontal extent covers all longitudes starting at -90 degrees such that the fine-mesh region is approximately centered on each panel. The color scales are identical for every panel and saturate at ± Density field obtained after one simulation day using the relative vorticity field from shallow-water test case 5, on a x generator grid, corresponding to the first four steps in Algorithm 3. Figure 6.1(a) has no smoothings applied, Figure 6.1(b) has 16 smoothings applied, Figure 6.1(c) has 64 smoothings applied, and Figure 6.1(d) has 128 smoothings applied. The smoothing operator is defined in (6.2). Red represents the minimum, where blue represents the maximum. To show transitions color represents log 2 (ρ 1/4 ) Three triangles with subdivision based on density values. Figure 6.2(a) shows a triangle whose density value is 1 4 providing no divisions. Figure 6.2(b) shows a triangle whose density value is 2 4 providing one division. Figure 6.2(c) shows a triangle whose density value is 4 4 providing two divisions AMR grids based on a 642 grid cell quasi-uniform grid. Color represents cell area, where Red is the minimum area and Purple is the maximum area. Presented are grids with 0, 16, 64, and 128 iterations of Laplacian smoothing applied Reference data fields for 642 quasi-uniform mesh. Shallow-water test case 5 was simulated for 1 day, plotted in Figure 7.2(a) is the fluid thickness field, Figure 7.2(b) is the potential vorticity field, and Figure 7.2(c) is the relative vorticity field Thickness fields from the 642 suite of AMR meshes. Figure 7.3(a) shows the thickness field from an unsmoothed AMR mesh. Figure 7.3(b) shows the thickness field from a mesh with 16 smoothings. Figure 7.3(c) shows the thickness field from a mesh with 64 smoothings. Figure 7.3(d) shows the thickness field from a mesh with 128 smoothings Potential vorticity fields from the 642 suite of AMR meshes. Figure 7.4(a) shows the potential vorticity field from an unsmoothed AMR mesh. Figure 7.4(b) shows the potential vorticity field from a mesh with 16 smoothings. Figure 7.4(c) shows the potential vorticity field from a mesh with 64 smoothings. Figure 7.4(d) shows the potential vorticity field from a mesh with 128 smoothings xi
13 7.5 Relative vorticity fields from the 642 suite of AMR meshes. Figure 7.5(a) shows the relative vorticity field from an unsmoothed AMR mesh. Figure 7.5(b) shows the relative vorticity field from a mesh with 16 smoothings. Figure 7.5(c) shows the relative vorticity field from a mesh with 64 smoothings. Figure 7.5(d) shows the relative vorticity field from a mesh with 128 smoothings AMR grids based on a 2562 grid cell quasi-uniform grid. Color represents cell area, where Red is the minimum area and Purple is the maximum area. Presented are grids with 0, 16, 64, and 128 iterations of Laplacian smoothing applied Reference data fields for 2562 quasi-uniform mesh. Shallow-water test case 5 was simulated for 1 day, plotted in figure 7.7(a) is the fluid thickness field, figure 7.7(b) is the potential vorticity field, and figure 7.7(c) is the relative vorticity field Thickness fields from the 2562 suite of AMR meshes. Figure 7.8(a) shows the thickness field from an unsmoothed AMR mesh. Figure 7.8(b) shows the thickness field from a mesh with 16 smoothings. Figure 7.8(c) shows the thickness field from a mesh with 64 smoothings. Figure 7.8(d) shows the thickness field from a mesh with 128 smoothings Potential vorticity fields from the 2562 suite of AMR meshes. Figure 7.9(a) shows the potential vorticity field from an unsmoothed AMR mesh. Figure 7.9(b) shows the potential vorticity field from a mesh with 16 smoothings. Figure 7.9(c) shows the potential vorticity field from a mesh with 64 smoothings. Figure 7.9(d) shows the potential vorticity field from a mesh with 128 smoothings Relative vorticity fields from the 2562 suite of AMR meshes. Figure 7.10(a) shows the relative vorticity field from an unsmoothed AMR mesh. Figure 7.10(b) shows the relative vorticity field from a mesh with 16 smoothings. Figure 7.10(c) shows the relative vorticity field from a mesh with 64 smoothings. Figure 7.10(d) shows the relative vorticity field from a mesh with 128 smoothings xii
14 ABSTRACT Spherical centroidal Voronoi tessellations (SCVT) are used in many applications in a variety of fields, one being climate modeling. They are a natural choice for spatial discretizations on the surface of the Earth. New modeling techniques have recently been developed that allow the simulation of ocean and atmosphere dynamics on arbitrarily unstructured meshes, including SCVTs. Creating ultra-high resolution SCVTs can be computationally expensive. A newly developed algorithm couples current algorithms for the generation of SCVTs with existing computational geometry techniques to provide the parallel computation of SCVTs and spherical Delaunay triangulations. Using this new algorithm, computing spherical Delaunay triangulations shows a speed up on the order of 4000 over other well known algorithms, when using 42 processors. As mentioned previously, newly developed numerical models allow the simulation of ocean and atmosphere systems on arbitrary Voronoi meshes providing a multiresolution modeling framework. A multi-resolution grid allows modelers to provide areas of interest with higher resolution with the hopes of increasing accuracy. However, one method of providing higher resolution lowers the resolution in other areas of the mesh which could potentially increase error. To determine the effect of multiresolution meshes on numerical simulations in the shallow-water context, a standard set of shallow-water test cases are explored using the Model for Prediction Across Scales (MPAS), a new modeling framework jointly developed by the Los Alamos National Laboratory and the National Center for Atmospheric Research. An alternative approach to multi-resolution modeling is Adaptive Mesh Refinement (AMR). AMR typically uses information about the simulation to determine xiii
15 optimal locations for degrees of freedom, however standard AMR techniques are not well suited for SCVTmeshes. In an effort to solve thisissue, a framework is developed to allow AMR simulations on SCVT meshes within MPAS. The resulting research contained in this dissertation ties together a newly developed parallel SCVT generator with a numerical method for use on arbitrary Voronoi meshes. Simulations are performed within the shallow-water context. New algorithms and frameworks are described and bench-marked. xiv
16 CHAPTER 1 INTRODUCTION Modeling the Earth s climate has been considered a grand-challenge problem due to the broad range of spatial and temporal scales required for robust simulation of its subcomponents. For example, the climate of the ocean is controlled by both basin scales of motion, O(10 4 ) km, and sub-mesoscale processes with O(10 1 ) km scales [2]. These scales are highly interacting, as is typical of nonlinear systems, in that the O(10 4 ) km global scales modify and are modified by the O(10 1 ) km local scales. For robust simulation of the climate, an accurate representation of the smallest scales is a requirement based on this strong inter-scale dependence. This broad scale interaction is present in both the atmosphere and the ocean creating a difficulty in accurately simulating the full climate system. One major deficiency in climate modeling today is resolving small-scale processes. These processes are resolved typically in one of two ways; either parameterization, or direct simulation. Direct simulation is computationally expensive as it requires a high enough spatial resolution to resolve even the smallest-scale processes. Currently the computational resources available are not sufficient to directly simulate all scales associated with the fundamental processes in the atmosphere and ocean, such as clouds and ocean eddies [22]. As an alternative to direct simulation many models use parameterizations of processes. However, parameterizing a process can be extremely difficult because it requires an a priori knowledge of the cross-scale interaction of the 1
17 process. This requires developers to have a greater understanding of the underlying physics associated with the physical process than those trying to perform direct simulations of the same process. Although parameterizations are indispensable tools, the underlying difficulty in developing accurate parameterizations leads climate modelers to increase model resolution, therefore allowing more direct simulations of small-scale processes. A novel technique in climate modeling is explored as part of this dissertation. This new technique, referred to as a multi-resolution method, is complementary to three existing branches of research that are active in the climate modeling community today. The first is global ultra high-resolution climate system modeling [18]. Global ultra high-resolution climate modeling attempts to pair ultra high-resolution climate systems with state-of-the art high performance computing systems to achieve simulations at unprecedented resolution. However, this approach has a disadvantage in that reducing horizontal grid spacing by a factor of two typically requires a factor of 2 3 increase in computing resources, where longitude, latitude, and time each account for a factor of 2 individually. This example is ignoring any extra expense from increases in vertical resolution. Based on this significant increase in computational expense, it is clear that global ultra-high resolution simulations are only able to represent a small portion of all the simulations performed. The second approach, intended to circumvent global high-resolution climate modeling, is called limited-area climate modeling. Limited-area climate modeling has been explored over the last two decades [12, 19, 34]. Typically this approach uses a high-resolution mesh only over an area of interest, thus only spanning a portion of the sphere. Utilizing a limited-area mesh reduces the computational requirements significantly; however one-way, non-interactive lateral boundary conditions are required. Typically these lateral boundary conditions are obtained from either reanalysis data or coarse-resolution global climate simulations. 2
18 The third approach currently being explored is referred to as multi-scale modeling. Multi-scale modeling couples models at different scales to create a full simulation. Previously, multi-scale modeling has been investigated with respect to atmospheric modeling[13]; however a preliminary exploration of this method with regards to ocean modeling is in progress[4]. Multi-scale methods are built under the assumption that a scale separation exists that can be exploited in modeling the physical system, meaning the fine-scale and coarse-scale processes act on temporal and spatial scales sufficiently far away from each other. However, this assumption remains unvalidated. As mentioned previously the work contained in this dissertation, and in[25], which hopes to become a fourth approach, attempts to address some of the existing computational challenges in modeling the climate system. This new method is informally referred to as a multi-resolution approach, and essentially merges traditional global climate modelling approaches with regional limited-area approaches. A global modeling framework is maintained in multi-resolution simulations in the sense that the entire spatial extent of the atmosphere and/or ocean is simulated within a single model; however arbitrary regions of local mesh refinement are allowed, similarly to limited area or multi-scale methods. A global, conforming mesh is employed similar to stretched-grid or conformal mapping approaches previously explored [9, 10]. Stretched-grid approaches require a deformation of the mesh through a continuous mapping, e.g. an increase of resolution in one region requires a decrease of resolution in other regions. Also, stretched-grid approaches are limited in their ability to place enhanced resolution in multiple regions. The multi-resolution approach developed in [25] and explored as part of this dissertation alleviates several of the disadvantages of stretched-grid methods. However, as with stretched-grid approaches, scale aware parameterizations need to be developed for use with multi-resolution methods. Multi-resolution approaches allow one or more regions with significantly higher grid-resolution than the remainder of the mesh, as can be seen in Figures 3.5 and
19 These meshes can be used to directly simulate processes in high resolution areas, while parameterizing those same processes in low resolution regions, similar to multi-scale methods. Following the motivation and requirements in [25], this multi-resolution method requires two key components: First, a finite-volume method capable of maintaining conservation properties when implemented on highly non-uniform grids, and second, a conforming variable-resolution mesh with exceptional mesh-quality characteristics. Before describing the spatial meshes that are used, the finite-volume scheme capable of conservative simulations on highly varying meshes is introduced. As described in [24, 31], a new finite-volume method has been developed which allows the use of Voronoi meshes to produce robust simulations of rotationally-dominated geophysical flows. Robust finite-volume techniques used in global atmosphere and ocean models often showcase their ability to constrain the spurious growth of nonlinear quantities, such as potential enstrophy and total energy [1]. This challenge is particularly difficult when implemented on non-uniform meshes. Combining the recent works of [24, 31] provides a finite-volume approach that allows for the conservation of nonlinear quantities, even when the underlying mesh is highly variable. Although results presented in [24, 31] only showcase quasi-uniform meshes, the numerical method described allows the use of arbitrary Voronoi meshes. As part of this dissertation the numerical method s ability to simulate on highly varying meshes is explored. Jointly developed by the Los Alamos National Laboratory (LANL) and the National Center for Atmospheric Research (NCAR), the Model for Prediction Across Scales (MPAS) provides a framework suitable for the rapid prototyping and development of dynamical cores. LANL has developed a shallow-water and a full three-dimensional ocean dynamical core for use in MPAS, while NCAR has developed an atmospheric model. MPAS implements the numerical method described in [24, 31] allowing the simulation on arbitrary Voronoi meshes, and will be used for the 4
20 exploration in this dissertation. In order to explore the model s ability to simulate on variable resolution meshes, a standard suite of test cases are used in the shallow-water system as described in [39]. Before describing their use in multi-resolution modeling, a brief history of Voronoi diagrams is provided. Voronoi diagrams have had many different names in their past such as Thiessen polygons, Wigner-Seitz unit cells, and Brillouin zones [21]. The use of Voronoi diagrams involves a wide range of applications from condensed matter physics, to measuring spatially distributed geophysical and meteorological data. Althoughtheirusetodayisbroad,theirpastusecanbetracedbacktoDescartes in Originally Dirichlet derived modern Voronoi diagrams, however only in 2 and 3 dimensional spaces. Georgy Fedoseevich Voronoi generalized this work in 1908 to arbitrary dimensions, providing the definition of what we call Voronoi diagrams today [33]. One version of these Voronoi diagrams, called a Spherical Centroidal Voronoi Tessellation (SCVT), fulfills the requirements of a conforming, variable-resolution mesh. Recently in climate modeling, Voronoi-like meshing of the sphere has found success in global atmosphere modeling [14, 32, 35]. Each of these examples motivates the use of Voronoi-like meshing through the ability to produce high-quality meshes of uniform resolution. In addition to the high-quality of Voronoi-like meshes, problematic grid singularities associated with other meshing approaches are eliminated. Recent work suggests that even though Voronoi meshes are well suited for uniform spherical meshes, they are perhaps even more valuable with respect to variable resolution meshes. As discussed in Chapter 2, the generation of variable-resolution SCVTs requires two key components. First, a point-density function must be defined over the surface of the sphere, providing high density in areas of interest. This density function will help to enforce the variable-resolution nature of the grid. Second, a centroid 5
21 constraint must be iteratively enforced in every Voronoi cell. Coupling these two together allows the creation of general variable-resolution meshes. However, current algorithms for the generation of SCVTs provide less than desired performance as the point set increases in size. In an effort to aid multi-resolution modeling, a new algorithm is developed as part of this dissertation to allow the parallel computation of SCVTs. SCVT generation involves two portions, first a triangulation step where all points are triangulated. Second, an integration step which enforces the centroidal constraint on the Voronoi diagram. In current algorithms, the performance bottleneck is the triangulation step, because of its sequential implementation. Previous research has been done in an attempt to parallelize planar triangulation computations [6], however this work does not directly translate onto the surface of the sphere. Combining existing computational geometry tools, such as stereographic projections and domain decomposition, this new algorithm provides the parallel computation of spherical Delaunay triangulations. One method yet to be explored using SCVTs in geophysical simulations is adaptive mesh refinement (AMR). AMR has previously been explored in the context of the shallow-water equations [5, 29]. However, the majority of work uses cubed sphere meshes that provide static degrees of freedom. Grid cells are used to represent the root nodes of quad-trees providing easily implemented coarsening and refining. Typically, some criterion is defined in order to determine if a grid cell should be coarsened or refined; however grid cells are not allowed to be coarser than their initial size. In order to satisfy the name of Adaptive Mesh Refinement, refinement of the meshes is performed adaptively as the simulation progresses. Usually a field of interest is used to define the refinement criteria, such as relative vorticity. As the simulation progresses, the field of interest propagates within the domain, providing new regions that need to be refined while previously refined regions might need to be coarsened. This process provides a usable framework typical of standard AMR techniques; however 6
22 this method does not translate easily to SCVT meshes. In order to relate AMR techniques to SCVT meshes and the MPAS framework, a new technique is explored providing AMR-like grid generation. Currently the tools to fully implement an AMR framework do not exist, however part of the work in this dissertation is intended to aid the creation of an AMR framework within the context of SCVTs. The parallel generation of SCVTs is described in detail in Chapter 2, and results from the new algorithm are presented in Chapter 3. Background material on the MPAS model, as well as the test cases used, are provided in Chapter 4. Results from the exploration of MPAS on variable-resolution meshes is provided in Chapter 5. A brief background on AMR and the new AMR framework are provided in Chapter 6. The results of this new AMR framework are presented in Chapter 7. Finally, this dissertation concludes with a discussion of the presented material in Chapter Personal Contributions This section explains my personal contributions to the work contained in this dissertation. In Chapters 2 and 3 my personal contributions are as follows: Developed and implemented algorithm for parallel computation of spherical Delaunay triangulations and spherical centroidal Voronoi tessellations; Developed and implemented load balancing algorithm for variable resolution grids; Benchmarked algorithm to produce results. In Chapters 4 and 5 my personal contributions are as follows: Wrote software for conversion from a point set and triangulation to MPAS grid; Wrote software for visualization of MPAS input/output/restart files; Generated all grids for simulations; Wrote software for computation of globally averaged diagnostic quantities; 7
23 Wrote initial condition generator for barotropic instability test case; Wrote software for computation of global error norms; Ran all 25 simulations and computed global error norms. In Chapters 6 and 7 my personal contributions are as follows: Developed AMR framework for SCVT meshes; Wrote software for refining SCVT meshes based on a field from the output of MPAS; Wrote software for mapping a density field and smoothing it; Wrote software for computation of global error norms; Ran all 8 simulations and computed global error norms. 8
24 CHAPTER 2 PARALLEL SCVT GENERATOR BACKGROUND This chapter provides the necessary background for, and describes the newly developed algorithm for the parallel generation of spherical centroidal Voronoi tessellations that was created as part of this dissertation work. Results for this new grid generator are presented in Section 3. To begin, constructs required for the definition of SCVTs are described, beginning with Delaunay triangulations and Voronoi tessellations. Stereographic projections and their associated properties are then introduced; followed by a detailed description of the parallel algorithm used for the construction of SCVTs. 2.1 Delaunay Triangulations A k-simplex is defined as a k-dimensional polytope which is the convex hull of its k +1 vertices. For example, a 2-simplex would be a triangle, and a 3-simplex would be a tetrahedron. A k-simplex is made up of what are referred to as s-faces, where an s-face is made up of any s+1 distinct vertices of the k-simplex. For example, a 2-face is a triangular face, a 1-face is an edge, and a 0-face is a vertex. Given a point set, P, in R d, the Delaunay triangulation of this point set, D(P), is the set of d-simplices such that: A point, p, in R d, is a vertex of a simplex in D(P), p P; 9
25 The intersection of two simplices in D(P), is either the empty set, or a common face; The interior of the circumscribing d-sphere through the d + 1 vertices of a particular simplex contains no other points from the set P. If the circumscribing d-sphere has more than d+1 points lying on its perimeter, the triangulation is Delaunay, but not unique. The Delaunay triangulation of a point set defined in R d is related to the convex hull of the point set when projected onto a paraboloid in R d+1 [6]. 2.2 Voronoi Tessellations The dual mesh of a Delaunay triangulation is called the Voronoi tessellation. Given a set of points, P, called generators, the Voronoi tessellation, V = V i, is defined as x x i < x x j x V i, (2.1) where V i represents a Voronoi cell, and x i P and x j P represent generators. This property, called the Voronoi property, states that every point contained inside a Voronoi cell is closer to its cell generator than to any other generator in the set P. To be a centroidal Voronoi tessellation, the cell generators x i are required to be the centers of mass for the cells, meaning x i = x i, with x i defined as x i = V i xρ(x)dx V i ρ(x)dx, (2.2) where ρ(x) defines a non-negative point-density function which can be used to create variable resolution meshes. ThecenterofmassandthegeneratorofaVoronoicellaregenerallynotcoincident. The requirement that x i and x i be the same can be imposed through one of many algorithms, such as Lloyd s algorithm[17]. Lloyd s algorithm imposes this by iterating 10
26 on the point set, moving each generator to its Voronoi cell s center of mass until they are identical. Lloyd s algorithm is more rigorously discussed in [7]. In general, the density function in (2.2) affects the grid spacing of the final SCVT. If we arbitrarily select two Voronoi cells from a tessellation, and index them i and j, their grid spacing and density are related as h i h j [ ] 1 ρ(xj ) d +2, (2.3) ρ(x i ) where d is the dimension of the simplical elements in the tessellation, ρ(x i ) is the density function as in (2.2) evaluated at a point x i V i, and h i is a measure of the local grid spacing at the point x i. Though (2.3) is an open conjecture, it has been supported through many numerical studies as can be seen further in [25]. Replacing all of the constructs defined in Sections 2.1 and 2.2 with their analogous components on the surface of a sphere creates the spherical complements to Delaunay triangulations and Voronoi tessellations. The spherical versions of Delaunay triangulations and Voronoi tessellations are used for the construction of SCVTs as opposed to planar CVTs which have been discussed above for simplicity. While planar CVTs tessellate a 2-dimensional region with polygons, an SCVT tessellates the surface of a 3-dimensional sphere with polygons. 2.3 Stereographic Projections Stereographic projections are special mappings between the surface of a sphere and a plane tangent to the sphere. Not only are stereographic projections a conformal mapping, meaning that angles are preserved, but the projections also preserve circles. As will be discussed below, preserving circles is a particularly important property of stereographic projections. Stereographic projections also map the interior of these circles to the interior of the mapped circles [3, 26]. Preserving circularity implies that the stereographic projection preserves Delaunay criteria as described in Section 2.1, 11
27 because Delaunay triangle circumcircles (along with their interiors) are preserved, and therefore Delaunay triangulations are preserved. This projection can be used to compute a triangulation of a portion of the sphere, by allowing the triangulation to be carried out in the more convenient geometry of the plane. To define the stereographic projection, we need to define the following quantities, all in Cartesian coordinates in R 3. C is the center of the sphere, typically the origin, T is the point of tangency (where the projection plane is tangent to the sphere), F is the focus point, which is a reflection about C of T, and P is a point on the surface of the sphere. The stereographic projection of P into a point Q in the plane defined by T is defined by s = 2 (C F) (C F) (C F) (P F) (2.4) Q = s P+(1 s) F. (2.5) Figure 2.1 illustrates the stereographic projection, using the variables defined for (2.4) and (2.5). For the purposes of this research, it is more useful to define the projection relative to T, rather than F for reasons that will be explained later. A simple substitution of T = C F produces s = 2 1 (T) (P+T) (2.6) Q = s P+(s 1) T (2.7) This projection can be used to project from R d to R d 1, and can be repeated until d 1 = 2. 12
28 Figure 2.1: Cross-sectional illustration of a stereographic projection from a sphere into a tangent plane. 13
29 2.4 Parallel Algorithm Details The parallel algorithm closely follows the layout of Lloyd s algorithm, with a few modifications. The key modification is computing a Delaunay triangulation in parallel, since all other portions are considered embarrassingly parallel. The idea of computing a planar triangulation in parallel has been discussed for several years [6]. Typically, such algorithms divide the point set up into smaller regions that can then be triangulated independently from each other. Each triangulation needs to be stitched together to form a global triangulation. This stitching, or merge step, is typically computed serially because it could involve modifying significant portions of each triangulation if the division was not performed correctly. The merge step is the main difference between most parallel algorithms. The main benefit of the algorithm here is that the merge step is done in parallel. To create a spherical triangulation in parallel, a similar technique is employed as in the planar triangulations. First,thesphereisdividedintoN overlappingregionsy k (T k,r k )fork = 1,...,N, which are defined by a geodesic arc length R k, and a tangent plane defined by the regions point of tangency T k. Each of these regions is owned by an independent processor, and these regions also have some connectivity, or list of neighbors, defined. On the sphere, these regions would look like overlapping umbrellas, as can be seen in Figure 2.2(a). Each region (or processor) would take from the global point set, p i P, the points that are inside of its region radius, where cos 1 (T k p i ) R k. Keep in mind, this sorting may cause one point to be in several regions, as in Figure 2.2, where Figure 2.2(a) shows an example domain decomposition with 12 regions that could be used on a set of generators shown triangulated in Figure 2.2(b). Since the end goal of this algorithm is to compute an SCVT, the regional triangulations do not need to be merged on every iteration because they overlap. After a spherical point set, ˆP k, is determined, the stereographic projection P k = S[ˆP k,t k ] of ˆP into the plane defined by the point of tangency T k is computed. Be- 14
30 cause a stereographic projection preserves circles (and their interiors), the projection also preserves the Delaunay criteria that every triangle s circumcircle needs to be empty. The newly projected point set is now triangulated using some planar triangulation algorithm, such as Triangle [28] which is used in this study. If the mapping from global point index to local point index is appropriately maintained, a simple map from local index to global index gives the approximate triangulation for the region on the sphere. One final step is needed to make this the true triangulation for the region, which is to remove all non-delaunay triangles. The criteria required to be a Delaunay triangle in the global triangulation is defined as cos 1 T k ĉ i + ˆr i < R k, (2.8) where T k is a region center, R k is a region radius, ˆr i is a triangle circumradius, and ĉ i is a triangle circumcenter. Since each region is unaware of the triangles and points outside of its radius, only triangles whose circumcircles are completely contained inside of the region radius R k are guaranteed to be Delaunay, as no other points from the point set can be in their circumcircle. Any triangle whose circumcircle extends outside of its regions radius may contain points that were not in ˆP k, and should be discarded from the region s triangulation because this triangle is not guaranteed to adhere to the Delaunay criteria for the entire point set. Figure 2.3 visualizes this point, where Figure 2.3(a) shows a projected planar triangulation P k before removing triangles that do not satisfy (2.8), and Figure 2.3(a) shows the exact same triangulation after removing these potentially non-delaunay triangles. After this step is complete, the regional triangulation is now exactly Delaunay. After the regional triangulation is computed, the integration step of Lloyd s algorithm can begin. The overlapping of regions is key to this portion of the algorithm, because if the overlap is not large enough some true Delaunay triangles might not be entirely in at least one region. 15
31 In Lloyd s algorithm, after the Delaunay triangulation of the point set is computed, every Voronoi cell center of mass must be computed by integration, so its generator can be replaced. This step typically requires the computation of the Voronoi diagram for a region in addition to the Delaunay triangulation previously computed. However, some careful geometry can reveal that one doesn t actually need the Voronoi diagram. A single triangle from a Delaunay triangulation contributes to the integration of three different Voronoi cells. As seen in Figure 2.4, if the triangle is split into three kites, each made up of two edge midpoints, the triangle s circumcenter, and a vertex of the triangle, each one contributes to the Voronoi cell associated with the triangle vertex that is part of the kite. Integrating each kite, and updating a portion of the centroid integral allows one to only use the Delaunay triangulation when computing a CVT or an SCVT, so that no mesh connectivity needs to be computed on an iteration basis. To make this algorithm parallel, one simply has to ensure that each generator is only updated by one region. This can be done using one of a variety of domain decomposition methods. The method used in this particular algorithm uses the set of generators from a coarse SCVT to define region centers. Each region then updates only the generators that are inside of its defined Voronoi cell based on (2.1), using region centers, or points of tangency, T k as x i and generators p i P as x. Since Voronoi cells are non-overlapping, each generator will only get updated by one region. As mentioned earlier, the overlapping of regions is necessary to ensure that the triangulation of all points contained inside each region s Voronoi cells is exact. In practice, a region radius corresponding to the maximum distance to any adjacent region center allows enough overlap for the triangulation to be exact, and is defined br R i = max j=1,...,n cos 1 (T i T j ), (2.9) where N is the number of region neighbors, T i is the region center of interest, T j is a neighboring region center, and R i is the geodesic arc distance for region i. 16
32 Whereas this heuristic allows the algorithm to work correctly, it may not be optimal for variable resolution grids, as some regions might contain many more points than they need to when they border both a fine and a coarse region. Once each of the generators is updated, each region needs to transfer its newly updated points only to its adjacent neighbors, not to all of the active processors. This limits each processor s communications to roughly 6 sends and receives, regardless of the total number of processors used. After this step is over, the convergence of the grid is checked, and the iterations continue, or stop depending on the result. 17
33 (a) 12 Generator SCVT (b) Generator Delaunay Triangulation Figure 2.2: Domain Decomposition Example. Figure 2.2(a) is an SCVT used for a 12 processor domain decomposition, where Figure 2.2(b) is a generator Delaunay triangulation computed using the 12 generator SCVT for parallelization. Each colored ring represents a regions radius R k, where region centers T k are the Voronoi cell center, at the center of each pentagonal structure in Figure 2.2(a). 18
34 (a) Before application of (2.8) (b) After application of (2.8) Figure 2.3: Triangulations in a plane after Stereographic projection. 2.3(a) is the triangulation before (2.8) is applied, and 2.3(b) is after it is applied 19
35 Figure 2.4: Triangle division used for integrating Voronoi cells using only the Delaunay triangulation without any adjacency information. Kite sections contribute to the Voronoi cell centered at the vertex that is part of the kite. A, B, C vertices are generators in the point set, where the point at the center of the triangle is the circumcenter of this triangle. Triangular regions that are colored similarly contribute to the same vertex. 20
36 2.4.1 Convergence Criteria When checking for convergence, two metrics are used. Currently, the L 2 norm (2.10) of the generator movement and the L norm (2.11) of generator movement are compared with some tolerance. If the norm of interest reaches the tolerance, the iteration process is deemed to have converged. The L is more strict, but both of these norms follow similar convergence paths when plotted against iteration number. There are other grid metrics that can be used, such as the clustering energy [8] as in (2.12), but in practice this tends to be less strict, and more computationally expensive, when compared with generator movement. L 2 = Initial Conditions Npts i=1 (xn i xn+1 i ) 2 (2.10) N pts L = max ( x n i x n+1 i ) i=1,...,n pts (2.11) N pts CE = (ρ(x) x x i 2 dx) V i (2.12) i=1 A variety of initial conditions can be used in an SCVT generator. The most obvious is Monte Carlo points [20]. These can either be uniformly distributed over the sphere, to create a quasi-uniform initial condition, or they can be sampled using the target point-density function, to potentially reduce the number of iterations required for convergence. In addition to using Monte Carlo initial conditions, one can use a bisection method to build fine grids from a coarse grid [14]. To create a bisection grid, a coarse grid will be converged, using as few points as possible. After this coarse grid is converged, the midpoint of every Voronoi cell edge, or Delaunay triangle edge is added to the set of points. This causes the overall grid spacing to be reduced by roughly a factor of two in every cell. It also makes the point set roughly four times 21
37 as large. In addition to Monte Carlo and bisection initial conditions, there are many other choices that can be used. 22
38 CHAPTER 3 PARALLEL SCVT GENERATOR RESULTS Two different types of grids are presented to show the robustness of this algorithm. To begin, quasi-uniform meshes are created, followed by more complicated variable resolution meshes, which cover the entire sphere. This method can also be used to create limited area grids on the sphere, however this is outside the scope of this dissertation. All of the results presented below were computed using Florida State University s High Performance Computing Facility. 3.1 Quasi-Uniform Results STRIPACK [23] is an ACM TOMS algorithm that computes Delaunay triangulations on a sphere. STRIPACK is a serial code used as a baseline for comparison in this study. It is currently one of the few well-known spherical triangulation libraries available, and is written in Fortran 77. Figure 3.1 shows the performance of STRI- PACK [23] as the number of generators is increased through bisection as mentioned in Section The green dashed line represents the portion of the code that performs the integration of the Voronoi cells and the red solid line represents the portion of the code that performs the Delaunay triangulation. It is clear that the majority of the time per iteration is spent in computing the Delaunay triangulation, and as the 23
39 number of generators increases the time spent computing a Delaunay triangulation grows more rapidly than the time to integrate all Voronoi cells. 1e+07 1e+06 Triangulation Integration Average time (ms) e+06 Number of Generators Figure 3.1: Timings for a STRIPACK based SCVT Generator at 162, 642, 10242, and generators. The red solid line represents the time spent in STRIPACK computing a triangulation, where the green dashed line represents the time spent integrating the Voronoi cells outside of STRI- PACK in one iteration of Lloyd s algorithm. Timings in this figure were computed using an Intel Core 2 Duo T8100 CPU with 3GB of RAM. Since most climate models are shifting towards global high resolution simulations, the target quasi-uniform grid for this research is a global 15km resolution grid, which corresponds to grid points, or Voronoi cells. Grids created based on a uniform Monte Carlo and bisection initial conditions are compared. The time for these grids to converge to an SCVT with a tolerance of 10 6 in the L 2 norm, as in (2.10), is presented. A threshold of 10 6 is the strictest convergence levels that the Monte Carlo grid can attain. For this reason, we use 10 6 as the convergence threshold for this study. However, the bisection grid can converge much further beyond this point. Table 3.1 shows timing results for the parallel algorithm comparing these two different options of initial conditions. It is clear from this table that bisection initial conditions provide a significant speedup in the overall cost to generate a grid, seeing as it takes 24
40 roughly 1 th of the time to converge a bisection grid compared to a Monte Carlo grid. 20 Based on the results presented in Table 3.1, only bisection initial conditions are used for the following experiments, unless otherwise specified. Table 3.1: Timing results for MPI-SCVT with bisection and Monte Carlo initial conditions and the speedup of bisection relative to Monte Carlo initial conditions Timed Portion Bisection (B) Monte Carlo (MC) Speedup MC B Total Time (ms) 3,526,041 70,581, Triangulation Time (ms) 73,684 21,164, Integration Time (ms) 235,016 12,211, Communication Time (ms) 3,152,376 33,713, Tables 3.2 and 3.3 compare the algorithm described in this dissertation (MPI- SCVT) with STRIPACK [23], for computing spherical Delaunay triangulations. The results in these tables compare the cost to compute a single triangulation of a generator (60km global) grid. Table 3.2 compares STRIPACK with the final triangulation routine in MPI-SCVT. This routine produces a full triangulation of the entire sphere, and is only called once, at the very end of the grid generation process. Table 3.2: Comparison of STRIPACK with Serial and Parallel versions of MPI-SCVT using final triangulations Algorithm Procs Regions Time (ms) Speedup STRIPACK Baseline MPI-SCVT MPI-SCVT Table 3.3 compares STRIPACK with the triangulation routine in MPI-SCVT that is called on every iteration. The results presented relative to MPI-SCVT in Table 3.3 are averages over 2000 iterations. It is clear from this table that we see a significant speedup over both the serial versions of MPI-SCVT and STRIPACK when using only 42 processors. 25
41 As was previously mentioned, the drastic different between Tables 3.2 and 3.3 is due to the different algorithms for computing triangulations. While Table 3.2 presents timings that are directly comparable to STRIPACK, Table 3.3 presents timings more useful in computing SCVTs. As a comparison with Figure 3.1, Figures 3.2 and 3.3 present timing graphs made from MPI-SCVT. From these three plots, it is clear that the increase in time to compute the Delaunay triangulation does not grow as fast with problem size as it did in STRIPACK. Two processors are used, because this is the minimum amount of parallelization that MPI-SCVT supports, and MPI-SCVT requires at least 2 regions because the stereographic projection has a singularity at the focus point. Eventually, at around generators, the triangulation becomes more expensive than the integration step at least for 2 processors. Figure 3.2 represents the timings of MPI-SCVT for 2 regions as the problem size increases. Figure 3.3(a) represents the timings for a generator grid, which is a global 120km resolution, where Figure 3.3(b) represents a generator grid, with a 60km resolution, and Figure 3.3(c) represents a generator grid with a 15km resolution. Table 3.3: Comparison of STRIPACK with serial and parallel versions of MPI-SCVT using per iteration triangulations Algorithm Procs Regions Time (ms) Speedup STRIPACK Baseline MPI-SCVT MPI-SCVT
42 Average Time (ms) 1e Triangulation Integration Communication e+06 1e+07 Number of Generators Figure 3.2: Timings for various portions of MPI-SCVT using 2 processors and 2 regions. As the problem size increases the slope of both the triangulation (Red-Solid) and the integration (Green-Dashed) remain constant. The triangulation doesn t become more expensive than the integration until after roughly generators, as compared to Figure 3.1 where triangulation was more expensive after only 2562 generators. Also, a triangulation using generators costs roughly the same using MPI-SCVT and 2 processors as a triangulation using generators in STRI- PACK. 27
43 10000 Average Time (ms) Triangulation Integration Communication Number of Processors (a) Generator Timings Average Time (ms) Triangulation Integration Communication Number of Processors (b) Generator Timings 1e+06 Average Time (ms) Triangulation Integration Communication Number of Processors (c) Generator Timings Figure 3.3: Timing results from MPI-SCVT vs. number of processors. Constant problem size, shown as parallelization is increased. Red solid lines represent the cost of computing a triangulation, where green dashed lines represent the cost of integrating all Voronoi cells, and blue dotted lines represent the cost of communicating each region s updated point set to its neighbors. 28
44 3.2 Variable Resolution Results Variable resolution grids here are only computed using MPI-SCVT. This is done because STRIPACK performs comparably in both the uniform case and variable resolution cases. The main issue with regards to variable resolution grids is the domain decomposition used for MPI-SCVT. For example, a poor choice of domain decomposition could force the overlap in regions to be significantly larger than it needs tobe. Thelargertheoverlapofregions, themorepointseachregionhasto, needlessly, triangulate. This is especially apparent when using variable resolution grids as will be seen later. Because of this, two simple domain decompositions are used on a grid with a highly varying density function applied, in addition to one, more complicated domain decomposition method. Timings are presented to determine which performs better, and gives better load balancing. The density function used to compute the grids in this section can be seen in Figure 3.4. Density 1 Density Distance from Center of Density Function (radians) Figure 3.4: Density function that creates a grid with resolutions that differ by a factor of 16 between the coarse and the fine region. The maximum value of the density function is 1, where the minimum value is ( 1 16 )4. The analytic form of the density function used in figure 3.4 is defined as ρ(x i ) = [ 1 tanh 2(1 γ) ( ) β xc x i 29 α ] +1 +γ, (3.1)
45 where x i is constrained to lie on the surface of the unit sphere. This function results in relatively large values of ρ within a distance β of the point x c where β is measured in radians and x c is also constrained to lie on the surface of the sphere. The function transitions to relatively small values of ρ across a radian distance of α. The distance between x c and x i is computed as x c x i = cos 1 (x c x i ) with a range from 0 to π. Figure 3.5 shows an example grid created using this density function, with x c set to be the center of the mountain defined in shallow-water test case number 5 from [39] with φ c = 3π 2, λ c = π 6 representing longitude and latitude respectively, γ = 1 164, β = π, and α = 0.15 with generators. This set of parameters used in (3.1) is 6 referred to as x16. It was previously mentioned in Section 2.4 that the heuristic used to determine the region radius does not provide good load balancing with respect to variable resolution grids. To resolve this issue, a new algorithm was developed. The new algorithm begins by sorting each point into a Voronoi cell. After all regions have their point sets, the union of this point set with the neighboring Voronoi cell s point sets gives the final point set used. This sort method is more expensive to perform, however the better load balancing reduces idle computing time from processors that have small loads. Timings using this new method in addition to two dot-product-based methods for domain decomposition can be seen in Table 3.4. Figure 3.6 shows the number of points that each processor has to triangulate on a per iteration basis. These timings and figures were computed using the exact same initial conditions, which was a converged x16 grid with generators, and they all used 42 processors, and 42 regions. Timings presented in Table 3.4 are averages over 3000 iterations. Based on Table 3.4 and Figure 3.6 there is a significant advantage to the Voronoi based decomposition in that it not only speeds up the overall cost per iteration, but it provides a more balanced load across the processors. In Table 3.4 note that the timings are taken relative to processor number 0, and as can be seen in Figure 3.6(a), 30
46 processor 0 has a very small load so the majority of its iteration time is spent waiting for the processors with large loads to finish and catch up which is included in the Communication column of the table. Table 3.4: Timings based on the domain decomposition used. Uniform uses a coarse quasi-uniform SCVT to define region centers and their associated radii, and sorts using a simple dot product. x16 uses a coarse x16 SCVT to define region centers and their associated radii, and sorts using a simple dot product. Voronoi uses a coarse x16 SCVT to define region centers and their associated radii, and sorts using a Voronoi cell based sort. Decomposition Triangulation Integration Communication Iteration Speedup Uniform Base x Voronoi
47 (a) Coarse Region (b) Transition Region (c) Fine Region Figure 3.5: Figures show a variable resolution grid created using a density function with the format defined in (3.1). All three figures are of the same grid, only the viewing perspective is changed. Figure 3.5(a) shows the coarse region of the grid, 3.5(b) shows the transition region of the grid, and 3.5(c) shows the fine region of the grid. 32
48 Number Of Points In Region Uniform Decomposition Region Number (a) Uniform Number Of Points In Region x16 Decomposition Region Number (b) x16 Number Of Points In Region Voronoi based Decomposition Region Number (c) Voronoi Figure 3.6: Number of points each processor has to triangulate. 3.6(a) uses a quasiuniform SCVT for its decomposition, with a simple dot product. 3.6(b) uses a x16 SCVT for its decomposition, with a simple dot product. 3.6(c) uses a x16 SCVT for its decomposition, with a more complicated sort based on the region s Voronoi diagram. 33
49 3.3 Grid Generator Performance To assess the overall performance of MPI-SCVT, some scalability results are presented in Figure 3.7. Figure 3.7(a) shows that this algorithm can easily under-saturate processors, and when this happens, communication ends up dominating the overall runtime for the algorithm, which can be seen in Figure 3.3(a), and scalability ends up being sub-linear. As the number of generators increases (as seen in Figures 3.7(b) and 3.7(c)) the limit for being under-saturated is higher. Currently in the algorithm, communications are done asynchronously using non-blocking sends and receives. Also, overall communications are reduced by only communicating with a region s neighbors. This is possible because points can only move within a region radius on any two subsequent iterations, and because of this can only move into another region which is overlapping the current region. More efficiency gains could be realized through improvements in the communication, and the integration algorithms, which could result in linear scaling. In theory, because all of the computation is local this algorithm should scale linearly very well, up to hundreds if not thousands of processors. 34
50 70 60 SpeedUp (Serial/Parallel) Linear Reference SpeedUp (Serial/Parallel) Linear Reference Speedup Speedup Number of Processors Number of Processors (a) Generator Speedup (b) Generator Speedup SpeedUp (Serial/Parallel) Linear Reference 50 Speedup Number of Processors (c) Generator Speedup Figure 3.7: Scalability results based on number of generators. Green is a linear reference where Red is the Speedup computed using parallel version of MPI- SCVT against a serial version 35
51 CHAPTER 4 NUMERICAL MODEL BACKGROUND Climate models are broken into sub-component models. These dynamical cores model the physics associated with various portions of the climate and are combined in intelligent ways to create full climate models. Dynamical cores can be used to represent the ocean, atmosphere, sea-ice, ice sheet, and other components of the climate. The work contained in this dissertation relates specifically to ocean models. Ocean models typically utilize equations that describe fluid dynamics with full 3-dimensional motion. These equations can be complicated to solve, and overly expensive for certain problems. Due to the cost of solving these equations, they can be less than desirable for model development. For this reason, a simplification of these equations is used as a starting point for ocean models, called the shallow-water equations. The shallow-water equations can be used to explore a less expensive system that can still capture some of the key physical features in the full ocean system. To explore the capabilities of their models, developers use a shallow-water model coupled with test cases that showcase the model s ability to simulate specific physical processes. For example, [39] provides test cases suitable for modeling anything from advection, to non-linear geostrophic flow, to flow over an isolated mountain. Combining these test cases together allows a developer to determine how well their numerical model performs in specific situations, and benchmark the overall conservation of the numer- 36
52 ical method. After the numerical method is explored in the shallow-water context, it can then be implemented in a full 3-dimensional system to simulate ocean processes. Once implemented similar benchmarks can be performed, though they are significantly more expensive. This chapter begins by giving a basic background into the shallow-water equations and the numerical method used for the research contained in this portion of the dissertation, followed by an introduction of several test cases which are used in the shallow water system to benchmark the numerical method. 4.1 Shallow-Water Equations and Numerical Method The shallow-water equations are described as follows: u t h t + (hu) = 0, (4.1) +ηk u = g (h+b) K, (4.2) where h represents the fluid layer thickness and u represents the fluid velocity along the surface of the sphere. The absolute vorticity, η, is defined as k ( u)+f and the kinetic energy, K, is defined as u 2. At all points on the surface of the sphere the 2 vector k points in the local vertical direction and we require k u = 0 at all points. The three parameters in the system are gravity, g, Coriolis parameter, f, and bottom topography, b. When using the shallow-water equations four quantities are expected to be conserved; these quantities are total mass, total energy, potential vorticity, and potential enstrophy. All of these conservation properties are explored in the results section using MPAS. 37
53 A more appropriate form of the continuous equations is expressed as: h t + F = 0, (4.3) u t +qf = g (h+b) K, (4.4) where F = hu, F = k hu and η = hq where q is the total potential vorticity. Using the definition of potential vorticity, potential enstrophy is defined as the thicknessweighted variance of potential vorticity by 1/2 q 2. The numerical method used in this research to model the shallow-water system is discussed at length in [24, 31]. An analysis of the linearized version of (4.1) and (4.2) is conducted in [31] in order to derive a numerical method that is able to reproduce stationary geostrophic modes found in the continuous system, even when the numerical method is implemented on variable resolution meshes such as those shown in Figure 3.5. [24] extends the analysis to the nonlinear shallow-water equations shown in (4.3) and (4.4) in order to derive a method that conserves total energy and potential vorticity while allowing for a physically-appropriate amount of potential enstrophy dissipation. The work in this dissertation, and in [25] focuses on variable resolution meshes, as seen in Figure 4.1, whereas both [24, 31] present results for quasi-uniform meshes, even though the method is suitable for arbitrary Voronoi tessellations. The numerical scheme is a standard finite-volume method that makes use of a C-grid staggering as shown in Figure 4.2. The discrete approximations of the divergence and gradient operator are shown in Figure 3 of [24], and are used throughout this derivation. The thickness field is defined on the Voronoi cells while all vorticity-related fields, such as relative vorticity, absolute vorticity and potential vorticity, are defined on the Delaunay triangles. Using a discrete approximation to the divergence operator, a discrete thickness equation is derived. The equation for the normal-component 38
54 velocity is derived by taking the inner product of n e (from Figure 4.2) and (4.4). The resulting discrete system is expressed as: h i t = [ F e] i, (4.5) u e t +F e q e = [ (g(h i +b i )+K i )] e (4.6) where F e = h e u e represents the mass flux across the edge of a Voronoi cell and F e represents the mass flux across the edge of each Delaunay cell. K i, h e, ˆq e and F e are defined following [24]. Also following [24], the anticipated potential vorticity method, [27], is used to dissipate potential enstrophy. The derivations in [24, 31] provide a numerical method that conserves total energy to within time-truncation error, conserves total potential vorticity to within machine round-off error and dissipates potential enstrophy at a rate that depends on a single parameter. As mentioned previously, this derivation was carried out for use on a general Voronoi mesh. In an effort to produce a framework suitable for the rapid prototyping and development of dynamical cores, this numerical method has been implemented in a joint effort between Los Alamos National Laboratory (LANL) and the National Center for Atmospheric Research (NCAR). This new framework is called the Model for Prediction Across Scales (MPAS). Currently LANL is using this framework to develop ocean and shallow-water models, and NCAR is developing an atmospheric model. For the purposes of this dissertation, the ocean and shallow-water models developed at LANL are used within MPAS. 39
55 (a) Quasi-Uniform Grid (x1) (b) Variable Resolution Grid (x2) (c) Variable Resolution Grid (x4) (d) Variable (x16) Resolution Grid Figure 4.1: Four members of a family of meshes constructed from (3.1). Each mesh uses 2562 grid points and only differ in the setting of the parameter γ. x1, x2, x4 and x16 shown in the top-left, top-right, bottom-left and bottomright, respectively. 40
56 Figure 4.2: C-grid staggering of variables for the finite-volume scheme used in MPAS. Fluid thickness, topography, and kinetic energy are stored at Voronoi cell centers. The normal component of the velocity field is defined at the mid-point of line segments connecting cell centers. Vorticity related fields such as relative, absolute, and potential vorticity are stored at Voronoi cell vertices. Derived fields, ĥe, ˆq e, and F e must be reconstructed at each velocity point. 41
57 4.2 Shallow-Water Test Cases The ocean modeling community tests their models using a variety of techniques. One technique is to apply test problems that showcase various features present in the ocean, and explore the errors associated with resolving these features. The test problems can involve anything from advection, to geostrophic flow, to Rossby-Haurwitz waves. There are several test problems generally accepted by the community for the testing of an ocean or shallow water dynamical core. One set of these test problems can be found in [39]. This section describes two test cases that are used to benchmark the MPAS shallow-water dynamical core defined in [39], along with the test problem defined in [11]. Some additional tests used to benchmark dynamical cores can be seen in [37, 38] Non-linear Geostrophic Flow (TC2) As defined in [39] this test case represents nonlinear geostrophic flow. Geostrophic flow is an extremely important physical process that naturally occurs in the ocean and atmosphere. It occurs when the nonlinear Coriolis force balances the horizontal pressure gradient. This leads to the momentum equation becoming steady state, taking the form of fk u = g (h+b) (4.7) by The initial conditions for the geostrophic flow defined for this test case are given u = u 0 (cos(λ)cos(α)+cos(φ)sin(λ)sin(α)) (4.8) v = u 0 sin(φ)sin(α) (4.9) gh = gh 0 (αωu 0 + u2 0 2 ) ( cos(φ)cos(λ)sin(α)+sin(λ)cos(α))2 (4.10) 42
58 where λ represents the latitude, φ represents the longitude, Ω represents the rotational rateoftheearth, andαrepresentstheanglebetweensolidbodyrotationandthepolar axis which is taken to be 0.0 in the simulations presented in Chapter 5. The velocity field described in (4.8) and (4.9) can also be written in a stream function form as ψ = au 0 (sin(λ)cos(α) cos(φ)cos(λ)sin(α)) (4.11) χ = 0 (4.12) These stream functions provide only zonal (u direction) flow, with no flow in the meridional (v) direction. To define the initial flow field, the stream function (4.11) is sampled at Delaunay cell points x v, and computing u e as k ψ. The thickness field is defined by sampling (4.10) at Voronoi cell points. Even though errors in u e are present at t = 0, this approach guarantees that the discrete divergence is identically zero at t = Zonal Flow Over an Isolated Mountain (TC5) Shallow-water test case number 5, as defined in [39], represents zonal flow over an isolated mountain. This test case begins with geostrophic flow as described in Section 4.2.1; however at the initial time step a mountain is added to the topography. The center of the mountain is placed at φ c = 3π, λ 2 c = π, with a height described by 6 h s = h s0 (1 r R ) (4.13) where, h s0 = 2000m, R = π/9, and r 2 = min(r 2,(φ φ c ) 2 +(λ λ c ) 2 ). This causes the zonal flow to interact with the added mountain, causing gravity and Rossby waves to propagate as the flow adjusts to the presence of the topographical mountain. This interaction leads to strong nonlinearity, and therefore makes this test case useful for exploration of a numerical method s conservative properties. 43
59 4.2.3 Barotropic Instability (BTI) As defined in [11], this test case starts with a barotropically unstable zonal flow that includes a simple perturbation added to induce the instability. The perturbation first causes global gravity waves to propagate around the sphere within a few hours. Secondly, it creates complex vortical dynamics which develop over a few days. This test case requires initial conditions of the form u(φ) = u max e n [ 0 ] for φ φ 0 1 exp ] (φ φ 0 )(φ φ 1 for φ ) 0 φ φ 1 0 for φ φ 1 (4.14) v(φ,λ) = 0 (4.15) [ ] gh(φ) = gh 0 au(φ ) f + tan(φ ) u(φ ) dφ (4.16) φ a [ where we take u max = 80 m, φ s 0 = π, φ 7 1 = π φ 4 2 0, and e n = exp (φ 1 φ 0 ], and a ) 2 is the radius of the Earth. In (4.16) h 0 is chosen such that the global average sea surface height is 10km. (4.14) is then used to derive a stream function, which is sampled at Delaunay cell locations as in TC2 in Section to define the flow field. The height field is generated based on (4.16). After the initial conditions are generated, a perturbation is added to the height field that will drive the barotropic instability throughout the system. This perturbation is defined as h (λ,φ) = ĥcos(φ)e (λ α )2 e [φ 2 φ β ] 2 for π < λ < π (4.17) where φ 2 = π, α = 1, β = 1, and ĥ = 120m
60 CHAPTER 5 NUMERICAL MODEL RESULTS 5.1 Shallow-Water Model Setup SCVTs are used, as described in Chapter 2, for the spatial discretizations used in the finite-volume scheme. These SCVTs are generated using (3.1) as the prescribed density function. 25 different grids are generated and used in this work, however only a subset of these are shown. Of the generated grids, 20 are variable resolution, and 5 are quasi-uniform. The quasi-uniform grids have grid spacings and generator counts that can be found in Table 5.1. Table 5.1: Table of grid sizes and spacings for quasi-uniform grids used in shallowwater exploration Generators Approx. Grid Spacing km km km km km The variable resolution grids used have the same number of generators as their quasi-uniform counterparts, but differ only in γ in the density function (3.1). The values used for γ can be found in Table 5.2. In these grids, is a distinct fine and coarse region that are connected by a smooth transition region. Based on the parameters used for the density function, the fine region has a radius of π/6 radians from the 45
61 center of the mountain as defined in TC5, the transition region extends past the fine region another π/9 radians, and the coarse region makes up the remainder of the sphere. γ is varied to give specific factors for the grid spacing between the coarse and fine region, as can be seen in (2.3). As an example, the x2 grid (seen in Table 5.2) has a factor of 2 between grid spacings in the coarse, and in the fine regions. Table 5.2: Minimum values and grid spacing factors Grid Name Grid Spacing Factor Minimum Value x x x x x Setting the grid points constant and varying the density function used to create the grids has advantages and disadvantages. In terms of disadvantages, making one region finer requires the rest of the sphere to become coarser, so a x grid has cells that are larger than any cell in a x grid. As far as advantages go, the refinement provided in the variable resolution grids can provide an accuracy increase in specific regions, similar to limited-area modeling approach s. Table 5.3 shows the approximate resolutions for the fine and coarse mesh regions when using the described density function. An example of the grids can also be seen in Figure 4.1. Table 5.3: Approximate mesh resolutions (km) of the fine-mesh (dx f ) and coarsemesh (dx c ) regions of the global domain for the x1 through x16 meshes as a function of the number of grid points. Grid Points x1(dx f, dx c ) x2(dx f,dx c ) x4(dx f,dx c ) x8(dx f,dx c ) x16(dx f,dx c ) 2562 (480, 480) (282, 537) (196, 737) (169, 1293) (163, 2419) (240, 240) (141, 169) (98, 368) (85, 648) (81, 1222) (120, 120) (70, 134) (49, 184) (42, 324) (40, 611) (60, 60) (35, 67) (25, 92) (21, 162) (20, 305) (30, 30) (16, 32) (12, 48) (10, 78) (9, 148) 46
62 All grid points are generated using the bisection method as described in Section Unique to x1, the grid points are also associated with the recursive bisectionprojection of an inscribed icosahedron [14]. This method results in a particularly uniform distribution of grid points resulting in a relatively small solution error. This special distribution of nodes is lost when producing the variable-resolution meshes. As a result, a relatively large cost, in terms of global error, is incurred by choosing to move away from the special quasi-uniform meshes, but very little additional cost is incurred by increasing the extent of the mesh variation. 5.2 Shallow Water Test Case Results Using the MPAS shallow-water dynamical core, three test cases are explored in this Section, as defined in Sections 4.2.1, 4.2.2, and The results in this Chapter are also published as [25] Shallow Water Test Case 5 The analysis of TC5 is presented first because it offers insight into the conservation properties of MPAS. TC5 contains a single mountain that is responsible for the evolution of the system. While the mountain is large in scale, it is still localized and, in that sense, is well suited for local mesh refinement. All of the meshes depicted in Figure 4.1 and Table 5.3 enhance resolution in the vicinity of the defined mountain. TC5 prescribes an analytic initial condition of large-scale geostrophic flow that would be in steady state, if not for the presence of the mountain. This mountain is centered at x c and extends π/9 radians in latitude and longitude. As described in Chapter 3 the variable resolution meshes created are also centered at x c and the fine-mesh region extends a distance of π/6 radians, meaning that the fine-mesh region includes all of the mountain. To begin, a qualitative assessment of TC5 is presented. Figure 5.1 shows the fluid 47
63 height field h i + b i at day 15 for the x1, x2, x4, and x16 meshes, with cells. As depicted, all four simulations appear to be identical. This is expected because the flow is characterized by large-scale Rossby waves that are well resolved on the coarse-mesh resolutions of all of the meshes. In the x16 simulation result, the coarse grid cells can clearly be seen. Based on the numerical scheme two quantities are conserved to round-off error in every simulation: the area-weighted global sum of thickness and the volume-weighted potential vorticity. As found throughout the simulation, t V = t t N i i=1 N v v=1 h i A i = 0, (5.1) q v h v A v =0, (5.2) to within round-off error in all simulations, where the quantity V represents the total fluid volume. In order to evaluate the energetics of the system, the total energy is computed following [24, Eq. (70)] as E = e A e [ĥe u 2 e 2 ] + i A i [ gh i ( 1 2 h i +b i )] E r. (5.3) where E r represents the unavailable potential energy, and has the form: E r = i [ ] g H Hi i A i 2 +b i (5.4) where H i = i A i(h i +b i ) i A b i (5.5) i hasbeensubtracted. Fromnowon, totalenergy implies totalavailableenergy. E r represents the potential energy of the fluid at rest, which is unavailable to the system. Figure 5.2 demonstrates the conservation of the total energy in the simulations. The figures show log 10 (E(t) E(0)) E(0) over the 15 day integration for the x1, x2, x4, x8 and 48
64 x16 meshes with grid points. At day 15, all solutions conserve total energy to within relative to total energy present at t = 0. This finding is orders of magnitude better than is required when considering the dissipation mechanisms present in the real atmosphere and ocean [31]. The total energy is conserved in a physically-appropriate manner, therefore the nonlinear Coriolis force neither creates nor destroys kinetic energy, and the exchange of energy between its potential and kinetic forms is equal and opposite. The degree to which the nonlinear Coriolis force is energetically-neutral is explored, by computing the time it would take for the nonlinear Coriolis force to double the kinetic energy in the system. With grid points, the time required for the nonlinear Coriolis force to double the kinetic energy is approximately 10 4 years for all meshes, which is in agreement with Figure 4 of [24]. The other important component in the total energy budget is the conservative exchange of energy between its potential and kinetic forms. The potential and kinetic energy equations each have a source term. These source terms are equal and opposite (see (15) and (16) of [24]). Following (65) and (67) from [24], the source term for kinetic and potential energy is explored, respectively. Since these RHS sources are algebraically equivalent in the discrete system, a very high degree of cancellation between the sources is expected. All 25 simulations show the time scale for doubling the kinetic energy of the system due to the imperfect cancellation of KE and PE sourcestermsisapproximately10 10 years. Thisisessentiallymachineprecisionroundoff error. With regards to conservation, the final quantity of interest is potential enstrophy. Figure5.4showslog 10 (R(t) R(0)) R(0) defined as where R is the global-integrated potential enstrophy R = 1 V N v v=1 q 2 vh v A v R r. (5.6) 49
65 Potential enstrophy also has a unavailable reservoir that is equal to the amount of potentialenstrophythatexistswhenthefluidisatrest. Thisunavailablereservoir, R r is removed from the computation in order to obtain a more representative evaluation of potential enstrophy conservation. Figure 5.3 shows the globally average potential enstrophy as a function of time over a 15 day simulation for each of the x1, x2, x4, x8, and x16 meshes. Figure 5.4 shows the relative change in globally-averaged potential enstrophy for the x1, x2, x4, x8 and x16 meshes with nodes. At day 15, the relative changes in globally-averaged potential enstrophy vary between 10 4 and for the X1 and X16 meshes, respectively. In these simulations, the x1 and x2 simulations show a monotonic decrease in globally-averaged potential enstrophy, while the x4, x8, and x16 simulations show a monotonic increase in globally-averaged potential enstrophy. A scale aware Anticipated Potential Vorticity method would clearly aid this discrepancy. In terms of formal L 2 global error norms, previous works using local mesh refinement with the shallow-water system all find that the solution error is relatively unchanged when adding resolution in a specific region (e.g. [5, 29, 36]). This means the solution error appears to be controlled by the coarse region of the mesh when using static mesh refinement. The global L 2 error norm for each of the 25 simulations, as a function of coarse-mesh resolution, is shown in Figure 5.5(b). Since TC5 does not have a known analytic solution, error norms are computed with respect to a T511 global spectral model [30]. For TC5 at T511, the global spectral model requires a scale-selective 4 dissipation of m 4 /s in order to prevent the accumulation of energy and potential enstrophy at the grid scale. Figure 5.5 shows the error norms for TC5. Figure 5.5(a) shows the normalized L 2 error as a function of number of generators, where Figure 5.5(b) shows the error as a function of grid spacing in the coarse-mesh region. Based on figure 5.5(b), the solution error appears to be controlled by the mesh resolution in the coarse region. 50
66 All of the simulations show the same convergence rate of approximately 1.5. Note these errors norms are plotted on a log log scale to emphasize the primary finding that the L 2 error is controlled by the coarse-mesh resolution. Looking at the results more closely, it is apparent that the variable resolution meshes provide a small, but measurable, improvement in solution error. 51
67 (a) x1 grid (b) x2 grid (c) x4 grid (d) x16 grid Figure 5.1: The fluid height, hi + bi, at day 15 for TC5. Starting at the upper left and moving clockwise shows results from the X1, X2, X16 and X4 meshes using cells. The black oval denotes the location of the mountain. The figures are generated by filling each Voronoi cell with a single color, i.e. there is no interpolation due to rendering. This allows the coarsemesh grid cells to be seen in the X4 and X16 simulations. All results are plotted with an identical color scheme with a maximum of 5975 m and a minimum of 5025 m. 52
68 Relative Change in Total Energy 1e-08 1e-09 1e-10 1e-11 x1 x2 1e-12 x4 x8 x16 1e e+06 Time (s) Figure 5.2: Log 10 oftherelative changein available total energyfor TC5 as afunction of time for the x1, x2, x4, x8 and x16 meshes with grid points. 53
69 Potential Enstrophy e-17 x e e e e e e e e e e+06 Time (s) Potential Enstrophy e-17 x e e e e e e e e e+06 Time (s) (a) x1 (b) x2 Potential Enstrophy e e e e e-17 x4 Potential Enstrophy 6.876e e e e e e e-17 x e e+06 Time (s) 6.862e e+06 Time (s) (c) x e e-17 x16 (d) x8 Potential Enstrophy 7.225e e e e e e e+06 Time (s) (e) x16 Figure 5.3: Globally averaged potential enstrophy as a function of time for x1, x2, x4, x8, and x16 meshes with grid points. Simulations are run for 15 days. Figures show decreasing potential enstrophy for x1 and x2 meshes, and increasing potential enstrophy for x4, x8, and x16 meshes. 54
70 Relative Change in Potential Enstrophy e-05 1e-06 x1 x2 1e-07 x4 x8 1e-08 x e+06 Time (s) Figure 5.4: Log 10 of the relative change in available potential enstrophy for TC5 as a function of time for the x1, x2, x4, x8 and x16 meshes with grid points. 55
71 0.01 Normalized L2 Error x1 x2 x4 x8 x16 1e e+06 Number of Generators (a) Normalized error as a function of number of generators 0.01 Normalized L2 Error x1 x2 x4 x8 x16 1e Coarse Grid Spacing (km) (b) Normalized error as a function of coarse-mesh grid spacing Figure 5.5: The L 2 error of the thickness field at day 15 for TC5 shown for the x1, x2, x4, x8andx16meshes. Figure5.5(a)showserrorsasafunctionofnumber of generators, and figure 5.5(b) shows errors as a function of coarse-mesh grid spacing. Error norms are computed against a T511 reference solution. 56
72 5.2.2 Shallow Water Test Case 2 Having confirmed the ability of the numerical model to simulate transient flows in a robust manner with TC5, TC2 is now used to measure the method s ability to maintain large-scale geostrophic balance. Because TC2 is steady-state, any deviation of the numerical solution from its initial condition is considered to be numerical error. While TC5 offers a reason for mesh refinement, no comparable reason is present in TC2. The motivation for evaluating the variable resolution meshes using TC2 is not to demonstrate the approaches utility, but rather to measure the cost of mesh refinement. Maintaining large-scale balance is an important property of any numerical model of the atmosphere or ocean. TC2 provides an environment to precisely measure, through the L 2 error norm, the impact of mesh refinement on maintaining geostrophic balance. Figure 5.6 plots the error norms for TC2. Figure 5.6(a) plots the normalized error norms as a function of number of generators where 5.6(b) shows the normalized L 2 error as a function of the coarse-mesh grid spacing. As found with TC5, essentially all of the variation in the L 2 error in the simulations is controlled by the coarse resolution grid spacing. For a given coarse resolution, solution error increases by approximately a factor of 2 between the x2 and x16 meshes. However, the solution error for the x1 mesh is approximately a factor of 10 smaller, regardless of the coarse mesh resolution. Unfortunately the rate of convergence for TC2 does not appear to be uniform. Meshes with minimum grid resolutions above 100 km show a convergence rate of approximately 1.9 with respect to the coarse mesh resolution. As the minimum resolution of the mesh becomes smaller and smaller, the rate of convergence becomes smaller. This reduction in convergence rate is likely caused by at least one the following: deficiencies in the structure of the grids, deficiencies in the manner in which error norms are computed, and/or deficiencies in the numerical model. Currently none of these possibilities have been excluded, and there is on-going research to de- 57
73 termine what the underlying cause of this issue is. It is expected that the 2nd-order convergence rate would continue indefinitely as resolution is increased. 58
74 0.1 Normalized L2 Error x1 x2 1e-05 x4 x8 x16 1e e+06 Number of Generators (a) Errors as a function of number of generators 0.1 Normalized L2 Error x1 x2 1e-05 x4 x8 x16 1e Coarse Grid Spacing (km) (b) Errors as a function of coarse-mesh grid spacing Figure 5.6: The L 2 error of the thickness field at day 12 for TC2 for the x1, x2, x4, x8 and x16 meshes. Figure 5.6(a) shows errors as a function of number of generators, and Figure 5.6(b) shows errors as a function of coarsemesh grid spacing. Error norms are computed against the analytic initial conditions. 59
75 5.2.3 Barotropic Instability Test Case The final test case explored in the shallow-water system is the growth of a barotropic instability on a zonally-symmetric zonal jet [11]. Figure 5.7 shows the relative vorticity field at day 6 for the x1, x2, x4, x8 and x16 meshes with cells. The fine-mesh region is coincident with the center of each panel. In addition, the envelope of the growing barotropic instability is roughly coincident with the fine mesh region at day 6, with parts of the wave system entering and exiting the fine-mesh region at this point in time. Test cases based on instabilities that grow on a zonally-symmetric base state are particularly challenging for MPAS. The test case is zonally symmetric and the instability is triggered by a small amplitude perturbation, however SCVT meshes used are not always zonally-symmetric and, as a result, lead to some truncation error which projects onto non-zero zonal wave numbers. This truncation error serves as an additional trigger for the instability and can lead to wave growth that is either too fast or not in the correct location. As the resolution is increased, the amplitude of the spurious forcing by truncation error diminishes and the instability is solely controlled by the perturbation contained in the initial conditions. In addition, the growth of the unstable waves depends strongly on the type and strength of the sub-grid scale closures that are either implicit in the underlying numerical formulation or explicitly added to the numerical models. For example, the x1 panel in Figure 5.7 agrees very closely with panel D in Figure 17 of [15], but is significantly different than panel D in Figure 9 of [11]. This is because the simulations presented here and in [15] do not use any explicit closure, whereas [11] uses hyper-diffusion on the RHS of the momentum equation. The strong correspondence of the x1 simulations with panel D in Figure 17 of [15] indicates that the x1 simulation is broadly representative of the instability when simulated in a system with minimal or no damping. The primary purpose here is 60
76 to understand how the use of variable resolution meshes alters the growth of the barotropic instability. First, focusing on the deep, tilted trough just right of center in each panel along with the ridge-trough-ridge system just upstream to the west one finds that these dominant features are present in all simulations with the same amplitude and phase. The x2 simulation is qualitatively equivalent to the x1 simulation in all respects. In addition, the x8 simulation is qualitatively equivalent to the x4 simulation in all respects. The x4 simulation differs from the x2 simulation only along the edges of the panels that corresponds to the center of the coarse-mesh regions. The primary difference between these two groups of simulations is that the x4/x8 simulations produce an additional ridge in the upstream wave. The x16 simulation is qualitatively different from the other simulations in all regions other than the fine-mesh region. The x16 simulation produces relatively strong ridge-trough systems in the coarsemesh region that are not present in the other simulations. It is important to note that the fine-mesh resolutions of the x8 and x16 simulations are essentially the same at approximately 10 km, yet the coarse-mesh resolution between these simulations differ by a factor of two (as in Table 5.3). The x16/ simulation is more similar to the x1/40962 simulation (not shown) than any of the other simulations with nodes. Since the coarse resolution of the x16/ simulation is comparable to the x1/40962 simulation, this finding is consistent with Figures 5.5(b) and 5.6(b) which demonstrate that the accuracy of the simulation is controlled primarily by the resolution in the coarse-mesh region. 61
77 Figure 5.7: Each panel depicts the relative vorticity field at day 6 for a barotropicallyunstable jet using cells. The panels differ only in the mesh used in the simulation. The vertical extent of each panel covers the northern hemisphere. The horizontal extent covers all longitudes starting at -90 degrees such that the fine-mesh region is approximately centered on each panel. The color scales are identical for every panel and saturate at ±
78 CHAPTER 6 ADAPTIVE MESH REFINEMENT BACKGROUND This chapter describes the framework used for the exploration of Adaptive Mesh Refinement (AMR) in the context of the shallow water equations using SCVT grids. Results from the described AMR framework are presented in Chapter AMR Background Adaptive Mesh Refinement is typically used as a means to get increased spatial accuracy without a significant increase in the computational cost. Typically, one would have to increase the global resolution of a mesh to increase the global accuracy, however AMR makes use of output data from simulations to generate new meshes that are better suited for that specific simulation. Because AMR meshes apply local refinement around features of interest they are a type of multi-resolution mesh. As a simulation progresses the meshes generated typically track features of interest. As was seen in Section error norms associated with multi-resolution meshes appear to be controlled by the coarse mesh resolution. Because of this, AMR SCVT meshes are only used with the motivation of reducing horizontal grid spacing in an area defined by simulation output. At a later point in time, scale aware parameterizations, which adapt to changes in grid spacing, may reduce the error norms by providing more accurate simulations on these multi-resolution AMR meshes. 63
79 The work in this portion of this dissertation follows two similar explorations[5, 29]. Both of these AMR approaches are implemented using cubed sphere grids that provide two beneficial features for implementing AMR. First, each cell can be thought of as the root of a quad tree allowing for local refinement simply by subdividing each cell into four sub-cells. Second, since the cells do not move over time, de-refinement is as simple as removing the sub-cells and replacing with the previous root cell. One disadvantage to cubed sphere grids is that they are non-conforming meshes and, because of this, have hanging nodes. The hanging nodes require interpolation schemes to remove spurious waves generated by reflection from the artificial boundary. Both [5, 29] use the absolute value of the relative vorticity field as the criteria for cell refinement. In their explorations they both use several of the standard shallowwater test cases found in [39] to test their AMR schemes. A common test between both explorations is shallow-water test case number 5, as defined in Section This test case is useful in testing AMR schemes due to the evolution of the vortical dynamics. As the vortices migrate around the sphere, the AMR scheme should adapt the grid by refining and derefining cells to compensate for this movement. 6.2 SCVT-AMR Framework A typical AMR framework for use on cubed sphere meshes with static grid points has a general format similar to the following pseudo-code: While Algorithm 1 is a typical AMR framework for use on structured grids with static grid points, it does not have a direct translation for use on SCVT meshes. As the focus of this dissertation is on multi-resolution meshes within SCVTs, a new framework is developed for use within this context, and is described as follows Currently, the tools required for the use of SCVTs in Algorithm 2 do not exist. Particularly difficult is re-mapping data between two SCVT meshes. There are methods of re-mapping data on SCVTs [16], however the implementations are not 64
80 mature enough to support this type of application. Due to this constraint, the framework presented in this dissertation only incorporates one time step of a typical AMR framework. This is done under the assumption that eventually the re-mapping tools will become mature enough to be combined with this AMR scheme, and will allow a comparison with previously implemented schemes which use Algorithm 1. The AMR framework used for a single time step is as follows: Following [5, 29] the relative vorticity field, ξ, is used to define both the pointdensity field and the refinement criteria. After one AMR time step, in this case one day, the output from MPAS shallow-water model is used to build a density field. In order to create a density field, several steps are required. To begin, the absolute value of the relative vorticity field, ξ, is cut off at a threshold comparable to [5, 29] of ξ > This step ensures only cells with extreme values of relative vorticity are refined, which ignores any relative vorticity in the mean flow. After the threshold is applied, the remaining relative vorticity field is rescaled, where this scaling is defined as ρ i = ξ i min N j=1 ξ j max N j=1 ξ j (γ 4 1.0)+1.0 (6.1) where ξ i represents the absolute value of the relative vorticity at cell i, N represents the number of cells, ρ i represents the density value at a cell, and γ represents an Algorithm 1 General AMR Framework t = 0 Initialize simulation while t < T do Iterate simulation for time of t Refine mesh based on chosen criteria, e.g. relative vorticity, ξ Map data from previous mesh to refined mesh end while Compute error norms 65
81 arbitrary scaling. Using the scaling defined in (6.1) and the cut off previously discussed, the density field has a minimum value of 1, and a maximum value defined by γ 4. The minimum grid spacing is then given as a factor of the coarse grid spacing, based on γ 4, as in (2.3). The resulting density field obtained by cutting off and mapping the relative vorticity field tends to have sharp gradients and can be very concentrated in certain areas. These sharp gradients cause issues when refinement is applied, as neighboring cells are allowed to differ by more than one level of refinement. In an attempt to remove these sharp gradients in the density field a Laplacian smoothing operator can be applied an arbitrary number of times. Laplacian smoothing will cause the density field to diffuse over the sphere, which will smooth out gradients in the density field. The motivation of this technique is that grids will be a higher quality if the density field has smooth gradients. The Laplacian smoothing operator is defined as ρ i = 1 2 ρ i + n 1 ( 2 n ρ j) (6.2) j=1 where n is the number of neighbors cell i has and ρ is the density defined at cell centers. This Laplacian smoothing operator replaces a cell value with a weighted average of its previous value and its neighbor s values. Because this operator smooths slowly, it may have to be applied many times before a reasonably smooth density field is obtained. Figure 6.1 illustrates this point with 4 plots. Presented are density fields with no smoothings (Figure 6.1(a)), 16 smoothings (Figure 6.1(b)), 64 smoothings (Figure 6.1(c)), and 128 smoothings (Figure 6.1(d)). 128 is used as the maximum numberofsmoothingsbecausemostofthefeaturespresentinthe0and16smoothings fields are not present anymore. Also, in the 128 smoothings case, refinement is applied within areas that do not appear to require it. 66
82 After Laplacian smoothing is applied, the grid refinement levels are validated to ensure only one level of refinement occurs across edges of Delaunay triangles. Although this could add more points than are required based on the refinement criteria, this technique is standard in the AMR techniques presented in [5, 29]. Cubed sphere AMR techniques maintain the coarse grid spacing of elements due to the static grid points. In an attempt to retain this advantage refinement can be used to intelligently add points to SCVTs. As was discussed previously, bisection provides a refinement in horizontal grid spacing of roughly a factor of two. In order to refine the reference mesh, Delaunay triangles are bisected based on the density value given from re-mapping and smoothing the relative vorticity field. This refinement procedure subdivides Delaunay triangles, adding points on edges, as well as the interior of triangles. The number of points added depends on the density in the triangle compared with the minimum density. One edge of a Delaunay triangle is subdivided n times, where n is defined as n = log 2 (ρ 1 4 n ) (6.3) where ρ n is the density value associated with the Delaunay triangle. The Delaunay triangle can either be refined when n > 1 or, if ξ > α. Both [5, 29] use ξ > α and set α = Because of the threshold on ξ the implemented method combines both these methods. Triangles are refined when n > 1, however n is only larger than 1 when ξ > α. As mentioned previously, refining triangles based on n > 1 causes the coarse mesh resolution to roughly be preserved, based on (2.3). Controlling γ from (6.1) allows control over the total number of points added to a mesh. Although low values of γ produce grids with less total points, they also produce grids with lower variances in horizontal grid spacing. Figure 6.2 shows three triangles with varying levels of division based on the density value of the triangle. Afteragridhasbeenrefinedandsmoothedusingacombinationof(6.1), (6.2), and 67
83 (6.3), the grid is no longer an SCVT. An SCVT generator, as described in Chapter 2, can be used to converge the point set to an SCVT. Before an SCVT generator can be used to iterate on a refined point set, a spatial density function needs to be defined in order to evaluate the point-density of each generator as they move around the mesh. There are several choices of spatial density functions, each with their own drawbacks and benefits. The main drawback is differences in computational cost. Some potential options for spatial density functions are piecewise constant, piecewise linear, and pointwise constant density functions. While pointwise constant density functions provide a benefit of having significantly lower computational cost, they have less dependence on the overlaying density function and can potentially move refined regions out of the area of interest. Piecewise constant density functions are almost as expensive as piecewise linear density functions, however they don t smooth the final point set over the mesh well, and end up with points clustered in reference Voronoi cells. Because of the drawbacks of piecewise and pointwise constant density functions, piecewise linear density functions are used. Before the refined mesh is output, a reference mesh is output, which contains points, density values associated with those points, and a triangulation of those points. The piecewise linear density function is defined as a barycentric interpolation within reference Delaunay triangles. In order to evaluate the density function at an arbitrary point, first the Delaunay triangle which contains the point must be determined. This is done through a combination of vector dot and cross products to check the orientation with each edge of the Delaunay triangle. After the in-out test is completed, the barycentric weights of the test point need to be computed. This computation is described as 68
84 α = Area(B,C,P) Area(A, B, C) β = Area(C,A,P) Area(A, B, C) γ = Area(A,B,P) Area(A, B, C) (6.4) (6.5) (6.6) (6.7) where A, B, and C are the vertices of the triangle, given in counter-clockwise order, P is the test point contained inside triangle ABC, and α, β, and γ are the barycentric weights for P associated with A, B, and C respectively. After the barycentric weights are computed, the density function is a simple map defined as follows ρ P = ρ A α+ρ B β +ρ C γ (6.8) where ρ is the density value, and α, β, and γ are the barycentric weights for point P. The resulting framework provides a method of producing AMR-like grids that maintain the specified coarse mesh resolution, while increasing resolution in areas of interest based on reference simulations. Using this scheme, and some yet-to-bedeveloped tools for re-mapping, a full AMR scheme can be implemented. Any of the fields present in these simulations can be used for computing the density field and refinement; relative vorticity is only used as a comparison to [5, 29]. 69
85 Algorithm 2 Full AMR Framework for SCVT meshes t = 0 Initialize simulation while t < T do Iterate simulation for time of t Convert field of interest, ξ, into a point-density field If desired, smooth point-density field Refine mesh based on point-density field Converge refined mesh to an SCVT as described in Chapter 2 Map data from previous SCVT to new SCVT end while Compute error norms Algorithm 3 Single time step SCVT AMR Framework t = 0 Initialize simulation Iterate simulation for time of t Convert field of interest, ξ, into a point-density field If desired, smooth point-density field Refine mesh based on point-density field Converge refined mesh to an SCVT as described in Chapter 2 Initialize simulation with newly converged SCVT mesh at t = 0 Iterate simulation for time of t Compute error norms 70
86 (a) No smoothing (b) 16 smoothings (c) 64 smoothings (d) 128 smoothings Figure 6.1: Density field obtained after one simulation day using the relative vorticity field from shallow-water test case 5, on a x generator grid, corresponding to the first four steps in Algorithm 3. Figure 6.1(a) has no smoothings applied, Figure 6.1(b) has 16 smoothings applied, Figure 6.1(c) has 64 smoothings applied, and Figure 6.1(d) has 128 smoothings applied. The smoothing operator is defined in (6.2). Red represents the minimum, where blue represents the maximum. To show transitions color represents log 2 (ρ 1/4 ) 71
87 (a) n = 1 (b) n = 2 (c) n = 3 Figure 6.2: Three triangles with subdivision based on density values. Figure 6.2(a) shows a triangle whose density value is 1 4 providing no divisions. Figure 6.2(b) shows a triangle whose density value is 2 4 providing one division. Figure 6.2(c) shows a triangle whose density value is 4 4 providing two divisions 72
88 CHAPTER 7 ADAPTIVE MESH REFINEMENT RESULTS To explore the potential of the AMR framework introduced in Chapter 6, results are presented in this chapter. To begin, a 642 generator quasi-uniform mesh is used as a reference mesh. After the 642 results are presented, a 2564 generator quasiuniform mesh is used to produce another set of AMR grids. These point sets are chosen due to their relatively small number of points, and large grid spacing. All of the results presented are computed using shallow-water test case number 5 involving geostrophic flow over an isolated mountain, implemented inside MPAS. Test case 5 was previously defined in Section Error norms are computed using a T511 high resolution spectral element solution, as was used for the shallow-water test case 5 results in Chapter Point Suite Tobegin,asuiteofresultsarepresentedbasedona642gridcellquasi-uniformgrid with roughly 960km grid spacing. Using this quasi-uniform reference grid, shallowwater test case 5, as defined in Section 4.2.2, is simulated for one day. After one simulation day, the relative vorticity field is mapped into a density field over the mesh using (6.1). Delaunay triangles are then refined based on their density values. The maximum density value is constrained using γ = 4. This provides four levels 73
89 of refinement within a mesh, reducing the 960km grid spacing to 120km in areas with extreme relative vorticity. Delaunay triangles are refined in the aforementioned manner, maintaining a fixed coarse grid resolution. Figure 7.1 shows four grids that make up the 642 grid cell suite. Figures 7.1(a), 7.1(b), 7.1(c), and 7.1(d) show 0, 16, 64, and 128 iterations of Laplacian smoothing on the density fields respectively. Color in these figures represents cell area, with red representing the smallest area, and purple representing the largest area. (a) Unsmoothed (b) 16 Smoothings (c) 64 Smoothings (d) 128 Smoothings Figure 7.1: AMR grids based on a 642 grid cell quasi-uniform grid. Color represents cell area, where Red is the minimum area and Purple is the maximum area. Presented are grids with 0, 16, 64, and 128 iterations of Laplacian smoothing applied. 74
90 Before exploring the results obtained from each simulation, reference data is shown for a qualitative comparison. Figure 7.2 shows the thickness, potential vorticity, and relative vorticity fields after one simulation day on the 642 quasi-uniform mesh. Again the relative vorticity field shown in Figure 7.2(c) was scaled to be the density field used to generate the meshes shown in Figure 7.1. (a) Thickness (b) Potential Vorticity (c) Relative Vorticity Figure 7.2: Reference data fields for 642 quasi-uniform mesh. Shallow-water test case 5 was simulated for 1 day, plotted in Figure 7.2(a) is the fluid thickness field, Figure 7.2(b) is the potential vorticity field, and Figure 7.2(c) is the relative vorticity field. The output fields from the four AMR grids after one simulation day using shallowwater test case 5 are presented in Figures 7.3, 7.4, and 7.5. Figure 7.3 shows the thickness fields for all four simulations, which appear qualitatively equivalent to the reference simulation. Figure 7.4 shows the potential vorticity fields for all four simu- 75
91 lations, which also appear qualitatively equivalent to the reference simulation. Figure 7.5 shows the relative vorticity fields for all four simulations. The relative vorticity fields appear to have an increase in noise as the number of smoothings applied to the mesh are increased. (a) Unsmoothed (b) 16 Smoothing (c) 64 Smoothing (d) 128 Smoothing Figure 7.3: Thickness fields from the 642 suite of AMR meshes. Figure 7.3(a) shows the thickness field from an unsmoothed AMR mesh. Figure 7.3(b) shows the thickness field from a mesh with 16 smoothings. Figure 7.3(c) shows the thickness field from a mesh with 64 smoothings. Figure 7.3(d) shows the thickness field from a mesh with 128 smoothings. As was seen in Section all conservation properties still hold on these AMR meshes. In order to explore the effect each AMR mesh has on the simulation error 76
92 norms are computed as was done in Section Table 7.1 lists the L 2 and L norms of the error in the thickness field of each AMR simulation at the end of one simulation day. Table 7.1: Error norms associated with the suite of AMR meshes based on the 642 grid point reference mesh. Presented are L 2 and L norms of the error in the thickness field, compared to a T511 reference simulation Grid L 2 L % Irreagular Cells Reference % Unsmoothed % 16 Smoothings % 64 Smoothings % 128 Smoothing % As can be seen in Table 7.1, all AMR meshes have slightly higher error than the reference mesh. Also, applying more iterations of Laplacian smoothing does not appear to aid the error norm much if at all. Most of the error in these meshes comes from the addition of pentagons and heptagons, or Voronoi cells with five and seven sides respectively. These irregular cells cause distortion in the area of the mesh surrounding them. Although the reference mesh has the minimum 12 pentagons, each of the other four meshes have more unneeded pentagons each with an additional septagon. Although it is an incredibly difficult problem, removing these extra pentagons and heptagons may potentially improve the error norms, and help this AMR scheme be more useful. 77
93 (a) Unsmoothed (b) 16 Smoothing (c) 64 Smoothing (d) 128 Smoothing Figure 7.4: Potential vorticity fields from the 642 suite of AMR meshes. Figure 7.4(a) shows the potential vorticity field from an unsmoothed AMR mesh. Figure 7.4(b) shows the potential vorticity field from a mesh with 16 smoothings. Figure 7.4(c) shows the potential vorticity field from a mesh with 64 smoothings. Figure 7.4(d) shows the potential vorticity field from a mesh with 128 smoothings. 78
94 (a) Unsmoothed (b) 16 Smoothing (c) 64 Smoothing (d) 128 Smoothing Figure 7.5: Relative vorticity fields from the 642 suite of AMR meshes. Figure 7.5(a) shows the relative vorticity field from an unsmoothed AMR mesh. Figure 7.5(b) shows the relative vorticity field from a mesh with 16 smoothings. Figure 7.5(c) shows the relative vorticity field from a mesh with 64 smoothings. Figure 7.5(d) shows the relative vorticity field from a mesh with 128 smoothings. 79
95 Point Suite As mentioned in Table 5.1 a 2562 generator quasi-uniform SCVT has a grid spacing of roughly 480km. Shallow-water test case 5 is simulated for one day, on the quasiuniform mesh, after which the relative vorticity field, ξ, is extracted and converted into a density field using (6.1). As was the case for the 642 grid point suite of meshes, γ = 4 is chosen to give four levels of refinement between the grid resolutions of the finest and coarsest grid regions as defined in (2.3). The factor 4 is chosen because it allows a large variation in grid spacing between the finest and coarsest grid regions without adding a significant number of points. Figure 6.1 shows the four meshes created as part of the 2562 grid point suite of AMR meshes. The four meshes presented consist of varying levels of Laplacian smoothing, with 0, 16, 64, and 128 applications of Laplacian smoothing. Each of these four meshes is colored by cell area, where red represents the smallest value, and purple represents the largest value. Figure 7.7 plots the thickness, relative vorticity, and potential vorticity fields on the quasi-uniform 2562 generator mesh after one simulation day. Figure 7.7 is provided as a reference for data presented on AMR grids based on the quasi-uniform 2562 generator mesh. Figures 7.8, 7.9, and 7.10 show the thickness, potential vorticity, and relative vorticity fields for all four AMR simulations based on the 2562 grid point reference mesh. All simulations are run for one simulation day using shallow-water test case 5. AswasseeninSection7.1, anincreaseinthenumberoftimeslaplaciansmoothing is applied to the mesh appears to increase the overall noise in the simulation. While the thickness and potential vorticity fields appear qualitatively similar to the reference simulation, the relative vorticity field appears to have significantly more noise. In order to determine the effect of this noise on the final simulations, the error norms are presented relative to a T511 reference simulation in Table
96 Table 7.2 shows the error norms from all 5 simulations to be essentially equivalent in the L 2 norm, and not significantly different in the L norm. As was the case in Section 7.1, all of the AMR grids have more pentagons and septagons than the reference mesh, and removing these may improve the error norm for the AMR simulations. Also, the grids presented as part of these results have distinct boundaries between levels of refinement in the final SCVT, which is evident from Figure 7.6. Smoothing out this boundary in the final density function may also improve the simulation results. Alternatively to the results presented in Table 7.1, Table 7.2 shows a slight decrease in both error norms(excluding the 16 smoothings case) as more smoothings are applied. As the number of points in the reference mesh increase, the resulting density function can capture more of the dynamics of the relative vorticity field, allowing for grids with smoother transition regions. This trend may continue to higher resolution reference grids. Table 7.2: Error norms for AMR grids based on 2562 grid point reference mesh. L 2 and L norms are computed with the thickness field relative to a T511 simulation. Grid L 2 L % Irregular cells Reference % Unsmoothed % 16 Smoothings % 64 Smoothings % 128 Smoothings % 81
97 (a) Unsmoothed (b) 16 Smoothings (c) 64 Smoothings (d) 128 Smoothings Figure 7.6: AMR grids based on a 2562 grid cell quasi-uniform grid. Color represents cell area, where Red is the minimum area and Purple is the maximum area. Presented are grids with 0, 16, 64, and 128 iterations of Laplacian smoothing applied. 82
98 (a) Thickness (b) Potential Vorticity (c) Relative Vorticity Figure 7.7: Reference data fields for 2562 quasi-uniform mesh. Shallow-water test case5wassimulatedfor1day, plottedinfigure7.7(a)isthefluidthickness field, figure 7.7(b) is the potential vorticity field, and figure 7.7(c) is the relative vorticity field. 83
99 (a) Unsmoothed (b) 16 Smoothing (c) 64 Smoothing (d) 128 Smoothing Figure 7.8: Thickness fields from the 2562 suite of AMR meshes. Figure 7.8(a) shows the thickness field from an unsmoothed AMR mesh. Figure 7.8(b) shows the thickness field from a mesh with 16 smoothings. Figure 7.8(c) shows the thickness field from a mesh with 64 smoothings. Figure 7.8(d) shows the thickness field from a mesh with 128 smoothings. 84
Parallel Quality Meshes for Earth Models
 Parallel Quality Meshes for Earth Models John Burkardt Department of Scientific Computing Florida State University... 04 October 2016, Virginia Tech... http://people.sc.fsu.edu/ jburkardt/presentations/......
Parallel Quality Meshes for Earth Models John Burkardt Department of Scientific Computing Florida State University... 04 October 2016, Virginia Tech... http://people.sc.fsu.edu/ jburkardt/presentations/......
Voronoi Diagram. Xiao-Ming Fu
 Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
13.472J/1.128J/2.158J/16.940J COMPUTATIONAL GEOMETRY
 13.472J/1.128J/2.158J/16.940J COMPUTATIONAL GEOMETRY Lecture 23 Dr. W. Cho Prof. N. M. Patrikalakis Copyright c 2003 Massachusetts Institute of Technology Contents 23 F.E. and B.E. Meshing Algorithms 2
13.472J/1.128J/2.158J/16.940J COMPUTATIONAL GEOMETRY Lecture 23 Dr. W. Cho Prof. N. M. Patrikalakis Copyright c 2003 Massachusetts Institute of Technology Contents 23 F.E. and B.E. Meshing Algorithms 2
Tiling Three-Dimensional Space with Simplices. Shankar Krishnan AT&T Labs - Research
 Tiling Three-Dimensional Space with Simplices Shankar Krishnan AT&T Labs - Research What is a Tiling? Partition of an infinite space into pieces having a finite number of distinct shapes usually Euclidean
Tiling Three-Dimensional Space with Simplices Shankar Krishnan AT&T Labs - Research What is a Tiling? Partition of an infinite space into pieces having a finite number of distinct shapes usually Euclidean
Outline of the presentation
 Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
Accuracy analysis of mimetic finite volume operators on geodesic grids and a consistent alternative
 Accuracy analysis of mimetic finite volume operators on geodesic grids and a consistent alternative Pedro S. Peixoto College of Engineering, Mathematics and Physical Sciences - University of Exeter Instituto
Accuracy analysis of mimetic finite volume operators on geodesic grids and a consistent alternative Pedro S. Peixoto College of Engineering, Mathematics and Physical Sciences - University of Exeter Instituto
A Constrained Delaunay Triangle Mesh Method for Three-Dimensional Unstructured Boundary Point Cloud
 International Journal of Computer Systems (ISSN: 2394-1065), Volume 03 Issue 02, February, 2016 Available at http://www.ijcsonline.com/ A Constrained Delaunay Triangle Mesh Method for Three-Dimensional
International Journal of Computer Systems (ISSN: 2394-1065), Volume 03 Issue 02, February, 2016 Available at http://www.ijcsonline.com/ A Constrained Delaunay Triangle Mesh Method for Three-Dimensional
Lecture 2 Unstructured Mesh Generation
 Lecture 2 Unstructured Mesh Generation MIT 16.930 Advanced Topics in Numerical Methods for Partial Differential Equations Per-Olof Persson (persson@mit.edu) February 13, 2006 1 Mesh Generation Given a
Lecture 2 Unstructured Mesh Generation MIT 16.930 Advanced Topics in Numerical Methods for Partial Differential Equations Per-Olof Persson (persson@mit.edu) February 13, 2006 1 Mesh Generation Given a
Conjectures concerning the geometry of 2-point Centroidal Voronoi Tessellations
 Conjectures concerning the geometry of 2-point Centroidal Voronoi Tessellations Emma Twersky May 2017 Abstract This paper is an exploration into centroidal Voronoi tessellations, or CVTs. A centroidal
Conjectures concerning the geometry of 2-point Centroidal Voronoi Tessellations Emma Twersky May 2017 Abstract This paper is an exploration into centroidal Voronoi tessellations, or CVTs. A centroidal
Computational Geometry
 Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
Manipulating the Boundary Mesh
 Chapter 7. Manipulating the Boundary Mesh The first step in producing an unstructured grid is to define the shape of the domain boundaries. Using a preprocessor (GAMBIT or a third-party CAD package) you
Chapter 7. Manipulating the Boundary Mesh The first step in producing an unstructured grid is to define the shape of the domain boundaries. Using a preprocessor (GAMBIT or a third-party CAD package) you
COMPUTING CONSTRAINED DELAUNAY
 COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS IN THE PLANE By Samuel Peterson, University of Minnesota Undergraduate The Goal The Problem The Algorithms The Implementation Applications Acknowledgments
COMPUTING CONSTRAINED DELAUNAY TRIANGULATIONS IN THE PLANE By Samuel Peterson, University of Minnesota Undergraduate The Goal The Problem The Algorithms The Implementation Applications Acknowledgments
Surface Reconstruction. Gianpaolo Palma
 Surface Reconstruction Gianpaolo Palma Surface reconstruction Input Point cloud With or without normals Examples: multi-view stereo, union of range scan vertices Range scans Each scan is a triangular mesh
Surface Reconstruction Gianpaolo Palma Surface reconstruction Input Point cloud With or without normals Examples: multi-view stereo, union of range scan vertices Range scans Each scan is a triangular mesh
A Polygon-based Line Integral Method for Calculating Vorticity, Divergence, and Deformation from Non-uniform Observations
 2.7 olygon-based Line Integral Method for Calculating Vorticity, Divergence, and Deformation from Non-uniform Observations Charles N. Helms and Robert E. Hart Florida State University, Tallahassee, Florida
2.7 olygon-based Line Integral Method for Calculating Vorticity, Divergence, and Deformation from Non-uniform Observations Charles N. Helms and Robert E. Hart Florida State University, Tallahassee, Florida
AMR Multi-Moment FVM Scheme
 Chapter 4 AMR Multi-Moment FVM Scheme 4.1 Berger s AMR scheme An AMR grid with the hierarchy of Berger s AMR scheme proposed in [13] for CFD simulations is given in Fig.4.1 as a simple example for following
Chapter 4 AMR Multi-Moment FVM Scheme 4.1 Berger s AMR scheme An AMR grid with the hierarchy of Berger s AMR scheme proposed in [13] for CFD simulations is given in Fig.4.1 as a simple example for following
Differential Geometry: Circle Packings. [A Circle Packing Algorithm, Collins and Stephenson] [CirclePack, Ken Stephenson]
![Differential Geometry: Circle Packings. [A Circle Packing Algorithm, Collins and Stephenson] [CirclePack, Ken Stephenson] Differential Geometry: Circle Packings. [A Circle Packing Algorithm, Collins and Stephenson] [CirclePack, Ken Stephenson]](/thumbs/85/92091407.jpg) Differential Geometry: Circle Packings [A Circle Packing Algorithm, Collins and Stephenson] [CirclePack, Ken Stephenson] Conformal Maps Recall: Given a domain Ω R 2, the map F:Ω R 2 is conformal if it
Differential Geometry: Circle Packings [A Circle Packing Algorithm, Collins and Stephenson] [CirclePack, Ken Stephenson] Conformal Maps Recall: Given a domain Ω R 2, the map F:Ω R 2 is conformal if it
Definitions. Topology/Geometry of Geodesics. Joseph D. Clinton. SNEC June Magnus J. Wenninger
 Topology/Geometry of Geodesics Joseph D. Clinton SNEC-04 28-29 June 2003 Magnus J. Wenninger Introduction Definitions Topology Goldberg s polyhedra Classes of Geodesic polyhedra Triangular tessellations
Topology/Geometry of Geodesics Joseph D. Clinton SNEC-04 28-29 June 2003 Magnus J. Wenninger Introduction Definitions Topology Goldberg s polyhedra Classes of Geodesic polyhedra Triangular tessellations
Optimal Compression of a Polyline with Segments and Arcs
 Optimal Compression of a Polyline with Segments and Arcs Alexander Gribov Esri 380 New York Street Redlands, CA 92373 Email: agribov@esri.com arxiv:1604.07476v5 [cs.cg] 10 Apr 2017 Abstract This paper
Optimal Compression of a Polyline with Segments and Arcs Alexander Gribov Esri 380 New York Street Redlands, CA 92373 Email: agribov@esri.com arxiv:1604.07476v5 [cs.cg] 10 Apr 2017 Abstract This paper
Quadrilateral Meshing by Circle Packing
 Quadrilateral Meshing by Circle Packing Marshall Bern 1 David Eppstein 2 Abstract We use circle-packing methods to generate quadrilateral meshes for polygonal domains, with guaranteed bounds both on the
Quadrilateral Meshing by Circle Packing Marshall Bern 1 David Eppstein 2 Abstract We use circle-packing methods to generate quadrilateral meshes for polygonal domains, with guaranteed bounds both on the
PS Computational Geometry Homework Assignment Sheet I (Due 16-March-2018)
 Homework Assignment Sheet I (Due 16-March-2018) Assignment 1 Let f, g : N R with f(n) := 8n + 4 and g(n) := 1 5 n log 2 n. Prove explicitly that f O(g) and f o(g). Assignment 2 How can you generalize the
Homework Assignment Sheet I (Due 16-March-2018) Assignment 1 Let f, g : N R with f(n) := 8n + 4 and g(n) := 1 5 n log 2 n. Prove explicitly that f O(g) and f o(g). Assignment 2 How can you generalize the
Preferred directions for resolving the non-uniqueness of Delaunay triangulations
 Preferred directions for resolving the non-uniqueness of Delaunay triangulations Christopher Dyken and Michael S. Floater Abstract: This note proposes a simple rule to determine a unique triangulation
Preferred directions for resolving the non-uniqueness of Delaunay triangulations Christopher Dyken and Michael S. Floater Abstract: This note proposes a simple rule to determine a unique triangulation
Discrete geometry. Lecture 2. Alexander & Michael Bronstein tosca.cs.technion.ac.il/book
 Discrete geometry Lecture 2 Alexander & Michael Bronstein tosca.cs.technion.ac.il/book Numerical geometry of non-rigid shapes Stanford University, Winter 2009 The world is continuous, but the mind is discrete
Discrete geometry Lecture 2 Alexander & Michael Bronstein tosca.cs.technion.ac.il/book Numerical geometry of non-rigid shapes Stanford University, Winter 2009 The world is continuous, but the mind is discrete
The ICON project: Design and performance of an unstructured grid approach for a global triangular grid model
 The ICON project: Design and performance of an unstructured grid approach for a global triangular grid model Luis Kornblueh, Luca Bonaventura, and Peter Sanders,... ICON : ICOsahedral, Nonhdyrostatic model
The ICON project: Design and performance of an unstructured grid approach for a global triangular grid model Luis Kornblueh, Luca Bonaventura, and Peter Sanders,... ICON : ICOsahedral, Nonhdyrostatic model
CS 532: 3D Computer Vision 14 th Set of Notes
 1 CS 532: 3D Computer Vision 14 th Set of Notes Instructor: Philippos Mordohai Webpage: www.cs.stevens.edu/~mordohai E-mail: Philippos.Mordohai@stevens.edu Office: Lieb 215 Lecture Outline Triangulating
1 CS 532: 3D Computer Vision 14 th Set of Notes Instructor: Philippos Mordohai Webpage: www.cs.stevens.edu/~mordohai E-mail: Philippos.Mordohai@stevens.edu Office: Lieb 215 Lecture Outline Triangulating
Using Semi-Regular 4 8 Meshes for Subdivision Surfaces
 Using Semi-Regular 8 Meshes for Subdivision Surfaces Luiz Velho IMPA Instituto de Matemática Pura e Aplicada Abstract. Semi-regular 8 meshes are refinable triangulated quadrangulations. They provide a
Using Semi-Regular 8 Meshes for Subdivision Surfaces Luiz Velho IMPA Instituto de Matemática Pura e Aplicada Abstract. Semi-regular 8 meshes are refinable triangulated quadrangulations. They provide a
Simple Mesh Examples to Illustrate Specific Finite Element Mesh Requirements
 Simple Mesh Examples to Illustrate Specific Finite Element Mesh Requirements Peter Fleischmann, Robert Kosik, Bernhard Haindl, and Siegfried Selberherr Institute for Microelectronics, TU Vienna, Gu6hausstrafie
Simple Mesh Examples to Illustrate Specific Finite Element Mesh Requirements Peter Fleischmann, Robert Kosik, Bernhard Haindl, and Siegfried Selberherr Institute for Microelectronics, TU Vienna, Gu6hausstrafie
Adaptive-Mesh-Refinement Pattern
 Adaptive-Mesh-Refinement Pattern I. Problem Data-parallelism is exposed on a geometric mesh structure (either irregular or regular), where each point iteratively communicates with nearby neighboring points
Adaptive-Mesh-Refinement Pattern I. Problem Data-parallelism is exposed on a geometric mesh structure (either irregular or regular), where each point iteratively communicates with nearby neighboring points
Parameterization of Triangular Meshes with Virtual Boundaries
 Parameterization of Triangular Meshes with Virtual Boundaries Yunjin Lee 1;Λ Hyoung Seok Kim 2;y Seungyong Lee 1;z 1 Department of Computer Science and Engineering Pohang University of Science and Technology
Parameterization of Triangular Meshes with Virtual Boundaries Yunjin Lee 1;Λ Hyoung Seok Kim 2;y Seungyong Lee 1;z 1 Department of Computer Science and Engineering Pohang University of Science and Technology
Surface Mesh Generation
 Surface Mesh Generation J.-F. Remacle Université catholique de Louvain September 22, 2011 0 3D Model For the description of the mesh generation process, let us consider the CAD model of a propeller presented
Surface Mesh Generation J.-F. Remacle Université catholique de Louvain September 22, 2011 0 3D Model For the description of the mesh generation process, let us consider the CAD model of a propeller presented
Shape Modeling and Geometry Processing
 252-0538-00L, Spring 2018 Shape Modeling and Geometry Processing Discrete Differential Geometry Differential Geometry Motivation Formalize geometric properties of shapes Roi Poranne # 2 Differential Geometry
252-0538-00L, Spring 2018 Shape Modeling and Geometry Processing Discrete Differential Geometry Differential Geometry Motivation Formalize geometric properties of shapes Roi Poranne # 2 Differential Geometry
Coupling of STAR-CCM+ to Other Theoretical or Numerical Solutions. Milovan Perić
 Coupling of STAR-CCM+ to Other Theoretical or Numerical Solutions Milovan Perić Contents The need to couple STAR-CCM+ with other theoretical or numerical solutions Coupling approaches: surface and volume
Coupling of STAR-CCM+ to Other Theoretical or Numerical Solutions Milovan Perić Contents The need to couple STAR-CCM+ with other theoretical or numerical solutions Coupling approaches: surface and volume
Lecture Tessellations, fractals, projection. Amit Zoran. Advanced Topics in Digital Design
 Lecture Tessellations, fractals, projection Amit Zoran Advanced Topics in Digital Design 67682 The Rachel and Selim Benin School of Computer Science and Engineering The Hebrew University of Jerusalem,
Lecture Tessellations, fractals, projection Amit Zoran Advanced Topics in Digital Design 67682 The Rachel and Selim Benin School of Computer Science and Engineering The Hebrew University of Jerusalem,
Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder]
![Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder] Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder]](/thumbs/93/111713975.jpg) Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder] Preliminaries Recall: Given a smooth function f:r R, the function
Differential Geometry: Circle Patterns (Part 1) [Discrete Conformal Mappinngs via Circle Patterns. Kharevych, Springborn and Schröder] Preliminaries Recall: Given a smooth function f:r R, the function
Glossary of dictionary terms in the AP geometry units
 Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
Möbius Transformations in Scientific Computing. David Eppstein
 Möbius Transformations in Scientific Computing David Eppstein Univ. of California, Irvine School of Information and Computer Science (including joint work with Marshall Bern from WADS 01 and SODA 03) Outline
Möbius Transformations in Scientific Computing David Eppstein Univ. of California, Irvine School of Information and Computer Science (including joint work with Marshall Bern from WADS 01 and SODA 03) Outline
Topological Issues in Hexahedral Meshing
 Topological Issues in Hexahedral Meshing David Eppstein Univ. of California, Irvine Dept. of Information and Computer Science Outline I. What is meshing? Problem statement Types of mesh Quality issues
Topological Issues in Hexahedral Meshing David Eppstein Univ. of California, Irvine Dept. of Information and Computer Science Outline I. What is meshing? Problem statement Types of mesh Quality issues
Scanning Real World Objects without Worries 3D Reconstruction
 Scanning Real World Objects without Worries 3D Reconstruction 1. Overview Feng Li 308262 Kuan Tian 308263 This document is written for the 3D reconstruction part in the course Scanning real world objects
Scanning Real World Objects without Worries 3D Reconstruction 1. Overview Feng Li 308262 Kuan Tian 308263 This document is written for the 3D reconstruction part in the course Scanning real world objects
VoroCrust: Simultaneous Surface Reconstruction and Volume Meshing with Voronoi cells
 VoroCrust: Simultaneous Surface Reconstruction and Volume Meshing with Voronoi cells Scott A. Mitchell (speaker), joint work with Ahmed H. Mahmoud, Ahmad A. Rushdi, Scott A. Mitchell, Ahmad Abdelkader
VoroCrust: Simultaneous Surface Reconstruction and Volume Meshing with Voronoi cells Scott A. Mitchell (speaker), joint work with Ahmed H. Mahmoud, Ahmad A. Rushdi, Scott A. Mitchell, Ahmad Abdelkader
Introduction to ANSYS ICEM CFD
 Lecture 4 Volume Meshing 14. 0 Release Introduction to ANSYS ICEM CFD 1 2011 ANSYS, Inc. March 21, 2012 Introduction to Volume Meshing To automatically create 3D elements to fill volumetric domain Generally
Lecture 4 Volume Meshing 14. 0 Release Introduction to ANSYS ICEM CFD 1 2011 ANSYS, Inc. March 21, 2012 Introduction to Volume Meshing To automatically create 3D elements to fill volumetric domain Generally
2) For any triangle edge not on the boundary, there is exactly one neighboring
 Triangulating Trimmed NURBS Surfaces Chang Shu and Pierre Boulanger Abstract. This paper describes techniques for the piecewise linear approximation of trimmed NURBS surfaces. The problem, called surface
Triangulating Trimmed NURBS Surfaces Chang Shu and Pierre Boulanger Abstract. This paper describes techniques for the piecewise linear approximation of trimmed NURBS surfaces. The problem, called surface
coding of various parts showing different features, the possibility of rotation or of hiding covering parts of the object's surface to gain an insight
 Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
10.1 Overview. Section 10.1: Overview. Section 10.2: Procedure for Generating Prisms. Section 10.3: Prism Meshing Options
 Chapter 10. Generating Prisms This chapter describes the automatic and manual procedure for creating prisms in TGrid. It also discusses the solution to some common problems that you may face while creating
Chapter 10. Generating Prisms This chapter describes the automatic and manual procedure for creating prisms in TGrid. It also discusses the solution to some common problems that you may face while creating
Ideas beyond Number. Teacher s guide to Activity worksheets
 Ideas beyond Number Teacher s guide to Activity worksheets Intended outcomes: Students will: extend their knowledge of geometrical objects, both 2D and 3D develop their skills in geometrical reasoning
Ideas beyond Number Teacher s guide to Activity worksheets Intended outcomes: Students will: extend their knowledge of geometrical objects, both 2D and 3D develop their skills in geometrical reasoning
Exploiting a database to predict the in-flight stability of the F-16
 Exploiting a database to predict the in-flight stability of the F-16 David Amsallem and Julien Cortial December 12, 2008 1 Introduction Among the critical phenomena that have to be taken into account when
Exploiting a database to predict the in-flight stability of the F-16 David Amsallem and Julien Cortial December 12, 2008 1 Introduction Among the critical phenomena that have to be taken into account when
Finite Volume Discretization on Irregular Voronoi Grids
 Finite Volume Discretization on Irregular Voronoi Grids C.Huettig 1, W. Moore 1 1 Hampton University / National Institute of Aerospace Folie 1 The earth and its terrestrial neighbors NASA Colin Rose, Dorling
Finite Volume Discretization on Irregular Voronoi Grids C.Huettig 1, W. Moore 1 1 Hampton University / National Institute of Aerospace Folie 1 The earth and its terrestrial neighbors NASA Colin Rose, Dorling
arxiv: v1 [math.na] 20 Sep 2016
![arxiv: v1 [math.na] 20 Sep 2016 arxiv: v1 [math.na] 20 Sep 2016](/thumbs/93/111453229.jpg) arxiv:1609.06236v1 [math.na] 20 Sep 2016 A Local Mesh Modification Strategy for Interface Problems with Application to Shape and Topology Optimization P. Gangl 1,2 and U. Langer 3 1 Doctoral Program Comp.
arxiv:1609.06236v1 [math.na] 20 Sep 2016 A Local Mesh Modification Strategy for Interface Problems with Application to Shape and Topology Optimization P. Gangl 1,2 and U. Langer 3 1 Doctoral Program Comp.
GEOMETRIC TOOLS FOR COMPUTER GRAPHICS
 GEOMETRIC TOOLS FOR COMPUTER GRAPHICS PHILIP J. SCHNEIDER DAVID H. EBERLY MORGAN KAUFMANN PUBLISHERS A N I M P R I N T O F E L S E V I E R S C I E N C E A M S T E R D A M B O S T O N L O N D O N N E W
GEOMETRIC TOOLS FOR COMPUTER GRAPHICS PHILIP J. SCHNEIDER DAVID H. EBERLY MORGAN KAUFMANN PUBLISHERS A N I M P R I N T O F E L S E V I E R S C I E N C E A M S T E R D A M B O S T O N L O N D O N N E W
A New Dynamical Core with Local Mesh Refinement. Todd Ringler
 A New Dynamical Core with Local Mesh Refinement Todd Ringler Los Alamos National Laboratory Theoretical Division LA-UR 09-05207 Climate, Ocean and Sea-Ice Modeling Project http://public.lanl.gov/ringler/ringler.html
A New Dynamical Core with Local Mesh Refinement Todd Ringler Los Alamos National Laboratory Theoretical Division LA-UR 09-05207 Climate, Ocean and Sea-Ice Modeling Project http://public.lanl.gov/ringler/ringler.html
Adaptive dynamic fracture simulation using potential-based cohesive zone modeling and polygonal finite elements
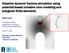 Adaptive dynamic fracture simulation using potential-based cohesive zone modeling and polygonal finite elements Sofie Leon University of Illinois Department of Civil and Environmental Engineering July
Adaptive dynamic fracture simulation using potential-based cohesive zone modeling and polygonal finite elements Sofie Leon University of Illinois Department of Civil and Environmental Engineering July
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass
 Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
Parallel Computation of Spherical Parameterizations for Mesh Analysis. Th. Athanasiadis and I. Fudos University of Ioannina, Greece
 Parallel Computation of Spherical Parameterizations for Mesh Analysis Th. Athanasiadis and I. Fudos, Greece Introduction Mesh parameterization is a powerful geometry processing tool Applications Remeshing
Parallel Computation of Spherical Parameterizations for Mesh Analysis Th. Athanasiadis and I. Fudos, Greece Introduction Mesh parameterization is a powerful geometry processing tool Applications Remeshing
Discrete representations of geometric objects: Features, data structures and adequacy for dynamic simulation. Part I : Solid geometry
 Discrete representations of geometric objects: Features, data structures and adequacy for dynamic simulation. Surfaces Part I : Solid geometry hachar Fleishman Tel Aviv University David Levin Claudio T.
Discrete representations of geometric objects: Features, data structures and adequacy for dynamic simulation. Surfaces Part I : Solid geometry hachar Fleishman Tel Aviv University David Levin Claudio T.
Computational Geometry. Algorithm Design (10) Computational Geometry. Convex Hull. Areas in Computational Geometry
 Computational Geometry Algorithm Design (10) Computational Geometry Graduate School of Engineering Takashi Chikayama Algorithms formulated as geometry problems Broad application areas Computer Graphics,
Computational Geometry Algorithm Design (10) Computational Geometry Graduate School of Engineering Takashi Chikayama Algorithms formulated as geometry problems Broad application areas Computer Graphics,
A New Progressive Lossy-to-Lossless Coding Method for 2.5-D Triangle Mesh with Arbitrary Connectivity
 A New Progressive Lossy-to-Lossless Coding Method for 2.5-D Triangle Mesh with Arbitrary Connectivity Dan Han University of Victoria October 31, 2016 New Mesh-Coding Method Dan Han 1 Outline 1 Introduction
A New Progressive Lossy-to-Lossless Coding Method for 2.5-D Triangle Mesh with Arbitrary Connectivity Dan Han University of Victoria October 31, 2016 New Mesh-Coding Method Dan Han 1 Outline 1 Introduction
arxiv:cs/ v1 [cs.cg] 19 Aug 1999
![arxiv:cs/ v1 [cs.cg] 19 Aug 1999 arxiv:cs/ v1 [cs.cg] 19 Aug 1999](/thumbs/85/91570185.jpg) Quadrilateral Meshing by Circle Packing Marshall Bern David Eppstein arxiv:cs/9908016v1 [cs.cg] 19 Aug 1999 Abstract We use circle-packing methods to generate quadrilateral meshes for polygonal domains,
Quadrilateral Meshing by Circle Packing Marshall Bern David Eppstein arxiv:cs/9908016v1 [cs.cg] 19 Aug 1999 Abstract We use circle-packing methods to generate quadrilateral meshes for polygonal domains,
Voronoi Diagrams in the Plane. Chapter 5 of O Rourke text Chapter 7 and 9 of course text
 Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
Chapter 8. Voronoi Diagrams. 8.1 Post Oce Problem
 Chapter 8 Voronoi Diagrams 8.1 Post Oce Problem Suppose there are n post oces p 1,... p n in a city. Someone who is located at a position q within the city would like to know which post oce is closest
Chapter 8 Voronoi Diagrams 8.1 Post Oce Problem Suppose there are n post oces p 1,... p n in a city. Someone who is located at a position q within the city would like to know which post oce is closest
Overview of Unstructured Mesh Generation Methods
 Overview of Unstructured Mesh Generation Methods Structured Meshes local mesh points and cells do not depend on their position but are defined by a general rule. Lead to very efficient algorithms and storage.
Overview of Unstructured Mesh Generation Methods Structured Meshes local mesh points and cells do not depend on their position but are defined by a general rule. Lead to very efficient algorithms and storage.
Automatic Delineation of Drainage Basins from Contour Elevation Data Using Skeleton Construction Techniques
 Summer School in New York, USA, Polytechnic University, July 21 25, 28 p. 1/16 Automatic Delineation of Drainage Basins from Contour Elevation Data Using Skeleton Construction Techniques Giovanni Moretti
Summer School in New York, USA, Polytechnic University, July 21 25, 28 p. 1/16 Automatic Delineation of Drainage Basins from Contour Elevation Data Using Skeleton Construction Techniques Giovanni Moretti
A numerical microscope for plasma physics
 A numerical microscope for plasma physics A new simulation capability developed for heavy-ion inertial fusion energy research will accelerate plasma physics and particle beam modeling, with application
A numerical microscope for plasma physics A new simulation capability developed for heavy-ion inertial fusion energy research will accelerate plasma physics and particle beam modeling, with application
Radial Basis Function-Generated Finite Differences (RBF-FD): New Opportunities for Applications in Scientific Computing
 Radial Basis Function-Generated Finite Differences (RBF-FD): New Opportunities for Applications in Scientific Computing Natasha Flyer National Center for Atmospheric Research Boulder, CO Meshes vs. Mesh-free
Radial Basis Function-Generated Finite Differences (RBF-FD): New Opportunities for Applications in Scientific Computing Natasha Flyer National Center for Atmospheric Research Boulder, CO Meshes vs. Mesh-free
An Introduction to Geometrical Probability
 An Introduction to Geometrical Probability Distributional Aspects with Applications A. M. Mathai McGill University Montreal, Canada Gordon and Breach Science Publishers Australia Canada China Prance Germany
An Introduction to Geometrical Probability Distributional Aspects with Applications A. M. Mathai McGill University Montreal, Canada Gordon and Breach Science Publishers Australia Canada China Prance Germany
Mathematics Standards for High School Geometry
 Mathematics Standards for High School Geometry Geometry is a course required for graduation and course is aligned with the College and Career Ready Standards for Mathematics in High School. Throughout
Mathematics Standards for High School Geometry Geometry is a course required for graduation and course is aligned with the College and Career Ready Standards for Mathematics in High School. Throughout
Geometry Foundations Planning Document
 Geometry Foundations Planning Document Unit 1: Chromatic Numbers Unit Overview A variety of topics allows students to begin the year successfully, review basic fundamentals, develop cooperative learning
Geometry Foundations Planning Document Unit 1: Chromatic Numbers Unit Overview A variety of topics allows students to begin the year successfully, review basic fundamentals, develop cooperative learning
ADAPTIVE TILE CODING METHODS FOR THE GENERALIZATION OF VALUE FUNCTIONS IN THE RL STATE SPACE A THESIS SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL
 ADAPTIVE TILE CODING METHODS FOR THE GENERALIZATION OF VALUE FUNCTIONS IN THE RL STATE SPACE A THESIS SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY BHARAT SIGINAM IN
ADAPTIVE TILE CODING METHODS FOR THE GENERALIZATION OF VALUE FUNCTIONS IN THE RL STATE SPACE A THESIS SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY BHARAT SIGINAM IN
The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a
 The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a coordinate system and then the measuring of the point with
The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a coordinate system and then the measuring of the point with
1.2 Numerical Solutions of Flow Problems
 1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
HOUGH TRANSFORM CS 6350 C V
 HOUGH TRANSFORM CS 6350 C V HOUGH TRANSFORM The problem: Given a set of points in 2-D, find if a sub-set of these points, fall on a LINE. Hough Transform One powerful global method for detecting edges
HOUGH TRANSFORM CS 6350 C V HOUGH TRANSFORM The problem: Given a set of points in 2-D, find if a sub-set of these points, fall on a LINE. Hough Transform One powerful global method for detecting edges
Russell County Pacing Guide
 August Experiment with transformations in the plane. 1. Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment based on the undefined notions of point, line, distance
August Experiment with transformations in the plane. 1. Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment based on the undefined notions of point, line, distance
Natural Inclusion of Boundary Points in a Mesh
 http://people.sc.fsu.edu/ jburkardt/presentations/ new orleans 2005.pdf... John 1 Max Gunzburger 2 Hoa Nguyen 2 Yuki Saka 2 1 School of Computational Science Florida State University 2 Department of Mathematics
http://people.sc.fsu.edu/ jburkardt/presentations/ new orleans 2005.pdf... John 1 Max Gunzburger 2 Hoa Nguyen 2 Yuki Saka 2 1 School of Computational Science Florida State University 2 Department of Mathematics
Voronoi diagram and Delaunay triangulation
 Voronoi diagram and Delaunay triangulation Ioannis Emiris & Vissarion Fisikopoulos Dept. of Informatics & Telecommunications, University of Athens Computational Geometry, spring 2015 Outline 1 Voronoi
Voronoi diagram and Delaunay triangulation Ioannis Emiris & Vissarion Fisikopoulos Dept. of Informatics & Telecommunications, University of Athens Computational Geometry, spring 2015 Outline 1 Voronoi
Lifting Transform, Voronoi, Delaunay, Convex Hulls
 Lifting Transform, Voronoi, Delaunay, Convex Hulls Subhash Suri Department of Computer Science University of California Santa Barbara, CA 93106 1 Lifting Transform (A combination of Pless notes and my
Lifting Transform, Voronoi, Delaunay, Convex Hulls Subhash Suri Department of Computer Science University of California Santa Barbara, CA 93106 1 Lifting Transform (A combination of Pless notes and my
Shrinkwrap developments for computational electromagnetics in ICE NITe
 Shrinkwrap developments for computational electromagnetics in ICE NITe Preparing CAD models for electromagnetic analysis remains a complex, time consuming process. Typically, the CAD model will contain
Shrinkwrap developments for computational electromagnetics in ICE NITe Preparing CAD models for electromagnetic analysis remains a complex, time consuming process. Typically, the CAD model will contain
Practical Linear Algebra: A Geometry Toolbox
 Practical Linear Algebra: A Geometry Toolbox Third edition Chapter 17: Breaking It Up: Triangles Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/pla
Practical Linear Algebra: A Geometry Toolbox Third edition Chapter 17: Breaking It Up: Triangles Gerald Farin & Dianne Hansford CRC Press, Taylor & Francis Group, An A K Peters Book www.farinhansford.com/books/pla
A Verification Study of ABAQUS AC3D8R Elements for Acoustic Wave Propagation
 A Verification Study of ABAQUS AC3D8R Elements for Acoustic Wave Propagation by Michael Robert Hubenthal A Project Submitted to the Graduate Faculty of Rensselaer Polytechnic Institute in Partial Fulfillment
A Verification Study of ABAQUS AC3D8R Elements for Acoustic Wave Propagation by Michael Robert Hubenthal A Project Submitted to the Graduate Faculty of Rensselaer Polytechnic Institute in Partial Fulfillment
3. Voronoi Diagrams. 3.1 Definitions & Basic Properties. Examples :
 3. Voronoi Diagrams Examples : 1. Fire Observation Towers Imagine a vast forest containing a number of fire observation towers. Each ranger is responsible for extinguishing any fire closer to her tower
3. Voronoi Diagrams Examples : 1. Fire Observation Towers Imagine a vast forest containing a number of fire observation towers. Each ranger is responsible for extinguishing any fire closer to her tower
Chapter 7 Practical Considerations in Modeling. Chapter 7 Practical Considerations in Modeling
 CIVL 7/8117 1/43 Chapter 7 Learning Objectives To present concepts that should be considered when modeling for a situation by the finite element method, such as aspect ratio, symmetry, natural subdivisions,
CIVL 7/8117 1/43 Chapter 7 Learning Objectives To present concepts that should be considered when modeling for a situation by the finite element method, such as aspect ratio, symmetry, natural subdivisions,
Data Representation in Visualisation
 Data Representation in Visualisation Visualisation Lecture 4 Taku Komura Institute for Perception, Action & Behaviour School of Informatics Taku Komura Data Representation 1 Data Representation We have
Data Representation in Visualisation Visualisation Lecture 4 Taku Komura Institute for Perception, Action & Behaviour School of Informatics Taku Komura Data Representation 1 Data Representation We have
Global non-hydrostatic modelling using Voronoi meshes: The MPAS model
 Global non-hydrostatic modelling using Voronoi meshes: The MPAS model William C. Skamarock, Joseph B. Klemp, Michael Duda, Laura Fowler and Sang-Hun Park National Center for Atmospheric Research Boulder,
Global non-hydrostatic modelling using Voronoi meshes: The MPAS model William C. Skamarock, Joseph B. Klemp, Michael Duda, Laura Fowler and Sang-Hun Park National Center for Atmospheric Research Boulder,
Applications of Generic Interpolants In the Investigation and Visualization of Approximate Solutions of PDEs on Coarse Unstructured Meshes
 Applications of Generic Interpolants In the Investigation and Visualization of Approximate Solutions of PDEs on Coarse Unstructured Meshes by Hassan Goldani Moghaddam A thesis submitted in conformity with
Applications of Generic Interpolants In the Investigation and Visualization of Approximate Solutions of PDEs on Coarse Unstructured Meshes by Hassan Goldani Moghaddam A thesis submitted in conformity with
This blog addresses the question: how do we determine the intersection of two circles in the Cartesian plane?
 Intersecting Circles This blog addresses the question: how do we determine the intersection of two circles in the Cartesian plane? This is a problem that a programmer might have to solve, for example,
Intersecting Circles This blog addresses the question: how do we determine the intersection of two circles in the Cartesian plane? This is a problem that a programmer might have to solve, for example,
Ocean Simulations using MPAS-Ocean
 Ocean Simulations using MPAS-Ocean Mark Petersen and the MPAS-Ocean development team Los Alamos National Laboratory U N C L A S S I F I E D Slide 1 Progress on MPAS-Ocean in 2010 MPAS-Ocean is a functioning
Ocean Simulations using MPAS-Ocean Mark Petersen and the MPAS-Ocean development team Los Alamos National Laboratory U N C L A S S I F I E D Slide 1 Progress on MPAS-Ocean in 2010 MPAS-Ocean is a functioning
Geometry Curriculum Map
 Quadrilaterals 7.1 Interior Angle Sum Theorem 7.2 Exterior Angle Sum Theorem 7.3 Using Interior and Exterior Angles to Solve Problems Define the Angle Sum Theorem. Illustrate interior angles with the Angle
Quadrilaterals 7.1 Interior Angle Sum Theorem 7.2 Exterior Angle Sum Theorem 7.3 Using Interior and Exterior Angles to Solve Problems Define the Angle Sum Theorem. Illustrate interior angles with the Angle
Seminar on. A Coarse-Grain Parallel Formulation of Multilevel k-way Graph Partitioning Algorithm
 Seminar on A Coarse-Grain Parallel Formulation of Multilevel k-way Graph Partitioning Algorithm Mohammad Iftakher Uddin & Mohammad Mahfuzur Rahman Matrikel Nr: 9003357 Matrikel Nr : 9003358 Masters of
Seminar on A Coarse-Grain Parallel Formulation of Multilevel k-way Graph Partitioning Algorithm Mohammad Iftakher Uddin & Mohammad Mahfuzur Rahman Matrikel Nr: 9003357 Matrikel Nr : 9003358 Masters of
Multigrid Pattern. I. Problem. II. Driving Forces. III. Solution
 Multigrid Pattern I. Problem Problem domain is decomposed into a set of geometric grids, where each element participates in a local computation followed by data exchanges with adjacent neighbors. The grids
Multigrid Pattern I. Problem Problem domain is decomposed into a set of geometric grids, where each element participates in a local computation followed by data exchanges with adjacent neighbors. The grids
Halftoning and quasi-monte Carlo
 Halftoning and quasi-monte Carlo Ken Hanson CCS-2, Methods for Advanced Scientific Simulations Los Alamos National Laboratory This presentation available at http://www.lanl.gov/home/kmh/ LA-UR-04-1854
Halftoning and quasi-monte Carlo Ken Hanson CCS-2, Methods for Advanced Scientific Simulations Los Alamos National Laboratory This presentation available at http://www.lanl.gov/home/kmh/ LA-UR-04-1854
Chapter 4. Clustering Core Atoms by Location
 Chapter 4. Clustering Core Atoms by Location In this chapter, a process for sampling core atoms in space is developed, so that the analytic techniques in section 3C can be applied to local collections
Chapter 4. Clustering Core Atoms by Location In this chapter, a process for sampling core atoms in space is developed, so that the analytic techniques in section 3C can be applied to local collections
arxiv:cs/ v1 [cs.cg] 26 Feb 2002
![arxiv:cs/ v1 [cs.cg] 26 Feb 2002 arxiv:cs/ v1 [cs.cg] 26 Feb 2002](/thumbs/79/79976714.jpg) The efficient generation of unstructured control volumes in 2D and 3D Jacek Leszczynski, Sebastian Pluta arxiv:cs/0202038v1 [cs.cg] 26 Feb 2002 Technical University of Czestochowa, Institute of Mathematics
The efficient generation of unstructured control volumes in 2D and 3D Jacek Leszczynski, Sebastian Pluta arxiv:cs/0202038v1 [cs.cg] 26 Feb 2002 Technical University of Czestochowa, Institute of Mathematics
Geometric Algorithms in Three Dimensions Tutorial. FSP Seminar, Strobl,
 Geometric Algorithms in Three Dimensions Tutorial FSP Seminar, Strobl, 22.06.2006 Why Algorithms in Three and Higher Dimensions Which algorithms (convex hulls, triangulations etc.) can be generalized to
Geometric Algorithms in Three Dimensions Tutorial FSP Seminar, Strobl, 22.06.2006 Why Algorithms in Three and Higher Dimensions Which algorithms (convex hulls, triangulations etc.) can be generalized to
A nodal based evolutionary structural optimisation algorithm
 Computer Aided Optimum Design in Engineering IX 55 A dal based evolutionary structural optimisation algorithm Y.-M. Chen 1, A. J. Keane 2 & C. Hsiao 1 1 ational Space Program Office (SPO), Taiwan 2 Computational
Computer Aided Optimum Design in Engineering IX 55 A dal based evolutionary structural optimisation algorithm Y.-M. Chen 1, A. J. Keane 2 & C. Hsiao 1 1 ational Space Program Office (SPO), Taiwan 2 Computational
Geometry. Cluster: Experiment with transformations in the plane. G.CO.1 G.CO.2. Common Core Institute
 Geometry Cluster: Experiment with transformations in the plane. G.CO.1: Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of
Geometry Cluster: Experiment with transformations in the plane. G.CO.1: Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of
Application of Finite Volume Method for Structural Analysis
 Application of Finite Volume Method for Structural Analysis Saeed-Reza Sabbagh-Yazdi and Milad Bayatlou Associate Professor, Civil Engineering Department of KNToosi University of Technology, PostGraduate
Application of Finite Volume Method for Structural Analysis Saeed-Reza Sabbagh-Yazdi and Milad Bayatlou Associate Professor, Civil Engineering Department of KNToosi University of Technology, PostGraduate
Advanced Algorithms Computational Geometry Prof. Karen Daniels. Fall, 2012
 UMass Lowell Computer Science 91.504 Advanced Algorithms Computational Geometry Prof. Karen Daniels Fall, 2012 Voronoi Diagrams & Delaunay Triangulations O Rourke: Chapter 5 de Berg et al.: Chapters 7,
UMass Lowell Computer Science 91.504 Advanced Algorithms Computational Geometry Prof. Karen Daniels Fall, 2012 Voronoi Diagrams & Delaunay Triangulations O Rourke: Chapter 5 de Berg et al.: Chapters 7,
Section 8.3: Examining and Repairing the Input Geometry. Section 8.5: Examining the Cartesian Grid for Leakages
 Chapter 8. Wrapping Boundaries TGrid allows you to create a good quality boundary mesh using a bad quality surface mesh as input. This can be done using the wrapper utility in TGrid. The following sections
Chapter 8. Wrapping Boundaries TGrid allows you to create a good quality boundary mesh using a bad quality surface mesh as input. This can be done using the wrapper utility in TGrid. The following sections
Multi-Domain Pattern. I. Problem. II. Driving Forces. III. Solution
 Multi-Domain Pattern I. Problem The problem represents computations characterized by an underlying system of mathematical equations, often simulating behaviors of physical objects through discrete time
Multi-Domain Pattern I. Problem The problem represents computations characterized by an underlying system of mathematical equations, often simulating behaviors of physical objects through discrete time
A Direct Simulation-Based Study of Radiance in a Dynamic Ocean
 A Direct Simulation-Based Study of Radiance in a Dynamic Ocean Lian Shen Department of Civil Engineering Johns Hopkins University Baltimore, MD 21218 phone: (410) 516-5033 fax: (410) 516-7473 email: LianShen@jhu.edu
A Direct Simulation-Based Study of Radiance in a Dynamic Ocean Lian Shen Department of Civil Engineering Johns Hopkins University Baltimore, MD 21218 phone: (410) 516-5033 fax: (410) 516-7473 email: LianShen@jhu.edu
University of Reading. Discretization On Non-uniform Meshes: Tests solving shallow-water equations
 University of Reading School of Mathematics, Meteorology and Physics Discretization On Non-uniform Meshes: Tests solving shallow-water equations By FAWZI B ALBUSAIDI August 2008 This dissertation is submitted
University of Reading School of Mathematics, Meteorology and Physics Discretization On Non-uniform Meshes: Tests solving shallow-water equations By FAWZI B ALBUSAIDI August 2008 This dissertation is submitted
COMPUTER AIDED GEOMETRIC DESIGN. Thomas W. Sederberg
 COMPUTER AIDED GEOMETRIC DESIGN Thomas W. Sederberg January 31, 2011 ii T. W. Sederberg iii Preface This semester is the 24 th time I have taught a course at Brigham Young University titled, Computer Aided
COMPUTER AIDED GEOMETRIC DESIGN Thomas W. Sederberg January 31, 2011 ii T. W. Sederberg iii Preface This semester is the 24 th time I have taught a course at Brigham Young University titled, Computer Aided
Curriki Geometry Glossary
 Curriki Geometry Glossary The following terms are used throughout the Curriki Geometry projects and represent the core vocabulary and concepts that students should know to meet Common Core State Standards.
Curriki Geometry Glossary The following terms are used throughout the Curriki Geometry projects and represent the core vocabulary and concepts that students should know to meet Common Core State Standards.
Driven Cavity Example
 BMAppendixI.qxd 11/14/12 6:55 PM Page I-1 I CFD Driven Cavity Example I.1 Problem One of the classic benchmarks in CFD is the driven cavity problem. Consider steady, incompressible, viscous flow in a square
BMAppendixI.qxd 11/14/12 6:55 PM Page I-1 I CFD Driven Cavity Example I.1 Problem One of the classic benchmarks in CFD is the driven cavity problem. Consider steady, incompressible, viscous flow in a square
