10. f(x) = 3 2 x f(x) = 3 x 12. f(x) = 1 x 2 + 1
|
|
|
- Aron Higgins
- 5 years ago
- Views:
Transcription
1 Relations and Functions.6. Eercises To see all of the help resources associated with this section, click OSttS Chapter b. In Eercises -, sketch the graph of the given function. State the domain of the function, identif an intercepts and test for smmetr. For help with these eercises, click on one or more of the resources below: Finding domain Graphing functions b plotting points Determining if a function is even, odd, or neither. f() =. f() =. f() = +. f() =. f() = 6. f() = 7. f() = ( )( + ) 8. f() = 9. f() = 0. f() = +. f() =. f() = + In Eercises - 0, sketch the graph of the given piecewise-defined function. For help with these eercises, click on the resource below: Graphing piecewise defined functions { if. f() = if > if < 0. f() = if 0 < < if > { if < 0 7. f() = if 0 if 9. f() = if < < if {. f() = if 0 if > 0 if 6. f() = if < < if { + if < 8. f() = if if 6 < < 0. f() = if < < if < < 9
2 .6 Graphs of Functions In Eercises -, determine analticall if the following functions are even, odd or neither. For help with these eercises, click on the resource below: Determining if a function is even, odd, or neither. f() = 7. f() = 7 +. f() = 7. f() =. f() = 6. f() = 6 7. f() = 8. f() = + 9. f() = f() = f() =. f() =. f() = 0. f() =. f() = 6. f() = 7. f() = + 9. f() = 0. f() = 8. f() = f() = For help with Eercises - 7, click obtaining information about a function from its graph. In Eercises - 7, use the graph of = f() given below to answer the question.. Find the domain of f.. Find the range of f.. Determine f( ).. Solve f() =.
3 Relations and Functions 6. List the -intercepts, if an eist. 7. List the -intercepts, if an eist. 8. Find the zeros of f. 9. Solve f() Find the number of solutions to f() =.. Does f appear to be even, odd, or neither?. List the intervals where f is increasing.. List the intervals where f is decreasing.. List the local maimums, if an eist.. List the local minimums, if an eist. 6. Find the maimum, if it eists. 7. Find the minimum, if it eists. In Eercises 8-7, use the graph of = f() given below to answer the question. 8. Find the domain of f. 9. Find the range of f. 60. Determine f(). 6. Solve f() =. 6. List the -intercepts, if an eist. 6. List the -intercepts, if an eist. 6. Find the zeros of f. 6. Solve f() Find the number of solutions to f() =. 67. Does f appear to be even, odd, or neither? 68. List the intervals where f is increasing. 69. List the intervals where f is decreasing. 70. List the local maimums, if an eist. 7. List the local minimums, if an eist. 7. Find the maimum, if it eists. 7. Find the minimum, if it eists.
4 .6 Graphs of Functions In Eercises 7-77, use our graphing calculator to approimate the local and absolute etrema of the given function. Approimate the intervals on which the function is increasing and those on which it is decreasing. Round our answers to two decimal places. For help with these eercises, click on resource below: Approimating relative etrema 7. f() = f() = / ( ) 76. f() = f() = 9 In Eercises 78-8, use the graphs of = f() and = g() below to find the function value. = f() = g() 78. (f + g)(0) 79. (f + g)() 80. (f g)() 8. (g f)() ( ) ( ) 8. (fg)() 8. (fg)() 8. f g () 8. g f () The graph below represents the height h of a Sasquatch (in feet) as a function of its age N in ears. Use it to answer the questions in Eercises N = h(n) 86. Find and interpret h(0).
5 6 Relations and Functions 87. How tall is the Sasquatch when she is ears old? 88. Solve h(n) = 6 and interpret. 89. List the interval over which h is constant and interpret our answer. 90. List the interval over which h is decreasing and interpret our answer. For Eercises 9-9, let f() = be the greatest integer function as defined in Eercise 7 in Section.. For help with these eercises, click on the resource below: The greatest integer function 9. Graph = f(). Be careful to correctl describe the behavior of the graph near the integers. 9. Is f even, odd, or neither? Eplain. 9. Discuss with our classmates which points on the graph are local minimums, local maimums or both. Is f ever increasing? Decreasing? Constant? In Eercises 9-9, use our graphing calculator to show that the given function does not have an etrema, neither local nor absolute. 9. f() = + 9. f() = In Eercise 7 in Section., we saw that the population of Sasquatch in Portage Count could be modeled b the function P (t) = 0t, where t = 0 represents the ear 80. Use t + our graphing calculator to analze the general function behavior of P. Will there ever be a time when 00 Sasquatch roam Portage Count? 97. Suppose f and g are both even functions. What can be said about the functions f + g, f g, fg and f g? What if f and g are both odd? What if f is even but g is odd? 98. One of the most important aspects of the Cartesian Coordinate Plane is its abilit to put Algebra into geometric terms and Geometr into algebraic terms. We ve spent most of this chapter looking at this ver phenomenon and now ou should spend some time with our classmates reviewing what we ve done. What major results do we have that tie Algebra and Geometr together? What concepts from Geometr have we not et described algebraicall? What topics from Intermediate Algebra have we not et discussed geometricall?
6 .6 Graphs of Functions 7 It s now time to thoroughl vet the pathologies induced b the precise definitions of local maimum and local minimum. We ll do this b providing ou and our classmates a series of Eercises to discuss. You will need to refer back to Definition.0 (Increasing, Decreasing and Constant) and Definition. (Maimum and Minimum) during the discussion. 99. Consider the graph of the function f given below. (a) Show that f has a local maimum but not a local minimum at the point (, ). (b) Show that f has a local minimum but not a local maimum at the point (, ). (c) Show that f has a local maimum AND a local minimum at the point (0, ). (d) Show that f is constant on the interval [, ] and thus has both a local maimum AND a local minimum at ever point (, f()) where < <. 00. Using Eample.6. as a guide, show that the function g whose graph is given below does not have a local maimum at (, ) nor does it have a local minimum at (, ). Find its etrema, both local and absolute. What s unique about the point (0, ) on this graph? Also find the intervals on which g is increasing and those on which g is decreasing.
7 8 Relations and Functions 0. We said earlier in the section that it is not good enough to sa local etrema eist where a function changes from increasing to decreasing or vice versa. As a previous eercise showed, we could have local etrema when a function is constant so now we need to eamine some functions whose graphs do indeed change direction. Consider the functions graphed below. Notice that all four of them change direction at an open circle on the graph. Eamine each for local etrema. What is the effect of placing the dot on the -ais above or below the open circle? What could ou sa if no function value were assigned to = 0? (a) Function I (b) Function II (c) Function III (d) Function IV Let f() = 0 +. Checkpoint Quiz.6. Find the domain of f. Write our answer using interval notation.. Find the - and -intercepts of the graph of = f().. Is f even, odd, or neither? Eplain.. Use a graphing utilit to graph = f(). From the graph, approimate the intervals over which f is increasing and the intervals over which it is decreasing. List the local maimums and minimums, if the eist, and approimate the range of f. For worked out solutions to this quiz, click the links below: Quiz Solution Part Quiz Solution Part
8 .6 Graphs of Functions 9.6. Answers. f() = -intercept: (, 0) -intercept: (0, ) No smmetr. f() = -intercept: (, 0) -intercept: ( 0, ) No smmetr. f() = + -intercept: None -intercept: (0, ) Even. f() = -intercepts: (, 0), (, 0) -intercept: (0, ) Even. f() = -intercept: None -intercept: (0, ) Even
9 0 Relations and Functions 6. f() = -intercept: (0, 0) -intercept: (0, 0) Odd f() = ( )( + ) -intercepts: (, 0), (0, 0), (, 0) -intercept: (0, 0) No smmetr 8. f() = Domain: [, ) -intercept: (, 0) -intercept: None No smmetr f() = Domain: (, ] -intercept: (, 0) -intercept: (0, ) No smmetr
10 .6 Graphs of Functions 0. f() = + Domain: [, ) -intercept: (, 0) -intercept: (0, ) No smmetr. f() = -intercept: (0, 0) -intercept: (0, 0) Odd f() = + -intercept: None -intercept: (0, ) Even
11 Relations and Functions odd. neither. even. even. even 6. neither 7. odd 8. odd 9. even 0. neither. neither. even. even and odd. odd. even 6. even 7. neither 8. odd 9. odd 0. even. even. [, ]. [, ]. f( ) =. = 6. (, 0), (, 0), (, 0) 7. (0, ) 8.,, 9. [, ], [, ] 0.
12 .6 Graphs of Functions. neither. [, ], [0, ]. [, 0], [, ]. f( ) =, f() =. f(0) = 6. f( ) = 7. f( ) = 8. [, ] 9. [, ) 60. f() = 6. = 6. (, 0), (0, 0), (, 0) 6. (0, 0) 6., 0, 6. [, 0] {} neither 68. [, ) 69. [, ], (, ] 70. none 7. f( ) =, f() = 7. none 7. f( ) = 7. No absolute maimum Absolute minimum f(.) 7.6 Local minimum at (.8, 9.) Local maimum at (0.,.7) Local minimum at (., 7.6) Increasing on [.8, 0.], [., ) Decreasing on (,.8], [0.,.] 76. Absolute maimum f(0) = Absolute minimum f(±) = 0 Local maimum at (0, ) No local minimum Increasing on [, 0] Decreasing on [0, ] 7. No absolute maimum No absolute minimum Local maimum at (0, 0) Local minimum at (.60,.8) Increasing on (, 0], [.60, ) Decreasing on [0,.60] 77. Absolute maimum f(.).0 Absolute minimum f(.).0 Local maimum (.,.0) Local minimum (.,.0) Increasing on [.,.] Decreasing on [,.], [., ] 78. (f + g)(0) = 79. (f + g)() = 80. (f g)() = 8. (g f)() = 0 ( ) ( ) 8. (fg)() = 9 8. (fg)() = 6 8. f g () = 0 8. g f () = 86. h(0) =, so the Sasquatch is feet tall at birth. 87. h() = 6, so the Saquatch is 6 feet tall when she is ears old. 88. h(n) = 6 when N = and N = 60. This means the Sasquatch is 6 feet tall when she is and 60 ears old. 89. h is constant on [0, ]. This means the Sasquatch s height is constant (at 6 feet) for these ears.
13 Relations and Functions 90. h is decreasing on [, 60]. This means the Sasquatch is getting shorter from the age of to the age of 60. (Sasquatchteoporosis, perhaps?) Note that f(.) =, but f(.) =, so f is neither even nor odd The graph of f() =.
Section 1.6: Graphs of Functions, from College Algebra: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative
 Section.6: Graphs of Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Section.6: Graphs of Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
1. y = f(x) y = f(x + 3) 3. y = f(x) y = f(x 1) 5. y = 3f(x) 6. y = f(3x) 7. y = f(x) 8. y = f( x) 9. y = f(x 3) + 1
 .7 Transformations.7. Eercises To see all of the help resources associated with this section, click OSttS Chapter b. Suppose (, ) is on the graph of = f(). In Eercises - 8, use Theorem.7 to find a point
.7 Transformations.7. Eercises To see all of the help resources associated with this section, click OSttS Chapter b. Suppose (, ) is on the graph of = f(). In Eercises - 8, use Theorem.7 to find a point
Section 4.4 Concavity and Points of Inflection
 Section 4.4 Concavit and Points of Inflection In Chapter 3, ou saw that the second derivative of a function has applications in problems involving velocit and acceleration or in general rates-of-change
Section 4.4 Concavit and Points of Inflection In Chapter 3, ou saw that the second derivative of a function has applications in problems involving velocit and acceleration or in general rates-of-change
4.6 Graphs of Other Trigonometric Functions
 .6 Graphs of Other Trigonometric Functions Section.6 Graphs of Other Trigonometric Functions 09 Graph of the Tangent Function Recall that the tangent function is odd. That is, tan tan. Consequentl, the
.6 Graphs of Other Trigonometric Functions Section.6 Graphs of Other Trigonometric Functions 09 Graph of the Tangent Function Recall that the tangent function is odd. That is, tan tan. Consequentl, the
3.2 Polynomial Functions of Higher Degree
 71_00.qp 1/7/06 1: PM Page 6 Section. Polnomial Functions of Higher Degree 6. Polnomial Functions of Higher Degree What ou should learn Graphs of Polnomial Functions You should be able to sketch accurate
71_00.qp 1/7/06 1: PM Page 6 Section. Polnomial Functions of Higher Degree 6. Polnomial Functions of Higher Degree What ou should learn Graphs of Polnomial Functions You should be able to sketch accurate
Name Date. In Exercises 1 6, graph the function. Compare the graph to the graph of ( )
 Name Date 8. Practice A In Eercises 6, graph the function. Compare the graph to the graph of. g( ) =. h =.5 3. j = 3. g( ) = 3 5. k( ) = 6. n = 0.5 In Eercises 7 9, use a graphing calculator to graph the
Name Date 8. Practice A In Eercises 6, graph the function. Compare the graph to the graph of. g( ) =. h =.5 3. j = 3. g( ) = 3 5. k( ) = 6. n = 0.5 In Eercises 7 9, use a graphing calculator to graph the
Module 3 Graphing and Optimization
 Module 3 Graphing and Optimization One of the most important applications of calculus to real-world problems is in the area of optimization. We will utilize the knowledge gained in the previous chapter,
Module 3 Graphing and Optimization One of the most important applications of calculus to real-world problems is in the area of optimization. We will utilize the knowledge gained in the previous chapter,
Name: Period: Date: Analyzing Graphs of Functions and Relations Guided Notes
 Analzing Graphs of Functions and Relations Guided Notes The graph of a function f is the set of ordered pairs(, f ), in the coordinate plane, such that is the domain of f. the directed distance from the
Analzing Graphs of Functions and Relations Guided Notes The graph of a function f is the set of ordered pairs(, f ), in the coordinate plane, such that is the domain of f. the directed distance from the
Chapter 1 Notes, Calculus I with Precalculus 3e Larson/Edwards
 Contents 1.1 Functions.............................................. 2 1.2 Analzing Graphs of Functions.................................. 5 1.3 Shifting and Reflecting Graphs..................................
Contents 1.1 Functions.............................................. 2 1.2 Analzing Graphs of Functions.................................. 5 1.3 Shifting and Reflecting Graphs..................................
The Sine and Cosine Functions
 Lesson -5 Lesson -5 The Sine and Cosine Functions Vocabular BIG IDEA The values of cos and sin determine functions with equations = sin and = cos whose domain is the set of all real numbers. From the eact
Lesson -5 Lesson -5 The Sine and Cosine Functions Vocabular BIG IDEA The values of cos and sin determine functions with equations = sin and = cos whose domain is the set of all real numbers. From the eact
Math 111 Lecture Notes
 A function f is even if for ever in the domain of f it holds that f( ) = f(). Visuall, an even function is smmetric about the -ais. A function f is odd if for ever in the domain of f it holds that f( )
A function f is even if for ever in the domain of f it holds that f( ) = f(). Visuall, an even function is smmetric about the -ais. A function f is odd if for ever in the domain of f it holds that f( )
2.3 Polynomial Functions of Higher Degree with Modeling
 SECTION 2.3 Polnomial Functions of Higher Degree with Modeling 185 2.3 Polnomial Functions of Higher Degree with Modeling What ou ll learn about Graphs of Polnomial Functions End Behavior of Polnomial
SECTION 2.3 Polnomial Functions of Higher Degree with Modeling 185 2.3 Polnomial Functions of Higher Degree with Modeling What ou ll learn about Graphs of Polnomial Functions End Behavior of Polnomial
End of Chapter Test. b. What are the roots of this equation? 8 1 x x 5 0
 End of Chapter Test Name Date 1. A woodworker makes different sizes of wooden blocks in the shapes of cones. The narrowest block the worker makes has a radius r 8 centimeters and a height h centimeters.
End of Chapter Test Name Date 1. A woodworker makes different sizes of wooden blocks in the shapes of cones. The narrowest block the worker makes has a radius r 8 centimeters and a height h centimeters.
4.2 Properties of Rational Functions. 188 CHAPTER 4 Polynomial and Rational Functions. Are You Prepared? Answers
 88 CHAPTER 4 Polnomial and Rational Functions 5. Obtain a graph of the function for the values of a, b, and c in the following table. Conjecture a relation between the degree of a polnomial and the number
88 CHAPTER 4 Polnomial and Rational Functions 5. Obtain a graph of the function for the values of a, b, and c in the following table. Conjecture a relation between the degree of a polnomial and the number
(0, 4) Figure 12. x + 3. d = c. = b. Figure 13
 80 CHAPTER EQUATIONS AND INEQUALITIES Plot both points, and draw a line passing through them as in Figure. Tr It # _, 0 Figure Find the intercepts of the equation and sketch the graph: = _ +. (0, (This
80 CHAPTER EQUATIONS AND INEQUALITIES Plot both points, and draw a line passing through them as in Figure. Tr It # _, 0 Figure Find the intercepts of the equation and sketch the graph: = _ +. (0, (This
Lesson 8.1 Exercises, pages
 Lesson 8.1 Eercises, pages 1 9 A. Complete each table of values. a) -3 - -1 1 3 3 11 8 5-1 - -7 3 11 8 5 1 7 To complete the table for 3, take the absolute value of each value of 3. b) - -3 - -1 1 3 3
Lesson 8.1 Eercises, pages 1 9 A. Complete each table of values. a) -3 - -1 1 3 3 11 8 5-1 - -7 3 11 8 5 1 7 To complete the table for 3, take the absolute value of each value of 3. b) - -3 - -1 1 3 3
2.1 The ReCTAngUlAR COORdInATe SySTemS And graphs
 7 CHAPTER equations ANd inequalities learning ObjeCTIveS In this section ou will: Plot ordered pairs in a Cartesian coordinate sstem. Graph equations b plotting points. Graph equations with a graphing
7 CHAPTER equations ANd inequalities learning ObjeCTIveS In this section ou will: Plot ordered pairs in a Cartesian coordinate sstem. Graph equations b plotting points. Graph equations with a graphing
College Algebra Final Exam Review. 5.) State the domain of the following functions. Then determine whether each function is a one-toone function.
 College Algebra Final Eam Review For # use the given graph f():.) Find f( )..) State the zeros, the domain, and the range. f().) State the local maimum and/or minimum..) State the intervals decreasing
College Algebra Final Eam Review For # use the given graph f():.) Find f( )..) State the zeros, the domain, and the range. f().) State the local maimum and/or minimum..) State the intervals decreasing
Essential Question How many turning points can the graph of a polynomial function have?
 .8 Analzing Graphs of Polnomial Functions Essential Question How man turning points can the graph of a polnomial function have? A turning point of the graph of a polnomial function is a point on the graph
.8 Analzing Graphs of Polnomial Functions Essential Question How man turning points can the graph of a polnomial function have? A turning point of the graph of a polnomial function is a point on the graph
Unit 2 Functions Analyzing Graphs of Functions (Unit 2.2)
 Unit 2 Functions Analzing Graphs of Functions (Unit 2.2) William (Bill) Finch Mathematics Department Denton High School Introduction Domain/Range Vert Line Zeros Incr/Decr Min/Ma Avg Rate Change Odd/Even
Unit 2 Functions Analzing Graphs of Functions (Unit 2.2) William (Bill) Finch Mathematics Department Denton High School Introduction Domain/Range Vert Line Zeros Incr/Decr Min/Ma Avg Rate Change Odd/Even
3.5 - Concavity. a concave up. a concave down
 . - Concavity 1. Concave up and concave down For a function f that is differentiable on an interval I, the graph of f is If f is concave up on a, b, then the secant line passing through points 1, f 1 and,
. - Concavity 1. Concave up and concave down For a function f that is differentiable on an interval I, the graph of f is If f is concave up on a, b, then the secant line passing through points 1, f 1 and,
Section 2.2: Absolute Value Functions, from College Algebra: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a
 Section.: Absolute Value Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Section.: Absolute Value Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Transformations of Functions. 1. Shifting, reflecting, and stretching graphs Symmetry of functions and equations
 Chapter Transformations of Functions TOPICS.5.. Shifting, reflecting, and stretching graphs Smmetr of functions and equations TOPIC Horizontal Shifting/ Translation Horizontal Shifting/ Translation Shifting,
Chapter Transformations of Functions TOPICS.5.. Shifting, reflecting, and stretching graphs Smmetr of functions and equations TOPIC Horizontal Shifting/ Translation Horizontal Shifting/ Translation Shifting,
1-1. Functions. Lesson 1-1. What You ll Learn. Active Vocabulary. Scan Lesson 1-1. Write two things that you already know about functions.
 1-1 Functions What You ll Learn Scan Lesson 1- Write two things that ou alread know about functions. Lesson 1-1 Active Vocabular New Vocabular Write the definition net to each term. domain dependent variable
1-1 Functions What You ll Learn Scan Lesson 1- Write two things that ou alread know about functions. Lesson 1-1 Active Vocabular New Vocabular Write the definition net to each term. domain dependent variable
y = f(x) x (x, f(x)) f(x) g(x) = f(x) + 2 (x, g(x)) 0 (0, 1) 1 3 (0, 3) 2 (2, 3) 3 5 (2, 5) 4 (4, 3) 3 5 (4, 5) 5 (5, 5) 5 7 (5, 7)
 0 Relations and Functions.7 Transformations In this section, we stud how the graphs of functions change, or transform, when certain specialized modifications are made to their formulas. The transformations
0 Relations and Functions.7 Transformations In this section, we stud how the graphs of functions change, or transform, when certain specialized modifications are made to their formulas. The transformations
Functions Project Core Precalculus Extra Credit Project
 Name: Period: Date Due: 10/10/1 (for A das) and 10/11/1(for B das) Date Turned In: Functions Project Core Precalculus Etra Credit Project Instructions and Definitions: This project ma be used during the
Name: Period: Date Due: 10/10/1 (for A das) and 10/11/1(for B das) Date Turned In: Functions Project Core Precalculus Etra Credit Project Instructions and Definitions: This project ma be used during the
REVIEW, pages
 REVIEW, pages 69 697 8.. Sketch a graph of each absolute function. Identif the intercepts, domain, and range. a) = ƒ - + ƒ b) = ƒ ( + )( - ) ƒ 8 ( )( ) Draw the graph of. It has -intercept.. Reflect, in
REVIEW, pages 69 697 8.. Sketch a graph of each absolute function. Identif the intercepts, domain, and range. a) = ƒ - + ƒ b) = ƒ ( + )( - ) ƒ 8 ( )( ) Draw the graph of. It has -intercept.. Reflect, in
Polynomial Functions I
 Name Student ID Number Group Name Group Members Polnomial Functions I 1. Sketch mm() =, nn() = 3, ss() =, and tt() = 5 on the set of aes below. Label each function on the graph. 15 5 3 1 1 3 5 15 Defn:
Name Student ID Number Group Name Group Members Polnomial Functions I 1. Sketch mm() =, nn() = 3, ss() =, and tt() = 5 on the set of aes below. Label each function on the graph. 15 5 3 1 1 3 5 15 Defn:
5.2 Graphing Polynomial Functions
 Locker LESSON 5. Graphing Polnomial Functions Common Core Math Standards The student is epected to: F.IF.7c Graph polnomial functions, identifing zeros when suitable factorizations are available, and showing
Locker LESSON 5. Graphing Polnomial Functions Common Core Math Standards The student is epected to: F.IF.7c Graph polnomial functions, identifing zeros when suitable factorizations are available, and showing
4.4. Concavity and Curve Sketching. Concavity
 4.4 Concavit and Curve Sketching 267 4.4 Concavit and Curve Sketching f' decreases CONCAVE DOWN 3 f' increases 0 CONCAVE UP FIGURE 4.25 The graph of ƒsd = 3 is concave down on s - q, 0d and concave up
4.4 Concavit and Curve Sketching 267 4.4 Concavit and Curve Sketching f' decreases CONCAVE DOWN 3 f' increases 0 CONCAVE UP FIGURE 4.25 The graph of ƒsd = 3 is concave down on s - q, 0d and concave up
Four Ways to Represent a Function: We can describe a specific function in the following four ways: * verbally (by a description in words);
 MA19, Activit 23: What is a Function? (Section 3.1, pp. 214-22) Date: Toda s Goal: Assignments: Perhaps the most useful mathematical idea for modeling the real world is the concept of a function. We eplore
MA19, Activit 23: What is a Function? (Section 3.1, pp. 214-22) Date: Toda s Goal: Assignments: Perhaps the most useful mathematical idea for modeling the real world is the concept of a function. We eplore
2.2 Absolute Value Functions
 . Absolute Value Functions 7. Absolute Value Functions There are a few was to describe what is meant b the absolute value of a real number. You ma have been taught that is the distance from the real number
. Absolute Value Functions 7. Absolute Value Functions There are a few was to describe what is meant b the absolute value of a real number. You ma have been taught that is the distance from the real number
Graphing square root functions. What would be the base graph for the square root function? What is the table of values?
 Unit 3 (Chapter 2) Radical Functions (Square Root Functions Sketch graphs of radical functions b appling translations, stretches and reflections to the graph of Analze transformations to identif the of
Unit 3 (Chapter 2) Radical Functions (Square Root Functions Sketch graphs of radical functions b appling translations, stretches and reflections to the graph of Analze transformations to identif the of
A Formal Definition of Limit
 5 CHAPTER Limits and Their Properties L + ε L L ε (c, L) c + δ c c δ The - definition of the it of f as approaches c Figure. A Formal Definition of Limit Let s take another look at the informal description
5 CHAPTER Limits and Their Properties L + ε L L ε (c, L) c + δ c c δ The - definition of the it of f as approaches c Figure. A Formal Definition of Limit Let s take another look at the informal description
ABSOLUTE EXTREMA AND THE MEAN VALUE THEOREM
 61 LESSON 4-1 ABSOLUTE EXTREMA AND THE MEAN VALUE THEOREM Definitions (informal) The absolute maimum (global maimum) of a function is the -value that is greater than or equal to all other -values in the
61 LESSON 4-1 ABSOLUTE EXTREMA AND THE MEAN VALUE THEOREM Definitions (informal) The absolute maimum (global maimum) of a function is the -value that is greater than or equal to all other -values in the
F8-18 Finding the y-intercept from Ordered Pairs
 F8-8 Finding the -intercept from Ordered Pairs Pages 5 Standards: 8.F.A., 8.F.B. Goals: Students will find the -intercept of a line from a set of ordered pairs. Prior Knowledge Required: Can add, subtract,
F8-8 Finding the -intercept from Ordered Pairs Pages 5 Standards: 8.F.A., 8.F.B. Goals: Students will find the -intercept of a line from a set of ordered pairs. Prior Knowledge Required: Can add, subtract,
Chapter 2: Introduction to Functions
 Chapter 2: Introduction to Functions Lesson 1: Introduction to Functions Lesson 2: Function Notation Lesson 3: Composition of Functions Lesson 4: Domain and Range Lesson 5: Restricted Domain Lesson 6:
Chapter 2: Introduction to Functions Lesson 1: Introduction to Functions Lesson 2: Function Notation Lesson 3: Composition of Functions Lesson 4: Domain and Range Lesson 5: Restricted Domain Lesson 6:
Graph each pair of functions on the same coordinate plane See margin. Technology Activity: A Family of Functions
 - What You ll Learn To analze translations To analze stretches, shrinks, and reflections...and Wh To analze a fabric design, as in Eample Families of Functions Check Skills You ll Need G for Help Lessons
- What You ll Learn To analze translations To analze stretches, shrinks, and reflections...and Wh To analze a fabric design, as in Eample Families of Functions Check Skills You ll Need G for Help Lessons
The Graph of an Equation
 60_0P0.qd //0 :6 PM Page CHAPTER P Preparation for Calculus Archive Photos Section P. RENÉ DESCARTES (96 60) Descartes made man contributions to philosoph, science, and mathematics. The idea of representing
60_0P0.qd //0 :6 PM Page CHAPTER P Preparation for Calculus Archive Photos Section P. RENÉ DESCARTES (96 60) Descartes made man contributions to philosoph, science, and mathematics. The idea of representing
1.5 LIMITS. The Limit of a Function
 60040_005.qd /5/05 :0 PM Page 49 SECTION.5 Limits 49.5 LIMITS Find its of functions graphicall and numericall. Use the properties of its to evaluate its of functions. Use different analtic techniques to
60040_005.qd /5/05 :0 PM Page 49 SECTION.5 Limits 49.5 LIMITS Find its of functions graphicall and numericall. Use the properties of its to evaluate its of functions. Use different analtic techniques to
Quadratic Inequalities
 TEKS FCUS - Quadratic Inequalities VCABULARY TEKS ()(H) Solve quadratic inequalities. TEKS ()(E) Create and use representations to organize, record, and communicate mathematical ideas. Representation a
TEKS FCUS - Quadratic Inequalities VCABULARY TEKS ()(H) Solve quadratic inequalities. TEKS ()(E) Create and use representations to organize, record, and communicate mathematical ideas. Representation a
3.5 - Concavity 1. Concave up and concave down
 . - Concavit. Concave up and concave down Eample: The graph of f is given below. Determine graphicall the interval on which f is For a function f that is differentiable on an interval I, the graph of f
. - Concavit. Concave up and concave down Eample: The graph of f is given below. Determine graphicall the interval on which f is For a function f that is differentiable on an interval I, the graph of f
Vertical and Horizontal Translations. Graph each pair of functions on the same coordinate plane See margin
 - Lesson Preview What You ll Learn BJECTIVE BJECTIVE To analze vertical translations To analze horizontal translations... And Wh To analze a fabric design, as in Eample BJECTIVE Vertical and Horizontal
- Lesson Preview What You ll Learn BJECTIVE BJECTIVE To analze vertical translations To analze horizontal translations... And Wh To analze a fabric design, as in Eample BJECTIVE Vertical and Horizontal
Sections 5.1, 5.2, 5.3, 8.1,8.6 & 8.7 Practice for the Exam
 Sections.1,.2,.3, 8.1,8.6 & 8.7 Practice for the Eam MAC 1 -- Sulivan 8th Ed Name: Date: Class/Section: State whether the function is a polnomial function or not. If it is, give its degree. If it is not,
Sections.1,.2,.3, 8.1,8.6 & 8.7 Practice for the Eam MAC 1 -- Sulivan 8th Ed Name: Date: Class/Section: State whether the function is a polnomial function or not. If it is, give its degree. If it is not,
Equations and Inequalities
 Equations and Inequalities Figure CHAPTER OUTLINE. The Rectangular Coordinate Sstems and Graphs. Linear Equations in One Variable. Models and Applications. Comple Numbers. Quadratic Equations.6 Other Tpes
Equations and Inequalities Figure CHAPTER OUTLINE. The Rectangular Coordinate Sstems and Graphs. Linear Equations in One Variable. Models and Applications. Comple Numbers. Quadratic Equations.6 Other Tpes
Graph the equation. 8) y = 6x - 2
 Math 0 Chapter Practice set The actual test differs. Write the equation that results in the desired transformation. 1) The graph of =, verticall compressed b a factor of 0.7 Graph the equation. 8) = -
Math 0 Chapter Practice set The actual test differs. Write the equation that results in the desired transformation. 1) The graph of =, verticall compressed b a factor of 0.7 Graph the equation. 8) = -
6. f(x) = x f(x) = x f(x) = x f(x) = 3 x. 10. f(x) = x + 3
 Section 9.1 The Square Root Function 879 9.1 Eercises In Eercises 1-, complete each of the following tasks. i. Set up a coordinate sstem on a sheet of graph paper. Label and scale each ais. ii. Complete
Section 9.1 The Square Root Function 879 9.1 Eercises In Eercises 1-, complete each of the following tasks. i. Set up a coordinate sstem on a sheet of graph paper. Label and scale each ais. ii. Complete
Re - do all handouts and do the review from the book. Remember to SHOW ALL STEPS. You must be able to solve analytically and then verify with a graph.
 Math 180 - Review Chapter 3 Name Re - do all handouts and do the review from the book. Remember to SHOW ALL STEPS. You must be able to solve analticall and then verif with a graph. Find the rational zeros
Math 180 - Review Chapter 3 Name Re - do all handouts and do the review from the book. Remember to SHOW ALL STEPS. You must be able to solve analticall and then verif with a graph. Find the rational zeros
Ready To Go On? Skills Intervention 9-1 Multiple Representations of Functions
 9A Read To Go On? Skills Intervention 9-1 Multiple Representations of Functions Using Multiple Representations to Solve Problems The table shows the sum of the interior angles of polgons and the number
9A Read To Go On? Skills Intervention 9-1 Multiple Representations of Functions Using Multiple Representations to Solve Problems The table shows the sum of the interior angles of polgons and the number
Polynomial and Rational Functions
 Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
0 COORDINATE GEOMETRY
 0 COORDINATE GEOMETRY Coordinate Geometr 0-1 Equations of Lines 0- Parallel and Perpendicular Lines 0- Intersecting Lines 0- Midpoints, Distance Formula, Segment Lengths 0- Equations of Circles 0-6 Problem
0 COORDINATE GEOMETRY Coordinate Geometr 0-1 Equations of Lines 0- Parallel and Perpendicular Lines 0- Intersecting Lines 0- Midpoints, Distance Formula, Segment Lengths 0- Equations of Circles 0-6 Problem
Intermediate Algebra. Gregg Waterman Oregon Institute of Technology
 Intermediate Algebra Gregg Waterman Oregon Institute of Technolog c 2017 Gregg Waterman This work is licensed under the Creative Commons Attribution 4.0 International license. The essence of the license
Intermediate Algebra Gregg Waterman Oregon Institute of Technolog c 2017 Gregg Waterman This work is licensed under the Creative Commons Attribution 4.0 International license. The essence of the license
SLOPE A MEASURE OF STEEPNESS through 2.1.4
 SLOPE A MEASURE OF STEEPNESS 2.1.2 through 2.1.4 Students used the equation = m + b to graph lines and describe patterns in previous courses. Lesson 2.1.1 is a review. When the equation of a line is written
SLOPE A MEASURE OF STEEPNESS 2.1.2 through 2.1.4 Students used the equation = m + b to graph lines and describe patterns in previous courses. Lesson 2.1.1 is a review. When the equation of a line is written
LESSON 3.1 INTRODUCTION TO GRAPHING
 LESSON 3.1 INTRODUCTION TO GRAPHING LESSON 3.1 INTRODUCTION TO GRAPHING 137 OVERVIEW Here s what ou ll learn in this lesson: Plotting Points a. The -plane b. The -ais and -ais c. The origin d. Ordered
LESSON 3.1 INTRODUCTION TO GRAPHING LESSON 3.1 INTRODUCTION TO GRAPHING 137 OVERVIEW Here s what ou ll learn in this lesson: Plotting Points a. The -plane b. The -ais and -ais c. The origin d. Ordered
9.1 Exercises. Section 9.1 The Square Root Function 879. In Exercises 1-10, complete each of the following tasks.
 Section 9. The Square Root Function 879 9. Eercises In Eercises -, complete each of the following tasks. i. Set up a coordinate sstem on a sheet of graph paper. Label and scale each ais. ii. Complete the
Section 9. The Square Root Function 879 9. Eercises In Eercises -, complete each of the following tasks. i. Set up a coordinate sstem on a sheet of graph paper. Label and scale each ais. ii. Complete the
2-3. Attributes of Absolute Value Functions. Key Concept Absolute Value Parent Function f (x)= x VOCABULARY TEKS FOCUS ESSENTIAL UNDERSTANDING
 - Attributes of Absolute Value Functions TEKS FOCUS TEKS ()(A) Graph the functions f() =, f() =, f() =, f() =,f() = b, f() =, and f() = log b () where b is,, and e, and, when applicable, analze the ke
- Attributes of Absolute Value Functions TEKS FOCUS TEKS ()(A) Graph the functions f() =, f() =, f() =, f() =,f() = b, f() =, and f() = log b () where b is,, and e, and, when applicable, analze the ke
4.1 Graph Quadratic Functions in
 4. Graph Quadratic Functions in Standard Form Goal p Graph quadratic functions. Your Notes VOCABULARY Quadratic function Parabola Verte Ais of smmetr Minimum and maimum value PARENT FUNCTION FOR QUADRATIC
4. Graph Quadratic Functions in Standard Form Goal p Graph quadratic functions. Your Notes VOCABULARY Quadratic function Parabola Verte Ais of smmetr Minimum and maimum value PARENT FUNCTION FOR QUADRATIC
9. f(x) = x f(x) = x g(x) = 2x g(x) = 5 2x. 13. h(x) = 1 3x. 14. h(x) = 2x f(x) = x x. 16.
 Section 4.2 Absolute Value 367 4.2 Eercises For each of the functions in Eercises 1-8, as in Eamples 7 and 8 in the narrative, mark the critical value on a number line, then mark the sign of the epression
Section 4.2 Absolute Value 367 4.2 Eercises For each of the functions in Eercises 1-8, as in Eamples 7 and 8 in the narrative, mark the critical value on a number line, then mark the sign of the epression
4.2 Graphs of Rational Functions
 0 Rational Functions. Graphs of Rational Functions In this section, we take a closer look at graphing rational functions. In Section., we learned that the graphs of rational functions ma have holes in
0 Rational Functions. Graphs of Rational Functions In this section, we take a closer look at graphing rational functions. In Section., we learned that the graphs of rational functions ma have holes in
1) y = 2x 7 2) (-2, 3) ( 3, -1) 3) table. 4) y 5 = ½ ( x 4) 5) 2x + 4y = 7 6) y = 5 7) 8) 9) (-1, 5) (0, 4) 10) y = -3x 7. 11) 2y = -3x 5 12) x = 5
 I SPY Slope! Geometr tetbook 3-6, pg 165 (), pg 172 (calculator) Name: Date: _ Period: Strategies: On a graph or a table rise ( Δ) Slope = run Δ ( ) Given 2 points Slope = 2 2 In an equation 1 1 1) = 2
I SPY Slope! Geometr tetbook 3-6, pg 165 (), pg 172 (calculator) Name: Date: _ Period: Strategies: On a graph or a table rise ( Δ) Slope = run Δ ( ) Given 2 points Slope = 2 2 In an equation 1 1 1) = 2
Using a Table of Values to Sketch the Graph of a Polynomial Function
 A point where the graph changes from decreasing to increasing is called a local minimum point. The -value of this point is less than those of neighbouring points. An inspection of the graphs of polnomial
A point where the graph changes from decreasing to increasing is called a local minimum point. The -value of this point is less than those of neighbouring points. An inspection of the graphs of polnomial
9. p(x) = x 3 8x 2 5x p(x) = x 3 + 3x 2 33x p(x) = x x p(x) = x 3 + 5x x p(x) = x 4 50x
 Section 6.3 Etrema and Models 593 6.3 Eercises In Eercises 1-8, perform each of the following tasks for the given polnomial. i. Without the aid of a calculator, use an algebraic technique to identif the
Section 6.3 Etrema and Models 593 6.3 Eercises In Eercises 1-8, perform each of the following tasks for the given polnomial. i. Without the aid of a calculator, use an algebraic technique to identif the
4 Using The Derivative
 4 Using The Derivative 4.1 Local Maima and Minima * Local Maima and Minima Suppose p is a point in the domain of f : f has a local minimum at p if f (p) is less than or equal to the values of f for points
4 Using The Derivative 4.1 Local Maima and Minima * Local Maima and Minima Suppose p is a point in the domain of f : f has a local minimum at p if f (p) is less than or equal to the values of f for points
Section 4.2 Graphing Lines
 Section. Graphing Lines Objectives In this section, ou will learn to: To successfull complete this section, ou need to understand: Identif collinear points. The order of operations (1.) Graph the line
Section. Graphing Lines Objectives In this section, ou will learn to: To successfull complete this section, ou need to understand: Identif collinear points. The order of operations (1.) Graph the line
14.1. It s very difficult to visualize a function f of three variables by its graph, since that
 + +@= + +@=4 SECTION 4. FUNCTIONS OF SEVERAL VARIABLES 86 It s ver difficult to visualie a function f of three variables b its graph, since that would lie in a four-dimensional space. However, we do gain
+ +@= + +@=4 SECTION 4. FUNCTIONS OF SEVERAL VARIABLES 86 It s ver difficult to visualie a function f of three variables b its graph, since that would lie in a four-dimensional space. However, we do gain
Chapter 3. Exponential and Logarithmic Functions. Selected Applications
 Chapter Eponential and Logarithmic Functions. Eponential Functions and Their Graphs. Logarithmic Functions and Their Graphs. Properties of Logarithms. Solving Eponential and Logarithmic Equations.5 Eponential
Chapter Eponential and Logarithmic Functions. Eponential Functions and Their Graphs. Logarithmic Functions and Their Graphs. Properties of Logarithms. Solving Eponential and Logarithmic Equations.5 Eponential
Precalculus Notes Unit 1 Day 1
 Precalculus Notes Unit Day Rules For Domain: When the domain is not specified, it consists of (all real numbers) for which the corresponding values in the range are also real numbers.. If is in the numerator
Precalculus Notes Unit Day Rules For Domain: When the domain is not specified, it consists of (all real numbers) for which the corresponding values in the range are also real numbers.. If is in the numerator
3.5 Rational Functions
 0 Chapter Polnomial and Rational Functions Rational Functions For a rational function, find the domain and graph the function, identifing all of the asmptotes Solve applied problems involving rational
0 Chapter Polnomial and Rational Functions Rational Functions For a rational function, find the domain and graph the function, identifing all of the asmptotes Solve applied problems involving rational
RELATIONS AND FUNCTIONS
 CHAPTER RELATINS AND FUNCTINS Long-distance truck drivers keep ver careful watch on the length of time and the number of miles that the drive each da.the know that this relationship is given b the formula
CHAPTER RELATINS AND FUNCTINS Long-distance truck drivers keep ver careful watch on the length of time and the number of miles that the drive each da.the know that this relationship is given b the formula
Graphing f ( x) = ax 2 + c
 . Graphing f ( ) = a + c Essential Question How does the value of c affect the graph of f () = a + c? Graphing = a + c Work with a partner. Sketch the graphs of the functions in the same coordinate plane.
. Graphing f ( ) = a + c Essential Question How does the value of c affect the graph of f () = a + c? Graphing = a + c Work with a partner. Sketch the graphs of the functions in the same coordinate plane.
PROBLEM SOLVING WITH EXPONENTIAL FUNCTIONS
 Topic 21: Problem solving with eponential functions 323 PROBLEM SOLVING WITH EXPONENTIAL FUNCTIONS Lesson 21.1 Finding function rules from graphs 21.1 OPENER 1. Plot the points from the table onto the
Topic 21: Problem solving with eponential functions 323 PROBLEM SOLVING WITH EXPONENTIAL FUNCTIONS Lesson 21.1 Finding function rules from graphs 21.1 OPENER 1. Plot the points from the table onto the
4 B. 4 D. 4 F. 3. What are some common characteristics of the graphs of cubic and quartic polynomial functions?
 .1 Graphing Polnomial Functions COMMON CORE Learning Standards HSF-IF.B. HSF-IF.C.7c Essential Question What are some common characteristics of the graphs of cubic and quartic polnomial functions? A polnomial
.1 Graphing Polnomial Functions COMMON CORE Learning Standards HSF-IF.B. HSF-IF.C.7c Essential Question What are some common characteristics of the graphs of cubic and quartic polnomial functions? A polnomial
REVIEW, pages
 REVIEW, pages 330 335 4.1 1. a) Use a table of values to graph = + 6-8. -5-4 -3 - -1 0 1 1 0-8 -1-1 -8 0 1 6 8 8 0 b) Determine: i) the intercepts ii) the coordinates of the verte iii) the equation of
REVIEW, pages 330 335 4.1 1. a) Use a table of values to graph = + 6-8. -5-4 -3 - -1 0 1 1 0-8 -1-1 -8 0 1 6 8 8 0 b) Determine: i) the intercepts ii) the coordinates of the verte iii) the equation of
PRACTICE FINAL - MATH 1210, Spring 2012 CHAPTER 1
 PRACTICE FINAL - MATH 2, Spring 22 The Final will have more material from Chapter 4 than other chapters. To study for chapters -3 you should review the old practice eams IN ADDITION TO what appears here.
PRACTICE FINAL - MATH 2, Spring 22 The Final will have more material from Chapter 4 than other chapters. To study for chapters -3 you should review the old practice eams IN ADDITION TO what appears here.
These are square roots, cube roots, etc. Intermediate algebra Class notes Radicals and Radical Functions (section 10.1)
 Intermediate algebra Class notes Radicals and Radical Functions (section 10.1) These are square roots, cube roots, etc. Worksheet: Graphing Calculator Basics: This will go over basic home screen and graphing
Intermediate algebra Class notes Radicals and Radical Functions (section 10.1) These are square roots, cube roots, etc. Worksheet: Graphing Calculator Basics: This will go over basic home screen and graphing
Section 9.3: Functions and their Graphs
 Section 9.: Functions and their Graphs Graphs provide a wa of displaing, interpreting, and analzing data in a visual format. In man problems, we will consider two variables. Therefore, we will need to
Section 9.: Functions and their Graphs Graphs provide a wa of displaing, interpreting, and analzing data in a visual format. In man problems, we will consider two variables. Therefore, we will need to
REMARKS. 8.2 Graphs of Quadratic Functions. A Graph of y = ax 2 + bx + c, where a > 0
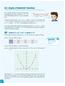 8. Graphs of Quadratic Functions In an earlier section, we have learned that the graph of the linear function = m + b, where the highest power of is 1, is a straight line. What would the shape of the graph
8. Graphs of Quadratic Functions In an earlier section, we have learned that the graph of the linear function = m + b, where the highest power of is 1, is a straight line. What would the shape of the graph
Chapter 1. Limits and Continuity. 1.1 Limits
 Chapter Limits and Continuit. Limits The its is the fundamental notion of calculus. This underling concept is the thread that binds together virtuall all of the calculus ou are about to stud. In this section,
Chapter Limits and Continuit. Limits The its is the fundamental notion of calculus. This underling concept is the thread that binds together virtuall all of the calculus ou are about to stud. In this section,
Section 1.5 Transformation of Functions
 Section.5 Transformation of Functions 6 Section.5 Transformation of Functions Often when given a problem, we try to model the scenario using mathematics in the form of words, tables, graphs and equations
Section.5 Transformation of Functions 6 Section.5 Transformation of Functions Often when given a problem, we try to model the scenario using mathematics in the form of words, tables, graphs and equations
CK-12 PreCalculus Concepts 1
 Chapter Functions and Graphs Answer Ke. Functions Families. - - - - - - - -. - - - - - - - - CK- PreCalculus Concepts Chapter Functions and Graphs Answer Ke. - - - - - - - -. - - - - - - - - 5. - - - -
Chapter Functions and Graphs Answer Ke. Functions Families. - - - - - - - -. - - - - - - - - CK- PreCalculus Concepts Chapter Functions and Graphs Answer Ke. - - - - - - - -. - - - - - - - - 5. - - - -
Solving Quadratics Algebraically Investigation
 Unit NOTES Honors Common Core Math 1 Day 1: Factoring Review and Solving For Zeroes Algebraically Warm-Up: 1. Write an equivalent epression for each of the problems below: a. ( + )( + 4) b. ( 5)( + 8)
Unit NOTES Honors Common Core Math 1 Day 1: Factoring Review and Solving For Zeroes Algebraically Warm-Up: 1. Write an equivalent epression for each of the problems below: a. ( + )( + 4) b. ( 5)( + 8)
12.2 Techniques for Evaluating Limits
 335_qd /4/5 :5 PM Page 863 Section Tecniques for Evaluating Limits 863 Tecniques for Evaluating Limits Wat ou sould learn Use te dividing out tecnique to evaluate its of functions Use te rationalizing
335_qd /4/5 :5 PM Page 863 Section Tecniques for Evaluating Limits 863 Tecniques for Evaluating Limits Wat ou sould learn Use te dividing out tecnique to evaluate its of functions Use te rationalizing
ACTIVITY: Representing Data by a Linear Equation
 9.2 Lines of Fit How can ou use data to predict an event? ACTIVITY: Representing Data b a Linear Equation Work with a partner. You have been working on a science project for 8 months. Each month, ou measured
9.2 Lines of Fit How can ou use data to predict an event? ACTIVITY: Representing Data b a Linear Equation Work with a partner. You have been working on a science project for 8 months. Each month, ou measured
1.2 Visualizing and Graphing Data
 6360_ch01pp001-075.qd 10/16/08 4:8 PM Page 1 1 CHAPTER 1 Introduction to Functions and Graphs 9. Volume of a Cone The volume V of a cone is given b V = 1 3 pr h, where r is its radius and h is its height.
6360_ch01pp001-075.qd 10/16/08 4:8 PM Page 1 1 CHAPTER 1 Introduction to Functions and Graphs 9. Volume of a Cone The volume V of a cone is given b V = 1 3 pr h, where r is its radius and h is its height.
1.2 Functions and Graphs
 Section.2 Functions and Graphs 3.2 Functions and Graphs You will be able to use the language, notation, and graphical representation of functions to epress relationships between variable quantities. Function,
Section.2 Functions and Graphs 3.2 Functions and Graphs You will be able to use the language, notation, and graphical representation of functions to epress relationships between variable quantities. Function,
A Picture Is Worth a Thousand Words
 Lesson 1.1 Skills Practice 1 Name Date A Picture Is Worth a Thousand Words Understanding Quantities and Their Relationships Vocabular Write a definition for each term in our own words. 1. independent quantit
Lesson 1.1 Skills Practice 1 Name Date A Picture Is Worth a Thousand Words Understanding Quantities and Their Relationships Vocabular Write a definition for each term in our own words. 1. independent quantit
Section 4.3 Features of a Line
 Section.3 Features of a Line Objectives In this section, ou will learn to: To successfull complete this section, ou need to understand: Identif the - and -intercepts of a line. Plotting points in the --plane
Section.3 Features of a Line Objectives In this section, ou will learn to: To successfull complete this section, ou need to understand: Identif the - and -intercepts of a line. Plotting points in the --plane
Lesson 2.1 Exercises, pages 90 96
 Lesson.1 Eercises, pages 9 96 A. a) Complete the table of values. 1 1 1 1 1. 1 b) For each function in part a, sketch its graph then state its domain and range. For : the domain is ; and the range is.
Lesson.1 Eercises, pages 9 96 A. a) Complete the table of values. 1 1 1 1 1. 1 b) For each function in part a, sketch its graph then state its domain and range. For : the domain is ; and the range is.
1.1. Parent Functions and Transformations Essential Question What are the characteristics of some of the basic parent functions?
 1.1 Parent Functions and Transformations Essential Question What are the characteristics of some of the basic parent functions? Identifing Basic Parent Functions JUSTIFYING CONCLUSIONS To be proficient
1.1 Parent Functions and Transformations Essential Question What are the characteristics of some of the basic parent functions? Identifing Basic Parent Functions JUSTIFYING CONCLUSIONS To be proficient
Problem 1: The relationship of height, in cm. and basketball players, names is a relation:
 Chapter - Functions and Graphs Chapter.1 - Functions, Relations and Ordered Pairs Relations A relation is a set of ordered pairs. Domain of a relation is the set consisting of all the first elements of
Chapter - Functions and Graphs Chapter.1 - Functions, Relations and Ordered Pairs Relations A relation is a set of ordered pairs. Domain of a relation is the set consisting of all the first elements of
Exponential Functions
 6. Eponential Functions Essential Question What are some of the characteristics of the graph of an eponential function? Eploring an Eponential Function Work with a partner. Cop and complete each table
6. Eponential Functions Essential Question What are some of the characteristics of the graph of an eponential function? Eploring an Eponential Function Work with a partner. Cop and complete each table
3-2. Families of Graphs. Look Back. OBJECTIVES Identify transformations of simple graphs. Sketch graphs of related functions.
 3-2 BJECTIVES Identif transformations of simple graphs. Sketch graphs of related functions. Families of Graphs ENTERTAINMENT At some circuses, a human cannonball is shot out of a special cannon. In order
3-2 BJECTIVES Identif transformations of simple graphs. Sketch graphs of related functions. Families of Graphs ENTERTAINMENT At some circuses, a human cannonball is shot out of a special cannon. In order
STRAND G: Relations, Functions and Graphs
 UNIT G Using Graphs to Solve Equations: Tet STRAND G: Relations, Functions and Graphs G Using Graphs to Solve Equations Tet Contents * * Section G. Solution of Simultaneous Equations b Graphs G. Graphs
UNIT G Using Graphs to Solve Equations: Tet STRAND G: Relations, Functions and Graphs G Using Graphs to Solve Equations Tet Contents * * Section G. Solution of Simultaneous Equations b Graphs G. Graphs
3 Limits Involving Infinity: Asymptotes LIMITS INVOLVING INFINITY. 226 Chapter 3 Additional Applications of the Derivative
 226 Chapter 3 Additional Applications of the Derivative 52. Given the function f() 2 3 3 2 2 7, complete the following steps: (a) Graph using [, ] b [, ] and [, ] b [ 2, 2]2. (b) Fill in the following
226 Chapter 3 Additional Applications of the Derivative 52. Given the function f() 2 3 3 2 2 7, complete the following steps: (a) Graph using [, ] b [, ] and [, ] b [ 2, 2]2. (b) Fill in the following
Algebra II Notes Linear Relations and Functions Unit 02. Special Functions
 Algebra II Notes Linear Relations and Functions Unit 0 Big Idea Special Functions This lesson examines three special functions; piecewise function usuall written with two or more algebraic expressions,
Algebra II Notes Linear Relations and Functions Unit 0 Big Idea Special Functions This lesson examines three special functions; piecewise function usuall written with two or more algebraic expressions,
Vocabulary. Term Page Definition Clarifying Example. dependent variable. domain. function. independent variable. parent function.
 CHAPTER 1 Vocabular The table contains important vocabular terms from Chapter 1. As ou work through the chapter, fill in the page number, definition, and a clarifing eample. dependent variable Term Page
CHAPTER 1 Vocabular The table contains important vocabular terms from Chapter 1. As ou work through the chapter, fill in the page number, definition, and a clarifing eample. dependent variable Term Page
is a plane curve and the equations are parametric equations for the curve, with parameter t.
 MATH 2412 Sections 6.3, 6.4, and 6.5 Parametric Equations and Polar Coordinates. Plane Curves and Parametric Equations Suppose t is contained in some interval I of the real numbers, and = f( t), = gt (
MATH 2412 Sections 6.3, 6.4, and 6.5 Parametric Equations and Polar Coordinates. Plane Curves and Parametric Equations Suppose t is contained in some interval I of the real numbers, and = f( t), = gt (
Putting the V in Absolute Value Defining Absolute Value Functions and Transformations
 1 Putting the V in Absolute Value Defining Absolute Value Functions and Transformations Warm Up The graph of f() 5 is shown. Graph each transformation. 1. g() 5 f() 1 5 2. h() 5 2? f() 2 3 Learning Goals
1 Putting the V in Absolute Value Defining Absolute Value Functions and Transformations Warm Up The graph of f() 5 is shown. Graph each transformation. 1. g() 5 f() 1 5 2. h() 5 2? f() 2 3 Learning Goals
Chapter Goals: Evaluate limits. Evaluate one-sided limits. Understand the concepts of continuity and differentiability and their relationship.
 MA123, Chapter 3: The idea of its (pp. 47-67) Date: Chapter Goals: Evaluate its. Evaluate one-sided its. Understand the concepts of continuit and differentiabilit and their relationship. Assignments: Assignment
MA123, Chapter 3: The idea of its (pp. 47-67) Date: Chapter Goals: Evaluate its. Evaluate one-sided its. Understand the concepts of continuit and differentiabilit and their relationship. Assignments: Assignment
Unconstrained and Constrained Optimization
 Unconstrained and Constrained Optimization Agenda General Ideas of Optimization Interpreting the First Derivative Interpreting the Second Derivative Unconstrained Optimization Constrained Optimization
Unconstrained and Constrained Optimization Agenda General Ideas of Optimization Interpreting the First Derivative Interpreting the Second Derivative Unconstrained Optimization Constrained Optimization
