Graph Terminology and Representations
|
|
|
- Arlene Warner
- 5 years ago
- Views:
Transcription
1 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Graph Terminology and Representations 1
2 Graphs A graph is a pair (V, E), where V is a set of nodes, called vertices E is a collection of pairs of vertices, called edges Vertices and edges are positions and store elements Example: A vertex represents an airport and stores the three-letter airport code An edge represents a flight route between two airports and stores the mileage of the route HNL SFO LAX ORD DFW LGA PVD MIA 2
3 Edge Types Directed edge ordered pair of vertices (u,v) first vertex u is the origin second vertex v is the destination e.g., a flight Undirected edge unordered pair of vertices (u,v) e.g., a flight route Directed graph all the edges are directed e.g., route network Undirected graph all the edges are undirected e.g., flight network ORD ORD flight AA miles PVD PVD 3
4 Applications Electronic circuits Printed circuit board Integrated circuit Transportation networks Highway network Flight network Computer networks Local area network Internet Web Databases Entity-relationship diagram cslab1a cslab1b math.brown.edu cs.brown.edu brown.edu qwest.net att.net cox.net John Paul David 4
5 Terminology End vertices (or endpoints) of an edge U and V are the endpoints of a Edges incident on a vertex a, d, and b are incident on V Adjacent vertices U and V are adjacent Degree of a vertex X has degree 5 Parallel edges h and i are parallel edges Loop j is a loop U a c V d W f b e X Y g h i Z j 5
6 Terminology (cont.) Path sequence of alternating vertices and edges begins with a vertex ends with a vertex each edge is preceded and followed by its endpoints Simple path path such that all its vertices and edges are distinct Examples P 1 =(V,b,X,h,Z) is a simple path P 2 =(U,c,W,e,X,g,Y,f,W,d,V) is a path that is not simple U a c V d P 2 W f b e P 1 X g Y h Z 6
7 Terminology (cont.) Cycle circular sequence of alternating vertices and edges each edge is preceded and followed by its endpoints Simple cycle cycle such that all its vertices and edges are distinct Examples C 1 =(V,b,X,g,Y,f,W,c,U,a,) is a simple cycle C 2 =(U,c,W,e,X,g,Y,f,W,d,V,a,) is a cycle that is not simple Edges can be dropped if no multiple edges. U a c V d C 2 W f b X e Y C 1 g h Z 7
8 Properties Property 1 S v deg(v) = 2m Proof: each edge is counted twice Property 2 In an undirected graph with no loops and no multiple edges m n (n - 1)/2 Proof: each vertex has degree at most (n - 1) What is the bound for a directed graph? Notation n m deg(v) number of vertices number of edges degree of vertex v Example n = 4 m = 6 deg(v) = 3 8
9 Vertices and Edges A graph is a collection of vertices and edges. A Vertex is can be an abstract unlabeled object or it can be labeled (e.g., with an integer number or an airport code) or it can store other objects An Edge can likewise be an abstract unlabeled object or it can be labeled (e.g., a flight number, travel distance, cost), or it can also store other objects. 9
10 Relations vs Graph A relation R on the set A is a subset of AA. There is 1-to-1 correspondence between R and (directed) G=(A, R). Example: Let A = {1, 2, 3, 4}. Which ordered pairs are in the relation R = {(a, b) a < b}? 1 2 R = { (1,2), (1,3), (1,4), (2,3), (2,4), (3,4) } 4 3
11 Representing Relations Using Digraphs Example: Display the digraph with V = {a, b, c, d}, E = {(a, b), (a, d), (b, b), (b, d), (c, a), (c, b), (d, b)}. a b d c An edge of the form (b, b) is called a loop.
12 Relations on a Set How many different relations can we define on a set A with n elements? A relation on a set A is a subset of AA. How many elements are in AA? The number of subsets that we can form out of a set with m elements is 2 m. Therefore, 2 n2 subsets can be formed out of AA. Answer: We can define 2 n2 different relations on A. As a result, we have that much directed graphs on n points. How many different undirected graphs over n points?
13 Properties of Relations Definition: A relation R on a set A is called reflexive if (a, a)r for every element aa. The graph that each node has a loop represents a reflexive relation. How many different loop-free directed graphs over n points?
14 Properties of Relations Definitions: A relation R on a set A is called symmetric if (b, a)r whenever (a, b)r for all a, ba. Every undirected graph represents a symmetric relation. A relation R on a set A is called antisymmetric if a = b whenever (a, b)r and (b, a)r. (N, ) is antisymmetric A relation R on a set A is called asymmetric if (a, b)r implies that (b, a)r for all a, ba. (N, <) is asymmetric What is the relation between antisymmetric and asymmetric? R is asymmetric iff R is antisymmetric and has no loops.
15 Properties of Relations Definition: A relation R on a set A is called transitive if whenever (a, b)r and (b, c)r, then (a, c)r for a, b, ca. Whenever there is a path that goes from a to b, then there is an edge (a, b) in the graph, then the graph represents a transitive relation. Are the following relation on {1, 2, 3} transitive? R = {(1, 1), (1, 2), (2, 2), (2, 1), (3, 3)}
16 Combining Relations Definition: Let R be a relation from a set A to a set B and S a relation from B to a set C. The composite of R and S is the relation consisting of ordered pairs (a, c), where aa, cc, and for which there exists an element bb such that (a, b)r and (b, c)s. We denote the composite of R and S by SR. If A = B = C, and S = R, then RR can be written as R 2. If R is represented by a graph, then (a, b) is in R 2 iff there is a path of length 2 from a to b. In general, (a, b) is in R k iff there is a path of length k from a to b.
17 Combining Relations Definition: Let R be a relation on the set A. The powers R k, k = 1, 2, 3,, are defined inductively by R 1 = R R k+1 = R k R In other words: R k = RR R (k times the letter R) The relation R* = R 1 R 2 R 3 R n-1, where n is the number of nodes, is called the transitive closure of R. To decide if (a, b) in R*, we need to decide if there is a path from a to b in G = (A, R).
18 Combining Relations Theorem: The relation R on a set A is transitive if and only if R k R for all positive integers k. Remember the definition of transitivity: Definition: A relation R on a set A is called transitive if whenever (a, b)r and (b, c)r, then (a, c)r for a, b, ca. The composite of R with itself contains exactly these pairs (a, c). Therefore, for a transitive relation R, RR does not contain any pairs that are not in R, so RR R. Since RR does not introduce any pairs that are not already in R, it must also be true that (RR)R R, and so on, so that R k R. 18
19 Equivalence Relations Equivalence relations are used to relate objects that are similar in some way. Definition: A relation on a set A is called an equivalence relation if it is reflexive, symmetric, and transitive. Two elements that are related by an equivalence relation R are called equivalent. The best representation of an equivalence relation is Sets.
20 Adjacency List Structure Incidence sequence for each vertex sequence of references to edge objects of incident edges Augmented edge objects references to associated positions in incidence sequences of end vertices 20
21 Adjacency Matrix Structure Edge list structure Augmented vertex objects Integer key (index) associated with vertex 2D-array adjacency array Reference to edge object for adjacent vertices Null for non nonadjacent vertices The old fashioned version just has 0 for no edge and 1 for edge 21
22 Graph Representations Option 1: Option 2: Class Node String: Name Boolean: Visited List<Node>: Neighbors List<Integer>: Costs End Node Class Node String: Name Boolean: Visited List<Edge>: Links End Node Class Edge Integer: Cost Node: tonode Node: fromnode End Link
23 Performance (All bounds are big-oh running times, except for Space ) n vertices, m edges no parallel edges no self-loops Edge List Adjacency List Adjacency Matrix Space n + m n + m n 2 incidentedges(v) m deg(v) n areadjacent (v, w) m min(deg(v), deg(w)) 1 insertvertex(o) 1 1 n 2 insertedge(v, w, o) removevertex(v) m deg(v) n 2 removeedge(e) 1 deg(v) 1 23
24 Subgraphs A subgraph S of a graph G is a graph such that The vertices of S are a subset of the vertices of G The edges of S are a subset of the edges of G A spanning subgraph of G is a subgraph that contains all the vertices of G Subgraph Spanning subgraph 24
25 Application: Web Crawlers A fundamental kind of algorithmic operation that we might wish to perform on a graph is traversing the edges and the vertices of that graph. A traversal is a systematic procedure for exploring a graph by examining all of its vertices and edges. For example, a web crawler, which is the data collecting part of a search engine, must explore a graph of hypertext documents by examining its vertices, which are the documents, and its edges, which are the hyperlinks between documents. A traversal is efficient if it visits all the vertices and edges in linear time. 25
26 Connectivity A graph is connected if there is a path between every pair of vertices A connected component of a graph G is a maximal connected subgraph of G Connected graph Non connected graph with two connected components 26
27 Trees and Forests A (free) tree is an undirected graph T such that T is connected T has no cycles This definition of tree is different from the one of a rooted tree A forest is an undirected graph without cycles The connected components of a forest are trees Tree Forest 27
28 Spanning Trees and Forests A spanning tree of a connected graph is a spanning subgraph that is a tree A spanning tree is not unique unless the graph is a tree Spanning trees have applications to the design of communication networks A spanning forest of a graph is a spanning subgraph that is a forest Graph Spanning tree 28
29 Depth-First Search Depth-first search (DFS) is a general technique for traversing a graph A DFS traversal of a graph G Visits all the vertices and edges of G Determines whether G is connected Computes the connected components of G Computes a spanning forest of G DFS on a graph with n vertices and m edges takes O(n + m ) time DFS can be further extended to solve other graph problems Find and report a path between two given vertices Find a cycle in the graph Depth-first search is to graphs what Euler tour is to binary trees 29
30 Depth-First Traversal with Marking Traverse(Node: node) <Process node> node.visited = True For each edge In Links If (Not edge.tonode.visited) Then Traverse(edge.toNode) End If end for End Traverse Complexity: O(n + m), n and m are the numbers of nodes and edges, resp.
31 Depth-First Traversal with Time-Stamp Traverse(Node: node) <Process node> node.starttime = ++time // time is global For Each edge In Links If (edge.tonode.starttime == 0) Then Traverse(edge.toNode) End If end for node.finishtime = ++time // optional End Traverse Color of a node: white if StartTime is undefined; gray if StartTime is defined but FinishTime is undefined; black if FinishTime is defined.
32 Example A unexplored vertex A A visited vertex unexplored edge B D E discovery edge back edge C A A B D E B D E C C 32
33 Example (cont.) A A B D E B D E C C A A B D E B D E C C 33
34 Non-Recursive DF Traversal DepthFirstTraverse(Node: start_node) start_node.visited = True // Visit this node. // Make a stack and put the start node in it. Stack[Node]: stack; stack.push(start_node); // Repeat as long as the stack isn t empty. While <stack isn t empty> Node node = stack.pop() // Get the next node from the stack. // Process the node s links. For each edge In node.links // if tonode hasn t been visited If (Not link.tonode.visited) Then // Mark the node as visited and set StartTime link.tonode.visited = True // Push the node onto the stack. stack.push(link.tonode) End If End for // Set FinishTime of node. Loop // Continue processing the stack until empty End DepthFirstTraverse 3 stages of a node: not visited (white), in stack (grey), exited stack (black)
35 Non-Recursive DF Traversal DepthFirstTraverse(Node: start_node) start_node.start = ++time // Visit this node. // Make a stack and put the start node in it. Stack[Node]: stack; stack.push(start_node); // Repeat as long as the stack isn t empty. While <stack isn t empty> Node node = stack.pop() // Get the next node from the stack. // Process the node s links. For each edge In node.links // if tonode hasn t been visited If (link.tonode.start < 1) Then // Mark the node as visited and set StartTime link.tonode.start = ++time // Push the node onto the stack. stack.push(link.tonode) End If End for // Set FinishTime of node. node.finish = ++time Loop // Continue processing the stack until empty End DepthFirstTraverse
36 Depth-First Search Example: d a i c b g h e f j
37 DFS and Maze Traversal The DFS algorithm is similar to a classic strategy for exploring a maze We mark each intersection, corner and dead end (vertex) visited We mark each corridor (edge ) traversed We keep track of the path back to the entrance (start vertex) by means of a rope (recursion stack) 37
38 Properties of DFS Property 1 DFS(G, v) visits all the vertices and edges in the connected component of v Property 2 The discovery (tree) edges labeled by DFS(G, v) form a spanning tree of the connected component of v B A C D E 38
39 The General DFS Algorithm Perform a DFS from each unexplored vertex: 39
40 Analysis of DFS Setting/getting a vertex/edge label takes O(1) time Each vertex is labeled twice once as UNEXPLORED once as VISITED Each edge is labeled twice once as UNEXPLORED once as DISCOVERY or BACK Method incidentedges is called once for each vertex DFS runs in O(n + m) time provided the graph is represented by the adjacency list structure Recall that S v deg(v) = 2m 40
41 Breadth-First Search Breadth-first search (BFS) is a general technique for traversing a graph A BFS traversal of a graph G Visits all the vertices and edges of G Determines whether G is connected Computes the connected components of G Computes a spanning forest of G BFS on a graph with n vertices and m edges takes O(n + m ) time BFS can be further extended to solve other graph problems Find and report a path with the minimum number of edges between two given vertices Find a simple cycle, if there is one 41
42 Example A unexplored vertex L 0 A A visited vertex unexplored edge L 1 B C D discovery edge cross edge E F L 0 A L 0 A L 1 B C D L 1 B C D E F E F 42
43 Example (cont.) L 0 A L 0 A L 1 B C D L 1 B C D E F L 2 E F L 0 A L 0 A L 1 B C D L 1 B C D L 2 E F L 2 E F 43
44 Example (cont.) L 0 A L 0 A L 1 B C D L 1 B C D L 2 E F L 2 E F L 0 A L 1 B C D L 2 E F 44
45 Properties Notation G s : connected component of s Property 1 BFS(G, s) visits all the vertices and edges of G s Property 2 The discovery edges labeled by BFS(G, s) form a spanning tree T s of G s Property 3 For each vertex v in L i The path of T s from s to v has i edges Every path from s to v in G s has at least i edges L 1 B L 0 L 2 B A E A E C C F F D D 45
46 BFS Algorithm The algorithm uses levels L i and a mechanism for setting and getting labels of vertices and edges. 46
47 Breadth-First Traversal BreadthFirstTraverse(Node: start_node) start_node.visited = True // Visit this node. // Make a stack and put the start node in it. Queue[Node]: queue; queue.add(start_node); // Repeat as long as the stack isn t empty. While <queue isn t empty> Node node = queue.remove() // Get the next node from the queue. // Process the node s links. For each edge In node.links // if tonode hasn t been visited If (Not link.tonode.visited) Then // Mark the node as visited and set StartTime link.tonode.visited = True // Push the node onto the stack. stack.push(link.tonode) End If End for // Set FinishTime of node. Loop // Continue processing the queue until empty End DepthFirstTraverse 3 stages of a node: not visited (white), in queue (grey), exited queue (black)
48 Analysis Setting/getting a vertex/edge label takes O(1) time Each vertex is labeled twice once as UNEXPLORED once as VISITED Each edge is labeled twice once as UNEXPLORED once as DISCOVERY or CROSS Each vertex is inserted once into a sequence L i Method incidentedges is called once for each vertex BFS runs in O(n + m) time provided the graph is represented by the adjacency list structure Recall that S v deg(v) = 2m 48
49 Applications We can use the BFS traversal algorithm, for a graph G, to solve the following problems in O(n + m) time Compute the connected components of G Compute a spanning forest of G Find a simple cycle in G, or report that G is a forest Given two vertices of G, find a path in G between them with the minimum number of edges, or report that no such path exists 49
50 DFS vs. BFS Applications DFS BFS Spanning forest, connected components, paths, cycles Shortest paths Biconnected components A L 0 A B C D L 1 B C D E F L 2 E F DFS BFS 50
51 DFS vs. BFS (cont.) Back edge (v,w) w is an ancestor of v in the tree of discovery edges Cross edge (v,w) w is in the same level as v or in the next level A L 0 A B C D L 1 B C D E F L 2 E F DFS BFS 51
52 Digraphs A digraph is a shorthand for directed graph whose edges are all directed Applications one-way streets flights task scheduling C E A D B 52
53 E Digraph Properties D A graph G=(V,E) such that Each edge goes in one direction: A Edge (a,b) goes from a to b, but not b to a If G is simple, m < n(n - 1) If we keep in-edges and out-edges in separate adjacency lists, we can perform listing of incoming edges and outgoing edges in time proportional to their size C B 53
54 Digraph Application Scheduling: edge (a,b) means task a must be completed before b can be started cs1210 cs2210 cs2230 cs2260 cs3330 cs3620 cs4640 cs2820 cs3640 cs3820 The good life cs4330, cs4340 cs4350, 54
55 Directed DFS We can specialize the traversal algorithms (DFS and BFS) to digraphs by traversing edges only along their direction In the directed DFS algorithm, we have four types of edges E D discovery (tree) edges back edges C forward edges B cross edges A directed DFS starting at a vertex s determines the vertices reachable from s A 55
56 Edge classification by DFS a Tree edges Forward edges Back edges Cross edges c b d The edge classification depends on the particular DFS tree!
57 Edge classification by DFS Both are valid Tree edges Forward edges Back edges Cross edges c b a c b a The edge classification depends on the particular DFS tree!
58 Edge classification by DFS Edge (u,v) of G is classified as: (1) Tree edge iff u discovers v during the DFS: P[v] = u i.e., v.starttime is undefined (v is white). If (u,v) is NOT a tree edge then it is: (2) Back edge iff u is a descendant of v in the DFS tree i.e., v.finishtime is undefined (v is grey). (3) Forward edge iff u is an ancestor of v in the DFS tree i.e., v.finishtime is defined (v is black) and u.starttime < v.starttime and P[v]!= u (4) Cross edge iff u is neither an ancestor nor a descendant of v i.e. v.finishtime is defined (v is black) and u.starttime > v.finishtime (v is black).
59 Reachability DFS tree rooted at v: vertices reachable from v via directed paths E D E D C A C B F A E C D F A B 59
60 DAGs and back edges Can there be a back edge in a DFS on a Directed Acyclic Graph (DAG)? NO! Back edges form a cycle! A graph G is a DAG <=> there is no back edge classified by DFS(G)
61 DAGs and Topological Ordering A directed acyclic graph (DAG) is a digraph that has no directed cycles A topological ordering of a digraph is a numbering v 1,, v n of the vertices such that for every edge (v i, v j ), we have i < j Example: in a task scheduling digraph, a topological ordering a task sequence that satisfies the precedence constraints Theorem A digraph admits a topological ordering if and only if it is a DAG v 2 v 1 B A B A D C E DAG G v 4 v 5 D E C v3 Topological ordering of G 61
62 Topological Sorting Number vertices, so that (u,v) in E implies u < v 1 wake up A typical student day 2 3 eat study computer sci. 4 5 nap more c.s. 7 play 8 write c.s. program 6 9 work out bake cookies 10 sleep 11 dream about graphs 62
63 Algorithm for Topological Sorting Note: This algorithm is different than the one in the book Algorithm TopologicalSort(G) H G // Temporary copy of G t 1 while H is not empty do Let v be a vertex with no ingoing edges Label v t t t + 1 Remove v from H Running time: O(n + m) 63
64 Implementation with DFS Simulate the algorithm by using depth-first search O(n+m) time. Algorithm topologicaldfs(g) Input dag G Output topological ordering of G t G.numVertices() for all u G.vertices() setlabel(u, UNEXPLORED) for all v G.vertices() if getlabel(v) = UNEXPLORED topologicaldfs(g, v) Algorithm topologicaldfs(g, v) Input graph G and a start vertex v of G Output labeling of the vertices of G in the connected component of v setlabel(v, VISITED) for all e G.outEdges(v) { outgoing edges } w opposite(v,e) if getlabel(w) = UNEXPLORED { e is a discovery edge } topologicaldfs(g, w) else { e is a forward or cross edge } Label v with topological number t t t - 1 Topological number = n finishtime
65 Topological Sorting Example 65
66 Topological Sorting Example 9 66
67 Topological Sorting Example
68 Topological Sorting Example
69 Topological Sorting Example
70 Topological Sorting Example
71 Topological Sorting Example
72 Topological Sorting Example
73 Topological Sorting Example
74 Topological Sorting Example
75 Strong Connectivity Each vertex can reach all other vertices a c g d e f b 75
76 Application: Networking A computer network can be modeled as a graph, where vertices are routers and edges are network connections between edges. A router can be considered critical if it can disconnect the network for that router to fail. It would be nice to identify which routers are critical. We can do such an identification by solving the biconnected components problem. 76
77 Strongly Connected Components Any directed graph can be partitioned into a unique set of strong components.
78 Strongly Connected Components The algorithm for finding the strong components of a directed graph G uses the transpose of the graph. The transpose G T has the same set of vertices V as graph G, but a new edge set consisting of the edges of G but with the opposite direction.
79 Strongly Connected Components Execute the depth-first search dfs() for the graph G which creates the list dfslist consisting of the vertices in G in the reverse order of their finishing times. Generate the transpose graph G T. Using the order of vertices in dfslist, make repeated calls to dfs() for vertices in G T. The list returned by each call is a strongly connected component of G.
80 Strongly Connected Components
81 Running Time of strongcomponents() Recall that the depth-first search has running time O(V+E), and the computation for G T is also O(V+E). It follows that the running time for the algorithm to compute the strong components is O(V+E).
82 Strongly Connected Components dfslist: [A, B, C, E, D, G, F] Using the order of vertices in dfslist, make successive calls to dfs() for graph G T Vertex A: dfs(a) returns the list [A, C, B] of vertices reachable from A in G T. Vertex E: The next unvisited vertex in dfslist is E. Calling dfs(e) returns the list [E]. Vertex D: The next unvisited vertex in dfslist is D; dfs(d) returns the list [D, F, G] whose elements form the last strongly connected component..
83 Strong Connectivity Algorithm Pick a vertex v in G Perform a DFS from v in G If there s a w not visited, print no G: a c g Let G be G with edges reversed d e Perform a DFS from v in G If there s a w not visited, print no f b Else, print yes Running time: O(n+m) G : a d c e g f b 83
84 Separation Edges and Vertices Definitions Let G be a connected graph A separation edge (bridge edge) of G is an edge whose removal disconnects G A separation (articulation) vertex of G is a vertex whose removal disconnects G Example DFW, LGA and LAX are separation vertices (DFW,LAX) is a separation edge SFO ORD LGA PVD HNL LAX DFW MIA 84
85 Finding Articulation (Separation) Points in a Graph A vertex v in an undirected graph G with more than two vertices is called an articulation point if there exist two vertices u and w different from v such that any path between u and w must pass through v. If G is connected, the removal of v and its incident edges will result in a disconnected subgraph of G. A graph is called biconnected if it is connected and has neither articulation points nor points of degree 1.
86 Finding Articulation (Separation) Points in a Graph Example: c, b, g, h are articulation points. d a i c b g h e f j
87 Finding Articulation (Separation) Points in a Graph To find the set of articulation points, we perform a depth-first search traversal on G. During the traversal, we maintain two labels with each vertex v V : [v] and [v]. [v] is simply v s start time in the depth-first search algorithm. [v] is initialized to [v], but may change later on during the traversal.
88 Finding Articulation (Separation) Points in a Graph For each vertex v visited, we let [v] be the minimum of the following: [v] [u] for each vertex u such that (v, u) is a back edge [w] for each vertex w such that (v, w) is a tree edge Thus, [v] is the smallest of those points that v can reach through back edges or tree edges.
89 Finding Articulation (Separation) Points in a Graph The articulation points are determined as follows: The root is an articulation point if and only if it has two or more children in the depth-first search tree. A vertex v other than the root is an articulation point if and only if v has a child w with [w][v].
90 Finding Articulation (Separation) Points in a Graph Input: A connected undirected graph G=(V, E); Output: Boolean array artpoint[1 n] indicates the articulation points of G, if any. 1. for each vertex vv 2. { [v] 0; artpoint[v] false; } 3. time 0; rootdegree 0; 4. dfs2(s); // s is the start vertex
91 Finding Articulation (Separation) Points in a Graph dfs2 (v) 2. [v] [v] ++time; 3. for each edge (v, w)e 4. if ([w] == 0) then // (v, w) is a tree edge 5. p[w] v; dfs2(w); 6. if (v==s) then // v is the root 7. rootdegreerootdegree+1; 8. if rootdegree==2 then artpoint[v] true; 9. else // v is not the root 10. [v]min{[v], [w]}; 11. if [w][v] then artpoint[v] true; 12. end if; 13. else if (p[v]!= w) // (v, w) is a back edge 14. then [v]min{[v], [w]}; 15. end if; 16. end for;
92 Finding Articulation (Separation) Points in a Graph Example: d a i c b g h e f j
93 How to find separation edges (bridges) in a Graph Example: (c, b), (g, h), (h, i), (h, j) are bridges. d a i c b g h e f j An edge (u, v) is a bridge if u and v are either separation (articulation) points or degree 1.
94 Biconnected Graph Equivalent definitions of a biconnected graph G Graph G has no separation edges and no separation vertices. For any two vertices u and v of G, there are two disjoint simple paths between u and v (i.e., two simple paths between u and v that share no other vertices or edges). For any two vertices u and v of G, there is a simple cycle containing u and v. Example SFO ORD PVD HNL LGA LAX DFW MIA 94
95 Biconnected Components Biconnected component of a graph G A maximal biconnected subgraph of G, or A subgraph consisting of a separation edge of G and its end vertices Interaction of biconnected components An edge belongs to exactly one biconnected component A nonseparation vertex belongs to exactly one biconnected component A separation vertex belongs to two or more biconnected components Example of a graph with four biconnected components HNL SFO LAX ORD DFW LGA MIA PVD RDU
96 Equivalence Classes An equivalence relation R on S induces a partition of the elements of S into equivalence classes. For undirected graph, connectivity is an equivalence relation on points, which generate classes of points (components). Let V be the set of vertices of an undirected graph G Define the relation C = { (v,w) VV such that G has a path from v to w} Relation C is an equivalence relation The equivalence classes of relation C are the vertices in each connected component of graph G For directed graph, strong connectivity is an equivalence classes on points (strongly connected components). 96
97 Biconnectivity Relation Edges e and f of connected graph G are biconnected if e = f, or G has a simple cycle containing e and f Theorem: The biconnectivity relation on the edges of a graph is an equivalence relation Proof Sketch: The reflexive and symmetric properties follow from the definition For the transitive property, consider two simple cycles sharing an edge a b c Equivalence classes of biconnected edges: {a} {b, c, d, e, f} {g, i, j} a b c d d e f f e g g j j i i 97
98 Biconnected Components The biconnected components of a graph G are the equivalence classes of edges with respect to the biconnectivity relation A biconnected component of G is the subgraph of G induced by an equivalence class of linked edges A separation edge is a single-element equivalence class of linked edges A separation vertex has incident edges in at least two distinct equivalence classes of linked edge HNL SFO LAX ORD DFW LGA MIA PVD RDU 98
Graphs 3/25/14 15:37 SFO LAX Goodrich, Tamassia, Goldwasser Graphs 2
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Graphs SFO 337 LAX 1843 1743 1233 802 DFW
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Graphs SFO 337 LAX 1843 1743 1233 802 DFW
Directed Graphs BOS Goodrich, Tamassia Directed Graphs 1 ORD JFK SFO DFW LAX MIA
 Directed Graphs BOS ORD JFK SFO LAX DFW MIA 2010 Goodrich, Tamassia Directed Graphs 1 Digraphs A digraph is a graph whose edges are all directed Short for directed graph Applications one-way streets flights
Directed Graphs BOS ORD JFK SFO LAX DFW MIA 2010 Goodrich, Tamassia Directed Graphs 1 Digraphs A digraph is a graph whose edges are all directed Short for directed graph Applications one-way streets flights
Graphs ADTs and Implementations
 Graphs ADTs and Implementations SFO 337 1843 802 ORD LAX 1233 DFW - 1 - Applications of Graphs Ø Electronic circuits cslab1a cslab1b q Printed circuit board math.brown.edu q Integrated circuit Ø Transportation
Graphs ADTs and Implementations SFO 337 1843 802 ORD LAX 1233 DFW - 1 - Applications of Graphs Ø Electronic circuits cslab1a cslab1b q Printed circuit board math.brown.edu q Integrated circuit Ø Transportation
Data Structures Lecture 14
 Fall 2018 Fang Yu Software Security Lab. ept. Management Information Systems, National hengchi University ata Structures Lecture 14 Graphs efinition, Implementation and Traversal Graphs Formally speaking,
Fall 2018 Fang Yu Software Security Lab. ept. Management Information Systems, National hengchi University ata Structures Lecture 14 Graphs efinition, Implementation and Traversal Graphs Formally speaking,
Graphs ORD SFO LAX DFW. Data structures and Algorithms
 SFO 143 ORD 337 1743 02 Graphs LAX 1233 DFW Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and
SFO 143 ORD 337 1743 02 Graphs LAX 1233 DFW Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and
CHAPTER 13 GRAPH ALGORITHMS
 CHPTER 13 GRPH LGORITHMS SFO LX ORD DFW 1 CKNOWLEDGEMENT: THESE SLIDES RE DPTED FROM SLIDES PROVIDED WITH DT STRUCTURES ND LGORITHMS IN C++, GOODRICH, TMSSI ND MOUNT (WILEY 2004) ND SLIDES FROM JORY DENNY
CHPTER 13 GRPH LGORITHMS SFO LX ORD DFW 1 CKNOWLEDGEMENT: THESE SLIDES RE DPTED FROM SLIDES PROVIDED WITH DT STRUCTURES ND LGORITHMS IN C++, GOODRICH, TMSSI ND MOUNT (WILEY 2004) ND SLIDES FROM JORY DENNY
Lecture 16: Directed Graphs
 Lecture 16: Directed Graphs ORD JFK BOS SFO LAX DFW MIA Courtesy of Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Directed Graphs Properties Algorithms for Directed Graphs DFS and
Lecture 16: Directed Graphs ORD JFK BOS SFO LAX DFW MIA Courtesy of Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Directed Graphs Properties Algorithms for Directed Graphs DFS and
CHAPTER 13 GRAPH ALGORITHMS ORD SFO LAX DFW
 SFO ORD CHAPTER 13 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES
SFO ORD CHAPTER 13 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES
CHAPTER 14 GRAPH ALGORITHMS ORD SFO LAX DFW
 SFO ORD CHAPTER 14 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016) GRAPH
SFO ORD CHAPTER 14 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016) GRAPH
DFS on Directed Graphs BOS. Outline and Reading ( 6.4) Digraphs. Reachability ( 6.4.1) Directed Acyclic Graphs (DAG s) ( 6.4.4)
 S on irected Graphs OS OR JK SO LX W MI irected Graphs S 1.3 1 Outline and Reading ( 6.4) Reachability ( 6.4.1) irected S Strong connectivity irected cyclic Graphs (G s) ( 6.4.4) Topological Sorting irected
S on irected Graphs OS OR JK SO LX W MI irected Graphs S 1.3 1 Outline and Reading ( 6.4) Reachability ( 6.4.1) irected S Strong connectivity irected cyclic Graphs (G s) ( 6.4.4) Topological Sorting irected
Graphs ORD SFO LAX DFW. Graphs 1
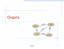 Graphs ORD 1843 SFO 802 1743 337 1233 LAX DFW Graphs 1 Outline and Reading Graphs ( 12.1) Definition Applications Terminology Properties ADT Data structures for graphs ( 12.2) Edge list structure Adjacency
Graphs ORD 1843 SFO 802 1743 337 1233 LAX DFW Graphs 1 Outline and Reading Graphs ( 12.1) Definition Applications Terminology Properties ADT Data structures for graphs ( 12.2) Edge list structure Adjacency
Digraphs ( 12.4) Directed Graphs. Digraph Application. Digraph Properties. A digraph is a graph whose edges are all directed.
 igraphs ( 12.4) irected Graphs OR OS digraph is a graph whose edges are all directed Short for directed graph pplications one- way streets flights task scheduling irected Graphs 1 irected Graphs 2 igraph
igraphs ( 12.4) irected Graphs OR OS digraph is a graph whose edges are all directed Short for directed graph pplications one- way streets flights task scheduling irected Graphs 1 irected Graphs 2 igraph
Graph Algorithms Using Depth First Search
 Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
Graphs. CS16: Introduction to Data Structures & Algorithms Spring 2018
 Graphs CS16: Introduction to Data Structures & Algorithms Spring 2018 Outline What is a Graph Terminology Properties Graph Types Representations Performance BFS/DFS Applications 2 What is a Graph A graph
Graphs CS16: Introduction to Data Structures & Algorithms Spring 2018 Outline What is a Graph Terminology Properties Graph Types Representations Performance BFS/DFS Applications 2 What is a Graph A graph
Graph Algorithms. Definition
 Graph Algorithms Many problems in CS can be modeled as graph problems. Algorithms for solving graph problems are fundamental to the field of algorithm design. Definition A graph G = (V, E) consists of
Graph Algorithms Many problems in CS can be modeled as graph problems. Algorithms for solving graph problems are fundamental to the field of algorithm design. Definition A graph G = (V, E) consists of
3.1 Basic Definitions and Applications
 Graphs hapter hapter Graphs. Basic efinitions and Applications Graph. G = (V, ) n V = nodes. n = edges between pairs of nodes. n aptures pairwise relationship between objects: Undirected graph represents
Graphs hapter hapter Graphs. Basic efinitions and Applications Graph. G = (V, ) n V = nodes. n = edges between pairs of nodes. n aptures pairwise relationship between objects: Undirected graph represents
Graphs ORD SFO LAX DFW Goodrich, Tamassia Graphs 1
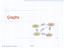 Graphs SFO 33 143 ORD 02 LAX 1233 DFW 2004 Goodrich, Tamassia Graphs 1 What is a Graph? (in computer science, it s not a data plot) General structure for representing positions with an arbitrary connectivity
Graphs SFO 33 143 ORD 02 LAX 1233 DFW 2004 Goodrich, Tamassia Graphs 1 What is a Graph? (in computer science, it s not a data plot) General structure for representing positions with an arbitrary connectivity
CS 220: Discrete Structures and their Applications. graphs zybooks chapter 10
 CS 220: Discrete Structures and their Applications graphs zybooks chapter 10 directed graphs A collection of vertices and directed edges What can this represent? undirected graphs A collection of vertices
CS 220: Discrete Structures and their Applications graphs zybooks chapter 10 directed graphs A collection of vertices and directed edges What can this represent? undirected graphs A collection of vertices
CSI 604 Elementary Graph Algorithms
 CSI 604 Elementary Graph Algorithms Ref: Chapter 22 of the text by Cormen et al. (Second edition) 1 / 25 Graphs: Basic Definitions Undirected Graph G(V, E): V is set of nodes (or vertices) and E is the
CSI 604 Elementary Graph Algorithms Ref: Chapter 22 of the text by Cormen et al. (Second edition) 1 / 25 Graphs: Basic Definitions Undirected Graph G(V, E): V is set of nodes (or vertices) and E is the
Graph Terminology and Representations
 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Graph Termiology ad Represetatios 2015 Goodrich ad Tamassia Graphs 1 Graphs A graph is
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Graph Termiology ad Represetatios 2015 Goodrich ad Tamassia Graphs 1 Graphs A graph is
Elementary Graph Algorithms. Ref: Chapter 22 of the text by Cormen et al. Representing a graph:
 Elementary Graph Algorithms Ref: Chapter 22 of the text by Cormen et al. Representing a graph: Graph G(V, E): V set of nodes (vertices); E set of edges. Notation: n = V and m = E. (Vertices are numbered
Elementary Graph Algorithms Ref: Chapter 22 of the text by Cormen et al. Representing a graph: Graph G(V, E): V set of nodes (vertices); E set of edges. Notation: n = V and m = E. (Vertices are numbered
Konigsberg Bridge Problem
 Graphs Konigsberg Bridge Problem c C d g A Kneiphof e D a B b f c A C d e g D a b f B Euler s Graph Degree of a vertex: the number of edges incident to it Euler showed that there is a walk starting at
Graphs Konigsberg Bridge Problem c C d g A Kneiphof e D a B b f c A C d e g D a b f B Euler s Graph Degree of a vertex: the number of edges incident to it Euler showed that there is a walk starting at
Data Structures. Elementary Graph Algorithms BFS, DFS & Topological Sort
 Data Structures Elementary Graph Algorithms BFS, DFS & Topological Sort 1 Graphs A graph, G = (V, E), consists of two sets: V is a finite non-empty set of vertices. E is a set of pairs of vertices, called
Data Structures Elementary Graph Algorithms BFS, DFS & Topological Sort 1 Graphs A graph, G = (V, E), consists of two sets: V is a finite non-empty set of vertices. E is a set of pairs of vertices, called
Graph. Vertex. edge. Directed Graph. Undirected Graph
 Module : Graphs Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS E-mail: natarajan.meghanathan@jsums.edu Graph Graph is a data structure that is a collection
Module : Graphs Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS E-mail: natarajan.meghanathan@jsums.edu Graph Graph is a data structure that is a collection
Graph Representation
 Graph Representation Adjacency list representation of G = (V, E) An array of V lists, one for each vertex in V Each list Adj[u] contains all the vertices v such that there is an edge between u and v Adj[u]
Graph Representation Adjacency list representation of G = (V, E) An array of V lists, one for each vertex in V Each list Adj[u] contains all the vertices v such that there is an edge between u and v Adj[u]
Graph Algorithms. Chapter 22. CPTR 430 Algorithms Graph Algorithms 1
 Graph Algorithms Chapter 22 CPTR 430 Algorithms Graph Algorithms Why Study Graph Algorithms? Mathematical graphs seem to be relatively specialized and abstract Why spend so much time and effort on algorithms
Graph Algorithms Chapter 22 CPTR 430 Algorithms Graph Algorithms Why Study Graph Algorithms? Mathematical graphs seem to be relatively specialized and abstract Why spend so much time and effort on algorithms
Copyright 2000, Kevin Wayne 1
 Chapter 3 - Graphs Undirected Graphs Undirected graph. G = (V, E) V = nodes. E = edges between pairs of nodes. Captures pairwise relationship between objects. Graph size parameters: n = V, m = E. Directed
Chapter 3 - Graphs Undirected Graphs Undirected graph. G = (V, E) V = nodes. E = edges between pairs of nodes. Captures pairwise relationship between objects. Graph size parameters: n = V, m = E. Directed
Graph Representations and Traversal
 COMPSCI 330: Design and Analysis of Algorithms 02/08/2017-02/20/2017 Graph Representations and Traversal Lecturer: Debmalya Panigrahi Scribe: Tianqi Song, Fred Zhang, Tianyu Wang 1 Overview This lecture
COMPSCI 330: Design and Analysis of Algorithms 02/08/2017-02/20/2017 Graph Representations and Traversal Lecturer: Debmalya Panigrahi Scribe: Tianqi Song, Fred Zhang, Tianyu Wang 1 Overview This lecture
Depth-First Search A B D E C
 epth-first Search Outline and Reading efinitions (6.1) Subgraph onnectivity Spanning trees and forests epth-first search (6.3.1) lgorithm xample Properties nalysis pplications of FS (6.5) Path finding
epth-first Search Outline and Reading efinitions (6.1) Subgraph onnectivity Spanning trees and forests epth-first search (6.3.1) lgorithm xample Properties nalysis pplications of FS (6.5) Path finding
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 4 Graphs Definitions Traversals Adam Smith 9/8/10 Exercise How can you simulate an array with two unbounded stacks and a small amount of memory? (Hint: think of a
Algorithm Design and Analysis LECTURE 4 Graphs Definitions Traversals Adam Smith 9/8/10 Exercise How can you simulate an array with two unbounded stacks and a small amount of memory? (Hint: think of a
Graph: representation and traversal
 Graph: representation and traversal CISC4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang! Acknowledgement The set of slides have use materials from the following resources Slides for textbook
Graph: representation and traversal CISC4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang! Acknowledgement The set of slides have use materials from the following resources Slides for textbook
Winter 2016 COMP-250: Introduction to Computer Science. Lecture 16, March 10, 2016
 Winter 2016-250: Introduction to Computer Science Lecture 16, March 10, 2016 GRAPHS Definitions Examples The Graph ADT PVD HNL LAX DFW STL FTL What is a Graph? Agraph G = (V,E) is composed of: V: set of
Winter 2016-250: Introduction to Computer Science Lecture 16, March 10, 2016 GRAPHS Definitions Examples The Graph ADT PVD HNL LAX DFW STL FTL What is a Graph? Agraph G = (V,E) is composed of: V: set of
Computer Science & Engineering 423/823 Design and Analysis of Algorithms
 s of s Computer Science & Engineering 423/823 Design and Analysis of Lecture 03 (Chapter 22) Stephen Scott (Adapted from Vinodchandran N. Variyam) 1 / 29 s of s s are abstract data types that are applicable
s of s Computer Science & Engineering 423/823 Design and Analysis of Lecture 03 (Chapter 22) Stephen Scott (Adapted from Vinodchandran N. Variyam) 1 / 29 s of s s are abstract data types that are applicable
Depth-First Search and Template Patterns
 Depth-First Search and Template Patterns A B D E C 1 Outline Template Patterns and Search Depth-first search Algorithm Example Properties Analysis Applications of DFS Path finding Cycle finding CS 4407,
Depth-First Search and Template Patterns A B D E C 1 Outline Template Patterns and Search Depth-first search Algorithm Example Properties Analysis Applications of DFS Path finding Cycle finding CS 4407,
Practical Session No. 12 Graphs, BFS, DFS, Topological sort
 Practical Session No. 12 Graphs, BFS, DFS, Topological sort Graphs and BFS Graph G = (V, E) Graph Representations (V G ) v1 v n V(G) = V - Set of all vertices in G E(G) = E - Set of all edges (u,v) in
Practical Session No. 12 Graphs, BFS, DFS, Topological sort Graphs and BFS Graph G = (V, E) Graph Representations (V G ) v1 v n V(G) = V - Set of all vertices in G E(G) = E - Set of all edges (u,v) in
Undirected Graphs. V = { 1, 2, 3, 4, 5, 6, 7, 8 } E = { 1-2, 1-3, 2-3, 2-4, 2-5, 3-5, 3-7, 3-8, 4-5, 5-6 } n = 8 m = 11
 Chapter 3 - Graphs Undirected Graphs Undirected graph. G = (V, E) V = nodes. E = edges between pairs of nodes. Captures pairwise relationship between objects. Graph size parameters: n = V, m = E. V = {
Chapter 3 - Graphs Undirected Graphs Undirected graph. G = (V, E) V = nodes. E = edges between pairs of nodes. Captures pairwise relationship between objects. Graph size parameters: n = V, m = E. V = {
 UNIT IV -NON-LINEAR DATA STRUCTURES 4.1 Trees TREE: A tree is a finite set of one or more nodes such that there is a specially designated node called the Root, and zero or more non empty sub trees T1,
UNIT IV -NON-LINEAR DATA STRUCTURES 4.1 Trees TREE: A tree is a finite set of one or more nodes such that there is a specially designated node called the Root, and zero or more non empty sub trees T1,
Lecture 3: Graphs and flows
 Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
W4231: Analysis of Algorithms
 W4231: Analysis of Algorithms 10/21/1999 Definitions for graphs Breadth First Search and Depth First Search Topological Sort. Graphs AgraphG is given by a set of vertices V and a set of edges E. Normally
W4231: Analysis of Algorithms 10/21/1999 Definitions for graphs Breadth First Search and Depth First Search Topological Sort. Graphs AgraphG is given by a set of vertices V and a set of edges E. Normally
LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS
 Department of Computer Science University of Babylon LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS By Faculty of Science for Women( SCIW), University of Babylon, Iraq Samaher@uobabylon.edu.iq
Department of Computer Science University of Babylon LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS By Faculty of Science for Women( SCIW), University of Babylon, Iraq Samaher@uobabylon.edu.iq
Graph Algorithms. Andreas Klappenecker. [based on slides by Prof. Welch]
![Graph Algorithms. Andreas Klappenecker. [based on slides by Prof. Welch] Graph Algorithms. Andreas Klappenecker. [based on slides by Prof. Welch]](/thumbs/81/84350835.jpg) Graph Algorithms Andreas Klappenecker [based on slides by Prof. Welch] 1 Directed Graphs Let V be a finite set and E a binary relation on V, that is, E VxV. Then the pair G=(V,E) is called a directed graph.
Graph Algorithms Andreas Klappenecker [based on slides by Prof. Welch] 1 Directed Graphs Let V be a finite set and E a binary relation on V, that is, E VxV. Then the pair G=(V,E) is called a directed graph.
COT 6405 Introduction to Theory of Algorithms
 COT 6405 Introduction to Theory of Algorithms Topic 14. Graph Algorithms 11/7/2016 1 Elementary Graph Algorithms How to represent a graph? Adjacency lists Adjacency matrix How to search a graph? Breadth-first
COT 6405 Introduction to Theory of Algorithms Topic 14. Graph Algorithms 11/7/2016 1 Elementary Graph Algorithms How to represent a graph? Adjacency lists Adjacency matrix How to search a graph? Breadth-first
Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1
 CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
Basic Graph Algorithms
 Basic Graph Algorithms 1 Representations of Graphs There are two standard ways to represent a graph G(V, E) where V is the set of vertices and E is the set of edges. adjacency list representation adjacency
Basic Graph Algorithms 1 Representations of Graphs There are two standard ways to represent a graph G(V, E) where V is the set of vertices and E is the set of edges. adjacency list representation adjacency
Minimum Spanning Trees Ch 23 Traversing graphs
 Next: Graph Algorithms Graphs Ch 22 Graph representations adjacency list adjacency matrix Minimum Spanning Trees Ch 23 Traversing graphs Breadth-First Search Depth-First Search 11/30/17 CSE 3101 1 Graphs
Next: Graph Algorithms Graphs Ch 22 Graph representations adjacency list adjacency matrix Minimum Spanning Trees Ch 23 Traversing graphs Breadth-First Search Depth-First Search 11/30/17 CSE 3101 1 Graphs
Graphs. Part I: Basic algorithms. Laura Toma Algorithms (csci2200), Bowdoin College
 Laura Toma Algorithms (csci2200), Bowdoin College Undirected graphs Concepts: connectivity, connected components paths (undirected) cycles Basic problems, given undirected graph G: is G connected how many
Laura Toma Algorithms (csci2200), Bowdoin College Undirected graphs Concepts: connectivity, connected components paths (undirected) cycles Basic problems, given undirected graph G: is G connected how many
CS 125 Section #6 Graph Traversal and Linear Programs 10/13/14
 CS 125 Section #6 Graph Traversal and Linear Programs 10/13/14 1 Depth first search 1.1 The Algorithm Besides breadth first search, which we saw in class in relation to Dijkstra s algorithm, there is one
CS 125 Section #6 Graph Traversal and Linear Programs 10/13/14 1 Depth first search 1.1 The Algorithm Besides breadth first search, which we saw in class in relation to Dijkstra s algorithm, there is one
Computer Science & Engineering 423/823 Design and Analysis of Algorithms
 Computer Science & Engineering 423/823 Design and Analysis of Algorithms Lecture 04 Elementary Graph Algorithms (Chapter 22) Stephen Scott (Adapted from Vinodchandran N. Variyam) sscott@cse.unl.edu Introduction
Computer Science & Engineering 423/823 Design and Analysis of Algorithms Lecture 04 Elementary Graph Algorithms (Chapter 22) Stephen Scott (Adapted from Vinodchandran N. Variyam) sscott@cse.unl.edu Introduction
Data Structures and Algorithms. Chapter 7. Graphs
 1 Data Structures and Algorithms Chapter 7 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
1 Data Structures and Algorithms Chapter 7 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
Scribes: Romil Verma, Juliana Cook (2015), Virginia Williams, Date: May 1, 2017 and Seth Hildick-Smith (2016), G. Valiant (2017), M.
 Lecture 9 Graphs Scribes: Romil Verma, Juliana Cook (2015), Virginia Williams, Date: May 1, 2017 and Seth Hildick-Smith (2016), G. Valiant (2017), M. Wootters (2017) 1 Graphs A graph is a set of vertices
Lecture 9 Graphs Scribes: Romil Verma, Juliana Cook (2015), Virginia Williams, Date: May 1, 2017 and Seth Hildick-Smith (2016), G. Valiant (2017), M. Wootters (2017) 1 Graphs A graph is a set of vertices
Suggested Study Strategy
 Final Exam Thursday, 7 August 2014,19:00 22:00 Closed Book Will cover whole course, with emphasis on material after midterm (hash tables, binary search trees, sorting, graphs) Suggested Study Strategy
Final Exam Thursday, 7 August 2014,19:00 22:00 Closed Book Will cover whole course, with emphasis on material after midterm (hash tables, binary search trees, sorting, graphs) Suggested Study Strategy
DFS & STRONGLY CONNECTED COMPONENTS
 DFS & STRONGLY CONNECTED COMPONENTS CS 4407 Search Tree Breadth-First Search (BFS) Depth-First Search (DFS) Depth-First Search (DFS) u d[u]: when u is discovered f[u]: when searching adj of u is finished
DFS & STRONGLY CONNECTED COMPONENTS CS 4407 Search Tree Breadth-First Search (BFS) Depth-First Search (DFS) Depth-First Search (DFS) u d[u]: when u is discovered f[u]: when searching adj of u is finished
Applications of BDF and DFS
 January 14, 2016 1 Deciding whether a graph is bipartite using BFS. 2 Finding connected components of a graph (both BFS and DFS) works. 3 Deciding whether a digraph is strongly connected. 4 Finding cut
January 14, 2016 1 Deciding whether a graph is bipartite using BFS. 2 Finding connected components of a graph (both BFS and DFS) works. 3 Deciding whether a digraph is strongly connected. 4 Finding cut
Cut vertices, Cut Edges and Biconnected components. MTL776 Graph algorithms
 Cut vertices, Cut Edges and Biconnected components MTL776 Graph algorithms Articulation points, Bridges, Biconnected Components Let G = (V;E) be a connected, undirected graph. An articulation point of
Cut vertices, Cut Edges and Biconnected components MTL776 Graph algorithms Articulation points, Bridges, Biconnected Components Let G = (V;E) be a connected, undirected graph. An articulation point of
MA/CSSE 473 Day 12. Questions? Insertion sort analysis Depth first Search Breadth first Search. (Introduce permutation and subset generation)
 MA/CSSE 473 Day 12 Interpolation Search Insertion Sort quick review DFS, BFS Topological Sort MA/CSSE 473 Day 12 Questions? Interpolation Search Insertion sort analysis Depth first Search Breadth first
MA/CSSE 473 Day 12 Interpolation Search Insertion Sort quick review DFS, BFS Topological Sort MA/CSSE 473 Day 12 Questions? Interpolation Search Insertion sort analysis Depth first Search Breadth first
Algorithms: Lecture 10. Chalmers University of Technology
 Algorithms: Lecture 10 Chalmers University of Technology Today s Topics Basic Definitions Path, Cycle, Tree, Connectivity, etc. Graph Traversal Depth First Search Breadth First Search Testing Bipartatiness
Algorithms: Lecture 10 Chalmers University of Technology Today s Topics Basic Definitions Path, Cycle, Tree, Connectivity, etc. Graph Traversal Depth First Search Breadth First Search Testing Bipartatiness
Lecture 14: Graph Representation, DFS and Applications
 Lecture 14: Graph Representation, FS and pplications SFO OR LX FW ourtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Graph Representation dge List djacency List djacency Matrix
Lecture 14: Graph Representation, FS and pplications SFO OR LX FW ourtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Graph Representation dge List djacency List djacency Matrix
Outline. Graphs. Divide and Conquer.
 GRAPHS COMP 321 McGill University These slides are mainly compiled from the following resources. - Professor Jaehyun Park slides CS 97SI - Top-coder tutorials. - Programming Challenges books. Outline Graphs.
GRAPHS COMP 321 McGill University These slides are mainly compiled from the following resources. - Professor Jaehyun Park slides CS 97SI - Top-coder tutorials. - Programming Challenges books. Outline Graphs.
22.3 Depth First Search
 22.3 Depth First Search Depth-First Search(DFS) always visits a neighbour of the most recently visited vertex with an unvisited neighbour. This means the search moves forward when possible, and only backtracks
22.3 Depth First Search Depth-First Search(DFS) always visits a neighbour of the most recently visited vertex with an unvisited neighbour. This means the search moves forward when possible, and only backtracks
Undirected Graphs. Hwansoo Han
 Undirected Graphs Hwansoo Han Definitions Undirected graph (simply graph) G = (V, E) V : set of vertexes (vertices, nodes, points) E : set of edges (lines) An edge is an unordered pair Edge (v, w) = (w,
Undirected Graphs Hwansoo Han Definitions Undirected graph (simply graph) G = (V, E) V : set of vertexes (vertices, nodes, points) E : set of edges (lines) An edge is an unordered pair Edge (v, w) = (w,
Representations of Graphs
 ELEMENTARY GRAPH ALGORITHMS -- CS-5321 Presentation -- I am Nishit Kapadia Representations of Graphs There are two standard ways: A collection of adjacency lists - they provide a compact way to represent
ELEMENTARY GRAPH ALGORITHMS -- CS-5321 Presentation -- I am Nishit Kapadia Representations of Graphs There are two standard ways: A collection of adjacency lists - they provide a compact way to represent
BACKGROUND: A BRIEF INTRODUCTION TO GRAPH THEORY
 BACKGROUND: A BRIEF INTRODUCTION TO GRAPH THEORY General definitions; Representations; Graph Traversals; Topological sort; Graphs definitions & representations Graph theory is a fundamental tool in sparse
BACKGROUND: A BRIEF INTRODUCTION TO GRAPH THEORY General definitions; Representations; Graph Traversals; Topological sort; Graphs definitions & representations Graph theory is a fundamental tool in sparse
CSE 417: Algorithms and Computational Complexity. 3.1 Basic Definitions and Applications. Goals. Chapter 3. Winter 2012 Graphs and Graph Algorithms
 Chapter 3 CSE 417: Algorithms and Computational Complexity Graphs Reading: 3.1-3.6 Winter 2012 Graphs and Graph Algorithms Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
Chapter 3 CSE 417: Algorithms and Computational Complexity Graphs Reading: 3.1-3.6 Winter 2012 Graphs and Graph Algorithms Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
Lecture 10. Elementary Graph Algorithm Minimum Spanning Trees
 Lecture 10. Elementary Graph Algorithm Minimum Spanning Trees T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo
Lecture 10. Elementary Graph Algorithm Minimum Spanning Trees T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo
CHAPTER 13 GRAPH ALGORITHMS
 CHAPTER 13 GRAPH ALGORITHMS SFO LAX ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 00) AND SLIDES FROM NANCY
CHAPTER 13 GRAPH ALGORITHMS SFO LAX ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 00) AND SLIDES FROM NANCY
Graphs. Graph G = (V, E) Types of graphs E = O( V 2 ) V = set of vertices E = set of edges (V V)
 Graph Algorithms Graphs Graph G = (V, E) V = set of vertices E = set of edges (V V) Types of graphs Undirected: edge (u, v) = (v, u); for all v, (v, v) E (No self loops.) Directed: (u, v) is edge from
Graph Algorithms Graphs Graph G = (V, E) V = set of vertices E = set of edges (V V) Types of graphs Undirected: edge (u, v) = (v, u); for all v, (v, v) E (No self loops.) Directed: (u, v) is edge from
Graphs ORD SFO LAX DFW
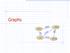 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graph Algorithms shortest paths, minimum spanning trees, etc.
 SFO ORD LAX Graph Algorithms shortest paths, minimum spanning trees, etc. DFW Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with
SFO ORD LAX Graph Algorithms shortest paths, minimum spanning trees, etc. DFW Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with
Part VI Graph algorithms. Chapter 22 Elementary Graph Algorithms Chapter 23 Minimum Spanning Trees Chapter 24 Single-source Shortest Paths
 Part VI Graph algorithms Chapter 22 Elementary Graph Algorithms Chapter 23 Minimum Spanning Trees Chapter 24 Single-source Shortest Paths 1 Chapter 22 Elementary Graph Algorithms Representations of graphs
Part VI Graph algorithms Chapter 22 Elementary Graph Algorithms Chapter 23 Minimum Spanning Trees Chapter 24 Single-source Shortest Paths 1 Chapter 22 Elementary Graph Algorithms Representations of graphs
Graph Algorithms. Textbook reading. Chapter 3 Chapter 4. CSci 3110 Graph Algorithms 1/41
 CSci 3110 Graph Algorithms 1/41 Graph Algorithms Textbook reading Chapter 3 Chapter 4 CSci 3110 Graph Algorithms 2/41 Overview Design principle: Learn the structure of a graph by systematic exploration
CSci 3110 Graph Algorithms 1/41 Graph Algorithms Textbook reading Chapter 3 Chapter 4 CSci 3110 Graph Algorithms 2/41 Overview Design principle: Learn the structure of a graph by systematic exploration
Graph Algorithms shortest paths, minimum spanning trees, etc.
 Graph Algorithms shortest paths, minimum spanning trees, etc. SFO ORD LAX DFW Graphs 1 Outline and Reading Graphs ( 1.1) Definition Applications Terminology Properties ADT Data structures for graphs (
Graph Algorithms shortest paths, minimum spanning trees, etc. SFO ORD LAX DFW Graphs 1 Outline and Reading Graphs ( 1.1) Definition Applications Terminology Properties ADT Data structures for graphs (
UNIT 5 GRAPH. Application of Graph Structure in real world:- Graph Terminologies:
 UNIT 5 CSE 103 - Unit V- Graph GRAPH Graph is another important non-linear data structure. In tree Structure, there is a hierarchical relationship between, parent and children that is one-to-many relationship.
UNIT 5 CSE 103 - Unit V- Graph GRAPH Graph is another important non-linear data structure. In tree Structure, there is a hierarchical relationship between, parent and children that is one-to-many relationship.
Announcements. HW3 is graded. Average is 81%
 CSC263 Week 9 Announcements HW3 is graded. Average is 81% Announcements Problem Set 4 is due this Tuesday! Due Tuesday (Nov 17) Recap The Graph ADT definition and data structures BFS gives us single-source
CSC263 Week 9 Announcements HW3 is graded. Average is 81% Announcements Problem Set 4 is due this Tuesday! Due Tuesday (Nov 17) Recap The Graph ADT definition and data structures BFS gives us single-source
Strongly connected: A directed graph is strongly connected if every pair of vertices are reachable from each other.
 Directed Graph In a directed graph, each edge (u, v) has a direction u v. Thus (u, v) (v, u). Directed graph is useful to model many practical problems (such as one-way road in traffic network, and asymmetric
Directed Graph In a directed graph, each edge (u, v) has a direction u v. Thus (u, v) (v, u). Directed graph is useful to model many practical problems (such as one-way road in traffic network, and asymmetric
Graphs Weighted Graphs. Reading: 12.5, 12.6, 12.7
 Graphs Weighted Graphs Reading: 1.5, 1.6, 1. Weighted Graphs, a.k.a. Networks In a weighted graph, each edge has an associated numerical value, called the weight or cost of the edge Edge weights may represent,
Graphs Weighted Graphs Reading: 1.5, 1.6, 1. Weighted Graphs, a.k.a. Networks In a weighted graph, each edge has an associated numerical value, called the weight or cost of the edge Edge weights may represent,
Chapter 14. Graphs Pearson Addison-Wesley. All rights reserved 14 A-1
 Chapter 14 Graphs 2011 Pearson Addison-Wesley. All rights reserved 14 A-1 Terminology G = {V, E} A graph G consists of two sets A set V of vertices, or nodes A set E of edges A subgraph Consists of a subset
Chapter 14 Graphs 2011 Pearson Addison-Wesley. All rights reserved 14 A-1 Terminology G = {V, E} A graph G consists of two sets A set V of vertices, or nodes A set E of edges A subgraph Consists of a subset
Definition Example Solution
 Section 11.4 Spanning Trees Definition: Let G be a simple graph. A spanning tree of G is a subgraph of G that is a tree containing every vertex of G. Example: Find the spanning tree of this simple graph:
Section 11.4 Spanning Trees Definition: Let G be a simple graph. A spanning tree of G is a subgraph of G that is a tree containing every vertex of G. Example: Find the spanning tree of this simple graph:
Depth-first search in undirected graphs What parts of the graph are reachable from a given vertex?
 Why graphs? Chapter 3. Decompositions of graphs Awiderangeofproblemscanbeexpressedwithclarityandprecisionin the concise pictorial language of graphs. Graph coloring. Graph connectivity and reachability.
Why graphs? Chapter 3. Decompositions of graphs Awiderangeofproblemscanbeexpressedwithclarityandprecisionin the concise pictorial language of graphs. Graph coloring. Graph connectivity and reachability.
Chapter 22 Elementary Graph Algorithms
 Chapter 22 Elementary Graph Algorithms Graph Representations Graph G = (V,E) Directed Undirected Adjacency Lists Adjacency Matrix Graph Representations Adjacency List: Undirected Memory: Adjacency: Graph
Chapter 22 Elementary Graph Algorithms Graph Representations Graph G = (V,E) Directed Undirected Adjacency Lists Adjacency Matrix Graph Representations Adjacency List: Undirected Memory: Adjacency: Graph
11/22/2016. Chapter 9 Graph Algorithms. Introduction. Definitions. Definitions. Definitions. Definitions
 Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Chapter 9 Graph Algorithms
 Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 7 Greedy Graph Algorithms Topological sort Shortest paths Adam Smith The (Algorithm) Design Process 1. Work out the answer for some examples. Look for a general principle
Algorithm Design and Analysis LECTURE 7 Greedy Graph Algorithms Topological sort Shortest paths Adam Smith The (Algorithm) Design Process 1. Work out the answer for some examples. Look for a general principle
CS 341: Algorithms. Douglas R. Stinson. David R. Cheriton School of Computer Science University of Waterloo. February 26, 2019
 CS 341: Algorithms Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo February 26, 2019 D.R. Stinson (SCS) CS 341 February 26, 2019 1 / 296 1 Course Information 2 Introduction
CS 341: Algorithms Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo February 26, 2019 D.R. Stinson (SCS) CS 341 February 26, 2019 1 / 296 1 Course Information 2 Introduction
Practical Session No. 12 Graphs, BFS, DFS Topological Sort
 Practical Session No. 12 Graphs, BFS, DFS Topological Sort Graphs and BFS Graph G = (V, E) Graph Representations (VG ) v1 v n V(G) = V - Set of all vertices in G E(G) = E - Set of all edges (u,v) in G,
Practical Session No. 12 Graphs, BFS, DFS Topological Sort Graphs and BFS Graph G = (V, E) Graph Representations (VG ) v1 v n V(G) = V - Set of all vertices in G E(G) = E - Set of all edges (u,v) in G,
Undirected Graphs. DSA - lecture 6 - T.U.Cluj-Napoca - M. Joldos 1
 Undirected Graphs Terminology. Free Trees. Representations. Minimum Spanning Trees (algorithms: Prim, Kruskal). Graph Traversals (dfs, bfs). Articulation points & Biconnected Components. Graph Matching
Undirected Graphs Terminology. Free Trees. Representations. Minimum Spanning Trees (algorithms: Prim, Kruskal). Graph Traversals (dfs, bfs). Articulation points & Biconnected Components. Graph Matching
DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI. Department of Computer Science and Engineering CS6301 PROGRAMMING DATA STRUCTURES II
 DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI Department of Computer Science and Engineering CS6301 PROGRAMMING DATA STRUCTURES II Anna University 2 & 16 Mark Questions & Answers Year / Semester: II / III
DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI Department of Computer Science and Engineering CS6301 PROGRAMMING DATA STRUCTURES II Anna University 2 & 16 Mark Questions & Answers Year / Semester: II / III
UNIT Name the different ways of representing a graph? a.adjacencymatrix b. Adjacency list
 UNIT-4 Graph: Terminology, Representation, Traversals Applications - spanning trees, shortest path and Transitive closure, Topological sort. Sets: Representation - Operations on sets Applications. 1. Name
UNIT-4 Graph: Terminology, Representation, Traversals Applications - spanning trees, shortest path and Transitive closure, Topological sort. Sets: Representation - Operations on sets Applications. 1. Name
Graphs: basic concepts and algorithms
 : basic concepts and algorithms Topics covered by this lecture: - Reminder Trees Trees (in-order,post-order,pre-order) s (BFS, DFS) Denitions: Reminder Directed graph (digraph): G = (V, E), V - vertex
: basic concepts and algorithms Topics covered by this lecture: - Reminder Trees Trees (in-order,post-order,pre-order) s (BFS, DFS) Denitions: Reminder Directed graph (digraph): G = (V, E), V - vertex
Graph Algorithms: Chapters Part 1: Introductory graph concepts
 UMass Lowell Computer Science 91.503 Algorithms Dr. Haim Levkowitz Fall, 2007 Graph Algorithms: Chapters 22-25 Part 1: Introductory graph concepts 1 91.404 Graph Review Elementary Graph Algorithms Minimum
UMass Lowell Computer Science 91.503 Algorithms Dr. Haim Levkowitz Fall, 2007 Graph Algorithms: Chapters 22-25 Part 1: Introductory graph concepts 1 91.404 Graph Review Elementary Graph Algorithms Minimum
CS2 Algorithms and Data Structures Note 10. Depth-First Search and Topological Sorting
 CS2 Algorithms and Data Structures Note 10 Depth-First Search and Topological Sorting In this lecture, we will analyse the running time of DFS and discuss a few applications. 10.1 A recursive implementation
CS2 Algorithms and Data Structures Note 10 Depth-First Search and Topological Sorting In this lecture, we will analyse the running time of DFS and discuss a few applications. 10.1 A recursive implementation
Algorithms (VII) Yijia Chen Shanghai Jiaotong University
 Algorithms (VII) Yijia Chen Shanghai Jiaotong University Review of the Previous Lecture Depth-first search in undirected graphs Exploring graphs explore(g, v) Input: G = (V, E) is a graph; v V Output:
Algorithms (VII) Yijia Chen Shanghai Jiaotong University Review of the Previous Lecture Depth-first search in undirected graphs Exploring graphs explore(g, v) Input: G = (V, E) is a graph; v V Output:
Strongly Connected Components
 Strongly Connected Components Let G = (V, E) be a directed graph Write if there is a path from to in G Write if and is an equivalence relation: implies and implies s equivalence classes are called the
Strongly Connected Components Let G = (V, E) be a directed graph Write if there is a path from to in G Write if and is an equivalence relation: implies and implies s equivalence classes are called the
Graph Theory. Many problems are mapped to graphs. Problems. traffic VLSI circuits social network communication networks web pages relationship
 Graph Graph Usage I want to visit all the known famous places starting from Seoul ending in Seoul Knowledge: distances, costs Find the optimal(distance or cost) path Graph Theory Many problems are mapped
Graph Graph Usage I want to visit all the known famous places starting from Seoul ending in Seoul Knowledge: distances, costs Find the optimal(distance or cost) path Graph Theory Many problems are mapped
Breadth-First Search L 1 L Goodrich, Tamassia, Goldwasser Breadth-First Search 1
 readth-irst Search 2013 Goodrich, Tamassia, Goldwasser readth-irst Search 1 readth-irst Search readth-first search (S) is a general technique for traversing a graph S traversal of a graph G Visits all
readth-irst Search 2013 Goodrich, Tamassia, Goldwasser readth-irst Search 1 readth-irst Search readth-first search (S) is a general technique for traversing a graph S traversal of a graph G Visits all
Graph and Digraph Glossary
 1 of 15 31.1.2004 14:45 Graph and Digraph Glossary A B C D E F G H I-J K L M N O P-Q R S T U V W-Z Acyclic Graph A graph is acyclic if it contains no cycles. Adjacency Matrix A 0-1 square matrix whose
1 of 15 31.1.2004 14:45 Graph and Digraph Glossary A B C D E F G H I-J K L M N O P-Q R S T U V W-Z Acyclic Graph A graph is acyclic if it contains no cycles. Adjacency Matrix A 0-1 square matrix whose
Lecture 10: Strongly Connected Components, Biconnected Graphs
 15-750: Graduate Algorithms February 8, 2016 Lecture 10: Strongly Connected Components, Biconnected Graphs Lecturer: David Witmer Scribe: Zhong Zhou 1 DFS Continued We have introduced Depth-First Search
15-750: Graduate Algorithms February 8, 2016 Lecture 10: Strongly Connected Components, Biconnected Graphs Lecturer: David Witmer Scribe: Zhong Zhou 1 DFS Continued We have introduced Depth-First Search
Design and Analysis of Algorithms
 Design and Analysis of Algorithms CS 5311 Lecture 19 Topological Sort Junzhou Huang, Ph.D. Department of Computer Science and ngineering CS5311 Design and Analysis of Algorithms 1 Topological Sort Want
Design and Analysis of Algorithms CS 5311 Lecture 19 Topological Sort Junzhou Huang, Ph.D. Department of Computer Science and ngineering CS5311 Design and Analysis of Algorithms 1 Topological Sort Want
Graph Search. Adnan Aziz
 Graph Search Adnan Aziz Based on CLRS, Ch 22. Recall encountered graphs several weeks ago (CLRS B.4) restricted our attention to definitions, terminology, properties Now we ll see how to perform basic
Graph Search Adnan Aziz Based on CLRS, Ch 22. Recall encountered graphs several weeks ago (CLRS B.4) restricted our attention to definitions, terminology, properties Now we ll see how to perform basic
Algorithms (VII) Yijia Chen Shanghai Jiaotong University
 Algorithms (VII) Yijia Chen Shanghai Jiaotong University Review of the Previous Lecture Depth-first search in undirected graphs Exploring graphs explore(g, v) Input: G = (V, E) is a graph; v V Output:
Algorithms (VII) Yijia Chen Shanghai Jiaotong University Review of the Previous Lecture Depth-first search in undirected graphs Exploring graphs explore(g, v) Input: G = (V, E) is a graph; v V Output:
GRAPHICAL ALGORITHMS. UNIT _II Lecture-12 Slides No. 3-7 Lecture Slides No Lecture Slides No
 GRAPHICAL ALGORITHMS UNIT _II Lecture-12 Slides No. 3-7 Lecture-13-16 Slides No. 8-26 Lecture-17-19 Slides No. 27-42 Topics Covered Graphs & Trees ( Some Basic Terminologies) Spanning Trees (BFS & DFS)
GRAPHICAL ALGORITHMS UNIT _II Lecture-12 Slides No. 3-7 Lecture-13-16 Slides No. 8-26 Lecture-17-19 Slides No. 27-42 Topics Covered Graphs & Trees ( Some Basic Terminologies) Spanning Trees (BFS & DFS)
