Graphs ORD SFO LAX DFW
|
|
|
- Laura Beatrice Jackson
- 5 years ago
- Views:
Transcription
1 Graphs SFO ORD LAX 1233 DFW
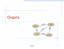
2 Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad store elemets Example: A vertex represets a airport ad stores the three-letter airport code A edge represets a flight route betwee two airports ad stores the mileage of the route HNL 2555 SFO LAX 2014 Goodrich, Tamassia, Goldwasser Graphs 802 ORD DFW LGA PVD MIA 2
3 Edge Types Directed edge ordered pair of vertices (u,v) first vertex u is the origi secod vertex v is the destiatio e.g., a flight Directed graph all the edges are directed e.g., route etwork Udirected edge uordered pair of vertices (u,v) e.g., a flight route Udirected graph all the edges are udirected e.g., flight etwork SFO LAX Soeyik Goodrich UA 120 AA 49 SW 45 ORD UA 877 DL 335 DFW AA 411 AA 523 AA 1387 Garg Goldwasser Tamassia Tollis NW 35 JFK AA 903 MIA BOS DL 247 Vitter Preparata Chiag Graphs 3
4 Applicatios Electroic circuits Prited circuit board Itegrated circuit Trasportatio etworks Highway etwork Flight etwork Computer etworks Local area etwork Iteret Web Databases Etity-relatioship diagram cslab1a cslab1b math.brow.edu cs.brow.edu brow.edu west.et att.et cox.et Joh Paul David 2014 Goodrich, Tamassia, Goldwasser Graphs 4
5 Termiology Ed vertices (or edpoits) of a edge U ad V are the edpoits of a Edges icidet o a vertex a a, d, ad b are icidet o V outgoig edges U icomig edges Adjacet vertices c U ad V are adjacet Degree of a vertex w X has degree 5 i-degree out-degree Parallel edges h ad i are parallel edges Self-loop j is a self-loop V d W f b e X Y g h i Z j Graphs 5
6 Questio What is the sum of degrees of all vertices? Graphs 6
7 Termiology (2) Path seuece of alteratig vertices ad edges begis with a vertex eds with a vertex each edge is preceded ad followed by its edpoits Simple path path such that all its vertices ad edges are distict Examples P 1 =(V,b,X,h,Z) is a simple path P 2 =(U,c,W,e,X,g,Y,f,W,d,V) is a path that is ot simple SFO U a c V d P 2 W b e f ORD P 1 X Y g h JFK BOS Z LAX DFW MIA 2014 Goodrich, Tamassia, Goldwasser Graphs 7
8 Termiology (3) Cycle circular seuece of alteratig vertices ad edges each edge is preceded ad followed by its edpoits Simple cycle cycle such that all its vertices ad edges are distict Examples C 1 =(V,b,X,g,Y,f,W,c,U,a, ) is a simple cycle C 2 =(U,c,W,e,X,g,Y,f,W,d,V,a, ) is a cycle that is ot simple U a c V d C 2 W f e b X Y C 1 g h Z 2014 Goodrich, Tamassia, Goldwasser Graphs 8
9 Termiology (4) BOS Reachable V is reachable from U if there is a path from U to V. Udirected graph reachability is symmetric Coected a graph is coected if, for ay two vertices, there is a path betwee them some path subgraph subset of vertices ad edges formig a graph SFO LAX DFW ORD JFK MIA coected Graphs ot coected 9
10 Termiology (5) Coected Compoet: maximal coected subgraph, e.g., the graph below has 3 coected compoets. Graphs 10
11 Termiology (6) Tree coected graph without cycles free tree Forest collectio of trees tree tree forest tree tree Graphs 11
12 Coectivity Let = # of vertices m = # of edges = 5 m = (5 4)/2 = 10 Complete graph all pairs of vertices are adjacet There (-1)/2 pairs of vertices ad so m=(-1)/2 if a graph is ot complete, m<(-1)/2 Graphs 12
13 Coectivity (2) = #vertices m= #edges For a tree m=-1 = 5 m = 4 Prove! Tree coected graph without cycles Graphs 13
14 Coectivity (3) = #vertices m= #edges For a tree m=-1 If m<-1, G is ot coected = 5 m = 3 Prove Graphs 14
15 Spaig Tree A spaig tree of G is a subgraph which is a tree cotais all vertices of G G spaig tree of G Failure of ay edge discoects system Graphs 15
16 Euler ad the Koeigsberg Bridges Gilliga s Isle? C Pregal River A D B Ca oe walk across each bridge exactly oce ad retur at the startig poit? I 1736, Euler proved that this is ot possible. Graphs 16
17 Graph Model (with parallel edges) Euleria Tour- path that traverses every edge exactly oce ad returs to the first vertex Euler s Theorem A graph has a Euleria tour if ad oly if all vertices have eve degree C A D Graphs B 17
18 Vertices ad Edges A graph is a collectio of vertices ad edges. We model the abstractio as a combiatio of three data types: Vertex, Edge, ad Graph. A Vertex is a lightweight object that stores a arbitrary elemet provided by the user (e.g., a airport code) We assume it supports a method, elemet(), to retrieve the stored elemet. A Edge stores a associated object (e.g., a flight umber, travel distace, cost), retrieved with the elemet( ) method Goodrich, Tamassia, Goldwasser Graphs 18
19 Edge List Structure Vertex object elemet referece to positio i vertex seuece Edge object elemet origi vertex object destiatio vertex object referece to positio i edge seuece Vertex seuece seuece of vertex objects Edge seuece seuece of edge objects 2014 Goodrich, Tamassia, Goldwasser Graphs 19
20 Performace vertices, m edges o parallel edges o self-loops Edge List Adjacecy List Adjacecy Matrix Space + m + m 2 icidetedges(v) m deg(v) areadjacet (v, w) m mi(deg(v), deg(w)) 1 isertvertex(o) isertedge(v, w, o) removevertex(v) m deg(v) 2 removeedge(e) Goodrich, Tamassia, Goldwasser Graphs 20
21 Adjacecy List Structure Icidece seuece for each vertex seuece of refereces to edge objects of icidet edges Augmeted edge objects refereces to associated positios i icidece seueces of ed vertices 2014 Goodrich, Tamassia, Goldwasser Graphs 21
22 Performace vertices, m edges o parallel edges o self-loops Edge List Adjacecy List Adjacecy Matrix Space + m + m 2 icidetedges(v) m deg(v) areadjacet (v, w) m mi(deg(v), deg(w)) 1 isertvertex(o) isertedge(v, w, o) removevertex(v) m deg(v) 2 removeedge(e) Goodrich, Tamassia, Goldwasser Graphs 22
23 Adjacecy Matrix Structure Edge list structure Augmeted vertex objects Iteger key (idex) associated with vertex 2D-array adjacecy array Referece to edge object for adjacet vertices Null for o oadjacet vertices The old fashioed versio just has 0 for o edge ad 1 for edge 2014 Goodrich, Tamassia, Goldwasser Graphs 23
24 Performace vertices, m edges o parallel edges o self-loops Edge List Adjacecy List Adjacecy Matrix Space + m + m 2 icidetedges(v) m deg(v) areadjacet (v, w) m mi(deg(v), deg(w)) 1 isertvertex(o) isertedge(v, w, o) removevertex(v) m deg(v) 2 removeedge(e) Goodrich, Tamassia, Goldwasser Graphs 24
25 Graph Search Algorithms Systematic search of every edge ad vertex of the graph Graph G = (V, E) is either directed or udirected Applicatios Compilers Networks Graphics Gamig 25
26 Breadth-First Search L 0 A L 1 B C D L 2 E F
27 Breadth-First Search Breadth-first search (BFS) is a geeral techiue for traversig a graph A BFS traversal of a graph G Visits all the vertices ad edges of G Determies whether G is coected Computes the coected compoets of G Computes a spaig forest of G BFS o a graph with vertices ad m edges takes O( + m ) time BFS ca be further exteded to solve other graph problems Fid ad report a path with the miimum umber of edges betwee two give vertices 2014 Goodrich, Tamassia, Goldwasser Breadth First Search 27
28 BFS Algorithm The algorithm uses a mechaism for settig ad gettig labels of vertices ad edges Algorithm BFS(G) Iput graph G Output labelig of the edges ad partitio of the vertices of G for all u G.vertices() setlabel(u, UNEXPLORED) for all e G.edges() setlabel(e, UNEXPLORED) for all v G.vertices() if getlabel(v) = UNEXPLORED BFS(G, v) Algorithm BFS(G, s) L 0 ew empty seuece L 0.addLast(s) setlabel(s, VISITED) i 0 while L i.isempty() L i +1 ew empty seuece for all v L i.elemets() for all e G.icidetEdges(v) if getlabel(e) = UNEXPLORED w opposite(v,e) if getlabel(w) = UNEXPLORED setlabel(e, DISCOVERY) setlabel(w, VISITED) L i +1.addLast(w) else setlabel(e, CROSS) i i Goodrich, Tamassia, Goldwasser 28 Breadth First Search
29 Example A uexplored vertex L 0 A A visited vertex uexplored edge L 1 B C D discovery edge cross edge E F L 0 A L 0 A L 1 B C D L 1 B C D E F E F 2014 Goodrich, Tamassia, Goldwasser Breadth First Search 29
30 Example (cot.) L 0 A L 0 A L 1 B C D L 1 B C D E F L 2 E F L 0 A L 0 A L 1 B C D L 1 B C D L 2 E F L 2 E F 2014 Goodrich, Tamassia, Goldwasser Breadth First Search 30
31 Example (cot.) L 0 A L 0 A L 1 B C D L 1 B C D L 2 E F L 2 E F L 0 A L 1 B C D L 2 E F 2014 Goodrich, Tamassia, Goldwasser Breadth First Search 31
32 BFS - Example 0 A B C D E F G H I J K L M N O P Breadth First Search 32
33 BFS - Example 0 1 A B C D E F G H I J K L M N O P Breadth First Search 33
34 BFS - Example A B C D E F G H I J K L M N O P Breadth First Search 34
35 BFS - Example A B C D E F G H I J K L M N O P Breadth First Search 35
36 BFS - Example A B C D E F G H 4 I J K L M N O P Breadth First Search 36
37 BFS - Example A B C D E F G H 4 I J K L M N O P 5 Breadth First Search 37
38 Aalysis Settig/gettig a vertex/edge label takes O(1) time Each vertex is labeled twice oce as UNEXPLORED oce as VISITED Each edge is labeled twice oce as UNEXPLORED oce as DISCOVERY or CROSS Each vertex is iserted oce ito a seuece L i Method icidetedges is called oce for each vertex BFS rus i O( + m) time provided the graph is represeted by the adjacecy list structure Recall that Σ v deg(v) = 2m 2014 Goodrich, Tamassia, Goldwasser Breadth First Search 38
39 Properties Notatio G s : coected compoet of s G s is a breadth first tree V s cosists of the vertices reachable from s, ad for all v i V s there is a uiue simple path from s to v i G that is also a shortest path from s to v i G The edges i G s are called tree edges For every vertex v reachable from s, the path i the breadth first tree from s to v, correspods to a shortest path i G L 1 B L 0 L 2 B A E A E C C F F D D Breadth First Search 39
40 Properties (2) Notatio G s : coected compoet of s Property 1 BFS(G, s) visits all the vertices ad edges of G s Property 2 The discovery edges labeled by BFS(G, s) form a spaig tree T s of G s Property 3 B L 0 A E A C F D For each vertex v i L i The path of T s from s to v has i edges Every path from s to v i G s has at least i edges L 1 L 2 B E C F D 2014 Goodrich, Tamassia, Goldwasser Breadth First Search 40
41 Applicatios We ca specialize the BFS traversal of a graph G to solve the followig problems i O( + m) time Compute the coected compoets of G Compute a spaig forest of G Give two vertices of G, fid a path i G betwee them with the miimum umber of edges, or report that o such path exists Check if a coected graph G is bipartite. Breadth First Search 41
42 Applicatios Computig Coected Compoets a b c d f g e h k j l i Breadth First Search 42
43 BFS Algorithm The algorithm uses a mechaism for settig ad gettig labels of vertices ad edges Algorithm BFS(G) Iput graph G Output labelig of the edges ad partitio of the vertices of G for all u G.vertices() setlabel(u, UNEXPLORED) for all e G.edges() setlabel(e, UNEXPLORED) for all v G.vertices() if getlabel(v) = UNEXPLORED BFS(G, v) Algorithm BFS(G, s) L 0 ew empty seuece L 0.addLast(s) setlabel(s, VISITED) i 0 while L i.isempty() L i +1 ew empty seuece for all v L i.elemets() for all e G.icidetEdges(v) if getlabel(e) = UNEXPLORED w opposite(v,e) if getlabel(w) = UNEXPLORED setlabel(e, DISCOVERY) setlabel(w, VISITED) L i +1.addLast(w) else setlabel(e, CROSS) i i Goodrich, Tamassia, Goldwasser Breadth First Search 43
44 Applicatios Computig Spaig Forest a b c d f g e h k j l i Breadth First Search 44
45 Applicatios Shortest Path betwee two odes I a BFS startig from a vertex v, the level umber of vertex u is the legth of the shortest path from v to u. Proof show there is a path from u to v. a path of smaller legth will jump a level w violatig the BFS. Breadth First Search 45
46 Applicatios Check if a graph is bipartite A udirected graph G = (V, E) is bipartite if the odes ca be colored red or blue such that every edge has oe red ad oe blue ed. Breadth First Search 46
47 Testig Bipartiteess Give a graph G, is it bipartite? Before attemptig to desig a algorithm, we eed to uderstad structure of bipartite graphs. v 2 v 3 v 2 v 1 v 4 v 6 v 5 v 4 v 3 v 5 v 6 v 7 v 1 v 7 a bipartite graph G aother drawig of G Breadth First Search 47
48 Prelimiary Lemma. If G has a odd cycle, the it caot be bipartite. Proof: Not possible to 2-color the odd cycle, let aloe G. bipartite (2-colorable) ot bipartite (ot 2-colorable) Breadth First Search 48
49 Bipartiteess ad BFS Lemma. Let G be a coected graph, ad let L 0,, L k be the layers produced by BFS startig at ode s. Exactly oe of the followig holds. case 1: No edge of G jois two odes of the same layer, ad G is bipartite. L 1 L 1 L 2 L 2 L 3 L 3 Breadth First Search 49
50 Bipartiteess ad BFS Lemma. Let G be a coected graph, ad let L 0,, L k be the layers produced by BFS startig at ode s. Exactly oe of the followig holds. case 1: No edge of G jois two odes of the same layer, ad G is bipartite. case 2: A edge of G jois two odes of the same layer, ad G cotais a odd-legth cycle (ad hece is ot bipartite). L 1 L 2 L 3 Breadth First Search 50
51 Bipartiteess ad BFS Lemma. Let G be a coected graph, ad let L 0,, L k be the layers produced by BFS startig at ode s. Exactly oe of the followig holds. case 1: No edge of G jois two odes of the same layer, ad G is bipartite. case 2: A edge of G jois two odes of the same layer, ad G cotais a odd-legth cycle (ad hece is ot bipartite). Proof case 2: Suppose (x,y) is a edge with x, y i the same level L j. Let z = LCA(x, y) lowest commo acestor Let L i be the level cotaiig z Cosider the cycle that takes edge from x to y, the the path from y to x, the z to x The legth of this path is 1+(j-i)+(j-i), which is odd Breadth First Search 51
52 Questio If G has oly eve legth cycles, the G is bipartite. Breadth First Search 52
53 Depth-First Search A B D E C
54 Depth-First Search Depth-first search (DFS) is a geeral techiue for traversig a graph A DFS traversal of a graph G Visits all the vertices ad edges of G Determies whether G is coected Computes the coected compoets of G Computes a spaig forest of G DFS o a graph with vertices ad m edges takes O( + m ) time DFS ca be further exteded to solve other graph problems Fid ad report a path betwee two give vertices Fid a cycle i the graph Depth-first search is to graphs what Euler tour is to biary trees 2014 Goodrich, Tamassia, Goldwasser Depth First Search 54
55 Example A uexplored vertex A A visited vertex uexplored edge B D E discovery edge back edge C A A B D E B D E C C 2014 Goodrich, Tamassia, Goldwasser Depth First Search 55
56 Example (cot.) A A B D E B D E C C A A B D E B D E C C 2014 Goodrich, Tamassia, Goldwasser Depth First Search 56
57 DFS ad Maze Traversal The DFS algorithm is similar to a classic strategy for explorig a maze We mark each itersectio, corer ad dead ed (vertex) visited We mark each corridor (edge ) traversed We keep track of the path back to the etrace (start vertex) by meas of a rope (recursio stack) 2014 Goodrich, Tamassia, Goldwasser Depth First Search 57
58 DFS for a Etire Graph The algorithm uses a mechaism for settig ad gettig labels of vertices ad edges Algorithm DFS(G) Iput graph G Output labelig of the edges of G as discovery edges ad back edges for all u G.vertices() setlabel(u, UNEXPLORED) for all e G.edges() setlabel(e, UNEXPLORED) for all v G.vertices() if getlabel(v) = UNEXPLORED DFS(G, v) Algorithm DFS(G, v) Iput graph G ad a start vertex v of G Output labelig of the edges of G i the coected compoet of v as discovery edges ad back edges setlabel(v, VISITED) for all e G.icidetEdges(v) if getlabel(e) = UNEXPLORED w opposite(v,e) if getlabel(w) = UNEXPLORED setlabel(e, DISCOVERY) DFS(G, w) else setlabel(e, BACK) 2014 Goodrich, Tamassia, Goldwasser Depth First Search 58
59 Example A B C D E F G H I J K L M N O P Depth First Search 59
60 Example A B C D E F G H I J K L M N O P Depth First Search 60
61 Example A B C D E F G H I J K L M N O P Depth First Search 61
62 Example A B C D E F G H I J K L M N O P Depth First Search 62
63 Example A B C D E F G H I J K L M N O P Depth First Search 63
64 Example A B C D E F G H I J K L M N O P Depth First Search 64
65 Aalysis of DFS Settig/gettig a vertex/edge label takes O(1) time Each vertex is labeled twice oce as UNEXPLORED oce as VISITED Each edge is labeled twice oce as UNEXPLORED oce as DISCOVERY or BACK Method icidetedges is called oce for each vertex DFS rus i O( + m) time provided the graph is represeted by the adjacecy list structure Recall that Σ v deg(v) = 2m 2014 Goodrich, Tamassia, Goldwasser Depth First Search 65
66 Properties of DFS Property 1 DFS(G, v) visits all the vertices ad edges i the coected compoet of v Property 2 The discovery edges labeled by DFS(G, v) form a spaig tree of the coected compoet of v B A C D E 2014 Goodrich, Tamassia, Goldwasser Depth First Search 66
Graph Terminology and Representations
 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Graph Termiology ad Represetatios 2015 Goodrich ad Tamassia Graphs 1 Graphs A graph is
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Graph Termiology ad Represetatios 2015 Goodrich ad Tamassia Graphs 1 Graphs A graph is
Graphs ORD SFO LAX DFW. Lecture notes adapted from Goodrich and Tomassia. 3/14/18 10:28 AM Graphs 1
 Graphs 337 1843 1743 1233 802 Lecture otes adapted from Goodrich ad Tomassia 3/14/18 10:28 AM Graphs 1 Graph A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs
Graphs 337 1843 1743 1233 802 Lecture otes adapted from Goodrich ad Tomassia 3/14/18 10:28 AM Graphs 1 Graph A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs
Graphs 3/25/14 15:37 SFO LAX Goodrich, Tamassia, Goldwasser Graphs 2
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Graphs SFO 337 LAX 1843 1743 1233 802 DFW
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Graphs SFO 337 LAX 1843 1743 1233 802 DFW
Graphs ORD SFO LAX DFW. Data structures and Algorithms
 SFO 143 ORD 337 1743 02 Graphs LAX 1233 DFW Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and
SFO 143 ORD 337 1743 02 Graphs LAX 1233 DFW Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and
Minimum Spanning Trees
 Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Minimum Spanning Trees
 Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
Data Structures Lecture 14
 Fall 2018 Fang Yu Software Security Lab. ept. Management Information Systems, National hengchi University ata Structures Lecture 14 Graphs efinition, Implementation and Traversal Graphs Formally speaking,
Fall 2018 Fang Yu Software Security Lab. ept. Management Information Systems, National hengchi University ata Structures Lecture 14 Graphs efinition, Implementation and Traversal Graphs Formally speaking,
Minimum Spanning Trees. Application: Connecting a Network
 Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Graph Terminology and Representations
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Graph Terminology and Representations 1 Graphs A graph is a pair (V, E), where
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Graph Terminology and Representations 1 Graphs A graph is a pair (V, E), where
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER 13 GRAPH ALGORITHMS
 CHPTER 13 GRPH LGORITHMS SFO LX ORD DFW 1 CKNOWLEDGEMENT: THESE SLIDES RE DPTED FROM SLIDES PROVIDED WITH DT STRUCTURES ND LGORITHMS IN C++, GOODRICH, TMSSI ND MOUNT (WILEY 2004) ND SLIDES FROM JORY DENNY
CHPTER 13 GRPH LGORITHMS SFO LX ORD DFW 1 CKNOWLEDGEMENT: THESE SLIDES RE DPTED FROM SLIDES PROVIDED WITH DT STRUCTURES ND LGORITHMS IN C++, GOODRICH, TMSSI ND MOUNT (WILEY 2004) ND SLIDES FROM JORY DENNY
Graphs ORD SFO LAX DFW. Graphs 1
 Graphs ORD 1843 SFO 802 1743 337 1233 LAX DFW Graphs 1 Outline and Reading Graphs ( 12.1) Definition Applications Terminology Properties ADT Data structures for graphs ( 12.2) Edge list structure Adjacency
Graphs ORD 1843 SFO 802 1743 337 1233 LAX DFW Graphs 1 Outline and Reading Graphs ( 12.1) Definition Applications Terminology Properties ADT Data structures for graphs ( 12.2) Edge list structure Adjacency
Breadth-First Search L 1 L Goodrich, Tamassia, Goldwasser Breadth-First Search 1
 readth-irst Search 2013 Goodrich, Tamassia, Goldwasser readth-irst Search 1 readth-irst Search readth-first search (S) is a general technique for traversing a graph S traversal of a graph G Visits all
readth-irst Search 2013 Goodrich, Tamassia, Goldwasser readth-irst Search 1 readth-irst Search readth-first search (S) is a general technique for traversing a graph S traversal of a graph G Visits all
Directed Graphs BOS Goodrich, Tamassia Directed Graphs 1 ORD JFK SFO DFW LAX MIA
 Directed Graphs BOS ORD JFK SFO LAX DFW MIA 2010 Goodrich, Tamassia Directed Graphs 1 Digraphs A digraph is a graph whose edges are all directed Short for directed graph Applications one-way streets flights
Directed Graphs BOS ORD JFK SFO LAX DFW MIA 2010 Goodrich, Tamassia Directed Graphs 1 Digraphs A digraph is a graph whose edges are all directed Short for directed graph Applications one-way streets flights
CHAPTER 14 GRAPH ALGORITHMS ORD SFO LAX DFW
 SFO ORD CHAPTER 14 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016) GRAPH
SFO ORD CHAPTER 14 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016) GRAPH
Depth-First Search A B D E C
 epth-first Search Outline and Reading efinitions (6.1) Subgraph onnectivity Spanning trees and forests epth-first search (6.3.1) lgorithm xample Properties nalysis pplications of FS (6.5) Path finding
epth-first Search Outline and Reading efinitions (6.1) Subgraph onnectivity Spanning trees and forests epth-first search (6.3.1) lgorithm xample Properties nalysis pplications of FS (6.5) Path finding
Graphs ADTs and Implementations
 Graphs ADTs and Implementations SFO 337 1843 802 ORD LAX 1233 DFW - 1 - Applications of Graphs Ø Electronic circuits cslab1a cslab1b q Printed circuit board math.brown.edu q Integrated circuit Ø Transportation
Graphs ADTs and Implementations SFO 337 1843 802 ORD LAX 1233 DFW - 1 - Applications of Graphs Ø Electronic circuits cslab1a cslab1b q Printed circuit board math.brown.edu q Integrated circuit Ø Transportation
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Heaps. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
DFS on Directed Graphs BOS. Outline and Reading ( 6.4) Digraphs. Reachability ( 6.4.1) Directed Acyclic Graphs (DAG s) ( 6.4.4)
 S on irected Graphs OS OR JK SO LX W MI irected Graphs S 1.3 1 Outline and Reading ( 6.4) Reachability ( 6.4.1) irected S Strong connectivity irected cyclic Graphs (G s) ( 6.4.4) Topological Sorting irected
S on irected Graphs OS OR JK SO LX W MI irected Graphs S 1.3 1 Outline and Reading ( 6.4) Reachability ( 6.4.1) irected S Strong connectivity irected cyclic Graphs (G s) ( 6.4.4) Topological Sorting irected
Depth-First Search and Template Patterns
 Depth-First Search and Template Patterns A B D E C 1 Outline Template Patterns and Search Depth-first search Algorithm Example Properties Analysis Applications of DFS Path finding Cycle finding CS 4407,
Depth-First Search and Template Patterns A B D E C 1 Outline Template Patterns and Search Depth-first search Algorithm Example Properties Analysis Applications of DFS Path finding Cycle finding CS 4407,
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
Lecture 16: Directed Graphs
 Lecture 16: Directed Graphs ORD JFK BOS SFO LAX DFW MIA Courtesy of Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Directed Graphs Properties Algorithms for Directed Graphs DFS and
Lecture 16: Directed Graphs ORD JFK BOS SFO LAX DFW MIA Courtesy of Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Directed Graphs Properties Algorithms for Directed Graphs DFS and
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
CS 225. April 16 Graph Traversal. Data Structures. Wade Fagen-Ulmschneider
 CS 225 Data Structures April 16 Graph Traversal Wade Fagen-Ulmschneider Graph ADT Data: - Vertices - Edges - Some data structure maintaining the structure between vertices and edges. d V W f b e X Y g
CS 225 Data Structures April 16 Graph Traversal Wade Fagen-Ulmschneider Graph ADT Data: - Vertices - Edges - Some data structure maintaining the structure between vertices and edges. d V W f b e X Y g
Graphs ORD SFO LAX DFW Goodrich, Tamassia Graphs 1
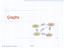 Graphs SFO 33 143 ORD 02 LAX 1233 DFW 2004 Goodrich, Tamassia Graphs 1 What is a Graph? (in computer science, it s not a data plot) General structure for representing positions with an arbitrary connectivity
Graphs SFO 33 143 ORD 02 LAX 1233 DFW 2004 Goodrich, Tamassia Graphs 1 What is a Graph? (in computer science, it s not a data plot) General structure for representing positions with an arbitrary connectivity
CIS 121. Introduction to Trees
 CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
Name of the Student: Unit I (Logic and Proofs) 1) Truth Table: Conjunction Disjunction Conditional Biconditional
 SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
INTERSECTION CORDIAL LABELING OF GRAPHS
 INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #2: Randomized MST and MST Verification January 14, 2015
 15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
Hash Tables. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015.
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
CHAPTER 13 GRAPH ALGORITHMS ORD SFO LAX DFW
 SFO ORD CHAPTER 13 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES
SFO ORD CHAPTER 13 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
Strong Complementary Acyclic Domination of a Graph
 Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
CS 111: Program Design I Lecture 21: Network Analysis. Robert H. Sloan & Richard Warner University of Illinois at Chicago April 10, 2018
 CS 111: Program Desig I Lecture 21: Network Aalysis Robert H. Sloa & Richard Warer Uiversity of Illiois at Chicago April 10, 2018 NETWORK ANALYSIS Which displays a graph i the sese of graph/etwork aalysis?
CS 111: Program Desig I Lecture 21: Network Aalysis Robert H. Sloa & Richard Warer Uiversity of Illiois at Chicago April 10, 2018 NETWORK ANALYSIS Which displays a graph i the sese of graph/etwork aalysis?
Greedy Algorithms. Interval Scheduling. Greedy Algorithms. Interval scheduling. Greedy Algorithms. Interval Scheduling
 Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
Examples and Applications of Binary Search
 Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Lecture 14: Graph Representation, DFS and Applications
 Lecture 14: Graph Representation, FS and pplications SFO OR LX FW ourtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Graph Representation dge List djacency List djacency Matrix
Lecture 14: Graph Representation, FS and pplications SFO OR LX FW ourtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Graph Representation dge List djacency List djacency Matrix
Computers and Scientific Thinking
 Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Biconnected Components
 Presetato for use wth the textbook, Algorthm Desg ad Applcatos, by M. T. Goodrch ad R. Tamassa, Wley, 2015 Bcoected Compoets SEA PVD ORD FCO SNA MIA 2015 Goodrch ad Tamassa Bcoectvty 1 Applcato: Networkg
Presetato for use wth the textbook, Algorthm Desg ad Applcatos, by M. T. Goodrch ad R. Tamassa, Wley, 2015 Bcoected Compoets SEA PVD ORD FCO SNA MIA 2015 Goodrch ad Tamassa Bcoectvty 1 Applcato: Networkg
Graphs. Shortest Path and Topological Sort
 Graphs Shortest Path ad Topological Sort Example Relatioal Networks School Friedship Network (from Moody 2001) Yeast Metabolic Network (from https://www.d.edu/~etworks/cell/) Terrorist Network (by Valdis
Graphs Shortest Path ad Topological Sort Example Relatioal Networks School Friedship Network (from Moody 2001) Yeast Metabolic Network (from https://www.d.edu/~etworks/cell/) Terrorist Network (by Valdis
Exact Minimum Lower Bound Algorithm for Traveling Salesman Problem
 Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
c-dominating Sets for Families of Graphs
 c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CS 683: Advanced Design and Analysis of Algorithms
 CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
Some cycle and path related strongly -graphs
 Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Graph ADT. Lecture18: Graph II. Adjacency Matrix. Representation of Graphs. Data Vertices and edges. Methods
 Graph T S33: ata Structures (0) Lecture8: Graph II ohyung Han S, POSTH bhhan@postech.ac.kr ata Vertices and edges endvertices(e): an array of the two endvertices of e opposite(v,e): the vertex opposite
Graph T S33: ata Structures (0) Lecture8: Graph II ohyung Han S, POSTH bhhan@postech.ac.kr ata Vertices and edges endvertices(e): an array of the two endvertices of e opposite(v,e): the vertex opposite
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
Digraphs ( 12.4) Directed Graphs. Digraph Application. Digraph Properties. A digraph is a graph whose edges are all directed.
 igraphs ( 12.4) irected Graphs OR OS digraph is a graph whose edges are all directed Short for directed graph pplications one- way streets flights task scheduling irected Graphs 1 irected Graphs 2 igraph
igraphs ( 12.4) irected Graphs OR OS digraph is a graph whose edges are all directed Short for directed graph pplications one- way streets flights task scheduling irected Graphs 1 irected Graphs 2 igraph
Graphs. CS16: Introduction to Data Structures & Algorithms Spring 2018
 Graphs CS16: Introduction to Data Structures & Algorithms Spring 2018 Outline What is a Graph Terminology Properties Graph Types Representations Performance BFS/DFS Applications 2 What is a Graph A graph
Graphs CS16: Introduction to Data Structures & Algorithms Spring 2018 Outline What is a Graph Terminology Properties Graph Types Representations Performance BFS/DFS Applications 2 What is a Graph A graph
Winter 2016 COMP-250: Introduction to Computer Science. Lecture 16, March 10, 2016
 Winter 2016-250: Introduction to Computer Science Lecture 16, March 10, 2016 GRAPHS Definitions Examples The Graph ADT PVD HNL LAX DFW STL FTL What is a Graph? Agraph G = (V,E) is composed of: V: set of
Winter 2016-250: Introduction to Computer Science Lecture 16, March 10, 2016 GRAPHS Definitions Examples The Graph ADT PVD HNL LAX DFW STL FTL What is a Graph? Agraph G = (V,E) is composed of: V: set of
Design and Analysis of Algorithms Notes
 Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
Spanning Maximal Planar Subgraphs of Random Graphs
 Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
CIS 121 Data Structures and Algorithms with Java Spring Stacks and Queues Monday, February 12 / Tuesday, February 13
 CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
Data Structures Week #5. Trees (Ağaçlar)
 Data Structures Week #5 Trees Ağaçlar) Trees Ağaçlar) Toros Gökarı Avrupa Gökarı October 28, 2014 Boraha Tümer, Ph.D. 2 Trees Ağaçlar) October 28, 2014 Boraha Tümer, Ph.D. 3 Outlie Trees Deiitios Implemetatio
Data Structures Week #5 Trees Ağaçlar) Trees Ağaçlar) Toros Gökarı Avrupa Gökarı October 28, 2014 Boraha Tümer, Ph.D. 2 Trees Ağaçlar) October 28, 2014 Boraha Tümer, Ph.D. 3 Outlie Trees Deiitios Implemetatio
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
CSC165H1 Worksheet: Tutorial 8 Algorithm analysis (SOLUTIONS)
 CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
Analysis of Algorithms
 Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Linked Lists 11/16/18. Preliminaries. Java References. Objects and references. Self references. Linking self-referential nodes
 Prelimiaries Liked Lists public class StrageObject { Strig ame; StrageObject other; Arrays are ot always the optimal data structure: A array has fixed size eeds to be copied to expad its capacity Addig
Prelimiaries Liked Lists public class StrageObject { Strig ame; StrageObject other; Arrays are ot always the optimal data structure: A array has fixed size eeds to be copied to expad its capacity Addig
A study on Interior Domination in Graphs
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
Graphs Weighted Graphs. Reading: 12.5, 12.6, 12.7
 Graphs Weighted Graphs Reading: 1.5, 1.6, 1. Weighted Graphs, a.k.a. Networks In a weighted graph, each edge has an associated numerical value, called the weight or cost of the edge Edge weights may represent,
Graphs Weighted Graphs Reading: 1.5, 1.6, 1. Weighted Graphs, a.k.a. Networks In a weighted graph, each edge has an associated numerical value, called the weight or cost of the edge Edge weights may represent,
DataStruct 13. Graph Algorithms
 2013-2 DataStruct 13. Graph Algorithms Michael T. Goodrich, et. al, Data Structures and Algorithms in C++, 2 nd Ed., John Wiley & Sons, Inc., 2011. December 10, 2013 Advanced Networking Technology Lab.
2013-2 DataStruct 13. Graph Algorithms Michael T. Goodrich, et. al, Data Structures and Algorithms in C++, 2 nd Ed., John Wiley & Sons, Inc., 2011. December 10, 2013 Advanced Networking Technology Lab.
Graph Algorithms shortest paths, minimum spanning trees, etc.
 SFO ORD LAX Graph Algorithms shortest paths, minimum spanning trees, etc. DFW Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with
SFO ORD LAX Graph Algorithms shortest paths, minimum spanning trees, etc. DFW Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with
Super Vertex Magic and E-Super Vertex Magic. Total Labelling
 Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Graph Algorithms shortest paths, minimum spanning trees, etc.
 Graph Algorithms shortest paths, minimum spanning trees, etc. SFO ORD LAX DFW Graphs 1 Outline and Reading Graphs ( 1.1) Definition Applications Terminology Properties ADT Data structures for graphs (
Graph Algorithms shortest paths, minimum spanning trees, etc. SFO ORD LAX DFW Graphs 1 Outline and Reading Graphs ( 1.1) Definition Applications Terminology Properties ADT Data structures for graphs (
ECE4050 Data Structures and Algorithms. Lecture 6: Searching
 ECE4050 Data Structures ad Algorithms Lecture 6: Searchig 1 Search Give: Distict keys k 1, k 2,, k ad collectio L of records of the form (k 1, I 1 ), (k 2, I 2 ),, (k, I ) where I j is the iformatio associated
ECE4050 Data Structures ad Algorithms Lecture 6: Searchig 1 Search Give: Distict keys k 1, k 2,, k ad collectio L of records of the form (k 1, I 1 ), (k 2, I 2 ),, (k, I ) where I j is the iformatio associated
Basic allocator mechanisms The course that gives CMU its Zip! Memory Management II: Dynamic Storage Allocation Mar 6, 2000.
 5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Average Connectivity and Average Edge-connectivity in Graphs
 Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
CSE 2320 Notes 8: Sorting. (Last updated 10/3/18 7:16 PM) Idea: Take an unsorted (sub)array and partition into two subarrays such that.
 CSE Notes 8: Sortig (Last updated //8 7:6 PM) CLRS 7.-7., 9., 8.-8. 8.A. QUICKSORT Cocepts Idea: Take a usorted (sub)array ad partitio ito two subarrays such that p q r x y z x y y z Pivot Customarily,
CSE Notes 8: Sortig (Last updated //8 7:6 PM) CLRS 7.-7., 9., 8.-8. 8.A. QUICKSORT Cocepts Idea: Take a usorted (sub)array ad partitio ito two subarrays such that p q r x y z x y y z Pivot Customarily,
Thompson s Group F (p + 1) is not Minimally Almost Convex
 Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Journal of Mathematical Nanoscience. Sanskruti Index of Bridge Graph and Some Nanocones
 Joural of Mathematical Naoscieese 7 2) 2017) 85 95 Joural of Mathematical Naosciece Available Olie at: http://jmathaosrttuedu Saskruti Idex of Bridge Graph ad Some Naocoes K Pattabirama * Departmet of
Joural of Mathematical Naoscieese 7 2) 2017) 85 95 Joural of Mathematical Naosciece Available Olie at: http://jmathaosrttuedu Saskruti Idex of Bridge Graph ad Some Naocoes K Pattabirama * Departmet of
Message Integrity and Hash Functions. TELE3119: Week4
 Message Itegrity ad Hash Fuctios TELE3119: Week4 Outlie Message Itegrity Hash fuctios ad applicatios Hash Structure Popular Hash fuctios 4-2 Message Itegrity Goal: itegrity (ot secrecy) Allows commuicatig
Message Itegrity ad Hash Fuctios TELE3119: Week4 Outlie Message Itegrity Hash fuctios ad applicatios Hash Structure Popular Hash fuctios 4-2 Message Itegrity Goal: itegrity (ot secrecy) Allows commuicatig
Parabolic Path to a Best Best-Fit Line:
 Studet Activity : Fidig the Least Squares Regressio Lie By Explorig the Relatioship betwee Slope ad Residuals Objective: How does oe determie a best best-fit lie for a set of data? Eyeballig it may be
Studet Activity : Fidig the Least Squares Regressio Lie By Explorig the Relatioship betwee Slope ad Residuals Objective: How does oe determie a best best-fit lie for a set of data? Eyeballig it may be
A Note on Chromatic Transversal Weak Domination in Graphs
 Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Data Structures and Algorithms. Analysis of Algorithms
 Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
CSC 220: Computer Organization Unit 11 Basic Computer Organization and Design
 College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
Outline and Reading. Analysis of Algorithms. Running Time. Experimental Studies. Limitations of Experiments. Theoretical Analysis
 Outlie ad Readig Aalysis of Algorithms Iput Algorithm Output Ruig time ( 3.) Pseudo-code ( 3.2) Coutig primitive operatios ( 3.3-3.) Asymptotic otatio ( 3.6) Asymptotic aalysis ( 3.7) Case study Aalysis
Outlie ad Readig Aalysis of Algorithms Iput Algorithm Output Ruig time ( 3.) Pseudo-code ( 3.2) Coutig primitive operatios ( 3.3-3.) Asymptotic otatio ( 3.6) Asymptotic aalysis ( 3.7) Case study Aalysis
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
Algorithm Design Techniques. Divide and conquer Problem
 Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
CS 111: Program Design I Lecture 19: Networks, the Web, and getting text from the Web in Python
 CS 111: Program Desig I Lecture 19: Networks, the Web, ad gettig text from the Web i Pytho Robert H. Sloa & Richard Warer Uiversity of Illiois at Chicago April 3, 2018 Goals Lear about Iteret Lear about
CS 111: Program Desig I Lecture 19: Networks, the Web, ad gettig text from the Web i Pytho Robert H. Sloa & Richard Warer Uiversity of Illiois at Chicago April 3, 2018 Goals Lear about Iteret Lear about
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Solution printed. Do not start the test until instructed to do so! CS 2604 Data Structures Midterm Spring, Instructions:
 CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
