Graphs ORD SFO LAX DFW. Data structures and Algorithms
|
|
|
- Claire Mason
- 5 years ago
- Views:
Transcription
1 SFO 143 ORD Graphs LAX 1233 DFW Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and Mount (Wiley, 2004)
2 Outline and Reading Data structures for graphs ( 13.2) Graph traversal ( 13.3) Depth-first search Breadth-first search Directed graphs ( 13.4) Shortest paths ( 13.6) Dijkstra's Algorithm Minimum spanning trees ( 13.7) Kruskal's Algorithm Prim-Jarnik Algorithm Graphs 2
3 Graph A graph is a pair (V, E), where V is a set of nodes, called vertices E is a collection of pairs of vertices, called edges Vertices and edges are positions and store elements Example: A vertex represents an airport and stores the three-letter airport code An edge represents a flight route between two airports and stores the mileage of the route HNL 2555 SFO 337 LAX ORD 02 DFW LGA PVD MIA Graphs 3
4 Edge Types Directed edge ordered pair of vertices (u,v) first vertex u is the origin second vertex v is the destination e.g., a flight Undirected edge unordered pair of vertices (u,v) e.g., a flight route Directed graph (Digraph) all the edges are directed e.g., flight network Undirected graph all the edges are undirected e.g., route network u ORD ORD (u,v) flight AA miles flight route 02 miles Weighted edge Weighted graph v DFW DFW all the edges are weighted Graphs 4
5 Applications Electronic circuits Printed circuit board Integrated circuit Transportation networks Highway network Flight network Computer networks Local area network Internet Web Databases Entity-relationship diagram Graphs 5
6 Terminology End vertices (or endpoints) of an edge U and V are the endpoints of a Edges incident on a vertex a, d, and b are incident on V Adjacent vertices U and V are adjacent a Degree of a vertex X has degree 5 U Parallel edges c h and i are parallel edges Self-loop j is a self-loop V d W f b e X Y g h i Z j Graphs 6
7 Terminology (cont.) V b h j Outgoing edges of a vertex h and b are the outgoing edges of X Incoming edges of a vertex d W e X g i Z e, g, and i are incoming edges of X In-degree of a vertex f Y X has in-degree 3 Out-degree of a vertex X has out-degree 2 Graphs 7
8 Terminology (cont.) Path sequence of alternating vertices and edges begins with a vertex ends with a vertex each edge is preceded and followed by its endpoints Simple path path such that all its vertices and edges are distinct Examples P 1 =(V,b,X,h,Z) is a simple path P 2 =(U,c,W,e,X,g,Y,f,W,d,V) is a path that is not simple U a c d P 2 V W f b e P 1 X Y g h Z Graphs
9 Terminology (cont.) Cycle circular sequence of alternating vertices and edges each edge is preceded and followed by its endpoints Simple cycle cycle such that all its vertices and edges are distinct Examples C 1 =(V,b,X,g,Y,f,W,c,U,a, ) is a simple cycle C 2 =(U,c,W,e,X,g,Y,f,W,d,V,a, ) is a cycle that is not simple U a c V d C 2 W f b X e Y C 1 g h Z Graphs 9
10 Properties of Undirected Graphs Property 1 Total degree Σ v deg(v) = 2m Proof: each edge is counted twice Property 2 Total number of edges In an undirected graph with no self-loops and no multiple edges m n (n 1)/2 Proof: each vertex has degree at most (n 1) Notation n m deg(v) number of vertices number of edges degree of vertex v Example n = 4 m = 6 deg(v) = 3 A graph with given number of vertices (4) and maximum number of edges Graphs 10
11 Properties of Directed Graphs Property 1 Total in-degree and out-degree Σ v in-deg(v) = m Σ v out-deg(v) = m Property 2 Total number of edges In an directed graph with no self-loops and no multiple edges m n (n 1) Notation n m deg(v) number of vertices number of edges degree of vertex v Example n = 4 m = 12 deg(v) = 6 A graph with given number of vertices (4) and maximum number of edges Graphs 11
12 Main Methods of the Graph ADT Vertices and edges are positions store elements Accessor methods endvertices(e): an array of the two end vertices of e opposite(v, e): the vertex opposite of v on e areadjacent(v, w): true iff v and w are adjacent replace(v, x): replace element at vertex v with x replace(e, x): replace element at edge e with x Update methods insertvertex(o): insert a vertex storing element o insertedge(v, w, o): insert an edge (v,w) storing element o removevertex(v): remove vertex v (and its incident edges) removeedge(e): remove edge e Iterator methods incidentedges(v): edges incident to v vertices(): all vertices in the graph edges(): all edges in the graph Graphs 12
13 Data Structures for Graphs Edge list structures Adjacency list structures Adjacency matrix structures Graphs 13
14 Edge List Structure Edge List (ORD, PVD) (ORD, DFW) Vertex Sequence 49 ORD 02 LGA An edge list can be stored in a sequence, a vector, a list or a dictionary such as a hash table (LGA, PVD) 142 (LGA, MIA) 1099 (DFW, LGA) 137 (DFW, MIA) 1120 PVD DFW MIA ORD 02 DFW LGA PVD MIA Graphs 14
15 Edge List Structure Vertex object element reference to position in vertex sequence Edge object element origin vertex object destination vertex object reference to position in edge sequence Vertex sequence sequence of vertex objects Edge sequence sequence of edge objects u a c b d v w z u v w z a b c d Graphs 15
16 Adjacency List Structure Edge List Adjacency List ORD 02 DFW 49 (ORD, PVD) ORD (ORD, PVD) (ORD, DFW) LGA PVD MIA 02 (ORD, DFW) LGA (LGA, PVD) (LGA, MIA) (LGA, DFW) 142 (LGA, PVD) PVD (PVD, ORD) (PVD, LGA) 1099 (LGA, MIA) DFW (DFW, ORD) (DFW, LGA) (DFW, MIA) 137 (DFW, LGA) MIA (MIA, LGA) (MIA, DFW) 1120 (DFW, MIA) Graphs 16
17 Adjacency List Structure Edge list structure Incidence sequence for each vertex sequence of references to edge objects of incident edges Augmented edge objects references to associated positions in incidence sequences of end vertices a v b u w u v w a b Graphs 17
18 Adjacency Matrix Structure Edge List Vertex Sequence 0:ORD 02 3:DFW :LGA :MIA 2:PVD 49 (ORD, PVD) 0 ORD (ORD, DFW) 1 LGA (LGA, PVD) (LGA, MIA) 2 3 PVD DFW (DFW, LGA) 4 MIA (DFW, MIA) Graphs 1
19 Adjacency Matrix Structure Edge list structure Augmented vertex objects Integer key (index) associated with vertex 2D-array adjacency array Reference to edge object for adjacent vertices Null for non nonadjacent vertices The old fashioned version just has 0 for no edge and 1 for edge u a 0 u 1 v 2 w a v 1 b 2 w b Graphs 19
20 Asymptotic Performance n vertices, m edges no parallel edges no self-loops Bounds are big-oh Edge List Adjacency List Adjacency Matrix Space n + m n + m n 2 incidentedges(v) adjacentvertices(v) m deg(v) n areadjacent (v, w) m min(deg(v), deg(w)) 1 insertvertex(o) 1 1 n 2 insertedge(v, w, o) removevertex(v) m deg(v) n 2 removeedge(e) Graphs 20
21 Graph Traversal Depth-First Search Bread-First Search Others Graphs 21
22 Depth-First Search A B D E C
23 Subgraphs A subgraph S of a graph G is a graph such that The vertices of S are a subset of the vertices of G The edges of S are a subset of the edges of G Subgraph A spanning subgraph of G is a subgraph that contains all the vertices of G Spanning subgraph Graphs 23
24 Connectivity A graph is connected if there is a path between every pair of vertices A connected component of a graph G is a maximal connected subgraph of G Connected graph Non-connected graph with two connected components Graphs 24
25 Trees and Forests A (free) tree is an undirected graph T such that T is connected T has no cycles This definition is different from that of a rooted tree A forest is an undirected graph without cycles The connected components of a forest are trees Tree Forest Graphs 25
26 Spanning Trees and Forests A spanning tree of a connected graph is a spanning subgraph that is a tree A spanning tree is not unique unless the graph is a tree Spanning trees have applications to the design of communication networks A spanning forest of a graph is a spanning subgraph that is a forest Graph Spanning tree Graphs 26
27 Depth-First Search Depth-first search (DFS) is a general technique for traversing a graph A DFS traversal of a graph G Visits all the vertices and edges of G Determines whether G is connected Computes the connected components of G Computes a spanning forest of G DFS on a graph with n vertices and m edges takes O(n + m ) time DFS can be further extended to solve other graph problems Find and report a path between two given vertices Find a cycle in the graph Depth-first search is to graphs what Euler tour is to binary trees Graphs 27
28 Example A A unexplored vertex visited vertex unexplored edge discovery edge back edge B A C D E A A B D E B D E C C Graphs 2
29 Example (cont.) A A B D E B D E C C A A B D E B D E C C Graphs 29
30 DFS and Maze Traversal The DFS algorithm is similar to a classic strategy for exploring a maze: We mark each intersection, corner and dead end (vertex) visited We mark each corridor (edge ) traversed We keep track of the path back to the entrance (start vertex) by means of a rope (recursion stack) Graphs 30
31 DFS Algorithm The algorithm uses a mechanism for setting and getting labels of vertices and edges Algorithm DFS(G) Input graph G Output labeling of the edges of G as discovery edges and back edges for all u G.vertices() setlabel(u, UNEXPLORED) for all e G.edges() setlabel(e, UNEXPLORED) for all v G.vertices() if getlabel(v) = UNEXPLORED DFS(G, v) Algorithm DFS(G, v) Input graph G and a start vertex v of G Output labeling of the edges of G in the connected component of v as discovery edges and back edges setlabel(v, VISITED) for all e G.incidentEdges(v) if getlabel(e) = UNEXPLORED w opposite(v,e) if getlabel(w) = UNEXPLORED setlabel(e, DISCOVERY) DFS(G, w) else setlabel(e, BACK) Graphs 31
32 Properties of DFS A B D E Property 1 DFS(G, v) visits all the vertices and edges in the connected component of v Property 2 The discovery edges labeled by DFS(G, v) form a spanning tree of the connected component of v C Graphs 32
33 Analysis of DFS Setting/getting a vertex/edge label takes O(1) time Each vertex is labeled twice once as UNEXPLORED once as VISITED Each edge is labeled twice once as UNEXPLORED once as DISCOVERY or BACK Method incidentedges is called once for each vertex DFS runs in O(n + m) time provided the graph is represented by the adjacency list structure B A C D E Recall that Σ v deg(v) = 2m Graphs 33
34 Path Finding We can specialize the DFS algorithm to find a path between two given vertices u and z We call DFS(G, u) with u as the start vertex We use a stack S to keep track of the path between the start vertex and the current vertex As soon as destination vertex z is encountered, we return the path as the contents of the stack Algorithm pathdfs(g, v, z) setlabel(v, VISITED) S.push(v) if v = z return S.elements() for all e G.incidentEdges(v) if getlabel(e) = UNEXPLORED w opposite(v,e) if getlabel(w) = UNEXPLORED setlabel(e, DISCOVERY) S.push(e) pathdfs(g, w, z) S.pop(e) else setlabel(e, BACK) S.pop(v) Graphs 34
35 Cycle Finding We can specialize the DFS algorithm to find a simple cycle We use a stack S to keep track of the path between the start vertex and the current vertex As soon as a back edge (v, w) is encountered, we return the cycle as the portion of the stack from the top to vertex w Algorithm cycledfs(g, v) setlabel(v, VISITED) S.push(v) for all e G.incidentEdges(v) if getlabel(e) = UNEXPLORED w opposite(v,e) S.push(e) if getlabel(w) = UNEXPLORED setlabel(e, DISCOVERY) cycledfs(g, w) S.pop(e) else T new empty stack repeat o S.pop() T.push(o) until o = w return T.elements() S.pop(v) Graphs 35
36 Breadth-First Search L 0 A L 1 B C D L 2 E F
37 Breadth-First Search Breadth-first search (BFS) is a general technique for traversing a graph A BFS traversal of a graph G Visits all the vertices and edges of G Determines whether G is connected Computes the connected components of G Computes a spanning forest of G BFS on a graph with n vertices and m edges takes O(n + m ) time BFS can be further extended to solve other graph problems Find and report a path with the minimum number of edges between two given vertices Find a simple cycle, if there is one Graphs 37
38 Example A A unexplored vertex visited vertex unexplored edge discovery edge cross edge L 1 L 0 B A E C F D L 0 A L 0 A L 1 B C D L 1 B C D E F E F Graphs 3
39 Example (cont.) A unexplored vertex visited vertex A unexplored edge discovery edge cross edge L 0 A L 0 A L 1 B C D L 1 B C D E F L 2 E F L 0 A L 0 A L 1 B C D L 1 B C D L 2 E F L 2 E F Graphs 39
40 Example (cont.) A unexplored vertex visited vertex A unexplored edge discovery edge cross edge L 0 A L 0 A L 1 B C D L 1 B C D L 2 E F L 2 E F L 0 A L 1 B C D L 2 E F Graphs 40
41 BFS Algorithm The algorithm uses a mechanism for setting and getting labels of vertices and edges Algorithm BFS(G) Input graph G Output labeling of the edges and partition of the vertices of G for all u G.vertices() setlabel(u, UNEXPLORED) for all e G.edges() setlabel(e, UNEXPLORED) for all v G.vertices() if getlabel(v) = UNEXPLORED BFS(G, v) Algorithm BFS(G, s) L 0 new empty sequence L 0.insertLast(s) setlabel(s, VISITED) i 0 while L i.isempty() L i +1 new empty sequence for all v L i.elements() for all e G.incidentEdges(v) if getlabel(e) = UNEXPLORED w opposite(v,e) if getlabel(w) = UNEXPLORED setlabel(e, DISCOVERY) setlabel(w, VISITED) L i +1.insertLast(w) else setlabel(e, CROSS) i i +1 Graphs 41
42 Properties L 0 A Notation G s : connected component of s Property 1 L 1 B L 2 E C F D BFS(G, s) visits all the vertices and edges of G s Property 2 The discovery edges labeled by BFS(G, s) form a spanning tree T s of G s Property 3 For each vertex v in L i The path of T s from s to v has i edges Every path from s to v in G s has at least i edges Graphs 42
43 Analysis Setting/getting a vertex/edge label takes O(1) time Each vertex is labeled twice once as UNEXPLORED once as VISITED Each edge is labeled twice once as UNEXPLORED once as DISCOVERY or CROSS Each vertex is inserted once into a sequence L i Method incidentedges() is called once for each vertex BFS runs in O(n + m) time provided the graph is represented by the adjacency list structure Recall that Σ v deg(v) = 2m Graphs 43
44 Applications Using the template method pattern, we can specialize the BFS traversal of a graph G to solve the following problems in O(n + m) time Compute the connected components of G Compute a spanning forest of G Find a simple cycle in G, or report that G is a forest Given two vertices of G, find a path in G between them with the minimum number of edges, or report that no such path exists Graphs 44
45 Directed Graphs BOS ORD JFK SFO LAX DFW MIA
46 E Digraphs D A digraph is a graph whose edges are all directed Short for directed graph Applications one-way streets flights task scheduling A graph G=(V,E) such that Each edge goes in one direction: Edge (a,b) goes from a to b, but not b to a. If G is simple, m < n*(n-1). C A B Graphs 46
47 Digraph Application Scheduling: edge (a,b) means task a must be completed before b can be started ics21 ics22 ics23 ics51 ics53 ics52 ics161 ics131 ics141 ics121 ics171 ics151 The good life Graphs 47
48 DAGs and Topological Ordering A directed acyclic graph (DAG) is a digraph that has no directed cycles A topological ordering of a digraph is a numbering v 1,, v n of the vertices such that for every edge (v i, v j ), we have i < j Example: in a task scheduling digraph, a topological ordering a task sequence that satisfies the precedence constraints Theorem A digraph admits a topological ordering if and only if it is a DAG v 2 v 1 B A B A D Graphs 4 C E DAG G v 4 v 5 D E C v3 Topological ordering of G
49 Topological Sorting Number vertices, so that (u,v) in E implies u < v wake up 2 3 eat study computer sci. 7 play 9 1 make cookies for professors nap write c.s. program 10 sleep A typical student day 4 5 more c.s. 6 work out 11 dream about graphs Graphs 49
50 Algorithm for Topological Sorting Method TopologicalSort(G) H G // Temporary copy of G n G.numVertices() while H is not empty do Let v be a vertex with no outgoing edges Label v n n n - 1 Remove v from H Running time: O(n + m). How? Graphs 50
51 Topological Sorting Algorithm using DFS Simulate the algorithm by using depth-first search Algorithm topologicaldfs(g) Input dag G Output topological ordering of G n G.numVertices() for all u G.vertices() setlabel(u, UNEXPLORED) for all e G.edges() setlabel(e, UNEXPLORED) for all v G.vertices() if getlabel(v) = UNEXPLORED topologicaldfs(g, v) O(n+m) time. Algorithm topologicaldfs(g, v) Input graph G and a start vertex v of G Output labeling of the vertices of G in the connected component of v setlabel(v, VISITED) for all e G.incidentEdges(v) if getlabel(e) = UNEXPLORED w opposite(v,e) if getlabel(w) = UNEXPLORED setlabel(e, DISCOVERY) topologicaldfs(g, w) else {e is a forward or cross edge} Label v with topological number n n n - 1 Graphs 51
52 Topological Sorting Example Graphs 52
53 Topological Sorting Example 9 Graphs 53
54 Topological Sorting Example 9 Graphs 54
55 Topological Sorting Example 7 9 Graphs 55
56 Topological Sorting Example Graphs 56
57 Topological Sorting Example Graphs 57
58 Topological Sorting Example Graphs 5
59 Topological Sorting Example Graphs 59
60 Topological Sorting Example Graphs 60
61 Topological Sorting Example Graphs 61
62 Shortest Paths 0 A B C D E F 3
63 Weighted Graphs In a weighted graph, each edge has an associated numerical value, called the weight of the edge Edge weights may represent distances, costs, etc. Example: In a flight route graph, the weight of an edge represents the distance in miles between the endpoint airports HNL 2555 SFO 337 LAX ORD 02 DFW LGA PVD MIA 1205 Graphs 63
64 Shortest Paths Given a weighted graph and two vertices u and v, we want to find a path of minimum total weight between u and v. Length of a path is the sum of the weights of its edges. Example: Shortest path between Providence and Honolulu Applications Internet packet routing Flight reservations Driving directions HNL 2555 SFO 337 LAX ORD 02 DFW LGA PVD MIA Graphs
65 Shortest Path Properties Property 1: A subpath of a shortest path is itself a shortest path Property 2: There is a tree of shortest paths from a start vertex to all the other vertices Example: Tree of shortest paths from Providence HNL 2555 SFO 337 LAX ORD 02 DFW LGA PVD MIA 1205 Graphs 65
66 Dijkstra s Algorithm The distance of a vertex v from a vertex s is the length of a shortest path between s and v Dijkstra s algorithm computes the distances of all the vertices from a given start vertex s Assumptions: the graph is connected the edges are undirected the edge weights are nonnegative We grow a cloud of vertices, beginning with s and eventually covering all the vertices We store with each vertex v a label d(v) representing the distance of v from s in the subgraph consisting of the cloud and its adjacent vertices At each step We add to the cloud the vertex u outside the cloud with the smallest distance label, d(u) We update the labels of the vertices adjacent to u Graphs 66
67 Edge Relaxation Consider an edge e = (u,z) such that u is the vertex most recently added to the cloud z is not in the cloud s d(u) = 50 u e 10 d(z) = 75 z The relaxation of edge e updates distance d(z) as follows: d(z) min{d(z),d(u) + weight(e)} s d(u) = 50 u e 10 d(z) = 60 z Graphs 67
68 Example B 0 A C 4 D 4 B 0 A C 4 D E F E F B 0 A C 4 D 3 B 7 0 A C 4 D E F E F Graphs 6
69 Example (cont.) B 7 0 A C 4 D E F B 7 0 A C 4 D E F Graphs 69
70 Dijkstra s Algorithm A priority queue stores the vertices outside the cloud Key: distance Element: vertex Locator-based methods insert(k,e) returns a locator replacekey(l,k) changes the key of an item We store two labels with each vertex: Distance (d(v) label) locator in priority queue Algorithm DijkstraDistances(G, s) Q new heap-based priority queue for all v G.vertices() if v = s setdistance(v, 0) else setdistance(v, ) l Q.insert(getDistance(v), v) setlocator(v,l) while Q.isEmpty() u Q.removeMin() for all e G.incidentEdges(u) { relax edge e } z G.opposite(u,e) r getdistance(u) + weight(e) if r < getdistance(z) setdistance(z,r) Q.replaceKey(getLocator(z),r) Graphs 70
71 Analysis of Dijkstra s Algorithm Graph operations Method incidentedges is called once for each vertex Label operations We set/get the distance and locator labels of vertex z O(deg(z)) times Setting/getting a label takes O(1) time Priority queue operations Each vertex is inserted once into and removed once from the priority queue, where each insertion or removal takes O(log n) time The key of a vertex in the priority queue is modified at most deg(w) times, where each key change takes O(log n) time Dijkstra s algorithm runs in O((n + m) log n) time provided the graph is represented by the adjacency list structure Recall that Σ v deg(v) = 2m The running time can also be expressed as O(m log n) since the graph is connected Graphs 71
72 Why Dijkstra s Algorithm Works Dijkstra s algorithm is based on the greedy method. It adds vertices by increasing distance. Suppose it didn t find all shortest distances. Let F be the first wrong vertex the algorithm processed. When the previous node, D, on the true shortest path was considered, its distance was correct. But the edge (D,F) was relaxed at that time! Thus, so long as d(f)>d(d), F s distance cannot be wrong. That is, there is no wrong vertex. B 7 A C E F 0 4 D 3 Graphs 72
73 Why It Doesn t Work for Negative-Weight Edges Dijkstra s algorithm is based on the greedy method. It adds vertices by increasing distance. If a node with a negative incident edge were to be added late to the cloud, it could mess up distances for vertices already in the cloud. 0 A B C D E F 4 C s true distance is 1, but it is already in the cloud with d(c)=5! Graphs 73
74 Bellman-Ford Algorithm Works even with negativeweight edges Must assume directed edges (for otherwise we would have negative-weight cycles) Iteration i finds all shortest paths that use i edges. Running time: O(n m). Can be extended to detect a negative-weight cycle if it exists How? Algorithm BellmanFord(G, s) for all v G.vertices() if v = s setdistance(v, 0) else setdistance(v, ) for i 1 to n-1 do for each e G.edges() { relax edge e } u G.origin(e) z G.opposite(u,e) r getdistance(u) + weight(e) if r < getdistance(z) setdistance(z,r) Graphs 74
75 Bellman-Ford Example Nodes are labeled with their d(v) values Graphs 75
76 DAG-based Algorithm Works even with negative-weight edges Uses topological order Doesn t use any fancy data structures Is much faster than Dijkstra s algorithm Running time: O(n+m). Algorithm DagDistances(G, s) for all v G.vertices() if v = s setdistance(v, 0) else setdistance(v, ) Perform a topological sort of the vertices for u 1 to n do {in topological order} for each e G.outEdges(u) { relax edge e } z G.opposite(u,e) r getdistance(u) + weight(e) if r < getdistance(z) setdistance(z,r) Graphs 76
77 DAG Example Nodes are labeled with their d(v) values Graphs (two steps)
78 Minimum Spanning Trees BOS SFO 337 LAX PVD ORD JFK BWI 1090 DFW MIA 2342
79 Minimum Spanning Trees Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning tree Spanning subgraph that is itself a (free) tree Minimum spanning tree (MST) Spanning tree of a weighted graph with minimum total edge weight Applications DEN 4 DFW 1 9 ORD 6 STL ATL PIT DCA 2 7 Communications networks Transportation networks Graphs 79
80 Cycle Property Cycle Property: Let T be a minimum spanning tree of a weighted graph G Let e be an edge of G that is not in T and C let be the cycle formed by e with T For every edge f of C, weight(f) weight(e) Proof: By contradiction If weight(f) > weight(e) we can get a spanning tree of smaller weight by replacing e with f f C f C Graphs e 4 7 Replacing f with e yields a better spanning tree e 4 7
81 Partition Property Partition Property: Consider a partition of the vertices of G into subsets U and V Let e be an edge of minimum weight across the partition There is a minimum spanning tree of G containing edge e Proof: Let T be an MST of G If T does not contain e, consider the cycle C formed by e with T and let f be an edge of C across the partition By the cycle property, weight(f) weight(e) Thus, weight(f) = weight(e) We obtain another MST by replacing f with e 2 2 U U 5 5 Graphs 1 f 7 e f e V 4 3 Replacing f with e yields another MST V 4 3
82 Kruskal s Algorithm A priority queue stores the edges outside the cloud Key: weight Element: edge At the end of the algorithm We are left with one cloud that encompasses the MST A tree T which is our MST Algorithm KruskalMST(G) for each vertex v in G do define a Cloud(v) of {v} let Q be a priority queue. Insert all edges into Q using their weights as the key T while T has fewer than n-1 edges do edge e = Q.removeMin() Let u, v be the endpoints of e if Cloud(v) Cloud(u) then Add edge e to T Merge Cloud(v) and Cloud(u) return T Graphs 2
83 Data Structure for Kruskal Algorithm The algorithm maintains a forest of trees An edge is accepted it if connects distinct trees We need a data structure that maintains a partition, i.e., a collection of disjoint sets, with the operations: -find(u): return the set storing u -union(u,v): replace the sets storing u and v with their union Graphs 3
84 Representation of a Partition Each set is stored in a sequence Each element has a reference back to the set operation find(u) takes O(1) time, and returns the set of which u is a member. in operation union(u,v), we move the elements of the smaller set to the sequence of the larger set and update their references the time for operation union(u,v) is min(n u,n v ), where n u and n v are the sizes of the sets storing u and v Whenever an element is processed, it goes into a set of size at least double, hence each element is processed at most log n times Graphs 4
85 Partition-Based Implementation A partition-based version of Kruskal s Algorithm performs cloud merges as unions and tests as finds. Algorithm Kruskal(G): Input: A weighted graph G. Output: An MST T for G. Let P be a partition of the vertices of G, where each vertex forms a separate set. Let Q be a priority queue storing the edges of G, sorted by their weights Let T be an initially-empty tree while Q is not empty do (u,v) Q.removeMinElement() if P.find(u)!= P.find(v) then return T Add (u,v) to T P.union(u,v) Running time: O((n+m)log n) Graphs 5
86 Kruskal Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 6
87 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 7
88 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs
89 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 9
90 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 90
91 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 91
92 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 92
93 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 93
94 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 94
95 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 95
96 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 96
97 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 97
98 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 9
99 Example BOS SFO ORD PVD JFK 14 BWI LAX 1235 DFW MIA Graphs 99
100 Prim-Jarnik s Algorithm Similar to Dijkstra s algorithm (for a connected graph) We pick an arbitrary vertex s and we grow the MST as a cloud of vertices, starting from s We store with each vertex v a label d(v) = the smallest weight of an edge connecting v to a vertex in the cloud At each step: We add to the cloud the vertex u outside the cloud with the smallest distance label We update the labels of the vertices adjacent to u Graphs 100
101 Prim-Jarnik s Algorithm (cont.) A priority queue stores the vertices outside the cloud Key: distance Element: vertex Locator-based methods insert(k,e) returns a locator replacekey(l,k) changes the key of an item We store three labels with each vertex: Distance Parent edge in MST Locator in priority queue Algorithm PrimJarnikMST(G) Q new heap-based priority queue s a vertex of G for all v G.vertices() if v = s : setdistance(v, 0) else : setdistance(v, ) setparent(v, ) l Q.insert(getDistance(v), v) setlocator(v,l) while Q.isEmpty() u Q.removeMin() for all e G.incidentEdges(u) z G.opposite(u,e) r weight(e) if r < getdistance(z) setdistance(z,r) setparent(z,e) Q.replaceKey(getLocator(z),r) Graphs 101
102 Graphs 102 Example B D C A F E B D C A F E B D C A F E B D C A F E
103 Example (contd.) 2 2 A 0 B D F C 3 E A 0 B D F C 3 E 7 3 Graphs 103
104 Analysis Graph operations Method incidentedges is called once for each vertex Label operations We set/get the distance, parent and locator labels of vertex z O(deg(z)) times Setting/getting a label takes O(1) time Priority queue operations Each vertex is inserted once into and removed once from the priority queue, where each insertion or removal takes O(log n) time The key of a vertex w in the priority queue is modified at most deg(w) times, where each key change takes O(log n) time Prim-Jarnik s algorithm runs in O((n + m) log n) time provided the graph is represented by the adjacency list structure Recall that Σ v deg(v) = 2m The running time is O(m log n) since the graph is connected Graphs 104
Graph Algorithms shortest paths, minimum spanning trees, etc.
 Graph Algorithms shortest paths, minimum spanning trees, etc. SFO ORD LAX DFW Graphs 1 Outline and Reading Graphs ( 1.1) Definition Applications Terminology Properties ADT Data structures for graphs (
Graph Algorithms shortest paths, minimum spanning trees, etc. SFO ORD LAX DFW Graphs 1 Outline and Reading Graphs ( 1.1) Definition Applications Terminology Properties ADT Data structures for graphs (
Graph Algorithms shortest paths, minimum spanning trees, etc.
 SFO ORD LAX Graph Algorithms shortest paths, minimum spanning trees, etc. DFW Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with
SFO ORD LAX Graph Algorithms shortest paths, minimum spanning trees, etc. DFW Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with
Graphs Weighted Graphs. Reading: 12.5, 12.6, 12.7
 Graphs Weighted Graphs Reading: 1.5, 1.6, 1. Weighted Graphs, a.k.a. Networks In a weighted graph, each edge has an associated numerical value, called the weight or cost of the edge Edge weights may represent,
Graphs Weighted Graphs Reading: 1.5, 1.6, 1. Weighted Graphs, a.k.a. Networks In a weighted graph, each edge has an associated numerical value, called the weight or cost of the edge Edge weights may represent,
Graphs ORD SFO LAX DFW. Graphs 1
 Graphs ORD 1843 SFO 802 1743 337 1233 LAX DFW Graphs 1 Outline and Reading Graphs ( 12.1) Definition Applications Terminology Properties ADT Data structures for graphs ( 12.2) Edge list structure Adjacency
Graphs ORD 1843 SFO 802 1743 337 1233 LAX DFW Graphs 1 Outline and Reading Graphs ( 12.1) Definition Applications Terminology Properties ADT Data structures for graphs ( 12.2) Edge list structure Adjacency
Shortest Paths D E. Shortest Paths 1
 Shortest Paths A 2 7 2 B C D 2 E F Shortest Paths Outline and Reading Weighted graphs ( 7.) Shortest path problem Shortest path properties Dijkstra s algorithm ( 7..) Algorithm Edge relaxation The Bellman-Ford
Shortest Paths A 2 7 2 B C D 2 E F Shortest Paths Outline and Reading Weighted graphs ( 7.) Shortest path problem Shortest path properties Dijkstra s algorithm ( 7..) Algorithm Edge relaxation The Bellman-Ford
Minimum Spanning Trees
 Minimum Spanning Trees 04 6 33 49 PVD 1 40 146 61 14 15 0 Minimum Spanning Trees 1 Minimum Spanning Trees ( 1.) Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning tree 1
Minimum Spanning Trees 04 6 33 49 PVD 1 40 146 61 14 15 0 Minimum Spanning Trees 1 Minimum Spanning Trees ( 1.) Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning tree 1
Prim & Kruskal Algorithm
 Prim & Kruskal Algorithm Minimum Spanning Tree Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning tree 1 10 PIT Spanning subgraph that is itself a (free) tree Minimum spanning
Prim & Kruskal Algorithm Minimum Spanning Tree Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning tree 1 10 PIT Spanning subgraph that is itself a (free) tree Minimum spanning
Minimum Spanning Trees
 Minimum Spanning Trees 04 6 33 135 49 1 40 146 61 14 15 0 111 34 Minimum Spanning Trees 1 Minimum Spanning Trees ( 1.) Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning
Minimum Spanning Trees 04 6 33 135 49 1 40 146 61 14 15 0 111 34 Minimum Spanning Trees 1 Minimum Spanning Trees ( 1.) Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning
Minimum Spanning Trees
 Minimum Spanning Trees 04 6 33 135 49 PVD 1 40 146 61 JFK 14 15 0 111 34 Minimum Spanning Trees 1 Outline and Reading Minimum Spanning Trees Definitions A crucial fact The Prim-Jarnik Algorithm Kruskal's
Minimum Spanning Trees 04 6 33 135 49 PVD 1 40 146 61 JFK 14 15 0 111 34 Minimum Spanning Trees 1 Outline and Reading Minimum Spanning Trees Definitions A crucial fact The Prim-Jarnik Algorithm Kruskal's
Graphs ORD SFO LAX DFW Goodrich, Tamassia Graphs 1
 Graphs SFO 33 143 ORD 02 LAX 1233 DFW 2004 Goodrich, Tamassia Graphs 1 What is a Graph? (in computer science, it s not a data plot) General structure for representing positions with an arbitrary connectivity
Graphs SFO 33 143 ORD 02 LAX 1233 DFW 2004 Goodrich, Tamassia Graphs 1 What is a Graph? (in computer science, it s not a data plot) General structure for representing positions with an arbitrary connectivity
CHAPTER 13 GRAPH ALGORITHMS
 CHAPTER 13 GRAPH ALGORITHMS SFO LAX ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 00) AND SLIDES FROM NANCY
CHAPTER 13 GRAPH ALGORITHMS SFO LAX ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 00) AND SLIDES FROM NANCY
Directed Graphs BOS Goodrich, Tamassia Directed Graphs 1 ORD JFK SFO DFW LAX MIA
 Directed Graphs BOS ORD JFK SFO LAX DFW MIA 2010 Goodrich, Tamassia Directed Graphs 1 Digraphs A digraph is a graph whose edges are all directed Short for directed graph Applications one-way streets flights
Directed Graphs BOS ORD JFK SFO LAX DFW MIA 2010 Goodrich, Tamassia Directed Graphs 1 Digraphs A digraph is a graph whose edges are all directed Short for directed graph Applications one-way streets flights
Data Structures Lecture 14
 Fall 2018 Fang Yu Software Security Lab. ept. Management Information Systems, National hengchi University ata Structures Lecture 14 Graphs efinition, Implementation and Traversal Graphs Formally speaking,
Fall 2018 Fang Yu Software Security Lab. ept. Management Information Systems, National hengchi University ata Structures Lecture 14 Graphs efinition, Implementation and Traversal Graphs Formally speaking,
CHAPTER 13 GRAPH ALGORITHMS
 CHPTER 13 GRPH LGORITHMS SFO LX ORD DFW 1 CKNOWLEDGEMENT: THESE SLIDES RE DPTED FROM SLIDES PROVIDED WITH DT STRUCTURES ND LGORITHMS IN C++, GOODRICH, TMSSI ND MOUNT (WILEY 2004) ND SLIDES FROM JORY DENNY
CHPTER 13 GRPH LGORITHMS SFO LX ORD DFW 1 CKNOWLEDGEMENT: THESE SLIDES RE DPTED FROM SLIDES PROVIDED WITH DT STRUCTURES ND LGORITHMS IN C++, GOODRICH, TMSSI ND MOUNT (WILEY 2004) ND SLIDES FROM JORY DENNY
Graph Terminology and Representations
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Graph Terminology and Representations 1 Graphs A graph is a pair (V, E), where
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Graph Terminology and Representations 1 Graphs A graph is a pair (V, E), where
Graphs 3/25/14 15:37 SFO LAX Goodrich, Tamassia, Goldwasser Graphs 2
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Graphs SFO 337 LAX 1843 1743 1233 802 DFW
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Graphs SFO 337 LAX 1843 1743 1233 802 DFW
Lecture 17: Weighted Graphs, Dijkstra s Algorithm. Courtesy of Goodrich, Tamassia and Olga Veksler
 Lecture 17: Weighted Graphs, Shortest Paths: Dijkstra s Algorithm A 4 B 7 C 1 D 3 5 3 9 5 E Courtesy of Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Weighted Graphs In a weighted graph, each
Lecture 17: Weighted Graphs, Shortest Paths: Dijkstra s Algorithm A 4 B 7 C 1 D 3 5 3 9 5 E Courtesy of Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Weighted Graphs In a weighted graph, each
Depth-First Search and Template Patterns
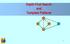 Depth-First Search and Template Patterns A B D E C 1 Outline Template Patterns and Search Depth-first search Algorithm Example Properties Analysis Applications of DFS Path finding Cycle finding CS 4407,
Depth-First Search and Template Patterns A B D E C 1 Outline Template Patterns and Search Depth-first search Algorithm Example Properties Analysis Applications of DFS Path finding Cycle finding CS 4407,
Routing & Congestion Control
 WIDE AREA NETWORK Routing & Congestion Control Introduction Congestion control and routing are major issues to be handled in Wide Area Networks. Congestion is handled at transport layer and routing is
WIDE AREA NETWORK Routing & Congestion Control Introduction Congestion control and routing are major issues to be handled in Wide Area Networks. Congestion is handled at transport layer and routing is
Lecture 16: Directed Graphs
 Lecture 16: Directed Graphs ORD JFK BOS SFO LAX DFW MIA Courtesy of Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Directed Graphs Properties Algorithms for Directed Graphs DFS and
Lecture 16: Directed Graphs ORD JFK BOS SFO LAX DFW MIA Courtesy of Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Directed Graphs Properties Algorithms for Directed Graphs DFS and
CHAPTER 14 GRAPH ALGORITHMS ORD SFO LAX DFW
 SFO ORD CHAPTER 14 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016) GRAPH
SFO ORD CHAPTER 14 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016) GRAPH
Weighted Graphs ( 12.5) Shortest Paths. Shortest Paths ( 12.6) Shortest Path Properties PVD ORD SFO LGA HNL LAX DFW MIA PVD PVD ORD ORD SFO SFO LGA
 Shortest Paths A Weighted Graphs (.) In a weighted graph, each edge has an associated numerical value, called the weight of the edge dge weights may represent, distances, costs, etc. xample: In a flight
Shortest Paths A Weighted Graphs (.) In a weighted graph, each edge has an associated numerical value, called the weight of the edge dge weights may represent, distances, costs, etc. xample: In a flight
DFS on Directed Graphs BOS. Outline and Reading ( 6.4) Digraphs. Reachability ( 6.4.1) Directed Acyclic Graphs (DAG s) ( 6.4.4)
 S on irected Graphs OS OR JK SO LX W MI irected Graphs S 1.3 1 Outline and Reading ( 6.4) Reachability ( 6.4.1) irected S Strong connectivity irected cyclic Graphs (G s) ( 6.4.4) Topological Sorting irected
S on irected Graphs OS OR JK SO LX W MI irected Graphs S 1.3 1 Outline and Reading ( 6.4) Reachability ( 6.4.1) irected S Strong connectivity irected cyclic Graphs (G s) ( 6.4.4) Topological Sorting irected
Dijkstra s Algorithm
 Dijkstra s Algorithm 7 1 3 1 Weighted Graphs In a weighted graph, each edge has an associated numerical value, called the weight of the edge Edge weights may represent, distances, costs, etc. Example:
Dijkstra s Algorithm 7 1 3 1 Weighted Graphs In a weighted graph, each edge has an associated numerical value, called the weight of the edge Edge weights may represent, distances, costs, etc. Example:
Depth-First Search A B D E C
 epth-first Search Outline and Reading efinitions (6.1) Subgraph onnectivity Spanning trees and forests epth-first search (6.3.1) lgorithm xample Properties nalysis pplications of FS (6.5) Path finding
epth-first Search Outline and Reading efinitions (6.1) Subgraph onnectivity Spanning trees and forests epth-first search (6.3.1) lgorithm xample Properties nalysis pplications of FS (6.5) Path finding
Outline and Reading. Minimum Spanning Tree. Minimum Spanning Tree. Cycle Property. Minimum Spanning Trees ( 12.7)
 Outline and Reading Minimum Spanning Tree PV 1 1 1 1 JK 1 15 SO 11 1 LX 15 Minimum Spanning Trees ( 1.) efinitions crucial fact Prim-Jarnik s lgorithm ( 1..) Kruskal s lgorithm ( 1..1) 111 // :1 PM Minimum
Outline and Reading Minimum Spanning Tree PV 1 1 1 1 JK 1 15 SO 11 1 LX 15 Minimum Spanning Trees ( 1.) efinitions crucial fact Prim-Jarnik s lgorithm ( 1..) Kruskal s lgorithm ( 1..1) 111 // :1 PM Minimum
CHAPTER 13 GRAPH ALGORITHMS ORD SFO LAX DFW
 SFO ORD CHAPTER 13 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES
SFO ORD CHAPTER 13 GRAPH ALGORITHMS LAX DFW ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES
Minimum Spanning Trees
 Minimum Spanning Trees 0 OS SO LX PV OR 0 JK 0 WI 00 W MI 00 Goodrich, Tamassia Minimum Spanning Trees Minimum Spanning Trees Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning
Minimum Spanning Trees 0 OS SO LX PV OR 0 JK 0 WI 00 W MI 00 Goodrich, Tamassia Minimum Spanning Trees Minimum Spanning Trees Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning
Graphs ADTs and Implementations
 Graphs ADTs and Implementations SFO 337 1843 802 ORD LAX 1233 DFW - 1 - Applications of Graphs Ø Electronic circuits cslab1a cslab1b q Printed circuit board math.brown.edu q Integrated circuit Ø Transportation
Graphs ADTs and Implementations SFO 337 1843 802 ORD LAX 1233 DFW - 1 - Applications of Graphs Ø Electronic circuits cslab1a cslab1b q Printed circuit board math.brown.edu q Integrated circuit Ø Transportation
Digraphs ( 12.4) Directed Graphs. Digraph Application. Digraph Properties. A digraph is a graph whose edges are all directed.
 igraphs ( 12.4) irected Graphs OR OS digraph is a graph whose edges are all directed Short for directed graph pplications one- way streets flights task scheduling irected Graphs 1 irected Graphs 2 igraph
igraphs ( 12.4) irected Graphs OR OS digraph is a graph whose edges are all directed Short for directed graph pplications one- way streets flights task scheduling irected Graphs 1 irected Graphs 2 igraph
CS2210 Data Structures and Algorithms
 S1 ata Structures and Algorithms Lecture 1 : Shortest Paths A 4 1 5 5 3 4 Goodrich, Tamassia Outline Weighted Graphs Shortest Paths Algorithm (ijkstra s) Weighted Graphs ach edge has an associated numerical
S1 ata Structures and Algorithms Lecture 1 : Shortest Paths A 4 1 5 5 3 4 Goodrich, Tamassia Outline Weighted Graphs Shortest Paths Algorithm (ijkstra s) Weighted Graphs ach edge has an associated numerical
CS 225. April 16 Graph Traversal. Data Structures. Wade Fagen-Ulmschneider
 CS 225 Data Structures April 16 Graph Traversal Wade Fagen-Ulmschneider Graph ADT Data: - Vertices - Edges - Some data structure maintaining the structure between vertices and edges. d V W f b e X Y g
CS 225 Data Structures April 16 Graph Traversal Wade Fagen-Ulmschneider Graph ADT Data: - Vertices - Edges - Some data structure maintaining the structure between vertices and edges. d V W f b e X Y g
Lecture 14: Graph Representation, DFS and Applications
 Lecture 14: Graph Representation, FS and pplications SFO OR LX FW ourtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Graph Representation dge List djacency List djacency Matrix
Lecture 14: Graph Representation, FS and pplications SFO OR LX FW ourtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Graph Representation dge List djacency List djacency Matrix
CHAPTER 14 GRAPH ALGORITHMS ORD SFO LAX DFW
 SO OR HPTR 1 GRPH LGORITHMS LX W KNOWLGMNT: THS SLIS R PT ROM SLIS PROVI WITH T STRUTURS N LGORITHMS IN JV, GOORIH, TMSSI N GOLWSSR (WILY 16) 6 OS MINIMUM SPNNING TRS SO 16 PV OR 1 1 16 61 JK 1 1 11 WI
SO OR HPTR 1 GRPH LGORITHMS LX W KNOWLGMNT: THS SLIS R PT ROM SLIS PROVI WITH T STRUTURS N LGORITHMS IN JV, GOORIH, TMSSI N GOLWSSR (WILY 16) 6 OS MINIMUM SPNNING TRS SO 16 PV OR 1 1 16 61 JK 1 1 11 WI
Graph ADT. Lecture18: Graph II. Adjacency Matrix. Representation of Graphs. Data Vertices and edges. Methods
 Graph T S33: ata Structures (0) Lecture8: Graph II ohyung Han S, POSTH bhhan@postech.ac.kr ata Vertices and edges endvertices(e): an array of the two endvertices of e opposite(v,e): the vertex opposite
Graph T S33: ata Structures (0) Lecture8: Graph II ohyung Han S, POSTH bhhan@postech.ac.kr ata Vertices and edges endvertices(e): an array of the two endvertices of e opposite(v,e): the vertex opposite
Winter 2016 COMP-250: Introduction to Computer Science. Lecture 16, March 10, 2016
 Winter 2016-250: Introduction to Computer Science Lecture 16, March 10, 2016 GRAPHS Definitions Examples The Graph ADT PVD HNL LAX DFW STL FTL What is a Graph? Agraph G = (V,E) is composed of: V: set of
Winter 2016-250: Introduction to Computer Science Lecture 16, March 10, 2016 GRAPHS Definitions Examples The Graph ADT PVD HNL LAX DFW STL FTL What is a Graph? Agraph G = (V,E) is composed of: V: set of
Graphs. CS16: Introduction to Data Structures & Algorithms Spring 2018
 Graphs CS16: Introduction to Data Structures & Algorithms Spring 2018 Outline What is a Graph Terminology Properties Graph Types Representations Performance BFS/DFS Applications 2 What is a Graph A graph
Graphs CS16: Introduction to Data Structures & Algorithms Spring 2018 Outline What is a Graph Terminology Properties Graph Types Representations Performance BFS/DFS Applications 2 What is a Graph A graph
Breadth-First Search L 1 L Goodrich, Tamassia, Goldwasser Breadth-First Search 1
 readth-irst Search 2013 Goodrich, Tamassia, Goldwasser readth-irst Search 1 readth-irst Search readth-first search (S) is a general technique for traversing a graph S traversal of a graph G Visits all
readth-irst Search 2013 Goodrich, Tamassia, Goldwasser readth-irst Search 1 readth-irst Search readth-first search (S) is a general technique for traversing a graph S traversal of a graph G Visits all
Suggested Study Strategy
 Final Exam Thursday, 7 August 2014,19:00 22:00 Closed Book Will cover whole course, with emphasis on material after midterm (hash tables, binary search trees, sorting, graphs) Suggested Study Strategy
Final Exam Thursday, 7 August 2014,19:00 22:00 Closed Book Will cover whole course, with emphasis on material after midterm (hash tables, binary search trees, sorting, graphs) Suggested Study Strategy
Graphs ORD SFO LAX DFW
 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
CS 341: Algorithms. Douglas R. Stinson. David R. Cheriton School of Computer Science University of Waterloo. February 26, 2019
 CS 341: Algorithms Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo February 26, 2019 D.R. Stinson (SCS) CS 341 February 26, 2019 1 / 296 1 Course Information 2 Introduction
CS 341: Algorithms Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo February 26, 2019 D.R. Stinson (SCS) CS 341 February 26, 2019 1 / 296 1 Course Information 2 Introduction
DataStruct 13. Graph Algorithms
 2013-2 DataStruct 13. Graph Algorithms Michael T. Goodrich, et. al, Data Structures and Algorithms in C++, 2 nd Ed., John Wiley & Sons, Inc., 2011. December 10, 2013 Advanced Networking Technology Lab.
2013-2 DataStruct 13. Graph Algorithms Michael T. Goodrich, et. al, Data Structures and Algorithms in C++, 2 nd Ed., John Wiley & Sons, Inc., 2011. December 10, 2013 Advanced Networking Technology Lab.
Graph Algorithms Introduction to Data Structures. Ananda Gunawardena 7/31/2011 1
 Graph Algorithms 15-121 Introduction to Data Structures Ananda Gunawardena 7/31/2011 1 In this lecture.. Main idea is finding the Shortest Path between two points in a Graph We will look at Graphs with
Graph Algorithms 15-121 Introduction to Data Structures Ananda Gunawardena 7/31/2011 1 In this lecture.. Main idea is finding the Shortest Path between two points in a Graph We will look at Graphs with
22 Elementary Graph Algorithms. There are two standard ways to represent a
 VI Graph Algorithms Elementary Graph Algorithms Minimum Spanning Trees Single-Source Shortest Paths All-Pairs Shortest Paths 22 Elementary Graph Algorithms There are two standard ways to represent a graph
VI Graph Algorithms Elementary Graph Algorithms Minimum Spanning Trees Single-Source Shortest Paths All-Pairs Shortest Paths 22 Elementary Graph Algorithms There are two standard ways to represent a graph
Minimum Spanning Trees Ch 23 Traversing graphs
 Next: Graph Algorithms Graphs Ch 22 Graph representations adjacency list adjacency matrix Minimum Spanning Trees Ch 23 Traversing graphs Breadth-First Search Depth-First Search 11/30/17 CSE 3101 1 Graphs
Next: Graph Algorithms Graphs Ch 22 Graph representations adjacency list adjacency matrix Minimum Spanning Trees Ch 23 Traversing graphs Breadth-First Search Depth-First Search 11/30/17 CSE 3101 1 Graphs
22 Elementary Graph Algorithms. There are two standard ways to represent a
 VI Graph Algorithms Elementary Graph Algorithms Minimum Spanning Trees Single-Source Shortest Paths All-Pairs Shortest Paths 22 Elementary Graph Algorithms There are two standard ways to represent a graph
VI Graph Algorithms Elementary Graph Algorithms Minimum Spanning Trees Single-Source Shortest Paths All-Pairs Shortest Paths 22 Elementary Graph Algorithms There are two standard ways to represent a graph
DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI. Department of Computer Science and Engineering CS6301 PROGRAMMING DATA STRUCTURES II
 DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI Department of Computer Science and Engineering CS6301 PROGRAMMING DATA STRUCTURES II Anna University 2 & 16 Mark Questions & Answers Year / Semester: II / III
DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI Department of Computer Science and Engineering CS6301 PROGRAMMING DATA STRUCTURES II Anna University 2 & 16 Mark Questions & Answers Year / Semester: II / III
Minimum-Spanning-Tree problem. Minimum Spanning Trees (Forests) Minimum-Spanning-Tree problem
 Minimum Spanning Trees (Forests) Given an undirected graph G=(V,E) with each edge e having a weight w(e) : Find a subgraph T of G of minimum total weight s.t. every pair of vertices connected in G are
Minimum Spanning Trees (Forests) Given an undirected graph G=(V,E) with each edge e having a weight w(e) : Find a subgraph T of G of minimum total weight s.t. every pair of vertices connected in G are
Part VI Graph algorithms. Chapter 22 Elementary Graph Algorithms Chapter 23 Minimum Spanning Trees Chapter 24 Single-source Shortest Paths
 Part VI Graph algorithms Chapter 22 Elementary Graph Algorithms Chapter 23 Minimum Spanning Trees Chapter 24 Single-source Shortest Paths 1 Chapter 22 Elementary Graph Algorithms Representations of graphs
Part VI Graph algorithms Chapter 22 Elementary Graph Algorithms Chapter 23 Minimum Spanning Trees Chapter 24 Single-source Shortest Paths 1 Chapter 22 Elementary Graph Algorithms Representations of graphs
2. True or false: even though BFS and DFS have the same space complexity, they do not always have the same worst case asymptotic time complexity.
 1. T F: Consider a directed graph G = (V, E) and a vertex s V. Suppose that for all v V, there exists a directed path in G from s to v. Suppose that a DFS is run on G, starting from s. Then, true or false:
1. T F: Consider a directed graph G = (V, E) and a vertex s V. Suppose that for all v V, there exists a directed path in G from s to v. Suppose that a DFS is run on G, starting from s. Then, true or false:
The big picture: from Perception to Planning to Control
 The big picture: from Perception to Planning to Control Perception Location, Map Signals: video, inertial, range Sensors Real World 1 Planning vs Control 0. In control we go from to A to B in free space
The big picture: from Perception to Planning to Control Perception Location, Map Signals: video, inertial, range Sensors Real World 1 Planning vs Control 0. In control we go from to A to B in free space
Copyright 2000, Kevin Wayne 1
 Chapter 3 - Graphs Undirected Graphs Undirected graph. G = (V, E) V = nodes. E = edges between pairs of nodes. Captures pairwise relationship between objects. Graph size parameters: n = V, m = E. Directed
Chapter 3 - Graphs Undirected Graphs Undirected graph. G = (V, E) V = nodes. E = edges between pairs of nodes. Captures pairwise relationship between objects. Graph size parameters: n = V, m = E. Directed
Chapter 9 Graph Algorithms
 Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
11/22/2016. Chapter 9 Graph Algorithms. Introduction. Definitions. Definitions. Definitions. Definitions
 Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Graph Algorithms. Textbook reading. Chapter 3 Chapter 4. CSci 3110 Graph Algorithms 1/41
 CSci 3110 Graph Algorithms 1/41 Graph Algorithms Textbook reading Chapter 3 Chapter 4 CSci 3110 Graph Algorithms 2/41 Overview Design principle: Learn the structure of a graph by systematic exploration
CSci 3110 Graph Algorithms 1/41 Graph Algorithms Textbook reading Chapter 3 Chapter 4 CSci 3110 Graph Algorithms 2/41 Overview Design principle: Learn the structure of a graph by systematic exploration
Outline. Graphs. Divide and Conquer.
 GRAPHS COMP 321 McGill University These slides are mainly compiled from the following resources. - Professor Jaehyun Park slides CS 97SI - Top-coder tutorials. - Programming Challenges books. Outline Graphs.
GRAPHS COMP 321 McGill University These slides are mainly compiled from the following resources. - Professor Jaehyun Park slides CS 97SI - Top-coder tutorials. - Programming Challenges books. Outline Graphs.
Graph Terminology and Representations
 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Graph Termiology ad Represetatios 2015 Goodrich ad Tamassia Graphs 1 Graphs A graph is
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Graph Termiology ad Represetatios 2015 Goodrich ad Tamassia Graphs 1 Graphs A graph is
Undirected Graphs. DSA - lecture 6 - T.U.Cluj-Napoca - M. Joldos 1
 Undirected Graphs Terminology. Free Trees. Representations. Minimum Spanning Trees (algorithms: Prim, Kruskal). Graph Traversals (dfs, bfs). Articulation points & Biconnected Components. Graph Matching
Undirected Graphs Terminology. Free Trees. Representations. Minimum Spanning Trees (algorithms: Prim, Kruskal). Graph Traversals (dfs, bfs). Articulation points & Biconnected Components. Graph Matching
Undirected Graphs. V = { 1, 2, 3, 4, 5, 6, 7, 8 } E = { 1-2, 1-3, 2-3, 2-4, 2-5, 3-5, 3-7, 3-8, 4-5, 5-6 } n = 8 m = 11
 Chapter 3 - Graphs Undirected Graphs Undirected graph. G = (V, E) V = nodes. E = edges between pairs of nodes. Captures pairwise relationship between objects. Graph size parameters: n = V, m = E. V = {
Chapter 3 - Graphs Undirected Graphs Undirected graph. G = (V, E) V = nodes. E = edges between pairs of nodes. Captures pairwise relationship between objects. Graph size parameters: n = V, m = E. V = {
Theory of Computing. Lecture 10 MAS 714 Hartmut Klauck
 Theory of Computing Lecture 10 MAS 714 Hartmut Klauck Seven Bridges of Königsberg Can one take a walk that crosses each bridge exactly once? Seven Bridges of Königsberg Model as a graph Is there a path
Theory of Computing Lecture 10 MAS 714 Hartmut Klauck Seven Bridges of Königsberg Can one take a walk that crosses each bridge exactly once? Seven Bridges of Königsberg Model as a graph Is there a path
CS 220: Discrete Structures and their Applications. graphs zybooks chapter 10
 CS 220: Discrete Structures and their Applications graphs zybooks chapter 10 directed graphs A collection of vertices and directed edges What can this represent? undirected graphs A collection of vertices
CS 220: Discrete Structures and their Applications graphs zybooks chapter 10 directed graphs A collection of vertices and directed edges What can this represent? undirected graphs A collection of vertices
Algorithm Analysis Graph algorithm. Chung-Ang University, Jaesung Lee
 Algorithm Analysis Graph algorithm Chung-Ang University, Jaesung Lee Basic definitions Graph = (, ) where is a set of vertices and is a set of edges Directed graph = where consists of ordered pairs
Algorithm Analysis Graph algorithm Chung-Ang University, Jaesung Lee Basic definitions Graph = (, ) where is a set of vertices and is a set of edges Directed graph = where consists of ordered pairs
Algorithm Design (8) Graph Algorithms 1/2
 Graph Algorithm Design (8) Graph Algorithms / Graph:, : A finite set of vertices (or nodes) : A finite set of edges (or arcs or branches) each of which connect two vertices Takashi Chikayama School of
Graph Algorithm Design (8) Graph Algorithms / Graph:, : A finite set of vertices (or nodes) : A finite set of edges (or arcs or branches) each of which connect two vertices Takashi Chikayama School of
Basic Graph Definitions
 CMSC 341 Graphs Basic Graph Definitions A graph G = (V,E) consists of a finite set of vertices, V, and a finite set of edges, E. Each edge is a pair (v,w) where v, w V. V and E are sets, so each vertex
CMSC 341 Graphs Basic Graph Definitions A graph G = (V,E) consists of a finite set of vertices, V, and a finite set of edges, E. Each edge is a pair (v,w) where v, w V. V and E are sets, so each vertex
Graphs and Network Flows ISE 411. Lecture 7. Dr. Ted Ralphs
 Graphs and Network Flows ISE 411 Lecture 7 Dr. Ted Ralphs ISE 411 Lecture 7 1 References for Today s Lecture Required reading Chapter 20 References AMO Chapter 13 CLRS Chapter 23 ISE 411 Lecture 7 2 Minimum
Graphs and Network Flows ISE 411 Lecture 7 Dr. Ted Ralphs ISE 411 Lecture 7 1 References for Today s Lecture Required reading Chapter 20 References AMO Chapter 13 CLRS Chapter 23 ISE 411 Lecture 7 2 Minimum
Lecture 6 Basic Graph Algorithms
 CS 491 CAP Intro to Competitive Algorithmic Programming Lecture 6 Basic Graph Algorithms Uttam Thakore University of Illinois at Urbana-Champaign September 30, 2015 Updates ICPC Regionals teams will be
CS 491 CAP Intro to Competitive Algorithmic Programming Lecture 6 Basic Graph Algorithms Uttam Thakore University of Illinois at Urbana-Champaign September 30, 2015 Updates ICPC Regionals teams will be
Graph Algorithms Using Depth First Search
 Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
Dijkstra s algorithm for shortest paths when no edges have negative weight.
 Lecture 14 Graph Algorithms II 14.1 Overview In this lecture we begin with one more algorithm for the shortest path problem, Dijkstra s algorithm. We then will see how the basic approach of this algorithm
Lecture 14 Graph Algorithms II 14.1 Overview In this lecture we begin with one more algorithm for the shortest path problem, Dijkstra s algorithm. We then will see how the basic approach of this algorithm
Shortest Path Problem
 Shortest Path Problem CLRS Chapters 24.1 3, 24.5, 25.2 Shortest path problem Shortest path problem (and variants) Properties of shortest paths Algorithmic framework Bellman-Ford algorithm Shortest paths
Shortest Path Problem CLRS Chapters 24.1 3, 24.5, 25.2 Shortest path problem Shortest path problem (and variants) Properties of shortest paths Algorithmic framework Bellman-Ford algorithm Shortest paths
CS521 \ Notes for the Final Exam
 CS521 \ Notes for final exam 1 Ariel Stolerman Asymptotic Notations: CS521 \ Notes for the Final Exam Notation Definition Limit Big-O ( ) Small-o ( ) Big- ( ) Small- ( ) Big- ( ) Notes: ( ) ( ) ( ) ( )
CS521 \ Notes for final exam 1 Ariel Stolerman Asymptotic Notations: CS521 \ Notes for the Final Exam Notation Definition Limit Big-O ( ) Small-o ( ) Big- ( ) Small- ( ) Big- ( ) Notes: ( ) ( ) ( ) ( )
Graph Algorithms. Chapter 22. CPTR 430 Algorithms Graph Algorithms 1
 Graph Algorithms Chapter 22 CPTR 430 Algorithms Graph Algorithms Why Study Graph Algorithms? Mathematical graphs seem to be relatively specialized and abstract Why spend so much time and effort on algorithms
Graph Algorithms Chapter 22 CPTR 430 Algorithms Graph Algorithms Why Study Graph Algorithms? Mathematical graphs seem to be relatively specialized and abstract Why spend so much time and effort on algorithms
Week 12: Minimum Spanning trees and Shortest Paths
 Agenda: Week 12: Minimum Spanning trees and Shortest Paths Kruskal s Algorithm Single-source shortest paths Dijkstra s algorithm for non-negatively weighted case Reading: Textbook : 61-7, 80-87, 9-601
Agenda: Week 12: Minimum Spanning trees and Shortest Paths Kruskal s Algorithm Single-source shortest paths Dijkstra s algorithm for non-negatively weighted case Reading: Textbook : 61-7, 80-87, 9-601
CSE 431/531: Algorithm Analysis and Design (Spring 2018) Greedy Algorithms. Lecturer: Shi Li
 CSE 431/531: Algorithm Analysis and Design (Spring 2018) Greedy Algorithms Lecturer: Shi Li Department of Computer Science and Engineering University at Buffalo Main Goal of Algorithm Design Design fast
CSE 431/531: Algorithm Analysis and Design (Spring 2018) Greedy Algorithms Lecturer: Shi Li Department of Computer Science and Engineering University at Buffalo Main Goal of Algorithm Design Design fast
Introduction to Algorithms. Lecture 11
 Introduction to Algorithms Lecture 11 Last Time Optimization Problems Greedy Algorithms Graph Representation & Algorithms Minimum Spanning Tree Prim s Algorithm Kruskal s Algorithm 2 Today s Topics Shortest
Introduction to Algorithms Lecture 11 Last Time Optimization Problems Greedy Algorithms Graph Representation & Algorithms Minimum Spanning Tree Prim s Algorithm Kruskal s Algorithm 2 Today s Topics Shortest
Chapter 14. Graphs Pearson Addison-Wesley. All rights reserved 14 A-1
 Chapter 14 Graphs 2011 Pearson Addison-Wesley. All rights reserved 14 A-1 Terminology G = {V, E} A graph G consists of two sets A set V of vertices, or nodes A set E of edges A subgraph Consists of a subset
Chapter 14 Graphs 2011 Pearson Addison-Wesley. All rights reserved 14 A-1 Terminology G = {V, E} A graph G consists of two sets A set V of vertices, or nodes A set E of edges A subgraph Consists of a subset
Lecture 3: Graphs and flows
 Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
UNIT 5 GRAPH. Application of Graph Structure in real world:- Graph Terminologies:
 UNIT 5 CSE 103 - Unit V- Graph GRAPH Graph is another important non-linear data structure. In tree Structure, there is a hierarchical relationship between, parent and children that is one-to-many relationship.
UNIT 5 CSE 103 - Unit V- Graph GRAPH Graph is another important non-linear data structure. In tree Structure, there is a hierarchical relationship between, parent and children that is one-to-many relationship.
Decreasing a key FIB-HEAP-DECREASE-KEY(,, ) 3.. NIL. 2. error new key is greater than current key 6. CASCADING-CUT(, )
 Decreasing a key FIB-HEAP-DECREASE-KEY(,, ) 1. if >. 2. error new key is greater than current key 3.. 4.. 5. if NIL and.
Decreasing a key FIB-HEAP-DECREASE-KEY(,, ) 1. if >. 2. error new key is greater than current key 3.. 4.. 5. if NIL and.
Lecture Summary CSC 263H. August 5, 2016
 Lecture Summary CSC 263H August 5, 2016 This document is a very brief overview of what we did in each lecture, it is by no means a replacement for attending lecture or doing the readings. 1. Week 1 2.
Lecture Summary CSC 263H August 5, 2016 This document is a very brief overview of what we did in each lecture, it is by no means a replacement for attending lecture or doing the readings. 1. Week 1 2.
Konigsberg Bridge Problem
 Graphs Konigsberg Bridge Problem c C d g A Kneiphof e D a B b f c A C d e g D a b f B Euler s Graph Degree of a vertex: the number of edges incident to it Euler showed that there is a walk starting at
Graphs Konigsberg Bridge Problem c C d g A Kneiphof e D a B b f c A C d e g D a b f B Euler s Graph Degree of a vertex: the number of edges incident to it Euler showed that there is a walk starting at
Chapter 9 Graph Algorithms
 Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures 3 Definitions an undirected graph G = (V, E) is a
Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures 3 Definitions an undirected graph G = (V, E) is a
UNIT Name the different ways of representing a graph? a.adjacencymatrix b. Adjacency list
 UNIT-4 Graph: Terminology, Representation, Traversals Applications - spanning trees, shortest path and Transitive closure, Topological sort. Sets: Representation - Operations on sets Applications. 1. Name
UNIT-4 Graph: Terminology, Representation, Traversals Applications - spanning trees, shortest path and Transitive closure, Topological sort. Sets: Representation - Operations on sets Applications. 1. Name
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 7 Greedy Graph Algorithms Topological sort Shortest paths Adam Smith The (Algorithm) Design Process 1. Work out the answer for some examples. Look for a general principle
Algorithm Design and Analysis LECTURE 7 Greedy Graph Algorithms Topological sort Shortest paths Adam Smith The (Algorithm) Design Process 1. Work out the answer for some examples. Look for a general principle
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 4 Graphs Definitions Traversals Adam Smith 9/8/10 Exercise How can you simulate an array with two unbounded stacks and a small amount of memory? (Hint: think of a
Algorithm Design and Analysis LECTURE 4 Graphs Definitions Traversals Adam Smith 9/8/10 Exercise How can you simulate an array with two unbounded stacks and a small amount of memory? (Hint: think of a
Chapter 9. Greedy Technique. Copyright 2007 Pearson Addison-Wesley. All rights reserved.
 Chapter 9 Greedy Technique Copyright 2007 Pearson Addison-Wesley. All rights reserved. Greedy Technique Constructs a solution to an optimization problem piece by piece through a sequence of choices that
Chapter 9 Greedy Technique Copyright 2007 Pearson Addison-Wesley. All rights reserved. Greedy Technique Constructs a solution to an optimization problem piece by piece through a sequence of choices that
Minimum Spanning Trees
 Minimum Spanning Trees Problem A town has a set of houses and a set of roads. A road connects 2 and only 2 houses. A road connecting houses u and v has a repair cost w(u, v). Goal: Repair enough (and no
Minimum Spanning Trees Problem A town has a set of houses and a set of roads. A road connects 2 and only 2 houses. A road connecting houses u and v has a repair cost w(u, v). Goal: Repair enough (and no
Chapter 4. Greedy Algorithms. Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
 Chapter 4 Greedy Algorithms Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 4.5 Minimum Spanning Tree Minimum Spanning Tree Minimum spanning tree. Given a connected
Chapter 4 Greedy Algorithms Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 4.5 Minimum Spanning Tree Minimum Spanning Tree Minimum spanning tree. Given a connected
Undirected Graphs. Hwansoo Han
 Undirected Graphs Hwansoo Han Definitions Undirected graph (simply graph) G = (V, E) V : set of vertexes (vertices, nodes, points) E : set of edges (lines) An edge is an unordered pair Edge (v, w) = (w,
Undirected Graphs Hwansoo Han Definitions Undirected graph (simply graph) G = (V, E) V : set of vertexes (vertices, nodes, points) E : set of edges (lines) An edge is an unordered pair Edge (v, w) = (w,
 CS6301 Programming and Data Structures II Unit -5 REPRESENTATION OF GRAPHS Graph and its representations Graph is a data structure that consists of following two components: 1. A finite set of vertices
CS6301 Programming and Data Structures II Unit -5 REPRESENTATION OF GRAPHS Graph and its representations Graph is a data structure that consists of following two components: 1. A finite set of vertices
CS420/520 Algorithm Analysis Spring 2009 Lecture 14
 CS420/520 Algorithm Analysis Spring 2009 Lecture 14 "A Computational Analysis of Alternative Algorithms for Labeling Techniques for Finding Shortest Path Trees", Dial, Glover, Karney, and Klingman, Networks
CS420/520 Algorithm Analysis Spring 2009 Lecture 14 "A Computational Analysis of Alternative Algorithms for Labeling Techniques for Finding Shortest Path Trees", Dial, Glover, Karney, and Klingman, Networks
Lecture 10. Elementary Graph Algorithm Minimum Spanning Trees
 Lecture 10. Elementary Graph Algorithm Minimum Spanning Trees T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo
Lecture 10. Elementary Graph Algorithm Minimum Spanning Trees T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo
1 Shortest Paths. 1.1 Breadth First Search (BFS) CS 124 Section #3 Shortest Paths and MSTs 2/13/2018
 CS Section # Shortest Paths and MSTs //08 Shortest Paths There are types of shortest paths problems: Single source single destination Single source to all destinations All pairs shortest path In today
CS Section # Shortest Paths and MSTs //08 Shortest Paths There are types of shortest paths problems: Single source single destination Single source to all destinations All pairs shortest path In today
Chapter 9 Graph Algorithms
 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures Chapter 9 Graph s 2 Definitions Definitions an undirected graph is a finite set
Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures Chapter 9 Graph s 2 Definitions Definitions an undirected graph is a finite set
CSE 100 Minimum Spanning Trees Prim s and Kruskal
 CSE 100 Minimum Spanning Trees Prim s and Kruskal Your Turn The array of vertices, which include dist, prev, and done fields (initialize dist to INFINITY and done to false ): V0: dist= prev= done= adj:
CSE 100 Minimum Spanning Trees Prim s and Kruskal Your Turn The array of vertices, which include dist, prev, and done fields (initialize dist to INFINITY and done to false ): V0: dist= prev= done= adj:
2 A Template for Minimum Spanning Tree Algorithms
 CS, Lecture 5 Minimum Spanning Trees Scribe: Logan Short (05), William Chen (0), Mary Wootters (0) Date: May, 0 Introduction Today we will continue our discussion of greedy algorithms, specifically in
CS, Lecture 5 Minimum Spanning Trees Scribe: Logan Short (05), William Chen (0), Mary Wootters (0) Date: May, 0 Introduction Today we will continue our discussion of greedy algorithms, specifically in
Topics. Trees Vojislav Kecman. Which graphs are trees? Terminology. Terminology Trees as Models Some Tree Theorems Applications of Trees CMSC 302
 Topics VCU, Department of Computer Science CMSC 302 Trees Vojislav Kecman Terminology Trees as Models Some Tree Theorems Applications of Trees Binary Search Tree Decision Tree Tree Traversal Spanning Trees
Topics VCU, Department of Computer Science CMSC 302 Trees Vojislav Kecman Terminology Trees as Models Some Tree Theorems Applications of Trees Binary Search Tree Decision Tree Tree Traversal Spanning Trees
Algorithms and Theory of Computation. Lecture 5: Minimum Spanning Tree
 Algorithms and Theory of Computation Lecture 5: Minimum Spanning Tree Xiaohui Bei MAS 714 August 31, 2017 Nanyang Technological University MAS 714 August 31, 2017 1 / 30 Minimum Spanning Trees (MST) A
Algorithms and Theory of Computation Lecture 5: Minimum Spanning Tree Xiaohui Bei MAS 714 August 31, 2017 Nanyang Technological University MAS 714 August 31, 2017 1 / 30 Minimum Spanning Trees (MST) A
CSE373: Data Structures & Algorithms Lecture 17: Minimum Spanning Trees. Dan Grossman Fall 2013
 CSE373: Data Structures & Algorithms Lecture 7: Minimum Spanning Trees Dan Grossman Fall 03 Spanning Trees A simple problem: Given a connected undirected graph G=(V,E), find a minimal subset of edges such
CSE373: Data Structures & Algorithms Lecture 7: Minimum Spanning Trees Dan Grossman Fall 03 Spanning Trees A simple problem: Given a connected undirected graph G=(V,E), find a minimal subset of edges such
CS 125 Section #6 Graph Traversal and Linear Programs 10/13/14
 CS 125 Section #6 Graph Traversal and Linear Programs 10/13/14 1 Depth first search 1.1 The Algorithm Besides breadth first search, which we saw in class in relation to Dijkstra s algorithm, there is one
CS 125 Section #6 Graph Traversal and Linear Programs 10/13/14 1 Depth first search 1.1 The Algorithm Besides breadth first search, which we saw in class in relation to Dijkstra s algorithm, there is one
Minimum Spanning Trees
 Minimum Spanning Trees Overview Problem A town has a set of houses and a set of roads. A road connects and only houses. A road connecting houses u and v has a repair cost w(u, v). Goal: Repair enough (and
Minimum Spanning Trees Overview Problem A town has a set of houses and a set of roads. A road connects and only houses. A road connecting houses u and v has a repair cost w(u, v). Goal: Repair enough (and
