Minimum Spanning Trees
|
|
|
- Myles Fowler
- 5 years ago
- Views:
Transcription
1 Miimum Spaig Trees
2 Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted graph with miimum total edge weight Applicatios ommuicatios etworks Trasportatio etworks A B 1 D 10 G E F 01 Goodrich, Tamassia, Goldwasser Miimum Spaig Trees
3 ycle Property ycle Property: Let T be a miimum spaig tree of a weighted graph G Let e be a edge of G that is ot i T ad let be the cycle formed by e with T f e For every edge f of, weight(f) weight(e) Proof: By cotradictio Replacig f with e yields a better spaig tree If weight(f) > weight(e) we ca get a spaig tree of smaller weight by replacig e with f f e 01 Goodrich, Tamassia, Goldwasser Miimum Spaig Trees
4 uts A cut i G is a partitio of the vertex set ito two parts U c Example: a w U- {a, e, b} w V {c, d, f} e Number of possible cuts w -1-1 Edges i the cut edges that coect vertices of oe partitio to vertices of the other partitio. b d V f Miimum Spaig Trees
5 Partitio Property Partitio Property: osider a partitio of the vertices of G ito subsets U ad V Let e be a edge of miimum weight across the partitio There is a miimum spaig tree of G cotaiig edge e Proof: Let T be a MST of G If T does ot cotai e, cosider the cycle formed by e with T ad let f be a edge of across the partitio By the cycle property, weight(f) weight(e) Thus, weight(f) = weight(e) We obtai aother MST by replacig f with e U U f e f e V Replacig f with e yields aother MST V 01 Goodrich, Tamassia, Goldwasser Miimum Spaig Trees
6 Prim-Jarik s Priciple Similar to Dijkstra s algorithm Utilizes the Partitio Property We pick a arbitrary vertex s ad we grow the MST as a cloud of vertices, startig from s A B D E F Miimum Spaig Trees
7 Prim-Jarik s Algorithm - Implemetatio Similar to Dijkstra s algorithm We pick a arbitrary vertex s ad we grow the MST as a cloud of vertices, startig from s We store with each vertex v label d(v) represetig the smallest weight of a edge coectig v to a vertex i the cloud At each step: We add to the cloud the vertex u outside the cloud with the smallest distace label We update the labels of the vertices adjacet to u 01 Goodrich, Tamassia, Goldwasser Miimum Spaig Trees
8 Example Miimum Spaig Trees B D A F E 0 B D A F E 0 B D A F E 0 B D A F E 0
9 Example (cotd.) A 0 B D F E A 0 B D F E Miimum Spaig Trees
10 Prim-Jarik Pseudo-code 01 Goodrich, Tamassia, Goldwasser Miimum Spaig Trees 10
11 Aalysis Graph operatios We cycle through the icidet edges oce for each vertex Label operatios We set/get the distace, paret ad locator labels of vertex z O(deg(z)) times Settig/gettig a label takes O(1) time Priority ueue operatios Each vertex is iserted oce ito ad removed oce from the priority ueue, where each isertio or removal takes O(log ) time The key of a vertex w i the priority ueue is modified at most deg(w) times, where each key chage takes O(log ) time Prim-Jarik s algorithm rus i O(( + m) log ) time provided the graph is represeted by the adjacecy list structure Recall that Σ v deg(v) = m The ruig time is O(m log ) sice the graph is coected 01 Goodrich, Tamassia, Goldwasser Miimum Spaig Trees 11
12 Kruskal s Priciple Greedy Algorithm greedily add the edge with miimum weight to the MST esure that the added edge does ot form a cycle 1 A B 11 E D G H F 01 Goodrich, Tamassia, Goldwasser Miimum Spaig Trees 1
13 Kruskal s Algorithm Maitai a partitio of the vertices ito clusters Iitially, sigle-vertex clusters Keep a MST for each cluster Merge closest clusters ad their MSTs A priority ueue stores the edges outside clusters Key: weight Elemet: edge At the ed of the algorithm Oe cluster ad oe MST 01 Goodrich, Tamassia, Goldwasser Miimum Spaig Trees 1
14 Example Miimum Spaig Trees 1 B G A F D 1 10 E H 11 B G A F D 1 10 E H 11 B G A F D 1 10 E H 11 B G A F D 1 10 E H 11
15 Example (cotd.) Miimum Spaig Trees 1 B G A F D 1 10 E H 11 B G A F D 1 10 E H 11 B G A F D 1 10 E H 11 four steps B G A F D 1 10 E H 11
16 Kruskal s Algorithm Miimum Spaig Trees 1
17 orrectess of Kruskal s Algorithm Let all the edges i the graph have distict weights Let the tree obtaied from Kruskal s algorithm cotai the edges g 1 <g <g <g -1 Let the Optimum MST have the edges f 1 <f <f...<f -1 Let i be the first edge that is differet betwee g s ad f s. w case1: g i <f i w case: f i <g i Merge Sort 1
18 Is the MST uiue? yes, if the edge weights are distict. o, otherwise. 01 Goodrich, Tamassia, Goldwasser Merge Sort 1
19 Data Structure for Kruskal s Algorithm The algorithm maitais a forest of trees A priority ueue extracts the edges by icreasig weight A edge is accepted it if coects distict trees We eed a data structure that maitais a partitio, i.e., a collectio of disjoit sets, with operatios: makeset(u): create a set cosistig of u fid(u): retur the set storig u uio(a, B): replace sets A ad B with their uio Total time O(m log + time for Uio* + time for Fid* m) 01 Goodrich, Tamassia, Goldwasser Miimum Spaig Trees 1
20 Kruskal s Algorithm Miimum Spaig Trees 0
21 Partitios with Uio-Fid Operatios makeset(x): reate a sigleto set cotaiig the elemet x ad retur the positio storig x i this set uio(a,b ): Retur the set A U B, destroyig the old A ad B fid(p): Retur the set cotaiig the elemet at positio p 01 Goodrich, Tamassia, Goldwasser Miimum Spaig Trees 1
22 List-based Implemetatio Each set is stored i a seuece represeted with a liked-list Each ode should store a object cotaiig the elemet ad a referece to the set ame 01 Goodrich, Tamassia, Goldwasser Miimum Spaig Trees
23 Aalysis of List-based Represetatio Uio mergig of two liked lists costat time Fid search through the list O() Total time O(m log )+O()+O(m). Miimum Spaig Trees
24 Tree-based Implemetatio Each elemet is stored i a ode, which cotais a poiter to a set ame A ode v whose set poiter poits back to v is also a set ame Each set is a tree, rooted at a ode with a selfreferecig set poiter For example: The sets 1,, ad : Goodrich, Tamassia, Goldwasser Miimum Spaig Trees 1
25 Uio-Fid Operatios To do a uio, simply make the root of oe tree poit to the root of the other To do a fid, follow set-ame poiters from the startig ode util reachig a ode whose set-ame poiter refers back to itself Goodrich, Tamassia, Goldwasser Miimum Spaig Trees
26 Uio-Fid Heuristic 1 Uio by size/rak: Whe performig a uio, make the root of smaller tree poit to the root of the larger Implies O( log ) time for performig uio-fid operatios: Each time we follow a poiter, we are goig to a subtree of size at least double the size of the previous subtree Thus, we will follow at most O(log ) poiters for ay fid Goodrich, Tamassia, Goldwasser Miimum Spaig Trees
27 Uio-Fid Heuristic Path compressio: After performig a fid, compress all the poiters o the path just traversed so that they all poit to the root Goodrich, Tamassia, Goldwasser Miimum Spaig Trees
28 Ed Semester Exam Thursday, November, losed book, closed otes exam Format Similar to the mid-semester exam - uestios w Defiitios/Examples w Algorithm Desig w Data Structure Desig w Data Structure Aalysis Write the solutio i the space provided i the aswer sheet. additioal sheets will be provided durig the exam. 01 Goodrich, Tamassia, Goldwasser Merge Sort
29 Searchig ad Search Tree Structures (chapter 11) Biary Search Trees isertio ad deletio operatios Balaced Search Trees AVL Trees operatios Red-Black Trees operatios (,) Trees multi-way search trees Splay Trees Splayig operatio
30 Strig Processig ad Dyamic Programmig (hapter 1) Patter Matchig Algorithms The Boyer-Moore Algorithm w Bad character ad good suffix rules The Kuth-Morris-Pratt algorithm w Failure fuctios Tries Stadard Tries ompressed Tries Suffix Tries w Prefix Matchig Huffma odig (covered before mid-semester) Dyamic Programmig Methodology 0
31 Sortig (hapter 1) Divide ad ouer Paradigm Merge Sort algorithm complexity aalysis Quick Sort/Radomized Quick Sort algorithm complexity aalysis I-Place partitioig Radix Sort Radix Exchage Sort Straight Radix Sort w Stable way Bucket sort 1
32 Graphs (hapter 1) Graphs Termiology Data Structures for represetig graphs edge list, adjacecy list, adjacecy map, adjacecy matrix Graph Traversals BFS, DFS Directed Graphs Trasitive losure Directed Acyclic Graphs topological order Shortest Paths weighted graphs, Dijkstra s algorithm, Bellma-ford algorithm Miimum Spaig Trees Prim-Jarik Algorithm, Kruskal s Algorithm, Data structure for Kruskal s algorithm.
33 Labs ad Quizzes - Lab - hopefully before this weeked - Lab - before the exam for sure. - Quiz - hopefully before this weeked - Quiz (tomorrow) - before this weeked
34 Good Luck
Minimum Spanning Trees
 Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Minimum Spanning Trees. Application: Connecting a Network
 Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Heaps. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
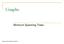 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs ORD SFO LAX DFW
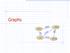 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
Greedy Algorithms. Interval Scheduling. Greedy Algorithms. Interval scheduling. Greedy Algorithms. Interval Scheduling
 Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
CIS 121 Data Structures and Algorithms with Java Spring Stacks and Queues Monday, February 12 / Tuesday, February 13
 CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
Graph Terminology and Representations
 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Graph Termiology ad Represetatios 2015 Goodrich ad Tamassia Graphs 1 Graphs A graph is
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Graph Termiology ad Represetatios 2015 Goodrich ad Tamassia Graphs 1 Graphs A graph is
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
Design and Analysis of Algorithms Notes
 Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #2: Randomized MST and MST Verification January 14, 2015
 15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
DATA STRUCTURES. amortized analysis binomial heaps Fibonacci heaps union-find. Data structures. Appetizer. Appetizer
 Data structures DATA STRUCTURES Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit distace, shortest paths, MST, max-flow,... amortized aalysis biomial heaps Fiboacci heaps uio-fid Dyamic
Data structures DATA STRUCTURES Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit distace, shortest paths, MST, max-flow,... amortized aalysis biomial heaps Fiboacci heaps uio-fid Dyamic
CSE 417: Algorithms and Computational Complexity
 Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Graphs ORD SFO LAX DFW. Lecture notes adapted from Goodrich and Tomassia. 3/14/18 10:28 AM Graphs 1
 Graphs 337 1843 1743 1233 802 Lecture otes adapted from Goodrich ad Tomassia 3/14/18 10:28 AM Graphs 1 Graph A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs
Graphs 337 1843 1743 1233 802 Lecture otes adapted from Goodrich ad Tomassia 3/14/18 10:28 AM Graphs 1 Graph A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Hash Tables. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015.
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Data Structures Week #5. Trees (Ağaçlar)
 Data Structures Week #5 Trees Ağaçlar) Trees Ağaçlar) Toros Gökarı Avrupa Gökarı October 28, 2014 Boraha Tümer, Ph.D. 2 Trees Ağaçlar) October 28, 2014 Boraha Tümer, Ph.D. 3 Outlie Trees Deiitios Implemetatio
Data Structures Week #5 Trees Ağaçlar) Trees Ağaçlar) Toros Gökarı Avrupa Gökarı October 28, 2014 Boraha Tümer, Ph.D. 2 Trees Ağaçlar) October 28, 2014 Boraha Tümer, Ph.D. 3 Outlie Trees Deiitios Implemetatio
Minimum Spanning Trees
 Minimum Spanning Trees 0 OS SO LX PV OR 0 JK 0 WI 00 W MI 00 Goodrich, Tamassia Minimum Spanning Trees Minimum Spanning Trees Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning
Minimum Spanning Trees 0 OS SO LX PV OR 0 JK 0 WI 00 W MI 00 Goodrich, Tamassia Minimum Spanning Trees Minimum Spanning Trees Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning
Major CSL Write your name and entry no on every sheet of the answer script. Time 2 Hrs Max Marks 70
 NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
Priority Queues. Binary Heaps
 Priority Queues Biary Heaps Priority Queues Priority: some property of a object that allows it to be prioritized with respect to other objects of the same type Mi Priority Queue: homogeeous collectio of
Priority Queues Biary Heaps Priority Queues Priority: some property of a object that allows it to be prioritized with respect to other objects of the same type Mi Priority Queue: homogeeous collectio of
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Data Structures Week #9. Sorting
 Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
CSE 2320 Notes 8: Sorting. (Last updated 10/3/18 7:16 PM) Idea: Take an unsorted (sub)array and partition into two subarrays such that.
 CSE Notes 8: Sortig (Last updated //8 7:6 PM) CLRS 7.-7., 9., 8.-8. 8.A. QUICKSORT Cocepts Idea: Take a usorted (sub)array ad partitio ito two subarrays such that p q r x y z x y y z Pivot Customarily,
CSE Notes 8: Sortig (Last updated //8 7:6 PM) CLRS 7.-7., 9., 8.-8. 8.A. QUICKSORT Cocepts Idea: Take a usorted (sub)array ad partitio ito two subarrays such that p q r x y z x y y z Pivot Customarily,
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
CS200: Hash Tables. Prichard Ch CS200 - Hash Tables 1
 CS200: Hash Tables Prichard Ch. 13.2 CS200 - Hash Tables 1 Table Implemetatios: average cases Search Add Remove Sorted array-based Usorted array-based Balaced Search Trees O(log ) O() O() O() O(1) O()
CS200: Hash Tables Prichard Ch. 13.2 CS200 - Hash Tables 1 Table Implemetatios: average cases Search Add Remove Sorted array-based Usorted array-based Balaced Search Trees O(log ) O() O() O() O(1) O()
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Administrative UNSUPERVISED LEARNING. Unsupervised learning. Supervised learning 11/25/13. Final project. No office hours today
 Admiistrative Fial project No office hours today UNSUPERVISED LEARNING David Kauchak CS 451 Fall 2013 Supervised learig Usupervised learig label label 1 label 3 model/ predictor label 4 label 5 Supervised
Admiistrative Fial project No office hours today UNSUPERVISED LEARNING David Kauchak CS 451 Fall 2013 Supervised learig Usupervised learig label label 1 label 3 model/ predictor label 4 label 5 Supervised
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
6.851: Advanced Data Structures Spring Lecture 17 April 24
 6.851: Advaced Data Structures Sprig 2012 Prof. Erik Demaie Lecture 17 April 24 Scribes: David Bejami(2012), Li Fei(2012), Yuzhi Zheg(2012),Morteza Zadimoghaddam(2010), Aaro Berstei(2007) 1 Overview Up
6.851: Advaced Data Structures Sprig 2012 Prof. Erik Demaie Lecture 17 April 24 Scribes: David Bejami(2012), Li Fei(2012), Yuzhi Zheg(2012),Morteza Zadimoghaddam(2010), Aaro Berstei(2007) 1 Overview Up
Algorithm Design Techniques. Divide and conquer Problem
 Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
Graphs. Shortest Path and Topological Sort
 Graphs Shortest Path ad Topological Sort Example Relatioal Networks School Friedship Network (from Moody 2001) Yeast Metabolic Network (from https://www.d.edu/~etworks/cell/) Terrorist Network (by Valdis
Graphs Shortest Path ad Topological Sort Example Relatioal Networks School Friedship Network (from Moody 2001) Yeast Metabolic Network (from https://www.d.edu/~etworks/cell/) Terrorist Network (by Valdis
of types having a total order and a predecessor and a successor function. In the
 J. Fuctioal Programmig 1 (1): 1{000, Jauary 1993 c 1993 Cambridge Uiversity Press 1 F U N C T I O N A L P E A R L S Diets for Fat Sets Marti Erwig FerUiversitat Hage, Praktische Iformatik IV 58084 Hage,
J. Fuctioal Programmig 1 (1): 1{000, Jauary 1993 c 1993 Cambridge Uiversity Press 1 F U N C T I O N A L P E A R L S Diets for Fat Sets Marti Erwig FerUiversitat Hage, Praktische Iformatik IV 58084 Hage,
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
Copyright 2016 Ramez Elmasri and Shamkant B. Navathe
 Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 19 Query Optimizatio Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio Query optimizatio Coducted by a query optimizer i a DBMS Goal:
Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 19 Query Optimizatio Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio Query optimizatio Coducted by a query optimizer i a DBMS Goal:
Examples and Applications of Binary Search
 Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
CIS 121. Introduction to Trees
 CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
Chapter 9. Greedy Technique. Copyright 2007 Pearson Addison-Wesley. All rights reserved.
 Chapter 9 Greedy Technique Copyright 2007 Pearson Addison-Wesley. All rights reserved. Greedy Technique Constructs a solution to an optimization problem piece by piece through a sequence of choices that
Chapter 9 Greedy Technique Copyright 2007 Pearson Addison-Wesley. All rights reserved. Greedy Technique Constructs a solution to an optimization problem piece by piece through a sequence of choices that
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
top() Applications of Stacks
 CS22 Algorithms ad Data Structures MW :00 am - 2: pm, MSEC 0 Istructor: Xiao Qi Lecture 6: Stacks ad Queues Aoucemets Quiz results Homework 2 is available Due o September 29 th, 2004 www.cs.mt.edu~xqicoursescs22
CS22 Algorithms ad Data Structures MW :00 am - 2: pm, MSEC 0 Istructor: Xiao Qi Lecture 6: Stacks ad Queues Aoucemets Quiz results Homework 2 is available Due o September 29 th, 2004 www.cs.mt.edu~xqicoursescs22
Minimum Spanning Trees
 Minimum Spanning Trees 04 6 33 49 PVD 1 40 146 61 14 15 0 Minimum Spanning Trees 1 Minimum Spanning Trees ( 1.) Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning tree 1
Minimum Spanning Trees 04 6 33 49 PVD 1 40 146 61 14 15 0 Minimum Spanning Trees 1 Minimum Spanning Trees ( 1.) Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning tree 1
BST Sequence of Operations
 Splay Trees Problems with BSTs Because the shape of a BST is determied by the order that data is iserted, we ru the risk of trees that are essetially lists 12 21 20 32 24 37 15 40 55 56 77 2 BST Sequece
Splay Trees Problems with BSTs Because the shape of a BST is determied by the order that data is iserted, we ru the risk of trees that are essetially lists 12 21 20 32 24 37 15 40 55 56 77 2 BST Sequece
ECE4050 Data Structures and Algorithms. Lecture 6: Searching
 ECE4050 Data Structures ad Algorithms Lecture 6: Searchig 1 Search Give: Distict keys k 1, k 2,, k ad collectio L of records of the form (k 1, I 1 ), (k 2, I 2 ),, (k, I ) where I j is the iformatio associated
ECE4050 Data Structures ad Algorithms Lecture 6: Searchig 1 Search Give: Distict keys k 1, k 2,, k ad collectio L of records of the form (k 1, I 1 ), (k 2, I 2 ),, (k, I ) where I j is the iformatio associated
quality/quantity peak time/ratio
 Semi-Heap ad Its Applicatios i Touramet Rakig Jie Wu Departmet of omputer Sciece ad Egieerig Florida Atlatic Uiversity oca Rato, FL 3343 jie@cse.fau.edu September, 00 . Itroductio ad Motivatio. relimiaries
Semi-Heap ad Its Applicatios i Touramet Rakig Jie Wu Departmet of omputer Sciece ad Egieerig Florida Atlatic Uiversity oca Rato, FL 3343 jie@cse.fau.edu September, 00 . Itroductio ad Motivatio. relimiaries
Analysis of Algorithms
 Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
Σ P(i) ( depth T (K i ) + 1),
 EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
Data Structures and Algorithms Part 1.4
 1 Data Structures ad Algorithms Part 1.4 Werer Nutt 2 DSA, Part 1: Itroductio, syllabus, orgaisatio Algorithms Recursio (priciple, trace, factorial, Fiboacci) Sortig (bubble, isertio, selectio) 3 Sortig
1 Data Structures ad Algorithms Part 1.4 Werer Nutt 2 DSA, Part 1: Itroductio, syllabus, orgaisatio Algorithms Recursio (priciple, trace, factorial, Fiboacci) Sortig (bubble, isertio, selectio) 3 Sortig
Minimum Spanning Trees
 Minimum Spanning Trees 04 6 33 135 49 1 40 146 61 14 15 0 111 34 Minimum Spanning Trees 1 Minimum Spanning Trees ( 1.) Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning
Minimum Spanning Trees 04 6 33 135 49 1 40 146 61 14 15 0 111 34 Minimum Spanning Trees 1 Minimum Spanning Trees ( 1.) Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning
1/27/12. Vectors: Outline and Reading. Chapter 6: Vectors, Lists and Sequences. The Vector ADT. Applications of Vectors. Array based Vector: Insertion
 Chater 6: ectors, Lists ad Sequeces ectors: Outlie ad Readig The ector ADT ( 6.1.1) Array-based imlemetatio ( 6.1.2) Nacy Amato Parasol Lab, Det. CSE, Texas A&M Uiversity Ackowledgemet: These slides are
Chater 6: ectors, Lists ad Sequeces ectors: Outlie ad Readig The ector ADT ( 6.1.1) Array-based imlemetatio ( 6.1.2) Nacy Amato Parasol Lab, Det. CSE, Texas A&M Uiversity Ackowledgemet: These slides are
EFFICIENT MULTIPLE SEARCH TREE STRUCTURE
 EFFICIENT MULTIPLE SEARCH TREE STRUCTURE Mohammad Reza Ghaeii 1 ad Mohammad Reza Mirzababaei 1 Departmet of Computer Egieerig ad Iformatio Techology, Amirkabir Uiversity of Techology, Tehra, Ira mr.ghaeii@aut.ac.ir
EFFICIENT MULTIPLE SEARCH TREE STRUCTURE Mohammad Reza Ghaeii 1 ad Mohammad Reza Mirzababaei 1 Departmet of Computer Egieerig ad Iformatio Techology, Amirkabir Uiversity of Techology, Tehra, Ira mr.ghaeii@aut.ac.ir
Copyright 2016 Ramez Elmasri and Shamkant B. Navathe
 Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 18 Strategies for Query Processig Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio DBMS techiques to process a query Scaer idetifies
Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 18 Strategies for Query Processig Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio DBMS techiques to process a query Scaer idetifies
Chapter 11. Friends, Overloaded Operators, and Arrays in Classes. Copyright 2014 Pearson Addison-Wesley. All rights reserved.
 Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Computers and Scientific Thinking
 Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
Solution printed. Do not start the test until instructed to do so! CS 2604 Data Structures Midterm Spring, Instructions:
 CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Graph Algorithms shortest paths, minimum spanning trees, etc.
 SFO ORD LAX Graph Algorithms shortest paths, minimum spanning trees, etc. DFW Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with
SFO ORD LAX Graph Algorithms shortest paths, minimum spanning trees, etc. DFW Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with
CMPT 125 Assignment 2 Solutions
 CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Basic allocator mechanisms The course that gives CMU its Zip! Memory Management II: Dynamic Storage Allocation Mar 6, 2000.
 5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Image Segmentation EEE 508
 Image Segmetatio Objective: to determie (etract) object boudaries. It is a process of partitioig a image ito distict regios by groupig together eighborig piels based o some predefied similarity criterio.
Image Segmetatio Objective: to determie (etract) object boudaries. It is a process of partitioig a image ito distict regios by groupig together eighborig piels based o some predefied similarity criterio.
Computer Science Foundation Exam. August 12, Computer Science. Section 1A. No Calculators! KEY. Solutions and Grading Criteria.
 Computer Sciece Foudatio Exam August, 005 Computer Sciece Sectio A No Calculators! Name: SSN: KEY Solutios ad Gradig Criteria Score: 50 I this sectio of the exam, there are four (4) problems. You must
Computer Sciece Foudatio Exam August, 005 Computer Sciece Sectio A No Calculators! Name: SSN: KEY Solutios ad Gradig Criteria Score: 50 I this sectio of the exam, there are four (4) problems. You must
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Sorting 9/15/2009. Sorting Problem. Insertion Sort: Soundness. Insertion Sort. Insertion Sort: Running Time. Insertion Sort: Soundness
 9/5/009 Algorithms Sortig 3- Sortig Sortig Problem The Sortig Problem Istace: A sequece of umbers Objective: A permutatio (reorderig) such that a ' K a' a, K,a a ', K, a' of the iput sequece The umbers
9/5/009 Algorithms Sortig 3- Sortig Sortig Problem The Sortig Problem Istace: A sequece of umbers Objective: A permutatio (reorderig) such that a ' K a' a, K,a a ', K, a' of the iput sequece The umbers
CSC165H1 Worksheet: Tutorial 8 Algorithm analysis (SOLUTIONS)
 CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
A graphical view of big-o notation. c*g(n) f(n) f(n) = O(g(n))
 ca see that time required to search/sort grows with size of We How do space/time eeds of program grow with iput size? iput. time: cout umber of operatios as fuctio of iput Executio size operatio Assigmet:
ca see that time required to search/sort grows with size of We How do space/time eeds of program grow with iput size? iput. time: cout umber of operatios as fuctio of iput Executio size operatio Assigmet:
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
Graphs Weighted Graphs. Reading: 12.5, 12.6, 12.7
 Graphs Weighted Graphs Reading: 1.5, 1.6, 1. Weighted Graphs, a.k.a. Networks In a weighted graph, each edge has an associated numerical value, called the weight or cost of the edge Edge weights may represent,
Graphs Weighted Graphs Reading: 1.5, 1.6, 1. Weighted Graphs, a.k.a. Networks In a weighted graph, each edge has an associated numerical value, called the weight or cost of the edge Edge weights may represent,
Elementary Data Structures. The Stack ADT ( 2.1.1) Applications of Stacks. Stacks, Queues, Vectors, Lists & Sequences Trees
 Elemetary Data Structures Stacks, Queues, ectors, Lists & Sequeces Trees The Stack ADT ( 2..) The Stack ADT stores arbitrary objects Isertios ad deletios follow the last-i first-out scheme Thik of a sprig-loaded
Elemetary Data Structures Stacks, Queues, ectors, Lists & Sequeces Trees The Stack ADT ( 2..) The Stack ADT stores arbitrary objects Isertios ad deletios follow the last-i first-out scheme Thik of a sprig-loaded
Data Structures and Algorithms. Analysis of Algorithms
 Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
Name of the Student: Unit I (Logic and Proofs) 1) Truth Table: Conjunction Disjunction Conditional Biconditional
 SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
1. SWITCHING FUNDAMENTALS
 . SWITCING FUNDMENTLS Switchig is the provisio of a o-demad coectio betwee two ed poits. Two distict switchig techiques are employed i commuicatio etwors-- circuit switchig ad pacet switchig. Circuit switchig
. SWITCING FUNDMENTLS Switchig is the provisio of a o-demad coectio betwee two ed poits. Two distict switchig techiques are employed i commuicatio etwors-- circuit switchig ad pacet switchig. Circuit switchig
Week 12: Minimum Spanning trees and Shortest Paths
 Agenda: Week 12: Minimum Spanning trees and Shortest Paths Kruskal s Algorithm Single-source shortest paths Dijkstra s algorithm for non-negatively weighted case Reading: Textbook : 61-7, 80-87, 9-601
Agenda: Week 12: Minimum Spanning trees and Shortest Paths Kruskal s Algorithm Single-source shortest paths Dijkstra s algorithm for non-negatively weighted case Reading: Textbook : 61-7, 80-87, 9-601
Pattern Recognition Systems Lab 1 Least Mean Squares
 Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Minimum Spanning Trees
 Minimum Spanning Trees 04 6 33 135 49 PVD 1 40 146 61 JFK 14 15 0 111 34 Minimum Spanning Trees 1 Outline and Reading Minimum Spanning Trees Definitions A crucial fact The Prim-Jarnik Algorithm Kruskal's
Minimum Spanning Trees 04 6 33 135 49 PVD 1 40 146 61 JFK 14 15 0 111 34 Minimum Spanning Trees 1 Outline and Reading Minimum Spanning Trees Definitions A crucial fact The Prim-Jarnik Algorithm Kruskal's
Chapter 9. Pointers and Dynamic Arrays. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
2. ALGORITHM ANALYSIS
 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times Lecture slides by Kevi Waye Copyright 2005 Pearso-Addiso
2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times Lecture slides by Kevi Waye Copyright 2005 Pearso-Addiso
The Magma Database file formats
 The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
How do we evaluate algorithms?
 F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
Spanning Maximal Planar Subgraphs of Random Graphs
 Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
Priority Queues and Heaps (Ch 5.5) Huffman Coding Trees (Ch 5.6) Binary Search Trees (Ch 5.4) Lec 5: Binary Tree. Dr. Patrick Chan
 ata Structure hapter Biary Trees r. Patrick ha School of om puter Sciece ad Egieerig South hia Uiversity of Techolog y Recursio recursio is a procedure which calls itself The recursive procedure call must
ata Structure hapter Biary Trees r. Patrick ha School of om puter Sciece ad Egieerig South hia Uiversity of Techolog y Recursio recursio is a procedure which calls itself The recursive procedure call must
Prim & Kruskal Algorithm
 Prim & Kruskal Algorithm Minimum Spanning Tree Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning tree 1 10 PIT Spanning subgraph that is itself a (free) tree Minimum spanning
Prim & Kruskal Algorithm Minimum Spanning Tree Spanning subgraph Subgraph of a graph G containing all the vertices of G Spanning tree 1 10 PIT Spanning subgraph that is itself a (free) tree Minimum spanning
THE PROBLEM THE PROBLEM (1) THE PROBLEM (2) THE MINIMUM ENERGY BROADCAST PROBLEM THE MINIMUM SPANNING TREE
 THE MINIMUM ENERGY BROADCAST PROBLEM I.E. THE MINIMUM SPANNING TREE PROBLEM Prof. Tiziaa Calamoeri Network Algorithms A.y. 05/ THE PROBLEM THE PROBLEM () THE PROBLEM () What does it meas sufficietly close?!
THE MINIMUM ENERGY BROADCAST PROBLEM I.E. THE MINIMUM SPANNING TREE PROBLEM Prof. Tiziaa Calamoeri Network Algorithms A.y. 05/ THE PROBLEM THE PROBLEM () THE PROBLEM () What does it meas sufficietly close?!
Using the Keyboard. Using the Wireless Keyboard. > Using the Keyboard
 1 A wireless keyboard is supplied with your computer. The wireless keyboard uses a stadard key arragemet with additioal keys that perform specific fuctios. Usig the Wireless Keyboard Two AA alkalie batteries
1 A wireless keyboard is supplied with your computer. The wireless keyboard uses a stadard key arragemet with additioal keys that perform specific fuctios. Usig the Wireless Keyboard Two AA alkalie batteries
A New Morphological 3D Shape Decomposition: Grayscale Interframe Interpolation Method
 A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
IMP: Superposer Integrated Morphometrics Package Superposition Tool
 IMP: Superposer Itegrated Morphometrics Package Superpositio Tool Programmig by: David Lieber ( 03) Caisius College 200 Mai St. Buffalo, NY 4208 Cocept by: H. David Sheets, Dept. of Physics, Caisius College
IMP: Superposer Itegrated Morphometrics Package Superpositio Tool Programmig by: David Lieber ( 03) Caisius College 200 Mai St. Buffalo, NY 4208 Cocept by: H. David Sheets, Dept. of Physics, Caisius College
Chapter 1. Introduction to Computers and C++ Programming. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 1 Itroductio to Computers ad C++ Programmig Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 1.1 Computer Systems 1.2 Programmig ad Problem Solvig 1.3 Itroductio to C++ 1.4 Testig
Chapter 1 Itroductio to Computers ad C++ Programmig Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 1.1 Computer Systems 1.2 Programmig ad Problem Solvig 1.3 Itroductio to C++ 1.4 Testig
Lower Bounds for Sorting
 Liear Sortig Topics Covered: Lower Bouds for Sortig Coutig Sort Radix Sort Bucket Sort Lower Bouds for Sortig Compariso vs. o-compariso sortig Decisio tree model Worst case lower boud Compariso Sortig
Liear Sortig Topics Covered: Lower Bouds for Sortig Coutig Sort Radix Sort Bucket Sort Lower Bouds for Sortig Compariso vs. o-compariso sortig Decisio tree model Worst case lower boud Compariso Sortig
Chapter 8. Strings and Vectors. Copyright 2014 Pearson Addison-Wesley. All rights reserved.
 Chapter 8 Strigs ad Vectors Overview 8.1 A Array Type for Strigs 8.2 The Stadard strig Class 8.3 Vectors Slide 8-3 8.1 A Array Type for Strigs A Array Type for Strigs C-strigs ca be used to represet strigs
Chapter 8 Strigs ad Vectors Overview 8.1 A Array Type for Strigs 8.2 The Stadard strig Class 8.3 Vectors Slide 8-3 8.1 A Array Type for Strigs A Array Type for Strigs C-strigs ca be used to represet strigs
A New Bit Wise Technique for 3-Partitioning Algorithm
 Special Issue of Iteratioal Joural of Computer Applicatios (0975 8887) o Optimizatio ad O-chip Commuicatio, No.1. Feb.2012, ww.ijcaolie.org A New Bit Wise Techique for 3-Partitioig Algorithm Rajumar Jai
Special Issue of Iteratioal Joural of Computer Applicatios (0975 8887) o Optimizatio ad O-chip Commuicatio, No.1. Feb.2012, ww.ijcaolie.org A New Bit Wise Techique for 3-Partitioig Algorithm Rajumar Jai
On Sorting an Intransitive Total Ordered Set Using Semi-Heap
 O Sortig a Itrasitive Total Ordered Set Usig Semi-Heap Jie Wu Departmet of Computer Sciece ad Egieerig Florida Atlatic Uiversity Boca Rato, FL jie@cse.fau.edu Abstract The problem of sortig a itrasitive
O Sortig a Itrasitive Total Ordered Set Usig Semi-Heap Jie Wu Departmet of Computer Sciece ad Egieerig Florida Atlatic Uiversity Boca Rato, FL jie@cse.fau.edu Abstract The problem of sortig a itrasitive
Minimum Spanning Tree
 Minimum Spanning Tree 1 Minimum Spanning Tree G=(V,E) is an undirected graph, where V is a set of nodes and E is a set of possible interconnections between pairs of nodes. For each edge (u,v) in E, we
Minimum Spanning Tree 1 Minimum Spanning Tree G=(V,E) is an undirected graph, where V is a set of nodes and E is a set of possible interconnections between pairs of nodes. For each edge (u,v) in E, we
