Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein

Transcription

1 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig the size of maximal matchigs (ad vertex covers) i a subliear umber of queries.. Implemetatio of the oracle.. Approximatig the average degree of a graph. Vertex cover approximatio usig Maximal matchig Cotiuig our effort from the last lecture to compute the vertex cover of a graph by simulatig a distributed algorithm we will try get a approximatio usig the graph maximal matchig.. Maximal matchig.. Matchig Matchig (M) of a graph G = (V, E) is a set of such that o two edges share a commo vertex... Maximal VS Maximum Maximal matchig (M M) is a matchig that caot be icreased without violatig the matchig. Maximum matchig is a matchig with maximum umber of edges. Example cosider the followig graph 0 Possible maximal matchig (red edges) 0 Possible maximum matchig (red edges) 0. Relatio betwee vertex cover ad M M Remider: V C is a set of vertices such that each edge of the graph is icidet to at least oe vertex of the set. V C MM : (u, v) MM at least u or v is i the V C (defiitio of V C). Sice the edges i the MM do t share a vertex it is clear that V C MM V C MM : We will create a V C from the MM. (u, v) MM we will add u, v to the V C. Oce we fiished

2 costructig the V C if exists a edge (u, v ) that is ot covered by the V C the we could have added this edge to the MM without violatig the Matchig cotradictig the assumptio of MM. We costructed a V C of size MM thus the optimal is less tha that. Assumig we ca compute the MM we get a approximatio to the V C. The algorithm that we will see will fid a approximatio to the MM i sub liear time thus yieldig a approximatio to the V C.. Greedy M M algorithm Data: G = (V, E) Result: M M ; for (u, v) E do if u or v is matched the M M (u, v) ed ed Algorithm : Maximal matchig algorithm Claim. M is a maximal matchig Proof: Lets assume that exists a edge e = (u, v) such that e / M ad {e} M is a matchig. Lets simulate the algorithm up to the poit that the algorithm ecouters the edge, sice M {e} is a matchig the algorithm will add the edge to M with cotradictio to the assumptio.. Oracle reductio framework Assume that we are give a oracle O such that give a edge e the oracle outputs "YES" if e MM ad "NO" else. Give that we have such a oracle we ca build a sub liear algorithm to estimate the MM. Data: G = (V, E), O Result: estimate of MM S 8 ɛ odes sampled iid; v S, defie X v ; for v S do if w N(v) such that O((v, w)) = "YES" the X v = else X v = 0 ed ed Output (( Xv S )) + ɛ ; Algorithm : Maximal matchig algorithm Claim. The expected output of the algorithm is MM + ɛ Proof: E[ X v ] = E[X v ] E[X v ] = S E[X v ] We sample iid the odes from the graph thus the probability of samplig a ode i the maximal matchig is MM. S E[X v ] = S MM

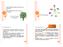
3 Plugig the result to the output of the algorithm E[(( S E[ X v )) S + ɛ )] = X v ] + ɛ = S E[ X v ] + ɛ S MM + ɛ S = MM + ɛ.. Boudig the error probability X v are idetically distributed Beroulli radom variables with p = MM probability > e ɛ S (p ɛ) S < X v < (p + ɛ) S therefore by Hoeffdig s iequality with ( MM ɛ) S < Takig S to be 0 ɛ yields that with probability > Sice the algorithm adds a additioal ɛ MM ɛ < S X v < ( MM + ɛ) S X v < MM + ɛ to the output result MM < S This completes the error boudig of the algorithm. Implemetatio of the oracle X v < MM + ɛ Remark. Give a order o the edges of the graph, the greedy sequetial algorithm for maximal matchig (defied earlier) determiistically outputs a uique maximal matchig. Defiitio. Give a order o the edges, the depedecy chai of edge e is the set of all adjacet edges to e that precede it i the order. Note that i the greedy sequetial algorithm, the decisio whether to iclude a edge i the matchig or ot depeds oly o the depedecy chai of this edge. Hece to implemet a oracle O M we ca cosider oly the depedecy chai of the queried edge ad check recursively whether the depedecy chai edges are i the matchig. The problem with this approach is that the depedecy chais ca be very log: Figure : Example for two differet rakigs that result i log depedecy chais. Note that i both cases i order to determie whether the edge marked e belogs to M the algorithm must recursively check all edges precedig it i the rakig To overcome the difficulty of log depedecy chais, we assig a radom orderig (rakig) to the edges. Formally, defie the rakig as r : E [0, ). We also assume edges have distict rakigs: e, e E, r(e) r(e ).

4 We ll see later that with this radom order the expected size of the depedecy chais is ot too log. The implemetatio of the oracle is as follows: Iput : A edge e ad rakig r : E [0, ) Output: "Yes" if e M ad "No" otherwise for every edge e adjacet to e do if r(e ) < r(e) the recursively ru this algorithm o e ; if received that e M the retur "No"; ed ed ed retur "Yes"; Algorithm : Oracle for determiig whether e M The correctess of this algorithm follows directly from the correctess of the greedy algorithm. Figure is a example of a executio of the algorithm. Claim. The expected umber of queries performed by the oracle algorithm is O( O(d) ). Corollary. The total query complexity of the algorithm usig this oracle is O( O(d) ɛ ) Proof of claim. For each e E cosider the tree of queries that are recursively called by the algorithm. The root of this tree is e, ad the childre of each ode i the tree are its adjacet edges (we allow edges to appear several times i the tree). By the algorithm, the paths i the tree that are explored are mootoe decreasig i rakig. Give a. The values of the edges are chose i.i.d from r : E [0, ). Therefore, each permutatio of the k + edges occurs with equal probability. Oly oe of these permutatios (r gives distict values for each edge) is mootoe decreasig, which meas that: path of legth k (correspodig to k + edges) the probability that it is mootoe decreasig is (k+)! P r[a path of legth k is explored] = (k + )! Every edge has up to d eighbors, so the umber of odes i the k-th level of the tree is bouded by (d) k. Therefore: which implies that: E[# of paths explored at distace k] E[total # of edges explored] k=0 (d)k (k + )! (d) k (k + )! ed d For each ode we must check all of its eighbors (of which there may be d), so the expected sample complexity of the oracle algorithm is bouded by: which is of course also O( O(d) ), as eeded. d E[total # of edges explored] = O(e d ) Remark. Our algorithm uses O() samples i the worst case. We ca boud the sample complexity by forcibly cuttig off the oracle (ad outputtig radomly) after it has used c O(d) samples for some costat c, which by Markov s iequality will esure that there is a low probability of this happeig, ad hece a low probability of error. Remark. There are some recet improvemets to this algorithm that have almost liear sample complexity i d.

5 Figure : The oracle will determie whether the edge 0. (bolded) is part of the maximal matchig. We ll cosider all its adjacet edges: this edge comes after 0., so we ll skip it we ll check it recursively: this edge comes after 0., so we ll skip it this edge comes after 0., so we ll skip it. 0. is part of the maximal matchig. 0. is part of the maximal matchig so 0. is t part of the maximal matchig we ll check it recursively: this edge comes after 0., so we ll skip it we ll check it recursively: this edge comes after 0., so we ll skip it this edge comes after 0., so we ll skip it. 0. is part of the maximal matchig. 0. is part of the maximal matchig so 0. is t part of the maximal matchig.. All the adjacet edges of 0. are t part of the maximal matchig, therefore 0. is part of the maximal matchig. Approximatig average degree For a give graph G, we would like to approximate the average degree, which is defied to be d = We will make several assumptios:. G is a simple graph: it does ot cotai multiple edges or loops.. G is ot "ultraspare", meaig: E = m = Ω(). v V d(v).. Our model is slightly differet to the graph model see before, which will allow us to make stroger queries: (a) Degree queries: retur d(v) for iput vertex v. (b) Neighbor queries: for iput vertex v ad idex j, retur the j-th eighbor of v.

6 A attempt at a aive solutio Radomly choose v,..., v s vertices, ad output s s i= d(v i). The problem with this approach is that for certai iput graphs the variace ca be very high. Cosider for example the star graph o vertices, where oe vertex has eighbors ad all the rest have oe eighbor. The average degree is which approaches. However, ay sample that we choose that does t happe to cotai the ceter will retur a estimate of, which is a bad multiplicative error. This allow us to coclude that we must make Ω() queries for this approach to be effective. I the ext lecture, we ll see a subliear algorithm for approximatig the average degree. 6