15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #2: Randomized MST and MST Verification January 14, 2015
|
|
|
- Winifred Matthews
- 5 years ago
- Views:
Transcription
1 15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets: Karger-Klai-Tarja algorithm ad MST Verificatio. Our settig is the same as last lecture. Let G = (V, E to be a simple graph with vertex set V ad edge set E, where V = ad E = m. We also assume that all the weights of edges are distict. I Lecture 1 we saw some determiistic algorithms fidig MST i time O(m log, O(m + log ad O(m log. Our goal i this lecture is to fid MST i the graph i O(m + expected time. Remember the two rules we metioed i Lecture 1: cut rule ad cycle rule. 1.1 Heavy & light Figure 2.1: Example of heavy ad light edges Take ay tree 1 i a graph. For example, i Figure 2.1 we pick the tree with black edges. The tree might ot be a MST, or eve ot be coected (a forest. Now look at ay other edge i the graph. The blue edge o the right side is heavier tha ay other edge i the cycle. The by cycle rule this edge will ot be i the MST of the graph. What about the red edge o the left side? This edge is ot the heaviest edgei the cycle, ad i fact this edge appears i the MST of the graph. Therefore we ca discard some edges which will ever appear i the MST based o ay give tree of a graph. Defiitio 2.1. Let T be a forest of graph G ad e E(G. If e create a cycle whe addig to T ad e is heaviest edge i the cycle, the we call edge e is T -heavy. Otherwise, edge e is T -light. Every edge should be either T -heavy or T -light. Notice that if a edge e does ot make a cycle, the e is T -light. If edge e is i the tree T, edge e is also T -light. I Figure 2.1, the red edge is T -light, the blue edge is T -heavy, ad all black edges are T -light. Fact 2.2. Edge e is T -light iff e MST(T {e}. 1 Here whe we talk about trees, i fact we mea trees or forests. Ad MST meas the miimum spaig forest if the graph is ot coected. 1
2 Fact 2.3. If T is a MST of G the edge e E(G is T -light iff e T. Therefore our idea is that pick a good tree/forest T, fid all the T -heavy edges ad get rid of them. Hopefully the umber of edges remaied is small. The we will fid the MST i remaiig edges. We wat to fid some tree T such that there are a lot of T -heavy edges. 1.2 Magic Blackbox How should we fid all the T -heavy edges? Here we first assume a magic blackbox: MST Verificatio. We ll show how to implemet MST Verificatio later. Theorem 2.4 (MST Verificatio. Give a tree T G, we ca output all the T -light edges i E(G i time O( V + E. This woderful blackbox ca output all the T -light edges i liear time. 2 Karger-Klai-Tarja Algorithm Suppose a graph G = (V, E has vertices ad m edges. KKT(G as followig. Here we will preset the algorithm 1. Ru 3 rouds of Borůvka s Algorithm o G to get a graph G = (V, E with /8 vertices ad m m edges. 2. E 1 a radom sample of edges E of G where each edge is picked idepedetly with probability 1/2. 3. T 1 KKT(G 1 = (V, E E 2 all the T 1 -light edges i E. 5. T 2 KKT(G 2 = (V, E Retur T 2 (combie with the edges chose i Step 1. Here the idea is that we radomly choose half of the edges ad fid the MST o those edges. We hope this tree T will have a lot of T -heavy edges therefore we ca discard these edges ad fid the MST o the remaiig graph. Theorem 2.5. KKT algorithm will retur MST(G. Proof. We ca prove it by iductio. For the basic case it is trivial, because we will fid the MST i Step 1. Otherwise i Step 3 we fid a MST T 1 of graph G 1, ad i E 2 just discard all the T 1 -heavy edges from the etire edges E (ot oly from E 1!! which are ot possible to be i the MST of G. Or i other words, MST(G E 2. Therefore what Step 5 returs is the MST of G 2, which is also the MST of G. Combie it with the edges we choose i Step 1, we get the MST of graph G. The key idea of this proof is that discardig heavy edges of ay tree i a graph will remai MST the same. Now we eed to deal with the complexity. 2
3 Claim 2.6. E[#E 1 ] = 1 2 m. This claim is trivial sice we pick each edge with probability 1/2. Claim 2.7. E[#E 2 ] 2. This meas graph G 2 will be hopefully very sparse. Figure 2.2: Illustratio of aother order of coi tossig How should we aalysis E[#E 2 ]? I Step 2 of KKG algorithm, we first flip a coi o each edge, the take all the edges tossig head ad fially i Step 3 we use KKG algorithm o this ew graph to get the MST of G 1. Let s thik of this process i aother order. First of all, Step 3 is to calculate the MST of the ew graph. It does ot matter if we use KKG algorithm or some other method, ad we will still get the same MST. The istead of first flippig cois for all edges the calculatig the MST. We ca do these two thigs simultaeously: We flip the cois for the edges i a icreasig order by weight, ad do Kruskal immediately after ay edge tossig head. We defie a coi toss is useful, if Kruskal algorithm would like to add this edge i the MST, ad defie a coi toss is useless if ot. For example, Figure 2.2(a gives a graph with coi toss result. The solid edges are the edges with tossig head, ad the dashed edges are the edges with tossig tail. Figure 2.2(b is the MST o all edges tossig head. Now let s check the usefuless of all these coi flips, as i Figure 2.2(c. I the begiig the MST is a empty set. The the coi flip of the first edge is useful, sice it should be added ito the MST. The tossig result is head, so we add this edge ito MST. The coi flip of the secod edge is useful, sice it should be added ito the MST. However the tossig result is tail, so sadly we ca ot add this edge ito MST. The coi flip of the third, forth, fifth edges are all useful, ad the tossig result are all head, so we add all of them ito the MST. The coi toss of sixth edge is useless, because we will ot add this edge ito MST sice it will creat a cycle, so is the seveth edge. Claim 2.8. T 1 = MST(G 1. e E is T 1 -light if ad oly if the coi flip of e is useful. 3
4 Proof. If the coi flip of e is useful, the at the momet we flip the coi by addig e ito the MST there is o cycle, which meas either e T 1 (coi tossig head, or there is o cycle i T 1 {e}, or edge e is ot the heaviest edge i the cycle of T 1 {e}. I ay of these cases, edge e is T 1 -light. O the other had, if the coi flip of e is useless, the at the momet we flip the coi there would be a cycle if we add e ito the MST, therefore edge e is T 1 -heavy. The we ca prove Claim 2.7. Proof of Claim 2.7. E[#E 2 ] = E[#useful coi flips] 1 1/2 2 The first iequality holds sice by each useful coi flip we may add a edge ito the MST of G 1 with probability 1/2, ad the fial T 1 = MST (G 1 has at most 1 edges. Therefore the expectatio of useful coi flips is at most 2( 1 2. Theorem 2.9. KKT(G = (V, E ca retur the MST i time O(m +. Proof. Let X G be the expect ruig time o graph G, ad X m, := max {X G} G=(V,E, V =, E =m I KKG algorithm, Step 1, 2, 4 ad 6 will be doe i liear time, so we assume the time cost of Step 1, 2, 4 ad 6 is at most cm. Step 3 will sped time X G1, ad Step 5 will sped time X G2. The we have X G cm + X G1 + X G2 cm + X m1, + X m 2, Here we assume that X m, c(2m +, the X G = cm + E[c(2m 1 + ] + E[c(2m 2 + ] c(m + m + 6 c(2m + The first iequality holds because E[m 1 ] 1 2 m ad E[m 2 ] 2. The secod iequality holds because /8 ad m m. 3 MST Verificatio Now we come back the implemet of the magic blackbox. Here we oly cosider about the trees (ot forests. Here we refie Theorem 2.4 as followig. Theorem 2.10 (MST Verificatio. Give T = (V, E where V = ad m pairs of vertices (u i, v i, we ca fid the heaviest edge o the path i T from u i to v i for all i i O(m + time. Tarja fid a algorithm i Time O(mα(m, usig Uio-Fid. Komlos fid how to do it with O(m + comparisos. Dixo-Rauch-Tarja o RAM machie with O(m. Here we will give the idea of Komlos. 4
5 Figure 2.3: Illustratio of balacig a tree 3.1 Balace the tree Suppose T = (V, E is a tree o vertices, ad we ru Boruvka s algorithm o T. (Let V 1 = V be the origial vertices at the begiig of roud 1, V i be the vertices i roud i, ad say there are L rouds so that V L+1 = 1. We build a tree T as follows: the vertices are the uio of all the V i. There is a edge from v V i to w V i+1 if the vertex v belogs to a compoet i roud i ad that is cotracted to form w V i+1 ; the weight of this edge (v, w is the mi-weight edge out of v i roud i. (Note that all vertices i V are ow leaves i T. Figure 2.3 shows a example of balacig a tree. Fact For odes u, v i a tree T, let maxwt T (u, v be the maximum weight of a edge o the (uique path betwee u, v i the tree T. For all u, v V, we have maxwt T (u, v = maxwt T (u, v This is a problem i Homework 1. I Figure 2.3, we have maxwt T (v 1, v 7 is 7 which is the weight of edge (v 4, v 6. We ca check that maxwt T (v 1, v 7 is also 7. Fact T has at most log 2 layers sice each vertex has at least 2 childre ad all leaves of T are at the bottom (the same level.. Here we ca make a balaced tree T based o tree T with some good properties. The we ca just query the heaviest edges of vertex pairs i tree T istead of T. Aother trick is that we ca assume that all queries are acestor-descet queries if we ca fid the least commo acestor quickly. Theorem 2.13 (Harel-Tarja. Give a tree T, we ca preprocess i O( time, ad aswer all LCA queries i O(1 time. 5
6 3.2 Get the aswer Now we have reduced our questio to how to aswer the acestor-descet queries efficietly. For each edge e = (u, v where v is the paret of u, we will look at all queries startig i subtree T u ad edig above vertex v. Say those queries go to w 1, w 2,..., w k. The the query strig is Q e = (w 1, w 2,..., w k. The we eed to calculate the aswer strig A e = (a 1, a 2,, a k where a i is the maximal weight amog the edges betwee w i ad u. Figure 2.4: Illustratio of queries ad aswers Figure 2.4 gives us a example. Suppose Q (b,a = (w 1, w 3, w 4, which meas there are three queries startig from some vertices i the subtree of b ad edig to w 1, w 3, w 4. The we get the aswer A (b,a = (a 1, a 3, a 4 = (6, 4, 4 sice the maximal weight of a edge o the path from w 1 to b is the weight of edge (w 1, w 2, ad the maximal weight of a edge o the path from either w 3, w 4 to b is from the weight of edge (w 3, w 4. Give the aswer of A (b,a, how should we fid the aswer of A (c,b efficietly? Say Q (c,b = (w 1, w 4, b. Comparig with Q (b,a, we may lose some queries sice they are from some other childre of vertex b, ad we may have some other queries edig at b which will ot cotai i Q (b,a. The easiest way is to update every query. Suppose the weight of edge (c, b is t. The we ca calculate A (c,b = (max{a 1, t}, max{a 4, t}, t = (max{6, 5}, max{4, 5}, 5 The trick is that if i Q e = (w 1, w 2,..., w k, w 1, w 2,..., w k is sorted from the top to the bottom. tha the aswers A e = (a 1, a 2,, a k should be o-icreasig, a 1 a 2 a k. Therefore we ca do biary search to reduce the umber of comparisos. Claim Give the questio strig Q e for e = (u, v where v is the paret of u, the aswer strig A e for e, we ca compute aswers A e for e = (w, u where w is a child of u, withi time log( A e
7 Theorem The total umber of comparisos for all queries t e log ( Q e + 1 O(m + Proof. Assume the umber of edges i level i is i. Here the level is couted from the bottom to the top, the edges coected to leaves are at level 0. log 2 (1 + Q e = i avg (log 2 (1 + Q e i log 2 (1 + avg = i log 2 (1 + i log 2 ( 1 + m i ( Q e Q e i ( m + = i log 2 + log 2 i The first iequality holds by Jese s iequality ad covexess of fuctio log 2 (1+x. The secod iequality holds sice the umber of all queries is m ad each query will oly appear o at most oe edge o ay particular level. Therefore we have t = e = i i log 2 (1 + Q e log 2 (1 + Q e ( m + i log 2 + log 2 i = log 2 m + + i i log 2 i m + log 2 + c = O( log m + + = O(m + 7
15-850: Advanced Algorithms CMU, Spring 2017 Lecture #2: Randomized MST and Directed MSTs January 27, 2017
 15-850: Advaced Algorithms CMU, Sprig 2017 Lecture #2: Radomized MST ad Directed MSTs Jauary 27, 2017 Lecturer: Aupam Gupta Scribe: Yu Zhao, Xiyu Wu 1 Prelimiaries I this lecture we itroduce the Karger-Klai-Tarja
15-850: Advaced Algorithms CMU, Sprig 2017 Lecture #2: Radomized MST ad Directed MSTs Jauary 27, 2017 Lecturer: Aupam Gupta Scribe: Yu Zhao, Xiyu Wu 1 Prelimiaries I this lecture we itroduce the Karger-Klai-Tarja
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
1 Minimum Spanning Trees: History
 15-850: Advanced Algorithms CMU, Fall 018 Lecture #1: Deterministic MSTs August 7, 018 Lecturer: Anupam Gupta Scribe: C.J. Argue and Xinyu Wu 1 Minimum Spanning Trees: History The minimum spanning tree
15-850: Advanced Algorithms CMU, Fall 018 Lecture #1: Deterministic MSTs August 7, 018 Lecturer: Anupam Gupta Scribe: C.J. Argue and Xinyu Wu 1 Minimum Spanning Trees: History The minimum spanning tree
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
Examples and Applications of Binary Search
 Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS 121 Data Structures and Algorithms with Java Spring Stacks and Queues Monday, February 12 / Tuesday, February 13
 CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
CIS 121. Introduction to Trees
 CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
Minimum Spanning Trees
 Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
CS 683: Advanced Design and Analysis of Algorithms
 CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
Greedy Algorithms. Interval Scheduling. Greedy Algorithms. Interval scheduling. Greedy Algorithms. Interval Scheduling
 Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
Minimum Spanning Trees
 Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Minimum Spanning Trees. Application: Connecting a Network
 Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
CSC165H1 Worksheet: Tutorial 8 Algorithm analysis (SOLUTIONS)
 CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Numerical Methods Lecture 6 - Curve Fitting Techniques
 Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
Major CSL Write your name and entry no on every sheet of the answer script. Time 2 Hrs Max Marks 70
 NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
CSC 220: Computer Organization Unit 11 Basic Computer Organization and Design
 College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Administrative UNSUPERVISED LEARNING. Unsupervised learning. Supervised learning 11/25/13. Final project. No office hours today
 Admiistrative Fial project No office hours today UNSUPERVISED LEARNING David Kauchak CS 451 Fall 2013 Supervised learig Usupervised learig label label 1 label 3 model/ predictor label 4 label 5 Supervised
Admiistrative Fial project No office hours today UNSUPERVISED LEARNING David Kauchak CS 451 Fall 2013 Supervised learig Usupervised learig label label 1 label 3 model/ predictor label 4 label 5 Supervised
CIS 121 Data Structures and Algorithms with Java Fall Big-Oh Notation Tuesday, September 5 (Make-up Friday, September 8)
 CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
prerequisites: 6.046, 6.041/2, ability to do proofs Randomized algorithms: make random choices during run. Main benefits:
 Itro Admiistrivia. Sigup sheet. prerequisites: 6.046, 6.041/2, ability to do proofs homework weekly (first ext week) collaboratio idepedet homeworks gradig requiremet term project books. questio: scribig?
Itro Admiistrivia. Sigup sheet. prerequisites: 6.046, 6.041/2, ability to do proofs homework weekly (first ext week) collaboratio idepedet homeworks gradig requiremet term project books. questio: scribig?
Massachusetts Institute of Technology Lecture : Theory of Parallel Systems Feb. 25, Lecture 6: List contraction, tree contraction, and
 Massachusetts Istitute of Techology Lecture.89: Theory of Parallel Systems Feb. 5, 997 Professor Charles E. Leiserso Scribe: Guag-Ie Cheg Lecture : List cotractio, tree cotractio, ad symmetry breakig Work-eciet
Massachusetts Istitute of Techology Lecture.89: Theory of Parallel Systems Feb. 5, 997 Professor Charles E. Leiserso Scribe: Guag-Ie Cheg Lecture : List cotractio, tree cotractio, ad symmetry breakig Work-eciet
Mathematical Stat I: solutions of homework 1
 Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Heaps. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Lecture 28: Data Link Layer
 Automatic Repeat Request (ARQ) 2. Go ack N ARQ Although the Stop ad Wait ARQ is very simple, you ca easily show that it has very the low efficiecy. The low efficiecy comes from the fact that the trasmittig
Automatic Repeat Request (ARQ) 2. Go ack N ARQ Although the Stop ad Wait ARQ is very simple, you ca easily show that it has very the low efficiecy. The low efficiecy comes from the fact that the trasmittig
Lecture Notes 6 Introduction to algorithm analysis CSS 501 Data Structures and Object-Oriented Programming
 Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
6.851: Advanced Data Structures Spring Lecture 17 April 24
 6.851: Advaced Data Structures Sprig 2012 Prof. Erik Demaie Lecture 17 April 24 Scribes: David Bejami(2012), Li Fei(2012), Yuzhi Zheg(2012),Morteza Zadimoghaddam(2010), Aaro Berstei(2007) 1 Overview Up
6.851: Advaced Data Structures Sprig 2012 Prof. Erik Demaie Lecture 17 April 24 Scribes: David Bejami(2012), Li Fei(2012), Yuzhi Zheg(2012),Morteza Zadimoghaddam(2010), Aaro Berstei(2007) 1 Overview Up
Thompson s Group F (p + 1) is not Minimally Almost Convex
 Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Switching Hardware. Spring 2018 CS 438 Staff, University of Illinois 1
 Switchig Hardware Sprig 208 CS 438 Staff, Uiversity of Illiois Where are we? Uderstad Differet ways to move through a etwork (forwardig) Read sigs at each switch (datagram) Follow a kow path (virtual circuit)
Switchig Hardware Sprig 208 CS 438 Staff, Uiversity of Illiois Where are we? Uderstad Differet ways to move through a etwork (forwardig) Read sigs at each switch (datagram) Follow a kow path (virtual circuit)
Solution printed. Do not start the test until instructed to do so! CS 2604 Data Structures Midterm Spring, Instructions:
 CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
Design and Analysis of Algorithms Notes
 Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Octahedral Graph Scaling
 Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Improved Random Graph Isomorphism
 Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Algorithm Design Techniques. Divide and conquer Problem
 Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
3. b. Present a combinatorial argument that for all positive integers n : : 2 n
 . b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
. b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
Priority Queues. Binary Heaps
 Priority Queues Biary Heaps Priority Queues Priority: some property of a object that allows it to be prioritized with respect to other objects of the same type Mi Priority Queue: homogeeous collectio of
Priority Queues Biary Heaps Priority Queues Priority: some property of a object that allows it to be prioritized with respect to other objects of the same type Mi Priority Queue: homogeeous collectio of
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
Chapter 4 The Datapath
 The Ageda Chapter 4 The Datapath Based o slides McGraw-Hill Additioal material 24/25/26 Lewis/Marti Additioal material 28 Roth Additioal material 2 Taylor Additioal material 2 Farmer Tae the elemets that
The Ageda Chapter 4 The Datapath Based o slides McGraw-Hill Additioal material 24/25/26 Lewis/Marti Additioal material 28 Roth Additioal material 2 Taylor Additioal material 2 Farmer Tae the elemets that
Data Structures Week #5. Trees (Ağaçlar)
 Data Structures Week #5 Trees Ağaçlar) Trees Ağaçlar) Toros Gökarı Avrupa Gökarı October 28, 2014 Boraha Tümer, Ph.D. 2 Trees Ağaçlar) October 28, 2014 Boraha Tümer, Ph.D. 3 Outlie Trees Deiitios Implemetatio
Data Structures Week #5 Trees Ağaçlar) Trees Ağaçlar) Toros Gökarı Avrupa Gökarı October 28, 2014 Boraha Tümer, Ph.D. 2 Trees Ağaçlar) October 28, 2014 Boraha Tümer, Ph.D. 3 Outlie Trees Deiitios Implemetatio
The Magma Database file formats
 The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
Lower Bounds for Sorting
 Liear Sortig Topics Covered: Lower Bouds for Sortig Coutig Sort Radix Sort Bucket Sort Lower Bouds for Sortig Compariso vs. o-compariso sortig Decisio tree model Worst case lower boud Compariso Sortig
Liear Sortig Topics Covered: Lower Bouds for Sortig Coutig Sort Radix Sort Bucket Sort Lower Bouds for Sortig Compariso vs. o-compariso sortig Decisio tree model Worst case lower boud Compariso Sortig
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
3D Model Retrieval Method Based on Sample Prediction
 20 Iteratioal Coferece o Computer Commuicatio ad Maagemet Proc.of CSIT vol.5 (20) (20) IACSIT Press, Sigapore 3D Model Retrieval Method Based o Sample Predictio Qigche Zhag, Ya Tag* School of Computer
20 Iteratioal Coferece o Computer Commuicatio ad Maagemet Proc.of CSIT vol.5 (20) (20) IACSIT Press, Sigapore 3D Model Retrieval Method Based o Sample Predictio Qigche Zhag, Ya Tag* School of Computer
CSE 417: Algorithms and Computational Complexity
 Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Σ P(i) ( depth T (K i ) + 1),
 EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
Pseudocode ( 1.1) Analysis of Algorithms. Primitive Operations. Pseudocode Details. Running Time ( 1.1) Estimating performance
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
University of Waterloo Department of Electrical and Computer Engineering ECE 250 Algorithms and Data Structures
 Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
The Closest Line to a Data Set in the Plane. David Gurney Southeastern Louisiana University Hammond, Louisiana
 The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
CMPT 125 Assignment 2 Solutions
 CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
The Adjacency Matrix and The nth Eigenvalue
 Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Computers and Scientific Thinking
 Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
ECE4050 Data Structures and Algorithms. Lecture 6: Searching
 ECE4050 Data Structures ad Algorithms Lecture 6: Searchig 1 Search Give: Distict keys k 1, k 2,, k ad collectio L of records of the form (k 1, I 1 ), (k 2, I 2 ),, (k, I ) where I j is the iformatio associated
ECE4050 Data Structures ad Algorithms Lecture 6: Searchig 1 Search Give: Distict keys k 1, k 2,, k ad collectio L of records of the form (k 1, I 1 ), (k 2, I 2 ),, (k, I ) where I j is the iformatio associated
One advantage that SONAR has over any other music-sequencing product I ve worked
 *gajedra* D:/Thomso_Learig_Projects/Garrigus_163132/z_productio/z_3B2_3D_files/Garrigus_163132_ch17.3d, 14/11/08/16:26:39, 16:26, page: 647 17 CAL 101 Oe advatage that SONAR has over ay other music-sequecig
*gajedra* D:/Thomso_Learig_Projects/Garrigus_163132/z_productio/z_3B2_3D_files/Garrigus_163132_ch17.3d, 14/11/08/16:26:39, 16:26, page: 647 17 CAL 101 Oe advatage that SONAR has over ay other music-sequecig
Pattern Recognition Systems Lab 1 Least Mean Squares
 Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Analysis Metrics. Intro to Algorithm Analysis. Slides. 12. Alg Analysis. 12. Alg Analysis
 Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Exact Minimum Lower Bound Algorithm for Traveling Salesman Problem
 Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Xiaozhou (Steve) Li, Atri Rudra, Ram Swaminathan. HP Laboratories HPL Keyword(s): graph coloring; hardness of approximation
 Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
Sorting 9/15/2009. Sorting Problem. Insertion Sort: Soundness. Insertion Sort. Insertion Sort: Running Time. Insertion Sort: Soundness
 9/5/009 Algorithms Sortig 3- Sortig Sortig Problem The Sortig Problem Istace: A sequece of umbers Objective: A permutatio (reorderig) such that a ' K a' a, K,a a ', K, a' of the iput sequece The umbers
9/5/009 Algorithms Sortig 3- Sortig Sortig Problem The Sortig Problem Istace: A sequece of umbers Objective: A permutatio (reorderig) such that a ' K a' a, K,a a ', K, a' of the iput sequece The umbers
n Some thoughts on software development n The idea of a calculator n Using a grammar n Expression evaluation n Program organization n Analysis
 Overview Chapter 6 Writig a Program Bjare Stroustrup Some thoughts o software developmet The idea of a calculator Usig a grammar Expressio evaluatio Program orgaizatio www.stroustrup.com/programmig 3 Buildig
Overview Chapter 6 Writig a Program Bjare Stroustrup Some thoughts o software developmet The idea of a calculator Usig a grammar Expressio evaluatio Program orgaizatio www.stroustrup.com/programmig 3 Buildig
Graphs ORD SFO LAX DFW
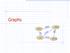 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Learning to Shoot a Goal Lecture 8: Learning Models and Skills
 Learig to Shoot a Goal Lecture 8: Learig Models ad Skills How do we acquire skill at shootig goals? CS 344R/393R: Robotics Bejami Kuipers Learig to Shoot a Goal The robot eeds to shoot the ball i the goal.
Learig to Shoot a Goal Lecture 8: Learig Models ad Skills How do we acquire skill at shootig goals? CS 344R/393R: Robotics Bejami Kuipers Learig to Shoot a Goal The robot eeds to shoot the ball i the goal.
Assignment 5; Due Friday, February 10
 Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
quality/quantity peak time/ratio
 Semi-Heap ad Its Applicatios i Touramet Rakig Jie Wu Departmet of omputer Sciece ad Egieerig Florida Atlatic Uiversity oca Rato, FL 3343 jie@cse.fau.edu September, 00 . Itroductio ad Motivatio. relimiaries
Semi-Heap ad Its Applicatios i Touramet Rakig Jie Wu Departmet of omputer Sciece ad Egieerig Florida Atlatic Uiversity oca Rato, FL 3343 jie@cse.fau.edu September, 00 . Itroductio ad Motivatio. relimiaries
Chapter 10. Defining Classes. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 10 Defiig Classes Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 10.1 Structures 10.2 Classes 10.3 Abstract Data Types 10.4 Itroductio to Iheritace Copyright 2015 Pearso Educatio,
Chapter 10 Defiig Classes Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 10.1 Structures 10.2 Classes 10.3 Abstract Data Types 10.4 Itroductio to Iheritace Copyright 2015 Pearso Educatio,
An Efficient Algorithm for Graph Bisection of Triangularizations
 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
Analysis of Algorithms
 Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
CS211 Fall 2003 Prelim 2 Solutions and Grading Guide
 CS11 Fall 003 Prelim Solutios ad Gradig Guide Problem 1: (a) obj = obj1; ILLEGAL because type of referece must always be a supertype of type of object (b) obj3 = obj1; ILLEGAL because type of referece
CS11 Fall 003 Prelim Solutios ad Gradig Guide Problem 1: (a) obj = obj1; ILLEGAL because type of referece must always be a supertype of type of object (b) obj3 = obj1; ILLEGAL because type of referece
1 Minimum Spanning Tree (MST)
 Lecture Notes CS:5360 Randomized Algorithms Lectures 10, 11, and 12: Sep 20, Sep 25, and Sep 27, 2018 Scribe: Hankyu Jang 1 Minimum Spanning Tree (MST) MST is another example of sampling. Input: An edge-weighted,
Lecture Notes CS:5360 Randomized Algorithms Lectures 10, 11, and 12: Sep 20, Sep 25, and Sep 27, 2018 Scribe: Hankyu Jang 1 Minimum Spanning Tree (MST) MST is another example of sampling. Input: An edge-weighted,
DATA STRUCTURES. amortized analysis binomial heaps Fibonacci heaps union-find. Data structures. Appetizer. Appetizer
 Data structures DATA STRUCTURES Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit distace, shortest paths, MST, max-flow,... amortized aalysis biomial heaps Fiboacci heaps uio-fid Dyamic
Data structures DATA STRUCTURES Static problems. Give a iput, produce a output. Ex. Sortig, FFT, edit distace, shortest paths, MST, max-flow,... amortized aalysis biomial heaps Fiboacci heaps uio-fid Dyamic
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Lecture 18. Optimization in n dimensions
 Lecture 8 Optimizatio i dimesios Itroductio We ow cosider the problem of miimizig a sigle scalar fuctio of variables, f x, where x=[ x, x,, x ]T. The D case ca be visualized as fidig the lowest poit of
Lecture 8 Optimizatio i dimesios Itroductio We ow cosider the problem of miimizig a sigle scalar fuctio of variables, f x, where x=[ x, x,, x ]T. The D case ca be visualized as fidig the lowest poit of
Load balanced Parallel Prime Number Generator with Sieve of Eratosthenes on Cluster Computers *
 Load balaced Parallel Prime umber Geerator with Sieve of Eratosthees o luster omputers * Soowook Hwag*, Kyusik hug**, ad Dogseug Kim* *Departmet of Electrical Egieerig Korea Uiversity Seoul, -, Rep. of
Load balaced Parallel Prime umber Geerator with Sieve of Eratosthees o luster omputers * Soowook Hwag*, Kyusik hug**, ad Dogseug Kim* *Departmet of Electrical Egieerig Korea Uiversity Seoul, -, Rep. of
OCR Statistics 1. Working with data. Section 3: Measures of spread
 Notes ad Eamples OCR Statistics 1 Workig with data Sectio 3: Measures of spread Just as there are several differet measures of cetral tedec (averages), there are a variet of statistical measures of spread.
Notes ad Eamples OCR Statistics 1 Workig with data Sectio 3: Measures of spread Just as there are several differet measures of cetral tedec (averages), there are a variet of statistical measures of spread.
Chapter 9. Pointers and Dynamic Arrays. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
Data Structures Week #9. Sorting
 Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
CRACKING CODING INTERVIEW
 CRACKING tlie CODING INTERVIEW 6th Editio 189 Programmig Questios ad Solutios GAYLE LAAKMANN MCDOWELL Fouder ad CEO, CareerCup.com CareerCup, LLC Palo Alto, CA CRACKING THE CODING INTERVIEW,SIXTH EDITION
CRACKING tlie CODING INTERVIEW 6th Editio 189 Programmig Questios ad Solutios GAYLE LAAKMANN MCDOWELL Fouder ad CEO, CareerCup.com CareerCup, LLC Palo Alto, CA CRACKING THE CODING INTERVIEW,SIXTH EDITION
Basic allocator mechanisms The course that gives CMU its Zip! Memory Management II: Dynamic Storage Allocation Mar 6, 2000.
 5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
15 UNSUPERVISED LEARNING
 15 UNSUPERVISED LEARNING [My father] advised me to sit every few moths i my readig chair for a etire eveig, close my eyes ad try to thik of ew problems to solve. I took his advice very seriously ad have
15 UNSUPERVISED LEARNING [My father] advised me to sit every few moths i my readig chair for a etire eveig, close my eyes ad try to thik of ew problems to solve. I took his advice very seriously ad have
