S p a t i a l D a t a M i n i n g. Spatial Clustering in the Presence of Obstacles
|
|
|
- Sophie Chapman
- 5 years ago
- Views:
Transcription
1 S p a t i a l D a t a M i n i n g Spatial Clustering in the Presence of Obstacles Milan Magdics Spring, 2007
2 I n t r o d u c t i o n Clustering in spatial data mining is to group similar objects based on their distance, connectivity, or their relative density in space Each of the clustering methods assume the existence of a distance measure between the objects A commonly used distance is the direct Euclidean distance
3 D i r e c t E u c l i d e a n d i s t a n c e The distance of two points is the length of the line connecting them d(a,b) = ((x 1 -x 2 ) 2 +(y 1 -y 2 ) 2 )
4 P r o b l e m s w i t h t h e E u c l i d e a n d i s t a n c e Sometimes the "real" distance differs largely from the direct Euclidean distance Many spatial applications have obstacles in presence
5 P r o b l e m s w i t h t h e E u c l i d e a n d i s t a n c e - E x a m p l e A bank planner wishes to locate 4 ATMs in an area to serve customers (represented by points in the figure). The task is to minimize the distance that customers have to travel to an ATM A common clustering method uses direct Euclidean distance, and can lead to distorted and useless results In this case, some of the clusters will be split by a large obstacle thus some customers will have to travel a long way
6 T h e C l u s t e r i n g w i t h O b s t r u c t e d D i s t a n c e ( C O D ) P r o b l e m Given a set P of n points {p 1,p 2,...,p n }, and a set O of m non-intersecting obstacles {o 1,o 2,...,o m } in a twodimensional region, R Each obstacle is represented by a simple polygon Let d(p j,p k ) denote the direct Euclidean distance between two points p j, p k by ignoring the obstacles, and d'(p j,p k ) denote the length of the shortest Euclidean path from p j to p k without cutting through any obstacles
7 T h e C l u s t e r i n g w i t h O b s t r u c t e d D i s t a n c e ( C O D ) P r o b l e m The problem of clustering with obstacle distance (COD) is to partition P into k clusters, Cl 1,...,Cl k, such that the following square-error function, E, is minimized E = i k = 1 p Cli (d'(p,c i ))2 where c i is the center of cluster Cl i that is determined by the clustering
8 H o w t o s o l v e t h i s p r o b l e m? The basic idea is to simply change the distance function and thus the COD problem could be handled by common clustering algorithms The article gives a partitioning-based algorithm, because it is a good choice to minimize overall travel distances to the cluster centers It uses k-medoids instead of k-means since the mean of a set of points is not well defined when obstacles are involved. This choice also guarantees that the center of the cluster cannot be inside an obstacle.
9 T h e C O D - C L A R A N S a l g o r i t h m The algorithm called COD-CLARANS is based on CLARANS and is designed for handling obstacles It not only changes the distance function, but also uses several optimizations for make the computations faster
10 T h e C O D - C L A R A N S a l g o r i t h m First it preprocesses the data and store certain information which will be needed later when calculating obstructed distances between objects and temporary cluster centers The main algorithm is similar to CLARANS Pruning function E' is a lower bound of the squared error E. It is used to avoid the computation of E in some cases or to speed it up by providing "focusing information"
11 P r e p r o c e s s i n g T h e B S P - t r e e A Binary-Space-Partition (BSP) tree is used to efficiently determine whether two points p and q are visible to each other within the region R By definition a point p is visible from a point q if the straight line joining them does not intersect any obstacles With the usage of the BSPtree, the set of all visible obstacle vertices from a point p (denoted by vis(p)) can be efficiently determined
12 P r e p r o c e s s i n g T h e V i s i b i l i t y G r a p h From the BSP-tree we can generate a Visibility Graph VG This graph contains a node for each vertex of the obstacles and two nodes are joined by an edge if and only if the corresponding vertices they represent are visible to each other Lemma: Let p and q be two points in the region and VG=(V,E) be the visibility graph of R. Let VG'=(V',E') be a visibility graph created from VG by adding two additional nodes p' and q' in V' representing p and q. E' contains an edge joining two nodes in V' if the points represented by the two nodes are mutually visible. The shortest path between the two nodes p and q will be a sub-path of VG'.
13 P r e p r o c e s s i n g T h e V i s i b i l i t y G r a p h In other words, if two points p and q are not visible to each other, the shortest path between them is by travelling through obstacle vertices, starting with an obstacle vertex visible from p or q and ending with an obstacle vertex visible from q or p
14 P r e p r o c e s s i n g - M i c r o - c l u s t e r i n g We perform micro-clustering to compress points that are close to each other into groups Instead of representing points individually, represent a microcluster as it's center and number of points in the group Micro-clusters are not split by obstacles Obstacles avoided by triangulating the region
15 P r e p r o c e s s i n g - M i c r o - c l u s t e r i n g All points within a triangle are mutually visible Using micro-clusters just approximates the squared error function, to control this, a radius of each is below user specified threshold, max_radius
16 P r e p r o c e s s i n g S p a t i a l J o i n I n d e x Each entry is a 3-tuple (p,q,d'(p,q)) where p and q are points and d' is the obstructed distance between p and q VV Index Compute an index entry for any pair of obstacles vertices All pairs shortest path in the visibility graph MV Index Compute an index entry of any pair of micro-cluster and obstacle vertex Can be done by using the VV Index and the BSP-tree, the idea is the same as in the lemma before MM Index Compute index entry for any pair of micro-clusters Can be done by using the MV Index and the BSP-tree Since the number of micro-clusters are usually large, it can be extremely huge
17 T h e M a i n F u n c t i o n The algorithm first randomly selects k points as the centers of the clusters Iteratively tries to find better centers A random center c random will replace a center c j if squared-error E is minimized Variable max_try bounds the new center tries for each dropped center
18 T h e M a i n F u n c t i o n Computing obstructed distance to Nearest Centers in remain (the centers by removing the selected center) has two phases In phase 1 find shortest obstructed distance between all vertices of obstacles and nearest cluster center N(v) of vertex v
19 T h e M a i n F u n c t i o n Computing obstructed distance to Nearest Centers in remain (the centers by removing the selected center) has two phases In phase 2, for each micro-cluster p, choose visible obstacle vertex v (use the BSP-tree for generating visible vertices) such that sum of distance between p and v and obstructed distance between v and N(v) is minimized
20 T h e M a i n F u n c t i o n Execution of phase 1 depends on whether VV is materialized Use visibility information (BSP-tree) and the index like before MV is materialized A simple minimum search in the index No spatial join index is materialized Use visibility graph and Dijkstra's algorithm
21 D i j k s t r a ' s a l g o r i t h m It gives the shortest path and the distance between two given points in a graph The weights of the edges are nonnegative The computation time is proportional to the number of edges in the graph Apply this algorithm to the visibility graph: First insert the k-1 cluster centers into the graph, connect them to the visible vertices Add a virtual node s and connect it with zero weight to each of the centers Run the algorithm with s as the source point and obstacle vertices as destination points the cluster center in the path will be the closest to the obstacle vertex
22 C o m p u t i n g l o w e r b o u n d E ' At this step we can use the previously computed Nearest Centers and their distances (using obstacled distance) For the new cluster center c random we use the direct Euclidean distance, which is much faster If direct Euclidean distance between a micro-cluster p and c random is shorter than obstructed distance d'(p,n(p)), then p is assigned to c random and Euclidean distance used to calculated estimated square error E' It can be proved that E' is a lower bound of E If E' is larger than the previously found best solution E, then we do not have to calculate the new E, because we have a worse solution Otherwise we have to compute the new squared error
23 C o m p u t i n g s q u a r e d e r r o r E We can make use of fact that if micro-cluster p is not assigned to c random when computing E', it will never be assigned to c random when computing E This is because the obstacled distance is greater or equal than the direct Euclidean distance Thus the only thing we need to do is to calculate the obstacled distances between the new cluster center c random and the micro-clusters that will be assigned to c random The obstructed distance of each micro-cluster to it's nearest center in remain is already computed
24 P e r f o r m a n c e S t u d y - M a i n r e s u l t s Decrease in quality of clusters not significant compared to decrease in number of micro-clusters Processing time of COD- CLARAN-VV and COD- CLARANS-MV minorly affected by max-radius
25 P e r f o r m a n c e S t u d y - M a i n r e s u l t s Algorithms that do not use pruning have longer execution time Spatial join indexes are useful in reducing the execution time COD-CLARANS scales well for large number of points
26 P e r f o r m a n c e S t u d y - M a i n r e s u l t s Comparing clusters generated by COD-CLARANS to ones generated by CLARANS: COD-CLARANS clusters better with obstacles Performance gap decreases with larger values of k Large k means that more other points are visible from the center, so the obstacled distance will be the same as the direct distance
27 C o n c l u s i o n Obstacles are a fact of real spatial data sets Propose COD-CLARANS Various types of pre-processed information enhance efficiency of COD-CLARANS Pushing handling of obstacles into COD-CLARANS algorithm and using pruning function E' instead of handling them in distance function level makes it more efficient Experiments show usefulness and scalability
28 Thank you!
Balanced COD-CLARANS: A Constrained Clustering Algorithm to Optimize Logistics Distribution Network
 Advances in Intelligent Systems Research, volume 133 2nd International Conference on Artificial Intelligence and Industrial Engineering (AIIE2016) Balanced COD-CLARANS: A Constrained Clustering Algorithm
Advances in Intelligent Systems Research, volume 133 2nd International Conference on Artificial Intelligence and Industrial Engineering (AIIE2016) Balanced COD-CLARANS: A Constrained Clustering Algorithm
Voronoi Diagrams in the Plane. Chapter 5 of O Rourke text Chapter 7 and 9 of course text
 Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
CS 532: 3D Computer Vision 14 th Set of Notes
 1 CS 532: 3D Computer Vision 14 th Set of Notes Instructor: Philippos Mordohai Webpage: www.cs.stevens.edu/~mordohai E-mail: Philippos.Mordohai@stevens.edu Office: Lieb 215 Lecture Outline Triangulating
1 CS 532: 3D Computer Vision 14 th Set of Notes Instructor: Philippos Mordohai Webpage: www.cs.stevens.edu/~mordohai E-mail: Philippos.Mordohai@stevens.edu Office: Lieb 215 Lecture Outline Triangulating
BBS654 Data Mining. Pinar Duygulu. Slides are adapted from Nazli Ikizler
 BBS654 Data Mining Pinar Duygulu Slides are adapted from Nazli Ikizler 1 Classification Classification systems: Supervised learning Make a rational prediction given evidence There are several methods for
BBS654 Data Mining Pinar Duygulu Slides are adapted from Nazli Ikizler 1 Classification Classification systems: Supervised learning Make a rational prediction given evidence There are several methods for
Data Mining Cluster Analysis: Basic Concepts and Algorithms. Lecture Notes for Chapter 8. Introduction to Data Mining
 Data Mining Cluster Analysis: Basic Concepts and Algorithms Lecture Notes for Chapter 8 Introduction to Data Mining by Tan, Steinbach, Kumar Tan,Steinbach, Kumar Introduction to Data Mining 4/18/004 1
Data Mining Cluster Analysis: Basic Concepts and Algorithms Lecture Notes for Chapter 8 Introduction to Data Mining by Tan, Steinbach, Kumar Tan,Steinbach, Kumar Introduction to Data Mining 4/18/004 1
Clustering Spatial Data in the Presence of Obstacles
 Clustering Spatial Data in the Presence of Obstacles Abstract. Clustering is a form of unsupervised machine learning. In this paper, we proposed the method to identify clusters in the presence of intersected
Clustering Spatial Data in the Presence of Obstacles Abstract. Clustering is a form of unsupervised machine learning. In this paper, we proposed the method to identify clusters in the presence of intersected
Fast Shortest Path Algorithm for Road Network and Implementation
 HONOURS PROJECT Page 1 Carleton University School of Computer Science COMP 4905 HONOURS PROJECT Fall Term, 2005 Fast Shortest Path Algorithm for Road Network and Implementation Author: Liang Dai Student
HONOURS PROJECT Page 1 Carleton University School of Computer Science COMP 4905 HONOURS PROJECT Fall Term, 2005 Fast Shortest Path Algorithm for Road Network and Implementation Author: Liang Dai Student
Effect of Physical Constraints on Spatial Connectivity in Urban Areas
 Effect of Physical Constraints on Spatial Connectivity in Urban Areas Yoav Vered and Sagi Filin Department of Transportation and Geo-Information Technion Israel Institute of Technology Motivation Wide
Effect of Physical Constraints on Spatial Connectivity in Urban Areas Yoav Vered and Sagi Filin Department of Transportation and Geo-Information Technion Israel Institute of Technology Motivation Wide
Overview. Efficient Simplification of Point-sampled Surfaces. Introduction. Introduction. Neighborhood. Local Surface Analysis
 Overview Efficient Simplification of Pointsampled Surfaces Introduction Local surface analysis Simplification methods Error measurement Comparison PointBased Computer Graphics Mark Pauly PointBased Computer
Overview Efficient Simplification of Pointsampled Surfaces Introduction Local surface analysis Simplification methods Error measurement Comparison PointBased Computer Graphics Mark Pauly PointBased Computer
Data Mining: Concepts and Techniques. Chapter March 8, 2007 Data Mining: Concepts and Techniques 1
 Data Mining: Concepts and Techniques Chapter 7.1-4 March 8, 2007 Data Mining: Concepts and Techniques 1 1. What is Cluster Analysis? 2. Types of Data in Cluster Analysis Chapter 7 Cluster Analysis 3. A
Data Mining: Concepts and Techniques Chapter 7.1-4 March 8, 2007 Data Mining: Concepts and Techniques 1 1. What is Cluster Analysis? 2. Types of Data in Cluster Analysis Chapter 7 Cluster Analysis 3. A
Ray Tracing: Intersection
 Computer Graphics as Virtual Photography Ray Tracing: Intersection Photography: real scene camera (captures light) photo processing Photographic print processing Computer Graphics: 3D models camera tone
Computer Graphics as Virtual Photography Ray Tracing: Intersection Photography: real scene camera (captures light) photo processing Photographic print processing Computer Graphics: 3D models camera tone
CLUSTERING. CSE 634 Data Mining Prof. Anita Wasilewska TEAM 16
 CLUSTERING CSE 634 Data Mining Prof. Anita Wasilewska TEAM 16 1. K-medoids: REFERENCES https://www.coursera.org/learn/cluster-analysis/lecture/nj0sb/3-4-the-k-medoids-clustering-method https://anuradhasrinivas.files.wordpress.com/2013/04/lesson8-clustering.pdf
CLUSTERING CSE 634 Data Mining Prof. Anita Wasilewska TEAM 16 1. K-medoids: REFERENCES https://www.coursera.org/learn/cluster-analysis/lecture/nj0sb/3-4-the-k-medoids-clustering-method https://anuradhasrinivas.files.wordpress.com/2013/04/lesson8-clustering.pdf
Querying visible points in large obstructed space
 DOI 10.1007/s10707-014-0213-7 Querying visible points in large obstructed space Jianqiu Xu Ralf Hartmut Güting Received: 24 September 2013 / Revised: 16 April 2014 / Accepted: 10 June 2014 Springer Science+Business
DOI 10.1007/s10707-014-0213-7 Querying visible points in large obstructed space Jianqiu Xu Ralf Hartmut Güting Received: 24 September 2013 / Revised: 16 April 2014 / Accepted: 10 June 2014 Springer Science+Business
Clustering in Data Mining
 Clustering in Data Mining Classification Vs Clustering When the distribution is based on a single parameter and that parameter is known for each object, it is called classification. E.g. Children, young,
Clustering in Data Mining Classification Vs Clustering When the distribution is based on a single parameter and that parameter is known for each object, it is called classification. E.g. Children, young,
4. Ad-hoc I: Hierarchical clustering
 4. Ad-hoc I: Hierarchical clustering Hierarchical versus Flat Flat methods generate a single partition into k clusters. The number k of clusters has to be determined by the user ahead of time. Hierarchical
4. Ad-hoc I: Hierarchical clustering Hierarchical versus Flat Flat methods generate a single partition into k clusters. The number k of clusters has to be determined by the user ahead of time. Hierarchical
6 Randomized rounding of semidefinite programs
 6 Randomized rounding of semidefinite programs We now turn to a new tool which gives substantially improved performance guarantees for some problems We now show how nonlinear programming relaxations can
6 Randomized rounding of semidefinite programs We now turn to a new tool which gives substantially improved performance guarantees for some problems We now show how nonlinear programming relaxations can
Testing Bipartiteness of Geometric Intersection Graphs David Eppstein
 Testing Bipartiteness of Geometric Intersection Graphs David Eppstein Univ. of California, Irvine School of Information and Computer Science Intersection Graphs Given arrangement of geometric objects,
Testing Bipartiteness of Geometric Intersection Graphs David Eppstein Univ. of California, Irvine School of Information and Computer Science Intersection Graphs Given arrangement of geometric objects,
Clustering part II 1
 Clustering part II 1 Clustering What is Cluster Analysis? Types of Data in Cluster Analysis A Categorization of Major Clustering Methods Partitioning Methods Hierarchical Methods 2 Partitioning Algorithms:
Clustering part II 1 Clustering What is Cluster Analysis? Types of Data in Cluster Analysis A Categorization of Major Clustering Methods Partitioning Methods Hierarchical Methods 2 Partitioning Algorithms:
CMSC 425: Lecture 9 Geometric Data Structures for Games: Geometric Graphs Thursday, Feb 21, 2013
 CMSC 425: Lecture 9 Geometric Data Structures for Games: Geometric Graphs Thursday, Feb 21, 2013 Reading: Today s materials is presented in part in Computational Geometry: Algorithms and Applications (3rd
CMSC 425: Lecture 9 Geometric Data Structures for Games: Geometric Graphs Thursday, Feb 21, 2013 Reading: Today s materials is presented in part in Computational Geometry: Algorithms and Applications (3rd
Olmo S. Zavala Romero. Clustering Hierarchical Distance Group Dist. K-means. Center of Atmospheric Sciences, UNAM.
 Center of Atmospheric Sciences, UNAM November 16, 2016 Cluster Analisis Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster)
Center of Atmospheric Sciences, UNAM November 16, 2016 Cluster Analisis Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster)
9.1. K-means Clustering
 424 9. MIXTURE MODELS AND EM Section 9.2 Section 9.3 Section 9.4 view of mixture distributions in which the discrete latent variables can be interpreted as defining assignments of data points to specific
424 9. MIXTURE MODELS AND EM Section 9.2 Section 9.3 Section 9.4 view of mixture distributions in which the discrete latent variables can be interpreted as defining assignments of data points to specific
Dijkstra's Algorithm
 Shortest Path Algorithm Dijkstra's Algorithm To find the shortest path from the origin node to the destination node No matrix calculation Floyd s Algorithm To find all the shortest paths from the nodes
Shortest Path Algorithm Dijkstra's Algorithm To find the shortest path from the origin node to the destination node No matrix calculation Floyd s Algorithm To find all the shortest paths from the nodes
1. Use the Trapezium Rule with five ordinates to find an approximate value for the integral
 1. Use the Trapezium Rule with five ordinates to find an approximate value for the integral Show your working and give your answer correct to three decimal places. 2 2.5 3 3.5 4 When When When When When
1. Use the Trapezium Rule with five ordinates to find an approximate value for the integral Show your working and give your answer correct to three decimal places. 2 2.5 3 3.5 4 When When When When When
Information Retrieval and Web Search Engines
 Information Retrieval and Web Search Engines Lecture 7: Document Clustering December 4th, 2014 Wolf-Tilo Balke and José Pinto Institut für Informationssysteme Technische Universität Braunschweig The Cluster
Information Retrieval and Web Search Engines Lecture 7: Document Clustering December 4th, 2014 Wolf-Tilo Balke and José Pinto Institut für Informationssysteme Technische Universität Braunschweig The Cluster
CSE 5243 INTRO. TO DATA MINING
 CSE 5243 INTRO. TO DATA MINING Cluster Analysis: Basic Concepts and Methods Huan Sun, CSE@The Ohio State University Slides adapted from UIUC CS412, Fall 2017, by Prof. Jiawei Han 2 Chapter 10. Cluster
CSE 5243 INTRO. TO DATA MINING Cluster Analysis: Basic Concepts and Methods Huan Sun, CSE@The Ohio State University Slides adapted from UIUC CS412, Fall 2017, by Prof. Jiawei Han 2 Chapter 10. Cluster
: Mesh Processing. Chapter 8
 600.657: Mesh Processing Chapter 8 Handling Mesh Degeneracies [Botsch et al., Polygon Mesh Processing] Class of Approaches Geometric: Preserve the mesh where it s good. Volumetric: Can guarantee no self-intersection.
600.657: Mesh Processing Chapter 8 Handling Mesh Degeneracies [Botsch et al., Polygon Mesh Processing] Class of Approaches Geometric: Preserve the mesh where it s good. Volumetric: Can guarantee no self-intersection.
CPSC 340: Machine Learning and Data Mining. Density-Based Clustering Fall 2016
 CPSC 340: Machine Learning and Data Mining Density-Based Clustering Fall 2016 Assignment 1 : Admin 2 late days to hand it in before Wednesday s class. 3 late days to hand it in before Friday s class. 0
CPSC 340: Machine Learning and Data Mining Density-Based Clustering Fall 2016 Assignment 1 : Admin 2 late days to hand it in before Wednesday s class. 3 late days to hand it in before Friday s class. 0
A visibility graph based method for path planning in dynamic environments
 A visibility graph based method for path planning in dynamic environments Hrvoje Kaluđer *, Mišel Brezak ** and Ivan Petrović** * TEB Elektronika d.o.o, Vončinina 2, 10000 Zagreb, Croatia hrvoje.kaluder@teb-elektronika.hr
A visibility graph based method for path planning in dynamic environments Hrvoje Kaluđer *, Mišel Brezak ** and Ivan Petrović** * TEB Elektronika d.o.o, Vončinina 2, 10000 Zagreb, Croatia hrvoje.kaluder@teb-elektronika.hr
Discrete geometry. Lecture 2. Alexander & Michael Bronstein tosca.cs.technion.ac.il/book
 Discrete geometry Lecture 2 Alexander & Michael Bronstein tosca.cs.technion.ac.il/book Numerical geometry of non-rigid shapes Stanford University, Winter 2009 The world is continuous, but the mind is discrete
Discrete geometry Lecture 2 Alexander & Michael Bronstein tosca.cs.technion.ac.il/book Numerical geometry of non-rigid shapes Stanford University, Winter 2009 The world is continuous, but the mind is discrete
Hidden Surface Elimination: BSP trees
 Hidden Surface Elimination: BSP trees Outline Binary space partition (BSP) trees Polygon-aligned 1 BSP Trees Basic idea: Preprocess geometric primitives in scene to build a spatial data structure such
Hidden Surface Elimination: BSP trees Outline Binary space partition (BSP) trees Polygon-aligned 1 BSP Trees Basic idea: Preprocess geometric primitives in scene to build a spatial data structure such
CSE 5243 INTRO. TO DATA MINING
 CSE 5243 INTRO. TO DATA MINING Cluster Analysis: Basic Concepts and Methods Huan Sun, CSE@The Ohio State University 09/25/2017 Slides adapted from UIUC CS412, Fall 2017, by Prof. Jiawei Han 2 Chapter 10.
CSE 5243 INTRO. TO DATA MINING Cluster Analysis: Basic Concepts and Methods Huan Sun, CSE@The Ohio State University 09/25/2017 Slides adapted from UIUC CS412, Fall 2017, by Prof. Jiawei Han 2 Chapter 10.
Week 8 Voronoi Diagrams
 1 Week 8 Voronoi Diagrams 2 Voronoi Diagram Very important problem in Comp. Geo. Discussed back in 1850 by Dirichlet Published in a paper by Voronoi in 1908 3 Voronoi Diagram Fire observation towers: an
1 Week 8 Voronoi Diagrams 2 Voronoi Diagram Very important problem in Comp. Geo. Discussed back in 1850 by Dirichlet Published in a paper by Voronoi in 1908 3 Voronoi Diagram Fire observation towers: an
Simple Silhouettes for Complex Surfaces
 Eurographics Symposium on Geometry Processing(2003) L. Kobbelt, P. Schröder, H. Hoppe (Editors) Simple Silhouettes for Complex Surfaces D. Kirsanov, P. V. Sander, and S. J. Gortler Harvard University Abstract
Eurographics Symposium on Geometry Processing(2003) L. Kobbelt, P. Schröder, H. Hoppe (Editors) Simple Silhouettes for Complex Surfaces D. Kirsanov, P. V. Sander, and S. J. Gortler Harvard University Abstract
PAM algorithm. Types of Data in Cluster Analysis. A Categorization of Major Clustering Methods. Partitioning i Methods. Hierarchical Methods
 Whatis Cluster Analysis? Clustering Types of Data in Cluster Analysis Clustering part II A Categorization of Major Clustering Methods Partitioning i Methods Hierarchical Methods Partitioning i i Algorithms:
Whatis Cluster Analysis? Clustering Types of Data in Cluster Analysis Clustering part II A Categorization of Major Clustering Methods Partitioning i Methods Hierarchical Methods Partitioning i i Algorithms:
Euclidean TSP Between Two Nested Convex Obstacles
 Euclidean TSP Between Two Nested Convex Obstacles August 11, 2005 Jeff Abrahamson, Dept. of Computer Science, Drexel University, Philadelphia, PA, USA, jeffa@cs.drexel.edu. Ali Shokoufandeh, Dept. of Computer
Euclidean TSP Between Two Nested Convex Obstacles August 11, 2005 Jeff Abrahamson, Dept. of Computer Science, Drexel University, Philadelphia, PA, USA, jeffa@cs.drexel.edu. Ali Shokoufandeh, Dept. of Computer
Computational Geometry
 Motivation Motivation Polygons and visibility Visibility in polygons Triangulation Proof of the Art gallery theorem Two points in a simple polygon can see each other if their connecting line segment is
Motivation Motivation Polygons and visibility Visibility in polygons Triangulation Proof of the Art gallery theorem Two points in a simple polygon can see each other if their connecting line segment is
Lecture 6: GIS Spatial Analysis. GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University
 Lecture 6: GIS Spatial Analysis GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University 1 Spatial Data It can be most simply defined as information that describes the distribution
Lecture 6: GIS Spatial Analysis GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University 1 Spatial Data It can be most simply defined as information that describes the distribution
Information Retrieval and Web Search Engines
 Information Retrieval and Web Search Engines Lecture 7: Document Clustering May 25, 2011 Wolf-Tilo Balke and Joachim Selke Institut für Informationssysteme Technische Universität Braunschweig Homework
Information Retrieval and Web Search Engines Lecture 7: Document Clustering May 25, 2011 Wolf-Tilo Balke and Joachim Selke Institut für Informationssysteme Technische Universität Braunschweig Homework
Clustering. CE-717: Machine Learning Sharif University of Technology Spring Soleymani
 Clustering CE-717: Machine Learning Sharif University of Technology Spring 2016 Soleymani Outline Clustering Definition Clustering main approaches Partitional (flat) Hierarchical Clustering validation
Clustering CE-717: Machine Learning Sharif University of Technology Spring 2016 Soleymani Outline Clustering Definition Clustering main approaches Partitional (flat) Hierarchical Clustering validation
arxiv: v1 [cs.cg] 8 Jan 2018
![arxiv: v1 [cs.cg] 8 Jan 2018 arxiv: v1 [cs.cg] 8 Jan 2018](/thumbs/76/73575871.jpg) Voronoi Diagrams for a Moderate-Sized Point-Set in a Simple Polygon Eunjin Oh Hee-Kap Ahn arxiv:1801.02292v1 [cs.cg] 8 Jan 2018 Abstract Given a set of sites in a simple polygon, a geodesic Voronoi diagram
Voronoi Diagrams for a Moderate-Sized Point-Set in a Simple Polygon Eunjin Oh Hee-Kap Ahn arxiv:1801.02292v1 [cs.cg] 8 Jan 2018 Abstract Given a set of sites in a simple polygon, a geodesic Voronoi diagram
Unsupervised Learning and Clustering
 Unsupervised Learning and Clustering Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr CS 551, Spring 2009 CS 551, Spring 2009 c 2009, Selim Aksoy (Bilkent University)
Unsupervised Learning and Clustering Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr CS 551, Spring 2009 CS 551, Spring 2009 c 2009, Selim Aksoy (Bilkent University)
University of Florida CISE department Gator Engineering. Clustering Part 2
 Clustering Part 2 Dr. Sanjay Ranka Professor Computer and Information Science and Engineering University of Florida, Gainesville Partitional Clustering Original Points A Partitional Clustering Hierarchical
Clustering Part 2 Dr. Sanjay Ranka Professor Computer and Information Science and Engineering University of Florida, Gainesville Partitional Clustering Original Points A Partitional Clustering Hierarchical
Algorithms for Euclidean TSP
 This week, paper [2] by Arora. See the slides for figures. See also http://www.cs.princeton.edu/~arora/pubs/arorageo.ps Algorithms for Introduction This lecture is about the polynomial time approximation
This week, paper [2] by Arora. See the slides for figures. See also http://www.cs.princeton.edu/~arora/pubs/arorageo.ps Algorithms for Introduction This lecture is about the polynomial time approximation
Unsupervised Learning Partitioning Methods
 Unsupervised Learning Partitioning Methods Road Map 1. Basic Concepts 2. K-Means 3. K-Medoids 4. CLARA & CLARANS Cluster Analysis Unsupervised learning (i.e., Class label is unknown) Group data to form
Unsupervised Learning Partitioning Methods Road Map 1. Basic Concepts 2. K-Means 3. K-Medoids 4. CLARA & CLARANS Cluster Analysis Unsupervised learning (i.e., Class label is unknown) Group data to form
Lecture 11 Combinatorial Planning: In the Plane
 CS 460/560 Introduction to Computational Robotics Fall 2017, Rutgers University Lecture 11 Combinatorial Planning: In the Plane Instructor: Jingjin Yu Outline Convex shapes, revisited Combinatorial planning
CS 460/560 Introduction to Computational Robotics Fall 2017, Rutgers University Lecture 11 Combinatorial Planning: In the Plane Instructor: Jingjin Yu Outline Convex shapes, revisited Combinatorial planning
9. Visible-Surface Detection Methods
 9. Visible-Surface Detection Methods More information about Modelling and Perspective Viewing: Before going to visible surface detection, we first review and discuss the followings: 1. Modelling Transformation:
9. Visible-Surface Detection Methods More information about Modelling and Perspective Viewing: Before going to visible surface detection, we first review and discuss the followings: 1. Modelling Transformation:
Geographical routing 1
 Geographical routing 1 Routing in ad hoc networks Obtain route information between pairs of nodes wishing to communicate. Proactive protocols: maintain routing tables at each node that is updated as changes
Geographical routing 1 Routing in ad hoc networks Obtain route information between pairs of nodes wishing to communicate. Proactive protocols: maintain routing tables at each node that is updated as changes
Data Mining and Data Warehousing Classification-Lazy Learners
 Motivation Data Mining and Data Warehousing Classification-Lazy Learners Lazy Learners are the most intuitive type of learners and are used in many practical scenarios. The reason of their popularity is
Motivation Data Mining and Data Warehousing Classification-Lazy Learners Lazy Learners are the most intuitive type of learners and are used in many practical scenarios. The reason of their popularity is
Computational Geometry
 Lecture 12: Lecture 12: Motivation: Terrains by interpolation To build a model of the terrain surface, we can start with a number of sample points where we know the height. Lecture 12: Motivation: Terrains
Lecture 12: Lecture 12: Motivation: Terrains by interpolation To build a model of the terrain surface, we can start with a number of sample points where we know the height. Lecture 12: Motivation: Terrains
Voronoi Diagram. Xiao-Ming Fu
 Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
Unsupervised Data Mining: Clustering. Izabela Moise, Evangelos Pournaras, Dirk Helbing
 Unsupervised Data Mining: Clustering Izabela Moise, Evangelos Pournaras, Dirk Helbing Izabela Moise, Evangelos Pournaras, Dirk Helbing 1 1. Supervised Data Mining Classification Regression Outlier detection
Unsupervised Data Mining: Clustering Izabela Moise, Evangelos Pournaras, Dirk Helbing Izabela Moise, Evangelos Pournaras, Dirk Helbing 1 1. Supervised Data Mining Classification Regression Outlier detection
CHAPTER 4 K-MEANS AND UCAM CLUSTERING ALGORITHM
 CHAPTER 4 K-MEANS AND UCAM CLUSTERING 4.1 Introduction ALGORITHM Clustering has been used in a number of applications such as engineering, biology, medicine and data mining. The most popular clustering
CHAPTER 4 K-MEANS AND UCAM CLUSTERING 4.1 Introduction ALGORITHM Clustering has been used in a number of applications such as engineering, biology, medicine and data mining. The most popular clustering
S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 165
 S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 165 5.22. You are given a graph G = (V, E) with positive edge weights, and a minimum spanning tree T = (V, E ) with respect to these weights; you may
S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 165 5.22. You are given a graph G = (V, E) with positive edge weights, and a minimum spanning tree T = (V, E ) with respect to these weights; you may
Clustering Part 4 DBSCAN
 Clustering Part 4 Dr. Sanjay Ranka Professor Computer and Information Science and Engineering University of Florida, Gainesville DBSCAN DBSCAN is a density based clustering algorithm Density = number of
Clustering Part 4 Dr. Sanjay Ranka Professor Computer and Information Science and Engineering University of Florida, Gainesville DBSCAN DBSCAN is a density based clustering algorithm Density = number of
Cluster Analysis. Ying Shen, SSE, Tongji University
 Cluster Analysis Ying Shen, SSE, Tongji University Cluster analysis Cluster analysis groups data objects based only on the attributes in the data. The main objective is that The objects within a group
Cluster Analysis Ying Shen, SSE, Tongji University Cluster analysis Cluster analysis groups data objects based only on the attributes in the data. The main objective is that The objects within a group
Lecture 3: Art Gallery Problems and Polygon Triangulation
 EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
Interactive Scientific Visualization of Polygonal Knots
 Interactive Scientific Visualization of Polygonal Knots Abstract Dr. Kenny Hunt Computer Science Department The University of Wisconsin La Crosse hunt@mail.uwlax.edu Eric Lunde Computer Science Department
Interactive Scientific Visualization of Polygonal Knots Abstract Dr. Kenny Hunt Computer Science Department The University of Wisconsin La Crosse hunt@mail.uwlax.edu Eric Lunde Computer Science Department
Planning: Part 1 Classical Planning
 Planning: Part 1 Classical Planning Computer Science 6912 Department of Computer Science Memorial University of Newfoundland July 12, 2016 COMP 6912 (MUN) Planning July 12, 2016 1 / 9 Planning Localization
Planning: Part 1 Classical Planning Computer Science 6912 Department of Computer Science Memorial University of Newfoundland July 12, 2016 COMP 6912 (MUN) Planning July 12, 2016 1 / 9 Planning Localization
Polygon Partitioning. Lecture03
 1 Polygon Partitioning Lecture03 2 History of Triangulation Algorithms 3 Outline Monotone polygon Triangulation of monotone polygon Trapezoidal decomposition Decomposition in monotone mountain Convex decomposition
1 Polygon Partitioning Lecture03 2 History of Triangulation Algorithms 3 Outline Monotone polygon Triangulation of monotone polygon Trapezoidal decomposition Decomposition in monotone mountain Convex decomposition
Lecture 2 The k-means clustering problem
 CSE 29: Unsupervised learning Spring 2008 Lecture 2 The -means clustering problem 2. The -means cost function Last time we saw the -center problem, in which the input is a set S of data points and the
CSE 29: Unsupervised learning Spring 2008 Lecture 2 The -means clustering problem 2. The -means cost function Last time we saw the -center problem, in which the input is a set S of data points and the
Computational Geometry
 Planar point location Point location Introduction Planar point location Strip-based structure Point location problem: Preprocess a planar subdivision such that for any query point q, the face of the subdivision
Planar point location Point location Introduction Planar point location Strip-based structure Point location problem: Preprocess a planar subdivision such that for any query point q, the face of the subdivision
LightSlice: Matrix Slice Sampling for the Many-Lights Problem
 LightSlice: Matrix Slice Sampling for the Many-Lights Problem SIGGRAPH Asia 2011 Yu-Ting Wu Authors Jiawei Ou ( 歐嘉蔚 ) PhD Student Dartmouth College Fabio Pellacini Associate Prof. 2 Rendering L o ( p,
LightSlice: Matrix Slice Sampling for the Many-Lights Problem SIGGRAPH Asia 2011 Yu-Ting Wu Authors Jiawei Ou ( 歐嘉蔚 ) PhD Student Dartmouth College Fabio Pellacini Associate Prof. 2 Rendering L o ( p,
CMU-Q Lecture 4: Path Planning. Teacher: Gianni A. Di Caro
 CMU-Q 15-381 Lecture 4: Path Planning Teacher: Gianni A. Di Caro APPLICATION: MOTION PLANNING Path planning: computing a continuous sequence ( a path ) of configurations (states) between an initial configuration
CMU-Q 15-381 Lecture 4: Path Planning Teacher: Gianni A. Di Caro APPLICATION: MOTION PLANNING Path planning: computing a continuous sequence ( a path ) of configurations (states) between an initial configuration
Institutionen för datavetenskap Department of Computer and Information Science
 Institutionen för datavetenskap Department of Computer and Information Science Final thesis K Shortest Path Implementation by RadhaKrishna Nagubadi LIU-IDA/LITH-EX-A--13/41--SE 213-6-27 Linköpings universitet
Institutionen för datavetenskap Department of Computer and Information Science Final thesis K Shortest Path Implementation by RadhaKrishna Nagubadi LIU-IDA/LITH-EX-A--13/41--SE 213-6-27 Linköpings universitet
Ray Tracing Acceleration Data Structures
 Ray Tracing Acceleration Data Structures Sumair Ahmed October 29, 2009 Ray Tracing is very time-consuming because of the ray-object intersection calculations. With the brute force method, each ray has
Ray Tracing Acceleration Data Structures Sumair Ahmed October 29, 2009 Ray Tracing is very time-consuming because of the ray-object intersection calculations. With the brute force method, each ray has
Spatial Analysis (Vector) II
 Spatial Analysis (Vector) II GEOG 300, Lecture 9 Dr. Anthony Jjumba 1 A Spatial Network is a set of geographic locations interconnected in a system by a number of routes is a system of linear features
Spatial Analysis (Vector) II GEOG 300, Lecture 9 Dr. Anthony Jjumba 1 A Spatial Network is a set of geographic locations interconnected in a system by a number of routes is a system of linear features
ECLT 5810 Clustering
 ECLT 5810 Clustering What is Cluster Analysis? Cluster: a collection of data objects Similar to one another within the same cluster Dissimilar to the objects in other clusters Cluster analysis Grouping
ECLT 5810 Clustering What is Cluster Analysis? Cluster: a collection of data objects Similar to one another within the same cluster Dissimilar to the objects in other clusters Cluster analysis Grouping
Hierarchical Clustering Lecture 9
 Hierarchical Clustering Lecture 9 Marina Santini Acknowledgements Slides borrowed and adapted from: Data Mining by I. H. Witten, E. Frank and M. A. Hall 1 Lecture 9: Required Reading Witten et al. (2011:
Hierarchical Clustering Lecture 9 Marina Santini Acknowledgements Slides borrowed and adapted from: Data Mining by I. H. Witten, E. Frank and M. A. Hall 1 Lecture 9: Required Reading Witten et al. (2011:
Ma/CS 6b Class 26: Art Galleries and Politicians
 Ma/CS 6b Class 26: Art Galleries and Politicians By Adam Sheffer The Art Gallery Problem Problem. We wish to place security cameras at a gallery, such that they cover it completely. Every camera can cover
Ma/CS 6b Class 26: Art Galleries and Politicians By Adam Sheffer The Art Gallery Problem Problem. We wish to place security cameras at a gallery, such that they cover it completely. Every camera can cover
Computer Graphics. Bing-Yu Chen National Taiwan University The University of Tokyo
 Computer Graphics Bing-Yu Chen National Taiwan University The University of Tokyo Hidden-Surface Removal Back-Face Culling The Depth-Sort Algorithm Binary Space-Partitioning Trees The z-buffer Algorithm
Computer Graphics Bing-Yu Chen National Taiwan University The University of Tokyo Hidden-Surface Removal Back-Face Culling The Depth-Sort Algorithm Binary Space-Partitioning Trees The z-buffer Algorithm
The Visibility Problem and Binary Space Partition. (slides by Nati Srebro)
 The Visibility Problem and Binary Space Partition (slides by Nati Srebro) The Visibility Problem b a c d e Algorithms Z-buffer: Draw objects in arbitrary order For each pixel, maintain distance to the
The Visibility Problem and Binary Space Partition (slides by Nati Srebro) The Visibility Problem b a c d e Algorithms Z-buffer: Draw objects in arbitrary order For each pixel, maintain distance to the
Cluster Analysis. CSE634 Data Mining
 Cluster Analysis CSE634 Data Mining Agenda Introduction Clustering Requirements Data Representation Partitioning Methods K-Means Clustering K-Medoids Clustering Constrained K-Means clustering Introduction
Cluster Analysis CSE634 Data Mining Agenda Introduction Clustering Requirements Data Representation Partitioning Methods K-Means Clustering K-Medoids Clustering Constrained K-Means clustering Introduction
22 Elementary Graph Algorithms. There are two standard ways to represent a
 VI Graph Algorithms Elementary Graph Algorithms Minimum Spanning Trees Single-Source Shortest Paths All-Pairs Shortest Paths 22 Elementary Graph Algorithms There are two standard ways to represent a graph
VI Graph Algorithms Elementary Graph Algorithms Minimum Spanning Trees Single-Source Shortest Paths All-Pairs Shortest Paths 22 Elementary Graph Algorithms There are two standard ways to represent a graph
Community Detection. Jian Pei: CMPT 741/459 Clustering (1) 2
 Clustering Community Detection http://image.slidesharecdn.com/communitydetectionitilecturejune0-0609559-phpapp0/95/community-detection-in-social-media--78.jpg?cb=3087368 Jian Pei: CMPT 74/459 Clustering
Clustering Community Detection http://image.slidesharecdn.com/communitydetectionitilecturejune0-0609559-phpapp0/95/community-detection-in-social-media--78.jpg?cb=3087368 Jian Pei: CMPT 74/459 Clustering
Lecture 11: Ray tracing (cont.)
 Interactive Computer Graphics Ray tracing - Summary Lecture 11: Ray tracing (cont.) Graphics Lecture 10: Slide 1 Some slides adopted from H. Pfister, Harvard Graphics Lecture 10: Slide 2 Ray tracing -
Interactive Computer Graphics Ray tracing - Summary Lecture 11: Ray tracing (cont.) Graphics Lecture 10: Slide 1 Some slides adopted from H. Pfister, Harvard Graphics Lecture 10: Slide 2 Ray tracing -
Chapter 7 TOPOLOGY CONTROL
 Chapter 7 TOPOLOGY CONTROL Distributed Computing Group Mobile Computing Winter 2005 / 2006 Overview Topology Control Gabriel Graph et al. XTC Interference SINR & Scheduling Complexity Distributed Computing
Chapter 7 TOPOLOGY CONTROL Distributed Computing Group Mobile Computing Winter 2005 / 2006 Overview Topology Control Gabriel Graph et al. XTC Interference SINR & Scheduling Complexity Distributed Computing
Mathematics Curriculum
 6 G R A D E Mathematics Curriculum GRADE 6 5 Table of Contents 1... 1 Topic A: Area of Triangles, Quadrilaterals, and Polygons (6.G.A.1)... 11 Lesson 1: The Area of Parallelograms Through Rectangle Facts...
6 G R A D E Mathematics Curriculum GRADE 6 5 Table of Contents 1... 1 Topic A: Area of Triangles, Quadrilaterals, and Polygons (6.G.A.1)... 11 Lesson 1: The Area of Parallelograms Through Rectangle Facts...
Road Map Methods. Including material from Howie Choset / G.D. Hager S. Leonard
 Road Map Methods Including material from Howie Choset The Basic Idea Capture the connectivity of Q free by a graph or network of paths. 16-735, Howie Choset, with significant copying from who loosely based
Road Map Methods Including material from Howie Choset The Basic Idea Capture the connectivity of Q free by a graph or network of paths. 16-735, Howie Choset, with significant copying from who loosely based
Delaunay Triangulations. Presented by Glenn Eguchi Computational Geometry October 11, 2001
 Delaunay Triangulations Presented by Glenn Eguchi 6.838 Computational Geometry October 11, 2001 Motivation: Terrains Set of data points A R 2 Height ƒ(p) defined at each point p in A How can we most naturally
Delaunay Triangulations Presented by Glenn Eguchi 6.838 Computational Geometry October 11, 2001 Motivation: Terrains Set of data points A R 2 Height ƒ(p) defined at each point p in A How can we most naturally
Configuration Space of a Robot
 Robot Path Planning Overview: 1. Visibility Graphs 2. Voronoi Graphs 3. Potential Fields 4. Sampling-Based Planners PRM: Probabilistic Roadmap Methods RRTs: Rapidly-exploring Random Trees Configuration
Robot Path Planning Overview: 1. Visibility Graphs 2. Voronoi Graphs 3. Potential Fields 4. Sampling-Based Planners PRM: Probabilistic Roadmap Methods RRTs: Rapidly-exploring Random Trees Configuration
6 ROUTING PROBLEMS VEHICLE ROUTING PROBLEMS. Vehicle Routing Problem, VRP:
 6 ROUTING PROBLEMS VEHICLE ROUTING PROBLEMS Vehicle Routing Problem, VRP: Customers i=1,...,n with demands of a product must be served using a fleet of vehicles for the deliveries. The vehicles, with given
6 ROUTING PROBLEMS VEHICLE ROUTING PROBLEMS Vehicle Routing Problem, VRP: Customers i=1,...,n with demands of a product must be served using a fleet of vehicles for the deliveries. The vehicles, with given
Hard clustering. Each object is assigned to one and only one cluster. Hierarchical clustering is usually hard. Soft (fuzzy) clustering
 An unsupervised machine learning problem Grouping a set of objects in such a way that objects in the same group (a cluster) are more similar (in some sense or another) to each other than to those in other
An unsupervised machine learning problem Grouping a set of objects in such a way that objects in the same group (a cluster) are more similar (in some sense or another) to each other than to those in other
Theorem 2.9: nearest addition algorithm
 There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
CHAPTER 4 VORONOI DIAGRAM BASED CLUSTERING ALGORITHMS
 CHAPTER 4 VORONOI DIAGRAM BASED CLUSTERING ALGORITHMS 4.1 Introduction Although MST-based clustering methods are effective for complex data, they require quadratic computational time which is high for
CHAPTER 4 VORONOI DIAGRAM BASED CLUSTERING ALGORITHMS 4.1 Introduction Although MST-based clustering methods are effective for complex data, they require quadratic computational time which is high for
Data Mining Algorithms
 for the original version: -JörgSander and Martin Ester - Jiawei Han and Micheline Kamber Data Management and Exploration Prof. Dr. Thomas Seidl Data Mining Algorithms Lecture Course with Tutorials Wintersemester
for the original version: -JörgSander and Martin Ester - Jiawei Han and Micheline Kamber Data Management and Exploration Prof. Dr. Thomas Seidl Data Mining Algorithms Lecture Course with Tutorials Wintersemester
Data Mining 4. Cluster Analysis
 Data Mining 4. Cluster Analysis 4.5 Spring 2010 Instructor: Dr. Masoud Yaghini Introduction DBSCAN Algorithm OPTICS Algorithm DENCLUE Algorithm References Outline Introduction Introduction Density-based
Data Mining 4. Cluster Analysis 4.5 Spring 2010 Instructor: Dr. Masoud Yaghini Introduction DBSCAN Algorithm OPTICS Algorithm DENCLUE Algorithm References Outline Introduction Introduction Density-based
CHAPTER VII INDEXED K TWIN NEIGHBOUR CLUSTERING ALGORITHM 7.1 INTRODUCTION
 CHAPTER VII INDEXED K TWIN NEIGHBOUR CLUSTERING ALGORITHM 7.1 INTRODUCTION Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called cluster)
CHAPTER VII INDEXED K TWIN NEIGHBOUR CLUSTERING ALGORITHM 7.1 INTRODUCTION Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called cluster)
Maps as Numbers: Data Models
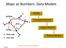 Maps as Numbers: Data Models vertices E Reality S E S arcs S E Conceptual Models nodes E Logical Models S Start node E End node S Physical Models 1 The Task An accurate, registered, digital map that can
Maps as Numbers: Data Models vertices E Reality S E S arcs S E Conceptual Models nodes E Logical Models S Start node E End node S Physical Models 1 The Task An accurate, registered, digital map that can
Efficient and Effective Clustering Methods for Spatial Data Mining. Raymond T. Ng, Jiawei Han
 Efficient and Effective Clustering Methods for Spatial Data Mining Raymond T. Ng, Jiawei Han 1 Overview Spatial Data Mining Clustering techniques CLARANS Spatial and Non-Spatial dominant CLARANS Observations
Efficient and Effective Clustering Methods for Spatial Data Mining Raymond T. Ng, Jiawei Han 1 Overview Spatial Data Mining Clustering techniques CLARANS Spatial and Non-Spatial dominant CLARANS Observations
Object-Based Classification & ecognition. Zutao Ouyang 11/17/2015
 Object-Based Classification & ecognition Zutao Ouyang 11/17/2015 What is Object-Based Classification The object based image analysis approach delineates segments of homogeneous image areas (i.e., objects)
Object-Based Classification & ecognition Zutao Ouyang 11/17/2015 What is Object-Based Classification The object based image analysis approach delineates segments of homogeneous image areas (i.e., objects)
Section 9.1. Points, Lines, Planes, and Angles. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 9.1 Points, Lines, Planes, and Angles What You Will Learn Points Lines Planes Angles 9.1-2 Basic Terms A point, line, and plane are three basic terms in geometry that are NOT given a formal definition,
Section 9.1 Points, Lines, Planes, and Angles What You Will Learn Points Lines Planes Angles 9.1-2 Basic Terms A point, line, and plane are three basic terms in geometry that are NOT given a formal definition,
Visible-Surface Detection Methods. Chapter? Intro. to Computer Graphics Spring 2008, Y. G. Shin
 Visible-Surface Detection Methods Chapter? Intro. to Computer Graphics Spring 2008, Y. G. Shin The Visibility Problem [Problem Statement] GIVEN: a set of 3-D surfaces, a projection from 3-D to 2-D screen,
Visible-Surface Detection Methods Chapter? Intro. to Computer Graphics Spring 2008, Y. G. Shin The Visibility Problem [Problem Statement] GIVEN: a set of 3-D surfaces, a projection from 3-D to 2-D screen,
Surface Simplification Using Quadric Error Metrics
 Surface Simplification Using Quadric Error Metrics Authors: Michael Garland & Paul Heckbert Presented by: Niu Xiaozhen Disclaimer: Some slides are modified from original slides, which were designed by
Surface Simplification Using Quadric Error Metrics Authors: Michael Garland & Paul Heckbert Presented by: Niu Xiaozhen Disclaimer: Some slides are modified from original slides, which were designed by
CS570: Introduction to Data Mining
 CS570: Introduction to Data Mining Scalable Clustering Methods: BIRCH and Others Reading: Chapter 10.3 Han, Chapter 9.5 Tan Cengiz Gunay, Ph.D. Slides courtesy of Li Xiong, Ph.D., 2011 Han, Kamber & Pei.
CS570: Introduction to Data Mining Scalable Clustering Methods: BIRCH and Others Reading: Chapter 10.3 Han, Chapter 9.5 Tan Cengiz Gunay, Ph.D. Slides courtesy of Li Xiong, Ph.D., 2011 Han, Kamber & Pei.
The Algorithm Design Manual
 Steven S. Skiena The Algorithm Design Manual With 72 Figures Includes CD-ROM THE ELECTRONIC LIBRARY OF SCIENCE Contents Preface vii I TECHNIQUES 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 1.10 2 2.1 2.2 2.3
Steven S. Skiena The Algorithm Design Manual With 72 Figures Includes CD-ROM THE ELECTRONIC LIBRARY OF SCIENCE Contents Preface vii I TECHNIQUES 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 1.10 2 2.1 2.2 2.3
Cluster Analysis. Prof. Thomas B. Fomby Department of Economics Southern Methodist University Dallas, TX April 2008 April 2010
 Cluster Analysis Prof. Thomas B. Fomby Department of Economics Southern Methodist University Dallas, TX 7575 April 008 April 010 Cluster Analysis, sometimes called data segmentation or customer segmentation,
Cluster Analysis Prof. Thomas B. Fomby Department of Economics Southern Methodist University Dallas, TX 7575 April 008 April 010 Cluster Analysis, sometimes called data segmentation or customer segmentation,
Computer Graphics. Bing-Yu Chen National Taiwan University
 Computer Graphics Bing-Yu Chen National Taiwan University Visible-Surface Determination Back-Face Culling The Depth-Sort Algorithm Binary Space-Partitioning Trees The z-buffer Algorithm Scan-Line Algorithm
Computer Graphics Bing-Yu Chen National Taiwan University Visible-Surface Determination Back-Face Culling The Depth-Sort Algorithm Binary Space-Partitioning Trees The z-buffer Algorithm Scan-Line Algorithm
Line Arrangements. Applications
 Computational Geometry Chapter 9 Line Arrangements 1 Line Arrangements Applications On the Agenda 2 1 Complexity of a Line Arrangement Given a set L of n lines in the plane, their arrangement A(L) is the
Computational Geometry Chapter 9 Line Arrangements 1 Line Arrangements Applications On the Agenda 2 1 Complexity of a Line Arrangement Given a set L of n lines in the plane, their arrangement A(L) is the
SAMPLING AND THE MOMENT TECHNIQUE. By Sveta Oksen
 SAMPLING AND THE MOMENT TECHNIQUE By Sveta Oksen Overview - Vertical decomposition - Construction - Running time analysis - The bounded moments theorem - General settings - The sampling model - The exponential
SAMPLING AND THE MOMENT TECHNIQUE By Sveta Oksen Overview - Vertical decomposition - Construction - Running time analysis - The bounded moments theorem - General settings - The sampling model - The exponential
University of Florida CISE department Gator Engineering. Clustering Part 4
 Clustering Part 4 Dr. Sanjay Ranka Professor Computer and Information Science and Engineering University of Florida, Gainesville DBSCAN DBSCAN is a density based clustering algorithm Density = number of
Clustering Part 4 Dr. Sanjay Ranka Professor Computer and Information Science and Engineering University of Florida, Gainesville DBSCAN DBSCAN is a density based clustering algorithm Density = number of
