Matrix representation of a solution of a combinatorial problem of the group theory
|
|
|
- Melina Jones
- 6 years ago
- Views:
Transcription
1 Matrix represetatio of a solutio of a combiatorial problem of the group theory Krasimir Yordzhev, Lilyaa Totia Faculty of Mathematics ad Natural Scieces South-West Uiversity 66 Iva Mihailov Str, 2700 Blagoevgrad, Bulgaria yordzhev@swubg, liliaa_totia@abvbg Abstract: A equivalece relatio i the symmetric group, where ³ 2 is a positive iteger has bee cosidered A algorithm for calculatio of the umber of the equivalece classes by this relatio for arbitrary iteger has bee described Keywords: Symmetric Group, Equivalece Relatio, Equivalece Classes, Directed Graph, Euler Fuctio, C++ Programmig Laguage S 1 INTRODUCTION The object of the preset study is to be received a algorithm for computer calculatio of some combiatorial characteristics of the symmetric group This algorithm has bee based o the theoretical elaboratios described closely i [3] ad [4] I our study with we deote the set of the positive itegers Let Î The with we deote the set = {1, 2,, With ì 1 2 ü S ï æ ö = is, s 1,2,,, is it fors t ï í Î = ¹ ý i1 i2 i ¹ ï çè î ø ïþ we deote the symmetric group o the set, i e the group of all oe-tooe mappigs a : of the set i oeself If mî, the with GCD(, m) we deote the greatest commo divisor of itegers ad m The ad m are relatively primes if ad oly if whe GCD(, m) =1
2 With j( ) we deote the Euler fuctio, i e the umber of elemets of that are relatively primes with (see more for example i [1] or [5]) By defiitio j(1) = 1 2 PRIOR INFORMATION Let be a positive iteger We cosider a elemet æ1 2 1 ö s - = ÎS ç çè2 3 1 ø I [3] the followig equivalece relatio had bee itroduced i : we say that abî, S are s - equivalet if the itegers ad l exist such that l a= s bs, that is equivalet to coditio that itegers ad l 1 1 exist such that s 1 l a = bs 1 The followig tas has bee put: To fid the umber of the equivalece classes by so defied equivalece relatio, with aother words the cardiality of the factor set Q = S/ s To be solved so puttig tas a directed graph with the set of vertices G {,, V Ì = a b a bî, 2 has bee costructed, formed by the ext mea: 1 For every iteger m Î such that 1, m V 2 If l, Î V, the divides GSD(, m ) = 1 Î exists, as i this vertex arcs do ot eter S a vertex 3 Let l, Î V ad let p is a prime divisor of The we receive the umber r that is equal to the remaider after the multiplicatio pl is divided ito We costruct a vertex p r Î V ad a arc with begi the vertex l, ad ed the, vertex p, r 4 Aother vertex ad aother arc i the graph G acceptig received by the mea described above do ot exist For example at = 12 the graph G12 is show o figure 1:
3 Fig 1: The graph G 12 We itroduce the followig partial order i the vertices set of the graph G : If v1, v2 ÎV, the v1< v2 if ad oly if whe a directed path with begi vertex v 1 ad ed vertex v 2 exists It is easily to see that by so itroduced order is semilattice with the uique maximal elemet Î V V V, ad j( ) i umber miimal elemets, each of id 1, m Î V, where j () is the Euler fuctio For more details of the graph theory see for example i [6] For each vertex l, Î V we defie the fuctio h (, ) that depeds o ad, but does ot deped o l 1 1 æ - æö ö h (, ) = ç 1! rhr (, ) - - ç å ç è è ø rt, < l, ø (1) ç( ) The followig assertio had bee demostrated i [3]: Theorem 1 [3] The umber of the equivalece classes by the s - equivalece is equal to (2) Q = å h (, ) l, ÎV Theorem 1 gives us a effective algorithm for the maual calculatio of Q Costructio of the graph G is ecessary for this object This approach gives relatively good results at relatively small values of as the experiece of authors has bee show With icrease of
4 probability of errors icreases repeatedly, because of the umber of classes icreases expoetially, accordig to formulas (1) ad (2) It had bee demostrate i [4] that all assertios cosidered i [3] are valid for a arbitrary elemet s Î S, o coditio that s is a cycle with legth It is easy to see that we ca reorgaize the formula (1) i the followig recursive id: (3) ç( ) æ ö -1 1 ç æö h (, ) = -1! - rt( r,, ) hr (, ) ç å for > 1 ç è ø r çè r< ø ad (4) h (,1) = 1, where the fuctio t( r,, ) gives as the umber of vertices rs, Î V, such that rs, <, Î V The followig assertio had bee demostrated i [4]: Theorem 2 [4] The umber of the vertices of id l, Î V is equal to j, where j m is the Euler fuctio ( ) ( ) As a cosequece of theorem 2 the formula (2) has bee reorgaized i the followig id: (5) Q = å h (, ) jç æ ö çè ø 3 MATRIX REPRESENTATION AND PROGRAM REALIZATION I this sectio we use program laguage C++ for descriptio of algorithms cosidered i the preset study The program was bee tested i a programmig eviromet Borlad C++ Builder
5 is a global costat iteger pa- ad may be used without explicit At the examples we cosider that rameter, equal to the order of the group S declaratio For usig theorem 1 as we avail ourselves of formulas (3) ad (4) it is coveiet to fill the elemets of the matrix M = m, cosistig of 4 rows ( ij ad q colums, where q is equal to the umber of all positive divisors of the iteger (icludig 1 ad ) Never the less the iteger will be writte dow i M, i our program realizatio we declare M as two-dimesioal array of type double because of fact that we expect to receive too large values at calculatio of the fuctio h (, ) accordig to formula (3) I the first row we write dow all itegers dividig without remaider the parameter That ca be realized with the help of the followig procedure, for example: void Divisors(it, it FirstRow[], it& q) { q = 1; FirstRow[0] = 1; for (it t = 2 ; t <= ; t++) { if (%t == 0) { FirstRow[q] = t; q++; As additioal effect of the wor of the fuctio Divisors we receive the umber q of all divisors of the global parameter It the ed the procedure receives a iteger array FirstRow, correctly filled with the divisors of We copy the values of the array FirstRow to first row of the array M We fill the secod row of M with the values of the Euler fuctio j ( ), where has bee tae from the correspodig compoet of the first row of M The fuctio j( m) ca be realized as we use a variety of the algorithm, ow as the Sieve of Eratosthees [2,5] it EulerFuctio(it m) { it t =1; it b[100]; for (it i=1; i <= m; i++) { b[i] = i; )
6 for (it i=2; i <= m; i++) { if (b[i] == 0) { cotiue; if (m%b[i] == 0) { for (it j=1; i*j<=m; j++) { b[i*j] = 0; else t++; retur t; We fill the third row of M with the values of the fuctio h) (,, accordig to formulas (3) ad (4), where has bee tae from the correspodig compoet of the first row of M Here we cosider agai that is a global costat parameter, ie it is ot ecessary to be preset i the list of formal parameters of the fuctio described below For simplicity of the expositio we will ot verify correctess of the data, ie whether divides This coditio has bee esured by the fact that has bee tae from the first row of the matrix M, where o coditio oly divisors of has bee writte dow We declare the type of the fuctio h(it), as well as some worig variables, which values are itegers with the type log double because of expectatio to receive to large values accordig to formula (3) For the calculatio of the fuctio h (, ), must first be calculated the fuctio t( r,, ) This ca be doe usig the followig algorithm: // Euclidea algorithm for fidig the greatest commo divisor of itegers a ad b: it GCD(it a, it b) { while (a!= b) if (a > b) { a = a-b; else b = b-a; retur a; //
7 // Fuctio examied whether l, is the vertex of V bool Vertex(it, it l, it ) { if ((<=0) (>) (l>) (%!= 0)) { retur false; else { if (( == )) { if (l == ) retur true; else for (it m=1; m<=; m++) { if ((GCD(m,) == 1) && (m*% == l)) retur true; retur false; // // The fuctio t( r,, ): it tau(it, it, it r) { it t=0; it p = /r; for (it s=1; s<; s++) { if (Vertex(r,s,) && (s*p% == %)) { t++; retur t; The a algorithm for obtaiig h (, ) accordig to formulas (3) ad (4) ca be realized usig the followig C++ fuctio: log double h(it, it ) { log double t; if ( == 1) { t=1;
8 else { log double fact = 1; for (it i=2; i <= -1; i++) { fact = fact*i; log double pow = 1; it p = /; for (it i=1; i<=-1; i++) { pow = pow*p ; log double sum = 0; for (it r=1; r<=-1; r++) { if (%r == 0) { sum = sum+r*tau(,,r)*h(,r); t = (fact*pow-sum)/; retur t; We receive the fourth row of M as multiply compoet by compoet the secod with the third rom Here we will sip the descriptio of the mai fuctio ad the iput ad output operatios as they are specific to differet programmig eviromets At = 12 the filled matrix M is show i table 1: Tab 1: Matrix M at = j ( ) h (, ) m j m3 j W e receive the fial result for the umber of the equivalece classes of S by the cosidered equivalece relatio as we add the elemets of the last row of the matrix M accordig to formula (5) We calculate from table 1: Q 12 = = Q
9 We show i table 2 the values of Q at 19 calculated by the algorithm described above: Tab 1: The umber of the 19 equivalece classes i cocerig to equivalece at Q Q Q S REFERENCES [1] Adreescu, T, Adrica, D, Feg, Z (2007) 104 Number Theory Problems Bosto: Birhauser [2] Reigold E W (1977) Combiatorial Algorithms Theory ad Practice New Jersey, Pretice-Hall [3] Yordzhev, K (2004) O a equivalece relatio i the set of the permutatio matrices, i Discrete Mathematics ad Applicatios, Blagoevgrad, SWU N Rilsi, [4] Yordzhev, K (to appear) O a Combiatorial Problem i the Symmetric Group [5] Мирчев, И, (1995) Теория на числата, Благоевград, ЮЗУ Н Рилски [6] Мирчев И, (2001) Графи Оптимизационни алгоритми в мрежи, Благоевград, ЮЗУ Н Рилски
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Chapter 3 Classification of FFT Processor Algorithms
 Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
AN EXAMPLE FOR THE USE OF BITWISE OPERATIONS IN PROGRAMMING
 AN EXAMPLE FOR THE USE OF BITWISE OPERATIONS IN PROGRAMMING Krasimir Yakov Yordzhev This piece of work presets a meaigful example for the advatages of usig bitwise operatios for creatig effective algorithms
AN EXAMPLE FOR THE USE OF BITWISE OPERATIONS IN PROGRAMMING Krasimir Yakov Yordzhev This piece of work presets a meaigful example for the advatages of usig bitwise operatios for creatig effective algorithms
BOOLEAN MATHEMATICS: GENERAL THEORY
 CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
9.1. Sequences and Series. Sequences. What you should learn. Why you should learn it. Definition of Sequence
 _9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
_9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
Outline and Reading. Analysis of Algorithms. Running Time. Experimental Studies. Limitations of Experiments. Theoretical Analysis
 Outlie ad Readig Aalysis of Algorithms Iput Algorithm Output Ruig time ( 3.) Pseudo-code ( 3.2) Coutig primitive operatios ( 3.3-3.) Asymptotic otatio ( 3.6) Asymptotic aalysis ( 3.7) Case study Aalysis
Outlie ad Readig Aalysis of Algorithms Iput Algorithm Output Ruig time ( 3.) Pseudo-code ( 3.2) Coutig primitive operatios ( 3.3-3.) Asymptotic otatio ( 3.6) Asymptotic aalysis ( 3.7) Case study Aalysis
Elementary Educational Computer
 Chapter 5 Elemetary Educatioal Computer. Geeral structure of the Elemetary Educatioal Computer (EEC) The EEC coforms to the 5 uits structure defied by vo Neuma's model (.) All uits are preseted i a simplified
Chapter 5 Elemetary Educatioal Computer. Geeral structure of the Elemetary Educatioal Computer (EEC) The EEC coforms to the 5 uits structure defied by vo Neuma's model (.) All uits are preseted i a simplified
Theory of Fuzzy Soft Matrix and its Multi Criteria in Decision Making Based on Three Basic t-norm Operators
 Theory of Fuzzy Soft Matrix ad its Multi Criteria i Decisio Makig Based o Three Basic t-norm Operators Md. Jalilul Islam Modal 1, Dr. Tapa Kumar Roy 2 Research Scholar, Dept. of Mathematics, BESUS, Howrah-711103,
Theory of Fuzzy Soft Matrix ad its Multi Criteria i Decisio Makig Based o Three Basic t-norm Operators Md. Jalilul Islam Modal 1, Dr. Tapa Kumar Roy 2 Research Scholar, Dept. of Mathematics, BESUS, Howrah-711103,
Polynomial Functions and Models. Learning Objectives. Polynomials. P (x) = a n x n + a n 1 x n a 1 x + a 0, a n 0
 Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
Chapter 4. Procedural Abstraction and Functions That Return a Value. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 4 Procedural Abstractio ad Fuctios That Retur a Value Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 4.1 Top-Dow Desig 4.2 Predefied Fuctios 4.3 Programmer-Defied Fuctios 4.4
Chapter 4 Procedural Abstractio ad Fuctios That Retur a Value Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 4.1 Top-Dow Desig 4.2 Predefied Fuctios 4.3 Programmer-Defied Fuctios 4.4
c-dominating Sets for Families of Graphs
 c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
MATHEMATICAL METHODS OF ANALYSIS AND EXPERIMENTAL DATA PROCESSING (Or Methods of Curve Fitting)
 MATHEMATICAL METHODS OF ANALYSIS AND EXPERIMENTAL DATA PROCESSING (Or Methods of Curve Fittig) I this chapter, we will eamie some methods of aalysis ad data processig; data obtaied as a result of a give
MATHEMATICAL METHODS OF ANALYSIS AND EXPERIMENTAL DATA PROCESSING (Or Methods of Curve Fittig) I this chapter, we will eamie some methods of aalysis ad data processig; data obtaied as a result of a give
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
Pattern Recognition Systems Lab 1 Least Mean Squares
 Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
CSC165H1 Worksheet: Tutorial 8 Algorithm analysis (SOLUTIONS)
 CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
Lecture Notes 6 Introduction to algorithm analysis CSS 501 Data Structures and Object-Oriented Programming
 Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
Super Vertex Magic and E-Super Vertex Magic. Total Labelling
 Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
How do we evaluate algorithms?
 F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
ENGI 4421 Probability and Statistics Faculty of Engineering and Applied Science Problem Set 1 Descriptive Statistics
 ENGI 44 Probability ad Statistics Faculty of Egieerig ad Applied Sciece Problem Set Descriptive Statistics. If, i the set of values {,, 3, 4, 5, 6, 7 } a error causes the value 5 to be replaced by 50,
ENGI 44 Probability ad Statistics Faculty of Egieerig ad Applied Sciece Problem Set Descriptive Statistics. If, i the set of values {,, 3, 4, 5, 6, 7 } a error causes the value 5 to be replaced by 50,
Project 2.5 Improved Euler Implementation
 Project 2.5 Improved Euler Implemetatio Figure 2.5.10 i the text lists TI-85 ad BASIC programs implemetig the improved Euler method to approximate the solutio of the iitial value problem dy dx = x+ y,
Project 2.5 Improved Euler Implemetatio Figure 2.5.10 i the text lists TI-85 ad BASIC programs implemetig the improved Euler method to approximate the solutio of the iitial value problem dy dx = x+ y,
CSE 417: Algorithms and Computational Complexity
 Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
What are we going to learn? CSC Data Structures Analysis of Algorithms. Overview. Algorithm, and Inputs
 What are we goig to lear? CSC316-003 Data Structures Aalysis of Algorithms Computer Sciece North Carolia State Uiversity Need to say that some algorithms are better tha others Criteria for evaluatio Structure
What are we goig to lear? CSC316-003 Data Structures Aalysis of Algorithms Computer Sciece North Carolia State Uiversity Need to say that some algorithms are better tha others Criteria for evaluatio Structure
Inductive Definition to Recursive Function
 PDS: CS 11002 Computer Sc & Egg: IIT Kharagpur 1 Iductive Defiitio to Recursive Fuctio PDS: CS 11002 Computer Sc & Egg: IIT Kharagpur 2 Factorial Fuctio Cosider the followig recursive defiitio of the factorial
PDS: CS 11002 Computer Sc & Egg: IIT Kharagpur 1 Iductive Defiitio to Recursive Fuctio PDS: CS 11002 Computer Sc & Egg: IIT Kharagpur 2 Factorial Fuctio Cosider the followig recursive defiitio of the factorial
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
3D Model Retrieval Method Based on Sample Prediction
 20 Iteratioal Coferece o Computer Commuicatio ad Maagemet Proc.of CSIT vol.5 (20) (20) IACSIT Press, Sigapore 3D Model Retrieval Method Based o Sample Predictio Qigche Zhag, Ya Tag* School of Computer
20 Iteratioal Coferece o Computer Commuicatio ad Maagemet Proc.of CSIT vol.5 (20) (20) IACSIT Press, Sigapore 3D Model Retrieval Method Based o Sample Predictio Qigche Zhag, Ya Tag* School of Computer
Convergence results for conditional expectations
 Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Chapter 9. Pointers and Dynamic Arrays. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
Examples and Applications of Binary Search
 Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
On Infinite Groups that are Isomorphic to its Proper Infinite Subgroup. Jaymar Talledo Balihon. Abstract
 O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
Reversible Realization of Quaternary Decoder, Multiplexer, and Demultiplexer Circuits
 Egieerig Letters, :, EL Reversible Realizatio of Quaterary Decoder, Multiplexer, ad Demultiplexer Circuits Mozammel H.. Kha, Member, ENG bstract quaterary reversible circuit is more compact tha the correspodig
Egieerig Letters, :, EL Reversible Realizatio of Quaterary Decoder, Multiplexer, ad Demultiplexer Circuits Mozammel H.. Kha, Member, ENG bstract quaterary reversible circuit is more compact tha the correspodig
Counting Regions in the Plane and More 1
 Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Some cycle and path related strongly -graphs
 Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
A New Morphological 3D Shape Decomposition: Grayscale Interframe Interpolation Method
 A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
Algorithm. Counting Sort Analysis of Algorithms
 Algorithm Coutig Sort Aalysis of Algorithms Assumptios: records Coutig sort Each record cotais keys ad data All keys are i the rage of 1 to k Space The usorted list is stored i A, the sorted list will
Algorithm Coutig Sort Aalysis of Algorithms Assumptios: records Coutig sort Each record cotais keys ad data All keys are i the rage of 1 to k Space The usorted list is stored i A, the sorted list will
3. b. Present a combinatorial argument that for all positive integers n : : 2 n
 . b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
. b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
Recursion. Computer Science S-111 Harvard University David G. Sullivan, Ph.D. Review: Method Frames
 Uit 4, Part 3 Recursio Computer Sciece S-111 Harvard Uiversity David G. Sulliva, Ph.D. Review: Method Frames Whe you make a method call, the Java rutime sets aside a block of memory kow as the frame of
Uit 4, Part 3 Recursio Computer Sciece S-111 Harvard Uiversity David G. Sulliva, Ph.D. Review: Method Frames Whe you make a method call, the Java rutime sets aside a block of memory kow as the frame of
Computer Science Foundation Exam. August 12, Computer Science. Section 1A. No Calculators! KEY. Solutions and Grading Criteria.
 Computer Sciece Foudatio Exam August, 005 Computer Sciece Sectio A No Calculators! Name: SSN: KEY Solutios ad Gradig Criteria Score: 50 I this sectio of the exam, there are four (4) problems. You must
Computer Sciece Foudatio Exam August, 005 Computer Sciece Sectio A No Calculators! Name: SSN: KEY Solutios ad Gradig Criteria Score: 50 I this sectio of the exam, there are four (4) problems. You must
Exact Minimum Lower Bound Algorithm for Traveling Salesman Problem
 Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
ABOUT A CONSTRUCTION PROBLEM
 INTERNATIONAL JOURNAL OF GEOMETRY Vol 3 (014), No, 14 19 ABOUT A CONSTRUCTION PROBLEM OVIDIU T POP ad SÁNDOR N KISS Abstract I this paper, we study the costructio of a polygo if we kow the midpoits of
INTERNATIONAL JOURNAL OF GEOMETRY Vol 3 (014), No, 14 19 ABOUT A CONSTRUCTION PROBLEM OVIDIU T POP ad SÁNDOR N KISS Abstract I this paper, we study the costructio of a polygo if we kow the midpoits of
Symmetric Class 0 subgraphs of complete graphs
 DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
Lecture 18. Optimization in n dimensions
 Lecture 8 Optimizatio i dimesios Itroductio We ow cosider the problem of miimizig a sigle scalar fuctio of variables, f x, where x=[ x, x,, x ]T. The D case ca be visualized as fidig the lowest poit of
Lecture 8 Optimizatio i dimesios Itroductio We ow cosider the problem of miimizig a sigle scalar fuctio of variables, f x, where x=[ x, x,, x ]T. The D case ca be visualized as fidig the lowest poit of
APPLICATION NOTE PACE1750AE BUILT-IN FUNCTIONS
 APPLICATION NOTE PACE175AE BUILT-IN UNCTIONS About This Note This applicatio brief is iteded to explai ad demostrate the use of the special fuctios that are built ito the PACE175AE processor. These powerful
APPLICATION NOTE PACE175AE BUILT-IN UNCTIONS About This Note This applicatio brief is iteded to explai ad demostrate the use of the special fuctios that are built ito the PACE175AE processor. These powerful
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
GPUMP: a Multiple-Precision Integer Library for GPUs
 GPUMP: a Multiple-Precisio Iteger Library for GPUs Kaiyog Zhao ad Xiaowe Chu Departmet of Computer Sciece, Hog Kog Baptist Uiversity Hog Kog, P. R. Chia Email: {kyzhao, chxw}@comp.hkbu.edu.hk Abstract
GPUMP: a Multiple-Precisio Iteger Library for GPUs Kaiyog Zhao ad Xiaowe Chu Departmet of Computer Sciece, Hog Kog Baptist Uiversity Hog Kog, P. R. Chia Email: {kyzhao, chxw}@comp.hkbu.edu.hk Abstract
Heaps. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Major CSL Write your name and entry no on every sheet of the answer script. Time 2 Hrs Max Marks 70
 NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
Running Time. Analysis of Algorithms. Experimental Studies. Limitations of Experiments
 Ruig Time Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects. The
Ruig Time Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects. The
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
A Generalized Set Theoretic Approach for Time and Space Complexity Analysis of Algorithms and Functions
 Proceedigs of the 10th WSEAS Iteratioal Coferece o APPLIED MATHEMATICS, Dallas, Texas, USA, November 1-3, 2006 316 A Geeralized Set Theoretic Approach for Time ad Space Complexity Aalysis of Algorithms
Proceedigs of the 10th WSEAS Iteratioal Coferece o APPLIED MATHEMATICS, Dallas, Texas, USA, November 1-3, 2006 316 A Geeralized Set Theoretic Approach for Time ad Space Complexity Aalysis of Algorithms
Running Time ( 3.1) Analysis of Algorithms. Experimental Studies. Limitations of Experiments
 Ruig Time ( 3.1) Aalysis of Algorithms Iput Algorithm Output A algorithm is a step- by- step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects.
Ruig Time ( 3.1) Aalysis of Algorithms Iput Algorithm Output A algorithm is a step- by- step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects.
Analysis of Algorithms
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Ruig Time Most algorithms trasform iput objects ito output objects. The
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Ruig Time Most algorithms trasform iput objects ito output objects. The
Data Structures and Algorithms. Analysis of Algorithms
 Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
9 x and g(x) = 4. x. Find (x) 3.6. I. Combining Functions. A. From Equations. Example: Let f(x) = and its domain. Example: Let f(x) = and g(x) = x x 4
 1 3.6 I. Combiig Fuctios A. From Equatios Example: Let f(x) = 9 x ad g(x) = 4 f x. Fid (x) g ad its domai. 4 Example: Let f(x) = ad g(x) = x x 4. Fid (f-g)(x) B. From Graphs: Graphical Additio. Example:
1 3.6 I. Combiig Fuctios A. From Equatios Example: Let f(x) = 9 x ad g(x) = 4 f x. Fid (x) g ad its domai. 4 Example: Let f(x) = ad g(x) = x x 4. Fid (f-g)(x) B. From Graphs: Graphical Additio. Example:
the beginning of the program in order for it to work correctly. Similarly, a Confirm
 I our sytax, a Assume statemet will be used to record what must be true at the begiig of the program i order for it to work correctly. Similarly, a Cofirm statemet is used to record what should be true
I our sytax, a Assume statemet will be used to record what must be true at the begiig of the program i order for it to work correctly. Similarly, a Cofirm statemet is used to record what should be true
LU Decomposition Method
 SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS LU Decompositio Method Jamie Traha, Autar Kaw, Kevi Marti Uiversity of South Florida Uited States of America kaw@eg.usf.edu http://umericalmethods.eg.usf.edu Itroductio
SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS LU Decompositio Method Jamie Traha, Autar Kaw, Kevi Marti Uiversity of South Florida Uited States of America kaw@eg.usf.edu http://umericalmethods.eg.usf.edu Itroductio
CS200: Hash Tables. Prichard Ch CS200 - Hash Tables 1
 CS200: Hash Tables Prichard Ch. 13.2 CS200 - Hash Tables 1 Table Implemetatios: average cases Search Add Remove Sorted array-based Usorted array-based Balaced Search Trees O(log ) O() O() O() O(1) O()
CS200: Hash Tables Prichard Ch. 13.2 CS200 - Hash Tables 1 Table Implemetatios: average cases Search Add Remove Sorted array-based Usorted array-based Balaced Search Trees O(log ) O() O() O() O(1) O()
Recursive Procedures. How can you model the relationship between consecutive terms of a sequence?
 6. Recursive Procedures I Sectio 6.1, you used fuctio otatio to write a explicit formula to determie the value of ay term i a Sometimes it is easier to calculate oe term i a sequece usig the previous terms.
6. Recursive Procedures I Sectio 6.1, you used fuctio otatio to write a explicit formula to determie the value of ay term i a Sometimes it is easier to calculate oe term i a sequece usig the previous terms.
A graphical view of big-o notation. c*g(n) f(n) f(n) = O(g(n))
 ca see that time required to search/sort grows with size of We How do space/time eeds of program grow with iput size? iput. time: cout umber of operatios as fuctio of iput Executio size operatio Assigmet:
ca see that time required to search/sort grows with size of We How do space/time eeds of program grow with iput size? iput. time: cout umber of operatios as fuctio of iput Executio size operatio Assigmet:
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
Algorithm Design Techniques. Divide and conquer Problem
 Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
BOOLEAN DIFFERENTIATION EQUATIONS APPLICABLE IN RECONFIGURABLE COMPUTATIONAL MEDIUM
 MATEC Web of Cofereces 79, 01014 (016) DOI: 10.1051/ mateccof/0167901014 T 016 BOOLEAN DIFFERENTIATION EQUATIONS APPLICABLE IN RECONFIGURABLE COMPUTATIONAL MEDIUM Staislav Shidlovskiy 1, 1 Natioal Research
MATEC Web of Cofereces 79, 01014 (016) DOI: 10.1051/ mateccof/0167901014 T 016 BOOLEAN DIFFERENTIATION EQUATIONS APPLICABLE IN RECONFIGURABLE COMPUTATIONAL MEDIUM Staislav Shidlovskiy 1, 1 Natioal Research
Last Class. Announcements. Lecture Outline. Types. Structural Equivalence. Type Equivalence. Read: Scott, Chapters 7 and 8. T2 y; x = y; n Types
 Aoucemets HW9 due today HW10 comig up, will post after class Team assigmet Data abstractio (types) ad cotrol abstractio (parameter passig) Due o Tuesday, November 27 th Last Class Types Type systems Type
Aoucemets HW9 due today HW10 comig up, will post after class Team assigmet Data abstractio (types) ad cotrol abstractio (parameter passig) Due o Tuesday, November 27 th Last Class Types Type systems Type
A New Bit Wise Technique for 3-Partitioning Algorithm
 Special Issue of Iteratioal Joural of Computer Applicatios (0975 8887) o Optimizatio ad O-chip Commuicatio, No.1. Feb.2012, ww.ijcaolie.org A New Bit Wise Techique for 3-Partitioig Algorithm Rajumar Jai
Special Issue of Iteratioal Joural of Computer Applicatios (0975 8887) o Optimizatio ad O-chip Commuicatio, No.1. Feb.2012, ww.ijcaolie.org A New Bit Wise Techique for 3-Partitioig Algorithm Rajumar Jai
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Abstract. Chapter 4 Computation. Overview 8/13/18. Bjarne Stroustrup Note:
 Chapter 4 Computatio Bjare Stroustrup www.stroustrup.com/programmig Abstract Today, I ll preset the basics of computatio. I particular, we ll discuss expressios, how to iterate over a series of values
Chapter 4 Computatio Bjare Stroustrup www.stroustrup.com/programmig Abstract Today, I ll preset the basics of computatio. I particular, we ll discuss expressios, how to iterate over a series of values
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
1.8 What Comes Next? What Comes Later?
 35 1.8 What Comes Next? What Comes Later? A Practice Uderstadig Task For each of the followig tables, CC BY Hiroaki Maeda https://flic.kr/p/6r8odk describe how to fid the ext term i the sequece, write
35 1.8 What Comes Next? What Comes Later? A Practice Uderstadig Task For each of the followig tables, CC BY Hiroaki Maeda https://flic.kr/p/6r8odk describe how to fid the ext term i the sequece, write
Solving Fuzzy Assignment Problem Using Fourier Elimination Method
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-768 Volume 3, Number 2 (207), pp. 453-462 Research Idia Publicatios http://www.ripublicatio.com Solvig Fuzzy Assigmet Problem Usig Fourier Elimiatio
Global Joural of Pure ad Applied Mathematics. ISSN 0973-768 Volume 3, Number 2 (207), pp. 453-462 Research Idia Publicatios http://www.ripublicatio.com Solvig Fuzzy Assigmet Problem Usig Fourier Elimiatio
CMPT 125 Assignment 2 Solutions
 CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
The Adjacency Matrix and The nth Eigenvalue
 Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
The Platonic solids The five regular polyhedra
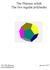 The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
EVALUATION OF TRIGONOMETRIC FUNCTIONS
 EVALUATION OF TRIGONOMETRIC FUNCTIONS Whe first exposed to trigoometric fuctios i high school studets are expected to memorize the values of the trigoometric fuctios of sie cosie taget for the special
EVALUATION OF TRIGONOMETRIC FUNCTIONS Whe first exposed to trigoometric fuctios i high school studets are expected to memorize the values of the trigoometric fuctios of sie cosie taget for the special
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Recursion. Recursion. Mathematical induction: example. Recursion. The sum of the first n odd numbers is n 2 : Informal proof: Principle:
 Recursio Recursio Jordi Cortadella Departmet of Computer Sciece Priciple: Reduce a complex problem ito a simpler istace of the same problem Recursio Itroductio to Programmig Dept. CS, UPC 2 Mathematical
Recursio Recursio Jordi Cortadella Departmet of Computer Sciece Priciple: Reduce a complex problem ito a simpler istace of the same problem Recursio Itroductio to Programmig Dept. CS, UPC 2 Mathematical
Copyright 2016 Ramez Elmasri and Shamkant B. Navathe
 Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 19 Query Optimizatio Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio Query optimizatio Coducted by a query optimizer i a DBMS Goal:
Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 19 Query Optimizatio Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio Query optimizatio Coducted by a query optimizer i a DBMS Goal:
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
Chapter 5. Functions for All Subtasks. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 5 Fuctios for All Subtasks Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 5.1 void Fuctios 5.2 Call-By-Referece Parameters 5.3 Usig Procedural Abstractio 5.4 Testig ad Debuggig
Chapter 5 Fuctios for All Subtasks Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 5.1 void Fuctios 5.2 Call-By-Referece Parameters 5.3 Usig Procedural Abstractio 5.4 Testig ad Debuggig
Analysis of Algorithms
 Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
Pseudocode ( 1.1) Analysis of Algorithms. Primitive Operations. Pseudocode Details. Running Time ( 1.1) Estimating performance
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
On Spectral Theory Of K-n- Arithmetic Mean Idempotent Matrices On Posets
 Iteratioal Joural of Sciece, Egieerig ad echology Research (IJSER), Volume 5, Issue, February 016 O Spectral heory Of -- Arithmetic Mea Idempotet Matrices O Posets 1 Dr N Elumalai, ProfRMaikada, 3 Sythiya
Iteratioal Joural of Sciece, Egieerig ad echology Research (IJSER), Volume 5, Issue, February 016 O Spectral heory Of -- Arithmetic Mea Idempotet Matrices O Posets 1 Dr N Elumalai, ProfRMaikada, 3 Sythiya
CSC 220: Computer Organization Unit 11 Basic Computer Organization and Design
 College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
Chapter 11. Friends, Overloaded Operators, and Arrays in Classes. Copyright 2014 Pearson Addison-Wesley. All rights reserved.
 Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Recursive Estimation
 Recursive Estimatio Raffaello D Adrea Sprig 2 Problem Set: Probability Review Last updated: February 28, 2 Notes: Notatio: Uless otherwise oted, x, y, ad z deote radom variables, f x (x) (or the short
Recursive Estimatio Raffaello D Adrea Sprig 2 Problem Set: Probability Review Last updated: February 28, 2 Notes: Notatio: Uless otherwise oted, x, y, ad z deote radom variables, f x (x) (or the short
. Perform a geometric (ray-optics) construction (i.e., draw in the rays on the diagram) to show where the final image is formed.
 MASSACHUSETTS INSTITUTE of TECHNOLOGY Departmet of Electrical Egieerig ad Computer Sciece 6.161 Moder Optics Project Laboratory 6.637 Optical Sigals, Devices & Systems Problem Set No. 1 Geometric optics
MASSACHUSETTS INSTITUTE of TECHNOLOGY Departmet of Electrical Egieerig ad Computer Sciece 6.161 Moder Optics Project Laboratory 6.637 Optical Sigals, Devices & Systems Problem Set No. 1 Geometric optics
Today s objectives. CSE401: Introduction to Compiler Construction. What is a compiler? Administrative Details. Why study compilers?
 CSE401: Itroductio to Compiler Costructio Larry Ruzzo Sprig 2004 Today s objectives Admiistrative details Defie compilers ad why we study them Defie the high-level structure of compilers Associate specific
CSE401: Itroductio to Compiler Costructio Larry Ruzzo Sprig 2004 Today s objectives Admiistrative details Defie compilers ad why we study them Defie the high-level structure of compilers Associate specific
Relationship between augmented eccentric connectivity index and some other graph invariants
 Iteratioal Joural of Advaced Mathematical Scieces, () (03) 6-3 Sciece Publishig Corporatio wwwsciecepubcocom/idexphp/ijams Relatioship betwee augmeted eccetric coectivity idex ad some other graph ivariats
Iteratioal Joural of Advaced Mathematical Scieces, () (03) 6-3 Sciece Publishig Corporatio wwwsciecepubcocom/idexphp/ijams Relatioship betwee augmeted eccetric coectivity idex ad some other graph ivariats
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
CS 11 C track: lecture 1
 CS 11 C track: lecture 1 Prelimiaries Need a CMS cluster accout http://acctreq.cms.caltech.edu/cgi-bi/request.cgi Need to kow UNIX IMSS tutorial liked from track home page Track home page: http://courses.cms.caltech.edu/courses/cs11/material
CS 11 C track: lecture 1 Prelimiaries Need a CMS cluster accout http://acctreq.cms.caltech.edu/cgi-bi/request.cgi Need to kow UNIX IMSS tutorial liked from track home page Track home page: http://courses.cms.caltech.edu/courses/cs11/material
