Enumerating pseudo-triangulations in the plane
|
|
|
- Easter Lane
- 5 years ago
- Views:
Transcription
1 Enumerating pseuo-triangulations in the plane Sergey Bereg Astrat A pseuo-triangle is a simple polygon with exatly three onvex verties. A pseuo-triangulation of a finite point set S in the plane is a partition of the onvex hull of S into interior isjoint pseuo-triangles whose verties are points of S. A pointe pseuo-triangulation is one whih has the least numer of pseuo-triangles. We stuy the graph G whose verties represent the pointe pseuo-triangulations an whose eges represent flips. We present an algorithm for enumerating pointe pseuo-triangulations in O(log n) time per pseuo-triangulation. Keywors: pseuo-triangulation, flip, enumeration, reverse searh. 1 Introution Pseuo-triangles an pseuo-triangulations have reeive muh attention reently eause of appliations in visiility [15, 16], ray shooting [15], ollision etetion [13], an rigi motion [7, 20]. There are many open questions relate to pseuo-triangulations [21]. A pseuo-triangle is a simple polygon with exatly three onvex verties. For a set S of n points in the plane, a pseuo-triangulation T is efine as partition of the onvex hull of S into interior isjoint pseuo-triangulations whose verties are points of S (eah point of S is a vertex of T an vie versa). A minimum or pointe pseuo-triangulation introue y Streinu [20] is a pseuotriangulation with the least numer of eges among all pseuo-triangulations of S. Streinu [20] showe that any pointe pseuo-triangulation has 2n 3 eges. Equivalently, we an efine a pointe pseuo-triangulation as a pseuo-triangulation with minimum numer of pseuo-triangles. Any pointe pseuo-triangulation has n 2 pseuo-triangles sine n f = n e n + 1 = n 2 y Euler s formula. Reent results on pseuo-triangulations inlue [1, 2, 12, 18]. Ranall et al. [18] gave lose form expressions for the numer of triangulations an the numer of pointe pseuo-triangulations when S has only one point insie its onvex hull. For a point set in general position, they prove an upper oun for the numer of pseuo-triangulations. Aihholzer et al. [1] investigate the numer of pseuo-triangulations generate y n points in the plane. They prove that the least numer of pseuo-triangulations is attaine when points are in onvex position. We otaine an algorithm [4] for enumeration of triangulations in O(log log n) time per triangulation. The algorithm is ase on flips, small moifiations of a triangulation. Pseuotriangulations amit flips as well, see Fig. 1. It allows us to efine, for a point set S, a graph of pseuo-triangulations whose verties are the pointe pseuo-triangulations of S an whose eges are the flips of interior pseuo-triangulation eges. Reently, Brönnimann et al. [6] esrie an Department of Computer Siene, University of Texas at Dallas, Box , Riharson, TX 75083, USA. esp@utallas.eu 1
2 algorithm for enumerating all pointe pseuo-triangulations using an effiient tehnique of Pohiola an Vegter [17] for fining a flip in O(1) amortize time. Unfortunately the omplexity of the algorithm is unknown 1 ut the require spae is quarati. It follows from the algorithm that the graph of pseuo-triangulations is onnete. (a) a () Figure 1: (a) Flip of triangles. () Flip of pseuo-triangles. Very reently, Rote et al. [19] introue a polytope of pointe pseuo-triangulations of a point set in the plane, efine as the polytope of infinitesimal expansive motions of the points sujet to ertain onstraints on the inrease of their istanes. The polytope possesses useful properties an its 1-skeleton is the graph of pseuo-triangulations. We present an algorithm for enumerating all pointe pseuo-triangulations in O(log n) time per pseuo-triangulation using linear spae. The algorithm is ase on reverse searh tehnique y Avis an Fukua [3]. As y-prout it implies that the graph of pointe pseuo-triangulations is onnete. Our algorithm an e use to list the verties of the polytope of pointe pseuotriangulations [19]. It also generates a spanning tree of the graph of pseuo-triangulations. Aihholzer et al. [2] onsiere the prolem of ounting the numer of pointe pseuo-triangulations of a point set. They showe that every pseuo-triangulation ontains a zigzag path. It is use to ount pointe pseuo-triangulations effiiently y enumerating zigzag paths in O(n 2 ) time per path. 2 Preliminaries Let S = {p 1, p 2,..., p n } e a set of n points in general position in the plane. We efine a onvex orer of the points as follows. Let S i = {p i, p i+1,..., p n } for i = 1,..., n. The orer (p 1, p 2,..., p n ) is onvex if every point p i, i = 1,..., n lies on the ounary of the onvex hull of S i. An example of the onvex orer is the lexiographial orer y (x, y)-oorinates. This orer is use, for example, 1 The authors onjeture that the running time is O(log n) per pseuo-triangulation. 2
3 in the inremental algorithm for onstruting the onvex hull. Let x(p i ) an y(p i ) enote the x- an y-oorinates of a point p i. A vertex of a polygon is onvex if its interior angle is less than π, otherwise the vertex is reflex. A polygon is alle a pseuo-triangle if it has exatly three onvex verties. A pseuo-quarangle has exatly four onvex verties. In general, a pseuo-k-gon has exatly k onvex verties. A sie of a pseuo-k-gon P onsists of verties an eges etween two onvex verties (the internal verties of a sie are reflex verties of P ). Let T 1 (P ), T 2 (P ),..., T k (P ) enote inary searh trees storing the verties of the sies of P in lokwise orer. Note that every onvex vertex of P partiipates in two trees an every reflex vertex is ontaine in one tree. The following lemma generalizes flips in triangulations to flips in pseuo-triangulations, see Fig. 1. Lemma 1 (Flips in a pseuo-quarangle) Every pseuo-quarangle Q has exatly two partitions into two pseuo-triangles whih are proue y two iagonals. The iagonals either interset properly or share a reflex vertex of the pseuo-quarangle. The iagonals an e ompute in O(log n) time if the verties of Q are store in four alane searh trees T i (Q), i = 1, 2, 3, 4 orresponing to the sies of Q. Proof: The existene of two iagonals has een shown y Rote et al. [19]. Let Q e a pseuoquarangle an let a,,, an e the onvex verties of Q in ounterlokwise orer. The partitions an e otaine y utting Q with the shortest paths from a to an from to in Q (see etails in Lemma 2.2 [19] an Lemma 2.1 [22]). Eah shortest path has exatly one ege insie Q, whih is a iagonal that splits Q into two pseuo-triangles, see Fig. 1 (). a a p q p q a p q a p q (a) () () () Figure 2: Four types of the shortest path etween a to. We show that the iagonals annot share a onvex vertex. Clearly, the shortest path etween a an avois the verties an sine they are onvex. Similarly the shortest path etween an avois the verties a an. Thus two shortest paths a an an share reflex verties only. We show that the iagonals interset. Let p e q e the enpoints of the iagonal from the shortest path a. The line pq is ommon tangent to two sies of Q, one is a or a an the other is or, see Fig. 2. Without loss of generality we an assume that the line pq is horizontal. In all four ases epite in Fig. 2 is aove the line pq an is elow the line pq. The shortest path ontains an ege p q suh that p lies aove or on the line pq an q lies elow or on the line pq. It an e verifie that p q is the seon iagonal an the iagonals interset. Computing iagonals. Eah iagonal is a itangent to two sies of Q. A itangent to two onvex polygons an e ompute in O(log n) time [14]. A sie of Q an e omplete to a onvex 3
4 a a a a (a) () () () Figure 3: Fining a iagonal of Q on the shortest path a. polygon y aing the straight line segment etween the sie enpoints. Let P a, P, P an P a enote the polygons orresponing to the sies a,, an a, respetively. We show how the sies of Q an foun in O(1) time. Suppose that we want to fin a iagonal of the geoesi a. Suppose that the point is elow a. Let a 1 e the ege of the sie a. Similarly we enote the eges a 1, 2, 2, see Fig. 3. We onsier the following ases epening on the loation the segment i i, i = 1, 2 relative to the segment a. If a interset oth 1 1 an 2 2, then a is the require iagonal, see Fig. 3 (a). If oth 1 1 an 2 2 lie on the same sie of the line a, say on the left sie (the ase of the right sie is symmetri), then the iagonal is a itangent of P a an P, see Fig. 3 (). Suppose that the line a separates the segments 1 1 an 2 2, say 1 1 lies to the left of a an 2 2 lies to the right of a. Then the iagonal is a itangent of P a an P, see Fig. 3 (). Suppose that the line a intersets only one of the segments 1 1 an 2 2, say 2 2. Suppose that 1 1 lies to the left of the line a (otherwise it is symmetri). Then the iagonal is a itangent of P a an P, see Fig. 3 (). Thus the iagonals an e foun in O(log n) time. The flip of an ege e in a pseuo-triangulation removes e an inserts another ege e. We all e a ual ege of e. A pseuo-triangulation of S is a partitioning of the onvex hull of S into pseuo-triangles with verties in S suh that eah point of S is a vertex of a pseuo-triangle. A pseuo-triangulation T is a minimum pseuo-triangulation or a pointe pseuo-triangulation if it ontains a minimum numer of eges. Streinu [20] prove that a pointe pseuo-triangulation of a n-point set ontains 2n 3 eges. Henneerg onstrution. Streinu [20] prove that the graph of a pointe pseuo-triangulation is minimally rigi. A minimally rigi graph [9, 23] an e onstrute using the Henneerg upates [10]. There are two types of graph upates: (I) attah a new vertex y two eges, an (II) elete an ege an attah a new vertex to the enpoints of the elete ege plus one other vertex. Figure 4 illustrates the Henneerg onstrution of type I. It an e use to generate a pointe pseuotriangulation of S. Let G e the graph of pointe pseuo-triangulations of S. Reall that its verties orrespon to pointe pseuo-triangulations an the eges orrespon to flips. Similarly the graph of triangulations G T is efine [11, 4]. These graphs share some properties though the graphs inue y the same point sets are ifferent in general. Both graphs G T an G are onnete (the onnetivity of G has een shown in [19] an follows from Theorem 3 elow). They oinie if the points of S are in onvex position. 4
5 CH p p (a) () Figure 4: The Henneerg onstrution of type I applie for a point p lying (a) outsie the onvex hull, an () insie a pseuo-triangle. Hurtao et al. [11] showe that there are 2n points in the plane an two triangulations that require more than (n 1) 2 flips to transform one into the other. Brönnimann et al. [6] showe that O(n 2 ) flips suffie to transform a pointe pseuo-triangulation into another one. Interestingly, the flip istane etween pseuo-triangulations is smaller than the one etween triangulations: reently, we improve the oun to O(n log n) [5]. 3 Tree of Pointe Pseuo-Triangulations Let onv(a) enote the onvex hull of a set A. Let (p 1, p 2,..., p n ) e a onvex orer of the points in S. A pointe pseuo-triangulation T ontains all the eges of onv(s) = onv(s 1 ). We efine an inex of T enote y inex(t ) as the largest k n 2 so that T has the eges of onv(s 1 ),..., onv(s k ). Clearly, k 1 for any pointe pseuo-triangulation. The pseuotriangulation T ontains onv(s k ). We efine a egree of T enote y egree(t ) as the numer of pseuo-triangles of T that are ontaine in S k an have p k as a vertex. With eah pointe pseuo-triangulation we assoiate a vetor α(t ) = (k, l) where k = inex(t ) an l = egree(t ), see Fig. 5 (a) for an example. The lexiographial orer of vetors α(t ) inues a partial orer on the set of pseuo-triangulations. Lemma 2 There is a unique pointe pseuo-triangulation with the lexio-largest vetor α. Proof: Let T e the pseuo-triangulation otaine y the Henneerg onstrution of type I applie for the points in the orer (p n, p n 1,..., p 1 ): start with the triangle p n p n 1 p n 2 an insert points p n 3,..., p 1. The pseuo-triangulation T is pointe (it an e easily verifie) y Theorem 3.1 [20]. We show that the vetor α of T is the lexio-largest vetor among all pointe pseuo-triangulations. The inex of T is n 2 sine T ontains the eges of onv(s i ), i = 1, 2,..., n 2. The inex of T has the maximum value. Any pseuo-triangulation T with inex n 2 ontains all the eges of onv(s i ), i = 1, 2,..., n 2 an, thus, is a supergraph of T. By the efinition of pointe pseuotriangulation T = T. The lemma follows. We enote y T max a pseuo-triangulation with the lexio-largest vetor. 5
6 p 2 p 1 p 4 p 5 p 8 p 7 p 3 p 1 p 4 p 6 p 2 p 3 p 6 p 7 p 8 p 5 (a) () Figure 5: (a) A pseuo-triangulation T with inex(t ) = 3 an α(t ) = (4, 3), () a pseuotriangulation with the lexio-largest vetor α(t ) = (6, 1). Theorem 3 For any pointe pseuo-triangulation T T max, there is a flip making a pseuotriangulation with lexio-larger vetor α. Proof: Let α(t ) = (k, l) e the vetor of T. Sine α(t ) is not the lexio-largest vetor, α(t ) (n 2, 1) an k < n 2. The egree of T, l, must e greater than 1; otherwise T has all the eges of the onvex hull of S k+1 an the first inex must e less than k. In other wors, there are at least two pseuo-triangles insie the onvex hull of S k that have the ommon vertex p k. Let 1 an 2 e two suh pseuo-triangles that share a ommon ege (p k, p i ). Let Q e the polygon whih is the union of 1 an 2. We show that Q is a pseuo-quarangle. Note that Q has at least three onvex verties p k, p k1 an p k2 where p k1 an p k2 are the onvex verties of 1 an 2 ifferent from p k an p i, see Fig. 6. On the other han, there are at most 6 aniates to e onvex verties of Q (the onvex verties of 1 an 2 ). Let γ 1 an γ 2 e the angles etween the segments inient to p i in the pseuo-triangle 1 an 2, respetively. The angles satisfy one of the the following ases. Case 1: γ 1 + γ 2 < π. The numer of onvex verties of Q is four sine p k an p i are the onvex verties of oth 1 an 2, see Fig. 6 (a). Case 2: γ 1 + γ 2 > π an γ 1, γ 2 < π. The numer of onvex verties of Q is three, see Fig. 6 (). It ontraits the fat that T is a pointe pseuo-triangulation. Case 3: γ 1 + γ 2 > π an one of the angles γ 1 or γ 2 is greater than π. The numer of onvex verties of Q is four, see Fig. 6 (). By Lemma 1 the polygon Q an e partitione into two pseuo-triangles in two ways an orresponing iagonals o not share the vertex p k. We show how a spanning tree T of G an e onstrute. It is possile to efine the tree using an approah similar to [4] whih is ase on a lexiographial orer of triangulations using ege vetors (note that the pointe pseuo-triangulations have a fixe numer of eges). Unfortunately, it is not lear how to traverse the resulting tree effiiently. We apply a ifferent approah for pseuo-triangulations. We restrit the orer of points to e monotone in some iretion. For simpliity, we assume that the points are sorte y x-oorinate an their x-oorinates are istint (we an slightly rotate the set of the points to ahieve this). The root of T orrespons to the pseuo-triangulation 6
7 p k2 p k1 p k1 p i p i γ 1 γ 2 p k2 γ 1 γ p k p k (a) () p k1 p k2 p k1 p i γ 1 γ 2 p i γ 1 γ 2 1 p k2 2 p k p k () Figure 6: Cases. (a) an () Q is a pseuo-quarangle. () Q is a pseuo-triangle. T max, see Fig. 5 (). Let T e a pseuo-triangulation istint from T max. Theorem 3 guarantees the existene of an ege whose flip inreases the vetor of T. Let v e the noe of G orresponing to T. We efine the parent noe of v as follows. Let e = (p a, p ), a < e an ege of T suh that (i) the flip of e inreases the vetor α(t ), an (ii) a is the least numer among the eges satisfying (i), an (iii) the vetor p a p has the maximum slope among the eges satisfying (i) an (ii). Clearly, e is well efine. Ausing notation, we all e parent ege of T an eges whose flips lea to the hilren of v as hil eges. The following lemma haraterizes the parent eges. Lemma 4 (Parent Ege) An ege e = (p a, p ), a < is the parent ege of a pseuo-triangulation T if an only if a = inex(t ) an e has the largest slope among the eges of T T max. Proof: Let k = inex(t ). First, we show that a k. Suppose to the ontrary that a < k. By the efinition of inex(t ), T inlues the eges of the polygons onv(s a ) an onv(s a+1 ). Their ifferene onv(s a ) onv(s a+1 ) is a pseuo-triangle, see Fig. 7. The interior of oes not ontain eges of T sine T is the pointe pseuo-triangulation. Let p i an p j e two ajaent verties of onv(s a ). Flip of either p a p i or p a p j in T estroys an introues a new ege inient to a vertex outsie onv(s a ). This flip ereases the vetor α(t ). The ontraition implies a k. 7
8 p i p a onv(s a+1 ) onv(s a ) p j Figure 7: Pseuo-triangle. By Theorem 3 there is an ege inient to p k satisfying the aove onition (i). The onition (ii) implies a = k. It follows from the proof of Theorem 3 that the flip of any ege (p a, p ), > a of T inreases α(t ). The lemma follows. The parent ege e of a pointe pseuo-triangulation T is non-vertial segment an is not an ege of the onvex hull of S. Thus it is inient to two pseuo-triangles of T, one ontains a nei. We enote y (T ) the pseuo-triangle of T that is inient to e parent an is aove e, i.e. an internal point p of the segment e enters (T ) y an infenitesimal motion upwar. An example of (T ) is epite in Fig. 9 where (p k, p u ) is the parent ege. Next we haraterize the hil eges in T. Theorem 5 (Chil Ege) Let v e a noe of T an let T e its pseuo-triangulation with α(t ) = (k, l). Let p k p j p m e the onvex verties of (T ) in lokwise orer. Let C e the sie of (T ) etween p j an p m. Let p j = p j1, p j2,..., p m e the verties of the sie C. An ege e = (p a, p ), a < is a hil ege of T if an only if e is not an ege of the onvex hull of S an one of the following onitions hols (i) a < k, or (ii) e is an ege of onv(s k ), or (iii) {a, } = {j r, j r+1 }, m / {a, } an oth p a an p are visile from p k in (T ), or (iv) (a) {a, } = {j r, j r+1 } an p jr is visile from p k in (T ), an () j r+1 = m or p jr+1 () the ual ege of e is inient to p k. is not visile from p k in (T ), an Proof: If). (i) If a < k then e is a hil ege sine its flip ereases the vetor α(t ), see the proof of Lemma 4. (ii) The ege e lies on the ounary of two pseuo-triangles, say 1 an 2. Sine e is an ege of onv(s k ), one of the pseuo-triangles, say 2, lies in onv(s k ) an the other lies outsie onv(s k ), see Fig. 8. Let x e the largest numer suh that 1 lies in onv(s x ). Note that 1 x < k sine 1 is ontaine in onv(s 1 ) ut not in onv(s k ). Also 1 = onv(s x ) onv(s x+1 ) sine T ontains all the eges of onv(s i ), i = 1,..., k. Let p x p y p z e the onvex verties of 1 an let p e the onvex vertex of 2 ifferent from p a an p, see Fig. 8. The ual ege of e is ontaine in the shortest path etween p x an p in 8
9 p x p y 1 e p p a 2 p k p t p z onv(s k ) onv(s x ) p Figure 8: Pseuo-triangle 1 with onvex vertex p z, x(p z ) < x(p k ). the pseuo-quarangle Q = 1 2. The shortest path p x p avois the onvex verties p x an p y of Q. Therefore the ual ege of e is inient to p x (sine p x is ajaent to p y an p z in Q). Let e = (p x, p t ) e the ual ege of e an let T e the pseuo-triangulation otaine from T y flipping e. The ege e is the parent ege of T y Lemma 7. (iii) Consier the thir ase. The pseuo-triangle (T ) ontains p jr p jr+1. Let 1 = p jr p jr+1 p e the pseuo-triangle of T on the other sie of p jr p jr+1, see Fig. 9. The union Q = (T ) 1 is a pseuo-quarangle sine p k, p j, p an p m are the onvex verties of Q. By Lemma 1, e an its ual ege interset either properly or at a vertex of e. Let q e the intersetion point. The ege e is ompletely visile from p k. Clearly, p k q is the part of the shortest path p k p in the pseuo-quarangle Q. Therefore the ual ege of e is inient to p k. Let (p k, p v ) e the ual ege of e. Let (p k, p u ) e the parent ege of T, see Fig. 9. We show that v / {u, j}. If v = u then the verties p u, p jr+1 an p m oinie. This is impossile sine j r+1 m. If v = j then p is aove the line passing through p k an p j. This is impossile sine p is ontaine in onv(s k ) an (p k, p j ) is its ege. Let T e the pseuo-triangulation otaine y flipping e in T. The parent ege of T is p k p v y Lemma 7. Thus e is a hil ege of T. (iv) The forth ase follows from the onition (). Only If). We show that e is not a hil ege of T if none of the onitions (i)-(iv) hols. This assumption implies that e lies in the interior onv(s k ). Let T e the pseuo-triangulation otaine from T y flipping e, let e e the ual ege of e an let (p k, p u ) e the parent ege of T. Suppose that e is not an ege of (T ). Then (T ) is a pseuo-triangle of T an (p k, p u ) is still the parent ege of T. Therefore e is not a hil ege. Suppose that e is an ege of the sie p j p m of (T ). If oth p a an p are not visile from p k, then e is not visile from p k an p k is not inient to e (y Lemma 1, e intersets e). Then e is not a hil ege. If oth p a an p are visile from p k an m / {a, }, then it is the ase (iii) an e is a hil ege. In the remaining ase e is not inient to p k y the onition (iv)(). Therefore e is not a hil ege. Suppose that e is an ege of the sie p k p m of (T ). Clearly, (p k, p u ) is not a hil ege sine its flip inreases the vetor of T. Suppose that e (p k, p u ). The ege e is not on the ounary of onv(s k ) y the onition (ii) (the hain p k p m annot atually ontain an ege of onv(s k ) sine 9
10 p j p jr e 1 p k p u (T ) p v p jr+1 p onv(s k ) p m Figure 9: The ual ege of e = (p jr, p jr+1 ) is (p k, p v ). p j p j p k p p a e e p p m onv(s k ) p k = p e p a e p p m onv(s k ) (a) () Figure 10: The ege e is not a hil ege of T. the internal verties of p k p m are reflex). Let e the pseuo-triangle with e on its ounary an ifferent from (T ). Let p e the onvex vertex of opposite to the sie of e, see Fig. 10. The ege e is a part of the shortest path from p j to p in the pseuo-quarangle Q = (T ). We show that e is not inient to p k (note that p may oinie with p k ). If p p k, then it follows from the fat that the shortest path p j p avois the onvex vertex p k of Q, see Fig. 10 (a). If p = p k, then it follows from e (p k, p u ), see Fig. 10 (). Theorem 6 (Height of T ) Let S e a set of n points in general position in the plane. The tree of pseuo-triangulations T has height at most ( n 2) 2. The oun is tight in the worst ase. Proof: The tree of pseuo-triangulations is onsistent with the partial orer on the set of pseuotriangulations. In orer to show the upper oun on the height of T it suffies to prove that the length of the partial orer on the set of vetors α(t ) is at most ( n 2) 2. This follows from the fat that there are ( n 2) possile vetors α() = (k, l) (note that every flip hanges α()). We ount all possile vetors α(). Let k e any integer from 1,..., n 3 an let T e a pseuotriangulation with inex k. The numer of possile pseuo-triangles of T in onv(s k ) inient to p k ranges from 2 to n k 1. Thus the numer of vetors α() for the fixe k is n k 2. If k = n 2, then the only pseuo-triangulation with inex k is T max. The total numer of vetors 10
11 p 2 p 3 p 4 p n 1 p 1 p n (a) () () () Figure 11: (a) n points on the ar. () Pseuo-triangulation with lexio-smallest α(). () Pseuotriangulation after n 3 flips. () T max. α() is n 2 n n k 2 = 1 + i = 1 + k=1 i=1 ( ) n 2. 2 It remains to prove the lower oun. We plae n points on the unit ar x 2 + y 2 = 1, y 0, see Fig. 11 (a). The pseuo-triangulation with the lexio-smallest vetor α(t ) = (1, n 2) is epite on Fig. 11 (). There are n 3 parent flips efore we otain a pseuo-triangulation with inex two, see Fig. 11 (). In general, there are n k 2 parent flips on pointe pseuo-triangulations of inex k. The theorem follows. An example of a spanning tree of pseuo-triangulations for a set of five points is illustrate in Fig Enumerating Pointe Pseuo-Triangulations We apply the reverse searh tehnique y Avis an Fukua [3]. A possile approah is to use a reursive proeure that proesses a noe of T. By Theorem 6 the spae requirement for this approah is Ω(n 2 ) in the worst ase. We show that the spae size an e reue to linear. We nee some properties of hil eges for an effiient algorithm. We lassify the hil eges aoring to the ases of Theorem 5, for example, the eges of type (i) orrespon to the ase (i). For every vertex p i S, i = 1, 2,..., n 2 we enote y e u i = (p i, p up(i) ) an e l i = (p i, p low(i) ) two eges of onv(s i ) inient to p i (e u i lies on the upper hull of S i an e l i lies on the lower hull of S i). Lemma 7 Let T e a pseuo-triangulation with inex k. (i) Let n 1 e the numer of hil eges of type (i) in T. Then k 2 n 1 2(k 2). (ii) The hil eges of type (ii) in T an e reporte in O(1) time per ege using the inex funtions up() an low(). Proof: (i) Let (p a, p ), a < e a hil ege of type (i). Then 2 a k 1. By the efinition of the inex of T, there are exatly two eges (p a, p 1 ) an (p a, p 2 ) in T satisfying i > a. This implies the upper oun for n 1. The lower oun follows from the fat that at least one of the eges (p a, p i ), i = 1, 2 lies insie the onvex hull of S (sine p 1 lies outsie onv(s a )). (ii) The eges e u k an el k are the eges of onv(s k) inient to p k. Let C up an C low e the upper hull an the lower hull of onv(s k ), respetively. We show how to fin eges of C up. Suppose that p i is the urrent vertex of C up. Note that p i an e inient to many eges, see Fig. 13. It turns out that the next vertex in C up is always p up(i). 11
12 p 1 p 2 p 3 p 5 (p 2, p 3 ) (p 2, p 4 ) p 4 (p 3, p 4 ) (p 3, p 5 ) (p 3, p 4 ) (p 3, p 5 ) (p 3, p 5 ) (p 2, p 3 ) (p 2, p 4 ) (p 3, p 5 ) (p 2, p 3 ) (p 3, p 5 ) Figure 12: A spanning tree of pseuo-triangulations for five points. The laels of tree eges are the parent eges. Let p j e the next vertex of onv(s k ), see Fig. 13. We laim that j = up(i). The point p up(i) lies in onv(s k ) sine p up(i) onv(s i ) onv(s k ). Thus, the slope of the segment p i p j is at least the slope of p i p up(i). Note that x(p j ) > x(p i ) (or j > i). On the other han, the slope of p i p up(i) is the maximum slope among the segments p i p l, l > i. Therefore p j = p up(i). Thus, the eges of C up an e foun using the funtion up(). The eges of C low an e foun similarly. Theorem 8 Let S e a set of n points in the plane. The pointe pseuo-triangulations of S an e reporte in O(log n) time per pseuo-triangulation using linear spae. Proof: The algorithm maintains ata strutures that allow an effiient traversal of T. There are stati ata strutures that store information aout the orer of the points an T max. The eges of the onvex hull onv(s) are store in a alane inary tree T onv in the lexio-graphial orer so that any ege (p i, p j ), i < j an e teste whether it is in onv(s) in O(log n) time. The eges of T max are store in a inary searh tree aoring to the lexio-graphial orer. We store the values up(i) an low(i) using two arrays. We store ynami strutures relate to the urrent pseuo-triangulation T. Let L t e the list of pseuo-triangles of T. With every sie s of a pseuo-triangle of T we assoiate a inary searh tree T s ( ) storing its points in ounterlokwise orer. We also assume that the operations of 12
13 p i p j p up(k) p k p low(k) onv(s k ) Figure 13: Fining the eges of C up. onatenation an split an e performe in O(log n) time using a union-split ata struture [8] for example. Note that a point p S an our in many trees T s ( ) (the numer of trees is atually at most the egree of p in T ). The preeessor an the suessor of a point p T s ( ) provie aess to the eges inient to p along the sie s. Every ege ours in two sets an we store it twie with pointers to eah other. We also store (i) L e, the list of eges in T. With every ege we store pointers to (at most) two inient pseuo-triangles. (ii) L, the list of eges of T T max in the lexiographial orer. For every point p S we store L 1 (p) the list of eges in T T max inient to p in the sorte orer y the slope. We apply the reverse searh tehnique [3] whih an e viewe as a epth-first traversal of the pseuo-triangulation tree T. For a urrent pseuo-triangulation T, the algorithm maintains its inex, the parent ege an the pseuo-triangle (T ). The value of inex(t ) an e ompute y fining the smallest element in L. The parent ege an e foun using L 1 (p k ). The pseuo-triangle (T ) an e foun y heking the pseuo-triangles inient to the parent ege. We traverse T as follows. The flip making a pseuo-triangulation of the parent is efine y the parent ege. The hil eges an e foun using Theorem 5. We esrie how the hil eges of eah type an e foun. Case (i). We show that the hil eges of type (i) an e foun in O(1) time per ege. The algorithm heks the verties p i, i = 2, 3,..., k 1 an the eges of onv(s i ) inient to p i. We use T onv to test whether an ege e is a hil ege. The total time is O(k) an the numer hil eges of type (i) is Ω(k) y Lemma 7 (i). Case (ii). The eges an e foun y Lemma 7 (ii). Cases (iii-iv). The algorithm traverses the eges of the sie p j p m of (T ) in the ounterlokwise orer (from p j to p m ). Let e = (p jr, p jr+1 ) e the urrent ege. We an etet if p jr an p jr+1 are visile from p k in O(log n) time. By Lemma 1 the ual ege of e an e foun in O(log n) time. Thus we an etet in O(log n) time if e has type (iii) or (iv). Note that the eges of types (iii) an (iv) form a ontinuous path p j p jl. We stop the searh if either e is the last ege of p j p m or e oes not satisfy the onitions (iii) an (iv). The linear spae an e ahieve using a non-reursive algorithm. For this, we maintain a oolean variale NewNoe iniating whether the urrent noe of T is visite for the first time. Depening on NewNoe we fin the hil ege y alling FinFirstChil() or FinNextChil(), see Algorithm 1. We store the urrent hil ege in ChilEge an the next hil ege in 13
14 NewChilEge. Both variales store pointers to the enpoints an the type of the ege so that next hil ege an e ompute. Clearly, the spae is linear. Algorithm 1 Enumeration of pointe pseuo-triangulations. 1: Compute T max, onv(s), T onv, up(), low(), the lists L t, L e, L, L 1 (p). {Initialization} 2: NewNoe = true; 3: loop {main loop} 4: if (NewNoe) then {we arrive at a new noe of T } 5: NewChilEge = FinFirstChil(); 6: else {ol noe of T } 7: NewChilEge = FinNextChil(); 8: en if 9: if (NewChilEge <> NULL) then {there is a new hil ege} 10: NewNoe=true; 11: ChilEge=NewChilEge; 12: Output(ChilEge); {new pseuo-triangulation} 13: Flip(ChilEge); 14: else {all hil eges are visite} 15: if (ParentEge = NULL) then {the root of T } 16: return; 17: en if 18: NewNoe=false; 19: ChilEge=Dual(ParentEge); 20: Output(ParentEge); 21: Flip(ParentEge); 22: en if 23: en loop 5 Conlusion We presente an algorithm for enumerating the pointe pseuo-triangulations of a set of n points in the plane. The algorithm uses flips to generate pseuo-triangulations an its running time is O(log n) per pseuo-triangulation. An interesting algorithmi question is to ount the numer of pseuo-triangulations without generating them. This might help to verify the onjeture [6, 18] that the numer of pseuo-triangulations for a finite set of points in the plane is at most the numer of its triangulations. Referenes [1] O. Aihholzer, F. Aurenhammer, H. Krasser, an B. Spekmann. Convexity minimizes pseuotriangulations. In Pro. 14th Cana. Conf. Comput. Geom., pp , [2] O. Aihholzer, G. Rote, B. Spekmann, an I. Streinu. The zigzag path of a pseuotriangulation. In Pro. 10th Workshop Algorithms Data Strut., pp ,
15 [3] D. Avis an K. Fukua. Reverse searh for enumeration. Disrete Appl. Math., 65:21 46, [4] S. Bespamyatnikh. An effiient algorithm for enumeration of triangulations. Comput. Geom. Theory Appl., 23(3): , 2002, [5] S. Bespamyatnikh. Transforming pseuo-triangulations. In Pro. International Conferene on Computational Siene, LNCS 2657, pp , 2003, link.asp?i=5t160n7unryyeku. [6] H. Brönnimann, L. Kettner, M. Pohiola, an J. Snoeyink. Counting an enumerating pseuotriangulations with the greey flip algorithm. In Fall Workshop on Comput. Geometry, [7] R. Connelly, E. D. Demaine, an G. Rote. Straightening polygonal ars an onvexifying polygonal yles. In Pro. 41th Annu. Sympos. on Foun. of Computer Siene, pp , [8] T. H. Cormen, C. E. Leiserson, R. L. Rivest, an C. Stein. Introution to Algorithms. MIT Press, Camrige, MA, 2n eition, [9] J. Graver, B. Servatius, an H. Servatius. Cominatorial Rigiity, volume 2. Amer. Math. So., Grauate Stuies in Mathematis, [10] L. Henneerg. Die graphishe Statik er starren Systeme. Leipzig, [11] F. Hurtao, M. Noy, an J. Urrutia. Flipping eges in triangulations. Disrete Comput. Geom., 22(3): , [12] L. Kettner, D. Kirkpatrik, an B. Spekmann. Tight egree ouns for pseuo-triangulations of points. In Pro. 13th Cana. Conf. Comput. Geom., pp , [13] D. Kirkpatrik, J. Snoeyink, an B. Spekmann. Kineti ollision etetion for simple polygons. In Pro. 16th Annu. ACM Sympos. Comput. Geom., pp , [14] M. H. Overmars an J. van Leeuwen. Maintenane of onfigurations in the plane. J. Comput. Syst. Si., 23: , [15] M. Pohiola an G. Vegter. Pseuo-triangulations: Theory an appliations. In Pro. 12th Annu. ACM Sympos. Comput. Geom., pp , [16] M. Pohiola an G. Vegter. Topologially sweeping visiility omplexes via pseuotriangulations. Disrete Comput. Geom., 16(4): , [17] M. Pohiola an G. Vegter. The visiility omplex. Int. J. Comput. Geom. Appl., 6(3): , [18] D. Ranall, G. Rote, F. Santos, an J. Snoeyink. Counting triangulations an pseuotriangulations of wheels. In Pro. 13th Cana. Conf. Comput. Geom., pp , [19] G. Rote, F. Santos, an I. Streinu. Expansive motions an the polytope of pointe pseuotriangulations. Disr. Comput. Geom. - The Gooman-Pollak Festshrift, pp , 2003, 15
16 [20] I. Streinu. A ominatorial approah to planar non-olliing root arm motion planning. In Pro. 41st Annu. IEEE Sympos. Foun. Comput. Si., pp , 2000, eu/~streinu/papers/motion.ps.gz. [21] I. Streinu. Foling arpenter s rulers, root arms, proteins: a rigiity theoreti approah. Invite talk, 10th Annual Fall Workshop on Computational Geometry, [22] I. Streinu. A ominatorial approah to planar non-olliing root arm motion planning. preprint, [23] W. Whiteley. Matrois from Disrete Geometry. in Matroi Theory, J. Bonin, J. Oxley an B. Servatius (es.), AMS Contemporary Mathematis,
Solutions to Tutorial 2 (Week 9)
 The University of Syney Shool of Mathematis an Statistis Solutions to Tutorial (Week 9) MATH09/99: Disrete Mathematis an Graph Theory Semester, 0. Determine whether eah of the following sequenes is the
The University of Syney Shool of Mathematis an Statistis Solutions to Tutorial (Week 9) MATH09/99: Disrete Mathematis an Graph Theory Semester, 0. Determine whether eah of the following sequenes is the
1 Disjoint-set data structure.
 CS 124 Setion #4 Union-Fin, Greey Algorithms 2/20/17 1 Disjoint-set ata struture. 1.1 Operations Disjoint-set ata struture enale us to effiiently perform operations suh as plaing elements into sets, querying
CS 124 Setion #4 Union-Fin, Greey Algorithms 2/20/17 1 Disjoint-set ata struture. 1.1 Operations Disjoint-set ata struture enale us to effiiently perform operations suh as plaing elements into sets, querying
Directed Rectangle-Visibility Graphs have. Abstract. Visibility representations of graphs map vertices to sets in Euclidean space and
 Direted Retangle-Visibility Graphs have Unbounded Dimension Kathleen Romanik DIMACS Center for Disrete Mathematis and Theoretial Computer Siene Rutgers, The State University of New Jersey P.O. Box 1179,
Direted Retangle-Visibility Graphs have Unbounded Dimension Kathleen Romanik DIMACS Center for Disrete Mathematis and Theoretial Computer Siene Rutgers, The State University of New Jersey P.O. Box 1179,
ON CHARACTERIZING TERRAIN VISIBILITY GRAPHS
 ON CHARACTERIZING TERRAIN VISIBILITY GRAPHS William Evans, and Noushin Saeedi Astrat. A terrain is an x-monotone polygonal line in the xy-plane. Two verties of a terrain are mutually visile if and only
ON CHARACTERIZING TERRAIN VISIBILITY GRAPHS William Evans, and Noushin Saeedi Astrat. A terrain is an x-monotone polygonal line in the xy-plane. Two verties of a terrain are mutually visile if and only
Keeping Things Simple: Finding Frequent Item Sets by Recursive Elimination
 Keeping Things Simple: Fining Frequent Item Sets y Reursive Elimination Christian Borgelt Department of Knowlege Proessing an Language Engineering Shool of Computer Siene, Otto-von-Guerike-University of
Keeping Things Simple: Fining Frequent Item Sets y Reursive Elimination Christian Borgelt Department of Knowlege Proessing an Language Engineering Shool of Computer Siene, Otto-von-Guerike-University of
10.2 Graph Terminology and Special Types of Graphs
 10.2 Grph Terminology n Speil Types of Grphs Definition 1. Two verties u n v in n unirete grph G re lle jent (or neighors) in G iff u n v re enpoints of n ege e of G. Suh n ege e is lle inient with the
10.2 Grph Terminology n Speil Types of Grphs Definition 1. Two verties u n v in n unirete grph G re lle jent (or neighors) in G iff u n v re enpoints of n ege e of G. Suh n ege e is lle inient with the
Math 2201 Unit 3: Acute Triangle Trigonometry. Ch. 3 Notes
 Rea Learning Goals, p. 17 text. Math 01 Unit 3: ute Triangle Trigonometry h. 3 Notes 3.1 Exploring Sie-ngle Relationships in ute Triangles (0.5 lass) Rea Goal p. 130 text. Outomes: 1. Define an aute triangle.
Rea Learning Goals, p. 17 text. Math 01 Unit 3: ute Triangle Trigonometry h. 3 Notes 3.1 Exploring Sie-ngle Relationships in ute Triangles (0.5 lass) Rea Goal p. 130 text. Outomes: 1. Define an aute triangle.
Advanced Algorithms for Fast and Scalable Deep Packet Inspection
 Avane Algorithms for Fast an Salale Deep Paket Inspetion Sailesh Kumar Washington University sailesh@arl.wustl.eu Jonathan Turner Washington University jon.turner@wustl.eu John Williams Ciso Systems jwill@iso.om
Avane Algorithms for Fast an Salale Deep Paket Inspetion Sailesh Kumar Washington University sailesh@arl.wustl.eu Jonathan Turner Washington University jon.turner@wustl.eu John Williams Ciso Systems jwill@iso.om
Vertex Unfoldings of Orthogonal Polyhedra: Positive, Negative, and Inconclusive Results
 CCCG 2018, Winnipeg, Canada, August 8 10, 2018 Vertex Unfoldings of Orthogonal Polyhedra: Positive, Negative, and Inonlusive Results Luis A. Garia Andres Gutierrrez Isaa Ruiz Andrew Winslow Abstrat We
CCCG 2018, Winnipeg, Canada, August 8 10, 2018 Vertex Unfoldings of Orthogonal Polyhedra: Positive, Negative, and Inonlusive Results Luis A. Garia Andres Gutierrrez Isaa Ruiz Andrew Winslow Abstrat We
The Happy Ending Problem
 The Happy Ending Problem Neeldhara Misra STATUTORY WARNING This doument is a draft version 1 Introdution The Happy Ending problem first manifested itself on a typial wintery evening in 1933 These evenings
The Happy Ending Problem Neeldhara Misra STATUTORY WARNING This doument is a draft version 1 Introdution The Happy Ending problem first manifested itself on a typial wintery evening in 1933 These evenings
Colouring contact graphs of squares and rectilinear polygons de Berg, M.T.; Markovic, A.; Woeginger, G.
 Colouring ontat graphs of squares and retilinear polygons de Berg, M.T.; Markovi, A.; Woeginger, G. Published in: nd European Workshop on Computational Geometry (EuroCG 06), 0 Marh - April, Lugano, Switzerland
Colouring ontat graphs of squares and retilinear polygons de Berg, M.T.; Markovi, A.; Woeginger, G. Published in: nd European Workshop on Computational Geometry (EuroCG 06), 0 Marh - April, Lugano, Switzerland
Incremental Mining of Partial Periodic Patterns in Time-series Databases
 CERIAS Teh Report 2000-03 Inremental Mining of Partial Periodi Patterns in Time-series Dataases Mohamed G. Elfeky Center for Eduation and Researh in Information Assurane and Seurity Purdue University,
CERIAS Teh Report 2000-03 Inremental Mining of Partial Periodi Patterns in Time-series Dataases Mohamed G. Elfeky Center for Eduation and Researh in Information Assurane and Seurity Purdue University,
3D convex hulls. Convex Hull in 3D. convex polyhedron. convex polyhedron. The problem: Given a set P of points in 3D, compute their convex hull
 Convex Hull in The rolem: Given set P of oints in, omute their onvex hull onvex hulls Comuttionl Geometry [si 3250] Lur Tom Bowoin College onvex olyheron 1 2 3 olygon olyheron onvex olyheron 4 5 6 Polyheron
Convex Hull in The rolem: Given set P of oints in, omute their onvex hull onvex hulls Comuttionl Geometry [si 3250] Lur Tom Bowoin College onvex olyheron 1 2 3 olygon olyheron onvex olyheron 4 5 6 Polyheron
Algorithms for External Memory Lecture 6 Graph Algorithms - Weighted List Ranking
 Algorithms for External Memory Leture 6 Graph Algorithms - Weighted List Ranking Leturer: Nodari Sithinava Sribe: Andi Hellmund, Simon Ohsenreither 1 Introdution & Motivation After talking about I/O-effiient
Algorithms for External Memory Leture 6 Graph Algorithms - Weighted List Ranking Leturer: Nodari Sithinava Sribe: Andi Hellmund, Simon Ohsenreither 1 Introdution & Motivation After talking about I/O-effiient
Register Allocation III. Interference Graph Allocators. Computing the Interference Graph (in MiniJava compiler)
 Register Alloation III Announements Reommen have interferene graph onstrution working by Monay Last leture Register alloation aross funtion alls Toay Register alloation options Interferene Graph Alloators
Register Alloation III Announements Reommen have interferene graph onstrution working by Monay Last leture Register alloation aross funtion alls Toay Register alloation options Interferene Graph Alloators
Triangle LMN and triangle OPN are similar triangles. Find the angle measurements for x, y, and z.
 1 Use measurements of the two triangles elow to find x and y. Are the triangles similar or ongruent? Explain. 1a Triangle LMN and triangle OPN are similar triangles. Find the angle measurements for x,
1 Use measurements of the two triangles elow to find x and y. Are the triangles similar or ongruent? Explain. 1a Triangle LMN and triangle OPN are similar triangles. Find the angle measurements for x,
Gray Codes for Reflectable Languages
 Gray Codes for Refletable Languages Yue Li Joe Sawada Marh 8, 2008 Abstrat We lassify a type of language alled a refletable language. We then develop a generi algorithm that an be used to list all strings
Gray Codes for Refletable Languages Yue Li Joe Sawada Marh 8, 2008 Abstrat We lassify a type of language alled a refletable language. We then develop a generi algorithm that an be used to list all strings
Outline. CS38 Introduction to Algorithms. Administrative Stuff. Administrative Stuff. Motivation/Overview. Administrative Stuff
 Outline CS38 Introdution to Algorithms Leture 1 April 1, 2014 administrative stuff motivation and overview of the ourse stale mathings example graphs, representing graphs graph traversals (BFS, DFS) onnetivity,
Outline CS38 Introdution to Algorithms Leture 1 April 1, 2014 administrative stuff motivation and overview of the ourse stale mathings example graphs, representing graphs graph traversals (BFS, DFS) onnetivity,
1 The Knuth-Morris-Pratt Algorithm
 5-45/65: Design & Analysis of Algorithms September 26, 26 Leture #9: String Mathing last hanged: September 26, 27 There s an entire field dediated to solving problems on strings. The book Algorithms on
5-45/65: Design & Analysis of Algorithms September 26, 26 Leture #9: String Mathing last hanged: September 26, 27 There s an entire field dediated to solving problems on strings. The book Algorithms on
Algorithms to Accelerate Multiple Regular Expressions Matching for Deep Packet Inspection
 Algorithms to Aelerate Multiple Regular Expressions Mathing for Deep Paket Inspetion Sailesh Kumar Washington University Computer Siene an Engineering St. Louis, MO 60-899 +--9-06 sailesh@arl.wustl.eu
Algorithms to Aelerate Multiple Regular Expressions Mathing for Deep Paket Inspetion Sailesh Kumar Washington University Computer Siene an Engineering St. Louis, MO 60-899 +--9-06 sailesh@arl.wustl.eu
Multitarget Data Association with Higher-Order Motion Models
 Multitarget Data Assoiation with Higher-Orer Motion Moels Robert T. Collins The Pennsylvania State University University Park, PA 16802, USA Abstrat We present an iterative approximate solution to the
Multitarget Data Assoiation with Higher-Orer Motion Moels Robert T. Collins The Pennsylvania State University University Park, PA 16802, USA Abstrat We present an iterative approximate solution to the
The four lines of symmetry have been drawn on the shape.
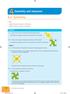 4Geometry an measures 4.1 Symmetry I an ientify refletion symmetry in 2D shapes ientify rotation symmetry in 2D shapes Example a i How many lines of symmetry oes this shape have? ii Colour two squares
4Geometry an measures 4.1 Symmetry I an ientify refletion symmetry in 2D shapes ientify rotation symmetry in 2D shapes Example a i How many lines of symmetry oes this shape have? ii Colour two squares
Planar Minimally Rigid Graphs and Pseudotriangulations. November 21, 2003
 Planar Minimally Rigid Graphs and Pseudotriangulations November 21, 2003 0 Planar Minimally Rigid Graphs and Pseudotriangulations I. Rigid Graphs. II. Robot Arms III. Pseudotriangles IV. Relationships
Planar Minimally Rigid Graphs and Pseudotriangulations November 21, 2003 0 Planar Minimally Rigid Graphs and Pseudotriangulations I. Rigid Graphs. II. Robot Arms III. Pseudotriangles IV. Relationships
An Efficient Image Distortion Correction Method for an X-ray Digital Tomosynthesis System
 An Effiient Image Distortion Corretion Metho for an X-ray Digital Tomosynthesis System J.Y. Kim Dept. of Mehatronis Engineering, Tongmyong University of Information Tehnology, 55 Yongang-ong, Nam-gu, Busan
An Effiient Image Distortion Corretion Metho for an X-ray Digital Tomosynthesis System J.Y. Kim Dept. of Mehatronis Engineering, Tongmyong University of Information Tehnology, 55 Yongang-ong, Nam-gu, Busan
Interconnection Styles
 Interonnetion tyles oftware Design Following the Export (erver) tyle 2 M1 M4 M5 4 M3 M6 1 3 oftware Design Following the Export (Client) tyle e 2 e M1 M4 M5 4 M3 M6 1 e 3 oftware Design Following the Export
Interonnetion tyles oftware Design Following the Export (erver) tyle 2 M1 M4 M5 4 M3 M6 1 3 oftware Design Following the Export (Client) tyle e 2 e M1 M4 M5 4 M3 M6 1 e 3 oftware Design Following the Export
Unsupervised Segmentation of Stereoscopic Video Objects: Proposal. and Comparison of Two Depth-Based Approaches
 Unsupervise Segmentation of Stereosopi Vieo Objets: Proposal an Comparison of Two Depth-Base Approahes Klimis S. Ntalianis an Athanasios S.Drigas Net Meia Lab, NCSR Demokritos, Athens, Greee E-mail: kntal@image.ntua.gr
Unsupervise Segmentation of Stereosopi Vieo Objets: Proposal an Comparison of Two Depth-Base Approahes Klimis S. Ntalianis an Athanasios S.Drigas Net Meia Lab, NCSR Demokritos, Athens, Greee E-mail: kntal@image.ntua.gr
LAB 4: Operations on binary images Histograms and color tables
 LAB 4: Operations on binary images Histograms an olor tables Computer Vision Laboratory Linköping University, Sween Preparations an start of the lab system You will fin a ouple of home exerises (marke
LAB 4: Operations on binary images Histograms an olor tables Computer Vision Laboratory Linköping University, Sween Preparations an start of the lab system You will fin a ouple of home exerises (marke
Sequential Incremental-Value Auctions
 Sequential Inremental-Value Autions Xiaoming Zheng and Sven Koenig Department of Computer Siene University of Southern California Los Angeles, CA 90089-0781 {xiaominz,skoenig}@us.edu Abstrat We study the
Sequential Inremental-Value Autions Xiaoming Zheng and Sven Koenig Department of Computer Siene University of Southern California Los Angeles, CA 90089-0781 {xiaominz,skoenig}@us.edu Abstrat We study the
Lecture 3: Art Gallery Problems and Polygon Triangulation
 EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
EECS 396/496: Computational Geometry Fall 2017 Lecture 3: Art Gallery Problems and Polygon Triangulation Lecturer: Huck Bennett In this lecture, we study the problem of guarding an art gallery (specified
Anchoring quartet-based phylogenetic distances and applications to species tree reconstruction
 Anhoring quartet-base phylogeneti istanes an appliations to speies tree reonstrution Erfan Sayyari an Siavash Mirarab Department of Eletrial an Computer Engineering University of California at San Diego
Anhoring quartet-base phylogeneti istanes an appliations to speies tree reonstrution Erfan Sayyari an Siavash Mirarab Department of Eletrial an Computer Engineering University of California at San Diego
Register Allocation III. Interference Graph Allocators. Coalescing. Granularity of Allocation (Renumber step in Briggs) Chaitin
 Register Alloation III Last time Register alloation aross funtion alls Toay Register alloation options Interferene Graph Alloators Chaitin Briggs CS553 Leture Register Alloation III 1 CS553 Leture Register
Register Alloation III Last time Register alloation aross funtion alls Toay Register alloation options Interferene Graph Alloators Chaitin Briggs CS553 Leture Register Alloation III 1 CS553 Leture Register
arxiv:math/ v1 [math.co] 21 Dec 2006
![arxiv:math/ v1 [math.co] 21 Dec 2006 arxiv:math/ v1 [math.co] 21 Dec 2006](/thumbs/72/66589081.jpg) Pseudo-Triangulations a Survey arxiv:math/0612672v1 [math.co] 21 Dec 2006 Günter Rote, Francisco Santos, and Ileana Streinu Abstract. A pseudo-triangle is a simple polygon with three convex vertices, and
Pseudo-Triangulations a Survey arxiv:math/0612672v1 [math.co] 21 Dec 2006 Günter Rote, Francisco Santos, and Ileana Streinu Abstract. A pseudo-triangle is a simple polygon with three convex vertices, and
1 Shortest Path Problems
 CS268: Geometric Algorithms Hanout #7 Design an Analysis Original Hanout #18 Stanfor University Tuesay, 25 February 1992 Original Lecture #8: 4 February 1992 Topics: Shortest Path Problems Scribe: Jim
CS268: Geometric Algorithms Hanout #7 Design an Analysis Original Hanout #18 Stanfor University Tuesay, 25 February 1992 Original Lecture #8: 4 February 1992 Topics: Shortest Path Problems Scribe: Jim
Exploiting Structure in Parsing to 1-Endpoint-Crossing Graphs
 Exploiting Struture in Parsing to 1-Enpoint-Crossing Graphs Roin Kurtz an Maro Kuhlmann Department of Computer an Information Siene Linköping University, Sween roin.kurtz@liu.se an maro.kuhlmann@liu.se
Exploiting Struture in Parsing to 1-Enpoint-Crossing Graphs Roin Kurtz an Maro Kuhlmann Department of Computer an Information Siene Linköping University, Sween roin.kurtz@liu.se an maro.kuhlmann@liu.se
LAMC Junior Circle April 15, Constructing Triangles.
 LAMC Junior Cirle April 15, 2012 Olga Radko radko@math.ula.edu Oleg Gleizer oleg1140@gmail.om Construting Triangles. Copyright: for home use only. This handout is a part of the book in preparation. Using
LAMC Junior Cirle April 15, 2012 Olga Radko radko@math.ula.edu Oleg Gleizer oleg1140@gmail.om Construting Triangles. Copyright: for home use only. This handout is a part of the book in preparation. Using
Inverse Design of Urban Procedural Models
 Inverse Design of Uran Proeural Moels Carlos A. Vanegas Purue University U.C. Berkeley Ignaio Garia-Dorao Purue University Daniel G. Aliaga Purue University Development site Paul Waell U.C. Berkeley Non-optimize
Inverse Design of Uran Proeural Moels Carlos A. Vanegas Purue University U.C. Berkeley Ignaio Garia-Dorao Purue University Daniel G. Aliaga Purue University Development site Paul Waell U.C. Berkeley Non-optimize
Searching for Entities: When Retrieval Meets Extraction
 Searhing for Entities: When Retrieval Meets Extration Qi Li, Daqing He Shool of Information Sienes, University of Pittsburgh Pittsburgh, Pennsylvania, U. S. {qili, aqing}@sis.pitt.eu Abstrat. Retrieving
Searhing for Entities: When Retrieval Meets Extration Qi Li, Daqing He Shool of Information Sienes, University of Pittsburgh Pittsburgh, Pennsylvania, U. S. {qili, aqing}@sis.pitt.eu Abstrat. Retrieving
Comparing Fisheye and Full-Zoom Techniques for Navigation of Hierarchically Clustered Networks
 Comparing Fisheye an Full-Zoom Tehniques for Navigation of Hierarhially Clustere Networks Doug Shaffer*, Zhengping Zuo, Lyn Bartram, John Dill, Shelli Dus, Saul Greenerg*, Mark Roseman* 1 * Dept of Computer
Comparing Fisheye an Full-Zoom Tehniques for Navigation of Hierarhially Clustere Networks Doug Shaffer*, Zhengping Zuo, Lyn Bartram, John Dill, Shelli Dus, Saul Greenerg*, Mark Roseman* 1 * Dept of Computer
SmartCuckoo: A Fast and Cost-Efficient Hashing Index Scheme for Cloud Storage Systems
 SmartCukoo: A Fast an Cost-Effiient Hashing Inex Sheme for Clou Storage Systems Yuanyuan Sun an Yu Hua, Huazhong University of Siene an Tehnology; Song Jiang, University of Texas, Arlington; Qiuyu Li,
SmartCukoo: A Fast an Cost-Effiient Hashing Inex Sheme for Clou Storage Systems Yuanyuan Sun an Yu Hua, Huazhong University of Siene an Tehnology; Song Jiang, University of Texas, Arlington; Qiuyu Li,
Drawing lines. Naïve line drawing algorithm. drawpixel(x, round(y)); double dy = y1 - y0; double dx = x1 - x0; double m = dy / dx; double y = y0;
 Naïve line drawing algorithm // Connet to grid points(x0,y0) and // (x1,y1) by a line. void drawline(int x0, int y0, int x1, int y1) { int x; double dy = y1 - y0; double dx = x1 - x0; double m = dy / dx;
Naïve line drawing algorithm // Connet to grid points(x0,y0) and // (x1,y1) by a line. void drawline(int x0, int y0, int x1, int y1) { int x; double dy = y1 - y0; double dx = x1 - x0; double m = dy / dx;
Fuzzy Pre-semi-closed Sets
 BULLETIN of the Malaysian Mathematial Sienes Soiety http://mathusmmy/bulletin Bull Malays Math Si So () 1() (008), Fuzzy Pre-semi-losed Sets 1 S Murugesan and P Thangavelu 1 Department of Mathematis, Sri
BULLETIN of the Malaysian Mathematial Sienes Soiety http://mathusmmy/bulletin Bull Malays Math Si So () 1() (008), Fuzzy Pre-semi-losed Sets 1 S Murugesan and P Thangavelu 1 Department of Mathematis, Sri
A Partial Sorting Algorithm in Multi-Hop Wireless Sensor Networks
 A Partial Sorting Algorithm in Multi-Hop Wireless Sensor Networks Abouberine Ould Cheikhna Department of Computer Siene University of Piardie Jules Verne 80039 Amiens Frane Ould.heikhna.abouberine @u-piardie.fr
A Partial Sorting Algorithm in Multi-Hop Wireless Sensor Networks Abouberine Ould Cheikhna Department of Computer Siene University of Piardie Jules Verne 80039 Amiens Frane Ould.heikhna.abouberine @u-piardie.fr
Dynamic Algorithms Multiple Choice Test
 3226 Dynami Algorithms Multiple Choie Test Sample test: only 8 questions 32 minutes (Real test has 30 questions 120 minutes) Årskort Name Eah of the following 8 questions has 4 possible answers of whih
3226 Dynami Algorithms Multiple Choie Test Sample test: only 8 questions 32 minutes (Real test has 30 questions 120 minutes) Årskort Name Eah of the following 8 questions has 4 possible answers of whih
HEXA: Compact Data Structures for Faster Packet Processing
 Washington University in St. Louis Washington University Open Sholarship All Computer Siene and Engineering Researh Computer Siene and Engineering Report Number: 27-26 27 HEXA: Compat Data Strutures for
Washington University in St. Louis Washington University Open Sholarship All Computer Siene and Engineering Researh Computer Siene and Engineering Report Number: 27-26 27 HEXA: Compat Data Strutures for
Data Structures in Java
 Data Strutures in Java Leture 8: Trees and Tree Traversals. 10/5/2015 Daniel Bauer 1 Trees in Computer Siene A lot of data omes in a hierarhial/nested struture. Mathematial expressions. Program struture.
Data Strutures in Java Leture 8: Trees and Tree Traversals. 10/5/2015 Daniel Bauer 1 Trees in Computer Siene A lot of data omes in a hierarhial/nested struture. Mathematial expressions. Program struture.
Enumerating Triangulations of Convex Polytopes
 Discrete Mathematics and Theoretical Computer Science Proceedings AA (DM-CCG), 2001, 111 122 Enumerating Triangulations of Convex Polytopes Sergei Bespamyatnikh Department of Computer Science, University
Discrete Mathematics and Theoretical Computer Science Proceedings AA (DM-CCG), 2001, 111 122 Enumerating Triangulations of Convex Polytopes Sergei Bespamyatnikh Department of Computer Science, University
A Support-Based Algorithm for the Bi-Objective Pareto Constraint
 Proeedings of the Twenty-Eighth AAAI Conferene on Artifiial Intelligene A Support-Based Algorithm for the Bi-Ojetive Pareto Constraint Renaud Hartert and Pierre Shaus UCLouvain, ICTEAM, Plae Sainte Bare
Proeedings of the Twenty-Eighth AAAI Conferene on Artifiial Intelligene A Support-Based Algorithm for the Bi-Ojetive Pareto Constraint Renaud Hartert and Pierre Shaus UCLouvain, ICTEAM, Plae Sainte Bare
1. Inversions. A geometric construction relating points O, A and B looks as follows.
 1. Inversions. 1.1. Definitions of inversion. Inversion is a kind of symmetry about a irle. It is defined as follows. he inversion of degree R 2 entered at a point maps a point to the point on the ray
1. Inversions. 1.1. Definitions of inversion. Inversion is a kind of symmetry about a irle. It is defined as follows. he inversion of degree R 2 entered at a point maps a point to the point on the ray
L11 Balanced Trees. Alice E. Fischer. Fall Alice E. Fischer L11 Balanced Trees... 1/34 Fall / 34
 L11 Balaned Trees Alie E. Fisher Fall 2018 Alie E. Fisher L11 Balaned Trees... 1/34 Fall 2018 1 / 34 Outline 1 AVL Trees 2 Red-Blak Trees Insertion Insertion 3 B-Trees Alie E. Fisher L11 Balaned Trees...
L11 Balaned Trees Alie E. Fisher Fall 2018 Alie E. Fisher L11 Balaned Trees... 1/34 Fall 2018 1 / 34 Outline 1 AVL Trees 2 Red-Blak Trees Insertion Insertion 3 B-Trees Alie E. Fisher L11 Balaned Trees...
Triangles. Learning Objectives. Pre-Activity
 Setion 3.2 Pre-tivity Preparation Triangles Geena needs to make sure that the dek she is building is perfetly square to the brae holding the dek in plae. How an she use geometry to ensure that the boards
Setion 3.2 Pre-tivity Preparation Triangles Geena needs to make sure that the dek she is building is perfetly square to the brae holding the dek in plae. How an she use geometry to ensure that the boards
Improved Bounds for Intersecting Triangles and Halving Planes
 Improved Bounds for Intersecting Triangles and Halving Planes David Eppstein Department of Information and Computer Science University of California, Irvine, CA 92717 Tech. Report 91-60 July 15, 1991 Abstract
Improved Bounds for Intersecting Triangles and Halving Planes David Eppstein Department of Information and Computer Science University of California, Irvine, CA 92717 Tech. Report 91-60 July 15, 1991 Abstract
Henneberg construction
 Henneberg construction Seminar über Algorithmen FU-Berlin, WS 2007/08 Andrei Haralevich Abstract: In this work will be explained two different types of steps of Henneberg construction. And how Henneberg
Henneberg construction Seminar über Algorithmen FU-Berlin, WS 2007/08 Andrei Haralevich Abstract: In this work will be explained two different types of steps of Henneberg construction. And how Henneberg
We P9 16 Eigenray Tracing in 3D Heterogeneous Media
 We P9 Eigenray Traing in 3D Heterogeneous Media Z. Koren* (Emerson), I. Ravve (Emerson) Summary Conventional two-point ray traing in a general 3D heterogeneous medium is normally performed by a shooting
We P9 Eigenray Traing in 3D Heterogeneous Media Z. Koren* (Emerson), I. Ravve (Emerson) Summary Conventional two-point ray traing in a general 3D heterogeneous medium is normally performed by a shooting
Polygon Simplification by Minimizing Convex Corners
 Polygon Simplification by Minimizing Convex Corners Yeganeh Bahoo 1, Stephane Durocher 1, J. Mark Keil 2, Saee Mehrabi 3, Sahar Mehrpour 1, an Debajyoti Monal 1 1 Department of Computer Science, University
Polygon Simplification by Minimizing Convex Corners Yeganeh Bahoo 1, Stephane Durocher 1, J. Mark Keil 2, Saee Mehrabi 3, Sahar Mehrpour 1, an Debajyoti Monal 1 1 Department of Computer Science, University
Pipelined Multipliers for Reconfigurable Hardware
 Pipelined Multipliers for Reonfigurable Hardware Mithell J. Myjak and José G. Delgado-Frias Shool of Eletrial Engineering and Computer Siene, Washington State University Pullman, WA 99164-2752 USA {mmyjak,
Pipelined Multipliers for Reonfigurable Hardware Mithell J. Myjak and José G. Delgado-Frias Shool of Eletrial Engineering and Computer Siene, Washington State University Pullman, WA 99164-2752 USA {mmyjak,
Facility Location: Distributed Approximation
 Faility Loation: Distributed Approximation Thomas Mosibroda Roger Wattenhofer Distributed Computing Group PODC 2005 Where to plae ahes in the Internet? A distributed appliation that has to dynamially plae
Faility Loation: Distributed Approximation Thomas Mosibroda Roger Wattenhofer Distributed Computing Group PODC 2005 Where to plae ahes in the Internet? A distributed appliation that has to dynamially plae
A Support-Based Algorithm for the Bi-Objective Pareto Constraint
 A Support-Based Algorithm for the Bi-Ojetive Pareto Constraint Renaud Hartert and Pierre Shaus UCLouvain, ICTEAM, Plae Sainte Bare 2, 1348 Louvain-la-Neuve, Belgium {renaud.hartert, pierre.shaus,}@ulouvain.e
A Support-Based Algorithm for the Bi-Ojetive Pareto Constraint Renaud Hartert and Pierre Shaus UCLouvain, ICTEAM, Plae Sainte Bare 2, 1348 Louvain-la-Neuve, Belgium {renaud.hartert, pierre.shaus,}@ulouvain.e
A DYNAMIC ACCESS CONTROL WITH BINARY KEY-PAIR
 Malaysian Journal of Computer Siene, Vol 10 No 1, June 1997, pp 36-41 A DYNAMIC ACCESS CONTROL WITH BINARY KEY-PAIR Md Rafiqul Islam, Harihodin Selamat and Mohd Noor Md Sap Faulty of Computer Siene and
Malaysian Journal of Computer Siene, Vol 10 No 1, June 1997, pp 36-41 A DYNAMIC ACCESS CONTROL WITH BINARY KEY-PAIR Md Rafiqul Islam, Harihodin Selamat and Mohd Noor Md Sap Faulty of Computer Siene and
The Geometry of Carpentry and Joinery
 The Geometry of Carpentry and Joinery Pat Morin and Jason Morrison School of Computer Science, Carleton University, 115 Colonel By Drive Ottawa, Ontario, CANADA K1S 5B6 Abstract In this paper we propose
The Geometry of Carpentry and Joinery Pat Morin and Jason Morrison School of Computer Science, Carleton University, 115 Colonel By Drive Ottawa, Ontario, CANADA K1S 5B6 Abstract In this paper we propose
On Optimal Total Cost and Optimal Order Quantity for Fuzzy Inventory Model without Shortage
 International Journal of Fuzzy Mathemat and Systems. ISSN 48-9940 Volume 4, Numer (014, pp. 193-01 Researh India Puliations http://www.ripuliation.om On Optimal Total Cost and Optimal Order Quantity for
International Journal of Fuzzy Mathemat and Systems. ISSN 48-9940 Volume 4, Numer (014, pp. 193-01 Researh India Puliations http://www.ripuliation.om On Optimal Total Cost and Optimal Order Quantity for
Reachability on a region bounded by two attached squares
 Reachability on a region bounded by two attached squares Ali Mohades mohades@cic.aku.ac.ir AmirKabir University of Tech., Math. and Computer Sc. Dept. Mohammadreza Razzazi razzazi@ce.aku.ac.ir AmirKabir
Reachability on a region bounded by two attached squares Ali Mohades mohades@cic.aku.ac.ir AmirKabir University of Tech., Math. and Computer Sc. Dept. Mohammadreza Razzazi razzazi@ce.aku.ac.ir AmirKabir
On Minimum Weight Pseudo-Triangulations
 On Minimum Weight Pseudo-Triangulations Oswin Aichholzer Franz Aurenhammer Thomas Hackl Bettina Speckmann Abstract In this note we discuss some structural properties of minimum weight pseudo-triangulations.
On Minimum Weight Pseudo-Triangulations Oswin Aichholzer Franz Aurenhammer Thomas Hackl Bettina Speckmann Abstract In this note we discuss some structural properties of minimum weight pseudo-triangulations.
On Unfolding Lattice Polygons/Trees and Diameter-4 Trees
 On Unfolding Lattice Polygons/Trees and Diameter-4 Trees Sheung-Hung Poon Department of Mathematics and Computer Science, TU Eindhoven, 5600 MB, Eindhoven, the Netherlands. spoon@win.tue.nl Abstract. We
On Unfolding Lattice Polygons/Trees and Diameter-4 Trees Sheung-Hung Poon Department of Mathematics and Computer Science, TU Eindhoven, 5600 MB, Eindhoven, the Netherlands. spoon@win.tue.nl Abstract. We
Abstract. We describe a parametric hybrid Bezier patch that, in addition. schemes are local in that changes to part of the data only aect portions of
 A Parametri Hyrid Triangular Bezier Path Stephen Mann and Matthew Davidhuk Astrat. We desrie a parametri hyrid Bezier path that, in addition to lending interior ontrol points, lends oundary ontrol points.
A Parametri Hyrid Triangular Bezier Path Stephen Mann and Matthew Davidhuk Astrat. We desrie a parametri hyrid Bezier path that, in addition to lending interior ontrol points, lends oundary ontrol points.
CleanUp: Improving Quadrilateral Finite Element Meshes
 CleanUp: Improving Quadrilateral Finite Element Meshes Paul Kinney MD-10 ECC P.O. Box 203 Ford Motor Company Dearborn, MI. 8121 (313) 28-1228 pkinney@ford.om Abstrat: Unless an all quadrilateral (quad)
CleanUp: Improving Quadrilateral Finite Element Meshes Paul Kinney MD-10 ECC P.O. Box 203 Ford Motor Company Dearborn, MI. 8121 (313) 28-1228 pkinney@ford.om Abstrat: Unless an all quadrilateral (quad)
arxiv: v1 [math.co] 15 Dec 2017
![arxiv: v1 [math.co] 15 Dec 2017 arxiv: v1 [math.co] 15 Dec 2017](/thumbs/95/123306327.jpg) Rectilinear Crossings in Complete Balance -Partite -Uniform Hypergraphs Rahul Gangopahyay Saswata Shannigrahi arxiv:171.05539v1 [math.co] 15 Dec 017 December 18, 017 Abstract In this paper, we stuy the
Rectilinear Crossings in Complete Balance -Partite -Uniform Hypergraphs Rahul Gangopahyay Saswata Shannigrahi arxiv:171.05539v1 [math.co] 15 Dec 017 December 18, 017 Abstract In this paper, we stuy the
Outline: Software Design
 Outline: Software Design. Goals History of software design ideas Design priniples Design methods Life belt or leg iron? (Budgen) Copyright Nany Leveson, Sept. 1999 A Little History... At first, struggling
Outline: Software Design. Goals History of software design ideas Design priniples Design methods Life belt or leg iron? (Budgen) Copyright Nany Leveson, Sept. 1999 A Little History... At first, struggling
Graphs, Trees. Pebbles, Robots
 Graphs, Trees Pebbles, Robots 1 Outline I. Robot Arms. II. Rigid Graphs. III. Characterizations of minimally rigid graphs. IV. Trees, Arboricity and Characterizations. V. The Pebbling Algorithm. VI. Applications:
Graphs, Trees Pebbles, Robots 1 Outline I. Robot Arms. II. Rigid Graphs. III. Characterizations of minimally rigid graphs. IV. Trees, Arboricity and Characterizations. V. The Pebbling Algorithm. VI. Applications:
Conflicts Analysis for Inter-Enterprise Business Process Model
 Conflits Analysis for nter-enterprise Business Proess Moel Wei DNG, Zhong TAN, Jian WANG, Jun ZHU, Haiqi LANG,Lei ZHANG {ingw, tianz, wangwj, zhujun, lianghq, lzhang}@n.ibm.om BM China Researh Lab, BM
Conflits Analysis for nter-enterprise Business Proess Moel Wei DNG, Zhong TAN, Jian WANG, Jun ZHU, Haiqi LANG,Lei ZHANG {ingw, tianz, wangwj, zhujun, lianghq, lzhang}@n.ibm.om BM China Researh Lab, BM
Fuzzy Meta Node Fuzzy Metagraph and its Cluster Analysis
 Journal of Computer Siene 4 (): 9-97, 008 ISSN 549-3636 008 Siene Publiations Fuzzy Meta Node Fuzzy Metagraph and its Cluster Analysis Deepti Gaur, Aditya Shastri and Ranjit Biswas Department of Computer
Journal of Computer Siene 4 (): 9-97, 008 ISSN 549-3636 008 Siene Publiations Fuzzy Meta Node Fuzzy Metagraph and its Cluster Analysis Deepti Gaur, Aditya Shastri and Ranjit Biswas Department of Computer
Learning Non-Linear Reconstruction Models for Image Set Classification
 Testing Training Learning Non-Linear Reonstrution Moels for Image Set Classifiation Munawar Hayat, Mohamme Bennamoun, Senian An Shool of Computer Siene an Software Enginnering The University of Western
Testing Training Learning Non-Linear Reonstrution Moels for Image Set Classifiation Munawar Hayat, Mohamme Bennamoun, Senian An Shool of Computer Siene an Software Enginnering The University of Western
Red-Black Trees 10/19/2009. Red-Black Trees. Example. Red-Black Properties. Black Height. Example
 lgorithms Red-lak Trees 13-2 Red-lak Trees Red-lak Trees ll binar searh tree operations take O(h) time, here h is the height of the tree Therefore, it is important to `balane the tree so that its height
lgorithms Red-lak Trees 13-2 Red-lak Trees Red-lak Trees ll binar searh tree operations take O(h) time, here h is the height of the tree Therefore, it is important to `balane the tree so that its height
PLANE-BASED CAMERA CALIBRATION WITHOUT DIRECT OPTIMIZATION ALGORITHMS. Jorge A. Sánchez, Eduardo A. Destefanis, Luis R. Canali
 PLANE-BASED CAMERA CALIBRAION WIHOU DIREC OPIMIZAION ALGORIHMS Jorge A. Sánhez, Euaro A. Destefanis, Luis R. Canali Centro e Investigaión en Informátia para Ingeniería, Univ. enológia Naional, Faulta Regional
PLANE-BASED CAMERA CALIBRAION WIHOU DIREC OPIMIZAION ALGORIHMS Jorge A. Sánhez, Euaro A. Destefanis, Luis R. Canali Centro e Investigaión en Informátia para Ingeniería, Univ. enológia Naional, Faulta Regional
Path Sharing and Predicate Evaluation for High-Performance XML Filtering*
 Path Sharing and Prediate Evaluation for High-Performane XML Filtering Yanlei Diao, Mihael J. Franklin, Hao Zhang, Peter Fisher EECS, University of California, Berkeley {diaoyl, franklin, nhz, fisherp}@s.erkeley.edu
Path Sharing and Prediate Evaluation for High-Performane XML Filtering Yanlei Diao, Mihael J. Franklin, Hao Zhang, Peter Fisher EECS, University of California, Berkeley {diaoyl, franklin, nhz, fisherp}@s.erkeley.edu
NONLINEAR BACK PROJECTION FOR TOMOGRAPHIC IMAGE RECONSTRUCTION. Ken Sauer and Charles A. Bouman
 NONLINEAR BACK PROJECTION FOR TOMOGRAPHIC IMAGE RECONSTRUCTION Ken Sauer and Charles A. Bouman Department of Eletrial Engineering, University of Notre Dame Notre Dame, IN 46556, (219) 631-6999 Shool of
NONLINEAR BACK PROJECTION FOR TOMOGRAPHIC IMAGE RECONSTRUCTION Ken Sauer and Charles A. Bouman Department of Eletrial Engineering, University of Notre Dame Notre Dame, IN 46556, (219) 631-6999 Shool of
Parametric Abstract Domains for Shape Analysis
 Parametri Abstrat Domains for Shape Analysis Xavier RIVAL (INRIA & Éole Normale Supérieure) Joint work with Bor-Yuh Evan CHANG (University of Maryland U University of Colorado) and George NECULA (University
Parametri Abstrat Domains for Shape Analysis Xavier RIVAL (INRIA & Éole Normale Supérieure) Joint work with Bor-Yuh Evan CHANG (University of Maryland U University of Colorado) and George NECULA (University
Figure 1. LBP in the field of texture analysis operators.
 L MEHODOLOGY he loal inary pattern (L) texture analysis operator is defined as a gray-sale invariant texture measure, derived from a general definition of texture in a loal neighorhood. he urrent form
L MEHODOLOGY he loal inary pattern (L) texture analysis operator is defined as a gray-sale invariant texture measure, derived from a general definition of texture in a loal neighorhood. he urrent form
LARGE-SCALE INVERSE MICROWAVE BACKSCATTER MODELING OF SEA ICE
 LARGE-SCALE INVERSE MICROWAVE BACKSCATTER MODELING OF SEA ICE Quinn P Remun Mirowave Earth Remote Sensing Laboratory Brigham Young University Provo Utah Abstrat Polar sea ie harateristi provie important
LARGE-SCALE INVERSE MICROWAVE BACKSCATTER MODELING OF SEA ICE Quinn P Remun Mirowave Earth Remote Sensing Laboratory Brigham Young University Provo Utah Abstrat Polar sea ie harateristi provie important
Chapter 2: Introduction to Maple V
 Chapter 2: Introdution to Maple V 2-1 Working with Maple Worksheets Try It! (p. 15) Start a Maple session with an empty worksheet. The name of the worksheet should be Untitled (1). Use one of the standard
Chapter 2: Introdution to Maple V 2-1 Working with Maple Worksheets Try It! (p. 15) Start a Maple session with an empty worksheet. The name of the worksheet should be Untitled (1). Use one of the standard
Pairwise alignment using shortest path algorithms, Gunnar Klau, November 29, 2005, 11:
 airwise alignment using shortest path algorithms, Gunnar Klau, November 9,, : 3 3 airwise alignment using shortest path algorithms e will iscuss: it graph Dijkstra s algorithm algorithm (GDU) 3. References
airwise alignment using shortest path algorithms, Gunnar Klau, November 9,, : 3 3 airwise alignment using shortest path algorithms e will iscuss: it graph Dijkstra s algorithm algorithm (GDU) 3. References
Automated Test Generation from Vulnerability Signatures
 Automated Test Generation from Vulneraility Signatures Adulaki Aydin, Muath Alkhalaf, and Tevfik Bultan Computer Siene Department University of California, Santa Barara Email: {aki,muath,ultan}@s.us.edu
Automated Test Generation from Vulneraility Signatures Adulaki Aydin, Muath Alkhalaf, and Tevfik Bultan Computer Siene Department University of California, Santa Barara Email: {aki,muath,ultan}@s.us.edu
This fact makes it difficult to evaluate the cost function to be minimized
 RSOURC LLOCTION N SSINMNT In the resoure alloation step the amount of resoures required to exeute the different types of proesses is determined. We will refer to the time interval during whih a proess
RSOURC LLOCTION N SSINMNT In the resoure alloation step the amount of resoures required to exeute the different types of proesses is determined. We will refer to the time interval during whih a proess
MITSUBISHI ELECTRIC RESEARCH LABORATORIES Cambridge, Massachusetts. Introduction to Matroids and Applications. Srikumar Ramalingam
 Cmrige, Msshusetts Introution to Mtrois n Applitions Srikumr Rmlingm MERL mm//yy Liner Alger (,0,0) (0,,0) Liner inepenene in vetors: v, v2,..., For ll non-trivil we hve s v s v n s, s2,..., s n 2v2...
Cmrige, Msshusetts Introution to Mtrois n Applitions Srikumr Rmlingm MERL mm//yy Liner Alger (,0,0) (0,,0) Liner inepenene in vetors: v, v2,..., For ll non-trivil we hve s v s v n s, s2,..., s n 2v2...
The Thresholding MLEM Algorithm
 Journal of Meial an Biologial Engineering, 24(2: 85-9 85 The Thresholing MLEM Algorithm Keh-Shih Chuang, Meei-Ling Jan,2 Jay Wu Sharon Chen Yu-Ching Ni Ying-Kai Fu 2 epartment of Nulear Siene, National
Journal of Meial an Biologial Engineering, 24(2: 85-9 85 The Thresholing MLEM Algorithm Keh-Shih Chuang, Meei-Ling Jan,2 Jay Wu Sharon Chen Yu-Ching Ni Ying-Kai Fu 2 epartment of Nulear Siene, National
Dynamic Restoration in Multi-layer IP/MPLS-over- Flexgrid Networks
 Dynami Restoration in Multi-layer IP/MPLS-over- Flexgri Networks Alberto Castro, Luis Velaso, Jaume Comellas, an Gabriel Junyent Universitat Politènia e Catalunya (UPC), Barelona, Spain E-mail: aastro@a.up.eu
Dynami Restoration in Multi-layer IP/MPLS-over- Flexgri Networks Alberto Castro, Luis Velaso, Jaume Comellas, an Gabriel Junyent Universitat Politènia e Catalunya (UPC), Barelona, Spain E-mail: aastro@a.up.eu
ECE 242 Fall Tilman Wolf 1. Character- by- character processing Special operators
 State Mahines University of Massahuse4s Amherst ECE 242 Data Strutures an Algorithms Leture 24 ECE 242 Fall 2013 2013 Tilman Wolf 1 Regular expressions Metho to esrie pa4erns of text Charater- y- harater
State Mahines University of Massahuse4s Amherst ECE 242 Data Strutures an Algorithms Leture 24 ECE 242 Fall 2013 2013 Tilman Wolf 1 Regular expressions Metho to esrie pa4erns of text Charater- y- harater
Bayesian Networks: Directed Markov Properties (Cont d) and Markov Equivalent DAGs
 Byesin Networks: Direte Mrkov Properties (Cont ) n Mrkov Equivlent DAGs Huizhen Yu jney.yu@s.helsinki.fi Dept. Computer Siene, Univ. of Helsinki Proilisti Moels, Spring, 2010 Huizhen Yu (U.H.) Byesin Networks:
Byesin Networks: Direte Mrkov Properties (Cont ) n Mrkov Equivlent DAGs Huizhen Yu jney.yu@s.helsinki.fi Dept. Computer Siene, Univ. of Helsinki Proilisti Moels, Spring, 2010 Huizhen Yu (U.H.) Byesin Networks:
Kinematic Analysis of a Family of 3R Manipulators
 Kinematic Analysis of a Family of R Manipulators Maher Baili, Philippe Wenger an Damien Chablat Institut e Recherche en Communications et Cybernétique e Nantes, UMR C.N.R.S. 6597 1, rue e la Noë, BP 92101,
Kinematic Analysis of a Family of R Manipulators Maher Baili, Philippe Wenger an Damien Chablat Institut e Recherche en Communications et Cybernétique e Nantes, UMR C.N.R.S. 6597 1, rue e la Noë, BP 92101,
OPERATING INSTRUCTIONS FOR. COPA (Computer Aided Photoelastic Analysis) PROGRAMME: VERSION 3. Philip Siegmann & Eann Patterson
 OPERATNG NSTRUCTONS FOR COPA (Computer Aie Photoelasti Analysis) PROGRAMME: VERSON 3 Philip Siegmann & Eann Patterson ntroution This oument aompanies a new piee of software initially proue in the Experimental
OPERATNG NSTRUCTONS FOR COPA (Computer Aie Photoelasti Analysis) PROGRAMME: VERSON 3 Philip Siegmann & Eann Patterson ntroution This oument aompanies a new piee of software initially proue in the Experimental
The influence of defeated arguments in defeasible argumentation
 The influene of efeate arguments in efeasible argumentation Bart Verheij University of Limburg, Department of Metajuriia P.O. Box 616, 6200 MD Maastriht, The Netherlans fax: +31 43 256538 email: bart.verheij@metajur.rulimburg.nl
The influene of efeate arguments in efeasible argumentation Bart Verheij University of Limburg, Department of Metajuriia P.O. Box 616, 6200 MD Maastriht, The Netherlans fax: +31 43 256538 email: bart.verheij@metajur.rulimburg.nl
Automatic Physical Design Tuning: Workload as a Sequence Sanjay Agrawal Microsoft Research One Microsoft Way Redmond, WA, USA +1-(425)
 Automati Physial Design Tuning: Workload as a Sequene Sanjay Agrawal Mirosoft Researh One Mirosoft Way Redmond, WA, USA +1-(425) 75-357 sagrawal@mirosoft.om Eri Chu * Computer Sienes Department University
Automati Physial Design Tuning: Workload as a Sequene Sanjay Agrawal Mirosoft Researh One Mirosoft Way Redmond, WA, USA +1-(425) 75-357 sagrawal@mirosoft.om Eri Chu * Computer Sienes Department University
XML Data Streams. XML Stream Processing. XML Stream Processing. Yanlei Diao. University of Massachusetts Amherst
 XML Stream Proessing Yanlei Diao University of Massahusetts Amherst XML Data Streams XML is the wire format for data exhanged online. Purhase orders http://www.oasis-open.org/ommittees/t_home.php?wg_abbrev=ubl
XML Stream Proessing Yanlei Diao University of Massahusetts Amherst XML Data Streams XML is the wire format for data exhanged online. Purhase orders http://www.oasis-open.org/ommittees/t_home.php?wg_abbrev=ubl
Particle Swarm Optimization for the Design of High Diffraction Efficient Holographic Grating
 Original Artile Partile Swarm Optimization for the Design of High Diffration Effiient Holographi Grating A.K. Tripathy 1, S.K. Das, M. Sundaray 3 and S.K. Tripathy* 4 1, Department of Computer Siene, Berhampur
Original Artile Partile Swarm Optimization for the Design of High Diffration Effiient Holographi Grating A.K. Tripathy 1, S.K. Das, M. Sundaray 3 and S.K. Tripathy* 4 1, Department of Computer Siene, Berhampur
Pebble Sets in Convex Polygons
 2 1 Pebble Sets in Convex Polygons Kevin Iga, Randall Maddox June 15, 2005 Abstract Lukács and András posed the problem of showing the existence of a set of n 2 points in the interior of a convex n-gon
2 1 Pebble Sets in Convex Polygons Kevin Iga, Randall Maddox June 15, 2005 Abstract Lukács and András posed the problem of showing the existence of a set of n 2 points in the interior of a convex n-gon
Predicting Project Outcome Leveraging Socio-Technical Network Patterns
 203 7th European Conferene on Software Maintenane an Reengineering Preiting Projet Outome Leveraging Soio-Tehnial Network Patterns Dii Surian, Yuan Tian, Davi Lo, Hong Cheng an Ee-Peng Lim Shool of Information
203 7th European Conferene on Software Maintenane an Reengineering Preiting Projet Outome Leveraging Soio-Tehnial Network Patterns Dii Surian, Yuan Tian, Davi Lo, Hong Cheng an Ee-Peng Lim Shool of Information
arxiv: v2 [cs.hc] 28 Apr 2018
![arxiv: v2 [cs.hc] 28 Apr 2018 arxiv: v2 [cs.hc] 28 Apr 2018](/thumbs/79/79076220.jpg) Clustrophile 2: Guie Visual Clustering Analysis Maro Cavallo an Çağatay Demiralp a arxiv:1804.03048v2 [s.hc] 28 Apr 2018 Fig. 1: Clustrophile 2 is an interative tool for guie exploratory lustering analysis.
Clustrophile 2: Guie Visual Clustering Analysis Maro Cavallo an Çağatay Demiralp a arxiv:1804.03048v2 [s.hc] 28 Apr 2018 Fig. 1: Clustrophile 2 is an interative tool for guie exploratory lustering analysis.
A Novel Validity Index for Determination of the Optimal Number of Clusters
 IEICE TRANS. INF. & SYST., VOL.E84 D, NO.2 FEBRUARY 2001 281 LETTER A Novel Validity Index for Determination of the Optimal Number of Clusters Do-Jong KIM, Yong-Woon PARK, and Dong-Jo PARK, Nonmembers
IEICE TRANS. INF. & SYST., VOL.E84 D, NO.2 FEBRUARY 2001 281 LETTER A Novel Validity Index for Determination of the Optimal Number of Clusters Do-Jong KIM, Yong-Woon PARK, and Dong-Jo PARK, Nonmembers
Adaptive Implicit Surface Polygonization using Marching Triangles
 Volume 20 (2001), Number 2 pp. 67 80 Adaptive Impliit Surfae Polygonization using Marhing Triangles Samir Akkouhe Eri Galin L.I.G.I.M L.I.G.I.M Eole Centrale de Lyon Université Claude Bernard Lyon 1 B.P.
Volume 20 (2001), Number 2 pp. 67 80 Adaptive Impliit Surfae Polygonization using Marhing Triangles Samir Akkouhe Eri Galin L.I.G.I.M L.I.G.I.M Eole Centrale de Lyon Université Claude Bernard Lyon 1 B.P.
A Compressed Breadth-First Search for Satisfiability
 A Compressed Breadth-First Searh for Satisfiaility DoRon B. Motter and Igor L. Markov Department of EECS, University of Mihigan, 1301 Beal Ave, Ann Aror, MI 48109-2122 dmotter, imarkov @ees.umih.edu Astrat.
A Compressed Breadth-First Searh for Satisfiaility DoRon B. Motter and Igor L. Markov Department of EECS, University of Mihigan, 1301 Beal Ave, Ann Aror, MI 48109-2122 dmotter, imarkov @ees.umih.edu Astrat.
Spanheight, A Natural Extension of Bandwidth and Treedepth
 Master s Thesis Spanheight, A Natural Extension of Banwith an Treeepth Author: N. van Roen Supervisor: Prof. r. Hans. L. Bolaener A thesis sumitte in fulfilment of the requirements for the egree of Master
Master s Thesis Spanheight, A Natural Extension of Banwith an Treeepth Author: N. van Roen Supervisor: Prof. r. Hans. L. Bolaener A thesis sumitte in fulfilment of the requirements for the egree of Master
