QEM Optimization, WS 2017/18 Part 4. Constrained optimization
|
|
|
- Dennis Powers
- 5 years ago
- Views:
Transcription
1 QEM Optimization, WS 2017/18 Part 4 Constrained optimization (about 4 Lectures) Supporting Literature: Angel de la Fuente, Mathematical Methods and Models for Economists, Chapter 7 Contents 4 Constrained Optimization 1 41 Equality Constrains: The Lagrange Problem Lagrange Problem: Mathematical Formulation The Simplest Case of EC: n=2, m= More variables: n 2, m = More Variables and More Constraints: n m 7 42 A Cookbook Procedure: How to use the Multidimensional Theorem of Lagrange Sufficient Conditions Global Sufficient Conditions Local Sufficient Conditions of 2nd Order Non-linear Programming and the (Karush-) Kuhn-Tucker Theorem: Optimization under Inequality Constraints Karush-Kuhn-Tucker (KKT) Theorem A Cookbook Procedure: How to use the Karush Kuhn Tucker Theorem Remarks on Applying KKT Method The Simplest Case of KKT: n = 2, m = The case n = m = Constrained Optimization 41 Equality Constrains: The Lagrange Problem Typical Example from Economics: 1
2 A consumer chooses how much of the available income I to spend on: goods units price per unit 1 x 1 p 1 n x n p n The consumer preferences are measured by the utility function u(x 1,, x n ) The consumer faces the problem of choosing (x 1,, x n ) in order to maximize u(x 1,, x n ) subject to the budget constraint p 1 x p n x n = I Mathematical formalization: maximize u(x 1,, x n ), subject to p 1 x p n x n = I We ignore for a moment that x 1,, x n 0 and that possibly not the whole income I may be spent To solve this and similar problems economists make use of the Lagrange multiplier method 411 Lagrange Problem: Mathematical Formulation Let U be a subset of R n and let m n Let moreover f : U R and g : U R m be functions (usually C 1 - or even C 2 -class) Equality Constraint (EC) Problem: maximize the objective function f(x) subject to g(x) = 0, ie find max x U, g(x)=0 f(x) The components of g = (g 1,, g m ) are called the constraint functions and the set D := {x U g(x) = 0} is called the constraint set The method is named after the Italian/French mathematician J L Lagrange ( ) In economics, the method was first implemented ( 1876) by the Danish economist H Westergard We are looking for points x D that are (local) maxima of f We could have a unique x or not x could exist or not exist at all Definition 411 A point x D is called a local max (resp min) for the EC problem if there exists ε > 0 such that for all x B ε (x ) D, one has f(x ) f(x) (resp f(x ) f(x)) Moreover, this point is a global max (resp min) if f(x ) f(x) (resp f(x ) f(x)) for all x D 2
3 412 The Simplest Case of EC: n=2, m=1 Let U R 2 be open and let f, g : U R be continuously differentiable We want to compute max {f(x 1, x 2 ) (x 1, x 2 ) U, g(x 1, x 2 ) = 0} Let (x 1, x 2) be some local maximiser for the EC problem (provided it exists) How do we find all such (x 1, x 2)? The Theorem of Lagrange (which will be precisely formulated later) gives the necessary conditions which should be satisfied by any local optima in this problem Based on the Lagrange Theorem, we should proceed as follows to find all possible candidates for (x 1, x 2) A Formal Scheme of the Lagrange Method (1) Write down the so-called Lagrangian function (or simple the Lagrangian ) L(x 1, x 2 ) := f(x 1, x 2 ) λg(x 1, x 2 ) with a constant λ R Lagrange multiplier (2) Take the partial derivatives of L(x 1, x 2 ) wrt x 1 and x 2 L(x 1, x 2 ) : = (x 1, x 2 ) λ g g(x 1, x 2 ), L(x 1, x 2 ) x 2 : = (x 1, x 2 ) λ g g(x 1, x 2 ) x 2 x 2 As will be explained below, a solution (x 1, x 2) to the EC problem can only be a point for which L(x 1, x 2 ) = L(x 1, x 2 ) = 0 x 2 for a suitable λ = λ(x 1, x 2) This leads to the next step: (3) Solve the system of three equations and find all possible solutions (x 1, x 2; λ ) U R L(x 1, x 2 ) = (x 1, x 2 ) λ g g(x 1, x 2 ) = 0, x 2 (x 1, x 2 ) λ g x 2 g(x 1, x 2 ) = 0, L(x λ 1, x 2 ) = g(x 1, x 2 ) = 0 x 2 L(x 1, x 2 ) = So, any candidate for local extrema (x 1, x 2) is a solution, with its own λ R, to the system L L L = 0, = 0, x 2 λ = 0 3
4 These 3 conditions are called the first order conditions for the EC problem were zero at (x 1, x 2), ie, (x 1, x 2) is a critical point of g The restriction that U does not contain critical points of g is called a constraint qualification in the domain U The restriction that g(x 1, x 2) 0 implies the constrain qualification in some neighborhood of the point (x 1, x 2) Remark 412 This procedure would not have worked if both g and g x 2 Remark 413 i A magic process!!! To solve the constraint problem for two variables (x 1, x 2 ) we transform it into the unconstrained problem in three variables by adding an artificial variable λ) ii The same scheme works whether we are minimising f(x 1, x 2 ) To distinguish max from min, one needs second order conditions Example 414 Maximize f(x 1, x 2 ) = x 1 x 2 subject to 2x 1 + x 2 = 100 Solution 415 Define g(x 1, x 2 ) = 2x 1 + x and the Lagrangian L(x 1, x 2 ) = x 1 x 2 λ (2x 1 + x 2 100) The 1st order conditions for the solutions of EC problem: Herefrom, L = x 2 2λ = 0, L x 2 = x 1 λ = 0, g(x 1, x 2 ) = 2x 1 + x = 0 The only candidate for the solution x 2 = 2λ, x 1 = λ, 2λ + 2λ = 100 λ = 25 x 1 = 25, x 2 = 50, λ = 25 The constrain qualification holds at all points (x, y) R 2 : g = 2, g x 2 = 1 The solution obtained can be confirmed by the substitution method: x 2 = 100 2x 1 = h(x 1 ) = x 1 (100 2x 1 ) = 2x 1 (50 x 1 ), h (x 1 ) = 4x = x 1 = 25, h (x 1 ) = 4 < 0 Therefore, x 1 = 25 is a max point for h = x 1 = 25, x 2 = 50 is a max point for f Justification of the EC scheme: An analytic argument 4
5 How to find a local max / min of f(x 1, x 2 ) subject to g(x 1, x 2 ) = 0 Let (x 1, x 2) U be a local extrema for the EC problem and let g(x 1, x 2) 0 Without loss of generality assume that g/ x 2 (x 1, x 2) 0 Then by the Implicit Function Theorem (IFT) the equation g(x 1, x 2 ) = 0 defines a differentiable function x 2 := i(x 1 ) such that g(x 1, i(x 1 )) = 0 near (x 1, x 2) U and Then i (x 1) = g/ g/ x 2 (x 1, x 2) h(x 1 ) := f(x 1, i(x 1 )) has a local extremum at the point x 1 By the Chain Rule 0 = h (x 1) = (x 1, x 2) + x 2 (x 1, x 2)i (x 1) = (x 1, x 2) x 2 (x 1, x 2) g/ g/ x 2 (x 1, x 2) Hence, Denoting we have and (x 1, x 2) = / x 2 g/ x 2 (x 1, x 2) g (x 1, x 2) (!!!) λ := / x 2 g/ x 2 (x 1, x 2) R, (x 1, x 2) λ (x 1, x 2) = 0 (x x 1, x 2) λ (x 2 x 1, x 2) = More variables: n 2, m = 1 Goal: Find min/max of f(x 1,, x n ) = 0 subject to g(x 1,, x n ) = 0 Define the Lagrangian with the multiplier λ R as L(x 1,, x n ) := f(x 1,, x n ) λg(x 1,, x n ) where (x 1,, x n ) U R n and U is open 5
6 Theorem 416 (Lagrange Theorem for a single constraint equation) Let U R n be open and let f, g : U R be continuously differentiable Let x = (x 1,, x n) U be a local extremum for f(x 1,, x n ) under the equality constraint g(x 1,, x n ) = 0 Suppose further that g(x ) 0, ie, at least one of g/ (x ) 0, 1 j n Then there exists a unique number λ R such that (x ) = λ g (x ), for all 1 j n, or f(x ) = λ g(x ) In particular, for any pair (i, j), where 1 i, j n, one has (x )/ (x ) = g (x )/ g (x ) x i x i Constraint qualification (CQ): We assume that g(x ) 0 The method in general fails if g(x ) = 0 All such critical points should be treated separately by calculating f(x ) The Theorem of Lagrange only provides necessary conditions for local optima x and, moreover, only for those which meet CQ, ie, g(x ) 0 These conditions are not sufficient! Counterexample 417 Maximize f(x 1, x 2 ) = x 2 subject to g(x 1, x 2 ) = x 3 2 x 2 1 = 0, with (x 1, x 2 ) U = R 2 Solution 418 Since x 3 2 = x 2 1 = x 2 0 Moreover, x 2 = 0 x 1 = 0 So, (x 1, x 2) = (0, 0) is the global max of f under the constraint g = 0 But g(x 1, x 2) = 0, ie, the constaint qualification does not hold Furthermore, f(x 1, x 2 ) = (0, 1) for all (x 1, x 2 ), and there cannot exist any λ R such that The Lagrange Theorem is not applicable Remark 419 f(x ) λ g(x ) = 0 (since 1 λ 0) i On the technical side: we need g(x ) 0 to apply IFT ii If g(x ) = 0, it still can happen that f(x ) = λ g(x ) = 0 (Suppose eg that f : U R has a strict global min/max in x and hence f(x ) = 0) iii It is also possible that the constraint qualifications holds, but the EC problem has no solutions, see the example below f(x 1, x 2 ) = x 2 1 x 2 2 subject to g(x 1, x 2 ) = 1 x 1 x 2 6
7 Then Define the Lagrangian Then 2x 1 + λ = 0 2x 2 + λ = 0 1 x 1 x 2 = 0 g(x 1, x 2 ) = ( 1, 1) 0 everywhere L(x 1, x 2 ) = f(x 1, x 2 ) λg(x 1, x 2 ) There are thus NO solutions to EC!! Indeed, put λ 0, x 1 = x 2, x 1 + x 2 = 1, or λ = 0, x 1 = x 2 = 0, x 1 + x 2 = 1 x 2 = 1 x 1 and h(x 1 ) := x 2 1 (1 x 1 ) 2 = 1 + 2x 1 Then there are NO local extrema!! 414 More Variables and More Constraints: n m Theorem 4110 (General Form of the Lagrange Theorem) Let U R n be open and let f : U R, g : U R m (m n) be continuously differentiable Suppose that x = (x 1,, x n) U is a local extremum for f(x 1,, x n ) under the equality constraints g 1 (x 1,, x n ) = 0, g m (x 1,, x n ) = 0 Suppose further that the matrix Dg(x ) has rank m Then there exists a unique vector λ = (λ 1,, λ m) R m such that In other words, f(x ) 1 n (x ) = m = λ 1 m DG(x ) m n i=1 λ i ( (x ),, ) (x ) = (λ x 1,, λ m) n g i (x ), for all 1 j n (product of 1 m and m n matrices), 7 g 1 (x ) g m (x ) g 1 x n (x ) g m (x )
8 Constraint Qualification: The rank of the Jacobian matrix g 1 (x g ) 1 x n (x ) Dg(x ) = g m (x ) is equal to the number of the constraints, ie, rank Dg(x ) = m g m (x ) This ensures that Dg(x ) contains an invertible m m submatrix, which will be used to determine λ R m Proof of Theorem 4110 The main ingredients of the proof are: i Implicit Function Theorem, and ii Chain Rule for Derivatives By assumption, there exists an m m submatrix of Dg(x ) with full rank, ie, its determinant is non-zero Without loss of generality, such submatrix can be chosen as D m g(x ) := g 1 (x ) g m (x ) g 1 x m (x ) g m x m (x ) (otherwise we can change the numbering of variables x 1,, x n ) So, we have det D m g(x ) 0, and hence there exists the inverse matrix [D m g(x )] 1 By the IFT there exist C 1 - functions i 1 (x m+1,, x n ),, i m (x m+1,, x n ) such that g (i 1 (x m+1,, x n ),, i m (x m+1,, x n ), x m+1,, x n ) = 0 near (x 1,, x n), and moreover Di(x m+1,, x }{{ n) = D m g(x } 1,, x n) m (n m) m n 1 D >m g(x 1,, x }{{ n), } n (n m) 8
9 where D >m g(x ) := g 1 x m+1 (x ) g m x m+1 (x ) Then (x m+1,, x n) is a local extrema of the C 1 -function g 1 x n (x ) g m x n (x ) h(x m+1,, x n ) := f (i 1 (x m+1,, x n ),, i m (x m+1,, x n ), x m+1,, x n ) Hence, by the Chain Rule or 0 = h(x m+1,, x n) R n m = m f(x 1,, x }{{ n) Di(x } m+1,, x n) + >m f(x 1,, x }{{ n) } 1 m m (n m) 1 (n m) = m f(x ) [D m g(x )] 1 D >m g(x ) + >m f(x ) 1 m m m m (n m) 1 (n m) where we set >m f(x ) 1 (n m) = m f(x ) [D m g(x )] 1 1 m m m = λ 1 m D >m g(x ) m (n m) D >m g(x ) m (n m) ( ) So, we have from ( ) R m λ := (λ 1,, λ m) := m f(x ) [D m g(x )] 1 ( ) 1 m 1 m m m (i) and respectively from ( ) (ii) which proves the theorem (x ) = m i=1 λ i g i (x ), for all m + 1 j n, m f(x ) [D m g(x )] 1 = λ 1 m m m 1 m m f(x ) 1 m (x ) = m = λ 1 m i=1 λ i D m g(x ) g i (x ), for all 1 j n, 9
10 42 A Cookbook Procedure: How to use the Multidimensional Theorem of Lagrange (1) Set up the Lagrangian function U (x 1,, x n ) L(x 1,, x n ) := f(x 1,, x n ) m with a vector of Lagrange multipliers λ = (λ 1,, λ m ) R m (2) Take the partial derivatives of L(x 1,, x n ) wrt x j, 1 j n, L(x 1,, x n ) := (x 1,, x n ) m i=1 λ i i=1 λ ig i (x 1,, x n ) g i (x 1,, x n ) (3) Find the set of all critical points (x 1,, x n) U for the Lagrangian L(x 1,, x n ) To this end, solve the system of (n + m) equations { L(x 1,, x n ) = 0, 1 j n, λ i L(x 1,, x n ) = g i (x 1,, x n ) = 0, 1 i m, with (n + m) unknowns (x 1,, x n ) U, (λ 1,, λ m ) R m Every critical point (x 1,, x n; λ 1,, λ m) U R m for L gives us the candidate (x 1,, x n) for the local extrema of the EC problem, provided this (x 1,, x n) satisfies the constraint qualification rank Dg(x ) = m To check whether x is a local (global) max / min, we need to evaluate f at each point x The points x at which the constraint qualification fails (ie, rank Dg(x ) < m) should be considered separately since the Lagrange Theorem is not applicable to them Example 421 (Economic / Numerical Example to EC) Maximize the Cobb-Douglas utility function u(x 1, x 2, x 3 ) = x 2 1x 3 2x 3, x 1, x 2, x 3 0 ( R + ), under the budjet constraint x 1 + x 2 + x 3 = 12 Solution 422 The global maximum exists by the Weierstrass theorem, since u is a continuous function defined on a compact domain D := { (x 1, x 2, x 3 ) R 3 + x 1 + x 2 + x 3 = 12 } If any of x 1, x 2, x 3 is zero, then u(x 1, x 2, x 3 ) = 0, which is not the max value 10
11 So, it is enough to solve the Lagrange optimization problem in the open domain Ů := { (x 1, x 2, x 3 ) R>0} 3 The Lagrangian is L(x 1, x 2, x 3 ) = x 2 1x 3 2x 3 λ(x 1 + x 2 + x 3 12) The 1st order conditions are L x 1 = 2x 1 x 3 2x 3 λ = 0, (i) L x 2 = 3x 2 1x 2 2x 3 λ = 0, (ii) L x 3 = x 2 1x 3 2 λ = 0, (iii) x 1 + x 2 + x 3 = 12, (iv) (i) + (ii) = x 2 = 3x 1 /2; (i) + (iii) = x 3 = x 1 /2 Inserting x 2 and x 3 in (iv) = x 1 + 3x 1 /2 + x 1 /2 = 12 = x 1 = 4, x 2 = 6, x 3 = 2 The Constraint Qualification in this (as well as in any other) point holds: g = g = g = 1 x 2 x 3 Answer: The only possible solution is (4, 6, 2), which is the global max point Example 423 (Harder Example) Determine the max/min of the objective function f(x, y) = x 2 + y 2 (square of distance from (0, 0) in R 2 ) subject to g(x, y) = x 2 + xy + y 2 3 = 0 Solution 424 The constraint g(x, y) = 0 defines an ellipse in R 2, so we should find points of the ellipse which have the minimal distance from (0, 0) The Lagrangian is L(x, y) = x 2 + y 2 λ(x 2 + xy + y 2 3), for (x, y) R 2 The 1st order conditions are L = 2x λ(2x + y), (i) x L = 2y λ(x + 2y), (ii) y x 2 + xy + y 2 3 = 0 (iii) We then have (i) = λ = 2y = 2x 2x+y if y 2x Inserting λ in (ii), we get 2x 2x + y (x + 2y) = y2 = x 2 x = ±y 11
12 (a) Suppose y = x Then (iii) = x 2 = 1, so x = 1 or x = 1 We have 2 solution candidates: (x, y) = (1, 1) and (x, y) = ( 1, 1) for λ = 2/3 (b) Suppose y = x Then (iii) = x 2 = 3, so x = 3 or x = 3 We have 2 solution candidates: (x, y) = ( 3, 3) and (x, y) = ( 3, 3) for λ = 2 (c) It remains to consider y = 2x Then (i) So, we have 4 candidates for the max/min problem: = x = y = 0, which contradicts (iii) f min = f(1, 1) = f( 1, 1) = 2 and f max = f( 3, 3) = f( 3, 3) = 6 Next, we check the constraint qualification at these points: g(x, y) = (2x + y, 2y + x) 0 The only point where g(x, y) = 0 is x = y = 0, but it does not satisfy the constraint g(x, y) = 0 Answer: (1, 1) and ( 1, 1) solve the min problem; ( 3, 3) and ( 3, 3) solve the max problem Example 425 (Economic Example) Suppose we have n resources with units x 1,, x n 0 and m consumers with their utility functions u 1 (x),, u m (x), x = (x 1,, x n ) R n + The vector x i := (x i1,, x in ) R n + describes the allocation received by the ith consumer, 1 i m Problem: Find under the resourse constraint m max x 1,,x n R n + m i=1 u i(x i ) x i = ω R n + (a given endowment vector), ie, i=1 m x ij = ω j 0, 1 j n i=1 Solution 426 The Weierstrass theorem says that the global maximum exists if each of the functions u 1 (x),, u m (x) are continuous The Lagrangian with the multiplier vector λ R n L(x1,, xn) = m u i(x i ) λ, m x i ω i=1 i=1 = m u i(x) n ( λ m ) j x ij ω j i=1 j=1 i=1 1st order conditions u i x ij (x i ) = λ j (independent of i) = u i x ij (x i ) u i x ik (x i ) = λ j λ k, for any pair of resourses k, j and any consumer i 12
13 The left-hand side is the so-called marginal rate of substitution (MRS) of resourse k for resourse j This relation is the same for all consumers, 1 i m 43 Sufficient Conditions 431 Global Sufficient Conditions The Lagrange multiplier method gives the necessary conditions They also will be sufficient in the following special case Concave / Convex Lagrangian Let everything be as in Theorem 42 Namely, let U R n be open and let f : U R, g : U R m (m n) be continuously differentiable Consider the Lagrangian L(x; λ) := f(x) m i=1 λ ig i (x) Let (x, λ ) U R be a critical point of L(x; λ), ie, it satisfies the 1st order conditions Theorem 431 The following hold i If L(x; λ ) is a concave function of x U, then x is the global maximum ii If L(x; λ ) is a convex function of x U, then x is the global minimum Proof By assumption, x obeys the constraint g(x) = 0 Let L(x; λ ) be concave on U Then by Theorem 36, for any x U, one has h(x) = L(x; λ ) L(x ; λ ) + x L(x ; λ ), x x R n = L(x ; λ ) + f(x ) m i=1 λ i g i (x ), x x R n = L(x ; λ ) + 0 = f(x ) λ, g(x ) R n = f(x ) 0 = f(x ) Remark 432 In particular, Theorem 431 holds if f is concave, g is convex and λ 0 Furthermore, all this applies to linear f, g which are both convex and concave 13
14 Example 433 (Economic Example) A firm uses inputs K > 0 of capital and L > 0 of labour, respectively, to produce a single output Q according to the Cobb-Douglas production function Q = K a L b, where a, b > 0 and a + b 1 The prices of capital and labour are r > 0 and w > 0, respectively Solve the cost minimising problem min {rk + wl} subject to K a L b = Q Solution 434 The Lagrangian is Note that L(K, L) = rk + wl λ ( K a L b Q ) f(k, L) := rk + wl is linear and g(k, L) := K a L b Q is concave The 1st order conditions are necessary and sufficient: Answer: r = λak a 1 L b, w = λbk a L b 1, K a L b = Q, K = Q 1 a+b = r = al w bk λ 0, L = K br ) b K a+b = Q ( aw br ( aw ) b a+b, L = K br ( ) a br aw = Q 1 a+b br a+b aw is the global solution of the Lagrange min problem 432 Local Sufficient Conditions of 2nd Order Theorem 435 Let U R n be open and let f : U R, g : U R m (m n) be twice continuously differentiable Define the Lagrangian Let x U be such that g(x ) = 0 and L(x; λ) := f(x) λ, g(x) R m D x L(x; λ ) = f(x ) λ Dg(x ) = 0 1 n 1 m m n 14 aw,
15 for some Lagrange multiplier λ R m, ie, (x, λ ) is a critical point of L(x; λ) Consider the matrix of 2nd partial derivatives of L(x; λ ) wrt x DxL(x; 2 λ ) := D 2 f(x) λ D 2 g(x ) n n 1 m m (n n) Suppose that D 2 xl(x; λ ) is negative definite subject to the constraint Dg(x ) h = 0, m n n 1 ie, for all x U and for all 0 h R n, one has D 2 x L(x; λ )h, h R n < 0 from the linear constraint subspace Z(x ) := {h R n Dg(x )h = 0} Then x is a strict local maximum of f(x) subject to g(x) = 0 (ie, there exists a ball B ε (x ) U such that f(x ) > f(x) for all x B ε (x ) satisfying the constraint g(x) = 0) Proof (Idea) By Taylor s formula and the IFT See eg Simon, Blume, Sect 193, or Sundarem, Sect 53 Example 436 (Illustrative Example with n = 2, m = 1 (see Section 42)) Find local max / min of f(x, y) = x 2 + y 2 subject to g(x, y) = x 2 + xy + y 2 3 = 0 Solution 437 We have seen that the 1st order conditions give 4 candidates Calculate (1, 1), ( 1, 1) with λ = 2/3, ( 3, 3), ( 3, 3) with λ = 2 g(x, y) = (2x + y, 2y + x), L(x, y) = x 2 + y 2 λ(x 2 + xy + y 2 3), ( ) 2 2λ λ D 2 L(x, y) = λ 2 2λ 15
16 i Let x = y = 1, λ = 2/3, and h = (h 1, h 2 ) 0 g(x, y ) = (3, 3), g(x, y ), h = 0 3h 1 + 3h 2 = 0 h 1 = h 2 D 2 x L(x; λ )h, h R n = (2 2λ )h 2 1 2λ h 1 h 2 + (2 2λ )h 2 2 = 8h 2 1/3 > 0 (for h 0) By Theorem 435, x = y = 1 is a local min The same holds for x = y = 1 ii Let x = y = 3, λ = 2, and h = (h 1, h 2 ) 0 g(x, y ) = ( 3, 3), g(x, y ), h = 0 h 1 = h 2 D 2 x L(x; λ )h, h R n = 8h 2 1 < 0 (for h 0) By Theorem 435, x = 3, y = 3 is a local maximum The same holds for x = 3, y = 3 44 Non-linear Programming and the (Karush-) Kuhn-Tucker Theorem: Optimization under Inequality Constraints In economics one usually meets inequality than equality constraints (certain variables should be nonnegative, budget constraints, etc) Formulation of the problem Let U R n be an open set and let n, m N (not necessarily m n) Find max x U f(x 1,, x n ) subject to m inequality constraints g 1 (x 1,, x n ) 0, g m (x 1,, x n ) 0 The points x U which satisfy these constraints are called admissible or feasible Respectively, D := {x U g 1 (x) 0,, g m (x) 0} is called admissible or feasible set A point x U is called a local maximum (resp minimum) of f under the above inequality constraints, if there exists a ball B ε (x ) U such that f(x ) f(x) (resp f(x ) f(x)) for all x D B ε (x ) 16
17 Remark 441 In general, it is possible that m > n, since we have some inequality constraints For the sake of concreteness we consider only the constraints with In principle, the problem can be solved by the Lagrange method We have to examine the critical points of L(x 1,, x n ) in the interior of the domain D and the behaviour of f(x 1,, x n ) on the boundary of D However, since the 1950s, the economists generally tacked this such problems by using an extension of the Lagrange multiplier method due to Karush Kuhn Tucker 441 Karush-Kuhn-Tucker (KKT) Theorem Albert Tucker ( ) was a Canadian-born American mathematician who made important contributions in topology, game theory, and non-linear programming He chaired the mathematics department of the Princeton University for about 20 years, one of the longest tenures Harold Kuhn (born 1925) is an American mathematician who studied game theory He won the 1980 John von Neumann Theory Prize along with David Gale and Albert Tucker He is known for his association with John Nash, as a fellow graduate student, a lifelong friend and colleague, and a key figure in getting Nash the attention of the Nobel Prize committee that led to Nash s 1994 Nobel Prize in Economics Kuhn and Nash both had long associations and collaborations with A Tucker, who was Nash s dissertation advisor Kuhn is credited as the mathematics consultant in the 2001 movie adaptation of Nash s life, A Beautiful Mind William Karush ( ) was a professor of California State University and is a mathematician best known for his contribution to Karush Kuhn Tucker conditions He was the first to publish the necessary conditions for the inequality constrained problem in his Masters thesis (Univ of Chicago, 1939), although he became renowned after a seminal conference paper by Kuhn and Tucker (1951) Definition 442 We say that the inequality constraint g i (x) 0 is effective (or active, binding) at a point x U if g i (x ) = 0 Respectively, the constraint g i (x) 0 is passive (inactive, not binding) at a point x U if g i (x ) < 0 Intuitively, only active constraints have effect on the local behaviour of an optimal solution If we know from the beginning which restrictions would be binding at an optimum, the Karush-Kuhn-Tucker problem would reduce to a Lagrange problem, in which we would take the active constraints as equalities and ignore the rest 17
18 Theorem 443 (Karush-Kuhn-Tucker Theorem or the 1st Order Necessary Conditions for Optima; without proof here) Let U R n be open and let f : U R and g : U R m, with m, n N, be continuously differentiable Suppose that x = (x 1,, x n) U is a local maximum for f(x 1,, x n ) under the inequality constraints g 1 (x 1,, x n ) 0, g m (x 1,, x n ) 0 Without loss of generality, suppose that the first p (0 p m) constraints are active at point x, while the others are inactive Furthermore, suppose that the Constraint Qualification (CQ) holds: the rank of the Jacobian matrix of the binding constraints (which is a p n matrix) is equal to p, ie, Dg p (x ) = g 1 (x ) g p (x ) rank Dg p (x ) = p g 1 x n (x ) g p x n (x ) Then there exists a nonnegative vector λ = (λ 1,, λ m) R m + such that (x, λ ) satisfy the following conditions hold: Remark 444 [KKT 1] (x ) = m g i i=1 λ i (x ), for all 1 j n; [KKT 2] λ i g i (x ) = 0, for all 1 i m i [KKT 2] is called the Complementary Slackness condition: if one of the inequalities λ i 0 or g i (x ) 0 is slack (ie, strict), the other cannot be! { λ i > 0 = g i (x ) = 0, g i (x ) < 0 = λ i = 0 It is also possible that both λ i = g i (x ) = 0 ii The Constraint Qualification (CQ) claims that the matrix Dg p (x ) is of full rank p, ie, there is no redundant binding constraints, both in the sense that there are fewer binding constraints than variables (ie, p n) and in the sense that the constraints which are binding are independent (otherwise, Dg p (x ) cannot have the full rank p) 18
19 By changing min f = max( f), we get the following: Corollary 445 Suppose f, g are defined as in Theorem 443 and x U is a local minimum Then the statement of Theorem 45 holds true with the only modification [KKT 1 ] (x ) = m i=1 λ i g i (x ), for all 1 j n 45 A Cookbook Procedure: How to use the Karush Kuhn Tucker Theorem (1) Set up the Lagrangian function U (x 1,, x n ) L(x 1,, x n ) := f(x 1,, x n ) m i=1 λ ig i (x 1,, x n ) with a vector of non-negative Lagrange multipliers λ = (λ 1,, λ m ) R m + (ie, all λ i 0, 1 i m) (2) Equate all 1st order partial derivatives of L(x 1,, x n ) wrt x j, 1 j n, to zero: [KKT 1] L(x 1,, x n ) = (x 1,, x n ) m (3) Require (x 1,, x n ) to satisfy the constraints i=1 λ i λ i L(x 1,, x n ) = g i (x 1,, x n ) 0, 1 i m Impose the Complementary Slackness Condition [KKT 2] λ i g i (x 1,, x n ) = 0, 1 i m, whereby λ i = 0 if g i (x 1,, x n ) < 0 and g i (x 1,, x n ) = 0 if λ i > 0 g i (x 1,, x n ) = 0 (4) Find all x = (x 1,, x n) U which together with the corresponding values of λ 1,, λ m satisfy Conditions [KKT 1], [KKT 2] These are the maxima solution candidates, at least one of which solves the problem (if it has a solution at all) For such x we should check the Constraint Qualification rank Dg p (x ) = p, otherwise the method can give a wrong answer Finally, compute all points x U where the Constraint Qualification fails and compare values of f at such points 19
20 451 Remarks on Applying KKT Method (1) The sign of λ i is important The multipliers λ i 0 correspond to the inequality constraints g i (x) 0, 1 i m Constraints g i (x) 0 formally lead to the multipliers λ i 0 in [KKT 1] (by setting g i := g i ) (2) λ i 0 correspond to the maximum problem In turn, the minimum problem max f(x) x U; g 1 (x) 0,,g m(x) 0 min f(x) x U; g 1 (x) 0,,g m(x) 0 leads to the following modification of the [KKT 1] (by setting f := f) [KKT 1 ] (x ) = m i=1 λ i g i (x ), for all 1 j n (3) Intuitively, the λ i means the sensitivity of the objective function f(x) wrt a small increase of the parameter c i in tne constraint g i (x) c i (4) Possible reasons leading to failure of the Karush-Kuhn-Tucker method: i The Constraint Qualification fails Even if an optimum x does exit but does not obey CQ, it may happen that x does not satisfy [KKT 1], [KKT 2] ii There exists no global optimum for the constrained problem at all Then there may exist solutions to [KKT 1], [KKT 2], which are however not global, or maybe even local, optima Example 451 (Worked Examples (with n = 2, m = 1)) Solve the problem: max f(x, y) for f(x, y) = x 2 + y 2 + y + 1 subject to g(x, y) = x 2 + y Solution 452 By the Weierstrass Theorem there exists a global maximum (x, y ) D of f(x, y) in the closed bounded domain (unit ball) D := { (x, y) R 2 x 2 + y 2 1 } The Lagrangian is defined for all (x, y) R 2 := U by L(x, y) := x 2 + y 2 + y + 1 λ(x 2 + y 2 1) 20
21 [KKT 1] [KKT 2] { L(x,y) { = 2x 2λx = 0, (i) x L(x,y) = 2y + 1 2λy = 0 (ii), y λ 0, x 2 + y 2 1, λ = 0 if x 2 + y 2 < 1, x 2 + y 2 = 1 if λ > 0 (iii) We should find all (x, y ) D which satisfy (i) (iii) for some λ 0 (i) 2x(1 λ) = 0 λ = 1 or x = 0 But λ = 1 = (ii) 2y + 1 2y = 0, contradiction Hence, x = 0 (a) Suppose x 2 + y 2 = 1 y = ±1 If y = 1 = (ii) If y = 1 = (ii) λ = 3/2, which solves (iii) λ = 1/2, which solves (iii) (b) Suppose x 2 + y 2 < 1; x = 0 = 1 < y < 1, λ = 0 Then by (ii) y = 1/2 We get 3 candidates: 1 (0, 1) with λ = 3/2 and f(0, 1) = 3; 2 (0, 1) with λ = 1/2 and f(0, 1) = 1; 3 (0, 1/2) with λ = 0 and f(0, 1/2) = 3/4 The point (0, 1/2) is inside D, ie, the constraint is not active At the points (0, 1) and (0, 1) the constraint is active, but g(x, y) = (2x, 2y) 0 and rankdg(x, y) = 1, ie, (CQ) holds The only point, where (CQ) could fail, ie, g(x, y) = 0, is x = y = 0 with f(0, 0) = 1 But this point is inside D, ie g(0, 0) < 0, and hence the constraint is passive Answer: x = 0, y = 1 is the solution (global maximum) Example 453 (Counterexample (KKT method fails)) Find max f(x, y) for f(x, y) = (x 2 + y 2 ) subject to g(x, y) = y 2 (x 1)
22 Solution 454 Elementary analysis: y 2 (x 1) 3 = x 1 In particular, the smallest possible value of x is 1, which corresponds to y = 0 So, is achieved at x = 1, y = 0 max f(x, y) = min g(x,y) 0 g(x,y) 0 (x2 + y 2 ) = 1 Now, we try to apply the Karush-Kuhn-Tucker method First we note that g(x, y ) = 0 and g(x, y ) = ( x g(x, y ), y g(x, y )) = (0, 0), ie, the Constrained Qualification fails Formally, we should find λ 0 such that { x f(x, y ) = λ x g(x, y ) = 0, y f(x, y ) = λ y g(x, y ) = 0, but we see that f(x, y ) = ( 2x, 2y ) = ( 2, 0) 0 The Kuhn-Tucker method gives no solutions / critical points, hence it is not applicable On the other hand, elementary analysis gives us the global maximum at the above point x = 1, y = The Simplest Case of KKT: n = 2, m = 1 Problem: Maximize f(x, y) subject to g(x, y) 0 Corollary 455 (Karush-Kuhn-Tucker Theorem with one inequality constraint) Let U be an open subset of R 2 and let f : U R and g : U R be continuously differentiable Suppose that (x, y ) U is a local maximum for f(x, y) under the inequality constraint g(x, y) 0 If g(x, y ) = 0 (ie, the constraint g is active at point (x, y )), suppose additionally that rank Dg(x ) = g(x ) = 1, ie, g x (x, y ) 0 ie, the Constraint Qualification (CQ) holds In any case, form the Lagrangian function or g y (x, y ) 0, L(x, y) := f(x, y) λg(x, y) Then, there exists a multiplier λ 0 such that L [KKT 1] x (x, y ) = x (x, y ) λ g x (x, y ) = 0, L y (x, y ) = y (x, y ) λ g y (x, y ) = 0; [KKT 2] λ g(x, y ) = 0, λ 0, g(x, y ) 0 22
23 Remark 456 (Why Does the Receipe Work? Geometrical Picture (n = 2, m = 1)) Since we do not know a priori whether or not the constraint will be binding at the maximizer, we cannot use the only condition [KKT 1], ie, x L(x, y) = y L(x, y) = 0 that we used with equality constraints We should complete the statement by the condition [KKT 2], which says that either the constraint is binding or its multiplier is zero (or sometime, both) Proof (Idea of Prooving Theorem 443) Case 1: Passive Constraint g(x, y ) < 0 The point p = (x, y ) is inside the feasible set D := {(x, y) U g(x, y) 0} This means that (x, y ) is an interior maximum of f(x, y) and thus In this case we set λ = 0 x (x, y ) = y (x, y ) = 0 Case 2: Binding Constraint g(x, y ) = 0 The point p = (x, y ) is on the boundary of the feasible set In other words, (x, y ) solves the Lagrange problem, ie, there exists a Lagrange multiplier λ R such that x (x, y ) = λ g x (x, y ), y (x, y ) = λ g y (x, y ), or f(x, y ) = λ g(x, y ) This time, however, the sign of λ is important! Let us show that λ 0 Recall from Sect 2, that f(x, y ) R 2 points in the direction in which f inreases most rapidly at the point (x, y ) In particular, g(x, y ) points to the set g(x, y) 0 and not to the set g(x, y) 0 Since (x, y ) maximizes f on the set g(x, y) 0, the gradient of f cannot point to the constraint set If did, we could increase f and still keep g(x, y) 0 So, f(x, y ) must point to the region where g(x, y) 0 This means that f(x, y ) and g(x, y ) must point in the same direction Thus, if f(x, y ) = λ g(x, y ), the multiplier λ must be 0 Corollary 457 (Trivial case (n = m = 1)) Let U R be open and let f, g C 1 (U) Suppose that x U is a local maximum for f(x) under the inequality constraint g(x) 0 23
24 If g(x ) = 0 (ie, the constraint is active at x ), suppose additionally that g (x ) 0 (ie, the CQ holds) Then there exists a multiplier λ 0 such that 453 The case n = m = 2 [KT 1] f (x ) = λ g (x ); [KT 2] λ g(x ) = 0, λ 0, g(x ) 0 Corollary 458 Let U R 2 be open and let f : U R, g 1 : U R, g 2 : U R be continuously differentiable Suppose that (x, y ) U is a local maximum for f(x, y) under the inequality constraints g 1 (x, y) 0, g 2 (x, y) 0 i If g 1 (x, y ) = g 2 (x, y ) = 0 (ie, both constraints are active at point (x, y )), suppose additionally that rankdg(x ) = 2, ie, g 1 x (x, y g ) 1 y (x, y ) det Dg(x, y ) = 0 g 2 x (x, y g ) 2 y (x, y ) (ie, the CQ holds) ii If g 1 (x, y ) = 0 and g 2 (x, y ) < 0, suppose additionally that rankdg 1 (x, y ) = 1, ie, at least one of g 1 x (x, y ) and g 1 y (x, y ) is not zero iii If g 1 (x, y ) < 0 and g 2 (x, y ) = 0, suppose respectively that rankdg 2 (x, y ) = 1, ie, at least one of g 2 x (x, y ) and g 2 y (x, y ) is not zero iv If both g 1 (x, y ) < 0 and g 2 (x, y ) < 0, no additional assumptions are needed (ie, the CQ holds automatically) In any case, form the Lagrangian function L(x, y) := f(x, y) λ 1 g 1 (x, y) λ 2 g 2 (x, y) Then there exists a multiplier λ = (λ 1, λ 2) R 2 + such that: [KKT 1] L x (x, y ) = x (x, y ) λ g 1 1 x (x, y ) λ g 2 2 x (x, y ) = 0, L y (x, y ) = y (x, y ) λ g 1 1 y (x, y ) λ g 2 2 y (x, y ) = 0; [KKT 2] λ 1g 1 (x, y ) = 0, λ 2g 2 (x, y ) = 0, λ 1 0, λ 2 0, g 1 (x, y ) 0, g 2 (x, y ) 0 24
25 Example 459 (More difficult: n = m = 2) Find min (e x y) subject to { e x + e y 6 y x Solution 4510 Rewrite the problem as max f(x, y) with f(x, y) := y e x where (x, y) R 2 =: U, subject to { g1 (x, y) := e x + e y 6 0 g 2 (x, y) := x y 0 Define the Lagrangian function with λ 1, λ 2 0 L(x, y) := y e x λ 1 (e x + e y 6) λ 2 (x y) The 1st order conditions [KKT-1] { e x λ 1 e x λ 2 = 0, (i) 1 λ 1 e y + λ 2 = 0 (ii) The Complementary Slackness [KKT-2] λ 1 (e x + e y 6) = 0; λ 1 0; λ 1 = 0 if e x + e y < 6, (iii) λ 2 (x y) = 0; λ 2 0; λ 2 = 0 if x < y; (iv) x y, e x + e y 6 From (ii) and then by (iii) λ = λ 1 e y = λ 1 > 0, e x + e y = 6 Suppose in (iv) that x = y, then e x = e y = 3 From (i) and (ii), we get { 1 3 3λ 1 λ 2 = 0, 1 3λ 1 + λ 2 = 0 = { λ1 = 2/9, λ 2 = 1/3, which contradicts to (iv) (since now λ 2 < 0) Hence x < y and λ 2 = 0, as well as e x + e y = 6 and λ 1 > 0 } (i) = λ 1 = e 2x, (ii) = λ 1 = e y = } y = 2x, e 2x + e x = e x = 2 or e x = 3 (impossible!) = 6 25
26 So, x = ln 2, y = 2x = ln 4, λ 1 = 1/4, λ 2 = 0 We showed that (x, y ) = (ln 2, ln 4) is the only candidate for a solution At this point the constraint g 1 (x, y) 0 is binding whereas the constraint g 2 (x, y) 0 is passive The (CQ) now reads as g 1 x (x, y ) = e x 0 or g 1 y (x, y ) = e y 0 and is satisfied Actually, (CQ) holds at all points (x, y) R 2 Namely, ( e x e y Dg(x, y) = 1 1 with det Dg(x, y) = (e x + e y ) < 0 and g 1 (x, y) 0, g 2 (x, y) 0 for all (x, y) R 2 The point (ln 2, ln 4) is the global minimum point we need to find ), 26
Lecture 2 Optimization with equality constraints
 Lecture 2 Optimization with equality constraints Constrained optimization The idea of constrained optimisation is that the choice of one variable often affects the amount of another variable that can be
Lecture 2 Optimization with equality constraints Constrained optimization The idea of constrained optimisation is that the choice of one variable often affects the amount of another variable that can be
EC5555 Economics Masters Refresher Course in Mathematics September Lecture 6 Optimization with equality constraints Francesco Feri
 EC5555 Economics Masters Refresher Course in Mathematics September 2013 Lecture 6 Optimization with equality constraints Francesco Feri Constrained optimization The idea of constrained optimisation is
EC5555 Economics Masters Refresher Course in Mathematics September 2013 Lecture 6 Optimization with equality constraints Francesco Feri Constrained optimization The idea of constrained optimisation is
5 Day 5: Maxima and minima for n variables.
 UNIVERSITAT POMPEU FABRA INTERNATIONAL BUSINESS ECONOMICS MATHEMATICS III. Pelegrí Viader. 2012-201 Updated May 14, 201 5 Day 5: Maxima and minima for n variables. The same kind of first-order and second-order
UNIVERSITAT POMPEU FABRA INTERNATIONAL BUSINESS ECONOMICS MATHEMATICS III. Pelegrí Viader. 2012-201 Updated May 14, 201 5 Day 5: Maxima and minima for n variables. The same kind of first-order and second-order
Demo 1: KKT conditions with inequality constraints
 MS-C5 Introduction to Optimization Solutions 9 Ehtamo Demo : KKT conditions with inequality constraints Using the Karush-Kuhn-Tucker conditions, see if the points x (x, x ) (, 4) or x (x, x ) (6, ) are
MS-C5 Introduction to Optimization Solutions 9 Ehtamo Demo : KKT conditions with inequality constraints Using the Karush-Kuhn-Tucker conditions, see if the points x (x, x ) (, 4) or x (x, x ) (6, ) are
Programming, numerics and optimization
 Programming, numerics and optimization Lecture C-4: Constrained optimization Łukasz Jankowski ljank@ippt.pan.pl Institute of Fundamental Technological Research Room 4.32, Phone +22.8261281 ext. 428 June
Programming, numerics and optimization Lecture C-4: Constrained optimization Łukasz Jankowski ljank@ippt.pan.pl Institute of Fundamental Technological Research Room 4.32, Phone +22.8261281 ext. 428 June
(1) Given the following system of linear equations, which depends on a parameter a R, 3x y + 5z = 2 4x + y + (a 2 14)z = a + 2
 (1 Given the following system of linear equations, which depends on a parameter a R, x + 2y 3z = 4 3x y + 5z = 2 4x + y + (a 2 14z = a + 2 (a Classify the system of equations depending on the values of
(1 Given the following system of linear equations, which depends on a parameter a R, x + 2y 3z = 4 3x y + 5z = 2 4x + y + (a 2 14z = a + 2 (a Classify the system of equations depending on the values of
Constrained Optimization
 Constrained Optimization Dudley Cooke Trinity College Dublin Dudley Cooke (Trinity College Dublin) Constrained Optimization 1 / 46 EC2040 Topic 5 - Constrained Optimization Reading 1 Chapters 12.1-12.3
Constrained Optimization Dudley Cooke Trinity College Dublin Dudley Cooke (Trinity College Dublin) Constrained Optimization 1 / 46 EC2040 Topic 5 - Constrained Optimization Reading 1 Chapters 12.1-12.3
Shiqian Ma, MAT-258A: Numerical Optimization 1. Chapter 2. Convex Optimization
 Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 2 Convex Optimization Shiqian Ma, MAT-258A: Numerical Optimization 2 2.1. Convex Optimization General optimization problem: min f 0 (x) s.t., f i
Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 2 Convex Optimization Shiqian Ma, MAT-258A: Numerical Optimization 2 2.1. Convex Optimization General optimization problem: min f 0 (x) s.t., f i
Applied Lagrange Duality for Constrained Optimization
 Applied Lagrange Duality for Constrained Optimization Robert M. Freund February 10, 2004 c 2004 Massachusetts Institute of Technology. 1 1 Overview The Practical Importance of Duality Review of Convexity
Applied Lagrange Duality for Constrained Optimization Robert M. Freund February 10, 2004 c 2004 Massachusetts Institute of Technology. 1 1 Overview The Practical Importance of Duality Review of Convexity
Unconstrained Optimization Principles of Unconstrained Optimization Search Methods
 1 Nonlinear Programming Types of Nonlinear Programs (NLP) Convexity and Convex Programs NLP Solutions Unconstrained Optimization Principles of Unconstrained Optimization Search Methods Constrained Optimization
1 Nonlinear Programming Types of Nonlinear Programs (NLP) Convexity and Convex Programs NLP Solutions Unconstrained Optimization Principles of Unconstrained Optimization Search Methods Constrained Optimization
MATHEMATICS II: COLLECTION OF EXERCISES AND PROBLEMS
 MATHEMATICS II: COLLECTION OF EXERCISES AND PROBLEMS GRADO EN A.D.E. GRADO EN ECONOMÍA GRADO EN F.Y.C. ACADEMIC YEAR 2011-12 INDEX UNIT 1.- AN INTRODUCCTION TO OPTIMIZATION 2 UNIT 2.- NONLINEAR PROGRAMMING
MATHEMATICS II: COLLECTION OF EXERCISES AND PROBLEMS GRADO EN A.D.E. GRADO EN ECONOMÍA GRADO EN F.Y.C. ACADEMIC YEAR 2011-12 INDEX UNIT 1.- AN INTRODUCCTION TO OPTIMIZATION 2 UNIT 2.- NONLINEAR PROGRAMMING
Lagrangian Multipliers
 Università Ca Foscari di Venezia - Dipartimento di Management - A.A.2017-2018 Mathematics Lagrangian Multipliers Luciano Battaia November 15, 2017 1 Two variables functions and constraints Consider a two
Università Ca Foscari di Venezia - Dipartimento di Management - A.A.2017-2018 Mathematics Lagrangian Multipliers Luciano Battaia November 15, 2017 1 Two variables functions and constraints Consider a two
Introduction to Constrained Optimization
 Introduction to Constrained Optimization Duality and KKT Conditions Pratik Shah {pratik.shah [at] lnmiit.ac.in} The LNM Institute of Information Technology www.lnmiit.ac.in February 13, 2013 LNMIIT MLPR
Introduction to Constrained Optimization Duality and KKT Conditions Pratik Shah {pratik.shah [at] lnmiit.ac.in} The LNM Institute of Information Technology www.lnmiit.ac.in February 13, 2013 LNMIIT MLPR
MTAEA Convexity and Quasiconvexity
 School of Economics, Australian National University February 19, 2010 Convex Combinations and Convex Sets. Definition. Given any finite collection of points x 1,..., x m R n, a point z R n is said to be
School of Economics, Australian National University February 19, 2010 Convex Combinations and Convex Sets. Definition. Given any finite collection of points x 1,..., x m R n, a point z R n is said to be
California Institute of Technology Crash-Course on Convex Optimization Fall Ec 133 Guilherme Freitas
 California Institute of Technology HSS Division Crash-Course on Convex Optimization Fall 2011-12 Ec 133 Guilherme Freitas In this text, we will study the following basic problem: maximize x C f(x) subject
California Institute of Technology HSS Division Crash-Course on Convex Optimization Fall 2011-12 Ec 133 Guilherme Freitas In this text, we will study the following basic problem: maximize x C f(x) subject
Bounded, Closed, and Compact Sets
 Bounded, Closed, and Compact Sets Definition Let D be a subset of R n. Then D is said to be bounded if there is a number M > 0 such that x < M for all x D. D is closed if it contains all the boundary points.
Bounded, Closed, and Compact Sets Definition Let D be a subset of R n. Then D is said to be bounded if there is a number M > 0 such that x < M for all x D. D is closed if it contains all the boundary points.
A Short SVM (Support Vector Machine) Tutorial
 A Short SVM (Support Vector Machine) Tutorial j.p.lewis CGIT Lab / IMSC U. Southern California version 0.zz dec 004 This tutorial assumes you are familiar with linear algebra and equality-constrained optimization/lagrange
A Short SVM (Support Vector Machine) Tutorial j.p.lewis CGIT Lab / IMSC U. Southern California version 0.zz dec 004 This tutorial assumes you are familiar with linear algebra and equality-constrained optimization/lagrange
Lecture 2 September 3
 EE 381V: Large Scale Optimization Fall 2012 Lecture 2 September 3 Lecturer: Caramanis & Sanghavi Scribe: Hongbo Si, Qiaoyang Ye 2.1 Overview of the last Lecture The focus of the last lecture was to give
EE 381V: Large Scale Optimization Fall 2012 Lecture 2 September 3 Lecturer: Caramanis & Sanghavi Scribe: Hongbo Si, Qiaoyang Ye 2.1 Overview of the last Lecture The focus of the last lecture was to give
Unconstrained Optimization
 Unconstrained Optimization Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 1 Denitions Economics is a science of optima We maximize utility functions, minimize
Unconstrained Optimization Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 1 Denitions Economics is a science of optima We maximize utility functions, minimize
Optimization III: Constrained Optimization
 Optimization III: Constrained Optimization CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Doug James (and Justin Solomon) CS 205A: Mathematical Methods Optimization III: Constrained Optimization
Optimization III: Constrained Optimization CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Doug James (and Justin Solomon) CS 205A: Mathematical Methods Optimization III: Constrained Optimization
Mathematical Programming and Research Methods (Part II)
 Mathematical Programming and Research Methods (Part II) 4. Convexity and Optimization Massimiliano Pontil (based on previous lecture by Andreas Argyriou) 1 Today s Plan Convex sets and functions Types
Mathematical Programming and Research Methods (Part II) 4. Convexity and Optimization Massimiliano Pontil (based on previous lecture by Andreas Argyriou) 1 Today s Plan Convex sets and functions Types
Mathematical and Algorithmic Foundations Linear Programming and Matchings
 Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
In other words, we want to find the domain points that yield the maximum or minimum values (extrema) of the function.
 1 The Lagrange multipliers is a mathematical method for performing constrained optimization of differentiable functions. Recall unconstrained optimization of differentiable functions, in which we want
1 The Lagrange multipliers is a mathematical method for performing constrained optimization of differentiable functions. Recall unconstrained optimization of differentiable functions, in which we want
1. Show that the rectangle of maximum area that has a given perimeter p is a square.
 Constrained Optimization - Examples - 1 Unit #23 : Goals: Lagrange Multipliers To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition).
Constrained Optimization - Examples - 1 Unit #23 : Goals: Lagrange Multipliers To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition).
Lagrangian Multipliers
 Università Ca Foscari di Venezia - Dipartimento di Economia - A.A.2016-2017 Mathematics (Curriculum Economics, Markets and Finance) Lagrangian Multipliers Luciano Battaia November 15, 2017 1 Two variables
Università Ca Foscari di Venezia - Dipartimento di Economia - A.A.2016-2017 Mathematics (Curriculum Economics, Markets and Finance) Lagrangian Multipliers Luciano Battaia November 15, 2017 1 Two variables
Introduction to optimization
 Introduction to optimization G. Ferrari Trecate Dipartimento di Ingegneria Industriale e dell Informazione Università degli Studi di Pavia Industrial Automation Ferrari Trecate (DIS) Optimization Industrial
Introduction to optimization G. Ferrari Trecate Dipartimento di Ingegneria Industriale e dell Informazione Università degli Studi di Pavia Industrial Automation Ferrari Trecate (DIS) Optimization Industrial
Kernels and Constrained Optimization
 Machine Learning 1 WS2014 Module IN2064 Sheet 8 Page 1 Machine Learning Worksheet 8 Kernels and Constrained Optimization 1 Kernelized k-nearest neighbours To classify the point x the k-nearest neighbours
Machine Learning 1 WS2014 Module IN2064 Sheet 8 Page 1 Machine Learning Worksheet 8 Kernels and Constrained Optimization 1 Kernelized k-nearest neighbours To classify the point x the k-nearest neighbours
Linear Programming. Larry Blume. Cornell University & The Santa Fe Institute & IHS
 Linear Programming Larry Blume Cornell University & The Santa Fe Institute & IHS Linear Programs The general linear program is a constrained optimization problem where objectives and constraints are all
Linear Programming Larry Blume Cornell University & The Santa Fe Institute & IHS Linear Programs The general linear program is a constrained optimization problem where objectives and constraints are all
Lecture Notes: Constraint Optimization
 Lecture Notes: Constraint Optimization Gerhard Neumann January 6, 2015 1 Constraint Optimization Problems In constraint optimization we want to maximize a function f(x) under the constraints that g i (x)
Lecture Notes: Constraint Optimization Gerhard Neumann January 6, 2015 1 Constraint Optimization Problems In constraint optimization we want to maximize a function f(x) under the constraints that g i (x)
Introduction to Machine Learning
 Introduction to Machine Learning Maximum Margin Methods Varun Chandola Computer Science & Engineering State University of New York at Buffalo Buffalo, NY, USA chandola@buffalo.edu Chandola@UB CSE 474/574
Introduction to Machine Learning Maximum Margin Methods Varun Chandola Computer Science & Engineering State University of New York at Buffalo Buffalo, NY, USA chandola@buffalo.edu Chandola@UB CSE 474/574
Lecture 25 Nonlinear Programming. November 9, 2009
 Nonlinear Programming November 9, 2009 Outline Nonlinear Programming Another example of NLP problem What makes these problems complex Scalar Function Unconstrained Problem Local and global optima: definition,
Nonlinear Programming November 9, 2009 Outline Nonlinear Programming Another example of NLP problem What makes these problems complex Scalar Function Unconstrained Problem Local and global optima: definition,
Local and Global Minimum
 Local and Global Minimum Stationary Point. From elementary calculus, a single variable function has a stationary point at if the derivative vanishes at, i.e., 0. Graphically, the slope of the function
Local and Global Minimum Stationary Point. From elementary calculus, a single variable function has a stationary point at if the derivative vanishes at, i.e., 0. Graphically, the slope of the function
Advanced Operations Research Techniques IE316. Quiz 1 Review. Dr. Ted Ralphs
 Advanced Operations Research Techniques IE316 Quiz 1 Review Dr. Ted Ralphs IE316 Quiz 1 Review 1 Reading for The Quiz Material covered in detail in lecture. 1.1, 1.4, 2.1-2.6, 3.1-3.3, 3.5 Background material
Advanced Operations Research Techniques IE316 Quiz 1 Review Dr. Ted Ralphs IE316 Quiz 1 Review 1 Reading for The Quiz Material covered in detail in lecture. 1.1, 1.4, 2.1-2.6, 3.1-3.3, 3.5 Background material
Lagrange multipliers. Contents. Introduction. From Wikipedia, the free encyclopedia
 Lagrange multipliers From Wikipedia, the free encyclopedia In mathematical optimization problems, Lagrange multipliers, named after Joseph Louis Lagrange, is a method for finding the local extrema of a
Lagrange multipliers From Wikipedia, the free encyclopedia In mathematical optimization problems, Lagrange multipliers, named after Joseph Louis Lagrange, is a method for finding the local extrema of a
Inverse and Implicit functions
 CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
Lecture 2 - Introduction to Polytopes
 Lecture 2 - Introduction to Polytopes Optimization and Approximation - ENS M1 Nicolas Bousquet 1 Reminder of Linear Algebra definitions Let x 1,..., x m be points in R n and λ 1,..., λ m be real numbers.
Lecture 2 - Introduction to Polytopes Optimization and Approximation - ENS M1 Nicolas Bousquet 1 Reminder of Linear Algebra definitions Let x 1,..., x m be points in R n and λ 1,..., λ m be real numbers.
minimise f(x) subject to g(x) = b, x X. inf f(x) = inf L(x,
 Optimisation Lecture 3 - Easter 2017 Michael Tehranchi Lagrangian necessity Consider the problem Let minimise f(x) subject to g(x) = b, x X. L(x, λ) = f(x) + λ (b g(x)) be the Lagrangian. Notice that for
Optimisation Lecture 3 - Easter 2017 Michael Tehranchi Lagrangian necessity Consider the problem Let minimise f(x) subject to g(x) = b, x X. L(x, λ) = f(x) + λ (b g(x)) be the Lagrangian. Notice that for
Chapter 3 Numerical Methods
 Chapter 3 Numerical Methods Part 1 3.1 Linearization and Optimization of Functions of Vectors 1 Problem Notation 2 Outline 3.1.1 Linearization 3.1.2 Optimization of Objective Functions 3.1.3 Constrained
Chapter 3 Numerical Methods Part 1 3.1 Linearization and Optimization of Functions of Vectors 1 Problem Notation 2 Outline 3.1.1 Linearization 3.1.2 Optimization of Objective Functions 3.1.3 Constrained
Solution Methods Numerical Algorithms
 Solution Methods Numerical Algorithms Evelien van der Hurk DTU Managment Engineering Class Exercises From Last Time 2 DTU Management Engineering 42111: Static and Dynamic Optimization (6) 09/10/2017 Class
Solution Methods Numerical Algorithms Evelien van der Hurk DTU Managment Engineering Class Exercises From Last Time 2 DTU Management Engineering 42111: Static and Dynamic Optimization (6) 09/10/2017 Class
EC 521 MATHEMATICAL METHODS FOR ECONOMICS. Lecture 2: Convex Sets
 EC 51 MATHEMATICAL METHODS FOR ECONOMICS Lecture : Convex Sets Murat YILMAZ Boğaziçi University In this section, we focus on convex sets, separating hyperplane theorems and Farkas Lemma. And as an application
EC 51 MATHEMATICAL METHODS FOR ECONOMICS Lecture : Convex Sets Murat YILMAZ Boğaziçi University In this section, we focus on convex sets, separating hyperplane theorems and Farkas Lemma. And as an application
Linear methods for supervised learning
 Linear methods for supervised learning LDA Logistic regression Naïve Bayes PLA Maximum margin hyperplanes Soft-margin hyperplanes Least squares resgression Ridge regression Nonlinear feature maps Sometimes
Linear methods for supervised learning LDA Logistic regression Naïve Bayes PLA Maximum margin hyperplanes Soft-margin hyperplanes Least squares resgression Ridge regression Nonlinear feature maps Sometimes
Outline. CS38 Introduction to Algorithms. Linear programming 5/21/2014. Linear programming. Lecture 15 May 20, 2014
 5/2/24 Outline CS38 Introduction to Algorithms Lecture 5 May 2, 24 Linear programming simplex algorithm LP duality ellipsoid algorithm * slides from Kevin Wayne May 2, 24 CS38 Lecture 5 May 2, 24 CS38
5/2/24 Outline CS38 Introduction to Algorithms Lecture 5 May 2, 24 Linear programming simplex algorithm LP duality ellipsoid algorithm * slides from Kevin Wayne May 2, 24 CS38 Lecture 5 May 2, 24 CS38
Math 5593 Linear Programming Lecture Notes
 Math 5593 Linear Programming Lecture Notes Unit II: Theory & Foundations (Convex Analysis) University of Colorado Denver, Fall 2013 Topics 1 Convex Sets 1 1.1 Basic Properties (Luenberger-Ye Appendix B.1).........................
Math 5593 Linear Programming Lecture Notes Unit II: Theory & Foundations (Convex Analysis) University of Colorado Denver, Fall 2013 Topics 1 Convex Sets 1 1.1 Basic Properties (Luenberger-Ye Appendix B.1).........................
EC422 Mathematical Economics 2
 EC422 Mathematical Economics 2 Chaiyuth Punyasavatsut Chaiyuth Punyasavatust 1 Course materials and evaluation Texts: Dixit, A.K ; Sydsaeter et al. Grading: 40,30,30. OK or not. Resources: ftp://econ.tu.ac.th/class/archan/c
EC422 Mathematical Economics 2 Chaiyuth Punyasavatsut Chaiyuth Punyasavatust 1 Course materials and evaluation Texts: Dixit, A.K ; Sydsaeter et al. Grading: 40,30,30. OK or not. Resources: ftp://econ.tu.ac.th/class/archan/c
Division of the Humanities and Social Sciences. Convex Analysis and Economic Theory Winter Separation theorems
 Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Winter 2018 Topic 8: Separation theorems 8.1 Hyperplanes and half spaces Recall that a hyperplane in
Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Winter 2018 Topic 8: Separation theorems 8.1 Hyperplanes and half spaces Recall that a hyperplane in
DM545 Linear and Integer Programming. Lecture 2. The Simplex Method. Marco Chiarandini
 DM545 Linear and Integer Programming Lecture 2 The Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 3. 4. Standard Form Basic Feasible Solutions
DM545 Linear and Integer Programming Lecture 2 The Marco Chiarandini Department of Mathematics & Computer Science University of Southern Denmark Outline 1. 2. 3. 4. Standard Form Basic Feasible Solutions
Lecture 10: SVM Lecture Overview Support Vector Machines The binary classification problem
 Computational Learning Theory Fall Semester, 2012/13 Lecture 10: SVM Lecturer: Yishay Mansour Scribe: Gitit Kehat, Yogev Vaknin and Ezra Levin 1 10.1 Lecture Overview In this lecture we present in detail
Computational Learning Theory Fall Semester, 2012/13 Lecture 10: SVM Lecturer: Yishay Mansour Scribe: Gitit Kehat, Yogev Vaknin and Ezra Levin 1 10.1 Lecture Overview In this lecture we present in detail
Elements of Economic Analysis II Lecture III: Cost Minimization, Factor Demand and Cost Function
 Elements of Economic Analysis II Lecture III: Cost Minimization, Factor Demand and Cost Function Kai Hao Yang 10/05/2017 1 Cost Minimization In the last lecture, we saw a firm s profit maximization problem.
Elements of Economic Analysis II Lecture III: Cost Minimization, Factor Demand and Cost Function Kai Hao Yang 10/05/2017 1 Cost Minimization In the last lecture, we saw a firm s profit maximization problem.
POLYHEDRAL GEOMETRY. Convex functions and sets. Mathematical Programming Niels Lauritzen Recall that a subset C R n is convex if
 POLYHEDRAL GEOMETRY Mathematical Programming Niels Lauritzen 7.9.2007 Convex functions and sets Recall that a subset C R n is convex if {λx + (1 λ)y 0 λ 1} C for every x, y C and 0 λ 1. A function f :
POLYHEDRAL GEOMETRY Mathematical Programming Niels Lauritzen 7.9.2007 Convex functions and sets Recall that a subset C R n is convex if {λx + (1 λ)y 0 λ 1} C for every x, y C and 0 λ 1. A function f :
Chapter 15 Introduction to Linear Programming
 Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
MATH2111 Higher Several Variable Calculus Lagrange Multipliers
 MATH2111 Higher Several Variable Calculus Lagrange Multipliers Dr. Jonathan Kress School of Mathematics and Statistics University of New South Wales Semester 1, 2016 [updated: February 29, 2016] JM Kress
MATH2111 Higher Several Variable Calculus Lagrange Multipliers Dr. Jonathan Kress School of Mathematics and Statistics University of New South Wales Semester 1, 2016 [updated: February 29, 2016] JM Kress
. Tutorial Class V 3-10/10/2012 First Order Partial Derivatives;...
 Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; 2 Application of Gradient; Tutorial Class V 3-10/10/2012 1 First Order
Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; 2 Application of Gradient; Tutorial Class V 3-10/10/2012 1 First Order
21-256: Lagrange multipliers
 21-256: Lagrange multipliers Clive Newstead, Thursday 12th June 2014 Lagrange multipliers give us a means of optimizing multivariate functions subject to a number of constraints on their variables. Problems
21-256: Lagrange multipliers Clive Newstead, Thursday 12th June 2014 Lagrange multipliers give us a means of optimizing multivariate functions subject to a number of constraints on their variables. Problems
Convex Optimization MLSS 2015
 Convex Optimization MLSS 2015 Constantine Caramanis The University of Texas at Austin The Optimization Problem minimize : f (x) subject to : x X. The Optimization Problem minimize : f (x) subject to :
Convex Optimization MLSS 2015 Constantine Caramanis The University of Texas at Austin The Optimization Problem minimize : f (x) subject to : x X. The Optimization Problem minimize : f (x) subject to :
LECTURE 18 - OPTIMIZATION
 LECTURE 18 - OPTIMIZATION CHRIS JOHNSON Abstract. In this lecture we ll describe extend the optimization techniques you learned in your first semester calculus class to optimize functions of multiple variables.
LECTURE 18 - OPTIMIZATION CHRIS JOHNSON Abstract. In this lecture we ll describe extend the optimization techniques you learned in your first semester calculus class to optimize functions of multiple variables.
Constrained and Unconstrained Optimization
 Constrained and Unconstrained Optimization Carlos Hurtado Department of Economics University of Illinois at Urbana-Champaign hrtdmrt2@illinois.edu Oct 10th, 2017 C. Hurtado (UIUC - Economics) Numerical
Constrained and Unconstrained Optimization Carlos Hurtado Department of Economics University of Illinois at Urbana-Champaign hrtdmrt2@illinois.edu Oct 10th, 2017 C. Hurtado (UIUC - Economics) Numerical
11 Linear Programming
 11 Linear Programming 11.1 Definition and Importance The final topic in this course is Linear Programming. We say that a problem is an instance of linear programming when it can be effectively expressed
11 Linear Programming 11.1 Definition and Importance The final topic in this course is Linear Programming. We say that a problem is an instance of linear programming when it can be effectively expressed
Constrained Optimization COS 323
 Constrained Optimization COS 323 Last time Introduction to optimization objective function, variables, [constraints] 1-dimensional methods Golden section, discussion of error Newton s method Multi-dimensional
Constrained Optimization COS 323 Last time Introduction to optimization objective function, variables, [constraints] 1-dimensional methods Golden section, discussion of error Newton s method Multi-dimensional
Computational Methods. Constrained Optimization
 Computational Methods Constrained Optimization Manfred Huber 2010 1 Constrained Optimization Unconstrained Optimization finds a minimum of a function under the assumption that the parameters can take on
Computational Methods Constrained Optimization Manfred Huber 2010 1 Constrained Optimization Unconstrained Optimization finds a minimum of a function under the assumption that the parameters can take on
Lagrange Multipliers and Problem Formulation
 Lagrange Multipliers and Problem Formulation Steven J. Miller Department of Mathematics and Statistics Williams College Williamstown, MA 01267 Abstract The method of Lagrange Multipliers (and its generalizations)
Lagrange Multipliers and Problem Formulation Steven J. Miller Department of Mathematics and Statistics Williams College Williamstown, MA 01267 Abstract The method of Lagrange Multipliers (and its generalizations)
Advanced Operations Research Techniques IE316. Quiz 2 Review. Dr. Ted Ralphs
 Advanced Operations Research Techniques IE316 Quiz 2 Review Dr. Ted Ralphs IE316 Quiz 2 Review 1 Reading for The Quiz Material covered in detail in lecture Bertsimas 4.1-4.5, 4.8, 5.1-5.5, 6.1-6.3 Material
Advanced Operations Research Techniques IE316 Quiz 2 Review Dr. Ted Ralphs IE316 Quiz 2 Review 1 Reading for The Quiz Material covered in detail in lecture Bertsimas 4.1-4.5, 4.8, 5.1-5.5, 6.1-6.3 Material
AM 221: Advanced Optimization Spring 2016
 AM 221: Advanced Optimization Spring 2016 Prof. Yaron Singer Lecture 2 Wednesday, January 27th 1 Overview In our previous lecture we discussed several applications of optimization, introduced basic terminology,
AM 221: Advanced Optimization Spring 2016 Prof. Yaron Singer Lecture 2 Wednesday, January 27th 1 Overview In our previous lecture we discussed several applications of optimization, introduced basic terminology,
PRIMAL-DUAL INTERIOR POINT METHOD FOR LINEAR PROGRAMMING. 1. Introduction
 PRIMAL-DUAL INTERIOR POINT METHOD FOR LINEAR PROGRAMMING KELLER VANDEBOGERT AND CHARLES LANNING 1. Introduction Interior point methods are, put simply, a technique of optimization where, given a problem
PRIMAL-DUAL INTERIOR POINT METHOD FOR LINEAR PROGRAMMING KELLER VANDEBOGERT AND CHARLES LANNING 1. Introduction Interior point methods are, put simply, a technique of optimization where, given a problem
Constrained Optimization and Lagrange Multipliers
 Constrained Optimization and Lagrange Multipliers MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Constrained Optimization In the previous section we found the local or absolute
Constrained Optimization and Lagrange Multipliers MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Constrained Optimization In the previous section we found the local or absolute
Lecture 7: Support Vector Machine
 Lecture 7: Support Vector Machine Hien Van Nguyen University of Houston 9/28/2017 Separating hyperplane Red and green dots can be separated by a separating hyperplane Two classes are separable, i.e., each
Lecture 7: Support Vector Machine Hien Van Nguyen University of Houston 9/28/2017 Separating hyperplane Red and green dots can be separated by a separating hyperplane Two classes are separable, i.e., each
Convexity Theory and Gradient Methods
 Convexity Theory and Gradient Methods Angelia Nedić angelia@illinois.edu ISE Department and Coordinated Science Laboratory University of Illinois at Urbana-Champaign Outline Convex Functions Optimality
Convexity Theory and Gradient Methods Angelia Nedić angelia@illinois.edu ISE Department and Coordinated Science Laboratory University of Illinois at Urbana-Champaign Outline Convex Functions Optimality
Kernel Methods & Support Vector Machines
 & Support Vector Machines & Support Vector Machines Arvind Visvanathan CSCE 970 Pattern Recognition 1 & Support Vector Machines Question? Draw a single line to separate two classes? 2 & Support Vector
& Support Vector Machines & Support Vector Machines Arvind Visvanathan CSCE 970 Pattern Recognition 1 & Support Vector Machines Question? Draw a single line to separate two classes? 2 & Support Vector
Department of Mathematics Oleg Burdakov of 30 October Consider the following linear programming problem (LP):
 Linköping University Optimization TAOP3(0) Department of Mathematics Examination Oleg Burdakov of 30 October 03 Assignment Consider the following linear programming problem (LP): max z = x + x s.t. x x
Linköping University Optimization TAOP3(0) Department of Mathematics Examination Oleg Burdakov of 30 October 03 Assignment Consider the following linear programming problem (LP): max z = x + x s.t. x x
Approximation Algorithms
 Approximation Algorithms Prof. Tapio Elomaa tapio.elomaa@tut.fi Course Basics A 4 credit unit course Part of Theoretical Computer Science courses at the Laboratory of Mathematics There will be 4 hours
Approximation Algorithms Prof. Tapio Elomaa tapio.elomaa@tut.fi Course Basics A 4 credit unit course Part of Theoretical Computer Science courses at the Laboratory of Mathematics There will be 4 hours
Distance-to-Solution Estimates for Optimization Problems with Constraints in Standard Form
 Distance-to-Solution Estimates for Optimization Problems with Constraints in Standard Form Philip E. Gill Vyacheslav Kungurtsev Daniel P. Robinson UCSD Center for Computational Mathematics Technical Report
Distance-to-Solution Estimates for Optimization Problems with Constraints in Standard Form Philip E. Gill Vyacheslav Kungurtsev Daniel P. Robinson UCSD Center for Computational Mathematics Technical Report
Section 4: Extreme Values & Lagrange Multipliers.
 Section 4: Extreme Values & Lagrange Multipliers. Compiled by Chris Tisdell S1: Motivation S2: What are local maxima & minima? S3: What is a critical point? S4: Second derivative test S5: Maxima and Minima
Section 4: Extreme Values & Lagrange Multipliers. Compiled by Chris Tisdell S1: Motivation S2: What are local maxima & minima? S3: What is a critical point? S4: Second derivative test S5: Maxima and Minima
Gate Sizing by Lagrangian Relaxation Revisited
 Gate Sizing by Lagrangian Relaxation Revisited Jia Wang, Debasish Das, and Hai Zhou Electrical Engineering and Computer Science Northwestern University Evanston, Illinois, United States October 17, 2007
Gate Sizing by Lagrangian Relaxation Revisited Jia Wang, Debasish Das, and Hai Zhou Electrical Engineering and Computer Science Northwestern University Evanston, Illinois, United States October 17, 2007
Contents. I Basics 1. Copyright by SIAM. Unauthorized reproduction of this article is prohibited.
 page v Preface xiii I Basics 1 1 Optimization Models 3 1.1 Introduction... 3 1.2 Optimization: An Informal Introduction... 4 1.3 Linear Equations... 7 1.4 Linear Optimization... 10 Exercises... 12 1.5
page v Preface xiii I Basics 1 1 Optimization Models 3 1.1 Introduction... 3 1.2 Optimization: An Informal Introduction... 4 1.3 Linear Equations... 7 1.4 Linear Optimization... 10 Exercises... 12 1.5
6. Lecture notes on matroid intersection
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
16.410/413 Principles of Autonomy and Decision Making
 16.410/413 Principles of Autonomy and Decision Making Lecture 17: The Simplex Method Emilio Frazzoli Aeronautics and Astronautics Massachusetts Institute of Technology November 10, 2010 Frazzoli (MIT)
16.410/413 Principles of Autonomy and Decision Making Lecture 17: The Simplex Method Emilio Frazzoli Aeronautics and Astronautics Massachusetts Institute of Technology November 10, 2010 Frazzoli (MIT)
Lagrange multipliers 14.8
 Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 Maximum? 1 1 Minimum? 3/2 Idea:
Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 Maximum? 1 1 Minimum? 3/2 Idea:
Part 4. Decomposition Algorithms Dantzig-Wolf Decomposition Algorithm
 In the name of God Part 4. 4.1. Dantzig-Wolf Decomposition Algorithm Spring 2010 Instructor: Dr. Masoud Yaghini Introduction Introduction Real world linear programs having thousands of rows and columns.
In the name of God Part 4. 4.1. Dantzig-Wolf Decomposition Algorithm Spring 2010 Instructor: Dr. Masoud Yaghini Introduction Introduction Real world linear programs having thousands of rows and columns.
minimize ½(x 1 + 2x 2 + x 32 ) subject to x 1 + x 2 + x 3 = 5
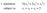 minimize ½(x 1 2 + 2x 2 2 + x 32 ) subject to x 1 + x 2 + x 3 = 5 In this Chapter We will study a new theory for constrained optimization Local optimality condition Easier to implement Deeper insights
minimize ½(x 1 2 + 2x 2 2 + x 32 ) subject to x 1 + x 2 + x 3 = 5 In this Chapter We will study a new theory for constrained optimization Local optimality condition Easier to implement Deeper insights
Lecture notes on the simplex method September We will present an algorithm to solve linear programs of the form. maximize.
 Cornell University, Fall 2017 CS 6820: Algorithms Lecture notes on the simplex method September 2017 1 The Simplex Method We will present an algorithm to solve linear programs of the form maximize subject
Cornell University, Fall 2017 CS 6820: Algorithms Lecture notes on the simplex method September 2017 1 The Simplex Method We will present an algorithm to solve linear programs of the form maximize subject
Machine Learning for Signal Processing Lecture 4: Optimization
 Machine Learning for Signal Processing Lecture 4: Optimization 13 Sep 2015 Instructor: Bhiksha Raj (slides largely by Najim Dehak, JHU) 11-755/18-797 1 Index 1. The problem of optimization 2. Direct optimization
Machine Learning for Signal Processing Lecture 4: Optimization 13 Sep 2015 Instructor: Bhiksha Raj (slides largely by Najim Dehak, JHU) 11-755/18-797 1 Index 1. The problem of optimization 2. Direct optimization
General properties of staircase and convex dual feasible functions
 General properties of staircase and convex dual feasible functions JÜRGEN RIETZ, CLÁUDIO ALVES, J. M. VALÉRIO de CARVALHO Centro de Investigação Algoritmi da Universidade do Minho, Escola de Engenharia
General properties of staircase and convex dual feasible functions JÜRGEN RIETZ, CLÁUDIO ALVES, J. M. VALÉRIO de CARVALHO Centro de Investigação Algoritmi da Universidade do Minho, Escola de Engenharia
1. Lecture notes on bipartite matching February 4th,
 1. Lecture notes on bipartite matching February 4th, 2015 6 1.1.1 Hall s Theorem Hall s theorem gives a necessary and sufficient condition for a bipartite graph to have a matching which saturates (or matches)
1. Lecture notes on bipartite matching February 4th, 2015 6 1.1.1 Hall s Theorem Hall s theorem gives a necessary and sufficient condition for a bipartite graph to have a matching which saturates (or matches)
Chapter II. Linear Programming
 1 Chapter II Linear Programming 1. Introduction 2. Simplex Method 3. Duality Theory 4. Optimality Conditions 5. Applications (QP & SLP) 6. Sensitivity Analysis 7. Interior Point Methods 1 INTRODUCTION
1 Chapter II Linear Programming 1. Introduction 2. Simplex Method 3. Duality Theory 4. Optimality Conditions 5. Applications (QP & SLP) 6. Sensitivity Analysis 7. Interior Point Methods 1 INTRODUCTION
An Introduction to Bilevel Programming
 An Introduction to Bilevel Programming Chris Fricke Department of Mathematics and Statistics University of Melbourne Outline What is Bilevel Programming? Origins of Bilevel Programming. Some Properties
An Introduction to Bilevel Programming Chris Fricke Department of Mathematics and Statistics University of Melbourne Outline What is Bilevel Programming? Origins of Bilevel Programming. Some Properties
Linear Programming: Introduction
 CSC 373 - Algorithm Design, Analysis, and Complexity Summer 2016 Lalla Mouatadid Linear Programming: Introduction A bit of a historical background about linear programming, that I stole from Jeff Erickson
CSC 373 - Algorithm Design, Analysis, and Complexity Summer 2016 Lalla Mouatadid Linear Programming: Introduction A bit of a historical background about linear programming, that I stole from Jeff Erickson
3.3 Optimizing Functions of Several Variables 3.4 Lagrange Multipliers
 3.3 Optimizing Functions of Several Variables 3.4 Lagrange Multipliers Prof. Tesler Math 20C Fall 2018 Prof. Tesler 3.3 3.4 Optimization Math 20C / Fall 2018 1 / 56 Optimizing y = f (x) In Math 20A, we
3.3 Optimizing Functions of Several Variables 3.4 Lagrange Multipliers Prof. Tesler Math 20C Fall 2018 Prof. Tesler 3.3 3.4 Optimization Math 20C / Fall 2018 1 / 56 Optimizing y = f (x) In Math 20A, we
CMU-Q Lecture 9: Optimization II: Constrained,Unconstrained Optimization Convex optimization. Teacher: Gianni A. Di Caro
 CMU-Q 15-381 Lecture 9: Optimization II: Constrained,Unconstrained Optimization Convex optimization Teacher: Gianni A. Di Caro GLOBAL FUNCTION OPTIMIZATION Find the global maximum of the function f x (and
CMU-Q 15-381 Lecture 9: Optimization II: Constrained,Unconstrained Optimization Convex optimization Teacher: Gianni A. Di Caro GLOBAL FUNCTION OPTIMIZATION Find the global maximum of the function f x (and
4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Mathematical programming (optimization) problem: min f (x) s.t. x X R n set of feasible solutions with linear objective function
4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Mathematical programming (optimization) problem: min f (x) s.t. x X R n set of feasible solutions with linear objective function
Some Advanced Topics in Linear Programming
 Some Advanced Topics in Linear Programming Matthew J. Saltzman July 2, 995 Connections with Algebra and Geometry In this section, we will explore how some of the ideas in linear programming, duality theory,
Some Advanced Topics in Linear Programming Matthew J. Saltzman July 2, 995 Connections with Algebra and Geometry In this section, we will explore how some of the ideas in linear programming, duality theory,
Lagrange multipliers October 2013
 Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 1 1 3/2 Example: Optimization
Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 1 1 3/2 Example: Optimization
3. The Simplex algorithmn The Simplex algorithmn 3.1 Forms of linear programs
 11 3.1 Forms of linear programs... 12 3.2 Basic feasible solutions... 13 3.3 The geometry of linear programs... 14 3.4 Local search among basic feasible solutions... 15 3.5 Organization in tableaus...
11 3.1 Forms of linear programs... 12 3.2 Basic feasible solutions... 13 3.3 The geometry of linear programs... 14 3.4 Local search among basic feasible solutions... 15 3.5 Organization in tableaus...
Characterizing Improving Directions Unconstrained Optimization
 Final Review IE417 In the Beginning... In the beginning, Weierstrass's theorem said that a continuous function achieves a minimum on a compact set. Using this, we showed that for a convex set S and y not
Final Review IE417 In the Beginning... In the beginning, Weierstrass's theorem said that a continuous function achieves a minimum on a compact set. Using this, we showed that for a convex set S and y not
Lecture 4: Convexity
 10-725: Convex Optimization Fall 2013 Lecture 4: Convexity Lecturer: Barnabás Póczos Scribes: Jessica Chemali, David Fouhey, Yuxiong Wang Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer:
10-725: Convex Optimization Fall 2013 Lecture 4: Convexity Lecturer: Barnabás Póczos Scribes: Jessica Chemali, David Fouhey, Yuxiong Wang Note: LaTeX template courtesy of UC Berkeley EECS dept. Disclaimer:
Convexity and Optimization
 Convexity and Optimization Richard Lusby Department of Management Engineering Technical University of Denmark Today s Material Extrema Convex Function Convex Sets Other Convexity Concepts Unconstrained
Convexity and Optimization Richard Lusby Department of Management Engineering Technical University of Denmark Today s Material Extrema Convex Function Convex Sets Other Convexity Concepts Unconstrained
Name. Final Exam, Economics 210A, December 2012 There are 8 questions. Answer as many as you can... Good luck!
 Name Final Exam, Economics 210A, December 2012 There are 8 questions. Answer as many as you can... Good luck! 1) Let S and T be convex sets in Euclidean n space. Let S + T be the set {x x = s + t for some
Name Final Exam, Economics 210A, December 2012 There are 8 questions. Answer as many as you can... Good luck! 1) Let S and T be convex sets in Euclidean n space. Let S + T be the set {x x = s + t for some
THREE LECTURES ON BASIC TOPOLOGY. 1. Basic notions.
 THREE LECTURES ON BASIC TOPOLOGY PHILIP FOTH 1. Basic notions. Let X be a set. To make a topological space out of X, one must specify a collection T of subsets of X, which are said to be open subsets of
THREE LECTURES ON BASIC TOPOLOGY PHILIP FOTH 1. Basic notions. Let X be a set. To make a topological space out of X, one must specify a collection T of subsets of X, which are said to be open subsets of
1.1 What is Microeconomics?
 1.1 What is Microeconomics? Economics is the study of allocating limited resources to satisfy unlimited wants. Such a tension implies tradeoffs among competing goals. The analysis can be carried out at
1.1 What is Microeconomics? Economics is the study of allocating limited resources to satisfy unlimited wants. Such a tension implies tradeoffs among competing goals. The analysis can be carried out at
Introduction to Optimization
 Introduction to Optimization Constrained Optimization Marc Toussaint U Stuttgart Constrained Optimization General constrained optimization problem: Let R n, f : R n R, g : R n R m, h : R n R l find min
Introduction to Optimization Constrained Optimization Marc Toussaint U Stuttgart Constrained Optimization General constrained optimization problem: Let R n, f : R n R, g : R n R m, h : R n R l find min
MATH 2400, Analytic Geometry and Calculus 3
 MATH 2400, Analytic Geometry and Calculus 3 List of important Definitions and Theorems 1 Foundations Definition 1. By a function f one understands a mathematical object consisting of (i) a set X, called
MATH 2400, Analytic Geometry and Calculus 3 List of important Definitions and Theorems 1 Foundations Definition 1. By a function f one understands a mathematical object consisting of (i) a set X, called
6.854 Advanced Algorithms. Scribes: Jay Kumar Sundararajan. Duality
 6.854 Advanced Algorithms Scribes: Jay Kumar Sundararajan Lecturer: David Karger Duality This lecture covers weak and strong duality, and also explains the rules for finding the dual of a linear program,
6.854 Advanced Algorithms Scribes: Jay Kumar Sundararajan Lecturer: David Karger Duality This lecture covers weak and strong duality, and also explains the rules for finding the dual of a linear program,
