5 Day 5: Maxima and minima for n variables.
|
|
|
- Dwain Strickland
- 5 years ago
- Views:
Transcription
1 UNIVERSITAT POMPEU FABRA INTERNATIONAL BUSINESS ECONOMICS MATHEMATICS III. Pelegrí Viader Updated May 14, Day 5: Maxima and minima for n variables. The same kind of first-order and second-order conditions we used to find unconstrained max/min for two variables are good for three or more variables. FIRST-ORDER NECESSARY CONDITIONS. If f(x, y, z,...) has a max/min at a point (x, y, z,...) interior to f s domain, then (x, y, z,...) is a stationary point for f, that is f x (x, y, z,...) = 0 f y (x, y, z,...) = 0 f z (x, y, z,...) = CONCAVITY/CONVEXITY: GLOBAL SUFFICIENT CONDITIONS. If f is defined on an open convex set S and (x, y,...) is a stationary point of S, then 1. If f is concave in S then (x, y,...) is a max (global on S); 2. If f is convex in S then (x, y,...) is a min (global on S); This is equivalent to saying: SECOND-ORDER GLOBAL SUFFICIENT CONDITIONS. If f is defined on an open convex set S and (x, y,...) is a stationary point of S, and H(x, y,...) is the Hessian of f: 1. If H(x, y,...) is positive (definite or semidefinite) for all (x, y,...) in S then (x, y,...) is a global min of f on S. 2. If H(x, y,...) is negative (definite or semidefinite) for all (x, y,...) in S then (x, y,...) is a global max of f on S. If we do not have information about all of the domain S but just for the Hessian at (x, y,...), then the max/min are local: SECOND-ORDER LOCAL SUFFICIENT CONDITIONS. If f is defined on an open set S and (x, y,...) is a stationary point of S, and H(x, y,...) is the Hessian of f at (x, y,...): 1. If H(x, y,...) is positive definite then (x, y,...) is a local min of f. 2. If H(x, y,...) is negative definite then (x, y,...) is a local max of f.. If H(x, y,...) is indefinite then (x, y,...) is a saddle point of f. 1
2 Remember that we can check the sign (PD, ND, etc.) of the Hessian using the leading principal minors method (LPM). In the case D n (x, y,...) 0 but D 1 (x, y,...), D 2 (x, y,...),...,d n (x, y,...) not following the pattern for positivity or negativity, then (x, y,...) is a saddle point. Examples. Find max/min of f(x, y, z) = x + y + z 2xy 2xz 2yz. The domain of this function is R. The stationary points come from solving x 2 2y 2z = 0 y 2 2x 2z = 0 z 2 2x 2y = 0 This system is not easy to solve. A possible method would be to solve E1 for y and replace in E2 and E. This leads to a 4th degree equation a bit tiresome to solve. The similarity of the equations makes us think of subtracting: E1 E2 produces which can be written x 2 y 2 + 2x 2y = 0 (x 2 y 2 ) + 2(x y) = 0 (x y) [(x + y) + 2] = 0. Similarly E2 E and E1 E produce (x z) [(x + z) + 2] = 0 and (y z) [(y + z) + 2] = 0. Factoring each one of these equations we have x y = 0 E1 (x + y) + 2 = 0 ; E2 x z = 0 (x + z) + 2 = 0 ; E All in all we can combine these equations in 8 possible ways (2 2 2). x y = 0 1. Case x z = 0. Solution (z, z, z). y z = 0 x y = 0 2. Case x z = 0. Solution ( 1/, 1/, 1/). (y + z) + 2 = 0 x y = 0. Case y z = 0. Solution ( 1/, 1/, 1/). (x + z) + 2 = 0 x z = 0 4. Case y z = 0. Solution ( 1/, 1/, 1/). (x + y) + 2 = 0 x y = 0 5. Case (x + z) + 2 = 0. Solution ( 2/ z, 2/ z, z). (y + z) + 2 = 0 2 y z = 0 (y + z) + 2 = 0.
3 6. Case 7. Case 8. Case x z = 0 (x + y) + 2 = 0 (y + z) + 2 = 0 y z = 0 (x + y) + 2 = 0 (x + z) + 2 = 0 (x + y) + 2 = 0 (x + z) + 2 = 0 (y + z) + 2 = 0. Solution ( 2/ y, y, 2/ y).. Solution (x, 2/ x, 2/ x).. Solution ( 1/, 1/, 1/) Let us check on the original system the solutions we have obtained (remember this is not a linear system and spurious solutions may appear. Any possible solution has to be checked in the original system). Case 1: (z, z, z) leads to z 2 4z = 0 which gives two actual solutions: (0, 0, 0) and (4/, 4/, 4/). Cases 2,, 4, and 8: ( 1/, 1/, 1/) is not good. Replacing in E1, for instance, we have ( 1/) 2 2( 1/) 2( 1/) = 5/ 0. Case 5: ( 2/ z, 2/ z, z) is not good either. Replacing in E1 we end up with z 2 +4z+8/ = 0 that has no real solutions. Similarly for cases 6 and 7. This means only two stationary points (0, 0, 0) and (4/, 4/, 4/). Classifying the stationary points. The Hessian is 6x y 2. The LPM are 2 2 6z D 1 (x, y, z) = 6x, D 2 (x, y, z) = 6xy 4, D (x, y, z) = 216xyz 24y 24x 24z 16 At (0, 0, 0) we have D 1 (0, 0, 0) = 0, D 2 (0, 0, 0) = 4 < 0, D (0, 0, 0) = 16 < 0 Thus, (0, 0, 0) is a saddle point as D (0, 0, 0) < 0, and D 1 (0, 0, 0) and D 2 (0, 0, 0) do not follow the pattern < 0, > 0. At (4/, 4/, 4/) we have D 1 (4/, 4/, 4/) = 8 > 0, D 2 (4/, 4/, 4/) = 60 > 0, D (4/, 4/, 4/) = 400 > 0 At (4/, 4/, 4/) we have a min (local). The value of this min is: f (4/, 4/, /) = 2/9 =.555 This is NOT a global min as (for instance) f(x, 0, 0) = x as x!
4 5.1 Extreme-Value Theorem. It is valid for n variables: If f is a continuous function on a compact set (closed and bounded), S, f reaches a global maximum and a global minimum at points of S. If f is differentiable, the way to proceed is the same as for one and two variables: 1. Find the stationary points of f that are interior to S. 2. Find the max/min of f at the boundary of S.. Make a list of values of f at each of the points found in 1 and Choose the max and the min from the list in. This may be a little more difficult to do than in the one or two variable case. Think of the boundary of S: it may be a piece of surface in R (or a hypersurface in R n ) and we have to study f restricted to this piece of surface. Kind of complicated. We will see that Khun-Tucker s method will help us to solve this problem. 6 Day 6: Lagrange 6.1 Review: Lagrange for two variables Remember that the general problem is max/min f(x, y) s.t. g(x, y) = c. ( ) Functions f, g are twice differentiable functions and 0 g. 0 (Sydsaeter & Hammond, Example 18.7) Max/min f(x, y) = 2x + y s.t. x + y = 5. Remark. Notice that the constraint is only defined for x 0 and y 0 and is not differentiable at points (25, 0) and (0, 25). These two points will be corners of the constraint which will be needed to be taken into consideration alongside any candidate coming from Lagrange s system. We write down the Lagrangian auxiliary function: L(x, y) = 2x + y λ( x + y 5). We solve the system L x = 0 L y = 0 g(x, y) = c that is 2 λ 1 2 x = 0 (E1) λ 1 2 = 0 (E2) y x + y = 5 (E) 4
5 We solve E1 and E2 for λ and we equate both results (we eliminate λ). We get 4 x = 6 y. We use this new equation with E: 4 x = 6 y x = y x + y = 5 2 and y 2 These last two equations imply x = 9, y = 4 (recall that x, y 0). + y = 5 y = 2 and x = Notice that we treat the two equations above as if x, y were the unknowns. In this way we avoid a lot of unnecessary algebra and cancelations. Consequently, there is only one candidate: (9, 4). Are there any other possible points? The remark above has to be considered. Let us have a look at the constraint: A (0, 25) x + y = 5 B (25, 0) We see clearly that the constraint is a curve defined only for 0 x 25 and 0 y 25. It is a closed and bounded set of points in R 2 : a compact. So, the EVT (Extreme-Value Theorem) guarantees that our continuous function f has a global max and a global min on the constraint. We notice that the constraint contains two extreme points, (0, 25) and (25, 0) at which g(x, y) has one infinite derivative! These two points, in consequence, have to be added to any list of candidates for max/min. We have now to compare f(0, 25) = 75; f(25, 0) = 50; f(9, 4) = 0. The max is 75 at (0, 25) and the min is 0 at (9, 4). Notice that we have been able to find max and min because the EVT ensured we had a solution. In this way, we have had no need to check the character of the candidate provided by Lagrange s method: (9, 4). We could also use the graphical method: 5
6 A (0, 25) max x + y = 5 2x + y = 0 f (9, 4) min (25, 0) B Or studied the convexity of the Lagrangian at (9, 4) with λ = 12 (The candidate. We cannot use this argument for corner points which are not candidates): L λ=12 (x, y) = 2x + y 12 x 12 y 60 a convex function as 2x + y 60 is linear (convex/concave) and 12 is a convex function of one variable. Lastly, the use of the bordered Hessian would have given information about (9, 4) but only LOCAL: 0 g x g 0 1/(2 x) 1/(2 y) y BH(x, y, λ) = g x L xx L xy = 1/(2 λ x) g y L xy L 4 x /2 0 yy 1/(2 λ y) 0 4 y /2 At (9, 4) and λ = /6 1/4 BH(9, 4, 12) = 1/6 1/27 0 < 0 min (local). 1/4 0 /8 6.2 Lagrange for n variables and m < n constraints. If we are interested in optimizing a three-variable function constrained by one or two constraints, we can use again Lagrange s method. Question: Find max/min of f(x, y, z) = x + 4y + z s.t. x 2 + y 2 + z 2 = 42 and x + 2y + z = 0. The two constraints are, respectively, the sphere of center (0, 0, 0) and radius 42 and a plane that goes through the sphere s center. Thus, the two constraints define a maximum circle on the sphere (think of the line of the equator on the Earth globe): 6
7 Sphere and plane. As such it is obviously a compact set. Our problem will have both a max and a min global solution. The Lagrangian is L(x, y, z) = x + 4y + z λ(x 2 + y 2 + z 2 42) µ(x + 2y + z). The candidates to max/min will come from solving the system of 5 equations and 5 unknowns 1 2λx µ = 0 4 2λy 2µ = 0 1 2λz µ = 0 x 2 + y 2 + z 2 = 42 x + 2y + z = 0 How do we solve this formidable system? It is not linear. We have to use substitution or some sort of reduction. The more sensible way to proceed is to solve E1 and E2 for λ and µ (eliminate λ and µ) and replace in E. In this way we will have a new equation in x, y, z to solve with the two constraints, E4 and E5. A little thinking, though, make things somewhat easier. If we want to solve E1, E2 and E for λ, µ we can write these three equations as if the unknowns were precisely λ, µ: 2x λ + µ = 1 2y λ + 2 µ = 4 2z λ + µ = 1 This is a 2-unknowns, λ and µ, -equations system. It will have a solution if and only if the rank of the system matrix equals that of the enlarged matrix. This implies that the determinant of the enlarged matrix must be 0: 2x 1 1 2y 2 4 = 20x + 4z + 4y = 0 or 5x + z + y = 0. 2z 1 This gives us the equation in x, y, z we sought in order to solve with E4 and E5. We now must solve 5x + y + z = 0 x + 2y + z = 0 x 2 + y 2 + z 2 = 42 We solve the first two equations for x, y in terms of z and we have x = z/11; y = 16z/11 Replacing in the third equation, z z z2 = 42 z = ± 11 7
8 We have two candidates: ( 1, 16 ), 11 λ = 14, µ = 6 7 and ( 1, 16, 11 ) We have found the corresponding values of λ and µ by solving λ 2 + µ = 1 λ 2 + µ = 1 2 λ + 2 µ = 4 and 2 λ + 2 µ = 4 22 λ + µ = 1 22 λ + µ = 1 The canceled equation is a linear combination of the other two. λ = 14, µ = 6 7. Remark. Check the note at the end of these notes for a general procedure to solve the Lagrangian systems. Using the EVT, we only need to find the value of f at each one of these points ( f 1, 16, 11 ) ( 1 = 18; f, 16 ), 11 = 18. ( 1 Global max is 18 at, 16 ) (, 11 and global min is 18 at 1, 16, 11 ). Alternatively, let us appeal to the concavity/convexity of the Lagrangian in its domain, R. For the candidate ( 1, 16, 11 ), the Lagrangian is L λ= /14,µ=6/7 (x, y, z) = = x + 4y + z + 14 (x2 + y 2 + z 2 42) 6 (x + 2y + z) = 7 = 1 14 (x2 + y 2 + z 2 + 2x + 2y 22z 126) a convex function in R (the sum of convex x 2 + y 2 + z 2 and linear 2x + 2y 22z 126). Our candidate then is a min (global). For the candidate ( 1, 16 ), 11, the Lagrangian is L λ=/14,µ=6/7 (x, y, z) = = x + 4y + z 14 (x2 + y 2 + z 2 42) 6 (x + 2y + z) = 7 = 1 14 ( x2 y 2 z 2 + 2x + 2y 22z 126) a concave function in R (the sum of concave x 2 y 2 z 2 and linear 2x + 2y 22z 126). Our candidate then is a max (global). 6. Interpretation of the Lagrange multipliers. As in the case of two variables, Lagrange multipliers can be interpreted as shadow prices of each constraint. Let us consider the problem of maximizing f(x, y,...) s.t. different constraints 8
9 g 1 (x, y,...) = c 1, g 2 (x, y,...) = c 2,... and let λ 1, λ 2,... be the corresponding multipliers. If the solution to our problem is f (maximum/minimum), we can imagine f as a function of c 1, c 2,.... Then λ i = f c i. So, if c i undergoes a change i (small compared to c i ) in its value, the max/min will change as f (c 1 + 1, c 2 + 2,...) f (c 1, c 2,...) + λ λ Question: In the problem above, max f(x, y, z) = x + 4y + z s.t. x 2 + y 2 + z 2 = 42 and x + 2y + z = 0 how will the max change if the constraints change to x 2 + y 2 + z 2 = 44 and x + 2y + z = 1? We had found that the max was f = 18 at and 2 = 1. ( 1, 16 ), 11 with λ = /14 and µ = 6/7. Now, 1 = 2 The new max will be ( 1) = Solving again the problem for the new RHS of the constraints we obtain a max (true value) of In the case of the min, its value was f = 18 and λ = /14 and µ = 6/7. Again, 1 = 2 and 2 = 1. The new min will be ( 1) = Solving again the problem for the new RHS of the constraints we obtain a min (true value) of Problems. x + 2y + z = 1 1. (a) Solve max/min f(x, y, z) = x 2 + y 2 + z 2 s.t. 2x y z = 4. x + 2y + z = 1.2 (b) How do the optimal values change if the constraints change to 2x y z =.9? 2. Solve max / min f(x, y, z) = x + y + z s.t. x 2 + y 2 + z 2 = 1 x y z = 1. A student used Lagrange with the problem max/min f(x, y, z) = x + y + z s.t. g(x, y, z) = c and she found the two points ( ) ( ) c c c c c c,, and,,. Which is the max and which the min? For each point, find the corresponding value of λ if c = 1. 9
10 7 Day 7: Kuhn-Tucker s method (KT). Kuhn-Tucker s method is a systematic method to solve general optimization problems of the form (standard): g 1 (x 1, x 2,...,x n ) c 1 g max/min f(x 1, x 2,...,x n ) s.t. 2 (x 1, x 2,...,x n ) c g m (x 1, x 2,...,x n ) c m Any point in R n that satisfies all the constraints is called a feasible (or admissible) point and the set of all feasible points, S, is the feasible set. If all the functions g i are differentiable, the feasible set is always a closed set (because of the = in which includes all the frontier curves). It may be bounded or not. Notice that all constraints are written using. If you are given a constraint like g(x, y,...) c, change it into g(x, y,...) c. As usual, we say that a constraint is active at a point (x, y,...) if g i (x, y,...) = c i. If g i (x, y,...) < c i, we say that the constraint is inactive. We assume all the functions involved are differentiable. KT establishes a protocol that helps us to obtain feasible candidate points to max/min. These candidates may be interior to S (all constraints inactive) or belong to the boundary of S (at least one constraint active). (See the figure below: P is an interior point to S and Q is a boundary point that makes two constraints active and the third inactive.) Q g 1 (x,y,...) c 1 S g 2 (x,y,...) c 2 P g (x,y,...) c KT uses Lagrange s method to study feasible points on the boundary of S. If we have m constraints, we use m Lagrange multipliers. We define L(x, y,...) = f(x, y,...) λ 1 [g 1 (x, y,...) c 1 ] λ m [g m (x, y,...) c m ] Let (x, y,...) be a candidate (solution to the Lagrangian system). Two possibilities: 1. Point (x, y,...) is interior to S. Then all constraints will be inactive and (x, y,...) will be a stationary point of L with λ 1 = λ 2 = = λ m = 0 (actually, it will be a stationary point of f as all the λ s are 0). 10
11 2. Point (x, y,...) belongs to the frontier of S, and as such, satisfies r constraints g i1 (x, y,...) = 0;...; g ir (x, y,...) = 0 leaving the other m r inactive (<). Then we have to solve the actual Lagrangian problem for λ i1,...,λ ir as multipliers and the other m r λ s = 0. In the first case, KT leads to a stationary point of f, interior to its domain S. All λ s are 0 and the candidate may be a max, a min or neither (a saddle point). In the second case, KT leads to a candidate for which the λ s outside λ i1,...,λ ir have to be 0. At the candidate, λ i1,...,λ ir may be positive, negative or 0. The candidate may be a candidate to max or a candidate to min or not a valid candidate to either thing. How do we tell? The shadow price interpretation of the λ s will help us to see how that works. We know that if f = f(x, y,...) is the optimal value (max or min) of our objective function, then λ i = f c i. If constraint j is active, increasing the value of c j, enlarges set S. That means that if our problem is a max one, f can only increase with c j : consequently λ j 0. If our problem is a min one, the enlargement of S can only produce a decrease in f. Consequently λ j 0. In any case, if g j is inactive at a solution (x, y,...), clearly λ j = 0 and if λ j 0, g j must be active. So, g j (x, y,...) c j and λ j cannot be 0 at the same time. KT imposes this condition and calls it the complementary slackness condition for each constraint. For a max candidate: For a min candidate: λ j 0 and λ j [g j (x, y,...) c j ] = 0. λ j 0 and λ j [g j (x, y,...) c j ] = 0. If some λ j are > 0 and some are < 0, the candidate is not valid. 7.1 Kuhn-Tucker: General procedure. 1. We define the Lagrangian auxiliary function: L(x 1,..., x n ) = f(x 1,...,x n ) λ 1 [g(x 1,...,x n ) c 1 ] λ m [g(x 1,...,x n ) c m ] 2. The candidates to max [min] will come from solving the system given by the KT conditions: (Block 1) L xi (x 1,...,x n ) = 0 (the n partial derivatives of L = 0); (Block 2) λ j [ ]0 and λ j [g j (x 1,...,x n ) c j ] = 0 (Complementary slackness); (Block ) g j (x 1,...,x n ) c j (Constraints). Block 1 are the usual first-order conditions that make our candidates stationary points for L. Block are the constraints that have to be satisfied: our candidates must be feasible points. And lastly block 2 are the special KT conditions that state that the multipliers have to be non-negative for a max candidate [respectively, non-positive for a min candidate] and must also satisfy the complementary slackness conditions. Notice that the complementary slackness max condition for constraint j says that either λ j > 0 or g j (x 1,...,x n ) < c j but not at the same time; that means that both cannot be inactive at the same time. 11
12 . We have to add to the list of candidates any extreme points not found in the previous process. Basically points where at least one of the g i (x, y,...) is not differentiable or points where the gradients of g i that are not independent vectors. We will not enter too deep into this area. 4. We establish the character of each candidate using either the EVT (if the domain is a compact) or considering the concavity/convexity of L in all its domain for the λ j specific for each candidate. If the problem is a two-variable problem, we can also use the graphical method. Remark. A good way of not forgetting any case in the KT protocol is to use the following simple schemes. Let A stand for ACTIVE and I stand for INACTIVE. Number of constraints: 2. Cases to study 2 2 = 4: AA; AI; IA; II. Number of constraints:. Cases to study = 8: the four cases above adding first an A and then an I: AAA; AIA; IAA; IIA and AAI; AII; IAI; III Each inactive case implies the corresponding λ = 0. Each active case, implies the corresponding constraint to be active (the = stands). Thus a case like AAI means that g 1 = c 1 ; g 2 = c 2 ; λ = 0. The best way to understand how KT works is with an example. We start with a simple two-variable one. Example 1. max/minf = x 2 + y 2 x s.t. x 2 + y 2 1. Notice that the constraint is the whole circle of center (0, 0) and radius 1. We can apply the EVT to this problem and solve it using the techniques we already know (stationary interior points, study of the function restricted to the boundary; list of values). Nevertheless, we are going to use KT. The Lagrangian is L(x, y) = x 2 + y 2 x λ (x 2 + y 2 1). The candidates will come from solving the system given by the KT conditions: 2x 1 2λx = 0 (Block 1) the two partial derivatives of L = 0; 2y 2λy = 0 [ (Block 2) λ 0 [λ 0] and λ x 2 + y 2 1 ] = 0 complementary slackness; (Block ) x 2 + y 2 1 constraints. Block 1 are the usual first-order conditions that make any candidates a stationary point for L. Block is the constraint that has to be satisfied: our candidates must be feasible points. And lastly, block 2 is the special Kuhn-Tucker condition that states that λ has to be non-negative for a max candidate [respectively, non-positive for a min candidate] and satisfy the complementary slackness condition which says that λ and x 2 + y 2 1 cannot be both different from zero. We proceed systematically in order to find candidates: 12
13 1. The constraint is active (A): x 2 + y 2 = 1. We solve B1 and B: 2x 1 2λx = 0 (E1) 2y 2λy = 0 (E2) x 2 + y 2 = 1 (E) From E2, y = 0 or λ = 1: Case y = 0. Replacing in E, x = ±1. For x = 1, from E1, λ = 1/2 0. Candidate to max: (1, 0), with λ = 1/2. For x = 1, from E1, λ = /2 0. Candidate to max: ( 1, 0), with λ = /2. Case λ = 1. Replacing in E1, 1 = 0. Impossible. We have no candidates from here. 2. The constraint is inactive (I): x 2 + y 2 < 1, and so λ = 0. We solve block one (B1) to find stationary points of L (or f) 2x 1 = 0 x = 1/2; y = 0. 2y = 0 The only stationary point is (1/2, 0) and λ = 0. It satisfies the constraint: (1/2) < 1. We have a candidate to max/min. Two ways of finishing our study. As S = (x, y) : x 2 + y 2 1} is a compact set, we apply the EVT to our candidates. The list of values is f(1/2, 0) = 1/4; f(1, 0) = 0; f( 1, 0) = 2. The global max is 2 at the (boundary) point ( 1, 0). The global min is 1/4 at the (interior) point (1/2, 0). Candidate (1/2, 0) is interior to the feasible region. For it, λ = 0. So, L λ=0 = f. And f is convex on its domain (it is the sum of convex x 2 +y 2 and linear x). So any stationary interior point is a global min on the whole domain: min = 1/4 at (1/2, 0). The global max has to be on the boundary: it must be either f(1, 0) = 0 or f( 1, 0) = 2. It is clearly 2 at ( 1, 0). 8 Day 8: Problems on KT max/min f(x, y, z) = 1 2 x y s.t. x + e x y + z 2 0 x 0 Notice that f is a three-variable function and that constraint 2 must be written x 0. Now, the Lagrangian is L(x, y, z) = 1 2 x y λ(x + e x y + z 2 ) µ( x) = 1 2 x y λ(x + e x y + z 2 ) + µx 1
14 and KT necessary conditions will be 1 2 λ(1 e x ) + µ = λ = 0 2λz = 0 λ [ ]0 and λ (x + e x y + z 2 ) = 0 Constraint 1 µ [ ]0 and µ ( x) = 0 Constraint 2 There are 4 different possibilities: 1. Constraint 1 is active and 2 is active: AA. The system is 1 2 λ(1 e x ) + µ = λ = 0 2λz = 0 x + e x y + z 2 = 0 x = 0 The only solution is x = 0; y = 1; z = 0; λ = 1; µ = 1/2. It is not a valid candidate as λ and µ have different signs. 2. Constraint 1 is active and 2 is inactive: AI. That means µ = λ(1 e x ) = λ = 0 2λz = 0 x + e x y + z 2 = 0 x > 0 We have immediately λ = 1; z = 0. From E1 we have e x = 1/2 and taking logarithms x = ln(1/2) which is x = ln 2. This satisfies constraint 2 and replacing in constraint 1 we get y = 1/2 + ln 2. We have a candidate to max: (ln 2, 12 + ln 2, 0 ) with λ = 1; µ = 0.. Constraint 1 is inactive and 2 is active: IA. That means λ = 0. The second equation in the system above becomes inconsistent: 1 = 0. No candidates. 4. Constraints 1 and 2 are inactive: II. That means λ = µ = 0. The second equation in the system above becomes inconsistent: 1 = 0. No candidates. We are left with a single candidate to max: (ln 2, 12 + ln 2, 0 ) with λ = 1; µ = 0. For λ = 1; µ = 0 the Lagrangian is L λ=1,µ=0 (x, y, z) = 1 2 x y (x + e x y + z 2 ) = 1 2 x e x z 2. This is concave as (1/2)x is linear and e linear and z 2 are concave (e linear and z 2 are convex). Our candidate is a global max. The value of the max is ln
15 8.1 Problems. Remember that you can use in order to find max/min. The syntax for our last problem would be: extrema x/2-y on x+exp(-x)-y+z^2<=0,x>=0 1. max/min f(x, y) = 1 x 2 y 2 s.t. 2. max/min f(x, y) = x 2 + y s.t. x 0 y 0 x x + y 2. max/min f(x, y) = x/2 y s.t. 4. max/min f(x, y) = x 2 + 2y s.t. 5. max/min f(x, y) = y x 2 s.t. x + e x y x 0 x 2 + y 2 5 y 0 y x 2 y 2 x y 0 6. max/min f(x, y, z) = x 2 + y 2 + e z s.t. x + y + z 1 e x+y+z 7. max/min f(x, y, z) = e x y + z 2 s.t. x + y + z 1 x 2 + y 2 8. Difficult problem An aircraft manufacturing firm can operate plants in either of two countries. In country A, its cost function as a function of output x 0 is C A (x) = ln(1 + x/100). In country B, its cost as a function of output y 0 is C B (y) = 2 ln(1+y/100). The firm allocates production between the two plants in order to minimize the total cost of producing at least q units of output worldwide where q > 0. (a) Show that the firm s cost-minimizing choices of x and y must solve a particular constrained optimization problem with non-negativity constraints. (b) Use the Lagrange multiplier method to show that there are one, two, or three solution candidates satisfying Kuhn-Tucker conditions, depending on the value of q. (c) Show that the firm uses only the plant in country A for levels of output below some critical level q, and only the plant in country B when q > q. (d) Find the firm s minimum cost as a function of q, and show that it is not differentiable at q. 8.2 Note on the solution of Lagrangian systems Let us consider the problem maxf(x, y, z) s.t. g(x, y, z) = c 1, h(x, y, z) = c 2. 15
16 We assume that f, g, and h are continuously differentiable on an open convex set S. We also assume that the gradients g, h are linearly independent in S. We will see later the necessity of this condition. The Lagrange function is L(x, y, z) = f(x, y, z) λ(g(x, y, z) c 1 ) µ(h(x, y, z) c 2 ). The candidates to max/min will come from solving the system of 5 equations and 5 unknowns f x (x, y, z) λ g x (x, y, z) µ h x (x, y, z) = 0 f y (x, y, z) λ g y (x, y, z) µ h y (x, y, z) = 0 f z (x, y, z) λ g z (x, y, z) µ h z (x, y, z) = 0 g(x, y, z) = c 1 h(x, y, z) = c 2. In order to eliminate λ and µ from the first equations, we consider them as a linear system in the unknowns λ and µ: λ g x + µ h x = f x λ g y + µ h y = f y λ g z + µ h z = f z The matrices of this system are A = g x g y h x h y and A = g x h x f x g y h y f y. g z h z g z h z f z The rank of these two matrices must coincide in order to have solutions for λ and µ. As for A, rank(a) = 2 (remember the assumption about the independence of the gradients of g and h). Thus rank(a ) = 2 which implies g x h x f x g y h y f y = 0. g z h z f z Let us call the above determinant, det(g, h, f ). This is the equation that must be solved together with the two constraints in order to find the Lagrange candidates: det(g, h, f ) = 0 g = 0 h = 0 Let (x, y, z ) be one of the solutions of this system. The corresponding values of λ and µ come from solving λ g x(x, y, z ) µ h x(x, y, z ) = f x(x, y, z ) λ g y (x, y, z ) µ h y (x, y, z ) = f y (x, y, z ) λ g z (x, y, z ) µ h z (x, y, z ) = f z (x, y, z ) One of the equations above is redundant. Assume it is the third. The values of λ and µ may be obtained by Cramer s rule: f x(x, y, z ) h x(x, y, z ) g x(x, y, z ) f x(x, y, z ) f y λ = (x, y, z ) h y (x, y, z ) g y g x (x, y, z ) h x (x, y, z ) ; µ = (x, y, z ) f y (x, y, z ) g x (x, y, z ) h x (x, y, z ). g y (x, y, z ) h y (x, y, z ) g y (x, y, z ) h y (x, y, z ) 16
(1) Given the following system of linear equations, which depends on a parameter a R, 3x y + 5z = 2 4x + y + (a 2 14)z = a + 2
 (1 Given the following system of linear equations, which depends on a parameter a R, x + 2y 3z = 4 3x y + 5z = 2 4x + y + (a 2 14z = a + 2 (a Classify the system of equations depending on the values of
(1 Given the following system of linear equations, which depends on a parameter a R, x + 2y 3z = 4 3x y + 5z = 2 4x + y + (a 2 14z = a + 2 (a Classify the system of equations depending on the values of
Lecture 2 Optimization with equality constraints
 Lecture 2 Optimization with equality constraints Constrained optimization The idea of constrained optimisation is that the choice of one variable often affects the amount of another variable that can be
Lecture 2 Optimization with equality constraints Constrained optimization The idea of constrained optimisation is that the choice of one variable often affects the amount of another variable that can be
Lagrangian Multipliers
 Università Ca Foscari di Venezia - Dipartimento di Management - A.A.2017-2018 Mathematics Lagrangian Multipliers Luciano Battaia November 15, 2017 1 Two variables functions and constraints Consider a two
Università Ca Foscari di Venezia - Dipartimento di Management - A.A.2017-2018 Mathematics Lagrangian Multipliers Luciano Battaia November 15, 2017 1 Two variables functions and constraints Consider a two
3.3 Optimizing Functions of Several Variables 3.4 Lagrange Multipliers
 3.3 Optimizing Functions of Several Variables 3.4 Lagrange Multipliers Prof. Tesler Math 20C Fall 2018 Prof. Tesler 3.3 3.4 Optimization Math 20C / Fall 2018 1 / 56 Optimizing y = f (x) In Math 20A, we
3.3 Optimizing Functions of Several Variables 3.4 Lagrange Multipliers Prof. Tesler Math 20C Fall 2018 Prof. Tesler 3.3 3.4 Optimization Math 20C / Fall 2018 1 / 56 Optimizing y = f (x) In Math 20A, we
EC5555 Economics Masters Refresher Course in Mathematics September Lecture 6 Optimization with equality constraints Francesco Feri
 EC5555 Economics Masters Refresher Course in Mathematics September 2013 Lecture 6 Optimization with equality constraints Francesco Feri Constrained optimization The idea of constrained optimisation is
EC5555 Economics Masters Refresher Course in Mathematics September 2013 Lecture 6 Optimization with equality constraints Francesco Feri Constrained optimization The idea of constrained optimisation is
Math 209 (Fall 2007) Calculus III. Solution #5. 1. Find the minimum and maximum values of the following functions f under the given constraints:
 Math 9 (Fall 7) Calculus III Solution #5. Find the minimum and maximum values of the following functions f under the given constraints: (a) f(x, y) 4x + 6y, x + y ; (b) f(x, y) x y, x + y 6. Solution:
Math 9 (Fall 7) Calculus III Solution #5. Find the minimum and maximum values of the following functions f under the given constraints: (a) f(x, y) 4x + 6y, x + y ; (b) f(x, y) x y, x + y 6. Solution:
Lagrangian Multipliers
 Università Ca Foscari di Venezia - Dipartimento di Economia - A.A.2016-2017 Mathematics (Curriculum Economics, Markets and Finance) Lagrangian Multipliers Luciano Battaia November 15, 2017 1 Two variables
Università Ca Foscari di Venezia - Dipartimento di Economia - A.A.2016-2017 Mathematics (Curriculum Economics, Markets and Finance) Lagrangian Multipliers Luciano Battaia November 15, 2017 1 Two variables
Unconstrained Optimization
 Unconstrained Optimization Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 1 Denitions Economics is a science of optima We maximize utility functions, minimize
Unconstrained Optimization Joshua Wilde, revised by Isabel Tecu, Takeshi Suzuki and María José Boccardi August 13, 2013 1 Denitions Economics is a science of optima We maximize utility functions, minimize
Constrained Optimization
 Constrained Optimization Dudley Cooke Trinity College Dublin Dudley Cooke (Trinity College Dublin) Constrained Optimization 1 / 46 EC2040 Topic 5 - Constrained Optimization Reading 1 Chapters 12.1-12.3
Constrained Optimization Dudley Cooke Trinity College Dublin Dudley Cooke (Trinity College Dublin) Constrained Optimization 1 / 46 EC2040 Topic 5 - Constrained Optimization Reading 1 Chapters 12.1-12.3
Bounded, Closed, and Compact Sets
 Bounded, Closed, and Compact Sets Definition Let D be a subset of R n. Then D is said to be bounded if there is a number M > 0 such that x < M for all x D. D is closed if it contains all the boundary points.
Bounded, Closed, and Compact Sets Definition Let D be a subset of R n. Then D is said to be bounded if there is a number M > 0 such that x < M for all x D. D is closed if it contains all the boundary points.
Unconstrained Optimization Principles of Unconstrained Optimization Search Methods
 1 Nonlinear Programming Types of Nonlinear Programs (NLP) Convexity and Convex Programs NLP Solutions Unconstrained Optimization Principles of Unconstrained Optimization Search Methods Constrained Optimization
1 Nonlinear Programming Types of Nonlinear Programs (NLP) Convexity and Convex Programs NLP Solutions Unconstrained Optimization Principles of Unconstrained Optimization Search Methods Constrained Optimization
Lagrange Multipliers and Problem Formulation
 Lagrange Multipliers and Problem Formulation Steven J. Miller Department of Mathematics and Statistics Williams College Williamstown, MA 01267 Abstract The method of Lagrange Multipliers (and its generalizations)
Lagrange Multipliers and Problem Formulation Steven J. Miller Department of Mathematics and Statistics Williams College Williamstown, MA 01267 Abstract The method of Lagrange Multipliers (and its generalizations)
21-256: Lagrange multipliers
 21-256: Lagrange multipliers Clive Newstead, Thursday 12th June 2014 Lagrange multipliers give us a means of optimizing multivariate functions subject to a number of constraints on their variables. Problems
21-256: Lagrange multipliers Clive Newstead, Thursday 12th June 2014 Lagrange multipliers give us a means of optimizing multivariate functions subject to a number of constraints on their variables. Problems
Section 4: Extreme Values & Lagrange Multipliers.
 Section 4: Extreme Values & Lagrange Multipliers. Compiled by Chris Tisdell S1: Motivation S2: What are local maxima & minima? S3: What is a critical point? S4: Second derivative test S5: Maxima and Minima
Section 4: Extreme Values & Lagrange Multipliers. Compiled by Chris Tisdell S1: Motivation S2: What are local maxima & minima? S3: What is a critical point? S4: Second derivative test S5: Maxima and Minima
Math 233. Lagrange Multipliers Basics
 Math 233. Lagrange Multipliers Basics Optimization problems of the form to optimize a function f(x, y, z) over a constraint g(x, y, z) = k can often be conveniently solved using the method of Lagrange
Math 233. Lagrange Multipliers Basics Optimization problems of the form to optimize a function f(x, y, z) over a constraint g(x, y, z) = k can often be conveniently solved using the method of Lagrange
Math 21a Homework 22 Solutions Spring, 2014
 Math 1a Homework Solutions Spring, 014 1. Based on Stewart 11.8 #6 ) Consider the function fx, y) = e xy, and the constraint x 3 + y 3 = 16. a) Use Lagrange multipliers to find the coordinates x, y) of
Math 1a Homework Solutions Spring, 014 1. Based on Stewart 11.8 #6 ) Consider the function fx, y) = e xy, and the constraint x 3 + y 3 = 16. a) Use Lagrange multipliers to find the coordinates x, y) of
MATH2111 Higher Several Variable Calculus Lagrange Multipliers
 MATH2111 Higher Several Variable Calculus Lagrange Multipliers Dr. Jonathan Kress School of Mathematics and Statistics University of New South Wales Semester 1, 2016 [updated: February 29, 2016] JM Kress
MATH2111 Higher Several Variable Calculus Lagrange Multipliers Dr. Jonathan Kress School of Mathematics and Statistics University of New South Wales Semester 1, 2016 [updated: February 29, 2016] JM Kress
Constrained Optimization and Lagrange Multipliers
 Constrained Optimization and Lagrange Multipliers MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Constrained Optimization In the previous section we found the local or absolute
Constrained Optimization and Lagrange Multipliers MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Constrained Optimization In the previous section we found the local or absolute
QEM Optimization, WS 2017/18 Part 4. Constrained optimization
 QEM Optimization, WS 2017/18 Part 4 Constrained optimization (about 4 Lectures) Supporting Literature: Angel de la Fuente, Mathematical Methods and Models for Economists, Chapter 7 Contents 4 Constrained
QEM Optimization, WS 2017/18 Part 4 Constrained optimization (about 4 Lectures) Supporting Literature: Angel de la Fuente, Mathematical Methods and Models for Economists, Chapter 7 Contents 4 Constrained
14.5 Directional Derivatives and the Gradient Vector
 14.5 Directional Derivatives and the Gradient Vector 1. Directional Derivatives. Recall z = f (x, y) and the partial derivatives f x and f y are defined as f (x 0 + h, y 0 ) f (x 0, y 0 ) f x (x 0, y 0
14.5 Directional Derivatives and the Gradient Vector 1. Directional Derivatives. Recall z = f (x, y) and the partial derivatives f x and f y are defined as f (x 0 + h, y 0 ) f (x 0, y 0 ) f x (x 0, y 0
Programming, numerics and optimization
 Programming, numerics and optimization Lecture C-4: Constrained optimization Łukasz Jankowski ljank@ippt.pan.pl Institute of Fundamental Technological Research Room 4.32, Phone +22.8261281 ext. 428 June
Programming, numerics and optimization Lecture C-4: Constrained optimization Łukasz Jankowski ljank@ippt.pan.pl Institute of Fundamental Technological Research Room 4.32, Phone +22.8261281 ext. 428 June
Lagrange multipliers October 2013
 Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 1 1 3/2 Example: Optimization
Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 1 1 3/2 Example: Optimization
(c) 0 (d) (a) 27 (b) (e) x 2 3x2
 1. Sarah the architect is designing a modern building. The base of the building is the region in the xy-plane bounded by x =, y =, and y = 3 x. The building itself has a height bounded between z = and
1. Sarah the architect is designing a modern building. The base of the building is the region in the xy-plane bounded by x =, y =, and y = 3 x. The building itself has a height bounded between z = and
EC422 Mathematical Economics 2
 EC422 Mathematical Economics 2 Chaiyuth Punyasavatsut Chaiyuth Punyasavatust 1 Course materials and evaluation Texts: Dixit, A.K ; Sydsaeter et al. Grading: 40,30,30. OK or not. Resources: ftp://econ.tu.ac.th/class/archan/c
EC422 Mathematical Economics 2 Chaiyuth Punyasavatsut Chaiyuth Punyasavatust 1 Course materials and evaluation Texts: Dixit, A.K ; Sydsaeter et al. Grading: 40,30,30. OK or not. Resources: ftp://econ.tu.ac.th/class/archan/c
Math 241, Final Exam. 12/11/12.
 Math, Final Exam. //. No notes, calculator, or text. There are points total. Partial credit may be given. ircle or otherwise clearly identify your final answer. Name:. (5 points): Equation of a line. Find
Math, Final Exam. //. No notes, calculator, or text. There are points total. Partial credit may be given. ircle or otherwise clearly identify your final answer. Name:. (5 points): Equation of a line. Find
MTAEA Convexity and Quasiconvexity
 School of Economics, Australian National University February 19, 2010 Convex Combinations and Convex Sets. Definition. Given any finite collection of points x 1,..., x m R n, a point z R n is said to be
School of Economics, Australian National University February 19, 2010 Convex Combinations and Convex Sets. Definition. Given any finite collection of points x 1,..., x m R n, a point z R n is said to be
Lagrange multipliers 14.8
 Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 Maximum? 1 1 Minimum? 3/2 Idea:
Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 Maximum? 1 1 Minimum? 3/2 Idea:
we wish to minimize this function; to make life easier, we may minimize
 Optimization and Lagrange Multipliers We studied single variable optimization problems in Calculus 1; given a function f(x), we found the extremes of f relative to some constraint. Our ability to find
Optimization and Lagrange Multipliers We studied single variable optimization problems in Calculus 1; given a function f(x), we found the extremes of f relative to some constraint. Our ability to find
Demo 1: KKT conditions with inequality constraints
 MS-C5 Introduction to Optimization Solutions 9 Ehtamo Demo : KKT conditions with inequality constraints Using the Karush-Kuhn-Tucker conditions, see if the points x (x, x ) (, 4) or x (x, x ) (6, ) are
MS-C5 Introduction to Optimization Solutions 9 Ehtamo Demo : KKT conditions with inequality constraints Using the Karush-Kuhn-Tucker conditions, see if the points x (x, x ) (, 4) or x (x, x ) (6, ) are
Constrained extrema of two variables functions
 Constrained extrema of two variables functions Apellidos, Nombre: Departamento: Centro: Alicia Herrero Debón aherrero@mat.upv.es) Departamento de Matemática Aplicada Instituto de Matemática Multidisciplnar
Constrained extrema of two variables functions Apellidos, Nombre: Departamento: Centro: Alicia Herrero Debón aherrero@mat.upv.es) Departamento de Matemática Aplicada Instituto de Matemática Multidisciplnar
Math 213 Exam 2. Each question is followed by a space to write your answer. Please write your answer neatly in the space provided.
 Math 213 Exam 2 Name: Section: Do not remove this answer page you will return the whole exam. You will be allowed two hours to complete this test. No books or notes may be used other than a onepage cheat
Math 213 Exam 2 Name: Section: Do not remove this answer page you will return the whole exam. You will be allowed two hours to complete this test. No books or notes may be used other than a onepage cheat
Math 233. Lagrange Multipliers Basics
 Math 33. Lagrange Multipliers Basics Optimization problems of the form to optimize a function f(x, y, z) over a constraint g(x, y, z) = k can often be conveniently solved using the method of Lagrange multipliers:
Math 33. Lagrange Multipliers Basics Optimization problems of the form to optimize a function f(x, y, z) over a constraint g(x, y, z) = k can often be conveniently solved using the method of Lagrange multipliers:
A Short SVM (Support Vector Machine) Tutorial
 A Short SVM (Support Vector Machine) Tutorial j.p.lewis CGIT Lab / IMSC U. Southern California version 0.zz dec 004 This tutorial assumes you are familiar with linear algebra and equality-constrained optimization/lagrange
A Short SVM (Support Vector Machine) Tutorial j.p.lewis CGIT Lab / IMSC U. Southern California version 0.zz dec 004 This tutorial assumes you are familiar with linear algebra and equality-constrained optimization/lagrange
Mathematical Programming and Research Methods (Part II)
 Mathematical Programming and Research Methods (Part II) 4. Convexity and Optimization Massimiliano Pontil (based on previous lecture by Andreas Argyriou) 1 Today s Plan Convex sets and functions Types
Mathematical Programming and Research Methods (Part II) 4. Convexity and Optimization Massimiliano Pontil (based on previous lecture by Andreas Argyriou) 1 Today s Plan Convex sets and functions Types
Local and Global Minimum
 Local and Global Minimum Stationary Point. From elementary calculus, a single variable function has a stationary point at if the derivative vanishes at, i.e., 0. Graphically, the slope of the function
Local and Global Minimum Stationary Point. From elementary calculus, a single variable function has a stationary point at if the derivative vanishes at, i.e., 0. Graphically, the slope of the function
LECTURE 18 - OPTIMIZATION
 LECTURE 18 - OPTIMIZATION CHRIS JOHNSON Abstract. In this lecture we ll describe extend the optimization techniques you learned in your first semester calculus class to optimize functions of multiple variables.
LECTURE 18 - OPTIMIZATION CHRIS JOHNSON Abstract. In this lecture we ll describe extend the optimization techniques you learned in your first semester calculus class to optimize functions of multiple variables.
Second Midterm Exam Math 212 Fall 2010
 Second Midterm Exam Math 22 Fall 2 Instructions: This is a 9 minute exam. You should work alone, without access to any book or notes. No calculators are allowed. Do not discuss this exam with anyone other
Second Midterm Exam Math 22 Fall 2 Instructions: This is a 9 minute exam. You should work alone, without access to any book or notes. No calculators are allowed. Do not discuss this exam with anyone other
In other words, we want to find the domain points that yield the maximum or minimum values (extrema) of the function.
 1 The Lagrange multipliers is a mathematical method for performing constrained optimization of differentiable functions. Recall unconstrained optimization of differentiable functions, in which we want
1 The Lagrange multipliers is a mathematical method for performing constrained optimization of differentiable functions. Recall unconstrained optimization of differentiable functions, in which we want
13.1. Functions of Several Variables. Introduction to Functions of Several Variables. Functions of Several Variables. Objectives. Example 1 Solution
 13 Functions of Several Variables 13.1 Introduction to Functions of Several Variables Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Objectives Understand
13 Functions of Several Variables 13.1 Introduction to Functions of Several Variables Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Objectives Understand
Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers
 In this section we present Lagrange s method for maximizing or minimizing a general function f(x, y, z) subject to a constraint (or side condition) of the form g(x, y, z) = k. Figure 1 shows this curve
In this section we present Lagrange s method for maximizing or minimizing a general function f(x, y, z) subject to a constraint (or side condition) of the form g(x, y, z) = k. Figure 1 shows this curve
Lagrange Multipliers
 Lagrange Multipliers Christopher Croke University of Pennsylvania Math 115 How to deal with constrained optimization. How to deal with constrained optimization. Let s revisit the problem of finding the
Lagrange Multipliers Christopher Croke University of Pennsylvania Math 115 How to deal with constrained optimization. How to deal with constrained optimization. Let s revisit the problem of finding the
. Tutorial Class V 3-10/10/2012 First Order Partial Derivatives;...
 Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; 2 Application of Gradient; Tutorial Class V 3-10/10/2012 1 First Order
Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; 2 Application of Gradient; Tutorial Class V 3-10/10/2012 1 First Order
Total. Math 2130 Practice Final (Spring 2017) (1) (2) (3) (4) (5) (6) (7) (8)
 Math 130 Practice Final (Spring 017) Before the exam: Do not write anything on this page. Do not open the exam. Turn off your cell phone. Make sure your books, notes, and electronics are not visible during
Math 130 Practice Final (Spring 017) Before the exam: Do not write anything on this page. Do not open the exam. Turn off your cell phone. Make sure your books, notes, and electronics are not visible during
Minima, Maxima, Saddle points
 Minima, Maxima, Saddle points Levent Kandiller Industrial Engineering Department Çankaya University, Turkey Minima, Maxima, Saddle points p./9 Scalar Functions Let us remember the properties for maxima,
Minima, Maxima, Saddle points Levent Kandiller Industrial Engineering Department Çankaya University, Turkey Minima, Maxima, Saddle points p./9 Scalar Functions Let us remember the properties for maxima,
Absolute extrema of two variables functions
 Absolute extrema of two variables functions Apellidos, Nombre: Departamento: Centro: Alicia Herrero Debón aherrero@mat.upv.es) Departamento de Matemática Aplicada Instituto de Matemática Multidisciplnar
Absolute extrema of two variables functions Apellidos, Nombre: Departamento: Centro: Alicia Herrero Debón aherrero@mat.upv.es) Departamento de Matemática Aplicada Instituto de Matemática Multidisciplnar
MATH Lagrange multipliers in 3 variables Fall 2016
 MATH 20550 Lagrange multipliers in 3 variables Fall 2016 1. The one constraint they The problem is to find the extrema of a function f(x, y, z) subject to the constraint g(x, y, z) = c. The book gives
MATH 20550 Lagrange multipliers in 3 variables Fall 2016 1. The one constraint they The problem is to find the extrema of a function f(x, y, z) subject to the constraint g(x, y, z) = c. The book gives
Optimizations and Lagrange Multiplier Method
 Introduction Applications Goal and Objectives Reflection Questions Once an objective of any real world application is well specified as a function of its control variables, which may subject to a certain
Introduction Applications Goal and Objectives Reflection Questions Once an objective of any real world application is well specified as a function of its control variables, which may subject to a certain
x 6 + λ 2 x 6 = for the curve y = 1 2 x3 gives f(1, 1 2 ) = λ actually has another solution besides λ = 1 2 = However, the equation λ
 Math 0 Prelim I Solutions Spring 010 1. Let f(x, y) = x3 y for (x, y) (0, 0). x 6 + y (4 pts) (a) Show that the cubic curves y = x 3 are level curves of the function f. Solution. Substituting y = x 3 in
Math 0 Prelim I Solutions Spring 010 1. Let f(x, y) = x3 y for (x, y) (0, 0). x 6 + y (4 pts) (a) Show that the cubic curves y = x 3 are level curves of the function f. Solution. Substituting y = x 3 in
Shiqian Ma, MAT-258A: Numerical Optimization 1. Chapter 2. Convex Optimization
 Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 2 Convex Optimization Shiqian Ma, MAT-258A: Numerical Optimization 2 2.1. Convex Optimization General optimization problem: min f 0 (x) s.t., f i
Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 2 Convex Optimization Shiqian Ma, MAT-258A: Numerical Optimization 2 2.1. Convex Optimization General optimization problem: min f 0 (x) s.t., f i
Convexity and Optimization
 Convexity and Optimization Richard Lusby Department of Management Engineering Technical University of Denmark Today s Material Extrema Convex Function Convex Sets Other Convexity Concepts Unconstrained
Convexity and Optimization Richard Lusby Department of Management Engineering Technical University of Denmark Today s Material Extrema Convex Function Convex Sets Other Convexity Concepts Unconstrained
Lagrange multipliers. Contents. Introduction. From Wikipedia, the free encyclopedia
 Lagrange multipliers From Wikipedia, the free encyclopedia In mathematical optimization problems, Lagrange multipliers, named after Joseph Louis Lagrange, is a method for finding the local extrema of a
Lagrange multipliers From Wikipedia, the free encyclopedia In mathematical optimization problems, Lagrange multipliers, named after Joseph Louis Lagrange, is a method for finding the local extrema of a
Introduction to Constrained Optimization
 Introduction to Constrained Optimization Duality and KKT Conditions Pratik Shah {pratik.shah [at] lnmiit.ac.in} The LNM Institute of Information Technology www.lnmiit.ac.in February 13, 2013 LNMIIT MLPR
Introduction to Constrained Optimization Duality and KKT Conditions Pratik Shah {pratik.shah [at] lnmiit.ac.in} The LNM Institute of Information Technology www.lnmiit.ac.in February 13, 2013 LNMIIT MLPR
Instructions and information
 Instructions and information. Check that this paper has a total of 5 pages including the cover page.. This is a closed book exam. Calculators and electronic devices are not allowed. Notes and dictionaries
Instructions and information. Check that this paper has a total of 5 pages including the cover page.. This is a closed book exam. Calculators and electronic devices are not allowed. Notes and dictionaries
Computational Methods. Constrained Optimization
 Computational Methods Constrained Optimization Manfred Huber 2010 1 Constrained Optimization Unconstrained Optimization finds a minimum of a function under the assumption that the parameters can take on
Computational Methods Constrained Optimization Manfred Huber 2010 1 Constrained Optimization Unconstrained Optimization finds a minimum of a function under the assumption that the parameters can take on
Chapter 3 Numerical Methods
 Chapter 3 Numerical Methods Part 1 3.1 Linearization and Optimization of Functions of Vectors 1 Problem Notation 2 Outline 3.1.1 Linearization 3.1.2 Optimization of Objective Functions 3.1.3 Constrained
Chapter 3 Numerical Methods Part 1 3.1 Linearization and Optimization of Functions of Vectors 1 Problem Notation 2 Outline 3.1.1 Linearization 3.1.2 Optimization of Objective Functions 3.1.3 Constrained
Convexity and Optimization
 Convexity and Optimization Richard Lusby DTU Management Engineering Class Exercises From Last Time 2 DTU Management Engineering 42111: Static and Dynamic Optimization (3) 18/09/2017 Today s Material Extrema
Convexity and Optimization Richard Lusby DTU Management Engineering Class Exercises From Last Time 2 DTU Management Engineering 42111: Static and Dynamic Optimization (3) 18/09/2017 Today s Material Extrema
Lecture 2 September 3
 EE 381V: Large Scale Optimization Fall 2012 Lecture 2 September 3 Lecturer: Caramanis & Sanghavi Scribe: Hongbo Si, Qiaoyang Ye 2.1 Overview of the last Lecture The focus of the last lecture was to give
EE 381V: Large Scale Optimization Fall 2012 Lecture 2 September 3 Lecturer: Caramanis & Sanghavi Scribe: Hongbo Si, Qiaoyang Ye 2.1 Overview of the last Lecture The focus of the last lecture was to give
Applied Lagrange Duality for Constrained Optimization
 Applied Lagrange Duality for Constrained Optimization Robert M. Freund February 10, 2004 c 2004 Massachusetts Institute of Technology. 1 1 Overview The Practical Importance of Duality Review of Convexity
Applied Lagrange Duality for Constrained Optimization Robert M. Freund February 10, 2004 c 2004 Massachusetts Institute of Technology. 1 1 Overview The Practical Importance of Duality Review of Convexity
minimize ½(x 1 + 2x 2 + x 32 ) subject to x 1 + x 2 + x 3 = 5
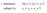 minimize ½(x 1 2 + 2x 2 2 + x 32 ) subject to x 1 + x 2 + x 3 = 5 In this Chapter We will study a new theory for constrained optimization Local optimality condition Easier to implement Deeper insights
minimize ½(x 1 2 + 2x 2 2 + x 32 ) subject to x 1 + x 2 + x 3 = 5 In this Chapter We will study a new theory for constrained optimization Local optimality condition Easier to implement Deeper insights
30. Constrained Optimization
 30. Constrained Optimization The graph of z = f(x, y) is represented by a surface in R 3. Normally, x and y are chosen independently of one another so that one may roam over the entire surface of f (within
30. Constrained Optimization The graph of z = f(x, y) is represented by a surface in R 3. Normally, x and y are chosen independently of one another so that one may roam over the entire surface of f (within
Solution 2. ((3)(1) (2)(1), (4 3), (4)(2) (3)(3)) = (1, 1, 1) D u (f) = (6x + 2yz, 2y + 2xz, 2xy) (0,1,1) = = 4 14
 Vector and Multivariable Calculus L Marizza A Bailey Practice Trimester Final Exam Name: Problem 1. To prepare for true/false and multiple choice: Compute the following (a) (4, 3) ( 3, 2) Solution 1. (4)(
Vector and Multivariable Calculus L Marizza A Bailey Practice Trimester Final Exam Name: Problem 1. To prepare for true/false and multiple choice: Compute the following (a) (4, 3) ( 3, 2) Solution 1. (4)(
MATHEMATICS II: COLLECTION OF EXERCISES AND PROBLEMS
 MATHEMATICS II: COLLECTION OF EXERCISES AND PROBLEMS GRADO EN A.D.E. GRADO EN ECONOMÍA GRADO EN F.Y.C. ACADEMIC YEAR 2011-12 INDEX UNIT 1.- AN INTRODUCCTION TO OPTIMIZATION 2 UNIT 2.- NONLINEAR PROGRAMMING
MATHEMATICS II: COLLECTION OF EXERCISES AND PROBLEMS GRADO EN A.D.E. GRADO EN ECONOMÍA GRADO EN F.Y.C. ACADEMIC YEAR 2011-12 INDEX UNIT 1.- AN INTRODUCCTION TO OPTIMIZATION 2 UNIT 2.- NONLINEAR PROGRAMMING
Worksheet 2.7: Critical Points, Local Extrema, and the Second Derivative Test
 Boise State Math 275 (Ultman) Worksheet 2.7: Critical Points, Local Extrema, and the Second Derivative Test From the Toolbox (what you need from previous classes) Algebra: Solving systems of two equations
Boise State Math 275 (Ultman) Worksheet 2.7: Critical Points, Local Extrema, and the Second Derivative Test From the Toolbox (what you need from previous classes) Algebra: Solving systems of two equations
Optimization problems with constraints - the method of Lagrange multipliers
 Monday, October 12 was Thanksgiving Holiday Lecture 13 Optimization problems with constraints - the method of Lagrange multipliers (Relevant section from the textbook by Stewart: 14.8) In Lecture 11, we
Monday, October 12 was Thanksgiving Holiday Lecture 13 Optimization problems with constraints - the method of Lagrange multipliers (Relevant section from the textbook by Stewart: 14.8) In Lecture 11, we
Introduction to optimization
 Introduction to optimization G. Ferrari Trecate Dipartimento di Ingegneria Industriale e dell Informazione Università degli Studi di Pavia Industrial Automation Ferrari Trecate (DIS) Optimization Industrial
Introduction to optimization G. Ferrari Trecate Dipartimento di Ingegneria Industriale e dell Informazione Università degli Studi di Pavia Industrial Automation Ferrari Trecate (DIS) Optimization Industrial
Lecture 25 Nonlinear Programming. November 9, 2009
 Nonlinear Programming November 9, 2009 Outline Nonlinear Programming Another example of NLP problem What makes these problems complex Scalar Function Unconstrained Problem Local and global optima: definition,
Nonlinear Programming November 9, 2009 Outline Nonlinear Programming Another example of NLP problem What makes these problems complex Scalar Function Unconstrained Problem Local and global optima: definition,
1. Suppose that the equation F (x, y, z) = 0 implicitly defines each of the three variables x, y, and z as functions of the other two:
 Final Solutions. Suppose that the equation F (x, y, z) implicitly defines each of the three variables x, y, and z as functions of the other two: z f(x, y), y g(x, z), x h(y, z). If F is differentiable
Final Solutions. Suppose that the equation F (x, y, z) implicitly defines each of the three variables x, y, and z as functions of the other two: z f(x, y), y g(x, z), x h(y, z). If F is differentiable
8(x 2) + 21(y 1) + 6(z 3) = 0 8x + 21y + 6z = 55.
 MATH 24 -Review for Final Exam. Let f(x, y, z) x 2 yz + y 3 z x 2 + z, and a (2,, 3). Note: f (2xyz 2x, x 2 z + 3y 2 z, x 2 y + y 3 + ) f(a) (8, 2, 6) (a) Find all stationary points (if any) of f. et f.
MATH 24 -Review for Final Exam. Let f(x, y, z) x 2 yz + y 3 z x 2 + z, and a (2,, 3). Note: f (2xyz 2x, x 2 z + 3y 2 z, x 2 y + y 3 + ) f(a) (8, 2, 6) (a) Find all stationary points (if any) of f. et f.
Department of Mathematics Oleg Burdakov of 30 October Consider the following linear programming problem (LP):
 Linköping University Optimization TAOP3(0) Department of Mathematics Examination Oleg Burdakov of 30 October 03 Assignment Consider the following linear programming problem (LP): max z = x + x s.t. x x
Linköping University Optimization TAOP3(0) Department of Mathematics Examination Oleg Burdakov of 30 October 03 Assignment Consider the following linear programming problem (LP): max z = x + x s.t. x x
22. LECTURE 22. I can define critical points. I know the difference between local and absolute minimums/maximums.
 . LECTURE Objectives I can define critical points. I know the difference between local and absolute minimums/maximums. In many physical problems, we re interested in finding the values (x, y) that maximize
. LECTURE Objectives I can define critical points. I know the difference between local and absolute minimums/maximums. In many physical problems, we re interested in finding the values (x, y) that maximize
302 CHAPTER 3. FUNCTIONS OF SEVERAL VARIABLES. 4. Function of several variables, their domain. 6. Limit of a function of several variables
 302 CHAPTER 3. FUNCTIONS OF SEVERAL VARIABLES 3.8 Chapter Review 3.8.1 Concepts to Know You should have an understanding of, and be able to explain the concepts listed below. 1. Boundary and interior points
302 CHAPTER 3. FUNCTIONS OF SEVERAL VARIABLES 3.8 Chapter Review 3.8.1 Concepts to Know You should have an understanding of, and be able to explain the concepts listed below. 1. Boundary and interior points
Linear Programming. Larry Blume. Cornell University & The Santa Fe Institute & IHS
 Linear Programming Larry Blume Cornell University & The Santa Fe Institute & IHS Linear Programs The general linear program is a constrained optimization problem where objectives and constraints are all
Linear Programming Larry Blume Cornell University & The Santa Fe Institute & IHS Linear Programs The general linear program is a constrained optimization problem where objectives and constraints are all
A small review, Second Midterm, Calculus 3, Prof. Montero 3450: , Fall 2008
 A small review, Second Midterm, Calculus, Prof. Montero 45:-4, Fall 8 Maxima and minima Let us recall first, that for a function f(x, y), the gradient is the vector ( f)(x, y) = ( ) f f (x, y); (x, y).
A small review, Second Midterm, Calculus, Prof. Montero 45:-4, Fall 8 Maxima and minima Let us recall first, that for a function f(x, y), the gradient is the vector ( f)(x, y) = ( ) f f (x, y); (x, y).
Multivariate Calculus Review Problems for Examination Two
 Multivariate Calculus Review Problems for Examination Two Note: Exam Two is on Thursday, February 28, class time. The coverage is multivariate differential calculus and double integration: sections 13.3,
Multivariate Calculus Review Problems for Examination Two Note: Exam Two is on Thursday, February 28, class time. The coverage is multivariate differential calculus and double integration: sections 13.3,
LECTURE 13: SOLUTION METHODS FOR CONSTRAINED OPTIMIZATION. 1. Primal approach 2. Penalty and barrier methods 3. Dual approach 4. Primal-dual approach
 LECTURE 13: SOLUTION METHODS FOR CONSTRAINED OPTIMIZATION 1. Primal approach 2. Penalty and barrier methods 3. Dual approach 4. Primal-dual approach Basic approaches I. Primal Approach - Feasible Direction
LECTURE 13: SOLUTION METHODS FOR CONSTRAINED OPTIMIZATION 1. Primal approach 2. Penalty and barrier methods 3. Dual approach 4. Primal-dual approach Basic approaches I. Primal Approach - Feasible Direction
Chapter 5 Partial Differentiation
 Chapter 5 Partial Differentiation For functions of one variable, y = f (x), the rate of change of the dependent variable can dy be found unambiguously by differentiation: f x. In this chapter we explore
Chapter 5 Partial Differentiation For functions of one variable, y = f (x), the rate of change of the dependent variable can dy be found unambiguously by differentiation: f x. In this chapter we explore
Chapter 15 Introduction to Linear Programming
 Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Lagrange Multipliers. Joseph Louis Lagrange was born in Turin, Italy in Beginning
 Andrew Roberts 5/4/2017 Honors Contract Lagrange Multipliers Joseph Louis Lagrange was born in Turin, Italy in 1736. Beginning at age 16, Lagrange studied mathematics and was hired as a professor by age
Andrew Roberts 5/4/2017 Honors Contract Lagrange Multipliers Joseph Louis Lagrange was born in Turin, Italy in 1736. Beginning at age 16, Lagrange studied mathematics and was hired as a professor by age
EXTRA-CREDIT PROBLEMS ON SURFACES, MULTIVARIABLE FUNCTIONS AND PARTIAL DERIVATIVES
 EXTRA-CREDIT PROBLEMS ON SURFACES, MULTIVARIABLE FUNCTIONS AND PARTIAL DERIVATIVES A. HAVENS These problems are for extra-credit, which is counted against lost points on quizzes or WebAssign. You do not
EXTRA-CREDIT PROBLEMS ON SURFACES, MULTIVARIABLE FUNCTIONS AND PARTIAL DERIVATIVES A. HAVENS These problems are for extra-credit, which is counted against lost points on quizzes or WebAssign. You do not
CS231A. Review for Problem Set 1. Saumitro Dasgupta
 CS231A Review for Problem Set 1 Saumitro Dasgupta On today's menu Camera Model Rotation Matrices Homogeneous Coordinates Vanishing Points Matrix Calculus Constrained Optimization Camera Calibration Demo
CS231A Review for Problem Set 1 Saumitro Dasgupta On today's menu Camera Model Rotation Matrices Homogeneous Coordinates Vanishing Points Matrix Calculus Constrained Optimization Camera Calibration Demo
Inverse and Implicit functions
 CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
Advanced Operations Research Techniques IE316. Quiz 1 Review. Dr. Ted Ralphs
 Advanced Operations Research Techniques IE316 Quiz 1 Review Dr. Ted Ralphs IE316 Quiz 1 Review 1 Reading for The Quiz Material covered in detail in lecture. 1.1, 1.4, 2.1-2.6, 3.1-3.3, 3.5 Background material
Advanced Operations Research Techniques IE316 Quiz 1 Review Dr. Ted Ralphs IE316 Quiz 1 Review 1 Reading for The Quiz Material covered in detail in lecture. 1.1, 1.4, 2.1-2.6, 3.1-3.3, 3.5 Background material
Introduction to Machine Learning
 Introduction to Machine Learning Maximum Margin Methods Varun Chandola Computer Science & Engineering State University of New York at Buffalo Buffalo, NY, USA chandola@buffalo.edu Chandola@UB CSE 474/574
Introduction to Machine Learning Maximum Margin Methods Varun Chandola Computer Science & Engineering State University of New York at Buffalo Buffalo, NY, USA chandola@buffalo.edu Chandola@UB CSE 474/574
California Institute of Technology Crash-Course on Convex Optimization Fall Ec 133 Guilherme Freitas
 California Institute of Technology HSS Division Crash-Course on Convex Optimization Fall 2011-12 Ec 133 Guilherme Freitas In this text, we will study the following basic problem: maximize x C f(x) subject
California Institute of Technology HSS Division Crash-Course on Convex Optimization Fall 2011-12 Ec 133 Guilherme Freitas In this text, we will study the following basic problem: maximize x C f(x) subject
REVIEW I MATH 254 Calculus IV. Exam I (Friday, April 29) will cover sections
 REVIEW I MATH 254 Calculus IV Exam I (Friday, April 29 will cover sections 14.1-8. 1. Functions of multivariables The definition of multivariable functions is similar to that of functions of one variable.
REVIEW I MATH 254 Calculus IV Exam I (Friday, April 29 will cover sections 14.1-8. 1. Functions of multivariables The definition of multivariable functions is similar to that of functions of one variable.
2 Second Derivatives. As we have seen, a function f (x, y) of two variables has four different partial derivatives: f xx. f yx. f x y.
 2 Second Derivatives As we have seen, a function f (x, y) of two variables has four different partial derivatives: (x, y), (x, y), f yx (x, y), (x, y) It is convenient to gather all four of these into
2 Second Derivatives As we have seen, a function f (x, y) of two variables has four different partial derivatives: (x, y), (x, y), f yx (x, y), (x, y) It is convenient to gather all four of these into
Paul's Online Math Notes Calculus III (Notes) / Applications of Partial Derivatives / Lagrange Multipliers Problems][Assignment Problems]
![Paul's Online Math Notes Calculus III (Notes) / Applications of Partial Derivatives / Lagrange Multipliers Problems][Assignment Problems] Paul's Online Math Notes Calculus III (Notes) / Applications of Partial Derivatives / Lagrange Multipliers Problems][Assignment Problems]](/thumbs/77/75726948.jpg) 1 of 9 25/04/2016 13:15 Paul's Online Math Notes Calculus III (Notes) / Applications of Partial Derivatives / Lagrange Multipliers Problems][Assignment Problems] [Notes] [Practice Calculus III - Notes
1 of 9 25/04/2016 13:15 Paul's Online Math Notes Calculus III (Notes) / Applications of Partial Derivatives / Lagrange Multipliers Problems][Assignment Problems] [Notes] [Practice Calculus III - Notes
Chapter II. Linear Programming
 1 Chapter II Linear Programming 1. Introduction 2. Simplex Method 3. Duality Theory 4. Optimality Conditions 5. Applications (QP & SLP) 6. Sensitivity Analysis 7. Interior Point Methods 1 INTRODUCTION
1 Chapter II Linear Programming 1. Introduction 2. Simplex Method 3. Duality Theory 4. Optimality Conditions 5. Applications (QP & SLP) 6. Sensitivity Analysis 7. Interior Point Methods 1 INTRODUCTION
Optimization III: Constrained Optimization
 Optimization III: Constrained Optimization CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Doug James (and Justin Solomon) CS 205A: Mathematical Methods Optimization III: Constrained Optimization
Optimization III: Constrained Optimization CS 205A: Mathematical Methods for Robotics, Vision, and Graphics Doug James (and Justin Solomon) CS 205A: Mathematical Methods Optimization III: Constrained Optimization
16.410/413 Principles of Autonomy and Decision Making
 16.410/413 Principles of Autonomy and Decision Making Lecture 17: The Simplex Method Emilio Frazzoli Aeronautics and Astronautics Massachusetts Institute of Technology November 10, 2010 Frazzoli (MIT)
16.410/413 Principles of Autonomy and Decision Making Lecture 17: The Simplex Method Emilio Frazzoli Aeronautics and Astronautics Massachusetts Institute of Technology November 10, 2010 Frazzoli (MIT)
Tangent Planes/Critical Points
 Tangent Planes/Critical Points Christopher Croke University of Pennsylvania Math 115 UPenn, Fall 2011 Problem: Find the tangent line to the curve of intersection of the surfaces xyz = 1 and x 2 + 2y 2
Tangent Planes/Critical Points Christopher Croke University of Pennsylvania Math 115 UPenn, Fall 2011 Problem: Find the tangent line to the curve of intersection of the surfaces xyz = 1 and x 2 + 2y 2
Introduction to Functions of Several Variables
 Introduction to Functions of Several Variables Philippe B. Laval KSU Today Philippe B. Laval (KSU) Functions of Several Variables Today 1 / 20 Introduction In this section, we extend the definition of
Introduction to Functions of Several Variables Philippe B. Laval KSU Today Philippe B. Laval (KSU) Functions of Several Variables Today 1 / 20 Introduction In this section, we extend the definition of
NOTATION AND TERMINOLOGY
 15.053x, Optimization Methods in Business Analytics Fall, 2016 October 4, 2016 A glossary of notation and terms used in 15.053x Weeks 1, 2, 3, 4 and 5. (The most recent week's terms are in blue). NOTATION
15.053x, Optimization Methods in Business Analytics Fall, 2016 October 4, 2016 A glossary of notation and terms used in 15.053x Weeks 1, 2, 3, 4 and 5. (The most recent week's terms are in blue). NOTATION
Winter 2012 Math 255 Section 006. Problem Set 7
 Problem Set 7 1 a) Carry out the partials with respect to t and x, substitute and check b) Use separation of varibles, i.e. write as dx/x 2 = dt, integrate both sides and observe that the solution also
Problem Set 7 1 a) Carry out the partials with respect to t and x, substitute and check b) Use separation of varibles, i.e. write as dx/x 2 = dt, integrate both sides and observe that the solution also
Linear methods for supervised learning
 Linear methods for supervised learning LDA Logistic regression Naïve Bayes PLA Maximum margin hyperplanes Soft-margin hyperplanes Least squares resgression Ridge regression Nonlinear feature maps Sometimes
Linear methods for supervised learning LDA Logistic regression Naïve Bayes PLA Maximum margin hyperplanes Soft-margin hyperplanes Least squares resgression Ridge regression Nonlinear feature maps Sometimes
Convexity Theory and Gradient Methods
 Convexity Theory and Gradient Methods Angelia Nedić angelia@illinois.edu ISE Department and Coordinated Science Laboratory University of Illinois at Urbana-Champaign Outline Convex Functions Optimality
Convexity Theory and Gradient Methods Angelia Nedić angelia@illinois.edu ISE Department and Coordinated Science Laboratory University of Illinois at Urbana-Champaign Outline Convex Functions Optimality
MEI Desmos Tasks for AS Pure
 Task 1: Coordinate Geometry Intersection of a line and a curve 1. Add a quadratic curve, e.g. y = x² 4x + 1 2. Add a line, e.g. y = x 3 3. Select the points of intersection of the line and the curve. What
Task 1: Coordinate Geometry Intersection of a line and a curve 1. Add a quadratic curve, e.g. y = x² 4x + 1 2. Add a line, e.g. y = x 3 3. Select the points of intersection of the line and the curve. What
R f da (where da denotes the differential of area dxdy (or dydx)
 Math 28H Topics for the second exam (Technically, everything covered on the first exam, plus) Constrained Optimization: Lagrange Multipliers Most optimization problems that arise naturally are not unconstrained;
Math 28H Topics for the second exam (Technically, everything covered on the first exam, plus) Constrained Optimization: Lagrange Multipliers Most optimization problems that arise naturally are not unconstrained;
Functions of Several Variables
 Chapter 3 Functions of Several Variables 3.1 Definitions and Examples of Functions of two or More Variables In this section, we extend the definition of a function of one variable to functions of two or
Chapter 3 Functions of Several Variables 3.1 Definitions and Examples of Functions of two or More Variables In this section, we extend the definition of a function of one variable to functions of two or
Solutions to assignment 3
 Math 9 Solutions to assignment Due: : Noon on Thursday, October, 5.. Find the minimum of the function f, y, z) + y + z subject to the condition + y + z 4. Solution. Let s define g, y, z) + y + z, so the
Math 9 Solutions to assignment Due: : Noon on Thursday, October, 5.. Find the minimum of the function f, y, z) + y + z subject to the condition + y + z 4. Solution. Let s define g, y, z) + y + z, so the
