10.2 AVL Trees. Definition of an AVL Tree. 438 Chapter 10. Search Trees
|
|
|
- Sandra Golden
- 5 years ago
- Views:
Transcription
1 438 Chapter 10. Search Trees 10. AVL Trees In theprevioussection,wediscussedwhatshouldbeanefficientmapdatastructure, but the worst-case performance it achieves for the various operations is linear time, which is no better than the performance of list- and array-based map implementations (such as the unordered lists and search tables discussed in Chapter 9). In this section, we describe a simple way of correcting this problem in order to achieve logarithmic time for all the fundamental map operations. Definition of an AVL Tree The simple correction is to add a rule to the binary search tree definition that maintains a logarithmic height for the tree. The rule we consider in this section is the following height-balance property, which characterizes the structure of a binary search tree T in terms of the heights of its internal nodes (recall from Section 7..1 that the height of a node v in a tree is the length of the longest path from v to an external node): Height-Balance Property: For every internal node v of T, the heights of the children of v differ by at most 1. Any binary search tree T that satisfies the height-balance property is said to be an AVL tree,namedaftertheinitialsofitsinventors,adel son-vel skiiandlandis. An example of an AVL tree is shown in Figure Figure 10.8: An exampleofanavltree.thekeysoftheentriesareshowninside the nodes, and the heights of the nodes are shown next to the nodes. An immediate consequence of the height-balance property is that a subtree of an AVL tree is itself an AVL tree. The height-balance property has also the important consequence of keeping the height small, as shown in the following proposition.
2 10.. AVL Trees 439 Proposition 10.: The height of an AVL tree storing n entries is O(log n). Justification: Instead of trying to find an upper bound on the height of an AVL tree directly, it turns out to be easier to work on the inverse problem of finding a lower bound on the minimum number of internal nodes n(h) of an AVL tree with height h. Weshowthatn(h) grows at least exponentially. From this, it is an easy step to derive that the height of an AVL tree storing n entries is O(logn). To start with, notice that n(1)=1andn()=, because an AVL tree of height 1musthaveatleastoneinternalnodeandanAVLtreeofheightmusthaveatleast two internal nodes. Now, for h 3, an AVL tree with height h and the minimum number of nodes is such that both its subtrees are AVL trees with the minimum number of nodes: one with height h 1andtheotherwithheighth. Taking the root into account, we obtain the following formula that relates n(h) to n(h 1) and n(h ), forh 3: n(h)=1 + n(h 1)+n(h ). (10.1) At this point, the reader familiar with the properties of Fibonacci progressions (Section..3 and Exercise C-4.17) already sees that n(h) is a function exponential in h. For the rest of the readers, we will proceed with our reasoning. Formula 10.1 implies that n(h) is a strictly increasing function of h. Thus,we know that n(h 1) > n(h ). Replacingn(h 1) with n(h ) in Formula 10.1 and dropping the 1, we get, for h 3, n(h) > n(h ). (10.) Formula 10. indicates that n(h) at least doubles each time h increases by, which intuitively means that n(h) grows exponentially. To show this fact in a formal way, we apply Formula 10. repeatedly, yielding the following series of inequalities: n(h) > n(h ) > 4 n(h 4) > 8 n(h 6). > i n(h i). (10.3) That is, n(h) > i n(h i),foranyintegeri, such that h i 1. Since we already know the values of n(1) and n(), wepicki so that h i is equal to either 1 or. That is, we pick h i = 1.
3 440 Chapter 10. Search Trees By substituting the above value of i in formula 10.3, we obtain, for h 3, ( ) n(h) > h h 1 n h + h 1 n(1) h 1. (10.4) By taking logarithms of both sides of formula 10.4, we obtain from which we get logn(h) > h 1, h < logn(h)+, (10.5) which implies that an AVL tree storing n entries has height at most log n+. By Proposition 10. and the analysis of binary search trees given in Section 10.1, the operation find, in a map implemented with an AVL tree,runs in time O(log n), where n is the number of entries in the map. Of course, we still have to show how to maintain the height-balance property after an insertion or removal Update Operations The insertion and removal operations for AVL trees are similar to those for binary search trees, but with AVL trees we must perform additional computations. Insertion An insertion in an AVL tree T begins as in an insert operation described in Section for a (simple) binary search tree. Recall that this operation always inserts the new entry at a node w in T that was previously an external node, and it makes w become an internal node with operation insertatexternal. Thatis, it adds two external node children to w. Thisactionmayviolatetheheight-balance property, however, for some nodes increase their heights by one. In particular, node w, andpossiblysomeofitsancestors,increasetheirheightsbyone.therefore,let us describe how to restructure T to restore its height balance. Given a binary search tree T,wesaythataninternalnodev of T is balanced if the absolute value of the difference between the heights of the children of v is at most 1, and we say that it is unbalanced otherwise. Thus, the height-balance property characterizing AVL trees is equivalent to saying that every internal node is balanced. Suppose that T satisfies the height-balance property, and hence is an AVL tree, prior to our inserting the new entry. As we have mentioned, after performing the
4 10.. AVL Trees 441 operation insertatexternal on T,the heights of some nodes of T,including w, increase. All such nodes are on the path of T from w to the root of T,andtheseare the only nodes of T that may have just become unbalanced. (See Figure 10.9(a).) Of course, if this happens, then T is no longer an AVL tree; hence, we need a mechanism to fix the unbalance that we have just caused. Figure 10.9: An exampleinsertionofanentrywithkey54intheavltreeof Figure 10.8: (a) after adding a new node for key 54, the nodes storing keys 78 and 44 become unbalanced; (b) a trinode restructuring restores the height-balance property. We show the heights of nodes next to them, and we identify the nodes x, y, andz participating in the trinode restructuring. We restore the balance of the nodes in the binary search tree T by a simple search-and-repair strategy. In particular, let z be the first node we encounter in going up from w toward the root of T such that z is unbalanced. (See Figure 10.9(a).) Also, let y denote the child of z with higher height (and note that node y must be an ancestor of w). Finally, let x be the child of y with higher height (there cannot be a tie and node x must be an ancestor of w). Also, node x is a grandchild of z and could be equal to w. Sincez became unbalanced because of an insertion in the subtree rooted at its child y, theheightofy is greater than its sibling. We now rebalance the subtree rooted at z by calling the trinode restructuring function, restructure(x), givenincodefragment10.1andillustratedinfigures 10.9 and A trinode restructuring temporarily renames the nodes x, y, and z as a, b, andc, sothata precedes b and b precedes c in an inorder traversal of T.Therearefourpossiblewaysofmappingx, y, andz to a, b, andc, asshown in Figure 10.10, which are unified into one case by our relabeling. The trinode restructuring then replaces z withthe node called b,makesthe children ofthis node be a and c, andmakesthechildrenofa and c be the four previous children of x, y, andz (other than x and y) whilemaintainingtheinorderrelationshipsofallthe nodes in T.
5 44 Chapter 10. Search Trees Algorithm restructure(x): Input: A node x of a binary search tree T that has both a parent y and a grandparent z Output: Tree T after a trinode restructuring (which corresponds to a single or double rotation) involving nodes x, y, and z 1: Let (a,b,c) be aleft-to-right(inorder)listingofthenodesx, y, andz, andlet (T 0,T 1,T,T 3 ) be a left-to-right (inorder) listing of the four subtrees of x, y, and z not rooted at x, y, orz. : Replace the subtree rooted at z with a new subtree rooted at b. 3: Let a be the left child of b and let T 0 and T 1 be the left and right subtrees of a, respectively. 4: Let c be the right child of b and let T and T 3 be the left and right subtrees of c, respectively. Code Fragment 10.1: The trinode restructuring operation in a binary search tree. The modification of a tree T caused by a trinode restructuring operation is often called a rotation,because of the geometric way wecan visualize the way it changes T.Ifb = y, thetrinoderestructuringmethodiscalledasingle rotation, foritcan be visualized as rotating y over z. (See Figure 10.10(a) and (b).) Otherwise, if b = x, the trinode restructuring operation is called a double rotation, for it can be visualized as first rotating x over y and then over z. (See Figure 10.10(c) and (d), and Figure 10.9.) Some computer researchers treat these two kinds of rotations as separate methods, each with two symmetric types. We have chosen, however, to unify these four types of rotations into a single trinode restructuring operation. No matter how we view it, though, the trinode restructuring method modifies parent-child relationships of O(1) nodes in T,whilepreservingtheinorder traversal ordering of all the nodes in T. In addition to its order-preserving property, a trinode restructuring changes the heights of several nodes in T,soastorestorebalance. Recallthatweexecutethe function restructure(x) because z, the grandparent of x, is unbalanced. Moreover, this unbalance is due to one of the children of x now having too large a height relative to the height of z s other child. As a result of a rotation, we move up the tall child of x while pushing down the short child of z. Thus,afterperforming restructure(x), allthenodesinthesubtreenowrootedatthenodewecalledb are balanced. (See Figure ) Thus, we restore the height-balance property locally at the nodes x, y, andz. Inaddition,sinceafterperformingthenewentryinsertion the subtree rooted at b replaces the one formerly rooted at z,whichwastallerbyone unit, all the ancestors of z that were formerly unbalanced become balanced. (See Figure 10.9.) (The justification of this fact is left as Exercise C ) Therefore, this one restructuring also restores the height-balance property globally.
6 10.. AVL Trees 443 (a) (b) (c) (d) Figure 10.10: Schematic illustration of a trinode restructuring operation (Code Fragment 10.1): (a) and (b) a single rotation; (c) and (d) a double rotation.
7 444 Chapter 10. Search Trees Removal As was the case for the insert map operation, we begin the implementation of the erase map operation on an AVL tree T by using the algorithm for performing this operation on a regular binary search tree. The added difficulty in using this approach with an AVL tree is that it may violate the height-balance property. In particular, after removing an internal node with operation removeaboveexternal and elevating one of its children into its place, there may be an unbalanced node in T on the path from the parent w of the previously removed node to the root of T. (See Figure 10.11(a).) In fact, there can be one such unbalanced node at most. (The justification of this fact is left as Exercise C ) Figure 10.11: Removal of the entry with key 3 from the AVL tree of Figure 10.8: (a) after removing the node storing key 3, the root becomes unbalanced; (b) a (single) rotation restores the height-balance property. As with insertion, we use trinode restructuring to restore balance in the tree T. In particular, let z be the first unbalanced node encountered going up from w toward the root of T.Also,lety be the child of z with larger height (note that node y is the child of z that is not an ancestor of w), and let x be the child of y defined as follows: if one of the children of y is taller than the other, let x be the taller child of y; else (both children of y have the same height), let x be the child of y on the same side as y (that is, if y is a left child, let x be the left child of y, elseletx be the right child of y). In any case, we then perform a restructure(x) operation, which restores the height-balance property locally, at the subtree that was formerly rooted at z and is now rooted at the node we temporarily called b. (SeeFigure10.11(b).) Unfortunately, this trinode restructuring may reduce the height of the subtree rooted at b by 1, which may cause an ancestor of b to become unbalanced. So, after rebalancing z, wecontinue walking up T looking for unbalanced nodes. If we find another, we perform a restructure operation to restore its balance, and continue marching up T looking for more, all the way to the root. Still, since the height of T is O(logn), wheren is the number of entries, by Proposition 10., O(logn) trinode restructurings are sufficient to restore the height-balance property.
8 Unbalanced Single rotation () Delete Unbalanced 7 Double rotation (15,7) Figure 6: AVL Deletion example.
CHAPTER 10 AVL TREES. 3 8 z 4
 CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
AVL Trees (10.2) AVL Trees
 AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
Chapter. Binary Search Trees. Contents
 Chapter 4 Balanced Binary Search Trees U.S. Navy Blue Angels, performing their delta formation during the Blues on the Bay Air Show at Marine Corps Base Hawaii in 2007. U.S. government photo by Petty Officer
Chapter 4 Balanced Binary Search Trees U.S. Navy Blue Angels, performing their delta formation during the Blues on the Bay Air Show at Marine Corps Base Hawaii in 2007. U.S. government photo by Petty Officer
Chapter 2: Basic Data Structures
 Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees (Ch. 9) > = Binary Search Trees 1
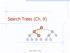 Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Chapter 10: Search Trees
 < 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
< 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
10/23/2013. AVL Trees. Height of an AVL Tree. Height of an AVL Tree. AVL Trees
 // AVL Trees AVL Trees An AVL tree is a binary search tree with a balance condition. AVL is named for its inventors: Adel son-vel skii and Landis AVL tree approximates the ideal tree (completely balanced
// AVL Trees AVL Trees An AVL tree is a binary search tree with a balance condition. AVL is named for its inventors: Adel son-vel skii and Landis AVL tree approximates the ideal tree (completely balanced
AVL Trees Goodrich, Tamassia, Goldwasser AVL Trees 1
 AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
CS350: Data Structures Red-Black Trees
 Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
AVL Tree Definition. An example of an AVL tree where the heights are shown next to the nodes. Adelson-Velsky and Landis
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
AVL Trees / Slide 2. AVL Trees / Slide 4. Let N h be the minimum number of nodes in an AVL tree of height h. AVL Trees / Slide 6
 COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
Part 2: Balanced Trees
 Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
Self-Balancing Search Trees. Chapter 11
 Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
AVL Trees. (AVL Trees) Data Structures and Programming Spring / 17
 AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
Balanced Binary Search Trees
 Balanced Binary Search Trees In the previous section we looked at building a binary search tree. As we learned, the performance of the binary search tree can degrade to O(n) for operations like getand
Balanced Binary Search Trees In the previous section we looked at building a binary search tree. As we learned, the performance of the binary search tree can degrade to O(n) for operations like getand
ECE 242 Data Structures and Algorithms. Trees IV. Lecture 21. Prof.
 ECE 22 Data Structures and Algorithms http://www.ecs.umass.edu/~polizzi/teaching/ece22/ Trees IV Lecture 2 Prof. Eric Polizzi Summary previous lectures Implementations BST 5 5 7 null 8 null null 7 null
ECE 22 Data Structures and Algorithms http://www.ecs.umass.edu/~polizzi/teaching/ece22/ Trees IV Lecture 2 Prof. Eric Polizzi Summary previous lectures Implementations BST 5 5 7 null 8 null null 7 null
COMP171. AVL-Trees (Part 1)
 COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
Search Trees. Chapter 11
 Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
Trees. Reading: Weiss, Chapter 4. Cpt S 223, Fall 2007 Copyright: Washington State University
 Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
Binary Search Trees. Analysis of Algorithms
 Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Data Structures Lesson 7
 Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
Balanced Search Trees. CS 3110 Fall 2010
 Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Binary search trees. We can define a node in a search tree using a Python class definition as follows: class SearchTree:
 Binary search trees An important use of binary trees is to store values that we may want to look up later. For instance, a binary search tree could be used to store a dictionary of words. A binary search
Binary search trees An important use of binary trees is to store values that we may want to look up later. For instance, a binary search tree could be used to store a dictionary of words. A binary search
Lesson 21: AVL Trees. Rotation
 The time required to perform operations on a binary search tree is proportional to the length of the path from root to leaf. This isn t bad in a well-balanced tree. But nothing prevents a tree from becoming
The time required to perform operations on a binary search tree is proportional to the length of the path from root to leaf. This isn t bad in a well-balanced tree. But nothing prevents a tree from becoming
Red-black tree. Background and terminology. Uses and advantages
 Red-black tree A red-black tree is a type of self-balancing binary search tree, a data structure used in computer science, typically used to implement associative arrays. The original structure was invented
Red-black tree A red-black tree is a type of self-balancing binary search tree, a data structure used in computer science, typically used to implement associative arrays. The original structure was invented
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Trees. (Trees) Data Structures and Programming Spring / 28
 Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Analysis of Algorithms
 Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
AVL Trees. Reading: 9.2
 AVL Trees Reading: 9.2 Balance Factor of a Node The difference in height of its two subtrees (h R -h L ) Balanced Node if -1 BF 1 Unbalanced Node if BF 1 h L h R Balance Factor of a Binar Tree Corresponds
AVL Trees Reading: 9.2 Balance Factor of a Node The difference in height of its two subtrees (h R -h L ) Balanced Node if -1 BF 1 Unbalanced Node if BF 1 h L h R Balance Factor of a Binar Tree Corresponds
Algorithms. Deleting from Red-Black Trees B-Trees
 Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
AVL Trees Outline and Required Reading: AVL Trees ( 11.2) CSE 2011, Winter 2017 Instructor: N. Vlajic
 1 AVL Trees Outline and Required Reading: AVL Trees ( 11.2) CSE 2011, Winter 2017 Instructor: N. Vlajic AVL Trees 2 Binary Searc Trees better tan linear dictionaries; owever, te worst case performance
1 AVL Trees Outline and Required Reading: AVL Trees ( 11.2) CSE 2011, Winter 2017 Instructor: N. Vlajic AVL Trees 2 Binary Searc Trees better tan linear dictionaries; owever, te worst case performance
Search Trees. COMPSCI 355 Fall 2016
 Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Search Trees - 2. Venkatanatha Sarma Y. Lecture delivered by: Assistant Professor MSRSAS-Bangalore. M.S Ramaiah School of Advanced Studies - Bangalore
 Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees. Undirected graph Directed graph Tree Binary search tree
 Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Fundamental Algorithms
 WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
9/29/2016. Chapter 4 Trees. Introduction. Terminology. Terminology. Terminology. Terminology
 Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
BRONX COMMUNITY COLLEGE of the City University of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE
 BRONX COMMUNITY COLLEGE of the City University of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI Section E01 AVL Trees AVL Property While BST structures have average performance of Θ(log(n))
BRONX COMMUNITY COLLEGE of the City University of New York DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE CSI Section E01 AVL Trees AVL Property While BST structures have average performance of Θ(log(n))
COSC160: Data Structures Balanced Trees. Jeremy Bolton, PhD Assistant Teaching Professor
 COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
CSCI2100B Data Structures Trees
 CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
CS350: Data Structures AVL Trees
 S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
Balanced Binary Search Trees
 Balanced Binary Search Trees Why is our balance assumption so important? Lets look at what happens if we insert the following numbers in order without rebalancing the tree: 3 5 9 12 18 20 1-45 2010 Pearson
Balanced Binary Search Trees Why is our balance assumption so important? Lets look at what happens if we insert the following numbers in order without rebalancing the tree: 3 5 9 12 18 20 1-45 2010 Pearson
13.4 Deletion in red-black trees
 Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Red-black trees (19.5), B-trees (19.8), trees
 Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
Balanced Binary Search Trees
 Balanced Binary Search Trees Pedro Ribeiro DCC/FCUP 2017/2018 Pedro Ribeiro (DCC/FCUP) Balanced Binary Search Trees 2017/2018 1 / 48 Motivation Let S be a set of comparable objects/items: Let a and b be
Balanced Binary Search Trees Pedro Ribeiro DCC/FCUP 2017/2018 Pedro Ribeiro (DCC/FCUP) Balanced Binary Search Trees 2017/2018 1 / 48 Motivation Let S be a set of comparable objects/items: Let a and b be
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
CS 206 Introduction to Computer Science II
 CS 206 Introduction to Computer Science II 04 / 26 / 2017 Instructor: Michael Eckmann Today s Topics Questions? Comments? Balanced Binary Search trees AVL trees Michael Eckmann - Skidmore College - CS
CS 206 Introduction to Computer Science II 04 / 26 / 2017 Instructor: Michael Eckmann Today s Topics Questions? Comments? Balanced Binary Search trees AVL trees Michael Eckmann - Skidmore College - CS
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
TREES. Trees - Introduction
 TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
Note that this is a rep invariant! The type system doesn t enforce this but you need it to be true. Should use repok to check in debug version.
 Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
Computational Optimization ISE 407. Lecture 16. Dr. Ted Ralphs
 Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
ECE250: Algorithms and Data Structures AVL Trees (Part A)
 ECE250: Algorithms and Data Structures AVL Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
ECE250: Algorithms and Data Structures AVL Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
Binary search trees (chapters )
 Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
Some Search Structures. Balanced Search Trees. Binary Search Trees. A Binary Search Tree. Review Binary Search Trees
 Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
Properties of red-black trees
 Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Data Structures in Java
 Data Structures in Java Lecture 10: AVL Trees. 10/1/015 Daniel Bauer Balanced BSTs Balance condition: Guarantee that the BST is always close to a complete binary tree (every node has exactly two or zero
Data Structures in Java Lecture 10: AVL Trees. 10/1/015 Daniel Bauer Balanced BSTs Balance condition: Guarantee that the BST is always close to a complete binary tree (every node has exactly two or zero
Multiway Search Trees. Multiway-Search Trees (cont d)
 Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
CSE 373 Midterm 2 2/27/06 Sample Solution. Question 1. (6 points) (a) What is the load factor of a hash table? (Give a definition.
 Question 1. (6 points) (a) What is the load factor of a hash table? (Give a definition.) The load factor is number of items in the table / size of the table (number of buckets) (b) What is a reasonable
Question 1. (6 points) (a) What is the load factor of a hash table? (Give a definition.) The load factor is number of items in the table / size of the table (number of buckets) (b) What is a reasonable
Section 5.5. Left subtree The left subtree of a vertex V on a binary tree is the graph formed by the left child L of V, the descendents
 Section 5.5 Binary Tree A binary tree is a rooted tree in which each vertex has at most two children and each child is designated as being a left child or a right child. Thus, in a binary tree, each vertex
Section 5.5 Binary Tree A binary tree is a rooted tree in which each vertex has at most two children and each child is designated as being a left child or a right child. Thus, in a binary tree, each vertex
13.4 Deletion in red-black trees
 The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
On k-dimensional Balanced Binary Trees*
 journal of computer and system sciences 52, 328348 (1996) article no. 0025 On k-dimensional Balanced Binary Trees* Vijay K. Vaishnavi Department of Computer Information Systems, Georgia State University,
journal of computer and system sciences 52, 328348 (1996) article no. 0025 On k-dimensional Balanced Binary Trees* Vijay K. Vaishnavi Department of Computer Information Systems, Georgia State University,
Computer Science 210 Data Structures Siena College Fall Topic Notes: Binary Search Trees
 Computer Science 10 Data Structures Siena College Fall 018 Topic Notes: Binary Search Trees Possibly the most common usage of a binary tree is to store data for quick retrieval. Definition: A binary tree
Computer Science 10 Data Structures Siena College Fall 018 Topic Notes: Binary Search Trees Possibly the most common usage of a binary tree is to store data for quick retrieval. Definition: A binary tree
Trees. A tree is a directed graph with the property
 2: Trees Trees A tree is a directed graph with the property There is one node (the root) from which all other nodes can be reached by exactly one path. Seen lots of examples. Parse Trees Decision Trees
2: Trees Trees A tree is a directed graph with the property There is one node (the root) from which all other nodes can be reached by exactly one path. Seen lots of examples. Parse Trees Decision Trees
Lecture 16 Notes AVL Trees
 Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Spring 2016) Frank Pfenning 1 Introduction Binary search trees are an excellent data structure to implement associative arrays,
Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Spring 2016) Frank Pfenning 1 Introduction Binary search trees are an excellent data structure to implement associative arrays,
Introduction. for large input, even access time may be prohibitive we need data structures that exhibit times closer to O(log N) binary search tree
 Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms
 Department of Informatics, University of Zürich Vertiefungsarbeit Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms Mirko Richter Matrikelnummer: 12-917-175 Email: mirko.richter@uzh.ch
Department of Informatics, University of Zürich Vertiefungsarbeit Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms Mirko Richter Matrikelnummer: 12-917-175 Email: mirko.richter@uzh.ch
Section 4 SOLUTION: AVL Trees & B-Trees
 Section 4 SOLUTION: AVL Trees & B-Trees 1. What 3 properties must an AVL tree have? a. Be a binary tree b. Have Binary Search Tree ordering property (left children < parent, right children > parent) c.
Section 4 SOLUTION: AVL Trees & B-Trees 1. What 3 properties must an AVL tree have? a. Be a binary tree b. Have Binary Search Tree ordering property (left children < parent, right children > parent) c.
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
Lecture 6: Analysis of Algorithms (CS )
 Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
(2,4) Trees Goodrich, Tamassia (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
(2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
Computer Science 210 Data Structures Siena College Fall Topic Notes: Binary Search Trees
 Computer Science 10 Data Structures Siena College Fall 016 Topic Notes: Binary Search Trees Possibly the most common usage of a binary tree is to store data for quick retrieval. Definition: A binary tree
Computer Science 10 Data Structures Siena College Fall 016 Topic Notes: Binary Search Trees Possibly the most common usage of a binary tree is to store data for quick retrieval. Definition: A binary tree
Outline. Definition. 2 Height-Balance. 3 Searches. 4 Rotations. 5 Insertion. 6 Deletions. 7 Reference. 1 Every node is either red or black.
 Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
CE 221 Data Structures and Algorithms
 CE 221 Data Structures and Algorithms Chapter 4: Trees (Binary) Text: Read Weiss, 4.1 4.2 Izmir University of Economics 1 Preliminaries - I (Recursive) Definition: A tree is a collection of nodes. The
CE 221 Data Structures and Algorithms Chapter 4: Trees (Binary) Text: Read Weiss, 4.1 4.2 Izmir University of Economics 1 Preliminaries - I (Recursive) Definition: A tree is a collection of nodes. The
AVL Trees. Version of September 6, AVL Trees Version of September 6, / 22
 VL Trees Version of September 6, 6 VL Trees Version of September 6, 6 / inary Search Trees x 8 4 4 < x > x 7 9 3 inary-search-tree property For every node x ll eys in its left subtree are smaller than
VL Trees Version of September 6, 6 VL Trees Version of September 6, 6 / inary Search Trees x 8 4 4 < x > x 7 9 3 inary-search-tree property For every node x ll eys in its left subtree are smaller than
/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/27/17
 01.433/33 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/2/1.1 Introduction In this lecture we ll talk about a useful abstraction, priority queues, which are
01.433/33 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/2/1.1 Introduction In this lecture we ll talk about a useful abstraction, priority queues, which are
Algorithms in Systems Engineering ISE 172. Lecture 16. Dr. Ted Ralphs
 Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
Recall from Last Time: AVL Trees
 CSE 326 Lecture 8: Getting to now AVL Trees Today s Topics: Balanced Search Trees AVL Trees and Rotations Splay trees Covered in Chapter 4 of the text Recall from Last Time: AVL Trees AVL trees are height-balanced
CSE 326 Lecture 8: Getting to now AVL Trees Today s Topics: Balanced Search Trees AVL Trees and Rotations Splay trees Covered in Chapter 4 of the text Recall from Last Time: AVL Trees AVL trees are height-balanced
Lecture 13: AVL Trees and Binary Heaps
 Data Structures Brett Bernstein Lecture 13: AVL Trees and Binary Heaps Review Exercises 1. ( ) Interview question: Given an array show how to shue it randomly so that any possible reordering is equally
Data Structures Brett Bernstein Lecture 13: AVL Trees and Binary Heaps Review Exercises 1. ( ) Interview question: Given an array show how to shue it randomly so that any possible reordering is equally
LECTURE 18 AVL TREES
 DATA STRUCTURES AND ALGORITHMS LECTURE 18 AVL TREES IMRAN IHSAN ASSISTANT PROFESSOR AIR UNIVERSITY, ISLAMABAD PROTOTYPICAL EXAMPLES These two examples demonstrate how we can correct for imbalances: starting
DATA STRUCTURES AND ALGORITHMS LECTURE 18 AVL TREES IMRAN IHSAN ASSISTANT PROFESSOR AIR UNIVERSITY, ISLAMABAD PROTOTYPICAL EXAMPLES These two examples demonstrate how we can correct for imbalances: starting
Search Structures. Kyungran Kang
 Search Structures Kyungran Kang (korykang@ajou.ac.kr) Ellis Horowitz, Sartaj Sahni and Susan Anderson-Freed, Fundamentals of Data Structures in C, 2nd Edition, Silicon Press, 2007. Contents Binary Search
Search Structures Kyungran Kang (korykang@ajou.ac.kr) Ellis Horowitz, Sartaj Sahni and Susan Anderson-Freed, Fundamentals of Data Structures in C, 2nd Edition, Silicon Press, 2007. Contents Binary Search
Unit III - Tree TREES
 TREES Unit III - Tree Consider a scenario where you are required to represent the directory structure of your operating system. The directory structure contains various folders and files. A folder may
TREES Unit III - Tree Consider a scenario where you are required to represent the directory structure of your operating system. The directory structure contains various folders and files. A folder may
The questions will be short answer, similar to the problems you have done on the homework
 Introduction The following highlights are provided to give you an indication of the topics that you should be knowledgeable about for the midterm. This sheet is not a substitute for the homework and the
Introduction The following highlights are provided to give you an indication of the topics that you should be knowledgeable about for the midterm. This sheet is not a substitute for the homework and the
Lecture 11: Multiway and (2,4) Trees. Courtesy to Goodrich, Tamassia and Olga Veksler
 Lecture 11: Multiway and (2,4) Trees 9 2 5 7 10 14 Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Multiway Seach Tree: a new type of search trees: for ordered d dictionary
Lecture 11: Multiway and (2,4) Trees 9 2 5 7 10 14 Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Multiway Seach Tree: a new type of search trees: for ordered d dictionary
Friday Four Square! 4:15PM, Outside Gates
 Binary Search Trees Friday Four Square! 4:15PM, Outside Gates Implementing Set On Monday and Wednesday, we saw how to implement the Map and Lexicon, respectively. Let's now turn our attention to the Set.
Binary Search Trees Friday Four Square! 4:15PM, Outside Gates Implementing Set On Monday and Wednesday, we saw how to implement the Map and Lexicon, respectively. Let's now turn our attention to the Set.
Chapter 4: Trees. 4.2 For node B :
 Chapter : Trees. (a) A. (b) G, H, I, L, M, and K.. For node B : (a) A. (b) D and E. (c) C. (d). (e).... There are N nodes. Each node has two pointers, so there are N pointers. Each node but the root has
Chapter : Trees. (a) A. (b) G, H, I, L, M, and K.. For node B : (a) A. (b) D and E. (c) C. (d). (e).... There are N nodes. Each node has two pointers, so there are N pointers. Each node but the root has
12 July, Red-Black Trees. Red-Black Trees
 1 BST work well if the data is inserted into the tree in random order. They work much slower if the data is inserted in already sorted order. When the values to be inserted are already ordered, a binary
1 BST work well if the data is inserted into the tree in random order. They work much slower if the data is inserted in already sorted order. When the values to be inserted are already ordered, a binary
Solutions. Suppose we insert all elements of U into the table, and let n(b) be the number of elements of U that hash to bucket b. Then.
 Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
CSC Design and Analysis of Algorithms
 CSC : Lecture 7 CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique CSC : Lecture 7 Transform and Conquer This group of techniques solves a problem by a
CSC : Lecture 7 CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique CSC : Lecture 7 Transform and Conquer This group of techniques solves a problem by a
CS 261 Data Structures. AVL Trees
 CS 261 Data Structures AVL Trees 1 Binary Search Tree Complexity of BST operations: proportional to the length of the path from a node to the root Unbalanced tree: operations may be O(n) E.g.: adding elements
CS 261 Data Structures AVL Trees 1 Binary Search Tree Complexity of BST operations: proportional to the length of the path from a node to the root Unbalanced tree: operations may be O(n) E.g.: adding elements
Lecture 5. Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
 Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
INF2220: algorithms and data structures Series 1
 Universitetet i Oslo Institutt for Informatikk I. Yu, D. Karabeg INF2220: algorithms and data structures Series 1 Topic Function growth & estimation of running time, trees Issued: 24. 08. 2016 Exercise
Universitetet i Oslo Institutt for Informatikk I. Yu, D. Karabeg INF2220: algorithms and data structures Series 1 Topic Function growth & estimation of running time, trees Issued: 24. 08. 2016 Exercise
Trees. Eric McCreath
 Trees Eric McCreath 2 Overview In this lecture we will explore: general trees, binary trees, binary search trees, and AVL and B-Trees. 3 Trees Trees are recursive data structures. They are useful for:
Trees Eric McCreath 2 Overview In this lecture we will explore: general trees, binary trees, binary search trees, and AVL and B-Trees. 3 Trees Trees are recursive data structures. They are useful for:
CSC 172 Data Structures and Algorithms. Fall 2017 TuTh 3:25 pm 4:40 pm Aug 30- Dec 22 Hoyt Auditorium
 CSC 172 Data Structures and Algorithms Fall 2017 TuTh 3:25 pm 4:40 pm Aug 30- Dec 22 Hoyt Auditorium Announcement Coming week: Nov 19 Nov 25 No Quiz No Workshop No New Lab Monday and Tuesday: regular Lab
CSC 172 Data Structures and Algorithms Fall 2017 TuTh 3:25 pm 4:40 pm Aug 30- Dec 22 Hoyt Auditorium Announcement Coming week: Nov 19 Nov 25 No Quiz No Workshop No New Lab Monday and Tuesday: regular Lab
Uses for Trees About Trees Binary Trees. Trees. Seth Long. January 31, 2010
 Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
