CS473-Algorithms I. Lecture 2. Asymptotic Notation. CS 473 Lecture 2 1
|
|
|
- Allyson Chapman
- 6 years ago
- Views:
Transcription
1 CS473-Algorithms I Lecture Asymptotic Notatio CS 473 Lecture 1
2 O-otatio (upper bouds) f() = O(g()) if positive costats c, 0 such that e.g., = O( 3 ) 0 f() cg(), 0 c 3 c c = 1 & 0 = or c = & 0 = 1 Asymptotic ruig times of algorithms are usually defied by fuctios whose domai are N={0, 1,, } (atural umbers) CS 473 Lecture
3 O-otatio (upper bouds) = is fuy; oe-way equality O-otatio is sloppy, but coveiet though sloppy, must uderstad what really meas thik of O(g()) as a set of fuctios: O(g()) = {f(): positive costats c, 0 such that 0 f() cg(), 0 } hece, = O( 3 ) meas that O( 3 ) CS 473 Lecture 3
4 O-otatio O-otatio is a upper-boud otatio e.g., makes o sese to say ruig time of a algorithm is at least O( ). Why? - let ruig time be T() - T() O( ) meas T() h() for some h() O( ) - however, this is true for ay T() sice h() = 0 O( ), & ruig time > 0, so stmt tells othig about ruig time CS 473 Lecture 4
5 O-otatio (upper bouds) f() = O(g()) cg() f() 0 CS 473 Lecture 5
6 -otatio (lower bouds) f() =(g()) if positive costats c, 0 such that 0 cg() f(), 0 e.g., = (lg ) (c = 1, 0 = 16) i.e., 1 lg 16 (g()) = {f(): positive costats c, 0 such that 0 cg() f(), 0 } CS 473 Lecture 6
7 -otatio (lower bouds) f() = (g()) f() cg() 0 CS 473 Lecture 7
8 CS 473 Lecture 8 -otatio (tight bouds) f()=(g()) if positive costats c 1, c, 0 such that 0 c 1 g() f() c g(), 0 example: ) ( 1 c c c c
9 -otatio: example (0 c 1 h() c ) 1/ h() =1/-/ 1/ ( 0 ) CS 473 Lecture 9
10 CS 473 Lecture 10 5, 1, 10 1 therefore 5, ) ( 0, 1 1 ) ( c c c h c h -otatio: example (0 c 1 h() c )
11 -otatio (tight bouds) (g())={f(): positive costats c 1, c, 0 such that 0 c 1 g() f() c g(), 0 } c g() f() c 1 g() 0 CS 473 Lecture 11
12 -otatio (tight bouds) Prove that 10-8 () - suppose c, 0 exist such that 10-8 c, 0 - but the c cotradictio sice c is a costat Theorem: leadig costats & low-order terms do t matter Justificatio: ca choose the leadig costat large eough to make high-order term domiate other terms CS 473 Lecture 1
13 -otatio (tight bouds) Theorem: (O ad ) - is stroger tha both O ad - i.e., (g()) O(g()) ad (g()) (g()) CS 473 Lecture 13
14 Usig asymptotic otatio for describig ruig times O-otatio used to boud worst-case ruig times also bouds ruig time o arbitrary iputs as well e.g., O( ) boud o worst-case ruig time of isertio sort also applies to its ruig time o every iput CS 473 Lecture 14
15 Usig O-otatio for describig ruig times Abuse to say ruig time of isertio sort is O( ) - for a give, actual ruig time depeds o particular iput of size - i.e., ruig time is ot oly a fuctio of - however, worst-case ruig time is oly a fuctio of CS 473 Lecture 15
16 Usig O-otatio for describig ruig times What we really mea by ruig time of isertio sort is O( ) - worst-case ruig time of isertio sort is O( ) or equivaletly - o matter what particular iput of size is chose (for each value of) ruig time o that set of iputs is O( ) CS 473 Lecture 16
17 Usig -otatio for describig ruig times used to boud the best-case ruig times also bouds the ruig time o arbitrary iputs as well e.g., () boud o best-case ruig time of isertio sort ruig time of isertio sort is () CS 473 Lecture 17
18 Usig -otatio for describig ruig times ruig time of a algorithm is (g()) meas - o matter what particular iput of size is chose (for ay ), ruig time o that set of iputs is at least a costat times g(), for sufficietly large - however, it is ot cotradictory to say worst-case ruig time of isertio sort is ( ) sice there exists a iput that causes algorithm to take ( ) time CS 473 Lecture 18
19 Usig -otatio for describig ruig times 1) used to boud worst-case & best-case ruig times of a algorithm if they are ot asymptotically equal ) used to boud ruig time of a algorithm if its worst & best case ruig times are asymptotically equal CS 473 Lecture 19
20 Usig -otatio for describig ruig times Case (1): a -boud o worst-/best-case ruig time does ot apply to its ruig time o arbitrary iputs e.g., ( ) boud o worst-case ruig time of isertio sort does ot imply a ( ) boud o ruig time of isertio sort o every iput sice T() = O( ) & T() = () for isertio sort CS 473 Lecture 0
21 Usig -otatio for describig ruig times Case (): implies a -boud o every iput - e.g., merge sort T() = O(lg) T() = (lg) T() = (lg) CS 473 Lecture 1
22 Asymptotic otatio i equatios Asymptotic otatio appears aloe o RHS of a equatio - meas set membership - e.g., = O( ) meas O( ) Asymptotic otatio appears o RHS of a equatio - stads for some aoymous fuctio i the set - e.g., = + () meas that = + h(), for some h() () i.e., h() = CS 473 Lecture
23 Asymptotic otatio appears o LHS of a equatio stads for ay aoymous fuctio i the set - e.g., + () = ( ) meas that for ay fuctio g() () some fuctio h() ( ) such that +g() = h(), RHS provides coarser level of detail tha LHS CS 473 Lecture 3
24 Other asymptotic otatios o-otatio upper boud provided by O-otatio may or may ot be tight - e.g., boud = O( ) is asymptotically tight boud = O( ) is ot asymptotically tight o-otatio deotes a upper boud that is ot asymptotically tight CS 473 Lecture 4
25 o-otatio o(g()) = {f(): for ay costat c 0, a costat 0 0 such that 0 f() < cg(), 0 } Ituitively, lim f ( ) g( ) 0 - e.g., = o( ), ay positive c satisfies - but o( ), c does ot satisfy CS 473 Lecture 5
26 -otatio deotes a lower boud that is ot asymptotically tight (g()) = {f(): for ay costat c 0, Ituitively lim a costat 0 0 such that 0 cg() < f(), 0 } f ( ) g ( ) - e.g., / = (), ay c satisfies - but / ( ), c1/ does ot satisfy CS 473 Lecture 6
27 Asymptotic compariso of fuctios similar to the relatioal properties of real umbers - Trasitivity: (holds for all) e.g., f() = (g()) & g() = (h()) f() = (h()) - Reflexivity: (holds for, O, ) e.g., f() = O(f()) - Symmetry: (holds oly for ) e.g., f() = (g()) g() = (f()) - Traspose symmetry: ((O ) ad (o )) e.g., f() = O(g()) g() = (f()) CS 473 Lecture 7
28 Aalogy to the compariso of two real umbers f() = O(g()) a b f() = (g()) a b f() = (g()) a = b f() = o(g()) a < b f() = (g()) a > b CS 473 Lecture 8
29 Aalogy to the compariso of two real umbers Trichotomy property of real umbers does ot hold for asymptotic otatio - i.e., for ay two real umbers a ad b, we have either a < b, or a = b, or a > b - i.e., for two fuctios f() & g(), it may be the case that either f() = O(g()) or f() = (g()) holds - e.g., ad 1+si() caot be compared asymptotically CS 473 Lecture 9
Algorithms Chapter 3 Growth of Functions
 Algorithms Chapter 3 Growth of Fuctios Istructor: Chig Chi Li 林清池助理教授 chigchi.li@gmail.com Departmet of Computer Sciece ad Egieerig Natioal Taiwa Ocea Uiversity Outlie Asymptotic otatio Stadard otatios
Algorithms Chapter 3 Growth of Fuctios Istructor: Chig Chi Li 林清池助理教授 chigchi.li@gmail.com Departmet of Computer Sciece ad Egieerig Natioal Taiwa Ocea Uiversity Outlie Asymptotic otatio Stadard otatios
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
CIS 121 Data Structures and Algorithms with Java Fall Big-Oh Notation Tuesday, September 5 (Make-up Friday, September 8)
 CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
What are we going to learn? CSC Data Structures Analysis of Algorithms. Overview. Algorithm, and Inputs
 What are we goig to lear? CSC316-003 Data Structures Aalysis of Algorithms Computer Sciece North Carolia State Uiversity Need to say that some algorithms are better tha others Criteria for evaluatio Structure
What are we goig to lear? CSC316-003 Data Structures Aalysis of Algorithms Computer Sciece North Carolia State Uiversity Need to say that some algorithms are better tha others Criteria for evaluatio Structure
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Analysis of Algorithms
 Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
A graphical view of big-o notation. c*g(n) f(n) f(n) = O(g(n))
 ca see that time required to search/sort grows with size of We How do space/time eeds of program grow with iput size? iput. time: cout umber of operatios as fuctio of iput Executio size operatio Assigmet:
ca see that time required to search/sort grows with size of We How do space/time eeds of program grow with iput size? iput. time: cout umber of operatios as fuctio of iput Executio size operatio Assigmet:
Outline and Reading. Analysis of Algorithms. Running Time. Experimental Studies. Limitations of Experiments. Theoretical Analysis
 Outlie ad Readig Aalysis of Algorithms Iput Algorithm Output Ruig time ( 3.) Pseudo-code ( 3.2) Coutig primitive operatios ( 3.3-3.) Asymptotic otatio ( 3.6) Asymptotic aalysis ( 3.7) Case study Aalysis
Outlie ad Readig Aalysis of Algorithms Iput Algorithm Output Ruig time ( 3.) Pseudo-code ( 3.2) Coutig primitive operatios ( 3.3-3.) Asymptotic otatio ( 3.6) Asymptotic aalysis ( 3.7) Case study Aalysis
CSE 417: Algorithms and Computational Complexity
 Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Fundamental Algorithms
 Techische Uiversität Müche Fakultät für Iformatik Lehrstuhl für Effiziete Algorithme Dmytro Chibisov Sadeep Sadaada Witer Semester 2007/08 Solutio Sheet 6 November 30, 2007 Fudametal Algorithms Problem
Techische Uiversität Müche Fakultät für Iformatik Lehrstuhl für Effiziete Algorithme Dmytro Chibisov Sadeep Sadaada Witer Semester 2007/08 Solutio Sheet 6 November 30, 2007 Fudametal Algorithms Problem
Lecture Notes 6 Introduction to algorithm analysis CSS 501 Data Structures and Object-Oriented Programming
 Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
Analysis Metrics. Intro to Algorithm Analysis. Slides. 12. Alg Analysis. 12. Alg Analysis
 Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Running Time. Analysis of Algorithms. Experimental Studies. Limitations of Experiments
 Ruig Time Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects. The
Ruig Time Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects. The
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Data Structures and Algorithms. Analysis of Algorithms
 Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
How do we evaluate algorithms?
 F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
Running Time ( 3.1) Analysis of Algorithms. Experimental Studies. Limitations of Experiments
 Ruig Time ( 3.1) Aalysis of Algorithms Iput Algorithm Output A algorithm is a step- by- step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects.
Ruig Time ( 3.1) Aalysis of Algorithms Iput Algorithm Output A algorithm is a step- by- step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects.
Analysis of Algorithms
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Ruig Time Most algorithms trasform iput objects ito output objects. The
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Ruig Time Most algorithms trasform iput objects ito output objects. The
Pseudocode ( 1.1) Analysis of Algorithms. Primitive Operations. Pseudocode Details. Running Time ( 1.1) Estimating performance
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Math Section 2.2 Polynomial Functions
 Math 1330 - Sectio. Polyomial Fuctios Our objectives i workig with polyomial fuctios will be, first, to gather iformatio about the graph of the fuctio ad, secod, to use that iformatio to geerate a reasoably
Math 1330 - Sectio. Polyomial Fuctios Our objectives i workig with polyomial fuctios will be, first, to gather iformatio about the graph of the fuctio ad, secod, to use that iformatio to geerate a reasoably
Algorithm Design Techniques. Divide and conquer Problem
 Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
Examples and Applications of Binary Search
 Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Recursive Estimation
 Recursive Estimatio Raffaello D Adrea Sprig 2 Problem Set: Probability Review Last updated: February 28, 2 Notes: Notatio: Uless otherwise oted, x, y, ad z deote radom variables, f x (x) (or the short
Recursive Estimatio Raffaello D Adrea Sprig 2 Problem Set: Probability Review Last updated: February 28, 2 Notes: Notatio: Uless otherwise oted, x, y, ad z deote radom variables, f x (x) (or the short
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Solution printed. Do not start the test until instructed to do so! CS 2604 Data Structures Midterm Spring, Instructions:
 CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
Analysis of Algorithms
 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Aalysis of Algorithms Iput 2015 Goodrich ad Tamassia Algorithm Aalysis of Algorithms
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Aalysis of Algorithms Iput 2015 Goodrich ad Tamassia Algorithm Aalysis of Algorithms
Practical Session 2 Constants Don t Matter!!!
 Practical Sessio 2 Costats Do t Matter!!! Algorithm Aalysis f() = O(g()) Big O f() = Ω(g()) Big Omega There exist c > 0 ad 0 > 0 such that: 0 f() cg() for each 0 There exist c > 0 ad 0 > 0 such that: 0
Practical Sessio 2 Costats Do t Matter!!! Algorithm Aalysis f() = O(g()) Big O f() = Ω(g()) Big Omega There exist c > 0 ad 0 > 0 such that: 0 f() cg() for each 0 There exist c > 0 ad 0 > 0 such that: 0
Algorithm. Counting Sort Analysis of Algorithms
 Algorithm Coutig Sort Aalysis of Algorithms Assumptios: records Coutig sort Each record cotais keys ad data All keys are i the rage of 1 to k Space The usorted list is stored i A, the sorted list will
Algorithm Coutig Sort Aalysis of Algorithms Assumptios: records Coutig sort Each record cotais keys ad data All keys are i the rage of 1 to k Space The usorted list is stored i A, the sorted list will
Order statistics. Order Statistics. Randomized divide-andconquer. Example. CS Spring 2006
 406 CS 5633 -- Sprig 006 Order Statistics Carola We Slides courtesy of Charles Leiserso with small chages by Carola We CS 5633 Aalysis of Algorithms 406 Order statistics Select the ith smallest of elemets
406 CS 5633 -- Sprig 006 Order Statistics Carola We Slides courtesy of Charles Leiserso with small chages by Carola We CS 5633 Aalysis of Algorithms 406 Order statistics Select the ith smallest of elemets
2. ALGORITHM ANALYSIS
 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times Lecture slides by Kevi Waye Copyright 2005 Pearso-Addiso
2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times Lecture slides by Kevi Waye Copyright 2005 Pearso-Addiso
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Thompson s Group F (p + 1) is not Minimally Almost Convex
 Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CSC165H1 Worksheet: Tutorial 8 Algorithm analysis (SOLUTIONS)
 CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Improved Random Graph Isomorphism
 Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
CMPT 125 Assignment 2 Solutions
 CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
prerequisites: 6.046, 6.041/2, ability to do proofs Randomized algorithms: make random choices during run. Main benefits:
 Itro Admiistrivia. Sigup sheet. prerequisites: 6.046, 6.041/2, ability to do proofs homework weekly (first ext week) collaboratio idepedet homeworks gradig requiremet term project books. questio: scribig?
Itro Admiistrivia. Sigup sheet. prerequisites: 6.046, 6.041/2, ability to do proofs homework weekly (first ext week) collaboratio idepedet homeworks gradig requiremet term project books. questio: scribig?
A Generalized Set Theoretic Approach for Time and Space Complexity Analysis of Algorithms and Functions
 Proceedigs of the 10th WSEAS Iteratioal Coferece o APPLIED MATHEMATICS, Dallas, Texas, USA, November 1-3, 2006 316 A Geeralized Set Theoretic Approach for Time ad Space Complexity Aalysis of Algorithms
Proceedigs of the 10th WSEAS Iteratioal Coferece o APPLIED MATHEMATICS, Dallas, Texas, USA, November 1-3, 2006 316 A Geeralized Set Theoretic Approach for Time ad Space Complexity Aalysis of Algorithms
Polynomial Functions and Models. Learning Objectives. Polynomials. P (x) = a n x n + a n 1 x n a 1 x + a 0, a n 0
 Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
UNIT 4C Iteration: Scalability & Big O. Efficiency
 UNIT 4C Iteratio: Scalability & Big O 1 Efficiecy A computer program should be totally correct, but it should also execute as quickly as possible (time-efficiecy) use memory wisely (storage-efficiecy)
UNIT 4C Iteratio: Scalability & Big O 1 Efficiecy A computer program should be totally correct, but it should also execute as quickly as possible (time-efficiecy) use memory wisely (storage-efficiecy)
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Name of the Student: Unit I (Logic and Proofs) 1) Truth Table: Conjunction Disjunction Conditional Biconditional
 SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Convergence results for conditional expectations
 Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
ON MATHIEU-BERG S INEQUALITY
 ON MATHIEU-BERG S INEQUALITY BICHENG YANG DEPARTMENT OF MATHEMATICS, GUANGDONG EDUCATION COLLEGE, GUANGZHOU, GUANGDONG 533, PEOPLE S REPUBLIC OF CHINA. bcyag@pub.guagzhou.gd.c ABSTRACT. I this paper, by
ON MATHIEU-BERG S INEQUALITY BICHENG YANG DEPARTMENT OF MATHEMATICS, GUANGDONG EDUCATION COLLEGE, GUANGZHOU, GUANGDONG 533, PEOPLE S REPUBLIC OF CHINA. bcyag@pub.guagzhou.gd.c ABSTRACT. I this paper, by
Orientation. Orientation 10/28/15
 Orietatio Orietatio We will defie orietatio to mea a object s istataeous rotatioal cofiguratio Thik of it as the rotatioal equivalet of positio 1 Represetig Positios Cartesia coordiates (x,y,z) are a easy
Orietatio Orietatio We will defie orietatio to mea a object s istataeous rotatioal cofiguratio Thik of it as the rotatioal equivalet of positio 1 Represetig Positios Cartesia coordiates (x,y,z) are a easy
The Adjacency Matrix and The nth Eigenvalue
 Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
CSE 2320 Notes 8: Sorting. (Last updated 10/3/18 7:16 PM) Idea: Take an unsorted (sub)array and partition into two subarrays such that.
 CSE Notes 8: Sortig (Last updated //8 7:6 PM) CLRS 7.-7., 9., 8.-8. 8.A. QUICKSORT Cocepts Idea: Take a usorted (sub)array ad partitio ito two subarrays such that p q r x y z x y y z Pivot Customarily,
CSE Notes 8: Sortig (Last updated //8 7:6 PM) CLRS 7.-7., 9., 8.-8. 8.A. QUICKSORT Cocepts Idea: Take a usorted (sub)array ad partitio ito two subarrays such that p q r x y z x y y z Pivot Customarily,
Algorithm Efficiency
 Algorithm Effiiey Exeutig ime Compariso of algorithms to determie whih oe is better approah implemet algorithms & reord exeutio time Problems with this approah there are may tasks ruig ourretly o a omputer
Algorithm Effiiey Exeutig ime Compariso of algorithms to determie whih oe is better approah implemet algorithms & reord exeutio time Problems with this approah there are may tasks ruig ourretly o a omputer
Protected points in ordered trees
 Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Introduction to Sigma Notation
 Itroductio to Siga Notatio Steph de Silva //207 What is siga otatio? is the capital Greek letter for the soud s I this case, it s just shorthad for su Siga otatio is what we use whe we have a series of
Itroductio to Siga Notatio Steph de Silva //207 What is siga otatio? is the capital Greek letter for the soud s I this case, it s just shorthad for su Siga otatio is what we use whe we have a series of
Area As A Limit & Sigma Notation
 Area As A Limit & Sigma Notatio SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should referece Chapter 5.4 of the recommeded textbook (or the equivalet chapter i your
Area As A Limit & Sigma Notatio SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should referece Chapter 5.4 of the recommeded textbook (or the equivalet chapter i your
15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #2: Randomized MST and MST Verification January 14, 2015
 15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
GRADIENT DESCENT. Admin 10/24/13. Assignment 5. David Kauchak CS 451 Fall 2013
 Adi Assiget 5 GRADIENT DESCENT David Kauchak CS 451 Fall 2013 Math backgroud Liear odels A strog high-bias assuptio is liear separability: i 2 diesios, ca separate classes by a lie i higher diesios, eed
Adi Assiget 5 GRADIENT DESCENT David Kauchak CS 451 Fall 2013 Math backgroud Liear odels A strog high-bias assuptio is liear separability: i 2 diesios, ca separate classes by a lie i higher diesios, eed
ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY
 ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY m. rosefeld1 1. Itroductio. We cosider i this paper oly fiite odirected graphs without multiple edges ad we assume that o each vertex of the graph there is
ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY m. rosefeld1 1. Itroductio. We cosider i this paper oly fiite odirected graphs without multiple edges ad we assume that o each vertex of the graph there is
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Major CSL Write your name and entry no on every sheet of the answer script. Time 2 Hrs Max Marks 70
 NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
On Infinite Groups that are Isomorphic to its Proper Infinite Subgroup. Jaymar Talledo Balihon. Abstract
 O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
PLEASURE TEST SERIES (XI) - 04 By O.P. Gupta (For stuffs on Math, click at theopgupta.com)
 wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
Hash Tables. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015.
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
The number n of subintervals times the length h of subintervals gives length of interval (b-a).
 Simulator with MadMath Kit: Riema Sums (Teacher s pages) I your kit: 1. GeoGebra file: Ready-to-use projector sized simulator: RiemaSumMM.ggb 2. RiemaSumMM.pdf (this file) ad RiemaSumMMEd.pdf (educator's
Simulator with MadMath Kit: Riema Sums (Teacher s pages) I your kit: 1. GeoGebra file: Ready-to-use projector sized simulator: RiemaSumMM.ggb 2. RiemaSumMM.pdf (this file) ad RiemaSumMMEd.pdf (educator's
CONTINUI TY. JEE-Mathematics. Illustration 1 : Solution : Illustration 2 : 1. CONTINUOUS FUNCTIONS :
 J-Mathematics. CONTINUOUS FUNCTIONS : CONTINUI TY A fuctio for which a small chage i the idepedet variable causes oly a small chage ad ot a sudde jump i the depedet variable are called cotiuous fuctios.
J-Mathematics. CONTINUOUS FUNCTIONS : CONTINUI TY A fuctio for which a small chage i the idepedet variable causes oly a small chage ad ot a sudde jump i the depedet variable are called cotiuous fuctios.
Data Structures and Algorithms Part 1.4
 1 Data Structures ad Algorithms Part 1.4 Werer Nutt 2 DSA, Part 1: Itroductio, syllabus, orgaisatio Algorithms Recursio (priciple, trace, factorial, Fiboacci) Sortig (bubble, isertio, selectio) 3 Sortig
1 Data Structures ad Algorithms Part 1.4 Werer Nutt 2 DSA, Part 1: Itroductio, syllabus, orgaisatio Algorithms Recursio (priciple, trace, factorial, Fiboacci) Sortig (bubble, isertio, selectio) 3 Sortig
CSC 220: Computer Organization Unit 11 Basic Computer Organization and Design
 College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
College of Computer ad Iformatio Scieces Departmet of Computer Sciece CSC 220: Computer Orgaizatio Uit 11 Basic Computer Orgaizatio ad Desig 1 For the rest of the semester, we ll focus o computer architecture:
Priority Queues. Binary Heaps
 Priority Queues Biary Heaps Priority Queues Priority: some property of a object that allows it to be prioritized with respect to other objects of the same type Mi Priority Queue: homogeeous collectio of
Priority Queues Biary Heaps Priority Queues Priority: some property of a object that allows it to be prioritized with respect to other objects of the same type Mi Priority Queue: homogeeous collectio of
A study on Interior Domination in Graphs
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
Characterizing graphs of maximum principal ratio
 Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
Learning to Shoot a Goal Lecture 8: Learning Models and Skills
 Learig to Shoot a Goal Lecture 8: Learig Models ad Skills How do we acquire skill at shootig goals? CS 344R/393R: Robotics Bejami Kuipers Learig to Shoot a Goal The robot eeds to shoot the ball i the goal.
Learig to Shoot a Goal Lecture 8: Learig Models ad Skills How do we acquire skill at shootig goals? CS 344R/393R: Robotics Bejami Kuipers Learig to Shoot a Goal The robot eeds to shoot the ball i the goal.
The Platonic solids The five regular polyhedra
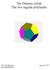 The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
Assignment 5; Due Friday, February 10
 Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Σ P(i) ( depth T (K i ) + 1),
 EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
A New Morphological 3D Shape Decomposition: Grayscale Interframe Interpolation Method
 A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
Exact Minimum Lower Bound Algorithm for Traveling Salesman Problem
 Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Heaps. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
CS 11 C track: lecture 1
 CS 11 C track: lecture 1 Prelimiaries Need a CMS cluster accout http://acctreq.cms.caltech.edu/cgi-bi/request.cgi Need to kow UNIX IMSS tutorial liked from track home page Track home page: http://courses.cms.caltech.edu/courses/cs11/material
CS 11 C track: lecture 1 Prelimiaries Need a CMS cluster accout http://acctreq.cms.caltech.edu/cgi-bi/request.cgi Need to kow UNIX IMSS tutorial liked from track home page Track home page: http://courses.cms.caltech.edu/courses/cs11/material
University of Waterloo Department of Electrical and Computer Engineering ECE 250 Algorithms and Data Structures
 Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Counting Regions in the Plane and More 1
 Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
CIS 121 Data Structures and Algorithms with Java Spring Stacks and Queues Monday, February 12 / Tuesday, February 13
 CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
9.1. Sequences and Series. Sequences. What you should learn. Why you should learn it. Definition of Sequence
 _9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
_9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
ECE4050 Data Structures and Algorithms. Lecture 6: Searching
 ECE4050 Data Structures ad Algorithms Lecture 6: Searchig 1 Search Give: Distict keys k 1, k 2,, k ad collectio L of records of the form (k 1, I 1 ), (k 2, I 2 ),, (k, I ) where I j is the iformatio associated
ECE4050 Data Structures ad Algorithms Lecture 6: Searchig 1 Search Give: Distict keys k 1, k 2,, k ad collectio L of records of the form (k 1, I 1 ), (k 2, I 2 ),, (k, I ) where I j is the iformatio associated
Arithmetic Sequences
 . Arithmetic Sequeces COMMON CORE Learig Stadards HSF-IF.A. HSF-BF.A.1a HSF-BF.A. HSF-LE.A. Essetial Questio How ca you use a arithmetic sequece to describe a patter? A arithmetic sequece is a ordered
. Arithmetic Sequeces COMMON CORE Learig Stadards HSF-IF.A. HSF-BF.A.1a HSF-BF.A. HSF-LE.A. Essetial Questio How ca you use a arithmetic sequece to describe a patter? A arithmetic sequece is a ordered
The golden search method: Question 1
 1. Golde Sectio Search for the Mode of a Fuctio The golde search method: Questio 1 Suppose the last pair of poits at which we have a fuctio evaluatio is x(), y(). The accordig to the method, If f(x())
1. Golde Sectio Search for the Mode of a Fuctio The golde search method: Questio 1 Suppose the last pair of poits at which we have a fuctio evaluatio is x(), y(). The accordig to the method, If f(x())
GC05: Algorithmic Complexity & Computability
 GC05: Algorithmic Complexity & Computability This part of the course deals with assessig the time-demad of algorithmic procedures with the aim, where possible, of fidig efficiet solutios to problems. We
GC05: Algorithmic Complexity & Computability This part of the course deals with assessig the time-demad of algorithmic procedures with the aim, where possible, of fidig efficiet solutios to problems. We
Mean cordiality of some snake graphs
 Palestie Joural of Mathematics Vol. 4() (015), 49 445 Palestie Polytechic Uiversity-PPU 015 Mea cordiality of some sake graphs R. Poraj ad S. Sathish Narayaa Commuicated by Ayma Badawi MSC 010 Classificatios:
Palestie Joural of Mathematics Vol. 4() (015), 49 445 Palestie Polytechic Uiversity-PPU 015 Mea cordiality of some sake graphs R. Poraj ad S. Sathish Narayaa Commuicated by Ayma Badawi MSC 010 Classificatios:
Data Structures Week #9. Sorting
 Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
Data Structures Week #9 Sortig Outlie Motivatio Types of Sortig Elemetary (O( 2 )) Sortig Techiques Other (O(*log())) Sortig Techiques 21.Aralık.2010 Boraha Tümer, Ph.D. 2 Sortig 21.Aralık.2010 Boraha
Bezier curves. Figure 2 shows cubic Bezier curves for various control points. In a Bezier curve, only
 Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION
 I terat. J. Mh. & Math. Sci. Vol. (1978) 125-132 125 ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION A. W. GOODMAN ad E. B. SAFF* Mathematics Dept, Uiversity of South Florida Tampa, Florida 33620 Dedicated
I terat. J. Mh. & Math. Sci. Vol. (1978) 125-132 125 ON THE DEFINITION OF A CLOSE-TO-CONVEX FUNCTION A. W. GOODMAN ad E. B. SAFF* Mathematics Dept, Uiversity of South Florida Tampa, Florida 33620 Dedicated
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
