Name of the Student: Unit I (Logic and Proofs) 1) Truth Table: Conjunction Disjunction Conditional Biconditional
|
|
|
- Dorthy Watkins
- 5 years ago
- Views:
Transcription
1 SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet: Brach: Uit I (Logic ad Proofs) 1) Truth Table: Cojuctio Disjuctio Coditioal Bicoditioal p q p q p q p q p q p q p q p q T T T T T T T T T T T T F F T F T T F F T F F T F F T T F T T F T F F F F F F F F T F F T F F T Negatio p p T F F T 2) Tautology ad Cotradictio: A Compoud propositio P P P P 1, 2, where P1 P2 tautology if it is true for every truth assigmet for P1, P2, P,, P variables are called P is called a Cotradictio if it is false for every truth assigmet for P1, P2, P If a propositio is either a tautology or a Cotradictio is called cotigecy 3) Laws of algebra of propositio: Name of Law Primal form Dual form Prepared by CGaesa, MSc, MPhil, (Ph: ) Page 1
2 Idempotet law p p p p p p Idetity law p F p Domiat law p T T p T p p F F Complemet law Commutative law p p T p p F p q q p p q q p Associative law p q r p q r p q r p q r Distributive law p q r p q p r p q r p q p r p p q p Absorptio law p p q p Demorga s law p q p q p q q p Double Negatio law p p 4) Equivalece ivolvig Coditioals: SlNo Propositios p q p q p q q p p q p q 4 p q p r p q r 5 p r q r p q r 5) Equivalece ivolvig Bicoditioals: SlNo Propositios p q 1 p q q p 2 p q p q Prepared by CGaesa, MSc, MPhil, (Ph: ) Page 2
3 p q 3 p q p q 4 p q p q 6) Tautological Implicatio: A B if ad oly if A B is tautology (ie) To prove A B, it eough to prove A B is tautology 7) The Theory of Ifereces: The aalysis of the validity of the formula from the give set of premises by usig derivatio is called theory of ifereces 8) Rules for ifereces theory: Rule P: A give premise may be itroduced at ay stage i the derivatio Rule T: A formula S may be itroduced i a derivatio if S is tautologically implied by oe or more of the precedig formulae i the derivatio Rule CP: If we ca drive S from R ad a set of give premises, the we ca derive R S from the set of premises aloe I such a case R is take as a additioal premise (assumed premise) Rule CP is also called the deductio theorem 9) Idirect Method of Derivatio: Wheever the assumed premise is used i the derivatio, the the method of derivatio is called idirect method of derivatio 10) Table of Logical Implicatios: Simplificatio Name of Law Primal form p q p p q q Additio Disjuctive Syllogism p p q q p q p p q q q p q p p Modus Poes p q q Modus Tolles p q q p Hypothetical Syllogism p q q r p r Prepared by CGaesa, MSc, MPhil, (Ph: ) Page 3
4 p q q p Uit II (Combiatorics) 1) Priciple of Mathematical Iductio: Let P ( ) be a statemet or propositio ivolvig for all positive itegers Step 1: P (1) is true Step2: Assume that Pk ( ) is true Step3: We have to prove Pk ( 1) is true 2) Priciple of Strog iductio Let P ( ) be a statemet or propositio ivolvig for all positive itegers Step 1: P (1) is true Step2: Assume that P ( ) is true for all itegers 1 k Step3: We have to prove Pk ( 1) is true 3) The Pigeohole Priciple: If pigeos are assiged to m pigeoholes ad m, tha at least oe pigeohole cotais two or more pigeos 4) The Exteded Pigeohole Priciple: If pigeos are assiged to m pigeoholes tha oe pigeohole must cotais at least 1 1 pigeos m 5) Recurrece relatio: A equatio that expresses a, the geeral term of the sequecea Prepared by CGaesa, MSc, MPhil, (Ph: ) Page 4 i terms of oe or more of the previous terms of the sequece, amely a 0, a 1, a 1, for all itegers is called a recurrece relatio fora or a differece equatio 6) Workig rule for solvig homogeeous recurrece relatio: Step 1: The give recurrece relatio of the form C ( ) a C ( ) a C ( ) a k k Step 2: Write the characteristic equatio of the recurrece relatio C0r k C1r C 0 1 kr k Step 3: Fid all the roots of the characteristic equatio amely r 1, r 2, r k Step 4: Case (i): If all the roots are distict the the geeral solutio is a b r b r b r k k Case (ii): If all the roots are equal the the geeral solutio is a b b b r
5 Uit III (Graph Theory) 1) Graph: A graph G=(V,E) cosists of two sets V v1, v2, v,,, called the set of edges of G E e1 e2 e, called the set of vertices ad 2) Simple graph: A graph is said to be simple graph if it has o loops ad parallel edges Otherwise it is multi graph 3) Regular graph: If every vertex of a simple graph has the same degree, the the graph is called a regular graph If every vertex i a regular graph has degree, the the graph is called -regular 4) Complete graph: A simple graph i which each pair of distict vertices is joied by a edge is called a complete graph The complete graph o vertices is deoted by K 5) Pedet vertex ad Pedet edge: A vertex with degree oe is called a pedet vertex ad the oly edge which is icidet with a pedet vertex is called the pedet edge 6) Matrix represetatio of a graph: There are two ways of represetig a graph by a matrix amely adjacet matrix ad icidece matrix as follows: Adjacecy matrices: by A ij Let G be a graph with vertices, the the adjacecy matrix, AG Aij 1, if ui, vj are adjacet 0, otherwise defied Icidece matrix: Let G be a graph with vertices, the the icidece matrix of G is a x e matrix B G ij B defied by B ij th th 1, if j edge is icidet o the i vert ex 0, otherwise 7) Bipartite graph: A graph G=(V,E) is called a bipartite graph if its vertex set V ca be partitioed ito two subsets V1 ad V2 such that each edge of G coects ad vertex of V 1 to a vertex of V 2 I other words, o edge joiig two vertices, i V 1 or two vertices i V 2 8) Isomorphism of a graph: The simple graphs G V, E ad G V, E are isomorphic if there is a oe to oe ad oto fuctio f from V1 to V 2 with the property that a ad b are adjacet i G1 if ad oly if f( a) ad f( b ) are adjacet i G 2, for all a ad b i V 1 Prepared by CGaesa, MSc, MPhil, (Ph: ) Page 5
6 9) Complemetary ad Self complemetary graph: Let G be a graph The complemet G of G is defied by ay two vertices are adjacet i G if ad oly if they are ot adjacet ig G is said to be a self complemetary graph if G is isomorphic tog 10) Coected graph: A graph G is said to be coected if there is at least oe path betwee every pair of vertices i G Otherwise G is discoected A discoected graph cosists of two or more coected sub graphs ad each of them is called a compoet It is deoted by ( G) 11) Strogly Coected ad Weakly Coected graph: 12) Cut edge: A cut edge of a graph G is a edge e such that ( G e) ( G) (ie) If G is coected ad e is a cut edge of G, the G eis discoected 13) Cut vertex: A cut vertex of a graph G is a vertex v such ( G v) ( G) (ie) If G is coected ad v is a cut vertex of G, the G vis discoected 14) Defie vertex coectivity The coectivity ( G) of G is the miimum k for which G has a k-vertex cut If G is either trivial or discoected the ( G) 0 15) Defie edge coectivity The edge coectivity ( G) of G is the miimum k for which G has a k-edge cut If G is either trivial or discoected the ( G) 0 16) Defie Euleria graph A path of graph G is called a Euleria path, if it icludes each edge of G exactly oce A circuit of a graph G is called a Euleria circuit, if it icludes each edge of G exactly oe A graph cotaiig a Euleria circuit is called a Euleria graph 17) Defie Hamiltoia graph A simple path i a graph G that passes through every vertex exactly oce is called a Hamilto path A circuit i a graph G that passes through every vertex exactly oce is called a Hamilto circuit A graph cotaiig a Hamiltoia circuit Uit IV (Algebraic Structures) 1) Semi group: If G is a o-empty set ad * be a biary operatio o G, the the algebraic system G,* is called a semi group, if G is closed uder * ad * is associative Example: If Z is the set of positive eve umbers, the Z, ad Z, are semi groups Prepared by CGaesa, MSc, MPhil, (Ph: ) Page 6
7 2) Mooid: If a semi group G,* has a idetity elemet with respect to the operatio *, the G,* is called a mooid It is deoted by G,*, e Example: If N is the set of atural umbers, the N, ad N, are mooids with the idetity elemets 0 ad 1 respectively Z, ad Z, are semi groups with out mooids, where Z is the set of all positive eve umbers 3) Sub semi groups: If G,* is a semi group ad H Gis called uder the operatio *, the H,* is called a sub semi group of G,* Example: If the set E of all eve o-egative itegers, the E, is a sub semi group of the semi group N,, where N is the set of atural umbers 4) Semi group homomorphism: If G,* ad G, are two semi groups, the a mappig f : G G is called a semi group homomorphism, if for ay a, b G, f ( a * b) f ( a) f ( b) A homomorphism f is called isomorphism if f is 1-1 ad oto 5) Group: If G is a o-empty set ad * is a biary operatio of G, the the algebraic system G,* is called a group if the followig coditios are satisfied (i) Closure property (ii) Associative property (iii) Existece of idetity elemet (iv) Existece of iverse elemet Example: Z, is a group ad Z, is ot a group 6) Abelia group: A group G,*, i which the biary operatio * is commutative, is called a commutative group or abelia group Example: The set of ratioal umbers excludig zero is a abelia group uder the multiplicatio 7) Coset: If H is a subgroup of a group G uder the operatio *, the the set ah, where a G, defie by ah a* h / h H is called the left coset of H i G geerated by the elemet a G Similarly the set Ha is called the right coset of H i G geerated by the elemet a G Prepared by CGaesa, MSc, MPhil, (Ph: ) Page 7
8 Example: G 1, 1, i, i be a group uder multiplicatio ad H 1, 1 is a subgroup of G The right cosets are 1H 1, 1, 1H 1,1, ih i, i ih i, i ad 8) Lagrage s theorem: The order of each subgroups of a fiite group is a divisor of a order of a group 9) Cyclic group: A group G,* is said to be cyclic, if ad elemet a G such that every elemet of 2 G geerated by a (ie) G a 1, a, a, a e Example: G 1, 1, i, i is a cyclic group uder the multiplicatio The geerator is i, because i 1, i 1, i, i i 10) Normal subgroup: A subgroup H of the group G is said to be ormal subgroup uder the operatio *, if for ay a G, ah Ha 11) Kerel of a homomorphism: If f is a group homomorphism from,* G ad, G, the the set of elemet of G, which are mapped ito e, the idetity elemet of G, is called the kerel of the homomorphism f ad deoted by ker f 12) Fudametal theorem of homomorphism: If f is a homomorphism of G o to G with kerel K, the G/ K is isomorphic to G 13) Cayley s theorem: Every fiite group of order is isomorphic to a permutatio group of degree 14) Rig: A algebraic system S,, is called a rig if the biary operatios ad o S satisfy the followig properties (i) S, is a abelia group (ii) S, is a semi group (iii) The operatio is distributive over Example: The set of all itegers Z, ad the set of all ratioal umbers R are rigs uder the usual additio ad usual multiplicatio 15) Commutative rig: 16) Itegral domai: A commutative rig without zero divisor is called Itegral domai Example: (i) R,, is a itegral domai, sice a, b R such that a 0, b 0 the 0 ab (ii),, Z is ot a itegral domai, Prepared by CGaesa, MSc, MPhil, (Ph: ) Page 8
9 because 2,3 Z10 ad Therefore 2 ad 5 are zero divisors 17) Field: A commutative reig S,, which has more tha oe elemet such that every ozero elemet of S has a multiplicative iverse i S is called a field Example: The rig of ratioal umbers Q,, is a field sice it is a commutative rig ad each o-zero elemet is iversible Uit V (Lattices ad Boolea algebra) 1) Partially ordered set (Poset): A relatio R o a set A is called a partial order relatio, if R is reflexive, atisymmetric ad trasitive The set A together with partial order relatio R is called partially ordered set or poset Example: The greater tha or equal to relatio is a partial orderig o the set of itegers Z 2) Lattice: A lattice is a partially ordered set L, i which every pair of elemets a, b L has a glb ad lub 3) Sub-lattice: 4) Geeral formula: glb a, b a* b a b i) ii) l ub a, b a b a b iii) iv) 5) Properties: Name of Law a * b a & a * b b a b a * b a If a b b Primal form Idempotet law a * a a Commutative law & a * b b* a a b a a b b Dual form a a a a b b a Associative law a * b* c a * b* c a b c a b c Prepared by CGaesa, MSc, MPhil, (Ph: ) Page 9
10 Distributive law p* q r p* q p* r p q* r p q* p r Absorptio law a* a b a * a a b a Complemet a* a 0 aa 1 Demorga s law * * a b a b a b a b Double Negatio law p p 6) Complemeted Lattices: A Lattice L,*, is said to be complemeted if for ay a L, there exist a L, such that a* a 0ad aa 1 7) Demorga s laws: Let L,*, be the complemeted lattice, the * a b a b * a b a b ad 8) Complete Lattice: A lattice L,*, is complete if for all o-empty subsets of L, there exists a glb ad lub 9) Lattice Homomorphism: Let L,*, ad S,, be two lattices A mappig g : L S homomorphism if g( a * b) g( a) g( b) ad g( a b) g( a) g( b) 10) Modular Lattice: A lattice L,*, is said to be modular if for ay a, b, c L i) ii) * * a c a b* c a b * c a c a b c a b c 11) Chai i Lattice: Let L, be a Chai if is called lattices i) a b or a c ad ii) a b ad a c 12) Coditio for the algebraic lattice: A lattice L,*, is said to be algebraic if it satisfies Commutative Law, Associative Law, Absorptio Law ad Existece of Idempotet elemet 13) Isotoe property: Prepared by CGaesa, MSc, MPhil, (Ph: ) Page 10
11 Let L,*, be a lattice The biary operatios * ad are said to possess isotoe b c a * b a * c property if a b a c 14) Boolea Algebra: A Boolea algebra is a lattice which is both complemeted ad distributive It is deoted by B,*, ---- All the Best ---- Prepared by CGaesa, MSc, MPhil, (Ph: ) Page 11
On Infinite Groups that are Isomorphic to its Proper Infinite Subgroup. Jaymar Talledo Balihon. Abstract
 O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
BOOLEAN MATHEMATICS: GENERAL THEORY
 CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Assignment 5; Due Friday, February 10
 Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Strong Complementary Acyclic Domination of a Graph
 Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
INTERSECTION CORDIAL LABELING OF GRAPHS
 INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
Some cycle and path related strongly -graphs
 Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
Symmetric Class 0 subgraphs of complete graphs
 DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
A Note on Chromatic Transversal Weak Domination in Graphs
 Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Super Vertex Magic and E-Super Vertex Magic. Total Labelling
 Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Copyright 2016 Ramez Elmasri and Shamkant B. Navathe
 Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 19 Query Optimizatio Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio Query optimizatio Coducted by a query optimizer i a DBMS Goal:
Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 19 Query Optimizatio Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio Query optimizatio Coducted by a query optimizer i a DBMS Goal:
The Adjacency Matrix and The nth Eigenvalue
 Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH
 J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
Thompson s Group F (p + 1) is not Minimally Almost Convex
 Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
CS 683: Advanced Design and Analysis of Algorithms
 CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
found that now considerable work has been done in this started with some example, which motivates the later results.
 8 Iteratioal Joural of Comuter Sciece & Emergig Techologies (E-ISSN: 44-64) Volume, Issue 4, December A Study o Adjacecy Matrix for Zero-Divisor Grahs over Fiite Rig of Gaussia Iteger Prajali, Amit Sharma
8 Iteratioal Joural of Comuter Sciece & Emergig Techologies (E-ISSN: 44-64) Volume, Issue 4, December A Study o Adjacecy Matrix for Zero-Divisor Grahs over Fiite Rig of Gaussia Iteger Prajali, Amit Sharma
Math 10C Long Range Plans
 Math 10C Log Rage Plas Uits: Evaluatio: Homework, projects ad assigmets 10% Uit Tests. 70% Fial Examiatio.. 20% Ay Uit Test may be rewritte for a higher mark. If the retest mark is higher, that mark will
Math 10C Log Rage Plas Uits: Evaluatio: Homework, projects ad assigmets 10% Uit Tests. 70% Fial Examiatio.. 20% Ay Uit Test may be rewritte for a higher mark. If the retest mark is higher, that mark will
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
A New Morphological 3D Shape Decomposition: Grayscale Interframe Interpolation Method
 A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
CIS 121. Introduction to Trees
 CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
CIS 121 Data Structures and Algorithms with Java Spring Stacks and Queues Monday, February 12 / Tuesday, February 13
 CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
Major CSL Write your name and entry no on every sheet of the answer script. Time 2 Hrs Max Marks 70
 NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
NOTE:. Attempt all seve questios. Major CSL 02 2. Write your ame ad etry o o every sheet of the aswer script. Time 2 Hrs Max Marks 70 Q No Q Q 2 Q 3 Q 4 Q 5 Q 6 Q 7 Total MM 6 2 4 0 8 4 6 70 Q. Write a
CIS 121 Data Structures and Algorithms with Java Fall Big-Oh Notation Tuesday, September 5 (Make-up Friday, September 8)
 CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
Graphs ORD SFO LAX DFW
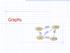 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
CS473-Algorithms I. Lecture 2. Asymptotic Notation. CS 473 Lecture 2 1
 CS473-Algorithms I Lecture Asymptotic Notatio CS 473 Lecture 1 O-otatio (upper bouds) f() = O(g()) if positive costats c, 0 such that e.g., = O( 3 ) 0 f() cg(), 0 c 3 c c = 1 & 0 = or c = & 0 = 1 Asymptotic
CS473-Algorithms I Lecture Asymptotic Notatio CS 473 Lecture 1 O-otatio (upper bouds) f() = O(g()) if positive costats c, 0 such that e.g., = O( 3 ) 0 f() cg(), 0 c 3 c c = 1 & 0 = or c = & 0 = 1 Asymptotic
UNIT 1 RECURRENCE RELATIONS
 UNIT RECURRENCE RELATIONS Structure Page No.. Itroductio 7. Objectives 7. Three Recurret Problems 8.3 More Recurreces.4 Defiitios 4.5 Divide ad Coquer 7.6 Summary 9.7 Solutios/Aswers. INTRODUCTION I the
UNIT RECURRENCE RELATIONS Structure Page No.. Itroductio 7. Objectives 7. Three Recurret Problems 8.3 More Recurreces.4 Defiitios 4.5 Divide ad Coquer 7.6 Summary 9.7 Solutios/Aswers. INTRODUCTION I the
South Slave Divisional Education Council. Math 10C
 South Slave Divisioal Educatio Coucil Math 10C Curriculum Package February 2012 12 Strad: Measuremet Geeral Outcome: Develop spatial sese ad proportioal reasoig It is expected that studets will: 1. Solve
South Slave Divisioal Educatio Coucil Math 10C Curriculum Package February 2012 12 Strad: Measuremet Geeral Outcome: Develop spatial sese ad proportioal reasoig It is expected that studets will: 1. Solve
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
A study on Interior Domination in Graphs
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
Force Network Analysis using Complementary Energy
 orce Network Aalysis usig Complemetary Eergy Adrew BORGART Assistat Professor Delft Uiversity of Techology Delft, The Netherlads A.Borgart@tudelft.l Yaick LIEM Studet Delft Uiversity of Techology Delft,
orce Network Aalysis usig Complemetary Eergy Adrew BORGART Assistat Professor Delft Uiversity of Techology Delft, The Netherlads A.Borgart@tudelft.l Yaick LIEM Studet Delft Uiversity of Techology Delft,
University of Waterloo Department of Electrical and Computer Engineering ECE 250 Algorithms and Data Structures
 Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Average Connectivity and Average Edge-connectivity in Graphs
 Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
International Journal of Pure and Applied Sciences and Technology
 It J Pure App Sci Techo 6( (0 pp7-79 Iteratioa Joura of Pure ad Appied Scieces ad Techoogy ISS 9-607 Avaiabe oie at wwwijopaasati Research Paper Reatioship Amog the Compact Subspaces of Rea Lie ad their
It J Pure App Sci Techo 6( (0 pp7-79 Iteratioa Joura of Pure ad Appied Scieces ad Techoogy ISS 9-607 Avaiabe oie at wwwijopaasati Research Paper Reatioship Amog the Compact Subspaces of Rea Lie ad their
ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY
 ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY m. rosefeld1 1. Itroductio. We cosider i this paper oly fiite odirected graphs without multiple edges ad we assume that o each vertex of the graph there is
ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY m. rosefeld1 1. Itroductio. We cosider i this paper oly fiite odirected graphs without multiple edges ad we assume that o each vertex of the graph there is
Compactness of Fuzzy Sets
 Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
On Spectral Theory Of K-n- Arithmetic Mean Idempotent Matrices On Posets
 Iteratioal Joural of Sciece, Egieerig ad echology Research (IJSER), Volume 5, Issue, February 016 O Spectral heory Of -- Arithmetic Mea Idempotet Matrices O Posets 1 Dr N Elumalai, ProfRMaikada, 3 Sythiya
Iteratioal Joural of Sciece, Egieerig ad echology Research (IJSER), Volume 5, Issue, February 016 O Spectral heory Of -- Arithmetic Mea Idempotet Matrices O Posets 1 Dr N Elumalai, ProfRMaikada, 3 Sythiya
Algorithm Design Techniques. Divide and conquer Problem
 Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
Algorithm Desig Techiques Divide ad coquer Problem Divide ad Coquer Algorithms Divide ad Coquer algorithm desig works o the priciple of dividig the give problem ito smaller sub problems which are similar
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
RTG Mini-Course Perspectives in Geometry Series
 RTG Mii-Course Perspectives i Geometry Series Jacob Lurie Lecture III: The Cobordism Hypothesis (1/27/2009) A quick review of ideas from previous lectures: The origial defiitio of a -dimesioal tqft provided
RTG Mii-Course Perspectives i Geometry Series Jacob Lurie Lecture III: The Cobordism Hypothesis (1/27/2009) A quick review of ideas from previous lectures: The origial defiitio of a -dimesioal tqft provided
Pseudocode ( 1.1) Analysis of Algorithms. Primitive Operations. Pseudocode Details. Running Time ( 1.1) Estimating performance
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
A log n lower bound to compute any function in parallel Reduction and broadcast in O(log n) time Parallel prefix (scan) in O(log n) time
 CS 267 Tricks with Trees Outlie A log lower boud to compute ay fuctio i parallel Reductio ad broadcast i O(log ) time Parallel prefix (sca) i O(log ) time Addig two -bit itegers i O(log ) time Multiplyig
CS 267 Tricks with Trees Outlie A log lower boud to compute ay fuctio i parallel Reductio ad broadcast i O(log ) time Parallel prefix (sca) i O(log ) time Addig two -bit itegers i O(log ) time Multiplyig
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
How do we evaluate algorithms?
 F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
Minimum Spanning Trees
 Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
9.1. Sequences and Series. Sequences. What you should learn. Why you should learn it. Definition of Sequence
 _9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
_9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
Minimum Spanning Trees. Application: Connecting a Network
 Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Matrix Partitions of Split Graphs
 Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
Minimum Spanning Trees
 Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
Graphs ORD SFO LAX DFW. Lecture notes adapted from Goodrich and Tomassia. 3/14/18 10:28 AM Graphs 1
 Graphs 337 1843 1743 1233 802 Lecture otes adapted from Goodrich ad Tomassia 3/14/18 10:28 AM Graphs 1 Graph A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs
Graphs 337 1843 1743 1233 802 Lecture otes adapted from Goodrich ad Tomassia 3/14/18 10:28 AM Graphs 1 Graph A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs
Computers and Scientific Thinking
 Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
Computers ad Scietific Thikig David Reed, Creighto Uiversity Chapter 15 JavaScript Strigs 1 Strigs as Objects so far, your iteractive Web pages have maipulated strigs i simple ways use text box to iput
ENERGY, DISTANCE ENERGY OF CONNECTED GRAPHS AND SKEW ENERGY OF CONNECTED DIGRAPHS WITH RESPECT TO ITS SPANNING TREES AND ITS CHORDS
 Iteratioal Joural of Combiatorial Graph Theory ad Applicatios Vol 4, No 2, (July-December 2011), pp 77-87 ENERGY, DISTANCE ENERGY OF CONNECTED GRAPHS AND SKEW ENERGY OF CONNECTED DIGRAPHS WITH RESPECT
Iteratioal Joural of Combiatorial Graph Theory ad Applicatios Vol 4, No 2, (July-December 2011), pp 77-87 ENERGY, DISTANCE ENERGY OF CONNECTED GRAPHS AND SKEW ENERGY OF CONNECTED DIGRAPHS WITH RESPECT
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
Convergence results for conditional expectations
 Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
A New Bit Wise Technique for 3-Partitioning Algorithm
 Special Issue of Iteratioal Joural of Computer Applicatios (0975 8887) o Optimizatio ad O-chip Commuicatio, No.1. Feb.2012, ww.ijcaolie.org A New Bit Wise Techique for 3-Partitioig Algorithm Rajumar Jai
Special Issue of Iteratioal Joural of Computer Applicatios (0975 8887) o Optimizatio ad O-chip Commuicatio, No.1. Feb.2012, ww.ijcaolie.org A New Bit Wise Techique for 3-Partitioig Algorithm Rajumar Jai
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
Mathematical Stat I: solutions of homework 1
 Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Fast Fourier Transform (FFT) Algorithms
 Fast Fourier Trasform FFT Algorithms Relatio to the z-trasform elsewhere, ozero, z x z X x [ ] 2 ~ elsewhere,, ~ e j x X x x π j e z z X X π 2 ~ The DFS X represets evely spaced samples of the z- trasform
Fast Fourier Trasform FFT Algorithms Relatio to the z-trasform elsewhere, ozero, z x z X x [ ] 2 ~ elsewhere,, ~ e j x X x x π j e z z X X π 2 ~ The DFS X represets evely spaced samples of the z- trasform
Theory of Fuzzy Soft Matrix and its Multi Criteria in Decision Making Based on Three Basic t-norm Operators
 Theory of Fuzzy Soft Matrix ad its Multi Criteria i Decisio Makig Based o Three Basic t-norm Operators Md. Jalilul Islam Modal 1, Dr. Tapa Kumar Roy 2 Research Scholar, Dept. of Mathematics, BESUS, Howrah-711103,
Theory of Fuzzy Soft Matrix ad its Multi Criteria i Decisio Makig Based o Three Basic t-norm Operators Md. Jalilul Islam Modal 1, Dr. Tapa Kumar Roy 2 Research Scholar, Dept. of Mathematics, BESUS, Howrah-711103,
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Behavioral Modeling in Verilog
 Behavioral Modelig i Verilog COE 202 Digital Logic Desig Dr. Muhamed Mudawar Kig Fahd Uiversity of Petroleum ad Mierals Presetatio Outlie Itroductio to Dataflow ad Behavioral Modelig Verilog Operators
Behavioral Modelig i Verilog COE 202 Digital Logic Desig Dr. Muhamed Mudawar Kig Fahd Uiversity of Petroleum ad Mierals Presetatio Outlie Itroductio to Dataflow ad Behavioral Modelig Verilog Operators
Elementary Educational Computer
 Chapter 5 Elemetary Educatioal Computer. Geeral structure of the Elemetary Educatioal Computer (EEC) The EEC coforms to the 5 uits structure defied by vo Neuma's model (.) All uits are preseted i a simplified
Chapter 5 Elemetary Educatioal Computer. Geeral structure of the Elemetary Educatioal Computer (EEC) The EEC coforms to the 5 uits structure defied by vo Neuma's model (.) All uits are preseted i a simplified
INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. 2 (2013), No. 1, 5-22 INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES NENAD U. STOJANOVIĆ Abstract. If above each side of a regular polygo
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 2 (2013), No. 1, 5-22 INSCRIBED CIRCLE OF GENERAL SEMI-REGULAR POLYGON AND SOME OF ITS FEATURES NENAD U. STOJANOVIĆ Abstract. If above each side of a regular polygo
Bezier curves. Figure 2 shows cubic Bezier curves for various control points. In a Bezier curve, only
 Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
c-dominating Sets for Families of Graphs
 c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
2 X = 2 X. The number of all permutations of a set X with n elements is. n! = n (n 1) (n 2) nn e n
 1 Discrete Mathematics revisited. Facts to remember Give set X, the umber of subsets of X is give by X = X. The umber of all permutatios of a set X with elemets is! = ( 1) ( )... 1 e π. The umber ( ) k
1 Discrete Mathematics revisited. Facts to remember Give set X, the umber of subsets of X is give by X = X. The umber of all permutatios of a set X with elemets is! = ( 1) ( )... 1 e π. The umber ( ) k
PLEASURE TEST SERIES (XI) - 04 By O.P. Gupta (For stuffs on Math, click at theopgupta.com)
 wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
Solution printed. Do not start the test until instructed to do so! CS 2604 Data Structures Midterm Spring, Instructions:
 CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
Algorithm. Counting Sort Analysis of Algorithms
 Algorithm Coutig Sort Aalysis of Algorithms Assumptios: records Coutig sort Each record cotais keys ad data All keys are i the rage of 1 to k Space The usorted list is stored i A, the sorted list will
Algorithm Coutig Sort Aalysis of Algorithms Assumptios: records Coutig sort Each record cotais keys ad data All keys are i the rage of 1 to k Space The usorted list is stored i A, the sorted list will
ON A GENERALIZED EULERIAN DISTRIBUTION
 A. Ist. Statist. Math. Vol. 43, No. 1, 197-206 (1991) ON A GENERALIZED EULERIAN DISTRIBUTION CH. A. CHARALAMBIDES Statistical Uit, Uiversity of Athes, Paepisteraiopolis, Athes 157 84, Greece (Received
A. Ist. Statist. Math. Vol. 43, No. 1, 197-206 (1991) ON A GENERALIZED EULERIAN DISTRIBUTION CH. A. CHARALAMBIDES Statistical Uit, Uiversity of Athes, Paepisteraiopolis, Athes 157 84, Greece (Received
Analysis Metrics. Intro to Algorithm Analysis. Slides. 12. Alg Analysis. 12. Alg Analysis
 Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Itro to Algorithm Aalysis Aalysis Metrics Slides. Table of Cotets. Aalysis Metrics 3. Exact Aalysis Rules 4. Simple Summatio 5. Summatio Formulas 6. Order of Magitude 7. Big-O otatio 8. Big-O Theorems
Image Segmentation EEE 508
 Image Segmetatio Objective: to determie (etract) object boudaries. It is a process of partitioig a image ito distict regios by groupig together eighborig piels based o some predefied similarity criterio.
Image Segmetatio Objective: to determie (etract) object boudaries. It is a process of partitioig a image ito distict regios by groupig together eighborig piels based o some predefied similarity criterio.
The Eigen-Cover Ratio of a Graph: Asymptotes, Domination and Areas
 The ige-cover Ratio of a Graph: Asymptotes, Domiatio ad Areas Paul August Witer ad Carol Lye Jessop Mathematics, UKZN, Durba, outh Africa-email: witerp@ukzacza Abstract The separate study of the two cocepts
The ige-cover Ratio of a Graph: Asymptotes, Domiatio ad Areas Paul August Witer ad Carol Lye Jessop Mathematics, UKZN, Durba, outh Africa-email: witerp@ukzacza Abstract The separate study of the two cocepts
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Design and Analysis of Algorithms Notes
 Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Fuzzy Minimal Solution of Dual Fully Fuzzy Matrix Equations
 Iteratioal Coferece o Applied Mathematics, Simulatio ad Modellig (AMSM 2016) Fuzzy Miimal Solutio of Dual Fully Fuzzy Matrix Equatios Dequa Shag1 ad Xiaobi Guo2,* 1 Sciece Courses eachig Departmet, Gasu
Iteratioal Coferece o Applied Mathematics, Simulatio ad Modellig (AMSM 2016) Fuzzy Miimal Solutio of Dual Fully Fuzzy Matrix Equatios Dequa Shag1 ad Xiaobi Guo2,* 1 Sciece Courses eachig Departmet, Gasu
Improved Random Graph Isomorphism
 Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Pattern Recognition Systems Lab 1 Least Mean Squares
 Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
prerequisites: 6.046, 6.041/2, ability to do proofs Randomized algorithms: make random choices during run. Main benefits:
 Itro Admiistrivia. Sigup sheet. prerequisites: 6.046, 6.041/2, ability to do proofs homework weekly (first ext week) collaboratio idepedet homeworks gradig requiremet term project books. questio: scribig?
Itro Admiistrivia. Sigup sheet. prerequisites: 6.046, 6.041/2, ability to do proofs homework weekly (first ext week) collaboratio idepedet homeworks gradig requiremet term project books. questio: scribig?
CSE 417: Algorithms and Computational Complexity
 Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Time CSE 47: Algorithms ad Computatioal Readig assigmet Read Chapter of The ALGORITHM Desig Maual Aalysis & Sortig Autum 00 Paul Beame aalysis Problem size Worst-case complexity: max # steps algorithm
Some new results on recursive aggregation rules
 Some ew results o recursive aggregatio rules Daiel Gómez Escuela de Estadística Uiversidad Complutese Madrid, 28040 Spai dagomez@estad.ucm.es Javier Motero Facultad de Matemáticas Uiversidad Complutese
Some ew results o recursive aggregatio rules Daiel Gómez Escuela de Estadística Uiversidad Complutese Madrid, 28040 Spai dagomez@estad.ucm.es Javier Motero Facultad de Matemáticas Uiversidad Complutese
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
