CONTINUI TY. JEE-Mathematics. Illustration 1 : Solution : Illustration 2 : 1. CONTINUOUS FUNCTIONS :
|
|
|
- Cory Carson
- 6 years ago
- Views:
Transcription
1 J-Mathematics. CONTINUOUS FUNCTIONS : CONTINUI TY A fuctio for which a small chage i the idepedet variable causes oly a small chage ad ot a sudde jump i the depedet variable are called cotiuous fuctios. Naively, we may say that a fuctio is cotiuous at a fied poit if we ca draw the graph of the fuctio aroud that poit without liftig the pe from the plae of the paper. a cotiuous a discotiuous a discotiuous a discotiuous a discotiuous Cotiuity of a fuctio at a poit : A fuctio f() is said to be cotiuous at = a, if Lim f( ) f( a). Symbolically f is cotiuous at = a if Lim f a h Lim f a h f a ( ) ( ), h > 0 h0 h0 a i.e. (LHL = a = RHL =a ) equals value of f at = a. It should be oted that cotiuity of a fuctio at = a ca be discussed oly if the fuctio is defied i the immediate eighbourhood of = a, ot ecessarily at = a.. Cotiuity at = 0 for the curve ca ot be discussed. o Illustratio : Solutio : Illustratio : si, If f() the fid whether f() is cotiuous or ot at =, where [ ] deotes [] greatest iteger fuctio. si, f() [], For cotiuity at =, we determie, f(), Now, f() = [] = f() = si so f() = f() = f() f() is cotiuous at = Cosider f() becomes cotiuous at = 0. 8 f() ad f(). = si = ad f() = [] = 8 4, 0 e si k4, 0 Defie the fuctio at = 0 if possible, so that f() h h h h h h ( ) ( ) Solutio : f(0 + ) = h0 = h h0 h h h (4 ) ( ) = = 4. h0 h h f(0 ) = e si k 4 = k4 0 f() is cotiuous at = 0, f(0 + ) = f(0 ) = f(0) 4. k4 k = f(0) = (4)() Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
2 Illustratio 3 : Let f() = Solutio : a( si ) b cos c d J-Mathematics 0 If f is cotiuous at = 0, the fid out the values of a, b, c ad d. Sice f() is cotiuous at = 0, so at = 0, both left ad right its must eist ad both must be equal to 3. Now Lim 0 If sice Now Do yourself - : a( si ) b cos 5 = 0 Lim (a b 5) a... 0 f() eists the a + b + 5 = 0 ad a b 0 0 c d ( d) = 3 0 So e d = 3 d = 3, eists ( d) d d 0 = e d Hece a =, b = 4, c = 0 ad d = 3. b c d = 3 (By the epasios of si ad cos) = 3 a = ad b = 4 3 = 0 c = 0 (i) (ii) If If cos ; 0 ƒ() fid the value of k if ƒ () is cotiuous at = 0. k; 0 ; the discuss the cotiuity of ƒ () at = ; ƒ() ta ( ) Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65. CONTINUITY OF TH FUNCTION IN AN INTRVAL : ( a ) A fuctio is said to be cotiuous i (a,b) if f is cotiuous at each & every poit belogig to (a, b). ( b ) A fuctio is said to be cotiuous i a closed iterval [a,b] if : (i) f is cotiuous i the ope iterval (a,b) (ii) f is right cotiuous at a i.e. Lim f f a a (iii) f is left cotiuous at b i.e. Lim f f b b Note : 9 = a fiite quatity a fiite quatity (i) Obseve that ƒ() a ad ƒ() b do ot make sese. As a cosequece of this defiitio, if ƒ() is defied oly at oe poit, it is cotiuous there, i.e., if the domai of ƒ() is a sigleto, ƒ() is a cotiuous fuctio. (ii) ample : Cosider ƒ() = a a. ƒ() is a sigleto fuctio defied oly at = a. Hece ƒ() is a cotiuous fuctio. All polyomials, trigoometrical fuctios, epoetial & logarithmic fuctios are cotiuous i their domais. (iii) If ƒ () & g() are two fuctios that are cotiuous at = c the the fuctio defied by : 3 F f g ; F K f, where K is ay real umber ; F f. g are also cotiuous at = c. f Further, if g(c) is ot zero, the F4 is also cotiuous at = c. g
3 J-Mathematics (iii) Some cotiuous fuctios : Fuctio f() Iterval i which f() is cotiuous Costat fuctio, is a iteger 0 ( ) ( ), is a positive iteger ( ) {0} a ( ) p() = a 0 + a + a a ( ) p(), where p() ad q() are polyomial i ( ) { : q() = 0} q() si, cos, e ( ) ta, sec ( ) {( + )/ : I} cot, cosec ( ) { : I} (0) (iv) Some Discotiuous Fuctios : Fuctios Poits of discotiuity [], {} ta, sec very Iteger 3,,... cot, cosec 0,,,... si, cos,, e/ = 0, 3, 0 Illustratio 4 : Discuss the cotiuity of f() = 3, , 3, 3, 0 Solutio : We write f() as f() = 3, , 3 As we ca see, f() is defied as a polyomial fuctio i each of itervals (, ), (,0), (0,3) ad (3,). Therefore, it is cotiuous i each of these four ope itervals. Thus we check the cotiuity at =,0,3. At the poit = f() = ( ) = + = f() = ( + 3) =. ( ) + 3 = 30 Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
4 J-Mathematics Therefore, f() does ot eist ad hece f() is discotiuous at =. Do yourself - : At the poit = 0 0 f() = 0 ( + 3) = 3 0 f() = 0 ( + 3) = 3 f(0) = = 3 Therefore f() is cotiuous at = 0. At the poit = 3 3 f() = 3 ( + 3) = = 3 f() = 3 ( 3 5) = = f(3) = = Therefore, f() is cotiuous at = 3. We fid that f() is cotiuous at all poits i R ecept at = (i) If ; 0 a ƒ() ; b 4b ; the fid the value of a & b if ƒ () is cotiuous i [0,) Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65 3 ; 0 (ii) Discuss the cotiuity of ƒ () = si ; log ; 3 3. RASONS OF DISCONTINUITY : ( a ) Limit does ot eist i.e. Lim f( ) Lim f( ) a a ( b ) f() is ot defied at = a ( c ) Lim f( ) f( a) a Geometrically, the graph of the fuctio will ehibit a break at = a, if the fuctio is discotiuous at = a. The graph as show is discotiuous at =, ad 3. i [0,3) Lim f() f() Lim f() does ot eist f() is ot defied at = 3 3
5 J-Mathematics 4. TYPS OF DISCONTINUITIS : Type- : (Removable type of discotiuities) : - I case Lim f( ) eists but is ot equal to f(a) the the fuctio is said to have a removable discotiuity or discotiuity of the first kid. I this case we ca redefie the fuctio such that Lim f f a classified as: a ( a ) Missig poit discotiuity : Where Lim a a ( ) & make it cotiuous at = a. Removable type of discotiuity ca be further f( ) eists but f(a) is ot defied. ( b ) Isolated poit discotiuity : Where Lim f( ) eists & f(a) also eists but; Lim f( ) f( a). a a, 0 Illustratio 5 : amie the fuctio, f() = / 4, 0. Discuss the cotiuity, ad if discotiuous remove, 0 the discotiuity by redefiig the fuctio (if possible). Solutio : Graph of f() is show, from graph it is see that y 0 f() = 0 f() =, but f(0) = /4 Thus, f() has removable discotiuity ad f() could be made cotiuous by takig f(0) = f() =, 0, 0, 0 /4 O y = f() before redefiig Do yourself -3 : ; 0 3 ; 4 (i) If ƒ(), the discuss the types of discotiuity for the fuctio. 5 ; 4 / 4 ; 4 Type- : (No-Removable type of discotiuities) :- I case Lim f( ) does ot eist the it is ot possible to make the fuctio cotiuous by redefiig it. Such a a discotiuity is kow as o-removable discotiuity or discotiuity of the d kid. No-removable type of discotiuity ca be further classified as : (i) Fiite type discotiuity : I such type of discotiuity left had it ad right had it at a poit eists but are ot equal. (ii) Ifiite type discotiuity : I such type of discotiuity atleast oe of the it viz. LHL ad RHL is tedig to ifiity. 3 Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
6 J-Mathematics ( i i i) Oscillatory type discotiuity : e.g. f si at = 0 si f y y=si( /) f() has o removable oscillatory type discotiuity at = 0 ample : From the adjacet graph ote that (i) f is cotiuous at = (ii) f has isolated discotiuity at = (iii) f has missig poit discotiuity at = (iv) f has o removable (fiite type) discotiuity at the origi. - 0 Note : I case of o-removable (fiite type) discotiuity the o-egative differece betwee the value of the RHL at = a & LHL at = a is called the jump of discotiuity. A fuctio havig a fiite umber of jumps i a give iterval I is called a piece wise cotiuous or sectioally cotiuous fuctio i this iterval. Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65 Illustratio 6 : Show that the fuctio, f() = = 0. Solutio : We have, f() = e 0, ; whe 0 / e / ; whe 0 0 f() = h0 f(0 + h) = h0 0 f() = h0 0 f() = 0 f() 0 / h e / h e / e / ; whe 0 e 0, ; whe 0 h e h = 0 0 e = h0 e e / h / h has o-removable discotiuity at = [ e /h ] = [ h 0 ; e /h 0] f(). Thus f() has o-removable discotiuity. cos {cot } Illustratio 7 : f() = ; fid jump of discotiuity, where [ ] deotes greatest iteger & [] { } deotes fractioal part fuctio. 33
7 J-Mathematics cos {cot } Solutio : f() = [] f() = cos {cot } = cos cot h cos tah h0 h0 = f() [] h h0 jump of discotiuity = = Do yourself -4 : (i) Discuss the type of discotiuity for ; ƒ() ; ( ) ; 5. TH INTRMDIAT VALU THORM : Suppose f() is cotiuous o a iterval I, ad a ad b are ay two poits of I. The if y 0 is a umber betwee f(a) ad f(b), there eists a umber c betwee a ad b such that y f(b) y 0 f(a) f(c) = y 0 Note that a fuctio f which is cotiuous i [a,b] possesses the followig properties : 34 0 a c b The fuctio f, beig cotiuous o [a,b] takes o every value betwee f(a) ad f(b) ( i ) If f(a) & f(b) posses opposite sigs, the there eists atleast oe root of the equatio (ii) f() = 0 i the ope iterval (a,b). If K is ay real umber betwee f(a) & f(b), the there eists atleast oe root of the equatio f() = K i the ope iterval (a,b). Note : I above cases the umber of roots is always odd. Illustratio 8 : Show that the fuctio, f() = ( a) ( b) +, takes the value a b Solutio : f() = ( a) ( b) + f(a) = a f(b) = b & a b (f(a), f(b)) Illustratio 9 : Let f : [0, ] for some 0 (a, b) By itermediate value theorem, there is atleast oe 0 (a, b) such that f( 0 ) = a b [0, ] oto [0, ] be a cotiuous fuctio, the prove that f() = for atleast oe. Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
8 J-Mathematics Solutio : Cosider g() = f() g(0) = f(0) 0 = f(0) 0 0 f() g() = f() 0 g(0). g() 0 g() = 0 has atleast oe root i [0, ] f() = for atleast oe [0, ] Do yourself -5 : (i) If ƒ () is cotiuous i [a,b] such that ƒ (c) = ƒ(a) 3ƒ(b) 5, the prove that c (a,b) 6. SOM IMPORTANT POINTS : ( a ) If f() is cotiuous & g() is discotiuous at = a the the product fuctio ( ) f( ). g( ) will ot ecessarily be discotiuous at = a, e.g. L M N si f g M 0 & 0 0 f() is cotiuous at = 0 & g() is discotiuous at = 0, but f().g() is cotiuous at = 0. ( b ) If f () ad g () both are discotiuous at = a the the product fuctio ( ) f( ). g( ) is ot ecessarily be discotiuous at = a, e.g. f g L NM 0 0 f() & g() both are discotiuous at = 0 but the product fuctio f.g() is still cotiuous at = 0 ( c ) If f () ad g () both are discotiuous at = a the f() ± g() is ot ecessarily be discotiuous at = a ( d ) A cotiuous fuctio whose domai is closed must have a rage also i closed iterval. (e) If f is cotiuous at = a & g is cotiuous at = f (a) the the composite g[f()] is cotiuous at = a. eg. si f & g cotiuous at = 0 are cotiuous at =0, hece the composite ( gof) si will also be Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65 Illustratio 0 : If f() = ad g(), the discuss the cotiuity of f(), g() ad fog () i R. Solutio : f() = f() is a ratioal fuctio it must be cotiuous i its domai ad f is ot defied at =. f is discotiuous at = g() = g() is also a ratioal fuctio. It must be cotiuous i its domai ad g is ot defied at =. g is discotiuous at = Now fog() will be discotiuous at = (poit of discotiuity of g()) Cosider g() = (whe g() = poit of discotiuity of f()) = = 3 fog() is discotiuous at = & = 3. 35
9 J-Mathematics Do yourself -6 : (i) Let ƒ () = [] & g() = sg() (where [.] deotes greatest iteger fuctio), the discuss the cotiuity of ƒ () ± g(), ƒ ().g() & ƒ() at = 0. g() (ii) If ƒ () = si & g() = ta the discuss the cotiuity of ƒ () ± g() ; ƒ() & ƒ () g() g() 7. SINGL POINT CONTINUITY : Fuctios which are cotiuous oly at oe poit are said to ehibit sigle poit cotiuity Illustratio : If ƒ Solutio : if Q if Q, fid the poits where ƒ() is cotiuous Let = a be the poit at which ƒ() is cotiuous. ƒ() ƒ() a a through ratioal through irratioal a = a a = 0 fuctio is cotiuous at = 0. Do yourself -7 : (i) If g if Q, the fid the poits where fuctio is cotiuous. 0 if Q (ii) If ƒ() ; Q ; Q, the fid the poits where fuctio is cotiuous. ANSWRS FOR DO YOURSLF. (i) (ii) discotiuous at =. (i) a= & b= (ii) Discotiuous at = & cotiuous at = 3. (i) Missig poit removable discotiuity at =, isolated poit removable discotiuity at = ( i ) Fiite type o-removable discotiuity at =, 6. (i) All are discotiuous at = 0. (ii) ƒ () g() & ƒ () ± g() are discotiuous at ( ) ; I ƒ() g() is discotiuous at = ; I 7. (i) = 0 (ii) 36 Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
10 J-Mathematics XRCIS - 0 CHCK YOUR GRASP SLCT TH CORRCT ALTRNATIV (ONLY ON CORRCT ANSWR). If, whe f 4, whe 3 5, whe 3, the correct statemet is - (A) f f 3 (B) f() is cotiuous at = 3 (C) f() is cotiuous at = (D) f() is cotiuous at = ad 3, 0 f e, the - 0, 0. If / (A) 0 (B) f f 0 0 (C) f() is discotiuous at = 0 (D) f() is cotiuous 3. If fuctio f() = 3, is cotiuous fuctio, the f(0) is equal to - (A) (B) /4 (C) /6 (D) /3 4. If a a, f, is cotiuous at =, the a is equal to - (A) 0 (B) (C) (D) 5. If f() = log( a) log( b), 0 k, 0, is cotiuous at = 0, the k is equal to - Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65 6. If (A) a + b (B) a b (C) b a (D) a + b [] [ ], f(), f is cotiuous at = the is (where [.] deotes greatest iteger) -, (A) (B) 0 (C) (D) 7. If f() = cos 4, 0 a, 0, the correct statemet is - 6 4, 0 (A) f() is discotiuous at = 0 for ay value of a (B) f() is cotiuous at = 0 whe a = 8 (C) f() is cotiuous at = 0 whe a = 0 (D) oe of these 37
11 J-Mathematics 8. Fuctio f() = log is discotiuous at - (A) oe poit (B) two poits (C) three poits (D) ifiite umber of poits 9. Which of the followig fuctios has fiite umber of poits of discotiuity i R (where [.] deotes greatest iteger) (A) ta (B) / (C) + [] (D) si [] 0. If f() = ta,, 0, 4 4 is a cotiuous fuctios, the f(/4) is equal to - (A) / (B) / (C) (D). The value of f(0), so that fuctio, f() = by - a a a a a a becomes cotiuous for all, is give (A) a a (B) a (C) a (D) a a. If e cos f(), 0 is cotiuous at = 0, the - (A) f(0) = 5 (B) [f(0)] = (C) {f(0)} = 0.5 (D) [f(0)].{f(0)}=.5 where [] ad {} deotes greatest iteger ad fractioal part fuctio. 3. Let f() = ( a cos ) b si, 0 ad f(0) =. The value of a ad b so that f is a cotiuous fuctio are - 3 (A) 5/, 3/ (B) 5/, 3/ (C) 5/, 3/ (D) oe of these 4. f is a cotiuous fuctio o the real lie. Give that ( f ) 3. f( ) The the value of fe 3j is - (A) ( 3 ) 3 38 (B) ( 3) (C) zero (D) caot be determied SLCT TH CORRCT ALTRNATIVS (ON OR MOR THAN ON CORRCT ANSWRS) 5. The value(s) of for which ƒ () = e si 4 9 is cotiuous, is (are) - (A) 3 (B) 3 (C) 5 (D) all (, 3] [3, ) 6. Which of the followig fuctio(s) ot defied at = 0 has/have removable discotiuity at the origi? (A) f() (B) cot (C) f() si (D) f() = si f() cos Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
12 J-Mathematics 7. Fuctio whose jump (o-egative differece of LHL & RHL) of discotiuity is greater tha or equal to oe, is/are - (A) / (e ) / ƒ () (e ) ( cos ) ; 0 ; 0 (B) g() = / 3 / ; ; ( ) (C) u() = si ; 0, ta 3 si ; 0 (D) v() = log 3 ( ) ; log / ( 5) ; 8. If ƒ(), the 7 66 ƒ is discotiuous at = (A) (B) 7 3 (C) 4 (D) 6, 0; Z 9. Let ƒ () = [] & g(), the (where [.] deotes greatest iteger fuctio) - ; R Z (A) Lim g() eists, but g() is ot cotiuous at =. (B) Lim f() does ot eist ad ƒ () is ot cotiuous at =. (C) gof is cotiuous for all. (D) fog is cotiuous for all. Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65 CHCK YOUR GRASP ANSWR KY X R CI S - Que A s. C C C A A A B C B A Que A s. B D C B A, B B,C,D A,C,D A,B,C A,B,C 39
13 J-Mathematics XRCIS - 0 BRAIN TASRS SLCT TH CORRCT ALTRNATIVS (ON OR MOR THAN ON CORRCT ANSWRS) if 0. Cosider the piecewise defied fuctio f() 0 if if 4 the cotiuity of this fuctio - (A) the fuctio is ubouded ad therefore caot be cotiuous (B) the fuctio is right cotiuous at = 0 choose the aswer which best describes (C) the fuctio has a removable discotiuity at 0 ad 4, but is cotiuous o the rest of the real lie (D) the fuctio is cotiuous o the etire real lie. f() is cotiuous at =0, the which of the followig are always true? (A) Lim f() 0 (B) f() is o cotiuous at = 0 (C) g() = f() is cotiuous at = 0 3. Idicate all correct alteratives if, f (A) ta (f ()) & f (C) ta (f ())& f () are both cotiuous (D) Lim (f() f(0)) , the o the iterval [0,] are both cotiuous (B) ta (f()) & f (D) ta (f()) is cotiuous but are both discotiuous 4. If f() = sg(cos si + 3), where sg ( ) is the sigum fuctio, the f() - (A) is cotiuous over its domai (C) has isolated poit discotiuity cos cos si e 5. f() ; g() ( ) 8 4 h() = f() for </ = g() for >/ the which of the followigs does ot holds? (A) h is cotiuous at = / f is ot (B) has a missig poit discotiuity (D) has irremovable discotiuity. (C) h has a removable discotiuity at = / (D) f g (B) h has a irremovable discotiuity at =/ 6. The umber of poits where f() = [si + cos] (where [ ] deotes the greatest iteger fuctio), (0, ) is ot cotiuous is - (A) 3 (B) 4 (C) 5 (D) 6 7. O the iterval I = [, ], the fuctio f() = the which oe of the followig hold good? ( )e ( 0) 0 ( 0) (A) is cotiuous for all values of I (B) is cotiuous for I (0) (C) assumes all itermediate values from f( ) & f() (D) has a maimum value equal to 3/e 8. If f() = cos cos ; where [] is the greatest iteger fuctio of, the f() is cotiuous at - (A) = 0 (B) = (C) = (D) oe of these Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
14 9. Give f() / cos e cot for 0 for 0 J-Mathematics where { } & [ ] deotes the fractioal part ad the itegral part fuctios respectively, the which of the followig statemet does ot hold good - (A) f (0 ) = 0 (B) f(0 + )=3 (C) f(0)=0 cotiuity of f at = 0 (D) irremovable discotiuity of f at = 0 0. Let f be a cotiuous fuctio o R. If f ( / 4 ) (si e )e (A) ot uique (B) (C) data sufficiet to fid f(0) (D) data isufficiet to fid f(0). Give f() = b ([] + []) + for = si ( ( a)) for < the f(0) is - where [] deotes the itegral part of, the for what values of a, b the fuctio is cotiuous at =? (A) a (3 / ); b R ; I (B) a 4 ; b R ; I (C) a 4 (3 / ) ; b R ; I (D) a 4 ; b R ; I [] log (+) for < < 0. Cosider f() = le e { } j where [*] & {*} are the greatest iteger fuctio & for 0 < < ta fractioal part fuctio respectively, the - (A) f(0) = l f is cotiuous at = 0 (B) f(0) = f is cotiuous at = 0 (C) f(0) = e f is cotiuous at = 0 (D) f has a irremovable discotiuity at = 0 Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65 3. Let a si for 0 ad f() m b cos for 0 ad m the - (A) f(0 ) f(0 + ) (B) f(0 + ) f(0) (C) f(0 ) f(0) (D) f is cotiuous at = 0 4. Cosider f Lim si si (A) f is cotiuous at = (B) f has a fiite discotiuity at = for 0, f()=0 the - (C) f has a ifiite or oscillatory discotiuity at = (D) f has a removable type of discotiuity at = BRAIN TASRS ANSWR KY X R CI S - Que A s. D C, D C, D C A,C,D C B,C,D B, C B, D B, C Que. 3 4 A s. A,C D A B 4
15 J-Mathematics XRCIS - 03 TRU / FALS. [] is discotiuous at ifiite poits. ([ ] deotes greatest iteger fuctio). si + si is ot cotiuous for all. 3. If f is cotiuous ad g is discotiuous at = a, the f().g() is discotiuous at = a. 4. There eists a cotiuous oto fuctio f : [0, ] [0, 0], but there eists o cotiuous oto fuctio g : [0, ] (0, 0) ta( / 4 ) 5. If f() = for, the the value which ca be give to f() at = so that the fuctio cos 4 4 becomes cotiuous every where i (0, /) is /4. 6. The fuctio f, defied by f() = is cotiuous for real. ta 7. f() = si is cotiuous at =. MISCLLANOUS TYP QUSTIONS 8. If f() is cotiuous i [0, ] ad f() = for all ratioal umbers i [0, ] the f =. MATCH TH COLUMN Followig questios cotais statemets give i two colums, which have to be matched. The statemets i Colum-I are labelled as A, B, C ad D while the statemets i Colum-II are labelled as p, q, r ad s. Ay give statemet i Colum-I ca have correct matchig with ON OR MOR statemet(s) i Colum-II.. Colum-I Colum-II (A) If f() = si{}; cos a ; where {.} deotes (p) the fractioal part fuctio, such that f() is cotiuous at =. If k = a (4 ) si 4 the k is (B) ( cos(si )) If the fuctio f() = is (q) 0 cotiuous at = 0, the f(0) is (C), Q f() =, the the values, Q (r) of at which f() is cotiuous (D) If f() = + { } + [], where [] ad {} (s) represets itegral ad fractioal part of, the the values of at which f() is discotiuous 4 Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
16 . Colum-I Colum-II J-Mathematics (A) If f() = /( ), the the poits at which (p) the fuctio fofof() is discotiuous (B) f(u) = u u, where u=. (q) 0 The values of at which 'f' is discotiuous (C) f() = u, where u =, 0, 0 (r) The umber of values of at which 'f' is discotiuous (D) The umber of value of at which the (s) fuctio f() = discotiuous ASSRTION & RASON is Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65 These questios cotais, Statemet I (assertio) ad Statemet II (reaso). (A) Statemet-I is true, Statemet-II is true ; Statemet-II is correct eplaatio for Statemet-I. (B) Statemet-I is true, Statemet-II is true ; Statemet-II is NOT a correct eplaatio for statemet-i. (C) Statemet-I is true, Statemet-II is false. (D) Statemet-I is false, Statemet-II is true.. Statemet-I : f() = si + [] is discotiuous at = 0 B e c a u s e Statemet-II : If g() is cotiuous & h() is discotiuous at = a, the g() + h() will ecessarily be discotiuous at = a (A) A (B) B (C) C (D) D si(a cos ) if (0,). Cosider ƒ () = 3 if 0 a b if 0 3. Let Statemet-I : If b = 3 ad a = 3 B e c a u s e the ƒ () is cotiuous i (, ) Statemet-II : If a fuctio is defied o a iterval I ad it eist at every poit of iterval I the fuctio is cotiuous i I. (A) A (B) B (C) C (D) D / cos e, 0 ƒ() 3 0, 0 the Statemet-I : ƒ () is cotiuous at = 0. B e c a u s e Statemet-II : / cos e. 0 4 (A) A (B) B (C) C (D) D 43
17 J-Mathematics 4. Statemet-I : The equatio B e c a u s e 3 si 3 has atleast oe solutio i [, ] 4 3 Statemet-II : If f:[a, b] R be a fuctio & let 'c' be a umber such that f(a) < c < f(b), the there is atleast oe umber (a, b) such that f() = c. (A) A (B) B (C) C (D) D e 5. Statemet-I : Rage of ƒ () = e e e 4 is ot R. B e c a u s e Statemet-II : Rage of a cotiuous eve fuctio ca ot be R. (A) A (B) B (C) C (D) D A B 6. Let ƒ () = 3A B (, ] 4 Statemet-I : ƒ () is cotiuous at all if A = 3 4, B = 4. B e c a u s e Statemet-II : Polyomial fuctio is always cotiuous. (A) A (B) B (C) C (D) D COMPRHNSION BASD QUSTIONS Comprehesio # If S ()... ( )( ) ( )( )...( ) ad > S () a b, 0 g(), 0 h : R R h() = O the basis of above iformatio, aswer the followig questios :. If g() is cotiuous at = 0 the a + b is equal to - (A) 0 (B) (C) (D) 3. If g() is cotiuous at = 0 the g'(0) is equal to - (A) 3. Idetify the icorrect optio - (B) h(6) 44 (C) a b (A) h() is surjective (B) domai of g() is [ /, ) (C) h() is bouded (D) = (D) does ot eist Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
18 J-Mathematics Comprehesio # A ma leaves his home early i the morig to have a walk. N He arrives at a juctio of road A & road B as show i figure. He takes the followig steps i later jourey : (a) km i orth directio Road B W S (b) chages directio & moves i orth-east directio for kms. Road A (c) chages directio & moves southwards for distace of km. (d) fially he chages the directio & moves i Home south-east directio to reach road A agai. Visible/Ivisible path :- The path traced by the ma i the directio parallel to road A & road B is called ivisible path, the remaiig path traced is visible. Visible poits :- The poits about which the ma chages directio are called visible poits ecept the poit from where he chages directio last time Now if road A & road B are take as -ais & y-ais the visible path & visible poit represets the graph of y = f(). O t he basis of above i format io, a swer t he fol low i g que st ios :. The value of at which the fuctio is discotiuous - (A) (B) 0 (C) (D) 3. The value of at which fof() is discotiuous - (A) 0 (B) (C) (D) 3 3. If f() is periodic with period 3, the f(9) is - (A) (B) 3 (C) 9 (D) oe of these Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65 MISCLLANOUS TYP QUSTION ANSWR KY XRCIS -3 Tr ue / False. T. F 3. F 4. T 5. F 6. F 7. F 8. T Match the Colum. (A) (p, r); (B) (s); (C) (s); (D) (p, q, r). (A) (q, s); (B) (p, r, s); (C) (q); (D) (q) Assertio & Reaso. A. C 3. A 4. C 5. A 6. B Comprehesio Based Questios Comprehesio # :. D. B 3. C Comprehesio # :. A. B,C 3. A 45
19 J-Mathematics XRCIS - 4 [A] CONCPTUAL SUBJCTIV XRCIS. If. Let, whe 0 5 4, whe 0 f() 3 4, whe 4 3, whe si for f a si b for cos for, discuss the cotiuity of f() i R. 3. Determie the values of a,b & c for which the fuctio is cotiuous at = 0. If f is cotiuous o, the fid the values of a & b. 46 si a si for 0 f c for 0 b / / 3 / for 0 b 4. Determie the kid of discotiuity of the fuctio y / at the poit = 0 f, 3 5. Suppose that 3 fbg 3 4 ad h 3 the K 3 (a) fid all zeros of f (b) fid the value of K that makes h cotiuous at =3 (c) usig the value of K foud i (b) determie whether h is a eve fuctio. 6. Draw the graph of the fuctio f, & discuss the cotiuity or discotiuity of f i the iterval. 7. si 3 A si B si If fbg b 0g is cotiuous at = 0, the fid A & B. Also fid f(0) (a) Let f( + y) = f() + f(y) for all, y & if the fuctio f() is cotiuous at = 0, the show that f() is cotiuous at all. (b) If f(. y) = f(). f(y) for all, y ad f() is cotiuous at =. Prove that f() is cotiuous for all ecept at = 0. Give f() amie the cotiuity at = 0 of the sum fuctio of the ifiite series : Show that : (a) a polyomial of a odd degree has at least oe real root (b) / a polyomial of a eve degree has at least two real roots if it attais at least oe value opposite i sig to the coefficiet of its highest-degree term. CONCPTUAL SUBJCTIV XRCIS ANSWR KY X R C IS - 4 ( A ). cotiuous every where ecept at = 0. a = b = 3. a = 3/, b 0, c = / 4. o-removable - fiite type 5. (a),, 3 (b) K= 5 (c) eve 6. f is cotiuous i 7. A = 4, B = 5, f( 0) = 9. discotiuous at = 0 Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
20 J-Mathematics XRCIS - 4 [B] BRAIN STORMING SUBJCTIV XRCIS. Give fbg F H G I r N r K J F H G I ta sec r K J ;, g r l f ta f ta. si ta Lim ; / 4 f ta K ; / 4 F HG I K J. Fid the value of k, if possible, where [ ] deotes the greatest iteger fuctio ad the domai of g() is 0, so that g() is cotiuous at / 4. Also state the poits of discotiuity of g() i b0, / 4g, if ay. 3 / 3, 0 ( ), 0. Let f()= ; g() /, 0 ( ), 0 3. Discuss the cotiuity of f i [0,] where f greater tha. Also draw the graph L N l 4. Discuss the cotiuity of the fuctio f Lim si Discuss the cotiuity of g(f()). for M 4 5 [ ] ; where [] is the greatest iteger ot [cos ] for at = a a a for 0 5. Cosider the fuctio g()= a where a > 0. a a for 0 Fid the value of a & g(0) so that the fuctio g() is cotiuous at = 0. Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65 si {}.si {} 3 6. Let f() = {} {} 7. Cosider aother fuctio g(); such that g() = f() for 0 f() for < 0 for 0 for 0 Discuss the cotiuity of the fuctios f() & g() at = 0. si ta a a f() ta si = ( ) ( ) sec cos for 0 where {} is the fractioal part of. for < 0, if f is cotiuous at = 0, fid a ow if g()= a.cot( a) for a, a 0, a > 0. If g is cotiuous at = a the show that g(e ) = e 47
21 J-Mathematics 8. Let [] deote the greatest iteger fuctio & f() be defied i a eighbourhood of by [] ep 4 4 6, f() 4 6 cos( ) A, ( ) ta( ) Fid the value of A & f() i order that f() may be cotiuous at =. 9. If g : [a, b] oto [a, b] is cotiuous show that there is some c [a, b] such that g(c) = c. e j e j 0. Let y... ad y Lim y. Discuss the cotiuity of b g y,, 3... ad y () at = 0 BRAIN STORMING SUBJCTIV XRCIS ANSWR KY X R C I S - 4 ( B ). k 0 ; g L NM b g l ta if 0 4. Hece g() is cotiuous everywhere. 0 if 4. gof is discotiuous at = 0, ad 3. the fuctio f is cotiuous everywhere i [0,] ecept for = 0,, & 4. discotiuous at = 5. a =, g(0)= 8 6. f(0 + ) = ; f(0 ) = 4 7. a = e 8. A = ; f() = / f is dicotiuous at = 0 ; g(0 + ) = g(0 ) = g(0) = g is cotiuous at = 0 0. y () is cotiuous at = 0 for all ad y () is discotiuous at = 0 48 Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
22 J-Mathematics XRCIS - 05 [A] J-[MAIN] : PRVIOUS YAR QUSTIONS. If f() = Q, the f is cotiuous at- [AI 00] Q () Oly at zero () oly at 0, (3) all real umbers (4) all ratioal umbers. If f() = e, 0 0, 0 the f() is- [AI 003] () discotiuous everywhere () cotiuous as well as differetiable for all (3) cotiuous for all but ot differetiable at =0 (4) either differetiable or cotiuous at = 0 3. Let f() = ta 4,, 0, 4, If f() is cotiuous i 0,, the f 4 is- [AI 004] () () / (3) / (4) 4. The fuctio f : R/{0} R give by f() = e ca be made cotiuous at = 0 by defiig f(0) as- [AI 007] () () (3) 0 (4) si(p ) si, 0 q, 0 5. The values of p ad q for which the fuctio f() =, 0 3 is cotiuous for all i R, are:- [AI 0] () p = 3, q = () p =, q = 3 (3) p =, q = 3 (4) p = 5, q = Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65 6. Defie F() as the product of two real fuctios f () =, IR, ad si, if 0 f () 0, if 0 as follows: f ().f () if 0 F() [AI 0] 0, if 0 Statemet- : F() is cotiuous o IR. Statemet- : f () ad f () are cotiuous o IR. () Stateme- is false, statemet- is true. () Stateme- i s true, statemet - i s true; Statemet- is correct eplaatio for statemet-. (3) Statemet- is true, statemet- is true, statemet- is ot a correct eplaatio for statemet- (4) Statemet- is true, statemet- is false 7. Cosider the fuctio, f() = + 5, R. Statemet : f'(4) = 0. Statemet : f is cotiuous i [, 5], differetiable i (, 5) ad f() = f(5). [AI 0] () Statemet is true, Statemet is false. () Statemet is false, Statemet is true. (3) Statemet is true, Statemet is true ; Statemet is a correct eplaatio for Statemet. (4) Statemet is true, Statemet is true ; Statemet is ot a correct eplaatio for Statemet. PRVIOUS YARS QUSTIONS ANSWR KY Q u e A s XRCIS-5 [A] 49
23 J-Mathematics XRCIS - 05 [B] J-[ADVANCD] : PRVIOUS YAR QUSTIONS. Discuss the cotiuity of the fuctio /( ) e /( ), ƒ() e, at =. [R 00 (Mais), 3]. For every iteger, let a ad b be real umbers. Let fuctio ƒ : IR IR be give by a si, for, ƒ(), for all itegers. b cos, for, If ƒ is cotiuous, the which of the followig holds(s) for all? [J 0, 4] (A) a b = 0 (B) a b = (C) a b + = (D) a b = PRVIOUS YARS QUSTIONS ANSWR KY. Discotiuous at = ; f( + ) = ad f( ) =. B,D 50 XRCIS-5 [B] Node-6\:\Data\04\Kota\J-Advaced\SMP\Maths\Uit#04\g\0.CONTINUITY\CONTINUITY.P65
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The Graphs of Polynomial Functions
 Sectio 4.3 The Graphs of Polyomial Fuctios Objective 1: Uderstadig the Defiitio of a Polyomial Fuctio Defiitio Polyomial Fuctio 1 2 The fuctio ax a 1x a 2x a1x a0 is a polyomial fuctio of degree where
Sectio 4.3 The Graphs of Polyomial Fuctios Objective 1: Uderstadig the Defiitio of a Polyomial Fuctio Defiitio Polyomial Fuctio 1 2 The fuctio ax a 1x a 2x a1x a0 is a polyomial fuctio of degree where
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
PLEASURE TEST SERIES (XI) - 04 By O.P. Gupta (For stuffs on Math, click at theopgupta.com)
 wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
9 x and g(x) = 4. x. Find (x) 3.6. I. Combining Functions. A. From Equations. Example: Let f(x) = and its domain. Example: Let f(x) = and g(x) = x x 4
 1 3.6 I. Combiig Fuctios A. From Equatios Example: Let f(x) = 9 x ad g(x) = 4 f x. Fid (x) g ad its domai. 4 Example: Let f(x) = ad g(x) = x x 4. Fid (f-g)(x) B. From Graphs: Graphical Additio. Example:
1 3.6 I. Combiig Fuctios A. From Equatios Example: Let f(x) = 9 x ad g(x) = 4 f x. Fid (x) g ad its domai. 4 Example: Let f(x) = ad g(x) = x x 4. Fid (f-g)(x) B. From Graphs: Graphical Additio. Example:
On Infinite Groups that are Isomorphic to its Proper Infinite Subgroup. Jaymar Talledo Balihon. Abstract
 O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
Numerical Methods Lecture 6 - Curve Fitting Techniques
 Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
NTH, GEOMETRIC, AND TELESCOPING TEST
 NTH, GEOMETRIC, AND TELESCOPING TEST Sectio 9. Calculus BC AP/Dual, Revised 08 viet.dag@humbleisd.et /4/08 0:0 PM 9.: th, Geometric, ad Telescopig Test SUMMARY OF TESTS FOR SERIES Lookig at the first few
NTH, GEOMETRIC, AND TELESCOPING TEST Sectio 9. Calculus BC AP/Dual, Revised 08 viet.dag@humbleisd.et /4/08 0:0 PM 9.: th, Geometric, ad Telescopig Test SUMMARY OF TESTS FOR SERIES Lookig at the first few
TANGENT & NORM AL. Here L is not tangent to C
 J-Mathematics TANGNT & NORM AL. TANGNT TO TH CURV AT A POINT : The tangent to the curve at 'P' is the line through P whose slope is limit of the secant slopes as Q P from either side.. MYTHS ABOUT TANGNT
J-Mathematics TANGNT & NORM AL. TANGNT TO TH CURV AT A POINT : The tangent to the curve at 'P' is the line through P whose slope is limit of the secant slopes as Q P from either side.. MYTHS ABOUT TANGNT
The Closest Line to a Data Set in the Plane. David Gurney Southeastern Louisiana University Hammond, Louisiana
 The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
Homework 1 Solutions MA 522 Fall 2017
 Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Homework 1 Solutios MA 5 Fall 017 1. Cosider the searchig problem: Iput A sequece of umbers A = [a 1,..., a ] ad a value v. Output A idex i such that v = A[i] or the special value NIL if v does ot appear
Math Section 2.2 Polynomial Functions
 Math 1330 - Sectio. Polyomial Fuctios Our objectives i workig with polyomial fuctios will be, first, to gather iformatio about the graph of the fuctio ad, secod, to use that iformatio to geerate a reasoably
Math 1330 - Sectio. Polyomial Fuctios Our objectives i workig with polyomial fuctios will be, first, to gather iformatio about the graph of the fuctio ad, secod, to use that iformatio to geerate a reasoably
CIS 121 Data Structures and Algorithms with Java Fall Big-Oh Notation Tuesday, September 5 (Make-up Friday, September 8)
 CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
Recursive Estimation
 Recursive Estimatio Raffaello D Adrea Sprig 2 Problem Set: Probability Review Last updated: February 28, 2 Notes: Notatio: Uless otherwise oted, x, y, ad z deote radom variables, f x (x) (or the short
Recursive Estimatio Raffaello D Adrea Sprig 2 Problem Set: Probability Review Last updated: February 28, 2 Notes: Notatio: Uless otherwise oted, x, y, ad z deote radom variables, f x (x) (or the short
Mathematical Stat I: solutions of homework 1
 Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Section 7.2: Direction Fields and Euler s Methods
 Sectio 7.: Directio ields ad Euler s Methods Practice HW from Stewart Tetbook ot to had i p. 5 # -3 9-3 odd or a give differetial equatio we wat to look at was to fid its solutio. I this chapter we will
Sectio 7.: Directio ields ad Euler s Methods Practice HW from Stewart Tetbook ot to had i p. 5 # -3 9-3 odd or a give differetial equatio we wat to look at was to fid its solutio. I this chapter we will
South Slave Divisional Education Council. Math 10C
 South Slave Divisioal Educatio Coucil Math 10C Curriculum Package February 2012 12 Strad: Measuremet Geeral Outcome: Develop spatial sese ad proportioal reasoig It is expected that studets will: 1. Solve
South Slave Divisioal Educatio Coucil Math 10C Curriculum Package February 2012 12 Strad: Measuremet Geeral Outcome: Develop spatial sese ad proportioal reasoig It is expected that studets will: 1. Solve
Math 3201 Notes Chapter 4: Rational Expressions & Equations
 Learig Goals: See p. tet.. Equivalet Ratioal Epressios ( classes) Read Goal p. 6 tet. Math 0 Notes Chapter : Ratioal Epressios & Equatios. Defie ad give a eample of a ratioal epressio. p. 6. Defie o-permissible
Learig Goals: See p. tet.. Equivalet Ratioal Epressios ( classes) Read Goal p. 6 tet. Math 0 Notes Chapter : Ratioal Epressios & Equatios. Defie ad give a eample of a ratioal epressio. p. 6. Defie o-permissible
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Math 10C Long Range Plans
 Math 10C Log Rage Plas Uits: Evaluatio: Homework, projects ad assigmets 10% Uit Tests. 70% Fial Examiatio.. 20% Ay Uit Test may be rewritte for a higher mark. If the retest mark is higher, that mark will
Math 10C Log Rage Plas Uits: Evaluatio: Homework, projects ad assigmets 10% Uit Tests. 70% Fial Examiatio.. 20% Ay Uit Test may be rewritte for a higher mark. If the retest mark is higher, that mark will
Solution printed. Do not start the test until instructed to do so! CS 2604 Data Structures Midterm Spring, Instructions:
 CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
CS 604 Data Structures Midterm Sprig, 00 VIRG INIA POLYTECHNIC INSTITUTE AND STATE U T PROSI M UNI VERSI TY Istructios: Prit your ame i the space provided below. This examiatio is closed book ad closed
Polynomial Functions and Models. Learning Objectives. Polynomials. P (x) = a n x n + a n 1 x n a 1 x + a 0, a n 0
 Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Intro to Scientific Computing: Solutions
 Itro to Scietific Computig: Solutios Dr. David M. Goulet. How may steps does it take to separate 3 objects ito groups of 4? We start with 5 objects ad apply 3 steps of the algorithm to reduce the pile
Itro to Scietific Computig: Solutios Dr. David M. Goulet. How may steps does it take to separate 3 objects ito groups of 4? We start with 5 objects ad apply 3 steps of the algorithm to reduce the pile
CMPT 125 Assignment 2 Solutions
 CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
CMPT 25 Assigmet 2 Solutios Questio (20 marks total) a) Let s cosider a iteger array of size 0. (0 marks, each part is 2 marks) it a[0]; I. How would you assig a poiter, called pa, to store the address
Pseudocode ( 1.1) Analysis of Algorithms. Primitive Operations. Pseudocode Details. Running Time ( 1.1) Estimating performance
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
9.1. Sequences and Series. Sequences. What you should learn. Why you should learn it. Definition of Sequence
 _9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
_9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
Assignment 5; Due Friday, February 10
 Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Chapter 9. Pointers and Dynamic Arrays. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
University of Waterloo Department of Electrical and Computer Engineering ECE 250 Algorithms and Data Structures
 Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
FURTHER INTEGRATION TECHNIQUES (TRIG, LOG, EXP FUNCTIONS)
 Mathematics Revisio Guides More Trigoometric ad Log Itegrals Page of 7 MK HOME TUITION Mathematics Revisio Guides Level: AS / A Level AQA : C Edexcel: C OCR: C OCR MEI: C FURTHER INTEGRATION TECHNIQUES
Mathematics Revisio Guides More Trigoometric ad Log Itegrals Page of 7 MK HOME TUITION Mathematics Revisio Guides Level: AS / A Level AQA : C Edexcel: C OCR: C OCR MEI: C FURTHER INTEGRATION TECHNIQUES
EVALUATION OF TRIGONOMETRIC FUNCTIONS
 EVALUATION OF TRIGONOMETRIC FUNCTIONS Whe first exposed to trigoometric fuctios i high school studets are expected to memorize the values of the trigoometric fuctios of sie cosie taget for the special
EVALUATION OF TRIGONOMETRIC FUNCTIONS Whe first exposed to trigoometric fuctios i high school studets are expected to memorize the values of the trigoometric fuctios of sie cosie taget for the special
Arithmetic Sequences
 . Arithmetic Sequeces COMMON CORE Learig Stadards HSF-IF.A. HSF-BF.A.1a HSF-BF.A. HSF-LE.A. Essetial Questio How ca you use a arithmetic sequece to describe a patter? A arithmetic sequece is a ordered
. Arithmetic Sequeces COMMON CORE Learig Stadards HSF-IF.A. HSF-BF.A.1a HSF-BF.A. HSF-LE.A. Essetial Questio How ca you use a arithmetic sequece to describe a patter? A arithmetic sequece is a ordered
Consider the following population data for the state of California. Year Population
 Assigmets for Bradie Fall 2016 for Chapter 5 Assigmet sheet for Sectios 5.1, 5.3, 5.5, 5.6, 5.7, 5.8 Read Pages 341-349 Exercises for Sectio 5.1 Lagrage Iterpolatio #1, #4, #7, #13, #14 For #1 use MATLAB
Assigmets for Bradie Fall 2016 for Chapter 5 Assigmet sheet for Sectios 5.1, 5.3, 5.5, 5.6, 5.7, 5.8 Read Pages 341-349 Exercises for Sectio 5.1 Lagrage Iterpolatio #1, #4, #7, #13, #14 For #1 use MATLAB
Convergence results for conditional expectations
 Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Test 4 Review. dy du 9 5. sin5 zdz. dt. 5 Ê. x 2 È 1, 3. 2cos( x) dx is less than using Simpson's. ,1 t 5 t 2. ft () t2 4.
 Name: Class: Date: ID: A Test Review Short Aswer. Fid the geeral solutio of the differetial equatio below ad check the result by differetiatio. dy du 9 u. Use the error formula to estimate the error i
Name: Class: Date: ID: A Test Review Short Aswer. Fid the geeral solutio of the differetial equatio below ad check the result by differetiatio. dy du 9 u. Use the error formula to estimate the error i
IMP: Superposer Integrated Morphometrics Package Superposition Tool
 IMP: Superposer Itegrated Morphometrics Package Superpositio Tool Programmig by: David Lieber ( 03) Caisius College 200 Mai St. Buffalo, NY 4208 Cocept by: H. David Sheets, Dept. of Physics, Caisius College
IMP: Superposer Itegrated Morphometrics Package Superpositio Tool Programmig by: David Lieber ( 03) Caisius College 200 Mai St. Buffalo, NY 4208 Cocept by: H. David Sheets, Dept. of Physics, Caisius College
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
OCR Statistics 1. Working with data. Section 3: Measures of spread
 Notes ad Eamples OCR Statistics 1 Workig with data Sectio 3: Measures of spread Just as there are several differet measures of cetral tedec (averages), there are a variet of statistical measures of spread.
Notes ad Eamples OCR Statistics 1 Workig with data Sectio 3: Measures of spread Just as there are several differet measures of cetral tedec (averages), there are a variet of statistical measures of spread.
Descriptive Statistics Summary Lists
 Chapter 209 Descriptive Statistics Summary Lists Itroductio This procedure is used to summarize cotiuous data. Large volumes of such data may be easily summarized i statistical lists of meas, couts, stadard
Chapter 209 Descriptive Statistics Summary Lists Itroductio This procedure is used to summarize cotiuous data. Large volumes of such data may be easily summarized i statistical lists of meas, couts, stadard
Parametric curves. Reading. Parametric polynomial curves. Mathematical curve representation. Brian Curless CSE 457 Spring 2015
 Readig Required: Agel 0.-0.3, 0.5., 0.6-0.7, 0.9 Parametric curves Bria Curless CSE 457 Sprig 05 Optioal Bartels, Beatty, ad Barsy. A Itroductio to Splies for use i Computer Graphics ad Geometric Modelig,
Readig Required: Agel 0.-0.3, 0.5., 0.6-0.7, 0.9 Parametric curves Bria Curless CSE 457 Sprig 05 Optioal Bartels, Beatty, ad Barsy. A Itroductio to Splies for use i Computer Graphics ad Geometric Modelig,
Integration: Reduction Formulas Any positive integer power of sin x can be integrated by using a reduction formula.
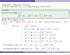 Itegratio: Reductio Formulas Ay positive iteger power of si x ca be itegrated by usig a reductio formula. Prove that for ay iteger 2, si xdx = 1 si 1 x cos x + 1 si Solutio. Weuseitegratiobyparts. Let
Itegratio: Reductio Formulas Ay positive iteger power of si x ca be itegrated by usig a reductio formula. Prove that for ay iteger 2, si xdx = 1 si 1 x cos x + 1 si Solutio. Weuseitegratiobyparts. Let
Counting Regions in the Plane and More 1
 Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
Coutig Regios i the Plae ad More 1 by Zvezdelia Stakova Berkeley Math Circle Itermediate I Group September 016 1. Overarchig Problem Problem 1 Regios i a Circle. The vertices of a polygos are arraged o
CS473-Algorithms I. Lecture 2. Asymptotic Notation. CS 473 Lecture 2 1
 CS473-Algorithms I Lecture Asymptotic Notatio CS 473 Lecture 1 O-otatio (upper bouds) f() = O(g()) if positive costats c, 0 such that e.g., = O( 3 ) 0 f() cg(), 0 c 3 c c = 1 & 0 = or c = & 0 = 1 Asymptotic
CS473-Algorithms I Lecture Asymptotic Notatio CS 473 Lecture 1 O-otatio (upper bouds) f() = O(g()) if positive costats c, 0 such that e.g., = O( 3 ) 0 f() cg(), 0 c 3 c c = 1 & 0 = or c = & 0 = 1 Asymptotic
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
Parabolic Path to a Best Best-Fit Line:
 Studet Activity : Fidig the Least Squares Regressio Lie By Explorig the Relatioship betwee Slope ad Residuals Objective: How does oe determie a best best-fit lie for a set of data? Eyeballig it may be
Studet Activity : Fidig the Least Squares Regressio Lie By Explorig the Relatioship betwee Slope ad Residuals Objective: How does oe determie a best best-fit lie for a set of data? Eyeballig it may be
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
Pattern Recognition Systems Lab 1 Least Mean Squares
 Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
2) Give an example of a polynomial function of degree 4 with leading coefficient of -6
 Math 165 Read ahead some cocepts from sectios 4.1 Read the book or the power poit presetatios for this sectio to complete pages 1 ad 2 Please, do ot complete the other pages of the hadout If you wat to
Math 165 Read ahead some cocepts from sectios 4.1 Read the book or the power poit presetatios for this sectio to complete pages 1 ad 2 Please, do ot complete the other pages of the hadout If you wat to
CS 683: Advanced Design and Analysis of Algorithms
 CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
An (or ) is a sequence in which each term after the first differs from the preceding term by a fixed constant, called the.
 Sectio.2 Arithmetic Sequeces ad Series -.2 Arithmetic Sequeces ad Series Arithmetic Sequeces Arithmetic Series Key Terms: arithmetic sequece (arithmetic progressio), commo differece, arithmetic series
Sectio.2 Arithmetic Sequeces ad Series -.2 Arithmetic Sequeces ad Series Arithmetic Sequeces Arithmetic Series Key Terms: arithmetic sequece (arithmetic progressio), commo differece, arithmetic series
Octahedral Graph Scaling
 Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Protected points in ordered trees
 Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Cubic Polynomial Curves with a Shape Parameter
 roceedigs of the th WSEAS Iteratioal Coferece o Robotics Cotrol ad Maufacturig Techology Hagzhou Chia April -8 00 (pp5-70) Cubic olyomial Curves with a Shape arameter MO GUOLIANG ZHAO YANAN Iformatio ad
roceedigs of the th WSEAS Iteratioal Coferece o Robotics Cotrol ad Maufacturig Techology Hagzhou Chia April -8 00 (pp5-70) Cubic olyomial Curves with a Shape arameter MO GUOLIANG ZHAO YANAN Iformatio ad
Compactness of Fuzzy Sets
 Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
It just came to me that I 8.2 GRAPHS AND CONVERGENCE
 44 Chapter 8 Discrete Mathematics: Fuctios o the Set of Natural Numbers (a) Take several odd, positive itegers for a ad write out eough terms of the 3N sequece to reach a repeatig loop (b) Show that ot
44 Chapter 8 Discrete Mathematics: Fuctios o the Set of Natural Numbers (a) Take several odd, positive itegers for a ad write out eough terms of the 3N sequece to reach a repeatig loop (b) Show that ot
COMP 558 lecture 6 Sept. 27, 2010
 Radiometry We have discussed how light travels i straight lies through space. We would like to be able to talk about how bright differet light rays are. Imagie a thi cylidrical tube ad cosider the amout
Radiometry We have discussed how light travels i straight lies through space. We would like to be able to talk about how bright differet light rays are. Imagie a thi cylidrical tube ad cosider the amout
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Algorithms Chapter 3 Growth of Functions
 Algorithms Chapter 3 Growth of Fuctios Istructor: Chig Chi Li 林清池助理教授 chigchi.li@gmail.com Departmet of Computer Sciece ad Egieerig Natioal Taiwa Ocea Uiversity Outlie Asymptotic otatio Stadard otatios
Algorithms Chapter 3 Growth of Fuctios Istructor: Chig Chi Li 林清池助理教授 chigchi.li@gmail.com Departmet of Computer Sciece ad Egieerig Natioal Taiwa Ocea Uiversity Outlie Asymptotic otatio Stadard otatios
Evaluation scheme for Tracking in AMI
 A M I C o m m u i c a t i o A U G M E N T E D M U L T I - P A R T Y I N T E R A C T I O N http://www.amiproject.org/ Evaluatio scheme for Trackig i AMI S. Schreiber a D. Gatica-Perez b AMI WP4 Trackig:
A M I C o m m u i c a t i o A U G M E N T E D M U L T I - P A R T Y I N T E R A C T I O N http://www.amiproject.org/ Evaluatio scheme for Trackig i AMI S. Schreiber a D. Gatica-Perez b AMI WP4 Trackig:
MATHEMATICAL METHODS OF ANALYSIS AND EXPERIMENTAL DATA PROCESSING (Or Methods of Curve Fitting)
 MATHEMATICAL METHODS OF ANALYSIS AND EXPERIMENTAL DATA PROCESSING (Or Methods of Curve Fittig) I this chapter, we will eamie some methods of aalysis ad data processig; data obtaied as a result of a give
MATHEMATICAL METHODS OF ANALYSIS AND EXPERIMENTAL DATA PROCESSING (Or Methods of Curve Fittig) I this chapter, we will eamie some methods of aalysis ad data processig; data obtaied as a result of a give
The Adjacency Matrix and The nth Eigenvalue
 Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
The number n of subintervals times the length h of subintervals gives length of interval (b-a).
 Simulator with MadMath Kit: Riema Sums (Teacher s pages) I your kit: 1. GeoGebra file: Ready-to-use projector sized simulator: RiemaSumMM.ggb 2. RiemaSumMM.pdf (this file) ad RiemaSumMMEd.pdf (educator's
Simulator with MadMath Kit: Riema Sums (Teacher s pages) I your kit: 1. GeoGebra file: Ready-to-use projector sized simulator: RiemaSumMM.ggb 2. RiemaSumMM.pdf (this file) ad RiemaSumMMEd.pdf (educator's
WebAssign Lesson 6-1b Geometric Series (Homework)
 WebAssig Lesso 6-b Geometric Series (Homework) Curret Score : / 49 Due : Wedesday, July 30 204 :0 AM MDT Jaimos Skriletz Math 75, sectio 3, Summer 2 204 Istructor: Jaimos Skriletz. /2 poitsrogac alcet2
WebAssig Lesso 6-b Geometric Series (Homework) Curret Score : / 49 Due : Wedesday, July 30 204 :0 AM MDT Jaimos Skriletz Math 75, sectio 3, Summer 2 204 Istructor: Jaimos Skriletz. /2 poitsrogac alcet2
Bezier curves. Figure 2 shows cubic Bezier curves for various control points. In a Bezier curve, only
 Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
Edited: Yeh-Liag Hsu (998--; recommeded: Yeh-Liag Hsu (--9; last updated: Yeh-Liag Hsu (9--7. Note: This is the course material for ME55 Geometric modelig ad computer graphics, Yua Ze Uiversity. art of
Graceful Labelings of Pendant Graphs
 Rose-Hulma Udergraduate Mathematics Joural Volume Issue Article 0 Graceful Labeligs of Pedat Graphs Alessadra Graf Norther Arizoa Uiversity, ag@au.edu Follow this ad additioal works at: http://scholar.rose-hulma.edu/rhumj
Rose-Hulma Udergraduate Mathematics Joural Volume Issue Article 0 Graceful Labeligs of Pedat Graphs Alessadra Graf Norther Arizoa Uiversity, ag@au.edu Follow this ad additioal works at: http://scholar.rose-hulma.edu/rhumj
Convex hull ( 凸殻 ) property
 Covex hull ( 凸殻 ) property The covex hull of a set of poits S i dimesios is the itersectio of all covex sets cotaiig S. For N poits P,..., P N, the covex hull C is the give by the expressio The covex hull
Covex hull ( 凸殻 ) property The covex hull of a set of poits S i dimesios is the itersectio of all covex sets cotaiig S. For N poits P,..., P N, the covex hull C is the give by the expressio The covex hull
Examples and Applications of Binary Search
 Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
Toy Gog ITEE Uiersity of Queeslad I the secod lecture last week we studied the biary search algorithm that soles the problem of determiig if a particular alue appears i a sorted list of iteger or ot. We
The Inverse z-transform
 The Iverse -Trasfor I sciece oe tries to tell people, i such a way as to be uderstood by everyoe, soethig that o oe ever ew before. But i poetry, it's the eact opposite. Paul Dirac Cotet ad Figures are
The Iverse -Trasfor I sciece oe tries to tell people, i such a way as to be uderstood by everyoe, soethig that o oe ever ew before. But i poetry, it's the eact opposite. Paul Dirac Cotet ad Figures are
Matrix Partitions of Split Graphs
 Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
CS Polygon Scan Conversion. Slide 1
 CS 112 - Polygo Sca Coversio Slide 1 Polygo Classificatio Covex All iterior agles are less tha 180 degrees Cocave Iterior agles ca be greater tha 180 degrees Degeerate polygos If all vertices are colliear
CS 112 - Polygo Sca Coversio Slide 1 Polygo Classificatio Covex All iterior agles are less tha 180 degrees Cocave Iterior agles ca be greater tha 180 degrees Degeerate polygos If all vertices are colliear
Civil Engineering Computation
 Civil Egieerig Computatio Fidig Roots of No-Liear Equatios March 14, 1945 World War II The R.A.F. first operatioal use of the Grad Slam bomb, Bielefeld, Germay. Cotets 2 Root basics Excel solver Newto-Raphso
Civil Egieerig Computatio Fidig Roots of No-Liear Equatios March 14, 1945 World War II The R.A.F. first operatioal use of the Grad Slam bomb, Bielefeld, Germay. Cotets 2 Root basics Excel solver Newto-Raphso
Reading. Parametric curves. Mathematical curve representation. Curves before computers. Required: Angel , , , 11.9.
 Readig Required: Agel.-.3,.5.,.6-.7,.9. Optioal Parametric curves Bartels, Beatty, ad Barsky. A Itroductio to Splies for use i Computer Graphics ad Geometric Modelig, 987. Fari. Curves ad Surfaces for
Readig Required: Agel.-.3,.5.,.6-.7,.9. Optioal Parametric curves Bartels, Beatty, ad Barsky. A Itroductio to Splies for use i Computer Graphics ad Geometric Modelig, 987. Fari. Curves ad Surfaces for
A study on Interior Domination in Graphs
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
SAMPLE VERSUS POPULATION. Population - consists of all possible measurements that can be made on a particular item or procedure.
 SAMPLE VERSUS POPULATION Populatio - cosists of all possible measuremets that ca be made o a particular item or procedure. Ofte a populatio has a ifiite umber of data elemets Geerally expese to determie
SAMPLE VERSUS POPULATION Populatio - cosists of all possible measuremets that ca be made o a particular item or procedure. Ofte a populatio has a ifiite umber of data elemets Geerally expese to determie
Strong Complementary Acyclic Domination of a Graph
 Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
CSC165H1 Worksheet: Tutorial 8 Algorithm analysis (SOLUTIONS)
 CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
CSC165H1, Witer 018 Learig Objectives By the ed of this worksheet, you will: Aalyse the ruig time of fuctios cotaiig ested loops. 1. Nested loop variatios. Each of the followig fuctios takes as iput a
( n+1 2 ) , position=(7+1)/2 =4,(median is observation #4) Median=10lb
 Chapter 3 Descriptive Measures Measures of Ceter (Cetral Tedecy) These measures will tell us where is the ceter of our data or where most typical value of a data set lies Mode the value that occurs most
Chapter 3 Descriptive Measures Measures of Ceter (Cetral Tedecy) These measures will tell us where is the ceter of our data or where most typical value of a data set lies Mode the value that occurs most
Thompson s Group F (p + 1) is not Minimally Almost Convex
 Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Fast Fourier Transform (FFT) Algorithms
 Fast Fourier Trasform FFT Algorithms Relatio to the z-trasform elsewhere, ozero, z x z X x [ ] 2 ~ elsewhere,, ~ e j x X x x π j e z z X X π 2 ~ The DFS X represets evely spaced samples of the z- trasform
Fast Fourier Trasform FFT Algorithms Relatio to the z-trasform elsewhere, ozero, z x z X x [ ] 2 ~ elsewhere,, ~ e j x X x x π j e z z X X π 2 ~ The DFS X represets evely spaced samples of the z- trasform
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
Outline and Reading. Analysis of Algorithms. Running Time. Experimental Studies. Limitations of Experiments. Theoretical Analysis
 Outlie ad Readig Aalysis of Algorithms Iput Algorithm Output Ruig time ( 3.) Pseudo-code ( 3.2) Coutig primitive operatios ( 3.3-3.) Asymptotic otatio ( 3.6) Asymptotic aalysis ( 3.7) Case study Aalysis
Outlie ad Readig Aalysis of Algorithms Iput Algorithm Output Ruig time ( 3.) Pseudo-code ( 3.2) Coutig primitive operatios ( 3.3-3.) Asymptotic otatio ( 3.6) Asymptotic aalysis ( 3.7) Case study Aalysis
Area As A Limit & Sigma Notation
 Area As A Limit & Sigma Notatio SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should referece Chapter 5.4 of the recommeded textbook (or the equivalet chapter i your
Area As A Limit & Sigma Notatio SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should referece Chapter 5.4 of the recommeded textbook (or the equivalet chapter i your
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Python Programming: An Introduction to Computer Science
 Pytho Programmig: A Itroductio to Computer Sciece Chapter 6 Defiig Fuctios Pytho Programmig, 2/e 1 Objectives To uderstad why programmers divide programs up ito sets of cooperatig fuctios. To be able to
Pytho Programmig: A Itroductio to Computer Sciece Chapter 6 Defiig Fuctios Pytho Programmig, 2/e 1 Objectives To uderstad why programmers divide programs up ito sets of cooperatig fuctios. To be able to
ENGI 4421 Probability and Statistics Faculty of Engineering and Applied Science Problem Set 1 Descriptive Statistics
 ENGI 44 Probability ad Statistics Faculty of Egieerig ad Applied Sciece Problem Set Descriptive Statistics. If, i the set of values {,, 3, 4, 5, 6, 7 } a error causes the value 5 to be replaced by 50,
ENGI 44 Probability ad Statistics Faculty of Egieerig ad Applied Sciece Problem Set Descriptive Statistics. If, i the set of values {,, 3, 4, 5, 6, 7 } a error causes the value 5 to be replaced by 50,
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
The Magma Database file formats
 The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
Chapter 11. Friends, Overloaded Operators, and Arrays in Classes. Copyright 2014 Pearson Addison-Wesley. All rights reserved.
 Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
