Data Structure: Search Trees 2. Instructor: Prof. Young-guk Ha Dept. of Computer Science & Engineering
|
|
|
- Lee Nicholson
- 6 years ago
- Views:
Transcription
1 Data Structure: Search Trees Instructor: Prof. Young-guk Ha Dept. of Computer Science & Engineering
2 Search Trees Tree data structures that can be used to implement a dictionary, especially an ordered dictionary Binary search trees AVL trees Multi-way search trees (2,4) trees Red-black trees 2
3 Multi-Way Search Trees MST
4 Multi-Way Search Trees A Multi-way Search Tree (MST) is an ordered tree s.t. eery internal node with d children stores d-1 entries (d 2) for a node with children 1, 2,, d storing keys k 1, k 2,, k d-1 keys in the node are ordered as k 1 k 2 k d-1 [eery key in the subtree of 1 ] k 1 k i-1 [eery key in the subtree of i ] k i (where 2 i d-1) [eery key in the subtree of d ] k d-1 The leaes store no entries and sere as placeholders just like BST k 1 k
5 Multi-Way Inorder Traersal We can extend the notion of the inorder traersal from binary trees to MSTs I.e., inorder traersal on an MST isits entry (k i, x i ) of node between the recursie traersals of subtrees rooted at children i and i+1 As in the case of BST, inorder traersal isits all the entries on the MST in an increasing order 1 2 k 1 k * Traersal order: [subtree of 1 ] k 1 [subtree of 2 ] k 2 [subtree of 3 ]
6 Multi-Way Searching Similar to the BST search To find an entry with key k, start from the root For each internal node with children 1,, d and keys k 1,, k d-1 if k is in node, the search terminates successfully if k < k 1, we continue the search in child 1 if k i-1 < k < k i (2 i d - 1), we continue the search in child i if k > k d-1, we continue the search in child d Reaching an external node terminates the search unsuccessfully Fail to search for 12 Successful search for 24 6
7 Implementation of MST MST implementation using a generic tree linked structure with secondary dictionaries D() storing entries of node key (k i ) alue parent [ Node ] 5 Dictionary D( i ) of entries k 1 k 1 D() [ Entry ] child ( i ) Values are not represented in the figure D( 1 ) 7 9 D( 2 ) 7
8 Analysis of Liked-Structure- Based MSTs The oerall space complexity is O(n), where n is the number of entries stored in an MST T Time complexity analysis Time spent at a node with d children O(log d), if D() is based on a search table O(d), if D() is based on a unsorted list Let d max denote the max number of children of any node in T and h the height of T, the search time is O(h*log d max ), if D() is based on a search table O(h*d max ), if D() is based on a unsorted list If d max is a constant, the running time is O(h), irrespectie of the implementation of the secondary dictionaries Thus, the primary efficiency goal for an MST is also to keep the height as small as possible 8
9 (2,4) Trees (2, 4)
10 Definition of (2,4) Tree A (2,4) Tree (also called tree) is a multi-way search tree with the following properties Size property: eery internal node has at most four children (d max = 4) i.e., D() search operations at any node are performed in O(1) time whether D() is sorted or not Depth property: all the external nodes hae the same depth enforces the important bound on the height Depending on the number of children (degree), each internal node of a (2,4) tree is called 2-node, 3-node or 4-node node 3-node 2-node
11 Height of a (2,4) Tree Theorem: height of a (2,4) tree storing n entries = O(log n) Proof Let h be the height of a (2,4) tree storing n entries Since there are at least 2 i entries at depth i = 0,, h - 1 and no entry at depth h (leaes), we hae n h-1 = 2 h - 1 By taking a log at the both sides, we get h log (n + 1), h = O(log n) Thus, searching a (2,4) tree with n entries takes O(log n) time Note search time of an MST is O(h*log d max ) and d max of a (2,4) tree is a constant (d max = 4) depth 0 1 # of entries h-1 h 2 h-1 (= 4)
12 Insertion Inserting an entry (k, x) into a (2,4) tree 1) Let denote a node that is the parent of the leaf z reached by unsuccessfully searching for k 2) Add a new child w to on the left of z 3) Insert a new entry (k, x) into the node between w and z E.g.) Insert key z w z 12
13 Insertion (cont.) Insertion preseres the depth property, but may iolate the size property E.g.) After inserting key 30, an oerflow occurs at node node becomes 5-node z * Oerflow: node becomes 5-node w z 13
14 Oerflow and Split We can handle an oerflow at 5-node with the split operation Let 1 5 be the children of and k 1 k 4 be the keys of 1) Node is replaced with nodes ' and " ' is a 3-node with keys k 1 k 2 and children " is a 2-node with key k 4 and children 4 5 2) Key k 3 is inserted into the parent u of Note the oerflow may propagate to the parent node u Then, split u If u is the root, create new root and split old root u u u ' 35 "
15 Sequential Insertion Example Initial tree insert(6) insert(12) insert(15) oerflow new root split oerflow split insert(3) insert(5) insert(10) insert(8) 15
16 Cascading Split Example insert(17) oerflow oerflow split new root split 16
17 Analysis of Insertion Let T be a (2,4) tree with n entries Tree T has O(log n) height Step 1 takes O(log n) time because we isit at most O(log n) nodes Step 2 takes O(1) time Step 3 takes O(log n) time because each split takes O(1) time and we perform at most O(log n) splits toward the root Thus, an insertion in a (2,4) tree takes O(log n) time Algorithm insert(k, o) 1) Search for key k to locate the insertion node 2) Add the new entry (k, x) at node 3) while isoerflow() // handling // oerflow if isroot() create a new empty root aboe split() parent() 17
18 Deletion If the entry to be deleted is at the node with leaf children Just remoe the entry and a leaf child Otherwise, if the node storing the entry to be deleted has no leaf children Replace the entry with its inorder successor (or, equialently predecessor) and then delete the replaced entry E.g., to delete key 24, replace it with 27 (inorder successor) replace
19 Underflow and Transfer Deleting an entry from a node may cause an underflow I.e., node becomes 1-node (with one child and no key) To handle an underflow at node with parent u, we need to consider the following two cases Case 1: one of adjacent siblings w of is a 3-node or a 4-node Perform the transfer operation (transfer a child of w to ia u) 1) Moe an entry from u to 2) Moe an entry from w to u Transfer operation does NOT propagate underflow u 4 9 u w 6 8 underflow w
20 Underflow and Fusion Case 2: all the adjacent siblings of are 2-nodes Perform the fusion operation 1) Merge with an adjacent sibling w 2) Moe an entry from u to the merged node ' as 3-node After a fusion, the underflow may propagate to parent u if u is a 2-node If u is the root, delete u Otherwise, perform fusion or transfer with u u 9 14 u 9 w underflow ' 20
21 Sequential Deletion Example remoe(4) transfer remoe(12) fusion remoe(13) 21
22 Propagating Fusion Example underflow propagated fusion remoe the root remoe(14) fusion 22
23 Analysis of Deletion Let T be a (2,4) tree with n entries Tree T has O(log n) height In a deletion operation We isit O(log n) nodes to locate the node with the entry to be deleted And then, we may handle an underflow with a series of O(log n) fusions, followed by at most one transfer Each fusion and transfer takes O(1) time Thus, deleting an entry from a (2,4) tree takes a total O(log n) time 23
24 Summarizing Performance of (2,4) Trees s is the number of entries returned 24
25 Red-Black Trees
26 Definition of Red-Black Tree A Red-black Tree is a binary search tree with each node colored red or black in a way that satisfies the following 4 properties Root Property: the root is black External Property: eery leaf is black Internal Property: the children of a red node are black Depth Property: all the leaes hae the same black depth* 9 Black depth = # of black ancestors
27 Red-Black Trees s. Other Search Trees In comparison with AVL trees and (2,4) trees Red-black trees hae the same logarithmic time performance But AVL and (2,4) trees may perform O(log n) physical restructurings while red-black trees performs O(1) restructurings I.e., restructuring in red-black trees does NOT propagate (cf. recoloring) A red-black tree can be represented as a (2,4) tree, ice ersa By merging eery red node into its parent This proides important intuition that will be used to perform restructuring or recoloring in red-black trees From red-black tree to (2,4) tree 27
28 From (2,4) to Red-Black Tree w 13 or 14 w w 6 8 z 28
29 Height of a Red-Black Tree Theorem Height of a red-black tree storing n entries = O(log n) Proof The red-black tree is at most twice as high as its associated (2,4) tree whose height is O(log n) Note one (2,4) tree node becomes two leels of red-black tree nodes at maximum Height of a red-black tree 2 * height of (2,4) tree = 2 * O(log n) = O(log n) The search algorithm of a red-black tree is the same as that of a binary search tree Thus, by the aboe theorem, searching in a red-black tree takes O(log n) time 29
30 A red-black tree can be implemented with a linked structure for binary trees Each node has an additional color indicator field The space requirement of a red-black tree storing n keys is O(n) Implementation of Red-Black Tree 6 8 B 6 B B color indicator 8 R B 30
31 Insertion To perform insert operation 1) Execute the insertion algorithm for binary search trees with the new node z 2) Color red the newly inserted node z unless it is the root We presere the root, external, and depth properties 3) Check the color of the parent node of z If the parent of z is black, we also presere the internal property and we are done If the parent of z is red, we iolated the internal property and need a reorganization of the tree this is called double red problem 31
32 Insertion Examples Example: an insertion of 4 done z 4 Example: an insertion of 4 causing a double red double red z 4 32
33 Remedying a Double Red Consider a double red with newly added child z and its parent (let w be the sibling of ) Case 1: If w is black The double red is an incorrect placement of keys in a 4-node Restructuring: we perform the 4-node realignment Case 2: If w is red The double red corresponds to an oerflow Recoloring: we perform the equialent of a split w 2 4 z 6 7 w 2 4 z
34 Restructuring A restructuring remedies a child-parent double red when the parent red node has a black sibling It is equialent to restoring the correct alignment of keys in a 4-node After the restructuring, the internal property is restored and the other properties are presered z w 2 4 z 6 7 tri-node restructuring w realignment
35 Restructuring (cont.) There are four restructuring configurations depending on whether the double red nodes are left or right children Same as the tri-node restructuring in AVL trees double rotation single rotation realignment 35
36 Recoloring A recoloring remedies a child-parent double red when the parent red node has a red sibling The parent and its sibling w become black and the grandparent u becomes red (unless it is the root) It is equialent to performing a split on a 5-node The double red iolation may propagate up after recoloring Because u may become red Need to check and continue remedy until the double red is finally resoled w 2 4 z u 6 7 recoloring w 2 u 4 z split
37 Insertion Examples insert(7) insert(12) after restructuring after recoloring insert(3) insert(5) insert(15) after restructuring insert(14) afrter recoloring insert(18) 37
38 Insertion Examples (cont.) after restructuring insert(16) Another double red after recoloring insert(17) after restructuring 38
39 Analysis of Insertion Algorithm insert(k, o) 1) We search for key k to locate the insertion node z 2) We add the new entry (k, o) at node z and color z red 3) while isdoublered(z) // remedy // double red if isblack(sibling(parent(z))) restructure(z) return else // if sibling(parent(z)) is red recolor(z) z parent(parent(z)) Recall that a red-black tree has O(log n) height Step 1 takes O(log n) time for a BST search Step 2 takes O(1) time Step 3 takes O(log n) time because we may perform O(log n) recolorings, each taking O(1) time, and at most one restructuring taking O(1) time Thus, an insertion in a red-black tree takes O(log n) time 39
40 Deletion To perform remoe operation 1) First execute the deletion algorithm for binary search trees 2) If the remoed node was red, we are done 3) Or if the remoed node was black, let be the remoed node, w the remoed external child of, and r the sibling of w (either external or internal) If r is red, we color r black and we are done If r is black, we will hae a double black problem, which iolates the depth property 40
41 Deletion Examples Example: deletion of r 7 w color r black 7 r black depth = 2 black depth = 2 Example: deletion of 8 causing a double black r w y double black r black depth = 1 black depth = 2 41
42 Remedying a Double Black Basically, a double black corresponds to an underflow from the iew of (2,4) trees The algorithm for remedying a double black node r with sibling y considers the following three cases Case 1: y is black and has a red child Perform a restructuring, equialent to a transfer of (2,4) trees, and we are done Case 2: y is black and its children are both black Perform a recoloring, equialent to a fusion of (2,4) trees Recoloring may propagate up the double black problem Case 3: y is red Perform an adjustment (actually a restructuring), equialent to a 3-node realignment in (2,4) trees After an adjustment either Case 1 or Case 2 needs to be applied according to the resulting configuration (note that, in this case, een if recoloring is applied, double-black is NOT propagated) 42
43 Restructuring after a Deletion Case 1: if y is black and has a red child x black depth -1 x 1-node r 1-node r transfer black depth +1 restructuring: (a) single or (b) double rotation r : either red or black 43
44 Recoloring after a Deletion Case 2: if y is black and its children are both black black depth -1 ` 2-node black depth -1 fusion recoloring black depth +1? fusion ` 1-node s? recoloring black depth -1 Recoloring propagates double black 44
45 Adjustment after a Deletion Case 3: if y is red black depth = 1 r realignment of a 3-node tri-node restructuring (adjustment)? r? s black depth = 1 * double-black is not resoled yet apply case 1 or 2 again according to the colors of node s and s s children (* note double black is not propagated after recoloring) 45
46 Deletion Examples remoe(12) remoe(3) after restructuring restructuring remoe(17) 46
47 Deletion Examples (cont.) remoe(18) recoloring remoe(15) remoe(16) adjustment after adjustment Double black is not resoled yet recoloring double black is resoled 47
48 Analysis of Deletion The deletion algorithm basically has the same procedure as the insertion algorithm A BST search takes O(log n) time A BST deletion takes O(1) time A reorganization procedure consisting of O(log n) recolorings, each taking O(1) time At most one adjustment (restructuring) taking O(1) time One additional restructuring or recoloring after the adjustment each taking O(1) time Thus, a deletion in a red-black tree also takes a total of O(log n) time 48
49 Summary of Red-Black Tree Reorganization Remedying double red after a insertion Red-black tree action (2,4) tree action Result Restructuring 4-node Realignment Double red remoed Recoloring Split Double red remoed or propagated up Remedying double black after a deletion Red-black tree action (2,4) tree action Result Restructuring Transfer Double black remoed Recoloring Adjustment Fusion 3-node Realignment Double black remoed or propagated up A restructuring or a recoloring follows 49
50 Performance of Red-Black Trees searches * s is the number of entries returned reorganization - O(1) restructurings - O(log n) recolorings Red-black, AVL, and (2,4) trees hae the same update operation (insertion and remoal) performance of O(log n) Howeer, red-black trees performs at most O(1) physical restructurings during the up-phase while AVL and (2,4) trees perform O(log n) restructurings 50
Red-Black Trees. 2/24/2006 Red-Black Trees 1
 Red-Black Trees 3 8 //00 Red-Black Trees 1 Outline and Reading From (,) trees to red-black trees ( 10.5) Red-black tree ( 10.5.1) Definition Height Insertion restructuring recoloring Deletion restructuring
Red-Black Trees 3 8 //00 Red-Black Trees 1 Outline and Reading From (,) trees to red-black trees ( 10.5) Red-black tree ( 10.5.1) Definition Height Insertion restructuring recoloring Deletion restructuring
Red-Black Trees Goodrich, Tamassia. Red-Black Trees 1
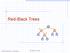 Red-Black Trees 3 8 00 Goodrich, Tamassia Red-Black Trees 1 From (,) to Red-Black Trees A red-black tree is a representation of a (,) tree by means of a binary tree hose nodes are colored red or black
Red-Black Trees 3 8 00 Goodrich, Tamassia Red-Black Trees 1 From (,) to Red-Black Trees A red-black tree is a representation of a (,) tree by means of a binary tree hose nodes are colored red or black
From (2,4) to Red-Black Trees
 Red-Black Trees 3/0/1 Presentation for use ith the textbook Data Structures and Algorithms in Jaa, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldasser, Wiley, 01 Red-Black Trees 3 8 01 Goodrich,
Red-Black Trees 3/0/1 Presentation for use ith the textbook Data Structures and Algorithms in Jaa, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldasser, Wiley, 01 Red-Black Trees 3 8 01 Goodrich,
Search Trees - 2. Venkatanatha Sarma Y. Lecture delivered by: Assistant Professor MSRSAS-Bangalore. M.S Ramaiah School of Advanced Studies - Bangalore
 Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Multi-Way Search Tree
 Presentation for se with the textbook Data Strctres and Algorithms in Jaa, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 204 (2,4) Trees 9 2 5 7 0 4 204 Goodrich, Tamassia,
Presentation for se with the textbook Data Strctres and Algorithms in Jaa, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 204 (2,4) Trees 9 2 5 7 0 4 204 Goodrich, Tamassia,
(2,4) Trees. 2/22/2006 (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
(2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
(2,4) Trees Goodrich, Tamassia (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
(2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Lecture 11: Multiway and (2,4) Trees. Courtesy to Goodrich, Tamassia and Olga Veksler
 Lecture 11: Multiway and (2,4) Trees 9 2 5 7 10 14 Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Multiway Seach Tree: a new type of search trees: for ordered d dictionary
Lecture 11: Multiway and (2,4) Trees 9 2 5 7 10 14 Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Multiway Seach Tree: a new type of search trees: for ordered d dictionary
Multi-Way Search Tree ( ) (2,4) Trees. Multi-Way Inorder Traversal. Multi-Way Search Tree ( ) Multi-Way Searching. Multi-Way Searching
 Mlti-Way Search Tree ( 0..) (,) Trees 9 5 7 0 (,) Trees (,) Trees Mlti-Way Search Tree ( 0..) A mlti-ay search tree is an ordered tree sch that Each internal node has at least to children and stores d
Mlti-Way Search Tree ( 0..) (,) Trees 9 5 7 0 (,) Trees (,) Trees Mlti-Way Search Tree ( 0..) A mlti-ay search tree is an ordered tree sch that Each internal node has at least to children and stores d
Multiway Search Trees. Multiway-Search Trees (cont d)
 Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
CS350: Data Structures Red-Black Trees
 Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
(2,4) Trees Goodrich, Tamassia. (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 (2,4) Trees 1 Multi-Way Search Tree ( 9.4.1) A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d 1 key-element items
(2,4) Trees 9 2 5 7 10 14 (2,4) Trees 1 Multi-Way Search Tree ( 9.4.1) A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d 1 key-element items
Trees. Courtesy to Goodrich, Tamassia and Olga Veksler
 Lecture 12: BT Trees Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline B-tree Special case of multiway search trees used when data must be stored on the disk, i.e. too large
Lecture 12: BT Trees Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline B-tree Special case of multiway search trees used when data must be stored on the disk, i.e. too large
Multi-way Search Trees. (Multi-way Search Trees) Data Structures and Programming Spring / 25
 Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
B-Trees and External Memory
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 and External Memory 1 1 (2, 4) Trees: Generalization of BSTs Each internal node
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 and External Memory 1 1 (2, 4) Trees: Generalization of BSTs Each internal node
B-Trees and External Memory
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 B-Trees and External Memory 1 (2, 4) Trees: Generalization of BSTs Each internal
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 B-Trees and External Memory 1 (2, 4) Trees: Generalization of BSTs Each internal
Algorithms. Deleting from Red-Black Trees B-Trees
 Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Search Trees. COMPSCI 355 Fall 2016
 Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
B Tree. Also, every non leaf node must have at least two successors and all leaf nodes must be at the same level.
 B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Self-Balancing Search Trees. Chapter 11
 Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
CMPS 2200 Fall 2017 Red-black trees Carola Wenk
 CMPS 2200 Fall 2017 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/13/17 CMPS 2200 Intro. to Algorithms 1 Dynamic Set A dynamic set, or dictionary, is a
CMPS 2200 Fall 2017 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/13/17 CMPS 2200 Intro. to Algorithms 1 Dynamic Set A dynamic set, or dictionary, is a
AVL Trees (10.2) AVL Trees
 AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
B-Trees. Disk Storage. What is a multiway tree? What is a B-tree? Why B-trees? Insertion in a B-tree. Deletion in a B-tree
 B-Trees Disk Storage What is a multiway tree? What is a B-tree? Why B-trees? Insertion in a B-tree Deletion in a B-tree Disk Storage Data is stored on disk (i.e., secondary memory) in blocks. A block is
B-Trees Disk Storage What is a multiway tree? What is a B-tree? Why B-trees? Insertion in a B-tree Deletion in a B-tree Disk Storage Data is stored on disk (i.e., secondary memory) in blocks. A block is
2-3 Tree. Outline B-TREE. catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } ADD SLIDES ON DISJOINT SETS
 Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
Lecture 6: Analysis of Algorithms (CS )
 Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Orthogonal range searching. Orthogonal range search
 CG Lecture Orthogonal range searching Orthogonal range search. Problem definition and motiation. Space decomposition: techniques and trade-offs 3. Space decomposition schemes: Grids: uniform, non-hierarchical
CG Lecture Orthogonal range searching Orthogonal range search. Problem definition and motiation. Space decomposition: techniques and trade-offs 3. Space decomposition schemes: Grids: uniform, non-hierarchical
CMPS 2200 Fall 2015 Red-black trees Carola Wenk
 CMPS 2200 Fall 2015 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/9/15 CMPS 2200 Intro. to Algorithms 1 ADT Dictionary / Dynamic Set Abstract data type
CMPS 2200 Fall 2015 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/9/15 CMPS 2200 Intro. to Algorithms 1 ADT Dictionary / Dynamic Set Abstract data type
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
CSCI 136 Data Structures & Advanced Programming. Lecture 25 Fall 2018 Instructor: B 2
 CSCI 136 Data Structures & Advanced Programming Lecture 25 Fall 2018 Instructor: B 2 Last Time Binary search trees (Ch 14) The locate method Further Implementation 2 Today s Outline Binary search trees
CSCI 136 Data Structures & Advanced Programming Lecture 25 Fall 2018 Instructor: B 2 Last Time Binary search trees (Ch 14) The locate method Further Implementation 2 Today s Outline Binary search trees
Trees. (Trees) Data Structures and Programming Spring / 28
 Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Properties of red-black trees
 Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Analysis of Algorithms
 Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
CSE 530A. B+ Trees. Washington University Fall 2013
 CSE 530A B+ Trees Washington University Fall 2013 B Trees A B tree is an ordered (non-binary) tree where the internal nodes can have a varying number of child nodes (within some range) B Trees When a key
CSE 530A B+ Trees Washington University Fall 2013 B Trees A B tree is an ordered (non-binary) tree where the internal nodes can have a varying number of child nodes (within some range) B Trees When a key
CS 3343 Fall 2007 Red-black trees Carola Wenk
 CS 3343 Fall 2007 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 334 Analysis of Algorithms 1 Search Trees A binary search tree is a binary tree.
CS 3343 Fall 2007 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 334 Analysis of Algorithms 1 Search Trees A binary search tree is a binary tree.
Search Trees. Chapter 11
 Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
TREES. Trees - Introduction
 TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
Multi-Way Search Tree
 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two and at most d children and stores d -1 data items (k i, D i ) Rule: Number of children = 1
Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two and at most d children and stores d -1 data items (k i, D i ) Rule: Number of children = 1
Dictionaries. Priority Queues
 Red-Black-Trees.1 Dictionaries Sets and Multisets; Opers: (Ins., Del., Mem.) Sequential sorted or unsorted lists. Linked sorted or unsorted lists. Tries and Hash Tables. Binary Search Trees. Priority Queues
Red-Black-Trees.1 Dictionaries Sets and Multisets; Opers: (Ins., Del., Mem.) Sequential sorted or unsorted lists. Linked sorted or unsorted lists. Tries and Hash Tables. Binary Search Trees. Priority Queues
CS Fall 2010 B-trees Carola Wenk
 CS 3343 -- Fall 2010 B-trees Carola Wenk 10/19/10 CS 3343 Analysis of Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
CS 3343 -- Fall 2010 B-trees Carola Wenk 10/19/10 CS 3343 Analysis of Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
13.4 Deletion in red-black trees
 Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Search Trees (Ch. 9) > = Binary Search Trees 1
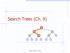 Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
AVL Trees Goodrich, Tamassia, Goldwasser AVL Trees 1
 AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
Lecture: Analysis of Algorithms (CS )
 Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
CHAPTER 10 AVL TREES. 3 8 z 4
 CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
Note that this is a rep invariant! The type system doesn t enforce this but you need it to be true. Should use repok to check in debug version.
 Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
Module 4: Dictionaries and Balanced Search Trees
 Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
CIS265/ Trees Red-Black Trees. Some of the following material is from:
 CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
Data Structure - Advanced Topics in Tree -
 Data Structure - Advanced Topics in Tree - AVL, Red-Black, B-tree Hanyang University Jong-Il Park AVL TREE Division of Computer Science and Engineering, Hanyang University Balanced binary trees Non-random
Data Structure - Advanced Topics in Tree - AVL, Red-Black, B-tree Hanyang University Jong-Il Park AVL TREE Division of Computer Science and Engineering, Hanyang University Balanced binary trees Non-random
CMPS 2200 Fall 2017 B-trees Carola Wenk
 CMPS 2200 Fall 2017 B-trees Carola Wenk 9/18/17 CMPS 2200 Intro. to Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
CMPS 2200 Fall 2017 B-trees Carola Wenk 9/18/17 CMPS 2200 Intro. to Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
Physical Level of Databases: B+-Trees
 Physical Level of Databases: B+-Trees Adnan YAZICI Computer Engineering Department METU (Fall 2005) 1 B + -Tree Index Files l Disadvantage of indexed-sequential files: performance degrades as file grows,
Physical Level of Databases: B+-Trees Adnan YAZICI Computer Engineering Department METU (Fall 2005) 1 B + -Tree Index Files l Disadvantage of indexed-sequential files: performance degrades as file grows,
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Chapter 2: Basic Data Structures
 Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Red-Black Trees. Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood
 Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
AVL Tree Definition. An example of an AVL tree where the heights are shown next to the nodes. Adelson-Velsky and Landis
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Trees. Truong Tuan Anh CSE-HCMUT
 Trees Truong Tuan Anh CSE-HCMUT Outline Basic concepts Trees Trees A tree consists of a finite set of elements, called nodes, and a finite set of directed lines, called branches, that connect the nodes
Trees Truong Tuan Anh CSE-HCMUT Outline Basic concepts Trees Trees A tree consists of a finite set of elements, called nodes, and a finite set of directed lines, called branches, that connect the nodes
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
Binary Search Trees. Analysis of Algorithms
 Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Augmenting Data Structures
 Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
CS 206 Introduction to Computer Science II
 CS 206 Introduction to Computer Science II 04 / 26 / 2017 Instructor: Michael Eckmann Today s Topics Questions? Comments? Balanced Binary Search trees AVL trees Michael Eckmann - Skidmore College - CS
CS 206 Introduction to Computer Science II 04 / 26 / 2017 Instructor: Michael Eckmann Today s Topics Questions? Comments? Balanced Binary Search trees AVL trees Michael Eckmann - Skidmore College - CS
M-ary Search Tree. B-Trees. B-Trees. Solution: B-Trees. B-Tree: Example. B-Tree Properties. Maximum branching factor of M Complete tree has height =
 M-ary Search Tree B-Trees Section 4.7 in Weiss Maximum branching factor of M Complete tree has height = # disk accesses for find: Runtime of find: 2 Solution: B-Trees specialized M-ary search trees Each
M-ary Search Tree B-Trees Section 4.7 in Weiss Maximum branching factor of M Complete tree has height = # disk accesses for find: Runtime of find: 2 Solution: B-Trees specialized M-ary search trees Each
Programming II (CS300)
 1 Programming II (CS300) Chapter 11: Binary Search Trees MOUNA KACEM mouna@cs.wisc.edu Fall 2018 General Overview of Data Structures 2 Introduction to trees 3 Tree: Important non-linear data structure
1 Programming II (CS300) Chapter 11: Binary Search Trees MOUNA KACEM mouna@cs.wisc.edu Fall 2018 General Overview of Data Structures 2 Introduction to trees 3 Tree: Important non-linear data structure
Chapter 10: Search Trees
 < 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
< 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
Search Trees. Undirected graph Directed graph Tree Binary search tree
 Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
An AVL tree with N nodes is an excellent data. The Big-Oh analysis shows that most operations finish within O(log N) time
 B + -TREES MOTIVATION An AVL tree with N nodes is an excellent data structure for searching, indexing, etc. The Big-Oh analysis shows that most operations finish within O(log N) time The theoretical conclusion
B + -TREES MOTIVATION An AVL tree with N nodes is an excellent data structure for searching, indexing, etc. The Big-Oh analysis shows that most operations finish within O(log N) time The theoretical conclusion
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Binary Trees, Binary Search Trees
 Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
Data Structures and Algorithms
 Data Structures and Algorithms CS245-2008S-19 B-Trees David Galles Department of Computer Science University of San Francisco 19-0: Indexing Operations: Add an element Remove an element Find an element,
Data Structures and Algorithms CS245-2008S-19 B-Trees David Galles Department of Computer Science University of San Francisco 19-0: Indexing Operations: Add an element Remove an element Find an element,
B-Trees. Version of October 2, B-Trees Version of October 2, / 22
 B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
Data Structures and Algorithms CMPSC 465
 Data Structures and Algorithms CMPSC 465 LECTURE 24 Balanced Search Trees Red-Black Trees Adam Smith 4/18/12 A. Smith; based on slides by C. Leiserson and E. Demaine L1.1 Balanced search trees Balanced
Data Structures and Algorithms CMPSC 465 LECTURE 24 Balanced Search Trees Red-Black Trees Adam Smith 4/18/12 A. Smith; based on slides by C. Leiserson and E. Demaine L1.1 Balanced search trees Balanced
M-ary Search Tree. B-Trees. Solution: B-Trees. B-Tree: Example. B-Tree Properties. B-Trees (4.7 in Weiss)
 M-ary Search Tree B-Trees (4.7 in Weiss) Maximum branching factor of M Tree with N values has height = # disk accesses for find: Runtime of find: 1/21/2011 1 1/21/2011 2 Solution: B-Trees specialized M-ary
M-ary Search Tree B-Trees (4.7 in Weiss) Maximum branching factor of M Tree with N values has height = # disk accesses for find: Runtime of find: 1/21/2011 1 1/21/2011 2 Solution: B-Trees specialized M-ary
The B-Tree. Yufei Tao. ITEE University of Queensland. INFS4205/7205, Uni of Queensland
 Yufei Tao ITEE University of Queensland Before ascending into d-dimensional space R d with d > 1, this lecture will focus on one-dimensional space, i.e., d = 1. We will review the B-tree, which is a fundamental
Yufei Tao ITEE University of Queensland Before ascending into d-dimensional space R d with d > 1, this lecture will focus on one-dimensional space, i.e., d = 1. We will review the B-tree, which is a fundamental
CSC 172 Data Structures and Algorithms. Fall 2017 TuTh 3:25 pm 4:40 pm Aug 30- Dec 22 Hoyt Auditorium
 CSC 172 Data Structures and Algorithms Fall 2017 TuTh 3:25 pm 4:40 pm Aug 30- Dec 22 Hoyt Auditorium Announcement Coming week: Nov 19 Nov 25 No Quiz No Workshop No New Lab Monday and Tuesday: regular Lab
CSC 172 Data Structures and Algorithms Fall 2017 TuTh 3:25 pm 4:40 pm Aug 30- Dec 22 Hoyt Auditorium Announcement Coming week: Nov 19 Nov 25 No Quiz No Workshop No New Lab Monday and Tuesday: regular Lab
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
Algorithms. Red-Black Trees
 Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Balanced search trees. DS 2017/2018
 Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
13.4 Deletion in red-black trees
 The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
Splay Trees. Splay Trees 1
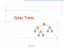 Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
Sorted Arrays. Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min
 Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
Chapter 12 Advanced Data Structures
 Chapter 12 Advanced Data Structures 2 Red-Black Trees add the attribute of (red or black) to links/nodes red-black trees used in C++ Standard Template Library (STL) Java to implement maps (or, as in Python)
Chapter 12 Advanced Data Structures 2 Red-Black Trees add the attribute of (red or black) to links/nodes red-black trees used in C++ Standard Template Library (STL) Java to implement maps (or, as in Python)
CSCI Trees. Mark Redekopp David Kempe
 CSCI 104 2-3 Trees Mark Redekopp David Kempe Trees & Maps/Sets C++ STL "maps" and "sets" use binary search trees internally to store their keys (and values) that can grow or contract as needed This allows
CSCI 104 2-3 Trees Mark Redekopp David Kempe Trees & Maps/Sets C++ STL "maps" and "sets" use binary search trees internally to store their keys (and values) that can grow or contract as needed This allows
Balanced Trees Part One
 Balanced Trees Part One Balanced Trees Balanced search trees are among the most useful and versatile data structures. Many programming languages ship with a balanced tree library. C++: std::map / std::set
Balanced Trees Part One Balanced Trees Balanced search trees are among the most useful and versatile data structures. Many programming languages ship with a balanced tree library. C++: std::map / std::set
Lec 17 April 8. Topics: binary Trees expression trees. (Chapter 5 of text)
 Lec 17 April 8 Topics: binary Trees expression trees Binary Search Trees (Chapter 5 of text) Trees Linear access time of linked lists is prohibitive Heap can t support search in O(log N) time. (takes O(N)
Lec 17 April 8 Topics: binary Trees expression trees Binary Search Trees (Chapter 5 of text) Trees Linear access time of linked lists is prohibitive Heap can t support search in O(log N) time. (takes O(N)
Intro to DB CHAPTER 12 INDEXING & HASHING
 Intro to DB CHAPTER 12 INDEXING & HASHING Chapter 12: Indexing and Hashing Basic Concepts Ordered Indices B+-Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing
Intro to DB CHAPTER 12 INDEXING & HASHING Chapter 12: Indexing and Hashing Basic Concepts Ordered Indices B+-Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing
CSIT5300: Advanced Database Systems
 CSIT5300: Advanced Database Systems L08: B + -trees and Dynamic Hashing Dr. Kenneth LEUNG Department of Computer Science and Engineering The Hong Kong University of Science and Technology Hong Kong SAR,
CSIT5300: Advanced Database Systems L08: B + -trees and Dynamic Hashing Dr. Kenneth LEUNG Department of Computer Science and Engineering The Hong Kong University of Science and Technology Hong Kong SAR,
Balanced Search Trees. CS 3110 Fall 2010
 Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Tree Traversal. Lecture12: Tree II. Preorder Traversal
 Tree Traersal (0F) Lecture: Tree II Process of isiting nodes in a tree systematically Some algorithms need to isit all nodes in a tree. Example: printing, counting nodes, etc. Implementation Can be done
Tree Traersal (0F) Lecture: Tree II Process of isiting nodes in a tree systematically Some algorithms need to isit all nodes in a tree. Example: printing, counting nodes, etc. Implementation Can be done
Trees. Reading: Weiss, Chapter 4. Cpt S 223, Fall 2007 Copyright: Washington State University
 Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
A red-black tree is a balanced binary search tree with the following properties:
 Binary search trees work best when they are balanced or the path length from root to any leaf is within some bounds. The red-black tree algorithm is a method for balancing trees. The name derives from
Binary search trees work best when they are balanced or the path length from root to any leaf is within some bounds. The red-black tree algorithm is a method for balancing trees. The name derives from
Motivation for B-Trees
 1 Motivation for Assume that we use an AVL tree to store about 20 million records We end up with a very deep binary tree with lots of different disk accesses; log2 20,000,000 is about 24, so this takes
1 Motivation for Assume that we use an AVL tree to store about 20 million records We end up with a very deep binary tree with lots of different disk accesses; log2 20,000,000 is about 24, so this takes
OPPA European Social Fund Prague & EU: We invest in your future.
 OPPA European Social Fund Prague & EU: We invest in your future. Data structures and algorithms Part 9 Searching and Search Trees II Petr Felkel 10.12. 2007 Topics Red-Black tree Insert Delete B-Tree Motivation
OPPA European Social Fund Prague & EU: We invest in your future. Data structures and algorithms Part 9 Searching and Search Trees II Petr Felkel 10.12. 2007 Topics Red-Black tree Insert Delete B-Tree Motivation
catch(...){ printf( "Assignment::SolveProblem() AAAA!"); }
 catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } ADD SLIDES ON DISJOINT SETS 2-3 Tree www.serc.iisc.ernet.in/~viren/courses/2009/ SE286/2-3Trees-mod.ppt Outline q Balanced Search Trees 2-3 Trees
catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } ADD SLIDES ON DISJOINT SETS 2-3 Tree www.serc.iisc.ernet.in/~viren/courses/2009/ SE286/2-3Trees-mod.ppt Outline q Balanced Search Trees 2-3 Trees
