TRIANGLE. The sides of a triangle (any type of triangle) are proportional to the sines of the angle opposite to them in triangle.
|
|
|
- Miles McCormick
- 5 years ago
- Views:
Transcription
1 19. SOLUTIONS OF TRINGLE 1. INTRODUTION In ny tringle, the side, opposite to the ngle is denoted by ; the side nd, opposite to the ngles nd respetively re denoted by b nd respetively. The semi-perimeter of the tringle is denoted by s nd its re by or S. In this hpter, we shll disuss vrious reltions between the sides, b, nd the ngles,, of. b. SINE RULE Figure 19.1 The sides of tringle (ny type of tringle) re proportionl to the sines of the ngle opposite to them in tringle b, sin sin sin sin sin sin Note: (i) The bove rule n lso be written s b (ii) The sine rule is very useful tool to express the sides of tringle in terms of sines of the ngle nd vie-vers b in the following mnner: k ( Let) ; k sin, b k sin, k sin sin sin sin sin sin sin Similrly, λ ( Let) ; sin λ, sin λ b, sin λ b 3. OSINE RULE b + + b + b In ny, os ; os ; os b b Note: In prtiulr 60 b + b 60 + b 60 + b b 4. PROJETION FORMULE Figure 19. If ny :(i) bos + os (ii) b os + os (iii) os + bos i.e. ny side of tringle is equl to the sum of the projetion of the other two sides on it.
2 19. Solutions of Tringle se I: When is n ute ngled tringle, D os D.os D.os nd D os D.os D bos then, D+D os + b os se II: When is n obtuse ngled tringle, D os D.os D D b.os nd os( 180 ) D.os then, nd D D bos + os Figure 19.3 Figure 19.4 Illustrtion 1: If 75, 45, then wht is the vlue of b+? (JEE MIN) Sol: Here, Therefore by using sine rule, we n solve the bove problem. Use sine rule b K sin75 sin45 sin60 k sin 75 b k sin 45 k sin 60 o o o 0 onsider, ( b + ) k ( sin45 + sin60 ) Illustrtion : In, if Sol: Here, by using osine rule k k k sin75 k sin 30 nd 3b, then find the vlue of. (JEE MIN) + b os we n esily solve the bove problem. + b 3 3b + b We hve os 3b b 0 OR b 0 ; 3b + b 0 ( b)( b) 0 Either b 30 or b 4b b Illustrtion 3: Prove tht sin( ) + bsin( ) + sin( ) 0 (JEE MIN) Sol: y sine rule i.e. b k we n simply prove the bove eqution. sin sin sin In eqution sin( ) + bsin( ) + sin( ) 0, putting k sin, b k sin, k sin k ( sin sin( ) sinsin( ) sinsin( ) ) (expnding ll terms gets nelled) (Using sin ( α β ) sin α. os β sin βos α) Illustrtion 4: Prove tht b sin sin (JEE MIN)
3 Mthemtis 19.3 ( ) b Sol: Given, sin( ) sin Tkin L.H.S., sin( ) (sinos ossin) sin( ) b sin Now using sine rule, sin sin sin k (sy) nd osine rule, b b b os +, nd os + b + b + b + b + b kb k k sin b RHS. b Illustrtion 5: The ngles of tringle re in 4:1:1 rtio. Find the rtio between its greter side nd perimeter? (JEE DVNED) Sol: Here, the ngles re 10, 30, 30. Therefore, by using sine rule, we will get the required rtio. ngles re 10, 30, 30. If the sides opposite to these ngles re, b nd respetively, will be the gretest side. b b Now from sine formul, ; sin10 sin30 sin30 3/ 1/ 1/ ; b k (sy) 3k 3 then 3k, perimeter ( + 3k ) ; Required rtio. + 3k + 3 Illustrtion 6: Solve bos + os in term of k where k is perimeter of the. (JEE DVNED) 1 + os θ Sol: We n solve the given problem simply by os θ b Here, bos + os ( 1 + os ) + (1 + os) [using projetion formul] b+ 1 + b+ + ; bos + os k [where k+b+, given] tn b Illustrtion 7: In ny tringle, show tht (JEE DVNED) + b + tn Sol: We n derive the vlues of, b nd using sine rule nd putting it to L.H.S. we n prove the bove problem. b We know tht, k sin sin sin k sin, b ksin, k sin (i) On putting the vlues of nd b from (1) on L.H.S., we get + os sin b k sin k sin sin sin L.H.S. + b k sin + k sin sin + sin + sin os tn + ot tn R.H.S. + tn
4 19.4 Solutions of Tringle 5. NPIER S NLOGY (LW OF TNGENTS) In ny, (i) b tn ot b+ (ii) b tn ot + b (iii) tn ot + Proof:(i) R.H.S. b ot k sin k sin ot [y the sine rule] b+ k sin + k sin + sin os.ot [y & D formule] + sin os sin sin ot sin + sin + tn.ot ot tn.tn.ot [y ondition identities] tn LHS Similrly, (ii) nd (iii) n be proved. Illustrtion 8: In ny tringle, if 30, b3 nd 3 3, then find nd. (JEE MIN) b Sol: y using formul, tn ot, we n esily obtin the vlues of nd. + b Here (i) Sine > b > nd (ii) b b + tn ot tn b b tn tn ; 3( 3 + 1) b π b tn ot tn + b + b 3( 3 1) ( 3 1) tn45 + tn30 [Using (1) ] tn tn( ) 3( 3 + 1) ( ) 1 tn45 tn30 1 ( ) tn ( ) ; ; 3 90 (iii) Solving (ii) nd (iii), we get 30 nd TRIGONOMETRI RTIOS OF HLF NGLES Sine, osine nd tngent of hlf the ngles of ny tringle re relted to their sides s given below. Note tht the perimeter of will be denoted by s i.e. s+b+ nd the re denoted by.
5 Mthemtis 19.5 Formule for (i) sin sin, sin, sin for ny ( s b)( s ) b (ii) sin ( s )( s ) (iii) sin ( s )( s b) b Formule for (i) os os, os, os for ny ss ( ) b (ii) os ss ( b) (iii) os ss ( ) b Formule for tn, tn, tn for ny s b s (i) tn ss s s (ii) tn ss b (iii) ( s )( s b) ( ) tn ss Illustrtion 9: In tringle, if s s b s, then find the vlue of s b s Sol: s we know, tn ss s s b s 3s + b + s ; Now tn tn (/ ). (JEE MIN). Therefore, by using this formul, we n solve the bove problem. ( s b)( s ) ss ( ) Illustrtion 10: In tringle, prove tht (+ b + ) tn + tn ot. (JEE MIN) s b s Sol: Here by using tn ss L.H.S. (+ b + ) tn + tn s s nd tn ss b s s b+ s s s s + b + b s s s b s s b lternte: L.H.S. s + s ( s ) s ( s b ) we n prove the bove problem. s b s s s s s b s s + s + ss ss b s s s b ( ) ( s )( s b) ss ot R.H.S. tn 1 1 s b s s + s s b s s b s s b.ot R.H.S. Illustrtion 11: In, if ot, ot, ot re in P, then prove tht the sides of re in.p. (JEE MIN) Sol: Here by using trigonometri rtios of hlf ngles formul, we n prove the bove illustrtion. Given ot, ot, ot re in.p.
6 19.6 Solutions of Tringle ss ( ) ss ( b ) ss ( ),, re in.p. ( s ), ( s b ), ( s ) re in.p., b, re in.p. Proved Illustrtion 1: In, the sides, b nd re in.p. Then wht is the vlue of tn + tn : ot? (JEE DVNED) Sol: Simply by using formul of tn, tn nd ot we n esily get the required result. tn + tn : ot s ( + ) : s ; s b s s s b s s b + : s s s s s s + b+ b: ; b : + b +.b. re in.p. ( ) + ( ) s s : s s b:+b+ :3 + b+ Illustrtion 13: In ny tringle, show tht ot + ot + ot ot. (JEE DVNED) + b Sol: Similr to the bove problem, by putting the vlues of problem. ot, ss ss b ss ot + ot + ot + + s b s s s s s b L.H.S. 1 ( )( )( ) s s s b s 1 ( )( )( ) s s s b s ( ) + ( ) + ( ) s s s s b s s { ( + + )} s 3s b 1 ( )( )( ) s s s b s ot nd 1 ( )( )( ) s s s b s ( s) s 3s ot we n prove the bove ( + + ) s s s b s s ot + ot + ot s s s b s ( )( )( ) (i) Now, R.H.S. L.H.S R.H.S + b + s s s ot ot ot ot + b + b + s s ss ( ) s s s s s b s s s b s + b+ s ; ot + b s s s b s (ii) From (i) nd (ii), we hve + b+ ot + ot + ot ot. + b Proved
7 Mthemtis RE OF TRINGLE If be the re of tringle, then bsin sin bsin Proof: Let be tringle. Then the following ses rise. se I: When D is n ute ngled tringle, sin 1 1 D sin ; D sin ; reof ; ( )( D ) ; sin D se-ii: When is n obtuse ngled tringle, sin( 180 ) ; D sin D sin re of ; () ( D ) ; sin ; So in eh se, sin (ii) Heron s formul s( s )( s b)( s ) Proof: 1 b sin os bsin.os ( s b)( s ) s( s ) b [y hlf ngle formul] s( s )( s b)( s ) b b Figure 19.5 Figure 19.6 (iii) 1 sinsin 1 b sinsin 1 sin sin sin sin sin ( + ) ( + ) ( + ) From the bove results, we obtin the following vlues of sin, sin nd sin b b (iv) sin s( s )( s b)( s ) (v) sin s( s )( s b)( s ) b b (vi) sin s( s )( s b)( s ) Further with the help of (iv), (v), (vi) we obtin sin sin sin b b Illustrtion 14: In ny tringle, prove tht Sol: We n prove the bove problem by using formul of re of tringle i.e. 1 os b + L.H.S. 4 ot 4. bsin. b os b. sin b 4 ot b +. (JEE MIN) 1 bsin nd b + R.H.S. b + os. b Illustrtion 15: In ny tringle, prove tht b sin sin. sin ( ) Sol: y putting k sin nd b k sin we n prove the bove illustrtion. b sin sin k sin k sin sin sin L.H.S.. sin sin( ) ( ) ( ) k sin sin sin sin sin( ) (JEE MIN)
8 19.8 Solutions of Tringle k sin + sin sinsin k [using sine formul k sin et.].sin ( + ) sinsin sin( ) 1 k sin k sin sin π ; + π ; 1 bsin R.H.S. Illustrtion 16: tree stnds vertilly on hill side whih mke n ngle of 15 o with the horizontl. From point on the ground 35m down the hill from the bse of the tree, the ngle of elevtion of the top of the tree is 60 o. Find the height of the tree. (JEE MIN) Sol: We n simply obtin the height of the tree from the given figure. P In QR, QR Qsin15 35sin15 ; R Qos15 35os15 In PR, PR tn60 ; PR R. 3 ; PQ + QR 3R R h h + 35sin os h 35 3 os15 sin ( 4) 35 m Hene, the height of the tree 35 m 60 o 15 o 35 m Figure 19.7 Q R Illustrtion 17: In ny tringle, prove tht 8 os + bos + os sinsin. (JEE DVNED) b Sol: we n solve this illustrtion by substituting s k sin, b k sin, nd k sin. k sin, b k sin, k sin (i) L.H.S. os + bos + os k sinos + k sinos + k sinos [using sine formul] k k sin os sinos + + { sin + sin} + sin k sin os ( ) + os ( π + ) k sinos sinos + k sin os os + k sin sinsin ( k sin ). sinsin sinsin 8 R.H.S. b ; b { } 1 sin sin ndsin b Illustrtion 18: The ngle of elevtion of the top point P of the vertil tower PQ of height h from point is 45 o nd from point, the ngle of elevtion is 60 o, where is point t distne d from the point mesured long the line whih mkes n ngle 30 with Q. Prove tht h d( 3 1) (JEE DVNED) Sol: y using sine rule in P, we n prove tht h d( 3 1) In the figure, PQ represents tower of height h. The ngle of elevtion of the point P from the point on the ground is
9 Mthemtis 19.9 PQ 45 ; P + Q 45 ; P P [Given Q 30 ] P (i) (Given) PH 45 ; P PH 45 + (given) P P 15 (ii) From (i) nd (ii), we hve P P So Pd; P d [Given d] gin PQ 45, Q 90 PQ 45 In PQ, PQ PQ Q PQ h P PQ + Q h + h P h P h pplying sine formul in P, we get d h sin15 h 3 1 d sin150 1 sin15 P sin150 d ( 3 1h ) d 45 o 30 o Figure 19.8 Illustrtion 19: lmp post is situted t the middle point M of the side of tringulr plot with 7m, 1 8m nd 9m. This lmp post subtends n ngle tn ( 3) t the point. Determine the height of the lmp post. (JEE DVNED) Sol: Here in post. MP PM tn PM, therefore by obtining the vlue of M we n find out the height of lmp M Here, is tringulr plot. lmp post PM is situted t the mid-point M of the side. Here PM subtends n 1 tn 3 t the point. 7m, b8m nd 9m ngle In, + b + os or os b os M M M 65 M In M, os ; os.m M 65 M [Using(i)] M M 7m In MP PM tn PM M Hene, the height of the lmp post 1m. 1 PM PM tn tn 3 3 PM 1m M 7 15 o P P h H Q (i) 9 M b8-1 tn (3) 7 Figure PROPERTIES OF TRINGLE 8.1 irumirle irle pssing through the verties of tringle is lled irumirle of the tringle. The entre of the irumirle is lled the irumentre of the tringle nd it is the point of intersetion of the perpendiulr bisetors of the sides of the tringle. The rdius of the irumirle is lled the irumrdius of the tringle nd is usully denoted by R nd is given by the following Figure 19.10
10 19.10 Solutions of Tringle b b formule: R Where is re of tringle nd sin sin sin 4 S 8. Inirle + b+ s. The irle whih n be insribed within the tringle so s to touh ll the three sides of the tringle is lled the inirle of the tringle. The entre of the inirle is lled the inentre of the tringle nd it is the point of intersetion of the internl bisetors of the ngles of the tringle. The rdius of the irle is lled the inrdius of the tringle nd is usully denoted by rin-rdius: The rdius r of the insribed irle of tringle is given by () (b) () r (ii) r ( s ) tn, r ( s b) tn s nd r ( s ) tn sin sin bsin sin sin sin r, r nd r os os os r 4R sin.sin.sin Figure entroid In, the mid-points of the sides, nd re D,E nd F respetively. The lines D, E nd F re lled medins of the tringle. The points of onurreny of three medins is lled the entroid. Generlly it is represented by G. lso, G D, G E nd G F Length of medins from Figure 9.1 b + D b + b 4 b b + 1 D D b Similrly, E + b nd F + b F D Figure 19.1 G E 8.4 pollonius Theorem + D + D Proof: D + D b + + b F E 8.5 Orthoentre O The point of intersetion of perpendiulrs drwn from the verties on the opposite sides of tringle is lled its orthoentre.let the perpendiulr D,E nd F from the verties, nd on the opposite sides, nd D of, respetively meet t O. Figure Then O is the orthoentre of the. The tringle DEF is lled the pedl Tringle of the.
11 Mthemtis entroid (G) of tringle is situted on the line joining its irumentre (O) nd orthoenter (H) show tht the line divides joining its irumentre (O) nd orthoenter (H) in the rtio 1:. Proof: Let L be perpendiulr from on, then H lies on L. If OD is perpendiulr from O on, then D is mid-point of. D is medin of. Let the line HO meet the medin D t G. Now, we shll prove tht G is the entroid of the. Obviously, OGD nd HG re similr tringles. OG GD OD R os 1 L D HG G H R os Figure GD G G is entroid of nd OG : HG 1 : The distnes of the orthoenter from the verties nd the sides: If O is the orthoenter nd DEF the pedl tringle of the, where D, E, F re the perpendiulrs drwn from,, on the opposite sides,, respetively, then (i) O R os, O R os nd O R os (ii) OD R osos, OER osos nd OF R osos, where R is irumrdius. H G O (iii) The irumrdius of the pedl tringle R (iv) The re of pedl tringle ososos. (v) The sides of the pedl tringle re os, bos nd os nd its ngles re π, π nd π. (vi) irumrdii of the tringles O, O, O nd re equl. MSTERJEE ONEPTS The irumentre, entroid nd orthoentre re olliner. In ny right ngled tringle, the orthoentre oinides with the vertex ontining the right ngle. The mid-point of the hypotenuse of right ngled tringle is equidistnt from the three verties of tringle. The mid-point of the hypotenuse of right ngled tringle is the irumentreof the tringle. The entroid of the tringle lies on the line joining the irumentre to the orthoentre nd divides it in the rtio 1: Vibhv Krishnn (JEE 009,IR ) 9. PEDL TRINGLE The tringle formed by the feet of the ltitudes on the side of tringle is lled pedl tringle. In n ute ngled tringle, orthoentre of is the in-entre of the pedl tringle DEF. F H E Proof: Points F,H,D nd re onyli π FDH FH E Similrly, points D, H, E nd re onyli D Figure 19.15
12 19.1 Solutions of Tringle π HDE HE F Thus, FDH HDE D is the ngle bisetor of FDE. Hene, ltitudes of re internl ngle bisetors of the pedl tringle. Thus, the orthoentre of is the inentre of the pedl tringle DEF. Sides of pedl tringle in ute ngled tringle In EF,F bos,e os y osine rule, EF E + F E Fos( EF) 3 EF b os + os bos EF os b + bos os EF os irumrdius of pedl tringle EF os os Let irumrdius be R' R ' R sin EDF sin π sinos sin R' R / MSTERJEE ONEPTS The irle irumsribing the pedl tringle of given tringle bisets the sides of the given tringle nd lso the lines joining the verties of the given tringle to the orthoenter of the given tringle. This irle is known s Nine point irle. The irumentre of the pedl tringle of given tringle bisets the line joining the irumentre of the tringle to the orthoentre. It lso psses through midpoint of the line segment from eh vertex to the orthoenter. Orthoenter of tringle is in entre of pedl tringle. Shriknt Ngori (JEE 009, IR 30) 10. ESRIED IRLES OF THE TRINGLE The irle whih touhes the sides nd two sides nd produed of tringle is lled the esribed irle opposite to the ngle. Its rdius is denoted byr 1. Similrly, r ndr 3 denote the rdii of the esribed irles opposite to the ngles nd respetively. The entres of the esribed irles re lled the ex-entres. The entre of the esribed irle opposite to the ngle is the point of intersetion of the externl bisetor of ngles nd. The internl bisetor lso psses through the sme point. This entre is generlly denoted by I 1. Formule for r 1,r,r 3 In ny, we hve (i) r 1,r,r s s b 3 s (ii) r 1 stn, r stn, r 3 stn os os os os os os (iii) r 1,r b,r 3 os os os (iv) r 1 4R sin os os, r 4R os sin os, r 3 4R os os sin Figure 19.16
13 Mthemtis MSTERJEE ONEPTS If I 1 is the entre of the esribed irle opposite to the ngle, then OI1 R 1 + 8sin.os.os ; OI R 1 + 8os.sin.os ; OI3 R 1 + 8os.os.sin Where R is irum rdius The Sum of the opposite ngles of yli qudrilterl is 180 o. In yli qudrilterl, the sum of the produts of the opposites is equl to the produt of digonls. This is known s Ptolemy s theorem. If the sum of the opposite sides of qudrilterl is equl, then nd only then irle n be insribed in the qudrilterl. If l 1, l nd l 3 re the entres of esribed irles whih re opposite to, nd respetively nd l is the entre of the inirle, then tringle is the pedl tringle of the tringle lll 13 nd l is the orthoenter of tringle lll 13. The irle irumsribing the pedl tringle of given tringle bisets the sides of the given tringle nd lso the lines joining the verties of the given tringle to the orthoenter of the given tringle. This irle is lso known s nine point irle. 1 + bd d + b b + d The irumrdius of yli qudrilterl, R 4 s s b s s d Nitish Jhwr (JEE 009, IR 7) 11. LENGTH OF NGLE ISETOR ND MEDINS If m nd β re the lengths of medin nd n ngle bisetor from the ngle then, b os 1 m b + nd β b+ 3. Note tht m + mb + m ( + b + ) 4 Illustrtion 0: The rtio of the irumrdius nd in rdius of n equilterl tringle is (JEE MIN) Sol: Here, s we know, ll ngles of n equilterl tringle re In rdius we n obtin the required rtio. 0 60, therefore by using formul of irumrdius nd r os + bos + os + b + os In n equilterl tringle, 60 R + b+ + b+ 0 Illustrtion 1: In, 18 nd b4m nd 30m then find the vlue of r 1, r nd r 3. (JEE MIN) Sol: s we know, r 1 s, r s b nd r 3 s. Hene, we n solve the bove problem by using this formul. 18m, b4m,30m; s b 7m + + ; s36m ut, s( s )( s b)( s ) sq. units Then, r 1 1m ; r s 18 18m s b 1 So, r 1,r, r 3 re 1m, 18m, nd 36m respetively. 16 ; r 3 36m s 6
14 19.14 Solutions of Tringle Illustrtion : If the exrdii of tringle re in HP, the orresponding sides re in (JEE MIN) Sol: Here, in this problem, r 1, r nd r 3 re in H.P s s b s,, re in.p.,, re in.p. s,s b,s re in.p. r r r 1 3, b, re in.p., b, re in.p. Illustrtion 3: Find the vlue of Sol: y using r 1 b b + +. (JEE DVNED) r r r 1 3 s, r s b nd r, we n solve the bove problem. 3 s ( b ) ( ) ( b) + + ( b ) + ( ) + ( b) r r r 1 3 ( s )( b ) + ( s b)( ) + ( s )( b) s s b s s b + + b b + b b + b 0 0 Illustrtion 4: Find the vlue of the r ot ot. (JEE DVNED) Sol: Here, in this problem, r4rsin/.sin/.sin/. y putting this vlue, we n solve the bove problem. rot/.ot/ os / os / 4R sin / sin /.sin /.. [s r4rsin/.sin/.sin/] sin / sin / 4R.sin/.os/.os/ r { s,r 4R sin/.os/.os/ } rot /.ot / r EXENTRL TRINGLE I 3 I The tringle formed by joining the three exentres I 1,I nd I 3 of is lled the exentrl or exentri tringle. Note tht: (i) The inentre I of is the orthoentre of the exentrl I13 II. (ii) is the pedl tringle of the III I 90 o (iii) The sides of the exentrl tringle re 4R os, 4R os nd 4R os nd π π π Its ngles re, nd. I 1 Figure (iv) Distne between the inentre nd exentre I I 1 4R sin ; I I 4R sin ; I I3 4R sin. m D n Figure 19.18
15 Mthemtis M-N THEOREM (RTIO FORMUL) If D be point on the side of () ( m n) ot mot not + θ α β (b) Proof: () Given tht, D m nd D θ D n D 180 θ ; D α nd D β suh tht D:D m:n nd D θ, αnd D β. m + n otθ not mot D 180 α+ 180 θ θ α nd D 180 ( θ+β) From D D D, sin α sin ( θ α) D D From D, or sin β sin 180 ( θ+β) dividing (i) by (ii), then ( θ+β) Dsinβ sin Dsinα sin θ α D D sinβ sin ( θ+β) m sinβ sin θ.osβ+ os θ.sinβ or n sinα sin θ.osα osθsinα or msinθsinβosα mos θ.sin α.sinβ nsinαsinθosβ+ nsinαosθsinβ motα motθ notβ+ notθ [dividing both sides by sin sin sin nd α β θ] or (b) Given D m nd D θ; D 180 θ; D nd D D n D θ+ θ ; D 180 ( θ+ ) nd now from nd from D D D. sin sin ( θ ) D D D, or sin 180 θ+ sin dividing (i) by (ii), then D. D ( ) sin( θ+ ) sin( θ ) D sin ( θ+ ) D sin sin m sinθ os + osθsin sin or, sin n sinθos osθsin sin or, msinθ ossin + mosθ sinsin nsinθsinos nosθsinsin or, mot + motθ not notθ [dividing both sides by sinsinsinθ ] or, ( m + n) otθ not mot m + n otθ motα notβ... (i)... (ii) (i)... (ii) Illustrtion 5: In tringle, if ot ot, ot ot nd ot ot b, then find the vlue of + +. (JEE MIN) s s b s Sol: Here, by using trigonometri rtios of hlf ngle, we n solve bove problem. ( ) ( ) ss ss b ot ot ; s b s s s Similrly So tht 1 1 b nd s s s b s b + s + + s s b s s s s 1 s s s
16 19.16 Solutions of Tringle 14. SOLUTION OF DIFFERENT TYPES OF TRINGLE In tringle, there re six elements- three sides nd three ngles. In plne geometry, we hve done tht if three of the elements re given, t lest one of whih must be side, then the other three elements n be uniquely determined. The proedure of determining unknown elements from the known elements is lled solving tringle. Solution of right ngled tringle se I: When two sides re given: Let the tringle be right ngled t. Then we n determine the remining elements s given in the tble. (i) (ii) Given, b, Required tn, 90, b sin sin, b os, 90 se II: When side nd n ute ngle re given: In this se, we n determine the remining elements s given in the tble. (i) Given, Required 90, b ot, sin (ii), 90, sin, b os Solution of tringle in generl se I: When three sides, b, re given: In this se, the remining elements re determined by using the following formule. s( s )( s b)( s ), where s + b + sin, sin, sin. OR tn, tn, tn b b ss ss b ss se II: When two sides, b nd the inluded ngle re given: In this se, we use the following formule: 1 b bsin, tn ot + b ; + 90 nd sin sin se III: When one side nd two ngle nd re given: In this se, we use the following formule to determine the remining elements sin 1 ; 180 ( + ) nd ; sin sin se IV: When two sides, b nd the opposite to one side is given: In this se, we use the following formule. b sin sin... (i) sin 180 ( + ), sin From (i), the following possibilities will rise: When is n ute ngle nd < bsin.
17 Mthemtis b In this se, the reltion sin sin gives tht sin > 1, whih is impossible. Hene no tringle is possible. When is n ute ngle nd bsin. In this se, only one tringle is possible whih is right ngled t. When is n ute ngle nd > bsin bsin In this se, there re two vlues of given by sin sy 1nd suh tht nd side n sin be obtined by using sin Some useful results: Solution of oblique tringles: The tringle whih re not right ngled re known s oblique tringles. The problems on solving n oblique tringle lie in the following tegories: () When three sides re given (b) When two side nd inluded ngle re given () When one side nd two ngles re given (d) When ll the three ngles re given (e) mbiguous se in solution of tringle When the three sides re given: When three sides, b, of tringle re given, then to solve it, we hve to find its three ngles,,. For this osine rule n be used. When two sides nd inluded ngle re given: Problem bsed on finding the ngles when ny two sides nd the ngles between them or ny two sides nd the differene of the opposite ngles to them re given, Npier s nlogy n be used. When one side nd two ngles re given: Problems bsed on finding the sides nd ngles when ny two nd side opposite to one of them re given, then sine rule n be used. When ll the three ngles re given: In this se unique solution of tringle is not possible. In this se only the rtio of the sides n be determined. b For this the formul, n be used sin sin sin mbiguous se in solution of tringles: When ny two sides nd one of the orresponding ngles re given, under ertin dditionl onditions, two tringles re possible. The se when two tringles re possible is lled the mbiguous se. In ft, when ny two sides nd the ngle opposite to one of them re given either no tringle is possible or only one tringle is possible or two tringles re possible. Now, we will disuss the se when two tringles re possible. Illustrtion 6: Solve the tringle, if b 7.95, 8.31, 4 47' (JEE MIN) Sol: y using sine rule i.e. sin sin, we n solve the given tringle. b sin sin sin 8.31 sin4 47' (i) To find sin b b sin '1'' nd 19 58'48''
18 19.18 Solutions of Tringle 50 1'1" I solution ' '1" 87 11'48" To find b sin sin bsin sin sin87 11'48" sin4 7' 19 58'48" II solution 180 (4 47' '48") 7 14'1" To find b sin sin bsin sin sin7 14'1" sin4 7' Two solutions re '1" '48" '48" Geometrilly, we drw the tringle with given dt,b nd ngle. () If N( sin) b (extly). The tringle is right ngled tringle. (b) If N( sin) > b, the tringle nnot be drwn. () If N( sin) < b <, two tringles re possible. (d) b>, only one tringle is possible. 7 14'1" N b Figure b Illustrtion 7: In tringle, b16m, 5m, nd 33 15'. Find the ngle. (JEE MIN) Sol: Simply by using sine rule, we n find out the ngle. We know tht, sin sin [Here, b16m, 5m, 33 15' ] b 5sin33 15' 1 sin sin ; sin ( ) 58 57' ; ' ; ' 11 3' b 16 PROLEM SOLVING TTIS In the pplition of sine rule, the following points re to be noted. We re given one side nd some other side x is to be found. oth these re in different tringles. We hoose ommon side y of these tringles. Then pply sine rule for nd y in one tringle nd for x nd y for the other tringle nd eliminte y. Thus, we will get the unknown side x in terms of. In the djoining figure, is the known side of nd x is the unknown side of tringle D. The ommon side of these tringles is y(sy). Now, pply sine rule. y y x y (i) nd. (ii) sinα sinβ sinθ sinγ x D Dividing (ii) by (i) we get, xsin α sin β sinβsinθ ; x sinθ sinγ sinαsinγ Figure 19.0 In se of generlized tringle problems, option verifition is very useful using equilterl, isoseles or right ngle tringle properties. So, it is dvised to remember properties of these tringles.
19 Mthemtis FORMULE SHEET () In, + + π () sin( + ) sin( π ) sin (b) os( + ) os ( π ) os () + π sin sin os + π (d) os os sin b (b) Sine rule: In, R Where R irumrdius nd, b, re sides of tringle. sin sin sin () b + + b + b osine rule: os, os, os b b (d) Trigonometri rtios of hlf ngles: () sin (e) re of tringle : ( s b)( s ) where s + b + ; (b) b bsin sin bsin (f) Heron s formul : s( s )( s b)( s ), where (g) irumirle Rdius : b b R sin sin sin 4 os + b+ s. ( ) ss ; () b ( s b)( s ) ( ) tn ss (h) Inirle Rdius : () r s (i) Rdius of the Esribed irle : () 1 3 r s tn ; (b) r ( s ) tn, r ( s b) tn nd r, r,r s s b s r stn, r stn, r stn os os os os os os r,r b,r os os os r 4R sin os os, r 4R os sin os, r 4R os os sin (b) 1 3 () 1 3 (d) 1 3 (j) Length of ngle bisetor nd Medin: b os 1 m b + nd β b+ m - length of medin, β - length of bisetor.
Line The set of points extending in two directions without end uniquely determined by two points. The set of points on a line between two points
 Lines Line Line segment Perpendiulr Lines Prllel Lines Opposite Angles The set of points extending in two diretions without end uniquely determined by two points. The set of points on line between two
Lines Line Line segment Perpendiulr Lines Prllel Lines Opposite Angles The set of points extending in two diretions without end uniquely determined by two points. The set of points on line between two
a c = A C AD DB = BD
 1.) SIMILR TRINGLES.) Some possile proportions: Geometry Review- M.. Sntilli = = = = =.) For right tringle ut y its ltitude = = =.) Or for ll possiilities, split into 3 similr tringles: ll orresponding
1.) SIMILR TRINGLES.) Some possile proportions: Geometry Review- M.. Sntilli = = = = =.) For right tringle ut y its ltitude = = =.) Or for ll possiilities, split into 3 similr tringles: ll orresponding
Pythagoras theorem and trigonometry (2)
 HPTR 10 Pythgors theorem nd trigonometry (2) 31 HPTR Liner equtions In hpter 19, Pythgors theorem nd trigonometry were used to find the lengths of sides nd the sizes of ngles in right-ngled tringles. These
HPTR 10 Pythgors theorem nd trigonometry (2) 31 HPTR Liner equtions In hpter 19, Pythgors theorem nd trigonometry were used to find the lengths of sides nd the sizes of ngles in right-ngled tringles. These
Right Angled Trigonometry. Objective: To know and be able to use trigonometric ratios in rightangled
 C2 Right Angled Trigonometry Ojetive: To know nd e le to use trigonometri rtios in rightngled tringles opposite C Definition Trigonometry ws developed s method of mesuring ngles without ngulr units suh
C2 Right Angled Trigonometry Ojetive: To know nd e le to use trigonometri rtios in rightngled tringles opposite C Definition Trigonometry ws developed s method of mesuring ngles without ngulr units suh
50 AMC LECTURES Lecture 2 Analytic Geometry Distance and Lines. can be calculated by the following formula:
 5 AMC LECTURES Lecture Anlytic Geometry Distnce nd Lines BASIC KNOWLEDGE. Distnce formul The distnce (d) between two points P ( x, y) nd P ( x, y) cn be clculted by the following formul: d ( x y () x )
5 AMC LECTURES Lecture Anlytic Geometry Distnce nd Lines BASIC KNOWLEDGE. Distnce formul The distnce (d) between two points P ( x, y) nd P ( x, y) cn be clculted by the following formul: d ( x y () x )
Section 10.4 Hyperbolas
 66 Section 10.4 Hyperbols Objective : Definition of hyperbol & hyperbols centered t (0, 0). The third type of conic we will study is the hyperbol. It is defined in the sme mnner tht we defined the prbol
66 Section 10.4 Hyperbols Objective : Definition of hyperbol & hyperbols centered t (0, 0). The third type of conic we will study is the hyperbol. It is defined in the sme mnner tht we defined the prbol
Final Exam Review F 06 M 236 Be sure to look over all of your tests, as well as over the activities you did in the activity book
 inl xm Review 06 M 236 e sure to loo over ll of your tests, s well s over the tivities you did in the tivity oo 1 1. ind the mesures of the numered ngles nd justify your wor. Line j is prllel to line.
inl xm Review 06 M 236 e sure to loo over ll of your tests, s well s over the tivities you did in the tivity oo 1 1. ind the mesures of the numered ngles nd justify your wor. Line j is prllel to line.
Doubts about how to use azimuth values from a Coordinate Object. Juan Antonio Breña Moral
 Douts out how to use zimuth vlues from Coordinte Ojet Jun Antonio Breñ Morl # Definition An Azimuth is the ngle from referene vetor in referene plne to seond vetor in the sme plne, pointing towrd, (ut
Douts out how to use zimuth vlues from Coordinte Ojet Jun Antonio Breñ Morl # Definition An Azimuth is the ngle from referene vetor in referene plne to seond vetor in the sme plne, pointing towrd, (ut
9.1 PYTHAGOREAN THEOREM (right triangles)
 Simplifying Rdicls: ) 1 b) 60 c) 11 d) 3 e) 7 Solve: ) x 4 9 b) 16 80 c) 9 16 9.1 PYTHAGOREAN THEOREM (right tringles) c If tringle is right tringle then b, b re the legs * c is clled the hypotenuse (side
Simplifying Rdicls: ) 1 b) 60 c) 11 d) 3 e) 7 Solve: ) x 4 9 b) 16 80 c) 9 16 9.1 PYTHAGOREAN THEOREM (right tringles) c If tringle is right tringle then b, b re the legs * c is clled the hypotenuse (side
Calculus Differentiation
 //007 Clulus Differentition Jeffrey Seguritn person in rowot miles from the nerest point on strit shoreline wishes to reh house 6 miles frther down the shore. The person n row t rte of mi/hr nd wlk t rte
//007 Clulus Differentition Jeffrey Seguritn person in rowot miles from the nerest point on strit shoreline wishes to reh house 6 miles frther down the shore. The person n row t rte of mi/hr nd wlk t rte
Math 4 Review for Quarter 2 Cumulative Test
 Mth 4 Review for Qurter 2 Cumultive Test Nme: I. Right Tringle Trigonometry (3.1-3.3) Key Fcts Pythgoren Theorem - In right tringle, 2 + b 2 = c 2 where c is the hypotenuse s shown below. c b Trigonometric
Mth 4 Review for Qurter 2 Cumultive Test Nme: I. Right Tringle Trigonometry (3.1-3.3) Key Fcts Pythgoren Theorem - In right tringle, 2 + b 2 = c 2 where c is the hypotenuse s shown below. c b Trigonometric
GEOMETRY 1 Basic definitions of some important term:
 GEOMETRY 1 Geometry: The branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogues. GEOMETRY WHT TO STUDY? LSSIFITION OF NGLES
GEOMETRY 1 Geometry: The branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogues. GEOMETRY WHT TO STUDY? LSSIFITION OF NGLES
Class-XI Mathematics Conic Sections Chapter-11 Chapter Notes Key Concepts
 Clss-XI Mthemtics Conic Sections Chpter-11 Chpter Notes Key Concepts 1. Let be fixed verticl line nd m be nother line intersecting it t fixed point V nd inclined to it t nd ngle On rotting the line m round
Clss-XI Mthemtics Conic Sections Chpter-11 Chpter Notes Key Concepts 1. Let be fixed verticl line nd m be nother line intersecting it t fixed point V nd inclined to it t nd ngle On rotting the line m round
Stained Glass Design. Teaching Goals:
 Stined Glss Design Time required 45-90 minutes Teching Gols: 1. Students pply grphic methods to design vrious shpes on the plne.. Students pply geometric trnsformtions of grphs of functions in order to
Stined Glss Design Time required 45-90 minutes Teching Gols: 1. Students pply grphic methods to design vrious shpes on the plne.. Students pply geometric trnsformtions of grphs of functions in order to
ANALYTICAL GEOMETRY. The curves obtained by slicing the cone with a plane not passing through the vertex are called conics.
 ANALYTICAL GEOMETRY Definition of Conic: The curves obtined by slicing the cone with plne not pssing through the vertex re clled conics. A Conic is the locus directrix of point which moves in plne, so
ANALYTICAL GEOMETRY Definition of Conic: The curves obtined by slicing the cone with plne not pssing through the vertex re clled conics. A Conic is the locus directrix of point which moves in plne, so
UNCORRECTED SAMPLE PAGES. Angle relationships and properties of 6geometrical figures 1. Online resources. What you will learn
 Online resoures uto-mrked hpter pre-test Video demonstrtions of ll worked exmples Intertive widgets Intertive wlkthroughs Downlodle HOTsheets ess to ll HOTmths ustrlin urriulum ourses ess to the HOTmths
Online resoures uto-mrked hpter pre-test Video demonstrtions of ll worked exmples Intertive widgets Intertive wlkthroughs Downlodle HOTsheets ess to ll HOTmths ustrlin urriulum ourses ess to the HOTmths
Geometrical reasoning 1
 MODULE 5 Geometril resoning 1 OBJECTIVES This module is for study y n individul teher or group of tehers. It: looks t pprohes to developing pupils visulistion nd geometril resoning skills; onsiders progression
MODULE 5 Geometril resoning 1 OBJECTIVES This module is for study y n individul teher or group of tehers. It: looks t pprohes to developing pupils visulistion nd geometril resoning skills; onsiders progression
TOPIC 10 THREE DIMENSIONAL GEOMETRY
 TOPIC THREE DIMENSIONAL GEOMETRY SCHEMATIC DIAGRAM Topi Conept Degree of importne Three Dimensionl Geometr (i Diretion Rtios n Diretion Cosines (iicrtesin n Vetor eqution of line in spe & onversion of
TOPIC THREE DIMENSIONAL GEOMETRY SCHEMATIC DIAGRAM Topi Conept Degree of importne Three Dimensionl Geometr (i Diretion Rtios n Diretion Cosines (iicrtesin n Vetor eqution of line in spe & onversion of
Math 142, Exam 1 Information.
 Mth 14, Exm 1 Informtion. 9/14/10, LC 41, 9:30-10:45. Exm 1 will be bsed on: Sections 7.1-7.5. The corresponding ssigned homework problems (see http://www.mth.sc.edu/ boyln/sccourses/14f10/14.html) At
Mth 14, Exm 1 Informtion. 9/14/10, LC 41, 9:30-10:45. Exm 1 will be bsed on: Sections 7.1-7.5. The corresponding ssigned homework problems (see http://www.mth.sc.edu/ boyln/sccourses/14f10/14.html) At
45 Wyner Math Academy I Spring 2016
 45 Wyner Math cademy I Spring 2016 HPTER FIVE: TRINGLES Review January 13 Test January 21 Other than circles, triangles are the most fundamental shape. Many aspects of advanced abstract mathematics and
45 Wyner Math cademy I Spring 2016 HPTER FIVE: TRINGLES Review January 13 Test January 21 Other than circles, triangles are the most fundamental shape. Many aspects of advanced abstract mathematics and
Paradigm 5. Data Structure. Suffix trees. What is a suffix tree? Suffix tree. Simple applications. Simple applications. Algorithms
 Prdigm. Dt Struture Known exmples: link tble, hep, Our leture: suffix tree Will involve mortize method tht will be stressed shortly in this ourse Suffix trees Wht is suffix tree? Simple pplitions History
Prdigm. Dt Struture Known exmples: link tble, hep, Our leture: suffix tree Will involve mortize method tht will be stressed shortly in this ourse Suffix trees Wht is suffix tree? Simple pplitions History
MA1008. Calculus and Linear Algebra for Engineers. Course Notes for Section B. Stephen Wills. Department of Mathematics. University College Cork
 MA1008 Clculus nd Liner Algebr for Engineers Course Notes for Section B Stephen Wills Deprtment of Mthemtics University College Cork s.wills@ucc.ie http://euclid.ucc.ie/pges/stff/wills/teching/m1008/ma1008.html
MA1008 Clculus nd Liner Algebr for Engineers Course Notes for Section B Stephen Wills Deprtment of Mthemtics University College Cork s.wills@ucc.ie http://euclid.ucc.ie/pges/stff/wills/teching/m1008/ma1008.html
SSC TIER II (MATHS) MOCK TEST - 21 (SOLUTION)
 007, OUTRM LINES, ST FLOOR, OPPOSITE MUKHERJEE NGR POLIE STTION, DELHI-0009 SS TIER II (MTHS) MOK TEST - (SOLUTION). () Let, totl no. of students Totl present students 8 7 9 7 5 5 Required frction 5 5.
007, OUTRM LINES, ST FLOOR, OPPOSITE MUKHERJEE NGR POLIE STTION, DELHI-0009 SS TIER II (MTHS) MOK TEST - (SOLUTION). () Let, totl no. of students Totl present students 8 7 9 7 5 5 Required frction 5 5.
CS 241 Week 4 Tutorial Solutions
 CS 4 Week 4 Tutoril Solutions Writing n Assemler, Prt & Regulr Lnguges Prt Winter 8 Assemling instrutions utomtilly. slt $d, $s, $t. Solution: $d, $s, nd $t ll fit in -it signed integers sine they re 5-it
CS 4 Week 4 Tutoril Solutions Writing n Assemler, Prt & Regulr Lnguges Prt Winter 8 Assemling instrutions utomtilly. slt $d, $s, $t. Solution: $d, $s, nd $t ll fit in -it signed integers sine they re 5-it
Math 227 Problem Set V Solutions. f ds =
 Mth 7 Problem Set V Solutions If is urve with prmetriztion r(t), t b, then we define the line integrl f ds b f ( r(t) ) dr dt (t) dt. Evlute the line integrl f(x,y,z)ds for () f(x,y,z) xosz, the urve with
Mth 7 Problem Set V Solutions If is urve with prmetriztion r(t), t b, then we define the line integrl f ds b f ( r(t) ) dr dt (t) dt. Evlute the line integrl f(x,y,z)ds for () f(x,y,z) xosz, the urve with
10.2 Graph Terminology and Special Types of Graphs
 10.2 Grph Terminology n Speil Types of Grphs Definition 1. Two verties u n v in n unirete grph G re lle jent (or neighors) in G iff u n v re enpoints of n ege e of G. Suh n ege e is lle inient with the
10.2 Grph Terminology n Speil Types of Grphs Definition 1. Two verties u n v in n unirete grph G re lle jent (or neighors) in G iff u n v re enpoints of n ege e of G. Suh n ege e is lle inient with the
5 ANGLES AND POLYGONS
 5 GLES POLYGOS urling rige looks like onventionl rige when it is extene. However, it urls up to form n otgon to llow ots through. This Rolling rige is in Pington sin in Lonon, n urls up every Friy t miy.
5 GLES POLYGOS urling rige looks like onventionl rige when it is extene. However, it urls up to form n otgon to llow ots through. This Rolling rige is in Pington sin in Lonon, n urls up every Friy t miy.
Review Packet #3 Notes
 SCIE 40, Fll 05 Miller Review Pket # Notes Prllel Lines If two prllel lines re onneted y third line (lled the trnsversl), the resulting ngles re either ongruent or supplementry. Angle pirs re nmed s follows:
SCIE 40, Fll 05 Miller Review Pket # Notes Prllel Lines If two prllel lines re onneted y third line (lled the trnsversl), the resulting ngles re either ongruent or supplementry. Angle pirs re nmed s follows:
4-1 NAME DATE PERIOD. Study Guide. Parallel Lines and Planes P Q, O Q. Sample answers: A J, A F, and D E
 4-1 NAME DATE PERIOD Pges 142 147 Prllel Lines nd Plnes When plnes do not intersect, they re sid to e prllel. Also, when lines in the sme plne do not intersect, they re prllel. But when lines re not in
4-1 NAME DATE PERIOD Pges 142 147 Prllel Lines nd Plnes When plnes do not intersect, they re sid to e prllel. Also, when lines in the sme plne do not intersect, they re prllel. But when lines re not in
9.1 apply the distance and midpoint formulas
 9.1 pply the distnce nd midpoint formuls DISTANCE FORMULA MIDPOINT FORMULA To find the midpoint between two points x, y nd x y 1 1,, we Exmple 1: Find the distnce between the two points. Then, find the
9.1 pply the distnce nd midpoint formuls DISTANCE FORMULA MIDPOINT FORMULA To find the midpoint between two points x, y nd x y 1 1,, we Exmple 1: Find the distnce between the two points. Then, find the
Lecture 12 : Topological Spaces
 Leture 12 : Topologil Spes 1 Topologil Spes Topology generlizes notion of distne nd loseness et. Definition 1.1. A topology on set X is olletion T of susets of X hving the following properties. 1. nd X
Leture 12 : Topologil Spes 1 Topologil Spes Topology generlizes notion of distne nd loseness et. Definition 1.1. A topology on set X is olletion T of susets of X hving the following properties. 1. nd X
MATHS LECTURE # 09. Plane Geometry. Angles
 Mthemtics is not specttor sport! Strt prcticing. MTHS LTUR # 09 lne eometry oint, line nd plne There re three sic concepts in geometry. These concepts re the point, line nd plne. oint fine dot, mde y shrp
Mthemtics is not specttor sport! Strt prcticing. MTHS LTUR # 09 lne eometry oint, line nd plne There re three sic concepts in geometry. These concepts re the point, line nd plne. oint fine dot, mde y shrp
PROBLEM OF APOLLONIUS
 PROBLEM OF APOLLONIUS In the Jnury 010 issue of Amerin Sientist D. Mkenzie isusses the Apollonin Gsket whih involves fining the rius of the lrgest irle whih just fits into the spe etween three tngent irles
PROBLEM OF APOLLONIUS In the Jnury 010 issue of Amerin Sientist D. Mkenzie isusses the Apollonin Gsket whih involves fining the rius of the lrgest irle whih just fits into the spe etween three tngent irles
Grade 7/8 Math Circles Geometric Arithmetic October 31, 2012
 Fculty of Mthemtics Wterloo, Ontrio N2L 3G1 Grde 7/8 Mth Circles Geometric Arithmetic Octoer 31, 2012 Centre for Eduction in Mthemtics nd Computing Ancient Greece hs given irth to some of the most importnt
Fculty of Mthemtics Wterloo, Ontrio N2L 3G1 Grde 7/8 Mth Circles Geometric Arithmetic Octoer 31, 2012 Centre for Eduction in Mthemtics nd Computing Ancient Greece hs given irth to some of the most importnt
Topics in Analytic Geometry
 Nme Chpter 10 Topics in Anltic Geometr Section 10.1 Lines Objective: In this lesson ou lerned how to find the inclintion of line, the ngle between two lines, nd the distnce between point nd line. Importnt
Nme Chpter 10 Topics in Anltic Geometr Section 10.1 Lines Objective: In this lesson ou lerned how to find the inclintion of line, the ngle between two lines, nd the distnce between point nd line. Importnt
Chapter 8: Right Triangle Trigonometry
 Haberman MTH 11 Setion I: The Trigonometri Funtions Chapter 8: Right Triangle Trigonometry As we studied in Part 1 of Chapter 3, if we put the same angle in the enter of two irles of different radii, we
Haberman MTH 11 Setion I: The Trigonometri Funtions Chapter 8: Right Triangle Trigonometry As we studied in Part 1 of Chapter 3, if we put the same angle in the enter of two irles of different radii, we
Fig.1. Let a source of monochromatic light be incident on a slit of finite width a, as shown in Fig. 1.
 Answer on Question #5692, Physics, Optics Stte slient fetures of single slit Frunhofer diffrction pttern. The slit is verticl nd illuminted by point source. Also, obtin n expression for intensity distribution
Answer on Question #5692, Physics, Optics Stte slient fetures of single slit Frunhofer diffrction pttern. The slit is verticl nd illuminted by point source. Also, obtin n expression for intensity distribution
Right Triangle Trigonometry
 Rigt Tringle Trigonometry Trigonometry comes from te Greek trigon (tringle) nd metron (mesure) nd is te study of te reltion between side lengts nd ngles of tringles. Angles A ry is strigt lf line tt stretces
Rigt Tringle Trigonometry Trigonometry comes from te Greek trigon (tringle) nd metron (mesure) nd is te study of te reltion between side lengts nd ngles of tringles. Angles A ry is strigt lf line tt stretces
Math 2201 Unit 3: Acute Triangle Trigonometry. Ch. 3 Notes
 Rea Learning Goals, p. 17 text. Math 01 Unit 3: ute Triangle Trigonometry h. 3 Notes 3.1 Exploring Sie-ngle Relationships in ute Triangles (0.5 lass) Rea Goal p. 130 text. Outomes: 1. Define an aute triangle.
Rea Learning Goals, p. 17 text. Math 01 Unit 3: ute Triangle Trigonometry h. 3 Notes 3.1 Exploring Sie-ngle Relationships in ute Triangles (0.5 lass) Rea Goal p. 130 text. Outomes: 1. Define an aute triangle.
Lesson 4.4. Euler Circuits and Paths. Explore This
 Lesson 4.4 Euler Ciruits nd Pths Now tht you re fmilir with some of the onepts of grphs nd the wy grphs onvey onnetions nd reltionships, it s time to egin exploring how they n e used to model mny different
Lesson 4.4 Euler Ciruits nd Pths Now tht you re fmilir with some of the onepts of grphs nd the wy grphs onvey onnetions nd reltionships, it s time to egin exploring how they n e used to model mny different
Introduction to Algebra
 INTRODUCTORY ALGEBRA Mini-Leture 1.1 Introdution to Alger Evlute lgeri expressions y sustitution. Trnslte phrses to lgeri expressions. 1. Evlute the expressions when =, =, nd = 6. ) d) 5 10. Trnslte eh
INTRODUCTORY ALGEBRA Mini-Leture 1.1 Introdution to Alger Evlute lgeri expressions y sustitution. Trnslte phrses to lgeri expressions. 1. Evlute the expressions when =, =, nd = 6. ) d) 5 10. Trnslte eh
Duality in linear interval equations
 Aville online t http://ijim.sriu..ir Int. J. Industril Mthemtis Vol. 1, No. 1 (2009) 41-45 Dulity in liner intervl equtions M. Movhedin, S. Slhshour, S. Hji Ghsemi, S. Khezerloo, M. Khezerloo, S. M. Khorsny
Aville online t http://ijim.sriu..ir Int. J. Industril Mthemtis Vol. 1, No. 1 (2009) 41-45 Dulity in liner intervl equtions M. Movhedin, S. Slhshour, S. Hji Ghsemi, S. Khezerloo, M. Khezerloo, S. M. Khorsny
Review Packet #3 Notes
 SCIE 40, Spring 0 Miller Review Pket # Notes Mpping Nottion We use mpping nottion to note how oordinte hnges. For exmple, if the point ( ) trnsformed under mpping nottion of ( x, y) ( x, y), then it eomes
SCIE 40, Spring 0 Miller Review Pket # Notes Mpping Nottion We use mpping nottion to note how oordinte hnges. For exmple, if the point ( ) trnsformed under mpping nottion of ( x, y) ( x, y), then it eomes
a < a+ x < a+2 x < < a+n x = b, n A i n f(x i ) x. i=1 i=1
 Mth 33 Volume Stewrt 5.2 Geometry of integrls. In this section, we will lern how to compute volumes using integrls defined by slice nlysis. First, we recll from Clculus I how to compute res. Given the
Mth 33 Volume Stewrt 5.2 Geometry of integrls. In this section, we will lern how to compute volumes using integrls defined by slice nlysis. First, we recll from Clculus I how to compute res. Given the
Lecture 8: Graph-theoretic problems (again)
 COMP36111: Advned Algorithms I Leture 8: Grph-theoreti prolems (gin) In Prtt-Hrtmnn Room KB2.38: emil: iprtt@s.mn..uk 2017 18 Reding for this leture: Sipser: Chpter 7. A grph is pir G = (V, E), where V
COMP36111: Advned Algorithms I Leture 8: Grph-theoreti prolems (gin) In Prtt-Hrtmnn Room KB2.38: emil: iprtt@s.mn..uk 2017 18 Reding for this leture: Sipser: Chpter 7. A grph is pir G = (V, E), where V
Chapter 2. Chapter 2 5. Section segments: AB, BC, BD, BE. 32. N 53 E GEOMETRY INVESTIGATION Answers will vary. 34. (a) N. sunset.
 Chpter 2 5 Chpter 2 32. N 53 E GEOMETRY INVESTIGATION Answers will vry. 34. () N Setion 2.1 2. 4 segments: AB, BC, BD, BE sunset sunrise 4. 2 rys: CD (or CE ), CB (or CA ) 6. ED, EC, EB W Oslo, Norwy E
Chpter 2 5 Chpter 2 32. N 53 E GEOMETRY INVESTIGATION Answers will vry. 34. () N Setion 2.1 2. 4 segments: AB, BC, BD, BE sunset sunrise 4. 2 rys: CD (or CE ), CB (or CA ) 6. ED, EC, EB W Oslo, Norwy E
2 Computing all Intersections of a Set of Segments Line Segment Intersection
 15-451/651: Design & Anlysis of Algorithms Novemer 14, 2016 Lecture #21 Sweep-Line nd Segment Intersection lst chnged: Novemer 8, 2017 1 Preliminries The sweep-line prdigm is very powerful lgorithmic design
15-451/651: Design & Anlysis of Algorithms Novemer 14, 2016 Lecture #21 Sweep-Line nd Segment Intersection lst chnged: Novemer 8, 2017 1 Preliminries The sweep-line prdigm is very powerful lgorithmic design
CHAPTER 5 RELATIONSHIPS WITHIN TRIANGLES
 HPTER 5 RELTIONSHIPS WITHIN TRINGLES In this chapter we address three ig IES: 1) Using properties of special segments in triangles 2) Using triangle inequalities to determine what triangles are possible
HPTER 5 RELTIONSHIPS WITHIN TRINGLES In this chapter we address three ig IES: 1) Using properties of special segments in triangles 2) Using triangle inequalities to determine what triangles are possible
Measurement and geometry
 Mesurement nd geometry 4 Geometry Geometry is everywhere. Angles, prllel lines, tringles nd qudrilterls n e found ll round us, in our homes, on trnsport, in onstrution, rt nd nture. This sene from Munih
Mesurement nd geometry 4 Geometry Geometry is everywhere. Angles, prllel lines, tringles nd qudrilterls n e found ll round us, in our homes, on trnsport, in onstrution, rt nd nture. This sene from Munih
6.3 Volumes. Just as area is always positive, so is volume and our attitudes towards finding it.
 6.3 Volumes Just s re is lwys positive, so is volume nd our ttitudes towrds finding it. Let s review how to find the volume of regulr geometric prism, tht is, 3-dimensionl oject with two regulr fces seprted
6.3 Volumes Just s re is lwys positive, so is volume nd our ttitudes towrds finding it. Let s review how to find the volume of regulr geometric prism, tht is, 3-dimensionl oject with two regulr fces seprted
ZZ - Advanced Math Review 2017
 ZZ - Advnced Mth Review Mtrix Multipliction Given! nd! find the sum of the elements of the product BA First, rewrite the mtrices in the correct order to multiply The product is BA hs order x since B is
ZZ - Advnced Mth Review Mtrix Multipliction Given! nd! find the sum of the elements of the product BA First, rewrite the mtrices in the correct order to multiply The product is BA hs order x since B is
Lesson 2: Right Triangle Trigonometry
 Lesson : Right Triangle Trigonometry lthough Trigonometry is used to solve many prolems, historially it was first applied to prolems that involve a right triangle. This an e extended to non-right triangles
Lesson : Right Triangle Trigonometry lthough Trigonometry is used to solve many prolems, historially it was first applied to prolems that involve a right triangle. This an e extended to non-right triangles
If f(x, y) is a surface that lies above r(t), we can think about the area between the surface and the curve.
 Line Integrls The ide of line integrl is very similr to tht of single integrls. If the function f(x) is bove the x-xis on the intervl [, b], then the integrl of f(x) over [, b] is the re under f over the
Line Integrls The ide of line integrl is very similr to tht of single integrls. If the function f(x) is bove the x-xis on the intervl [, b], then the integrl of f(x) over [, b] is the re under f over the
Lily Yen and Mogens Hansen
 SKOLID / SKOLID No. 8 Lily Yen nd Mogens Hnsen Skolid hs joined Mthemticl Myhem which is eing reformtted s stnd-lone mthemtics journl for high school students. Solutions to prolems tht ppered in the lst
SKOLID / SKOLID No. 8 Lily Yen nd Mogens Hnsen Skolid hs joined Mthemticl Myhem which is eing reformtted s stnd-lone mthemtics journl for high school students. Solutions to prolems tht ppered in the lst
Convex Hull Algorithms. Convex hull: basic facts
 CG Leture D Conve Hull Algorithms Bsi fts Algorithms: Nïve, Gift wrpping, Grhm sn, Quik hull, Divide-nd-onquer Lower ound 3D Bsi fts Algorithms: Gift wrpping, Divide nd onquer, inrementl Conve hulls in
CG Leture D Conve Hull Algorithms Bsi fts Algorithms: Nïve, Gift wrpping, Grhm sn, Quik hull, Divide-nd-onquer Lower ound 3D Bsi fts Algorithms: Gift wrpping, Divide nd onquer, inrementl Conve hulls in
1. Inversions. A geometric construction relating points O, A and B looks as follows.
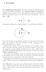 1. Inversions. 1.1. Definitions of inversion. Inversion is a kind of symmetry about a irle. It is defined as follows. he inversion of degree R 2 entered at a point maps a point to the point on the ray
1. Inversions. 1.1. Definitions of inversion. Inversion is a kind of symmetry about a irle. It is defined as follows. he inversion of degree R 2 entered at a point maps a point to the point on the ray
Vocabulary Check. 410 Chapter 4 Trigonometry
 40 pter 4 Trigonometr etion 4.8 pplitions n Moels You soul e le to solve rigt tringles. You soul e le to solve rigt tringle pplitions. You soul e le to solve pplitions of simple rmoni motion. Voulr ek.
40 pter 4 Trigonometr etion 4.8 pplitions n Moels You soul e le to solve rigt tringles. You soul e le to solve rigt tringle pplitions. You soul e le to solve pplitions of simple rmoni motion. Voulr ek.
Name Date Class. cot. tan. cos. 1 cot 2 csc 2
 Fundmentl Trigonometric Identities To prove trigonometric identit, use the fundmentl identities to mke one side of the eqution resemle the other side. Reciprocl nd Rtio Identities csc sec sin cos Negtive-Angle
Fundmentl Trigonometric Identities To prove trigonometric identit, use the fundmentl identities to mke one side of the eqution resemle the other side. Reciprocl nd Rtio Identities csc sec sin cos Negtive-Angle
Algebra II Notes Unit Ten: Conic Sections
 Sllus Ojective: 0. The student will sketch the grph of conic section with centers either t or not t the origin. (PARABOLAS) Review: The Midpoint Formul The midpoint M of the line segment connecting the
Sllus Ojective: 0. The student will sketch the grph of conic section with centers either t or not t the origin. (PARABOLAS) Review: The Midpoint Formul The midpoint M of the line segment connecting the
Tight triangulations: a link between combinatorics and topology
 Tight tringultions: link between ombintoris nd topology Jonthn Spreer Melbourne, August 15, 2016 Topologil mnifolds (Geometri) Topology is study of mnifolds (surfes) up to ontinuous deformtion Complited
Tight tringultions: link between ombintoris nd topology Jonthn Spreer Melbourne, August 15, 2016 Topologil mnifolds (Geometri) Topology is study of mnifolds (surfes) up to ontinuous deformtion Complited
MTH 146 Conics Supplement
 105- Review of Conics MTH 146 Conics Supplement In this section we review conics If ou ne more detils thn re present in the notes, r through section 105 of the ook Definition: A prol is the set of points
105- Review of Conics MTH 146 Conics Supplement In this section we review conics If ou ne more detils thn re present in the notes, r through section 105 of the ook Definition: A prol is the set of points
Graphing Conic Sections
 Grphing Conic Sections Definition of Circle Set of ll points in plne tht re n equl distnce, clled the rdius, from fixed point in tht plne, clled the center. Grphing Circle (x h) 2 + (y k) 2 = r 2 where
Grphing Conic Sections Definition of Circle Set of ll points in plne tht re n equl distnce, clled the rdius, from fixed point in tht plne, clled the center. Grphing Circle (x h) 2 + (y k) 2 = r 2 where
MATH 25 CLASS 5 NOTES, SEP
 MATH 25 CLASS 5 NOTES, SEP 30 2011 Contents 1. A brief diversion: reltively prime numbers 1 2. Lest common multiples 3 3. Finding ll solutions to x + by = c 4 Quick links to definitions/theorems Euclid
MATH 25 CLASS 5 NOTES, SEP 30 2011 Contents 1. A brief diversion: reltively prime numbers 1 2. Lest common multiples 3 3. Finding ll solutions to x + by = c 4 Quick links to definitions/theorems Euclid
EXPONENTIAL & POWER GRAPHS
 Eponentil & Power Grphs EXPONENTIAL & POWER GRAPHS www.mthletics.com.u Eponentil EXPONENTIAL & Power & Grphs POWER GRAPHS These re grphs which result from equtions tht re not liner or qudrtic. The eponentil
Eponentil & Power Grphs EXPONENTIAL & POWER GRAPHS www.mthletics.com.u Eponentil EXPONENTIAL & Power & Grphs POWER GRAPHS These re grphs which result from equtions tht re not liner or qudrtic. The eponentil
Chapter 11 Trigonometry
 hapter 11 Trigonometry Sec. 1 Right Triangle Trigonometry The most difficult part of Trigonometry is spelling it. Once we get by that, the rest is a piece of cake. efore we start naming the trigonometric
hapter 11 Trigonometry Sec. 1 Right Triangle Trigonometry The most difficult part of Trigonometry is spelling it. Once we get by that, the rest is a piece of cake. efore we start naming the trigonometric
Solutions to Math 41 Final Exam December 12, 2011
 Solutions to Mth Finl Em December,. ( points) Find ech of the following its, with justifiction. If there is n infinite it, then eplin whether it is or. ( ) / ln() () (5 points) First we compute the it:
Solutions to Mth Finl Em December,. ( points) Find ech of the following its, with justifiction. If there is n infinite it, then eplin whether it is or. ( ) / ln() () (5 points) First we compute the it:
Geometry Unit 3 Practice
 Lesson 17-1 1. Find the image of each point after the transformation (x, y) 2 x y 3, 3. 2 a. (6, 6) b. (12, 20) Geometry Unit 3 ractice 3. Triangle X(1, 6), Y(, 22), Z(2, 21) is mapped onto XʹYʹZʹ by a
Lesson 17-1 1. Find the image of each point after the transformation (x, y) 2 x y 3, 3. 2 a. (6, 6) b. (12, 20) Geometry Unit 3 ractice 3. Triangle X(1, 6), Y(, 22), Z(2, 21) is mapped onto XʹYʹZʹ by a
Angle Properties in Polygons. Part 1 Interior Angles
 2.4 Angle Properties in Polygons YOU WILL NEED dynmic geometry softwre OR protrctor nd ruler EXPLORE A pentgon hs three right ngles nd four sides of equl length, s shown. Wht is the sum of the mesures
2.4 Angle Properties in Polygons YOU WILL NEED dynmic geometry softwre OR protrctor nd ruler EXPLORE A pentgon hs three right ngles nd four sides of equl length, s shown. Wht is the sum of the mesures
)
 Chpter Five /SOLUTIONS Since the speed ws between nd mph during this five minute period, the fuel efficienc during this period is between 5 mpg nd 8 mpg. So the fuel used during this period is between
Chpter Five /SOLUTIONS Since the speed ws between nd mph during this five minute period, the fuel efficienc during this period is between 5 mpg nd 8 mpg. So the fuel used during this period is between
Chapter 4 Fuzzy Graph and Relation
 Chpter 4 Fuzzy Grph nd Reltion Grph nd Fuzzy Grph! Grph n G = (V, E) n V : Set of verties(node or element) n E : Set of edges An edge is pir (x, y) of verties in V.! Fuzzy Grph ~ n ( ~ G = V, E) n V :
Chpter 4 Fuzzy Grph nd Reltion Grph nd Fuzzy Grph! Grph n G = (V, E) n V : Set of verties(node or element) n E : Set of edges An edge is pir (x, y) of verties in V.! Fuzzy Grph ~ n ( ~ G = V, E) n V :
N-Level Math (4045) Formula List. *Formulas highlighted in yellow are found in the formula list of the exam paper. 1km 2 =1000m 1000m
 *Formul highlighted in yellow re found in the formul lit of the em pper. Unit Converion Are m =cm cm km =m m = m = cm Volume m =cm cm cm 6 = cm km/h m/ itre =cm (ince mg=cm ) 6 Finncil Mth Percentge Incree
*Formul highlighted in yellow re found in the formul lit of the em pper. Unit Converion Are m =cm cm km =m m = m = cm Volume m =cm cm cm 6 = cm km/h m/ itre =cm (ince mg=cm ) 6 Finncil Mth Percentge Incree
Inequalities in Triangles Geometry 5-5
 Inequalities in Triangles Geometry 5-5 Name: ate: Period: Theorem 5-10 Theorem 5-11 If two sides of a triangle are not If two angles of a triangle are not congruent, then the larger angle congruent, then
Inequalities in Triangles Geometry 5-5 Name: ate: Period: Theorem 5-10 Theorem 5-11 If two sides of a triangle are not If two angles of a triangle are not congruent, then the larger angle congruent, then
and vertically shrinked by
 1. A first exmple 1.1. From infinite trnsltion surfe mp to end-periodi mp. We begin with n infinite hlf-trnsltion surfe M 0 desribed s in Figure 1 nd n ffine mp f 0 defined s follows: the surfe is horizontlly
1. A first exmple 1.1. From infinite trnsltion surfe mp to end-periodi mp. We begin with n infinite hlf-trnsltion surfe M 0 desribed s in Figure 1 nd n ffine mp f 0 defined s follows: the surfe is horizontlly
Chapter44. Polygons and solids. Contents: A Polygons B Triangles C Quadrilaterals D Solids E Constructing solids
 Chpter44 Polygons nd solids Contents: A Polygons B Tringles C Qudrilterls D Solids E Constructing solids 74 POLYGONS AND SOLIDS (Chpter 4) Opening prolem Things to think out: c Wht different shpes cn you
Chpter44 Polygons nd solids Contents: A Polygons B Tringles C Qudrilterls D Solids E Constructing solids 74 POLYGONS AND SOLIDS (Chpter 4) Opening prolem Things to think out: c Wht different shpes cn you
Chapter 7. Right Triangles and Trigonometry
 hapter 7 Right Triangles and Trigonometry 7.1 pply the Pythagorean Theorem 7.2 Use the onverse of the Pythagorean Theorem 7.3 Use Similar Right Triangles 7.4 Special Right Triangles 7.5 pply the Tangent
hapter 7 Right Triangles and Trigonometry 7.1 pply the Pythagorean Theorem 7.2 Use the onverse of the Pythagorean Theorem 7.3 Use Similar Right Triangles 7.4 Special Right Triangles 7.5 pply the Tangent
MATH STUDENT BOOK. 12th Grade Unit 3
 MTH STUDENT OOK 12th Grade Unit 3 MTH 1203 RIGHT TRINGLE TRIGONOMETRY INTRODUTION 3 1. SOLVING RIGHT TRINGLE LENGTHS OF SIDES NGLE MESURES 13 INDIRET MESURE 18 SELF TEST 1: SOLVING RIGHT TRINGLE 23 2.
MTH STUDENT OOK 12th Grade Unit 3 MTH 1203 RIGHT TRINGLE TRIGONOMETRY INTRODUTION 3 1. SOLVING RIGHT TRINGLE LENGTHS OF SIDES NGLE MESURES 13 INDIRET MESURE 18 SELF TEST 1: SOLVING RIGHT TRINGLE 23 2.
Ray surface intersections
 Ry surfce intersections Some primitives Finite primitives: polygons spheres, cylinders, cones prts of generl qudrics Infinite primitives: plnes infinite cylinders nd cones generl qudrics A finite primitive
Ry surfce intersections Some primitives Finite primitives: polygons spheres, cylinders, cones prts of generl qudrics Infinite primitives: plnes infinite cylinders nd cones generl qudrics A finite primitive
Geometry/Trig 2 Unit 3 Review Packet Answer Key
 Unit 3 Review Pcket nswer Key Section I Nme the five wys to prove tht prllel lines exist. 1. If two lines re cut y trnsversl nd corresponding ngles re congruent, then the lines re prllel.. If two lines
Unit 3 Review Pcket nswer Key Section I Nme the five wys to prove tht prllel lines exist. 1. If two lines re cut y trnsversl nd corresponding ngles re congruent, then the lines re prllel.. If two lines
8.2 Areas in the Plane
 39 Chpter 8 Applictions of Definite Integrls 8. Ares in the Plne Wht ou will lern out... Are Between Curves Are Enclosed Intersecting Curves Boundries with Chnging Functions Integrting with Respect to
39 Chpter 8 Applictions of Definite Integrls 8. Ares in the Plne Wht ou will lern out... Are Between Curves Are Enclosed Intersecting Curves Boundries with Chnging Functions Integrting with Respect to
Answer Key Lesson 6: Workshop: Angles and Lines
 nswer Key esson 6: tudent Guide ngles nd ines Questions 1 3 (G p. 406) 1. 120 ; 360 2. hey re the sme. 3. 360 Here re four different ptterns tht re used to mke quilts. Work with your group. se your Power
nswer Key esson 6: tudent Guide ngles nd ines Questions 1 3 (G p. 406) 1. 120 ; 360 2. hey re the sme. 3. 360 Here re four different ptterns tht re used to mke quilts. Work with your group. se your Power
Integration. October 25, 2016
 Integrtion October 5, 6 Introduction We hve lerned in previous chpter on how to do the differentition. It is conventionl in mthemtics tht we re supposed to lern bout the integrtion s well. As you my hve
Integrtion October 5, 6 Introduction We hve lerned in previous chpter on how to do the differentition. It is conventionl in mthemtics tht we re supposed to lern bout the integrtion s well. As you my hve
Chapter Spline Method of Interpolation More Examples Electrical Engineering
 Chpter. Spline Method of Interpoltion More Exmples Electricl Engineering Exmple Thermistors re used to mesure the temperture of bodies. Thermistors re bsed on mterils chnge in resistnce with temperture.
Chpter. Spline Method of Interpoltion More Exmples Electricl Engineering Exmple Thermistors re used to mesure the temperture of bodies. Thermistors re bsed on mterils chnge in resistnce with temperture.
called the vertex. The line through the focus perpendicular to the directrix is called the axis of the parabola.
 Review of conic sections Conic sections re grphs of the form REVIEW OF CONIC SECTIONS prols ellipses hperols P(, ) F(, p) O p =_p REVIEW OF CONIC SECTIONS In this section we give geometric definitions
Review of conic sections Conic sections re grphs of the form REVIEW OF CONIC SECTIONS prols ellipses hperols P(, ) F(, p) O p =_p REVIEW OF CONIC SECTIONS In this section we give geometric definitions
Width and Bounding Box of Imprecise Points
 Width nd Bounding Box of Impreise Points Vhideh Keikh Mrten Löffler Ali Mohdes Zhed Rhmti Astrt In this pper we study the following prolem: we re given set L = {l 1,..., l n } of prllel line segments,
Width nd Bounding Box of Impreise Points Vhideh Keikh Mrten Löffler Ali Mohdes Zhed Rhmti Astrt In this pper we study the following prolem: we re given set L = {l 1,..., l n } of prllel line segments,
Unit #9 : Definite Integral Properties, Fundamental Theorem of Calculus
 Unit #9 : Definite Integrl Properties, Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Unit #9 : Definite Integrl Properties, Fundmentl Theorem of Clculus Gols: Identify properties of definite integrls Define odd nd even functions, nd reltionship to integrl vlues Introduce the Fundmentl
Congruent triangle: all pairs of corresponding parts are congruent. Congruent Polygons: all pairs of corresponding parts are congruent.
 Notes Page 1 3.1 Notes Wednesday, October 01, 2008 8:33 PM efinitions: 2. ongruent triangle: all pairs of corresponding parts are congruent. ongruent Polygons: all pairs of corresponding parts are congruent.
Notes Page 1 3.1 Notes Wednesday, October 01, 2008 8:33 PM efinitions: 2. ongruent triangle: all pairs of corresponding parts are congruent. ongruent Polygons: all pairs of corresponding parts are congruent.
Matrices and Systems of Equations
 Mtrices Mtrices nd Sstems of Equtions A mtri is rectngulr rr of rel numbers. CHAT Pre-Clculus Section 8. m m m............ n n n mn We will use the double subscript nottion for ech element of the mtri.
Mtrices Mtrices nd Sstems of Equtions A mtri is rectngulr rr of rel numbers. CHAT Pre-Clculus Section 8. m m m............ n n n mn We will use the double subscript nottion for ech element of the mtri.
Honors Thesis: Investigating the Algebraic Properties of Cayley Digraphs
 Honors Thesis: Investigting the Algebri Properties of Cyley Digrphs Alexis Byers, Wittenberg University Mthemtis Deprtment April 30, 2014 This pper utilizes Grph Theory to gin insight into the lgebri struture
Honors Thesis: Investigting the Algebri Properties of Cyley Digrphs Alexis Byers, Wittenberg University Mthemtis Deprtment April 30, 2014 This pper utilizes Grph Theory to gin insight into the lgebri struture
B. Definition: The volume of a solid of known integrable cross-section area A(x) from x = a
 Mth 176 Clculus Sec. 6.: Volume I. Volume By Slicing A. Introduction We will e trying to find the volume of solid shped using the sum of cross section res times width. We will e driving towrd developing
Mth 176 Clculus Sec. 6.: Volume I. Volume By Slicing A. Introduction We will e trying to find the volume of solid shped using the sum of cross section res times width. We will e driving towrd developing
Adjacency. Adjacency Two vertices u and v are adjacent if there is an edge connecting them. This is sometimes written as u v.
 Terminology Adjeny Adjeny Two verties u nd v re djent if there is n edge onneting them. This is sometimes written s u v. v v is djent to nd ut not to. 2 / 27 Neighourhood Neighourhood The open neighourhood
Terminology Adjeny Adjeny Two verties u nd v re djent if there is n edge onneting them. This is sometimes written s u v. v v is djent to nd ut not to. 2 / 27 Neighourhood Neighourhood The open neighourhood
SOAR2001 GEOMETRY SUMMER 2001
 SR2001 GEMETRY SUMMER 2001 1. Introduction to plane geometry This is the short version of the notes for one of the chapters. The proofs are omitted but some hints are given. Try not to use the hints first,
SR2001 GEMETRY SUMMER 2001 1. Introduction to plane geometry This is the short version of the notes for one of the chapters. The proofs are omitted but some hints are given. Try not to use the hints first,
MATH 2530: WORKSHEET 7. x 2 y dz dy dx =
 MATH 253: WORKSHT 7 () Wrm-up: () Review: polr coordintes, integrls involving polr coordintes, triple Riemnn sums, triple integrls, the pplictions of triple integrls (especilly to volume), nd cylindricl
MATH 253: WORKSHT 7 () Wrm-up: () Review: polr coordintes, integrls involving polr coordintes, triple Riemnn sums, triple integrls, the pplictions of triple integrls (especilly to volume), nd cylindricl
Introduction Transformation formulae Polar graphs Standard curves Polar equations Test GRAPHS INU0114/514 (MATHS 1)
 POLAR EQUATIONS AND GRAPHS GEOMETRY INU4/54 (MATHS ) Dr Adrin Jnnett MIMA CMth FRAS Polr equtions nd grphs / 6 Adrin Jnnett Objectives The purpose of this presenttion is to cover the following topics:
POLAR EQUATIONS AND GRAPHS GEOMETRY INU4/54 (MATHS ) Dr Adrin Jnnett MIMA CMth FRAS Polr equtions nd grphs / 6 Adrin Jnnett Objectives The purpose of this presenttion is to cover the following topics:
Year 10 Practice Assessment Task 3 (Note: All hints except the cosine rule will not be in exam, so memorise)
 Year 10 Practice ssessment Task 3 (Note: ll hints except the cosine rule will not be in exam, so memorise) 1)! 5 m 35 6 m The area of this triangle is closest to () 8 6 m 2 () 12 3 m 2 () 17 2 m 2 (D)
Year 10 Practice ssessment Task 3 (Note: ll hints except the cosine rule will not be in exam, so memorise) 1)! 5 m 35 6 m The area of this triangle is closest to () 8 6 m 2 () 12 3 m 2 () 17 2 m 2 (D)
Hyperbolas. Definition of Hyperbola
 CHAT Pre-Clculus Hyperols The third type of conic is clled hyperol. For n ellipse, the sum of the distnces from the foci nd point on the ellipse is fixed numer. For hyperol, the difference of the distnces
CHAT Pre-Clculus Hyperols The third type of conic is clled hyperol. For n ellipse, the sum of the distnces from the foci nd point on the ellipse is fixed numer. For hyperol, the difference of the distnces
such that the S i cover S, or equivalently S
 MATH 55 Triple Integrls Fll 16 1. Definition Given solid in spce, prtition of consists of finite set of solis = { 1,, n } such tht the i cover, or equivlently n i. Furthermore, for ech i, intersects i
MATH 55 Triple Integrls Fll 16 1. Definition Given solid in spce, prtition of consists of finite set of solis = { 1,, n } such tht the i cover, or equivlently n i. Furthermore, for ech i, intersects i
3 4. Answers may vary. Sample: Reteaching Vertical s are.
 Chpter 7 Answers Alterntive Activities 7-2 1 2. Check students work. 3. The imge hs length tht is 2 3 tht of the originl segment nd is prllel to the originl segment. 4. The segments pss through the endpoints
Chpter 7 Answers Alterntive Activities 7-2 1 2. Check students work. 3. The imge hs length tht is 2 3 tht of the originl segment nd is prllel to the originl segment. 4. The segments pss through the endpoints
Improper Integrals. October 4, 2017
 Improper Integrls October 4, 7 Introduction We hve seen how to clculte definite integrl when the it is rel number. However, there re times when we re interested to compute the integrl sy for emple 3. Here
Improper Integrls October 4, 7 Introduction We hve seen how to clculte definite integrl when the it is rel number. However, there re times when we re interested to compute the integrl sy for emple 3. Here
CHAPTER 5 RELATIONSHIPS WITHIN TRIANGLES
 HPTR 5 RLTIONSHIPS WITHIN TRINGLS In this chapter we address three ig IS: 1) Using properties of special segments in triangles ) Using triangle inequalities to determine what triangles are possible 3)
HPTR 5 RLTIONSHIPS WITHIN TRINGLS In this chapter we address three ig IS: 1) Using properties of special segments in triangles ) Using triangle inequalities to determine what triangles are possible 3)
[Prakash* et al., 5(8): August, 2016] ISSN: IC Value: 3.00 Impact Factor: 4.116
![[Prakash* et al., 5(8): August, 2016] ISSN: IC Value: 3.00 Impact Factor: 4.116 [Prakash* et al., 5(8): August, 2016] ISSN: IC Value: 3.00 Impact Factor: 4.116](/thumbs/84/89299493.jpg) [Prksh* et l 58: ugust 6] ISSN: 77-9655 I Vlue: Impt Ftor: 6 IJESRT INTERNTIONL JOURNL OF ENGINEERING SIENES & RESERH TEHNOLOGY SOME PROPERTIES ND THEOREM ON FUZZY SU-TRIDENT DISTNE Prveen Prksh* M Geeth
[Prksh* et l 58: ugust 6] ISSN: 77-9655 I Vlue: Impt Ftor: 6 IJESRT INTERNTIONL JOURNL OF ENGINEERING SIENES & RESERH TEHNOLOGY SOME PROPERTIES ND THEOREM ON FUZZY SU-TRIDENT DISTNE Prveen Prksh* M Geeth
