Lecture 5: May 24, 2007
|
|
|
- Chloe Perkins
- 5 years ago
- Views:
Transcription
1 Analysis of Gene Expression Data Spring Semester, 2007 Lecture 5: May 24, 2007 Lecturer: Ron Shamir Scribe: Shelly Mahlev and Shaul Karni Introduction As we have seen in previous lectures, the technology of DNA chips allows the measurement of mrna levels simultaneously for thousands of genes. The abundance of readily available data allows us the option to try to extract information, not easily seen while analyzing a single test, from the results of a multitude of tests. The results of DNA chip experiments are usually organized together in a gene expression matrix, with rows corresponding to genes and columns corresponding to conditions. A bicluster can be defined as a submatrix spanned by a subset of genes and a subset of conditions in which the genes have joint behavior in the corresponding conditions. Different algorithmic approaches to the biclustering problem use different measures for the quality of a given biclustering solution. Hence, the definition of the goal function of each algorithm is part of its description. There are two important themes regarding biclustering algorithms: 1. Data normalization. A common preprocessing step before applying any clustering algorithm is to normalize the rows or columns of the gene expression matrix, depending on the dimension on which the clustering is applied (rows/columns). In biclustering algorithms, for which the two dimensions are considered, the question of how normalization should be done is not simple. Some of the biclustering algorithms do not refer to the normalization problem and assume that the given data is normalized. 2. Eliminating redundancies when searching for all (or many) biclusters. Usually in clustering solutions, each gene/condition participates in at most one cluster, in biclustering solutions genes and conditions are often part of several biclusters. A bicluster algorithm should eliminate redundancies ( similar biclusters) from its output. This lecture can be viewed as a direct continuation of Lecture 4 which already described the notion of biclustering and presented Cheng and Church s biclustering algorithm. In this lecture, we will first recollect on Cheng and Church s algorithm (section 5.2) and then describe three more biclustering algorithms. First, we will describe the elegant simple Iterative 1 Based in part on a scribe by Itamar Elem and Seagull Chalamish, March 2005; Michal Ozery-Flato and Israel Steinfeld, May 2004; Irit Gat and Amos Tanay, May 2002.
2 2 Analysis of Gene Expression Data c Tel Aviv Univ. Signature Algorithm (section 5.3). Then, the hierarchical Coupled Two Way Clustering algorithm (section 5.4). And finally, we will describe the Statistical Algorithmic Method for Biclustering Analysis (section 5.5), a fast, combinatorial, statistically based algorithm. 5.2 Cheng and Church s algorithm First, let s briefly describe Cheng and Church s algorithm [4]. For a full description, the reader should refer to Lecture 4. Cheng and Church [4] implicitly assume that (gene, condition) pairs in a good bicluster have a constant expression level, plus possibly additive row and column specific effects. After removing row, column and submatrix averages, the residual level should be as small as possible. More formally, given the gene expression matrix E, a subset of genes I and a subset of conditions J, we define e Ij = P i I,j J e ij I J P i I e ij I as column subset average, e ij = P j J e ij J as row subset average and e IJ = as submatrix average. We define the residue score of an element e ij in a submatrix E IJ as RS IJ (i, j) = e ij e Ij e ij + e IJ and the mean square residue score of the entire submatrix as H(I, J) = RS IJ (i,j) 2 i I,j J. Given the I J score definition, the maximum bicluster problem seeks a bicluster of maximum size among all biclusters with score not exceeding a threshold δ. The size can be defined in several ways, for example as the number of cells in the matrix ( I J ) or the number of rows plus number of columns ( I + J ). To discover more than one bicluster, Cheng and Church suggested repeated application of the biclustering algorithm on modified matrices. The modification includes randomization of the values in the cells of the previously discovered biclusters, preventing the correlative signal in them to be beneficial for any other bicluster in the matrix. This has the obvious effect of precluding the identification of biclusters with significant overlaps. 5.3 The Iterative Signature Algorithm In the Iterative Signature Algorithm (ISA), the goal is to find a bicluster in which the conditions induce a correlated expression of the genes in the bicluster. I.e., the expression profiles of the genes in the bicluster are the most similar to each other when compared over its conditions. Conversely, the patterns of gene expression obtained under the conditions of the bicluster are most similar to each other when compared only over its genes. The degree of similarity is determined by a pair of threshold parameters. The gene threshold constrains the gene set, while the condition threshold constrains the condition set. Importantly, distinct biclusters may share common genes and conditions. Therefore, for each condition the average gene expression over all the genes of the bicluster should be exceptionally different (unusually high or low), and for each gene the average gene expression over all biclusters conditions
3 The Iterative Signature Algorithm 3 should be surprising as well. This intuition is formalized using a simple linear model for gene expression assuming normally distributed expression levels for each gene or condition as shown below Normalization The algorithm, presented in Figure 5.1, uses two normalized copies, E C and E G, of the original gene expression matrix E. The matrix E G (E C ) results from E by normalizing each column (row) so that the expression level of a random condition (gene) has mean 0 and variance 1. Note that the normalized matrices E G and E C in general are not equal Bicluster definition Suppose G = {g} is a set of independent random variables, where each random variable g G has mean 0 and variance 1. In this case, the average of all the random variables in G 1 (i.e. G g G g ) has a mean and a variance equal to 0 and 1 respectively. For G G G and C C we define: e G G c = 1 E G gc G (5.1) g G e C gc = 1 E C gc C (5.2) c C Note that e G Gc = ec gc = 0 due to the normalization made in EG and E C. For a fixed C (G ) let σ G (σ C ) be the standard deviation of the means {e C gc : g G} ({e G G c : c C}). The standard deviation σ 1 1 G (σ C ) can be predicted as ( ) as G ec gc C (e G G c ) being a linear sum of C ( G ) independent standard random variables. Alternatively, the standard deviations, σ G and σ C, can be estimated directly from the data, correcting for possible biases in the statistics of the specific condition and gene sets used. Given a set of genes G and a threshold parameter T C define: ISA(G ) = {c C : e G G c > T C σ C } (5.3) Given a set of conditions C and a threshold parameter T G define: ISA(C ) = {g G : e C gc > T Gσ G } (5.4) A (perfect) bicluster B = (G, C ) is required to have: ISA(G ) = C, ISA(C ) = G (5.5)
4 4 Analysis of Gene Expression Data c Tel Aviv Univ. The above definition states that for each condition c in the bicluster the average expression level of the genes in the bicluster, e G G c, is above a certain threshold T C. Conversely, for each gene g in the bicluster the average expression level over the conditions of the bicluster, e C gc, is also above some threshold T G. This reciprocal dependence between the genes and the conditions associated with a bicluster implies that, considering only the genes of the bicluster, its conditions are exactly those for which the coexpression is the most stringent. In other words, in a bicluster, the z-score of each gene, measured w.r.t. the conditions of the bicluster, and the z-score of each condition, measured w.r.t. the genes of the bicluster, should exceed a threshold. As we shall see below, ISA will not discover biclusters for which the conditions (5.5) hold strictly, but will use a relaxed version Searching for biclusters Define a directed bipartite graph B(G, C, E) as follows. G = {G : G G}, C = {C : C C}, E = {(G, C ) : ISA(G ) = C, G G, C C} {(G, C ) : ISA(C ) = G, G G, C C}, that is, every node in the graph is either a subset of conditions or a subset of genes. The goal is to find a cycle as small as possible following the conditions (5.5), and therefore a (perfect) bicluster is a cycle of size 2. However, as we mentioned before, the algorithm searches for an approximation of a (perfect) bicluster. The algorithm starts from an arbitrary set of genes G 0 = G in. The set may be randomly generated or selected based on some prior knowledge. The algorithm then repeatedly applies the update equations: C i = ISA(G i ), G i+1 = ISA(C i ) (5.6) Let g n be a binary vector of size G for which g n (i) bicluster is a pair (G n, C n ) satisfying: = 1 iff i G n. An approximated g n g n i g n + g n i < ɛ (5.7) for all i > 0 smaller than some m. The ISA thus searches for a series of gene sets {G i } which converges to an approximated fixed point that is considered to be a bicluster. The actual fixed point depends on both the initial set G in and the threshold parameters T C, T G. The ISA algorithm can be generalized by assigning weights for each gene/condition such that genes/conditions with a significant behavior (higher z-score) will have larger weights. In this case, there are two changes to the algorithm: 1. the simple means, e G G c and ec gc, are replaced by weighted means. 2. The vector g n (see 5.7) has real-valued elements and is defined as follows: g (i) weight(i) if i G n, otherwise g n (i) = 0. n =
5 The Iterative Signature Algorithm 5 ISA(G, C, E, G in, T G, T C, m, ɛ): \ G : genes. C : conditions. E : Gene expression matrix. G in : Initial gene set. T G, T C : gene and condition z-score thresholds. m, ɛ: stopping criteria. \ Construct matrix E C. Construct matrix E G. Initialize counter n = 0. Initialize the current genes set G = G in and compute g 0 based on G While ( true) do Compute e G G c for c C. C = {c C : e G G c > T C } G Compute e C gc for g G. G = {g G : e C gc > T G } C n = n + 1 Compute g n from G. If (n < m 1) continue. Initialize counter i = 1 while i < m If ( gn g n i g n+g n i ɛ) break i = i + 1 If i == m break Report G, C Applications Figure 5.1: The ISA algorithm for finding a single bicluster. There are a few difficulties and redundancies that we have to take into account: Starting from different seeds yields different fixed points (biclusters). Using different thresholds changes the graph structure and gives a different number of fixed points. There is need to filter similar solutions and report a short list of significant biclusters. The following practical applications take the above into consideration: Start from genes with a known functional annotation and refine them into a bicluster. Start from genes with known transcription factor binding sites.
6 6 Analysis of Gene Expression Data c Tel Aviv Univ. Start from a set of sequence orthologs, to find similar genes from different species. Start from a random set (the algorithm might end up reporting an empty bicluster). Therefore, to generate a representative set of biclusters, do the following: 1. Run ISA with different seeds. 2. Run ISA with variant thresholds (see equations 5.3 and 5.4). This action affects the ISA function and consequently the traversed bipartite graph. Scanning over different values for (T C, T G ) reveals the modular structure at different resolutions: Lower thresholds yield larger biclusters whose coregulation is relatively loose, while higher thresholds lead to smaller, tightly coregulated biclusters. After eliminating redundancies (similar solutions), the set of fixed points can be analyzed as a set of biclusters Discussion on ISA ISA is an elegant algorithm which has quite a fast implementation. It offers a satisfying simple solution to the normalization problem. It is known to have good empirical results in several cases. However, there are some difficulties in the use of ISA: 1. The size of a bicluster depends critically on the associated set of two thresholds that determine the similarity between the genes and conditions of the module, respectively, and there is no scheme for choosing the values of the thresholds. 2. Finding good seeds for the algorithm can be problematic. 3. We cannot know if we found all or even most of the existing (approximated) biclusters. 4. Since the algorithm uses Z-score statistics, it implicitly assumes that the data (genes and conditions) have normal distribution. However, if the data have non-normal behavior, then the algorithm may fail. For instance, assume that the data contains a gene g and a condition c for which the expression level is much higher than all the other levels (E gc is extremely high). In this case, if a set of genes G contains g then c ISA(G ) and vice versa: c C implies g ISA(C ). Hence, we can get a bicluster in which there are a condition and a gene which have no relevance to the other genes/conditions in the bicluster. 5. Redundancies are a general problem of biclustering, that most methods do not deal with. ISA, for example, might find two overlapping biclusters as significant biclusters.
7 The Iterative Signature Algorithm 7 Figure 5.2: Modular organization of yeast expression data. The iterative signature algorithm was applied to genome wide yeast expression data gathered by more than 1000 DNA-chip experiments. (a) The figure shows the identified biclusters at three different gene thresholds t G =1.8,2.1,2.4. For each threshold the corresponding biclusters are displayed in a plane, such that their distance reflects their correlation with respect to conditions. Moving to a higher threshold, corresponding biclusters are kept in the same position in each plane, while the new biclusters are placed such that their position reflects best their correlation with the other biclusters. The leftmost plane corresponds to the lowest threshold (t G = 1.8), where only five fixed points exist. The corresponding biclusters can be associated with central functions of the yeast organism: protein synthesis, cell cycle (G 1, mating, amino-acid biosynthesis, and stress response. Different gray scales were used to indicate which of the fixed points that emerge at higher thresholds are related to these five central biclusters (i.e., they would converge to the respective module at the lowest threshold). (b) The pie charts show the number of random input sets that converged to the respective fixed point. The gray scales are as in (a).
8 8 Analysis of Gene Expression Data c Tel Aviv Univ. 5.4 Coupled two-way clustering Coupled two-way clustering (CTWC), introduced by Getz, Levine and Domany [8] is another algorithm for finding biclusters. The main idea is to identify subsets of the genes and conditions, such that when one of these is used to cluster the other, stable and significant partitions emerge. This algorithm is based on iterative clustering, that performs a search for such subsets. A straightforward approach to finding pairs of subsets, (G, C ), that lead to meaningful clusters, could be to take all possible submatrices of the original data and apply the standard (uncoupled) two-way clustering procedure to every one of them. By keeping track of all stable clusters that are formed in this process, and storing the identity of both genes and conditions that define the particular submatrix, one is guaranteed to find every possible stable partition in the data. This approach is, of course, impossible to implement, because the number of such submatrices grows exponentially with the size of the problem. CTWC provides an efficient heuristic to generate such pairs of genes and conditions subsets by an iterative process that severely restricts the possible candidates for such subsets; Only those submatrices whose rows (columns) belong to genes (conditions) that were identified (in a previous iteration) as a stable cluster were considered and tested. This algorithm does not define any goal function or other measure for the quality of a given biclustering solution. Instead it defines a generic scheme for transforming a one-dimensional clustering algorithm into a biclustering algorithm. The iterative process is initialized with the full matrixi.e., the sets of all genes (g 0 ) and of all conditions (s 0 ) are used to perform standard two-way clustering. Denote by gi 1 and s 1 i stable clusters of genes and conditions found in this first step. Every pair (gi n, gj m ) (made of clusters obtained so far) defines a submatrix of the expression data; for every such submatrix two-way clustering was performed. The resulting stable gene (or condition) clusters are denoted by gk 2 (or s2 l ). Each cluster is stored. Together with each new cluster we also store pointers that identify the pair of parent clusters (gi n, s m j ) that were used in the clustering process that generated it. These steps are iterated further, using pairs of all previously found clusters. Note that every pair is treated only once; the process is terminated when no new clusters that satisfy some criteria (such as stability, critical size, etc.) are found. The problem with this algorithm is that its success depends on the clustering algorithm that was used, and therefore the CTWC procedure might miss significant biclusters. 5.5 SAMBA We next describe SAMBA (Statistical Algorithmic Method for Bicluster Analysis) [16]. The motivation underlying its development is the need for a fast biclustering method that would produce statistically significant results as part of its design. The key point in the understanding of SAMBA is the statistical model used by the bicluster scoring scheme. The
9 SAMBA 9 normalization is done by translating the gene expression matrix to a weighted bipartite graph, using a statistical model for the data. The hope is that a model which captures the essential features of the data would guarantee high quality results Data Modeling The intuitive notion of a bicluster is a subset of genes that exhibit similar expression patterns over a subset of conditions. Following this intuition, the authors defined a bicluster as a subset of genes that jointly respond across a subset of conditions, where a gene is termed responding in some condition if its expression level changes significantly at that condition w.r.t. its normal level. The expression data is modeled as a bipartite graph whose two parts correspond to conditions and genes with edges spanned between the parts where significant expression changes occur. Later, we shall assign weights to the vertex pairs of the bipartite graph according to a statistical model, so that heavy subgraphs would correspond to significant biclusters. We can tag each edge to incorporate the direction of regulation (up or down), as we shall see later. For now assume edges are not tagged. Formally, given an input gene expression data, we form a bipartite graph G = (U, V, E) (e.g. Figure 5.3). In this graph, U is the set of conditions, V is the set of genes, and (u, v) E iff v responds in condition u, i.e., if the expression level of v changes significantly in u. This discretization can be further developed using a discretisation function, adding edges according to the expression level of v.a bicluster corresponds to a subgraph H = (U, V, E ) of G, and represents a subset V of genes that are coregulated under a subset of conditions U (see Figure 5.3). The weight of a subgraph (bicluster) is the sum of the weights of gene-condition pairs in it (edges and non-edges). In order to assign statistical meaning to the weight of a subgraph, the authors developed statistical models for the bipartite graph representation of expression data. Using these models one can derive scoring schemes for assessing the significance of an observed subgraph (corresponding to a bicluster). This is done so that the score can be expressed as a sum of independent contributions from each of the node pairs (condition-gene) in the subgraph. Using this model, we can reduce the biclustering problem to the problem of finding heavy subgraphs in a bipartite graph A Simple Model The first statistical model we present is a simplistic one, and is presented as a motivation for the more sophisticated model that will follow. Let H = (U, V, E ) be a subgraph of G. Denote U = m, V = n, E = k. The model assumes that edges occur independently with an equal probability p, where p = E (edge density). We shall now calculate P (H) U V the p value of H (i.e. the tail of a binomial distribution). Then, the probability of observing
10 10 Analysis of Gene Expression Data c Tel Aviv Univ. Figure 5.3: Source: [16]. SAMBA model : Gene expression data is modeled using a bipartite graph whose two sides correspond to the set of conditions U and the set of genes V. An edge (u, v) indicates the response of gene v in condition u. A statistical model assigns weights to the edges and non-edges of the graph. A: Part of the graph showing the condition tup1 deletion and its effect on the genes gal7 (response) and ecm11 (no response). B: A heavy subgraph (shaded) representing a significant bicluster. a graph at least as dense as H according to this model is: P (H) = nm k =k ( nm This can then be bounded, assuming that p < 1/2 by : P (H) = nm k =k ( nm k k ) p k (1 p) nm k (5.8) ) p k (1 p) nm k 2 nm p k (1 p) nm k (5.9) Our goal is to find a subgraph H with the lowest P (H). Seeking a minimal weighted subgraph H, is equivalent to minimizing the logarithm of the upper bound: (1 + log p) + (l + log(1 p)) (5.10) edges non edges Which is the sum of the edges and the sum of non-edges A Refined Model The simple model presented above is actually far from reality. In fact, if we look at the degree distribution of real gene expression data, we can identify a very non uniform behavior,
11 SAMBA 11 where some of the conditions and genes have very high degrees and others very low degrees. Because, a simple random graph model would result in very high scores for the bicluster defined by all high degree nodes in the graph, we next describe a refined null model that takes into account the variability of the degrees in G. This model incorporates the characteristic behavior of each specific condition and gene. This behavior may reflect some experiment artifact (some genes are more likely to have noisy measurements) or some biological actual meaning (some of the genes participate in many of the cellular pathways). Let H = (U, V, E ) be a subgraph of G and denote E = (U V ) \ E. For a vertex w U V let d G w denote its degree in G. The refined null model assumes that the occurrence of each edge (u, v) is an independent Bernoulli variable with parameter p (u,v). The probability p (u,v) is the fraction of bipartite graphs with degree sequence identical to G that contain the edge (u, v), or p (u,v) = {G = (U, V, E ) w, d G w = d G w, (u, v) E } (5.11) {G = (U, V, E ) w, d G = d G w} We can estimate p (u,v) using a Monte-Carlo Markov Chain process, starting from the original graph and performing a sequence of random edge swaps that preserve the degrees (A formal proof of a sampling lemma in the space of fixed degree graphs is however still an open problem). The probability of observing H is thus P (H) = ( (u,v) E p (u,v) ) ( (u,v) E (1 p (u,v) )). However, we cannot simply compare subgraphs according to this probability, since it improves (decreases) as the size of H increases (decreases). To overcome this problem, we use a likelihood ratio to capture the significance of biclusters. The null model is as stated above. For the alternative model we assume that each edge of a bicluster occurs with constant probability p c > max (u,v) U V p (u,v). This model reflects our belief that biclusters represent approximately uniform relations between their elements. The log likelihood ratio for H is therefore: log L(H) = (u,v) E log p c p (u,v) + w (u,v) E log 1 p c 1 p (u,v) Setting the weight of each edge (u, v) to log pc p (u,v) > 0 and the weight of each non-edge (u, v) to log < 0, we conclude that the score of H is simply its weight. 1 pc 1 p (u,v) Finding heavy subgraphs Having assigned weights for edges in our model bipartite graph, such that the weight of a subgraph encode some reasonable likelihood ratio, we now turn to the problem of identifying the maximum likelihood bicluster, which is, under our formulation, the heaviest subgraph. The computational problem of finding the largest node biclique (the one with the largest number of vertices) in a bipartite graph has an elegant polynomial time algorithm (using
12 12 Analysis of Gene Expression Data c Tel Aviv Univ. matching). Our problem, however, is more closely related to the problem of finding the largest edge biclique (the biclique with the largest number of edges) which is NP-hard for both unweighted [13] and weighted graphs [9]. In fact, the problem of finding the heaviest bipartite subgraph when edges are assigned positive weights and non edges negative weights is hard as well (by reduction from CLIQUE). We thus enforce additional limitation on our graph, namely, restrict the degree of the genes side, so that a gene that responds in more then d conditions is ignored. This enables us to develop a polynomial algorithm which is later used as the basis for a practical implementation that can avoid the degree restriction. Note that according to the statistical model, genes with high degree contribute less to the significance of a bicluster, so running the algorithm without them may not be a very restricting limitation. Maximum Bounded Biclique We start by describing an O( V 2 d )-time algorithm to find a maximum weight biclique in a bipartite graph whose gene vertices have d-bounded degree. This algorithm will be a key component in the algorithms that follow. Let G = (U, V, E) be a bipartite graph. We say that G has d-bounded gene side, if every v V has degree at most d. Let w : U V R be a weight function. For a pair of subsets U U, V V we denote by w(u, V ) the weight of the subgraph induced on U V, i.e., w(u, V ) = u U,v V w((u, v)). The neighborhood of a vertex v, denoted N(v), is the set of vertices adjacent to v in G. We denote V = n throughout. Problem 5.1 (Maximum Bounded Biclique) Given a weighted bipartite graph G with a d-bounded gene side, find a maximum weight complete subgraph of G. Theorem 5.1 The maximum bounded biclique problem can be solved in O(n2 d ) time and space. Proof: Observe that a maximum bounded biclique H = (U, V, E ) in G must have U d. If not, it s easy to show that there must be a vertex in U whose removal will give a better biclique, with contradiction to the assumption that H is maximal. Figure 5.5 describes a hash-table based algorithm that for each vertex v V scans all O(2 d ) subsets of its neighbors, thereby identifying the heaviest biclique. Each hash entry corresponds to a subset of conditions and records the total weight of edges from adjacent gene vertices. An iteration over subsets of N(v) can be done in O(2 d ) time. Hence, the algorithm spends O(n2 d ) time on the hashing and finding U best. Since U best d, computing V best can be done in O(nd) time, so the total running time is O(n2 d ). The space complexity is O(n2 d ) due to the hash-table. Note that the algorithm can be adapted to give the k condition subsets that induce solutions of highest weight in O(n2 d log k) time using a priority queue data structure.
13 SAMBA 13 Figure 5.4: Example of the hashing technique, in which a maximal Biclique, is found for a subgraph. Each row stands for a subset of genes, and a score (for the row). The score is initialized as zero, and for every condition that is connected to all genes in the subset, the size of the subset is added to it. Thus, the score of a subset is the number of genes multiplied by the number of conditions connected to the whole subset. The maximal biclique is the genes in the row with the highest score, and the conditions that are connected to the whole subset. Finding Heavy Subgraphs Algorithm We will now show how to extend the latter algorithm to find heavy subgraphs which are not necessarily complete. For simplicity we shall describe the algorithm assuming that each edge has weight +1 and each non-edge has weight 1. Extension to more general weights can be done in a similar manner. Formally, given a bipartite graph G = (U, V, E) define a weight function w : U V { 1, 1} such that w((u, v)) = 1 for (u, v) E, and w((u, v)) = 1 for (u, v) (U V ) \ E. Consider the following problem: Problem 5.2 (Maximum Bounded Bipartite Subgraph) Given a bipartite graph G with d-bounded gene side, find a maximum weight subgraph of G. Lemma 5.2 Let H = (U, V, E ) be a maximum weight subgraph of G. Then every vertex in H is connected to at least half the vertices on the other side of H. Proof: Follows from the choice of weights, since if a vertex v V has less than U /2 neighbors, then removing v from H will result in a heavier subgraph. The proof for u U is symmetric. Lemma 5.3 Let H = (U, V, E ) be a maximum weight subgraph of G. For each set X U there exists a subset Y X with Y X /2 such that Y N(v) for some v V.
14 14 Analysis of Gene Expression Data c Tel Aviv Univ. MaxBoundBiClique(U, V, E, d): Initialize a hash table weight; weight best 0 For all v V do For all S N(v) do weight[s] weight[s]+ w(s, {v}) If (weight[s] > weight best ) U best S weight best weight[s] Compute V best = u Ubest N(u) Output (U best, V best ) Figure 5.5: Source: [16]. An algorithm for the maximum bounded biclique problem. Proof: Assume there exists X U such that all subsets X N(v), v V are of size smaller than X /2. Then the weight of the subgraph induced on (U \ X, V ) exceeds that of H, a contradiction. Corollary 5.4 A maximum weight subgraph of G has at most 2d vertices from U. Proof: let X be U, since Y N(v) then d Y. From lemma 5.3 we know Y U /2, so we get U 2d. Lemma 5.5 Let H = (U, V, E ) be a maximum weight subgraph of G. Then U can be covered by at most log(2d) sets, each of which is contained in the neighborhood of some vertex in V. Proof: Denote U = t. By Lemma 5.3 there exists a subset Y U with Y t/2, such that Y N(v) for some v V. The same holds for the set U \ Y, and we can continue in this manner until we cover U. By construction we have at most log t sets in the cover. Since t 2d by Corollary 5.4, the result follows. Lemma 5.5 implies an algorithm to find a maximum weight subgraph. The algorithm tests all collections of at most log(2d) subsets of neighborhoods of vertices in V. Since there are O(n2 d ) such subsets we have: Corollary 5.6 The maximum bounded bipartite subgraph problem can be solved in O((n2 d ) log(2d) ) time.
15 SAMBA Incorporating the Direction of Expression Changes In our discussion so far, the underlying bipartite graph used for modeling the data contained edges for significantly changed genes, but ignored the type of change (increase or decrease in the expression level). We can integrate additional information into the model by associating a sign of up or down with each edge. We now have three types of binary relations in our bipartite graphs: An up edge, a down edge or no edge. It is reasonable to look for a bicluster in which the conditions tend to affect genes in a consistent way, i.e., two clustered conditions should either have always the same effect or always the opposite effect on each of the genes. This leads to the definition of a consistent biclique: Given a bipartite graph G = (U, V, E) with edge sign function c : E { 1, 1}, we say that an induced biclique H = (U, V, E ) is consistent if there exists an assignment τ : U V { 1, 1} such that for every v V, u U we have c((u, v)) = τ(u)τ(v). The maximum consistent biclique problem in degree-bounded graphs can be solved in polynomial time by reduction to the standard maximum biclique problem: Lemma 5.7 There is an O(n2 d )-time algorithm for the maximum consistent bounded biclique problem on graphs with d-bounded gene side. Proof: Given G and c, we construct the graph G = (U U, V V, E ), where U and V are copies of U and V, respectively, and E = {(u, v), (u, v) (u, v) E, c((u, v)) = 1} {(u, v), (u, v) (u, v) E, c((u, v)) = 1}. Suppose that (U, V ) induce a consistent biclique in G of size k with a sign assignment τ. Then {v U V τ(v) = 1} {v v U V, τ(v) = 1} induce a biclique of size k in G. Conversely, if (U, V ) induce a biclique in G, then no pair u, u is contained in it, so {v U V v U V or v U V } induce a consistent biclique in G of the same size, where τ(v) = 1 if v U V and τ(v) = 1 if v U V. The claim thus follows from Theorem 5.1. We can use similar ideas to handle consistent subgraphs. All we need is to ensure that the sum of weights of edges from a node to two opposite sign neighbors is negative. Given this condition, the algorithms from previous sections can be applied directly and generate consistent subgraphs The SAMBA Algorithm The scoring scheme and combinatorial algorithms developed above can be combined to create the practical SAMBA algorithm (Figure 5.6). We cannot apply the theoretical algorithm directly on large data sets since for reasonable degree bounds (e.g. 60), 2 d is too large. The suggested solution avoids hashing all subsets of incoming neighbors per gene and exhaust only subset of small size (typically 4 6 conditions). The heaviest condition sets are then used as kernels that are extended by a local search procedure.
16 16 Analysis of Gene Expression Data c Tel Aviv Univ. SAMBA thus works as follows: We first form the bipartite graph and calculate vertex pair weights using one of the weighting methods described above. We consider a gene to be up (down) regulated in a condition if its standardized level with mean 0 and variance 1 is above 1 (below -1). Depending on the data, we may choose to work with signed or unsigned graphs. In the second phase of the algorithm we apply the hashing technique of the algorithm previously shown (Figure 5.5) to find the heaviest bicliques in the graph. In fact, SAMBA looks for the k best bicliques intersecting every given condition or gene. We ignore genes with degree exceeding some threshold d, and hash for each gene only subsets of its neighbors of size ranging from N 1 to N 2. The third phase of the algorithm performs a local improvement procedure on the biclusters derived from the previous phase. The procedure iteratively applies the best modification to the bicluster (addition or deletion of a single vertex) until no score improvement is possible. To avoid similar biclusters whose vertex sets differ only slightly, a greedy algorithm is applied. We iterate over all generated biclusters, ordered by their score, and filter out biclusters whose intersection with a previous solution (number of shared conditions times number of shared genes) is above L%. An implementation of SAMBA can handle large data sets in a few minutes (15,000 genes, 500 conditions, d = 40, N 1 = 4, N 2 = 6, K = 20, L = 30) Validating Biclustering Quality As the reader may have noted, for many applications in computational biology, it is hard to compare different algorithms and methodologies and state clearly which one is better. It is however, very important for any scientific discipline to have means for evaluating the quality of a given result and to make sure the field is indeed making progress. Described below are two examples of general methodologies for assessing algorithms performance : comparative analysis, which matches algorithmic results with some external knowledge, and intrinsic validation, which uses randomization to evaluate the significance of the signals discovered. Comparative analysis One way for evaluating bicluster algorithms is by using prior biological knowledge as some form of a gold standard that we can compare our set of biclusters to. A correspondence plot depicts the distribution of p-values of the produced biclusters, using for evaluation a known (putatively correct) classification of conditions (e.g., to various cancer types) or a given gene annotation. We describe the plot when a classification is given. For each value of p on a logarithmic scale, the plot presents the fraction of biclusters whose p-value is at most p out of the k best biclusters.
17 SAMBA 17 SAMBA(U, V, E, w, d, N 1, N 2, k): U : conditions. V : genes. E : graph edges. w : edge/non-edge weights. N 1, N 2 : hashed set size limits. k : max biclusters per gene/condition. Initialize a hash table weight. For all v V with N(v) d do For all S N(v) with N 1 S N 2 do weight[s] weight[s] + w(s, {v}). For each v V set best[v][1... k] to the k heaviest S such that v S. For each v V, i {1..k} S = best[v][i] V u S N(u). B S V. Do { a = argmax x V U (w(b x)) b = argmax x B (w(b x)) if w(b a) > w(b b) then B = B a else B = B b } While improving Store B. Post process to filter overlapping biclusters. Figure 5.6: The practical biclustering algorithm. p-values are calculated according to the known classification as follows: Suppose prior knowledge partitions the m conditions into k classes, C 1,..., C k. Let B be a bicluster with b conditions, out of which b j belong to class C j. The p-value of B, assuming its most abundant class is C i, is calculated as p(b) = b ( Ci )( m Ci ) ( k=b i k b k / m ) b. Hence, the p-value measures the probability of obtaining at least b i elements from the class in a random set of size b. One should note, that high quality biclusters can also identify phenomena that are not covered by the given classification. Nevertheless, we expect a large fraction of the biclusters to conform to the known classification. As an example for the usage of correspondence plots, we present the analysis of outputs from SAMBA algorithm compared to Cheng and Church s algorithm. Running on the same data set (the lymphoma data of [2]), a collection of biclusters from both algorithm were analyzed using the known classification of conditions to different clinical types (DLBCL, CLL, FL and more). As a reference, a correspondence plot calculated on a random annotation of the 96 samples (preserving class sizes) was added. The results (Figure 5.7(A)) clearly indicate that SAMBA s biclusters are much more concordant with the biological information.
18 18 Analysis of Gene Expression Data c Tel Aviv Univ. Intrinsic validation A second method for validating the quality of biclusters is by analyzing the results on random data sets. We should make sure that the results we consider as statistically significant are not obtained from random data. The details of randomization may be critical to the integrity of such test. Assume we are using a uniformly random graph model (the simple model described above) and we randomize the data according to it. Then the artifact we have mentioned before, causing the identification of high degree nodes as biclusters would not be discovered since the random graph model will follow our originally restricting assumption. Figure 5.7(B) describes the results of a randomization test done on SAMBA using a degree preserving random graph model. The analysis was done on two data sets, first the real data was biclustered and the significance of each bicluster was calculated. Then the same procedure was done with a random graph preserving all vertex degrees. It can be seen that significance values on the random data are well separated from those computed on the original data and, furthermore, only two random biclusters have significance values below zero. The scatter plot not only demonstrates that heavy biclusters are non random but also provides empirical evidence to the relation of the SAMBA likelihood score and the more formal significance measure. A B Figure 5.7: Source: [16]. A: Performance of different weighting schemes and algorithms. Correspondence plots for SAMBA, the algorithm of Cheng and Church [4], and random biclusters. Likelihood weights use p c = 0.9. For each value of p on a logarithmic scale, the plot presents the fraction of biclusters whose p-value is at most p out of the (say) 100 best biclusters. B: Scatter plots of significance values of biclusters (x-axis) vs. their log likelihood (weight) on synthetic and real data. x-axis: significance value, y-axis: bicluster weight Source Heterogeneity SAMBA can be used to evaluate several data sources, separately or combined. The more information we can add to the graph, the more precise our results will be, this is because
19 SAMBA 19 true results will be amplified by the new properties added. Thus, different types of datasets are used in conjunction to produce more accurate results. Examples of other data that can be added include transcription factor binding profiles, protein-protein interaction data and phenotype profiles. Figure 5.8: Example of a variety of sources combined to produce a better result using the SAMBA algorithm Functional Annotation using biclusters The output of a bicluster algorithm is a collection of significant local signals in the data. Such signals may be used in diverse applications. One example for an application of biclusters is for automatic annotation of genes. The budding yeast, which is one of the most characterized eukaryotes up to date, contains about 6,200 genes, only half of which have a known function. We can use a large database of gene expression and a set of derived biclusters to try and associate unknown genes with a function. The idea is simple, whenever a significant fraction of the characterized genes in a bicluster share a common functional class, it is likely that the other genes in the bicluster are also related to this class. A compiled data set of yeast gene expression, including 515 conditions for the 6,200 yeast ORFs was used to test this idea [10, 6, 7, 14, 11]. The data was collected from five different experiments. Analysis by SAMBA generated 2,406 biclusters ranging over 4,961 genes and 515 conditions. The source for the known functional annotation was the SGD database [1], which includes 3,000 annotations from the Gene Ontology [5] vocabulary.
20 20 Analysis of Gene Expression Data c Tel Aviv Univ. Figure 5.9: Example of a SAMBA bicluster based on different properties. Other then the gene expression profile, transcription factor binding profiles and different cell growth conditions are combined in this bicluster. On the left, two GO annotations are added to show the quality of the results. The bicluster set was filtered to include only those biclusters in which more than 60% of their annotated members had the same class. Out of those, only biclusters that were functionally enriched (p-value below 10 4 ) were used. The unannotated genes in those biclusters were now assigned to the most abundant class. Note that each gene may be annotated more than once, as is the case for the curated GO annotations. For cross validation, 100 runs were performed and in each one 30% of the annotations were hidden. The overall average success rate in annotating the hidden genes was calculated. The results of these runs are summarized in Figure 5.10(A,B). Overall, 81.5% of the test set annotations matched those known from SGD, demonstrating that we can extrapolate functional annotation using biclusters Global Transcriptional Network Another application that can be applied on the biclusters is identification of Transcription Factor (TF) binding sites. Genes in the same biological modules, that is genes that are expressed corporately under some conditions related to a biological process, might be derived by one or more common TFs. TFs are important for understanding the biological regulation mechanism. In several cases, TF binding property can even explain the apparent biological coregulation. In Figure 5.11 we can see a process-tf map derived from samba biclustering results. The biological modules are represented by ovals and the TFs by circles. An edge
21 Summary 21 A B C Figure 5.10: Source: [16]. Yeast functional annotation. A: Annotation specificity. The table depicts the annotation accuracy measured using 70:30 cross-validation. Rows represent classes assigned using our method and columns represent SGD GO classes. Cell (x, y) contains the percentage of genes annotated x that belong to GO class y. Higher percentages are darker. B: Annotation sensitivity calculated w.r.t. annotated genes only. Cell (x, y) contains the percentage of SAMBA annotated genes that belong to GO class y and were annotated x. C: Annotation of unknown genes. The table shows for each functional class its size in the SGD GO annotation, the number of genes that belong to this class and were annotated by SAMBA, and the number of unknown genes assigned to this class by SAMBA. between a process and a TF represents an enrichment of the TF in the module s genes. This map enables us to generally view the Transcriptional regulation mechanism. As can be seen, some TFs can coregulate several processes. For example MBP1 that has considerable representation in the DNA metabolism and Cell Cycle processes SAMBA - Discussion The SAMBA algorithm is fast and allows simultaneous normalization of genes and conditions and integration of heterogenous data. It is well suited for query based usage. Disadvantages of SAMBA: discretisation and redundancies. 5.6 Summary In this and the previous lectures, we have reviewed some methods for biclustering. In each of these methods we focused on the discovery of one, presumingly best, bicluster. To obtain a set of biclusters we had to apply our algorithm many times, possibly in parallel. A different approach may be to try and discover a multiple biclustering model for the entire data. This
22 22 Analysis of Gene Expression Data c Tel Aviv Univ. Figure 5.11: Source: [15] Functional modules and their transcription factors in s.cerevisiee. Modules with significant functional enrichment for a particular process (with p value 0.01) are grouped and plotted as ovals with the process name. TFs with binding profiles associated with any of these modules are marked as green circles and connected to the associated process. Modules enriched in more than one process may appear in several places in the figure. The thickness of the connecting lines is inversely proportional to the p-value of the functional enrichment in the associated module. The map was automatically generated by SAMBA using no prior biological knowledge. Key abbreviations: Met: Metabolism, AA: Amino Acid, Tran: Transport. approach has the advantage of enabling a global view of the data and reducing overfitting and redundancies. On the other hand, as biclusters are by definition local patterns, a global approach to biclustering is not a trivial task. A family of methods using a basically global approach is based on probabilistic models. For example, we can model each sub column and row as having a typical value distribution, which may be different from the background. We can then model the entire data set by tiling it with a small number of biclusters, each having a characteristic distribution. To discover such tiling, it is possible to use variants of the EM algorithm. As we have seen, the many possible definitions of the biclustering problem have a central importance in the design and implementation of algorithms for solving it. As for now, there is no single solution that is accepted as a standard. As gene expression data accumulates rapidly, the need for a robust and efficient biclustering algorithms is nevertheless increasing.
23 Bibliography [1] [2] A. A. Alizadeh, M. B. Eisen, R. E. Davis, C. Ma, I. S. Lossos, A. Rosenwald, J. C. Boldrick, H. Sabet, T. Tran, X. Yu, J. I. Powell, L. Yang, G. E. Marti, T. Moore, J. Hudson, L. Lu, D. B. Lewis, R. Tibshirani, G. Sherlock, W. C. Chan, T. C. Greiner, D. D. Weisenburger, J. O. Armitage, R. Warnke, and L. M. Staudt. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature, 403(6769): , [3] S. Bergmann, J. Ihmels, and N. Barkai. Iterative signature algorithm for the analysis of large-scale gene expression data. Phys Rev E Stat Nonlin Soft Matter Phys, 67(3 Pt 1): , [4] Y. Cheng and G.M. Church. Biclustering of expression data. In Proc. ISMB 00, pages AAAI Press, [5] The Gene Ontology Consortium. Gene Ontology: tool for the unification of biology. Nature Genetics, 25:25 29, [6] A. P. Gasch et al. Genomic expression programs in the response of yeast cells to environmental changes. Mol Biol Cell, 11: , [7] A.P. Gasch et al. Genomic expression responses to DNA-damaging agents and the regulatory role of the yeast ATR homolog mec1p. Mol. Biol. Cell, 12(10): , [8] G. Getz, E. Levine, and E. Domany. Coupled two-way clustering analysis of gene microarray data. Proc. Natl. Acad. Sci. USA, 97(22): , [9] Dorit S. Hochbaum. Approximating clique and biclique problems. Journal of Algorithms, 29(1): , [10] TR. Hughes et al. Functional discovery via a compendium of expression profiles. Cell, 102:109 26,
24 24 BIBLIOGRAPHY [11] T. Ideker, J.A. Thorsson, V. Ranish, R. Christmas, J. Buhler, J.K. Eng, R. Bumgarner, D.R. Goodlett, R. Aebersold, and Hood L. Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science, 291:929 34, [12] J. Ihmels, G. Friedlander, S. Bergmann, O. Sarig, Y. Ziv, and N. Barkai. Revealing modular organization in the yeast transcriptional network. Nature Genetics, 31(4):370 7, [13] R. Peeters. The maximum edge biclique problem is NP-complete. citeseer.nj.nec.com/peeters00maximum.html. [14] P. T. Spellman, G. Sherlock, et al. Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell, 9: , [15] A. Tanay, R. Sharan, M. Kupiec, and R. Shamir. Revealing modularity and organization in the yeast molecular network by integrated analysis of highly heterogeneous genomewide data. Proc Natl Acad Sci U S A., 101(9):2981 6, [16] A. Tanay, R. Sharan, and R. Shamir. Discovering statistically significant biclusters in gene expression data. Bioinformatics, 18(Suppl 1):S136 44, 2002.
Biclustering algorithms ISA and SAMBA
 Biclustering algorithms ISA and SAMBA Slides with Amos Tanay 1 Biclustering Clusters: global. partition of genes according to common exp pattern across all conditions conditions Genes have multiple functions
Biclustering algorithms ISA and SAMBA Slides with Amos Tanay 1 Biclustering Clusters: global. partition of genes according to common exp pattern across all conditions conditions Genes have multiple functions
Biclustering Algorithms for Gene Expression Analysis
 Biclustering Algorithms for Gene Expression Analysis T. M. Murali August 19, 2008 Problems with Hierarchical Clustering It is a global clustering algorithm. Considers all genes to be equally important
Biclustering Algorithms for Gene Expression Analysis T. M. Murali August 19, 2008 Problems with Hierarchical Clustering It is a global clustering algorithm. Considers all genes to be equally important
BIOINFORMATICS. Discovering statistically significant biclusters in gene expression data. Amos Tanay, Roded Sharan and Ron Shamir
 BIOINFORMATICS Electronic edition http://www.bioinformatics.oupjournals.org VOLUME 18 NUMBER Suppl. 1 JULY 2002 PAGES S136 S144 Discovering statistically significant biclusters in gene expression data
BIOINFORMATICS Electronic edition http://www.bioinformatics.oupjournals.org VOLUME 18 NUMBER Suppl. 1 JULY 2002 PAGES S136 S144 Discovering statistically significant biclusters in gene expression data
BIMAX. Lecture 11: December 31, Introduction Model An Incremental Algorithm.
 Analysis of DNA Chips and Gene Networks Spring Semester, 2009 Lecturer: Ron Shamir BIMAX 11.1 Introduction. Lecture 11: December 31, 2009 Scribe: Boris Kostenko In the course we have already seen different
Analysis of DNA Chips and Gene Networks Spring Semester, 2009 Lecturer: Ron Shamir BIMAX 11.1 Introduction. Lecture 11: December 31, 2009 Scribe: Boris Kostenko In the course we have already seen different
Biclustering for Microarray Data: A Short and Comprehensive Tutorial
 Biclustering for Microarray Data: A Short and Comprehensive Tutorial 1 Arabinda Panda, 2 Satchidananda Dehuri 1 Department of Computer Science, Modern Engineering & Management Studies, Balasore 2 Department
Biclustering for Microarray Data: A Short and Comprehensive Tutorial 1 Arabinda Panda, 2 Satchidananda Dehuri 1 Department of Computer Science, Modern Engineering & Management Studies, Balasore 2 Department
Identifying network modules
 Network biology minicourse (part 3) Algorithmic challenges in genomics Identifying network modules Roded Sharan School of Computer Science, Tel Aviv University Gene/Protein Modules A module is a set of
Network biology minicourse (part 3) Algorithmic challenges in genomics Identifying network modules Roded Sharan School of Computer Science, Tel Aviv University Gene/Protein Modules A module is a set of
Iterative Signature Algorithm for the Analysis of Large-Scale Gene Expression Data. By S. Bergmann, J. Ihmels, N. Barkai
 Iterative Signature Algorithm for the Analysis of Large-Scale Gene Expression Data By S. Bergmann, J. Ihmels, N. Barkai Reasoning Both clustering and Singular Value Decomposition(SVD) are useful tools
Iterative Signature Algorithm for the Analysis of Large-Scale Gene Expression Data By S. Bergmann, J. Ihmels, N. Barkai Reasoning Both clustering and Singular Value Decomposition(SVD) are useful tools
Missing Data Estimation in Microarrays Using Multi-Organism Approach
 Missing Data Estimation in Microarrays Using Multi-Organism Approach Marcel Nassar and Hady Zeineddine Progress Report: Data Mining Course Project, Spring 2008 Prof. Inderjit S. Dhillon April 02, 2008
Missing Data Estimation in Microarrays Using Multi-Organism Approach Marcel Nassar and Hady Zeineddine Progress Report: Data Mining Course Project, Spring 2008 Prof. Inderjit S. Dhillon April 02, 2008
Clustering Jacques van Helden
 Statistical Analysis of Microarray Data Clustering Jacques van Helden Jacques.van.Helden@ulb.ac.be Contents Data sets Distance and similarity metrics K-means clustering Hierarchical clustering Evaluation
Statistical Analysis of Microarray Data Clustering Jacques van Helden Jacques.van.Helden@ulb.ac.be Contents Data sets Distance and similarity metrics K-means clustering Hierarchical clustering Evaluation
Contents. ! Data sets. ! Distance and similarity metrics. ! K-means clustering. ! Hierarchical clustering. ! Evaluation of clustering results
 Statistical Analysis of Microarray Data Contents Data sets Distance and similarity metrics K-means clustering Hierarchical clustering Evaluation of clustering results Clustering Jacques van Helden Jacques.van.Helden@ulb.ac.be
Statistical Analysis of Microarray Data Contents Data sets Distance and similarity metrics K-means clustering Hierarchical clustering Evaluation of clustering results Clustering Jacques van Helden Jacques.van.Helden@ulb.ac.be
FISA: Fast Iterative Signature Algorithm for the analysis of large-scale gene expression data
 FISA: Fast Iterative Signature Algorithm for the analysis of large-scale gene expression data Seema Aggarwal Department of Computer Science University of Delhi saggarwal@mh.du.ac.in and Neelima Gupta Department
FISA: Fast Iterative Signature Algorithm for the analysis of large-scale gene expression data Seema Aggarwal Department of Computer Science University of Delhi saggarwal@mh.du.ac.in and Neelima Gupta Department
/ Computational Genomics. Normalization
 10-810 /02-710 Computational Genomics Normalization Genes and Gene Expression Technology Display of Expression Information Yeast cell cycle expression Experiments (over time) baseline expression program
10-810 /02-710 Computational Genomics Normalization Genes and Gene Expression Technology Display of Expression Information Yeast cell cycle expression Experiments (over time) baseline expression program
MSCBIO 2070/02-710: Computational Genomics, Spring A4: spline, HMM, clustering, time-series data analysis, RNA-folding
 MSCBIO 2070/02-710:, Spring 2015 A4: spline, HMM, clustering, time-series data analysis, RNA-folding Due: April 13, 2015 by email to Silvia Liu (silvia.shuchang.liu@gmail.com) TA in charge: Silvia Liu
MSCBIO 2070/02-710:, Spring 2015 A4: spline, HMM, clustering, time-series data analysis, RNA-folding Due: April 13, 2015 by email to Silvia Liu (silvia.shuchang.liu@gmail.com) TA in charge: Silvia Liu
6 Randomized rounding of semidefinite programs
 6 Randomized rounding of semidefinite programs We now turn to a new tool which gives substantially improved performance guarantees for some problems We now show how nonlinear programming relaxations can
6 Randomized rounding of semidefinite programs We now turn to a new tool which gives substantially improved performance guarantees for some problems We now show how nonlinear programming relaxations can
p v P r(v V opt ) = Algorithm 1 The PROMO algorithm for module identification.
 BIOINFORMATICS Vol. no. 6 Pages 1 PROMO : A Method for identifying modules in protein interaction networks Omer Tamuz, Yaron Singer, Roded Sharan School of Computer Science, Tel Aviv University, Tel Aviv,
BIOINFORMATICS Vol. no. 6 Pages 1 PROMO : A Method for identifying modules in protein interaction networks Omer Tamuz, Yaron Singer, Roded Sharan School of Computer Science, Tel Aviv University, Tel Aviv,
e-ccc-biclustering: Related work on biclustering algorithms for time series gene expression data
 : Related work on biclustering algorithms for time series gene expression data Sara C. Madeira 1,2,3, Arlindo L. Oliveira 1,2 1 Knowledge Discovery and Bioinformatics (KDBIO) group, INESC-ID, Lisbon, Portugal
: Related work on biclustering algorithms for time series gene expression data Sara C. Madeira 1,2,3, Arlindo L. Oliveira 1,2 1 Knowledge Discovery and Bioinformatics (KDBIO) group, INESC-ID, Lisbon, Portugal
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science Algorithms For Inference Fall 2014
 Suggested Reading: Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Probabilistic Modelling and Reasoning: The Junction
Suggested Reading: Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Probabilistic Modelling and Reasoning: The Junction
Matching Algorithms. Proof. If a bipartite graph has a perfect matching, then it is easy to see that the right hand side is a necessary condition.
 18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
Biclustering with δ-pcluster John Tantalo. 1. Introduction
 Biclustering with δ-pcluster John Tantalo 1. Introduction The subject of biclustering is chiefly concerned with locating submatrices of gene expression data that exhibit shared trends between genes. That
Biclustering with δ-pcluster John Tantalo 1. Introduction The subject of biclustering is chiefly concerned with locating submatrices of gene expression data that exhibit shared trends between genes. That
CS Introduction to Data Mining Instructor: Abdullah Mueen
 CS 591.03 Introduction to Data Mining Instructor: Abdullah Mueen LECTURE 8: ADVANCED CLUSTERING (FUZZY AND CO -CLUSTERING) Review: Basic Cluster Analysis Methods (Chap. 10) Cluster Analysis: Basic Concepts
CS 591.03 Introduction to Data Mining Instructor: Abdullah Mueen LECTURE 8: ADVANCED CLUSTERING (FUZZY AND CO -CLUSTERING) Review: Basic Cluster Analysis Methods (Chap. 10) Cluster Analysis: Basic Concepts
Exploratory data analysis for microarrays
 Exploratory data analysis for microarrays Jörg Rahnenführer Computational Biology and Applied Algorithmics Max Planck Institute for Informatics D-66123 Saarbrücken Germany NGFN - Courses in Practical DNA
Exploratory data analysis for microarrays Jörg Rahnenführer Computational Biology and Applied Algorithmics Max Planck Institute for Informatics D-66123 Saarbrücken Germany NGFN - Courses in Practical DNA
Gene regulation. DNA is merely the blueprint Shared spatially (among all tissues) and temporally But cells manage to differentiate
 Gene regulation DNA is merely the blueprint Shared spatially (among all tissues) and temporally But cells manage to differentiate Especially but not only during developmental stage And cells respond to
Gene regulation DNA is merely the blueprint Shared spatially (among all tissues) and temporally But cells manage to differentiate Especially but not only during developmental stage And cells respond to
Analysis of Biological Networks: Protein modules Color Coding
 Analysis of Biological Networks: Protein modules Color Coding Lecturer: Eithan Hirsh Scribe: Shelly Mahleb and Benny Davidovich Lecture 6, November 30, 2006 1 Introduction In this lecture we present: Color
Analysis of Biological Networks: Protein modules Color Coding Lecturer: Eithan Hirsh Scribe: Shelly Mahleb and Benny Davidovich Lecture 6, November 30, 2006 1 Introduction In this lecture we present: Color
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings
 On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
Analysis of Biological Networks: Network Modules Identication
 Analysis of Biological Networks: Network Modules Identication Lecturer: Roded Sharan Scribe: Regina Ring and Constantin Radchenko Lecture 4, March 25, 2009 In this lecture we complete the discussion of
Analysis of Biological Networks: Network Modules Identication Lecturer: Roded Sharan Scribe: Regina Ring and Constantin Radchenko Lecture 4, March 25, 2009 In this lecture we complete the discussion of
EECS730: Introduction to Bioinformatics
 EECS730: Introduction to Bioinformatics Lecture 15: Microarray clustering http://compbio.pbworks.com/f/wood2.gif Some slides were adapted from Dr. Shaojie Zhang (University of Central Florida) Microarray
EECS730: Introduction to Bioinformatics Lecture 15: Microarray clustering http://compbio.pbworks.com/f/wood2.gif Some slides were adapted from Dr. Shaojie Zhang (University of Central Florida) Microarray
1. Lecture notes on bipartite matching
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans February 5, 2017 1. Lecture notes on bipartite matching Matching problems are among the fundamental problems in
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans February 5, 2017 1. Lecture notes on bipartite matching Matching problems are among the fundamental problems in
2. Background. 2.1 Clustering
 2. Background 2.1 Clustering Clustering involves the unsupervised classification of data items into different groups or clusters. Unsupervised classificaiton is basically a learning task in which learning
2. Background 2.1 Clustering Clustering involves the unsupervised classification of data items into different groups or clusters. Unsupervised classificaiton is basically a learning task in which learning
On the Max Coloring Problem
 On the Max Coloring Problem Leah Epstein Asaf Levin May 22, 2010 Abstract We consider max coloring on hereditary graph classes. The problem is defined as follows. Given a graph G = (V, E) and positive
On the Max Coloring Problem Leah Epstein Asaf Levin May 22, 2010 Abstract We consider max coloring on hereditary graph classes. The problem is defined as follows. Given a graph G = (V, E) and positive
Joint Entity Resolution
 Joint Entity Resolution Steven Euijong Whang, Hector Garcia-Molina Computer Science Department, Stanford University 353 Serra Mall, Stanford, CA 94305, USA {swhang, hector}@cs.stanford.edu No Institute
Joint Entity Resolution Steven Euijong Whang, Hector Garcia-Molina Computer Science Department, Stanford University 353 Serra Mall, Stanford, CA 94305, USA {swhang, hector}@cs.stanford.edu No Institute
PCP and Hardness of Approximation
 PCP and Hardness of Approximation January 30, 2009 Our goal herein is to define and prove basic concepts regarding hardness of approximation. We will state but obviously not prove a PCP theorem as a starting
PCP and Hardness of Approximation January 30, 2009 Our goal herein is to define and prove basic concepts regarding hardness of approximation. We will state but obviously not prove a PCP theorem as a starting
Computational Genomics and Molecular Biology, Fall
 Computational Genomics and Molecular Biology, Fall 2015 1 Sequence Alignment Dannie Durand Pairwise Sequence Alignment The goal of pairwise sequence alignment is to establish a correspondence between the
Computational Genomics and Molecular Biology, Fall 2015 1 Sequence Alignment Dannie Durand Pairwise Sequence Alignment The goal of pairwise sequence alignment is to establish a correspondence between the
Biclustering Algorithms: A Survey
 Biclustering Algorithms: A Survey Amos Tanay Λ Roded Sharan y Ron Shamir Λ May 2004 Abstract Analysis of large scale geonomics data, notably gene expression, has initially focused on clustering methods.
Biclustering Algorithms: A Survey Amos Tanay Λ Roded Sharan y Ron Shamir Λ May 2004 Abstract Analysis of large scale geonomics data, notably gene expression, has initially focused on clustering methods.
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret
 Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret Greedy Algorithms (continued) The best known application where the greedy algorithm is optimal is surely
Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret Greedy Algorithms (continued) The best known application where the greedy algorithm is optimal is surely
Data Mining Technologies for Bioinformatics Sequences
 Data Mining Technologies for Bioinformatics Sequences Deepak Garg Computer Science and Engineering Department Thapar Institute of Engineering & Tecnology, Patiala Abstract Main tool used for sequence alignment
Data Mining Technologies for Bioinformatics Sequences Deepak Garg Computer Science and Engineering Department Thapar Institute of Engineering & Tecnology, Patiala Abstract Main tool used for sequence alignment
Mathematical and Algorithmic Foundations Linear Programming and Matchings
 Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Mean Square Residue Biclustering with Missing Data and Row Inversions
 Mean Square Residue Biclustering with Missing Data and Row Inversions Stefan Gremalschi a, Gulsah Altun b, Irina Astrovskaya a, and Alexander Zelikovsky a a Department of Computer Science, Georgia State
Mean Square Residue Biclustering with Missing Data and Row Inversions Stefan Gremalschi a, Gulsah Altun b, Irina Astrovskaya a, and Alexander Zelikovsky a a Department of Computer Science, Georgia State
Vertical decomposition of a lattice using clique separators
 Vertical decomposition of a lattice using clique separators Anne Berry, Romain Pogorelcnik, Alain Sigayret LIMOS UMR CNRS 6158 Ensemble Scientifique des Cézeaux Université Blaise Pascal, F-63 173 Aubière,
Vertical decomposition of a lattice using clique separators Anne Berry, Romain Pogorelcnik, Alain Sigayret LIMOS UMR CNRS 6158 Ensemble Scientifique des Cézeaux Université Blaise Pascal, F-63 173 Aubière,
FastA & the chaining problem
 FastA & the chaining problem We will discuss: Heuristics used by the FastA program for sequence alignment Chaining problem 1 Sources for this lecture: Lectures by Volker Heun, Daniel Huson and Knut Reinert,
FastA & the chaining problem We will discuss: Heuristics used by the FastA program for sequence alignment Chaining problem 1 Sources for this lecture: Lectures by Volker Heun, Daniel Huson and Knut Reinert,
Mining Deterministic Biclusters in Gene Expression Data
 Mining Deterministic Biclusters in Gene Expression Data Zonghong Zhang 1 Alvin Teo 1 BengChinOoi 1,2 Kian-Lee Tan 1,2 1 Department of Computer Science National University of Singapore 2 Singapore-MIT-Alliance
Mining Deterministic Biclusters in Gene Expression Data Zonghong Zhang 1 Alvin Teo 1 BengChinOoi 1,2 Kian-Lee Tan 1,2 1 Department of Computer Science National University of Singapore 2 Singapore-MIT-Alliance
Biclustering Bioinformatics Data Sets. A Possibilistic Approach
 Possibilistic algorithm Bioinformatics Data Sets: A Possibilistic Approach Dept Computer and Information Sciences, University of Genova ITALY EMFCSC Erice 20/4/2007 Bioinformatics Data Sets Outline Introduction
Possibilistic algorithm Bioinformatics Data Sets: A Possibilistic Approach Dept Computer and Information Sciences, University of Genova ITALY EMFCSC Erice 20/4/2007 Bioinformatics Data Sets Outline Introduction
Graphs and Network Flows IE411. Lecture 21. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Characterizing Graphs (3) Characterizing Graphs (1) Characterizing Graphs (2) Characterizing Graphs (4)
 S-72.2420/T-79.5203 Basic Concepts 1 S-72.2420/T-79.5203 Basic Concepts 3 Characterizing Graphs (1) Characterizing Graphs (3) Characterizing a class G by a condition P means proving the equivalence G G
S-72.2420/T-79.5203 Basic Concepts 1 S-72.2420/T-79.5203 Basic Concepts 3 Characterizing Graphs (1) Characterizing Graphs (3) Characterizing a class G by a condition P means proving the equivalence G G
6. Lecture notes on matroid intersection
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Module 7. Independent sets, coverings. and matchings. Contents
 Module 7 Independent sets, coverings Contents and matchings 7.1 Introduction.......................... 152 7.2 Independent sets and coverings: basic equations..... 152 7.3 Matchings in bipartite graphs................
Module 7 Independent sets, coverings Contents and matchings 7.1 Introduction.......................... 152 7.2 Independent sets and coverings: basic equations..... 152 7.3 Matchings in bipartite graphs................
FastA and the chaining problem, Gunnar Klau, December 1, 2005, 10:
 FastA and the chaining problem, Gunnar Klau, December 1, 2005, 10:56 4001 4 FastA and the chaining problem We will discuss: Heuristics used by the FastA program for sequence alignment Chaining problem
FastA and the chaining problem, Gunnar Klau, December 1, 2005, 10:56 4001 4 FastA and the chaining problem We will discuss: Heuristics used by the FastA program for sequence alignment Chaining problem
Random projection for non-gaussian mixture models
 Random projection for non-gaussian mixture models Győző Gidófalvi Department of Computer Science and Engineering University of California, San Diego La Jolla, CA 92037 gyozo@cs.ucsd.edu Abstract Recently,
Random projection for non-gaussian mixture models Győző Gidófalvi Department of Computer Science and Engineering University of California, San Diego La Jolla, CA 92037 gyozo@cs.ucsd.edu Abstract Recently,
Discrete mathematics , Fall Instructor: prof. János Pach
 Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
Triclustering in Gene Expression Data Analysis: A Selected Survey
 Triclustering in Gene Expression Data Analysis: A Selected Survey P. Mahanta, H. A. Ahmed Dept of Comp Sc and Engg Tezpur University Napaam -784028, India Email: priyakshi@tezu.ernet.in, hasin@tezu.ernet.in
Triclustering in Gene Expression Data Analysis: A Selected Survey P. Mahanta, H. A. Ahmed Dept of Comp Sc and Engg Tezpur University Napaam -784028, India Email: priyakshi@tezu.ernet.in, hasin@tezu.ernet.in
The Encoding Complexity of Network Coding
 The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
Clustering Techniques
 Clustering Techniques Bioinformatics: Issues and Algorithms CSE 308-408 Fall 2007 Lecture 16 Lopresti Fall 2007 Lecture 16-1 - Administrative notes Your final project / paper proposal is due on Friday,
Clustering Techniques Bioinformatics: Issues and Algorithms CSE 308-408 Fall 2007 Lecture 16 Lopresti Fall 2007 Lecture 16-1 - Administrative notes Your final project / paper proposal is due on Friday,
MCL. (and other clustering algorithms) 858L
 MCL (and other clustering algorithms) 858L Comparing Clustering Algorithms Brohee and van Helden (2006) compared 4 graph clustering algorithms for the task of finding protein complexes: MCODE RNSC Restricted
MCL (and other clustering algorithms) 858L Comparing Clustering Algorithms Brohee and van Helden (2006) compared 4 graph clustering algorithms for the task of finding protein complexes: MCODE RNSC Restricted
ECS 234: Data Analysis: Clustering ECS 234
 : Data Analysis: Clustering What is Clustering? Given n objects, assign them to groups (clusters) based on their similarity Unsupervised Machine Learning Class Discovery Difficult, and maybe ill-posed
: Data Analysis: Clustering What is Clustering? Given n objects, assign them to groups (clusters) based on their similarity Unsupervised Machine Learning Class Discovery Difficult, and maybe ill-posed
9/29/13. Outline Data mining tasks. Clustering algorithms. Applications of clustering in biology
 9/9/ I9 Introduction to Bioinformatics, Clustering algorithms Yuzhen Ye (yye@indiana.edu) School of Informatics & Computing, IUB Outline Data mining tasks Predictive tasks vs descriptive tasks Example
9/9/ I9 Introduction to Bioinformatics, Clustering algorithms Yuzhen Ye (yye@indiana.edu) School of Informatics & Computing, IUB Outline Data mining tasks Predictive tasks vs descriptive tasks Example
E-Companion: On Styles in Product Design: An Analysis of US. Design Patents
 E-Companion: On Styles in Product Design: An Analysis of US Design Patents 1 PART A: FORMALIZING THE DEFINITION OF STYLES A.1 Styles as categories of designs of similar form Our task involves categorizing
E-Companion: On Styles in Product Design: An Analysis of US Design Patents 1 PART A: FORMALIZING THE DEFINITION OF STYLES A.1 Styles as categories of designs of similar form Our task involves categorizing
DNA chips and other techniques measure the expression level of a large number of genes, perhaps all
 INESC-ID TECHNICAL REPORT 1/2004, JANUARY 2004 1 Biclustering Algorithms for Biological Data Analysis: A Survey* Sara C. Madeira and Arlindo L. Oliveira Abstract A large number of clustering approaches
INESC-ID TECHNICAL REPORT 1/2004, JANUARY 2004 1 Biclustering Algorithms for Biological Data Analysis: A Survey* Sara C. Madeira and Arlindo L. Oliveira Abstract A large number of clustering approaches
Chapter 15 Introduction to Linear Programming
 Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Approximation Algorithms
 Approximation Algorithms Prof. Tapio Elomaa tapio.elomaa@tut.fi Course Basics A 4 credit unit course Part of Theoretical Computer Science courses at the Laboratory of Mathematics There will be 4 hours
Approximation Algorithms Prof. Tapio Elomaa tapio.elomaa@tut.fi Course Basics A 4 credit unit course Part of Theoretical Computer Science courses at the Laboratory of Mathematics There will be 4 hours
Chapter 2 Basic Structure of High-Dimensional Spaces
 Chapter 2 Basic Structure of High-Dimensional Spaces Data is naturally represented geometrically by associating each record with a point in the space spanned by the attributes. This idea, although simple,
Chapter 2 Basic Structure of High-Dimensional Spaces Data is naturally represented geometrically by associating each record with a point in the space spanned by the attributes. This idea, although simple,
EE512 Graphical Models Fall 2009
 EE512 Graphical Models Fall 2009 Prof. Jeff Bilmes University of Washington, Seattle Department of Electrical Engineering Fall Quarter, 2009 http://ssli.ee.washington.edu/~bilmes/ee512fa09 Lecture 11 -
EE512 Graphical Models Fall 2009 Prof. Jeff Bilmes University of Washington, Seattle Department of Electrical Engineering Fall Quarter, 2009 http://ssli.ee.washington.edu/~bilmes/ee512fa09 Lecture 11 -
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
LECTURES 3 and 4: Flows and Matchings
 LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
1 Homophily and assortative mixing
 1 Homophily and assortative mixing Networks, and particularly social networks, often exhibit a property called homophily or assortative mixing, which simply means that the attributes of vertices correlate
1 Homophily and assortative mixing Networks, and particularly social networks, often exhibit a property called homophily or assortative mixing, which simply means that the attributes of vertices correlate
On Covering a Graph Optimally with Induced Subgraphs
 On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
Clustering. Lecture 6, 1/24/03 ECS289A
 Clustering Lecture 6, 1/24/03 What is Clustering? Given n objects, assign them to groups (clusters) based on their similarity Unsupervised Machine Learning Class Discovery Difficult, and maybe ill-posed
Clustering Lecture 6, 1/24/03 What is Clustering? Given n objects, assign them to groups (clusters) based on their similarity Unsupervised Machine Learning Class Discovery Difficult, and maybe ill-posed
5 Matchings in Bipartite Graphs and Their Applications
 5 Matchings in Bipartite Graphs and Their Applications 5.1 Matchings Definition 5.1 A matching M in a graph G is a set of edges of G, none of which is a loop, such that no two edges in M have a common
5 Matchings in Bipartite Graphs and Their Applications 5.1 Matchings Definition 5.1 A matching M in a graph G is a set of edges of G, none of which is a loop, such that no two edges in M have a common
Estimating Error-Dimensionality Relationship for Gene Expression Based Cancer Classification
 1 Estimating Error-Dimensionality Relationship for Gene Expression Based Cancer Classification Feng Chu and Lipo Wang School of Electrical and Electronic Engineering Nanyang Technological niversity Singapore
1 Estimating Error-Dimensionality Relationship for Gene Expression Based Cancer Classification Feng Chu and Lipo Wang School of Electrical and Electronic Engineering Nanyang Technological niversity Singapore
Semi-Supervised Clustering with Partial Background Information
 Semi-Supervised Clustering with Partial Background Information Jing Gao Pang-Ning Tan Haibin Cheng Abstract Incorporating background knowledge into unsupervised clustering algorithms has been the subject
Semi-Supervised Clustering with Partial Background Information Jing Gao Pang-Ning Tan Haibin Cheng Abstract Incorporating background knowledge into unsupervised clustering algorithms has been the subject
Gene expression & Clustering (Chapter 10)
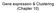 Gene expression & Clustering (Chapter 10) Determining gene function Sequence comparison tells us if a gene is similar to another gene, e.g., in a new species Dynamic programming Approximate pattern matching
Gene expression & Clustering (Chapter 10) Determining gene function Sequence comparison tells us if a gene is similar to another gene, e.g., in a new species Dynamic programming Approximate pattern matching
Clustering gene expression data
 Clustering gene expression data 1 How Gene Expression Data Looks Entries of the Raw Data matrix: Ratio values Absolute values Row = gene s expression pattern Column = experiment/condition s profile genes
Clustering gene expression data 1 How Gene Expression Data Looks Entries of the Raw Data matrix: Ratio values Absolute values Row = gene s expression pattern Column = experiment/condition s profile genes
Vertex 3-colorability of claw-free graphs
 Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Clustering and Visualisation of Data
 Clustering and Visualisation of Data Hiroshi Shimodaira January-March 28 Cluster analysis aims to partition a data set into meaningful or useful groups, based on distances between data points. In some
Clustering and Visualisation of Data Hiroshi Shimodaira January-March 28 Cluster analysis aims to partition a data set into meaningful or useful groups, based on distances between data points. In some
Genomics - Problem Set 2 Part 1 due Friday, 1/26/2018 by 9:00am Part 2 due Friday, 2/2/2018 by 9:00am
 Genomics - Part 1 due Friday, 1/26/2018 by 9:00am Part 2 due Friday, 2/2/2018 by 9:00am One major aspect of functional genomics is measuring the transcript abundance of all genes simultaneously. This was
Genomics - Part 1 due Friday, 1/26/2018 by 9:00am Part 2 due Friday, 2/2/2018 by 9:00am One major aspect of functional genomics is measuring the transcript abundance of all genes simultaneously. This was
Lectures by Volker Heun, Daniel Huson and Knut Reinert, in particular last years lectures
 4 FastA and the chaining problem We will discuss: Heuristics used by the FastA program for sequence alignment Chaining problem 4.1 Sources for this lecture Lectures by Volker Heun, Daniel Huson and Knut
4 FastA and the chaining problem We will discuss: Heuristics used by the FastA program for sequence alignment Chaining problem 4.1 Sources for this lecture Lectures by Volker Heun, Daniel Huson and Knut
3 No-Wait Job Shops with Variable Processing Times
 3 No-Wait Job Shops with Variable Processing Times In this chapter we assume that, on top of the classical no-wait job shop setting, we are given a set of processing times for each operation. We may select
3 No-Wait Job Shops with Variable Processing Times In this chapter we assume that, on top of the classical no-wait job shop setting, we are given a set of processing times for each operation. We may select
11.1 Facility Location
 CS787: Advanced Algorithms Scribe: Amanda Burton, Leah Kluegel Lecturer: Shuchi Chawla Topic: Facility Location ctd., Linear Programming Date: October 8, 2007 Today we conclude the discussion of local
CS787: Advanced Algorithms Scribe: Amanda Burton, Leah Kluegel Lecturer: Shuchi Chawla Topic: Facility Location ctd., Linear Programming Date: October 8, 2007 Today we conclude the discussion of local
CLUSTERING IN BIOINFORMATICS
 CLUSTERING IN BIOINFORMATICS CSE/BIMM/BENG 8 MAY 4, 0 OVERVIEW Define the clustering problem Motivation: gene expression and microarrays Types of clustering Clustering algorithms Other applications of
CLUSTERING IN BIOINFORMATICS CSE/BIMM/BENG 8 MAY 4, 0 OVERVIEW Define the clustering problem Motivation: gene expression and microarrays Types of clustering Clustering algorithms Other applications of
Special course in Computer Science: Advanced Text Algorithms
 Special course in Computer Science: Advanced Text Algorithms Lecture 8: Multiple alignments Elena Czeizler and Ion Petre Department of IT, Abo Akademi Computational Biomodelling Laboratory http://www.users.abo.fi/ipetre/textalg
Special course in Computer Science: Advanced Text Algorithms Lecture 8: Multiple alignments Elena Czeizler and Ion Petre Department of IT, Abo Akademi Computational Biomodelling Laboratory http://www.users.abo.fi/ipetre/textalg
Exact Algorithms Lecture 7: FPT Hardness and the ETH
 Exact Algorithms Lecture 7: FPT Hardness and the ETH February 12, 2016 Lecturer: Michael Lampis 1 Reminder: FPT algorithms Definition 1. A parameterized problem is a function from (χ, k) {0, 1} N to {0,
Exact Algorithms Lecture 7: FPT Hardness and the ETH February 12, 2016 Lecturer: Michael Lampis 1 Reminder: FPT algorithms Definition 1. A parameterized problem is a function from (χ, k) {0, 1} N to {0,
arxiv: v1 [math.co] 4 Apr 2011
![arxiv: v1 [math.co] 4 Apr 2011 arxiv: v1 [math.co] 4 Apr 2011](/thumbs/94/118782109.jpg) arxiv:1104.0510v1 [math.co] 4 Apr 2011 Minimal non-extensible precolorings and implicit-relations José Antonio Martín H. Abstract. In this paper I study a variant of the general vertex coloring problem
arxiv:1104.0510v1 [math.co] 4 Apr 2011 Minimal non-extensible precolorings and implicit-relations José Antonio Martín H. Abstract. In this paper I study a variant of the general vertex coloring problem
Lecture Note: Computation problems in social. network analysis
 Lecture Note: Computation problems in social network analysis Bang Ye Wu CSIE, Chung Cheng University, Taiwan September 29, 2008 In this lecture note, several computational problems are listed, including
Lecture Note: Computation problems in social network analysis Bang Ye Wu CSIE, Chung Cheng University, Taiwan September 29, 2008 In this lecture note, several computational problems are listed, including
Comparing the strength of query types in property testing: The case of testing k-colorability
 Comparing the strength of query types in property testing: The case of testing k-colorability Ido Ben-Eliezer Tali Kaufman Michael Krivelevich Dana Ron Abstract We study the power of four query models
Comparing the strength of query types in property testing: The case of testing k-colorability Ido Ben-Eliezer Tali Kaufman Michael Krivelevich Dana Ron Abstract We study the power of four query models
Theorem 2.9: nearest addition algorithm
 There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
Polynomial-Time Approximation Algorithms
 6.854 Advanced Algorithms Lecture 20: 10/27/2006 Lecturer: David Karger Scribes: Matt Doherty, John Nham, Sergiy Sidenko, David Schultz Polynomial-Time Approximation Algorithms NP-hard problems are a vast
6.854 Advanced Algorithms Lecture 20: 10/27/2006 Lecturer: David Karger Scribes: Matt Doherty, John Nham, Sergiy Sidenko, David Schultz Polynomial-Time Approximation Algorithms NP-hard problems are a vast
Optimal Detector Locations for OD Matrix Estimation
 Optimal Detector Locations for OD Matrix Estimation Ying Liu 1, Xiaorong Lai, Gang-len Chang 3 Abstract This paper has investigated critical issues associated with Optimal Detector Locations for OD matrix
Optimal Detector Locations for OD Matrix Estimation Ying Liu 1, Xiaorong Lai, Gang-len Chang 3 Abstract This paper has investigated critical issues associated with Optimal Detector Locations for OD matrix
10-701/15-781, Fall 2006, Final
 -7/-78, Fall 6, Final Dec, :pm-8:pm There are 9 questions in this exam ( pages including this cover sheet). If you need more room to work out your answer to a question, use the back of the page and clearly
-7/-78, Fall 6, Final Dec, :pm-8:pm There are 9 questions in this exam ( pages including this cover sheet). If you need more room to work out your answer to a question, use the back of the page and clearly
Lecture notes on the simplex method September We will present an algorithm to solve linear programs of the form. maximize.
 Cornell University, Fall 2017 CS 6820: Algorithms Lecture notes on the simplex method September 2017 1 The Simplex Method We will present an algorithm to solve linear programs of the form maximize subject
Cornell University, Fall 2017 CS 6820: Algorithms Lecture notes on the simplex method September 2017 1 The Simplex Method We will present an algorithm to solve linear programs of the form maximize subject
Integrated Analysis of Gene Expression and Other Data
 Analysis of DNA Chips and Gene Networks Fall Semester, 2010 Lecture 14: January 21, 2010 Lecturer: Prof. Ron Shamir Scribe: David Ze evi Integrated Analysis of Gene Expression and Other Data 14.1 Introduction
Analysis of DNA Chips and Gene Networks Fall Semester, 2010 Lecture 14: January 21, 2010 Lecturer: Prof. Ron Shamir Scribe: David Ze evi Integrated Analysis of Gene Expression and Other Data 14.1 Introduction
Clustering Using Graph Connectivity
 Clustering Using Graph Connectivity Patrick Williams June 3, 010 1 Introduction It is often desirable to group elements of a set into disjoint subsets, based on the similarity between the elements in the
Clustering Using Graph Connectivity Patrick Williams June 3, 010 1 Introduction It is often desirable to group elements of a set into disjoint subsets, based on the similarity between the elements in the
Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1
 CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
Data mining, 4 cu Lecture 8:
 582364 Data mining, 4 cu Lecture 8: Graph mining Spring 2010 Lecturer: Juho Rousu Teaching assistant: Taru Itäpelto Frequent Subgraph Mining Extend association rule mining to finding frequent subgraphs
582364 Data mining, 4 cu Lecture 8: Graph mining Spring 2010 Lecturer: Juho Rousu Teaching assistant: Taru Itäpelto Frequent Subgraph Mining Extend association rule mining to finding frequent subgraphs
Chordal Graphs: Theory and Algorithms
 Chordal Graphs: Theory and Algorithms 1 Chordal graphs Chordal graph : Every cycle of four or more vertices has a chord in it, i.e. there is an edge between two non consecutive vertices of the cycle. Also
Chordal Graphs: Theory and Algorithms 1 Chordal graphs Chordal graph : Every cycle of four or more vertices has a chord in it, i.e. there is an edge between two non consecutive vertices of the cycle. Also
1. Lecture notes on bipartite matching February 4th,
 1. Lecture notes on bipartite matching February 4th, 2015 6 1.1.1 Hall s Theorem Hall s theorem gives a necessary and sufficient condition for a bipartite graph to have a matching which saturates (or matches)
1. Lecture notes on bipartite matching February 4th, 2015 6 1.1.1 Hall s Theorem Hall s theorem gives a necessary and sufficient condition for a bipartite graph to have a matching which saturates (or matches)
Monotone Paths in Geometric Triangulations
 Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
Integer Programming Theory
 Integer Programming Theory Laura Galli October 24, 2016 In the following we assume all functions are linear, hence we often drop the term linear. In discrete optimization, we seek to find a solution x
Integer Programming Theory Laura Galli October 24, 2016 In the following we assume all functions are linear, hence we often drop the term linear. In discrete optimization, we seek to find a solution x
Application of Hierarchical Clustering to Find Expression Modules in Cancer
 Application of Hierarchical Clustering to Find Expression Modules in Cancer T. M. Murali August 18, 2008 Innovative Application of Hierarchical Clustering A module map showing conditional activity of expression
Application of Hierarchical Clustering to Find Expression Modules in Cancer T. M. Murali August 18, 2008 Innovative Application of Hierarchical Clustering A module map showing conditional activity of expression
Computational Molecular Biology
 Computational Molecular Biology Erwin M. Bakker Lecture 3, mainly from material by R. Shamir [2] and H.J. Hoogeboom [4]. 1 Pairwise Sequence Alignment Biological Motivation Algorithmic Aspect Recursive
Computational Molecular Biology Erwin M. Bakker Lecture 3, mainly from material by R. Shamir [2] and H.J. Hoogeboom [4]. 1 Pairwise Sequence Alignment Biological Motivation Algorithmic Aspect Recursive
2 The Fractional Chromatic Gap
 C 1 11 2 The Fractional Chromatic Gap As previously noted, for any finite graph. This result follows from the strong duality of linear programs. Since there is no such duality result for infinite linear
C 1 11 2 The Fractional Chromatic Gap As previously noted, for any finite graph. This result follows from the strong duality of linear programs. Since there is no such duality result for infinite linear
