Voronoi diagram of 3D spheres: theory and applications
|
|
|
- Lewis Cummings
- 6 years ago
- Views:
Transcription
1 Voronoi diagram of 3D spheres: theory and applications Donguk KIM 1, Youngsong CHO 1, Cheol-Hyung CHO 1, Joonghyun RYU 1 Chong-Min KIM 1 and Deok-Soo KIM 2 1) Voronoi Diagram Research Center, Hanyang University, Seoul, KOREA 2) Department of Industrial Engineering, Hanyang University, Seoul, KOREA Corresponding Author : Deok-Soo KIM, dskim@hanyang.ac.kr ABSTRACT Voronoi diagrams have several important applications in science and engineering. While the properties and algorithms for the ordinary Voronoi diagram of point set have been well-known, their counterparts for a set of spheres have not been sufficiently studied. In this paper, we present the definition, properties and algorithms for the Voronoi diagram of 3D spheres based on the Euclidean distance from the surface of spheres. Then, we show how such a Voronoi diagram can be used for solving various important geometric problems in biological systems. Key words: Voronoi diagram, Euclidean, algorithm, molecular surface, interaction interface 1 INTRODUCTION Since its introduction in the early 20th century, the Voronoi diagram has been one of the central topics in computational geometry as well as in other disciplines in science and engineering. The ordinary Voronoi diagram for a point set and its construction have been studied extensively in both 2 and higher dimensions [13]. However, the construction of the Voronoi diagram for spheres in Euclidean distance metric, often referred to as an additively weighted Voronoi diagram [13], has not been explored sufficiently even though the potential impact of this Voronoi diagram on diverse applications can be significant [1,5,11,15,17]. There are many important applications for such a Voronoi diagram. For example, the structural analysis of protein requires an efficient computational tool to analyze the spatial structure among its atoms [5,6,15]. In the design of new material, a similar analysis is fundamental as well [10,12]. Despite of its applicability to various problems, the previous studies are very limited [2,18,4,10]. Recently, Kim et al. reported on the details of an edge-tracing algorithm and its full implementation for constructing the whole Voronoi diagram with discussions on various applications including the analysis of protein structures [6 8]. In this paper, we present properties and two algorithms for Voronoi diagram of 3D spheres based on the Euclidean distance from the surface of spheres. Then, we show how such a Voronoi diagram can be used for solving various important geometric problems in biological systems. 2 DEFINITIONS RELATED TO THE EUCLIDEAN VORONOI DIAGRAMS FOR SPHERES Let S = {s 1, s 2,, s n } be a set of generators where s i is a three dimensional spherical ball. Hence, s i = (c i, r i ) where c i = (x i, y i, z i ) and r i denote the center and radius of a ball,
2 respectively. We assume that no ball is completely contained inside another ball while other types of intersections between balls are allowed. Associated with each ball s i, there is a corresponding region VR i, called a Voronoi region for s i, where VR i = {p dist(p, c i ) r i dist(p, c j ) r j, i j}. Then, VD(S)= {VR 1, VR 2,, VR n } is called the Euclidean Voronoi diagram for S. In this paper, the ordinary L 2 -distance from the surface of balls is used to define Euclidean Voronoi diagrams. Illustrated in Fig. 1(a) and (b) are fifteen balls with three different radii and the Voronoi region corresponding to the largest ball in the center. Fig. 1(c) shows the Voronoi diagram of a subset of protein with 67 atoms, which form an alpha-helix, downloaded from PDB [14]. (a) (b) (c) Figure 1. Voronoi diagrams 3 ALGORITHMS FOR VD(S) A Voronoi vertex is the center of an empty sphere simultaneously tangent to four balls. A Voronoi edge is defined as the locus of points equi-distant from three nearby balls, and it can be easily shown that an edge is always a conic curve and can be conveniently represented, if necessary, in a rational quadratic Bézier form [8]. Two topologically neighboring balls define a Voronoi face as a locus of points equi-distant from two nearby balls, and the face is a segment of a hyperboloid of two sheets and its equation can be easily obtained [5,8]. 3.1 Edge-Tracing Algorithm The idea of the edge-tracing algorithm is simple as it constructs Voronoi edges in the order of a depth-first search. The algorithm first locates a true Voronoi vertex v 0 by computing an empty tangent sphere defined by four appropriate nearby balls. Given v 0, four edges e 0, e 1, e 2, and e 3 emanating from v 0 can be easily identified and pushed into a stack called an Edge-stack. Hence, these edges have v 0 as their starting vertices. After popping an edge from the stack, the algorithm computes the end vertex of the popped edge. Note that the end vertex can be found by computing an empty sphere tangent to four balls: three balls which define the popped edge and one of the (n 3) candidate balls. If an empty tangent sphere is found, the center of the sphere may become the end vertex of the popped edge. Once the end vertex of edge is found, it is also possible to define three new edges emanating from this new vertex. Hence, these new edges starting from the new vertex just computed are created and pushed into the Edge-stack. By following this process until the Edge-stack is empty, the computation of the Voronoi diagram of a connected graph is completed.
3 Given an initial Voronoi vertex to start with, the edge-tracing algorithm runs in O(mn) time in the worst-case, where m is the number of edges and n is the number of balls. The algorithm iterates O(m) times since it traces all edges once for each edge. For each edge, it is necessary to do O(n) scans through all candidate balls once to compute a valid tangent sphere. 3.2 Region-Expansion Algorithm The region-expansion algorithm extends its precursor in 2D and adapts the idea of discrete event simulation. Let VD(P ) be an ordinary Voronoi diagram of the centers of balls. The algorithm constructs VD(S) by expanding Voronoi regions for one ball after another via a series of edge-flips, starting from VD(P ). After choosing a point generator c i, which is the center of a spherical ball s i, and the corresponding Voronoi region VR i, the algorithm continuously enlarges the point generator c i to the ball s i. Then, the corresponding region VR i expands according to the enlargement of the corresponding generator. Repeating the process for all generators constructs a correct Voronoi diagram if the topology is consistently and correctly maintained. The computation necessary to expand a Voronoi region, starting from a center point to a complete ball, takes O(n 2 log n) time in the worst-case since there can be O(n 2 ) number of edges and sorting is necessary according to the event time of each edge. Therefore, the whole Voronoi diagram can be constructed by the region-expansion algorithm in O(n 3 log n) time in the worst-case. We believe, however, that there should be a tighter bound for the worst-case time complexity and the expected time complexity can be much lower. 4 APPLICATIONS OF VD(S) IN BIOLOGICAL PROBLEMS 4.1 Computation of Molecular Surfaces A protein is usually modelled as a set of hard spheres in order to represent atoms in a space-filling model where their radii are the van der Waals radii [3,9]. Given such a model, there are usually two kinds of surfaces involved: a solvent accessible surface(sas) and a molecular surface(ms). A SAS, first defined by Lee and Richards [9], is the set of centers of a spherical probe rolling around the protein. A probe is used for the computational convenience of a small molecule which interacts with the protein. A MS, also known as a Connolly surface, consists of the most inward points on the probe toward the interior of a protein when the probe is in contact with two or more atoms in the protein [3,16]. It is well-known that atoms located at the boundary of a protein determine the function of the protein. Hence, knowledge of a molecular surface is important in the study of protein functions since the surface has a direct relation with other atoms. The molecular surface consists of two groups: a solvent contact surface(scs) and a reentrant surface(rs). A SCS consists of points on the van der Waals atoms which are touchable by a probe. A RS is defined as points on the inward part of the surface of a probe, where the probe is in contact with atoms [16]. An RS, known as a blending surface in CAGD community, consists of two types of blending surface patches: rolling blending and link blending. These blending surface patches can be computed by rolling a spherical probe in every possible direction while keeping tangential contact with the atoms. It turns out that a VD(S) conveniently stores all information necessary for the computation of the molecular surface of a protein. Shown in Fig. 2(a) is a subset of protein data downloaded from PDB [14] which forms an α-helix. In the model, there are 41 C s, 14 N s, and 12 O s.
4 Fig. 2(b), (c) and (d) show the molecular surfaces defined by different probes with radii of 1.4Å, 4Å, and 8Å, respectively. Note that all molecular surfaces are computed from the identical Euclidean Voronoi diagram of the model in Fig. 2(a). (a) (b) (c) (d) Figure 2. Molecular surfaces 4.2 Analyzing Interaction Interfaces A protein is a macromolecule consisting of the permutation of 20 different kinds of amino acids. Amino acids are linearly connected to one another via peptide bonds to form chains. When a protein consists of two chains, it is called a dimer as shown in Fig. 3(a). Shown in Fig. 3(b) and (c) are examples of a trimer (three chains) and a tetramer (four chains), respectively. Since interaction among chains is critical for protein functions, understanding the interaction is getting more important and the geometric properties of the interactions are getting more attention. (a) (b) (c) Figure 3. Protein examples: (a) a dimer, (b) a trimer, and (c) a tetramer. The interaction interface IIF is defined in this paper as follows. Let A = {a 1, a 2,..., a m }, B = {b 1, b 2,..., b n } be two chains in a protein, where a i and b j are atoms with appropriate centers and radii. The interaction interface between two chains A and B is defined as IIF (A, B) = {p dist(p, A) = dist(p, B)}, where dist(p, A) denotes the minimum Euclidean distance from p to the surfaces of all van der Waals atoms in the set A. Then, IIF (A, B) is a subset of Voronoi faces in VD(A B). Hence, IIF (A, B) can be easily located by simply
5 checking each Voronoi face with its generating atom types. Note that IIF (A, B) expands to infinity. The infinite Voronoi faces in IIF (A, B) are biologically less significant since proteins, as well as IIF (A, B), are usually hydrated. Hence, we define a trimmed interaction interface IIF (A, B) against a probe of a water molecule. Fig. 4(a) and (b) illstrate the van der Waals atoms of a dimer 1bh8 downloaded from PDB and the corresponding IIF (A, B), respectively. To analyze the topology and geometry of an interaction interface, we define a base surface BS(A, B) which is defined as a smooth surface fitted through the trimming curve of IIF (A, B) with a certain minimality condition. Fig. 4(c) shows the base surface BS(A, B) of IIF (A, B) in Fig. 4(b). Once an interface and its corresponding base surface are obtained, various analyses can be done on the interaction behavior between chains in the protein. (a) (b) (c) Figure 4. A dimer (PDB ID: 1bh8): (a) van der Waals model, (b) IIF, and (c) BS. 5 CONCLUSIONS In this paper, we have presented properties and two algorithms for Voronoi diagram of 3D spheres based on the Euclidean distance from the surface of spheres. We have also shown how such a Voronoi diagram can be used for solving various important geometric problems in biological systems by illustrating two examples: the computation of surfaces defined on a protein, and the extraction and characterization of interaction interfaces between multiple proteins. ACKNOWLEDGEMENTS This research was supported by the Creative Research Initiatives from the Ministry of Science and Technology in Korea. REFERENCES 1. Angelov, B., Sadoc, J.-F., Jullien, R., Soyer, A., Mornon, J.-P., Chomilier, J.: Nonatomic solvent-driven Voronoi tessellation of proteins: an open tool to analyze protein folds. Proteins: Structure, Function, and Genetics 49(4) (2002) Aurenhammer, F.: Power diagrams: properties, algorithms and applications. SIAM Journal of Computing 16 (1987) Connolly, M, L.: Molecular surfaces: a review. Network Sci. (1996). 4. Gavrilova, M.: Proximity and Applications in General Metrics. Ph.D. thesis: The University of Calgary, Dept. of Computer Science, Calgary, AB, Canada (1998).
6 5. Goede, A., Preissner, R., Frömmel, C.: Voronoi cell: new method for allocation of space among atoms: elimination of avoidable errors in calculation of atomic volume and density. Journal of Computational Chemistry 18(9) (1997) Kim, D.-S., Cho, Y., Kim, D., Cho, C.-H.: Protein structure analysis using Euclidean Voronoi diagram of atoms. Proc. International Workshop on Biometric Technologies (BT 2004) (2004) Kim, D.-S., Cho, Y., Kim, D.: Edge-tracing algorithm for Euclidean Voronoi diagram of 3D spheres. Proc. 16th Canadian Conference on Computational Geometry (2004) Kim, D.-S., Cho, Y., Kim, D.: Euclidean Voronoi diagram of 3D balls and its computation via tracing edges. Computer-Aided Design (in printing). 9. Lee, B., Richards, F.M.: The interpretation of protein structures: estimation of static accessibility. Journal of Molecular Biology, 55 (1971) Luchnikov, V.A., Medvedev, N.N., Oger, L., Troadec, J.-P.: Voronoi-Delaunay analyzis of voids in systems of nonspherical particles. Physical review E 59(6) (1999) Montoro, J.C.G., Abascal, J.L.F.: The Voronoi polyhedra as tools for structure determination in simple disordered systems. The Journal of Physical Chemistry 97(16) (1993) Naberukhin, Y.I., Voloshin, V.P., Medvedev, N.N.: Geometrical analysis of the structure of simple liquids: percolation approach. Molecular Physics 73 (1991) Okabe, A., Boots, B., Sugihara, K., Chiu, S.N.: Spatial Tessellations: Concepts and Applications of Voronoi Diagrams. 2nd ed. Chichester: John Wiley & Sons, (1999). 14. RCSB Protein Data Bank. (2004). 15. Richards, F.M.: The interpretation of protein structures: total volume, group volume distributions and packing density. Journal of Molecular Biology 82 (1974) Richards, F. M.: Areas, volumes, packing and protein structure. Annu. Rev. Biophys. Bioeng. 6 (1977) Voloshin, V.P., Beaufils, S., Medvedev, N.N.: Void space analysis of the structure of liquids. Journal of Molecular Liquids (2002) Will, H.-M.: Computation of Additively Weighted Voronoi Cells for Applications in Molecular Biology. Ph.D. thesis, ETH, Zurich (1999).
Geometry of molecules
 Geometry of molecules 1 MOLECULAR GEOMETRY AND ITS APPLICATION TO NANO INFORMATICS AND MOLECULAR DESIGN Sep 29, 2014 The 11th Korea-U.S. Forum on Nanotechnology: Nanomanufacturing, Nanocomposites and Nanoinformatics
Geometry of molecules 1 MOLECULAR GEOMETRY AND ITS APPLICATION TO NANO INFORMATICS AND MOLECULAR DESIGN Sep 29, 2014 The 11th Korea-U.S. Forum on Nanotechnology: Nanomanufacturing, Nanocomposites and Nanoinformatics
International Journal of Computational Geometry & Applications c World Scientific Publishing Company
 International Journal of Computational Geometry & Applications c World Scientific Publishing Company EUCLIDEAN VORONOI DIAGRAM FOR CIRCLES IN A CIRCLE DONGUK KIM Voronoi Diagram Research Center, Hanyang
International Journal of Computational Geometry & Applications c World Scientific Publishing Company EUCLIDEAN VORONOI DIAGRAM FOR CIRCLES IN A CIRCLE DONGUK KIM Voronoi Diagram Research Center, Hanyang
Molecular Surface Representation
 Molecular Surface Representation Applications to docking 1 Motivation Studies of protein folding (Lee and Richards). Prediction of biomolecular recognition. Detection of drug binding cavities. Molecular
Molecular Surface Representation Applications to docking 1 Motivation Studies of protein folding (Lee and Richards). Prediction of biomolecular recognition. Detection of drug binding cavities. Molecular
A Sweep-Line Algorithm for the Inclusion Hierarchy among Circles
 Japan J. Indust. Appl. Math., 23 (2006), 127 138 Area 3 A Sweep-Line Algorithm for the Inclusion Hierarchy among Circles Deok-Soo Kim 1,, Byunghoon Lee 2 and Kokichi Sugihara 3 1 Department of Industrial
Japan J. Indust. Appl. Math., 23 (2006), 127 138 Area 3 A Sweep-Line Algorithm for the Inclusion Hierarchy among Circles Deok-Soo Kim 1,, Byunghoon Lee 2 and Kokichi Sugihara 3 1 Department of Industrial
Molecular Shapes and Surfaces *
 OpenStax-CNX module: m11616 1 Molecular Shapes and Surfaces * Lydia E. Kavraki This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 1.0 Topics in this Module
OpenStax-CNX module: m11616 1 Molecular Shapes and Surfaces * Lydia E. Kavraki This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 1.0 Topics in this Module
1 Proximity via Graph Spanners
 CS273: Algorithms for Structure Handout # 11 and Motion in Biology Stanford University Tuesday, 4 May 2003 Lecture #11: 4 May 2004 Topics: Proximity via Graph Spanners Geometric Models of Molecules, I
CS273: Algorithms for Structure Handout # 11 and Motion in Biology Stanford University Tuesday, 4 May 2003 Lecture #11: 4 May 2004 Topics: Proximity via Graph Spanners Geometric Models of Molecules, I
A sweepline algorithm for Euclidean Voronoi diagram of circles
 Computer-Aided Design 38 (2006) 260 272 www.elsevier.com/locate/cad A sweepline algorithm for Euclidean Voronoi diagram of circles Li Jin a, Donguk Kim b, Lisen Mu a, Deok-Soo Kim c, Shi-Min Hu a, * a
Computer-Aided Design 38 (2006) 260 272 www.elsevier.com/locate/cad A sweepline algorithm for Euclidean Voronoi diagram of circles Li Jin a, Donguk Kim b, Lisen Mu a, Deok-Soo Kim c, Shi-Min Hu a, * a
On a Nearest-Neighbour Problem in Minkowski and Power Metrics
 On a Nearest-Neighbour Problem in Minkowski and Power Metrics M.L. Gavrilova Dept of Comp. Science, University of Calgary Calgary, AB, Canada, T2N1N4 marina@cpsc.ucalgary.ca Abstract. The paper presents
On a Nearest-Neighbour Problem in Minkowski and Power Metrics M.L. Gavrilova Dept of Comp. Science, University of Calgary Calgary, AB, Canada, T2N1N4 marina@cpsc.ucalgary.ca Abstract. The paper presents
66 III Complexes. R p (r) }.
 66 III Complexes III.4 Alpha Complexes In this section, we use a radius constraint to introduce a family of subcomplexes of the Delaunay complex. These complexes are similar to the Čech complexes but differ
66 III Complexes III.4 Alpha Complexes In this section, we use a radius constraint to introduce a family of subcomplexes of the Delaunay complex. These complexes are similar to the Čech complexes but differ
Robot Motion Planning Using Generalised Voronoi Diagrams
 Robot Motion Planning Using Generalised Voronoi Diagrams MILOŠ ŠEDA, VÁCLAV PICH Institute of Automation and Computer Science Brno University of Technology Technická 2, 616 69 Brno CZECH REPUBLIC Abstract:
Robot Motion Planning Using Generalised Voronoi Diagrams MILOŠ ŠEDA, VÁCLAV PICH Institute of Automation and Computer Science Brno University of Technology Technická 2, 616 69 Brno CZECH REPUBLIC Abstract:
Laguerre Tessellations
 Voronoi Tessellation Applications of Voronoi tessellations Laguerre tessellation Voronoi cells vs. Laguerre cells Normal tessellations are LT Claudia Lautensack 1 2 1 University of Applied Sciences, Darmstadt,
Voronoi Tessellation Applications of Voronoi tessellations Laguerre tessellation Voronoi cells vs. Laguerre cells Normal tessellations are LT Claudia Lautensack 1 2 1 University of Applied Sciences, Darmstadt,
The Contour-Buildup Algorithm to Calculate the Analytical Molecular Surface
 JOURNAL OF STRUCTURAL BIOLOGY 116, 138 143 (1996) ARTICLE NO. 0022 The Contour-Buildup Algorithm to Calculate the Analytical Molecular Surface MAXIM TOTROV Skirball Institute of Biomolecular Medicine,
JOURNAL OF STRUCTURAL BIOLOGY 116, 138 143 (1996) ARTICLE NO. 0022 The Contour-Buildup Algorithm to Calculate the Analytical Molecular Surface MAXIM TOTROV Skirball Institute of Biomolecular Medicine,
Fast Computation of Generalized Voronoi Diagrams Using Graphics Hardware
 Fast Computation of Generalized Voronoi Diagrams Using Graphics Hardware paper by Kennet E. Hoff et al. (University of North Carolina at Chapel Hill) presented by Daniel Emmenegger GDV-Seminar ETH Zürich,
Fast Computation of Generalized Voronoi Diagrams Using Graphics Hardware paper by Kennet E. Hoff et al. (University of North Carolina at Chapel Hill) presented by Daniel Emmenegger GDV-Seminar ETH Zürich,
CS612 - Algorithms in Bioinformatics
 Spring 2016 Docking April 17, 2016 Docking Docking attempts to find the best matching between two molecules Docking A More Serious Definition Given two biological molecules determine: Whether the two molecules
Spring 2016 Docking April 17, 2016 Docking Docking attempts to find the best matching between two molecules Docking A More Serious Definition Given two biological molecules determine: Whether the two molecules
Mathematical Analysis and Calculation of Molecular Surfaces
 Mathematical Analysis and Calculation of Molecular Surfaces Chaoyu Quan, Benjamin Stamm To cite this version: Chaoyu Quan, Benjamin Stamm. Mathematical Analysis and Calculation of Molecular Surfaces. Journal
Mathematical Analysis and Calculation of Molecular Surfaces Chaoyu Quan, Benjamin Stamm To cite this version: Chaoyu Quan, Benjamin Stamm. Mathematical Analysis and Calculation of Molecular Surfaces. Journal
Algorithms and Modern Computer Science
 Algorithms and Modern Computer Science Dr. Marina L. Gavrilova Dept of Comp. Science, University of Calgary, AB, Canada, T2N1N4 My Research Interests Computer modeling and simulation Computational geometry
Algorithms and Modern Computer Science Dr. Marina L. Gavrilova Dept of Comp. Science, University of Calgary, AB, Canada, T2N1N4 My Research Interests Computer modeling and simulation Computational geometry
Solutions to Exercise 4 Algebraic Curve, Surface Splines IV: Molecular Models
 Solutions to Exercise 4 Algebraic Curve, Surface Splines IV: Molecular Models CS384R, CAM 395T, BME 385J: Fall 2007 Question 1. Describe the LEG (Labelled Embedded Graph) atomic representations as per
Solutions to Exercise 4 Algebraic Curve, Surface Splines IV: Molecular Models CS384R, CAM 395T, BME 385J: Fall 2007 Question 1. Describe the LEG (Labelled Embedded Graph) atomic representations as per
Aspect-Ratio Voronoi Diagram with Applications
 Aspect-Ratio Voronoi Diagram with Applications Tetsuo Asano School of Information Science, JAIST (Japan Advanced Institute of Science and Technology), Japan 1-1 Asahidai, Nomi, Ishikawa, 923-1292, Japan
Aspect-Ratio Voronoi Diagram with Applications Tetsuo Asano School of Information Science, JAIST (Japan Advanced Institute of Science and Technology), Japan 1-1 Asahidai, Nomi, Ishikawa, 923-1292, Japan
NURBS based B-rep Models for Macromolecules and their Properties
 NURBS based B-rep Models for Macromolecules and their Properties C.Bajaj H.Y.Lee R.Merkert V.Pascucci Department of Computer Sciences, Purdue University, West Lafayette, Indiana I Introduction We consider
NURBS based B-rep Models for Macromolecules and their Properties C.Bajaj H.Y.Lee R.Merkert V.Pascucci Department of Computer Sciences, Purdue University, West Lafayette, Indiana I Introduction We consider
Fuzzy Voronoi Diagram
 Fuzzy Voronoi Diagram Mohammadreza Jooyandeh and Ali Mohades Khorasani Mathematics and Computer Science, Amirkabir University of Technology, Hafez Ave., Tehran, Iran mohammadreza@jooyandeh.info,mohades@aut.ac.ir
Fuzzy Voronoi Diagram Mohammadreza Jooyandeh and Ali Mohades Khorasani Mathematics and Computer Science, Amirkabir University of Technology, Hafez Ave., Tehran, Iran mohammadreza@jooyandeh.info,mohades@aut.ac.ir
Algebraic Geometry of Segmentation and Tracking
 Ma191b Winter 2017 Geometry of Neuroscience Geometry of lines in 3-space and Segmentation and Tracking This lecture is based on the papers: Reference: Marco Pellegrini, Ray shooting and lines in space.
Ma191b Winter 2017 Geometry of Neuroscience Geometry of lines in 3-space and Segmentation and Tracking This lecture is based on the papers: Reference: Marco Pellegrini, Ray shooting and lines in space.
Dynamic Maintenance and Visualization of Molecular Surfaces Chandrajit L. Bajaj Valerio Pascucci Department of Computer Sciences and TICAM University
 Dynamic Maintenance and Visualization of Molecular Surfaces Chandrajit L. Bajaj Valerio Pascucci Department of Computer Sciences and TICAM University of Texas, Austin, TX 78712 Robert J. Holt Arun N. Netravali
Dynamic Maintenance and Visualization of Molecular Surfaces Chandrajit L. Bajaj Valerio Pascucci Department of Computer Sciences and TICAM University of Texas, Austin, TX 78712 Robert J. Holt Arun N. Netravali
The Voronoi Diagram of Planar Convex Objects
 The Voronoi Diagram of Planar Convex Objects Memelaos Karavelas, Mariette Yvinec To cite this version: Memelaos Karavelas, Mariette Yvinec. The Voronoi Diagram of Planar Convex Objects. European Symposium
The Voronoi Diagram of Planar Convex Objects Memelaos Karavelas, Mariette Yvinec To cite this version: Memelaos Karavelas, Mariette Yvinec. The Voronoi Diagram of Planar Convex Objects. European Symposium
Optimization Techniques in an Event-Driven Simulation of a Shaker Ball Mill
 Optimization Techniques in an Event-Driven Simulation of a Shaker Ball Mill Marina Gavrilova 1, Jon Rokne 1, Dmitri Gavrilov 2, and Oleg Vinogradov 3 1 Dept of Comp. Science, Universit of Calgary, Calgary,
Optimization Techniques in an Event-Driven Simulation of a Shaker Ball Mill Marina Gavrilova 1, Jon Rokne 1, Dmitri Gavrilov 2, and Oleg Vinogradov 3 1 Dept of Comp. Science, Universit of Calgary, Calgary,
Robot Motion Planning in Eight Directions
 Robot Motion Planning in Eight Directions Miloš Šeda and Tomáš Březina Abstract In this paper, we investigate the problem of 8-directional robot motion planning where the goal is to find a collision-free
Robot Motion Planning in Eight Directions Miloš Šeda and Tomáš Březina Abstract In this paper, we investigate the problem of 8-directional robot motion planning where the goal is to find a collision-free
Generating Tool Paths for Free-Form Pocket Machining Using z-buffer-based Voronoi Diagrams
 Int J Adv Manuf Technol (1999) 15:182 187 1999 Springer-Verlag London Limited Generating Tool Paths for Free-Form Pocket Machining Using z-buffer-based Voronoi Diagrams Jaehun Jeong and Kwangsoo Kim Department
Int J Adv Manuf Technol (1999) 15:182 187 1999 Springer-Verlag London Limited Generating Tool Paths for Free-Form Pocket Machining Using z-buffer-based Voronoi Diagrams Jaehun Jeong and Kwangsoo Kim Department
Computational Structural Bioinformatics II: Molecular Models. Chandrajit Bajaj
 Computational Structural Bioinformatics II: Molecular Models Chandrajit Bajaj September 14, 2010 2 Contents 1 Introduction 5 2 Spatial Occupancy 7 2.1 Surface Representations...............................................
Computational Structural Bioinformatics II: Molecular Models Chandrajit Bajaj September 14, 2010 2 Contents 1 Introduction 5 2 Spatial Occupancy 7 2.1 Surface Representations...............................................
The Voronoi diagram of circles made easy
 The Voronoi diagram of circles made easy François Anton Department of Informatics and Mathematical Modelling Technical University of Denmark, Richard Petersens Plads DK-2800 Kongens Lyngby, Denmark E-mail:
The Voronoi diagram of circles made easy François Anton Department of Informatics and Mathematical Modelling Technical University of Denmark, Richard Petersens Plads DK-2800 Kongens Lyngby, Denmark E-mail:
LATEST TRENDS on APPLIED MATHEMATICS, SIMULATION, MODELLING
 3D surface reconstruction of objects by using stereoscopic viewing Baki Koyuncu, Kurtuluş Küllü bkoyuncu@ankara.edu.tr kkullu@eng.ankara.edu.tr Computer Engineering Department, Ankara University, Ankara,
3D surface reconstruction of objects by using stereoscopic viewing Baki Koyuncu, Kurtuluş Küllü bkoyuncu@ankara.edu.tr kkullu@eng.ankara.edu.tr Computer Engineering Department, Ankara University, Ankara,
Other Voronoi/Delaunay Structures
 Other Voronoi/Delaunay Structures Overview Alpha hulls (a subset of Delaunay graph) Extension of Voronoi Diagrams Convex Hull What is it good for? The bounding region of a point set Not so good for describing
Other Voronoi/Delaunay Structures Overview Alpha hulls (a subset of Delaunay graph) Extension of Voronoi Diagrams Convex Hull What is it good for? The bounding region of a point set Not so good for describing
Chapter 4 Concepts from Geometry
 Chapter 4 Concepts from Geometry An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Line Segments The line segment between two points and in R n is the set of points on the straight line joining
Chapter 4 Concepts from Geometry An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Line Segments The line segment between two points and in R n is the set of points on the straight line joining
Quality Mesh Generation for Molecular Skin Surfaces Using Restricted Union of Balls
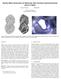 Quality Mesh Generation for Molecular Skin Surfaces Using Restricted Union of Balls Ho-Lun Cheng Xinwei Shi School of Computing National University of Singapore Figure 1: Molecular models of the molecule
Quality Mesh Generation for Molecular Skin Surfaces Using Restricted Union of Balls Ho-Lun Cheng Xinwei Shi School of Computing National University of Singapore Figure 1: Molecular models of the molecule
Voronoi-Delaunay analysis of voids in systems of nonspherical particles
 PHYSICAL REVIEW E VOLUME 59, NUMBER 6 JUNE 1999 Voronoi-Delaunay analysis of voids in systems of nonspherical particles V. A. Luchnikov, 1, * N. N. Medvedev, 1, L. Oger, 2, and J.-P. Troadec 2, 1 Institute
PHYSICAL REVIEW E VOLUME 59, NUMBER 6 JUNE 1999 Voronoi-Delaunay analysis of voids in systems of nonspherical particles V. A. Luchnikov, 1, * N. N. Medvedev, 1, L. Oger, 2, and J.-P. Troadec 2, 1 Institute
The Duality of Geodesic Voronoi/Delaunay Diagrams For An Intrinsic Discrete Laplace-Beltrami Operator on Simplicial Surfaces
 CCCG 2014, Halifax, Nova Scotia, August 11 13, 2014 The Duality of Geodesic Voronoi/Delaunay Diagrams For An Intrinsic Discrete Laplace-Beltrami Operator on Simplicial Surfaces Yong-Jin Liu, Chun-Xu Xu
CCCG 2014, Halifax, Nova Scotia, August 11 13, 2014 The Duality of Geodesic Voronoi/Delaunay Diagrams For An Intrinsic Discrete Laplace-Beltrami Operator on Simplicial Surfaces Yong-Jin Liu, Chun-Xu Xu
Roadmap Methods vs. Cell Decomposition in Robot Motion Planning
 Proceedings of the 6th WSEAS International Conference on Signal Processing, Robotics and Automation, Corfu Island, Greece, February 16-19, 007 17 Roadmap Methods vs. Cell Decomposition in Robot Motion
Proceedings of the 6th WSEAS International Conference on Signal Processing, Robotics and Automation, Corfu Island, Greece, February 16-19, 007 17 Roadmap Methods vs. Cell Decomposition in Robot Motion
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass
 Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
Tutorial 3 Comparing Biological Shapes Patrice Koehl and Joel Hass University of California, Davis, USA http://www.cs.ucdavis.edu/~koehl/ims2017/ What is a shape? A shape is a 2-manifold with a Riemannian
CS133 Computational Geometry
 CS133 Computational Geometry Voronoi Diagram Delaunay Triangulation 5/17/2018 1 Nearest Neighbor Problem Given a set of points P and a query point q, find the closest point p P to q p, r P, dist p, q dist(r,
CS133 Computational Geometry Voronoi Diagram Delaunay Triangulation 5/17/2018 1 Nearest Neighbor Problem Given a set of points P and a query point q, find the closest point p P to q p, r P, dist p, q dist(r,
Computational Geometry
 Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
Computational Geometry 600.658 Convexity A set S is convex if for any two points p, q S the line segment pq S. S p S q Not convex Convex? Convexity A set S is convex if it is the intersection of (possibly
Definitions. Topology/Geometry of Geodesics. Joseph D. Clinton. SNEC June Magnus J. Wenninger
 Topology/Geometry of Geodesics Joseph D. Clinton SNEC-04 28-29 June 2003 Magnus J. Wenninger Introduction Definitions Topology Goldberg s polyhedra Classes of Geodesic polyhedra Triangular tessellations
Topology/Geometry of Geodesics Joseph D. Clinton SNEC-04 28-29 June 2003 Magnus J. Wenninger Introduction Definitions Topology Goldberg s polyhedra Classes of Geodesic polyhedra Triangular tessellations
3. The three points (2, 4, 1), (1, 2, 2) and (5, 2, 2) determine a plane. Which of the following points is in that plane?
 Math 4 Practice Problems for Midterm. A unit vector that is perpendicular to both V =, 3, and W = 4,, is (a) V W (b) V W (c) 5 6 V W (d) 3 6 V W (e) 7 6 V W. In three dimensions, the graph of the equation
Math 4 Practice Problems for Midterm. A unit vector that is perpendicular to both V =, 3, and W = 4,, is (a) V W (b) V W (c) 5 6 V W (d) 3 6 V W (e) 7 6 V W. In three dimensions, the graph of the equation
Figure 1: An Area Voronoi Diagram of a typical GIS Scene generated from the ISPRS Working group III/3 Avenches data set. 2 ARRANGEMENTS 2.1 Voronoi Di
 Qualitative Spatial Relations using Arrangements for Complex Images M. Burge and W. Burger Johannes Kepler University, Department of Systems Science Computer Vision Laboratory, A-4040 Linz, Austria burge@cast.uni-linz.ac.at
Qualitative Spatial Relations using Arrangements for Complex Images M. Burge and W. Burger Johannes Kepler University, Department of Systems Science Computer Vision Laboratory, A-4040 Linz, Austria burge@cast.uni-linz.ac.at
In what follows, we will focus on Voronoi diagrams in Euclidean space. Later, we will generalize to other distance spaces.
 Voronoi Diagrams 4 A city builds a set of post offices, and now needs to determine which houses will be served by which office. It would be wasteful for a postman to go out of their way to make a delivery
Voronoi Diagrams 4 A city builds a set of post offices, and now needs to determine which houses will be served by which office. It would be wasteful for a postman to go out of their way to make a delivery
A Constrained Delaunay Triangle Mesh Method for Three-Dimensional Unstructured Boundary Point Cloud
 International Journal of Computer Systems (ISSN: 2394-1065), Volume 03 Issue 02, February, 2016 Available at http://www.ijcsonline.com/ A Constrained Delaunay Triangle Mesh Method for Three-Dimensional
International Journal of Computer Systems (ISSN: 2394-1065), Volume 03 Issue 02, February, 2016 Available at http://www.ijcsonline.com/ A Constrained Delaunay Triangle Mesh Method for Three-Dimensional
Crystal Voronoi Diagram and Its Applications to Collision-Free Paths
 Crystal Voronoi Diagram and Its Applications to Collision-Free Paths Kei Kobayashi 1 and Kokichi Sugihara 2 1 University of Tokyo, Hongo, Bunkyo-ku, Tokyo 113-8656, Japan, kkoba@stat.t.u-tokyo.ac.jp 2
Crystal Voronoi Diagram and Its Applications to Collision-Free Paths Kei Kobayashi 1 and Kokichi Sugihara 2 1 University of Tokyo, Hongo, Bunkyo-ku, Tokyo 113-8656, Japan, kkoba@stat.t.u-tokyo.ac.jp 2
An efficient implementation of the greedy forwarding strategy
 An efficient implementation of the greedy forwarding strategy Hannes Stratil Embedded Computing Systems Group E182/2 Technische Universität Wien Treitlstraße 3 A-1040 Vienna Email: hannes@ecs.tuwien.ac.at
An efficient implementation of the greedy forwarding strategy Hannes Stratil Embedded Computing Systems Group E182/2 Technische Universität Wien Treitlstraße 3 A-1040 Vienna Email: hannes@ecs.tuwien.ac.at
Planes Intersecting Cones: Static Hypertext Version
 Page 1 of 12 Planes Intersecting Cones: Static Hypertext Version On this page, we develop some of the details of the plane-slicing-cone picture discussed in the introduction. The relationship between the
Page 1 of 12 Planes Intersecting Cones: Static Hypertext Version On this page, we develop some of the details of the plane-slicing-cone picture discussed in the introduction. The relationship between the
Chapter 8. Voronoi Diagrams. 8.1 Post Oce Problem
 Chapter 8 Voronoi Diagrams 8.1 Post Oce Problem Suppose there are n post oces p 1,... p n in a city. Someone who is located at a position q within the city would like to know which post oce is closest
Chapter 8 Voronoi Diagrams 8.1 Post Oce Problem Suppose there are n post oces p 1,... p n in a city. Someone who is located at a position q within the city would like to know which post oce is closest
Visualization of pinfold simulations
 Visualization of pinfold simulations Sebastian Pötzsch Faculty of Mathematics and Computer Science University of Leipzig Overview 1. Introduction 1.1 Protein folding problem 1.2 HP-model 1.3 Pinfold simulation
Visualization of pinfold simulations Sebastian Pötzsch Faculty of Mathematics and Computer Science University of Leipzig Overview 1. Introduction 1.1 Protein folding problem 1.2 HP-model 1.3 Pinfold simulation
A fast approximation of the Voronoi diagram for a set of pairwise disjoint arcs
 A fast approximation of the Voronoi diagram for a set of pairwise disjoint arcs Dmytro Kotsur Taras Shevchenko National University of Kyiv 64/13, Volodymyrska, st., Kyiv, Ukraine dkotsur@gmail.com Vasyl
A fast approximation of the Voronoi diagram for a set of pairwise disjoint arcs Dmytro Kotsur Taras Shevchenko National University of Kyiv 64/13, Volodymyrska, st., Kyiv, Ukraine dkotsur@gmail.com Vasyl
NEW VERSION PROGRAM SUMMARY
 ARVO-CL:The OpenCL Version of the ARVO Package An Efficient Tool for Computing the Accessible Surface Area and the Excluded Volume of Proteins via Analytical Equations Ján Buša Jr. a,b,c,, Shura Hayryan
ARVO-CL:The OpenCL Version of the ARVO Package An Efficient Tool for Computing the Accessible Surface Area and the Excluded Volume of Proteins via Analytical Equations Ján Buša Jr. a,b,c,, Shura Hayryan
A parallel algorithm for constructing Voronoi diagrams based on point-set adaptive grouping
 CONCURRENCY AND COMPUTATION: PRACTICE AND EXPERIENCE Concurrency Computat.: Pract. Exper. 2014; 26:434 446 Published online 26 February 2013 in Wiley Online Library (wileyonlinelibrary.com)..3005 A parallel
CONCURRENCY AND COMPUTATION: PRACTICE AND EXPERIENCE Concurrency Computat.: Pract. Exper. 2014; 26:434 446 Published online 26 February 2013 in Wiley Online Library (wileyonlinelibrary.com)..3005 A parallel
Shape Space from Deformation
 Shape Space from Deformation Ho-Lun Cheng Ý, Herbert Edelsbrunner Þ and Ping Fu Ü Abstract The construction of shape spaces is studied from a mathematical and a computational viewpoint. A program is outlined
Shape Space from Deformation Ho-Lun Cheng Ý, Herbert Edelsbrunner Þ and Ping Fu Ü Abstract The construction of shape spaces is studied from a mathematical and a computational viewpoint. A program is outlined
Unit 3 Functions of Several Variables
 Unit 3 Functions of Several Variables In this unit, we consider several simple examples of multi-variable functions, quadratic surfaces and projections, level curves and surfaces, partial derivatives of
Unit 3 Functions of Several Variables In this unit, we consider several simple examples of multi-variable functions, quadratic surfaces and projections, level curves and surfaces, partial derivatives of
JET 2 User Manual 1 INSTALLATION 2 EXECUTION AND FUNCTIONALITIES. 1.1 Download. 1.2 System requirements. 1.3 How to install JET 2
 JET 2 User Manual 1 INSTALLATION 1.1 Download The JET 2 package is available at www.lcqb.upmc.fr/jet2. 1.2 System requirements JET 2 runs on Linux or Mac OS X. The program requires some external tools
JET 2 User Manual 1 INSTALLATION 1.1 Download The JET 2 package is available at www.lcqb.upmc.fr/jet2. 1.2 System requirements JET 2 runs on Linux or Mac OS X. The program requires some external tools
Smallest Intersecting Circle for a Set of Polygons
 Smallest Intersecting Circle for a Set of Polygons Peter Otfried Joachim Christian Marc Esther René Michiel Antoine Alexander 31st August 2005 1 Introduction Motivated by automated label placement of groups
Smallest Intersecting Circle for a Set of Polygons Peter Otfried Joachim Christian Marc Esther René Michiel Antoine Alexander 31st August 2005 1 Introduction Motivated by automated label placement of groups
Voronoi Diagrams in the Plane. Chapter 5 of O Rourke text Chapter 7 and 9 of course text
 Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
Math 734 Aug 22, Differential Geometry Fall 2002, USC
 Math 734 Aug 22, 2002 1 Differential Geometry Fall 2002, USC Lecture Notes 1 1 Topological Manifolds The basic objects of study in this class are manifolds. Roughly speaking, these are objects which locally
Math 734 Aug 22, 2002 1 Differential Geometry Fall 2002, USC Lecture Notes 1 1 Topological Manifolds The basic objects of study in this class are manifolds. Roughly speaking, these are objects which locally
3.2 THREE DIMENSIONAL OBJECT REPRESENTATIONS
 3.1 THREE DIMENSIONAL CONCEPTS We can rotate an object about an axis with any spatial orientation in threedimensional space. Two-dimensional rotations, on the other hand, are always around an axis that
3.1 THREE DIMENSIONAL CONCEPTS We can rotate an object about an axis with any spatial orientation in threedimensional space. Two-dimensional rotations, on the other hand, are always around an axis that
be a polytope. has such a representation iff it contains the origin in its interior. For a generic, sort the inequalities so that
 ( Shelling (Bruggesser-Mani 1971) and Ranking Let be a polytope. has such a representation iff it contains the origin in its interior. For a generic, sort the inequalities so that. a ranking of vertices
( Shelling (Bruggesser-Mani 1971) and Ranking Let be a polytope. has such a representation iff it contains the origin in its interior. For a generic, sort the inequalities so that. a ranking of vertices
Tiling Three-Dimensional Space with Simplices. Shankar Krishnan AT&T Labs - Research
 Tiling Three-Dimensional Space with Simplices Shankar Krishnan AT&T Labs - Research What is a Tiling? Partition of an infinite space into pieces having a finite number of distinct shapes usually Euclidean
Tiling Three-Dimensional Space with Simplices Shankar Krishnan AT&T Labs - Research What is a Tiling? Partition of an infinite space into pieces having a finite number of distinct shapes usually Euclidean
Distributed Algorithm for Voronoi Partition of Wireless Sensor Networks with a Limited Sensing Range
 sensors Article Distributed Algorithm for Voronoi Partition of Wireless Sensor Networks with a Limited Sensing Range Chenlong He 1, * ID, Zuren Feng 1 and Zhigang Ren 2 1 State Key Laboratory for Manufacturing
sensors Article Distributed Algorithm for Voronoi Partition of Wireless Sensor Networks with a Limited Sensing Range Chenlong He 1, * ID, Zuren Feng 1 and Zhigang Ren 2 1 State Key Laboratory for Manufacturing
The Crust and Skeleton Applications in GIS
 The Crust and Skeleton Applications in GIS Christopher Gold and Maciek Dakowicz School of Computing, University of Glamorgan Pontypridd CF37 1DL Wales UK christophergold@voronoi.com Abstract This paper
The Crust and Skeleton Applications in GIS Christopher Gold and Maciek Dakowicz School of Computing, University of Glamorgan Pontypridd CF37 1DL Wales UK christophergold@voronoi.com Abstract This paper
Solid Modeling Lecture Series. Prof. Gary Wang Department of Mechanical and Manufacturing Engineering The University of Manitoba
 Solid Modeling 25.353 Lecture Series Prof. Gary Wang Department of Mechanical and Manufacturing Engineering The University of Manitoba Information complete, unambiguous, accurate solid model Solid Modeling
Solid Modeling 25.353 Lecture Series Prof. Gary Wang Department of Mechanical and Manufacturing Engineering The University of Manitoba Information complete, unambiguous, accurate solid model Solid Modeling
Voronoi Diagrams and Delaunay Triangulation slides by Andy Mirzaian (a subset of the original slides are used here)
 Voronoi Diagrams and Delaunay Triangulation slides by Andy Mirzaian (a subset of the original slides are used here) Voronoi Diagram & Delaunay Triangualtion Algorithms Divide-&-Conquer Plane Sweep Lifting
Voronoi Diagrams and Delaunay Triangulation slides by Andy Mirzaian (a subset of the original slides are used here) Voronoi Diagram & Delaunay Triangualtion Algorithms Divide-&-Conquer Plane Sweep Lifting
Voronoi Diagram. Xiao-Ming Fu
 Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
Voronoi Diagram Xiao-Ming Fu Outlines Introduction Post Office Problem Voronoi Diagram Duality: Delaunay triangulation Centroidal Voronoi tessellations (CVT) Definition Applications Algorithms Outlines
Computation of tunnels in protein molecules using Delaunay triangulation
 Computation of tunnels in protein molecules using Delaunay triangulation Petr Medek Faculty of Informatics Masaryk University Botanická 68a 60 00 Brno, Czech Republic medek@fi.muni.cz Petr Beneš Faculty
Computation of tunnels in protein molecules using Delaunay triangulation Petr Medek Faculty of Informatics Masaryk University Botanická 68a 60 00 Brno, Czech Republic medek@fi.muni.cz Petr Beneš Faculty
Characterization of the formation structure in team sports. Tokyo , Japan. University, Shinjuku, Tokyo , Japan
 Characterization of the formation structure in team sports Takuma Narizuka 1 and Yoshihiro Yamazaki 2 1 Department of Physics, Faculty of Science and Engineering, Chuo University, Bunkyo, Tokyo 112-8551,
Characterization of the formation structure in team sports Takuma Narizuka 1 and Yoshihiro Yamazaki 2 1 Department of Physics, Faculty of Science and Engineering, Chuo University, Bunkyo, Tokyo 112-8551,
Data Structures for Approximate Proximity and Range Searching
 Data Structures for Approximate Proximity and Range Searching David M. Mount University of Maryland Joint work with: Sunil Arya (Hong Kong U. of Sci. and Tech) Charis Malamatos (Max Plank Inst.) 1 Introduction
Data Structures for Approximate Proximity and Range Searching David M. Mount University of Maryland Joint work with: Sunil Arya (Hong Kong U. of Sci. and Tech) Charis Malamatos (Max Plank Inst.) 1 Introduction
Topological estimation using witness complexes. Vin de Silva, Stanford University
 Topological estimation using witness complexes, Acknowledgements Gunnar Carlsson (Mathematics, Stanford) principal collaborator Afra Zomorodian (CS/Robotics, Stanford) persistent homology software Josh
Topological estimation using witness complexes, Acknowledgements Gunnar Carlsson (Mathematics, Stanford) principal collaborator Afra Zomorodian (CS/Robotics, Stanford) persistent homology software Josh
Lecture 1 Discrete Geometric Structures
 Lecture 1 Discrete Geometric Structures Jean-Daniel Boissonnat Winter School on Computational Geometry and Topology University of Nice Sophia Antipolis January 23-27, 2017 Computational Geometry and Topology
Lecture 1 Discrete Geometric Structures Jean-Daniel Boissonnat Winter School on Computational Geometry and Topology University of Nice Sophia Antipolis January 23-27, 2017 Computational Geometry and Topology
Molecular Distance Geometry and Atomic Orderings
 Molecular Distance Geometry and Atomic Orderings Antonio Mucherino IRISA, University of Rennes 1 Workshop Set Computation for Control ENSTA Bretagne, Brest, France December 5 th 2013 The Distance Geometry
Molecular Distance Geometry and Atomic Orderings Antonio Mucherino IRISA, University of Rennes 1 Workshop Set Computation for Control ENSTA Bretagne, Brest, France December 5 th 2013 The Distance Geometry
Geometry Optimization Made Simple with Translation and Rotation Coordinates
 Geometry Optimization Made Simple with Translation and Rotation Coordinates Lee-Ping Wang 1 and Chenchen Song 2, 3 1) Department of Chemistry, University of California; 1 Shields Ave; Davis, CA 95616.
Geometry Optimization Made Simple with Translation and Rotation Coordinates Lee-Ping Wang 1 and Chenchen Song 2, 3 1) Department of Chemistry, University of California; 1 Shields Ave; Davis, CA 95616.
CURVILINEAR MESH GENERATION IN 3D
 CURVILINEAR MESH GENERATION IN 3D Saikat Dey, Robert M. O'Bara 2 and Mark S. Shephard 2 SFA Inc. / Naval Research Laboratory, Largo, MD., U.S.A., dey@cosmic.nrl.navy.mil 2 Scientific Computation Research
CURVILINEAR MESH GENERATION IN 3D Saikat Dey, Robert M. O'Bara 2 and Mark S. Shephard 2 SFA Inc. / Naval Research Laboratory, Largo, MD., U.S.A., dey@cosmic.nrl.navy.mil 2 Scientific Computation Research
The Voronoi diagram of circles and its application to the visualization of the growth of particles
 The Voronoi diagram of circles and its application to the visualization of the growth of particles François Anton 1, Darka Mioc 2, and Christopher Gold 3 1 Department of Informatics and Mathematical Modelling
The Voronoi diagram of circles and its application to the visualization of the growth of particles François Anton 1, Darka Mioc 2, and Christopher Gold 3 1 Department of Informatics and Mathematical Modelling
Measuring Lengths The First Fundamental Form
 Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
2) For any triangle edge not on the boundary, there is exactly one neighboring
 Triangulating Trimmed NURBS Surfaces Chang Shu and Pierre Boulanger Abstract. This paper describes techniques for the piecewise linear approximation of trimmed NURBS surfaces. The problem, called surface
Triangulating Trimmed NURBS Surfaces Chang Shu and Pierre Boulanger Abstract. This paper describes techniques for the piecewise linear approximation of trimmed NURBS surfaces. The problem, called surface
Computation of Voronoi Diagrams and Delaunay Triangulation via Parametric Linear Programming
 Computation of Voronoi Diagrams and Delaunay Triangulation via Parametric Linear Programming Saša V. Raković, Pascal Grieder and Colin Jones September 14, 2004 Abstract This note illustrates how Voronoi
Computation of Voronoi Diagrams and Delaunay Triangulation via Parametric Linear Programming Saša V. Raković, Pascal Grieder and Colin Jones September 14, 2004 Abstract This note illustrates how Voronoi
6. Concluding Remarks
 [8] K. J. Supowit, The relative neighborhood graph with an application to minimum spanning trees, Tech. Rept., Department of Computer Science, University of Illinois, Urbana-Champaign, August 1980, also
[8] K. J. Supowit, The relative neighborhood graph with an application to minimum spanning trees, Tech. Rept., Department of Computer Science, University of Illinois, Urbana-Champaign, August 1980, also
CAD & Computational Geometry Course plan
 Course plan Introduction Segment-Segment intersections Polygon Triangulation Intro to Voronoï Diagrams & Geometric Search Sweeping algorithm for Voronoï Diagrams 1 Voronoi Diagrams Voronoi Diagrams or
Course plan Introduction Segment-Segment intersections Polygon Triangulation Intro to Voronoï Diagrams & Geometric Search Sweeping algorithm for Voronoï Diagrams 1 Voronoi Diagrams Voronoi Diagrams or
Voronoi and Radical Tessellations of Packings of Spheres
 Voronoi and Radical Tessellations of Packings of Spheres A. Gervois 1, L. Oger 2, P. Richard 2, and J.P. Troadec 2 1 Service de Physique Théorique, Direction des Sciences de la Matière, CEA/Saclay, F91191
Voronoi and Radical Tessellations of Packings of Spheres A. Gervois 1, L. Oger 2, P. Richard 2, and J.P. Troadec 2 1 Service de Physique Théorique, Direction des Sciences de la Matière, CEA/Saclay, F91191
VORONOI DIAGRAM PETR FELKEL. FEL CTU PRAGUE Based on [Berg] and [Mount]
![VORONOI DIAGRAM PETR FELKEL. FEL CTU PRAGUE Based on [Berg] and [Mount] VORONOI DIAGRAM PETR FELKEL. FEL CTU PRAGUE Based on [Berg] and [Mount]](/thumbs/88/116547690.jpg) VORONOI DIAGRAM PETR FELKEL FEL CTU PRAGUE felkel@fel.cvut.cz https://cw.felk.cvut.cz/doku.php/courses/a4m39vg/start Based on [Berg] and [Mount] Version from 9.11.2017 Talk overview Definition and examples
VORONOI DIAGRAM PETR FELKEL FEL CTU PRAGUE felkel@fel.cvut.cz https://cw.felk.cvut.cz/doku.php/courses/a4m39vg/start Based on [Berg] and [Mount] Version from 9.11.2017 Talk overview Definition and examples
Chapter 7 Spatial Operation
 7.1 Introduction Chapter 7 Spatial Operation Q: What is spatial operation? A: Spatial operation is computational manipulation of spatial objects that deepen our understanding of spatial phenomena. In spatial
7.1 Introduction Chapter 7 Spatial Operation Q: What is spatial operation? A: Spatial operation is computational manipulation of spatial objects that deepen our understanding of spatial phenomena. In spatial
GEOMETRIC LIBRARY. Maharavo Randrianarivony
 GEOMETRIC LIBRARY Maharavo Randrianarivony During the last four years, I have maintained a numerical geometric library. The constituting routines, which are summarized in the following list, are implemented
GEOMETRIC LIBRARY Maharavo Randrianarivony During the last four years, I have maintained a numerical geometric library. The constituting routines, which are summarized in the following list, are implemented
On Merging Straight Skeletons
 On Merging Straight Skeletons Franz Aurenhammer 1 and Michael Steinkogler 2 1 Institute for Theoretical Computer Science, University of Technology, Graz, Austria auren@igi.tugraz.at 2 Institute for Theoretical
On Merging Straight Skeletons Franz Aurenhammer 1 and Michael Steinkogler 2 1 Institute for Theoretical Computer Science, University of Technology, Graz, Austria auren@igi.tugraz.at 2 Institute for Theoretical
Polyhedra with Spherical Faces and Quasi-Fuchsian Fractals
 Topology and Computer 2017 Polyhedra with Spherical Faces and Quasi-Fuchsian Fractals Kento Nakamura Graduate School of Advanced Mathematical Science, Meiji University Sphairahedron sphaira- (= spherical)
Topology and Computer 2017 Polyhedra with Spherical Faces and Quasi-Fuchsian Fractals Kento Nakamura Graduate School of Advanced Mathematical Science, Meiji University Sphairahedron sphaira- (= spherical)
Observing Information: Applied Computational Topology.
 Observing Information: Applied Computational Topology. Bangor University, and NUI Galway April 21, 2008 What is the geometric information that can be gleaned from a data cloud? Some ideas either already
Observing Information: Applied Computational Topology. Bangor University, and NUI Galway April 21, 2008 What is the geometric information that can be gleaned from a data cloud? Some ideas either already
Advanced Algorithms Computational Geometry Prof. Karen Daniels. Fall, 2012
 UMass Lowell Computer Science 91.504 Advanced Algorithms Computational Geometry Prof. Karen Daniels Fall, 2012 Voronoi Diagrams & Delaunay Triangulations O Rourke: Chapter 5 de Berg et al.: Chapters 7,
UMass Lowell Computer Science 91.504 Advanced Algorithms Computational Geometry Prof. Karen Daniels Fall, 2012 Voronoi Diagrams & Delaunay Triangulations O Rourke: Chapter 5 de Berg et al.: Chapters 7,
Part 3 - Changing Colors and Display Formats
 Part 3 - Changing Colors and Display Formats http://cbm.msoe.edu/newwebsite/learntomodel Introduction One of the most powerful features of Jmol is the ability to completely customize how your structure
Part 3 - Changing Colors and Display Formats http://cbm.msoe.edu/newwebsite/learntomodel Introduction One of the most powerful features of Jmol is the ability to completely customize how your structure
Contents. Preface... VII. Part I Classical Topics Revisited
 Contents Preface........................................................ VII Part I Classical Topics Revisited 1 Sphere Packings........................................... 3 1.1 Kissing Numbers of Spheres..............................
Contents Preface........................................................ VII Part I Classical Topics Revisited 1 Sphere Packings........................................... 3 1.1 Kissing Numbers of Spheres..............................
Divided-and-Conquer for Voronoi Diagrams Revisited. Supervisor: Ben Galehouse Presenter: Xiaoqi Cao
 Divided-and-Conquer for Voronoi Diagrams Revisited Supervisor: Ben Galehouse Presenter: Xiaoqi Cao Outline Introduction Generalized Voronoi Diagram Algorithm for building generalized Voronoi Diagram Applications
Divided-and-Conquer for Voronoi Diagrams Revisited Supervisor: Ben Galehouse Presenter: Xiaoqi Cao Outline Introduction Generalized Voronoi Diagram Algorithm for building generalized Voronoi Diagram Applications
Offset Triangular Mesh Using the Multiple Normal Vectors of a Vertex
 285 Offset Triangular Mesh Using the Multiple Normal Vectors of a Vertex Su-Jin Kim 1, Dong-Yoon Lee 2 and Min-Yang Yang 3 1 Korea Advanced Institute of Science and Technology, sujinkim@kaist.ac.kr 2 Korea
285 Offset Triangular Mesh Using the Multiple Normal Vectors of a Vertex Su-Jin Kim 1, Dong-Yoon Lee 2 and Min-Yang Yang 3 1 Korea Advanced Institute of Science and Technology, sujinkim@kaist.ac.kr 2 Korea
Automatic Pipeline Generation by the Sequential Segmentation and Skelton Construction of Point Cloud
 , pp.43-47 http://dx.doi.org/10.14257/astl.2014.67.11 Automatic Pipeline Generation by the Sequential Segmentation and Skelton Construction of Point Cloud Ashok Kumar Patil, Seong Sill Park, Pavitra Holi,
, pp.43-47 http://dx.doi.org/10.14257/astl.2014.67.11 Automatic Pipeline Generation by the Sequential Segmentation and Skelton Construction of Point Cloud Ashok Kumar Patil, Seong Sill Park, Pavitra Holi,
4 Basis, Subbasis, Subspace
 4 Basis, Subbasis, Subspace Our main goal in this chapter is to develop some tools that make it easier to construct examples of topological spaces. By Definition 3.12 in order to define a topology on a
4 Basis, Subbasis, Subspace Our main goal in this chapter is to develop some tools that make it easier to construct examples of topological spaces. By Definition 3.12 in order to define a topology on a
Unit Activity Correlations to Common Core State Standards. Geometry. Table of Contents. Geometry 1 Statistics and Probability 8
 Unit Activity Correlations to Common Core State Standards Geometry Table of Contents Geometry 1 Statistics and Probability 8 Geometry Experiment with transformations in the plane 1. Know precise definitions
Unit Activity Correlations to Common Core State Standards Geometry Table of Contents Geometry 1 Statistics and Probability 8 Geometry Experiment with transformations in the plane 1. Know precise definitions
An Optimal Algorithm for the Euclidean Bottleneck Full Steiner Tree Problem
 An Optimal Algorithm for the Euclidean Bottleneck Full Steiner Tree Problem Ahmad Biniaz Anil Maheshwari Michiel Smid September 30, 2013 Abstract Let P and S be two disjoint sets of n and m points in the
An Optimal Algorithm for the Euclidean Bottleneck Full Steiner Tree Problem Ahmad Biniaz Anil Maheshwari Michiel Smid September 30, 2013 Abstract Let P and S be two disjoint sets of n and m points in the
FEATURE-PRESERVING ADAPTIVE MESH GENERATION FOR MOLECULAR MODELING
 FEATURE-PRESERVING ADAPTIVE MESH GENERATION FOR MOLECULAR MODELING ZEYUN YU, MICHAEL HOLST, AND ANDREW MCCAMMON Department of Mathematics, Department of Chemistry and Biochemistry University of California,
FEATURE-PRESERVING ADAPTIVE MESH GENERATION FOR MOLECULAR MODELING ZEYUN YU, MICHAEL HOLST, AND ANDREW MCCAMMON Department of Mathematics, Department of Chemistry and Biochemistry University of California,
Planar Graphs. 1 Graphs and maps. 1.1 Planarity and duality
 Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
Planar Graphs In the first half of this book, we consider mostly planar graphs and their geometric representations, mostly in the plane. We start with a survey of basic results on planar graphs. This chapter
What is Internet COMPUTER NETWORKS AND NETWORK-BASED BIOINFORMATICS RESOURCES
 What is Internet COMPUTER NETWORKS AND NETWORK-BASED BIOINFORMATICS RESOURCES Global Internet DNS Internet IP Internet Domain Name System Domain Name System The Domain Name System (DNS) is a hierarchical,
What is Internet COMPUTER NETWORKS AND NETWORK-BASED BIOINFORMATICS RESOURCES Global Internet DNS Internet IP Internet Domain Name System Domain Name System The Domain Name System (DNS) is a hierarchical,
The transition from order to disorder in Voronoi Diagrams with applications
 Applied Physics Research; Vol. 10, No. 6; 2018 ISSN 1916-9639 E-ISSN 1916-9647 Published by Canadian Center of Science and Education The transition from order to disorder in Voronoi Diagrams with applications
Applied Physics Research; Vol. 10, No. 6; 2018 ISSN 1916-9639 E-ISSN 1916-9647 Published by Canadian Center of Science and Education The transition from order to disorder in Voronoi Diagrams with applications
Geometric Steiner Trees
 Geometric Steiner Trees From the book: Optimal Interconnection Trees in the Plane By Marcus Brazil and Martin Zachariasen Part 2: Global properties of Euclidean Steiner Trees and GeoSteiner Marcus Brazil
Geometric Steiner Trees From the book: Optimal Interconnection Trees in the Plane By Marcus Brazil and Martin Zachariasen Part 2: Global properties of Euclidean Steiner Trees and GeoSteiner Marcus Brazil
