Adaptive Moving Mesh Modeling for Two Dimensional Groundwater Flow and Transport
|
|
|
- Lauren Logan
- 6 years ago
- Views:
Transcription
1 Contemporary Mathematics Adaptive Moving Mesh Modeling for Two Dimensional Groundwater Flow and Transport Weizhang Huang and Xiaoyong Zhan Abstract. An adaptive moving mesh method is presented for numerical simulation of two dimensional groundwater flow and transport problems. A selection of problems are considered, including advection dominated chemical transport and reaction, solute transport from contamination sources, transport of nonaqueous phase liquids NAPLs) in an aquifer, and coupling of groundwater flow with NAPL transport. Numerical results show that the adaptive moving mesh method is able to capture sharp moving fronts and detect the emerging of new fronts. 1. Introduction Groundwater resources are vital to the natural environment, social welfare, and economic health. In the past two decades, numerical simulation has proved to be an effective tool for simulating and predicting behaviors of chemical contamination in the subsurface that can degrade groundwater quality. Indeed, a variety of algorithms and software have been developed for the numerical simulation of groundwater flow and transport, e.g., see [25, 31] and references therein. Meanwhile, the quest for more accurate and efficient numerical methods remains active. This is especially true for problems exhibiting sharp moving fronts, for which conventional methods tend to produce oscillatory solutions and excessive numerical dispersion in regions around sharp fronts. It has been amply demonstrated that, by placing more mesh nodes in the regions around sharp fronts than in the rest of the domain, mesh adaptation provides an effective tool in reducing numerical dispersion and oscillation while enhancing the efficiency and accuracy of numerical simulation. Roughly speaking, mesh adaptation can be cast into two main categories, the refinement method and the dynamic or moving mesh method. The first type of method is conceptually simpler. It achieves mesh adaptivity by adding or removing mesh nodes locally. The refinement method has been successfully applied to a number of groundwater problems in one and two dimensions. For example, Yeh et al. [29] combine the method of characteristics with local mesh refinement and effectively avoid the numerical dispersion and 1991 Mathematics Subject Classification. 65M50, 65M60, 86A05. 1 c 0000 copyright holder)
2 2 WEIZHANG HUANG AND XIAOYONG ZHAN oscillation problem in solving advection-dispersion equations. Trompert [26] applies local-uniform-mesh refinement to modeling transport in heterogeneous media. On the other hand, the moving mesh method [11,14,23] achieves mesh adaptivity by relocating the node positions while keeping the number of mesh nodes and the mesh connectivity fixed throughout the entire solution process. Since the size of computation and data structure are kept fixed, it is much easier to implement the moving mesh method than the refinement method. Moreover, the moving mesh method often works better because the relocation of node positions improves the alignment of mesh elements with the solution and thus the simulation accuracy. Unfortunately, it has been known that it is difficult to formulate a reliable moving mesh method in multi-dimensions. So far, the moving mesh method has been successfully applied to groundwater modeling only in one dimension; see [8 10, 17, 30]. Progress has been made recently in developing more reliable moving mesh methods in multi-dimensions. The development has mainly focused on the variational approach where the node positions are obtained by minimizing a functional measuring some difficulty in approximating the physical solution. Such a functional can be formulated as the energy functional of harmonic mappings [3,7,20,28] or based on a Jabobian weighting [18], interpolation error estimates [12,16], or a combination of various mesh properties [1, 2]. The reader is also referred to [4] for brief comparison of variational-type moving mesh methods with those based on mesh velocity. In this work, we focus on a particular variational-type moving mesh method, the so-called moving mesh PDE MMPDE) approach developed by Huang et al. [14, 15]. With this approach, adaptive moving meshes are generated as images of a fixed computational mesh in the auxiliary domain through a time dependent coordinate transformation. The transformation is obtained as the solution of the gradient flow equation of an adaptation functional which is related to the wellknown equidistribution principle [6] and measures the difficulty in approximating the solution. Since the mesh nodes are continuously relocated and dynamically adapted to solution behavior, the MMPDE moving mesh method provides an ideal adaptive strategy to capture evolving sharp fronts without using a large number of grid points. In [17], the method has been used to model a range of one dimensional groundwater problems, including of advection dominated chemical transport and reaction, non-linear infiltration in soil, and the coupling of density dependent flow and transport. The objective of this paper is to investigate the applicability of the MMPDE moving mesh method to two dimensional groundwater flow and transport problems. Although the moving mesh method has been successfully applied to a number of one dimensional groundwater problems [8 10, 17, 30], there lacks in published work in two dimensions. Moreover, it is far from clear that the method is necessarily able to capture sharp two dimensional moving fronts. This is because two dimensional moving fronts have far more complicated structures and thus more difficult to simulate and track. For demonstration purpose, a range of problems common in groundwater flow and transport are considered. They include advection dominated chemical transport and reaction, solute transport from contamination sources, transport of nonaqueous phase liquids NAPLs) in an aquifer, and coupling of groundwater flow with NAPL transport. The paper is organized as follows. The MMPDE moving mesh method and its implementation are presented in section 2. In section 3, the groundwater problems
3 MOVING MESH MODELING FOR GROUNDWATER FLOW AND TRANSPORT 3 are described. The simulation results using the adaptive moving mesh method are also given in the same section. Finally, the summary and comments are given in Section The MMPDE moving mesh method The MMPDE moving mesh method is developed in [14] in one dimension and in [15] for multi-dimensional problems. The basic idea is to define the time-dependent coordinate transformation needed for generating adaptive meshes as the solution of an MMPDE moving mesh PDE), which in turn is defined as the gradient flow equation of an adaptation functional measuring the difficulty in approximating the physical solution. The physical PDE is discretized and integrated with the quasi- Lagrange approach where the effect of mesh movement is reflected by extra terms involving mesh velocity in the transformed physical PDE. For the clarity of presentation, the MMPDE moving mesh method is described for the following simplified version of the advection-dispersion-reaction equation ADRE), one of typical mathematical models describing chemical transport in the subsurface: 2.1) R C t = x D C ) + D C ) C V 1 x y y x V C 2 y λrc, where C = Ct,x,y) is the concentration of a certain type of chemical, D = Dt,x,y) is the dispersivity, V = V 1 t,x,y),v 2 t,x,y)) is the Darcy velocity, R is the retardation factor, and λ is the reaction factor. It should be emphasized that the method can be straightforwardly applied to other systems Spatial discretization on a moving mesh. In a moving mesh method, the mesh is generated as the image of a uniform logical mesh under the coordinate transformation denoted by x = xt,ξ,η), y = yt,ξ,η)) from the logical domain Ω c ) to the physical domain Ω). As a common practice, we choose the logical domain as the the unit square, i.e., Ω c = 0,1) 0,1). Given two positive integers J and K, let ξ = 1/J and η = 1/K. With the uniform logical mesh being denoted by 2.2) ξ j = j ξ, η k = k η j = 0,...,J, k = 0,...,K the moving mesh can be written as 2.3) x j,k t) = xt,ξ j,η k ), y j,k t) = yt,ξ j,η k ) j = 0,...,J, k = 0,...,K. Finite differences are used for the spatial discretization of equation 2.1). To this end, 2.1) is first transformed from the physical coordinates to the logical ones. Let c = ct,ξ,η) = Ct,xt,ξ,η),yt,ξ,η)). Then, 2.1) can be written in the new coordinates as 2.4) R c t = D c ) + D c ) V 1 x t ) c x x y y x V 2 y t ) c y λrc, where x t,y t ) is the mesh velocity. Note that the partial derivatives with respect to x and y in 2.4) should be understood through the chain-rule, viz., 2.5) x = ξ x ξ + η x η, y = ξ y ξ + η y η,
4 4 WEIZHANG HUANG AND XIAOYONG ZHAN with the transformation relations being given by J = x ξ y η x η y ξ and [ ] [ ] 1 ξx ξ 2.6) y xξ x = η = 1 [ ] y η x η. η x η y y ξ y η J y ξ x ξ The approximation of the partial derivatives using central finite differences on the uniform logical mesh is standard. For example, c c x = ξ x j,k ξ + η c x η) j,k ξ x j,k c j+1,k c j 1,k 2 ξ c j,k+1 c j,k 1 + η x j,k, 2 η where ξ x j,k and η x j,k are calculated through 2.6). Some cautions may be needed when discretizing the second order derivatives. Consider the first term on the righthand side of 2.4). In the new coordinates it reads as x D c x ) = ξ x ξ Dξ x c ξ + Dη c x η ) + η x η Dξ x c ξ + Dη c x η To obtain a compact and stable scheme, we use half-point differences for approximating the outer differentiation, [ D c x x) j,k ξ ] x j,k c Dξ x ξ ξ + Dη c c x Dξ x η) j+ 1 2,k ξ + Dη c x η) j 1 2 [,k + η ] x j,k c Dξ x η ξ + Dη c c x Dξ x η) ξ + Dη c x. η) j,k+ 1 2 ). j,k 1 2 The remaining differentiation can be approximated by the standard central differencing and averaging, e.g., c ξ 1 [ cj+1,k c j 1,k + c ] j+1,k±1 c j 1,k±1, j,k± ξ 2 ξ 2 c η 1 [ cj,k+1 c j,k 1 + c ] j±1,k+1 c j±1,k 1. j± 1 2,k 2 2 η 2 η It is noted that the effect of mesh movement is reflected in the transformed equation 2.4) via the terms containing mesh velocity x t,y t ). For this reason, 2.4) is often said to be of the quasi-lagrange form. With this quasi-lagrange approach, there is no need for interpolation of the physical variable from the old mesh to the new mesh. This is in contrast to the so-called mesh rezoning approach, where the physical variable is interpolated from the old mesh to the new mesh and the physical PDE is discretized and integrated on the new mesh that is considered fixed in the current time step); see [11,20] for more discussion on this approach The MMPDE approach of mesh movement. The idea of the MM- PDE approach is to determine the time-dependent coordinate transformation needed for generating adaptive meshes as the solution of an MMPDE, which in turn is defined as the gradient flow equation of an adaptation functional measuring the difficulty in approximating the physical solution. To measure the difficulty in the
5 MOVING MESH MODELING FOR GROUNDWATER FLOW AND TRANSPORT 5 numerical approximation of the solution, we define the so-called arc-length monitor function as [ ] 1 + C 2.7) Mx,y) = I + C C) T 2 = x C x C y C x C y 1 + Cy 2. Generally we expect that the mesh is generated such that it closely satisfies the socalled equidistribution principle or the mesh density is approximately proportional to the square root of the determinant of the monitor function e.g., see [16]). In this sense, the monitor function 2.7) places more mesh nodes in the regions of large gradient of the solution C. It is known that the arc-length monitor function is the simplest but not the best for all cases. The reader is referred to [16] for a more sophisticated definition of the monitor function based on interpolation error. Given the monitor function, the adaptation functional is defined for the inverse coordinate transformation as 2.8) I[ξ,η] = 1 ξ) T M 1 ξ + η) T M 1 η ) dxdy, 2 Ω where = / x, / y) is the gradient operator. The MMPDE is then defined [13] as the gradient flow equation of I[ξ,η], 2.9) ξ t = 1 τp M 1 ξ ), η t = 1 τp M 1 η ), where p = pt,x,y) is a positive function cf. its definition in 2.11)) and τ > 0 is a user-prescribed parameter for adjusting the time scale of mesh movement. The final form of the MMPDE is obtained by interchanging the roles of the independent and dependent variables in 2.9), 2.10) where 2.11) u = 1 J x t = 1 τp y t = 1 τp [ y η x η [ a 11 2 x [ a 11 2 y ξ 2 + 2a 2 x 12 ξ η + a 2 x 22 η 2 + b x 1 ξ + b x 2 η ξ 2 + 2a 2 y 12 ξ η + a 2 y 22 η 2 + b y 1 ξ + b y 2 η ], v = 1 [ yξ J x ξ ], J = x ξ y η x η y ξ, a 11 = u T M 1 u, a 12 = u T M 1 v, a 22 = v T M 1 v, b 1 = u T 1 1 M M u + v ξ η p = a a b2 1 + b2 2. ), b 2 = v T 1 M u + v ξ ], ], M 1 Central finite differences are used to discretize the mesh equation 2.10) on the uniform logical mesh. In our computation, τ is taken as τ = 0.01, and this value seems to work well for all the tested cases Time integration and solution procedure. In principle, the physical PDE 2.4) and the MMPDE 2.10) can be integrated in time either simultaneously or alternately. However, alternating solution seems more realistic in multidimensions since it voids the highly nonlinear coupling of the mesh and physical solution and preserves many structures such as ellipticity and sparsity in each of the mesh and physical PDEs. The following alternating procedure is used in our η ),
6 6 WEIZHANG HUANG AND XIAOYONG ZHAN computations. Here, t is the time step size associated with the physical PDE and t mesh for that related to the MMPDE. Alternating Procedure: Assume that the physical solution c n, the mesh x n,y n ), and a time step size t n are given at time t = t n. i) Compute the monitor function M n x,y)=mt n,x,y) using c n and x n,y n ). The solution derivatives used in M are calculated using a gradient recovery technique similar to that developed by Zienkiewicz and Zhu [32, 33] based on the nodal values of the computed solution. M n is understood as a continuous function in the sense of interpolation. ii) Integrate the MMPDE 2.10) over the time period [t n,t n + t n ] using variable step size t mesh,n and monitor function Mx,y) = M n x,y). The MMPDE is discretized in time using the backward Euler scheme with the coefficients a 11, a 12, a 22, b 1, and b 2 being calculated at t n. More than one sub-step may be needed for the integration to reach t = t n + t n. When this happens, the monitor function is updated for each sub-step via linear interpolation. The obtained mesh is denoted by x n+1,y n+1 ). iii) Integrate the physical PDE 2.4) with a fixed or variable step size. The equation is discretized in time using the Singly Diagonally Implicit Runge- Kutta scheme [5]. The mesh and mesh velocity are calculated using linear interpolation: xt) = t t n t n x n+1 + t n + t n t t n x n, yt) = t t n t n y n+1 + t n + t n t t n y n. iv) When a variable step size is used in step iii), the physical PDE may actually be integrated over a smaller step ˆ t n < t n. In this case, the mesh at the actual new time level t n+1 = t n + ˆ t n should be updated as x n+1,y n+1 ) := xt n+1 ),yt n+1 )). v) Go to the next step with the step size predicted by the physical PDE solver. 3. Applications Example 3.1: Advection dominated chemical transport and reaction. Contaminant in form of ions, molecules, or particles undergoes multiple and complicated processes including transport, chemical, and biological ones in water environment. The transport process is mainly due to advection and dispersion. The chemical process covers acid-base reactions, solution, volatilization, precipitation, solute reactions, oxidation-reduction reactions, hydrolysis reaction, isotropic reactions, adsorption, and desorption. The biological process covers bacterias and virus activities. A quantitative description of these processes is prerequisite to the successful protection of water quality. The advection-dispersion-reaction equation ADRE), Eq. 2.1), is one of most commonly used mathematical models describing these processes in geohydrology [19]. The equation can become advectiondominated or dispersion-dominated depending on the magnitude of the aquifer permeability and Darcy velocity. The challenge in the numerical solution of this equation is to capture the chemical transport and reaction front without introducing erroneous instability and numerical dispersion while maintaining reasonable computational efficiency. The physical domain is taken as Ω = 0,1) 0,1) in our computations.
7 MOVING MESH MODELING FOR GROUNDWATER FLOW AND TRANSPORT 7 We now consider a case which essentially is one-dimensional. We choose this test example because it has the exact solution and can be used to verify the computer code. Moreover, the one dimensional version of the ADRE with the same exact solution has been used as an example for testing the one dimensional MM- PDE moving mesh method in [17]. For this case, the physical parameters are taken as Dt,x,y) = D = 10 5, V 1 t,x,y) = V = 1, V 2 t,x,y) = 0, and R = 1.1, and λ = 1.1. The initial and boundary conditions are defined as 3.1) C0,x,y) = 0, Ct,0,y) = 1, Ct,1,y) = C, C y C t,x,0) = t,x,1) = 0, y where C is a constant taken as the value at x = 1 of the exact solution [19,27] Cx,t) = 1 ) [ ) V x V 2 2 exp + 4DλRx exp erfc 2D 2D ) V 2 + 4DλRx + exp erfc 2D x ) V 2 + 4DλRt/R 4Dt/R x + )] V 2 + 4DλRt/R. 4Dt/R A typical adaptive mesh and the solution obtained thereon are shown in Fig. 1. The chemical reaction front is captured with the adaptive moving mesh. The results are in good agreement with the one dimensional ones obtained in [17]. Figure 1. Example 3.1. Adaptive moving mesh first row) and computed solution second row) for ADRE.
8 8 WEIZHANG HUANG AND XIAOYONG ZHAN Example 3.2: Solute transport from contamination sources in a heterogeneous aquifer. Solute transport from contamination sources in a heterogeneous aquifer is studied in this example. The governing equation is given by ADRE 2.1). The physical parameters are taken as Dt,x,y) = D = 10 5, R = 1, λ = 0, and V 1 t,x,y) = x 2 y 2 ), V 2 t,x,y) = 0. We first consider the case with a single source. The boundary conditions on the south, north, and east sides of the domain are flux free and the initial condition is zero everywhere. The source is placed on the west side of the domain. The adaptive mesh and the computed concentration of the contaminant are presented in Fig. 2. It can be seen that the concentration of the mesh nodes follows correctly with that of the contaminant, which is moving southeast due to the non-uniform Darcy velocity in the aquifer. We now consider a case where three contamination sources, one on the west boundary and the other two inside the domain, are disposed in different time intervals. The results are shown in Fig. 3. The mesh adapts well to the concentration variations and automatically captures the emerging of new peaks. This example demonstrates that the adaptive moving mesh method provides a useful tool to detect unknown or unexpected pollution sources in water environment. Figure 2. Example 3.2. Adaptive moving mesh first row) and computed solution second row) for ADRE with a single contamination source. Example 3.3. Transport of nonaqueous phase liquids NAPLs) in an aquifer. The system of governing equations becomes more complicated for
9 MOVING MESH MODELING FOR GROUNDWATER FLOW AND TRANSPORT 9 Figure 3. Example 3.2. Adaptive moving mesh first row) and computed solution second row) for ADRE with multiple contamination sources. multiphase flow and transport in groundwater environment; e.g. see [21, 24] and references therein. Here we consider a specific case where nonaqueous phase liquids NAPLs) are dissolved into the aqueous phase [22]. The physical process is described by two PDEs, one for the volumetric fraction of NAPL or NAPL content, 3.2) θ n t = k na C a C a ) ρ n, and the other for the NAPL dissolved in water, θ a C a ) 3.3) = D C a q a C a ) + k na Ca C a ), t where the subscripts a and n represent the aqueous and nonaqueous phases, respectively, the superscript indicates an equilibrium condition with the companion phase involved in the mass transfer, θ = θt,x,y) is the volumetric fraction, C a = C a t,x,y) is the concentration of the NAPL dissolved in water, ρ is density, k na is a mass transfer coefficient representing a mass transfer process referenced to a loss by the nonaqueous phase and a gain by the aqueous phase, q a is water flux, and D is the dispersivity. It is noted that θ n +θ a = n, where n is the porosity considered to be constant here. The reader is referred to [22] for the derivations of the governing equations and the corresponding initial and boundary conditions. The values of the physical parameters are taken as those given in Table 15.1 of [22]. In particular, the water flux is taken as a constant vector in the x-direction. The parameter values are representative of conditions encountered in the two-dimensional physical experiements. The physical scenario of this case is that the aqueous phase
10 10 WEIZHANG HUANG AND XIAOYONG ZHAN is being flushed from the left boundary and the dissolved NAPL is being eluted from the right boundary. The left and right boundary conditions are a specified flux for the aqueous phase, while the top and bottom boundary conditions are noflow. The initial residual NAPL saturation and other parameters are homogeneous, a typical laboratory condition, except that a perturbation in the residual NAPL saturation near the left boundary where a portion of the boundary is NAPL free, indicating that a clean water is flushing in. The development of this perturbation into a dissolution profile is then observed. The obtained results are shown in Fig. 4 for mesh evolution, NAPL, and dissolved NAPL in water. It can be observed that a clean inflow from the west boundary washes out NAPL and reduces dissolved NAPL in water in a channel zone with time. The movements of the front and the boundary of the channel are captured correctly with the adaptive mesh. Once again the results show that the adaptive moving mesh method holds a great promise for solving multiphase flow and transport problems such as NAPL dissolution. Example 3.4. Coupling of groundwater flow and NAPL transport. A more realistic modeling of the NAPL transport requires consideration of the coupling with the water flow. In this situation, in addition to equations 3.2) and 3.3), another equation is needed for the aqueous phase pressure p a = p a t,x,y), viz., ) k kra 1 3.4) 0 = µ p a ρ a g x) + 1 ) k na Ca C a ), ρ a ρ n where k is permeability, k ra is relative permeability, µ is viscosity, g is the gravity constant, and x is the vertical coordinate. Unlike the previous example, the water flux in the equation 3.3) is now given by Darcy s law, q a = k k ra µ p a ρ a g x). The values of other physical parameters are taken from Table 15.1 of [22]. Similar phenomena can be observed from the computational results cf. Fig. 5). This seems reasonable since the water flux remains stable and has a similar profile as the one used in Example 3.3 as far as the water pressure gradient is maintained. 4. Summary and comments The MMPDE moving mesh PDE) moving mesh method developed in [14,15] has been presented and applied to the numerical simulation of groundwater flow and transport problems. A range of problems have been considered, including advection dominated chemical transport and reaction, solute transport from contamination sources, transport of nonaqueous phase liquids NAPLs) in an aquifer, and coupling of groundwater flow with NAPL transport. Numerical results have demonstrated that the MMPDE moving mesh method is able to capture sharp moving fronts and detect the emerging of new fronts. This consolidates the findings in a previous work [17] for one dimensional groundwater problems. It should be pointed out that the investigations presented in this work are still at a preliminary stage and more work has yet to be done. For example, we have used a simple adaptation functional 2.8) and the arc-length monitor function 2.7) for mesh movement. For more precise control of mesh adaptation and for better
11 MOVING MESH MODELING FOR GROUNDWATER FLOW AND TRANSPORT 11 Figure 4. Example 3.3. Adaptive moving mesh first row), NAPL second row), and dissolved NAPL in water third row) for the NAPL problem. simulation accuracy, it would be better to use more sophisticated functionals and monitor functions such as those developed in [12,16] based on interpolation error. Acknowledgements The work was partially supported by the National Science Foundation through grants DMS and DMS and by the Kansas Geological Survey. The simulations were performed with a SGI-Origin 2000 multi-processor computer in the Kansas Center for Advanced Scientific Computing, The University of Kansas. It is acknowledged that L. Zheng participated in this investigation at the early stage.
12 12 WEIZHANG HUANG AND XIAOYONG ZHAN Figure 5. Example 3.4. Adaptive moving mesh first row), NAPL second row), dissolved NAPL in water third row), and aqueous phase pressure fourth row) for the NAPL-flow coupling problem.
13 MOVING MESH MODELING FOR GROUNDWATER FLOW AND TRANSPORT 13 References 1. J. U. Brackbill, An adaptive grid with directional control, J. Comput. Phys ), J. U. Brackbill and J. S. Saltzman, Adaptive zoning for singular problems in two dimensions, J. Comput. Phys ), W. Cao, W. Huang, and R. D. Russell, An r-adaptive finite element method based upon moving mesh pdes, J. Comp. Phys ), , Approaches for generating moving adaptive meshes: location versus velocity, Appl. Numer. Math ), J. R. Cash, Diagonally implicit runge-kutta formulae with error estimates, J. Inst. Math. Appl ), C. de Boor, Good approximation by splines with variable knots, Spline Functions and Approximation Theory A. Meir and A. Sharma, eds.), Birkhäuser Verlag, Basel und Stuttgart, 1973, pp A. S. Dvinsky, Adaptive grid generation from harmonic maps on riemannian manifolds, J. Comput. Phys ), A. Gamliel and L. M. Abriola, A one-dimensional moving grid solution for the coupled nonlinear equations governing multi-phase flow in porous media. 1: Model development, Int. J. Numer. Meth. Fluids ), , A one-dimensional moving grid solution for the coupled nonlinear equations governing multi-phase flow in porous media. 2: Example simulations and sensitivity analysis, Int. J. Numer. Meth. Fluids ), G. Gottardi and M. Venutelli, Moving finite element model for one-dimensional infiltration in unsaturated soil, Water Resour. Res ), D. F. Hawken, J. J. Gottlieb, and J. S. Hansen, Review of some adaptive node-movement techniques in finite element and finite difference solutions of PDEs, J. Comput. Phys ), W. Huang, Measuring mesh qualities and application to variational mesh adaptation, to appear in SIAM J. Sci. Comput. 13., Practical aspects of formulation and solution of moving mesh partial differential equations, J. Comput. Phys ), W. Huang, Y. Ren, and R. D. Russell, Moving mesh partial differential equations MMPDEs) based upon the equidistribution principle, SIAM J. Numer. Anal ), W. Huang and R. D. Russell, A high dimensional moving mesh strategy, Appl. Numer. Math ), W. Huang and W. Sun, Variational mesh adaptation II: error estimates and monitor functions, J. Comput. Phys ), W. Huang, L. Zheng, and X. Zhan, Adaptive moving mesh methods for simulating onedimensional groundwater problems with sharp moving fronts, Int. J. Numer. Meth. Engng ), P. M. Knupp, Jacobian-weighted elliptic grid generation, SIAM J. Sci. Comput ), T. Lee, Applied mathematics in hydrology, Lewis Publishers, R. Li, T. Tang, and P. W. Zhang, Moving mesh methods in multiple dimensions based on harmonic maps, J. Comput. Phys ), C. T. Miller, G. Christakos, P. T. Imhoff, J. F. McBride, J. A. Pedit, and J. A. Trangenstein, Multiphase flow and transport modeling in heterogeneous porous media: Challenges and approaches, Adv. Water Resour ), C. T. Miller, S. N. Gleyzer, and P. T. Imhoff, Numerical modeling of napl dissolution fingering in porous media, Physical nonequilibrium in soils modeling and application H. M. Selim and L. Ma, eds.), Ann Arbor Press, Chelsea, Michigan, K. Miller and R. N. Miller, Moving finite elements I, SIAM J. Numer. Anal ), T. F. Russell, Modeling of multiphase multicontaminant transport in the subsurface, Rev. Geophys ), , Supplement D. R. Shier and K. T. Wallenius, Applied mathematical modeling: A multidisciplinary approach, Chapman & Hall/CRC, London, Boca Raton, 2000.
14 14 WEIZHANG HUANG AND XIAOYONG ZHAN 26. R. Trompert, Local-uniform grid refinement and transport in heterogeneous porous media, Adv. Water Resour ), E. J. Wexler, Analytical solutions for one-, two-, and three-dimensional solute transport in ground-water systems with uniform flow, U.S. Geological Survey, Book 3, Techniques of Water- Resources Investigations, 1992, p A. M. Winslow, Adaptive mesh zoning by the equipotential method, Tech. Report UCID-19062, Lawrence Livemore Laboratory, G. T. Yeh, J. Chang, and T. E. Short, An exact peak capturing and oscillation-free scheme to solve advection-dispersion transport equations, Water Resour. Res ), P. A. Zegeling, J. G. Verwer, and J. C. H. Van Eijkeren, Application of a moving grid method to a class of 1D brine transport problems in porous media, Int. J. Numer. Meth. Fluids ), C. Zheng and G. D. Bennett, Applied contaminant transport modeling: Theory and practice, Van Nostrand Reinhold, New York, O. C. Zienkiewicz and J. Z. Zhu, The superconvergence patch recovery and a posteriori error estimates. part 1: The recovery technique, Int. J. Numer. Methods Engrg ), , The superconvergence patch recovery and a posteriori error estimates. part 2: Error esimates and adaptivity, Int. J. Numer. Methods Engrg ), Department of Mathematics, The University of Kansas, Lawrence, KS 66045, USA address: huang@math.ku.edu Kansas Geological Survey, The University of Kansas, Lawrence, KS 66047, USA address: xyz@ku.edu
A Moving Mesh Method for Time dependent Problems Based on Schwarz Waveform Relaxation
 A Moving Mesh Method for Time dependent Problems Based on Schwarz Waveform Relaation Ronald D. Haynes, Weizhang Huang 2, and Robert D. Russell 3 Acadia University, Wolfville, N.S., Canada. ronald.haynes@acadiau.ca
A Moving Mesh Method for Time dependent Problems Based on Schwarz Waveform Relaation Ronald D. Haynes, Weizhang Huang 2, and Robert D. Russell 3 Acadia University, Wolfville, N.S., Canada. ronald.haynes@acadiau.ca
A Moving Mesh Method for Time Dependent Problems based on Schwarz Waveform Relaxation
 A Moving Mesh Method for Time Dependent Problems based on Schwarz Waveform Relaation Ronald D. Haynes, Weizhang Huang 2, and Robert D. Russell 3 Acadia University, Wolfville, N.S., Canada ronald.haynes@acadiau.ca
A Moving Mesh Method for Time Dependent Problems based on Schwarz Waveform Relaation Ronald D. Haynes, Weizhang Huang 2, and Robert D. Russell 3 Acadia University, Wolfville, N.S., Canada ronald.haynes@acadiau.ca
lecture 8 Groundwater Modelling -1
 The Islamic University of Gaza Faculty of Engineering Civil Engineering Department Water Resources Msc. Groundwater Hydrology- ENGC 6301 lecture 8 Groundwater Modelling -1 Instructor: Dr. Yunes Mogheir
The Islamic University of Gaza Faculty of Engineering Civil Engineering Department Water Resources Msc. Groundwater Hydrology- ENGC 6301 lecture 8 Groundwater Modelling -1 Instructor: Dr. Yunes Mogheir
IMPROVING THE NUMERICAL ACCURACY OF HYDROTHERMAL RESERVOIR SIMULATIONS USING THE CIP SCHEME WITH THIRD-ORDER ACCURACY
 PROCEEDINGS, Thirty-Seventh Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, California, January 30 - February 1, 2012 SGP-TR-194 IMPROVING THE NUMERICAL ACCURACY OF HYDROTHERMAL
PROCEEDINGS, Thirty-Seventh Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, California, January 30 - February 1, 2012 SGP-TR-194 IMPROVING THE NUMERICAL ACCURACY OF HYDROTHERMAL
Robust and Efficient Adaptive Moving Mesh Solution of the 2-D Euler equations
 Contemporary Mathematics Robust and Efficient Adaptive Moving Mesh Solution of the -D Euler equations P. A. Zegeling, W. D. de Boer, and H. Z. Tang Abstract. In this paper we describe an adaptive moving
Contemporary Mathematics Robust and Efficient Adaptive Moving Mesh Solution of the -D Euler equations P. A. Zegeling, W. D. de Boer, and H. Z. Tang Abstract. In this paper we describe an adaptive moving
Homogenization and numerical Upscaling. Unsaturated flow and two-phase flow
 Homogenization and numerical Upscaling Unsaturated flow and two-phase flow Insa Neuweiler Institute of Hydromechanics, University of Stuttgart Outline Block 1: Introduction and Repetition Homogenization
Homogenization and numerical Upscaling Unsaturated flow and two-phase flow Insa Neuweiler Institute of Hydromechanics, University of Stuttgart Outline Block 1: Introduction and Repetition Homogenization
Groundwater in Hydrologic Cycle
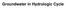 Groundwater in Hydrologic Cycle Types of Terrestrial Water Surface Water Soil Moisture Ground water Pores Full of Combination of Air and Water Unsaturated Zone / Zone of Aeration / Vadose (Soil Water)
Groundwater in Hydrologic Cycle Types of Terrestrial Water Surface Water Soil Moisture Ground water Pores Full of Combination of Air and Water Unsaturated Zone / Zone of Aeration / Vadose (Soil Water)
CS205b/CME306. Lecture 9
 CS205b/CME306 Lecture 9 1 Convection Supplementary Reading: Osher and Fedkiw, Sections 3.3 and 3.5; Leveque, Sections 6.7, 8.3, 10.2, 10.4. For a reference on Newton polynomial interpolation via divided
CS205b/CME306 Lecture 9 1 Convection Supplementary Reading: Osher and Fedkiw, Sections 3.3 and 3.5; Leveque, Sections 6.7, 8.3, 10.2, 10.4. For a reference on Newton polynomial interpolation via divided
Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Computation in Astrophysics Seminar (Spring 2006) L. J. Dursi
 Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Eulerian Grid Methods The methods covered so far in this course use an Eulerian grid: Prescribed coordinates In `lab frame' Fluid elements flow
Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Eulerian Grid Methods The methods covered so far in this course use an Eulerian grid: Prescribed coordinates In `lab frame' Fluid elements flow
The WENO Method in the Context of Earlier Methods To approximate, in a physically correct way, [3] the solution to a conservation law of the form u t
![The WENO Method in the Context of Earlier Methods To approximate, in a physically correct way, [3] the solution to a conservation law of the form u t The WENO Method in the Context of Earlier Methods To approximate, in a physically correct way, [3] the solution to a conservation law of the form u t](/thumbs/88/114600770.jpg) An implicit WENO scheme for steady-state computation of scalar hyperbolic equations Sigal Gottlieb Mathematics Department University of Massachusetts at Dartmouth 85 Old Westport Road North Dartmouth,
An implicit WENO scheme for steady-state computation of scalar hyperbolic equations Sigal Gottlieb Mathematics Department University of Massachusetts at Dartmouth 85 Old Westport Road North Dartmouth,
BACK AND FORTH ERROR COMPENSATION AND CORRECTION METHODS FOR REMOVING ERRORS INDUCED BY UNEVEN GRADIENTS OF THE LEVEL SET FUNCTION
 BACK AND FORTH ERROR COMPENSATION AND CORRECTION METHODS FOR REMOVING ERRORS INDUCED BY UNEVEN GRADIENTS OF THE LEVEL SET FUNCTION TODD F. DUPONT AND YINGJIE LIU Abstract. We propose a method that significantly
BACK AND FORTH ERROR COMPENSATION AND CORRECTION METHODS FOR REMOVING ERRORS INDUCED BY UNEVEN GRADIENTS OF THE LEVEL SET FUNCTION TODD F. DUPONT AND YINGJIE LIU Abstract. We propose a method that significantly
Solve Non-Linear Parabolic Partial Differential Equation by Spline Collocation Method
 Solve Non-Linear Parabolic Partial Differential Equation by Spline Collocation Method P.B. Choksi 1 and A.K. Pathak 2 1 Research Scholar, Rai University,Ahemdabad. Email:pinalchoksey@gmail.com 2 H.O.D.
Solve Non-Linear Parabolic Partial Differential Equation by Spline Collocation Method P.B. Choksi 1 and A.K. Pathak 2 1 Research Scholar, Rai University,Ahemdabad. Email:pinalchoksey@gmail.com 2 H.O.D.
AN ADAPTIVE MESH REDISTRIBUTION ALGORITHM FOR CONVECTION-DOMINATED PROBLEMS. Zheng-Ru Zhang and Tao Tang
 COMMUNICATIONS ON Website: http://aimsciences.org PURE AND APPLIED ANALYSIS Volume, Number 3, september pp. 34 357 AN ADAPTIVE MESH REDISTRIBUTION ALGORITHM FOR CONVECTION-DOMINATED PROBLEMS Zheng-Ru Zhang
COMMUNICATIONS ON Website: http://aimsciences.org PURE AND APPLIED ANALYSIS Volume, Number 3, september pp. 34 357 AN ADAPTIVE MESH REDISTRIBUTION ALGORITHM FOR CONVECTION-DOMINATED PROBLEMS Zheng-Ru Zhang
Fully discrete Finite Element Approximations of Semilinear Parabolic Equations in a Nonconvex Polygon
 Fully discrete Finite Element Approximations of Semilinear Parabolic Equations in a Nonconvex Polygon Tamal Pramanick 1,a) 1 Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati
Fully discrete Finite Element Approximations of Semilinear Parabolic Equations in a Nonconvex Polygon Tamal Pramanick 1,a) 1 Department of Mathematics, Indian Institute of Technology Guwahati, Guwahati
Control Volume Finite Difference On Adaptive Meshes
 Control Volume Finite Difference On Adaptive Meshes Sanjay Kumar Khattri, Gunnar E. Fladmark, Helge K. Dahle Department of Mathematics, University Bergen, Norway. sanjay@mi.uib.no Summary. In this work
Control Volume Finite Difference On Adaptive Meshes Sanjay Kumar Khattri, Gunnar E. Fladmark, Helge K. Dahle Department of Mathematics, University Bergen, Norway. sanjay@mi.uib.no Summary. In this work
arxiv: v1 [math.na] 1 Apr 2015
![arxiv: v1 [math.na] 1 Apr 2015 arxiv: v1 [math.na] 1 Apr 2015](/thumbs/72/66321511.jpg) Stochastic domain decomposition for time dependent adaptive mesh generation Alexander Bihlo, Ronald D. Haynes and Emily J. Walsh arxiv:1504.00084v1 [math.na] 1 Apr 015 Department of Mathematics and Statistics,
Stochastic domain decomposition for time dependent adaptive mesh generation Alexander Bihlo, Ronald D. Haynes and Emily J. Walsh arxiv:1504.00084v1 [math.na] 1 Apr 015 Department of Mathematics and Statistics,
Mid-Year Report. Discontinuous Galerkin Euler Equation Solver. Friday, December 14, Andrey Andreyev. Advisor: Dr.
 Mid-Year Report Discontinuous Galerkin Euler Equation Solver Friday, December 14, 2012 Andrey Andreyev Advisor: Dr. James Baeder Abstract: The focus of this effort is to produce a two dimensional inviscid,
Mid-Year Report Discontinuous Galerkin Euler Equation Solver Friday, December 14, 2012 Andrey Andreyev Advisor: Dr. James Baeder Abstract: The focus of this effort is to produce a two dimensional inviscid,
The Immersed Interface Method
 The Immersed Interface Method Numerical Solutions of PDEs Involving Interfaces and Irregular Domains Zhiiin Li Kazufumi Ito North Carolina State University Raleigh, North Carolina Society for Industrial
The Immersed Interface Method Numerical Solutions of PDEs Involving Interfaces and Irregular Domains Zhiiin Li Kazufumi Ito North Carolina State University Raleigh, North Carolina Society for Industrial
Solving Partial Differential Equations on Overlapping Grids
 **FULL TITLE** ASP Conference Series, Vol. **VOLUME**, **YEAR OF PUBLICATION** **NAMES OF EDITORS** Solving Partial Differential Equations on Overlapping Grids William D. Henshaw Centre for Applied Scientific
**FULL TITLE** ASP Conference Series, Vol. **VOLUME**, **YEAR OF PUBLICATION** **NAMES OF EDITORS** Solving Partial Differential Equations on Overlapping Grids William D. Henshaw Centre for Applied Scientific
Toward reservoir simulation on geological grid models
 1 Toward reservoir simulation on geological grid models JØRG E. AARNES and KNUT ANDREAS LIE SINTEF ICT, Dept. of Applied Mathematics, P.O. Box 124 Blindern, NO-0314 Oslo, Norway Abstract We present a reservoir
1 Toward reservoir simulation on geological grid models JØRG E. AARNES and KNUT ANDREAS LIE SINTEF ICT, Dept. of Applied Mathematics, P.O. Box 124 Blindern, NO-0314 Oslo, Norway Abstract We present a reservoir
Collocation and optimization initialization
 Boundary Elements and Other Mesh Reduction Methods XXXVII 55 Collocation and optimization initialization E. J. Kansa 1 & L. Ling 2 1 Convergent Solutions, USA 2 Hong Kong Baptist University, Hong Kong
Boundary Elements and Other Mesh Reduction Methods XXXVII 55 Collocation and optimization initialization E. J. Kansa 1 & L. Ling 2 1 Convergent Solutions, USA 2 Hong Kong Baptist University, Hong Kong
Investigating The Stability of The Balance-force Continuum Surface Force Model of Surface Tension In Interfacial Flow
 Investigating The Stability of The Balance-force Continuum Surface Force Model of Surface Tension In Interfacial Flow Vinh The Nguyen University of Massachusetts Dartmouth Computational Science Training
Investigating The Stability of The Balance-force Continuum Surface Force Model of Surface Tension In Interfacial Flow Vinh The Nguyen University of Massachusetts Dartmouth Computational Science Training
Boundary/Contour Fitted Grid Generation for Effective Visualizations in a Digital Library of Mathematical Functions
 Boundary/Contour Fitted Grid Generation for Effective Visualizations in a Digital Library of Mathematical Functions Bonita Saunders Qiming Wang National Institute of Standards and Technology Bureau Drive
Boundary/Contour Fitted Grid Generation for Effective Visualizations in a Digital Library of Mathematical Functions Bonita Saunders Qiming Wang National Institute of Standards and Technology Bureau Drive
The Level Set Method applied to Structural Topology Optimization
 The Level Set Method applied to Structural Topology Optimization Dr Peter Dunning 22-Jan-2013 Structural Optimization Sizing Optimization Shape Optimization Increasing: No. design variables Opportunity
The Level Set Method applied to Structural Topology Optimization Dr Peter Dunning 22-Jan-2013 Structural Optimization Sizing Optimization Shape Optimization Increasing: No. design variables Opportunity
Groundwater hydraulics numerical modelling
 Groundwater hydraulics numerical modelling Martin Šanda, B673 martin.sanda@fsv.cvut.cz Martina Sobotková, B609 martina.sobotkova@fsv.cvut.cz CTU in Prague, FCE, Dept. of Irrigation, Drainage and landscape
Groundwater hydraulics numerical modelling Martin Šanda, B673 martin.sanda@fsv.cvut.cz Martina Sobotková, B609 martina.sobotkova@fsv.cvut.cz CTU in Prague, FCE, Dept. of Irrigation, Drainage and landscape
Module 1: Introduction to Finite Difference Method and Fundamentals of CFD Lecture 13: The Lecture deals with:
 The Lecture deals with: Some more Suggestions for Improvement of Discretization Schemes Some Non-Trivial Problems with Discretized Equations file:///d /chitra/nptel_phase2/mechanical/cfd/lecture13/13_1.htm[6/20/2012
The Lecture deals with: Some more Suggestions for Improvement of Discretization Schemes Some Non-Trivial Problems with Discretized Equations file:///d /chitra/nptel_phase2/mechanical/cfd/lecture13/13_1.htm[6/20/2012
Second International Workshop on Scientific Computing and Applications. Kananaskis, Canada, May 28 - June 1, 2000
 Second International Workshop on Scientific Computing and Applications. Kananaskis, Canada, May 28 - June 1, 2000 Program May 28 (Sunday) 19:00-21:00 Registration and reception Session Chairman: Y. Wong
Second International Workshop on Scientific Computing and Applications. Kananaskis, Canada, May 28 - June 1, 2000 Program May 28 (Sunday) 19:00-21:00 Registration and reception Session Chairman: Y. Wong
Determination of Free Surface in Steady-State Seepage through a Dam with Toe Drain by the Boundary Element Method
 Determination of Free Surface in Steady-State Seepage through a Dam with Toe Drain by the Boundary Element Method Somchart Chantasiriwan Faculty of Engineering, Thammasat University, Rangsit Campus, Pathum
Determination of Free Surface in Steady-State Seepage through a Dam with Toe Drain by the Boundary Element Method Somchart Chantasiriwan Faculty of Engineering, Thammasat University, Rangsit Campus, Pathum
MATHEMATICAL ANALYSIS, MODELING AND OPTIMIZATION OF COMPLEX HEAT TRANSFER PROCESSES
 MATHEMATICAL ANALYSIS, MODELING AND OPTIMIZATION OF COMPLEX HEAT TRANSFER PROCESSES Goals of research Dr. Uldis Raitums, Dr. Kārlis Birģelis To develop and investigate mathematical properties of algorithms
MATHEMATICAL ANALYSIS, MODELING AND OPTIMIZATION OF COMPLEX HEAT TRANSFER PROCESSES Goals of research Dr. Uldis Raitums, Dr. Kārlis Birģelis To develop and investigate mathematical properties of algorithms
TOUGHREACT Example: Aqueous Transport with Adsorption and Decay
 403 Poyntz Avenue, Suite B Manhattan, KS 66502 USA +1.785.770.8511 www.thunderheadeng.com TOUGHREACT Example: Aqueous Transport with Adsorption and Decay PetraSim 2016.1 Table of Contents Overview...1
403 Poyntz Avenue, Suite B Manhattan, KS 66502 USA +1.785.770.8511 www.thunderheadeng.com TOUGHREACT Example: Aqueous Transport with Adsorption and Decay PetraSim 2016.1 Table of Contents Overview...1
Department of Computing and Software
 Department of Computing and Software Faculty of Engineering McMaster University Assessment of two a posteriori error estimators for steady-state flow problems by A. H. ElSheikh, S.E. Chidiac and W. S.
Department of Computing and Software Faculty of Engineering McMaster University Assessment of two a posteriori error estimators for steady-state flow problems by A. H. ElSheikh, S.E. Chidiac and W. S.
Numerical Simulation of Coupled Fluid-Solid Systems by Fictitious Boundary and Grid Deformation Methods
 Numerical Simulation of Coupled Fluid-Solid Systems by Fictitious Boundary and Grid Deformation Methods Decheng Wan 1 and Stefan Turek 2 Institute of Applied Mathematics LS III, University of Dortmund,
Numerical Simulation of Coupled Fluid-Solid Systems by Fictitious Boundary and Grid Deformation Methods Decheng Wan 1 and Stefan Turek 2 Institute of Applied Mathematics LS III, University of Dortmund,
ENERGY-224 Reservoir Simulation Project Report. Ala Alzayer
 ENERGY-224 Reservoir Simulation Project Report Ala Alzayer Autumn Quarter December 3, 2014 Contents 1 Objective 2 2 Governing Equations 2 3 Methodolgy 3 3.1 BlockMesh.........................................
ENERGY-224 Reservoir Simulation Project Report Ala Alzayer Autumn Quarter December 3, 2014 Contents 1 Objective 2 2 Governing Equations 2 3 Methodolgy 3 3.1 BlockMesh.........................................
Application of Finite Volume Method for Structural Analysis
 Application of Finite Volume Method for Structural Analysis Saeed-Reza Sabbagh-Yazdi and Milad Bayatlou Associate Professor, Civil Engineering Department of KNToosi University of Technology, PostGraduate
Application of Finite Volume Method for Structural Analysis Saeed-Reza Sabbagh-Yazdi and Milad Bayatlou Associate Professor, Civil Engineering Department of KNToosi University of Technology, PostGraduate
Anisotropic quality measures and adaptation for polygonal meshes
 Anisotropic quality measures and adaptation for polygonal meshes Yanqiu Wang, Oklahoma State University joint work with Weizhang Huang Oct 2015, POEMs, Georgia Tech. 1 / 23 Consider the following function
Anisotropic quality measures and adaptation for polygonal meshes Yanqiu Wang, Oklahoma State University joint work with Weizhang Huang Oct 2015, POEMs, Georgia Tech. 1 / 23 Consider the following function
Introduction to C omputational F luid Dynamics. D. Murrin
 Introduction to C omputational F luid Dynamics D. Murrin Computational fluid dynamics (CFD) is the science of predicting fluid flow, heat transfer, mass transfer, chemical reactions, and related phenomena
Introduction to C omputational F luid Dynamics D. Murrin Computational fluid dynamics (CFD) is the science of predicting fluid flow, heat transfer, mass transfer, chemical reactions, and related phenomena
NUMERICAL VISCOSITY. Convergent Science White Paper. COPYRIGHT 2017 CONVERGENT SCIENCE. All rights reserved.
 Convergent Science White Paper COPYRIGHT 2017 CONVERGENT SCIENCE. All rights reserved. This document contains information that is proprietary to Convergent Science. Public dissemination of this document
Convergent Science White Paper COPYRIGHT 2017 CONVERGENT SCIENCE. All rights reserved. This document contains information that is proprietary to Convergent Science. Public dissemination of this document
Skåne University Hospital Lund, Lund, Sweden 2 Deparment of Numerical Analysis, Centre for Mathematical Sciences, Lund University, Lund, Sweden
 Volume Tracking: A New Method for Visualization of Intracardiac Blood Flow from Three-Dimensional, Time-Resolved, Three-Component Magnetic Resonance Velocity Mapping Appendix: Theory and Numerical Implementation
Volume Tracking: A New Method for Visualization of Intracardiac Blood Flow from Three-Dimensional, Time-Resolved, Three-Component Magnetic Resonance Velocity Mapping Appendix: Theory and Numerical Implementation
1 Exercise: Heat equation in 2-D with FE
 1 Exercise: Heat equation in 2-D with FE Reading Hughes (2000, sec. 2.3-2.6 Dabrowski et al. (2008, sec. 1-3, 4.1.1, 4.1.3, 4.2.1 This FE exercise and most of the following ones are based on the MILAMIN
1 Exercise: Heat equation in 2-D with FE Reading Hughes (2000, sec. 2.3-2.6 Dabrowski et al. (2008, sec. 1-3, 4.1.1, 4.1.3, 4.2.1 This FE exercise and most of the following ones are based on the MILAMIN
Post Processing, Visualization, and Sample Output
 Chapter 7 Post Processing, Visualization, and Sample Output Upon successful execution of an ADCIRC run, a number of output files will be created. Specifically which files are created depends upon how the
Chapter 7 Post Processing, Visualization, and Sample Output Upon successful execution of an ADCIRC run, a number of output files will be created. Specifically which files are created depends upon how the
Fluent User Services Center
 Solver Settings 5-1 Using the Solver Setting Solver Parameters Convergence Definition Monitoring Stability Accelerating Convergence Accuracy Grid Independence Adaption Appendix: Background Finite Volume
Solver Settings 5-1 Using the Solver Setting Solver Parameters Convergence Definition Monitoring Stability Accelerating Convergence Accuracy Grid Independence Adaption Appendix: Background Finite Volume
Challenges and recent progress in developing numerical methods for multi-material ALE Hydrocodes
 Challenges and recent progress in developing numerical methods for multi-material ALE Hydrocodes ICFD 25 year Anniversary Conference 15-16 th September 2008 Oxford University Andrew Barlow AWE Introduction
Challenges and recent progress in developing numerical methods for multi-material ALE Hydrocodes ICFD 25 year Anniversary Conference 15-16 th September 2008 Oxford University Andrew Barlow AWE Introduction
Phase-field simulation of two-phase micro-flows in a Hele-Shaw cell
 Computational Methods in Multiphase Flow III 7 Phase-field simulation of two-phase micro-flows in a Hele-Shaw cell Y. Sun & C. Beckermann Department of Mechanical and Industrial Engineering, University
Computational Methods in Multiphase Flow III 7 Phase-field simulation of two-phase micro-flows in a Hele-Shaw cell Y. Sun & C. Beckermann Department of Mechanical and Industrial Engineering, University
Verification Manual. 1D / 2D / 3D Contaminant Transport Modeling Software. SoilVision Systems Ltd. Saskatoon, Saskatchewan, Canada
 1D / 2D / 3D Contaminant Transport Modeling Software Verification Manual Written by: Robert Thode, P.Eng., B.Sc.G.E. Edited by: Murray Fredlund, P.Eng., Ph.D. SoilVision Systems Ltd. Saskatoon, Saskatchewan,
1D / 2D / 3D Contaminant Transport Modeling Software Verification Manual Written by: Robert Thode, P.Eng., B.Sc.G.E. Edited by: Murray Fredlund, P.Eng., Ph.D. SoilVision Systems Ltd. Saskatoon, Saskatchewan,
Chapter 6. Petrov-Galerkin Formulations for Advection Diffusion Equation
 Chapter 6 Petrov-Galerkin Formulations for Advection Diffusion Equation In this chapter we ll demonstrate the difficulties that arise when GFEM is used for advection (convection) dominated problems. Several
Chapter 6 Petrov-Galerkin Formulations for Advection Diffusion Equation In this chapter we ll demonstrate the difficulties that arise when GFEM is used for advection (convection) dominated problems. Several
A NURBS-BASED APPROACH FOR SHAPE AND TOPOLOGY OPTIMIZATION OF FLOW DOMAINS
 6th European Conference on Computational Mechanics (ECCM 6) 7th European Conference on Computational Fluid Dynamics (ECFD 7) 11 15 June 2018, Glasgow, UK A NURBS-BASED APPROACH FOR SHAPE AND TOPOLOGY OPTIMIZATION
6th European Conference on Computational Mechanics (ECCM 6) 7th European Conference on Computational Fluid Dynamics (ECFD 7) 11 15 June 2018, Glasgow, UK A NURBS-BASED APPROACH FOR SHAPE AND TOPOLOGY OPTIMIZATION
1.2 Numerical Solutions of Flow Problems
 1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
HYDRUS (2D/3D) Software Package for Simulating the Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes
 HYDRUS (2D/3D) Software Package for Simulating the Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media User Manual Version 1.02 March 2007 PC-Progress,
HYDRUS (2D/3D) Software Package for Simulating the Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media User Manual Version 1.02 March 2007 PC-Progress,
INVERSE PROBLEMS IN GROUNDWATER MODELING
 INVERSE PROBLEMS IN GROUNDWATER MODELING Theory and Applications of Transport in Porous Media Series Editor: Jacob Bear, Technion - Israel Institute of Technology, Haifa, Israel Volume 6 The titles published
INVERSE PROBLEMS IN GROUNDWATER MODELING Theory and Applications of Transport in Porous Media Series Editor: Jacob Bear, Technion - Israel Institute of Technology, Haifa, Israel Volume 6 The titles published
Existence and Dynamics of Bounded Traveling Wave Solutions to Getmanou Equation
 Commun. Theor. Phys. 70 (2018) 672 676 Vol. 70, No. 6, December 1, 2018 Existence and Dynamics of Bounded Traveling Wave Solutions to Getmanou Equation Zhen-Shu Wen ( 温振庶 ) School of Mathematical Sciences,
Commun. Theor. Phys. 70 (2018) 672 676 Vol. 70, No. 6, December 1, 2018 Existence and Dynamics of Bounded Traveling Wave Solutions to Getmanou Equation Zhen-Shu Wen ( 温振庶 ) School of Mathematical Sciences,
Multi-Mesh CFD. Chris Roy Chip Jackson (1 st year PhD student) Aerospace and Ocean Engineering Department Virginia Tech
 Multi-Mesh CFD Chris Roy Chip Jackson (1 st year PhD student) Aerospace and Ocean Engineering Department Virginia Tech cjroy@vt.edu May 21, 2014 CCAS Program Review, Columbus, OH 1 Motivation Automated
Multi-Mesh CFD Chris Roy Chip Jackson (1 st year PhD student) Aerospace and Ocean Engineering Department Virginia Tech cjroy@vt.edu May 21, 2014 CCAS Program Review, Columbus, OH 1 Motivation Automated
On a nested refinement of anisotropic tetrahedral grids under Hessian metrics
 On a nested refinement of anisotropic tetrahedral grids under Hessian metrics Shangyou Zhang Abstract Anisotropic grids, having drastically different grid sizes in different directions, are efficient and
On a nested refinement of anisotropic tetrahedral grids under Hessian metrics Shangyou Zhang Abstract Anisotropic grids, having drastically different grid sizes in different directions, are efficient and
Corrected/Updated References
 K. Kashiyama, H. Ito, M. Behr and T. Tezduyar, "Massively Parallel Finite Element Strategies for Large-Scale Computation of Shallow Water Flows and Contaminant Transport", Extended Abstracts of the Second
K. Kashiyama, H. Ito, M. Behr and T. Tezduyar, "Massively Parallel Finite Element Strategies for Large-Scale Computation of Shallow Water Flows and Contaminant Transport", Extended Abstracts of the Second
Modeling Ground Water Problems Using the Complex Polynomial Method
 Modeling Ground Water Problems Using the Complex Polynomial Method A. W. Bohannon and T. V. Hromadka, AS-0020 Abstract Numerical methods for solving the governing partial differential equations involved
Modeling Ground Water Problems Using the Complex Polynomial Method A. W. Bohannon and T. V. Hromadka, AS-0020 Abstract Numerical methods for solving the governing partial differential equations involved
Moving Finite Element Simulations for Reaction-Diffusion Systems
 Advances in Applied Mathematics and Mechanics Adv. Appl. Math. Mech., Vol. 4, No. 3, pp. 365-381 DOI: 10.4208/aamm.10-m11180 June 2012 Moving Finite Element Simulations for Reaction-Diffusion Systems Guanghui
Advances in Applied Mathematics and Mechanics Adv. Appl. Math. Mech., Vol. 4, No. 3, pp. 365-381 DOI: 10.4208/aamm.10-m11180 June 2012 Moving Finite Element Simulations for Reaction-Diffusion Systems Guanghui
1. Mathematical Modelling
 1. describe a given problem with some mathematical formalism in order to get a formal and precise description see fundamental properties due to the abstraction allow a systematic treatment and, thus, solution
1. describe a given problem with some mathematical formalism in order to get a formal and precise description see fundamental properties due to the abstraction allow a systematic treatment and, thus, solution
Numerical Methods for PDEs : Video 11: 1D FiniteFebruary Difference 15, Mappings Theory / 15
 22.520 Numerical Methods for PDEs : Video 11: 1D Finite Difference Mappings Theory and Matlab February 15, 2015 22.520 Numerical Methods for PDEs : Video 11: 1D FiniteFebruary Difference 15, Mappings 2015
22.520 Numerical Methods for PDEs : Video 11: 1D Finite Difference Mappings Theory and Matlab February 15, 2015 22.520 Numerical Methods for PDEs : Video 11: 1D FiniteFebruary Difference 15, Mappings 2015
MODELING MIXED BOUNDARY PROBLEMS WITH THE COMPLEX VARIABLE BOUNDARY ELEMENT METHOD (CVBEM) USING MATLAB AND MATHEMATICA
 A. N. Johnson et al., Int. J. Comp. Meth. and Exp. Meas., Vol. 3, No. 3 (2015) 269 278 MODELING MIXED BOUNDARY PROBLEMS WITH THE COMPLEX VARIABLE BOUNDARY ELEMENT METHOD (CVBEM) USING MATLAB AND MATHEMATICA
A. N. Johnson et al., Int. J. Comp. Meth. and Exp. Meas., Vol. 3, No. 3 (2015) 269 278 MODELING MIXED BOUNDARY PROBLEMS WITH THE COMPLEX VARIABLE BOUNDARY ELEMENT METHOD (CVBEM) USING MATLAB AND MATHEMATICA
Lecture 3.2 Methods for Structured Mesh Generation
 Lecture 3.2 Methods for Structured Mesh Generation 1 There are several methods to develop the structured meshes: Algebraic methods, Interpolation methods, and methods based on solving partial differential
Lecture 3.2 Methods for Structured Mesh Generation 1 There are several methods to develop the structured meshes: Algebraic methods, Interpolation methods, and methods based on solving partial differential
An Investigation into Iterative Methods for Solving Elliptic PDE s Andrew M Brown Computer Science/Maths Session (2000/2001)
 An Investigation into Iterative Methods for Solving Elliptic PDE s Andrew M Brown Computer Science/Maths Session (000/001) Summary The objectives of this project were as follows: 1) Investigate iterative
An Investigation into Iterative Methods for Solving Elliptic PDE s Andrew M Brown Computer Science/Maths Session (000/001) Summary The objectives of this project were as follows: 1) Investigate iterative
New Mexico Tech Hyd 510
 Numerics Motivation Modeling process (JLW) To construct a model we assemble and synthesize data and other information to formulate a conceptual model of the situation. The model is conditioned on the science
Numerics Motivation Modeling process (JLW) To construct a model we assemble and synthesize data and other information to formulate a conceptual model of the situation. The model is conditioned on the science
MESHLESS SOLUTION OF INCOMPRESSIBLE FLOW OVER BACKWARD-FACING STEP
 Vol. 12, Issue 1/2016, 63-68 DOI: 10.1515/cee-2016-0009 MESHLESS SOLUTION OF INCOMPRESSIBLE FLOW OVER BACKWARD-FACING STEP Juraj MUŽÍK 1,* 1 Department of Geotechnics, Faculty of Civil Engineering, University
Vol. 12, Issue 1/2016, 63-68 DOI: 10.1515/cee-2016-0009 MESHLESS SOLUTION OF INCOMPRESSIBLE FLOW OVER BACKWARD-FACING STEP Juraj MUŽÍK 1,* 1 Department of Geotechnics, Faculty of Civil Engineering, University
Three Dimensional Numerical Simulation of Turbulent Flow Over Spillways
 Three Dimensional Numerical Simulation of Turbulent Flow Over Spillways Latif Bouhadji ASL-AQFlow Inc., Sidney, British Columbia, Canada Email: lbouhadji@aslenv.com ABSTRACT Turbulent flows over a spillway
Three Dimensional Numerical Simulation of Turbulent Flow Over Spillways Latif Bouhadji ASL-AQFlow Inc., Sidney, British Columbia, Canada Email: lbouhadji@aslenv.com ABSTRACT Turbulent flows over a spillway
Observations on the fifth-order WENO method with non-uniform meshes
 Observations on the fifth-order WENO method with non-uniform meshes Rong Wang, a, Hui Feng, b, Raymond J. Spiteri a,, a Department of Computer Science, University of Saskatchewan, Saskatoon, SK, S7N 5C9,
Observations on the fifth-order WENO method with non-uniform meshes Rong Wang, a, Hui Feng, b, Raymond J. Spiteri a,, a Department of Computer Science, University of Saskatchewan, Saskatoon, SK, S7N 5C9,
PTE 519 Lecture Note Finite Difference Approximation (Model)
 PTE 519 Lecture Note 3 3.0 Finite Difference Approximation (Model) In this section of the lecture material, the focus is to define the terminology and to summarize the basic facts. The basic idea of any
PTE 519 Lecture Note 3 3.0 Finite Difference Approximation (Model) In this section of the lecture material, the focus is to define the terminology and to summarize the basic facts. The basic idea of any
PHT3D Transport and Mineral Reactions
 v. 10.3 GMS 10.3 Tutorial PHT3D Geochemical Reactions Objectives Learn about transport and mineral reactions in PHT3D. Prerequisite Tutorials MT3DMS Grid Approach Required Components Grid Module MODFLOW
v. 10.3 GMS 10.3 Tutorial PHT3D Geochemical Reactions Objectives Learn about transport and mineral reactions in PHT3D. Prerequisite Tutorials MT3DMS Grid Approach Required Components Grid Module MODFLOW
An explicit and conservative remapping strategy for semi-lagrangian advection
 An explicit and conservative remapping strategy for semi-lagrangian advection Sebastian Reich Universität Potsdam, Potsdam, Germany January 17, 2007 Abstract A conservative semi-lagrangian advection scheme
An explicit and conservative remapping strategy for semi-lagrangian advection Sebastian Reich Universität Potsdam, Potsdam, Germany January 17, 2007 Abstract A conservative semi-lagrangian advection scheme
Numerical and theoretical analysis of shock waves interaction and reflection
 Fluid Structure Interaction and Moving Boundary Problems IV 299 Numerical and theoretical analysis of shock waves interaction and reflection K. Alhussan Space Research Institute, King Abdulaziz City for
Fluid Structure Interaction and Moving Boundary Problems IV 299 Numerical and theoretical analysis of shock waves interaction and reflection K. Alhussan Space Research Institute, King Abdulaziz City for
MATLAB. Advanced Mathematics and Mechanics Applications Using. Third Edition. David Halpern University of Alabama CHAPMAN & HALL/CRC
 Advanced Mathematics and Mechanics Applications Using MATLAB Third Edition Howard B. Wilson University of Alabama Louis H. Turcotte Rose-Hulman Institute of Technology David Halpern University of Alabama
Advanced Mathematics and Mechanics Applications Using MATLAB Third Edition Howard B. Wilson University of Alabama Louis H. Turcotte Rose-Hulman Institute of Technology David Halpern University of Alabama
The vertical stratification is modeled by 4 layers in which we work with averaged concentrations in vertical direction:
 Numerical methods in smog prediction M. van Loon Center for Mathematics and Computer Science, dep. AW, P.O. Boz ^072 J(%%? GB Ams
Numerical methods in smog prediction M. van Loon Center for Mathematics and Computer Science, dep. AW, P.O. Boz ^072 J(%%? GB Ams
Using a Single Rotating Reference Frame
 Tutorial 9. Using a Single Rotating Reference Frame Introduction This tutorial considers the flow within a 2D, axisymmetric, co-rotating disk cavity system. Understanding the behavior of such flows is
Tutorial 9. Using a Single Rotating Reference Frame Introduction This tutorial considers the flow within a 2D, axisymmetric, co-rotating disk cavity system. Understanding the behavior of such flows is
SEAWAT 4 Tutorial - Example Problem
 SEAWAT 4 Tutorial - Example Problem Introduction About SEAWAT-4 SEAWAT-4 is the latest release of SEAWAT computer program for simulation of threedimensional, variable-density, transient ground-water flow
SEAWAT 4 Tutorial - Example Problem Introduction About SEAWAT-4 SEAWAT-4 is the latest release of SEAWAT computer program for simulation of threedimensional, variable-density, transient ground-water flow
Development of the Compliant Mooring Line Model for FLOW-3D
 Flow Science Report 08-15 Development of the Compliant Mooring Line Model for FLOW-3D Gengsheng Wei Flow Science, Inc. October 2015 1. Introduction Mooring systems are common in offshore structures, ship
Flow Science Report 08-15 Development of the Compliant Mooring Line Model for FLOW-3D Gengsheng Wei Flow Science, Inc. October 2015 1. Introduction Mooring systems are common in offshore structures, ship
MIDAS Geotechnical Training Series
 MIDAS Geotechnical Training Series Fully Coupled vs Consolidation Analysis Seongwan Bae Angel F. Martinez MIDAS Information Technology Integrated Solver Optimized for the next generation 6-bit platform
MIDAS Geotechnical Training Series Fully Coupled vs Consolidation Analysis Seongwan Bae Angel F. Martinez MIDAS Information Technology Integrated Solver Optimized for the next generation 6-bit platform
Development of a Maxwell Equation Solver for Application to Two Fluid Plasma Models. C. Aberle, A. Hakim, and U. Shumlak
 Development of a Maxwell Equation Solver for Application to Two Fluid Plasma Models C. Aberle, A. Hakim, and U. Shumlak Aerospace and Astronautics University of Washington, Seattle American Physical Society
Development of a Maxwell Equation Solver for Application to Two Fluid Plasma Models C. Aberle, A. Hakim, and U. Shumlak Aerospace and Astronautics University of Washington, Seattle American Physical Society
CS-184: Computer Graphics Lecture #21: Fluid Simulation II
 CS-184: Computer Graphics Lecture #21: Fluid Simulation II Rahul Narain University of California, Berkeley Nov. 18 19, 2013 Grid-based fluid simulation Recap: Eulerian viewpoint Grid is fixed, fluid moves
CS-184: Computer Graphics Lecture #21: Fluid Simulation II Rahul Narain University of California, Berkeley Nov. 18 19, 2013 Grid-based fluid simulation Recap: Eulerian viewpoint Grid is fixed, fluid moves
Partial Differential Equations
 Simulation in Computer Graphics Partial Differential Equations Matthias Teschner Computer Science Department University of Freiburg Motivation various dynamic effects and physical processes are described
Simulation in Computer Graphics Partial Differential Equations Matthias Teschner Computer Science Department University of Freiburg Motivation various dynamic effects and physical processes are described
Finite Element Convergence for Time-Dependent PDEs with a Point Source in COMSOL 4.2
 Finite Element Convergence for Time-Dependent PDEs with a Point Source in COMSOL 4.2 David W. Trott and Matthias K. Gobbert Department of Mathematics and Statistics, University of Maryland, Baltimore County,
Finite Element Convergence for Time-Dependent PDEs with a Point Source in COMSOL 4.2 David W. Trott and Matthias K. Gobbert Department of Mathematics and Statistics, University of Maryland, Baltimore County,
Driven Cavity Example
 BMAppendixI.qxd 11/14/12 6:55 PM Page I-1 I CFD Driven Cavity Example I.1 Problem One of the classic benchmarks in CFD is the driven cavity problem. Consider steady, incompressible, viscous flow in a square
BMAppendixI.qxd 11/14/12 6:55 PM Page I-1 I CFD Driven Cavity Example I.1 Problem One of the classic benchmarks in CFD is the driven cavity problem. Consider steady, incompressible, viscous flow in a square
Sweeping Jet Flushing Method for EDM
 International Conference on Multidisciplinary Research & Practice P a g e 192 Sweeping Jet Flushing Method for EDM Kishor K Kulkarni # Production Engineering, ShivajiUniversity/Ashokrao Mane Group of Institution
International Conference on Multidisciplinary Research & Practice P a g e 192 Sweeping Jet Flushing Method for EDM Kishor K Kulkarni # Production Engineering, ShivajiUniversity/Ashokrao Mane Group of Institution
Simulation in Computer Graphics. Particles. Matthias Teschner. Computer Science Department University of Freiburg
 Simulation in Computer Graphics Particles Matthias Teschner Computer Science Department University of Freiburg Outline introduction particle motion finite differences system of first order ODEs second
Simulation in Computer Graphics Particles Matthias Teschner Computer Science Department University of Freiburg Outline introduction particle motion finite differences system of first order ODEs second
The Level Set Method. Lecture Notes, MIT J / 2.097J / 6.339J Numerical Methods for Partial Differential Equations
 The Level Set Method Lecture Notes, MIT 16.920J / 2.097J / 6.339J Numerical Methods for Partial Differential Equations Per-Olof Persson persson@mit.edu March 7, 2005 1 Evolving Curves and Surfaces Evolving
The Level Set Method Lecture Notes, MIT 16.920J / 2.097J / 6.339J Numerical Methods for Partial Differential Equations Per-Olof Persson persson@mit.edu March 7, 2005 1 Evolving Curves and Surfaces Evolving
An Error Indicator Monitor Function for an r-adaptive Finite-Element Method
 Journal of Computational Physics 170, 871 892 (2001) doi:10.1006/jcph.2001.6770, available online at http://www.idealibrary.com on An Error Indicator Monitor Function for an r-adaptive Finite-Element Method
Journal of Computational Physics 170, 871 892 (2001) doi:10.1006/jcph.2001.6770, available online at http://www.idealibrary.com on An Error Indicator Monitor Function for an r-adaptive Finite-Element Method
A Singular Example for the Averaged Mean Curvature Flow
 To appear in Experimental Mathematics Preprint Vol. No. () pp. 3 7 February 9, A Singular Example for the Averaged Mean Curvature Flow Uwe F. Mayer Abstract An embedded curve is presented which under numerical
To appear in Experimental Mathematics Preprint Vol. No. () pp. 3 7 February 9, A Singular Example for the Averaged Mean Curvature Flow Uwe F. Mayer Abstract An embedded curve is presented which under numerical
A novel model for biolm growth and its resolution by using the hybrid immersed interface-level set method
 A novel model for biolm growth and its resolution by using the hybrid immersed interface-level set method Juan A. Asenjo & Carlos Conca Applied Mathematics Group - Basic Sciences Department - University
A novel model for biolm growth and its resolution by using the hybrid immersed interface-level set method Juan A. Asenjo & Carlos Conca Applied Mathematics Group - Basic Sciences Department - University
Gradient Free Design of Microfluidic Structures on a GPU Cluster
 Gradient Free Design of Microfluidic Structures on a GPU Cluster Austen Duffy - Florida State University SIAM Conference on Computational Science and Engineering March 2, 2011 Acknowledgements This work
Gradient Free Design of Microfluidic Structures on a GPU Cluster Austen Duffy - Florida State University SIAM Conference on Computational Science and Engineering March 2, 2011 Acknowledgements This work
CFD MODELING FOR PNEUMATIC CONVEYING
 CFD MODELING FOR PNEUMATIC CONVEYING Arvind Kumar 1, D.R. Kaushal 2, Navneet Kumar 3 1 Associate Professor YMCAUST, Faridabad 2 Associate Professor, IIT, Delhi 3 Research Scholar IIT, Delhi e-mail: arvindeem@yahoo.co.in
CFD MODELING FOR PNEUMATIC CONVEYING Arvind Kumar 1, D.R. Kaushal 2, Navneet Kumar 3 1 Associate Professor YMCAUST, Faridabad 2 Associate Professor, IIT, Delhi 3 Research Scholar IIT, Delhi e-mail: arvindeem@yahoo.co.in
Understanding and Using MINC
 Understanding and Using MINC Background In TOUGH2, the MINC (Multiple Interacting Continua) approach is used to model flow in fractured media. It is a generalization of the classical double-porosity concept
Understanding and Using MINC Background In TOUGH2, the MINC (Multiple Interacting Continua) approach is used to model flow in fractured media. It is a generalization of the classical double-porosity concept
CHAPTER 1. Introduction
 ME 475: Computer-Aided Design of Structures 1-1 CHAPTER 1 Introduction 1.1 Analysis versus Design 1.2 Basic Steps in Analysis 1.3 What is the Finite Element Method? 1.4 Geometrical Representation, Discretization
ME 475: Computer-Aided Design of Structures 1-1 CHAPTER 1 Introduction 1.1 Analysis versus Design 1.2 Basic Steps in Analysis 1.3 What is the Finite Element Method? 1.4 Geometrical Representation, Discretization
Australian Journal of Basic and Applied Sciences, 3(2): , 2009 ISSN
 Australian Journal of Basic and Applied Sciences, 3(2): 1334-1339, 2009 ISSN 1991-8178 Comparison of Direct and Indirect Boundary Element Methods for the Calculation of Potential Flow Around an Elliptic
Australian Journal of Basic and Applied Sciences, 3(2): 1334-1339, 2009 ISSN 1991-8178 Comparison of Direct and Indirect Boundary Element Methods for the Calculation of Potential Flow Around an Elliptic
The 3D DSC in Fluid Simulation
 The 3D DSC in Fluid Simulation Marek K. Misztal Informatics and Mathematical Modelling, Technical University of Denmark mkm@imm.dtu.dk DSC 2011 Workshop Kgs. Lyngby, 26th August 2011 Governing Equations
The 3D DSC in Fluid Simulation Marek K. Misztal Informatics and Mathematical Modelling, Technical University of Denmark mkm@imm.dtu.dk DSC 2011 Workshop Kgs. Lyngby, 26th August 2011 Governing Equations
NIA CFD Seminar, October 4, 2011 Hyperbolic Seminar, NASA Langley, October 17, 2011
 NIA CFD Seminar, October 4, 2011 Hyperbolic Seminar, NASA Langley, October 17, 2011 First-Order Hyperbolic System Method If you have a CFD book for hyperbolic problems, you have a CFD book for all problems.
NIA CFD Seminar, October 4, 2011 Hyperbolic Seminar, NASA Langley, October 17, 2011 First-Order Hyperbolic System Method If you have a CFD book for hyperbolic problems, you have a CFD book for all problems.
New Basis Functions and Their Applications to PDEs
 Copyright c 2007 ICCES ICCES, vol.3, no.4, pp.169-175, 2007 New Basis Functions and Their Applications to PDEs Haiyan Tian 1, Sergiy Reustkiy 2 and C.S. Chen 1 Summary We introduce a new type of basis
Copyright c 2007 ICCES ICCES, vol.3, no.4, pp.169-175, 2007 New Basis Functions and Their Applications to PDEs Haiyan Tian 1, Sergiy Reustkiy 2 and C.S. Chen 1 Summary We introduce a new type of basis
Continuum-Microscopic Models
 Scientific Computing and Numerical Analysis Seminar October 1, 2010 Outline Heterogeneous Multiscale Method Adaptive Mesh ad Algorithm Refinement Equation-Free Method Incorporates two scales (length, time
Scientific Computing and Numerical Analysis Seminar October 1, 2010 Outline Heterogeneous Multiscale Method Adaptive Mesh ad Algorithm Refinement Equation-Free Method Incorporates two scales (length, time
Training Manual FEFLOW 7.1
 Training Manual FEFLOW 7.1 Groundwater Modeling with FEFLOW 7.1 August 24, 2017 DHI WASY GmbH Groundwater Modelling Centre FEFLOW Services Contents 3 Contents Preface i 0.1 Scope and structure of this
Training Manual FEFLOW 7.1 Groundwater Modeling with FEFLOW 7.1 August 24, 2017 DHI WASY GmbH Groundwater Modelling Centre FEFLOW Services Contents 3 Contents Preface i 0.1 Scope and structure of this
A Quintic Spline method for fourth order singularly perturbed Boundary Value Problem of Reaction-Diffusion type
 A Quintic Spline method for fourth order singularly perturbed Boundary Value Problem of Reaction-Diffusion type Jigisha U. Pandya and Harish D. Doctor Asst. Prof., Department of Mathematics, Sarvajanik
A Quintic Spline method for fourth order singularly perturbed Boundary Value Problem of Reaction-Diffusion type Jigisha U. Pandya and Harish D. Doctor Asst. Prof., Department of Mathematics, Sarvajanik
ABSTRACTS OF PUBLICATIONS. is modified to take into account the subgrid-scale solution and solved as a large linear system of
 ABSTRACTS OF PUBLICATIONS T. Arbogast, Numerical subgrid upscaling of two-phase flow in porous media, submitted. We present a locally mass conservative scheme for the approximation of two-phase flow in
ABSTRACTS OF PUBLICATIONS T. Arbogast, Numerical subgrid upscaling of two-phase flow in porous media, submitted. We present a locally mass conservative scheme for the approximation of two-phase flow in
2.7 Cloth Animation. Jacobs University Visualization and Computer Graphics Lab : Advanced Graphics - Chapter 2 123
 2.7 Cloth Animation 320491: Advanced Graphics - Chapter 2 123 Example: Cloth draping Image Michael Kass 320491: Advanced Graphics - Chapter 2 124 Cloth using mass-spring model Network of masses and springs
2.7 Cloth Animation 320491: Advanced Graphics - Chapter 2 123 Example: Cloth draping Image Michael Kass 320491: Advanced Graphics - Chapter 2 124 Cloth using mass-spring model Network of masses and springs
Eulerian Techniques for Fluid-Structure Interactions - Part II: Applications
 Published in Lecture Notes in Computational Science and Engineering Vol. 103, Proceedings of ENUMATH 2013, pp. 755-762, Springer, 2014 Eulerian Techniques for Fluid-Structure Interactions - Part II: Applications
Published in Lecture Notes in Computational Science and Engineering Vol. 103, Proceedings of ENUMATH 2013, pp. 755-762, Springer, 2014 Eulerian Techniques for Fluid-Structure Interactions - Part II: Applications
Adaptive numerical methods
 METRO MEtallurgical TRaining On-line Adaptive numerical methods Arkadiusz Nagórka CzUT Education and Culture Introduction Common steps of finite element computations consists of preprocessing - definition
METRO MEtallurgical TRaining On-line Adaptive numerical methods Arkadiusz Nagórka CzUT Education and Culture Introduction Common steps of finite element computations consists of preprocessing - definition
