CS2210 Data Structures and Algorithms. Lecture 9: AVL TREES definition, properties, insertion
|
|
|
- Natalie Harvey
- 6 years ago
- Views:
Transcription
1 CS2210 Data Structures and Algorithms Lecture 9: AVL TREES definition, roerties, insertion v
2 BST Performance BST ith n nodes and of height h methods find, insert and remove take O(h) time h is O(n) in the orst case and O(log n) in the best case orst case best case 2
3 Balanced Tree Motivation Need to insure height h of BST is O(log n) then orst case comleit for find, insert, remove is O(log n) height h is O(log n) for a balanced tree Informall, a tree is balanced, if for an node the sie of its left subtree not too different from sie of the right subtree or, equivalentl, left and right subtree heights are not too different More formall, a tree is balanced if its height is O(log n) 3
4 Balanced Trees Comlete tree is an eamle of a balanced tree used for a riorit queue hea suorts insert and removemin, but it does not suort find and remove thus hea does not ork for an ordered dictionar There are other eamles of balanced trees that suort find, insert, remove AVL trees 4
5 Definition: Height of a Node height a tree node v is the height of the subtree rooted at node v recall that tree height is the maimum over tree node deths
6 Definition: AVL Tree Inventors: Adel'son-Vel'skii and Landis (1962) "An algorithm for organiation of information", Doklad Akademii Nauk USSR AVL Tree is BST that satisfies the height-balance roert for ever node v, the heights of its left and right children differ b at most 1 Height-balance roert ensures that height is logarithmic in the number of nodes 6
7 Height of an AVL Tree Theorem: Height h of AVL tree storing n kes is O(log n) Proof: Let n(h) be number of internal nodes in smallest AVL tree of height h n(1) = 1 and n(2) = 2 8 n(h) = 1 + n(h-1) + n(h-2) 2 4 h-2 h-1 smallest AVL tree of height h > 1 + n(h-2) + n(h-2) > 2n(h-2) solving: n(h) > 2n(h-2), n(h) > 4n(h-4), n(h) > 8n(n-6),,n(h) > 2 i n(h-2i) base case: h-2i=1, solving for i, e get i=(h-1)/2 therefore n(h) > 2 (h-1)/2 n(1)=2 (h-1)/2 take logarithms of both sides: h < 2log n(h) + 1 h
8 Oerations in AVL Tree The height of an AVL tree is O(log n) Thus find is O(log n) erformed just like in BST since AVL tree is BST Have to sho ho to insert and remove in AVL trees, hile maintaining 1. the height-balance roert 2. the binar search tree order 8
9 Insertion in an AVL Tree Insertion starts as in BST eanding at eternal node Eamle: insert 54 before inserting after inserting insertion node 9
10 Insertion in an AVL Tree After inserting at eternal, heightbalance roert is likel lost Need to restructure the tree Will use ictorial notation
11 Rebalancing After Insertion Node is unbalanced if difference in heights of its left and right children is more than 1 After insertion, onl heights of ancestors of insertion node could change if change, increase b eactl 1 Need to check onl ancestors of Follo the ath from to the root, udating the heights and correcting an unbalanced nodes in about 50% of the cases, insertion causes no unbalance 11
12 Rebalancing After Insertion Suose is the first unbalanced node on the ath from to the root Height difference beteen the left and the right child of is more than 1 tree as balanced before the insertion insertion can change height onl b 1 Thus this height difference is eactl 2 One subtree has height, other height +2 as inserted into the higher subtree the higher subtree could be on the left as ell +2
13 Rebalancing After Insertion Let S be the higher subtree could be either on the left or on the right of as balanced before insertion, so height of S as +1 before insertion S +2 S had at least one internal node before insertion, since its height is +1 Therefore S has a non-leaf root Let be the root of S +1 S before insertion
14 Rebalancing After Insertion Let be the root of S balanced after insertion Eand structure of S before insertion Case 1: both subtrees of S have height +1 S before insertion Case 2: one subtree of S has height, another height 1 ill be inserted in higher subtree -1 imossible, since ould become unbalanced after insertion
15 Before/After Insertion Structure S before insertion S after insertion +1 could have been inserted into the right subtree of 15
16 Eanded Picture after Insertion S S S could be either the left or right subtree of could have been inserted either in left or right subtrees of Let R be the higher subtree of
17 Rebalancing After Insertion Let R be the higher subtree of R contains, hich is an internal node therefore R has at least one internal node Let be the root of R +1 height of R ent from before insertion to +1 after insertion as balanced before insertion and stas balanced after insertion both subtrees of had height -1 before insertion After insertion, one subtree of has height, the other height -1 R R before insertion R after insertion
18 Eanded Picture after Insertion +2-1 could be either left or right child of could be either left or right child of
19 Before Insertion vs after Insertion
20 Rebalance BST order is reserved all kes in gre subtree larger than all kes in ello subtree smaller than
21 Rebalance This case is hen to the right of, to the left of Three other cases to the right of, to the right of to the left of, to the left of to the left of, to the right of
22 Rebalance, other cases to the right of, is to the right of
23 Rebalance, other cases to the left of, is to the left of
24 Rebalance, other cases to the left of, is to the right of
25 Trinode Restructuring trinode restructuring handles all cases Call node as the middle (has middle ke) node as the smallest (has smallest ke) nodes as the largest (has largest ke) Make middle node ne subtree arent smallest node its left child largest node its right child subtrees of middle node are orhaned left subtree, if resent, goes to the ne left child right subtree, if resent, goes to the ne right child
26 PseudoCode for Trinode Restructuring Algorithm TriNodeRestructure(,,) Inut: Unbalanced node, is the taller child of, is the taller child of Outut: osition of the node that goes in the lace of in the tree structure if.right() = and.left() = then a = ; b = ; c = if.right() = and.right() = then a = ; b = ; c = if.left() = and.left() = then a = ; b = ; c = if.left() = and.right() = then a = ; b = ; c = if ( = root) then root = b; //root changes after trinoderestructure b.arent = null else // reconnect arent of to the node relacing if.arent.left() = then MakeLeftChild(.arent, b); else MakeRightChild(.arent, b); if b.left() and b.left() // left orhan resent MakeRightChild(a, b.leftchild); if b.right() and b.right() //right orhan resent MakeLeftChild(c, b.rightchild); MakeLeftChild(b,a); MakeRightChild(b,c); return b
27 PseudoCode for Trinode Restructuring Algorithm TriNodeRestructure(,,) Inut: Unbalanced node, is the taller child of, is the taller child of Outut: osition of the node that goes in the lace of in the tree structure if.right() = and.left() = if.right() = and.right() = if.left() = and.left() = if.left() = and.right() = then a = ; b = ; c = then a = ; b = ; c = then a = ; b = ; c = then a = ; b = ; c = a b c -1
28 PseudoCode for Trinode Restructuring Algorithm TriNodeRestructure(,,) Inut: Unbalanced node, is the taller child of, is the taller child of Outut: osition of the node that goes in the lace of in the tree structure if ( = root ) then root = b; //root changes after trinoderestructure b.arent = null else // reconnect arent of to the node relacing if.arent.left() = then MakeLeftChild(.arent, b) else MakeRightChild(.arent,b) a b c -1 root a b c -1 root
29 Trinode Restructuring Algorithm TriNodeRestructure(,,) Inut: Unbalanced node, is the taller child of, is the taller child of Outut: osition of the node that goes in the lace of in the tree structure a b d c if ( = root ) then -1 root = b; //root changes after trinoderestructure b.arent = null eventuall ant this else // reconnect arent of to the node relacing if.arent.left() = then MakeLeftChild(.arent, b) else MakeRightChild(.arent, b) a d b c -1 a b d c -1
30 Trinode Restructuring a b d c Algorithm TriNodeRestructure(,,) Inut: Unbalanced node, is the taller child of, is the taller child of Outut: osition of the node that goes in the lace of in the tree structure if b.left() and b.left() // left orhan resent MakeRightChild(a, b.leftchild); if b.right() and b.right() //right orhan resent MakeLeftChild(c, b.rightchild); -1 eventuall ant this a b d c a b d c -1-1
31 Trinode Restructuring a b d c Algorithm TriNodeRestructure(,,) Inut: Unbalanced node, is the taller child of, is the taller child of Outut: osition of the node that goes in the lace of in the tree structure if b.left() and b.left() // left orhan resent MakeRightChild(a, b.leftchild); if b.right() and b.right() //right orhan resent MakeLeftChild(c, b.rightchild); -1 eventuall ant this a b d c a b d c -1-1
32 PseudoCode for Trinode Restructuring Algorithm TriNodeRestructure(,,) Inut: Unbalanced node, is the taller child of, is the taller child of Outut: osition of the node that goes in the lace of in the tree structure MakeLeftChild(b,a) MakeRightChild(b,c) return b a b d c a b d c -1-1
33 PseudoCode for Trinode Restructuring MakeLeftChild(a,b) makes node b left child of node a a.leftchild = b b.arent = a MakeRightChild(a,b) makes node b right child of node a a.rightchild = b b.arent = a Trinode restructuring is O(1) constant number of comarisons and assignments 33
34 Insertion and Trinode Restructuring before insert after insert, before trinode restructure after insert and trinode restructure After one trinode restructure, height-balance roert is restored globall can sto checking ancestor ath after trinode restructure
35 Insertion into AVL Tree Algorithm AVLtreeInsert(k,o) Inut: ke k and value o; Outut: node here the entr as inserted = TreeInsert(k,o,T.root) // holds osition of ne entr (k,o) // no need to check and if needed, restore height-balance roert = hile ( null) // traverse u the tree, checking for imbalance setheight() // reset the height of since it ma have changed if getheight(.left)-getheight(.right) > 1 then =TriNodeRestructure(tallerChild(tallerChild()),tallerChild(),) setheight(.left); setheight(.right); setheight(); break // eit hile loo, tree is balanced after 1 trinoderestructure = arent() return setheight() = 1+ma(.left.height,.right.height) tallerchild(v) returns the child of v ith larger height
36 Insertion Eamle Continued after inserting after inserting
37 Inserting in AVL Tree, Summar After inserting into at node, go u the tree, folloing ancestor ath from, checking if an node on this ath has become unbalanced If an unbalanced node is found, erform tri-node restructuring tree becomes balanced and and can return from insert right after trinode restructuring Trace at most one ath in the tree, erforminc constant number of oerations at each node, thus insert is O(log n) 37
CS2210 Data Structures and Algorithms. Lecture 10: AVL TREES deletion
 CS2210 Data Strctres and Algorithms Lectre 10: AVL TREES deletion v 6 3 8 4 Review of Removal in BST Case 2: node v storing entr to be removed has no leaf child relace entr at v with entr whose ke k reserves
CS2210 Data Strctres and Algorithms Lectre 10: AVL TREES deletion v 6 3 8 4 Review of Removal in BST Case 2: node v storing entr to be removed has no leaf child relace entr at v with entr whose ke k reserves
Search Trees. Chapter 11
 Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
AVL Trees Goodrich, Tamassia, Goldwasser AVL Trees 1
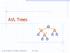 AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Tree Definition. An example of an AVL tree where the heights are shown next to the nodes. Adelson-Velsky and Landis
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
AVL Trees. Reading: 9.2
 AVL Trees Reading: 9.2 Balance Factor of a Node The difference in height of its two subtrees (h R -h L ) Balanced Node if -1 BF 1 Unbalanced Node if BF 1 h L h R Balance Factor of a Binar Tree Corresponds
AVL Trees Reading: 9.2 Balance Factor of a Node The difference in height of its two subtrees (h R -h L ) Balanced Node if -1 BF 1 Unbalanced Node if BF 1 h L h R Balance Factor of a Binar Tree Corresponds
AVL Trees (10.2) AVL Trees
 AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
COMP171. AVL-Trees (Part 1)
 COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
Height of a Heap. Heaps. 1. Insertion into a Heap. Heaps and Priority Queues. The insertion algorithm consists of three steps
 Heaps A heap is a binary tree storing keys at its nodes and satisfying the folloing properties:! Heap-Order: " for every internal node v other than the root, key(v)! key(parent(v))! Complete Binary Tree:
Heaps A heap is a binary tree storing keys at its nodes and satisfying the folloing properties:! Heap-Order: " for every internal node v other than the root, key(v)! key(parent(v))! Complete Binary Tree:
Chapter 2: Basic Data Structures
 Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Search Trees (Ch. 9) > = Binary Search Trees 1
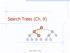 Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
Splay Trees. Splay Trees 1
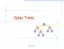 Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
COSC160: Data Structures Balanced Trees. Jeremy Bolton, PhD Assistant Teaching Professor
 COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
AVL Trees / Slide 2. AVL Trees / Slide 4. Let N h be the minimum number of nodes in an AVL tree of height h. AVL Trees / Slide 6
 COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
Splay Trees Goodrich, Tamassia, Dickerson. Splay Trees 1
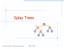 Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored
Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
CS350: Data Structures AVL Trees
 S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
Chapter 10: Search Trees
 < 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
< 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
CSI33 Data Structures
 Outline Department of Mathematics and Computer Science Bronx Community College November 21, 2018 Outline Outline 1 C++ Supplement 1.3: Balanced Binary Search Trees Balanced Binary Search Trees Outline
Outline Department of Mathematics and Computer Science Bronx Community College November 21, 2018 Outline Outline 1 C++ Supplement 1.3: Balanced Binary Search Trees Balanced Binary Search Trees Outline
CHAPTER 10 AVL TREES. 3 8 z 4
 CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
ECE250: Algorithms and Data Structures AVL Trees (Part A)
 ECE250: Algorithms and Data Structures AVL Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
ECE250: Algorithms and Data Structures AVL Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
B Tree. Also, every non leaf node must have at least two successors and all leaf nodes must be at the same level.
 B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
Splay Trees 3/20/14. Splay Trees. Splay Trees are Binary Search Trees. note that two keys of equal value may be wellseparated (7,T) (1,Q) (1,C) (5,H)
 Spla Trees 3/20/14 Presentation for use with the tetbook Data Structures and Algorithms in Java, 6 th edition, b M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wile, 2014 Spla Trees v 6 3 8 4 2013
Spla Trees 3/20/14 Presentation for use with the tetbook Data Structures and Algorithms in Java, 6 th edition, b M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wile, 2014 Spla Trees v 6 3 8 4 2013
Priority Queue ADT ( 7.1) Heaps and Priority Queues 2. Comparator ADT ( 7.1.4) Total Order Relation. Using Comparators in C++
 Heaps and Priority Queues Priority Queue ADT (.) A priority queue stores a collection of items An item is a pair (key, element) Main methods of the Priority Queue ADT insertitem(k, o) inserts an item ith
Heaps and Priority Queues Priority Queue ADT (.) A priority queue stores a collection of items An item is a pair (key, element) Main methods of the Priority Queue ADT insertitem(k, o) inserts an item ith
AVL Trees. (AVL Trees) Data Structures and Programming Spring / 17
 AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
search(i): Returns an element in the data structure associated with key i
 CS161 Lecture 7 inary Search Trees Scribes: Ilan Goodman, Vishnu Sundaresan (2015), Date: October 17, 2017 Virginia Williams (2016), and Wilbur Yang (2016), G. Valiant Adated From Virginia Williams lecture
CS161 Lecture 7 inary Search Trees Scribes: Ilan Goodman, Vishnu Sundaresan (2015), Date: October 17, 2017 Virginia Williams (2016), and Wilbur Yang (2016), G. Valiant Adated From Virginia Williams lecture
Balanced Search Trees. CS 3110 Fall 2010
 Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Algorithms and Data Structures
 Ordered Dictionaries and Binary Search Trees Page 1 BFH-TI: Softwareschule Schweiz Ordered Dictionaries and Binary Search Trees Dr. CAS SD01 Ordered Dictionaries and Binary Search Trees Page Outline Ordered
Ordered Dictionaries and Binary Search Trees Page 1 BFH-TI: Softwareschule Schweiz Ordered Dictionaries and Binary Search Trees Dr. CAS SD01 Ordered Dictionaries and Binary Search Trees Page Outline Ordered
Priority Queues and Heaps. More Data Structures. Priority Queue ADT ( 2.4.1) Total Order Relation. Sorting with a Priority Queue ( 2.4.
 More Data Structures Priority Queues and Heaps Priority Queues, Comparators, Locators, Dictionaries More Data Structures v. More Data Structures v. Priority Queue ADT (.4.) Total Order Relation A priority
More Data Structures Priority Queues and Heaps Priority Queues, Comparators, Locators, Dictionaries More Data Structures v. More Data Structures v. Priority Queue ADT (.4.) Total Order Relation A priority
Data Structures in Java
 Data Structures in Java Lecture 10: AVL Trees. 10/1/015 Daniel Bauer Balanced BSTs Balance condition: Guarantee that the BST is always close to a complete binary tree (every node has exactly two or zero
Data Structures in Java Lecture 10: AVL Trees. 10/1/015 Daniel Bauer Balanced BSTs Balance condition: Guarantee that the BST is always close to a complete binary tree (every node has exactly two or zero
Some Search Structures. Balanced Search Trees. Binary Search Trees. A Binary Search Tree. Review Binary Search Trees
 Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
CS 261 Data Structures. AVL Trees
 CS 261 Data Structures AVL Trees 1 Binary Search Tree Complexity of BST operations: proportional to the length of the path from a node to the root Unbalanced tree: operations may be O(n) E.g.: adding elements
CS 261 Data Structures AVL Trees 1 Binary Search Tree Complexity of BST operations: proportional to the length of the path from a node to the root Unbalanced tree: operations may be O(n) E.g.: adding elements
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presentation for use ith the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Ch.03 Binary Search Trees Binary Search Binary search can perform nearest neighbor queries
Presentation for use ith the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Ch.03 Binary Search Trees Binary Search Binary search can perform nearest neighbor queries
Balanced Binary Search Trees
 Balanced Binary Search Trees Pedro Ribeiro DCC/FCUP 2017/2018 Pedro Ribeiro (DCC/FCUP) Balanced Binary Search Trees 2017/2018 1 / 48 Motivation Let S be a set of comparable objects/items: Let a and b be
Balanced Binary Search Trees Pedro Ribeiro DCC/FCUP 2017/2018 Pedro Ribeiro (DCC/FCUP) Balanced Binary Search Trees 2017/2018 1 / 48 Motivation Let S be a set of comparable objects/items: Let a and b be
CSCI 136 Data Structures & Advanced Programming. Lecture 25 Fall 2018 Instructor: B 2
 CSCI 136 Data Structures & Advanced Programming Lecture 25 Fall 2018 Instructor: B 2 Last Time Binary search trees (Ch 14) The locate method Further Implementation 2 Today s Outline Binary search trees
CSCI 136 Data Structures & Advanced Programming Lecture 25 Fall 2018 Instructor: B 2 Last Time Binary search trees (Ch 14) The locate method Further Implementation 2 Today s Outline Binary search trees
Trees. Reading: Weiss, Chapter 4. Cpt S 223, Fall 2007 Copyright: Washington State University
 Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
Analysis of Algorithms
 Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
More Binary Search Trees AVL Trees. CS300 Data Structures (Fall 2013)
 More Binary Search Trees AVL Trees bstdelete if (key not found) return else if (either subtree is empty) { delete the node replacing the parents link with the ptr to the nonempty subtree or NULL if both
More Binary Search Trees AVL Trees bstdelete if (key not found) return else if (either subtree is empty) { delete the node replacing the parents link with the ptr to the nonempty subtree or NULL if both
10.2 AVL Trees. Definition of an AVL Tree. 438 Chapter 10. Search Trees
 438 Chapter 10. Search Trees 10. AVL Trees In theprevioussection,wediscussedwhatshouldbeanefficientmapdatastructure, but the worst-case performance it achieves for the various operations is linear time,
438 Chapter 10. Search Trees 10. AVL Trees In theprevioussection,wediscussedwhatshouldbeanefficientmapdatastructure, but the worst-case performance it achieves for the various operations is linear time,
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
More BSTs & AVL Trees bstdelete
 More BSTs & AVL Trees bstdelete if (key not found) return else if (either subtree is empty) { delete the node replacing the parents link with the ptr to the nonempty subtree or NULL if both subtrees are
More BSTs & AVL Trees bstdelete if (key not found) return else if (either subtree is empty) { delete the node replacing the parents link with the ptr to the nonempty subtree or NULL if both subtrees are
Data Structures and Algorithms
 Data Structures and Algorithms Spring 2009-2010 Outline BST Trees (contd.) 1 BST Trees (contd.) Outline BST Trees (contd.) 1 BST Trees (contd.) The bad news about BSTs... Problem with BSTs is that there
Data Structures and Algorithms Spring 2009-2010 Outline BST Trees (contd.) 1 BST Trees (contd.) Outline BST Trees (contd.) 1 BST Trees (contd.) The bad news about BSTs... Problem with BSTs is that there
Red-Black Trees Goodrich, Tamassia. Red-Black Trees 1
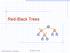 Red-Black Trees 3 8 00 Goodrich, Tamassia Red-Black Trees 1 From (,) to Red-Black Trees A red-black tree is a representation of a (,) tree by means of a binary tree hose nodes are colored red or black
Red-Black Trees 3 8 00 Goodrich, Tamassia Red-Black Trees 1 From (,) to Red-Black Trees A red-black tree is a representation of a (,) tree by means of a binary tree hose nodes are colored red or black
Part 2: Balanced Trees
 Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
AVL Trees. See Section 19.4of the text, p
 AVL Trees See Section 19.4of the text, p. 706-714. AVL trees are self-balancing Binary Search Trees. When you either insert or remove a node the tree adjusts its structure so that the remains a logarithm
AVL Trees See Section 19.4of the text, p. 706-714. AVL trees are self-balancing Binary Search Trees. When you either insert or remove a node the tree adjusts its structure so that the remains a logarithm
Binary Trees. Binary Search Trees
 Binar Trees A binar tree is a rooted tree where ever node has at most two children. When a node has onl one child, we still distinguish whether this is the left child or the right child of the parent.
Binar Trees A binar tree is a rooted tree where ever node has at most two children. When a node has onl one child, we still distinguish whether this is the left child or the right child of the parent.
Data Structures Lesson 7
 Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
From (2,4) to Red-Black Trees
 Red-Black Trees 3/0/1 Presentation for use ith the textbook Data Structures and Algorithms in Jaa, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldasser, Wiley, 01 Red-Black Trees 3 8 01 Goodrich,
Red-Black Trees 3/0/1 Presentation for use ith the textbook Data Structures and Algorithms in Jaa, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldasser, Wiley, 01 Red-Black Trees 3 8 01 Goodrich,
Trees. A tree is a directed graph with the property
 2: Trees Trees A tree is a directed graph with the property There is one node (the root) from which all other nodes can be reached by exactly one path. Seen lots of examples. Parse Trees Decision Trees
2: Trees Trees A tree is a directed graph with the property There is one node (the root) from which all other nodes can be reached by exactly one path. Seen lots of examples. Parse Trees Decision Trees
Fundamental Algorithms
 WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
Lesson 21: AVL Trees. Rotation
 The time required to perform operations on a binary search tree is proportional to the length of the path from root to leaf. This isn t bad in a well-balanced tree. But nothing prevents a tree from becoming
The time required to perform operations on a binary search tree is proportional to the length of the path from root to leaf. This isn t bad in a well-balanced tree. But nothing prevents a tree from becoming
Search Structures. Kyungran Kang
 Search Structures Kyungran Kang (korykang@ajou.ac.kr) Ellis Horowitz, Sartaj Sahni and Susan Anderson-Freed, Fundamentals of Data Structures in C, 2nd Edition, Silicon Press, 2007. Contents Binary Search
Search Structures Kyungran Kang (korykang@ajou.ac.kr) Ellis Horowitz, Sartaj Sahni and Susan Anderson-Freed, Fundamentals of Data Structures in C, 2nd Edition, Silicon Press, 2007. Contents Binary Search
3137 Data Structures and Algorithms in C++
 3137 Data Structures and Algorithms in C++ Lecture 4 July 17 2006 Shlomo Hershkop 1 Announcements please make sure to keep up with the course, it is sometimes fast paced for extra office hours, please
3137 Data Structures and Algorithms in C++ Lecture 4 July 17 2006 Shlomo Hershkop 1 Announcements please make sure to keep up with the course, it is sometimes fast paced for extra office hours, please
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
AVL trees and rotations
 AVL trees and rotations Part of written assignment 5 Examine the Code of Ethics of the ACM Focus on property rights Write a short reaction (up to 1 page single-spaced) Details are in the assignment Operations
AVL trees and rotations Part of written assignment 5 Examine the Code of Ethics of the ACM Focus on property rights Write a short reaction (up to 1 page single-spaced) Details are in the assignment Operations
CSC 172 Data Structures and Algorithms. Fall 2017 TuTh 3:25 pm 4:40 pm Aug 30- Dec 22 Hoyt Auditorium
 CSC 172 Data Structures and Algorithms Fall 2017 TuTh 3:25 pm 4:40 pm Aug 30- Dec 22 Hoyt Auditorium Announcement Coming week: Nov 19 Nov 25 No Quiz No Workshop No New Lab Monday and Tuesday: regular Lab
CSC 172 Data Structures and Algorithms Fall 2017 TuTh 3:25 pm 4:40 pm Aug 30- Dec 22 Hoyt Auditorium Announcement Coming week: Nov 19 Nov 25 No Quiz No Workshop No New Lab Monday and Tuesday: regular Lab
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
In a postorder traversal, a node is visited after its descendants Application: compute space used by files in a directory and its subdirectories 9 1
 What is a Tree Trees Stock Fraud Make Money Fast! Winning Lotto / Bank Robbery In computer science, a tree is an abstract model of a hierarchical structure A tree consists of nodes ith a parent-child relation
What is a Tree Trees Stock Fraud Make Money Fast! Winning Lotto / Bank Robbery In computer science, a tree is an abstract model of a hierarchical structure A tree consists of nodes ith a parent-child relation
Binary Search Trees. Analysis of Algorithms
 Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Inf 2B: AVL Trees. Lecture 5 of ADS thread. Kyriakos Kalorkoti. School of Informatics University of Edinburgh
 Inf 2B: AVL Trees Lecture 5 of ADS thread Kyriakos Kalorkoti School of Informatics University of Edinburgh Dictionaries A Dictionary stores key element pairs, called items. Several elements might have
Inf 2B: AVL Trees Lecture 5 of ADS thread Kyriakos Kalorkoti School of Informatics University of Edinburgh Dictionaries A Dictionary stores key element pairs, called items. Several elements might have
10/23/2013. AVL Trees. Height of an AVL Tree. Height of an AVL Tree. AVL Trees
 // AVL Trees AVL Trees An AVL tree is a binary search tree with a balance condition. AVL is named for its inventors: Adel son-vel skii and Landis AVL tree approximates the ideal tree (completely balanced
// AVL Trees AVL Trees An AVL tree is a binary search tree with a balance condition. AVL is named for its inventors: Adel son-vel skii and Landis AVL tree approximates the ideal tree (completely balanced
Chapter. Binary Search Trees. Contents
 Chapter 4 Balanced Binary Search Trees U.S. Navy Blue Angels, performing their delta formation during the Blues on the Bay Air Show at Marine Corps Base Hawaii in 2007. U.S. government photo by Petty Officer
Chapter 4 Balanced Binary Search Trees U.S. Navy Blue Angels, performing their delta formation during the Blues on the Bay Air Show at Marine Corps Base Hawaii in 2007. U.S. government photo by Petty Officer
Binary search trees (chapters )
 Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Computer Science 210 Data Structures Siena College Fall Topic Notes: Binary Search Trees
 Computer Science 10 Data Structures Siena College Fall 018 Topic Notes: Binary Search Trees Possibly the most common usage of a binary tree is to store data for quick retrieval. Definition: A binary tree
Computer Science 10 Data Structures Siena College Fall 018 Topic Notes: Binary Search Trees Possibly the most common usage of a binary tree is to store data for quick retrieval. Definition: A binary tree
Balanced BST. Balanced BSTs guarantee O(logN) performance at all times
 Balanced BST Balanced BSTs guarantee O(logN) performance at all times the height or left and right sub-trees are about the same simple BST are O(N) in the worst case Categories of BSTs AVL, SPLAY trees:
Balanced BST Balanced BSTs guarantee O(logN) performance at all times the height or left and right sub-trees are about the same simple BST are O(N) in the worst case Categories of BSTs AVL, SPLAY trees:
CS 310: Tree Rotations and AVL Trees
 CS 310: Tree Rotations and AVL Trees Chris Kauffman Week 12-2 Practice/Demo Sites jgrasp is so-so for seeing tree operations Play with Blanced Binary Search Trees online using the following applets (titles
CS 310: Tree Rotations and AVL Trees Chris Kauffman Week 12-2 Practice/Demo Sites jgrasp is so-so for seeing tree operations Play with Blanced Binary Search Trees online using the following applets (titles
CS Transform-and-Conquer
 CS483-11 Transform-and-Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
CS483-11 Transform-and-Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
Binary search trees (chapters )
 Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
Lecture 16 Notes AVL Trees
 Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Fall 2015) Frank Pfenning 1 Introduction Binar search trees are an ecellent data structure to implement associative arras, maps,
Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Fall 2015) Frank Pfenning 1 Introduction Binar search trees are an ecellent data structure to implement associative arras, maps,
Balanced Search Trees
 Balanced Search Trees Computer Science E-22 Harvard Extension School David G. Sullivan, Ph.D. Review: Balanced Trees A tree is balanced if, for each node, the node s subtrees have the same height or have
Balanced Search Trees Computer Science E-22 Harvard Extension School David G. Sullivan, Ph.D. Review: Balanced Trees A tree is balanced if, for each node, the node s subtrees have the same height or have
DATA STRUCTURES AND ALGORITHMS
 LECTURE 13 Babeş - Bolyai University Computer Science and Mathematics Faculty 2017-2018 In Lecture 12... Binary Search Trees Binary Tree Traversals Huffman coding Binary Search Tree Today Binary Search
LECTURE 13 Babeş - Bolyai University Computer Science and Mathematics Faculty 2017-2018 In Lecture 12... Binary Search Trees Binary Tree Traversals Huffman coding Binary Search Tree Today Binary Search
Introduction to Programming: Lecture 13
 Introduction to Programming: Lecture 13 K Narayan Kumar Chennai Mathematical Institute http://www.cmi.ac.in/~kumar 9 October 2012 Balanced search trees... Ideally, for each node size of left and right
Introduction to Programming: Lecture 13 K Narayan Kumar Chennai Mathematical Institute http://www.cmi.ac.in/~kumar 9 October 2012 Balanced search trees... Ideally, for each node size of left and right
BINARY SEARCH TREES cs2420 Introduction to Algorithms and Data Structures Spring 2015
 BINARY SEARCH TREES cs2420 Introduction to Algorithms and Data Structures Spring 2015 1 administrivia 2 -assignment 7 due tonight at midnight -asking for regrades through assignment 5 and midterm must
BINARY SEARCH TREES cs2420 Introduction to Algorithms and Data Structures Spring 2015 1 administrivia 2 -assignment 7 due tonight at midnight -asking for regrades through assignment 5 and midterm must
Balanced Binary Search Trees
 Balanced Binary Search Trees In the previous section we looked at building a binary search tree. As we learned, the performance of the binary search tree can degrade to O(n) for operations like getand
Balanced Binary Search Trees In the previous section we looked at building a binary search tree. As we learned, the performance of the binary search tree can degrade to O(n) for operations like getand
Dictionaries. Priority Queues
 Red-Black-Trees.1 Dictionaries Sets and Multisets; Opers: (Ins., Del., Mem.) Sequential sorted or unsorted lists. Linked sorted or unsorted lists. Tries and Hash Tables. Binary Search Trees. Priority Queues
Red-Black-Trees.1 Dictionaries Sets and Multisets; Opers: (Ins., Del., Mem.) Sequential sorted or unsorted lists. Linked sorted or unsorted lists. Tries and Hash Tables. Binary Search Trees. Priority Queues
SEARCHING. the dictionary ADT. binary search. binary search trees. Searching
 the dictionary ADT binary search binary search trees SEARCHING 44 17 78 32 50 88 48 62 1 The Dictionary ADT a dictionary is an abstract model of a database like a priority queue, a dictionary stores key-element
the dictionary ADT binary search binary search trees SEARCHING 44 17 78 32 50 88 48 62 1 The Dictionary ADT a dictionary is an abstract model of a database like a priority queue, a dictionary stores key-element
Data Structure - Advanced Topics in Tree -
 Data Structure - Advanced Topics in Tree - AVL, Red-Black, B-tree Hanyang University Jong-Il Park AVL TREE Division of Computer Science and Engineering, Hanyang University Balanced binary trees Non-random
Data Structure - Advanced Topics in Tree - AVL, Red-Black, B-tree Hanyang University Jong-Il Park AVL TREE Division of Computer Science and Engineering, Hanyang University Balanced binary trees Non-random
Module 4: Priority Queues
 Module 4: Priority Queues CS 240 Data Structures and Data Management T. Biedl K. Lanctot M. Sepehri S. Wild Based on lecture notes by many previous cs240 instructors David R. Cheriton School of Computer
Module 4: Priority Queues CS 240 Data Structures and Data Management T. Biedl K. Lanctot M. Sepehri S. Wild Based on lecture notes by many previous cs240 instructors David R. Cheriton School of Computer
Search Trees - 2. Venkatanatha Sarma Y. Lecture delivered by: Assistant Professor MSRSAS-Bangalore. M.S Ramaiah School of Advanced Studies - Bangalore
 Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees. COMPSCI 355 Fall 2016
 Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
CSCI2100B Data Structures Trees
 CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
Solutions. Suppose we insert all elements of U into the table, and let n(b) be the number of elements of U that hash to bucket b. Then.
 Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
Red-black trees (19.5), B-trees (19.8), trees
 Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
AVL Trees. Version of September 6, AVL Trees Version of September 6, / 22
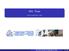 VL Trees Version of September 6, 6 VL Trees Version of September 6, 6 / inary Search Trees x 8 4 4 < x > x 7 9 3 inary-search-tree property For every node x ll eys in its left subtree are smaller than
VL Trees Version of September 6, 6 VL Trees Version of September 6, 6 / inary Search Trees x 8 4 4 < x > x 7 9 3 inary-search-tree property For every node x ll eys in its left subtree are smaller than
AVL Trees Heaps And Complexity
 AVL Trees Heaps And Complexity D. Thiebaut CSC212 Fall 14 Some material taken from http://cseweb.ucsd.edu/~kube/cls/0/lectures/lec4.avl/lec4.pdf Complexity Of BST Operations or "Why Should We Use BST Data
AVL Trees Heaps And Complexity D. Thiebaut CSC212 Fall 14 Some material taken from http://cseweb.ucsd.edu/~kube/cls/0/lectures/lec4.avl/lec4.pdf Complexity Of BST Operations or "Why Should We Use BST Data
Augmenting Data Structures
 Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
8.1. Optimal Binary Search Trees:
 DATA STRUCTERS WITH C 10CS35 UNIT 8 : EFFICIENT BINARY SEARCH TREES 8.1. Optimal Binary Search Trees: An optimal binary search tree is a binary search tree for which the nodes are arranged on levels such
DATA STRUCTERS WITH C 10CS35 UNIT 8 : EFFICIENT BINARY SEARCH TREES 8.1. Optimal Binary Search Trees: An optimal binary search tree is a binary search tree for which the nodes are arranged on levels such
Week 3 Web site:
 Week 3 Web site: https://pages.cs.wisc.edu/~deppeler/cs400/ (announcements and resources) Canvas: https://canvas.wisc.edu/ (modules, assignments, grades) Top Hat join code: X-Team Exercise #1: (in-class
Week 3 Web site: https://pages.cs.wisc.edu/~deppeler/cs400/ (announcements and resources) Canvas: https://canvas.wisc.edu/ (modules, assignments, grades) Top Hat join code: X-Team Exercise #1: (in-class
Lecture 9: Balanced Binary Search Trees, Priority Queues, Heaps, Binary Trees for Compression, General Trees
 Lecture 9: Balanced Binary Search Trees, Priority Queues, Heaps, Binary Trees for Compression, General Trees Reading materials Dale, Joyce, Weems: 9.1, 9.2, 8.8 Liang: 26 (comprehensive edition) OpenDSA:
Lecture 9: Balanced Binary Search Trees, Priority Queues, Heaps, Binary Trees for Compression, General Trees Reading materials Dale, Joyce, Weems: 9.1, 9.2, 8.8 Liang: 26 (comprehensive edition) OpenDSA:
Note that this is a rep invariant! The type system doesn t enforce this but you need it to be true. Should use repok to check in debug version.
 Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
Heaps. 2/13/2006 Heaps 1
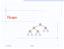 Heaps /13/00 Heaps 1 Outline and Reading What is a heap ( 8.3.1) Height of a heap ( 8.3.) Insertion ( 8.3.3) Removal ( 8.3.3) Heap-sort ( 8.3.) Arraylist-based implementation ( 8.3.) Bottom-up construction
Heaps /13/00 Heaps 1 Outline and Reading What is a heap ( 8.3.1) Height of a heap ( 8.3.) Insertion ( 8.3.3) Removal ( 8.3.3) Heap-sort ( 8.3.) Arraylist-based implementation ( 8.3.) Bottom-up construction
AVL trees and rotations
 / AVL trees and rotations This week, you should be able to perform rotations on height-balanced trees, on paper and in code write a rotate() method search for the kth item in-order using rank } Term project
/ AVL trees and rotations This week, you should be able to perform rotations on height-balanced trees, on paper and in code write a rotate() method search for the kth item in-order using rank } Term project
We will show that the height of a RB tree on n vertices is approximately 2*log n. In class I presented a simple structural proof of this claim:
 We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
Lecture 16 Notes AVL Trees
 Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Spring 2016) Frank Pfenning 1 Introduction Binary search trees are an excellent data structure to implement associative arrays,
Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Spring 2016) Frank Pfenning 1 Introduction Binary search trees are an excellent data structure to implement associative arrays,
