3/1/2016. Calculus: A Reminder. Calculus: A Reminder. Calculus: A Reminder. Calculus: A Reminder. Calculus: A Reminder. Calculus: A Reminder
|
|
|
- Donna Hart
- 6 years ago
- Views:
Transcription
1 1 Intermediate Microeconomics W3211 Lecture 5: Choice and Demand Introduction Columbia Universit, Spring 2016 Mark Dean: 2 The Stor So Far. 3 Toda s Aims 4 We have now have had a first attempt at solving the consumer problem Provides a recipe based on finding three tpes of solution Corner solutions Tangenc points Kinks 1. Provide some more mathematicall sophisticated tools to find tangenc points Varian Ch. 5 appendix, Feldman and Serrano Ch. 3 appendix 2. Introduce the concept of a demand function, which measures how the amount of good a consumer purchaces changes with Prices Varian Ch. 6, Feldman and Serrano Ch Discuss how demand changes with income Varian Ch. 6, Feldman and Serrano Ch. 4 Solving the Consumer s Problem 6 One of the reasons that calculus is so useful is that it allows us to find the optimal solutions for constrained and unconstrained optimization problems Calculus and the Consumer s Problem 1: Constrained to unconstrained problems This relies on derivatives Onl works for finding points of tangenc Not corner solutions Not kinks So these tools are useful, but don t forget ou still need to worr about other solutions 5 1
2 7 8 f(x) Imagine ou have an unconstrained optimization problem Choose x to maximize f(x) How can ou use calculus to solve this? f'(x) f''(x) f(x) A maximum of the function will occur where it is flat i.e. where the derivative is zero Is it alwas the case that the derivative being zero means that ou have found a maximum? f'(x) f''(x) Flat points of the function occur either at maxima or minima To differentiate between the two, check the second derivative If ou have found a point at which The first derivative is zero The second derivative is negative Then ou have found a local maximum However ou still have to worr about Other local maxima 2
3 13 14 Flat points of the function occur either at maxima or minima To differentiate between the two, check the second derivative If ou have found a point at which The first derivative is zero The second derivative is negative Then ou have found a local maximum However ou still have to worr about Other local maxima Corner solutions Flat points of the function occur either at maxima or minima To differentiate between the two, check the second derivative If ou have found a point at which The first derivative is zero The second derivative is negative Then ou have found a local maximum However ou still have to worr about Other local maxima Corner solutions Kinks From Constrained to Unconstrained Problems How does this help us? Tells us how to solve unconstrained optimization problems But we have a constrained optimization problem Choose, to Maximize, Subject to Answer: We can substitute in using the budget constraint to make it an unconstrained problem Note in order to do so we are assuming the budget constrain holds with equalit Monotonic preferences 17 From Constrained to Unconstrained Problems An example: Choose, to Maximize, = Subject to Using the budget constraint we get Substitute this into the utilit function = Can choose an (such that and are greater than or equal to zero) to maximize utilit Don t have to worr about the budget constraint adjusts automaticall to changes in 18 3
4 From Constrained to Unconstrained Problems 19 The Advantages of This Approach 20 Problem becomes Choose to Maximize = Taking derivatives gives 2 )= )=2 Second derivative is negative, so first order condition will give us a local maximum 2 0 Implies (using the budget constraint for ) and Unsurprisingl, gives the same answer as the recipe from last week What is the advantage of this approach? One thing is the second order conditions Helps us to identif when we have found a local minima Consider concave preferences, = + You should check ou agree, but these preferences give utilit that looks like The Advantages of This Approach 21 The Advantages of This Approach 22 So a tangenc point is actuall a minimum The second order conditions can help us spot this Choose, to Maximize, = + Subject to Becomes Choose to Maximize = Taking derivatives gives )=2 2 )=22 0 Second order condition fails, tells us we have a maximum Karush Kuhn Tucker 24 Mathematicians have developed even more powerful tools for solving constrained optimization problems We won t have time to go over them thoroughl in this class Calculus and the Consumer s Problem 2: Karush Kuhn Tucker The ultimate tool for constrained optimization problems But I want ou to be aware of them, for two reasons 1. The can make it easier to solve problems we will deal with 2. You will certainl need them if ou take economics further You will not need to use these techniques to solve questions in exams But ou should use them if ou want You ma need them to solve homework questions 23 4
5 Karush Kuhn Tucker 25 Karush Kuhn Tucker 26 Imagine ou have a constrained optimization problem Choose, to Maximize, Subject to f, 0 Choose,, to Maximize,,, f, How do we solve this problem? (in our case f, ) Treat it like an unconstrained optimization problem It turns out that ou can solve this problem b solving a related unconstrained maximization problem Take first derivatives and set them to zero! Choose,, to Maximize,,, f, is the Lagrange Multiplier You can treat it just like another thing to choose (like and ) Karush Kuhn Tucker 27 Karush Kuhn Tucker 28 A worked example:,, Choose, to Maximize, = Subject to First set up the Lagrange Function,, Then take derivatives Then take derivatives First two equations gives the (ver familiar looking!) Last equation gives the (ver familiar looking) Advantages of Karush Kuhn Tucker 29 Karush Kuhn Tucker 30 Wh have I bothered to tell ou this? What is the advantage of this approach? Imagine that we had three goods Choose,, to Maximize,, Subject to Substitution method won t work (we have too man unknowns) Can t draw indifference curves in two dimensions,,,,, Then take derivatives However the KKT approach will still work Four equations, four unknowns will generall be able to find a solution 5
6 A Word of Warning 31 Are KKT solutions alwas the solutions to the consumer s problem? No! KKT conditions find points of tangenc But the usual caveats appl Tangenc are neither necessar or sufficienc for optimalit Solutions ma still be at corners or kinks, or preferences ma be nonmonotonic Also, KKT conditions ma pick out minima instead of maxima Just as when we use differentiation to solve unconstrained optimization problems There are equivalent second order conditions, but ou don t need to worr about them for this course Demand Or, the effect of prices and income Remember this! I will tr to fool ou, and I will catch some of ou! 32 Defining Demand 33 Defining Demand 34 We now know how to solve the consumer s problem This solution depends on budget constraint The prices of the two goods, and the income We define the amount that the consumer will bu, given prices and incomes, as their demand,, Is the amount that the consumer will bu of good one if prices are and and income is * This is the demand function for Similarl,,,is the demand function for * More generall,, is the demand function for good i if the vector of prices p In the next half a lecture, we will think about how demand changes with prices and income How Does Demand Change with? 36 Question 1: how does,, change with? Keeping prices fixed Demand 1: The effect of income on demand 35 6
7 37 38 < < < < < < < < offer curve The curve that unites the optimal choices for various levels of income is called income offer curve or income expansion path Axes are and < < offer curve A plot of quantit demanded against income is called an curve. Axes are and Traditionall is on the vertical axis 7
8 43 44 < < < < offer curve offer curve * * 45 < < offer curve * 46 < < offer curve * < < offer curve * 47 and Cobb- Douglas Preferences * An example of computing the equations of curves; the Cobb-Douglas case. Ux ( 1, x2) x1 a x b 2. The ordinar demand equations are * a * b x1 ; x2. ( a b) p1 ( a b) p2 48 8
9 and Cobb- Douglas Preferences * a * b x1 ; x2. ( a b) p1 ( a b) p2 Rearranged to isolate, these are: ( a b) p 1 * a ( a b) p * 2 b curve for curve for 49 and Cobb- Douglas Preferences ( a b) p 1 * a curve * * for ( a b) p 2 * b curve for 50 and Perfectl- Complementar Preferences Another example of computing the equations of curves; the perfectl-complementar case. Ux ( 1, x2) min x1, x2. The ordinar demand equations are * * x1 x2. p1 p2 51 and Perfectl- Complementar Preferences * * x1 x2. p1 p2 Rearranged to isolate, these are: * ( p1p2) x1 * ( p1p2) x2 curve for curve for < < 9
10 55 56 < < < < < < 57 < < 58 * x * 1 < < 59 ( p1p2) x * 2 60 * ( p x 1 p2) * 1 * x * 1 * 10
11 61 62 Some properties of the curves that we have seen so far: 1. The are straight lines 2. The are upward sloping Is this true in general? Some properties of the curves that we have seen so far: 1. The are straight lines 2. The are upward sloping Is this true in general? Homotheticit It turns out the linear curves come from preferences which are homothetic A consumer s preferences are homothetic if and onl if (, ) ( 1, 2 ) (k,k ) (k 1,k 2 ) for ever k > 0. That is, the consumer s MRS is the same anwhere on a straight line drawn from the origin. i.e. draw a straight line from the origin The slope of indifference curves is the same everwhere along that line MRS the same along a straight line As prices don t change, tangenc point the same along a straight line Offer curve and Engle Curves are straight lines -- A Nonhomothetic Example Are preferences alwas homothetic? No, in fact ou have come across an example of onhomothetic preferences: Quasilinear. For example: 65 Quasi-linear Indifference Curves Each curve is a verticall shifted cop of the others. Each curve intersects both axes. 66 Ux ( 1, x2) x1 x2. 11
12 ; Quasilinear Utilit 67 ; Quasilinear Utilit 68 curve for ~ ~ ~ * ; Quasilinear Utilit curve for 69 ; Quasilinear Utilit 70 curve for * * curve for ~ ~ ~ * Some properties of the curves that we have seen so far: 1. The are straight lines 2. The are upward sloping A good for which quantit demanded rises with income is called normal. Therefore a normal good s curve is positivel sloped. Is this true in general? 12
13 Normal goods offer curve 73 * It is possible to construct examples in which this is not the case 74 * : inferior goods
14 79 80 offer curve 81 curve for 82 curve for * curve for * * 83 Inferior Goods 84 A good for which quantit demanded falls as income increases is called income inferior. Therefore an income inferior good s curve is negativel sloped. So good can be inferior goods But wait: wh? Examples? 14
15 Inferior Goods 85 Elasticit of Demand 86 So good can be inferior goods How do we mathematicall describe the effect of income on demand? But wait: wh? Derivative of the demand function?,, Examples? Cheap objects: the wealthier ou are the less ou bu of them Ramen noodles Often we will instead use the income elasticit of demand,, We can thing of this as the effect of a percentage change in income on the percentage change in demand Elasticit of Demand 87 What is the advantage of using elasticities? One is that the do not depend on the units Imagine that we measure the demand for potatoes in kilos rather than pounds The demand at a given price would change So would the derivation of the demand function However, the elasticit would not change A percentage change is the same whether demand is measured in kilos or pounds Summar Equivalent concept of price elasticit of demand,, 88 Summar 89 Toda we have done the following 1. Provide some more mathematicall sophisticated tools to find tangenc points Derivative based approach Karush Kuhn Tucker Conditions 2. Defined the concept of demand, and shown how the demand for a particular good can change with income 15
Algebra I Notes Linear Functions & Inequalities Part I Unit 5 UNIT 5 LINEAR FUNCTIONS AND LINEAR INEQUALITIES IN TWO VARIABLES
 UNIT LINEAR FUNCTIONS AND LINEAR INEQUALITIES IN TWO VARIABLES PREREQUISITE SKILLS: students must know how to graph points on the coordinate plane students must understand ratios, rates and unit rate VOCABULARY:
UNIT LINEAR FUNCTIONS AND LINEAR INEQUALITIES IN TWO VARIABLES PREREQUISITE SKILLS: students must know how to graph points on the coordinate plane students must understand ratios, rates and unit rate VOCABULARY:
The principal behavioral postulate is. most preferred alternative from those
 Chapter 5 Choice Economic Rationality The principal behavioral postulate is that a decisionmaker chooses its most preferred alternative from those available to it. The available choices constitute the
Chapter 5 Choice Economic Rationality The principal behavioral postulate is that a decisionmaker chooses its most preferred alternative from those available to it. The available choices constitute the
ABSOLUTE EXTREMA AND THE MEAN VALUE THEOREM
 61 LESSON 4-1 ABSOLUTE EXTREMA AND THE MEAN VALUE THEOREM Definitions (informal) The absolute maimum (global maimum) of a function is the -value that is greater than or equal to all other -values in the
61 LESSON 4-1 ABSOLUTE EXTREMA AND THE MEAN VALUE THEOREM Definitions (informal) The absolute maimum (global maimum) of a function is the -value that is greater than or equal to all other -values in the
Topic 2 Transformations of Functions
 Week Topic Transformations of Functions Week Topic Transformations of Functions This topic can be a little trick, especiall when one problem has several transformations. We re going to work through each
Week Topic Transformations of Functions Week Topic Transformations of Functions This topic can be a little trick, especiall when one problem has several transformations. We re going to work through each
Roberto s Notes on Integral Calculus Chapter 3: Basics of differential equations Section 6. Euler s method. for approximate solutions of IVP s
 Roberto s Notes on Integral Calculus Chapter 3: Basics of differential equations Section 6 Euler s method for approximate solutions of IVP s What ou need to know alread: What an initial value problem is.
Roberto s Notes on Integral Calculus Chapter 3: Basics of differential equations Section 6 Euler s method for approximate solutions of IVP s What ou need to know alread: What an initial value problem is.
Homework 2 Solutions
 Homework 2 Solutions Econ 5 - Stanford Universit - Winter Quarter 215/16 Januar 22, 216 Eercise 1: Based on Varian, Microeconomics, 8e, Problem 4.1 A college football coach sas that given an two linemen,
Homework 2 Solutions Econ 5 - Stanford Universit - Winter Quarter 215/16 Januar 22, 216 Eercise 1: Based on Varian, Microeconomics, 8e, Problem 4.1 A college football coach sas that given an two linemen,
LINEAR TOPICS Notes and Homework: DUE ON EXAM
 NAME CLASS PERIOD LINEAR TOPICS Notes and Homework: DUE ON EXAM VOCABULARY: Make sure ou know the definitions of the terms listed below. These will be covered on the exam. Axis Scatter plot b Slope Coordinate
NAME CLASS PERIOD LINEAR TOPICS Notes and Homework: DUE ON EXAM VOCABULARY: Make sure ou know the definitions of the terms listed below. These will be covered on the exam. Axis Scatter plot b Slope Coordinate
Section Graphs and Lines
 Section 1.1 - Graphs and Lines The first chapter of this text is a review of College Algebra skills that you will need as you move through the course. This is a review, so you should have some familiarity
Section 1.1 - Graphs and Lines The first chapter of this text is a review of College Algebra skills that you will need as you move through the course. This is a review, so you should have some familiarity
MATH SPEAK - TO BE UNDERSTOOD AND MEMORIZED
 FOM 11 T9 GRAPHING LINEAR EQUATIONS REVIEW - 1 MATH SPEAK - TO BE UNDERSTOOD AND MEMORIZED 1) -INTERCEPT = the point where the graph touches or crosses the -ais. It occurs when = 0. ) -INTERCEPT = the
FOM 11 T9 GRAPHING LINEAR EQUATIONS REVIEW - 1 MATH SPEAK - TO BE UNDERSTOOD AND MEMORIZED 1) -INTERCEPT = the point where the graph touches or crosses the -ais. It occurs when = 0. ) -INTERCEPT = the
Math 1525 Excel Lab 9 Fall 2000 This lab is designed to help you discover how to use Excel to identify relative extrema for a given function.
 Math 1525 Excel Lab 9 Fall 2 This lab is designed to help ou discover how to use Excel to identif relative extrema for a given function. Example #1. Stud the data table and graph below for the function
Math 1525 Excel Lab 9 Fall 2 This lab is designed to help ou discover how to use Excel to identif relative extrema for a given function. Example #1. Stud the data table and graph below for the function
Pre-Algebra Notes Unit 8: Graphs and Functions
 Pre-Algebra Notes Unit 8: Graphs and Functions The Coordinate Plane A coordinate plane is formed b the intersection of a horizontal number line called the -ais and a vertical number line called the -ais.
Pre-Algebra Notes Unit 8: Graphs and Functions The Coordinate Plane A coordinate plane is formed b the intersection of a horizontal number line called the -ais and a vertical number line called the -ais.
Transformations of Functions. 1. Shifting, reflecting, and stretching graphs Symmetry of functions and equations
 Chapter Transformations of Functions TOPICS.5.. Shifting, reflecting, and stretching graphs Smmetr of functions and equations TOPIC Horizontal Shifting/ Translation Horizontal Shifting/ Translation Shifting,
Chapter Transformations of Functions TOPICS.5.. Shifting, reflecting, and stretching graphs Smmetr of functions and equations TOPIC Horizontal Shifting/ Translation Horizontal Shifting/ Translation Shifting,
MATHEMATICAL METHODS UNITS 3 AND Sketching Polynomial Graphs
 Maths Methods 1 MATHEMATICAL METHODS UNITS 3 AND 4.3 Sketching Polnomial Graphs ou are required to e ale to sketch the following graphs. 1. Linear functions. Eg. = ax + These graphs when drawn will form
Maths Methods 1 MATHEMATICAL METHODS UNITS 3 AND 4.3 Sketching Polnomial Graphs ou are required to e ale to sketch the following graphs. 1. Linear functions. Eg. = ax + These graphs when drawn will form
y = f(x) x (x, f(x)) f(x) g(x) = f(x) + 2 (x, g(x)) 0 (0, 1) 1 3 (0, 3) 2 (2, 3) 3 5 (2, 5) 4 (4, 3) 3 5 (4, 5) 5 (5, 5) 5 7 (5, 7)
 0 Relations and Functions.7 Transformations In this section, we stud how the graphs of functions change, or transform, when certain specialized modifications are made to their formulas. The transformations
0 Relations and Functions.7 Transformations In this section, we stud how the graphs of functions change, or transform, when certain specialized modifications are made to their formulas. The transformations
LINEAR PROGRAMMING. Straight line graphs LESSON
 LINEAR PROGRAMMING Traditionall we appl our knowledge of Linear Programming to help us solve real world problems (which is referred to as modelling). Linear Programming is often linked to the field of
LINEAR PROGRAMMING Traditionall we appl our knowledge of Linear Programming to help us solve real world problems (which is referred to as modelling). Linear Programming is often linked to the field of
3x 4y 2. 3y 4. Math 65 Weekly Activity 1 (50 points) Name: Simplify the following expressions. Make sure to use the = symbol appropriately.
 Math 65 Weekl Activit 1 (50 points) Name: Simplif the following epressions. Make sure to use the = smbol appropriatel. Due (1) (a) - 4 (b) ( - ) 4 () 8 + 5 6 () 1 5 5 Evaluate the epressions when = - and
Math 65 Weekl Activit 1 (50 points) Name: Simplif the following epressions. Make sure to use the = smbol appropriatel. Due (1) (a) - 4 (b) ( - ) 4 () 8 + 5 6 () 1 5 5 Evaluate the epressions when = - and
GRAPHING WORKSHOP. A graph of an equation is an illustration of a set of points whose coordinates satisfy the equation.
 GRAPHING WORKSHOP A graph of an equation is an illustration of a set of points whose coordinates satisfy the equation. The figure below shows a straight line drawn through the three points (2, 3), (-3,-2),
GRAPHING WORKSHOP A graph of an equation is an illustration of a set of points whose coordinates satisfy the equation. The figure below shows a straight line drawn through the three points (2, 3), (-3,-2),
Quadratic Functions In Standard Form In Factored Form In Vertex Form Transforming Graphs. Math Background
 Graphing In Standard Form In Factored Form In Vertex Form Transforming Graphs Math Background Previousl, ou Identified and graphed linear functions Applied transformations to parent functions Graphed quadratic
Graphing In Standard Form In Factored Form In Vertex Form Transforming Graphs Math Background Previousl, ou Identified and graphed linear functions Applied transformations to parent functions Graphed quadratic
In other words, we want to find the domain points that yield the maximum or minimum values (extrema) of the function.
 1 The Lagrange multipliers is a mathematical method for performing constrained optimization of differentiable functions. Recall unconstrained optimization of differentiable functions, in which we want
1 The Lagrange multipliers is a mathematical method for performing constrained optimization of differentiable functions. Recall unconstrained optimization of differentiable functions, in which we want
Algebra I Notes Unit Six: Graphing Linear Equations and Inequalities in Two Variables, Absolute Value Functions
 Sllabus Objective.4 The student will graph linear equations and find possible solutions to those equations using coordinate geometr. Coordinate Plane a plane formed b two real number lines (axes) that
Sllabus Objective.4 The student will graph linear equations and find possible solutions to those equations using coordinate geometr. Coordinate Plane a plane formed b two real number lines (axes) that
LESSON 3.1 INTRODUCTION TO GRAPHING
 LESSON 3.1 INTRODUCTION TO GRAPHING LESSON 3.1 INTRODUCTION TO GRAPHING 137 OVERVIEW Here s what ou ll learn in this lesson: Plotting Points a. The -plane b. The -ais and -ais c. The origin d. Ordered
LESSON 3.1 INTRODUCTION TO GRAPHING LESSON 3.1 INTRODUCTION TO GRAPHING 137 OVERVIEW Here s what ou ll learn in this lesson: Plotting Points a. The -plane b. The -ais and -ais c. The origin d. Ordered
Name: NOTES 5: LINEAR EQUATIONS AND THEIR GRAPHS. Date: Period: Mrs. Nguyen s Initial: LESSON 5.1 RATE OF CHANGE AND SLOPE. A. Finding rates of change
 NOTES : LINEAR EQUATIONS AND THEIR GRAPHS Name: Date: Period: Mrs. Nguen s Initial: LESSON. RATE OF CHANGE AND SLOPE A. Finding rates of change vertical change Rate of change = = change in x The rate of
NOTES : LINEAR EQUATIONS AND THEIR GRAPHS Name: Date: Period: Mrs. Nguen s Initial: LESSON. RATE OF CHANGE AND SLOPE A. Finding rates of change vertical change Rate of change = = change in x The rate of
Learning Objectives for Section Graphs and Lines. Cartesian coordinate system. Graphs
 Learning Objectives for Section 3.1-2 Graphs and Lines After this lecture and the assigned homework, ou should be able to calculate the slope of a line. identif and work with the Cartesian coordinate sstem.
Learning Objectives for Section 3.1-2 Graphs and Lines After this lecture and the assigned homework, ou should be able to calculate the slope of a line. identif and work with the Cartesian coordinate sstem.
Mathematics Stage 5 PAS5.1.2 Coordinate geometry
 Mathematics Stage PAS.. Coordinate geometr Part Graphing lines Acknowledgments This publication is copright New South Wales Department of Education and Training (DET), however it ma contain material from
Mathematics Stage PAS.. Coordinate geometr Part Graphing lines Acknowledgments This publication is copright New South Wales Department of Education and Training (DET), however it ma contain material from
A Short SVM (Support Vector Machine) Tutorial
 A Short SVM (Support Vector Machine) Tutorial j.p.lewis CGIT Lab / IMSC U. Southern California version 0.zz dec 004 This tutorial assumes you are familiar with linear algebra and equality-constrained optimization/lagrange
A Short SVM (Support Vector Machine) Tutorial j.p.lewis CGIT Lab / IMSC U. Southern California version 0.zz dec 004 This tutorial assumes you are familiar with linear algebra and equality-constrained optimization/lagrange
Graphing Linear Equations
 Graphing Linear Equations Question 1: What is a rectangular coordinate system? Answer 1: The rectangular coordinate system is used to graph points and equations. To create the rectangular coordinate system,
Graphing Linear Equations Question 1: What is a rectangular coordinate system? Answer 1: The rectangular coordinate system is used to graph points and equations. To create the rectangular coordinate system,
Increasing/Decreasing Behavior
 Derivatives and the Shapes of Graphs In this section, we will specifically discuss the information that f (x) and f (x) give us about the graph of f(x); it turns out understanding the first and second
Derivatives and the Shapes of Graphs In this section, we will specifically discuss the information that f (x) and f (x) give us about the graph of f(x); it turns out understanding the first and second
15.4 Constrained Maxima and Minima
 15.4 Constrained Maxima and Minima Question 1: Ho do ou find the relative extrema of a surface hen the values of the variables are constrained? Question : Ho do ou model an optimization problem ith several
15.4 Constrained Maxima and Minima Question 1: Ho do ou find the relative extrema of a surface hen the values of the variables are constrained? Question : Ho do ou model an optimization problem ith several
Lagrange multipliers. Contents. Introduction. From Wikipedia, the free encyclopedia
 Lagrange multipliers From Wikipedia, the free encyclopedia In mathematical optimization problems, Lagrange multipliers, named after Joseph Louis Lagrange, is a method for finding the local extrema of a
Lagrange multipliers From Wikipedia, the free encyclopedia In mathematical optimization problems, Lagrange multipliers, named after Joseph Louis Lagrange, is a method for finding the local extrema of a
5.1 Introduction to the Graphs of Polynomials
 Math 3201 5.1 Introduction to the Graphs of Polynomials In Math 1201/2201, we examined three types of polynomial functions: Constant Function - horizontal line such as y = 2 Linear Function - sloped line,
Math 3201 5.1 Introduction to the Graphs of Polynomials In Math 1201/2201, we examined three types of polynomial functions: Constant Function - horizontal line such as y = 2 Linear Function - sloped line,
2.2 Absolute Value Functions
 . Absolute Value Functions 7. Absolute Value Functions There are a few was to describe what is meant b the absolute value of a real number. You ma have been taught that is the distance from the real number
. Absolute Value Functions 7. Absolute Value Functions There are a few was to describe what is meant b the absolute value of a real number. You ma have been taught that is the distance from the real number
Sketching graphs of polynomials
 Sketching graphs of polynomials We want to draw the graphs of polynomial functions y = f(x). The degree of a polynomial in one variable x is the highest power of x that remains after terms have been collected.
Sketching graphs of polynomials We want to draw the graphs of polynomial functions y = f(x). The degree of a polynomial in one variable x is the highest power of x that remains after terms have been collected.
Implicit differentiation
 Roberto s Notes on Differential Calculus Chapter 4: Basic differentiation rules Section 5 Implicit differentiation What ou need to know alread: Basic rules of differentiation, including the chain rule.
Roberto s Notes on Differential Calculus Chapter 4: Basic differentiation rules Section 5 Implicit differentiation What ou need to know alread: Basic rules of differentiation, including the chain rule.
Student Page. Algebra/ Day #4 90 Minute Class Functions, Patterns and X-Y Tables
 Student Page Algebra/ Da #4 90 Minute Class Functions, Patterns and X-Y Tables Definition: A relation is an set of ordered pairs Ex: # {(,), (-7,6), (-,4)} # { (0,8), (-, ), (0,6)} Definition: A function
Student Page Algebra/ Da #4 90 Minute Class Functions, Patterns and X-Y Tables Definition: A relation is an set of ordered pairs Ex: # {(,), (-7,6), (-,4)} # { (0,8), (-, ), (0,6)} Definition: A function
Section 2.2: Absolute Value Functions, from College Algebra: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a
 Section.: Absolute Value Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Section.: Absolute Value Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Math-2. Lesson 3-1. Equations of Lines
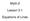 Math-2 Lesson 3-1 Equations of Lines How can an equation make a line? y = x + 1 x -4-3 -2-1 0 1 2 3 Fill in the rest of the table rule x + 1 f(x) -4 + 1-3 -3 + 1-2 -2 + 1-1 -1 + 1 0 0 + 1 1 1 + 1 2 2 +
Math-2 Lesson 3-1 Equations of Lines How can an equation make a line? y = x + 1 x -4-3 -2-1 0 1 2 3 Fill in the rest of the table rule x + 1 f(x) -4 + 1-3 -3 + 1-2 -2 + 1-1 -1 + 1 0 0 + 1 1 1 + 1 2 2 +
5 Day 5: Maxima and minima for n variables.
 UNIVERSITAT POMPEU FABRA INTERNATIONAL BUSINESS ECONOMICS MATHEMATICS III. Pelegrí Viader. 2012-201 Updated May 14, 201 5 Day 5: Maxima and minima for n variables. The same kind of first-order and second-order
UNIVERSITAT POMPEU FABRA INTERNATIONAL BUSINESS ECONOMICS MATHEMATICS III. Pelegrí Viader. 2012-201 Updated May 14, 201 5 Day 5: Maxima and minima for n variables. The same kind of first-order and second-order
Understand the Slope-Intercept Equation for a Line
 Lesson Part : Introduction Understand the Slope-Intercept Equation for a Line Focus on Math Concepts CCLS 8.EE..6 How can ou show that an equation in the form 5 mx b defines a line? You have discovered
Lesson Part : Introduction Understand the Slope-Intercept Equation for a Line Focus on Math Concepts CCLS 8.EE..6 How can ou show that an equation in the form 5 mx b defines a line? You have discovered
Objectives. Materials
 Activity 13 Objectives Understand what a slope field represents in terms of Create a slope field for a given differential equation Materials TI-84 Plus / TI-83 Plus Graph paper Introduction One of the
Activity 13 Objectives Understand what a slope field represents in terms of Create a slope field for a given differential equation Materials TI-84 Plus / TI-83 Plus Graph paper Introduction One of the
Unit 3, Lesson 3.1 Creating and Graphing Equations Using Standard Form
 Unit 3, Lesson 3.1 Creating and Graphing Equations Using Standard Form Imagine the path of a basketball as it leaves a player s hand and swooshes through the net. Or, imagine the path of an Olympic diver
Unit 3, Lesson 3.1 Creating and Graphing Equations Using Standard Form Imagine the path of a basketball as it leaves a player s hand and swooshes through the net. Or, imagine the path of an Olympic diver
L3 Rigid Motion Transformations 3.1 Sequences of Transformations Per Date
 3.1 Sequences of Transformations Per Date Pre-Assessment Which of the following could represent a translation using the rule T (, ) = (, + 4), followed b a reflection over the given line? (The pre-image
3.1 Sequences of Transformations Per Date Pre-Assessment Which of the following could represent a translation using the rule T (, ) = (, + 4), followed b a reflection over the given line? (The pre-image
The big picture and a math review
 The big picture and a math review Intermediate Micro Topic 1 Mathematical appendix of Varian The big picture Microeconomics Study of decision-making under scarcity Individuals households firms investors
The big picture and a math review Intermediate Micro Topic 1 Mathematical appendix of Varian The big picture Microeconomics Study of decision-making under scarcity Individuals households firms investors
Algebra I. Linear Equations. Slide 1 / 267 Slide 2 / 267. Slide 3 / 267. Slide 3 (Answer) / 267. Slide 4 / 267. Slide 5 / 267
 Slide / 67 Slide / 67 lgebra I Graphing Linear Equations -- www.njctl.org Slide / 67 Table of ontents Slide () / 67 Table of ontents Linear Equations lick on the topic to go to that section Linear Equations
Slide / 67 Slide / 67 lgebra I Graphing Linear Equations -- www.njctl.org Slide / 67 Table of ontents Slide () / 67 Table of ontents Linear Equations lick on the topic to go to that section Linear Equations
Increasing/Decreasing Behavior
 Derivatives and the Shapes of Graphs In this section, we will specifically discuss the information that f (x) and f (x) give us about the graph of f(x); it turns out understanding the first and second
Derivatives and the Shapes of Graphs In this section, we will specifically discuss the information that f (x) and f (x) give us about the graph of f(x); it turns out understanding the first and second
EC422 Mathematical Economics 2
 EC422 Mathematical Economics 2 Chaiyuth Punyasavatsut Chaiyuth Punyasavatust 1 Course materials and evaluation Texts: Dixit, A.K ; Sydsaeter et al. Grading: 40,30,30. OK or not. Resources: ftp://econ.tu.ac.th/class/archan/c
EC422 Mathematical Economics 2 Chaiyuth Punyasavatsut Chaiyuth Punyasavatust 1 Course materials and evaluation Texts: Dixit, A.K ; Sydsaeter et al. Grading: 40,30,30. OK or not. Resources: ftp://econ.tu.ac.th/class/archan/c
a) y = x 3 + 3x 2 2 b) = UNIT 4 CURVE SKETCHING 4.1 INCREASING AND DECREASING FUNCTIONS
 UNIT 4 CURVE SKETCHING 4.1 INCREASING AND DECREASING FUNCTIONS We read graphs as we read sentences: left to right. Plainly speaking, as we scan the function from left to right, the function is said to
UNIT 4 CURVE SKETCHING 4.1 INCREASING AND DECREASING FUNCTIONS We read graphs as we read sentences: left to right. Plainly speaking, as we scan the function from left to right, the function is said to
Math Analysis Chapter 1 Notes: Functions and Graphs
 Math Analysis Chapter 1 Notes: Functions and Graphs Day 6: Section 1-1 Graphs Points and Ordered Pairs The Rectangular Coordinate System (aka: The Cartesian coordinate system) Practice: Label each on the
Math Analysis Chapter 1 Notes: Functions and Graphs Day 6: Section 1-1 Graphs Points and Ordered Pairs The Rectangular Coordinate System (aka: The Cartesian coordinate system) Practice: Label each on the
STRAND G: Relations, Functions and Graphs
 UNIT G Using Graphs to Solve Equations: Tet STRAND G: Relations, Functions and Graphs G Using Graphs to Solve Equations Tet Contents * * Section G. Solution of Simultaneous Equations b Graphs G. Graphs
UNIT G Using Graphs to Solve Equations: Tet STRAND G: Relations, Functions and Graphs G Using Graphs to Solve Equations Tet Contents * * Section G. Solution of Simultaneous Equations b Graphs G. Graphs
3.1. 3x 4y = 12 3(0) 4y = 12. 3x 4y = 12 3x 4(0) = y = x 0 = 12. 4y = 12 y = 3. 3x = 12 x = 4. The Rectangular Coordinate System
 3. The Rectangular Coordinate System Interpret a line graph. Objectives Interpret a line graph. Plot ordered pairs. 3 Find ordered pairs that satisfy a given equation. 4 Graph lines. 5 Find x- and y-intercepts.
3. The Rectangular Coordinate System Interpret a line graph. Objectives Interpret a line graph. Plot ordered pairs. 3 Find ordered pairs that satisfy a given equation. 4 Graph lines. 5 Find x- and y-intercepts.
Name Class Date. subtract 3 from each side. w 5z z 5 2 w p - 9 = = 15 + k = 10m. 10. n =
 Reteaching Solving Equations To solve an equation that contains a variable, find all of the values of the variable that make the equation true. Use the equalit properties of real numbers and inverse operations
Reteaching Solving Equations To solve an equation that contains a variable, find all of the values of the variable that make the equation true. Use the equalit properties of real numbers and inverse operations
PATTERNS AND ALGEBRA. He opened mathematics to many discoveries and exciting applications.
 PATTERNS AND ALGEBRA The famous French philosopher and mathematician René Descartes (596 65) made a great contribution to mathematics in 67 when he published a book linking algebra and geometr for the
PATTERNS AND ALGEBRA The famous French philosopher and mathematician René Descartes (596 65) made a great contribution to mathematics in 67 when he published a book linking algebra and geometr for the
UNIT P1: PURE MATHEMATICS 1 QUADRATICS
 QUADRATICS Candidates should able to: carr out the process of completing the square for a quadratic polnomial, and use this form, e.g. to locate the vertex of the graph of or to sketch the graph; find
QUADRATICS Candidates should able to: carr out the process of completing the square for a quadratic polnomial, and use this form, e.g. to locate the vertex of the graph of or to sketch the graph; find
Math Analysis Chapter 1 Notes: Functions and Graphs
 Math Analysis Chapter 1 Notes: Functions and Graphs Day 6: Section 1-1 Graphs; Section 1- Basics of Functions and Their Graphs Points and Ordered Pairs The Rectangular Coordinate System (aka: The Cartesian
Math Analysis Chapter 1 Notes: Functions and Graphs Day 6: Section 1-1 Graphs; Section 1- Basics of Functions and Their Graphs Points and Ordered Pairs The Rectangular Coordinate System (aka: The Cartesian
Section 4.3: How Derivatives Affect the Shape of the Graph
 Section 4.3: How Derivatives Affect the Shape of the Graph What does the first derivative of a function tell you about the function? Where on the graph below is f x > 0? Where on the graph below is f x
Section 4.3: How Derivatives Affect the Shape of the Graph What does the first derivative of a function tell you about the function? Where on the graph below is f x > 0? Where on the graph below is f x
 Specific Objectives Students will understand that that the family of equation corresponds with the shape of the graph. Students will be able to create a graph of an equation by plotting points. In lesson
Specific Objectives Students will understand that that the family of equation corresponds with the shape of the graph. Students will be able to create a graph of an equation by plotting points. In lesson
SNAP Centre Workshop. Graphing Lines
 SNAP Centre Workshop Graphing Lines 45 Graphing a Line Using Test Values A simple way to linear equation involves finding test values, plotting the points on a coordinate plane, and connecting the points.
SNAP Centre Workshop Graphing Lines 45 Graphing a Line Using Test Values A simple way to linear equation involves finding test values, plotting the points on a coordinate plane, and connecting the points.
Section 18-1: Graphical Representation of Linear Equations and Functions
 Section 18-1: Graphical Representation of Linear Equations and Functions Prepare a table of solutions and locate the solutions on a coordinate system: f(x) = 2x 5 Learning Outcome 2 Write x + 3 = 5 as
Section 18-1: Graphical Representation of Linear Equations and Functions Prepare a table of solutions and locate the solutions on a coordinate system: f(x) = 2x 5 Learning Outcome 2 Write x + 3 = 5 as
CHAPTER 5: LINEAR EQUATIONS AND THEIR GRAPHS Notes#26: Section 5-1: Rate of Change and Slope
 Name: Date: Period: CHAPTER : LINEAR EQUATIONS AND THEIR GRAPHS Notes#: Section -: Rate of Change and Slope A. Finding rates of change vertical change Rate of change change in x The rate of change is constant
Name: Date: Period: CHAPTER : LINEAR EQUATIONS AND THEIR GRAPHS Notes#: Section -: Rate of Change and Slope A. Finding rates of change vertical change Rate of change change in x The rate of change is constant
Essential Question: How do you graph an exponential function of the form f (x) = ab x? Explore Exploring Graphs of Exponential Functions. 1.
 Locker LESSON 4.4 Graphing Eponential Functions Common Core Math Standards The student is epected to: F-IF.7e Graph eponential and logarithmic functions, showing intercepts and end behavior, and trigonometric
Locker LESSON 4.4 Graphing Eponential Functions Common Core Math Standards The student is epected to: F-IF.7e Graph eponential and logarithmic functions, showing intercepts and end behavior, and trigonometric
F8-18 Finding the y-intercept from Ordered Pairs
 F8-8 Finding the -intercept from Ordered Pairs Pages 5 Standards: 8.F.A., 8.F.B. Goals: Students will find the -intercept of a line from a set of ordered pairs. Prior Knowledge Required: Can add, subtract,
F8-8 Finding the -intercept from Ordered Pairs Pages 5 Standards: 8.F.A., 8.F.B. Goals: Students will find the -intercept of a line from a set of ordered pairs. Prior Knowledge Required: Can add, subtract,
Using Characteristics of a Quadratic Function to Describe Its Graph. The graphs of quadratic functions can be described using key characteristics:
 Chapter Summar Ke Terms standard form of a quadratic function (.1) factored form of a quadratic function (.1) verte form of a quadratic function (.1) concavit of a parabola (.1) reference points (.) transformation
Chapter Summar Ke Terms standard form of a quadratic function (.1) factored form of a quadratic function (.1) verte form of a quadratic function (.1) concavit of a parabola (.1) reference points (.) transformation
Modeling with CMU Mini-FEA Program
 Modeling with CMU Mini-FEA Program Introduction Finite element analsis (FEA) allows ou analze the stresses and displacements in a bod when forces are applied. FEA determines the stresses and displacements
Modeling with CMU Mini-FEA Program Introduction Finite element analsis (FEA) allows ou analze the stresses and displacements in a bod when forces are applied. FEA determines the stresses and displacements
Tangent line problems
 You will find lots of practice problems and homework problems that simply ask you to differentiate. The following examples are to illustrate some of the types of tangent line problems that you may come
You will find lots of practice problems and homework problems that simply ask you to differentiate. The following examples are to illustrate some of the types of tangent line problems that you may come
The Graph Scale-Change Theorem
 Lesson 3-5 Lesson 3-5 The Graph Scale-Change Theorem Vocabular horizontal and vertical scale change, scale factor size change BIG IDEA The graph of a function can be scaled horizontall, verticall, or in
Lesson 3-5 Lesson 3-5 The Graph Scale-Change Theorem Vocabular horizontal and vertical scale change, scale factor size change BIG IDEA The graph of a function can be scaled horizontall, verticall, or in
Implicit Differentiation - the basics
 x x 6 Implicit Differentiation - the basics Implicit differentiation is the name for the method of differentiation that we use when we have not explicitl solved for in terms of x (that means we did not
x x 6 Implicit Differentiation - the basics Implicit differentiation is the name for the method of differentiation that we use when we have not explicitl solved for in terms of x (that means we did not
Demo 1: KKT conditions with inequality constraints
 MS-C5 Introduction to Optimization Solutions 9 Ehtamo Demo : KKT conditions with inequality constraints Using the Karush-Kuhn-Tucker conditions, see if the points x (x, x ) (, 4) or x (x, x ) (6, ) are
MS-C5 Introduction to Optimization Solutions 9 Ehtamo Demo : KKT conditions with inequality constraints Using the Karush-Kuhn-Tucker conditions, see if the points x (x, x ) (, 4) or x (x, x ) (6, ) are
Chapter 1. Linear Equations and Straight Lines. 2 of 71. Copyright 2014, 2010, 2007 Pearson Education, Inc.
 Chapter 1 Linear Equations and Straight Lines 2 of 71 Outline 1.1 Coordinate Systems and Graphs 1.4 The Slope of a Straight Line 1.3 The Intersection Point of a Pair of Lines 1.2 Linear Inequalities 1.5
Chapter 1 Linear Equations and Straight Lines 2 of 71 Outline 1.1 Coordinate Systems and Graphs 1.4 The Slope of a Straight Line 1.3 The Intersection Point of a Pair of Lines 1.2 Linear Inequalities 1.5
EXAMPLE A {(1, 2), (2, 4), (3, 6), (4, 8)}
 Name class date Understanding Relations and Functions A relation shows how one set of things is related to, or corresponds to, another set. For instance, the equation A 5 s shows how the area of a square
Name class date Understanding Relations and Functions A relation shows how one set of things is related to, or corresponds to, another set. For instance, the equation A 5 s shows how the area of a square
1 MATH 253 LECTURE NOTES for FRIDAY SEPT. 23,1988: edited March 26, 2013.
 1 MATH 253 LECTURE NOTES for FRIDAY SEPT. 23,1988: edited March 26, 2013. TANGENTS Suppose that Apple Computers notices that every time they raise (or lower) the price of a $5,000 Mac II by $100, the number
1 MATH 253 LECTURE NOTES for FRIDAY SEPT. 23,1988: edited March 26, 2013. TANGENTS Suppose that Apple Computers notices that every time they raise (or lower) the price of a $5,000 Mac II by $100, the number
Concept: Slope of a Line
 Concept: Slope of a Line Warm Up Name: The following suggested activities would serve as a review to consolidate previous learning. While promoting rich mathematical dialog, the will also provide students
Concept: Slope of a Line Warm Up Name: The following suggested activities would serve as a review to consolidate previous learning. While promoting rich mathematical dialog, the will also provide students
Lecture 2 Optimization with equality constraints
 Lecture 2 Optimization with equality constraints Constrained optimization The idea of constrained optimisation is that the choice of one variable often affects the amount of another variable that can be
Lecture 2 Optimization with equality constraints Constrained optimization The idea of constrained optimisation is that the choice of one variable often affects the amount of another variable that can be
1. Show that the rectangle of maximum area that has a given perimeter p is a square.
 Constrained Optimization - Examples - 1 Unit #23 : Goals: Lagrange Multipliers To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition).
Constrained Optimization - Examples - 1 Unit #23 : Goals: Lagrange Multipliers To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition).
2. Suppose we drew many tangent lines for this second curve. How do the slopes of these tangent lines change as we look from left to right?
 Do now as a warm up: 1. Suppose we drew many tangent lines for this first curve. How do the slopes of these tangent lines change as we look from left to right? 2. Suppose we drew many tangent lines for
Do now as a warm up: 1. Suppose we drew many tangent lines for this first curve. How do the slopes of these tangent lines change as we look from left to right? 2. Suppose we drew many tangent lines for
3.2 Exercises. rise y (ft) run x (ft) Section 3.2 Slope Suppose you are riding a bicycle up a hill as shown below.
 Section 3.2 Slope 261 3.2 Eercises 1. Suppose ou are riding a biccle up a hill as shown below. Figure 1. Riding a biccle up a hill. a) If the hill is straight as shown, consider the slant, or steepness,
Section 3.2 Slope 261 3.2 Eercises 1. Suppose ou are riding a biccle up a hill as shown below. Figure 1. Riding a biccle up a hill. a) If the hill is straight as shown, consider the slant, or steepness,
Partial Fraction Decomposition
 Section 7. Partial Fractions 53 Partial Fraction Decomposition Algebraic techniques for determining the constants in the numerators of partial fractions are demonstrated in the eamples that follow. Note
Section 7. Partial Fractions 53 Partial Fraction Decomposition Algebraic techniques for determining the constants in the numerators of partial fractions are demonstrated in the eamples that follow. Note
Sec 4.1 Coordinates and Scatter Plots. Coordinate Plane: Formed by two real number lines that intersect at a right angle.
 Algebra I Chapter 4 Notes Name Sec 4.1 Coordinates and Scatter Plots Coordinate Plane: Formed by two real number lines that intersect at a right angle. X-axis: The horizontal axis Y-axis: The vertical
Algebra I Chapter 4 Notes Name Sec 4.1 Coordinates and Scatter Plots Coordinate Plane: Formed by two real number lines that intersect at a right angle. X-axis: The horizontal axis Y-axis: The vertical
5.2 Graphing Polynomial Functions
 Locker LESSON 5. Graphing Polnomial Functions Common Core Math Standards The student is epected to: F.IF.7c Graph polnomial functions, identifing zeros when suitable factorizations are available, and showing
Locker LESSON 5. Graphing Polnomial Functions Common Core Math Standards The student is epected to: F.IF.7c Graph polnomial functions, identifing zeros when suitable factorizations are available, and showing
MA123, Chapter 6: Extreme values, Mean Value Theorem, Curve sketching, and Concavity
 MA123, Chapter 6: Etreme values, Mean Value Theorem, Curve sketching, and Concavit Chapter Goals: Appl the Etreme Value Theorem to find the global etrema for continuous function on closed and bounded interval.
MA123, Chapter 6: Etreme values, Mean Value Theorem, Curve sketching, and Concavit Chapter Goals: Appl the Etreme Value Theorem to find the global etrema for continuous function on closed and bounded interval.
4.1 The Coordinate Plane
 4. The Coordinate Plane Goal Plot points in a coordinate plane. VOCABULARY Coordinate plane Origin -ais -ais Ordered pair -coordinate -coordinate Quadrant Scatter plot Copright McDougal Littell, Chapter
4. The Coordinate Plane Goal Plot points in a coordinate plane. VOCABULARY Coordinate plane Origin -ais -ais Ordered pair -coordinate -coordinate Quadrant Scatter plot Copright McDougal Littell, Chapter
9.1 Linear Inequalities in Two Variables Date: 2. Decide whether to use a solid line or dotted line:
 9.1 Linear Inequalities in Two Variables Date: Key Ideas: Example Solve the inequality by graphing 3y 2x 6. steps 1. Rearrange the inequality so it s in mx ± b form. Don t forget to flip the inequality
9.1 Linear Inequalities in Two Variables Date: Key Ideas: Example Solve the inequality by graphing 3y 2x 6. steps 1. Rearrange the inequality so it s in mx ± b form. Don t forget to flip the inequality
Section 4.3 Features of a Line
 Section.3 Features of a Line Objectives In this section, ou will learn to: To successfull complete this section, ou need to understand: Identif the - and -intercepts of a line. Plotting points in the --plane
Section.3 Features of a Line Objectives In this section, ou will learn to: To successfull complete this section, ou need to understand: Identif the - and -intercepts of a line. Plotting points in the --plane
Chapter12. Coordinate geometry
 Chapter1 Coordinate geometr Contents: A The Cartesian plane B Plotting points from a table of values C Linear relationships D Plotting graphs of linear equations E Horizontal and vertical lines F Points
Chapter1 Coordinate geometr Contents: A The Cartesian plane B Plotting points from a table of values C Linear relationships D Plotting graphs of linear equations E Horizontal and vertical lines F Points
Unit 2 Functions Analyzing Graphs of Functions (Unit 2.2)
 Unit 2 Functions Analzing Graphs of Functions (Unit 2.2) William (Bill) Finch Mathematics Department Denton High School Introduction Domain/Range Vert Line Zeros Incr/Decr Min/Ma Avg Rate Change Odd/Even
Unit 2 Functions Analzing Graphs of Functions (Unit 2.2) William (Bill) Finch Mathematics Department Denton High School Introduction Domain/Range Vert Line Zeros Incr/Decr Min/Ma Avg Rate Change Odd/Even
Constrained Optimization
 Constrained Optimization Dudley Cooke Trinity College Dublin Dudley Cooke (Trinity College Dublin) Constrained Optimization 1 / 46 EC2040 Topic 5 - Constrained Optimization Reading 1 Chapters 12.1-12.3
Constrained Optimization Dudley Cooke Trinity College Dublin Dudley Cooke (Trinity College Dublin) Constrained Optimization 1 / 46 EC2040 Topic 5 - Constrained Optimization Reading 1 Chapters 12.1-12.3
Graphing Review. Math Tutorial Lab Special Topic
 Graphing Review Math Tutorial Lab Special Topic Common Functions and Their Graphs Linear Functions A function f defined b a linear equation of the form = f() = m + b, where m and b are constants, is called
Graphing Review Math Tutorial Lab Special Topic Common Functions and Their Graphs Linear Functions A function f defined b a linear equation of the form = f() = m + b, where m and b are constants, is called
20 Calculus and Structures
 0 Calculus and Structures CHAPTER FUNCTIONS Calculus and Structures Copright LESSON FUNCTIONS. FUNCTIONS A function f is a relationship between an input and an output and a set of instructions as to how
0 Calculus and Structures CHAPTER FUNCTIONS Calculus and Structures Copright LESSON FUNCTIONS. FUNCTIONS A function f is a relationship between an input and an output and a set of instructions as to how
9. p(x) = x 3 8x 2 5x p(x) = x 3 + 3x 2 33x p(x) = x x p(x) = x 3 + 5x x p(x) = x 4 50x
 Section 6.3 Etrema and Models 593 6.3 Eercises In Eercises 1-8, perform each of the following tasks for the given polnomial. i. Without the aid of a calculator, use an algebraic technique to identif the
Section 6.3 Etrema and Models 593 6.3 Eercises In Eercises 1-8, perform each of the following tasks for the given polnomial. i. Without the aid of a calculator, use an algebraic technique to identif the
Forms of Linear Equations
 6. 1-6.3 Forms of Linear Equations Name Sec 6.1 Writing Linear Equations in Slope-Intercept Form *Recall that slope intercept form looks like y = mx + b, where m = slope and b = y=intercept 1) Writing
6. 1-6.3 Forms of Linear Equations Name Sec 6.1 Writing Linear Equations in Slope-Intercept Form *Recall that slope intercept form looks like y = mx + b, where m = slope and b = y=intercept 1) Writing
1 Teaching Objective(s) *Lesson Plan designed for 3-5 days The student will: II (c): complete a function based on a given rule.
 ! "# Teaching Objective(s) *Lesson Plan designed for 3-5 das The student will: II (c): complete a function based on a given rule. II (e): appl the principles of graphing in the coordinate sstem. II (f):
! "# Teaching Objective(s) *Lesson Plan designed for 3-5 das The student will: II (c): complete a function based on a given rule. II (e): appl the principles of graphing in the coordinate sstem. II (f):
3.6 Graphing Piecewise-Defined Functions and Shifting and Reflecting Graphs of Functions
 76 CHAPTER Graphs and Functions Find the equation of each line. Write the equation in the form = a, = b, or = m + b. For Eercises through 7, write the equation in the form f = m + b.. Through (, 6) and
76 CHAPTER Graphs and Functions Find the equation of each line. Write the equation in the form = a, = b, or = m + b. For Eercises through 7, write the equation in the form f = m + b.. Through (, 6) and
Chapter 4: Utility Function
 Econ Microeconomic Analysis Chapter : Utility Function Instructor: Hiroki Watanabe Spring Watanabe Econ Utility Function / Introduction Utility Function Indifference Curves Examples Trinity Now We Know
Econ Microeconomic Analysis Chapter : Utility Function Instructor: Hiroki Watanabe Spring Watanabe Econ Utility Function / Introduction Utility Function Indifference Curves Examples Trinity Now We Know
Tangents of Parametric Curves
 Jim Lambers MAT 169 Fall Semester 2009-10 Lecture 32 Notes These notes correspond to Section 92 in the text Tangents of Parametric Curves When a curve is described by an equation of the form y = f(x),
Jim Lambers MAT 169 Fall Semester 2009-10 Lecture 32 Notes These notes correspond to Section 92 in the text Tangents of Parametric Curves When a curve is described by an equation of the form y = f(x),
Exponential Functions. Christopher Thomas
 Mathematics Learning Centre Eponential Functions Christopher Thomas c 1998 Universit of Sdne Mathematics Learning Centre, Universit of Sdne 1 1 Eponential Functions 1.1 The functions =2 and =2 From our
Mathematics Learning Centre Eponential Functions Christopher Thomas c 1998 Universit of Sdne Mathematics Learning Centre, Universit of Sdne 1 1 Eponential Functions 1.1 The functions =2 and =2 From our
Module 2, Section 2 Graphs of Trigonometric Functions
 Principles of Mathematics Section, Introduction 5 Module, Section Graphs of Trigonometric Functions Introduction You have studied trigonometric ratios since Grade 9 Mathematics. In this module ou will
Principles of Mathematics Section, Introduction 5 Module, Section Graphs of Trigonometric Functions Introduction You have studied trigonometric ratios since Grade 9 Mathematics. In this module ou will
Week 3. Topic 5 Asymptotes
 Week 3 Topic 5 Asmptotes Week 3 Topic 5 Asmptotes Introduction One of the strangest features of a graph is an asmptote. The come in three flavors: vertical, horizontal, and slant (also called oblique).
Week 3 Topic 5 Asmptotes Week 3 Topic 5 Asmptotes Introduction One of the strangest features of a graph is an asmptote. The come in three flavors: vertical, horizontal, and slant (also called oblique).
slope rise run Definition of Slope
 The Slope of a Line Mathematicians have developed a useful measure of the steepness of a line, called the slope of the line. Slope compares the vertical change (the rise) to the horizontal change (the
The Slope of a Line Mathematicians have developed a useful measure of the steepness of a line, called the slope of the line. Slope compares the vertical change (the rise) to the horizontal change (the
Did you ever think that a four hundred year-old spider may be why we study linear relationships today?
 Show Me: Determine if a Function is Linear M8221 Did you ever think that a four hundred year-old spider may be why we study linear relationships today? Supposedly, while lying in bed Rene Descartes noticed
Show Me: Determine if a Function is Linear M8221 Did you ever think that a four hundred year-old spider may be why we study linear relationships today? Supposedly, while lying in bed Rene Descartes noticed
Name: Date: Absolute Value Transformations
 Name: Date: Absolute Value Transformations Vocab: Absolute value is the measure of the distance awa from zero on a number line. Since absolute value is the measure of distance it can never be negative!
Name: Date: Absolute Value Transformations Vocab: Absolute value is the measure of the distance awa from zero on a number line. Since absolute value is the measure of distance it can never be negative!
Graphing. I ll put this information together with some other techniques into a step-by-step graphing procedure. Here it is:
 Graphing 1010005 Calculus provides information which is useful in graphing curves. The first derivative y tells where a curve is increasing and where a curve is decreasing. The second derivative y tells
Graphing 1010005 Calculus provides information which is useful in graphing curves. The first derivative y tells where a curve is increasing and where a curve is decreasing. The second derivative y tells
CCNY Math Review Chapter 2: Functions
 CCN Math Review Chapter : Functions Section.1: Functions.1.1: How functions are used.1.: Methods for defining functions.1.3: The graph of a function.1.: Domain and range.1.5: Relations, functions, and
CCN Math Review Chapter : Functions Section.1: Functions.1.1: How functions are used.1.: Methods for defining functions.1.3: The graph of a function.1.: Domain and range.1.5: Relations, functions, and
