Variable Resolution Spatial Interpolation Using the Simple Recursive Point Voronoi Diagram
|
|
|
- Roy Randall
- 6 years ago
- Views:
Transcription
1 Geographical Analysis ISSN Using the Simple Recursive Point Voronoi Diagram Robert Feick, 1 Barry Boots 2 1 Department of Geography, School of Planning, University of Waterloo, Waterloo, ON, Canada, 2 Department of Geography and Environmental Studies, Wilfrid Laurier University, Waterloo, ON, Canada This article introduces a procedure for progressively increasing the density of an initial point set that can be used as a basis for interpolating surfaces of variable resolution from sparse samples of data sites. The procedure uses the Simple Recursive Point Voronoi Diagram in which Voronoi concepts are used to tessellate space with respect to a given set of generator points. The construction is repeated every time with a new generator set, which comprises members selected from the previous generator set plus features of the current tessellation. We show how this procedure can be implemented in Arc/Info and present an illustration of its application using three known surfaces and alternative generator point configurations. Initial results suggest that the procedure has considerable potential and we discuss further methods for evaluating and extending it. Introduction Spatial data consist of measurements (data values) of an attribute taken at specific locations (data sites) in a geographic space (study region). In much of the data collected in the environmental sciences, the attribute is assumed to be spatially continuous (possibly piecewise) so that the data values can be considered as a sampling of the attribute at the data sites. Suppose that our primary aim is to use the data to interpolate the values of the attribute at locations other than the data sites, thus enabling us to create a visual representation of the underlying surface (Watson 1992). This task can be considered as a specific instance of the more general problem of approximating surfaces that arises in a variety of applications in computeraided design, computer graphics, computer vision, and finite element methods. In some applications, where the number of data sites is very large, it may not be necessary to use all the data sites in order to capture the fundamental features of the Correspondence: Robert Feick, Department of Geography, University of Waterloo, Waterloo, Canada ON N2L 3G1 rdfeick@fes.uwaterloo.ca Submitted: November 11, Revised version accepted: June 6, Geographical Analysis 37 (2005) r 2005 The Ohio State University 225
2 Geographical Analysis surface. Instead, a representative subset of data sites, which enables the surface to be represented with a prespecified level of accuracy, can be selected. This can be achieved either by a process of simplification (also referred to as decimation or coarsening) in which we start with the complete set of data sites and remove some of them or by a process of refinement when we start with an insufficient subset of data sites and add additional ones (see Garland [1999] and De Floriani and Magillo [2002] for reviews). However, there are also situations where the data sites are sparse and there is no possibility of supplementing their number by increasing the size of the sample. Typically, this applies to most historical data. Further, notwithstanding advances in remote sensing and global positioning system data collection methods, in some instances it can still be impractical or too costly to collect appropriately detailed data. In addition, with historical data, we may also lack knowledge of the sampling design, although some characteristics may be inferred from the spatial distribution of data sites. Much less attention has been applied to this situation, which is the focus of this article. We propose a procedure for progressively increasing the density of an initial point set that provides a basis for interpolating surfaces of variable resolution from sparse samples of data sites. The procedure makes use of the simple recursive point Voronoi diagram (SRPVD). Our proposal is motivated by both practical and conceptual considerations. Practically, the procedure can be fully automated and implemented within existing commercial off-the-shelf (COTS) software. Conceptually, it is supported by recognition of the dual relationships between Voronoi and Delaunay constructions. The latter have a long history of use in terrain modeling and visualization, with the Delaunay triangulation being the most popular method of constructing a triangulated irregular network (TIN; Hutchinson and Gallant 1999). In part, this is because it is the only triangulation that satisfies both local and global max min angle criteria (Sibson 1978; Okabe et al. 2000, p. 93). Wang et al. (2001) also demonstrate that the basic Delaunay triangulation even outperforms data-dependent triangulations in modeling terrain surfaces. Further, several recursive forms of Delaunay triangulations have already been used as top-down, multiresolution TIN models in the refinement process described above (see De Floriani, Marzano, and Puppo 1996; De Floriani et al for reviews). These include strictly hierarchical TINs (HTINs), which involve the recursive subdivision of the initial triangle(s) into a set of nested triangles (De Floriani and Puppo 1992, 1995), and nonnested, pyramidal TINs (PTINs) in which a new structure is computed every time new points are inserted (De Floriani, Falcidieno, and Pienovi 1985; De Floriani 1989; Voightmann, Becker, and Hinrichs 1994). It will become apparent below that, in essence, the SRPVD is a dual form of PTIN. We begin our presentation by describing recursive Voronoi diagrams in general terms and providing a specific definition of the SRPVD. We then show how these constructions can be used to create surfaces of varying spatial resolution. In the third main section we describe how these procedures can be implemented in Arc/ 226
3 Robert Feick and Barry Boots Info. This is followed in the fourth section by an application of the procedure to point samples drawn from three known topographic surfaces using three different sampling designs. We conclude by discussing outstanding issues and directions for future work. Recursive Voronoi diagrams The basic Voronoi concept involves tessellating an m-dimensional space with respect to a finite set of objects by assigning all locations in the space to the closest member of the object set. This concept can also be applied recursively by tessellating the space with respect to a given set of generators and then repeating the construction every time with a new generator set consisting of objects selected from the previous generator set plus features of the current tessellation. More formally, consider a finite set of n distinct generators, G. First, construct the Voronoi diagram V(G) ofg. Next, extract a set of features Q from V(G) and create a new set of generators G 0 that comprises Q plus selected members of G. Then construct the Voronoi diagram V(G 0 )ofg 0. This step is then repeated a number of times. At each step, the number of generators that are retained may range from none to all. Boots and Shiode (2003) show that such recursive constructions provide an integrative conceptual framework for a number of disparate procedures in spatial analysis and modeling. Simple recursive point Voronoi diagram In this article, we consider a specific form of recursive Voronoi diagram, the SRPVD, in which the initial set of generators consists of n distinct points G (0) 5 {g (0)1, g (0)2,...,g (0)n }. The construction of this diagram involves the following steps: 0. define the initial set of generators G (0) ; 1. generate the ordinary Voronoi diagram V(G (0) )ofg (0) ; 2. extract all m(0) Voronoi vertices Q (0) 5 {q (0)1, q (0)2,...,q (0)m(0) }ofv(g (0) ); 3. create a new set of generator points G (1) 5 G (0) 1Q (0) ;and 4. repeat steps 1 through 3. We call the result of the kth construction, V(G (k) ), the kth generation of the SRPVD. Similarly, we call its generator set G (k) and its vertices Q (k) the kth generation of the point set and the kth generation of the vertices, respectively. The results of applying these steps for five recursions to an initial generator set consisting of five points are shown in Fig. 1. Note that the Voronoi polygons at generation k are either entirely contained within a Voronoi polygon at generation (k 1), that is, V(G (k)i ) V(G (k 1)i ), or are composed of pieces of three polygons from generation (k 1), that is, V(G (k)i ) 5 (V(G (k)i ) \ V(G (k 1)l )) [ (V(G (k)i ) \ V(G (k 1)m )) [ (V(G (k)i ) \ V(G (k 1)n )) (see Fig. 2). As noted above, a recursive 227
4 Geographical Analysis Figure 1. The first five recursions of a simple recursive point Voronoi diagram. Voronoi structure will have a dual recursive Delaunay structure. The recursive Delaunay construction that is equivalent to the SRPVD is defined as follows: 0. define the initial set of generators G (0) ; 1. generate the Delaunay triangulation D (0) of G (0) ; 2. identify the circumcenters C (0) 5 {c (0)1,...,c (0)m } of all the triangles of D (0) ; 3. create a new set of generator points G (1) 5 G (0) 1C (0) ; and 4. repeat steps 1 and 3. Figure 2. Simple recursive point Voronoi diagram generations
5 Robert Feick and Barry Boots From this description, it will be seen that our procedure is similar to the refinement strategies that have been used in some of the other application areas noted in the Introduction. A common feature of these strategies is that they start with a triangulation of the data sites, insert one or more points in each triangle, and then build another triangulation. While our procedure inserts new points at the circumcenters of the triangles, others insert points at other locations within the triangles or on their edges (e.g., Scarlatos and Pavlidis 1992; De Floriani and Puppo 1995; Cignoni, Puppo, and Scopigno 1997; Klein and Straer 1997). Using the SRPVD to construct variable resolution surfaces Using the SRPVD, the following procedure can be used to produce topographic surfaces that have increasing spatial resolution: Let G (0) be an initial set of generators, each with an associated data value, and label the set of data values D (0). Generate V(G (0) ). Extract the set Q (0) consisting of the m (0) vertices of V(G (0) ). Extrapolate data values for Q (0) using Sibson s natural neighbor interpolation (Sibson 1981) and D (0). Label extrapolated values D (1). If desired, create surface representation from D (0) 1D (1). Let G (1) 5 G (0) 1Q (0). Generate V(G (1) ). Extract the set Q (1) consisting of the m (1) vertices of V(G (1) ). Extrapolate data values for Q (1) using Sibson s natural neighbor interpolation and D (0) 1D (1). Label extrapolated values D (2). If desired, create surface representation from D (0) 1D (1) 1D (2).. Let G (k) 5 G (k 1) 1Q (k 1). Generate V(G (k) ). Extract the set Q (k) consisting of the m (k) vertices of V(G (k) ). Extrapolate data values for Q (k) using Sibson s natural neighbor interpolation and D ð0þ þ D ð1þ þþd ðkþ. Label extrapolated values D (k11). If desired, create surface representation from D ð0þ þ D ð1þ þþd ðkþ1þ. We use Sibson s interpolation procedure because the input it requires is readily obtained from two successive generations of the SRPVD. For generators in the general quadratic position, each interpolated value in D (k11) will be interpolated from three values in D ð0þ þ D ð1þ þþd ðkþ.ifd (k11)i is the interpolated value at Q (k)i and V(Q (k)i ) is the Voronoi polygon of Q (k)i, and V(Q (k)i ) is the area of V(Q (k)i ), 229
6 Geographical Analysis then Note that: D ðkþ1þi ¼ X3 p¼1 jvðq ðkþi Þj ¼ X3 jvðq ðkþi Þ\VðQ ðk 1Þp Þj D ðkþp jvðq ðkþi Þj p¼1 jvðq ðkþi Þ\VðQ ðk 1Þp Þj ð1þ By selecting vertices exclusively, an entire set of interpolated values can be generated in one pass. Further, vertices may be considered as locally optimal sites for new data interpolation locations because they maximize the distance from triples of existing interpolation locations. Operationalizing SRPVD construction in Arc/Info The SRPVD constructions described in this article were built with the Arc/Info 8.3 geographical information system platform. The input consists of a set of generator seed points, the G (0) generator set described in the previous section, and an associated set of attribute values. These data, which we refer to as Gen_i_Pts, were used as the basis for each of five Voronoi recursions. The general procedure for generating the SRPVD construction is as follows with specific Arc/Info commands identified for reference in Courier font: 1. Create a Voronoi polygon coverage for Generation i (Gen_i_VD) Gen_i_Pts using Thiessen. 2. Build node and line topology for Gen_i_VD. 3. Add a Gen field to the node attribute table of the Gen_i_VD coverage to track the age of each point. The value of the Gen field is set to i for all nodes. 4. Convert all nodes in Gen_i_VD to a point coverage (VD_i_Pts) using Node- Point. 5. Create Gen_i11_Pts coverage by Appending Gen_i_Pts and the VD_i_Pts. 6. Repeat steps 1 5 based on the updated Gen_i11_Pts coverage for k generations. Fig. 2 illustrates this procedure for generations 0 2. In practice, although the Voronoi structure is not bounded in a conceptual sense, a spatial limit needs to be established to minimize the impact of edge effects on subsequent analyses. This is discussed further in the next section. Next, attribute values for the new data points created using the process described above are interpolated on a generation-by-generation basis. The interpolation procedure is summarized below and is also illustrated in Fig. 3: 1. Union Gen_i_VD and Gen_i11_VD Voronoi polygon coverages to create a Union_i_i11 polygon coverage. 230
7 Robert Feick and Barry Boots Figure 3. Interpolation procedure example. 2. Establish relates between Union_i_i11, Gen_i_VD, and Gen_i11_VD. Calculate the ratio of each Union_i_i11 polygon s area relative to the area of the corresponding parent VD_i polygon (see shaded polygons in Fig. 3). Store the value in a PercentArea field. 3. Calculate the attribute value being interpolated for each Union_i_i11 polygon as PercentArea the attribute value recorded for the parent Gen_i_VD polygon. Store the value in a CalcAttribute field. 4. Use statistics on the Union_i_i11 coverage to create a summary table (Gen_i_stats) that lists the sum of the CalcAttribute field for each Gen_ i11_vd polygon. 5. Reselect the Gen_i11_VD and Gen_i11_Pts features for generation i11 and transfer the corresponding interpolated values from the Gen_i_stats table using relates. Illustrations To demonstrate our procedure, we applied it to known second-, third-, and fourthorder surfaces shown in Figs For convenience, these surfaces are referred to as Surfaces A, B, and C. The elevation ranges of these surfaces are 4185, 3194, and 2414 units, respectively. Three initial generator sets (sets of data sites) were considered for each surface in order to investigate the impact of generator set configuration on the results. The 121 points in the generator sets were arranged according to a randomly jittered square (JS), a stratified random (SR), and a triangular grid (TG) sampling design. Figs. 4 6 each illustrate one of these generator point configurations. 231
8 Geographical Analysis Figure 4. Surface A with jittered square generator set. Figure 5. Surface B with stratified random generator set. 232
9 Robert Feick and Barry Boots Figure 6. Surface C with triangular grid generator set. We used the procedure described in the section on Using the SRPVD to construct variable resolution surfaces to generate additional data sites and data values up to the 5th generation of the SRPVD. Column 2 in Table 2 ( All points ) lists the number of the data sites by generation from the initial point set (generation 0) to generation 5. The corresponding data for Surfaces B and C are provided in Tables 3 and 4. We undertook a series of error analyses to assess the performance of our procedure by comparing the elevation values calculated for new data points with values generated using the trend surface coefficients listed in Table 1. We recognize that our procedure, like all interpolation procedures, is subject to edge effects. Consequently, although we allowed new data points to be generated beyond the boundary of the convex hull of the sample points, we did not consider associated with such points. Columns 3, 6, and 9 ( Points examined ) in Tables 2 4 list the number of data points that remain in the analysis. As the JS, SR, and TG generator sets produce unique convex hulls, the number of points examined differs slightly across the three sample configurations. Note that the remaining content of Tables 2 4 (i.e., Extreme error columns) is discussed later in this section. To examine overall performance, we calculated both the mean absolute error (MAE) and the root-mean-squared error (RMSE) by generation (see Figs. 7 9). MAE is less sensitive to large than RMSE and so gives a better picture of the overall performance of the interpolation. Figs. 7 9 show MAE and RMSE by generation for 233
10 Geographical Analysis Table 1 Coefficients of Trend Surfaces Coefficient Surface A Surface B Surface C Constant 12, x y x E E 006 xy E E E 006 y E E E 005 x E E E 011 x 2 y E E E 011 xy E E E 011 y E E E 011 x E E 017 x 3 y E E 017 x 2 y E E 017 xy E E 017 y E E 016 x E 023 x 4 y E 023 x 3 y E 023 x 2 y E 023 xy E 022 y E 023 Surfaces A C. Note that as the elevation ranges differ across the three surfaces, MAE and RMSE are expressed as percentages to permit comparisons of error. Figs. 7 9 show that the average MAE over all generations is relatively small at less than 1.5 percent of the elevation ranges. For all three surfaces, there is a noticeable reduction in MAE between the first two generations, after which MAE stabilizes. The MAE values for the TG sample design prove to be an exception to this general statement as they increase from generation 2 to 3 before stabilizing. The behavior of RMSE is more variable, in part, reflecting its sensitivity to extreme. Nevertheless, the average RMSE for the JS and SR samples are still relatively low at approximately 2 percent of their elevation ranges. The RMSE (and, to a lesser extent, the MAE) values for the SR generator set were affected by three generation 5 data points that were assigned very low elevation values in the interpolation procedure. Some 15 generation 5 data points in the TG generator runs were also affected by this problem which caused the TG RMSE values on all three surfaces to increase noticeably at generation 5. The cause of these particular is the subject of ongoing investigation. Given the large number of data points associated with the later generations of the SRPVD construction, we focused further analyses on absolute of at least 5 percent of the elevation range of a surface. We label these extreme. The 234
11 Robert Feick and Barry Boots Table 2 Simple Recursive Point Voronoi Diagram (SRPVD) Generated Data Points and Extreme Errors by Generation (Gen.) Surface A Gen. All points Jittered square Stratified Random Triangular Grid Points # examined Extreme % Extreme Points # examined Extreme % Extreme Points # examined Extreme % Extreme ,764 16, , , Totals 29,645 24, , , With Surface A, an SRPVD data point is classed as an extreme error if its interpolated value deviates (1 or ) by 209 m from the corresponding trend surface value. number of extreme associated with Surfaces A C are listed in Tables 2 4 by generation and by generator set (i.e., JS, SR, TG). As the number of data points differ across generations and across sampling designs, the tables also report extreme as percentages of the number of points examined. The last rows in Tables 2 4 show that when an entire set of points (generations 1 5) is considered, extreme account for between 1.8 and 8.1 percent of the data points. Interestingly, the RS sampling design appeared to perform the best across all three surfaces, followed closely by the JS generator set. In contrast, the TG sample proved to have the highest number of extreme. We anticipated that would be most evident in the earliest generations because, on average, these points would be furthest from the initial generator points. When the proportion of extreme are considered, this assumption appears to be valid for the JS and RS samples on Surfaces A and B as the highest Table 3 Simple Recursive Point Voronoi Diagram (SRPVD) Generated Data Points and Extreme Errors by Generation (Gen.) Surface B Gen. All points Jittered square Stratified random Triangular grid Points # examined Extreme % Extreme Points # examined Extreme % Extreme Points # examined Extreme % Extreme ,764 16, , , Totals 29,645 24, , , With Surface B, an SRPVD data point is classed as an extreme error if its interpolated value deviates (1 or ) by 160 m from the corresponding trend surface value. 235
12 Geographical Analysis Table 4 Simple Recursive Point Voronoi Diagram (SRPVD) Generated Data Points and Extreme Errors by Generation (Gen.) Surface C Gen. All points Jittered square Stratified random Triangular grid Points # Extreme % examined Extreme Points # Extreme % examined Extreme Points # Extreme % examined Extreme ,764 16, , , Totals 29,645 24, , , With Surface C, an SRPVD data point is classed as an extreme error if its interpolated value deviates (1 or ) by 121 m from the corresponding trend surface value. percent of extreme is found in generation 1. Tables 2 4 indicate that this claim cannot be made for the TG sample as only one extreme error was recorded across all three surfaces up to generation 2, after which the proportion of extreme increased substantially. We also expected that the magnitude of would be highest in the earlier generations. However, the greatest occurred in generation 5 in all cases. This suggests that are propagated with advancing generations. This effect is most evident with increasing proximity to the edge of the study area (i.e., the convex hull). By generation 5, the SRPVD procedure produces relatively dense Figure 7. Mean absolute error (MAE) and root-mean-squared error (RMSE) Surface A. 236
13 Robert Feick and Barry Boots Figure 8. Mean absolute error (MAE) and root-mean-squared error (RMSE) Surface B. concentrations of new data points in this area; hence, edge effects could be more pronounced at this level. In addition to examining the overall level of interpolation error, we were interested in the spatial distribution of error. In Figs , the extreme associated with selected surface and generator set combinations are displayed in Figure 9. Mean absolute error (MAE) and root-mean-squared error (RMSE) Surface C. 237
14 Geographical Analysis Figure 10. Surface A extreme jittered square generators. three dimensions (see for the complete set of figures). Positive (overestimates) are shown as dark-colored extrusions above the surface in these figures, while negative (underestimates) are shown as light extrusions that extend below the surface. No vertical exaggeration was applied to the surfaces; however, the magnitude of the was multiplied by 3 to produce Z-values that could be more easily visualized. For convenience, Surfaces A C are shown extending somewhat beyond the convex hulls associated with the JS, RS, and TG generator sets. Figs show that negative are both more common and generally of a greater magnitude than positive. As underestimation is more evident as surface complexity increases, we suspect that at least part of this tendency is related to the generator sets being insufficient in size to capture topographic variations adequately. The figures also show that most of the extreme are concentrated around the edges of the convex hulls formed by the initial generator points. This is particularly apparent for the TG generator set (see Fig. 13) as all of the extreme for all three surfaces are found in proximity to the periphery of the study area. This suggests that the associated with the TG sample are at least partially an artifact of the original point configuration given that the generators were located on a nonequilateral triangular grid. The presence of the 15 most pronounced extreme Figure 11. Surface A extreme stratified random generators. 238
15 Robert Feick and Barry Boots Figure 12. Surface B extreme stratified random generators. does account for the high RMSE values evident for generations 3 5 of the TG generator set as well. The interior in the JS and RS figures show no obvious spatial distribution although there is a tendency for them to be located in small local clusters. While some of these clusters appear to be associated with initial generator points, this does not appear to be a general tendency. Indeed, we had anticipated that there might be a positive relationship between error magnitude at a generated location and the distance of that location to the nearest initial generator point. However, with the exception of the 1st generation of some surface and sample design combinations, this relationship was not found. As an example, Fig. 16 shows the situation for Surface A and the JS generator set. In this figure, the distance of each extreme error point to the nearest generator point (generation 0) is plotted. Based on the arrangement of the JS generator points, the furthest a new data point could be from a generator point would be approximately 25,000 m. In contrast, the largest concentration of extreme occurs at distances between 7000 and 12,000 m. Discussion and conclusions The primary aim of this article was to introduce an automated method, based on the SRPVD, for progressively increasing the density of an initial point set, thus providing a basis for interpolating surfaces of variable resolution from sparse samples of Figure 13. Surface B extreme Triangular grid generators. 239
16 Geographical Analysis Figure 14. Surface C extreme jittered square generators. data sites. As we show, an attractive feature of this procedure is that it can be readily implemented in Arc/Info. In our illustrative examples, absolute in excess of 5 percent of the variable ranges generally occurred at less than 5 percent of the generated data sites. Clearly, the global error measurements (e.g., MAE, RMSE, extreme error counts) discussed were affected by the general problem of interpolating data values near a study area boundary. However, the lack of systematic relationships between error values and characteristics of either the underlying surface or the initial point set suggests that the procedure may be robust with respect to these features. Further, the observation that, after an initial change, the average level of error remains relatively constant may be a desirable feature for those who require a multiresolution hierarchical data set with little variation in accuracy at different levels. For example, in hydrological modelling, one may wish to use a finer spatial resolution for detailed model runs while maintaining consistency with coarser resolutions used for cruder models. However, in order to confirm our initial findings much more testing needs to be carried out. For example, we need to further explore the sensitivity of the results for a given surface to different spatial sampling designs for selecting the generator points and to different sizes of generator point sets. We also need to consider a range of surfaces with different characteristics, especially more complex surfaces. Also, of course, we need to compare the performance of the procedure relative to other COTS interpolation procedures. Figure 15. Surface C extreme stratified random generators. 240
17 Robert Feick and Barry Boots Figure 16. Surface A extreme and generator proximity jittered square generators. Notwithstanding the need for further testing, there are several ways the procedure may be refined and extended. For example, it is possible, and probably desirable, not to add all the Voronoi vertices of a given generation to the generator set for the next generation. In the present context, there are at least two circumstances where this would be appropriate. First, we may wish to constrain the new generators to those within a specific distance range of existing generators. If the potential new generators are very close to existing ones, we can expect that they may add little new information and thus may be discarded. Similarly, if a potential new generator is more than some specified distance from an existing generator it may be unwise to extend interpolation to that generator. One means of identifying such an upper limit would be to use the characteristics of the semi-variogram of the initial data points, perhaps limiting new generators to those whose distance to existing generators is less than half of the range of the semi-variogram. A similar strategy has been used successfully in the choice of control points in classification of spatial imagery into classes (Shine and Wakefield 1999) and in two other articles in this issue (Goovaerts 2005; Kyriakidis and Yoo 2005). We may also wish to relate the addition of new generators to the nature of local changes in attribute values. While it is useful to have increased resolution in areas where there are marked changes in attribute values, little is gained by increasing the resolution in areas where there is little variation. There has already been some initial consideration of such a generator constrained recursive point Voronoi diagram (Boots et al. 2002). Although we illustrated our procedure using quantitative data, it is also applicable to categorical data. In this case, instead of a single value being interpolated at each generated point, a vector of fuzzy membership values (FMVs) for classes can be interpolated (Lowell 1994) and equation (1) will need to be adjusted accord- 241
18 Geographical Analysis ingly. FMV surfaces can then be generated for each class. Alternatively, at each recursion, each polygon can be labeled with the value of its generator and these values mapped to create a piecewise continuous surface (choropleth map). Acknowledgements We are grateful for the helpful comments of three anonymous reviewers and the guest editor, which led to improvements in both the article s content and presentation. References Boots, B., R. D. Feick, N. Shiode, and S. Roberts. (2002). Investigating Recursive Point Voronoi Diagrams. In Geographic Information Science: Second International Conference, GIScience 2002, Boulder, CO, USA, September Lecture Notes in Computer Science, Vol. 2478: 1 21, edited by M. J. Egenhofer and D. M. Mark. Berlin, Germany: Springer-Verlag. Boots, B., and N. Shiode. (2003). Recursive Voronoi Diagrams. Environment and Planning B: Planning and Design 30, Cignoni, P., E. Puppo, and R. Scopigno. (1997). Representation and Visualization of Terrain Surfaces at Variable Resolutions. The Visual Computer 13, De Floriani, L. (1989). A Pyramidal Data Structure for Triangle-Based Surface Description. IEEE Computer Graphics and Applications 9, De Floriani, L., B. Falcidieno, and C. Pienovi. (1985). Delaunay-Based Representation of Surfaces Defined over Arbitrarily Shaped Domains. Computer Vision, Graphics, and Image Processing 32, De Floriani, L., and P. Magillo. (2002). Multiresolution Mesh Representation: Models and Data Structures. In Multiresolution in Geometric Modelling, , edited by M. Floater, A. Iske, and E. Quak. Berlin, Germany: Springer-Verlag. De Floriani, L., P. Magillo, S. Bussi, and E. Bailey. (2000). Triangle-Based Surface Models. In Intelligent Systems and Robotics, , edited by G. W. Zobrist and C. Y. Ho. Australia: Gordon and Breach Scientific Publishers. De Floriani, L., P. Marzano, and E. Puppo. (1996). Multiresolution Models for Terrain Surface Description. The Visual Computer 12, De Floriani, L., and E. Puppo. (1992). A Hierarchical Triangle-Based Model for Terrain Description. In Theories and Methods of Spatio-Temporal Reasoning in Geographic Space. Lecture Notes in Computer Science, Vol. 639: , edited by A. Frank, I. Campari, and U. Formentini. Berlin, Germany: Springer-Verlag. De Floriani, L., and E. Puppo. (1995). Hierarchical Triangulation for Multi-Resolution Surface Description. ACM Transactions on Graphics 14, Garland, M. (1999). Multiresolution Modeling: Survey & Future Opportunities. Eurographics 99, STAR State of the Art Reports, Goovaerts, P. (2005). Exploring Scale-Dependent Correlations Between Cancer Mortality Rates Using Factorial Kriging and Population Weighted Semivariograms: A Simulation Study. Geographical Analysis 37,
19 Robert Feick and Barry Boots Hutchinson, M. F., and J. C. Gallant. (1999). Representation of Terrain. In Geographical Information Systems: Principles, Techniques, Applications, and Management, Vol. 1, 2nd ed , edited by P. A. Longley, M. F. Goodchild, D. J. Maguire, and D. W. Rhind. New York: Wiley. Klein, R., and W. Straer. (1997). Generation of Multiresolution Models from CAD Data for Real Time Rendering. In Theory and Practice of Geometric Modeling (Blaueuren II), edited by R. Klein, W. Straer, and R. Rau. Berlin, Germany: Springer-Verlag. Kyriakidis, P. C., and E.-H. Yoo. (2005). Geostatistical Prediction/Simulation of Point Values from Areal Data. Geographical Analysis 37, Lowell, K. E. (1994). A Fuzzy Surface Cartographic Representation for Forestry Based on Voronoi Diagram Area Stealing. Canadian Journal of Forest Research 24, Okabe, A., B. Boots, K. Sugihara, and S. N. Chiu. (2000). Spatial Tessellations: Concepts and Applications of Voronoi Diagrams, 2nd ed. Chichester, UK: Wiley. Scallatos, L. L., and T. Pavlidis. (1992). Hierarchical Triangulation Using Cartographic Coherence. CVGIP: Graphical Models and Image Processing 54(2), Shine, J. A., and G. I. Wakefield. (1999). A Comparison of Supervised Imagery Classification Using Analyst-Chosen and Geostatistically-Chosen Training Sets. Geocomputation 99 (CD-ROM). Sibson, R. (1978). Locally Equiangular Triangulations. The Computer Journal 21, Sibson, R. (1981). A Brief Description of Natural Neighbour Interpolation. In Interpreting Multivariate Data, edited by V. Barnett. New York: Wiley. Voightmann, A., L. Becker, and K. Hinrichs. (1994). Hierarchical Surface Representations Using Constrained DELAUNEY (sic) Triangulations. In Advances in GIS Research: International Symposium on Spatial Data Handling, Vols 1 & 2: Wang, K., C. P. Lo, G. A. Brook, and H. A. Arabnia. (2001). Comparison of Existing Triangulation Methods for Regularly and Irregularly Spaced Height Fields. International Journal of Geographical Information Science 15, Watson, D. F. (1992). Contouring: A Guide to the Analysis and Display of Spatial Data. Oxford, UK: Pergamon Press. 243
Variable Resolution Spatial Interpolation Using the Simple Recursive Point Voronoi Diagram B. Boots 1 and R.D. Feick 2
 Variable Resolution Spatial Interpolation Using the Simple Recursive Point Voronoi Diagram B. Boots 1 and R.D. Feick 2 1 Department of Geography and Environmental Studies, Wilfrid Laurier University, Waterloo,
Variable Resolution Spatial Interpolation Using the Simple Recursive Point Voronoi Diagram B. Boots 1 and R.D. Feick 2 1 Department of Geography and Environmental Studies, Wilfrid Laurier University, Waterloo,
IMPROVING THE ACCURACY OF DIGITAL TERRAIN MODELS
 STUDIA UNIV. BABEŞ BOLYAI, INFORMATICA, Volume XLV, Number 1, 2000 IMPROVING THE ACCURACY OF DIGITAL TERRAIN MODELS GABRIELA DROJ Abstract. The change from paper maps to GIS, in various kinds of geographical
STUDIA UNIV. BABEŞ BOLYAI, INFORMATICA, Volume XLV, Number 1, 2000 IMPROVING THE ACCURACY OF DIGITAL TERRAIN MODELS GABRIELA DROJ Abstract. The change from paper maps to GIS, in various kinds of geographical
Geostatistics 2D GMS 7.0 TUTORIALS. 1 Introduction. 1.1 Contents
 GMS 7.0 TUTORIALS 1 Introduction Two-dimensional geostatistics (interpolation) can be performed in GMS using the 2D Scatter Point module. The module is used to interpolate from sets of 2D scatter points
GMS 7.0 TUTORIALS 1 Introduction Two-dimensional geostatistics (interpolation) can be performed in GMS using the 2D Scatter Point module. The module is used to interpolate from sets of 2D scatter points
Algorithm That Mimics Human Perceptual Grouping of Dot Patterns
 Algorithm That Mimics Human Perceptual Grouping of Dot Patterns G. Papari and N. Petkov Institute of Mathematics and Computing Science, University of Groningen, P.O.Box 800, 9700 AV Groningen, The Netherlands
Algorithm That Mimics Human Perceptual Grouping of Dot Patterns G. Papari and N. Petkov Institute of Mathematics and Computing Science, University of Groningen, P.O.Box 800, 9700 AV Groningen, The Netherlands
Preferred directions for resolving the non-uniqueness of Delaunay triangulations
 Preferred directions for resolving the non-uniqueness of Delaunay triangulations Christopher Dyken and Michael S. Floater Abstract: This note proposes a simple rule to determine a unique triangulation
Preferred directions for resolving the non-uniqueness of Delaunay triangulations Christopher Dyken and Michael S. Floater Abstract: This note proposes a simple rule to determine a unique triangulation
The Effect of Changing Grid Size in the Creation of Laser Scanner Digital Surface Models
 The Effect of Changing Grid Size in the Creation of Laser Scanner Digital Surface Models Smith, S.L 1, Holland, D.A 1, and Longley, P.A 2 1 Research & Innovation, Ordnance Survey, Romsey Road, Southampton,
The Effect of Changing Grid Size in the Creation of Laser Scanner Digital Surface Models Smith, S.L 1, Holland, D.A 1, and Longley, P.A 2 1 Research & Innovation, Ordnance Survey, Romsey Road, Southampton,
Triangulation Based Volume Calculation Andrew Y.T Kudowor and George Taylor Department of Geomatics University of Newcastle
 Triangulation Based Volume Calculation Andrew Y.T Kudowor and George Taylor Department of Geomatics University of Newcastle ABSTRACT Delaunay triangulation is a commonly used method for generating surface
Triangulation Based Volume Calculation Andrew Y.T Kudowor and George Taylor Department of Geomatics University of Newcastle ABSTRACT Delaunay triangulation is a commonly used method for generating surface
Class #2. Data Models: maps as models of reality, geographical and attribute measurement & vector and raster (and other) data structures
 Class #2 Data Models: maps as models of reality, geographical and attribute measurement & vector and raster (and other) data structures Role of a Data Model Levels of Data Model Abstraction GIS as Digital
Class #2 Data Models: maps as models of reality, geographical and attribute measurement & vector and raster (and other) data structures Role of a Data Model Levels of Data Model Abstraction GIS as Digital
Dijkstra's Algorithm
 Shortest Path Algorithm Dijkstra's Algorithm To find the shortest path from the origin node to the destination node No matrix calculation Floyd s Algorithm To find all the shortest paths from the nodes
Shortest Path Algorithm Dijkstra's Algorithm To find the shortest path from the origin node to the destination node No matrix calculation Floyd s Algorithm To find all the shortest paths from the nodes
Comparing different interpolation methods on two-dimensional test functions
 Comparing different interpolation methods on two-dimensional test functions Thomas Mühlenstädt, Sonja Kuhnt May 28, 2009 Keywords: Interpolation, computer experiment, Kriging, Kernel interpolation, Thin
Comparing different interpolation methods on two-dimensional test functions Thomas Mühlenstädt, Sonja Kuhnt May 28, 2009 Keywords: Interpolation, computer experiment, Kriging, Kernel interpolation, Thin
M. Andrea Rodríguez-Tastets. I Semester 2008
 M. -Tastets Universidad de Concepción,Chile andrea@udec.cl I Semester 2008 Outline refers to data with a location on the Earth s surface. Examples Census data Administrative boundaries of a country, state
M. -Tastets Universidad de Concepción,Chile andrea@udec.cl I Semester 2008 Outline refers to data with a location on the Earth s surface. Examples Census data Administrative boundaries of a country, state
RECOMMENDATION ITU-R P DIGITAL TOPOGRAPHIC DATABASES FOR PROPAGATION STUDIES. (Question ITU-R 202/3)
 Rec. ITU-R P.1058-1 1 RECOMMENDATION ITU-R P.1058-1 DIGITAL TOPOGRAPHIC DATABASES FOR PROPAGATION STUDIES (Question ITU-R 202/3) Rec. ITU-R P.1058-1 (1994-1997) The ITU Radiocommunication Assembly, considering
Rec. ITU-R P.1058-1 1 RECOMMENDATION ITU-R P.1058-1 DIGITAL TOPOGRAPHIC DATABASES FOR PROPAGATION STUDIES (Question ITU-R 202/3) Rec. ITU-R P.1058-1 (1994-1997) The ITU Radiocommunication Assembly, considering
Extraction of representative learning set from measured geospatial data
 Extraction of representative learning set from measured geospatial data Béla Paláncz 1, Lajos Völgyesi 2, Piroska Zaletnyik 2, Levente Kovács 3 1 Department of Photogrammetry and Geoinformatics, Faculty
Extraction of representative learning set from measured geospatial data Béla Paláncz 1, Lajos Völgyesi 2, Piroska Zaletnyik 2, Levente Kovács 3 1 Department of Photogrammetry and Geoinformatics, Faculty
Scope and Sequence for the New Jersey Core Curriculum Content Standards
 Scope and Sequence for the New Jersey Core Curriculum Content Standards The following chart provides an overview of where within Prentice Hall Course 3 Mathematics each of the Cumulative Progress Indicators
Scope and Sequence for the New Jersey Core Curriculum Content Standards The following chart provides an overview of where within Prentice Hall Course 3 Mathematics each of the Cumulative Progress Indicators
Creating Surfaces. Steve Kopp Steve Lynch
 Steve Kopp Steve Lynch Overview Learn the types of surfaces and the data structures used to store them Emphasis on surface interpolation Learn the interpolation workflow Understand how interpolators work
Steve Kopp Steve Lynch Overview Learn the types of surfaces and the data structures used to store them Emphasis on surface interpolation Learn the interpolation workflow Understand how interpolators work
Lecture 6: GIS Spatial Analysis. GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University
 Lecture 6: GIS Spatial Analysis GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University 1 Spatial Data It can be most simply defined as information that describes the distribution
Lecture 6: GIS Spatial Analysis GE 118: INTRODUCTION TO GIS Engr. Meriam M. Santillan Caraga State University 1 Spatial Data It can be most simply defined as information that describes the distribution
6. Concluding Remarks
 [8] K. J. Supowit, The relative neighborhood graph with an application to minimum spanning trees, Tech. Rept., Department of Computer Science, University of Illinois, Urbana-Champaign, August 1980, also
[8] K. J. Supowit, The relative neighborhood graph with an application to minimum spanning trees, Tech. Rept., Department of Computer Science, University of Illinois, Urbana-Champaign, August 1980, also
Outline of the presentation
 Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
Surface Reconstruction Petra Surynková Charles University in Prague Faculty of Mathematics and Physics petra.surynkova@mff.cuni.cz Outline of the presentation My work up to now Surfaces of Building Practice
Scalar Visualization
 Scalar Visualization 5-1 Motivation Visualizing scalar data is frequently encountered in science, engineering, and medicine, but also in daily life. Recalling from earlier, scalar datasets, or scalar fields,
Scalar Visualization 5-1 Motivation Visualizing scalar data is frequently encountered in science, engineering, and medicine, but also in daily life. Recalling from earlier, scalar datasets, or scalar fields,
Flexible Lag Definition for Experimental Variogram Calculation
 Flexible Lag Definition for Experimental Variogram Calculation Yupeng Li and Miguel Cuba The inference of the experimental variogram in geostatistics commonly relies on the method of moments approach.
Flexible Lag Definition for Experimental Variogram Calculation Yupeng Li and Miguel Cuba The inference of the experimental variogram in geostatistics commonly relies on the method of moments approach.
LATEST TRENDS on APPLIED MATHEMATICS, SIMULATION, MODELLING
 3D surface reconstruction of objects by using stereoscopic viewing Baki Koyuncu, Kurtuluş Küllü bkoyuncu@ankara.edu.tr kkullu@eng.ankara.edu.tr Computer Engineering Department, Ankara University, Ankara,
3D surface reconstruction of objects by using stereoscopic viewing Baki Koyuncu, Kurtuluş Küllü bkoyuncu@ankara.edu.tr kkullu@eng.ankara.edu.tr Computer Engineering Department, Ankara University, Ankara,
Shape fitting and non convex data analysis
 Shape fitting and non convex data analysis Petra Surynková, Zbyněk Šír Faculty of Mathematics and Physics, Charles University in Prague Sokolovská 83, 186 7 Praha 8, Czech Republic email: petra.surynkova@mff.cuni.cz,
Shape fitting and non convex data analysis Petra Surynková, Zbyněk Šír Faculty of Mathematics and Physics, Charles University in Prague Sokolovská 83, 186 7 Praha 8, Czech Republic email: petra.surynkova@mff.cuni.cz,
17/07/2013 RASTER DATA STRUCTURE GIS LECTURE 4 GIS DATA MODELS AND STRUCTURES RASTER DATA MODEL& STRUCTURE TIN- TRIANGULAR IRREGULAR NETWORK
 RASTER DATA STRUCTURE GIS LECTURE 4 GIS DATA MODELS AND STRUCTURES Space is subdivided into regular grids of square grid cells or other forms of polygonal meshes known as picture elements (pixels) the
RASTER DATA STRUCTURE GIS LECTURE 4 GIS DATA MODELS AND STRUCTURES Space is subdivided into regular grids of square grid cells or other forms of polygonal meshes known as picture elements (pixels) the
The Crust and Skeleton Applications in GIS
 The Crust and Skeleton Applications in GIS Christopher Gold and Maciek Dakowicz School of Computing, University of Glamorgan Pontypridd CF37 1DL Wales UK christophergold@voronoi.com Abstract This paper
The Crust and Skeleton Applications in GIS Christopher Gold and Maciek Dakowicz School of Computing, University of Glamorgan Pontypridd CF37 1DL Wales UK christophergold@voronoi.com Abstract This paper
Watershed Sciences 4930 & 6920 GEOGRAPHIC INFORMATION SYSTEMS
 HOUSEKEEPING Watershed Sciences 4930 & 6920 GEOGRAPHIC INFORMATION SYSTEMS Quizzes Lab 8? WEEK EIGHT Lecture INTERPOLATION & SPATIAL ESTIMATION Joe Wheaton READING FOR TODAY WHAT CAN WE COLLECT AT POINTS?
HOUSEKEEPING Watershed Sciences 4930 & 6920 GEOGRAPHIC INFORMATION SYSTEMS Quizzes Lab 8? WEEK EIGHT Lecture INTERPOLATION & SPATIAL ESTIMATION Joe Wheaton READING FOR TODAY WHAT CAN WE COLLECT AT POINTS?
Filling Space with Random Line Segments
 Filling Space with Random Line Segments John Shier Abstract. The use of a nonintersecting random search algorithm with objects having zero width ("measure zero") is explored. The line length in the units
Filling Space with Random Line Segments John Shier Abstract. The use of a nonintersecting random search algorithm with objects having zero width ("measure zero") is explored. The line length in the units
On the Selection of an Interpolation Method for Creating a Terrain Model (TM) from LIDAR Data
 On the Selection of an Interpolation Method for Creating a Terrain Model (TM) from LIDAR Data Tarig A. Ali Department of Technology and Geomatics East Tennessee State University P. O. Box 70552, Johnson
On the Selection of an Interpolation Method for Creating a Terrain Model (TM) from LIDAR Data Tarig A. Ali Department of Technology and Geomatics East Tennessee State University P. O. Box 70552, Johnson
Hierarchical Representation of 2-D Shapes using Convex Polygons: a Contour-Based Approach
 Hierarchical Representation of 2-D Shapes using Convex Polygons: a Contour-Based Approach O. El Badawy, M. S. Kamel Pattern Analysis and Machine Intelligence Laboratory, Department of Systems Design Engineering,
Hierarchical Representation of 2-D Shapes using Convex Polygons: a Contour-Based Approach O. El Badawy, M. S. Kamel Pattern Analysis and Machine Intelligence Laboratory, Department of Systems Design Engineering,
2) For any triangle edge not on the boundary, there is exactly one neighboring
 Triangulating Trimmed NURBS Surfaces Chang Shu and Pierre Boulanger Abstract. This paper describes techniques for the piecewise linear approximation of trimmed NURBS surfaces. The problem, called surface
Triangulating Trimmed NURBS Surfaces Chang Shu and Pierre Boulanger Abstract. This paper describes techniques for the piecewise linear approximation of trimmed NURBS surfaces. The problem, called surface
Terrain Modeling Using Voronoi Hierarchies
 Terrain Modeling Using Voronoi Hierarchies Martin Bertram 1, Shirley E. Konkle 2, Hans Hagen 1, Bernd Hamann 3,and Kenneth I. Joy 3 1 University of Kaiserslautern, Department of Computer Science, P.O.
Terrain Modeling Using Voronoi Hierarchies Martin Bertram 1, Shirley E. Konkle 2, Hans Hagen 1, Bernd Hamann 3,and Kenneth I. Joy 3 1 University of Kaiserslautern, Department of Computer Science, P.O.
SOME stereo image-matching methods require a user-selected
 IEEE GEOSCIENCE AND REMOTE SENSING LETTERS, VOL. 3, NO. 2, APRIL 2006 207 Seed Point Selection Method for Triangle Constrained Image Matching Propagation Qing Zhu, Bo Wu, and Zhi-Xiang Xu Abstract In order
IEEE GEOSCIENCE AND REMOTE SENSING LETTERS, VOL. 3, NO. 2, APRIL 2006 207 Seed Point Selection Method for Triangle Constrained Image Matching Propagation Qing Zhu, Bo Wu, and Zhi-Xiang Xu Abstract In order
Surface Creation & Analysis with 3D Analyst
 Esri International User Conference July 23 27 San Diego Convention Center Surface Creation & Analysis with 3D Analyst Khalid Duri Surface Basics Defining the surface Representation of any continuous measurement
Esri International User Conference July 23 27 San Diego Convention Center Surface Creation & Analysis with 3D Analyst Khalid Duri Surface Basics Defining the surface Representation of any continuous measurement
Prentice Hall Pre-Algebra 2004 Correlated to: Hawaii Mathematics Content and Performance Standards (HCPS) II (Grades 9-12)
 Hawaii Mathematics Content and Performance Standards (HCPS) II (Grades 9-12) NUMBER AND OPERATIONS STANDARD 1: Students understand numbers, ways of representing numbers, relationships among numbers, and
Hawaii Mathematics Content and Performance Standards (HCPS) II (Grades 9-12) NUMBER AND OPERATIONS STANDARD 1: Students understand numbers, ways of representing numbers, relationships among numbers, and
Chapter 1. Introduction
 Introduction 1 Chapter 1. Introduction We live in a three-dimensional world. Inevitably, any application that analyzes or visualizes this world relies on three-dimensional data. Inherent characteristics
Introduction 1 Chapter 1. Introduction We live in a three-dimensional world. Inevitably, any application that analyzes or visualizes this world relies on three-dimensional data. Inherent characteristics
Contents of Lecture. Surface (Terrain) Data Models. Terrain Surface Representation. Sampling in Surface Model DEM
 Lecture 13: Advanced Data Models: Terrain mapping and Analysis Contents of Lecture Surface Data Models DEM GRID Model TIN Model Visibility Analysis Geography 373 Spring, 2006 Changjoo Kim 11/29/2006 1
Lecture 13: Advanced Data Models: Terrain mapping and Analysis Contents of Lecture Surface Data Models DEM GRID Model TIN Model Visibility Analysis Geography 373 Spring, 2006 Changjoo Kim 11/29/2006 1
Voronoi Diagrams in the Plane. Chapter 5 of O Rourke text Chapter 7 and 9 of course text
 Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
Voronoi Diagrams in the Plane Chapter 5 of O Rourke text Chapter 7 and 9 of course text Voronoi Diagrams As important as convex hulls Captures the neighborhood (proximity) information of geometric objects
Algorithms for GIS. Spatial data: Models and representation (part I) Laura Toma. Bowdoin College
 Algorithms for GIS Spatial data: Models and representation (part I) Laura Toma Bowdoin College Outline Spatial data in GIS applications Point data Networks Terrains Planar maps and meshes Data structures
Algorithms for GIS Spatial data: Models and representation (part I) Laura Toma Bowdoin College Outline Spatial data in GIS applications Point data Networks Terrains Planar maps and meshes Data structures
1. Estimation equations for strip transect sampling, using notation consistent with that used to
 Web-based Supplementary Materials for Line Transect Methods for Plant Surveys by S.T. Buckland, D.L. Borchers, A. Johnston, P.A. Henrys and T.A. Marques Web Appendix A. Introduction In this on-line appendix,
Web-based Supplementary Materials for Line Transect Methods for Plant Surveys by S.T. Buckland, D.L. Borchers, A. Johnston, P.A. Henrys and T.A. Marques Web Appendix A. Introduction In this on-line appendix,
demonstrate an understanding of the exponent rules of multiplication and division, and apply them to simplify expressions Number Sense and Algebra
 MPM 1D - Grade Nine Academic Mathematics This guide has been organized in alignment with the 2005 Ontario Mathematics Curriculum. Each of the specific curriculum expectations are cross-referenced to the
MPM 1D - Grade Nine Academic Mathematics This guide has been organized in alignment with the 2005 Ontario Mathematics Curriculum. Each of the specific curriculum expectations are cross-referenced to the
Investigation of Sampling and Interpolation Techniques for DEMs Derived from Different Data Sources
 Investigation of Sampling and Interpolation Techniques for DEMs Derived from Different Data Sources FARRAG ALI FARRAG 1 and RAGAB KHALIL 2 1: Assistant professor at Civil Engineering Department, Faculty
Investigation of Sampling and Interpolation Techniques for DEMs Derived from Different Data Sources FARRAG ALI FARRAG 1 and RAGAB KHALIL 2 1: Assistant professor at Civil Engineering Department, Faculty
Statistical surfaces and interpolation. This is lecture ten
 Statistical surfaces and interpolation This is lecture ten Data models for representation of surfaces So far have considered field and object data models (represented by raster and vector data structures).
Statistical surfaces and interpolation This is lecture ten Data models for representation of surfaces So far have considered field and object data models (represented by raster and vector data structures).
Geostatistics 3D GMS 7.0 TUTORIALS. 1 Introduction. 1.1 Contents
 GMS 7.0 TUTORIALS Geostatistics 3D 1 Introduction Three-dimensional geostatistics (interpolation) can be performed in GMS using the 3D Scatter Point module. The module is used to interpolate from sets
GMS 7.0 TUTORIALS Geostatistics 3D 1 Introduction Three-dimensional geostatistics (interpolation) can be performed in GMS using the 3D Scatter Point module. The module is used to interpolate from sets
Learn the various 3D interpolation methods available in GMS
 v. 10.4 GMS 10.4 Tutorial Learn the various 3D interpolation methods available in GMS Objectives Explore the various 3D interpolation algorithms available in GMS, including IDW and kriging. Visualize the
v. 10.4 GMS 10.4 Tutorial Learn the various 3D interpolation methods available in GMS Objectives Explore the various 3D interpolation algorithms available in GMS, including IDW and kriging. Visualize the
Middle School Math Course 3 Correlation of the ALEKS course Middle School Math 3 to the Illinois Assessment Framework for Grade 8
 Middle School Math Course 3 Correlation of the ALEKS course Middle School Math 3 to the Illinois Assessment Framework for Grade 8 State Goal 6: Number Sense 6.8.01: 6.8.02: 6.8.03: 6.8.04: 6.8.05: = ALEKS
Middle School Math Course 3 Correlation of the ALEKS course Middle School Math 3 to the Illinois Assessment Framework for Grade 8 State Goal 6: Number Sense 6.8.01: 6.8.02: 6.8.03: 6.8.04: 6.8.05: = ALEKS
DATA MODELS IN GIS. Prachi Misra Sahoo I.A.S.R.I., New Delhi
 DATA MODELS IN GIS Prachi Misra Sahoo I.A.S.R.I., New Delhi -110012 1. Introduction GIS depicts the real world through models involving geometry, attributes, relations, and data quality. Here the realization
DATA MODELS IN GIS Prachi Misra Sahoo I.A.S.R.I., New Delhi -110012 1. Introduction GIS depicts the real world through models involving geometry, attributes, relations, and data quality. Here the realization
Controlling the spread of dynamic self-organising maps
 Neural Comput & Applic (2004) 13: 168 174 DOI 10.1007/s00521-004-0419-y ORIGINAL ARTICLE L. D. Alahakoon Controlling the spread of dynamic self-organising maps Received: 7 April 2004 / Accepted: 20 April
Neural Comput & Applic (2004) 13: 168 174 DOI 10.1007/s00521-004-0419-y ORIGINAL ARTICLE L. D. Alahakoon Controlling the spread of dynamic self-organising maps Received: 7 April 2004 / Accepted: 20 April
Geometric Considerations for Distribution of Sensors in Ad-hoc Sensor Networks
 Geometric Considerations for Distribution of Sensors in Ad-hoc Sensor Networks Ted Brown, Deniz Sarioz, Amotz Bar-Noy, Tom LaPorta, Dinesh Verma, Matthew Johnson, Hosam Rowaihy November 20, 2006 1 Introduction
Geometric Considerations for Distribution of Sensors in Ad-hoc Sensor Networks Ted Brown, Deniz Sarioz, Amotz Bar-Noy, Tom LaPorta, Dinesh Verma, Matthew Johnson, Hosam Rowaihy November 20, 2006 1 Introduction
Students will understand 1. that numerical expressions can be written and evaluated using whole number exponents
 Grade 6 Expressions and Equations Essential Questions: How do you use patterns to understand mathematics and model situations? What is algebra? How are the horizontal and vertical axes related? How do
Grade 6 Expressions and Equations Essential Questions: How do you use patterns to understand mathematics and model situations? What is algebra? How are the horizontal and vertical axes related? How do
Möbius Transformations in Scientific Computing. David Eppstein
 Möbius Transformations in Scientific Computing David Eppstein Univ. of California, Irvine School of Information and Computer Science (including joint work with Marshall Bern from WADS 01 and SODA 03) Outline
Möbius Transformations in Scientific Computing David Eppstein Univ. of California, Irvine School of Information and Computer Science (including joint work with Marshall Bern from WADS 01 and SODA 03) Outline
ON ESTIMATING PARTIAL DERIVATIVES FOR BIVARIATE INTERPOLATION OF SCATTERED DATA
 ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 4, Number, Winter 984 ON ESTIMATING PARTIAL DERIVATIVES FOR BIVARIATE INTERPOLATION OF SCATTERED DATA HIROSHI AKIMA ABSTRACT. The method for estimating partial
ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 4, Number, Winter 984 ON ESTIMATING PARTIAL DERIVATIVES FOR BIVARIATE INTERPOLATION OF SCATTERED DATA HIROSHI AKIMA ABSTRACT. The method for estimating partial
SHAPE, SPACE & MEASURE
 STAGE 1 Know the place value headings up to millions Recall primes to 19 Know the first 12 square numbers Know the Roman numerals I, V, X, L, C, D, M Know the % symbol Know percentage and decimal equivalents
STAGE 1 Know the place value headings up to millions Recall primes to 19 Know the first 12 square numbers Know the Roman numerals I, V, X, L, C, D, M Know the % symbol Know percentage and decimal equivalents
The Regular Hierarchical Surface Model (RHSM)
 The Regular Hierarchical Surface Model (RHSM) Joseph W. Wright 1 2, Antoni B. Moore * 1 and Gregory H. Leonard 1 1 School of Surveying, University of Otago, PO Box 56, Dunedin, New Zealand 2 Cardno, Wellington,
The Regular Hierarchical Surface Model (RHSM) Joseph W. Wright 1 2, Antoni B. Moore * 1 and Gregory H. Leonard 1 1 School of Surveying, University of Otago, PO Box 56, Dunedin, New Zealand 2 Cardno, Wellington,
Middle School Math Course 3
 Middle School Math Course 3 Correlation of the ALEKS course Middle School Math Course 3 to the Texas Essential Knowledge and Skills (TEKS) for Mathematics Grade 8 (2012) (1) Mathematical process standards.
Middle School Math Course 3 Correlation of the ALEKS course Middle School Math Course 3 to the Texas Essential Knowledge and Skills (TEKS) for Mathematics Grade 8 (2012) (1) Mathematical process standards.
GIS Data Models. 4/9/ GIS Data Models
 GIS Data Models 1 Conceptual models of the real world The real world can be described using two conceptually different models: 1. As discrete objects, possible to represent as points, lines or polygons.
GIS Data Models 1 Conceptual models of the real world The real world can be described using two conceptually different models: 1. As discrete objects, possible to represent as points, lines or polygons.
PITSCO Math Individualized Prescriptive Lessons (IPLs)
 Orientation Integers 10-10 Orientation I 20-10 Speaking Math Define common math vocabulary. Explore the four basic operations and their solutions. Form equations and expressions. 20-20 Place Value Define
Orientation Integers 10-10 Orientation I 20-10 Speaking Math Define common math vocabulary. Explore the four basic operations and their solutions. Form equations and expressions. 20-20 Place Value Define
Chapter 2 Basic Structure of High-Dimensional Spaces
 Chapter 2 Basic Structure of High-Dimensional Spaces Data is naturally represented geometrically by associating each record with a point in the space spanned by the attributes. This idea, although simple,
Chapter 2 Basic Structure of High-Dimensional Spaces Data is naturally represented geometrically by associating each record with a point in the space spanned by the attributes. This idea, although simple,
The Farthest Point Delaunay Triangulation Minimizes Angles
 The Farthest Point Delaunay Triangulation Minimizes Angles David Eppstein Department of Information and Computer Science UC Irvine, CA 92717 November 20, 1990 Abstract We show that the planar dual to the
The Farthest Point Delaunay Triangulation Minimizes Angles David Eppstein Department of Information and Computer Science UC Irvine, CA 92717 November 20, 1990 Abstract We show that the planar dual to the
Lesson 5 overview. Concepts. Interpolators. Assessing accuracy Exercise 5
 Interpolation Tools Lesson 5 overview Concepts Sampling methods Creating continuous surfaces Interpolation Density surfaces in GIS Interpolators IDW, Spline,Trend, Kriging,Natural neighbors TopoToRaster
Interpolation Tools Lesson 5 overview Concepts Sampling methods Creating continuous surfaces Interpolation Density surfaces in GIS Interpolators IDW, Spline,Trend, Kriging,Natural neighbors TopoToRaster
DIGITAL TERRAIN MODELLING. Endre Katona University of Szeged Department of Informatics
 DIGITAL TERRAIN MODELLING Endre Katona University of Szeged Department of Informatics katona@inf.u-szeged.hu The problem: data sources data structures algorithms DTM = Digital Terrain Model Terrain function:
DIGITAL TERRAIN MODELLING Endre Katona University of Szeged Department of Informatics katona@inf.u-szeged.hu The problem: data sources data structures algorithms DTM = Digital Terrain Model Terrain function:
Computational Geometry
 Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
Proceedings of the 5th WSEAS International Conference on Telecommunications and Informatics, Istanbul, Turkey, May 27-29, 2006 (pp )
 A Rapid Algorithm for Topology Construction from a Set of Line Segments SEBASTIAN KRIVOGRAD, MLADEN TRLEP, BORUT ŽALIK Faculty of Electrical Engineering and Computer Science University of Maribor Smetanova
A Rapid Algorithm for Topology Construction from a Set of Line Segments SEBASTIAN KRIVOGRAD, MLADEN TRLEP, BORUT ŽALIK Faculty of Electrical Engineering and Computer Science University of Maribor Smetanova
D-Optimal Designs. Chapter 888. Introduction. D-Optimal Design Overview
 Chapter 888 Introduction This procedure generates D-optimal designs for multi-factor experiments with both quantitative and qualitative factors. The factors can have a mixed number of levels. For example,
Chapter 888 Introduction This procedure generates D-optimal designs for multi-factor experiments with both quantitative and qualitative factors. The factors can have a mixed number of levels. For example,
Agile Mind Mathematics 6 Scope and Sequence, Indiana Academic Standards for Mathematics
 In the three years prior Grade 6, students acquired a strong foundation in numbers and operations, geometry, measurement, and data. Students are fluent in multiplication of multi-digit whole numbers and
In the three years prior Grade 6, students acquired a strong foundation in numbers and operations, geometry, measurement, and data. Students are fluent in multiplication of multi-digit whole numbers and
Figure 1: An Area Voronoi Diagram of a typical GIS Scene generated from the ISPRS Working group III/3 Avenches data set. 2 ARRANGEMENTS 2.1 Voronoi Di
 Qualitative Spatial Relations using Arrangements for Complex Images M. Burge and W. Burger Johannes Kepler University, Department of Systems Science Computer Vision Laboratory, A-4040 Linz, Austria burge@cast.uni-linz.ac.at
Qualitative Spatial Relations using Arrangements for Complex Images M. Burge and W. Burger Johannes Kepler University, Department of Systems Science Computer Vision Laboratory, A-4040 Linz, Austria burge@cast.uni-linz.ac.at
A Polygon-based Line Integral Method for Calculating Vorticity, Divergence, and Deformation from Non-uniform Observations
 2.7 olygon-based Line Integral Method for Calculating Vorticity, Divergence, and Deformation from Non-uniform Observations Charles N. Helms and Robert E. Hart Florida State University, Tallahassee, Florida
2.7 olygon-based Line Integral Method for Calculating Vorticity, Divergence, and Deformation from Non-uniform Observations Charles N. Helms and Robert E. Hart Florida State University, Tallahassee, Florida
Contour Simplification with Defined Spatial Accuracy
 Contour Simplification with Defined Spatial Accuracy Bulent Cetinkaya, Serdar Aslan, Yavuz Selim Sengun, O. Nuri Cobankaya, Dursun Er Ilgin General Command of Mapping, 06100 Cebeci, Ankara, Turkey bulent.cetinkaya@hgk.mil.tr
Contour Simplification with Defined Spatial Accuracy Bulent Cetinkaya, Serdar Aslan, Yavuz Selim Sengun, O. Nuri Cobankaya, Dursun Er Ilgin General Command of Mapping, 06100 Cebeci, Ankara, Turkey bulent.cetinkaya@hgk.mil.tr
Lab 12: Sampling and Interpolation
 Lab 12: Sampling and Interpolation What You ll Learn: -Systematic and random sampling -Majority filtering -Stratified sampling -A few basic interpolation methods Data for the exercise are in the L12 subdirectory.
Lab 12: Sampling and Interpolation What You ll Learn: -Systematic and random sampling -Majority filtering -Stratified sampling -A few basic interpolation methods Data for the exercise are in the L12 subdirectory.
Year 8 Review 1, Set 1 Number confidence (Four operations, place value, common indices and estimation)
 Year 8 Review 1, Set 1 Number confidence (Four operations, place value, common indices and estimation) Place value Digit Integer Negative number Difference, Minus, Less Operation Multiply, Multiplication,
Year 8 Review 1, Set 1 Number confidence (Four operations, place value, common indices and estimation) Place value Digit Integer Negative number Difference, Minus, Less Operation Multiply, Multiplication,
KS4 Course Outline: Mathematics
 6+ Topic Index Sheet, Autumn Term Year 10 D Factorise an expression eg. 6a+8 = 2(3a+4); a 2-3a = a(a - 3) 104 C Factorise an expression with 2 or more factors eg. 4x 3 + 6xy = 2x(2x 2 +3y) 104 D Write
6+ Topic Index Sheet, Autumn Term Year 10 D Factorise an expression eg. 6a+8 = 2(3a+4); a 2-3a = a(a - 3) 104 C Factorise an expression with 2 or more factors eg. 4x 3 + 6xy = 2x(2x 2 +3y) 104 D Write
A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3
 A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3 ANDREW J. HANSON AND JI-PING SHA In this paper we present a systematic and explicit algorithm for tessellating the algebraic surfaces (real 4-manifolds) F
A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3 ANDREW J. HANSON AND JI-PING SHA In this paper we present a systematic and explicit algorithm for tessellating the algebraic surfaces (real 4-manifolds) F
Mathematics Scope & Sequence Grade 8 Revised: June 2015
 Mathematics Scope & Sequence 2015-16 Grade 8 Revised: June 2015 Readiness Standard(s) First Six Weeks (29 ) 8.2D Order a set of real numbers arising from mathematical and real-world contexts Convert between
Mathematics Scope & Sequence 2015-16 Grade 8 Revised: June 2015 Readiness Standard(s) First Six Weeks (29 ) 8.2D Order a set of real numbers arising from mathematical and real-world contexts Convert between
Maps as Numbers: Data Models
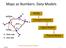 Maps as Numbers: Data Models vertices E Reality S E S arcs S E Conceptual Models nodes E Logical Models S Start node E End node S Physical Models 1 The Task An accurate, registered, digital map that can
Maps as Numbers: Data Models vertices E Reality S E S arcs S E Conceptual Models nodes E Logical Models S Start node E End node S Physical Models 1 The Task An accurate, registered, digital map that can
This strand involves properties of the physical world that can be measured, the units used to measure them and the process of measurement.
 ICAS MATHEMATICS ASSESSMENT FRAMEWORK ICAS Mathematics assesses mathematical skills in a range of contexts. The content of the papers is divided into the strands of: and, and, and, and, and and. The content
ICAS MATHEMATICS ASSESSMENT FRAMEWORK ICAS Mathematics assesses mathematical skills in a range of contexts. The content of the papers is divided into the strands of: and, and, and, and, and and. The content
Study on Delaunay Triangulation with the Islets Constraints
 Intelligent Information Management, 2010, 2, 375-379 doi:10.4236/iim.2010.26045 Published Online June 2010 (http://www.scirp.org/journal/iim) Study on Delaunay Triangulation with the Islets Constraints
Intelligent Information Management, 2010, 2, 375-379 doi:10.4236/iim.2010.26045 Published Online June 2010 (http://www.scirp.org/journal/iim) Study on Delaunay Triangulation with the Islets Constraints
Solve problems involving proportional reasoning. Number Sense and Algebra
 MFM 1P - Grade Nine Applied Mathematics This guide has been organized in alignment with the 2005 Ontario Mathematics Curriculum. Each of the specific curriculum expectations are cross-referenced to the
MFM 1P - Grade Nine Applied Mathematics This guide has been organized in alignment with the 2005 Ontario Mathematics Curriculum. Each of the specific curriculum expectations are cross-referenced to the
Module 1 Lecture Notes 2. Optimization Problem and Model Formulation
 Optimization Methods: Introduction and Basic concepts 1 Module 1 Lecture Notes 2 Optimization Problem and Model Formulation Introduction In the previous lecture we studied the evolution of optimization
Optimization Methods: Introduction and Basic concepts 1 Module 1 Lecture Notes 2 Optimization Problem and Model Formulation Introduction In the previous lecture we studied the evolution of optimization
3D Finite Element Software for Cracks. Version 3.2. Benchmarks and Validation
 3D Finite Element Software for Cracks Version 3.2 Benchmarks and Validation October 217 1965 57 th Court North, Suite 1 Boulder, CO 831 Main: (33) 415-1475 www.questintegrity.com http://www.questintegrity.com/software-products/feacrack
3D Finite Element Software for Cracks Version 3.2 Benchmarks and Validation October 217 1965 57 th Court North, Suite 1 Boulder, CO 831 Main: (33) 415-1475 www.questintegrity.com http://www.questintegrity.com/software-products/feacrack
Exploiting a database to predict the in-flight stability of the F-16
 Exploiting a database to predict the in-flight stability of the F-16 David Amsallem and Julien Cortial December 12, 2008 1 Introduction Among the critical phenomena that have to be taken into account when
Exploiting a database to predict the in-flight stability of the F-16 David Amsallem and Julien Cortial December 12, 2008 1 Introduction Among the critical phenomena that have to be taken into account when
University of Florida CISE department Gator Engineering. Clustering Part 5
 Clustering Part 5 Dr. Sanjay Ranka Professor Computer and Information Science and Engineering University of Florida, Gainesville SNN Approach to Clustering Ordinary distance measures have problems Euclidean
Clustering Part 5 Dr. Sanjay Ranka Professor Computer and Information Science and Engineering University of Florida, Gainesville SNN Approach to Clustering Ordinary distance measures have problems Euclidean
Montana City School GRADE 5
 Montana City School GRADE 5 Montana Standard 1: Students engage in the mathematical processes of problem solving and reasoning, estimation, communication, connections and applications, and using appropriate
Montana City School GRADE 5 Montana Standard 1: Students engage in the mathematical processes of problem solving and reasoning, estimation, communication, connections and applications, and using appropriate
THE METHODS OF TRIANGULATION
 THE METHODS OF TRIANGULATION Abstract M. Varshosaz, Assistant Professor, Faculty of Geodesy & Geomatics Eng., K.N. Toosi University of Technology K.N. Toosi University of Technology, Vali_Asr St, Tehran,
THE METHODS OF TRIANGULATION Abstract M. Varshosaz, Assistant Professor, Faculty of Geodesy & Geomatics Eng., K.N. Toosi University of Technology K.N. Toosi University of Technology, Vali_Asr St, Tehran,
Neighbourhood Operations Specific Theory
 Neighbourhood Operations Specific Theory Neighbourhood operations are a method of analysing data in a GIS environment. They are especially important when a situation requires the analysis of relationships
Neighbourhood Operations Specific Theory Neighbourhood operations are a method of analysing data in a GIS environment. They are especially important when a situation requires the analysis of relationships
Spatial Patterns Point Pattern Analysis Geographic Patterns in Areal Data
 Spatial Patterns We will examine methods that are used to analyze patterns in two sorts of spatial data: Point Pattern Analysis - These methods concern themselves with the location information associated
Spatial Patterns We will examine methods that are used to analyze patterns in two sorts of spatial data: Point Pattern Analysis - These methods concern themselves with the location information associated
Lecture 25: Bezier Subdivision. And he took unto him all these, and divided them in the midst, and laid each piece one against another: Genesis 15:10
 Lecture 25: Bezier Subdivision And he took unto him all these, and divided them in the midst, and laid each piece one against another: Genesis 15:10 1. Divide and Conquer If we are going to build useful
Lecture 25: Bezier Subdivision And he took unto him all these, and divided them in the midst, and laid each piece one against another: Genesis 15:10 1. Divide and Conquer If we are going to build useful
Grades 7 & 8 Pre-Algebra/Course 3,
 Grades 7 & 8 Pre-Algebra/Course 3, TERM 1 - AUGUST/SEPTEMBER/OCTOBER Algebra Tools Solving Equations Integers Solving Multi-Step Equations and Inequalities TERM 2 NOVEMBER/DECEMBER/JANUARY Functions &
Grades 7 & 8 Pre-Algebra/Course 3, TERM 1 - AUGUST/SEPTEMBER/OCTOBER Algebra Tools Solving Equations Integers Solving Multi-Step Equations and Inequalities TERM 2 NOVEMBER/DECEMBER/JANUARY Functions &
Middle School Math Course 2
 Middle School Math Course 2 Correlation of the ALEKS course Middle School Math Course 2 to the Indiana Academic Standards for Mathematics Grade 7 (2014) 1: NUMBER SENSE = ALEKS course topic that addresses
Middle School Math Course 2 Correlation of the ALEKS course Middle School Math Course 2 to the Indiana Academic Standards for Mathematics Grade 7 (2014) 1: NUMBER SENSE = ALEKS course topic that addresses
Spectral Coding of Three-Dimensional Mesh Geometry Information Using Dual Graph
 Spectral Coding of Three-Dimensional Mesh Geometry Information Using Dual Graph Sung-Yeol Kim, Seung-Uk Yoon, and Yo-Sung Ho Gwangju Institute of Science and Technology (GIST) 1 Oryong-dong, Buk-gu, Gwangju,
Spectral Coding of Three-Dimensional Mesh Geometry Information Using Dual Graph Sung-Yeol Kim, Seung-Uk Yoon, and Yo-Sung Ho Gwangju Institute of Science and Technology (GIST) 1 Oryong-dong, Buk-gu, Gwangju,
A Modified Longest Side Bisection Triangulation
 A Modified Longest Side Bisection Triangulation Christoph Stamm Stephan Eidenbenz Renato Pajarola Computer Science Department Institute of Theoretical Computer Science ETH Zurich, Switzerland E-mail: stamm@inf.ethz.ch
A Modified Longest Side Bisection Triangulation Christoph Stamm Stephan Eidenbenz Renato Pajarola Computer Science Department Institute of Theoretical Computer Science ETH Zurich, Switzerland E-mail: stamm@inf.ethz.ch
Eye Detection by Haar wavelets and cascaded Support Vector Machine
 Eye Detection by Haar wavelets and cascaded Support Vector Machine Vishal Agrawal B.Tech 4th Year Guide: Simant Dubey / Amitabha Mukherjee Dept of Computer Science and Engineering IIT Kanpur - 208 016
Eye Detection by Haar wavelets and cascaded Support Vector Machine Vishal Agrawal B.Tech 4th Year Guide: Simant Dubey / Amitabha Mukherjee Dept of Computer Science and Engineering IIT Kanpur - 208 016
GTPS Curriculum Mathematics Grade 8
 4.2.8.B2 Use iterative procedures to generate geometric patterns: Fractals (e.g., the Koch Snowflake); Self-similarity; Construction of initial stages; Patterns in successive stages (e.g., number of triangles
4.2.8.B2 Use iterative procedures to generate geometric patterns: Fractals (e.g., the Koch Snowflake); Self-similarity; Construction of initial stages; Patterns in successive stages (e.g., number of triangles
CHAPTER 6 MODIFIED FUZZY TECHNIQUES BASED IMAGE SEGMENTATION
 CHAPTER 6 MODIFIED FUZZY TECHNIQUES BASED IMAGE SEGMENTATION 6.1 INTRODUCTION Fuzzy logic based computational techniques are becoming increasingly important in the medical image analysis arena. The significant
CHAPTER 6 MODIFIED FUZZY TECHNIQUES BASED IMAGE SEGMENTATION 6.1 INTRODUCTION Fuzzy logic based computational techniques are becoming increasingly important in the medical image analysis arena. The significant
Review of Cartographic Data Types and Data Models
 Review of Cartographic Data Types and Data Models GIS Data Models Raster Versus Vector in GIS Analysis Fundamental element used to represent spatial features: Raster: pixel or grid cell. Vector: x,y coordinate
Review of Cartographic Data Types and Data Models GIS Data Models Raster Versus Vector in GIS Analysis Fundamental element used to represent spatial features: Raster: pixel or grid cell. Vector: x,y coordinate
Announcements. Data Sources a list of data files and their sources, an example of what I am looking for:
 Data Announcements Data Sources a list of data files and their sources, an example of what I am looking for: Source Map of Bangor MEGIS NG911 road file for Bangor MEGIS Tax maps for Bangor City Hall, may
Data Announcements Data Sources a list of data files and their sources, an example of what I am looking for: Source Map of Bangor MEGIS NG911 road file for Bangor MEGIS Tax maps for Bangor City Hall, may
Compressing 2-D Shapes using Concavity Trees
 Compressing 2-D Shapes using Concavity Trees O. El Badawy 1 and M. S. Kamel 2 1 Dept. of Systems Design Engineering. 2 Dept. of Electrical and Computer Engineering. Pattern Analysis and Machine Intelligence
Compressing 2-D Shapes using Concavity Trees O. El Badawy 1 and M. S. Kamel 2 1 Dept. of Systems Design Engineering. 2 Dept. of Electrical and Computer Engineering. Pattern Analysis and Machine Intelligence
Finding a (Buffon s) needle in a hierarchical triangular haystack
 Post-Conference Paper Presented at: International Conference on Discrete Global Grids NCGIA-Santa Barbara, CA, March 6-8, 000 http://www.ncgia.ucsb.edu/globalgrids/ Finding a (Buffon s) needle in a hierarchical
Post-Conference Paper Presented at: International Conference on Discrete Global Grids NCGIA-Santa Barbara, CA, March 6-8, 000 http://www.ncgia.ucsb.edu/globalgrids/ Finding a (Buffon s) needle in a hierarchical
An Experiment in Visual Clustering Using Star Glyph Displays
 An Experiment in Visual Clustering Using Star Glyph Displays by Hanna Kazhamiaka A Research Paper presented to the University of Waterloo in partial fulfillment of the requirements for the degree of Master
An Experiment in Visual Clustering Using Star Glyph Displays by Hanna Kazhamiaka A Research Paper presented to the University of Waterloo in partial fulfillment of the requirements for the degree of Master
Using level-2 fuzzy sets to combine uncertainty and imprecision in fuzzy regions
 Using level-2 fuzzy sets to combine uncertainty and imprecision in fuzzy regions Verstraete Jörg Abstract In many applications, spatial data need to be considered but are prone to uncertainty or imprecision.
Using level-2 fuzzy sets to combine uncertainty and imprecision in fuzzy regions Verstraete Jörg Abstract In many applications, spatial data need to be considered but are prone to uncertainty or imprecision.
Surface Analysis with 3D Analyst
 2013 Esri International User Conference July 8 12, 2013 San Diego, California Technical Workshop Surface Analysis with 3D Analyst Khalid H. Duri Esri UC2013. Technical Workshop. Why use 3D GIS? Because
2013 Esri International User Conference July 8 12, 2013 San Diego, California Technical Workshop Surface Analysis with 3D Analyst Khalid H. Duri Esri UC2013. Technical Workshop. Why use 3D GIS? Because
Delaunay Triangulations. Presented by Glenn Eguchi Computational Geometry October 11, 2001
 Delaunay Triangulations Presented by Glenn Eguchi 6.838 Computational Geometry October 11, 2001 Motivation: Terrains Set of data points A R 2 Height ƒ(p) defined at each point p in A How can we most naturally
Delaunay Triangulations Presented by Glenn Eguchi 6.838 Computational Geometry October 11, 2001 Motivation: Terrains Set of data points A R 2 Height ƒ(p) defined at each point p in A How can we most naturally
Averages and Variation
 Averages and Variation 3 Copyright Cengage Learning. All rights reserved. 3.1-1 Section 3.1 Measures of Central Tendency: Mode, Median, and Mean Copyright Cengage Learning. All rights reserved. 3.1-2 Focus
Averages and Variation 3 Copyright Cengage Learning. All rights reserved. 3.1-1 Section 3.1 Measures of Central Tendency: Mode, Median, and Mean Copyright Cengage Learning. All rights reserved. 3.1-2 Focus
